2020届中考数学压轴题全揭秘 专题15 动点综合问题(含解析)
2020中考数学压轴题十五 动点综合问题(附答案解析)

2020中考数学压轴题十五 动点综合问题(附答案解析)【典例分析】【考点1】动点之全等三角形问题 【例1】如图,直线443y x =-+与x 轴和y 轴分别交于,A B 两点,另一条直线过点A 和点(7,3)C . (1)求直线AC 的函数表达式;(2)求证: AB AC ⊥;(3)若点P 是直线AC 上的一个动点,点Q 是x 轴上的一个动点,且以,,P Q A 为顶点的三角形与AOB ∆全等,求点Q 的坐标.【答案】(1) 3944y x =-;(2) 222AB AD BD +=; (3) 点Q 的坐标为(7,0)或(8,0)或(1,0)-或(2,0)-【解析】(1)在y=-43x+4中,令y=0,则0=-43x+4,求得A(3,0),设直线AC对应的函数关系式为y=kx+b,解方程组即可得到结论;(2)在直线ABy=-43x+4中,得到k1=-43,在直线AC y=34x−94中,得到k2=34,由于k1•k2=-1,即可得到结论;(3)根据勾股定理得到AB=5,①当∠AQP=90°时,如图1,由全等三角形的性质得到AQ=OB=4,于是得到Q1(7,0),Q2(-1,0),②当∠APQ=90°时,如图2,根据全等三角形的性质得到AQ=AB=5,于是得到Q3(8,0),Q4(-2,0),③当∠PAQ=90°时,这种情况不存在.【详解】(1)在y=-43x+4中,令y=0,则0=-43x+4,∴x=3,∴A(3,0),设直线AC对应的函数关系式为y=kx+b,则:0337k bk b+⎧⎨+⎩==,解得:3494kb⎧⎪⎪⎨⎪-⎪⎩==,∴直线AC对应的函数关系式为y=34x-94.(2) 在直线ABy=-43x+4中,∵k1=-43,在直线AC y=34x−94中,k2=34,∴k1•k2=-1,∴AB⊥AC;(3)在y=-43x+4中,令x=0,则y=4,∴OA=3,OB=4,由勾股定理得AB=5,①当∠AQP=90°时,如图1,∵△AOB≌△AQP,∴AQ=OB=4,∴Q1(7,0),Q2(-1,0),②当∠APQ=90°时,如图2,∵△AOB≌△AQP,∴AQ=AB=5,∴Q3(8,0),Q4(-2,0).③当∠PAQ=90°时,这种情况不存在,综上所述:点Q的坐标为:(7,0)(8,0)(-1,0)(-2,0).【点睛】考查了一次函数综合题,待定系数法求函数的解析式,勾股定理的应用和全等三角形的性质等知识,分类讨论是解题关键,以防遗漏.【变式1-1】)如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时,△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)【答案】0;4;8;12【解析】此题要分两种情况:①当P在线段BC上时,②当P在BQ上,再分别分两种情况AC=BP或AC =BN进行计算即可.【详解】解:①当P在线段BC上,AC=BP时,△ACB≌△PBN,。
中考数学压轴题专题解析---直角三角形中的动点问题

(3)点 E 的坐标是 或 】 ( 10, 8) ( 16, 35)
2、动点直角三角形 SAS 问题 例2.已知:如图,抛物线 y
4 2 x mx 4 与 y 轴交于点 C,与 x 轴交于点 A、B, 5
(点 A 在点 B 的左侧)且满足 OC 4OA .设抛物线的对称轴与 x 轴交于点 M. (1)求抛物线的解析式及点 M 的坐标; (2)联接 CM ,点 Q 是射线 CM 上的一个动点,当 QMB 与 COM 相似时,求 直线 AQ 的解析式. y
BQ 2 BM
(5, 6) 即Q
∴AQ: (ii)当 COM BQM 90 时, COM ∽BQM 同理 Q( ∴AQ: )
】 例 3.如 图 , 在 RtABC 中 , C 90 , AB 5 , tan B 点,点 E 是 AB 边上的动点, DF DE 交射线 AC 于点 F . (1)求 AC 和 BC 的长; (2)当 EF BC 时,求 BE 的长; (3)联结 EF ,当 DEF 和 ABC 相似时,求 BE 的长.
① 综合①、②,当 DEF 和 ABC 相似时, BE 的长为
5 40 或 . 】 2 9
3、动点直角三角形三角比问题 例 4.已知:如图,在 Rt ABC 中, C 90 , BC 2 , AC 4 , P 是斜边 AB 上的一个动点, PD AB ,交边 AC 于点 D (点 D 与点 A 、 C 都不重合) , E 是射 线 DC 上一点,且 EPD A .设 A 、 P 两点的距离为 x , BEP 的面积为 y . (1)求证: AE 2 PE ; (2)求 y 关于 x 的函数解析式,并写出它的定义域; (3)当 BEP 与 ABC 相似时,求 BEP 的面积.
2020年中考数学压轴题精讲:动点产生的相似三角形问题

2020年中考数学压轴题精讲:动点产生的相似三角形问题例1:如图1,在平面直角坐标系中,双曲线(k≠0)与直线y=x+2都经过点A(2, m).(1)求k与m的值;(2)此双曲线又经过点B(n, 2),过点B的直线BC与直线y=x+2平行交y轴于点C,联结AB、AC,求△ABC的面积;(3)在(2)的条件下,设直线y=x+2与y轴交于点D,在射线CB上有一点E,如果以点A、C、E所组成的三角形与△ACD相似,且相似比不为1,求点E的坐标.图1满分解答(1)将点A(2, m)代入y=x+2,得m=4.所以点A的坐标为(2, 4).将点A(2, 4)代入kyx=,得k=8.(2)将点B(n, 2),代入8yx=,得n=4.所以点B的坐标为(4, 2).设直线BC为y=x+b,代入点B(4, 2),得b=-2.所以点C的坐标为(0,-2).由A(2, 4) 、B(4, 2) 、C (0,-2),可知A、B两点间的水平距离和竖直距离都是2,B、C两点间的水平距离和竖直距离都是4.所以AB=22,BC=42,∠ABC=90°.所以S△ABC=12BA BC⋅=122422⨯⨯=8.(3)由A(2, 4) 、D(0, 2) 、C (0,-2),得AD=22,AC=210.由于∠DAC+∠ACD=45°,∠ACE+∠ACD=45°,所以∠DAC=∠ACE.所以△ACE与△ACD相似,分两种情况:①如图3,当CE ADCA AC=时,CE=AD=22.图2此时△ACD≌△CAE,相似比为1.②如图4,当CE ACCA AD=时,21021022=.解得CE=102.此时C、E两点间的水平距离和竖直距离都是10,所以E(10, 8).图3 图4例2:如图1,Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.(1)若△BPQ与△ABC相似,求t的值;(2)如图2,连接AQ、CP,若AQ⊥CP,求t的值;(3)试证明:PQ的中点在△ABC的一条中位线上.图1 图2满分解答(1)Rt△ABC中,AC=6,BC=8,所以AB=10.△BPQ与△ABC相似,存在两种情况:①如果BP BABQ BC=,那么510848tt=-.解得t=1.②如果BP BCBQ BA=,那么588410tt=-.解得3241t=.图3 图4(2)作PD ⊥BC ,垂足为D .在Rt △BPD 中,BP =5t ,cos B =45,所以BD =BP cos B =4t ,PD =3t . 当AQ ⊥CP 时,△ACQ ∽△CDP .所以AC CD QC PD =,即68443t t t -=.解得78t =.图5 图6(3)如图4,过PQ 的中点H 作BC 的垂线,垂足为F ,交AB 于E . 由于H 是PQ 的中点,HF //PD ,所以F 是QD 的中点. 又因为BD =CQ =4t ,所以BF =CF . 因此F 是BC 的中点,E 是AB 的中点.所以PQ 的中点H 在△ABC 的中位线EF 上.例3:如图1,已知抛物线211(1)444by x b x =-++(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 是左侧),与y 轴的正半轴交于点C .(1)点B 的坐标为______,点C 的坐标为__________(用含b 的代数式表示); (2)请你探索在第一象限内是否存在点P ,使得四边形PCOB 的面积等于2b ,且△PBC 是以点P 为直角顶点的等腰直角三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由;(3)请你进一步探索在第一象限内是否存在点Q ,使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.图1满分解答(1)B 的坐标为(b , 0),点C 的坐标为(0,4b ). (2)如图2,过点P 作PD ⊥x 轴,PE ⊥y 轴,垂足分别为D 、E ,那么△PDB ≌△PEC . 因此PD =PE .设点P 的坐标为(x, x). 如图3,联结OP .所以S 四边形PCOB =S △PCO +S △PBO =1152428b x b x bx ⨯⋅+⨯⋅==2b .解得165x =.所以点P 的坐标为(1616,55).图2 图3(3)由2111(1)(1)()4444b y x b x x x b =-++=--,得A (1, 0),OA =1. ①如图4,以OA 、OC 为邻边构造矩形OAQC ,那么△OQC ≌△QOA . 当BA QA QA OA=,即2QA BA OA =⋅时,△BQA ∽△QOA . 所以2()14bb =-.解得843b =±Q 为(1,23+.②如图5,以OC 为直径的圆与直线x =1交于点Q ,那么∠OQC =90°。
2020年广东中考数学压轴题:动点问题

2020年广东省中考数学压轴题:动点问题如图1,已知梯形OABC ,抛物线分别过点O (0,0)、A (2,0)、B (6,3).(1)直接写出抛物线的对称轴、解析式及顶点M 的坐标;(2)将图1中梯形OABC 的上下底边所在的直线OA 、CB 以相同的速度同时向上平移,分别交抛物线于点O 1、A 1、C 1、B 1,得到如图2的梯形O 1A 1B 1C 1.设梯形O 1A 1B 1C 1的面积为S ,A 1、 B 1的坐标分别为 (x 1,y 1)、(x 2,y 2).用含S 的代数式表示x 2-x 1,并求出当S =36时点A 1的坐标;(3)在图1中,设点D 的坐标为(1,3),动点P 从点B 出发,以每秒1个单位长度的速度沿着线段BC 运动,动点Q 从点D 出发,以与点P 相同的速度沿着线段DM 运动.P 、Q 两点同时出发,当点Q 到达点M 时,P 、Q 两点同时停止运动.设P 、Q 两点的运动时间为t ,是否存在某一时刻t ,使得直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴围成的三角形相似?若存在,请求出t 的值;若不存在,请说明理由.图1 图2满分解答(1)抛物线的对称轴为直线1x =,解析式为21184y x x =-,顶点为M (1,18-). (2) 梯形O 1A 1B 1C 1的面积12122(11)3()62x x S x x -+-⨯3==+-,由此得到1223s x x +=+.由于213y y -=,所以22212211111138484y y x x x x -=--+=.整理,得212111()()384x x x x ⎡⎤-+-=⎢⎥⎣⎦.因此得到2172x x S -=. 当S =36时,212114,2.x x x x +=⎧⎨-=⎩ 解得126,8.x x =⎧⎨=⎩ 此时点A 1的坐标为(6,3).(3)设直线AB 与PQ 交于点G ,直线AB 与抛物线的对称轴交于点E ,直线PQ 与x 轴交于点F ,那么要探求相似的△GAF 与△GQE ,有一个公共角∠G .在△GEQ 中,∠GEQ 是直线AB 与抛物线对称轴的夹角,为定值.在△GAF 中,∠GAF 是直线AB 与x 轴的夹角,也为定值,而且∠GEQ ≠∠GAF . 因此只存在∠GQE =∠GAF 的可能,△GQE ∽△GAF .这时∠GAF =∠GQE =∠PQD .由于3tan4GAF∠=,tan5DQ tPQDQP t∠==-,所以345tt=-.解得207t=.图3 图4。
2020年全国中考数学压轴题全解全析

2020年全国中考数学压轴题全解全析一年一度的中考就要开始了,中考数学中的压轴题向来是广大师生非常关注的,因为这些试题往往在很大程度上决定了考分的高下,为了帮助大家迎接今年的中考,特别制作了此资料,希望能对大家有一定的帮助。
1、(北京课改B 卷)我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;(2)探究:当等对角线四边形中两条对角线所夹锐角为60o时,这对60o角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.[解] (1)答案不唯一,如正方形、矩形、等腰梯形等等.(2)结论:等对角线四边形中两条对角线所夹锐角为60o时,这对60o角所对的两边之和大于或等于一条对角线的长.已知:四边形ABCD 中,对角线AC ,BD 交于点O ,AC BD =,且60AOD ∠=o.求证:BC AD AC +≥.证明:过点D 作DF AC ∥,在DF 上截取DE ,使DE AC =. 连结CE ,BE .故60EDO ∠=o ,四边形ACED 是平行四边形. 所以BDE △是等边三角形,CE AD =. 所以DE BE AC ==.①当BC 与CE 不在同一条直线上时(如图1), 在BCE △中,有BC CE BE +>. 所以BC AD AC +>.②当BC 与CE 在同一条直线上时(如图2), 则BC CE BE +=. 因此BC AD AC +=.综合①、②,得BC AD AC +≥.即等对角线四边形中两条对角线所夹角为60o时,这对60o角所对的两边之和大于或等于其中一条对角线的长.[点评]本题是一道探索题,是近年来中考命题的热点问题,在第2小题中要求学生先猜想可能的结论,再进行证明,这对学生的确有较高的能力要求,而在探索结论前可以自己先画几个草图,做到心中有数再去努力求证;很多学生往往会忽略特殊情况没有进行讨论,应当予以关注,总之这是一道新课标形势下的优秀压轴题。
2020年东营市中考数学压轴题型讲练——几何图形中运动变化问题

2020年东营市中考数学压轴题型讲练——几何图形中运动变化问题【题型导引】题型一:动点问题动态型试题一般是指以几何知识和图形为背景,渗透运动变化观点的一类试题,常见的运动对象有点动、线动、图动;其运动形式有平动、旋转、翻折、滚动等.动态型试题其特点是集几何、代数知识于一体,数形结合,有较强的综合性.题目灵活多变,动中有静,动静结合.(1)动中求静,即在运动变化中探索问题中的不变性;(2)动静互化,抓住“静”的瞬间,找出导致图形或变化规律发生改变的特殊时刻;同时在运动变化的过程中寻找不变性及变化规律.题型二:动线问题动线问题主要和旋转变换结合,在处理此类问题上要注意进行转化,化动为静,利用变换的性质解答即可。
题型三:动面问题面的转动问题注意转化为静态问题来研究,转动后的与之前的在性质上形成新的图形,结合图形特点进行解答。
【典例解析】类型一:动点问题例题1:(2019•湖南衡阳•3分)如图,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC 和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与△ABC的重叠部分面积为S.则S关于t的函数图象大致为()A.B.C.D.【解答】解:∵在直角三角形ABC中,∠C=90°,AC=BC,∴△ABC是等腰直角三角形,∵EF⊥BC,ED⊥AC,∴四边形EFCD是矩形,∵E是AB的中点,∴EF=AC,DE=BC,∴EF=ED,∴四边形EFCD是正方形,设正方形的边长为a,如图1当移动的距离<a时,S=正方形的面积﹣△EE′H的面积=a2﹣t2;当移动的距离>a时,如图2,S=S△AC′H=(2a﹣t)2=t2﹣2at+2a2,∴S关于t的函数图象大致为C选项,故选:C.技法归纳:解答此类问题的策略可以归纳为三步:“看”“写” “选”.(1)“看”就是认真观察几何图形,彻底弄清楚动点从何点开始出发,运动到何点停止,整个运动过程分为不同的几段,何点(时刻)是特殊点(时刻),这是准确解答的前提和关键;(2)“写”就是计算、写出动点在不同路段的函数解析式,注意一定要注明自变量的取值范围,求出在特殊点的函数数值和自变量的值;(3)“选”就是根据解析式选择准确的函数图象或答案,多用排除法。
中考专题动点综合问题-2020年中考数学
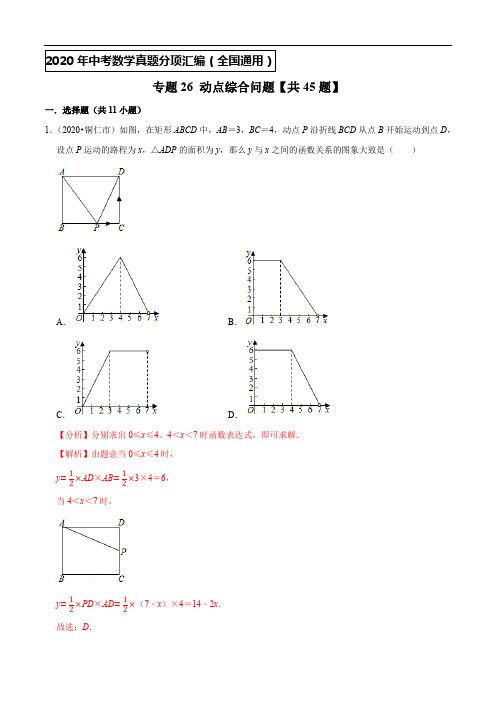
2020年中考数学真题分项汇编(全国通用)专题26 动点综合问题【共45题】一.选择题(共11小题)1.(2020•铜仁市)如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是()A.B.C.D.【分析】分别求出0≤x≤4、4<x<7时函数表达式,即可求解.【解析】由题意当0≤x≤4时,y=12×AD×AB=12×3×4=6,当4<x<7时,y=12×PD×AD=12×(7﹣x)×4=14﹣2x.故选:D.2.(2020•安徽)如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC在直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为()A.B.C.D.【分析】分为0<x≤2、2<x≤4两种情况,然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式,于是可求得问题的答案.【解析】如图1所示:当0<x≤2时,过点G作GH⊥BF于H.∵△ABC和△DEF均为等边三角形,∴△GEJ为等边三角形.∴GH=√32EJ=√32x,∴y=12EJ•GH=√34x2.当x=2时,y=√3,且抛物线的开口向上.如图2所示:2<x≤4时,过点G作GH⊥BF于H.y =12FJ •GH =√34(4﹣x )2,函数图象为抛物线的一部分,且抛物线开口向上.故选:A .3.(2020•江西)在平面直角坐标系中,点O 为坐标原点,抛物线y =x 2﹣2x ﹣3与y 轴交于点A ,与x 轴正半轴交于点B ,连接AB ,将Rt △OAB 向右上方平移,得到Rt △O 'A 'B ',且点O ',A '落在抛物线的对称轴上,点B '落在抛物线上,则直线A 'B '的表达式为( )A .y =xB .y =x +1C .y =x +12D .y =x +2【分析】求得A 、B 的坐标以及抛物线的对称轴,根据题意设出A ′(1,n ),则B ′(4,n +3),把B ′(4,n +3)代入抛物线解析式求得n ,即可求得A ′、B ′的坐标,然后根据待定系数法即可求得直线A 'B '的表达式.【解析】如图,∵抛物线y =x 2﹣2x ﹣3与y 轴交于点A ,与x 轴正半轴交于点B ,令y =0,解得x =﹣1或3,令x =0,求得y =﹣3,∴A (3,0),B (0,﹣3),∵抛物线y =x 2﹣2x ﹣3的对称轴为直线x =−−22×1=1, ∴A ′的横坐标为1,设A ′(1,n ),则B ′(4,n +3),∵点B '落在抛物线上,∴n +3=16﹣8﹣3,解得n =2,∴A ′(1,2),B ′(4,5),设直线A 'B '的表达式为y =kx +b ,∴{k +b =24k +b =5, 解得{k =1b =1∴直线A 'B '的表达式为y =x +1,故选:B .4.(2020•衡阳)如图1,在平面直角坐标系中,▱ABCD在第一象限,且BC∥x轴.直线y=x从原点O出发沿x轴正方向平移,在平移过程中,直线被▱ABCD截得的线段长度n与直线在x轴上平移的距离m 的函数图象如图2所示.那么▱ABCD的面积为()A.3B.3√2C.6D.6√2【分析】根据函数图象中的数据可以分别求得平行四边形的边AD的长和边AD边上的高BM的长,从而可以求得平行四边形的面积.【解析】过B作BM⊥AD于点M,分别过B,D作直线y=x的平行线,交AD于E,如图1所示,由图象和题意可得,AE=6﹣4=2,DE=7﹣6=1,BE=2,∴AB=2+1=3,∵直线BE平行直线y=x,∴BM=EM=√2,∴平行四边形ABCD的面积是:AD•BM=3×√2=3√2.故选:B.5.(2020•辽阳)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2√2,CD⊥AB于点D.点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F.设点P 运动的路程为x,四边形CEPF的面积为y,则能反映y与x之间函数关系的图象是()A.B.C.D.【分析】根据Rt△ABC中,∠ACB=90°,AC=BC=2√2,可得AB=4,根据CD⊥AB于点D.可得AD=BD=2,CD平分角ACB,点P从点A出发,沿A→D→C的路径运动,运动到点C停止,分两种情况讨论:根据PE⊥AC,PF⊥BC,可得四边形CEPF是矩形和正方形,设点P运动的路程为x,四边形CEPF的面积为y,进而可得能反映y与x之间函数关系式,从而可以得函数的图象.【解析】∵在Rt△ABC中,∠ACB=90°,AC=BC=2√2,∴AB=4,∠A=45°,∵CD⊥AB于点D,∴AD=BD=2,∵PE⊥AC,PF⊥BC,∴四边形CEPF是矩形,∴CE=PF,PE=CF,∵点P运动的路程为x,∴AP=x,则AE=PE=x•sin45°=√22x,∴CE=AC﹣AE=2√2−√22x,∵四边形CEPF的面积为y,∴当点P从点A出发,沿A→D路径运动时,即0<x<2时,y=PE•CE=√22x(2√2−√22x)=−12x2+2x=−12(x﹣2)2+2,∴当0<x<2时,抛物线开口向下;当点P沿D→C路径运动时,即2≤x<4时,∵CD是∠ACB的平分线,∴PE=PF,∴四边形CEPF是正方形,∵AD=2,PD=x﹣2,∴CP=4﹣x,y=12(4﹣x)2=12(x﹣4)2.∴当2≤x<4时,抛物线开口向上,综上所述:能反映y与x之间函数关系的图象是:A.故选:A.6.(2020•孝感)如图,在四边形ABCD中,AD∥BC,∠D=90°,AB=4,BC=6,∠BAD=30°.动点P沿路径A→B→C→D从点A出发,以每秒1个单位长度的速度向点D运动.过点P作PH⊥AD,垂足为H.设点P运动的时间为x(单位:s),△APH的面积为y,则y关于x的函数图象大致是()A.B.C.D.【分析】分别求出点P在AB上运动、点P在BC上运动、点P在CD上运动时的函数表达式,进而求解.【解析】①当点P在AB上运动时,y=12AH×PH=12×AP sin A×AP cos A=12×x2×√34=√38x2,图象为二次函数;②当点P在BC上运动时,如下图,由①知,BH′=AB sin A=4×12=2,同理AH′=2√3,则y=12×AH×PH=12(2√3+x﹣4)×2=2√3−4+x,为一次函数;③当点P在CD上运动时,同理可得:y=12×(2√3+6)×(4+6+2﹣x)=(3+√3)(12﹣x),为一次函数;故选:D.7.(2020•淄博)如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是()A.12B.24C.36D.48【分析】由图2知,AB=BC=10,当BP⊥AC时,y的值最小,即△ABC中,BC边上的高为8(即此时BP=8),即可求解.【解析】由图2知,AB=BC=10,当BP⊥AC时,y的值最小,即△ABC中,BC边上的高为8(即此时BP=8),当y=8时,PC=√BC2−BP2=√102−82=6,△ABC的面积=12×AC×BP=12×8×12=48,故选:D.8.(2020•广元)如图,AB,CD是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→B→O的路线匀速运动,设∠APD=y(单位:度),那么y与点P运动的时间(单位:秒)的关系图是()A.B.C.D.【分析】根据图示,分三种情况:(1)当点P沿O→C运动时;(2)当点P沿C→B运动时;(3)当点P沿B→O运动时;分别判断出y的取值情况,进而判断出y与点P运动的时间x(单位:秒)的关系图是哪个即可.【解析】(1)当点P沿O→C运动时,当点P在点O的位置时,y=90°,当点P在点C的位置时,∵OA=OC,∴y=45°,∴y由90°逐渐减小到45°;(2)当点P沿C→B运动时,根据圆周角定理,可得y≡90°÷2=45°;(3)当点P沿B→O运动时,当点P在点B的位置时,y=45°,当点P在点O的位置时,y=90°,∴y由45°逐渐增加到90°.故选:B.9.(2020•金昌)如图①,正方形ABCD中,AC,BD相交于点O,E是OD的中点.动点P从点E出发,沿着E→O→B→A的路径以每秒1个单位长度的速度运动到点A,在此过程中线段AP的长度y随着运动时间x的函数关系如图②所示,则AB的长为()A.4√2B.4C.3√3D.2√2【分析】连接AE,由题意DE=OE,设DE=OE=x,则OA=OD=2x,AE=2√5,在Rt△AEO中,利用勾股定理构建方程即可解决问题.【解析】如图,连接AE.∵四边形ABCD是正方形,∴AC⊥BD,OA=OC=OD=OB,由题意DE=OE,设DE=OE=x,则OA=OD=2x,∵AE=2√5,∴x2+(2x)2=(2√5)2,解得x=2或﹣2(不合题意舍弃),∴OA=OD=4,∴AB =AD =4√2,故选:A .10.(2020•台州)如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v (单位:m /s )与运动时间t (单位:s )的函数图象如图2,则该小球的运动路程y (单位:m )与运动时间t (单位:s )之间的函数图象大致是( )A .B .C .D .【分析】小球从左侧的斜坡滚下是匀变速运动,运动的路程y 是t 的二次函数,图象是先缓后陡,由此即可判断.【解析】小球从左侧的斜坡滚下是匀变速运动,运动的路程y 是t 的二次函数,图象是先缓后陡, 在右侧上升时,情形与左侧相反,故选:C . 11.(2020•河南)如图,在△ABC 中,∠ACB =90°,边BC 在x 轴上,顶点A ,B 的坐标分别为(﹣2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,点D 的坐标为( )A .(32,2)B .(2,2)C .(114,2) D .(4,2)【分析】根据已知条件得到AC =6,OC =2,OB =7,求得BC =9,根据正方形的性质得到DE =OC =OE =2,求得O ′E ′=O ′C ′=2,根据相似三角形的性质得到BO ′=3,于是得到结论.【解析】如图,设正方形D ′C ′O ′E ′是正方形OCDE 沿x 轴向右平移后的正方形,∵顶点A ,B 的坐标分别为(﹣2,6)和(7,0),∴AC =6,OC =2,OB =7,∴BC =9,∵四边形OCDE 是正方形,∴DE =OC =OE =2,∴O ′E ′=O ′C ′=2,∵E ′O ′⊥BC ,∴∠BO ′E ′=∠BCA =90°,∴E ′O ′∥AC ,∴△BO ′E ′∽△BCA ,∴E′O′AC=BO′BC , ∴26=BO′9,∴BO ′=3,∴OC ′=7﹣2﹣3=2,∴当点E 落在AB 边上时,点D 的坐标为(2,2),故选:B .二.填空题(共11小题)12.(2020•通辽)如图①,在△ABC 中,AB =AC ,∠BAC =120°,点E 是边AB 的中点,点P 是边BC上一动点,设PC =x ,P A +PE =y .图②是y 关于x 的函数图象,其中H 是图象上的最低点.那么a +b 的值为 4+2√3 .【分析】点A关于BC的对称点为点A′,连接A′E交BC于点P,此时y最小,进而求解.【解析】如图,将△ABC沿BC折叠得到△A′BC,则四边形ABA′C为菱形,菱形的对角线交于点O,设菱形的边长为2m,在△ABC中,BC=2BO=2×AC sin∠OAC=4m×sin60°=2√3m,从图②看,AB+BE=3√3=3m,解得:m=√3;点A关于BC的对称点为点A′,连接A′E交BC于点P,此时y最小,∵AB=AC,∠BAC=120°,则∠BAA′=60°,故AA′B为等边三角形,∵E是AB的中点,故A′E⊥AB,而AB∥A′C,故∠P A′C为直角,则a=PC=A′Ccos∠BCA′=2mcos30°=4√33m,此时b=AA′=2m,则a+b=2m+4√33m=4+2√3.故答案为4+2√3.13.(2020•连云港)如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y=34x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为2.【分析】如图,连接OB ,取OA 的中点M ,连接CM ,过点M 作MN ⊥DE 于N .首先证明点C 的运动轨迹是以M 为圆心,1为半径的⊙M ,设⊙M 交MN 于C ′.求出MN ,当点C 与C ′重合时,△C ′DE 的面积最小.【解析】如图,连接OB ,取OA 的中点M ,连接CM ,过点M 作MN ⊥DE 于N .∵AC =CB ,AM =OM ,∴MC =12OB =1,∴点C 的运动轨迹是以M 为圆心,1为半径的⊙M ,设⊙M 交MN 于C ′.∵直线y =34x ﹣3与x 轴、y 轴分别交于点D 、E ,∴D (4,0),E (0,﹣3),∴OD =4,OE =3,∴DE =2+42=5,∵∠MDN =∠ODE ,∠MND =∠DOE ,∴△DNM ∽△DOE ,∴MNOE =DMDE ,∴MN 3=35, ∴MN =95,当点C 与C ′重合时,△C ′DE 的面积最小,最小值=12×5×(95−1)=2, 故答案为2.14.(2020•福建)设A ,B ,C ,D 是反比例函数y =kx 图象上的任意四点,现有以下结论:①四边形ABCD 可以是平行四边形;②四边形ABCD 可以是菱形;③四边形ABCD 不可能是矩形;④四边形ABCD 不可能是正方形.其中正确的是 ①④ .(写出所有正确结论的序号)【分析】如图,过点O 任意作两条直线分别交反比例函数的图象于A ,C ,B ,D ,得到四边形ABCD .证明四边形ABCD 是平行四边形即可解决问题.【解析】如图,过点O 任意作两条直线分别交反比例函数的图象于A ,C ,B ,D ,得到四边形ABCD .由对称性可知,OA =OC ,OB =OD ,∴四边形ABCD 是平行四边形,当OA =OC =OB =OD 时,四边形ABCD 是矩形.∵反比例函数的图象在一,三象限,∴直线AC 与直线BD 不可能垂直,∴四边形ABCD 不可能是菱形或正方形,故选项①④正确,故答案为①④,15.(2020•淮安)如图,等腰△ABC 的两个顶点A (﹣1,﹣4)、B (﹣4,﹣1)在反比例函数y =k1x (x <0)的图象上,AC=BC.过点C作边AB的垂线交反比例函数y=k1x(x<0)的图象于点D,动点P从点D出发,沿射线CD方向运动3√2个单位长度,到达反比例函数y=k2x(x>0)图象上一点,则k2=1.【分析】用待定系数求得反比例函数y=k1x,再与直线y=x联立方程组求得D点坐标,再题意求得运动后P点的坐标,最后将求得的P点坐标代入y=k2x(x>0)求得结果.【解析】把A(﹣1,﹣4)代入y=k1x中得,k1=4,∴反比例函数y=k1x为y=4x,∵A(﹣1,﹣4)、B(﹣4,﹣1),∴AB的垂直平分线为y=x,联立方程驵{y=4xy=x,解得{x=−2y=−2,或{x=2y=2,∵AC=BC,CD⊥AB,∴CD是AB的垂直平分线,∵CD与反比例函数y=k1x(x<0)的图象于点D,∴D(﹣2,﹣2),∵动点P从点D出发,沿射线CD方向运动3√2个单位长度,到达反比例函数y=k2x(x>0)图象上一点,∴设移动后的点P的坐标为(m,m)(m>﹣2),则(x+2)2+(x+2)2=(3√2)2,∴x=1,∴P(1,1),把P (1,1)代入y =k2x (x >0)中,得k 2=1, 故答案为:1.16.(2020•德州)如图,在矩形ABCD 中,AB =√3+2,AD =√3.把AD 沿AE 折叠,使点D 恰好落在AB边上的D ′处,再将△AED ′绕点E 顺时针旋转α,得到△A 'ED ″,使得EA ′恰好经过BD ′的中点F .A ′D ″交AB 于点G ,连接AA ′.有如下结论:①A ′F 的长度是√6−2;②弧D 'D ″的长度是5√312π;③△A ′AF ≌△A ′EG ;④△AA ′F ∽△EGF .上述结论中,所有正确的序号是 ①②④ .【分析】由折叠的性质可得∠D =∠AD 'E =90°=∠DAD ',AD =AD ',可证四边形ADED '是正方形,可得AD =AD '=D 'E =DE =√3,AE =√2AD =√6,∠EAD '=∠AED '=45°,由勾股定理可求EF 的长,由旋转的性质可得AE =A 'E =√6,∠D 'ED ''=α,∠EA 'D ''=∠EAD '=45°,可求A 'F =√6−2,可判断①;由锐角三角函数可求∠FED '=30°,由弧长公式可求弧D 'D ″的长度,可判断②;由等腰三角形的性质可求∠EAA '=∠EA 'A =52.5°,∠A 'AF =7.5°,可判断③;由“HL ”可证Rt △ED 'G ≌Rt △ED ''G ,可得∴∠D 'GE =∠D ''GE =52.5°,可证△AF A '∽△EFG ,可判断④,即可求解.【解析】∵把AD 沿AE 折叠,使点D 恰好落在AB 边上的D ′处, ∴∠D =∠AD 'E =90°=∠DAD ',AD =AD ',∴四边形ADED '是矩形,又∵AD =AD '=√3,∴四边形ADED '是正方形,∴AD =AD '=D 'E =DE =√3,AE =√2AD =√6,∠EAD '=∠AED '=45°,∴D 'B =AB ﹣AD '=2,∵点F 是BD '中点,∴D 'F =1,∴EF =√D′E 2+D′F 2=√3+1=2,∵将△AED ′绕点E 顺时针旋转α,∴AE =A 'E =√6,∠D 'ED ''=α,∠EA 'D ''=∠EAD '=45°,∴A 'F =√6−2,故①正确;∵tan∠FED'=D′FD′E=1√3=√33,∴∠FED'=30°∴α=30°+45°=75°,∴弧D'D″的长度=75°×π×√3180°=5√312π,故②正确;∵AE=A'E,∠AEA'=75°,∴∠EAA'=∠EA'A=52.5°,∴∠A'AF=7.5°,∵∠AA'F≠∠EA'G,∠AA'E≠∠EA'G,∠AF A'=120°≠∠EA'G,∴△AA'F与△A'GE不全等,故③错误;∵D'E=D''E,EG=EG,∴Rt△ED'G≌Rt△ED''G(HL),∴∠D'GE=∠D''GE,∵∠AGD''=∠A'AG+∠AA'G=105°,∴∠D'GE=52.5°=∠AA'F,又∵∠AF A'=∠EFG,∴△AF A'∽△EFG,故④正确,故答案为:①②④.17.(2020•东营)如图,在Rt△AOB中,OB=2√3,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为2√2.【分析】连接OP、OQ,作OP′⊥AB于P′,根据切线的性质得到OQ⊥PQ,根据勾股定理得到PQ=√OP2−1,根据垂线段最短得到当OP⊥AB时,OP最小,根据直角三角形的性质、勾股定理计算即可.【解析】连接OP、OQ,作OP′⊥AB于P′,∵PQ是⊙O的切线,∴OQ⊥PQ,∴PQ=√OP2−OQ2=√OP2−1,当OP最小时,线段PQ长度的最小,当OP⊥AB时,OP最小,在Rt△AOB中,∠A=30°,∴OA=OBtanA=6,在Rt△AOP′中,∠A=30°,∴OP′=12OA=3,∴线段PQ长度的最小值=√32−1=2√2,故答案为:2√2.18.(2020•广东)有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC =90°,点M,N分别在射线BA,BC上,MN长度始终保持不变,MN=4,E为MN的中点,点D到BA,BC的距离分别为4和2.在此滑动过程中,猫与老鼠的距离DE的最小值为2√5−2.【分析】如图,连接BE,BD.求出BE,BD,根据DE≥BD﹣BE求解即可.【解析】如图,连接BE,BD.由题意BD =√22+42=2√5,∵∠MBN =90°,MN =4,EM =NE ,∴BE =12MN =2,∴点E 的运动轨迹是以B 为圆心,2为半径的弧,∴当点E 落在线段BD 上时,DE 的值最小,∴DE 的最小值为2√5−2.故答案为2√5−2.19.(2020•鄂州)如图,半径为2cm 的⊙O 与边长为2cm 的正方形ABCD 的边AB 相切于E ,点F 为正方形的中心,直线OE 过F 点.当正方形ABCD 沿直线OF 以每秒(2−√3)cm 的速度向左运动 1或(11+6√3) 秒时,⊙O 与正方形重叠部分的面积为(23π−√3)cm 2.【分析】分两种情形:如图1中,当点A ,B 落在⊙O 上时,如图2中,当点C ,D 落在⊙O 上时,分别求解即可解决问题.【解析】如图1中,当点A ,B 落在⊙O 上时,⊙O 与正方形重叠部分的面积为(23π−√3)cm 2此时,运动时间t =(2−√3)÷(2−√3)=1(秒)如图2中,当点C ,D 落在⊙O 上时,⊙O 与正方形重叠部分的面积为(23π−√3)cm 2此时,运动时间t=[4+2﹣(2−√3)]÷(2−√3)=(11+6√3)(秒),综上所述,满足条件的t的值为1秒或(11+6√3)秒.故答案为1或(11+6√3).20.(2020•鄂州)如图,已知直线y=−√3x+4与x、y轴交于A、B两点,⊙O的半径为1,P为AB上一动点,PQ切⊙O于Q点.当线段PQ长取最小值时,直线PQ交y轴于M点,a为过点M的一条直线,则点P到直线a的距离的最大值为2√3.【分析】在直线y=−√3x+4上,x=0时,y=4,y=0时,x=4√33,可得OB=4,OA=4√33,得角OBA=30°,根据PQ切⊙O于Q点可得OQ⊥PQ,由OQ=1,因此当OP最小时PQ长取最小值,此时OP ⊥AB,若使点P到直线a的距离最大,则最大值为PM,且M位于x轴下方,过点P作PE⊥y轴于点E,根据勾股定理和特殊角30度即可求出PM的长.【解析】如图,在直线y=−√3x+4上,x=0时,y=4,当y=0时,x=4√3 3,∴OB=4,OA=4√3 3,∴tan∠OBA=OAOB=√33,∴∠OBA=30°,由PQ切⊙O于Q点可知:OQ⊥PQ,∴PQ=√OP2−OQ2,由于OQ=1,因此当OP最小时PQ长取最小值,此时OP⊥AB,∴OP=12OB=2,此时PQ=√22−12=√3,BP=√42−22=2√3,∴OQ=12OP,即∠OPQ=30°,若使点P到直线a的距离最大,则最大值为PM,且M位于x轴下方,过点P作PE⊥y轴于点E,∴EP=12BP=√3,∴BE=√(2√3)2−(√3)2=3,∴OE=4﹣3=1,∵OE=12OP,∴∠OPE=30°,∴∠EPM=30°+30°=60°,即∠EMP=30°,∴PM=2EP=2√3.故答案为:2√3.21.(2020•成都)如图,在矩形ABCD中,AB=4,BC=3,E,F分别为AB,CD边的中点.动点P从点E出发沿EA向点A运动,同时,动点Q从点F出发沿FC向点C运动,连接PQ,过点B作BH⊥PQ 于点H,连接DH.若点P的速度是点Q的速度的2倍,在点P从点E运动至点A的过程中,线段PQ 长度的最大值为3√2,线段DH长度的最小值为√13−√2.【分析】连接EF交PQ于M,连接BM,取BM的中点O,连接OH,OD,过点O作ON⊥CD于N.首先利用相似三角形的性质证明EM=2FN,推出EM=2,FN=1,当点P与A重合时,PQ的值最大,解直角三角形求出OD,OH即可解决问题.【解析】连接EF交PQ于M,连接BM,取BM的中点O,连接OH,OD,过点O作ON⊥CD于N.∵四边形ABCD是矩形,DF=CF,AE=EB,∴四边形ADFE是矩形,∴EF=AD=3,∵FQ∥PE,∴△MFQ∽△MEP,∴MFME =FQPE,∵PE=2FQ,∴EM=2MF,∴EM=2,FM=1,当点P与A重合时,PQ的值最大,此时PM=√AE2+ME2=√22+22=2√2,MQ=√FQ2+MF2=√12+12=√2,∴PQ=3√2,∵MF∥ON∥BC,MO=OB,∴FN=CN=1,DN=DF+FN=3,ON=12(FM+BC)=2,∴OD=√DN2+ON2=√32+22=√13,∵BH⊥PQ,∴∠BHM=90°,∵OM=OB,∴OH=12BM=12×√22+22=√2,∵DH≥OD﹣OH,∴DH≥√13−√2,∴DH的最小值为√13−√2,故答案为3√2,√13−√2.22.(2020•泰州)如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,若以1cm为半径的⊙O与直线a相切,则OP的长为3cm或5cm.【分析】当点O在点H的左侧⊙O与直线a相切时,OP=PH﹣OH;当点O在点H的右侧⊙O与直线a相切时,OP=PH+OH,即可得出结果.【解析】∵直线a⊥b,O为直线b上一动点,∴⊙O与直线a相切时,切点为H,∴OH=1cm,当点O在点H的左侧,⊙O与直线a相切时,如图1所示:OP=PH﹣OH=4﹣1=3(cm);当点O在点H的右侧,⊙O与直线a相切时,如图2所示:OP=PH+OH=4+1=5(cm);∴⊙O与直线a相切,OP的长为3cm或5cm,故答案为:3cm或5cm.三.解答题(共23小题)23.(2020•临沂)如图,菱形ABCD的边长为1,∠ABC=60°,点E是边AB上任意一点(端点除外),线段CE的垂直平分线交BD,CE分别于点F,G,AE,EF的中点分别为M,N.(1)求证:AF=EF;(2)求MN+NG的最小值;(3)当点E在AB上运动时,∠CEF的大小是否变化?为什么?【分析】(1)连接CF,根据垂直平分线的性质和菱形的对称性得到CF=EF和CF=AF即可得证;(2)连接AC,根据菱形对称性得到AF+CF最小值为AC,再根据中位线的性质得到MN+NG的最小值为AC的一半,即可求解;(3)延长EF,交DC于H,利用外角的性质证明∠AFC=∠FCE+∠FEC+∠F AE+∠FEA,再由AF=CF =EF,得到∠AEF=∠EAF,∠FEC=∠FCE,从而推断出∠AFD=∠F AE+∠ABF=∠F AE+∠CEF,从而可求出∠ABF=∠CEF=30°,即可证明.【解析】(1)连接CF,∵FG垂直平分CE,∴CF=EF,∵四边形ABCD为菱形,∴A和C关于对角线BD对称,∴CF=AF,∴AF =EF ;(2)连接AC ,∵M 和N 分别是AE 和EF 的中点,点G 为CE 中点,∴MN =12AF ,NG =12CF ,即MN +NG =12(AF +CF ),当点F 与菱形ABCD 对角线交点O 重合时, AF +CF 最小,即此时MN +NG 最小,∵菱形ABCD 边长为1,∠ABC =60°,∴△ABC 为等边三角形,AC =AB =1,即MN +NG 的最小值为12;(3)不变,理由是:延长EF ,交DC 于H ,∵∠CFH =∠FCE +∠FEC ,∠AFH =∠F AE +∠FEA ,∴∠AFC =∠FCE +∠FEC +∠F AE +∠FEA ,∵点F 在菱形ABCD 对角线BD 上,根据菱形的对称性可得:∠AFD =∠CFD =12∠AFC ,∵AF =CF =EF ,∴∠AEF =∠EAF ,∠FEC =∠FCE ,∴∠AFD=∠F AE+∠ABF=∠F AE+∠CEF,∴∠ABF=∠CEF,∵∠ABC=60°,∴∠ABF=∠CEF=30°,为定值.24.(2020•金华)如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F,已知OB=8.(1)求证:四边形AEFD为菱形.(2)求四边形AEFD的面积.(3)若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P,Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.【分析】(1)根据邻边相等的四边形是菱形证明即可.(2)连接DE,求出△ADE的面积即可解决问题.(3)首先证明AK=3DK,①当AP为菱形的一边,点Q在x轴的上方,有图2,图3两种情形.②当AP为菱形的边,点Q在x轴的下方时,有图4,图5两种情形.③如图6中,当AP为菱形的对角线时,有图6一种情形.分别利用相似三角形的性质求解即可.【解答】(1)证明:如图1中,∵AE∥DF,AD∥EF,∴四边形AEFD是平行四边形,∵四边形ABOC是正方形,∴AC=AB=OC=OB,∠ACE=∠ABD=90°,∵E,D分别是OC,OB的中点,∴CE=BD,∴△CAE≌△ABD(SAS),∴AE=AD,∴四边形AEFD是菱形.(2)解:如图1中,连接DE.∵S△ADB=S△ACE=12×8×4=16,S△EOD=12×4×4=8,∴S△AED=S正方形ABOC﹣2S△ABD﹣S△EOD=64﹣2×16﹣8=24,∴S菱形AEFD=2S△AED=48.(3)解:如图1中,连接AF,设AF交DE于K,∵OE=OD=4,OK⊥DE,∴KE=KD,∴OK=KE=KD=2√2,∵AO=8√2,∴AK=6√2,∴AK=3DK,①当AP 为菱形的一边,点Q 在x 轴的上方,有图2,图3两种情形:如图2中,设AG 交PQ 于H ,过点H 作HN ⊥x 轴于N ,交AC 于M ,设AM =t .∵菱形P AQG ∽菱形ADFE ,∴PH =3AH ,∵HN ∥OQ ,QH =HP ,∴ON =NP , ∴HN 是△PQO 的中位线,∴ON =PN =8﹣t ,∵∠MAH =∠PHN =90°﹣∠AHM ,∠PNH =∠AMH =90°,∴△HMA ∽△PNH ,∴AMNH =MHPN =AHPH =13, ∴HN =3AM =3t ,∴MH =MN ﹣NH =8﹣3t ,∵PN =3MH ,∴8﹣t =3(8﹣3t ),∴t =2,∴OP =2ON =2(8﹣t )=12,∴P (12,0).如图3中,过点H 作HI ⊥y 轴于I ,过点P 作PN ⊥x 轴交IH 于N ,延长BA 交IN 于M .同法可证:△AMH ∽△HNP ,∴AMHN =MHPN =AHHP =13,设MH =t , ∴PN =3MH =3t ,∴AM =BM ﹣AB =3t ﹣8,∵HI 是△OPQ 的中位线,∴OP =2IH ,∴HI =HN ,∴8+t =9t ﹣24,∴t =4,∴OP =2HI =2(8+t )=24,∴P (24,0).②当AP 为菱形的边,点Q 在x 轴的下方时,有图4,图5两种情形:如图4中,QH =3PH ,过点H 作HM ⊥OC 于M ,过D 点P 作PN ⊥MH 于N .∵MH 是△QAC 的中位线,∴MH =12AC =4, 同法可得:△HPN ∽△QHM ,∴NPHM =HN MQ =PH QH =13, ∴PN =13HM =43,∴OM =PN =43,设HN =t ,则MQ =3t ,∵MQ =MC ,∴3t =8−43,∴t =209, ∴OP =MN =4+t =569,∴点P 的坐标为(569,0).如图5中,QH =3PH ,过点H 作HM ⊥x 轴于M 交AC 于I ,过点Q 作QN ⊥HM 于N .∵IH 是△ACQ 的中位线,∴CQ =2HI ,NQ =CI =4,同法可得:△PMH ∽△HNQ ,∴MHNQ =PMHN =PHHQ =13,则MH =13NQ =43, 设PM =t ,则HN =3t ,∵HN =HI ,∴3t =8+43,∴t =289,∴OP =OM ﹣PM =QN ﹣PM =4﹣t =89,∴P (89,0). ③如图6中,当AP 为菱形的对角线时,有图6一种情形:过点H 作HM ⊥y 轴于于点M ,交AB 于I ,过点P 作PN ⊥HM 于N .∵HI ∥x 轴,AH =HP ,∴AI =IB =4,∴PN =IB =4,同法可得:△PNH ∽△HMQ ,∴PNHM =HNMQ =PHHQ =13, ∴MH =3PN =12,HI =MH ﹣MI =4,∵HI 是△ABP 的中位线,∴BP =2IH =8,∴OP =OB +BP =16,∴P (16,0),综上所述,满足条件的点P 的坐标为(12,0)或(24,0)或(569,0)或(89,0)或(16,0). 25.(2020•连云港)筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋)中写道:“水能利物,轮乃曲成”.如图,半径为3m 的筒车⊙O 按逆时针方向每分钟转56圈,筒车与水面分别交于点A 、B ,筒车的轴心O 距离水面的高度OC 长为2.2m ,筒车上均匀分布着若干个盛水筒.若以某个盛水筒P 刚浮出水面时开始计算时间.(1)经过多长时间,盛水筒P 首次到达最高点?(2)浮出水面3.4秒后,盛水筒P 距离水面多高?(3)若接水槽MN 所在直线是⊙O 的切线,且与直线AB 交于点M ,MO =8m .求盛水筒P 从最高点开始,至少经过多长时间恰好在直线MN 上.(参考数据:cos43°=sin47°≈1115,sin16°=cos74°≈1140,sin22°=cos68°≈38)【分析】(1)如图1中,连接OA .求出∠AOC 的度数,以及旋转速度即可解决问题.(2)如图2中,盛水筒P 浮出水面3.4秒后,此时∠AOP =3.4×5°=17°,过点P 作PD ⊥OC 于D ,解直角三角形求出CD 即可.(3)如图3中,连接OP ,解直角三角形求出∠POM ,∠COM ,可得∠POH 的度数即可解决问题.【解析】(1)如图1中,连接OA .由题意,筒车每秒旋转360°×56÷60=5°,在Rt △ACO 中,cos ∠AOC =OC OA =2.23=1115. ∴∠AOC =43°,∴180−435=27.4(秒).答:经过27.4秒时间,盛水筒P 首次到达最高点.(2)如图2中,盛水筒P 浮出水面3.4秒后,此时∠AOP =3.4×5°=17°,∴∠POC =∠AOC +∠AOP =43°+17°=60°,过点P 作PD ⊥OC 于D ,在Rt △POD 中,OD =OP •cos60°=3×12=1.5(m ), 2.2﹣1.5=0.7(m ),答:浮出水面3.4秒后,盛水筒P 距离水面0.7m .(3)如图3中,∵点P 在⊙O 上,且MN 与⊙O 相切,∴当点P 在MN 上时,此时点P 是切点,连接OP ,则OP ⊥MN ,在Rt △OPM 中,cos ∠POM =OP OM =38,∴∠POM =68°,在Rt △COM 中,cos ∠COM =OC OM =2.28=1140, ∴∠COM =74°,∴∠POH =180°﹣∠POM ﹣∠COM =180°﹣68°﹣74°=38°,∴需要的时间为385=7.6(秒),答:盛水筒P 从最高点开始,至少经过7.6秒恰好在直线MN 上.26.(2020•潍坊)如图1,在△ABC 中,∠A =90°,AB =AC =√2+1,点D ,E 分别在边AB ,AC 上,且AD =AE =1,连接DE .现将△ADE 绕点A 顺时针方向旋转,旋转角为α(0°<α<360°),如图2,连接CE ,BD ,CD .(1)当0°<α<180°时,求证:CE =BD ;(2)如图3,当α=90°时,延长CE 交BD 于点F ,求证:CF 垂直平分BD ;(3)在旋转过程中,求△BCD 的面积的最大值,并写出此时旋转角α的度数.【分析】(1)利用“SAS ”证得△ACE ≌△ABD 即可得到结论;(2)利用“SAS ”证得△ACE ≌△ABD ,推出∠ACE =∠ABD ,计算得出AD =BC =√2+2,利用等腰三角形“三线合一”的性质即可得到结论;(3)观察图形,当点D 在线段BC 的垂直平分线上时,△BCD 的面积取得最大值,利用等腰直角三角形的性质结合三角形面积公式即可求解.【解答】(1)证明:如图2中,根据题意:AB =AC ,AD =AE ,∠CAB =∠EAD =90°,∵∠CAE +∠BAE =∠BAD +∠BAE =90°,∴∠CAE =∠BAD ,在△ACE 和△ABD 中,{AC =AB ∠CAE =∠BAD AE =AD,∴△ACE ≌△ABD (SAS ),∴CE =BD ;(2)证明:如图3中,根据题意:AB =AC ,AD =AE ,∠CAB =∠EAD =90°,在△ACE 和△ABD 中,{AC =AB ∠CAE =∠BAD AE =AD,∴△ACE ≌△ABD (SAS ),∴∠ACE =∠ABD ,∵∠ACE +∠AEC =90°,且∠AEC =∠FEB ,∴∠ABD +∠FEB =90°,∴∠EFB =90°,∴CF ⊥BD ,∵AB =AC =√2+1,AD =AE =1,∠CAB =∠EAD =90°,∴BC =√2AB =√2+2,CD =AC +AD =√2+2,∴BC =CD ,∵CF ⊥BD , ∴CF 是线段BD 的垂直平分线;(3)解:△BCD 中,边BC 的长是定值,则BC 边上的高取最大值时△BCD 的面积有最大值,∴当点D 在线段BC 的垂直平分线上时,△BCD 的面积取得最大值,如图4中:∵∵AB =AC =√2+1,AD =AE =1,∠CAB =∠EAD =90°,DG ⊥BC 于G ,∴AG =12BC =√2+22,∠GAB =45°,∴DG =AG +AD =√2+22+1=√2+42,∠DAB =180°﹣45°=135°,∴△BCD 的面积的最大值为:12BC ⋅DG =12(√2+2)(√2+42)=3√2+52, 旋转角α=135°.27.(2020•苏州)如图,已知∠MON =90°,OT 是∠MON 的平分线,A 是射线OM 上一点,OA =8cm .动点P 从点A 出发,以1cm /s 的速度沿AO 水平向左作匀速运动,与此同时,动点Q 从点O 出发,也以1cm /s 的速度沿ON 竖直向上作匀速运动.连接PQ ,交OT 于点B .经过O 、P 、Q 三点作圆,交OT 于点C ,连接PC 、QC .设运动时间为t (s ),其中0<t <8.(1)求OP +OQ 的值;(2)是否存在实数t ,使得线段OB 的长度最大?若存在,求出t 的值;若不存在,说明理由.(3)求四边形OPCQ 的面积.【分析】(1)由题意得出OP =8﹣t ,OQ =t ,则可得出答案;(2)如图,过点B 作BD ⊥OP ,垂足为D ,则BD ∥OQ .设线段BD 的长为x ,则BD =OD =x ,OB =√2BD =√2x ,PD =8﹣t ﹣x ,得出PDOP =BDOQ ,则8−t−x8−t =x t ,解出x =8t−t 28.由二次函数的性质可得出答案; (3)证明△PCQ 是等腰直角三角形.则S △PCQ =12PC •QC =12×√22PQ ⋅√22PQ =14PQ 2.在Rt △POQ 中,PQ 2=OP 2+OQ 2=(8﹣t )2+t 2.由四边形OPCQ 的面积S =S △POQ +S △PCQ 可得出答案.【解析】(1)由题意可得,OP =8﹣t ,OQ =t ,∴OP +OQ =8﹣t +t =8(cm ).(2)当t =4时,线段OB 的长度最大.如图,过点B 作BD ⊥OP ,垂足为D ,则BD ∥OQ .∵OT 平分∠MON ,∴∠BOD =∠OBD =45°,∴BD =OD ,OB =√2BD .设线段BD 的长为x ,则BD =OD =x ,OB =√2BD =√2x ,PD =8﹣t ﹣x ,∵BD ∥OQ ,∴PD OP =BD OQ , ∴8−t−x 8−t =xt ,∴x =8t−t 28.∴OB=√2⋅8t−t28=−√28(t−4)2+2√2.当t=4时,线段OB的长度最大,最大为2√2cm.(3)∵∠POQ=90°,∴PQ是圆的直径.∴∠PCQ=90°.∵∠PQC=∠POC=45°,∴△PCQ是等腰直角三角形.∴S△PCQ=12PC•QC=12×√22PQ⋅√22PQ=14PQ2.在Rt△POQ中,PQ2=OP2+OQ2=(8﹣t)2+t2.∴四边形OPCQ的面积S=S△POQ+S△PCQ=12OP⋅OQ+14PQ2,=12t(8−t)+14[(8−t)2+t2],=4t−12t2+12t2+16﹣4t=16.∴四边形OPCQ的面积为16cm2.28.(2020•黑龙江)如图,在平面直角坐标系中,矩形ABCD的边AB长是x2﹣3x﹣18=0的根,连接BD,∠DBC=30°,并过点C作CN⊥BD,垂足为N,动点P从B点以每秒2个单位长度的速度沿BD方向匀速运动到D点为止;点M沿线段DA以每秒√3个单位长度的速度由点D向点A匀速运动,到点A为止,点P与点M同时出发,设运动时间为t秒(t>0).(1)线段CN=3√3;(2)连接PM和MN,求△PMN的面积s与运动时间t的函数关系式;(3)在整个运动过程中,当△PMN是以PN为腰的等腰三角形时,直接写出点P的坐标.【分析】(1)解方程求出AB的长,由直角三角形的性质可求BD,BC的长,CN的长;(2)分三种情况讨论,由三角形的面积可求解;(3)分两种情况讨论,由等腰三角形的性质和勾股定理可求解.【解析】(1)∵AB长是x2﹣3x﹣18=0的根,∴AB=6,∵四边形ABCD是矩形,∴AD=BC,AB=CD=6,∠BCD=90°,∵∠DBC=30°,∴BD=2CD=12,BC=√3CD=6√3,∵∠DBC=30°,CN⊥BD,∴CN=12BC=3√3,故答案为:3√3.(2)如图,过点M作MH⊥BD于H,∵AD∥BC,∴∠ADB=∠DBC=30°,∴MH=12MD=√32t,∵∠DBC=30°,CN⊥BD,∴BN=√3CN=9,当0<t<92时,△PMN的面积s=12×(9﹣2t)×√32t=−√32t2+9√34t;当t=92时,点P与点N重合,s=0,当92<t≤6时,△PMN的面积s=12×(2t﹣9)×√32t=√32t2−9√34t;(3)如图,过点P作PE⊥BC于E,当PN =PM =9﹣2t 时,∵PM 2=MH 2+PH 2,∴(9﹣2t )2=(√32t )2+(12﹣2t −32t )2, ∴t =3或t =73,∴BP =6或143,当BP =6时,∵∠DBC =30°,PE ⊥BC ,∴PE =12BP =3,BE =√3PE =3√3,∴点P (3√3,3),当BP =143时,同理可求点P (7√33,73), 当PN =NM =9﹣2t 时,∵NM 2=MH 2+NH 2,∴(9﹣2t )2=(√32t )2+(32t ﹣3)2, ∴t =3或24(不合题意舍去),∴BP =6,∴点P (3√3,3),综上所述:点P 坐标为(3√3,3)或(7√33,73). 29.(2020•河北)如图1和图2,在△ABC 中,AB =AC ,BC =8,tan C =34.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且AM =CN =2.点P 从点M 出发沿折线MB ﹣BN 匀速移动,到达点N 时停止;而点Q 在AC 边上随P 移动,且始终保持∠APQ =∠B .(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=94,请直接写出点K被扫描到的总时长.【分析】(1)如图1中,过点A作AH⊥BC于H.解直角三角形求出AH即可.(2)利用相似三角形的性质求解即可.(3)分两种情形:当0≤x≤3时,当3<x≤9时,分别画出图形求解即可.(4)求出CK的长度,以及CQ的最大值,利用路程与速度的关系求解即可.【解析】(1)如图1中,过点A作AH⊥BC于H.∵AB=AC,AH⊥BC,∴BH=CH=4,∠B=∠C,∴tan∠B=tan∠C=AHBH=34,∴AH=3,AB=AC=√AH2+BH2=√32+42=5.∴当点P在BC上时,点P到A的最短距离为3.(2)如图1中,∵∠APQ=∠B,∴PQ∥BC,∴△APQ∽△ABC,。
决胜2020年中考数学压轴题全揭秘——以三角形为载体的几何综合问题(含答案)

以三角形为载体的几何综合问题【考点1】关于三角形角度计算与证明的综合问题【例1】(2020•衢州)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是()A.60°B.65°C.75°D.80°【分析】根据OC=CD=DE,可得∠O=∠ODC,∠DCE=∠DEC,根据三角形的外角性质可知∠DCE=∠O+∠ODC=2∠ODC,进一步根据三角形的外角性质可知∠BDE=3∠ODC=75°,即可求出∠ODC的度数,进而求出∠CDE的度数.【解析】∵OC=CD=DE,∴∠O=∠ODC,∠DCE=∠DEC,∴∠DCE=∠O+∠ODC=2∠ODC,∵∠O+∠OED=3∠ODC=∠BDE=75°,∵∠CDE+∠ODC=180°﹣∠BDE=105°,∴∠CDE=105°﹣∠ODC=80°.故选:D.点评:本题主要考查了等腰三角形的性质以及三角形的外角性质,理清各个角之间的关系是解答本题的关键.【例2】(2020•杭州)如图,在△ABC中,AC<AB<BC.(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.【分析】(1)根据线段垂直平分线的性质可知PA=PB,根据等腰三角形的性质可得∠B=∠BAP,根据三角形的外角性质即可证得APC=2∠B;(2)根据题意可知BA=BQ,根据等腰三角形的性质可得∠BAQ=∠BQA,再根据三角形的内角和公式即可解答.【解析】(1)证明:∵线段AB的垂直平分线与BC边交于点P,∴PA=PB,∴∠B=∠BAP,∵∠APC=∠B+∠BAP,∴∠APC=2∠B;(2)根据题意可知BA=BQ,∴∠BAQ=∠BQA,∵∠AQC=3∠B,∠AQC=∠B+∠BAQ,∴∠BQA=2∠B,∵∠BAQ+∠BQA+∠B=180°,∴∠B =36°.点评:本题主要考查了等腰三角形的性质、垂直平分线的性质以及三角形的外角性质,难度适中. 【考点2】关于三角形的线段计算综合问题【例3】(2020•绍兴)如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )A .245B .325C .12√3417D .20√3417【分析】设DE =x ,则AD =8﹣x ,由长方体容器内水的体积得出方程,解方程求出DE ,再由勾股定理求出CD ,过点C 作CF ⊥BG 于F ,由△CDE ∽△CBF 的比例线段求得结果即可. 【解析】过点C 作CF ⊥BG 于F ,如图所示:设DE =x ,则AD =8﹣x ,根据题意得:12(8﹣x +8)×3×3=3×3×6,解得:x =4, ∴DE =4, ∵∠E =90°,由勾股定理得:CD =2+CE 2=√42+32=5, ∵∠BCE =∠DCF =90°,∵∠DEC =∠BFC =90°, ∴△CDE ∽△CBF , ∴CE CF =CD CB ,即3CF=58,∴CF =245. 故选:A .点评:本题考查了勾股定理的应用、长方体的体积、梯形的面积的计算方法;熟练掌握勾股定理,由长方体容器内水的体积得出方程是解决问题的关键.【例4】(2020•浙江自主招生)如图,等边三角形ABC 中,AO 是∠BAC 的平分线,D 为AO 上一点,以CD 为一边且在CD 下方作等边三角形CDE ,连结BE ,延长BE 至点Q ,P 为BQ 上一点,连结CP ,CQ ,使CP =CQ =5,若BC =8时,则PQ 的长为 6 .【分析】根据SAS 即可证得△ACD ≌△BCE ,过点C 作CH ⊥BQ 于H ,由等边三角形的性质,即可求得∠DAC =30°,则根据等腰三角形与直角三角形中的勾股定理即可求得PQ 的长. 【解析】过点C 作CH ⊥BQ 于H ,∵△ABC 是等边三角形,AO 是角平分线,∵△ABC与△DCE是等边三角形,∴AC=BC,DC=EC,∠ACB=∠DCE=60°,∴∠ACD+∠DCB=∠ECB+∠DCB=60°,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS);∴∠PBC=∠DAC=30°,∴在Rt△BHC中,CH=12BC=12×8=4,∵PC=CQ=5,CH=4,∴PH=QH=3,∴PQ=6.故答案为:6.点评:此题考查了全等三角形的判定与性质,等腰三角形、等边三角形以及直角三角形的性质等知识,熟练掌握全等三角形的判定是解题的关键.【考点3】全等三角形的计算与证明【例5】(2020•温州)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED 的延长线于点F.(1)求证:△BDE≌△CDF.(2)当AD⊥BC,AE=1,CF=2时,求AC的长.【分析】(1)根据平行线的性质得到∠B=∠FCD,∠BED=∠F,由AD是BC边上的中线,得到BD=CD,于是得到结论;(2)根据全等三角形的性质得到BE=CF=2,求得AB=AE+BE=1+2=3,于是得到结论.【解答】(1)证明:∵CF∥AB,∴∠B=∠FCD,∠BED=∠F,∵AD是BC边上的中线,∴BD=CD,∴△BDE≌△CDF(AAS);(2)解:∵△BDE≌△CDF,∴BE=CF=2,∴AB=AE+BE=1+2=3,∵AD⊥BC,BD=CD,∴AC=AB=3.点评:本题考查了全等三角形的判定和性质,平行线的性质,熟练掌握全等三角形的判定和性质是解题的关键.【考点4】三角形与旋转变换综合问题【例6】(2020•绍兴)如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.(1)在旋转过程中,①当A,D,M三点在同一直线上时,求AM的长.②当A,D,M三点为同一直角三角形的顶点时,求AM的长.(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2,此时∠AD2C=135°,CD2=60,求BD2的长.【分析】(1)①分两种情形分别求解即可.②显然∠MAD不能为直角.当∠AMD为直角时,根据AM2=AD2﹣DM2,计算即可,当∠ADM=90°时,根据AM2=AD2+DM2,计算即可.(2)连接CD.首先利用勾股定理求出CD1,再利用全等三角形的性质证明BD2=CD1即可.【解析】(1)①AM=AD+DM=40,或AM=AD﹣DM=20.②显然∠MAD不能为直角.当∠AMD为直角时,AM2=AD2﹣DM2=302﹣102=800,∴AM=20√2或(﹣20√2舍弃).当∠ADM=90°时,AM2=AD2+DM2=302+102=1000,∴AM=10√10或(﹣10√10舍弃).综上所述,满足条件的AM的值为20√2或10√10.(2)如图2中,连接CD.由题意:∠D1AD2=90°,AD1=AD2=30,∴∠AD2D1=45°,D1D2=30√2,∵∠AD2C=135°,∴∠CD2D1=90°,∴CD1=√CD22+D1D22=30√6,∵∠BAC=∠A1AD2=90°,∴∠BAC﹣∠CAD2=∠D2AD1﹣∠CAD2,∴∠BAD2=∠CAD1,∵AB=AC,AD2=AD1,∴△BAD2≌△CAD1(SAS),∴BD2=CD1=30√6.点评:本题属于四边形综合题,考查了等腰直角三角形的性质,勾股定理,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.【考点5】以三角形为载体的几何综合探究问题【例7】(2018•舟山)已知,△ABC中,∠B=∠C,P是BC边上一点,作∠CPE=∠BPF,分别交边AC,AB 于点E,F.(1)若∠CPE=∠C(如图1),求证:PE+PF=AB.(2)若∠CPE≠∠C,过点B作∠CBD=∠CPE,交CA(或CA的延长线)于点D.试猜想:线段PE,PF和BD之间的数量关系,并就∠CPE>∠C情形(如图2)说明理由.(3)若点F与A重合(如图3),∠C=27°,且PA=AE.①求∠CPE的度数;②设PB=a,PA=b,AB=c,试证明:b=a2−c2 c.【分析】(1)只要证明PF=BF,PE=AF即可解决问题;(2)结论:BD=PE+PF.如图1中,作BG∥CD交EP的延长线于G.只要证明BD=EG,PF=PG即可解决问题;(3)①设∠CPE=∠BPF=x,根据三角形内角和定理构建方程即可解决问题;②延长BA到M,使得AM=AP.连接PM.由△ABP∽△PBM,可得BPAB =BMBP,推出PB2=BA•BM,又PB=a,PA=AM=b,AB=c,可得a2=c(b+c)解决问题;【解答】(1)证明:如图1中,∵∠B=∠C,∠CPE=∠BPF,∠CPE=∠C,∴∠B=∠BPF=∠CPE,∠BPF=∠C,∴PF=BF,PE∥AF,PF∥AE,∴四边形AEPF是平行四边形,∴PE=AF,∴PE+PF=AF+BF=AB.(2)结论:BD=PE+PF.理由:如图1中,作BG∥CD交EP的延长线于G.∴∠ABC=∠C=∠CBG,∵∠CPE=∠BPF,∴∠BPF=∠CPE=∠BPG,∵BP=BP,∴△FBP≌△GBP(ASA),∴PF=PG,∵∠CBD=∠CPE,∴PE∥BD,∴四边形BDEG是平行四边形,∴BD=EG=PG+PE=PF+PE.(3)①设∠CPE=∠BPF=x,∵∠C=27°,PA=AE,∴∠APE=∠PEA=∠C+∠CPE=27°+x,∵∠BPA+∠APE+∠CPE=180°,∴x+x+27°+x=180°,∴x=51°,即∠CPE=51°.②延长BA到M,使得AM=AP.连接PM.∵∠C=27°,∠BPA=∠CPE=51°,∴∠BAP=180°﹣27°﹣51°=102°=∠M+∠APM,∵AM=AP,∴∠M=∠APM=51°,∴∠M=∠BPA,∵∠B=∠B,∴△ABP∽△PBM,∴BPAB =BMBP,∴PB2=BA•BM,∵PB=a,PA=AM=b,AB=c,∴a2=c(b+c),∴b=a2−c2 c.点评:本题考查三角形综合题、等腰三角形的判定和性质、平行四边形的判定和性质、全等三角形的判定和性质.相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.【例8】(2018•台州)如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.(1)如图1,求证:∠CAE=∠CBD;(2)如图2,F是BD的中点,求证:AE⊥CF;(3)如图3,F,G分别是BD,AE的中点,若AC=2√2,CE=1,求△CGF的面积.【分析】(1)直接判断出△ACE≌△BCD即可得出结论;(2)先判断出∠BCF=∠CBF,进而得出∠BCF=∠CAE,即可得出结论;(3)先求出BD=3,进而求出CF=32,同理:EG=32,再利用等面积法求出ME,进而求出GM,最后用面积公式即可得出结论.【解析】(1)在△ACE和△BCD中,{AC=BC∠ACB=∠ACB=90°CE=CD,∴△ACE≌△BCD,∴∠CAE=∠CBD;(2)如图2,记AE与CF的交点为M,在Rt△BCD中,点F是BD的中点,∴CF=BF,∴∠BCF=∠CBF,由(1)知,∠CAE=∠CBD,∴∠BCF=∠CAE,∴∠CAE+∠ACF=∠BCF+∠ACF=∠ACB=90°,∴∠AMC=90°,∴AE⊥CF;(3)如图3,记AE与CF的交点为M,∵AC=2√2,∴BC=AC=2√2,∵CE=1,∴CD=CE=1,在Rt△BCD中,根据勾股定理得,BD=√CD2+BC2=3,∵点F是BD中点,∴CF=DF=12BD=32,同理:EG=12AE=32,连接EF,过点F作FH⊥BC,∵∠ACB=90°,点F是BD的中点,∴FH=12CD=12,∴S △CEF =12CE •FH =12×1×12=14, 由(2)知,AE ⊥CF ,∴S △CEF =12CF •ME =12×32ME =34ME ,∴34ME =14, ∴ME =13,∴GM =EG ﹣ME =32−13=76, ∴S △CFG =12CF •GM =12×32×76=78. 点评:此题是三角形综合题,主要考查了全等三角形的判定和性质,直角三角形的性质,三角形的中位线定理,三角形的面积公式,勾股定理,作出辅助线求出△CFG 的边CF 上的是解本题的关键.【考点5】以三角形为载体的几何阅读创新题【例9】(2018•绍兴)数学课上,张老师举了下面的例题:例1 等腰三角形ABC 中,∠A =110°,求∠B 的度数.(答案:35°)例2 等腰三角形ABC 中,∠A =40°,求∠B 的度数,(答案:40°或70°或100°)张老师启发同学们进行变式,小敏编了如下一题:变式 等腰三角形ABC 中,∠A =80°,求∠B 的度数.(1)请你解答以上的变式题.(2)解(1)后,小敏发现,∠A 的度数不同,得到∠B 的度数的个数也可能不同,如果在等腰三角形ABC 中,设∠A =x °,当∠B 有三个不同的度数时,请你探索x 的取值范围.【分析】(1)由于等腰三角形的顶角和底角没有明确,因此要分类讨论;(2)分两种情况:①90≤x <180;②0<x <90,结合三角形内角和定理求解即可.【解析】(1)若∠A 为顶角,则∠B =(180°﹣∠A )÷2=50°;若∠A 为底角,∠B 为顶角,则∠B =180°﹣2×80°=20°;若∠A 为底角,∠B 为底角,则∠B =80°;故∠B =50°或20°或80°;(2)分两种情况:①当90≤x <180时,∠A 只能为顶角,∴∠B 的度数只有一个;②当0<x <90时,若∠A 为顶角,则∠B =(180−x 2)°;若∠A 为底角,∠B 为顶角,则∠B =(180﹣2x )°;若∠A 为底角,∠B 为底角,则∠B =x °.当180−x2≠180﹣2x 且180﹣2x ≠x 且180−x2≠x ,即x ≠60时,∠B 有三个不同的度数.综上所述,可知当0<x <90且x ≠60时,∠B 有三个不同的度数.点评:本题考查了等腰三角形的性质及三角形内角和定理,进行分类讨论是解题的关键.一.选择题(共5小题)1.(2020•衢州模拟)在我国古代数学著作《九章算术》“勾股”章中有一题:“今有开门去阃(k ǔn )一尺,不合二寸,问门广几何?”大意是说:如图,推开双门(AD 和BC ),门边缘D ,C 两点到门槛AB 的距离为1尺(1尺=10寸),双门间的缝隙CD 为2寸,那么门的宽度(两扇门的和)AB 为( )A .103寸B .102寸C .101寸D .100寸【分析】画出直角三角形,根据勾股定理即可得到结论.【解答】解:设OA =OB =AD =BC =r ,过D 作DE ⊥AB 于E ,则DE =10,OE =12CD =1,AE =r ﹣1.在Rt △ADE 中, AE 2+DE 2=AD 2,即(r ﹣1)2+102=r 2,解得2r =101.故门的宽度(两扇门的和)AB 为101寸.故选:C .2.(2020•拱墅区校级一模)如图,在△ABC 中,∠C =90°,D 是BC 边上一点,∠ADC =3∠BAD ,BD =4,DC =3.则AB 的值为( )A .5+3√2B .2+2√15C .7√2D .√113【分析】延长CB 到E ,使得BE =BA .设BE =AB =a .利用相似三角形的性质,勾股定理构建方程即可解决问题.【解答】解:如图,延长CB 到E ,使得BE =BA .设BE =AB =a .∵BE =BA ,∴∠E =∠BAE ,∵∠ADC =∠ABD +∠BAD =2∠E +∠BAD =3∠BAD ,∴∠BAD =∠E ,∵∠ADB =∠EDA ,∴△ADB ∽△EDA ,∴AD ED=DB AD , ∴AD 2=4(4+a )=16+4a ,∵AC 2=AD 2﹣CD 2=AB 2﹣BC 2,∴16+4a ﹣32=a 2﹣72,解得a =2+2√15或2﹣2√15(舍弃).∴AB =2+2√15,故选:B .3.(2020•温州模拟)如图,已知∠ACB =∠DBC ,添加以下条件,不能判定△ABC ≌△DCB 的是( )A .∠ABC =∠DCB B .∠ABD =∠DCAC .AC =DBD .AB =DC【分析】根据全等三角形的判定定理 逐个判断即可.【解答】解:A 、∵在△ABC 和△DCB 中{∠ABC =∠DCBBC =CB ∠ACB =∠DBC∴△ABC ≌△DCB (ASA ),故本选项不符合题意; B 、∵∠ABD =∠DCA ,∠DBC =∠ACB ,∴∠ABD +∠DBC =∠ACD +∠ACB ,即∠ABC =∠DCB ,∵在△ABC 和△DCB 中{∠ABC =∠DCBBC =CB ∠ACB =∠DBC∴△ABC ≌△DCB (ASA ),故本选项不符合题意; C 、∵在△ABC 和△DCB 中{BC =CB ∠ACB =∠DBC AC =DB∴△ABC ≌△DCB (SAS ),故本选项不符合题意;D 、根据∠ACB =∠DBC ,BC =BC ,AB =DC 不能推出△ABC ≌△DCB ,故本选项符合题意;故选:D .4.(2020•周村区一模)如图,在△ABC 中,∠B =50°,∠C =30°,分别以点A 和点C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N ,作直线MN 交BC 于点D ,连接AD ,则∠BAD 的度数为( )A.50°B.60°C.70°D.80°【分析】根据内角和定理求得∠BAC=95°,由中垂线性质知DA=DC,即∠DAC=∠C=30°,从而得出答案.【解答】解:在△ABC中,∵∠B=50°,∠C=30°,∴∠BAC=180°﹣∠B﹣∠C=100°,由作图可知MN为AC的中垂线,∴DA=DC,∴∠DAC=∠C=30°,∴∠BAD=∠BAC﹣∠DAC=70°,故选:C.5.(2020•黄岩区模拟)如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB 与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB =AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有()A.1个B.2个C.3个D.4个【分析】利用角平分线的性质以及已知条件对①②③④进行一一判断,从而求解.【解答】解:∵PA平分∠CAB,PB平分∠CBE,∴∠PAB=12∠CAB,∠PBE=12∠CBE,∵∠CBE=∠CAB+∠ACB,∠PBE=∠PAB+∠APB,∴∠ACB=2∠APB;故①正确;过P作PM⊥AB于M,PN⊥AC于N,PS⊥BC于S,∴PM=PN=PS,∴PC 平分∠BCD ,∵S △PAC :S △PAB =(12AC •PN ):(12AB •PM )=AC :AB ;故②正确; ∵BE =BC ,BP 平分∠CBE∴BP 垂直平分CE (三线合一),故③正确;∵PG ∥AD ,∴∠FPC =∠DCP∵PC 平分∠DCB ,∴∠DCP =∠PCF ,∴∠PCF =∠CPF ,故④正确.故选:D .二.填空题(共4小题)6.(2020•温州模拟)如图,已知OP 平分∠AOB ,CP ∥OA ,PD ⊥OA 于点D ,PE ⊥OB 于点E .CP =254,PD =6.如果点M 是OP 的中点,则DM 的长是 5 .【分析】由角平分线的性质得出∠AOP =∠BOP ,PC =PD =6,∠PDO =∠PEO =90°,由勾股定理得出CE =√CP 2−PE 2=74,由平行线的性质得出∠OPC =∠AOP ,得出∠OPC =∠BOP ,证出CO =CP =254,得出OE =CE +CO =8,由勾股定理求出OP =√OE 2+PE 2=10,再由直角三角形斜边上的中线性质即可得出答案.【解答】解:∵OP 平分∠AOB ,PD ⊥OA 于点D ,PE ⊥OB 于点E ,∴∠AOP =∠BOP ,PC =PD =6,∠PDO =∠PEO =90°,∴CE =√CP 2−PE 2=√(254)2−62=74,∵CP ∥OA ,∴∠OPC =∠AOP ,∴∠OPC =∠BOP ,∴OE =CE +CO =74+254=8, ∴OP =√OE 2+PE 2=√82+62=10,在Rt △OPD 中,点M 是OP 的中点,∴DM =12OP =5;故答案为:5.7.(2020•温岭市校级一模)在半径为2的⊙O 中,弦AB =2√2,连接OA ,OB .在直线OB 上取一点K ,使tan ∠BAK =12,则△OAK 的面积为 23或6 .【分析】由勾股定理的逆定理得出△AOB 是等腰直角三角形,得出∠OBA =45°,分两种情况:①点K 在线段OB 上时;②点K 在线段OB 延长线上时;由三角函数定义和等腰直角三角形的性质求出BK ,得出OK ,再由三角形面积公式即可得出答案.【解答】解:∵OA =OB =2,AB =2√2,∴OA 2+OB 2=AB 2,∴△AOB 是等腰直角三角形,∴∠OBA =45°,分两种情况:①点K 在线段OB 上时,如图1所示:作KD ⊥AB 于D ,则DB =DK ,∵tan ∠BAK =12,∴DK AD =12, ∴AD =2DK =2DB ,∴DK =13AB =2√23,∴OK =OB ﹣BK =23,∴S △OAK =12OA •OK =12×2×23=23; ②点K 在线段OB 延长线上时,如图2所示:作KD ⊥AB 于D ,则DB =DK ,∵tan ∠BAK =12,∴DK AD =12, ∴AD =2DK ,∵DK =DB ,∴DB =AB =2√2,∴BK =√2DB =4,∴OK =OB +BK =6,∴S △OAK =12OA •OK =12×2×6=6;故答案为:23或6.8.(2020•萧山区一模)如图,CE 、BF 分别是△ABC 的高线,连接EF ,EF =6,BC =10,D 、G 分别是EF 、BC 的中点,则DG 的长为 4 .【分析】连接EG、FG,根据直角三角形的性质得到EG=FG=12BC=5,根据等腰三角形的性质求出ED,根据勾股定理计算,得到答案.【解答】解:连接EG、FG,∵CE,BF分别是△ABC的高线,∴∠BEC=90°,∠BFC=90°,∵G是BC的中点,∴EG=FG=12BC=5,∵D是EF的中点,∴ED=12EF=3,GD⊥EF,由勾股定理得,DG=√GE2−DE2=4,故答案为:4.9.(2020•海宁市二模)如图,四边形ABCD中,∠ABC=∠BCD=90°,AB=1,AE⊥AD,交BC于点E,EA 平分∠BED.(1)CD的长是 2 ;(2)当点F是AC中点时,四边形ABCD的周长是5+√3.【分析】(1)如图,延长DA ,CB 交于点H ,由“ASA ”可证△ADE ≌△AHE ,可得AH =AD ,由平行线分线段成比例可求解;(2)如图2中,作AH ⊥CD 于H ,利用垂径定理证明以及线段的垂直平分线的性质证明△ADC 是等边三角形即可解决问题.【解答】解:(1)如图1中,延长DA ,CB 交于点H ,∵EA 平分∠BED ,∴∠AEH =∠AED ,且AE =AE ,∠EAH =∠EAD =90°,∴△ADE ≌△AHE (ASA )∴AH =AD ,∵∠ABC =∠BCD =90°,∴AB ∥CD , ∴AB CD =AHDH ,且AB =1,AH =AD =12HD , ∴CD =2,故答案为:2.(2)如图2中,作AH ⊥CD 于H ,∵∠DAE =∠DCE =90°,∴A,D,C,E四点共圆,设圆心为O,则点O是线段DE的中点,∵AF=CF,∴DE⊥AC,∴DA=DC,∵∠ABC=∠BCH=∠AHC=90°,∴四边形ABCH是矩形,∴CH=AB=1,∵CD=2,∴CH=HD=1,∵AH⊥CD,∴AD=AC,∴AD=CD=AC=2,∴BC=√AC2−AB2=√22−12=√3,∴四边形ABCD的周长为2+2+1+√3=5+√3.故答案为5+√3.三.解答题(共11小题)10.(2020•拱墅区校级一模)在△ABC和△DBE中,CA=CB,EB=ED,点D在AC上.(1)如图1,若∠ABC=∠DBE=60°,求证:∠ECB=∠A;(2)如图2,设BC与DE交于点F.当∠ABC=∠DBE=45°时,求证:CE∥AB;(3)在(2)的条件下,若tan∠DEC=12时,求EFDF的值.【分析】(1)根据SAS可证明△ABD≌△CBE.得出∠A=∠ECB;(2)得出△ABC和△DBE都是等腰直角三角形,证明△ABD∽△CBE,则∠BAD=∠BCE=45°,可得出结论;(3)过点D作DM⊥CE于点M,过点D作DN∥AB交CB于点N,设DM=MC=a,得出DN=2a,CE=a,证明△CEF ∽△DNF ,可得出答案.【解答】(1)证明:∵CA =CB ,EB =ED ,∠ABC =∠DBE =60°,∴△ABC 和△DBE 都是等边三角形,∴AB =BC ,DB =BE ,∠A =60°.∵∠ABC =∠DBE =60°,∴∠ABD =∠CBE ,∴△ABD ≌△CBE (SAS ).∴∠A =∠ECB ;(2)证明:∵∠ABC =∠DBE =45°,CA =CB ,EB =ED ,∴△ABC 和△DBE 都是等腰直角三角形,∴∠CAB =45°, ∴AB BC =√2,DB BE =√2, ∴ABBC =DBBE ,∵∠ABC =∠DBE ,∴∠ABD =∠CBE ,∴△ABD ∽△CBE ,∴∠BAD =∠BCE =45°,∵∠ABC =45°,∴∠ABC =∠BCE ,∴CE ∥AB ;(3)解:过点D 作DM ⊥CE 于点M ,过点D 作DN ∥AB 交CB 于点N ,∵∠ACB =90°,∠BCE =45°,∴∠DCM =45°,∴∠MDC =∠DCM =45°,∴DM =MC ,设DM=MC=a,∴DC=√2a,∵DN∥AB,∴△DCN为等腰直角三角形,∴DN=√2DC=2a,∵tan∠DEC=DMME=12,∴ME=2DM,∴CE=a,∴CEDN =a2a=12,∵CE∥DN,∴△CEF∽△DNF,∴EFDF =CEDN=12.11.(2020•天台县模拟)某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC 的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.【特例探究】(1)如图1,当∠PAB=45°,AB=6√2时,AC=6√5,BC=6√5;如图2,当sin∠PAB=12,AB=4时,AC=2√13,BC=2√7;【归纳证明】(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.【拓展证明】(3)如图4,在△ABC中,AB=4√3,BC=2√5,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.【分析】(1)如图1,由等腰直角三角形的性质得到AP=BP=6,根据三角形中位线的性质和平行线分线段成比例定理可得PE=PF=3,利用勾股定理可得AC和BC的长;如图2,根据特殊三角函数值可得∠BAP =30°,计算PB和AP的长,同理由中线的性质和勾股定理可得结论;(2)设PF=m,PE=n则AP=2m,PB=2n,根据勾股定理分别列等式,可得结论;(3)如图4,作辅助线,证明四边形EFCG是平行四边形,得Q是FG的中点,根据中垂三角形的定义可知:△FCG是中垂三角形,利用(2)中三边的关系可得GF的长.【解答】(1)解:如图1,∵AF⊥BE,∴∠APB=∠APE=∠BPF=90°,∵∠PAB=45°,AB=6√2,∴AP=PB=6,如图1,连接EF,∵AF,BE是△ABC的中线,∴EF是△ABC的中位线,∴EF∥AB.且EF=12AB,∴PE PB =PF PA =12, ∴PE =PF =3,由勾股定理得:AE =BF =√AP 2+PE 2=√62+32=3√5,∴AC =BC =2AE =6√5,如图2,∵sin ∠PAB =12,AB =4,AF ⊥BE ,∴∠PAB =30°,∴BP =12AB =2,AP =2√3,∵AF 、BE 是△ABC 的中线,∴PE =12PB =1,PF =12AP =√3,由勾股定理得:AE =√PE 2+AP 2=√12+(2√3)2=√13, BF =√PF 2+PB 2=√(√3)2+22=√7,∴AC =2AE =2√13,BC =2BF =2√7,故答案为:6√5,6√5,2√13,2√7;(2)解:猜想:AB 2、BC 2、AC 2三者之间的关系是:AC 2+BC 2=5AB 2,证明:如图3,设 PF =m ,PE =n 则AP =2m ,PB =2n ,在Rt △APB 中,(2m )2+(2n )2=AB 2①,在Rt △APE 中,(2m )2+n 2=(AC 2)2②, 在Rt △BPF 中,m 2+(2n )2=(BC 2)2③,由①得:m 2+n 2=AB 24,由②+③得:5( m 2+n 2)=AC 2+BC 24, ∴AC 2+BC 2=5AB 2;(3)解:如图4,连接CG ,EF ,过点F 作FN ∥BG 交CG 于点N ,FG 与AC 交于点Q ,∵FN∥BG,BG⊥AC,∴FN⊥AC,∵F是BC的中点,∴N是CG的中点,∵D、E分别是AB、AC的中点,∴DE=FC,DE∥FC,∵ED=EG,∴EG=FC,EG∥FC,∴四边形EFCG是平行四边形,∴Q是FG的中点,∴△FCG是中垂三角形,∵AB=4√3,BC=2√5,∴CG=EF=BD=2√3,FC=√5,由(2)中结论可知:5FC2=CG2+FG2,即5×5=(2√3)2+FG2,∴GF=√13.12.(2020•拱墅区校级模拟)如图,在Rt△ABC中,∠CAB=90°,AF为BC边上的中线,DE经过△ABC的重心G,且∠ADE=∠C.(1)问:线段AG是△ADE的高线还是中线?请说明理由.(2)若AB=6,AC=8,求AD的长.【分析】(1)说明∠DAG+∠ADE=90°可得结论;(2)先根据重心的性质:重心到顶点的距离等于它到对边中点距离的2倍,可得AG的长,根据等角的三角函数列式可得结论.【解答】解:(1)∵∠CAB=90°,AF为BC边上的中线,∴AF=12BC=CF,∴∠C=∠FAC,∵∠ADE=∠C,∴∠ADE=∠FAC,∵∠FAC+∠DAG=90°,∴∠DAG+∠ADE=90°,∴∠AGD=90°∴线段AG是△ADE的高线;(2)在Rt△ABC中,AB=6,AC=8,∴BC=√AC2+AB2=√62+82=10,∵AF为BC边上的中线,∴AF=5,∵G为△ABC的重心,∴AG=23×5=103,∵∠ADE=∠C,∴sin∠ADG=AGAD=sin∠C=AB BC,∴103AD=610,AD=509.13.(2020•温州模拟)如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.(1)如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;(2)如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;(3)当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.【分析】(1)根据等腰三角形的性质得到∠BAC=110°,根据三角形的外角的性质即可得到结论;(2)根据三角形的外角的性质得到∠E=75°﹣18°=57°,于是得到结论;(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β,①如图1,当点D在点B的左侧时,∠ADC=x°﹣α,②如图2,当点D在线段BC上时,∠ADC=x°+α,③如图3,当点D在点C 右侧时,∠ADC=x°﹣α,根据题意列方程组即可得到结论.【解答】解:(1)∵∠B=∠C=35°,∴∠BAC=110°,∵∠BAD=80°,∴∠DAE=30°,∴∠ADE=∠AED=75°,∴∠CDE=180°﹣35°﹣30°﹣75°=40°;(2)∵∠ACB=75°,∠CDE=18°,∴∠E=75°﹣18°=57°,∴∠ADE=∠AED=57°,∴∠ADC=39°,∵∠ABC=∠ADB+∠DAB=75°,∴∠BAD=36°;(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β①如图1,当点D在点B的左侧时,∠ADC=x°﹣α,∴{y°=x°+α(1)y°=x°−α+β(2),(1)﹣(2)得2α﹣β=0,∴2α=β;②如图2,当点D在线段BC上时,∠ADC=x°+α,∴{x°=y°+α(1)x°+α=y°+β(2),(2)﹣(1)得α=β﹣α,∴2α=β;③如图3,当点D在点C右侧时,∠ADC=x°﹣α,∴{x°−α+y°+β=180°(1) y°+x°+α=180°(2),(2)﹣(1)得2α﹣β=0,∴2α=β.综上所述,∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.14.(2020•上城区模拟)如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).(1)若点P在AC上,且满足PA=PB时,求出此时t的值;(2)若点P恰好在∠BAC的角平分线上,求t的值;(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.【分析】(1)设存在点P,使得PA=PB,此时PA=PB=2t,PC=4﹣2t,根据勾股定理列方程即可得到结论;(2)当点P在∠CAB的平分线上时,如图1,过点P作PE⊥AB于点E,此时BP=7﹣2t,PE=PC=2t﹣4,BE=5﹣4=1,根据勾股定理列方程即可得到结论;(3)在Rt△ABC中,根据勾股定理得到AC=4cm,根据题意得:AP=2t,当P在AC上时,△BCP为等腰三角形,得到PC=BC,即4﹣2t=3,求得t=12,当P在AB上时,△BCP为等腰三角形,若CP=PB,点P在BC的垂直平分线上,如图2,过P作PE⊥BC于E,求得t=194,若PB=BC,即2t﹣3﹣4=3,解得t=5,③PC=BC,如图3,过C作CF⊥AB于F,由射影定理得;BC2=BF•AB,列方程32=2t−3−42×5,即可得到结论.【解答】解:(1)设存在点P,使得PA=PB,此时PA=PB=2t,PC=4﹣2t,在Rt△PCB中,PC2+CB2=PB2,即:(4﹣2t)2+32=(2t)2,解得:t=25 16,∴当t=2516时,PA=PB;(2)当点P在∠BAC的平分线上时,如图1,过点P作PE⊥AB于点E,此时BP=7﹣2t,PE=PC=2t﹣4,BE=5﹣4=1,在Rt△BEP中,PE2+BE2=BP2,即:(2t﹣4)2+12=(7﹣2t)2,解得:t=8 3,当t=6时,点P与A重合,也符合条件,∴当t=83或6时,P在△ABC的角平分线上;(3)在Rt△ABC中,∵AB=5cm,BC=3cm,∴AC=4cm,根据题意得:AP=2t,当P在AC上时,△BCP为等腰三角形,∴PC=BC,即4﹣2t=3,∴t=1 2,当P在AB上时,△BCP为等腰三角形,①CP=PB,点P在BC的垂直平分线上,如图2,过P作PE⊥BC于E,∴BE=12BC=32,∴PB=12AB,即2t﹣3﹣4=52,解得:t=194,②PB=BC,即2t﹣3﹣4=3,解得:t=5,③PC=BC,如图3,过C作CF⊥AB于F,∴BF=12BP,∵∠ACB=90°,由射影定理得;BC2=BF•AB,即32=2t−3−42×5,解得:t=53 10,∴当t=12,5,5310或194时,△BCP为等腰三角形.15.(2020•杭州模拟)定义:若一个三角形一条边上的高等于这条边长的一半,则称该三角形为“半高”三角形,这条高称为“半高”.(1)如图1,△ABC中,∠ACB=90°,BC=2AC,点P在AB上,PD⊥AC于点D,PE⊥BC于点E,连接BD,DE求证:△BDE是“半高”三角形;(2)如图2,△ABC是“半高”三角形,且BC边上的高是“半高”,点P在AB上,PQ∥BC交AC于点Q,PM⊥BC于点M,QN⊥BC于点N.①请探究BM,PM,CN之间的等量关系,并说明理由;②若△ABC的面积等于16,求MQ的最小值.【分析】(1)根据新定义“半高”三角形进行证明;(2)①利用新定义的概念进行转化;②将MQ的长度根据勾股定理用二次函数表示出来,利用二次函数的性质进行求解.【解答】(1)证明:∵PE⊥BC,∴∠PEC=∠PEB=90°=∠ACB,又∵∠PBE=∠ABC,∴△PBE~△ABC,∴PEBE =ACBC=12,∴BE=2PE,∵PD⊥AC,∴∠PDC=90°,∴四边形CEPD为矩形,∴DC=PE,∴BE=2DC,∴△BDE是“半高”三角形.(2)解:①BM+CN=2PM.理由如下:如图2,过A作AE⊥BC于E,交PQ于D,∵△ABC 是“半高”三角形,且BC 边上的高是“半高”, ∴BC =2AE ∵PQ ∥BC , ∴△APQ ~△ABC , ∴AD AE =PQ BC, 即AD AE=PQ 2AE,∴PQ =2AD ,∴BC ﹣PQ =2AE ﹣2AD =2(AE ﹣AD ), ∵PQ ∥BC ,PM ⊥BC ,QN ⊥BC , ∴四边形MNQP 是矩形, ∴PQ =MN ,PM =DE =QN , ∴BC ﹣MN =2PM , 即BM +CN =2PM .②∵S △ABC =12BC ×AE =14BC 2=16, ∴BC =8, 设PM =x , 由①得PQ =8﹣2x ,∴MQ 2=x 2+(8﹣2x )2=5x 2﹣32x +64=5(x −165)2+645, ∴当x =165时,MQ 2取得最小值645,则MQ 取得最小值为8√55.16.(2020•南浔区二模)(1)尝试探究如图1,等腰Rt △ABC 的两个顶点B ,C 在直线MN 上,点D 是直线MN 上一个动点(点D 在点C 的右边),BC =3,BD =m ,在△ABC 同侧作等腰Rt △ADE ,∠ABC =∠ADE =90°,EF ⊥MN 于点F ,连接CE .①求DF 的长;②在判断AC ⊥CE 是否成立时,小明同学发现可以由以下两种思路解决此问题: 思路一:先证CF =EF ,求出∠ECF =45°,从而证得结论成立.思路二:先求DF ,EF 的长,再求CF 的长,然后证AC 2+CE 2=AE 2,从而证得结论成立.请你任选一种思路,完整地书写本小题的证明过程.(如用两种方法作答,则以第一种方法评分) (2)拓展探究将(1)中的两个等腰直角三角形都改为有一个角为30°的直角三角形,如图2,∠ABC =∠ADE =90°,∠BAC =∠DAE =30°,BC =3,BD =m ,当4≤m ≤6时,求CE 长的范围. 【分析】(1)①根据AAS 证明△ABD ≌△DFE ,可得结论; ②思路一:先证CF =EF ,求出∠ECF =45°,从而证得结论成立.思路二:先求DF ,EF 的长,再求CF 的长,然后证AC 2+CE 2=AE 2,从而证得结论成立.(2)如图2,作EF ⊥MN ,同理证明AC ⊥CE ,则无论m 取何大于3的数,AC ⊥CE 总成立,即点E 在一条直线上运动,可得结论.【解答】解:(1)①在等腰Rt △ABC 和等腰Rt △ADE 中,∠ABC =∠ADE =90°, ∴∠ADB +∠EDF =90°, ∵EF ⊥MN ,∴∠DEF +∠EDF =90°, ∴∠ADB =∠DEF , 在△ABD 和△DFE 中, {∠ADB =∠DEF∠ABD =∠DFE AD =DE ,∴△ABD ≌△DFE (AAS ), ∴DF =AB =BC =3; ②证明:思路一:由①得△ABD≌△DFE(AAS),∴DF=AB=BC=3,EF=BD=m,∴CF=CD+DF=CD+BC=BD=m,∴CF=EF,∵EF⊥MN,∴∠ECF=45°,∵∠ACB=45°,∴∠ACE=90°,即AC⊥CE;思路二:由①得△ABD≌△DFE(AAS),∴DF=AB=BC=3,EF=BD=m,∴CF=CD+DF=CD+BC=BD=m,由勾股定理得:DE2=DF2+EF2=32+m2=9+m2,∴AE2=2DE2=2(9+m2),AC2=32+32=18,CE2=CF2+EF2=2m2,∴AC2+CE2=AE2,∴∠ACE=90°,即AC⊥CE;(2)如图2,作EF⊥MN,∴∠DEF+∠EDF=90°,∵∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD∽△DFE,∴EF BD=DF AB =DE AD=tan30°=√33, ∴EF =√3m3,DF =3,∴CF =CD +DF =CD +BC =BD =m , ∴在Rt △CEF 中,tan ∠ECF =√33, ∴∠ECF =30°,CE =2EF =2√3m3, ∴∠ACE =90°, 即AC ⊥CE ,∴无论m 取何大于3的数,AC ⊥CE 总成立,即点E 在一条直线上运动, ∴4≤m ≤6时,CE 长的范围是8√33≤CE ≤4√3. 17.(2020•瑞安市三模)如图,在等腰△ABC 中,AB =BC ,点D 是AC 边的中点,延长BD 至点E ,使得DE =BD ,连结CE .(1)求证:△ABD ≌△CED .(2)当BC =5,CD =3时,求△BCE 的周长.【分析】(1)利用全等三角形的判定定理SAS 证得结论;(2)利用勾股定理求得BD =4,然后利用三角形的周长公式解答. 【解答】(1)证明:∵AB =BC ,点D 是AC 边的中点, ∴AD =CD ,∠ADB =∠CDE =90°. 又∵DE =BD ,∴△ABD ≌△CED (SAS );(2)解:∵BD =√BC 2−CD 2=√52−32=4, ∴BE =2BD =8. 又∵CE =AB =BC =5,∴BC +CE +BE =5+5+8=18,即△BCE 的周长为18.18.(2020•黄岩区二模)如图,△ABC 和△ADE 是两个不全等的等腰直角三角形,其中点B 与点D 是直角顶点,现固定△ABC,而将△ADE绕点A在平面内旋转.(1)如图1,当点D在CA延长线上时,点M为EC的中点,求证:△DMB是等腰三角形.(2)如图2,当点E在CA延长线上时,M是EC上一点,若△DMB是等腰直角三角形,∠DMB为直角,求证:点M是EC的中点.(3)如图3,当△ADE绕点A旋转任意角度时,线段EC上是否都存在点M,使△BMD为等腰直角三角形,若不存在,请举出反例;若存在,请予以证明.【分析】(1)利用直角三角形斜边上的中线等于斜边的一半得出BM=DM=12EC,即可得出答案;(2)根据AAS证明△DFM≌∠MGB,得FM=BG,DF=MG,根据线段的和表示EM和MC,可得结论;(3)线段EC上都存在中点M,使△BMD为等腰直角三角形,作辅助线,构建全等三角形,证明△DFM≌∠MGB(SAS),得BM=DM,∠FMD=∠GBM,再证明∠DMB=90°,可得结论.【解答】证明:(1)如图1,∵∠EDC=90°,点M为EC的中点,∴DM=12EC.同理可得:BM=12EC.∴DM=BM,∴△DMB是等腰三角形;(2)证明:过点D作DF⊥EA,过点B作BG⊥AC,∴∠DFM=∠BGM=90°,∴∠FDM+∠DMF=90°,∵△DMB是等腰直角三角形,∴DM=BM,∠DMB=90°,∴∠BMG+∠DMF=90°,∴∠FDM=∠BMG,∴△DFM≌∠MGB(AAS),∴FM=BG,DF=MG,∵BG=GC,DF=EF,∴FM=GC,MG=EF,∵EM=EF+FM,MC=MG+GC,∴EM=MC,∴点M是EC的中点;(3)线段EC上都存在中点M,使△BMD为等腰直角三角形,理由是:取AE中点F,AC中点G,连接FD,FM,BG,GM,∵点M是EC的中点,点G是AC的中点,∴GM=12AE,GM∥AE,∵F是AE中点,∴AF=12AE,∴AF∥GM,AF=GM,∴四边形AFMG是平行四边形,∴∠AFM=∠AGM,∴∠EFM=∠MGC.∴∠DFM=∠BGM,∵GM=AF=DF,∴DF=GM,同理可得BG=FM,∴△DFM≌∠MGB(SAS),∴BM=DM,∠FMD=∠GBM,∵FM∥AC,∴∠FMG=∠CGM,∴∠DMB=∠FMD+∠FMG+∠GMB,=∠GBM+∠CGM+∠GMB,=180°﹣∠BGC,=90°,∴△BMD是等腰直角三角形.19.(2020•余杭区二模)如图,在正方形ABCD中,点E,F分别在BC,AB上,且DE=DF,连结AC,分别交DE,DF于点M,N.(1)求证:△ADF≌△CDE;(2)设△DMN和△AFN的面积分别为S1和S2;①若∠ADF=∠EDF,求S2:S1的值.②若S2=2S1,求tan∠ADF.【分析】(1)根据HL证明三角形全等即可.(2)①如图,作NH ⊥AB 于H .设FH =a .利用参数表示S 2,S 1即可.②如图,作NH ⊥AB 于H .易证∠ADF =∠HNF ,设tan ∠ADF =tan ∠FNH =k ,设NH =AH =b ,则FH =kb ,利用面积关系构建方程求出k 即可解决问题.【解答】(1)证明:∵四边形ABCD 是正方形,∴AB =BC =CD =AD ,∠DAF =∠DCE =∠ADC =90°,∵DF =DE ,∴Rt △ADF ≌Rt △CDE (HL ).(2)①如图,作NH ⊥AB 于H .设FH =a .∵Rt △ADF ≌Rt △CDE (HL ),∵∠ADF =∠CDE ,∵∠ADF =∠DEF ,∴∠ADF =∠EDF =∠CDE =30°,∴∠AFD =60°,∵∠NHF =90°,∴∠FNH =30°,∴HN =√3a ,∵∠NAH =45°,∠AHN =90°,∴∠NAH =∠ANH =45°,∴HA =HN =√3a ,∴AF =(1+√3)a ,AD =√3AF =(3+√3)a ,∴S 2=12•AF •NH =12•(1+√3)a ⋅√3a =3+√32a 2, ∵∠ADN =∠CDM ,AD =DC ,∠DAN =∠DCM =45°,∴△ADN ≌△CDM (ASA ),∴S △ADN =S △DCM ,∴S 1=S △ADC ﹣2S △ADN =12•[(3+√3)a ]2﹣2×12•(3+√3)a •√3a =3a 2,∴S 2S 1=3+√32a 23a 2=3+√36.。
决胜2020年中考数学压轴题专题15 动点综合问题(含答案)
专题15 动点综合问题【典例分析】【考点1】动点之全等三角形问题【例1】如图,直线443y x=-+与x轴和y轴分别交于,A B两点,另一条直线过点A和点(7,3) C.(1)求直线AC的函数表达式;(2)求证: AB AC⊥;(3)若点P是直线AC上的一个动点,点Q是x轴上的一个动点,且以,,P Q A为顶点的三角形与AOB∆全等,求点Q的坐标.【变式1-1】)如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s 的速度沿射线CQ 运动,点N 为射线BM 上一动点,满足PN=AB,随着P 点运动而运动,当点P 运动_______秒时,△BCA 与点P 、N 、B 为顶点的三角形全等.(2个全等三角形不重合)【考点2】动点之直角三角形问题 【例2】(模型建立)(1)如图1,等腰直角三角形ABC 中,90ACB ∠=o,CB CA =,直线ED 经过点C ,过A 作AD ED ⊥于点D ,过B 作BE ED ⊥于点E .求证:BEC CDA ∆≅∆; (模型应用)(2)已知直线1l:443y x =+与坐标轴交于点A 、B ,将直线1l 绕点A 逆时针旋转45o 至直线2l,如图2,求直线2l的函数表达式;(3)如图3,长方形ABCO ,O 为坐标原点,点B 的坐标为()8,6-,点A 、C 分别在坐标轴上,点P 是线段BC 上的动点,点D 是直线26y x =-+上的动点且在第四象限.若APD ∆是以点D 为直角顶点的等腰直角三角形,请直接写出点D 的坐标.【变式2-1】(2019·辽宁中考模拟)如图,已知二次函数y =ax2+bx+4的图象与x 轴交于点A(4,0)和点D(﹣1,0),与y 轴交于点C ,过点C 作BC 平行于x 轴交抛物线于点B ,连接AC(1)求这个二次函数的表达式;(2)点M 从点O 出发以每秒2个单位长度的速度向点A 运动;点N 从点B 同时出发,以每秒1个单位长度的速度向点C 运动,其中一个动点到达终点时,另一个动点也随之停动,过点N 作NQ 垂直于BC 交AC 于点Q ,连结MQ.①求△AQM的面积S与运动时间t之间的函数关系式,写出自变量的取值范围;当t为何值时,S有最大值,并求出S的最大值;②是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.【变式2-2】如图,四边形ABCD是正方形,以DC为边向外作等边△DCE,连接AE交BD 于点F,交CD于点G,点P是线段AE上一动点,连接DP、BP.(1)求∠AFB的度数;(2)在点P从A到E的运动过程中,若DP平分∠CDE,求证:AG•DP=DG•BD;(3)已知AD=6,在点P从A到E的运动过程中,若△DBP是直角三角形,请求DP的长.【考点3】动点之等腰三角形问题【例3】(2019·湖南中考真题)如图一,在射线DE的一侧以AD为一条边作矩形ABCD,53AD=5CD=,点M是线段AC上一动点(不与点A重合),连结BM,过点M作BM的垂线交射线DE于点N,连接BN.(1)求CAD ∠的大小;(2)问题探究:动点M 在运动的过程中,①是否能使AMN ∆为等腰三角形,如果能,求出线段MC 的长度;如果不能,请说明理由. ②MBN ∠的大小是否改变?若不改变,请求出MBN ∠的大小;若改变,请说明理由. (3)问题解决:如图二,当动点M 运动到AC 的中点时,AM 与BN 的交点为F ,MN 的中点为H ,求线段FH 的长度.【变式3-1】如图①,已知正方形ABCD 边长为2,点P 是AD 边上的一个动点,点A 关于直线BP 的对称点是点Q ,连结PQ 、DQ 、CQ 、BQ .设AP=x.(1)当1x =时,求BP 长;(2)如图②,若PQ 的延长线交CD 边于E ,并且90CQD ∠=o,求证:CEQ ∆为等腰三角形;(3)若点P 是射线AD 上的一个动点,则当CDQ ∆为等腰三角形时,求x 的值.【变式3-2】(2019·河南中考模拟)如图,抛物线y=ax2+bx+3交y 轴于点A ,交x 轴于点B (-3,0)和点C (1,0),顶点为点M . (1)求抛物线的解析式;(2)如图,点E 为x 轴上一动点,若△AME 的周长最小,请求出点E 的坐标;(3)点F 为直线AB 上一个动点,点P 为抛物线上一个动点,若△BFP 为等腰直角三角形,请直接写出点P 的坐标.【变式3-3】(2019·广西中考真题)已知抛物线2y mx =和直线y x b =-+都经过点()2,4M -,点O 为坐标原点,点P 为抛物线上的动点,直线y x b =-+与x 轴、y 轴分别交于AB 、两点. (1)求m b 、的值;(2)当PAM ∆是以AM 为底边的等腰三角形时,求点P 的坐标; (3)满足(2)的条件时,求sin BOP ∠的值. 【考点4】动点之相似三角形问题【例4】在边长为4的正方形ABCD 中,动点E 以每秒1个单位长度的速度从点A 开始沿边AB 向点B 运动,动点F 以每秒2个单位长度的速度从点B 开始沿边BC 向点C 运动,动点E 比动点F 先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F 的运动时间为t 秒.()1如图1,连接DE ,AF ,若DE AF ⊥,求t 的值 ()2如图2,连接,EF DF ,当t 为何值时,?EBF DCF V :V【变式4-1】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),BC=34AC(1)求过点A,B的直线的函数表达式;(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D 的坐标;(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.【变式4-2】如图,已知抛物线2y ax bx c =++经过A(-3,0)、B(8,0)、C(0,4)三点,点D是抛物线上的动点,连结AD与y轴相交于点E,连结AC,CD.(1)求抛物线所对应的函数表达式;(2)当AD平分∠CAB时.①求直线AD所对应的函数表达式;②设P是x轴上的一个动点,若△PAD与△CAD相似,求点P的坐标.【考点5】动点之平行四边形问题(含特殊四边形)【例5】(2019·广东中考模拟)如图,点O是平面直角坐标系的原点,点A33),AC⊥OA 与x轴的交点为C.动点M3A向点O运动.同时,动点N以每秒3个单位长度由点O向点C运动,当一动点先到终点时,另一动点立即停止运动.(1)写出∠AOC的值;(2)用t表示出四边形AMNC的面积;(3)求点P的坐标,使得以O、N、M、P为顶点的四边形是特殊的平行四边形?【变式5-1】(2019·江西中考真题)在图1,2,3中,已知,,点为线段上的动点,连接,以为边向上作菱形,且.(1)如图1,当点与点重合时,________°;(2)如图2,连接.①填空:_________(填“>”,“<”,“=”);②求证:点在的平分线上;(3)如图3,连接,,并延长交的延长线于点,当四边形是平行四边形时,求的值.【变式5-2】(2019·湖南中考真题)如图,二次函数213y x bx c=-++的图象过原点,与x轴的另一个交点为() 8,0【变式5-3】.如图,在平面直角坐标系中,AOB ∆的顶点O 是坐标原点,点A 坐标为()1,3,A 、B 两点关于直线y x =对称,反比例函数()0ky x x =>图象经过点A ,点P 是直线y x=上一动点.(1)B 点的坐标为______;(2)若点C 是反比例函数图象上一点,是否存在这样的点C ,使得以A 、B 、C 、P 四点为顶点的四边形是平行四边形?若存在,求出点C 坐标;若不存在,请说明理由; (3)若点Q 是线段OP 上一点(O 不与O 、P 重合),当四边形AOBP 为菱形时,过点Q 分别作直线OA 和直线AP 的垂线,垂足分别为E 、F ,当QE QF QB ++的值最小时,求出Q 点坐标.【考点6】动点之线段面积问题【例6】如图已知平面内有一动点A ,x 轴上有一定点B (4,0),连接AB ,且将线段AB 绕B 点逆时针旋转90°得到线段BC .①当A 点坐标为(1,1)时,求C 点坐标;②当A 点在直线x=1上滑动时,求在此运动过程中△BOC 的面积是否发生变化,若不变,请求出面积,若变化,请说明理由;③若总条件中的动点A 改为直线y=x 上的动点A ,其余条件都不变,请直接写出当A 点在直线y=x 上滑动时,点D (0,-2)到C 点的最短距离.【变式6-1】(2019·山东中考模拟)如图,抛物线2y x bx c =-++交x 轴于点()30A -,和点B ,交y 轴于点()0,3C .(1)求抛物线的函数表达式; (2)若点P 在抛物线上,且4AOP BOCS S ∆∆=,求点P 的坐标;(3)如图,设点Q 是线段AC 上的一动点,作DQ x ⊥轴,交抛物线于点D ,求线段DQ 长度的最大值,并求出DAC ∆面积的最大值.【变式6-2】如图,矩形ABCD 中,3,4AD AB ==,点P 是对角线AC 上一动点(不与A C 、重合),连接PB ,过点P 作PE PB ⊥,交射线DC 于点E ,以线段,PE PB 为邻边作矩形BPEF ,过点P 作GH CD ⊥。
2020年全国中考数学压轴题全析全解(2)

2020年全国中考数学压轴题全解全析11、(河北卷)如图,在Rt △ABC 中,∠C =90°,AC =12,BC =16,动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P ,Q 分别从点A ,C 同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,△PCQ 关于直线PQ 对称的图形是△PDQ .设运动时间为t (秒).(1)设四边形PCQD 的面积为y ,求y 与t 的函数关系式; (2)t 为何值时,四边形PQBA 是梯形?(3)是否存在时刻t ,使得PD ∥AB ?若存在,求出t 的值;若不存在,请说明理由; (4)通过观察、画图或折纸等方法,猜想是否存在时刻t ,使得PD ⊥AB ?若存在,请估计t 的值在括号中的哪个时间段内(0≤t ≤1;1<t ≤2;2<t ≤3;3<t ≤4);若不存在,请简要说明理由. [解] (1)由题意知 CQ =4t ,PC =12-3t ,∴S △PCQ =t t CQ PC 246212+-=⋅. ∵△PCQ 与△PDQ 关于直线PQ 对称,∴y=2S △PCQ t t 48122+-=. (2)当CQCP CA CB=时,有PQ ∥AB ,而AP 与BQ 不平行,这时四边形PQBA 是梯形, ∵CA =12,CB =16,CQ =4t , CP =12-3t ,∴16412312tt =-,解得t =2. ∴当t =2秒时,四边形PQBA 是梯形.(3)设存在时刻t ,使得PD ∥AB ,延长PD 交BC 于点M ,如图2,若PD ∥AB ,则∠QMD =∠B ,又∵∠QDM =∠C =90°,∴Rt △QMD ∽Rt △ABC ,从而ACQD AB QM =, ∵QD =CQ =4t ,AC =12,AB=20,∴QM =203t . 若PD ∥AB ,则CP CMCA CB=,得20412331216t t t +-=, 解得t =1211. ∴当t =1211秒时,PD ∥AB .(4)存在时刻t ,使得PD ⊥AB .P图2图7D 时间段为:2<t ≤3.[点评]这是一道非常典型的动态几何问题,考查相似形、图形变换等知识,难度比起2005年河北非课改区的那道压轴题略有降低,但仍保留了足够的区分度,在解第3小题时应当先假设结论存在,再根据已知求解,若出现矛盾,则说明结论不存在,第4小题应该通过画图来判断时间段。
2020年中考数学压轴题(含答案)
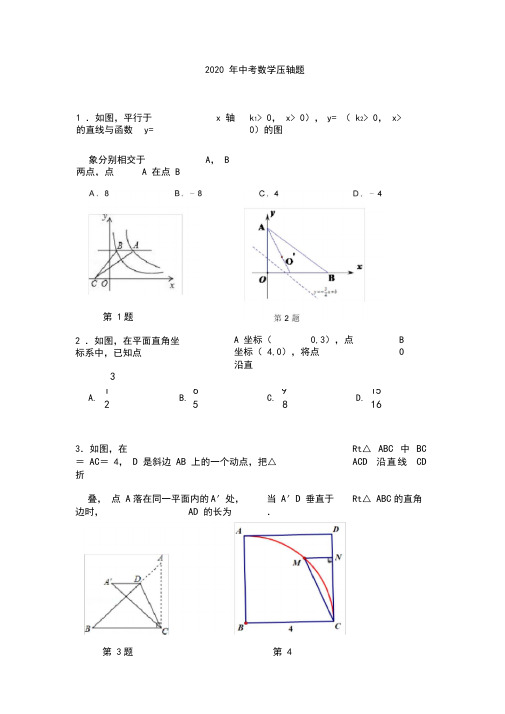
2020 年中考数学压轴题3.如图,在Rt △ ABC 中 BC = AC = 4, D 是斜边 AB 上的一个动点,把△ ACD 沿直线 CD折叠, 点 A 落在同一平面内的 A ′处, 当 A ′D 垂直于Rt △ ABC 的直角边时, AD 的长为.1 .如图,平行于 x 轴的直线与函数 y= 象分别相交于 A , B两点,点 A 在点 B k 1> 0, x> 0), y= ( k 2> 0, x>0)的图第 1题2 .如图,在平面直角坐标系中,已知点3 A 坐标( 0,3),点 B 坐标( 4,0),将点 O沿直1 A.26 B. 5 9 C.8 15 D.16第 3题 第 4题4. 如图,在正方形ABCD 中, AB=4 ,以 B 为圆心,BA 长为半径画弧,点M 为弧上一点,MN ⊥ CD 于 N,连接CM ,则 CM - MN 的最大值为.三、解答题B⌒D=A⌒D,DE⊥ BC,垂足为E.5.如图,四边形ABCD 是⊙ O的内接四边形,AC 为直径,( 1 )求证:CD 平分∠ACE;( 2 )判断直线ED 与⊙ O 的位置关系,并说明理由;(3)若CE=2 ,AC= 8,阴影部分的面积为.6.如图,抛物线y=ax2+bx+ c(a< 0,a、b、 c 为常数)与x轴交于A、C两点,与y 轴交于B 点,A(﹣6,0),C( 1 ,0),B(0,).( 1 )求该抛物线的函数关系式与直线AB 的函数关系式;( 2)已知点M (m, 0)是线段OA 上的一个动点,过点M作x轴的垂线l,分别与直线AB 和抛物线交于 D 、 E 两点,当m 为何值时,△ BDE 恰好是以DE 为底边的等腰三角形?( 3 )在( 2 )问条件下,当△BDE 恰妤是以DE 为底边的等腰三角形时,动点M 相应位置记为点M ′,将OM ′绕原点O 顺时针旋转得到ON(旋转角在0°到 90 °之间);i:探究:线段OB 上是否存在定点P(P 不与O、B 重合),无论ON 如何旋转,始终保持不变,若存在,试求出 P 点坐标:若不存在,请说明理由;NA + NB )的最小值.【答案与解析】一、选择题 1. A 2. D 二、填空题3. 【分析】由等腰直角三角形的性质和勾股定理得出 AB = 4 ,∠ B =∠ A ′ CB = 45 °,①如图 1 , 当 A ′D ∥ BC , 设 AD = x , 根据折叠的性质得到∠ A ′=∠ A =∠ A ′CB = 45°, A ′D = AD= x ,推出 A ′C ⊥ AB ,求得 BH =BC = 2 , DH =A ′D =x ,然后列方程即可得到结果,②如图 2,当 A ′D ∥ AC ,根据折叠的性质得到 AD = A ′D , AC = A ′C ,∠ ACD=∠ A ′CD ,根据平行线的性质得到∠ A ′DC =∠ACD ,于是得到∠ A ′DC =∠A ′CD ,推出 A ′ii :试求出此旋转过程中,D =A′C,于是得到AD =AC= 2.【解答】解:Rt△ ABC 中,BC=AC= 4,∴ AB= 4 ,∠ B=∠A′CB= 45°,①如图 1 ,当A′D∥ BC,设AD=x,∵把△ ACD 沿直线CD 折叠,点 A 落在同一平面内的 A ′处,A′=∠A=∠A′CB= 45°,A′D=AD=x,B= 45∴ A′C⊥ AB,∴ BH=BC= 2 ,DH=A′D=x,∴ x+ x+2 = 4 ,∴ x= 4 ﹣ 4 ,∴ AD = 4 ﹣ 4 ;②如图 2 ,当A′D∥ AC,∵把△ ACD 沿直线CD 折叠,点 A 落在同一平面内的 A ′处,∴ AD=A′D,AC=A′C,∠ ACD =∠ A′CD,∵∠ A′DC=∠ ACD,∴∠ A′DC=∠ A′CD,∴ A′D=A′C,∴ AD =AC = 4 ,综上所述:AD 的长为: 4 ﹣ 4 或 4.4. 2三、解答题5、( 1 )Q B?D ?AD, ∠ BAD ∠ ACDQ 四边形ABCD内接于圆O,∠ BAD +∠ BCD 180又 Q ∠ BCD +∠ DCE 180°, ∠ DCE ∠ BAD∠ ACD ∠ DCE 即 CD 平分∠ ACE( 2 )直线 ED 与⊙ O 相切。
决胜2020年中考数学压轴题全揭秘——操作类探究问题(含答案)
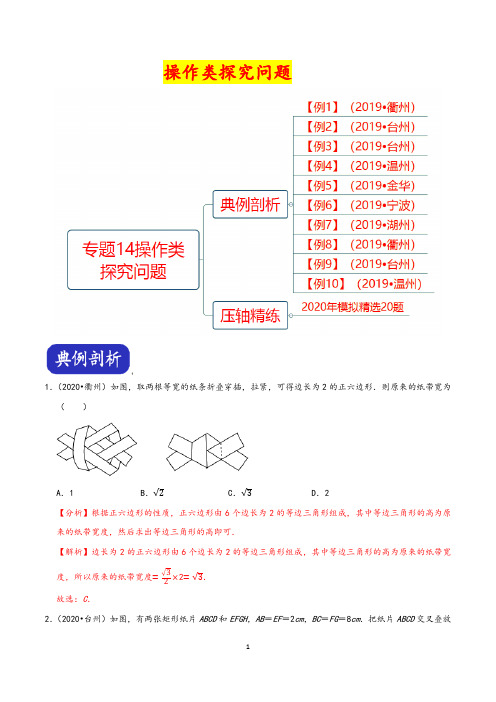
操作类探究问题1.(2020•衢州)如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为()A.1 B.√2C.√3D.2【分析】根据正六边形的性质,正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,然后求出等边三角形的高即可.【解析】边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,所以原来的纸带宽度=√32×2=√3.故选:C.2.(2020•台州)如图,有两张矩形纸片ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.把纸片ABCD交叉叠放在纸片EFGH 上,使重叠部分为平行四边形,且点D 与点G 重合.当两张纸片交叉所成的角α最小时,tan α等于( )A .14B .12C .817D .815【分析】由“ASA ”可证△CDM ≌△HDN ,可证MD =DN ,即可证四边形DNKM 是菱形,当点B 与点E 重合时,两张纸片交叉所成的角a 最小,可求CM =154,即可求tan α的值. 【解析】如图,∵∠ADC =∠HDF =90°∴∠CDM =∠NDH ,且CD =DH ,∠H =∠C =90° ∴△CDM ≌△HDN (ASA )∴MD =ND ,且四边形DNKM 是平行四边形 ∴四边形DNKM 是菱形 ∴KM =DM∵sin α=sin ∠DMC =CDMD∴当点B 与点E 重合时,两张纸片交叉所成的角a 最小, 设MD =a =BM ,则CM =8﹣a , ∵MD 2=CD 2+MC 2, ∴a 2=4+(8﹣a )2, ∴a =174∴CM=15 4∴tanα=tan∠DMC=CDMC=815故选:D.3.(2020•台州)如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为()A.√2:1 B.3:2 C.√3:1 D.√2:2【分析】如图,作DC⊥EF于C,DK⊥FH于K,连接DF.求出△DFN与△DNK的面积比即可.【解析】如图,作DC⊥EF于C,DK⊥FH于K,连接DF.由题意:四边形DCFK是正方形,∠CDM=∠MDF=∠FDN=∠NDK,∴∠CDK=∠DKF=90°,DK=FK,DF=√2DK,∴S△DFNS△DNK =FNNK=DFDK=√2(角平分线的性质定理,可以用面积法证明),∴SA型SB型=2S△DFN2S△DNK=√2,∴图案中A型瓷砖的总面积与B型瓷砖的总面积之比为√2:1,故选:A.4.(2020•温州)如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N,欧几里得在《几何原本》中利用该图解释了(a+b)(a﹣b)=a2﹣b2,现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S 1,图中阴影部分的面积为S 2.若点A ,L ,G 在同一直线上,则S 1S 2的值为( )A .√22B .√23C .√24D .√26【分析】如图,连接AL ,GL ,PF .利用相似三角形的性质求出a 与b 的关系,再求出面积比即可. 【解析】如图,连接AL ,GL ,PF .由题意:S 矩形AMLD =S 阴=a 2﹣b 2,PH =√a 2−b 2, ∵点A ,L ,G 在同一直线上,AM ∥GN , ∴△AML ∽△GNL , ∴AM GN=ML NL, ∴a+b a−b=a−b b,整理得a =3b ,∴S 1S 2=12⋅(a−b)⋅√a 2−b 2a −b =2√2b 28b =√24,故选:C .5.(2020•金华)将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM ,GN 是折痕.若正方形EFGH 与五边形MCNGF 的面积相等,则FM GF的值是( )A .√5−√22B .√2−1C .12D .√22【分析】连接HF ,设直线MH 与AD 边的交点为P ,根据剪纸的过程以及折叠的性质得PH =MF 且正方形EFGH 的面积=15×正方形ABCD 的面积,从而用a 分别表示出线段GF 和线段MF 的长即可求解.【解析】连接HF ,设直线MH 与AD 边的交点为P ,如图:由折叠可知点P 、H 、F 、M 四点共线,且PH =MF , 设正方形ABCD 的边长为2a , 则正方形ABCD 的面积为4a 2,∵若正方形EFGH 与五边形MCNGF 的面积相等∴由折叠可知正方形EFGH 的面积=15×正方形ABCD 的面积=45a 2, ∴正方形EFGH 的边长GF =√45a 2=2√55a ∴HF =√2GF =2√105a ∴MF =PH =2a−2√105a 2=5−√105a∴FM GF=5−√105a ÷2√55a =√5−√22故选:A .6.(2020•宁波)如图所示,矩形纸片ABCD 中,AD =6cm ,把它分割成正方形纸片ABFE 和矩形纸片EFCD 后,分别裁出扇形ABF 和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB 的长为( )A .3.5cmB .4cmC .4.5cmD .5cm【分析】设AB =xcm ,则DE =(6﹣x )cm ,根据扇形的弧长等于圆锥底面圆的周长列出方程,求解即可. 【解析】设AB =xcm ,则DE =(6﹣x )cm , 根据题意,得90πx 180=π(6﹣x ),解得x =4. 故选:B .二.填空题(共4小题)7.(2020•湖州)七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为4√2的正方形ABCD 可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH 内拼成如图2所示的“拼搏兔”造型(其中点Q 、R 分别与图2中的点E 、G 重合,点P 在边EH 上),则“拼搏兔”所在正方形EFGH 的边长是 4√5 .【分析】如图2中,连接EG ,GM ⊥EN 交EN 的延长线于M ,利用勾股定理解决问题即可. 【解析】如图2中,连接EG ,作GM ⊥EN 交EN 的延长线于M .在Rt △EMG 中,∵GM =4,EM =2+2+4+4=12,∴EG =√EM 2+GM 2=√122+42=4√10, ∴EH =EG√2=4√5, 故答案为4√5.8.(2020•衢州)如图,由两个长为2,宽为1的长方形组成“7”字图形(1)将一个“7”字图形按如图摆放在平面直角坐标系中,记为“7”字图形ABCDEF ,其中顶点A 位于x 轴上,顶点B ,D 位于y 轴上,O 为坐标原点,则OB OA的值为12.(2)在(1)的基础上,继续摆放第二个“7”字图形得顶点F 1,摆放第三个“7”字图形得顶点F 2,依此类推,…,摆放第n 个“7”字图形得顶点F n ﹣1,…,则顶点F 2020的坐标为 (6062√55,405√5) .【分析】(1)先证明△AOB ∽△BCD ,所以OB OA=DC BC,因为DC =1,BC =2,所有OB OA=12;(2)利用三角形相似与三角形全等依次求出F 1,F 2,F 3,F 4的坐标,观察求出F 2020的坐标. 【解析】(1)∵∠ABO +∠DBC =90°,∠ABO +∠OAB =90°, ∴∠DBC =∠OAB , ∵∠AOB =∠BCD =90°, ∴△AOB ∽△BCD , ∴OB OA=DC BC,∵DC =1,BC =2, ∴OB OA=12,故答案为12;(2)解:过C 作CM ⊥y 轴于M ,过M 1作M 1N ⊥x 轴,过F 作FN 1⊥x 轴.根据勾股定理易证得BD =√22+12=√5,CM =OA =2√55,DM =OB =AN =√55, ∴C (2√55,√5),∵AF =3,M 1F =BC =2, ∴AM 1=AF ﹣M 1F =3﹣2=1, ∴△BOA ≌ANM 1(AAS ), ∴NM 1=OA =2√55, ∵NM 1∥FN 1, ∴M 1N FN 1=AM 1AF, 2√55FN 1=13,∴FN 1=6√55, ∴AN 1=3√55,∴ON 1=OA +AN 1=2√55+3√55=5√55 ∴F (5√55,6√55), 同理,F 1(8√55,7√55),即(1×3+55√5,6+15√5) F 2(11√55,8√55),即(2×3+55√5,6+25√5) F 3(14√55,9√55),即(3×3+55√5,6+35√5) F 4(17√55,10√55),即(4×3+55√5,6+45√5) …F 2020(2020×3+55√5,6+20205√5),即(60625√5,405√5), 故答案为即(60625√5,405√5). 9.(2020•台州)如图,直线l 1∥l 2∥l 3,A ,B ,C 分别为直线l 1,l 2,l 3上的动点,连接AB ,BC ,AC ,线段AC 交直线l 2于点D .设直线l 1,l 2之间的距离为m ,直线l 2,l 3之间的距离为n ,若∠ABC =90°,BD =4,且m n=23,则m +n 的最大值为253.【分析】延长AB 交l 3于E ,根据已知条件得到DB CE=m m+n,求得CE =10,∠CBE =90°,设m =2x ,n=3x ,构造以CE 为直径的半圆,则点B 在其弧上运动,易知BG ≤B ′G ′=5,得到3x ≤5,由m +n =5x ≤253,于是得到结论.【解析】延长AB 交l 3于E ,∵m n=23,易知DB CE=m m+n,∵BD =4, ∴CE =10, ∵∠ABC =90°, ∴∠CBE =90°, 设m =2x ,n =3x ,构造以CE 为直径的半圆,则点B 在其弧上运动,易知BG ≤B ′G ′=5, 即3x ≤5,∴x ≤53,∵m +n =5x ≤253, ∴m +n 的最大值为253.故答案为:253.10.(2020•温州)三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB =∠AOE =90°,菱形的较短对角线长为2cm .若点C 落在AH 的延长线上,则△ABE 的周长为 12+8√2 cm .【分析】连接IC ,连接CH 交OI 于K ,则A ,H ,C 在同一直线上,CI =2,根据△COH 是等腰直角三角形,即可得到∠CKO =90°,即CK ⊥IO ,设CK =OK =x ,则CO =IO =√2x ,IK =√2x ﹣x ,根据勾股定理即可得出x 2=2+√2,再根据S 菱形BCOI =IO ×CK =12IC ×BO ,即可得出BO =2√2+2,进而得到△ABE 的周长. 【解析】如图所示,连接IC ,连接CH 交OI 于K ,则A ,H ,C 在同一直线上,CI =2,∵三个菱形全等, ∴CO =HO ,∠AOH =∠BOC , 又∵∠AOB =∠AOH +∠BOH =90°, ∴∠COH =∠BOC +∠BOH =90°, 即△COH 是等腰直角三角形,∴∠HCO =∠CHO =45°=∠HOG =∠COK , ∴∠CKO =90°,即CK ⊥IO ,设CK =OK =x ,则CO =IO =√2x ,IK =√2x ﹣x , ∵Rt △CIK 中,(√2x ﹣x )2+x 2=22, 解得x 2=2+√2,又∵S菱形BCOI=IO×CK=12IC×BO,∴√2x2=12×2×BO,∴BO=2√2+2,∴BE=2BO=4√2+4,AB=AE=√2BO=4+2√2,∴△ABE的周长=4√2+4+2(4+2√2)=12+8√2,故答案为:12+8√2.1.(2020•奉化区模拟)如图,矩形ABCD中,AD=6,AB=4,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G,FH⊥BC,垂足为H,连接BF、DG.以下结论:①BF∥ED;②BH=3FH;③tan∠GEB=3 4;④S△BFG=0.6,其中正确的个数是()A.1 B.2 C.3 D.4【分析】根据正方形的性质、折叠的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理依次对各个选项进行判断、计算,即可得出答案.【解析】①∵AB=4,E为AB的中点,∴AE=BE=2,∵将△ADE沿DE翻折得到△FDE,∴AD=DF,AE=EF=2,∠AED=∠DEF,∴AE=EF=BE,∴∠EBF=∠EFB,∵∠AEF=∠EBF+∠EFB,∴∠AED=∠EBF,∴BF ∥ED , 故①正确; ②∵BF ∥ED , ∴∠ABF =∠AED ,∵∠ABF +∠FBH =90°,∠AED +∠ADE =90°, ∴∠FBH =∠ADE ,∴tan ∠FBH =FHBH =tan ∠ADE =AEAD =26=13, ∴FH BH=13,∴BH =3FH , 故②正确;③过点E 作EM ⊥BF 于点M ,如图,∵AE =EF =BE , ∴∠FEM =12∠BEF , ∵∠DEF =12∠AEF ,∴∠FEM +∠DEF =12×180°=90°, ∵∠DEF +∠EDF =90°, ∴∠FEM =∠EDF , ∵∠EMF =∠DFE =90°, ∴△EFM ∽△DEF , ∴FM EF=EF ED,∴FM =√105, ∴BF =2FM =2√105,∵∠HBF +∠EBM =∠EBM +∠BEM =90°, ∴∠HBF =∠BEM =∠FEM =∠FDE , ∵∠BHF =∠DFE =90°, ∴△BHF ∽△DFE , ∴FH EF=BH DF,∵BH =3FH , ∴FH =25,BH =65, 设HG =x , ∵FH ⊥BC , ∴FH ∥BE , ∴△GFH ∽△GEB ,∴HG BG=HF BE,即xx+65=252,解得,x =310,∴BG =BH +HG =32, ∴tan ∠GEB =BG EB =34, 故③正确;④S △BFG =12BG ⋅FH =0.3, 故④错误; 综上共有3个正确. 故选:C .2.(2020•宁波模拟)如图,将矩形ABCD 沿EF 折叠,使顶点C 恰好落在AB 边的中点C ′上,点D 落在D ′处,C′D′交AE于点M,若AB=6,BC=9,则AM的长为()A.2 B.94C.52D.114【分析】先根据勾股定理求出BF,再根据△AMC′∽△BC′F求出AM即可.【解析】∵四边形ABCD是矩形,∴∠A=∠B=∠C=90°,根据折叠的性质可知,FC=FC′,∠C=∠FC′M=90°,设BF=x,则FC=FC′=9﹣x,∵BF2+BC′2=FC′2,∴x2+32=(9﹣x)2,解得:x=4,∴BF=4,∵∠FC′M=90°,∴∠AC′M+∠BC′F=90°,又∵∠BFC′+BC′F=90°,∴∠AC′M=∠BFC′,∵∠A=∠B=90°,∴△AMC′∽△BC′F,∴AMBC′=AC′BF,即AM3=34,∴AM=9 4;故选:B.3.(2020•宁波模拟)如图,梯形ABCD 被分割成两个小梯形①②,和一个小正方形③,去掉③后,①和②可剪拼成一个新的梯形,若EF ﹣AD =2,BC ﹣EF =1,则AB 的长是( )A .6B .3√5C .9D .3√10【分析】连接AH 交EF 于点K ,根据EF ﹣AD =2,BC ﹣EF =1,可得BC ﹣AD =3,由图象剪拼观察可得,AD =HC ,四边形AHCD 是平行四边形,再证明△AEK ∽△ABH ,可得AB 的长.【解析】如图,连接AH 交EF 于点K , ∵EF ﹣AD =2,BC ﹣EF =1, ∴BC ﹣AD =3, 由图象剪拼观察可知:AD =HC ,∴四边形AHCD 是平行四边形, ∴BC ﹣AD =BC ﹣HC =3,KF =AD ,EK =2,∵③为正方形, ∴EB =BH =3, ∵△AEK ∽△ABH , ∴AE AB=EK BH,即AB−3AB=23,解得AB =9. 故选:C .4.(2020•黄岩区模拟)如图,矩形纸片ABCD 中,AB =6,BC =8,E 是边CD 上一点,连接AE .折叠该纸片,使点A 落在AE 上的G 点,并使折痕经过点B ,得到折痕BF ,点F 在AD 上.若DE =4,则AF 的长为( )A .163B .4C .3D .2【分析】由矩形的性质可得AB =CD =6,AD =BC =8,∠BAD =∠D =90°,通过证明△ABF ∽△DAE ,可得AF AB=DE AD,即可求解.【解析】设BF 与AE 交于点H ,∵四边形ABCD 为矩形,∴AB =CD =6,AD =BC =8,∠BAD =∠D =90°,由折叠及轴对称的性质可知,△ABF ≌△GBF ,BF 垂直平分AG , ∴BF ⊥AE ,AH =GH , ∴∠BAH +∠ABH =90°, 又∵∠FAH +∠BAH =90°, ∴∠ABH =∠FAH , 又∵∠BAD =∠D =90°, ∴△ABF ∽△DAE , ∴AF AB=DE AD,∴AF =48×6=3, 故选:C .5.(2020•路桥区模拟)如图,在矩形ABCD 中,将△ABE 沿着BE 翻折,使点A 落在BC 边上的点F 处,再将△DEG 沿着EG 翻折,使点D 落在EF 边上的点H 处.若点A ,H ,C 在同一直线上,AB =1,则AD 的长为( )A .32B .√5+12C .√2D .√5−1【分析】由折叠的性质可得AB =BF =1,AE =EF ,∠ABE =∠FBE ,∠A =∠EFB =90°,DE =EH ,可证四边形CDEF 是矩形,可得DE =FC ,由平行线分线段成比例可得HF AB=CF BC,可求AD 的长.【解析】连接AC ,∵四边形ABCD 是矩形,∴∠A =∠C =∠ADC =∠ABC =90°,AD =BC ,∵将△ABE 沿着BE 翻折,使点A 落在BC 边上的点F 处,再将△DEG 沿着EG 翻折,使点D 落在EF 边上的点H 处,∴AB =BF =1,AE =EF ,∠ABE =∠FBE ,∠A =∠EFB =90°,DE =EH , ∴AB ∥EF ,∠FEB =∠EBF =45°, ∴EF =BF =1=AE ,∵∠EFC =∠C =∠ADC =90°, ∴四边形CDEF 是矩形, ∴DE =FC ,∴DE =EH =FC =AD ﹣AE =AD ﹣1, ∴HF =1﹣(AD ﹣1)=2﹣AD , ∵点A ,H ,C 在同一直线上,EF ∥AB ,∴HF AB =CF BC,∴2−AD1=AD−1AD,∴AD =1+√52或1−√52(舍去) ∴AD =1+√52, 故选:B .6.(2020•宁波模拟)如图,四边形ABCD 是轴对称图形,对角线BD 所在的直线是它的对称轴,∠A =∠C =90°,AB ≠AD ,若把这个轴对称图形沿对角线BD 剪开成两个三角形后,再把这两个三角形的一边完全重合在一起,重新拼成一个中心对称图形,则拼法共有( )A .0种B .1种C .2种D .3种【分析】直接利用旋转的性质结合中心对称图形的性质得出符合题意的答案. 【解析】如图所示:3种拼法都是中心对称图形. 故选:D .7.(2020•柯桥区模拟)如图,矩形ABCD 的对角线AC 与BD 交于点O ,AD =1,DC =√3,矩形OGHM 的边OM 经过点D ,边OG 交CD 于点P ,将矩形OGHM 绕点O 逆时针方向旋转α(0°<α<60°),OM ′交AD 于点F ,OG ′交CD 于点E ,设DF =y ,EP =x ,则y 与x 的关系为( )A .y =√3xB .y =√32xC .y =√33xD .y =12x【分析】由矩形的性质和余角的性质可得∠ODC =∠OCD ,由锐角三角函数可得AD DC=OP DO,通过证明△DOP∽△POE ,可得PEDF=PO DO,即可求解.【解析】∵四边形ABCD 是矩形,∴AC =BD ,AO =CO ,BO =DO ,∠ADC =90°, ∴DO =CO , ∴∠ODC =∠OCD , ∵四边形OGHM 是矩形, ∴∠MOG =90°, ∴∠ODC +∠OPD =90°, 又∵∠ODC +∠ODF =90°, ∴∠OPD =∠ODF , ∵∠ODC =∠OCD , ∴tan ∠OCD =tan ∠ODC , ∴AD DC=OP DO,∵AD =1,DC =√3, ∴OP DO=√3,∵将矩形OGHM 绕点O 逆时针方向旋转α, ∴∠DOF =∠POE , 又∵∠OPD =∠ODF ,∴△DFO∽△PEO,∴PEDF =PODO,∴xy =√3,∴y=√3x,故选:A.8.(2020•路桥区模拟)如图,Rt△ABC中,∠C=90°,BC=6,DE是△ABC的中位线,点D在AB上,把点B绕点D按顺时针方向旋转α(0°<α<180°)角得到点F,连接AF,BF.下列结论:①△ABF是直角三角形;②若△ABF和△ABC全等,则α=2∠BAC或2∠ABC;③若α=90°,连接EF,则S△DEF=4.5;其中正确的结论是()A.①②B.①③C.①②③D.②③【分析】由三角形中位线定理和旋转的性质可得AD=BD=DF,可得△ABF是直角三角形,可判断①;由全等三角形的性质和等腰三角形的性质,可得∠BDF=α=2∠DAF,∠DAF=∠BAC或∠DAF=∠ABC,可判断②;过点B作BN⊥DE,交ED的延长线于N,过点F作FH⊥DE,交交ED的延长线于H,由“AAS”可证△DFH≌△BDN,可得DN=FH=3,由三角形面积公式可得S△DEF=4.5,可判断③,即可求解.【解析】∵DE是△ABC的中位线,∴AD=DB,∵把点B绕点D按顺时针方向旋转α(0°<α<180°)角得到点F,∴BD=DF,∴BD=AD=DF,∴△ABF是直角三角形,故①正确,∵AD=BD=DF,∴∠DAF=∠DFA,∴∠BDF=α=2∠DAF,若△ABF和△ABC全等,且∠AFB=∠C=90°,∴∠DAF=∠BAC或∠DAF=∠ABC,∴α=2∠BAC或2∠ABC,故②正确,如图,过点B作BN⊥DE,交ED的延长线于N,过点F作FH⊥DE,交交ED的延长线于H,∵BC=6,DE是△ABC的中位线,∴DE∥BC,DE=12BC=3,∵BN⊥DE,∠C=90°,∴∠NEC+∠C=180°,∴∠C=∠NEC=90°,又∵BN⊥DE,∴四边形BCEN是矩形,∴BC=NE=6,∴DN=3,∵把点B绕点D按顺时针方向旋转90°,∴DF=DB,∠FDB=90°,∴∠FDH+∠BDN=90°,又∵∠FDH+∠F=90°,∴∠F=∠BDN,又∵DF=BD,∠FHD=∠BND=90°,∴△DFH≌△BDN(AAS),∴DN=FH=3,∴S△DEF=4.5,故③正确,故选:C .二.填空题(共6小题)9.(2020•下城区一模)如图,在矩形ABCD 中,点E 是边DC 上一点,连结BE ,将△BCE 沿BE 对折,点C 落在边AD 上点F 处,BE 与对角线AC 交于点M ,连结FM .若FM ∥CD ,BC =4.则AF = 2√5−2【分析】由对折的性质得∠BCM =∠BFM ,BC =BF ,再由FM ∥CD ,证明∠BFM =ABF ,从而得△ABF ∽△BCA ,由相似三角形的性质求得AB ,进而由勾股定理得AF .【解析】∵四边形ABCD 是矩形,∴∠ABC =∠BAD =90°,AB ∥CD ,∵FM ∥CD ,∴FM ∥AB ,∴∠ABF =∠BFM ,由折叠的性质得,BF =BC =4,∠BFM =∠ACB ,∴∠ABF =∠ACB ,∴△ABF ∽△BCA ,∴AB BC =BF CA , ∴AB 4=√AB 2+42, 即AB 216=16AB +16,∴AB 2=8√5−8,∴AF =√BF 2−AB 2=√16−8√5+8=√24−8√5=√(2√5−2)2=2√5−2.故答案为:2√5−2.10.(2020•柯桥区模拟)如图,在等腰三角形ABC 中,AC =BC =4,∠A =30°,点D 为AC 的中点,点E 为边AB 上一个动点,连接DE ,将△ADE 沿直线DE 折叠,点A 落在点F 处.当直线EF 与直线AC 垂直时,则AE 的长为 2√33或2√3 .【分析】当直线EF与直线AC垂直时,如图1,如图2,根据折叠的性质得到和等腰三角形的判定和性质定理以及直角三角形的性质健康得到结论.【解析】∵AC=4,点D为AC的中点,∴AD=12AC=2,①当直线EF与直线AC垂直时,如图1,∵将△ADE沿直线DE折叠,点A落在点F处,∴∠F=∠A=30°,∠AED=∠FED,∵∠AGE=90°,∴∠AEG=60°,∴∠AED=∠FED=30°,∴AD=DE=2,过D作DM⊥AE与M,∴AE=2AM=2×√32×2=2√3;当直线EF与直线AC垂直时,如图2,∵将△ADE沿直线DE折叠,点A落在点F处,∴∠F=∠A=30°,∠ADE=∠FDE,∵∠AGE =∠FGE =90°,∴∠FGD =60°,∴∠ADE =∠FDE =30°,∴∠A =∠ADE ,∴AE =DE ,∴AG =12AD =1, ∴AE =2√33,综上所述,2√33或2√3, 故答案为:2√33或2√3. 11.(2020•瓯海区二模)如图是一个可调节花盆支架,外围是一个圆形框架,如图1,支架AC ,BD 的长度均为14cm ,端点C ,D 固定在花盆圆形套圈的直径两端,端点A ,B 可在外围圆形框架上移动,整个花盆支架始终成轴对称,已知花盆高EF =15cm ,圆形套圈的直径CD =20cm ,且EF 被CD 平分为上下比为1:2,当端点A ,B 向上调节至最高时,AC ,BD 和CD 同一直线上(如图2所示),此时,花盆底到圆形框架最低点的距离为FG =6cm ,则圆形框架的半径为 26 cm ,为了整体美观要求,花盆底到圆形框架最低点的距离FG 要最大,则此时FG 为 (16﹣2√11) cm .【分析】如图2中,设圆心为O ,连接OG ,交花盆的上底于E ,交花盆的下底于F ,交AB 于T .连接OA ,设OA =OG =r .在Rt △AOT 中,利用勾股定理构建方程即可解决问题.如图1中,如图1中,连接OG 交CD 于T ,连接OC ,OB ,观察图象可知:当,O ,C ,A 共线,O ,D ,B 共线时,OC =OD =26﹣14=12最小,此时OE 的值最小,FG 的值最大.【解析】如图2中,设圆心为O ,连接OG ,交花盆的上底于E ,交花盆的下底于F ,交AB 于T .连接OA ,设OA =OG =r .由题意AB=AC+CD+BD=14+20+14=48(cm),FG=6cm,TF=23EF=10(cm),∴TG=TF+FG=16(m).在Rt△AOT中,∵OA2=OT2+AT2,∴r2=(r﹣16)2+242,解得r=26.如图1中,连接OG交CD于T,连接OC,OB,观察图象可知:当,O,C,A共线,O,D,B共线时,OC=OD=26﹣14=12最小,此时OE的值最小,FG 的值最大,在Rt△OCT中,CT=10,OC=12,∴OT=√OC2−CT2=√122−102=2√11(cm),∵TF=23EF=10(cm),∴FG=OG﹣OT﹣TF=26﹣2√11−10=(16﹣2√11)cm.故答案为26,(16﹣2√11).12.(2020•温州一模)如图,在矩形ABCD中,BC=8,E为BC中点,将△ABE沿AE翻折后,得到△AEF,再将CE折向FE,使点C与点F重合,折痕为EG.若CG=3,则AG=253.【分析】由折叠的性质可得AB =AF ,∠B =∠AFE =90°,FG =CG =3,∠C =∠EFG =90°,可证点A ,点F ,点G 三点共线,由勾股定理可求AB 的长,即可求解.【解析】∵将△ABE 沿AE 翻折后,得到△AEF ,再将CE 折向FE ,使点C 与点F 重合,∴AB =AF ,∠B =∠AFE =90°,FG =CG =3,∠C =∠EFG =90°,∴∠AFE +∠GFE =180°,∴点A ,点F ,点G 三点共线,∵AD 2+DG 2=AG 2,∴64+(AB ﹣3)2=(AB +3)2,∴AB =163, ∴AG =AF +FG =253,故答案为:253.13.(2020•杭州模拟)如图,矩形ABCD 中,AB =8,AD =6,E 为AB 边上一点,将△BEC 沿着CE 翻折,使点B 落在点F 处,连接AF ,当△AEF 为直角三角形时,BE = 3或6 .【分析】分三种情况讨论,由折叠的性质和勾股定理可BE 的长.【解析】如图,若∠AEF =90°,∵∠B =∠BCD =90°=∠AEF∴四边形BCFE 是矩形∵将△BEC 沿着CE 翻折∴CB=CF∴四边形BCFE是正方形∴BE=BC=AD=6,如图,若∠AFE=90°,∵将△BEC沿着CE翻折∴CB=CF=6,∠B=∠EFC=90°,BE=EF∵∠AFE+∠EFC=180°∴点A,点F,点C三点共线∴AC=√AB2+BC2=10,∴AF=AC﹣CF=4∵AE2=AF2+EF2,∴(8﹣BE)2=16+BE2,∴BE=3,(3)若∠EAF=90°,∵CD=8>CF=6∴点F不可能落在直线AD上,∴不存在∠EAF=90°,综上所述:BE=3或614.(2020•余杭区二模)如图,已知矩形ABCD,E,F分别是边AB,CD的中点,M,N分别是边AD,AB上两点,将△AMN沿MN对折,使点A落在点E上.若AB=a,BC=b,且N是FB的中点,则ba 的值为√22.【分析】由题意可证四边形ADEF 是矩形,可得AD =EF =b ,∠EFB =90°,由折叠性质可得AN =EN =34a ,由勾股定理可求解.【解析】∵四边形ABCD 是矩形∴AB =CD ,AB ∥CD ,∠A =90°∵E ,F 分别是边AB ,CD 的中点,N 是FB 的中点,∴DE =AF =BF =12AB =12a ,FN =14AB =14a ,∴AN =AF +FN =34a∵AF =DE ,DC ∥AB ,∠A =90°∴四边形ADEF 是矩形∴AD =EF =b ,∠EFB =90°∵将△AMN 沿MN 对折,使点A 落在点E 上∴AN =EN =34a ,在Rt △EFN 中,EN 2=EF 2+FN 2,∴916a 2=b 2+116a 2,∴b =√22a ∴b a =√22故答案为:√22 三.解答题(共6小题)15.(2020•江干区模拟)已知一张正方形ABCD 纸片,边长AB =2,按步骤进行折叠,如图1,先将正方形纸片ABCD 对折,得到折痕EF ;再折出矩形BCFE 的对角线BF .(1)如图2,将CF 边折到BF 上,得到折痕FM ,点C 的对应点为C ',求CM 的长.(2)如图3,将AB 边折到BF 上,得到折痕BN ,点A 的对应点为A ',求AN 的长.【分析】(1)由折叠的性质可得CF =C 'F =1,∠C =∠FC 'M =90°,CM =C 'M ,可得BC '=√5−1,由锐角三角函数可得CF BC =C ′M BC ′,即可求解;(2)由折叠的性质可得AB =A 'B =2,AN =A 'N ,∠A =∠NA 'F =90°,由勾股定理可列方程,可求解.【解析】∵将正方形纸片ABCD 对折,∴CF =DF =1,∴BF =√CF 2+BC 2=√1+4=√5,(1)∵将CF 边折到BF 上,∴CF =C 'F =1,∠C =∠FC 'M =90°,CM =C 'M ,∴BC '=√5−1,∵tan ∠FBC =CF BC =C ′M BC ′, ∴12=√5−1, ∴C 'M =√5−12, ∴CM =√5−12;(2)如图,连接NF ,∵将AB 边折到BF 上,∴AB =A 'B =2,AN =A 'N ,∠A =∠NA 'F =90°,∴A 'F =√5−2,∵NF2=DN2+DF2,NF2=A'N2+A'F2,∴(2﹣AN)2+1=AN2+(√5−2)2,∴AN=√5−1.16.(2020•宁波模拟)如图,平行四边形纸片ABCD中,折叠纸片使点D落在AB上的点E处,得折痕AF,再折叠纸片使点C落在EF上的G点,得折痕FH.(1)请说明:∠AFH=90°;(2)请说明:GH∥AB.【分析】(1)根据折叠的性质得到∠DFA=∠EFA,∠CFH=∠GFH,根据平角的定义即可得到结论;(2)根据平行四边形的性质得到AB∥CD,求得∠DFA=∠FAE,得到AD=DF,推出四边形ADFE是平行四边形,根据平行四边形的性质得到AD∥EF,推出四边形BCFE是平行四边形,于是得到结论.【解析】(1)∵折叠纸片使点D落在AB上的点E处,∴∠DFA=∠EFA,∵折叠纸片使点C落在EF上的G点,∴∠CFH=∠GFH,∵∠DFA+∠EFA+∠GFH+∠CFH=180°,∴∠EFA+∠GFH=12×180°=90°,∴∠AFH=90°;(2)∵四边形ABCD是平行四边形,∴AB∥CD,∴∠DFA=∠FAE,∵∠DAF=∠EAF,∴∠DAF=∠DFA,∴AD=DF,由折叠的性质得,AD=AE,∴AE=DF,∵AE∥DF,∴四边形ADFE是平行四边形,∴AD∥EF,∴EF∥BC,∴四边形BCFE是平行四边形,∴∠C=∠BEF,由折叠的性质的,∠C=∠FGH,∴∠FGH=∠BEF,∴GH∥AB.17.(2020•上虞区一模)如图,在平行四边形ABCD中,AB=4√2,BC=8,∠B=60°,将平行四边形ABCD 沿EF折叠,点D恰好落在边AB的中点D′处,折叠后点C的对应点为C′,D′C′交BC于点G,∠BGD′=32°.(1)求∠D′EF的度数;(2)求线段AE的长.【分析】(1)由平行四边形的性质可得∠B=∠D=60°,AD∥BC,可得∠DEF=∠EFB,由折叠的性质可得∠D=∠ED'G=60°,∠DEF=∠D'EF,由四边形内角和定理可求∠D′EF的度数;(2)过点E作EH⊥AB于点H,设AE=x,可得AH=x2,HE=√32x,由勾股定理可求x的值,即可求线段AE的长.【解析】(1)∵四边形ABCD是平行四边形∴∠B=∠D=60°,AD∥BC∴∠DEF=∠EFB∵将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处∴∠D=∠ED'G=60°,∠DEF=∠D'EF,∴∠D'EF=∠EFB,∵∠BGD ′=32°∴∠D 'GF =148°∵∠D 'GF +∠EFB +∠D 'EF +∠ED 'G =360°∴∠D 'EF =76°(2)过点E 作EH ⊥AB 于点H ,设AE =x ,∵AD ∥BC∴∠HAD =∠B =60°,且EH ⊥AB∴AH =x 2,HE =√32x ,∵点D '是AB 中点∴AD '=12AB =2√2∵HE 2+D 'H 2=D 'E 2,∴34x 2+(2√2+x 2)2=(8﹣x )2, ∴x =112−14√231∴AE =112−14√231 18.(2020•萧山区模拟)如图,在矩形ABCD 中,2AB >BC ,点E 和点F 为边AD 上两点,将矩形沿着BE 和CF 折叠,点A 和点D 恰好重合于矩形内部的点G 处,(1)当AB =BC 时,求∠GEF 的度数;(2)若AB =√2,BC =2,求EF 的长.【分析】(1)由折叠的性质可得AB=BG,CD=CG;∠EGB=∠A=90°=∠FGC,可得BG=BC=GC,可得∠BGC=60°,∠ABG=30°,由四边形内角和可求∠AEG=360°﹣∠A﹣∠BGE﹣∠ABG=150°,可求∠GEF的度数;(2)由折叠的性质可得AB=BG,CD=CG,AE=EG,DF=FG,由勾股定理的逆定理可得∠BGC=90°,可得∠GBC=45°,由四边形内角和可求∠AEG=360°﹣∠A﹣∠BGE﹣∠ABG=135°,可求∠FEG=45°,由线段关系可求EF的长.【解析】(1)当AB=BC时,矩形ABCD为正方形由折叠得,AB=BG,CD=CG;∠EGB=∠A=90°=∠FGC,∵AB=BC=CD∴BG=BC=GC∴∠BGC=60°∴∠ABG=30°∴∠AEG=360°﹣∠A﹣∠BGE﹣∠ABG=150°∴∠GEF=30°(2)在矩形ABCD中,AB=CD=√2由折叠得,AB=BG,CD=CG,AE=EG,DF=FG∴BG=GC=√2,∵BG2+CG2=4,BC2=4,∴BG2+CG2=BC2,∴∠BGC=90°,且BG=CG,∴∠GBC=45°∴∴∠AEG=360°﹣∠A﹣∠BGE﹣∠ABG=135°∴∠FEG=45°,同理可得∠EFG=45°,∴△EGF为等腰直角三角形设EG=x,则AE=FD=x,EF=√2x,得(2+√2)x=2,∴x=2−√2∴EF=√2x=2√2−219.(2020•义乌市校级模拟)在△ABC中,沿着中位线DE剪切后,用得到的△ADE和四边形DBCE可以拼成平行四边形DBCF,剪切线与拼图如图1所示.仿照上述的方法,按要求完成下列操作设计,并在规定位置画出图示.(画图工具不限,剪切线用实线表示,拼接线用虚线表示,要求写出简要的说明)(1)将平行四边形ABCD剪切成两个图形,再将它们拼成一个矩形,剪切线与拼图画在图2的位置;(2)将梯形ABCD剪切成两个图形,再将它们拼成一个平行四边形,剪切线与拼图画在图3的位置.【分析】(1)过点A作AE⊥BC,再把△ABE剪切,然后移到△DCF的位置即可;(2)过AB的中点作GF∥DC,再把△BGF剪切,然后旋转到△AEG的位置即可;【解析】(1)如图:过点A作AE⊥BC,再把△ABE剪切,然后移到△DCF的位置即可;(2)如图:过AB的中点作GF∥DC,再把△BGF剪切,然后旋转到△AEG的位置即可;20.(2020•新昌县一模)在平面直角坐标系中,已知点A(0,4),B(4,4),点M,N是射线OC上两动点(OM<ON),且运动过程中始终保持∠MAN=45°,小明用几何画板探究其中的线段关系.(1)探究发现:当点M,N均在线段OB上时(如图1),有OM2+BN2=MN2.他的证明思路如下:第一步:将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.第二步:证明△APM≌△ANM,得MP=MM.第一步:证明∠POM=90°,得OM2+OP2=MP2.最后得到OM2+BN2=MN2.请你完成第二步三角形全等的证明.(2)继续探究:除(1)外的其他情况,OM2+BN2=MN2的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)新题编制:若点B是MN的中点,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).【分析】(1)将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.证明△APM≌△ANM,再利用勾股定理即可解决问题.(2)如图2中,当点M,N在OB的延长线上时结论仍然成立.证明方法类似(1).(3)如图3中,若点B是MN的中点,求MN的长.利用(2)中结论,构建方程即可解决问题.【解析】(1)如图1中,将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.∵点A(0,4),B(4,4),∴OA=AB,∠OAB=90°,∵∠NAP=∠OAB=90°,∠MAN=45°,∴∠MAN=∠MAP,∵MA=MA,AN=AP,∴△MAN≌△MAP(SAS).(2)如图2中,结论仍然成立.理由:如图2中,将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.∵∠NAP=∠OAB=90°,∠MAN=45°,∴∠MAN=∠MAP,∵MA=MA,AN=AP,∴△MAN≌△MAP(SAS),∴MN=PM,∵∠ABN=∠AOP=135°,∠AOB=45°,∴∠MOP=90°,∴PM2=OM2+OP2,∴OM2+BN2=MN2.(3)如图3中,若点B是MN的中点,求MN的长.设MN=2x,则BM=BN=x,∵OA=AB=4,∠OAB=90°,∴OB=4√2,∴OM=4√2−x,∵OM2+BN2=MN2.∴(4√2−x)2+x2=(2x)2,解得x=﹣2√2+2√6或﹣2√2−2√6(舍弃)∴MN=﹣4√2+4√6.。
专题15动点综合问题(解析版)
CD 于点 G,点 P 是线段 AE 上一动点,连接 DP、BP. (1)求∠AFB 的度数; (2)在点 P 从 A 到 E 的运动过程中,若 DP 平分∠CDE,求证:AG•DP=DG•BD; (3)已知 AD=6,在点 P 从 A 到 E 的运动过程中,若△ DBP 是直角三角形,请求 DP 的长.
【变式 2-1】(2019·辽宁中考模拟)如图,已知二次函数 y=ax2+bx+4 的图象与 x 轴交于点 A(4,0)和点
D(﹣1,0),与 y 轴交于点 C,过点 C 作 BC 平行于 x 轴交抛物线于点 B,连接 AC
(1)求这个二次函数的表达式;
(2)点 M 从点 O 出发以每秒 2 个单位长度的速度向点 A 运动;点 N 从点 B 同时出发,以每秒 1 个单位长度
【答案】(1)见解析;(2)y=−7x−21;(3)D(4,−2)或( 20 , 22 ). 33
【解析】(1)根据△ ABC 为等腰直角三角形,AD⊥ED,BE⊥ED,可判定 BEC CDA ;
(2)①过点 B 作 BC⊥AB,交 l2 于 C,过 C 作 CD⊥y 轴于 D,根据△ CBD≌△BAO,得出 BD=AO=3, CD=OB=4,求得 C(−4,7),最后运用待定系数法求直线 l2 的函数表达式; (3)根据△ APD 是以点 D 为直角顶点的等腰直角三角形,当点 D 是直线 y=−2x+6 上的动点且在第四象 限时,分两种情况:当点 D 在矩形 AOCB 的内部时,当点 D 在矩形 AOCB 的外部时,设 D(x,−2x+6), 分别根据△ ADE≌△DPF,得出 AE=DF,据此列出方程进行求解即可. 【详解】解:(1)证明:∵△ABC 为等腰直角三角形, ∴CB=CA,∠ACD+∠BCE=90°, 又∵AD⊥ED,BE⊥ED, ∴∠D=∠E=90°,∠EBC+∠BCE=90°, ∴∠ACD=∠EBC,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的速度向点 C 运动,其中一个动点到达终点时,另一个动点也随之停动,过点 N 作 NQ 垂直于 BC 交 AC
于点 Q,连结 MQ.
①求△ AQM 的面积 S 与运动时间 t 之间的函数关系式,写出自变量的取值范围;当 t 为何值时,S 有最大 值,并求出 S 的最大值; ②是否存在点 M,使得△ AQM 为直角三角形?若存在,求出点 M 的坐标;若不存在,说明理由.
【例 2】(模型建立) (1)如图 1,等腰直角三角形 ABC 中,ACB 90 ,CB CA ,直线 ED 经过点 C ,过 A 作 AD ED 于点 D ,过 B 作 BE ED 于点 E .求证: BEC CDA ;
(模型应用)
(2)已知直线 l1 : y
4 3
x
4
与坐标轴交于点
AQ=OB=4,于是得到 Q1(7,0),Q2(-1,0),②当∠APQ=90°时,如图 2,根据全等三角形
的性质得到 AQ=AB=5,于是得到 Q3(8,0),Q4(-2,0),③当∠PAQ=90°时,这种情况不存
在.
【详解】(1)在 y=- 4 x+4 中, 3
令 y=0,则 0=- 4 x+4, 3
【答案】(1)见解析;(2)y=−7x−21;(3)D(4,−2)或( 20 , 22 ). 33
【解析】(1)根据△ ABC 为等腰直角三角形,AD⊥ED,BE⊥ED,可判定 BEC CDA ;
(2)①过点 B 作 BC⊥AB,交 l2 于 C,过 C 作 CD⊥y 轴于 D,根据△ CBD≌△ BAO,得出 BD=AO=3, CD=OB=4,求得 C(−4,7),最后运用待定系数法求直线 l2 的函数表达式; (3)根据△ APD 是以点 D 为直角顶点的等腰直角三角形,当点 D 是直线 y=−2x+6 上的动点且在第四象 限时,分两种情况:当点 D 在矩形 AOCB 的内部时,当点 D 在矩形 AOCB 的外部时,设 D(x,−2x+6), 分别根据△ ADE≌△DPF,得出 AE=DF,据此列出方程进行求解即可. 【详解】解:(1)证明:∵△ABC 为等腰直角三角形, ∴CB=CA,∠ACD+∠BCE=90°, 又∵AD⊥ED,BE⊥ED, ∴∠D=∠E=90°,∠EBC+∠BCE=90°, ∴∠ACD=∠EBC,
∴x=3,
∴A(3,0),
设直线 AC 对应的函数关系式为 y=kx+b,
则:
0=3k 3=7k
b b
,解得:
k=
3 4
b=
9 4
,
∴直线 AC 对应的函数关系式为 y= 3 x- 9 . 44
(2) 在直线 ABy=- 4 x+4 中, 3
∵k1=- 4 , 3
在直线 ACy= 3 x− 9 中,k2= 3 ,
3
3
3
综上所述,D 点坐标为:(4,−2)或( 20 , 22 )
3
3
【点睛】本题属于一次函数综合题,主要考查了点的坐标、矩形的性质、待定系数法、等腰直角三角形的
性质以及全等三角形等相关知识的综合应用,解决问题的关键是作辅助线构造全等三角形,运用全等三角
形的性质进行计算,解题时注意分类思想的运用.
可得答案;
②分类讨论直角三角形的直角顶点,然后解出 t,求得 M 坐标.
【详解】(1)∵二次函数的图象经过 A(4,0)和点 D(﹣1,0),
∴
16a 4b a b 4
4 0
0
,
解得
a b
1 3
,
所以,二次函数的解析式为 y=﹣x2+3x+4.
(2)①延长 NQ 交 x 轴于点 P,
∵BC 平行于 x 轴,C(0,4)
44
4
∴k1•k2=-1,
∴AB⊥AC;(3)在 y=- 4 x+4 中, 3
令 x=0,则 y=4,
∴OA=3,OB=4,由勾股定理得 AB=5,
①当∠AQP=90°时,如图 1,∵△AOB≌△AQP, ∴AQ=OB=4, ∴Q1(7,0),Q2(-1,0), ②当∠APQ=90°时,如图 2,∵△AOB≌△AQP, ∴AQ=AB=5, ∴Q3(8,0),Q4(-2,0). ③当∠PAQ=90°时,这种情况不存在, 综上所述:点 Q 的坐标为:(7,0)(8,0)(-1,0)(-2,0).
2020 届中考数学压轴题全揭秘
专题 15 动点综合问题
【典例分析】
【考点 1】动点之全等三角形问题
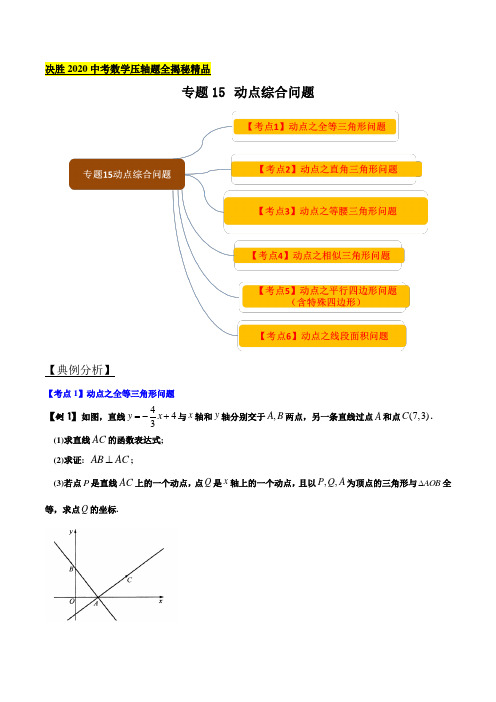
【例 1】如图,直线 y 4 x 4 与 x 轴和 y 轴分别交于 A, B 两点,另一条直线过点 A 和点 C(7,3) . 3
(1)求直线 AC 的函数表达式; (2)求证: AB AC ; (3)若点 P 是直线 AC 上的一个动点,点 Q 是 x 轴上的一个动点,且以 P,Q, A 为顶点的三角形与 AOB 全 等,求点 Q 的坐标.
关系式为 y=kx+b,解方程组即可得到结论;
(2)在直线 ABy=- 4 x+4 中,得到 k1=- 4 ,在直线 ACy= 3 x− 9 中,得到 k2= 3 ,由于 k1•k2=-1,
3
3
44
4
即可得到结论;
(3)根据勾股定理得到 AB=5,①当∠AQP=90°时,如图 1,由全等三角形的性质得到
【点睛】考查了一次函数综合题,待定系数法求函数的解析式,勾股定理的应用和全等三角形的性质等知 识,分类讨论是解题关键,以防遗漏.
【变式 1-1】)如图,CA⊥BC,垂足为 C,AC=2Cm,BC=6cm,射线 BM⊥BQ,垂足为 B,动点 P 从 C 点出发以
1cm/s 的速度沿射线 CQ 运动,点 N 为射线 BM 上一动点,满足 PN=AB,随着 P 点运动而运动,当点 P 运动 _______秒时,△ BCA 与点 P、N、B 为顶点的三角形全等.(2 个全等三角形不重合)
【变式 2-1】(2019·辽宁中考模拟)如图,已知二次函数 y=ax2+bx+4 的图象与 x 轴交于点 A(4,0)和点
D(﹣1,0),与 y 轴交于点 C,过点 C 作 BC 平行于 x 轴交抛物线于点 B,连接 AC
(1)求这个二次函数的表达式;
(2)点 M 从点 O 出发以每秒 2 个单位长度的速度向点 A 运动;点 N 从点 B 同时出发,以每秒 1 个单位长度
A
、
B
,将直线
l1
绕点
A
逆时针旋转
45
至直线 l2 ,如图 2,
求直线 l2 的函数表达式;
(3)如图 3,长方形 ABCO, O 为坐标原点,点 B 的坐标为 8, 6 ,点 A 、C 分别在坐标轴上,点 P 是
线段 BC 上的动点,点 D 是直线 y 2x 6 上的动点且在第四象限.若 APD 是以点 D 为直角顶点的等腰 直角三角形,请直.接.写出点 D 的坐标.
∴PQ 是底边 MA 的中线,
∴PQ=AP= 1 MA, 2
∴1+t= 1 (4﹣2t), 2
解得,t= 1 , 2
∴M 的坐标为(1,0).
Ⅱ.若∠QMA=90°,此时 QM 与 QP 重合.
∴QM=QP=MA,
∴1+t=4﹣2t,
∴t=1,
∴点 M 的坐标为(2,0).
所以,使得△ AQM 为直角三角形的点 M 的坐标分别为(1,0)和(2,0). 【点睛】此题考查了待定系数法求解析式,还考查了三角形的面积,要注意利用点的坐标的意义表示线段 的长度,从而求出线段之间的关系还要注意求最大值可以借助于二次函数.
【变式 2-2】如图,四边形 ABCD 是正方形,以 DC 为边向外作等边△ DCE,连接 AE 交 BD 于点 F,交
CD 于点 G,点 P 是线段 AE 上一动点,连接 DP、BP. (1)求∠AFB 的度数; (2)在点 P 从 A 到 E 的运动过程中,若 DP 平分∠CDE,求证:AG•DP=DG•BD; (3)已知 AD=6,在点 P 从 A 到 E 的运动过程中,若△ DBP 是直角三角形,请求 DP 的长.
∴B(3,4),NP⊥OA.
根据题意,经过 t 秒时,NB=t,OM=2t,
则 CN=3﹣t,AM=4﹣2t.
∵∠BCA=∠MAQ=45°,
∴QN=CN=3﹣t,
∴PQ=NP﹣NQ=4﹣(1﹣t)=1+t,
∴S△ AMQ= 1 AM×PQ= 1 (4-2t)(1+t)
2
2
=﹣t2+t+2.
∴S=-t2+t+2=-(t- 1 )2+ 9 . 24
【答案】(1)
y 3 x 9 ;(2) 44
AB2 AD2 BD2 ; (3) 点 Q 的坐标为 (7, 0) 或 (8, 0) 或 (1, 0) 或 (2, 0)
【解析】(1)在 y=- 4 x+4 中,令 y=0,则 0=- 4 x+4,求得 A(3,0),设直线 AC 对应的函数
3
3
由(1)可得,△ ADE≌△DPF,则 DF=AE,即:12−2x=8−x, 解得 x=4, ∴−2x+6=−2, ∴D(4,−2), 此时,PF=ED=4,CP=6=CB,符合题意; 当点 D 在矩形 AOCB 的外部时,如图,过 D 作 x 轴的平行线 EF,交直线 OA 于 E,交直线 BC 于 F,
【答案】0;4;8;12 【解析】此题要分两种情况:①当 P 在线段 BC 上时,②当 P 在 BQ 上,再分别分两种情况 AC=BP 或 AC =BN 进行计算即可. 【详解】解:①当 P 在线段 BC 上,AC=BP 时,△ ACB≌△PBN,
∵AC=2, ∴BP=2, ∴CP=6−2=4, ∴点 P 的运动时间为 4÷1=4(秒); ②当 P 在线段 BC 上,AC=BN 时,△ ACB≌△NBP, 这时 BC=PN=6,CP=0,因此时间为 0 秒; ③当 P 在 BQ 上,AC=BP 时,△ ACB≌△PBN, ∵AC=2, ∴BP=2, ∴CP=2+6=8, ∴点 P 的运动时间为 8÷1=8(秒); ④当 P 在 BQ 上,AC=NB 时,△ ACB≌△NBP, ∵BC=6, ∴BP=6, ∴CP=6+6=12, 点 P 的运动时间为 12÷1=12(秒), 故答案为:0 或 4 或 8 或 12. 【点睛】本题考查三角形全等的判定方法,判定两个三角形全等时必须有边的参与,若有两边一角对应相 等时,角必须是两边的夹角. 【考点 2】动点之直角三角形问题
