专题07 反比例函数问题-决胜2018中考数学压轴题全揭秘精品(解析版)
2018年全国各地中考数学试题《反比例函数》解答题试题汇编含答案解析

2018年全国各地中考数学试题《反比例函数》解答题试题汇编(含答案解析)1.如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.(1)求该反比例函数的解析式;(2)若△ABC的面积为6,求直线AB的表达式.2.如图,在平面直角坐标系中有三点(1,2),(3,1),(﹣2,﹣1),其中有两点同时在反比例函数y=的图象上,将这两点分别记为A,B,另一点记为C.(1)求出k的值;(2)求直线AB对应的一次函数的表达式;(3)设点C关于直线AB的对称点为D,P是x轴上的一个动点,直接写出PC+PD 的最小值(不必说明理由).3.如图,反比例函数y=(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,CA∥y轴,∠ABC=90°.(1)求k的值及点B的坐标;(2)求tanC的值.4.如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.(1)求双曲线的解析式;(2)求点C的坐标,并直接写出y1<y2时x的取值范围.5.设P(x,0)是x轴上的一个动点,它与原点的距离为y1.(1)求y1关于x的函数解析式,并画出这个函数的图象;(2)若反比例函数y2=的图象与函数y1的图象相交于点A,且点A的纵坐标为2.①求k的值;②结合图象,当y1>y2时,写出x的取值范围.6.如图,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=(k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=,B(m,﹣2).(1)求一次函数和反比例函数的解析式.(2)结合图象直接写出:当y1>y2时,x的取值范围.7.已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.(1)当y1﹣y2=4时,求m的值;(2)如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x 轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).8.如图,直线y=3x﹣5与反比例函数y=的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.(1)求k和n的值;(2)求△AOB的面积.9.如图,已知反比例函数y=(x>0)的图象与一次函数y=﹣x+4的图象交于A和B(6,n)两点.(1)求k和n的值;(2)若点C(x,y)也在反比例函数y=(x>0)的图象上,求当2≤x≤6时,函数值y的取值范围.10.如图,一次函数y1=k1x+b(k1≠0)的图象分别与x轴,y轴相交于点A,B,与反比例函数y2=的图象相交于点C(﹣4,﹣2),D(2,4).(1)求一次函数和反比例函数的表达式;(2)当x为何值时,y1>0;(3)当x为何值时,y1<y2,请直接写出x的取值范围.11.如图,已知一次函数y1=k1x+b(k1≠0)与反比例函数y2=(k2≠0)的图象交于A(4,1),B(n,﹣2)两点.(1)求一次函数与反比例函数的解析式;(2)请根据图象直接写出y1<y2时x的取值范围.12.如图,矩形ABCD的两边AD、AB的长分别为3、8,E是DC的中点,反比例函数y=的图象经过点E,与AB交于点F.(1)若点B坐标为(﹣6,0),求m的值及图象经过A、E两点的一次函数的表达式;(2)若AF﹣AE=2,求反比例函数的表达式.13.如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=,且点B的坐标为(n,﹣2).(1)求一次函数与反比例函效的解析式;(2)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E 点坐标.14.如图,一次函数y=mx+b的图象与反比例函数y=的图象交于A(3,1),B (﹣,n)两点.(1)求该反比例函数的解析式;(2)求n的值及该一次函数的解析式.15.如图,在平面直角坐标系xOy中,一次函数y=x+b的图象经过点A(﹣2,0),与反比例函数y=(x>0)的图象交于B(a,4).(1)求一次函数和反比例函数的表达式;(2)设M是直线AB上一点,过M作MN∥x轴,交反比例函数y=(x>0)的图象于点N,若A,O,M,N为顶点的四边形为平行四边形,求点M的坐标.16.已知反比例函数y=的图象与一次函数y=kx+m的图象交于点(2,1).(1)分别求出这两个函数的解析式;(2)判断P(﹣1,﹣5)是否在一次函数y=kx+m的图象上,并说明原因.17.在平面直角坐标系中,反比例函数y=(k≠0)图象与一次函数y=x+2图象的一个交点为P,且点P的横坐标为1,求该反比例函数的解析式.18.如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.(1)求此反比例函数的表达式;=S△BOC,求点P的坐标.(2)若点P在x轴上,且S△ACP19.小明根据学习函数的经验,对函数y=x +的图象与性质进行了探究. 下面是小明的探究过程,请补充完整:(1)函数y=x +的自变量x 的取值范围是 .(2)下表列出了y 与x 的几组对应值,请写出m ,n 的值:m= ,n= ;(3)如图,在平面直角坐标系xOy 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(4)结合函数的图象,请完成:①当y=﹣时,x= .②写出该函数的一条性质 .③若方程x +=t 有两个不相等的实数根,则t 的取值范围是 .20.如图,已知点D 在反比例函数y=的图象上,过点D 作DB ⊥y 轴,垂足为B (0,3),直线y=kx +b 经过点A (5,0),与y 轴交于点C ,且BD=OC ,OC :OA=2:5.(1)求反比例函数y=和一次函数y=kx +b 的表达式;(2)直接写出关于x 的不等式>kx +b 的解集.21.参照学习函数的过程与方法,探究函数y=的图象与性质. 因为y=,即y=﹣+1,所以我们对比函数y=﹣来探究. 列表:y= 描点:在平面直角坐标系中,以自变量x 的取值为横坐标,以y=相应的函数值为纵坐标,描出相应的点,如图所示:(1)请把y 轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;(2)观察图象并分析表格,回答下列问题:①当x <0时,y 随x 的增大而 ;(填“增大”或“减小”)②y=的图象是由y=﹣的图象向 平移 个单位而得到; ③图象关于点 中心对称.(填点的坐标)(3)设A (x 1,y 1),B (x 2,y 2)是函数y=的图象上的两点,且x 1+x 2=0,试求y1+y2+3的值.22.如图所示,四边形ABCD是菱形,边BC在x轴上,点A(0,4),点B(3,0),双曲线y=与直线BD交于点D、点E.(1)求k的值;(2)求直线BD的解析式;(3)求△CDE的面积.23.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A 作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.(1)求反比例函数y=的表达式;(2)求点B的坐标;(3)求△OAP的面积.24.如图,已知点A在反比例函数y=(x>0)的图象上,过点A作AC⊥x轴,垂足是C,AC=OC.一次函数y=kx+b的图象经过点A,与y轴的正半轴交于点B.(1)求点A的坐标;(2)若四边形ABOC的面积是3,求一次函数y=kx+b的表达式.25.如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.(1)求一次函数与反比例函数的解析式;(2)记两函数图象的另一个交点为E,求△CDE的面积;(3)直接写出不等式kx+b≤的解集.26.如图,已知双曲线y1=与直线y2=ax+b交于点A(﹣4,1)和点B(m,﹣4).(1)求双曲线和直线的解析式;(2)直接写出线段AB的长和y1>y2时x的取值范围.27.如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=(a≠0)的图象在第二象限交于点A(m,2).与x轴交于点C(﹣1,0).过点A作AB⊥x轴于点B,△ABC的面积是3.(1)求一次函数和反比例函数的解析式;(2)若直线AC与y轴交于点D,求△BCD的面积.28.如图,函数y=x的图象与函数y=(x>0)的图象相交于点P(2,m).(1)求m,k的值;(2)直线y=4与函数y=x的图象相交于点A,与函数y=(x>0)的图象相交于点B,求线段AB长.29.如图,已知反比例函数y=(m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).(1)求反比例函数与一次函数的表达式;(2)一次函数的图象分别与x轴、y轴交于A、B两点,与反比例函数图象的另一个交点为P点,连结OP、OQ,求△OPQ的面积.30.如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x 轴的正半轴上,顶点C的坐标为(1,).(1)求图象过点B的反比例函数的解析式;(2)求图象过点A,B的一次函数的解析式;(3)在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.31.如图,在平面直角坐标系中,一次函数y=k1x+b的图象与反比例函数y=的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.(1)求k2,n的值;(2)请直接写出不等式k1x+b的解集;(3)将x轴下方的图象沿x轴翻折,点A落在点A′处,连接A′B,A′C,求△A′BC 的面积.32.如图,直线y=kx+b(k≠0)与双曲线y=(m≠0)交于点A(﹣,2),B (n,﹣1).(1)求直线与双曲线的解析式.=3,求点P的坐标.(2)点P在x轴上,如果S△ABP33.一次函数y=kx+b的图象经过点A(﹣2,12),B(8,﹣3).(1)求该一次函数的解析式;(2)如图,该一次函数的图象与反比例函数y=(m>0)的图象相交于点C(x1,y1),D(x2,y2),与y轴交于点E,且CD=CE,求m的值.34.如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣x+与边AB,BC分别相交于点M,N,函数y=(x>0)的图象过点M.(1)试说明点N也在函数y=(x>0)的图象上;(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═(x >0)的图象仅有一个交点时,求直线M'N′的解析式.35.探究函数y=x+(x>0)与y=x+(x>0,a>0)的相关性质.(1)小聪同学对函数y=x+(x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为,它的另一条性质为;(2)请用配方法求函数y=x+(x>0)的最小值;(3)猜想函数y=x+(x>0,a>0)的最小值为.36.如图,点M在函数y=(x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=(x>0)的图象于点B、C.(1)若点M的坐标为(1,3).①求B、C两点的坐标;②求直线BC的解析式;(2)求△BMC的面积.37.如图,一次函数y=﹣x+的图象与反比例函数y=(k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.(1)求反比例函数的解析式;(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.38.设一次函数y=kx+b(k,b是常数,k≠0)的图象过A(1,3),B(﹣1,﹣1)两点.(1)求该一次函数的表达式;(2)若点(2a+2,a2)在该一次函数图象上,求a的值.(3)已知点C(x1,y1)和点D(x2,y2)在该一次函数图象上,设m=(x1﹣x2)(y1﹣y2),判断反比例函数y=的图象所在的象限,说明理由.39.反比例函数y=(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).(1)求反比例函数的解析式及B点的坐标;(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.40.在平面直角坐标系xOy中,函数y=(x>0)的图象G经过点A(4,1),直线l:y=+b与图象G交于点B,与y轴交于点C.(1)求k的值;(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,B之间的部分与线段OA,OC,BC围成的区域(不含边界)为w.①当b=﹣1时,直接写出区域W内的整点个数;②若区域W内恰有4个整点,结合函数图象,求b的取值范围.1.如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.(1)求该反比例函数的解析式;(2)若△ABC的面积为6,求直线AB的表达式.【分析】(1)把A的坐标代入反比例函数的解析式即可求得;(2)作AD⊥BC于D,则D(2,b),即可利用a表示出AD的长,然后利用三角形的面积公式即可得到一个关于b的方程求得b的值,进而求得a的值,根据待定系数法,可得答案.【解答】解:(1)由题意得,k=xy=2×3=6∴反比例函数的解析式为y=.(2)设B点坐标为(a,b),如图,作AD⊥BC于D,则D(2,b)∵反比例函数y=的图象经过点B(a,b)∴b=∴AD=3﹣.=BC•AD∴S△ABC=a(3﹣)=6解得a=6∴b==1∴B(6,1).设AB的解析式为y=kx+b,将A(2,3),B(6,1)代入函数解析式,得,解得,直线AB的解析式为y=﹣x+4.【点评】本题考查了反比例函数,利用待定系数法求反比例函数的解析式,正确利用a,b表示出BC,AD的长度是关键.2.如图,在平面直角坐标系中有三点(1,2),(3,1),(﹣2,﹣1),其中有两点同时在反比例函数y=的图象上,将这两点分别记为A,B,另一点记为C.(1)求出k的值;(2)求直线AB对应的一次函数的表达式;(3)设点C关于直线AB的对称点为D,P是x轴上的一个动点,直接写出PC+PD 的最小值(不必说明理由).【分析】(1)确定A、B、C的坐标即可解决问题;(2)理由待定系数法即可解决问题;(3)作D关于x轴的对称点D′(0,﹣4),连接CD′交x轴于P,此时PC+PD的值最小,最小值=CD′的长;【解答】解:(1)∵反比例函数y=的图象上的点横坐标与纵坐标的积相同,∴A(1,2),B(﹣2,﹣1),C(3,1)∴k=2.(2)设直线AB的解析式为y=mx+n,则有,解得,∴直线AB的解析式为y=x+1(3)∵C、D关于直线AB对称,∴D(0,4)作D关于x轴的对称点D′(0,﹣4),连接CD′交x轴于P,此时PC+PD的值最小,最小值=CD′==【点评】本题考查反比例函数图形上的点的特征,一次函数的性质、反比例函数的性质、轴对称最短问题等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会利用轴对称解决最短问题.3.如图,反比例函数y=(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,CA∥y轴,∠ABC=90°.(1)求k的值及点B的坐标;(2)求tanC的值.【分析】(1)先利用正比例函数解析式确定A(1,2),再把A点坐标代入y=中求出k得到反比例函数解析式为y=,然后解方程组得B点坐标;(2)作BD⊥AC于D,如图,利用等角的余角相等得到∠C=∠ABD,然后在在Rt△ABD中利用正切的定义求解即可.【解答】解:(1)把A(1,a)代入y=2x得a=2,则A(1,2),把A(1,2)代入y=得k=1×2=2,∴反比例函数解析式为y=,解方程组得或,∴B点坐标为(﹣1,﹣2);(2)作BD⊥AC于D,如图,∴∠BDC=90°,∵∠C+∠CBD=90°,∠CBD+∠ABD=90°,∴∠C=∠ABD,在Rt△ABD中,tan∠ABD===2,即tanC=2.【点评】本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.4.如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.(1)求双曲线的解析式;(2)求点C的坐标,并直接写出y1<y2时x的取值范围.【分析】(1)作高线AC,根据等腰直角三角形的性质和点A的坐标的特点得:x=2x﹣2,可得A的坐标,从而得双曲线的解析式;(2)一次函数和反比例函数解析式列方程组,解出可得点C的坐标,根据图象可得结论.【解答】解:(1)∵点A在直线y1=2x﹣2上,∴设A(x,2x﹣2),过A作AC⊥OB于C,∵AB⊥OA,且OA=AB,∴OC=BC,∴AC=OB=OC,∴x=2x﹣2,x=2,∴A(2,2),∴k=2×2=4,∴;(2)∵,解得:,,∴C(﹣1,﹣4),由图象得:y1<y2时x的取值范围是x<﹣1或0<x<2.【点评】此题考查了反比例函数和一次函数的综合;熟练掌握通过求点的坐标进一步求函数解析式的方法;通过观察图象,从交点看起,函数图象在上方的函数值大.5.设P(x,0)是x轴上的一个动点,它与原点的距离为y1.(1)求y1关于x的函数解析式,并画出这个函数的图象;(2)若反比例函数y2=的图象与函数y1的图象相交于点A,且点A的纵坐标为2.①求k的值;②结合图象,当y1>y2时,写出x的取值范围.【分析】(1)写出函数解析式,画出图象即可;(2)①分两种情形考虑,求出点A坐标,利用待定系数法即可解决问题;②利用图象法分两种情形即可解决问题;【解答】解:(1)由题意y1=|x|.函数图象如图所示:(2)①当点A在第一象限时,由题意A(2,2),∴2=,∴k=4.同法当点A在第二象限时,k=﹣4,②观察图象可知:当k>0时,x>2时,y1>y2或x<0时,y1>y2.当k<0时,x<﹣2时,y1>y2或x>0时,y1>y2.【点评】本题考查反比例函数图象上点的特征,正比例函数的应用等知识,解题的关键是学会利用图象法解决问题,属于中考常考题型.6.如图,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=(k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=,B(m,﹣2).(1)求一次函数和反比例函数的解析式.(2)结合图象直接写出:当y1>y2时,x的取值范围.【分析】(1)求得A(2,3),把A(2,3)代入y2=可得反比例函数的解析式为y=,求得B(﹣3,﹣2),把A(2,3),B(﹣3,﹣2)代入一次函数y1=ax+b,可得一次函数的解析式为y=x+1.(2)由图可得,当y1>y2时,x的取值范围为﹣3<x<0或x>2.【解答】解:(1)∵OC=2,tan∠AOC=,∴AC=3,∴A(2,3),把A(2,3)代入y2=可得,k=6,∴反比例函数的解析式为y=,把B(m,﹣2)代入反比例函数,可得m=﹣3,∴B(﹣3,﹣2),把A(2,3),B(﹣3,﹣2)代入一次函数y1=ax+b,可得,解得,∴一次函数的解析式为y=x+1.(2)由图可得,当y1>y2时,x的取值范围为﹣3<x<0或x>2.【点评】本题考查一次函数与反比例函数的交点问题,解题的关键是学会利用待定系数法确定函数解析式,知道两个函数图象的交点坐标可以利用解方程组解决,学会利用图象确定自变量取值范围.7.已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.(1)当y1﹣y2=4时,求m的值;(2)如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x 轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).【分析】(1)先根据反比例函数的图象经过点A(﹣4,﹣3),利用待定系数法求出反比例函数的解析式为y=,再由反比例函数图象上点的坐标特征得出y1==,y2==,然后根据y1﹣y2=4列出方程﹣=4,解方程即可求出m 的值;(2)设BD与x轴交于点E.根据三角形PBD的面积是8列出方程••PE=8,求出PE=4m,再由E(2m,0),点P在x轴上,即可求出点P的坐标.【解答】解:(1)设反比例函数的解析式为y=,∵反比例函数的图象经过点A(﹣4,﹣3),∴k=﹣4×(﹣3)=12,∴反比例函数的解析式为y=,∵反比例函数的图象经过点B(2m,y1),C(6m,y2),∴y1==,y2==,∵y1﹣y2=4,∴﹣=4,∴m=1;(2)设BD与x轴交于点E.∵点B(2m,),C(6m,),过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,∴D(2m,),BD=﹣=.∵三角形PBD的面积是8,∴BD•PE=8,∴••PE=8,∴PE=4m,∵E(2m,0),点P在x轴上,∴点P坐标为(﹣2m,0)或(6m,0).【点评】本题考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征以及三角形的面积,正确求出双曲线的解析式是解题的关键.8.如图,直线y=3x﹣5与反比例函数y=的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.(1)求k和n的值;(2)求△AOB的面积.【分析】(1)先求出B点的坐标,再代入反比例函数解析式求出即可;(2)先求出直线与x轴、y轴的交点坐标,再求出即可.【解答】解:(1)∵点B(n,﹣6)在直线y=3x﹣5上,∴﹣6=3n﹣5,解得:n=﹣,∴B (﹣,﹣6),∵反比例函数y=的图象过点B ,∴k ﹣1=﹣×(﹣6),解得:k=3;(2)设直线y=3x ﹣5分别与x 轴、y 轴交于C 、D ,当y=0时,3x ﹣5=0,x=,即OC=,当x=0时,y=﹣5,即OD=5,∵A (2,m )在直线y=3x ﹣5上,∴m=3×2﹣5=1,即A (2,1),∴△AOB 的面积S=S △BOD +S △COD +S △AOC =××5+×5+×1=.【点评】本题考查了用待定系数法求反比例函数的解析式,反比例函数与一次函数的交点问题、函数图象上点的坐标特征等知识点,能求出反比例函数的解析式是解此题的关键.9.如图,已知反比例函数y=(x >0)的图象与一次函数y=﹣x +4的图象交于A 和B (6,n )两点.(1)求k 和n 的值;(2)若点C(x,y)也在反比例函数y=(x>0)的图象上,求当2≤x≤6时,函数值y的取值范围.【分析】(1)利用一次函数图象上点的坐标特征可求出n值,进而可得出点B 的坐标,再利用反比例函数图象上点的坐标特征即可求出k值;(2)由k=6>0结合反比例函数的性质,即可求出:当2≤x≤6时,1≤y≤3.【解答】解:(1)当x=6时,n=﹣×6+4=1,∴点B的坐标为(6,1).∵反比例函数y=过点B(6,1),∴k=6×1=6.(2)∵k=6>0,∴当x>0时,y随x值增大而减小,∴当2≤x≤6时,1≤y≤3.【点评】本题考查了一次函数图象上点的坐标特征、反比例函数图象上点的坐标特征以及反比例函数的性质,解题的关键是:(1)利用一次(反比例)函数图象上点的坐标特征,求出n、k的值;(2)利用一次函数的性质找出当x>0时,y 随x值增大而减小.10.如图,一次函数y1=k1x+b(k1≠0)的图象分别与x轴,y轴相交于点A,B,与反比例函数y2=的图象相交于点C(﹣4,﹣2),D(2,4).(1)求一次函数和反比例函数的表达式;(2)当x为何值时,y1>0;(3)当x为何值时,y1<y2,请直接写出x的取值范围.【分析】(1)将C、D两点代入一次函数的解析式中即可求出一次函数的解析式,然后将点D代入反比例函数的解析式即可求出反比例函数的解析式;(2)根据一元一次不等式的解法即可求出答案.(3)根据图象即可求出答案该不等式的解集.【解答】解:(1)∵一次函数y1=k1x+b的图象经过点C(﹣4,﹣2),D(2,4),∴,解得.∴一次函数的表达式为y1=x+2.∵反比例函数的图象经过点D(2,4),∴.∴k2=8.∴反比例函数的表达式为.(2)由y1>0,得x+2>0.∴x>﹣2.∴当x>﹣2时,y1>0.(3)x<﹣4或0<x<2.【点评】本题考查反比例函数与一次函数的综合问题,解题的关键是熟练运用待定系数法以及数形结合的思想,本题属于中等题型.11.如图,已知一次函数y1=k1x+b(k1≠0)与反比例函数y2=(k2≠0)的图象交于A(4,1),B(n,﹣2)两点.(1)求一次函数与反比例函数的解析式;(2)请根据图象直接写出y1<y2时x的取值范围.【分析】(1)由点A的坐标利用反比例函数图象上点的坐标特征可求出k2的值,进而可得出反比例函数的解析式,由点B的纵坐标结合反比例函数图象上点的坐标特征可求出点B的坐标,再由点A、B的坐标利用待定系数法,即可求出一次函数的解析式;(2)根据两函数图象的上下位置关系,找出y1<y2时x的取值范围.【解答】解:(1)∵反比例函数y2=(k2≠0)的图象过点A(4,1),∴k2=4×1=4,∴反比例函数的解析式为y2=.∵点B(n,﹣2)在反比例函数y2=的图象上,∴n=4÷(﹣2)=﹣2,∴点B的坐标为(﹣2,﹣2).将A(4,1)、B(﹣2,﹣2)代入y1=k1x+b,,解得:,∴一次函数的解析式为y=x﹣1.(2)观察函数图象,可知:当x<﹣2和0<x<4时,一次函数图象在反比例函数图象下方,∴y1<y2时x的取值范围为x<﹣2或0<x<4.【点评】本题考查了待定系数法求一次函数解析式以及反比例函数图象上点的坐标特征,解题的关键是:(1)利用反比例函数图象上点的坐标特征求出点B的坐标;(2)根据两函数图象的上下位置关系,找出不等式y1<y2的解集.12.如图,矩形ABCD的两边AD、AB的长分别为3、8,E是DC的中点,反比例函数y=的图象经过点E,与AB交于点F.(1)若点B坐标为(﹣6,0),求m的值及图象经过A、E两点的一次函数的表达式;(2)若AF﹣AE=2,求反比例函数的表达式.【分析】(1)根据矩形的性质,可得A,E点坐标,根据待定系数法,可得答案;(2)根据勾股定理,可得AE的长,根据线段的和差,可得FB,可得F点坐标,根据待定系数法,可得m的值,可得答案.【解答】解:(1)点B坐标为(﹣6,0),AD=3,AB=8,E为CD的中点,∴点A(﹣6,8),E(﹣3,4),函数图象经过E点,∴m=﹣3×4=﹣12,设AE的解析式为y=kx+b,,解得,一次函数的解析是为y=﹣x;(2)AD=3,DE=4,∴AE==5,∵AF﹣AE=2,∴AF=7,BF=1,设E点坐标为(a,4),则F点坐标为(a﹣3,1),∵E,F两点在函数y=图象上,∴4a=a﹣3,解得a=﹣1,∴E(﹣1,4),∴m=﹣1×4=﹣4,∴y=﹣.【点评】本题考查了反比例函数,解(1)的关键是利用待定系数法,又利用了矩形的性质;解(2)的关键利用E,F两点在函数y=图象上得出关于a的方程.13.如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=,且点B的坐标为(n,﹣2).(1)求一次函数与反比例函效的解析式;(2)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E 点坐标.【分析】(1)由垂直的定义及锐角三角函数定义求出AO的长,利用勾股定理求出OD的长,确定出A坐标,进而求出m的值确定出反比例解析式,把B的坐标代入反比例解析式求出n的值,确定出B坐标,利用待定系数法求出一次函数解析式即可;(2)分类讨论:当AO为等腰三角形腰与底时,求出点E坐标即可.【解答】解:(1)∵一次函数y=kx+b与反比例函数y=图象交于A与B,且AD ⊥x轴,∴∠ADO=90°,在Rt△ADO中,AD=4,sin∠AOD=,∴=,即AO=5,根据勾股定理得:DO==3,∴A(﹣3,4),代入反比例解析式得:m=﹣12,即y=﹣,把B坐标代入得:n=6,即B(6,﹣2),代入一次函数解析式得:,解得:,即y=﹣x+2;(2)当OE3=OE2=AO=5,即E2(0,﹣5),E3(0,5);当OA=AE1=5时,得到OE1=2AD=8,即E1(0,8);当AE4=OE4时,由A(﹣3,4),O(0,0),得到直线AO解析式为y=﹣x,中点坐标为(﹣1.5,2),∴AO垂直平分线方程为y﹣2=(x+),令x=0,得到y=,即E4(0,),综上,当点E(0,8)或(0,5)或(0,﹣5)或(0,)时,△AOE是等腰三角形.【点评】此题考查了反比例函数与一次函数的交点问题,熟练掌握各自的性质是解本题的关键.14.如图,一次函数y=mx+b的图象与反比例函数y=的图象交于A(3,1),B (﹣,n)两点.(1)求该反比例函数的解析式;(2)求n的值及该一次函数的解析式.【分析】(1)根据反比例函数y=的图象经过A(3,1),即可得到反比例函数的解析式为y=;(2)把B(﹣,n)代入反比例函数解析式,可得n=﹣6,把A(3,1),B(﹣,﹣6)代入一次函数y=mx+b,可得一次函数的解析式为y=2x﹣5.【解答】解:(1)∵反比例函数y=的图象经过A(3,1),∴k=3×1=3,∴反比例函数的解析式为y=;(2)把B(﹣,n)代入反比例函数解析式,可得﹣n=3,解得n=﹣6,∴B(﹣,﹣6),把A(3,1),B(﹣,﹣6)代入一次函数y=mx+b,可得,解得,∴一次函数的解析式为y=2x﹣5.【点评】本题考查了利用图象解决一次函数和反比例函数的问题.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.15.如图,在平面直角坐标系xOy中,一次函数y=x+b的图象经过点A(﹣2,0),与反比例函数y=(x>0)的图象交于B(a,4).(1)求一次函数和反比例函数的表达式;(2)设M是直线AB上一点,过M作MN∥x轴,交反比例函数y=(x>0)的图象于点N,若A,O,M,N为顶点的四边形为平行四边形,求点M的坐标.【分析】(1)根据一次函数y=x+b的图象经过点A(﹣2,0),可以求得b的值,从而可以解答本题;(2)根据平行四边形的性质和题意,可以求得点M的坐标,注意点M的横坐标大于0.【解答】解:(1)∵一次函数y=x+b的图象经过点A(﹣2,0),∴0=﹣2+b,得b=2,∴一次函数的解析式为y=x+2,∵一次函数的解析式为y=x+2与反比例函数y=(x>0)的图象交于B(a,4),∴4=a+2,得a=2,∴4=,得k=8,即反比例函数解析式为:y=(x>0);(2)∵点A(﹣2,0),∴OA=2,设点M(m﹣2,m),点N(,m),当MN∥AO且MN=AO时,四边形AOMN是平行四边形,||=2,解得,m=2或m=+2,∴点M的坐标为(﹣2,)或(,2+2).【点评】本题考查反比例函数与一次函数的交点问题,解答本题的关键是明确题意,利用数形结合的思想解答.16.已知反比例函数y=的图象与一次函数y=kx+m的图象交于点(2,1).(1)分别求出这两个函数的解析式;(2)判断P(﹣1,﹣5)是否在一次函数y=kx+m的图象上,并说明原因.【分析】(1)将点(2,1)代入y=,求出k的值,再将k的值和点(2,1)代入解析式y=kx+m,即可求出m的值,从而得到两个函数的解析式;(2)将x=﹣1代入(1)中所得解析式,若y=﹣5,则点P(﹣1,﹣5)在一次函数图象上,否则不在函数图象上.【解答】解:(1)∵y=经过(2,1),∴2=k.∵y=kx+m经过(2,1),∴1=2×2+m,∴m=﹣3.∴反比例函数和一次函数的解析式分别是:y=和y=2x﹣3.(2)当x=﹣1时,y=2x﹣3=2×(﹣1)﹣3=﹣5.∴点P(﹣1,﹣5)在一次函数图象上.【点评】本题考查了反比例函数与一次函数的交点问题,解题的关键是知道函数图象的交点坐标符合两个函数的解析式.17.在平面直角坐标系中,反比例函数y=(k≠0)图象与一次函数y=x+2图象的一个交点为P,且点P的横坐标为1,求该反比例函数的解析式.【分析】先求出P点的坐标,再把P点的坐标代入反比例函数的解析式,即可求出答案.【解答】解:∵把x=1代入y=x+2得:y=3,即P点的坐标是(1,3),把P点的坐标代入y=得:k=3,即反比例函数的解析式是y=.【点评】本题考查了用待定系数法求反比例函数的解析式和函数图象上点的坐标特征,能求出P点的坐标是解此题的关键.18.如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.(1)求此反比例函数的表达式;(2)若点P在x轴上,且S=S△BOC,求点P的坐标.△ACP。
专题07 反比例函数问题-决胜2018中考数学压轴题全揭秘精品(原卷版)

一、选择题1.(2017滨州,第12题,3分)在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线1yx=相交于点A、B,且AC+BC=4,则△OAB的面积为()A.23+3或23﹣3B.2 +1或2﹣1C.23﹣3D.2﹣12.(2017广西桂林市,第11题,3分)一次函数y=﹣x+1(0≤x≤10)与反比例函数1yx=(﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1,y1),(x2,y2)是图象上两个不同的点,若y1=y2,则x1+x2的取值范围是()A.﹣8910≤x≤1B.﹣8910≤x≤899C.﹣899≤x≤8910D.1≤x≤89103.(2017新疆乌鲁木齐市,第10题,4分)如图,点A(a,3),B(b,1)都在双曲线3yx=上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为()A.52B.62C.21022+D.824.(2017江苏省泰州市,第6题,3分)如图,P为反比例函数kyx=(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是()A .2B .4C .6D .85.(2017湖北省十堰市,第10题,3分)如图,直线36y x =-分别交x 轴,y 轴于A ,B ,M 是反比例函数ky x=(x >0)的图象上位于直线上方的一点,MC ∥x 轴交AB 于C ,MD ⊥MC 交AB 于D ,AC •BD =43,则k 的值为( )A .﹣3B .﹣4C .﹣5D .﹣66.(2017湖北省咸宁市,第8题,3分)在平面直角坐标系xOy 中,将一块含有45°角的直角三角板如图放置,直角顶点C 的坐标为(1,0),顶点A 的坐标为(0,2),顶点B 恰好落在第一象限的双曲线上,现将直角三角板沿x 轴正方向平移,当顶点A 恰好落在该双曲线上时停止运动,则此时点C 的对应点C ′的坐标为( )A .(32,0) B .(2,0) C .(52,0) D .(3,0)7.(2017湖北省荆州市,第10题,3分)规定:如果关于x 的一元二次方程20ax bx c ++=(a ≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论: ①方程2280x x +-=是倍根方程;②若关于x 的方程220x ax ++=是倍根方程,则a =±3;③若关于x 的方程260ax ax c -+=(a ≠0)是倍根方程,则抛物线26y ax ax c =-+与x 轴的公共点的坐标是(2,0)和(4,0); ④若点(m ,n )在反比例函数4y x=的图象上,则关于x 的方程250mx x n ++=是倍根方程. 上述结论中正确的有( )A .①②B .③④C .②③D .②④8.(2017湖北省荆门市,第12题,3分)已知:如图,在平面直角坐标系xOy 中,等边△AOB 的边长为6,点C 在边OA 上,点D 在边AB 上,且OC =3BD ,反比例函数ky x=(k ≠0)的图象恰好经过点C 和点D ,则k 的值为( )A .81325 B . 81316 C . 8135 D .81349.(2017怀化,第10题,4分)如图,A ,B 两点在反比例函数1k y x=的图象上,C ,D 两点在反比例函数2k y x=的图象上,AC ⊥y 轴于点E ,BD ⊥y 轴于点F ,AC =2,BD =1,EF =3,则12k k -的值是( )A.6B.4C.3D.210.(2017辽宁省营口市,第8题,3分)如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数kyx=的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为()A.33yx=-B.3yx=-C.3yx=-D.3yx=11.(2017辽宁省锦州市,第8题,2分)如图,矩形OABC中,A(1,0),C(0,2),双曲线kyx=(0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF,则k值为()A.23B.1C.43D.212.(2017贵州省黔西南州,第10题,4分)如图,点A是反比例函数1yx=(x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比例函数图象上移动时,点B也在某一反比例函数kyx=图象上移动,则k的值为()A.﹣4B.4C.﹣2D.213.(2017四川省乐山市,第10题,3分)如图,平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别落在x 、y 轴上,点B 坐标为(6,4),反比例函数xy 6=的图象与AB 边交于点D ,与BC 边交于点E ,连结DE ,将△BDE 沿DE 翻折至△B 'DE 处,点B '恰好落在正比例函数y =kx 图象上,则k 的值是( )A .52-B .211-C .51-D .241- 14.(2017四川省达州市,第10题,3分)已知函数()()12030x xy x x⎧->⎪⎪=⎨⎪<⎪⎩的图象如图所示,点P 是y 轴负半轴上一动点,过点P 作y 轴的垂线交图象于A ,B 两点,连接OA 、OB .下列结论: ①若点M 1(x 1,y 1),M 2(x 2,y 2)在图象上,且x 1<x 2<0,则y 1<y 2; ②当点P 坐标为(0,﹣3)时,△AOB 是等腰三角形; ③无论点P 在什么位置,始终有S △AOB =7.5,AP =4BP ;④当点P 移动到使∠AOB =90°时,点A 的坐标为(26,6-). 其中正确的结论个数为( )A .1B .2C .3D .415.(2017临沂,第14题,3分)如图,在平面直角坐标系中,反比例函数ky x=(x >0)的图象与边长是6的正方形OABC 的两边AB ,BC 分别相交于M ,N 两点,△OMN 的面积为10.若动点P 在x 轴上,则PM +PN 的最小值是( )A .62B .10C .226D .22916.(2017山东省威海市,第12题,3分)如图,正方形ABCD 的边长为5,点A 的坐标为(﹣4,0),点B 在y 轴上,若反比例函数xky =(k ≠0)的图象过点C ,则该反比例函数的表达式为( )A .x y 3=B .x y 4=C . x y 5=D .xy 6= 17.(2016吉林省长春市)如图,在平面直角坐标系中,点P (1,﹣4)、Q (m ,n )在函数ky x =(x >0)的图象上,当m >1时,过点P 分别作x 轴、y 轴的垂线,垂足为点A ,B ;过点Q 分别作x 轴、y 轴的垂线,垂足为点C 、D .QD 交PA 于点E ,随着m 的增大,四边形ACQE 的面积( )A .减小B .增大C .先减小后增大D .先增大后减小 18.(2016天津市)若点A (﹣5,1y ),B (﹣3,2y ),C (2,3y )在反比例函数3y x=的图象上,则1y ,2y ,3y 的大小关系是( )A .132y y y <<B .123y y y <<C .321y y y <<D .213y y y << 19.(2016宁夏)正比例函数11y k x =的图象与反比例函数22k y x=的图象相交于A ,B 两点,其中点B 的横坐标为﹣2,当12y y <时,x 的取值范围是( )A .x <﹣2或x >2B .x <﹣2或0<x <2C .﹣2<x <0或0<x <2D .﹣2<x <0或x >220.(2016四川省乐山市)如图,在反比例函数2y x=-的图象上有一动点A ,连接AO 并延长交图象的另一支于点B ,在第一象限内有一点C ,满足AC =BC ,当点A 运动时,点C 始终在函数ky x=的图象上运动.若tan ∠CAB =2,则k 的值为( )A .2B .4C .6D .821.(2016山东省临沂市)如图,直线y =﹣x +5与双曲线ky x=(x >0)相交于A ,B 两点,与x 轴相交于C 点,△BOC 的面积是52.若将直线y =﹣x +5向下平移1个单位,则所得直线与双曲线ky x=(x >0)的交点有( )A .0个B .1个C .2个D .0个,或1个,或2个 22.(2016山东省日照市)正比例函数11y k x =(1k >0)与反比例函数22k y x=(2k >0)图象如图所示,则不等式21k k x x>的解集在数轴上表示正确的是( )A .B .C .D .23.(2016山东省济宁市)如图,O 为坐标原点,四边形OACB 是菱形,OB 在x 轴的正半轴上,sin ∠AOB =45,反比例函数48y x=在第一象限内的图象经过点A ,与BC 交于点F ,则△AOF 的面积等于( )A .60B .80C .30D .40 24.(2016山东省淄博市)反比例函数a y x =(a >0,a 为常数)和2y x=在第一象限内的图象如图所示,点M在ayx=的图象上,MC⊥x轴于点C,交2yx=的图象于点A;MD⊥y轴于点D,交2yx=的图象于点B,当点M在ayx=的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的个数是()A.0B.1C.2D.325.(2016山东省烟台市)反比例函数16tyx-=的图象与直线y=﹣x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是()A.t<16B.t>16C.t≤16D.t≥1626.(2016湖北省十堰市)如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线kyx=上(k>0,x>0),则k的值为()A.253B.183C.93D.927.(2016湖北省宜昌市)函数21yx=+的图象可能是()A .B .C .D .28.(2016湖南省株洲市)已知,如图一次函数1y ax b =+与反比例函数2ky x=的图象如图示,当12y y <时,x 的取值范围是( )A .x <2B .x >5C .2<x <5D .0<x <2或x >529.(2016甘肃省兰州市)如图,A ,B 两点在反比例函数1k y x =的图象上,C 、D 两点在反比例函数2ky x=的图象上,AC⊥x 轴于点E ,BD⊥x 轴于点F ,AC=2,BD=3,EF=103,则21k k -=( )A .4B .143 C .163D .630.(2016湖北省荆州市)如图,在Rt △AOB 中,两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,将△AOB 绕点B 逆时针旋转90°后得到△A ′O ′B .若反比例函数ky x=的图象恰好经过斜边A ′B的中点C ,S △ABO =4,tan ∠BAO =2,则k 的值为( )A .3B .4C .6D .831.(2016辽宁省抚顺市)如图,矩形ABCD 的顶点D 在反比例函数ky x=(x <0)的图象上,顶点B ,C 在x 轴上,对角线AC 的延长线交y 轴于点E ,连接BE ,若△BCE 的面积是6,则k 的值为( )A .﹣6B .﹣8C .﹣9D .﹣1232.(2016黑龙江省大庆市)已知A (1x ,1y )、B (2x ,2y )、C (3x ,3y )是反比例函数2y x=上的三点,若123x x x <<,213y y y <<,则下列关系式不正确的是( ) A .12x x <0 B .13x x <0 C .23x x <0 D .12x x +<033.(2015宿迁)在平面直角坐标系中,点A ,B 的坐标分别为(﹣3,0),(3,0),点P 在反比例函数xy 2=的图象上,若△P AB 为直角三角形,则满足条件的点P 的个数为( ) A .2个 B .4个 C .5个 D .6个 34.(2015眉山)如图,A 、B 是双曲线xky =上的两点,过A 点作AC ⊥x 轴,交OB 于D 点,垂足为C .若△ADO 的面积为1,D 为OB 的中点,则k 的值为( ) A .34 B .38C .3D .435.(2015内江)如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线kyx=与正方形ABCD有公共点,则k的取值范围为()A.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<1636.(2015孝感)如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数1yx=的图象上.若点B在反比例函数kyx=的图象上,则k的值为()A.﹣4B.4C.﹣2D.237.(2015宜昌)如图,市煤气公司计划在地下修建一个容积为410m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是()A .B .C .D .38.(2015三明)如图,已知点A 是双曲线2y x=在第一象限的分支上的一个动点,连接AO 并延长交另一分支于点B ,过点A 作y 轴的垂线,过点B 作x 轴的垂线,两垂线交于点C ,随着点A 的运动,点C 的位置也随之变化.设点C 的坐标为(m ,n ),则m ,n 满足的关系式为( )A .2n m =-B .2n m =-C .4n m =-D .4n m=- 39.(2015乌鲁木齐)如图,在直角坐标系xOy 中,点A ,B 分别在x 轴和y 轴,34OA OB =.∠AOB 的角平分线与OA 的垂直平分线交于点C ,与AB 交于点D ,反比例函数ky x=的图象过点C .当以CD 为边的正方形的面积为27时,k 的值是( )A .2B .3C .5D .740.(2015重庆市)如图,在平面直角坐标系中,菱形ABCD 在第一象限内,边BC 与x 轴平行,A ,B 两点的纵坐标分别为3,1.反比例函数3y x=的图象经过A ,B 两点,则菱形ABCD 的面积为( )A .2B .4C .22D .4241.(2015临沂)在平面直角坐标系中,直线2y x =-+与反比例函数1y x=的图象有唯一公共点,若直线y x b =-+与反比例函数1y x=的图象有2个公共点,则b 的取值范围是( )A .b >2B .﹣2<b <2C .b >2或b <﹣2D .b <﹣242.(2015滨州)如图,在x 轴的上方,直角∠BOA 绕原点O 按顺时针方向旋转,若∠BOA 的两边分别与函数1y x=-、2y x =的图象交于B 、A 两点,则∠OAB 的大小的变化趋势为( )A .逐渐变小B .逐渐变大C .时大时小D .保持不变 二、填空题43.(2017云南省,第6题,3分)已知点A (a ,b )在双曲线5y x=上,若a 、b 都是正整数,则图象经过B (a ,0)、C (0,b )两点的一次函数的解析式(也称关系式)为 .44.(2017内蒙古通辽市,第17题,3分)如图,直线333--=x y 与x ,y 轴分别交于点A ,B ,与反比例函数xky =的图象在第二象限交于点C ,过点A 作x 轴的垂线交该反比例函数图象于点D .若AD =AC ,则点D 的坐标为 .45.(2017四川省成都市,第24题,4分)在平面直角坐标系xOy 中,对于不在坐标轴上的任意一点P (x ,y ),我们把点P (1x ,1y),称为点P 的“倒影点”,直线1y x =-+ 上有两点A 、B ,它们的倒影点A ′,B ′均在反比例函数ky x=的图象上,若AB =22 ,则k = . 46.(2017山东省日照市,第16题,4分)如图,在平面直角坐标系中,经过点A 的双曲线ky x=(x >0)同时经过点B ,且点A 在点B 的左侧,点A 的横坐标为2,∠AOB =∠OBA =45°,则k 的值为 .47.(2017江苏省南通市,第18题,3分)如图,四边形OABC 是平行四边形,点C 在x 轴上,反比例函数ky x=(x >0)的图象经过点A (5,12),且与边BC 交于点D .若AB =BD ,则点D 的坐标为 .48.(2017江苏省宿迁市,第16题,3分)如图,矩形ABOC 的顶点O 在坐标原点,顶点B ,C 分别在x ,y 轴的正半轴上,顶点A 在反比例函数ky x=(k 为常数,k >0,x >0)的图象上,将矩形ABOC 绕点A 按逆时针方向旋转90°得到矩形AB ′O ′C ′,若点O 的对应点O ′恰好落在此反比例函数图象上,则COBO 的值是 .49.(2017江苏省常州市,第18题,2分)如图,已知点A 是一次函数12y x =(x ≥0)图象上一点,过点A 作x 轴的垂线l ,B 是l 上一点(B 在A 上方),在AB 的右侧以AB 为斜边作等腰直角三角形ABC ,反比例函数ky x=(x >0)的图象过点B ,C ,若△OAB 的面积为6,则△ABC 的面积是 .50.(2017江苏省盐城市,第16题,3分)如图,曲线l 是由函数6y x=在第一象限内的图象绕坐标原点O 逆时针旋转45°得到的,过点A (42-,42),B (22,22)的直线与曲线l 相交于点M 、N ,则△OMN 的面积为 .51.(2017江苏省连云港市,第15题,3分)设函数3y x =与y =﹣2x ﹣6的图象的交点坐标为(a ,b ),则12a b+的值是 .52.(2017江苏省连云港市,第16题,3分)如图,已知等边三角形OAB与反比例函数kyx=(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则BDDC的值为.(已知sin15°=624-)53.(2017浙江省宁波市,第17题,4分)已知△ABC的三个顶点为A(﹣1,﹣1),B(﹣1,3),C(﹣3,﹣3),将△ABC向右平移m(m>0)个单位后,△ABC某一边的中点恰好落在反比例函数3yx=的图象上,则m的值为.54.(2017浙江省温州市,第15题,5分)如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数kyx=(k≠0)的图象恰好经过点A′,B,则k的值为.55.(2017浙江省湖州市,第16题,4分)如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数1yx=和9yx=在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交1yx=的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是.56.(2017金华,第15题,4分)如图,已知点A(2,3)和点B(0,2),点A在反比例函数kyx=的图象上,做射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.57.(2017湖北省孝感市,第16题,3分)如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数kyx=(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为.58.(2017湖北省荆州市,第18题,3分)如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x 轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数kyx=(x<0)的图象交AB于点N,S矩形OABC =32,tan∠DOE=12,则BN的长为.59.(2017湖北省鄂州市,第15题,3分)如图,AC ⊥x 轴于点A ,点B 在y 轴的正半轴上,∠ABC =60°,AB =4,BC =23,点D 为AC 与反比例函数ky x=的图象的交点.若直线BD 将△ABC 的面积分成1:2的两部分,则k 的值为 .60.(2017湖南省株洲市,第17题,3分)如图所示是一块含30°,60°,90°的直角三角板,直角顶点O 位于坐标原点,斜边AB 垂直于x 轴,顶点A 在函数11k y x =(x >0)的图象上,顶点B 在函数22ky x=(x >0)的图象上,∠ABO =30°,则12k k = .61.(2017贵州省遵义市,第18题,4分)如图,点E ,F 在函数2y x=的图象上,直线EF 分别与x 轴、y 轴交于点A 、B ,且BE :BF =1:3,则△EOF 的面积是 .62.(2017辽宁省盘锦市,第16题,3分)在平面直角坐标系中,点P的坐标为(0,﹣5),以P为圆心的圆与x轴相切,⊙P的弦AB(B点在A点右侧)垂直于y轴,且AB=8,反比例函数kyx=(k≠0)经过点B,则k= .63.(2017黑龙江省齐齐哈尔市,第18题,3分)如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=43,反比例函数kyx=的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于.64.(2017山东省济南市,第20题,3分)如图,过点O的直线AB与反比例函数kyx=的图象交于A,B两点,A(2,1),直线BC∥y轴,与反比例函数3kyx-=(x<0)的图象交于点C,连接AC,则△ABC的面积为.65.(2017山东省莱芜市,第15题,4分)直线y=kx+b与双曲线6yx=-交于A(﹣3,m),B(n,﹣6)两点,将直线y=kx+b向上平移8个单位长度后,与双曲线交于D,E两点,则S△ADE= .66.(2016云南省昆明市)如图,反比例函数kyx=(k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE 的面积为2,则k的值为.67.(2016内蒙古包头市)如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数kyx=(x<0)的图象经过点A,若S△ABO=3,则k的值为.68.(2016内蒙古呼和浩特市)已知函数1yx=-,当自变量的取值为﹣1<x<0或x≥2,函数值y的取值.69.(2016四川省内江市)如图,点A在双曲线5yx=上,点B在双曲线8yx=上,且AB∥x轴,则△OAB的面积等于.70.(2016四川省眉山市)如图,已知点A是双曲线6yx=在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线kyx=上运动,则k的值是.71.(2016四川省达州市)如图,在平面直角坐标系中,矩形ABCD的边AB:B C=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数kyx=(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为.72.(2016山东省滨州市)如图,已知点A、C在反比例函数y=的图象上,点B,D在反比例函数y=的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=,CD=,AB与CD间的距离为6,则a ﹣b的值是.73.(2016广东省深圳市)如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将▱ABCO绕点A逆时针旋转得到▱ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点D在反比例函数kyx=(x<0)的图象上,则k的值为.74.(2016广西南宁市)如图所示,反比例函数ky x=(k ≠0,x >0)的图象经过矩形OABC 的对角线AC 的中点D .若矩形OABC 的面积为8,则k 的值为 .75.(2016江西省)如图,直线l ⊥x 轴于点P ,且与反比例函数11k y x =(x >0)及22ky x=(x >0)的图象分别交于点A ,B ,连接OA ,OB ,已知△OAB 的面积为2,则12k k -= .76.(2016陕西省)已知一次函数y =2x +4的图象分别交x 轴、y 轴于A 、B 两点,若这个一次函数的图象与一个反比例函数的图象在第一象限交于点C ,且AB =2BC ,则这个反比例函数的表达式为 .77.(2016江苏省宿迁市)如图,在平面直角坐标系中,一条直线与反比例函数8y x=(x >0)的图象交于两点A 、B ,与x 轴交于点C ,且点B 是AC 的中点,分别过两点A 、B 作x 轴的平行线,与反比例函数2y x=(x >0)的图象交于两点D 、E ,连接DE ,则四边形ABED 的面积为 .78.(2016江苏省扬州市)如图,点A 在函数4y x=(x >0)的图象上,且OA =4,过点A 作AB ⊥x 轴于点B ,则△ABO 的周长为 .79.(2016浙江省丽水市)如图,一次函数y =﹣x +b 与反比例函数4y x=(x >0)的图象交于A ,B 两点,与x 轴、y 轴分别交于C ,D 两点,连结OA ,OB ,过A 作AE ⊥x 轴于点E ,交OB 于点F ,设点A 的横坐标为m .(1)b = (用含m 的代数式表示); (2)若4OAF EFBC S S +=△四边形,则m 的值是 .80.(2016浙江省宁波市)如图,点A 为函数9y x =(x >0)图象上一点,连结OA ,交函数1y x=(x >0)的图象于点B ,点C 是x 轴上一点,且AO =AC ,则△ABC 的面积为 .81.(2016浙江省绍兴市)如图,已知直线l:y=﹣x,双曲线1yx=,在l上取一点A(a,﹣a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为.82.(2016浙江省温州市)如图,点A,B在反比例函数kyx=(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE 的面积的2倍,则k的值是.83.(2016浙江省湖州市)已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P 向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.(1)k的值是;(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数4yx-=图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若127 9SS=,则b的值是.84.(2016浙江省衢州市)如图,正方形ABCD的顶点A,B在函数kyx=(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.(1)当k=2时,正方形A′B′C′D′的边长等于.(2)当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是.85.(2016贵州省黔东南州)如图,点A是反比例函数11yx=(x>0)图象上一点,过点A作x轴的平行线,交反比例函数2kyx=(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为.86.(2016湖北省荆门市)如图,已知点A(1,2)是反比例函数kyx=图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△P AB是等腰三角形,则点P的坐标是 .87.(2016湖北省鄂州市)如图,已知直线1y k x b =+与x 轴、y 轴相交于P 、Q 两点,与2k y x=的图象相交于A (﹣2,m )、B (1,n )两点,连接OA 、OB ,给出下列结论:①12k k <0;②m +12n =0;③S △AOP =S △BOQ ;④不等式21k k x b x+>的解集是x <﹣2或0<x <1,其中正确的结论的序号是 .88.(2016湖北省随州市)如图,直线y =x +4与双曲线ky x=(k ≠0)相交于A (﹣1,a )、B 两点,在y 轴上找一点P ,当P A +PB 的值最小时,点P 的坐标为 .89.(2016湖北省孝感市)如图,已知双曲线ky x=与直线y =﹣x +6相交于A ,B 两点,过点A 作x 轴的垂线与过点B 作y 轴的垂线相交于点C ,若△ABC 的面积为8,则k 的值为 .90.(2016辽宁省葫芦岛市)如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=25,反比例函数kyx=的图象经过点B,则k的值为.91.(2016黑龙江省齐齐哈尔市)如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数kyx=的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k= .92.(2015南宁)如图,点A在双曲线23yx=(0x>)上,点B在双曲线kyx=(0x>)上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k= .93.(2015桂林)如图,以▱ABCO 的顶点O 为原点,边OC 所在直线为x 轴,建立平面直角坐标系,顶点A 、C 的坐标分别是(2,4)、(3,0),过点A 的反比例函数ky x=的图象交BC 于D ,连接AD ,则四边形AOCD 的面积是 .94.(2015贵港)如图,已知点A 1,A 2,…,A n 均在直线1y x =-上,点B 1,B 2,…,B n 均在双曲线1y x=-上,并且满足:A 1B 1⊥x 轴,B 1A 2⊥y 轴,A 2B 2⊥x 轴,B 2A 3⊥y 轴,…,A n B n ⊥x 轴,B n A n +1⊥y 轴,…,记点A n 的横坐标为a n (n 为正整数).若11a =-,则a 2015= .95.(2015南京)如图,过原点O 的直线与反比例函数1y ,2y 的图象在第一象限内分别交于点A ,B ,且A 为OB 的中点,若函数11y x=,则2y 与x 的函数表达式是 .96.(2015攀枝花)如图,若双曲线ky x=(0k >)与边长为3的等边△AOB (O 为坐标原点)的边OA 、AB 分别交于C 、D 两点,且OC =2BD ,则k 的值为 .97.(2015荆门)如图,点1A ,2A 依次在93(0)y x x=>的图象上,点1B ,2B 依次在x 轴的正半轴上,若11A OB △,212A B B △均为等边三角形,则点2B 的坐标为 .98.(2015烟台)如图,矩形OABC 的顶点A 、C 的坐标分别是(4,0)和(0,2),反比例函数ky x=(x >0)的图象过对角线的交点P 并且与AB ,BC 分别交于D ,E 两点,连接OD ,OE ,DE ,则△ODE 的面积为 .三、解答题99.(2017内蒙古呼和浩特市,第23题,7分)已知反比例函数21k y x--=(k 为常数).(1)若点P 1(132-,y 1)和点P 2(12-,y 2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y 1和y 2的大小;(2)设点P (m ,n )(m >0)是其图象上的一点,过点P 作PM ⊥x 轴于点M .若tan ∠POM =2,PO =5(O为坐标原点),求k 的值,并直接写出不等式210k kx x++>的解集. 100.(2017内蒙古赤峰市,第21题,10分)如图,一次函数313y x =-+的图象与x 轴、y 轴分别交于点A 、B ,以线段AB 为边在第一象限作等边△ABC . (1)若点C 在反比例函数ky x=的图象上,求该反比例函数的解析式; (2)点P (23,m )在第一象限,过点P 作x 轴的垂线,垂足为D ,当△P AD 与△OAB 相似时,P 点是否在(1)中反比例函数图象上?如果在,求出P 点坐标;如果不在,请加以说明.101.(2017四川省自贡市,第24题,10分)[探究函数xx y 4+=的图象与性质] (1)函数xx y 4+=的自变量x 的取值范围是 ; (2)下列四个函数图象中函数xx y 4+=的图象大致是 ;(3)对于函数xx y 4+=,求当x >0时,y 的取值范围. 请将下列的求解过程补充完整. 解:∵x >0 ∴x x y 4+==222()()x x + =22()x x-+ . ∵22()x x-≥0,∴y ≥ . [拓展运用](4)若函数259x x y x-+=,则y 的取值范围 .102.(2017宁夏,第24题,8分)直线y =kx +b 与反比例函数6y x=(x >0)的图象分别交于点 A (m ,3)和点B (6,n ),与坐标轴分别交于点C 和点D . (1)求直线AB 的解析式;(2)若点P 是x 轴上一动点,当△COD 与△ADP 相似时,求点P 的坐标.103.(2017济宁,第22题,11分)定义:点P 是△ABC 内部或边上的点(顶点除外),在△P AB ,△PBC ,△PCA 中,若至少有一个三角形与△ABC 相似,则称点P 是△ABC 的自相似点.例如:如图1,点P 在△ABC 的内部,∠PBC =∠A ,∠PCB =∠ABC ,则△BCP ∽△ABC ,故点P 是△ABC 的自相似点.请你运用所学知识,结合上述材料,解决下列问题:在平面直角坐标系中,点M是曲线33yx=(x>0)上的任意一点,点N是x轴正半轴上的任意一点.(1)如图2,点P是OM上一点,∠ONP=∠M,试说明点P是△MON的自相似点;当点M的坐标是(3,3),点N的坐标是(3,0)时,求点P的坐标;(2)如图3,当点M的坐标是(3,3),点N的坐标是(2,0)时,求△MON的自相似点的坐标;(3)是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.104.(2017山东省淄博市,第22题,8分)如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数kyx=(k>0)的图象经过BC边的中点D(3,1).(1)求这个反比例函数的表达式;(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.①求OF的长;②连接AF,BE,证明四边形ABEF是正方形.105.(2017山东省聊城市,第23题,8分)如图,分别位于反比例函数1yx=,kyx=在第一象限图象上的两点A、B,与原点O在同一直线上,且13 OAOB=.(1)求反比例函数kyx=的表达式;(2)过点A作x轴的平行线交kyx=的图象于点C,连接BC,求△ABC的面积.106.(2017江苏省苏州市,第25题,8分)如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数kyx=(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=52.(1)若OA=4,求k的值;(2)连接OC,若BD=BC,求OC的长.107.(2017湖北省恩施州,第21题,8分)如图,∠AOB=90°,反比例函数2yx=-(x<0)的图象过点A(﹣1,a),反比例函数kyx=(k>0,x>0)的图象过点B,且AB∥x轴.(1)求a和k的值;(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线kyx=于另一点,求△OBC的面积.108.(2017黄冈,第23题,12分)月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)(1)请求出y(万件)与x(元/件)之间的函数关系式;(2)求出第一年这种电子产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值.(3)假设公司的这种电子产品第一年恰好按年利润s(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格x(元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.109.(2017湖南省株洲市,第24题,8分)如图所示,Rt△P AB的直角顶点P(3,4)在函数kyx=(x>0)的图象上,顶点A、B在函数tyx=(x>0,0<t<k)的图象上,P A∥x轴,连接OP,OA,记△OP A的面积为S△OP A,△P AB的面积为S△P AB,设w=S△OP A﹣S△P AB.①求k的值以及w关于t的表达式;②若用w max和w min分别表示函数w的最大值和最小值,令T=w max+a2﹣a,其中a为实数,求T min.110.(2017四川省攀枝花市,第21题,8分)如图,在平面直角坐标系中,坐标原点O是菱形ABCD的对称中心.边AB与x轴平行,点B(1,-2),反比例函数kyx=(k≠0)的图象经过A,C两点.(1)求点C的坐标及反比例函数的解析式.(2)直线BC与反比例函数图象的另一交点为E,求以O,C,E为顶点的三角形的面积.111.(2017山东省济南市,第26题,9分)如图1,▱OABC的边OC在y轴的正半轴上,OC=3,A(2,1),反比例函数kyx=(x>0)的图象经过的B.(1)求点B的坐标和反比例函数的关系式;(2)如图2,直线MN分别与x轴、y轴的正半轴交于M,N两点,若点O和点B关于直线MN成轴对称,求线段ON的长;(3)如图3,将线段OA延长交kyx=(x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,请探究线段ED与BF的数量关系,并说明理由.。
2018年中考数学押轴题解析-文档资料

2018年中考数学押轴题解析以下是查字典数学网为您推荐的 2018年中考数学押轴题解析,希望本篇文章对您学习有所帮助。
2018年中考数学押轴题解析一、选择题1. (2018福建龙岩4分)如图,矩形ABCD中,AB=1,BC=2,把矩形ABCD 绕AB所在直线旋转一周所得圆柱的侧面积为【】A. B. C. D.2【答案】B。
【考点】矩形的性质,旋转的性质。
【分析】把矩形ABCD 绕AB所在直线旋转一周所得圆柱是以BC=2为底面半径,AB=1为高。
所以,它的侧面积为。
故选B。
2. (2018福建南平4分)如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别和AE、AF折叠,点B、D恰好都将在点G处,已知BE=1,则EF的长为【】A. B. C. D.3【答案】B。
【考点】翻折变换(折叠问题),正方形的性质,折叠的性质,勾股定理。
【分析】∵正方形纸片ABCD的边长为3,C=90,BC=CD=3。
根据折叠的性质得:EG=BE=1,GF=DF。
设DF=x,则EF=EG+GF=1+x,FC=DC-DF=3-x,EC=BC-BE=3-1=2。
在Rt△EFC中,EF2=EC2+FC2,即(x+1)2=22+(3-x)2,解得:。
DF= ,EF=1+ 。
故选B。
3. (2018福建宁德4分)如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥HG,EH∥FG,则四边形EFGH的周长是【】A.10B.13C.210D.2134. (2018福建莆田4分)如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按ABC-DA一的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是【】A.(1,-1)B.(-1,1)C.(-1,-2)D.(1,-2)【答案】B。
2018-2019年全国中考数学真题《反比例函数》分类汇编解析
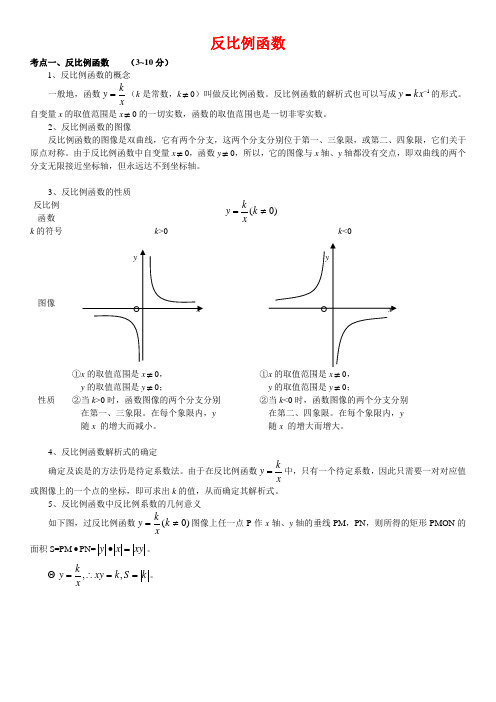
反比例函数考点一、反比例函数(3~10分)1、反比例函数的概念一般地,函数xky=(k是常数,k≠0)叫做反比例函数。
反比例函数的解析式也可以写成1-=kxy的形式。
自变量x的取值范围是x≠0的一切实数,函数的取值范围也是一切非零实数。
2、反比例函数的图像反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限,它们关于原点对称。
由于反比例函数中自变量x≠0,函数y≠0,所以,它的图像与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
3、反比例函数的性质反比例函数)0(≠=kxkyk的符号k>0 k<0图像性质①x的取值范围是x≠0,y的取值范围是y≠0;②当k>0时,函数图像的两个分支分别在第一、三象限。
在每个象限内,y随x的增大而减小。
①x的取值范围是x≠0,y的取值范围是y≠0;②当k<0时,函数图像的两个分支分别在第二、四象限。
在每个象限内,y随x的增大而增大。
4、反比例函数解析式的确定确定及诶是的方法仍是待定系数法。
由于在反比例函数xky=中,只有一个待定系数,因此只需要一对对应值或图像上的一个点的坐标,即可求出k的值,从而确定其解析式。
5、反比例函数中反比例系数的几何意义如下图,过反比例函数)0(≠=kxky图像上任一点P作x轴、y轴的垂线PM,PN,则所得的矩形PMON的面积S=PM∙PN=xyxy=∙。
kSkxyxky==∴=,,。
一、选择题1.(2017·山东省菏泽市·3分)如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为()A.36 B.12 C.6 D.32.(2017·山东省济宁市·3分)如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=,反比例函数y=在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于()A.60 B.80 C.30 D.403.(2017·福建龙岩·4分)反比例函数y=﹣的图象上有P1(x1,﹣2),P2(x2,﹣3)两点,则x1与x2的大小关系是()A.x1>x2 B.x1=x2 C.x1<x2 D.不确定4.(2017贵州毕节3分)如图,点A为反比例函数图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为()A.﹣4 B.4 C.﹣2 D.25.(2017海南3分)某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是()A.该村人均耕地面积随总人口的增多而增多B.该村人均耕地面积y与总人口x成正比例C.若该村人均耕地面积为2公顷,则总人口有100人D.当该村总人口为50人时,人均耕地面积为1公顷6.(2017河南)如图,过反比例函数y=(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为()A.2 B.3 C.4 D.57. (2017·黑龙江龙东·3分)已知反比例函数y=,当1<x<3时,y的最小整数值是()A.3 B.4 C.5 D.68.(2017·湖北荆州·3分)如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB 绕点B逆时针旋转90°后得到△A′O′B.若反比例函数的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO =2,则k的值为()A .3B .4C .6D .8二、 填空题1. (2017·江西·3分)如图,直线l ⊥x 轴于点P ,且与反比例函数y 1=(x >0)及y 2=(x >0)的图象分别交于点A ,B ,连接OA ,OB ,已知△OAB 的面积为2,则k 1﹣k 2= .2. (2017·辽宁丹东·3分)反比例函数y=的图象经过点(2,3),则k = . 3.(2017·四川内江)如图10,点A 在双曲线y =5x 上,点B 在双曲线y =8x上,且AB ∥x 轴,则△OAB 的面积等于______.3.(2017·山东省滨州市·4分)如图,已知点A 、C 在反比例函数y=的图象上,点B ,D 在反比例函数y=的图象上,a >b >0,AB ∥CD ∥x 轴,AB ,CD 在x 轴的两侧,AB=,CD=,AB 与CD 间的距离为6,则a ﹣b 的值是 .4. (2017·云南省昆明市·3分)如图,反比例函数y =(k ≠0)的图象经过A ,B 两点,过点A 作AC ⊥x 轴,垂足为C ,过点B 作BD ⊥x 轴,垂足为D ,连接AO ,连接BO 交AC 于点E ,若OC =CD ,四边形BDCE 的面积为2,则k 的值为 .5. (2017·浙江省湖州市·4分)已知点P 在一次函数y =kx +b (k ,b 为常数,且k <0,b >0)的图象上,将点P 向左平移1个单位,再向上平移2个单位得到点Q ,点Q 也在该函数y =kx +b 的图象上.图10(1)k 的值是 ;(2)如图,该一次函数的图象分别与x 轴、y 轴交于A ,B 两点,且与反比例函数y =图象交于C ,D 两点(点C 在第二象限内),过点C 作CE ⊥x 轴于点E ,记S 1为四边形CEOB 的面积,S 2为△OAB 的面积,若=,则b 的值是 .6. (2017·浙江省绍兴市·5分)如图,已知直线l :y =﹣x ,双曲线y =,在l 上取一点A (a ,﹣a )(a >0),过A 作x 轴的垂线交双曲线于点B ,过B 作y 轴的垂线交l 于点C ,过C 作x 轴的垂线交双曲线于点D ,过D 作y 轴的垂线交l 于点E ,此时E 与A 重合,并得到一个正方形ABCD ,若原点O 在正方形ABCD 的对角线上且分这条对角线为1:2的两条线段,则a 的值为 .7.(2017广西南宁3分)如图,在4×4正方形网格中,有3个小正方形已经涂黑,若再涂黑任意一个白色的小正方形(2017•南宁)如图所示,反比例函数y =(k ≠0,x >0)的图象经过矩形OABC 的对角线AC 的中点D .若矩形OABC 的面积为8,则k 的值为 .8.(2017·黑龙江齐齐哈尔·3分)如图,已知点P (6,3),过点P 作PM ⊥x 轴于点M ,PN ⊥y 轴于点N ,反比例函数y =的图象交PM 于点A ,交PN 于点B .若四边形OAPB 的面积为12,则k = .9.(2017·湖北荆门·3分)如图,已知点A (1,2)是反比例函数y =图象上的一点,连接AO 并延长交双曲线的另一分支于点B ,点P 是x 轴上一动点;若△P AB 是等腰三角形,则点P 的坐标是 _______________ .10.(2017·湖北荆州·3分)若12x m ﹣1y 2与3xy n+1是同类项,点P (m ,n )在双曲线上,则a 的值为 . 三、 解答题1. (2017·湖北武汉·8分)已知反比例函数xy 4=. (1) 若该反比例函数的图象与直线y =kx +4(k ≠0)只有一个公共点,求k 的值; (2) 如图,反比例函数xy 4=(1≤x ≤4)的图象记为曲线C 1,将C 1向左平移2个单位长度,得曲线C 2,请在图中画出C 2,并直接写出C 1平移至C 2处所扫过的面积.2. (2017·吉林·7分)如图,在平面直径坐标系中,反比例函数y=(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD=(1)点D的横坐标为(用含m的式子表示);(2)求反比例函数的解析式.3.(2017·四川泸州)如图,一次函数y=kx+b(k<0)与反比例函数y=的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)(1)求反比例函数的解析式;(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.4.(2017·四川南充)如图,直线y=x+2与双曲线相交于点A(m,3),与x轴交于点C.(1)求双曲线解析式;(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.5.(2017·四川攀枝花)如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y=(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,(1)求反比例函数y=的解析式;(2)求cos∠OAB的值;(3)求经过C、D两点的一次函数解析式.6.(2017·四川宜宾)如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于A(2,﹣1),B(,n)两点,直线y=2与y轴交于点C.(1)求一次函数与反比例函数的解析式;(2)求△ABC的面积.7.(2017·湖北黄石·12分)如图1所示,已知:点A(﹣2,﹣1)在双曲线C:y=上,直线l1:y=﹣x+2,直线l2与l1关于原点成中心对称,F1(2,2),F2(﹣2,﹣2)两点间的连线与曲线C在第一象限内的交点为B,P是曲线C上第一象限内异于B的一动点,过P作x轴平行线分别交l1,l2于M,N两点.(1)求双曲线C及直线l2的解析式;(2)求证:PF2﹣PF1=MN=4;(3)如图2所示,△PF1F2的内切圆与F1F2,PF1,PF2三边分别相切于点Q,R,S,求证:点Q与点B重合.(参考公式:在平面坐标系中,若有点A(x1,y1),B(x2,y2),则A、B两点间的距离公式为AB=.)8.(2017·青海西宁·2分)如图,一次函数y=x+m的图象与反比例函数y=的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).(1)求m及k的值;(2)求点C的坐标,并结合图象写出不等式组0<x+m≤的解集.9.(2017·广西百色·6分)△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.(1)求过点B′的反比例函数解析式;(2)求线段CC′的长.10..(2017·贵州安顺·10分)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)m(m≠0)的图象交于A、B两点,与x轴交于C点,点A的图象与反比例函数y=x的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.(1)求该反比例函数和一次函数的解析式;(2)求点B的坐标.11. (2017·浙江省湖州市)湖州市菱湖镇某养鱼专业户准备挖一个面积为2000平方米的长方形鱼塘.(1)求鱼塘的长y(米)关于宽x(米)的函数表达式;(2)由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米,鱼塘的长为多少米?12. (2017·重庆市A卷·10分)在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH =,点B的坐标为(m,﹣2).(1)求△AHO的周长;(2)求该反比例函数和一次函数的解析式.13. (2017·重庆市B卷·10分)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=.(1)求反比例函数的解析式;(2)连接OB,求△AOB的面积.14.(2017·山东省菏泽市·3分)如图,在平面直角坐标系xOy中,双曲线y=与直线y=﹣2x+2交于点A(﹣1,a).(1)求a,m的值;(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.15.(2017·山东省德州市·4分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?16.(2017·山东省东营市·9分)如图,在平面直角坐标系中,直线AB 与x 轴交于点B ,与y 轴交于点A ,与反比例函数y =x m 的图象在第二象限交于点C ,CE ⊥x 轴,垂足为点E ,tan ∠ABO =12,OB =4,OE =2.(1)求反比例函数的解析式;(2)若点D 是反比例函数图象在第四象限上的点,过点D 作DF ⊥y 轴,垂足为点F ,连接OD 、BF ,如果S △BAF =4S △DFO ,求点D 的坐标.答案反比例函数一、选择题1.(2017·山东省菏泽市·3分)如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为()A.36 B.12 C.6 D.3【考点】反比例函数系数k的几何意义;等腰直角三角形.【分析】设△OAC和△BAD的直角边长分别为a、b,结合等腰直角三角形的性质及图象可得出点B的坐标,根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论.【解答】解:设△OAC和△BAD的直角边长分别为a、b,则点B的坐标为(a+b,a﹣b).∵点B在反比例函数y=的第一象限图象上,∴(a+b)×(a﹣b)=a2﹣b2=6.∴S△OAC﹣S△BAD=a2﹣b2=(a2﹣b2)=×6=3.故选D.【点评】本题考查了反比例函数系数k的几何意义、等腰三角形的性质以及面积公式,解题的关键是找出a2﹣b2的值.本题属于基础题,难度不大,解决该题型题目时,设出等腰直角三角形的直角边,用其表示出反比例函数上点的坐标是关键.2.(2017·山东省济宁市·3分)如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=,反比例函数y=在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于()A.60 B.80 C.30 D.40【考点】反比例函数与一次函数的交点问题.【分析】过点A作AM⊥x轴于点M,过点F作FN⊥x轴于点N,设OA=a,BF=b,通过解直角三角形分别找出点A、F的坐标,结合反比例函数图象上点的坐标特征即可求出a、b的值,通过分割图形求面积,最终找出△AOF 的面积等于梯形AMNF的面积,利用梯形的面积公式即可得出结论.【解答】解:过点A作AM⊥x轴于点M,过点F作FN⊥x轴于点N,如图所示.设OA=a,BF=b,在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=,∴AM=OA•sin∠AOB=a,OM==a,∴点A的坐标为(a,a).∵点A在反比例函数y=的图象上,∴a×a==48,解得:a=10,或a=﹣10(舍去).∴AM=8,OM=6.∵四边形OACB是菱形,∴OA=OB=10,BC∥OA,∴∠FBN=∠AO B.在Rt△BNF中,BF=b,sin∠FBN=,∠BNF=90°,∴FN=BF•sin∠FBN=b,BN==b,∴点F的坐标为(10+b,b).∵点B在反比例函数y=的图象上,∴(10+b)×b=48,解得:b=,或b=(舍去).∴FN=,BN=﹣5,MN=OB+BN﹣OM=﹣1.S△AOF=S△AOM+S梯形AMNF﹣S△OFN=S梯形AMNF=(AM+FN)•MN=(8+)×(﹣1)=×(+1)×(﹣1)=40.故选D.3.(2017·福建龙岩·4分)反比例函数y=﹣的图象上有P1(x1,﹣2),P2(x2,﹣3)两点,则x1与x2的大小关系是()A.x1>x2 B.x1=x2 C.x1<x2 D.不确定【考点】反比例函数图象上点的坐标特征.【分析】直接利用反比例函数的增减性进而分析得出答案.【解答】解:∵反比例函数y=﹣的图象上有P1(x1,﹣2),P2(x2,﹣3)两点,∴每个分支上y随x的增大而增大,∵﹣2>﹣3,∴x1>x2,故选:A.4.(2017贵州毕节3分)如图,点A为反比例函数图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO 的面积为()A.﹣4 B.4 C.﹣2 D.2【考点】反比例函数系数k的几何意义.【分析】根据反比例函数系数k的几何意义:在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变,可计算出答案.【解答】解:△ABO的面积为:×|﹣4|=2,故选D.5.(2017海南3分)某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是()A.该村人均耕地面积随总人口的增多而增多B.该村人均耕地面积y与总人口x成正比例C.若该村人均耕地面积为2公顷,则总人口有100人D.当该村总人口为50人时,人均耕地面积为1公顷【考点】反比例函数的应用;反比例函数的图象.【分析】解:如图所示,人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数关系是反比例函数,它的图象在第一象限,根据反比例函数的性质可推出A,B错误,再根据函数解析式求出自变量的值与函数值,有可判定C,D.【解答】解:如图所示,人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数关系是反比例函数,它的图象在第一象限,∴y随x的增大而减小,∴A,B错误,设y=(k>0,x>0),把x=50时,y=1代入得:k=50,∴y=,把y=2代入上式得:x=25,∴C错误,把x=1代入上式得:y=,∴D正确,故答案为:D.【点评】本题主要考查了反比例函数的性质,图象,求函数值与自变量的值,根据图象找出正确信息是解题的关键.6.(2017河南)如图,过反比例函数y=(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为()A.2 B.3 C.4 D.5【考点】反比例函数系数k的几何意义;反比例函数的性质.【分析】根据点A在反比例函数图象上结合反比例函数系数k的几何意义,即可得出关于k的含绝对值符号的一元一次方程,解方程求出k值,再结合反比例函数在第一象限内有图象即可确定k值.【解答】解:∵点A是反比例函数y=图象上一点,且AB⊥x轴于点B,∴S△AOB=|k|=2,解得:k=±4.∵反比例函数在第一象限有图象,∴k=4.故选C.【点评】本题考查了反比例函数的性质以及反比例函数系数k的几何意义,解题的关键是找出关于k的含绝对值符号的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k的几何意义找出关于k的含绝对值符号的一元一次方程是关键.7. (2017·黑龙江龙东·3分)已知反比例函数y=,当1<x<3时,y的最小整数值是()A.3 B.4 C.5 D.6【考点】反比例函数的性质.【分析】根据反比例函数系数k>0,结合反比例函数的性质即可得知该反比例函数在x>0中单调递减,再结合x 的取值范围,可得出y的取值范围,取其内的最小整数,本题得解.【解答】解:在反比例函数y=中k=6>0,∴该反比例函数在x>0内,y随x的增大而减小,当x=3时,y==2;当x=1时,y==6.∴当1<x<3时,2<y<6.∴y的最小整数值是3.故选A.8.(2017·湖北荆州·3分)如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB 绕点B逆时针旋转90°后得到△A′O′B.若反比例函数的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO =2,则k的值为()A.3 B.4 C.6 D.8【分析】先根据S△ABO=4,tan∠BAO=2求出AO、BO的长度,再根据点C为斜边A′B的中点,求出点C的坐标,点C的横纵坐标之积即为k值.【解答】解:设点C坐标为(x,y),作CD⊥BO′交边BO′于点D,∵tan∠BAO=2,∴=2,∵S△ABO=•AO•BO=4,∴AO=2,BO=4,∵△ABO≌△A′O′B,∴AO=A′0′=2,BO=BO′=4,∵点C为斜边A′B的中点,CD⊥BO′,∴CD=A′0′=1,BD=BO′=2,∴x=BO﹣CD=4﹣1=3,y=BD=2,∴k=x•y=3•2=6.故选C..【点评】本题考查了反比例函数图象上点的坐标特征,解答本题的关键在于读懂题意,作出合适的辅助线,求出点C的坐标,然后根据点C的横纵坐标之积等于k值求解即可.二、填空题1. (2017·江西·3分)如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1﹣k2=4.【考点】反比例函数与一次函数的交点问题;反比例函数系数k的几何意义.【分析】由反比例函数的图象过第一象限可得出k1>0,k2>0,再由反比例函数系数k的几何意义即可得出S△OAP=k1,S△OBP=k2,根据△OAB的面积为2结合三角形之间的关系即可得出结论.【解答】解:∵反比例函数y1=(x>0)及y2=(x>0)的图象均在第一象限内,∴k1>0,k2>0.∵AP⊥x轴,∴S△OAP=k1,S△OBP=k2.∴S△OAB=S△OAP﹣S△OBP=(k1﹣k2)=2,解得:k1﹣k2=4.故答案为:4.2. (2017·辽宁丹东·3分)反比例函数y=的图象经过点(2,3),则k=7.【考点】反比例函数图象上点的坐标特征.【分析】根据点的坐标以及反比例函数图象上点的坐标特征即可得出关于k的一元一次方程,解方程即可得出结论.【解答】解:∵反比例函数y=的图象经过点(2,3),∴k﹣1=2×3,解得:k=7.故答案为:7.3.(2017·四川内江)如图10,点A在双曲线y=5x上,点B在双曲线y=8x上,且AB∥x轴,则△OAB的面积等于______.[答案]3 2[考点]反比例函数,三角形的面积公式。
中考数学与反比例函数有关的压轴题附答案解析

中考数学与反比例函数有关的压轴题附答案解析一、反比例函数1.如图,在平面直角坐标系中,反比例函数y= 的图象与一次函数y=ax+b的图象交于点A(﹣2,3)和点B(m,﹣2).(1)求反比例函数和一次函数的解析式;(2)直线x=1上有一点P,反比例函数图象上有一点Q,若以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,直接写出点Q的坐标.【答案】(1)解:∵点A(﹣2,3)在反比例函数y= 的图形上,∴k=﹣2×3=﹣6,∴反比例函数的解析式为y=﹣,∵点B在反比例函数y=﹣的图形上,∴﹣2m=﹣6,∴m=3,∴B(3,﹣2),∵点A,B在直线y=ax+b的图象上,∴,∴,∴一次函数的解析式为y=﹣x+1(2)解:∵以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,∴AB=PQ,AB∥PQ,设直线PQ的解析式为y=﹣x+c,设点Q(n,﹣),∴﹣ =﹣n+c,∴c=n﹣,∴直线PQ的解析式为y=﹣x+n﹣,∴P(1,n﹣﹣1),∴PQ2=(n﹣1)2+(n﹣﹣1+ )2=2(n﹣1)2,∵A(﹣2,3).B(3,﹣2),∴AB2=50,∵AB=PQ,∴50=2(n﹣1)2,∴n=﹣4或6,∴Q(﹣4. )或(6,﹣1)【解析】【分析】(1)先利用待定系数法求出反比例函数解析式,进而求出点B的坐标,再用待定系数法求出直线解析式;(2)先判断出AB=PQ,AB∥PQ,设出点Q的坐标,进而得出点P的坐标,即可求出PQ,最后用PQ=AB建立方程即可得出结论.2.抛物线y= +x+m的顶点在直线y=x+3上,过点F(﹣2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.(1)先通过配方求抛物线的顶点坐标(坐标可用含m的代数式表示),再求m的值;(2)设点N的横坐标为a,试用含a的代数式表示点N的纵坐标,并说明NF=NB;(3)若射线NM交x轴于点P,且PA•PB= ,求点M的坐标.【答案】(1)解:y= x2+x+m= (x+2)2+(m﹣1)∴顶点坐标为(﹣2,m﹣1)∵顶点在直线y=x+3上,∴﹣2+3=m﹣1,得m=2;(2)解:过点F作FC⊥NB于点C,∵点N在抛物线上,∴点N的纵坐标为: a2+a+2,即点N(a, a2+a+2)在Rt△FCN中,FC=a+2,NC=NB﹣CB= a2+a,∴NF2=NC2+FC2=( a2+a)2+(a+2)2,=( a2+a)2+(a2+4a)+4,而NB2=( a2+a+2)2,=( a2+a)2+(a2+4a)+4∴NF2=NB2,NF=NB(3)解:连接AF、BF,由NF=NB,得∠NFB=∠NBF,由(2)的思路知,MF=MA,∴∠MAF=∠MFA,∵MA⊥x轴,NB⊥x轴,∴MA∥NB,∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°,∴2∠MAF+2∠NBF=180°,∠MAF+∠NBF=90°,∵∠MAB+∠NBA=180°,∴∠FBA+∠FAB=90°,又∵∠FAB+∠MAF=90°,∴∠FBA=∠MAF=∠MFA,又∵∠FPA=∠BPF,∴△PFA∽△PBF,∴ = ,PF2=PA×PB= ,过点F作FG⊥x轴于点G,在Rt△PFG中,PG= = ,∴PO=PG+GO= ,∴P(﹣,0)设直线PF:y=kx+b,把点F(﹣2,2)、点P(﹣,0)代入y=kx+b,解得k= ,b= ,∴直线PF:y= x+ ,解方程 x2+x+2= x+ ,得x=﹣3或x=2(不合题意,舍去),当x=﹣3时,y= ,∴M(﹣3,).【解析】【分析】(1)利用配方法将二次函数化成顶点式,写出顶点坐标,由顶点再直线y=x+3上,建立方程求出m的值。
中考数学压轴题专题复习——反比例函数的综合及详细答案

的坐标是(7,﹣3)时,对应的函数解析式是 y=﹣ x2+ ; f、当点 A 在 x 轴负半轴上,点 B 在 y 轴负半轴上,点 C 坐标为(3,4)时,另一个顶点 D
3.已知点 A,B 分别是 x 轴、y 轴上的动点,点 C,D 是某个函数图象上的点,当四边形 ABCD(A,B,C,D 各点依次排列)为正方形时,我们称这个正方形为此函数图象的“伴侣 正方形”. 例如:在图 1 中,正方形 ABCD 是一次函数 y=x+1 图象的其中一个“伴侣正方形”.
(1)如图 1,若某函数是一次函数 y=x+1,求它的图象的所有“伴侣正方形”的边长;
∵ 反比例函数 ∴ k=1×2=2,
的图象过点 A(1,2).
∴ 反比例函数关系式是:y=
(2)解:反比例函数 y= ,当 x>0 时,y 随 x 的增大而减少, 而当 x=1 时,y=2,当
x=6 时,y= ,
∴ 当 1≤x≤6 时,反比例函数 y 的值: ≤y≤2 【解析】【分析】(1)根据题意首先把点 B(﹣1,0)代入一次函数 y=x+b 求出一次函数 解析式,又点 A(1,n)在一次函数 y=x+b 的图象上,再利用一次函数解析式求出点 A 的 坐标,然后利用代入系数法求出反比例函数解析式,(2)根据反比例函数的性质分别求出 当 x=1,x=6 时的 y 值,即可得到答案.
(3)解:∠ PAQ=∠ PBQ. 理由如下:
过点 Q 作 QT⊥x 轴于 T,设 AQ 交 x 轴于 D,QB 的延长线交 x 轴于 E,如图 3. 可设点 Q 为(c, ),直线 AQ 的解析式为 y=px+q,则有
最新-2018年全国中考数学压轴题全析全解 精品

2018年全国中考数学压轴题全析全解1、(2018重庆)如图1所示,一张三角形纸片ABC ,∠ACB=90°,AC=8,BC=6.沿斜边AB 的中线CD 把这张纸片剪成11AC D ∆和22BC D ∆两个三角形(如图2所示).将纸片11AC D ∆沿直线2D B (AB )方向平移(点12,,,A D D B 始终在同一直线上),当点1D 于点B 重合时,停止平移.在平移过程中,11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P. (1) 当11AC D ∆平移到如图3所示的位置时,猜想图中的1D E 与2D F 的数量关系,并证明你的猜想;(2) 设平移距离21D D 为x ,11AC D ∆与22BC D ∆重叠部分面积为y ,请写出y 与x 的函数关系式,以及自变量的取值范围;(3)对于(2)中的结论是否存在这样的x 的值,使重叠部分的面积等于原ABC ∆面积的14. 若存在,求x 的值;若不存在,请说明理由.[解](1)12D E D F =.因为1122C D C D ∥,所以12C AFD ∠=∠.又因为90ACB ∠=︒,CD 是斜边上的中线,所以,DC DA DB ==,即112221C D C D BD AD === 所以,1C A ∠=∠,所以2AFD A ∠=∠ 所以,22AD D F =.同理:11BD D E =.又因为12AD BD =,所以21AD BD =.所以12D E D F =CB D A 图1122图3C 2D 2C 1BD 1A 图2P(2)因为在Rt ABC ∆中,8,6AC BC ==,所以由勾股定理,得10.AB = 即1211225AD BD C D C D ====又因为21D D x =,所以11225D E BD D F AD x ====-.所以21C F C E x == 在22BC D ∆中,2C 到2BD 的距离就是ABC ∆的AB 边上的高,为245. 设1BED ∆的1BD 边上的高为h ,由探究,得221BC D BED ∆∆∽,所以52455h x-=. 所以24(5)25x h -=.121112(5)225BED S BD h x ∆=⨯⨯=- 又因为1290C C ∠+∠=︒,所以290FPC ∠=︒.又因为2C B ∠=∠,43sin ,cos 55B B ==. 所以234,55PC x PF x == ,22216225FC P S PC PF x ∆=⨯=而2212221126(5)22525BC D BED FC P ABC y S S S S x x ∆∆∆∆=--=--- 所以21824(05)255y x x x =-+≤≤ (3) 存在. 当14ABC y S ∆=时,即218246255x x -+= 整理,得2320250.x x -+=解得,125,53x x ==.即当53x =或5x =时,重叠部分的面积等于原ABC ∆面积的142、(2018浙江金华)如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D .(1)求直线AB 的解析式; (2)若S 梯形OBCD,求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P,O,B 为顶点的 三角形与△OBA 相似.若存在,请求出所有符合条件 的点P 的坐标;若不存在,请说明理由.[解] (1)直线AB 解析式为:y=33-x+3.(2)方法一:设点C坐标为(x ,33-x+3),那么OD =x ,CD =33-x+3. ∴OBCD S 梯形=()2CD CD OB ⨯+=3632+-x . 由题意:3632+-x =334,解得4,221==x x (舍去) ∴ C(2,33) 方法二:∵ 23321=⨯=∆OB OA S AOB ,OBCD S 梯形=334,∴63=∆ACD S . 由OA=3OB ,得∠BAO =30°,AD=3CD .∴ ACD S ∆=21CD ×AD =223CD =63.可得CD =33. ∴ AD=1,OD =2.∴C (2,33). (3)当∠OBP =Rt ∠时,如图①若△BOP ∽△OBA ,则∠BOP =∠BAO=30°,BP=3OB=3,∴1P (3,33). ②若△BPO ∽△OBA ,则∠BPO =∠BAO=30°,OP=33OB=1. ∴2P (1,3).当∠OPB =Rt ∠时③ 过点P 作OP ⊥BC 于点P(如图),此时△PBO ∽△OBA ,∠BOP =∠BAO =30°过点P 作PM ⊥OA 于点M .方法一: 在Rt △PBO 中,BP =21OB =23,OP =3BP =23. ∵ 在Rt △P MO 中,∠OPM =30°, ∴ OM =21OP =43;PM =3OM =433.∴3P (43,433).方法二:设P(x ,33-x+3),得OM =x ,PM =33-x+3 由∠BOP =∠BAO,得∠POM =∠ABO .∵tan ∠POM==OMPM =x x 333+-,tan ∠ABOC=OBOA =3.∴33-x+3=3x ,解得x =43.此时,3P (43,433).④若△POB ∽△OBA(如图),则∠OBP=∠BAO =30°,∠POM =30°. ∴ PM =33OM =43. ∴ 4P (43,43)(由对称性也可得到点4P 的坐标). 当∠OPB =Rt ∠时,点P 在x轴上,不符合要求.综合得,符合条件的点有四个,分别是:1P (3,33),2P (1,3),3P (43,433),4P (43,43).3、(2018山东济南)如图1,已知Rt ABC △中,30CAB ∠=,5BC =.过点A 作AE AB ⊥,且15AE =,连接BE 交AC 于点P . (1)求PA 的长;(2)以点A 为圆心,AP 为半径作⊙A ,试判断BE 与⊙A 是否相切,并说明理由;(3)如图2,过点C 作CD AE ⊥,垂足为D .以点A 为圆心,r 为半径作⊙A ;以点C 为圆心,R 为半径作⊙C .若r 和R 的大小是可变化的,并且在变化过程中保持⊙A 和⊙C 相.切.,且使D 点在⊙A 的内部,B 点在⊙A 的外部,求r 和R 的变化范围.[解]CD图1图2(1) 在Rt ABC △中,305CAB BC ∠==,, 210AC BC ∴==.AE BC ∥,APE CPB ∴△∽△. ::3:1PA PC AE BC ∴==. :3:4PA AC ∴=,3101542PA ⨯==. (2)BE 与⊙A 相切.在Rt ABE △中,AB =15AE =,tanAE ABE AB ∴∠===60ABE ∴∠= . 又30PAB ∠=,9090ABE PAB APB ∴∠+∠=∴∠=,, BE ∴与⊙A 相切.(3)因为5AD AB ==,r 的变化范围为5r <<当⊙A 与⊙C 外切时,10R r +=,所以R 的变化范围为105R -<<;当⊙A 与⊙C 内切时,10R r -=,所以R 的变化范围为1510R <<+ 4、(2018山东烟台)如图,已知抛物线L 1: y=x 2-4的图像与x 有交于A 、C 两点, (1)若抛物线l 2与l 1关于x 轴对称,求l 2的解析式; (2)若点B 是抛物线l 1上的一动点(B 不与A 、C 重合),以AC 为对角线,A 、B 、C 三点为顶点的平行四边形的第四个顶点定为D ,求证:点D 在l 2上;(3)探索:当点B 分别位于l 1在x 轴上、下两部分的图像上时,平行四边形ABCD 的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
中考数学综合题专题复习【反比例函数】专题解析附答案

一、反比例函数真题与模拟题分类汇编(难题易错题)1.如图.一次函数y=x+b的图象经过点B(﹣1,0),且与反比例函数(k为不等于0的常数)的图象在第一象限交于点A(1,n).求:(1)一次函数和反比例函数的解析式;(2)当1≤x≤6时,反比例函数y的取值范围.【答案】(1)解:把点B(﹣1,0)代入一次函数y=x+b得: 0=﹣1+b,∴b=1,∴一次函数解析式为:y=x+1,∵点A(1,n)在一次函数y=x+b的图象上,∴n=1+1,∴n=2,∴点A的坐标是(1,2).∵反比例函数的图象过点A(1,2).∴k=1×2=2,∴反比例函数关系式是:y=(2)解:反比例函数y= ,当x>0时,y随x的增大而减少,而当x=1时,y=2,当x=6时,y= ,∴当1≤x≤6时,反比例函数y的值:≤y≤2【解析】【分析】(1)根据题意首先把点B(﹣1,0)代入一次函数y=x+b求出一次函数解析式,又点A(1,n)在一次函数y=x+b的图象上,再利用一次函数解析式求出点A的坐标,然后利用代入系数法求出反比例函数解析式,(2)根据反比例函数的性质分别求出当x=1,x=6时的y值,即可得到答案.2.心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y 随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?【答案】(1)解:设线段AB所在的直线的解析式为y1=k1x+20,把B(10,40)代入得,k1=2,∴y1=2x+20.设C、D所在双曲线的解析式为y2= ,把C(25,40)代入得,k2=1000,∴当x1=5时,y1=2×5+20=30,当,∴y1<y2∴第30分钟注意力更集中.(2)解:令y1=36,∴36=2x+20,∴x1=8令y2=36,∴,∴∵27.8﹣8=19.8>19,∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.【解析】【分析】(1)根据一次函数和反比例函数的应用,用待定系数法求出线段AB所在的直线的解析式,和C、D所在双曲线的解析式;把x1=5时和进行比较得到y1<y2,得出第30分钟注意力更集中;(2)当y1=36时,得到x1=8,当y2=36,得到,由27.8﹣8=19.8>19,所以经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.3.抛物线y= +x+m的顶点在直线y=x+3上,过点F(﹣2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.(1)先通过配方求抛物线的顶点坐标(坐标可用含m的代数式表示),再求m的值;(2)设点N的横坐标为a,试用含a的代数式表示点N的纵坐标,并说明NF=NB;(3)若射线NM交x轴于点P,且PA•PB= ,求点M的坐标.【答案】(1)解:y= x2+x+m= (x+2)2+(m﹣1)∴顶点坐标为(﹣2,m﹣1)∵顶点在直线y=x+3上,∴﹣2+3=m﹣1,得m=2;(2)解:过点F作FC⊥NB于点C,∵点N在抛物线上,∴点N的纵坐标为: a2+a+2,即点N(a, a2+a+2)在Rt△FCN中,FC=a+2,NC=NB﹣CB= a2+a,∴NF2=NC2+FC2=( a2+a)2+(a+2)2,=( a2+a)2+(a2+4a)+4,而NB2=( a2+a+2)2,=( a2+a)2+(a2+4a)+4∴NF2=NB2,NF=NB(3)解:连接AF、BF,由NF=NB,得∠NFB=∠NBF,由(2)的思路知,MF=MA,∴∠MAF=∠MFA,∵MA⊥x轴,NB⊥x轴,∴MA∥NB,∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°,∴2∠MAF+2∠NBF=180°,∠MAF+∠NBF=90°,∵∠MAB+∠NBA=180°,∴∠FBA+∠FAB=90°,又∵∠FAB+∠MAF=90°,∴∠FBA=∠MAF=∠MFA,又∵∠FPA=∠BPF,∴△PFA∽△PBF,∴ = ,PF2=PA×PB= ,过点F作FG⊥x轴于点G,在Rt△PFG中,PG= = ,∴PO=PG+GO= ,∴P(﹣,0)设直线PF:y=kx+b,把点F(﹣2,2)、点P(﹣,0)代入y=kx+b,解得k= ,b= ,∴直线PF:y= x+ ,解方程 x2+x+2= x+ ,得x=﹣3或x=2(不合题意,舍去),当x=﹣3时,y= ,∴M(﹣3,).【解析】【分析】(1)利用配方法将二次函数化成顶点式,写出顶点坐标,由顶点再直线y=x+3上,建立方程求出m的值。
中考数学反比例函数-经典压轴题附答案解析
中考数学反比例函数 -经典压轴题附答案解析一、反比例函数1.如图,矩形 OABC 的顶点 A 、 C 分别在 x 、y 轴的正半轴上,点 D 为 BC 边上的点,反比2)将矩形 OABC 的进行折叠,使点 O 于点 D 重合,折痕分别与 x 轴、 y 轴正半轴交于点 F ,G ,求折痕 FG 所在直线的函数关系式. 【答案】 (1)∵反比例函数 y= (k ≠0)在第一象限内的图象经过点E (3, ), ∴反比例函数的表达式为 y= .又∵点 D (m ,2)在反比例函数 y= 的图象上, ∴2m=2 ,解得: m=1(2)解:设 OG=x ,则 CG=OC ﹣OG=2﹣x ,∵点 D ( 1, 2), ∴CD=1.在 Rt △CDG 中,∠DCG=9°0,CG=2﹣x ,CD=1,DG=OG=x , ∴CD 2+CG 2=DG 2 ,即 1+( 2﹣ x ) 2=x 2 ,解得: x= ,∴点 G (0, ).过点 F 作 FH ⊥ CB 于点 H ,如图所示.D (m ,2)和 AB 边上的点E (3,由折叠的特性可知: ∠GDF=∠GOF=9°0 ,OG=DG ,OF=DF . ∵∠ CGD+∠CDG=90 ,°∠CDG+∠ HDF=90 ,° ∴∠ CGD=∠HDF ,∵∠ DCG=∠ FHD=90 ,°∴△ GCD ∽△DHF ,∴ =2 ,∴DF=2GD= ,∴点 F 的坐标为( ,0).设折痕 FG 所在直线的函数关系式为 y=ax+b ,∴折痕 FG 所在直线的函数关系式为 y=﹣ x+【解析】 【分析】( 1)由点 E 的坐标利用反比例函数图象上点的坐标特征即可求出 k 值, 再由点 B 在反比例函数图象上,代入即可求出 m 值;( 2)设 OG=x ,利用勾股定理即可得 出关于 x 的一元二次方程,解方程即可求出 x 值,从而得出点 G 的坐标.再过点 F 作 FH ⊥CB 于点 H ,由此可得出 △GCD ∽△DHF ,根据相似三角形的性质即可求出线段 DF 的长 度,从而得出点 F 的坐标,结合点 G 、 F 的坐标利用待定系数法即可求出结论.∴有 ,解得:2.如图,一次函数y=kx+b 的图象交反比例函数y= (x> 0)的图象于A(4,-8)、 B (m,-2)两点,交x 轴于点C.(1)求反比例函数与一次函数的关系式;(2)根据图象回答:当x 为何值时,一次函数的值大于反比例函数的值?(3)以O、A、B、P为顶点作平行四边形,请直接写出点P 的坐标.【答案】(1)解:∵反比例函数y= (x>0)的图象于A(4,-8),∴k=4 ×(-8)=-32.∵双曲线y= 过点B(m,-2),∴m=16 .由直线y=kx+b 过点 A , B 得:,解得,反比例函数关系式为,一次函数关系式为(2)解:观察图象可知,当0<x<4或x>16时,一次函数的值大于反比例函数的值(3)解:∵ O(0,0),A(4,-8)、B(16,-2),分三种情况:① 若OB∥AP,OA∥ BP,∵O(0,0),A(4,-8),∴由平移规律,点B(16,-2)向右平移 4 个单位,向下平移8 个单位得到P 点坐标为(20,-10);② 若OP∥ AB,OA∥ BP,∵A(4,-8),B(16,-2),∴由平移规律,点O(0,0)向右平移12 个单位,向上平移 6 个单位得到P 点坐标为(12,6);③ 若OB∥ AP,OP∥AB,∵B(16,-2),A(4,-8),∴由平移规律,点O(0,0)向左平移12 个单位,向下平移 6 个单位得到P 点坐标为(- 12,-6);∴以O,A,B,P为顶点作平行四边形,第四个顶点P的坐标为(12,6)或(-12,-6)或(20,-10)【解析】【分析】(1)将点A(4,-8),B(m ,-2)代入反比例函数y= (x> 0)中,可求k、a;再将点A(4,-8),B(m,-2)代入y=kx+b 中,列方程组求k、b 即可;(2)根据两函数图象的交点,图象的位置可确定一次函数的值大于反比例函数的值时x 的范围;(3)根据平行四边形的性质,即可直接写出.3.如图,已知A(3,m),B(﹣2,﹣3)是直线AB 和某反比例函数的图象的两个交点.(1)求直线AB 和反比例函数的解析式;(2)观察图象,直接写出当x 满足什么范围时,直线AB 在双曲线的下方;(3)反比例函数的图象上是否存在点C,使得△OBC 的面积等于△OAB 的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点 C 的坐标.【答案】(1)解:设反比例函数解析式为y= ,把B(﹣2,﹣3)代入,可得k=﹣2×(﹣ 3 )=6,∴反比例函数解析式为y= ;把A(3,m)代入y= ,可得3m=6,即m=2 ,∴A(3,2),设直线AB 的解析式为y=ax+b,把A(3,2),B(﹣2,﹣3)代入,可得解得,∴直线AB 的解析式为y=x﹣1(2)解:由题可得,当x满足:x<﹣2或0<x<3时,直线AB在双曲线的下方(3)解:存在点C.如图所示,延长AO 交双曲线于点C1 ,∵点 A 与点C1 关于原点对称,∴AO=C1O,∴△ OBC1的面积等于△ OAB的面积,此时,点C1的坐标为(﹣3,﹣2);如图,过点C1作BO的平行线,交双曲线于点C2 ,则△OBC2的面积等于△ OBC1的面积,∴△ OBC2的面积等于△ OAB的面积,由B(﹣2,﹣3)可得OB 的解析式为y= x ,可设直线C1C2 的解析式为y= x+b',把C1(﹣3,﹣2)代入,可得﹣2= ×(﹣3)+b',解得b'= ,∴直线C1C2 的解析式为y= x+ ,解方程组,可得C2();如图,过 A 作OB的平行线,交双曲线于点C3 ,则△OBC3 的面积等于△ OBA的面积,设直线AC3 的解析式为y= x+ ,把A(3,2)代入,可得2= ×3+ ,解得=﹣,∴直线AC3 的解析式为y= x﹣,解方程组,可得C3();综上所述,点C的坐标为(﹣3,﹣2),(()).【解析】【分析】(1)用待定系数法求出反比例函数解析式,一次函数解析式,将已知的点A,B 的坐标代入设的函数解析式列出关于待定系数的方程(组)求出系数,再回代到解析式(2)结合图像判断直线AB 在双曲线的交点坐标为A,B,X 取值范围为双曲线所在象限交点的横坐标,第一象限为为小于横坐标大于零,第三象限为小于横坐标(3)结合已知条件根据同底等高、等底同高作出与原三角形面积相等的三角形,再结合已知条件用待定系数法求出与双曲线有交点的直线的解析式,得出点的坐标,注意要考虑满足条件的所有点 C 的坐标。
2018中考反比例函数(含解析)

2018中考数学:反比例函数一.选择题(共21小题)1.(2018•玉林)等腰三角形底角与顶角之间的函数关系是()A.正比例函数 B.一次函数C.反比例函数D.二次函数【分析】根据一次函数的定义,可得答案.【解答】解:设等腰三角形的底角为y,顶角为x,由题意,得y=﹣x+90°,故选:B.2.(2018•怀化)函数y=kx﹣3与y=(k≠0)在同一坐标系内的图象可能是()A.B.C.D.【分析】根据当k>0、当k<0时,y=kx﹣3和y=(k≠0)经过的象限,二者一致的即为正确答案.【解答】解:∵当k>0时,y=kx﹣3过一、三、四象限,反比例函数y=过一、三象限,当k<0时,y=kx﹣3过二、三、四象限,反比例函数y=过二、四象限,∴B正确;故选:B.3.(2018•永州)在同一平面直角坐标系中,反比例函数y=(b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是()A.B.C.D.【分析】直接利用二次函数图象经过的象限得出a,b的值取值范围,进而利用反比例函数的性质得出答案.【解答】解:A、抛物线y=ax2+bx开口方向向上,则a>0,对称轴位于y轴的右侧,则a、b异号,即b<0.所以反比例函数y=的图象位于第二、四象限,故本选项错误;B、抛物线y=ax2+bx开口方向向上,则a>0,对称轴位于y轴的左侧,则a、b同号,即b>0.所以反比例函数y=的图象位于第一、三象限,故本选项错误;C、抛物线y=ax2+bx开口方向向下,则a<0,对称轴位于y轴的右侧,则a、b异号,即b>0.所以反比例函数y=的图象位于第一、三象限,故本选项错误;D、抛物线y=ax2+bx开口方向向下,则a<0,对称轴位于y轴的右侧,则a、b异号,即b>0.所以反比例函数y=的图象位于第一、三象限,故本选项正确;故选:D.4.(2018•菏泽)已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+a与反比例函数y=在同一平面直角坐标系中的图象大致是()A.B.C.D.【分析】直接利用二次函数图象经过的象限得出a,b,c的取值范围,进而利用一次函数与反比例函数的性质得出答案.【解答】解:∵二次函数y=ax2+bx+c的图象开口向上,∴a>0,∵该抛物线对称轴位于y轴的右侧,∴a、b异号,即b<0.∵当x=1时,y<0,∴a+b+c<0.∴一次函数y=bx+a的图象经过第一、二、四象限,反比例函数y=的图象分布在第二、四象限,故选:B.5.(2018•大庆)在同一直角坐标系中,函数y=和y=kx﹣3的图象大致是()A.B.C.D.【分析】根据一次函数和反比例函数的特点,k≠0,所以分k>0和k<0两种情况讨论.当两函数系数k取相同符号值,两函数图象共存于同一坐标系内的即为正确答案.【解答】解:分两种情况讨论:①当k>0时,y=kx﹣3与y轴的交点在负半轴,过一、三、四象限,反比例函数的图象在第一、三象限;②当k<0时,y=kx﹣3与y轴的交点在负半轴,过二、三、四象限,反比例函数的图象在第二、四象限.故选:B.6.(2018•香坊区)对于反比例函数y=,下列说法不正确的是()A.点(﹣2,﹣1)在它的图象上B.它的图象在第一、三象限C.当x>0时,y随x的增大而增大D.当x<0时,y随x的增大而减小【分析】根据反比例函数的性质用排除法解答.【解答】解:A、把点(﹣2,﹣1)代入反比例函数y=得﹣1=﹣1,故A选项正确;B、∵k=2>0,∴图象在第一、三象限,故B选项正确;C、当x>0时,y随x的增大而减小,故C选项错误;D、当x<0时,y随x的增大而减小,故D选项正确.故选:C.7.(2018•衡阳)对于反比例函数y=﹣,下列说法不正确的是()A.图象分布在第二、四象限B.当x>0时,y随x的增大而增大C.图象经过点(1,﹣2)D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2【分析】根据反比例函数图象的性质对各选项分析判断后利用排除法求解.【解答】解:A、k=﹣2<0,∴它的图象在第二、四象限,故本选项正确;B、k=﹣2<0,当x>0时,y随x的增大而增大,故本选项正确;C、∵﹣=﹣2,∴点(1,﹣2)在它的图象上,故本选项正确;D、点A(x1,y1)、B(x2、y2)都在反比例函数y=﹣的图象上,若x1<x2<0,则y1<y2,故本选项错误.故选:D.8.(2018•柳州)已知反比例函数的解析式为y=,则a的取值范围是()A.a≠2B.a≠﹣2 C.a≠±2D.a=±2【分析】根据反比例函数解析式中k是常数,不能等于0解答即可.【解答】解:由题意可得:|a|﹣2≠0,解得:a≠±2,故选:C.9.(2018•德州)给出下列函数:①y=﹣3x+2;②y=;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是()A.①③B.③④C.②④D.②③【分析】分别利用一次函数、正比例函数、反比例函数、二次函数的增减性分析得出答案.【解答】解:①y=﹣3x+2,当x>1时,函数值y随自变量x增大而减小,故此选项错误;②y=,当x>1时,函数值y随自变量x增大而减小,故此选项错误;③y=2x2,当x>1时,函数值y随自变量x增大而减小,故此选项正确;④y=3x,当x>1时,函数值y随自变量x增大而减小,故此选项正确;故选:B.10.(2018•嘉兴)如图,点C在反比例函数y=(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为()A.1 B.2 C.3 D.4【分析】根据题意可以设出点A的坐标,从而以得到点C和点B的坐标,再根据△AOB的面积为1,即可求得k的值.【解答】解:设点A的坐标为(a,0),∵过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,∴点C(﹣a,),∴点B(0,),∴=1,解得,k=4,故选:D.11.(2018•温州)如图,点A,B在反比例函数y=(x>0)的图象上,点C,D在反比例函数y=(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为,则k的值为()A.4 B.3 C.2 D.【分析】先求出点A,B的坐标,再根据AC∥BD∥y轴,确定点C,点D的坐标,求出AC,BD,最后根据,△OAC与△ABD的面积之和为,即可解答.【解答】解:∵点A,B在反比例函数y=(x>0)图象上,点A,B的横坐标分别为1,2,∴点A的坐标为(1,1),点B的坐标为(2,),∵AC∥BD∥y轴,∴点C,D的横坐标分别为1,2,∵点C,D在反比例函数y=(k>0)的图象上,∴点C的坐标为(1,k),点D的坐标为(2,),∴AC=k﹣1,BD=,∴S△OAC=(k﹣1)×1=,S△ABD=•×(2﹣1)=,∵△OAC与△ABD的面积之和为,∴,解得:k=3.故选:B.12.(2018•宁波)如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为()A.8 B.﹣8 C.4 D.﹣4【分析】设A(a,h),B(b,h),根据反比例函数图象上点的坐标特征得出ah=k1,bh=k2.根据三角形的面积公式得到S△ABC=AB•y A=(a﹣b)h=(ah﹣bh)=(k1﹣k2)=4,求出k1﹣k2=8.【解答】解:∵AB∥x轴,∴A,B两点纵坐标相同.设A(a,h),B(b,h),则ah=k1,bh=k2.∵S△ABC=AB•y A=(a﹣b)h=(ah﹣bh)=(k1﹣k2)=4,∴k1﹣k2=8.故选:A.13.(2018•郴州)如图,A,B是反比例函数y=在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是()A.4 B.3 C.2 D.1【分析】先根据反比例函数图象上点的坐标特征及A,B两点的横坐标,求出A(2,2),B(4,1).再过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,根据反比例函数系数k的几何意义得出S△AOC=S△BOD=×4=2.根据S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,得出S△AOB=S梯形ABDC,利用梯形面积公式求出S梯形ABDC=(BD+AC)•CD=(1+2)×2=3,从而得出S△AOB=3.【解答】解:∵A,B是反比例函数y=在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,∴当x=2时,y=2,即A(2,2),当x=4时,y=1,即B(4,1).如图,过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,则S△AOC=S△BOD=×4=2.∵S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,∴S△AOB=S梯形ABDC,∵S梯形ABDC=(BD+AC)•CD=(1+2)×2=3,∴S△AOB=3.故选:B.14.(2018•无锡)已知点P(a,m),Q(b,n)都在反比例函数y=的图象上,且a<0<b,则下列结论一定正确的是()A.m+n<0 B.m+n>0 C.m<n D.m>n【分析】根据反比例函数的性质,可得答案.【解答】解:y=的k=﹣2<0,图象位于二四象限,∵a<0,∴P(a,m)在第二象限,∴m>0;∵b>0,∴Q(b,n)在第四象限,∴n<0.∴n<0<m,即m>n,故D正确;故选:D.15.(2018•淮安)若点A(﹣2,3)在反比例函数y=的图象上,则k的值是()A.﹣6 B.﹣2 C.2 D.6【分析】根据待定系数法,可得答案.【解答】解:将A(﹣2,3)代入反比例函数y=,得k=﹣2×3=﹣6,故选:A.16.(2018•岳阳)在同一直角坐标系中,二次函数y=x2与反比例函数y=(x>0)的图象如图所示,若两个函数图象上有三个不同的点A(x1,m),B(x2,m),C(x3,m),其中m为常数,令ω=x1+x2+x3,则ω的值为()A.1 B.m C.m2D.【分析】三个点的纵坐标相同,由图象可知y=x2图象上点横坐标互为相反数,则x1+x2+x3=x3,再由反比例函数性质可求x3.【解答】解:设点A、B在二次函数y=x2图象上,点C在反比例函数y=(x>0)的图象上.因为AB两点纵坐标相同,则A、B关于y轴对称,则x1+x2=0,因为点C(x3,m)在反比例函数图象上,则x3=,∴ω=x1+x2+x3=x3=, 故选:D.17.(2018•遵义)如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=(x >0)的图象上,则经过点B的反比例函数解析式为()A.y=﹣B.y=﹣C.y=﹣D.y=【分析】直接利用相似三角形的判定与性质得出=,进而得出S△AOD=2,即可得出答案.【解答】解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,∵∠BOA=90°,∴∠BOC+∠AOD=90°,∵∠AOD+∠OAD=90°,∴∠BOC=∠OAD,又∵∠BCO=∠ADO=90°,∴△BCO∽△ODA,∴=tan30°=,∴=,∵×AD×DO=xy=3,∴S△BCO=×BC×CO=S△AOD=1,∴S△AOD=2,∵经过点B的反比例函数图象在第二象限,故反比例函数解析式为:y=﹣.故选:C.18.(2018•湖州)如图,已知直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是()A.(﹣1,﹣2)B.(﹣1,2) C.(1,﹣2) D.(﹣2,﹣1)【分析】直接利用正比例函数的性质得出M,N两点关于原点对称,进而得出答案.【解答】解:∵直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点,∴M,N两点关于原点对称,∵点M的坐标是(1,2),∴点N的坐标是(﹣1,﹣2).故选:A.19.(2018•江西)在平面直角坐标系中,分别过点A(m,0),B(m+2,0)作x轴的垂线l1和l2,探究直线l1,直线l2与双曲线y=的关系,下列结论错误的是()A.两直线中总有一条与双曲线相交B.当m=1时,两直线与双曲线的交点到原点的距离相等C.当﹣2<m<0时,两直线与双曲线的交点在y轴两侧D.当两直线与双曲线都有交点时,这两交点的最短距离是2【分析】A、由m、m+2不同时为零,可得出:两直线中总有一条与双曲线相交;B、找出当m=1时两直线与双曲线的交点坐标,利用两点间的距离公式可得出:当m=1时,两直线与双曲线的交点到原点的距离相等;C、当﹣2<m<0时,0<m+2<2,可得出:当﹣2<m<0时,两直线与双曲线的交点在y轴两侧;D、由y与x之间一一对应结合两交点横坐标之差为2,可得出:当两直线与双曲线都有交点时,这两交点的距离大于2.此题得解.【解答】解:A、∵m、m+2不同时为零,∴两直线中总有一条与双曲线相交;B、当m=1时,点A的坐标为(1,0),点B的坐标为(3,0),当x=1时,y==3,∴直线l1与双曲线的交点坐标为(1,3);当x=3时,y==1,∴直线l2与双曲线的交点坐标为(3,1).∵=,∴当m=1时,两直线与双曲线交点到原点的距离相等;C、当﹣2<m<0时,0<m+2<2,∴当﹣2<m<0时,两直线与双曲线的交点在y轴两侧;D、∵m+2﹣m=2,且y与x之间一一对应,∴当两直线与双曲线都有交点时,这两交点的距离大于2.故选:D.20.(2018•铜仁市)如图,已知一次函数y=ax+b和反比例函数y=的图象相交于A(﹣2,y1)、B(1,y2)两点,则不等式ax+b<的解集为()A.x<﹣2或0<x<1;B.x<﹣2 C.0<x<1 D.﹣2<x<0或x>1【分析】根据一次函数图象与反比例函数图象的上下位置关系结合交点坐标,即可得出不等式的解集.【解答】解:观察函数图象,发现:当﹣2<x<0或x>1时,一次函数图象在反比例函数图象的下方,∴不等式ax+b<的解集是﹣2<x<0或x>1.故选:D.21.(2018•聊城)春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过5min的集中药物喷洒,再封闭宿舍10min,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x (min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是()A.经过5min集中喷洒药物,室内空气中的含药量最高达到10mg/m3B.室内空气中的含药量不低于8mg/m3的持续时间达到了11minC.当室内空气中的含药量不低于5mg/m3且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效D.当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内【分析】利用图中信息一一判断即可;【解答】解:A、正确.不符合题意.B、由题意x=4时,y=8,∴室内空气中含药量不低于8mg/m3的持续时间达到了11min,正确,不符合题意;C、y=5时,x=2.5或24,24﹣2.5=21.5<35,故本选项错误,符合题意;D、正确.不符合题意,故选:C.二.填空题(共9小题)22.(2018•上海)已知反比例函数y=(k是常数,k≠1)的图象有一支在第二象限,那么k的取值范围是k<1.【分析】由于在反比例函数y=的图象有一支在第二象限,故k﹣1<0,求出k的取值范围即可.【解答】解:∵反比例函数y=的图象有一支在第二象限,∴k﹣1<0,解得k<1.故答案为:k<1.23.(2018•齐齐哈尔)已知反比例函数y=的图象在第一、三象限内,则k的值可以是1.(写出满足条件的一个k的值即可)【分析】根据反比例函数的性质:反比例函数y=的图象在第一、三象限内,则可知2﹣k>0,解得k 的取值范围,写出一个符合题意的k即可.【解答】解:由题意得,反比例函数y=的图象在第一、三象限内,则2﹣k>0,故k<2,满足条件的k可以为1,故答案为:1.24.(2018•连云港)已知A(﹣4,y1),B(﹣1,y2)是反比例函数y=﹣图象上的两个点,则y1与y2的大小关系为y1<y2.【分析】根据反比例函数的性质和题目中的函数解析式可以判断y1与y2的大小,从而可以解答本题.【解答】解:∵反比例函数y=﹣,﹣4<0,∴在每个象限内,y随x的增大而增大,∵A(﹣4,y1),B(﹣1,y2)是反比例函数y=﹣图象上的两个点,﹣4<﹣1,∴y1<y2,故答案为:y1<y2.25.(2018•南京)已知反比例函数y=的图象经过点(﹣3,﹣1),则k=3.【分析】根据反比例函数y=的图象经过点(﹣3,﹣1),可以求得k的值.【解答】解:∵反比例函数y=的图象经过点(﹣3,﹣1),∴﹣1=,解得,k=3,故答案为:3.26.(2018•陕西)若一个反比例函数的图象经过点A(m,m)和B(2m,﹣1),则这个反比例函数的表达式为.【分析】设反比例函数的表达式为y=,依据反比例函数的图象经过点A(m,m)和B(2m,﹣1),即可得到k的值,进而得出反比例函数的表达式为.【解答】解:设反比例函数的表达式为y=,∵反比例函数的图象经过点A(m,m)和B(2m,﹣1),∴k=m2=﹣2m,解得m1=﹣2,m2=0(舍去),∴k=4,∴反比例函数的表达式为.故答案为:.27.(2018•东营)如图,B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为y=.【分析】设A坐标为(x,y),根据四边形OABC为平行四边形,利用平移性质确定出A的坐标,利用待定系数法确定出解析式即可.【解答】解:设A坐标为(x,y),∵B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,∴x+5=0+3,y+0=0﹣3,解得:x=﹣2,y=﹣3,即A(﹣2,﹣3),设过点A的反比例解析式为y=,把A(﹣2,﹣3)代入得:k=6,则过点A的反比例解析式为y=,故答案为:y=28.(2018•成都)设双曲线y=(k>0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径“,当双曲线y=(k>0)的眸径为6时,k的值为.【分析】以PQ为边,作矩形PQQ′P′交双曲线于点P′、Q′,联立直线AB及双曲线解析式成方程组,通过解方程组可求出点A、B的坐标,由PQ的长度可得出点P的坐标(点P在直线y=﹣x上找出点P的坐标),由图形的对称性结合点A、B和P的坐标可得出点P′的坐标,再利用反比例函数图象上点的坐标特征即可得出关于k的一元一次方程,解之即可得出结论.【解答】解:以PQ为边,作矩形PQQ′P′交双曲线于点P′、Q′,如图所示.联立直线AB及双曲线解析式成方程组,,解得:,,∴点A的坐标为(﹣,﹣),点B的坐标为(,).∵PQ=6,∴OP=3,点P的坐标为(﹣,).根据图形的对称性可知:AB=OO′=PP′,∴点P′的坐标为(﹣+2,+2).又∵点P′在双曲线y=上,∴(﹣+2)•(+2)=k,解得:k=.故答案为:.29.(2018•安顺)如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+n=0;③S△AOP=S△BOQ;④不等式k1x+b的解集是x<﹣2或0<x<1,其中正确的结论的序号是②③④.【分析】根据一次函数和反比例函数的性质得到k1k2>0,故①错误;把A(﹣2,m)、B(1,n)代入y=中得到﹣2m=n故②正确;把A(﹣2,m)、B(1,n)代入y=k1x+b得到y=﹣mx﹣m,求得P(﹣1,0),Q(0,﹣m),根据三角形的面积公式即可得到S△AOP=S△BOQ;故③正确;根据图象得到不等式k1x+b的解集是x<﹣2或0<x<1,故④正确.【解答】解:由图象知,k1<0,k2<0,∴k1k2>0,故①错误;把A(﹣2,m)、B(1,n)代入y=中得﹣2m=n,∴m+n=0,故②正确;把A(﹣2,m)、B(1,n)代入y=k1x+b得,∴,∵﹣2m=n,∴y=﹣mx﹣m,∵已知直线y=k1x+b与x轴、y轴相交于P、Q两点,∴P(﹣1,0),Q(0,﹣m),∴OP=1,OQ=m,∴S△AOP=m,S△BOQ=m,∴S△AOP=S△BOQ;故③正确;由图象知不等式k1x+b的解集是x<﹣2或0<x<1,故④正确;故答案为:②③④.30.(2018•安徽)如图,正比例函数y =kx 与反比例函数y =的图象有一个交点A (2,m ),AB ⊥x 轴于点B .平移直线y =kx ,使其经过点B ,得到直线l ,则直线l 对应的函数表达式是 y =x ﹣3 .【分析】首先利用图象上点的坐标特征得出A 点坐标,进而得出正比例函数解析式,再利用平移的性质得出答案.【解答】解:∵正比例函数y =kx 与反比例函数y =的图象有一个交点A (2,m ),∴2m =6,解得:m =3,故A (2,3),则3=2k ,解得:k =,故正比例函数解析式为:y =x ,∵AB ⊥x 轴于点B ,平移直线y =kx ,使其经过点B ,∴B (2,0),∴设平移后的解析式为:y =x +b ,则0=3+b ,解得:b =﹣3,故直线l 对应的函数表达式是:y =x ﹣3.故答案为:y =x ﹣3.三.解答题(共20小题)31.(2018•贵港)如图,已知反比例函数y =(x >0)的图象与一次函数y =﹣x +4的图象交于A 和B(6,n )两点.(1)求k 和n 的值;(2)若点C (x ,y )也在反比例函数y =(x >0)的图象上,求当2≤x ≤6时,函数值y 的取值范围.【分析】(1)利用一次函数图象上点的坐标特征可求出n 值,进而可得出点B 的坐标,再利用反比例函数图象上点的坐标特征即可求出k 值;(2)由k =6>0结合反比例函数的性质,即可求出:当2≤x ≤6时,1≤y ≤3.【解答】解:(1)当x=6时,n=﹣×6+4=1,∴点B的坐标为(6,1).∵反比例函数y=过点B(6,1),∴k=6×1=6.(2)∵k=6>0,∴当x>0时,y随x值增大而减小,∴当2≤x≤6时,1≤y≤3.32.(2018•泰安)如图,矩形ABCD的两边AD、AB的长分别为3、8,E是DC的中点,反比例函数y=的图象经过点E,与AB交于点F.(1)若点B坐标为(﹣6,0),求m的值及图象经过A、E两点的一次函数的表达式;(2)若AF﹣AE=2,求反比例函数的表达式.【分析】(1)根据矩形的性质,可得A,E点坐标,根据待定系数法,可得答案;(2)根据勾股定理,可得AE的长,根据线段的和差,可得FB,可得F点坐标,根据待定系数法,可得m的值,可得答案.【解答】解:(1)点B坐标为(﹣6,0),AD=3,AB=8,E为CD的中点,∴点A(﹣6,8),E(﹣3,4),函数图象经过E点,∴m=﹣3×4=﹣12,设AE的解析式为y=kx+b,,解得,一次函数的解析是为y=﹣x;(2)AD=3,DE=4,∴AE==5,∵AF﹣AE=2,∴AF=7,BF=1,设E点坐标为(a,4),则F点坐标为(a﹣3,1),∵E,F两点在函数y=图象上,∴4a=a﹣3,解得a=﹣1,∴E(﹣1,4),∴m=﹣1×4=﹣4,∴y=﹣.33.(2018•岳阳)如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,A C.(1)求该反比例函数的解析式;(2)若△ABC的面积为6,求直线AB的表达式.【分析】(1)把A的坐标代入反比例函数的解析式即可求得;(2)作AD⊥BC于D,则D(2,b),即可利用a表示出AD的长,然后利用三角形的面积公式即可得到一个关于b方程求得b的值,进而求得a的值,根据待定系数法,可得答案.【解答】解:(1)由题意得,k=xy=2×3=6∴反比例函数的解析式为y=.(2)设B点坐标为(a,b),如图,作AD⊥BC于D,则D(2,b)∵反比例函数y=的图象经过点B(a,b),∴b=,∴AD=3﹣.∴S△ABC=BC•AD=a(3﹣)=6,解得a=6,∴b==, ∴B(6,1).设AB的解析式为y=kx+b,将A(2,3),B(6,1)代入函数解析式,得,解得,直线AB的解析式为y=﹣x+4.34.(2018•柳州)如图,一次函数y=mx+b的图象与反比例函数y=的图象交于A(3,1),B(﹣,n)两点.(1)求该反比例函数的解析式;(2)求n的值及该一次函数的解析式.【分析】(1)根据反比例函数y=的图象经过A(3,1),即可得到反比例函数的解析式为y=;(2)把B(﹣,n)代入反比例函数解析式,可得n=﹣6,把A(3,1),B(﹣,﹣6)代入一次函数y=mx+b,可得一次函数的解析式为y=2x﹣5.【解答】解:(1)∵反比例函数y=的图象经过A(3,1),∴k=3×1=3,∴反比例函数的解析式为y=;(2)把B(﹣,n)代入反比例函数解析式,可得﹣n=3,解得n=﹣6,∴B(﹣,﹣6),把A(3,1),B(﹣,﹣6)代入一次函数y=mx+b,可得,解得,∴一次函数的解析式为y=2x﹣5.35.(2018•白银)如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.(1)求此反比例函数的表达式;(2)若点P在x轴上,且S△ACP=S△BOC,求点P的坐标.【分析】(1)利用点A在y=﹣x+4上求a,进而代入反比例函数y=求k.(2)联立方程求出交点,设出点P坐标表示三角形面积,求出P点坐标.【解答】解:(1)把点A(﹣1,a)代入y=x+4,得a=3,∴A(﹣1,3),把A(﹣1,3)代入反比例函数y=,∴k=﹣3,∴反比例函数的表达式为y=﹣(2)联立两个函数的表达式得,解得或,∴点B的坐标为B(﹣3,1)当y=x+4=0时,得x=﹣4,∴点C(﹣4,0),设点P的坐标为(x,0)∵S△ACP=S△BOC,∴解得x1=﹣6,x2=﹣2,∴点P(﹣6,0)或(﹣2,0)36.(2018•菏泽)如图,已知点D在反比例函数y=的图象上,过点D作DB⊥y轴,垂足为B(0,3),直线y=kx+b经过点A(5,0),与y轴交于点C,且BD=OC,OC:OA=2:5.(1)求反比例函数y=和一次函数y=kx+b的表达式;(2)直接写出关于x的不等式>kx+b的解集.【分析】(1)由OC、OA、BD之间的关系结合点A、B的坐标可得出点C、D的坐标,由点D的坐标利用反比例函数图象上点的坐标特征可求出a值,进而可得出反比例函数的表达式,再由点A、C的坐标利用待定系数法,即可求出一次函数的表达式;(2)将一次函数表达式代入反比例函数表达式中,利用根的判别式△<0可得出两函数图象无交点,再观察图形,利用两函数图象的上下位置关系即可找出不等式>kx+b的解集.【解答】解:(1)∵BD=OC,OC:OA=2:5,点A(5,0),点B(0,3),∴OA=5,OC=BD=2,OB=3,又∵点C在y轴负半轴,点D在第二象限,∴点C的坐标为(0,﹣2),点D的坐标为(﹣2,3).∵点D(﹣2,3)在反比例函数y=的图象上,∴a=﹣2×3=﹣6,∴反比例函数的表达式为y=﹣.将A(5,0)、B(0,﹣2)代入y=kx+b,,解得:,∴一次函数的表达式为y=x﹣2.(2)将y=x﹣2代入y=﹣,整理得:x2﹣2x+6=0,∵△=(﹣2)2﹣4××6=﹣<0,∴一次函数图象与反比例函数图象无交点.观察图形,可知:当x<0时,反比例函数图象在一次函数图象上方,∴不等式>kx+b的解集为x<0.37.(2018•湘西州)反比例函数y=(k为常数,且k≠0)图象过点A(1,3)、B(3,m).(1)求反比例函数的解析式及B点的坐标;(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.【分析】(1)先把A点坐标代入y=求出k得到反比例函数解析式;然后把B(3,m)代入反比例函数解析式求出m得到B点坐标;(2)作A点关于x轴的对称点A′,连接BA′交x轴于P点,则A′(1,﹣3),利用两点之间线段最短可判断此时此时PA+PB的值最小,再利用待定系数法求出直线BA′的解析式,然后求出直线与x轴的交点坐标即可得到P点坐标.【解答】解:(1)把A(1,3)代入y=得k=1×3=3,∴反比例函数解析式为y=;把B(3,m)代入y=得3m=3,解得m=1,∴B点坐标为(3,1);(2)作A点关于x轴的对称点A′,连接BA′交x轴于P点,则A′(1,﹣3),∵PA+PB=PA′+PB=BA′,∴此时此时PA+PB的值最小,设直线BA′的解析式为y=mx+n,把A′(1,﹣3),B(3,1)代入得,解得,∴直线BA′的解析式为y=2x﹣5,当y=0时,2x﹣5=0,解得x=,∴P点坐标为(,0).38.(2018•大庆)如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.(1)求反比例函数y=的表达式;(2)求点B的坐标;(3)求△OAP的面积.【分析】(1)将点A的坐标代入解析式求解可得;(2)利用勾股定理求得AB=OA=5,由AB∥x轴即可得点B的坐标;(3)先根据点B坐标得出OB所在直线解析式,求得直线与双曲线交点P的坐标,再利用割补法求解可得.【解答】解:(1)将点A(4,3)代入y=,得:k=12,则反比例函数解析式为y=;(2)如图,过点A作AC⊥x轴于点C,则OC=4、AC=3,∴OA==5,∵AB∥x轴,且AB=OA=5,∴点B的坐标为(9,3);(3)∵点B坐标为(9,3),∴OB所在直线解析式为y=x,由可得点P坐标为(6,2),过点P作PD⊥x轴,延长DP交AB于点E,则点E坐标为(6,3),∴AE=2、PE=1、PD=2,则△OAP的面积=×(2+6)×3﹣×6×2﹣×2×1=5.39.(2018•枣庄)如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.(1)求一次函数与反比例函数的解析式;(2)记两函数图象的另一个交点为E,求△CDE的面积;(3)直接写出不等式kx+b≤的解集.【分析】(1)根据三角形相似,可求出点C坐标,可得一次函数和反比例函数解析式;(2)联立解析式,可求交点坐标;(3)根据数形结合,将不等式转化为一次函数和反比例函数图象关系.【解答】解:(1)由已知,OA=6,OB=12,OD=4∵CD⊥x轴,∴OB∥CD,∴△ABO∽△ACD,∴,∴,∴CD=20∴点C坐标为(﹣4,20),∴n=xy=﹣80,∴反比例函数解析式为:y=﹣把点A(6,0),B(0,12)代入y=kx+b得:解得:∴一次函数解析式为:y=﹣2x+12(2)当﹣=﹣2x+12时,解得x1=10,x2=﹣4当x=10时,y=﹣8,∴点E坐标为(10,﹣8),∴S△CDE=S△CDA+S△EDA=(3)不等式kx+b≤,从函数图象上看,表示一次函数图象不低于反比例函数图象∴由图象得,x≥10,或﹣4≤x<040.(2018•杭州)设一次函数y=kx+b(k,b是常数,k≠0)的图象过A(1,3),B(﹣1,﹣1)两点.(1)求该一次函数的表达式;(2)若点(2a+2,a2)在该一次函数图象上,求a的值.(3)已知点C(x1,y1)和点D(x2,y2)在该一次函数图象上,设m=(x1﹣x2)(y1﹣y2),判断反比例函数y=的图象所在的象限,说明理由.【分析】(1)根据一次函数y=kx+b(k,b是常数,k≠0)的图象过A(1,3),B(﹣1,﹣1)两点,可以求得该函数的表达式;(2)根据(1)中的解析式可以求得a的值;(3)根据题意可以判断m的正负,从而可以解答本题.【解答】解:(1)∵一次函数y=kx+b(k,b是常数,k≠0)的图象过A(1,3),B(﹣1,﹣1)两点,∴,得,即该一次函数的表达式是y=2x+1;(2)点(2a+2,a2)在该一次函数y=2x+1的图象上,∴a2=2(2a+2)+1,解得,a=﹣1或a=5,即a的值是﹣1或5;(3)反比例函数y=的图象在第一、三象限,理由:∵点C(x1,y1)和点D(x2,y2)在该一次函数y=2x+1的图象上,m=(x1﹣x2)(y1﹣y2),假设x1<x2,则y1<y1,此时m=(x1﹣x2)(y1﹣y2)>0,假设x1>x2,则y1>y1,此时m=(x1﹣x2)(y1﹣y2)>0,由上可得,m>0,∴m+1>0,∴反比例函数y=的图象在第一、三象限.41.(2018•杭州)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).(1)求v关于t的函数表达式.(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?【分析】(1)直接利用vt=100进而得出答案;(2)直接利用要求不超过5小时卸完船上的这批货物,进而得出答案.【解答】解:(1)由题意可得:100=vt,则v=;(2)∵不超过5小时卸完船上的这批货物,∴t≤5,则v≥=20,答:平均每小时至少要卸货20吨.42.(2018•河北)如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t (秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.(1)求k,并用t表示h;(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.【分析】(1)用待定系数法解题即可;(2)根据题意,分别用t表示x、y,再用代入消元法得出y与x之间的关系式;(3)求出甲距x轴1.8米时的横坐标,根据题意求出乙位于甲右侧超过4.5米的v乙.【解答】解:(1)由题意,点A(1,18)带入y=,得:18=,∴k=18设h=at2,把t=1,h=5代入∴a=5,∴h=5t2(2)∵v=5,AB=1,∴x=5t+1,∵h=5t2,OB=18,∴y=﹣5t2+18。
各地2018年中考数学试卷精选汇编 反比例函数(含解析)

【分析】根据反比例函数 y= 的图象经过点(﹣3,﹣1),可以求得 k 的值.
【解答】解:∵反比例函数 y= 的图象经过点(﹣3,﹣1),
∴﹣1= ,
解得,k=3, 故答案为:3. 【点评】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质 解答.
②∵S△AOP= ·AP·yA= ·( -a)·b=6- ab,
S△BOP= ·BP·xB= ·( ∴S△AOP=S△BOP. 故②正确; ③作 PD⊥OB,PE⊥OA,
-b)·a=6- ab,
∵OA=OB,S△AOP=S△BOP. ∴PD=PE, ∴OP平分∠AOB, 故③正确;
④∵S△BOP=6∴ab=4,
在函数 y= 图象的概率是( )
A. B. C. D.
【分析】根据反比例函数图象上点的坐标特征可得出 mn=6,列表找出所有 mn的值,根据表格中 mn=6所占 比例即可得出结论. 【解答】解:∵点(m,n)在函数 y= 的图象上,
∴mn=6.
列表如下:
m ﹣﹣ ﹣ 2 2 2 3 3 3 ﹣ ﹣ ﹣
14. (2018·广东深圳·3 分)如图,
是函数
上两点,为一动点,作
轴,
轴,下列说法正确的是(
)
①
;②
;③若
,则 平分
;④若
,则
A. ① ③ ③ ④ 【答案】B 【考点】反比例函数系数 k 的几何意义,三角形的面积,角的平分线判定
B. ②
C.
②
D. ③④
【解析】【解答】解:设 P(a,b),则 A( ,b),B(a, ),①∴AP= -a,BP= -b, ∵a≠b, ∴AP≠BP,OA≠OB, ∴△AOP和△BOP不一定全等, 故①错误;
2018挑战中考数学压轴题全套含答案及解析

第一部分函数图象中点的存在性问题§1.1 因动点产生的相似三角形问题例1 2014年市中考第28题例2 2014年市中考第21题例3 2015年湘西州中考第26题例4 2015年市中考第25题例5 2016年市中考第26题例6 2016年市中考第24题例7 2016年市崇明县中考模拟第25题例8 2016年市黄浦区中考模拟第26题§1.2 因动点产生的等腰三角形问题例9 2014年市中考第26题例10 2014年市第25题例11 2014年市中考第26题例12 2014年市中考第27题例13 2015年市中考第22题例14 2015年市中考第26题例15 2016年市中考第26题例16 2016年市长宁区金山区中考模拟第25题例17 2016年省中考第23题§1.3 因动点产生的直角三角形问题例19 2015年市中考第21题例20 2015年市中考第26题例21 2016年市中考第26题例22 2016年市松江区中考模拟第25题例23 2016年义乌市市中考第24题§1.4 因动点产生的平行四边形问题例24 2014年市中考第24题例25 2014年市中考第20题例26 2014年市中考第25题例27 2015年市中考第25题例28 2015年黄冈市中考第24题例29 2016年市中考第26题例30 2016年市嘉定区宝山区中考模拟中考第24题例31 2016年市徐汇区中考模拟第24题§1.5 因动点产生的面积问题例32 2014年市中考第25题例33 2014年永州市中考第25题例35 2015年市中考第26题例36 2015年株洲市中考第23题例37 2015年市中考第28题例38 2016年市中考第22题例39 2016年永州市中考第26题例40 2016年市中考第26题例41 2016年省中考第25题§1.6 因动点产生的相切问题例42 2014年市中考第27题例43 2014年株洲市中考第23题例44 2015年市中考第25题例45 2015年湘西州中考第25题例46 2016年市中考第25题例47 2016年市中考第26题例48 2016年市闵行区中考模拟第24题例49 2016年市普陀区中考模拟中考第25题§1.7 因动点产生的线段和差问题例50 2014年市中考第26题例51 2014年湘西州中考第25题例53 2015年市中考第28题例54 2015年市中考第25题例55 2016年市中考第26题例56 2016年市中考第24题例57 2016年市中考第21题第二部分图形运动中的函数关系问题§2.1 由比例线段产生的函数关系问题例1 2014年市中考第26题例2 2014年市中考第25题例3 2014年市中考第25题例4 2015年市中考第25题例5 2015年市中考第26题例6 2015年市中考第25题例7 2015年市中考第26题例8 2016年市中考第25题例9 2016年湘西州中考第26题例10 2016年市静安区青浦区中考模拟第25题例11 2016年市中考第27题第三部分图形运动中的计算说理问题§3.1 代数计算及通过代数计算进行说理问题例1 2014年市中考第25题例2 2014年市中考第23题例3 2014年市中考第26题例4 2014年株洲市中考第24题例5 2015年市中考第27题例6 2015年市中考第25题例7 2015年永州市中考第26题例8 2015年市中考第25题例9 2015年株洲市中考第24题例10 2016年市中考第22题例11 2016年市中考第25题例12 2016年株洲市中考第26题例13 2016年市中考第25题例14 2016年市中考第26题§3.2 几何证明及通过几何计算进行说理问题例15 2014年市中考第26题例16 2014年市中考第26题例17 2014年市中考第23题例18 2015年市中考第26题例19 2015年市中考第20题例20 2015年永州市中考第27题例21 2015年市中考第23题例22 2016年市中考第25题例23 2016年市中考第25题例24 2016年永州市中考第27题例25 2016年市中考第23题例26 2016年株洲市中考第25题例27 2016年市中考第25题第四部分图形的平移、翻折与旋转§4.1 图形的平移例1 2015年市中考第15题例2 2015年市中考第14题例3 2015年株洲市中考第14题例4 2016年市虹口区中考模拟第18题§4.2 图形的翻折例5 2016年市奉贤区中考模拟第18题例6 2016年市静安区青浦区中考模拟第18题例7 2016年市闵行区中考模拟第18题例8 2016年市浦东新区中考模拟第18题例8 2016年市普陀区中考模拟第18题例10 2016年市中考第15题例11 2016年市中考第14题例12 2016年市中考第18题例13 2016年市中考第15题例14 2016年市中考第12题§4.3 图形的旋转例15 2016年昂立教育中学生三模联考第18题例16 2016年市崇明县中考模拟第18题例17 2016年市黄浦区中考模拟第18题例18 2016年市嘉定区宝山区中考模拟第18题例19 2016年市闸北区中考模拟第18题例20 2016年市中考第13题例21 2016年株洲市中考第4题§4.4 三角形例22 2016年省中考第10题例23 2016年市中考第10题例24 2016年省中考第16题例25 2016年市中考第10题例27 2016年市中考第10题例28 2016年省中考第14题例29 2016年江市中考第11题例30 2016年市中考第18题§4.5 四边形例31 2016年湘西州中考第11题例32 2016年市中考第4题例33 2016年市中考第6题例34 2016年市中考第16题例35 2016年市中考第14题例36 2016年市中考第13题例37 2016年市中考第18题例38 2016年市中考第17题例39 2016年市中考第15题§4.6 圆例40 2016年滨州市中考第16题例41 2016年市中考第17题例42 2016年市中考第16题例43 2016年市中考第17题例45 2016年市中考第18题例46 2016年市中考第9题例47 2016年宿迁市中考第16题例48 2016年市中考第17题例49 2016年市中考第18题例50 2016年湘西州中考第18题例51 2016年永州市中考第20题§4.7 函数的图象及性质例52 2015年荆州市中考第9题例53 2015年市中考第12题例54 2015年市中考第12题例55 2015年市中考第10题例56 2015年市中考第10题例57 2015年呼和浩特市中考第10题例58 2016年市中考第18题例59 2016年市中考第19题例60 2016年市中考第15题例61 2016年株洲市中考第9题例62 2016年永州市中考第19题例63 2016年市中考第8题例64 2016年市中考第16题例65 2016年市中考第14题例66 2016年株洲市中考第10题例67 2016年株洲市中考第17题例68 2016年东营市中考第15题例69 2016年市中考第13题例70 2016年市中考第16题例71 2016年宿迁市中考第15题例72 2016年市中考第14题例73 2016年义乌市市中考第9题例74 2016年市中考第12题例75 2016年市中考第16题§1.1 因动点产生的相似三角形问题课前导学相似三角形的判定定理有3个,其中判定定理1和判定定理2都有对应角相等的条件,因此探求两个三角形相似的动态问题,一般情况下首先寻找一组对应角相等.判定定理2是最常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验.如果已知∠A =∠D ,探求△ABC 与△DEF 相似,只要把夹∠A 和∠D 的两边表示出来,按照对应边成比例,分AB DE AC DF =和AB DF AC DE=两种情况列方程. 应用判定定理1解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等. 应用判定定理3解题不多见,根据三边对应成比例列连比式解方程(组).还有一种情况,讨论两个直角三角形相似,如果一组锐角相等,其中一个直角三角形的锐角三角比是确定的,那么就转化为讨论另一个三角形是直角三角形的问题.求线段的长,要用到两点间的距离公式,而这个公式容易记错.理解记忆比较好. 如图1,如果已知A 、B 两点的坐标,怎样求A 、B 两点间的距离呢?我们以AB 为斜边构造直角三角形,直角边与坐标轴平行,这样用勾股定理就可以求斜边AB 的长了.水平距离BC 的长就是A 、B 两点间的水平距离,等于A 、B 两点的横坐标相减;竖直距离AC 就是A 、B 两点间的竖直距离,等于A 、B 两点的纵坐标相减.图1例 1 2014年省市中考第28题二次函数y =a x 2+b x +c (a ≠0)的图象与x 轴交于A (-3, 0)、B (1, 0)两点,与y 轴交于点C (0,-3m )(m >0),顶点为D .(1)求该二次函数的解析式(系数用含m 的代数式表示);(2)如图1,当m =2时,点P 为第三象限抛物线上的一个动点,设△APC 的面积为S ,试求出S 与点P 的横坐标x 之间的函数关系式及S 的最大值;(3)如图2,当m 取何值时,以A 、D 、C 三点为顶点的三角形与△OBC 相似?图1 图2动感体验请打开几何画板文件名“1428”,拖动点P 运动,可以体验到,当点P 运动到AC 的中点的正下方时,△APC 的面积最大.拖动y 轴上表示实数m 的点运动,抛物线的形状会改变,可以体验到,∠ACD 和∠ADC 都可以成为直角.思路点拨1.用交点式求抛物线的解析式比较简便.2.连结OP ,△APC 可以割补为:△AOP 与△COP 的和,再减去△AOC .3.讨论△ACD 与△OBC 相似,先确定△ACD 是直角三角形,再验证两个直角三角形是否相似.4.直角三角形ACD 存在两种情况.图文解析(1)因为抛物线与x 轴交于A (-3, 0)、B (1, 0)两点,设y =a (x +3)(x -1).代入点C (0,-3m ),得-3m =-3a .解得a =m .所以该二次函数的解析式为y =m (x +3)(x -1)=mx 2+2mx -3m .(2)如图3,连结OP .当m =2时,C (0,-6),y =2x 2+4x -6,那么P (x , 2x 2+4x -6).由于S △AOP =1()2P OA y ⨯-=32-(2x 2+4x -6)=-3x 2-6x +9, S △COP =1()2P OC x ⨯-=-3x ,S △AOC =9, 所以S =S △APC =S △AOP +S △COP -S △AOC =-3x 2-9x =23273()24x -++. 所以当32x =-时,S 取得最大值,最大值为274.图3 图4 图5(3)如图4,过点D 作y 轴的垂线,垂足为E .过点A 作x 轴的垂线交DE 于F . 由y =m (x +3)(x -1)=m (x +1)2-4m ,得D (-1,-4m ).在Rt △OBC 中,OB ∶OC =1∶3m .如果△ADC 与△OBC 相似,那么△ADC 是直角三角形,而且两条直角边的比为1∶3m .①如图4,当∠ACD =90°时,OA OC EC ED =.所以331m m =.解得m =1. 此时3CA OC CD ED ==,3OC OB =.所以CA OC CD OB =.所以△CDA ∽△OBC . ②如图5,当∠ADC =90°时,FA FD ED EC =.所以421m m=.解得2m =. 此时222DA FD DC EC m===,而3232OC m OB ==.因此△DCA 与△OBC 不相似. 综上所述,当m =1时,△CDA ∽△OBC .考点伸展第(2)题还可以这样割补:如图6,过点P 作x 轴的垂线与AC 交于点H .由直线AC :y =-2x -6,可得H (x ,-2x -6).又因为P (x , 2x 2+4x -6),所以HP =-2x 2-6x .因为△PAH 与△PCH 有公共底边HP ,高的和为A 、C 两点间的水平距离3,所以S =S △APC =S △APH +S △CPH=32(-2x 2-6x ) =23273()24x -++. 图6例2 2014年省市中考第21题如图1,在直角梯形ABCD中,AB//CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.2·1·c·n·j·y(1)求AD的长;(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.动感体验图1请打开几何画板文件名“1421”,拖动点P在AB上运动,可以体验到,圆心O的运动轨迹是线段BC的垂直平分线上的一条线段.观察S随点P运动的图象,可以看到,S有最小值,此时点P看上去象是AB的中点,其实离得很近而已.思路点拨1.第(2)题先确定△PCB是直角三角形,再验证两个三角形是否相似.2.第(3)题理解△PCB的外接圆的圆心O很关键,圆心O在确定的BC的垂直平分线上,同时又在不确定的BP的垂直平分线上.而BP与AP是相关的,这样就可以以AP 为自变量,求S的函数关系式.图文解析(1)如图2,作CH⊥AB于H,那么AD=CH.在Rt△BCH中,∠B=60°,BC=4,所以BH=2,CH=23.所以AD=23.(2)因为△APD是直角三角形,如果△APD与△PCB相似,那么△PCB一定是直角三角形.①如图3,当∠CPB=90°时,AP=10-2=8.所以APAD =23=43,而PCPB=3.此时△APD与△PCB不相似.图2 图3 图4 ②如图4,当∠BCP=90°时,BP=2BC=8.所以AP=2.所以AP AD =23=3.所以∠APD =60°.此时△APD ∽△CBP . 综上所述,当x =2时,△APD ∽△CBP .(3)如图5,设△ADP 的外接圆的圆心为G ,那么点G 是斜边DP 的中点.设△PCB 的外接圆的圆心为O ,那么点O 在BC 边的垂直平分线上,设这条直线与BC 交于点E ,与AB 交于点F .设AP =2m .作OM ⊥BP 于M ,那么BM =PM =5-m .在Rt △BEF 中,BE =2,∠B =60°,所以BF =4.在Rt △OFM 中,FM =BF -BM =4-(5-m )=m -1,∠OFM =30°,所以OM =3(1)m -. 所以OB 2=BM 2+OM 2=221(5)(1)3m m -+-. 在Rt △ADP 中,DP 2=AD 2+AP 2=12+4m 2.所以GP 2=3+m 2.于是S =S 1+S 2=π(GP 2+OB 2)=22213(5)(1)3m m m π⎡⎤++-+-⎢⎥⎣⎦=2(73285)3m m π-+. 所以当167m =时,S 取得最小值,最小值为1137π.图5 图6考点伸展关于第(3)题,我们再讨论个问题.问题1,为什么设AP =2m 呢?这是因为线段AB =AP +PM +BM =AP +2BM =10. 这样BM =5-m ,后续可以减少一些分数运算.这不影响求S 的最小值.问题2,如果圆心O 在线段EF 的延长线上,S 关于m 的解析式是什么?如图6,圆心O 在线段EF 的延长线上时,不同的是FM =BM -BF =(5-m )-4=1-m .此时OB 2=BM 2+OM 2=221(5)(1)3m m -+-.这并不影响S 关于m 的解析式.例 3 2015年省湘西市中考第26题如图1,已知直线y =-x +3与x 轴、y 轴分别交于A 、B 两点,抛物线y =-x 2+bx +c 经过A 、B 两点,点P 在线段OA 上,从点O 出发,向点A 以每秒1个单位的速度匀速运动;同时,点Q 在线段AB 上,从点A 出发,向点B 以每秒2个单位的速度匀速运动,连结PQ ,设运动时间为t 秒.(1)求抛物线的解析式;(2)问:当t 为何值时,△APQ 为直角三角形;(3)过点P 作PE //y 轴,交AB 于点E ,过点Q 作QF //y 轴,交抛物线于点F ,连结EF ,当EF //PQ 时,求点F 的坐标;(4)设抛物线顶点为M ,连结BP 、BM 、MQ ,问:是否存在t 的值,使以B 、Q 、M 为顶点的三角形与以O 、B 、P 为顶点的三角形相似?若存在,请求出t 的值;若不存在,请说明理由. 图1动感体验请打开几何画板文件名“15湘西26”,拖动点P 在OA 上运动,可以体验到,△APQ 有两个时刻可以成为直角三角形,四边形EPQF 有一个时刻可以成为平行四边形,△MBQ 与△BOP 有一次机会相似.思路点拨1.在△APQ 中,∠A =45°,夹∠A 的两条边AP 、AQ 都可以用t 表示,分两种情况讨论直角三角形APQ .2.先用含t 的式子表示点P 、Q 的坐标,进而表示点E 、F 的坐标,根据PE =QF 列方程就好了.3.△MBQ 与△BOP 都是直角三角形,根据直角边对应成比例分两种情况讨论. 图文解析(1)由y =-x +3,得A (3, 0),B (0, 3).将A (3, 0)、B (0, 3)分别代入y =-x 2+bx +c ,得930,3.b c c -++=⎧⎨=⎩ 解得2,3.b c =⎧⎨=⎩ 所以抛物线的解析式为y =-x 2+2x +3.(2)在△APQ 中,∠PAQ =45°,AP =3-t ,AQ =2t .分两种情况讨论直角三角形APQ :①当∠PQA =90°时,AP =2AQ .解方程3-t =2t ,得t =1(如图2).②当∠QPA =90°时,AQ =2AP .解方程2t =2(3-t ),得t =1.5(如图3).图2 图3(3)如图4,因为PE //QF ,当EF //PQ 时,四边形EPQF 是平行四边形.所以EP =FQ .所以y E -y P =y F -y Q .因为x P =t ,x Q =3-t ,所以y E =3-t ,y Q =t ,y F =-(3-t )2+2(3-t )+3=-t 2+4t . 因为y E -y P =y F -y Q ,解方程3-t =(-t 2+4t )-t ,得t =1,或t =3(舍去).所以点F 的坐标为(2, 3).图4 图5(4)由y =-x 2+2x +3=-(x -1)2+4,得M (1, 4).由A (3, 0)、B (0, 3),可知A 、B 两点间的水平距离、竖直距离相等,AB =2. 由B (0, 3)、M (1, 4),可知B 、M 两点间的水平距离、竖直距离相等,BM 2 所以∠MBQ =∠BOP =90°.因此△MBQ 与△BOP 相似存在两种可能: ①当BM OB BQ OP =23322t t=-.解得94t =(如图5). ②当BM OP BQ OB =23322t t =-.整理,得t 2-3t +3=0.此方程无实根. 考点伸展第(3)题也可以用坐标平移的方法:由P (t , 0),E (t , 3-t ),Q(3-t , t ),按照P →E 方向,将点Q 向上平移,得F (3-t , 3).再将F (3-t , 3)代入y =-x 2+2x +3,得t =1,或t =3.§1.2 因动点产生的等腰三角形问题课前导学我们先回顾两个画图问题:1.已知线段AB =5厘米,以线段AB 为腰的等腰三角形ABC 有多少个?顶点C 的轨迹是什么?2.已知线段AB =6厘米,以线段AB 为底边的等腰三角形ABC 有多少个?顶点C 的轨迹是什么?已知腰长画等腰三角形用圆规画圆,圆上除了两个点以外,都是顶点C .已知底边画等腰三角形,顶角的顶点在底边的垂直平分线上,垂足要除外.在讨论等腰三角形的存在性问题时,一般都要先分类.如果△ABC 是等腰三角形,那么存在①AB =AC ,②BA =BC ,③CA =CB 三种情况. 解等腰三角形的存在性问题,有几何法和代数法,把几何法和代数法相结合,可以使得解题又好又快.几何法一般分三步:分类、画图、计算.哪些题目适合用几何法呢?如果△ABC 的∠A (的余弦值)是确定的,夹∠A 的两边AB 和AC 可以用含x 的式子表示出来,那么就用几何法.①如图1,如果AB =AC ,直接列方程;②如图2,如果BA =BC ,那么1cos 2AC AB A =∠;③如图3,如果CA =CB ,那么1cos 2AB AC A =∠. 代数法一般也分三步:罗列三边长,分类列方程,解方程并检验.如果三角形的三个角都是不确定的,而三个顶点的坐标可以用含x 的式子表示出来,那么根据两点间的距离公式,三边长(的平方)就可以罗列出来.图1 图2 图3例 9 2014年市中考第26题如图1,抛物线y =ax 2+bx +c (a 、b 、c 是常数,a ≠0)的对称轴为y 轴,且经过(0,0)和1(,)16a 两点,点P 在该抛物线上运动,以点P 为圆心的⊙P 总经过定点A (0, 2). (1)求a 、b 、c 的值;(2)求证:在点P 运动的过程中,⊙P 始终与x 轴相交;(3)设⊙P 与x 轴相交于M (x 1, 0)、N (x 2, 0)两点,当△AMN 为等腰三角形时,求圆心P 的纵坐标.图1动感体验请打开几何画板文件名“1426”,拖动圆心P 在抛物线上运动,可以体验到,圆与x 轴总是相交的,等腰三角形AMN 存在五种情况.思路点拨1.不算不知道,一算真奇妙,原来⊙P 在x 轴上截得的弦长MN =4是定值.2.等腰三角形AMN 存在五种情况,点P 的纵坐标有三个值,根据对称性,MA =MN 和NA =NM 时,点P 的纵坐标是相等的.图文解析(1)已知抛物线的顶点为(0,0),所以y =ax 2.所以b =0,c =0.将1(,)16a 代入y =ax 2,得2116a =.解得14a =(舍去了负值). (2)抛物线的解析式为214y x =,设点P 的坐标为21(,)4x x . 已知A (0, 2),所以222411(2)4416PA x x x =+-+>214x . 而圆心P 到x 轴的距离为214x ,所以半径PA >圆心P 到x 轴的距离. 所以在点P 运动的过程中,⊙P 始终与x 轴相交.(3)如图2,设MN 的中点为H ,那么PH 垂直平分MN .在Rt △PMH 中,2241416PM PA x ==+,22411()416PH x x ==,所以MH 2=4. 所以MH =2.因此MN =4,为定值.等腰△AMN 存在三种情况:①如图3,当AM =AN 时,点P 为原点O 重合,此时点P 的纵坐标为0.图2 图3 ②如图4,当MA =MN 时,在Rt △AOM 中,OA =2,AM =4,所以OM =23.此时x =OH =232+.所以点P 的纵坐标为22211(232)(31)42344x =+=+=+. 如图5,当NA =NM 时,根据对称性,点P 的纵坐标为也为423+.图4 图5③如图6,当NA =NM =4时,在Rt △AON 中,OA =2,AN =4,所以ON =23.此时x =OH =232-.所以点P 的纵坐标为22211(232)(31)42344x =-=-=-. 如图7,当MN =MA =4时,根据对称性,点P 的纵坐标也为423-.图6 图7考点伸展如果点P 在抛物线214y x =上运动,以点P 为圆心的⊙P 总经过定点B (0, 1),那么在点P 运动的过程中,⊙P 始终与直线y =-1相切.这是因为:设点P 的坐标为21(,)4x x .已知B (0, 1),所以2114PB x ==+. 而圆心P 到直线y =-1的距离也为2114x +,所以半径PB =圆心P 到直线y =-1的距离.所以在点P 运动的过程中,⊙P 始终与直线y =-1相切.例 10 2014年省市中考第25题如图1,在平面直角坐标系中,O 为坐标原点,抛物线y =ax 2+bx +c (a ≠0)过O 、B 、C 三点,B 、C 坐标分别为(10, 0)和1824(,)55-,以OB 为直径的⊙A 经过C 点,直线l 垂直x 轴于B 点.(1)求直线BC 的解析式;(2)求抛物线解析式及顶点坐标;(3)点M 是⊙A 上一动点(不同于O 、B ),过点M 作⊙A 的切线,交y 轴于点E ,交直线l 于点F ,设线段ME 长为m ,MF 长为n ,请猜想mn 的值,并证明你的结论;(4)若点P 从O 出发,以每秒1个单位的速度向点B 作直线运动,点Q 同时从B 出发,以相同速度向点C 作直线运动,经过t (0<t ≤8)秒时恰好使△BPQ 为等腰三角形,请求出满足条件的t 值. 图图1 动感体验请打开几何画板文件名“1425”,拖动点M 在圆上运动,可以体验到,△EAF 保持直角三角形的形状,AM 是斜边上的高.拖动点Q 在BC 上运动,可以体验到,△BPQ 有三个时刻可以成为等腰三角形.思路点拨1.从直线BC 的解析式可以得到∠OBC 的三角比,为讨论等腰三角形BPQ 作铺垫.2.设交点式求抛物线的解析式比较简便.3.第(3)题连结AE 、AF 容易看到AM 是直角三角形EAF 斜边上的高.4.第(4)题的△PBQ 中,∠B 是确定的,夹∠B 的两条边可以用含t 的式子表示.分三种情况讨论等腰三角形.图文解析(1)直线BC 的解析式为31542y x =-. (2)因为抛物线与x 轴交于O 、B (10, 0)两点,设y =ax (x -10). 代入点C 1824(,)55-,得241832()555a -=⨯⨯-.解得524a =. 所以2255255125(10)(5)2424122424y x x x x x =-=-=--. 抛物线的顶点为125(5,)24-. (3)如图2,因为EF 切⊙A 于M ,所以AM ⊥EF . 由AE =AE ,AO =AM ,可得Rt △AOE ≌Rt △AME .所以∠1=∠2.同理∠3=∠4.于是可得∠EAF =90°.所以∠5=∠1.由tan ∠5=tan ∠1,得MA ME MF MA=. 所以ME ·MF =MA 2,即mn =25.图2(4)在△BPQ 中,cos ∠B =45,BP =10-t ,BQ =t . 分三种情况讨论等腰三角形BPQ : ①如图3,当BP =BQ 时,10-t =t .解得t =5.②如图4,当PB =PQ 时,1cos 2BQ BP B =∠.解方程14(10)25t t =-,得8013t =. ③如图5,当QB =QP 时,1cos 2BP BQ B =∠.解方程14(10)25t t -=,得5013t =.图3 图4 图5考点伸展在第(3)题条件下,以EF 为直径的⊙G 与x 轴相切于点A .如图6,这是因为AG 既是直角三角形EAF 斜边上的中线,也是直角梯形EOBF 的中位线,因此圆心G 到x 轴的距离等于圆的半径,所以⊙G 与x 轴相切于点A .图6例11 2014年省市中考第26题在平面直角坐标系中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C.(1)若m=2,n=1,求A、B两点的坐标;(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,-1),求∠ACB的大小;(3)若m=2,△ABC是等腰三角形,求n的值.动感体验请打开几何画板文件名“1426”,点击屏幕左下方的按钮(2),拖动点A在x轴正半轴上运动,可以体验到,△ABC保持直角三角形的形状.点击屏幕左下方的按钮(3),拖动点B在x轴上运动,观察△ABC的顶点能否落在对边的垂直平分线上,可以体验到,等腰三角形ABC有4种情况.思路点拨1.抛物线的解析式可以化为交点式,用m,n表示点A、B、C的坐标.2.第(2)题判定直角三角形ABC,可以用勾股定理的逆定理,也可以用锐角的三角比.3.第(3)题讨论等腰三角形ABC,先把三边长(的平方)罗列出来,再分类解方程.图文解析(1)由y=x2-(m+n)x+mn=(x-m)(x-n),且m>n,点A位于点B的右侧,可知A(m, 0),B(n, 0).若m=2,n=1,那么A(2, 0),B(1, 0)..(2)如图1,由于C(0, mn),当点C的坐标是(0,-1),mn=-1,OC=1.若A、B两点分别位于y轴的两侧,那么OA·OB=m(-n)=-mn=1.所以OC2=OA·OB.所以OC OB.OA OC所以tan ∠1=tan ∠2.所以∠1=∠2.又因为∠1与∠3互余,所以∠2与∠3互余.所以∠ACB =90°.图1 图2 图3(3)在△ABC 中,已知A (2, 0),B (n , 0),C (0, 2n ).讨论等腰三角形ABC ,用代数法解比较方便:由两点间的距离公式,得AB 2=(n -2)2,BC 2=5n 2,AC 2=4+4n 2.①当AB =AC 时,解方程(n -2)2=4+4n 2,得43n =-(如图2). ②当CA =CB 时,解方程4+4n 2=5n 2,得n =-2(如图3),或n =2(A 、B 重合,舍去).③当BA =BC 时,解方程(n -2)2=5n 2,得51n +=-(如图4),或51n -=(如图5).图4 图5考点伸展第(2)题常用的方法还有勾股定理的逆定理.由于C (0, mn ),当点C 的坐标是(0,-1),mn =-1.由A (m , 0),B (n , 0),C (0,-1),得AB 2=(m -n )2=m 2-2mn +n 2=m 2+n 2+2, BC 2=n 2+1,AC 2=m 2+1.所以AB 2=BC 2+AC 2.于是得到Rt △ABC ,∠ACB =90°.第(3)题在讨论等腰三角形ABC 时,对于CA =CB 的情况,此时A 、B 两点关于y轴对称,可以直接写出B (-2, 0),n =-2.例 12 2014年省市中考第27题如图1,在△ABC 中,∠ACB =90°,AC =4cm ,BC =3cm .如果点P 由点B 出发沿BA 方向向点A 匀速运动,同时点Q 由点A 出发沿AC 方向向点C 匀速运动,它们的速度均为1cm/s .连结PQ ,设运动时间为t (s )(0<t <4),解答下列问题:(1)设△APQ 的面积为S ,当t 为何值时,S 取得最大值?S 的最大值是多少?(2)如图2,连结PC ,将△PQC 沿QC 翻折,得到四边形PQP ′C ,当四边形PQP ′C 为菱形时,求t 的值;(3)当t 为何值时,△APQ 是等腰三角形?图1 图2动感体验请打开几何画板文件名“1427”,拖动点Q 在AC 上运动,可以体验到,当点P 运动到AB 的中点时,△APQ 的面积最大,等腰三角形APQ 存在三种情况.还可以体验到,当QC =2HC 时,四边形PQP ′C 是菱形.思路点拨1.在△APQ 中,∠A 是确定的,夹∠A 的两条边可以用含t 的式子表示.2.四边形PQP ′C 的对角线保持垂直,当对角线互相平分时,它是菱形,.图文解析(1)在Rt △ABC 中,AC =4,BC =3,所以AB =5,sin A =35,cos A =45. 作QD ⊥AB 于D ,那么QD =AQ sin A =35t . 所以S =S △APQ =12AP QD ⋅=13(5)25t t -⨯=23(5)10t t --=23515()+1028t --. 当52t =时,S 取得最大值,最大值为158.(2)设PP ′与AC 交于点H ,那么PP ′⊥QC ,AH =AP cos A =4(5)5t -.如果四边形PQP ′C 为菱形,那么PQ =PC .所以QC =2HC . 解方程4424(5)5t t ⎡⎤-=⨯--⎢⎥⎣⎦,得2013t =.图3 图4(3)等腰三角形APQ 存在三种情况:①如图5,当AP =AQ 时,5-t =t .解得52t =. ②如图6,当PA =PQ 时,1cos 2AQ AP A =.解方程14(5)25t t =-,得4013t =. ③如图7,当QA =QP 时,1cos 2AP AQ A =.解方程14(5)25t t -=,得2513t =.图5 图6 图7考点伸展在本题情境下,如果点Q 是△PP ′C 的重心,求t 的值.如图8,如果点Q 是△PP ′C 的重心,那么QC =23HC . 解方程2444(5)35t t ⎡⎤-=⨯--⎢⎥⎣⎦,得6023t =.图8例 13 2015年省市中考第22题如图1,已知Rt △ABC 中,∠C =90°,AC =8,BC =6,点P 以每秒1个单位的速度从A 向C 运动,同时点Q 以每秒2个单位的速度从A →B →C 方向运动,它们到C 点后都停止运动,设点P 、Q 运动的时间为t 秒.(1)在运动过程中,求P 、Q 两点间距离的最大值;(2)经过t 秒的运动,求△ABC 被直线PQ 扫过的面积S 与时间t 的函数关系式;(3)P ,Q 两点在运动过程中,是否存在时间t ,使得△PQC 为等腰三角形.若存在,求出此时的t 值,若不存在,请说明理由.(24.25≈,结果保留一位小数)图1动感体验请打开几何画板文件名“1522”,拖动点P 在AC 上运动,可以体验到,PQ 与BD 保持平行,等腰三角形PQC 存在三种情况.思路点拨1.过点B 作QP 的平行线交AC 于D ,那么BD 的长就是PQ 的最大值.2.线段PQ 扫过的面积S 要分两种情况讨论,点Q 分别在AB 、BC 上.3.等腰三角形PQC 分三种情况讨论,先罗列三边长.图文解析(1)在Rt △ABC 中,AC =8,BC =6,所以AB =10.如图2,当点Q 在AB 上时,作BD //PQ 交AC 于点D ,那么22AB AQ t AD AP t===. 所以AD =5.所以CD =3. 如图3,当点Q 在BC 上时,16228CQ t CP t-==-. 又因为623CB CD ==,所以CQ CB CP CD =.因此PQ //BD .所以PQ 的最大值就是BD . 在Rt △BCD 中,BC =6,CD =3,所以BD =35.所以PQ 的最大值是35.图2 图3 图4(2)①如图2,当点Q 在AB 上时,0<t ≤5,S △ABD =15.由△AQP ∽△ABD ,得2()AQPABDS AP S AD =△△.所以S =S △AQP =215()5t ⨯=235t . ②如图3,当点Q 在BC 上时,5<t ≤8,S △ABC =24. 因为S △CQP =12CQ CP ⋅=1(162)(8)2t t --=2(8)t -,所以S =S △ABC -S △CQP =24-(t -8)2=-t 2+16t -40.(3)如图3,当点Q 在BC 上时,CQ =2CP ,∠C =90°,所以△PQC 不可能成为等腰三角形.当点Q 在AB 上时,我们先用t 表示△PQC 的三边长:易知CP =8-t .如图2,由QP //BD ,得QP AP BD AD =,即535t =.所以35QP t =. 如图4,作QH ⊥AC 于H .在Rt △AQH 中,QH =AQ sin ∠A =65t ,AH =85t . 在Rt △CQH 中,由勾股定理,得CQ =22QH CH +=2268()(8)55t t +-. 分三种情况讨论等腰三角形PQC :(1)①当PC =PQ 时,解方程358t t -=,得6510t =-≈3.4(如图5所示). ②当QC =QP 时,226835()(8)55t t t +-=.整理,得2111283200t t -+=. 所以(11t -40)(t -8)=0.解得4011t =≈3.6(如图6所示),或t =8(舍去). ③当CP =CQ 时,22688()(8)55t t t -=+-.整理,得25160t t -=.解得165t ==3.2(如图7所示),或t =0(舍去). 综上所述,当t 的值约为3.4,3.6,或等于3.2时,△PQC 是等腰三角形.图5 图6 图7考点伸展第(1)题求P 、Q 两点间距离的最大值,可以用代数计算说理的方法:①如图8,当点Q 在AB 上时,PQ =22QH PH +=2268()()55t t t +-=35t . 当Q 与B 重合时,PQ 最大,此时t =5,PQ 的最大值为35.②如图9,当点Q 在BC 上时,PQ =22CQ CP +=22(2)CP CP +=5(8)t -. 当Q 与B 重合时,PQ 最大,此时t =5,PQ 的最大值为35.综上所述,PQ 的最大值为35.图8 图9§1.3 因动点产生的直角三角形问题课前导学我们先看三个问题:1.已知线段AB ,以线段AB 为直角边的直角三角形ABC 有多少个?顶点C 的轨迹是什么?2.已知线段AB ,以线段AB 为斜边的直角三角形ABC 有多少个?顶点C 的轨迹是什么?3.已知点A (4,0),如果△OAB 是等腰直角三角形,求符合条件的点B 的坐标.图1 图2 图3如图1,点C 在垂线上,垂足除外.如图2,点C 在以AB 为直径的圆上,A 、B 两点除外.如图3,以OA为边画两个正方形,除了O、A两点以外的顶点和正方形对角线的交点,都是符合题意的点B,共6个.解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根.一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程.有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.如图4,已知A(3, 0),B(1,-4),如果直角三角形ABC的顶点C在y轴上,求点C的坐标.我们可以用几何的方法,作AB为直径的圆,快速找到两个符合条件的点C.如果作BD⊥y轴于D,那么△AOC∽△CDB.设OC=m,那么341mm-=.这个方程有两个解,分别对应图中圆与y轴的两个交点.图4例19 2015年省市中考第21题如图1,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y轴的对称点分别为点A′、B′.(1)求m的值及抛物线E2所表示的二次函数的表达式;(2)如图1,在第一象限,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;(3)如图2,P为第一象限的抛物线E1上与点A不重合的一点,连结OP并延长与抛物线E2相交于点P′,求△PAA′与△P′BB′的面积之比.。
中考数学复习---《反比例函数综合》压轴题练习(含答案解析)
中考数学复习---《反比例函数综合》压轴题练习(含答案解析)一.反比例函数系数k的几何意义(共4小题)1.(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图像上.若BD∥y轴,点D的横坐标为3,则k1+k2=()A.36B.18C.12D.9【答案】B【解答】解:连接AC交于E,延长BD交x轴于F,连接OD、OB,如图:∵四边形ABCD是正方形,∴AE=BE=CE=DE,设AE=BE=CE=DE=m,D(3,a),∵BD∥y轴,∴B(3,a+2m),A(3+m,a+m),∵A,B都在反比例函数y=(k1>0)的图像上,∴k1=3(a+2m)=(3+m)(a+m),∵m≠0,∴m=3﹣a,∴B(3,6﹣a),∵B(3,6﹣a)在反比例函数y=(k1>0)的图像上,D(3,a)在y=(k2>0)的图像上,∴k1=3(6﹣a)=18﹣3a,k2=3a,∴k1+k2=18﹣3a+3a=18;故选:B.2.(2022•通辽)如图,点D是▱OABC内一点,AD与x轴平行,BD与y轴平行,BD=,∠BDC=120°,S△BCD=,若反比例函数y=(x<0)的图像经过C,D两点,则k的值是()A.﹣6B.﹣6C.﹣12D.﹣12【答案】C【解答】解:过点C作CE⊥y轴,延长BD交CE于点F,∵四边形OABC为平行四边形,∴AB∥OC,AB=OC,∴∠COE=∠1,∵BD与y轴平行,∴∠1=∠ABD,∠ADB=90°,∴∠COE=∠ABD,在△COE和△ABD中,,∴△COE≌△ABD(AAS),∴OE=BD=,∵S△BDC=BD•CF=,∴CF=9,∵∠BDC=120°,∴∠CDF=60°,∴DF=3,点D的纵坐标为4,设C(m,),则D(m+9,4),∵反比例函数y=(x<0)的图像经过C,D两点,∴k=m=4(m+9),∴m=﹣12,∴k=﹣12,故选:C.3.(2022•宜宾)如图,△OMN是边长为10的等边三角形,反比例函数y=(x >0)的图像与边MN、OM分别交于点A、B(点B不与点M重合).若AB ⊥OM于点B,则k的值为.【答案】9【解答】解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,如图,∵△OMN是边长为10的等边三角形,∴OM=ON=MN=10,∠MON=∠M=∠MNO=60°设OC=b,则BC=,OB=2b,∴BM=OM﹣OB=10﹣2b,B(b,b),∵∠M=60°,AB⊥OM,∴AM=2BM=20﹣4b,∴AN=MN﹣AM=10﹣(20﹣4b)=4b﹣10,∵∠AND=60°,∴DN==2b﹣5,AD=AN=2b﹣5,∴OD=ON﹣DN=15﹣2b,∴A(15﹣2b,2b﹣5),∵A、B两点都在反比例函数y=(x>0)的图像上,∴k=(15﹣2b)(2b﹣5)=b•b,解得b=3或5,当b=5时,OB=2b=10,此时B与M重合,不符题意,舍去,∴b=3,∴k=b•b=9,故答案为:9.4.(2022•乐山)如图,平行四边形ABCD的顶点A在x轴上,点D在y=(k >0)上,且AD⊥x轴,CA的延长线交y轴于点E.若S△ABE=,则k=.【答案】3【解答】解:设BC与x轴交于点F,连接DF、OD,∵四边形ABCD为平行四边形,∴AD∥BC,∴S△ODF=S△EBC,S△ADF=S△ABC,∴S△OAD=S△ABE=,∴k=3,故答案为:3.二.反比例函数图像上点的坐标特征(共4小题)5.(2022•宿迁)如图,点A在反比例函数y=(x>0)的图像上,以OA为一边作等腰直角三角形OAB,其中∠OAB=90°,AO=AB,则线段OB长的最小值是()A.1B.C.2D.4【答案】C【解答】解:∵三角形OAB是等腰直角三角形,∴当OB最小时,OA最小,设A点坐标为(a,),∴OA=,∵≥0,即:﹣4≥0,∴≥4,∵≥0,两边同时开平方得:a﹣=0,∴当a=时,OA有最小值,解得a1=,a2=﹣(舍去),∴A点坐标为(,),∴OA=2,∵三角形OAB是等腰直角三角形,OB为斜边,∴OB=OA=2.故选:C.6.(2022•枣庄)如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为()A.4B.﹣4C.﹣3D.3【答案】C【解答】解:如图,过点C作CE⊥y轴于E,在正方形ABCD中,AB=BC,∠ABC=90°,∴∠ABO+∠CBE=90°,∵∠OAB+∠ABO=90°,∴∠OAB=∠CBE,∵点A的坐标为(4,0),∴OA=4,∵AB=5,∴OB==3,在△ABO和△BCE中,,∴△ABO≌△BCE(AAS),∴OA=BE=4,CE=OB=3,∴OE=BE﹣OB=4﹣3=1,∴点C的坐标为(﹣3,1),∵反比例函数y=(k≠0)的图像过点C,∴k=xy=﹣3×1=﹣3,故选:C.7.(2022•江西)已知点A在反比例函数y=(x>0)的图像上,点B在x 轴正半轴上,若△OAB为等腰三角形,且腰长为5,则AB的长为.【答案】5或2或【解答】解:当AO=AB时,AB=5;当AB=BO时,AB=5;当OA=OB时,设A(a,)(a>0),B(5,0),∵OA=5,∴=5,解得:a1=3,a2=4,∴A(3,4)或(4,3),∴AB==2或AB==;综上所述,AB的长为5或2或.故答案为:5或2或.8.(2022•宁波)如图,四边形OABC为矩形,点A在第二象限,点A关于OB的对称点为点D,点B,D都在函数y=(x>0)的图像上,BE⊥x 轴于点E.若DC的延长线交x轴于点F,当矩形OABC的面积为9时,的值为,点F的坐标为.【答案】,(,0).【解答】解:如图,方法一:作DG⊥x轴于G,连接OD,设BC和OD交于I,设点B(b,),D(a,),由对称性可得:△BOD≌△BOA≌△OBC,∴∠OBC=∠BOD,BC=OD,∴OI=BI,∴DI=CI,∴=,∵∠CID=∠BIO,∴△CDI∽△BOI,∴∠CDI=∠BOI,∴CD∥OB,∴S△BOD=S△AOB=S矩形AOCB=,∵S△BOE=S△DOG==3,S四边形BOGD=S△BOD+S△DOG=S梯形BEGD+S△BOE,∴S梯形BEGD=S△BOD=,∴•(a﹣b)=,∴2a2﹣3ab﹣2b2=0,∴(a﹣2b)•(2a+b)=0,∴a=2b,a=﹣(舍去),∴D(2b,),即:(2b,),在Rt△BOD中,由勾股定理得,OD2+BD2=OB2,∴[(2b)2+()2]+[(2b﹣b)2+(﹣)2]=b2+()2,∴b=,∴B(,2),D(2,),∵直线OB的解析式为:y=2x,∴直线DF的解析式为:y=2x﹣3,当y=0时,2﹣3=0,∴x=,∴F(,0),∵OE=,OF=,∴EF=OF﹣OE=,∴=,方法二:如图,连接BF,BD,作DG⊥x轴于G,直线BD交x轴于H,由上知:DF∥OB,∴S△BOF=S△BOD=,∵S△BOE=|k|=3,∴==,设EF=a,FG=b,则OE=2a,∴BE=,OG=3a+b,DG=,∵△BOE∽△DFG,∴=,∴=,∴a=b,a=﹣(舍去),∴D(4a,),∵B(2a,),∴==,∴GH=EG=2a,∵∠ODH=90°,DG⊥OH,∴△ODG∽△DHG,∴,∴,∴a=,∴3a=,∴F(,0)故答案为:,(,0).三.待定系数法求反比例函数解析式(共1小题)9.(2022•湖州)如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图像经过点C的反比例函数的解析式是y=,则图像经过点D的反比例函数的解析式是.【答案】y=﹣【解答】解:如图,过点C作CT⊥y轴于点T,过点D作DH⊥CT交CT的延长线于点H.∵tan∠ABO==3,∴可以假设OB=a,OA=3a,∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠AOB=∠BTC=90°,∴∠ABO+∠CBT=90°,∠CBT+∠BCT=90°,∴∠ABO=∠BCT,∴△AOB≌△BTC(AAS),∴BT=OA=3a,OB=TC=a,∴OT=BT﹣OB=2a,∴C(a,2a),∵点C在y=上,∴2a2=1,同法可证△CHD≌△BTC,∴DH=CT=a,CH=BT=3a,∴D(﹣2a,3a),设经过点D的反比例函数的解析式为y=,则有﹣2a×3a=k,∴k=﹣6a2=﹣3,∴经过点D的反比例函数的解析式是y=﹣.故答案为:y=﹣.四.反比例函数与一次函数的交点问题(共2小题)10.(2022•怀化)如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图像于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a 的值为()A.8B.9C.10D.11【答案】D【解答】解:设点B的坐标为(m,),∵S△BCD=5,且a>1,∴×m×=5,解得:a=11,故选:D.11.(2022•巴中)将双曲线y=向右平移2个单位,再向下平移1个单位,得到的新双曲线与直线y=k i(x﹣2)﹣1(k i>0,i=1,2,3, (1011)相交于2022个点,则这2022个点的横坐标之和为.【答案】4044【解答】解:直线y=k i(x﹣2)﹣1(k i>0,i=1,2,3,⋅⋅⋅,1011)可由直线y=k i x(k i>0,i=1,2,3,⋅⋅⋅,1011)向右平移2个单位,再向下平移1个单位得到,∴直线y=k i x(k i>0,i=1,2,3,⋅⋅⋅,1011)到直线y=k i(x﹣2)﹣1(k i>0,i=1,2,3,⋅⋅⋅,1011)的平移方式与双曲线双曲线的相同,∴新双曲线与直线y=k i(x﹣2)﹣1(k i>0,i=1,2,3,⋅⋅⋅,1011)的交点也可以由双曲线与直线y=k i x(k i>0,i=1,2,3,⋅⋅⋅,1011)的交点以同样的方式平移得到,设双曲线与直线y=k i x(k i>0,i=1,2,3,⋅⋅⋅,1011)的交点的横坐标为x i,x'i,(i=1,2,3,⋅⋅⋅,1011),则新双曲线与直线y=k i(x﹣2)﹣1(k i>0,i=1,2,3,⋅⋅⋅,1011)的交点的横坐标为x i+2,x'i+2(i=1,2,3,⋅⋅⋅,1011),根据双曲线与直线y=k i x(k i>0,i=1,2,3,⋅⋅⋅,1011)图像都关于原点对称,可知双曲线与直线y=k i x(k i>0,i=1,2,3,⋅⋅⋅,1011)的交点也关于原点对称,∴x i+x'i=0,(i=1,2,3,⋅⋅⋅,1011),∴(x i+2)+(x'i+2)=4(i=1,2,3,⋅⋅⋅,1011),即新双曲线与直线y=k i(x﹣2)﹣1(k i>0,i=1,2,3,⋅⋅⋅,1011)的交点的横坐标之和都是4,∴这2022个点的横坐标之和为:4×1011=4044.故答案是:4044.。
中考数学反比例函数-经典压轴题附答案

中考数学反比例函数-经典压轴题附答案一、反比例函数1.如图,反比例函数y= 的图象与一次函数y=kx+b的图象交于A、B两点,点A的坐标为(2,3n),点B的坐标为(5n+2,1).(1)求反比例函数与一次函数的表达式;(2)将一次函数y=kx+b的图象沿y轴向下平移a个单位,使平移后的图象与反比例函数y= 的图象有且只有一个交点,求a的值;(3)点E为y轴上一个动点,若S△AEB=5,则点E的坐标为________.【答案】(1)解:∵A、B在反比例函数的图象上,∴2×3n=(5n+2)×1=m,∴n=2,m=12,∴A(2,6),B(12,1),∵一次函数y=kx+b的图象经过A、B两点,∴,解得,∴反比例函数与一次函数的表达式分别为y= ,y=﹣ x+7.(2)解:设平移后的一次函数的解析式为y=﹣ x+7﹣a,由,消去y得到x2+(2a﹣14)x+24=0,由题意,△=0,(21a﹣14)2﹣4×24=0,解得a=7±2 .(3)(0,6)或(0,8)【解析】【解答】(3)设直线AB交y轴于K,则K(0,7),设E(0,m),由题意,PE=|m﹣7|.∵S△AEB=S△BEP﹣S△AEP=5,∴ ×|m﹣7|×(12﹣2)=5.∴|m﹣7|=1.∴m1=6,m2=8.∴点E的坐标为(0,6)或(0,8).故答案为(0,6)或(0,8).【分析】(1)由A、B在反比例函数的图象上,得到n,m的值和A、B的坐标,用待定系数法求出反比例函数与一次函数的表达式;(2)由将一次函数y=kx+b的图象沿y轴向下平移a个单位,得到平移后的一次函数的解析式,由平移后的图象与反比例函数的图象有且只有一个交点,得到方程组求出a的值;(3)由点E为y轴上一个动点和S△AEB=5,求出点E的坐标.2.如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y= 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.(1)求双曲线和抛物线的解析式;(2)计算△ABC的面积;(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.【答案】(1)解:把点A的坐标代入双曲线的解析式得:k=﹣1×4=﹣4.所以双曲线的解析式为y=﹣.设点B的坐标为(m,﹣m).∵点B在双曲线上,∴﹣m2=﹣4,解得m=2或m=﹣2.∵点B在第四象限,∴m=2.∴B(2,﹣2).将点A、B、C的坐标代入得:,解得:.∴抛物线的解析式为y=x2﹣3x.(2)解:如图1,连接AC、BC.令y=0,则x2﹣3x=0,∴x=0或x=3,∴C(3,0),∵A(﹣1,4),B(2,﹣2),∴直线AB的解析式为y=﹣2x+2,∵点D是直线AB与x轴的交点,∴D(1,0),∴S△ABC=S△ADC+S△BDC= ×2×4+ ×2×2=6;(3)解:存在,理由:如图2,由原抛物线的解析式为y=x2﹣3x=(x﹣)2﹣,∴原抛物线的顶点坐标为(,﹣),∴抛物线向左平移个单位,再向上平移个单位,而平移前A(﹣1,4),B(2,﹣2),∴平移后点A(﹣,),B(,),∴点A关于y轴的对称点A'(,),连接A'B并延长交y轴于点P,连接AP,由对称性知,∠APE=∠BPE,∴△APB的内切圆的圆心在y轴上,∵B(,),A'(,),∴直线A'B的解析式为y=3x﹣,∴P(0,﹣).【解析】【分析】(1)首先将点A的坐标代入反比例函数的解析式求得k的值,然后再求得B的值,最后根据点A的坐标求出双曲线的解析式,进而得出点B的坐标,最后,将点A、B、O三点的坐标代入抛物线的解析式,求得a、b、c的值即可;(2)由点A和点B的坐标可求得直线AB的解析式,然后将y=0可求得点D的横坐标,最后用三角形的面积和求解即可;(3)先确定出平移后点A,B的坐标,进而求出点A关于y轴的对称点的坐标,求出直线BA'的解析式即可得出点P的坐标.3.如图,在平面直角坐标系中,平行四边形的边,顶点坐标为,点坐标为 .(1)点的坐标是________,点的坐标是________(用表示);(2)若双曲线过平行四边形的顶点和,求该双曲线的表达式;(3)若平行四边形与双曲线总有公共点,求的取值范围.【答案】(1);(2)解:∵双曲线过点和点,∴,解得,∴点的坐标为,点的坐标为,把点的坐标代入,解得,∴双曲线表达式为(3)解:∵平行四边形与双曲线总有公共点,∴当点在双曲线,得到,当点在双曲线,得到,∴的取值范围 .【解析】【分析】(1)由四边形ABCD为平行四边形,得到A与B纵坐标相同,C与D纵坐标相同,横坐标相差2,得出B、C坐标即可;(2)根据B与D在反比例图象上,得到C与D横纵坐标乘积相等,求出b的值确定出B坐标,进而求出k的值,确定出双曲线解析式;(3)抓住两个关键点,将A坐标代入双曲线解析式求出b的值;将C坐标代入双曲线解析式求出b的值,即可确定出平行四边形与双曲线总有公共点时b的范围.4.如图,过原点O的直线与双曲线交于上A(m,n)、B,过点A的直线交x轴正半轴于点D,交y轴负半轴于点E,交双曲线于点P.(1)当m=2时,求n的值;(2)当OD:OE=1:2,且m=3时,求点P的坐标;(3)若AD=DE,连接BE,BP,求△PBE的面积.【答案】(1)解:∵点A(m,n)在双曲线y=上,∴mn=6,∵m=2,∴n=3;(2)解:由(1)知,mn=6,∵m=3,∴n=2,∴A(3,2),∵OD:OE=1:2,设OD=a,则OE=2a,∵点D在x轴坐标轴上,点E在y轴负半轴上,∴D(a,0),E(0,﹣2a),∴直线DE的解析式为y=2x﹣2a,∵点A(3,2)在直线y=2x﹣2a上,∴6﹣2a=2,∴a=2,∴直线DE的解析式为y=2x﹣4①,∵双曲线的解析式为y=②,联立①②解得,(点A的横纵坐标,所以舍去)或,∴P(﹣2,﹣3);(3)解:∵AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,A(m,n),∴E(0,﹣n),D( m,0),∴直线DE的解析式为y= x﹣n,∵mn=6,∴m=,∴y= x﹣n③,∵双曲线的解析式为y=④,联立③④解得,∴(点A的横纵坐标,所以舍去)或,∴P(﹣2m,﹣2n),∵A(m,n),∴直线AB的解析式为y=x⑤.联立④⑤解得,(点A的横纵坐标,所以舍去)或∴B(﹣m,﹣n),∵E(0,﹣n),∴BE∥x轴,∴S△PBE= BE×|y E﹣y P|= ×m×|﹣n﹣(﹣2n)|= mn=3.【解析】【分析】(1)把A(2,n)代入解析式即可求出n;(2)先求出A点坐标,设OD=a,则OE=2a,得D(a,0),E(0,﹣2a),直线DE的解析式为y=2x﹣2a,把点A(3,2)代入求出a,再联立两函数即可求出交点P;(3)由AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,故A(m,n),E(0,﹣n),D( m,0),求得直线DE 的解析式为y= x﹣n,又mn=6,得y= x﹣n,与y=联立得,即为P点坐标,由直线AB的解析式为y= x与双曲线联立解得B (﹣m,﹣n),再根据S△PBE= BE×|y E﹣y P|= ×m×|﹣n﹣(﹣2n)|求出等于3.5.如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.(1)求直线AB和反比例函数的解析式;(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.【答案】(1)解:设反比例函数解析式为y= ,把B(﹣2,﹣3)代入,可得k=﹣2×(﹣3)=6,∴反比例函数解析式为y= ;把A(3,m)代入y= ,可得3m=6,即m=2,∴A(3,2),设直线AB 的解析式为y=ax+b,把A(3,2),B(﹣2,﹣3)代入,可得,解得,∴直线AB 的解析式为y=x﹣1(2)解:由题可得,当x满足:x<﹣2或0<x<3时,直线AB在双曲线的下方(3)解:存在点C.如图所示,延长AO交双曲线于点C1,∵点A与点C1关于原点对称,∴AO=C1O,∴△OBC1的面积等于△OAB的面积,此时,点C1的坐标为(﹣3,﹣2);如图,过点C1作BO的平行线,交双曲线于点C2,则△OBC2的面积等于△OBC1的面积,∴△OBC2的面积等于△OAB的面积,由B(﹣2,﹣3)可得OB的解析式为y= x,可设直线C1C2的解析式为y= x+b',把C1(﹣3,﹣2)代入,可得﹣2= ×(﹣3)+b',解得b'= ,∴直线C1C2的解析式为y= x+ ,解方程组,可得C2();如图,过A作OB的平行线,交双曲线于点C3,则△OBC3的面积等于△OBA的面积,设直线AC3的解析式为y= x+ ,把A(3,2)代入,可得2= ×3+ ,解得 =﹣,∴直线AC3的解析式为y= x﹣,解方程组,可得C3();综上所述,点C的坐标为(﹣3,﹣2),(()).【解析】【分析】(1)用待定系数法求出反比例函数解析式,一次函数解析式,将已知的点A,B的坐标代入设的函数解析式列出关于待定系数的方程(组)求出系数,再回代到解析式(2)结合图像判断直线AB在双曲线的交点坐标为A,B,X取值范围为双曲线所在象限交点的横坐标,第一象限为为小于横坐标大于零,第三象限为小于横坐标(3)结合已知条件根据同底等高、等底同高作出与原三角形面积相等的三角形,再结合已知条件用待定系数法求出与双曲线有交点的直线的解析式,得出点的坐标,注意要考虑满足条件的所有点C的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.(2017滨州,第12题,3分)在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线1yx=相交于点A、B,且AC+BC=4,则△OAB的面积为()A.23+3或23﹣3B.2 +1或2﹣1C.23﹣3D.2﹣1【答案】A.【分析】根据题意表示出AC,BC的长,进而得出等式求出m的值,进而得出答案.点睛:此题主要考查了反比例函数与一次函数的交点,正确表示出各线段长是解题关键.考点:反比例函数与一次函数的交点问题.2.(2017广西桂林市,第11题,3分)一次函数y=﹣x+1(0≤x≤10)与反比例函数1yx=(﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1,y1),(x2,y2)是图象上两个不同的点,若y1=y2,则x1+x2的取值范围是()A .﹣8910≤x ≤1 B .﹣8910≤x ≤899 C .﹣899≤x ≤8910 D .1≤x ≤8910【答案】B .【分析】由x 的取值范围结合y 1=y 2可求出y 的取值范围,根据y 关于x 的关系式可得出x 关于y 的关系式,利用做差法求出x =1﹣y +1y 再﹣9≤y ≤﹣110中的单调性,依此单调性即可求出x 1+x 2的取值范围. 【解析】当x =﹣10时,1y x ==﹣110; 当x =10时,y =﹣x +1=﹣9,∴﹣9≤y 1=y 2≤﹣110. 设x 1<x 2,则y 2=﹣x 2+1、y 1=11x ,∴x 2=1﹣y 2,x 1=11y ,∴x 1+x 2=1﹣y 2+11y . 设x =1﹣y +1y (﹣9≤y ≤﹣110),﹣9≤y m <y n ≤﹣110,则x n ﹣x m =y m ﹣y n +11n m y y -=(y m ﹣y n )(1+1m n y y )<0,∴x =1﹣y +1y 中x 值随y 值的增大而减小,∴1﹣(﹣110)﹣10=﹣8910≤x ≤1﹣(﹣9)﹣19 =899. 故选B .点睛:本题考查了反比例函数图象上点的坐标特征以及一次函数图象上点的坐标特征,找出x =1﹣y +1y在﹣9≤y ≤﹣110中的单调性是解题的关键. 考点:反比例函数图象上点的坐标特征;一次函数图象上点的坐标特征.学科#网3.(2017新疆乌鲁木齐市,第10题,4分)如图,点A (a ,3),B (b ,1)都在双曲线3y x=上,点C ,D ,分别是x 轴,y 轴上的动点,则四边形ABCD 周长的最小值为( )A .52B .62C . 21022+D .82 【答案】B .【分析】先把A 点和B 点的坐标代入反比例函数解析式中,求出a 与b 的值,确定出A 与B 坐标,再作A 点关于y 轴的对称点P ,B 点关于x 轴的对称点Q ,根据对称的性质得到P 点坐标为(﹣1,3),Q 点坐标为(3,﹣1),PQ 分别交x 轴、y 轴于C 点、D 点,根据两点之间线段最短得此时四边形P ABQ 的周长最小,然后利用两点间的距离公式求解可得.【解析】分别把点A (a ,3)、B (b ,1)代入双曲线3y x=得:a =1,b =3,则点A 的坐标为(1,3)、B 点坐标为(3,1),作A 点关于y 轴的对称点P ,B 点关于x 轴的对称点Q ,所以点P 坐标为(﹣1,3),Q 点坐标为(3,﹣1),连结PQ 分别交x 轴、y 轴于C 点、D 点,此时四边形ABCD 的周长最小,四边形ABCD 周长=DA +DC +CB +AB =DP +DC +CQ +AB =PQ +AB =22(13)(31)--++ +22(13)(31)-+-=4222+ =62,故选B .点睛:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、熟练运用两点之间线段最短解决有关几何图形周长最短的问题是解题的关键.考点:反比例函数图象上点的坐标特征;轴对称﹣最短路线问题;最值问题;动点型;综合题. 4.(2017江苏省泰州市,第6题,3分)如图,P 为反比例函数ky x=(k >0)在第一象限内图象上的一点,过点P 分别作x 轴,y 轴的垂线交一次函数y =﹣x ﹣4的图象于点A 、B .若∠AOB =135°,则k 的值是( )A.2B.4C.6D.8【答案】D.【分析】作BF⊥x轴,OE⊥AB,CQ⊥AP,易证△BOE∽△AOD,根据相似三角形对应边比例相等的性质即可求出k的值.∵当x=0时,y=﹣x﹣4=﹣4,∴OC=DQ=4,GE=OE=22OC=22;同理可证:BG=2BF=2PD=2kn,∴BE=BG+EG=222kn+;∵∠AOB=135°,∴∠OBE+∠OAE=45°,∵∠DAO+∠OAE=45°,∴∠DAO=∠OBE,在△BOE和△AOD中,∵∠DAO=∠OBE,∠BEO=∠ADO,∴△BOE∽△AOD;∴OE BEOD AD=,即222224knn+=+;整理得:nk+2n2=8n+2n2,化简得:k=8.故选D.点睛:本题主要考查了相似三角形的判定与性质及反比例函数图象上点的坐标特征,解题的关键是正确作出辅助线,构造相似三角形.考点:反比例函数图象上点的坐标特征;一次函数图象上点的坐标特征;综合题. 5.(2017湖北省十堰市,第10题,3分)如图,直线36y x =-分别交x 轴,y 轴于A ,B ,M 是反比例函数ky x=(x >0)的图象上位于直线上方的一点,MC ∥x 轴交AB 于C ,MD ⊥MC 交AB 于D ,AC •BD =43,则k 的值为( )A .﹣3B .﹣4C .﹣5D .﹣6 【答案】A .【分析】过点D 作DE ⊥y 轴于点E ,过点C 作CF ⊥x 轴于点F ,然后求出OA 与OB 的长度,即可求出∠OAB 的正弦值与余弦值,再设M (x ,y ),从而可表示出BD 与AC 的长度,根据AC •BD =43出k 的值.【解析】过点D 作DE ⊥y 轴于点E ,过点C 作CF ⊥x 轴于点F ,令x =0代入36y x =-,∴y =﹣6,∴B(0,﹣6),∴OB =6,令y =0代入36y x =-,∴x =3230),∴OA =3知:AB =43sin ∠OAB =3OB AB =,cos ∠OAB =12OA AB =.设M (x ,y ),∴CF =﹣y ,ED =x ,∴sin ∠OAB =CF AC ,∴AC =23y ,∵cos ∠OAB =cos ∠EDB =EDDB,∴BD =2x ,∵AC •BD =4323 y ×2x =43xy =﹣3,∵M 在反比例函数的图象上,∴k =xy =﹣3,故选A .点睛:本题考查反比例函数与一次函数的综合问题,解题的关键是根据∠OAB的锐角三角函数值求出BD、AC,本题属于中等题型.考点:反比例函数与一次函数的交点问题.6.(2017湖北省咸宁市,第8题,3分)在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为()A.(32,0)B.(2,0)C.(52,0)D.(3,0)【答案】C.【分析】过点B作BD⊥x轴于点D,易证△ACO≌△BCD(AAS),从而可求出B的坐标,进而可求出反比例函数的解析式,根据解析式与A的坐标即可得知平移的单位长度,从而求出C的对应点.点睛:本题考查反比例函数的综合问题,涉及全等三角形的性质与判定,反比例函数的解析式,平移的性质等知识,综合程度较高,属于中等题型.考点:反比例函数图象上点的坐标特征;坐标与图形变化﹣平移;综合题.学科#网7.(2017湖北省荆州市,第10题,3分)规定:如果关于x 的一元二次方程20ax bx c ++=(a ≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论: ①方程2280x x +-=是倍根方程;②若关于x 的方程220x ax ++=是倍根方程,则a =±3;③若关于x 的方程260ax ax c -+=(a ≠0)是倍根方程,则抛物线26y ax ax c =-+与x 轴的公共点的坐标是(2,0)和(4,0); ④若点(m ,n )在反比例函数4y x=的图象上,则关于x 的方程250mx x n ++=是倍根方程. 上述结论中正确的有( )A .①②B .③④C .②③D .②④ 【答案】C .【分析】①通过解方程得到该方程的根,结合“倍根方程”的定义进行判断;②设x 2=2x 1,得到x 1x 2=2x 12=2,得到当x 1=1时,x 2=2,当x 1=﹣1时,x 2=﹣2,于是得到结论;③根据“倍根方程”的定义即可得到结论; ④若点(m ,n )在反比例函数4y x=的图象上,得到mn =4,然后解方程250mx x n ++=即可得到正确的结论;【解析】①由2280x x +-=,得(x +4)(x -2)=0,解得x 1=-4,x 2=2,∵x 1≠2x 2,或x 2≠2x 1,∴方程2280x x +-=不是倍根方程.故①错误;②关于x 的方程220x ax ++=是倍根方程,∴设x 2=2x 1,∴x 1x 2=2x 12=2,∴x 1=±1,当x 1=1时,x 2=2,当x 1=﹣1时,x 2=﹣2,∴x 1+x 2=﹣a =±3,∴a =±3,故②正确;③关于x 的方程260ax ax c -+=(a ≠0)是倍根方程,∴x 2=2x 1,∵抛物线26y ax ax c =-+的对称轴是直线x =3,∴抛物线26y ax ax c =-+与x 轴的交点的坐标是(2,0)和(4,0),故③正确; ④∵点(m ,n )在反比例函数4y x =的图象上,∴mn =4,解250mx x n ++=得x 1=﹣2m ,x 2=﹣8m,∴x 2=4x 1,∴关于x 的方程250mx x n ++=不是倍根方程; 故选C .点睛:本题考查了反比例函数图象上点的坐标特征,根与系数的关系,正确的理解倍根方程的定义是解题的关键.考点:反比例函数图象上点的坐标特征;根的判别式;根与系数的关系;抛物线与x 轴的交点;综合题. 8.(2017湖北省荆门市,第12题,3分)已知:如图,在平面直角坐标系xOy 中,等边△AOB 的边长为6,点C 在边OA 上,点D 在边AB 上,且OC =3BD ,反比例函数ky x=(k ≠0)的图象恰好经过点C 和点D ,则k 的值为( )A .81325 B . 81316 C . 8135 D .8134【答案】A .【分析】过点C 作CE ⊥x 轴于点E ,过点D 作DF ⊥x 轴于点F ,设BD =a ,则OC =3a ,根据等边三角形的性质结合解含30度角的直角三角形,可找出点C 、D 的坐标,再利用反比例函数图象上点的坐标特征即可求出a 、k 的值,此题得解.【解析】过点C 作CE ⊥x 轴于点E ,过点D 作DF ⊥x 轴于点F ,如图所示. 设BD =a ,则OC =3a .∵△AOB 为边长为6的等边三角形,∴∠COE =∠DBF =60°,OB =6. 在Rt △COE 中,∠COE =60°,∠CEO =90°,OC =3a ,∴∠OCE =30°,∴OE =32a ,CE =22OC OE - =33a ,∴点C (32a ,332 a ).同理,可求出点D 的坐标为(6﹣12a ,32a ).∵反比例函数k y x =(k ≠0)的图象恰好经过点C 和点D ,∴k =32a ×33a =(6﹣12a )×3a ,∴a =65,k =813.故选A .点睛:本题考查了反比例函数图象上点的坐标特征、等边三角形的性质以及解含30度角的直角三角形,根据等边三角形的性质结合解含30度角的直角三角形,找出点C 、D 的坐标是解题的关键. 考点:反比例函数图象上点的坐标特征;等边三角形的性质;综合题. 9.(2017怀化,第10题,4分)如图,A ,B 两点在反比例函数1k yx的图象上,C ,D 两点在反比例函数2k yx的图象上,AC ⊥y 轴于点E ,BD ⊥y 轴于点F ,AC =2,BD =1,EF =3,则12k k 的值是( )A.6B.4C.3D.2【答案】D.【分析】由反比例函数的性质可知S△AOE=S△BOF=12k1,S△COE=S△DOF=﹣12k2,结合S△AOC=S△AOE+S△COE和S△BOD=S△DOF+S△BOF可求得k1﹣k2的值.点睛:本题考查反比例函数图象上的点的坐标特征,解题的关键是利用参数,构建方程组解决问题,属于中考常考题型.考点:反比例函数图象上点的坐标特征.10.(2017辽宁省营口市,第8题,3分)如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数kyx的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为()A.33y=-B.3y=-C.3yx=-D.3y=【答案】A.【分析】过点C作CD⊥x轴于D,设菱形的边长为a,根据菱形的性质和三角函数分别表示出C,以及点A 向下平移2个单位的点,再根据反比例函数图象上点的坐标特征得到方程组求解即可.【解析】过点C作CD⊥x轴于D,设菱形的边长为a,在Rt△CDO中,OD=a•cos60°=12a,CD=a•sin60°=3a,则C(﹣12a,3a),点A向下平移2个单位的点为(﹣12a﹣a,3a﹣2),即(﹣32a,3a﹣2),则:31232322kaakaa⎧=⎪⎪-⎪⎨⎪-=⎪-⎪⎩,解得:2333ak⎧=⎪⎨=-⎪⎩.故反比例函数解析式为33y=-.故选A.点睛:本题考查的是反比例函数综合题目,考查了反比例函数解析式的求法、坐标与图形性质、菱形的性质、平移的性质等知识;本题综合性强,有一定难度.考点:反比例函数图象上点的坐标特征;菱形的性质;坐标与图形变化﹣平移.11.(2017辽宁省锦州市,第8题,2分)如图,矩形OABC中,A(1,0),C(0,2),双曲线kyx=(0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF,则k值为()A .23B .1C .43D .2 【答案】A .【分析】设E 点坐标为(1,m ),则F 点坐标为(2m ,2),根据三角形面积公式得到S △BEF =1(1)22m -(2﹣m ),根据反比例函数k 的几何意义得到S △OFC =S △OAE =12m ,由于S △OEF =S 矩形ABCO ﹣S △OCF ﹣S △OEA ﹣S △BEF ,列方程即可得到结论.【解析】∵四边形OABC 是矩形,BA ⊥OA ,A (1,0),∴设E 点坐标为(1,m ),则F 点坐标为(2m ,2),则S △BEF =1(1)22m -(2﹣m ),S △OFC =S △OAE =12m ,∴S △OEF =S 矩形ABCO ﹣S △OCF ﹣S △OEA ﹣S △BEF =2﹣12m ﹣12m ﹣1(1)22m -(2﹣m ),∵S △OEF =2S △BEF ,∴2﹣12m ﹣12m ﹣1(1)22m -(2﹣m )=12(1)22m ⨯-(2﹣m ),整理得23(2)204m m -+-=,解得m 1=2(舍去),m 2=23,∴E 点坐标为(1,23);∴k =23,故选A .点睛:本题考查了反比例函数k 的机几何意义和矩形的性质;会利用面积的和差计算不规则图形的面积. 考点:反比例函数系数k 的几何意义.12.(2017贵州省黔西南州,第10题,4分)如图,点A 是反比例函数1y x=(x >0)上的一个动点,连接OA ,过点O 作OB ⊥OA ,并且使OB =2OA ,连接AB ,当点A 在反比例函数图象上移动时,点B 也在某一反比例函数k y x=图象上移动,则k 的值为( )A .﹣4B .4C .﹣2D .2【答案】A .【分析】过A 作AC ⊥x 轴于点C ,过B 作BD ⊥x 轴于点D ,可设A (x ,1x ),由条件证得△AOC ∽△OBD ,从而可表示出B 点坐标,则可求得得到关于k 的方程,可求得k 的值.点睛:本题主要考查反比例函数图象上点的坐标特征,利用条件构造三角形相似,用A 点坐标表示出B 点坐标是解题的关键.考点:反比例函数图象上点的坐标特征.学科#网13.(2017四川省乐山市,第10题,3分)如图,平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别落在x 、y 轴上,点B 坐标为(6,4),反比例函数xy 6 的图象与AB 边交于点D ,与BC 边交于点E ,连结DE ,将△BDE 沿DE 翻折至△B 'DE 处,点B '恰好落在正比例函数y =kx 图象上,则k 的值是( )A .52-B .211-C .51-D .241- 【答案】B . 【分析】根据矩形的性质得到,CB ∥x 轴,AB ∥y 轴,于是得到D (6,1),E (32,4),根据勾股定理得到ED 的长,连接BB ′,交ED 于F ,过B ′作B ′G ⊥BC 于G ,根据轴对称的性质得到BF =B ′F ,BB ′⊥ED 求得BB ′的长,设EG =x ,则BG =92﹣x 根据勾股定理即可得到结论. 【解析】∵矩形OABC ,∴CB ∥x 轴,AB ∥y 轴,∵点B 坐标为(6,4),∴D 的横坐标为6,E 的纵坐标为4,∵D ,E 在反比例函数x y 6=的图象上,∴D (6,1),E (32,4),∴BE =6﹣32=92,BD =4﹣1=3,∴ED =22BE BD +=3132,连接BB ′,交ED 于F ,过B ′作B ′G ⊥BC 于G ,∵B ,B ′关于ED 对称,∴BF =B ′F ,BB ′⊥ED ,∴BF •ED =BE •BD ,即3132BF =3×92,∴BF =13,∴BB ′=13,设EG =x ,则BG =92﹣x ,∵BB ′2﹣BG 2=B ′G 2=EB ′2﹣GE 2,∴222299()()()2213x x --=-,∴x =4526,∴EG =4526,∴CG =4213,∴B ′G =5413,∴B ′(4213,﹣213),∴k =211-.故选B .点睛:本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,熟练掌握折叠的性质是解题的关键. 考点:反比例函数与一次函数的交点问题;翻折变换(折叠问题);综合题.14.(2017四川省达州市,第10题,3分)已知函数()()123xxyxx⎧->⎪⎪=⎨⎪<⎪⎩的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:①若点M1(x1,y1),M2(x2,y2)在图象上,且x1<x2<0,则y1<y2;②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;④当点P移动到使∠AOB=90°时,点A的坐标为(26,6-).其中正确的结论个数为()A.1B.2C.3D.4【答案】C.【分析】①错误.因为x1<x2<0,函数y随x是增大而减小,所以y1>y2;②正确.求出A、B两点坐标即可解决问题;③正确.设P(0,m),则B(3m,m),A(﹣12m,m),可得PB=﹣3m,P A=﹣12m,推出P A=4PB,S AOB=S △OPB+S△OP A=31222+=7.5;④正确.设P(0,m),则B(3m,m),A(﹣12m,m),推出PB=﹣3m,P A=﹣12m,OP=﹣m,由△OPB ∽△APO,可得OP2=PB•P A,列出方程即可解决问题;【解析】①错误.∵x1<x2<0,函数y随x是增大而减小,∴y1>y2,故①错误.②正确.∵P(0,﹣3),∴B(﹣1,﹣3),A(4,﹣3),∴AB=5,OA2234+5,∴AB=AO,∴△AOB 是等腰三角形,故②正确.③正确.设P(0,m),则B(3m,m),A(﹣12m,m),∴PB=﹣3m,P A=﹣12m,∴P A=4PB,∵S AOB=S△OPB+S △OP A=31222+=7.5,故③正确.④正确.设P (0,m ),则B (3m ,m ),A (﹣12m ,m ),∴PB =﹣3m,P A =﹣12m ,OP =﹣m ,∵∠AOB =90°,∠OPB =∠OP A =90°,∴∠BOP +∠AOP =90°,∠AOP +∠OP A =90°,∴∠BOP =∠OAP ,∴△OPB ∽△APO ,∴OP PB AP OP =,∴OP 2=PB •P A ,∴m 2=﹣3m•(﹣12m ),∴m 4=36,∵m <0,∴m =﹣6,∴A (26,﹣6),故④正确,∴②③④正确,故选C . 点睛:本题考查反比例函数综合题、等腰三角形的判定、两点间距离公式、相似三角形的判定和性质、待定系数法等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数,构建方程解决问题,属于中考选择题中的压轴题.考点:反比例函数综合题;综合题.15.(2017临沂,第14题,3分)如图,在平面直角坐标系中,反比例函数k y x =(x >0)的图象与边长是6的正方形OABC 的两边AB ,BC 分别相交于M ,N 两点,△OMN 的面积为10.若动点P 在x 轴上,则PM +PN 的最小值是( )A .62B .10C .26D .29【答案】C . 【分析】由正方形OABC 的边长是6,得到点M 的横坐标和点N 的纵坐标为6,求得M (6,6k ),N (6k ,6),根据三角形的面积列方程得到M (6,4),N (4,6),作M 关于x 轴的对称点M ′,连接NM ′交x 轴于P ,则NM ′的长=PM +PN 的最小值,根据勾股定理即可得到结论.【解析】∵正方形OABC 的边长是6,∴点M 的横坐标和点N 的纵坐标为6,∴M (6,6k ),N (6k ,6),∴BN =6﹣6k ,BM =6﹣6k ,∵△OMN 的面积为10,∴6×6﹣12×6×6k ﹣12×6×6k ﹣12×2(6)6k -=10,∴k =24,∴M (6,4),N (4,6),作M 关于x 轴的对称点M ′,连接NM ′交x 轴于P ,则NM ′的长=PM +PN 的最小值,∵AM =AM ′=4,∴BM ′=10,BN =2,∴NM 22'BN BN +22102+226C .点睛:本题考查了反比例函数的系数k 的几何意义,轴对称﹣最小距离问题,勾股定理,正方形的性质,正确的作出图形是解题的关键.考点:反比例函数系数k 的几何意义;轴对称﹣最短路线问题;最值问题;综合题.16.(2017山东省威海市,第12题,3分)如图,正方形ABCD 的边长为5,点A 的坐标为(﹣4,0),点B 在y 轴上,若反比例函数x k y =(k ≠0)的图象过点C ,则该反比例函数的表达式为( )A .x y 3=B .x y 4=C . x y 5=D .xy 6= 【答案】A .【解析】如图,过点C 作CE ⊥y 轴于E ,在正方形ABCD 中,AB =BC ,∠ABC =90°,∴∠ABO +∠CBE =90°,∵∠OAB +∠ABO =90°,∴∠OAB =∠CBE ,∵点A 的坐标为(﹣4,0),∴OA =4,∵AB =5,∴OB 2254-=3,在△ABO 和△BCE 中,∵∠OAB =∠CBE ,∠AOB =∠BEC ,AB =BC ,∴△ABO ≌△BCE (AAS ),∴OA =BE =4,CE =OB =3,∴OE =BE ﹣OB =4﹣3=1,∴点C 的坐标为(3,1),∵反比例函数xk y =(k ≠0)的图象过点C ,∴k=xy=3×1=3,∴反比例函数的表达式为xy3=.故选A.点睛:本题考查的是反比例函数图象上点的坐标特点,涉及到正方形的性质,全等三角形的判定与性质,反比例函数图象上的点的坐标特征,作辅助线构造出全等三角形并求出点D的坐标是解题的关键.考点:待定系数法求反比例函数解析式;反比例函数图象上点的坐标特征;正方形的性质;综合题.17.(2016吉林省长春市)如图,在平面直角坐标系中,点P(1,﹣4)、Q(m,n)在函数kyx=(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积()A.减小B.增大C.先减小后增大D.先增大后减小【答案】B.【分析】首先利用m和n表示出AC和AQ的长,则四边形ACQE的面积即可利用m、n表示,然后根据函数的性质判断.【解析】AC=m﹣1,CQ=n,则S四边形ACQE=AC•CQ=(m﹣1)n=mn﹣n.∵Q(m,n)在函数kyx=(x>0)的图象上,∴mn=k=﹣4(常数),∴S四边形ACQE=AC•CQ=(m﹣1)n=﹣4﹣n,∵当m>1时,n随m的增大而减小,∴S四边形ACQE=﹣4﹣n随m的增大而增大.故选B.考点:反比例函数系数k的几何意义.18.(2016天津市)若点A (﹣5,1y ),B (﹣3,2y ),C (2,3y )在反比例函数3y x =的图象上,则1y ,2y ,3y 的大小关系是( )A .132y y y <<B .123y y y <<C .321y y y <<D .213y y y <<【答案】D .【分析】直接利用反比例函数图象的分布,结合增减性得出答案.【解析】∵点A (﹣5,1y ),B (﹣3,2y ),C (2,3y )在反比例函数3y x=的图象上,∴A ,B 点在第三象限,C 点在第一象限,每个图象上y 随x 的增大减小,∴3y 一定最大,1y >2y ,∴213y y y <<.故选D .考点:反比例函数图象上点的坐标特征.19.(2016宁夏)正比例函数11y k x =的图象与反比例函数22k y x=的图象相交于A ,B 两点,其中点B 的横坐标为﹣2,当12y y <时,x 的取值范围是( )A .x <﹣2或x >2B .x <﹣2或0<x <2C .﹣2<x <0或0<x <2D .﹣2<x <0或x >2【答案】B .【分析】由正、反比例函数的对称性结合点B 的横坐标,即可得出点A 的横坐标,再根据两函数图象的上下关系结合交点的横坐标,即可得出结论.【解析】∵正比例和反比例均关于原点O 对称,且点B 的横坐标为﹣2,∴点A 的横坐标为2. 观察函数图象,发现:当x <﹣2或0<x <2时,一次函数图象在反比例函数图象的下方,∴当12y y <时,x 的取值范围是x <﹣2或0<x <2.故选B .考点:反比例函数与一次函数的交点问题.学科#网20.(2016四川省乐山市)如图,在反比例函数2yx=-的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数kyx=的图象上运动.若tan∠CAB=2,则k的值为()A.2B.4C.6D.8【答案】D.【分析】连接OC,过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,通过角的计算找出∠AOE=∠COF,结合“∠AEO=90°,∠CFO=90°”可得出△AOE∽△COF,根据相似三角形的性质得出AE OE AO CF OF CO==,再由tan∠CAB=AOCO=2,可得出CFOF=8,由此即可得出结论.【解析】连接OC,过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,如图所示.由直线AB与反比例函数2yx=-的对称性可知A、B点关于O点对称,∴AO=BO.又∵AC=BC,∴CO⊥AB.∵∠AOE+∠EOC=90°,∠EOC+∠COF=90°,∴∠AOE=∠COF,又∵∠AEO=90°,∠CFO=90°,∴△AOE∽△COF,∴AE OE AO CF OF CO==.∵tan∠CAB=AOCO=2,∴CF=2AE,OF=2OE.又∵AE•OE=|﹣2|=2,CF•OF=|k|,∴k=±8.∵点C在第一象限,∴k=8.故选D.考点:反比例函数图象上点的坐标特征;反比例函数的性质;相似三角形的判定与性质.21.(2016山东省临沂市)如图,直线y=﹣x+5与双曲线kyx=(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是52.若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线kyx=(x>0)的交点有()A.0个B.1个C.2个D.0个,或1个,或2个【答案】B.【分析】令直线y=﹣x+5与y轴的交点为点D,过点O作OE⊥直线AC于点E,过点B作BF⊥x轴于点F,通过令直线y=﹣x+5中x、y分别等于0,得出线段OD、OC的长度,根据正切的值即可得出∠DCO=45°,再结合做的两个垂直,可得出△OEC与△BFC都是等腰直角三角形,根据等腰直角三角形的性质结合面积公式即可得出线段BC的长,从而可得出BF、CF的长,根据线段间的关系可得出点B的坐标,根据反比例函数图象上点的坐标特征即可得出反比例函数系数k的值,根据平移的性质找出平移后的直线的解析式将其代入反比例函数解析式中,整理后根据根的判别式的正负即可得出结论.【解析】令直线y=﹣x+5与y轴的交点为点D,过点O作OE⊥直线AC于点E,过点B作BF⊥x轴于点F,如图所示.将直线y =﹣x +5向下平移1个单位得到的直线的解析式为y =﹣x +5﹣1=﹣x +4,将y =﹣x +4代入到4y x=中,得:44x x -+=,整理得:2440x x -+=,∵△=16﹣4×4=0,∴平移后的直线与双曲线4y x=只有一个交点.故选B .考点:反比例函数与一次函数的交点问题;反比例函数图象上点的坐标特征;一次函数的应用;反比例函数的应用.22.(2016山东省日照市)正比例函数11y k x =(1k >0)与反比例函数22k y x=(2k >0)图象如图所示,则不等式21k k x x>的解集在数轴上表示正确的是( )A .B .C .D .【答案】B .【分析】由图象可以知道,当x =﹣2或x =2时,两个函数的函数值是相等的,再根据函数的增减性可以判断出不等式21k k x x>的解集,即可得出结论. 【解析】两个函数图象的另一个交点坐标为(﹣2,﹣1),当﹣2<x <0或x >2时,直线11y k x =在22k y x=(2k >0)图象的上方,故不等式21k k x x>的解集为x <﹣1或x >2.故选B . 考点:在数轴上表示不等式的解集;反比例函数与一次函数的交点问题.23.(2016山东省济宁市)如图,O 为坐标原点,四边形OACB 是菱形,OB 在x 轴的正半轴上,sin ∠AOB =45,反比例函数48y x=在第一象限内的图象经过点A ,与BC 交于点F ,则△AOF 的面积等于( )A .60B .80C .30D .40 【答案】D .【分析】过点A 作AM ⊥x 轴于点M ,过点F 作FN ⊥x 轴于点N ,设OA =a ,BF =b ,通过解直角三角形分别找出点A 、F 的坐标,结合反比例函数图象上点的坐标特征即可求出a 、b 的值,通过分割图形求面积,最终找出△AOF 的面积等于梯形AMNF 的面积,利用梯形的面积公式即可得出结论. 【解析】过点A 作AM ⊥x 轴于点M ,过点F 作FN ⊥x 轴于点N ,如图所示.设OA =a ,BF =b ,在Rt △OAM 中,∠AMO =90°,OA =a ,sin ∠AOB =45,∴AM =OA •sin ∠AOB =45a ,OM =22OA AM -=35a ,∴点A 的坐标为(35a ,45a ).∵点A 在反比例函数48y x=的图象上,∴35a ×45a =21225a =48,解得:a =10,或a =﹣10(舍去),∴AM =8,OM =6.∵四边形OACB 是菱形,∴OA =OB =10,BC ∥OA ,∴∠FBN =∠AOB .在Rt △BNF 中,BF =b ,sin ∠FBN =45,∠BNF =90°,∴FN =BF •sin ∠FBN =45b ,BN =22BF FN -=35b ,∴点F 的坐标为(10+35b ,45b ).∵点B 在反比例函数48y x =的图象上,∴(10+35b )×45b =48,解得:b =56125-,或b =56125--(舍去),∴FN =4(615)-,BN =615-,MN =OB +BN ﹣OM =611-. S △AOF =S △AOM +S 梯形AMNF ﹣S △OFN =S梯形AMNF =12(AM +FN )•MN =12(8+4(615)-)×(611-)=40.故选D .考点:反比例函数与一次函数的交点问题;综合题.24.(2016山东省淄博市)反比例函数a y x =(a >0,a 为常数)和2y x=在第一象限内的图象如图所示,点M 在a y x =的图象上,MC ⊥x 轴于点C ,交2y x =的图象于点A ;MD ⊥y 轴于点D ,交2y x=的图象于点B ,当点M 在ay x=的图象上运动时,以下结论:①S △ODB =S △OCA ;②四边形OAMB 的面积不变;③当点A 是MC 的中点时,则点B 是MD 的中点. 其中正确结论的个数是( )A .0B .1C .2D .3 【答案】D .【分析】①由反比例系数的几何意义可得答案;②由四边形OAMB 的面积=矩形OCMD 面积﹣(三角形ODB 面积+面积三角形OCA ),解答可知;③连接OM,点A是MC的中点可得△OAM和△OAC的面积相等,根据△ODM的面积=△OCM的面积、△ODB与△OCA的面积相等解答可得.【解析】①由于A、B在同一反比例函数2yx=图象上,则△ODB与△OCA的面积相等,都为12×2=1,正确;②由于矩形OCMD、三角形ODB、三角形OCA为定值,则四边形MAOB的面积不会发生变化,正确;③连接OM,点A是MC的中点,则△OAM和△OAC的面积相等,∵△ODM的面积=△OCM的面积=12 a,△ODB与△OCA的面积相等,∴△OBM与△OAM的面积相等,∴△OBD和△OBM面积相等,∴点B一定是MD的中点.正确;故选D.考点:反比例函数的图象;反比例函数的性质;反比例函数的应用.25.(2016山东省烟台市)反比例函数16tyx-=的图象与直线y=﹣x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是()A.t<16B.t>16C.t≤16D.t≥16【答案】B.【分析】将一次函数解析式代入到反比例函数解析式中,整理得出关于x的一元二次方程,由两函数图象有两个交点,且两交点横坐标的积为负数,结合根的判别式以及根与系数的关系即可得出关于k的一元一次不等式组,解不等式组即可得出结论.考点:反比例函数与一次函数的交点问题.学科#网26.(2016湖北省十堰市)如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A ,B 重合),作CD ⊥OB 于点D ,若点C ,D 都在双曲线ky x=上(k >0,x >0),则k 的值为( )A.253 B .183 C .93 D .9 【答案】C .【分析】过点A 作AE ⊥OB 于点E ,根据正三角形的性质以及三角形的边长可找出点A 、B 、E 的坐标,再由CD ⊥OB ,AE ⊥OB 可找出CD ∥AE ,即得出BD BC BE BA =,令该比例BD BCBE BA==n ,根据比例关系找出点D 、C 的坐标,利用反比例函数图象上点的坐标特征即可得出关于k 、n 的二元一次方程组,解方程组即可得出结论.【解析】过点A 作AE ⊥OB 于点E ,如图所示.∵△OAB 为边长为10的正三角形,∴点A 的坐标为(10,0)、点B 的坐标为(5,53),点E 的坐标为(52,532).∵CD ⊥OB ,AE ⊥OB ,∴CD ∥AE ,∴BD BC BE BA=.设BD BC BE BA ==n (0<n <1),∴点D 的坐标为(1052n -,103532n-),点C 的坐标为(5+5n ,5353n -).∵点C 、D 均在反比例函数k y x =图象上,∴105103532(55)(5353)n nk k n n ⎧--=⨯⎪⎨⎪=+⨯-⎩,解得:4593n k ⎧=⎪⎨⎪=⎩.故选C .考点:反比例函数图象上点的坐标特征;平行线的性质;等边三角形的性质.27.(2016湖北省宜昌市)函数21y x =+的图象可能是( ) A . B .C .D .【答案】C .【分析】函数21y x =+是反比例2y x =的图象向左移动一个单位,根据反比例函数的图象特点判断即可. 【解析】函数21y x =+是反比例2y x =的图象向左移动一个单位,即函数21y x =+是图象是反比例2y x=的图象双曲线向左移动一个单位.故选C . 考点:反比例函数的图象;函数的平移.28.(2016湖南省株洲市)已知,如图一次函数1y ax b =+与反比例函数2ky x=的图象如图示,当12y y <时,x 的取值范围是( )A .x <2B .x >5C .2<x <5D .0<x <2或x >5 【答案】D .【分析】根据图象得出两交点的横坐标,找出一次函数图象在反比例图象下方时x 的范围即可. 【解析】根据题意得:当12y y <时,x 的取值范围是0<x <2或x >5.故选D . 考点:反比例函数与一次函数的交点问题.29.(2016甘肃省兰州市)如图,A,B两点在反比例函数1kyx=的图象上,C、D两点在反比例函数2kyx=的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=103,则21k k-= ()A.4B.143C.163D.6【答案】A.【分析】设A(m,1km),B(n,1kn)则C(m,2km),D(n,2kn),根据题意列出方程组即可解决问题.【解析】设A(m,1km),B(n,1kn)则C(m,2km),D(n,2kn),由题意:122110323n mk kmk kn⎧-=⎪⎪-⎪=⎨⎪-⎪=⎪⎩,解得21k k-=4.故选A.考点:反比例函数图象上点的坐标特征.30.(2016湖北省荆州市)如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数kyx=的图象恰好经过斜边A′B 的中点C,S△ABO=4,tan∠BAO=2,则k的值为()A.3B.4C.6D.8【答案】C.【分析】先根据S△ABO=4,tan∠BAO=2求出AO、BO的长度,再根据点C为斜边A′B的中点,求出点C 的坐标,点C的横纵坐标之积即为k值.考点:反比例函数图象上点的坐标特征.31.(2016辽宁省抚顺市)如图,矩形ABCD的顶点D在反比例函数kyx=(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是6,则k的值为()A.﹣6B.﹣8C.﹣9D.﹣12【答案】D.【分析】先设D(a,b),得出CO=﹣a,CD=AB=b,k=ab,再根据△BCE的面积是6,得出BC×OE=12,最后根据AB∥OE,得出BC ABOC EO=,即BC•EO=AB•CO,求得ab的值即可.【解析】设D(a,b),则CO=﹣a,CD=AB=b,∵矩形ABCD的顶点D在反比例函数kyx=(x<0)的图象上,∴k=ab,∵△BCE的面积是6,∴12×BC×OE=6,即BC×OE=12,∵AB∥OE,∴BC ABOC EO=,即BC•EO=AB•CO,∴12=b×(﹣a),即ab=﹣12,∴k=﹣12,故选D.。
