2016天津中考数学压轴题及答案解析
天津市2016年中考数学试题含答案分解

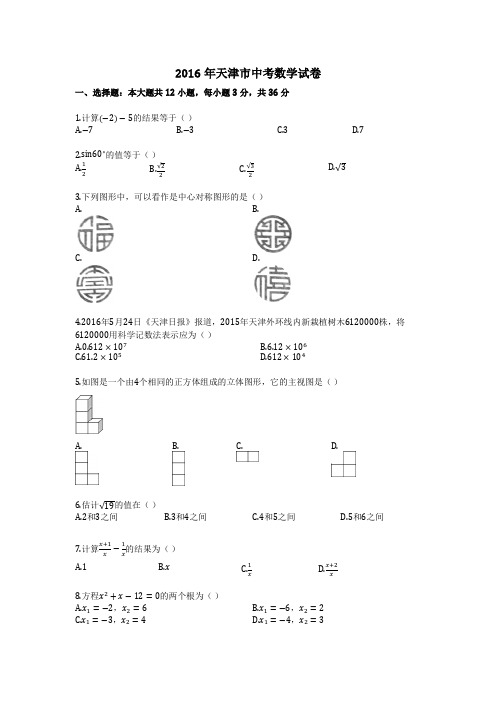
2016年天津市初中毕业生学业考试试卷数学、选择题(本大题共12小题,每小题3分,共3636分,在每小题给出的 四个选项中,只有一个是符合题目要求的)(1)计算(-2)-5的结果等于(3)下列图形中,可以看作是中心对称图 形的是(A) ( B ) (C )(4) 2016年5月24日《天津日报》报道,2015年天津外环线内新栽植树木(A )-7(2)sin60的值等于(B )-3(C ) 3(D) 7XIAl2 26120 000株,将6120 000用科学记数法表示应为(A) -a < 0 < -b(A) 0.612 X 107(B) 6.12 X 06 (D ) 612 X 1044个相同的正方体组成的立体图形,它的主视第(5)题图(B)(C )(D)(6)估计6的值在(A ) 2和3之间(B)3和4之间 (C ) 4和5之间(D) 5和6之间x , 1(7)计算丄的结果为x x(B ) x(C)(D)(8)方程x 2,2x-12=0的两个根为(A) X 1= -2,X 2=6(B )X 1= -6,X 2=2 (C) x 1= -3,x 2=4 (D) x 1=-4, X 2=3(9) 实数a ,b 在数轴上的对应点的位置如图所示, 把-a ,-b ,0按照从小到大的顺序排列,正确的是a 0 b第(9)题图(C ) 61.2 X 105(B)0 < -a < -b(C)-b < 0 < -a(D)0 < -b < -a(10) 如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B, AB ' 与DC相交于点E,则下列结论一定正确的是第(10)题图(B)ZACD= ZB 'CD(C)AD=AE ( D) AE=CE3 (11) 若点A (-5, y i), B (-3, y2), C (2 , y)在反比例函数y 二—错误!x未找到引用源。
天津中考数学第24题(几何压轴题)思路分析及真题练习

天津中考数学第24题(几何压轴题)思路分析及真题练习思路分析:观察近几年的中考真题可以发现,每年倒数第二题的出题形式,都是将几何图形放在平面直角坐标系中。
但是,由于解析几何要到高中才学,所以坐标系在这里其实只能起到一个确定点的坐标的作用。
当然,如果把直线看成一次函数图像,一次函数解析式就是直线方程,也就可以将直线交点问题,转化为方程组求解问题,但在这道题中通常都不需要这样做。
题目每年都会对几何图形进行变换,近六年的变换规律是:旋转、对称、旋转、对称、旋转、平移,明年应该大概率是旋转。
因为无论是对称变换、旋转变换还是平移变换,图形的大小和形状都不会发生改变,所以每年的题目都会涉及到全等。
由于在图形变换的过程中,全等的判定通常都是比较容易的,所以本题对全等的考察又主要在全等性质的应用上。
题目设问无论是点的坐标、线段的长还是图形的面积,其核心都是求距离。
所有的距离又都可以转化为求两点间的距离或求点到直线间的距离。
任意两点之间的距离公式虽然要高中才学,但我们可以将两点之间的距离转化为求一个直角三角形的斜边长,用勾股定理求解。
因此,我们会发现每年的题目中几乎都会涉及到勾股定理。
任意点到任意直线的距离公式也要到高中才会学习,但对于一些特殊情况,我们现在就可以做了。
每年的第一问,都是送分问,用一次勾股定理基本都可以解决。
第二问和第三问,解题的关键是要抓住全等的性质和特殊三角形。
第三问通常也会和其它知识点结合,但涉及的都是一些基础知识点,基本功扎实的同学,问题都不大。
最后提醒一下,当对图形进行旋转变换时,尤其需要注意其与圆的结合。
在研究点、直线、圆和圆的位置关系时,只需要研究它们和圆心的位置关系即可。
而在旋转变换时,旋转中心自然就是圆心。
真题练习参考答案。
2016年天津市中考数学试卷(word版)及答案

机密★启用前2016年天津市初中毕业生学业测试试卷数学本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。
第Ⅰ卷为第1页至第3页,第Ⅱ卷为第4页至第8页。
试卷满分120分。
测试时间100分钟。
答卷前,请你务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上,并在规定位置粘贴测试用条形码。
答题时,务必将答案涂写在“答题卡”上,答案答在试卷上无效。
测试结束后,将本试卷和“答题卡”一并交回。
祝你测试顺利!第Ⅰ卷注意事项:1.每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
2.本卷共12题,共36分。
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)(1)计算(-2)-5的结果等于(A)-7 (B)-3(C)3 (D)7(2)sin60 的值等于(A)12(B2(C 3(D3(3)下列图形中,可以看作是中心对称图形的是(A ) (B ) (C ) (D )(4)据2016年5月24日《天津日报》报道,2015年天津外环线内新栽植树木6 120 000株.将6 120 000用科学记数法表示应为 (A )70.61210⨯ (B )66.1210⨯(C )561.210⨯(D )461210⨯(5)右图是一个由4个相同的正方体组成的立体图形,它的主视图是(A ) (B )(C ) (D ) (6)估计19的值在(A )2和3之间 (B )3和4之间 (C )4和5之间 (D )5和6之间(7)计算11x x x+-的结果为 (A )1 (B )x(C )1x(D )2x x+ (8)方程2120x x +-=的两个根为(A )1226x x =-=, (B )1262x x =-=,(C )1234x x =-=,(D )1243x x =-=,(9)实数a b ,在数轴上的对应点的位置如图所示,把a -,第(5)题abb -,0按照从小到大的顺序排列,正确的是(A )0a b -<<- (B )0a b <-<- (C )0b a -<<- (D )0b a <-<-(10)如图,把一张矩形纸片ABCD 沿对角线AC 折叠,点B 的对应点为B ′,AB ′和DC 相交于点E ,则下列结论一定正确的是(A )∠DAB ′=∠CAB ′ (B )∠ACD =∠B ′CD (C )AD =AE(D )AE =CE(11)若点A 1(5)y -,,B 2(3)y -,,C 3(2)y ,在反比例函数3y x=的图象上,则123y y y ,,的大小关系是(A )132y y y << (B )123y y y << (C )321y y y << (D )213y y y <<(12)已知二次函数2()1y x h =-+(h 为常数),在自变量x 的值满足1≤x ≤3的情况下,和其对应的函数值y 的最小值为5,则h 的值为(A )1或-5 (B )-1或5 (C )1或-3 (D )1或3 机密★启用前2016年天津市初中毕业生学业测试试卷数 学第(10)题第(9)题EB'B第Ⅱ卷注意事项:1.用黑色字迹的签字笔将答案写在“答题卡”上(作图可用2B 铅笔)。
2016年天津市中考数学试卷-答案

∵点 C 与点 B 关于 x 轴对称,∴C (0, 3) , 设直线 O′C 的解析式为 y kx b ,
把 O′ (3
3
,
9
)
,C
(0,
3)
代入得
3
3 2
k
b
9 2
,解得
k
5
3 2
,
22
b 3
b 3
∴直线 O′C 的解析式为 y 5 3 x-3 , 2
当 y 0 时, 5 3 x-3 0 ,解得 x 3 3 ,
24563 ∴这组数据的平均数为 1.61. ∵在这组数据中,1.65 出现了 6 次,出现的次数最多 ∴这组数据的众数为 1.65. ∵将这组数据从小到大排列,其中处于中间的两个数都是 1.60,有 1.60 1.60 1.60
2 ∴这组数据的中位数为 1.60. (Ⅲ)将成绩从高到低排序后,取第 9 名的成绩,可判断1.65m 能否进入复赛,因为1.65m>1.60m ,故能 进入复赛. 【考点】扇形统计图和条形统计图 21.【答案】(Ⅰ) 36 (Ⅱ) 30 【解析】(Ⅰ)如图,连接 OC.
(元),当租用甲货车 x 辆时,租用甲种货车的费用为: 400x (元),则租用乙种货车 (8 x) 辆,租用乙种
货车的费用为: 280 (8 x) ﹣280x 2240 (元);
(Ⅱ)当租用甲种货车 x 辆时,两种货车的总费用为 y 400x (280x 2240)120x 2240 ,
22 (Ⅲ)∵ △ABO 绕点 B 逆时针旋转120 ,得△ABO ,点 P 的对应点为 P , ∴ BP BP ,∴ OP BP OP BP , 如图,作 B 点关于 x 轴的对称点 C,连结 O′C 交 x 轴于 P 点,
天津中考数学压轴题全搞定

九年级数学冲刺讲义二次函数12题1. 已知关于x的函数同时满足下列三个条件:①函数的图象不经过第二象限;②当x<2时,对应的函数值y<0;③当x<2时,函数值y随x的增大而增大.你认为符合要求的函数的解析式可以是:(写出一个即可,答案不唯一).2.已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a﹣b+c≥0;④的最小值为3.其中,正确结论的个数为()A.1个B.2个C.3个D.4个3.已知抛物线y=﹣x2+x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为()A.B.C.D.4.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为()A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或35.已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,有下列结论:①b2﹣4ac>0;②abc<0;③m>2.其中,正确结论的个数是()A.0 B.1 C.2 D.36.若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1、x2,且x1≠x2,有下列结论:①x1=2,x2=3;②m>﹣;③二次函数y=(x﹣x1)(x﹣x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是()A.0 B.1 C.2 D.37.已知二次函数y=ax 2+bx+c (a≠0)的图象如图所示,有下列结论:①b 2﹣4ac >0;②abc >0;③8a+c >0;④9a+3b+c <0其中,正确结论的个数是( )A .1B .2C .3D .48.已知二次函数y=ax 2+bx+c (a≠0)的图象如图所示,有下列5个结论:①abc >0;②b <a+c ;③4a+2b+c >0;④2c <3b ;⑤a+b >m (am+b )(m≠1的实数).其中正确的结论有( )A .2个B .3个C .4个D .5个9. 已知抛物线y=x 2-(2m-1)x+2m 不经过第三象限,且当x>2时,函数值y 随x 的增大而增大,则实数m 的取值范围是( )A.0≤m≤1.5B.m≥1.5C.0≤m≤1D.0<m≤1.5网格题18题1. 如图,在下列网格中,每个小正方形的边长都是1,点A 、B 、Q 、P 均为格点。
2016年天津市中考数学试卷

2016年天津市中考数学试卷一、选择题:本大题共12小题,每题3分,共36分1.计算(−2)−5的结果等于〔〕A.−7B.−3C.3D.72.sin60∘的值等于〔〕A.1 2B.√22C.√32D.√33.以下图形中,可以看作是中心对称图形的是〔〕A. B.C. D.4.2016年5月24日《天津日报》报道,2015年天津外环线内新栽植树木6120000株,将6120000用科学记数法表示应为〔〕A.0.612×107B.6.12×106C.61.2×105D.612×1045.如图是一个由4个相同的正方体组成的立体图形,它的主视图是〔〕A. B. C. D.6.估计√19的值在〔〕A.2和3之间B.3和4之间C.4和5之间D.5和6之间7.计算x+1x −1x的结果为〔〕A.1B.xC.1x D.x+2x8.方程x2+x−12=0的两个根为〔〕A.x1=−2,x2=6B.x1=−6,x2=2C.x1=−3,x2=4D.x1=−4,x2=39.实数a ,b 在数轴上的对应点的位置如下图,把−a ,−b ,0按照从小到大的顺序排列,正确的选项是〔 〕A.−a <0<−bB.0<−a <−bC.−b <0<−aD.0<−b <−a10.如图,把一张矩形纸片ABCD 沿对角线AC 折叠,点B 的对应点为B′,AB′与DC 相交于点E ,则以下结论一定正确的选项是〔 〕A.∠DAB′=∠CAB′B.∠ACD =∠B′CDC.AD =AED.AE =CE11.假设点A(−5, y 1),B(−3, y 2),C(2, y 3)在反比例函数y =3x 的图象上,则y 1,y 2,y 3的大小关系是〔 〕 A.y 1<y 3<y 2 B.y 1<y 2<y 3 C.y 3<y 2<y 1 D.y 2<y 1<y 312.已知二次函数y =(x −ℎ)2+1〔ℎ为常数〕,在自变量x 的值满足1≤x ≤3的情况下,与其对应的函数值y 的最小值为5,则ℎ的值为〔 〕 A.1或−5 B.−1或5 C.1或−3 D.1或3 二、填空题:本大题共6小题,每题3分,共18分13.计算(2a)3的结果等于________.14.计算(√5+√3)(√5−√3)的结果等于________.15.不透明袋子中装有6个球,其中有1个红球、2个绿球和3个黑球,这些球除颜色外无其他差异,从袋子中随机取出1个球,则它是绿球的概率是________.16.假设一次函数y =−2x +b 〔b 为常数〕的图象经过第二、三、四象限,则b 的值可以是________〔写出一个即可〕.17.如图,在正方形ABCD 中,点E ,N ,P ,G 分别在边AB ,BC ,CD ,DA 上,点M ,F ,Q 都在对角线BD 上,且四边形MNPQ 和AEFG 均为正方形,则S 正方形MNPQS正方形AEFG的值等于________.18.如图,在每个小正方形的边长为1的网格中,A ,E 为格点,B ,F 为小正方形边的中点,C 为AE ,BF 的延长线的交点.(1)AE 的长等于________;(2)假设点P 在线段AC 上,点Q 在线段BC 上,且满足AP =PQ =QB ,请在如下图的网格中,用无刻度的直尺,画出线段PQ ,并简要说明点P ,Q 的位置是如何找到的〔不要求证明〕________.三、综合题:本大题共7小题,共66分19.解不等式{x +2≤6,3x −2≥2x,,请结合题意填空,完成此题的解答.(1)解不等式①,得________;(2)解不等式②,得________;(3)把不等式①和②的解集在数轴上表示出来;(4)原不等式组的解集为________.20.在一次中学生田径运动会上,根据参加男子跳高初赛的运发动的成绩〔单位:m 〕,绘制出如下的统计图①和图②,请根据相关信息,解答以下问题:(1)图1中a 的值为________;(2)求统计的这组初赛成绩数据的平均数、众数和中位数;(3)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m 的运发动能否进入复赛.21.在⊙O中,AB为直径,C为⊙O上一点.(1)如图1.过点C作⊙O的切线,与AB的延长线相交于点P,假设∠CAB=27∘,求∠P的大小;(2)如图2,D为AC^上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,假设∠CAB=10∘,求∠P的大小.22.小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63m,∠A=45∘,∠B=37∘,求AC,CB的长.〔结果保留小数点后一位〕参考数据:sin37∘≈0.60,cos37∘≈0.80,tan37∘≈0.75,√2取1.414.23.公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元(1)设租用甲种货车x辆〔x为非负整数〕,试填写表格.表一:(2)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.24.在平面直角坐标系中,O为原点,点A(4, 0),点B(0, 3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.(I)如图①,假设α=90∘,求AA′的长;(II)如图②,假设α=120∘,求点O′的坐标;(III)在(II)的条件下,边OA上的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标〔直接写出结果即可〕).25.已知抛物线C:y=x2−2x+1的顶点为P,与y轴的交点为Q,点F(1, 12(I)求点P,Q的坐标;(II)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.①求抛物线C′的解析式;②假设点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.答案1. 【答案】A【解析】根据减去一个数等于加上这个数的相反数进行计算即可得解.【解答】解:(−2)−5=(−2)+(−5)=−(2+5)=−7,故选:A.2. 【答案】C【解析】直接利用特殊角的三角函数值求出答案..【解答】解:sin60∘=√32故选:C.3. 【答案】B【解析】根据中心对称图形的概念求解.【解答】解:A、不是中心对称图形,因为找不到任何这样的一点,旋转180度后它的两部分能够重合;即不满足中心对称图形的定义,故此选项错误;B、是中心对称图形,故此选项正确;C、不是中心对称图形,因为找不到任何这样的一点,旋转180度后它的两部分能够重合;即不满足中心对称图形的定义,故此选项错误;D、不是中心对称图形,因为找不到任何这样的一点,旋转180度后它的两部分能够重合;即不满足中心对称图形的定义,故此选项错误.故选:B.4. 【答案】B【解析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.【解答】解:6120000=6.12×106,故选:B.5. 【答案】A【解析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解答】解:从正面看易得第一层有2个正方形,第二层左边有一个正方形,第三层左边有一个正方形.故选A.6. 【答案】C【解析】直接利用二次根式的性质得出√19的取值范围.【解答】解:∵√16<√19<√25,∴√19的值在4和5之间.故选:C.7. 【答案】A【解析】根据同分母分式相加减,分母不变,分子相加减计算即可得解.【解答】解:x+1x −1x=x+1−1x=1.故选A.8. 【答案】D【解析】将x2+x−12分解因式成(x+4)(x−3),解x+4=0或x−3=0即可得出结论.【解答】解:x2+x−12=(x+4)(x−3)=0,则x+4=0,或x−3=0,解得:x1=−4,x2=3.故选D.9. 【答案】C【解析】根据数轴得出a<0<b,求出−a>−b,−b<0,−a>0,即可得出答案.【解答】解:∵从数轴可知:a<0<b,∴−a>−b,−b<0,−a>0,∴−b<0<−a,故选C.10. 【答案】D【解析】根据翻折变换的性质可得∠BAC=∠CAB′,根据两直线平行,内错角相等可得∠BAC=∠ACD,从而得到∠ACD=∠CAB′,然后根据等角对等边可得AE=CE,从而得解.【解答】解:∵矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,∴∠BAC=∠CAB′,∵AB // CD,∴∠BAC=∠ACD,∴∠ACD=∠CAB′,∴AE=CE,所以,结论正确的选项是D选项.故选D.11. 【答案】D【解析】直接利用反比例函数图象的分布,结合增减性得出答案.【解答】解:∵点A(−5, y1),B(−3, y2),C(2, y3)在反比例函数y=3x的图象上,∴A,B点在第三象限,C点在第一象限,每个图象上y随x的增大减小,∴y3一定最大,y1>y2,∴y2<y1<y3.故选:D.12. 【答案】B【解析】由解析式可知该函数在x=ℎ时取得最小值1、x>ℎ时,y随x的增大而增大、当x<ℎ时,y随x的增大而减小,根据1≤x≤3时,函数的最小值为5可分如下两种情况:①假设ℎ<1≤x≤3,x=1时,y取得最小值5;②假设1≤x≤3<ℎ,当x=3时,y取得最小值5,分别列出关于ℎ的方程求解即可.【解答】解:∵当x>ℎ时,y随x的增大而增大,当x<ℎ时,y随x的增大而减小,∴①假设ℎ<1≤x≤3,x=1时,y取得最小值5,可得:(1−ℎ)2+1=5,解得:ℎ=−1或ℎ=3〔舍〕;②假设1≤x≤3<ℎ,当x=3时,y取得最小值5,可得:(3−ℎ)2+1=5,解得:ℎ=5或ℎ=1〔舍〕.综上,ℎ的值为−1或5,故选:B.13. 【答案】8a3【解析】根据幂的乘方与积的乘方运算法则进行计算即可.【解答】解:(2a)3=8a3.故答案为:8a3.14. 【答案】2【解析】先套用平方差公式,再根据二次根式的性质计算可得.【解答】解:原式=(√5)2−(√3)2=5−3=2,故答案为:2.15. 【答案】13【解析】由题意可得,共有6种等可能的结果,其中从口袋中任意摸出一个球是绿球的有2种情况,利用概率公式即可求得答案.【解答】解:∵在一个不透明的口袋中有6个除颜色外其余都相同的小球,其中1个红球、2个绿球和3个黑球,∴从口袋中任意摸出一个球是绿球的概率是26=13,故答案为:13.16. 【答案】−1【解析】根据一次函数的图象经过第二、三、四象限,可以得出k<0,b<0,随便写出一个小于0的b值即可.【解答】解:∵一次函数y=−2x+b〔b为常数〕的图象经过第二、三、四象限,∴k<0,b<0.故答案为:−1.17. 【答案】89【解析】根据辅助线的性质得到∠ABD=∠CBD=45∘,四边形MNPQ和AEFG均为正方形,推出△BEF与△BMN是等腰直角三角形,于是得到FE=BE=AE=12AB,BM=MN= QM,同理DQ=MQ,即可得到结论.【解答】解:在正方形ABCD中,∵∠ABD=∠CBD=45∘,∵四边形MNPQ和AEFG均为正方形,∴∠BEF=∠AEF=90∘,∠BMN=∠QMN=90∘,∴△BEF与△BMN是等腰直角三角形,∴FE=BE=AE=12AB,BM=MN=QM,同理DQ=MQ,∴MN=13BD=√23AB,∴S正方形MNPQ S正方形AEFG =(√23AB)2(12AB)2=89,故答案为:89.18. 【答案】√5;; (2)如图,AC与网格线相交,得到P,取格点M,连接AM,并延长与BC交于Q,连接PQ,则线段PQ即为所求.故答案为:AC与网格线相交,得到P,取格点M,连接AM,并延长与BC交于Q,连接PQ,则线段PQ即为所求.【解析】(1)根据勾股定理即可得到结论;; (2)取格点M,连接AM,并延长与BC交于Q,连接PQ,则线段PQ即为所求.【解答】解:(1)AE=√22+12=√5;; (2)如图,AC与网格线相交,得到P,取格点M,连接AM,并延长与BC交于Q,连接PQ,则线段PQ即为所求.19. 【答案】x≤4;; (2)解不等式②,得x≥2.故答案为:x≥2.; (3)把不等式①和②的解集在数轴上表示为:;; (4)原不等式组的解集为:.故答案为:2≤x≤4.【解析】分别求出各不等式的解集,再在数轴上表示出来即可.; ; ;【解答】解:(1)解不等式①,得x≤4.; (2)解不等式②,得x≥2.; (3)把不等式①和②的解集在数轴上表示为:;; (4)原不等式组的解集为:.20. 【答案】25;; (2)观察条形统计图得:=1.61;x=1.50×2+1.55×4+1.60×5+1.65×6+1.70×32+4+5+6+3∵在这组数据中,1.65出现了6次,出现的次数最多,∴这组数据的众数是1.65;将这组数据从小到大排列为,其中处于中间的两个数都是1.60,则这组数据的中位数是1.60.; (3)能;∵共有20个人,中位数是第10、11个数的平均数,∴根据中位数可以判断出能否进入前9名;∵1.65m>1.60m,∴能进入复赛.【解析】(1)用整体1减去其它所占的百分比,即可求出a的值;; (2)根据平均数、众数和中位数的定义分别进行解答即可;; (3)根据中位数的意义可直接判断出能否进入复赛.【解答】解:(1)根据题意得:1−20%−10%−15%−30%=25%;则a的值是25;; (2)观察条形统计图得:=1.61;x=1.50×2+1.55×4+1.60×5+1.65×6+1.70×32+4+5+6+3∵在这组数据中,1.65出现了6次,出现的次数最多,∴这组数据的众数是1.65;将这组数据从小到大排列为,其中处于中间的两个数都是1.60,则这组数据的中位数是1.60.; (3)能;∵共有20个人,中位数是第10、11个数的平均数,∴根据中位数可以判断出能否进入前9名;∵1.65m>1.60m,∴能进入复赛.21. 【答案】解:(1)如图,连接OC,∵⊙O与PC相切于点C,∴OC⊥PC,即∠OCP=90∘,∵∠CAB=27∘,∴∠COB=2∠CAB=54∘,在Rt△AOE中,∠P+∠COP=90∘,∴∠P=90∘−∠COP=36∘;; (2)∵E为AC的中点,∴OD⊥AC,即∠AEO=90∘,在Rt△AOE中,由∠EAO=10∘,得∠AOE=90∘−∠EAO=80∘,∠AOD=40∘,∴∠ACD=12∵∠ACD是△ACP的一个外角,∴∠P=∠ACD−∠A=40∘−10∘=30∘.【解析】(1)连接OC,首先根据切线的性质得到∠OCP=90∘,利用∠CAB=27∘得到∠COB=2∠CAB=54∘,然后利用直角三角形两锐角互余即可求得答案;; (2)根据E为AC 的中点得到OD⊥AC,从而求得∠AOE=90∘−∠EAO=80∘,然后利用圆周角定理求得∠AOD=40∘,最后利用三角形的外角的性质求解即可.∠ACD=12【解答】解:(1)如图,连接OC,∵⊙O与PC相切于点C,∴OC⊥PC,即∠OCP=90∘,∵∠CAB=27∘,∴∠COB=2∠CAB=54∘,在Rt△AOE中,∠P+∠COP=90∘,∴∠P=90∘−∠COP=36∘;; (2)∵E为AC的中点,∴OD⊥AC,即∠AEO=90∘,在Rt△AOE中,由∠EAO=10∘,得∠AOE=90∘−∠EAO=80∘,∠AOD=40∘,∴∠ACD=12∵∠ACD是△ACP的一个外角,∴∠P=∠ACD−∠A=40∘−10∘=30∘.22. 【答案】AC的长约为38.2cm,CB的长约等于45.0m.【解析】根据锐角三角函数,可用CD表示AD,BD,AC,BC,根据线段的和差,可得关于CD的方程,根据解方程,可得CD的长,根据AC=√2CD,CB=CD,可得答案.0.60【解答】解:过点C作CD⊥AB垂足为D,在Rt△ACD中,tanA=tan45∘=CDAD=1,CD=AD,sinA=sin45∘=CDAC =√22,AC=√2CD.在Rt△BCD中,tanB=tan37∘=CDBD ≈0.75,BD=CD0.75;sinB=sin37∘=CDBC ≈0.60,CB=CD0.60.∵AD+BD=AB=63,∴CD+CD0.75=63,解得CD≈27,AC=√2CD≈1.414×27=38.178≈38.2,CB=CD0.60≈270.60=45.0,23. 【答案】表一:315,45x,30,−30x+240;表二:1200,400x,1400,−280x+2240;; (2)能完成此项运送任务的最节省费用的租车方案是甲车6辆,乙车2辆,理由:当租用甲种货车x辆时,设两种货车的总费用为y元,则两种货车的总费用为:y=400x+(−280x+2240)=120x+2240,又∵45x+(−30x+240)≥330,解得x≥6,∵120>0,∴在函数y=120x+2240中,y随x的增大而增大,∴当x=6时,y取得最小值,即能完成此项运送任务的最节省费用的租车方案是甲种货车6辆,乙种货车2辆.【解析】(1)根据计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元,可以分别把表一和表二补充完整;; (2)由(1)中的数据和公司有330台机器需要一次性运送到某地,可以解答此题.【解答】解:(1)由题意可得,在表一中,当甲车7辆时,运送的机器数量为:45×7=315〔台〕,则乙车8−7=1辆,运送的机器数量为:30×1=30〔台〕,当甲车x辆时,运送的机器数量为:45×x=45x〔台〕,则乙车(8−x)辆,运送的机器数量为:30×(8−x)=−30x+240〔台〕,在表二中,当租用甲货车3辆时,租用甲种货车的费用为:400×3=1200〔元〕,则租用乙种货车8−3=5辆,租用乙种货车的费用为:280×5=1400〔元〕,当租用甲货车x辆时,租用甲种货车的费用为:400×x=400x〔元〕,则租用乙种货车(8−x)辆,租用乙种货车的费用为:280×(8−x)=−280x+2240〔元〕,; (2)能完成此项运送任务的最节省费用的租车方案是甲车6辆,乙车2辆,理由:当租用甲种货车x辆时,设两种货车的总费用为y元,则两种货车的总费用为:y=400x+(−280x+2240)=120x+2240,又∵45x+(−30x+240)≥330,解得x≥6,∵120>0,∴在函数y=120x+2240中,y随x的增大而增大,∴当x=6时,y取得最小值,即能完成此项运送任务的最节省费用的租车方案是甲种货车6辆,乙种货车2辆.24. 【答案】解:(1)如图①,∵点A(4, 0),点B(0, 3),∴OA=4,OB=3,∴AB=√32+42=5,∵△ABO绕点B逆时针旋转90∘,得△A′BO′,∴BA=BA′,∠ABA′=90∘,∴△ABA′为等腰直角三角形,∴AA′=√2BA=5√2;(2)作O′H⊥y轴于H,如图②,∵△ABO绕点B逆时针旋转120∘,得△A′BO′,∴BO=BO′=3,∠OBO′=120∘,∴∠HBO′=60∘,在Rt△BHO′中,∵∠BO′H=90∘−∠HBO′=30∘,∴BH=12BO′=32,O′H=√3BH=3√32,∴OH=OB+BH=3+32=92,∴O′点的坐标为(3√32, 92 );(3)∵△ABO绕点B逆时针旋转120∘,得△A′BO′,点P的对应点为P′,∴BP=BP′,∴O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,则O′P+BP=O′P+PC=O′C,此时O′P+BP的值最小,∵点C与点B关于x轴对称,∴C(0, −3),设直线O′C的解析式为y=kx+b,把O′(3√32, 92),C(0, −3)代入得{3√32k+b=92b=−3,解得{k=5√33b=−3,∴直线O′C的解析式为y=5√33x−3,当y=0时,5√33x−3=0,解得x=3√35,则P(3√35, 0),∴OP=3√35,∴O′P′=OP=3√35,作P′D⊥O′H于D,∵∠BO′A′=∠BOA=90∘,∠BO′H=30∘,∴∠DP′O′=30∘,∴O′D=12O′P′=3√310,P′D=√3O′D=910,∴DH=O′H−O′D=3√32−3√310=6√35,∴P′点的坐标为(6√35, 275).【解析】(1)如图①,先利用勾股定理计算出AB=5,再根据旋转的性质得BA=BA′,∠ABA′=90∘,则可判定△ABA′为等腰直角三角形,然后根据等腰直角三角形的性质求AA′的长;(2)作O′H⊥y轴于H,如图②,利用旋转的性质得BO=BO′=3,∠OBO′=120∘,则∠HBO′=60∘,再在Rt△BHO′中利用含30度的直角三角形三边的关系可计算出BH和O′H的长,然后利用坐标的表示方法写出O′点的坐标;(3)由旋转的性质得BP=BP′,则O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,易得O′P+BP=O′C,利用两点之间线段最短可判断此时O′P+BP的值最小,接着利用待定系数法求出直线O′C的解析式为y=5√33x−3,从而得到P(3√35, 0),则O′P′=OP=3√35,作P′D⊥O′H于D,然后确定∠DP′O′=30∘后利用含30度的直角三角形三边的关系可计算出P′D和DO′的长,从而可得到P′点的坐标.【解答】解:(1)如图①,∵点A(4, 0),点B(0, 3),∴OA=4,OB=3,∴AB=√32+42=5,∵△ABO绕点B逆时针旋转90∘,得△A′BO′,∴BA=BA′,∠ABA′=90∘,∴△ABA′为等腰直角三角形,∴AA′=√2BA=5√2;(2)作O′H⊥y轴于H,如图②,∵△ABO绕点B逆时针旋转120∘,得△A′BO′,∴BO=BO′=3,∠OBO′=120∘,∴∠HBO′=60∘,在Rt△BHO′中,∵∠BO′H=90∘−∠HBO′=30∘,∴BH=12BO′=32,O′H=√3BH=3√32,∴OH=OB+BH=3+32=92,∴O′点的坐标为(3√32, 92 );(3)∵△ABO绕点B逆时针旋转120∘,得△A′BO′,点P的对应点为P′,∴BP=BP′,∴O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,则O′P+BP=O′P+PC=O′C,此时O′P+BP的值最小,∵点C与点B关于x轴对称,∴C(0, −3),设直线O′C的解析式为y=kx+b,把O′(3√32, 92),C(0, −3)代入得{3√32k+b=92b=−3,解得{k=5√33b=−3,∴直线O′C的解析式为y=5√33x−3,当y=0时,5√33x−3=0,解得x=3√35,则P(3√35, 0),∴OP=3√35,∴O′P′=OP=3√35,作P′D⊥O′H于D,∵∠BO′A′=∠BOA=90∘,∠BO′H=30∘,∴∠DP′O′=30∘,∴O′D=12O′P′=3√310,P′D=√3O′D=910,∴DH=O′H−O′D=3√32−3√310=6√35,∴P′点的坐标为(6√35, 275).25. 【答案】解:(I)∵y=x2−2x+1=(x−1)2∴顶点P(1, 0),∵当x=0时,y=1,∴Q(0, 1),; (II)①设抛物线C′的解析式为y=x2−2x+m,∴Q′(0, m)其中m>1,∴OQ′=m ,∵F(1, 12),过F 作FH ⊥OQ′,如图:∴FH =1,Q′H =m −12,在Rt △FQ′H 中,FQ′2=(m −12)2+1=m 2−m +54,∵FQ′=OQ′,∴m 2−m +54=m 2,∴m =54,∴抛物线C′的解析式为y =x 2−2x +54,②设点A(x 0, y 0),则y 0=x 02−2x 0+54, 过点A 作x 轴的垂线,与直线Q′F 相交于点N ,则可设N(x 0, n),∴AN =y 0−n ,其中y 0>n ,连接FP ,∵F(1, 12),P(1, 0),∴FP ⊥x 轴,∴FP // AN ,∴∠ANF =∠PFN ,连接PK ,则直线Q′F 是线段PK 的垂直平分线,∴FP =FK ,有∠PFN =∠AFN ,∴∠ANF =∠AFN ,则AF =AN ,根据勾股定理,得,AF 2=(x 0−1)2+(y 0−12)2,∴(x 0−1)2+(y 0−12)2=(x 20 −2x 0+54)+y 20 −y 0=y 20 , ∴AF =y 0,∴y 0=y 0−n ,∴n =0,∴N(x 0, 0),设直线Q′F 的解析式为y =kx +b ,则{b =54k +b =12, 解得{k =−34b =54, ∴y =−34x +54,由点N 在直线Q′F 上,得,0=−34x 0+54,∴x 0=53,将x 0=53代入y 0=x 20 −2x 0+54, ∴y 0=2536,∴A(53, 2536)【解析】(1)令x =0,求出抛物线与y 轴的交点,抛物线解析式化为顶点式,求出点P 坐标;(2)①设出Q′(0, m),表示出Q′H ,根据FQ′=OQ′,用勾股定理建立方程求出m ,即可. ②根据AF =AN ,用勾股定理,(x −1)2+(y −12)2=(x 2−2x +54)+y 2−y =y 2,求出AF =y ,再求出直线Q′F 的解析式,即可.;【解答】解:(I)∵y =x 2−2x +1=(x −1)2∴顶点P(1, 0),∵当x =0时,y =1,∴Q(0, 1),; (II)①设抛物线C′的解析式为y =x 2−2x +m ,∴Q′(0, m)其中m >1,∴OQ′=m ,∵F(1, 12),过F 作FH ⊥OQ′,如图:∴FH =1,Q′H =m −12,在Rt △FQ′H 中,FQ′2=(m −12)2+1=m 2−m +54, ∵FQ′=OQ′,∴m 2−m +54=m 2,∴m =54,∴抛物线C′的解析式为y =x 2−2x +54,②设点A(x 0, y 0),则y 0=x 02−2x 0+54, 过点A 作x 轴的垂线,与直线Q′F 相交于点N ,则可设N(x 0, n),∴AN =y 0−n ,其中y 0>n ,连接FP ,∵F(1, 12),P(1, 0),∴FP ⊥x 轴,∴FP // AN ,∴∠ANF =∠PFN ,连接PK ,则直线Q′F 是线段PK 的垂直平分线, ∴FP =FK ,有∠PFN =∠AFN ,∴∠ANF =∠AFN ,则AF =AN ,根据勾股定理,得,AF 2=(x 0−1)2+(y 0−12)2,∴(x 0−1)2+(y 0−12)2=(x 20 −2x 0+54)+y 20 −y 0=y 20 , ∴AF =y 0,∴y 0=y 0−n ,∴n =0,∴N(x 0, 0),设直线Q′F 的解析式为y =kx +b ,则{b =54k +b =12, 解得{k =−34b =54, ∴y =−34x +54,由点N 在直线Q′F 上,得,0=−34x 0+54, ∴x 0=53,将x 0=53代入y 0=x 20 −2x 0+54, ∴y 0=2536,∴A(53, 2536)。
中考数学压轴题解析

中(Zhong)考数学压轴题解析一.解(Jie)答题1.如(Ru)图,在(Zai)△ABC中(Zhong)(BC>AC),∠ACB=90°,点(Dian)D在(Zai)AB边(Bian)上,DE⊥AC于点E.(1)若=,AE=2,求EC的长;(2)设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P.问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由.2.阅读理解:如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.简单应用:(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是;(2)当图③中的∠BCD=120°时,∠AEB′=°;(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有个(包含四边形ABCD).拓展提升:当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.3.在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E.DF与线段AC(或AC的延长线)相交于点F.(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB;(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,作DN⊥AC于点N,若DN⊥AC于点N,若DN=FN,求证:BE+CF=(BE﹣CF).4.如(Ru)图(Tu)1,在(Zai)△ABC中(Zhong),∠ACB=90°,AC=BC,∠EAC=90°,点(Dian)M为(Wei)射线(Xian)AE上任意一(Yi)点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.(1)直接写出∠NDE的度数;(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=,其他条件不变,求线段AM的长.5.如图,在▱ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将▱ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.(1)当点H与点C重合时.①填空:点E到CD的距离是;②求证:△BCE≌△GCF;③求△CEF的面积;(2)当点H落在射线BC上,且CH=1时,直线EH与直线CD交于点M,请直接写出△MEF的面积.6.如图,在平面直角坐(Zuo)标系中,四边形(Xing)OABC的(De)顶点(Dian)O是坐标原(Yuan)点,点(Dian)A 在(Zai)第一象限,点(Dian)C在第四象限,点B的坐标为(60,0),OA=AB,∠OAB=90°,OC=50.点P是线段OB上的一个动点(点P不与点O、B重合),过点P与y轴平行的直线l交边OA或边AB于点Q,交边OC或边BC于点R,设点P横坐标为t,线段QR的长度为m.已知t=40时,直线l恰好经过点C.(1)求点A和点C的坐标;(2)当0<t<30时,求m关于t的函数关系式;(3)当m=35时,请直接写出t的值;(4)直线l上有一点M,当∠PMB+∠POC=90°,且△PMB的周长为60时,请直接写出满足条件的点M 的坐标.7.如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.求证:∠APB是∠MON的智慧角.(2)如图1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,连结AB,用含α的式子分别表示∠APB的度数和△AOB的面积.(3)如图3,C是函数y=(x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.8.如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.(1)求抛物线的解析式;(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.9.已(Yi)知抛物线(Xian)y=x2+c与(Yu)x轴(Zhou)交于(Yu)A(﹣1,0),B两(Liang)点,交(Jiao)y轴(Zhou)于点C.(1)求抛物线的解析式;(2)点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG.求n的值并直接写出m的取值范围(利用图1完成你的探究).(3)如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长.10.如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含端点),过点P作PF⊥BC于点F,点D、E的坐标分别为(0,6),(﹣4,0),连接PD、PE、DE.(1)请直接写出抛物线的解析式;(2)小明探究点P的位置发现:当P与点A或点C重合时,PD与PF的差为定值,进而猜想:对于任意一点P,PD与PF的差为定值,请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE周长最小时“好点”的坐标.11.如图,已知二次函数y=x2+(1﹣m)x﹣m(其中0<m<1)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC(1)∠ABC的度数(Shu)为;(2)求(Qiu)P点坐标(Biao)(用含(Han)m的代数式(Shi)表示);(3)在坐标轴上(Shang)是否存在着点(Dian)Q(与(Yu)原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由.12.如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D和点C关于抛物线的对称轴对称,直线AD与y轴交于点E.(1)求直线AD的解析式;(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是以AM为边的矩形.若点T和点Q关于AM所在直线对称,求点T的坐标.13.如图,在平面直角坐标系中,抛物线y=﹣x2﹣x+2与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.(1)填空:点A的坐标为(,),点B的坐标为(,),点C的坐标为(,),点D的坐标为(,);(2)点P是线段BC上的动点(点P不与点B、C重合)①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标;②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长;③若点Q是线段AB上的动点(点Q不与点A、B重合),点R是线段AC上的动点(点R不与点A、C 重合),请直接写出△PQR周长的最小值.2016中考数学压(Ya)轴题参考答案与试题(Ti)解析一.解答(Da)题1.(2015•杭州)如(Ru)图,在(Zai)△ABC中(Zhong)(BC>AC),∠ACB=90°,点(Dian)D在(Zai)AB边上,DE⊥AC于点E.(1)若=,AE=2,求EC的长;(2)设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P.问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由.【分析】(1)易证DE∥BC,由平行线分线段成比例定理列比例式即可求解;(2)分三种情况讨论:①若∠CFG=∠ECD,此时线段CP是△CFG的FG边上的中线;②若∠CFG=∠EDC,此时线段CP为△CFG的FG边上的高线;③当CD为∠ACB的平分线时,CP既是△CFG的FG边上的高线又是中线.【解答】解:(1)∵∠ACB=90°,DE⊥AC,∴DE∥BC,∴,∵,AE=2,∴EC=6;(2)①如图1,若∠CFG=∠ECD,此时线段CP是△CFG的FG边上的中线.证明:∵∠CFG+∠CGF=90°,∠ECD+∠PCG=90°,又∵∠CFG=∠ECD,∴∠CGF=∠PCG,∴CP=PG,∵∠CFG=∠ECD,∴CP=FP,∴PF=PG=CP,∴线段CP是△CFG的FG边上的中线;②如图2,若∠CFG=∠EDC,此时线段CP为△CFG的FG边上的高线.证明:∵DE⊥AC,∴∠EDC+∠ECD=90°,∵∠CFG=∠EDC,∴∠CFG+∠ECD=90°,∴∠CPF=90°,∴线段CP为△CFG的FG边上的高线.③如图3,当CD为∠ACB的平分线时,CP既是△CFG的FG边上的高线又是中线.【点(Dian)评】本题主要考查了平行线分线段成比例定理、等腰三角形的判定、三角形的有关概念,分类讨论,能全面(Mian)的思考问题是解决问题的关键.2.(2015•淮安(An))阅读理解:如(Ru)图(Tu)①,如果四(Si)边形(Xing)ABCD满(Man)足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.简单应用:(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是正方形;(2)当图③中的∠BCD=120°时,∠AEB′=80°;(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有5个(包含四边形ABCD).拓展提升:当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.【分析】(1)由平行四边形、矩形、菱形、正方形的性质和“完美筝形”的定义容易得出结论;(2)先证出∠AEB′=∠BCB′,再求出∠BCE=∠ECF=40°,即可得出结果;(3)由折叠的性质得出BE=B′E,BC=B′C,∠B=∠CB′E=90°,CD=CD′,FD=FD′,∠D=∠CD′F=90°,即可得出四边形EBCB′、四边形FDCD′是“完美筝形”;由题意得出∠OD′E=∠OB′F=90°,CD′=CB′,由菱形的性质得出AE=AF,CE=CF,再证明△OED′≌△OFB′,得出OD′=OB′,OE=OF,证出∠AEB′=∠AFD′=90°,即可得出四边形CD′OB′、四边形AEOF是“完美筝形”;即可得出结论;当图③中的∠BCD=90°时,四边形ABCD是正方形,证明A、E、B′、F四点共圆,得出,由圆周角定理即可得出∠AB′E的度数.【解答】解:(1)①∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠A=∠C≠90°,∠B=∠D≠90°,∴AB≠AD,BC≠CD,∴平行四边形不一定为“完美筝形”;②∵四(Si)边形(Xing)ABCD是矩(Ju)形,∴∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,∴AB≠AD,BC≠CD,∴矩形不一(Yi)定为(Wei)“完(Wan)美筝形(Xing)”;③∵四(Si)边形ABCD是菱形,∴AB=BC=CD=AD,∠A=∠C≠90°,∠B=∠D≠90°,∴菱形不一定为“完美筝形”;④∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,∴正方形一定为“完美筝形”;∴在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是正方形;故答案为:正方形;(2)根据题意得:∠B′=∠B=90°,∴在四边形CBEB′中,∠BEB′+∠BCB′=180°,∵∠AEB′+∠BEB′=180°,∴∠AEB′=∠BCB′,∵∠BCE=∠ECF=∠FCD,∠BCD=120°,∴∠BCE=∠ECF=40°,∴∠AEB′=∠BCB′=40°+40°=80°;故答案为:80;(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有5个;理由如下;根据题意得:BE=B′E,BC=B′C,∠B=∠CB′E=90°,CD=CD′,FD=FD′,∠D=∠CD′F=90°,∴四边形EBCB′、四边形FDCD′是“完美筝形”;∵四边形ABCD是“完美筝形”,∴AB=AD,CB=CD,∠B=∠D=90°,∴CD′=CB′,∠CD′O=∠CB′O=90°,∴∠OD′E=∠OB′F=90°,∵四边形AECF为菱形,∴AE=AF,CE=CF,AE∥CF,AF∥CE,∴D′E=B′F,∠AEB′=∠CB′E=90°,∠AFD′=∠CD′F=90°,在△OED′和△OFB′中,,∴△OED′≌△OFB′(AAS),∴OD′=OB′,OE=OF,∴四边形CD′OB′、四边形AEOF是“完美筝形”;∴包含四边形ABCD,对应图③中的“完美筝形”有5个;故答案为:5;当图③中的∠BCD=90°时,如图所示:四边形ABCD是正方形,∴∠BAD=90°,∵∠EB′F=90°,∴∠BAD+∠EB′F=180°,∴A、E、B′、F四点共圆,∵AE=AF,∴,∴∠AB′E=∠AB′F=∠EB′F=45°.【点(Dian)评】本题是四(Si)边形综合题目,考查了平行四边形、矩形、菱形、正方形的性质、“完(Wan)美筝形(Xing)”的判定与性质、全等(Deng)三角形的判定与性质、四点共圆、圆周角定理等知识;本题难度较大,综合性强,熟练掌握(Wo)“完(Wan)美筝形(Xing)”的定义,并能进行推理论证与计算是解决问题的关键.3.(2015•重庆)在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E.DF与线段AC(或AC的延长线)相交于点F.(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB;(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,作DN⊥AC于点N,若DN⊥AC于点N,若DN=FN,求证:BE+CF=(BE﹣CF).【分析】(1)如图1,易求得∠B=60°,∠BED=90°,BD=2,然后运用三角函数的定义就可求出BE的值;(2)过点D作DM⊥AB于M,作DN⊥AC于N,如图2,易证△MBD≌△NCD,则有BM=CN,DM=DN,进而可证到△EMD≌△FND,则有EM=FN,就可得到BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=BC=AB;(3)过点D作DM⊥AB于M,如图3.同(1)可得:∠B=∠ACD=60°,同(2)可得:BM=CN,DM=DN,EM=FN.由DN=FN可得DM=DN=FN=EM,从而可得BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM,BE﹣CF=BM+EM﹣CF=BM+NF﹣CF=BM+NC=2BM.然后在Rt△BMD中,运用三角函数就可得到DM=BM,即BE+CF=(BE﹣CF).【解答】解:(1)如图1,∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠B=∠C=60°,BC=AC=AB=4.∵点D是线段BC的中点,∴BD=DC=BC=2.∵DF⊥AC,即∠AFD=90°,∴∠AED=360°﹣60°﹣90°﹣120°=90°,∴∠BED=90°,∴BE=BD×cos∠B=2×cos60°=2×=1;(2)过(Guo)点(Dian)D作(Zuo)DM⊥AB于(Yu)M,作(Zuo)DN⊥AC于(Yu)N,如(Ru)图(Tu)2,则有∠AMD=∠BMD=∠AND=∠CND=90°.∵∠A=60°,∴∠MDN=360°﹣60°﹣90°﹣90°=120°.∵∠EDF=120°,∴∠MDE=∠NDF.在△MBD和△NCD中,,∴△MBD≌△NCD,∴BM=CN,DM=DN.在△EMD和△FND中,,∴△EMD≌△FND,∴EM=FN,∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=BC=AB;(3)过点D作DM⊥AB于M,如图3.同(1)可得:∠B=∠ACD=60°.同(2)可得:BM=CN,DM=DN,EM=FN.∵DN=FN,∴DM=DN=FN=EM,∴BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM,BE﹣CF=BM+EM﹣CF=BM+NF﹣CF=BM+NC=2BM.在Rt△BMD中,DM=BM•tanB=BM,∴BE+CF=(BE﹣CF).【点(Dian)评】本题主要考查了等边三角形的判定与性质、四边形的内角和定理、全等三角形的判定与性质、三角函数的定义、特殊角的三角函数值等知(Zhi)识,通过证明三角形全等得到(Dao)BM=CN,DM=DN,EM=FN是解(Jie)决本题的关键.4.(2015•济(Ji)南)如图(Tu)1,在(Zai)△ABC中(Zhong),∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.(1)直接写出∠NDE的度数;(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=,其他条件不变,求线段AM的长.【分析】(1)根据题意证明△MAC≌△NBC即可;(2)与(1)的证明方法相似,证明△MAC≌△NBC即可;(3)作GK⊥BC于K,证明AM=AG,根据△MAC≌△NBC,得到∠BDA=90°,根据直角三角形的性质和已知条件求出AG的长,得到答案.【解答】解:(1)∵∠ACB=90°,∠MCN=90°,∴∠ACM=∠BCN,在(Zai)△MAC和(He)△NBC中(Zhong),,∴△MAC≌△NBC,∴∠NBC=∠MAC=90°,又(You)∵∠ACB=90°,∠EAC=90°,∴∠NDE=90°;(2)不(Bu)变,在(Zai)△MAC≌△NBC中(Zhong),,∴△MAC≌△NBC,∴∠N=∠AMC,又(You)∵∠MFD=∠NFC,∠MDF=∠FCN=90°,即∠NDE=90°;(3)作GK⊥BC于K,∵∠EAC=15°,∴∠BAD=30°,∵∠ACM=60°,∴∠GCB=30°,∴∠AGC=∠ABC+∠GCB=75°,∠AMG=75°,∴AM=AG,∵△MAC≌△NBC,∴∠MAC=∠NBC,∴∠BDA=∠BCA=90°,∵BD=,∴AB=+,AC=BC=+1,设BK=a,则GK=a,CK=a,∴a+a=+1,∴a=1,∴KB=KG=1,BG=,AG=,∴AM=.【点(Dian)评】本题考查的是矩形的判定和(He)性质以及三角形全等的判定和性质,正确作出辅助线、利用方程的思想是解题的关键,注意旋转的性质的灵活运用.5.(2015•沈(Shen)阳)如图,在(Zai)▱ABCD中(Zhong),AB=6,BC=4,∠B=60°,点(Dian)E是(Shi)边(Bian)AB上的一点,点F是边CD上一点,将▱ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.(1)当点H与点C重合时.①填空:点E到CD的距离是2;②求证:△BCE≌△GCF;③求△CEF的面积;(2)当点H落在射线BC上,且CH=1时,直线EH与直线CD交于点M,请直接写出△MEF的面积.【分析】(1)①解直角三角形即可;②根据平行四边形的性质和折叠的性质得出∠B=∠G,∠BCE=∠GCF,BC=GC,然后根据AAS即可证明;③过E点作EP⊥BC于P,设BP=m,则BE=2m,通过解直角三角形求得EP=m,然后根据折叠的性质和勾股定理求得EC,进而根据三角形的面积就可求得;(2)过E点作EQ⊥BC于Q,通过解直角三角形求得EP=n,根据折叠的性质和勾股定理求得EH,然后根据三角形相似对应边成比例求得MH,从而求得CM,然后根据三角形面积公式即可求得.【解答】解:(1)如图1,①作CK⊥AB于K,∵∠B=60°,∴CK=BC•sin60°=4×=2,∵C到AB的距离和E到CD的距离都是平行线AB、CD间的距离,∴点E到CD的距离是2,故答案为2;②∵四边形ABCD是平行四边形,∴AD=BC,∠D=∠B,∠A=∠BCD,由折叠(Die)可知,AD=CG,∠D=∠G,∠A=∠ECG,∴BC=GC,∠B=∠G,∠BCD=∠ECG,∴∠BCE=∠GCF,在(Zai)△BCE和(He)△GCF中(Zhong),,∴△BCE≌△GCF(ASA);③过(Guo)E点(Dian)作(Zuo)EP⊥BC于(Yu)P,∵∠B=60°,∠EPB=90°,∴∠BEP=30°,∴BE=2BP,设BP=m,则BE=2m,∴EP=BE•sin60°=2m×=m,由折叠可知,AE=CE,∵AB=6,∴AE=CE=6﹣2m,∵BC=4,∴PC=4﹣m,在RT△ECP中,由勾股定理得(4﹣m)2+(m)2=(6﹣2m)2,解得m=,∴EC=6﹣2m=6﹣2×=,∵△BCE≌△GCF,∴CF=EC=,∴S△CEF=××2=;(2)①当H在BC的延长线上,且位于C点的右侧时,如图2,过E点作EQ⊥BC于Q,∵∠B=60°,∠EQB=90°,∴∠BEQ=30°,∴BE=2BQ,设BQ=n,则BE=2n,∴QE=BE•sin60°=2n×=n,由折叠可知,AE=HE,∵AB=6,∴AE=HE=6﹣2n,∵BC=4,CH=1,∴BH=5,∴QH=5﹣n,在Rt△EHQ中,由勾股定理得(5﹣n)2+(n)2=(6﹣2n)2,解得n=,∴AE=HE=6﹣2n=,∵AB∥CD,∴△CMH∽△BEH,∴=,即(Ji)=,∴MH=,∴EM=﹣=∴S△EMF=××2=.②如(Ru)图(Tu)3,当(Dang)H在(Zai)线段(Duan)BC上(Shang)时,过(Guo)E点作EQ⊥BC于Q,∵∠B=60°,∠EQB=90°,∴∠BEQ=30°,∴BE=2BQ,设BQ=n,则BE=2n,∴QE=BE•sin60°=2n×=n,由折叠可知,AE=HE,∵AB=6,∴AE=HE=6﹣2n,∵BC=4,CH=1,∴BH=3∴QH=3﹣n在Rt△EHQ中,由勾股定理得(3﹣n)2+(n)2=(6﹣2n)2,解得n=∴BE=2n=3,AE=HE=6﹣2n=3,∴BE=BH,∴∠B=60°,∴△BHE是等边三角形,∴∠BEH=60°,∵∠AEF=∠HEF,∴∠FEH=∠AEF=60°,∴EF∥BC,∴DF=CF=3,∵AB∥CD,∴△CMH∽△BEH,∴=,即=,∴CM=1∴EM=CF+CM=4∴S△EMF=×4×2=4.综上,△MEF的面积为或4.【点(Dian)评】本题是四边形综合题,考查了解直角三角形,平行四边形的性质,折(Zhe)叠的性质勾股定理的应用,三角形相似的判定和性质,三角形面积等,熟练掌握性质定理是解题的关键.6.(2015•沈(Shen)阳)如图,在平面直角坐标系中,四边形(Xing)OABC的(De)顶点(Dian)O是坐(Zuo)标原点,点(Dian)A在第一象限,点C在第四象限,点B的坐标为(60,0),OA=AB,∠OAB=90°,OC=50.点P是线段OB上的一个动点(点P不与点O、B重合),过点P与y轴平行的直线l交边OA 或边AB于点Q,交边OC或边BC于点R,设点P横坐标为t,线段QR的长度为m.已知t=40时,直线l恰好经过点C.(1)求点A和点C的坐标;(2)当0<t<30时,求m关于t的函数关系式;(3)当m=35时,请直接写出t的值;(4)直线l上有一点M,当∠PMB+∠POC=90°,且△PMB的周长为60时,请直接写出满足条件的点M 的坐标.【分析】(1)利用等腰三角形的性质以及勾股定理结合B点坐标得出A,C点坐标;(2)利用锐角三角函数关系结合(1)中所求得出PR,QP的长,进而求出即可;(3)利用(2)中所求,利用当0<t<30时,当30≤t≤60时,分别利用m与t的关系式求出即可;(4)利用相似三角形的性质,得出M点坐标即可.【解答】解:(1)如图1,过点A作AD⊥OB,垂足为D,过点C作CE⊥OB,垂足为E,∵OA=AB,∴OD=DB=OB,∵∠OAB=90°,∴AD=OB,∵点(Dian)B的坐标(Biao)为:(60,0),∴OB=60,∴OD=OB=×60=30,∴点(Dian)A的坐(Zuo)标为:(30,30),∵直(Zhi)线(Xian)l平(Ping)行于(Yu)y轴且当t=40时,直线l恰好过点C,∴OE=40,在Rt△OCE中,OC=50,由勾股定理得:CE===30,∴点C的坐标为:(40,﹣30);(2)如图2,∵∠OAB=90°,OA=AB,∴∠AOB=45°,∵直线l平行于y轴,∴∠OPQ=90°,∴∠OQP=45°,∴OP=QP,∵点P的横坐标为t,∴OP=QP=t,在Rt△OCE中,OE=40,CE=30,∴tan∠EOC=,∴tan∠POR==,∴PR=OP•tan∠POR=t,∴QR=QP+PR=t+t=t,∴当0<t<30时,m关于t的函数关系式为:m=t;(3)由(2)得:当0<t<30时,m=35=t,解得:t=20;如图3,当30≤t≤40时,m=35显然不可能;当40<t<60时,∵OP=t,则BP=QP=60﹣t,∵PR∥CE,∴△BPR∽△BEC,∴=,∴=,解得:PR=90﹣t,则(Ze)m=60﹣t+90﹣t=35,解(Jie)得:t=46,综上(Shang)所述:t的(De)值为(Wei)20或(Huo)46;(4)如(Ru)图(Tu)4,当∠PMB+∠POC=90°且△PMB的周长为60时,此时t=40,直线l恰好经过点C,则∠MBP=∠COP,故此时△BMP∽△OCP,则=,即=,解得:x=15,故M1(40,15),同理可得:M2(40,﹣15),综上所述:符合题意的点的坐标为:M1(40,15),M2(40,﹣15).【点(Dian)评】此题主要考查了一次函数综合以及相似三角形的判(Pan)定与性质和勾股定理等知识,利用分类讨论以及数形结合得出是解题关键.7.(2015•宁(Ning)波)如图(Tu)1,点(Dian)P为(Wei)∠MON的(De)平分线上一点,以(Yi)P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.求证:∠APB是∠MON的智慧角.(2)如图1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,连结AB,用含α的式子分别表示∠APB的度数和△AOB的面积.(3)如图3,C是函数y=(x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.【分析】(1)由角平分线求出∠AOP=∠BOP=∠MON=45°,再证出∠OAP=∠OPB,证明△AOP∽△POB,得出对应边成比例,得出OP2=OA•OB,即可得出结论;(2)由∠APB是∠MON的智慧角,得出,证出△AOP∽△POB,得出对应角相等∠OAP=∠OPB,即可得出∠APB=180°﹣α;过点A作AH⊥OB于H,由三角形的面积公式得出:S△AOB=OB•AH,即可得出S△AOB=2sinα;(3)设点C(a,b),则ab=3,过点C作CH⊥OA于H;分两种情况:①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,BC=2CA不可能;当得A在x轴的正半轴上时;先求出,由平行线得出△ACH∽△ABO,得出比例式:=,得出OB=3b,OA=,求出OA•OB=,根据∠APB是∠AOB的智慧角,得出OP,即可得出点P的坐标;②当点B在y轴的负半轴上时;由题意得出:AB=CA,由AAS证明△ACH≌△ABO,得出OB=CH=b,OA=AH=a,得出OA•OB=,求出OP,即可得出点P的坐标.【解答】(1)证明:∵∠MON=90°,P为∠MON的平分线上一点,∴∠AOP=∠BOP=∠MON=45°,∵∠AOP+∠OAP+∠APO=180°,∴∠OAP+∠APO=135°,∵∠APB=135°,∴∠APO+∠OPB=135°,∴∠OAP=∠OPB,∴△AOP∽△POB,∴,∴OP2=OA•OB,∴∠APB是(Shi)∠MON的智慧(Hui)角;(2)解(Jie):∵∠APB是(Shi)∠MON的智慧(Hui)角,∴OA•OB=OP2,∴,∵P为(Wei)∠MON的平分线上(Shang)一点,∴∠AOP=∠BOP=α,∴△AOP∽△POB,∴∠OAP=∠OPB,∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°﹣α,即(Ji)∠APB=180°﹣α;过点A作AH⊥OB于H,连接AB;如图1所示:则S△AOB=OB•AH=OB•OAsinα=OP2•sinα,∵OP=2,∴S△AOB=2sinα;(3)设点C(a,b),则ab=3,过点C作CH⊥OA于H;分两种情况:①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,如图2所示:BC=2CA不可能;当点A在x轴的正半轴上时,如图3所示:∵BC=2CA,∴,∵CH∥OB,∴△ACH∽△ABO,∴=,∴OB=3b,OA=,∴OA•OB=•3b==,∵∠APB是∠AOB的智慧角,∴OP===,∵∠AOB=90°,OP平分∠AOB,∴点P的坐标为:(,);②当点B在y轴的负半轴上时,如图4所示:∵BC=2CA,∴AB=CA,在(Zai)△ACH和(He)△ABO中(Zhong),,∴△ACH≌△ABO(AAS),∴OB=CH=b,OA=AH=a,∴OA•OB=a•b=,∵∠APB是(Shi)∠AOB的智慧(Hui)角,∴OP===,∵∠AOB=90°,OP平(Ping)分(Fen)∠AOB,∴点(Dian)P的坐标为:(,﹣);综上所述:点P的坐标为:(,),或(,﹣).。
2016年中考数学压轴题及解析分类汇编

中考数学压轴题及解析分类汇编问题中考数学压轴:等腰三角形问题中考数学压轴:直角三角形问题问题中考数学压轴:梯形问题中考数学压轴:面积问题2016中考数学压轴题:函数相似三角形问题(一)例1、直线113y x=-+分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△COD,抛物线y=ax2+bx+c经过A、C、D三点.(1) 写出点A、B、C、D的坐标;(2) 求经过A、C、D三点的抛物线表达式,并求抛物线顶点G的坐标;(3) 在直线BG上是否存在点Q,使得以点A、B、Q为顶点的三角形与△COD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.图1思路点拨1.图形在旋转过程中,对应线段相等,对应角相等,对应线段的夹角等于旋转角.2.用待定系数法求抛物线的解析式,用配方法求顶点坐标.3.第(3)题判断∠ABQ =90°是解题的前提.4.△ABQ 与△COD 相似,按照直角边的比分两种情况,每种情况又按照点Q 与点B 的位置关系分上下两种情形,点Q 共有4个.满分解答(1)A (3,0),B (0,1),C (0,3),D (-1,0).(2)因为抛物线y =ax 2+bx +c 经过A (3,0)、C (0,3)、D (-1,0) 三点,所以930,3,0.a b c c a b c ++=⎧⎪=⎨⎪-+=⎩ 解得1,2,3.a b c =-⎧⎪=⎨⎪=⎩所以抛物线的解析式为y =-x 2+2x +3=-(x -1)2+4,顶点G 的坐标为(1,4).(3)如图2,直线BG 的解析式为y =3x +1,直线CD 的解析式为y =3x +3,因此CD //BG . 因为图形在旋转过程中,对应线段的夹角等于旋转角,所以AB ⊥CD .因此AB ⊥BG ,即∠ABQ =90°.因为点Q 在直线BG 上,设点Q 的坐标为(x ,3x +1),那么BQ ==. Rt △COD 的两条直角边的比为1∶3,如果Rt △ABQ 与Rt △COD 相似,存在两种情况: ①当3BQ BA =3=.解得3x =±.所以1(3,10)Q ,2(3,8)Q --.②当13BQ BA =13=.解得13x =±.所以31(,2)3Q ,41(,0)3Q -.图2 图3考点伸展第(3)题在解答过程中运用了两个高难度动作:一是用旋转的性质说明AB ⊥BG ;二是BQ =.我们换个思路解答第(3)题:如图3,作GH ⊥y 轴,QN ⊥y 轴,垂足分别为H 、N .通过证明△AOB ≌△BHG ,根据全等三角形的对应角相等,可以证明∠ABG =90°. 在Rt △BGH 中,sin 1∠=,cos 1∠=①当3BQ BA=时,BQ = 在Rt △BQN 中,sin 13QN BQ =⋅∠=,cos 19BN BQ =⋅∠=.当Q 在B 上方时,1(3,10)Q ;当Q 在B 下方时,2(3,8)Q --.②当13BQ BA =时,BQ =31(,2)3Q ,41(,0)3Q -. 例2、 Rt △ABC 在直角坐标系内的位置如图1所示,反比例函数(0)k y k x=≠在第一象限内的图像与BC 边交于点D (4,m ),与AB 边交于点E (2,n ),△BDE 的面积为2.(1)求m与n的数量关系;(2)当tan∠A=12时,求反比例函数的解析式和直线AB的表达式;(3)设直线AB与y轴交于点F,点P在射线FD上,在(2)的条件下,如果△AEO 与△EFP相似,求点P的坐标.图1思路点拨1.探求m与n的数量关系,用m表示点B、D、E的坐标,是解题的突破口.2.第(2)题留给第(3)题的隐含条件是FD//x轴.3.如果△AEO与△EFP相似,因为夹角相等,根据对应边成比例,分两种情况.满分解答(1)如图1,因为点D(4,m)、E(2,n)在反比例函数kyx=的图像上,所以4,2.m kn k=⎧⎨=⎩整理,得n=2m.(2)如图2,过点E作EH⊥BC,垂足为H.在Rt△BEH中,tan∠BEH=tan∠A=12,EH=2,所以BH=1.因此D(4,m),E(2,2m),B(4,2m+1).已知△BDE的面积为2,所以11(1)2222BD EH m⋅=+⨯=.解得m=1.因此D(4,1),E(2,2),B(4,3).因为点D(4,1)在反比例函数kyx=的图像上,所以k=4.因此反比例函数的解析式为4yx =.设直线AB 的解析式为y =kx +b ,代入B (4,3)、E (2,2),得34,22.k b k b =+⎧⎨=+⎩ 解得12k =,1b =.因此直线AB 的函数解析式为112y x =+.图2 图3 图4(3)如图3,因为直线112y x =+与y 轴交于点F (0,1),点D 的坐标为(4,1),所以FD // x 轴,∠EFP =∠EAO .因此△AEO 与△EFP 相似存在两种情况:①如图3,当EA EF AO FP ==.解得FP =1.此时点P 的坐标为(1,1).②如图4,当EA FPAO EF ==.解得FP =5.此时点P 的坐标为(5,1).考点伸展本题的题设部分有条件“Rt △ABC 在直角坐标系内的位置如图1所示”,如果没有这个条件限制,保持其他条件不变,那么还有如图5的情况:第(1)题的结论m 与n 的数量关系不变.第(2)题反比例函数的解析式为12y x =-,直线AB 为172y x =-.第(3)题FD 不再与x 轴平行,△AEO 与△EFP 也不可能相似.图52016中考数学压轴题函数相似三角形问题(二)例3、如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、B1的坐标分别为(x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1 图2思路点拨1.第(2)题用含S 的代数式表示x 2-x 1,我们反其道而行之,用x 1,x 2表示S .再注意平移过程中梯形的高保持不变,即y 2-y 1=3.通过代数变形就可以了.2.第(3)题最大的障碍在于画示意图,在没有计算结果的情况下,无法画出准确的位置关系,因此本题的策略是先假设,再说理计算,后验证.3.第(3)题的示意图,不变的关系是:直线AB 与x 轴的夹角不变,直线AB 与抛物线的对称轴的夹角不变.变化的直线PQ 的斜率,因此假设直线PQ 与AB 的交点G 在x 轴的下方,或者假设交点G 在x 轴的上方.满分解答(1)抛物线的对称轴为直线1x =,解析式为21184y x x =-,顶点为M (1,18-). (2) 梯形O 1A 1B 1C 1的面积12122(11)3()62x x S x x -+-⨯3==+-,由此得到1223s x x +=+.由于213y y -=,所以22212211111138484y y x x x x -=--+=.整理,得212111()()384x x x x ⎡⎤-+-=⎢⎥⎣⎦.因此得到2172x x S -=. 当S =36时,212114,2.x x x x +=⎧⎨-=⎩ 解得126,8.x x =⎧⎨=⎩ 此时点A 1的坐标为(6,3). (3)设直线AB 与PQ 交于点G ,直线AB 与抛物线的对称轴交于点E ,直线PQ 与x 轴交于点F ,那么要探求相似的△GAF 与△GQE ,有一个公共角∠G .在△GEQ 中,∠GEQ 是直线AB 与抛物线对称轴的夹角,为定值.在△GAF 中,∠GAF 是直线AB 与x 轴的夹角,也为定值,而且∠GEQ ≠∠GAF .因此只存在∠GQE =∠GAF 的可能,△GQE ∽△GAF .这时∠GAF =∠GQE =∠PQD . 由于3tan 4GAF ∠=,tan 5DQ t PQD QP t∠==-,所以345t t =-.解得207t =.图3 图4例4、 如图1,已知点A (-2,4) 和点B (1,0)都在抛物线22y mx mx n =++上.(1)求m 、n ;(2)向右平移上述抛物线,记平移后点A 的对应点为A ′,点B 的对应点为B ′,若四边形A A ′B ′B 为菱形,求平移后抛物线的表达式;(3)记平移后抛物线的对称轴与直线AB ′ 的交点为C ,试在x 轴上找一个点D ,使得以点B ′、C 、D 为顶点的三角形与△ABC 相似.图1思路点拨1.点A 与点B 的坐标在3个题目中处处用到,各具特色.第(1)题用在待定系数法中;第(2)题用来计算平移的距离;第(3)题用来求点B ′ 的坐标、AC 和B ′C 的长.2.抛物线左右平移,变化的是对称轴,开口和形状都不变.3.探求△ABC 与△B ′CD 相似,根据菱形的性质,∠BAC =∠CB ′D ,因此按照夹角的两边对应成比例,分两种情况讨论.满分解答(1) 因为点A (-2,4) 和点B (1,0)都在抛物线22y mx mx n =++上,所以444,20.m m n m m n -+=⎧⎨++=⎩ 解得43m =-,4n =. (2)如图2,由点A (-2,4) 和点B (1,0),可得AB =5.因为四边形A A ′B ′B 为菱形,所以A A ′=B ′B = AB =5.因为438342+--=x x y ()2416133x =-++,所以原抛物线的对称轴x =-1向右平移5个单位后,对应的直线为x =4. 因此平移后的抛物线的解析式为()3164342,+--=x y .图2(3) 由点A (-2,4) 和点B ′ (6,0),可得A B ′=如图2,由AM //CN ,可得''''B N B C B M B A =,即28=.解得'B C =AC =ABC 与△B ′CD 中,∠BAC =∠CB ′D .①如图3,当''AB B C AC B D ==,解得'3B D =.此时OD =3,点D 的坐标为(3,0).②如图4,当''AB B D AC B C ==,解得5'3B D =.此时OD =133,点D 的坐标为(133,0).图3 图4考点伸展在本题情境下,我们还可以探求△B ′CD 与△AB B ′相似,其实这是有公共底角的两个等腰三角形,容易想象,存在两种情况.我们也可以讨论△B ′CD 与△C B B ′相似,这两个三角形有一组公共角∠B ,根据对应边成比例,分两种情况计算.2016中考数学压轴题函数相似三角形问题(三)例5 、 如图1,抛物线经过点A (4,0)、B (1,0)、C (0,-2)三点. (1)求此抛物线的解析式;(2)P 是抛物线上的一个动点,过P 作PM ⊥x 轴,垂足为M ,是否存在点P ,使得以A 、P 、M 为顶点的三角形与△OAC 相似?若存在,请求出符合条件的 点P 的坐标;若不存在,请说明理由;(3)在直线AC 上方的抛物线是有一点D ,使得△DCA 的面积最大,求出点D 的坐标.,图1思路点拨1.已知抛物线与x 轴的两个交点,用待定系数法求解析式时,设交点式比较简便. 2.数形结合,用解析式表示图象上点的坐标,用点的坐标表示线段的长. 3.按照两条直角边对应成比例,分两种情况列方程. 4.把△DCA 可以分割为共底的两个三角形,高的和等于OA . 满分解答(1)因为抛物线与x 轴交于A (4,0)、B (1,0)两点,设抛物线的解析式为)4)(1(--=x x a y ,代入点C 的 坐标(0,-2),解得21-=a .所以抛物线的解析式为22521)4)(1(212-+-=---=x x x x y .(2)设点P 的坐标为))4)(1(21,(---x x x . ①如图2,当点P 在x 轴上方时,1<x <4,)4)(1(21---=x x PM ,x AM -=4. 如果2==CO AOPM AM ,那么24)4)(1(21=----x x x .解得5=x 不合题意. 如果21==CO AO PM AM ,那么214)4)(1(21=----x x x .解得2=x . 此时点P 的坐标为(2,1).②如图3,当点P 在点A 的右侧时,x >4,)4)(1(21--=x x PM ,4-=x AM .解方程24)4)(1(21=---x x x ,得5=x .此时点P 的坐标为)2,5(-.解方程214)4)(1(21=---x x x ,得2=x 不合题意.③如图4,当点P 在点B 的左侧时,x <1,)4)(1(21--=x x PM ,x AM -=4. 解方程24)4)(1(21=---x x x ,得3-=x .此时点P 的坐标为)14,3(--.解方程214)4)(1(21=---x x x ,得0=x .此时点P 与点O 重合,不合题意.综上所述,符合条件的 点P 的坐标为(2,1)或)14,3(--或)2,5(-.图2 图3 图4 (3)如图5,过点D 作x 轴的垂线交AC 于E .直线AC 的解析式为221-=x y . 设点D 的横坐标为m )41(<<m ,那么点D 的坐标为)22521,(2-+-m m m ,点E 的坐标为)221,(-m m .所以)221()22521(2---+-=m m m DE m m 2212+-=.因此4)221(212⨯+-=∆m m S DAC m m 42+-=4)2(2+--=m .当2=m 时,△DCA 的面积最大,此时点D 的坐标为(2,1).图5 图6考点伸展第(3)题也可以这样解:如图6,过D 点构造矩形OAMN ,那么△DCA 的面积等于直角梯形CAMN 的面积减去△CDN 和△ADM 的面积.设点D 的横坐标为(m ,n ))41(<<m ,那么42)4(21)2(214)22(21++-=--+-⨯+=n m m n n m n S . 由于225212-+-=m m n ,所以m m S 42+-=. 例6 、 如图1,△ABC 中,AB =5,AC =3,cos A =310.D 为射线BA 上的点(点D 不与点B 重合),作DE //BC 交射线CA 于点E ..(1) 若CE =x ,BD =y ,求y 与x 的函数关系式,并写出函数的定义域; (2) 当分别以线段BD ,CE 为直径的两圆相切时,求DE 的长度;(3) 当点D 在AB 边上时,BC 边上是否存在点F ,使△ABC 与△DEF 相似?若存在,请求出线段BF 的长;若不存在,请说明理由.图1 备用图 备用图思路点拨1.先解读背景图,△ABC 是等腰三角形,那么第(3)题中符合条件的△DEF 也是等腰三角形.2.用含有x 的式子表示BD 、DE 、MN 是解答第(2)题的先决条件,注意点E 的位置不同,DE 、MN 表示的形式分两种情况.3.求两圆相切的问题时,先罗列三要素,再列方程,最后检验方程的解的位置是否符合题意.4.第(3)题按照DE 为腰和底边两种情况分类讨论,运用典型题目的结论可以帮助我们轻松解题. 满分解答(1)如图2,作BH ⊥AC ,垂足为点H .在Rt △ABH 中,AB =5,cosA =310AH AB =,所以AH =32=12AC .所以BH 垂直平分AC ,△ABC 为等腰三角形,AB =CB =5. 因为DE //BC ,所以AB AC DB EC =,即53y x=.于是得到53y x =,(0x >). (2)如图3,图4,因为DE //BC ,所以DE AE BC AC =,MN AN BC AC =,即|3|53DE x -=,1|3|253x MN -=.因此5|3|3x DE -=,圆心距5|6|6x MN -=.图2 图3 图4在⊙M 中,115226M r BD y x ===,在⊙N 中,1122N r CE x ==. ①当两圆外切时,5162x x +5|6|6x -=.解得3013x =或者10x =-. 如图5,符合题意的解为3013x =,此时5(3)15313x DE -==. ②当两圆内切时,5162x x -5|6|6x -=. 当x <6时,解得307x =,如图6,此时E 在CA 的延长线上,5(3)1537x DE -==; 当x >6时,解得10x =,如图7,此时E 在CA 的延长线上,5(3)3533x DE -==.图5 图6 图7(3)因为△ABC 是等腰三角形,因此当△ABC 与△DEF 相似时,△DEF 也是等腰三角形.如图8,当D 、E 、F 为△ABC 的三边的中点时,DE 为等腰三角形DEF 的腰,符合题意,此时BF =2.5.根据对称性,当F 在BC 边上的高的垂足时,也符合题意,此时BF =4.1.如图9,当DE 为等腰三角形DEF 的底边时,四边形DECF 是平行四边形,此时12534BF =.图8 图9 图10 图11考点伸展:第(3)题的情景是一道典型题,如图10,如图11,AH 是△ABC 的高,D 、E 、F 为△ABC 的三边的中点,那么四边形DEHF 是等腰梯形.例 7 如图1,在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b ).平移二次函数2tx y -=的图象,得到的抛物线F 满足两个条件:①顶点为Q ;②与x 轴相交于B 、C 两点(∣OB ∣<∣OC ∣),连结A ,B .(1)是否存在这样的抛物线F ,使得OC OB OA⋅=2?请你作出判断,并说明理由;(2)如果AQ ∥BC ,且tan ∠ABO =23,求抛物线F 对应的二次函数的解析式.思路点拨1.数形结合思想,把OC OB OA⋅=2转化为212t x x =⋅.2.如果AQ ∥BC ,那么以OA 、AQ 为邻边的矩形是正方形,数形结合得到t =b . 3.分类讨论tan ∠ABO =23,按照A 、B 、C 的位置关系分为四种情况.A 在y 轴正半轴时,分为B 、C 在y 轴同侧和两侧两种情况;A 在y 轴负半轴时,分为B 、C 在y 轴同侧和两侧两种情况. 满分解答(1)因为平移2tx y -=的图象得到的抛物线F 的顶点为Q (t ,b ),所以抛物线F 对应的解析式为b t x t y +--=2)(.因为抛物线与x 轴有两个交点,因此0>b t .令0=y ,得-=t OB t b,+=t OC tb . 所以-=⋅t OC OB (|||||tb)( +t t b )|-=2|t 22|OA t tb ==.即22b t t t -=±.所以当32t b =时,存在抛物线F 使得||||||2OC OB OA ⋅=.(2)因为AQ //BC ,所以t =b ,于是抛物线F 为t t x t y +--=2)(.解得1,121+=-=t x t x .①当0>t 时,由||||OC OB <,得)0,1(-t B .如图2,当01>-t 时,由=∠ABO tan 23=||||OB OA =1-t t ,解得3=t .此时二次函数的解析式为241832-+-=x x y .如图3,当01<-t 时,由=∠ABO tan 23=||||OB OA =1+-t t ,解得=t 53.此时二次函数的解析式为-=y 532x +2518x +12548.图2 图3②如图4,如图5,当0<t 时,由||||OC OB <,将t -代t ,可得=t 53-,3-=t .此时二次函数的解析式为=y 532x +2518x -12548或241832++=x x y .图4 图5考点伸展第(2)题还可以这样分类讨论:因为AQ //BC ,所以t =b ,于是抛物线F 为2()y t x t t =--+.由3tan 2OA ABO OB ∠==,得23OB OA =. ①把2(,0)3B t 代入2()y t x t t =--+,得3t =±(如图2,图5).②把2(,0)3B t -代入2()y t x t t =--+,得35t =±(如图3,图4).2016中考数学压轴题函数等腰三角形问题(一)例1、如图1,已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P (0,m )是线段OC 上一动点(C 点除外),直线PM 交AB 的延长线于点D .(1)求点D 的坐标(用含m 的代数式表示); (2)当△APD 是等腰三角形时,求m 的值;(3)设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ,过点O 作直线ME 的垂线,垂足为H (如图2).当点P 从O 向C 运动时,点H 也随之运动.请直接写出点H 所经过的路长(不必写解答过程).图1 图2思路点拨1.用含m 的代数式表示表示△APD 的三边长,为解等腰三角形做好准备. 2.探求△APD 是等腰三角形,分三种情况列方程求解.3.猜想点H 的运动轨迹是一个难题.不变的是直角,会不会找到不变的线段长呢?Rt △OHM 的斜边长OM 是定值,以OM 为直径的圆过点H 、C . 满分解答(1)因为PC //DB ,所以1CP PM MCBD DM MB===.因此PM =DM ,CP =BD =2-m .所以AD =4-m .于是得到点D 的坐标为(2,4-m ).(2)在△APD 中,22(4)AD m =-,224AP m =+,222(2)44(2)PD PM m ==+-. ①当AP =AD 时,2(4)m -24m =+.解得32m =(如图3). ②当PA =PD 时,24m +244(2)m =+-.解得43m =(如图4)或4m =(不合题意,舍去).③当DA =DP 时,2(4)m -244(2)m =+-.解得23m =(如图5)或2m =(不合题意,舍去).综上所述,当△APD 为等腰三角形时,m 的值为32,43或23.图3 图4 图5(3)点H.考点伸展第(2)题解等腰三角形的问题,其中①、②用几何说理的方法,计算更简单:①如图3,当AP=AD时,AM垂直平分PD,那么△PCM∽△MBA.所以12 PC MBCM BA==.因此12PC=,32m=.②如图4,当PA=PD时,P在AD的垂直平分线上.所以DA=2PO.因此42m m-=.解得43m=.第(2)题的思路是这样的:如图6,在Rt△OHM中,斜边OM为定值,因此以OM为直径的⊙G经过点H,也就是说点H在圆弧上运动.运动过的圆心角怎么确定呢?如图7,P与O重合时,是点H运动的起点,∠COH=45°,∠CGH=90°.图6 图7例2 如图1,已知一次函数y =-x +7与正比例函数43y x = 的图象交于点A ,且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l //y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒. ①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形?若存在,求t 的值;若不存在,请说明理由.图1思路点拨1.把图1复制若干个,在每一个图形中解决一个问题.2.求△APR 的面积等于8,按照点P 的位置分两种情况讨论.事实上,P 在CA 上运动时,高是定值4,最大面积为6,因此不存在面积为8的可能.3.讨论等腰三角形APQ ,按照点P 的位置分两种情况讨论,点P 的每一种位置又要讨论三种情况.满分解答(1)解方程组7,4,3y x y x =-+⎧⎪⎨=⎪⎩得3,4.x y =⎧⎨=⎩ 所以点A 的坐标是(3,4).令70y x =-+=,得7x =.所以点B 的坐标是(7,0).(2)①如图2,当P 在OC 上运动时,0≤t <4.由8A P R A C P P O RC O R A S S S S =--=△△△梯形,得1113+7)44(4)(7)8222t t t t -⨯-⨯⨯--⨯-=(.整理,得28120t t -+=.解得t =2或t =6(舍去).如图3,当P 在CA 上运动时,△APR 的最大面积为6.因此,当t =2时,以A 、P 、R 为顶点的三角形的面积为8.图2 图3 图4②我们先讨论P 在OC 上运动时的情形,0≤t <4.如图1,在△AOB 中,∠B =45°,∠AOB >45°,OB =7,AB =OB >AB .因此∠OAB >∠AOB >∠B .如图4,点P 由O 向C 运动的过程中,OP =BR =RQ ,所以PQ //x 轴.因此∠AQP =45°保持不变,∠PAQ 越来越大,所以只存在∠APQ =∠AQP 的情况. 此时点A 在PQ 的垂直平分线上,OR =2CA =6.所以BR =1,t =1. 我们再来讨论P 在CA 上运动时的情形,4≤t <7. 在△APQ 中, 3cos 5A ∠=为定值,7AP t =-,5520333AQ OA OQ OA OR t =-=-=-. 如图5,当AP =AQ 时,解方程520733t t -=-,得418t =.如图6,当QP =QA 时,点Q 在PA 的垂直平分线上,AP =2(OR -OP ).解方程72[(7)(4)]t t t -=---,得5t =.如7,当PA =PQ 时,那么12cos AQ A AP∠=.因此2cos AQ AP A =⋅∠.解方程52032(7)335t t -=-⨯,得22643t =. 综上所述,t =1或418或5或22643时,△APQ 是等腰三角形.图5 图6 图7考点伸展当P在CA上,QP=QA时,也可以用2cos=⋅∠来求解.AP AQ A2016中考数学压轴题函数等腰三角形问题(二)例3 如图1,在直角坐标平面内有点A(6, 0),B(0, 8),C(-4, 0),点M、N分别为线段AC和射线AB上的动点,点M以2个单位长度/秒的速度自C向A方向作匀速运动,点N以5个单位长度/秒的速度自A向B方向作匀速运动,MN交OB于点P.(1)求证:MN∶NP为定值;(2)若△BNP与△MNA相似,求CM的长;(3)若△BNP是等腰三角形,求CM的长.图1思路点拨1.第(1)题求证MN∶NP的值要根据点N的位置分两种情况.这个结论为后面的计算提供了方便.2.第(2)题探求相似的两个三角形有一组邻补角,通过说理知道这两个三角形是直角三角形时才可能相似.3.第(3)题探求等腰三角形,要两级(两层)分类,先按照点N 的位置分类,再按照顶角的顶点分类.注意当N 在AB 的延长线上时,钝角等腰三角形只有一种情况.4.探求等腰三角形BNP ,N 在AB 上时,∠B 是确定的,把夹∠B 的两边的长先表示出来,再分类计算.满分解答(1)如图2,图3,作NQ ⊥x 轴,垂足为Q .设点M 、N 的运动时间为t 秒. 在Rt △ANQ 中,AN =5t ,NQ =4t ,AQ =3t .在图2中,QO =6-3t ,MQ =10-5t ,所以MN ∶NP =MQ ∶QO =5∶3. 在图3中,QO =3t -6,MQ =5t -10,所以MN ∶NP =MQ ∶QO =5∶3.(2)因为△BNP 与△MNA 有一组邻补角,因此这两个三角形要么是一个锐角三角形和一个钝角三角形,要么是两个直角三角形.只有当这两个三角形都是直角三角形时才可能相似.如图4,△BNP ∽△MNA ,在Rt △AMN 中,35AN AM =,所以531025t t =-.解得3031t =.此时CM 6031=.图2 图3 图4(3)如图5,图6,图7中,OP MPQN MN=,即245OP t =.所以85OP t =. ①当N 在AB 上时,在△BNP 中,∠B 是确定的,885BP t =-,105BN t =-.(Ⅰ)如图5,当BP =BN 时,解方程881055t t -=-,得1017t =.此时CM 2017=.(Ⅱ)如图6,当NB =NP 时,45BE BN =.解方程()1848105255t t ⎛⎫-=- ⎪⎝⎭,得54t =.此时CM 52=. (Ⅲ)当PB =PN 时,1425BN BP =.解方程()1481058255t t ⎛⎫-=- ⎪⎝⎭,得t 的值为负数,因此不存在PB =PN 的情况.②如图7,当点N 在线段AB 的延长线上时,∠B 是钝角,只存在BP =BN 的可能,此时510BN t =-.解方程885105t t -=-,得3011t =.此时CM 6011=.图5 图6 图7考点伸展如图6,当NB =NP 时,△NMA 是等腰三角形,1425BN BP =,这样计算简便一些.例4、如图1,在矩形ABCD 中,AB =m (m 是大于0的常数),BC =8,E 为线段BC 上的动点(不与B 、C 重合).连结DE ,作EF ⊥DE ,EF 与射线BA 交于点F ,设CE =x ,BF =y .(1)求y 关于x 的函数关系式;(2)若m =8,求x 为何值时,y 的值最大,最大值是多少? (3)若12y m=,要使△DEF 为等腰三角形,m 的值应为多少?图1思路点拨1.证明△DCE ∽△EBF ,根据相似三角形的对应边成比例可以得到y 关于x 的函数关系式.2.第(2)题的本质是先代入,再配方求二次函数的最值.3.第(3)题头绪复杂,计算简单,分三段表达.一段是说理,如果△DEF 为等腰三角形,那么得到x =y ;一段是计算,化简消去m ,得到关于x 的一元二次方程,解出x 的值;第三段是把前两段结合,代入求出对应的m 的值.满分解答(1)因为∠EDC 与∠FEB 都是∠DEC 的余角,所以∠EDC =∠FEB .又因为∠C =∠B =90°,所以△DCE ∽△EBF .因此DC EB CE BF =,即8m xx y-=.整理,得y 关于x 的函数关系为218y x x m m=-+. (2)如图2,当m =8时,2211(4)288y x x x =-+=--+.因此当x =4时,y 取得最大值为2.(3) 若12y m =,那么21218x x m m m=-+.整理,得28120x x -+=.解得x =2或x =6.要使△DEF 为等腰三角形,只存在ED =EF 的情况.因为△DCE ∽△EBF ,所以CE =BF ,即x =y .将x =y =2代入12y m =,得m =6(如图3);将x =y =6代入12y m=,得m =2(如图4).图2 图3 图4考点伸展本题中蕴涵着一般性与特殊性的辩证关系,例如: 由第(1)题得到218y x x m m =-+221116(8)(4)x x x m m m=--=--+, 那么不论m 为何值,当x =4时,y 都取得最大值.对应的几何意义是,不论AB 边为多长,当E 是BC 的中点时,BF 都取得最大值.第(2)题m =8是第(1)题一般性结论的一个特殊性.再如,不论m 为小于8的任何值,△DEF 都可以成为等腰三角形,这是因为方程218x x x m m=-+总有一个根8x m =-的.第(3)题是这个一般性结论的一个特殊性.2016中考数学压轴题函数相似三角形问题(三)例5 已知:如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3,过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .(1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为56,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由;(3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在成立,请说明理由.图1思路点拨1.用待定系数法求抛物线的解析式,这个解析式在第(2)、(3)题的计算中要用到. 2.过点M 作MN ⊥AB ,根据对应线段成比例可以求FA 的长. 3.将∠EDC 绕点D 旋转的过程中,△DCG 与△DEF 保持全等.4.第(3)题反客为主,分三种情况讨论△PCG 为等腰三角形,根据点P 的位置确定点Q 的位置,再计算点Q 的坐标.满分解答(1)由于OD 平分∠AOC ,所以点D 的坐标为(2,2),因此BC =AD =1. 由于△BCD ≌△ADE ,所以BD =AE =1,因此点E 的坐标为(0,1).设过E 、D 、C 三点的抛物线的解析式为c bx ax y ++=2,那么⎪⎩⎪⎨⎧=++=++=.039,224,1c b a c b a c 解得65-=a ,613=b 1=c .因此过E 、D 、C 三点的抛物线的解析式为1613652++-=x x y .(2)把56=x 代入1613652++-=x x y ,求得512=y .所以点M 的坐标为⎪⎭⎫⎝⎛512,56.如图2,过点M 作MN ⊥AB ,垂足为N ,那么DADNFA MN =,即25622512-=-FA .解得1=FA . 因为∠EDC 绕点D 旋转的过程中,△DCG ≌△DEF ,所以CG =EF =2.因此GO =1,EF=2GO .(3)在第(2)中,GC =2.设点Q 的坐标为⎪⎭⎫ ⎝⎛++-161365,2x x x . ①如图3,当CP =CG =2时,点P 与点B (3,2)重合,△PCG 是等腰直角三角形.此时G Q Q x x y -=,因此11613652-=++-x x x 。
2016年天津市中考数学试卷
2016年天津市中考数学试卷一、选择题:本大题共12小题,每小题3分,共36分1.计算的结果等于()A. B. C. D.2.的值等于()A. B. C. D.3.下列图形中,可以看作是中心对称图形的是()A. B.C. D.4.年月日《天津日报》报道,年天津外环线内新栽植树木株,将用科学记数法表示应为()A. B.C. D.5.如图是一个由个相同的正方体组成的立体图形,它的主视图是()A. B. C. D.6.估计的值在()A.和之间B.和之间C.和之间D.和之间7.计算的结果为()A. B. C. D.8.方程的两个根为()A.,B.,C.,D.,9.实数,在数轴上的对应点的位置如图所示,把,,按照从小到大的顺序排列,正确的是()A. B.C. D.10.如图,把一张矩形纸片沿对角线折叠,点的对应点为,与相交于点,则下列结论一定正确的是()A. B.C. D.11.若点,,在反比例函数的图象上,则,,的大小关系是()A. B.C. D.12.已知二次函数(为常数),在自变量的值满足的情况下,与其对应的函数值的最小值为,则的值为()A.或B.或C.或D.或二、填空题:本大题共6小题,每小题3分,共18分13.计算的结果等于________.14.计算的结果等于________.15.不透明袋子中装有个球,其中有个红球、个绿球和个黑球,这些球除颜色外无其他差别,从袋子中随机取出个球,则它是绿球的概率是________.16.若一次函数(为常数)的图象经过第二、三、四象限,则的值可以是________(写出一个即可).17.如图,在正方形中,点,,,分别在边,,,上,点,,的值等于________.都在对角线上,且四边形和均为正方形,则正方形正方形18.如图,在每个小正方形的边长为的网格中,,为格点,,为小正方形边的中点,为,的延长线的交点.的长等于________;若点在线段上,点在线段上,且满足,请在如图所示的网格中,用无刻度的直尺,画出线段,并简要说明点,的位置是如何找到的(不要求证明)________.三、综合题:本大题共7小题,共66分19.解不等式,请结合题意填空,完成本题的解答.解不等式①,得________;解不等式②,得________;把不等式①和②的解集在数轴上表示出来;原不等式组的解集为________.20.在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:图中的值为________;求统计的这组初赛成绩数据的平均数、众数和中位数;根据这组初赛成绩,由高到低确定人进入复赛,请直接写出初赛成绩为的运动员能否进入复赛.21.在中,为直径,为上一点.如图.过点作的切线,与的延长线相交于点,若,求的大小;如图,为上一点,且经过的中点,连接并延长,与的延长线相交于点,若,求的大小.22.小明上学途中要经过,两地,由于,两地之间有一片草坪,所以需要走路线,,如图,在中,,,,求,的长.(结果保留小数点后一位)参考数据:,,,取.23.公司有台机器需要一次性运送到某地,计划租用甲、乙两种货车共辆,已知每辆甲种货车一次最多运送机器台、租车费用为元,每辆乙种货车一次最多运送机器台、租车费用为元设租用甲种货车辆(为非负整数),试填写表格.表一:表二:给出能完成此项运送任务的最节省费用的租车方案,并说明理由.24.在平面直角坐标系中,为原点,点,点,把绕点逆时针旋转,得,点,旋转后的对应点为,,记旋转角为.如图①,若,求的长;如图②,若,求点的坐标;在的条件下,边上的一点旋转后的对应点为,当取得最小值时,求点的坐标(直接写出结果即可)25.已知抛物线的顶点为,与轴的交点为,点.求点,的坐标;将抛物线向上平移得到抛物线,点平移后的对应点为,且.①求抛物线的解析式;②若点关于直线的对称点为,射线与抛物线相交于点,求点的坐标.答案1. 【答案】A【解析】根据减去一个数等于加上这个数的相反数进行计算即可得解.【解答】解:,故选:.2. 【答案】C【解析】直接利用特殊角的三角函数值求出答案.【解答】解:.故选:.3. 【答案】B【解析】根据中心对称图形的概念求解.【解答】解:、不是中心对称图形,因为找不到任何这样的一点,旋转度后它的两部分能够重合;即不满足中心对称图形的定义,故此选项错误;、是中心对称图形,故此选项正确;、不是中心对称图形,因为找不到任何这样的一点,旋转度后它的两部分能够重合;即不满足中心对称图形的定义,故此选项错误;、不是中心对称图形,因为找不到任何这样的一点,旋转度后它的两部分能够重合;即不满足中心对称图形的定义,故此选项错误.故选:.4. 【答案】B【解析】科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值大于时,是正数;当原数的绝对值小于时,是负数.【解答】解:,故选:.5. 【答案】A【解析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解答】解:从正面看易得第一层有个正方形,第二层左边有一个正方形,第三层左边有一个正方形.故选.6. 【答案】C【解析】直接利用二次根式的性质得出的取值范围.【解答】解:∵,∴的值在和之间.故选:.7. 【答案】A【解析】根据同分母分式相加减,分母不变,分子相加减计算即可得解.【解答】解:.故选.8. 【答案】D【解析】将分解因式成,解或即可得出结论.【解答】解:,则,或,解得:,.故选.9. 【答案】C【解析】根据数轴得出,求出,,,即可得出答案.【解答】解:∵从数轴可知:,∴ ,,,∴ ,故选.10. 【答案】D【解析】根据翻折变换的性质可得,根据两直线平行,内错角相等可得,从而得到,然后根据等角对等边可得,从而得解.【解答】解:∵矩形纸片沿对角线折叠,点的对应点为,∴ ,∵ ,∴ ,∴ ,∴ ,所以,结论正确的是选项.故选.11. 【答案】D【解析】直接利用反比例函数图象的分布,结合增减性得出答案.【解答】解:∵点,,在反比例函数的图象上,∴ ,点在第三象限,点在第一象限,每个图象上随的增大减小,∴ 一定最大,,∴ .故选:.12. 【答案】B【解析】由解析式可知该函数在时取得最小值、时,随的增大而增大、当时,随的增大而减小,根据时,函数的最小值为可分如下两种情况:①若,时,取得最小值;②若,当时,取得最小值,分别列出关于的方程求解即可.【解答】解:∵当时,随的增大而增大,当时,随的增大而减小,∴①若,时,取得最小值,可得:,解得:或(舍);②若,当时,取得最小值,可得:,解得:或(舍).综上,的值为或,故选:.13. 【答案】【解析】根据幂的乘方与积的乘方运算法则进行计算即可.【解答】解:.故答案为:.14. 【答案】【解析】先套用平方差公式,再根据二次根式的性质计算可得.【解答】解:原式,故答案为:.15. 【答案】【解析】由题意可得,共有种等可能的结果,其中从口袋中任意摸出一个球是绿球的有种情况,利用概率公式即可求得答案.【解答】解:∵在一个不透明的口袋中有个除颜色外其余都相同的小球,其中个红球、个绿球和个黑球,∴从口袋中任意摸出一个球是绿球的概率是,故答案为:.16. 【答案】【解析】根据一次函数的图象经过第二、三、四象限,可以得出,,随便写出一个小于的值即可.【解答】解:∵一次函数(为常数)的图象经过第二、三、四象限,∴ ,.故答案为:.17. 【答案】【解析】根据辅助线的性质得到,四边形和均为正方形,推出与是等腰直角三角形,于是得到,,同理,即可得到结论.【解答】解:在正方形中,∵ ,∵四边形和均为正方形,∴ ,,∴ 与是等腰直角三角形,∴,,同理,∴,∴正方形,正方形故答案为:.18. 【答案】;; 如图,与网格线相交,得到,取格点,连接,并延长与交于,连接,则线段即为所求.故答案为:与网格线相交,得到,取格点,连接,并延长与交于,连接,则线段即为所求.【解析】根据勾股定理即可得到结论;; 取格点,连接,并延长与交于,连接,则线段即为所求.【解答】解:;; 如图,与网格线相交,得到,取格点,连接,并延长与交于,连接,则线段即为所求.19. 【答案】;; 解不等式②,得.故答案为:.; 把不等式①和②的解集在数轴上表示为:;; 原不等式组的解集为:.故答案为:.【解析】分别求出各不等式的解集,再在数轴上表示出来即可.; ; ;【解答】解:解不等式①,得.; 解不等式②,得.; 把不等式①和②的解集在数轴上表示为:;; 原不等式组的解集为:.20. 【答案】;; 观察条形统计图得:;∵在这组数据中,出现了次,出现的次数最多,∴这组数据的众数是;将这组数据从小到大排列为,其中处于中间的两个数都是,则这组数据的中位数是.; 能;∵共有个人,中位数是第、个数的平均数,∴根据中位数可以判断出能否进入前名;∵ ,∴能进入复赛.【解析】用整体减去其它所占的百分比,即可求出的值;; 根据平均数、众数和中位数的定义分别进行解答即可;; 根据中位数的意义可直接判断出能否进入复赛.【解答】解:根据题意得:;则的值是;; 观察条形统计图得:;∵在这组数据中,出现了次,出现的次数最多,∴这组数据的众数是;将这组数据从小到大排列为,其中处于中间的两个数都是,则这组数据的中位数是.; 能;∵共有个人,中位数是第、个数的平均数,∴根据中位数可以判断出能否进入前名;∵ ,∴能进入复赛.21. 【答案】解:如图,连接,∵ 与相切于点,∴ ,即,∵ ,∴ ,在中,,∴ ;; ∵ 为的中点,∴ ,即,在中,由,得,∴,∵ 是的一个外角,∴ .【解析】连接,首先根据切线的性质得到,利用得到,然后利用直角三角形两锐角互余即可求得答案;; 根据为的中点得到,从而求得,然后利用圆周角定理求得,最后利用三角形的外角的性质求解即可.【解答】解:如图,连接,∵ 与相切于点,∴ ,即,∵ ,∴ ,在中,,∴ ;; ∵ 为的中点,∴ ,即,在中,由,得,∴,∵ 是的一个外角,∴ .22. 【答案】的长约为,的长约等于.【解析】根据锐角三角函数,可用表示,,,,根据线段的和差,可得关于的方程,根据解方程,可得的长,根据,,可得答案.【解答】解:过点作垂足为,在中,,,,.在中,,;,.∵ ,∴,解得,,,23. 【答案】表一:,,,;表二:,,,;; 能完成此项运送任务的最节省费用的租车方案是甲车辆,乙车辆,理由:当租用甲种货车辆时,设两种货车的总费用为元,则两种货车的总费用为:,又∵ ,解得,∵ ,∴在函数中,随的增大而增大,∴当时,取得最小值,即能完成此项运送任务的最节省费用的租车方案是甲种货车辆,乙种货车辆.【解析】根据计划租用甲、乙两种货车共辆,已知每辆甲种货车一次最多运送机器台、租车费用为元,每辆乙种货车一次最多运送机器台、租车费用为元,可以分别把表一和表二补充完整;; 由中的数据和公司有台机器需要一次性运送到某地,可以解答本题.【解答】解:由题意可得,在表一中,当甲车辆时,运送的机器数量为:(台),则乙车辆,运送的机器数量为:(台),当甲车辆时,运送的机器数量为:(台),则乙车辆,运送的机器数量为:(台),在表二中,当租用甲货车辆时,租用甲种货车的费用为:(元),则租用乙种货车辆,租用乙种货车的费用为:(元),当租用甲货车辆时,租用甲种货车的费用为:(元),则租用乙种货车辆,租用乙种货车的费用为:(元),; 能完成此项运送任务的最节省费用的租车方案是甲车辆,乙车辆,理由:当租用甲种货车辆时,设两种货车的总费用为元,则两种货车的总费用为:,又∵ ,解得,∵ ,∴在函数中,随的增大而增大,∴当时,取得最小值,即能完成此项运送任务的最节省费用的租车方案是甲种货车辆,乙种货车辆.24. 【答案】解:如图①,∵点,点,∴ ,,∴,∵ 绕点逆时针旋转,得,∴ ,,∴ 为等腰直角三角形,∴;作轴于,如图②,∵ 绕点逆时针旋转,得,∴ ,,∴ ,在中,∵ ,∴,,∴,∴ 点的坐标为;∵ 绕点逆时针旋转,得,点的对应点为,∴ ,∴ ,作点关于轴的对称点,连结交轴于点,如图②,则,此时的值最小,∵点与点关于轴对称,∴ ,设直线的解析式为,把,代入得,解得,∴直线的解析式为,当时,,解得,则,∴,∴,作于,∵ ,,∴ ,∴,,∴,∴ 点的坐标为.【解析】如图①,先利用勾股定理计算出,再根据旋转的性质得,,则可判定为等腰直角三角形,然后根据等腰直角三角形的性质求的长;作轴于,如图②,利用旋转的性质得,,则,再在中利用含度的直角三角形三边的关系可计算出和的长,然后利用坐标的表示方法写出点的坐标;由旋转的性质得,则,作点关于轴的对称点,连结交轴于点,如图②,易得,利用两点之间线段最短可判断此时的值最小,接着利用待定系数法求出直线的解析式为,从而得到,则,作于,然后确定后利用含度的直角三角形三边的关系可计算出和的长,从而可得到点的坐标.【解答】解:如图①,∵点,点,∴ ,,∴,∵ 绕点逆时针旋转,得,∴ ,,∴ 为等腰直角三角形,∴;作轴于,如图②,∵ 绕点逆时针旋转,得,∴ ,,∴ ,在中,∵ ,∴,,∴,∴ 点的坐标为;∵ 绕点逆时针旋转,得,点的对应点为,∴ ,∴ ,作点关于轴的对称点,连结交轴于点,如图②,则,此时的值最小,∵点与点关于轴对称,∴ ,设直线的解析式为,把,代入得,解得,∴直线的解析式为,当时,,解得,则,∴,∴,作于,∵ ,,∴ ,∴,,∴,∴ 点的坐标为.25. 【答案】解: ∵∴顶点,∵当时,,∴ ,; ①设抛物线的解析式为,∴ 其中,∴ ,∵,过作,如图:∴ ,,在中,,∵ ,∴ ,∴ ,∴抛物线的解析式为,②设点,则,过点作轴的垂线,与直线相交于点,则可设,∴ ,其中,连接,∵,,∴ 轴,∴ ,∴ ,连接,则直线是线段的垂直平分线,∴ ,有,∴ ,则,根据勾股定理,得,,∴ ,∴ ,∴ ,∴ ,∴ ,设直线的解析式为,则,解得,∴ ,由点在直线上,得,,∴ ,将代入,∴ ,∴【解析】令,求出抛物线与轴的交点,抛物线解析式化为顶点式,求出点坐标;①设出,表示出,根据,用勾股定理建立方程求出,即可.②根据,用勾股定理,,求出,再求出直线的解析式,即可.;【解答】解: ∵∴顶点,∵当时,,∴ ,; ①设抛物线的解析式为,∴ 其中,∴ ,∵,过作,如图:∴ ,,在中,,∵ ,∴ ,∴ ,∴抛物线的解析式为,②设点,则,过点作轴的垂线,与直线相交于点,则可设,∴ ,其中,连接,∵,,∴ 轴,∴ ,∴ ,连接,则直线是线段的垂直平分线,∴ ,有,∴ ,则,根据勾股定理,得,,∴ ,∴ ,∴ ,∴ ,∴ ,设直线的解析式为,则,解得,∴ ,由点在直线上,得,,∴ ,将代入,∴ ,∴。
2016年天津市中考数学试卷(word版,含答案)

2016年天津市中考数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题3分,共36分1.计算(﹣2)﹣5的结果等于()A.﹣7 B.﹣3 C.3 D.7A.2.sin60°的值等于()A.B.C.D.C.3.下列图形中,可以看作是中心对称图形的是()A.B.C. D.B.4.2016年5月24日《天津日报》报道,2015年天津外环线内新栽植树木6120000株,将6120000用科学记数法表示应为()A.0.612×107B.6.12×106 C.61.2×105 D.612×104B.5.如图是一个由4个相同的正方体组成的立体图形,它的主视图是()A.B. C.D.A.6.估计的值在()A.2和3之间B.3和4之间C.4和5之间D.5和6之间C.7.计算﹣的结果为()A.1 B.x C.D.A.8.方程x2+x﹣12=0的两个根为()A.x1=﹣2,x2=6 B.x1=﹣6,x2=2 C.x1=﹣3,x2=4 D.x1=﹣4,x2=3D.9.实数a,b在数轴上的对应点的位置如图所示,把﹣a,﹣b,0按照从小到大的顺序排列,正确的是()A.﹣a<0<﹣b B.0<﹣a<﹣b C.﹣b<0<﹣a D.0<﹣b<﹣aC.10.如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是()A.∠DAB′=∠CAB′B.∠ACD=∠B′CD C.AD=AE D.AE=CED.11.若点A(﹣5,y1),B(﹣3,y2),C(2,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是()A.y1<y3<y2B.y1<y2<y3C.y3<y2<y1D.y2<y1<y3D.12.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为()A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或3B.二、填空题:本大题共6小题,每小题3分,共18分13.计算(2a)3的结果等于8a3.14.计算(+)(﹣)的结果等于2.15.不透明袋子中装有6个球,其中有1个红球、2个绿球和3个黑球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是绿球的概率是.16.若一次函数y=﹣2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是﹣1(写出一个即可).17.如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于.18.如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.(Ⅰ)AE的长等于;(Ⅱ)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明)AC与网格线相交,得到P,取格点M,连接AM,并延长与BC交予Q,连接PQ,则线段PQ即为所求.三、综合题:本大题共7小题,共66分19.解不等式,请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得x≤4;(Ⅱ)解不等式②,得x≥2;(Ⅲ)把不等式①和②的解集在数轴上表示出来;(Ⅳ)原不等式组的解集为2≤x≤4.解:(I)解不等式①,得x≤4.故答案为:x≤4;(II)解不等式②,得x≥2.故答案为:x≥2.(III)把不等式①和②的解集在数轴上表示为:;(IV)原不等式组的解集为:.故答案为:2≤x≤4.20.在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:(Ⅰ)图1中a的值为25;(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.解:(Ⅰ)根据题意得:1﹣20%﹣10%﹣15%﹣30%=25%;则a的值是25;故答案为:25;(Ⅱ)观察条形统计图得:==1.61;∵在这组数据中,1.65出现了6次,出现的次数最多,∴这组数据的众数是1.65;将这组数据从小到大排列为,其中处于中间的两个数都是1.60,则这组数据的中位数是1.60.(Ⅲ)能;∵共有20个人,中位数是第10、11个数的平均数,∴根据中位数可以判断出能否进入前9名;∵1.65m>1.60m,∴能进入复赛.21.在⊙O中,AB为直径,C为⊙O上一点.(Ⅰ)如图1.过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P 的大小;(Ⅱ)如图2,D为上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.解:(Ⅰ)如图,连接OC,∵⊙O与PC相切于点C,∴OC⊥PC,即∠OCP=90°,∵∠CAB=27°,∴∠COB=2∠CAB=54°,在Rt△AOE中,∠P+∠COP=90°,∴∠P=90°﹣∠COP=36°;(Ⅱ)∵E为AC的中点,∴OD⊥AC,即∠AEO=90°,在Rt△AOE中,由∠EAO=10°,得∠AOE=90°﹣∠EAO=80°,∴∠ACD=∠AOD=40°,∵∠ACD是△ACP的一个外角,∴∠P=∠ACD﹣∠A=40°﹣10°=30°.22.小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63m,∠A=45°,∠B=37°,求AC,CB的长.(结果保留小数点后一位)参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,取1.414.解:过点C作CD⊥AB垂足为D,在Rt△ACD中,tanA=tan45°==1,CD=AD,sinA=sin45°==,AC=CD.在Rt△BCD中,tanB=tan37°=≈0.75,BD=;sinB=sin37°=≈0.60,CB=.∵AD+BD=AB=63,∴CD+=63,解得CD≈27,AC=CD≈1.414×27=38.178≈38.2,CB=≈=45.0,答:AC的长约为38.2cm,CB的长约等于45.0m.23.公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元(Ⅰ)设租用甲种货车x辆(x为非负整数),试填写表格.表一:租用甲种货车的数量/辆 3 7 x租用的甲种货车最多运送机器的数量/台135 31545x租用的乙种货车最多运送机器的数量/台150 30﹣30x+240表二:租用甲种货车的数量/辆 3 7 x租用甲种货车的费用/元12002800 400x租用乙种货车的费用/元1400280 ﹣280x+2240(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.解:(Ⅰ)由题意可得,在表一中,当甲车7辆时,运送的机器数量为:45×7=315(台),则乙车8﹣7=1辆,运送的机器数量为:30×1=30(台),当甲车x辆时,运送的机器数量为:45×x=45x(台),则乙车(8﹣x)辆,运送的机器数量为:30×(8﹣x)=﹣30x+240(台),在表二中,当租用甲货车3辆时,租用甲种货车的费用为:400×3=1200(元),则租用乙种货车8﹣3=5辆,租用乙种货车的费用为:280×5=1400(元),当租用甲货车x辆时,租用甲种货车的费用为:400×x=400x(元),则租用乙种货车(8﹣x)辆,租用乙种货车的费用为:280×(8﹣x)=﹣280x+2240(元),故答案为:表一:315,45x,30,﹣30x+240;表二:1200,400x,1400,﹣280x+2240;(Ⅱ)能完成此项运送任务的最节省费用的租车方案是甲车6辆,乙车2辆,理由:当租用甲种货车x辆时,设两种货车的总费用为y元,则两种货车的总费用为:y=400x+(﹣280x+2240)=120x+2240,又∵45x+(﹣30x+240)≥330,解得x≥6,∵120>0,∴在函数y=120x+2240中,y随x的增大而增大,∴当x=6时,y取得最小值,即能完成此项运送任务的最节省费用的租车方案是甲种货车6辆,乙种货车2辆.24.在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.(Ⅰ)如图①,若α=90°,求AA′的长;(Ⅱ)如图②,若α=120°,求点O′的坐标;(Ⅲ)在(Ⅱ)的条件下,边OA上的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)解:(1)如图①,∵点A(4,0),点B(0,3),∴OA=4,OB=3,∴AB==5,∵△ABO绕点B逆时针旋转90°,得△A′BO′,∴BA=BA′,∠ABA′=90°,∴△ABA′为等腰直角三角形,∴AA′=BA=5;(2)作O′H⊥y轴于H,如图②,∵△ABO绕点B逆时针旋转120°,得△A′BO′,∴BO=BO′=3,∠OBO′=120°,∴∠HBO′=60°,在Rt△BHO′中,∵∠BO′H=90°﹣∠HBO′=30°,∴BH=BO′=,O′H=BH=,∴OH=OB+BH=3+=,∴O′点的坐标为(,);(3)∵△ABO绕点B逆时针旋转120°,得△A′BO′,点P的对应点为P′,∴BP=BP′,∴O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,则O′P+BP=O′P+PC=O′C,此时O′P+BP的值最小,∵点C与点B关于x轴对称,∴C(0,﹣3),设直线O′C的解析式为y=kx+b,把O′(,),C(0,﹣3)代入得,解得,∴直线O′C的解析式为y=x﹣3,当y=0时,x﹣3=0,解得x=,则P(,0),∴OP=,∴O′P′=OP=,作P′D⊥O′H于D,∵∠BO′A=∠BOA=90°,∠BO′H=30°,∴∠DP′O′=30°,∴O′D=O′P′=,P′D=O′D=,∴DH=O′H﹣O′D=﹣=,∴P′点的坐标为(,).25.已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1,).(Ⅰ)求点P,Q的坐标;(Ⅱ)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.①求抛物线C′的解析式;②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.解:(Ⅰ)∵y=x2﹣2x+1=(x﹣1)2∴顶点P(1,0),∵当x=0时,y=1,∴Q(0,1),(Ⅱ)①设抛物线C′的解析式为y=x2﹣2x+m,∴Q′(0,m)其中m>1,∴OQ′=m,∵F(1,),过F作FH⊥OQ′,如图:∴FH=1,Q′H=m﹣,在Rt△FQ′H中,FQ′2=(m﹣)2+1=m2﹣m+,∵FQ′=OQ′,∴m2﹣m+=m2,∴m=,∴抛物线C′的解析式为y=x2﹣2x+,②设点A(x0,y0),则y0=x02﹣2x0+,过点A作x轴的垂线,与直线Q′F相交于点N,则可设N(x0,n),∴AN=y0﹣n,其中y0>n,连接FP,∵F(1,),P(1,0),∴FP⊥x轴,∴FP∥AN,∴∠ANF=∠PFN,连接PK,则直线Q′F是线段PK的垂直平分线,∴FP=FK,有∠PFN=∠AFN,∴∠ANF=∠AFN,则AF=AN,根据勾股定理,得,AF2=(x0﹣1)2+(y0﹣)2,∴(x0﹣1)2+(y0﹣)2=(x﹣2x0+)+y﹣y0=y,∴AF=y0,∴y0=y0﹣n,∴n=0,∴N(x0,0),设直线Q′F的解析式为y=kx+b,则,解得,∴y=﹣x+,由点N在直线Q′F上,得,0=﹣x0+,∴x0=,将x0=代入y0=x﹣2x0+,∴y0=,∴A(,)第11页(共11页)。
天津市2016年中考数学试题含答案

2016年天津市初中毕业生学业考试试卷数学第Ⅰ卷一、选择题(本大题共12小题,每小题3分,共3636分,在每小题给出的四个选项中,只有一个是符合题目要求的) (1)计算(-2)-5的结果等于(A )-7(B )-3(C )3(D )7(2)sin60o 的值等于(A )21(B )22 (C )23 (D )3(3)下列图形中,可以看作是中心对称图形的是(A )(B )(C )(D )(4)2016年5月24日《天津日报》报道,2015年天津外环线内新栽植树木6120 000株,将6120 000用科学记数法表示应为(A )0.612×107(B )6.12×106(C )61.2×105(D )612×104(5)右图是一个由4个相同的正方体组成的立体图形,它的主视图是(A )(B )(C )(D )(6)估计6的值在(A )2和3之间 (B )3和4之间 (C )4和5之间(D )5和6之间(7)计算xx x 11-+的结果为(A )1 (B )x (C )x1(D )xx 2+ (8)方程01222=-+x x 的两个根为(A )x 1= -2,x 2=6 (B )x 1= -6,x 2=2 (C )x 1= -3,x 2=4(D )x 1= -4,x 2=3(9)实数a ,b 在数轴上的对应点的位置如图所示,把-a ,-b ,0按照从小到大的顺序排列,正确的是(A )-a < 0 < -b第(5)题图第(9)题图a 0 b(B )0 < -a < -b (C )-b < 0 < -a (D )0 < -b < -a(10)如图,把一张矩形纸片ABCD 沿对角线AC 折叠,点B 的对应点为B ’,AB ’与DC 相交于点E ,则下列结论一定正确的是(A )∠DAB ’=∠CAB ’ (B )∠ACD=∠B ’CD (C )AD=AE(D )AE=CE(11)若点A (-5,y 1),B (-3,y 2),C (2,y 3)在反比例函数xy 3错误!未找到引用源。
中考数学压轴题 (附答案)

一、中考数学压轴题1.附加题:在平面直角坐标系中,抛物线21y ax a =-与y 轴交于点A ,点A 关于x 轴的对称点为点B ,(1)求抛物线的对称轴;(2)求点B 坐标(用含a 的式子表示);(3)已知点11,P a ⎛⎫ ⎪⎝⎭,(3,0)Q ,若抛物线与线段PQ 恰有一个公共点,结合函数图像,求a 的取值范围. 2.已知:如图,AB 为O 的直径,弦CD AB ⊥垂足为E ,点H 为弧AC 上一点.连接DH 交AB 于点F ,连接HA 、BD ,点G 为DH 上一点,连接AG ,HAG BDC ∠=∠. (1)如图1,求证:AG HD ⊥;(2)如图2,连接HC ,若HC HF =,求证:HC HA =;(3)如图3,连接HO 交AG 于点K ,若点F 为DG 的中点,HC 2HG =,求KG AK的值.3.如图,已知抛物线()2y ax bx 2a 0=+-≠与x 轴交于A 、B 两点,与y 轴交于C 点,直线BD 交抛物线于点D ,并且()D 2,3,()B 4,0-.(1)求抛物线的解析式;(2)已知点M 为抛物线上一动点,且在第三象限,顺次连接点B 、M 、C ,求BMC 面积的最大值;(3)在(2)中BMC 面积最大的条件下,过点M 作直线平行于y 轴,在这条直线上是否存在一个以Q 点为圆心,OQ 为半径且与直线AC 相切的圆?若存在,求出圆心Q 的坐标;若不存在,请说明理由.4.如图,已知正方形ABCD 中,4,BC AC BD =、相交于点O ,过点A 作射线AM AC ⊥,点E 是射线AM 上一动点,连接OE 交AB 于点F ,以OE 为一边,作正方形OEGH ,且点A 在正方形OEGH 的内部,连接DH .(1)求证:EDO EAO ∆≅∆;(2)设BF x =,正方形OEGH 的边长为y ,求y 关于x 的函数关系式,并写出定义域;(3)连接AG ,当AEG ∆是等腰三角形时,求BF 的长.5.如图①,四边形ABCD 中,//,90AB CD ADC ∠=︒.(1)动点M 从A 出发,以每秒1个单位的速度沿路线A B C D →→→运动到点D 停止,设运动时间为a ,AMD ∆的面积为,S S 关于a 的函数图象如图②所示,求AD CD 、的长.(2)如图③动点P 从点A 出发,以每秒2个单位的速度沿路线A D C →→运动到点C 停止,同时,动点Q 从点C 出发,以每秒5个单位的速度沿路线C D A →→运动到点A 停止,设运动时间为t ,当Q 点运动到AD 边上时,连接CP CQ PQ 、、,当CPQ ∆的面积为8时,求t 的值.6.在平面直角坐标系xOy 中,对于点A 和图形M ,若图形M 上存在两点P ,Q ,使得3AP AQ =,则称点A 是图形M 的“倍增点”.(1)若图形M 为线段BC ,其中点()2,0B -,点()2,0C ,则下列三个点()1,2D -,()1,1E -,()0,2F 是线段BC 的倍增点的是_____________;(2)若O 的半径为4,直线l :2y x =-+,求直线l 上O 倍增点的横坐标的取值范围;(3)设直线1y x =-+与两坐标轴分别交于G ,H ,OT 的半径为4,圆心T 是x 轴上的动点,若线段GH 上存在T 的倍增点,直接写出圆心T 的横坐标的取值范围.7.∠MON=90°,点A ,B 分别在OM 、ON 上运动(不与点O 重合).(1)如图①,AE 、BE 分别是∠BAO 和∠ABO 的平分线,随着点A 、点B 的运动,∠AEB= °(2)如图②,若BC 是∠ABN 的平分线,BC 的反向延长线与∠OAB 的平分线交于点D ①若∠BAO=60°,则∠D= °.②随着点A ,B 的运动,∠D 的大小会变吗?如果不会,求∠D 的度数;如果会,请说明理由.(3)如图③,延长MO 至Q ,延长BA 至G ,已知∠BAO ,∠OAG 的平分线与∠BOQ 的平分线及其延长线相交于点E 、F ,在△AEF 中,如果有一个角是另一个角的3倍,求∠ABO 的度数.8.对于平面直角坐标系xOy 中的任意点()P x y ,,如果满足x y a += (x ≥0,a 为常数),那么我们称这样的点叫做“特征点”.(1)当2≤a ≤3时,①在点(1,2),(1,3),(2.5,0)A B C 中,满足此条件的特征点为__________________;②⊙W 的圆心为(,0)W m ,半径为1,如果⊙W 上始终存在满足条件的特征点,请画出示意图,并直接写出m 的取值范围;(2)已知函数()10Z x x x=+>,请利用特征点求出该函数的最小值.9.如图,平面上存在点P 、点M 与线段AB .若线段AB 上存在一点Q ,使得点M 在以PQ 为直径的圆上,则称点M 为点P 与线段AB 的共圆点.已知点P (0,1),点A (﹣2,﹣1),点B (2,﹣1).(1)在点O (0,0),C (﹣2,1),D (3,0)中,可以成为点P 与线段AB 的共圆点的是 ;(2)点K 为x 轴上一点,若点K 为点P 与线段AB 的共圆点,请求出点K 横坐标x K 的取值范围;(3)已知点M (m ,﹣1),若直线y =12x +3上存在点P 与线段AM 的共圆点,请直接写出m 的取值范围.10.如图一,矩形ABCD 中,AB=m ,BC=n ,将此矩形绕点B 顺时针方向旋转θ(0°<θ<90°)得到矩形A 1BC 1D 1,点A 1在边CD 上.(1)若m=2,n=1,求在旋转过程中,点D 到点D 1所经过路径的长度;(2)将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2,点D 2在BC 的延长线上,设边A 2B 与CD 交于点E ,若161A E EC=-,求n m 的值. (3)如图二,在(2)的条件下,直线AB 上有一点P ,BP=2,点E 是直线DC 上一动点,在BE 左侧作矩形BEFG 且始终保持BE n BG m =,设AB=33,试探究点E 移动过程中,PF 是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.11.如图,抛物线2y x bx c =-++与x 轴相交于A 、B 两点,与y 轴相交于点C ,且点B 与点C 的坐标分别为()3,0B ,()0,3C ,点M 是抛物线的顶点.(1)求二次函数的关系式.(2)点P 为线段MB 上一个动点,过点P 作PD x ⊥轴于点D .若OD m =,PCD 的面积为S .①求S 与m 的函数关系式,写出自变量m 的取值范围.②当S 取得最值时,求点P 的坐标.(3)在MB 上是否存在点P ,使PCD 为直角三角形?如果存在,请直接写出点P 的坐标;如果不存在,请说明理由.12.如图1,平面直角坐标系xoy 中,A (-4,3),反比例函数(0)k y k x=<的图象分别交矩形ABOC 的两边AC ,BC 于E ,F (E ,F 不与A 重合),沿着EF 将矩形ABOC 折叠使A ,D 重合.(1)①如图2,当点D 恰好在矩形ABOC 的对角线BC 上时,求CE 的长;②若折叠后点D 落在矩形ABOC 内(不包括边界),求线段CE 长度的取值范围. (2)若折叠后,△ABD 是等腰三角形,请直接写出此时点D 的坐标.13.综合与探究:如图1,在平面直角坐标系xOy 中,四边形OABC 是边长为4的菱形,60C ︒∠=(1)把菱形OABC 先向右平移4个单位后,再向下平移()03m m <<个单位,得到菱形''''O A B C ,在向下平移的过程中,易知菱形''''O A B C 与菱形OABC 重叠部分的四边形'AEC F 为平行四边形,如图2.试探究:当m 为何值时,平行四边形'AEC F 为菱形:(2)如图,在()1的条件下,连接''',AC B O G 、为CE 的中点J 为EB 的中点,H 为AC 上一动点,I 为''B O 上一动点,连接,,,GH HI IJ 求GH HI IJ ++的最小值,并直接写出此时,H I 点的坐标.14.(1)探究发现数学活动课上,小明说“若直线21y x =-向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”经过一番讨论,小组成员展示了他们的解答过程:在直线21y x =-上任取点()01A -,, 向左平移3个单位得到点()31,'--A 设向左平移3个单位后所得直线所对应的函数表达式为2y x n =+.因为2y x n =+过点()31,'--A , 所以61n -+=-,所以5n =,填空:所以平移后所得直线所对应函数表达式为(2)类比运用已知直线21y x =-,求它关于x 轴对称的直线所对应的函数表达式;(3)拓展运用将直线21y x =-绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .15.已知:菱形 ABCD ,点 E 在线段 BC 上,连接 DE ,点 F 在线段 AB 上,连接 CF 、DF , CF 与 DE 交于点 G ,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.(1)求证:CD=CF ;(2)设∠CED = x ,∠DCF = y ,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围) (3)在(2)的条件下,当 x =45°时,以 CD 为底边作等腰△CDK ,顶角顶点 K 在菱形 ABCD 的内部,连接 GK ,若 GK ∥CD ,CD =4 时,求线段 KG 的长.16.如图,抛物线214y x bx c =++与x 轴交于点A (-2,0),交y 轴于点B (0,52-).直线32y kx =+过点A 与y 轴交于点C ,与抛物线的另一个交点是D .(1) 求抛物线214y x bx c =++与直线32y kx =+的解析式; (2)点P 是抛物线上A 、D 间的一个动点,过P 点作PM ∥CE 交线段AD 于M 点.①过D 点作DE ⊥y 轴于点E ,问是否存在P 点使得四边形PMEC 为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;②作PN ⊥AD 于点N ,设△PMN 的周长为m ,点P 的横坐标为x ,求m 关于x 的函数关系式,并求出m 的最大值.17.如图,在等边△ABC 中,AB =BC =AC =6cm ,点P 从点B 出发,沿B →C 方向以1.5cm/s 的速度运动到点C 停止,同时点Q 从点A 出发,沿A →B 方向以1cm/s 的速度运动,当点P 停止运动时,点Q 也随之停止运动,连接PQ ,过点P 作BC 的垂线,过点Q 作BC 的平行线,两直线相交于点M .设点P 的运动时间为x (s ),△MPQ 与△ABC 重叠部分的面积为y (cm 2)(规定:线段是面积为0的图形).(1)当x = (s )时,PQ ⊥BC ;(2)当点M 落在AC 边上时,x = (s );(3)求y 关于x 的函数解析式,并写出自变量x 的取值范围.18.在平行四边形ABCD 中,60B ∠=︒,点E ,F 分别在边AB ,AD 上,且60ECF ∠=︒.(1)如图1,若AB BC =,求证:AE AF BC +=;(2)如图2,若4AB BC ==,且点E 为AB 的中点,连接BF 交CE 于点M ,求FM ;(3)如图3,若AB kBC =,探究线段BE 、DF 、BC 三之间的数量关系,说明理由.19.ABC 内接于O ,AB BC =,连接BO ;(1)如图1,连接CO 并延长交O 于点M ,连接AM ,求证://AM BO ;(2)如图2,延长BO 交AC 于点H ,点F 为BH 上一点,连接AF ,若AH HF AB BF =,求证:BAF HAF ∠=∠;(3)在(2)的条件下,如图3,点E 为AB 上一点,点D 为O 上一点,连接ED 、OE ,若CBD 3ABH 90∠+∠=︒,若OF 3=,FH 4=,13623EBD S ∆=,连接OE ,求线段OE 的长.20.如图①,△ABC 是等腰直角三角形,在两腰AB 、AC 外侧作两个等边三角形ABD 和ACE ,AM 和AN 分别是等边三角形ABD 和ACE 的角平分线,连接CM 、BN ,CM 与AB 交于点P .(1)求证:CM =BN ;(2)如图②,点F 为角平分线AN 上一点,且∠CPF =30°,求证:△APF ∽△AMC ; (3)在(2)的条件下,求PF BN的值. 21.如图,在平面直角坐标系xOy 中,已知Rt ABC 的直角顶点()0,12C ,斜边AB 在x 轴上,且点A 的坐标为()9,0-,点D 是AC 的中点,点E 是BC 边上的一个动点,抛物线212y ax bx =++过D ,C ,E 三点.(1)当//DE AB 时,①求抛物线的解析式;②平行于对称轴的直线x m =与x 轴,DE ,BC 分别交于点F ,H ,G ,若以点D ,H ,F 为顶点的三角形与GHE △相似,求点m 的值.(2)以E 为等腰三角形顶角顶点,ED 为腰构造等腰EDG △,且G 点落在x 轴上.若在x 轴上满足条件的G 点有且只有一个时,请直接写出....点E 的坐标. 22.如图,直角梯形ABCD 中,1//,90,60,3,9,AD BC A C AD cm BC cm O ︒︒∠∠====的圆心1O 从点A 开始沿折线——A D C 以1/cm s 的速度向点C 运动,2O 的圆心2O 从点B 开始沿BA 边以3/cm s 的速度向点A 运动,1O 半径为22,cm O 的半径为4cm ,若12,O O 分别从点A 、点B 同时出发,运动的时间为ts(1)请求出2O 与腰CD 相切时t 的值; (2)在03s t s ≤<范围内,当t 为何值时,1O 与2O 外切?23.在平面直角坐标系xOy 中,点A 、B 为反比例函数()4x 0xy =>的图像上两点,A 点的横坐标与B 点的纵坐标均为1,将()4x 0xy =>的图像绕原点O 顺时针旋转90°,A 点的对应点为A’,B 点的对应点为B’.(1)点A’的坐标是 ,点B’的坐标是 ;(2)在x 轴上取一点P ,使得PA+PB 的值最小,直接写出点P 的坐标. 此时在反比例函数()4x 0xy =>的图像上是否存在一点Q ,使△A’B’Q 的面积与△PAB 的面积相等,若存在,求出点Q 的横坐标;若不存在,请说明理由;(3)连接AB’,动点M 从A 点出发沿线段AB’以每秒1个单位长度的速度向终点B’运动;动点N 同时从B’点出发沿线段B’A’以每秒1个单位长度的速度向终点A’运动.当其中一个点停止运动时,另一个点也随之停止运动.设运动的时间为t 秒,试探究:是否存在使△MNB’为等腰直角三角形的t 值.若存在,求出t 的值;若不存在,说明理由.24.(操作发现)如图1,ABC ∆为等腰直角三角形,90ACB ∠=︒,先将三角板的90︒角与ACB ∠重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0︒且小于45︒),旋转后三角板的一直角边与AB 交于点D .在三角板另一直角边上取一点F ,使CF CD =,线段AB 上取点E ,使45DCE ∠=︒,连接AF ,EF .(1)请求出EAF ∠的度数? (2)DE 与EF 相等吗?请说明理由;(类比探究)如图2,ABC ∆为等边三角形,先将三角板中的60︒角与ACB ∠重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0︒且小于30).旋转后三角板的一直角边与AB 交于点D .在三角板斜边上取一点F ,使CF CD =,线段AB 上取点E ,使30DCE ∠=︒,连接AF ,EF .(3)直接写出EAF∠=_________度;(4)若1AE =,2BD =,求线段DE 的长度.25.问题背景:如图(1),ABC 内接于O ,过点A 作O 的切线l ,在l 上任取一个不同于点A 的点P ,连接PB PC 、,比较BPC ∠与BAC ∠的大小,并说明理由.问题解决:如图(2),A (0,2)、B (0,4),在x 轴正半轴上是否存在一点P ,使得cos APB ∠最小?若存在,求出点P 的坐标;若不存在,请说明理由.拓展应用:如图(3),四边形ABCD 中,//AB CD ,AD CD ⊥于D ,E 是AB 上一点,AE AD =,P 是DE 右侧四边形ABCD 内一点,若8AB =,11CD =,tan 2C =,9DEPS=,求sin APB ∠的最大值.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题 1.B解析:(1)直线x=0;(2)B (0,1a );(3)2-≤a ≤13-或13≤a 2 【解析】 【分析】(1)根据抛物线的表达式直接得出对称轴即可;(2)根据题意得出点A 的坐标,再利用关于x 轴对称的点的坐标规律得出点B 坐标; (3)分a >0和a <0两种情况分别讨论,画图图像,求出a 的范围. 【详解】解:(1)在抛物线21y ax a=-中, 002a-=, ∴对称轴为直线x=0,即y 轴; (2)∵抛物线与y 轴交于点A ,∴A (0,1a-), ∵点A 关于x 轴的对称点为点B ,∴B (0,1a); (3)当a >0时,点A (0,1a-)在y 轴负半轴上, 当点P 恰好在抛物线上时,代入得:11a a a-=,解得:2a=或2-(舍),当点Q恰好在抛物线上时,代入得:190 aa-=,解得:13a=或13-(舍),∴当13≤a≤2时,抛物线与线段PQ恰有一个公共点;当a<0时,点A(0,1a-)在y轴正半轴上,同理可知:当点P恰好在抛物线上时,代入得:11aa a -=,解得:2a=(舍)或2-,当点Q恰好在抛物线上时,代入得:190 aa-=,解得:13a=(舍)或13-,∴当2-≤a≤13-时,抛物线与线段PQ只有一个公共点;综上:若抛物线与线段PQ恰有一个公共点,a的取值范围是2-≤a≤13 -或13≤a2.【点睛】本题是一道二次函数的综合题目,主要考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,画出相应的函数图象,利用分类讨论的方法和数形结合的思想解答.2.A解析:(1)详见解析;(2)详见解析;(3)15KG AK = 【解析】 【分析】(1)根据同弧所对的圆周角相等,进行角度计算,得90AHG HAG ∠+∠=︒,进而得到90AGH ∠=︒,即可证明AG HD ⊥;(2)连接AC 、AD 、CF ,根据同弧所对的圆周角相等,进行角度计算,得HFA HAF ∠=∠,进而得到HF HA =,再根据已知HC HF =,得到HC HA =; (3)在DH 上截取DT HC =,过点C 作CM HD ⊥于点M ,通过证明AHC ≌ATD 得到AH AT =,进而得到HG CH GD +=,再根据F 为DG 中点,得到GF DF =,通过勾股定理逆用,证明90HCF ∠=︒,再通过解ACE △得1tan 3CAB ∠=,解△CDH 得1tan 2CDF ∠=,求得OF 、OH ,逆用勾股定理证明90HOF ∠=︒,易求1tan 2KHG ∠=,1tan 3HAG ∠=,最后求得KGAK的值. 【详解】(1)证明:如图,设HAG ∠为α,∵HAG BDC ∠=∠, ∴HAG BDC α∠=∠=, ∵CD AB ⊥,∴90BDC DBE ∠+∠=︒ ∴90DBE α∠=︒-,∵AHG ∠与ABD ∠为同对弧AD 所对的圆周角, ∴90AHG ABD α∠=∠=︒-, ∴90AHG HAG ∠+∠=︒,∴18090AGH AHG HAG ∠=︒-∠-∠=︒ ∴AG HD ⊥(2)如图,连接AC 、AD 、CF ,∵AB 为直径,AB CD ⊥, ∴CE DE =, ∴AB 垂直平分CD , ∴AC AD =,FC FD =,∴ACD ADC ∠=∠,FCD FDC ∠=∠,∴ACD FCD ADC FDC ∠-∠=∠-∠,即ACF ADF ∠=∠, 设FCD FDC α∠=∠=,ACF ADF β∠=∠=, ∵ADH ∠与ACH ∠为同对弧AH 所对的圆周角, ∴ADH ACH β∠=∠=, ∴2HCF HCA ACF β∠=∠+∠=, ∵HFC FCD FDC ∠=∠+∠, ∴2HFC α∠=, ∵HC HF =, ∴HCF HFC ∠=∠, ∴22αβ=, ∴αβ=, ∵AB 为直径, ∴90ADB ∠=︒, ∴90HDB β∠=︒-,∵HAB ∠与为HDB ∠同对弧BH 所对的圆周角, ∴90HAB HDB β∠=∠=︒-, ∵AB CD ⊥,∴9090BFD αβ∠=︒-=︒-, ∵9090HFA BFD αβ∠=∠=︒-=︒-, ∴HFA HAF ∠=∠, ∴HF HA =, ∴HC HA =;(3)如图,在DH 上截取DT HC =,∵ADH ∠与ACH ∠同对弧AH 所对的圆周角, ∴ADH ACH ∠=∠, ∵AB 为直径,且AB CD ⊥ ∴AC =AD , ∴AC AD =, ∴AHC ≌ATD , ∴AH AT =, ∵AG HT ⊥, ∴HG TG =,∴HG CH GT DT GD +=+=, 设2HG k =,则4CH k =,GD 6k =, ∵F 为DG 中点, ∴3GF DF k ==,∴5HF HG GF k =+=,FD =CF =3k ,在HCF 中,由勾股定理逆定理得90HCF ∠=︒, 过点C 作CM HD ⊥于点M , 由△HCF 面积,可求CM =125k , ∴229=5MF CF CM k -=, ∴1tan 2CM CM CDF MD MF FD ∠===+, 解ACE △得1tan 3CAB ∠=, 易求OF ,OH ,由勾股定理逆定理得90HOF ∠=︒, 易求1tan 2KHG ∠=,1tan 3HAG ∠=, ∴15KG AK =. 【点睛】本题考查圆与三角形综合,主要考查知识点有同弧所对的圆周角相等,垂径定理,三角形全等的判定与性质,勾股定理的逆用,解直角三角形,锐角三角函数等,知识点跨度大,计算量多;熟练掌握圆的性质和三角形相关知识是解决本题的关键.3.B解析:(1)213y x x 222=+-;(2)4;(3)存在,Q 的坐标为()2,4-或()2,1-- 【解析】 【分析】()1根据题意将()D 2,3、()B 4,0-的坐标代入抛物线表达式,即可求解;()2由题意设点M 的坐标为213x,x x 222⎛⎫+- ⎪⎝⎭,则点1K x,x 22⎛⎫-- ⎪⎝⎭,BMC1SMK OB 2=⋅⋅,即可求解; ()3由题意和如图所示可知,1tan QHN 2∠=,在RtQNH 中,QH m 6=+,222QN OQ (2)m m 4==-+=+,2QN m 4sin QHN QH5∠+===,进行分析计算即可求解. 【详解】解:()1将()D 2,3、()B 4,0-的坐标代入抛物线表达式得:422316420a b a b +-=⎧⎨--=⎩,解得:1232a b ⎧=⎪⎪⎨⎪=⎪⎩, 则抛物线的解析式为:213y x x 222=+-; ()2过点M 作y 轴的平行线,交直线BC 于点K ,将点B 、C 的坐标代入一次函数表达式:y k'x b'=+得:04'''2k b b =-+⎧⎨=-⎩,解得:1'2'2k b ⎧=-⎪⎨⎪=-⎩, 则直线BC 的表达式为:1y x 22=--, 设点M 的坐标为213x,x x 222⎛⎫+- ⎪⎝⎭,则点1K x,x 22⎛⎫-- ⎪⎝⎭, 22BMC1113SMK OB 2x 2x x 2x 4x 2222⎛⎫=⋅⋅=----+=-- ⎪⎝⎭, a 10=-<,BMC S∴有最大值,当bx 22a=-=-时, BMCS最大值为4,点M 的坐标为()2,3--;()3如图所示,存在一个以Q 点为圆心,OQ 为半径且与直线AC 相切的圆,切点为N ,过点M 作直线平行于y 轴,交直线AC 于点H ,点M 坐标为()2,3--,设:点Q 坐标为()2,m -, 点A 、C 的坐标为()1,0、()0,2-,OA 1tan OCA OC 2∠==, QH //y 轴, QHN OCA ∠∠∴=, 1tan QHN 2∠∴=,则sin QHN 5∠=将点A 、C 的坐标代入一次函数表达式:y mx n =+得:02m n n +=⎧⎨=-⎩,则直线AC 的表达式为:y 2x 2=-, 则点()H 2,6--,在Rt QNH 中,QH m 6=+,QN OQ ===QN sin QHNQHm 6∠===+, 解得:m 4=或1-,即点Q 的坐标为()2,4-或()2,1--. 【点睛】本题考查的是二次函数知识的综合运用,涉及到解直角三角形、圆的基本知识,本题难点是()3,核心是通过画图确定圆的位置,本题综合性较强.4.A解析:(1)详见解析;(2)y =(04x <<);(3)当AEG ∆是等腰三角形时,2BF =或43【解析】 【分析】(1)根据正方形的性质得到∠AOD=90°,AO=OD ,∠EOH=90°,OE=OH ,由全等三角形的性质即可得到结论;(2)如图1,过O 作ON ⊥AB 于N ,根据等腰直角三角形的性质得到122AN BN ON AB ====,根据勾股定理得到OF ===线段成比例定理即可得到结论;(3)①当AE=EG 时,△AEG 是等腰三角形,②当AE=AG 时,△AEG 是等腰三角形,如图2,过A 作AP ⊥EG 于P ③当GE=AG 时,△AEG 是等腰三角形,如图3,过G 作GQ ⊥AE 于Q ,根据相似三角形的性质或全等三角形的性质健即可得到结论. 【详解】(1)∵四边形ABCD 是正方形,,OA OD AC BD ∴=⊥,90AOD ∴∠=︒,∵四边形OEGH 是正方形,,90OE OH EOH ∴=∠=︒,AOD EOH ∴∠=∠,AOD AOH EOH AOH ∴∠-∠=∠-∠, 即HOD EOA ∠=∠, HDO EAO ∴∆≅∆.(2)如图1,过O 作ON⊥AB 于N ,则122AN BN ON AB ====, ∵BF=x, ∴AF=4-x , ∴FN=2-x , ∴()222222248OF FN ON x x x =+=-+=-+,∴248EF y x x =--+, ∵AM⊥A C , ∴AE∥OB, ∴BF OF AF EF=, ∴2248448x x x x y x x -+=---+, ∴()244804x x y x -+≤=<;(3)①当AE=EG 时,△AEG 是等腰三角形,则AE=OE , ∵∠EAO=90°, ∴这种情况不存在;②当AE=AG 时,△AEG 是等腰三角形, 如图2,过A 作AP⊥EG 于P ,则AP∥OE,∴∠PAE=∠AEO,∴△APE∽△EAO,∴PE AE OA OE=,∵AE=AG,∴241482x xPE y-+==,()22248xAE yx-=-=,∴()22222224448448xx xxx xxx---+=+,解得:x=2,②当GE=AG时,△AEG是等腰三角形,如图3,过G作GQ⊥AE于Q,∴∠GQE=∠EAO=90°,∴∠GEQ+∠EGQ=∠GEQ+∠AEO=90°,∴∠EGQ=∠AEO,∵GE=OE,∴△EGQ≌△OEA(AAS),∴22EQ AO==∴24242()xAE ExQ-===,∴43x=,∴BF=2或43.【点睛】本题考查了四边形的综合题,正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,等腰三角形的性质,勾股定理,正确的作出辅助线构造全等三角形是解题的关键.5.C解析:(1)12,16AD CD ==;(2)277和297. 【解析】 【分析】(1)根据题意由函数图象可知动点M 从A 出发,以每秒1个单位的速度从C 到D 耗时16秒求出CD ,再利用三角形面积公式求得AD 即可;(2)由题意可知只能有P 和Q 点都在AD 边上,此时分当P 在Q 上方时以及当P 在Q 下方时两种情况运用数形结合思维进行分析得出答案. 【详解】解:(1)由函数图象可知动点M 从A 出发,以每秒1个单位的速度从C 到D 耗时36-20=16秒,即CD=16,而此时AMD ∆的面积为96,又因为90ADC ∠=︒,即有11169622CD AD AD =⨯=,解得12AD =. 所以12,16AD CD ==.(2)由题意可知Q 运动到点A 停止的时间为285,而P 运动到点D 停止的时间为6, 所以只能有P 和Q 点都在AD 边上,此时以PQ 为底边,CD 为高,设运动时间为t ,则AP=2t ,QD=5t-16,(162855t ≤<), ①当P 在Q 上方时,则有PQ=AD-AP-QD= 122516287t t t --+=-,可知CPQ ∆的面积为8时即11(287)16822PQ CD t =⨯-⨯=,解得277t =(满足条件);②当P 在Q 下方时,则有PQ=QD-(AD-AP )= 516(122)728t t t ---=-, 可知CPQ ∆的面积为8时即11(728)16822PQ CD t =⨯-⨯=,解得297t =(满足条件). 所以当CPQ ∆的面积为8时,t 的值为277和297. 【点睛】本题考查四边形动点问题和一次函数结合,熟练掌握四边形动点问题的解决办法和一次函数图象的相关性质,运用数形结合思维分析是解题的关键.6.A解析:(1)()1,1E -;(2)12m -≤≤-或01m ≤≤3)9t ≤≤. 【解析】 【分析】(1)首先要理解点A 是图形M 的“倍增点”的定义,将三个点逐一代入验证即可; (2)分两种情况:①点"倍增点”在O 的外部,分别求得“倍增点”横坐标的最大值和最小值,②点"倍增点"在O 的内部,依次求得“倍增点"横坐标的最大值和最小值,即可确定“倍增点”横坐标的范围;(3)分别求得线段GH 两端点为T "倍增点”时横坐标的最大值和最小值即可. 【详解】(1)()1,2D -到线段BC 的距离为2,22(12)(20)1332DC =--+-=<⨯ ∴()1,2D -不是线段BC 的倍增点;()1,1E -到线段BC 的距离为1,22(12)(10)103EC =--+-=>,∴在线段BC 上必存在一点P 使EP=3,∴()1,1E -是线段BC 的倍增点;()0,2F 到线段BC 的距离为2,22(02)(20)2232FC =-+-=<⨯ ∴()0,2F 不是线段BC 的倍增点;综上,()1,1E -是线段BC 的倍增点; (2)设直线l 上“倍增点”的横坐标为m , 当点在O 外时,222(2)8,m m +-+≤解方程222(2)8m m +-+=, 得1131m =+,2131m =- 当点在O 内部时,22224(2)3(44(2))m m m m ++-+≥--+-+解得:m≥0或m≤-2∴直线l 上“倍增点”的橫坐标的取值范围为1312m -≤≤-或0131m ≤≤+;(3)如图所示,当点G(1,0)为T "倍增点"时, T(9,0),此时T 的横坐标为最大值, 当点H(0,1)为T “倍增点”时,则T(63-,0),此时T 的横坐标为最小值;∴圆心T(t, 0)的横坐标的取值范围为:639t -≤≤.【点睛】在正确理解点A 是图形M 的“倍增点”定义的基础上,利用(1)判断是否是倍增点的不等关系式,即可列不等式组求解范围.7.A解析:(1)135°;(2)①45°,②不发生变化,45°;(3)60°或45° 【解析】 【分析】(1)利用三角形内角和定理、两角互余、角平分线性质即可求解; (2)①利用对顶角相等、两角互余、两角互补、角平分线性质即可求解; ②证明和推理过程同①的求解过程;(3)由(2)的证明求解思路,不难得出EAF ∠=90°,如果有一个角是另一个角的3倍,所以不确定是哪个角是哪个角的三倍,所以需要分情况讨论;值得注意的是,∠MON=90°,所以求解出的∠ABO 一定要小于90°,注意解得取舍. 【详解】(1)()11801802118090180451352AEB EBA BAE OBA BAO ∠=︒-∠-∠=︒-∠+∠=︒-⨯︒=︒-︒=︒(2)①如图所示AD 与BO 交于点E ,()9060301180307521909030602180180756045OBA DBO NBC DEB OEA OAB D DBE DEB ∠=︒-︒=︒∠=∠=︒-︒=︒∠=∠=︒-∠=︒-︒=︒∠=︒-∠-∠=︒-︒-︒=︒②∠D 的度数不随A 、B 的移动而发生变化设BAD α∠=,因为AD 平分∠BAO ,所以2BAO α∠=,因为∠AOB=90°,所以180902ABN ABO AOB BAO α∠=︒-∠=∠+∠=+。
2016年天津市中考数学试卷(含详细答案)

绝密★启用前天津市2016年初中毕业生会考学业考试数学本试卷满分120分,考试时间100分钟.第Ⅰ卷(选择题共36分)一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算(2)5--的结果等于()A.7-B.3-C.3D.72.sin60的值等于()A .12B .22C.32D.33.下列图形中,可以看作是中心对称图形的是 ()A B C D4.2016年5月24日《天津日报》报道,2015年天津外环线内新栽植树木6 120 000株.将6120000用科学记数法表示应为 ( )A.70.61210⨯B.66.1210⨯C.561.210⨯D.461210⨯5.如图是一个由4个相同的正方体组成的立体图形,它的主视图是()A B C D6.估计19的值在 ()A.2和3之间B.3和4之间C.4和5之间D.5和6之间7.计算11xx x+-的结果为 ()A.1B.xC.1xD.2xx+8.方程2120x x+-=的两个根为 ()A.12x=-,26x=B.16x=-,22x=C.13x=-,24x=D.14x=-,23x=9.实数a,b在数轴上的对应点的位置如图所示.把a-,b-,0按照从小到大的顺序排列,正确的是 ( )A.0a b--<<B.0a b--<<C.0b a--<<D.0b a--<<10.如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B',AB'与DC相交于点E,则下列结论一定正确的是( )A.DA CB BA∠=∠''B.ACD CB D∠=∠'C.AD AE=D.AE CE=11.若点1()5,A y-,2()3,B y-,3(2,)C y在反比例函数3yx=的图象上,则1y,2y,3y的大小关系是()A.132y y y<<B.123y y y<<C.321y y y<<D.213y y y<<12.已知二次函数2()1y x h=-+(h为常数),在自变量x的值满足13x≤≤的情况下,与其对应的函数值y的最小值为5,则h的值为()A.1或5-B.1-或5C.1或3-D.1或3第Ⅱ卷(非选择题共84分)二、填空题(本大题共6小题,每小题3分,共18分.请把答案填写在题中的横线上)13.计算3(2)a的结果等于.14.计算(53)(53)+-的结果等于.15.不透明袋子中装有6个球,其中有1个红球、2个绿球和3个黑球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是绿球的概率是.毕业学校_____________姓名________________考生号_____________________________________________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷第1页(共28页)数学试卷第2页(共28页)数学试卷第4页(共28页)16.若一次函数2y x b=-+(b为常数)的图象经过第二、三、四象限,则b的值可以是(写出一个即可).17.如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则MNPQAEFGSS正方形正方形的值等于.18.如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.(1)AE的长等于;(2)若点P在线段AC上,点Q在线段BC上,且满足AP PQ PB==,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明).三、解答题(本大题共7小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)19.(本小题满分8分)解不等式组26,322,xx x+⎧⎨-⎩≥①②≤请结合题意填空,完成本题的解答.(1)解不等式①得;(2)解不等式②得;(3)把不等式①和②的解集在数轴上表示出来:(4)原不等式组的解集为.20.(本小题满分8分)在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:(1)图1中a的值为;(2)求统计的这组初赛成绩数据的平均数、众数和中位数;(3)根据这组初赛成绩,由高到低确定9人能进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.21.(本小题满分10分)在O中,AB为直径,C为O上一点.(1)如图①,过点C作O的切线,与AB的延长线相交于点P,若27CAB∠=,求P∠的大小;(2)如图②,D为AC上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若10CAB∠=,求P∠的大小.数学试卷第3页(共28页)数学试卷 第5页(共28页) 数学试卷 第6页(共28页)22.(本小题满分10分)小明上学途中要经过A ,B 两地,由于A ,B 两地之间有一片草坪,所以需要走路线AC ,CB .如图,在ABC △中,63m AB =,45A ∠=,37B ∠=,求AC ,CB 的长(结果保留小数点后一位).参考数据:sin370.60≈,cos370.80≈,tan370.75≈取1.414.23.(本小题满分10分)公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆.已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元.(1)设租用甲种货车x 辆(x 为非负整数),试填写下表.(2)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.24.(本小题满分10分)在平面直角坐标系中,O 为原点,点()4,0A ,点()0,3B 把ABO △绕点B 逆时针旋转,得A BO ''△,点A ,O 旋转后的对应点为A ',O '.记旋转角为α.(1)如图1,若90α=,求AA '的长; (2)如图2,若120α=,求点O '的坐标;(3)在(2)的条件下,边OA 上的一点P 旋转后的对应点为P ',当O P BP ''+取得最小值时,求点P '的坐标(直接写出结果即可).25.(本小题满分10分)已知抛物线C :221y x x =-+的顶点为P ,与y 轴的交点为Q ,点1(1,)2F . (1)求点P ,Q 的坐标;(2)将抛物线C 向上平移得抛物线C ',点Q 平移后的对应点为Q ',且FQ OQ ''=. ①求抛物线C '的解析式;②若点P 关于直线Q F '的对称点为K ,射线FK 与抛物线C '相交于点A ,求点A 的坐标.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷第7页(共28页)数学试卷第8页(共28页)333=a a.8+53)(55/ 14PQ即为所求.数学试卷第11页(共28页)数学试卷第12页(共28页)(Ⅲ)(Ⅲ)把不等式①和②的解集在数轴上表示为:;7/ 14数学试卷 第15页(共28页)数学试卷 第16页(共28页)54.+∠COP 36︒. (Ⅱ)∵E 为AC 的中点,【解析】如图,过点C 作⊥CD AB ,垂足为D .9 / 1445, tan37︒tan37tan363631+7≈︒︒141427.00⨯=的长约等于38.2cm 【考点】解直角三角形数学试卷 第19页(共28页)数学试卷 第20页(共28页)90得到的, (Ⅱ)如图,根据题意,3cos cos602∠'='︒=B O BC O B ,92+=BC ,点的坐标为339(,)22.。
2016年中考数学压轴题及解析分类汇编

2016年中考数学压轴题及解析分类汇编中考数学压轴题及解析分类汇编2016年中考数学压轴题及解析分类汇编2016中考数学压轴:相似三角形问题2016中考数学压轴题函数相似三角形问题(一)2016中考数学压轴题函数相似三角形问题(二)2016中考数学压轴题函数相似三角形问题(三)2016中考数学压轴:等腰三角形问题2016中考数学压轴题函数等腰三角形问题(一)2016中考数学压轴题函数等腰三角形问题(二)2016中考数学压轴题函数等腰三角形问题(三)2016中考数学压轴:直角三角形问题2016中考数学压轴题函数直角三角形问题(一)2016中考数学压轴题函数直角三角形问题(二)2016中考数学压轴题函数直角三角形问题(三)2016中考数学压轴:平行四边形问题2016中考数学压轴题函数平行四边形问题(一)2016中考数学压轴题函数平行四边形问题(二)2016中考数学压轴题函数平行四边形问题(三)2016中考数学压轴:梯形问题2016中考数学压轴题函数梯形问题(一) 2016中考数学压轴题函数梯形问题(二) 2016中考数学压轴题函数梯形问题(三) 2016中考数学压轴:面积问题2016中考数学压轴题函数面积问题(一) 2016中考数学压轴题函数面积问题(二) 2016中考数学压轴题函数面积问题(三)2016中考数学压轴题:函数相似三角形问题(一)例1、直线113y x =-+分别交x 轴、y 轴于A 、B 两点,△AOB 绕点O 按逆时针方向旋转90°后得到△COD ,抛物线y =ax 2+bx +c 经过A 、C 、D 三点.(1) 写出点A 、B 、C 、D 的坐标;(2) 求经过A 、C 、D 三点的抛物线表达式,并求抛物线顶点G 的坐标;(3) 在直线BG 上是否存在点Q ,使得以点A 、B 、Q 为顶点的三角形与△COD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.图1思路点拨1.图形在旋转过程中,对应线段相等,对应角相等,对应线段的夹角等于旋转角.2.用待定系数法求抛物线的解析式,用配方法求顶点坐标.3.第(3)题判断∠ABQ =90°是解题的前提.4.△ABQ 与△COD 相似,按照直角边的比分两种情况,每种情况又按照点Q 与点B 的位置关系分上下两种情形,点Q 共有4个. 满分解答(1)A (3,0),B (0,1),C (0,3),D (-1,0).(2)因为抛物线y =ax 2+bx +c 经过A (3,0)、C (0,3)、D (-1,0) 三点,所以930,3,0.a b c c a b c ++=⎧⎪=⎨⎪-+=⎩ 解得1,2,3.a b c =-⎧⎪=⎨⎪=⎩所以抛物线的解析式为y =-x 2+2x +3=-(x -1)2+4,顶点G 的坐标为(1,4).(3)如图2,直线BG 的解析式为y =3x+1,直线CD 的解析式为y =3x +3,因此CD //BG .因为图形在旋转过程中,对应线段的夹角等于旋转角,所以AB ⊥CD .因此AB ⊥BG ,即∠ABQ =90°.因为点Q 在直线BG 上,设点Q 的坐标为(x ,3x +1),那么22(3)10BQ x x x =+=±.Rt △COD 的两条直角边的比为1∶3,如果Rt △ABQ 与Rt △COD 相似,存在两种情况:①当3BQ BA=时,10310x ±=.解得3x =±.所以1(3,10)Q ,2(3,8)Q --.②当13BQ BA =时,101310x ±=.解得13x =±.所以31(,2)3Q ,41(,0)3Q -.图2 图3考点伸展第(3)题在解答过程中运用了两个高难度动作:一是用旋转的性质说明AB ⊥BG ;二是BQ ==.我们换个思路解答第(3)题:如图3,作GH ⊥y 轴,QN ⊥y 轴,垂足分别为H 、N .通过证明△AOB ≌△BHG ,根据全等三角形的对应角相等,可以证明∠ABG =90°.在Rt △BGH 中,sin 1∠=,cos 1∠= ①当3BQ BA=时,BQ =. 在Rt △BQN 中,sin 13QN BQ =⋅∠=,cos 19BN BQ =⋅∠=. 当Q 在B 上方时,1(3,10)Q ;当Q 在B 下方时,2(3,8)Q --. ②当13BQ BA =时,BQ =同理得到31(,2)3Q ,41(,0)3Q -.例2、 Rt △ABC 在直角坐标系内的位置如图1所示,反比例函数(0)k y k x=≠在第一象限内的图像与BC 边交于点D (4,m ),与AB 边交于点E (2,n ),△BDE 的面积为2.(1)求m 与n 的数量关系;(2)当tan ∠A =12时,求反比例函数的解析式和直线AB 的表达式;(3)设直线AB 与y 轴交于点F ,点P 在射线FD 上,在(2)的条件下,如果△AEO 与△EFP 相似,求点P 的坐标.图1思路点拨1.探求m 与n 的数量关系,用m 表示点B 、D 、E 的坐标,是解题的突破口.2.第(2)题留给第(3)题的隐含条件是FD //x 轴.3.如果△AEO 与△EFP 相似,因为夹角相等,根据对应边成比例,分两种情况.满分解答(1)如图1,因为点D (4,m )、E (2,n )在反比例函数k y x =的图像上,所以4,2.m k n k =⎧⎨=⎩整理,得n =2m .(2)如图2,过点E 作EH ⊥BC ,垂足为H .在Rt △BEH 中,tan ∠BEH =tan ∠A =12,EH =2,所以BH =1.因此D (4,m ),E (2,2m ),B (4,2m +1).已知△BDE 的面积为2,所以11(1)2222BD EH m ⋅=+⨯=.解得m =1.因此D (4,1),E (2,2),B (4,3).因为点D (4,1)在反比例函数k y x=的图像上,所以k =4.因此反比例函数的解析式为4y x=.设直线AB 的解析式为y =kx +b ,代入B (4,3)、E (2,2),得34,22.k b k b =+⎧⎨=+⎩解得12k =,1b =. 因此直线AB 的函数解析式为112y x =+.图2图3 图4(3)如图3,因为直线112y x =+与y 轴交于点F (0,1),点D 的坐标为(4,1),所以FD // x 轴,∠EFP =∠EAO .因此△AEO 与△EFP 相似存在两种情况:①如图3,当EA EF AO FP=时,2552FP =.解得FP =1.此时点P 的坐标为(1,1).②如图4,当EA FP AO EF =255=.解得FP =5.此时点P 的坐标为(5,1).考点伸展本题的题设部分有条件“Rt △ABC 在直角坐标系内的位置如图1所示”,如果没有这个条件限制,保持其他条件不变,那么还有如图5的情况:第(1)题的结论m 与n 的数量关系不变.第(2)题反比例函数的解析式为12y x=-,直线AB 为172y x =-.第(3)题FD 不再与x 轴平行,△AEO 与△EFP 也不可能相似.图52016中考数学压轴题函数相似三角形问题(二) 例3、如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、B1的坐标分别为(x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1图2思路点拨1.第(2)题用含S的代数式表示x2-x1,我们反其道而行之,用x1,x2表示S.再注意平移过程中梯形的高保持不变,即y 2-y 1=3.通过代数变形就可以了.2.第(3)题最大的障碍在于画示意图,在没有计算结果的情况下,无法画出准确的位置关系,因此本题的策略是先假设,再说理计算,后验证.3.第(3)题的示意图,不变的关系是:直线AB 与x 轴的夹角不变,直线AB 与抛物线的对称轴的夹角不变.变化的直线PQ 的斜率,因此假设直线PQ 与AB 的交点G 在x 轴的下方,或者假设交点G 在x 轴的上方.满分解答(1)抛物线的对称轴为直线1x =,解析式为21184y x x =-,顶点为M (1,18-). (2) 梯形O 1A 1B 1C 1的面积12122(11)3()62x x S x x -+-⨯3==+-,由此得到1223s x x +=+.由于213y y -=,所以22212211111138484y y x x x x -=--+=.整理,得212111()()384x x x x ⎡⎤-+-=⎢⎥⎣⎦.因此得到2172x x S -=.当S =36时,212114,2.x x x x +=⎧⎨-=⎩ 解得126,8.x x =⎧⎨=⎩ 此时点A 1的坐标为(6,3).(3)设直线AB 与PQ 交于点G ,直线AB 与抛物线的对称轴交于点E ,直线PQ 与x 轴交于点F ,那么要探求相似的△GAF 与△GQE ,有一个公共角∠G .在△GEQ 中,∠GEQ 是直线AB 与抛物线对称轴的夹角,为定值.在△GAF 中,∠GAF 是直线AB 与x 轴的夹角,也为定值,而且∠GEQ ≠∠GAF .因此只存在∠GQE =∠GAF 的可能,△GQE ∽△GAF .这时∠GAF =∠GQE =∠PQD . 由于3tan 4GAF ∠=,tan 5DQ t PQD QP t ∠==-,所以345t t =-.解得207t =.图3 图4例4、如图1,已知点A (-2,4) 和点B (1,0)都在抛物线22=++上.y mx mx n(1)求m、n;(2)向右平移上述抛物线,记平移后点A 的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;(3)记平移后抛物线的对称轴与直线AB′的交点为C,试在x轴上找一个点D,使得以点B′、C、D为顶点的三角形与△ABC相似.图1思路点拨1.点A 与点B 的坐标在3个题目中处处用到,各具特色.第(1)题用在待定系数法中;第(2)题用来计算平移的距离;第(3)题用来求点B ′ 的坐标、AC 和B ′C 的长.2.抛物线左右平移,变化的是对称轴,开口和形状都不变.3.探求△ABC 与△B ′CD 相似,根据菱形的性质,∠BAC =∠CB ′D ,因此按照夹角的两边对应成比例,分两种情况讨论.满分解答(1) 因为点A (-2,4) 和点B (1,0)都在抛物线22y mxmx n =++上,所以444,20.m m n m m n -+=⎧⎨++=⎩ 解得43m =-,4n =.(2)如图2,由点A (-2,4) 和点B (1,0),可得AB =5.因为四边形A A ′B ′B 为菱形,所以A A ′=B ′B = AB =5.因为438342+--=x x y ()2416133x =-++,所以原抛物线的对称轴x=-1向右平移5个单位后,对应的直线为x =4.因此平移后的抛物线的解析式为()3164342,+--=x y .图2(3) 由点A (-2,4) 和点B ′ (6,0),可得A B ′=5如图2,由AM //CN ,可得''''B N B C B M B A=,即2845=.解得'5B C =35AC =质,在△ABC 与△B ′CD 中,∠BAC =∠CB ′D .①如图3,当''AB B C AC B D =时,5'35B D =,解得'3B D =.此时OD =3,点D 的坐标为(3,0).②如图4,当''AB B D AC B C=时,355=,解得5'3B D =.此时OD =133,点D 的坐标为(133,0).图3图4考点伸展在本题情境下,我们还可以探求△B ′CD 与△AB B ′相似,其实这是有公共底角的两个等腰三角形,容易想象,存在两种情况.我们也可以讨论△B′CD与△C B B′相似,这两个三角形有一组公共角∠B,根据对应边成比例,分两种情况计算.2016中考数学压轴题函数相似三角形问题(三)例5 、如图1,抛物线经过点A(4,0)、B (1,0)、C(0,-2)三点.(1)求此抛物线的解析式;(2)P是抛物线上的一个动点,过P作PM ⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.,图1思路点拨1.已知抛物线与x 轴的两个交点,用待定系数法求解析式时,设交点式比较简便.2.数形结合,用解析式表示图象上点的坐标,用点的坐标表示线段的长.3.按照两条直角边对应成比例,分两种情况列方程.4.把△DCA 可以分割为共底的两个三角形,高的和等于OA . 满分解答(1)因为抛物线与x 轴交于A (4,0)、B (1,0)两点,设抛物线的解析式为)4)(1(--=x x a y ,代入点C 的 坐标(0,-2),解得21-=a .所以抛物线的解析式为22521)4)(1(212-+-=---=x xx x y .(2)设点P 的坐标为))4)(1(21,(---x x x .①如图2,当点P 在x 轴上方时,1<x <4,)4)(1(21---=x x PM ,x AM -=4.如果2==COAOPM AM ,那么24)4)(1(21=----xx x .解得5=x 不合题意.如果21==CO AO PM AM ,那么214)4)(1(21=----x x x .解得2=x .此时点P 的坐标为(2,1).②如图3,当点P 在点A 的右侧时,x >4,)4)(1(21--=x x PM ,4-=x AM .解方程24)4)(1(21=---x x x ,得5=x .此时点P 的坐标为)2,5(-.解方程214)4)(1(21=---x x x ,得2=x 不合题意.③如图4,当点P 在点B 的左侧时,x <1,)4)(1(21--=x x PM ,x AM -=4.解方程24)4)(1(21=---xx x ,得3-=x .此时点P 的坐标为)14,3(--.解方程214)4)(1(21=---x x x ,得0=x .此时点P 与点O重合,不合题意.综上所述,符合条件的 点P 的坐标为(2,1)或)14,3(--或)2,5(-.图2 图3图4(3)如图5,过点D 作x 轴的垂线交AC 于E .直线AC 的解析式为221-=x y . 设点D 的横坐标为m )41(<<m ,那么点D 的坐标为)22521,(2-+-m mm ,点E 的坐标为)221,(-m m .所以)221()22521(2---+-=m m mDE m m 2212+-=.因此4)221(212⨯+-=∆m m SDACm m 42+-=4)2(2+--=m .当2=m 时,△DCA 的面积最大,此时点D 的坐标为(2,1).图5图6 考点伸展第(3)题也可以这样解:如图6,过D 点构造矩形OAMN ,那么△DCA 的面积等于直角梯形CAMN 的面积减去△CDN 和△ADM 的面积.设点D 的横坐标为(m ,n ))41(<<m ,那么42)4(21)2(214)22(21++-=--+-⨯+=n m m n n m n S .由于225212-+-=m mn ,所以mmS 42+-=.例6 、 如图1,△ABC 中,AB =5,AC =3,cos A =310.D 为射线BA 上的点(点D 不与点B 重合),作DE //BC 交射线CA 于点E ..(1) 若CE =x ,BD =y ,求y 与x 的函数关系式,并写出函数的定义域;(2) 当分别以线段BD ,CE 为直径的两圆相切时,求DE 的长度;(3) 当点D 在AB 边上时,BC 边上是否存在点F ,使△ABC 与△DEF 相似?若存在,请求出线段BF 的长;若不存在,请说明理由.图1备用图 备用图 思路点拨1.先解读背景图,△ABC 是等腰三角形,那么第(3)题中符合条件的△DEF 也是等腰三角形.2.用含有x 的式子表示BD 、DE 、MN 是解答第(2)题的先决条件,注意点E 的位置不同,DE 、MN 表示的形式分两种情况.3.求两圆相切的问题时,先罗列三要素,再列方程,最后检验方程的解的位置是否符合题意.4.第(3)题按照DE 为腰和底边两种情况分类讨论,运用典型题目的结论可以帮助我们轻松解题. 满分解答(1)如图2,作BH ⊥AC ,垂足为点H .在Rt △ABH 中,AB =5,cosA =310AH AB ,所以AH =32=12AC .所以BH 垂直平分AC ,△ABC 为等腰三角形,AB =CB =5.因为DE //BC ,所以AB AC DB EC =,即53y x=.于是得到53yx =,(0x >). (2)如图3,图4,因为DE //BC ,所以DE AEBC AC=,MN AN BC AC =,即|3|53DE x -=,1|3|253x MN -=.因此5|3|3x DE -=,圆心距5|6|6x MN -=.图2图3 图4在⊙M 中,115226MrBD y x ===,在⊙N 中,1122N r CE x==.①当两圆外切时,5162x x +5|6|6x -=.解得3013x =或者10x =-.如图5,符合题意的解为3013x =,此时5(3)15313x DE -==.②当两圆内切时,5162x x -5|6|6x -=. 当x <6时,解得307x =,如图6,此时E 在CA 的延长线上,5(3)1537x DE -==; 当x >6时,解得10x =,如图7,此时E 在CA 的延长线上,5(3)3533x DE -==.图5图6 图7(3)因为△ABC是等腰三角形,因此当△ABC与△DEF相似时,△DEF也是等腰三角形.如图8,当D、E、F为△ABC的三边的中点时,DE为等腰三角形DEF的腰,符合题意,此时BF=2.5.根据对称性,当F在BC边上的高的垂足时,也符合题意,此时BF=4.1.如图9,当DE为等腰三角形DEF的底边时,四边形DECF是平行四边形,此时125BF .34图8 图9图10 图11考点伸展:第(3)题的情景是一道典型题,如图10,如图11,AH是△ABC的高,D、E、F为△ABC的三边的中点,那么四边形DEHF是等腰梯形.例 7 如图1,在直角坐标系xOy中,设点A(0,t),点Q(t,b).平移二次函数2tx=y-的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B、C两点(∣OB∣<∣OC∣),连结A,B.(1)是否存在这样的抛物线F,使得2?请你作出判断,并说明理由;OC=OA⋅OB3,求(2)如果AQ∥BC,且tan∠ABO=2抛物线F对应的二次函数的解析式.思路点拨1.数形结合思想,把OC OB OA⋅=2转化为212t x x =⋅.2.如果AQ ∥BC ,那么以OA 、AQ 为邻边的矩形是正方形,数形结合得到t =b .3.分类讨论tan ∠ABO =23,按照A 、B 、C 的位置关系分为四种情况.A 在y 轴正半轴时,分为B 、C 在y 轴同侧和两侧两种情况;A 在y 轴负半轴时,分为B 、C 在y 轴同侧和两侧两种情况.满分解答(1)因为平移2tx y -=的图象得到的抛物线F 的顶点为Q (t ,b ),所以抛物线F 对应的解析式为b t x t y +--=2)(.因为抛物线与x 轴有两个交点,因此0>b t .令0=y ,得-=t OB t b ,+=t OC t b . 所以-=⋅t OC OB (|||||t b )( +t t b )|-=2|t 22|OA t t b ==.即22b tt t -=±.所以当32t b =时,存在抛物线F 使得||||||2OC OB OA ⋅=.(2)因为AQ //BC ,所以t =b ,于是抛物线F 为t t x t y +--=2)(.解得1,121+=-=t x t x .①当0>t 时,由||||OC OB <,得)0,1(-t B .如图2,当01>-t 时,由=∠ABO tan 23=||||OB OA =1-t t ,解得3=t .此时二次函数的解析式为241832-+-=x x y .如图3,当01<-t 时,由=∠ABO tan 23=||||OB OA =1+-t t ,解得=t 53.此时二次函数的解析式为-=y 532x +2518x +12548.图2图3②如图4,如图5,当0<t 时,由||||OC OB <,将t -代t ,可得=t 53-,3-=t .此时二次函数的解析式为=y 532x +2518x -12548或241832++=x x y .图4图5考点伸展第(2)题还可以这样分类讨论:因为AQ //BC ,所以t =b ,于是抛物线F 为2()y t x t t =--+.由3tan 2OA ABO OB ∠==,得23OB OA =.①把2(,0)3B t 代入2()y t x t t =--+,得3t =±(如图2,图5). ②把2(,0)3B t -代入2()y t x t t =--+,得35t =±(如图3,图4).2016中考数学压轴题函数等腰三角形问题(一)例1、如图1,已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P (0,m )是线段OC 上一动点(C 点除外),直线PM 交AB 的延长线于点D .(1)求点D 的坐标(用含m 的代数式表示);(2)当△APD 是等腰三角形时,求m 的值;(3)设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ,过点O 作直线ME 的垂线,垂足为H (如图2).当点P 从O 向C 运动时,点H 也随之运动.请直接写出点H 所经过的路长(不必写解答过程).图1 图2思路点拨1.用含m的代数式表示表示△APD的三边长,为解等腰三角形做好准备.2.探求△APD是等腰三角形,分三种情况列方程求解.3.猜想点H的运动轨迹是一个难题.不变的是直角,会不会找到不变的线段长呢?Rt△OHM的斜边长OM是定值,以OM为直径的圆过点H、C.满分解答(1)因为PC//DB,所以1CP PM MC===.因此BD DM MBPM=DM,CP=BD=2-m.所以AD=4-m.于是得到点D的坐标为(2,4-m).(2)在△APD 中,22(4)AD m =-,224AP m =+,222(2)44(2)PD PM m ==+-. ①当AP =AD 时,2(4)m -24m =+.解得32m =(如图3). ②当PA =PD 时,24m +244(2)m =+-.解得43m =(如图4)或4m =(不合题意,舍去).③当DA =DP 时,2(4)m -244(2)m =+-.解得23m =(如图5)或2m =(不合题意,舍去).综上所述,当△APD 为等腰三角形时,m的值为32,43或23.图3图4 图5(3)点H 5.考点伸展第(2)题解等腰三角形的问题,其中①、②用几何说理的方法,计算更简单:①如图3,当AP =AD 时,AM 垂直平分PD ,那么△PCM ∽△MBA .所以12PC MB CM BA ==.因此12PC =,32m =.②如图4,当PA =PD 时,P 在AD 的垂直平分线上.所以DA =2PO .因此42m m -=.解得43m =. 第(2)题的思路是这样的:如图6,在Rt △OHM 中,斜边OM 为定值,因此以OM 为直径的⊙G 经过点H ,也就是说点H 在圆弧上运动.运动过的圆心角怎么确定呢?如图7,P 与O 重合时,是点H 运动的起点,∠COH =45°,∠CGH =90°.图6 图7例2 如图1,已知一次函数y =-x +7与正比例函数43y x 的图象交于点A ,且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l //y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒.①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形?若存在,求t 的值;若不存在,请说明理由.图1思路点拨1.把图1复制若干个,在每一个图形中解决一个问题.2.求△APR 的面积等于8,按照点P 的位置分两种情况讨论.事实上,P 在CA 上运动时,高是定值4,最大面积为6,因此不存在面积为8的可能.3.讨论等腰三角形APQ ,按照点P 的位置分两种情况讨论,点P 的每一种位置又要讨论三种情况.满分解答(1)解方程组7,4,3y x y x =-+⎧⎪⎨=⎪⎩ 得3,4.x y =⎧⎨=⎩ 所以点A 的坐标是(3,4).令70y x =-+=,得7x =.所以点B 的坐标是(7,0).(2)①如图2,当P 在OC 上运动时,0≤t <4.由8APR ACP POR CORA S S S S =--=△△△梯形,得1113+7)44(4)(7)8222t t t t -⨯-⨯⨯--⨯-=(.整理,得28120tt -+=.解得t =2或t =6(舍去).如图3,当P 在CA 上运动时,△APR 的最大面积为6.因此,当t =2时,以A 、P 、R 为顶点的三角形的面积为8.图2 图3 图4②我们先讨论P 在OC 上运动时的情形,0≤t <4.如图1,在△AOB 中,∠B =45°,∠AOB >45°,OB =7,42AB =OB >AB .因此∠OAB >∠AOB >∠B .如图4,点P 由O 向C 运动的过程中,OP =BR =RQ ,所以PQ //x 轴.因此∠AQP =45°保持不变,∠PAQ 越来越大,所以只存在∠APQ =∠AQP 的情况.此时点A 在PQ 的垂直平分线上,OR =2CA =6.所以BR =1,t =1.我们再来讨论P 在CA 上运动时的情形,4≤t <7.在△APQ 中,3cos 5A ∠=为定值,7AP t =-,5520333AQ OA OQ OA OR t =-=-=-.如图5,当AP =AQ 时,解方程520733t t -=-,得418t =.如图6,当QP =QA 时,点Q 在PA 的垂直平分线上,AP =2(OR -OP ).解方程72[(7)(4)]t t t -=---,得5t =.如7,当PA =PQ 时,那么12cos AQ A AP∠=.因此2cos AQ AP A=⋅∠.解方程52032(7)335t t -=-⨯,得22643t =. 综上所述,t =1或418或5或22643时,△APQ 是等腰三角形.图5 图6 图7考点伸展当P在CA上,QP=QA时,也可以用AP AQ A=⋅∠来求解.2cos2016中考数学压轴题函数等腰三角形问题(二)例3 如图1,在直角坐标平面内有点A(6, 0),B(0, 8),C(-4, 0),点M、N分别为线段AC和射线AB上的动点,点M以2个单位长度/秒的速度自C向A方向作匀速运动,点N以5个单位长度/秒的速度自A向B方向作匀速运动,MN交OB于点P.(1)求证:MN∶NP为定值;(2)若△BNP与△MNA相似,求CM的长;(3)若△BNP是等腰三角形,求CM的长.图1思路点拨1.第(1)题求证MN∶NP的值要根据点N的位置分两种情况.这个结论为后面的计算提供了方便.2.第(2)题探求相似的两个三角形有一组邻补角,通过说理知道这两个三角形是直角三角形时才可能相似.3.第(3)题探求等腰三角形,要两级(两层)分类,先按照点N的位置分类,再按照顶角的顶点分类.注意当N在AB的延长线上时,钝角等腰三角形只有一种情况.4.探求等腰三角形BNP,N在AB上时,∠B是确定的,把夹∠B的两边的长先表示出来,再分类计算.满分解答(1)如图2,图3,作NQ⊥x轴,垂足为Q.设点M、N的运动时间为t秒.在Rt△ANQ中,AN=5t,NQ=4t,AQ=3t.在图2中,QO=6-3t,MQ=10-5t,所以MN∶NP=MQ∶QO=5∶3.在图3中,QO=3t-6,MQ=5t-10,所以MN∶NP=MQ∶QO=5∶3.(2)因为△BNP与△MNA有一组邻补角,因此这两个三角形要么是一个锐角三角形和一个钝角三角形,要么是两个直角三角形.只有当这两个三角形都是直角三角形时才可能相似.如图4,△BNP ∽△MNA ,在Rt △AMN中,35AN AM =,所以531025t t =-.解得3031t =.此时CM 6031=.图2 图3图4(3)如图5,图6,图7中,OP MP QN MN =,即245OP t =.所以85OP t =. ①当N 在AB 上时,在△BNP 中,∠B 是确定的,885BP t =-,105BN t =-.(Ⅰ)如图5,当BP =BN 时,解方程881055t t -=-,得1017t =.此时CM 2017=.(Ⅱ)如图6,当NB =NP 时,45BE BN =.解方程()1848105255t t ⎛⎫-=- ⎪⎝⎭,得54t =.此时CM 52=. (Ⅲ)当PB =PN 时,1425BN BP =.解方程()1481058255t t ⎛⎫-=- ⎪⎝⎭,得t 的值为负数,因此不存在PB=PN 的情况.②如图7,当点N 在线段AB 的延长线上时,∠B 是钝角,只存在BP =BN 的可能,此时510BN t =-.解方程885105t t -=-,得3011t =.此时CM 6011=.图5图6 图7 考点伸展如图6,当NB =NP 时,△NMA 是等腰三角形,1425BN BP ,这样计算简便一些.例4、如图1,在矩形ABCD 中,AB =m (m 是大于0的常数),BC =8,E 为线段BC 上的动点(不与B 、C 重合).连结DE ,作EF ⊥DE ,EF 与射线BA 交于点F ,设CE =x ,BF =y .(1)求y关于x的函数关系式;(2)若m=8,求x为何值时,y的值最大,最大值是多少?(3)若12,要使△DEF为等腰三角形,mym的值应为多少?图1思路点拨1.证明△DCE∽△EBF,根据相似三角形的对应边成比例可以得到y关于x的函数关系式.2.第(2)题的本质是先代入,再配方求二次函数的最值.3.第(3)题头绪复杂,计算简单,分三段表达.一段是说理,如果△DEF为等腰三角形,那么得到x=y;一段是计算,化简消去m,得到关于x的一元二次方程,解出x的值;第三段是把前两段结合,代入求出对应的m的值.满分解答(1)因为∠EDC 与∠FEB 都是∠DEC 的余角,所以∠EDC =∠FEB .又因为∠C =∠B =90°,所以△DCE ∽△EBF .因此DC EBCE BF=,即8m x x y -=.整理,得y 关于x 的函数关系为218y xx m m=-+.(2)如图2,当m =8时,2211(4)288y x x x =-+=--+.因此当x =4时,y 取得最大值为2.(3) 若12y m =,那么21218xx m mm=-+.整理,得28120x x -+=.解得x =2或x =6.要使△DEF 为等腰三角形,只存在ED =EF 的情况.因为△DCE ∽△EBF ,所以CE =BF ,即x =y .将x =y =2代入12y m =,得m =6(如图3);将x =y =6代入12y m=,得m =2(如图4).。
专题12 压轴题-2017版[中考15年]天津市2002-2016年中考数学试题分项(原卷版)
![专题12 压轴题-2017版[中考15年]天津市2002-2016年中考数学试题分项(原卷版)](https://img.taocdn.com/s3/m/6db6fb6627284b73f24250bf.png)
2017版[中考15年]天津市2002-2016年中考数学试题分类解析专题12:押轴题编辑一、选择题1.(天津市2002年3分)已知四边形ABCD 的对角线AC 与BD 相交于点O ,若S ΔAOB =4,S ΔCOD =9,则四边形ABCD 的面积S 四边形ABCD 的最小值为【 】(A )21 (B )25 (C )26 (D )362. (天津市2003年3分)在△ABC 中,已知AB =2a ,∠A =30°,CD 是AB 边的中线,若将△ABC 沿CD 对折起来,折叠后两个小△ACD 与△BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的14,有如下结论:①AC 边的长可以等于a ; ②折叠前的△ABC 的面积可以等于232a ; ③折叠后,以A 、B 为端点的线段AB 与中线CD 平行且相等。
其中,正确结论的个数是【 】(A )0个 (B )1个 (C )2个 (D )3个3. (天津市2004年3分)如图,正△ABC 内接于⊙O ,P 是劣弧BC 上任意一点,PA 与BC 交于点E ,有如下结论:① PA=PB+PC ; ② 111PA PB PC=+;③ PA·PE=PB·PC.其中,正确结论的个数为【 】(A) 3个 (B) 2个 (C) 1个 (D) 0个4.(天津市2005年3分)若关于x 的一元二次方程2x 2-2x +3m -1=0的两个实数根x 1,x 2,且x 1·x 2 >x 1+x 2-4,则实数m 的取值范围是【 】(A )m >53- (B ) m≤12 (C) m <53- (D) 53-<m≤125.(天津市2006年3分)已知实数a ,b ,c 满足a 2+b 2=1,b 2+c 2=2,c 2+a 2=2,则ab +bc +ca 的 最小值为【 】(A )52 (B) 132+ (C) 12- (D) 132- 6.(天津市2007年3分)已知二次函数2y ax bx c(a 0)=++≠的图象如图所示,有下列5个结论:① abc 0>;② b a c <+;③ 4a 2b c 0++>;④ 2c 3b <;⑤ a b m(am b)+>+,(m 1≠的实数)其中正确的结论有【 】A. 2个B. 3个C. 4个D. 5个7. (天津市2008年3分)在平面直角坐标系中,已知点A (4-,0),B (2,0),若点C 在一次函数1=22y x -+ 的图象上,且△ABC 为直角三角形,则满足条件的点C 有【 】A .1个B .2个C .3个D .4个8.(天津市2009年3分)在平面直角坐标系中,先将抛物线22y x x =+-关于x 轴作轴对称变换,再将所得的抛物线关于y 轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为【 】A .22y x x =--+B .22y x x =-+-C .22y x x =-++D .22y x x =++9. (天津市2010年3分)已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列结论:①240b ac ->;②0abc >;③80a c +>;④930a b c ++<.其中,正确结论的个数是【 】(A )1 (B )2 (C )3 (D )410.(天津市2011年3分)若实数x 、y 、z 满足2()4()()0x z x y y z ----=.则下列式子一定成立的是【 】 (A)0x y z ++= (B) 20x y z +-= (C) 20y z x +-= (D) 2=0x z y +-11. (2012天津市3分)若关于x 的一元二次方程(x -2)(x -3)=m 有实数根x 1,x 2,且x 1≠x 2,有下列结论:①x 1=2,x 2=3; ②1m 4>-; ③二次函数y=(x -x 1)(x -x 2)+m 的图象与x 轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是【 】(A )0 (B )1 (C )2 (D )312.(2013年天津市3分)如图,是一对变量满足的函数关系的图象,有下列3个不同的问题情境:①小明骑车以400米/分的速度匀速骑了5分,在原地休息了4分,然后以500米/分的速度匀速骑回出发地,设时间为x 分,离出发地的距离为y 千米;②有一个容积为6升的开口空桶,小亮以1.2升/分的速度匀速向这个空桶注水,注5分后停止,等4分后,再以2升/分的速度匀速倒空桶中的水,设时间为x 分,桶内的水量为y 升;③矩形ABCD 中,AB=4,BC=3,动点P 从点A 出发,依次沿对角线AC 、边CD 、边DA 运动至点A 停止,设点P 的运动路程为x ,当点P 与点A 不重合时,y=S △ABP ;当点P 与点A 重合时,y=0.其中,符合图中所示函数关系的问题情境的个数为【 】A .0B .1C .2D .3二、填空题1. (天津市2002年3分)如图,在四边形ABCD 中,对角线AC 与BD 相交于点E ,若AC 平分∠DAB ,且AB=AE ,AC=AD ,有如下四个结论:①AC ⊥BD ;②BC=DE ;③1DBC=DAB 2∠∠, ④ΔABE 是正三角形。
2010—2016天津中考数学压轴题(学生版)

20010年—2016年天津中考压轴题解析3.(2010·天津)在平面直角坐标系中,已知抛物线2=-++与x轴交于点A、B(点A在点By x bx c的左侧),与y轴的正半轴交于点C,顶点为E.(Ⅰ)若2c=,求此时抛物线顶点E的坐标;b=,3(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足S△BCE= S△ABC,求此时直线BC的解析式;(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足S△BCE= 2S△AOC,且顶点E 恰好落在直线43=-+上,求此时抛物线的解析式.y x4.(2011·天津)已知抛物线1C :21112y x x =-+.点F (1,1). (Ⅰ) 求抛物线1C 的顶点坐标;(Ⅱ) ①若抛物线1C 与y 轴的交点为A .连接AF ,并延长交抛物线1C 于点B ,求证:112AF BF+= ②抛物线1C 上任意一点P (P P x y ,))(01P x <<).连接PF .并延长交抛物线1C 于点Q (Q Q x y ,), 试判断112PF QF+=是否成立?请说明理由; (Ⅲ) 将抛物线1C 作适当的平移.得抛物线2C :221()2y x h =-,若2x m <≤时.2y x ≤恒成立,求m 的最大值.5.(2012·天津)已知抛物线y =ax 2+bx +c (0<2a <b )的顶点为P (x 0,y 0),点A (1,y A )、B (0,y B )、 C (–1,y C )在该抛物线上.(Ⅰ)当a =1,b =4,c =10时,①求顶点P 的坐标;②求AB Cy y y -的值;(Ⅱ)当y 0≥0恒成立时,求AB Cy y y -的最小值.6.(2013·天津)已知抛物线y1=ax2+bx+c(a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:(Ⅰ)求y1与x之间的函数关系式;(Ⅱ)若经过点T(0,t)作垂直于y轴的直线l′,A为直线l′上的动点,线段AM的垂直平分线交直线l于点B,点B关于直线AM的对称点为P,记P(x,y2).(1)求y2与x之间的函数关系式;(2)当x取任意实数时,若对于同一个x,有y1<y2恒成立,求t的取值范围.7.(2014·天津)在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E、点F、点M 都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.(Ⅰ)若点M的坐标为(1,–1).①当点F的坐标为(1,1)时,如图,求点P的坐标;②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式;(Ⅱ)若点M (1,m),点F(1,t),其中t ≠0.过点P作PQ⊥l于点Q,当OQ=PQ时,试用含t的式子表示m.8.(2015·天津)已知二次函数y=x2+bx+c(b,c为常数).(Ⅰ)当b=2,c= –3时,求二次函数的最小值;(Ⅱ)当c=5时,若在函数值y=l的情况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;(Ⅲ)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.9.(2016年)已知抛物线C :221y x x =-+的顶点为P ,与y 轴的交点为Q ,点F (1,12). (Ⅰ)求点P ,Q 的坐标;(Ⅱ)将抛物线C 向上平移得到抛物线C ′,点Q 平移后的对应点为Q ′,且FQ ′=OQ ′. ① 求抛物线C ′的解析式;② 若点P 关于直线Q ′F 的对称点为K ,射线FK 与抛物线C ′相交于点A ,求点A 的坐标.解析版3.(2010·天津)在平面直角坐标系中,已知抛物线2y x bx c =-++与x 轴交于点A 、B (点A 在点B 的左侧),与y 轴的正半轴交于点C ,顶点为E . (Ⅰ)若2b =,3c =,求此时抛物线顶点E 的坐标;(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC 中满足S △BCE = S △ABC ,求此时直线BC 的解析式;(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC 中满足S △BCE = 2S △AOC ,且顶点E恰好落在直线43y x =-+上,求此时抛物线的解析式.解:(Ⅰ)当2b =,3c =时,抛物线的解析式为223y x x =-++,即2(1)4y x =--+.∴ 抛物线顶点E 的坐标为(1,4). .................2分(Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点E 在对称轴1x =上,有2b =, ∴ 抛物线的解析式为22y x x c =-++(0c >).∴ 此时,抛物线与y 轴的交点为0( )C c ,,顶点为1( 1)E c +,. ∵ 方程220x x c-++=的两个根为11x=21x =+∴ 此时,抛物线与x 轴的交点为10()A ,10()B +. 如图,过点E 作EF ∥CB 与x 轴交于点F ,连接CF ,则S △BCE = S △BCF .∵ S △BCE = S △ABC , ∴ S △BCF = S△ABC . ∴ BF AB == 设对称轴1x =与x 轴交于点D , 则12DF AB BF =+= 由EF ∥CB ,得EFD CBO ∠=∠. ∴ Rt △EDF ∽Rt △COB .有ED CODF OB=. ∴.结合题意,解得 54c =. ∴ 点54(0 )C ,,52( 0)B ,.设直线BC 的解析式为y mx n =+,则5,450.2n m n ⎧=⎪⎪⎨⎪=+⎪⎩ 解得 1,25.4m n ⎧=-⎪⎪⎨⎪=⎪⎩ ∴ 直线BC 的解析式为1524y x =-+. .....................6分(Ⅲ)根据题意,设抛物线的顶点为( )E h k ,,(0h >,0k >) 则抛物线的解析式为2()y x h k =--+, 此时,抛物线与y 轴的交点为2(0 )C h k -+,, 与x轴的交点为0()A h -,0()B h +0h >) 过点E 作EF ∥CB 与x 轴交于点F ,连接CF , 则S △BCE = S △BCF . 由S △BCE = 2S △AOC ,∴ S △BCF = 2S △AOC .得2)BF AO h ==. 设该抛物线的对称轴与x 轴交于点D . 则122DF AB BF h =+=. 于是,由Rt △EDF ∽Rt △COB ,有ED CODF OB=. ∴2=,即2220h k -+=.结合题意,解得h =① ∵ 点( )E h k ,在直线43y x =-+上,有43k h =-+. ② ∴1=. 有1k =,12h =.∴ 抛物线的解析式为234y x x =-++. ..........10分4.(2011·天津)已知抛物线1C :21112y x x =-+.点F (1,1). (Ⅰ) 求抛物线1C 的顶点坐标;(Ⅱ) ①若抛物线1C 与y 轴的交点为A .连接AF ,并延长交抛物线1C 于点B ,求证:112AF BF+= ②抛物线1C 上任意一点P (P P x y ,))(01P x <<).连接PF .并延长交抛物线1C 于点Q (Q Q x y ,),试判断112PF QF+=是否成立?请说明理由; (Ⅲ) 将抛物线1C 作适当的平移.得抛物线2C :221()2y x h =-,若2x m <≤时.2y x ≤恒成立,求m 的最大值.解 (I )∵2211111(1)222y x x x =-+=-+, ∴抛物线1C 的顶点坐标为(112, ).(II )①根据题意,可得点A (0,1), ∵F (1,1).∴AB ∥x 轴.得AF =BF =1,112AF BF+= ②112PF QF+=成立. 理由如下:如图,过点P (P P x y ,)作PM ⊥AB 于点M ,则FM =1P x -,PM =1P y -(01P x <<) ∴Rt △PMF 中,由勾股定理,得22222(1)(1)P P PF FM PM x y =+=-+-又点P (P P x y ,)在抛物线1C 上, 得211(1)22P P y x =-+,即2(1)21P P x y -=- ∴22221(1)P P P PF y y y =-+-=即P PF y =.过点Q (Q Q x y ,)作QN ⊥AB ,与AB 的延长线交于点N , 同理可得Q QF y =.图文∠PMF =∠QNF =90°,∠MFP =∠NFQ , ∴△PMF ∽△QNF 有PF PMQF QN= 这里11P PM y PF =-=-,11Q QN y QF =-=-x∴11PF PFQF QF -=- 即112PF QF+= (Ⅲ) 令3y x =,设其图象与抛物线2C 交点的横坐标为0x ,x 0′,且0x < x 0′, ∵抛物线2C 可以看作是抛物线212y x =左右平移得到的, 观察图象.随着抛物线2C 向右不断平移,0x ,x 0′ 的值不断增大, ∴当满足2x m <≤,.2y x ≤恒成立时,m 的最大值在x 0′ 处取得. 可得当02x =时.所对应的x 0′ 即为m 的最大值.于是,将02x =带入21()2x h x -=,有21(2)22h -=解得4h =或0h =(舍) ∴221(4)2y x =-此时,23y y =,得21(4)2x x -=解得02x =,x 0′=8 ∴m 的最大值为8.5.(2012·天津)已知抛物线y =ax 2+bx +c (0<2a <b )的顶点为P (x 0,y 0),点A (1,y A )、B (0,y B )、 C (–1,y C )在该抛物线上.(Ⅰ)当a =1,b =4,c =10时,①求顶点P 的坐标;②求AB Cy y y -的值;(Ⅱ)当y 0≥0恒成立时,求AB Cy y y -的最小值.解:(Ⅰ)若a =1,b =4,c =10,此时抛物线的解析式为y =x 2+4x +10.①∵y =x 2+4x +10=(x +2)2+6,∴抛物线的顶点坐标为P (–2,6). ②∵点A (1,y A )、B (0,y B )、C (–1,y C )在抛物线y =x 2+4x +10上,∴y A =15,y B =10,y C =7.∴155107A B C y y y ==--.(Ⅱ)由0<2a <b ,得012bx a=--<. 由题意,如图过点A 作AA 1⊥x 轴于点A 1, 则AA 1=y A ,OA 1=1.连接BC ,过点C 作CD ⊥y 轴于点D ,则BD =y B -y C ,CD =1.过点A 作AF ∥BC ,交抛物线于点E (x 1,y E ), 交x 轴于点F (x 2,0).则∠F AA 1=∠CBD .∴Rt △AF A 1∽Rt △BCD . ∴11AA FA BD CD=,即22111A B C y x x y y -==--. 过点E 作EG ⊥AA 1于点G ,易得△AEG ∽△BCD . ∴AG EGBD CD=,即A E B C y y y y --=1–x 1. ∵点A (1,y A )、B (0,y B )、C (–1,y C )、E (x 1,y E )在抛物线y =ax 2+bx +c 上, ∴y A =a +b +c ,y B =c ,y C =a –b +c ,y E =ax 12+bx 1+c ,∴2111()()1()a b c ax bx c x c a b c ++-++=---+,化简,得x 12+x 1–2=0, 解得x 1= –2(x 1=1舍去).∵y 0≥0恒成立,根据题意,有x 2≤x 1<–1. 则1–x 2≥1–x 1,即1–x 2≥3.∴AB Cy y y -的最小值为3.解法2:(Ⅱ)解:设m >0,由于b >2a >0,令b =2a +m 当y 0≥0恒成立时,应有b 2–4ac ≤0 ∴(2a +m )2–4ac ≤0 ∵a >0∴c ≥2(2)4a m a +=2(2)4a m a +–2m +2m =2(2)4a m a -+2m∵2(2)4a m a-≥0∴c ≥2m∵点A (1,y A )、B (0,y B )、C (–1,y C )在抛物线y =ax 2+bx +c 上 ∴y A =a +b +c , y B =c , y C = a –b +c ∴A B C y y y -=()a b c c a b c ++--+= a b cb a++-代入b =2a +m ,得A B C y y y -= 22a a m c a m a ++++-= 2a m a c a m ++++= 21a ca m+++∵c ≥2m , ∴A B C y y y -= 21a c a m +++≥221a ma m +++=3∴AB Cy y y -的最小值为3解法3:A (1,a +b +c )、B (0,c )、C (–1,a –b +c )由B (0,c )、C (–1,a –b +c )得直线BC 为y =(b –a )x +c ∵AE ∥BC ∴设直线AE 为y =(b –a )x +m将A (1,a +b +c )代入上式,得m =2a +c . ∴直线AE 为y =(b –a )x +2a +c由()2–2y b a x a c y ax bx c⎧=++⎪⎨=++⎪⎩得x 2+x –2=0. 解得E 点横坐标为x 1=–2(x 1=1舍去)∵y 0≥0恒成立,根据题意,有x 2≤x 1<-1. 则1-x 2≥1-x 1,即1-x 2≥3.∴AB Cy y y -的最小值为3.6.(2013·天津)已知抛物线y 1=ax 2+bx +c (a ≠0)的对称轴是直线l ,顶点为点M .若自变量x 和函数值y 1的部分对应值如下表所示: (Ⅰ)求y 1与x 之间的函数关系式;(Ⅱ)若经过点T (0,t )作垂直于y 轴的直线l ′,A 为直线l ′上的动点,线段AM 的垂直平分线交直线l 于点B ,点B 关于直线AM 的对称点为P ,记P (x ,y 2). (1)求y 2与x 之间的函数关系式;(2)当x解:(Ⅰ)∵抛物线经过点(0,94),∴c =94.∴y 1=ax 2+bx +94,∵点(–1,0)、(3,0)在抛物线y 1=ax 2+bx +94上, ∴90499304a b a b ⎧-+=⎪⎪⎨⎪++=⎪⎩,解得,3432a b ⎧=-⎪⎪⎨⎪=⎪⎩∴y 1与x 之间的函数关系式为:y 1= –34x 2+32x +94;(II )∵y 1= –34x 2+32x +94,∴y 1= –34(x –1)2+3,∴直线l 为x =1,顶点M (1,3). ①由题意得,t ≠3,如图,记直线l 与直线l ′交于点C (1,t ),当点A 与点C 不重合时, ∵由已知得,AM 与BP 互相垂直平分, ∴四边形ANMP 为菱形, ∴P A ∥l ,又∵点P (x ,y 2), ∴点A (x ,t ) (x ≠1), ∴PM =P A =|y 2–t |,过点P 作PQ ⊥l 于点Q ,则点Q (1,y 2), ∴QM =|y 2–3|,PQ =AC =|x –1|, 在Rt △PQM 中,∵PM 2=QM 2+PQ 2,即(y 2–t )2=(y 2–3)2+(x –1)2,整理得,y 2=162t -(x –1)2+32t +, 即y 2=162t -x 2–13t-x +21062t t --,∵当点A 与点C 重合时,点B 与点P 重合, ∴P (1,32t +), ∴P 点坐标也满足上式,∴y 2与x 之间的函数关系式为y 2=162t -x 2–13t-x +21062t t -- (t ≠3);②根据题意,借助函数图象:当抛物线y 2开口方向向上时,6–2t >0,即t <3时,抛物线y 1的顶点M (1,3),抛物线y 2的顶点(1,32t +), ∵3>32t +,∴不合题意,当抛物线y 2开口方向向下时,6–2t <0,即t >3时,y 1–y 2= –34(x –1)2+3–[162t -(x –1)2+32t +]=3114(3)t t --(x –1)2+32t-, 若3t –11≠0,要使y 1<y 2恒成立, 只要抛物线y =3114(3)t t --(x –1)2+32t -开口方向向下,且顶点(1,32t-)在x 轴下方,∵3–t <0,只要3t –11>0,解得t >113,符合题意; 若3t –11=0,y 1–y 2= –13<0,即t =113也符合题意.综上,可以使y 1<y 2恒成立的t 的取值范围是t ≥113.7.(2014·天津) 在平面直角坐标系中,O 为原点,直线l :x =1,点A (2,0),点E 、点F 、点M 都在直线l 上,且点E 和点F 关于点M 对称,直线EA 与直线OF 交于点P . (Ⅰ)若点M 的坐标为(1,–1).① 当点F 的坐标为(1,1)时,如图,求点P 的坐标; ② 当点F 为直线l 上的动点时,记点P (x ,y ),求y 关于x 的函数解析式;(Ⅱ)若点M (1,m ),点F (1,t ),其中t ≠0.过点P 作 PQ ⊥l 于点Q ,当OQ =PQ 时,试用含t 的式子表示m .解:(Ⅰ) ①∵点O (0,0),点F (1,1).∴直线OF 的解析式为y =x 设直线EA 的解析式为y =kx +b由点E 和点F 关于点M (1,–1)对称,得点E (1,–3) 又点A (2,0).点E 在直线EA 上. ∴203k b k b +=⎧⎨+=-⎩解得36k b =⎧⎨=-⎩∴直线EA 的解析式为y =3x –6 ∵点P 是直线OF 与直线EA 的交点,有36y x y x =⎧⎨=-⎩.解得33x y =⎧⎨=⎩∴点P 坐标为(3,3) ②由已知,设点F (1,t ) ∴直线OF 的解析式为y =tx 设直线EA 的解析式为y =kx +b由点E 和点F 关于点M (1,–1)对称,得点E (1,–2–t ) 又点A 、点E 在直线EA 上∴202k b k b t +=⎧⎨+=--⎩解得22(2)k t b t =+⎧⎨=-+⎩∴直线EA 的解析式为y =(2+t )x –2(2+t ) ∵点P 为直线OF 与直线EA 的交点 ∴tx =(2+t )x –2(2+t ),化简,得t =x –2 有y =tx =(x –2)x =x 2–2x∴y 关于x 的函数解析式为y =x 2–2x (Ⅱ)根据题意,同(Ⅰ)可得 直线OF 的解析式为y =tx直线EA 的解析式为y =(t –2m )x –2(t –2m ) ∵点P 为直线OF 与直线EA 的交点 ∴tx =(t –2m )x –2(t –2m ),m ≠0化简,得2tx m =-. 有y =tx =22t t m -∴点P 坐标为(2tm -,22t t m -)∵PQ ⊥l 于点Q ,点Q (1,22t t m-)∴OQ 2=221(2)t t m +-,PQ 2=2(1)t m- ∵OQ =PQ∴221(2)t t m +-=2(1)t m- 化简,得t (t –2m )(t 2–2mt –1)=0. 又t ≠0 ∴t –2m =0或t 2–2mt –1=0∴m =2t或212t m t -=即为所求.8.(2015·天津)已知二次函数y =x 2+bx +c (b ,c 为常数).(Ⅰ)当b =2,c = –3时,求二次函数的最小值;(Ⅱ)当c =5时,若在函数值y =l 的情况下,只有一个自变量x 的值与其对应,求此时二次函数的解析 式;(Ⅲ)当c =b 2时,若在自变量x 的值满足b ≤x ≤b +3的情况下,与其对应的函数值y 的最小值为21, 求此时二次函数的解析式.解:(Ⅰ)当b =2,c = –3时,二次函数的解析式为y =x 2+2x –3=(x +1)2–4,∴当x = –1时,二次函数取得最小值–4;(Ⅱ)当c =5时,二次函数的解析式为y =x 2+bx +5, 由题意得,x 2+bx +5=1有两个相等是实数根, ∴△=b 2–16=0,解得,b 1=4,b 2= –4,∴次函数的解析式y =x 2+4x +5,y =x 2–4x +5; (Ⅲ)当c =b 2时,二次函数解析式为y =x 2+bx +b 2, 图象开口向上,对称轴为直线x = –b2 ,①当–b2<b ,即b >0时,在自变量x 的值满足b ≤x ≤b +3的情况下,y 随x 的增大而增大, ∴当x =b 时,y =b 2+b •b +b 2=3b 2为最小值, ∴3b 2=21,解得,b 1= –7 (舍去),b 2=7 ; ②当b ≤–b2 ≤b +3时,即–2≤b ≤0,∴x = –b 2 ,y =34b 2为最小值,∴34b 2=21,解得,b 1= –27 (舍去),b 2=27 (舍去); ③当–b2>b +3,即b <–2,在自变量x 的值满足b ≤x ≤b +3的情况下,y 随x 的增大而减小, 故当x =b +3时,y =(b +3)2+b (b +3)+b 2=3b 2+9b +9为最小值, ∴3b 2+9b +9=21.解得,b 1=1(舍去),b 2=﹣4; ∴b =7 时,解析式为:y =x 2+7x +7b = –4时,解析式为:y =x 2–4x +16.综上可得,此时二次函数的解析式为y =x 2+7x +7或y =x 2–4x +16.本题考查了二次函数的最值:当a >0时,抛物线在对称轴左侧,y 随x 的增大而减少;在对称轴右侧,y 随x 的增大而增大,因为图象有最低点,所以函数有最小值,当x = –b2a 时,y = 4ac –b 24a ;当a <0时,抛物线在对称轴左侧,y 随x 的增大而增大;在对称轴右侧,y 随x 的增大而减少,因为图象有最高点,所以函数有最大值,当x = –b2a 时,y = 4ac –b 24a ;确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.9.(2016年)已知抛物线C :221y x x =-+的顶点为P ,与y 轴的交点为Q ,点F (1,12). (Ⅰ)求点P ,Q 的坐标;(Ⅱ)将抛物线C 向上平移得到抛物线C ′,点Q 平移后的对应点为Q ′,且FQ ′=OQ ′. ③ 求抛物线C ′的解析式;④ 若点P 关于直线Q ′F 的对称点为K ,射线FK 与抛物线C ′相交于点A ,求点A 的坐标.由点N 在直线Q ′F 上,得035044x -+=,解得053x =. 将053x =代入2000524y x x =-+,得02536y =.∴点A 的坐标为525()336,(Ⅱ) ②解法二:设K 00()x y ,. 连接Q ′P 、Q ′K 、FP . 由P 、K 关于直线Q ′F 对称,有Q ′K =Q ′P ,FK =FP ,因此,Q ′K 2=Q ′P 2,FK 2= FP 2.2.221.81.61.41.210.80.60.40.20.20.4y50.51 1.52 2.5xNAK Q'FQ O P根据勾股定理,得2222002220055()1()4411(1)()()22x y x y ⎧+-=+⎪⎪⎨⎪-+-=⎪⎩.解方程组,得0037251625x y ⎧=⎪⎪⎨⎪=⎪⎩,即点K 的坐标为3716(2525, 设直线FK 的解析式为y kx b =+,代入F 1(1)2,及K 3716()2525,, 得1237162525k b k b ⎧+=⎪⎪⎨⎪+=⎪⎩,解方程组得,724524k b ⎧=⎪⎪⎨⎪=⎪⎩,即直线FK 的解析式为752424y x =+. 点A 为射线FK 与抛物线C ′的交点,把752424y x =+代入2524y x x =-+, 得方程2552502424x x -+=,解得1255138x x ==<,(舍去). 此时,2536y =, 即点A 的坐标为525()336,.。
2016年天津市中考数学试卷

一、选择题:本大题共 12 小题,每小题 3 分,共 36 分 1. (3 分)计算(﹣2)﹣5 的结果等于( A.﹣7 B.﹣3 ) D . √3 ) ) C.3 D .7
2. (3 分)sin60°的值等于( A.
1
√2 √3 C. 2 2 2 3. (3 分)下列图形中,可以看作是中心对称图形的是(
第5页(共25页)
23. (10 分)公司有 330 台机器需要一次性运送到某地,计划租用甲、乙两种货 车共 8 辆,已知每辆甲种货车一次最多运送机器 45 台、租车费用为 400 元, 每辆乙种货车一次最多运送机器 30 台、租车费用为 280 元 (Ⅰ)设租用甲种货车 x 辆(x 为非负整数) ,试填写表格. 表一: 租用甲种货车的数量/辆 租用的甲种货车最多运送机器的数量/台 租用的乙种货车最多运送机器的数量/台 表二: 租用甲种货车的数量/辆 租用甲种货车的费用/元 租用乙种货车的费用/元 3 7 2800 280 x 3 135 150 7 x
B.
A.
B.
C.
D.
4. (3 分)2016 年 5 月 24 日《天津日报》报道,2015 年天津外环线内新栽植树 木 6120000 株,将 6120000 用科学记数法表示应为( A.0.612×107 B.6.12×106 C.61.2×105 ) D.612×104 )
5. (3 分) 如图是一个由 4 个相同的正方体组成的立体图形, 它的主视图是 (
(Ⅰ)解不等式①,得 (Ⅱ)解不等式②,得
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为
.
20. (8 分)在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成 绩(单位:m) ,绘制出如下的统计图①和图②,请根据相关信息,解答下列 问题:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016天津中考数学压轴题及答案解析
2016年天津中考数学压轴题及答案解析,更多2016中考真题答案、2016中考志愿填报、2016中考成绩查询、2016中考分数线等信息,请及时关注2016年中考真题及答案※中考作文※成绩查询
选择压轴题
今年的选择压轴题考查的内容沿用了2015天津中考数学试卷的最后一道大题,也就是区间最值问题,难度不大。
填空压轴题
今年的填空压轴题已经是连续第五年考察格点作图问题,同学们平日的练习以及各级各类考试中都会涉及到,难度还没有到想不出来的地步,如果用。
