高一函数大题训练及答案
高一数学函数习题(练习题以及答案

一、 求函数的定义域1、求下列函数的定义域:⑴y =⑵y =⑶01(21)111y x x =+-++-2、设函数f x ()的定义域为[]01,,则函数f x ()2的定义域为_ _ _;函数f x ()-2的定义域为________;3、若函数(1)f x +的定义域为[]-23,,则函数(21)f x -的定义域是 ;函数1(2)f x+的定义域为 。
4、 知函数f x ()的定义域为 [1,1]-,且函数()()()F x f x m f x m =+--的定义域存在,求实数m 的取值范围。
二、求函数的值域5、求下列函数的值域:⑴223y x x =+- ()x R ∈ ⑵223y x x =+- [1,2]x ∈ ⑶311x y x -=+ ⑷311x y x -=+ (5)x ≥ ⑸y = ⑹ 225941x x y x +=-+ ⑺31y x x =-++ ⑻2y x x =- ⑼y ⑽4y =⑾y x =-6、已知函数222()1x ax bf x x ++=+的值域为[1,3],求,a b 的值。
三、求函数的解析式1、 已知函数2(1)4f x x x -=-,求函数()f x ,(21)f x +的解析式。
2、 已知()f x 是二次函数,且2(1)(1)24f x f x x x ++-=-,求()f x 的解析式。
3、已知函数()f x 满足2()()34f x f x x +-=+,则()f x = 。
4、设()f x 是R 上的奇函数,且当[0,)x ∈+∞时,()(1f x x =+,则当(,0)x ∈-∞时()f x =____ _()f x 在R 上的解析式为5、设()f x 与()g x 的定义域是{|,1}x x R x ∈≠±且,()f x 是偶函数,()g x 是奇函数,且1()()1f xg x x +=-,求()f x 与()g x 的解析表达式四、求函数的单调区间6、求下列函数的单调区间:⑴ 223y x x =++ ⑵y = ⑶ 261y x x =--7、函数()f x 在[0,)+∞上是单调递减函数,则2(1)f x -的单调递增区间是8、函数236xy x -=+的递减区间是 ;函数y =的递减区间是五、综合题9、判断下列各组中的两个函数是同一函数的为 ( ) ⑴3)5)(3(1+-+=x x x y , 52-=x y ; ⑵111-+=x x y , )1)(1(2-+=x x y ;⑶x x f =)(, 2)(x x g =; ⑷x x f =)(, ()g x =; ⑸21)52()(-=x x f , 52)(2-=x x f 。
高一函数练习题和答案

函数练习1函数(一)1.下列各组函数中,表示相同函数的是 ( )A f(x)=x 与g(x)=xx 2Bf(x)=|x|与 g(x)=2x Cf(x)=12-x 与g(x)=1-x ?1+xDf(x)=x 0与g(x)=1 1. 函数y=x--113的定义域为 ( )A (-∞,1]B(-∞,0) (0,1]C(-∞,0) (0,1)D[1,+∞)2. 下列函数中值域是R +的是 ( )A y=2x+1(x>0)By=x 2Cy=112-x Dy=x2 3. 函数y=22++-x x 的定义域为__________,值域为_____________.4. 已知f(x)=x 2+1,则f[f(-1)]=______________________ 5. 求下列函数的定义域;(1)y=x111+; (2)y=xx x -+||)1(07.用可围成32m 墙的砖头,沿一面旧墙围猪舍四间(其平面图为连成一排大小相同的四个长方形,如图),应怎样围,才能使猪舍的总面积最大?最大面积是多少?函数练习2函数(二)1. 下面四个函数:(1)y=1-x(2)y=2x-1(3)y=x 2-1(4)y=x5,其中的函数有 ( )A 1个B 2个C 3个D 4个2. 下列图象能作为函数图象的是 ( ) A B C D3. (1)数集{x|4≤x<16}用区间表示为_________;(2)数集{x||x|≤3}用区间表示为_______;(3)数集{x|x ∈R ,且x ≠0}用区间表示为_______;4. 已知f(x)=⎪⎩⎪⎨⎧--3210x )0()0()0(<=>x x x ,求f{f[f(5)]}的值。
5. 已知f(x)的定义域为(0,1)求f(x 2)的定义域 6.若2f(x)+f(-x)=3x+1,求f(x)的解析式。
函数练习3函数的单调性1.若函数y=(2k+1)x+6在(-∞,+∞)上是减函数,则()Ak>21Bk<21Ck>-21Dk<-212.函数y=-x 2+4x-7在区间(-1,3)上是()A 增函数B 减函数C 先是增函数后是减函数D 先是减函数后是函数 3.函数y=x1的单调区间是____________。
(完整)高一数学第一学期函数压轴[大题]练习[含答案及解析],推荐文档
![(完整)高一数学第一学期函数压轴[大题]练习[含答案及解析],推荐文档](https://img.taocdn.com/s3/m/0e4f6c50eff9aef8941e06cb.png)
10. (本题 16 分)已知函数 f (x) log9 (9x 1) kx ( k R )是偶函数.
(1)求 k 的值;
(2)若函数 y f (x) 的图象与直线 y 1 x b 没有交点,求 b 的取值范围; 2
(3)设 h(x) log9
f
1 ()
2
.
1 x2
25
(1) 求实数 a , b 的值;
(2) 用定义证明:函数 f (x) 在区间 (1,1) 上是增函数;
(3) 解关于 t 的不等式 f (t 1) f (t) 0 .
4. (14 分)定义在 R 上的函数 f(x)对任意实数 a,b R ,均有 f(ab)=f(a)+f(b)成立,且当 x>1 时,f(x)
技术资料.整理分享
WORD 格式.可编辑
13.(本小题满分 16 分)
设 a 0 , b 0 ,已知函数 f (x) ax b . x 1
(Ⅰ)当 a b 时,讨论函数 f (x) 的单调性(直接写结论);
(Ⅱ)当 x 0 时,(i)证明 f (1) f ( b ) [ f ( b )]2 ;
6. (12 分)设函数 f (x) loga (x 3a)(a 0,且a 1) ,当点 P(x, y) 是函数 y f (x) 图象上的点时,
点 Q(x 2a, y) 是函数 y g(x) 图象上的点. (1)写出函数 y g(x) 的解析式; (2)若当 x [a 2, a 3] 时,恒有 | f (x) g(x) |„ 1 ,试确定 a 的取值范围; (3)把 y g(x) 的图象向左平移 a 个单位得到 y h(x) 的图象,函数
WORD 格式.可编辑
高一函数练习题及答案

高一函数练习题及答案高一函数练习题及答案高一阶段是学习数学的重要时期,其中函数是一个重要的内容。
函数作为数学的一个基础概念,对于学生来说是一个相对抽象的概念。
因此,通过练习题的方式来巩固和提高对函数的理解和运用能力是非常必要的。
本文将为大家提供一些高一函数练习题及答案,希望能够帮助大家更好地掌握函数的知识。
一、选择题1. 设函数f(x) = 2x + 3,那么f(4)的值是多少?A. 7B. 11C. 9D. 8答案:B. 11解析:将x = 4代入函数f(x) = 2x + 3中,得到f(4) = 2 × 4 + 3 = 8 + 3 = 11。
2. 已知函数g(x) = x^2 + 3x - 2,求g(-1)的值是多少?A. -6B. -2C. 2D. 6答案:C. 2解析:将x = -1代入函数g(x) = x^2 + 3x - 2中,得到g(-1) = (-1)^2 + 3 × (-1) - 2 = 1 - 3 - 2 = -4。
3. 函数h(x) = 3x^2 - 2x + 1,求h(2)的值是多少?A. 9B. 11C. 15D. 19答案:A. 9解析:将x = 2代入函数h(x) = 3x^2 - 2x + 1中,得到h(2) = 3 × 2^2 - 2 × 2 + 1 = 3 × 4 - 4 + 1 = 12 - 4 + 1 = 9。
二、填空题1. 设函数f(x) = 2x + 3,求f(-1)的值是多少?答案:1解析:将x = -1代入函数f(x) = 2x + 3中,得到f(-1) = 2 × (-1) + 3 = -2 + 3 = 1。
2. 已知函数g(x) = x^2 + 3x - 2,求g(0)的值是多少?答案:-2解析:将x = 0代入函数g(x) = x^2 + 3x - 2中,得到g(0) = 0^2 + 3 × 0 - 2 = 0 - 2 = -2。
高一数学函数经典练习题(含答案详细)

高一数学函数经典练习题(含答案详细)一、求函数的定义域1、求下列函数的定义域:⑴ $y=\frac{x^2-2x-15}{x+3-3}$答案:首先化简得到 $y=\frac{x^2+2x-15}{x}$。
然后根据分式的定义,分母不能为零,即 $x\neq0$。
同时,分子中有$x-5$ 和 $x+3$ 两个因式,因此 $x\leq-3$ 或 $x\geq5$。
综合起来得到定义域为 $\{x|x\leq-3 \text{ 或 } x\geq5 \text{ 或 }x\neq0\}$。
⑵ $y=1-\frac{x-1}{2x+2}$答案:首先化简得到 $y=\frac{x+1}{2x+2}$。
然后根据分式的定义,分母不能为零,即 $x\neq-1$。
同时,分子中有 $x-1$ 和 $x+1$ 两个因式,因此 $x\geq0$。
综合起来得到定义域为 $\{x|x\geq0 \text{ 且 } x\neq-1\}$。
2、设函数 $f(x)$ 的定义域为 $[0,1]$,则函数 $f(x^2)$ 的定义域为 _。
_。
_;函数 $x-2f(x-2)$ 的定义域为答案:对于 $f(x^2)$,$x^2\in[0,1]$,因此 $x\in[-1,1]$。
综合起来得到定义域为 $\{x|-1\leq x\leq1\}$。
对于 $x-2f(x-2)$,$x-2(x-2)\in[0,1]$,即 $2\leq x\leq3$。
因此定义域为 $\{x|2\leq x\leq3\}$。
3、若函数 $f(x+1)$ 的定义域为 $[-2,3]$,则函数 $f(2x-1)$ 的定义域是;函数 $f(\frac{x+2}{x})$ 的定义域为。
答案:对于 $f(2x-1)$,$2x-1\in[-2,3]$,因此 $-1\leqx\leq2$。
综合起来得到定义域为 $\{x|-1\leq x\leq2\}$。
对于 $f(\frac{x+2}{x})$,$x\neq0$ 且 $\frac{x+2}{x}\in[-2,3]$,即 $-2x\leq x+2\leq3x$,解得 $-3\leq x\leq-1$ 或$x\geq2$。
高一数学第一学期函数压轴(大题)练习(含答案)

高一数学第一学期函数压轴(大题)练习(含答案)1.已知不等式 $2(\log_2 x)^2+7\log_2 x+3\leqslant 0$,求函数 $f(x)=\log_2 x\cdot \log_2 x$ 的最大值、最小值及相应的$x$ 值。
2.已知定义域为 $\mathbb{R}$ 的函数$f(x)=\dfrac{2x+1}{x^2+1}$ 是奇函数。
1)求 $a$ 的值;2)判断并证明该函数在定义域 $\mathbb{R}$ 上的单调性;3)若对任意的 $t\in\mathbb{R}$,不等式 $f(t-2t)+f(2t-k)<0$ 恒成立,求实数 $k$ 的取值范围。
3.已知定义在区间 $(-1,1)$ 上的函数 $f(x)=\dfrac{(1-a)x^2+b}{1-x^2}$。
1)求实数 $a,b$ 的值;2)用定义证明:函数$f(x)$ 在区间$(-1,1)$ 上是增函数;3)解关于 $t$ 的不等式 $\dfrac{(1-a)t^2+b}{1-t^2}>0$。
4.定义在 $\mathbb{R}^+$ 上的函数 $f(x)$ 对任意实数$a,b\in \mathbb{R}^+$,均有 $f(ab)=f(a)+f(b)$ 成立,且当$x>1$ 时,$f(x)<0$。
1)求 $f(1)$;2)求证:$f(x)$ 为减函数;3)当 $f(4)=-2$ 时,解不等式$f(x)+f\left(\dfrac{1}{2}x\right)>0$。
5.已知函数$f(x)=x-2bx+\dfrac{4}{b}$,定义域为$[1,4]$,$b\geqslant 1$。
I)求 $f(x)$ 的最小值 $g(b)$;II)求 $g(b)$ 的最大值 $M$。
6.设函数 $f(x)=\log_a (x-3)$,$a>0$ 且 $a\neq 1$,当点$P(x,y)$ 是函数 $y=f(x)$ 图象上的点时,点 $Q(x-2a,-y)$ 是函数 $y=g(x)$ 图象上的点。
高一数学函数试题及答案

函数与基本初等函数一、选择题1.下列函数中,在其定义域内既是奇函数又是减函数的是( )A .y =-x 3,x ∈R B .y =sin x ,x ∈RC .y =x ,x ∈RD .y =(12)x ,x ∈R2.若函数y =f (x )是函数y =a x (a >0,且a ≠1)的反函数,且f (2)=1,则f (x )=( )A .log 2x B.12x C .log 12x D .2x -23.已知函数f (x )=ax 3+bx 2+c 是奇函数,则( )A .b =c =0B .a =0C .b =0,a ≠0D .c =0 4.函数f (x +1)为偶函数,且x <1时,f (x )=x 2+1, 则x >1时,f (x )的解析式为( )A .f (x )=x 2-4x +4B .f (x )=x 2-4x +5C .f (x )=x 2-4x -5D .f (x )=x 2+4x +55.函数f (x )=3x 21-x+lg(3x +1)的定义域是( )A .(-13,+∞)B .(-13,1)C .(-13,13) D .(-∞,-13) 6.若定义在R 上的函数f (x )满足:对任意x 1,x 2∈R 有f (x 1+x 2)=f (x 1)+f (x 2)+1,则下列说法一定正确的是( )A .f (x )为奇函数B .f (x )为偶函数C .f (x )+1为奇函数D .f (x )+1为偶函数7.设奇函数f (x )在(0,+∞)内为增函数,且f (1)=0,则不等式f (x )-f (-x )x<0的解集为( )A .(-1,0)∪(1,+∞)B .(-∞,-1)∪(0,1)C .(-∞,-1)∪(1,+∞)D .(-1,0)∪(0,1)8.设a ,b ,c 均为正数,且2a =log 12a ,(12)b =log 12b ,(12)c =log 2c ,则( )A .a <b <cB .c <b <aC .c <a <bD .b <a <c二、填空题9.函数y =log 12x +2的定义域是____________.10.已知函数f (x )=a x +b 的图象经过点(-2,134),其反函数y =f -1(x )的图象经过点(5,1),则f (x )的解析式是________.11.函数f (x )=ln 1+ax1+2x(a ≠2)为奇函数,则实数a 等于________.12.方程x 2-2ax +4=0的两根均大于1,则实数a 的范围是________.13.若函数f (x )=(x +a )(bx +2a )(常数a ,b ∈R )是偶函数,且它的值域为(-∞,4],则该函数的解析式f (x )=________.14.函数f (x )=log 0.5(3x 2-ax +5)在(-1,+∞)上是减函数,则实数a 的取值范围是________. 三、解答题15.设f (x )是奇函数,g (x )是偶函数,并且f (x )-g (x )=x 2-x ,求f (x ),g (x ).16.设不等式2(log 12x )2+9(log 12x )+9≤0的解集为M ,求当x ∈M 时,函数f (x )=(log 2x 2)(log 2x8)的最大、最小值.17.已知函数f (x )的图象与函数h (x )=x +1x+2的图象关于点A (0,1)对称.18.设函数f (x )=ax 2+1bx +c是奇函数(a ,b ,c 都是整数),且f (1)=2,f (2)<3.(1)求a ,b ,c 的值;(2)当x <0,f (x )的单调性如何?用单调性定义证明你的结论.参考答案1 B 在其定义域内是奇函数但不是减函数;C 在其定义域内既是奇函数又是增函数;D 在其定义域内不是奇函数,只是减函数;故选A.2 函数y =a x (a >0,且a ≠1)的反函数是f (x )=log a x ,又f (2)=1,即log a 2=1,所以,a =2,故f (x )=log 2x ,选A.3 ∵f (x )是奇函数,∴f (0)=0,∴c =0.∴-ax 3-bx 2=-ax 3+bx 2,∴b =0,故选A. 4 因为f (x +1)为偶函数,所以f (-x +1)=f (x +1),即f (x )=f (2-x );当x >1时,2-x <1,此时,f (2-x )=(2-x )2+1,即f (x )=x 2-4x +5. 5 ⎩⎨⎧1-x >03x +1>0,解得-13<x<1.故选B.6 令x =0,得f (0)=2f (0)+1,f (0)=-1,所以f (x -x )=f (x )+f (-x )+1=-1,而f (x )+f (-x )+1+1=0,即 f (x )+1=-,所以f (x )+1为奇函数,故选C. 7因为f (x )是奇函数,所以f (-x )=-f (x ),于是不等式变为2f (x )x<0,根据函数的单调性和奇偶性,画出函数的示意图(图略),可知不等式2f (x )x <0的解集为(-1,0)∪(0,1). 8如下图:∴a <b <c . A9 (0,4] 10 f (x )=2x +3 11依题意有f (-x )+f (x )=ln1-ax1-2x+ln 1+ax 1+2x =0,即1-ax 1-2x ·1+ax 1+2x =1,故1-a 2x 2=1-4x 2,解得a 2=4,但a ≠2,故a =-2.12 解法一:利用韦达定理,设方程x 2-2ax +4=0的两根为x 1、x 2,则⎩⎨⎧(x 1-1)(x 2-1)>0,(x 1-1)+(x 2-1)>0,解之得2≤a <52. 13 f (x )=(x +a )(bx +2a )=bx 2+(2a +ab )x +2a 2是偶函数,则其图象关于y 轴对称.∴2a +ab =0⇒b =-2,∴f (x )=-2x 2+2a 2,且值域为(-∞,4],∴2a 2=4,∴f (x )=-2x 2+4. -2x 2+414设g (x )=3x 2-ax +5,已知⎩⎨⎧a 6≤-1,g (-1)≥0,解得-8≤a ≤-6.15 f (x )为奇函数,∴f (-x )=-f (x );g (x )为偶数,∴g (-x )=g (x ).f (x )-g (x )=x 2-x∴f (-x )-g (-x )=x 2+x从而-f (x )-g (x )=x 2+x ,即f (x )+g (x )=-x 2-x ,16 ∵2(log 12x )2+9(log 12x )+9≤0,∴(2log 12x +3)(log 12x +3)≤0.∴-3≤log 12x ≤-32.即log 12(12)-3≤log 12x ≤log 12(12)-32∴(12)-32≤x ≤(12)-3,即22≤x ≤8.从而M =.又f (x )=(log 2x -1)(log 2x -3)=log 22x -4log 2x +3=(log 2x -2)2-1.∵22≤x ≤8,∴32≤log 2x ≤3.∴当log 2x =2,即x =4时y min =-1;当log 2x =3,即x =8时,y max =0.⎩⎨⎧ f (x )-g (x )=x 2-x f (x )+g (x )=-x 2-x ⇒⎩⎨⎧f (x )=-xg (x )=-x 2 17 (1)求f (x )的解析式;(2)若g (x )=f (x )·x +ax ,且g (x )在区间(0,2]上为减函数,求实数a 的取值范围.(1)设f (x )图象上任意一点的坐标为(x ,y ),点(x ,y )关于点A (0,1)的对称点(-x,2-y )在h (x )的图象上.∴2-y =-x +1-x +2,∴y =x +1x ,即f (x )=x +1x .(2)g (x )=(x +1x )·x +ax ,即g (x )=x 2+ax +1.g (x )在(0,2]上递减⇒-a 2≥2,∴a ≤-4.18 (1)由f (x )=ax 2+1bx +c是奇函数,得f (-x )=-f (x )对定义域内x 恒成立,则a (-x )2+1b (-x )+c =-ax 2+1bx +c ⇒-bx +c =-(bx +c )对定义域内x 恒成立,即c =0.又⎩⎨⎧f (1)=2f (2)<3⇒⎩⎪⎨⎪⎧a +1b =2 ①4a +12b <3 ②由①得a =2b -1代入②得2b -32b<0⇒0<b <32,又a ,b ,c 是整数,得b =a =1.(2)由(1)知,f (x )=x 2+1x =x +1x,当x <0,f (x )在(-∞,-1]上单调递增,在上单调递增.同理,可证f (x )在[-1,0)上单调递减.。
高一数学函数经典练习题(含答案)
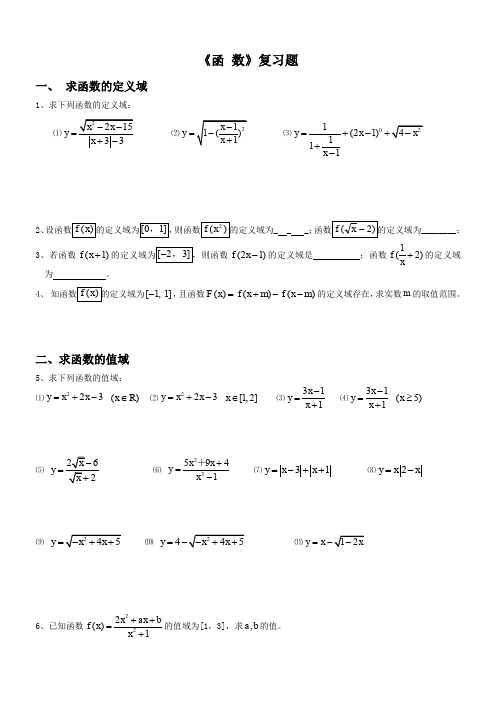
《函 数》复习题一、 求函数的定义域1、求下列函数的定义域:⑴33y x =+-⑵y =⑶01(21)111y x x =+-++-2、_ _ _;________;3、若函数(1)f x+(21)f x -的定义域是 ;函数1(2)f x+的定义域为 。
4、 [1,1]-,且函数()()()F x f x m f x m =+--的定义域存在,求实数m 的取值范围。
二、求函数的值域5、求下列函数的值域:⑴223y x x =+- ()x R ∈ ⑵223y x x =+- [1,2]x ∈ ⑶311x y x -=+ ⑷311x y x-=+ (5)x ≥⑸ y =⑹ 225941x x y x +=-+ ⑺31y x x =-++⑻2y x x =-⑼y ⑽4y = ⑾y x =-6、已知函数222()1x ax bf x x ++=+的值域为[1,3],求,a b 的值。
三、求函数的解析式1、 已知函数2(1)4f x x x -=-,求函数()f x ,(21)f x +的解析式。
2、 已知()f x 是二次函数,且2(1)(1)24f x f x x x ++-=-,求()f x 的解析式。
3、已知函数()f x 满足2()()34f x f x x +-=+,则()f x = 。
4、设()f x 是R 上的奇函数,且当[0,)x ∈+∞时, ()(1f x x =+,则当(,0)x ∈-∞时()f x =____ _()f x 在R 上的解析式为5、设()f x 与()g x 的定义域是{|,1}x x R x ∈≠±且,()f x 是偶函数,()g x 是奇函数,且1()()1f xg x x +=-,求()f x 与()g x 的解析表达式四、求函数的单调区间6、求下列函数的单调区间:⑴ 223y x x =++ ⑵y =⑶ 261y x x =--7、函数()f x 在[0,)+∞上是单调递减函数,则2(1)f x -的单调递增区间是8、函数236xy x -=+的递减区间是 ;函数y =的递减区间是五、综合题9、判断下列各组中的两个函数是同一函数的为 ( ) ⑴3)5)(3(1+-+=x x x y , 52-=x y ; ⑵111-+=x x y , )1)(1(2-+=x x y ;⑶x x f =)(, 2)(x x g =; ⑷x x f =)(, ()g x =; ⑸21)52()(-=x x f , 52)(2-=x x f 。
高一函数练习题及答案

高一函数练习题及答案1. 已知函数f(x)=2x-1,求f(-3)的值。
答案:将-3代入函数f(x)=2x-1,得到f(-3)=2*(-3)-1=-7。
2. 函数y=x^2-4x+3的顶点坐标是什么?答案:首先将函数转化为顶点式,y=(x-2)^2-1,顶点坐标为(2,-1)。
3. 判断函数f(x)=|x-1|+|x-2|的奇偶性。
答案:f(-x)=|-x-1|+|-x-2|=|x+1|+|x+2|=f(x),所以f(x)是偶函数。
4. 若函数f(x)=x^3-3x^2+2x+1,求f(a)+f(-a)的值。
答案:f(a)+f(-a)=a^3-3a^2+2a+1+(-a)^3-3(-a)^2+2(-a)+1=0。
5. 函数y=x^2-2x+1的图像与x轴的交点坐标是什么?答案:令y=0,解得x^2-2x+1=0,解得x=1,所以与x轴的交点坐标为(1,0)。
6. 已知函数g(x)=x^2+3x+2,求g(x)的反函数。
答案:首先解出g(x)的表达式,令y=x^2+3x+2,解得x=(-3±√(3^2-4*1*2))/2=-1,-2,所以g(x)的反函数为g^(-1)(x)={-1,-2}。
7. 函数f(x)=x^2-4x+3在区间[0,3]上的最大值和最小值分别是多少?答案:函数f(x)=x^2-4x+3的顶点为(2,-1),所以最小值为-1;在区间[0,3]上,f(0)=3,f(3)=0,所以最大值为3。
8. 已知函数h(x)=x^3-6x^2+9x+2,求h(2)的值。
答案:将2代入函数h(x)=x^3-6x^2+9x+2,得到h(2)=2^3-6*2^2+9*2+2=-2。
9. 函数y=x^2-6x+8的图像与直线y=k相切,求k的值。
答案:首先求导数y'=2x-6,设切点为(x0,y0),则y'|x=x0=2x0-6,切线的斜率为2x0-6。
又因为切线过切点,所以y0=x0^2-6x0+8,将y'|x=x0代入得k-y0=(2x0-6)(x0-y0),解得k=-4。
高一函数大题训练和答案

(3)在直角坐标系中.求定点A(–3,1)到此函数图象上任意一点P的距离|AP|的最小值。
函数大题专练答案
1、已知关于 的不等式 .其中 。
⑴试求不等式的解集 ;
⑵对于不等式的解集 .若满足 (其中 为整数集)。试探究集合 能否为有限集?若能.求出使得集合 中元素个数最少的 的所有取值.并用列举法表示集合 ;若不能.请说明理由。
②若
当 时. 是 上的减函数.所以 .即 .所以
6、设 .求满足下列条件的实数 的值:至少有一个正实数 .使函数 的定义域和值域相同。
解:(1)若 .则对于每个正数 . 的定义域和值域都是
故 满足条件
(2)若 .则对于正数 . 的定义域为 .
但 的值域 .故 .即 不合条件;
(3)若 .则对正数 .定义域 .
由条件可知 .即 .
解得 .
. .
(2)当 时. .
即 .
. .
.
故 的取值范围是 .
4.设函数 是定义在 上的偶函数.若当 时.
(1)求 在 上的解析式.
(2)请你作出函数 的大致图像.
(3)当 时.若 .求 的取值范围.
(4)若关于 的方程 有7个不同实数解.求 满足的条件.
[解](1)当 时. .
(Ⅱ)对于(I)中你认为属于集合A的函数 .不等式 .是否对于任意的 总成立?若不成立.为什么?若成立.请证明你的结论.
解:(1)函数 不属于集合A. 因为 的值域是 ,所以函数 不属于集合A.(或 .不满足条件.)
在集合A中, 因为:① 函数 的定义域是 ;② 函数 的值域是 ;③ 函数 在 上是增函数.
高一函数试题及答案

高一函数试题及答案一、选择题(每题3分,共30分)1. 函数f(x) = 2x^2 - 3x + 5在区间[1, 3]上的最大值是()。
A. 7B. 11C. 13D. 152. 下列哪个函数是奇函数?A. y = x^2B. y = x^3C. y = |x|D. y = sin(x)3. 已知函数f(x) = x^2 + 2ax + 1在区间(-∞, 1)上单调递减,则a 的取值范围是()。
A. a < 1B. a ≤ -1C. a > -1D. a ≥ -14. 函数f(x) = √x在区间[0, +∞)上是()。
A. 单调递增函数B. 单调递减函数C. 常数函数D. 非单调函数5. 若函数f(x) = |x - 1| + |x - 2| + |x - 3|的最小值为2,则x 的取值范围是()。
A. x ≥ 3B. x ≤ 1C. 1 ≤ x ≤ 2D. x ∈ R6. 函数f(x) = log2(x)的图像与x轴的交点坐标是()。
A. (1, 0)B. (0, 1)C. (2, 1)D. (1, 1)7. 已知函数f(x) = sin(x)在区间[0, π]上的最大值为1,则其最小值为()。
A. -1B. 0C. πD. 不存在8. 函数f(x) = 2^x在R上的单调性是()。
A. 单调递增B. 单调递减C. 先增后减D. 非单调9. 已知函数f(x) = x^3 - 3x^2 + x - 5的零点个数是()。
A. 1B. 2C. 3D. 410. 函数f(x) = (x - 1)^2在x = 1处的导数是()。
A. 0B. 1C. 2D. 3二、填空题(每题4分,共20分)11. 函数f(x) = x^2 - 4的顶点坐标是_________。
12. 函数f(x) = 1/x的图像关于_________对称。
13. 若函数f(x) = 2x - 3与g(x) = x/2 + 1的图像有交点,则交点的横坐标x的取值范围是_________。
高一函数的试题及答案

高一函数的试题及答案一、选择题(每题5分,共20分)1. 函数f(x) = 2x + 3的值域是什么?A. (-∞, +∞)B. [3, +∞)C. [0, +∞)D. (-∞, 3]2. 下列哪个函数是奇函数?A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = sin(x)3. 如果函数f(x) = 3x - 5在x = 2处的导数为a,那么a的值是多少?A. 1B. 3C. 5D. 74. 函数g(x) = 1/x在区间(-∞, 0)上是单调递增还是递减?A. 单调递增B. 单调递减C. 先增后减D. 先减后增二、填空题(每题4分,共16分)5. 若f(x) = x^2 + 1,求f(-2)的值。
答案:______6. 函数h(x) = √x的定义域是_____7. 函数y = 2x^2 + 3x + 1的顶点坐标是_____8. 函数f(x) = 1/(2x - 1)的渐近线是_____三、解答题(每题8分,共24分)9. 已知函数f(x) = x^2 - 4x + 4,求f(x)的最小值,并说明x的取值范围。
10. 求函数y = 3x + 2的反函数,并证明你的答案是正确的。
11. 已知函数f(x) = 2x - 1,如果f(x) = 5,求x的值。
四、综合题(每题10分,共40分)12. 函数f(x) = x^3 - 3x^2 + 2x,求f'(x)和f''(x),并讨论f(x)的凹凸性。
13. 已知函数g(x) = 2x^2 + 3x - 5,求g(x)的极值点,并说明极值点的性质。
14. 函数y = ln(x) + 2x - 6,求y的导数,并讨论y的增减性。
15. 已知函数h(x) = x^2 + 2x - 8,求h(x)的值域。
答案:1. A2. C3. B4. B5. 56. [0, +∞)7. (-3/2, -25/4)8. y = 0 和 x = 1/29. 最小值为0,当x = 2时取得。
高一函数试题及答案

高一函数试题及答案### 高一函数试题及答案一、选择题1. 函数f(x) = 2x^2 - 3x + 5的图像的对称轴是()A. x = 1B. x = -3C. x = 3/4D. x = 02. 若f(x) = ax + b,且f(0) = 2,f(1) = 5,则f(x)的表达式为()A. f(x) = 3x + 2B. f(x) = 3x - 1C. f(x) = x + 2D. f(x) = x - 1二、填空题1. 若函数f(x) = x^2 + 2x + 1,则f(-1) = _______。
2. 函数g(x) = x^3 - 3x^2 + 2x的导数为 g'(x) = _______。
三、解答题1. 已知函数y = 3x^2 - 2x + 1,求其在区间[-1, 2]上的最大值和最小值。
2. 已知函数f(x) = x^2 + 2x - 8,若f(x) = 0,求x的值。
答案一、选择题1. C解析:对于二次函数f(x) = ax^2 + bx + c,其对称轴的x坐标为 -b/(2a)。
将f(x) = 2x^2 - 3x + 5中的系数代入,得对称轴为 x =3/4。
2. A解析:由f(0) = 2得b = 2,由f(1) = 5得a + b = 5,解得a = 3。
因此,f(x) = 3x + 2。
二、填空题1. 1解析:将x = -1代入f(x) = x^2 + 2x + 1,得f(-1) = (-1)^2 +2*(-1) + 1 = 1。
2. 3x^2 - 6x + 2解析:对g(x) = x^3 - 3x^2 + 2x求导,得g'(x) = 3x^2 - 6x + 2。
三、解答题1. 解:函数y = 3x^2 - 2x + 1的导数为y' = 6x - 2。
令y' = 0,得x = 1/3。
在区间[-1, 2]上,当x = 1/3时,函数取得极小值,即最小值为y(1/3) = 3*(1/3)^2 - 2*(1/3) + 1 = 7/9。
高一函数练习题及答案

高一函数练习题及答案1. 定义域问题给定函数 \( f(x) = \frac{1}{x} \),求其定义域。
2. 函数值问题已知 \( g(x) = 3x - 2 \),求 \( g(5) \)。
3. 函数的奇偶性判断函数 \( h(x) = x^3 - 2x \) 的奇偶性。
4. 函数的单调性分析函数 \( k(x) = x^2 + 3x + 2 \) 在 \( (-\infty, -1.5) \) 和 \( (-1.5, +\infty) \) 上的单调性。
5. 复合函数已知 \( f(x) = x^2 \) 和 \( g(x) = x + 3 \),求 \( f(g(x)) \)。
6. 反函数问题求函数 \( m(x) = 2x + 1 \) 的反函数。
7. 函数的图像变换若 \( n(x) = x^2 \),求 \( n(2x - 1) \) 的图像与 \( n(x) \) 的图像之间的关系。
8. 函数的极值问题求函数 \( p(x) = -x^3 + 3x^2 - 2x \) 的极值点。
9. 函数的连续性判断函数 \( q(x) = \frac{x^2 - 1}{x - 1} \) 在 \( x = 1 \) 处是否连续。
10. 函数的应用问题某工厂生产的产品数量与成本之间的关系由函数 \( r(x) = 100x + 500 \) 给出,其中 \( x \) 代表产品数量,求当产品数量为 50 时的成本。
答案1. 定义域为 \( x \neq 0 \) 的所有实数。
2. \( g(5) = 3 \times 5 - 2 = 13 \)。
3. 函数 \( h(x) \) 是奇函数,因为 \( h(-x) = (-x)^3 - 2(-x) = -x^3 + 2x = -h(x) \)。
4. 函数 \( k(x) \) 在 \( (-\infty, -1.5) \) 上单调递减,在\( (-1.5, +\infty) \) 上单调递增。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中函数大题专练1、已知关于x 的不等式2(4)(4)0kx k x --->,其中k R ∈。
⑴试求不等式的解集A ;⑵对于不等式的解集A ,若满足A Z B =I (其中Z 为整数集)。
试探究集合B 能否为有限集?若能,求出使得集合B 中元素个数最少的k 的所有取值,并用列举法表示集合B ;若不能,请说明理由。
2、对定义在[0,1]上,并且同时满足以下两个条件的函数()f x 称为G 函数。
① 对任意的[0,1]x ∈,总有()0f x ≥;② 当12120,0,1x x x x ≥≥+≤时,总有1212()()()f x x f x f x +≥+成立。
已知函数2()g x x =与()21xh x a =⋅-是定义在[0,1]上的函数。
(1)试问函数()g x 是否为G 函数?并说明理由; (2)若函数()h x 是G 函数,求实数a 的值;(3)在(2)的条件下,讨论方程(21)()xg h x m -+=()m R ∈解的个数情况。
3.已知函数||212)(x x x f -=. (1)若2)(=x f ,求x 的值;(2)若0)()2(2≥+t mf t f t 对于[2,3]t ∈恒成立,求实数m 的取值范围. 4.设函数)(x f 是定义在R 上的偶函数.若当0x ≥时,11,()0,f x x⎧-⎪=⎨⎪⎩0;0.x x >= (1)求)(x f 在(,0)-∞上的解析式.(2)请你作出函数)(x f 的大致图像.(3)当0a b <<时,若()()f a f b =,求ab 的取值范围.(4)若关于x 的方程0)()(2=++c x bf x f 有7个不同实数解,求,b c 满足的条件.5.已知函数()(0)||bf x a x x =-≠。
(1)若函数()f x 是(0,)+∞上的增函数,求实数b 的取值范围;(2)当2b =时,若不等式()f x x <在区间(1,)+∞上恒成立,求实数a 的取值范围; (3)对于函数()g x 若存在区间[,]()m n m n <,使[,]x m n ∈时,函数()g x 的值域也是[,]m n ,则称()g x 是[,]m n 上的闭函数。
若函数()f x 是某区间上的闭函数,试探求,a b 应满足的条件。
6、设bx ax x f +=2)(,求满足下列条件的实数a 的值:至少有一个正实数b ,使函数)(x f 的定义域和值域相同。
7.对于函数)(x f ,若存在R x ∈0 ,使00)(x x f =成立,则称点00(,)x x 为函数的不动点。
(1)已知函数)0()(2≠-+=a b bx ax x f 有不动点(1,1)和(-3,-3)求a 与b 的值; (2)若对于任意实数b ,函数)0()(2≠-+=a b bx ax x f 总有两个相异的不动点,求a 的取值范围;(3)若定义在实数集R 上的奇函数)(x g 存在(有限的)n 个不动点,求证:n 必为奇数。
8.设函数)0(1)(≠+=x xx x f ,的图象为1C 、1C 关于点A (2,1)的对称的图象为2C ,2C 对应的函数为)(x g .(1)求函数)(x g y =的解析式;(2)若直线b y =与2C 只有一个交点,求b 的值并求出交点的坐标.9.设定义在),0(+∞上的函数)(x f 满足下面三个条件:①对于任意正实数a 、b ,都有()()()1f a b f a f b ⋅=+-; ②(2)0f =;③当1>x 时,总有()1f x <. (1)求)21()1(f f 及的值;(2)求证:),0()(+∞在x f 上是减函数.10. 已知函数)(x f 是定义在[]2,2-上的奇函数,当)0,2[-∈x 时,321)(x tx x f -=(t 为常数)。
(1)求函数)(x f 的解析式;(2)当]6,2[∈t 时,求)(x f 在[]0,2-上的最小值,及取得最小值时的x ,并猜想)(x f 在[]2,0上的单调递增区间(不必证明);(3)当9≥t 时,证明:函数)(x f y =的图象上至少有一个点落在直线14=y 上。
11.记函数()272++-=x x x f 的定义域为A ,()()()[]()R a b ax b x x g ∈>+-=,012lg 的定义域为B ,(1)求A : (2)若B A ⊆,求a 、b 的取值范围12、设()()1,011≠>-+=a a a a x f xx 。
(1)求()x f 的反函数()x f 1-:(2)讨论()x f1-在()∞+.1上的单调性,并加以证明:(3)令()x x g a log 1+=,当[]()()n m n m <+∞⊂,1,时,()x f1-在[]n m ,上的值域是()()[]m g n g ,,求a 的取值范围。
13.集合A 是由具备下列性质的函数)(x f 组成的:(1) 函数)(x f 的定义域是[0,)+∞; (2) 函数)(x f 的值域是[2,4)-;(3) 函数)(x f 在[0,)+∞上是增函数.试分别探究下列两小题:(Ⅰ)判断函数1()2(0)f x x =≥,及21()46()(0)2x f x x =-⋅≥是否属于集合A ?并简要说明理由.(Ⅱ)对于(I )中你认为属于集合A 的函数)(x f ,不等式)1(2)2()(+<++x f x f x f ,是否对于任意的0≥x 总成立?若不成立,为什么?若成立,请证明你的结论.14、设函数f(x)=ax 2+bx+1(a,b 为实数),F(x)=⎩⎨⎧<->)0()()0()(x x f x x f(1)若f(-1)=0且对任意实数x 均有f(x)0≥成立,求F(x)表达式。
(2)在(1)的条件下,当x []2,2-∈时,g(x)=f(x)-kx 是单调函数,求实数k 的取值范围。
(3)(理)设m>0,n<0且m+n>0,a>0且f(x)为偶函数,求证:F(m)+F(n)>0。
15.函数f(x)=bax x+(a ,b 是非零实常数),满足f(2)=1,且方程f(x)=x 有且仅有一个解。
(1)求a 、b 的值;(2)是否存在实常数m ,使得对定义域中任意的x ,f(x)+f(m –x)=4恒成立?为什么? (3)在直角坐标系中,求定点A(–3,1)到此函数图象上任意一点P 的距离|AP|的最小值。
函数大题专练答案1、已知关于x 的不等式2(4)(4)0kx k x --->,其中k R ∈。
⑴试求不等式的解集A ;⑵对于不等式的解集A ,若满足A Z B =I (其中Z 为整数集)。
试探究集合B 能否为有限集?若能,求出使得集合B 中元素个数最少的k 的所有取值,并用列举法表示集合B ;若不能,请说明理由。
解:(1)当0k =时,(,4)A =-∞;当0k >且2k ≠时,4(,4)(,)A k k=-∞++∞U ; 当2k =时,(,4)(4,)A =-∞+∞U ;(不单独分析2k =时的情况不扣分)当0k <时,4(,4)A k k=+。
(2) 由(1)知:当0k ≥时,集合B 中的元素的个数无限;当0k <时,集合B 中的元素的个数有限,此时集合B 为有限集。
因为44k k+≤-,当且仅当2k =-时取等号,所以当2k =-时,集合B 的元素个数最少。
此时()4,4A =-,故集合{}3,2,1,0,1,2,3B =---。
2、对定义在[0,1]上,并且同时满足以下两个条件的函数()f x 称为G 函数。
① 对任意的[0,1]x ∈,总有()0f x ≥;② 当12120,0,1x x x x ≥≥+≤时,总有1212()()()f x x f x f x +≥+成立。
已知函数2()g x x =与()21xh x a =⋅-是定义在[0,1]上的函数。
(1)试问函数()g x 是否为G 函数?并说明理由; (2)若函数()h x 是G 函数,求实数a 的值;(3)在(2)的条件下,讨论方程(21)()xg h x m -+=()m R ∈解的个数情况。
解:(1) 当[]0,1x ∈时,总有2g x x 0()=≥,满足①,当12120,0,1x x x x ≥≥+≤时,22221212121212g x x x x 2x x x x g x g x +=++≥+=+()()(),满足② (2)若a 1<时,h 0a 10()=-<不满足①,所以不是G 函数;若a 1≥时,h x ()在x 01[,]∈上是增函数,则h x 0≥(),满足①由1212h x x h x h x +≥+()()() ,得1212x x x x a 21a 21a 21+⋅-≥⋅-+⋅-,即12xx a 121211[()()]---≤,因为 12120,0,1x x x x ≥≥+≤所以 1x0211≤-≤ 2x0211≤-≤ 1x 与2x 不同时等于1 11xx021211()()∴≤--<11x x 1a 12121()()∴≤---当12x x 0==时,11x x 1112121min ()()()=--- a 1∴≤, 综合上述:a 1{}∈(3)根据(2)知: a=1,方程为xx42m -=,由x 02110x 1⎧≤-≤⎨≤≤⎩ 得 x 01∈[,] 令x 2t 12=∈[,],则2211m t t t 24=-=--()由图形可知:当m 02∈[,]时,有一解;当m 02∈-∞⋃+∞(,)(,)时,方程无解。
3.已知函数||212)(x x x f -=. (1)若2)(=x f ,求x 的值;(2)若0)()2(2≥+t mf t f t 对于[2,3]t ∈恒成立,求实数m 的取值范围.[解] (1)当0<x 时,0)(=x f ;当0≥x 时,x x x f 212)(-=. 由条件可知 2212=-x x ,即 012222=-⋅-x x , 解得 212±=x .02>x Θ,()21log 2+=∴x .(2)当]2,1[∈t 时,021*******≥⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-t t tt t m , 即 ()()121242--≥-t t m .0122>-t Θ, ∴ ()122+-≥t m . ()2[2,3],12[65,17]t t ∈∴-+∈--Q ,故m 的取值范围是[17,)-+∞.(1)若函数()f x 是(0,)+∞上的增函数,求实数b 的取值范围;(2)当2b =时,若不等式()f x x <在区间(1,)+∞上恒成立,求实数a 的取值范围; (3)对于函数()g x 若存在区间[,]()m n m n <,使[,]x m n ∈时,函数()g x 的值域也是[,]m n ,则称()g x 是[,]m n 上的闭函数。
