第01章 质点运动学(2)
大学物理第一章-质点运动学和第二章-质点动力学基础

i
k
j
这样:A B ( Ax i Ay j Az k ) ( Bx i B y j Bz k )
矢量的数积(数乘): mA mAx i mAy j mAz k
z
Δr r ( A)
o
A
B
r ( B) y
x rA x Ai y A j rB xB i yB j 位移 r rB rA ( x x )i ( y y ) j B A B A 三维空间
r ( xB x A )i ( yB y A ) j ( zB z A )k 2 2 2 r x y z 位移的大小为
瞬时加速度 与瞬时速度的定义相类似,瞬时加速速度是一个 极限值 2 v
a lim
t 0
d r d v dt dt2 t
瞬时加速度简称加速度,它是矢量,在直角坐 标系中用分量表示:
2 d vx d x ax 2 dt dt d vy d2 y ay dt dt2 d vz d 2 z az dt dt2
§1-1
参考系与坐标系
时间
要定量描述物体的位臵与运动情况,就要运用 数学手段,采用固定在参考系上的坐标系。
常用的坐标系有直角坐标系 (x,y,z) ,极坐标系 (,),球坐标系(R,, ),柱坐标系(R, ,z )。 z z
z y x o x
o
R y R
参考方向
2. 空间和时间
切向单位矢量
法向单位矢量 n
et
显然,轨迹上各点处,自然坐标轴的方位不断变化。
大学物理第1章质点运动学

二、位置矢量 、位移、速度、加速度
1. 位置矢量 在选定的参考系中 建立坐标系如图,在时 刻t,质点P在坐标系中 的位置可用坐标 (x,y,z) 表示,也可用矢量 r ( t ) 来表示,该矢量称位置 矢量。
y
P( x , y , z )
r( t )
j
0
k i
x
z
r x2 y2 z2
r xi y j zk
d ( xi y j zk ) dt dx dy dz i j k dt dt dt
A AB
B
0
r( t2 )
x
z
v v x v y vz
v v
称速率。
v x i v y j vz k
例1 设质点的运动方程为 r(t ) x(t )i y(t ) j ,其中
v
v a 的方向 沿半径指向圆心, 称向心加速度。a n R t 0 时 0 a vA
t 0
t
t
R
R 2
二、变速圆周运动
vA vA
在三角形CDE中,取CE上一点F,
v B 使CF = CD = vA,则FE = vB - vA
vA
C
v v B v B v A v v A v v v B A 令 令 o v v B v DF DF FE 令v n v t A FE v n vt DF FE v n v t 令 v v FE Alim v v v v B DF Av v B a nv v t t改变了速度方向 a lim 令t 0 v 令 v t 0 t lim a D 0 t v DF a lim DF v t v改变了速度大小 FE v n FE vtn nt t v t t 0 v n v t lim an at v v limvt 0 v vt at t 0t t n an v lim v t lim v na t 0 t a nt t lim a tt lim t t t a n a t v t t 0 t 0 t t a n 0 v n E v t v n t F vB lim a n av t t 0 t lim t an at
第1章-质点运动学

位移
rrrBArxBxBAii
rA
yA
yB
j j
y
yB A r
r y A A
rB
B
yB yA
(xB xA)i ( yB yA) j
xi yj
o
xA
xB x
xB xA
若质点r 在 (三x维B 空x间A中)i运动( yB
yA)
j
(zB
z A )k
位移的大小为 r x2 y2 z2
23
1-2 求解运动学问题举例
例3 有 一个球体在某液体中竖直下落, 其初速度
为 v0 10 j , 它的加速度为 a 1.0v j. 问:(1)经
过多少时间后可以认为小球已停止运动, (2)此球体
在停止运动前经历的路程有多长?
解:由加速度定义
v dv 1.0
t
dt
,
v v0
0
a dv 1.0v dt
v v2
位矢量
t
0,
t 0
0,
tv
rv
a
dv dt
v2 r
en
2ren
法向单 位矢量
vB
r
o
en
v
vB
vA et r
vA
31
1-3 圆周运动
三alitlami tm 变00速litdmdv圆vvvt0tt周nt运vtavt动dvdttrev2ttleeit切mntv向a0nn加aaevn速tntneen度t 和法向v加2v速tove度2vnrevtv1vn1
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
物理 质点运动学(2)

t2
t1
t
dx vdt
x2
x1
dx vdt
t1
t2
1
3.几种特殊的直线运动
⒈匀速直线运动
⒉匀变速直线运动
a 恒量,
a 0, v v0 , x x0 vt .
v v0 at (1)
1 2 x x0 v0 t at 2 (2)
v v0 2a( x x0 )
2 0
射程 y
根据轨迹方程的极值条件, 求得最大射高为: v
v0
v sin h 2g
2 0 2
g Ov 0y
0x
v
h H
x
1
抛体运动分类: 自由落体:v0=0 平抛: v0 0 0 v 上(下)抛: 0 0 2 斜抛: v 0 0 ,0
1
习题册P1-
习题5
提示
灯距地面高度为h1,一个人身高为h2,在灯下以 匀速率v沿水平直线行走,如图所示。试计算他的头 顶在地上的影子M点沿地面移动的速度大小 关键:寻找运动方程(利用几何关系等) 找出人和M点位置关系式
1
一、 抛体运动
在空中所做的运动称抛体运动。
1-5抛体运动
抛体运动: 从地面上某点向空中抛出的物体
dx( t ) d r 2 ( t ) h2 vx dt dt
v0
h
x
r(t )
dr( t ) v 0 r 2 h2 dt
r
x( t ) h x( t )
2
2
x(t t ) x (t )
方向:水平向左(即负号表示沿x轴负方向)
1
加速度为
大学物理习题答案

大学物理习题答案大学物理习题答案Final revision by standardization team on December 10, 2020.B 班级学号姓名第1章质点运动学1-2 已知质点的运动方程为r i 3j 6k e e t t -=++。
(1)求:自t =0至t =1质点的位移。
(2)求质点的轨迹方程。
解:(1) ()k j i r 630++= ()k j i r 6e 3e 1-1++=质点的位移为()j i r-+-=3e31e ?(2) 由运动方程有t x e =,t y -=e 3, 6=z 消t 得轨迹方程为1=xy 且6=z1-3运动质点在某瞬时位于矢径()y x,r 的端点处,其速度的大小为( D )(A)dt dr (B)dt d r(C)dt d r (D)22+??? ??dt dy dt dx1-5某质点的运动方程为k j i r 251510t t ++-=,求:t =0,1时质点的速度和加速度。
解:由速度和加速度的定义得k j r v t dt d 1015+==, k va 10==dtd 所以 t =0,1时质点的速度和加速度为 015==t jv 11015=+=t kj v 1010,ka ==t1-8 一质点在平面上运动,已知质点的运动方程为j i r 2235t t +=,则该质点所作运动为[ B ](A) 匀速直线运动 (B) 匀变速直线运动 (C) 抛体运动 (D) 一般的曲线运动*1-6一质点沿Ox 轴运动,坐标与时间之间的关系为t t x 233-=(SI)。
则质点在4s 末的瞬时速度为142m ·s -1 ,瞬时加速度为72m ·s -2 ;1s 末到4s 末的位移为 183m ,平均速度为61m ·s -1 ,平均加速度为45m ·s -2。
解题提示:瞬时速度计算dt dxv =,瞬时加速度计算22dtx d a =;位移为()()14x x x -=?,平均速度为()()1414--=x x v ,平均加速度为 ()()1414--=v v a1-11 已知质点沿Ox 轴作直线运动,其瞬时加速度的变化规律为t a x 3=2s m -?。
第01章(质点运动学)习题答案

思 考 题1-1 什么是矢径?矢径和对初始位置的位移矢量之间有何关系?怎样选取坐标原点才能够 使两者一致?答:矢径即位置矢量,是从坐标原点O 指向质点所在处P 的有向线段。
位移 r vD 和矢径r v不同,矢径确定某一时刻质点的位置,位移则描述某段时间内始未质点位置的变化。
矢径是相对坐标原点的,位移矢量是相对初始位置的。
对于相对静止的不同坐标系来说,位矢依 赖于坐标系的选择,而位移则与所选取的坐标系无关。
若取初始位置为坐标原点才能够使两 者一致。
1-2 在下列各图中质点 M 作曲线运动,指出哪些运动是不可能的?答:(A) 质点只要作曲线运动,肯定有法向加速度,不可能加速度为零。
(C) 在质点作曲线运动时,加速度的方向总是指向轨迹曲线凹的一侧。
(D) 质点只要作曲线运动,肯定有法向加速度,不可能只有切向加速度。
1-3 下列说法哪一条是正确的?(A) 加速度恒定不变时,物体运动方向也不变. (B) 平均速率等于平均速度的大小.(C) 不管加速度如何,平均速率表达式总可以写成 ( ) 2 / 2 1 v v v += ,其中 v 1、v 2 分 别为初、末速率.(D) 运动物体速率不变时,速度可以变化.答:加速度恒定不变时,意味着速度的大小和方向的变化是恒定的。
不是物体运动方向 不变。
平均速率不等于平均速度的大小。
若速率的变化是线性的(加速度恒定)平均速率表 达式才可以写成 ( ) 2 / 2 1 v v v + = , 否则不可以。
只有运动物体速率不变时, 速度可以变化. 才 是正确的。
1-4 如图所示,质点作曲线运动,质点的加速度 a 是恒矢量(a 1=a 2=a 3=a ).试问质点是否能作匀变速率运动? 答:质点作匀变速率运动要求切向加速度是恒量,如图 所示, 质点作曲线运动, 质点的加速度 a 是恒矢量(a 1=a 2=a 3=a) 则切向分量不一样,质点不能作匀变速率运动。
1-5 以下五种运动形式中,加速度 a 保持不变的运动是哪一a 3M 1M 2M 3a 3a 3思考题 1-4图aMMMvva =0 (A)(B)(C)(D)a vM av思考题 1-2图种或哪几种?(A) 单摆的运动. (B) 匀速率圆周运动.(C) 行星的椭圆轨道运动. (D) 抛体运动. (E) 圆锥摆运动.答:加速度a 保持不变(意味加速度 a 的大小和方向都保持不变)的运动是抛体运动。
大学物理 第1章 质点运动学习题解答

第1章质点运动学习题解答1-1 如图所示,质点自A 点沿曲线运动到B 点,A 点和B 点的矢径分别为A r 和B r。
试在图中标出位移r∆和路程s ∆,同时对||r ∆和r ∆的意义及它们与矢径的关系进行说明。
解:r∆和s ∆如图所示。
||r∆是矢径增量的模||A B r r -,即位移的大小;r ∆是矢径模的增量A B A B r r r r -=-||||,即矢径长度的变化量。
1-2 一质点沿y 轴作直线运动,其运动方程为32245t t y -+=(SI )。
求在计时开始的头3s 内质点的位移、平均速度、平均加速度和所通过的路程。
解:32245t t y -+=,2624t v -=,t a 12-=)(18)0()3(m y y y =-=∆)/(63s m yv =∆=)/(183)0()3(2s m v v a -=-=s t 2=时,0=v ,质点作反向运动)(46|)2()3(|)0()2(m y y y y s =-+-=∆1-3 一质点沿x 轴作直线运动,图示为其t v -曲线图。
设0=t 时,m 5=x 。
试根据t v -图画出:(1)质点的t a -曲线图;(2)质点的t x -曲线图。
解:⎪⎩⎪⎨⎧≤≤-≤≤+≤≤+-=)106( 5.775)62( 5.215)20( 2020t t t t t t v(1)dtdva =,可求得: ⎪⎩⎪⎨⎧≤≤-≤≤+≤≤+-=)106( 5.775)62( 5.215)20( 2020t t t t t t v质点的t a -曲线图如右图所示 (2)dtdxv = ,⎰⎰=t x vdt dx 00, 可求得:20≤≤t 时,⎰⎰+-=txdt t dx 05)2020(, 520102+-=t t x62≤≤t 时,⎰⎰⎰+++-=txdt t dt t dx 2205)5.215()2020(, 3015452-+=t t x 106≤≤t 时,⎰⎰⎰⎰-++++-=txdt t dt t dt t dx 662205)5.775()5.215()2020(,210754152-+-=t t x ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤-+-≤≤-+≤≤+-=∴)106( 21075415)62( 301545)20( 52010222t t t t t t t t t x质点的t x -曲线图如右图所示。
(完整版)大学物理质点运动学习题及答案(2)

第1章 质点运动学 习题及答案1.|r ∆|与r ∆ 有无不同?t d d r 和dr dt 有无不同? t d d v 和dv dt有无不同?其不同在哪里?试举例说明. 解: |r ∆|与r ∆ 不同. |r ∆|表示质点运动位移的大小,而r ∆则表示质点运动时其径向长度的增量;t d d r 和dr dt 不同. t d d r 表示质点运动速度的大小,而dr dt则表示质点运动速度的径向分量;t d d v 和dv dt 不同. t d d v 表示质点运动加速度的大小, 而dv dt则表示质点运动加速度的切向分量. 2.质点沿直线运动,其位置矢量是否一定方向不变?质点位置矢量方向不变,质点是否一定做直线运动?解: 质点沿直线运动,其位置矢量方向可以改变;质点位置矢量方向不变,质点一定做直线运动.3.匀速圆周运动的速度和加速度是否都恒定不变?圆周运动的加速度是否总是指向圆心,为什么? 解: 由于匀速圆周运动的速度和加速度的方向总是随时间发生变化的,因此,其速度和加速度不是恒定不变的;只有匀速圆周运动的加速度总是指向圆心,故一般来讲,圆周运动的加速度不一定指向圆心.4.一物体做直线运动,运动方程为2362x t t =-,式中各量均采用国际单位制,求:(1)第二秒内的平均速度(2)第三秒末的速度;(3)第一秒末的加速度;(4)物体运动的类型。
解: 由于: 232621261212x(t )t t dx v(t )t t dtdv a(t )t dt=-==-==- 所以:(1)第二秒内的平均速度: 1(2)(1)4()21x x v ms --==- (2)第三秒末的速度: 21(3)1236318()v ms -=⨯-⨯=-(3)第一秒末的加速度:2(1)121210()a ms -=-⨯=(4)物体运动的类型为变速直线运动。
5.一质点运动方程的表达式为2105(t t t =+r i j ),式中的,t r 分别以m,s 为单位,试求;(1)质点的速度和加速度;(2)质点的轨迹方程。
大学物理答案第一章
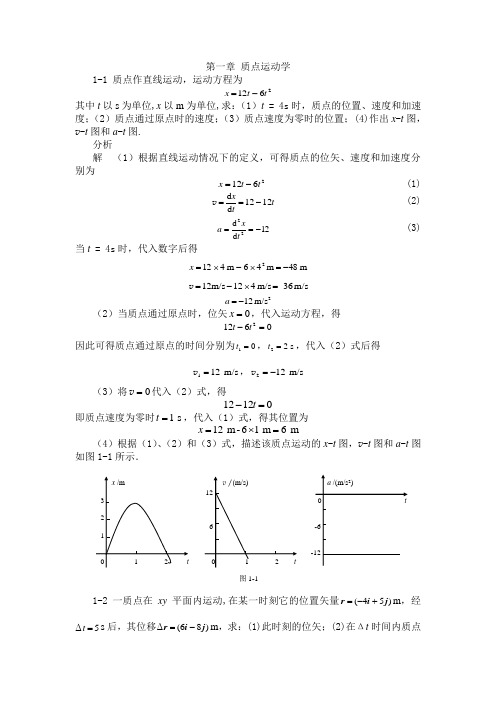
第一章 质点运动学1-1 质点作直线运动,运动方程为2612t t x -=其中t 以s 为单位,x 以m 为单位,求:(1)t = 4s 时,质点的位置、速度和加速度;(2)质点通过原点时的速度;(3)质点速度为零时的位置;(4)作出x -t 图,v -t 图和a -t 图.分析解 (1)根据直线运动情况下的定义,可得质点的位矢、速度和加速度分别为2612t t x -= (1)t tx 1212d d -==v (2) 12d d 22-==tx a (3) 当t = 4s 时,代入数字后得m 48m 46m 4122-=⨯-⨯=xm/s -36m/s 412m/s 12=⨯-=v2m/s 12-=a(2)当质点通过原点时,位矢0=x ,代入运动方程,得06122=-t t因此可得质点通过原点的时间分别为01=t ,s 22=t ,代入(2)式后得m/s 121=v ,m/s 122-=v(3)将0=v 代入(2)式,得01212=-t即质点速度为零时s 1=t ,代入(1)式,得其位置为m 6m 16-m 12=⨯=x(4)根据(1)、(2)和(3)式,描述该质点运动的x -t 图,v -t 图和a -t 图如图1-1所示.1-2 一质点在xy 平面内运动,在某一时刻它的位置矢量)54(j i r +-=m ,经5Δ=t s 后,其位移)86(Δj i r -=m ,求:(1)此时刻的位矢;(2)在Δt 时间内质点图1-1的平均速度.(i 、j 分别为x 、y 方向的单位矢.)分析解 (1)据题意,在t t ∆+时刻,该质点的位矢为m 32m )8-(6m )54(1)(j i j i j i r r r -=++-=∆+=(2)在Δt 时间内质点的平均速度为m/s )1.6-(1.2m/s 586j i j i r v =-=∆∆=t 1-3 质点在xy 平面上运动,运动方程为t y t x 4sin ,4cos 3ππ== 其中t 以s 为单位,x ,y 以m 为单位.(1)求质点运动轨道的正交坐标方程并在xy 平面上绘出质点的轨道;(2)求出质点的速度和加速度表示式,由此求出质点在轨道上运动的方向并证明质点的加速度指向坐标原点;(3)求t = 1 s 时质点的位置和速度与加速度的大小和方向.分析解 (1)质点的运动方程为 t x 43πcos = (1) t y 4πsin = (2) (1)式两边同乘以3并平方后与(2)式的平方相加,得正交坐标方程为 1322=+y x 上式表明质点的运动轨道是一个椭圆,如图1-2所示.(2)由(1)和(2)式可得质点速度和加速度的x ,y 方向分量分别为t t x 443d d ππsin -==x v (3) t t y 44d d ππcos ==y v (4) t t a x 4163d d 2ππcos -==x v (5) t t a y 416d d 2ππsin -==yv (6)则质点速度为 j i v t t 44443ππππcos sin +-= 当t =0时,由运动方程(1)和(2)式,得知质点位于横坐标上3的位置,图1-2由(3)和(4)式,知040>==πy x v v ,,即表明质点在椭圆上沿反时针方向运动. 质点加速度为 j i a 2t t 41641632ππππsin cos --= 由(1)和(2)式得t 时刻质点的位矢为j i r t t 44ππsin cos += (7) 位矢r 与x 轴的夹角ϕ由下式确定:t x y 433πϕtan tan == 而加速度a 与x 轴的夹角α则由下式确定:t a a x y433παtan tan == 即有ϕαtan tan =,注意到在曲线运动中加速度始终指向曲线凹的一侧,则得πϕα+=,表明a 与r 方向相反,指向原点,如图1-2所示.(3)当t = 1 s 时,由(1)--(2)式得m 26=x m 22=y m/s 86π-=x v m/s 82π=y v 22m/s 326π-=x a 22m/s 322π-=y a 速度的大小 m/s 42π=+=2y 2xv v v 速度v 与x 轴的夹角θ则由下式确定:33-==x yv v θtan 注意到此时v x <0,v y >0,则 πθ6533=-=)a r c t a n (. 加速度的大小 22m/s 162π=+=2y 2x a a a对于夹角α有 33==x ya a αtan 又因a x <0,a y <0,则 πα6733==)a r c t a n (. 1-4 质点沿直线运动,其速度2323++=t t v ,如果t = 2时,x = 4,求t = 3时质点的位置、速度和加速度.(其中v 以m/s 为单位,t 以s 为单位,x 以m 为单位)分析解 速度表示式对t 积分,得034241d x t t t t x +++==⎰v 将t = 2 s 时,x = 4 m 代入上式,得积分常数120-=x m ,则1224134-++=t t t x 速度表示式对t 求导数,得t t ta 63d d 2+==v 因此t = 3 s 时质点的位置、速度和加速度分别为m 2541m 12m 32m 3m 34134.=-⨯++⨯=x m/s 56m/s 2m/s 33m/s 323=+⨯+=v2222m/s 45m/s 36m/s 33=⨯+⨯=a1-5 质点沿直线运动,加速度24t a -=,如果当t = 3时,x = 9,v = 2,求质点的运动方程.(其中a 以m/s 2为单位,t 以s 为单位,x 以m 为单位,v 以m/s 为单位)分析解 加速度表示式对t 积分,得03431d v v ++-==⎰t t t a 0242121d x t t t t x +++-==⎰0v v 将t =3 s 时,x = 9 m ,v = 2 m/s 代入以上二式,得积分常数m/s 10-=v ,7500.=x m ,则14313-+-=t t v 750212124.+-+-=t t t x 1-6 质点以不变的速率5m/s 运动,速度的方向与x 轴间夹角等于t 弧度(t为时间的数值),当t = 0时,x = 0,y = 5m ,求质点的运动方程及轨道的正交坐标方程,并在xy 平面上描画出它的轨道.分析解 设质点的速率为v ,与x 轴间夹角为t 弧度,则速度的分量为t t x x cos v v ==d d t ty y s i n v v ==d d 以上两式分别积分,得1C t x +=sin v 2C t y +-=c o s v初始条件为t = 0时,x = 0,y = 5m ,代入以上两式后,得01=C m 102=C因此运动方程为t x sin 5= 105+-=t y cos从中消去t ,得质点运动轨道的正交坐标方程为251022=-+)(y x这是圆心在y 轴上10m 处的圆,半径为5m ,如图1-3所示.1-7 在离水面高度为h 的岸上,有人用绳子拉船靠岸,人以0v 的速率收绳,求当船离岸边的距离为s 时,船的速度和加速度.分析解 选如图1-4所示的直角坐标系,设t 时刻绳长为l ,船的速度为v ,则此时船的x ,y 方向坐标分别为22h l x -= h y =由速度定义得0d d d d ===th t y y v t l hl l t x d d d d 22-===x v v图1-3 图1-4因绳长l 随时间减小的速率等于人的收绳速率,即0d d v =-tl ,则当s x =时,船的速度为022022v v v s h s h l l+-=--= 其中负号表明船的速度方向沿x 轴的负向.又由加速度的定义得0d d ==t a yy v2023222022d d d d v v v x )(h l h h l l t t a a x --=⎪⎪⎭⎫ ⎝⎛--=== 当s x =时,加速度为 2032v sh a -= 其中负号表明船的加速度方向也沿x 轴的负向,且船作变加速直线运动.1-8 当物体以非常高的速度穿过空气时,由空气阻力产生的反向加速度大小与物体速度的平方成正比,即2v k a -=,其中k 为常量.若物体不受其它力作用沿x 方向运动,通过原点时的速度为0v ,试证明在此后的任意位置x 处其速度为x k -=e 0v v分析证 根据加速度的定义,得2v v k a t-==d d 因 tt x x t a d d d d d d d d v v v v ===,代入上式,整理后得 x d d 1-k v v= 应用初始条件0=x 时,0v v =,上式两边分别对v 和x 积分⎰⎰-=x x 0d d 10k v v vv 得 kx -=0v v ln 即有 x k -=e 0v v1-9 一支气枪竖直向上发射,发射速度为29.4m /s ,若发射两粒子弹的间隔时间为4s ,求二子弹将在距发射点多高的地方彼此相遇?分析解 以发射点为原点,竖直向上为y 坐标正向,第一粒子弹发射后的t 时刻,其位置为20121gt t y -=v (1) 其中0v 为发射速度,第二粒子弹此时(设4>t s )的位置为2024214)()(---=t g t y v (2) 当二子弹相遇时,21y y =,由(1)和(2)式得s 5s 2s 8942920=+=+=..g t v 将上式代入(1)式,得m 524m 58921m 5429212201...=⨯⨯-⨯=-=gt t y v 1-10 A 车通过某加油站后其行驶路程x 与时间t 的关系可以表示为24.02t t x +=(其中t 以s 为单位,x 以m 为单位)在A 车离开10 s 后B 车通过该加油站时速度为12 m/s ,且具有与A 车相同的加速度.求:(1)B 车离开加油站后追上A 车所需时间;(2)两车相遇时各自的速度.分析解 (1)令B 车通过该加油站时0=t ,则A 车的运动方程为2A 1040102)(.)(+++=t t xB 车的运动方程为2B 4012t t x .+=两车相遇时有B A x x =,由以上两式得2240121040102t t t t .)(.)(+=+++解得 s 30=t(2)根据速度的定义,相遇时两车速度分别为m/s 3410802d d A A =+⨯+==)(.t tx v m/s 368012d d B B =+==t tx .v 1-11 一升降机以加速度1.22m /s 2上升,当上升速度为2.44m /s 时,有一螺帽自升降机的天花板松落,天花板与升降机底面相距2.74m ,计算:(1)螺帽从天花板落到底面所需的时间;(2)螺帽相对于升降机外固定柱子的下降距离. 分析解 (1)以升降机外固定柱子为参考系,竖直向上为y 坐标正向,螺帽松落时升降机底面位置为原点.螺帽松落后从m 7420.=y 处以初速度m /s4420.=v 作竖直上抛运动,升降机底面则从原点以同样的初速度作向上的加速运动,加速度2m/s 221.=a ,它们的运动方程分别为螺帽: 200121gt t y y -+=v 底面: 20221at t y +=v 螺帽落到底面上时,21y y =,由以上两式可得s 0.705s 22189742220=+⨯=+=...a g y t (2)螺帽相对于升降机外固定柱子的下降距离为m 7150m 70508921m 7050442 2122010.....=⨯⨯+⨯-=+-=-=gt t y y s v 1-12 一小球自h = 4.9m 处落到一倾角θ= 45°的斜面上,设小球与斜面碰撞后速率不变,方向如图所示.求小球第二次与斜面碰撞时,离第一次碰撞处的距离L 为若干? 分析 解 以小球与斜面第一次相撞点为原点取直角坐标系如图1-5所示.第一次相撞后小球作平抛运动,初速度为0v .此前,小球为自由落体,因此有 gh 20=v小球作平抛运动的运动方程为t x 0v = 221gt y = 由于斜面倾角θ= 45°,当小球第二次碰到斜面时,应有y x =,则由以上二式解得 gt 02v =两次碰撞点之间的距离为m 27.7m 459444200=︒⨯=====sin .sin sin sin sin θθθθh g t x L 2v v 1-13 消防队员用水龙头喷射10 m 外的着火竖墙,水龙头每分钟喷水量为图1-5280 kg ,水喷出时速度为26 m/s ,与地面交角为45º。
第1章 质点运动学

第1章 质点运动学1.1 一质点沿直线运动,运动方程为x (t ) = 6t 2 - 2t 3.试求: (1)第2s 内的位移和平均速度;(2)1s 末及2s 末的瞬时速度,第2s 内的路程; (3)1s 末的瞬时加速度和第2s 内的平均加速度.解:(1)质点在第1s 末的位移大小为x (1) = 6×12 - 2×13 = 4(m). 在第2s 末的位移大小为x (2) = 6×22 - 2×23 = 8(m). 在第2s 内的位移大小为Δx = x (2) – x (1) = 4(m),经过的时间为Δt = 1s ,所以平均速度大小为v =Δx /Δt = 4(m·s -1).(2)质点的瞬时速度大小为v (t ) = d x /d t = 12t - 6t 2, 因此v (1) = 12×1 - 6×12 = 6(m·s -1),v (2) = 12×2 - 6×22 = 0, 质点在第2s 内的路程等于其位移的大小,即Δs = Δx = 4m .(3)质点的瞬时加速度大小为a (t ) = d v /d t = 12 - 12t , 因此1s 末的瞬时加速度为a (1) = 12 - 12×1 = 0,第2s 内的平均加速度为a = [v (2) - v (1)]/Δt = [0 – 6]/1 = -6(m·s -2). [注意]第几秒内的平均速度和平均加速度的时间间隔都是1秒.1.2 一质点作匀加速直线运动,在t = 10s 内走过路程s = 30m ,而其速度增为n = 5倍.试证加速度为22(1)(1)n sa n t -=+.并由上述数据求出量值.证:依题意得v t = nv o ,根据速度公式v t = v o + at ,得a = (n – 1)v o /t ------- (1) 根据速度与位移的关系式 v t 2 = v o 2 + 2as , 得a = (n 2 – 1)v o 2/2s ------- (2) (1}平方之后除以 (2)式证得22(1)(1)n sa n t -=+.计算得加速度为22(51)30(51)10a -=+= 0.4(m·s -2).1.3 一人乘摩托车跳越一个大矿坑,他以与水平成22.5°的夹角的初速度65m·s -1从西边起跳,准确地落在坑的东边.已知东边比西边低70m ,忽略空气阻力,且取g = 10m·s -2.问: (1)矿坑有多宽?他飞越的时间多长?(2)他在东边落地时的速度?速度与水平面的夹角?解:方法一:分步法.(1)夹角用θ表示,人和车(他)在竖直方向首先做竖直上抛运动,初速度的大小为v y 0 = v 0sin θ = 24.87(m·s -1).取向上的方向为正,根据匀变速直线运动的速度公式v t - v 0 = at ,这里的v 0就是v y 0,a = -g ;当他达到最高点时,v t = 0,所以上升到最高点的时间为t 1 = v y 0/g = 2.49(s).再根据匀变速直线运动的速度和位移的关系式v t 2 - v 02 = 2a s , 可得上升的最大高度为h 1 = v y 02/2g = 30.94(m).他从最高点开始再做自由落体运动,下落的高度为h 2 = h 1 + h = 100.94(m). 根据自由落体运动公式s = gt 2/2,得下落的时间为图1.32t =. 因此他飞越的时间为t = t 1 + t 2 = 6.98(s).他飞越的水平速度为v x 0 = v 0cos θ = 60.05(m·s -1), 所以矿坑的宽度为x = v x 0t = 419.19(m).(2)根据自由落体速度公式可得他落地的竖直速度大小为v y = gt = 69.8(m·s -1), 落地速度为v = (v x 2 + v y 2)1/2 = 92.08(m·s -1), 与水平方向的夹角为φ = arctan(v y /v x ) = 49.30º,方向斜向下.方法二:一步法.取向上的方向为正,他在竖直方向的位移为y = v y 0t - gt 2/2,移项得时间的一元二次方程201sin 02gt v t y θ-+=,解得0(sin t v g θ=. 这里y = -70m ,根号项就是他落地时在竖直方向的速度大小,由于时间应该取正值,所以公式取正根,计算时间为t = 6.98(s). 由此可以求解其他问题.1.4 一个正在沿直线行驶的汽船,关闭发动机后,由于阻力得到一个与速度反向、大小与船速平方成正比例的加速度,即d v /d t = -kv 2,k 为常数. (1)试证在关闭发动机后,船在t 时刻的速度大小为011kt v v =+; (2)试证在时间t 内,船行驶的距离为01ln(1)x v kt k=+. 证:(1)分离变量得2d d vk t v=-, 积分020d d vtv vk t v =-⎰⎰, 可得 011kt v v =+. (2)公式可化为001v v v kt=+,由于v = d x/d t ,所以00001d d d(1)1(1)v x t v kt v kt k v kt ==+++ 积分 00001d d(1)(1)xtx v kt k v kt =++⎰⎰.因此 01ln(1)x v kt k=+. 证毕. [讨论] 当力是速度的函数时,即f = f (v ),根据牛顿第二定律得f = ma .由于a = d 2x /d t 2,而 d x /d t = v ,所以 a = d v /d t ,分离变量得方程 d d ()m vt f v =, 解方程即可求解.在本题中,k 已经包括了质点的质量.如果阻力与速度反向、大小与船速的n 次方成正比,则d v /d t = -kv n . (1)如果n = 1,则得d d vk t v=-,积分得ln v = -kt + C . 当t = 0时,v = v 0,所以C = ln v 0,因此ln v/v 0 = -kt ,得速度为 v = v 0e -kt .而d v = v 0e -kt d t ,积分得0e `ktv x C k-=+-. 当t = 0时,x = 0,所以C` = v 0/k ,因此 0(1-e )ktv x k -=.(2)如果n ≠1,则得d d n vk t v=-,积分得11n v kt C n -=-+-.当t = 0时,v = v 0,所以101n v C n-=-,因此11011(1)n n n kt v v --=+-. 如果n = 2,就是本题的结果.如果n ≠2,可得1(2)/(1)020{[1(1)]1}(2)n n n n n v kt x n v k----+--=-, 读者不妨自证.1.5 一质点沿半径为0.10m 的圆周运动,其角位置(以弧度表示)可用公式表示:θ = 2 + 4t 3.求:(1)t = 2s 时,它的法向加速度和切向加速度;(2)当切向加速度恰为总加速度大小的一半时,θ为何值? (3)在哪一时刻,切向加速度和法向加速度恰有相等的值?解:(1)角速度为ω = d θ/d t = 12t 2 = 48(rad·s -1), 法向加速度为 a n = rω2 = 230.4(m·s -2);角加速度为 β = d ω/d t = 24t = 48(rad·s -2), 切向加速度为 a t = rβ = 4.8(m·s -2). (2)总加速度为a = (a t 2 + a n 2)1/2,当a t = a /2时,有4a t 2 = a t 2 + a n 2,即n a a =2r r ω=, 即22(12)24t = 解得36t =.所以3242(13)t θ=+=+=3.154(rad).(3)当a t = a n 时,可得rβ = rω2,即 24t = (12t 2)2, 解得 t = (1/6)1/3 = 0.55(s).1.6 一飞机在铅直面内飞行,某时刻飞机的速度为v = 300m·s -1,方向与水平线夹角为30°而斜向下,此后飞机的加速度为a =m·s -2,方向与水平前进方向夹角为30°而斜向上,问多长时间后,飞机又回到原来的高度?在此期间飞机在水平方向飞行的距离为多少? 解:建立水平和垂直坐标系,飞机的初速度的大小为v 0x = v 0cos θ,v 0y = v 0sin θ.加速度的大小为a x = a cos α,a y = a sin α.运动方程为2012x x x v t a t =+,2012y y y v t a t =-+.即 201cos cos 2x v t a t θα=⋅+⋅,201sin sin 2y v t a t θα=-⋅+⋅.令y = 0,解得飞机回到原来高度时的时间为t = 0(舍去);02sin sin v t a θα==.将t 代入x 的方程求得x = 9000m .[注意]选择不同的坐标系,例如x 方向沿着a 的方向或者沿着v 0的方向,也能求出相同的结果.1.7 一个半径为R = 1.0m 的轻圆盘,可以绕一水平轴自由转动.一根轻绳绕在盘子的边缘,其自由端拴一物体A .在重力作用下,物体A 从静止开始匀加速地下降,在Δt = 2.0s 内下降的距离h = 0.4m .求物体开始下降后3s 末,圆盘边缘上任一点的切向加速度与法向加速度.解:圆盘边缘的切向加速度大小等于物体A 下落加速度. 由于212t h a t =∆,所以a t = 2h /Δt 2 = 0.2(m·s -2). 物体下降3s 末的速度为v = a t t = 0.6(m·s -1),这也是边缘的线速度,因此法向加速度为2n v a R== 0.36(m·s -2).1.8 一升降机以加速度1.22m·s -2上升,当上升速度为2.44m·s -1时,有一螺帽自升降机的天花板上松落,天花板与升降机的底面相距2.74m .计算: (1)螺帽从天花板落到底面所需的时间;(2)螺帽相对于升降机外固定柱子的下降距离.解:在螺帽从天花板落到底面时,升降机上升的高度为21012h v t at =+; 螺帽做竖直上抛运动,位移为22012h v t gt =-. 由题意得h = h 1 - h 2,所以21()2h a g t =+,解得时间为t =.算得h 2 = -0.716m ,即螺帽相对于升降机外固定柱子的下降距离为0.716m .[注意]以升降机为参考系,钉子下落时相对加速度为a + g ,而初速度为零,可列方程 h = (a + g )t 2/2,由此可计算钉子落下的时间,进而计算下降距离.1.9 有一架飞机从A 处向东飞到B 处,然后又向西飞回到A 处.已知气流相对于地面的速度为u ,AB 之间的距离为l ,飞机相对于空气的速率v 保持不变.(1)如果u = 0(空气静止),试证来回飞行的时间为02l t v =; (2)如果气流的速度向东,证明来回飞行的总时间为01221/t t u v =-;(3)如果气流的速度向北,证明来回飞行的总时间为2t =.证:(1)飞机飞行来回的速率为v ,路程为2l ,所以飞行时间为t 0 = 2l /v . (2)飞机向东飞行顺风的速率为v + u ,向西飞行逆风的速率为v - u ,所以飞行时间为1222l l vlt v u v u v u=+=+-- 022222/1/1/t l v u v u v ==--. (3)飞机相对地的速度等于相对风的速度加风相对地的速度.为了使飞机沿着AB 之间的直线飞行,就要使其相对地的速度偏向北方,可作矢量三角形,其中沿AB方向的速度大小为V =,所以飞行时间为22l t V ==== 证毕.AAB vv + uv - uABvu uvv1.10 如图所示,一汽车在雨中沿直线行驶,其速度为v 1,下落雨的速度方向与铅直方向的夹角为θ,偏向于汽车前进方向,速度为v 2.今在车后放一长方形物体,问车速v 1为多大时此物体刚好不会被雨水淋湿?解:雨对地的速度2v r 等于雨对车的速度3v r 加车对地的速度1v r,由此可作矢量三角形.根据题意得tan α = l/h . 方法一:利用直角三角形.根据直角三角形得v 1 = v 2sin θ + v 3sin α,其中v 3 = v ⊥/cos α,而v ⊥ = v 2cos θ,因此v 1 = v 2sin θ + v 2cos θsin α/cos α, 即 12(sin cos )lv v hθθ=+. 证毕. 方法二:利用正弦定理.根据正弦定理可得12sin()sin(90)v v θαα=+︒-,所以12sin()cos v v θαα+=2sin cos cos sin cos v θαθαα+=2(sin cos tan )v θθα=+, 即 12(sin cos )lv v hθθ=+.方法三:利用位移关系.将雨滴的速度分解为竖直和水平两个分量,在t 时间内,雨滴的位移为l = (v 1 – v 2sin θ)t ,h = v 2cos θ∙t .两式消去时间t 即得所求. 证毕.图1.101h l α。
大学物理学(第二版) 第01章 运动学

P2 (x2 , y2 , z2 )
注意 r r 位矢长度的变化
r x22 y22 z22 x12 y12 z12
讨论 (1)位移与位置矢量
位移表示某段时间内质点位置的变 化,是个过程量;位置矢量表示某个时
y
s
p1
'
s r
p2
刻质点的位置,是个状态量. (2)位移与路程
r(t1) r(t2)
(2)选取不同的参考系或在同一参考系上建立不同的坐标系时,
它的方向和数值一般是不同的,故具有相对性.
(3)在质点运动过程中位矢是随时间而改变的,故还具有瞬时性.
2.运动方程
运动方程:质点在运动时,其位置矢量的大小和方向均随时间
发生变化,对于任一时刻t,都有一个完全确定的位置矢量与之
对应,也就是说,位置矢量是时间t的函数,即 r r(t)
2.路程 质点所经过的实际运动轨迹的长度为质点所经历的路
程,记作△S .
位移的物理意义
A)确切反映物体在空间中位置的 变化,与路径无关,只决定于质
y P1 rs P2
点的始末位置.
B)反映了运动的矢量性和叠加性.
r
xi
yj
zk
r x2 y2 z2
z
r(t1)
r
r(t2 )
O
x P1(x1, y1, z1)
P1P2 两点间的路程s是不唯一的,可 O
z 以是 s 或 s ,而位移 r 是唯一的.
x
一般情况下,位移与路程并不相等:只有当质点作单方向的
直线运动时,路程与位移的大小才是相等的;此外,在 t 0的
第1章 质点运动学
本章内容
1.1 质点 参考系 坐标系 时空 1.2 描述质点运动的物理量 1.3 加速度为恒矢量时的质点运动 1.4 曲线运动 1.5 运动描述的相对性 伽利略坐标变换
02质点运动学二解答

2 3
只适用于匀加速率运动
S υ 2υ1 3 2 2 a = 6t ,υ1 = 0, S1 = 0 υ 2 = 3t , S 2 = t υ = =t ≠ = t t 2 2
质点运动学二
第一章 质点运动学
4.下列说法中,哪一个是正确的? .下列说法中,哪一个是正确的? (A) 一质点在某时刻的瞬时速度是 一质点在某时刻的瞬时速度是2m/s,说明它 , 在此后1s内一定要经过 的路程. 内一定要经过2m的路程 在此后 内一定要经过 的路程. (B) 斜向上抛的物体,在最高点处的速度最小, 斜向上抛的物体,在最高点处的速度最小, 加速度最大. 加速度最大. (C) 物体作曲线运动时,有可能在某时刻的法向 物体作曲线运动时, 加速度为零. 加速度为零. (D) 物体加速度越大,则速度越大. 物体加速度越大,则速度越大.
0 = υ 3 + υ 2 + υ1
质点运动学二
第一章 质点运动学
υ 5. 两条直路交叉成α角,两辆汽车分别以速率υ1和υ2沿 两条路行驶,一车相对另一车的速度大小为_______. 两条路行驶,一车相对另一车的速度大小为 υ1 υ2-1 α α υ2 υ2 υ2-1 υ1
υ 21 = υ 2 υ 1
风-人 人
υ风-地 地
二、填空题
√1.在水平飞行的飞机上向前发射一颗炮弹,发射后 .在水平飞行的飞机上向前发射一颗炮弹, 飞机的速度为υ0,炮弹相对于飞机的速度为υ.略去空 气阻力, 以地球为参考系,炮弹的轨迹方程为__, 气阻力,则(1) 以地球为参考系,炮弹的轨迹方程为 , (2) 以飞机为参考系,炮弹的轨迹方程为 以飞机为参考系,炮弹的轨迹方程为______. . (设两种参考系中坐标原点均在发射处,x轴沿速度方向 设两种参考系中坐标原点均在发射处, 轴沿速度方向 设两种参考系中坐标原点均在发射处 向前, 轴竖直向下 轴竖直向下) 向前,y轴竖直向下
01质点运动学2

C
解:由速度、加速度、速率和切向加速度定义
dv a dt ds v dt
dr v dt
dv at dt
2.下面各种判断中, 错误的是 (A)质点作直线运动时,加速度的方向和运动方向总是一致的; (B)质点作匀速率圆周运动时,加速度的方向总是指向圆心; (C)质点作斜抛运动时,加速度的方向恒定; (D)质点作曲线运动时,加速度的方向总是指向曲线凹的一边。
v0 bt
2
R
。
解:根据自然坐标速度,切向和法向加速度定义,得
ds v v0 bt dt dv at b dt
v0 bt v an R R
2
2
4.第十三届国际度量衡会议上决定采用 原子的跃迁辐射 作 为计时标准。
三、计算题
1.一个质点沿半径为0.1 m的圆周运动,其角位置 2 4 2t (SI),求 (1)t 时刻的角速度ω和角加速度β; (2)在什么时刻,总加速度与半径成45 。 解:(1)
2 4 1/ 2
d v v2 v2 ; (C) ; (D) 。 R dt R
B
解:由切向加速度和法向加速度定义
dv at dt
v an R
2 12 n
2
a a a
2 t
d v v 2 d t R
2 4
an at
0.4 1.6t t 0.5s
2.质点在重力场中作斜上抛运动,初速度的大小为v0,与水 平方向成α角。求 (1)质点到达抛出点的同一高度时的切向加速度at 和法向加 速度an ; (2)该时刻质点所在处轨迹的曲率半径ρ(忽略空气阻力)。
大学物理第一章课后习题答案

第一章质点运动学1.1一质点沿y 方向运动,它在任意时刻t 的位置由式1052+=t y 给出,式中t 以s 计,y 以m 计算下列各段时间内质点的平均速度大小:(1)2s 到3s (2)2s 到2.1s (3)2s 到2.001s (4)2s 到2.0001s 解:(1)令质点的始末时刻为s t 21=,s t 32=,则质点的平均速度大小为:{}sm sm t t y y /25)23(]10)2(5[10)3(5221212=−+−+=−−=υ(2)令质点的始末时刻为s t 21=,s t 1.22=,则质点的平均速度大小为:{}sm sm t t y y /5.20)21.2(]10)2(5[10)1.2(5221211=−+−+=−−=υ(3)令质点的始末时刻为s t 21=,s t 001.22=,则质点的平均速度大小为:{}sm smt t y y /005.20)2001.2(]10)2(5[10)001.2(5221212=−+−+=−−=υ(4)令质点的始末时刻为s t 21=,s t 0001.22=,则质点的平均速度大小为:sm smt t y y /0005.20)20001.2(]10)2(510)0001.2(5[221212=−−−+=−−=υ1.2一质点沿Ox 轴运动,其运动方程为2653t t x +−=;式中t 以s 计,x 以m 计,试求:(1)质点的初始位置和初始速度;(2)质点在任一时刻的速度和加速度;(3)质点做什么运动;(4)做出t x −图和t −υ图;(5)质点做匀加速直线运动吗?解:(1)设质点初始时刻00=t ,则质点的初始位置为:mm x 3]06053[20=×+×−=即质点的初始位置在Ox 轴正方向3m 处。
因为质点的速度为:tdt dx125+−==υ所以质点的初始速度为:220/5/)0125(s m s m dt dxt −=×+−===υ质点的初始速度大小为2/5s m ,方向沿Ox 轴负方向。
第1章 质点运动学

dr υ= dt
方向: 方向:切线方向
速度是位置矢量对时间的一阶导数
第一章 质点运动学 9
3) 平均速率和瞬时速率 平均速率
S υ= t
S dS υ = lim = dt 0 t → t
运动路径
P (t1 )
瞬时速率 讨论
υ
r
s
Q(t2 )
速度的矢量性、瞬时性和相对性。 1) 速度的矢量性、瞬时性和相对性。 2) 速度和速率的区别
∫
∫
第一章 质点运动学
18
§1-4 用自然坐标表示平面曲线运 动中的速度和加速度
自然坐标系 (用自然坐标 表示质点位置) 用自然坐标S表示质点位置 表示质点位置)
设质点作曲线运动,且轨迹已知, 设质点作曲线运动,且轨迹已知,则 选参考点和正方向即可建立自然坐标。 选参考点和正方向即可建立自然坐标。运 动方程为: 动方程为: s = s(t) 单位切向量τ : 长度为 ,沿切向指向运动方向 长度为1, 单位法向量 n: 长度为 ,沿法向指向凹的一侧 长度为1,
S = Rωt
第一章 质点运动学 7
§1-2 质点的位移、速度和加速度 质点的位移、
一、位移
描述质点位置变化的物理量 几何描述: 几何描述: PQ 数学描述: 数学描述: r
= r ( t + t ) r ( t )
r( t )
P S Q r
r ( t + t )
r
讨论 (1) 位移是矢量(有大小,有方向) 位移是矢量(有大小,有方向) 位移不同于路程 r ≠ S (2) 位移与坐标选取无关 (3) 由质点的始末位置确定, 由质点的始末位置确定, 与中间运动过程无关 (4) 分清 r 与r 的区别
大学物理习题册及解答(第二版)第一章 质点的运动

2 t =2
= −16m/s
2
dv a= =10 −18t dt
t =2
= −26m/s
2.一质点在 一质点在Oxy平面上运动,运动方程为 平面上运动, 一质点在 平面上运动 运动方程为x=3t, y=3t2-5(SI), 求(1)质 质 点运动的轨道方程,并画出轨道曲线 并画出轨道曲线;(2)t1=0s和 t2=120s时质点的 点运动的轨道方程 并画出轨道曲线 和 时质点的 的速度、加速度。 的速度、加速度。 解:(1)从运动方程中消去时间就得到轨道方程 从运动方程中消去时间就得到轨道方程
s = v2t
h = H 2,
1 ∴ H' = H 2
Qd s d h
2
2 H2
= −4 H < 0
所以上条件为S极大的条件
5.河水自西向东流动,速度为10km/h.一轮船在水中航行,船 相对于河水的航向为北偏西300,相对于水的航速为20km/h.此 时风向为正西,风速为10km/h.试求在船上观察到的烟囱冒出 的烟缕的飘向.(设烟离开烟囱后很快就获得与风相同的速度)
dθ 则其切向加速度为 a = Rα = R = 0.1m/ s dt
2 t 2
π 1 θ = + t (SI) 4 2
2
2
6 在一个转动的齿轮上,一个齿尖P沿半径为R的圆周运动,其路 程S随时间的变化规律为 S = v 0 t + 1 2 bt 2 ,其中v0和b都是正的常 量.则t时刻齿尖P的速度大小为v0 + bt,加速度大小为 .
v1 = 2 gh
h
v v2
因为完全弹性碰撞,小 S 2 1 球弹射的速度大小为: v2的方向是沿水平方向,故小球与斜面碰撞后作平抛运动,弹出 的水平距离为:
质点运动学

et (t)
A
Δs
Δθ
Δθ
Δ et
o
B
et (t + Δt)
dθ 1 en (t) = v dt ρ o' det dθ 1 v =v en = v en 切向加速度分量 an dt dt ρ 2 dv v2 d s 1 ds 2 a= et + en = et + ( ) en 2 dt ρ dt ρ dt
ds v = vet = et dt
dv d(vet ) a= = dt dt det dv = et + v dt dt
反映速度大小的变化
反映速度方向的变化
dv d s 切向加速度分量: a t = = 2 dt dt
2
det v ? dt
t时间内: Δet
Δθ 大小: Δet = 2 et sin( ) 2 当 Δt 0 有 Δθ 0 Δθ 大小: Δet = 2 Δθ 2
lim Δr = dr ——元位移 记: Δ t 0
Δt 0
lim Δr = dr ——元位移的大小
A B
Δr
3、Δ r 与Δ r 的区别
——标量 = rB Δr = r B -r A A
Δr Δr
(三角形的两边之差小于第三边)
rA
o
rB
二、速度
7/8班
A
Δr
et
Δs
Δr 平均速度: v = Δt Δs 平均速率: v = Δt
2
2
2
极坐标系:
随时间变化 横向单位矢量 径向单位矢量
eθ
极径
er
极角
极点
r θ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4)上升为 h 高度时的切向加速度和法向加速度?
v 2ti j (m / s) 2 a 2i (m / s )
y
an
at
由 y t (m) 知 : 气球上升为 h 高度时: t = h (s)
自然坐标系: a at et an en O at et an en 2i
0 a2
a3
12
例 1-5 有一质点沿半径为 R=2(m)圆轨道作圆 周运动,t 时刻的角位置
2
t (弧度),求
2
t=1(s)时质点的速度和加速度。
解:先考察角量
角速度:
d
t ( rad / s )
dt d 2 ( rad / s ) 角加速度: dt
t ( rad / s )
s
v
ds
d
( R ) R
d dt d dt
dt dt R d dt
1 R
θ:角位置
ω:角速度
at
an
dv dt 2 v
R
R
R
2 2
d dt
R R
2
α:角加速度
【思考】质点能否按图示的加速度沿圆周运动?如 果能,分别表示什么情形?
a4
a1
(v ' cos V ) v ' sin
2 2 2
v ' V 2Vv ' cos
2 2
tan
vy vx
v ' sin v ' cos V
作业: 1-19、1-20
加速度:
ds v vet et dt d ( vet ) dv a dt dt dv det et v dt dt
et
e t
et
Δ
P
P s
en
en
O
det dt
lim
et t
et et 'et
2
2
2
at
a
an
en
P
dv d s et et 切向加速度: at 2 dt dt
反映速度大小的变化
v 1 ds 2 法向加速度: an en ( ) en dt
反映速度方向的变化
2
例 1-4:一热气球以 1 m/s 的速度从地面匀速上升, 由于风的影响,气球的水平速度随着上升的高度而 增大,其关系式为 vx=2y (SI单位),如图所示。求: (1)气球运动方程;(2)轨道方程;(3)加速 度;(4)上升为 h 高度时的切向加速度和法向加 速度的大小。 y
1.自然坐标系下的 速度和加速度
自然坐标系 坐标:s =s(t)
切向 e t
v
P
s
速度:
v lim
t 0
法向 e n
r t
t 0 r set
O
s lim et t 0 t ds 速率: v dt
ds v et vet dt
例 1-6
如图, 一物体沿倾角为 的斜面下滑, 设当
物体相对斜面的速度大小为 v ' 时, 斜面对地的速度大 小为 V,求此时物体对地的速度大小和方向。
V
v'
O
x
y
解: v v 'V
v x v ' cos V v y v ' sin
v
et
e t
et
Δ
P
d ds ds dt
2
Δ
Δs
P s O
d dt
v
ρ
en
en
v dv a et en dt
dv d dv a et v et v en dt dt dt dt
det
et
v dv a et en dt d s 1 ds 2 et ( ) en 2 dt dt a at et an en
a
作业: 1-15、1-16
1.运动描述的相对性:
两 个 相 对 平 动 的 参 照 系
u
P(x,y,z) (x’,y’,z’)
x
y
[S]
y
[S]
r
O
r0
O
r
r ro r
x
对质点位置(矢量)描述的相对性!
利用速度和加速度定义:
dr dt
dro dt
( rad / s )
2
再看线量: 速度: v R Rt (m / s)
at R R ( m / s ) 加速度: 2 2 2 2 an R Rt ( m / s )
2
当 t 1( s ) 时,
,再代入 R 2(m) 2 et P v v 2et (m / s) en 2 2 O a (2et 2 en ) (m / s )
写成分量形式:
v u v
x x ' ut y y ' z z' t t '
——伽利略时空坐标变换
——伽利略速度变换
设O点和O′点开始计时:t =t’
r0 ut uti
r r 'uti
en
O
d lim lim en en t 0 t t 0 t dt dt det
dv d dv a et v et v en dt dt dt dt
曲率半径:ρ
t 0 :
s 0; 0
s
解:(1)运动方程:
v y 1 v x 2 y y t O t t 2 t 2 x v x dt 2tdt t 0 t 0 0 2 r t i t j (运动方程)
x
(2)轨道方程:
y t 2 xt
t 0
et et 'et
t 0 :
大小:et et
et
e t
et
方向: 0 : et || en
et en
det et
en
: et '、 et 之间夹角
Δ
P
P s
at dv dt2Fra bibliotek ax
at an 4
4h 4h 1
2
2
2
d
2t
dt
2
1
4t 4t 1
2
(m / s )
2
an
4 at
2 4h 1
2
(m / s )
2
2.圆周运动
圆周运动:
v dv a et en dt
2
s R
θ O R
dr dt
2 d r
r ro r dr dro v ;u dt dt
t:S参考系时间
如果 t = t’,则:
2 d r
dt
2
2 d ro
dt
2
dt
2
v'
dr ' dt '
dr ' dt
v u v a a0 a
u :牵引速度 du :牵引加速度 ao dt
2.伽利略坐标变换
相 对 运 动 沿 S 的 x 轴
y
y
r ro r
[S]
[S]
u
y
y
P
r
x
O
r r0
O
x
z
z'
设O点和O′点开始计时:t =t’
r0 ut uti
r r 'uti
y
2
x y ( y 0)
(3)速度、加速度:
dx dy v i j 2ti j dt dt 2 2 d x d y a i j 2i 2 2 dt dt O (m / s) (m / s )
2
x
2 r t i t j (运动方程)
