1985年高考理科数学试题
1985年山东高考卷

1985年山东高考卷注意事项:1、答第1卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2、选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在本试卷上,否则无效。
第一部分:听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试题卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B.£9.18.C.£9.15.答案是C。
1、What is the man‘s job?A.A barber.B.A pilot.C.A taxi driver.2、Where should the woman turn right?A. At the colored sign.B. At Joe‘s Garage.C. After two miles.3、What does the woman think the man should do?A. Change the smaller offices into large ones.B. Turn the meeting room into offices.C. Move the offices to another building.4、What time is it now?A. 7:15.B.7:30.C.7:50.5、How does the man feel at the moment?A. Great.B. Terrible.C. Better.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
三角函数(1985年2003年高考试题集)

三角函数(1985年——2003年高考试题集)一、选择题 1. t an x =1是x =45π的 。
(85(2)3分)A.必要条件B.充分条件C.充要条件D.既不充分也不必要条件 2. 函数y =2sin2xcos2x 是 。
(86(4)3分)A.周期为2π的奇函数 B.周期为2π的偶函数 C.周期为4π的奇函数D.周期为4π的偶函数3. 函数y =cosx -sin 2x -cos2x +417的最小值是 。
(86广东) A.47 B.2 C.49D.417 E.4194. 函数y =cos 4x -sin 4x 的最小正周期是 。
(88(6),91(3)3分)A.πB.2πC.2πD.4π5. 要得到函数y =sin(2x -3π)的图象,只须将函数y =sin2x 的图象 。
(87(6)3分)A.向左平移3π B.向右平移3π C.向左平移6π D.向右平移6π6. 若α是第四象限的角,则π-α是 。
(89上海)A.第一象限的角B.第二象限的角C.第三象限的角D.第四象限的角7. t an 70°+tan50°-3tan70°tan50°的值是 。
(90广东)A.3B.33C.-33D.-38. 要得到函数y =cos(2x -4π)的图象,只需将函数y =sin2x 的图象 。
(89上海)A.向左平移8π个单位 B.向右平移8π个单位 C.向左平移4π个单位 D.向右平移4π个单位9. 函数y =cotx|cotx ||tanx |tanx cosx|cosx ||sinx |sinx +++的值域是 。
(90(6)3分)A.{-2,4}B.{-2,0,4}C.{-2,0,2,4}D.{-4,-2,0,4} 10. 若函数y =sin(ωx)cos(ωx)(ω>0)的最小正周期是4π,那么常数ω为 。
(92(2)3)A.4B.2C.21 D.41注:原考题中无条件“ω>0”,则当ω取负值时也可能满足条件 11. 在直角三角形中两锐角为A 和B ,则sinAsinB 。
1985年上海高考

1985年全国普通高等学校招生统一考试上海 物理试卷考生注意:(1)全卷共八大题,在120分钟内答完。
(2)第五、六、七、八题要求写出必要的文字说明、方程式和重要演算步骤.只写出最后答案,而未写出主要演算过程的,不能得分,有数值计算的题,答案必须明确写出数值和单位.(3)本卷中重力加速度g 取10米/秒2.一.(20分)本题有5个小题。
每小题4分。
把答案填写在题中横线上空白处,不要求写出演算过程。
1.在真空中有两个点电荷,电量分别是q 1和q 2,当它们相距为r 时,它们间相互作用力的大小已知是F 。
如果它们的电量保持不变,而距离变为2r,则它们之间的相互作用力的大小是 F 。
如果它们之间的距离r 保持不变,而电量分别变为2q 1和3q 2,则它们之间的相互作用力的大小是 F.2.照明用的交流电电压为220伏特,这是指电压的 值;当接入一个电阻为1100欧姆的电热丝时,通过电热丝的电流的最大值是 安培。
3.一个质点的简谐振动图象如图所示。
从图中可以看出,振动的振幅是 米,频率是 赫兹。
4.设氢原子基态的能量是E 1,某一激发态的能量是E 2,当氢原子从这一激发态跃迁到基态时,它辐射出的光子的频率ν= ;在真空中的波长λ= 。
(光在真空中的速度记作c ,普朗克恒量记作h 。
)5.(1)平衡下列核反应方程式:Be 94+He 42→C 126+ 。
(2)铋210的半衰期是5天,12克的铋210经过20天以后还剩下 克。
二.(12分)本题有4个小题,每小题3分。
每小题选出一个正确的答案,把它的号码填写在题后的方括号内:选对的,得3分;选错的或不选的得0分;如果选了两个或两个以上的答案,不论其中有没有对的,均得0分。
6.水平地面上有一块重量是2牛顿的静止石块。
一个小孩用10牛顿的力踢石块,使石块滑行了1米的距离,则小孩对石块所做的功是()(A)10焦耳(B)2焦耳(C)12焦耳(D)条件不足,无法确定7.对于一定质量的理想气体,正确的是()(A)如果体积V减小,气体分子在单位时间内作用于器壁单位面积的总冲量一定增大(B)如果压强p增大,气体分子在单位时间内作用于器壁单位面积的总冲量一定增大(C)如果温度T不变,气体分子在单位时间内作用于器壁单位面积的总冲量一定不变(D)如果密度不变,气体分子在单位时间内作用于器壁单位面积的总冲量一定不变8.有一电场的电场线分布如图所示,场中A、B两点的电场强度的大小和电势分别用E A、E B和U A、U B表示。
三角函数(1985年高考试题集)

三角函数(1985年——2003年高考试题集)一、选择题 1. t an x =1是x =45π的 。
(85(2)3分) A.必要条件B.充分条件C.充要条件D.既不充分也不必要条件2. 函数y =2sin2xcos2x 是 。
(86(4)3分)A.周期为2π的奇函数 B.周期为2π的偶函数C.周期为4π的奇函数D.周期为4π的偶函数3. 函数y =cosx -sin 2x -cos2x +417的最小值是 。
(86广东) A.47 B.2C.49D.417 E.4194. 函数y =cos 4x -sin 4x 的最小正周期是 。
(88(6),91(3)3分)A.πB.2πC.2πD.4π5. 要得到函数y =sin(2x -3π)的图象,只须将函数y =sin2x 的图象 。
(87(6)3分) A.向左平移3π B.向右平移3π C.向左平移6π D.向右平移6π6. 若α是第四象限的角,则π-α是 。
(89上海)A.第一象限的角B.第二象限的角C.第三象限的角D.第四象限的角7. t an 70°+tan50°-3tan70°tan50°的值是 。
(90广东) A.3B.33C.-33 D.-38. 要得到函数y =cos(2x -4π)的图象,只需将函数y =sin2x 的图象 。
(89上海) A.向左平移8π个单位 B.向右平移8π个单位 C.向左平移4π个单位 D.向右平移4π个单位9. 函数y =cotx|cotx ||tanx |tanx cosx |cosx ||sinx |sinx +++的值域是 。
(90(6)3分)A.{-2,4}B.{-2,0,4}C.{-2,0,2,4}D.{-4,-2,0,4}10. 若函数y =sin(ωx)cos(ωx)(ω>0)的最小正周期是4π,那么常数ω为 。
(92(2)3)A.4B.2C.21 D.41 注:原考题中无条件“ω>0”,则当ω取负值时也可能满足条件 11. 在直角三角形中两锐角为A 和B ,则sinAsinB 。
1985年全国高等学校统一招生数学试题

1985年全国高等学校统一招生数学试题
康庄;家骏;文立
【期刊名称】《数学教学通讯》
【年(卷),期】1984(000)003
【总页数】4页(P48-51)
【作者】康庄;家骏;文立
【作者单位】
【正文语种】中文
【中图分类】G6
【相关文献】
1.2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(文科类) [J],
2.2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(理工农医类)[J],
3.2005年普通高等学校招生全国统一考试(广东卷)数学试题和参考答案 [J], 无
4.2007年普通高等学校招生全国统一考试(重庆卷)——数学试题(文史类)[J], 无
5.2007年普通高等学校招生全国统一考试(重庆卷)——数学试题卷(理工农医类) [J], 无
因版权原因,仅展示原文概要,查看原文内容请购买。
1985年2003年高考试题集

三角函数(1985年——2003年高考试题集)一、选择题1. t an x =1是x =45π的 。
(85(2)3分) A.必要条件 B.充分条件 C.充要条件 D.既不充分也不必要条件2. 函数y =2sin2xcos2x 是 。
(86(4)3分)A.周期为2π的奇函数B.周期为2π的偶函数 C.周期为4π的奇函数 D.周期为4π的偶函数 3. 函数y =cosx -sin 2x -cos2x +417的最小值是 。
(86广东) A.47 B.2 C.49 D.417 E.419 4. 函数y =cos 4x -sin 4x 的最小正周期是 。
(88(6),91(3)3分)A.πB.2πC.2π D.4π 5. 要得到函数y =sin(2x -3π)的图象,只须将函数y =sin2x 的图象 。
(87(6)3分) A.向左平移3π B.向右平移3π C.向左平移6π D.向右平移6π 6. 若α是第四象限的角,则π-α是 。
(89上海)A.第一象限的角B.第二象限的角C.第三象限的角D.第四象限的角7. t an 70°+tan50°-3tan70°tan50°的值是 。
(90广东) A.3 B.33 C.-33 D.-38. 要得到函数y =cos(2x -4π)的图象,只需将函数y =sin2x 的图象 。
(89上海) A.向左平移8π个单位 B.向右平移8π个单位 C.向左平移4π个单位 D.向右平移4π个单位 9. 函数y =cotx|cotx ||tanx |tanx cosx |cosx ||sinx |sinx +++的值域是 。
(90(6)3分) A.{-2,4} B.{-2,0,4} C.{-2,0,2,4} D.{-4,-2,0,4}10. 若函数y =sin(ωx)cos(ωx)(ω>0)的最小正周期是4π,那么常数ω为 。
(92(2)3)A.4B.2C.21D.41 注:原考题中无条件“ω>0”,则当ω取负值时也可能满足条件11. 在直角三角形中两锐角为A 和B ,则sinAsinB 。
1985年吉林省高考数学试卷

1985年吉林省高考数学试卷一、选择题(在下列各题的四个备选答案中,只有一个是符合题意的,请将正确答案前的字母写在答题纸上;本题共32分,每小题4分)1、已知⊙O的直径为3cm,点P到圆心O的距离OP=2cm,则点P()A、在⊙O外B、在⊙O上C、在⊙O内D、不能确定2、已知△ABC中,∠C=90°,AC=6,BC=8,则cose的值是()A、0.6B、0.75C、0.8D、0.853、△ABC中,点M、N分别在两边AB、AC上,MN∥BC,则下列比例式中,不正确的是()A、1B、2C、3D、44、既是中心对称图形又是轴对称图形的是()A、1B、-1C、2D、-25、已知⊙O1、⊙O2的半径分别是1cm、4cm,O1O2=cm,则⊙O1和⊙O2的位置关系是()A、外离B、外切C、内切D、相交6、某二次函数y=ax2+bx+c的图像,则下列结论正确的是()A、ao,b0,c0B、a0,b0,c;0C、a0,b0,c0D、a0,b0,c07、下列命题中,正确的是()A、平面上三个点确定一个圆B、等弧所对的圆周角相等C、平分弦的直径垂直于这条弦D、与某圆一条半径垂直的直线是该圆的切线8、把抛物线y=-x2+4x-3先向左平移3个单位,再向下平移2个单位,则变换后的抛物线解析式是()A、y=-(x+3)2-2B、y=-(x+1)2-1C、y=-x2+x-5D、前三个答案都不正确二、填空题(本题共16分,每小题4分)9、已知两个相似三角形面积的比是2∶1,则它们周长的比_____。
10、在反比例函数y=中,当x0时,y随x的增大而增大,则k的取值范围是_________。
11、水平相当的甲乙两人进行羽毛球比赛,规定三局两胜,则甲队战胜乙队的概率是_________;甲队以2∶0战胜乙队的概率是________。
12、已知⊙O的直径AB为6cm,弦CD与AB相交,夹角为30°,交点M恰好为AB的一个三等分点,则CD的长为_________cm。
1985年北京高考数学

1985年北京高考数学一、选择题(在下列各题的四个备选答案中,只有一个是符合题意的,请将正确答案前的字母写在答题纸上;本题共32分,每小题4分)1、已知⊙O的直径为3cm,点P到圆心O的距离OP=2cm,则点P()A、在⊙O外B、在⊙O上C、在⊙O内D、不能确定2、已知△ABC中,∠C=90°,AC=6,BC=8,则cose的值是()A、0.6B、0.75C、0.8D、0.853、△ABC中,点M、N分别在两边AB、AC上,MN∥BC,则下列比例式中,不正确的是()A、1B、2C、3D、44、既是中心对称图形又是轴对称图形的是()A、1B、-1C、2D、-25、已知⊙O1、⊙O2的半径分别是1cm、4cm,O1O2=cm,则⊙O1和⊙O2的位置关系是()A、外离B、外切C、内切D、相交6、某二次函数y=ax2+bx+c的图像,则下列结论正确的是()A、ao,b0,c0B、a0,b0,c;0C、a0,b0,c0D、a0,b0,c07、下列命题中,正确的是()A、平面上三个点确定一个圆B、等弧所对的圆周角相等C、平分弦的直径垂直于这条弦D、与某圆一条半径垂直的直线是该圆的切线8、把抛物线y=-x2+4x-3先向左平移3个单位,再向下平移2个单位,则变换后的抛物线解析式是()A、y=-(x+3)2-2B、y=-(x+1)2-1C、y=-x2+x-5D、前三个答案都不正确二、填空题(本题共16分,每小题4分)9、已知两个相似三角形面积的比是2∶1,则它们周长的比_____。
10、在反比例函数y=中,当x0时,y随x的增大而增大,则k的取值范围是_________。
11、水平相当的甲乙两人进行羽毛球比赛,规定三局两胜,则甲队战胜乙队的概率是_________;甲队以2∶0战胜乙队的概率是________。
12、已知⊙O的直径AB为6cm,弦CD与AB相交,夹角为30°,交点M恰好为AB的一个三等分点,则CD的长为_________cm。
1985年全国高考数学试题及答案解析

(1)解法一:由原对数方程得
因为log0.25a=-log4a,上式变成
由此得到
解这个方程,得到
x1=0,x2=7.
检验:把x=0代入原方程,左右两边都等于0;故x=0是原方程的根.但当x=7时,由于3-x<0,1-x<0,它们的对数无意义;故x=7不是原方程的根,应舍去.
当n=k+1时,可得
即
也成立.
从而不等式对所有的正整数n都成立.
证法二:直接证明.
由于不等式
对所有的正整数k成立,把它对k从1到n(n≥1)求和,得到
又因
以及
因此不等式
对所有的正整数n都成立.
(2)由(1)及bn的定义知
于是
八、设a,b是两个实数,
解法二:设直线PA和QB的交点为M(x,y).
当点M与点P及点Q都不重合时,直线PM的方程是
(x+2)(Y-2)=(y-2)(X+2),
直线பைடு நூலகம்M的方程是
x(Y-2)=(y-2)X.
由方程组
解得直线PM和直线l的交点A的坐标为
由方程组
解得直线QM和直线l的交点B的坐标为
根据题意,线段AB两端点A,B的横坐标有如下关系:
1985年全国高考数学试题及答案解析
(理工农医类)
一、本题每一个小题都给出代号为A,B,C,D的四个结论,其中只有一个结论是正确的,把正确结论的代号写在题后的括号内.
(1)如果正方体ABCD_A′B′C′D′的棱长为a,那么四面体
A′_ABD的体积是
【】
[Key]一、本题考查基本概念和基本运算.
(1)D;
一九八五年的高考数学试卷

一、选择题(本大题共20小题,每小题5分,共100分)1. 下列各数中,无理数是()A. $\sqrt{2}$B. $\frac{1}{3}$C. $\pi$D. $\sqrt{9}$2. 已知函数$f(x)=2x-3$,则$f(-1)$的值为()A. -1B. 1C. 2D. 33. 如果$a^2+b^2=5$,且$a-b=2$,那么$ab$的值为()A. 1B. 2C. 3D. 44. 在直角坐标系中,点$A(2,3)$关于直线$x+y=1$的对称点为()A. $(-1,1)$B. $(-1,-1)$C. $(1,-1)$D. $(1,1)$5. 下列命题中,正确的是()A. 函数$y=x^2$在$x=0$处有极小值B. 函数$y=\log_2x$在$x=1$处有极大值C. 函数$y=\sqrt{x}$在$x=0$处有极小值D. 函数$y=3^x$在$x=0$处有极小值6. 已知等差数列$\{a_n\}$的前$n$项和为$S_n$,且$a_1=1$,$S_3=6$,则$a_4$的值为()A. 2B. 3C. 4D. 57. 如果复数$z$满足$|z-1|=|z+1|$,那么$z$对应的点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限8. 在$\triangle ABC$中,若$A=45^\circ$,$B=60^\circ$,则$C$的度数为()A. $45^\circ$B. $60^\circ$C. $75^\circ$D. $90^\circ$9. 若$|x+2|=|x-2|$,则$x$的取值范围是()A. $x \leq -2$B. $x \geq 2$C. $x \leq 2$或$x \geq -2$D. $x = 0$10. 下列函数中,奇函数是()A. $y=x^2$B. $y=x^3$C. $y=\frac{1}{x}$D. $y=\sqrt{x}$11. 如果$a+b=5$,$ab=6$,那么$a^2+b^2$的值为()A. 19B. 20C. 21D. 2212. 在$\triangle ABC$中,若$a:b:c=1:2:3$,则$\cos A$的值为()A. $\frac{1}{3}$B. $\frac{2}{3}$C. $\frac{1}{2}$D. $\frac{3}{2}$13. 已知$sinA=0.6$,$cosB=0.8$,那么$sin(A+B)$的值为()A. 0.4B. 0.5C. 0.6D. 0.714. 下列各对数式中,正确的是()A. $\log_2(8)=3$B. $\log_5(25)=2$C. $\log_4(16)=2$D. $\log_3(9)=1$15. 下列各三角函数式中,正确的是()A. $\sin^2x+\cos^2x=1$B. $\tan^2x+\sec^2x=1$C. $\cos^2x+\csc^2x=1$D. $\cot^2x+\sec^2x=1$16. 已知等比数列$\{a_n\}$的前$n$项和为$S_n$,且$a_1=1$,$S_4=10$,则$a_5$的值为()A. 5B. 10C. 20D. 4017. 下列各函数中,是单调递增函数的是()A. $y=x^2$B. $y=x^3$C. $y=\frac{1}{x}$D. $y=\sqrt{x}$18. 如果复数$z$满足$|z-1|=|z+1|$,那么$z$对应的点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限19. 在$\triangle ABC$中,若$A=45^\circ$,$B=60^\circ$,则$C$的度数为()A. $45^\circ$B. $60^\circ$C. $75^\circ$D. $90^\circ$20. 若$|x+2|=|x-2|$,则$x$的取值范围是()A. $x \leq -2$B. $x \geq 2$C. $x \leq 2$或$x \geq -2$D. $x = 0$二、填空题(本大题共10小题,每小题5分,共50分)21. 若$a+b=5$,$ab=6$,则$a^2+b^2=$______。
1985年高考数学试题及答案

1985年普通高等学校招生全国统一考试理科数学试题及答案考生注意:这份试题共八道大题,满分120分第九题是附加题,满分10分,不计入总分一.(本题满分15分)本题共有5小题,每小题都给出代号为A ,B ,C ,D 的四个结论,其中只有一个结论是正确的,把正确结论的代号写在题后的圆括号内,选对的得3分、不选,选错或者选出的代号超过一个的(不论是否都写在圆括号内),一律得0分(1)如果正方体ABCD-A 'B 'C 'D '的棱长为a ,那么四面体A '-ABD 的体积是 ( D )6(D) 4(C) 3(B)2)(3333a a a a A (2)π==451x tgx 是的 ( A ) (A )必要条件 (B )充分条件(C )充分必要条件 (D )既不充分又不必要的条件 (3)在下面给出的函数中,哪一个函数既是区间)2,0(π上的增函数又是以π为周期的偶函数? ( B ) (A )).(2R x x y ∈= (B ))(|sin |R x x y ∈= (C ))(2cos R x x y ∈= (D ))(2sin R x e y x ∈=(4)极坐标方程)0(sin >θ=ρa a 的图象是 ( C )(A) X2(5)用1,2,3,4,5这五个数字,可以组成比20000大,并且百位数不是数字3的没有重复数字的五位数,共有 ( B )(A )96个 (B(C (D )64个二.(本题满分20分)本题共5小题,每一个小题满分4分只要求直接写出结果)集(1)求方程16sin(2=π+x 解答:}.,6]1)1[(|{Z k k x x k ∈π--+π=(2)设1||≤a ,求)arccos(arccos a a -+的值答:π(3)求曲线64162+-=x y 的焦点答:(0,0)(4)设(3x-1)6=a 6x 6+a 5x 5+a 4x 4+a 3x 3+a 2x 2+a 1x+a 0,求a 6+a 5+a 4+a 3+a 2 +a 1+a 0的值(C) O X(B) (D) a X答:64(或26)(5)设函数f(x)的定义域是[0,1],求函数f(x 2)的定义域答:[-1,1]三.(本题满分14分)(1)解方程).12(log )1(log )3(log )3(log 25.0425.04++-=++-x x x x 解:由原对数方程得,312log 312log 13log 425.04⎪⎭⎫⎝⎛++-=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛--x x x x x x1)3)(1()12)(3(,031213log 4=+-+-=⎪⎭⎫ ⎝⎛++⋅--x x x x x x x x 由此得到 解这个方程,得到x 1=0,x 2=7. 检验:x=7是增根,x=0是原方程的根(2)解不等式.152+>+x x解:⎪⎩⎪⎨⎧++>+≥+≥+⎩⎨⎧<+≥+125201052010522x x x x x x x 或 解得}.225|{<≤-x x 四.(本题满分15分)如图,设平面AC 和BD 相交于BC ,它们所成的一个二面角为450,P 为平面AC 内的一点,Q 为面BD 内的一点MQ 是直线PQ 在平面BD 内的射影,并且M 在BC 上又设PQ 与平面BD 所成的角为β,∠CMQ=θ(00<θ<900),线段PM 的长为a ,求线段PQ 的长解:自点P 作平面BD 的垂线,垂足为R ,由于直线MQ 是直线PQ 在平面BD 内的射影,所以R 在MQ 上,过R 作BC 的垂线,设垂足为N ,则PN ⊥BC (三垂线定理)因此∠PNR 是所给二面角的平面角,所以∠PNR=450由于直线MQ 是直线PQ 在平面BD 内的射影,所以∠PQR=β 在Rt △PNR 中,NR=PRctg450,所以NR=PR 在Rt △MNR 中,MR=θ=θsin 1sin 1PR NR在Rt △PMR 中,sin 11(sin 22222222θ+=θ+=+=PR PR PR MR PR a又已知00<θ<900,所以.sin 1sin 2θ+θ=a PR在Rt △PRQ 中,.sin 1sin sin sin 12θ+βθ=β=a PR PQ 故线段PQ 五.(本题满分15分)设O 为复平面的原点,Z 1和Z 2为复平面内的两动点,并且满足:(1)Z 1和Z 2所对应的复数的辐角分别为定值θ和-θ)20(π<θ<, (2)△OZ 1Z 2的面积为定值S求△OZ 1Z 2的重心Z 所对应的复数的模的最小值AB Q D解:设Z 1,Z 2和Z 对应的复数分别为z 1,z 2和z ,其中).sin (),sin (2211θ-θ=θ+θ=i co r z i co r z由于Z 是△OZ 1Z 2的重心,根据复数加法的几何意义,则有.sin )(cos )(3212121θ-+θ+=+=i r r r r z z z 于是θ+-=θ-+θ+θ-=θ-+θ+=22122122212212221222122212cos 4)(sin )(cos 4cos )(sin )(cos )(|3|r r r r r r r r r r r r r r z 又知△OZ 1Z 2的面积为定值S 及)20(02sin π<θ<>θ ,所以.32||,||,2sin 24)(2sin cos 8)(|3|,2sin 2,2sin 2121221222122121θ=θ==θ+-=θθ+-=θ==θSctg z z S r r Sctg r r S r r z S r r S r r 最小值且最小时故当由此即六.(本题满分15分)已知两点P (-2,2),Q (0,2)以及一条直线:L:y=x ,设长为2的线段AB 在直线L 上移动,如图PA 和QB 的交点M 的轨迹方程(要求把结果写成普通方程)解:由于线段AB 在直线y=x 上移动,且AB 的长2,所以可设点A 和B 分别是(a ,a )和(a +1,a +1),其中a 为参数YZ 2于是可得:直线PA 的方程是)1()2()2(222-≠++-=-a x a a y直线QB 的方程是)2()1(112-≠+-=-a x a a y 1.当,0,1122时即=+-=+-a a a a a 直线PA 和QB2.当0≠a 时,直线PA 与QB相交,设交点为M(x,y),由(2)式得.2632,2232,221,)121(2+---=-+-+-=+∴+-=++-=-y x x y a y x y x a y x x a x a y 将上述两式代入(1)式,得(*)18)1(8)1(0822)2(236322222-=+-+=+-+-++---=-y x y x y x x y x x y y 即整理得当a =-2或a =-1时,直线PA 和QB 仍然相交,并且交点坐标也满足(*)式所以(*)式即为所求动点的轨迹方程注:考生没指出“a =0”及“a =-2或a =-1”时的情形不扣分七.(本题满分14分)设)2,1()1(3221 =+++⋅+⋅=n n n a n(1)证明不等式2)1(2)1(2+<<+n a n n n 对所有的正整数n 都成立(2)设),2,1()1( =+=n n n a b n n 用定义证明.21lim =∞→n n b YXM(1)证一:用数学归纳法略证二:由不等式2122)1()1(+=++<+<k k k k k k 对所有正整数k 成立,把它对k 从1到n (n ≥1)求和,得到212252321++++<<+++n a n n 又因,2)1(21+=+++n n n 以及 .2)1(2)1(,2)1()]12(531[21212252322+<<++=+++++<++++n a n n n n n n 因此不等式 对所有的正整数n 都成立(2)由(1)及b n 的定义知nb b n n n b n n n 212121,21212121<-=-+=+<<于是 对任意指定的正数ε,要使ε<-21n b ,只要使ε<n 21,即只要使 .21ε>n 取N 是ε21的整数部分,则数列b n 的第N 项以后所有的项都满足<-21n b 根据极限的定义,证得.21lim =∞→n n b 八.(本题满分12分) 设a ,b 是两个实数,A={(x,y)|x=n,y=n a +b,n 是整数}, B={(x,y)|x=m,y=3m 2+15,m 是整数}, C={(x,y)|x 2+y 2≤144},是平面XOY 内的点集合,讨论是否存在a 和b 使得(1)A ∩B ≠φ(φ表示空集), (2)(a ,b)∈C 同时成立解:如果实数a 和b 使得(1)成立,于是存在整数m 和n 使得(n,n a +b)=(m,3m 2+15), 即⎩⎨⎧+=+=.153,2m b na m n 由此得出,存在整数n 使得n a +b=3n 2+15, 或写成n a +b-(3n 2+15)=0这个等式表明点P (a ,b)在直线L :nx+y-(3n 2+15)=0上,记从原点到直线L 的距离为d ,于是12)1221(611532222≥+++=++=n n n n d 当且仅当3,12122==+n n 即时上式中等号才成立由于n 是整数,因此32≠n ,所以上式中等号不可能成立即12>d因为点P 在直线L 上,点P 到原点的距离22b a +必满足.1222>≥+d b a而(2)成立要求a 2+b 2≤144,即1222≤+b a 由此可见使得(1)成立的a 和b 必不能使(2)成立所以,不存在实数a 和b 使得(1),(2)同时成立 九.(附加题,本题满分10分,)已知曲线y=x 3-6x 2+11x-6.在它对应于]2,0[∈x 的弧段上求一点P ,使得曲线在该点的切线在y 轴上的截距为最小,并求出这个最小值解:已知曲线方程是y=x 3-6x 2+11x-6,因此y '=3x 2-12x+11在曲线上任取一点P(x0,y0),则点P处切线的斜率是y'|x=x0=3x02-12x0+11点P处切线方程是y=(3x02-12x0+11)(x-x0)+y0设这切线与y轴的截距为r,则r=(3x02-12x0+11)(-x0)+(x03-6x02+11x0-6)=-2x03+6x02-6根据题意,要求r(它是以x0为自变量的函数)在区间[0,2]上的最小值因为r'=-6x02+12x0=-6x0(x0-2)当0<x0<2时r'>0,因此r是增函数,故r在区间[0,2]的左端点x0=0处取到最小值即在点P(0,-6)处切线在y轴上的截距最小这个最小值是r最小值=-6。
1985—1999年立体几何

1985年高考试题选(立体几何)1.(1985·全国卷·文理科)如果正方体1111ABCD A B C D -的棱长为a ,那么四面体1A ABD -的体积为A .32aB .33aC .34aD .36a2.(1985·全国卷·理科)如图,设平面AC 和BD 相交于BC ,它们所成的一个二面角为45,P 为面AC 内的一点,Q 为面BD 内的一点.已知直线MQ 是直线PQ 在平面BD 内的射影,并且M 在BC 上,又设PQ 与平面BD 所成的角为β,CMQ θ∠=(02πθ<<),线段PM 的长为a ,求线段PQ 的长.3.(1985·全国卷·理科)设一个三棱锥V ABC -的三个侧面与底面所成的二面角都是β,它的高是h .求这个三棱锥底面的内接圆半径.1986年高考试题选(立体几何)1.(1986·全国卷·理科)在正方形123SG G G 中,E ,F 分别是12G G 及23G G 的中点,D 是EF 的中点,现在沿SE 、SF 及EF 把这个正方形折成一个四面体,使1G ,2G ,3G 三点重合,重合后的点记为G .那么,在四面体S EFG -中必有 A .SG EFG ⊥∆所在平面 B .SD EFG ⊥∆所在平面 C .GF SEF ⊥∆所在平面 D .GD SEF ⊥∆所在平面ABCDA 1B 1C 1D 1ABCPQM2.(1986·全国卷·文科)已知正方体的对角线长为a ,那么,这个正方形的全面积为A.2 B .22a C.2 D.2 3.(1986·全国卷·文理科)如图,AB 是圆O 的直径,PA 垂直于圆O 所在的平面,C 是圆周上不同于A ,B 的任意一点.求证:平面PAC 垂直于平面PBC .1987年高考试题选(立体几何)1.(1987·全国卷·理科)已知E ,F ,G ,H 为空间中的四个点,设命题甲:点E ,F ,G ,H 不共面;命题乙:直线EF 和GH 不相交.那么 A .甲是乙的充分条件,但不是必要条件 B .甲是乙的必要条件,但不是充分条件 C .甲是乙的充要条件D .甲不是乙的充分条件,也不是乙的必要条件2.(1987·全国卷·理科)一个正三棱台的下底和上底的周长分别为30cm 和12cm ,而侧面积等于两底面积之差,求斜高.3.(1987·全国卷·文科)圆锥底面面积为3π,母线与底面所成的角为60,求它的体积.4.(1987·全国卷·文理科)如图,三棱锥P ABC -中,已知PA BC ⊥,PA BC =l =,PA ,BC 的公垂线ED =h .求证:三棱锥P ABC -的体积216V l h =.SG 2G 1G 3EF DBO1988年高考试题选(立体几何)1.(1988·全国卷·文理科)如图,正四棱台中,11A D 所在的直线与1BB 所在的直线是A .相交直线B .平行直线C .不互相垂直的异面直线D .互相垂直的异面直线2.(1988·全国卷·理科)如图,二面角AB αβ--的平面角是锐角,C 是面α内的一点(它不在棱AB 上),点D 是点C 在面β上的射影,点E 是棱AB 上满足CEB ∠为锐角的任意一点,那么A .CEB DEB ∠>∠ B .CEB DEB ∠=∠C .CEB DEB ∠<∠D .CEB ∠,DEB ∠的大小关系不能确定2.(1988·全国卷·文科)已知二面角AB αβ--的平面角是锐角θ,α内的一点C 到β的距离为3,点C 到棱AB 的距离为4,那么tan θ的值等于ABCDEPB A CDA 1C 1 B 1D 1 AB CDEαβA .34B .35C.7 D.34.(1988·全国卷·文理科)如图,已知四棱锥S ABCD -的底面是边长为1的正方形,侧棱SB垂直于底面,并且SB =α表示ASD ∠,求sin α的值.5.(1988·全国卷·文科)一个直角三角形的两条直角边的长分别为3cm 和4cm ,将这个直角三角形以斜边为轴旋转一周,求所得旋转体的体积. 6.(1988·全国卷·理科)如图,正三棱锥S ABC -的侧面是边长为a 的正三角形,D 是SA 的中点,E 是BC 的中点,求SDE ∆绕直线SE 旋转一周所得到的旋转体的体积.1989年高考试题选(立体几何)1.(1989,高为2,那么它的侧面积是A. B. C. D. 2.(1989·全国卷·文理科)已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧,且相距为1,那么这个球的半径是A .2B .3C .4D .5AB CDS3.(1989·全国卷·理科)如图,已知圆柱的底面半径是3,高是4,A,B两点分别在两底面的圆周上,并且5AB=,那么直线AB与轴OO'之间的距离等于 .4.(1989·全国卷·文科)如图,P是二面角ABαβ--棱AB上的一点,分别在α,β上引射线PM,PN,如果45BPM BPN∠=∠=,60MPN∠=,那么二面角ABαβ--的大小是 .5.(1989·全国卷·文理科)如图,在平行六面体1111ABCD A B C D-中,已知5AB=,4AD=,13AA=,AB AD⊥,113A AB A ADπ∠=∠=.(Ⅰ)求证:顶点1A在底面ABCD的射影O在BAD∠的平分线上;(Ⅱ)求这个平行六面体的体积.1990年高考试题选(立体几何)1.(1990·全国卷·文理科)如果轴截面为正方形的圆柱的侧面积是S,那么圆柱的体积等于A C2.(1990·全国卷·文理科)如图,正三棱锥S ABC-的侧棱与底面边长相等,如果E,F分别为SC,AB的中点,那么异面直线EF与SA所成的角等于ABOO'A BCDOA1B1C1D1αβA BPMNA .90B .60C .45D .303.(1990·全国卷·文理科)如图,三棱柱111ABC A B C -中,若E ,F 分别为AB ,AC 的中点,平面11EB C F 将三棱柱分成体积为1V ,2V 的两部分,那么1V :2V = .4.(1990·全国卷·文理科)如图,在三棱锥S ABC -中,SA ⊥底面ABC ,AB BC ⊥,DE 垂直平分SC ,且分别交AC ,SC 于D ,E ,又SA AB =,SB BC =.求以BD 为棱,以BDE 与BDC 为面的二面角的度数.1991年高考试题选(立体几何)1.(1991·全国卷·文理科)如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线共有A .12对B .24对C .36对D .48对 2.(1991·全国卷·文理科)如果三棱锥S ABC -的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点S 在底面的射影O 在ABC ∆内,那么OABCSEFA ABDCES是ABC ∆的A .垂心B .重心C .外心D .内心 3.(1991·全国卷·理科)已知正三棱台上底面边长为2,下底面边长为4,且侧棱与底面所成的角是45,那么这个正三棱台的体积等于 .4.(1991·全国卷·文理科)在球面上有四个点P ,A ,B ,C ,如果PA ,PB ,PC 两两互相垂直,且PA PB =PC a ==,那么这个球面的面积是 . 5.(1991·全国卷·文科)在长方体1111ABCD A B C D -中,已知顶点A 上三条棱2,如果对角线1AC 与过A 的相邻三个面所成的角分别为α,β,γ,那么2cos α+22cos cos βγ+= .6.(1991·全国卷·理科)已知ABCD 是边长为4的正方形,E ,F 分别是AB ,AD 的中点,GC 垂直于ABCD 所在的平面,且2GC =,求点B 到平面EFG 的距离.7.(1991·全国卷·理科)如图,在三棱台111ABC A B C -中,已知1AA ⊥底面ABC ,111AA A B ==11B C a =,1BB BC ⊥,且1BB 和底面ABC 所成的角是45,求这个棱台的体积.1992年高考试题选(立体几何)1.(1992·全国卷·文理科)已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是A .6:5B .5:4C .4:3D .3:2 2.(1992·全国卷·文理科)在四棱锥的四个侧面中,直角三角形最多可有 A .1个 B .2个 C .3个 D .4个 3.(1992·全国卷·文理科)在棱长为1的正方体1111ABCD A B C D -中,M 和N 分别为11A B 和1BB 的中点,那么直线AM 与CN 所成角的余弦值是 AB.35 D .25A BCA 1B 1C 14.(1992·全国卷·文理科)长方体的全面积为11,十二条棱长度之和为24,则这个长方体的一条对角线长为A ..5 D .6 5.(1992·全国卷·文科)已知1111ABCD ABCD -是棱长为a 的正方体,E ,F 分别为棱1AA ,1CC 的中点,求四棱锥11A EBFD -的体积.6.(1992·全国卷·理科)已知:两条异面直线a ,b 所成的角为θ,它们的公垂线段1AA 的长度为d .在直线a ,b 上分别取点E ,F ,设1A E m =,AF n =.求证:EF =1993年高考试题选(立体几何)1.(1993时,圆锥的轴截面顶角是A .45B .60C .90D .120 2.(1993·全国卷·文理科)若正棱锥的底面边长与侧棱长相等,则该棱锥一点不是A .三棱锥B .四棱锥C .五棱锥D .六棱锥 3.(1993·全国卷·文理科)如果圆柱轴截面的周长l 为定值,那么圆柱体积的最大值是A .3()6l πB .3()3l πC .3()4lπ D .31()44l π4.(1993·全国卷·理科)已知异面直线a 与b 所成的角为50,P 为空间一定点,则过点P 且与a ,b 所成的角都是30的直线有且仅有A .1条B .2条C .3条D .4条 5.(1993·全国卷·文科)在正方体1111A B C D ABCD -中,M ,N 分别是棱1A A 和1B B 的中点,若θ为直线CM 与1D N 所成的角,则sin θ=A .19B .23C 6.(1993·全国卷·文理科)在半径为30cm 的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为120,若要光源恰好照亮整个广场,则其高度应为 m (精确到0.1m ).7.(1993·全国卷·文理科)如图,111A B C ABC -是直三棱柱,过点1A ,B ,1C 的平面和平面ABC 的交线记作l .(Ⅰ)判定直线11A C 和l 的位置关系,并加以证明;(Ⅱ)若11A A =,4AB =,3BC =,90ABC ∠=,求顶点1A 到直线l 的距离.1994年高考试题选(立体几何)1.(1994·全国卷·文理科)已知正六棱台的上、下底面边长分别为2和4,高为2,则其体积为A. B...2.(1994·全国卷·文理科)对于直线m ,n 和平面α,β,αβ⊥的一个充分条件是A .m n ⊥,m ∥n ,n ∥βB .m n ⊥,m αβ=,n α⊆C .m ∥n ,n β⊥,m β⊆D .m ∥n ,m α⊥,n β⊥ 3.(1994·全国卷·文理科)已知过球面上A ,B ,C 三点的截面和球心的距离等于球半径的一半,且2AB BC CA ===,则球面面积是A .169π B .83π C .4π D .649π4.(1994·全国卷·文理科)设圆锥底面圆周上两点A ,B 间的距离为2,圆锥顶点到直线AB的距离为,AB 和圆锥的轴的距离为1,则该圆锥的体积为 .5.(1994·全国卷·理科)如图,已知111A B C ABC -是正三棱柱,D 是AC 中点.(Ⅰ)证明1AB ∥平面1DBC ;ABCEFDA 1B 1C 1(Ⅱ)假设1AB 1BC ⊥,求以1BC 为棱,1DBC 与1CBC 为面的二面角α的度数.6.(1994·全国卷·文科)如图,已知111A B C ABC -是正三棱柱,D 是AC 中点.(Ⅰ)证明1AB ∥平面1DBC ;(Ⅱ)假设1AB 1BC ⊥,2BC =,求线段1AB 在侧面11B BCC 上的射影长.1995年高考试题选(立体几何)1.(1995·全国卷·文理科)正方体的全面积是2a ,它的顶点都在球面上,这个球的表面积是 A .23a π B .22a π C .22a π D .23a π2.(1995·全国卷·文理科)已知直线l ⊥平面α,直线m ⊂平面β,有下面四个命题:①α∥βl m ⇒⊥;②l αβ⊥⇒∥m ;③l ∥m αβ⇒⊥;④l m ⊥⇒α∥β.其中正确的两个命题是A .①与②B .③与④C .②与④D .①与③3.(1995·全国卷·理科)如图,111A B C ABC -是直三棱柱,90BCA ∠=,点1D ,1F 分别是11A B ,11A C 的中点,若1BC CA CC ==,则1BD 与1AF 所成的角A BCA 1B 1C 1D A BCA 1B 1C 1 D的余弦值是 A.10 B .12C.15 D.103.(1995·全国卷·文科)如图,1111A B C D ABCD -是正方体,1111114A B B E D F ==, 则1BE 与1DF 所成的角的余弦值是 A .1517 B .12 C .817D.4.(1995·全国卷·文理科)已知圆台上、下底面圆周都在球面上,且下底面过球心,母线与底面所成的角为3π,则圆台的体积与球的体积之比为 .5.(1995·全国卷·文理科)如图,圆柱的轴截面ABCD 是正方形,点E 在底面的圆周上,AF DE ⊥,F 是垂足. (Ⅰ)求证:AF DB ⊥;(Ⅱ)如果圆柱与三棱锥D ABE -的体积的比等于3π,求直线DE 与平ABCD 所成的角.ABCA 1B 1D 1 F 1C 1ABCA 1B 1D 1E 1F 1C 1D1996年高考试题选(立体几何)1.(1996·全国卷·文理科)如果直线l ,m 与平面α,β,γ满足:l βγ=,l ∥α,m α⊂和m γ⊥,那么必有A .αγ⊥且l m ⊥B .αγ⊥且m ∥βC .m ∥β且l m ⊥D .α∥β且αγ⊥2.(1996·全国卷·文理科)将边长为a 的正方形ABCD 沿对角线AC 折起,使得BD a =,则三棱锥D ABC -的体积为A .36aB .312a C3.(1996·全国卷·理科)母线长为l 的圆锥体积最大时,其侧面展开图圆心角ϕ等于 A.3 B.3CD.3 4.(1996·全国卷·文科)圆锥的母线长为1,侧面展开图圆心角为240,则该圆锥的体积是 A.81 B .881π C.81 D .1081π 4.(1996·全国卷·文理科)如图,正方形ABCD 所在平面与正方形ABEF 所在平面成60的二面角,则异面直线AD 与BF 所成角的余弦值是 .5.(1996·全国卷·文理科)如图,在正三棱柱111ABC A B C -中,E 在1BB 上,截面1A EC ⊥侧面11AAC C . (Ⅰ)求证:1BE EB =;ABCDE F注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ). (Ⅰ)证明:在截面1A EC 内,过E 作1EG A C ⊥,G 是垂足. ①∵∴EG ⊥侧面1AC ;取AC 的中点F ,连接BF ,FG ,由AB BC =,BF AC ⊥, ②∵∴BF ⊥侧面1AC ;得BF ∥EG ,BF ,EG 确定一个平面,交侧面1AC 于FG . ③∵∴BE ∥FG ,四边形BEFG 是平行四边形,BE FG =, ④∵∴FG ∥1AA ,1AA C ∆∽FGC ∆,⑤∵∴111122FG AA BB ==,112BE BB =,故1BE EB =(Ⅱ)若111AA A B =,求平面1A EC 与平面111A B C 所成二面角(锐角)的度数.7.(1996·全国卷·文理科)如图,在正三棱柱111ABC A B C -中,113AB AA =a =,E ,F 分别是1BB ,1CC 上的点.且BE a =,2CF a =.(Ⅰ)求证:平面AEF ⊥平面ACF ; (Ⅱ)求三棱锥1A AEF -的体积.1997年高考试题选(立体几何)1.(1997·全国卷·文理科)已知三棱锥D ABC -的三个测面与底面全等,且AB AC ==2BC =,则以BC 为棱,面BCD 与面BCA 为面的二面角的大小ABCEA 1B 1C 1是 A.arccos3 B .1arccos 3 C .2πD .23π 2.(1997·全国卷·文理科)长方体一个顶点上三条棱的长分别为3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是A. B. C .50π D .200π 3.(1997·全国卷·文理科)圆台上,下底面积分别为π,4π,侧面积为6π,这个圆台的体积是 AB. CD4.(1997·全国卷·文理科)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有A .150种B .147种C .144种D .141种 5.(1997·全国卷·文理科)已知m ,l 是直线,α,β是平面,给出下列命题: ①若l 垂直于α内的两条相交直线,则l ⊥α; ②若l 平行于α,则l 平行与α内的所有直线; ③若m α⊂,l β⊂,且l m ⊥,则αβ⊥; ④若l β⊂,且l α⊥,则αβ⊥; ⑤若m α⊂,l β⊂,且α∥β,则m ∥l .其中正确的命题的序号是 .(注:把你认为正确的命题的序号都.写上) 6.(1997·全国卷·文理科)如图,在正方体1111ABCD A B C D -中,E ,F 分别是1BB ,CD 的中点. (Ⅰ)证明:1AD D F ⊥; (Ⅱ)求AE 与1D F 所成的角; (Ⅲ)证明:面AED ⊥面1A FD ;(Ⅳ)设12AA =,求三棱锥11F A ED -的体积.A BCDA 1B 1C 1D 1EF1998年高考试题选(立体几何)1.(1998·全国卷·文理科)已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为A .120B .150C .180D .240 2.(1998·全国卷·文理科)如果棱台的两底面积分别是S ,S ',中截面的面积是0S ,那么A.=.0S =.02S S S '=+ D .202S SS '= 3.(1998·全国卷·文理科)球面上有3个点,其中任意两点的球面距离都等于大圆周长的16,经过这3个点的小圆的周长为4π,那么这个球的半径为A...2 D4.(1998·全国卷·文理科)如图,在直四棱柱1111A B C D ABCD -中,当底面四边形ABCD 满足条件 时,有111AC B D ⊥. (注:填上一种你认为正确的一种条件即可,不必考虑所有可能的情形.)5.(1998·全国卷·文理)已知斜三棱柱111ABC A B C -的侧面11A ACC 与底面垂直,90ABC ∠=,2BC =,AC =11AA A C ⊥,11AA A C =. (Ⅰ)求侧棱1AA 与底面ABC 所成角的大小; (Ⅱ)求侧面11A ABB 与底面ABC 所成二面角的大小; (Ⅲ)求顶点C 到侧面11A ABB 的距离.A BCDA 1B 1C 1D 11999年高考试题选(立体几何)1.(1999·全国卷·文理科)如图,在多面体ABCDEF 中,已知面ABCD 是边长为3的正方形,EF ∥AB ,32EF =,EF 与面AC 的距离为2,则该多面体的体积为A .29B .5C .6D .2152.(1999·全国卷·文理科)如果圆台的上底面半径为5,下底面半径为R ,中截面把圆台分为上、下两个圆台,它们的侧面积的比为1:2,那么R = A .10 B .15 C .20 D .25 3.(1999·全国卷·文理科)若干毫升水倒入底面半径为cm 2的圆柱形器皿中,量得水面的高度为cm 6,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是A .cm 36B .cm 6C .cm 3182D .cm 3123 4.(1999·全国卷·文理科)α,β是两个不同的平面,m ,n 是平面α及β之外的两条不同直线,给出四个论断:①m ⊥n ,②α⊥β,③n ⊥β,④m ⊥α, 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题: .5.(1999·全国卷·文理科)如图,已知正四棱柱1111D C B A ABCD -,点E 在棱D D 1上,截面EAC ∥B D 1,且面EAC 与底面ABCD 所成的角为45,AB a =. (Ⅰ)求截面EAC 的面积;ABCA 1B 1C 1ABCDEF(Ⅱ)求异面直线11B A 与AC 之间的距离; (Ⅲ)求三棱锥EAC B 1的体积.ABCDE A 1B 1C 1D 1。
DA1985年广东数学(理工类).doc
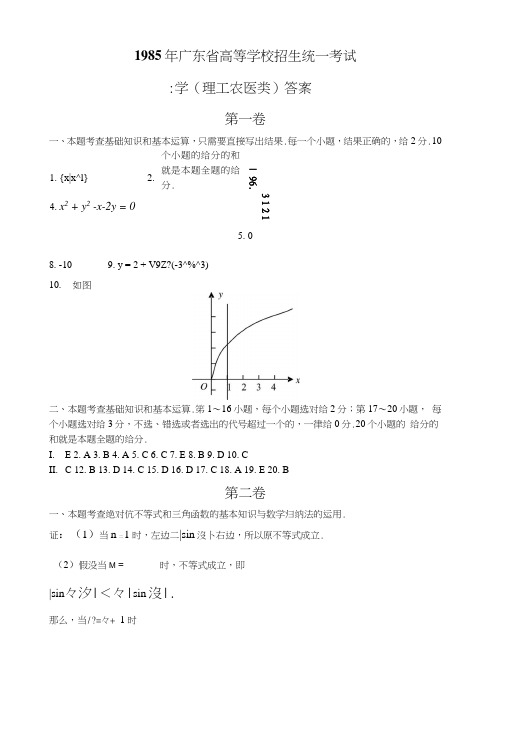
1985年广东省高等学校招生统一考试:学(理工农医类)答案第一卷一、本题考查基础知识和基本运算,只需要直接写出结果.每一个小题,结果正确的,给2 分.10个小题的给分的和就是本题全题的给分.5. 08. -10 9. y = 2 + V9Z?(-3^%^3)10. 如图二、本题考查基础知识和基本运算.笫1〜16小题,每个小题选对给2分;第17〜20小题, 每个小题选对给3分,不选、错选或者选出的代号超过一个的,一律给0分.20个小题的 给分的和就是本题全题的给分.I. E 2. A 3. B 4. A 5. C 6. C 7. E 8. B 9. D 10. CII. C 12. B 13. D 14. C 15. D 16. D 17. C 18. A 19. E 20. B第二卷一、本题考查绝对伉不等式和三角函数的基本知识与数学归纳法的运用. 证:(1)当n 二1时,左边二|sin 沒卜右边,所以原不等式成立.(2)假没当M = 时,不等式成立,即|sin 々汐|<々|sin 沒|.那么,当/?=々+ 1时3 1 2 1 | 96.1. {x|x^l}2.4. x 2 + y 2 -x-2y = 0| s'm(k +1)^ |=| sin k3 cos 6 + cos kd sin 6 \ sin kdcos沒 | +1 cos 々汐sin 沒 | =| sin k3\\ cos沒 | +1 cos據 || sin 沒 |sin 々汐 | +1 sin 沒 | sin 汐 | +1 sin 汐 |= (々 + l)|sin 沒 |.这就是说,原不等式对于/2 = & + 1成立. 根裾(1)和(2),原不等式对于任意自然数n 都成立.二、本题考查空间的两条直线的位罝关系,二面角人小的计算以及空间想象能力和逻辑推理 能力.(1) 证:•••/15(? — 451(?1是直三棱住,/. 丄底而y4fiC .•••C£c 平面 AfiC ,•••C£iA4I .又芯是等腰三角形/15C 底边A5的中点,/.C£丄故C£丄平而V AB, c=平面 ABB }A }t :. C£ 丄 .(2) 证:•••(?£ 丄 AS, C£ 丄 Ag,•••C£ 丄平面过£作££> 丄 AB,,垂足为 £>,£Z)c 平面?ISSA, /.C£ 丄 ££). 故££>是C£和Ag 所在的异而直线的距离. 在 RtA/lBfijDRtA/lDE 中,ZA 公共, 人 AABB,⑺△/AD£,即 £D 二AE叫. 'BB, AB, AB,••MC 二BC 二2,ZACB 二90°,/. AB = 272, AE = -AB = y/2 .2又在RtAABB,屮,BB'=4, A AB } == Vs + 16 = 2^6 .(3)解:Y££>丄C£丄侧而连结CZ),依三垂线定理有CD 丄,故ZCD£是截面CAB,和侧面ABB,4所成的二而角的平面角,且力锐角.C£是RtAAfiCED2A /62^3丁(cm)的斜边上的中线,故C£ = 1/IS =人,2义 ED =,于是,在 RtACED 中,tgZCDE = — = —3ED 2故截面CAB,和侧面ABB,A,所成的较小的二面角等于arctg三、本题考查二次函数与对数函数的基本性质,不等式的证明和不等式的解法(1)证:当meM 时,有m 〉l ,从而对所有的实数x 都有 X 2 - 4A /U -+ 4m 2 + mH ——-—= (x- 2m)2+ m H ——-—m H ——-—> 0对所有的实数x 都有意义.反之,如果/00对所有的实数x 都有意义,则对所有的实数X ,都有Af^T — "2 + 1 即"__或 m-i由于上式左端的分子总是正数,所以它的分母m-1〉0,即m 〉l,从而me A/ (2)解:因为以3为底的对数函数是增函数,所以,从①式得又因为/(2m) = log:(3)证:当meAl 时,有m 〉l ,所以m-\——-—=(m-l)H ——; + 1》2' (m-1) ------- h l =32m-\ 于是,当me A/时,函数/(x) = log. x 2 - 4z?tv + 4m 2 + m +x 2 - 4/?1¥ + 4m 2 +m +m-\〉0,而当x = 2m 时,上戎变为m +"2 — 1>0 >0.f ⑽=log(x-2m)2 +m +m-\彡 log 3m-\所以,当me W 时,/⑺的最小值是log.777 +m-i卜.式两端取以3为底的对数,得log. log. 3 = 1.m-l于是,根据(2)的结果可知,对每一个me Al, /(X)的最小值都不小于1.四、本题考查二次曲线的基础知识,曲线参数方程的应用,以及逻辑推理能力和计算能力. (1)证:将曲线I ,II 的方程化为直角坐标方程(x-m)2 y 2 2 A 3^(4 3I 2)当m = 4时,椭圆I 屮心的坐标力(4,0),长轴在;v 轴上,长半轴长==短半轴长b =忑,从而,半焦距C = A /V 2 =1,焦点坐标(4士G 0)即为(5,0)和(3,0),准线方程2x = 4±f-,即为x = 8和 % = 0 .由抛物线II 的方程可知:该抛物线以x 轴力对称轴,开II 向右,顶点的坐标力即为x = 0.所以,椭圆I 的左焦点和左准线分别与抛物线II 的焦点和准线重合. (2)证:将曲线I ,II 的直角坐标方程联立(*)] 4 3 V / Z 2 \y 2 =6 x ——.②2那么,曲线I, II 有交点o 方程组(*)有实数解%,>,.这时,(%,y)为交点. 将②代入①,整理得%2+(8 — 2m)x + m 2—16 = 0;③又由于X-— = 1彡0,故方程组(*)有实数解<=> 方程③有不小于一的实根. 2 6 2 方程③的两个根为x, = -(4-m) + 2^/2(4 - m),=_(4 _ /zz) - 2^2(4 - ni).可见,当且仅当4一时,又2是实根,且这时x 2<0.,焦点至顶点的距离是*4,从而焦点的坐标为3 p—-------------------2 23由此可知:厕有不小于,实根㉞满足不等式组4 — m X),-(4-m) + 2V2(4^m)彡 、 2解此不等式组的解集综合起來,即得:当且仅当时,椭圆I 与抛物线II 有交点.(3)因为椭圆I 屮心的坐标力(m ,0),所以,曲线I ,II 的交点(%,>’)满足题设,等价于x ,y满足x 2 + y 2=(x —m)2 + y 2,即是m(m -2x) = Q, ①由(2)的证明可知,曲线I ,II 的交点横平标是将它代入①式,得知所求的m 值应满足方程解方程:由"2 = 0得叫=0,由8-爪-4^/2(4-爪)二0.即m 2 +16m — 64 = 0 ,得’712=86/^_1)6[_去,备+1) G [―,(应舍去)直接检验可知,当m 二0或8(^-1)时,曲线I, II 的交点满足题设条件,故所求的m 的 值是0和8(^ — 1).五、木题考查利用导数求函数极伉和讨论方程的不同的实根个数的能力.(1)解:f\x) = 5/ -5 = 5(/ -1) •令/W = 0,即5(/—1) = 0,这个方程的实根是x = ±l .而 /(-l) = -l + 5 + C 二 C + 4,x = (m -4) + 2^/2(4-771),■[一丄4m[8-m-4^2(4-m)] = 0,/(l) = l-5 + C = C-4.函数/(JV)的变化怙况如下表所示:所以/(%)的极大值是/(—I) = C + 4, /(%)的极小值是/(I) = C-4.(2)证:用反证法证明.假如方程/(x) = 0的不同实根个数大于3,则至少可找到四个不同的实数七 < x2 < < x4,使得/(x,) = /(%2) = f(x3) = /(x4) = 0,根据微分中值定理,有x2),使得由式①及%2〉七,可知/(3) = 0.这表明方程/(x) = 0在区间(什易)屮至少有一个实根沒1;同理可证:方程/\x) = 0在区间(x2, %3), (%3, %4)中分别有实根巧,A .显然,有即方程/Xr) = O至少有三个不同的实根,这与(1)中所得的结果相矛盾,从而,方程/(x) = 0的不同实根的个数不大于3.。
1985福建高考数学

1985福建高考数学一、说明1985年是福建省高考历史上非常重要的一年,因为那一年的高考出现了数学题目中的“一题多解”事件,引起了广泛的争议和讨论。
二、事件回顾当年的数学试卷中,有一道只有两行字的填空题:已知$\frac{a}{b}+\frac{c}{d}=1$,且 $a$,$b$,$c$,$d$均为正整数,求$a+b+c+d$ 的值。
但如果仅从这道题目中可以发现很多的数学技巧,例如杨辉三角,质因数分解等。
然而,当时这道题引起了一些考生之间的争议,因为这道题目出现了“一题多解”的情况。
三、讨论与评价1. 辩方观点一些考生认为,由于题目中条件不足以唯一决定各个变量的取值,因此这道题目应当存在多个不同的解法。
他们认为,考试大纲并没有明确规定一题只能有一种解法,所以即使存在多种解法,也应该能够得分。
2. 正方观点另外一些考生则持相反意见,认为这道数学题目中应该只存在一种正确的答案。
他们认为,这是因为这道题目中用语不明确,因此导致了考生之间对于求解方法的理解存在争议。
因此,如果存在多种解法,就会导致评分的不公正。
3. 官方回应最后,高考主管部门也对此事进行了回应。
据官方表示,根据高考考试原则和规定,题目应该要具有唯一的解法,多解的情况应该予以惩罚。
但由于当时没有明确规定,考试成绩受到了影响,所以对于当时的这道数学题目,评分标准进行了调整,以免因此影响到了考生的公正评分。
四、结语虽然这起“一题多解”的事件在当时引起了一些争议和争端,但对于数学教育而言,这道题目的出现更多的是为了向考生展示同一个问题不同解法的奥妙所在,以及激发学生的创造力和想象力。
因此,这起事件也可以看做是福建省高考数学史上的一件趣闻。
1985年全国统一高考数学考试卷(理科)

1985年全国统一高考数学试卷〔理科〕一、选择题〔共5小题,每一小题3分,总分为15分〕的体积是〔〕π为周期的偶函数?〔〕5.〔3分〕用1,2,3,4,5这五个数字,可以组成比20000大,并且百位数不是数字3的没有重复二、解答题〔共13小题,总分为90分〕6.〔4分〕求方程解集.7.〔4分〕设|a|≤1,求arccosa+arccos〔﹣a〕的值.8.〔4分〕求曲线y2=﹣16x+64的焦点.9.〔4分〕设〔3x﹣1〕6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,求a6+a5+a4+a3+a2+a1+a0的值.10.〔4分〕设函数f〔x〕的定义域是[0,1],求函数f〔x2〕的定义域.11.〔7分〕解方程log4〔3﹣x〕+log〔3+x〕=log4〔1﹣x〕+log〔2x+1〕.12.〔7分〕解不等式13.〔15分〕如图,设平面AC和BD相交于BC,它们所成的一个二面角为45°,P为平面AC的一点,Q为面BD的一点,直线MQ是直线PQ在平面BD的射影,并且M在BC上又设PQ与平面BD 所成的角为β,∠CMQ=θ〔0°<θ<90°〕,线段PM的长为a,求线段PQ的长.14.〔15分〕设O为复平面的原点,Z1和Z2为复平面的两动点,并且满足:〔1〕Z1和Z2所对应的复数的辐角分别为定值θ和﹣θ;〔2〕△OZ1Z2的面积为定值S求△OZ1Z2的重心Z所对应的复数的模的最小值.15.〔15分〕两点P〔﹣2,2〕,Q〔0,2〕以与一条直线:L:y=x,设长为的线段AB在直线L上移动,如图,求直线PA和QB的交点M的轨迹方程.〔要求把结果写成普通方程〕16.〔14分〕设,〔1〕证明不等式对所有的正整数n都成立;〔2〕设,用定义证明17.〔12分〕设a,b是两个实数,A={〔x,y〕|x=n,y=na+b,n是整数},B={〔x,y〕|x=m,y=3m2+15,m是整数},C={〔x,y〕|x2+y2≤144},是平面XOY的点集合,讨论是否存在a和b使得〔1〕A∩B≠φ〔φ表示空集〕,〔2〕〔a,b〕∈C同时成立.18.曲线y=x3﹣6x2+11x﹣6.在它对应于x∈[0,2]的弧段上求一点P,使得曲线在该点的切线在y轴上的截距为最小,并求出这个最小值.1985年全国统一高考数学试卷〔理科〕参考答案与试题解析一、选择题〔共5小题,每一小题3分,总分为15分〕的体积是〔〕A.B.C.D.2.〔3分〕的〔〕A.必要条件B.充分条件C.充分必要条件D.既不充分又不必要的条件π为周期的偶函数?〔〕5.〔3分〕用1,2,3,4,5这五个数字,可以组成比20000大,并且百位数不是数字3的没有重复二、解答题〔共13小题,总分为90分〕6.〔4分〕求方程解集.7.〔4分〕设|a|≤1,求arccosa+arccos〔﹣a〕的值.8.〔4分〕求曲线y2=﹣16x+64的焦点.9.〔4分〕设〔3x﹣1〕6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,求a6+a5+a4+a3+a2+a1+a0的值.10.〔4分〕设函数f〔x〕的定义域是[0,1],求函数f〔x2〕的定义域.11.〔7分〕解方程log4〔3﹣x〕+log〔3+x〕=log4〔1﹣x〕+log〔2x+1〕.考点:对数的运算性质;对数函数的定义域.专题:计算题.分析:把方程移项,再化为同底的对数,利用对数性质解出自变量的值,由于不是恒等变形,注意验根.解答:解:由原对数方程得,解这个方程,得到x1=0,x2=7.检验:x=7是增根,故x=0是原方程的根.点评:此题考查对数的运算性质,对数函数的定义域.12.〔7分〕解不等式考点:其他不等式的解法.专题:计算题;分类讨论.分析:分类讨论,当时不等式成立,解出不等式解集即可,当时,将不等式的两边平方,解出解集即可,最后求出两个解集的并集即可.解答:解:,解得;〔4分〕或,解得﹣1≤x<2;〔8分〕综上所述,解得〔12分〕点评:此题主要考查根号下的不等式的求解.13.〔15分〕如图,设平面AC和BD相交于BC,它们所成的一个二面角为45°,P为平面AC的一点,Q为面BD的一点,直线MQ是直线PQ在平面BD的射影,并且M在BC上又设PQ与平面BD所成的角为β,∠CMQ=θ〔0°<θ<90°〕,线段PM的长为a,求线段PQ的长.考点:平面与平面之间的位置关系.专题:计算题.分析:过点P作平面BD的垂线,垂足为R,由PQ与平面BD所成的角为β,要求PQ,可根据,故我们要先求PR值,而由二面角的平面角为45°,我们可得NR=PR,故我们要先根据MR=,与a2=PR2+MR2,求出NR的值.解答:解:自点P作平面BD的垂线,垂足为R,由于直线MQ是直线PQ在平面BD的射影,所以R在MQ上,过R作BC的垂线,设垂足为N,如此PN⊥BC〔三垂线定理因此∠PNR是所给二面角的平面角,所以∠PNR=45°由于直线MQ是直线PQ在平面BD的射影,所以∠PQR=β在Rt△PNR中,NR=PRcot45°,所以NR=PR.在Rt△MNR中,MR=,在Rt△PMR中,,又0°<θ<90°,所以.在Rt△PRQ中,.故线段PQ的长为.点评:此题考查的知识点是平面与平面间的位置关系,二面角,解三角形,根据条件由未知的结论利用分析法寻求解题思路是解题的关键.14.〔15分〕设O为复平面的原点,Z1和Z2为复平面的两动点,并且满足:〔1〕Z1和Z2所对应的复数的辐角分别为定值θ和﹣θ;〔2〕△OZ1Z2的面积为定值S求△OZ1Z2的重心Z所对应的复数的模的最小值.考点:复数的根本概念;复数求模.专题:综合题.分析:设出Z1,Z2和Z对应的复数分别为z1,z2和z,由于Z是△OZ1Z2的重心,表示其关系,求解即可.解答:解:设Z1,Z2和Z对应的复数分别为z1,z2和z,其中z1=r1〔coθ+isinθ〕,z2=r2〔coθ﹣isinθ〕.由于Z是△OZ1Z2的重心,根据复数加法的几何意义,如此有3z=z1+z2=〔r1+r2〕cosθ+〔r1﹣r2〕isinθ.于是|3z|2=〔r1+r2〕2cos2θ+〔r1﹣r2〕2sin2θ=〔r1﹣r2〕2cos2θ+4r1r2cos2θ+〔r1﹣r2〕2sin2θ=〔r1﹣r2〕2+4r1r2cos2θ又知△OZ1Z2的面积为定值S与,所以,即由此,故当r1=r2=时,|z|最小,且|z|最小值=.点评:此题考查复数的根本概念,复数求模,是中档题.15.〔15分〕两点P〔﹣2,2〕,Q〔0,2〕以与一条直线:L:y=x,设长为的线段AB在直线L上移动,如图,求直线PA和QB的交点M的轨迹方程.〔要求把结果写成普通方程〕考点:轨迹方程.专题:计算题;交轨法.分析:根据题意,设点A和B分别是〔a,a〕和〔a+1,a+1〕,直线PA的方程是,直线QB的方程直线PA和QB平行,无交点〔2〕当a≠0时,直线PA与QB相交,设交点为M〔x,y〕,由〔2〕式得,∴将上述两式代入〔1〕式,得整理得x2﹣y2+2x﹣2y+8=0,即当a=﹣2或a=﹣1时,直线PA和QB仍然相交,并且交点坐标也满足〔*〕式所以〔*〕式即为所求动点的轨迹方程.点评:此题考查轨迹方程的求法,解题时要认真审题,仔细分析,注意挖掘题设中的隐含条件,合理地选取公式.16.〔14分〕设,〔1〕证明不等式对所有的正整数n都成立;〔2〕设,用定义证明考点:不等式的证明;极限与其运算.专题:证明题.分析:〔1〕考虑a n和式的通项,先对其进展放缩,结合数列的求和公式即可证得;〔2〕欲用定义证明即证对任意指定的正数ε,要使.解答:证:〔1〕由不等式17.〔12分〕设a,b是两个实数,A={〔x,y〕|x=n,y=na+b,n是整数},B={〔x,y〕|x=m,y=3m2+15,m是整数},C={〔x,y〕|x2+y2≤144},是平面XOY的点集合,讨论是否存在a和b使得〔1〕A∩B≠φ〔φ表示空集〕,〔2〕〔a,b〕∈C同时成立.18.曲线y=x3﹣6x2+11x﹣6.在它对应于x∈[0,2]的弧段上求一点P,使得曲线在该点的切线在y轴上的截距为最小,并求出这个最小值.。
1985年高考数学题

1986年高考数学题1. 已知平面直角坐标系上直线L: $2x-y+3=0$ , M($\frac{7}{4}$,1) , 点P到L的距离为 $\frac{1}{2}$ 。
求:(1) 直线L的斜率;(2) 点P到直线L的垂线方程。
2. 若函数$f(x)=ax^2+bx+c$ ($a \neq 0$)的图象恰与x轴相切,且过点(1,2),则a,b,c 的值满足的关系为________。
3. 已知3阶矩阵$A = \begin{pmatrix}1 & -2 & 2\\2 & 2 & -1\\0 & 1 & 0\end{pmatrix}$ 。
求:(1) A的伴随矩阵;(2) $A^{-1}$ 。
以下是这三道题目的解答:1.(1)直线L的斜率为 $k = \frac{2}{1} = 2$。
(2)设点P到直线L的垂线为直线N,则直线N的斜率为 $-\frac{1}{2}$,直线N的方程为 $y-1 = -\frac{1}{2}(x-\frac{7}{4})$ 或 $x+2y-{\frac{15}{4}}=0$。
2.因为函数$f(x)$与x轴相切,所以$f(1) = 0$ 且 $f'(1) = 0$。
解得:$a+b+c=2$ 且 $2a+b=0$。
因为 $a \neq 0$,所以可以解得 $a = 1$ 且 $b = -2$,进而得到 $c = 3$。
因此,a,b,c的值满足 $a=1, b=-2, c=3$。
3.(1)A的伴随矩阵为 $A^*=\begin{pmatrix}-1 & 1 & 4\\-2 & 2 & 5\\-2 & 2 & 4\end{pmatrix}$。
(2)A的行列式为 $|A|=1$,所以 A 可逆。
根据矩阵求逆的公式,可以得到 $A^{-1}=\frac{1}{|A|}A^*=\begin{pmatrix}-1 & 1 & 4\\-2 & 2 & 5\\-2 & 2 & 4\end{pmatrix}$。
高考数学普通高等学校招生全国统一考试85

高考数学普通高等学校招生全国统一考试85高考数学普通高等学校招生全国统一考试85数学试题(文史类)分选择题和非选择题两部分. 满分150分. 考试时间120分钟.注意事项:1.答题前,务必将自己的姓名.准考证号填写在答题卡规定的位置上.2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦擦干净后,再选涂其他答案标号.3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.4.所有题目必须在答题卡上作答,在试题卷上答题无效.5.考试结束后,将试题卷和答题卡一并交回.参考公式:如果事件A.B互斥,那么P(A+B)=P(A)+P(B)如果事件A.B相互独立,那么P(A·B)=P(A)·P(B)如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率第一部分(选择题共50分)一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个备选项中,只有一项是符合题目要求的.1.圆关于原点(0,0)对称的圆的方程为( )A. B.C. D.解:∵圆的圆心(-2,0)关于原点对称的点为(2,0),∴圆关于原点对称的圆为(_-2)2+y2=5,选(A).2. ( )A.B. C.D.解:,选(D)3.若函数是定义在R上的偶函数,在上是减函数,且,则使得的取值范围是( )A. B.C.D.(-2,2)解:∵函数是定义在R上的偶函数,在上是减函数,且,∴f(-2)=0, 在上的_的取值范围是,又由对称性,∴在R上f_)_lt;0仰_的取值范围为(-2,2),选(D)4.设向量a=(-1,2),b=(2,-1),则(a·b)(a+b)等于( )A.(1,1) B.(-4,-4) C.-4D.(-2,-2)解:(a·b)(a+b)=[-2+(-2)](1,1)=(-4,-4),选(B)5.不等式组的解集为( )A.B.C.D.解∵_-2_lt;2的解集为(0,4),log2(_2-1)_gt;1的解集为,∴不等式组的解集,选(C)6.已知均为锐角,若的( )A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件解:∵由.均为锐角,得0_lt;α_lt;α+β_lt; ∴sin(α+β)_gt;sinα,但.均为锐角,sinα_lt;sin(α+β),不一定能推出α+β_lt;,如α=,β=就是一个反例,选(C)7.对于不重合的两个平面,给定下列条件:①存在平面,使得α.β都垂直于;②存在平面,使得α.β都平行于;③存在直线,直线,使得;④存在异面直线l.m,使得其中,可以判定α与β平行的条件有( )A.1个B.2个C.3个D.4个解:命题①③是真命题,选(B)8.若展开式中含的项的系数等于含_的项的系数的8倍,则n等于( )A.5 B.7 C.9 D.11解:的项的系数为,_的项的系数为,由题意得=8解之得n=5,选(A)一了9.若动点在曲线上变化,则的最大值为 ( )A. B.C.D.解:由题意可设_=2cosα,y=bsinα,则_2+2y=4cos2α+2bsinα=-4sin2α+2bsinα+4=-2(sin2α-bsinα-2)=-2(sinα-)2+4+,∴的最大值为,选(A)10.有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各连接中点,已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )A.4 B.5C.6 D.7解:k层塔形的各层立方体的边长,增加的表面积以及k层塔形的表面积一览表如下:第k个立方体边长aka!=2a2=a3=1a4=a5=a6=第k层立方体增加的面积bk b1=24b2=8b3=4b4=2b5=1b6=K层塔形的表面积SkS1=24S2=32S3=36S4=38S5=39S6=由上表可以看出要使塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是6层,选(C)第二部分(非选择题共100分)二.填空题:本大题共6小题,每小题4分,共24分. 把答案填写在答题卡相应位置上.11.若集合,则.解:∵A=(-4,3),B=(2,5),∴A∩B={_2_lt;__lt;3}12.曲线在点(1,1)处的切线与_轴.直线所围成的三角形的面积为.解:∵=3_2,∵在(1,1)处切线为y-1=3(_-1),令y=0,得切线与_轴交点(),切线与直线_=2交于(2,4),∴曲线处的切线与_轴.直线所围成的三角形的面积为S=..13.已知均为锐角,且.解:由已知得1-tanαtanβ=tanα-tanβ,∴tanα=.14.若的最大值是.解:令_=2cosα,y=2sinα,则_-y=2cosα-2sinα=2sin()≤2,∴若的最大值是215.若10把钥匙中只有2把能打开某锁,则从中任取2把能将该锁打开的概率为.解;P=16.已知是圆为圆心)上一动点,线段AB的垂直平分线交BF于P,则动点P的轨迹方程为.解:由题意可知,动点P的轨迹是椭圆,这个椭圆的焦点是A(-,0)和F(,0),定长2a=圆F的半径2,因而动点P的轨迹方程为三.解答题:本大题共6小题,共76分. 解答应写出文字说明.证明过程或演算步骤.17.(本小题满分13分)若函数的最大值为,试确定常数a的值.18.(本小题满分13分)加工某种零件需经过三道工序,设第一.二.三道工序的合格率分别为..,且各道工序互不影响.(Ⅰ)求该种零件的合格率;(Ⅱ)从该种零件中任取3件,求恰好取到一件合格品的概率和至少取到一件合格品的概率.19.(本小题满分13分)设函数R.(1)若处取得极值,求常数a的值;(2)若上为增函数,求a的取值范围.20.(本小题满分13分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC. 已知求(Ⅰ)异面直线PD与EC的距离;(Ⅱ)二面角E—PC—D的大小.21.(本小题满分12分)已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(1)求双曲线C的方程;(2)若直线与双曲线C恒有两个不同的交点A和B,且(其中O为原点). 求k的取值范围.22.(本小题满分12分)数列记(Ⅰ)求b1.b2.b3.b4的值;(Ⅱ)求数列的通项公式及数列的前n项和数学试题(文史类)答案一.选择题:每小题5分,满分50分.1.A2.D3.D4.B5.C6.B7.B 8.A 9.A10.C二.填空题:每小题4分,满分24分. 11.12.13.1 14. 15. 16.三.解答题:满分76分.17.(本小题13分)解:因为的最大值为的最大值为1,则所以18.(本小题13分)(Ⅰ)解:;(Ⅱ)解法一: 该种零件的合格品率为,由独立重复试验的概率公式得: 恰好取到一件合格品的概率为,至少取到一件合格品的概率为解法二:恰好取到一件合格品的概率为,至少取到一件合格品的概率为19.(本小题13分)解:(Ⅰ)因取得极值, 所以解得经检验知当为极值点.(Ⅱ)令当和上为增函数,故当上为增函数.当上为增函数,从而上也为增函数.综上所述,当上为增函数.20.(本小题13分)解法一:(Ⅰ)因PD⊥底面,故PD⊥DE,又因EC⊥PE,且DE是PE在面ABCD内的射影,由三垂直线定理的逆定理知EC⊥DE,因此DE是异面直线PD与EC的公垂线.设DE=_,因△DAE∽△CED,故(负根舍去).从而DE=1,即异面直线PD与EC的距离为1.(Ⅱ)过E作EG⊥CD交CD于G,作GH⊥PC交PC于H,连接EH. 因PD⊥底面, 故PD⊥EG,从而EG⊥面PCD.因GH⊥PC,且GH是EH在面PDC内的射影,由三垂线定理知EH⊥PC.因此∠EHG为二面角的平面角.在面PDC中,PD=,CD=2,GC=因△PDC∽△GHC,故,又故在即二面角E—PC—D的大小为解法二:(Ⅰ)以D为原点,..分别为_.y.z轴建立空间直角坐标系.由已知可得D(0,0,0),P(0,0,,C(0,2,0)设由,即由,又PD⊥DE,故DE是异面直线PD与CE的公垂线,易得,故异面直线PD. CE的距离为1.(Ⅱ)作DG⊥PC,可设G(0,y,z).由得即作EF⊥PC于F,设F(0,m,n),则由,又由F在PC上得因故平面E—PC—D的平面角的大小为向量的夹角.故即二面角E—PC—D的大小为21.(本小题12分)解:(Ⅰ)设双曲线方程为由已知得故双曲线C的方程为(Ⅱ)将由直线l与双曲线交于不同的两点得即①设,则而于是②由①.②得故k的取值范围为22.(本小题12分)解法一:(I)(II)因,故猜想因,(否则将代入递推公式会导致矛盾)故的等比数列.,解法二:(Ⅰ)由整理得(Ⅱ)由所以解法三: (Ⅰ)同解法一(Ⅱ)从而。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1985年高考理科数学试题(理工农医类)一、本题每一个小题都给出代号为A,B,C,D的四个结论,其中只有一个结论是正确的,把正确结论的代号写在题后的括号内.(1)如果正方体ABCD1A′B′C′D′的棱长为a,那么四面体A′1ABD的体积是【】[Key] 一、本题考查基本概念和基本运算.(1)D;(A)必要条件(B)充分条件(C)充分必要条件(D)既不充分又不必要的条件【】[Key] (2)A;(A)y=x2(x∈R)(B)y=│sinx│(x∈R)(C)y=cos2x(x∈R)(D)y=e sin2x(x∈R)【】[Key] (3)B;(4)极坐标方程ρ=asinθ(a>0)的图象是【】[Key] (4)C;(5)用1,2,3,4,5这五个数字,可以组成比20000大,并且百位数不是数字3的没有重复数字的五位数,共有(A)96个(B)78个(C)72个(D)64个【】[Key] (5)B.二、只要求直接写出结果.(2)设│a│≤1,求arccosa+arccos(-a)的值.(3)求曲线y2=-16x+64的焦点.(5)设函数f(x)的定义域是[0,1],求函数f(x2)的定义域.[Key] 二、本题考查基础知识和基本运算,只需直接写出结果.(2)π;(3)(0,0);(4)64(或26);(5)[-1,1](或{x│-1≤x≤1},或-1≤x≤1).三、(1)解方程log4(3-x)+log0.25(3+x)=log4(1-x)+log0.25(2x+1).[Key] 三、本题考查对数方程、无理不等式的解法和分析问题的能力.(1)解法一:由原对数方程得因为log0.25a=-log4a,上式变成由此得到解这个方程,得到x1=0,x2=7.检验:把x=0代入原方程,左右两边都等于0;故x=0是原方程的根.但当x=7时,由于3-x<0,1-x<0,它们的对数无意义;故x=7不是原方程的根,应舍去.因此,原对数方程的根是x=0.对原方程变形,同解法一,得x1=0,x2=7.2x+5>x2+2x+1,x2<4,即-2<x<2.但由条件x≥-1,因此-1≤x<2也是原不等式的解.综合(i),(ii),得出原不等式的解集是四、如图,设平面AC和BD相交于BC,它们所成的一个二面角为45°,P为面AC内的一点,Q为面BD内的一点.已知直线MQ是直线PQ在平面BD内的射影,并且M在BC上.又设PQ与平面BD所成的角为β,∠CMQ=θ(0°<θ<90°)线段PM的长为a.求线段PQ的长.[Key] 四、本题考查三垂线定理、二面角、斜线与平面所成的角、解三角形、空间想象能力和综合运用知识的能力.解法一:自点P作平面BD的垂线,垂足为R,由于直线MQ是直线PQ在平面BD内的射影,所以R 在MQ上,过R作BC的垂线,设垂足为N,则PN⊥BC.(三垂线定理)因此∠PNR是所给二面角的平面角,所以∠PNR=45°.由于直线MQ是直线PQ在平面BD内的射影,所以∠PQR=β.在Rt△PNR中,NR=PRctg45°,所以NR=PR.又已知0°<θ<90°,所以解法二:同解法一,得∠PQR=β.设:∠PMR=α则在Rt△PMR中,MR=acosα,PR=asinα,在Rt△MNR中,NR=MRsinθ=acosα·sinθ.又在Rt△PNR中,由于∠PNR=45°,所以PR=NR.于是asinα=acosα·sinθ,tgα=sinθ,在△PMQ中,应用正弦定理得五、设O为复平面的原点,Z1和Z2为复平面内的两个动点,并且满足:(2)△OZ1Z2的面积为定值S.求△OZ1Z2的重心Z所对应的复数的模的最小值.[Key] 五、本题考查复数的概念、复数运算的几何意义、三角恒等式、不等式以及灵活运用知识的能力.解法一:设Z1、Z2和Z对应的复数分别为z1、z2和z,其中z1=r1(cosθ+isinθ),z2=r2(cosθ-isinθ).由于Z是△OZ1Z2的重心,根据复数加法的几何意义,则有3z=z1+z2=(r1+r2)cosθ+(r1-r2)isinθ.于是│3z│2=(r1+r2)2cos2θ+(r1-r2)2sin2θ=(r1-r2)2cos2θ+4r1r2cos2θ+(r1-r2)2sin2θ=(r1-r2)2+4r1r2cos2θ.解法二:同解法一,得3z=(r1+r2)cosθ+(r1-r2)isinθ.于是│3z│2=(r1+r2)2cos2θ+(r1-r2)2sin2θ.又已知△OZ1Z2的面积为S,且r1为三角形边长,r1>0,以及sin2>θ(因[Key] 六、本题考查直线方程、两点间的距离公式、参数方程以及轨迹方程的求法.2.当a≠0时,直线PA与QB相交,设交点为M(x,y),由(2)式得将上述两式代入(1)式,得整理得x2-y2+2x-2y+8=0,(*)当a=-2或a=-1时,直线PA和QB仍然相交,并且交点坐标也满足(*)式.所以(*)式即为所求动点的轨迹方程.解法二:设直线PA和QB的交点为M(x,y).当点M与点P及点Q都不重合时,直线PM的方程是(x+2)(Y-2)=(y-2)(X+2),直线QM的方程是x(Y-2)=(y-2)X.由方程组解得直线PM和直线l的交点A的坐标为由方程组解得直线QM和直线l的交点B的坐标为根据题意,线段AB两端点A,B的横坐标有如下关系:从而得x2-y2+2x-2y+8=0,(*)即又因点M与点P或点Q重合时,M点的坐标也满足(*)式.所以(*)式即为所求动点M的轨迹方程.(1)证明不等式对所有的正整数n都成立.[Key] 七、本题考查数列和极限的基础知识,证明不等式的基本方法.(1)证法一:用数学归纳法.假设当n=k(k≥1)时不等式成立,即当n=k+1时,可得即也成立.从而不等式对所有的正整数n都成立.证法二:直接证明.由于不等式对所有的正整数k成立,把它对k从1到n(n≥1)求和,得到又因以及因此不等式对所有的正整数n都成立.(2)由(1)及b n的定义知于是八、设a,b是两个实数,A={(x,y)│x=n,y=na+b,n是整数},B={(x,y)│x=,m,y=3m2+15,m是整数},C={(x,y)│x2+y2≤144}是平面XOY内的点集合.讨论是否存在a和b使得(2)(a,b)∈C同时成立.[Key] 八、本题考查集合的基本知识,不等式的证明以及分析问题的能力.解法一:如果实数a和b使得(1)成立,于是存在整数m和n使得(n,na+b)=(m,3m2+15),即由此得出,存在整数n使得na+b=3n2+15,或写成na+b-(3n2+15)=0.这个等式表明点P(a,b)在直线l:nx+y-(3n2+15)=0上,记从原点到直线l的距离为d,于是当且仅当时上式中等号才成立.由于n是整数,因此n2≠3,所以上式中等号不可能成立.即d>12.所以,不存在实数a和b使得(1),(2)同时成立.解法二:如果实数a和b使得(1),(2)同时成立.同解法一,由于(1)成立,知存在整数n使得na+b=3n2+15,即b=3n2+15-an.(*)由(2)成立,得a2+b2≤144.把(*)式代入上式,得关于a的不等式(1+n2)a2-2n(3n2+15)a+(3n2+15)2-144≤0.(**)它的判别式Δ=4n2(3n2+15)2-4(1+n)2[(3n2+15)2-144]=-36(n2-3)2.但n是整数,n2-3≠0,因而Δ<0.又因1+n2>0,故(**)式不可能有实数解a,这就表明,不存在实数a和b使得(1)、(2)同时成立.解法三:如果实数a和b使(1)、(2)同时成立.同解法一,由(1)成立知,必存在整数n使得3n2-an-(b-15)=0.(*)于是,它的判别式非负,即Δ=a2+12b-180≥0,(**)由(**)得12b-180≥-a2.由(2)成立知a2+b2≤144,(***)即-a2≥b2-144.因此,12b-180≥b2-144,即(b-6)2≤0,由此得出b=6.把b=6代入判别式(**),得出a2≥108,但把b=6代入(***),得出a2≤108,因而必有a2=108.此时,从(*)式可解出所以,不存在实数a和b使得(1),(2)同时成立.九、(附加题,不计入总分)已知曲线y=x3-6x2+11x-6.在它对应于x∈[0,2]的弧段上求一点P,使得曲线在该点的切线在y 轴上的截距为最小,并求出这个最小值.[Key] 九、(本题分数不计入总分)本题考查导数的几何意义,利用导数解决函数的最大值、最小值问题的能力.解:已知曲线方程是y=x3-6x2+11x-6,因此y′=3x2-12x+11.在曲线上任取一点P(x0,y0),则点P处切线的斜率是点P处切线方程是设这切线与y轴的截距为r,则根据题意,要求r(它是以x0为自变量的函数)在区间[0,2]上的最小值.因为当0<x0<2时r′>0,因此r是增函数,故r在区间[0,2]的左端点x0=0处取到最小值.即在点P(0,-6)处切线在y轴上的截距最小.这个最小值是r最小值=-6.。
