28.1.1锐角三角函数(3)--三角函数值
28.1.1锐角三角函数公开课教案

28.1.1锐角三角函数学校矿泉中学授课陆叙波时间设计理念注重学生经历观察、操作等探索过程,强调学生对知识的感觉与对新知识的理解与认知。
鼓励学生自主探索与合作交流,培养学生概括的能力,使知识形成体系,并渗透数学思想方法。
教学目标1、知识目标:使学生知道当直角三角形的锐角固定时,它的对边与斜边的比值都固定这一事实,进而认识正弦(sinA).2、技能目标:经历当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一事实,发展学生的形象思维.3、情感态度与价值观:使学生体验数学活动充满着探索与创造,能积极参与数学学习活动重点使学生知道当锐角固定时,它的对边与斜边的比值是固定值这一事实,认识正弦(sinA).难点学生很难想到对任意锐角,它的对边与斜边的比值是固定值的事实,关键在于教师引导学生比较、分析,得出结论.方法体验、探索式教学课型新授课教学过程教学环节教学内容师生活动设计意图一、观察发现问题:为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?思考:1.在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?2.若斜坡与水平面所成角的度数是45°,结果会如何呢?3.若斜坡与水平面所成角的度数是40°,结果会如何呢?4.若已知出水口高度为40m,斜坡上铺设的水管长50m,那么斜坡与水平面所成角的度数是多少呢?教师提出问题,给学生一定的时间进行思考,之后可让学生进行交流。
得到在直角三角形中,如果一个锐角是30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都是12由实际需要引出新知.前两个问题学生很容易回答.主要是引起学生的回忆,并使学生意识到,本章要用到这些知识.后两个问题的设计却使学生感到疑惑,这对九年级这些好奇、好胜的学生来说,起到激起学生的学习兴趣的作用.二、探究1.请每一位同学拿出自己的三角板,分别测量并教师提出问在培养学生。
28.1 .1 锐角三角函数

cos 60 1 (3) ; 1 sin 60 tan 30
1 2005 0 (4) 2 sin 45 cos 60 ( 1 ) ( 1 2). 2
3、在Rt△ABC中,∠C = 90°,若sinA = cosA ,则tanA =
4、如果α是锐角,且sin2α+cos2 35º =1,那么α= 5、已知sinα+cosα= ,则sinα·cosα= 2 。
度。
6、若sinA=1/3,则cosA=
。
练习1:
如图,在Rt△DEF中, 若∠F=90°,EF=3,DE=5
则sin∠A=___.
4 5、如图,在△ABC中, AB=CB=5,sinA= , 5 求△ABC 的面积。
B
5
5
A
C
28.1锐角三角函数(2)
——余弦 正切
复习与探究:
B c A b a C
在 Rt ABC中, C 90
1.锐角正弦的定义
∠A的正弦: s inA
A的 对 边 BC a 斜边 AB c
方法一:从特殊到一般,仿照正弦的研究过程;
方法二:根据相似三角形的性质来说明。
如图,在Rt△ABC中,∠C=90°, ★我们把锐角A的邻边与斜边的比叫做∠A的
余弦(cosine),记作cosA, 即
B 斜边c A 对边a C
A的邻边 b cos A 斜边 c
邻边b
★我们把锐角A的对边与邻边的比叫做∠A的 正切(tangent),记作tanA, 即
1 2 3 2 解:原式 ( ) ( ) 2 2
2 sin 2 60表示(sin 60) ,
九年级数学下册第28章锐角三角函数28-1锐角三角函数3特殊角的三角函数值新版新人教版

5 [2023·枣庄]如图所示,桔槔是一种原始的汲水工具, 它是在一根竖立的架子上加上一根细长的杠杆,末端 悬挂一重物,前端悬挂水桶,当人把水桶放入水中打 满水以后,由于杠杆末端的重力作用, 便能轻易把水提升至所需处,
若已知:杠杆 AB=6 米,AO∶OB=2∶1,支架 OM⊥ EF,OM=3 米,AB 可以绕着点 O 自由旋转,当点 A 旋 转到如图所示位置时∠AOM=45°,此时点 B 到水平地 面 EF 的距离为_(_3_+___2_)_米.(结果保留根号)
第28章 锐角三角函数
28.1.3 特殊角的三角函数值
1 [2023·天津]sin 45°+ 22的值等于( B ) A.1 B. 2 C. 3 D.2
2 [2023·深圳]爬坡时坡面与水平面夹角为 α,则每爬 1 m
耗能(1.025-cos α)J,如图,若某人爬了 1 000 m,该坡
角为 30°,则他耗能( )
sin A=ac,cos B=ac,tan A=ab,故 A 不一定成立; sin2 A+cos2 A=ac2+bc2=cc22=1,故 B 一定成立; sin2 A+sin2 B=ac2+bc2=cc22=1,故 C 一定成立;
tan A·tan B=ab·ba=1,故 D 一定成立. 【答案】A
C.锐角三角形 D.不能确定
9 (母题:教材 P70 习题 T10) 在 Rt△ ABC 中,∠C=90°,
下列式子不一定成立的是( )
A.tan
A=csions
A B
C.sin2 A+sin2 B=1
B.sin2 A+cos2 A=1 D.tan A·tan B=1
【点拨】 设∠A,∠B,∠C 所对的边分别为 a,b,c,则
锐角三角函数公式

• 利用正弦函数和余弦函数,计算电场强度和磁场强度 • 利用正切函数和余切函数,计算电场强度和磁场强度
04
锐角三角函数的计算器法与编程实现
计算器法求解锐角三角函数
利用科学计算器直接计算锐角三角函数的值
• 输入角的大小,直接计算正弦值、余弦值、正切值和余切值 • 利用计算器的其他功能,进行角度的转换和运算
角度和差公式
• 通过角度和差公式,将任意角与锐角联系起来 • 利用锐角三角函数的性质,推导出角度和差公式的三角函数表达式
03
锐角三角函数的应用
测量问题中的应用
测量高度
• 利用正切函数,计算物体的高度 • 利用余切函数,计算物体的高度
测量距离
• 利用正弦函数和余弦函数,计算物体的距离 • 利用正切函数和余切函数,计算物体的距离
解题技巧
• 利用三角函数的性质,简化计算过程 • 通过角度的转换,将复杂问题转化为简单问题
锐角三角函数的学习方法与建议
学习方法
• 理解锐角三角函数的定义与性质,掌握公式的推导过程 • 熟练掌握锐角三角函数的应用,解决实际问题
学习建议
• 多做练习,提高计算能力和解题技巧 • 注重归纳总结,形成完整的知识体系
余弦函数的取值范围与特殊值
• 取值范围:[-1, 1] • 特殊值:cos(0) = 1, cos(π/2) = 0, cos(π) = -1
余切函数的取值范围与特殊值
• 取值范围:实数集 • 特殊值:cot(0) = ∞, cot(π/2) = 0, cot(π) = -1
02
锐角三角函数的公式推导
正弦公式与余弦公式的推导
正弦公式的推导
• 利用单位圆的性质,将圆周角与弧度制联系起来 • 通过正弦函数的定义,将正弦值与单位圆上的点联系起 来
锐角三角函数知识点总结

锐角三角函数知识点总结一、引言数学是一门抽象而理性的学科,而三角函数则是数学中一个重要而又有趣的分支。
在这篇文章中,我将为你总结锐角三角函数的基本知识,并探讨其在数学和实际应用中的重要性。
二、什么是锐角三角函数在介绍锐角三角函数之前,我们先了解一下什么是锐角。
锐角是指角度小于90度的角。
而锐角三角函数是用来描述锐角三角形中角度和边长之间的关系的函数。
锐角三角函数一共有三个主要函数:正弦(sine)、余弦(cosine)和正切(tangent)。
三、正弦函数正弦函数是最基本的锐角三角函数之一。
它定义了角度和斜边与斜边的比值之间的关系。
正弦函数的基本公式为:sinθ = 对边/斜边,其中θ表示角度。
正弦函数的值域在-1到1之间。
四、余弦函数余弦函数也是锐角三角函数的一部分。
它定义了角度和邻边与斜边的比值之间的关系。
余弦函数的基本公式为:cosθ = 邻边/斜边。
余弦函数的值域同样在-1到1之间。
五、正切函数正切函数是锐角三角函数中的最后一个函数。
它定义了角度和对边与邻边的比值之间的关系。
正切函数的基本公式为:tanθ = 对边/邻边。
与正弦和余弦函数不同,正切函数的定义域是全体实数。
六、锐角三角函数的性质除了上述的基本定义,锐角三角函数还有一些重要的性质。
其中一些性质包括周期性、奇偶性和特殊角度的值。
1. 周期性:正弦函数、余弦函数、正切函数都是周期函数。
正弦函数和余弦函数的最小正周期为2π,而正切函数的最小正周期为π。
2. 奇偶性:正弦函数是奇函数,余弦函数是偶函数,正切函数则既不是奇函数也不是偶函数。
3. 特殊角度的值:锐角三角函数在某些特殊的角度下有确定的值,比如sin30°=1/2,cos45°=√2/2等。
七、锐角三角函数的应用锐角三角函数在数学和实际应用中有着广泛的应用。
一些常见的应用包括:几何学中的三角测量、物理学中的运动分析、工程学中的结构分析等。
1. 几何学中的三角测量:锐角三角函数被广泛应用于三角测量中,比如测量两点间的距离、测量船和灯塔之间的角度等。
28.1.1锐角三角函数---特殊的三角函数值

?
思考
两块三角尺中有几个不同的锐角? 两块三角尺中有几个不同的锐角? 分别求出这几个锐角的正弦值余弦值正 切值. 切值.
设图中,每个三角尺较 短的边长为1,利用勾股 定理和三角函数的定义可 以求出这些三角函数值.
300、450、600角 的正弦值、余弦值和正切值、余切值如下表:
三角函数 正弦sinα 锐角α
0 ’ ” 键,进一步得到 还可以利用 2nd F 07’08.97 这说明锐角A精确到1 的结果为 08.97”( ∠ A=30007 08.97 (这说明锐角A精确到1’的结果为 的结果为30 9 ). 3007’,精确到1”的结果为3007’9”). ,精确到1 的结果为
怎样验算求出 ∠A=3007’9”的 是否正确?
例4.(1)如图,在Rt△ABC中, 4.(1)如图, Rt△ABC中 如图 ,BC=√3,求 的度数. ∠C=900,AB=√6 ,BC=√3,求∠A的度数.
解: (1)在 中 图 , BC 3 2 Qsin A = = = AB 2 6 0 ∴∠A = 45
(2)如图,己知圆锥的高AO等于圆锥的底面半径 (2)如图,己知圆锥的高AO等于圆锥的底面半径 如图 AO OB的 OB的√3倍,求α.
B 一个锐角的正弦,等于它的余角的余弦( 一个锐角的正弦,等于它的余角的余弦(或一个 锐角的余弦等于它的余角的正弦); 锐角的余弦等于它的余角的正弦); 一个锐角的正切,等于它的余角的余切( 一个锐角的正切,等于它的余角的余切(或一个 锐角的余切等于它的余角的正切); 锐角的余切等于它的余角的正切); A c a b ┌ C
例4.(1)如图,在Rt△ABC中, 4.(1)如图, Rt△ABC中 如图 ,BC=√3,求 的度数. ∠C=900,AB=√6 ,BC=√3,求∠A的度数. (2)如图,己知圆锥的高AO等于圆锥的底面半径 (2)如图,己知圆锥的高AO等于圆锥的底面半径 如图 AO OB的√3倍,求α. OB的
锐角三角函数公式表

锐角三角函数公式表
1. 正弦函数(Sine Function):sinθ= 对边/斜边
例如,在一个直角三角形中,如果一条直角边长为3,斜边长为5,则正弦值为sinθ= 3/5。
2. 余弦函数(Cosine Function):cosθ= 邻边/斜边
例如,在同样一个直角三角形中,如果另一条直角边长为4,斜边长度仍然是5,则余弦值为cosθ=4/5。
3. 正切函数(Tangent Function):tanθ= 对辺/邻辺
例如,在一个30-60-90度特殊的等腰直角三角形中, 如果短腿长度是1,则长腿长度就会是栗子号数学常数√3。
因此在这个特殊的情况下tan(30°)= sin(30°)/cos(30°)= (1/(2)) /(√3/(2))= √3 / 3.
4. 余切函数(Cotangent Function): cot θ=邻辺/对辺,即cot θ=1/tan θ
例如,在上述相同的等腰直角三角形中,如果短脚長度是2 ,那麼長脚長度就是2√3。
因此在这个特殊的情况下cot(60°)=1/tan(60°) = (√3 / 3)/ (1/2) = √3 * 2。
5. 正割函数(Secant Function): sec θ=1/cos θ
例如,如果cosθ=0.6,则secθ=1/cosθ=5/3。
6.余割函數(Cosecant function): csc θ=1/sin θ
例如,如果sinθ=0.8,则cscθ=1/sinθ=5/4。
这些公式和举例可以帮助我们更好地理解锐角三角函数及其应用。
常见三角函数值表

数据处理技巧
• 数据筛选与排序
• 数据拟合与插值
• 数据可视化
数据存储与查询
• 建立数据文件
• 设计数据查询接口
• 提供数据查询服务
⌛️
三角函数值表的应用场景与优势
应用场景
• 教育与教学
• 科学研究
• 工程与产品设计
优势
• 提高计算效率
• 减少误差
• 方便数据查询与共享
04
三角函数值表的比较与评估
不同来源的三角函数值表的比较
纸质三角函数值表
⌛️
• 传统方法与工具
• 信息量有限
• 查询速度慢
网络三角函数值表
• 实时更新与维护
电子三角函数值表
• 便捷访问与共享
• 丰富的应用场景
• 数字化方法与工具
• 信息量大
• 查询速度快
三角函数值表的准确性评估
01
误差来源分析
• 测量误差
• 计算误差
• 数据处理误差
01
计算机技术
• 数据处理与计算
• 数据存储与查询
• 数据可视化
02
信息技术
• 网络传输与共享
• 数据库建设与维护
• 信息系统开发与应用
03
人工智能技术
• 数据分析与挖掘
• 误差分析与控制
• 智能计算与优化
未来三角函数值表的发展趋势与前景
发展趋势
• 更高的计算精度
• 更广泛的应用场景
• 更智能化的数据处理
三角函数值表在实际应用中的案例
测量问题
• 测量建筑物的高度
• 测量物体的距离
• 测量角度的大小
物理学问题
高中必背三角函数值表

高中必背三角函数值表引言在高中数学的学习过程中,三角函数是一个非常重要的概念。
掌握三角函数的各种性质和数值是解决各类三角函数问题的关键。
其中,掌握三角函数值表是非常基础也非常重要的一部分,它可以帮助我们快速准确地计算各种三角函数的值。
本文将对高中必背的三角函数值表进行总结和归纳,希望能够帮助读者更好地掌握这一知识点。
正弦函数值表正弦函数是三角函数中的一个重要概念,下面是正弦函数在特定角度下的取值表格:角度(度)0°30°45°60°90°正弦值00.5√2/2√3/21在实际计算中,通过掌握这个值表,我们可以快速得到特定角度下正弦函数的值。
余弦函数值表余弦函数是另一个重要的三角函数,下面是余弦函数在特定角度下的取值表格:角度(度)0°30°45°60°90°余弦值1√3/2√2/20.50掌握这个表格能够帮助我们迅速计算出特定角度下余弦函数的值。
正切函数值表正切函数在三角函数中也扮演着重要的角色,下面是正切函数在特定角度下的取值表格:角度(度)0°30°45°60°正切值0√3/31√3正切函数的值表对于解决与三角函数有关的问题非常有帮助,熟记这些数值将事半功倍。
总结三角函数值表是高中数学学习中不可或缺的基础知识,掌握这些表格将为我们解决各类三角函数问题提供便利。
通过努力记忆和实践运用,我们可以更快更准确地计算出各种三角函数的值,为数学学习打下坚实的基础。
希望本文的内容能对读者在学习三角函数时有所帮助。
参考•高中数学教科书这篇文档对高中必背的三角函数值表进行了总结和归纳,希望能够帮助读者更好地掌握这一重要知识点。
初中九年级数学中考锐角三角函数知识点总结

九年级数学中,锐角三角函数是一个重要的知识点。
锐角三角函数是指对于锐角的正弦、余弦和正切函数。
下面我将对锐角三角函数的基本概念、性质和应用进行总结。
一、基本概念1.弧度和角度:角度是常用的角度度量单位,弧度是角度的另一种度量单位。
1个弧度对应360°/2π≈57.3°。
角度和弧度之间的关系式:弧度=角度×π/180°。
2.锐角:指角度小于90°的角。
3. 三角函数:对于一个锐角A,定义其正弦(sin A)为对边与斜边的比值,余弦(cos A)为邻边与斜边的比值,正切(tan A)为对边与邻边的比值。
二、性质1.正弦函数的性质:(1)对于锐角A,0 < A < 90°,sin A > 0;(2)sin A = sin (180° - A) = sin (A + 360°);(3)sin (90° - A) = cos A;(4)sin A ≠ 0,当且仅当A是锐角。
2.余弦函数的性质:(1)对于锐角A,0 < A < 90°,cos A > 0;(2)cos A = cos (180° - A) = cos (360° + A);(3)cos (90° - A) = sin A;(4)cos A ≠ 0,当且仅当A是锐角。
3.正切函数的性质:(1)对于锐角A,0 < A < 90°,tan A > 0;(2)tan A = tan (180° + A);(3)tan (90° - A) = 1/tan A;(4)tan A ≠ 0,当且仅当A是锐角。
4.三角函数的关系:(1)sin^2 A + cos^2 A = 1;(2)tan A = sin A / cos A。
三、应用1.解三角形:利用已知角的正弦、余弦和正切的值,可以求解未知边长或角度的三角形问题。
28.1.1锐角三角函数
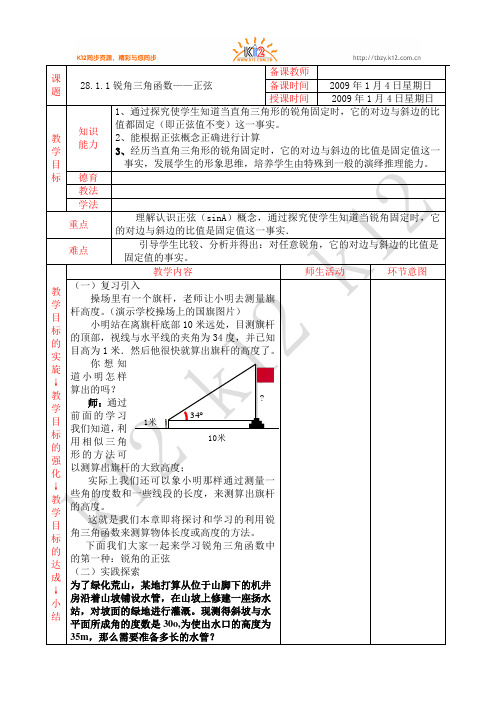
如图,在 例 1 如图 在 sin 的值. 的值
中,
,求 sin 求
和
解答按课本 (四)巩固再现 1.﹙2006 海南﹚三角形在正方形 网格纸中的位置如图所ห้องสมุดไป่ตู้,则 sin α的值是﹙ ﹚
α
A. 3
4
B. 4
3
C. 3
5
D. 4
5
2. (2005 厦门市)如图,在直角△ o ABC 中,∠C=90 ,若 AB=5,AC= 4,则 sinA=( ) A. 3 4 3 5 D. 4 3 B. 4 5
系 分析:由于∠C=∠C` =90o,∠A=∠A`=α,所以
Rt△ABC∽Rt△A`B`C`,
,即 结论:在直角三角形中,当锐角 A 的度数一定 时,不管三角形的大小如何,∠A 的对边与斜边 的比也是一个固定值。 认识正弦 如图,在 Rt△ABC 中,∠A、∠B、∠C 所对的边分别记为 a、b、c。 师 : 在 Rt △ ABC 中,∠C=90°,我们 把锐角 A 的对边与斜边的比叫做∠A 的正弦 记 正弦。 正弦 作 sinA。 板书:sinA= ∠A的对边 a = (举例说明: ∠A的斜边 c
课 题
教 学 目 标
教 学 目 标 的 实 旋 ↓ 教 学 目 标 的 强 化 ↓ 教 学 目 标 的 达 成 ↓ 小 结
备课教师 28.1.1 锐角三角函数——正弦 备课时间 2009 年 1 月 4 日星期日 授课时间 2009 年 1 月 4 日星期日 1、通过探究使学生知道当直角三角形的锐角固定时,它的对边与斜边的比 值都固定(即正弦值不变)这一事实。 知识 2、能根据正弦概念正确进行计算 能力 3、经历当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一 事实,发展学生的形象思维,培养学生由特殊到一般的演绎推理能力。 德育 教法 学法 理解认识正弦(sinA)概念,通过探究使学生知道当锐角固定时,它 重点 的对边与斜边的比值是固定值这一事实. 引导学生比较、分析并得出:对任意锐角,它的对边与斜边的比值是 难点 固定值的事实。 教学内容 师生活动 环节意图 (一)复习引入 操场里有一个旗杆,老师让小明去测量旗 杆高度。 (演示学校操场上的国旗图片) 小明站在离旗杆底部 10 米远处,目测旗杆 的顶部,视线与水平线的夹角为 34 度,并已知 目高为 1 米.然后他很快就算出旗杆的高度了。 你想知 道小明怎样 算出的吗? ? 师:通过 34 ° 前面的学习 1米 我们知道, 利 10米 用相似三角 形的方法可 以测算出旗杆的大致高度; 实际上我们还可以象小明那样通过测量一 些角的度数和一些线段的长度,来测算出旗杆 的高度。 这就是我们本章即将探讨和学习的利用锐 角三角函数来测算物体长度或高度的方法。 下面我们大家一起来学习锐角三角函数中 的第一种:锐角的正弦 (二)实践探索 为了绿化荒山, 为了绿化荒山,某地打算从位于山脚下的机井 房沿着山坡铺设水管, 房沿着山坡铺设水管,在山坡上修建一座扬水 对坡面的绿地进行灌溉。 站,对坡面的绿地进行灌溉。现测得斜坡与水 为使出水口的高度为 平面所成角的度数是 30o,为使出水口的高度为 35m,那么需要准备多长的水管? ,那么需要准备多长的水管?
锐角三角函数知识点

锐角三角函数知识点锐角三角函数是九年级学生在学习了函数概念以及反比例函数、一次函数、二次函数之后学习的又一种形式的函数,本文是店铺整理锐角三角函数知识点的资料,仅供参考。
锐角三角函数的定义锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),(余割csc)都叫做角A的锐角三角函数。
正弦等于对边比斜边余弦等于邻边比斜边正切等于对边比邻边余切等于邻边比对边正割等于斜边比邻边余割等于斜边比对边正切与余切互为倒数它的本质是任意角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。
另一种定义是在直角三角形中,但并不完全。
现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
由于三角函数的周期性,它并不具有单值函数意义上的反函数。
它有六种基本函数(初等基本表示):函数名正弦余弦正切余切正割余割在平面直角坐标系xOy中,从点O引出一条射线OP,设旋转角为θ,设OP=r,P点的坐标为(x,y)有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y(斜边为r,对边为y,邻边为x。
)以及两个不常用,已趋于被淘汰的函数:正矢函数versinθ =1-cosθ余矢函数coversθ =1-sinθ锐角三角函数的性质1、锐角三角函数定义锐角角A的正弦,余弦和正切都叫做角A的锐角三角函数2、互余角的三角函数间的关系。
sin(90°-α)=cosα, cos(90°-α)=sinα,tan(90°-α)=cotα, cot(90°-α)=tanα.3、同角三角函数间的关系平方关系:sin2α+cos2α=1倒数关系:cotα=(或tanα·cotα=1)商的关系:tanα= , cotα=.(这三个关系的证明均可由定义得出)4、三角函数值(1)特殊角三角函数值(2)0°~90°的任意角的三角函数值,查三角函数表。
《锐角的三角函数》 知识清单

《锐角的三角函数》知识清单一、锐角三角函数的定义在直角三角形中,我们把锐角的对边与斜边的比叫做正弦(sin),锐角的邻边与斜边的比叫做余弦(cos),锐角的对边与邻边的比叫做正切(tan)。
以一个锐角为∠A 的直角三角形为例。
假设∠C = 90°,∠A 所对的边为 a,∠A 的邻边为 b,斜边为 c。
那么正弦 sinA =对边/斜边= a/c;余弦 cosA =邻边/斜边= b/c;正切 tanA =对边/邻边= a/b。
需要注意的是,三角函数的值只与角的大小有关,而与三角形的大小无关。
二、特殊锐角的三角函数值我们需要牢记一些特殊锐角(30°、45°、60°)的三角函数值。
当∠A = 30°时,sinA = 1/2,cosA =√3/2,tanA =√3/3;当∠A = 45°时,sinA = cosA =√2/2,tanA = 1;当∠A = 60°时,sinA =√3/2,cosA = 1/2,tanA =√3。
这些特殊值在解题中经常会用到,所以一定要熟练记忆。
三、锐角三角函数的关系1、平方关系sin²A + cos²A = 1这意味着,如果已知一个锐角的正弦值,可以通过这个关系式求出它的余弦值;反之亦然。
2、商数关系tanA = sinA / cosA这个关系常用于将正切转化为正弦和余弦的形式进行计算。
四、锐角三角函数的应用锐角三角函数在实际生活中有广泛的应用,比如:1、测量物体的高度如果知道一个物体与观测点的水平距离以及观测点看物体顶部的仰角,就可以利用正切函数求出物体的高度。
2、测量河流的宽度在河的一岸选择一个观测点,测出对岸某一点的俯角以及观测点到对岸的距离,通过三角函数可以计算出河流的宽度。
3、计算斜坡的坡度坡度是斜坡的垂直高度与水平距离的比值,通常用正切值来表示。
五、解直角三角形解直角三角形是指在直角三角形中,由已知元素求出未知元素的过程。
28.1.1锐角三角函数教案

(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“锐角三角函数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
五、教学反思
今天在教授《锐角三角函数》这一章节时,我发现学生们对于三角函数的概念和应用表现出很大的兴趣。在导入新课环节,通过提出与日常生活相关的问题,成功引起了学生的好奇心,这是一个很好的开始。但在教学过程中,我也注意到了一些需要改进的地方。
首先,理论介绍环节,虽然我尽可能用简洁明了的语言解释锐角三角函数的定义,但仍有部分学生显得有些困惑。我意识到,对于这部分学生来说,可能需要更多的具体例子和直观图形来帮助他们理解。在接下来的教学中,我打算增加一些图示和动画,让学生更直观地感受三角函数的变化。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解锐角三角函数的基本概念。锐角三角函数是指在直角三角形中,锐角的对边、邻边、斜边的比值。它们是解决直角三角形相关问题的重要工具。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了如何利用锐角三角函数计算直角三角形中的未知角度和边长。
解决方法:设置多个实际问题,引导学生运用三角函数解决,培养学生的数学应用意识。
(3)计算过程中的细节处理:学生在计算过程中容易忽视单位换算、精确度等问题,需要教师在教学中强调。
举例:在计算过程中,注意角度与弧度的转换,以及精确到小数点后几位等。
(4)空间想象力的培养:在直角三角形中,学生需要具备一定的空间想象力,才能更好地理解三角函数的应用。
人教版初中数学九年级下册 28.1 锐角三角函数(第1课时)课件 【经典初中数学课件】

18
21
78°
83°
β
24
G
E
F
H
α
x
118°
【例题】
例2.已知四边形ABCD与四边形A1B1C1D1相似,且A1B1:B1C1:C1D1:D1A1=7:8:11:14,若四边形ABCD的周长为40,求四边形ABCD的各边的长.
当堂检测,反馈提高
1.△ABC与△DEF相似,且相似比是 ,则△DEF 与△ABC与的相似比是( ). A. B. C. D. 2.下列所给的条件中,能确定相似的有( ) (1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形. A.3个 B.4个 C.5个 D.6个 3.已知四边形ABCD和四边形A1B1C1D1相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,如果四边形A1B1C1D1的最短边的长是6cm,那么四边形A1B1C1D1中最长的边长是多少?
小结: 1、谈谈你的收获。 2.你有哪些困惑。 3.学会了哪些解决问题的方法。
27.1 图形的相似
图形的相似
图形的相似
图形的相似
图形的相似
图形的相似
观察下面两张照片,你发现有什么相同与不同?
想一想:我们刚才所见到的图形有什么相同和不同的地方?
相同点:形状相同. 不同点:大小不一定相同.
A
C
B
┌
【解析】在Rt△ABC中,
【尝试应用】
1.判断对错:
A
10m
6m
B
C
(1)如图 sin A= ( ) ②sin B= . ( ) ③sin A=0.6m. ( ) ④sin B=0.8. ( )
锐角三角函数公式大全表格

锐角三角函数公式大全表格1. 正弦函数(sin):正弦函数表示一个角的对边与斜边的比值。
它的公式为:sinθ = 对边 / 斜边2. 余弦函数(cos):余弦函数表示一个角的邻边与斜边的比值。
它的公式为:cosθ = 邻边 / 斜边3. 正切函数(tan):正切函数表示一个角的对边与邻边的比值。
它的公式为:tanθ = 对边 / 邻边4. 余切函数(cot):余切函数表示一个角的邻边与对边的比值。
它的公式为:cotθ = 邻边 / 对边5. 正割函数(sec):正割函数表示一个角的斜边与邻边的比值的倒数。
它的公式为:secθ = 斜边 / 邻边6. 余割函数(csc):余割函数表示一个角的斜边与对边的比值的倒数。
它的公式为:cscθ = 斜边 / 对边7.和差化积公式:sin(α ± β) = sinαcosβ ± cosαsinβcos(α ± β) = cosαcosβ ∓ sinαsinβtan(α ± β) = (tanα ± tanβ) / (1 ∓ tanαtanβ)8.二倍角公式:sin2θ = 2sinθcosθcos2θ =cos^2θ - sin^2θ = 2cos^2θ - 1 = 1 - 2sin^2θtan2θ = (2tanθ) / (1 - tan^2θ)9.平方和差公式:sin^2α + sin^2β = 1 - 2sinαsinβcos(α + β)cos^2α + cos^2β = 1 + 2cosαcosβcos(α + β)10.半角公式:sin(θ/2) = ±√[(1 - cosθ) / 2]cos(θ/2) = ±√[(1 + cosθ) / 2]tan(θ/2) = ±√[(1 - cosθ) / (1 + cosθ)]这些公式是锐角三角函数的基础,它们可以用于解决各种和角度有关的问题。
28.1 锐角三角函数(3)

2、互余两角的三角函数性质 在Rt△ABC中,当∠C=90°,
则有sinA= cosB ,cosA= sinB ,tanA.tanB= 1 .
一副三角尺有几个不同的锐角?
你能求出这几个锐角的正弦值、余弦值和 正切值吗?
新知探索:
B
1
2
C
30.0 A
3
sin30°=
A的对边 斜边
1 2
cos30°=
例1.计算:
(1)cos260°+sin260 °
(2) csoins4455°°+tan45°
练习1:
当锐角α>30°,则cosα的值 ( )
例2、(1)如图,在Rt△ABC中,∠C=90°, AB= 6 , BC= 3 。求∠A的度数。
B
A
6
3
A
C
(1)
O B
(2)
(2)如图,已知圆锥的高AO等于圆锥的底面 半径OB的 3 倍,求α.
例3.求适合下列各式的锐角α
( 1 ) 3 t a n α 3
( 2 )2 c o s α 1 2
1
(3) 3tan2 4 tan 3 0
练习2:
在Rt△ABC中,C 90,且sinA cosB 3. 则tan A ?
例4、如图,在△ABC中,A 30,tan B 3 , 2
AC 2 3.求AB的长。
α的正弦值随着角度的增大而增大,
α的余弦值随着角度的增大而减少, α的正切值随着角度的增大而增大。
且0 <sinα< 1, 0 <cosα< 1
3、三角函数值和角之间是对应的,知道三角函数值可以求角的
度数,知道角的度数可以求出三角函数值。
4、通过三角函数值可以把边和角有机地联系在一起,由边求角, 由角求边。
28、1 锐角三角函数——特殊角的三角涵数应用及用计算器求角的三角涵数值 —21学年数学九年级下册

求∠A的度数; B
解: 在图中,
sin A BC 3 2 , AB 6 2
6
3
A 45;
A
C
(2)如图,AO是圆锥的高,OB是底面半径,AO= 3 OB,
求 的度数.
解: 在图中,
A
tan AO 3OB 3 ,
OB OB
60.
O B
当堂练习
1. 3 tan(α+20°)=1,锐角α的度数应是( D ) A.40° B.30° C.20° D.10°
DE⊥AB于点E,BC=1,AC= 3 ,则∠D的度数
为 30 .
状元成才路
课堂小结
锐角 锐角A 三角函数
sin A
cos A
tan A
30°
1 2 3 2 3 3
45°
2 2 2 2 1
60°
3 2 1 2 3
课堂小结
用计算器求 锐角三角函 数值及锐角
用计算器求锐角 的三角函数值或 角的度数
利用计算器 探索锐三角 函数的新知
不同的计算器操作步 骤可能有所不同
sin = cos(90? ) cos = sin(90? )
sin2 + cos2 1 tan tan(90 ) 1
正弦值随着角度的增大(或减小)而增大(或减小); 余弦值随着角度的增大(或减小)而减小(或增大); 正切值随着角度的增大(或减小)而增大(或减小).
tan 30 a 3 3a 3
sin 60 3a 3 2a 2
cos 60 a 1
2a 2
60°
tan 60 3a 3 a
设两条直角边长为a,则斜边长= a2 a2 2a
sin 45 a 2 2a 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
要能记 住有多 好
2
正切tanα
3 3
1
3
这张表还可以看出许多 知识之间的内在联系?
例1 计算: (1)sin300+cos450;
(2) sin2600+cos2600-tan450.
( 3 ) 12 3 tan 30 ( 2010 ) ( ) 2
0 0
1
1
计算:
(1)sin600-cos450; (2)cos600+tan600;
300,450,600角的三角函数值
锐角三角函数定义
脑中有“图”,心中有 “式”
直角三角形中边与角的关系:锐角三角函数.
在直角三角形中,若一个锐角确定,那么这个角的对边,邻 边和斜边之间的比值也随之确定.
sin A sin B a c b c , cos B , cos A b c a c ,
课堂小结
看图说话: 直角三角形三边的关系. 直角三角形两锐角的关系. 直角三角形边与角之间的关系. A 特殊角300,450,600角的三角函 数值. 互余两角之间的三角函数关系. 同角之间的三角函数关系.
450
B
00
┌
┌
3
做一做
sin60°=
3
60°
3
B
2 A 1 C
2
1 2
cos60°=
tan60°=
3
做一做
sin45 ° =
B
2 2 2 2
2
45°
1 C
cos45°=
A 1
tan45°=
1
特殊角的三角函数值表
锐角α 三角函数 正弦sinα 余弦cosα
300
1 2
3 2
450
2 2
2 2
600
3 2 1
B c
,
a A b ┌ C
tanA= a
b
tanB=
b a
锐角A的正弦、余弦、和正切统称∠A的三角函数
如图,观察一副三角板: 它们其中有几个锐角?分别是多少度? (1)sin300等于多少? (2)cos300等于多少? (3)tan300等于多少?
1 2
3
300
450
2
3
2
3
450
┌ 600 1
老师提示:将实际问题数学化. O
2.5
B
C D A
1.某商场有一自动扶梯,其倾斜角为300,高为 7m,扶梯的长度是多少?
2.如图,河岸AD,BC互相平行,桥AB垂直于两岸.桥 长12m,在C处看桥两端A,B,夹角∠BCA=600. 求B,C间的距离(结果精确到1m).
A
B
┐
C
3.如图,身高1.5m的小丽用一个两锐角分别是300 和600 的三角尺测量一棵树的高度.已知她与树之 间的距离为5m,那么这棵树大约有多高?
3
4
2 2
2 2
sin 45 sin 60 2 cos 45 .
0 0 0
sin
2
30 cos
0
2
60 2 cos
0
2
45 .
0
例2 如图:一个小孩荡秋千,秋千链子的长度为
2.5m,当秋千向两边摆动时,摆角恰好为600,且两边
摆动的角度相同,求它摆至最高位置时与其摆至最低 位置时的高度之差(结果精确到0.01m).
