锐角三角函数特殊值表及巧记方法
锐角三角函数值记忆法

30、 45、 60角的正弦值、余弦值、正切值的记忆法
1.口诀法:可用“一二三、三二一、三九二十七”来帮助记忆,如下表:
2.数形定义法:如右图,在含 30角的直角三角形中,三边的比为1︰3︰2,即 30角的对边(或 60角的邻边)为“1”,
60角的对边(或 30角的邻边)为“3”,斜边为“2”;再利用锐角三角函数的定义得到,213030sin ==斜边角的对边 ,233030cos ==斜边角的邻边
30tan =角的邻边角的对边 3030=33,同样可得 60角的三角函数值。
在等腰直角三角形中,三边的比为1︰1︰2,即 45角的对边或邻边都是“1”, 斜边是“
2”; 再由锐角三角函数的定义得,222
14545sin ===斜边角的对边 ,22214545cos ===斜边角的邻边 1454545tan ==角的邻边角的邻边 。
60 ︒
45 ︒ 45 ︒ 30 ︒ 2
1 1
2
3 1。
特殊角的三角函数值的巧记

特殊角的三角函数值的巧记特殊角的三角函数值在计算,求值,解直角三角形和今后的学习中,常常会用到,所以一定要熟记.要在理解的基础上,采用巧妙的方法加强记忆.这里关键的问题还是要明白和掌握这些三角函数值是怎样求出的,既便遗忘了,自己也能推算出来,切莫死记硬背.那么怎样才能更好地记熟它们呢?下面介绍几种方法,供同学们借鉴。
1、“三角板”记法根据含有特殊角的直角三角形的知识,利用你手里的一套三角板,就可以帮助你记住30°、45°、60°角的三角函数值.我们不妨称这种方法为“三角板”记法.首先,如图所标明的那样,先把手中一套三角板的构造特点弄明白,记清它们的边角是什么关系.对左边第一块三角板,要抓住在直角三角形中,30°角的对边是斜边的一半的特点,再应用勾股定理.可以知道在这个直角三角形中30°角的对边、邻边、斜边的比是掌握了这个比例关系,就可以依定义求出30°、60°角的任意一个锐角三角函数值,如:001sin 30,cos302== 求60°角的三角函数值,还应抓住60°角是30°角的余角这一特点.在右边那块三角板中,应注意在直角三角形中,若有一锐角为45°,则此三角形是等腰直角三角形,且两直角边与斜边的比是1∶1,那么,就不难记住:00sin 45cos 45==,00tan 45cot 451==。
这种方法形象、直观、简单、易记,同时巩固了三角函数的定义.二、列表法:说明:正弦值随角度变化,即0˚ →30˚→45˚ →60˚ →90˚变化;值从0→21→22→23→1变化,其余类似记忆. 三、口诀记忆法口诀是:“一、二、三,三、二、一,三、九、二十七,弦是二,切是三,分子根号不能删.”前三句中的1,2,3;3,2,1;3,9,27,分别是30°,45°,60°角的正弦、余弦、正切值中分子根号内的值.弦是二、切是三是指正弦、余弦的分母为2,正切的分母为3.最后一句,讲的是各函数值中分子都加上根号,不能丢掉.如tan60°=3=tan45°=13=.这种方法有趣、简单、易记. 四、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:①有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
(完整版)三角函数特殊角值表

角度 函数 0 30 45 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 2π sin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan√3/31√3-√3-1-√3/31、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=21,sin45°=cos45°=22, tan30°=cot60°=33, tan 45°=cot45°=1正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y2、列表法:说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从02122 23 1变化,其余类似记忆.3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:① 有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A 若45°<A <90°,则sin A >cos A ;tan A >cot A . 4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为2m 形式,正切、余切值可表示为3m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.30˚ 123145˚ 1212 60˚ 3函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin(A)=a/c余弦函数cos(A)=b/c正切函数tan(A)=a/b余切函数cot(A)=b/a其中a为对边,b为邻边,c为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.7320二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin 22sin cos cos 2cos 2sin 22cos 2112sin 2αααααααα==-=-=-2tan tan 21tan 2ααα=--sin 33sin 4sin 3cos34cos33cos .3tan tan 3tan 313tan 2αααααααααα=-=--=--三角函数的和差化积公式 三角函数的积化和差公式sin sin 2sincos 22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+--化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)22sin cos sin()a x b x a b x φ±=+±其中φ角所在的象限由a 、b 的符号确定,φ角的值由tan ba φ=确定六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
三角函数特殊角值表

角度 函数 0 3045 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 2π sin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan√3/31√3-√3-1-√3/31、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=21,sin45°=cos45°=22, tan30°=cot60°=33, tan 45°=cot45°=1正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y2、列表法:说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从021 22 23 1变化,其余类似记忆. 3、规律记忆法:观察表中的数值特征,可总结为以下记忆规律: ① 有界性:〔锐角三角函数值都是正值〕即当0°<α<90°时,那么0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:〔锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小〕,即当0<A <B <90°时,那么sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:假设0°<α<45°,那么sin A <cos A ;tan A <cot A 假设45°<A <90°,那么sin A >cos A ;tan A >cot A . 4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为2m 形式,正切、余切值可表示为3m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.30˚ 123145˚1212 60˚ 3函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin〔A〕=a/c余弦函数cos〔A〕=b/c正切函数tan〔A〕=a/b余切函数cot〔A〕=b/a其中a为对边,b为邻边,c为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.7320二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin 22sin cos cos 2cos 2sin 22cos 2112sin 2αααααααα==-=-=- 2tan tan 21tan 2ααα=--sin 33sin 4sin 3cos34cos33cos .3tan tan 3tan 313tan 2αααααααααα=-=--=--三角函数的和差化积公式三角函数的积化和差公式sin sin 2sincos 22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 化asinα ±bcosα为一个角的一个三角函数的形式〔辅助角的三角函数的公式〕22sin cos sin()a x b x a b x φ±=+±其中φ角所在的象限由a 、b 的符号确定,φ角的值由tan ba φ=确定六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
(完整版)特殊角的三角函数值的巧记

特殊角的三角函数值的巧记特殊角的三角函数值在计算,求值,解直角三角形和今后的学习中,常常会用到,所以一定要熟记.要在理解的基础上,采用巧妙的方法加强记忆.这里关键的问题还是要明白和掌握这些三角函数值是怎样求出的,既便遗忘了,自己也能推算出来,切莫死记硬背.那么怎样才能更好地记熟它们呢?下面介绍几种方法,供同学们借鉴。
1、“三角板”记法根据含有特殊角的直角三角形的知识,利用你手里的一套三角板,就可以帮助你记住30°、45°、60°角的三角函数值.我们不妨称这种方法为“三角板”记法.首先,如图所标明的那样,先把手中一套三角板的构造特点弄明白,记清它们的边角是什么关系.对左边第一块三角板,要抓住在直角三角形中,30°角的对边是斜边的一半的特点,再应用勾股定理.可以知道在这个直角三角形中30°角的对边、邻边、斜边的比是3掌握了这个比例关系,就可以依定义求出30°、60°角的任意一个锐角三角函数值,如:0013sin 30,cos302== 求60°角的三角函数值,还应抓住60°角是30°角的余角这一特点.在右边那块三角板中,应注意在直角三角形中,若有一锐角为45°,则此三角形是等腰直角三角形,且两直角边与斜边的比是1∶12,那么,就不难记住:002sin 45cos 452==,00tan 45cot 451==。
这种方法形象、直观、简单、易记,同时巩固了三角函数的定义.二、列表法:说明:正弦值随角度变化,即0˚ →30˚→45˚ →60˚ →90˚变化;值从0→21→22→23→1变化,其余类似记忆. 三、口诀记忆法口诀是:“一、二、三,三、二、一,三、九、二十七,弦是二,切是三,分子根号不能删.”前三句中的1,2,3;3,2,1;3,9,27,分别是30°,45°,60°角的正弦、余弦、正切值中分子根号内的值.弦是二、切是三是指正弦、余弦的分母为2,正切的分母为3.最后一句,讲的是各函数值中分子都加上根号,不能丢掉.如tan60°==tan45°=13=.这种方法有趣、简单、易记. 四、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:①有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
三角函数特殊角值表

三角函数特殊值1、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=21sin45°=cos45°=22tan30°=cot60°=33tan 45°=cot45°=1230˚ 1 23145˚ 12 12 60˚ 3说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从023 1变化,其余类似记忆.3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:① 有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A 若45°<A <90°,则sin A >cos A ;tan A >cot A .4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为2m 形式,正切、余切值可表示为3m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.巧记特殊角的三角函数值初学三角函数,记忆特殊角三角函数值易错易混。
若在理解掌握的基础上,经过变形,使其呈现某种规律,再配以歌诀,则可浅显易记,触目成诵。
仔细观察表1,你会发现重要的规律。
表1中,三角函数值的前三行,分子被开方数排列特征依次为“1,2,3,3,2,1,3,9,27”。
“一二三,三二一,三九二十七”。
记此歌诀即可。
观察表2也可发现重要的规律。
三角函数值表及记忆方法

只想上传这一个表 下面的都就是无用的话 不用瞧了。
1、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=
2
1
sin45°=cos45°=22
2 30˚ 45˚ 60˚ 90˚
23 1变化,其余类似记忆.
3、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为
2m 形式,正切、余切值可表示为3
m
形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.
4、规律记忆法:观察表中的数值特征,可总结为下列记忆规律: ① 有界性:(锐角三角函数值都就是正值)即当0°<α<90°时,
则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A 若45°<A <90°,则sin A >cos A ;tan A >cot A .。
三角函数记忆顺口溜 记忆的方法和技巧

三角函数记忆顺口溜记忆的方法和技巧
三角函数是基本初等函数之一,是以角度为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
也可以等价地用与单位圆有关的各种线段的长度来定义。
1 三角函数记忆口诀三角函数是函数,象限符号坐标注。
函数图像单位圆,周期奇偶增减现。
同角关系很重要,化简证明都需要。
正六边形顶点处,从上到下弦切割;
中心记上数字一,连结顶点三角形。
向下三角平方和,倒数关系是对角,顶点任意一函数,等于后面两根除。
诱导公式就是好,负化正后大化小,变成锐角好查表,化简证明少不了。
二的一半整数倍,奇数化余偶不变,将其后者视锐角,符号原来函数判。
两角和的余弦值,化为单角好求值,余弦积减正弦积,换角变形众公式。
和差化积须同名,互余角度变名称。
计算证明角先行,注意结构函数名,保持基本量不变,繁难向着简易变。
逆反原则作指导,升幂降次和差积。
条件等式的证明,方程思想指路明。
万能公式不一般,化为有理式居先。
公式顺用和逆用,变形运用加巧用;
一加余弦想余弦,一减余弦想正弦,幂升一次角减半,升幂降次它为范;
三角函数反函数,实质就是求角度,先求三角函数值,再判角取值范围;
利用直角三角形,形象直观好换名,简单三角的方程,化为最简求解集。
1 三角函数万能公式怎幺记1)正弦:1 加切方除切倍。
要注意‘除’的含义。
2)余弦:阴阳相比是余弦。
初中锐角三角函数知识点总结

锐角三角函数及其应用榆林第六中学 高启鹏一、锐角三角函数中考考点归纳考点一、锐角三角函数1、锐角三角函数的定义如图,在Rt △ABC 中,∠C 为直角,则∠A 为△ABC 中的一锐角,则有∠A 的正弦:斜边的对边A A ∠=sin c a =∠A 的余弦:斜边的邻边A A ∠=cos cb =∠A的正切:的邻边的对边A tan ∠∠=A A ba =2、特殊角的三角函数值(1)图表记忆法 (2)规律记忆法:30°、45°、60°角的正弦值的分母都是2,分子依次为1、23;30°、45°、60°角余弦值恰好是60°、45°、 30°角的正弦值。
邻边C(3)口诀记忆法口诀是:“一、二、三,三、二、一,三、九、二十七,弦比二,切比三,分子根号不能删.”前三句中的1,2,3;3,2,1;3,9,27,分别是30°,45°,60°角的正弦、余弦、正切值中分子根号内的值.弦比二、切比三是指正弦、余弦的分母为2,正切的分母为3.最后一句,讲的是各函数值中分子都加上根号,不能丢掉.如tan60°=3=tan45°=13=.这种方法有趣、简单、易记. 考点二、解直角三角形1、由直角三角形中的已知元素求出其他未知元素的过程,叫做解直角三角形。
2、解直角三角形的类型和解法如下表:考点三、锐角三角函数的实际应用(高频考点)仰角、俯角、坡度(坡比)、坡角、方向角仰角、俯角在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角。
坡度(坡比)、坡角坡面的铅直高度h和水平宽度l的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角α叫坡角,方向角指北或指南的方向线与目标方向线所成的小于90°的锐角叫做方向角.注意:东北方向指北偏东45°方向,东南方向指南偏东45°方向,西北方向指北偏西45°方向,西南方向指南偏西45°方向.我们一般画图的方位为上北下南,左西右东.lhi==αtan二、锐角三角函数常见考法(一)、锐角三角函数以选择题的形式出现.例1、(2016?陕西)已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为()A. B. C. D.2【考点】抛物线与x轴的交点;锐角三角函数的定义.【解析】先求出A、B、C坐标,作CD⊥AB于D,根据tan∠ACD=即可计算.【解答】解:令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,不妨设A(﹣3,0),B(1,0),∵y=﹣x2﹣2x+3=﹣(x+1)2+4,∴顶点C(﹣1,4),如图所示,作CD⊥AB于D.在RT△ACD中,tan∠CAD===2,故答案为D.(二)、锐角三角函数以填空题的形式出现.例2、(2016?陕西)请从以下两个小题中任选一个作答,若多选,则按第一题计分.A.一个多边形的一个外角为45°,则这个正多边形的边数是8 .B.运用科学计算器计算:3sin73°52′≈.(结果精确到)【考点】计算器—三角函数;近似数和有效数字;计算器—数的开方;多边形内角与外角.【解析】(1)根据多边形内角和为360°进行计算即可;(2)先分别求得3和sin73°52′的近似值,再相乘求得计算结果.【解答】解:(1)∵正多边形的外角和为360°∴这个正多边形的边数为:360°÷45°=8(2)3sin73°52′≈×≈故答案为:8,例3、(2015?陕西)如图,有一滑梯AB,其水平宽度AC为米,铅直高度BC为米,则∠A的度数约为°(用科学计算器计算,结果精确到°).【考点】解直角三角形的应用-坡度坡角问题.【解析】直接利用坡度的定义求得坡角的度数即可.【解答】解:∵tan∠A==≈,∴∠A=°,故答案为:°.【点评】本题考查了坡度坡角的知识,解题时注意坡角的正切值等于铅直高度与水平宽度的比值,难度不大.例4、(2014?陕西)用科学计算器计算:+3tan56°≈(结果精确到)【考点】计算器—三角函数;计算器—数的开方.【分析】先用计算器求出′、tan56°的值,再计算加减运算.【解答】解:≈,tan56°≈,则+3tan56°≈+3×≈故答案是:.【点评】本题考查了计算器的使用,要注意此题是精确到.例5、(2014?陕西)如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为2﹣.【考点】旋转的性质【分析】利用正方形和旋转的性质得出A′D=A′E,进而利用勾股定理得出BD的长,进而利用锐角三角函数关系得出DE的长即可.【解答】解:由题意可得出:∠BDC=45°,∠DA′E=90°,∴∠DEA′=45°,∴A′D=A′E,∵在正方形ABCD中,AD=1,∴AB=A′B=1,∴BD=,∴A′D=﹣1,∴在Rt△DA′E中,DE==2﹣.故答案为:2﹣.【点评】此题主要考查了正方形和旋转的性质以及勾股定理、锐角三角函数关系等知识,得出A′D的长是解题关键.(三)、锐角三角函数定义以解答题的形式出现例6、(12分)(2015?陕西)如图,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.(1)如图①,点M是四边形ABCD边AD上的一点,则△BMC的面积为24;(2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值;(3)如图③,在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由.【考点】四边形综合题..【专题】综合题.【解析】(1)如图①,过A作AE⊥BC,可得出四边形AECF为矩形,得到EC=AD,BE=BC﹣EC,在直角三角形ABE中,求出AE的长,即为三角形BMC的高,求出三角形BMC面积即可;(2)如图②,作点C关于直线AD的对称点C′,连接C′N,C′D,C′B交AD于点N′,连接CN′,则BN+NC=BN+NC′≥BC′=BN′+CN′,可得出△BNC 周长的最小值为△BN′C的周长=BN′+CN′+BC=BC′+BC,求出即可;(3)如图③所示,存在点P,使得cos∠BPC的值最小,作BC的中垂线PQ交BC于点Q,交AD于点P,连接BP,CP,作△BPC的外接圆O,圆O与直线PQ交于点N,则PB=PC,圆心O在PN上,根据AD与BC平行,得到圆O与AD 相切,根据PQ=DC,判断得到PQ大于BQ,可得出圆心O在BC上方,在AD上任取一点P′,连接P′B,P′C,P′B交圆O于点M,连接MC,可得∠BPC=∠BMC≥∠BP′C,即∠BPC最小,cos∠BPC的值最小,连接OB,求出即可.【解答】解:(1)如图①,过A作AE⊥BC,∴四边形AECD为矩形,∴EC=AD=8,BE=BC﹣EC=12﹣8=4,在Rt△ABE中,∠ABE=60°,BE=4,∴AB=2BE=8,AE==4,则S △BMC=BC?AE=24;故答案为:24;(2)如图②,作点C关于直线AD的对称点C′,连接C′N,C′D,C′B交AD于点N′,连接CN′,则BN+NC=BN+NC′≥BC′=BN′+CN′,∴△BNC周长的最小值为△BN′C的周长=BN′+CN′+BC=BC′+BC,∵AD∥BC,AE⊥BC,∠ABC=60°,∴过点A作AE⊥BC,则CE=AD=8,∴BE=4,AE=BE?tan60°=4,∴CC′=2CD=2AE=8,∵BC=12,∴BC′==4,∴△BNC周长的最小值为4+12;(3)如图③所示,存在点P,使得cos∠BPC的值最小,作BC的中垂线PQ交BC于点Q,交AD于点P,连接BP,CP,作△BPC的外接圆O,圆O与直线PQ交于点N,则PB=PC,圆心O在PN上,∵AD∥BC,∴圆O与AD相切于点P,∵PQ=DC=4>6,∴PQ>BQ,∴∠BPC<90°,圆心O在弦BC的上方,在AD上任取一点P′,连接P′B,P′C,P′B交圆O于点M,连接MC,∴∠BPC=∠BMC≥∠BP′C,∴∠BPC最大,cos∠BPC的值最小,连接OB,则∠BON=2∠BPN=∠BPC,∵OB=OP=4﹣OQ,在Rt△BOQ中,根据勾股定理得:OQ2+62=(4﹣OQ)2,解得:OQ=,∴OB=,∴cos∠BPC=cos∠BOQ==,则此时cos∠BPC的值为.【点评】此题属于四边形综合题,涉及的知识有:勾股定理,矩形的判定与性质,对称的性质,圆的切线的判定与性质,以及锐角三角函数定义,熟练掌握定理及性质是解本题的关键.例7、(10分)(2014年陕西省)已知抛物线C:y=﹣x2+bx+c经过A(﹣3,0)和B(0,3)两点,将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.(1)求抛物线C的表达式;(2)求点M的坐标;(3)将抛物线C平移到C′,抛物线C′的顶点记为M′,它的对称轴与x 轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?【考点】二次函数图象与几何变换;二次函数的性质;待定系数法求二次函数解析式;平行四边形的性质.菁优网版权所有【分析】(1)直接把A(﹣3,0)和B(0,3)两点代入抛物线y=﹣x2+bx+c,求出b,c的值即可;(2)根据(1)中抛物线的解析式可得出其顶点坐标;(3)根据平行四边形的定义,可知有四种情形符合条件,如解答图所示.需要分类讨论.【解答】解:(1)∵抛物线y=﹣x2+bx+c经过A(﹣3,0)和B(0,3)两点,∴,解得,故此抛物线的解析式为:y=﹣x2﹣2x+3;(2)∵由(1)知抛物线的解析式为:y=﹣x2﹣2x+3,∴当x=﹣=﹣=﹣1时,y=4,xKb om∴M(﹣1,4).(3)由题意,以点M、N、M′、N′为顶点的平行四边形的边MN的对边只能是M′N′,∴MN∥M′N′且MN=M′N′.∴MN?NN′=16,∴NN′=4.i)当M、N、M′、N′为顶点的平行四边形是?MNN′M′时,将抛物线C向左或向右平移4个单位可得符合条件的抛物线C′;ii)当M、N、M′、N′为顶点的平行四边形是?MNM′N′时,将抛物线C先向左或向右平移4个单位,再向下平移8个单位,可得符合条件的抛物线C′.∴上述的四种平移,均可得到符合条件的抛物线C′.【点评】本题考查了抛物线的平移变换、平行四边形的性质、待定系数法及二次函数的图象与性质等知识点.第(3)问需要分类讨论,避免漏解.例8、(12分)(2014?陕西)问题探究(1)如图①,在矩形ABCD中,AB=3,BC=4,如果BC边上存在点P,使△APD为等腰三角形,那么请画出满足条件的一个等腰三角形△APD,并求出此时BP的长;(2)如图②,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F 分别为边AB、AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长;问题解决(3)有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳,已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长,若不存在,请说明理由.【考点】圆的综合题;全等三角形的判定与性质;等边三角形的性质;勾股定理;三角形中位线定理;矩形的性质;正方形的判定与性质;直线与圆的位置关系;特殊角的三角函数值.菁优网版权所有【专题】压轴题;存在型.【分析】(1)由于△PAD是等腰三角形,底边不定,需三种情况讨论,运用三角形全等、矩形的性质、勾股定理等知识即可解决问题.(2)以EF为直径作⊙O,易证⊙O与BC相切,从而得到符合条件的点Q唯一,然后通过添加辅助线,借助于正方形、特殊角的三角函数值等知识即可求出BQ长.(3)要满足∠AMB=60°,可构造以AB为边的等边三角形的外接圆,该圆与线段CD的交点就是满足条件的点,然后借助于等边三角形的性质、特殊角的三角函数值等知识,就可算出符合条件的DM长.【解答】解:(1)①作AD的垂直平分线交BC于点P,如图①,则PA=PD.∴△PAD是等腰三角形.∵四边形ABCD是矩形,∴AB=DC,∠B=∠C=90°.∵PA=PD,AB=DC,∴Rt△ABP≌Rt△DCP(HL).∴BP=CP.∵BC=4,∴BP=CP=2.②以点D为圆心,AD为半径画弧,交BC于点P′,如图①,.则DA=DP′.∴△P′AD是等腰三角形.∵四边形ABCD是矩形,∴AD=BC,AB=DC,∠C=90°.∵AB=3,BC=4,∴DC=3,DP′=4.∴CP′==.∴BP′=4﹣.③点A为圆心,AD为半径画弧,交BC于点P″,如图①,则AD=AP″.∴△P″AD是等腰三角形.同理可得:BP″=.综上所述:在等腰三角形△ADP中,若PA=PD,则BP=2;若DP=DA,则BP=4﹣;若AP=AD,则BP=.(2)∵E、F分别为边AB、AC的中点,∴EF∥BC,EF=BC.∵BC=12,∴EF=6.以EF为直径作⊙O,过点O作OQ⊥BC,垂足为Q,连接EQ、FQ,如图②.∵AD⊥BC,AD=6,∴EF与BC之间的距离为3.∴OQ=3∴OQ=OE=3.∴⊙O与BC相切,切点为Q.∵EF为⊙O的直径,∴∠EQF=90°.过点E作EG⊥BC,垂足为G,如图②.∵EG⊥BC,OQ⊥BC,∴EG∥OQ.∵EO∥GQ,EG∥OQ,∠EGQ=90°,OE=OQ,∴四边形OEGQ是正方形.∴GQ=EO=3,EG=OQ=3.∵∠B=60°,∠EGB=90°,EG=3,∴BG=.∴BQ=GQ+BG=3+.∴当∠EQF=90°时,BQ的长为3+.(3)在线段CD上存在点M,使∠AMB=60°.理由如下:以AB为边,在AB的右侧作等边三角形ABG,作GP⊥AB,垂足为P,作AK⊥BG,垂足为K.设GP与AK交于点O,以点O为圆心,OA为半径作⊙O,过点O作OH⊥CD,垂足为H,如图③.则⊙O是△ABG的外接圆,∵△ABG是等边三角形,GP⊥AB,∴AP=PB=AB.∵AB=270,∴AP=135.∵ED=285,∴OH=285﹣135=150.∵△ABG是等边三角形,AK⊥BG,∴∠BAK=∠GAK=30°.∴OP=AP?tan30°=135×=45.∴OA=2OP=90.∴OH<OA.∴⊙O与CD相交,设交点为M,连接MA、MB,如图③.∴∠AMB=∠AGB=60°,OM=OA=90..∵OH⊥CD,OH=150,OM=90,∴HM===30.∵AE=400,OP=45,∴DH=400﹣45.若点M在点H的左边,则DM=DH+HM=400﹣45+30.∵400﹣45+30>340,∴DM>CD.∴点M不在线段CD上,应舍去.若点M在点H的右边,则DM=DH﹣HM=400﹣45﹣30.∵400﹣45﹣30<340,∴DM<CD.∴点M在线段CD上.综上所述:在线段CD上存在唯一的点M,使∠AMB=60°,此时DM的长为(400﹣45﹣30)米.X|k | B| 1 . c |O |m【点评】本题考查了垂直平分线的性质、矩形的性质、等边三角形的性质、正方形的判定与性质、直线与圆的位置关系、圆周角定理、三角形的中位线定理、全等三角形的判定与性质、勾股定理、特殊角的三角函数值等知识,考查了操作、探究等能力,综合性非常强.而构造等边三角形及其外接圆是解决本题的关键.三、三角函数易错点解析三角函数是初中数学的重要内容,三角函数是学生在初中阶段第一次接触角函数,这部分知识的学习对于学生来说有一定的难度,下面就三角函数教学中容易出现的几种“错误”进行分析:1.对应关系混淆【1】如图9,先进村准备在坡角为α的山坡上栽树,要求相邻两树之间的图9水平距离为a 米,那么这两树在坡面上的距离AB 为 ( )A. a a cos 米B.αcos a 米 C. a a sin 米 D. αsin a 米 解析:分别过点B ,A 作平行水平面的直线和垂直于水平面的直线相交于点C 。
特殊角三角函数值的记忆规律

特殊角三角函数值的记忆规律
一、特殊角三角函数值表
二、记忆规律:
1、sin α的值随α
的增大而增大,依次为:222
.
2、cos α的值随α,22. 温馨提示:00030,45,60千万不要把分母弄成3吆!
3、互余角的三角函数关系:00sin30cos60=,00sin 45cos 45=,00sin 60cos30= 温馨提示:根据互余角的三角函数关系,只要记住030和045的正弦值就可以了, 060和045的正余弦值分别根据045030和045的余正弦值去推导,可以收到事半功倍的效果.
4、sin tan cos ααα
= 5、借助三角形记忆: 2 1 0
30060
THANKS !!!
致力为企业和个人提供合同协议,策划案计划书,学习课件等等
打造全网一站式需求
欢迎您的下载,资料仅供参考。
三角函数特殊角值表完整

0
说明:正弦值随角度变化,即0˚30˚ 45˚ 60˚ 90˚变化;值从0
1变化,其余类似记忆.
3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:
1有界性:(锐角三角函数值都是正值)即当0°< <90°时,
则0<sin <1; 0<cos <1 ; tan >0 ; cot >0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A<B<90°时,则sinA<sinB;tanA<tanB; cosA>cosB;cotA>cotB;特别地:若0°< <45°,则sinA<cosA;tanA<cotA
若45°<A<90°,则sinA>cosA;tanA>cotA.
4、口决记忆法:观察表中的数值特征
正弦、余弦值可表示为 形式,正切、余切值可表示为 形式,有关m的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.
巧记特殊角的三角函数值
初学三角函数,记忆特殊角三角函数值易错易混。若在理解掌握的基础上,经过变形,使其呈现某种规律,再配以歌诀,则可浅显易记,触目成诵。
=1+cos(A-B)[cos(A+B-2 )-cos(A+B-2 )-cos(A-B)]
=1- cos2(A-B)= sin2(A-B)
∴原式的值只与A-B的值有关,而与 的值无关.参考答案:
一、单选题
1.B 2.C 3.C 4.A 5.D 6.B 7.B 8.C 9.B
二、填充题
1. 2. 3. 4.-1 5.1 6.115° 7. 135°
三角函数特殊值
角度
函数
0
30
45
60
90
120
特殊三角函数值记忆口诀

特殊三角函数值记忆口诀
三角函数在数学中占有重要的地位,而特殊角的三角函数值是我们在解题中经常需要用到的。
为了便于记忆和应用,我们可以使用口诀来帮助我们记忆这些特殊角的三角函数值。
下面就为大家整理了一些特殊角的三角函数值记忆口诀:
正弦值口诀
•正弦30度,约根儿2除4;
•正弦45度,根儿2除2;
•正弦60度,根儿3除2。
余弦值口诀
•余弦30度,根儿3除2;
•余弦45度,根儿2除2;
•余弦60度,约根儿2除4。
正切值口诀
•正切30度,约1除根儿3;
•正切45度,1;
•正切60度,根儿3。
余切值口诀
•余切30度,根儿3;
•余切45度,1;
•余切60度,约1除根儿3。
这些口诀可以帮助我们在需要用到特殊角的三角函数值时快速记忆,提高我们解题的效率和准确性。
希望大家能多加练习,牢记这些口诀,更加熟练地运用特殊三角函数值在数学问题中。
特殊角的三角函数值记忆口诀手指记忆法一只手

特殊角的三角函数值记忆口诀手指记忆法一只手在学习三角函数时,我们经常要记忆各种特殊角的正弦、余弦、正切值。
为了方便记忆和计算,我们可以利用特殊角的数值特点以及一只手指记忆法。
这种方法既方便,又能在没有工具的情况下随时进行计算。
首先,我们将标注每个手指代表一个特殊角,从食指到小指分别表示0度、30度、45度、60度和90度。
然后,根据特殊角的数值特点,我们可以得到每个角的正弦、余弦、正切值。
•食指(0度):在三角函数中,sine 0等于0、cos 0等于1、tan 0等于0。
•中指(30度):sine 30等于1/2、cos 30等于√3/2、tan 30等于1/√3。
•无名指(45度):sine 45等于√2/2、cos 45等于√2/2、tan 45等于1。
•无名指(60度):sine 60等于√3/2、cos 60等于1/2、tan 60等于√3。
•小指(90度):sine 90等于1、cos 90等于0、tan 90为不存在。
通过这种手指记忆法,我们可以快速获取各个特殊角的正弦、余弦、正切值,不仅可以加深对三角函数的理解,还能方便日常计算。
充分利用我们自己的身体构架能够帮助我们更好地学习和应用知识。
在学习过程中,我们也可以通过手指记忆法来检验自己的记忆和掌握程度,通过不断重复练习,可以加深记忆,提高记忆的持久性。
特殊角的三角函数值记忆口诀手指记忆法一只手,让学习过程更加生动有趣,同时也提高我们记忆和理解的效率。
总结来说,特殊角的三角函数值记忆口诀手指记忆法一只手是一种简单有效的学习方法,可以帮助我们更好地掌握三角函数知识,并在需要时快速计算得出结果。
通过这种方法,我们可以轻松应对关于特殊角的计算,进一步提高学习效率和成绩。
希望这种方法对大家学习三角函数有所帮助。
高中特殊角的三角函数值记忆口诀

高中特殊角的三角函数值记忆口诀
在高中数学学习中,三角函数是一个重要的概念,而特殊角的三角函数值更是需要我们掌握的基础知识。
为了方便记忆和应用,我们可以通过一些口诀来帮助我们快速地计算出特殊角的三角函数值。
0度角(0°)
•正弦值:0
•余弦值:1
•正切值:0
•余切值:无穷
30度角(π/6)
•正弦值:1/2
•余弦值:√3/2
•正切值:1/√3
•余切值:√3
45度角(π/4)
•正弦值:√2/2
•余弦值:√2/2
•正切值:1
•余切值:1
60度角(π/3)
•正弦值:√3/2
•余弦值:1/2
•正切值:√3
•余切值:1/√3
90度角(π/2)
•正弦值:1
•余弦值:0
•正切值:无穷
•余切值:0
通过以上口诀,我们可以方便地记忆和运用特殊角的三角函数值,有助于我们在解决数学问题时更加高效和准确。
对于高中学生来说,掌握这些基础知识是非常重要的,希望大家能够通过不断练习和应用,提高自己的数学能力。
让学生快速记住特殊三角函数值的两种巧妙方法
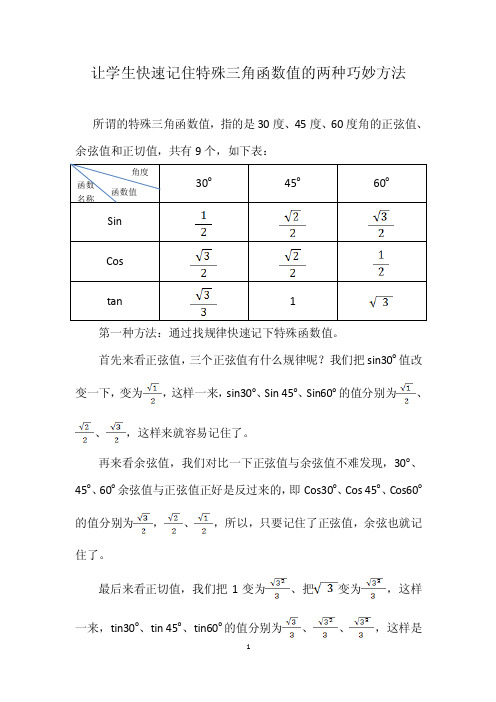
让学生快速记住特殊三角函数值的两种巧妙方法所谓的特殊三角函数值,指的是30度、45度、60度角的正弦值、余弦值和正切值,共有9个,如下表:第一种方法:通过找规律快速记下特殊函数值。
首先来看正弦值,三个正弦值有什么规律呢?我们把sin30o 值改变一下,变为,这样一来,sin30o 、Sin 45o 、Sin60o 的值分别为、、,这样来就容易记住了。
再来看余弦值,我们对比一下正弦值与余弦值不难发现,30o 、45o 、60o 余弦值与正弦值正好是反过来的,即Cos30o 、Cos 45o 、Cos60o 的值分别为,、,所以,只要记住了正弦值,余弦也就记住了。
最后来看正切值,我们把1变为、把变为,这样一来,tin30o 、tin 45o 、tin60o 的值分别为、、,这样是不是好记了?第二种方法:通过画图快速求出特殊三角函数值 首先画出第一幅图:有一个锐角为30度 的直角三角形ABC 。
如图:在Rt △ABC 中,∠A=30o ,∠C=90o 。
由已知条件得∠B=60o ,我们假设BC=1,根据“在直角三角形,30度角所对的直角边是斜边的一半”,所以得AB=2,在根据勾股定理求出AC=,所以sinA =sin30o ==; sinB =sin60o ==; cosA =cos30o ==;cosB =cos60o ==; tinA =tin30o ===;tinB =tin60o ===我们画出了第一幅图就把6个特殊函数值求了出来,接下来我在画第二幅图:有一个锐角为45度的直角三角形ABC 。
如图:在Rt △ABC 中,∠A=45o ,∠C=90o 。
由已知条件得∠B=45o ,我们假设BC=1,ABC BCA所以AC=1,根据勾股定理得AB=。
所以sinA=sin45o==;cosA=cos45o==;tinA=tin45o===1。
这样一来我们通过画两幅图就可以轻而易举的把9个特殊的三角函数值求出来了。
特殊角的三角函数值的巧记

特殊角的三角函数值的巧记特殊角的三角函数值在计算,求值,解直角三角形和今后的学习中,常常会用到,所以一定要熟记•要在理解的根底上,采用巧妙的方法加强记忆•这里关键的问题还是要明白和掌握这些三角函数值是怎样求出的,既便遗忘了,自己也能推算出来,切莫死记硬背.那么怎样才能更好地记熟它们呢?下面介绍几种方法,供同学们借鉴。
1、三角板〞记法根据含有特殊角的直角三角形的知识,利用你手里的一套三角板,就可以帮助你记住30° 45° 60°角的三角函数值•我们不妨称这种方法为三角板〞记法.首先,如图所标明的那样,先把手中一套三角板的构造特点弄明白,记清它们的边角是什么关系.-aa对左边第一块三角板,要抓住在直角三角形中,30°角的对边是斜边的一半的特点,再应用勾股定理•可以知道在这个直角三角形中30°角的对边、邻边、斜边的比是1: 3:2.掌握了这个比例关系,就可以依定义求出30° 60°角的任意一个锐角三角函数值,如:sin30°-,cos30 0 32 2求60°角的三角函数值,还应抓住60°角是30°角的余角这一特点.在右边那块三角板中,应注意在直角三角形中,假设有一锐角为45°那么此三角形是等腰直角三角形,且两直角边与斜边的比是 1 : 1 :2,那么,就不难记住:sin 45° cos45°-, tan45° cot 45° 1。
这种方法形象、直观、简单、2易记,同时稳固了三角函数的定义.二、列表法:说明:正弦值随角度变化,即0? f 30?- 45? f 60? f 90?变化;值从0-1f 二f 仝fl变化,其余类似记忆.2 2 2三、口诀记忆法口诀是:一、二、三,三、二、一,三、九、二十七,弦是二,切是三,分子根号不能删.〞前三句中的1, 2, 3; 3, 2,1; 3, 9, 27,分别是30° 45°60°角的正弦、余弦、正切值中分子根号内的值.弦是二、切是三是指正弦、余弦的分母为2,正切的分母为3.最后一句,讲的是各函数值中分子都加上根号,不能丢掉.如tan60 =—―― . 3 , tan45 = -— 1 .这种方法有趣、简单、易记.3 3四、规律记忆法:观察表中的数值特征,可总结为以下记忆规律:①有界性:〔锐角三角函数值都是正值〕即当0°< v 90°时,那么0< sin < 1 ;0< cos < 1 ; tan >0 ;cot >0。
