浙教版八年级下册5.1矩形同步练习(无答案)
初中数学浙教版八年级下册5.1 矩形(1) 同步训练

初中数学浙教版八年级下册5.1 矩形(1)同步训练一、基础夯实(共9题;共28分)1.如图,在矩形AOBC中,A(-2,0),B(0,1).若正比例函数y=kx的图象经过点C,则k的值为()A. -B.C. -2D. 22.如图,矩形ABCD的对角线交于点O.若∠BAO=55°,则∠AOD等于( )A. 110°B. 115°C. 120°D. 125°3.矩形不一定具有的性质是()A. 对角线互相平分B. 对角线互相垂直C. 对角线相等D. 是轴对称图形4.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法不一定成立的是()A. ∠ABC=90°B. AC=BDC. OA=OBD. OA=AD5.如图,矩形的对角线,交于点,,,则的长为()A. 4cmB. 4cmC. 2cmD. 2cm6.已知一个矩形的对角线的长为4,它们的夹角是60°,则这个矩形的较短的边长为________,面积为________.7.如图,矩形ABCD中,点E,F分别是AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N,连接AM, CN,MN,若AB=2,BC=3,则图中阴影部分的面积为________.8.如图,E为矩形ABCD内一点,且EB=EC,求证:AE=ED.9.如图,在矩形ABCD中,对角线AC与BD交于点O,DE∥AC交BA的延长线于点E.(1)求证:BD=DE;(2)若∠ACB=30°,BD=8,求四边形BCDE的面积.二、提高特训(共6题;共13分)10.如图,已知矩形ABCD的对角线AC的长为10cm,连接各边中点E,F,G,H得四边形EFGH,则四边形EFGH的周长为( ).A. 20cmB. 20 cmC. 20 cmD. 25 cm11.如图,▱ABCD的对角线AC、BD相交于点O,则下列条件中不能判定四边形ABCD为矩形的是()A. AB=ADB. OA=OBC. AC=BDD. DC⊥BC12.如图,将两根相同的矩形木条沿虚线剪开得到四根完全一样的木条,然后重新围城一个矩形画框.已知矩形木条的两边分别为,且,则围城的矩形画框的内框的面积为()A. B. C. D.13.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E.若∠ADE=22.5°,BD=4,则OE的长为________.14.如图,在矩形ABCD中,对角线AC、BD交于点O,DE平分∠ADC.若∠AOB=60°,则∠COE的大小为________ .15.如图所示,矩形ABCD的对角线相交于点O,OF⊥AD于点F,OF=2cm,AE⊥BD于点E,且BE﹕BD=1﹕4,求AC的长.答案解析部分一、基础夯实二、提高特训。
八年级数学下册《5.1 矩形(第1课时)》同步练习 浙教版(2021学年)

浙江省绍兴市绍兴县杨汛桥镇八年级数学下册《5.1 矩形(第1课时)》同步练习(新版)浙教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(浙江省绍兴市绍兴县杨汛桥镇八年级数学下册《5.1 矩形(第1课时)》同步练习(新版)浙教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为浙江省绍兴市绍兴县杨汛桥镇八年级数学下册《5.1 矩形(第1课时)》同步练习(新版)浙教版的全部内容。
5。
1 矩形(第1课时)课堂笔记有一个角是的叫做矩形;矩形的个角都是直角;矩形的对角线;矩形既是对称图形,又是对称图形,它至少有条对称轴。
课时训练A组基础训练1.下面图形中,既是中心对称图形,又是轴对称图形的是( )A。
等腰三角形ﻩB。
平行四边形C。
等边三角形ﻩ D. 矩形2。
已知一矩形的周长是24cm,相邻两边之比是1∶2,那么这个矩形的面积是()A.24cm2ﻩB。
32cm2 ﻩC。
48cm2 D。
128cm2 3。
矩形具有而一般的平行四边形不具有的特征是( )A. 对角线相等ﻩB。
对边相等C. 对角相等D。
对角线互相平分1AE,AE=2,则AC等于( )4。
如图,E为矩形ABCD的边BC的中点,且BE=2A.3ﻩB. 22ﻩC. 6D。
75。
如图,在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE等于( )A. 15°ﻩB. 22.5°ﻩC.30°ﻩD。
45°6。
如图,在矩形ABCD中,∠DBC=29°,将矩形沿直线BD折叠,顶点C落在点E处,则∠ABE的度数是( )A。
29°B。
八年级数学下册5.1矩形同步练习新版浙教版【word版】.doc

5.1矩形一、选择题1.过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是()A. 对角线相等的四边形B. 对角线垂直的四边形C. 对角线互相平分且相等的四边形D. 对角线互相垂直平分的四边形2.如图,要使▱ABCD成为矩形,需添加的条件是( )A. AB=BCB. AO=BOC. ∠1=∠2D. AC⊥BD3.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC 于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是()A. 2.5B. 2.4C. 2.2D. 24.不能判断四边形ABCD是矩形的是(0为对角线的交点)()A. AB=CD,AD=BC,∠A=90°B. OA=OB=OC=ODC. AB CD,AC=BDD. AB CD,OA=OC,OB=OD5.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是()A. 3B. 5C. 2.4D. 2.56.矩形ABCD的周长为56,对角线AC,BD交于点O,△ABO与△BCO的周长差为4,则AB的长是()A. 12B. 22C. 16D. 267.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为()A. B. 8 C.D. 68.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为()A. 30°B. 60°C. 90°D. 120°9.已知:如图,在▱ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE 交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是()A. 菱形B. 矩形C. 平行四边形 D. 正方形10.如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是()A. B. 2C. 2D. 4二、填空题11.如图,在矩形ABCD中,已知∠DBC=45°,∠DBC的平分线交DC于点E,作EF⊥BD于点F,作FG⊥BC于点G,则=________.12.如图,矩形ABCD中,O是两对角线的交点,AE⊥BD,垂足为E.若OD=2OE,AE= ,则AD的长为________13.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为________14.已知矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4,则矩形对角线的长是________.15.工人师傅在做矩形零件时,常用测量平行四边形的两条对角线是否相等来检查直角的精确度,这是根据________.16.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为________ .17.如图,矩形ABCD的面积为6,它的两条对角线交于点,以AB、A为两邻边作平行四边形AB,平行四边形AB的对角线交于点,同样以AB、A为两邻边作平行四边形AB,……,依次类推,则平行四边形AB的面积为________.三、解答题18.如图所示,M是▱ABCD的中点,且MB=MC,求证:▱ABCD是矩形.19.如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.20.已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,(1)求证:四边形ADCE是平行四边形;(2)当△ABC满足什么条件时,平行四边形ADCE是矩形?21.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?。
浙教版 八年级下册第五章特殊的平行四边形第一节矩形同步习题( 答案不全)

(浙教版)八年级下册第五章特殊的平行四边形第一节矩形同步习题一、单选题1.矩形具有而平行四边形不一定具有的性质是( ) A .对角线互相垂直 B .对角线相等C .对角线互相平分D .对角相等2.检查一个门框(已知两组对边分别相等)是不是矩形,不可用的方法是( ) A .测量两条对角线是否相等 B .用重锤线检查竖门框是否与地面垂直 C .测量两条对角线是否互相平分D .测量门框的三个角是否都是直角3.如图,矩形ABCD 的两条对角线相交于点O ,∠AOB =60°,AO =4,则AB 的长是( )A .4B .5C .6D .84.如图,△ABC 中,∠ACB =90°,AD =DB ,CD =4,则AB 等于( )A .8B .6C .4D .25.如图,在Rt ABC ∆中,90ABC ∠=︒,BD 是AC 的中线,BD=5,则以下结论正确的是( )A .5AB = B .10AB =C .10BC =D .10AC =6.已知:如图,矩形ABCD 中,AB =5,BC =12,对角线AC 、BD 相交于点O ,点P 是线段AD 上任意一点,且PE ⊥AC 于点E ,PF ⊥BD 于点F ,则PE +PF 等于( )A .6013B .5013C .185D .1257.如图,在直角坐标系中,将矩形OABC 沿OB 对折,使点A 落在A 1处,已知AB=1,则点A 1的坐标是( )A .32)B .3)C .(32D .(128.矩形ABCD 与CEFG ,如图放置,点B ,C ,E 共线,点C ,D ,G 共线,连接AF ,取AF 的中点H ,连接GH .若BC=EF=2,CD=CE=1,则GH=( )A .1B .23C D 9.如图,在Rt △ABC 中,∠BAC=90°,AB=5,AC=12,P 为边BC 上一动点(P 不与B 、C 重合),PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的取值范围是( )A .3013≤AM <6 B .5≤AM <12 C .125≤AM <12D .125≤AM <6 10.如图所示,矩形ABCD 中,AE 平分BAD ∠交BC 于E ,15CAE ︒∠=,则下面的结论:①ODC ∆是等边三角形;②=2BC AB ;③135AOE ︒∠=;④AOE COE S S ∆∆=,其中正确结论有( )A .1个B .2个C .3个D .4个二、填空题11.如图,在平行四边形ABCD 中,添加一个条件________使平行四边形ABCD 是矩形.12.矩形的两条对角线的夹角为60,较短的边长为12cm ,则对角线长为________cm .13.如图,已知在ABC ∆中,90,ACB ∠=︒CD 是AB 边上的中线,6AB =,则CD 的长度是_______.14.如图,E 是矩形ABCD 的对角线的交点,点F 在边AE 上,且DF =DC ,若∠ADF =25°,则∠ECD =___°.15.矩形ABCD 的对角线AC 、BD 相交于点O ,∠AOD =120°,AC =8,则△ABC 的周长为_____. 16.如图,矩形ABCD 中将其沿EF 翻折后,D 点恰落在B 处,∠BFE = 65°,则∠AEB =____________.17.如图,在Rt △ABC 中,∠BAC =90°,且BA =6,AC =8,点D 是斜边BC 上的一个动点,过点D 分别作DM ⊥AB 于点M ,DN ⊥AC 于点N ,连接MN ,则线段MN 的最小值为_____.18.如图,将平行四边形ABCD 的边DC 延长到E ,使CE CD =,连接AE 交BC 于F ,AFC n D ∠∠=,当n =______时,四边形ABEC 是矩形.19.如图,在Rt △ABC 中,∠BAC =90º,BC =4,E 、F 分别是BC ,AC 的中点,延长BA 到点D ,使AD=12AB ,则DF=_______.20.如图,点P 是矩形ABCD 的对角线AC 上一点,过点P 作EF ∥BC ,分别交AB ,CD 于点E ,F ,连接PB ,PD .若AE =2,PF =8.则图中阴影部分的面积为___.三、解答题21.如图,在矩形ABCD 中,AE ∥BD ,且交CB 的延长线于点E ,求证:∠EAB =∠CAB .22.已知:在矩形ABCD 中,BD 是对角线,AE BD ⊥于点E ,CF BD ⊥于点F .求证:AE CF =23.如图,在△ABC 中,∠BAC =90°,AC =5,AB =12,∠BAC 的平分线与BC 的垂直平分线DG 交于点D ,DE ⊥AC 的延长线于点E ,DF ⊥AB 于点F .(1)求证:CE =BF ; (2)求DG 的长.24.如图,在四边形ABCD 中,对角线AC ,BD 相交于点O ,AO =CO ,BO =DO ,且∠ABC +∠ADC =180°.(1)求证:四边形ABCD 是矩形;(2)若∠ADF :∠FDC =3:2,DF ⊥AC ,求∠BDF 的度数.25.如图,ABCD 的面积为60DAB ︒∠=.点P 从点D 出发,以每秒1个单位的速度向点C 运动:点Q 从点B 同时出发,以每秒3个单位的速度向点A 运动.规定其中一个点到达端点时,另一个点也随之停止运动。
浙教版八年级数学下册《5.1矩形(1)》同步练习(含答案)
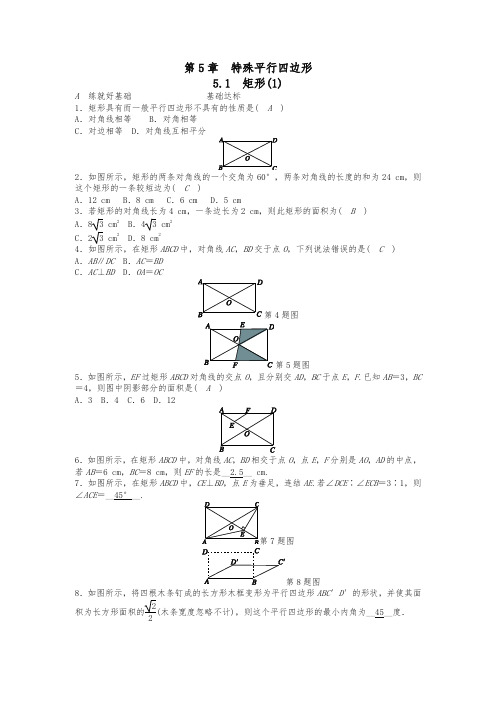
第5章特殊平行四边形5.1 矩形(1)A练就好基础基础达标1.矩形具有而一般平行四边形不具有的性质是( A)A.对角线相等B.对角相等C.对边相等 D.对角线互相平分224 cm,则这个矩形的一条较短边为( C)A.12 cm B.8 cm C.6 cm D.5 cm3.若矩形的对角线长为4 cm,一条边长为2 cm,则此矩形的面积为( B)A.8 3 cm2 B.4 3 cm2C.2 3 cm2 D.8 cm24.如图所示,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( C) A.AB∥DC B.AC=BDC.AC⊥BD D.OA=OC4题图5题图5.如图所示,EF过矩形ABCD对角线的交点O,且分别交AD,BC于点E,F.已知AB=3,BC =4,则图中阴影部分的面积是( A)A.3 B.4 C.6 D.126.如图所示,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=6 cm,BC=8 cm,则EF的长是__2.5__ cm.7.如图所示,在矩形ABCD中,CE⊥BD,点E为垂足,连结AE.若∠DCE∶∠ECB=3∶1,则∠ACE=__45°__.7题图8题图8.如图所示,将四根木条钉成的长方形木框变形为平行四边形ABC′D′的形状,并使其面积为长方形面积的22(木条宽度忽略不计),则这个平行四边形的最小内角为__45__度.解:过点C′作AB的垂线,垂足是点E,如图所示:∵将四根木条钉成的矩形木框变形为平行四边形木框ABC′D′的形状,并使其面积为矩形木框的22,∴C′E=22BC=22BC′,∴BC′=2C′E,∴∠C′BE=∠D′AB=45°.9.如图所示,已知矩形ABCD的对角线AC与BD交于点O.(1)求证:∠ACD=∠ABD.(2)若矩形ABCD的面积为120 cm2,周长为46 cm,求AC的长.解:(1)证明:在矩形ABCD中,易得∠DCB=∠ABC=90°,OC=OB,∴∠OBC=∠OCB.∴∠DCB-∠OCB=∠ABC-∠OBC,∴∠ACD=∠ABD.(2)在Rt△ABC中,AC=AB2+BC2=17.10.如图所示,BD为矩形ABCD的一条对角线,延长BC至点E,使CE=BD,连结AE,若AB =1,∠AEB=15°,求AD的长度.解:如图,连结AC,∵四边形ABCD是矩形,∴AD∥BE,AC=BD,且∠ADB=∠CAD,∴∠E=∠DAE.又∵BD=CE,∴CE=CA,∴∠E=∠CAE.∵∠CAD=∠CAE+∠DAE=30°,∴∠ADB=30°,∴BD=2AB=2,∴AD=BD2-AB2= 3.B更上一层楼能力提升11.如图所示,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1,S2,则S1,S2的大小关系是( A)A.S1=S2B.S1>S2C.S1<S2 D.3S1=2S212.如图所示,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为AB上一动点,且PE⊥AC于点E,PF⊥BC于点F,则线段EF长度的最小值是__2.4__.12题图13题图13.如图所示,在矩形ABCD 中,AC ,BD 相交于点O ,AE 平分∠BAD 交BC 于点E .若∠CAE =15°,则∠BOE 的度数是__75°__.14.2018·威海矩形ABCD 与CEFG ,如图放置,点B ,C ,E 共线,点C ,D ,G 共线,连结AF ,取AF 的中点H ,连结GH .若BC =EF =2,CD =CE =1,求GH 的长.解:如图,延长GH 交AD 于点P ,∵四边形ABCD 和四边形CEFG 都是矩形,∴∠ADC =∠ADG =∠CGF =90°,AD =BC =2,GF =CE =1,∴AD ∥GF ,∴∠GFH =∠PAH .又∵H 是AF 的中点,∴AH =FH .在△APH 和△FGH 中,∵⎩⎪⎨⎪⎧∠PAH =∠GFH ,AH =FH ,∠AHP =∠FHG ,∴△APH ≌△FGH (ASA ),∴AP =GF =1,GH =PH =12PG , ∴PD =AD -AP =1.∵CG =2,CD =1,∴DG =1,∴GH =12PG =12×PD 2+DG 2=22. 15.如图所示,在矩形ABCD 中,E ,F 分别是边BC ,AB 上的点,且EF =ED ,EF ⊥ED . 求证:AE 平分∠BAD .证明:∵四边形ABCD 是矩形,∴∠B =∠C =∠BAD =90°,AB =CD,∴∠BEF +∠BFE =90°.∵EF ⊥ED ,∴∠BEF +∠CED =90°.∴∠BFE =∠CED .又∵EF =ED ,∴△EBF ≌△DCE (AAS ).∴BE =CD .∴BE =AB ,∴∠BAE =∠BEA =45°.∴∠EAD =45°.∴∠BAE =∠EAD .∴AE 平分∠BAD .C 开拓新思路 拓展创新16.如图所示,四边形ABCD 是矩形,P 是矩形外一点,且PA =PB .(1)求证:PD =PC .(2)若△PAB 的面积为S 1,△PCD 的面积为S 2,则矩形ABCD 的面积为________.解:(1)证明:∵四边形ABCD 是矩形,∴AD =BC ,∠DAB =∠ABC =90°.∵PA =PB ,∴∠PAB =∠PBA ,∴∠PAD =∠PBC .在△APD 和△BPC 中,∵⎩⎪⎨⎪⎧PA =PB ,∠PAD =∠PBC ,AD =BC ,∴△APD ≌△BPC (SAS ),∴PD =PC .(2)2(S 1-S 2)。
浙教版数学 八年级下第五章 5.1矩形的性质 同步练习

浙教版数学八年级下册第五章5. 1矩形的性质同步练习第Ⅰ卷(选择题)一.选择题(共10小题,3*10=30)1. 如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为( ) A.1 B.2 C.3 D.42.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )A.∠ABC=90°B.AC=BDC.OA=OB D.OA=AD3. 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6 cm,则AB的长是( ) A.3 cm B.6 cm C.10 cm D.12 cm4.如图,矩形纸片ABCD 中,AB =4,BC =6,将△ABC 沿AC 折叠,使点B 落在点E 处,CE 交AD 于点F ,则DF 的长等于( ) A .35 B .53 C .73 D .545.在矩形ABCD 中,点O 是BC 的中点,∠AOD =90°,矩形ABCD 的周长为30 cm ,则AB 的长为( ) A .3 cm B .4 cm C .5 cm D .6 cm6.如图,矩形ABCD 的两条对角线相交于点O ,∠AOD =60°,AD =2,则AC 的长是( ) A .2 B .4 C .2 3 D .4 37.如图,四边形ABCD 和四边形AEFC 是两个矩形,点B 在边EF 上,若矩形ABCD 和矩形AEFC 的面积分别是S 1,S 2,则S 1,S 2的大小关系是( ) A .S 1>S 2 B .S 1=S 2 C .S 1<S 2 D .3S 1=2S 28.如图,在矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,则重叠部分△AFC 的面积为( ) A .12 B .10 C .8 D .6是( )A .3B .5C .5 2D .52210.如图,在△ABC 中,AB =AC ,D 为BC 中点,四边形ABDE 是平行四边形,AC ,DE 相交于点O. 若∠AOE =60°,AE =4,则矩形ADCE 对角线的长是( ). A .4 B .6 C .8 D .10第Ⅱ卷(非选择题)二.填空题(共6小题,3*8=24)11.在矩形ABCD 中,点O 是BC 的中点,∠AOD =90°,矩形ABCD 的周长为30 cm ,则AB 的长为_______cm .12. 如图,在矩形纸片ABCD 中,E 是AD 的中点,且AE =1,BE 的垂直平分线MN 恰好过点C ,则AB 的长为_______.13.如图,矩形OBCD 的顶点C 的坐标为(1,3),则对角线BD 的长等于______.14.如图,矩形ABCD的两条对角线交于点O,过点O作AC的垂线EF,分别交AD,BC于点E,F,连结CE,已知△CDE的周长为24 cm,则矩形ABCD的周长是______cm.15.如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为_______.16.如图,矩形ABCD中,AB=3 cm,BC=4 cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F,G.则PF+PG的长为____cm.17. 如图,矩形ABCD中,AB=2,BC=4,点A,B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是__________________________.18.如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点B的坐标是__________.三.解答题(共7小题,46分)19. (6分)如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连结AF,DE交于点O.求证:(1)△ABF≌△DCE;(2)△AOD是等腰三角形.20.(6分)如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.(1)求证:BD=BE;(2)若∠DBC=30°,BO=4,求四边形ABED的面积..21.(6分)如图,在矩形ABCD中,E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.22.(6分)如图,在矩形ABCD中,E,F分别是AD,BC的中点,CE,AF分别交BD于G,H两点.求证:(1)四边形AFCE是平行四边形;(2)EG=FH.23.(6分)在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.求证:DF=DC.24. (8分)如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD,若∠EAO=15°,求∠BOE的度数.25.(8分)如图,在矩形ABCD中,AB=12 cm,BC=6 cm,点P沿AB从点A开始向点B以2 cm/s的速度移动,点Q沿DA边从点D开始向点A以1 cm/s的速度移动,如果P,Q同时出发,用t(s)表示移动的时间(0≤t≤6).(1)当t为何值时,△QAP为等腰三角形?(2)求四边形QAPC的面积,并探索一个与计算结果有关的结论.2参考答案 1-5 BDABC 6-10 BBBDC 11. 5 12. 3 13. 10 14. 48 15. 14 16. 317. (23+1,2) 18. (2,23)19. 解:(1)∵四边形ABCD 是矩形,∴AB =DC ,∠ABF =∠DCE =90°,又∵BE =CF ,∴BE +EF =CF +EF ,∴BF =CE ,∴△ABF ≌△DCE(SAS )(2)∵△ABF ≌△DCE ,∴∠DEF =∠AFE ,又∵AD ∥BC ,∴∠OAD =∠AFE ,∠ODA =∠DEF ,∴∠OAD =∠ODA ,∴OA =OD ,∴△AOD 是等腰三角形20. 解:(1)∵AB ∥CD ,BE ∥AC ,∴四边形ABEC 是平行四边形,∴AC =BE ,又∵BD =AC ,∴BD =BE (2)S 四边形ABED =24 321. 解:易证△BEF ≌△CDE ,∴BE =CD =AB ,∴△ABE 是等腰直角三角形,∴∠BAE =45°,从而∠BAE =12∠BAD ,∴AE 平分∠BAD22. 解:(1)∵四边形ABCD 是矩形,∴AD ∥BC ,AD =BC ,∵E ,F 分别是AD ,BC 的中点,∴AE =12AD ,CF =12BC ,∴AE =CF ,∴四边形AFCE 是平行四边形(2)∵四边形AFCE 是平行四边形,∴CE ∥AF ,∴∠DGE =∠AHD =∠BHF ,∵AD ∥BC ,∴∠EDG =∠FBH ,又∵DE =BF ,∴△DEG ≌△BFH(AAS),∴EG =FH23. 解:连结DE ,∵AE =AD =CD ,∴∠ADE =∠DEF ,∵AD ∥BC ,∴∠DEC =∠ADE ,∴∠DEF =∠DEC ,又∵∠DFE =∠DCE =90°,DE =DE ,∴△DEF ≌△DEC ,∴DF =DC24.解:∵AE 平分∠BAD ,∴∠BAE =45°,从而∠OAB =45°+15°=60°,易证OA =OB ,∴△AOB 是等边三角形,∴OB =AB ,易证△ABE 是等腰直角三角形,∴BE =AB ,∴OB =BE ,∴∠BOE =∠BEO ,又∵∠OBE =90°-60°=30°,∴∠BOE =75°25. 解:(1)由DQ =t cm ,得AQ =(6-t) cm ,AP =2t cm ,若△QAP 为等腰三角形,则只能是AQ =(2)S 四边形QAPC =S 矩形ABCD -S △CDQ -S △BPC =12×6-12×12t -12×(12-2t)×6=72-6t -36+6t =36(cm 2).结论:四边形QAPC 的面积始终不变,为36 cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩形(1)
1.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是()
A.∠ABC=90°
B.AC=BD
C.OA=OB
D.OA=AD
2.如图,矩形ABCD的两条对角线交于点O.若∠AOD=120°,AB=6,则AC的长为()
A.8
B.10
C.12
D.18
3.如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为cm.
4.如图,在平面直角坐标系中,点O为坐标原点,矩形OABC中,A(10,0)、C(0,4),D为OA的中点,P为BC边上一点.若∠POD为等腰三角形,则所有满足条件的点P的坐标为.
5.如图,E 、F 是矩形ABCD 对角线AC 上的两点,试添加一个条件: (∠DFE=∠BEF 除外)使得BE∠DF.
6.若矩形ABCD 的两邻边长分别为一元二次方程01272
+-x x 的两个实数根,则矩形ABCD 的对角线长为 .
7.如图,四边形ABCD 为矩形,H 、F 分别为AD 、BC 边的中点,四边形EFGH 为矩形,E 、G 分别在AB 、CD 边上,则图中四个直角三角形面积之和与矩形EFGH 的面积之比为 .
8.如图,在矩形ABCD 中,AD =12,AB =5,P 是边AD 上异于点A 和D 的任意一点,PE∠BD 于点E ,PF∠AC 于点F ,则PE +PF= .
9.如图,在矩形ABCD 中,点O 在边AB 上,∠AOC=∠BOD.求证:AO=OB.
10.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别在边AD、BC 上,且DE=CF,连结OE、OF.求证:OE=OF.
11.如图,在矩形ABCD中,F是CD中点,连结AF并延长,交BC的延长线于点E,连结AC、DE.
(1)求证:∠ADF∠∠ECF;
(2)若AB=1,BC=2,求四边形ACED的面积.
12.如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF∠AE,垂足为F,连结DE.求证:BE=AF.。
