cos的功率谱函数
通信原理习题解答

W
Pd
n0 4
B
1
W
第5章
5. 已知调制信号 m(t) = cos2000t + cos4000t ,载波为 cos104t,进行单边带调制,试确定该上边带信号的表示 式,并画出其频谱图。
解:m(t)的Hilbert变换为
mˆ (t) sin 2000πt sin 4000πt
则上边带信号为
sUSB
j2πf
1 (2 jsin0.2πf ) j2πf
0.2 sin0.2πf 0.2Sa(0.2πf ) 0.2πf
(2)频谱图如图所示。
3. 已知f (t)的频谱F(f )如图所示,画出 f(t)cos2f0t的频谱函数 图。设f0=3fx。
解:设 f1 (t) f (t) cos 2πf0t 根据傅里叶变换的频移性质直接画出其频谱函数F1(f )。
第一章
1. 通信系统的主要性能指标是什么? 解:通信系统的主要性能指标有有效性和可靠性。
在模拟通信系统中,系统的传输有效性通常用每路信号 的有效传输带宽来衡量。可靠性通常用通信系统的输出 信噪比来衡量。 数字通信系统的有效性可以用码元传输速率或信息传 输速率来衡量。数字通信系统的传输可靠性通常用差错 率来衡量。差错率有两种表述方法:误码率及误信率。
解(1)DSB: B=2fx=30 kHz
Si Ni
S0 N0
/ GDSB
105 / 2 510 4
Ni n0B 2 10 12 30 103 6 10 8 (W)
Si 5104 6 108 3 (mW) S 105 Si 300 (W)
(2)SSB: B=fx=15 kHz
Si Ni
S0 N0
/ GAM
第21讲 频带传输:MSK、功率谱密度

= E [b(t )b(t + τ ) ] E [ cos(2ωc t + ωcτ + 2θ ) ]
E [b(t )b(t + τ ) cos(2ωc t + ωcτ + 2θ )]
1 Rs (τ ) = Tb
∫
Rs (t , t + τ )dt
1 1 = cos(ωcτ ) Tb 2
因为 xk = 0, ±π
xk =
2
+ xk −1
所以 bI = ±1 bQ = ±1 2nπ (a2 n −1 − a2 n ) bI (2 n ) = cos x2 n = cos x2 n −1 + = cos x2 n −1 = bI (2 n −1) 2 即 bI 在 (2n − 1)Ts ≤ t ≤ (2n + 1)Ts 范围内取值不变 同理: 同理:bQ (2 n +1) = bQ (2 n ) 即 bQ 在 2nTs ≤ t ≤ (2n + 2)Ts 范围内取值不变
频带传输系统
f' 恒包络连续相位调制— 恒包络连续相位调制—MSK
∆f
二进制频移键控信号: 二进制频移键控信号:
π A cos(2f1 f1t ) s2FSK (t ) = A cos(2π f 2t ) 则两个波形间的频率间隔: 则两个波形间的频率间隔:f ' = f1 − f 2
"1" "0"
则载波的角度为:Φ = ω dt = 则载波的角度为: ∫ ∫
−∞ t t −∞
Φ = ∫ ω dt
−∞
t
[ 2π f c + 2π hb(τ )] dτ
功率谱计算[资料]
![功率谱计算[资料]](https://img.taocdn.com/s3/m/0a7a52056fdb6f1aff00bed5b9f3f90f76c64d0e.png)
功率谱计算功率谱估计在现代信号处理中是一个很重要的课题,涉及的问题很多。
在这里,结合matlab,我做一个粗略介绍。
功率谱估计可以分为经典谱估计方法与现代谱估计方法。
经典谱估计中最简单的就是周期图法,又分为直接法与间接法。
直接法先取N点数据的傅里叶变换(即频谱),然后取频谱与其共轭的乘积,就得到功率谱的估计;间接法先计算N点样本数据的自相关函数,然后取自相关函数的傅里叶变换,即得到功率谱的估计.都可以编程实现,很简单。
在matlab中,周期图法可以用函数periodogram实现。
但是周期图法估计出的功率谱不够精细,分辨率比较低。
因此需要对周期图法进行修正,可以将信号序列x(n)分为n个不相重叠的小段,分别用周期图法进行谱估计,然后将这n段数据估计的结果的平均值作为整段数据功率谱估计的结果。
还可以将信号序列x(n)重叠分段,分别计算功率谱,再计算平均值作为整段数据的功率谱估计。
这2种称为分段平均周期图法,一般后者比前者效果好。
加窗平均周期图法是对分段平均周期图法的改进,即在数据分段后,对每段数据加一个非矩形窗进行预处理,然后在按分段平均周期图法估计功率谱。
相对于分段平均周期图法,加窗平均周期图法可以减小频率泄漏,增加频峰的宽度。
welch法就是利用改进的平均周期图法估计估计随机信号的功率谱,它采用信号分段重叠,加窗,FFT等技术来计算功率谱。
与周期图法比较,welch法可以改善估计谱曲线的光滑性,大大提高谱估计的分辨率。
matlab中,welch法用函数psd实现。
调用格式如下:[Pxx,F] = PSD(X,NFFT,Fs,WINDOW,NOVERLAP)X:输入样本数据NFFT:FFT点数Fs:采样率WINDOW:窗类型NOVERLAP,重叠长度现代谱估计主要针对经典谱估计分辨率低和方差性不好提出的,可以极大的提高估计的分辨率和平滑性。
可以分为参数模型谱估计和非参数模型谱估计。
参数模型谱估计有AR模型,MA模型,ARMA模型等;非参数模型谱估计有最小方差法和MUSIC法等。
数字频带传输的功率谱和带宽总结
(1)当基带信号为矩形波时:
2 PSk f
传输带宽:
B2 PSK 2B基带 2 Bnull 2 RB
(2)当对基带信号作无 ISI 滤波时 :
Hf
f
0 fN
2 PSK f
B f N 1
f
0
fc B
fc
fc B
传输带宽: B2 PSK 2B基带 2 f N 1 RB 1
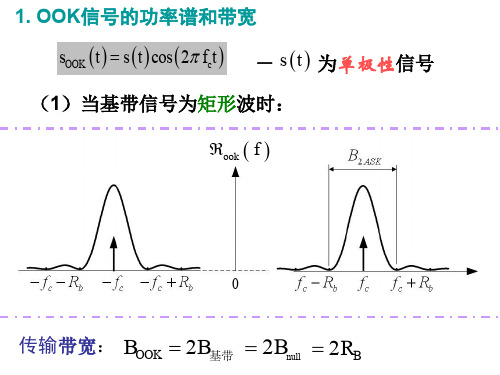
1. OOK信号的功率谱和带宽
sOOK t s t cos 2 fct
- s t 为单极性信号
(1)当基带信号为矩形波时:
ook f
0
传输带宽: BOOK 2B基带 2 Bnull 2 RB
(2)当对基带信号作无 ISI 滤波时 :
Hf
f
0 fN
QPSK f
f N 1
f
0
ff c f N 1
传输带宽: BQPSK 2 f N 1 RB 1
4. DQPSK、OQPSK、 DQPSK 信号的功率谱和带宽 4
与QPSK的完全一样。 5. MPSK、MDPSK信号的功率谱和带宽
f
0 fN
OOK f
B f N 1
f
0
fc B
fc
fc B
传输带宽: BOOK 2B基带 2 f N 1 RB 1
2. BPSK信号的功率谱和带宽
s2 PSK t s t cos 2 fct
- s t 为双极性信号
与BPSK的完全一样。
总结: OOK、MPSK 、MDPSK的功率谱和带宽完全一样。
功率谱密度估计方法的MATLAB实现

功率谱密度估计方法的MATLAB实现功率谱密度估计是信号处理领域中常用的一种方法,用于分析信号的频率特性。
MATLAB提供了多种功率谱密度估计方法的函数,包括传统的傅里叶变换方法和更现代的自相关方法。
以下是一些常见的功率谱密度估计方法及其MATLAB实现。
1.傅里叶变换方法:傅里叶变换方法是最常用的功率谱密度估计方法之一、MATLAB提供了`pwelch`函数来实现傅里叶变换方法的功率谱密度估计。
以下是一个简单的使用例子:```matlabfs = 1000; % 采样率t = 0:1/fs:1-1/fs; % 时间序列x = cos(2*pi*50*t) + randn(size(t)); % 生成一个包含50 Hz 正弦波和噪声的信号[Pxx, f] = pwelch(x, [],[],[], fs); % 估计功率谱密度plot(f, 10*log10(Pxx)); % 画出功率谱密度曲线xlabel('Frequency (Hz)');ylabel('Power Spectral Density (dB/Hz)');```2.自相关方法:自相关方法是另一种常用的功率谱密度估计方法。
MATLAB提供了`pcov`函数来实现自相关方法的功率谱密度估计。
以下是一个简单的使用例子:```matlabfs = 1000; % 采样率t = 0:1/fs:1-1/fs; % 时间序列x = cos(2*pi*50*t) + randn(size(t)); % 生成一个包含50 Hz 正弦波和噪声的信号[Rxx, lags] = xcorr(x, 'biased'); % 估计自相关函数[Pxx, f] = pcov(Rxx, [], fs, length(x)); % 估计功率谱密度plot(f, 10*log10(Pxx)); % 画出功率谱密度曲线xlabel('Frequency (Hz)');ylabel('Power Spectral Density (dB/Hz)');```3.周期图方法:周期图方法是一种能够处理非平稳信号的功率谱密度估计方法。
【精品】扩频通信习题解答

扩频通信习题参考解答1 在高斯噪声干扰信道中,要求在干扰噪声功率比信号平均功率大100 倍的情况下工作,输出信噪比不小于10dB,信息传输速率Rb=8kb/s,系统采用直扩BPSK 调制,试求所需传输通道的最小带宽解:S 10dB ,忽略系统的实现执行损耗,即Lsys 0dB ,系统要求干扰N out容限M j 100 20dB ,则系统的处理增益为S G P M j Lsys N out 20dB 10dB 30dB 1000扩频码的码速率为Rc Rb G P 8kb/s 1000 8000b/s 8Mb/s传输通道的带宽为BRF 2 Rc 16MHz 2 某系统的最大带宽BRF=1.2MHz,一信号的速率Rb=6kHz,设系统采用直扩BPSK 调制,该信号通过这个系统时,输出的信噪比最大能改善多少解:速率为Rb=6kHz 的信号,BPSK 调制后,经信号的带宽为Bb12kHz,这样,系统的扩频增益为BRF GP Bb 1.2MHz 100 20dB 12kHz信号通过系统时,输出的信噪比最大能改善20dB。
3 一白色高斯噪声干扰信道,信道带宽为4MHz,当干扰比信号噪大30dB时,要求输出信噪比最小为10dB 的情况下,允许的最大信息传输速率为多少解:在忽略系统的实现执行损耗,即Lsys 0dB ,M j 30dB ,则处理增益为S G P M j Lsys N out 30dB 10dB 40dB 10000扩频码速率为BRF Rc 2 2Mb/s信息码速率为Rc Rb GP 2Mb/s 0.2kb/s 10000在要求的条件下,允许的信息传输速率不能大于0.2kb/s。
4 用一码速率为Rc=5Mb/s 的伪码序列,进行直接序列扩频,扩频后信号带宽是多少?若信息码速率为10k/s,则系统处理增益是多少?解:BRF 2 Rc 2 5 10MHz Rc GP Rb 5Mb/s 500 27dB 10kb/s 5 要求某系统在干扰噪声功率比信号功率大300 倍的环境下工作,系统需要多大的干扰容限?若要求输出信噪比为10dB,则系统的最小处理增益是多少?解:系统需要的干扰容限M j 300 24.8dB ,在忽略系统的实现执行损耗,即Lsys 0dB ,系统的最小处理增益为S G P M j Lsys N out 24.8dB 10dB 34.8dB 3000 6 一个FH/DS 混合系统,扩频码速率Rc20Mb/s,频率数为100,数据信息速率为9.6kb/s,试求该系统的处理增益是多少?解:直扩增益为R G PDS c Rb 20Mb/s 2000 33dB 9.6kb/s跳频增益为G PFH N 100 20dB假设各频点间的频率间隔为40MHz,即在跳频时频谱不会发生重叠,这样,系统的处理增益为G P G PDS G PFH 2000 100 200000 33dB 20dB 53dB 7 BPSK 直接序列扩频系统的发射信号功率谱是怎样的?主瓣与旁瓣带宽之比是多少?与主瓣峰值相比,第一旁瓣的峰值功率电平是多少?主瓣包含的信号功率占总信号功率的百分比是多少?解:2 sin x BPSK 直接序列扩频系统的发射信号功率谱具有形状,主瓣带宽为xBRF Rc 0 Rc (单边),第一旁瓣带宽为2 Rc Rc Rc (单边),第二旁瓣带宽为3Rc 2 Rc Rc (单边),……,主瓣与旁瓣带宽相等。
韦尔奇功率谱密度

韦尔奇功率谱密度
韦尔奇功率谱密度:是一种描述随机振动过程特征的方法,它能够反映随机振动的功率关于频率的分布密度。
在工程技术问题中,广泛采用功率谱密度函数来描述一个随机振动过程的特征。
功率谱密度函数的计算可以通过傅里叶变换求得,对于一个能量信号s(t),其频谱密度S(w)可以通过傅里叶变换求得,即S(w)=F(s(t))。
能量信号的频谱密度S(f)和功率信号C(jnw)的频谱主要区别在于:
1.S(f)是连续谱,而C(jnw)是离散谱;
2.S(f)的单位是幅度/频率,而C(jnw)的单位是幅度;
3.能量信号的能量有限,并连续地分布在频率轴上,每个频率点上的信号
幅度是无穷小的,只有df上才有确定的非0振幅;而功率信号的功率
有限。
此外,为了能够从频率域描述一个随机振动过程的特征,需要采用功率谱密度函数。
随机振动--第7章-功率谱密度

根据Parseval 定理
xT t dt
2
T 2 T 2
1 xT t dt 2
2
X T d
2
2 1 T 1 1 2 2 X T d T xT t dt 2 T T 2
19
T , xT t x t
1 lim T T
T 2 T 2
f x
22
tt dt S x f df
一方面,此式表示平均功率 的时间结构,即各个瞬时的功 率x 2 t 对于平均功率的贡献。 另一方面,又表示了平均功率的频率结构,即各种频率的功 率成分Sx(f)df对于平均功率的贡献,因此称为功率谱。
S x Rx e
j
d
j
1 Rx 2
S x e
d
维纳—辛钦关系式
10
7.2 自功率谱密度函数
定义:用符号Sx(ω)记作Rx(τ)的傅立叶变换 S x Rx e j d
16
(5) 导数过程的自谱
Sx S x
2
17
从Parseval 定理角度来定义功率谱密度
——信号在时域的总能量等与它在频域的总能量
x t dt X f
2
2
2 1 df X d 2
18
设 x t 是平稳随机过程的一个样本函数,一般情 况下它不一定能满足绝对可积的条件,为此引入 辅助函数: T T x t , - t 2 2 xT t T 0 , t 2
功率谱密度与互功率谱密度

2 1 X T d Tlim 2T
确定信号的功率谱是确定信号频谱的一个转 换,也是一个确定的不随时间变化函数。
确定信号的相关函数的定义: 确定信号X(t)的相关函数:R(x(t1),x(t2))=1。 所以确定信号的功率P=x(t)*x(t)是一确定的随时间变 化的函数。 相关函数与功率谱的关系: 确定信号的功率谱S=E[P]=R(P)=R(0),是一个确定的常 量。
26/117 2018/9/11
例3.10 讨论(加性)单频干扰 。若实平稳随机 信号 X(t) 受到加性的独立随机正弦分量 Z(t) 的干扰,已知 A,ω0 为常数,Θ是在 [0,2π) 上 均匀分布的随机变量。试求:
(1) 受扰后的信号 Y(t) 的相关函数 RY(t +τ, t) ; (2) 信号 X(t),Y(t) 是否联合平稳? 如果是,求 SY(ω),SXY(ω)
随机信号的相关函数的定义: 自相关函数: Rx(t1,t2)=E[X(t1),X(t2)] 随机信号与相关函数的关系:
PX ARX t , t
相关函数与功率谱的关系:
S(w)=E[P x]=E[ A[Rx( t, t)]]
14/117
2018/9/11
确定信号与随机信号的功率谱密度的区别:
2 1 S X , lim X T , T 2T
12/117 2018/9/11
随机信号的频谱与功率谱的区别与联系:
区别: 随机信号X(t)的频谱是随机过程样本的傅里叶变换。 对于随机信号而言,频谱也是一个“随机过程” (随机的频域序列)。 随机信号X(t)的功率谱是随机过程统计平均的概念。 联系: 随机信号X(t)的频谱与功率谱都是随机过程样本关 于w,ξ 的函数,且二者之间存在着相应的变换关 系。
功率谱密度的性质

( )
2
[ ( 0 ) ( 0 )]
6
单边功率谱GX(w)与双边功率谱SX(w)的关系
只用正频率部分来表示功率谱密度
G X ( ) 2S X ( ) 0 0 0
S ( ) 2 R ( ) cos d 0 X X 1 RX ( ) S X ( ) cos d 0
CXY ( ) RXY ( ) mX mY
RXY ( ) RYX ( ) mX mY
S XY () FT[ RXY ( )] FT[mX mY ] 2mX mY ()
5、 互谱密度的幅度平方满足 : S XY ( ) S X ( ) SY ( )
根据功率谱密度的性质来判断
(1) 该函数非负的实函数且 为偶函数, 故它是功率 谱密度的正确表达式 .
(2) 该函数虽为实偶函数 , 但它可为负数 , 故不可能 成为功率谱密度的正确 表达式.
(3) 该函数虽满足非负的实 函数, 但它不是偶函数 , 故它不能成为功率谱密 度的正确表达式 .
2
2 2 例2.3.1 已知平稳随机过程的功 率谱密度为S X ( ) 4 3 2 2 求自相关函数 RX ( )和平均功率W .
16
如果平稳过程N (t )的数学期望为零, 并在整个频率 N0 范围内的功率谱为常数S N ( ) ( ) 2 则称它是白噪声过程, 简称白噪声.
N0 白噪声的自相关函数为 : RN ( ) ( ) 2
1 0 白噪声的相关系数为 : rN ( ) 0 0
f X ( x1 , x2 , )
1 1 r ( )
2
e
功率谱密度曲线

二、自相关检测 三、互相关检测
一、相关函数的定义与计算
• 能量有限信号的自相关函数
R( ) Rxx ( ) x(t ) x (t )dt x (t ) x(t )dt
功率有限信号的自相关函数 1 T2 R( ) Rxx ( ) lim T x(t ) x (t )dt T T 2 两个能量有限信号的互相关函数
R()
0
二、自相关检测
• 基本原理 • 利用信号周期性和噪声随机性的特点,通过自相关或 互相关运算,达到去除噪声的目的基本原理 • 是从强噪声中提取弱信号的重要手段。 实现方法 混有噪声的信号 fi t Si t ni t 送入相关接收机 两个通道(不延时和延时)相乘器积分器
2 1 x0 lim cos( ) T 0 T T 2 2 x0 cos( ) 2
3、噪声的相关函数
• 随机噪声是一种前后独立的平稳随机过程,其相关 函数随τ的增加而减小,如红色曲线所示。 • 对于白噪声,其相关性很小。相关函数函数随τ的 增加而迅速减小如蓝色曲线所示。
●白噪声:当其通过一个电压传输系数为Kv,
带宽为B= f 2- f 1的系统后, 则输出噪声为 :
E
2 n0 f2 f `1 2 Eni K df f in 2 v
2 v
功率谱密度的性质

性质 1 : 宽平稳高斯过程一定是 严平稳高斯过程
11
性质2 : 若平稳高斯过程在任意 两个不同时刻 是不相关的 , 那么也一定是互相独立 的
两个高斯变量 X 1和X 2的联合概率密度 f X ( x1 , x2 ) 1 21 2 1 r 2
2
2
e
( x1 m1 ) 2 2 r ( x1 m1 )( x2 m2 ) ( x2 m2 ) 2 1 [ ] 2 2 2 2 (1 r ) 1 2 1 2
( )
2
[ ( 0 ) ( 0 )]
6
单边功率谱GX(w)与双边功率谱SX(w)的关系
只用正频率部分来表示功率谱密度
G X ( ) 2S X ( ) 0 0 0
S ( ) 2 R ( ) cos d 0 X X 1 RX ( ) S X ( ) cos d 0
RX () 0, 且呈振荡形式, 也可引入 函数解决
1 S X ( ) FT [ RX ( )] FT [ (1 cos 0 )] 2 1 1 FT [ ] FT [ cos 0 ] 2 2 1 1 2 ( ) [ ( 0 ) ( 0 )] 2 2
2.3.2 功率谱密度的性质
1 、S X ()为非负实函数, 即 : S X () 0
1 2 S X ( ) lim E[ X T ( ) ] T 2T
X T ( ) 0, 故S X ( ) 0
2
2、 若X (t )实平稳, 则S X ()是偶函数,即: S X () X (t ), Y (t )互相正交, 互谱密度为零.
RXY ( ) 0 S XY () FT[ RXY ( )] 0
《通信原理》樊昌信__课后习题答案

《通信原理》樊昌信__课后习题答案第⼀章概论1.3 某个信息源由A 、B 、C 、D 等4个符号组成。
这些符号分别⽤⼆进制码组00、01、10、11表⽰。
若每个⼆进制码元⽤宽度为5ms 的脉冲传输,试分别求出在下列条件下的平均信息速率。
(1)这4个符号等概率出现;(2)这4个符号出现的概率分别为1/4、1/4、3/16、5/16。
解:每秒可传输的⼆进制位为:()20010513=?÷-每个符号需要2位⼆进制,故每秒可传输的符号数为: 1002200=÷ (1) 4个符号等概率出现时每个符号包含的平均信息量为: bit 24log 2=故平均信息速率为:s b R b /2002100=?=(2)每个符号包含的平均信息量为:bit 977.11651log 1651631log 163411log 41411log 412222=+++故平均信息速率为: s b R b /7.197977.1100=?=1.6 设⼀个信号源输出四进制等概率信号,其码元宽度为125s µ。
试求码元速率和信息速率。
解:码元速率为:()baud R B 80001012516=?÷=- 信息速率为:s kb R R B b /16280004log 2=?==第⼆章信号2.2 设⼀个随机过程X (t )可以表⽰成:()()∞<<∞-+=t t t X θπ2cos 2其中θ在(0,2π)之间服从均匀分布,判断它是功率信号还是能量信号?并求出其功率谱密度或能量谱密度。
解:它的能量⽆限,功率有界,所以是⼀个功率信号。
`()[]()[]()()()πτθπτθππτπθπθπτπθπππ2cos 4224cos 2cos 22122cos 22cos 22020=+++=+++=?d t d t t由维纳-⾟钦关系有:()()ττωωτd e R P j X -+∞∞-?=()()[]πωδπωδπ222++-=2.3 设有⼀信号可表⽰为:()()??>≥-=000exp 4t t t t x试问它是功率信号还是能量信号?并求出其功率谱密度或能量谱密度。
第5章 功率谱分析及其应用3

2 xy
Gxy 2 Gx Gy
相干函数是表示两个信号在频域内的相似 性。
随机信号的功率谱密度
▪ 频率响应函数的定义
H
Gxy Gx
▪ 谱相干函数的性质
2
Sxy ( f ) Sx ( f )Sy ( f )
油管振动自谱
第五章 信号分析技术
机械工程测试技术基础
§5.2 功率谱分析及其应用
一、自功率谱密度函数
1 定义
Sx ( f )
Rx
(
)e
j
2
f
d
称 Sx(f) 为 x(t) 的自功率谱密度函数
7
第五章 信号分析技术
机械工程测试技术基础
2 功率谱分析及其应用
2.1 自功率谱密度函数
1 定义 ➢ 根据维纳—辛钦公式,平稳随机过程的功率谱密
Sy f Sx f
测量中经常用这个公式计算频率响应函数的幅值, 但无法计算它的相位、实部和虚部。
随机信号的功率谱密度
▪ 互功率谱密度函数定义
➢
如果互相关函数满足付氏变换条件
Rxy
d
Sxy
R xy
e j d
Rxy
1
2
S xy
e j d
▪ 单边互谱密度函数
Gxy
➢ 虚部
Qxy
2
R xy
sin d
Gxy Gxy e jxy
Gxy Cxy 2 Qxy 2
xy
arctan
Qxy Cxy
第五章 信号分析技术
机械工程测试技术基础
matlab 互功率谱密度

matlab 互功率谱密度
互功率谱密度(Cross Power Spectral Density,CPSD)是一种描述两个信号之间频率依赖性的统计量。
在 MATLAB 中,可以使用`cpsd`函数来计算两个信号的互功率谱密度。
下面是一个示例代码:
```matlab
% 生成两个信号
s1 = sin(2*pi*5*t);
s2 = cos(2*pi*10*t);
% 计算互功率谱密度
cpsd(s1, s2, 512, 1024, 2);
在上述示例中,我们生成了两个正弦信号`s1`和`s2`,然后使用`cpsd`函数计算它们的互功率谱密度。
其中,`512`和`1024`分别表示频谱的分辨率和频率范围,`2`表示使用 Hanning 窗进行平滑处理。
需要注意的是,`cpsd`函数返回的是一个复数矩阵,其中每一行和每一列对应于一
个频率点。
实部表示互功率谱密度的幅度,虚部表示相位。
如果你想进一步了解互功率谱密度的概念和应用,可以查阅相关的信号处理文献或书籍。
u形功率谱

U形功率谱一、引言功率谱密度(Power Spectral Density,简称PSD)是信号处理和统计学中的重要概念,用于描述随机信号在不同频率下的功率分布。
U形功率谱是一种常见的功率谱形状,因其类似于英文字母“U”而得名。
这种谱形在许多领域都有应用,如语音信号处理、振动分析、雷达信号处理等。
本文将对U形功率谱进行详细介绍。
二、U形功率谱的定义U形功率谱是一种具有单峰、双峰或三峰的功率谱形状,通常可以表示为一系列频率的函数。
其数学表达式可以根据实际应用的具体情况进行定义。
通常情况下,U形功率谱可以被定义为高斯函数或洛斯密图斯函数等形式。
三、U形功率谱的特性1.单峰U形功率谱:单峰U形功率谱只有一个峰值,通常出现在低频段。
这种谱形的特点是中频段和高频段的功率较小,而低频段的功率较大。
这种谱形常用于描述周期性信号或具有特定频率成分的信号。
2.双峰U形功率谱:双峰U形功率谱有两个峰值,通常分别出现在低频和高频段。
这种谱形的特点是中频段的功率较小,而低频段和高频段的功率较大。
这种谱形常用于描述具有两个主要频率成分的信号,如语音信号中的基频和泛音等。
3.三峰U形功率谱:三峰U形功率谱有三个峰值,通常分别出现在低频、中频和高频段。
这种谱形的特点是各频段的功率相对均衡,但中频段的功率略高于低频段和高频段。
这种谱形常用于描述具有多个频率成分的信号,如振动信号中的不同模态等。
四、U形功率谱的应用1.语音信号处理:语音信号是一种典型的具有U形功率谱的信号。
通过分析语音信号的U形功率谱,可以对语音信号进行滤波、降噪、压缩和识别等处理。
2.振动分析:振动信号中的U形功率谱可用于描述结构在不同频率下的振动响应。
通过对U形功率谱的分析,可以确定结构的固有频率、阻尼比等参数,从而对结构的健康状况进行评估和预测。
3.雷达信号处理:雷达信号的回波通常具有U形功率谱特性。
通过对雷达回波信号的U形功率谱进行分析,可以提取目标的位置、速度和距离等信息,从而实现目标的检测和跟踪。
FFT结果的物理意义

[原创]FFT结果的物理意义FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。
有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在圈圈就根据实际经验来说说FFT结果的具体物理意义。
一个模拟信号,经过ADC采样之后,就变成了数字信号。
采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此罗嗦了。
采样得到的数字信号,就可以做FFT变换了。
N个采样点,经过FFT之后,就可以得到N个点的FFT结果。
为了方便进行FFT 运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。
那么FFT之后结果就是一个为N点的复数。
每一个点就对应着一个频率点。
这个点的模值,就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。
而第一个点就是直流分量,它的模值就是直流分量的N倍。
而每个点的相位呢,就是在该频率下的信号的相位。
第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。
例如某点n所表示的频率为:Fn=(n-1)*Fs/N。
由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。
1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。
matlab随机相位余弦波的相关函数和功率谱密度

在MATLAB中可以利用以下步骤生成随机相位余弦波和计算其功率谱密度:1. 首先创建一个余弦波信号。
在此例中,设定信号频率、采样频率和采样点数,然后生成原始余弦波:f = 10; % 信号频率 (Hz)fs = 1000; % 采样频率 (Hz)n = 1024; % 采样点数t = (0:n-1)/fs; % 时间序列x = cos(2*pi*f*t); % 余弦波信号1. 生成随机相位,并将其应用于余弦波信号:phi = 2*pi*rand(1,1); % 生成一个位于 [0, 2*pi] 区间的随机相位x_rand = cos(2*pi*f*t + phi); % 应用随机相位的余弦波信号1. 计算随机相位余弦波信号的功率谱密度。
在MATLAB中,可使用`periodogram`或`pwelch`函数来实现。
以下展示了使用`periodogram`函数的例子:[pxx, fxx] = periodogram(x_rand, [], [], fs); % 计算功率谱密度1. 最后,绘制随机相位余弦波和其功率谱密度:figure;subplot(2,1,1);plot(t, x_rand);xlabel('Time (s)');ylabel('Amplitude');title('Random Phase Cosine Wave');grid on;subplot(2,1,2);plot(fxx, pxx);xlabel('Frequency (Hz)');ylabel('Power/Frequency (dB/Hz)');title('Power Spectral Density (PSD)');grid on;以上代码展示了如何在MATLAB中生成随机相位余弦波,以及如何计算其功率谱密度。
使用这些概念和函数,可以进一步进行信号处理和分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cos的功率谱函数
正弦信号的功率怎么求
功率=UI=UU/R
对于正弦信号,算电压时是幅度的二分之根号2倍,所以功率=UU/2R
关于正弦交流电的平均功率
交流电的平均功率为
P平=(∫uidt)/T,T是交流电的周期,∫是积分符号
平均功回率等于瞬时功率在一个周答期内的平均值。
P平=(1/T)∫[6+4sin(ωt+30度)][3+(根号23)
sin(ωt-15度)]dt
在积分时,角度要用弧度为单位,30度=π/6,15度=π/12周期T=2π/ω
剩下的就是求出积分了,时间t的积分区间是一个周期。
余弦信号功率扩展:
一个正弦信号可表示为x(t)=Asin(ωt+φ)=Acos(ωt+φ-
π/2)。
式中,A为振幅,ω为角频率(弧度/秒),φ为初始相角(弧度)。
正弦信号是周期信号,其周期T为:T=2π/ω=1/f。
均方值(记为E[X2(t)],在工程上表示信号的平均功率,其平方根称有效值。
随机信号的强度,可以用其均方值来描述。
对于平稳的遍历性随机过程,随机信号的均方值用样本函版数平方值的时
间平均来表示。
余弦信号平均功率是0.5
cosx的平方=0.5+0.5(cos2x)
其中第二项的平均值显然为0。
