幂指函数高一期中复习
高一数学指对幂函数重点知识归纳

(每日一练)高一数学指对幂函数重点知识归纳单选题1、已知函数f(x)=te x−lnx+lnt对任意x∈(0,+∞)都有f(x)≥0,则正数t的最小值为()A.e2B.1e2C.e D.1e答案:D解析:转化f(x)≥0为e x+lnt+x+lnt≥e lnx+lnx,令g(x)=x+lnx,则g(x+lnt)≥g(lnx),结合g(x)的单调性分析即得解根据题意得f(x)=te x−lnx+lnt=e x+lnt−lnx+lnt≥0,即e x+lnt+x+lnt≥x+lnx=e lnx+lnx,令g(x)=x+lnx,则g(x+lnt)≥g(lnx),由于y=x,y=lnx都在(0,+∞)单调递增故g(x)在x∈(0,+∞)上单调递增,所以x+lnt≥lnx,所以lnt≥lnx−x在(0,+∞)上恒成立,令ℎ(x)=lnx−x,ℎ′(x)=1x −1=1−xx(x>0)令ℎ′(x)>0∴x<1,故函数ℎ(x)在(0,1)单调递增;令ℎ′(x)<0∴x>1,故函数ℎ(x)在(1,+∞)单调递减故ℎ(x)max=ℎ(1)=−1所以lnt ≥(lnx −x)max =−1,即t ≥1e ,所以正数t 的最小值为1e .故选:D2、中国的5G 技术领先世界,5G 技术的数学原理之一便是著名的香农公式:C =Wlog 2(1+S N ).它表示:在受噪声干扰的信道中,最大信息传递速度C 取决于信道带宽W ,信道内信号的平均功率S ,信道内部的高斯噪声功率N 的大小,其中S N 叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计.按照香农公式,若不改变带宽W ,而将信噪比S N 从1000提升至4000,则C 大约增加了( )附:lg2≈0.3010 A .10%B .20%C .50%D .100%答案:B解析:根据题意,计算出log 24000log 21000的值即可; 当S N =1000时,C =Wlog 21000,当S N=4000时,C =Wlog 24000, 因为log 24000log 21000=lg4000lg1000=3+2lg23≈3.60203≈1.2所以将信噪比S N 从1000提升至4000,则C 大约增加了20%,故选:B.小提示:本题考查对数的运算,考查运算求解能力,求解时注意对数运算法则的运用.3、函数f(x)=(6−x −x 2)32的单调递减区间为( )A .[−12,2]B .[−3,−12]C .[−12,+∞)D .(−∞,−12]答案:A解析:f(x)=√(6−x−x2)3,由6−x−x2≥0结合函数y=6−x−x2的递减区间可得结果. f(x)=(6−x−x2)32=√(6−x−x2)3,由6−x−x2≥0得−3≤x≤2,又6−x−x2=−(x+12)2+254,所以函数f(x)的单调递减区间为[−12,2].故选:A.4、已知f(x)=a−x(a>0,且a≠1),且f(−2)>f(−3),则a的取值范围是()A.(0,+∞)B.(1,+∞)C.(-∞,1)D.(0,1)答案:D解析:由a>0,且a≠1,排除AC;利用指数函数的单调性排除B,确定D.由a>0,且a≠1,排除AC;∵f(x)=a−x=(1a )x ,当a>1时,0<1a<1,f(x)为单调递减函数,∴f(−2)<f(−3),与已知矛盾矛盾,故B错误;当0<a<1时,1a>1,f(x)为单调递增函数,∴f(−2)>f(−3),符合题意.故选:D.5、若a>1,b<0,且a b+a−b=2√2,则a b−a−b=()A.-2B.-4C.2D.4答案:A解析:对a b+a−b=2√2两边平方,可得a2b+a−2b的值,进而可计算出(a b−a−b)2,再根据已知条件判断出a b−a−b的符号,开方即可.a b+a−b=2√2,则(a b+a−b)2=a2b+2+a−2b=8,故a2b+a−2b=6,(a b−a−b)2=a2b+a−2b−2=4,a>1,b<0,故a b−a−b<0,故a b−a−b=−2.故选:A小提示:本题考查指数幂的运算,考查完全平方公式的应用,属于基础题.。
高一数学复习考点知识与题型专题讲解12--- 幂函数

高一数学复习考点知识与题型专题讲解3.3 幂函数【考点梳理】知识点一幂函数的概念一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.知识点二五个幂函数的图象与性质1.在同一平面直角坐标系内函数(1)y=x;(2)y=12x;(3)y=x2;(4)y=x-1;(5)y=x3的图象如图.2.五个幂函数的性质y=x y=x2y=x312y xy=x-1定义域R R R[0,+∞){x|x≠0}值域R[0,+∞)R[0,+∞){y|y≠0}奇偶性奇偶奇非奇非偶奇单调性增在[0,+∞) 上增,增增在(0,+∞)上减,在(-∞,0] 上减在(-∞,0)上减知识点三 一般幂函数的图象特征1.所有的幂函数在(0,+∞)上都有定义,并且图象都过点(1,1).2.当α>0时,幂函数的图象通过原点,并且在区间[0,+∞)上是增函数.特别地,当α>1时,幂函数的图象下凸;当0<α<1时,幂函数的图象上凸. 3.当α<0时,幂函数的图象在区间(0,+∞)上是减函数.4.幂指数互为倒数的幂函数在第一象限内的图象关于直线y =x 对称.5.在第一象限,作直线x =a (a >1),它同各幂函数图象相交,按交点从下到上的顺序,幂指数按从小到大的顺序排列.【题型归纳】题型一:幂函数的定义1.(2020·江苏省平潮高级中学高一月考)如果幂函数()22233m m y m m x --=-+的图象不过原点,则实数m 的取值为( ) A .1B .2C .1或2D .无解2.(2021·云南省玉溪第一中学高一月考)已知幂函数()y f x =的图象过点()33,,则该函数的解析式为( )A .2y x =B .2y x =C .3y x =D .y x =3.(2020·江苏镇江市·)已知幂函数()2()33m f x m m x =--在区间()0,∞+上是单调递增函数,则实数m 的值是( )A .-1或4B .4C .-1D .1或4题型二:幂函数的值域问题4.(2021·全国高一课时练习)已知幂函数()f x x α=的图像过点(8,4),则()f x x α= 的值域是( )A .(),0-∞B .()(),00,-∞⋃+∞C .()0,∞+D .[)0,+∞5.(2020·湖南衡阳市·高一月考)函数2y x -=在区间1,22⎡⎤⎢⎥⎣⎦上的最小值是( )A .14B .14-C .4D .4-6.(2018·南京市第三高级中学高一期中)以下函数12y x =,2y x =,23y x =,1y x -=中,值域为[0,)+∞的函数共( )个 A .1B .2C .3D .4题型三:幂函数的定点和图像问题7.(2021·高邮市临泽中学高一月考)已知幂函数1()(21)a g x a x +=-的图象过函数1()(0,1)2x b f x m m m -=->≠的图象所经过的定点,则b 的值等于( )A .12±B .22±C .2D .2± 8.(2020·南宁市银海三美学校高一月考)函数23y x =的图象是( )A .B .C .D .9.(2019·宁都县宁师中学高一月考)已知函数y =x a ,y =x b ,y =x c 的图象如图所示,则a ,b ,c 的大小关系为( )A .c <b <aB .a <b <cC .b <c <aD .c <a <b题型四:幂函数的单调性问题(比较大小、解不等式、参数)10.(2021·江西宜春市·高安中学高一月考)已知 1.13a =, 1.14b =,0.93c =,则a ,b ,c 的大小关系为( )A .c a b <<B .c b a <<C .b a c <<D .b c a <<11.(2020·江苏省平潮高级中学高一月考)幂函数223a a y x --=是奇函数,且在()0+∞,是减函数,则整数a 的值是( ) A .0B .0或2C .2D .0或1或212.(2020·江西鹰潭一中)已知幂函数12()f x x =,若()()132f a f a +<-,则实数a 的取值范围是( )A .[)1,3-B .21,3⎡⎫-⎪⎢⎣⎭C .[)1,0-D .21,3⎛⎤- ⎥⎝⎦题型五:幂函数的奇偶性问题13.(2020·江西南昌市·南昌十中高一月考)已知幂函数y =f (x )经过点(3,3),则f (x )( )A .是偶函数,且在(0,+∞)上是增函数B .是偶函数,且在(0,+∞)上是减函数C .是奇函数,且在(0,+∞)上是减函数D .是非奇非偶函数,且在(0,+∞)上是增函数14.(2021·吴县中学)有四个幂函数:①()2f x x -=;②()1f x x -=;③()3f x x =;④()3f x x =,某向学研究了其中的一个函数,并给出这个函数的三个性质:(1)()f x 为偶函数;(2)()f x 的值域为()(),00,-∞⋃+∞;(3)()f x 在(),0-∞上是增函数.如果给出的三个性质中,有两个正确,一个错误,则他研究的函数是( ) A .①B .②C .③D .④15.(2020·乌苏市第一中学高一月考)已知112,1,,,1,2,322α⎧⎫∈---⎨⎬⎩⎭,若幂函数()f x x α=为偶函数,且在(0,)+∞上递减,则a =( ) A .1-,12-B .1,3C .2-D .12,2【双基达标】一、单选题16.(2021·镇远县文德民族中学校高一月考)已知幂函数()()21f x m x =-,则实数m 等于( )A .2B .1C .0D .任意实数17.(2020·南京市第十三中学高一月考)函数 85y x =的图象是( )A .B .C .D .18.(2021·全国高一课时练习)下列结论中,正确的是( ) A .幂函数的图象都经过点(0,0),(1,1) B .幂函数的图象可以出现在第四象限C .当幂指数α取1,3,12时,幂函数y =x α是增函数 D .当α=-1时,幂函数y =x α在其整个定义域上是减函数19.(2021·全国高一单元测试)已知幂函数()f x 的图象过点1(2,)2,则f (4)的值是( ) A .64B .42C .24D .1420.(2021·全国高一专题练习)函数()()()102121f x x x -=-+-的定义域是( ) A .(],1-∞B .11,,122⎛⎫⎛⎫-∞⋃ ⎪ ⎪⎝⎭⎝⎭C .(),1-∞-D .1,12⎛⎫⎪⎝⎭21.(2021·全国高一课前预习)已知幂函数()3m f x x -=(m ∈N *)为奇函数,且在区间(0,+∞)上是减函数,则m 等于( ) A .1B .2C .1或2D .322.(2021·全国)幂函数()f x 满足:对任意12x x R ∈、,当且仅当12x x =时,有12()()f x f x =,则(1)(0)(1)f f f -++=( ). A .1-B .0C .1D .223.(2021·全国)下列比较大小中正确的是( ).A .0.50.532()()23<B .1123()()35---<-C .3377( 2.1)( 2.2)--<-D .443311()()23-<24.(2019·云南昭通市第一中学高一月考)已知函数()f x x =,若(1)(102)f a f a+<-,则a 的取值范围是( )A .(0,5)B .(5,)+∞C .[1,3)-D .(3,5)25.(2021·全国)幂函数1y x -=,及直线,1,1y x y x ===将直角坐标系第一象限分成八个“卦限: I, II, III,IV, V, VI, VII, VIII (如图所示),那么,而函数13y x -=的图象在第一象限中经过的“卦限”是( )A .IV,VII B . IV,VIII C . III, VIII D . III, VII 【高分突破】一:单选题26.(2021·全国高一课前预习)幂函数2266()(33)m m f x m m x -+=-+在(0,)+∞上单调递增,则m的值为( ) A .1B .2C .3D .1或227.(2021·浙江)下列函数中,在其定义域内既是奇函数又是减函数的是( ) A .()y x x R =-∈B .3()y x x x R =--∈ C .1()()2x y x R =∈D .1y x=-(x R ∈,且0)x ≠28.(2021·全国高一课时练习)点(,8)m 在幂函数()(1)n f x m x =-的图象上,则函数()g x n x x m =-+-的值域为( )A .0,2⎡⎤⎣⎦B .1,2⎡⎤⎣⎦C .2,2⎡⎤⎣⎦D .[]2,329.(2021·全国高一课时练习)如图,①②③④对应四个幂函数的图像,其中②对应的幂函数是( )A .3y x =B .2y x =C .y x =D .y x =30.(2021·全国高一课时练习)已知幂函数()()2133m f x m m x +=-+的图象关于原点对称,则满足()()132m ma a +>-成立的实数a 的取值范围为( )A .22,33⎛⎫- ⎪⎝⎭B .22,3⎛⎫-- ⎪⎝⎭C .22,3⎛⎫- ⎪⎝⎭D .2,43⎛⎫ ⎪⎝⎭31.(2021·全国高一课时练习)设11,,1,2,32α⎧⎫∈-⎨⎬⎩⎭则“()f x x α=的图象经过()1,1--”是“()f x x α=为奇函数”的( )A .充分不必要件B .必要不充分条件C .充要条件D .既不充分也不必要条件32.(2021·浙江高一期末)已知实数a ,b 满足等式35a b =,给出下列五个关系式:①1b a <<;②1a b <<-;③01b a <<<;④10a b -<<<;⑤a b =,其中,可能成立的关系式有( ) A .1个B .2个C .3个D .5个33.(2021·全国高一单元测试)已知函数1a y ax b =-+-是幂函数,直线20(0,0)mx ny m n -+=>>过点(,)a b ,则11n m ++的取值范围是( ) A .11,,333⎫⎫⎛⎛-∞⋃ ⎪ ⎪⎝⎝⎭⎭B .(1,3)C .1,33⎡⎤⎢⎥⎣⎦D .1,33⎛⎫ ⎪⎝⎭二、多选题34.(2021·全国高一课时练习)下列关于幂函数y x α=的性质,描述正确的有( ) A .当1α=-时函数在其定义域上是减函数B .当0α=时函数图象是一条直线 C .当2α=时函数是偶函数D .当3α=时函数在其定义域上是增函数35.(2021·全国高一课时练习)已知函数()21m m y m x -=-为幂函数,则该函数为( ) A .奇函数B .偶函数C .区间()0,∞+上的增函数D .区间()0,∞+上的减函数36.(2021·全国高一课时练习)已知幂函数223()(1)m m f x m m x +-=--,对任意12,(0,)x x ∈+∞,且12x x ≠,都满足1212()()0f x f x x x ->-,若,a b ∈R 且()()0f a f b +<,则下列结论可能成立的有( )A .0a b +> 且0ab <B .0a b +< 且0ab <C .0a b +< 且0ab >D .以上都可能37.(2021·全国高一专题练习)已知幂函数9()5m f x m x ⎛⎫=+ ⎪⎝⎭,则下列结论正确的有( )A .()13216f -=B .()f x 的定义域是RC .()f x 是偶函数D .不等式()()12f x f -≥的解集是[)(]1,11,3-38.(2020·江苏常州市·常州高级中学高一期中)若函数()f x 同时满足:①对于定义域上的任意x ,恒有()()0f x f x +-=;②对于定义城上的任意1x ,2x ,当12x x ≠时,恒有()()12120f x f x x x -<-,则称函数()f x 为“理想函数”.下列四个函数中,能被称为“理想函数”的有( ) A .()2121x f x x -=+B .()3f x x =-C .()f x x =-D .()22,0,,0x x f x x x ⎧-≥=⎨<⎩三、填空题39.(2021·湖南邵阳市·高一期末)已知幂函数()y f x =的图象过点()2,2,则()5f =______.40.(2021·雄县第二高级中学高一期末)已知幂函数()f x 过定点18,2⎛⎫ ⎪⎝⎭,且满足()()2150f a f ++->,则a 的范围为________.41.(2021·全国高一课时练习)不等式()()1133312a a -<+的解集为______42.(2021·上海上外浦东附中高一期末)已知幂函数()223()m m f x x m Z --=∈的图像关于y 轴对称,与x 轴及y 轴均无交点,则由m 的值构成的集合是__________.43.(2021·全国高一单元测试)已知112,1,,1,,2,322k ⎧⎫∈---⎨⎬⎩⎭,若幂函数()kf x x =为奇函数,且在()0,∞+上单调递减,则k =______.四、解答题44.(2021·全国高一课时练习)已知函数()()21212223m f x m m xn -=+-+-是幂函数,求2m n -的值.45.(2021·全国高一课时练习)已知函数()()()()1221a a f x a a x -+=--是幂函数()a R ∈,且()()12f f <.(1)求函数()f x 的解析式;(2)试判断是否存在实数b ,使得函数()()32g x f x bx =-+在区间[]1,1-上的最大值为6,若存在,求出b 的值;若不存在,请说明理由.46.(2021·全国高一专题练习)已知幂函数()()1222mf x m m x =--在()0,∞+上单调递减.(1)求实数m 的值.(2)若实数a 满足条件()()132f a f a ->+,求a 的取值范围.47.(2021·江西省乐平中学高一开学考试)已知幂函数()()()22322k k f x m m x k -=-+∈Z 是偶函数,且在()0,∞+上单调递增. (1)求函数()f x 的解析式;(2)若()()212f x f x -<-,求x 的取值范围: (3)若实数()*,,a b a b ∈R 满足237a b m +=,求3211a b +++的最小值.【答案详解】1.C 【详解】由幂函数的定义得m 2-3m +3=1,解得m =1或m =2;当m =1时,m 2-m -2=-2,函数为y =x -2,其图象不过原点,满足条件; 当m =2时,m 2-m -2=0,函数为y =x 0,其图象不过原点,满足条件. 综上所述,m =1或m =2. 故选:C. 2.D 【详解】设()f x x α=,依题意()13332f αα==⇒=,所以()f x x =. 故选:D 3.B 【详解】幂函数()2()33mf x m m x =--在(0,)+∞上是增函数则2331m m m ⎧--=⎨>⎩ ,解得4m = 故选:B 4.D【详解】幂函数()f x x α=的图像过点(8,4),84α∴=,解得23α=,2332(0)f x x x ∴==≥,∴()f x 的值域是[)0,+∞. 故选:D. 5.A 【详解】∵函数2y x -=在区间1,22⎡⎤⎢⎥⎣⎦上是减函数,∴2min 124y -==, 故选:A. 6.C 【详解】函数12y x x ==,其定义域为[0,)+∞,值域为[0,)+∞; 函数2y x =的定义域为R ,值域为[0,)+∞; 函数2323y x x ==,20x ≥Q ,∴函数值域为[0,)+∞;函数331y x x -==,值域为(,0)(0,)-∞+∞. ∴值域为[0,)+∞的函数共3个.故选:C. 7.B 【详解】由于1()(21)a g x a x +=-为幂函数,则211a -=,解得:1a =,则2()g x x =; 函数1()(0,1)2x b f x m m m -=->≠,当x b = 时,11()22b b f b a -=-=,故()f x 的图像所经过的定点为1,2b ⎛⎫ ⎪⎝⎭, 所以1()2g b =,即212b =,解得:22b =±, 故选:B. 8.C 【详解】首先由分数指数幂运算公式可知()21233x x ⎛⎫=⎪⎝⎭,则()()23y f x x ==,()()f x f x -=,且函数的定义域为R ,所以函数是偶函数,关于y 轴对称,故排除AD ,因为2013<<,所以23y x =在第一象限的增加比较缓慢,故排除B , 故选:C 9.A试题:由幂函数图像特征知,1a >,01b <<,0c <,所以选A . 10.A 【详解】由题意,构造函数 1.13,x y y x ==,由指数函数和幂函数的性质, 可知两个函数在(0,)+∞单调递增;由于0.9 1.10.9 1.133c a <∴<∴<;由于 1.1 1.13434a b <∴<∴<;综上:c a b << 故选:A 11.B由于幂函数223a a y x --=是奇函数,且在(0,)+∞是减函数,故2230a a --<,且223a a --是奇数,且a 是整数,13a -<<∴,a Z ∈,当0a =时,2233a a --=-,是奇数,; 当1a =时,2234a a --=-,不是奇数; 当2a =时,2233a a --=-,是奇数; 故0a =或2. 故答选:B 12.B 【详解】因为幂函数()12f x x =是增函数,且定义域为[)0,+∞,由()()132f a f a +<-得13210320a aa a +<-⎧⎪+≥⎨⎪-≥⎩,解得213a -≤<.所以实数a 的取值范围是21,3⎡⎫-⎪⎢⎣⎭故选:B 13.D 【详解】设幂函数的解析式为y x α=, 将点()3,3的坐标代入解析式得33α=,解得12α=, ∴12y x =,函数的定义域为[)0,+∞,是非奇非偶函数,且在()0,+∞上是增函数,14.A 【详解】对于①,函数()2f x x -=为偶函数,且()2210f x x x -==>,该函数的值域为()0,∞+, 函数()2f x x -=在()0,∞+上为减函数,该函数在(),0-∞上为增函数,①满足条件;对于②,函数()11x x f x -==为奇函数,且()10f x x=≠,该函数的值域为()(),00,-∞⋃+∞, 函数()f x 在(),0-∞上为减函数,②不满足条件;对于③,函数()3f x x =的定义域为R ,且()()33f x x x f x -=-=-=-,该函数为奇函数, 当0x ≥时,()30f x x =≥;当0x <时,()30f x x =<,则函数()f x 的值域为R , 函数()3f x x =在()0,∞+上为增函数,该函数在(),0-∞上也为增函数,③不满足条件;对于④,函数()3f x x =为奇函数,且函数()3f x x =的值域为R ,该函数在(),0-∞上为增函数,④不满足条件. 故选:A. 15.C 【详解】112,1,,,1,2,322α⎧⎫∈---⎨⎬⎩⎭若幂函数()f x x α=为偶函数,且在(0,)+∞上递减,则0α<且2,k k Z α=∈, 所以2a =-. 故选:C 16.A因为函数()()21f x m x =-为幂函数,所以m -1=1,则m =2.故选:A. 17.A 【详解】由幂函数85y x =可知: 85y x =是定义域为R 的偶函数,在(0,+∞)上单调递增,且当x >1时,函数值增长的比较快. 故选:A 18.C 【详解】当幂指数α=-1时,幂函数y =x -1的图象不经过原点,故A 错误;因为所有的幂函数在区间(0,+∞)上都有定义,且y =x α(α∈R)>0,所以幂函数的图象不可能出现在第四象限,故B 错误; 当α>0时,y =x α是增函数,故C 正确;当α=-1时,y =x -1在区间(-∞,0),(0,+∞)上是减函数,但在整个定义域上不是减函数,故D 错误. 故选:C. 19.D 【详解】幂函数()a f x x =的图象过点1(2,)2,122a ∴=,解得1a =-,1()f x x∴=, f ∴(4)14=, 故选:D . 20.B 【详解】因为()()()()121121211f x x x x x-=-+-=+--, 则有10210x x ->⎧⎨-≠⎩,解得1x <且12x ≠,因此()f x 的定义域是11,,122⎛⎫⎛⎫-∞⋃ ⎪ ⎪⎝⎭⎝⎭. 故选:B. 21.B 【详解】因为()3m f x x -=在(0,+∞)上是减函数,所以m -3<0,所以m <3. 又因为m ∈N *,所以1m =或2.又因为()3m f x x -=是奇函数,所以m -3是奇数, 所以m =2. 故选:B. 22.B 【详解】设()a f x x =,由已知,函数()f x 的定义域为R ,∴0a >,又∵对任意12x x R ∈、,当且仅当12x x =时,有12()()f x f x =,即y 与x 一一对应,()f x 必定不是偶函数,∴必定为奇函数,∴答案为0,故选:B. 23.C 【详解】A 选项,0.5y x =在[0)+∞,上是递增函数,0.50.523()()32<,错, B 选项,1y x -=在()0-∞,上是递减函数,1123()()35--->-,错, C 选项,37y x =在()0-∞,上是递增函数, 337721( 2.1)()10-=-,33775( 2.2)()11--=-,3377( 2.1)( 2.2)--<-,对,D 选项,43y x =在[0)+∞,上是递增函数, 443311()()22-=,443311()()23>,443311()()23->,错,故选:C . 24.C 【详解】()f x x =的定义域为[)0,+∞,且在[)0,+∞单调递增,所以(1)(102)f a f a +<-可化为:1010201102a a a a +≥⎧⎪-≥⎨⎪+<-⎩,解得:13x -≤<. 故a 的取值范围是[1,3)-. 故选:C 25.B【详解】对于幂函数13y x -=,因为103-< ,所以13y x -=在第一象限单调递减, 根据幂函数的性质可知:在直线1x =的左侧,幂函数的指数越大越接近y 轴 ,因为113->-,所以13y x -=的图象比1y x -=的图象更接近y 轴 ,所以进过第IV 卦限, 在直线1x =的右侧,幂函数的指数越小越接近x 轴,因为1103-<-<, 所以13y x -=的图象位于1y x -=和1y =之间,所以经过VIII 卦限,所有函数13y x -=的图象在第一象限中经过的“卦限”是IV,VIII , 故选:B 26.A 【详解】解:幂函数2266()(33)m m f x m m x -+=-+在(0,)+∞上单调递增,2331m m ∴-+=,且2660m m -+>,解2331m m -+=得1m =或2m =,当1m =时26610m m -+=>符合题意; 当2m =时26620m m -+=-<不符合题意; 故选:A . 27.B 【详解】解:对于A 选项,()()f x x x f x -=--=-=,为偶函数,故错误;对于B 选项,()()()()33f x x x x x f x -=----=+=-,为奇函数,且函数3,y x y x =-=-均为减函数,故3()y x x x R =--∈为减函数,故正确; 对于C 选项,指数函数没有奇偶性,故错误;对于D 选项,函数为奇函数,在定义域上没有单调性,故错误.故选:B28.B【详解】解:因为点(,8)m 在幂函数()(1)n f x m x =-的图象上,所以11m -=,即2m =,()()228n f m f ===,所以3n =, 故()32g x x x =-+-,[]2,3x ∈, ()()22()12321256g x x x x x =+--=+-+-, 因为[]2,3x ∈,所以21560,4x x ⎡⎤-+-∈⎢⎥⎣⎦, 所以[]2()1,2g x ∈, 所以函数()g x n x x m =-+-的值域为1,2⎡⎤⎣⎦.故选:B.29.C【详解】 解:由图知:①表示y x =,②表示y x =,③表示2y x =,④表示3y x =.故选:C.30.D【详解】由题意得:2331m m -+=,得1m =或2m =当1m =时,2()f x x =图象关于y 轴对称,不成立;当2m =时,3()f x x =是奇函数,成立;所以不等式转化为22(1)(32)a a +>-,即231480a a -+<,解得243a <<.故选:D31.C【详解】 由11,,1,2,32α⎧⎫∈-⎨⎬⎩⎭,由()f x x α=的图像经过()1,1--,则α的值为11,3-,,此时()f x x α=为奇函数. 又当()f x x α=为奇函数时,则α的值为11,3-,,此时()f x x α=的图象经过()1,1--. 所以“()f x x α=的图象经过()1,1--”是“()f x x α=为奇函数”的充要条件故选:C32.C【详解】在同一坐标系中画出函数3y x =和5y x =的图像,如图所示:数形结合可知,在(1)处1a b <<-;在(2)处10b a -<<<;在(3)处01a b <<<; 在(4)处1b a <<;在1a b ==或1a b ==-也满足,故①②⑤对故选:C.33.D【详解】由1a y ax b =-+-是幂函数,知:1,1a b =-=,又(,)a b 在20mx ny -+=上,∴2m n +=,即20n m =->,则1341111n m m m m +-==-+++且02m <<, ∴11(,3)13n m +∈+. 故选:D.34.CD【详解】对于A 选项,1y x =,在(,0)-∞和(0,)+∞上递减,不能说在定义域上递减,故A 选项错误.对于B 选项,0y x =,0x ≠,图像是:直线1y =并且除掉点(0,1),故B 选项错误. 对于C 选项,2y x =,定义域为R ,是偶函数,所以C 选项正确.对于D 选项,3y x =,函数在其定义域上是增函数,所以D 选项正确.故选:CD35.BC【详解】由()21m m y m x -=-为幂函数,得11m -=,即m =2,则该函数为2y x =,故该函数为偶函数,且在区间()0,∞+上是增函数,故选:BC .36.BC【详解】因为223()(1)m m f x m m x +-=--为幂函数,所以211m m --=,解得:m =2或m =-1.因为任意12,(0,)x x ∈+∞,且12x x ≠,都满足1212()()0f x f x x x ->-, 不妨设12x x >,则有12())0(f x f x ->,所以()y f x =为增函数,所以m =2,此时3()f x x =因为()33()()f x x x f x -=-=-=-,所以3()f x x =为奇函数.因为,a b ∈R 且()()0f a f b +<,所以()()f a f b <-.因为()y f x =为增函数,所以a b <-,所以0a b +<.故BC 正确.故选:BC37.ACD【详解】 因为函数是幂函数,所以915m +=,得45m =-,即()45f x x -=, ()()()45451322216f --⎡⎤-=-=-=⎣⎦,故A 正确;函数的定义域是{}0x x ≠,故B 不正确; ()()f x f x -=,所以函数是偶函数,故C 正确;函数()45f x x -=在()0,∞+是减函数,不等式()()12f x f -≥等价于12x -≤,解得:212x -≤-≤,且10x -≠,得13x -≤≤,且1x ≠,即不等式的解集是[)(]1,11,3-,故D 正确.故选:ACD38.BCD【详解】对于①对于定义域内的任意x ,恒有()()0f x f x +-=,即()()f x f x -=-,所以()f x 是奇函数;对于②对于定义域内的任意1x ,2x ,当12x x ≠时,恒有()()12120f x f x x x -<-, ()f x 在定义域内是减函数; 对于A :()2121x f x x -=+,()113f =,()13f -=,故不是奇函数,所以不是“理想函数”; 对于 B :()3f x x =-是奇函数,且是减函数,所以是“理想函数”;对于C :()f x x =-是奇函数,并且在R 上是减函数,所以是“理想函数”;对于D :()22,0,0x x f x x x x x ⎧-≥==-⎨<⎩,()||()f x x x f x -==-, 所以()22,0,0x x f x x x ⎧-≥=⎨<⎩是奇函数; 根据二次函数的单调性,()f x 在(,0)-∞,(0,)+∞都是减函数,且在0x =处连续,所以()22,0,0x x f x x x ⎧-≥=⎨<⎩在R 上是减函数, 所以是“理想函数”.故选:BCD.39.5【详解】设()f x x α=,则()12222f αα==⇒=, 所以()(),55f x x f ==. 故答案为:540.()22-,【详解】设幂函数()y f x x α==,其图象过点18,2⎛⎫ ⎪⎝⎭, 所以182α=,即3122α-=,解得:13α=-,所以()13f x x -=, 因为()()()13f x x f x --=-=-,所以()13f x x -=为奇函数,且在()0-∞,和()0+∞,上单调递减, 所以()()2150f a f ++->可化为()()()2155f a f f +>--=, 可得215a +<,解得:22a -<<,所以a 的范围为()22-,, 故答案为:()22-,. 41.()4,-+∞【详解】 解:因为幂函数13y x =在R 上为增函数,()()1133312a a -<+, 所以312a a -<+,解得4a >-,所以不等式的解集为()4,-+∞,故答案为:()4,-+∞42.{}1,1,3-【详解】由幂函数()f x 与x 轴及y 轴均无交点,得2230m m -≤-,解得13m -≤≤,又m Z ∈,即{}1,0,1,2,3m ∈-,()223()m m f x x m Z --=∈的图像关于y 轴对称, 即函数为偶函数,故223m m --为偶数, 所以{}1,1,3m ∈-,故答案为:{}1,1,3-.43.1-【详解】由题意知,幂函数()k f x x =在(0)+∞,上单调递减, 则k 为负数,则k =-2,-1,12-,又由函数()k f x x =为奇函数,则k =-1,故答案为:-144.-6【详解】因为()()21212223m f x m m x n -=+-+-是幂函数,所以22221,10,230,m m m n ⎧+-=⎪-≠⎨⎪-=⎩,解得3,3,2m n =-⎧⎪⎨=⎪⎩, 所以323262m n -=--⨯=-.45.(1)()2f x x =;(2)存在,2b =±. 解:因为函数()()()()1221a a f x a a x -+=--是幂函数,所以211a a --=,解得2a =或1a =-,当2a =时,()4f x x -=,则()()12f f >,故不符题意,当1a =-时,()2f x x =,则()()12f f <,符合题意,所以()2f x x =;(2)由(1)得 ()()()22232233g x f x bx x bx x b b =-+=-++=--++, 函数图像开口向下,对称轴为:x b =,当1b ≤-时,函数()g x 在区间[]1,1-上递减,则()()11236max g x g b =-=--+=,解得2b =-,符合题意; 当1b ≥时,函数()g x 在区间[]1,1-上递增,则()()11236max g x g b ==-++=,解得2b =,符合题意;当11b -<<时,()()22236max g x g b b b ==-++=,解得3b =±,不符题意, 综上所述,存在实数2b =±满足题意.46.(1)1m =-;(2)32,,123⎛⎫⎛⎫-∞-- ⎪ ⎪⎝⎭⎝⎭. 【详解】解:(1)()f x 是幂函数,2221m m ∴--=,解得:3m =或1m =-, 3m =时,()13f x x =在(0,)+∞上单调递增,1m =-时,()1f x x=在(0,)+∞递减, 故1m =-;(2)若实数a 满足条件()()132f a f a ->+,则10320a a ->⎧⎨+<⎩或10320132a a a a ->⎧⎪+>⎨⎪-<+⎩或10320132a a a a-<⎧⎪+<⎨⎪-<+⎩,解得:32a <-或213a -<<,故a 的取值范围是32,,123⎛⎫⎛⎫-∞-- ⎪ ⎪⎝⎭⎝⎭. 47.(1)2()f x x =;(2)(1,1)-;(3)2.【详解】(1)()f x 是幂函数,则2221m m -+=,1m =,又()f x 是偶函数,所以23(3)k k k k -=-是偶数,()f x 在(0,)+∞上单调递增,则230k k ->,03k <<,所以1k =或2. 所以2()f x x =;(2)由(1)偶函数()f x 在[0,)+∞上递增, (21)(2)f x f x -<-22(21)(2)212f x f x x x ⇔-<-⇔-<-11x ⇔-<<. 所以x 的范围是(1,1)-.(3)由(1)237a b +=,2(1)3(1)12a b +++=,0,0a b >>, []3213219(1)2(1)2(1)3(1)121112111211b a a b a b a b a b ++⎛⎫⎛⎫+=++++=++ ⎪ ⎪++++++⎝⎭⎝⎭ 19(1)4(1)12221211b a a b ⎛⎫++≥+⨯= ⎪ ⎪++⎝⎭,当且仅当9(1)4(1)11b a a b ++=++,即2,1a b ==时等号成立. 所以3211a b +++的最小值是2.。
高一数学知识点幂函数的总结

高一数学知识点幂函数的总结高一数学知识点幂函数的总结「篇一」不过作为集合大小的定义,我们希望能够比较任意两个集合的大小。
所以,对于任何给定的两个集合A和B,或者A比B大,或者B比A大,或者一样大,这三种情况必须有一种正确而且只能有一种正确。
这样的偏序关系被称为“全序关系”。
最后,新的定义必须保持原来有限集合间的大小关系。
有限集合间的大小关系是很清楚的,所谓的“大”,也就是集合中的元素更多,有五个元素的集合要比有四个元素的集合大,在新的扩充了的集合定义中也必须如此。
这个要求是理所当然的,否则我们没有理由将新的定义作为老定义的扩充。
经过精心的整理,有关“高一数学学习:集合大小定义的基本要求三”的内容已经呈现给大家,祝大家学习愉快!学好高中数学也需阅读积累阅读,在语文中要抓住精炼的或生动形象的词与句,而在数学中,则应抓住关键的词语。
比如在初二课本第一学期第21章第五节反比例函数性质的第一条:“当k>0时,函数图像的两个分支分别在第一、三象限内,在每个象限内,自变量x逐渐增大时,y的值则随着逐渐减小。
&rdquo 高中历史;这句话中,关键词语是“在每个象限内”,反比例函数的图像为双曲线,而这个性质是对于其中某一分支而言,并不是对整个函数来说的。
所以在做题时,应注意到这一点。
从这一实例来看,我们不难发现阅读时抓住关键词语的重要性。
积累,在语文中有利于写作,在数学中有利于解题。
积累包括两方面:一、概念知识,二、错误的题目。
脑子中多一些概念就多了一些思考的方法,多了一些解题的突破口,在做较难的题目时,也就得心应手了。
积累错误的题目,指挑选一些自己平时易错或难懂的题目,记在本子上,在复习时,翻看这本本子就能更加清楚地了解自己在哪些方面还有所欠缺,应特别注意。
所以积累对学好数学起着极大的作用。
自主复习最好各科交替进行大部分区县都将实行全区统考,并将考生成绩进行大排队。
这次考试将成为考生填报高考志愿的重要参考依据。
高一数学指对幂函数高频考点知识梳理

(每日一练)高一数学指对幂函数高频考点知识梳理单选题1、已知55<84,134<85.设a =log 53,b =log 85,c =log 138,则( )A .a <b <cB .b <a <cC .b <c <aD .c <a <b答案:A解析:由题意可得a 、b 、c ∈(0,1),利用作商法以及基本不等式可得出a 、b 的大小关系,由b =log 85,得8b =5,结合55<84可得出b <45,由c =log 138,得13c =8,结合134<85,可得出c >45,综合可得出a 、b 、c 的大小关系.由题意可知a 、b 、c ∈(0,1),a b =log 53log 85=lg3lg5⋅lg8lg5<1(lg5)2⋅(lg3+lg82)2=(lg3+lg82lg5)2=(lg24lg25)2<1,∴a <b ; 由b =log 85,得8b =5,由55<84,得85b <84,∴5b <4,可得b <45;由c =log 138,得13c =8,由134<85,得134<135c ,∴5c >4,可得c >45. 综上所述,a <b <c .故选:A.小提示:本题考查对数式的大小比较,涉及基本不等式、对数式与指数式的互化以及指数函数单调性的应用,考查推理能力,属于中等题.2、一种药在病人血液中的量保持1500mg 以上才有效,而低于500mg 病人就有危险.现给某病人注射了这种药2500mg ,如果药在血液中以每小时20%的比例衰减,为了充分发挥药物的利用价值,那么从现在起经过( )小时向病人的血液补充这种药,才能保持疗效.(附:1g2=0.301,1g3=0.4771,答案采取四舍五入精确到0.1h)A.2.3小时B.3.5小时C.5.6小时D.8.8小时答案:A解析:药在血液中以每小时20%的比例衰减,根据指数函数模型列方程或不等式求解.设从现在起经过x小时向病人的血液补充这种药,才能保持疗效.则2500×0.8x=1500,0.8x=0.6,lg0.8x=lg0.6,xlg0.8=lg0.6,x=lg0.6lg0.8=lg610lg810=lg2+lg3−13lg2−1=0.301+0.4771−13×0.301−1≈2.3.故选:A.3、若a=2√3,b=log2√3, c=log√32,则实数a,b,c之间的大小关系为()A.a>c>b B.a>b>c C.c>a>b D.b>a>c答案:A解析:利用中间1和2进行比较可得答案.因为2√3>21=2,log2√3<log22=1,log√3√3<log√32<log√33=2;所以a>c>b.故选:A.小提示:本题主要考查比较指数式和对数式的大小,一般是利用函数的单调性结合中间值进行比较,侧重考查数学抽象的核心素养.4、下列函数中为偶函数的是( )A .y =cosxB .y =sinxC .y =x 3D .y =2x答案:A解析:对四个选项一一验证:对于A :利用奇偶性的定义进行证明;对于B :取特殊值f (π2),f (−π2)否定结论;对于C :取特殊值f (1),f (−1)否定结论;对于D :取特殊值f (1),f (−1)否定结论.对于A :y =cosx 的定义域为R.因为f (−x )=cos (−x )=cosx =f (x ),所以y =cosx 为偶函数.故A 正确;对于B :对于y =sinx ,f (π2)=sin π2=1,f (−π2)=sin (−π2)=−1,不满足f (−x )=f (x ),故y =sinx 不是偶函数.故B 错误;对于C :对于y =x 3,f (1)=13=1,f (−1)=(−1)3=−1,不满足f (−x )=f (x ),故y =x 3不是偶函数.故C 错误;对于D :对于y =2x ,f (1)=21=2,f (−1)=2−1=12,不满足f (−x )=f (x ),故y =2x 不是偶函数.故D 错误; 故选:A.5、指数函数y =a x 的图象经过点(3,18),则a 的值是( )A .14B .12C .2D .4答案:B解析:将已知点的坐标代入指数函数的表达式,求得a 的值. 因为y =a x 的图象经过点(3,18), 所以a 3=18,解得a =12,故选:B.。
单元复习 幂函数、指数函数与对数函数-高一数学(苏教版2019必修第一册)

故 f(x)=lg
+1
(2)由(1)知,f(x)=lg 1- (-1<x<1),
-+1
1-
1+ -1
1+
所以 f(-x)=lg1-(-)=lg1+=lg 1- =-lg 1- =-f(x),
所以 f(x)为奇函数.
+1
(3)原不等式可化为 lg 1- ≥lg(3x+1)(-1<x<1),
改进数学模型.
题型探究
一、直观想象
在本章中,函数图象的识别及应用均突出体现了直观想象的核心素养.
图象的识别
[例 1]
m
n
(1)已知函数 y=x (m,n∈N *,且互质)的图象如图所示,
那么下面说法正确的是
(
)
m
A.m,n 是奇数, n <1
m
B.m 是偶数,n 是奇数, n >1
m
C.m 是偶数,n 是奇数, n <1
m
n
是奇数.根据函数图象,当 x∈(1,+∞)时,y=x 的图象在 y=x 图象的下方,
m
n
m
所以 n <1.故选 C.
(2)当 0<a<1 时,函数 y=ax 的图象过定点(0,1),在 R 上单调递减,
1
于是函数 y=ax的图象过定点(0,1),在 R 上单调递增,函数ຫໍສະໝຸດ 1 1
1
y=logax+2的图象过定点2,0,在-2,+∞上单调递减.
是由函数 f(x)=ax 的图象向下平移一个单位长度,再将 x 轴下方的图象翻折到 x 轴上
方得到,分 a>1 和 0<a<1 两种情况作图,如图.当 a>1 时,直线 g(x)=2a 与函数 f(x)
人教版高一数学指对幂函数重点知识点大全

(每日一练)人教版高一数学指对幂函数重点知识点大全单选题1、方程log2x=log4(2x+3)的解为()A.−1B.1C.3D.−1或3答案:C解析:根据对数运算性质化为同底的对数方程,结合对数真数大于零可求得结果.∵log2x=log4(2x+3)=12log2(2x+3)=log2√2x+3,∴{x>02x+3>0x=√2x+3,解得:x=3.故选:C.2、中国的5G技术领先世界,5G技术的数学原理之一便是著名的香农公式:C=Wlog2(1+SN),它表示:在受噪声干扰的信道中,最大信息传递速率C取决于信道带宽W、信道内信号的平均功率S、信道内部的高斯噪声功率N的大小,其中SN 叫做信噪比.按照香农公式,若不改变带宽W,而将信噪比SN从1000提升至5000,则C大约增加了()(附:lg2≈0.3010)A.20%B.23%C.28%D.50%答案:B解析:利用对数减法与换底公式可求得结果.将信噪比S N 从1000提升至5000,C 大约增加了Wlog 2(1+5000)−Wlog 2(1+1000)Wlog 2(1+1000)=log 25001−log 21001log 21001 ≈lg5000lg2−lg1000lg2lg1000lg2=lg53=lg 1023=1−lg23≈0.2330.所以,C 大约增加了23%.故选:B3、若2x =3,2y =4,则2x+y 的值为( )A .7B .10C .12D .34答案:C解析:根据指数幂的运算性质直接进行求解即可.因为2x =3,2y =4,所以2x+y =2x ⋅2y =3×4=12,故选:C填空题4、函数y =log 0.4(−x 2+3x +4)的值域是________.答案:[−2,+∞)解析:先求出函数的定义域为(−1,4),设f (x )=−x 2+3x +4=−(x −32)2+254,x ∈(−1,4),根据二次函数的性质求出单调性和值域,结合对数函数的单调性,以及利用复合函数的单调性即可求出y =log 0.4(−x 2+3x +4)的单调性,从而可求出值域.解:由题可知,函数y =log 0.4(−x 2+3x +4),则−x 2+3x +4>0,解得:−1<x <4,所以函数的定义域为(−1,4),设f (x )=−x 2+3x +4=−(x −32)2+254,x ∈(−1,4), 则x ∈(−1,32)时,f (x )为增函数,x ∈(32,4)时,f (x )为减函数,可知当x =32时,f (x )有最大值为254, 而f (−1)=f (4)=0,所以0<f (x )≤254,而对数函数y =log 0.4x 在定义域内为减函数,由复合函数的单调性可知,函数y =log 0.4(−x 2+3x +4)在区间(−1,32)上为减函数,在(32,4)上为增函数,∴y ≥log 0.4254=−2,∴函数y =log 0.4(−x 2+3x +4)的值域为[−2,+∞).所以答案是:[−2,+∞).小提示:关键点点睛:本题考查对数型复合函数的值域问题,考查对数函数的单调性和二次函数的单调性,利用“同增异减”求出复合函数的单调性是解题的关键,考查了数学运算能力.5、若幂函数y =f(x)的图像经过点(18,2),则f(−18)的值为_________. 答案:−2解析:根据已知求出幂函数的解析式f(x)=x −13,再求出f(−18)的值得解.设幂函数的解析式为f(x)=x a ,由题得2=(18)a =2−3a ,∴−3a =1,∴a =−13,∴f(x)=x −13.所以f(−18)=(−18)−13=(−12)3×(−13)=−2.所以答案是:−2.小提示:本题主要考查幂函数的解析式的求法和函数值的求法,意在考查学生对这些知识的理解掌握水平.。
幂函数函数知识点归纳总结

幂函数函数知识点归纳总结《幂函数函数知识点归纳总结:嘿,这可真有趣!》嘿,各位小伙伴们!今天咱来唠唠幂函数这个神奇的玩意儿,那可是高中数学里特别重要的一部分啊!咱先说说啥是幂函数。
简单说呢,就是那种形式像是y = x^a 的家伙,这里的a 可是个关键角色。
就好比是给x 披上不同的“外衣”,让它变得有了各种不同的性格。
这幂函数啊,有那么几个关键点得记牢。
首先就是幂指数a,它要是正数呢,那图像就雄赳赳气昂昂地往上走,越来越高。
要是负数呢,图像就垂头丧气地往下走,还会和坐标轴玩“暧昧”,怎么都不肯远离。
然后呢,当a 是奇数时,图像就是个对称美,左边右边都长得一样。
就像照镜子,这对称得让人看着就舒服。
嘿,你别说,学幂函数的时候还有些好玩的事儿。
有一次,我在做题,看到一个幂函数图像,怎么看都觉得它像个调皮的小鬼在那扭来扭去,还冲我做鬼脸呢!不过,咱可不能被它吓住,得找到它的规律,把它给收服喽。
还有啊,幂函数的性质也很有意思。
比如它的定义域,有时候是全体实数,有时候又得避开一些数,就像走在路上得避开那些坑坑洼洼的地方一样。
值域呢,也会跟着幂指数变来变去,一会儿大,一会儿小。
学习幂函数的时候,我还经常和同学们一起讨论,你一言我一语的,就像在开一场热闹的派对。
有时候会为了一个小问题争得面红耳赤,但最后搞清楚了,那感觉真是爽歪歪!就好像解开了一个大大的谜团,心里特别有成就感。
总之呢,幂函数知识点虽然有些让人头疼,但也有很多有趣的地方。
只要咱认真学,多做题,多和它“打交道”,就一定能把它拿下!把幂函数这个家伙彻底收服,让它为我们的数学之路增添一份乐趣和挑战。
小伙伴们,加油吧!让我们在幂函数的世界里尽情遨游,探索更多的奥秘!。
高一数学幂函数知识点
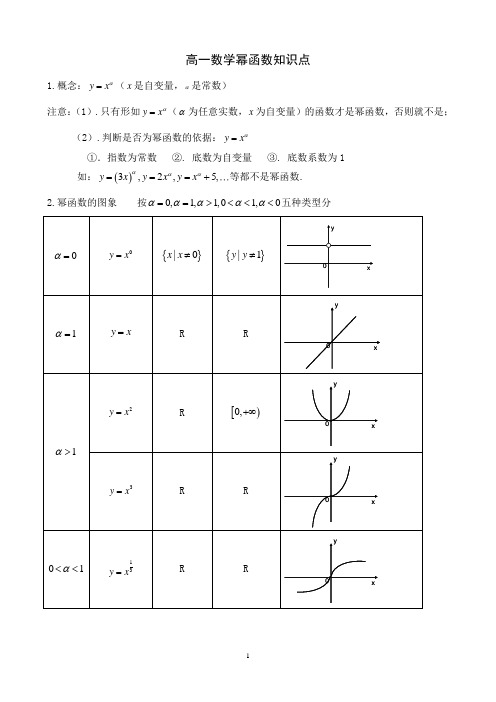
高一数学幂函数知识点1.概念:y x α=(x 是自变量,α是常数)注意:(1).只有形如y x α=(α为任意实数,x 为自变量)的函数才是幂函数,否则就不是; (2).判断是否为幂函数的依据:y x α=①.指数为常数 ②. 底数为自变量 ③. 底数系数为1 如:()3,2,5,y x y x y x ααα===+等都不是幂函数.2.幂函数的图象 按0,1,1,01,0ααααα==><<<五种类型分3.幂函数y x α=在第一象限图象特征(1).当1α>时,图象过(0,0),(1,1),下凸递增,如3y x = (2).当01α<<时,图象过(0,0),(1,1),上凸递增,如12y x =(3).当0α<时,图象过(1,1),下凸递减,且以两坐标轴为渐近线.如12y x -= 4.幂函数的性质(1).所有的幂函数在()0,+∞上都有意义,图象都过(1,1). (2).如果0α>,则幂函数过原点,在()0,+∞上单调递增.(3).如果0α<,图象在()0,+∞上单调递减,在第一象限内,当x 从右边趋向于原点时,图象在y 轴右方无限逼近y 轴;当x 趋向于+∞时,图象在x 轴上方无限逼近x 轴. (4).①.当α为奇数时,幂函数为奇数 ②.当α为偶数时,幂函数为偶数 ③.当(),,pp q p q N qα+=∈为互质,时a. 若q 为奇数,则当p 为奇数时p q y x =为奇函数,当p 为偶数时p qy x =为偶函数 b. 若q 为偶数,则p 必为奇数,此时pqy x =为非奇非偶函数 (5).幂函数的定义域①.当N α+∈时,定义域为R ②.当0α=时,定义域为{}|,0x x R x ∈≠ ③.当α为负整数时,定义域为{}|,0x x R x ∈≠ ④.当(),,1,,pp q N q p q qα+=∈>且互质时 a. q 为偶数时,定义域为[)0,+∞ b. q 为奇数时,定义域为R ⑤.当()-,,1,,pp q N q p q qα+=∈>且互质时 a. q 为偶数,定义域为()0,+∞ b. q 为奇数,定义域为{}|,0x x R x ∈≠.。
高中数学高一(上)幂函数与指数函数复习教学案【解析】

化简得 又因为
所以2007年后的第7年即2014年,该国会出现粮食危机。
(2)设2007年后的第 年该国出现粮食危机,则此时人口总量为 人
化简得
而当 时,
当 时,
所以2007年的第8年即2015年,该国会出现粮食危机。
(3)设2007年后的第 年该国出现粮食危机,则 年后人口总量为 人
①将 的图像向左平移一个单位即可得到函数 的图像;将 的图像向右平移一个单位就得到函数 的图像。
②将 的图像向上平移一个单位就得到函数 的图像,将 的图像向下平移一个单位就得到函数 的图像。
(2)对称变换:
①函数 的图像与 的图像关于 轴对称;
②函数 的图像与 的图像关于 轴对称;
③函数 的图像与 的图像关于原点对称。
【例1】函数 ,当 时, 单调递增,求实数 的取值范围。
【解】
的两条渐近线为
单调递减,所以其图像必在“新坐标”系中的二、四象限
【点拨】利用函数单调性定义求解是解此题的关键。
变式练习:指出函数 的定义域、值域及单调区间。
答案:定义域[1,3],值域 ,[1,2]单调递增,[2,3]单调递减。
专题二有关幂函数奇偶性的问题
【答案】B
变式练习:若函数 分别是R上的奇函数,偶函数,且满足 ,则有()
A、f(2)<f(3)<g(0) B、g(0)<f(3)<f(2) C、f(2)<g(0)<f(3) D、g(0)<f(2)<f(3)
答案:D
专题三幂函数图像及应用
幂函数 的图像和性质比较复杂,要重点掌握 的幂函数的性质。
高一数学指对幂函数考点总结

(每日一练)高一数学指对幂函数考点总结单选题1、函数y =2x −2−x ( )A .是R 上的减函数B .是R 上的增函数C .在(−∞,0)上是减函数,在(0,+∞)上是增函数D .无法判断其单调性答案:B解析:利用指数函数的单调性结合单调性的性质可得出结论.因为指数函数f (x )=2x 为R 上的增函数,指数函数g (x )=2−x =(12)x 为R 上的减函数, 故函数y =2x −2−x 是R 上的增函数.故选:B.2、已知集合M ={y ∣y =3x }, N ={x ∣y =√1−x},则M ∩N =( )A .{x ∣0<x <1}B .{x ∣0<x ⩽1}C .{x ∣x ⩽1}D .{x ∣x >0}答案:B解析:先分别求出集合M,N ,再求交集即可.M ={y ∣y =3x }=(0,+∞),N ={x ∣y =√1−x}=(−∞,1]所以M ∩N =(0,1]故选:B小提示:本题考查指数函数的值域问题,集合求交集运算,属于基础题.3、已知函数f(x)=a 2x−6+3(a >0且a ≠1)的图像经过定点A ,且点A 在角θ的终边上,则sinθ−cosθsinθ+cosθ=()A .−17B .0C .7D .17答案:D解析:由题知A(3,4),进而根据三角函数定义结合齐次式求解即可.解:令2x −6=0得x =3,故定点A 为A(3,4),所以由三角函数定义得tanθ=43,所以sinθ−cosθsinθ+cosθ=tanθ−1tanθ+1=43−143+1=17故选:D4、已知函数y =f(x −2)的图象关于直线x =2对称,在x ∈(0,+∞)时,f (x )单调递减,若a =f(4ln3),b =f(2−e ),c =f(ln 1π)(其中e 为自然对数的底数,π为圆周率),则a ,b ,c 的大小关系为( )A .a >c >bB .a >b >cC .c >a >bD .b >c >a答案:D解析:由题意得到函数f (x )的图象关于y 轴对称,满足f (x )=f (−x ),求得c =f(lnπ),结合4ln3>41=4>lnπ>lne =1>2−e >0和函数的单调性,即可求解.由函数y=f(x−2)的图象关于直线x=2对称,可得函数f(x)的图象关于y轴对称,即函数f(x)为偶函数,满足f(x)=f(−x),则c=f(ln1π)=f(−lnπ)=f(lnπ),又由4ln3>41=4>lnπ>lne=1>2−e>0,因为x∈(0,+∞)时,f(x)单调递减,可得f(4ln3)<f(ln1π)<f(2−e),所以b>c>a. 故选:D.5、已知f(x)={2x−2,x≥0−x2+3,x<0,若f(a)=2,则实数a的值为()A.-1B.-1或-2C.-1或2D.-1或1或2答案:C解析:根据f(x)={2x−2,x≥0−x2+3,x<0,分a≥0,a<0讨论求解.因为f(x)={2x−2,x≥0−x2+3,x<0,当a≥0时,2a−2=2,即2a=4=22,解得a=2,当a<0时,−a2+3=2,则a2=1,解得a=−1或a=1(舍去)综上:实数a的值为-1或2,故选:C.。
《幂函数》专题复习与训练

《3.3 幂函数》专题复习与训练【新课导入】1.幂函数的概念一般地,函数y =x α叫做幂函数,其中x 是自变量,α是常数. 2.幂函数的图象在同一平面直角坐标系中,画出幂函数y =x ,y =x 2,y =x 3,y =x 12,y =x-1的图象如图所示:3.幂函数的性质1.下列函数中不是幂函数的是( ) A .y =x B .y =x 3 C .y =3xD .y =x -1C [只有y =3x 不符合幂函数y =x α的形式,故选C.] 2.已知f (x )=(m +1)x m 2+2是幂函数,则m =( ) A .2 B .1 C .3 D .0 D [由题意可知m +1=1,即m =0,∴f(x )=x 2.]3.已知幂函数f (x )=x α的图象过点⎝⎛⎭⎪⎫2,22,则f (4)=________.12 [由f (2)=22可知2α=22,即α=-12, ∴f (4)=4-12=12.]【合作探究】 幂函数的概念【例1】 已知y =(m 2+2m -2)xm 2-1+2n -3是幂函数,求m ,n 的值.[解]由题意得⎩⎨⎧m 2+2m -2=1,m 2-1≠0,2n -3=0,解得⎩⎨⎧m =-3,n =32,所以m =-3,n =32.判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y =x α(α为常数)的形式,即函数的解析式为一个幂的形式,且需满足:(1)指数为常数;(2)底数为自变量;(3)系数为1.1.(1)在函数y =1x2,y =2x 2,y =x 2+x ,y =1中,幂函数的个数为( )A .0B .1C .2D .3(2)若函数f (x )是幂函数,且满足f (4)=3f (2),则f ⎝ ⎛⎭⎪⎫12的值等于________.(1)B (2)13 [(1)∵y =1x2=x -2,∴是幂函数;y =2x 2由于出现系数2,因此不是幂函数; y =x 2+x 是两项和的形式,不是幂函数;y =1=x 0(x ≠0),可以看出,常函数y =1的图象比幂函数y =x 0的图象多了一个点(0,1),所以常函数y =1不是幂函数.(2)设f (x )=x α,∵f (4)=3f (2),∴4α=3×2α,解得α=log 23,∴f ⎝ ⎛⎭⎪⎫12=⎝ ⎛⎭⎪⎫12log 23=13.]幂函数的图象及应用【例2】 点(2,2)与点⎝ ⎛⎭⎪⎫-2,-12分别在幂函数f (x ),g (x )的图象上,问当x 为何值时,有:(1)f (x )>g (x );(2)f (x )=g (x );(3)f (x )<g (x ).[解] 设f(x)=xα,g(x)=xβ.∵(2)α=2,(-2)β=-1 2,∴α=2,β=-1,∴f(x)=x2,g(x)=x-1.分别作出它们的图象,如图所示.由图象知,(1)当x∈(-∞,0)∪(1,+∞)时,f(x)>g(x);(2)当x=1时,f(x)=g(x);(3)当x∈(0,1)时,f(x)<g(x).解决幂函数图象问题应把握的两个原则(1)依据图象高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图象越靠近x轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图象越远离x轴(简记为指大图高).(2)依据图象确定幂指数α与0,1的大小关系,即根据幂函数在第一象限内的图象(类似于y=x-1或y=x 12或y=x3)来判断.2.(1)若四个幂函数y=x a,y=x b,y=x c,y=x d在同一坐标系中的图象如图,则a,b,c,d的大小关系是( )A.d>c>b>aB.a>b>c>dC.d>c>a>bD.a>b>d>c(2)函数y=x 12-1的图象关于x轴对称的图象大致是( )A B C D(1)B(2)B[(1)令a=2,b=12,c=-13,d=-1,正好和题目所给的形式相符合.在第一象限内,x=1的右侧部分的图象,图象由下至上,幂指数增大,所以a>b>c>d.故选B.(2)y=x 12的图象位于第一象限且为增函数,所以函数图象是上升的,函数y=x 12-1的图象可看作由y=x12的图象向下平移一个单位得到的(如选项A中的图所示),将y=x 12-1的图象关于x轴对称后即为选项B.]幂函数性质的综合应用[探究问题]1.幂函数y=xα在(0,+∞)上的单调性与α有什么关系?提示:当α>0时,幂函数y=xα在(0,+∞)上单调递增;当α<0时,幂函数y=xα在(0,+∞)上单调递减.2.2.3-0.2和2.2-0.2可以看作哪一个函数的两个函数值?二者的大小关系如何?提示:2.3-0.2和2.2-0.2可以看作幂函数f(x)=x-0.2的两个函数值,因为函数f(x)=x-0.2在(0,+∞)上单调递减,所以2.3-0.2<2.2-0.2.【例3】比较下列各组中幂值的大小:(1)0.213,0.233;(2)1.212,0.9-12, 1.1.[思路点拨] 构造幂函数,借助其单调性求解.[解] (1)∵函数y=x3是增函数,且0.21<0.23,∴0.213<0.233.(2)0.9-12=⎝ ⎛⎭⎪⎫10912, 1.1=1.112.∵1.2>109>1.1,且y =x 12在[0,+∞)上单调递增,∴1.212>⎝ ⎛⎭⎪⎫10912>1.112,即1.212>0.9-12> 1.1.把本例的各组数据更换如下,再比较其大小关系:(1)⎝ ⎛⎭⎪⎫250.5与⎝ ⎛⎭⎪⎫130.5;(2)⎝ ⎛⎭⎪⎫-23-1与⎝ ⎛⎭⎪⎫-35-1.[解] (1)因为幂函数y =x 0.5在[0,+∞)上是单调递增的, 又25>13, 所以⎝ ⎛⎭⎪⎫250.5>⎝ ⎛⎭⎪⎫130.5.(2)因为幂函数y =x -1在(-∞,0)上是单调递减的,又-23<-35,所以⎝ ⎛⎭⎪⎫-23-1>⎝ ⎛⎭⎪⎫-35-1.比较幂的大小时若指数相同,则利用幂函数的单调性比较大小;若底数、指数均不同,则考虑用中间值法比较大小,这里的中间值可以是“0”或“1”.1.判断一个函数是否为幂函数,其关键是判断其是否符合y =x α(α为常数)的形式.2.幂函数的图象是幂函数性质的直观反映,会用类比的思想分析函数y =x α(α为常数)同五个函数(y =x ,y =x 2,y =x 3,y =x -1,y =x 12)图象与性质的关系.3.幂函数的单调性是比较幂值大小关系的重要依据,要学会用幂函数的图象及性质处理幂值大小的比较问题.【课堂达标】 1.思考辨析(1)幂函数的图象都过点(0,0),(1,1).( ) (2)幂函数的图象一定不能出现在第四象限.( )(3)当幂指数α取1,3,12时,幂函数y =x α是增函数.( )(4)当幂指数α=-1时,幂函数y =x α在定义域上是减函数.( ) [答案] (1)× (2)√ (3)√ (4)×2.幂函数的图象过点(2,2),则该幂函数的解析式是( ) A .y =x -1B .y =x 12 C .y =x 2D .y =x 3B [设f (x )=x α,则2α=2, ∴α=12,∴f (x )=x 12.选B.]3.函数y =x 54的图象是( )A B C DC [∵函数y =x 54是非奇非偶函数,故排除A 、B 选项.又54>1,故选C.]4.比较下列各组数的大小:(1)3-52与3.1-52;(2)4.125,3.8-23,(-1.9)-35.[解] (1)因为函数y =x-52在(0,+∞)上为减函数,又3<3.1,所以3-52>3.1-52. (2)4.125>125=1,0<3.8-23<1-23=1,而(-1.9)-35<0,所以4.125>3.8-23>(-1.9)-35.《幂函数》专题训练[合格基础练]一、选择题1.已知幂函数f (x )=k ·x α的图象过点⎝ ⎛⎭⎪⎫12,2,则k +α等于( )A.12 B .1 C.32D .2 A [∵幂函数f (x )=kx α(k ∈R ,α∈R )的图象过点⎝ ⎛⎭⎪⎫12,2,∴k =1,f ⎝ ⎛⎭⎪⎫12=⎝ ⎛⎭⎪⎫12α=2,即α=-12,∴k +α=12.]2.如图所示,给出4个幂函数的图象,则图象与函数的大致对应是( )A .①y =x 13,②y =x 2,③y =x 12,④y =x -1B .①y =x 3,②y =x 2,③y =x 12,④y =x -1C .①y =x 2,②y =x 3,③y =x 12,④y =x -1D .①y =x 3,②y =x 12,③y =x 2,④y =x -1B [因为y =x 3的定义域为R 且为奇函数,故应为图①;y =x 2为开口向上的抛物线且顶点为原点,应为图②.同理可得出选项B 正确.]3.幂函数的图象过点(3, 3),则它的单调递增区间是( ) A .[-1,+∞) B .[0,+∞) C .(-∞,+∞)D .(-∞,0)B [设幂函数为f (x )=x α,因为幂函数的图象过点(3, 3),所以f (3)=3α=3=312,解得α=12,所以f (x )=x 12,所以幂函数的单调递增区间为[0,+∞),故选B.]4.设α∈⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫-1,1,12,3,则使函数y =x α的定义域是R ,且为奇函数的所有α的值是( )A .1,3B .-1,1C .-1,3D .-1,1,3A [当α=-1时,y =x -1的定义域是{x |x ≠0},且为奇函数;当α=1时,函数y =x 的定义域是R ,且为奇函数;当α=12时,函数y =x 12的定义域是{x |x ≥0},且为非奇非偶函数;当α=3时,函数y =x 3的定义域是R 且为奇函数.故选A.]5.幂函数f (x )=x α的图象过点(2,4),那么函数f (x )的单调递增区间是( )A .(-2,+∞)B .[-1,+∞)C .[0,+∞)D .(-∞,-2)C [由题意得4=2α,即22=2α,所以α=2.所以f (x )=x 2. 所以二次函数f (x )的单调递增区间是[0,+∞).]二、填空题6.已知幂函数f (x )=x m 的图象经过点⎝⎛⎭⎪⎫3,13,则f (6)=________.136 [依题意13=(3)m=3m 2,所以m 2=-1,m =-2, 所以f (x )=x -2,所以f (6)=6-2=136.] 7.若幂函数f (x )=(m 2-m -1)x 2m -3在(0,+∞)上是减函数,则实数m =________.-1 [∵f (x )=(m 2-m -1)x 2m -3为幂函数, ∴m 2-m -1=1,∴m =2或m =-1.当m =2时,f (x )=x ,在(0,+∞)上为增函数,不合题意,舍去;当m =-1时,f (x )=x -5,符合题意.综上可知,m =-1.]8.若幂函数y =x mn (m ,n ∈N *且m ,n 互质)的图象如图所示,则下列说法中正确的是________.①m ,n 是奇数且m n <1;②m 是偶数,n 是奇数,且m n>1;③m 是偶数,n 是奇数,且m n <1;④m ,n 是偶数,且m n>1.③ [由题图知,函数y =x mn 为偶函数,m 为偶数,n 为奇数,又在第一象限向上“凸”,所以mn<1,选③.]三、解答题9.已知函数f (x )=(m 2+2m )·x m 2+m -1,m 为何值时,函数f (x )是:(1)正比例函数;(2)反比例函数;(3)幂函数.[解] (1)若函数f (x )为正比例函数,则⎩⎨⎧m 2+m -1=1,m 2+2m ≠0,∴m =1.(2)若函数f (x )为反比例函数,则 ⎩⎨⎧m 2+m -1=-1,m 2+2m ≠0,∴m =-1.(3)若函数f (x )为幂函数,则m 2+2m =1,∴m =-1± 2. 10.已知幂函数y =f (x )经过点⎝ ⎛⎭⎪⎫2,18.(1)试求函数解析式;(2)判断函数的奇偶性并写出函数的单调区间.[解] (1)由题意,得f (2)=2α=18,即α=-3,故函数解析式为f (x )=x-3.(2)∵f (x )=x -3=1x3,∴要使函数有意义,则x ≠0,即定义域为(-∞,0)∪(0,+∞),关于原点对称.∵f (-x )=(-x )-3=-x -3=-f (x ), ∴该幂函数为奇函数.当x >0时,根据幂函数的性质可知f (x )=x -3在(0,+∞)上为减函数,∵函数f (x )是奇函数,∴在(-∞,0)上也为减函数,故其单调减区间为(-∞,0),(0,+∞).[等级过关练]1.函数y =x -2在区间⎣⎢⎡⎦⎥⎤12,2上的最大值是( )A.14 B .-1 C .4D .-4C [函数y =x -2在区间⎣⎢⎡⎦⎥⎤12,2上为减函数,所以当x =12时有最大值4.] 2.给出幂函数:①f (x )=x ;②f (x )=x 2;③f (x )=x 3;④f (x )=x ;⑤f (x )=1x .其中满足条件f ⎝ ⎛⎭⎪⎫x 1+x 22>f (x 1)+f (x 2)2(x 1>x 2>0)的函数的个数是( )A .1个B .2个C .3个D .4个A [①函数f (x )=x 的图象是一条直线,故当x 1>x 2>0时,f ⎝⎛⎭⎪⎫x 1+x 22=f (x 1)+f (x 2)2;②函数f (x )=x 2的图象是凹形曲线,故当x 1>x 2>0时,f ⎝ ⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2;③在第一象限,函数f (x )=x 3的图象是凹形曲线,故当x 1>x 2>0时,f ⎝⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2;④函数f (x )=x 的图象是凸形曲线,故当x 1>x 2>0时,f ⎝ ⎛⎭⎪⎫x 1+x 22>f (x 1)+f (x 2)2;⑤在第一象限,函数f (x )=1x的图象是一条凹形曲线,故当x 1>x 2>0时,f ⎝ ⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2.故仅有函数f (x )=x 满足当x 1>x 2>0时, f ⎝ ⎛⎭⎪⎫x 1+x 22>f (x 1)+f (x 2)2.故选A.]3.幂函数f (x )=x 3m -5(m ∈N )在(0,+∞)上是减函数,且f (-x )=f (x ),则m 可能等于________.1 [∵幂函数f (x )=x 3m -5(m ∈N )在(0,+∞)上是减函数,∴3m -5<0,即m <53,又m ∈N ,∴m =0,1;∵f (-x )=f (x ),∴f (x )为偶函数.当m =0时,f (x )=x -5是奇函数;当m =1时,f (x )=x -2是偶函数,故m =1.]4.已知幂函数f (x )=x 12,若f (10-2a )<f (a +1),则a 的取值范围是________.3<a ≤5 [因为f (x )=x 12=x (x ≥0), 易知f (x )在(0,+∞)上为增函数, 又f (10-2a )<f (a +1),所以⎩⎨⎧a +1≥0,10-2a ≥0,a +1>10-2a ,解得⎩⎨⎧a ≥-1,a ≤5,a >3,所以3<a ≤5.]5.已知幂函数f (x )=x α的图象过点⎝ ⎛⎭⎪⎫2,12,函数g (x )=(x -2)f (x )⎝ ⎛⎭⎪⎫12≤x ≤1,求函数g (x )的最大值与最小值.[解] 因为f (x )的图象过点⎝ ⎛⎭⎪⎫2,12,所以12=2α,所以α=-1,所以f (x )=x -1, 所以g (x )=(x -2)·x -1=x -2x =1-2x. 又g (x )=1-2x 在⎣⎢⎡⎦⎥⎤12,1上是增函数,所以g (x )min =g ⎝ ⎛⎭⎪⎫12=-3,g (x )max =g (1)=-1.。
(完整版)高一数学幂函数题型复习总结,推荐文档

知识点一、幂的运算法则
初中知识点:(1) am an
(2) am n
指数幂与根式的互化: n am
1
练习: x3
例:计算
5 x2
am an
am bm
1 n am
x
2 3
an
1 4 x3
练习:
1
知识点二、幂函数图象
画图注意事项 1 定义域:偶次方根被开方数 0 ,奇次方根被开方数 R ,分母 0 . 2 奇偶性:判断 f (x) 与 f (x) 相等?相反数? 3 闲着描描点!极限情况靠想象!快快慢慢!增增减减!秒悟! 1、初级练场:常见幂函数图象:
1
(8) y x 4
3
(9) y x 2
总结:横看成岭侧成峰!
3
(1) (2)
4
5
3
3
2
练习:画函数图象 y x 3 , y x 2 , y x 5 , y x 4 , y x 5
知识点三、幂函数图象性质的应用
1、幂函数的定义
4
2、幂函数的图像
3、幂函数比较大小
1
1
例 1、(1)1.52
3、 4、比较大小 5、
7
“
”
“
”
At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!
高一数学幂函数、指数函数复习(教师版)

学科教师辅导讲义解:因为)(322Z m x y m m ∈=--的图象与x,y 轴都无交点,所以,2230m m --<,所以,m 可取0,1,2。
因为)(322Z m x y m m ∈=--的图象关于y 轴对称 所以m=14、下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系..6543212132323123---======x y x y x y x y x y x y );();()(;);();()((A ) (B ) (C ) (D ) (E ) (F ) 解:六个幂函数的定义域,奇偶性,单调性如下: (1)323x x y ==定义域[0,,既不是奇函数也不是偶函数,在[0,是增函数;.),0(16),0(15),0(14),0[3),0[22133223232331上减函数函数,在既不是奇函数也不是偶定义域为)(是减函数;是奇函数,在定义域)(是减函数;是偶函数,在定义域)(是增函数;,是偶函数,在定义域为)(是增函数;,是奇函数,在定义域为)(+∞==+∞==+∞==+∞==+∞==+--+--+-R xx y UR R x x y UR R x x y R x x y R x x y 通过上面分析,可以得出(1)↔(A ),(2)↔(F ),(3)↔(E ),(4)↔(C ),(5)↔(D ),(6)↔(B ).5、由于对某种商品开始收税,使其定价比原定价上涨x 成(即上涨率为10x),涨价后,商品卖出个数减少bx 成,税率是新定价的a 成,这里a,b 均为正常数,且a <10,设售货款扣除税款后,剩余y 元,要使y 最大,求x 的值.解:设原定价A 元,卖出B 个,则现在定价为A(1+10x ), 现在卖出个数为B(1-10bx),现在售货金额为A(1+10x ) B(1-10bx )=AB(1+10x )(1-10bx ),应交税款为AB(1+10x )(1-10bx )·10a,12.值域为()0,+∞的函数一定是 ( ) A 115xy -= B 113xy -⎛⎫= ⎪⎝⎭C 12y x =-D 112xy ⎛⎫=- ⎪⎝⎭13.函数21113x y -⎛⎫=- ⎪⎝⎭的定义域是 ( )A )1,2⎡+∞⎢⎣ B 1,2⎛⎤-∞ ⎥⎦⎝C (),-∞+∞D ](,1-∞14.由于油船漏油,导致海洋污染,污染面积()2y km 与时间t (小时)的关系是ty a =,如图,有如下叙述 ①这个指数函数的底数为2;②5个小时,污染面积就会超过302km③污染面积从24km 到212km 需经过1.5个小时;④每小时新增的污染面积相等其中正确的是 ( )A ①④B ①②③④C ②③④D ①②三、解答题15.求函数13932xx x y +=++的最大值16.已知函数()112x x f x a a ⎛⎫=+ ⎪⎝⎭,其中0,1a a >≠,判断()()f a b f a b ++-与()()2f a f b 的大小。
人教版高一数学指对幂函数高频考点知识梳理

(每日一练)人教版高一数学指对幂函数高频考点知识梳理单选题1、下列各组函数中,表示同一个函数的是( )A .y =1与y =x 0B .y =x 与y =(√x)2C .y =2log 2x 与y =log 2x 2D .y =ln 1+x 1−x 与y =ln (1+x )−ln (1−x )答案:D解析:分别计算每个选项中两个函数的定义域和对应关系,定义域和对应关系都相同的是同一个函数,即可得正确选项.对于A :y =1定义域为R ,y =x 0定义域为{x|x ≠0},定义域不同不是同一个函数,故选项A 不正确;对于B :y =x 定义域为R ,y =(√x)2的定义域为{x|x ≥0},定义域不同不是同一个函数,故选项B 不正确;对于C :y =2log 2x 的定义域为{x|x >0},y =log 2x 2定义域为{x|x ≠0},定义域不同不是同一个函数,故选项C 不正确;对于D :由1+x 1−x >0可得(x +1)(x −1)<0,解得:−1<x <1,所以y =ln 1+x 1−x 的定义域为{x|−1<x <1},由{1+x >01−x >0可得−1<x <1,所以函数y =ln (1+x )−ln (1−x )的定义域为{x|−1<x <1}且y =ln (1+x )−ln (1−x )=ln 1+x 1−x ,所以两个函数定义域相同对应关系也相同是同一个函数,故选项D 正确, 故选:D.2、函数y =ln (3−4x )+1x 的定义域是( )A .(−∞,34)B .(0,34) C .(−∞,0)∪(0,34)D .(34,+∞) 答案:C解析:根据具体函数定义域的求解办法列不等式组求解.由题意,{3−4x >0x ≠0 ⇒x <34且x ≠0,所以函数的定义域为(−∞,0)∪(0,34). 故选:C3、已知集合M ={y ∣y =3x }, N ={x ∣y =√1−x},则M ∩N =( )A .{x ∣0<x <1}B .{x ∣0<x ⩽1}C .{x ∣x ⩽1}D .{x ∣x >0}答案:B解析:先分别求出集合M,N ,再求交集即可.M ={y ∣y =3x }=(0,+∞),N ={x ∣y =√1−x}=(−∞,1]所以M ∩N =(0,1]故选:B小提示:本题考查指数函数的值域问题,集合求交集运算,属于基础题.填空题4、方程5x+2−5x−1=12425的解是__________.答案:x =−1解析:令5x=t,t∈(0,+∞),可将原方程化为关于t的一元一次方程,解出t,继而可得x的值.∵5x+2−5x−1=12425,可令5x=t,t∈(0,+∞),∴25t−15t=12425,解得t=15,故而x=−1,即方程的解为x=−1,故答案为x=−1.小提示:本题主要考查了指数方程的解法,转化为一元一次方程是解题的关键,属于基础题.5、若函数f(x)=log|x+1|a(a>0,a≠1)在区间(−1,0)上有f(x)>0,则f(x)的单调减区间是_______.答案:(−1,+∞)解析:由题意当x∈(−1,0)时,|x+1|∈(0,1),又f(x)>0,得0<a<1.则根据复合函数的单调性即可求出f(x)的单调减区间.解:因为x∈(−1,0),所以|x+1|∈(0,1),又f(x)>0,所以0<a<1.根据复合函数单调性法则:f(x)的单调减区间为y=|x+1|的单调增区间,又y=|x+1|>0,所以f(x)的单调减区间为(−1,+∞).故答案为(−1,+∞).小提示:本题考查对数函数的取值范围,考查求复合函数的单调区间,解题的关键是注意函数的定义域,属于基础题.。
高一上学期期中考后,幂函数及函数要点总结

高一上学期期中考后,幂函数及函数要点总结重要性:高一数学一共六个章节,其中函数就占了其中三个章节,分别是函数的基本性质、幂函数、指数函数和对数函数、三角函数,高一数学学习的主线就是函数。
除此之外,高二上的数列,高二下的坐标平面山的直线、圆锥曲线等章节中都大量蕴含着函数中的基本思想和思维方式。
尤其直线方程、圆锥曲线等解析几何问题本身就是函数的延伸。
高考中所占分值:高一部分的函数类占分大约40分(满分150),高二部分类函数的解析几何部分所占分值大约为25-30分。
初高中函数的区别:1、内容上:初中所学的有正反比例函数、一次函数、二次函数。
主要着重点在于函数的概念、图像的画法、性质方面仅侧重于单调性。
高中所学有函数的基本性质(包含解析式的基本求法、定义域的求法、值域的求法、对抽象函数关系的理解、函数的奇偶性、单调性)、幂函数、指数函数、对数函数(以上三类为高中的基本函数,侧重点在于三种不同函数的图像画法、单调性等问题)、三角函数(侧重在于函数的周期性、对称性、函数的平移、拉伸)。
2、难度上:初中函数着力点还在于对具体函数关系的理解,对基本图像和性质的认识。
相较而言高中函数的特点是抽象化、复杂化、容量大。
打个比方相当于初中学函数是要求十分钟内跑500米,高中函数的负重情况下要求五分钟内跑1000米。
其实不仅仅是函数,由于初高中难度跨越比较大(尤其上海),初中接近满分上了高中却在及格线上挣扎的同学比比皆是。
因而对学生的学习习惯和学习能力有了远高于初中的要求。
本阶段常见的难点:(1)解析式的求法、值域的求法不能针对不同题型熟练应用不同方法。
高中范围内针对解析式的求法和值域的求法,分别都有4-5中常规不同方法,分别对应不同的题型。
但理解不透彻、题型分类不清晰的同学,对具体题型难以短时间内找准准确的方法来应用。
(2)函数的定义域求法(尤其是抽象函数定义域的求法)。
要点不在于x的取值范围是什么,而在于整个括号内的取值范围。
高一数学幂函数知识点归纳整理

高一数学幂函数知识点归纳整理高一数学幂函数知识点归纳整理形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。
定义域和值域:当a为不同的数值时,幂函数的定义域的不同情况如下:如果a为任意实数,则函数的定义域为大于0的所有实数;如果a为负数,则x肯定不能为0,不过这时函数的定义域还必须根[据q的奇偶性来确定,即如果同时q为偶数,则x不能小于0,这时函数的定义域为大于0的所有实数;如果同时q为奇数,则函数的定义域为不等于0的所有实数。
当x为不同的数值时,幂函数的值域的不同情况如下:在x大于0时,函数的值域总是大于0的实数。
在x小于0时,则只有同时q为奇数,函数的值域为非零的实数。
而只有a为正数,0才进入函数的值域性质:对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性:首先我们知道如果a=p/q,q和p都是整数,则x^(p/q)=q次根号(x的p次方),如果q是奇数,函数的定义域是R,如果q是偶数,函数的定义域是[0,+∞)。
当指数n是负整数时,设a=-k,则x=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞)。
因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道:排除了为0与负数两种可能,即对于x0,则a可以是任意实数;排除了为0这种可能,即对于x0和x0的所有实数,q不能是偶数;排除了为负数这种可能,即对于x为大于且等于0的所有实数,a就不能是负数。
总结起来,就可以得到当a为不同的数值时,幂函数的定义域的不同情况如下:如果a为任意实数,则函数的定义域为大于0的所有实数;如果a为负数,则x肯定不能为0,不过这时函数的定义域还必须根据q的奇偶性来确定,即如果同时q为偶数,则x不能小于0,这时函数的定义域为大于0的所有实数;如果同时q为奇数,则函数的定义域为不等于0的所有实数。
人教版高一数学指对幂函数总结(重点)超详细

(每日一练)人教版高一数学指对幂函数总结(重点)超详细单选题1、已知f(x)=a−x(a>0,且a≠1),且f(−2)>f(−3),则a的取值范围是()A.(0,+∞)B.(1,+∞)C.(-∞,1)D.(0,1)答案:D解析:由a>0,且a≠1,排除AC;利用指数函数的单调性排除B,确定D.由a>0,且a≠1,排除AC;∵f(x)=a−x=(1a )x ,当a>1时,0<1a<1,f(x)为单调递减函数,∴f(−2)<f(−3),与已知矛盾矛盾,故B错误;当0<a<1时,1a>1,f(x)为单调递增函数,∴f(−2)>f(−3),符合题意.故选:D.2、①函数值域为[0,+∞);②函数为偶函数;③函数在[0,+∞)上f(x1)−f(x2)x1−x2>0恒成立;④若任意x1≥0,x2≥0都有f(x1)+f(x2)2≥f(x1+x22).已知函数:①y1=2|x|−1;②y2=(12)|x|;③y3=x2;④y4=x12.其中同时满足以上四个条件的函数有()个A.0B.1C.2D.3答案:C解析:分别作出①y 1=2|x |−1;②y 2=(12)|x |;③y 3=x 2;④y 4=x 12四个函数的图象,再根据图象逐一判断四个函数是否满足①②③④四个条件即可求解.分别作出①y 1=2|x |−1;②y 2=(12)|x |;③y 3=x 2;④y 4=x 12四个函数的图象:由图知,四个函数的值域都是[0,+∞)都满足①;由图知:①y 1=2|x |−1;②y 2=(12)|x |;③y 3=x 2图象关于y 轴对称,都是偶函数,④y 4=x 12的定义域为[0,+∞)不关于原点对称,既不是奇函数也不是偶函数,故④y 4=x 12不满足条件②;排除函数④y 4=x 12; 条件③:函数在[0,+∞)上f (x 1)−f (x 2)x 1−x 2>0恒成立;由函数单调性的定义可知:函数在[0,+∞)上单调递增,由四个函数图象可知,①y 1=2|x |−1,③y 3=x 2,④y 4=x 12满足条件③,函数②y 2=(12)|x |不满足条件③,排除函数②y 2=(12)|x |; 对于条件④:函数①y1=2|x|−1:如图任意x1≥0,x2≥0都有f(x1)+f(x2)2≥f(x1+x22),故函数①y1=2|x|−1满足条件④,函数③y3=x2:如图任意x1≥0,x2≥0都有f(x1)+f(x2)2≥f(x1+x22),故函数③y3=x2满足条件④,所以同时满足以上四个条件的函数有函数①y1=2|x|−1、函数③y3=x2,共有2个,故选:C3、已知函数f(x)=log a x(a>0,a≠1),则y=f(|x|−1)的图象可能是()A.B.C.D.答案:B解析:利用奇偶性定义判断y =f(|x|−1)的奇偶性,结合x =3、x =32的函数值符号,排除错误选项即可. 由题意,y =g(x)=f(|x|−1)=log a (|x|−1),∴g(−x)=log a (|−x|−1)=g(x),即g(x)为偶函数,排除A 、D ; 当x =3时,y =g(3)=log a (|3|−1)=log a 2, 当x =32时,y =g(32)=log a (|32|−1)=−log a 2, ∴x =3、x =32对应函数值异号,排除C ; 故选:B 填空题4、函数f (x )=log 12(x 2−5x +6)的单调递减区间为___________.答案:(3,+∞) 解析:利用对数型复合函数性质求解即可.由题知:x 2−5x +6>0,解得x >3或x <2. 令t =x 2−5x +6,则y =log 12t 为减函数.所以t ∈(−∞,2),t =x 2−5x +6为减函数,f (x )=log 12(x 2−5x +6)为增函数,t ∈(3,+∞),t =x 2−5x +6为增函数,f (x )=log 12(x 2−5x +6)为减函数.所以函数f (x )=log 12(x 2−5x +6)的单调递减区间为(3,+∞).所以答案是:(3,+∞)5、已知函数f (x )为偶函数,当x ≥0时,f (x )=3|x−1|,若直线y =a 与函数y =f (x )的图象有4个交点,则实数a 的取值范围是______.答案:(1,3)解析:根据函数为偶函数得到函数的解析式,画出函数图像,根据图像得到答案. 当x<0时,−x>0,则f(x)=f(−x)=3|−x−1|=3|x+1|,故f(x)={3|x−1|,x∈[0,+∞)3|x+1|,x∈(−∞,0),f(1)=f(−1)=1,f(0)=3,由题知f(x)的图像如图所示.因为直线y=a与函数y=f(x)的图象有4个交点,所以实数a的取值范围是(1,3).所以答案是:(1,3).。
高一数学幂的运算指数函数复习

(2)
(3)
注意:
底数的约定:
3.1.2指数函数
1、指数函数的定义:
注意:(1)定义域:
(2)底数:
(3)形式的严格性:
如: 、 、 、 是不是指数函数?
2、指数函数的图象和性质:
a>1
0<a<1
图
象
性
质
(1)定义域:
(2)值域:
(3)过点(,),即:x=时,y=
(4)在R上是函数
(4)在R上是函数
思考:
3.1.1有理指数幂及其运算
1、幂的运算性质:
(1)
(2)
(3)
(4)
规定:
零指数幂:
负整数指数幂:
2、分数指数幂:
(1)
(2)
(3)
分数指数幂是根式的另一种表示,根式的运算可利用分数指数幂与根式之间的关系转化为分数指数幂的运算.
当指数的范围由整数集 扩大有理数集Q到之后,幂的运算性质可由5条合并为3条,即:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一第一学期数学期末复习——幂指函数
1. 若已知幂函数的图像过(8,4),则该函数的值域为____________
2. 函数()()432112x x y -+=
的定义域是__________
3. 若幂函数()32221----=m m
x m m y 在()+∞,0上为减函数,则实数m 的取值范围为__________
4.若函数m y x +=2的图象不经过第二象限,则m 的取值范围为__________
5.已知函数14)(-+=x a
x f 的图像恒过定点P ,则P 点坐标是__________
6.若指数函数x a x f )1()(2-=在R 上是减函数,则实数a 的取值范围为__________
7.不等式15122<⎪
⎭⎫ ⎝⎛-+x x 的解集是__________
8函数()012
41<+-=+x y x x 的值域是__________
9.函数2221++-⎪
⎭⎫ ⎝⎛=x x y 的单调递减区间是__________
10.若函数a y x 242
--=有4个零点,则实数a 的取值范围为__________
11.幂函数k x y =(1)图像恒过(1,1)和(0,0) (2)0>k 时,函数单调递增(3)第四象限无图像 (4)}1,0{∈k 时图像为直线;其中正确的序号为 ( )
A.(1)(2)(3)(4)
B. (2) (3)(4)
C. (2)(3)
D. (3)
12.对幂函数k x y =,⎭
⎬⎫⎩⎨⎧--∈2,2,32,31,21,3k ,其中定义域为R 的函数有( ) A.2 B.3 C.4 D.5
13.下列函数在定义域上是奇函数,且在区间()0,∞-上是增函数的是( ) A.21
x y = B.31x y = C.2-=x y D.3
4x y =
14.函数()01,10<<-<<=+b a a y b x 的大致图像为( )
A B C D
15.已知0,≠>ab b a ,给出下列不等式○122b a >,○2b
a 22>,○3
b a 11<,○,43131b a >,○5b a ⎪⎭
⎫ ⎝⎛<⎪⎭⎫ ⎝⎛3131其中恒成立的个数是( ) A .4 B.5 C.6 D.7
16.已知幂函数)(42Z m x y m m ∈=- 的图像关于y 轴对称,且在区间()+∞,0上为减函数
(1) 求m 的值和函数)(x f 的解析式
(2) 解关于x 不等式)21()2(x f x f -<+
17.若函数x
a y =在[]2,1上的最大值比最小值大2,求实数a 的值
18.已知x x x
x x f --+-=10
101010)((1)判断函数的奇偶性;(2)求函数)(x f 的值域;(3)证明)(x f 在区间()+∞∞-,上是增函数。
19.若函数)(1
22)(R a a x f x ∈+-=。
(1) 若函数)(x f y =为奇函数,求实数a 的值;
(2) 判断函数的单调性,无需证明;
(3) 若不等式a x f 21)(>
在区间()3,1上都成立,求实数a 的取值范围 (4)。
