2012高考全国卷数学文科试卷及其规范标准答案
2012年新课标高考数学文科试卷带详解

2012年普通高等学校招生全国统一考试文科数学第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1. 已知集合A ={x |x 2-x -2<0},B ={x |-1<x <1}则 ( ) A. A ⊂≠B B. B ⊂≠A C..A =B D. A ∩B =∅ 【测量目标】不等式的运算和集合的包含关系.【考查方式】通过解不等式判断集合的包含关系. 【参考答案】B【试题解析】:由题意得,2={|20}{|12}A x x x x x --<=-<<,则B 是A 的真子集.2. 复数z =-3+i2+i 的共轭复数是 ( )A. 2+iB. 2-iC. -1+iD. -1-i 【测量目标】复数的四则运算及共轭复数的概念. 【考查方式】通过运算直接考查共轭复数. 【参考答案】D【试题解析】由题意得,()()3i 2i 3i 1i 2i 5z -+--+===-++,则1i z =--,故选D 3.在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线y =12x +1上,则这组样本数据的样本相关系数为 ( ) A. -1 B . 0 C . 2 D. 1【测量目标】线性回归方程与样本系数的的关系式. 【考查方式】通过给出方程求样本系数. 【参考答案】D【试题解析】:由题意得,根据线性相关性的检验可知,此时数据密切相关,此时数据的样本相关系数为1,故选D.4.设F 1、F 2是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,P 为直线x =3a2上一点,△F 1PF 2是底角为30的等腰三角形,则E 的离心率为 ( )A. 12B. 23C. 34 D .45【测量目标】:椭圆的简单几何性质.【考查方式】将椭圆与三角函数知识结合起来考查. 【参考答案】C【试题解析】:由题意得,如图所示12212060F F P MF P ∠=⇒∠=,在直角2MF P △中,2sin60PM PF == , 又232F M a c =-,且2tan 603322PM F M a c a c==⇒=--所以34c e a ==,故选C . 5. 已知正三角形ABC 的顶点A (1,1),B (1,3),顶点C 在第一象限,若点(x ,y )在△ABC 内部,则z x y =-+的取值范围是 ( ) A.(1-3,2) B.(0,2) C.(3-1,2) D.(0,1+3) 【测量目标】二元线性规划的最优解.【考查方式】利用线性约束条件通过直线平移求最值. 【参考答案】A【试题解析】由题意得,正三角形ABC 的边长为2,所以顶点C的坐标为()12C , 当取点三角形ABC 的顶点()1,3B 时目标函数取得最大值,最大值为max 2z =,当取点()12C +时,目标函数有最小值,此时最小值为min 1z =所以目标函数的取值范围为()12,故选A.6.如果执行下边的程序框图,输入正整数N (N ≥2)和实数a 1,a 2,…,a N ,输出A,B ,则 ( ) A.A+B 为a 1,a 2,…,a N 的和 B.2A B+为a 1,a 2,…,a N 的算术平均数 C.A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数 D.A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数 【测量目标】程序框图的算法流程. 【考查方式】直接考查程序框图的算法. 【参考答案】C【试题解析】:由题意得,根据给定的程序框图可知,此程序框图是计算123,,,,N a a a a 的最大值与最小值的算法框图,A 表示计算123,,,,N a a a a 最大值,B 表示计算123,,,,N a a a a 的最小值,故选C.7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为 ( ) A.6 B.9 C.12 D.18【测量目标】利用三视图求体积.【考查方式】通过观察三视图判断图形. 【参考答案】B【试题解析】由题意得,根据三视图的规则,原几何体表示底面为直角边长为直角三角形,高为3的三棱锥,所以几何体的体积为11139332V Sh ==⨯⨯=,故选B.8.平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为 ( ) A.6π B.43π C.46π D.63π【测量目标】球体体积的计算方法.【考查方式】通过平面截球求出球的半径和体积. 【参考答案】B【试题解析】:由题意得,连接球心与截面小圆的圆心1OO ,则1OO α⊥平面,则1OO = 根据球的性质得,球的半径R == 所以球的体积为3344ππ33V R ===,故B .9.已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin(ωx+φ)图像的两条相邻的对称轴,则φ=( )A.π4B.π3C.π2D.3π4【测量目标】三角函数的周期和图像.【考查方式】通过相邻对称轴的距离求出ω和ϕ. 【参考答案】A【试题解析】由题意得,直线π4x =和5π4x =是函数()f x 图象的两条相邻的对称轴, 则函数周期满足π2π12TT ω=⇒=⇒=,即函数()sin()f x x ϕ=+, 又ππππ()sin()1π,4442f k k ϕϕ=+=±⇒+=+∈Z ,即ππ,4k k ϕ=+∈Z ,当0k =时,π4ϕ=,故选A.10.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB |=43,则C 的实轴长为 ( ) A. 2 B.2 2 C.4 D.8 【测量目标】等轴双曲线的概念和抛物线的相关概念. 【考查方式】等轴双曲线与抛物线结合考查. 【参考答案】C【试题解析】:由题意得,设等轴双曲线的方程为22221x y a a-=抛物线216y x =的准线方程为4x =-,代入双曲线的方程得,所以=2a =4,所以选C 11.当0<x ≤12时,4x <log a x ,则a 的取值范围是 ( )A.(0,22) B.(22,1) C.(1,2) D.(2,2) 【测量目标】对数函数与指数函数的图像与性质.【考查方式】通过不等式比较大小求出范围. 【参考答案】B【试题解析】:由题意得,当01a <<时,要使得14log ,(0)2xa x x <<…,即当102x <…时,函数4xy =在函数log a y x =图象的下方,又当12x =时,1242=,即函数4xy =过点1(,2)2,把点1(,2)2代入函数log a y x =得2a =,即12a <<,当1a >时,不符合题意,舍去,所以实数a 的取值范围是12a <<,故选B. 12.数列{a n }满足a n +1+(-1)n a n =2n -1,则{a n }的前60项和为 ( ) A.3690 B.3660 C.1845 D.1830 【测量目标】数列的通项公式和求和公式. 【考查方式】给出数列的递推关系求和. 【参考答案】D【试题解析】:由题意得,由1(1)21n n n a a n ++-=-得21(1)21n n n a a n ++=-++=1(1)[(1)21]21n n n a n n ---+-++(1)(21)21n n a n n =-+--++即2(1)(21)21n n n a a n n ++=--++ 也有31(1)(21)23n n n a a n n +++=--+++两式相加得1232(1)44n n n n n a a a a n ++++++=--++设k 为整数,则41414243442(1)4(41)41610k k k k k a a a a k k ++++++++=--+++=+ 于是141460414243440()(1610)1830k k k k k k S aa a a k ++++===+++=+=∑∑第Ⅱ卷本卷包括必考题和选考题两部分.第13题-第21题为必考题,每个试题考生都必须作答,第22-24题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13.曲线y =x (3ln x +1)在点(1,1)处的切线方程为________. 【测量目标】导数的几何意义.【考查方式】通过点在曲线上求出斜率和直线. 【参考答案】43y x =-【试题解析】:由题意得,(3ln 1)3ln 3ln 4y x x x x x y x '=+=+⇒=+,所以1|4x y ='=, 由点斜式方程得14(1)y x -=-,整理得43y x =-.14.等比数列{a n }的前n 项和为S n ,若S 3+3S 2=0,则公比q =_______. 【测量目标】等比数列求和公式的简单运用. 【考查方式】通过等式直接考查. 【参考答案】-2【试题解析】:设等比数列的首项为1a ,公比为q ,由题意得,3230S S +=,则221(44)0440a q q q q ++=⇒++=,解得2q =-.15.已知向量a,b 夹角为45,且|a |=1,|2a -b |=10,则|b |= . 【测量目标】平面向量的数量积与向量的模. 【考查方式】通过给出向量的模和角度直接考查.【参考答案】:【试题解析】:由题意得,222224444cos 45-=-+=-+ a b a b b a b b ,则244cos 4510-+=⇒=a b b b16.设函数f (x )=(x +1)2+sin xx 2+1的最大值为M ,最小值为m ,则M+m=____.【测量目标】函数奇偶性的判断和性质. 【考查方式】利用奇偶性求函数最值. 【参考答案】2【试题解析】:由题意得,函数()22222(1)sin 21sin 2sin 1111x x x x x x xf x x x x ++++++===++++,设()22sin 1x x g x x +=+,则()()222()sin()2sin ()11x x x xg x g x x x -+-+-==-=--++, 所以函数()g x 为奇函数,(步骤1)设当x a =时,()g x 有最大值()g a ,则当x a =-时,()g x 有最小值()g a -, 又()()1f x g x =+,则当x a =时,()f x 有最大值()1g a +,则当x a =-时,()f x 有最小值()1g a -+, 即()1,()1M g a m g a =+=-+,所以2M m +=(步骤2)三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知,,a b c 分别为ABC △个内角三,,A B C 所对的边,sin cos c C c A =-. (1)求A ;(2)若2a =,ABC △b ,c .【测量目标】正弦定理的运用.【考查方式】通过给出三角函数关系式直接考查.【试题解析】(1)∵sin cos c C c A -,∴sin sin sin cos C A C C A =-,(步骤1) ∵0πC <<,∴sin 0C ≠,cos 1A A -=,∴1cos )12A A -=, ∴π1sin()62A -=,(步骤2)∵0πA <<,∴π3A =.(步骤3)(2)∵1sin 2S bc A ==4bc =.①(步骤4)∵222cos a b c bc A =+-,∴228b c +=,②由①②解得2b c ==.(步骤5)18.(本小题满分12分)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.(1)若花店一天购进17枝玫瑰花,求当天的利润y (单位:元)关于当天需求量n (单位:枝,n ∈N )的函数解析式.(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.【测量目标】独立事件的概率分布列和期望.【考查方式】通过对实际问题的考查去求概率相关知识.【试题解析】(1)当日需求量17n …时,利润85y =;(步骤1) 当日需求量17n <时,利润1085y n =-,(步骤2)∴y 关于n 的解析式为1085,17,()85,17,y n n n y n =-<⎧∈⎨= ⎩N ….(步骤3)(2)(i)这100天中有10天的日利润为55元,20天的日利润为65元,16天的日利润为75元,54天的日利润为85元, ∴这100天的平均利润为1(5510652075168554)76.4100⨯+⨯+⨯+⨯=.(步骤4)(ii)利润不低于75元,当且仅当日需求不少于16枝, 故当天的利润不少于75元的概率为0.160.160.150.130.10.7P =++++=.(步骤5) 19.(本小题满分12分)如图,三棱柱111ABC A B C -中,侧棱垂直底面,90ACB ∠=,112AC BC AA ==,D 是棱1AA 的中点.(1)证明:平面1BDC ⊥平面BDC ;(2)平面1BDC 分此棱柱为两部分,求这两部分体积的比.【测量目标】空间几何体内面面垂直的判定及体积公式.【考查方式】由线面垂直得到面面垂直,根据棱柱体积公式计算. . 【试题解析】(1)由题设知1BC CC ⊥,BC AC ⊥,1CC AC C = ,∴BC ⊥平面11ACC A , (步骤1) 又∵1DC ⊂平面11ACC A ,∴1DC BC ⊥,由题设知1145A DC ADC ∠=∠=,∴190CDC ∠= ,即1DC DC ⊥,(步骤2) 又∵BC DC C ⊥=, ∴1DC ⊥平面BDC , ∵1DC ⊂平面1BDC ,∴平面1BDC ⊥平面BDC .(步骤3) (2)设棱锥1B DACC -的体积为1V ,1AC =, 由题意得,1112111322V +=⨯⨯⨯=,(步骤4) 由三棱柱111ABC A B C -的体积1V =, ∴11():1:1V V V -=,∴平面1BDC 分此棱柱为两部分体积之比为1:1.(步骤5) 20.(本小题满分12分)设抛物物线C :22(0)x py p =>的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于,B D 两点.(1)若90BFD ∠=,ABD △的面积为p 的值及圆F 的方程;(2)若,,A B F 三点在同一条直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 距离的比值.【测量目标】抛物线与圆的标准方程及简单几何性质. 【考查方式】考查分类讨论的思想.【试题解析】设准线l 于y 轴的焦点为E ,圆F 的半径为r , 则FE p =,FA FB FD r ===,E 是BD 的中点, (1)∵90BFD ∠=,∴FA FB FD ===,2BD p =,(步骤1)点A 到直线l的距离d FA ==,∵ABD △的面积为∴11222ABD S BD d p ==⨯= △2) 解得2p =,∴(0,1)F , FA =,∴圆F 的方程为:22(1)8x y +-=.(步骤3) (2)∵,,A B F 三点在同一条直线m 上, ∴AB 是圆F 的直径,90ADB ∠=,由抛物线定义知12AD FA AB ==, ∴30ABD ∠=,∴m 的斜率为3或3-∴直线m 的方程为:2py x =+,(步骤4)∴原点到直线m 的距离14d p =,设直线n 的方程为:3y x b =±+,由22y x b x py⎧=+⎪⎨⎪=⎩,得220x px pb ±-=,(步骤5) ∵n 与C 只有一个公共点,∴24803p pb ∆=+=,∴6p b =-,∴直线n 的方程为:6py x =-,(步骤6) ∴原点到直线n 的距离2d p =,∴坐标原点到m ,n 距离的比值为3.(步骤7)21.(本小题满分12分)设函数()e 2xf x ax =--. (1)求()f x 的单调区间;(2)若1a =,k 为整数,且当0x >时,()()10x k f x x '-++>,求k 的最大值 【测量目标】利用导数求函数的单调区间及最值.【考查方式】直接考查单调区间及考查构造函数的思想.【试题解析】(1)()f x 的定义域为(,)-∞+∞,()e x f x a '=-,(步骤1) 若0a …时,则()0f x '>,∴()f x 在(,)-∞+∞上单调递增.(步骤2) 若0a >时,令()0f x '=,解得ln x a =,当(,ln )x a ∈-∞时,()0f x '<,当(ln ,)x a ∈+∞时,()0f x '>,∴()f x 在(,ln )a -∞上单调递减,在(ln ,)a +∞上单调递增.(步骤3) (2)若1a =,()()1()(e 1)1x x k f x x x k x '-++=--++∴当0x >时,()()10x k f x x '-++>等价于1(0)e 1xx k x x +<+>-.① 令1()(0)e 1x x g x x x +=+>-,22(e 1)(1)e e (e 2)()1(e 1)(e 1)xx x x x x x x g x --+--'=+=--, 由(1)知,()e 2x h x x =--在(0,)+∞上单调递增.(步骤4) ∵(1)0,(2)0h h <>,∴()h x 在(0,)+∞上存在唯一零点. ∴()g x '在(0,)+∞上存在唯一零点.(步骤5) 设其零点为a ,则(1,2)a ∈.当(0,)x a ∈时,()0g x '<,当(,)x a ∈+∞时,()0g x '>, ∴()g x 在(0,)+∞上的最小值为()g a ,(步骤6) ∵()0g a '=,∴e 2aa =+,∴()1(2,3)g a a =+∈. 由于①等价于()k g a <,∴整数k 的最大值为2.(步骤7)请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号.22.(本小题满分10分)选修4-1:几何证明选讲如图,D ,E 分别为△ABC 边AB ,AC 的中点,直线DE 交△ABC 的外接圆于F ,G 两点,若CF//AB ,证明:(Ⅰ)CD=BC ;(Ⅱ)△BCD ∽△GBD【测量目标】圆和相似三角形的概念和性质.【考查方式】通过性质和判定定理去求相关问题.【试题解析】(I )因为D,E 分别为AB,AC 的中点,所以DE //BC.又已知CF AB ,故四边形BCFD 是平行四边形,所以CF=BD=AD .而CF AD ,连接AF ,所以ADCF 是平行四边形,故CD=AF .(步骤1)因为CF AB ,所以BC=AF ,故CD=BC (步骤2)(II)因为FG BC ,故GB =CF .由(I )可知BD=CF ,所以GB=BD .而∠DGB=∠EFG=∠DBC,故△BCD ∽△GBD.23.(本小题满分10分)选修4—4;坐标系与参数方程已知曲线C 1的参数方程是2cos 3sin x y ϕϕ=⎧⎨=⎩ (φ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程是ρ=2.正方形ABCD 的顶点都在C 2上,且A 、B 、C 、D 以逆时针次序排列,点A 的极坐标为(2,π3) (Ⅰ)求点A 、B 、C 、D 的直角坐标;(Ⅱ)设P 为C 1上任意一点,求|PA| 2+ |PB|2 + |PC| 2+ |PD|2的取值范围.【测量目标】曲线参数方程与极坐标方程互化.【考查方式】通过给出方程进行互化.【试题解析】(I )由已知可得A (2cosπ3,2sin π3),B (2cos(ππ+32),2sin(ππ+32)), C (2cos(π+π3),2sin(π+π3)),D (2cos(π3π+32),2sin(π3π+32)), 即A (1B(C (1-,,D1-)(II)设P (2cos ϕ,3sin ϕ),令S =2222||||||||PA PB PC PD +++,则S =1622cos 36sin ϕϕ++16=32+202sin ϕ因为0…2sin ϕ…1,所以S 的取值范围是[32,52]24.(本小题满分10分)选修4—5:不等式选讲已知函数f (x ) = |x + a | + |x -2|.(Ⅰ)当a =-3时,求不等式f (x )≥3的解集;(Ⅱ)若f (x )≤|x -4|的解集包含[1,2],求a 的取值范围.【测量目标】含有绝对值的不等式的解集.【考查方式】给出等式进行化简变换.【试题解析】(I)当a =3-时,25,2()1,2325,3x x f x x x x -+⎧⎪=<⎨⎪-⎩……<当2x …时,由()3f x …得253x -+…,解得1x …;(步骤1) 当23x <<时,()3f x …无解;(步骤2)当3x …时,由()3f x …得25x -3…;解得4x …;所以()3f x …的解集为{|1}{|4}x x x x 剠(步骤3)(II)()|4|f x x -…|4|x ⇔-|2|x --||x a +…当[1,2]x ∈时,|4|x -|2|x --||x a +…⇔4(2)x x ---||x a +…⇔2a x --…2a -…(步骤4) 由条件得21a --…且22a -…,即30a -剟故满足条件的a 的取值范围为[3,0]-.(步骤5)。
2012年高考试题:文科数学(全国卷)——含答案及解析

2012年普通高等学校招生全国统一考试文科数学(必修+选修Ⅰ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
考试结束后,将本卷和答题卡一并交回。
第Ⅰ卷注意事项:1、答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2、每小题选出答案后,用2B 铅笔把答题卡上对应题目答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
3、第Ⅰ卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
一、选择题(1)已知集合{|}{|}{|}{|}A x xB x xC x xD x x ==是平行四边形,是矩形,是正方形,是菱形,则( ).()()()()A A B B C B C D C D A D⊆⊆⊆⊆【考点】集合【难度】容易【点评】本题考查集合之间的运算关系,即包含关系。
在高一数学强化提高班上学期课程讲座1,第一章《集合》中有详细讲解,在高考精品班数学(文)强化提高班中有对集合相关知识的总结讲解。
(2)函数1(1)y x x =+-≥的反函数为( ). 2()1(0)A yx x =-≥ 2()1(1)B yx x =-≥ 2()1(0)C yx x =+≥ 2()1(1)D yx x =+≥ 【考点】反函数【难度】容易【点评】本题考查反函数的求解方法,注意反函数的定义域即为原函数的值域。
在高一数学强化提高班上学期课程讲座1,第二章《函数与初等函数》中有详细讲解,在高考精品班数学(文)强化提高班中有对函数相关知识的总结讲解。
(3)若函数()s i n [0,2]3x fx ϕϕ+=∈(π)是偶函数,则ϕ=( ).()2A π 2()3B π 3()2C π 5()3D π 【考点】三角函数与偶函数的结合【难度】中等【点评】本题考查三角函数变换,及偶函数的性质。
2012年(全国卷II)(含答案)高考文科数学

2012年普通高等学校招生全国统一考试(2全国卷)数学(文)试题一、选择题 ( 本大题 共 12 题, 共计 60 分)1.已知集合A ={x |x 是平行四边形},B ={x |x 是矩形},C ={x |x 是正方形},D ={x |x 是菱形},则( )A .AB B .CB C .DC D .AD2.函数1y x =+x ≥-1)的反函数为( ) A .y =x 2-1(x ≥0) B .y =x 2-1(x ≥1) C .y =x 2+1(x ≥0) D .y =x 2+1(x ≥1) 3.若函数()sin 3x f x ϕ+=(φ∈[0,2π])是偶函数,则φ=( ) A .π2B .2π3C .3π2D .5π34.已知α为第二象限角,3sin 5α=,则sin2α=( ) A .2425-B .1225-C .1225D .2425 5.椭圆的中心在原点,焦距为4,一条准线为x =-4,则该椭圆的方程为( )A .2211612x y += B .221128x y += C .22184x y += D .221124x y += 6.已知数列{a n }的前n 项和为S n ,a 1=1,S n =2a n +1,则S n =( )A .2n -1B .13()2n -C .12()3n -D .112n -7. 6位选手依次演讲,其中选手甲不在第一个也不在最后一个演讲,则不同的演讲次序共有( )A .240种B .360种C .480种D .720种8.已知正四棱柱ABCD -A 1B 1C 1D 1中,AB =2,122CC =E 为CC 1的中点,则直线AC 1与平面BED 的距离为( )A.2 BC .2D.19.△ABC中,AB边的高为CD.若CB=a ,CA=b,a·b=0,|a|=1,|b|=2,则AD=()A.1133-a b B.2233-a bC.3355-a b D.4455-a b10.已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=()A.14B.35C.34D.4511.已知x=ln π,y=log52,12=ez-,则()A.x<y<z B.z<x<yC.z<y<x D.y<z<x12.正方形ABCD的边长为1,点E在边AB上,点F在边BC上,AE=BF=13.动点P从E出发沿直线向F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当点P第一次碰到E时,P与正方形的边碰撞的次数为() A.8 B.6 C.4 D.3二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.13.(x+12x)8的展开式中x2的系数为__________.14.若x,y满足约束条件10,30,330, x yx yx y-+≥⎧⎪+-≤⎨⎪+-≥⎩则z=3x-y的最小值为__________.15.当函数y=sin x x(0≤x<2π)取得最大值时,x=__________.16.已知正方体ABCD-A1B1C1D1中,E,F分别为BB1,CC1的中点,那么异面直线AE与D1F所成角的余弦值为__________.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.△ABC中,内角A,B,C成等差数列,其对边a,b,c满足2b2=3ac,求A.18.已知数列{a n}中,a1=1,前n项和23n nnS a+=.(1)求a2,a3;(2)求{a n}的通项公式.19.如图,四棱锥P-ABCD中,底面ABCD为菱形,P A⊥底面ABCD,AC=P A=2,E是PC上的一点,PE=2EC.(1)证明:PC⊥平面BED;(2)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小.20.乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.(1)求开始第4次发球时,甲、乙的比分为1比2的概率;(2) 求开始第5次发球时,甲得分领先的概率.21.已知函数f(x)=13x3+x2+ax.(1)讨论f(x)的单调性;(2)设f(x)有两个极值点x1,x2,若过两点(x1,f(x1)),(x2,f(x2))的直线l与x 轴的交点在曲线y=f(x)上,求a的值.22.已知抛物线C:y=(x+1)2与圆M:(x-1)2+(y-12)2=r2(r>0)有一个公共点A,且在A处两曲线的切线为同一直线l.(1)求r;(2)设m,n是异于l且与C及M都相切的两条直线,m,n的交点为D,求D到l的距离.2012年普通高等学校招生全国统一考试(2全国卷)数学(文)试题答案解析:1. B ∵正方形组成的集合是矩形组成集合的子集, ∴C B .2. A ∵1y x =+∴y 2=x +1, ∴x =y 2-1,x ,y 互换可得:y =x 2-1. 又∵10y x =+≥.∴反函数中x ≥0,故选A 项. 3.C ∵()sin3x f x ϕ+=是偶函数,∴f (0)=±1. ∴sin 13ϕ=±.∴ππ32k ϕ=+(k ∈Z).∴φ=3k π+3π2(k ∈Z). 又∵φ∈[0,2π],∴当k =0时,3π2ϕ=.故选C 项. 4.A ∵3sin 5α=,且α为第二象限角, ∴24cos 1sin 5αα=-=--.∴3424sin22sin cos 25525ααα⎛⎫==⨯⨯-=- ⎪⎝⎭.故选A 项. 5. C ∵焦距为4,即2c =4,∴c =2.又∵准线x =-4,∴24a c-=-.∴a 2=8.∴b 2=a 2-c 2=8-4=4.∴椭圆的方程为22184x y +=,故选C 项.6.B 当n =1时,S 1=2a 2,又因S 1=a 1=1,所以21 2a=,213 122S=+=.显然只有B项符合.7.C由题意可采用分步乘法计数原理,甲的排法种数为14A,剩余5人进行全排列:55A,故总的情况有:14A·55A=480种.故选C 项.8.D连结AC交BD于点O,连结OE,∵AB=2,∴AC=又1CC=AC=CC1.作CH⊥AC1于点H,交OE于点M.由OE为△ACC1的中位线知,CM⊥OE,M为C H的中点.由BD⊥AC,EC⊥BD知,BD⊥面EOC,∴CM⊥BD.∴CM⊥面BDE.∴HM为直线AC1到平面BDE的距离.又△AC C1为等腰直角三角形,∴CH=2.∴HM=1.9.D∵a·b=0,∴a⊥b.又∵|a|=1,|b|=2,∴||5AB=.∴||5CD==.∴2||25AD ==. ∴4544445()5555AD AB AB ===-=-a b a b .10. C 设|PF 2|=m ,则|PF 1|=2m , 由双曲线定义|PF 1|-|PF 2|=2a , ∴2m -m=.∴m 又24c ==, ∴由余弦定理可得cos ∠F 1PF 2=2221212||||432||||4PF PF c PF PF +-=.11. D ∵x =ln π>1,y =log 52>1log 2=,121e2z -==>=,且12e -<e 0=1,∴y <z <x . 12. B 如图,由题意:tan ∠BEF =12, ∴2112KX =,∴X 2为HD 中点,2312X D X D =,∴313X D =, 4312X C X C =,∴413X C =, 5412X H X H =,∴512X H =, 5612X A X A =,∴613X A =,∴X 6与E 重合,故选B 项. 13.答案:7 解析:∵(x +12x )8展开式的通项为T r +1=8C r x 8-r(12x)r =C r 82-r x 8-2r,令8-2r =2,解得r =3.∴x 2的系数为38C 2-3=7.14.答案:-1解析:由题意画出可行域,由z =3x -y 得y =3x -z ,要使z 取最小值,只需截距最大即可,故直线过A (0,1)时,z 最大.∴z max =3×0-1=-1. 15.答案:5π6解析:y =sin xx=1π2(sin )2sin()23x x x =-. 当y 取最大值时,ππ2π32x k -=+,∴x =2k π+5π6.又∵0≤x <2π,∴5π6x =. 16.答案:35解析:设正方体的棱长为a .连结A 1E ,可知D 1F ∥A 1E ,∴异面直线AE 与D 1F 所成的角可转化为AE 与A 1E 所成的角, 在△AEA 1中,2222213cos 5a a a a a AEA ⎛⎫⎛⎫+++- ⎪ ⎪∠==. 17.解:由A ,B ,C 成等差数列及A +B +C =180°,得B =60°,A +C =120°.由2b 2=3ac 及正弦定理得2sin 2B =3sin A sin C , 故1sin sin 2A C =.cos(A +C )=cos A cos C -sin A sin C =cos A cos C -12, 即cos A cos C -12=12-,cos A cos C =0, cos A =0或cos C =0,所以A =90°或A =30°.18.解:(1)由2243S a =得3(a 1+a 2)=4a 2,解得a 2=3a 1=3; 由3353S a =得3(a 1+a 2+a 3)=5a 3,解得a 3=32(a 1+a 2)=6. (2)由题设知a 1=1.当n >1时有a n =S n -S n -1=12133n n n n a a -++-, 整理得111n n n a a n -+=-. 于是a 1=1,a 2=31a 1,a 3=42a 2,… a n -1=2nn -a n -2,a n =11n n +-a n -1.将以上n 个等式两端分别相乘,整理得(1)2n n n a +=. 综上,{a n }的通项公式(1)2n n n a +=. 19.解法一:(1)证明:因为底面ABCD 为菱形,所以BD ⊥AC .又P A ⊥底面ABCD , 所以PC ⊥BD . 设AC ∩BD =F ,连结EF .因为AC =P A =2,PE =2EC ,故PC =3EC =,FC = 从而PC FC =,ACEC =, 因为PC ACFC EC=,∠FCE =∠PCA , 所以△FCE ∽△PCA ,∠FEC =∠P AC =90°, 由此知PC ⊥EF .PC 与平面BED 内两条相交直线BD ,EF 都垂直,所以PC ⊥平面BED .(2)在平面P AB 内过点A 作AG ⊥PB ,G 为垂足.因为二面角A -PB -C 为90°,所以平面P AB ⊥平面PBC . 又平面P AB ∩平面PBC =PB ,故AG ⊥平面PBC ,AG ⊥BC . BC 与平面P AB 内两条相交直线P A ,AG 都垂直, 故BC ⊥平面P AB ,于是BC ⊥AB ,所以底面ABCD 为正方形,AD =2,2222PD PA AD =+=. 设D 到平面PBC 的距离为d .因为AD ∥BC ,且AD 平面PBC ,BC 平面PBC ,故AD ∥平面PBC ,A ,D 两点到平面PBC 的距离相等,即d =AG 2.设PD 与平面PBC 所成的角为α,则1sin 2d PD α==. 所以PD 与平面PBC 所成的角为30°.解法二:(1)证明:以A 为坐标原点,射线AC 为x 轴的正半轴,建立如图所示的空间直角坐标系A -xyz .设C (220,0),D 2,b,0),其中b >0, 则P (0,0,2),E (23,0,23),B 2b,0). 于是PC =(220,-2),BE =(23,b ,23),DE =(23,-b ,23),从而0PC BE ⋅=,0PC DE ⋅=, 故PC ⊥BE ,PC ⊥DE .又BE ∩DE =E ,所以PC ⊥平面BDE .(2)AP =(0,0,2),AB =b,0). 设m =(x ,y ,z )为平面P AB 的法向量, 则m ·AP =0,m ·AB =0,即2z =0-by =0, 令x =b ,则m =(b,0).设n =(p ,q ,r )为平面PBC 的法向量,则n ·PC =0,n ·BE =0,即20r -=且2033bq r ++=,令p =1,则r =q b =-,n =(1,b-). 因为面P AB ⊥面PBC ,故m·n =0,即20b b-=,故b = 于是n =(1,-1),DP =(2),1cos ,2||||DP DP DP ⋅==n n n ,〈n ,DP 〉=60°. 因为PD 与平面PBC 所成角和〈n ,DP 〉互余,故PD 与平面PBC 所成的角为30°.20.解:记A i 表示事件:第1次和第2次这两次发球,甲共得i 分,i =0,1,2;B i 表示事件:第3次和第4次这两次发球,甲共得i 分,i =0,1,2; A 表示事件:第3次发球,甲得1分;B 表示事件:开始第4次发球时,甲、乙的比分为1比2;C 表示事件:开始第5次发球时,甲得分领先.(1)B =A 0·A +A 1·A , P (A )=0.4,P (A 0)=0.42=0.16,P (A 1)=2×0.6×0.4=0.48, P (B )=P (A 0·A +A 1·A )=P(A0·A)+P(A1·A)=P(A0)P(A)+P(A1)P(A)=0.16×0.4+0.48×(1-0.4)=0.352.(2) P(B0)=0.62=0.36,P(B1)=2×0.4×0.6=0.48,P(B2)=0.42=0.16,P(A2)=0.62=0.36.C=A1·B2+A2·B1+A2·B2P(C)=P(A1·B2+A2·B1+A2·B2)=P(A1·B2)+P(A2·B1)+P(A2·B2)=P(A1)P(B2)+P(A2)P(B1)+P(A2)P(B2)=0.48×0.16+0.36×0.48+0.36×0.16=0.307 2.21.解:(1)f′(x)=x2+2x+a=(x+1)2+a-1.①当a≥1时,f′(x)≥0,且仅当a=1,x=-1时,f′(x)=0,所以f(x)是R上的增函数;②当a<1时,f′(x)=0有两个根x1=-1x2=-1当x∈(-∞,-1时,f′(x)>0,f(x)是增函数;当x∈(-11时,f′(x)<0,f(x)是减函数;当x∈(-1∞)时,f′(x)>0,f(x)是增函数.(2)由题设知,x1,x2为方程f′(x)=0的两个根,故有a<1,x12=-2x1-a,x22=-2x2-a.因此f(x1)=13x13+x12+ax1=13x1(-2x1-a)+x12+ax1=13x12+23ax1=13(-2x1-a)+23ax1=23(a-1)x1-3a.同理,f(x2)=23(a-1)x2-3a.因此直线l 的方程为y =23(a -1)x -3a . 设l 与x 轴的交点为(x 0,0),得02(1)ax a =-, 22322031()[][](12176)32(1)2(1)2(1)24(1)a a a a f x a a a a a a =++=-+----. 由题设知,点(x 0,0)在曲线y =f (x )上,故f (x 0)=0, 解得a =0或23a =或34a =.22.解:(1)设A (x 0,(x 0+1)2),对y =(x +1)2求导得y ′=2(x +1), 故l 的斜率k =2(x 0+1).当x 0=1时,不合题意,所以x 0≠1. 圆心为M (1,12),MA 的斜率2001(1)21x k'x +-=-.由l ⊥MA 知k ·k ′=-1, 即2(x 0+1)·2001(1)21x x +--=-1,解得x 0=0,故A (0,1), r =|MA |=,即2r =. (2)设(t ,(t +1)2)为C 上一点,则在该点处的切线方程为y -(t +1)2=2(t +1)(x -t ),即y =2(t +1)x -t 2+1.若该直线与圆M 相切,则圆心M=化简得t 2(t 2-4t -6)=0,解得t 0=0,12t =22t =抛物线C 在点(t i ,(t i +1)2)(i =0,1,2)处的切线分别为l ,m ,n ,其方程分别为y =2x +1,①y =2(t 1+1)x -t 12+1,② y =2(t 2+1)x -t 22+1,③ ②-③得1222t t x +==. 将x =2代入②得y =-1,故D (2,-1). 所以D 到l的距离d ==.。
2012年新课标全国卷高考文科数学试题及答案

一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1、已知集合,,那么集合是()A.B.C.D.2、如图是某班50位学生期中考试数学成绩的频率分布直方图,其中成绩分组区间是:,,,,,,则图中的值等于()A. B.C. D.3、已知圆的极坐标方程是,那么该圆的直角坐标方程是()A.B.C.D.4、已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为()A.1B.2C.3D.45、阅读程序框图,运行相应的程序,当输入的值为时,输出的值为()A.B.C.D.6、已知,那么的值为()A.B.C.D.7、过抛物线焦点的直线交抛物线于,两点,若,则的中点到轴的距离等于()A.B.C.D.8、已知函数是定义在上的奇函数,且当时,(其中是的导函数),若,,,则,,的大小关系是()A.B.C.D.第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分.9、已知向量,,若,则 ________.10、若复数是纯虚数,则实数的值为________.11、各项均为正数的等比数列的前项和为,若,,则的值为________,的值为________.12、如图,为⊙的直径,切⊙于点,且过点的割线交的延长线于点,若,,则 ________,________.13、 5名志愿者到3个不同的地方参加义务植树,则每个地方至少有一名志愿者的方案共有________种.14、在数列中,若对任意的,都有(为常数),则称数列为比等差数列,称为比公差.现给出以下命题:①等比数列一定是比等差数列,等差数列不一定是比等差数列;②若数列满足,则数列是比等差数列,且比公差;③若数列满足,,(),则该数列不是比等差数列;④若是等差数列,是等比数列,则数列是比等差数列.其中所有真命题的序号是________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15、(本小题共13分)已知函数.⑴求的最小正周期;⑵当时,求的取值范围.16、(本小题共13分)某校高三年级同学进行体育测试,测试成绩分为优秀、良好、合格三个等级.测试结果如下表:(单位:人)优秀良好合格男女按优秀、良好、合格三个等级分层,从中抽取人,其中成绩为优的有人.⑴求的值;⑵若用分层抽样的方法,在合格的同学中按男女抽取一个容量为的样本,从中任选人,记为抽取女生的人数,求的分布列及数学期望.17、(本小题共14分)如图,是等边三角形,,,将沿折叠到的位置,使得.⑴求证:;⑵若,分别是,的中点,求二面角的余弦值.18、(本小题共14分)已知函数().⑴求的单调区间;⑵如果是曲线上的任意一点,若以为切点的切线的斜率恒成立,求实数的最小值;⑶讨论关于的方程的实根情况.19、(本小题共13分)已知椭圆:()的离心率,原点到过点,的直线的距离是.⑴求椭圆的方程;⑵若椭圆上一动点关于直线的对称点为,求的取值范围.⑶如果直线()交椭圆于不同的两点,,且,都在以为圆心的圆上,求的值.20、(本小题共13分)已知数列,,,,().⑴求,;⑵是否存在正整数,使得对任意的,有;⑶设,问是否为有理数,说明理由.北京市东城区2012-2013学年度第二学期高三综合练习(二)数学参考答案(理科)一、选择题(本大题共8小题,每小题5分,共40分)(1)B (2)C (3)A (4)D(5)D (6)B (7)D (8)C二、填空题(本大题共6小题,每小题5分,共30分)(9)(10)(11)(12)(13)(14)①③注:两个空的填空题第一个空填对得3分,第二个空填对得2分.三、解答题(本大题共6小题,共80分)(15)(共13分)解:(Ⅰ)因为.所以的最小正周期.(Ⅱ)因为,所以.所以的取值范围是.………………………………13分(16)(共13分)解:(Ⅰ)设该年级共人,由题意得,所以.则.(Ⅱ)依题意,所有取值为.,,.的分布列为:.………………………………………13分(17)(共14分)(Ⅰ)证明:因为所以,又因为,且,所以平面,因为平面,所以.(Ⅱ)因为△是等边三角形,,,不防设,则,又因为,分别为,的中点,由此以为原点,,,所在直线为坐标轴建立空间直角坐标系.则有,,,,,.所以,.设平面的法向量为.则即令,则.所以.又平面的一个法向量为.所以.所以二面角的余弦值为.………………………………14分(18)(共14分)解:(Ⅰ) ,定义域为,则.因为,由得,由得,所以的单调递增区间为,单调递减区间为.(Ⅱ)由题意,以为切点的切线的斜率满足,所以对恒成立.又当时,,所以的最小值为.(Ⅲ)由题意,方程化简得+令,则.当时,,当时,,所以在区间上单调递增,在区间上单调递减.所以在处取得极大值即最大值,最大值为.所以当,即时,的图象与轴恰有两个交点,方程有两个实根,当时,的图象与轴恰有一个交点,方程有一个实根,当时,的图象与轴无交点,方程无实根.……14分(19)(共13分)解: (Ⅰ)因为,,所以.因为原点到直线:的距离,解得,.故所求椭圆的方程为.(Ⅱ)因为点关于直线的对称点为,所以解得,.所以.因为点在椭圆 : 上,所以.因为,所以.所以的取值范围为.(Ⅲ)由题意消去,整理得.可知.设,,的中点是,则,.所以.所以.即.又因为,所以.所以.………………………………13分(20)(共13分)解:(Ⅰ);.(Ⅱ)假设存在正整数,使得对任意的,有.则存在无数个正整数,使得对任意的,有.设为其中最小的正整数.若为奇数,设(),则.与已知矛盾.若为偶数,设(),则,而从而.而,与为其中最小的正整数矛盾.综上,不存在正整数,使得对任意的,有.(Ⅲ)若为有理数,即为无限循环小数,则存在正整数,,对任意的,且,有.与(Ⅱ)同理,设为其中最小的正整数.若为奇数,设(),当时,有.与已知矛盾.若为偶数,设(),当时,有,而从而.而,与为其中最小的正整数矛盾.故不是有理数.……………………………………………………13分。
2012年全国高考文科数学试题及答案-新课标word版

绝密*启用前2012年普通高等学校招生全国统一考试(新课标卷)文科数学注息事项:1。
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2。
问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效。
3。
回答第Ⅱ卷时。
将答案写在答题卡上。
写在本试卷上无效·4。
考试结束后.将本试卷和答且卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
1、已知集合A={x|x2-x-2<0},B={x|-1〈x<1},则(A)A错误!B (B)B错误!A (C)A=B (D)A∩B=(2)复数z=错误!的共轭复数是(A)2+i (B)2-i (C)-1+i (D)-1-i3、在一组样本数据(x1,y1),(x2,y2),…,(x n,y n)(n≥2,x1,x2,…,x n不全相等)的散点图中,若所有样本点(x i,y i)(i=1,2,…,n)都在直线y=错误!x+1上,则这组样本数据的样本相关系数为(A)-1 (B)0 (C)错误!(D)1(4)设F1、F2是椭圆E:错误!+错误!=1(a〉b〉0)的左、右焦点,P为直线x=错误!上一点,△F1PF2是底角为30°的等腰三角形,则E的离心率为( )(A)错误!(B)错误!(C)错误!(D)错误!5、已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是(A)(1-错误!,2)(B)(0,2)(C)(错误!-1,2) (D)(0,1+错误!)(6)如果执行右边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,a N,输出A,B,则(A)A+B为a1,a2,…,a N的和(B)错误!为a1,a2,…,a N的算术平均数(C)A和B分别是a1,a2,…,a N中最大的数和最小的数(D)A和B分别是a1,a2,…,a N中最小的数和最大的数(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A)6(B)9(C)12(D)18(8)平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为错误!,则此球的体积为(A)错误!π(B)4错误!π(C)4错误!π(D)6错误!π(9)已知ω>0,0〈φ〈π,直线x=错误!和x=错误!是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=(A)错误!(B)错误!(C)错误!(D)错误!(10)等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,|AB|=4错误!,则C的实轴长为(A)错误!(B)2错误!(C)4 (D)8(11)当0〈x≤错误!时,4x〈log a x,则a的取值范围是(A)(0,错误!)(B)(错误!,1) (C)(1,错误!)(D)(错误!,2)(12)数列{a n}满足a n+1+(-1)n a n=2n-1,则{a n}的前60项和为(A)3690 (B)3660 (C)1845 (D)1830第Ⅱ卷本卷包括必考题和选考题两部分。
2012年高考新课标全国卷文科数学试题(附答案)

2012年普通高等学校招生全国统一考试(新课标全国卷)文科数学试题一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合A={x |x 2−x −2<0},B={x |−1<x <1},则(A )A ⊂≠B (B )B ⊂≠A (C )A=B (D )A ∩B=∅ (2)复数z =32ii-++的共轭复数是 (A )2i + (B )2i - (C )1i -+ (D )1i --(3)在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线112y x =+上,则这组样本数据的样本相关系数为(A )−1 (B )0 (C )12(D )1(4)设1F ,2F 是椭圆E :2222x y a b+=1(a >b >0)的左、 右焦点,P 为直线32ax =上一点,△21F PF 是底角为030的等腰三角形,则E 的离心率为 (A )12 (B )23 (C )34 D .45(5)已知正三角形ABC 的顶点A (1,1),B (1,3),顶点C 在第一象限,若点(x ,y )在△ABC内部,则z x y =-+的取值范围是(A )(1-3,2) (B )(0,2) (C )(3-1,2) (D )(0,1+3) (6)如果执行右边的程序框图,输入正整数N (N ≥2)和实数1a ,2a ,…,N a ,输出A ,B ,则 (A )A +B 为1a ,2a ,…,N a 的和 (B )2A B+为1a ,2a ,…,N a 的算术平均数 (C )A 和B 分别为1a ,2a ,…,N a 中的最大数和最小数(D )A 和B 分别为1a ,2a ,…,N a 中的最小数和最大数 (7)如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为 (A )6 (B )9 (C )12 (D )18(8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为(A )6π (B )43π (C )46π (D )63π (9)已知ω>0,0ϕπ<<,直线x =4π和x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=(A )π4 (B )π3 (C )π2 (D )3π4(10)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于A 、B 两点,||AB =43,则C 的实轴长为(A )2 (B )22 (C )4 (D )8 (11)当0<x ≤12时,4log xa x <,则a 的取值范围是(A )(0,22) (B )(22,1) (C )(1,2) (D )(2,2) (12)数列{n a }满足1(1)21nn n a a n ++-=-,则{n a }的前60项和为(A )3690 (B )3660 (C )1845 (D )1830二.填空题:本大题共4小题,每小题5分。
2012年高考新课标全国卷文科数学试题附答案
学习资料收集于网络,仅供参考 2012年普通高等学校招生全国统一考试(新课标全国卷)文科数学试题分,在每小题给同的四个选项中,只有一项是符一、选择题:本大题共12小题,每小题5 合题目要求的。
2 |?1<x<1},则?x?2<0},B={xx|A={(1)已知集合x??∩B=?(D)A (C)A=B (A)AA B (B)B??i?3?=的共轭复数是(2)复数z i2?i1???i1?i?2?i2 C ())(D(A)(B)不全相等)的,xx,x,…,…,(x,y)(n≥2,,(3)在一组样本数据(x,y),(xy)n121nn12211y??x 上,则这组样本)(i=1,2,…,n)都在直线,散点图中,若所有样本点(xy ii2数据的样本相关系数为11)(D )0 (C)B?(A)1 (222yxa b?FFE是椭圆>:0=1((4)设)的,>2122baa3PFF?x P上一点,△为直线左、右焦点,122030E的离心率为的等腰三角形,则是底角为4231D.(B)C(A))(5423ABC在第一象限,若点(x,y)在△)已知正三角形ABC的顶点A(1,1),B(1,3),顶点C(5y??x?z内部,则的取值范围是3) (0,1+ (D)(C)(3-1,2) 2) B (1(A),-32) ()(0,NN和实2)≥(6)如果执行右边的程序框图,输入正整数(aaaBA,输出,数,,则,…,N12aaa BA+的和为,,…,(A)N12BA?aaa,…,B(),的算术平均数为N122aaa BA中的最大数,…,)(C和分别为,N12和最小数学习资料.学习资料收集于网络,仅供参考aaaBA,(D)中的最小数和最大数和,…,分别为N12,粗线画出的是)如图,网格上小正方形的边长为1(7某几何体的三视图,则此几何体的体积为(A)6B)9 ()12 (C18(D)??,则此球的体积2到平面(8)平面的距离为截球O的球面所得圆的半径为1,球心O 为(D)π6C()346π(A()6πB)43π??5?????xx)x?f(?x?)?sin(0图像的两条=是函数,直线9)已知和>0,=(44?=相邻的对称轴,则3ππππ(D))(C A()(B)44322x CC x16y?A、的中心在原点,焦点在轴上,的准线交于与抛物线(10)等轴双曲线C34|AB|B两点,=,则的实轴长为2228 D))((C)4 (A)(B1x xxlog4?,则a的取值范围是(11)当0<时,≤2a222) ,)( (D1) ,(C)2(1(A)(0,,) (B)2) (22n aa1n??1)a?2a?(项和为的前,则{60}(12)数列{}满足nnn1n?1830 D)()(C1845 (A)3690 (B)36605分。
2012年高考新课标全国卷文科数学试题附答案

2012年一般高等学校招生全国统一考试(新课标全国卷)文科数学试题一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合A={x |x 2−x −2<0},B={x |−1<x <1},则(A )A ̹B (B )B ̹A (C )A=B (D )A ∩B=Æ(2)复数z =32ii-++的共轭复数是 (A )2i + (B )2i - (C )1i -+ (D )1i -- (3)在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若全部样本点(x i ,y i )(i =1,2,…,n )都在直线112y x =+上,则这组样本数据的样本相关系数为(A )−1 (B )0 (C )12(D )1(4)设1F ,2F 是椭圆E :2222x y a b+=1(a >b >0)的左、 右焦点,P 为直线32ax =上一点,△21F PF 是底角为030的等腰三角形,则E 的离心率为 (A )12(B )23(C )34D .45(5)已知正三角形ABC 的顶点A (1,1),B (1,3),顶点C 在第一象限,若点(x ,y )在△ABC 内部,则z x y =-+的取值范围是 (A )(1-3,2) (B )(0,2) (C )(3-1,2) (D )(0,1+3)(6)假如执行右边的程序框图,输入正整数N (N ≥2)与实数1a ,2a ,…,N a ,输出A ,B ,则(A )A +B 为1a ,2a ,…,N a 的与 (B )2A B+为1a ,2a ,…,N a 的算术平均数(C )A 与B 分别为1a ,2a ,…,N a 中的最大数与最小数(D )A 与B 分别为1a ,2a ,…,N a 中的最小数与最大数(7)如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为 (A )6 (B )9 (C )12 (D )18(8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的间隔为2,则此球的体积为(A )6π (B )43π (C )46π (D )63π(9)已知ω>0,0ϕπ<<,直线x =4π与x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=(A )π4 (B )π3 (C )π2 (D )3π4(10)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x=的准线交于A 、B 两点,||AB =C 的实轴长为 (A(B ) (C )4 (D )8 (11)当0<x ≤12时,4log x a x <,则a 的取值范围是(A )(0,22) (B )(22,1) (C )(1,2) (D )(2,2)(12)数列{n a }满意1(1)21n n n a a n ++-=-,则{n a }的前60项与为 (A )3690 (B )3660 (C )1845 (D )1830二.填空题:本大题共4小题,每小题5分。
2012年全国高考文科数学试题及答案-新课标word版

绝密 * 启用前2012 年普通高等学校招生全国统一考试(新课标卷)文科数学注息事项 :1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题 )两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动 .用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效.3.回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效·4.考试结束后 .将本试卷和答且卡一并交回。
第Ⅰ卷一、选择题:本大题共 12 小题,每小题 5 分,在每小题给同的四个选项中,只有一项是符合题目要求的。
1、已知集合 A={x| x 2- x - 2<0}, B={x| -1<x<1},则( A )A B(B )B A(C )A=B(D )A ∩B=- 3+i ( 2)复数z =的共轭复数是 2+i( A ) 2+i( B )2- i( C )- 1+i( D )- 1- i3、在一组样本数据( x 1 ,y 1 ),(x 2 ,y 2 ),⋯,( x n ,y n )( n ≥ 2,x 1,x 2, ⋯ ,x n 不全相等)的散点图中,若所有样本点( x i , y i ) (i=1,2, ⋯ , n) 都在直线 1y= x+1 上,则这组样本数据的样本相关系数为2(A )- 1(B )0(C )1( D )12223a上一点,△ F( 4)设 F 、 F 是椭圆 E :x2y 2是底角12a +b= 1(a>b>0)的左、右焦点, P 为直线 x= 2 1PF 2为 30°的等腰三角形,则 E 的离心率为()( A )12342 (B )3 ( C )4 (D ) 55、已知正三角形 ABC 的顶点 A(1,1),B(1,3),顶点 C 在第一象限,若点( x ,y )在△ ABC 内部,则z=-x+y 的取值范围是 ( A )(1- 3, 2)( B ) (0, 2) ( C )( 3-1,2) ( D ) (0, 1+ 3)( 6)如果执行右边的程序框图,输入正整数 N(N ≥2)和实数 a 1,a 2,⋯,a N ,输出 A,B ,则( A )A+B 为 a 1,a 2,⋯,a N 的和 ( B )A + B为 a 1,a 2,⋯ ,a N 的算术平均数2( C )A 和 B 分别是 a 1,a 2,⋯ ,a N 中最大的数和最小的数( D ) A 和 B 分别是 a 1,a 2,⋯ ,a N 中最小的数和最大的数开始输入 N ,a 1,a 2,⋯,a Nk=1,A=a 1,B=a 1x =a kk=k+1是x > A否A=x是x<B否B=x否k ≥ N是输出 A ,B结束( 7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积 为 ( A )6 ( B )9 ( C )12( D ) 18(8)平面 α 截球 O 的球面所得圆的半径为 1,球心 O 到平面 α的距离为 2,则此球的体积为( A ) 6π ( B ) 4 3π (C ) 4 6π (D ) 6 3ππ 5π( 9)已知 ω>0, 0<φ<π,直线 x= 和 x=是函数 f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=44( A )πππ3π4(B ) 3(C ) 2(D ) 4( 10)等轴双曲线 C 的中心在原点,焦点在 x 轴上, C 与抛物线 y 2=16x 的准线交于 A ,B 两点,|AB|=4 3,则 C 的实轴长为(A ) 2(B )2 2(C )4(D )8(11)当 0<x ≤1时, 4x <log a x ,则 a 的取值范围是2( A )(0, 22,1) (C ) (1, 2) (D )( 2, 2) 2 ) (B )( 2( 12)数列 {a n }满足 a n+1 + (- 1)n a n = 2n - 1,则 {a n }的前 60 项和为 ( A )3690( B ) 3660( C )1845( D )1830第Ⅱ卷本卷包括必考题和选考题两部分。
2012年全国新课标高考文科数学真题及答案(Word版)

绝密*启用前2012年普通高等学校招生全国统一考试 文科数学 注息事项:1. 本试卷分第I 卷(选择题)和第n 卷 号填写在本试卷和答题卡相应位置上。
2. 问答第I 卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动 擦干净后,再选涂其它答案标号。
写在本试卷上无效3.回答第n 卷时。
将答案写在答题卡上 .写在本试卷上无效•4. 考试结束后.将本试卷和答且卡一并交回。
1y i ) (i=1,2,…,n)都在直线y=2x+1上,则这组样本数据的样本相关系数为x 2 y 2 3aF 2是椭圆E :耸+ y^= 1(a>b>0)的左、右焦点,P 为直线x=3a 上一点,△ F 1PF 2是底角为30°a b 2 的等腰三角形,则 E 的离心率为()(A) 1 ( B ) 2 (C ) 4( D ) 4 5、已知正三角形 ABC 的顶点A(1,1),B(1,3),顶点C 在第一象限,若点(x ,丫)在厶ABC 内部,贝U z= —x+y 的取值范围是 (A ) (1 — 3, 2) ( B ) (0, 2)( C ) ( 3— 1, 2)( D ) (0,1+ 3)(6)如果执行右边的程序框图,输入正整数 N(N >2)和实数a 1,a 2,…,a N ,输出A,B ,则(A)A+B 为 a 1,a 2,…,a N 的和 A + B(B)—2 —为a1,a 2,…,a N 的算术平均数(A )— 1(B) 0 (D) 1(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证.用橡皮 、选择题: 本大题共 12小题, 每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
1、已知集合 A={ x|x 2— x — 2<0}, B={ x|— 1<x<1},(A) A B(B ) B A (C ) A=B(D ) A n B=(2)复数 z =—的共轭复数是2+i(A) 2+i( B ) 2 — i(C )— 1+i (D )— 1— i3、在一组样本数据(X 1, y 1), (x 2, y 2),…,(x n .y n ) ( n > 2, X 1,x 2,…,X n 不全相等)的散点图中,若所有样本点(X i ,(4)设 F 1、(C) A和B分别是a i,a2,…,a N中最大的数和最小的数(D) A和B分别是a i,a2,…,a N中最小的数和最大的数(7) 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A) 6(B) 9(C) 12(D)18(8) 平面a截球0的球面所得圆的半径为1球心O到平面a的距离为,2,则此球的体积为(A) 6n ( B) 4 3n (C) 4 6n (D) 6 3n(9) 已知3>0, 0< o <n直线x=4和x=5^函数f(x)=sin( ®x+妨图像的两条相邻的对称轴,贝Un n n 3 n(A ) 4 (B) 3 ( C) 2 ( D) G(10) 等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=l6x的准线交于A , B两点, 则C的实轴长为(A ) 2 (B) 2 2 (C) 4 ( D) 8(11) 当0<x< 2时,4x<|og a x,贝y a的取值范围是(A ) (0,子) (B)(今,1) (C) (1 , 2) ( D) (.2, 2)(12) 数列{a n}满足a n+1 + (- 1)n a n = 2n- 1,则{a n}的前60项和为(A) 3690 ( B) 3660 (C) 1845 ( D) 1830本卷包括必考题和选考题两部分。
2012年普通高等学校招生全国统一考试 数学试卷含答案(文科)

2012年普通高等学校招生全国统一考试(课标全国卷)文数本卷满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={x|x2-x-2<0},B={x|-1<x<1},则( )A.A⫋BB.B⫋AC.A=BD.A∩B=⌀2.复数z=-的共轭复数是( )A.2+iB.2-IC.-1+iD.-1-i3.在一组样本数据(x1,y1),(x2,y2),…,(x n,y n)(n≥2,x1,x2,…,x n不全相等)的散点图中,若所有样本点(x i,y i)(i=1,2,…,n)都在直线y=x+1上,则这组样本数据的样本相关系数为( )A.-1B.0C.D.14.设F1、F2是椭圆E:+=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )A. B. C. D.5.已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是( )A.(1-,2)B.(0,2)C.(-1,2)D.(0,1+)6.如果执行如图的程序框图,输入正整数N(N≥2)和实数a1,a2,…,a N,输出A,B,则( )A.A+B为a1,a2,…,a N的和B.为a1,a2,…,a N的算术平均数C.A和B分别是a1,a2,…,a N中最大的数和最小的数D.A和B分别是a1,a2,…,a N中最小的数和最大的数7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A.6B.9C.12D.188.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )A. B.4 C.4 D.69.已知ω>0,0<φ<π,直线x=和x=是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则φ=( )A. B. C. D.10.等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,|AB|=4,则C的实轴长为( )A. B.2 C.4 D.811.当0<x≤时,4x<log a x,则a的取值范围是( )A.,B.,C.(1,D.(,2)12.数列{a n}满足a n+1+(-1)n a n=2n-1,则{a n}的前60项和为( )A.3 690B.3 660C.1 845D.1 830第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.曲线y=x(3ln x+1)在点(1,1)处的切线方程为.14.等比数列{a n}的前n项和为S n,若S3+3S2=0,则公比q= .15.已知向量a,b夹角为45°,且|a|=1,|2a-b|=,则|b|= .16.设函数f(x)=()的最大值为M,最小值为m,则M+m= .三、解答题(解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)已知a,b,c分别为△ABC三个内角A,B,C的对边,c=(Ⅰ)求A;(Ⅱ)若a=2,△ABC的面积为,求b,c.18.(本小题满分12分)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数; (ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.19.(本小题满分12分)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点. (Ⅰ)证明:平面BDC1⊥平面BDC;(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比.20.(本小题满分12分)设抛物线C:x2=2py(p>0)的焦点为F,准线为l.A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.(Ⅰ)若∠BFD=90°,△ABD的面积为4,求p的值及圆F的方程;(Ⅱ)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.21.(本小题满分12分)设函数f(x)=e x-ax-2.(Ⅰ)求f(x)的单调区间;(Ⅱ)若a=1,k为整数,且当x>0时,(x-k)f '(x)+x+1>0,求k的最大值.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.22.(本小题满分10分)选修4—1:几何证明选讲如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点.若CF∥AB,证明:(Ⅰ)CD=BC;(Ⅱ)△BCD∽△GBD.23.(本小题满分10分)选修4—4:坐标系与参数方程已知曲线C1的参数方程是,(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为,.(Ⅰ)求点A,B,C,D的直角坐标;(Ⅱ)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.24.(本小题满分10分)选修4—5:不等式选讲已知函数f(x)=|x+a|+|x-2|.(Ⅰ)当a=-3时,求不等式f(x)≥3的解集;(Ⅱ)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.2012年普通高等学校招生全国统一考试(课标全国卷)一、选择题1.B A={x|-1<x<2},B={x|-1<x<1},则B⫋A,故选B.评析本题考查了集合的关系以及二次不等式的解法.=-=-1+i,=-1-i,故选D.2.D z=-=(-)(-)()(-)评析本题考查了复数的运算,易忽略共轭复数而错选.3.D 所有点均在直线上,则样本相关系数最大即为1,故选D.评析本题考查了线性回归,掌握线性回归系数的含义是解题关键,本题易错选C.4.C 设直线x=a与x轴交于点Q,由题意得∠PF2Q=60°,|F2P|=|F1F2|=2c,|F2Q|=a-c,∴a-c=×2c,e==,故选C.评析本题考查了椭圆的基本性质,考查了方程的思想,灵活解三角形对求解至关重要. 5.A 由题意知区域为△ABC(不含边界).当直线-x+y-z=0过点C(1+,2)时,z min=1-;当过点B(1,3)时,z max=2.故选A.评析本题考查了简单的线性规划,考查了数形结合的思想.正确理解直线的斜率、截距的几何意义是求解的关键.6.C 不妨令N=3,a1<a2<a3,则有k=1,A=a1,B=a1;x=a2,A=a2;x=a3,A=a3,故输出A=a3,B=a1,选C. 评析本题考查了流程图,考查了由一般到特殊的转化思想.7.B 由三视图可得,该几何体为三棱锥S-ABC,其中底面△ABC为等腰三角形,底边AC=6,AC 边上的高为3,SB⊥底面ABC,且SB=3,所以该几何体的体积V=××6×3×3=9.故选B.评析本题考查了三视图和三棱锥的体积,考查了空间想象能力.由三视图正确得到该几何体的直观图是求解的关键.8.B 如图,设平面α截球O所得圆的圆心为O1,则|OO1|=,|O1A|=1,∴球的半径R=|OA|==.∴球的体积V=πR3=4π.故选B.评析本题考查了球的基础知识,利用勾股定理求球的半径是关键.9.A 由题意得=2-,∴ω=1,∴f(x)=sin(x+φ),则+φ=kπ+(k∈Z),φ=kπ+(k∈Z),又0<φ<π,∴φ=,故选A.评析本题考查了三角函数的图象和性质,掌握相邻对称轴的距离为周期的一半是关键.10.C 由题意可得A(-4,2).∵点A在双曲线x2-y2=a2上,∴16-12=a2,a=2,∴双曲线的实轴长2a=4.故选C.评析本题考查了双曲线和抛物线的基础知识,考查了方程的数学思想,要注意双曲线的实轴长为2a.11.B 易知0<a<1,则函数y=4x与y=log a x的大致图象如图,则只需满足log a>2,解得a>,故选B.评析本题考查了利用数形结合解指数、对数不等式.12.D 当n=2k时,a2k+1+a2k=4k-1,当n=2k-1时,a2k-a2k-1=4k-3,∴a2k+1+a2k-1=2,∴a2k+1+a2k+3=2,∴a2k-1=a2k+3,∴a1=a5=…=a61.∴a1+a2+a3+…+a60=(a2+a3)+(a4+a5)+…+(a60+a61)=3+7+11+…+(2×60-1)=()=30×61=1 830.评析本题考查了数列求和及其综合应用,考查了分类讨论及等价转化的数学思想.二、填空题13.答案y=4x-3解析y'=3ln x+1+x·=3ln x+4,k=y'|x=1=4,切线方程为y-1=4(x-1),即y=4x-3.评析本题考查了导数的几何意义,考查了运算求解能力.14.答案-2解析由S 3+3S2=0得4a1+4a2+a3=0,有4+4q+q2=0,解得q=-2.评析本题考查了等比数列的运算,直接利用定义求解可达到事半功倍的效果.15.答案3解析把|2a-b|=两边平方得4|a|2-4|a|·|b|·cos 45°+|b|2=10.∵|a|=1,∴|b|2-2|b|-6=0.∴|b|=3或|b|=-(舍去).评析本题考查了向量的基本运算,考查了方程的思想.通过“平方”把向量问题转化为数量问题是求解的关键.16.答案 2解析f(x)==1+,令g(x)=,则g(x)为奇函数,有g(x)max+g(x)min=0,故M+m=2.评析本题考查了函数性质的应用,运用了奇函数的值域关于原点对称的特征,考查了转化与化归的思想方法.三、解答题17.解析(Ⅰ)由c=asin C-c·cos A及正弦定理得·sin A·sin C-cos A·sin C-sin C=0.由于sin C≠0,所以sin-=.又0<A<π,故A=.(Ⅱ)△ABC的面积S=bcsin A=,故bc=4.而a2=b2+c2-2bccos A,故b2+c2=8.解得b=c=2.评析本题考查了正、余弦定理和三角公式,考查了方程的思想,灵活利用正、余弦定理是求解关键,正确的转化是本题的难点.18.解析(Ⅰ)当日需求量n≥17时,利润y=85.当日需求量n<17时,利润y=10n-85.所以y关于n的函数解析式为y=-,,,(n∈N).(Ⅱ)(i)这100天中有10天的日利润为55元,20天的日利润为65元,16天的日利润为75元,54天的日利润为85元,所以这100天的日利润的平均数为(55×10+65×20+75×16+85×54)=76.4.(ii)利润不低于75元当且仅当日需求量不少于16枝.故当天的利润不少于75元的概率为P=0.16+0.16+0.15+0.13+0.1=0.7.评析本题考查概率统计,考查运用样本频率估计总体概率及运算求解能力.19.解析(Ⅰ)证明:由题设知BC⊥CC 1,BC⊥AC,CC1∩AC=C,所以BC⊥平面ACC1A1.又DC1⊂平面ACC1A1,所以DC1⊥BC.由题设知∠A1DC1=∠ADC=45°,所以∠CDC1=90°,即DC1⊥DC.又DC∩BC=C,所以DC1⊥平面BDC.又DC1⊂平面BDC1,故平面BDC1⊥平面BDC.(Ⅱ)设棱锥B-DACC1的体积为V1,AC=1.由题意得V1=××1×1=.又三棱柱ABC-A1B1C1的体积V=1,所以(V-V1)∶V1=1∶1.故平面BDC1分此棱柱所得两部分体积的比为1∶1.评析本题考查了线面垂直的判定,考查了体积问题,同时考查了空间想象能力,属中档难度.20.解析(Ⅰ)由已知可得△BFD为等腰直角三角形,|BD|=2p,圆F的半径|FA|=p.由抛物线定义可知A到l的距离d=|FA|=p.因为△ABD的面积为4所以|BD|·d=4即·2p·p=4解得p=-2(舍去),p=2.所以F(0,1),圆F的方程为x2+(y-1)2=8.(Ⅱ)因为A,B,F三点在同一直线m上,所以AB为圆F的直径,∠ADB=90°.由抛物线定义知|AD|=|FA|=|AB|,所以∠ABD=30°,m的斜率为或-.当m的斜率为时,由已知可设n:y=x+b,代入x2=2py得x2-px-2pb=0.由于n与C只有一个公共点,故Δ=p2+8pb=0.解得b=-.因为m的截距b1=,||||=3,所以坐标原点到m,n距离的比值为3.当m的斜率为-时,由图形对称性可知,坐标原点到m,n距离的比值为3.评析本题考查了直线、圆、抛物线的位置关系,考查了分类讨论的方法和数形结合的思想.21.解析(Ⅰ)f(x)的定义域为(-∞,+∞), f '(x)=e x-a.若a≤0,则f '(x)>0,所以f(x)在(-∞,+∞)上单调递增.若a>0,则当x∈(-∞,ln a)时, f '(x)<0;当x∈(ln a,+∞)时, f '(x)>0,所以, f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.(Ⅱ)由于a=1,所以(x-k)f '(x)+x+1=(x-k)(e x-1)+x+1.故当x>0时,(x-k)f '(x)+x+1>0等价于k<-+x(x>0).①令g(x)=-+x,则g'(x)=--(-)+1=(--)(-).由(Ⅰ)知,函数h(x)=e x-x-2在(0,+∞)上单调递增.而h(1)<0,h(2)>0,所以h(x)在(0,+∞)上存在唯一的零点.故g'(x)在(0,+∞)上存在唯一的零点.设此零点为α,则α∈(1,2).当x∈(0,α)时,g'(x)<0;当x∈(α,+∞)时,g'(x)>0.所以g(x)在(0,+∞)上的最小值为g(α).又由g'(α)=0,可得eα=α+2,所以g(α)=α+1∈(2,3).由于①式等价于k<g(α),故整数k的最大值为2.评析本题考查了函数与导数的综合应用,判断出导数的零点范围是求解第(Ⅱ)问的关键.22.证明(Ⅰ)因为D,E分别为AB,AC的中点,所以DE∥BC.又已知CF∥AB,故四边形BCFD是平行四边形,所以CF=BD=AD.而CF∥AD,连结AF,所以四边形ADCF是平行四边形,故CD=AF.因为CF∥AB,所以BC=AF,故CD=BC.(Ⅱ)因为FG∥BC,故GB=CF.由(Ⅰ)可知BD=CF,所以GB=BD.而∠DGB=∠EFC=∠DBC,故△BCD∽△GBD.评析本题考查了直线和圆的位置关系,处理好平行的关系是关键.23.解析(Ⅰ)由已知可得A ,,B2cos+,2sin+,C2cos+π,2sin+π,D2cos+,2sin+,即A(1,),B(-,1),C(-1,-),D(,-1).(Ⅱ)设P(2cos φ,3sin φ),令S=|PA|2+|PB|2+|PC|2+|PD|2,则S=16cos2φ+36sin2φ+16=32+20sin2φ.因为0≤sin2φ≤1,所以S的取值范围是[32,52].评析本题考查了曲线的参数方程和极坐标方程.考查了函数的思想方法,正确“互化”是关键,难点是建立函数S=f(φ).24.解析(Ⅰ)当a=-3时,f(x)=-,, ,,-,.当x≤2时,由f(x)≥3得-2x+5≥3,解得x≤1;当2<x<3时, f(x)≥3无解;当x≥3时,由f(x)≥3得2x-5≥3,解得x≥4.所以f(x)≥3的解集为{x|x≤1或x≥4}.(Ⅱ)f(x)≤|x-4|⇔|x-4|-|x-2|≥|x+a|.当x∈[1,2]时,|x-4|-|x-2|≥|x+a|⇔4-x-(2-x)≥|x+a|⇔-2-a≤x≤2-a.由条件得-2-a≤1且2-a≥2,即-3≤a≤0.故满足条件的a的取值范围为[-3,0].评析本题考查了含绝对值不等式的解法,运用零点法分类讨论解含绝对值的不等式,考查了运算求解能力.。
2012年文数高考试题答案及解析-全国

2012 年一般高等学校招生全国一致考试文科数学(必修 +选修Ⅱ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第第 3 至第 4 页。
考试结束,务势必试卷和答题卡一并上交。
1 至2 页,第Ⅱ卷第Ⅰ卷注意事项:全卷满分150 分,考试时间120 分钟。
考生注意事项:1.答题前,考生在答题卡上务必用直径0.5 毫米黑色墨水署名笔将自己的姓名、准考据填写清楚,并贴好条形码。
请仔细批准该条形码上的准考据、姓名和科目。
2.没小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标涂黑,如需变动,用橡皮擦洁净后,再选涂其余答案标。
在试题卷上作答无效。
.........3.第 I 卷共 12 小题,每题 5 分,共 60 分。
在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
一、选择题( 1 )已知会合 A { x | x是平行四边形}, B{ x | x是矩形} , C{ x | x是正方形},D { x | x 是菱形 } ,则(A)A B(B)C B(C)D C(D)A D【分析】依据四边形的定义和分类可知选 B.【答案】 B( 2)函数y x 1( x1) 的反函数为( A )y x21( x0)(B)y x21( x 1)( C)y x21( x0)( D)y x21( x 1)【分析】由于 x1因此y x10 .由 y x 1 得, x 1 y2,因此 x y 2 1 ,因此反函数为y x 21(x0) ,选A.【答案】 B( 3)若函数f ()sinx([0,2])是偶函数,则x3( A )235( B)(C)( D)2x3x2x3【分析】函数 f (x)) ,由于函数 f ( x)) 为偶函数,因此sin sin(sin(33333k,因此33k, k ,[0,2],因此当k0时,3,选C.322Z 又2【答案】 C( 4)已知为第二象限角,sin 3,则sin 2 5( A)24( B)12(C)12(D)2425252525【分析】由于为第二象限,因此cos0 ,即cos1sin 24,因此43125sin 22sin cos,选 B.5525【答案】 B( 5)椭圆的中心在原点,焦距为 4 ,一条准线为 x 4 ,则该椭圆的方程为(A) x2y21(B) x2y211612128(C) x2y21(D) x2y2184124【分析】椭圆的焦距为4,因此2c 4, c 2 由于准线为x 4 ,因此椭圆的焦点在x 轴上,且a2 4 ,所以a24c8 , b2 a 2 c 28 4 4,因此椭圆的方程为cx 2y 21,选C.84【答案】 C( 6)已知数列{ a n}的前n项和为S n,a11, S n2a n1, ,则S n( A)2n 1( B)(3)n 1( C)(2)n 1( D)1 232n 1【分析】由于 a n 1 S n 1S n,因此由 S n2a n 1得,S n2(S n1 S n ) ,整理得 3S n2S n 1,S n13,因此数列{S n }是以S a 1 为首项,公比q3的等比数列,因此因此S n2112S n(3) n 1,选B.2【答案】 B(7)6位选手挨次演讲,此中选手甲不再第一个也不再最后一个演讲,则不一样的演讲序次共有( A)240种(B)360种(C)480种(D)720种【分析】先排甲,有 4 种方法,节余 5 人全摆列有A55120 种,因此不一样的演讲序次有4 120 480种,选 C.【答案】 C( 8)已知正四棱柱 ABCD A 1B 1C 1 D 1 中 , AB 2 , CC 1 2 2 , E 为 CC 1的中点,则直线AC 1 与平面 BED 的距离为(A ) 2(B ) 3 (C ) 2(D )1【分析】连结 AC,BD 交于点 O ,连结 OE ,由于 O,E 是中点,因此 OE// AC 1 ,且OE1AC 1 ,因此 AC 1 // BDE ,即直线 AC 1 与平面 BED 的距离等于点 C 到平面 BED 的距2离,过 C 做CF OE 于 F ,则 CF 即为所求距离 .由于底面边长为2 ,高为2 2,因此 AC 2 2,OC 2,CE2 ,OE2 , 因此利用等积法得CF1,选 D.【答案】 D( ) ABC 中, AB 边的高为CD ,若 CB a ,CAb ,a b 0 ,| a | 1,|b | 2,则 AD9( A ) 1 a 1b( B ) 2a2 b ( C )3 a 3b( D ) 4a4 b333 35 555【分析】如图,在直角三角形中,CB1, CA 2, AB5 ,则CD2 ,因此 ADCA 2 CD 24 44 , 因此5 55AD 4 ,即 AD 4AB4(a b)4 a 4b ,选 D.AB 55555【答案】 D( 10)已知 F 1 、 F 2 为双曲线 C : x 2 y 2 2 的左、右焦点,点 P 在 C 上, | PF 1 | 2 | PF 2 |,则 cos F 1PF 2(A )1(B )3(C )3(D )44545【分析】双曲线的方程为x 2y 2b2,c 2 ,由于 |PF 1|=|2PF2| ,因此点21 ,因此 a2P 在双曲线的右支上,则有|PF 1|-|PF 2|=2a= 2 2 ,因此解得 |PF 2|= 2 2 , |PF 1 |= 4 2 ,因此根据余弦定理得cosF 1 PF 2 (2 2) 2 (4 2 )21432 2 2 4 2,选 C.4【答案】 C1( 11)已知 x ln , y log 5 2 , z e 2 ,则( A ) x yz( B ) z x y( C ) zy x( D ) y z x11 , 11【 解 析 】 xln1 ,y log 5 211, z e 21,因此log 2 52e 2ey z x ,选 D.【答案】 D( 12)正方形 ABCD 的边长为 1,点 E 在边 AB 上,点 F 在边 BC 上, AEBF1 。
2012年全国高考文科数学试题及答案-新课标word版

绝密*启用前2012年普通高等学校招生全国统一考试(新课标卷)文科数学注息事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2.问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效.3。
回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
1、已知集合A={x |x 2-x -2〈0},B={x |-1〈x 〈1},则(A )A 错误!B (B )B 错误!A (C )A=B (D)A ∩B=(2)复数z =错误!的共轭复数是(A )2+i (B)2-i (C )-1+i (D )-1-i3、在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线y =错误!x +1上,则这组样本数据的样本相关系数为(A)-1 (B)0 (C )错误! (D )1(4)设F 1、F 2是椭圆E :错误!+错误!=1(a >b >0)的左、右焦点,P 为直线x =错误!上一点,△F 1PF 2是底角为30°的等腰三角形,则E 的离心率为( )(A )12 (B )错误! (C)错误! (D)错误!5、已知正三角形ABC 的顶点A(1,1),B (1,3),顶点C 在第一象限,若点(x,y )在△ABC 内部,则z =-x+y 的取值范围是(A )(1-3,2) (B )(0,2) (C)(错误!-1,2) (D)(0,1+错误!)(6)如果执行右边的程序框图,输入正整数N (N ≥2)和实数a 1,a 2,…,a N ,输出A ,B ,则(A )A+B 为a 1,a 2,…,a N 的和(B )错误!为a 1,a 2,…,a N 的算术平均数(C )A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数(D )A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A)6(B)9(C)12(D)18(8)平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为错误!,则此球的体积为(A)错误!π(B)4错误!π(C)4错误!π(D)6错误!π(9)已知ω>0,0<φ<π,直线x=错误!和x=错误!是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=(A)错误!(B)错误!(C)错误!(D)错误!(10)等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,|AB|=4错误!,则C的实轴长为(A)错误!(B)2错误!(C)4 (D)8(11)当0〈x≤错误!时,4x<log a x,则a的取值范围是(A)(0,错误!)(B)(错误!,1)(C)(1,错误!) (D)(错误!,2)(12)数列{a n}满足a n+1+(-1)n a n=2n-1,则{a n}的前60项和为(A)3690 (B)3660 (C)1845 (D)1830第Ⅱ卷本卷包括必考题和选考题两部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密*启用前
2012年普通高等学校招生全国统一考试
文科数学
注息事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效.
3.回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效·
4.考试结束后.将本试卷和答且卡一并交回。
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
1、已知集合A={x |x 2-x -2<0},B={x |-1<x <1},则
(A )A ⊂≠B (B )B ⊂≠A (C )A=B (D )A ∩B=∅
(2)复数z =-3+i 2+i 的共轭复数是
(A )2+i (B )2-i (C )-1+i (D )-1-i
3、在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点
图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线y =12x +1上,则这组样本数据的样本相关系
数为
(A )-1 (B )0 (C )12 (D )1
(4)设F 1、F 2是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,P 为直线x =3a 2上一点,△F 1PF 2是底
角为30°的等腰三角形,则E 的离心率为( )
(A )12 (B )23 (C )34 (D )45
5、已知正三角形ABC 的顶点A(1,1),B(1,3),顶点C 在第一象限,若点(x ,y )在△ABC 内部,则z =-x+y 的取值范围是
(A )(1-3,2) (B )(0,2) (C )(3-1,2) (D )(0,1+3)
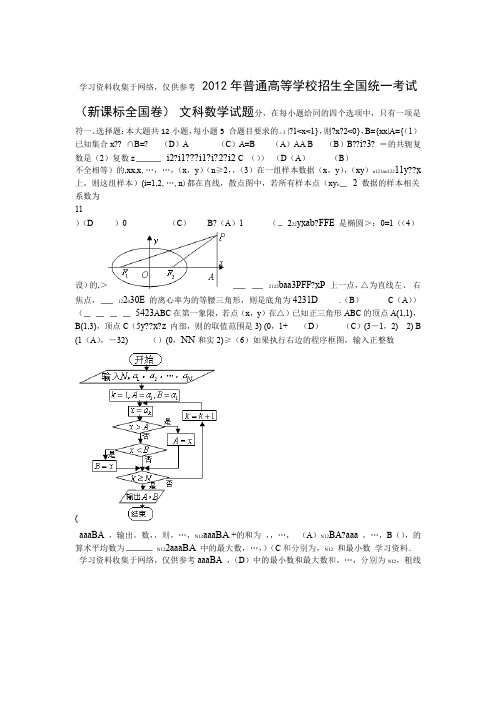
(6)如果执行右边的程序框图,输入正整数N(N ≥2)和实数a 1,a 2,…,a N ,输出A,B ,则
(A )A+B 为a 1,a 2,…,a N 的和
(B )A +B 2为a 1,a 2,…,a N 的算术平均数
(C )A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数
(D )A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数
(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为
(A)6
(B)9
(C)12
(D)18
(8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为
(A )6π (B )43π (C )46π (D )63π
(9)已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则
φ=
(A )π4 (B )π3 (C )π2 (D )3π4
(10)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB|=43,则C 的实轴长为
(A ) 2 (B )2 2 (C )4 (D )8
(11)当0<x ≤12时,4x <log a x ,则a 的取值范围是
(A )(0,22) (B )(22,1) (C )(1,2) (D )(2,2)
(12)数列{a n }满足a n +1+(-1)n a n =2n -1,则{a n }的前60项和为
(A )3690 (B )3660 (C )1845 (D )1830
第Ⅱ卷
本卷包括必考题和选考题两部分。
第13题-第21题为必考题,每个试题考生都必须作答,第22-24题为选考题,考生根据要求作答。
二.填空题:本大题共4小题,每小题5分。
(13)曲线y =x (3ln x +1)在点(1,1)处的切线方程为________
(14)等比数列{a n }的前n 项和为S n ,若S 3+3S 2=0,则公比q =_______
(15)已知向量a ,b 夹角为45° ,且|a |=1,|2a -b |=10,则|b |=
(16)设函数f (x )=(x +1)2+sin x x 2+1的最大值为M ,最小值为m ,则M+m =____
三、解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)
已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,c = 3a sinC -c cosA
(1) 求A
(2) 若a =2,△ABC 的面积为3,求b ,c
18.(本小题满分12分)
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。
如果当天卖不完,剩下的玫瑰花做垃圾处理。
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y (单位:元)关于当天需求量n (单位:枝,n ∈N )的函数解析式。
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
(1)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
(2)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率。
(19)(本小题满分12分)
如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=1
2AA 1,D 是棱AA 1的中点 (I)证明:平面BDC 1⊥平面BDC
(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比。
(20)(本小题满分12分)
设抛物线C :x 2=2py (p >0)的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于B ,D 两点。
B 1
C B A
D C 1 A 1
(I )若∠BFD =90°,△ABD 的面积为42,求p 的值及圆F 的方程;
(II )若A ,B ,F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 距离的比值。
(21)(本小题满分12分)
设函数f (x )= e x -ax -2
(Ⅰ)求f (x )的单调区间
(Ⅱ)若a =1,k 为整数,且当x >0时,(x -k ) f ´(x )+x +1>0,求k 的最大值
请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,D ,E 分别为△ABC 边AB ,AC 的中点,直线DE 交△ABC 的外接圆于F ,G 两点,若CF//AB ,证明:
F
G
(Ⅰ)CD=BC ;
(Ⅱ)△BCD ∽△GBD
(23)(本小题满分10分)选修4—4;坐标系与参数方程
已知曲线C 1的参数方程是⎩⎪⎨⎪⎧
x =2cos φy =3sin φ(φ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程是ρ=2.正方形ABCD 的顶点都在C 2上,且A 、B 、C 、
D 以逆时针次序排列,点A 的极坐标为(2,π3)
(Ⅰ)求点A 、B 、C 、D 的直角坐标;
(Ⅱ)设P 为C 1上任意一点,求|PA| 2+ |PB|2 + |PC| 2+ |PD|2的取值范围。
(24)(本小题满分10分)选修4—5:不等式选讲 已知函数f (x ) = |x + a | + |x -2|.
(Ⅰ)当a =-3时,求不等式f (x )≥3的解集;
(Ⅱ)若f (x )≤|x -4|的解集包含[1,2],求a 的取值范围。
!-。
