论本源性质
毛泽东思想的产生

毛泽东思想的产生,形成有它的社会历史条件,它是20世纪中国社会历史和革命运动发展的必然结果。
俄国十月革命给中国送来了马克思列宁主义,经过新文化运动洗礼的中国,为马列主义的传播准备了条件。
李大钊,毛泽东等中国先进的知识分子经过比较鉴别,终于接受了马克思主义。
毛泽东思想正是在这种时代条件和马克思主义广泛传播的前提下产生的;毛泽东思想的本源是马克思列宁主义,而次源则是中国优秀的传统文化。
毛泽东思想产生,形成的过程,也就是马列主义和中国优秀文化传统融会贯通的过程。
所以马克思列宁主义和中国优秀的传统文化是麻醉的思想形成的思想理论渊源。
中国工人阶级队伍的不断发展壮大,工人运动不断发展,迫切学要新的本阶级的思想武器的知道和革命政党的领导,这就为马列主义传入中国和毛泽东思想的产生创造了社会条件,奠定了阶级基础;而中国共产党成立后领导的人民革命运动则是毛泽东思想形成的时间基础。
毛泽东思想的形成,发展有一个历史过程。
大革命时期中国共产党人不断尝试把马克思列宁主义同中国实际相结合,提出了关于新民主主义革命的基本思想,标志着毛泽东思想已经萌芽。
20世纪20年代后期和30年代前期,以毛泽东为代表的中国共产党人,不但在时间上为开辟一条农村包围城市的革命道路奠定了极为坚实的基础,初步形成了关于农村包围城市,武装夺取政权的中国革命新道路的理论,并解决了与这条新道路相关的一系列革命的基本问题,特别是关于《反对本本主义》一文已初步包含了实事求是,群众路线,独立自主毛泽东思想活的灵魂的三个方面,这标志着土地革命战争时期毛泽东思想已基本形成;土地革命后期和抗日战争时期,即从遵义会议到中共七大,毛泽东思想得到系统的总结和多方面展开而到达成熟,并被确立为党的指导思想;解放战争时期和新中国建立后,毛泽东思想继续得到发展。
毛泽东领导全党对适合中国国情的社会主义建设道路的探索,也取得了可喜的成果。
马克思列宁主义同中国实际相结合有两次历史性飞跃,产生了凉亭大理论成果。
传播学概论论述题完整总结

1.试述传播活动的演变过程答:首先,传播活动是随着人类社会生活与信息交流的推进而不断发展和完善的。
(1)最早的传播方式是原始的、简单的,不仅信息的内容并不复杂,而且表达信息的符号和传递信息的载体也相当简单。
在古代,简单的社会生活内容并不要求有复杂的传播形式。
而到了近代和现代,简单的传播形式就无法表达复杂的生活内容。
(2)由此可见,传播的内容和形式是统一的、一致的。
正是出于社会发展的需求,加上生产力发展促进传播技术不断更新,传播才一步步发展起来。
其次,尽管人类社会的传播方式最早是十分简单和原始的,但同时却是多通道的、多样化的,也就是说人类对听觉系统和视觉系统及这两类系统的信息符号是并用的,既有口头语言,也有手势语和各种图像、图形的符号集。
(1)目前,在有些民族如澳洲土著居民中,还使用着一种十分复杂特殊的手势语。
可是,随着文字的产生,特别是15世纪中期印刷机的出现,人类兼用的视听两种通道开始分离,社会信息沟通以视觉通道为主。
(2)本世纪以来,传播活动发生了根本性的变革。
广播电视相继问世,听觉通道、视觉通道和原来的印刷媒介的视觉通道、文字符号都共同被全社会所使用。
到今天,网络传播又成了时代的宠儿。
(3)这些都一再说明了,正是出于社会需要和实际可能,传播活动才能得以不断完善,朝着复杂化、多样化、多层次和日益改善的方向发展。
2.试述传播学和新闻学的差异答:传播学和新闻学的不同之处主要是:(1)传播学重视理论研究,而新闻学重视业务研究。
初期的新闻学著作大都是有关业务方面即采访、写作、编辑等内容的,后来研究领域虽有所拓宽,进而总结和评述新闻事业(主要是报业)的历史,但新闻理论的专著却并不多。
而新闻理论多半论述新闻的本质、本源和特性,以及新闻事业的性质、任务和作用等,研究的角度、范围都很有限。
由此可见,新闻学的研究路线是:实务一历史一理论。
传播事业的发展及其对社会的巨大影响,要求学者们跳出以往单学科研究的狭隘圈子,从社会整体和宏观的角度,借助政治学、心理学、社会学、语言学、文化人类学和信息科学等研究方法和理论研究成果,对人类与社会的信息交流活动进行全面的跨学科的研究。
历史根本原因分析

历史根本原因分析的五种方法历史根本原因分析的五种方法根本原因,指本质的原因,是事物的本源,是导致历史事件发生的不以人的意志为转移的必然因素。
根据辩证唯物主义和历史唯物主义的有关原理,我们可以把历史根本原因的分析方法概括成五个入手。
一、从生产力与生产关系的矛盾入手生产力决定生产关系,生产力水平决定生产关系的性质,生产力的发展决定生产关系的变革。
生产关系一定要适合生产力状况的规律是不以人的意志为转移的客观规律。
生产力和生产关系的矛盾是任何社会发展的根本动力。
所以抓住生产力的发展以及生产力与生产关系的矛盾,许多历史现象产生、发展的根本原因就迎刃而解了。
如原始社会,氏族公社代替原始人群、父系氏族公社代替母系氏族公社、定居生活代替游牧生活、家庭的形成、私有财产的出现、阶级的逐渐产生等的历史根源都是由于生产力的发展。
春秋末期井田制的瓦解、明朝中后期“机户”的出现、世界近代史上包买商的产生、工场代替作坊、工厂代替工场、垄断资本主义的形成等也都是生产力发展的必然结果。
在阶级社会里,生产力和生产关系的矛盾,集中地体现为阶级矛盾和阶级斗争,一切社会革命最深刻的根源在于新的生产力和腐朽的生产关系之间的矛盾冲突。
如16世纪尼德兰革命、17世纪英国资产阶级革命、18世纪法国大革命等中外近代史上的一切资产阶级性质的革命或者改革运动都是资本主义经济的发展受到了诸如封建专制、殖民统治、奴隶制度、分裂割据、封建主义与殖民主义双重压迫等落后的腐朽的生产关系的阻碍,双方矛盾激化的产物。
二、从经济基础和上层建筑的矛盾入手经济基础决定上层建筑,经济基础的需要决定上层建筑的建立,经济基础的性质决定上层建筑的性质,经济基础的变更决定上层建筑的变更。
上层建筑反作用于经济基础,它为经济基础服务,保护和帮助经济基础的形成、巩固和发展。
政治制度、法律制度是上层建筑的重要组成部分,分析它们产生和发展的根本原因自然应当从与这一制度相联系的经济基础入手。
深入探究有效类比凸显本源引出性质——2011年高考四川卷理科21题的研究性学习案例
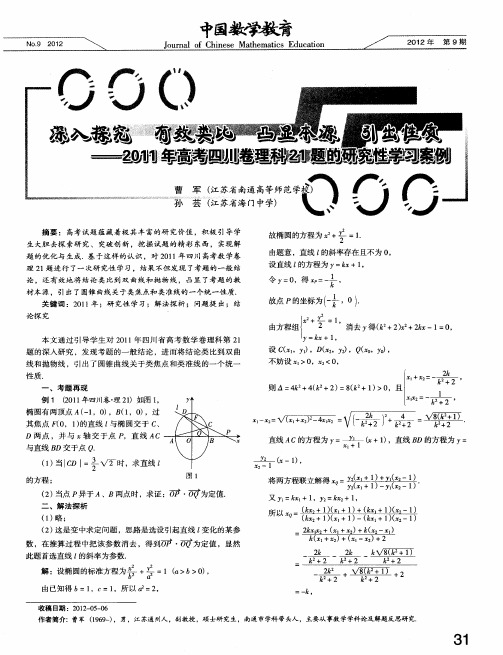
轴交 于点 P,设直线 AC与直 线 B D交 于点 p,当点 P异于 A、 B两点时 , ・ 是否为定值?
直线 B D的方程为 '=—z ( , —b , )
t ’ t
证 明 :设 尸 m, ) ( ( 0 m≠0 , (o Y) C x,, , x, 2, ) 0 x, o, ( )) o(: Y) ,
注意到定 ̄o- - F・
=z b与定点 C O t f )在 ' ( , )(≠0 , 轴上
考题中椭圆的6 c , ̄ = =1
形探索如下问题.
:F・ - o -
: 中的定值也为 的位置无关 ,而当直线 Z 1 绕着点 C O )t )旋转时 ,点 P的 ( ,t(≠o
之变化 ,故还可以选设点 P的横 坐标 m ( m≠0 为参 变量 ,转 )
N . O2 O9 2 1
J u n l o hn s te t s E u ain o r a f C ie e Mah mai d c t c o
21 0 2年
第 9期
摘 要 :高考试题 蕴藏 着极 其丰 富的研 究价值 ,积极 引导学 生 大胆去探 索研 究、突破创 新 ,挖掘 试题 的精 彩 东西 ,实现解 题 的优化 与生成.基 于这样 的认 识 ,对 2 1 0 1年四川 高考数 学卷 理 2 题进 行 了一次研 究性 学习,结果 不但发现 了考题 的一般 结 1 论 ,还有 效地将 结论 类 比到 双曲线和抛 物线 ,凸显 了考题 的教
直线 A c的方程为 '= ,
( +b , )
设直线 z 的方程 为 y x+c =k ,用解 答考题 同样 的解法 ,通
比较文学的本体论与方法论

比较文学的本体论与方法论(一)比较文学的本体论1.本体现在讨论中所使用的本体一概念,其基本内涵即源自于“essentia”,在康德及其以后的哲学那里固定下来,意指万物恒定不变的基点、本源。
2.本体论本体论是指从哲学的高度研究万物创生的基点——本源——终极存在的学问。
3.比较文学本体论借用本体与本体论这两个概念,使其转型到比较文学基本原理的建构中,来设问与回答“比较文学的本体是什么”,以此成立比较文学本体论,即设问与回答比较文学研究作为一门学科的成立它所安身立命的基点是什么,对比较文学研究的基点——本源做终极意义上本体论追问。
4.比较文学的本质或性质比较文学的本质或性质是研究,是文学研究,是作为一门学科对两个民族以上的文学和文学与其他相关学科进行汇通性的学术研究。
这是比较文学的本质或性质。
5.比较文学的本体:比较文学研究的基点——本体就是比较视域,比较视域就是比较文学的本体。
(二)比较视域1.不同于民族文学研究和国别文学研究的是,比较文学研究在学科成立的意义上非常强调主体性,这种主体性即是比较文学研究主体的比较视域。
2.视域:“视域”在比较文学这里是指一种多元观察的、多视点透视的研究视野,我们把它总称为“视域”。
3.在古汉语中,“比”有两种基本意义涉及比较文学原理的建构(1)“比”在“密”的原初意义上引申为“亲近”、“亲合”、“和协”、“齐同”、“并列”与“相连接”,这样一条意义链正契合比较视域对两种民族文学关系或文学与其他相关学科关系进行透视所获取的内在意义。
(2)“比”在古汉语中的第二种基本意义就相当于现代汉语的“比较”人们在这个层面上对“比”与“比较”的理解、使用在日常生活中是最为普泛的,一些初涉比较文学的学者往往从这一字面上提取意义,去理解比较文学,最终导致对比较文学产生望文生义的误解,认为比较文学就是把两种文学现象拿过来进行对比。
4.比较视域的含义(1)比较视域是比较文学在学科成立上安身立命的本体,是比较文学研究主体在两种文学关系之间或文学与其他相关学科关系之间的内在透视,这种透视是跨越两种及两种以上民族文化知识的内在汇通,也是跨越文学与其他相关学科知识的内在汇通。
简单解释本体论和认识论

简单解释本体论和认识论
本体论和认识论是哲学中的两个重要分支,它们探讨的是关于世界和人类认识的问题。
本体论主要研究存在的本质和结构,探讨世界的本源和基础,而认识论则主要研究人类知识和认识的来源、性质和限制。
本体论认为,存在是基本的和不可分割的,世界是由物质和精神两个方面构成的。
物质是指有形的实体,而精神则是指思维、意识、灵魂等无形的实体。
本体论认为世界存在于自己的本质之中,世界的本质是一种实体或者实在性,这种实体或实在性可以被人类认识和探究。
认识论则探讨人类认识的本质以及人类如何获得知识。
认识论认为人类认识的来源包括经验和理性。
经验是通过感官获得的知识,而理性则是通过推理和思考获得的知识。
认识论认为人类的知识是有限的,人类对于世界的认识和理解是逐步深入和完善的。
综上所述,本体论和认识论都是哲学中重要的分支学科,它们从不同的角度探讨了世界和人类认识的问题。
两者相互关联,相互补充,为人类认识世界提供了深刻的思考和理论基础。
- 1 -。
辩论赛人性本善一辩稿

今天我方的观点人性本善,今天我们讨论的对象只限于社会人,与自然人有着明显区别,且我方解“本”为本质本源之意,人性本善,就是说人本质有做善事的倾向。
哲学家康德主张,人不分聪明才智、贫富美丑都具有理性。
孟子认为人性本善,所以进一步又加了一句,每个人都有恻隐之心。
而佛家说,一心迷是真身,一心觉则是佛。
正因为人性本善,所以人随时随地都可以放下屠刀、立地成佛。
首先,人性本善,就是主张人性的根源点是善的,有善端才会有善行,才会有恻隐之心。
著名电影《辛德勒的名单》中的主角辛德勒本身是一个纳粹党人,是一个不择手段谋取利益的商人,可以说,他是一个谈不上“善”的人,但他在看到纳粹集中营中犹太人的悲惨遭遇之后,还是产生了恻隐之心,之后也才有了他救助那么多犹太人的善行,辛德勒在这万恶的环境中产生了恻隐之心难道不正是人性本善的体现吗?第二,我方不否认在人类社会中存在有恶行,但是恶行的产生则是由外在环境所造成,所以恶是结果而不是原因。
譬如社会上常见的小偷,若不是生活所迫,找不到工作,哪会去偷?若你作为一个有正当工作稳定收入的青年,你会去偷吗?答案当然是否定的。
所以说,恶行的产生是由外在环境所造成的。
如果硬要说恶是因不是果,也就是说人性本恶,那么人世间能产生真正的道德吗?公交车上我们可以经常看到年轻人自觉为老人、孕妇、小孩让座,所人性本恶,那么他们又为何自觉让座?难不成法律中明确要求公交车上年轻人必须为老人、孕妇、小孩让座?我遍观法律,却没有这一条!所以说,正是因为人性本善,世间才产生了真正的道德啊!这便证明了,恶是结果而不是原因,恶行的产生是由外在环境所造成。
纵观人类历史社会,没有产生一个绝对权威的君主,但是舍己为人的事情在不断地发生。
而在生活当中,不仅仅只有泰丽莎修女的善行,为善不为人知的生徒小民更是比比皆是。
由此可见,人性的根源点是善的,有善端才有善行,才会产生出恻隐之心,恶行是由外在环境所造成的。
所以我方坚定地认为,人性本善。
史学概论重点资料复习

史学概论复习资料辑要1、史学本体论:历史学的本体论就是关于历史现象存在的本源和性质的观点或理论,其核心就是人们通常所说的社会历史观。
在西方非马克思主义的史学本体论体系中,长期存在着人本主义和科学主义两大思潮的分歧和斗争。
2、史学认识论:史学认识论是关于人们的历史认识的性质和特点的观点或理论,研究的问题诸如人们的历史认识是怎样产生或形成的?人们对历史的认识是否受到社会生活的影响和制约等3、史学方法论:史学方法论是关于历史研究方法的性质和特点的观点和理论,研究的问题例如历史研究方法是否存在着导向性方法和技术性方法的区别?历史研究方法与自然科学和其他人文社会科学研究方法有何异同等。
4、《史学要论》:李大钊著。
《史学要论》是他运用唯物史观研究史学理论的成果,是我国第一部马克思主义史学概论。
他阐述什么是历史和历史学、历史学的系统、历史学的科学地位、历史学与其它学科的关系以及历史学研究的任务等问题,介绍马克思主义的历史学理论,批判地主资产阶级旧史学,并倡导史学革命,提出要以唯物史观“改作”、“重作”全部历史。
5、合力英雄史观合力:历史最终的结果总是从许多单个的意志的相互冲突中产生出来的,而其中每一个意志,又是由于许多特殊的生活条件,才成为它所成为的那样。
这样就有无数互相交错的力量,有无数个力的平行四边形,而由此就产生出一个合力,即历史结果,而这个结果又可以看作一个作为整体的、不自觉地和不自主地起着作用的力量的产物。
英雄史观:代表人物卡莱尔,尼采等。
认为时势造英雄,英雄造时势。
历史发展取决于伟大人物的活动。
6、马克思主义史学如何看待历史的客观实在性?历史本身是客观地存在着的,它独立于认识者、研究者的主体意识之外。
人类历史是以往经历过的客观存在的过程,它有自己独特的从低级向高级发展的运动规律。
人类历史及其发展规律可以被认识,只是它被认识的途径、特点、方法与其它学科有差别罢了。
7、人类社会历史有无规律?如果有,如何正确理解?有。
立法理念论

立法理念论陈兴良立法是人的一种实践活动,因而不能离开一定的理论指导。
只有科学地确立了立法理念,才能正确地界定立法的本质,并有效地指导立法活动。
一、法本源论立法是创制法律,因而正确地认识法的本源具有十分重要的意义。
对于法本源的认识,在人类历史上经历了一个神性到人性的演变过程。
在古代社会,由于宗教神学的影响,往往不能科学地认识法现象,因而把法看作神法,这种神性的法本源观念对于古代立法产生了深远的影响。
应该说,这种法的神本源论是当时君权神授观念的必然产物。
关于中国古代是否存在神权法思想,在学术上存在不同观点。
美国汉学家布迪等人认为中国古代不存在神权法思想,指出:中国的历史理论和哲学理论皆具有一个显著特征,即注重现实的社会生活。
这一特征在中国历史的早期即已显露出来。
一般说来,中国的理论家们在阐释人世间的现象时,宁可采用理性主义(或在它看来是合乎理性的)原则,而不借助超自然的学说。
早期中国文献中所反映出的中国神话的遭遇,即是一个很好的例证。
在我们所接触到的文献中,有一些零碎的史料表明,人们根据“神话即是历史”的原则,将神话中的神、半神半人及妖怪们转虚为实,变成似乎在历史上确实存在过的贤明君主、英雄或者叛逆者。
所以,当我们再回到法律领域,而发现法律也完全具有世俗性质的时候,应该不会感到意外。
〔1〕英国学者梅因也有类似的观点,认为人类社会有一时期,法律规范尚未脱离宗教规范而单独存在,在中国则已超过此点。
对此,我国著名学者瞿同祖表示了不同看法,指出:从表面上来观察,我们确不易见宗教在中国法律史上的地位。
根据历史材料,我们实无像汉穆拉比(Hammurabi),摩奴(Manu)或摩西(Moses)法一类出自神授的法律。
在我们祖先的意识形态中,根本没有像希腊人那样以为每一法律皆为神所拟定的观念。
同时我们的法律也不曾依赖巫术宗教的力量来维持。
没有一条所知的法律是附有咒诅的。
握有司法权的人也非具有巫术或是神权的人。
在中国法律制裁与宗教制裁或仪式制裁是分开的。
数是万物的本源

数是万物的本源
数是万物的本原是由古希腊早期著名的哲学家毕达哥拉斯提出来的。
在他看来,世间万物皆是数,数乃是万物的原型,一切物质都是模仿数的,属于数的摹本,数的原则统治着所有现象,数量关系决定着事物的性质,所有事物遵照既定的数量比例构成和谐的秩序。
他认为,一作为万物的本原,产生出二,二是从属于一的不定质料,而一是原因。
从完满的一和不定的二中产生了各种数目;数产生点,点产生线,线产生面,面产生体,体产生所有形体。
毕达哥拉斯还将数的元素分为奇偶,在他看来,奇是有限的,偶是无限的,这个数便是由这两种元素构成的,而且由一产生出所有数目。
所以,有限与无限就是宇宙的两大根本原则,世界也是由它们组成的。
毕达哥拉斯将数作为物质世界的基础,还将一些非物质的事物也归于数,赋予数神秘的色彩。
毕达哥拉斯所提出的数的本原论,在人类认识史上是一个非常大的进步。
它标志着人类已不满足使用具体形象的东西来解释世界的产生、存在与发展,标志着人类尝试透过繁杂的现象世界,把握事物间某种数的“比例”关系,孕育着数的规律,可是这个命题本身也带有数的绝对化倾向。
史学概论复习题答案

史学概论复习题答案一,名词解释1.历史本体论:历史学的本体论就是关于历史现象(历史过程中出现的个人,人群,事件和过程)存在的本源和性质的观点或理论,其核心是社会历史观。
2.历史认识论:史学认识论是关于人们的历史认识的性质和特点的观点和理论。
3.兰克学派:兰克学派是由德国史学家兰克开创的学派,其主要观点有:a,科学历史学:一是“客观主义”的态度,二是科学研究的方法。
b,史学本体论:他强调精英人物的目的、意志和动机体现着时代精神,决定着历史的进程。
c,史学研究方法:他强调从精心考证过的第一手史料中领悟精英人物的思想、目的和动机,进而对历史人物和事件作出具体的“个别描述”,而避免进行任何总体性或理论性的概括,认为这样才能恢复历史的本来面目。
4.年鉴学派:年鉴学派是由吕西安·费弗尔和马克·布洛赫于1929年创立的,它得名于是年发刊的《经济与社会史年鉴》。
他们追求总体史学,反对政治史;提倡运用跨学科和回溯复原的研究方法;关注各个不同历史时期的特点,广泛采用各种文字与文字史料进行研究。
为现当代法国史学和世界史学留下了宝贵的史学遗产。
年鉴学派的第二阶段是布罗代尔时代,他在继承总体史的基础上提出长时段、中时段和短时段的三种历史时段理论。
第三个阶段是年鉴——新史学派,代表人物勒高夫和拉杜里,他们热衷于研究历史人类学和心态史,重视历史认识论与方法论的更新。
5.校法四例:1931年陈垣发表《元章典校补释例》,其中总结校勘学方法为“校法四例”。
即对校法(以同书的祖本与别本对校),本校法(以同一本书前后互校),他校法(以他书校本书)和理校法(根据书本的体制和遣词造句的特点或事物的常理校对),为以后校勘学的发展奠定了基础。
6.二重证据法:王国维1925年提出了“二重证据法”,以作为古文献的“纸上材料”与考古所得的“地下新材料”相结合以考证古史的方法,将乾嘉学派的考据方法与西方资产阶级革命以来的科学新方法相结合,“不绌旧以就新,亦不绌新以从旧”,取得了杰出的学术成就,被认为是20世纪中国考古学和考据学的重大革新。
高校学位授予权本源 性质与司法审查

在法律上,高校学位授予权的地位具有双重性。一方面,高校作为教育事业 单位,享有学术自由和自主管理权,因此学位授予权是高校自主管理权的体现; 另一方面,高校学位授予权受到国家法律法规的约束和监督,因此它也是一种受 限制的权力。
在实践中,高校学位授予权面临着诸多挑战。例如,学生学位申请的门槛逐 渐降低,但学位含金量却受到了质疑;又如,一些高校出现了学术不端行为,严 重影响了学位授予的公正性和权威性。针对这些问题,高校需要不断完善学位授 予制度,提高学术水平和教学质量。
文献综述
自20世纪80年代以来,我国高校学位授予权经历了从无到有、逐步发展的过 程。早期的研究主要集中在学位授予权的申请、审批和监管等方面。随着高等教 育的快速发展,学者们开始学位授予权的制度体系问题。一些研究表明,我国高 校学位授予权在实践过程中存在一定的乱象,如审批不严、监管不到位等。此外, 对于学位授予权的性质、地位和作用等问题,学界也进行了深入探讨。
司法审查与高校学位授予权 权力。在许多国家,司法审查已成为保障公民权利、维护公正和促进法治的重要 手段。那么,高校学位授予权是否属于司法审查的范围呢?
根据相关法律法规,高校学位授予权受到国家法律法规的约束和监督。当学 生对高校的学位授予行为产生异议时,可以通过行政诉讼等途径进行维权。在此 情况下,司法机关可以依据法律法规对高校的学位授予行为进行审查,以保障学 生的合法权益。
高校学位授予权本源 性质与司 法审查
目录
01 高校学位授予权本源
02
高校学位授予权的性 质
03
司法审查与高校学位 授予权
04 结论
05 参考内容
随着高等教育的普及和深入,高校学位授予权的本源、性质与司法审查逐渐 成为教育界和法律界共同的热点问题。本次演示将详细阐述高校学位授予权的来 源、性质及司法审查,以期为进一步研究打下基础。
元素 规则 法则 本源法则

元素规则法则本源法则元素、规则、法则,这些词汇都是我们日常生活和学习中经常听到的。
它们都与事物的本质和运行规律息息相关。
本文将以元素、规则和法则为主题,讨论它们的意义和应用。
我们来谈谈元素。
元素是构成事物的基本成分,可以是物质的或非物质的。
在化学中,元素是指不能通过化学反应分解成其他物质的单一物质。
例如,氢、氧、铁等都是化学元素。
在自然界和宇宙中,元素是构成一切物质的基本单位。
无论是星球、植物还是人类,都是由不同的元素组成的。
元素的存在和相互作用决定了事物的性质和变化。
接下来,我们来探讨规则。
规则是描述事物行为或运行方式的准则或规范。
规则可以是自然界的规律,也可以是人类社会的准则。
在自然界中,有许多规则可以被观察到和验证。
例如,万有引力定律描述了物体之间相互吸引的规律;光的折射定律描述了光在介质中传播时的规则。
在人类社会中,法律和道德规范是人们行为的基本规则。
规则的存在和遵守保证了事物的有序运行和社会的和谐发展。
我们来讨论法则。
法则是指导事物发展和运行的基本原则。
法则是对规律的总结和概括,是对事物运行的普遍规律的描述。
法则具有普遍性和稳定性,能够指导人们认识和改造世界。
例如,能量守恒定律描述了能量在系统中不会被创造或消失,只会转化的基本原则;达尔文的进化论描述了生物进化的基本法则。
法则的存在和应用推动了人类的科学研究和社会进步。
元素、规则、法则是我们认识世界和解决问题的基础。
它们相互联系,相互作用。
元素是构成事物的基本成分,规则是事物运行的准则,法则是事物发展的原则。
在科学研究中,我们通过分析事物的元素和规律,总结出法则,从而更好地认识和掌握事物的本质和运行规律。
在日常生活中,我们遵守规则和法律,以保持社会的秩序和稳定。
在不同领域和学科中,元素、规则和法则的应用也各有不同。
在化学中,我们通过研究元素的性质和规律,设计和合成新的物质。
在物理学中,我们通过研究规则和法则,揭示宇宙的奥秘。
在社会科学中,我们通过研究社会规则和法律,改善社会的发展和人民的生活。
《矛盾是一切问题的本源》的看法

《矛盾是一切问题的本源》的看法《矛盾是一切问题的本源》主要是关于人类世界观和方法论的的哲学著作,世界观就是人类对整个世界最普遍问题的根本观点和看法,这里最普遍的问题包括:世界的本源是什么;世界处于什么状态;是否是普遍联系之中;是否是发展的;如果是发展的,又是如何发展的;发展的动力是什么。
用这种看待世界的根本观点和看法来分析问题和解决问题,就是方法论。
对于世界的本源是什么的问题,有两种答案:物质的和精神的,唯物主义者认为物质第一,精神第二,而唯心主义者认为反之。
对于世界是否是普遍联系的,是否是发展的以及发展的动力源于哪里,这些问题的回答又可分为辩证法和形而上学两种。
形而上学的世界观是世界上一切事物,一切事物的形态和种类,都是永远彼此孤立和永远不变化的;如果有变化,也只是数量的增减和场所的变更;并且这种增减和变更的原因,不在事物的内部而在事物的外部,即是由于外力的推动。
辩证法认为世界上没有什么事物是绝对孤立的,任何事物只有在一定的联系中才能存在和发展,并且事物的普遍联系是不以人的意志为转移的,是客观世界的本性。
这种“联系”指的是一切事物之间以及事物内部要素之间的相互依赖、相互影响、相互制约和相互作用;事物的这种相互作用的“联系”,使事物原有状态或性质处于不断发生变化之中,但是这种变化的总趋势表现为前进向上性的发展,并且这种变化和发展是永恒的、无始无终的;客观的物质世界的发展动力源于事物之间和事物内部要素间的相互作用,事物内部要素间的相互作用是事物发展的根本动力,而事物间的外力作用是第二位的动力,即外力是通过内力来起作用的。
《矛盾是一切问题的本源》所主张的世界观和方法论是唯物的和辩证法的,即唯物辩证法,并把事物之间和事物内部因素间的相互依赖、相互影响、相互制约和相互作用的关系,称为对立统一的关系,并用我们中国人所理解的“矛盾”这一概念来称呼,估计这也是《矛盾是一切问题的本源》名字的由来。
首先《矛盾是一切问题的本源》先论述了“矛盾”现象是普遍存在,并且是客观存在的。
深圳市本源生活商业有限公司介绍企业发展分析报告

Enterprise Development专业品质权威Analysis Report企业发展分析报告深圳市本源生活商业有限公司免责声明:本报告通过对该企业公开数据进行分析生成,并不完全代表我方对该企业的意见,如有错误请及时联系;本报告出于对企业发展研究目的产生,仅供参考,在任何情况下,使用本报告所引起的一切后果,我方不承担任何责任:本报告不得用于一切商业用途,如需引用或合作,请与我方联系:深圳市本源生活商业有限公司1企业发展分析结果1.1 企业发展指数得分企业发展指数得分深圳市本源生活商业有限公司综合得分说明:企业发展指数根据企业规模、企业创新、企业风险、企业活力四个维度对企业发展情况进行评价。
该企业的综合评价得分需要您得到该公司授权后,我们将协助您分析给出。
1.2 企业画像类别内容行业体育-文艺创作与表演资质空产品服务是:互联网销售(除销售需要许可的商品);1.3 发展历程2工商2.1工商信息2.2工商变更2.3股东结构2.4主要人员2.5分支机构2.6对外投资2.7企业年报2.8股权出质2.9动产抵押2.10司法协助2.11清算2.12注销3投融资3.1融资历史3.2投资事件3.3核心团队3.4企业业务4企业信用4.1企业信用4.2行政许可-工商局4.3行政处罚-信用中国4.4行政处罚-工商局4.5税务评级4.6税务处罚4.7经营异常4.8经营异常-工商局4.9采购不良行为4.10产品抽查4.11产品抽查-工商局4.12欠税公告4.13环保处罚4.14被执行人5司法文书5.1法律诉讼(当事人)5.2法律诉讼(相关人)5.3开庭公告5.4被执行人5.5法院公告5.6破产暂无破产数据6企业资质6.1资质许可6.2人员资质6.3产品许可6.4特殊许可7知识产权7.1商标7.2专利7.3软件著作权7.4作品著作权7.5网站备案7.6应用APP7.7微信公众号8招标中标8.1政府招标8.2政府中标8.3央企招标8.4央企中标9标准9.1国家标准9.2行业标准9.3团体标准9.4地方标准10成果奖励10.1国家奖励10.2省部奖励10.3社会奖励10.4科技成果11土地11.1大块土地出让11.2出让公告11.3土地抵押11.4地块公示11.5大企业购地11.6土地出租11.7土地结果11.8土地转让12基金12.1国家自然基金12.2国家自然基金成果12.3国家社科基金13招聘13.1招聘信息感谢阅读:感谢您耐心地阅读这份企业调查分析报告。
高考本源探究之函数及其性质
高考本源探究—函数及其性质高考本源课题组 刘 臻函数是高中数学的主线,其不仅灵活而且抽象!学好函数要把握好函数中两种思维是直觉思维与抽象思维,这里分为如下五部分作介绍:一、初等函数,二、函数性质,三、函数图像,四、特殊函数,五、数学思维.1.1、初等函数之二次函数【17全国Ⅰ理21】已知函数2()e (2)e x x f x a a x =+--. (Ⅰ)讨论()f x 的单调性;(Ⅱ)若()f x 有两个零点,求a 的取值范围.【示例分析】'2()2e (2)e 1xxf x a a =+--,因式分解:'()(e 1)(2e 1)xxf x a =-+ 再对参数进行分类讨论,得到函数单调性. 【14全国Ⅱ理21】已知()e e 2xxf x x -=+-.(Ⅰ)讨论()f x 的单调性;(Ⅱ)设()(2)4()g x f x bf x =-,当0x >时,()0g x >,求b 的取值范围.【示例分析】整体思想:视e ex x -+为整体.化简22()(ee )4(e e )(84)xx x x g x b b x --=---+-求导'22()2(e e )4(e e )84x x x x g x b b --=+-++-22[(e e )2(e e )44]x x x xb b --=+-++-2[(e e )2][(e e )(22)]x x x x b --=+-+--讨论:依据e e 2x x-+≥与22b -大小关系分类.1.2、初等函数之三次函数【高考1】(13全国新课标10)已知函数33y x x c =-+的图像与x 轴恰有两个公共点,则c =A.2-或2B. 9-或3C. 1-或1D. 3-或1【高考2】(13新课标理10/文11)已知函数32()f x x bx cx d =+++,下列结论中错误的是A .0R x ∃∈,有0()0f x =B . 函数()f x 的图像是中心对称函数C . 若0x 是函数()f x 的极小值点,则()f x 在区间0(,)x -∞单调递减D . 若0x 是函数()f x 的极值点,则'0()0f x =【高考3】(14全国Ⅱ文12)已知函数32()31f x ax x =-+,若函数()f x 存在唯一的零点0x ,且00x >,则实数a 的取值范围是A .(2,)+∞B . (1,)+∞C . (,2)-∞-D . (,1)-∞-【例题1】(武汉2月调研)函数32()367f x x x x =-+-的图像是中心对称函数,则其对称中心为______. 【分析】巧用导数处理函数的对称中心 如图所示:设00(,)x y 是函数的对称中心,且点11(,)x y 、22(,)x y 是函数上关于对称中心对称两点,由 对称性可知,函数在1x 、2x 处的切线斜率相等,设斜率为k 则'2()366f x x x k =-+=,且'1()f x k =、'2()f x k = 知1x 、2x 是23660x x k -+-=的两根,则12022x x x +== 即01x =,0()(1)3f x f ==-,知(1,3)-为函数的对称中心.【分析】6139(2)(2)1y x x x x x =-+-=-+-+,这是不容易直接想到的,但可以借助于导数,三次函数对称中心的横坐标是一阶导数的对称轴横坐标(或二阶导数的零点),待定系数便可很快的找到对称中心. 即326139y x x x =-+-,'231213y x x =-+,''612y x x =-,知对称中心横坐标为2,所以可得3236139(2)(2)1y x x x x x=-+-=-+-+,此函数由3()f x x x =+向右平移2单位,向上平移一单位得到,研究直线'l 与3()f x x x =+交点依次为''',(),A B O C ,且''''||=|AB BC '()B O 中心对称,设'l 方程:y kx =,'00(,)A x y ,则00220030005y kx x y y x x=⎧⎪+=⎨⎪=+⎩,消元得到3260k k k -+-=,试根得 2(2)(3)0k k k -++=,即得2k =,也即'l 方程:2y x = 再平移回去:l 方程:2(2)123y x x =-+=-,故选B .【反思】充分利用函数对称的特性:两点关于对称中心对称,则这两点处的切线平行,这样转化为研究导函数,将三次函数降为二次函数,利用函数与方程思想,找到对称两点的中点横坐标(二次函数的对称轴),进而找到对称中心坐标.1.3、初等函数之指数与对数函数【高考1】(05大纲Ⅲ文6/理6)若ln 22a =,ln 33b =,ln 55c =,则 A .c b a >> B .b c a >> C .a c b >> D .b a c >> 【高考2】(13课标Ⅱ理8)设3log 6a =,5log 10b =,7log 14c =,则A .a b c <<B .c a b <<C .c b a <<D .b a c << 【高考3】(16课标Ⅰ文81<,则A .log log a b c c < C .c c a b < D .a bc c >【高考4】(17全国Ⅰ理,,x y z 235x y z ==,则A .235x y z <<B .523z x y <<C .352y z x << 【高考5】(18全国Ⅰ理8)设1a b >>,01c <<,则A .cca b < B .ccab ba < C .log log b a a c b c < D .log log a b c c < 【高考6】(18全国Ⅲ12)设0.2log 0.3a =,2log 0.3b =,则A .0a b ab +<<B .0ab a b <+<C .0a b ab +<<D .0ab a b <<+【例题1】(17全国Ⅰ理11)设,,x y z 为正数,且235x y z==,则( D )A .235x y z <<B .523z x y <<C .352y z x <<D .325y x z << 【分析】思路一:架设桥梁,化归统一形式比较大小.令235x y z k ===,由,,x y z 为正数,知1k >,可得2log x k =、3log y k =、5log z k = (既顺应了题设中“相等”,又将变量化归统一到相同变量,实现了减元,自然之道) ∴222log x k k ==、333log y k k ==、555log z k k ==∴2x =、3y =、5z =,从而问题归结到比较的大小,化同底指数知<325y x z =<=<=,故选D .【分析】研究函数()f x x=(必须掌握的熟悉函数),在(0,e)x ∈上递增,在(e,)x ∈+∞上递减;即有(5)(4)(3)(e)f f f f <<<,所以ln 5ln 4ln 2ln 35423<=<,故c a b <<.其真数满足z x y =<=(经典一直在默默地传承)【再分析】本题含有高等数学背景,即问题的实质可归结为讨论幂指函数1xy x =在0x >上的单调性,对函数两边先取常用对数得1ln ln y x x =,再两边同时对x 求导,'22111ln y x y x x =-+,得到1'21ln x x y x x -=,知函数在(0,e)上单调递增,在(e,+)∞<<当两对数的底数和真数不同,又不是明显的一正一负或可以选择中间常量对比的情况,如5log 3和6log 4,两对数符号相同,且难以通过中间常量进行判断比较大小,这时我们如何办呢?【例题2】(13新课标Ⅱ理8) 设3log 6a =,5log 10b =,7log 14c =,则 ( C )A .c b a >>B .b c a >>C .a b c >>D .a c b >>【命题预期】设9log 10a =,lg11b =,则,a b 的大小关系是________.【分析】由9log 10a =,10log 11b =知1a >、1b >由9log 10a =,知910a =;由10log 11b =知1011b=,所以9101110a b=<=(底数小的指数函数小于底数大的指数函数),根据指数函数图像,还是不能判断大小! 仔细想想:要是底数大的指数式小于底数小的指数式,就能比较大小 试着将两对数分离出同一个常数,再比较指数大小:9991010101010log 10log 91log 991111log 11log 101log 1010a b ==⨯=+==⨯=+,设91010log 911log 10m n ==,即10191991111011010m n ==+==+,即910m n>(底数大的指数式小于底数小的指数式,就能比较大小)即m n >,所以a b >.于y x =对称这一特性,利用该特性可以应用数形结合思想解决.思路一:利用指对函数的对称性,数形结合解决(过程略);222log (1)5x x +-=可变形为25log (1)2x x -=-; 则225xx +=可变形为1522x x -=-(向同结构转化) 换元简化:令10x t -=>, 12,t t 分别是方程322tt =-,23log 2t t =-两根,即12,t t 分别是32y t =-与2t y =和2log y t =交点,A B 的横坐标,如图:由图像对称特性可知,交点,A B 关于点P 对称,而易知34P x =,故1232t t +=,所以12127(1)(1)2x x t t +=+++=.思路二:化异求同,函数思想解决:由11225xx +=,即1115202x x -+-=,说明1x 是函数15()22x f x x -=+-的一个零点; 由22222log (1)5x x +-=,即252212x x --=,则27()122752()022x x --+--=,说明272x -也是函数15()22x f x x -=+-的一个零点;而15()22x f x x -=+-,'1()2ln 21x f x -=+,即此函数单调递增,有唯一零点,故1272x x =-,即1272x x +=.2.1、函数性质之奇偶性、对称性【高考14新课标Ⅰ文5理3】()f x ,()g x 是定义在R 上的函数,()()()h x f x g x =+,则“()f x ,()g x 均为偶函数”是“()h x 为偶函数的”A .充要条件B .充分不必要条件C .必要不充分条件D . 既不充分也不必要条件【高考15新课标Ⅱ文12】设函数21()ln(1||)1f x x x =+-+,则使得()(21)f x fx >-成立的x 的取值范围是 B .1(,)(1,)3-∞+∞ C .11(,)33- D .11(,)(,)33-∞+∞【高考16新课标Ⅲ文16】已知函数()f x 为偶函数,当0x <时,1()x f x e x --=-,则曲线()y f x =在(1,2)处的切线方程___________.20x y -=【高考16新课标Ⅲ理15】已知函数()f x 为偶函数,当0x <时,()ln()3f x x x =-+,则曲线()y f x =在(1,3)-处的切线方程___________.210x y ++=【分析】221222()2xf x x x++++==⋅,而函数222x xy -=++是偶函数,函数y x =是奇函数,故原函数为奇函数.【知识拓展】符号函数1,0sgn()0,01,0x x x x -<⎧⎪==⎨⎪>⎩,有sgn()sgn()xx -=-,sgn()sgn()(0)ax x a =>,知其为奇函数,借此可速判断分段函数的奇偶性.例如:22223,0()0,0(+3)sgn()223,0x x x f x x x x x x x x ⎧---<⎪===-⎨⎪-+>⎩为奇函数.【例题2】(17全国Ⅰ文9)已知函数()ln ln(2)f x x x =+-,则( C )A .函数()f x 在(0,2)上单调递增B .函数()f x 在(0,2)上单调递减C .函数()f x 图像关于1x =对称D .函数()f x 图像关于点(1,0)对称 【分析】思路一:对称问题的代数形式入手:发现(2)ln ln(2)()f x x x f x -=+-=,即(2)()f x f x -=,即函数()f x 图像关于1x =对称; 对函数求导:'112(1)()2(2)x f x x x x x -=-=--,在(0,2)x ∈上不单调. 思路二:化简变形,平移化归为偶函数2()ln ln(2)ln[(2)]ln[(1)1]f x x x x x x =+-=-=--+,(0,2)x ∈而2()ln(1)g x x =-+,(1,1)x ∈-是偶函数,关于y 轴对称,()(1)f x g x =-,可知函数关于1x =对称.破解轴对称问题微课程【引例】(07全国理14)若函数()(1)()f x x x a =++为偶函数,则实数a = ______.【分析】思路一:从代数性质上推导,对任意R x ∈,恒有(1)()()()(1)()x x a f x f x x x a -+-+=-==++恒成立,即2(1)0a x +=,此式与变量无关,得1a =-;思路二:从几何图像对称性质上推导,发现()(1)()f x x x a =++一个已知的零点1x =-,函数为偶函数,其图像关于y 轴对称,零点也必有一个对称零点1x =,即得1a =-.(从中你有何感触)【例题3】(13全国Ⅰ理16)若函数22()(1)()f x x x ax b =-++的图像关于直线2x =-对称,则()f x 的最大值是______.【分析】思路一:运用一般到特殊思想,挖掘特殊的点对的对称性(对象函数是有两个已知零点的一元四次函数,类比二次函数轴对称知已知的对应零点必然对称) 由22()(1)()f x x x ax b =-++,知(1)(1)0f f -==,则-3,-5也为函数零点得(19)(93)0(125)(255)0a b a b --+=⎧⎨--+=⎩ ,815a b =⎧⎨=⎩,即22()(1)(815)f x x x x =-++.又图象关于2x =-对称得出2x =-是函数的一个极值点(三次函数发现一个因式,大大降低分解因式难度)∴'22()2(815)(1)(28)f x x x x x x =-+++-+4(2)(22x x x =-+++∴列表可看出()f x 在2x =-2x =-(2(216f f -=-=. 【再分析】利用函数思想,转化类比二次函数求最值同法一:知()(1)(1)(3)(5)f x x x x x =-+++(发现函数零点的等距,换元构造) 思路二:得()[3(2)][3(2)][(2)1][(2)1]f x x x x x =-++++-++2222[9(2)][(2)1][(2)5]1616x x x =-++-=-+-+≤(类比二次函数处理最值手段)思路三:回归偶函数,左右平移不改变函数的值域将函数往右平移2个单位可得(2)[1(2)][1(2)][(2)3][(2)5]f x x x x x -=--+--+-+1616)5()1)(9(2222≤+--=--=x x x+4022(2012f +【分析一】利用对称中心的充要条件,待定中心【分析二】利用函数平移,回归奇函数对称性【分析三】利用求导,从一阶导函数对称轴(二阶导函数零点)探寻函数对称中心 【分析四】分解函数,探寻函数对称中心设32()3g x x x =-,则'2()36g x x x =-,''()66g x x =-,知''(1)0g =,而(1)2g =-,得函数()g x 的对称中心为(12)-,; 再设()sin(π)h x x =-,知()h x 的一个对称中心是(10),, 所以()()()f x g x h x =+的对称中心为(12)-,.(以下同解法一,过程略) 【反思】1、对称性性质在教学中多以让学生记忆的方式学习为主,这样容易使得学生对这些性质的理解不到位,仅会生般硬套公式而不能灵活应用,陷入解题困境.如函数()f x 关于直线x a =成轴对称图形,其充要条件是()(2)f x f a x =-,学生首先想到的是代数形式,而系列点的对称才是对称性问题的本质,特殊的点对对称的图像特征是我们破解函数对称性问题优先的思考方向.2、理论依据:设函数()()()f x g x h x =+,若()g x 的对称中心为(,)a b ,()h x 的对称中心为(,)a c ,则函数()()()f x g x h x =+的对称中心为(,)a b c +.简略证明:()g x 的对称中心为(,)a b ,知()(2)2g x g a x b +-=,()h x 的对称中心为(,)a c ,则()(2)2h x h a x c +-=,所以()(2)()()(2)(2)2()f x f a x g x h x g a x h a x b c +-=++-+-=+,即()()()f x g x h x =+对称中心为(,)a b c +,得证.但要注意,若两个函数图像对称中心的横坐标不相等,不能得出一般性结论.2.2、函数性质之周期性概念及应用【例题1】若()y f x =既是周期函数,又是奇函数,则其导函数 ( B )A .既是周期函数,又是奇函数B .既是周期函数,又是偶函数C .不是周期函数,但是奇函数D .不是周期函数,但是偶函数 很多小伙伴做对了,也不敢确定答案,准确地说,只是“猜”对了!思路一:特殊化,一般这类问题学生都是通过特殊化思想去验证的,如可举例:()sin f x x =,其导函数既是周期函数,又是奇函数.思路二:一般化,由周期性知()()f x f x T =+,对恒等式两边求导,''()()f x f x T =+;由奇函数知()()f x f x -=-, 对恒等式两边求导,''()()f x f x --=-;所以,'()y f x =既是周期函数,又是偶函数(现在总放心了吧).对于定义在R 上的函数()f x ,若存在正数a ,对于任意的R x ∈,均有b a x f x f 2)2()(=++,(b a x f a x f 2)4()2(=+++, 两式作差得0)()4(=-+x f a x f ),知T 为函数()f x 的一个正周期.对于具有两个对称性的抽象函数,其一定有周期性. ,0)(0,)+∞上的零点个数为(【分析】从题源可以发现:(1)分段函数中含有形如1()(2)2f x f x =-性质神似函数的周期性,但外面有一个倍数关系,依然可以考虑利用周期性的思想,在作图时,以一个“周期”图像为基础,其余各部分按照倍数调整图像即可.进一步推广还有一种形如11()()22f x f x =性质,也可类比周期性,仍以一个“周期”图像为基础,只是下一个区间长度发生变化而已.(2)周期性函数或类周期性函数作图时,若函数图像不连续,则要注意每个“周期”的边界值是属于哪一段周期,在图像中要准确标出,这是利用数形结合解题的一个易错点.2.3、函数性质之单调性概念及应用【高考13大纲理9】若函数21()f x x ax x =++在1(+)2∞,是增函数,则a 的取值范围是 A .[1,0]- B .[1,)-+∞ C .[0,3] D .[3,)+∞ 【高考14课标Ⅱ理11】若函数()ln f x kx x =-在区间(1+)∞,单调递增,则k 的取值范围是A .(,2]-∞-B .(,1]-∞-C .[2,)+∞D .[1,)+∞【高考16全国Ⅰ文12】若函数1()sin 2sin 3f x x x a x =-+在(+)-∞∞,单调递增,则a 的取值范围是A .[1,1]-B .1[1,]3-D .1[1,]3--【高考17课标Ⅱ文8】函数2()ln(28)f x x x =--的单调递增区间是A .(,2)-∞-B .(,1)-∞-C .(1,)+∞D .(4,)+∞【例题1】(18全国Ⅰ文12)设函数2,0()1,0x x f x x -⎧≤=⎨>⎩,则满足(1)(2)f x f x +<的x 的取值范围是 ( D )A .(,1)-∞-B .(0,)+∞C .(1,0)-D .(,0)-∞【分析】问题看似简单,却深刻地考察函数单调性概念,很多学生认为函数是单调递减的,不等式可转化为12x x +>得出错解,问题出在哪?单调性一定是要指明区间的,这个被忽略.【例题2】(07天津文10改)设函数22,0()0,0,0x x f x x x x ⎧-<⎪==⎨⎪>⎩,且对于任意的[,2]x t t ∈+,不等式()2()f x t f x +≥恒成立,求实数t 的取值范围.【分析】回归符号函数模型:2()sgn()f x x x =⋅,显然函数为奇函数,且函数在R 上单调递增,根据符号函数性质:222()2sgn())))f x x x f =⋅=⋅= ,化归转化抽象不等式:()2()f x t f x +≥恒成立,可转化为())f x t f +≥恒成立, 利用单调性转化:x t +≥对[,2]x t t ∈+恒成立,即1)x t ≤对[,2]x t t ∈+恒成立, 恒成立问题转化:1)(2)t t +≤,解得)t ∈+∞.【反思】解题的核心关键在于将抽象不等式的变形为函数两应变量的大小关系,再根据具体函数抽象化方法,利用其性质解题,否则就需要要讨论、再代入具体函数的繁琐的计算.3.1、函数图像之图像变换【分析】函数()f x 先整体往右平移1个单位,变换本质是1x x →+,得到(1)y f x =-;重新赋予变换后的函数一个新的抽象函数名称,令()(1)g x f x =-, 将所有点的横坐标压缩为原来的12倍,变换实质是2x x →,得到(2)(21)g x f x =-,故选B .【例题2】函数(21)y f x =-为奇函数,则下列推断正确的是( A )A .(21)(21)0f x f x -+--=B .(21)(21)0f x f x -+-+=C .(21)(21)0f x f x ----=D .(21)(21)0f x f x ---+=【分析】抽象函数具体模型验证是快速可行方法,但原理学生还是不懂,面对抽象复合函数,根据整体代换思想重新赋予其一个新的抽象函数,可发现问题本源.令()(21)g x f x =-,然后隐去(21)f x -,回到最简函数()g x ,由于是奇函数,有()()g x g x -=-, 而()(21)g x f x -=--,所以(21)(21)f x f x -=---,即(21)(21)0f x f x -+--=.【命题预期】函数(21)y f x =-关于点(1,2)中心对称,则下列推断正确的是( D )A .(21)(23)4f x f x -+--=B .(21)(23)2f x f x -+-+=C .(2)(23)4f x f x +-+=D .(2)(22)4f x f x +-+=【分析】令()(21)g x f x =-,然后隐去(21)f x -,回到最简函数()g x ,由于()g x 关于点(1,2)中心对称,有()(2)4g x g x +-=,而(2)[2(2)1](23)g x f x f x -=--=-+,所以(21)(23)4f x f x -+-+=,也即(2)(22)4f x f x +-+=. 【反思】函数图像变换的实质是“替换”,我们要清楚每一步的确切“替换”,在每一步变换前赋予一个新的抽象函数名称,准确找到变换过程中的“替换”,依此类推,一步变换赋予一个新抽象函数名称(即函数每到一个新地方改名换姓以新面孔出现),这样每一步变换就尽在我们掌控之中.3.2、利用函数性质画图像 【例题】(10山东理11)函数22x y x =-的图像大致是【分析】思路一:直接研究函数设2()2xf x x =-,则'()2ln 22xf x x =-,''2()2ln 22xf x =-(ln 20.6935≈) 显然二阶导函数''()f x 是R 上单调递增函数,''2(2)2(2ln 21)0f =-<,''2(3)2(4ln 21)0f =->即二阶导函数''()f x 在(2,3)上有一零点, 不妨设为0x (形式上虚设,运算上代换),有022ln 220x -=,即0222ln 2x =,知在0(,)x -∞时,''()0f x <,即'()f x 递减;知在0()x ∞,+时,''()0f x >,即'()f x 递增;且'(0)ln 20f =>、'(1)2(ln 21)0f =-<,'3(3)8(ln 2)04f =-<,'(4)8(2ln 21)0f =-> 发现'()f x 有且只有两个零点,不妨设为12,x x (形式上虚设,运算上代换),且111(0,1)2ln22x x x ∈=、222(3,4)2ln 22x x x ∈=,知在1(,)x -∞时,'()0f x >,即()f x 递增;在12()x x ,时,'()0f x <,即'()f x 递减; 在2()x +∞,时,'()0f x >,即()f x 递增;且122211111111222222222222()2()(2)0ln 2ln 222()2()(3)0ln 2ln 2x x x f x x x x x x x x f x x x x x x x =-=-=->->=-=-=-<-<,即()f x 在12()x x ,只有一个零点, 结合正负处极限值,知()f x 在1(,)x -∞只有一个零点,()f x 在2()x +∞,只有一个零点,()f x 在R 上有且只有三个零点,一个在(1,0)-,一个为2、一个为4.思路二:转化与化归研究函数转化与化归:研究方程22xx =的根,其中0x =不是方程的根,两边同时取对数后,也即2ln 2ln x x =,也即研究ln 2ln ||2x x =,即研究ln 20.3452y =≈与ln ||x y x =的图像公共点个数, 而ln ||x y x =是奇函数,只需要研究0x >时图像,结合对称性画出另一侧图像:ln x y x =(0x >)(大熟悉了,导数中基本型函数),'21ln x y x -=,知其先增后减,max10.345ey =>, 如图(复杂函数作趋势图像):观察图像(心中有图胜千言万语),显然是三个交点.函数的“难题”是由“原味”的初等函数“灵动”组合而成的,通过函数组合教学,实现解一题通一类.【命题预期】函数2x y a x =-(1a >)恰有三个不同零点,求实数a 的取值范围.【分析】转化与化归:研究方程2x a x =的根,也即研究x y a =与2y x =图像三个公共点问题(此处对函数图像的准确性要求很高,几何直观难办到).按例题思路二的方法,分离变量,向熟悉函数转化:其中0x =不是方程2x a x =的根,两边同取对数,也即2ln ln x a x =,也即研究ln ln ||2a x x =,即研究ln 02a y =>与ln ||x y x=的图像公共点个数,而ln ||x y x=是奇函数,只需要研究0x >时图像,结合对称性画出另一侧图像: ln x y x =(0x >)(大熟悉了,导数中基本型函数),'21ln x y x -=,知其先增后减,max 1ey =, 如例题中图(复杂函数作趋势图像):得2ln ea <,即2e 1e a <<.【反思】动态函数直接利用几何直观无法达到目的,转化为常数函数与静态函数,想到分离变量,两边同时取对数就并非“无源之水”,这就是数学思维碰撞!3.3、函数图像之穿针引线绘图如在近年高考试题中多次出现“乘积结构”类型的有难度的函数试题,从这些试题“乘积结构”的特征出发,巧用“穿针引线”绘函数图像,可快速解决.穿针引线绘图像微课程 【例题1】(12浙江理17)设R a ∈,若0x >时,均有2[(1)1](1)0a x x ax ----≥,则实数a = _______. 【分析】思路一、代数法解不等式分析设2()[(1)1](1)f x a x x ax =----,()(1)1g x a x =--,2()1h x x ax =-- 当x →+∞时,2()1h x x ax =--开口向上,知()h x →+∞,由条件0x >时,均有2[(1)1](1)0a x x ax ----≥,知当x →+∞时,()g x →+∞,得10a -> 知11x a =-是210x ax --=的根,得0a =(舍去)或32a =. 思路二、图像法解不等式分析设2()[(1)1](1)f x a x x ax =----,()(1)1g x a x =--,2()1h x x ax =-- 当x →+∞时,2()1h x x ax =--开口向上,知()h x →+∞,由条件0x >时,均有2[(1)1](1)0a x x ax ----≥,知当x →+∞时,()g x →+∞,得10a -> 由(0)10h =-<,知()h x 有两个一正一负零点,不妨设为120x x <<,()g x 的零点为3101x a =>- 若32101x x a =>>-,由“穿针引线”,画出()f x 的图像如图3,知()f x 在23(,)x x 上()0f x <(不合); 若32101x x a <=<-,由“穿针引线”,画出()f x 的图像如图4,知()f x 在32(,)x x 上()0f x <(不合); 要满足题设条件,由穿针引线法(图5)知,只有3211x x a ==-,即1()01h a =-把311x a =-代入210x ax --=,求得32a =.【命题预期】(13浙江理8)已知e 为自然对数的底数,设函数()(e 1)(1)(1,2)x k f x x k =--=,则( ) A .当1k =时,()f x 在1x =处取得极小值 B .当1k =时,()f x 在1x =处取得极大值 C .当2k =时,()f x 在1x =处取得极小值 D .当2k =时,()f x 在1x =处取得极大值【反思】1、试题编制过程应该是将两个简单的函数1(1)1y a x =--与221y x ax =--拼接在一起,两函数含有同一参数a ,且都过同一定点(0,1),画出两函数图像,要使120y y ⋅≥在0x >恒成立,必须有且只有直线零点经过二次函数另一零点!根据试题源头分析,解决这个问题策略是将两函数重新拆开,根据图像直观分析.2、在平面直角坐标中,利用穿针引线法可画出解析式为乘积式(已因式分解找到了零点)的函数的大体图像,仍同用“穿针引线”法解高次不等式类似,保证函数最高次幂系数为正,“ 遇奇直穿,遇偶折回”的原则,用直观的图像可突破代数的抽象,解题效率得到大大提高.4.1、特殊函数之抽象函数【例题1】已知函数()f x 对任意的实数,x y 均有()()()f x y f x f y +=+,且当0x >时,()0f x >,(1)2f -=-,则()f x 在[12]x ∈-,上的值域为__________.【分析】用变量x 替换y ,得(2)2()f x f x =,即()2()2x f x f =(这还是个恒等式,用运动眼光看到是自变量成倍数关系时,应变量也是倍数关系,好象是个正比例函数,又(1)2f -=-这时很多同学会以2y x =作原型函数)猜测()f x kx =,又(1)2f -=-,得()2f x x =,检验满足0x >时,()0f x >,所以()f x 在[12]x ∈-,上的值域为[24]x ∈-,. 【知识拓展】用变量x 替换y ,得(2)2()f x f x =,即()2()2xf x f =设12,R x x ∈,11()2()2x f x f =,22()2()2x f x f =,即11()()22f x x f =,22()()22f x xf = 得1212()()()()2222f x f x x x f f +=+, 1212()()()()222f x f x x xf f +=+ 对任意12,R x x ∈,有1212()()()f x x f x f x +=+,即1212()()()222x x x xf f f +=+ 所以1212()()()22f x f x x xf ++=,说明函数图像上任意两点的中点也在此两点连线上 所以()f x 图像是直线,又取120x x ==得(0)0f =,即直线还过原点所以()(R)f x kx k =∈,得证.【例题2】设函数()f x 是实数集R 上的单调递增函数,若()()(2)g x f x f x =--,且12()()0g x g x +>,求证:122x x +>.【分析】先判断函数()g x 的单调性:(抽象函数的单调性判定一般只能用单调性定义)设任意12R x x ∈,,且12x x <,∴1222x x ->-(预设自变量大小关系,判断应变量大小关系是否一致)()f x 是实数集R 上的单调递增函数,∴12()()f x f x <,21(2)(2)f x f x -<-∴121122()()()(2)[()(2)]g x g x f x f x f x f x -=-----1221[()()]+[(2)(2)]0f x f x f x f x =----<(方向明确,判断应变量大小关系) ∴12()()g x g x <,即()g x 为实数R 上的单调递增函数;又22222()[()(2)](2)()g x f x f x f x f x -=---=--(验证猜想22()(2)g x g x -=-是否成立) 而22222(2)(2)[2(2)](2)()g x f x f x f x f x -=----=--,得22()(2)g x g x -=-, 由12()()0g x g x +>,得122()()(2)g x g x g x >-=-,即12()(2)g x g x >-, 且()g x 为实数R 上的单调递增函数,得122x x >-,即122x x +>得证.有极大值1(1)ef =,画函数大致图像: 结合条件12()()f x f x =,知1201x x <<<,121x ->要证明结论 122x x +> ⇔ 212x x >-,逆用单调性 ⇔21()(2)f x f x <-,由条件12()()f x f x = 变量化一 ⇔11()(2)f x f x <-,即证11(2)11e(2)e x x x x ---⋅<-⋅(注意定义变化101x <<)等价变形 ⇔11112(2)e 0e e x x x x -+<,构造函数2(2)e ()e ex x x xg x -=+,(0,1)x ∈(发现函数零点(1)0g =) 研究新构造函数:22'222(1)e 1(1)(e e )(1)()(e e)(e e)e e e ex x x x x x x x x x x g x ++-----=+==+- 分析导函数知:在(0,1)x ∈上有'()0g x >,正用函数单调性:在(0,1)x ∈上有()(1)0g x g <=,原命题得证.4.2、特殊函数之分段函数【例题1】(15湖南15)已知函数32,(),x x af x x x a ⎧≤=⎨>⎩,若存在实数b ,使得()()g x f x b =-有两个零点,则实数a 的取值范围是___________.【分析】图像直观发现分段函数性质:试题难点是分类界点的确定,由32x x =,得到界点为01,.(1)当0a < (2)当01a ≤≤ (3)当1a > 显然只有在0a <或1a >时,函数()f x 不单调,()()g x f x b =-有可能有两个零点.(1)当1a ≤时,1()f x x x =-,在[1,4]x ∈上递增,则15()4g a =; (2)当14a <<时,12(),1()1,4a x x a xf x x a x x ⎧-+≤≤⎪⎪=⎨⎪-<≤⎪⎩,在[1,]x a ∈上递减,则()22g a a =-;在(,4]x a ∈上递增,则15()4g a =;继续比较154与22a -的大小,分界点为238:(二级讨论)当2318a ≤≤时,15()4g a =;当2348a <<时,()22g a a =-; (3)当4a ≥时,1()2()f x a x x =-+,在[1,4]x ∈上递减,则()22g a a =-;综上所述:1523,48()2322,8a g a a a ⎧≤⎪⎪=⎨⎪->⎪⎩.【反思】绝对值函数是高中数学重要内容,如果绝对值函数中带有参变量,那这类问题比较复杂.其方法是先把绝对值函数先写成分段函数形式,通过研究分段函数的“整体”图像,找到分类讨论的“界点”(依据),画龙贵于点睛,分类讨论难于找界点.4.3、特殊函数之复合函数【例题1】设函数22,0(),0x x x f x x x ⎧+<=⎨-≥⎩,若(())2f f a ≤,则实数a 的取值范围是_________.【分析】问题的内层与外层函数是同一个函数,其核心是要把(())2f f a ≤转化为关于a 不等式,由已知函数()f x 的表达式.思路一:借助代数推理,由外到内剥离整体换元()f a t =剥离内层函数,先解不等式()2f t ≤,得出t 范围,再将换元代回,计算a 范围.由分段函数讨论:202t t t <⎧⎨+≤⎩或202t t ≥⎧⎨-≤⎩,即20t -≤<或0t ≥,即2t ≥- 解决完内层函数,再回到外层函数考虑, ()2t f a =≥-,再次同样对分段函数讨论:202a a a <⎧⎨+≥-⎩或202a a ≥⎧⎨-≥-⎩,得0a <或0a ≤≤,即a ≤为所求.思路二:借助几何直观,由外到内的深入函数22,0(),0x x x f x x x ⎧+<=⎨-≥⎩,图像如图:观察外层函数图像,由(())2f f a ≤,知()2f a ≥-再观察内层函数图像,由()2f a ≥-,知a ≤.【反思】解决复合函数[()]y f g x =问题的核心就是如何转化为单层函数问题,转化的主要方式是由内而外的剥离,先将内层函数整体()t g x =换元,再转化研究()y f t =(其中函数的变化特点是函数()t g x =的值域是函数()y f t =的定义域).5.数学思维之整体思维思路一:变量代换后分类讨论令4x t x+=,由[14]x ∈,,知[45]t ∈,,问题转化为函数()||g t t a a =-+在[45]t ∈,最大值为5, 讨论(一)对参数a 分(1)4a ≤、(2)45a <<、(3)5a ≥进行类讨论求最值.讨论(二)抓住函数图像特征,优化讨论,()||g t t a a =-+为V 型函数,max ()max{(4),(5)}g t g g =,再对(4)(5)g g ≤与(4)(5)g g >分类讨论.思路二:从不等式恒成立问题视角转化问题转化为4||5x a a x +-+≤对[14]x ∈,恒成立,即455a x a a x -≤+-≤-对[14]x ∈,恒成立, 即42545a x x x a ax ⎧-≤+⎪⎪⎨⎪+-≤-⎪⎩,根据且命题的恒成立处理原则得92a ≤.【例题2】(08浙江理15)已知t 为常数,函数2()|2|f x x x t =--在区间[03],上最大值为2,则实数t 的值为________. 【分析】思路一:优化讨论max ()max{(0),(1),(3)}f x f f f =,以三个值大小为依据确定讨论的界.思路二:采用整体换元,令22x x m -=,由[03]x ∈,,得[13]m ∈-,,问题转化为||y m t =-在[13]m ∈-,上,函数最大值为2.函数的几何意义可视为数轴上两点间距离,即数轴上任意动点到区间[13]-,上任意动点最大距离为2,只有落在区间[13]-,的中点满足题意,即1t =.思路三:从不等式恒成立问题视角转化问题转化为2|2|2x x t --≤对[03]x ∈,恒成立,即2222x x t -≤--≤对[14]x ∈,恒成立,即222222t x x x x t⎧≤-+⎨--≤⎩对[03]x ∈,恒成立,即1t =. 【命题预期】已知t 为常数,函数2()||f x x tx t =--在区间[03],上最大值为2,则实数t 的值为________.【分析】这时采用整体换元就无法应对了,但还是可以从优化讨论或恒成立问题转化下手.【反思】换元法就是通过引入一个或几个新变量来替换原来的某些变量的解题方法,我们都深刻知道换元关键是要注意新变元定义的变化,换元仅是一种变量代换,即整体思维,但它可以把复杂函数变为简单函数,化难为易、化繁为简,快速实现未知向已知转换.。
社会主义先进文化的本源探析

中国特色社会主义理论与实践研究课程论文社会主义先进文化的本源分析【摘要】:文化是多元的,这是社会生活多元性决定的;而用先进修饰文化,就是意识形态和价值观的问题。
那么,在当前,什么是先进文化呢?江泽民在“七一”讲话中明确指出:“在当代中国,发展先进文化,就是发展有中国特色社会主义的文化,就是建设社会主义精神文明。
”可见,中国先进文化与中国特色社会主义文化、社会主义精神文明这三个概念的内涵是一致的。
当代中国的先进文化,就是以马克思主义为指导,以培养有理想、有道德、有文化、有纪律的公民为目标的,面向现代化、面向世界、面向未来的,民族的科学的大众的,健康向上的,具有中国风格、中国特色的社会主义文化和文明。
【关键词】:本源马克思主义社会主义先进文化一、中国特色的社会主义先进文化的内涵(一)马克思主义文化观马克思主义认为,文化是在人改造自然的对象化劳动中产生的,是以人化为基础,以人的本质或本质力量的对象化为实质的,它包括物质文化、精神文化等因素,是一个广义的文化概念。
文化在本质上是实践的,马克思概括道:“社会生活在本质上是实践的。
”据此引申,也可以说文化在本质上是实践的。
因为人的社会生活与其价值意识不可分离,而“人化”趋向又是社会实践的必趋之势,因此,社会生活的本质与文化相容并成为一个整体。
我们可以说,马克思的文化观是以“每个人的自由发展”和“一切人的自由发展”为价值枢纽的。
在经济、政治和文化这三者的关系中,经济是基础,是最终起决定作用的因素;政治是经济的集中反映,被经济所决定,又对经济起着巨大的反作用;文化则是一定的经济和政治的反映,并给经济和政治以重大的影响。
一定的社会,都是一定的经济、政治和文化的统一体,这三个方面的相互联系和相互作用推动社会不断发展前进。
这是马克思主义文化观的基本原理。
(二)文化结构人类直接相关的生产有物质生产和物质性入口生产这两种。
那么,与之相应的生产能力和所创造的财富也应该有两种:一种是物质生产能力和所创造的物质财富;另外一种是物质性人口生产能力和所创造的物质性人口财富。
本质的哲学名词解释

本质的哲学名词解释
本质的哲学是一种研究事物本质的哲学流派。
它关注事物的本质属性和本体特点,探讨事物存在的根本性质和内在规律,力图揭示事物的真正本质和核心。
本质的哲学认为事物的本质是其存在的固有属性,是决定其独特性和特征的根本要素。
它追求回归事物真实的本质,超越表面现象和外在显现,探索事物的本源、本质和本格。
本质的哲学强调理性思维,注重思考和解剖,试图通过思辨和辩证的方法揭示事物的本质特征。
本质的哲学涉及的主要问题包括:事物的存在与本质关系、主体与客体的关系、事物发展的内在定律、精神与物质的关系等。
它通过对现象背后的真实本质进行分析和探索,希望能够揭示事物的根本规律,为人们认识和改造世界提供理论指导。
本质的哲学在哲学史上有多种代表性派别,如古希腊的本质论派、黑格尔的本质辩证法、康德的本质批判等,它们对本质的概念和研究方法有不同的理解和表达。
在现代哲学中,本质的哲学被视为一种重要的思维方式和研究取向,对认识世界和人类自身具有重要意义。
史学概论期末考点

1、什么是史学的本体论、认识论、方法论?历史学本体论:关于历史现象存在的本源和性质观点或理论,核心是社会历史观(也即是对客观历史本质的反思)。
历史学认识论和方法论则是对历史学作为一门学科在对客观历史的认识和研究方法上的理论思考。
也有学者把史学本体论称为历史理论,认识论和方法论称为历史学理论或史学理论。
历史认识论是关于历史认识的理论,它与历史本体论、历史方法论或史学方法论共同构成了历史哲学。
具体说来,它是关于历史认识主体认识其客体的过程、特征、方法等等的理论,它主要涉及历史认识主体(人、特别是史学家)和历史认识客体(即客观历史)各自的特点,二者之间的关系,涉及历史认识过程的特点、历史认识正误的原因及其检验方法,还涉及历史认识如何对实践乃至对现实发展进程的影响。
2、历史广义、狭义之分广义:自然史、人类史,指客观世界运动发展的过程。
狭义:人类史(指人类社会发生、发展的过程)3、自然史和人类史的关系(不同)。
①自然史与人类史相比,在时间上要久远得多,在范围上也要广泛得多。
②人类史是人类自己创造的,而自然史则不然,自然是没有意识的存在。
4、唯物史观与唯心史观的区别历史唯物主义和历史唯心主义是两种根本对立的历史观。
历史唯心主义认为:社会意识第一性,存在第二性,社会意识决定社会存在。
历史唯心主义把人们的思想动机、英雄人物的意志或某种超自然的神秘力量看做是社会历史发展的根本原因。
它否认社会发展的客观规律。
否认人民群众在历史上的决定作用。
而历史唯物主义认为:存在第一性,意识第二性,社会意识是存在的派生物。
社会的基本矛盾是历史发展的根本动力,肯定了社会发展的客观规律,认为人民群众才是历史的创造者。
5、唯心史观代表观点历史唯心主义有两种基本形态:主观唯心主义和客观唯心主义。
主观唯心主义把人们的思想动机主要是少数的英雄人物的意志看作是历史发展的根本动力,用主观精神解释社会的发展。
客观唯心主义则从社会外部寻找某种神秘的精神力量,把诸如上帝、神等所谓的客观精神看作是历史发展的决定力量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《论本源性质》
所有事物都是由其对立物或中间物产生并消失在对立物或中间物。
另一个说法是所有事物都是由本源产生。
我认为如果连对立性也是由本源产生,那么本源就不具有对立性而是具有独立性。
在各种情况中变化的都必定有一件事物作为变化的基础。
如果将一件变化的事物的变化前称为前现象,变化后未完成变化的状态称为后现象。
那么变化后未完成变化的状态可以称为变化后完成的状态的前现象,可知某一事物在变化的情况下必然会出现既是前现象又是后现象的中间部分,既相对于前又相对于后,依靠于之前可独立于之后,依靠于之后可独立于之前。
比如一个不认识字的人从来不认识字,不认识字的时候是前现象,学会认字是后现象。
那么学习认字的过程既是前现象的后现象又是后现象的前现象。
如果去掉学习认字的过程,那么从不认字到认识字根本无法完成。
而不认字又可以作为其它事物的后现象,认识字又可作为其它事物的前现象,我将它称为“前后互换”。
在亚里士多德的《物理学》中将绝对产生事物的方式大致分为:(1)形状的改变、(2)添加减少、(3)性质改变。
那么如果要证明本源是不变的话就要证明本源不具有形状、本源不具有数量、本源不具有性质。
从而可以知道本源既不是圆的也不是方的,因为本源不具有形状。
本源既不是一个也不是多个,因为本源不具有数量。
本源既不是金做的也不是银做的,因为本源不具有性质。
如果引入前面所讲的“前后互换”的概念的话,本源既是圆的又是方的,本源既是一个也是多个,本源既是银做的也是金做的。
从而可以引出本源可见也不可见,存在于万物之中却具有独立性。
就如人格至尊首神所说的“众生在我之中,我却不在众生之中。
”
万事万物都有个静止转为运动,运动转为静止的过程。
比如将一个棍子扶持竖立在地上,此时的棍子是静止的,而如果我们放开手静止的棍子就变为了运动的棍子,倒在地上停止运动后又变为静止了。
然而造成万事万物的变化也不是没有原因的,佛教称之为缘起,也就是由因缘产生。
再比如冰变成水,冰是不能无缘无故就变成水的,而是由于温度过高而引起的。
本源既是万物的起源又是一切的初始,既是每一个事物的材料又是规定事物的形状、状态、形式。
而在物质发生变化时却不变化。
从而可知(1)本源虽然是一切的初始但又存在于一切之中。
、(2)本源是物质的形状、状态、形式,是物质的前现象又是物质的后现象。
(3)是物质变化的原因,既是创造又是毁
灭。
这样便可知道一切事物都是没有偶然的,都是必然的。
一个看似偶然的事情是由之前的必然的事物产生。
那么这个偶然也就是必然,对于之前的必然来说是必然的,对于由这个看似偶然的必然所产生的必然的事物又是必然的。
那么这个必然的概念是具有假设性还是必然性?如果具有必然性,那么必然是必然发生的,如果具有假设性,那么这个必然很可能是非必然的。
就像是生孩子是注定生出谁还是可能生出谁。
从因果的角度来说,生孩子是具有必然性,那么必然会生出谁。
因为事物都具有必然性,那么必然性也是必然的,可知物质的变化也是必然的,究竟物质的变化是有限和无限的?因为这关系到了本源是有限还是无限。
事实上一件事物既可以作为有限对待也可以作为无限对待。
比如冰变成水,如果只看冰变成水,那么变成水后变化就完成了,也就是有限的。
但是如果是看水分子的话,那么水分子的间距变化了,而且分子本身一直都有在运动。
具有必然的事物既是存在又是不存在。
存在的事物会因为必然性的变化而消失为不存在,而不存在的事物又可变为存在。
比如有座“雕像”,它是存在的。
当我们打碎它时,“雕像”不存在了。
当我们用它的碎石再做一个雕像时,“雕像”又存在了。
所以可知事物的存在与不存在,有限和无限是因为人所赋予的概念的不同。
那么可以得出本源的存在与不存在和有限与无限也是会随着人所赋予的概念的不同而发生改变。
那么本源究竟会不会变化呢,我想既是会也是不会吧。
构成万物的材料是本源,而事物本身在变化那么本源也必将变化。
但是根据能量守恒定律,不管物质怎么变化,能量的总和是无法改变的。
再说了“变化”这件事还是由本源构成的呢。
如果要拿一个图形来形容本源,我认为圆最合适。
为什么呢?因为在圆上做往返运动可以无停留的无限循环下去,而在直线构成的图形上做往返运动必然会发生停留也就是无法完成永恒的连续运动。
参考文献:①《薄伽梵歌》巴帝维丹达书籍出版有限公司, 2009.
②亚里士多德《物理学》商务印刷出版社, 1997.。
