高等土力学土中水及渗流计算(193页)
高等土力学04土中水及渗流计算

深基坑中渗透影响水土压力及支护结构的内力
采油工业 地下水污染 :废水、固体垃圾、放射性废料· · · · 生物力学
渗流的工程应用
§4.1 导言
仁者乐山 智者乐水
98洪水中的险情和溃口
长江出险:6100多处; 松花江与嫩江:9500多处;60-70%为管涌 历史上长江干堤决口的90%由于堤基管涌所导致 98·8·7:九江城防管涌决口,形成61米宽溃口 98·8·4:江西江新洲管涌引起溃口,淹没区4.1 万人,78km2
仁者乐山 智者乐水
总水头:单位重量水体所具有的能量
位置水头Z:水体的位置势能(任选基准面)
u v2 h= z+ + w 2g
压力水头u/w:水体的压力势能(u孔隙水压力)
流速水头V2/(2g):水体的动能(对渗流多处于层流≈0)
u 渗流的总水头: h = z + w
也称测管水头,是渗流的总驱动能,渗流 总是从水头高处流向水头低处
T T
kxx k = k yx kzx
{i}为由其三个水力坡 降分量组成的向量 对各向同性材料,其 方向同流速方向一致 对于各向异性材料, 其方向同流速方向不 一致
v = vx i = ix
重力势 g 压力势 p 基质势 m 溶质势 0
A hA
0
10
20
w(%)
A = g + m = whA + m = 0
m = - whA
§4.2 饱和土的渗透性和基本方程 - 土中水的势能
仁者乐山 智者乐水
土中水的势能:
重力势 g 压力势 p 基质势 m 溶质势 0
渗流力计算公式

渗流力计算公式
1. 基本概念。
- 渗流力是一种体积力,它是由于土中渗流的存在而产生的作用于土骨架上的力。
- 当水在土孔隙中流动时,会对土颗粒施加拖曳力,这个拖曳力就是渗流力。
2. 公式推导。
- 假设土样的横截面积为A,长度为L,土颗粒间的孔隙率为n,水力坡降为i,水的重度为γ_w。
- 作用在土样两端的水头差为Δ h,则水力坡降i=(Δ h)/(L)。
- 渗流速度v = ki(达西定律,k为渗透系数)。
- 单位时间内通过土样的渗流水体积Q = vA。
- 渗流水的重量G_w=γ_wQ=γ_wvA。
- 渗流力J等于渗流水的重量除以土颗粒的体积V_s。
- 因为土颗粒的体积V_s=(1 - n)AL,所以渗流力J=(γ_wvA)/((1 - n)AL)。
- 又因为v = ki,所以J=(γ_wkiA)/((1 - n)AL)=(γ_wi)/(1 - n)。
- 在一般的土力学分析中,如果忽略土颗粒的孔隙率n对渗流力计算的影响(当孔隙率较小时),渗流力J=γ_wi。
3. 公式应用。
- 在土坡稳定分析中,渗流力是一个重要的因素。
例如,当土坡中存在渗流时,渗流力会使土坡的下滑力增加,从而降低土坡的稳定性。
土力学土的渗透性及渗流

8
2、渗流量的计算及渗透变形控制问题
基坑围护结构下的渗流
板桩墙
基坑
透水层
渗流问题:
1. 渗流量? 2. 渗透破坏? 3. 渗水压力?
不透水层
9
基坑开挖降水
井点降水
10
管井降水
11
工程实例 湖南浯溪水电站二期基坑出现管涌
12
2、渗流量的计算及渗透变形控制问题
水井渗流 Q
天然水面
含水层
渗流问题:
38
三、成层土的平均渗透系数
天然土层多呈层状
✓确立各层的k ✓考虑渗流方向
等效渗透系数
39
水平渗流 将土层简化为均质土,便于计算
总流量等于各土层流量之和 (各层的水力梯度相等)
条件:
im
i
h L
Q q j kxiH
q j v j H j k jiH j
等效渗透系数:
m
Q kxiH i k j H j j 1
P1 = γwhw
P2 = γwh2
R + P2 = W + P1
R + γwh2 = L(γ + γw) + γwhw
R = ? R = γ L
0
45
静水中的土体 R = γ L
渗流中的土体
ab
P1
W A=1
P2 R
W = Lγsat=L(γ + γw)
贮水器 hw L 土样
0
Δh
h1 h2
0 滤网
非线性流(紊流) 地下水的渗流速度与 水力梯度成非线性关系
线性稳定流
线性非稳定流
非线性稳定流 非线性非稳定流
我们现在需要掌握和理解的达西定律
高等土力学-土中水及渗流计算

仁者乐山 智者乐水
1856年法国工程师达西(Darcy)提出达西定律 1889年俄国的茹可夫斯基推导了渗流的微分方程 1901年劳(Low)给出了粘土颗粒表面结合水形成
的机理
1910年理查森首先提出了有限差分法
1922年巴甫洛夫斯基提出了求解渗流场的电模拟法 20世纪60年代之后,计算渗流力学发展。非饱和土、
历史上长江干堤决口的90%由于堤基管涌所导致 98·8·1:簰州湾,管涌引起决口,44人丧生;造成
31米深冲坑
98·8·7:九江城防管涌决口,形成61米宽溃口 98·8·4:江西江新洲管涌引起溃口,淹没区4·1万
人,78km2
98长江洪水中的险情和溃口
第四章 土中水及渗流计算 4.1 导言
第四章 渗流计算 4.2 土中水形态及对土性影响-毛细现象
仁者乐山 智者乐水
毛 细 管
hc
T
hc wΒιβλιοθήκη 4Tcosd
0
4T cos
ua-uw
hc wd
d
土中毛细水
第四章 渗流计算 4.2 土中水形态及对土性影响-毛细现象
毛细力与 孔隙半径
仁者乐山 智者乐水
不同曲率半径情况下 毛细管中的水-气分 界面
当水量较小时,气水交界面位于 小孔隙处,其弯液面曲率半径较 小。随着水量增加,弯液面曲率 半径逐渐增加
第四章 渗流计算 4.2 土中水形态及对土性影响-基质吸力
仁者乐山 智者乐水
pc
pa
pw
20 rk
cos
空气 水 固体颗粒
小孔隙对应大的基质吸力 多相界面在小孔隙(曲率半径最小)
处最易达到平衡
湿润流体相和固体表面附着力最大,
通常首先占据小孔隙
2 土力学 第二章 土的渗透性及水的渗流
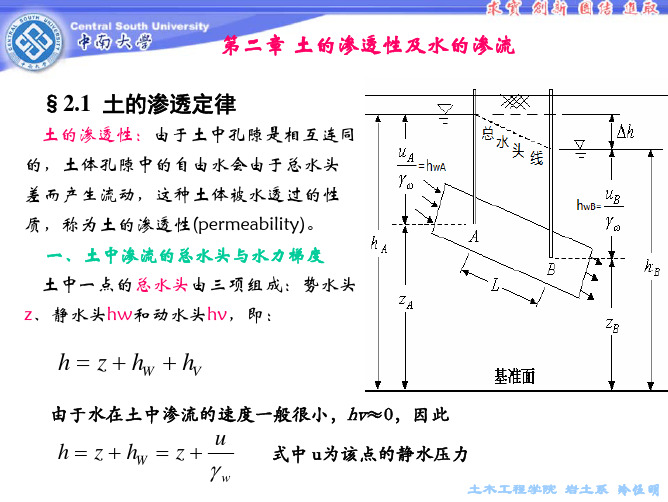
二、临界水力梯度及渗透破坏 当土中水向上渗流时,渗透力垂直向上而与土样重力方向相反,若渗透力 等于土样浮度,即
j = iγ w = γ , 得临界水力梯度: i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此,若土中水向上渗流: ⑴若i>icr,会发生流土破坏,即“管涌”; ⑵若i=icr,流土处于临界状态,即“悬浮”; ⑶若i<icr,不会发生流土破坏。
h = z + hW + hV
由于水在土中渗流的速度一般很小,hv≈0,因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
A、B两点的总水头可分别表示为:
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差:
作业题:P54: 2-7,2-9 补题1:什么是渗透力、临界水力梯度?
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性:由于土中孔隙是相互连同 的,土体孔隙中的自由水会由于总水头 差而产生流动,这种土体被水透过的性 质,称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成:势水头 z、静水头hw和动水头hv,即:
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得,只能通过试验确定。 测定k值室内方法:定水头法、变水头法。 (1)定水头法 保持总水头差Δh不变,在t时间内,量得透过土样的水量为Q,求k: 根据达西定律
土力学第二章 土的渗透性及水的渗流1
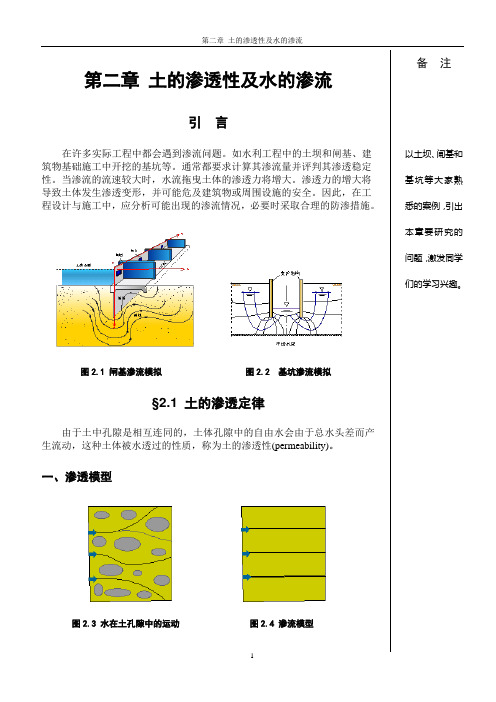
第二章土的渗透性及水的渗流引言在许多实际工程中都会遇到渗流问题。
如水利工程中的土坝和闸基、建筑物基础施工中开挖的基坑等。
通常都要求计算其渗流量并评判其渗透稳定性。
当渗流的流速较大时,水流拖曳土体的渗透力将增大。
渗透力的增大将导致土体发生渗透变形,并可能危及建筑物或周围设施的安全。
因此,在工程设计与施工中,应分析可能出现的渗流情况,必要时采取合理的防渗措施。
图2.1 闸基渗流模拟图2.2 基坑渗流模拟§2.1 土的渗透定律由于土中孔隙是相互连同的,土体孔隙中的自由水会由于总水头差而产生流动,这种土体被水透过的性质,称为土的渗透性(permeability)。
一、渗透模型图2.3 水在土孔隙中的运动图2.4 渗流模型备注以土坝、闸基和基坑等大家熟悉的案例,引出本章要研究的问题,激发同学们的学习兴趣。
121. 不考虑渗流路径的迂回曲折,只分析它的主要流向;2. 不考虑土体中颗粒的影响,认为孔隙和土粒所占的空间之总和均为渗流所充满;3. 在同一过水断面,渗流模型的流量等于真实渗流的流量;4. 在任意截面上,渗流模型的压力与真实渗流的压力相等;5. 体积内,渗流模型所受到的阻力与真实渗流所受到的阻力相等。
二、土中渗流的总水头与水力梯度图2.5 渗流中的位置、压力和总水头液体流动应满足:连续原理和能量方程,即伯努里(D.Bernoulli)方程。
水头:单位重量水体所具有的能量,包括动能和位能。
gv uz h 22++=ωγ A 、B 两点的总水头可分别表示为:g vu z h A AA 221++=ωγg vu z h B BB 222++=ωγ式中A z 、B z —分别表示A 点和B 点相对于任意选定的基准面的高度,代表单位重量液体所具有的位能,故称为位置水头。
B A u u 、—分别为A 点和B 点的水压力,在土力学中称为孔隙水压力。
代表单位重量液体所具有的压力势能。
备 注结合水力学内容介绍。
高等土力学4.6_渗流的数值计算.

N 2 x
h3
N 3 x
h3
C21h1 C22h2
C23h3
iz
h z
C31h1Leabharlann C32h2C33h3
h
ix iz
x h
C21 C31
z
C22 C32
C23 C33
h1 h2 h3
vx vz
k 0
0
k
iixz
h t
N
h t
e
2. 单元渗流矩阵
I(h)
e1 m
Pije
K
h
P
h t
S
h t
F
0
Fij
e1
Fije
整体平衡方程
自由水面
可压缩部分
K
h
P
h t
S
h t
F
0
已知结点的部分
K
h
P
h t
S
h t
F
0
这样就可对式多元联立方程组用不同的数 学方法求解,得到各单元结点水头; 然后可用式(4.6.15)求单元域内任一点水 头值,从而得到有限元数值分析的解; 对于三维渗流计算方法是一样的;
a3z1 a3z2
h3 a1 a2 x3 a3z3
设:
CC1211
(x2 z3 (z2
x3z2 )/ z3 )/ 2 Ae
2 Ae
C12 (x3z1 x1z3 )/ C22 (z3 z1 )/ 2 Ae
2 Ae
C13 (x1z2 x2 z1 )/ 2 Ae C23 (z1 z2 )/ 2 Ae
1. 渗流场的离散与插值函数 图4-73 有限单元网格划分
假设单元的水头函数值在1、2、3结点上的值分别 为h1,h2,h3,在单元内部的值可用线性插值求得:
土木工程中的渗流场计算方法

土木工程中的渗流场计算方法引言在土木工程领域中,渗流现象的研究和计算是非常重要的。
渗流是指水流通过多孔介质的过程,它在土壤力学、水力学和地下水模拟等方面都起着关键作用。
正确计算渗流场是土木工程设计和施工的基础,因此对于渗流场计算方法的研究和应用具有重要意义。
一、概述渗流场计算的基本原理是根据多孔介质流动的守恒方程和边界条件,采用数值计算方法求解物理场的分布情况。
基本的渗流方程可以用Darcy定律表示,即流体在多孔介质中的流动速度与渗透率和渗压梯度成正比。
针对不同的土体和工程条件,有多种计算方法可以应用于渗流场的计算。
二、有限差分法有限差分法是计算渗流场的常用方法之一。
它将物理场离散化为有限个节点,利用有限差分近似代替偏导数,建立离散方程组,并通过数值迭代方法求解。
有限差分法计算简单、直观,适用于大部分渗流问题。
但是,在处理复杂边界条件和非线性问题时,有限差分法的精度和稳定性可能受到限制。
三、有限元法有限元法是另一种常用的渗流场计算方法。
它将物理场离散化为有限个单元,利用有限元的形函数对物理场进行近似,并通过建立离散方程组求解。
有限元法在处理各向异性介质和非线性问题时较有优势,且可以较好地处理边界条件。
然而,相比于有限差分法,有限元法需要更多的计算资源和复杂的数值算法,计算成本较高。
四、边界元法边界元法是一种较为特殊的渗流场计算方法。
它基于格林函数的理论,将边界上的渗流问题转化为边界上的边值问题,然后利用边界条件和格林函数进行求解。
边界元法适用于处理特殊形状和边界条件的问题,对于模拟地下水流动和地下水污染传输等问题有广泛应用。
然而,边界元法对网格划分和边界处理较为敏感,需要细致的几何建模和数值计算。
五、数值模拟软件随着计算机技术的不断进步,数值模拟软件在土木工程中的应用越来越广泛。
目前市面上有许多专业的渗流模拟软件,如FLAC、SEEP/W和MODFLOW等。
这些软件通过图形界面和高效的求解算法,实现了快速、准确地计算渗流场。
土力学系列土的渗透性和渗流PPT课件

流入和流出相等:
adh= k(h/L)Adt
即 dt aLdh kAh
整理并积分得
由此求得渗透系数:
第24页/共47页
2021/6/9
变水头渗透试验装置
第25页/共47页
3.现场抽水试验
▪ 粗颗粒土或成层的土,室内试验时不易取得原状土样; ▪ 小土样不能反映天然土层的结构性。
第3页/共47页
图3-1 渗流模型
渗流模型基本假定:
➢ 不考虑渗流路径的迂回曲折,只分析它的主要流向; ➢ 认为孔隙和土粒所占的空间之总和均为渗流所充满。
第4页/共47页
➢ 同一过水断面,渗流模型的流量等于真实渗流的流量; ➢ 任一界面上,渗流模型的压力与真实渗流的压力相等; ➢ 相同体积内,渗流模型所受阻力与真实渗流相等。
图3-1 渗流模型
第5页/共47页
1.渗流速度 断面面积为A,通过的渗透流流量为q,则平均流速为:
v=q/A
真实渗流仅发生在孔隙面积A内,因此真实流速为:
于是
v0=q/A
v/v0=A/A=n
“模型的平均流速要小于真实流速”
第6页/共47页
2.水头
能 量 是 用 水 头 来 表 示 , Bernoulli’s Equation:
图3-12 流土示意图
第42页/共47页
▪ 比较和区别: ✓ 流砂现象发生在土体表面渗流逸出处,不发生于土体内部 ✓ 管涌可以发生在渗流逸出处,也可能发生在土体内部
第43页/共47页
例3-4:
(1)由渗透力计算公式得j=wi 而 故
第44页/共47页
(2) 由 可得
即 发生流土现象。
而
第45页/共47页
高等土力学(李广信)4

4.1.3 土中水和渗流问题的研究历史
1.1901劳(Low)年给出了粘土颗粒表面结合水 形成的机理;
2.1856年,法国工程师达西(Darcy)提出了线性 渗流的达西定律;
3.1910年理查森(L. F. Richardson)首先提出了 有限差分法;
4.20世纪60年代之后, 渗流计算发展:非饱和土、 固结与变形耦合计算、与极限分析耦合、混合 流、污染物扩散……
4.1.1岩土中的水及其运动
蒸发
图4-1 土中水
滞水 潜水
图流的生态与工程意义
1.土中水是地球生命的源泉 2.渗漏:我国渠系中水的利用系数平均不足0.5 3.渗透破坏:土坝中有39%是由于渗透引起的 ;堤防
60%~70%是由于“管涌”等渗透变形引起的 4.深基坑中渗透影响水土压力及支护结构的内力,也是其
失事的主要原因 5.采油工业 6.地下水的污染 :废水、固体垃圾、放射性废料……
98长江洪水中的险情和溃口
1)长江出险:6100多处 2)98.8.1:簰州湾,管涌引起决口,44人丧生;造
成31米深冲坑 3)98.8.4:江西江新洲管涌引起溃口,淹没区4.1
万人,78km2 4)98.8.7:九江城防由于管涌决口,形成61米宽溃
第4章 土中水与土的 渗透及其计算
第4章 土中水与土的渗透及其计算
4.1 概述 4.2 土中水的形态及其对土性的影响 4.3 土的渗透性 4.4 二维渗流与流网 4.5 有关渗流的一些工程问题 4.6 渗流的数值计算
4.1 概述
4.1.1岩土中的水及其运动 4.1.2 渗流的工程意义 4.1.3 土中水和渗流问题的研究历史
口 5)松花江与嫩江:9500多处 6) 60 %~70%所谓的管涌 7)历史上长江干堤决口90%由于堤基管涌
土木工程中的渗流计算与防渗措施

土木工程中的渗流计算与防渗措施渗流是土木工程中常见的问题,对于工程建设的安全和可持续发展至关重要。
为了有效地控制土壤和地下水中的渗流,需要进行准确的渗流计算,并采取相应的防渗措施。
本文将介绍土木工程中的渗流计算方法,并讨论常用的防渗措施。
渗流计算是通过数学模型和实验方法来确定土体中水分和地下水的流动规律。
常用的渗流计算方法包括单位流量法、播种法、渗透仪法等。
其中,单位流量法是一种简单而有效的渗流计算方法,通过测量单位时间内通过水平单位面积的流量来估计土壤渗透能力。
该方法适用于土壤渗透能力较弱的情况。
播种法是利用植物根系的渗透能力来测定土壤的渗流能力,适用于土壤渗透能力较强的情况。
渗透仪法是一种实验方法,通过在实验室中模拟土壤渗流条件来测定土壤的渗透性。
根据渗透仪法可以确定土壤的渗透能力和压力头等参数,为工程设计提供有效的依据。
在土木工程中,为了控制渗流并保证工程安全,需要采取一系列的防渗措施。
常用的防渗措施包括降低水头、加固土体、构筑物理屏障和采取地下水位管理等措施。
降低水头是通过减少或控制水的输入量来降低渗流压力,常用的方法包括排水、防渗帷幕等。
加固土体是通过改变土壤的物理性质或增加土体的抗渗能力来达到防渗的目的,常见的做法包括土工合成材料的使用、土壤改良等。
构筑物理屏障是通过建造物理隔离层来隔离地下水流动,常用的屏障材料包括土工膜、混凝土墙等。
地下水位管理是通过控制地下水位来控制渗流,常见的方法包括设置排水系统、进行水平补给等。
除了以上常用的防渗措施,还有一些新型的防渗技术在土木工程中得到了广泛应用。
例如,渗流过程中常出现的裂缝和孔隙是渗流的主要通道,可以通过注浆、灌浆等方法来封堵这些通道,减少渗流量。
此外,还可以利用化学方法,如灌浆材料、地下水固化剂等,来增加土壤的抗渗能力,从而实现地下渗流的控制。
在土木工程中,渗流计算和防渗措施的选择需要综合考虑工程的实际情况和需求。
根据地质环境、水文条件和工程用途等因素,选取合适的渗流计算方法,并结合经济、技术和环保等因素,选择适当的防渗措施。
土力学土的渗透性与渗透问题

设饱和土体内某一研究平面的 总面积为A,其中粒间接触面积之 和为As ,则该平面内由孔隙水所占 面积为 Aw =A-As.若由外荷(和/或 自重)在该研究平面上所引起的法 向总应力为,如图所示,那么,它 必将由该面上的孔隙水和粒间接触 面共同来分担,即该面上的总法向 力等于孔隙水所承担的力和粒间所 承担的力之和,于是可以写成:
式中,右端第一项Psv/A为全部竖向 粒间作用力之和除以横断面积A,它 代表全面积A上的平均竖直向粒间应力,并定义为有效应力,习惯上用 ‘ 表示。有端第二项中的As/A,试验研究表明,粒间接触面积As不超过 0.03A,故 As/A可忽略不计。于是上式可简化为:
=‘ 十 u 即为著名的有效应力原理
第18页/共26页
(1)几何条件 土中粗颗粒所构成的孔隙直径必须大于细颗粒的直径,才可能让细 颗粒在其中移动,这是管涌产生的必要条件。 (2)水力条件 渗透力能够带动细颗粒在孔隙间滚动或移动是发生管涌的水力条件, 可用管涌的水力坡降表示。 流土现象发生在土体表面渗流渗出处,不发生在土体内部。而管涌 现象可以发生在渗流逸出处,也可以发生于土体的内部。
渗流量之和,即 将达西定律代入上式可得沿水平方向的等效渗透系数kx:
(二)竖直向渗流 竖直渗流的特点: (1)根据水流连续原理,流经各土层的流速与流经等效土层的流速
相同,即 (2)流经等效土层H的总水头损失h等于各层上的水头损失之和,即 将达西定律代入上式可得沿竖直方向的等效渗透系数kz:
第9页/共26页
测管水头:位置水头与压力水头之和 h= z+ u/w
测管水头代表的是单位重量液体所具有的总势能
伯努里方程用于土中渗流时有两点需要指出: (1)饱和土体中两点间是否出现渗流,完全是由总水头差决定。只有当 两点间的总水头差时,才会发生水从总水头高的点向总水头低的点 流动。 (2)由于土中渗流阻力大,故流速 v 在一般情况下都很小,因而形成的 流速水头也很小,为简便起见可以忽略。渗流中任一点的总水头就可 用测管水头来代替。 水力坡降
高等土力学复习资料(最终版)

为水密度,则式左可化为
nwdxdydz
t
dt
w
1
n
1 w
u t
dxdydz
(1)
由u
w
g
h
z
代入可得:
vx x
vy y
vz z
w
g
1
n 1 w
h
t
(u
wg h
z)
vx x
vy y
vz z
Ss
h t
(定义 Ss
w
g
1
n 1 w
为单位储存量)
2、渗流原理的基本假定:连续介质假定(P150) 液体(如地下水、石油)在土孔隙或其他透水性介质(如水工建筑)中的流动问题称为渗流。 土体的渗透特性表现为非均质和非连续性。但为了研究问题方便,常将水假想成充满整个介质空
二、发生曼德尔-克雷尔效应的机理是什么?为什么拟三维固结理论不能描述这一效应?(P339)
曼德尔效应:按比奥理论求解饱和土的固结问题时会出现一种现象:在不变的荷重施加于土体上 后的某时段内,土体内的孔隙水压力不是下降,而是继续上升,而且超过应有的压力值。即中心部位 孔隙压力高于外压力。同样的边界条件,用太沙基理论(扩散理论)分析时不会出现该现象。
vzdxd y
w
vx
vx x
dx
d
y
d
z
vy
vy y
dy
dxdz
vz
vz z
dz
d
x
d
y
nwd x d y d z t
dt
化简得:
w
vx x
vy y
vz z
dxdydz
nwd x d y d z t
第2讲 土中水与土中渗流的计算

2.3.2 静水条件下的孔隙水压力
地面 自由水面 地下水位 海底面
z
z
图2.5 静水条件下的孔隙水压力
孔隙水压力就是水力学中的静水压力U=rwz u—孔隙水压力,kPa; rw—水的重度,kN/m3; Z—从地下水位或自由水面算起计算点的深度,m.
地下水位以上毛细饱和区孔隙水压力也属于静水条件下的.理论上毛细饱和区 孔隙水压力值为负;在实际工程计算中,毛细饱和区负的孔隙水压力值是忽略 不计的.
klnh1h2alft2t1对一个实验装置afl是不变的试验时只要测定t1时的h1t2时的h2便可代入公式求得k值a水柱截面积lh2图24变水头渗透试验装置326渗透系数的原位测定方法?原位试验是在现场对土层进行测试能获得较为符合实际情况的土性参数对于难以取得土样的粗颗粒土尤有重要实用意义
3 土的渗透性及水的渗流
3.4.1有效应力表达式
以∑Fin表示所有法向分量之和,若 通过截面a-a内孔隙水与土骨架传递 的总法向力为P,根据法向力的平衡 条件可以写出: P= ∑Fin+u (A-As) (1) As为考虑颗粒接触点所占的面积.将 (1)式两端除以A,得: P/A= ∑Fin/A+u(1-As/A) (2) 总应力记为
3.2.2 土中渗流的总水头差与水力梯度
考察A、B两点水流动情况,
总水头线
Z— 位置水头 hw — 静水头 h=Z+hw --总水头 动水头或速度水头忽略不计
hwA
hwB
A 总水头差:△h=hA-hB
Байду номын сангаасB L
ZA
基准面
单位流程的水头损失即为渗流的 水力梯度
ZB i = △h/L (水力坡降)
3.2.3 达西渗透定律 • V=k i
土中水与土的渗透及其计算
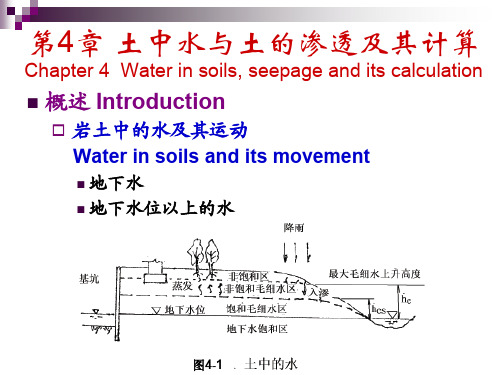
Chapter 4 Water in soils, seepage and its calculation
概述 Introduction
岩土中的水及其运动 Water in soils and its movement
地下水 地下水位以上的水
图4-1
渗流的工程意义 Engineering significance of seepage
非饱和土的渗透性
Permeability of unsaturated soil 非饱和土中孔隙水与气的三种不同形态
水封闭 双开敞 气封闭
图4-16
水和气体流动的广义达西定律
ka a va kaia a y k w w vw k wiw w y
渗漏 水利工程
渗透破坏 石油和采矿工程、环境工程
土中水和渗流问题的研究历史
Research history of water in soils and seepage
土中水的研究
年Low给出了粘土颗粒表面结合水形成的机理; 1960 年Martin得出了不同厚度结合水的密度分布, 1959年给出了物理模型以说明土的冻胀机理; 1975 年Mitchell在出版的Fundamentals of Soil Behavior一书中,对于土中水的形态及其对土性的 影响作了较全面的总结和阐述。
通过土体1和2的流量相等,得 则 则微分方程在土体1 中的定解为: (b) 土体2 的边界条件为 可求得微分方程在土体2中的定解为: (c)
若将测管水头基准面选在 h2的水面位置,微分方程的 解可进一步简化为
土体1中
高等土力学渗流

2.压力势p
3.基质势m
3.溶质势0
:静水压力势;渗流压力势;超静水压力势
土中水的总势能:
g p m 0
A点: A g m w hA m 0 m w hA B点: B g m w hB m 0 m w hB
1、粗粒土 Reynold试验:
Re vd10来自当Re≤10时,层流区, v ki
200>Re>5时,过渡区, ki 0.74 v Re>200时,紊流区,
v ki 0.5
适用于:中砂、细砂、粉砂;
不适用:粗砂、砾石、卵石等。
2、粘性土(非线性渗透)
v a c b
0
I0
I
v k I I 0
p p K p sat z 2c K p
pw 0
2、不同渗流情况下的水土压力
3、超静孔隙水压力对水土压力的影响
4.6 渗流的数值计算
4.6.1 渗流的基本微分方程
1、不可压缩土体:
h h kx kz 0 x x z z
4.5 有关渗流的一些工程问题
4.5.1 渗透力与渗透变形及其防治
1、渗透力
p dAdh w F
F dh f w dAdl dl dh j f w wi dl
2、渗透变形 流砂(流土) 管涌 3、渗透变形的防治 采用不透水材料或完全阻断渗流路径,或者增加渗透路径,减少水力坡降; 在渗流出逸处布置减压、压重或反滤层防止流土和管涌的发生。
4.2.2 毛细水与土中吸力
1、毛细水和毛细水上升高度
4T cos hc w 0 d
土的渗流
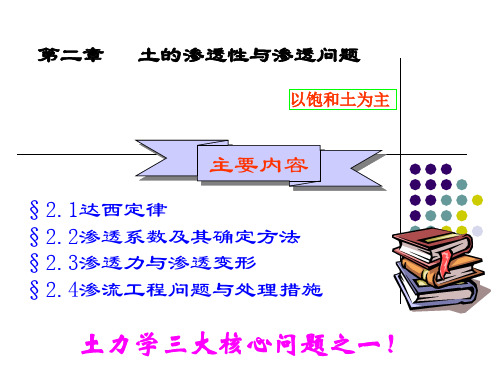
密实粘土 i
(区别较大)
适用条件
层流(线性流) ——大部分砂土,粉土;疏松的 粘土及砂性较重的粘性土
v vcr
o
v kim (m 1)
i
两种特例
粗粒土: ①砾石类土中的渗流不符合达西定律 ②砂土中渗透速度:vcr=0.3-0.5cm/s 粘性土: 致密的粘土 (粘滞阻力 )
v
v k (i ib )
d5 icr 2.2Gs 11 n d 20
2
3.流土与管涌的判别——与土的类别、颗粒级配以及 水力条件等因素有关 。 粘性土由于粒间具有粘聚力,粘结较紧,一般不出现管涌而 只发生流土破坏;一般认为不均匀系数Cu>10的匀粒砂土,在 一定的水力梯度下,局部地区较易发生流土破坏。
竖直向渗透系数:
H kz Hi k i
=0.03m/day
§2.3
渗透力与渗透变形
一、渗透力和临界水力坡降
1.渗透力—渗透水流施加于单位土粒上的拖曳力
动水压力
h
1 h1 2 h2
沿水流方向放臵两个测压 管,测压管水面高差h 土样 土粒对水流 面积 的阻力应为
F w hA
根据牛顿第三定律,试样的 总渗流力J和土粒对水流的阻 力F大小相等,方向相反
二、达西定律适用范围与起始水力坡降
讨论: 砂土的渗透速度与水
力梯度呈线性关系 a、密实的粘土,需要克服 结合水的粘滞阻力后才能 发生渗透; b、渗透系数与水力坡降的 规律还偏离达西定律而呈 非线性关系。
v v=ki O v
砂土i 虚直线简化源自v k (i ib )
0
起始水 力坡降 ib
达西定律适用于层 流,不适用于紊流
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
h
h
静水压力势
超静水压力势
渗流压力势
h
等势线
§4.2 饱和土的渗透性和基本方程 - 土中水的势能
土中水的势能:
重力势 g 压力势 p 基质势 m 溶质势 0
基质势又称为广义毛细势,由气 水界面的收缩膜,即表面张力引 起,它是一种广义的压力势(发 生在非饱和区,压力值小于0)
高 出
100
水
渗流的总水头: h = z + u gw
也称测管水头,是渗流的总驱动能,渗流 总是从水头高处流向水头低处
渗流问题的水头
§4.2 饱和土的渗透性和基本方程 - 达西定律
Q
L
A
Q
h1 h2
Q = k A (h1 - h2 ) L
v = Q =ki A
vs
=
v n
《高等土力学》之四
土中水及渗流计算
第四章 土中水及渗流计算
渗流及其特点
水力学
• 不可压缩粘滞性流体 Navier-Stokes 方程 • 对无粘性的理想流体 Euler 方程
渗流为水的流动问题,为什么需要进
行专门的研究?
渗流有些什么特征?
第四章 土中水及渗流计算
4.1 导言 4.2 饱和土的渗透性和基本方程 4.3 饱和土二维渗流与流网 4.4 饱和渗流数值计算方法 4.5 非饱和土水的形态和基质吸力 4.6 非饱和土土水特征曲线 4.7 非饱和土的渗透性和数值计算 4.8 有关渗流的一些工程问题
上层滞水 潜水
不透水层
不透水层
承压水
不透水层
三种形态的地下水
§4.1 导言
土中水 - 使大地充满生机
§4.1 导言
地球生命的源泉 渗漏:渠系中水的利用系数平均不足0.5 渗透破坏:土石坝破坏有39%由渗透所导致
堤防60-70%由于“管涌”等渗透变形引起
深基坑中渗透影响水土压力及支护结构的内力 采油工业 地下水污染 :废水、固体垃圾、放射性废料···· 生物力学
g = zg w
其中,z为所考虑点相对于
基准面的竖向距离,在基准 面以上取正值,之下取负值。
§4.2 饱和土的渗透性和基本方程 - 土中水的势能
土中水的势能:
重力势 g 压力势 p 基质势 m 溶质势 0
压力势由所受到的压力所决定, 某点的压力势可以用与该点连通 的测压管中的水位确定。可分:
的机理
1910年理查森首先提出了有限差分法 1922年巴甫洛夫斯基提出了求解渗流场的电模拟法 20世纪60年代之后,计算渗流力学发展。非饱和土、
固结与变形耦合计算、与极限分析耦合、混合流、 污染物扩散····
土中水和渗流问题的研究历史
第四章 土中水及渗流计算
4.1 导言 4.2 饱和土的渗透性和基本方程 4.3 饱和土二维渗流与流网 4.4 饱和渗流数值计算方法 4.5 非饱和土水的形态和基质吸力 4.6 非饱和土土水特征曲线 4.7 非饱和土的渗透性和数值计算 4.8 有关渗流的一些工程问题
§4.1 导言
江西省江新洲洲头 北侧堤坝崩岸原貌
治理管涌
§4.1 导言
长江的塌岸
§4.1 导言
建于1989年 高71米
长265米 1993年8月27
日垮坝 死300余人
渗透破坏:青海沟后水库溃口
§4.1 导言
1856年法国工程师达西(Darcy)提出达西定律 1889年俄国的茹可夫斯基推导了渗流的微分方程 1901年劳(Low)给出了粘土颗粒表面结合水形成
§4.2 饱和土的渗透性和基本方程
土中水的势能 达西定律与土的渗透性 广义达西定律 饱和稳定渗流的数学描述 饱和非稳定渗流的数学描述
饱和土的渗透性和基本方程
§4.2 饱和土的渗透性和基本方程 - 土中水的势能
土中水的势能:
重力势 g 压力势 p 基质势 m 溶质势 0
重力势为水的势能,单位体 积水的重力势可表示为:
岩土中的水及其运动
§4.1 导言
毛细带:
地下水位以上一定范 围,饱和、非饱和
• 上升高度取决于土
体的孔隙特性
• 随上升高度增加,
饱和度减少
• 水相压力大气压,
随高度减小
• 性质复杂
入渗
降水
非饱和区 非饱和毛细区 饱和毛细区
地下水饱和区
蒸发 地下水位
毛细水最大 上升高度
岩土中的水及其运动
§4.1 导言
降水 蒸发
地下水位
毛细水最大 上升高度
岩土中的水及其运动
§4.1 导言
地下水位:
孔隙水压力=大气压
地下水饱和区: • 位于地下水位以下 • 来自饱和度=1 • 水相压力大气压,
随深度增加
• 同一种土渗透系数
为常数
入渗
非饱和区 非饱和毛细区 饱和毛细区 地下水饱和区
降水 蒸发
地下水位
毛细水最大 上升高度
面
A
的
距 离
50
hA
(cm)
0 10 20 w(%)
A = g + m = g whA + m = 0
m = -g whA
§4.2 饱和土的渗透性和基本方程 - 土中水的势能
土中水的势能:
重力势 g 压力势 p 基质势 m 溶质势 0
溶质势是半透膜上渗透压力的 反作用,总是负值,也叫作渗 析吸力。它实际上是水中离子 和分子渗析扩散的驱动势能, 与一般水体的宏观流动有一定 的区别。纯水中溶质势设为零,
渗流的工程应用
§4.1 导言
98洪水中的险情和溃口
长江出险:6100多处;
松花江与嫩江:9500多处;60-70%为管涌
历史上长江干堤决口的90%由于堤基管涌所导致 98·8·7:九江城防管涌决口,形成61米宽溃口 98·8·4:江西江新洲管涌引起溃口,淹没区4.1
万人,78km2
1993美国密西西比管涌
即o=0,溶解有离子的溶液中 溶质势o<0 。离子浓度越大, 溶解的离子价位越高, o的
绝对值越高。
§4.2 饱和土的渗透性和基本方程 - 土中水的势能
总水头:单位重量水体所具有的能量 h = z + u + v2
g w 2g
位置水头Z:水体的位置势能(任选基准面) 压力水头u/gw:水体的压力势能(u孔隙水压力) 流速水头V2/(2g):水体的动能(对渗流多处于层流≈0)
§4.1 导言
岩土中的水及其运动 渗流的工程应用 土中水和渗流问题的研
究历史
导言
§4.1 导言
地面:地下水输入和
输出的界面
非饱和带(包气带):
浅层非饱和区,
• 位于地下水位和毛
细区以上
• 水饱和度1 • 水相压力大气压 • 渗透系数与含水量
相关
入渗
非饱和区 非饱和毛细区 饱和毛细区 地下水饱和区
