新疆维吾尔自治区2012届高三数学第二次适应性检测 理 新人教A版
2012年乌鲁木齐市二模数学答案Microsoft Word 文档

乌鲁木齐地区2012年高三年级第二次诊断性测验文理科数学试题参考答案及评分标准一、选择题(共12小题,每小题5分,共60分)1.(文科)选B .【解析】()()()()31324121112i i i i i ii i ----===-++-.(理科)选D .【解析】()()()()()21234432543434325i i i i z i ii i ---+-====---+.2.选A .【解析】运行此程序后输出的值1133y -==.3.选B . 【解析】若l ∥α,则l 与α内的直线平行或异面,排除A 、C ;若l ∥m ,l 不 在平面α内,则l ∥α,故排除D . 4.(文科)选C .【解析】由已知易得12⋅=-a b ,∴1cos ,2〈〉=-a b ,2,3π〈〉=a b .(理科)选B .【解析】由题知:3322882C a C a =,解得1a =.5.选C .【解析】不妨设正方形的边长为2,则22c =,21a =-,∴离心率22c e a=12=.6.选C . 【解析】直线34240x y +-=与坐标轴的两个交点为()8,0A ,()0,6B ,由题知A B 为圆的直径,且10AB =,∴圆的半径是5.7.(文科)选A .【解析】原式11sin cos sin 2cos 244222πππαααα⎛⎫⎛⎫⎛⎫=++=+==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()21112sin24α-=.(理科)选B .【解析】()f x 的最小正周期为6,由题意知:5= ,解得2A =.8.选D .【解析】作出可行区域,如图,由题可知点()22,a 应在点()2,4的上方或与其重合,故2a ≥4,∴a ≥2或a ≤-2,又0a >且1a ≠,∴a ≥2.9.选B .【解析】可知21=x x π-,31=2x x π+,∵2231=x x x ,∴()()2111=2x x x ππ-⋅+,解得1=4x π,∴sin42b π==.10.(文科)选B .【解析】设切点1,ln 2a a a ⎛⎫-+ ⎪⎝⎭,112y x '=-+,∴11122a -+= ,1a =,故切点11,2⎛⎫-⎪⎝⎭在直线12y x b =+上,有1122b -=+,∴1b =-. (理科)选C .【解析】设切点(),2ln a a +,1y x'=,∴12ln a k aa+==,∴1a e -=,k e =.11.选D .【解析】方程可化为2211x x x --=+或2211x x x --=--,即2320x x --=或20x x -=,所有解之和为4.12.选A .【解析】,02p F ⎛⎫⎪⎝⎭,设211,2y P y p ⎛⎫ ⎪⎝⎭,222,2y Q y p ⎛⎫ ⎪⎝⎭12()y y ≠.由抛物线定义及||||PF QF =,得22221212122222y y p p y y y y pp+=+⇒=⇒=-,∴1||2||2PQ y ==⇒1||1y =,又1||2222p PF p p=+=⇒=±.二、填空题(共4小题,每小题5分,共20分)13.(文科)填13.【解析】由正弦定理得134sin 53B π==.(理科)填79.【解析】由正弦定理得sin 134sin 53B π==,2cos 212sin B B =-2171239⎛⎫=-⨯= ⎪⎝⎭.14.(文科)填41n -.【解析】由题n ≥2时,1n n n a S S -=-22n n =+-22(1)n -(1)n --=41n -,又13411a ==⨯-,∴41n a n =-.(理科)填6.【解析】∵()199599182a a S a +===,∴52a =.设等差数列{}n a 的公差为d ,则()()()1311111121034a a a a a d a d a d ++=++++=+=536a =.15.填3π.【解析】底面正三角形内切圆半径就是球O的半径1322R =⋅=,∴球O 的表面积243S R ππ==.16.(文科)填500.【解析】设这个学校高一年级的学生人数为x ,有1001260x=,解得500x =.(理科)填12.【解析】记A C B D 、的交点为O ,由于PQ PO O Q =+,∴A P P Q ⋅=()AP PO O Q AP PO ⋅+=⋅,而当P 在线段O C (不含端点O )上时,AP PO ⋅< 0,∴考虑P 在线段A O上有AP PO +=AP PO AP PO ⋅⋅=≤22AP PO ⎛⎫+⎪ ⎪⎝⎭12=,当且仅当2AP PO ==时等号成立.三、解答题(共70分) 17.(本小题满分12分) (文科)(1)()22sin sin cos sin 1f x x x x x =++=+, ∴()f x 的最小正周期为2π;…5分(2)()f x 在,62ππ⎡⎤-⎢⎥⎣⎦上为增函数,在2,23ππ⎡⎤⎢⎥⎣⎦上为减函数,又263f f ππ⎛⎫⎛⎫-< ⎪ ⎪⎝⎭⎝⎭, ∴6x π=-时,()f x 有最小值1sin 1662f ππ⎛⎫⎛⎫-=-+= ⎪ ⎪⎝⎭⎝⎭; 2x π=时,()f x 有最大值sin 1222f ππ⎛⎫=+=⎪⎝⎭. …12分 (理科)(1)请参照(文科)(2)的解答; …6分(2)由题知A 、B 为锐角,∴24sin 25A =,4sin 5B =,()243744sin sin sin cos cos sin 2552555C A B A B A B =+=+=⨯+⨯=,∴()9sin 15f C C =+=. …12分18.(本小题满分12分)(1)过E 作EF AB ⊥,垂足为F ,连结C F ,112B F B E BC ===,∴45BCF ABD ∠==∠,∴BD C F ⊥.∵ AD PAB ⊥平面,∴EF AD ⊥,∴EF ABCD ⊥面, ∴EF BD ⊥,∴BD CEF ⊥面,∴B D C E ⊥; …6分 (2)(文科)取A B 的中点G ,连结P G ,则P G ⊥A B ,又P G A D ⊥, ∴P G ⊥平面A B C D ,四棱锥P A B C D -的体积1()1(41)432323AD BC AB V PG +⋅+=⋅⋅=⋅⨯=…12分 (理科)如图所示,建立空间直角坐标系A xyz -,可取(1,0,0)=m 为平面A B C D 的一个法向量.设平面EAC 的一个法向量为(,,)l m n =n .则0AC ⋅= n ,0AE ⋅=n ,其中(0,4,1)A C =,3,0)AE =,∴40,30.m n m +=⎧⎪+=∴,4.l n m ⎧=⎪⎨=-⎪⎩ 不妨取1m =-,则1,4)=-n .cos ,10⋅〈〉===⋅m n m n m n.∴二面角E A C B --10…12分19.(本小题满分12分)(1)6名男应征者的平均身高是181cm ,9名女应征者身高的中位数为168cm ;…4分 (2)(文科)能进入下一环节的男生有3人,女生有4人.记满足条件的3名男生分别为123,,a a a ,4名女生分别为1234,,,b b b b ,则从中任取2人可以表示为:()12,a a ,()13,a a ,()11,a b ,()12,a b ,()13,a b ,()14,a b ,()23,a a ,()21,a b ,()22,a b ,()23,a b ,()24,a b ,()31,a b ,()32,a b ,()33,a b ,()34,a b ,()12,b b ,()13,b b ,()14,b b ,()23,b b ,()24,b b ,()34,b b ,即基本事件共21个.∴至多有一位男生的概率186217P ==. …12分(理科)能进入下一环节的男生3人,女生4人.X 的可能取值是0,1,2. 则()2427207C P X C===;()114327417C C P X C===;()2327127C P X C===.∴X 的分布列为2416=0+1+2=7777E X ⨯⨯⨯. …12分20.(本小题满分12分) (文科) (1)由题知c =2a ==,∴a =222862b a c =-=-=,∴椭圆C 的方程为22182xy+=; …6分(2)过点(2,1)P 的直线1l 或2l 的方程可设为()12y k x -=-,由()2212,1.82y k x x y ⎧-=-⎪⎨+=⎪⎩消去y 得:()()22221482161640k x k k x k k ++-+--= (*) 其判别式△()()()()2222282414161641621k kk k k k ⎡⎤=--+--=+⎣⎦. ①当点A 、B 中有一点与P 重合,不妨设B 与P 重合,则直线2l 与椭圆C 只有一个交点,∴ 由△()216210k =+=,解得12k =-为2l 的斜率. 由于直线1l 、2l 倾斜角互补,∴12A B A P k k k ==-=.②当点A 、B 中没有点与P 重合,不妨设直线1l 的方程为()12y k x -=-,1l 与椭圆C 相交于不同两点()2,1P 、()11,A x y ,则由(*)式得21216164214k k x k--=+,∴21288214k k x k--=+.同理2l 与椭圆C 相交于不同两点()2,1P 、()22,B x y ,得22288214k k x k+-=+,于是1221614k x x k--=+,()121228414k y y k x x k k--=+-=+,∴212122811416214AB ky y k k k x x k --+===--+. 综合①②,都有12AB k =. …12分(理科)(1)请参照文科(2)的解答; …6分(2)当点A 、B 中有一点与P 重合,不妨设B 与P 重合, 由(1)知1l 的方程为()1122y x -=-,即12yx =,此时椭圆与直线都是关于原点对称的图形,由对称性知()2,1A --,∴AB = 当点A 、B 中没有点与P 重合,14AB k ===+14kk==+≤14k k=,即12k =时取等号)等号取得就是点A 、B中有一点与P 重合的情况,∴AB <综上,A B 取最大值为A B 的方程为12y x =,由对称性知此时焦点到直线A B 的距离为5. …12分21.(本小题满分12分)(1)显然()f x 在R 上连续,且()1x m f x e -'=-,令()0f x '=,得x m =.当(),x m ∈-∞时,1x m e -<,()0f x '<; 当(),+x m ∈∞时,1x m e ->,()0f x '>. 所以,当x m =时,()f m 为极小值,也是最小值.令()1f m m =-≥0,得m ≤1时,有()f x ≥0; …6分 (2)当1m >时,()10f m m =-<,由(1)知()f x 在[]0,2m 上至多有两个零点.因为(0)0m f e -=>,()()00f f m ⋅<,所以()f x 在()0,m 上有一个零点; 又(2)2m f m e m =-,令()2mg m em =-,因为()20mg m e '=->在1m >时成立,所以()g m 在(1,)+∞上单调递增,()(1)20g m g e >=->,即(2)0f m >.∴ ()(2)0f m f m ⋅<,所以()f x 在(),2m m 上也有一个零点;故()f x 在[]0,2m 上有两个零点. …12分22.(本小题满分10分)选修4-1:几何证明选讲(1)连结A C ,由O D 是半径,A D D C =O D AC ⇒⊥,又∵=90BCA ∠⇒B C A C ⊥,于是有O D ∥B C . …5分(2)由(1)及E A A O =,2ED =,知23O D E D E O B CE CE B===,∴3E C =.∵23ED EC EA EB EA ⋅=⋅=,∴2323EA =⨯,即EA =1C D E C E D =-=,33222BC O D EA ===.∴周长=22AD C D BC BA +++=+. …10分23.(本小题满分10分)选修4-4:坐标系与参数方程(1)l 表示过点()3,0倾斜角为120的直线,曲线C 表示以(),0C a '为圆心,a 为半径的圆.∵l 与C 相切,∴()132a a =-,1a ⇒=.于是曲线C 的方程为2cos ρθ=,∴22cos ρρθ=,于是222x y x +=故所求C 的直角坐标方程为2220x y x +-=; …5分 (2)∵30POC OPC ''∠=∠=,∴O P =.∴切点P的极坐标为,6π⎛⎫⎪⎝⎭. …10分24.(本小题满分10分)选修4-5:不等式选讲 (1)不等式可化为:1x +≤2,解得:3-≤x ≤1.故不等式()f x ≤2的解集为{|3x -≤x ≤}1; …5分 (2)()()f x f x +-=2,2,11,2,.x x x x x ⎧⎪-<<⎨⎪-⎩≥1,≤-1 当x ≥1时,()()f x f x +-=22x ≥, 当11x -<<时,()()f x f x +-=2, 当1x -≤时,()()f x f x +-=22x -≥,故()()f x f x +-2≥(“=”在11x -≤≤时成立).∴a ≤2,即a 的最大值为2. …10分以上各题的其它解法,限于篇幅,从略.请相应评分.。
新疆维吾尔自治区2022届高三普通高考第二次适应性检测数学(理)试题(含答案解析)

新疆维吾尔自治区2022届高三普通高考第二次适应性检测数学(理)试题学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.设z 是复数z 的共轭复数,若复数z 在复平面内对应的点为()4,2,则iz=( ) A .24i +B .24i -C .24i --D .24i -+2.已知集合{}31,A a a n n ==-∈Z ,{}31,B b b n n ==+∈Z ,全集U =Z ,则()U A B ⋂=( )A .AB .BC .∅D .Z3.已知命题p :x ∀∈N ,22x x <;命题q :x ∃∈R ,sin cos 1x x +>,下列命题中为假命题的是( ) A .p q ∨B .()¬p q ∧C .()()¬¬p q ∨D .()¬p q ∨ 4.我国著名数学家华罗庚曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来研究函数图象的特征.我们从这个商标中抽象出一个函数的图象如图,其对应的函数解析式可能是( )A .()11f x x =- B .()211f x x =- C .()11tan2f x xπ=-D .()11f x x =- 5.设l 是直线,α,β是两个不同的平面,则下列命题正确的是( ) A .若//l α,l β//,则//αβ B .若//l α,l β⊥,则αβ⊥ C .若//αβ,//l α,则l β//D .若αβ⊥,l α⊥,则l β⊥6.已知数列{}n a 的各项为互异正数,且其倒数构成公差为3的等差数列,则112231nn na a a a a a a a --=++⋅⋅⋅+( )A .16B .13C .3D .67.某几何体的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为( )A .43B .83C .163D .3238.把1,2,3,4,5这五个数随机排成一列,组成一个数列,要求该数列恰好先减后增,则这样的数列有( ) A .13个B .14个C .15个D .16个9.某数学兴趣小组要测量校园内国旗杆CD 的高度,测量的同学在地面选择了A ,B 两个观测点,且A ,B ,C 三点在同一直线上,如图所示.在A 处测得国旗杆顶端D 的仰角为α,在B 处测得国旗杆顶端D 的仰角为β.若AB a ,则国旗杆CD 的高度为( )A .()sin sin sin a αββα-B .()sin sin sin a αβαβ-C .()sin sin sin a ββαα-D .()sin sin sin a αβαβ-10.若函数()32e lnf x x ax x x =-+-有两个零点,则a 的取值范围为( )A .10,2e ⎛⎤ ⎥⎝⎦B .1,2e ⎛⎫+∞ ⎪⎝⎭C .21,12e ⎛⎤-∞+ ⎥⎝⎦D .1,2e ⎛⎫-∞ ⎪⎝⎭11.已知点P 是双曲线2213y x -=上的动点,1F ,2F 分别为其左,右焦点,O 为坐标原点.则12PF PF OP+的最大值是( )A .7B .6C .5D .412.实数x ,y ,z 分别满足212022log 21x =,2122y =,2021z =,则x ,y ,z 的大小关系为( ) A .x y z >> B .x z y >>C .z x y >>D .y x z >>二、填空题13.已知向量()2,1a =,()1,2b =,若()a b b λ+⊥,则λ=______.14.若F 为抛物线22y px =的焦点,M 为抛物线上一点,N 为抛物线准线与坐标轴的交点,且72MF p =,MNF的面积为______. 15.在正项等比数列{}n a 中,31a =,456a a +=,则满足123123n n a a a a a a a a +++⋅⋅⋅+<⋅⋅⋅的最小正整数n 的值为______.16.已知正方体1111ABCD A B C D -的棱长为1,M 、N 分别为棱1AA 、11A D 的中点,P 为棱11A B 上的动点,Q 为线段11B D 的中点.则下列结论中正确序号为______.①MN CP ⊥;①//AQ 平面MNP ;①PDQ ∠的余弦值的取值范围是⎣⎦;①①1APC三、解答题17.设ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c ,且sin sin 2cos 1b C c B A =+-(1)求角A 的大小;(2)若2b =,1c =,D 为AB 的中点,求CD 的长.18.如图,在三棱柱111ABC A B C -中,平面11A ACC ⊥平面ABC ,ABC 是正三角形,D 是AB 的中点.11AA A C =,直线1A B 与平面11A ACC 所成的角为45︒.(1)求证:1BC ∥平面1A CD ; (2)求二面角1A CD C --的正弦值.19.2021年8月8日是我国第13个“全民健身日”,社会上参与全民健身活动的人越来越多,小明也有大量好友参与了“健步团”,他随机选取了其中的40人,记录了他们某一天的走路步数,并将数据整理如下:(1)若在小明该日走路不超过7000步的好友中任选2人,求至少有1名男性的概率; (2)如果每人一天的走路步数超过8000步就会被系统评定为“健步型”,否则为“良好型”,根据题意完成下面的22⨯列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关附:参考公式()()()()()22n ad bc K a b c d a c b d -=++++. 临界值表:20.设函数()1e ln 1xa f x a x -=--,其中0a > (1)当1a =时,讨论()f x 单调性;(2)证明:()f x 有唯一极值点0x ,且()00f x ≥.21.已知椭圆C :()222210x y a b a b+=>>经过点163,5M ⎛⎫ ⎪⎝⎭,过椭圆C 的右焦点()3,0作斜率为k 的直线l 交椭圆于A ,B 两点,记MA ,MB 的斜率为1k ,2k (1)求椭圆C 的标准方程; (2)若120k k +=,求实数k 的值22.在平面直角坐标系xOy 中,圆C 的方程为()()22228x y -+-=,直线l 的参数方程为12x y ⎧=⎪⎨=⎪⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系 (1)求直线l 的普通方程和圆C 的极坐标方程;(2)若点P 的直角坐标为()1,2,直线l 与圆C 相交于A 、B 两点,求22PA PB +的值.23.已知函数()13f x x x =-++ (1)求不等式()6f x ≥的解集;(2)设函数()f x 的最小值为m ,若正数a ,b 满足2ab a b m =++,求ab 的最小值参考答案:1.C 【解析】 【分析】利用复数的几何意义和复数的除法运算求解. 【详解】解:因为复数z 在复平面内对应的点为()4,2, 所以42i z =+,则42i z =-, 所以42i24i iiz-==--, 故选:C 2.A 【解析】 【分析】根据集合的描述判断集合,A B 的关系,进而判断,U A B 的包含关系,即可得答案. 【详解】由题设,{...,4,1,2,5,8,...}A =--,{...,5,2,1,4,7,...}B =--, 所以A B =∅,而{...,4,3,1,0,2,3,5,6,8,...}UB =---,则U A B ≠⊂, 所以()UAB A =.故选:A 3.D 【解析】 【分析】先判断出命题,p q 的真假,再根据复合命题的判断方法判断即可 【详解】当2x =时,22x x =,所以命题p 为假命题,则p ⌝为真命题,当4x π=时,sincos144ππ+=,所以命题q 为真命题,则q ⌝为假命题,所以p q ∨为真命题,()¬p q ∧为真命题,()()¬¬p q ∨为真命题,()¬p q ∨为假命题, 故选:D4.D 【解析】 【分析】由定义域判断A ;利用特殊函数值:(0)f 、2()3f 的符号判断B 、C ;利用奇偶性定义及区间单调性判断D. 【详解】A :函数的定义域为{|1}x x ≠,不符合;B :由1(0)101f ==--,不符合; C :由2()03f =<,不符合; D :11()()|||1||||1|f x f x x x -===---且定义域为{|1}x x ≠±,()f x 为偶函数, 在(0,1)上1()1f x x=-单调递增,(1,)+∞上1()1f x x =-单调递减,结合偶函数的对称性知:(1,0)-上递减,(,1)-∞-上递增,符合. 故选:D 5.B 【解析】 【分析】根据各选项中线面、面面的位置关系,结合平面的基本性质判断线面、面面关系即可. 【详解】A :若//l α,l β//,则,αβ可能平行、相交,错误;B :若//l α,过l 的平面γ且m γα=,则//l m ,而l β⊥即m β⊥,又m α⊂,则αβ⊥,正确;C :若//αβ,//l α,则l β//或l β⊂,错误;D :若αβ⊥,l α⊥,则l β//或l β⊂,错误. 故选:B 6.C 【解析】 【分析】根据等差数列的定义进行求解即可.【详解】因为数列{}n a 的各项为互异正数,且其倒数构成公差为3的等差数列, 所以有11111113(2,)33n n n n n n n n n n a a n n N a a a a a a a a *-------=≥∈⇒-=⇒=, 所以1112311212231133333n n n n nn n na a a a a aa a a a a a a a a a a a a a -----==⋅=---++⋅⋅⋅+-++⋅⋅⋅+, 故选:C 7.C 【解析】 【分析】由三视图还原几何体为三棱锥,再应用棱锥的体积公式求体积即可. 【详解】由三视图知:如下图示,几何体为三棱锥A ECD -,而AB ⊥面BCDE ,24AB BC CD ===,所以111164423323A ECD ECDV AB S -=⋅=⨯⨯⨯⨯=. 故选:C 8.B 【解析】 【分析】1为该数列递减和递增的分界点,分情况讨论即可. 【详解】从2,3,4,5中任选1个排在1的左侧,其余排在右侧,共有4个先减后增的数列;从2,3,4,5中任选2个排在1的左侧,其余排在右侧,共有24C =6个先减后增的数列;从2,3,4,5中任选3个排在1的左侧,其余排在右侧,共有34C =4个先减后增的数列;①共有4+6+4=14个先减后增的数列. 故选:B. 9.A 【解析】 【分析】先在ABD △中,利用正弦定理求得BD ,再在DBC △中,由sin CD BD β=求解. 【详解】解:在ABD △中,由正弦定理得sin sin AB BDADB BAD=∠∠,即()sin sin a BDαβα=-, 所以()sin sin a BD αβα=-,在DBC △中,()sin sin sin sin a CD BD αβββα==-,故选:A 10.B 【解析】 【分析】问题转化为函数32()g x x ax ex =-+,()ln h x x =的图像有两个交点 作出草图,寻求临界相切的情况即可 【详解】问题转化为函数32()e g x x ax x =-+,()ln h x x =的图像有两个交点 作出草图,寻求临界相切的情况设切点的横坐标为0x .则()()()()0000g x h x g x h x ''⎧=⎪⎨=⎪⎩,即320000200e ln 132e x ax x x x ax x ⎧-+=⎪⎨-+=⎪⎩消去a 得3000e 2ln 10x x x -+-=设3()e 2ln 1x x x x ϕ=-+-22232111()3e 3e 33ee 0x xx x x x x xϕ'=-+=++-⋅=> 即()x ϕ在(0,)+∞上单调递增注意到110ϕ=-= 所以唯一切点的恒坐标为0x 代入解得12ea = 显然当()()32320000000011,e e 2e 2e a g x x ax x x x x h x ⎛⎫>=-+<-+= ⎪⎝⎭此时必有两个交点,所以a 的取值范围为1,2e ⎛⎫+∞⎪⎝⎭故选:B 11.D 【解析】 【分析】设(,)P x y 在右支上,根据双曲线的性质求得2||PF ex a =-、1||PF ex a =+且||OP =12PF PF OP+=,结合x 的范围求范围,即可得结果.【详解】由双曲线的对称性,假设(,)P x y 在右支上,即x a ≥, 由P 到2a x c =的距离为2a d x c =-,而2||PF =所以22||cxa PF a adx x x x c cc c-====----c e a ==, 综上,2||PF ex a =-,同理1||PF ex a =+,则12PF PF OP+==对于双曲线2213y x -=,有2233y x =-且2e =,所以12PF PF OP +==1≥x,即124PF PF OP +≤=. 故选:D 【点睛】关键点点睛:双曲线上点到焦点距离与到2a x c=±距离的比值为e ,求焦半径2||PF 、1||PF ,进而结合已知双曲线求目标式范围.12.B 【解析】 【分析】由题意得22212120x ⎛⎫= ⎪⎝⎭,21log 22y =,20log 21z =,然后y 与z 作差结合基本不等式比较大小,构造函数ln ()xf x x=,可判断其在(e,)+∞上单调递减,则(21)(20)f f <,化简可得21202120<,则2021log 2120z >=,则可比较出z 与y 的大小即可 【详解】由题意得22212120x ⎛⎫= ⎪⎝⎭,21log 22y =,20log 21z =,则 2021lg 21lg 22log 21log 22lg 20lg 21z y -=-=-2lg 21lg 20lg 22lg 20lg 21-⋅=⋅,因为2211lg 20lg 22(lg 20lg 22)lg 44022⎡⎤⎛⎫⋅<+= ⎪⎢⎥⎣⎦⎝⎭,所以222111lg 21lg 440lg 21lg 440lg 21lg 440lg 21lg 20lg 222220lg 20lg 21lg 20lg 21lg 20lg 21⎛⎫⎛⎫⎛⎫-+- ⎪ ⎪⎪-⋅⎝⎭⎝⎭⎝⎭>=>⋅⋅⋅, 所以z y >, 设ln ()xf x x=,则21ln ()x f x x -'=,当(e,)x ∈+∞时,()0f x '<,所以()f x 在(e,)+∞上单调递减,所以(21)(20)f f <,即ln 21ln 202120<,所以20ln 2121ln 20<, 所以2021ln 21ln 20<,所以20212120<,所以21202120<,所以2021log 2120z >=, 因为222121212020x ⎛⎫=>⎪⎝⎭,所以>x z , 所以x z y >>, 故选:B 【点睛】关键点点睛:此题考查对数与指数的互化,考查基本不等式的应用,考查导数的应用,解题的关键是构造函数ln ()xf x x=判断出其单调性,可得20212120<,再转化为2021log 2120>,考查数学转化思想和计算能力,属于难题 13.45-##0.8-【解析】 【分析】根据平面向量运算的坐标表示公式,结合平面向量垂直的性质进行求解即可. 【详解】 因为()1,2b =,所以(),2b λλλ=,而()2,1a =, 所以(2,12)a b λλλ+=++,而()1,2b =,所以由()()4022(12)05a b b a b b λλλλλ+⊥⇒+⋅=⇒+++=⇒=-,故答案为:45-14.2y = 【解析】【分析】根据抛物线的定义,结合三角形面积公式进行求解即可. 【详解】由题意可知:(,0),(,0)22p pF N -,准线方程为2p x =-,设200(,)2y M y p , 因为72MF p =,所以2220007()6222y p p y p y p --=⇒=⇒=, 因为MNF的面积为,FN p =,所以012p y p p ⋅⋅===所以抛物线的方程为2y =,故答案为:2y = 15.7 【解析】 【分析】先根据已知列方程组求得通项公式,然后由等比数列前n 项和与指数运算化简不等式,通过放缩转化为指数不等式求解,然后验证可得. 【详解】设数列{}n a 的公比为q ,则由题知323316a a q a q =⎧⎨+=⎩,解得2q 或3q =-(舍去),所以3332n n n a a q --==,得212a -=由等比数列求和公式得321222(12)12124n n n a a a a --+++-=⋅⋅=⋅-+-,又(5)2101(3)212322n n n n a a a a ---+++⋅⋅⋅+-=⋅⋅⋅=,所以(5)221224n n n ---<, 不等式(5)22(5)2222n n n n n n ---<⇔-<,解得n >7,n n ≥∈N , 因为当6n =时,6(65)622112162844---=->=,综上,n 的最小正整数为7. 故答案为:7 16.①① 【解析】 【分析】①连接11,AD BC ,根据正方体性质有1//MN BC ,结合CP 在面11BCC B 上的投影为1CB 即可判断;①①构建空间直角坐标系,求面MNP 的法向量及方向向量AQ ,利用空间向量夹角的坐标表示判断线面关系,同理求线线角的关于参数m 的余弦值,结合导数求最值,即可判断余弦值的范围;①将问题转化为求1C P AP +的最小值,展开正方体侧面研究最小情况即可判断. 【详解】①连接11,AD BC ,即11//AD BC ,又M 、N 分别为1AA 、11A D 的中点,则1//MN AD ,所以1//MN BC ,而CP 在面11BCC B 上的投影为1CB ,又11CB BC ⊥,即CP 1BC ⊥, 所以MN CP ⊥,正确;①如下图示,1(1,0,)2M ,1(,0,1)2N ,(1,,1)P m ,则1(0,,)2MP m =,1(,,0)2NP m =,若(,,)n x y z =是面MNP 的一个法向量,则022z MP n my x NP n my ⎧⋅=+=⎪⎪⎨⎪⋅=+=⎪⎩,令2x z m ==即(2,1,2)n m m =-,而(1,0,0)A ,11(,,1)22Q ,则11(,,1)22AQ =-,所以11222AQ n m m m ⋅=--+=-,仅当12m =时AQ n ⊥,即//AQ 平面MNP ,故错误;①如下图,(1,,1)P m ,11(,,1)22Q ,(0,0,0)D ,故DP =(1,),1m ,DQ =11(,,1)22,所以32m DP DQ +⋅=,且2||DP m =6||2DQ=,则cos PDQ∠=令267()2m f m m +=+(01)m ≤≤,则22271216()66()(2)m f m m -++'=+,而(0)30f '=>,8(1)09f '=-<,所以,存在0()0f m '=,则0(0,)m 上()0f m '>,()f m 递增;0(,1)m 上()0f m '<,()f m 递减;所以[0,1]上有0()()f m f m ≤, 由7(0)2f =时cos PDQ ∠=13(1)3f =时cos PDQ ∠=,故0()f m 时cos PDQ ∠>①由①1APC 周长为11C P AP AC ++,而1AC 1C P AP +最小, 将11ABB A 与1111B A D C 展开成一个平面,如下图示:当1,,A P C 共线时,1C P AP +. 故答案为:①① 【点睛】关键点点睛:①①构建空间直角坐标系,利用向量法判断线面关系、求线线角余弦值关于参数的表达式,进而应用导数判断最值. 17.(1)3A π=【解析】 【分析】(1)由正弦定理化简求解 (2)由余弦定理求解a ,然后求解 (1) 因为sin sin b cB C=,所以sin sin b C c B = 又sin sin 2cos 1b C c B A =+- 所以1cos 2A =,()0,A π∈,所以3A π=. (2)在ABC 中,由2222cos a b c bc A =+-得a =222b a c =+,故2B π=在Rt CBD △中CD == 18.(1)证明见解析(2)sin θ 【解析】 【分析】(1)连接1AC 交1A C 于点E ,连接DE ,证得1DE BC ∥,再根据线面平行的判定定理即可得证;(2)解:取AC 中点O ,连接1OA 、OB ,则1OA AC ⊥,根据面面垂直的性质可得1OA ⊥平面ABC ,如图,建立空间直角坐标系O xyz -,设2AB =,1OA a =,根据直线1A B 与平面11A ACC 所成的角求得a ,再利用向量法即可得出答案. (1)证明:连接1AC 交1A C 于点E ,连接DE , 因为四边形11ACC A 是平行四边形, 所以E 是1AC 的中点,又D 是AB 的中点, 所以1DE BC ∥,又1BC ⊄平面1A CD ,DE ⊂平面1A CD , 所以1BC ∥面1A CD ; (2)解:取AC 中点O ,连接1OA 、OB , 因为11AA A C =,所以1OA AC ⊥,因为平面11A ACC ⊥平面ABC ,1OA 平面11A ACC , 平面11A ACC ⋂平面ABC AC =, 所以1OA ⊥平面ABC ,因为ABC 是正三角形,O 是AC 的中点,所以OB AC ⊥, 如图,建立空间直角坐标系O xyz -, 设2AB =,1OA a =, 则()0,1,0A -,)B,()0,1,0C,1,02D ⎫-⎪⎝⎭,()10,0,A a ,()10,2,C a , 所以()13,0,A B a =-,又平面1A ACC 的一个法向量()1,0,0n =,所以1113cos ,sin 453A Bn A B n A B na ⋅===︒=+ 因为0a >,所以a =又(1CC =,33,022CD ⎛⎫=- ⎪ ⎪⎝⎭,设平面1CC D 的一个法向()1,,n x y z =,则11100n CC n CD ⎧⋅=⎪⎨⋅=⎪⎩,即0302y x y ⎧=-=, 令3x =,得31x y z =⎧⎪=⎨⎪=-⎩所以()13,3,1n =-,又平面ACD 的一个法向量()20,0,1n =,所以12cos ,n n =设二面角1A CD C --的平面角为θ, 则sin θ=即二面角1A CD C --【点睛】19.(1)910(2)列联表见解析,没有95%以上的把握认为“评定类型”与“性别”有关 【解析】 【分析】(1)根据古典概型公式计算即可; (2)填表后计算2K 即可判断. (1)用A 表示“任选2人中至少有1名男性”这一事件,则()21133225910C C C P A C +== (2)由题意得22⨯列联表为:由表中数据可得()224014126840 3.636 3.8412020221811K ⨯⨯-⨯==≈<⨯⨯⨯故没有95%以上的把握认为“评定类型”与“性别”有关.20.(1)()f x 在0,1上单调递减,在()1,+∞上单调递增; (2)证明见解析. 【解析】 【分析】(1)首先确定()f x 定义域,再应用二阶导数的符号判断f x 的单调性,进而分区间判断fx 的符号,即可确定()f x 的单调性.(2)求()f x 的二阶导,根据其符号知fx 在()0,+∞上单调递增,令0fx得到ln 1x x a +=,构造()ln 1xh x x a=+-结合其单调性,注意利用导数研究()ln 1x x x ϕ=-+的符号,再用放缩法判断1a h a ⎛⎫ ⎪+⎝⎭、()1e a h +的符号,即可判断零点0x 的唯一性,进而得到00011ln ln x x a x -==-,结合基本不等式求证()00f x ≥. (1)当1a =时,()1e ln 1xf x x -=--,定义域为()0,+∞,则()11e x f x x -'=-,()121e 0x f x x -+'=>',所以fx 在()0,+∞上单调递增,又()10f '=,当01x <<时,0f x,所以()f x 在区间0,1上单调递减;当1x >时,0fx,所以()f x 在区间()1,+∞上单调递增.综上,()f x 在0,1上单调递减,在()1,+∞上单调递增. (2)由题意,()11e xaf x x -='-,()1211e 0x af x a x-=⋅+'>',则f x 在()0,+∞上单调递增,至多有一个零点,令()ln 1x x x ϕ=-+,其中1x >,则()111xx x xϕ-'=-=, 当()0,1x ∈时,()0ϕ'>x ,()ϕx 单调递增. 当()1,x ∈+∞时,()0ϕ'<x ,()ϕx 单调递减,所以()()10x ϕϕ≤=,即ln 10x x -+≤,于是ln 1≤-x x ,令0f x ,则e e x a x ⋅=,两边取自然对数可得ln 1x x a+=, 令()ln 1x h x x a=+-,则()h x 在()0,+∞上单调递增. 故11ln 1111011111a a a h a a a a a ⎛⎫=+-≤-+-=-< ⎪+++++⎝⎭,又()11111e e ln e e 10a a a a h a a a++++=+⋅-=+>, 所以()h x 在()0,+∞上有唯一零点0x ,则f x 有唯一零点0x ,即()f x 有唯一极值点0x . 下证()00f x ≥:因为()01001e 0x a f x x -'=-=,所以0101e x a x -=,可得00011ln ln x x a x -==-, 所以()010000eln 11120x a x a f x a x x a -=--=+--≥=,当且仅当0x a =时等号成立, 综上,()f x 有唯一极值点0x 且()00f x ≥,得证.【点睛】关键点点睛:第二问,利用二阶导数研究一阶导数的单调性,根据零点所得的等量关系构造()ln 1x h x x a =+-,结合单调性、零点存在性定理判断f x 零点的唯一性,进而利用基本不等式证明不等式.21.(1)2212516x y += (2)35k = 【解析】【分析】(1)依题意得到方程组2222292561259a b c a b ⎧+=⎪⎨⎪=-=⎩,解得2a 、2b ,即可求出椭圆方程;(2)设直线l 的方程为()3y k x =-,()11,A x y ,()22,B x y ,联立直线与椭圆方程,消元、列出韦达定理,表示出1k ,2k ,根据120k k +=得到方程,解得k 即可;(1)解:由已知得2222292561259a b c a b ⎧+=⎪⎨⎪=-=⎩,解得222516a b ⎧=⎨=⎩, 所以椭圆C 的标准方程为2212516x y +=. (2)解:由题意,设直线l 的方程为()3y k x =-联立方程组()22312516y k x x y ⎧=-⎪⎨+=⎪⎩得()222216251502254000k x k x k +-+-= 设()11,A x y ,()22,B x y ,则21221501625k x x k +=+,21222254001625k x x k -=+. 又1111653y k x -=-,2221653y k x -=-, 所以()()()()122112121616335533y x y x k k x x ⎛⎫⎛⎫--+-- ⎪ ⎪⎝⎭⎝⎭+=-- 由()113y k x =-,()223y k x =-,得()()()122121536256005162533k k k k x x -+==+-- 解得35k =. 22.(1)l :10x y -+=,C:4πρθ⎛⎫=+ ⎪⎝⎭; (2)16﹒【解析】【分析】(1)根据l 的参数方程,消去参数t 即可得其普通方程;将x =ρcos θ,y =ρsin θ代入圆的直角坐标方程化简即可得其极坐标方程;(2)将直线l 的参数方程化为标准形式,代入圆的方程化简,利用直线参数方程参数的几何意义,结合韦达定理即可求解.(1)将直线l的参数方程12x y ⎧=⎪⎨=⎪⎩,消去参数t ,得直线l 的普通方程为10x y -+=;由圆C 的直角坐标方程()()22228x y -+-=得2244x y x y +=+,即24cos 4sin ρρθρθ=+, 故圆C的极坐标方程为4πρθ⎛⎫=+ ⎪⎝⎭. (2)将直线l的参数方程化为12x y ⎧=⎪⎪⎨⎪='⎩'⎪(t '为参数), 代入()()22228x y -+-=得270t ''-=,设A 、B 对应的参数分别为1t '、2t ',则12t t ''+127t t ''⋅=-, 故()()22222212121222716PA PB t t t t t t ''''+=+=+-=-⨯-=''.23.(1){|4x x ≤-或2}x ≥;(2)4.【解析】【分析】(1)分类讨论求绝对值不等式的解集,然后取并集.(2)利用绝对三角不等式求()f x 的最小值m ,再应用基本不等式求ab 的范围,注意端点值成立的条件,即可得最小值.(1)由()22,34,3122,1x x f x x x x --≤-⎧⎪=-<<⎨⎪+≥⎩且()6f x ≥,则2263x x --≥⎧⎨≤-⎩或2261x x +≥⎧⎨≥⎩,解得4x ≤-或2x ≥, 所以原不等式的解集为{|4x x ≤-或2}x ≥.(2)由()()()13134f x x x x x =-++≥--+=,则4m =,所以244ab a b =++≥,即20ab ≥21-(舍), 所以4ab ≥,当且仅当2a b ==时取等号,故ab 的最小值为4.。
2023届新疆维吾尔自治区乌鲁木齐市等5地二模理科数学2答案

新疆维吾尔自治区2023年普通高考第二次适应性检测理科数学参考答案第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.题号123456789101112答案CBCCBCDAAABD第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.13.514.2315.-16.3033-三、解答题:共70分,解答应写出文字说明,证明过程或演算步骤.17.解:(1)由已知得⎩⎨⎧-=-=++②① )1( )1(11n n n n a p S a p S ,①②-得n n n pa pa a -=++11*()n ∈N ,所以n n pa a p =-+1)1(,又因为1≠p ,所以11-=+p pa a n n ,当1=n 时,111,1pa pa p a p =-=-故.所以数列{}n a 是首项为1-p p ,公比为1-p p 的等比数列.……………………6分(2)由(1)知nn a 2=,所以22)12(21-=-=+n nn S ,故121121(21)12)(12(42111---=--=+++n n n n n n b ,所以123n nT b b b b =+++⋯+122311111111()2212121212121n n +=-+-+⋯+-------)1211(211--=+n ,又因为*n ∈N ,所以01211>-+n ,所以21<n T .…………………………12分18.解:(1)作AD EF //交P A 于F ,作//EM PA 交AD 于M ,连接CM ,FQ ,易得//EF MA .因为||||||||||||DE DM BQ EP MA QC ==,且DM MA BQ QC +=+,所以//AM QC ,又//EF MA ,所以//EF CQ .故四边形EFQC 是平行四边形,所以//CE FQ ,又FQ ⊂平面P AQ ,CE ⊄平面P AQ ,所以//CE 平面P AQ .………………………………………………………………6分(2)以A 为坐标原点,AB 方向为x 轴,AD 方向为y 轴,AP 方向为z 轴建立坐标系,设)40( ||<<=t t BQ ,则)0,0,0(A ,)0,4,0(D ,)4,0,0(P ,)0,,2(t Q .设平面PAQ 的一个法向量为1111(,,)x y z =n ,)4,0,0(=AP ,(2,,0)AQ t =,则有111402t 0z x y =⎧⎨+=⎩,令t x =1,则1(,2,0)t =-n .设平面PQD 的一个法向量为2222(,,)x y z =n ,)4,4,0(-=PD ,(2,,4)PQ t =-,则有22222440240y z x ty z -=⎧⎨+-=⎩,令22y =,则2(4,2,2)t =-n .若存在二面角D PQ A --是直二面角,则120⋅=n n ,即24t t 40--=,解得2=t ,(2,2,0)Q .故存在点Q 是BC 的中点时,使得二面角D PQ A --是直二面角,此时||1.||BQ CQ =…………………………………………………………………12分19.解:(1)由于甲队每场比赛平局的概率都是41,所以甲队三场比赛打平的场次,即随机变量X 服从二项分布,由题意得1~(3,4X B ,其分布列如下:00331327(0)((,4464P X C ===11231327(1)((,4464P X C ===2213139(2)((,4464P X C ===3303131(3)()(,4464P X C ===X 0123P64276427649641数学期望13()3.44E X =⨯=………………………………………………6分(2)由已知得不同的对阵情况共有633=A 种,每种可能性出现的概率均为1.6设甲队第二轮对阵乙队至少连续获胜两场的概率为1p ,甲队第二轮对阵丙队至少连续获胜两场的概率为2p ,甲队第二轮对阵丁队至少连续获胜两场的概率为3p ,则211111111111311511;6236436234643272p =⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=311111112111111111;6246346342624318p =⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=因为321p p p >>,所以甲队在第二轮对阵乙队时,p 的取值最大,最大值为1.12……………………………………………………………………………………12分111111112111311111;6326426324642312p =⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=20.解:(1)由题意知()e e(ln )x f x x x x =-+,()0,x ∈+∞,e()(1)(e x f x x x'=+-所以,易见e e ()xp x x=-在()0,x ∈+∞上递增,且(1)0p =,所以当()0,1x ∈时,()0p x <,即()0f x '<,()f x 在()0,1上单调递减,当()1,x ∈+∞时,()0p x >,即()0f x '>,()f x 在()1,+∞上单调递增,故()(1)0f x f ≥=,所以)(x f 的最小值为0.………………………………5分(2)原不等式等价于()()l e n 21xx x x b x -+≥-+在()0,x ∈+∞上恒成立,即ln e 1x x x x bx +--≥在()0,x ∈+∞上恒成立,也即e ln 1x x x x b x +--≥在()0,x ∈+∞上恒成立.令()ln 1e x x x x t x x +--=,()0,x ∈+∞,所以()22ln e x x xt x x+'=,令()2e ln xx x x ϕ=+,则()x ϕ是()0,∞+上的增函数,又因为12e 1e 10e ϕ-⎛⎫=-< ⎪⎝⎭,()e 10ϕ=>,所以()x ϕ在区间()0,1上存在唯一的零点0x ,即0020e n 0l xx x +=,由0200ln 0x x e x +=得01000ln 000ln 111e ln ln e x x x x x x x x ⎛⎫=-=⋅=⋅ ⎪⎝⎭,又由函数()e x q x x =在区间()0,∞+上单调递增,上式即()001lnq x q x ⎛⎫= ⎪⎝⎭所以0001lnln x x x ==-,00e 1x x =,当()00,x x ∈时,()0t x '<,()t x 单调递减,当()0,x x ∈+∞时,()0t x '>,()t x 单调递增,所以()000000min000ln 111()2e x x x x x x t x t x x x +--+-=+===,所以2b ≤.…………………………………………………………………………12分21.解:(1)因为||||AB MN =,所以点O 到AB 的距离等于点O 到MN 的距离,该距离等于2p,所以2AB p =.由||2AB p ==解得2p =,所以抛物线C 的方程为24x y =.………4分(2)由(1)可知准线l 的方程为1y =-,设点(,1)D m -,(,1)E n -,00(,)P x y 则直线PD 的方程为00(1)()()(1)y x m x m y +-=-+,整理得0000(1)()()(1)0y x x m y x m m y +-----+=.因为直线PD 和圆O 相切,所以点O 到直线PD 的距离等于1,1,=整理得2000(1)2(1)0y m x m y -+-+=,同理有2000(1)2(1)0y n x n y -+-+=,因为01y >,所以,m n 是一元二次方程2000(1)2(1)0y x x x y -+-+=的两个根,则0021x m n y -+=-,00(1)1y mn y -+=-,故0||||DE m n =-=又因为2004,x y =所以||DE =.因为点P 到准线l 的距离为01,y +所以12PDES =⨯△…………………………………9分令01(t 0)y t -=>,则PDES △因为44t t +≥,所以PDE S ≥=△当且仅当2t =时等号成立.综上,△PDE面积的最小值为………………………………………12分二选一试题22.解:(1)因为曲线C 的参数方程为()2cos 22sin x y θθθ=+⎧⎨=⎩为参数,故曲线C 的直角坐标方程为2240y x x +-=.又cos ,sin x y ρθρθ==,故曲线C 的极坐标方程为4cos ρθ=.……5分(2)设直线l 的倾斜角为α,则直线l 的参数方程为1cos 1sin x t y t αα=+⋅⎧⎨=+⋅⎩(t 为参数),代入()2224x y -+=得()22sin cos 20t t αα+--=.设点P 对应的参数为1t ,点Q 对应的参数为2t ,则()12122sin cos 2t t t t αα⎧+=--⎨⋅=-⎩(*),因为:2:3PM PQ =,所以122t t =,所以122t t =-,代入*式整理可得223sin 8sin cos 3cos 0αααα-+=,解得4tan 3α±=,所以直线l的斜率为43+或43.………………10分23.解:(1)原不等式为 |1||4|7x x +++≤,当4x ≤-时,147x x ----≤,得6x ≥-,所以64x -≤≤-;当41x -<≤-时,147x x --++≤恒成立,所以41x -<≤-;当1x >-时,147x x +++≤,得1x ≤,所以11x -<≤.综上,不等式的解集为 61{|}x x -≤≤.………………………………………5分(2)因为,m n 为正实数,()2()0m n f x mn +-≥即为()2mnf x m n≥+又213m n m m m n mn n m n m ++=+=+335m n n m =++≥+=,当且仅当m nn m =时等号成立,即41m n ==时等号成立,所以2mn m n +的最大值为15.又因为()()|4||3|f x x a x a a ≥+-+=(当x a =-时取等号),要使()2mn f x m n ≥+恒成立,只需 |31|5a ≥.所以115a ≤-或151a ≥.……………………………………………………10分以上解法仅供参考,如有其他方法,酌情给分。
2012年新疆维吾尔自治区普通高考第二次适应性检测试卷语文参考答案

2012年新疆维吾尔自治区普通高考第二次适应性检测试卷语文参考答案一、基础知识(每题3分,共48分)1.下列各组词语中加点字的读音,全都正确的一组是A.修葺(qì)瞭(liào)望纰(pī)漏濒危(pín)痉(jìng)挛B.眩(xuàn)晕渲(xuàn)染忖度(cǔn)羞赧(nǎn)创(chuānɡ)伤C.横(hénɡ)财档(dàng) 次稽(jī)查喑(ān)哑嫉(jí)妒D.骁(xiāo)勇祛(qù)除屠戮(lù)裨(pì)益粗犷(kuàng)2.下列各组词语中,没有错别字的一组是A. 关注寥廓耽搁草菅民命黄粱一梦人才辈出B.收讫彩排端祥顾名思义真知灼见弊帚自珍C.思辨筹画愚腐无的放矢篷头垢面甘之如饴D.流览跻身沉缅和盘托出融会贯通礼上往来3. 下列句子中,加点的成语使用不正确的一项是A. 据报道,近日科学家们发现了迄今已知的两个最大的黑洞,它们的质量是太阳的100亿倍,整个太阳系在它们面前都显得相形见绌。
B. 尽管如今搞收藏的人越来越多,但社会上不少拍卖会却与平民无关,普通的收藏者只能望洋兴叹,因为一般的藏品进不了拍卖会的门槛。
C.姜文在电影《关云长》中饰演曹操,他的表演栩栩如生,极具个性,有人评论他诠释了一个前所未有的带有“姜文”印记的曹操。
D.孙家栋院士如数家珍地向前来参观的人们介绍了我国绕月探测工程五大系统的特点,并特别强调这五大系统处处是“中国制造”。
4.下列句子中,没有语病的一句是A.为加强校车安全管理,防止校车安全事故不再发生,国务院法制办起草公布了《校车安全条例(草案征求意见稿)》。
B.中科院紫金山天文台研究员王思潮介绍,本次月全食是继今年1月10日之后我国境内观测条件最好的一次月全食。
C.地沟油不仅脏而且危害极大,其中含有多种有毒有害物质,会使人导致肠癌、胃癌等恶性疾病,严重威胁身体健康。
新疆乌鲁木齐市等5地2023届高三高考第二次适应性检测数学(文)试题(含答案与解析)

新疆维吾尔自治区2023年普通高考第二次适应性检测数学(文科)(卷面分值:150分;考试时间:120分钟)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,答题前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号,写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}Z 12A x x =∈-≤≤,{}128x B x =≤≤,则A B = ()A. []0,2B. {}0,1C. {}0,1,2D. []1,3-2. 复数z 满足11i 3z <--<,则z 的范围是( )A.)3-+B.C. )3⎡⎣D.3. 人们用分贝(dB )来划分声音的等级,声音的等级()d x (单位:dB )与声音强度x (单位:2W /m )满足()1210lg10xd x -=⋅.一般两人正常交谈时,声音的等级约为60dB ,燃放烟花爆竹时声音的等级约为150dB ,那么燃放烟花爆竹时声音强度约为两人正常交谈时声音强度的( ) A 710倍B. 810倍C. 910倍D. 1010倍4. 为了研究某公司工作人员人数x (单位:名)和月销售量y (单位:万元)的关系,从该公司随机抽取10名工作人员,根据测量数据的散点图可以看出y 与x 之间有线性相关关系,设其回归直线方程为y bx a =+$$$.已知101320i i x ==∑,1012400i i y ==∑,5b= .若该公司工作人员为25名,据此估计其月销售量为( ) A. 195B. 200C. 205D. 210.5. 如图,在长方体1111ABCD A B C D -中,若E ,F ,G ,H 分别是棱11A B ,1BB ,1CC ,11C D 上的动点,且//EH FG ,则必有( )A. 1BD EH ⊥B. AD FG ∥C. 平面11BB D D ⊥平面EFGHD. 平面11//A BCD 平面EFGH6. 已知向量a ,b 满足1a = ,(),2b m m =-r ,cos a b θ= (θ为a 与b的夹角),则a b - 的最小值为( )A.B.C. 1D. 27. 如图所示的程序框图,输入3个数据5log 2a =,8log 3b =,12c =,则输出的a 为( )A. 1B.12C. 8log 3D. 5log 28. 已知A ,B 为双曲线E :()222210,0x y a b a b-=>>的两个焦点,C ,D 在双曲线上,且四边形ABCD 为正方形,则22b a=( )A. 2+B.1+C. 2-D.1-9. 如图所示的曲线为函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>><⎪⎝⎭的部分图象,将()y f x =图象上的所有点的横坐标伸长到原来的32倍,再将所得曲线向左平移π8个单位长度,得到函数()y g x =的图象,则( )A. 直线π2x =为()g x 图象的一条对称轴 B. 点3π,08⎛⎫⎪⎝⎭为()g x 图象的一个对称中心 C. 函数()g x 的最小正周期为2π D. 函数()g x 在5π13π,2424⎡⎤⎢⎥⎣⎦上单调递减 10. 已知函数()()2πsin 22cos 106f x x x ωωω⎛⎫=++-> ⎪⎝⎭在[]0,π内有且仅有2个零点,则ω的取值范围是( ) A 54,63⎡⎫⎪⎢⎣⎭B. 54,63⎛⎤ ⎥⎝⎦C. 513,36⎫⎡⎪⎢⎣⎭D. 513,36⎛⎤⎥⎝⎦11. 已知四边形ABCD 的对角线AC ,BD的长分别为6,且BD 垂直平分AC 把△ACD 沿AC 折起,使得点D 到达点P ,则三棱锥P -ABC 体积最大时,其外接球半径为( ) A. 2B.C.D.12. 设()f x 是定义在R 上的以2为周期的偶函数,在区间[]1,2上单调递减,且满足()π1f =,()2π0f =,则不等式组()0101x f x ≤≤⎧⎨≤≤⎩的解集为( )A. 1,12⎡⎤⎢⎥⎣⎦B. []0,4π-C. []2π6,1-D. []2π6,4π--第Ⅱ卷本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须作答,.第22题~第23题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13. 已知椭圆C :2218x y a +=的焦距为8,则C 的离心率e =______________.14. 魏晋时期数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”(如图),在注中,刘徽对“牟合方盖”有以下的描述:“取立方棋八枚,皆令立方一寸,积之为立方二寸.规之为圆囷,径二寸,高二寸.又复横规之,则其形有似牟合方盖矣.八棋皆似阳马,圆然也.按合盖者,方率也.丸其中,即圆率也.”牟合方盖的发现有着重大的历史意义.通过计算得知正方体内切球的体积与“牟合方盖”的体积之比应为π:4.若在该正方体内任取一点,则此点取自“牟合方盖”内的概率是_____________.15. 在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若π3A =,224sin 2C b a a +=,则tan C =_____________.16. 对于三次函数()()320ax bx d a f x cx =+++≠,给出定义:设()f x '是()y f x =的导数,()x ϕ是()y f x ='的导数,若方程()0x ϕ=有实数解0x ,则称点()()00,x f x 为曲线()y f x =的“拐点”,可以发现,任何一个三次函数都有“拐点”.设函数()322343g x x x x =-+-,则1220232023g g ⎛⎫⎛⎫+++⎪ ⎪⎝⎭⎝⎭20222023g ⎛⎫= ⎪⎝⎭_____________. 三、解答题:共70分,解答应写出文字说明,证明过程或演算步骤.17. 已知非零数列{}n a 的前n 项和为n S ,且满足()1n n S p a =-,其中p 为常数,且1p ≠. (1)证明:数列{}n a 是等比数列; (2)若2p =,12n n n n S b S S ++=,数列{}n b 的前n 项和为n T ,证明:12n T <.18. 如图,三棱柱111ABC A B C -的所有棱长均为1,且点1A 在底面上的射影是AC 的中点D .1AB 与1A B 交于点E ,1BC 与1B C 交于点F.(1)证明:11A B B C ⊥; (2)求几何体ABCFE 的体积.19. 从2023年起,某市中考考试科目将改为“3科必考+3科选考+体育”.其中3科必考科目为语文、数学和外语,满分都为100分.3科选考科目应在物理和生化(生物、化学合为一科)两科中选择1或2科,在历史、地理和思想品德三科中选择1或2科,每科原始满分都为100分,所选的三科成绩,将由高到低分别按照100%,80%,60%的系数折算成最后分数,三科折算后的实际满分为100分,80分,60分,体育成绩为40分,中考满分为580分.已知甲,乙两名考生在选考科目中选择每一科的可能性都相同. (1)若甲、乙两名考生的中考考试科目和原始分数成绩单如下:科目 语文 数学 英语 物理 生化 地理 体育 甲的分数 92 97 96 100 80 60 40 乙的分数92979680808040请分别计算甲、乙两名考生的中考总分; (2)求甲考生在选考科目中选考历史的概率. 20. 已知()()e ln xf x x a x x =-+.(1)当e a =时,求()f x 的最小值;(2)当1a =时,有()()21f x b x -+≥恒成立,求b 的取值范围. 21. 在平面直角坐标系xOy 中,抛物线G 准线方程为=2y-. (1)求抛物线G 的标准方程;(2)过抛物线焦点F 作互相垂直的两条直线1l 和2l ,1l 与抛物线交于P ,Q 两点,2l 与抛物线交于C ,D 两点,M ,N 分别是线段PQ ,CD 的中点,求△FMN 面积的最小值.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请用2B 铅笔在答题卡上把所选题目的题号涂黑. [选修4-4:坐标系与参数方程]的的22. 已知曲线C 的方程为2cos 22sin x y θθ=+⎧⎨=⎩(θ为参数),以坐标原点O 为极点,x 轴正半轴为极轴,建立极坐标系.(1)求曲线C 的极坐标方程;(2)过()1,1M 作直线l 交曲线C 于P 、Q 两点,且:2:3PM PQ =,求直线l 的斜率.[选修4-5:不等式选讲]23. 已知函数()4f x x a x a =+++. (1)当1a =时,求不等式()7f x ≤解集;(2)对于任意的正实数m ,n ,且13n m =-,若()()20m n f x mn +-≥恒成立,求实数a 的范围.参考答案一、选择题:本大题共12小题,每小题5分,每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}Z 12A x x =∈-≤≤,{}128x B x =≤≤,则A B = ()A. []0,2B. {}0,1C. {}0,1,2D. []1,3-【答案】C 【解析】【分析】先由集合的表示方法和指数函数的性质化简集合,A B ,再利用集合交集的定义求解即可. 【详解】因{}{}Z 121,0,1,2A x x =∈-≤≤=-, 由指数函数的性质可得{}03B x x =≤≤, 所以{}0,1,2A B = , 故选:C2. 复数z 满足11i 3z <--<,则z 的范围是( )A.)3-+B.C. )3⎡⎣D.【答案】B 【解析】【分析】根据题意,得到2i 4i z +<<+,结合复数模的计算公式,即可求解.的为【详解】由11i 3z <--<,可得2i 4i z +<<+,又由2i i +=+=z <<,即z ∈.故选:B3. 人们用分贝(dB )来划分声音的等级,声音的等级()d x (单位:dB )与声音强度x (单位:2W /m )满足()1210lg10xd x -=⋅.一般两人正常交谈时,声音的等级约为60dB ,燃放烟花爆竹时声音的等级约为150dB ,那么燃放烟花爆竹时声音强度约为两人正常交谈时声音强度的( ) A 710倍B. 810倍C. 910倍D. 1010倍【答案】C 【解析】【分析】根据解析式分别求出对于声音强度可得.【详解】分别记正常交谈和燃放烟花爆竹时的声音强度分别为12,x x , 则有12121210lg60,10lg 1501010x x --⋅=⋅=, 解得631210,10x x -==,则39261101010x x -==. 故选:C4. 为了研究某公司工作人员人数x (单位:名)和月销售量y (单位:万元)的关系,从该公司随机抽取10名工作人员,根据测量数据的散点图可以看出y 与x 之间有线性相关关系,设其回归直线方程为y bx a =+$$$.已知101320i i x ==∑,1012400i i y ==∑,5b= .若该公司工作人员为25名,据此估计其月销售量为( ) A. 195 B. 200 C. 205 D. 210【答案】C 【解析】【分析】计算x 、y ,根据回归方程的性质求出a ∧的值,再利用回归方程计算25x =时y ∧的值.【详解】根据题意,计算10132110i i x x ===∑,101240110i i y y ===∑,ˆ5b =; ∴ˆ24053280a y bx∧=-=-⨯=, ∴ 580y x =+,当25x =时,可得52580205y =⨯+=$,..所以估计其月销售量约为205. 故选:C .5. 如图,在长方体1111ABCD A B C D -中,若E ,F ,G ,H 分别是棱11A B ,1BB ,1CC ,11C D 上的动点,且//EH FG ,则必有( )A. 1BD EH ⊥B. AD FG ∥C. 平面11BB D D ⊥平面EFGHD. 平面11//A BCD 平面EFGH【答案】B 【解析】【分析】根据题意,结合图形,分别判断选项中的命题是否正确即可. 【详解】若点E 与1A 重合,点H 与点1D 重合,则1BD 与EH 的夹角便是1BD 与11A D 的夹角,显然1BD 与11A D 的夹角不是π2, 所以1BD EH ⊥错误,A 错误;当FG 与11B C 重合时,由11//AD B C 可得AD FG ∥, 当FG 与11B C 不重合时,因为//EH FG ,EH ⊂平面1111D C B A ,FG ⊄平面1111D C B A , 所以//FG 平面1111D C B A ,FG ⊂平面11BCC B , 平面11BCC B 平面111111A B C D B C =, 所以11//FG B C ,又11//AD B C , 所以AD FG ∥,B 正确;当平面EFGH 与平面11BCC B 重合时,平面11BB D D 与平面11BCC B 不垂直,C 错误; 当FG 与BC 重合时,平面11A BCD 与平面EFGH 相交,D 错误. 故选;B.6. 已知向量a ,b 满足1a = ,(),2b m m =-r ,cos a b θ= (θ为a 与b的夹角),则a b - 的最小值为( )A.B.C. 1D. 2【答案】C 【解析】【分析】由平面向量数量积的运算,结合平面向量的模长的计算公式求解即可.【详解】因为向量a ,b 满足1a = ,(),2b m m =-r ,cos a b θ= (θ为a 与b的夹角),则cos 1a b a b θ⋅=⋅⋅=,则222222121a b a b a b b b -=+-⋅=+-=-()()2222212432111m m m m m =+--=-+=-+≥,当且仅当1m =时取等号,即2a b - 的最小值为1,即a b - 的最小值为1.故选:C .7. 如图所示的程序框图,输入3个数据5log 2a =,8log 3b =,12c =,则输出的a 为( )A. 1B.12C. 8log 3D. 5log 2【答案】D 【解析】【分析】由程序框图可知,输出结果为a 、b 、c 中的最小值,然后将12分别化为5和8为底的对数比较大小可得.【详解】由程序框图可知,输出结果为a 、b 、c 中的最小值, 因为12551log 2log 52a =<=,所以a c <,又128881log 3log log 82b =>==,所以bc > 所以b c a >>. 故选:D8. 已知A ,B 为双曲线E :()222210,0x y a b a b-=>>的两个焦点,C ,D 在双曲线上,且四边形ABCD 为正方形,则22b a=( )A. 2+B.1+ C. 2-D.1-【答案】A 【解析】【分析】利用已知条件列出方程组,求解得关于a ,c 的等式关系,转化为离心率的式子,即可求得. 【详解】解:如图,正方形的顶点A ,B 为双曲线的焦点,顶点C ,D 在双曲线上则(,0),(,0)A c B c -,故2(,b C c a由正方形ABCD 得:AB BC =,所以22b c a=,则2222ac b c a ==-即:2220c ac a --=,两边同除2a 得:2210e e --=,解得:1=+e 或1=+e (舍), )2222113b e a=+==+,则222b a=+.故选:A .9. 如图所示的曲线为函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象,将()y f x =图象上的所有点的横坐标伸长到原来的32倍,再将所得曲线向左平移π8个单位长度,得到函数()y g x =的图象,则( )A. 直线π2x =为()g x 图象的一条对称轴 B. 点3π,08⎛⎫⎪⎝⎭为()g x 图象的一个对称中心 C. 函数()g x 的最小正周期为2π D. 函数()g x 在5π13π,2424⎡⎤⎢⎥⎣⎦上单调递减 【答案】A 【解析】【分析】先由函数的图象求出()f x 的解析式,再结合题意求出()g x ,结合余弦函数的图象性质即可求解 【详解】由图象知2A =,又π2π5π63212+=,所以()f x 的一个最低点为5π,212⎛⎫- ⎪⎝⎭, 而()f x 的最小正周期为2π2π033T =-=, 所以2π3Tω==, 又5π5π2sin 321212f ϕ⎛⎫⎛⎫=⨯+=- ⎪ ⎪⎝⎭⎝⎭,则5πsin 3112ϕ⎛⎫⨯+=- ⎪⎝⎭, 所以()5π3π2π42k k ϕ+=+∈Z ,即()π2π4k k ϕ=+∈Z , 又π2ϕ<,所以π4ϕ=, 所以()π2sin 34f x x ⎛⎫=+⎪⎝⎭,将函数()y f x =图象上的所有点的横坐标伸长到原来的32得π2sin 24y x ⎛⎫=+ ⎪⎝⎭的图象,再把所得曲线向左平移π8个单位长度得π2sin 22cos 22y x x ⎛⎫=+= ⎪⎝⎭,即()2cos 2g x x =. 因为ππ2cos 22222g cos π⎛⎫=⨯==-⎪⎝⎭, 所以直线π2x =是()g x 图象的一条对称轴,故A 正确;因为3π3π3π2cos 22cos 884g ⎛⎫=⨯==⎪⎝⎭, 所以3π,08⎛⎫⎪⎝⎭不是()g x 图象的一个对称中心,故B 错误; 函数()g x 在周期2ππ2T ==,故C 错误; 由()2π2π2πk x k k ≤≤+∈Z 得()πππ2k x k k ≤≤+∈Z , 所以()g x 在ππ,π2k k ⎡⎤+⎢⎥⎣⎦()k ∈Z 上单调递减, 当5π13π,2424x ⎡⎤∈⎢⎥⎣⎦时,可知()g x 在5ππ,242⎡⎤⎢⎥⎣⎦递减,在π13π,224⎡⎤⎢⎥⎣⎦递增,所以D 错误. 故选:A.10. 已知函数()()2πsin 22cos 106f x x x ωωω⎛⎫=++-> ⎪⎝⎭在[]0,π内有且仅有2个零点,则ω的取值范围是( ) A. 54,63⎡⎫⎪⎢⎣⎭B. 54,63⎛⎤ ⎥⎝⎦C. 513,36⎫⎡⎪⎢⎣⎭D. 513,36⎛⎤⎥⎝⎦【答案】A 【解析】【分析】把函数化成sin()y A x ωϕ=+的形式,再利用正弦函数的性质求解作答.【详解】依题意,()132cos 2cos 22cos 222f x x x x x x ωωωωω=++=+π)3x ω=+,当[0,π]x ∈时,πππ2,2π333x ωω⎡⎤+∈+⎢⎥⎣⎦,因为()f x 在[]0,π内有且仅有2个零点, 于是π2π2π3π3ω≤+<,解得5463ω≤<,所以ω的取值范围是54[,)63. 故选:A11. 已知四边形ABCD 的对角线AC ,BD 的长分别为6,且BD 垂直平分AC 把△ACD 沿AC 折起,使得点D 到达点P ,则三棱锥P -ABC 体积最大时,其外接球半径为( )A. 2B.C.D.【答案】B 【解析】【分析】设,AC BD 交于点E ,由三棱锥P -ABC 体积最大可得PE ⊥平面ABC ,3PE BE ==,后作出三棱锥P -ABC 球心O ,利用几何知识即可求得外接球半径.【详解】如图,设,AC BD 交于点E ,6,BE x DE PE x ===-, 要使三棱锥P -ABC 体积最大,则PE ⊥平面ABC ,其体积为:()()2116336ABC S PE AC BE PE x x x ⋅=⋅⋅=-=--+ 则当3x =,即3PE BE ==时,三棱锥P -ABC 体积最大. 注意到此时,PAC BAC ≅ ,且均为等边三角形,设BAC 外心为1O ,PAC △外心为2O ,过12,O O 分别作平面BAC ,平面PAC 垂线,交点为O , 则O 为三棱锥P -ABC 外接球球心.又2O 为PAC △重心,则2113O E PE ==, 结合四边形21O EO O 是矩形,则121O O O E ==.又BAC 外接圆半径为11223O A O B BE ===,则三棱锥P -ABC 外接球半径为OA ===.故选:B【点睛】结论点睛:本题有更一般的结论,若在三棱锥P -ABC 中,平面PAC ⊥平面BAC ,则三棱锥P -ABC 外接球半径r =12,r r 分别为,PAC BAC 外接圆半径,l 为,PAC BAC 交线长度.12. 设()f x 是定义在R 上的以2为周期的偶函数,在区间[]1,2上单调递减,且满足()π1f =,()2π0f =,则不等式组()0101x f x ≤≤⎧⎨≤≤⎩的解集为( )A. 1,12⎡⎤⎢⎥⎣⎦B. []0,4π-C. []2π6,1-D. []2π6,4π--【答案】D 【解析】【分析】根据题意,由函数的周期性与奇偶性分析可得()()2f x f x -=+,则函数()f x 关于直线1x =对称,据此可得()f x 在[]0,1上递增,且()41f π-=,()260f π-=,则进而分析()0101x f x ≤≤⎧⎨≤≤⎩可得答案.【详解】根据题意,()f x 为周期为2的偶函数, 则()()2f x f x =+且()()=f x f x -, 则有()()2f x f x -=+, 则函数()f x 关于直线1x =对称,又由()f x 在区间[]1,2上单调递减,且()π1f =,()2π0f =, 因为周期为2得()12fπ-=,()260f π-=,又()f x 关于直线1x =对称,则()4π1f -=,则()f x 在[]0,1上递增,且()2π60f -=,()4π1f -=,则()[]012π6,4π01x f x ≤≤⎧⇒--⎨≤≤⎩,即不等式组的解集为[]2π6,4π--. 故选:D .第Ⅱ卷本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须作答,第22题~第23题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13. 已知椭圆C :2218x y a +=的焦距为8,则C 的离心率e =______________.【解析】【分析】根据给定椭圆的方程和焦距,求出长半轴长即可作答.【详解】因为椭圆C :2218x y a +=的焦距为8,则半焦距4c =,根据方程可知,284<,所以焦点在x 轴上,因此短半轴长为==,所以C 的离心率e ==.14. 魏晋时期数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”(如图),在注中,刘徽对“牟合方盖”有以下的描述:“取立方棋八枚,皆令立方一寸,积之为立方二寸.规之为圆囷,径二寸,高二寸.又复横规之,则其形有似牟合方盖矣.八棋皆似阳马,圆然也.按合盖者,方率也.丸其中,即圆率也.”牟合方盖的发现有着重大的历史意义.通过计算得知正方体内切球的体积与“牟合方盖”的体积之比应为π:4.若在该正方体内任取一点,则此点取自“牟合方盖”内的概率是_____________.【答案】23【解析】【分析】设正方体的棱长为2a ,用a 表示出“牟合方盖”的体积,再利用几何概型计算作答. 【详解】设正方体的棱长为2a ,则该正方体内切球半径为a ,令 “牟合方盖”的体积为V ,于是34ππ34aV =,解得3163V a =,而正方体的体积为3(2)a , 所以在该正方体内任取一点,此点取自“牟合方盖”内的概率是3331623(2)83aV a a ==. 故答案为:2315. 在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若π3A =,224sin 2C b a a +=,则tan C =_____________.【答案】-【解析】【分析】由正弦定理和两角和的正弦公式化简即可得出答案. 【详解】由正弦定理可得:1cos sin 2sin 4sin 2C B A A -+=⋅, 因为π3A =,所以sin A =,所以()sin 1cos B C +=-,πsin 3C C ⎛⎫+= ⎪⎝⎭,1sin 2C C C +=1sin 2C C =-,则tan C =-.故答案为:-16. 对于三次函数()()320ax bx d a f x cx =+++≠,给出定义:设()f x '是()y f x =的导数,()x ϕ是()y f x ='的导数,若方程()0x ϕ=有实数解0x ,则称点()()00,x f x 为曲线()y f x =的“拐点”,可以发现,任何一个三次函数都有“拐点”.设函数()322343g x x x x =-+-,则1220232023g g ⎛⎫⎛⎫+++⎪ ⎪⎝⎭⎝⎭20222023g ⎛⎫= ⎪⎝⎭_____________. 【答案】-3033 【解析】分析】由题意对已知函数进行二次求导,证明函数关于点1,02⎛⎫ ⎪⎝⎭中心对称,即()1()0g x g x -+=,由此可得到结果.【详解】因为()322343g x x x x =-+-,所以()2664g x x x '=-+,设()2664h x x x =-+,则()126h x x '=-,令()1260h x x '=-=,可得12x =, 又32311115323432222222g x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫+=+-+++-=+-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭32311115323432222222g x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫-=---+--=--- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以11322g x g x ⎛⎫⎛⎫++-=- ⎪ ⎪⎝⎭⎝⎭,即()()13g x g x +-=-, 所以1202222021101110123202320232023202320232023g g g g g g ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=+=⋅⋅⋅=+=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,所以1220223033202320232023g g g ⎛⎫⎛⎫⎛⎫+++=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故答案为:3033-.【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.三、解答题:共70分,解答应写出文字说明,证明过程或演算步骤.17. 已知非零数列{}n a 的前n 项和为n S ,且满足()1n n S p a =-,其中p 为常数,且1p ≠. (1)证明:数列{}n a 是等比数列; (2)若2p =,12n n n n S b S S ++=,数列{}n b 的前n 项和为n T ,证明:12n T <.【答案】(1)证明见解析(2)证明见解析 【解析】【【分析】(1)利用11n n n a S S ++=-的思想,即可推出11n n a pa p +=-,得证; (2)若2p =,由(1)知数列{}n a 是首项为2,公比为2的等比数列,根据等比数列前n 项和公式求出n S ,即可得出n b ,再利用裂项法求和,即可得证.【小问1详解】由已知得()()1111n n n n S p a S p a ++⎧=-⎪⎨=-⎪⎩①②,②-①得()*11n n n a pa pa n ++=-∈N ,所以()11n n p a pa +-=,又因为1p ≠,所以11n n a pa p +=-, 当1n =时,11a pa p =-,故11p a p =-. 所以数列{}n a 是首项为1p p -,公比为1pp -的等比数列.【小问2详解】若2p =,由(1)知数列{}n a 是首项为2,公比为2的等比数列, 所以()12122212n n n S +-==--,故()()11121112212142121n n n n n n b +++⎛⎫==- ⎪----⎝⎭,所以123n n T b b b b =++++1223111111112212121212121n n +⎛⎫-+-++- ⎪------⎝=⎭1111221n +⎛⎫=- ⎪-⎝⎭, 又因为*n ∈N ,所以11021n +>-,所以12n T <. 18. 如图,三棱柱111ABC A B C -的所有棱长均为1,且点1A 在底面上的射影是AC 的中点D .1AB 与1A B 交于点E ,1BC 与1B C 交于点F .(1)证明:11A B B C ⊥; (2)求几何体ABCFE 的体积. 【答案】(1)见解析 (2)332【解析】【分析】(1)连接BD ,利用等腰三角形的三线合一得BD AC ⊥,再利用线面垂直的判定得AC ⊥平面1A BD ,从而1A B AC ⊥,再利用菱形性质得11A B AB ⊥,最后再次利用线面垂直的判定和性质即可得到答案;(2)通过棱锥体积公式求得118B ABC V -=三棱锥,再利用其与几何体ABCFE 的体积的关系即可. 【小问1详解】因为点1A 在底面上的射影是AC 的中点D ,所以1A D AC ⊥, 连接BD ,因为ABC 是边长为1的正三角形,所以BD AC ⊥,因为11,,A D BD D A D BD =⊂ 平面1A BD ,所以AC ⊥平面1A BD , 因为1A B ⊂平面1A BD ,所以1A B AC ⊥.因为四边形11ABB A 是边长为1的菱形,所以11A B AB ⊥,又因为11,,AB AC A AB AC =⊂ 平面1AB C ,所以1A B ⊥平面1AB C , 因为1B C ⊂平面1AB C ,所以11A B B C ⊥.【小问2详解】因为三棱柱111ABC A B C -的所有棱长均为1, 且点1A 在底面上的射影是AC 的中点D ,所以三棱柱的高为1A D =.又ABC 的面积为1112⨯⨯=,所以 11138B ABC V -==三棱锥 由题可知,点E 为1AB 的中点,点F 为1B C 的中点, 所以梯形AEFC 的面积是1AB C V 的面积的34, 所以143233841343ABCFE B AEFC B AB C B ABC V V V V ---====⨯=几何体四棱锥三棱锥三棱锥. 19. 从2023年起,某市中考考试科目将改为“3科必考+3科选考+体育”.其中3科必考科目为语文、数学和外语,满分都为100分.3科选考科目应在物理和生化(生物、化学合为一科)两科中选择1或2科,在历史、地理和思想品德三科中选择1或2科,每科原始满分都为100分,所选的三科成绩,将由高到低分别按照100%,80%,60%的系数折算成最后分数,三科折算后的实际满分为100分,80分,60分,体育成绩为40分,中考满分为580分.已知甲,乙两名考生在选考科目中选择每一科的可能性都相同. (1)若甲、乙两名考生的中考考试科目和原始分数成绩单如下:科目 语文 数学 英语 物理 生化 地理 体育 甲的分数 92 97 96 100 80 60 40 乙的分数92979680808040请分别计算甲、乙两名考生的中考总分; (2)求甲考生在选考科目中选考历史的概率. 【答案】(1)甲总分525分,乙总分517分(2)59【解析】【分析】(1)直接根据总分计算方式代入计算即可;(2)写出所有情况,再得到满足题意的情况数,最后得到概率值. 【小问1详解】甲的总分9297961008080%6060%40525=++++⨯+⨯+=;乙的总分929796808080%8060%40517=++++⨯+⨯+=. 【小问2详解】设物理、生化、历史、地理、思想品德五科分别为A ,B ,C ,D ,E . 从五科中选考三科且历史,地理,思想品德三科不能同时被选, 有ABC ,ABD ,ABE ,ACD ,ACE ,ADE ,BCD ,BCE ,BDE 共9个基本事件,设“甲同学在选考科目中选中历史”为事件M , 则M 中包含,,,,ABC ACD ACE BCD BCE 共5个基本事件, 所以5()9P M =. 则甲考生在选考科目中选考历史的概率为59. 20. 已知()()e ln xf x x a x x =-+.(1)当e a =时,求()f x 的最小值;(2)当1a =时,有()()21f x b x -+≥恒成立,求b 的取值范围. 【答案】(1)0 (2)2b ≤【解析】【分析】(1)求函数()f x 的定义域和导函数,根据()ee x p x x=-的单调性确定函数()f x '的取值规律,由此判断函数()f x 的单调性,求其最值;(2)已知条件等价于等价于e ln 1x x x x b x +--≥在()0,x ∈+∞上恒成立,利用导数求函数()e ln 1x x x x t x x+--=的最小值可得b 的取值范围. 【小问1详解】由题意知()()e e ln xf x x x x =-+,()0,x ∈+∞,所以()()e '1e x f x x x ⎛⎫=+- ⎪⎝⎭, 易见()ee xp x x=-在()0,x ∈+∞上递增,且()10p =, 所以当()0,1x ∈时,()0p x <,即()'0f x <,()f x 在()0,1上单调递减, 当()1,x ∈+∞时,()0p x >,即()'0f x >,()f x 在()1,+∞上单调递增, 故()()10f x f ≥=,所以()f x 的最小值为0.【小问2详解】由已知()()e ln 21xx x x b x -+≥-+在()0,x ∈+∞上恒成立,即e ln 1x x x x bx +--≥在()0,x ∈+∞上恒成立,也即e ln 1x x x x b x +--≥在()0,x ∈+∞上恒成立.令()e ln 1x x x x t x x +--=,()0,x ∈+∞,所以()22e ln 'x x xt x x+=, 令()2e ln xx x x ϕ=+,则()x ϕ是()0,∞+上的增函数,又因为12e 1e 10e ϕ-⎛⎫=-< ⎪⎝⎭,()1e 0ϕ=>,所以()x ϕ在区间()0,1上存在唯一的零点0x ,即0020e n 0l xx x +=,由0020e n 0l x x x +=得001ln 000000ln 111e ln ln e x x x x x x x x ⎛⎫=-=⋅=⋅ ⎪⎝⎭, 又由函数()e xq x x =在区间()0,∞+上单调递增,上式等价于()001lnq x q x ⎛⎫= ⎪⎝⎭所以0001lnln x x x ==-,001e x x =, 当()00,x x ∈时,()'0t x <,()t x 单调递减, 当()0,x x ∈+∞时,()'0t x >,()t x 单调递增, 所以()()0000000min 00e ln 1112x x x x x x t x t x x x +--++-====,所以2b ≤.【点睛】对于恒成立问题,常用到以下两个结论: (1)()a f x ≥恒成立⇔()max a f x ≥; (2)()a f x ≤恒成立⇔()min a f x ≤.21. 在平面直角坐标系xOy 中,抛物线G 的准线方程为=2y -. (1)求抛物线G 的标准方程;(2)过抛物线的焦点F 作互相垂直的两条直线1l 和2l ,1l 与抛物线交于P ,Q 两点,2l 与抛物线交于C ,D 两点,M ,N 分别是线段PQ ,CD 的中点,求△FMN 面积的最小值.【答案】(1)28x y =(2)16 【解析】【分析】(1)根据题意得22p-=-,解出p 值即可; (2)设直线1l 的方程为()()11222,,,,y kx P x y Q x y =+,联立直线与抛物线方程,得到韦达定理式,根据中点公式求出()24,42M k k +,通过代换得到244,2N k k ⎛⎫-+ ⎪⎝⎭,写出面积表达式,利用基本不等式即可求出最值. 【小问1详解】设抛物线标准方程为22x py =,其中0p >, 由题意得22p-=-,解得4p =,则焦点()0,2F , 故抛物线G 标准方程为28x y =. 【小问2详解】(0,2)F ,由题意知直线12,l l 的斜率都存在且不为0,设直线1l 的方程为()()11222,,,,y kx P x y Q x y =+, 则直线2l 的方程为12y x k=-+, 由282x y y kx ⎧=⎨=+⎩得28160x kx --=,则264640k ∆=+>, 所以12128,16x x k x x +==-, 所以()21214,2422M M M x x x k y kx k =+==+=+, 所以()24,42M k k +. 用1k -替换k 可得22,44N N x y k k =-=+,所以244,2N k k ⎛⎫-+ ⎪⎝⎭.所以1||||2FMNS FM FN =====8216≥=⨯=,当且仅当221k k =,即1k =±时等号成立, 所以FMN 面积的最小值为16.【点睛】关键点睛:本题第二问的关键是设直线方程,然后将其与抛物线方程联立,得到韦达定理式,求出()24,42M k k +,而N 的坐标无需再次联立方程,用1k-替换k 即可,最后得到面积表达式,再利用基本不等式即可求出最值.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请用2B 铅笔在答题卡上把所选题目的题号涂黑. [选修4-4:坐标系与参数方程]22. 已知曲线C 的方程为2cos 22sin x y θθ=+⎧⎨=⎩(θ为参数),以坐标原点O 为极点,x 轴正半轴为极轴,建立极坐标系.(1)求曲线C 的极坐标方程;(2)过()1,1M 作直线l 交曲线C 于P 、Q 两点,且:2:3PM PQ =,求直线l 的斜率. 【答案】(1)4cos ρθ=(2 【解析】【分析】(1)将曲线C 的参数方程化为普通方程,再转化为极坐标方程即可;(2)设直线l 的倾斜角为α,写出直线l 的参数方程,代入曲线C 的普通方程,可得出关于t 的二次方程,列出韦达定理,设点P 对应的参数为1t ,点Q 对应的参数为2t ,由已知可得出122t t =,代入韦达定理可得出关于tan α的二次方程,解出tan α的值,即可得出直线l 的斜率. 【小问1详解】因为曲线C 的参数方程为2cos 22sin x y θθ=+⎧⎨=⎩(θ为参数),所以22cos 2sin x y θθ-=⎧⎨=⎩,消去参数θ,可得()2224x y -+=, 故曲线C 的普通方程为2240x y x +-=. 又cos x ρθ=,sin y ρθ=,故曲线C 的极坐标方程为24cos 0ρρθ-=,即4cos ρθ=. 【小问2详解】设直线l 的倾斜角为α,则直线l 的参数方程为1cos 1sin x t y t αα=+⎧⎨=+⎩(t 为参数),代入()2224x y -+=,得()22sin cos 20t t αα+--=.()24sin cos 80αα∆=-+>,设点P 对应的参数为1t ,点Q 对应的参数为2t ,则()12122sin cos 2t t t t αα⎧+=--⎨⋅=-⎩(*),因为:2:3PM PQ =,所以122t t =,所以122t t =-,代入(*)式整理,可得()2224sin cos 1sin cos αααα-==+, 可得223sin 8sin cos 3cos 0αααα-+=, 若cos 0α=,则sin 0α=,与22sin cos 1αα+=矛盾,故cos 0α≠,可得23tan 8tan 30αα-+=,解得tan α=所以直线l[选修4-5:不等式选讲]23. 已知函数()4f x x a x a =+++. (1)当1a =时,求不等式()7f x ≤的解集;(2)对于任意的正实数m ,n ,且13n m =-,若()()20m n f x mn +-≥恒成立,求实数a 的范围.【答案】(1){}61x x -≤≤(2)115a ≤-或151a ≥【解析】【分析】(1)分4x ≤-,41x -<≤-,1x >-几种情况去掉绝对值,即可解不等式;(2)()()20m n f x mn +-≥恒成立,等价于()2m axmn f x m n ⎛⎫≥ ⎪+⎝⎭,利用基本不等式可得215m axmn m n ⎛⎫= ⎪+⎝⎭,又()3f x a ≥,即可得答案. 【小问1详解】原不等式为147x x +++≤,当4x ≤-时,147x x ----≤,得6x ≥-,所以64x -≤≤-; 当41x -<≤-时,147x x --++≤恒成立,所以41x -<≤-; 当1x >-时,147x x +++≤,得1x ≤,所以11x -<≤. 综上,不等式的解集为{}61x x -≤≤; 【小问2详解】因m ,n 为正实数,()()20m n f x mn +-≥恒成立,即为()2m axmn f x m n ⎛⎫≥ ⎪+⎝⎭,又213m n m m m nmn n m n m ++=+=+=3m n n m ++35≥+=,当且仅当m n n m =,即41m n ==时等号成立, 所以2mn m n+的最大值为15.又因为()()43f x x a x a a ≥+-+=(当()()40x a x a ++≤时取等号), 要使()2mn f x m n≥+恒成立,只需135a ≥. 所以115a ≤-或151a ≥.为。
新疆维吾尔自治区2024届高三第二次适应性检测数学试题含答案

新疆维吾尔自治区2024年普通高考第二次适应性检测数学(卷面分值:150分考试时间:120分钟)注意事项:1.本试卷分选择题和非选择题两部分,答题前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号,写在本试卷上无效.3.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z 满足4+=z z ,且2i -=z z ,则=zA B .C .2D2.已知集合{==∣P x y ,{}2==∣Q y y x ,则下列选项中正确的是A .=R P QB .⊆Q PC .=∅P Q D .⊆P Q3.若函数()11-=-ax f x x 的图象关于点()1,2对称,则=a A .2-B .1-C .1D .24.已知直线=+y kx m (m 为常数)与圆224+=x y 交于点M ,N ,当k 变化时,若MN 的最小值为2,则=mA .1±B .C .D .2±5.设{}n a 是等差数列,下列结论中正确的是A .若120+>a a ,则230+>a a B .若130+<a a ,则120+<a aC .若120<<a a ,则2>a D .若10<a ,则()()21410--<a a a a 6.过点()1,4且与曲线()32=++f x x x 相切的直线方程为A .40-=x y B .7490-+=x y C .40-=x y 或7490-+=x y D .40-=x y 或47240-+=x y7.设0,2πα⎛⎫∈ ⎪⎝⎭,0,2πβ⎛⎫∈ ⎪⎝⎭,且1tan tan cos αββ=+,则A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=8.已知椭圆22198+=x y 的左、右焦点分别为1F ,2F ,M 为椭圆上不与左右顶点重合的任意一点,I ,G 分别为12ΔMF F 的内心和重心,则12⋅=IG F FA .0B .1C .D .3二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.下列结论正确的是A .若样本数据126,,, x x x 的方差为2,则数据12621,21,,21--- x x x 的方差为8B .若随机变量()21,ξσ~N ,()20.21ξ-=P ,则()40.79ξ=p C .已知经验回归方程为ˆˆ 1.8=+ybx ,且2=x ,20=y ,则ˆ9.1=b D .根据分类变量X 与Y 成对样本数据,计算得到29.632χ=,依据小概率值0.001α=的2χ独立性检验()0.00110.828=x ,可推断“X 与Y 有关联”,此推断犯错误的概率不大于0.00110.已知α,β是两个平面,m ,n 是两条直线,则下列命题正确的是A .如果αβ∥,α⊂m ,那么β∥m B .如果α⊥m ,α∥n ,那么⊥m n C .如果⊥m n ,α⊥m ,β∥n ,那么αβ⊥D .如果∥m n ,αβ∥,那么m 与α所成的角和n 与β所成的角相等11.已知函数()f x 是定义在R 上的奇函数,且()()20++=f x f x ,若[]0,2∈x 时,()=f x ,函数()()4=--g x g x .若()=y f x 与()=y g x 恰有2024个交点()11,x y ,()22,x y ,,()20242024,x y ,则下列说法正确的是A .()20241=f B .函数()f x 的图象关于直线1=x 对称C .()202414048=+=∑iii x yD .当实数,,610106⎛⎫⎛⎫∈-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭k 时,关于x 的方程()()+=f x f x kx 恰有四个不同的实数根三、填空题:本大题共3小题,每小题5分,共15分.12.已知向量()1,3= a ,()3,4= b ,若()()-⊥+ma b a b ,则=m _________.13.某学校组织学生参加劳动实践活动,其中2名男生和4名女生参加农场体验活动,体验活动结束后,农场主与6名同学站成一排合影留念,则2名男生相邻且农场主站在正中间的排列数为_________.(用数字作答)14.我国古代数学著作《九章算术》中记载了一种称为“羡除”的几何体,该几何体的一种结构是三个面均为梯形,其他两面为三角形的五面体.如图所示,四边形ABCD ,ABFE ,CDEF 均为等腰梯形,∥∥AB CD EF ,6=AB ,8=CD ,10=EF ,EF 到平面ABCD 的距离为5,CD 与AB 间的距离为10,则这个羡除的体积=V _________.四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)如图,ABC △中,点D 为边BC 上一点,且满足=AD CDAB BC.(1)证明:π∠+∠=BAC DAC ;(2)若2=AB ,1=AC ,=BC AD 的长度.16.(15分)某人工智能研究实验室开发出一款全新聊天机器人棋型,它能够通过学习和理解人类的语言来进行对话.聊天机器人棋型的开发主要采用RLHF (人类反馈强化学习)技术,在测试它时,如果输入的问题没有语法错误,则它的回答被采纳的概率为90%,当出现语法错误时,它的回答被采纳的概率为50%.(1)在某次测试中输入了7个问题,聊天机器人棋型的回答有5个被采纳,现从这7个问题中抽取4个,以ξ表示抽取的问题中回答被采纳的问题个数,求ξ的分布列和数学期望;(2)设输入的问题出现语法错误的概率为p ,若聊天机器人棋型的回答被采纳的概率为80%,求p 的值.17.(15分)已知椭圆2222:1(0)+=>>x y C a b a b的左焦点为F ,C 上任意一点到F 的距离的最大值和最小值之积为1,离心率为3.(1)求C 的方程;(2)设过点11,3⎛⎫⎪⎝⎭R 的直线l 与C 交于M ,N 两点,若动点P 满足λ= PM MR ,λ=- PN NR ,动点Q在椭圆C 上,求PQ 的最小值.18.(17分)在圆柱1OO 中,AB 是圆O 的一条直径,CD 是圆柱1OO 的母线,其中点C 与A ,B 不重合,M ,N 是线段BD 的两个三等分点,==BM MN ND ,2=AB ,3=CD .(1)若平面COM 和平面CAN 的交线为l ,证明:∥l 平面ABD ;(2)设平面COM 、平面CAN 和底面圆O 所成的锐二面角分别为α和β,平面ABD 和底面圆O 所成的锐二面角为γ,若αβ=,求tan γ的值.19.(17分)已知函数()()ln 1e =--xf x x a x ,其中∈R a .(1)讨论()f x 的极值点个数,并说明理由;(2)若10e<<a ,设0x 为()f x 的极值点,1x 为()f x 的零点,且11>x ,求证:0012ln +>x x x .新疆维吾尔自治区2024年普通高考第二次适应性检测数学参考答案一、选择题:本大题共8小题,每小题5分,共40分.1.D2.B3.D4.C5.C6.C7.B8.A二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.AC10.ABD11.BCD三、填空题:本大题共3小题,每小题5分,共15分.12.8513.19214.200四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.解:(1)在ABC △中,由正弦定理得sin sin =∠AB CBC BAC,在ADC △中,由正弦定理得sin sin =∠AD CCD DAC,又=AD CD AB BC ,故sin sin sin sin =∠∠C C DAC BAC,sin sin ∴∠=∠BAC DAC ,由于∠>∠BAC DAC ,因此π∠+∠=BAC DAC .(2)由2=AB ,1=AC,=BC 2224171cos 22212+-+-∠===-⋅⨯⨯AB AC BC BAC AB AC ,又∠BAC 为三角形的内角,则120∠=BAC ,由(1)知60∠=DAC ,故60∠=DAB .因为=+ABC ABD ADC S S S △△△,所以111sin120sin60sin60222⋅⋅⋅=⋅⋅⋅+⋅⋅⋅ AB AC AB AD AD AC ,故23=AD .16.解:(1)易知ξ的所有取值为2,3,4,()2252471022357ξ====C C P C ,()3152472043357ξ====C C P C ,()405247514357ξ====C C P C ,故ξ的分布列为:ξ234P274717则()241202347777ξ=⨯+⨯+⨯=E .(2)记“输入的问题没有语法错误”为事件A ,记“输入的问题有语法错误”为事件B ,记“回答被采纳”为事件C ,由已知得,()0.8=P C ,()0.9=∣P CA ,()0.5=∣P C B ,()=P B p ,()1=-P A p ,()()()()()()()()0.910.5=+=⋅+⋅=-+ ∣∣P C P AC P BC P A P C A P B P C B p p0.90.4=-p ,0.90.40.8∴-=p ,解得0.25=p .17.解:(1)设(),E x y ,(),0-F c ,则==+cEF x aa.又因为-a x a,所以22max min||1⋅=-=EF EF a c,即21=b,又椭圆的离心率e3==ca,所以3=c a,则2222221133-=-==a c a a a,解得23=a,故C的方程为2213+=x y.(2)设()11,M x y,()22,N x y,()00,P x y,因为λ=PM MR,所以()1010111,1,3λ⎛⎫--=--⎪⎝⎭x x y y x y,若1λ=-,则=-PM MR,即P与R重合,与=PN NR矛盾,若1λ=,则=-PN NR,即P与R重合,与=PM MR矛盾,故1λ≠±,于是1113,11λλλλ++==++yxx y,将点013,11λλλλ⎛⎫+⎪+⎪++⎪⎝⎭yxM代入2213+=x y,化简得()2220000566183990λλ-++-++-=x y x y,同理可得,()2220000566183990λλ--+-++-=x y x y,故λ,λ-为方程()2220000566183990-++-++-=x x y x x y的两根,于是0066180+-=x y,即0030+-=x y,动点P在定直线1:30+-=l x y上.令直线2:0(0)+-=>l x y m m,当2l与T相切时,记1l,2l的距离为d,则PQ d ,联立2213+-=⎧⎪⎨+=⎪⎩x y mx y可得2246330-+-=x mx m,由()22Δ(6)16330=--=m m,解得2=±m,又0>m,则2=m,此时,解得32=x,12=y,即切点为31,22⎛⎫⎪⎝⎭,直线1l,2l的距离为22==d,故PQ的最小值为2.18.(1)证明:由已知易得M 是BN 的中点,O 是BA 的中点,∴∥OM AN ,又⊆ AN 平面CAN ,OM Ú平面CAN ,∴∥OM 平面CAN ,又⊆ OM 平面COM ,平面 COM 平面=CAN l ,由线面平行的性质定理可得,∥l OM又⊆ OM 平面ABD ,l Ú平面ABD ,∴∥l 平面ABD(2)解:以O 为坐标原点, OA 方向为x 轴,底面圆O 所在平面内垂直于OA 方向为y 轴,1 OO 方向为z轴建立如图所示空间直角坐标系.由对称性,不妨设(0)θθπ∠=<<AOC ,易得底面圆O 的半径为1,则:()0,0,0O ,()1,0,0A ,()1,0,0-B ,()cos ,sin ,0θθC ,()cos ,sin ,3θθD ,cos 2sin ,,133θθ-⎛⎫ ⎪⎝⎭M ,2cos 12sin ,,233θθ-⎛⎫ ⎪⎝⎭N ,易知底面圆O 的一个法向量为()10,0,1=n ,cos 2sin ,,133θθ-⎛⎫= ⎪⎝⎭OM ,()cos ,sin ,0θθ=OC ,设平面COM 的一个法向量为()2,,=n x y z ,则cos 2sin 033cos sin 0θθθθ-⎧++=⎪⎨⎪+=⎩x y z x y ,令sin θ=x ,解得22sin sin ,cos ,3θθθ⎛⎫=- ⎪⎝⎭n ,12122sin 3cos θα⋅∴==n n n n .()cos 1,sin ,0θθ=- AC ,2cos 42sin ,,233θθ-⎛⎫= ⎪⎝⎭AN ,设平面CAN 的一个法向量为()3,,=n a b c ,则()2cos 42sin 2033cos 1sin 0θθθθ-⎧++=⎪⎨⎪-+=⎩a b c a b,令sin θ=a ,解得3sin sin ,1cos ,3θθθ⎛⎫=- ⎪⎝⎭n ,1313sin 3cos θβ⋅∴==n n n n .0,2παβ⎛⎫∈ ⎪⎝⎭、,且αβ=,2sin sin 33cos cos θθαβ∴=⇒=221117sin 22cos sin cos 4998θθθθ⇒+=-+⇒=,sin 8θ∴==,过点C 作AB 的垂线,垂足为E 点.因为CD 为圆柱的母线,所以⊥CD 平面ABC ,又⊆AB 平面ABC ,所以⊥CD AB ,又= CE CD C ,所以⊥AB 平面CED ,故⊥AB DE ,所以∠DEC 为平面ABD 和底面圆O 所成锐二面角的平面角.815tan sin 5γθ∴===CD CD CE.19.(1)解:由已知,()f x 的定义域为()0,+∞,()211e e -=-'=x x ax f x ax x x①当0a 时,21e 0->x ax ,从而()0'>f x ,所以()f x 在()0,+∞内单调递增,无极值点;②当0>a 时,令()21e =-xg x ax ,则由于()g x 在[)0,+∞上单调递减,()010=>g,10=-<g ,所以存在唯一的()00,∈+∞x ,使得()00=g x ,所以当()00,∈x x 时,()0>g x ,即()0'>f x ;当()0,∈+∞x x 时,()0<g x ,即()0'<f x ,所以0x 是()f x 的唯一极值点.所以当0>a 时,()f x 在()0,+∞上有且仅有一个极值点.综上所述,当0a 时,函数()f x 无极值点;当0>a 时,函数()f x 只有一个极值点.(2)证明:由题意得()()0100⎧=⎪⎨=⎩'⎪f x f x ,即()0120111e 0ln 1e 0⎧-=⎪⎨--=⎪⎩xx ax x a x 从而()012011e ln 1e =-xxx x x ,即101121ln e --=x x x x x .令()ln 1ϕ=-+x x x ,其中0>x ,则()1ϕ'-=xx x,当()0,1∈x 时,()0ϕ'>x ,()ϕx 单调递增,当()1,∈+∞x 时,()0ϕ'<x ,()ϕx 单调递减,故()()10ϕϕ=x ,则ln 10-+x x ,于是ln 1-x x .因为当11>x 时,11ln 1<-x x ,又101>>x x ,故1011201e 1--<-x x x x x ,即102e -<x x x ,两边取对数,得1020lneln -<x x x ,于是1002ln -<x x x ,整理得0012ln +>x x x .以上解法仅供参考,如有其他方法,酌情给分.参考答案解析1.D 法一:=+z a bi ,2422=⎧∴⎨=⎩a bi i ,2=a ,1=b,∴=z .法二:42+=⎧⎨-=⎩z z z z i,242∴=+z i ,2=+z i,∴=z 2.B{1==⇒-∣P x y x ,≠ P Q R (A 误)⊆Q P (B 正确){}20==⇒Q y y x y ,{}:1≠∅ ∣P Q xx (C 误)(D 错误)3.D ()1111--==---ax a f x a x x 关于()1.2对称则2=a 4.C2=r .直线过()0,m,则==m解析如图:即=mN (当且仅当=h m 时取得最小值)5.C A .12113120230+=+>⇒+=+>a a a d a a a d (误)B .131********+=+<⇒+=+<a a a d a a a d (误)C .1322+=a a a应用一般不等式有:2132=+a a a2∴a 又21> a a 故不存在123==a a a使原式取等情况,2∴>a D .10<a 与后式214<<a a a 或412<<a a a 无关且2a 、4a 只可能同时大于或小于1a (误)6.()f x 切线,()()2000:31-=+-l y y x x x ,有:()()200300031142⎡+-=-⎢=++⎢⎣x x y y x x 解得0014=⎧⎨=⎩x y 或001298⎧=-⎪⎪⎨⎪=⎪⎩x y 代入l 可得C .7.B1tan tan cos αββ=+,sin cos sin cos cos αββαα=+,()sin cos sin 2παβαα⎛⎫-==- ⎪⎝⎭22παβ∴-=-或22ππαβα⋅+⋅=(舍),22παβ∴-=8.A法一:I :内心:()22,x y G 重心:,33⎛⎫⎪⎝⎭m m x y G联立解分线上点到角两边距离相等不难求得:23=m x x 12∴⊥IG F F ,120∴⋅=IG F F法二:设M 恰在上顶点,120∴⋅= IG F F 9.AC A :2228⨯=,正确B :仍为0.21,错误C :代入得ˆ202 1.8=+b,ˆ9.1=b ,正确D :9.63210.828<,错误10.ABDC :α与β可呈任意关系,错误11.BCD ()f x 为奇函数:()()()2-=-=+f x f x f x ,()()2∴-=+f x f x ,()∴f x 有对称轴1=x .() f x 有对称中心:()0,0,4∴=T ()()40+-=g x g x ,()∴g x 有对称中心(2,0)A :()()202400==f f (误),B 正确C :() f x 为奇函数且()f x 有对称中心()2,0,0∴=∑i y ,220244048=⨯=∑i x D :图象为:求切线即可,D 正确12.()3,34-=--ma b m m ,()4,7+=a b 41221280∴-+-=m m ,85=m 13.组合:1343222192⨯⨯⨯⨯=C A 种121211(68)1052007732-==⨯⨯+⨯⨯=E ABCD。
2012东北三校二模--理科数学

东北三省三校2012届高三数学第二次联考试题 理 新人教A 版本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,共24题,满分150分,考试结束后,请将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔记清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第I 卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.设集合{1,2,3}M =,{2,3,4}N =,则( C )A .M N ⊆B .N M ⊆C .{2,3}M N =D .{1,4,5}M N = 2.已知1(z i i =-是虚数单位),则24z z+=( ) A.2 B .2i C .24i + D .24i -3.在30的展开式中,x 的幂指数是整数的项共有( ) A .4项 B .5项 C .6项 D .7项4.向量AB 与向量(3,4)a =- 的夹角为π,||10AB =,若点A 的坐标是(1,2),则点B 的坐标为( )A .(-7,8)C .(-5,10)5A .34 B .45C .56D .676.已知4sin cos (0)34πθθθ+=<<,则sin cos θθ-的值为( )A .3 B .3- C .13 D .13-7.若,*m n N ∈,则a b >“”是“m nm n n m m n a b a b ab +++>+”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件8.一个几何体的三视图如图所示(单位长度:cm )的体积为33cm,则该几何体的高h 为( ) A .cm π B.(cm πC .(cm π+D .(3cm π+9.若抛物线2y 2(0)px p =>的值为( )A .2B .18C .2或18D .4或1610.设函数()2sin+4f x x πωω=()(>0)与函数()cos(2)(||)2g x x πφφ=+≤的对称轴完全相同,则φ的值为( )A .4π B .4π- C .2π D .2π-11.已知半径为5的球O 被互相垂直的两个平面所截,得到的两个圆的公共弦为4,若其中的一圆的半径为4,则另一圆的半径为( )AC.12.设()f x 在区间(,)-∞+∞可导,其导数为'()f x ,给出下列四组条件( ) ①()p f x :是奇函数,':()q f x 是偶函数②()p f x :是以T 为周期的函数,':()q f x 是以T 为周期的函数③()p f x :在区间(,)-∞+∞上为增函数,':()0q f x >在(,)-∞+∞恒成立 ④()p f x :在0x 处取得极值,'0:()0q f x =A .①②③B .①②④C .①③④D .②③④第II 卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分。
新疆乌鲁木齐市等5地2023届高三高考第二次适应性检测数学(理)试题
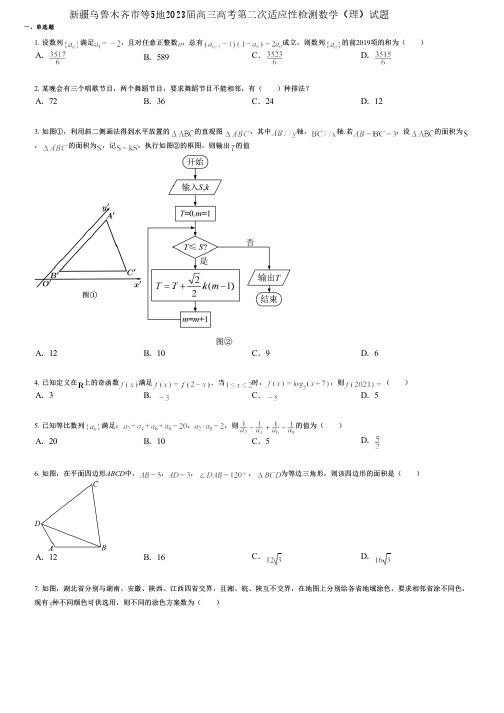
一、单选题1. 设数列满足,且对任意正整数,总有成立,则数列的前2019项的和为( )A.B .589C.D.2. 某晚会有三个唱歌节目,两个舞蹈节目,要求舞蹈节目不能相邻,有( )种排法?A .72B .36C .24D .123. 如图①,利用斜二侧画法得到水平放置的的直观图,其中轴,轴.若,设的面积为,的面积为,记,执行如图②的框图,则输出的值A .12B .10C .9D .64. 已知定义在上的奇函数满足.当时,,则( )A .3B.C.D .55. 已知等比数列满足:,,则的值为( )A .20B .10C .5D.6. 如图,在平面四边形ABCD 中,,,,为等边三角形,则该四边形的面积是()A .12B .16C.D.7. 如图,湖北省分别与湖南、安徽、陕西、江西四省交界,且湘、皖、陕互不交界,在地图上分别给各省地域涂色,要求相邻省涂不同色,现有种不同颜色可供选用,则不同的涂色方案数为( )新疆乌鲁木齐市等5地2023届高三高考第二次适应性检测数学(理)试题A.B.C.D.8. 在给出的①;②;③.三个不等式中,正确的个数为()A.0个B.1个C.2个D.3个9. 已知复数的实部为3,其中为虚数单位,则复数的虚部为()A.B.C.D.10. 长方体的8个顶点在同一个球面上,且AB=2,AD=,,则顶点A、B间的球面距离是A.B.C.D.11.将函数的图象向左平移个单位长度,得到函数的图象,有下述四个结论:①若是偶函数,则;②当时,满足的的取值范围为;③若在区间上恰有一个极值点,则的取值范围为;④当时,若,则的最小值为.其中所有正确结论的个数为()A.B.C.D.12. 在的二项展开式中,x的系数为( )A.10B.-10C.40D.-40 13. 已知函数在区间上的图象如图所示,则()A.B.C.2D.14. 已知函数的大致图象如下,下列选项中为自然对数的底数,则函数的解析式可能为()二、多选题A.B.C.D.15. 已知在高为2的正四棱锥中,,则正四棱锥外接球的体积为( )A.B.C.D.16. 某几何体的三视图如图所示,则该几何体的表面积是().A.B.C .6D.17.在正方体中,点分别是棱的中点,则下列说法正确的是( )A .过三点的平面截正方体的截面图形是矩形B .过三点的平面截正方体的截面图形是等腰梯形C.平面D .若,则平面平面18.已知函数的图象关于直线对称,则( )A.是奇函数B.的最小正周期是πC .的一个对称中心是D .的一个递增区间是19. 如图是一个正方体的展开图,如果将它还原为正方体,则以下正确的是().A.B.C.D.20. 已知函数在处有极值,且极值为8,则( )A.有三个零点B.三、填空题C .曲线在点处的切线方程为D .函数为奇函数21. 已知事件A ,B是相互独立事件,且,则( )A.B.C.D.22. 已知定义在R上的函数满足,且为奇函数,,.下列说法正确的是( )A .3是函数的一个周期B.函数的图象关于直线对称C .函数是偶函数D.23. 筒车是我国古代发明的一种灌溉工具,因其经济又环保,至今还在农业生产中得到使用(图1),明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图2).现有一个半径为3米的筒车按逆时针方向每分钟旋转1圈,筒车的轴心距离水面的高度为2米,设筒车上的某个盛水筒P到水面的距离为(单位:米)(在水面下则为负数),若以盛水筒P 刚浮出水面为初始时刻,经过t 秒后,下列命题正确的是( )(参考数据:)A .,其中,且B .,其中,且C .当时,盛水筒再次进入水中D .当时,盛水筒到达最高点24. 已知集合,若对于任意,存在,使得成立,则称集合M 是“完美对点集”.给出下列四个集合:①;②;③;④.其中是“完美对点集”的序号为( )A .①B .②C .③D .④25. 若命题“,”为假命题,则的取值范围为______.26.已知,分别为双曲线:左、右焦点,过点的直线与双曲线的左、右两支分别交于,两点,且四、解答题五、解答题,,则双曲线的离心率是______.27. 已知,是两个单位向量,,且,则与的夹角为_________.28. 已知一组数据,,,,,则该组数据的方差是______.29.抛物线的焦点为,经过其准线与轴的交点的直线与抛物线切于点,则外接圆的标准方程为___________.30. 在中,若,,,则____.31. 已知单位向量,,满足,则与的夹角是______.32.已知双曲线的中心在原点且对称轴为坐标轴,的一条渐近线与焦点为的抛物线交于点,且,则双曲线的离心率为__________.33.已知函数.(1)化简并求函数的最小正周期;(2)求使函数取得最大值的集合.34. 已知函数.(1)当时,讨论函数的单调性;(2)若不等式在上恒成立,求实数的取值范围.35. 已知为锐角,,求的值.36. 已知数列是公比为2的等比数列,数列是等差数列,.(1)求数列的通项公式;(2)设,求数列的前项和.37.如图,在多面体中,四边形为菱形,且∠ABC =60°,AE ⊥平面 ABCD ,AB =AE =2DF ,AE DF.(1)证明:平面AEC ⊥平面 CEF ;(2)求平面ABE 与平面CEF 夹角的余弦值.38. 化简或求值:(1);(2).39. 年月,习近平总书记对制止餐饮浪费行为作出重要指示,要求进一步加强宣传教育,切实培养节约习惯,在全社会营造浪费可耻、节约光荣的氛围.为贯彻总书记指示,大庆市某学校食堂从学生中招募志愿者,协助食堂宣传节约粮食的相关活动.现已有高一人,高二人,高三人报名参加志愿活动.根据活动安排,拟采用分层抽样的方法,从已报名的志愿者中抽取名志愿者,参加为期天的第一期志愿活动.(1)第一期志愿活动需从高一、高二、高三报名的学生中各抽取多少人?(2)现在要从第一期志愿者中的高二、高三学生中抽取人去粘贴宣传标语,设这人中含有高二学生人,求随机变量的分布列;(3)食堂每天约有人就餐,其中一组志愿者的任务是记录学生每天倒掉的剩菜剩饭的重量(单位:公斤),以天为单位来衡量宣传节约粮食的效果.在一个周期内,这组志愿者记录的数据如下:前天剩菜剩饭的重量为:后天剩菜剩饭的重量为:借助统计中的图、表、数字特征等知识,分析宣传节约粮食活动的效果(选择一种方法进行说明即可).40. 有一种画椭圆的工具如图1所示.定点是滑槽的中点,短杆绕转动,长杆通过处铰链与连接,上的栓子可沿滑槽滑动,且,.当栓子在滑槽内做往复运动时,带动绕转动一周(不动时,也不动),处的笔尖画出的曲线记为.以为原点,所在的直线为轴,建立如图2所示的平面直角坐标系.(1)求曲线的方程;(2)在平面直角坐标系中,过点的动直线与曲线交于、两点,是否存在异于点的定点,使得平分?若存在,求点坐标;若不存在,说明理由.41. 已知是函数图象的一条对称轴.(1)求的值;(2)求函数的单调增区间;(3)作出函数在上的图象简图(列表,画图).42. 已知函数,(且)的图象经过点.(1)求的值,并在直角坐标系中画出的图象;(2)若在区间上是单调函数,求的取值范围.43. 某省参加2021年普通高考统考报名的所有考生均可选考英语口试科目,考生自愿参加,不作为统一要求.考生卷面成绩采用百分制.某市从六、解答题参加高三英语口语考试的1000名学生中随机抽取100名学生,将其英语口试成绩(均为整数)分成六组,…后得到如下部分频率分布直方图,已知第二组与第三组的频数之和等于第四组的频数.(1)求频率分布直方图中未画出矩形的总面积;(2)预估该市本次参加高三英语口语考试的1000名学生中成绩处于的人数;(3)用分层抽样的方法在高分(不低于80分)段的学生中抽取一个容量为12的样本,将该样本看成一个总体,再从中任取3人,记这3人中成绩低于90分的人数为,求随机变量的分布列及数学期望.44. 已知等腰直角,,点,分别为边,的中点,沿将折起,得到四棱锥,平面平面.(Ⅰ)过点的平面平面,平面与棱锥的面相交,在图中画出交线;设平面与棱交于点,写出的值(不必说出画法和求值理由);(Ⅱ)求证:平面平面.45. 已知函数,其中a ,b 为常数,为自然对数底数,.(1)当时,若函数,求实数b 的取值范围;(2)当时,若函数有两个极值点,,现有如下三个命题:①;②;③;请从①②③中任选一个进行证明.(注:如果选择多个条件分别解答,按第一个解答计分)46. 如图,几何体中,平面平面,四边形为边长为2的正方形,在等腰梯形中,,,.(1)求证:;(2)求二面角的余弦值.七、解答题47.在中,内角所对的边分别为,且.(1)证明:;(2)若,求.48. 如图,三棱柱中,平面平面,和都是正三角形,是的中点.(1)求证:平面;(2)求二面角的余弦值.49. 如图,△ABC 内接于圆O ,AB 是圆O 的直径,,,设AE 与平面ABC 所成的角为,且,四边形DCBE 为平行四边形,DC平面ABC .(1)求三棱锥C -ABE 的体积;(2)证明:平面ACD平面ADE ;(3)在CD 上是否存在一点M ,使得MO ∥平面ADE?证明你的结论.50. 在三棱锥中,底面是边长为的等边三角形,点在底面上的射影为棱的中点,且与底面所成角为,点为线段上一动点.(1)求证:;(2)是否存在点,使得二面角的余弦值为,若存在,求出点的位置;若不存在,请说明理由.51.某企业拟生产甲、乙两种产品,根据市场调研预测,甲产品的利润与投资额的算术平方根成正比,其关系如图1,乙产品的利润与投资额成正比,其关系如图2.(1)分别将甲、乙两种产品的利润表示为投资额的函数关系式;(2)如果企业将筹集到的160万元资金全部投入到甲、乙两种产品的生产中,试问:怎样分配这160万元的投资才能使该企业获得最大利润,最大利润是多少?52. 经市场调查,某商品每吨的价格为万元时,该商品的月供给量为吨,;月需求量为吨,,当该商品的需求量大于供给量时,销售量等于供给量;当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.(1)已知,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);(2)记需求量与供给量相等时的价格为均衡价格,若该商品的均衡价格不低于每吨6万元,求实数的取值范围.53. 四户村民甲、乙、丙、丁把自己不宜种粮的承包土地流转给农村经济合作社,甲、乙、丙、丁分别获得所有流转土地年总利润7%,7%,10%,6%的流转收益.该土地全部种植了苹果树,2022年所产苹果在电商平台销售并售完,所售苹果单个质量(单位:g,下同)在区间[100,260]上,苹果分装在A,B,C,D4种不同的箱子里,共5000箱,装箱情况如下表.把这5000箱苹果按单个质量所在区间以箱为单位得到的频率分布直方图如下图.苹果箱种类A B C D每箱利润(元)40506070苹果单个质量区间[100,140)[140,180)[180,220)[220,260](1)根据频率分布直方图,求a和甲、乙、丙、丁2022年所获土地流转收益(单位:万元):(2)在甲、乙、丙、丁中随机抽取2户,求这2户中恰有1户2022年土地流转收益超过2万元的概率.54. 南昌市教育局组织中学生足球比赛,共有实力相当的8支代表队(含有一中代表队,二中代表队)参加比赛,比赛规则如下:第一轮:抽签分成四组,每组两队进行比赛,胜队进入第二轮,第二轮:将四队分成两组,每组两队进行比赛,胜队进入第三轮,第三轮:两队进行决赛,胜队获得冠军.现记ξ=0表示整个比赛中一中代表队与二中代表队没有相遇,ξ=i表示恰好在第i轮比赛时一中代表队与二中代表队相遇(i=1,2,3).(1)求ξ的分布列;(2)求.55. 2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有采购成本分别为万元/辆和万元/辆的两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:使用寿命年数5年6年7年8年总计型出租车(辆)10204525100型出租车(辆)153********(1)填写下表,并判断是否有的把握认为出租车的使用寿命年数与汽车车型有关?使用寿命不高于年使用寿命不低于年总计型八、解答题型总计(2)从和的车型中各随机抽取车,以表示这车中使用寿命不低于年的车数,求的分布列和数学期望;(3)根据公司要求,采购成本由出租公司负责,平均每辆出租车每年上交公司万元,其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?附:,.0.0500.0100.0013.8416.63510.82856. 在十四运射击选拔赛中,某代表队甲、乙两人所得成绩如下表所示:甲9.810.31010.59.9乙10.29.910.110.210.1(1)分别求出甲、乙两人成绩的平均数与方差;(2)根据(1)的结果,你认为甲、乙两人中谁更适合参加最终比赛?57. 已知函数,其中.(1)求函数的零点个数;(2)证明:是函数存在最小值的充分而不必要条件.58. 已知定义在上的函数.(1)判断的奇偶性并证明;(2)已知不等式,对所有恒成立,求关于的函数的最小值.59. 已知四棱锥的底面为菱形,是等边三角形,平面平面,,分别是棱,上的动点.(1)若是的中点,且∥平面,证明:是的中点;(2)若,,,求三棱锥的体积.60.设椭圆:的离心率为,上一点到右焦点距离的最小值为1.(1)求椭圆的方程;(2)过点且倾斜角为的直线交椭圆于,两点,求的面积.61.已知数列的前n项和为,,,.(1)求;(2)令,证明:.62. 椭圆的两个焦点,点在椭圆上,且,且.(1)求椭圆的方程.(2)以此椭圆的上顶点为直角顶点作椭圆的内接等腰直角三角形,这样的直角三角形是否存在?若存在,请说明有几个;若不存在,请说明理由.。
新疆乌鲁木齐市2012届高三第三次诊断性测验理科数学试卷(高清扫描版).pdf

故, ∴.
由切割线定理有,∴.
…10分
23.选修4-4:坐标系与参数方程
(1)设曲线上任意一点,由变换得代入得,所以曲线是以为圆心,半径为的圆.
∴的极坐标方程为;
…5分
(2)曲线的直角坐标方程为,由得或所以交点为或,两点的坐标均满足曲线的直角
坐标方程.
∴直线与曲线的交点也在曲线上.
由题知,化简得
,即是点的轨迹的方程;
…6分
(2)设,,,可得
两式相减,得
变形可得,即,
其中表示的中点与坐标原点连线的斜率,
又,∴,∥.
同理,∥,其中为的中点.
∴为的中点.
…12分,,,则
……①, ……②, ……③.
由,化为
,即
……(*)
若轴,得,由(*)及②可得
,∴,∴为的中点.
若与轴不垂直,可设其方程为.
由消去,得
∴,.
,
,代入(*)化简得
,即,∵,∴.
故过原点,由对称性知为的中点.
…12分,.
设切点,则,即 .
∴,又.
∴,易知,故.
由,得.
因此当时, ,于是单调递减;
当时,,于是单调递增.
所以的减区间是,增区间是;
2012年乌鲁木齐地区高三年级第次诊断性测验
理科数学试题参考答案及评分标准
CADBDCBDCCA B1.选C.【解析】由题知,∴.
2.选A.【解析】,∴,.时,,满足题意;时,由,满足题意.
,过点的最长弦(直径)斜率为,且最长弦与最短弦垂直,∴过点的最短弦所在直线的斜率为,倾斜角是.与相交
…6分
(2)由.
若≤时,,于是在上单调递增,因此不可能有两个零点;若时,易得的减区间是,增区间是.
浙江省嘉兴市2012届高三数学二模测试试题 理 新人教A版

12012年高三教学测试(二)理科数学 试题卷注意事项:1.本科考试分试题卷和答题卷,考生须在答题卷上作答.答题前,请在答题卷的密封线内填写学校、班级、学号、姓名;2.本试题卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页,全卷满分150分,考试时间120分钟.参考公式:如果事件A ,B 互斥,那么 )()()(B P A P B A P +=+.如果事件A ,B 相互独立,那么 )()()(B P A P B A P ⋅=⋅.如果事件A 在一次试验中发生的概率是p , 那么n次独k 次的概率),,2,1,0()1()(n k p p C k P k n kk n n Λ=-=- .球的表面积公式 24R S π=,其中R 表示球的半径. 球的体积公式334R V π=, 其中R 表示球的半径. 棱柱的体积公式Sh V =,其中S 表示棱柱的底面积,h 表示棱柱的高.棱锥的体积公式Sh V 31=, 其中S 表示棱锥的底面积,h 表示棱锥的高.棱台的体积公式)(312211S S S S h V ++=, 其中21,S S 分别表示棱台的上、下底面积,h 表示棱台的高.第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合}21{<≤-=x x M ,}0log |{2>=x x N ,则=N M YA .),1[+∞-B .),1(+∞C .)2,1(-D . )2,0(2.若复数i 2i-+a (i 为虚数单位)是纯虚数,则实数a 的值为 A .-2B .2C .21-D .213.已知非零向量a ρ、b ρ,则b a ρρ=是0)()(=-⋅+b a b a ρρρρ的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.下列函数中,最小正周期为π的奇函数是A .x y 2cos =B .x y 2sin =C .x y 2tan =D .)2π2sin(-=x y5.某程序框图如图所示,则该程序运行后输出的值是A .-8B .-2C .-1D .06.已知直线m 和平面α、β,则下列结论一定成立的是A .若α//m ,βα//,则β//mB .若α⊥m ,βα⊥,则β//mC .若α//m ,βα⊥,则β⊥mD .若α⊥m ,βα//,则β⊥m7.有6个人站成前后两排,每排3人,若甲、乙两人左右、前后均不相邻,则不同的站法种数为 A .240B .384C .480D .768(第5题)8.设实数y x ,满足:⎪⎩⎪⎨⎧≥+≤-+≥++0201053x y x y x ,则yx z 42+=的最小值是A .41 B . 21C .1D .89.设双曲线)0,0(12222>>=-b a b y a x 的右焦点为F ,过点F 作与x 轴垂直的直线l 交两渐近线于A 、B 两点,与双曲线的其中一个交点为P ,设O 为坐标原点,若)R ,(∈+=n m OB n OA m OP ,且92=mn ,则该双曲线的离心率为 A .223 B .553 C .423 D .8910.已知函数t t x x f t --=2)()((R ∈t ),设b a <,⎩⎨⎧≥<=)()(),()()(),()(x f x f x f x f x f x f x f b a b b a a ,若函数b a x x f -++)(有四个零点,则a b -的取值范围是A .)52,0(+B .)32,0(+C .),52(+∞+D .),32(+∞+第Ⅱ卷二、填空题(本大题共7小题,每小题4分,共28分) 11.不等式0||22≤-x x 的解集是 ▲ . 12.若二项式6)1(xax -展开式中的常数项为60,则实数a 的值为 ▲ .13.已知等差数列}{n a 的前n 项和为n S ,且3513a a a =+,1410=a ,则=12S ▲ . 14.在ABC ∆中,角C B A ,,的对边分别为c b a ,,,若C a c b cos 21=-,则=A ▲ .15.某几何体的三视图如图所示,则这个几何体的体积是 ▲ . 16.已知抛物线y x 42=的焦点为F ,经过F 的直线与抛物线相交于A 、B 两点,则以AB 为直径的圆在x 轴上所截得的弦长的最小值是 ▲ .17.甲、乙两人进行“石头、剪子、布”游戏.开始时每人拥有3张卡片,每一次“出手”(双方同时):若分出胜11负,则负者给对方一张卡片;若不分胜负,则不动卡片.规定:当一人拥有6张卡片或“出手”次数达到6次时游戏结束.设游戏结束时“出手”次数为ξ,则=ξE ▲ . 三、解答题(本大题共5小题,共72分) 18.(本题满分14分)已知函数1cos sin 3cos )(2+-=x x x x f . (Ⅰ)求函数)(x f 的单调递增区间; (Ⅱ)若65)(=θf ,)3π23π(,∈θ,求θ2sin 的值.19.(本题满分14分)在等差数列}{n a 和等比数列}{n b 中,11=a ,21=b ,0>n b (∈n *N ),且221,,b a b 成等差数列,2,,322+a b a 成等比数列.(Ⅰ)求数列}{n a 、}{n b 的通项公式; (Ⅱ)设n b n a c =,数列}{n c 的前n 和为n S ,若t a nS nS n n n +>++242恒成立,求常数t 的取值范围.20.(本题满分14分)如图,三棱柱111C B A ABC -的各棱长均为2,侧面11B BCC ⊥底面ABC ,侧棱1BB 与底面ABC 所成的角为︒60.(Ⅰ)求直线C A 1与底面ABC 所成的角;(Ⅱ)在线段11C A 上是否存在点P ,使得平面⊥CP B 1平面11A ACC ?若存在,求出P C 1的长;若不存在,请说明理由.A1A 1B 1C21.(本题满分15分)已知点P 是圆122=+y x 上任意一点,过点P 作y 轴的垂线,垂足为Q ,点R 满足RQ =,记点R 的轨迹为曲线C .(Ⅰ)求曲线C 的方程;(Ⅱ)设A )1,0(,点M 、N 在曲线C 上,且直线AM 与直线AN 的斜率之积为32,求AMN ∆的面积的最大值.22.(本题满分15分)已知a 为常数,R ∈a ,函数x ax x x f ln )(2-+=,x x g e )(=.(其中e 是自然对数的底数)(Ⅰ)过坐标原点O 作曲线)(x f y =的切线,设切点为),(00y x P ,求证:10=x ; (Ⅱ)令)()()(x g x f x F =,若函数)(x F 在区间]1,0(上是单调函数,求a 的取值范围.2012年高三教学测试(二)理科数学 参考答案一、选择题(本大题共10小题,每小题5分,共50分) 1.A ; 2.D ; 3.A ; 4.B ; 5.C ; 6.D ;7.B ;8.B ;9.C ;10.C .9.提示:),(),,(a bcc B a bc c A -,代入OB n OA m OP +=,得))(,)((abc n m c n m P -+,代入双曲线方程,得142=mn e ,即可得423=e ; 10.提示:作函数)(xf 的图象,且解方程)()(x f x f b a =得21-+=b a x ,即交点))21(,21(2a ab b a P ----+,又函数b a x x f -++)(有四个零点,即函数)(x f 的图象与直线a b x y l -+-=:有四个不同的交点,由图象知,点P 在l 的上方,所以+-+21b a 0)()21(2>-----a b a a b ,解得52+>-a b . 二、填空题(本大题共7小题,每小题4分,共28分)11.]2,2[-;12.2±;13.84;14.3π;15.337;16.32;17.950.17.提示:272)31(2)3(3=⋅==ξP ,272)31(2)4(413=⋅⋅==C P ξ, 272])31()31([2)5(513524=⋅+⋅⋅==C C P ξ,2721)5(1)6(=≤-==ξξP P . 三、解答题(本大题共5小题,第18-20题各14分,第21、22题各15分,共72分) 18.(本题满分14分)已知函数1cos sin 3cos )(2+-=x x x x f . (Ⅰ)求函数)(x f 的单调递增区间; (Ⅱ)若65)(=θf ,)3π23π(,∈θ,求θ2sin 的值.解:(Ⅰ)1cos sin 3cos )(2+-=x x x x f12sin 2322co 1+-+=x x s 23)32cos(++=πx .…4分由πππππ22322+≤+≤+k x k ,得653ππππ+≤≤+k x k (Z k ∈). ∴函数)(x f 的单调递增区间是]65,3[ππππ++k k (Z k ∈).…6分 (Ⅱ)∵65)(=θf ,∴6523)32cos(=++πx ,32)32cos(-=+πθ. …8分∵⎪⎭⎫⎝⎛∈323ππθ,,∴)35,(32πππθ∈+,35)32(cos 1)32(sin 2-=+--=+πθπθ. …11分∴)32cos(23)32sin(21)332sin(2sin πθπθππθθ+-+=-+=6532-=. …14分 19.(本题满分14分)在等差数列}{n a 和等比数列}{n b 中,11=a ,21=b ,0>n b (∈n *N ),且221,,b a b 成等差数列,2,,322+a b a 成等比数列.(Ⅰ)求数列}{n a 、}{n b 的通项公式; (Ⅱ)设n b n a c =,数列}{n c 的前n 和为n S ,若t a nS nS n n n +>++242恒成立,求常数t 的取值范围.解:(Ⅰ)设等差数列}{n a 的公差为d ,等比数列}{n b 的公比为)0(>q q . 由题意,得⎩⎨⎧++=+=+)23)(1()2(22)1(22d d q qd ,解得3==q d . …3分∴23-=n a n ,132-⋅=n n b . …7分 (Ⅱ)23223-⋅=-⋅=n n n b c .…9分 ∴n n c c c S +++=Λ21n n 2)333(221-+++=Λ3231--=+n n .…11分∴133333241122+=--=++++n n n n n n S n S . …12分∴t n n +->+2313恒成立,即min )333(+-<n t n .令333)(+-=n n f n ,则0332)()1(>-⋅=-+n n f n f ,所以)(n f 单调递增. 故3)1(=<f t ,即常数t 的取值范围是)3,(-∞. …14分20.(本题满分14分)如图,三棱柱111C B A ABC -的各棱长均为2,侧面11B BCC ⊥底面ABC ,侧棱1BB 与底面ABC 所成的角为︒60.(Ⅰ)求直线C A 1与底面ABC 所成的角;(Ⅱ)在线段11C A 上是否存在点P ,使得平面⊥CP B 1平面11A ACC ?若存在,求出P C 1的长;若不存在,请说明理由.解:(Ⅰ)过1B 作BC O B ⊥1于O , ∵侧面11B BCC ⊥平面ABC ,∴⊥O B 1平面ABC ,∴=∠BC B 1︒60.又∵11B BCC 是菱形,∴O 为BC 的中点.…2分以O 为坐标原点,如图建立空间直角坐标系,则)0,0,3(-A ,)0,1,0(-B ,)0,1,0(C ,)3,1,3(1-A ,)3,0,0(1B ,)3,2,0(1C ∴)3,0,3(1-=CA ,又底面ABC 的法向量)1,0,0(=n ρ…4分设直线C A 1与底面ABC 所成的角为θ,则22sin ==θ,∴︒=45θ 所以,直线C A 1与底面ABC 所成的角为︒45. …7分(Ⅱ)假设在线段11C A 上存在点P ,设P C 1=11A C λ,则)0,1,3(1--=λC ,)3,1,3(11λλ--=+=C CC ,)3,1,0(1-=B .…8分设平面CP B 1的法向量),,(z y x =,则⎪⎩⎪⎨⎧=+-+-=⋅=-=⋅03)1(3031z y x CP m z y B λλ.令1=z ,则3=y ,λλ-=2x , )1,3,2(λλ-=∴. …10分设平面11A ACC 的法向量),,(z y x n =,则⎪⎩⎪⎨⎧=--=⋅=+=⋅03031z y C C n y x令1=z ,则3-=y ,1=x ,)1,3,1(-=∴.…12分要使平面⊥CP B 1平面11A ACC ,则=⋅)1,3,2(λλ-)1,3,1(-⋅=022=--λλ. 32=∴λ. 341=∴P C .…14分121.(本题满分15分)已知点P 是圆122=+y x 上任意一点,过点P 作y 轴的垂线,垂足为Q ,点R满足RQ =,记点R 的轨迹为曲线C .(Ⅰ)求曲线C 的方程;(Ⅱ)设A )1,0(,点M 、N 在曲线C 上,且直线AM 与直线AN 的斜率之积为32,求AMN ∆的面积的最大值.解:(I )设),(y x R ,),(00y x P ,则),0(0y Q .ΘRQ =,⎪⎩⎪⎨⎧==∴y y x x 0033,1220=+y x Θ,故点R 的轨迹方程:1322=+y x .…6分(Ⅱ)(1)当直线MN 的斜率不存在时,设:MN )33(<<-=t t x . 则)31,(2t t M -,)31,(2t t N --,31=⋅∴AN AM K k ,不合题意.…7分(2)当直线MN 的斜率存在时,设b kx y l MN +=:,),(11y x M ,),(22y x N 联立方程⎪⎩⎪⎨⎧=++=1322y x bkx y ,得0336)31(222=-+++b kbx x k . 0)13(1222>+-=∆∴b k ,221316k kb x x +-=+,22213133k b x x +-=.…9分又32)1())(1(11212212122211=-++-+=-⋅-=⋅x x b x x b k x x k x y x y k k ANAM ,即0)1(3))(1(3)23(221212=-++-+-b x x b k x x k .将221316k kbx x +-=+,22213133k b x x +-=⋅代入上式,得3-=b .∴直线MN 过定点)3,0(-T . …11分∴21221214)(2||||21x x x x x x AT S AMN-+=-⋅=∆22318334k k +-⋅= . …13分令)0(832>=-t t k ,即8322+=t k ,∴619193183222≤+=+=+-tt t t k k .当且仅当3=t 时,332)(max =∆ABC S . …15分22.(本题满分15分)已知a 为常数,R ∈a ,函数x ax x x f ln )(2-+=,x x g e )(=.(其中e 是自然对数的底数)(Ⅰ)过坐标原点O 作曲线)(x f y =的切线,设切点为),(00y x P ,求证:10=x ; (Ⅱ)令)()()(x g x f x F =,若函数)(x F 在区间]1,0(上是单调函数,求a 的取值范围. 解:(I )xa x x f 12)(-+='(0>x ). …2分所以切线的斜率0002000ln 12x x ax x x a x k -+=-+=, 整理得01ln 020=-+x x .…4分显然,10=x 是这个方程的解,又因为1ln 2-+=x x y 在),0(+∞上是增函数, 所以方程01ln 2=-+x x 有唯一实数解.故10=x .…6分(Ⅱ)xe xax x x g x f x F ln )()()(2-+==,xe x x a x a x x F ln 1)2()(2+-+-+-='. …8分设x x a x a x x h ln 1)2()(2+-+-+-=,则a x xx x h -+++-='2112)(2. 易知)(x h '在]1,0(上是减函数,从而a h x h -='≥'2)1()(.…10分(1)当02≥-a ,即2≤a 时,0)(≥'x h ,)(x h 在区间)1,0(上是增函数. 0)1(=h Θ,0)(≤∴x h 在]1,0(上恒成立,即0)(≤'x F 在]1,0(上恒成立. )(x F ∴在区间]1,0(上是减函数.所以,2≤a 满足题意. …12分(2)当02<-a ,即2>a 时,设函数)(x h '的唯一零点为0x ,则)(x h 在),0(0x 上递增,在)1,(0x 上递减. 又∵0)1(=h ,∴0)(0>x h . 又∵0ln )2()(2<+-+-+-=----a a a a a e e a e a e e h , ∴)(x h 在)1,0(内有唯一一个零点x ',当),0(x x '∈时,0)(<x h ,当)1,(x x '∈时,0)(>x h .11 从而)(x F 在),0(x '递减,在)1,(x '递增,与在区间]1,0(上是单调函数矛盾. ∴2>a 不合题意.综合(1)(2)得,2≤a . …15分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新疆维吾尔自治区2012年普通高考第二次适应性检测
数学试题(理科)
注意事项:
1.本试卷分第I 卷选择题.和第Ⅱ卷非选择题.两部分。
答题前,考生务必将自己的
姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答第I 卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第I 卷
一、选择题:本大题共12小题,每小题5分,每小题给出的四个选项中,只有一项是符合
题目要求的。
1.复数
1a i
i
--的实部与虚部的和为-1,则a 的值为 A . -2
B . -1
C .l
D .2
2.下列函数既是偶函数,在(,0)2
π
-上又是减函数的是
A .y=sin2x
B .y= cos2sc
C .||
x y e =
D .y =
3.同时掷两颗骰子,向上的点数和为10的概率是 A .
1
36
B .
1
18
C .
1
16
D .
112
4.根据如下框图,输出的x 的值为
A .6
B .64
C .210
D .480
5.已知角α的顶点与直角坐标的原点重合,始边为x 轴的正半轴,终边落在直线y=kx 上,
此直线过点A (k – 1,k 2
+1),则cos2α的值为
A .0
B .
2
C .—
2
D .2
±
6.已知一个几何体的三视图和尺寸大小如下,则它的体积为
A .12(1)π+
B .12(10)π+
C .12(20)π+
D .12(30)π+
7.设{a n }为公比q>1的等比数列,若45a a 和,是方程4x 2
—8x +3 =0的两根,则78a a +等
于
A .6
B .18
C .54
D .8.已知()|4||6|f x x x =+--的最大值为n ,则二项式2
(n x
+展开式中常数项等于
A .21
B .28
C .36
D .45
9.由曲线y=x 2
+2和直线y=3x 所围成的平面图形的面积为
A .16
-
B .
16
C .
13
D .
12
10.已知双曲线22221(0,0)x y a b a b
-=>>的左顶点是圆22
220x y x ++-=的圆心,一条
渐近线
的方程为y=2x ,则双曲线的焦距为
A .5
B C D .11.已知A 、B 、C 是圆2
2
2
:O x y r +=上三点,且,OA OB OC AB OC +=⋅
则等于
A .0
B .
12 C .
32
D .—
32
12.半径为1的球内切于一圆锥,则圆锥体积的最小值为 A .2π
B .
83
π
C .3π
D .
113
π
第Ⅱ卷
本卷包括必考题和选考题两部分。
第13题~第21题为必考题,每个试题考生都必须作
答。
第22题~第24题为选考题,考生根据要求作答。
二、填空题:本大题共4小题,每小题5分。
13.已知实数x 、y 满足020
,10y x y x y ≤≤⎧⎪
-≤⎨⎪-+≥⎩
且Z=x+y ,则Z 的取值范围是 . 14.已知等差数列{n a }是递增数列,且*
780,,,0n n a n N n S S S ≠∈⋅<其前项和为若,则
在
812
128
,,,S S S a a a 中最大的是 。
15.某人用10万元买了一辆小汽车用来跑出租,已知这辆汽车从启用的第一年起连续使用,第n 年的保养维修费力2000(n -1)元,使用它直到“报废最合算”(所谓“报废最合算”是指使用的这辆汽车的年平均耗资最少)为止,则最佳报废时间为____年。
16.已知随机变量X 服从正态分布2
(,),(22)0.92N P X μσμσμσ-<<+=且,
()0.68,3,2,(57)P X P X μσμσμσ-<<+===<<若则= 。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17.本小题满分12分.
已知A 、B 、C 是三角形ABC 的三个内角,向量m=1(,
)22
-,n=(cosA ,sinA )
, 且m ·n =1.2
(I )求角A ;
(II )若sin2B +3cos2B=-1,求tanC .
18.本小题满分12分. 如图(一),在直角梯形ABCD 中,AD ∥BC ,AB ⊥AD ,AD= 2AB= 2BC ,E 为AD 中点,
沿CE 折叠,使面DEC ⊥面ABCE ,在图(二)中. (I )证明:AC ⊥BD
(Ⅱ)求DE 与面ACD 所成角的余弦值.
19.本小题满分12分.
目前全世界都使用体重指数(BMI )来衡量一个人胖或不胖,计算的方法是:BMI=
体重(kg )除以身高(m )的平方,世界卫生组织拟定的标准是:BMI 在18.5—24.9时属正常范围,BMI 大于25为超重,BMI 大于30为肥胖,在某所高中随机抽取16名学生,测得身高、体重、BMI 值如下表:表中身高单位为cm ,体重单位为kg .
(I )若从这16人中随机选取4人,求至多有一人是肥胖的概率;
(Ⅱ)以这16人的样本数据来估计这所高中学校的整体数据,若从该校任选4人,ξ表
示抽到肥胖学生的人数,求ξ的分布列及数学期望.
20.本小题满分12分.
已知椭圆G 的方程为22
221(0)x y a b a b
+=>>,它与x 轴交于A 、B 两点,与y 轴
正半轴交于C 点,点D (0,4),若3,||AC BC BD ⋅=-=
(I )求椭圆G 的方程;
(II )过点D 的直线l 交椭圆G 于M ,N 两点,若∠NMO =90°,求|MN|的长.
21.本小题满分l2分.
已知5ln()1
[,0),()ln(),().22
x x f x x bx g x x -∈-=--+=+- (I )当b= -l 时,求证:()()f x g x >;
(II )是否存在实数b ,使()f x 的最小值是2,若存在求出b 的值,若不存在说明理由,
请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分。
作答时请写清题号。
22.本小题满分10分.选修4-1:几何证明选讲
如图,在梯形ABCD 中,AD ∥BC ,AB =DC ,过点D 作AC 的平行线DE 交BA 的延长线于E ,AC 交BD 于F .
(I )求证:△AFB ≌△DFC ; (II )求证:DE ·DC =AE ·BD .
23.本小题满分10分.选修4-4:坐标系与参数方程
已知直线l
的参数方程为()x t
t y =⎧⎪⎨
=⎪⎩为参数,若以直角坐标系xoy 的原点O 点为极点,以x 轴正半轴为极轴,选取相同的长度单位建立极坐标系,曲线C 的极坐标方程为2sin()4
π
ρθ=+
,若直线l 与曲线C 交于A 、B 两点.
(I )求直线l 的倾斜角及l 与坐标轴所围成的三角形的面积;
(II )求| AB|.
24.本小题满分10分.选修4-5:不等式选讲 设函数()1|23|.f x x =-- (I )求不等式()f x ≥3x+l 的解集;
(II )若不等式()0f x mx -≥的解集非空,求m 的取值范围。
