2021高考数学浙江专用一轮习题：专题6+第38练+等差数列

合集下载

2021年高考数学一轮复习讲练测(浙江版)专题6.2 等差数列及其前n项和(测)

班级__________ 姓名_____________ 学号___________ 得分__________一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的.） 1．【浙江省高三第一次五校联考】在等差数列{}n a 中，53a =，62a =-，则348a a a ++等于（）A. 1B. 2C. 3D. 4 【答案】C. 【解析】试题分析：∵等差数列{}n a ，∴3847561a a a a a a +=+=+=，∴3483a a a ++=.2．【辽宁省沈阳市东北育才学校高三八模】等差数列{}n a 中，564a a +=，则10122log (222)a a a⋅=（）A.10B.20C.40D.22log 5+【答案】B 【解析】试题分析：由于10121056125()54222222a a a a a a a a ++++⨯⋅⋅⋅===，所以10125422log (222)log 220.a a a ⨯⋅⋅⋅==选B.3．数列{}n a 为等差数列，满足242010a a a +++=，则数列{}n a 前21项的和等于（）A ．212B ．21C ．42D ．84 【答案】B 【解析】4．各项均为正数的等差数列}{n a 中，4936a a =，则前12项和12S 的最小值为（）（A ）78 （B ）48 （C ）60 （D ）72 【答案】D 【解析】试题分析：由于11212494912()6()12722a a S a a a a +==+≥=，当且仅当496a a ==时取等号，所以12S 的最小值为72，选D.5．【改编题】已知n S 是等差数列{}n a 的前n 项和，则=-nnn S S S 32（） A. 30 B. 3 C. 300 D.31【答案】D【解析】由于)(2)(231212n n n n n a a n a a n S S +=+=-+，)(23313n n a a n S +=，所以3132=-n n n S S S .6．【改编题】已知n S 是公差d 不为零的等差数列}{n a 的前n 项和，且83S S =，k S S =7（7≠k ），则k 的值为（）A. 3B.4C.5D.6 【答案】B7．【2022新课标I 学易大联考二】已知数列{}n a 的前n 项和n S 满足21(1)22n n nS n S n n +-+=+*()n N ∈，13a =，则数列{}n a 的通项n a =（）A ．41n -B ．21n +C ．3nD ．2n +【命题意图】本题考查数列前n 项和n S 与通项n a 间的关系、等差数列通项公式等基础学问，意在考查同学的规律思维力量、运算求解力量，以及转化思想的应用．【答案】A【解析】由21(1)22n n nS n S n n +-+=+，得121n n S S n n+-=+，则数列{}n S n 是首项为131S=，公差为2的等差数列，则32(1)21nS n n n=+-=+，即22n S n n =+，则当2n ≥时，1n n n a S S -=-＝2222(1)(1)41n n n n n +----=-．又当1n =时，113a S ==，满足41n a n =-，故选A ．8．【2022新课标II 学易大联考一】《九章算术》有这样一个问题：今有女子善织，日增等尺，七日织二十一尺，其次日、第五日、第八日所织之和为十五尺，问第十日所织尺数为（） A ．6 B ．9 C ．12 D ．15【命题意图】本题主要考查等差数列的通项公式与前n 项和公式，是基础题.【答案】D【解析】由题知该女每天所织尺数等差数列，设为{}n a ，n S 是其前n 项和，则7S =177()2a a +=47a =21，所以4a =3，由于258a a a ++=53a =15，所以5a =5，所以公差54d a a =-=2，所以10a =55a d +=15，故选D.9．某企业为节能减排，用9万元购进一台新设备用于生产. 第一年需运营费用2万元，从其次年起，每年运营费用均比上一年增加2万元，该设备每年生产的收入均为11万元. 设该设备使用了()n n N *∈年后，盈利总额达到最大值（盈利额等于收入减去成本），则n 等于（）A.4B.5C.6D.7 【答案】A10．【原创题】已知等差数列}{n a 中，59914,90a a S +==, 则12a 的值是（） A ． 15 B ．12-C ．32-D ．32【答案】B【解析】由已知得，597214a a a +==，故77a =，又19959()9902a a S a +===，故510a =，则7532a a d -=-=，32d =-，故125217102a a d =+=-12=-．11．【原创题】已知等差数列765)1()1()1(53}{x x x n a a n n +++++-=，则，的开放式中4x 项的系数是数列}{n a 中的（）A ．第9项B ．第10项C ．第19项D ．第20项【答案】D ．【解析】由二项式定理得567(1)(1)(1)x x x +++++的开放式中4x 项的系数为44456776551555123C C C ⨯⨯++=++=⨯⨯，由3555n -=，得20n =，故选D ．12．【2022浙江理6】如图所示，点列{}{},n n A B 分别在某锐角的两边上，且1n n A A +=12n n A A ++，2n n A A +≠，n ∈*N ，112n n n n B B B B +++=，2n n B B +≠，n ∈*N （P Q ≠表示点P 与点Q 不重合）.若n n n d A B =，n S 为1n n n A B B +△的面积，则（）.S nB 1B 2B nB 3B n+1A n+1A 3A nS 1S 2A 2A 1••••••••••••••••••A. {}n S 是等差数列B.2{}n S 是等差数列C.{}n d 是等差数列D.2{}n d 是等差数列【答案】A ．那么11121(tan )2n n S h A A B B θ=+⋅.由题目中条件知112n n n n A A A A +++=，则()1121n A A n A A =-. 所以()1121211tan 2n S h n A A B B θ=⎡+-⋅⎤⎣⎦，其中θ为定值，所以n S 为等差数列.故选A. 二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上.）13．【2022江苏8】已知{}n a 是等差数列，n S 是其前n 项和．若2123a a +=-，510S =，则9a 的值是．【答案】20【解析】设公差为d ，则由题意可得()2111351010a a d a d ⎧++=-⎪⎨+=⎪⎩，解得143a d =-⎧⎨=⎩，则948320a =-+⨯=．14.【2022北京理12】已知{}n a 为等差数列，n S 为其前n 项和，若16a =，350a a +=，则6S =__________. 【答案】615．如图，有一个形如六边形的点阵，它的中心是一个点（算第．．1．层．），第2层每边有两个点，第3层每边有三个点，依次类推．（1）试问第n 层()2n N n *∈≥且的点数为___________个；（2）假如一个六边形点阵共有169个点，那么它一共有_____层．【答案】(1) ()61n -；(2)8.【解析】试题分析：（1）由题意知：11a =，26a =，312a =，418a =，…， ∴数列{}n a 是从第2项起成等差数列，∴2(2)66n a a n d n =+-=-.（2）由(1)(666)11692n n n S -+-=+=，∴8n =.16．【2021届江苏省盐城市高三第三次模拟考试】设n S 是等差数列{}n a 的前n 项和，若数列{}n a 满足2n n a S An Bn C +=++且0A >，则1B C A+-的最小值为．【答案】23 【解析】所以1B C A+-的最小值为23故答案为3三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．【2022届广东省惠州市高三第一次调研考试】（本题10分）已知{}n a 为等差数列，且满足138a a +=，2412a a +=．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）记{}n a 的前n 项和为n S ，若31,,k k a a S +成等比数列，求正整数k 的值．【答案】（Ⅰ）2n a n =;（Ⅱ）2k = 【解析】∴3236a =⨯=，12(1)k a k +=+，2k S k k =+因 31,,k k a a S + 成等比数列，所以213k ka a S +=，从而22(22)6()k k k +=+，即 220k k --=，*k N ∈,解得2k = 或1k =-（舍去） ∴ 2k =18．【2022届宁夏银川一中高三上学期第一次月考】等差数列{}n a 中，13a =，前n 项和为n S ，等比数列{}n b 各项均为正数，11b =，且2212b S +=，{}n b 的公比22S q b = （1）求n a 与n b ；（2）求nS S S 11121+++ ．【答案】（1）n n a n 3)1(33=-+=,13-=n n b （2）23(1)n nS n =+【解析】试题分析：（1）由{}n b 的公比22S q b =及2212b S +=可解得3,q =由11b =则n b 可求，又由22Sq b = 可得3,6,91222=-===a a d a S 则n a 可求；（2）由（1）可得3(1)2n n n S +=则12211()3(1)31)n S n n n n ==-++，故由裂项相消法可求n S S S 11121+++12111211111(1)32231n S S S n n +++=-+-++-+ 212(1)313(1)n n n =-=++ 19．【2022全国甲理17】n S 为等差数列{}n a 的前n 项和，且11a =，728S =．记[]lg n n b a =，其中[]x 表示不超过的最大整数，如[]0.90=，[]lg 991=．（1）求1b ，11b ，101b ；（2）求数列{}n b 的前1000项和．【答案】（1）0,1,2；（2）1893．【解析】（1）设{}n a 的公差为d ，74728S a ==，所以44a =，所以4113a a d -==，所以1(1)n a a n d n =+-=．所以[][]11lg lg10b a ===，[][]1111lg lg111b a ===，[][]101101lg lg1012b a ===．（2）当0lg 1n a <≤时，129n =⋅⋅⋅，，，；当1lg 2n a <≤时，101199n =⋅⋅⋅，，，；当2lg 3n a <≤时，100101999n =⋅⋅⋅，，，；当lg 3n a =时，1000n =．所以1000121000=T b b b =++⋅⋅⋅+[][][]121000lg lg lg =a a a ++⋅⋅⋅+091902900311893⨯+⨯+⨯+⨯=． 20．【江苏省盐城市高三第三次模拟考试】设函数21()1+f x px qx=+（其中220p q +≠），且存在无穷数列{}n a ，使得函数在其定义域内还可以表示为212()1n n f x a x a x a x =+++++．（1）求2a （用,p q 表示）；（2）当1,1p q =-=-时，令12n n n n a b a a ++=，设数列{}n b 的前n 项和为n S ，求证：32n S <；（3）若数列{}n a 是公差不为零的等差数列，求{}n a 的通项公式．【答案】（1）22a p q =-；（2）证明见解析；（3）1n a n =+．【解析】列{}n a 的通项公式．试题解析：（1）由题意，得2212(1)(1)1n n px qx a x a x a x +++++++=，明显2,x x 的系数为0，所以121+0++0a p a a p q =⎧⎨=⎩，从而1a p =-，22a p q =-．（2）由1,1p q =-=-，考虑(3)nx n ≥的系数，则有120n n n a pa qa --++=，得1212120(3)n n n a a a a a n --=⎧⎪=⎨⎪--=≥⎩，即21n n n a a a ++=+，所以210p q +=-=，即2,1p q =-=，由（1）知12a =，23a =，所以1n a n =+． 21.【2022年山西高三四校联考】（本小题满分12分）在等差数列}{n a 中，11,552==a a ，数列}{n b 的前n 项和n n a n S +=2.（Ⅰ）求数列}{n a ，}{n b 的通项公式；（Ⅱ）求数列⎩⎨⎧⎭⎬⎫+11n n b b 的前n 项和n T ．【答案】（I ）12+=n a n ，⎩⎨⎧≥+==)2(,12)1(,4n n n b n ；（II ）)32(2016+-=n n T n ．【解析】（I ）由11,552==a a 可求得数列}{n a 的首项及公差，从而求得n a ，对于数列}{n b ，可先令1=n ，由1111b a S =+=，先求得1b ，再由1,1>-=-n S S b n n n 来求得}{n b 的通项；（II ）有第一问可求得⎩⎨⎧≥+==)2(,12)1(,4n n n b n ，可先求得⎩⎨⎧⎭⎬⎫+11n n b b 的通项公式，在利用拆项法求n T ．试题解析：（1）设等差数列}{n a 的首项为1a ，公差为d ，则⎩⎨⎧=+==+=11451512d a a d a a∴⎩⎨⎧==231d a ∴122)1(3+=⨯-+=n n a n …………（3分）所以)32(201615101201)32151(21201)32112191717151(21201+-=+-+=+-+=+-+++-+-+=n n n n n n n T nn=1仍旧适合上式， …………（10分）综上，)32(201615101201+-=+-+=n n n n T n …………（12分）22.【2022年江西师大附中高三二模】（本小题满分12分）在公比为2的等比数列{}n a 中，2a 与5a 的等差中项是93. （Ⅰ）求1a 的值；（Ⅱ）若函数1sin 4y a x πφ⎛⎫=+⎪⎝⎭，φπ<，的一部分图像如图所示，()11,M a -，()13,N a -为图像上的两点，设MPN β∠=，其中P 与坐标原点O 重合，πβ<<0，求()tan φβ-的值.【答案】（I ）13a =；（II ）32-+．【解析】试题分析：（I ）n a 为公比为2的等比数列，所以258a a =代入等差中项关系式31825=+a a 中，求出2a ，如图，连接MN ，在MPN ∆中，由余弦定理得222412283cos 2283PM PN MNPM PNβ+-+-===-又∵πβ<<0 ∴ 56βπ= -------------9分∴ 12πφβ-=-∴ ()tan tantan 231246πππφβ⎛⎫-=-=--=-+ ⎪⎝⎭-------------12分。

2021年高中数学一轮复习第六章数列6.2等差数列及其前n项和学案

§6.2 等差数列及其前n 项和考纲展示►1.理解等差数列的概念.2.掌握等差数列的通项公式与前n 项和公式.3.能在具体的问题情境中识别数列的等差关系，并能用有关知识解决相应的问题.4.了解等差数列与一次函数、二次函数的关系.考点1 等差数列的基本运算1.等差数列的有关概念 (1)等差数列的定义一般地，如果一个数列从第________项起，每一项与它的前一项的差等于________，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，通常用字母________表示，定义表达式为a n －a n －1＝d (常数)(n ∈N *，n ≥2)或a n ＋1－a n ＝d (常数)(n ∈N *)．(2)等差中项若三个数a ，A ，b 成等差数列，则A 叫做a 与b 的等差中项，且有A ＝a ＋b2.答案：(1)2 同一个常数 d 2．等差数列的有关公式 (1)等差数列的通项公式如果等差数列{a n }的首项为a 1，公差为d ，那么它的通项公式是________． (2)等差数列的前n 项和公式设等差数列{a n }的公差为d ，其前n 项和S n ＝na 1＋n n －12d 或S n ＝n a 1＋a n2.答案：(1)a n ＝a 1＋(n －1)d(1)[教材习题改编]已知等差数列－5，－2,1，…，则该数列的第20项为________．答案：52(2)[教材习题改编]在100以内的正整数中有________个能被6整除的数．答案：16 知三求二．等差数列中，有五个基本量，a 1，d ，n ，a n ，S n ，这五个基本量通过________，____________联系起来，如果已知其中三个量，利用这些公式，便可以求出其余两个的值，这其间主要是通过方程思想，列方程组求解．答案：通项公式前n 项和公式[典题1] (1)设S n 为等差数列{a n }的前n 项和，S 8＝4a 3，a 7＝－2，则a 9＝( ) A ．－6B ．－4C ．－2D ．2[答案] A[解析] 解法一(常规解法)：设公差为d ，则8a 1＋28d ＝4a 1＋8d ，即a 1＝－5d ，a 7＝a 1＋6d ＝－5d ＋6d ＝d ＝－2，所以a 9＝a 7＋2d ＝－6.解法二(结合性质求解)：根据等差数列的定义和性质，可得S 8＝4(a 3＋a 6)，又S 8＝4a 3，所以a 6＝0，又a 7＝－2，所以a 8＝－4，a 9＝－6.(2)[2017·河北武邑中学高三期中]等差数列{a n }中，S n 是其前n 项和，a 1＝－9，S 99－S 77＝2，则S 10＝( )A ．0B ．－9C ．10D ．－10[答案] A[解析] 因为⎩⎨⎧⎭⎬⎫S n n 是等差数列，且公差为d ＝1，故S 1010＝a 11＋1×(10－1)＝－9＋9＝0，故选A.(3)[2017·河北唐山模拟]设等差数列{a n }的前n 项和为S n ，S 3＝6，S 4＝12，则S 6＝________.[答案] 30[解析] 解法一：设数列{a n }的首项为a 1，公差为d ，由S 3＝6，S 4＝12，可得⎩⎪⎨⎪⎧S 3＝3a 1＋3d ＝6，S 4＝4a 1＋6d ＝12，解得⎩⎪⎨⎪⎧a 1＝0，d ＝2，则S 6＝6a 1＋15d ＝30.解法二：∵等差数列{a n }，故可设S n ＝An 2＋Bn ，由S 3＝6，S 4＝12，可得⎩⎪⎨⎪⎧S 3＝9A ＋3B ＝6，S 4＝16A ＋4B ＝12，解得⎩⎪⎨⎪⎧A ＝1，B ＝－1，即S n ＝n 2－n ，则S 6＝36－6＝30.[点石成金] 等差数列运算的解题思路及答题步骤 (1)解题思路由等差数列的前n 项和公式及通项公式可知，若已知a 1，d ，n ，a n ，S n 中的三个便可求出其余两个，即“知三求二”，“知三求二”的实质是方程思想，即建立方程组求解．(2)答题步骤步骤一：结合所求结论，寻找已知与未知的关系；步骤二：根据已知条件列方程求出未知量；步骤三：利用前n 项和公式求得结果．考点2 等差数列的判断与证明等差数列的概念的两个易误点：同一个常数；常数.(1)在数列{a n }中，若a 1＝1，a n ＋1＝a n ＋2，则该数列的通项公式为a n ＝__________. 答案：2n －1解析：由a n ＋1＝a n ＋2，知{a n }为等差数列，其公差为2，故a n ＝1＋(n －1)×2＝2n －1. (2)若数列{a n }满足a 1＝1，a n ＋1－a n ＝n ，则数列{a n }的通项公式为a n ＝__________. 答案：1＋n n －12解析：由a n ＋1－a n ＝n ，得a 2－a 1＝1，a 3－a 2＝2，…，a n －a n －1＝n －1，各式相加，得a n－a 1＝1＋2＋…＋n －1＝n －11＋n －12＝nn －12，故a n ＝1＋n n －12.[典题2] 若数列{a n }的前n 项和为S n ，且满足a n ＋2S n S n －1＝0(n ≥2)，a 1＝12.(1)求证：⎩⎨⎧⎭⎬⎫1S n 是等差数列；(2)求数列{a n }的通项公式．(1)[证明] 当n ≥2时，由a n ＋2S n S n －1＝0，得S n －S n －1＝－2S n S n －1，所以1S n －1S n －1＝2.又1S 1＝1a 1＝2，故⎩⎨⎧⎭⎬⎫1S n 是首项为2，公差为2的等差数列． (2)[解] 由(1)，可得1S n ＝2n ，∴S n ＝12n .当n ≥2时，a n ＝S n －S n －1＝12n －12n －1＝n －1－n2n n －1＝－12n n －1.当n ＝1时，a 1＝12不适合上式．故a n＝⎩⎪⎨⎪⎧12，n ＝1，－12n n －1，n ≥2.[题点发散1] 若将母题条件变为：数列{a n }的前n 项和为S n (n ∈N *)，2S n －na n ＝n .求证：{a n}为等差数列．证明：∵2S n－na n＝n，①∴当n≥2时，2S n－1－(n－1)a n－1＝n－1，②①－②，得(2－n)a n＋(n－1)a n－1＝1，则(1－n)a n＋1＋na n＝1，∴2a n＝a n－1＋a n＋1(n≥2)，∴数列{a n}为等差数列．[题点发散2] 若母题变为：已知数列{a n}中，a1＝2，a n＝2－1a n－1(n≥2，n∈N*)，设b n＝1a n－1(n∈N*)．求证：数列{b n}是等差数列．证明：∵a n＝2－1a n－1，∴a n＋1＝2－1a n.∴b n＋1－b n＝1a n＋1－1－1a n－1＝12－1a n－1－1a n－1＝a n－1a n－1＝1，∴{b n}是首项为b1＝12－1＝1，公差为1的等差数列．[点石成金] 等差数列的判定与证明方法n n34 117，a2＋a5＝22.(1)求数列{a n}的通项公式；(2)若数列{b n }满足b n ＝S nn ＋c，是否存在非零实数c 使得{b n }为等差数列？若存在，求出c的值；若不存在，请说明理由．解：(1)设等差数列{a n }的公差为d ，且d ＞0，由等差数列的性质，得a 2＋a 5＝a 3＋a 4＝22，所以a 3，a 4是关于x 的方程x 2－22x ＋117＝0的解，所以a 3＝9，a 4＝13，易知a 1＝1，d ＝4，故通项为a n ＝1＋(n －1)×4＝4n －3. (2)由(1)知，S n ＝n 1＋4n －32＝2n 2－n ，所以b n ＝S nn ＋c ＝2n 2－n n ＋c.解法一：所以b 1＝11＋c ，b 2＝62＋c，b 3＝153＋c(c ≠0)．由2b 2＝b 1＋b 3，解得c ＝－12.当c ＝－12时，b n ＝2n 2－nn －12＝2n ，当n ≥2时，b n －b n －1＝2.故当c ＝－12时，数列{b n }为等差数列．解法二：由b n ＝S nn ＋c＝n 1＋4n －32n ＋c＝2n ⎝ ⎛⎭⎪⎫n －12n ＋c，∵c ≠0，∴可令c ＝－12，得到b n ＝2n .∵b n ＋1－b n ＝2(n ＋1)－2n ＝2(n ∈N *)， ∴数列{b n }是公差为2的等差数列．即存在一个非零常数c ＝－12，使数列{b n }为等差数列．考点3 等差数列的性质及应用等差数列的常用性质(1)通项公式的推广：a n ＝a m ＋________(n ，m ∈N *)．(2)若{a n }为等差数列，且k ＋l ＝m ＋n (k ，l ，m ，n ∈N *)，则____________． (3)若{a n }是等差数列，公差为d ，则{a 2n }也是等差数列，公差为________． (4)若{a n }，{b n }是等差数列，公差为d ，则{pa n ＋qb n }也是等差数列．(5)若{a n }是等差数列，公差为d ，则a k ，a k ＋m ，a k ＋2m ，…(k ，m ∈N *)是公差为________的等差数列．(6)数列S m ，S 2m －S m ，S 3m －S 2m ，…也是等差数列． (7)S 2n －1＝(2n －1)a n .(8)若n 为偶数，则S 偶－S 奇＝nd2；若n 为奇数，则S 奇－S 偶＝a 中(中间项)．答案：(1)(n －m )d (2)a k ＋a l ＝a m ＋a n (3)2d (5)md等差数列的基本公式：通项公式；前n 项和公式．(1)等差数列{a n }中，a 2＋a 3＝1，a 5－2a 1＝27，则a 5＝________. 答案：13解析：设等差数列的公差为d ，则有2a 1＋3d ＝1,4d －a 1＝27，解得d ＝5，a 1＝－7，所以a 5＝a 1＋4d ＝13.(2)等差数列{a n }的首项为1，公差为4，前n 项和为120，则n ＝________. 答案：8解析：a n ＝1＋(n －1)×4＝4n －3，所以S n ＝n 1＋4n －32＝120，解得n ＝8或n ＝－152(舍去).等差数列运算的两个方法：应用性质；巧妙设元．(1)在等差数列{a n }中，已知a 4＋a 10＝12，则该数列前13项和S 13＝__________. 答案：78解析：由等差数列的性质与前n 项和公式，得S 13＝13a 1＋a 132＝13a 4＋a 102＝78.(2)已知等差数列{a n }前三项的和为－3，前三项的积为8，则{a n }的通项公式是__________．答案：a n ＝－3n ＋5或a n ＝3n －7解析：设等差数列{a n }的前三项为a 2－d ，a 2，a 2＋d ，由题意得⎩⎪⎨⎪⎧3a 2＝－3，a 2－d a 2a 2＋d ＝8，解得⎩⎪⎨⎪⎧a 2＝－1，d ＝－3 或⎩⎪⎨⎪⎧a 2＝－1，d ＝3，所以a n ＝2－3(n －1)＝－3n ＋5或a n ＝－4＋3(n －1)＝3n －7. 故a n ＝－3n ＋5或a n ＝3n －7.[典题3] [2017·河南洛阳统考]设等差数列{a n }的前n 项和为S n ，若S 3＝9，S 6＝36，则a 7＋a 8＋a 9＝( )A ．63B ．45C ．36D ．27[答案] B[解析] 由{a n }是等差数列，得S 3，S 6－S 3，S 9－S 6为等差数列，即2(S 6－S 3)＝S 3＋(S 9－S 6)，得到S 9－S 6＝2S 6－3S 3＝45，故选B.[点石成金] 在等差数列{a n }中，数列S m ，S 2m －S m ，S 3m －S 2m 也成等差数列．等差数列的性质是解题的重要工具.1.[2017·宁夏银川模拟]已知等差数列{a n }的公差为d (d ≠0)，且a 3＋a 6＋a 10＋a 13＝32.若a m ＝8，则m ＝( )A ．8B ．12C ．6D ．4答案：A解析：由a 3＋a 6＋a 10＋a 13＝32，得 (a 3＋a 13)＋(a 6＋a 10)＝32，即4a 8＝32， ∴a 8＝8，∴m ＝8.故选A.2．已知等差数列{a n }的前n 项和为S n ，且S 10＝10，S 20＝30，则S 30＝________. 答案：60解析：∵S 10，S 20－S 10，S 30－S 20成等差数列， ∴2(S 20－S 10)＝S 10＋S 30－S 20， ∴40＝10＋S 30－30，∴S 30＝60.考点4 等差数列前n 项和的最值问题[典题4] 在等差数列{a n }中，a 1＝29，S 10＝S 20，则数列{a n }的前n 项和S n 的最大值为( ) A ．S 15 B ．S 16 C ．S 15或S 16 D ．S 17 [答案] A[解析]∵a 1＝29，S 10＝S 20，∴10a 1＋10×92d ＝20a 1＋20×192d ，解得d ＝－2， ∴S n ＝29n ＋n n －12×(－2)＝－n 2＋30n＝－(n －15)2＋225.∴当n ＝15时，S n 取得最大值．[题点发散1] 若将条件“a 1＝29，S 10＝S 20”改为“a 1>0，S 5＝S 12”，如何求解？解：解法一：设等差数列{a n }的公差为d ，由S 5＝S 12，得5a 1＋10d ＝12a 1＋66d ，解得d ＝－18a 1<0.所以S n ＝na 1＋n n －12d＝na 1＋n n －12·⎝ ⎛⎭⎪⎫－18a 1＝－116a 1(n 2－17n )＝－116a 1⎝ ⎛⎭⎪⎫n －1722＋28964a 1.因为a 1>0，n ∈N *，所以当n ＝8或n ＝9时，S n 有最大值．解法二：设等差数列{a n }的公差为d ，同解法一得d ＝－18a 1<0.设此数列的前n 项和最大，则⎩⎪⎨⎪⎧a n ≥0，a n ＋1≤0，即⎩⎪⎨⎪⎧a n＝a 1＋n －1·⎝ ⎛⎭⎪⎫－18a 1≥0，a n ＋1＝a 1＋n ·⎝ ⎛⎭⎪⎫－18a 1≤0，解得⎩⎪⎨⎪⎧n ≤9，n ≥8，即8≤n ≤9，又n ∈N *，所以当n ＝8或n ＝9时，S n 有最大值．解法三：设等差数列{a n }的公差为d ，同解法一得d ＝－18a 1<0.由于S n ＝na 1＋n n －12d ＝d 2n 2＋⎝ ⎛⎭⎪⎫a 1－d 2n ，设f (x )＝d2x 2＋⎝ ⎛⎭⎪⎫a 1－d 2x ，则函数y ＝f (x )的图象为开口向下的抛物线，由S 5＝S 12知，抛物线的对称轴为x ＝172(如图所示)，由图可知，当1≤n ≤8时，S n 单调递增；当n ≥9时，S n 单调递减．又n ∈N *，所以当n ＝8或n ＝9时，S n 最大．[题点发散2] 若将条件“a 1＝29，S 10＝S 20”改为“a 3＝12，S 12>0，S 13<0”，如何求解？解：因为a 3＝a 1＋2d ＝12，所以a 1＝12－2d ，所以⎩⎪⎨⎪⎧S 12＝12a 1＋66d >0，S 13＝13a 1＋78d <0，即⎩⎪⎨⎪⎧144＋42d >0，156＋52d <0，解得－247<d <－3.故公差d 的取值范围为⎝ ⎛⎭⎪⎫－247，－3. 解法一：由d <0可知，{a n }为递减数列，因此，在1≤n ≤12中，必存在一个自然数n ，使得a n ≥0，a n ＋1<0，此时对应的S n 就是S 1，S 2，…，S 12中的最大值．由于⎩⎪⎨⎪⎧S 12＝6a 6＋a 7>0，S 13＝13a 7<0，于是a 7<0，从而a 6>0，因此S 6最大．解法二：由d <0可知{a n }是递减数列，令⎩⎪⎨⎪⎧a n ＝a 3＋n －3d ≥0，a n ＋1＝a 3＋n －2d <0，可得⎩⎪⎨⎪⎧n ≤3－12d ，n >2－12d.由－247<d <－3，可得⎩⎨⎧n ≤3－12d <3＋123＝7，n >2－12d >2＋12247＝5.5，所以5.5<n <7，故n ＝6，即S 6最大．[题点发散3] 若将“a 1＝29，S 10＝S 20”改为“a 5>0，a 4＋a 7<0”，如何求解？解：∵⎩⎪⎨⎪⎧a 4＋a 7＝a 5＋a 6<0，a 5>0，∴⎩⎪⎨⎪⎧a 5>0，a 6<0，∴S n 的最大值为S 5.[点石成金] 求等差数列前n 项和的最值的方法(1)运用配方法转化为二次函数，借助二次函数的单调性以及数形结合的思想，从而使问题得解．(2)通项公式法：求使a n ≥0(a n ≤0)成立时最大的n 的值即可．一般地，等差数列{a n }中，若a 1>0，且S p ＝S q (p ≠q )，则①若p ＋q 为偶数，则当n ＝p ＋q2时，S n 最大； ②若p ＋q 为奇数，则当n ＝p ＋q －12或n ＝p ＋q ＋12时，S n 最大.1.等差数列{a n }的前n 项和为S n ，已知a 5＋a 7＝4，a 6＋a 8＝－2，则当S n 取最大值时，n ＝( )A ．5B ．6C ．7D ．8答案：B解析：依题意，得2a 6＝4,2a 7＝－2，a 6＝2＞0，a 7＝－1＜0.又数列{a n }是等差数列，因此在该数列中，前6项均为正数，自第7项起以后各项均为负数，于是当S n 取最大值时，n ＝6，故选B.2．[2017·安徽望江中学模拟]设数列{a n }是公差d ＜0的等差数列，S n 为前n 项和，若S 6＝5a 1＋10d ，则S n 取最大值时，n ＝( )A ．5B ．6C ．5或6D ．11 答案：C解析：由题意，得S 6＝6a 1＋15d ＝5a 1＋10d ，所以a 6＝0，故当n ＝5或6时，S n 最大，故选C.[方法技巧] 1.在遇到三个数成等差数列问题时，可设三个数为：(1)a ，a ＋d ，a ＋2d ；(2)a －d ，a ，a ＋d ；(3)a －d ，a ＋d ，a ＋3d 等，可视具体情况而定．2．数列{a n }为等差数列．(1)若项数为偶数2n ，则S 2n ＝n (a 1＋a 2n )＝n (a n ＋a n ＋1)；S 偶－S 奇＝nd ；S 奇S 偶＝a na n ＋1. (2)若项数为奇数2n －1，则S 2n －1＝(2n －1)a n ；S 奇－S 偶＝a n ；S 奇S 偶＝n n －1.3．若数列{a n }与{b n }均为等差数列，且前n 项和分别是S n 和T n ，则S 2m －1T 2m －1＝a m b m. 4．若a m ＝n ，a n ＝m (m ≠0)，则a m ＋n ＝0. [易错防范] 1.公差不为0的等差数列的前n 项和公式是n 的二次函数，且常数项为0.若某数列的前n 项和公式是常数项不为0的二次函数，则该数列不是等差数列，它从第二项起成等差数列．2．求等差数列的前n 项和S n 的最值时，需要注意“自变量n 为正整数”这一隐含条件．若对称轴取不到，需考虑最接近对称轴的自变量n (n 为正整数)；若对称轴对应在两个正整数的中间，此时应有两个符合题意的n 值．真题演练集训1．[2016·新课标全国卷Ⅰ]已知等差数列{a n }前9项的和为27，a 10＝8，则a 100＝( )A ．100B ．99C ．98D ．97 答案：C解析：由等差数列性质知，S 9＝9a 1＋a 92＝9×2a 52＝9a 5＝27，解得a 5＝3，而a 10＝8，因此公差d ＝a 10－a 510－5＝1，∴a 100＝a 10＋90d ＝98，故选C.2．[2015·北京卷]设{a n }是等差数列，下列结论中正确的是( )A ．若a 1＋a 2＞0，则a 2＋a 3＞0B ．若a 1＋a 3＜0，则a 1＋a 2＜0C ．若0＜a 1＜a 2，则a 2＞a 1a 3D ．若a 1＜0，则(a 2－a 1)(a 2－a 3)＞0答案：C解析：A ，B 选项易举反例．C 中若0＜a 1＜a 2，∴a 3＞a 2＞a 1＞0，∵a 1＋a 3>2a 1a 3，又2a 2＝a 1＋a 3，∴2a 2>2a 1a 3，即a 2>a 1a 3成立．D 中，若a 1<0，则(a 2－a 1)(a 2－a 3)＝d ·(－d )＝－d 2≤0，故D 选项错误．故选C.3．[2016·江苏卷]已知{a n }是等差数列，S n 是其前n 项和．若a 1＋a 22＝－3，S 5＝10，则a 9的值是________．答案：20解析：设等差数列{a n }公差为d ，由题意，得⎩⎪⎨⎪⎧ a 1＋a 1＋d 2＝－3，5a 1＋5×42d ＝10，解得⎩⎪⎨⎪⎧ a 1＝－4，d ＝3，则a 9＝a 1＋8d ＝－4＋8×3＝20.4．[2016·新课标全国卷Ⅱ]S n 为等差数列{a n }的前n 项和，且a 1＝1，S 7＝28.记b n ＝[lg a n ]，其中[x ]表示不超过x 的最大整数，如[0.9]＝0，[lg 99]＝1.(1)求b 1，b 11，b 101；(2)求数列{b n }的前1 000项和．解：(1)设{a n }的公差为d ，据已知有7＋21d ＝28，解得d ＝1.所以{a n }的通项公式为a n ＝n .b 1＝[lg 1]＝0，b 11＝[lg 11]＝1，b 101＝[lg 101]＝2.(2)因为b n ＝⎩⎪⎨⎪⎧ 0，1≤n <10，1，10≤n <100，2，100≤n <1 000，3，n ＝1 000，所以数列{b n }的前1 000项和为1×90＋2×900＋3×1＝1 893.课外拓展阅读巧用三点共线解等差数列问题1．等差数列的求解由等差数列与一次函数的关系可知：对于公差为d (d ≠0)的等差数列{a n }，其通项公式为a n ＝dn ＋(a 1－d )，则点(n ，a n )(n ∈N *)共线，又d ＝a n －a m n －m(n ≠m )，所以d 为过(m ，a m )，(n ，a n )两点的直线的斜率．由此可用三点共线解决等差数列问题．[典例1] 若数列{a n }为等差数列，a p ＝q ，a q ＝p (p ≠q )，则a p ＋q ＝________.[思路分析][解析] 解法一：设数列{a n }的公差为d ，因为a p ＝a q ＋(p －q )d ，所以q ＝p ＋(p －q )d ，即q －p ＝(p －q )d .因为p ≠q ，所以d ＝－1.所以a p ＋q ＝a p ＋(p ＋q －p )d ＝q ＋q (－1)＝0.解法二：因为数列{a n }为等差数列，所以点(n ，a n )(n ∈N *)在一条直线上．不妨设p <q ，记点A (p ，q )，B (q ，p )，则直线AB的斜率k ＝p －q q －p＝－1，如图所示，由图知OC ＝p ＋q ，即点C 的坐标为(p ＋q,0)，故a p ＋q ＝0.[答案] 0[典例2] 已知{a n }为等差数列，且a 100＝304，a 300＝904，求a 1 000.[思路分析][解] 因为{a n }为等差数列，则(100,304)，(300,904)，(1 000，a 1 000)三点共线，所以904－304300－100＝a 1 000－9041 000－300，解得a 1 000＝3 004.2．等差数列前n 项和的求解在等差数列前n 项和公式的变形S n ＝d 2n 2＋⎝ ⎛⎭⎪⎫a 1－d 2n 中，两边同除以n 得S n n ＝d 2n ＋⎝ ⎛⎭⎪⎫a 1－d 2.该式说明对任意n ∈N *，所有的点⎝ ⎛⎭⎪⎫n ，S n n 都在同一条直线上，从而对m ，n ∈N *(m ≠n )有S n n －S m m n －m ＝d 2(常数)，即数列⎩⎨⎧⎭⎬⎫S n n 是一个等差数列． [典例3] 已知在等差数列{a n }中，S n ＝33，S 2n ＝44，求这个数列的前3n 项的和S 3n .[解] 由题意知，⎝⎛⎭⎪⎫n ，33n ，⎝ ⎛⎭⎪⎫2n ，442n ，⎝ ⎛⎭⎪⎫3n ，S 3n 3n 三点在同一条直线上，从而有442n －33n 2n －n ＝S 3n 3n －442n 3n －2n，解得S 3n ＝33. 所以该数列的前3n 项的和为33.。

2021版高考数学一轮复习浙江专用精练：6.3 等比数列(试题部分) Word版含解析

姓名，年级：时间：6.3 等比数列探考情悟真题【考情探究】考点内容解读5年考情预测热度考题示例考向关联考点等比数列的有关概念及运算1.理解等比数列的有关概念.2.掌握等比数列的通项公式.3。

掌握等比数列的前n项和公式。

4.了解等比数列与指数函数之间的关系.2015浙江文，10,6分等比数列的通项公式★★★等比数列的性质及应用能利用等比数列的性质解决有关问题.2018浙江，10,4分等比数列的性质不等式的性质★★★分析解读1。

考查等比数列的定义与判定，通项公式，前n项和公式，等比数列的性质等知识。

2.预计2021年高考试题中，对等比数列的考查仍以概念、性质、通项公式、前n项和公式等知识为主，以中档题形式出现,复习时要足够重视。

破考点练考向【考点集训】考点一等比数列的有关概念及运算1.（2019浙江衢州、湖州、丽水三地教学质量检测,4）已知等比数列｛a n｝满足a1+a3=—2a2,则公比q=（）A.—1 B。

1 C.—2 D。

2答案 A2.（2018浙江嘉兴期末,11）各项均为实数的等比数列{a n｝，若a1=1，a5=9，则a3= ，公比q= .答案3；±√3考点二等比数列的性质及应用1。

（2019浙江高考信息优化卷(一）,4)已知等比数列{a n ｝的公比为q,前n 项和为S n ,则“q>1”是“S 4+S 6〉2S 5”的（ )A 。

充分不必要条件B 。

必要不充分条件 C.充分必要条件 D.既不充分也不必要条件答案 D2.(2018浙江杭州二中期中,6）已知等比数列｛a n ｝的前n 项积为T n ,log 2a 3+log 2a 7=2,则T 9的值为( ) A 。

±512 B.512 C 。

±1 024 D 。

1 024 答案 B3.（2020届浙江镇海中学期中，15）已知｛a n }是等比数列,且a n 〉0,a 2a 4+2a 3a 5+a 4a 6=25，则a 4的最大值为 . 答案52炼技法提能力【方法集训】方法1 等比数列中“基本量法”的解题方法1.（2019浙江高考“超级全能生”联考，11)中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关，初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数，请公仔细算相还。

2021届高三数学总复习第一轮——等差数列

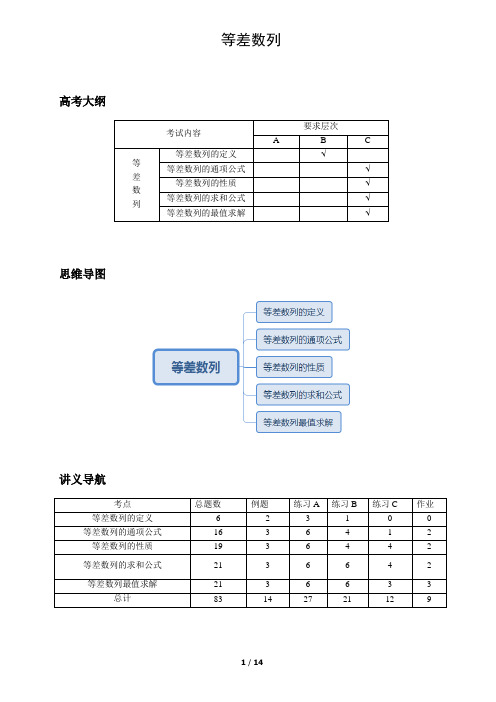
等差数列高考大纲思维导图讲义导航知识梳理一、等差数列的定义如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列．这个常数叫做等差数列的公差，公差常用字母d表示二、等差数列的通项公式等差数列是常见数列的一种，数列从第二项起，每一项与它的前一项的差等于同一个常数，已知等差数列的首项a1，公差d，那么第n项为a n＝a1+（n﹣1）d，或者已知第m项为a m，则第n项为a n＝a m+（n﹣m）d．三、等差数列的性质（1）若公差d＞0，则为递增等差数列；若公差d＜0，则为递减等差数列；若公差d＝0，则为常数列；（2）有穷等差数列中，与首末两端“等距离”的两项和相等，并且等于首末两项之和；（3）m，n∈N+，则a m＝a n+（m﹣n）d；（4）若s，t，p，q∈N*，且s+t＝p+q，则a s+a t＝a p+a q，其中a s，a t，a p，a q是数列中的项，特别地，当s+t＝2p时，有a s+a t＝2a p；（5）若数列{a n}，{b n}均是等差数列，则数列{ma n+kb n}仍为等差数列，其中m，k均为常数．（6）a n，a n﹣1，a n﹣2，…，a2，a1仍为等差数列，公差为﹣d．（7）从第二项开始起，每一项是与它相邻两项的等差中项，也是与它等距离的前后两项的等差中项，即2a n+1＝a n+a n+2，2a n＝a n﹣m+a n+m，（n≥m+1，n，m∈N+）（8）a m，a m+k，a m+2k，a m+3k，…仍为等差数列，公差为kd（首项不一定选a1）．四、等差数列的求和公式等差数列的前n项和公式等差数列的前n项和的公式：①()12nnn a aS+=；②()112nn nS na d-=+．五、等差数列最值求解等差数列前n项和的最值问题可转化为项的正负问题，也可转化为二次函数最值问题.例题讲解一、等差数列定义的理解例1．下面数列中，是等差数列的有( ) ①4,5,6,7,8…②3,0，－3,0，－6，…③0,0,0,0…④110，210，310，410，… A ．1个 B ．2个C ．3个D ．4个例2．下列数列中不是等差数列的为（） A.0，0，0，0，0 B.0，1-，2-，3-，4- C.2，3，4，5，6 D.0，1，2，1，0二、等差数列通项公式例1．在等差数列{}n a 中，已知32a =，5815a a +=，则10(a = ) A ．64 B ．26C ．18D ．13例2．在等差数列{}n a 中，214a =，55a =，则公差(d = )A ．2-B ．3-C ．2D ．3例3．已知{}n a 是等差数列，124a a +=，7828a a +=，则公差等于( ) A ．2 B ．4 C ．6 D ．8三、等差数列的性质例1．等差数列{}n a 中，已知21016a a +=，则468(a a a ++= ) A ．16 B ．20 C ．24 D ．28例2．等差数列{}n a 中，若4681012120a a a a a ++++=，则91113a a -的值是( )A ．14B ．15C ．16D ．17例3．已知等差数列{}n a 单调递增且满足1104a a +=，则8a 的取值范围是( )A ．(2,4)B ．(,2)-∞C ．(2,)+∞D ．(4,)+∞四、等差数列的求和公式例1．已知等差数列{}n a 的前n 项和为n S ，若33S a =，且30a ≠，则43(S S = ) A ．1B ．53C ．83D ．3例2．等差数列{}n a 中，14739a a a ++=，36927a a a ++=，则数列{}n a 前9项的和9S 等于( ) A ．99 B ．66C ．144D ．297例3．设{}n a 是任意等差数列，它的前n 项和、前2n 项和与前4n 项和分别为X ，Y ，Z ，则下列等式中恒成立的是( )A ．23X Z Y +=B ．44X Z Y +=C ．237X Z Y +=D ．86X Z Y +=六、等差数列最值求解例1．已知等差数列{}n a 中，39a a =，公差0d <，则使其前n 项和n S 取得最大值的自然数n 是（）． A.4或5 B.5或6 C.6或7 D.不存在例2．设等差数列{a n }的前n 项和为S n ，若a 2=−3，S 5=−10，则a 5=__________，S n 的最小值_______．例3．在各项均为正数的等比数列{a n }中，214a =，且a 4+a 5=6a 3．练习A1．下列说法中正确的是（）A.若a ，b ，c 成等差数列，则222,,a b c 成等差数列B.若a ，b ，c 成等差数列，则222log ,log ,log a b c 成等差数列C.若a ，b ，c 成等差数列，则a+2，b+2，c+2成等差数列D.若a ，b ，c 成等差数列，则2,2,2a b c 成等差数列2．已知下列各数列，其中为等差数列的个数为（） 1 4，5，6，7，8，... 2 3，0，-3，0，-6，... 3 0，0，0，0， (4)1234,,,,10101010… A.1 B.2C.3D.43．已若{}n a 是等差数列，则由下列关系确定的数列{}n b 也一定是等差数列的是（）A. 2n n b a =B. 2n n b a n =+C. 1n n n b a a +=+D. n n b na =4．已知数列{}n a 为等差数列，且39a =，53a =，则9a 等于( )A ．9-B ．6-C ．3-D ．275．已知等差数列{}n a 中，1232a a a ++=，3456a a a ++=，则91011a a a ++的值为( ) A ．18 B ．16 C ．14 D ．126．等差数列{}n a 中，若46101290a a a a +++=，则10141(3a a -= )A ．15B ．30C ．45D ．607．等差数列{}n a 中，31a =-，1117a =-，则7a 等于( )A ．9-B ．8-C ．92-D ．4-8．在等差数列{}n a 中，公差为12，1359960a a a a +++⋯+=，则246100(a a a a +++⋯+= ) A ．60 B ．70 C ．75 D ．859．已知等差数列{}n a 满足12910a a a ++⋯+=，则有( )A ．3890a a +=B ．2900a a +<C ．1910a a +>D ．4646a =10．已知数列{}n a 为等差数列，且17132a a a π++=，则7tan (a = )A．BC． D．11．已知0a >，0b >，并且1a ，12，1b成等差数列，则9a b +的最小值为( ) A ．16 B ．9C ．5D ．412．等差数列{}n a 中，已知21016a a +=，则468(a a a ++= ) A ．16 B ．20C ．24D ．2813．在等差数列{}n a 中，若4681012120a a a a a ++++=，则10122a a -的值为( ) A ．20 B ．22C ．24D ．2814．等差数列{}n a 中，156a a +=，65a =，那么9a 的值是( ) A ．7- B ．7 C ．113-D ．11315．已知等比数列{}n a 中，各项都是正数，且1321,,22a a a 成等差数列，则8967a a a a ++等于( )A．1+B．1-C．3+D．3-16．已知等差数列{}n a 的前n 项和为n S ，若33S a =，且30a ≠，则43(S S = ) A ．1B ．53C ．83D ．317．设等差数列{}n a 的前n 项和n S ，若4104a a +=，则13(S = ) A ．13 B ．14C ．26D ．5218．设n S 是等差数列{}n a 的前n 项和，若1353a a a ++=，则5(S = ) A ．5 B ．7C ．9D ．1019．在等差数列{}n a 中，若351024a a a ++=，则此数列的前13项的和等于( ) A ．8 B ．13C ．16D ．2620．在等差数列{}n a 中，若14739a a a ++=，36927a a a ++=，则9(S = ) A ．66 B ．99C ．144D ．29721．已知{}n a 为等差数列，n S 为其前n 项和．若312S =，244a a +=，则6(S = ) A ．6 B ．12C ．15D ．1822．等差数列{}n a 前n 项和为n S ，111a =-，466a a +=-．则当n S 取最小值时，(n = ) A ．6 B ．7C ．8D ．923．数列{}n a 的通项公式为2328n a n n =-，则数列{}n a 各项中最小项是( )A ．第4项B ．第5项C ．第6项D ．第7项24．已知数列{}n a 是等差数列，若91130a a +<，10110a a <，且数列{}n a 的前n 项和n S 有最大值，那么当n S 得最小正值时，n 等于( ) A ．20 B ．17 C ．19 D ．2125．已知n S 是等差数列*{}()n a n N ∈的前n 项和，且564S S S >>，以下有四个命题：①数列{}n a 中的最大项为10S ②数列{}n a 的公差0d < ③100S >④110S <其中正确的序号是( )A ．②③B ．②③④C ．②④D ．①③④26．在等差数列{}n a 中，128a =-，公差4d =，若前n 项和n S 取得最小值，则n 的值为( ) A ．7 B ．8C ．7或8D ．8或927．数列{}n a 是首项为111a =，公差为2d =-的等差数列，那么使前n 项和n S 最大的n 值为( ) A ．4 B ．5C ．6D ．7练习B1．设{}n a 为等差数列，则下列数列中，成等差数列的个数为( )①2{}na ②{}n pa ③{}n pa q + ④{}(n na p 、q 为非零常数） A ．1 B ．2C ．3D ．42．等差数列{}n a 的公差0d >，前n 项和为n S ，则对2n >时有( ) A ．1nn S a a n<< B ．1nn S a a n <<C ．1n n Sa a n<<D ．1,,n n Sa a n的大小不确定3．设等差数列{}n a 的前n 项和为n S ，在同一个坐标系中，()n a f n =及()n S g n =的部分图象如图所示，则( )A ．当4n =时，n S 取得最大值B ．当3n =时，n S 取得最大值C ．当4n =时，n S 取得最小值D ．当3n =时，n S 取得最小值4．已知数列{}n a 是等差数列，n S 为其前n 项和．若3916S S =，则612(S S = )A ．110B ．310C ．510D ．7105．设等差数列{}n a 的前n 项和为n S ，且满足100S >，110S <，则下列数值最大的是( )A ．4SB ．5SC ．6SD ．7S6．等差数列{}n a 与{}n b 的前n 项和分别为n S 与n T ，若3221n n S n T n -=+，则77(ab = ) A ．3727B ．3828C ．3929D ．40307．一个有限项的等差数列，前4项之和为40，最后4项之和是80，所有项之和是210，则此数列的项数为( ) A ．10 B ．12 C ．14 D ．168．已知点(n ，*)()n a n N ∈都在直线3240x y --=上，那么在数列n a 中有79(a a += )A ．790a a +>B ．790a a +<C ．790a a +=D ．790a a =9．已知等差数列{}n a 满足3243a a =，则{}n a 中一定为零的项是( )A ．6aB ．8aC ．10aD ．12a10．在等差数列{}n a 中，15a =，470a a +=，则数列{}n a 中为正数的项的个数为( ) A ．4 B ．5 C ．6 D ．711．已知数列{}n a 中，132(3n n a a ++= *)n N ∈，且356820a a a a +++=，那么10a 等于( ) A ．8 B ．5 C ．263D ．712．若等差数列{}n a 的公差为d ，前n 项和为n S ，记nn S b n=，则( ) A ．数列{}n b 是等差数列，{}n b 的公差也为dB ．数列{}n b 是等差数列，{}n b 的公差为2dC ．数列{}n n a b +是等差数列，{}n n a b +的公差为dD ．数列{}n n a b -是等差数列，{}n n a b -的公差为2d13．等差数列{}n a 中，已知113a =，254a a +=，33n a =，则n 为( )A ．48B ．49C ．50D ．5114．若等差数列的首项是24-，且从第10项开始大于零，则公差d 的取值范围是( )A ．83d > B ．3d < C ．833d < D ．833d <15．在数列{}n a 中，若1332()n n a a n N +=+∈，且247920a a a a +++=，则10a 为( ) A ．5 B ．7C ．8D ．1016．等差数列{}n a 前n 项和为n S ，111a =-，466a a +=-．则当n S 取最小值时，(n = ) A ．6 B ．7C ．8D ．917．在各项均为正数的等比数列{}n a 中，63a =，则48(a a += )A ．有最小值6B ．有最大值6C ．有最大值9D ．有最小值318．已知实数序列1a ，2a ，⋯，n a 满足：任何连续3项之和均为负数，且任何4项之和均为正数，则n 的最大值是( ) A ．4 B ．5C ．6D ．719．已知n S 是等差数列*{}()n a n N ∈的前n 项和，且564S S S >>，以下有四个命题：①数列{}n a 中的最大项为10S ②数列{}n a 的公差0d < ③100S >④110S <其中正确的序号是( )A ．②③B ．②③④C ．②④D ．①③④20．已知各项均为正数的等比数列{}n a 中，如果21a =，那么这个数列前3项的和3S 的取值范围是( )A ．(-∞，1]-B ．[1，)+∞C ．[2，)+∞D ．[3，)+∞21．已知等差数列{}n a 的前n 项和为n S ，且110a =，56S S ，下列四个命题中，假命题是( )A ．公差d 的最大值为2-B ．70S <C ．记n S 的最大值为K ，K 的最大值为30D ．20162017a a >练习C1．已知||0x y >>．将四个数,,x x y x y -+( )A ．当0x >时，存在满足已知条件的x ，y ，四个数构成等比数列B ．当0x >时，存在满足已知条件的x ，y ，四个数构成等差数列C ．当0x <时，存在满足已知条件的x ，y ，四个数构成等比数列D ．当0x <时，存在满足已知条件的x ，y ，四个数构成等差数列2．等差数列{}n a 的公差0d >，前n 项和为n S ，则对2n >时有( )A ．1nn S a a n<< B ．1nn S a a n<<C ．1nn S a a n<< D ．1,,nn S a a n的大小不确定3．设等差数列{}n a 的前n 项和为n S ，在同一个坐标系中，()n a f n =及()n S g n =的部分图象如图所示，则( )A ．当4n =时，n S 取得最大值B ．当3n =时，n S 取得最大值C ．当4n =时，n S 取得最小值D ．当3n =时，n S 取得最小值4．等差数列，的前项和分别为，，若，则 A ． B ．C ．D ．5．在等差数列中，，其前项和为，若，则 A ． B ．C ．2008D ．20096．设为等差数列，则下列数列中，成等差数列的个数为① ② ③ ④、为非零常数） A ．1 B ．2 C ．3 D ．47．设表示等差数列的前项和，已知，那么等于 A ．B ．C ．D ．8．等差数列中，，，则该数列前项之和为{}n a {}n b n n S n T 231n n S n T n =+(n na b =)232131n n --2131n n ++2134n n -+{}n a 12007a =-n n S 20082006220082006S S -=2009(S =)2009-2008-{}n a ()2{}na {}n pa {}n pa q +{}(n na p q n S {}n a n 51013S S =1020SS ()193101813{}n a 1m a k =1()k a m k m=≠mk ()A ．B ．C ．D ．9．设数列为等差数列，其前项和为，已知，，若对任意，都有成立，则的值为A ．22B ．21C ．20D ．1910．设等差数列的公差为，前项和为．若，则的最小值为 A ．10 B ．C ．D ．二．填空题（共2小题） 11．在等差数列中，，若它的前项和有最大值，则使取得最小正数的 19 ．12．已知两个等差数列、的前项和分别为和，若，则使为整数的正整数的个数是 5个．课后练习1．等差数列中，若，则．2．设等差数列的前项和为，若，，则 0 ，的最小值为．3．等差数列中，，，则取最大值时， 6或7 ．4．已知等差数列的前项和为，能够说明“若数列是递减数列，则数列是递减数列”是假命题的数列的一个通项公式为（答案不唯一）．5．设等差数列的前项和为，若，，则数列的公差等于．6．若等差数列满足，则12mk-2mk12mk +12mk+{}n a n n S 14799a a a ++=25893a a a ++=*n N ∈n k S S k (){}n a d n n S 11a d ==8n nS a +()927212+{}n a 11101a a <-n n S n S n ={}n a {}n b n n A n B 7453n n A n B n +=+n na b {}n a 31110a a +=678a a a ++={}n a n n S 23a =-510S =-5a =n S {}n a 10a >49S S =n S n ={}n a n n S {}n a {}n S {}n a 27n a n =-+{}n a n n S 1122S =71a ={}n a 1-{}n a 1461,52a a a =+=2019a =20192二．解答题（共3小题）7．在等差数列中，已知，，．（Ⅰ）求数列的通项公式；（Ⅱ）求．8．设等差数列满足，．（1）求的通项公式；（2）求的前项和及使得最大的序号的值．9．已知为等差数列，，． ( I ) 求数列的通项公式以及前项和．（Ⅱ）求使得的最小正整数的值．{}n a 1312a a +=2418a a +=*n N ∈{}n a 3693n a a a a +++⋯+{}n a 35a =109a =-{}n a {}n a n n S n S n {}n a 112a =-562a a ={}n a n n S 14n S >n。

(浙江版)高考数学一轮复习专题6.2等差数列及其前n项和(练)(2021学年)

(浙江版）２018年高考数学一轮复习专题６.２等差数列及其前n项和(练）编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望((浙江版)２018年高考数学一轮复习专题6.2 等差数列及其前n项和（练))的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步，以下为（浙江版)20１8年高考数学一轮复习专题6．2 等差数列及其前n项和（练）的全部内容。

第02节等差数列及其前n 项和A 基础巩固训练1。

设公差不为零的等差数列{}n a 的前n 项和为n S ,若4232()a a a =+,则74S a =（） A.74B.145C.7 D ．14 【答案】Ｃ.2．【２０18届宁夏银川一中高三上第二次月考】等差数列{a }n 中, n S 为n a 的前n 项和, 820a =, 756S =,则12a =( )Ａ。

２8 B. 32 C ． 36 Ｄ。

4０【答案】B 【解析】()177412847565682408322a a S a a a a +=⇒=⇒=∴=-=-=，选B 。

3.【20１７届江西省上饶市二模】已知数列{}n a 的前 n 项和记为 n S ，满足1785,3a a ==,且122n n n a a a ++=+，要使得n S 取到最大值，则n =（ )A 。

13 Ｂ. 14 C. 15或16 D 。

16 【答案】C【解析】由于122n n n a a a ++=+,故数列为等差数列,依题意有7181757,33a a d d d =+=+==-,所以()21131266n n n n n S na d -=+⋅=-+,开口向下且对称轴为312n =，故15n =或16时取得最大值.4.【２０18届福建省德化一中、永安一中、漳平一中高三上三校联考】已知等差数列{}n a 中, 315,a a 是方程2610x x --=的两根，则9a =_____【答案】3【解析】等差数列{}n a 中, 315962a a a +==,93a ∴=,故填３。

2021年高考数学一轮复习讲练测(浙江版)专题6.1 数列的概念及其简单表示(测)

第01节数列的概念与简洁表示法班级__________ 姓名_____________ 学号___________ 得分__________一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的.） 1．已知数列：2，0，2，0，2，0，．前六项不适合．．．下列哪个通项公式( ) A ．n a ＝()111n ++- B ．n a ＝2|sin2n π| C ．n a ＝()11n-- D ．n a ＝2sin 2n π 【答案】D故选D.2．【改编题】已知数列{}n a ，则“11n n a a +>-”是“数列{}n a 为递增数列”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件【答案】B【解析】由题意，若“数列{}n a 为递增数列”，则11n n n a a a +>>-，但11n n a a +>-不能推出1n n a a +>，如11, 1.5n n a a +==，则不能推出“数列{}n a 为递增数列”，所以“11n n a a +>-”是“数列{}n a 为递增数列”的必要而不充分条件.故选B.3．【改编题】已知数列}{n a 的前n 项和为nS ，且)1(2+=n n a S ，则5a = （）A ．16-B ．32-C ．32D ．64-【答案】B ．【解析】当1n =时，111122,2a S a a ==+∴=-．当2n ≥时，由22n n S a =+得1122n n S a --=+，两式作差得：12n n a a -=，∴数列{}n a 是以2-为首项，2为公比的等比数列，∴452232a =-⨯=-，故选B ．4．【山西晋城市2022届高三下学期第三次模拟考试】已知数列{}n a 的前n 项和为n S ,且满足111,2nn n a a a +==,则20S =（）A ．3066B ．3063C ．3060D ．3069 【答案】D 【解析】5．【太原市2022年高三班级模拟试题（三）】设等差数列{}n a 的前n 项和为n S ，若6726a a =+，则9S 的值为（）A ．27B ．36C ．45D ．54 【答案】D 【解析】试题分析：由6726a a =+得641=+d a ,故54)4(92899119=+=⨯+=d a d a S ,故应选D. 6．【太原市2022年高三班级模拟试题（三）】已知{}n a 满足11a =，*11()()4n n n a a n N ++=∈，21123444n n n S a a a a -=++++，则54n n n S a -=（）A ．1n -B ．nC ．2nD ．2n 【答案】B 【解析】试题分析：由*11()()4n n n a a n N ++=∈得:1441=++n n n n a a ,取n n ,,3,2,1⋅⋅⋅=,得到n 个等式并两边相加得:n a a a a a a a n nn n =+⋅⋅⋅++++⋅⋅⋅++++)444()4444(132233221,由于21123444n n n S a a a a -=++++,则n a S S n n n n =+-++)41(41,而n n n n a a 4141-=+,所以n a S n n n =-45,应选B.7．【原创题】已知函数()f x 满足：(1)3,(2)6,(3)10,(4)15,f f f f ====，则(12)f 的值为（）A ．54B ．65C ．77D ．91【答案】D ．故选D ．8．【2022年安庆市高三二模】数列{}n a 满足：11n n a a λ+=-（n *∈Ν,λ∈R 且0λ≠）,若数列{}1n a -是等比数列,则λ的值等于（）A ．1B ．1-C ．12D ．2 【答案】D【解析】由11n n a a λ+=-,得1212()n n n a a a λλλ+-=-=-.由于数列{1}n a -是等比数列,所以21λ=,得2λ=.故选D.9．【浙江省杭州外国语学校高三上学期期中考试】已知函数()f x =⎩⎨⎧>+-≤-)0(,1)1()0(,12x x f x x ,把函数()()g x f x x =-的零点按从小到大的挨次排列成一个数列,则该数列的通项公式为（）A ．2)1(-=n n a nB ．1-=n a nC ．)1(-=n n a nD ．22-=n n a【答案】B 【解析】试题分析：当(]0,∞-∈x 时，由()()012=--=-=x x x f x g x，得12+=x x，令x y 2=，1+=x y ，在同一个坐标系内作出两函数在区间(]0,∞-上的图象，由图象易知交点为()1,0，故得到函数的零点为0=x .当(]1,0∈x 时，(]0,11-∈-x ，()()11211211--=+-=+-=x x x f x f ，由()()021=-=-=-x x x f x g x ，得x x =-12，令12-=x y ，x y =，在同一个坐标系内作出两函数在区间(]1,0上的图象，由图象易知交点为()1,1，故函数的零点为1=x .当(]2,1∈x 时，(]1,01∈-x ，10．【2022年江西省四校高三一模测试】已知数列{}n a 是等比数列，数列{}n b 是等差数列，若1611161133,7a a a b b b π⋅⋅=-++=,则3948tan 1b b a a +-⋅的值是（）A.1B. 22 C . 22- D. 3【答案】D 【解析】试题分析：数列{}n a 是等比数列，数列{}n b 是等差数列，，且1611161133,7a a a b b b π⋅⋅=-++=(3366667,3,37,3,3a b a b ππ∴=-=∴=-=,3948tan 1b b a a +-⋅6262tan1b a =-()2723tan13π⨯=-7tantan 2tan 3333ππππ⎛⎫==--=-= ⎪⎝⎭11.【2022年江西师大附中鹰潭一中联考】已知等差数列}{n a 的前n 项和为n S ，满足95S S =，且01>a ，则n S 中最大的是（）A ．6SB ．7SC ．8SD ．15S 【答案】B【解析】由95S S =,得()67897820a a a a a a +++=+=,由01>a 知,0,087<>a a ,所以7S 最大，故B 正确. 12．【浙江省桐乡第一等四校高三上学期期中理考】已知函数()121f x x =--，[0,1]x ∈.定义：1()()f x f x =，21()(())f x f f x =，……，1()(())n n f x f f x -=，2,3,4,n =满足()n f x x =的点[0,1]x ∈称为()f x 的n 阶不动点.则()f x 的n 阶不动点的个数是（）A.2n 个B.22n 个 C.2(21)n -个 D.2n 个【答案】D. 【解析】二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上.）13．【2022年河北石家庄高三二模】数列{}n a 满足：1132,51++⋅=-=n n n n a a a a a ，则数列{}1+⋅n n a a 前10项的和为______.【答案】1021【解析】令2n =,23232a a a a -=⋅,解得213a =,令1n =,则12122a a a a -=⋅,解得11a =,对112n n n n a a a a ++-=⋅两边除以1n n a a +⋅,得1112n na a +-=,故数列1n a ⎧⎫⎨⎬⎩⎭是以111a =为首项,公差为2的等差数列,所以()()111111121,,21212122121n n n n n a a a a n n n n n +⎛⎫=-=⋅==- ⎪--⋅+-+⎝⎭,故其前10项的和为1111111110112335192122121⎛⎫⎛⎫-+-++-=-= ⎪ ⎪⎝⎭⎝⎭. 14．【2022年江西九江高三模拟】已知数列{}n a 各项均不为0，其前n 项和为n S ，且112,1+==n n n a a S a ，则=n S ______.【答案】2)1(+n n15．【陕西省西安长安区一中高三上学期第三次质检】把正整数按肯定的规章排成了如图所示的三角形数表．124357681012911131517141618202224设(),ij a i j N +∈是位于这个三角形数表中从上往下数第i 行、从左往右数第j 个数，如5211a =．则87a = ．【答案】38【解析】试题分析由三角形数表可以看出其奇数行为奇数列，偶数行为偶数列，故87a 表示第8行的第7个数字，即第2+4+6+7=19个正偶数．故8721938a =⨯=.16．【2022年4月湖北省七市（州）教科研协作体高三联合考试】已知数列{}n a 的首项11a =，且对任意*n N ∈，1,n n a a +是方程230n x nx b -+=的两实根，则21n b -= .【答案】(31)(32)n n -- 【解析】三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17．【湖南省2022届高考冲刺卷数学（理）试题（三）】（本小题满分10分）已知数列{}n a 中,()111,3nn n a a a n N a *+==∈+.（1）求证：112n a ⎧⎫+⎨⎬⎩⎭是等比数列, 并求{}n a 的通项公式n a ；（2）数列{}n b 满足()312nn n n n b a =-,数列{}nb 的前n 项和为n T ,若不等式()112n n n n T λ--<+对一切n N *∈恒成立, 求λ的取值范围. 【答案】（1）231n n a =-（2）()2,3- 【解析】试题分析：（1）证明等比数列，一般从定义动身，即证相邻项的比值是一个与项数无关的非零常数，即1311122=3111122n n n n n a a a a a ++++=++，由112n a ⎧⎫+⎨⎬⎩⎭通项11133,22n n a -+=⨯得231n n a =-（2）先代入化简得12n n nb -=，所以用错位相减法求和1242n n n T -+=-，对不等式恒成立问题，一般转化为对应函数最值问题，由于有符号数列，所以分类争辩：若n 为偶数, 则min 12(4)32n λ-<-=；若n 为奇数, 则min 12(4)222n λλ--<-=⇒>-，因此求交集得λ的取值范围试题解析：（1）由数列{}n a 中, ()111,3nn n a a a n N a *+==∈+,可得1131311111,322n n n n n n a a a a a a ++⎛⎫+==+∴+=+ ⎪⎝⎭,112n a ⎛⎫∴+ ⎪⎝⎭是首项为32,公比为3的等比数18．【2022届高三班级第四次四校联考】（本小题满分12分）已知数列}{n a 的前n 项和为n S ，且)(12*∈-=N n S n n(1) 求数列}{n a 的通项公式；(2) 若1232212+⨯-=+nn nn b ，且数列{n b }的前n 项和为n T ，求证：1<n T 。

2021年高考数学一轮复习讲练测(浙江版)专题6.1 数列的概念及其简单表示(练)

A 基础巩固训练1．数列{}n a 的前n 项积为2n ，那么当2n ≥时，{}n a 的通项公式为( )A ．n a =21n -B ．n a =2n C ．na =()221n n+ D ．n a =()221n n -【答案】D【解析】设数列{}n a 的前n 项积为n T ，则n T ＝2n ，当2n ≥时，n a =1n n T T -＝()221n n -. 2．设函数()f x ）定义为如下数表，且对任意自然数n 均有x n+1=02014(),6,n f x x x =若则的值为( )A ．1B ．2C ．4D ．5 【答案】D 【解析】3．【2022辽宁大连双基测试】数列{}n a 前n 项和2nn S =，则n a = .【答案】12,12,2n n n -=⎧⎨≥⎩【解析】当2n ≥时，2n n S =，112n n S --=，两式相减，得11222n n n n a --=-=．又当1n =时，12a =，不满足12n n a -=，所以n a =12,12,2n n n -=⎧⎨≥⎩． 4．【2021届山东枣庄市第三高三其次次模考】观看下列等式1=1 2+3+4=9 3+4+5+6+7=25 4+5+6+7+8+9+10=49照此规律，第n 个等式为．【答案】()()()()2123221n n n n n +++++⋅⋅⋅+-=-【解析】由题意可知第1行，第1个数是1，共1个，和是1的平方；第2行，第1个数是2，连续3个数，和是3的平方；第3行，第1个数是3，连续5个数，和是5的平方，照此规律，第n 个等式，第1个数是n ，连续2n-1个数，和是2n-1的平方，即()()()()2123221n n n n n +++++⋅⋅⋅+-=-.5．【2021届甘肃兰州第一高三12月月考数学试卷】数列{}n a 满足*32132(,1)23n na a a a n N n n++++=-∈≥,则n a =________．【答案】11, 123,2n n n n -=⎧⎨⋅≥⎩【解析】B 力量提升训练1．若在数列{}n a 中，对任意正整数n ，都有221n n a a p ++=（常数），则称数列{}n a 为“等方和数列”，称p 为“公方和”，若数列{}n a 为“等方和数列”，其前n 项和为n S ，且“公方和”为1，首项11a =，则2014S 的最大值与最小值之和为（）A 、2014B 、1007C 、1-D 、2 【答案】D【解析】由221n n a a p ++=得2212n n a a p +++=，两等式相减得：222n n a a +=.又“公方和”为1，首项11a =，所以2222223520132420141,0a a a a a a ========.所以2014S 的最大值为1007，最小值为-1005，其和为2.选D.2．【2022新课标II 押题卷1】已知数列{}n a 的首项1a m =，其前n 项和为n S ，且满足2132n n S S n n ++=+，若对n N *∀∈，1n n a a +<恒成立，则m 的取值范围是_______．【命题意图】本题考查数列递推公式、数列性质等基础学问，意在考查转化与化归、规律思维力量和基本运算力量．【答案】15(,)43-3．【2022北京东城区二模】成等差数列的三个正数的和等于，并且这三个数分别加上、、后成为等比数列中的、、，则数列的通项公式为（）A ．B ．C ．D ．【答案】A【解析】设三个数为：由题得：所以所以。

高考数学一轮复习(浙江版)专题6.2等差数列及其前n项和(测)含解析

一、选择题（本大题共10小题，每小题4分，在每小题给出的四个选择中，只有一个是符合题目要求的.）1．【2018届河南省郑州外国语学校调研】在等差数列中，已知是函数的两个零点，则的前10项和等于( )A． -18 B． 9 C． 18 D． 20【答案】D【解析】2．【2018届福建省三明市第一中学适应性练习（一）】已知是等差数列的前项和，且，，则（）A． 2 B． 3 C． 4 D． 5【答案】B【解析】，解得或者（舍去）3.【2018届安徽省六安市第一中学适应性考试】已知等差数列的前项和为，若，则（）A． B． C． D．【答案】D【解析】设等差数列的公差为d，，化为.则.故选：D.4．【2018届河北省武邑中学四模】设等差数列的前项和为.若，，则（）A． B． C． D．【答案】D【解析】又.可得，则故选D.5．【黑龙江省2018年仿真模拟（七）】在数列中，若，且对任意正整数、，总有，则的前项和为（）A． B． C． D．【答案】C【解析】6．【2018届陕西省黄陵中学6月模拟】已知等差数列的前项和为，且，，则“取得最小值”的一个充分不必要条件是（）A ．或 B ．或或 C ．D ．【答案】C 【解析】7．已知等差数列{}n a 中， 1311,1a a ==-，则{}n a 的前n 项和n S 的最大值是（） A. 15 B. 20 C. 26 D. 30 【答案】C 【解析】51351a a d -==-- ，所以通项公式()11314n a a n d n =+-=-+，当101430{{01130n n a n a n +≥-≥⇒≤-≤ ，解得111433n ≤≤ 即4n = ，即前4项和最大， ()4434113262S ⨯=⨯+⨯-=，故选C. 8．【2018届广东省珠海市高三摸底考试】对大于1的自然数 m 的三次幂可用奇数进行以下形式的“分裂”：3331373152{ 3{9 4{ (517)1119，，，.仿此，若3m 的“分裂数”中有一个是2017，则m 的值为( )A. 44B. 45C. 46D. 47 【答案】C【解析】由题意，从23到m 3，正好用去从3开始的连续奇数共()()212342m m m +-+++⋯+=个，2017从3开始的第1008个奇数，据此可得46m = . 本题选择C 选项.9．某企业为节能减排，用9万元购进一台新设备用于生产. 第一年需运营费用2万元，从第二年起，每年运营费用均比上一年增加2万元，该设备每年生产的收入均为11万元. 设该设备使用了()n n N *∈年后，盈利总额达到最大值（盈利额等于收入减去成本），则n 等于（） A.4 B.5 C.6 D.7 【答案】A10．【2018届湖北省荆州市荆州中学高考模拟】已知等差数列的前项和为．若，，则（）A ． 35B ． 42C ． 49D ． 63 【答案】B 【解析】已知数列为等差数列，则其前项和性质有、、也是等差，由题意得，，则，，故选.二、填空题（本大题共7小题，共36分.把答案填在题中的横线上.） 11.【2018届江苏省扬州树人学校模拟（四）】已知等差数列的前项和为，且，则__________．【答案】.【解析】∵等差数列中，∴，∴．设等差数列的公差为，则．12.已知{}n a是等差数列，n S是其前n项和．若2123a a+=-，510S=，则9a的值是．【答案】20【解析】设公差为d，则由题意可得()21113 51010a a da d⎧++=-⎪⎨+=⎪⎩，解得14 3a d =-⎧⎨=⎩，则948320a=-+⨯=．13.【上海市2018年5月高考模练习（一）】等差数列，，记，则当__________时，取得最大值【答案】4【解析】14.【2018届浙江省台州中学高考模拟】已知数列为等差数列，为的前项和，，若，，则__________．__________．【答案】 -12【解析】分析：首先根据题中的条件，结合等差数列的通项公式和求和公式，建立关于其首项与公差所满足的等量关系式，解方程组，求得其值，之后再借助于等差数列的通项公式和求和公式求得相应的结果.详解：设等差数列的公差为，则由已知得：，即，解得，所以，.15.【2018届江西省赣州市崇义中学高三上第二次月考】等差数列{}n a 满足113n n n a a a n -+++= ()2n ≥，函数()2xf x =， ()2log n n b f a =，则数列{}n b 的前项和为________【答案】()12n n +【解析】等差数列{}n a 满足()1132,33n n n n a a a n n a n -+++=≥∴=，即n a n =，函数()()2,2x n n f x f a =∴=，则12...n b b b +++= ()()()()22122log ...log 22...2nn f a f a f a ⎡⎤⋅=⨯⨯⨯⎣⎦()12...21log 22nn n ++++==，故答案为()12n n +.16．【2017届四川省广元市高三第三次统考】若数列是正项数列，且，则等于____________. A. B.C.D.【答案】17.【2018届宁夏平罗中学第四次（5月）模拟】已知数列的前项和为,且,,时,,则的通项公式___________．【答案】.【解析】由得．又，，∴．二、解答题（本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.）18.【福建省闽侯第二中学、连江华侨中学等五校教学联合体联考】已知为等差数列的前项和，且，．（1）求数列的通项公式；（2）设，求数列的前项和．【答案】（1）；（2）【解析】（1）设等差数列的公差为，则由已知，得，解得,故；（2）由已知可得，．19.【2018届江西省横峰中学、铅山一中、德兴一中第一次月考】已知等差数列{}n a 的前n 项和为n S ，且5645,60S S ==.（Ⅰ）求数列{}n a 的通项公式n a ；（Ⅱ）若数列{}n b 满足()1*n n n b b a n N +-=∈，且13b =，求1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T . 【答案】(1) 23n a n =+ (2) 222352,4128n n n nb n n T n n +=+=++20.【2018届山东省临沂市沂水县第一中学第三轮考试】已知公差不为0的等差数列的前三项的和为15，且.（1）求数列的通项公式；（2）设，数列的前项和为，若恒成立，求实数的最小值.【答案】（1）；（2）【解析】（1）依题意，即，即，故.又，即，故.故数列的通项公式.（2）依题意，.则，故恒成立，则，所以实数的最小值为.21.【2018届江苏省盐城中学全仿真模拟】已知正项数列的前项和为，其中.(I)若，求数列的通项公式；(I)若，求证: 是等差数列.【答案】(1)；(2)证明见解析.【解析】当时有.两式相减得，整理得.又恒成立，则，所以是等差数列.22．【2018届黑龙江省齐齐哈尔八中高三第二次月考】(1)在等差数列中，已知，前项和为，且，求当取何值时，取得最大值，并求出它的最大值；(2)已知数列的通项公式是，求数列的前项和．【答案】（1）；（2）.。

2021年高考数学一轮复习讲练测(浙江版)专题6.3 等比数列及其前n项和(测)

班级__________ 姓名_____________ 学号___________ 得分__________一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的.） 1. 【2022届陕西省高三下学期教学质检二数学（理）】已知等比数列{}n a 的前n 项和为n S ．若321510,9S a a a =+=，则1a =（）。

A ．19 B ．19- C ．13D ．13-【答案】A 【解析】试题分析：由已知可得⎪⎩⎪⎨⎧==+91041211q a q a a ，解之得⎪⎩⎪⎨⎧==3911q a ,应选A 。

2.【2022届福建厦门外国语学校高三5月适应性数学】我国明朝有名数学家程大位在其名著《算法统宗》中记载了如下数学问题：“远看巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯”。

诗中描述的这个宝塔古称浮屠，本题说它一共有7层，每层悬挂的红灯数是上一层的2倍，共有381盏灯，那么塔顶有（）盏灯。

A ．2B ．3C ．5D ．6【答案】B【解析】3. 【海淀区高三年纪其次学期其中练习】在数列{}n a 中，“12,2,3,4,n n a a n -==”是“{}n a 是公比为2的等比数列”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【答案】B4. 【原创题】设等比数列{}n a 的前n 项和为n S ，满足0,1n a q >>，且3520a a +=，2664a a ⋅=，则5S =（）A ．31B ．36C ．42D ．48 【答案】A【解析】由已知得，3564a a ⋅=，又3520a a +=，则354,16a a ==，故24q =，2q =，11a =，所以55123112S -==-.5. 【改编题】函数21(3)y x =--图象上存在不同的三点到原点的距离构成等比数列，则以下不行能．．．成为公比的数是（） A ．21B 2．1 D ．33【答案】A【解析】函数21(3)y x =--2，最大值为4，故2122q ≤≤，即22q ≤≤122<，因此选A. 6.【2022届四川凉山州高三第三次诊断数学】《庄子·天下篇》中记述了一个有名命题：“一尺之棰，日取其半，万世不竭．”反映这个命题本质的式子是( )A ．21111122222n n +++⋅⋅⋅+=- B ．211112222n +++⋅⋅⋅++⋅⋅⋅<C ．21111222n ++⋅⋅⋅+=D ．21111222n ++⋅⋅⋅++⋅⋅⋅<【答案】D 【解析】试题分析：据已知可得每次截取的长度构造一个以12为首项，以12为公比的等比数列， 21111112222n n ++⋅⋅⋅++⋅⋅⋅=-<.故反映这个命题本质的式子是21111222n ++⋅⋅⋅++⋅⋅⋅<.故选D7.【2022届安徽省安庆市高三第三次模拟考试数学】在等比数列{}n a 中，若720,2n a a >=，则31112a a +的最小值为（）A ．22B ．4C ．8D ．16 【答案】B 【解析】试题分析：由于720,2n a a >=，所以由基本不等式可得，231131171222224a a a a a +≥==，故选B. 8.【2022年高考冲刺卷（5）【浙江卷】理科】已知S n 是单调递减的等比数列{a n }的前n 项和，则（）A ．S 2m ·S 2n ≤2n m S +，S 2m +S 2n ≤2S m +n B ．S 2m ·S 2n ≤2n m S +，S 2m +S 2n ≥2S m +n C ．S 2m ·S 2n ≥2n m S +，S 2m +S 2n ≤2S m +nD ．S 2m ·S 2n ≥2n m S +，S 2m +S 2n ≥2S m +n【命题意图】这是一道数列的问题，主要考查了等比数列的概念、通项公式和前n 项和公式以及不等式等基础学问，还考查了基本运算力量．【答案】B9.设等比数列}{n a 的前n 项和为n S ，若15m S -=,-11m S =,121m S +=，则=m （） A.3 B.4C.5D. 6【答案】C【解析】由已知得，116m m m S S a --==-，1132m m m S S a ++-==，故公比2q =-，又11m m a a qS q-=-11=-，故11a =-，又1116m m a a q-=⋅=-，代入可求得5m =． 10.【2022届河北省衡水高三下练习五】在等比数列{}n a 中，若25234535,44a a a a a a =-+++=，则23451111a a a a +++=（） A ．1 B ．34- C ．53- D ．43- 【答案】C 【解析】试题分析：由于数列{}n a 为等比数列，所以2534234523452534251111a a a a a a a a a a a a a a a a a a ++++++++=+=⋅⋅⋅ 554334==--，故选C ．11．若数列{}n a 满足211n n n na a k a a ++++=（k 为常数），则称数列{}n a 为“等比和数列”，k 称为公比和，已知数列{}n a 是以3为公比和的等比和数列，其中11a =，22a =，则2015a = （）A. 1B. 2C. 10062D. 10072【答案】D 【解析】所以100720152=a .12．已知等差数列{}n a 的公差0d ≠，且1313,,a a a 成等比数列，若11,n a S =是数列{}n a 的前n 项的和，则*216()3n n S n N a +∈+的最小值为（）A ．4B ．3C ．232-D ．92【答案】A ．【解析】试题分析：∵11a =，1313,,a a a 成等比数列，∴2(12)1(112)d d +=⋅+．得2d =或0d =（舍去），∴21n a n =-，∴2(121)2nn n S n +-==，∴2216216322n n S n a n ++=++．令1t n =+，则216926243n n S t a t +=+-≥-=+，故选A. 二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上.）13. 【改编题】设n S 是等比数列}{n a 的前n 项和，若,13221=+a a 433a a =，则=+n n a S 2 ．【答案】1【解析】设等比数列}{n a 的公比为q ，由已知得，4313a q a ==，故1112313a a +⋅=，解得113a =，故 11332211113nn n n n n a S a a a a -+=+=-+=-．14. 【改编题】已知数列1,,9a 是等比数列，数列121,,,9b b 是等差数列，则12ab b +的值为 .【答案】310．【解析】1,,9a 成等比数列，219,3a a ∴=⨯∴=．又121,,,9b b 是等差数列，121231910,10a b b b b +=+=∴=+． 15.【2022届上海市七宝高三模拟理科数学试卷】设()cos 2()cxf x ax bx x R =++∈，,,a b c R ∈且为常数，若存在一公差大于0的等差数列{}n x （*n N ∈），使得{()}n f x 为一公比大于1的等比数列，请写出满足条件的一组,,a b c 的值________.【答案】0,0,0a b c ≠=>（答案不唯一，一组即可）【解析】试题分析：由题设可取1,0,1===c b a ,此时xx x f 2cos )(+=,存在数列25,23,2πππ,满足题设,应填答案1,0,1===c b a .16．已知{}n a 满足()*+∈⎪⎭⎫⎝⎛=+=N n a a a nn n 41,111， +⋅+⋅+=232144a a a S n 14-⋅n n a 类比课本中推导等比数列前项和公式的方法，可求得=-n n n a S 45___________．【答案】n ．【解析】三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．【2022全国丙17】（本题满分10分）已知数列{}n a 的前n 项和1n S a =+，1n n S a λ=+.其中0λ≠. （1）证明{}n a 是等比数列，并求其通项公式；（2）若53132S =，求λ. 【答案】（1）()1*111n n a n λλλ-⎛⎫=∈ ⎪--⎝⎭N ；（2）1λ=-.【解析】（1）由题意得1111a S a λ==+，故1λ≠，111a λ=-，10a ≠. 由1n n S a λ=+，111n n S a λ++=+，得11n n n a a a λλ++=-，即()11n n a a λλ+-=.由10a ≠，0λ≠，得0n a ≠，所以11n n a a λλ+=-.因此{}n a 是首项为11λ-，公比为1λλ-的等比数列. 于是()1*111n n a n λλλ-⎛⎫=∈ ⎪--⎝⎭N .（2）由（1）得11nn S λλ⎛⎫=- ⎪-⎝⎭.由53132S =，得5311132λλ⎛⎫-= ⎪-⎝⎭，即51132λλ⎛⎫= ⎪-⎝⎭，解得1λ=-. 18.【改编题】已知等比数列{n a }的公比为q ，且满足1n n a a +<，1a +2a +3a =913，1a 2a 3a =271.（1）求数列{n a }的通项公式；（2）记数列{n a n ⋅-)12(}的前n 项和为n T ，求.n T故数列{n a }的通项公式为n a =131-n （n *N ∈） ………………6分（2）由（1）知n a n ⋅-)12(=1312--n n ，所以n T =1+33+235+⋯+1312--n n ①31n T =31+233+335+…+1332--n n +n n 312- ② ①－② 得：32n T =1+32+232+332+⋯+132-n －nn 312-=12+（31+231+331+⋯+131-n ）－nn 312- =12+311)311(311--⋅-n －n n 312-=2－131-n －n n 312-,所以nT =3－131-+n n . 19．各项为正的数列{}n a 满足112a =,21,()n n n a a a n λ*+=+∈N ，（1）取1n a λ+=，求证：数列1n n a a +⎧⎫⎨⎬⎩⎭是等比数列，并求其公比；（2）取2λ=时令12n n b a =+，记数列{}n b 的前n 项和为n S ，数列{}n b 的前n 项之积为n T ，求证：对任意正整数n ，12n n n T S ++为定值．【答案】(1) 证明见解析，公比为1+52（2）定值为2 【解析】（2）由21111122222()n nn n n n n n n n a a a a a a a b a a +++=+⇒=+⇒==+ 所以+1121122311111111122222()()()()()()()n n n n n n n n a a a a T b b b a a a a a +++=⋅=== 211+1+1122111===222n n n n n n n n n n n n a a a a b a a a a a a a +++-=-所以12111111=2n n n n S a a a a a a ++=+++=--，故+12n n n T S +2=为定值． 20．已知数列{}n a 的前n 项和为n S ，10a =，1231n n a a a a n a ++++++=，*n ∈N ．（Ⅰ) 求证：数列{1}n a +是等比数列；（Ⅱ) 设数列{}n b 的前n 项和为n T ，11b =，点1(,)n n T T +在直线112x y n n -=+上，若不等式1212911122n n nb b bm a a a a +++≥-++++对于*n ∈N 恒成立，求实数m 的最大值．【答案】（Ⅰ)详见解析; （Ⅱ) 6116. 【解析】试题解析：（Ⅰ)由1231n n a a a a n a ++++++=，得12311(2)n n a a a a n a n -+++++-=≥ ，两式相减得121n n a a +=+，所以112(1)n n a a ++=+ （2n ≥)，由于10a =，所以111a +=，21211a a =+=，2112(1)a a +=+ 所以{1}n a +是以1为首项，公比为2的等比数列（Ⅱ)由（Ⅰ)得121n n a -=-，由于点1(,)n n T T +在直线112x y n n -=+上，所以1112n n T T n n +-=+，又11232527(4)(4)222n n n n n n ++------=，故当3n ≤时，25{4}2nn --单调递减；当3n =时，323531428⨯--=；当4n ≥时，25{4}2nn --单调递增；当4n =时，4245614216⨯--=；则2542nn --的最小值为6116，所以实数m的最大值是6116 21.【2022届河南新乡名校学术联盟高三高考押题四理数学试卷】已知等比数列{}n a 中，11a =，且()24331a a a +=+．（1）求数列{}n a 的通项公式；（2）设32333431log log log log n n b a a a a +=+++⋅⋅⋅+，求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和．【答案】（1）13n n a -=；（2）21nn +．【解析】试题分析：（1）用公比q 表示出234,,a a a ，即可求出q ，从而得通项公式；（2）由（1）13n n a -=，因此故()1211211n b n n n n ⎛⎫==- ⎪++⎝⎭12111111111122211223111n n b b b n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫++⋅⋅⋅+=-+-+⋅⋅⋅+-=-=⎪ ⎪ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，所以数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和为21nn +． 22.【2022届湖南师大附中高三上学期月考六数学（理）试卷】设数列{}n x 的前n 项和为n S ，若存在非零常数p ，使对任意n *∈N 都有2nnS p S =成立，则称数列{}n x 为“和比数列”．（1）若数列{}n a 是首项为2，公比为4的等比数列，推断数列{}2log n a 是否为“和比数列”；（2）设数列{}n b 是首项为2，且各项互不相等的等差数列，若数列{}n b 是“和比数列”，求数列{}n b 的通项公式．【答案】（1）是，证明见解析；（2）()24142n b n n =+-=- 【解析】试题分析：（1）已知可得121242n n n a --=⋅=2log 21n a n ⇒=-()21212n n S n n +-⇒=⋅=24n n SS ⇒=；（2）由已知可得前n 项和()122n n n n d -T =+()()()()222148*********n n n n n d n d p n n n d n d-++-T ⇒===-T +-+恒成立()222142n n n n d -T =+，所以()()()()222148*********n n n n n d n d n n n d n d-++-T ==-T +-+由于{}n b 是“和比数列”，则存在非零常数p ，使()()822141n dp n d+-=+-恒成立．即()()822141n d p n d +-=+-⎡⎤⎣⎦，即()()()4240p dn p d -+--=恒成立．所以()()()40240p d p d -=⎧⎪⎨--=⎪⎩由于0d ≠，则4p =，4d =所以数列{}n b 的通项公式是()24142n b n n =+-=-。

浙江专用2021届高考数学一轮复习专题六数列6.2等差数列试题含解析

§6.2 等差数列基础篇固本夯基【基础集训】考点一等差数列的有关概念及运算1.已知等差数列{a n }中,a 2=1,前5项和S 5=-15,则数列{a n }的公差为( ) A.-3 B.-52 C.-2 D.-4答案 D2.已知在等差数列{a n }中,a 1=1,a 3=2a+1,a 5=3a+2,若S n =a 1+a 2+…+a n ,且S k =66,则k 的值为 ( ) A.9 B.11 C.10 D.12 答案 B3.设等差数列{a n }满足3a 8=5a 15,且a 1>0,S n 为其前n 项和,则数列{S n }的最大项为( ) A.S 23 B.S 24 C.S 25 D.S 26 答案 C4.已知数列{a n }满足a 1=12,且a n+1=2an2+a n.(1)求证:数列{1a n}是等差数列;(2)若b n =a n a n+1,求数列{b n }的前n 项和S n . 解析 (1)证明:易知a n ≠0,∵a n+1=2a n 2+a n,∴1an+1=2+a n 2a n,∴1an+1-1a n=12,又∵a 1=12,∴1a 1=2,∴数列{1a n}是以2为首项,12为公差的等差数列.(2)由(1)知,1a n=2+12(n-1)=n+32,即a n =2n+3,∴b n =4(n+3)(n+4)=4(1n+3-1n+4),∴S n =4[(14-15)+(15-16)+…+(1n+3-1n+4)] =4(14-1n+4)=nn+4.考点二等差数列的性质5.设S n 是等差数列{a n }的前n 项和,若a 6a 5=911,则S11S 9=( )A.1B.-1C.2D.12答案 A6.(2018河北唐山第二次模拟,7)设{a n }是任意等差数列,它的前n 项和、前2n 项和与前4n 项和分别为X,Y,Z,则下列等式中恒成立的是( ) A.2X+Z=3Y B.4X+Z=4YC.2X+3Z=7YD.8X+Z=6Y 答案 D7.已知数列{a n }是公差为d 的等差数列,S n 为其前n 项和,若S 2 0172 017-S 1717=100,则d 的值为( )A.120B.110C.10D.20答案 B8.在等差数列{a n }中,a 3+a 7=37,则a 2+a 4+a 6+a 8= . 答案 749.已知A n 及B n 是等差数列{a n }、{b n }的前n 项和,且An B n =3n+14n+1,则a 11b 11= .答案648510.已知数列{a n }是等差数列.(1)前四项和为21,末四项和为67,且各项和为286,求项数;(2)项数为奇数,奇数项和为44,偶数项和为33.求数列的中间项和项数.解析 (1)由已知得a 1+a 2+a 3+a 4=21,a n-3+a n-2+a n-1+a n =67,∴a 1+a 2+a 3+a 4+a n-3+a n-2+a n-1+a n =88,∴a 1+a n =884=22.∵S n =286,∴n (a 1+a n )2=286,∴11n=286,∴n=26.(2)解法一:设项数为2k+1,则a 1+a 3+…+a 2k+1=44=k+12(a 1+a 2k+1),a 2+a 4+…+a 2k =33=k2(a 2+a 2k ),又∵a 1+a 2k+1=a 2+a 2k ,∴k+1k=4433,∴k=3,项数为7,∴中间项为a 1+a 2k+12=11.解法二:记等差数列{a n }的中间项为a 中,奇数项和为S 奇,偶数项和为S 偶,前n 项和为S n .根据题意得{S 偶+S 奇=S n ,S 奇-S 偶=a 中,∴S n =77,a 中=11,又na 中=S n ,∴n=7.综合篇知能转换【综合集训】考法一等差数列的判定与证明1.(2018山东济宁一模,11)设数列{a n }满足a 1=1,a 2=2,且2na n =(n-1)a n-1+(n+1)a n+1(n≥2且n∈N *),则a 18=( ) A.259 B.269 C.3 D.289答案 B2.(2019河北冀州模拟,9)已知{a n },{b n }均为等差数列,且a 2=4,a 4=6,b 3=3,b 7=9,由{a n },{b n }的公共项组成新数列{c n },则c 10=( )A.18B.24C.30D.36 答案 C3.设数列{a n }的前n 项和为S n ,且S n =2n-1.数列{b n }满足b 1=2,b n+1-2b n =8a n . (1)求数列{a n }的通项公式;(2)证明数列{bn2n }为等差数列,并求{b n }的通项公式. 解析 (1)当n=1时,a 1=S 1=21-1=1;当n≥2时,a n=S n-S n-1=(2n-1)-(2n-1-1)=2n-1. 因为a1=1适合上式,所以a n=2n-1(n∈N*).(2)因为b n+1-2b n=8a n,所以b n+1-2b n=2n+2,即b n+12n+1-b n2n=2.又b121=1,所以{b n2n}是首项为1,公差为2的等差数列,所以b n2n=1+2(n-1)=2n-1.所以b n=(2n-1)×2n.考法二等差数列前n项和的最值问题4.(2018江西赣中南五校联考,4)在等差数列{a n}中,已知a3+a8>0,且S9<0,则S1、S2、…、S9中最小的是( )A.S5B.S6C.S7D.S8答案 A5.(2018广东汕头模拟,8)已知等差数列{a n}的前n项和为S n,a1=9,S99-S55=-4,则S n取最大值时的n为( )A.4B.5C.6D.4或5答案 B6.(2018湖南永州三模,11)已知数列{a n}是等差数列,前n项和为S n,满足a1+5a3=S8,给出下列结论:①a10=0;②S10最小;③S7=S12;④S20=0.其中一定正确的结论是( )A.①②B.①③④C.①③D.①②④答案 C7.(2018广东深圳期末,14)设等差数列{a n}的前n项和为S n,若a1=-11,a4+a6=-6,则当S n取最小值时,n= .答案 6【五年高考】考点一等差数列的有关概念及运算1.(2016课标Ⅰ,3,5分)已知等差数列{a n}前9项的和为27,a10=8,则a100=( )A.100B.99C.98D.97答案 C2.(2018课标Ⅰ,4,5分)记S n为等差数列{a n}的前n项和.若3S3=S2+S4,a1=2,则a5=( )A.-12B.-10C.10D.12答案 B3.(2017课标Ⅰ,4,5分)记S n为等差数列{a n}的前n项和.若a4+a5=24,S6=48,则{a n}的公差为( )A.1B.2C.4D.8答案 C4.(2017课标Ⅲ,9,5分)等差数列{a n}的首项为1,公差不为0.若a2,a3,a6成等比数列,则{a n}前6项的和为( )A.-24B.-3C.3D.8答案 A5.(2019课标Ⅰ,9,5分)记S n为等差数列{a n}的前n项和.已知S4=0,a5=5,则( )A.a n=2n-5B.a n=3n-10C.S n=2n2-8nD.S n=12n2-2n答案 A6.(2019课标Ⅲ,14,5分)记S n为等差数列{a n}的前n项和,若a1≠0,a2=3a1,则S10S5= .答案 47.(2018北京,9,5分)设{a n}是等差数列,且a1=3,a2+a5=36,则{a n}的通项公式为.答案 a n =6n-38.(2019江苏,8,5分)已知数列{a n }(n∈N *)是等差数列,S n 是其前n 项和.若a 2a 5+a 8=0,S 9=27,则S 8的值是 . 答案 169.(2019北京,10,5分)设等差数列{a n }的前n 项和为S n .若a 2=-3,S 5=-10,则a 5= ,S n 的最小值为 . 答案 0;-1010.(2018课标Ⅱ,17,12分)记S n 为等差数列{a n }的前n 项和,已知a 1=-7,S 3=-15. (1)求{a n }的通项公式; (2)求S n ,并求S n 的最小值.解析 (1)设{a n }的公差为d,由题意得3a 1+3d=-15. 由a 1=-7得d=2.所以{a n }的通项公式为a n =2n-9.(2)由(1)得S n =n 2-8n=(n-4)2-16.所以当n=4时,S n 取得最小值,最小值为-16.11.(2016天津,18,13分)已知{a n }是各项均为正数的等差数列,公差为d.对任意的n∈N *,b n 是a n 和a n+1的等比中项.(1)设c n =b n+12-b n 2,n∈N *,求证:数列{c n }是等差数列; (2)设a 1=d,T n =∑k=12n(-1)kb k 2,n∈N *,求证:∑k=1n1T k<12d 2.证明 (1)由题意得b n 2=a n a n+1,有c n =b n+12-b n 2=a n+1·a n+2-a n a n+1=2da n+1,因此c n+1-c n =2d(a n+2-a n+1)=2d 2, 所以{c n }是等差数列.(2)T n =(-b 12+b 22)+(-b 32+b 42)+…+(-b 2n -12+b 2n 2) =2d(a 2+a 4+…+a 2n )=2d·n (a 2+a 2n )2=2d 2n(n+1). 所以∑k=1n1T k =12d 2∑k=1n1k (k+1)=12d 2∑k=1n(1k -1k+1)=12d 2·(1-1n+1)<12d 2. 考点二等差数列的性质12.(2015广东,10,5分)在等差数列{a n }中,若a 3+a 4+a 5+a 6+a 7=25,则a 2+a 8= . 答案 10教师专用题组考点一等差数列的有关概念及运算1.(2016浙江,6,5分)如图,点列{A n },{B n }分别在某锐角的两边上,且|A n A n+1|=|A n+1A n+2|,A n ≠A n+2,n∈N *,|B n B n+1|=|B n+1B n+2|,B n ≠B n+2,n∈N *.(P≠Q 表示点P 与Q 不重合)若d n =|A n B n |,S n 为△A n B n B n+1的面积,则( )A.{S n }是等差数列B.{S n 2}是等差数列C.{d n }是等差数列D.{d n 2}是等差数列答案 A2.(2015浙江,3,5分)已知{a n }是等差数列,公差d 不为零,前n 项和是S n .若a 3,a 4,a 8成等比数列,则( )A.a1d>0,dS4>0B.a1d<0,dS4<0C.a1d>0,dS4<0D.a1d<0,dS4>0答案 B3.(2013课标Ⅰ,7,5分)设等差数列{a n}的前n项和为S n,若S m-1=-2,S m=0,S m+1=3,则m=( )A.3B.4C.5D.6答案 C4.(2016江苏,8,5分)已知{a n}是等差数列,S n是其前n项和.若a1+a22=-3,S5=10,则a9的值是.答案205.(2014课标Ⅰ,17,12分)已知数列{a n}的前n项和为S n,a1=1,a n≠0,a n a n+1=λS n-1,其中λ为常数,(1)证明:a n+2-a n=λ;(2)是否存在λ,使得{a n}为等差数列?并说明理由.解析(1)证明:由题设a n a n+1=λS n-1,知a n+1a n+2=λS n+1-1.两式相减得,a n+1(a n+2-a n)=λa n+1.由于a n+1≠0,所以a n+2-a n=λ.(2)存在.由a1=1,a1a2=λa1-1,可得a2=λ-1,由(1)知,a3=λ+1.令2a2=a1+a3,解得λ=4.故a n+2-a n=4,由此可得,{a2n-1}是首项为1,公差为4的等差数列,a2n-1=1+(n-1)·4=4n-3;{a2n}是首项为3,公差为4的等差数列,a2n=3+(n-1)·4=4n-1.所以a n=2n-1,a n+1-a n=2.因此存在λ=4,使得{a n}为等差数列.思路分析(1)已知a n a n+1=λS n-1,用n+1代替n得a n+1·a n+2=λS n+1-1,两式相减得结论.(2)利用a1=1,a2=λ-1,a3=λ+1及2a2=a1+a3,得λ=4.进而得a n+2-a n=4.故数列{a n}的奇数项和偶数项分别组成公差为4的等差数列,分别求通项公式,进而求出{a n}的通项公式,从而证出等差数列.方法总结对于含a n、S n的等式的处理,往往可转换为关于a n的递推式或关于S n的递推式;对于存在性问题,可先探求参数的值再证明.考点二等差数列的性质6.(2015陕西,13,5分)中位数为1 010的一组数构成等差数列,其末项为2 015,则该数列的首项为.答案 57.(2013课标Ⅱ,16,5分)等差数列{a n}的前n项和为S n.已知S10=0,S15=25,则nS n的最小值为.答案-49【三年模拟】一、单项选择题(每题5分,共40分)1.(2020届云南陆良第二次教学质量摸底考,3)已知{a n}为等差数列,若a3+a4+a8=12,则S9=( )A.24B.27C.36D.54答案 C2.(2020届四川宜宾四中开学考,4)已知等差数列{a n}中,a2、a2 016是方程x2-2x-2=0的两根,则S2 017=( )A.-2 017B.-1 008C.1 008D.2 017答案 D3.(2020届河北邯郸大名一中第六周周测,4)设{a n}是等差数列,则下列结论一定正确的是( )A.若a1+a2>0,则a2+a3>0B.若a1+a3<0,则a2+a3<0C.若0<a1<a2,则a2>√a1a3D.(a2-a1)(a2-a3)<0答案 C4.(2019 5·3原创冲刺卷一,4)已知等差数列{a n}的前n项和为S n,S2=3,S3=6,则S2n+1=( )A.(2n+1)(n+1)B.(2n+1)(n-1)C.(2n-1)(n+1)D.(2n+1)(n+2)答案 A5.(2018安徽合肥第二次教学质量检测,5)中国古诗词中,有一道“八子分绵”的数学名题:“九百九十六斤绵,赠分八子作盘缠,次第每人多十七,要将第八数来言”.题意是:把996斤绵分给8个儿子作盘缠,按照年龄从大到小的顺序依次分绵,年龄小的比年龄大的多17斤绵,那么第8个儿子分到的绵是( )A.174斤B.184斤C.191斤D.201斤答案 B6.(2019湖北宜昌一模,8)等差数列{a n}的前n项和为S n,若公差d>0,(S8-S5)(S9-S5)<0,则( )A.a7=0B.|a7|=|a8|C.|a7|>|a8|D.|a7|<|a8|答案 D7.(2018湖南三湘名校教育联盟第三次联考,5)已知等差数列{a n}的各项都为整数,且a1=-5,a3a4=-1,则|a1|+|a2|+…+|a10|=( )A.70B.58C.51D.40答案 B8.(2018安徽淮北一模,9)S n是等差数列{a n}的前n项和,S2 018<S2 016,S2 017<S2 018,则S n<0时n的最大值是( )A.2 017B.2 018C.4 033D.4 034答案 D二、多项选择题(每题5分,共10分)9.(改编题)设等差数列{a n}满足a3+a7=36,a4a6=275,则( )A.a n=7n-17B.a n=-7n+53C.a n a n+1的最小值为-12D.a n a n+1无最小值答案ABC10.(改编题)记S n为等比数列{a n}的前n项和,已知S2=2,S3=-6,则( )A.a n=(-2)nB.S n+1,S n,S n+2成等差数列C.a n=-2nD.S n+1,S n,S n+2不成等差数列答案AB三、填空题(每题5分,共15分)11.(2020届河北邯郸大名一中周测,14)设等差数列{a n}的前n项和为S n,若a2=3,S4=16,则数列{a n}的公差d= .答案 212.(2019上海嘉定(长宁)二模,11)已知有穷数列{a n}共有m项,记数列{a n}的所有项的和为S(1),第二项及以后所有项的和为S(2),……,第n(1≤n≤m)项及以后所有项的和为S(n),若S(n)是首项为1,公差为2的等差数列的前n项和,则当1≤n<m时,a n= .答案-2n-113.(2018河南六市第一次联考,16)已知正项数列{a n}的前n项和为S n,若{a n}和{√S n}都是等差数列,且公差相等,则a2= .答案34四、解答题(共25分)14.(2020届四川宜宾四中开学考,18)已知数列{a n}的首项a1=1,2a n a n+1=a n-a n+1(n∈N*).(1)证明:数列{1a n}是等差数列;(2)设b n=a n a n+1,数列{b n}的前n项和为S n,求证:S n<12.证明(1)由于a1=1,2a n a n+1=a n-a n+1,显然a n a n+1≠0,所以两边同除以a n a n+1可得,1a n+1-1a n=2,所以数列{1a n}是1为首项,2为公差的等差数列.(2)由(1)知,1a n=1+(n-1)×2=2n -1,所以a n =12n -1.所以b n =a n a n+1=1(2n -1)(2n+1)=12(12n -1-12n+1),所以S n =12[(1-13)+(13-15)+…+(12n -1-12n+1)]=12(1-12n+1)<12.15.(2019湖北武汉外国语学校3月模拟,17)若数列{a n }的前n 项和为S n ,首项a 1>0且2S n =a n 2+a n (n∈N *). (1)求数列{a n }的通项公式;(2)若a n >0(n∈N *),令b n =1a n (a n +2),求数列{b n }的前n 项和T n .解析 (1)当n=1时,2S 1=a 12+a 1=2a 1,又a 1>0,则a 1=1,当n≥2时,a n =S n -S n-1=a n 2+a n 2-a n -12+a n -12,即(a n +a n-1)(a n -a n-1-1)=0⇒a n =-a n-1或a n =a n-1+1,∴a n =(-1)n-1或a n =n. (2)∵a n >0,∴a n =n,∴b n =1n (n+2)=12(1n -1n+2),∴T n =12[(1-13)+(12-14)+…+(1n -1n+2)]=121+12-1n+1-1n+2=34-2n+32(n+1)(n+2).。

浙江专用高考数学一轮总复习专题6数列6.2等差数列课件

(3)数列{an}的前n项和Sn=An2+Bn(A,B为常数)是{an}成等差数列的② 充要条件 .
(4)等差数列的单调性
③ d>0 ⇔{an}为递增数列,Sn有最小值. ④ d<0 ⇔{an}为递减数列,Sn有最大值.
d=0⇔{an}为常数列. (5)若{an}和{bn}均是等差数列,则{man+kbn}仍为等差数列,m,k为常数. (6)等差数列中依次k项的和成等差数列,即Sk,S2k-Sk,S3k-S2k,…成等差数列, 公差为k2d. (7)项数为偶数2n的非零等差数列{an},有 S2n=n(a1+a2n)=n(a2+a2n-1)=…=n(an+an+1)(an与an+1为中间的两项),
3n 6
4
.
解题导引
(1)
(2) (3)
解析 (1)证明:当b=1时,an+1= an2 2an 3 +1,由题意得(an+1-1)2-(an-1)2=2, 又(a1-1)2=0,∴数列{(an-1)2}是首项为0,公差为2的等差数列.
(2)显然an>0,an+1= an2 2an 3 -1. ∵f(x)= x2 2x 3 -1在x∈[0,1]上单调递减,
2 2
5 2 3 2
2
2
a2n1
1 2
<
1 4
a2
n1
1 2
,
∴
a1
1 2
+
a3
1 2
+…+
a2n1
1 2
<
1 2
+
1 2
×
1 4
+…+

2021届高考数学(浙江专用)一轮试题：§6.1 数列的概念及其表示 Word版含解析

专题六数列【考情探究】课标解读考情分析备考指导主题内容一、数列的概念及其表示1.了解数列的概念和几种简单的表示方法(列表、图象、通项公式).2.了解数列是自变量为正整数的一类函数.从近几年高考情况来看,数列问题每年都考查,难度中等.考查内容主要集中在两个方面:一是以选择题或填空题的形式考查等差、等比数列的运算和性质,题目多为常规试题;二是等差、等比数列的通项与求和问题,近两年结合概率、统计、函数、不等式等进行综合考查,涉及内容较为全面,题型新颖、方法灵活多变.1.解决等差(比)数列的基本问题时,要灵活利用等差、等比数列的定义、通项公式及前n项和公式,利用基本量法求解.2.数列的通项与求和是高考常考内容,其中求通项是求和的基础.3.重视方程、函数、分类讨论思想的应用.(1)方程思想:等差(比)数列中,由五个量a1,d(q),n,a n,S n中的三个量可求出其余两个量,要求选用公式要恰当,善于应用性质,减少计算量.(2)函数思想:在等差数列中,当d≠0时,a n与自变量n为一次函数关系.S n与n的关系:当d=0时,S n=na1为一次函数;当d≠0时,S n=d2n2+(a1-d2)n为二次函数.在等比数列中,通项公式a n=a1q n-1可化为a n=a1q·q n,这是指数型函数.(3)分类讨论思想:当q=1时,{a n}的前n项和S n=na1;当q≠1时,{a n}的前n项和S n=a1(1-q n)1-q=a1-a n q1-q.等比数列的前n项和公式涉及对公比q的分类讨论,此处是易错点.二、等差数列1.理解等差数列的概念.2.掌握等差数列的通项公式与前n项和公式.3.能在具体的问题情境中识别数列的等差关系,并能用等差数列的有关知识解决相应问题.4.了解等差数列与一次函数的关系.三、等比数列1.理解等比数列的概念.2.掌握等比数列的通项公式与前n项和公式.3.能在具体问题情境中识别数列的等比关系,并能用等比数列的有关知识解决相应问题.4.了解等比数列与指数函数的关系.四、数列求和及综合应用1.掌握数列求和的几种常见方法.2.能在具体的问题情境中识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.【真题探秘】§6.1 数列的概念及其表示基础篇固本夯基【基础集训】考点数列的概念及其表示1.数列1,23,35,47,59,…的一个通项公式a n =( ) A.n2n+1B.n 2n -1 C.n 2n -3D.n2n+3答案 B2.已知数列{a n }满足:∀m,n ∈N *,都有a n ·a m =a n+m ,且a 1=12,那么a 5=( ) A.132B.116C.14D.12答案 A3.已知数列{a n }的前n 项和为S n ,且a 1=1,S n =(n+1)a n2,则a 2 017=( )A.2 016B.2 017C.4 032D.4 034 答案 B4.在数列{a n }中,a 1=-14,a n =1-1a n -1(n ≥2,n ∈N *),则a 2 018的值为( )A.-14B.5C.45D.54答案 B5.已知数列{a n }满足a n+1=a n -a n-1(n ≥2),a 1=m,a 2=n,S n 为数列{a n }的前n 项和,则S 2 017的值为( ) A.2 017n-m B.n-2 017m C.m D.n 答案 C综合篇知能转换【综合集训】考法一利用S n 与a n 的关系求通项公式1.(2018山东省实验中学期中,5)若数列{a n }满足a 1+a 2+a 3+…+a n =3n-2,那么这个数列的通项公式为( ) A.a n =2×3n-1B.a n =3×(12)n -1C.a n =3n-2D.a n ={1,n =12×3n -1,n ≥2。

[创新方案](浙江专版)2021届高考数学一轮复习 5.5 数列的综合

[创新方案]（浙江专版）2021届高考数学一轮复习 5.5 数列的综合[创新方案]（浙江专版）2021届高考数学一轮复习5.5数列的综合限时训练（31）序列的综合(限时：50分钟满分：106分)一、多项选择题（本大题共8个子题，每个子题5分，共40分）1.等差数列{an}中，a3＋a11＝8，数列{bn}是等比数列，且b7＝a7，则b6b8的值()a．2c．8b、 4d.1622.让项数为8的等比序列的中间两项等于2x+7x+4=0的两项，则序列项的乘积为（）a．64c．32b、 3d.163．数列{an}是公差不为0的等差数列，且a1，a3，a7为等比数列{bn}中连续的三项，则数列{bn}的公比为()a、 2c.2b．41d.二*4.（2022年泉州模拟）如果A1=1，log2an+1=log2an+1（n∈ n），其前n项之和为Sn，则Sn>1025的最小n值为（）a．9c．11b、 10d.12*5.（2022杭州模拟）在正项比例序列{an}中，有两项am，an（m，n）∈ n）所以aman=4a1,15且a7＝a6＋2a5，则＋的最小值是()mn7a。

4c。

二百五十六b．1＋25d.三536.根据市场调查结果，预测从年初开始的n个月内，一种家用商品的累计需求Sn （10000件）大致满足Sn=（21n-n-5）（n=1,2，？，12）的关系。

根据这一预测，今年的需求90超过1.5万件的月份是()a、 5月和6月约7日和8月b．6、7月d．8、9月n217.序列{an}an=n的一般项？cosa.470c.49522nπ3－sin2nπ？3.，其前n项和为sn，则s30为()b、公元490年510*8.（2022株洲模拟）在序列{an}中，对于任何n∈ n、有一种叫做“等差比序列”的序列。

以下是“等差比序列”的判断：①k不可能为0；② 算术序列必须是算术比率序列；③ 等比序列必须是等差比序列；an＋2－an＋1=K（K是常数），那么an＋1－an④通项公式为an＝ab＋c(a≠0，b≠0,1)的数列一定是等差比数列．其中正确的判断为()a．①②b。

2021年高考数学分项汇编专题6 数列(含解析)文

2021年高考数学分项汇编专题6 数列（含解析）文一．基础题组1. 【xx课标全国Ⅰ，文6】设首项为1，公比为的等比数列{a n}的前n项和为S n，则( )．A．S n＝2a n－1 B．S n＝3a n－2 C．S n＝4－3a n D．S n＝3－2a n【答案】：D2. 【xx全国1，文6】已知数列{a n}的前n项和为S n，a1＝1，S n＝2a n＋1，则S n＝( )A．2n－1 B． C． D．【答案】B3. 【2011全国1，文6】设为等差数列的前项和，若，公差，，则 ( )（A）8 （B）7 （C）6 （D）5【答案】D4. 【xx全国1，文4】已知各项均为正数的等比数列{a n}中，a1a2a3＝5，a7a8a9＝10，则a4a5a6等于( ) A．5 B．7 C．6 D．4【答案】：A5. 【xx全国1，文7】已知等比数列满足，则（）A．64 B．81 C．128 D．243【答案】A6. 【xx全国卷Ⅰ,文14】设等差数列{a n}的前n项和为S n.若S9=72,则a2+a4+a9=__________. 【答案】:247. 【xx全国1，文17】已知是递增的等差数列，，是方程的根。

（I）求的通项公式；（II）求数列的前项和.8. 【xx全国1，文18】已知数列{a n}中，a1＝1，前n项和.(1)求a2，a3；(2)求{a n}的通项公式．9. 【2011全国1，文17】10. 【xx全国1，文17】记等差数列{a n}的前n项和为S n，设S3＝12，且2a1，a2，a3＋1成等比数列，求S n.11. 【xx全国卷Ⅰ,文17】设等差数列{a n}的前n项和为S n,公比是正数的等比数列{b n}的前n项和为T n,已知a1=1,b1=3,a3+b3=17,T3-S3=12,求{a n},{b n}的通项公式.12. 【xx全国1，文19】在数列中，，．（Ⅰ）设．证明：数列是等差数列；（Ⅱ）求数列的前项和．13. 【xx全国1，文21】（本小题满分12分）设是等差数列，是各项都为正数的等比数列，且，，（Ⅰ）求、的通项公式；（Ⅱ）求数列的前n项和。

(浙江版)高考数学一轮复习专题6.2等差数列及其前n项和(讲)(2021学年)

（浙江版)2018年高考数学一轮复习专题6．2 等差数列及其前n项和（讲) 编辑整理:尊敬的读者朋友们：这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（浙江版)20１8年高考数学一轮复习专题6.２等差数列及其前n项和(讲))的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(浙江版）2018年高考数学一轮复习专题6．2 等差数列及其前ｎ项和（讲)的全部内容。

第0２节等差数列及其前ｎ项和【考纲解读】【知识清单】一．等差数列的有关概念１．定义:等差数列定义:一般地，如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列，这个常数叫做等差数列的公差,公差通常用字母d 表示．用递推公式表示为1(2)n n a a d n --=≥或1(1)n n a a d n +-=≥。

２.等差数列的通项公式:1(1)n a a n d =+-;说明:等差数列(通常可称为A P 数列)的单调性:d 0>为递增数列,0d =为常数列,0d < 为递减数列.３。

等差中项的概念：定义：如果a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项,其中2a bA += 。

a ,A ,b 成等差数列⇔2a bA +=。

4。

等差数列的前n 和的求和公式：11()(1)22n n n a a n n S na d +-==+。

5。

要注意概念中的“从第2项起＂．如果一个数列不是从第２项起,而是从第3项或第4项起,每一项与它前一项的差是同一个常数，那么此数列不是等差数列. 6。

注意区分等差数列定义中同一个常数与常数的区别. 对点练习:【20１7届浙江省温州市二模】在等差数列中，若，则___＿__＿。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

10．(2019·丽水模拟)已知等差数列{an}的公差 d≠0，且 a1，a3，a9 构成等比数列{bn}的前 3
1
项，则 a1＋a3＋a9 ＝______；若 d＝2，则数列{bn}的前 n 项的和 Sn＝______. a2＋a4＋a10
11．设公差不为零的等差数列{an}的前 n 项和为 Sn，若 a2＋am＝18，S13＝117，则 m 等于( )
∴a2＋am＝a1＋a13，∵数列{an}的公差不为零，∴am＝a12，即 m＝12.] 12．D [由 an＋2＝2an＋1－an(n∈N*)，得 an＋2－an＋1＝an＋1－an， ∴数列{an}为等差数列，设其公差为 d， ∵a1＝8，a4＝2，∴3d＝2－8＝－6，解得 d＝－2，
∴a10＝a1＋9d＝8－18＝－10，S5＝5a1＋5×4d＝40－20＝20， 2
A．10 B．6 C．8 D．12
4．在等差数列{an}中，Sn 是其前 n 项和，若 a3＋a8＝5，S9＝45，则 S11 等于( )
A．0 B．10 C．20 D．25
5．在等差数列{an}中，若 S1＝1，S5＝15，则2S2001199 等于(
)
A．2 019
B．1
C．1 009
D．1 010
∴λ＝aS150＝－2100＝－2.] 13．A [由等差数列的求和公式及性质，
可得
S2
020＝2
020(a1＋a2 2
020)
＝1 010(a1 010＋a1 011)>0，
所以 a1 010＋a1 011>0，同理可得 a1 011<0，所以 a1 010>0，a1 011<0，且 a1 010>|a1 011|，d<0，对任意正整数 n，都有|an|≥|ak|，则 k＝1 011.]
020＝ 4×2
3
＝
020－1 8
3 .] 079
15.2 2 7 6n－5
16．an＝ n 119 解析由题意得数列{a2n}为等差数列，首项为 1，公差为 1，an>0. ∴a2n＝1＋(n－1)＝n. 则数列{an}的通项公式为 an＝ n.
又1＝ an＋an＋1
1＝ n＋ n＋1
n＋1－
n.
6．设
Sn
是等差数列{an}的前
n
项和，若S4＝1，则 S8 等于( S8 5 S16
)
A.1 B.1 C. 5 D. 5 3 5 13 22
7．(2020·温州模拟)在等差数列{an}中，已知 a7>0，a3＋a9<0，则{an}的前 n 项和 Sn 的最小值
为( )
A．S4 B．S5 C．S6 D．S7
14．A [由题意知数列{an}满足：
an＝2aann－－22－ana－n1－1(n∈N*，n>2)，
可得 1 ＋ 1 ＝ 2 ， an an－2 an－1
1 所以数列 an 是等差数列，
其公差 d＝ 1 － 1 ＝7－1＝4，
a2 a1 3
3
所以 1 ＝1＋4(n－1)＝4n－1，
an
3
3
3
a2
数 n，都有|an|≥|ak|，则 k 的值为( )
A．1 011 B．1 007 C．1 008 D．1 009
14．(2020·浙江省宁波市慈溪市月考)已知数列{an}满足：an＝ an－2an－1 (n∈N*，n>2)，若 a1 2an－2－an－1
＝1，a2＝37，则 a2 020 等于(
)
A. 3 B. 3 C. 5 D. 5 8 079 6 054 6 058 4 036
15．在数列{an}中，已知 a1＝2，an＋1＝3aan＋n 1(n∈N*)，则 a2＝________，an＝________.
16．(2019·浙江省名校协作体联考)已知数列{an}中，a1＝1，an＝ a2n－1＋1(n≥2，n∈N*)，则
8．将正整数按如图所示进行排列，则图中
B．第 45 行第 83 列
C．第 44 行第 84 列
D．第 45 行第 84 列
9．已知数列{an}满足：a1＝1，a2＝1， 2 ＝ 1 ＋ 1 (n∈N*)，则 a2 020＝________. 2 an＋1 an an＋2
1．已知数列{an}是等差数列，数列{bn}分别满足下列各式，其中数列{bn}必为等差数列的是
() A．bn＝|an|
B．bn＝a2n
C．bn＝a1n
D．bn＝－a2n
2．在等差数列{an}中，已知 a1＝2，a2＋a3＝16，则 a4＋a5＋a6 等于( )
A．50 B．52 C．54 D．56
3．等差数列 1＋x,2x＋2,5x＋1，…的第四项等于( )
A．10 B．11 C．12 D．13
12．已知数列{an}的前 n 项和为 Sn，a1＝8，a4＝2 且满足 an＋2＝2an＋1－an(n∈N*)，若 S5＝λa10，
则λ的值为( )
A．－1 B．－3 C．－1 D．－2
3
2
13．(2020·杭州调研)设等差数列{an}的前 n 项和为 Sn，且满足 S2 020>0，S2 021<0，对任意正整
数列{an}的通项公式为________；若 1 ＋ 1 ＋…＋ 1 <10，则 n 的最大值为
a1＋a2 a2＋a3
an＋an＋1
________．
2
答案精析
1．D 2.C 3.C 4.A 5.D 6.D 7.C
8．D 9. 1 10.13 3n－1 2 020 16
11．C [∵S13＝117，∴13a1＋a13＝117，∴a1＋a13＝18.∵a2＋am＝18， 2
∴ 1 ＋ 1 ＋…＋ 1
a1＋a2 a2＋a3
an＋an＋1
＝ 2－1＋ 3－ 2＋…＋ n＋1－ n
＝ n＋1－1<10，
∴ n＋1<11，解得 n<120，则 n 的最大值为 119.
4