同济大学结构力学第9章 超静定结构的实用计算方法与概念分析
结构力学第9章__力矩分配法(新)

9-2 单结点的力矩分配——基本运算
①求固端弯矩; ②将会交于结点的固端弯矩之和按分配系数分配给每一个杆端。 ③各杆按各自的传递系数向远端传递。 ④将固端弯矩和分配(或传递的弯矩)相加,得杆端最后弯矩。
9-2 单结点的力矩分配——基本运算
例题
12kN/m
i
6m
16kN
2i
3m
3m
0.4 0.6
固端弯矩 -36
第9章 渐进法及超静定力的影响线 9-1 力矩分配法的基本概念 9-2 单结点的力矩分配法 9-3 多结点的力矩分配法 9-4 计算结果的校核
9-1力矩分配法的基本概念
M
4
2 i12 1
i14
i13
3
4i12Δ1
2i12Δ1
i13Δ1 i13Δ1
3i14Δ1
M12 4i121 M13 i131 M14 3i141
M
1 M21 2 M12 M31 M13 M41 0 M14
9-1力矩分配法的基本概念
1 转动刚度:梁端发生单位转角产生的弯矩。
M ik Sik 1
4iik 远端为固定端
S ik
3iik iik
远端为铰支端 远端为平行支链杆
0 远端为自由端
2 分配系数:与转动刚度成正比
ik
96 64 → 32
-23.6 ← -47.3 -47.3 → -23.6 14.2 9.4 → 4.7
-1.2 ← 0.7 0.5 →
-2.3 -2.3 → -1.2 0.3
-0.1 -0.2
200.9 -200.9
237.3 -237.3 87.7
200.9
237.3
87.7
同济大学结构力学

金茂大厦421m
西尔斯大厦 442m
同济大学结构力学
学习方法 1、采用课堂讲课和自学教材相结合的方法,以讲课为主,有部分内容给大家自学,目的是培养大家自学的能 力。在自学过程中,不能理解的内容,大家可以相互讨论,当然也可将看不懂的问题和我一起探讨。 2、希望同学们应以讲课内容为主,作简单笔记,在学习理论、概念的同时,一定要作相当数量的习题,通过 手算的方法和技巧来掌握力学的概念以及分析和计算的方法。
几何特征:其横截面上两个方向的尺寸远小于长度。 典型形式:梁、刚架、拱和珩架。 (b)板壳结构——也称薄壁结构。 几何特征:其厚度远小于其余两个方向上的尺度。 典型形式:房屋建筑中的楼板、壳体屋盖及飞机和轮船的外 壳等。 (c)实体结构——也称三维连续体结构。 几何特征:结构的长、宽、高三个方向的尺寸大小相仿。 典型形式:重力式挡土墙、水工建筑中的重力坝等。
人类建筑师总想将摩天大楼越盖越高,美国有527米高的芝加哥西尔斯大厦,加拿大有553米高的多 伦多CN电视塔,阿联酋迪拜市正在建造一座高达807米的世界最高楼。然而这些摩天大楼和日本大成 建筑公司蓝图中的“X-Seed 4000”摩天巨塔相比,却全都是“小巫见大巫”。
美国“高层建筑及城市居住委员会”设定了4个衡量标准:最高一层地板的高度、最高一层屋顶的高度、 大厦尖顶的高度及大厦最高点的高度。
吉隆坡的双子塔452m
台北市的101大楼508m
芝加哥“螺旋之尖”摩天大楼的建设方案获得了政府批 准,“螺旋之尖”摩天大楼全高610米,建成后将是全 美最高的大楼,它也将是世界各大城市里高楼建筑的一 个典范。
结构力学超静定结构计算

SAB= 3i
M A1B ?
SAB= i
SAB M S
A
MAD
C
M
? MAB
m? 0
? M AD ? 3iAD? A ? SAD? A
1
M AC ?
M ? (SAB ? SAC ? SAD )? A
SAC M S
A
MAC
A
? ? A
?
SAB ?
M SAC
?
法相同,即都假设对杆端顺时针旋转为正号、对结点
或附加刚臂逆时针旋转为正号。作用于结点的外力偶 荷载、作用于附加刚臂的约束反力矩,也假定为对结
点或附加刚臂顺时针旋转为正号。
一、转动刚度 S:表示杆端对转动的抵抗能力。
在数值上 = 仅使杆件近端产生单位转角时所需在杆端施加 的力矩。
SAB=4i
1
SAB=3i
A
?A
B
CAB ?
M BA M AB
?
0
? MAB= iAB A
A
?A
MBA = - iAB ?A
B
CAB ?
M BA M AB
?
?1
在结点上的外力矩按各杆分配系数分配给各杆近端截面,各杆远 端弯矩分别等于各杆近端弯矩乘以传递系数。
单结点的力矩分配
——基本运算
A MAB
B
MBA
= MBC
MB
固端弯矩带本身符号 C
-MC
锁住1结点,用单结点
1
2
+
的力矩分配法,对2结 点的不平衡力矩进行分
…
配。
§2 多结点的力矩分配 ——渐近运算
超静定结构的计算

第二节力法
这样,原结构的内力计算问题就转变为基本结构在多余未知 力多的X余基1未本及知未荷力知载量Xq共1就,同是其作多余用余的下未计的知算内力就力。迎计刃算而问解题了了。。因只此要,设力法法求计出算
(二)力法方程 基本结构在月端不再受约束限制,因此在荷载y作用下月点
竖1小因5向-不此10位同基(d移而本)]向异结。下 , 构显由 的[然图于 变在15形X二-11位是者0(c移取共)]状代,同态了在作应被X用1与拆下作原去B用点结约下竖构束月向完对点位全原竖移一结向将致构位随,的移X即作向1的B用上点大,[图 的余方竖未向向知产位力生移X的1位△共移1同必应作须与用为原下零结,,构在也在拆就X除是1方约说向束基的处本位沿结移多构相余在等未已。知知即力荷X:载1作与用多 △1=0 这就是基本结构应满足的变形谐调条件,又称位移条件。
用结所构示11、上。产则12生△、的11、1沿3 △表X11示2方、单向△位的13可力相以X应1表=位1示移, X为,2=如1,X图3=151-分12别(c作),(用d)于, (基c),本(d) 11 11X1、12 12 X 2、13 13 X 3,上面儿何条件(15-2)
中的第一式可以写为:
下一页 返回
第一节超静定结构基本知识
(1)去掉支座处的一根链杆或者切断一根链杆,相当于去掉一 个约束,如图15-3 (a),(b)所示的两个结构都多出来一个约束, 都是一次超静定结构。
(2)去掉一个铰支座或内部的一个单铰,相当于去掉两个约束。 图15-4 (a), (b)所示的两个刚架都多出来两个约束,都是二次 超静定结构。
上一页 下一页 返回
第二节力法
用力法计算超静定结构在支座移动所引起的内力时,其基本 原理和解题步骤与荷载作用的情况相同,只是力法方程中自 由项的计算有所不同,它表示基本结构由于支座移动在多余 约第束五处节沿“多支余 座未 移知 动力 时方 静向 定所 结引 构起 的的 位位 移移 计算△”iC,所可述用方第法十求四得帝。 此外,还应注意力法方程等号右侧为基本结构在拆除约束处 沿多余未知力方向的位移条件,也就是原结构在多余未知力 方正向值的,已否知则实 取际 负位 值移 。值△i,当△i与多余未知力方向一致时取
同济大学朱慈勉-结构力学第9章-弯矩分配法
• 弯矩分配法中,结点转动在远端产生的弯矩可通过近端弯矩乘以传递系数得到。
• 远端为固定支座:CAB 1 2
A 1 i
A SAB 4i
M BA 2i B
• 远端为铰支座: CAB 0
A 1 i
A SAB 3i
M BA 0 B
• 远端为定向滑动支座:CAB 1
A 1 i
i2
4m
C
4m
3m 2m
B
A
C
BA AB AC AD CA
0.3 0.4 0.3
60
48
0 3.6 4.8 3.6 2.4
【解】 ⑴计算分配系数:
SAB 2 3 6, SAC 2 4 8, SAD 1.5 46 6
AB
6 20
0.3,
AC
8 20
•
M
u A
M
g AB
M
g AC
M
g AD
1 ql2 8
2019/12/5
q
q
M
u A
B
A
C
B
A
C
B
M
u A
A
C
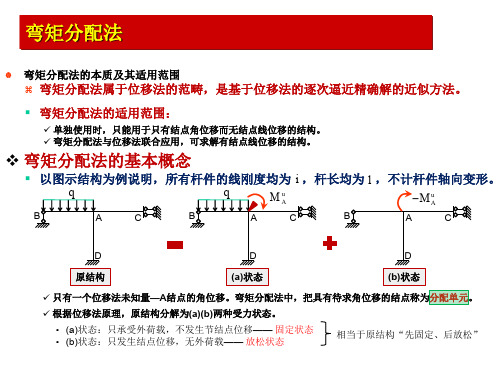
D 原结构
D (a)固定状态
D (b)放松状态
放松状态内力分析
放松状态就是原结构承受结点不平衡力矩的反向力矩(相当于解除约束)。 放松状态的内力可借助转动刚度、分配系数、传递系数等概念计算。
相当于原结构“先固定、后放松”
q
q
M
u A
B
A
C
B
A
C
B
静定超静定判断及计算

目的和意义
目的
理解静定与超静定的概念,掌握判断方法,能够进行相应的计算。
意义
在实际工程中,正确判断结构和系统的静定或超静定状态对于确保结构安全、节约材料和降低成本具有重要意义。
02
静定与超静定的基本概念
静定结构的定义
静定结构
在任何外界影响下,其平衡位置都是稳定的 ,且在受到微小扰动后能自动恢复到原来的 平衡状态。
内力计算的方法
静定结构的内力计算通常采用截面法或节点法进行。截面法是通过 截取结构的一部分进行分析,节点法则是对结构的节点进行受力分 析。
内力的表示方法
内力可以用实线和虚线表示,实线表示实际受力方向,虚线表示实际 受力反方向。
静定结构的位移计算
1
位移计算的意义
在结构分析中,位移是一个重要的参数 。通过计算位移,可以了解结构的变形 情况,从而评估结构的稳定性和安全性 。
本文的研究成果已被广泛应用于建筑、机械、航空航天等工程领 域,解决了众多实际工程问题,取得了显著的经济和社会效益。
对未来研究的展望
深入研究复杂结构体系
随着科技的发展,复杂结构体系在工程中越来越常见,未 来研究可进一步探讨复杂结构体系的静定与超静定问题, 提高工程结构的稳定性和安全性。
引入先进计算技术
计算公式
自由度数 = 刚片数 - 约束数。
判断标准
若自由度数等于0,则结构为静定;若自由度数不等于0,则结 构为超静定。
几何法判断
定义
几何法判断是指通过分析结构的几何形状来判断结构是否为静定或超静定的一种方法。
判断标准
若结构的几何形状满足静定结构的条件(即所有刚片都是相互平行的),则结构为静定;否则为超静 定。
01
结构力学课后解答:第9章__超静定结构的实用计算方法与概念分析

习 题9-2解:设EI=6,则5.1,1==BC AB i i 53.05.13145.1347.05.131414=⨯+⨯⨯==⨯+⨯⨯=BC BA μμ结点 A BC 杆端 AB BA BC 分配系数 固端 0.47 0.53 绞支 固端弯矩 -60 60 -30 0 分配传递 -7.05 -14.1 -15.9 0 最后弯矩-67.0545.9-45.9()()()逆时针方向215.216005.6721609.4522131m KN EI EI m M m M i AB AB BA BA B ⋅-=⎥⎦⎤⎢⎣⎡+---=⎥⎦⎤⎢⎣⎡---=θ(b)解:设EI=9,则3,31,1====BE BD BC AB i i i i12.0141333331316.0141333331436.01413333333=⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==BC BA BE BD μμμμ结点 A BC杆端 AB BA BC BD BE 分配系数 固端 0.16 0.12 0.36 0.36 绞支 固端弯矩0 45 -90 0 分配传递 3.6 7.2 5.4 16.216.20 最后弯矩 3.6 7.25.461.2 -73.8()()()顺时针方向22.1606.32102.732131m KN EI EI m M m M i AB AB BA BA B ⋅=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡---=θ9-3 (a) 解:B为角位移节点设EI=8,则1==BC AB i i ,5.0==BC BA μμ 固端弯矩()m KN l b l Pab M BA ⋅=⨯⨯⨯⨯=+=4882124432222 m KN l M BC ⋅-=⋅+-=582621892 结点力偶直接分配时不变号结点 A BC 杆端 AB BA BC 分配系数 铰接 0.5 0.5 固端弯矩 0 48 -58 12 分配传递0 50 50 5 5 12 最后弯矩103-312(b) 解:存在B 、C 角位移结点设EI=6,则1===CD BC AB i i i73741413145.0141414==⨯+⨯⨯==⨯+⨯⨯==BC CB BC BA μμμμ固端弯矩:mKN M M M m KN M m KN M CDCB BC BA AB ⋅-=⨯+⨯-===⋅-=⋅-=14021808640080802结点 A BC杆端 AB BA BC CB CD 分配系数 固结 0.5 0.5 4/7 3/7 固端弯矩-80 80 0 0 -140 分配传递-20 -40 -40 -2047.5 91.4 68.6 -11.4 -22.8 -22.8 -11.4 3.25 6.5 4.9 -0.82-1.63-1.63-0.820.6 0.45 最后弯矩-112.2215.57-15.4866.28-66.05(c) 解:B 、C 为角位移结点51411,5441454414,51411=+==+==+==+=CD CBBC BA μμμμ固端弯矩:mKN M mKN M mKN M mKN M mKN M mKN M DC CD CB BC BA AB ⋅-=⨯-=⋅-=⨯-=⋅=⨯=⋅-=⨯-=⋅=⨯=⋅=⨯=10065242003524501252450125241283424646424222222结点 A BCD 杆端 AB BA BC CB CD 滑动 分配系数 滑动 0.2 0.8 0.8 0.2 -100固端弯矩64 128 -50 50 -200 分配传递15.6 -15.6 -62.4 -31.272.48 144.96 36.24 -36.24 14.5 -14.5 -58 -29 11.6 23.2 5.8 -5.8 2.32-2.32-9.28-4.643.7 0.93 -0.93 最后弯矩96.4295.58-95.6157.02-157.03-142.9796.42(d) 解:11313141413114131414145.0141414=⨯+⨯+⨯⨯===⨯+⨯+⨯⨯===⨯+⨯⨯=DBDE DCCD CA μμμμμ 固端弯矩:mKN M mKN M ED DE ⋅=⋅-=⨯-=383812422 结点 A CD E 杆端 AC CA CD DC DB DE ED 分配系数 固结 0.5 0.5 4/11 3/11 4/11 固结 固端弯矩0 0 0 0 0 -2.67 2.67 分配传递-5 -10 -10 -546/33 92/33 69/33 92/33 46/33 -0.35 - 23/33- 23/33-0.35 0.127 0.096 0.127 0.064 最后弯矩-5.35-10.7-9.3-2.442.190.254.12(e) 解:当D 发生单位转角时:()()2414-=⨯⨯=m EI K Y C 则())假设12(441==⨯=-m EI EIM DC73,74,3716,379,371216,12,16,9,12=====∴=====∴EB ED DE DA DC DE EB DE DA DC S S S S S μμμμμ 结点D EB 杆端 DC DA DE ED EB BE 分配系数 12/37 9/37 16/37 4/7 3/7 固结 固端弯矩0 0 -9 9 0 0 分配传递-2.57 -5.14 -3.86 -1.93 3.75 2.81 5 -2.5 -0.72 -1.43 -1.07 -0.54 0.230.18 0.31 0.16 最后弯矩3.982.99-6.985-5-2.47(f) 解:截取对称结构为研究对象。
结构力学 力法计算超静定结构

Δ1 = 0 称为位移协调条件。
( 3 – 1)
情景二 力法的基本原理和典型方程
知识链接
Δ1 = 0 的物理意义:基本结构在荷载与 X1 的共同作用下,B 处所产 生的竖向位移应等于原结构 B 处的实际竖向位移(因原结构 B 处无
竖向位移,故 Δ = 1 0 )。根据叠加原理,基本结构在 q 与 X1 的 共同作用下,产生的 B 处竖向位移 Δ1,应等于 q 与 X1 分别单独作 用在基本结构 B处的竖向位移的叠加,即
情景二 力法的基本原理和典型方程 知识链接
情景二 力法的基本原理和典型方程
知识链接 2.力法原理
如图 3 – 17a 所示一次超静定梁,去掉支座 B,用多余未知力 X1 代 替,得如图 3 – 17b 所示的基本结构。由前述知,只要设法求出多 余未知力 X1,则其余支反力和内力的计算就与静定结构完全相同。 但仅靠平衡条件无法求出 X1,因为在基本结构中除 X1 外还有三个 支座反力未知,故平衡方程数目少于未知力数,其解值是不定的。 为求出未知力 X1,将图 3 – 17a 所示超静定梁与图 3 – 17b 所示静 定梁的受力条件和变形条件进行比较。
Δ11=δ11X11,于是上述位移条件(3–2)可写成
δ11X11 + Δ1P= 0
(3-3)
此方程为力法的基本方程。δ11 和 Δ1P 都是静定结构在已知力作用下 的位移,完全可以由项目二中所述方法求得,于是多余未知力 X 1 即可
由式(3–3)求得。这种以多余未知力为基本知量,通过基本结构,利
用计算静定结构的位移,达到求解超静定结构的方法称为力法。 为了计算 δ11 和 Δ1P ,分别作基本结构在荷载作用下的弯矩图 MP 和
由于原结构在b点的位移为零因此基本结构在荷载和多余未知力共同作用下b点沿x1x2x3方向的水平位移竖向位移和角位移也都应该为零即b处应满足位移条件102030项目实施情景二力法的基本原理和典型方程x11单独作用时沿x1x2x3方向位移分别为112131
结构力学第9章

(a) A
l/ 3
m
k1
2l /3
2l
(c)
9
A
X 1=1
M 1图
(b)
B
A
(d)
B
A
F=1
B
X1
F=1
B
2l 9
M P图
解: 本题的重点是求柔度系数, 用力法, 取图b的
基本体系。力法典型方程为
1
1X1
1P
X1 k1
应用图乘法求出系数并代入方程解得 X 1
8 89
, 因此
X1 4l3 , 1 267EI
当外荷载的频率很大时 (θ>>ω),体系振动很快,因此 惯性力很大,弹性力和阻尼力相对来说比较小,动荷载主 要与惯性力平衡。
当外荷载接近自振频率时(θ ≈ ω),弹性力和惯性力都 接近于零,这时动荷载主要由阻尼力相平衡。
6. 多自由度体系主振型的正交性 当ω i ≠ ω j 时,两个主振型具有正交性,即质量正交 和刚度正交。
(1) 简谐动荷载作用在质体上,内力动力系数与位移
动力系数相同。 动力系数
ymax ys t
1
1
2 2
计算时,只须将干扰力幅值当作静荷载按静力方法
算出相应的位移、内力,再乘以动力系数 即可。
(2) 简谐动荷载不作用在质体上,结构没有一个统一
的动力系数。
计算结构的位移和内力时,
应先算出质体上的惯性力,并
k1 267EI
m 4ml3
另解:体系简化成并联弹簧体系(图b),设梁在
质点m处的刚度系数为k2,k2=1/2 ,由M 图(图c)可 求得2
112 l l 2 l 212 l 2 l 2 l 2 4 l3 2 E (2 I 9 3 9 3 2 9 3 9 3 ) 2E 4I 3
《结构力学(Ⅰ)》课程教学大纲

《结构⼒学(Ⅰ)》课程教学⼤纲《结构⼒学(Ⅰ)》课程教学⼤纲⼀、课程性质与⽬的《结构⼒学》课程是⼟建、⽔利类专业本科⽣的⼀门重要的专业基础课程。
本课程的任务是在学习理论⼒学和材料⼒学等课程的基础上进⼀步掌握有关杆系结构受⼒分析的基本概念、基本原理和基本⽅法,了解各类结构的受⼒性能,为学习有关专业课程以及进⾏结构设计和科学研究打好⼒学基础,培养结构分析与计算等⽅⾯的能⼒。
课程的⽬的主要有:1、了解杆系结构的构造规律。
2、掌握静定和超静定结构内⼒分析的概念、原理与⽅法,掌握结构位移的计算⽅法。
3、了解结构矩阵分析⽅法。
本课程采⽤英语教学。
⼆、课程基本要求1、使学⽣具备系统的结构⼒学知识,对常见的杆系结构具有选择计算简图的初步能⼒,并能根据具体问题选择恰当的分析、计算⽅法,为学习有关专业课程,为毕业后从事结构设计、施⼯和科研⼯作打好理论基础。
2、提⾼学⽣的结构分析能⼒,具有对各种静定、超静定结构进⾏计算的能⼒,具有对计算结果进⾏校核以及对内⼒分布的合理性作出判断的能⼒,初步具备使⽤电⼦计算机进⾏结构分析的能⼒。
3、培养学⽣的综合分析能⼒和科学作风。
三、课程基本内容(⼀)绪论1.结构⼒学的研究对象及任务。
2.荷载的分类。
结点及⽀座的分类。
3.结构的计算简图及其分类。
4.结构⼒学的基本假设。
(⼆)平⾯体系的⼏何构造分析1.⼏何构造分析的⽬的。
⾃由度的概念。
2.平⾯体系的⾃由度计算。
3.平⾯体系的⼏何构造分析。
4.瞬变体系的特征。
5.静定与超静定结构的⼏何构造特征。
(三)静定结构1.多跨静定梁和静定刚架的⼏何构造。
在直接荷载及结点荷载作⽤下的内⼒分析以及内⼒图的绘制。
2.拱的基本受⼒特征。
三铰拱的内⼒计算⽅法。
三铰拱的压⼒线与合理拱轴线。
3.静定平⾯桁架的⼏何构造及其分类。
⽤结点法及截⾯法计算桁架的内⼒。
结点法与截⾯法的联合应⽤。
各类平⾯梁式桁架的⽐较。
组合结构的计算。
4.静定结构的⼀般性质。
(四)静定结构的影响线1.移动荷载和影响线的概念。
结构力学 超静定结构总论

超静定结构总论
• 基本解法的分类和比较 • 基本解法的推广和联合应用
• 混合法与近似法 • 超静定结构的特性 • 关于计算简图的补充讨论
§14-1 超静定结构解法的分类和比较
手 基本形式
算
能量形式
渐近形式
力法类型 力法
余能法 (渐近力法)
位移法类型 位移法 势能法
力矩分配法、无剪力分配法
电算 矩阵形式
变形条件:
11X1 12X 2 133 144 1P 0
21X1 22X 2 233 244 2P 0
X2 X1
平衡条件: M B 0, M BA M BC M BD 0
M D 0, M DB M DE M DF 0
六个多余 未知力, 两个结点 位移。用 位移法作。
A
θ3 B
C
θ4
DF E
对称问题按位
P移法或力矩分源自配法计算,反对称问题按力
法或无剪切分
配法计算。
P/2 P/2
对 称
P/2 P/2
反 对 称
§14-3 混合法
混合法的基本特点是:基本未知量中既有位移,又有力。
两个多余 未知力, 五个结点 位移。用 力法作。
合理的方法是混合法:
基本未知量:X1 X2θ3θ4 基本方程:变形条件、平衡条件。
2)忽略每层梁的竖向荷载对其它各层的影响,把多层刚架
分成一层一层地计算。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
除底层柱底外,其余各柱端是 弹性固定端。故将上层各柱的 i×0.9,传递系数改为1/3。
二、反弯点法 (适用于水平荷载作用下的强梁弱柱结构)
假设:横梁为刚性梁;结点无转角。柱的反弯点在其中点。
结构力学超静定结构总论

110.3
由几何关系,得 12 7
由图乘法,得
D1P
1 3
5 160
3 4
3
1 3
41605 3400
§12-2 分区混合法
(4)求杆端弯矩
由杆件的刚度方程,得
M BA
4iAB2
4
3 4
2
32
M BC
4iBC2
4
1 4
2
2
由平衡条件,得
M BD 7 X1 160
故
42 7 X1 160 0
§12-4 结构计算简图续论
2 交叉体系的荷载传递方式及其简化 (1)矩形楼板的简化计算
矩形楼板
两个方向分别取1m 宽板带计算
§12-4 结构计算简图续论
短边方向的简图
长边方向的简图
根据两个简图跨中挠度相等的条件,得
q1 q2 l2 l1 4
§12-4 结构计算简图续论
故,实际工程中将板分成两类: ▲双向板:长短边之比<2,板上的荷载沿两个方向传递。 ▲单向板:长短边之比≥2,板上的荷载沿短边方向传递。 (2)拱坝的简化计算
m2
FP EI
M M1X1 M22 MP
§12-2 分区混合法
4 混合分区的典型方程
k
k
X
DP FP
0 0
——a区与力X相应的柔度矩阵
k ——b区与位移Δ相应的刚度矩阵
——由位移Δ引起的沿力X方向的位移影响系数矩阵
k ——由力X 引起的沿位移Δ方向的约束力影响系数矩阵
EI
EA
GA
度改变内力分布
§12-3 超静定结构的特性
3 温度和沉陷等变形因素的影响
11 X1 12 X 2 L 1n X n 1t 1c 0 21 X1 22 X 2 L 2n X n 2t 2c 0
超静定结构的实用计算方法与概念分析.doc

习 题9-1 试说出何为杆端转动刚度、弯矩分配系数和传递系数,为什么弯矩分配法一般只能用于无结点线位移的梁和刚架计算。
9-2 试用弯矩分配法计算图示梁和刚架,作出M 图,并求刚结点B 的转角φB 。
(a)解:设EI=6,则5.1,1==B C A B i i53.05.13145.1347.05.131414=⨯+⨯⨯==⨯+⨯⨯=B CB A μμ结点 A BC 杆端 AB BA BC 分配系数 固端 0. 47 0.53 绞支 固端弯矩 -60 60 -30 0 分配传递 -7.05 -14.1 -15.9 0 最后弯矩-67.0545.9-45.9()()()逆时针方向215.216005.6721609.4522131m KN EIEI m M m M i AB AB BA BA B ⋅-=⎥⎦⎤⎢⎣⎡+---=⎥⎦⎤⎢⎣⎡---=θ9067.545.940(b)解:设EI=9,则3,31,1====B E B D B C A B i i i i9m9m 40kN C6mAD B EEIEI2EI2EI3m 3m 20k N /m2m6m2m20kN/m ABC EI EI 40kN12.0141333331316.0141333331436.01413333333=⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==B CB A B E B D μμμμ 结点 A BC 杆端 AB BA BC BD BE 分配系数 固端 0.16 0.12 0.36 0.36 绞支 固端弯矩 0 0 0 45 -90 0 分配传递 3.6 7.2 5.4 16.2 16.2 0 最后弯矩3.67.25.461.2-73.8()()()顺时针方向22.1606.32102.732131m KN EIEI m M m M i AB AB BA BA B ⋅=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡---=θ6061.27.23.65.473.8909-3 试用弯矩分配法计算图示刚架,并作出M 图。
