高考数学刷题首选卷 考点测试 平面向量的概念及线性运算 理含解析.doc
高考冲刺:平面向量的概念及线性运算含解析答案(教师版+学生版)
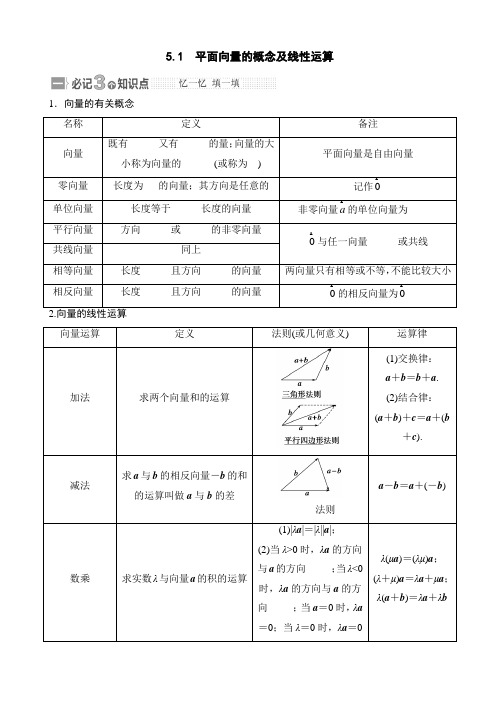
5.1 平面向量的概念及线性运算1.向量的有关概念与任一向量______两向量只有相等或不等,或几何意义) 运算律3.向量共线定理如果有一个实数λ,使b =λa (a ≠0),那么b 与a 是共线向量;反之,如果b 与a (a ≠0)是共线向量,那么有且只有一个实数λ,使b =λa .1.作两个向量的差时,要注意向量的方向是指向被减向量的终点;2.在向量共线的重要条件中易忽视“a ≠0”,否则λ可能不存在,也可能有无数个; 3.要注意向量共线与三点共线的区别与联系. 考点自测1.D 是△ABC 的边AB 上的中点,若CD =x BA +y BC ,则x +y =________. 2.已知a 与b 是两个不共线向量,且向量a +λb 与-(b -3a )共线,则λ=________. 3.在ABCD 中,AB →=a ,AD →=b ,AN →=3NC →,M 为BC 的中点,则MN →=____________.(用a ,b 表示)题型一 平面向量的概念 例1 给出下列命题:①若|a |=|b |,则a =b ;②若A ,B ,C ,D 是不共线的四点,则“AB →=DC →”是“四边形ABCD 为平行四边形”的充要条件;③若a =b ,b =c ,则a =c ;④a =b 的充要条件是|a |=|b |且a ∥b . 其中正确命题的序号是________.题型二 平面向量的线性运算例2 (1)在平行四边形ABCD 中,AC 与BD 相交于点O ,E 是线段OD 的中点,AE 的延长线与CD 交于点F ,若AC →=a ,BD →=b ,则AF →=________.(用a ,b 表示)(2)在△ABC 中,AB →=c ,AC →=b ,若点D 满足BD →=2DC →,则AD →=________(用b ,c 表示).变式训练1 (2013·江苏)设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC .若DE →=λ1AB →+λ2AC →(λ1,λ2为实数),则λ1+λ2的值为________.题型三 共线定理的应用例3 设两个非零向量a 与b 不共线,(1)若AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ),求证:A 、B 、D 三点共线; (2)试确定实数k ,使k a +b 和a +k b 共线.题型四 方程思想在平面向量的线性运算中的应用例4 如图所示,在△ABO 中,OC →=14OA →,OD →=12OB →,AD 与BC 相交于点M ,设OA →=a ,OB →=b .试用a 和b 表示向量OM →.变式训练2 如图,在平面四边形ABCD 中,,E F 分别是,AD BC 的中点,求证:2AB DC EF +=.1.向量的中线公式若P 为线段AB 的中点,O 为平面内一点,则OP =12(OA +OB ).2.三点共线等价关系A ,P ,B 三点共线⇔AP =λAB (λ≠0)⇔ OP =(1-t )·OA +t OB (O 为平面内异于A ,P ,B 的任一点,t ∈R )⇔OP =x OA +y OB (O 为平面内异于A ,P ,B 的任一点,x ∈R ,y ∈R ,x +y =1). 课堂练习1.下列命题中,正确的是________.(填序号) ①有向线段就是向量,向量就是有向线段;②向量a 与向量b 平行,则a 与b 的方向相同或相反; ③向量AB →与向量CD →共线,则A 、B 、C 、D 四点共线; ④如果a ∥b ,b ∥c ,那么a ∥c ;⑤两个向量不能比较大小,但它们的模能比较大小.2.在△ABC 中,若BM →=3MA →,CM →=λ1AC →+λ2BC →(其中λ1,λ2为实数),则λ1+λ2=________. 3.已知D 为三角形ABC 的边BC 的中点,点P 满足P A →+BP →+CP →=0,AP →=λPD →,则实数λ的值为________.4.已知平面上不共线的四点O ,A ,B ,C ,若OA →-4OB →+3OC →=0,则|AB →||BC →|=________.5.已知a ,b 不共线,OA =a ,OB =b ,OC =c ,OD =d ,OE =e ,设t ∈R , 如果3a =c,2b =d ,e =t (a +b ),是否存在实数t 使C ,D ,E 三点在一条直线上?若存在,求出实数t 的值,若不存在,请说明理由.5.1 平面向量的概念及线性运算(作业)1、已知向量a =(2,4),b =(-1,1),则2a -b =________.2、设a ,b 不共线,AB →=2a +p b ,BC →=a +b ,CD →=a -2b ,若A ,B ,D 三点共线, 则实数p 的值是________.3、已知点O 为△ABC 外接圆的圆心,且OA →+OB →+OC →=0,则△ABC 的内角A =________.4、在△ABC 中,AB =2,BC =3,∠ABC =60°,AD 为BC 边上的高,O 为AD 的中点,若AO →=λAB →+μBC →,则λ+μ=________.5、命题:①如果非零向量a 与b 的方向相同或相反,那么a +b 的方向必与a ,b 之一方向相同; ②三角形ABC 中,必有AB →+BC →+CA →=0;③若AB →+BC →+CA →=0,则A ,B ,C 为三角形的三个顶点; ④若a ,b 均为非零向量,则|a +b |与|a |+|b |一定相等. 其中假命题的序号为________.6、设O 是△ABC 内部一点,且OA →+OC →=-2OB →,则△AOB 与△AOC 的面积之比为________.7、在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,且3a BC +4b CA +5c AB =0, 则a ∶b ∶c =________.8、在△ABC 中,已知D 是AB 边上一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ=________.9、如图,经过△OAB 的重心G 的直线与OA ,OB 分别交于点P ,Q ,设OP →=mOA →,OQ →=nOB →,m ,n ∈R ,则1n +1m的值为________.10、如图所示,在△ABC 中,点O 是BC 的中点.过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若AB →=mAM →,AC →=nAN →,则m +n 的值为________.11、如图所示,在△ABC 中,D 、F 分别是BC 、AC 的中点,AE →=23AD →,AB →=a ,AC →=b .(1)用a 、b 表示向量AD →,AE →,AF →,BE →,BF →;(2)求证:B ,E ,F 三点共线.12、已知O ,A ,B 是不共线的三点,且OP →=mOA →+nOB →(m ,n ∈R ). (1)若m +n =1,求证:A ,P ,B 三点共线; (2)若A ,P ,B 三点共线,求证:m +n =1.5.1 平面向量的概念及线性运算1.向量的有关概念(的和三角形法则(1)|λa|=|λ||a|;如果有一个实数λ,使b =λa (a ≠0),那么b 与a 是共线向量;反之,如果b 与a (a ≠0)是共线向量,那么有且只有一个实数λ,使b =λa .1.作两个向量的差时,要注意向量的方向是指向被减向量的终点;2.在向量共线的重要条件中易忽视“a ≠0”,否则λ可能不存在,也可能有无数个; 3.要注意向量共线与三点共线的区别与联系.1.D 是△ABC 的边AB 上的中点,若CD =x BA +y BC ,则x +y =________. 解析:∵CD =BD -BC =12BA -BC ,则x =12,y =-1∴x +y =-12.答案:-122.已知a 与b 是两个不共线向量,且向量a +λb 与-(b -3a )共线,则λ=________. 解析:由题意知a +λb =k [-(b -3a )],所以⎩⎪⎨⎪⎧λ=-k ,1=3k ,解得⎩⎨⎧k =13,λ=-13.答案:-133.在▱ABCD 中,AB →=a ,AD →=b ,AN →=3NC →,M 为BC 的中点,则MN →=____________.(用a ,b 表示) 答案 -14a +14b解析 由AN →=3NC →得AN →=34AC →=34(a +b ),AM →=a +12b ,所以MN →=AN →-AM →=34(a +b )-⎝⎛⎭⎫a +12b =-14a +14b .题型一 平面向量的概念 例1 给出下列命题:①若|a |=|b |,则a =b ;②若A ,B ,C ,D 是不共线的四点,则“AB →=DC →”是“四边形ABCD 为平行四边形”的充要条件;③若a =b ,b =c ,则a =c ;④a =b 的充要条件是|a |=|b |且a ∥b . 其中正确命题的序号是________. 答案 ②③解析 ①不正确.两个向量的长度相等,但它们的方向不一定相同. ②正确.∵AB →=DC →,∴|AB →|=|DC →|且AB →∥DC →,又∵A ,B ,C ,D 是不共线的四点,∴四边形ABCD 为平行四边形;反之,若四边形ABCD 为平行四边形,则AB →∥DC →且|AB →|=|DC →|,因此,AB →=DC →.故“AB →=DC →”是“四边形ABCD 为平行四边形”的充要条件.③正确.∵a =b ,∴a ,b 的长度相等且方向相同;又b =c , ∴b ,c 的长度相等且方向相同, ∴a ,c 的长度相等且方向相同,故a =c .④不正确.当a ∥b 且方向相反时,即使|a |=|b |,也不能得到a =b ,故“|a |=|b |且a ∥b ”不是“a =b ”的充要条件,而是必要不充分条件. 综上所述,正确命题的序号是②③.思维升华 (1)相等向量具有传递性,非零向量的平行也具有传递性. (2)共线向量即为平行向量,它们均与起点无关.(3)向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象的移动混为一谈.(4)非零向量a 与a |a |的关系:a|a |是a 方向上的单位向量.题型二 平面向量的线性运算例2 (1)在平行四边形ABCD 中,AC 与BD 相交于点O ,E 是线段OD 的中点,AE 的延长线与CD 交于点F ,若AC →=a ,BD →=b ,则AF →=________.(用a ,b 表示)(2)在△ABC 中,AB →=c ,AC →=b ,若点D 满足BD →=2DC →,则AD →=________(用b ,c 表示). 答案 (1)23a +13b (2)23b +13c解析 (1)如图,AF →=AD →+DF →,由题意知, DE ∶BE =1∶3=DF ∶AB , ∴DF →=13AB →,∴AF →=12a +12b +13(12a -12b )=23a +13b .(2)∵BD →=2DC →,∴AD →-AB →=BD →=2DC →=2(AC →-AD →), ∴3AD →=2AC →+AB →, ∴AD →=23AC →+13AB →=23b +13c .思维升华 (1)解题的关键在于熟练地找出图形中的相等向量,并能熟练运用相反向量将加减法相互转化.(2)用几个基本向量表示某个向量问题的基本技巧:①观察各向量的位置;②寻找相应的三角形或多边形;③运用法则找关系;④化简结果.变式训练1 (2013·江苏)设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC .若DE →=λ1AB →+λ2AC →(λ1,λ2为实数),则λ1+λ2的值为________.解析 由题意,得DE →=DB →+BE →=12AB →+23BC →=12AB →+23(AC →-AB →)=-16AB →+23AC →,则λ1=-16,λ2=23,即λ1+λ2=12.题型三 共线定理的应用例3 设两个非零向量a 与b 不共线,(1)若AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ),求证:A 、B 、D 三点共线; (2)试确定实数k ,使k a +b 和a +k b 共线.(1)证明 ∵AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ), ∴BD →=BC →+CD →=2a +8b +3(a -b ) =2a +8b +3a -3b =5(a +b )=5AB →. ∴AB →、BD →共线,又∵它们有公共点B , ∴A 、B 、D 三点共线. (2)解 ∵k a +b 和a +k b 共线, ∴存在实数λ,使k a +b =λ(a +k b ), 即k a +b =λa +λk b .∴(k -λ)a =(λk -1)b . ∵a 、b 是两个不共线的非零向量, ∴k -λ=λk -1=0,∴k 2-1=0.∴k =±1.思维升华 (1)证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系.当两向量共线且有公共点时,才能得出三点共线.(2)向量a 、b 共线是指存在不全为零的实数λ1,λ2,使λ1a +λ2b =0成立,若λ1a +λ2b =0,当且仅当λ1=λ2=0时成立,否则向量a 、b 不共线. 题型四 方程思想在平面向量的线性运算中的应用例4 如图所示,在△ABO 中,OC →=14OA →,OD →=12OB →,AD 与BC 相交于点M ,设OA →=a ,OB →=b .试用a 和b 表示向量OM →.思维点拨 (1)用已知向量来表示另外一些向量是用向量解题的基本要领,要尽可能地转化到平行四边形或三角形中去. (2)既然OM →能用a 、b 表示,那我们不妨设出OM →=m a +n b . (3)利用向量共线建立方程,用方程的思想求解. 规范解答解 设OM →=m a +n b ,则AM →=OM →-OA →=m a +n b -a =(m -1)a +n b . AD →=OD →-OA →=12OB →-OA →=-a +12b .[3分]又∵A 、M 、D 三点共线,∴AM →与AD →共线. ∴存在实数t ,使得AM →=tAD →, 即(m -1)a +n b =t ⎝⎛⎭⎫-a +12b .[6分] ∴(m -1)a +n b =-t a +12t b .∴⎩⎪⎨⎪⎧m -1=-t ,n =t 2,消去t 得,m -1=-2n , 即m +2n =1.① [9分]又∵CM →=OM →-OC →=m a +n b -14a =⎝⎛⎭⎫m -14a +n b , CB →=OB →-OC →=b -14a =-14a +b .又∵C 、M 、B 三点共线, ∴CM →与CB →共线.[12分] ∴存在实数t 1,使得CM →=t 1CB →, 即(m -14)a +n b =t 1⎝⎛⎭⎫-14a +b .∴⎝⎛⎭⎫m -14a +n b =-14t 1a +t 1b , ∴⎩⎪⎨⎪⎧m -14=-14t 1,n =t 1.消去t 1得,4m +n =1.②由①②得m =17,n =37,∴OM →=17a +37b .[14分]温馨提醒 (1)本题考查了向量的线性运算,知识要点清楚,但解题过程复杂,有一定的难度.(2)易错点是,找不到问题的切入口,想不到利用待定系数法求解.(3)数形结合思想是向量加法、减法运算的核心,向量是一个几何量,是有“形”的量,因此在解决向量有关问题时,多数习题要结合图形进行分析、判断、求解,这是研究平面向量最重要的方法与技巧.如本题易忽视A 、M 、D 三点共线和B 、M 、C 三点共线这个几何特征.(4)方程思想是解决本题的关键,要注意体会.变式训练2 如图,在平面四边形ABCD 中,,E F 分别是,AD BC 的中点,求证:2AB DC EF +=.1.向量的中线公式若P 为线段AB 的中点,O 为平面内一点,则OP =12(OA +OB ).2.三点共线等价关系A ,P ,B 三点共线⇔AP =λAB (λ≠0)⇔ OP =(1-t )·OA +t OB (O 为平面内异于A ,P ,B 的任一点,t ∈R )⇔OP =x OA +y OB (O 为平面内异于A ,P ,B 的任一点,x ∈R ,y ∈R ,x +y =1).方法与技巧1.向量的线性运算要满足三角形法则和平行四边形法则,做题时,要注意三角形法则与平行四边形法则的要素.向量加法的三角形法则要素是“首尾相接,指向终点”;向量减法的三角形法则要素是“起点重合,指向被减向量”;平行四边形法则要素是“起点重合”. 2.证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.3.对于三点共线有以下结论:对于平面上的任一点O ,OA →,OB →不共线,满足OP →=xOA →+yOB →(x ,y ∈R ),则P ,A ,B 共线⇔x +y =1. 失误与防范1.解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是要考虑向量的方向;二是考虑零向量是否也满足条件.要特别注意零向量的特殊性.2.在利用向量减法时,易弄错两向量的顺序,从而求得所求向量的相反向量,导致错误.1.下列命题中,正确的是________.(填序号) ①有向线段就是向量,向量就是有向线段;②向量a 与向量b 平行,则a 与b 的方向相同或相反; ③向量AB →与向量CD →共线,则A 、B 、C 、D 四点共线; ④如果a ∥b ,b ∥c ,那么a ∥c ;⑤两个向量不能比较大小,但它们的模能比较大小. 答案 ⑤解析 ①不正确,向量可以用有向线段表示,但向量不是有向线段,有向线段也不是向量; ②不正确,若a 与b 中有一个为零向量,零向量的方向是不确定的,故两向量方向不一定相同或相反;③不正确,共线向量所在的直线可以重合,也可以平行; ④不正确,如果b =0,则a 与c 不一定平行;⑤正确,向量既有大小,又有方向,不能比较大小;向量的模均为实数,可以比较大小. 2.在△ABC 中,若BM →=3MA →,CM →=λ1AC →+λ2BC →(其中λ1,λ2为实数),则λ1+λ2=________. 解析 由题意可得CM →=CB →+BM →=CB →+34BA →=CB →+34(CA →-CB →)=-34AC →-14BC →,所以λ1+λ2=-34-14=-1.3.已知D 为三角形ABC 的边BC 的中点,点P 满足P A →+BP →+CP →=0,AP →=λPD →,则实数λ的值为________.解析 如图所示,由AP →=λPD →,且P A →+BP →+CP →=0,则P 是以AB 、AC 为邻边的平行四边形的第四个顶点,因此AP →=-2PD →,则λ=-2.4.已知平面上不共线的四点O ,A ,B ,C ,若OA →-4OB →+3OC →=0,则|AB →||BC →|=________.解析 OA →-4OB →+3OC →=0⇒OA →-OB →-3(OB →-OC →)=0⇒BA →=3CB →,所以|AB →||BC →|=3.5.已知a ,b 不共线,OA =a ,OB =b ,OC =c ,OD =d ,OE =e ,设t ∈R ,如果3a =c,2b =d ,e =t (a +b ),是否存在实数t 使C ,D ,E 三点在一条直线上?若存在,求出实数t 的值,若不存在,请说明理由.解:由题设知,CD =d -c =2b -3a ,CE =e -c =(t -3)a +t b ,C ,D ,E 三点在一条直线上的充要条件是存在实数k ,使得CE =k CD ,即(t -3)a +t b =-3k a +2k b ,整理得(t -3+3k )a =(2k -t )b .因为a ,b 不共线,所以有⎩⎪⎨⎪⎧t -3+3k =0,t -2k =0,解之得t =65.故存在实数t =65使C ,D ,E 三点在一条直线上.5.1 平面向量的概念及线性运算(作业)1.已知向量a =(2,4),b =(-1,1),则2a -b =________.解析 2a -b =(4,8)-(-1,1)=(5,7).2.设a ,b 不共线,AB →=2a +p b ,BC →=a +b ,CD →=a -2b ,若A ,B ,D 三点共线,则实数p 的值是________.解析 ∵BC →=a +b ,CD →=a -2b , ∴BD →=BC →+CD →=2a -b .又∵A ,B ,D 三点共线,∴AB →,BD →共线. 设AB →=λBD →, ∴2a +p b =λ(2a -b ),∴2=2λ,p =-λ,∴λ=1,p =-1.3. 已知点O 为△ABC 外接圆的圆心,且OA →+OB →+OC →=0,则△ABC 的内角A =________. 解析 由OA →+OB →+OC →=0,知点O 为△ABC 的重心, 又O 为△ABC 外接圆的圆心, ∴△ABC 为等边三角形,A =60°.4.在△ABC 中,AB =2,BC =3,∠ABC =60°,AD 为BC 边上的高,O 为AD 的中点,若AO →=λAB →+μBC →,则λ+μ=________. 解析 ∵AD →=AB →+BD →=AB →+13BC →,∴2AO →=AB →+13BC →,即AO →=12AB →+16BC →.故λ+μ=12+16=23.5.命题:①如果非零向量a 与b 的方向相同或相反,那么a +b 的方向必与a ,b 之一方向相同; ②三角形ABC 中,必有AB →+BC →+CA →=0;③若AB →+BC →+CA →=0,则A ,B ,C 为三角形的三个顶点; ④若a ,b 均为非零向量,则|a +b |与|a |+|b |一定相等.其中假命题的序号为________. 答案 ①③④解析 ①若a 与b 长度相等,方向相反,则a +b =0;③A ,B ,C 三点可能在一条直线上;④|a |+|b |≥|a +b |.6. 设O 是△ABC 内部一点,且OA →+OC →=-2OB →,则△AOB 与△AOC 的面积之比为________. 解析 设D 为AC 的中点,连结OD ,则OA →+OC →=2OD →. 又OA →+OC →=-2OB →,所以OD →=-OB →,即O 为BD 的中点,从而容易得△AOB 与△AOC 的面积之比为1∶2.7.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,且3a BC +4b CA +5c AB =0, 则a ∶b ∶c =________.解析:在△ABC 中有BC +CA +AB =0,又3a BC +4b CA +5c AB =0,消去AB 得 (3a -5c ) BC +(4b -5c ) CA =0, 从而3a -5c =0,4b -5c =0, 故a ∶b ∶c =20∶15∶12.8.在△ABC 中,已知D 是AB 边上一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ=________.解析 由图知CD →=CA →+AD →,① CD →=CB →+BD →,② 且AD →+2BD →=0.①+②×2得:3CD →=CA →+2CB →, ∴CD →=13CA →+23CB →,∴λ=23.9如图,经过△OAB 的重心G 的直线与OA ,OB 分别交于点P ,Q ,设OP →=mOA →,OQ →=nOB →,m ,n ∈R ,则1n +1m的值为________.解析 设OA →=a ,OB →=b ,由题意知OG →=23×12(OA →+OB →)=13(a +b ),PQ →=OQ →-OP →=n b -m a ,PG →=OG →-OP →=(13-m )a +13b ,由P 、G 、Q 三点共线得,存在实数λ,使得PQ →=λPG →,即n b -m a =λ(13-m )a +13λb ,从而⎩⎨⎧-m =λ(13-m ),n =13λ,消去λ得1n +1m=3.10如图所示,在△ABC 中,点O 是BC 的中点.过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若AB →=mAM →,AC →=nAN →,则m +n 的值为________.解析 ∵O 是BC 的中点,∴AO →=12(AB →+AC →).又∵AB →=mAM →,AC →=nAN →,∴AO →=m 2AM →+n 2AN →.∵M ,O ,N 三点共线,∴m 2+n2=1.则m +n =2.11如图所示,在△ABC 中,D 、F 分别是BC 、AC 的中点,AE →=23AD →,AB →=a ,AC →=b .(1)用a 、b 表示向量AD →,AE →,AF →,BE →,BF →; (2)求证:B ,E ,F 三点共线.(1)解 延长AD 到G ,使AD →=12AG →,连结BG ,CG ,得到▱ABGC , 所以AG →=a +b ,AD →=12AG →=12(a +b ),AE →=23AD →=13(a +b ),AF →=12AC →=12b ,BE →=AE →-AB →=13(a +b )-a =13(b -2a ).BF →=AF →-AB →=12b -a =12(b -2a ).(2)证明 由(1)可知BE →=23BF →,又因为BE →,BF →有公共点B ,所以B ,E ,F 三点共线.12.已知O ,A ,B 是不共线的三点,且OP →=mOA →+nOB →(m ,n ∈R ). (1)若m +n =1,求证:A ,P ,B 三点共线; (2)若A ,P ,B 三点共线,求证:m +n =1. 证明 (1)若m +n =1,则OP →=mOA →+(1-m )OB →=OB →+m (OA →-OB →), ∴OP →-OB →=m (OA →-OB →), 即BP →=mBA →,∴BP →与BA →共线.又∵BP →与BA →有公共点B ,则A ,P ,B 三点共线. (2)若A ,P ,B 三点共线,则存在实数λ,使BP →=λBA →, ∴OP →-OB →=λ(OA →-OB →). 又OP →=mOA →+nOB →.故有mOA →+(n -1)OB →=λOA →-λOB →, 即(m -λ)OA →+(n +λ-1)OB →=0.∵O ,A ,B 不共线,∴OA →,OB →不共线,∴⎩⎪⎨⎪⎧m -λ=0,n +λ-1=0,∴m +n =1.。
高考数学一轮复习学案:5.1 平面向量的概念及线性运算(含答案)

高考数学一轮复习学案:5.1 平面向量的概念及线性运算(含答案)5.1平面向量的概念及线性运算平面向量的概念及线性运算最新考纲考情考向分析1.了解向量的实际背景2.理解平面向量的概念,理解两个向量相等的含义3.理解向量的几何表示4.掌握向量加法.减法的运算,并理解其几何意义5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义6.了解向量线性运算的性质及其几何意义.主要考查平面向量的线性运算加法.减法.数乘向量及其几何意义.共线向量定理常与三角函数.解析几何交汇考查,有时也会有创新的新定义问题;题型以选择题.填空题为主,属于中低档题目偶尔会在解答题中作为工具出现.1向量的有关概念名称定义备注向量既有大小,又有方向的量;向量的大小叫做向量的长度或称模平面向量是自由向量零向量长度为0的向量;其方向是任意的记作0单位向量长度等于1个单位长度的向量非零向量a的单位向量为a|a|平行向量共线向量方向相同或相反的非零向量0与任一向量平行或共线相等向量长度相等且方向相同的向量两向量只有相等或不等,不能比较大小相反向量长度相等且方向相反的向量0的相反向量为02.向量的线性运算向量运算定义法则或几何意义运算律加法求两个向量和的运算3交换律abba;4结合律abcabc减法求a与b的相反向量b的和的运算abab数乘求实数与向量a的积的运算6|a||||a|;7当0时,a与a的方向相同;当0时,a与a的方向相反;当0时,a08aa;9aaa;10abab3.共线向量定理向量aa0与b共线,当且仅当有唯一一个实数,使ba.知识拓展1一般地,首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量,即A1A2A2A3A3A4An1AnA1An,特别地,一个封闭图形,首尾连接而成的向量和为零向量2若P为线段AB的中点,O为平面内任一点,则OP12OAOB3.OAOBOC,为实数,若点A,B,C共线,则1.题组一思考辨析1判断下列结论是否正确请在括号中打“”或“”1向量与有向线段是一样的,因此可以用有向线段来表示向量2|a|与|b|是否相等与a,b的方向无关3若ab,bc,则ac.4若向量AB与向量CD是共线向量,则A,B,C,D四点在一条直线上5当两个非零向量a,b共线时,一定有ba,反之成立6若两个向量共线,则其方向必定相同或相反题组二教材改编2P86例4已知ABCD的对角线AC和BD相交于点O,且OAa,OBb,则DC______,BC________.用a,b表示答案baab 解析如图,DCABOBOAba,BCOCOBOAOBab.3P108B组T5在平行四边形ABCD中,若|ABAD||ABAD|,则四边形ABCD的形状为________答案矩形解析如图,因为ABADAC,ABADDB,所以|AC||DB|.由对角线长相等的平行四边形是矩形可知,四边形ABCD是矩形题组三易错自纠4对于非零向量a,b,“ab0”是“ab”的A充分不必要条件B必要不充分条件C充要条件D既不充分也不必要条件答案A解析若ab0,则ab,所以ab.若ab,则ab0不一定成立,故前者是后者的充分不必要条件5设向量a,b不平行,向量ab 与a2b平行,则实数____________.答案12解析向量a,b不平行,a2b0,又向量ab与a2b平行,则存在唯一的实数,使aba2b 成立,即aba2b,则,12,解得12.6设D,E分别是ABC的边AB,BC上的点,AD12AB,BE23BC.若DE1AB2AC1,2为实数,则12的值为________答案12解析DEDBBE12AB23BC12AB23BAAC16AB23AC,116,223,即1212.题型一题型一平面向量的概念平面向量的概念1给出下列四个命题若|a||b|,则ab;若A,B,C,D是不共线的四点,则ABDC是四边形ABCD为平行四边形的充要条件;若ab,bc,则ac;ab的充要条件是|a||b|且ab.其中正确命题的序号是ABCD答案A解析不正确两个向量的长度相等,但它们的方向不一定相同;正确ABDC,|AB||DC|且ABDC,又A,B,C,D是不共线的四点,四边形ABCD为平行四边形,反之,若四边形ABCD为平行四边形,则ABDC且|AB||DC|,ABDC;正确ab,a,b的长度相等且方向相同,又bc,b,c的长度相等且方向相同,a,c的长度相等且方向相同,故ac;不正确当ab且方向相反时,即使|a||b|,也不能得到ab,故|a||b|且ab不是ab的充要条件,而是必要不充分条件综上所述,正确命题的序号是.故选A.2设a0为单位向量,若a为平面内的某个向量,则a|a|a0;若a与a0平行,则a|a|a0;若a与a0平行且|a|1,则aa0.上述命题中,假命题的个数是A0B1C2D3答案D解析向量是既有大小又有方向的量,a与|a|a0的模相同,但方向不一定相同,故是假命题;若a与a0平行,则a与a0的方向有两种情况一是同向,二是反向,反向时a|a|a0,故也是假命题综上所述,假命题的个数是3.思维升华向量有关概念的关键点1向量定义的关键是方向和长度2非零共线向量的关键是方向相同或相反,长度没有限制3相等向量的关键是方向相同且长度相等4单位向量的关键是长度都是一个单位长度5零向量的关键是长度是0,规定零向量与任何向量共线题型二题型二平面向量的线性运算平面向量的线性运算命题点1向量的线性运算典例1在ABC中,ABc,ACb,若点D满足BD2DC,则AD等于A.23b13cB.53c23bC.23b13cD.13b23c答案A解析BD2DC,ADABBD2DC2ACAD,3AD2ACAB,AD23AC13AB23b13c.2xx青海西宁一模如图,在ABC中,点D在BC 边上,且CD2DB,点E在AD边上,且AD3AE,则用向量AB,AC表示CE为A.29AB89ACB.29AB89ACC.29AB79ACD.29AB79AC答案B解析由平面向量的三角形法则及向量共线的性质可得CEAEAC13ADAC13AB13BCAC13AB13ACABAC29AB89AC.命题点2根据向量线性运算求参数典例1在ABC中,点M,N满足AM2MC,BNNC.若MNxAByAC,则x________,y______.答案1216解析MNMCCN13AC12CB13AC12ABAC12AB16ACxAByAC,x12,y16.2在ABC中,点D在线段BC的延长线上,且BC3CD,点O 在线段CD上与点C,D不重合,若AOxAB1xAC,则x的取值范围是A.0,12B.0,13C.12,0D.13,0答案D解析设COyBC,AOACCOACyBCACyACAByAB1yAC.BC3CD,点O在线段CD上与点C,D不重合,y0,13,AOxAB1xAC,xy,x13,0.思维升华平面向量线性运算问题的常见类型及解题策略1向量加法或减法的几何意义向量加法和减法均适合三角形法则2求已知向量的和一般共起点的向量求和用平行四边形法则;求差用三角形法则;求首尾相连向量的和用三角形法则3求参数问题可以通过研究向量间的关系,通过向量的运算将向量表示出来,进行比较,求参数的值跟踪训练1如图,在正方形ABCD中,点E是DC的中点,点F是BC上的一个靠近点B的三等分点,那么EF等于A.12AB13ADB.14AB12ADC.13AB12DAD.12AB23AD答案D解析在CEF中,有EFECCF.因为点E为DC 的中点,所以EC12DC.因为点F为BC上的一个靠近点B的三等分点,所以CF23CB.所以EF12DC23CB12AB23DA12AB23AD,故选D.2如图,直线EF与平行四边形ABCD的两边AB,AD分别交于E,F两点,且与对角线AC交于点K,其中,AE25AB,AF12AD,AKAC,则的值为______答案29解析AE25AB,AF12AD,AB52AE,AD2AF.由向量加法的平行四边形法则可知,ACABAD,AKACABAD52AE2AF52AE2AF,E,F,K三点共线,5221,29.题型三题型三共线向量定理的应用共线向量定理的应用典例设两个非零向量a与b不共线1若ABab,BC2a8b,CD3ab,求证A,B,D三点共线;2试确定实数k,使kab和akb共线1证明ABab,BC2a8b,CD3ab,BDBCCD2a8b3ab2a8b3a3b5ab5AB,AB,BD共线又它们有公共点B,A,B,D三点共线2解假设kab与akb共线,则存在实数,使kabakb,即kak1b.又a,b是两个不共线的非零向量,kk10.消去,得k210,k1.引申探究若将本例1中“BC2a8b”改为“BCamb”,则m为何值时,A,B,D三点共线解BCCDamb3ab4am3b,即BD4am3b.若A,B,D三点共线,则存在实数,使BDAB.即4am3bab4,m3,解得m7.故当m7时,A,B,D三点共线思维升华1证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系当两向量共线且有公共点时,才能得出三点共线2向量a,b 共线是指存在不全为零的实数1,2,使1a2b0成立,若1a2b0,当且仅当120时成立,则向量a,b不共线跟踪训练1xx资阳模拟已知向量ABa3b,BC5a3b,CD3a3b,则AA,B,C三点共线BA,B,D三点共线CA,C,D三点共线DB,C,D三点共线答案B解析BDBCCD2a6b2a3b2AB,BD,AB共线,又有公共点B,A,B,D三点共线故选B.2已知A,B,C是直线l上不同的三个点,点O不在直线l 上,则使等式x2OAxOBBC0成立的实数x的取值集合为A0BC1D0,1答案C解析BCOCOB,x2OAxOBOCOB0,即OCx2OAx1OB,A,B,C三点共线,x2x11,即x2x0,解得x0或x1.当x0时,x2OAxOBBC0,此时B1,C两点重合,不合题意,舍去故x1.故选C.容易忽视的零向量典例下列叙述错误的是________填序号若非零向量a与b方向相同或相反,则ab与a,b之一的方向相同;|a||b||ab|a与b方向相同;向量b与向量a共线的充要条件是有且只有一个实数,使得ba;ABBA0;若ab,则ab.错解展示中两个向量的和仍是一个向量,所以ABBA0.错误答案现场纠错解析对于,当ab0时,其方向任意,它与a,b的方向都不相同对于,当a,b之一为零向量时结论不成立对于,当a0且b0时,有无数个值;当a0但b0或a0但b0时,不存在对于,由于两个向量之和仍是一个向量,所以ABBA0.对于,当0时,不管a与b的大小与方向如何,都有ab,此时不一定有ab.故均错答案纠错心得在考虑向量共线问题时,要注意考虑零向量.。
高考数学 平面向量的概念及线性运算、平面向量基本定理及坐标表示 高考真题

专题六 平面向量6.1 平面向量的概念及线性运算、平面向量基本定理及坐标表示考点一 平面向量的概念及线性运算1.(2022全国乙文,3,5分)已知向量a =(2,1),b =(-2,4),则|a -b |= ( )A.2B.3C.4D.5答案D 由题意知a -b =(4,-3),所以|a -b |=√42+(−3)2=5,故选D .2.(2022新高考Ⅰ,3,5分)在△ABC 中,点D 在边AB 上,BD =2DA.记CA ⃗⃗⃗⃗⃗ =m ,CD ⃗⃗⃗⃗⃗ =n ,则CB ⃗⃗⃗⃗⃗ = ( )A.3m -2nB.-2m +3nC.3m +2nD.2m +3n答案B 由题意可知,DA ⃗⃗⃗⃗⃗ =CA ⃗⃗⃗⃗⃗ −CD ⃗⃗⃗⃗⃗ =m -n ,又BD =2DA ,所以BD ⃗⃗⃗⃗⃗⃗ =2DA ⃗⃗⃗⃗⃗ =2(m -n ),所以CB ⃗⃗⃗⃗⃗ =CD ⃗⃗⃗⃗⃗ +DB⃗⃗⃗⃗⃗⃗ =n -2(m -n )=3n -2m ,故选B .3.(2015课标Ⅰ理,7,5分)设D 为△ABC 所在平面内一点,BC ⃗⃗⃗⃗ =3CD ⃗⃗⃗⃗ ,则( ) A.AD ⃗⃗⃗⃗ =-13AB ⃗⃗⃗⃗ +43AC ⃗⃗⃗⃗ B.AD ⃗⃗⃗⃗ =13AB ⃗⃗⃗⃗ -43AC ⃗⃗⃗⃗ C.AD⃗⃗⃗⃗ =43AB ⃗⃗⃗⃗ +13AC ⃗⃗⃗⃗ D.AD ⃗⃗⃗⃗ =43AB ⃗⃗⃗⃗ -13AC ⃗⃗⃗⃗ 答案 A AD⃗⃗⃗⃗ =AB ⃗⃗⃗⃗ +BD ⃗⃗⃗⃗ =AB ⃗⃗⃗⃗ +BC ⃗⃗⃗⃗ +CD ⃗⃗⃗⃗ =AB ⃗⃗⃗⃗ +43BC ⃗⃗⃗⃗ =AB ⃗⃗⃗⃗ +43(AC ⃗⃗⃗⃗ -AB ⃗⃗⃗⃗ )=-13AB ⃗⃗⃗⃗ +43AC ⃗⃗⃗⃗ .故选A. 4.(2014课标Ⅰ文,6,5分)设D,E,F 分别为△ABC 的三边BC,CA,AB 的中点,则EB ⃗⃗⃗⃗ +FC ⃗⃗⃗⃗ =( ) A.AD ⃗⃗⃗⃗ B.12AD ⃗⃗⃗⃗ C.BC ⃗⃗⃗⃗ D.12BC⃗⃗⃗⃗ 答案 A 设AB⃗⃗⃗⃗ =a,AC ⃗⃗⃗⃗ =b,则EB ⃗⃗⃗⃗ =-12b+a,FC ⃗⃗⃗⃗ =-12a+b,从而EB ⃗⃗⃗⃗ +FC ⃗⃗⃗⃗ =(−12b +a )+(−12a +b )=12(a+b)=AD ⃗⃗⃗⃗ ,故选A.5.(2015课标Ⅱ理,13,5分)设向量a ,b 不平行,向量λa +b 与a +2b 平行,则实数λ= . 答案12解析 由于a ,b 不平行,所以可以以a ,b 作为一组基底,于是λa +b 与a +2b 平行等价于λ1=12,即λ=12.6.(2015北京理,13,5分)在△ABC 中,点M,N 满足AM⃗⃗⃗⃗⃗ =2MC ⃗⃗⃗⃗⃗ ,BN ⃗⃗⃗⃗ =NC ⃗⃗⃗⃗ .若MN ⃗⃗⃗⃗⃗ =x AB ⃗⃗⃗⃗ +y AC ⃗⃗⃗⃗ ,则x = ,y = .答案12;-16解析 由AM⃗⃗⃗⃗⃗ =2MC ⃗⃗⃗⃗⃗ 知M 为AC 上靠近C 的三等分点,由BN ⃗⃗⃗⃗ =NC ⃗⃗⃗⃗ 知N 为BC 的中点,作出草图如下:则有AN⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗ +AC ⃗⃗⃗⃗ ),所以MN ⃗⃗⃗⃗⃗ =AN ⃗⃗⃗⃗ -AM ⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗ +AC ⃗⃗⃗⃗ )-23·AC ⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗ -16AC ⃗⃗⃗⃗ , 又因为MN ⃗⃗⃗⃗⃗ =x AB ⃗⃗⃗⃗ +y AC⃗⃗⃗⃗ ,所以x=12,y=-16. 7.(2013江苏,10,5分)设D,E 分别是△ABC 的边AB,BC 上的点,AD=12AB,BE=23BC.若DE⃗⃗⃗⃗ =λ1AB ⃗⃗⃗⃗ +λ2AC ⃗⃗⃗⃗ (λ1,λ2为实数),则λ1+λ2的值为 . 答案12解析 DE ⃗⃗⃗⃗ =DB ⃗⃗⃗⃗ +BE ⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗ +23BC ⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗ +23(AC ⃗⃗⃗⃗ -AB ⃗⃗⃗⃗ )=-16AB ⃗⃗⃗⃗ +23AC ⃗⃗⃗⃗ , ∵DE⃗⃗⃗⃗ =λ1AB ⃗⃗⃗⃗ +λ2AC ⃗⃗⃗⃗ ,∴λ1=-16,λ2=23,故λ1+λ2=12. 考点二 平面向量的基本定理及坐标运算1.(2015课标Ⅰ文,2,5分)已知点A(0,1),B(3,2),向量AC⃗⃗⃗⃗ =(-4,-3),则向量BC ⃗⃗⃗⃗ =( ) A.(-7,-4) B.(7,4) C.(-1,4) D.(1,4)答案 A 根据题意得AB ⃗⃗⃗⃗ =(3,1),∴BC ⃗⃗⃗⃗ =AC ⃗⃗⃗⃗ -AB⃗⃗⃗⃗ =(-4,-3)-(3,1)=(-7,-4).故选A. 2.(2014北京文,3,5分)已知向量a =(2,4),b =(-1,1),则2a -b =( ) A.(5,7) B.(5,9) C.(3,7) D.(3,9)答案 A 由a =(2,4)知2a =(4,8),所以2a -b =(4,8)-(-1,1)=(5,7).故选A. 3.(2014广东文,3,5分)已知向量a =(1,2),b =(3,1),则b -a =( ) A.(-2,1) B.(2,-1) C.(2,0) D.(4,3) 答案 B b -a =(3,1)-(1,2)=(2,-1).故答案为B.4.(2014福建理,8,5分)在下列向量组中,可以把向量a =(3,2)表示出来的是( )A.e 1=(0,0),e 2=(1,2)B.e 1=(-1,2),e 2=(5,-2)C.e 1=(3,5),e 2=(6,10)D.e 1=(2,-3),e 2=(-2,3) 答案 B 设a=k 1e 1+k 2e 2,A 选项,∵(3,2)=(k 2,2k 2),∴{k 2=3,2k 2=2,无解.B 选项,∵(3,2)=(-k 1+5k 2,2k 1-2k 2), ∴{−k 1+5k 2=3,2k 1−2k 2=2,解之得{k 1=2,k 2=1. 故B 中的e 1,e 2可把a 表示出来. 同理,C 、D 选项同A 选项,无解.5.(2021全国乙文,13,5分)已知向量a =(2,5),b =(λ,4),若a ∥b ,则λ= .答案85解题指导:利用“若a =(x 1,y 1),b =(x 2,y 2),则a ∥b ⇔x 1y 2=x 2y 1”解题.解析由已知a ∥b 得2×4=5λ,∴λ=85.解题关键:记准两平面向量共线的充要条件是解这类问题的关键.6.(2017山东文,11,5分)已知向量a =(2,6),b =(-1,λ).若a ∥b ,则λ= . 答案 -3解析 本题考查向量平行的条件. ∵a=(2,6),b =(-1,λ),a ∥b , ∴2λ-6×(-1)=0,∴λ=-3.7.(2016课标Ⅱ文,13,5分)已知向量a =(m,4),b =(3,-2),且a ∥b ,则m= . 答案 -6解析 因为a ∥b ,所以m 3=4−2,解得m=-6. 易错警示 容易把两个向量平行与垂直的条件混淆. 评析 本题考查了两个向量平行的充要条件.8.(2014陕西,13,5分)设0<θ<π2,向量a =(sin 2θ,cos θ),b =(cos θ,1),若a ∥b ,则tan θ= . 答案12解析∵a∥b,∴sin 2θ×1-cos2θ=0,∴2sin θcos θ-cos2θ=0,∵0<θ<π2,∴cos θ>0,∴2sin θ=cos θ,∴tan θ=1 2 .。
2023届高考数学复习:历年经典好题专项(平面向量的概念及线性运算)练习(附答案)

A.√3
B.2√3
C.3√3
D.4√3
)
)
10.(多选)设 M 是△ABC 所在平面内一点,则下列说法正确的是(
A.若⃗
1 ⃗
2
1 ⃗
,则
2
⃗
M 是边 BC 的中点
B.若⃗=2⃗
⃗ ,则点 M 在边 BC 的延长线上
C.若⃗=-⃗
⃗,则 M 是△ABC 的重心
1
1
D.若⃗=x⃗+y⃗ ,且 x+y= ,则△MBC 的面积是△ABC 面积的
2
2
1
4
11.(历年山东德州高三模拟)设向量 a,b 不平行,向量 a+ λb 与-a+b 平行.则实数 λ=
.
12.(历年浙江杭州二中高二期中)在等腰梯形 ABCD 中,设⃗=a,⃗=b,⃗ =2⃗,M 为 BC 的中点,则
2
3
1
3
A. a+ b
2
3
1
3
C. a- b
2
3
)
(
)
1
3
B.- a+ b
2
3
1
3
D.- a- b
5.(历年四川宜宾叙州区第一中学月考)在▱ABCD 中,若|⃗
A.▱ABCD 为菱形
(
⃗|=|⃗
⃗|,则必有(
)
B.▱ABCD 为矩形
C.▱ABCD 为正方形 D.▱ABCD 为梯形
6.设 a,b 是非零向量,则“a=2b”是“|a+b|≥|a|+|b|”的
A.充分不必要条件
高考数学一轮总复习 专题5.1 平面向量的概念及线性运算练习(含解析)理

专题5.1 平面向量的概念及线性运算真题回放1.【2017年高考新课标Ⅱ卷文4题】设非零向量a ,b 满足+=-b b a a 则 ( ) A.a ⊥b B. =b a C. a ∥b D. >b a 【答案】A2.【2016年高考山东理8题】已知非零向量m ,n 满足4|m |=3|n |,cos ,m n =13.若n ⊥(t m +n ),则实数t 的值为 (A )4 (B )–4(C )94(D )–94【答案】B【考点】平面向量的数量积【名师点睛】本题主要考查平面向量的数量积、平面向量的坐标运算.解答本题,关键在于能从n ⊥(t m +n )出发,转化成为平面向量的数量积的计算.本题能较好地考查考生转化与化归思想、基本运算能力等.3.【2016年高考北京理4题】设,a b 是向量,则“||||=a b ”是“||||+=-a b a b ”的 (A ) 充分而不必要条件 (B )必要而不充分条件(C ) 充分必要条件 (D )既不充分也不必要条件 【答案】D【考点】充要条件,向量运算【名师点睛】由向量数量积的定义||||cos θ⋅=⋅⋅a b a b (θ为a ,b 的夹角)可知,数量积的值、模的乘积、夹角知二可求一,再考虑到数量积还可以用坐标表示,因此又可以借助坐标进行运算.当然,无论怎样变化,其本质都是对数量积定义的考查.求解夹角与模的题目在近几年高考中出现的频率很高,应熟练掌握其解法. 考点分析融会贯通题型一 平面向量的概念典例1 (2016-2017年河北武邑中学高二文周考)点C 在线段AB上,且,则ACuuu r 等于( )【答案】D【解析】因为点C 在线段AB 上,所以AC uuu r 等于 D.考点:向量的相等. 解题技巧与方法总结平面向量的概念问题需要牢牢抓住平行向量(共线向量)、相等向量、相反向量的概念及特征,需要注意平行向量可以包含两个向量重合的情况,这点需要与直线平行加以区别【变式训练1】(2016-2017学年河北武邑中学高一上学期月考)下列说法正确的是( ) A .零向量没有方向 B .单位向量都相等 C .任何向量的模都是正实数 D .共线向量又叫平行向量 【答案】D考点:向量的概念.【变式训练2】设a r是非零向量,λ是非零实数,下列结论中正确的是( )A .a r 与λa r的方向相反 B .a r 与2λa r 的方向相同 C .|-λa r |≥| a r|D .|-λa r |≥| λ|·a r【答案】B【解析】对于A ,当λ>0时,a r 与λa r 的方向相同,当λ<0时,a r 与λa r的方向相反,B 正确;对于C ,|-λa r |=|-λ|| a r |,由于|-λ|的大小不确定,故|-λa r |与| a r|的大小关系不确定;对于D ,|λ| a r 是向量,而|-λa r|表示长度,两者不能比较大小.【变式训练3】(2015-2016学年江西上饶铅山县一中高一下学期期中)下列关系式正确的是 ( )A. 0AB BA +=uu u r uu r rB. a b ⋅r r是一个向量 C. AB AC BC -=uu u r uuu r uu u r D. 00AB ⋅=uu u r r【答案】D 【解析】试题分析:A 相反向量的和为零向量,所以A 不正确;B 两向量的数量积是一个实数,所以B 不正确;C 根据向量的减法的三角形法则,得CB AC =-AB ,故C 不正确;D 零与任何向量的数量积等等于零向量,故D 正确.考点:平面向量的线性运算;向量的数量积的定义及其性质.1.向量:既有大小又有方向的量叫作向量.向量的大小叫向量的长度(或模).2.几个特殊的向量(1)零向量:长度为零的向量,记作0,其方向是任意的. (2)单位向量:长度等于1个单位长度的向量.(3)平行向量:方向相同或相反的非零向量,平行向量又称为共线向量,规定0与任一向量共线.(4)相等向量:长度相等且方向相同的向量. (5)相反向量:长度相等且方向相反的向量.典例2 (青海省平安县第一高级中学2015~2016课后练习)设向量,a b rr 不平行,向量a b λ+r r 与2a b +r r平行,则实数λ=___________【答案】12考点:向量平行的条件 解题技巧与方法总结(1)证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.(2)向量,a b r r共线是指存在不全为零的实数12,λλ,使120a b λλ+=r r r 成立;若120a b λλ+=r r r ,当且仅当12λλ==0时成立,则向量,a b r r不共线.【变式训练1】(青海省平安县第一高级中学2015~2016课后练习)已知向量i r 与j r不共线,且,,1AB i m j AD ni j m =+=+≠u u u r r r u u u r r r,若,,A B D 三点共线,则实数,m n 满足的条件是( )A. 1m n +=B. 1m n +=-C. 1mn =D. 1mn =-【解析】法一:Q ,,1AB i m j AD ni j m =+=+≠u u u r r r u u u r r r,若,,A B D 三点共线且,,A B D 三点共线所以存在非零实数λ,使AB AD λ=uu u r uuu r即()i m j ni j λ+=+r r r rQ i r 与j r不共线所以1n m λλ=⎧⎨=⎩1n m λλ⎧=⎪⇒⎨⎪=⎩∴1mn =法二:由题可得, AB CD uu u r uu u rP∴AB AD λ=uu u r uuu r∴11m n = ∴1mn =考点:向量共线定理【变式训练2】已知(1,0),(2,1)a b ==r r(1) 当k 为何值时,ka b -r r 与2a b +r r共线?(2) 若23AB a b =+uu u r r r ,BC a mb =+uu u r r r,且,,A B C 三点共线,求m 的值【答案】1-232(2)Q ,,A B C 三点共线AB BC ∴u u u r u u u rP故存在实数λ,使得AB BC λ=uu u r uu u r()23a b a mb λ+=+r r r r∴2λ=,32m =考点:向量的运算法则、共线定理 知识链接:平行向量:方向相同或相反的非零向量,平行向量又称为共线向量,规定0与任一向量共线. 两个向量共线定理:向量b 与非零向量a 共线⇔有且只有一个实数λ,使得b =λa . 题型二 向量的线性运算 命题点1 简单的向量线性运算典例 (吉林省吉林大学附属中学2017届高三第五次摸底考试数学(理))在梯形ABCD 中,3AB DC =uu u r uuu r ,则BC uu u r等于( )【答案】D解题技巧与方法总结(1)解题的关键在于熟练地找出图形中的相等向量,并能熟练运用相反向量将加减法相互转化.(2)用几个基本向量表示某个向量问题的基本技巧: ①观察各向量的位置; ②寻找相应的三角形或多边形; ③运用法则找关系;④化简结果.【变式训练1】(河南省商丘市九校2016-2017学年高一下学期期中)如图12,e e u r u r为互相垂直的单位向量,向量a b c ++r r r可表示为( )A. 1223e e +u r u rB. 1232e e +u r u rC. 1232e e -u r u rD. 1233e e --u r u r【答案】B【解析】 1212122,2,2a e e b e e c e e =+=-=+u r u r u r u r u r u r r r r ,故 1232a b c e e ++=+u r u rr r r .知识链接:平面向量的基本定理如果12,e e u r u r是一个平面内的两个不共线向量,那么对这一平面内的任一向量,有且只有一对实数21,λλ使:1122a e e λλ=+r u r u r 其中不共线的向量12,e e u r u r叫做表示这一平面内所有向量的一组基底【变式训练2】(北京市东城区2017届高三5月综合练习(二模)数学理)设,a b rr 是非零向量,则“,a b rr 共线”是“ )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件 【答案】B命题点2 向量线性运算运用典例 (山东省淄博市临淄中学2016-2017学年高二上学期期末考试数学(理)试题)如图在空间四边形 OABC 中,点M 在OA 上,且 2OM MA = , N 为BC 中点,则MN uuu r等于( )A.121232OA OB OC -+uu ruu u r uuu r B.211322OA OB OC -++uu r uuu r uuu r C.111222OA OB OC +-uu ruu u r uuu r D.221332OA OB OC+-uu ruu u r uuu r【答案】B【名师点睛】进行向量的运算时,要尽可能转化到平行四边形或三角形中,选用从同一点出发的基本量或首尾相接的向量,运用向量的加减运算及数乘来求解,充分利用相等的向量,相反的向量和线段的比例关系,把未知向量转化为与已知向量有直接关系的向量来解决 【变式训练1】如图所示,已知AB 是圆O 的直径,点C ,D 是半圆弧的两个三等分点,AB →=a ,AC →=b ,则AD →=( )A .a -12b B.12a -bC .a +12b D.12a +b【答案】D【解析】连接CD ,由点C ,D 是半圆弧的三等分点,得CD ∥AB 且CD →=12AB →=12a ,所以AD →=AC →+CD →=b +12a .【变式训练2】如图所示,设P 、Q 为△ABC 内的两点,且=+,=+,则△ABP与△ABQ 的面积之比为 .【答案】知识链接:1.向量加法:求两个向量和的运算叫做向量的加法,例AB BC AC +=uu u r uu u r uuu r(1)0+0a a a =+=r r r r r;(2)向量加法满足交换律与结合律;2.向量加法有“三角形法则”与“平行四边形法则”:(1)用平行四边形法则时,两个已知向量是要共始点的,和向量是始点与已知向量的始点重合的那条对角线,而差向量是另一条对角线,方向是从减向量指向被减向量(2) 三角形法则的特点是“首尾相接”,由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和;差向量是从减向量的终点指向被减向量的终点当两个向量的起点公共时,用平行四边形法则;当两向量是首尾连接时,用三角形法则. 向量加法的三角形法则可推广至多个向量相加:AB BC CD PQ QR AR +++++=u u u r u u u r u u u r u u u r u u u r u u u rL ,但这时必须“首尾相连”. 3.向量的减法 :向量a r 加上b r 的相反向量叫做a r 与b r的差,记作:()a b a b -=+-r r r r 求两个向量差的运算,叫做向量的减法4.作图法:a b -r r 可以表示为从b r 的终点指向a r 的终点的向量(a r 、b r有共同起点)命题点3 向量线性运算求参数值或取值范围典例 1(黑龙江省齐齐哈尔市第一中学校2016-2017学年高一3月月考数学(理)试题)已知在ABC ∆中,点在边上,且2,CD DB CD r AB sAC ==+u u u r u u u r u u u r u u u r u u u r,则的值为( ) A. 0 B. D. 3- 【答案】A【解析】分析试题由已知可得:()22223333CD CB AB AC AB AC ==-=-uu u r uu r uu u r uuu r uuu r uuu r ,所以=点睛:向量的线性运算,注意理解加法的三角形法则和平行四边形法则以及减法法则的运用. 【变式训练1】(2013·江苏卷)设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC.若DE →=λ1AB →+λ2AC →(λ1,λ2为实数),则λ1+λ2的值为________.【答案】12【变式训练2】在△ABC 中,M 为边BC 上任意一点,N 为AM 的中点,AN →=λAB →+μAC →,则λ+μ的值为 ( )A. 12B. 13C. 14D .1【答案】A【解析】∵M 为BC 上任意一点,∴可设AM →=x AB →+y AC →(x +y =1).∵N 为AM 的中点,∴AN →=12AM →=12x AB →+12y AC →=λ AB →+μ AC →,∴λ+μ=12(x +y )=12.知识链接:三点共线的性质定理:(1)若平面上三点A 、B 、C 共线,则AB →=λBC →.(2)若平面上三点A 、B 、C 共线,O 为不同于A 、B 、C 的任意一点,则OC →=λOA →+μOB →,且λ+μ=1.典例2【2014届广东省东莞市高三第二次模拟考试】如图所示,A 、B 、C 是圆O 上的三点,CO 的延长线与线段AB 交于圆内一点D ,若OC =uuu r xOA yOB +uu r uu u r,则 ( )A.01x y <+<B.1x y +>C.1x y +<-D.10x y -<+<【答案】C【变式训练】(2014北京东城高三期末)在直角梯形ABCD 中,90,30,2,A B A BB C ∠=︒∠=︒==,点E 在线段CD 上,若AE AD AB μ=+uu u r uuu r uu u r,则实数μ的取值范围是 .【答案】102⎡⎤⎢⎥⎣⎦, 【解析】由题意可求得1,AD CD ==2AB DC =uu u r uuu r.因为点E 在线段CD 上,所以DE DC λ=uuu r uuu r(01λ≤≤).因为AE AD DE =+uu u r uuu r uuu r ,又AE AD AB μ=+uu u r uuu r uu u r =2AD DC μ+u u u r u u u r =2AD DE μλ+uuur uuu r ,所以2μλ=1,即μ=2λ.因为0≤λ≤1,所以0≤μ≤12.知识交汇例1 如图,经过△OAB 的重心G 的直线与OA ,OB 分别交于点P ,Q ,设OP →=mOA →,OQ →=nOB →,m ,n ∈R ,则1n +1m的值为________.【答案】3【交汇技巧】本题将向量的共线定理与三角形重心的性质进行结合,三角形重心是三条边中线的交点,另外本题还结合了方程思想,通过消去λ得到m ,n 之间的关系例2 已知点O 为△ABC 外接圆的圆心,且0OA OB CO ++=uu r uu u r uu u r r,则△ABC 的内角A 等于( )A .30°B .60°C .90°D .120°【答案】A【解析】 由0OA OB CO ++=uu r uu u r uu u r r 得OA OB OC +=uu r uu u r uuu r,由O 为△ABC 外接圆的圆心,结合向量加法的几何意义知四边形OACB 为菱形,且∠CAO =60°,故A =30°.【交汇技巧】三角形外接圆的圆心是三角形三条边垂直平分线的交点,到三个顶点距离相等,结合0OA OB CO ++=uu r uu u r uu u r r可得四边形OACB 为平行四边形的条件,得出四边形OACB 为菱形,从而求出角A 的大小 练习检测1.【山东省淄博实验中学2015届高三第一学期第一次诊断考试试题,文10】在ABC ∆中,点,M N 分别是,AB AC 上,且32,5AM MB AN AC ==uuu r uuu r uuu r uuu r,线段CM 与BM 相交于点P ,且,AB a AC b ==u u u r r u u u r r,则AP uu u r 用a r 和b r 表示为( )A .4193AP a b =+uu u r r rB .4293AP a b =+uu u r r rC . 2493AP a b =+uu u r r rD .4377AP a b =+uu u r r r【答案】A2.(江西省南昌市重点学校2016-2017学年高一4月检测)已知ABC ∆的边BC 上有一点D 满足3BD DC =uu u r uuu r ,则AD uuu r可表示为( )A. 23AD AB AC =-+uuu r uu u r uuu rB.【答案】C【解析】如图所示,3.(2015届北京市156中学高三上学期期中考试理科)如图,向量b a -等于( )(A )2124e e -- (B )2142e e --(C )213e e - (D )213e e - 【答案】C点评:12,e e u r u r 是两个单位向量,从图上将,a b r r用单位向量表示出来4.已知点O ,A ,B 不在同一条直线上,点P 为该平面上一点,且2OP →=2OA →+BA →,则 ( )A .点P 在线段AB 上B .点P 在线段AB 的反向延长线上C .点P 在线段AB 的延长线上D .点P 不在直线AB 上 【答案】B【解析】因为2OP →=2OA →+BA →,所以2AP →=BA →,所以点P 在线段AB 的反向延长线上,故选B. 5.(2016-2017学年天津市静海县第一中学高二上学期期末五校联考理)如图,在三棱柱111ABC A B C -中,M 为11A C 的中点,若1,,AB a BC b AA c ===uu u r r uu u r r uuu r r,则BM uuu r 可表示为( )A. 1122a b c -++r r rB. 1122a b c ++r r rC. 1122a b c --+r r rD. 1122a b c -+r r r【答案】A【解析】()111222BN BA BC a b =+=-+uuu r uu r uu u r r r Q1122BM BN NM a b c ∴=+=-++uuu r uuu r uuur r r r,故本题正确答案为A6.(江西省赣州市十四县(市)2017届高三下学期期中联考(理))如图,平行四边形ABCD的两条对角线相交于点O ,点E , F 分别在边AB , AD 上,直线EF 交AC 于点K , AK AO λ=uuu r,则λ等于( )【答案】C7.在△ABC 中,E ,F 分别为AC ,AB 的中点,BE 与CF 相交于G 点,设AB →=a ,AC →=b ,试用a ,b 表示AG →.8.设点O 在ABC V 内部,且有40OA OB OC ++=uu r uu u r uuu r r,求△ABC 的面积与△OBC 的面积之比.【答案】S △ABC ∶S △OBC =3∶2.【解析】取BC 的中点D,连接OD,则+=2,4++=0,∴4=-(+)=-2,∴=-.∴O 、A 、D 三点共线,且||=2||,∴O 是中线AD 上靠近A 点的一个三等分点, ∴S △ABC ∶S △OBC =3∶2.9.在任意四边形ABCD 中,E 是AD 的中点,F 是BC 中点,求证:()1=+2EF AB DC uu u r uu u r uuu r法二:连接EB EC uu r uu u r , 则=+EC ED DC uu u r uu u r uuu r()()11==+++=22EF EC EB ED DC EA AB +uu u r uu u r uu r uu u r uuu r uu r uu u r ()1+2AB DC uuu r uuu r。
新高考数学(理)之平面向量 专题01 平面向量的概念及线性运算(解析版)

新高考数学(理)平面向量01平面向量的概念及线性运算【考点讲解】一、具本目标:1.平面向量的实际背景及基本概念(1)了解向量的实际背景.(2)理解平面向量的概念和两个向量相等的含义.(3)理解向量的几何表示.2.向量的线性运算(1)掌握向量加法、减法的运算,并理解其几何意义.(2)掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.(3)了解向量线性运算的性质及其几何意义.备考情况:1.以考查向量的线性运算、共线为主,主要是在理解含义的基础上,进一步解题,比如利用向量的线性运算求参数.2.单独考查平面向量的实际背景及基本概念的题目极少.3.备考重点:(1) 理解相关概念是基础,掌握线性运算的方法是关键;(2) 注意与平面几何、三角函数、解析几何等交汇问题,注意运用数形结合的思想方法.二、知识概述:1.向量的概念1.向量:既有大小又有方向的量叫向量;向量的大小叫做向量的模.2.零向量:长度等于0的向量,其方向是任意的.3.单位向量:长度等于1个单位的向量.4.平行向量:方向相同或相反的非零向量,又叫共线向量,规定:0与任一向量共线.5.相等向量:长度相等且方向相同的向量.6.相反向量:长度相等且方向相反的向量.2.平面向量的线性运算一.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算三角形法则平行四边形法则交换律:abba+=+结合律:()()c bacba++=++减法求a与b的相反向量-b的和的运算叫做a与b的差三角形法则二.向量的数乘运算及其几何意义1.定义:实数λ与向量a 的积是一个向量,这种运算叫向量的数乘,记作λa ,它的长度与方向规定如下: ①|λa |=|λ||a |;②当λ>0时,λa 的方向与a 的方向相同;当λ<0时,λa 的方向与a 的方向相反;当λ=0时,λa =0. 2.运算律:设λ,μ是两个实数,则:①()()a a λμλμ=;②() a a a λμλμ+=+;③()a b a b λλλ+=+.3.向量共线定理:如果有一个实数λ,使()0λ≠r r r r=ba a ,那么rb 与r a 是共线向量; 反之,如果r b 与r a ()0≠r r a 是共线向量,那么有且只有一个实数λ,使λr r=ba . 4.三点共线的性质定理:(1)若平面上三点、、A B C 共线,则AB →=λBC →.(2)若平面上三点A B C 、、共线,O 为不同于A B C 、、的任意一点,则OC →=λOA →+μOB →,且λμ+=1. 【温馨提示】(1)如果两个向量起点相同,终点相同,那么这两个向量相等;但两个相等向量,不一定有相同的起点和终点.(2)零向量和单位向量是两个特殊的向量.它们的模确定,但方向不确定.. (3)两个重要的结论:①向量相等具有传递性,非零向量的平行具有传递性; ②向量可以平移,平移后的向量与原向量是相等向量.1.【2019年高考全国II 卷文数】已知向量a =(2,3),b =(3,2),则|a -b |=( ) A .2B .2C .52D .50【解析】由已知,(2,3)(3,2)(1,1)-=-=-a b ,所以22||(1)12-=-+=a b ,故选A. 【答案】A2.【2018年全国理Ⅰ】在中,为边上的中线,为的中点,则( )A .B .C .D .【解析】本题考点是向量的和及向量的线性运算,由题意可知:AD EB21=,()AC AB AD +=21.所以有()⎪⎭⎫ ⎝⎛+-=-=-=AC AB AB AD AB AE AB EB 212121=AC AB 4143-=.【答案】A3.【2017年高考全国II 卷文数】设非零向量a ,b 满足+=-a b a b ,则( )A .a ⊥bB .=a bC .a ∥bD .>a b【解析】由向量加法与减法的几何意义可知,以非零向量a ,b 的模长为边长的平行四边形是矩形,从而可得a ⊥b .故选A. 【答案】A4.【2017年高考北京卷文数】设m ,n 为非零向量,则“存在负数λ,使得λ=m n ”是“0<⋅m n ”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件ABC △AD BC E AD EB =u u u r3144AB AC -u u ur u u u r 1344AB AC -u u ur u u u r 3144AB AC +u u ur u u u r 1344AB AC +u u ur u u u r 【真题分析】【解析】若0λ∃<,使λ=m n ,则两向量,m n 反向,夹角是180︒, 那么cos180⋅=︒=m n m n 0-<m n ;若0⋅<m n ,那么两向量的夹角为(]90,180︒︒,并不一定反向,即不一定存在负数λ,使得λ=m n ,所以是充分而不必要条件,故选A. 【答案】A5.【2019优选题】设向量()()6,4,2x b a ==与向量)共线,则实数x =( )A.2B.3C.4D.6【解析】本题考点是向量的坐标表示以及向量共线的性质的应用,因为两向量平行,所以有, 有2∶4=x ∶6,解得x =3,选B. 【答案】B6. 【2019优选题】设D ,E ,F 分别为△ABC 的三边BC ,CA ,AB 的中点,则EB FC +=u u u r u u u r( ). A .AD u u u r B .12AD u u u r C .BC uuu r D .12BC uuur【解析】本题的考点是平面向量的加法、减法法则,线段中点的性质,考查转化能力,用向量法表示三角形中线的性质要引起重视,由题意可知D ,E ,F 分别是BC ,CA ,AB 的中点,所以有以下结论:()()1122EB FC BA BC CA CB +=-+-+u u u r u u u r u u u r u u u r u u u r u u u r ()()1112222BA CA AB AC AD AD =-+=+=⨯=u u u r u u u r u u u r u u u r u u ur u u u r ,故选A.【答案】A7. 【2019优选题】设D 为∆ABC 中BC 边上的中点,且O 为AD 边上靠近点A 的三等分点,则( )A. 5166BO AB AC =-+u u u r u u ur u u u r B . 1162BO AB AC =-u u u r u u u r u u u rC. 5166BO AB AC =-u u u r u u u r u u u rD. 1162BO AB AC =-+u u u r u u ur u u u r【解析】本题考点是平面向量的加减法运算法则,由题意可知在三角形BAO 中:()11513666BO AO AB AD AB AB AC AB AB AC =-=-=+-=-+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r ,故选A.【答案】A8. 【2019优选题】在平行四边形ABCD 中,a AB=,b AC =,EC DE 2=,则=BE ()A .a b 31-B .a b 32-C .a b 34-D .a b 31+【解析】因为AB DE AD AB AE BE-+=-=,所以AB AB AB AC AB AB BC BE -+-=-+=3232=a b 34-,故选C . 【答案】C9. 【2019优选题】设D 为ABC ∆所在平面内一点3BC CD =u u u r u u u r,则( )A.1433AD AB AC =-+u u u r u u ur u u u r B.1433AD AB AC =-u u u r u u u r u u u rC.4133AD AB AC =+u u u u u r u u u r u u u rD.4133AD AB AC =-u u u u u u u ru u u r u u u r【解析】本题考点是向量的线性运算,由题意可知11()33AD AC CD AC BC AC AC AB =+=+=+-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r =1433AB AC -+u u ur u u u r ,故选A.【答案】A10.【2017年高考山东卷文数】已知向量a =(2,6),b =(1,)λ- ,若∥a b ,则λ=________. 【解析】由∥a b 可得162 3.λλ-⨯=⇒=- 【答案】3-11.【2018年高考全国III 卷】已知向量()=1,2a ,()=2,2-b ,()=1,λc .若()2∥c a +b ,则λ=___________. 【解析】由题可得()24,2+=a b ,()2Q ∥c a +b ,()=1,λc ,420λ∴-=,即12λ=,故答案为12. 【答案】1212.【2019优选题】已知O A B ,,是不共线的三点,且OP →=m OA →+n OB →(m n ∈R ,). (1)若m n +=1,求证:A P B ,,三点共线; (2)若A P B ,,三点共线,求证:m n +=1. 【证明】 (1)若m n +=1,则OP →=m OA →+(1m -)OB →=OB →+m (OA →-OB →),∴OP →-OB →=m (OA →-OB →), 即BP →=m BA →,∴BP →与BA →共线.又∵BP →与BA →有公共点B ,则A P B ,,三点共线. (2)若A P B ,,三点共线,则存在实数λ,使BP →=λBA →, ∴OP →-OB →=λ(OA →-OB →).又OP →=m OA →+n OB →.故有m OA →+(n -1)OB →=λOA →-λOB →, 即(m λ-)OA →+(1n λ+-)OB →=0r. ∵O A B ,,不共线,∴OA →,OB →不共线,∴⎩⎪⎨⎪⎧m -λ=0,n +λ-1=0,∴m n +=1.1.设M 为□ABCD 对角线的交点,O 为□ABCD 所在平面内任意一点,则OA OB OC OD +++u u u r u u u r u u u r u u u r等于 ( )A.OMB.OM 2C.OM 3D.OM 4 【解析】本题的考点是平面向量的线性运算,相反向量的和向量是零向量.由已知得,1111,,,,2222OA OM CA OB OM DB OC OM AC OD OM BD =+=+=+=+u u u r u u u u r u u u r u u u r u u u u r u u u r u u u r u u u u r u u u r u u u r u u u u r u u u r而,,CA AC DB BD =-=-u u u r u u u r u u u r u u u r所以4OA OB OC OD OM +++=u u u r u u u r u u u r u u u r u u u u r .【答案】D2.设D 为ABC ∆所在平面内一点3BC CD =u u u r u u u r,则( )(A )1433AD AB AC =-+u u u r u u ur u u u r (B)1433AD AB AC =-u u u r u u u r u u u r(C )4133AD AB AC =+u u u u u r u u u r u u u r (D)4133AD AB AC =-u u u u u u u ru u u r u u u r【解析】本题考点是平面向量的线性运算,由题知11()33AD AC CD AC BC AC AC AB =+=+=+-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r =1433AB AC -+u u ur u u u r ,故选A【答案】A3.已知O 为ABC ∆所在平面内一点且满足:230OA OB OC ++=u u u r u u u r u u u r r,则AOB ∆与AOC ∆的面积之比为( ) A .1 B.32 C. 23D .2 【模拟考场】【错解】 据题意O 为ABC ∆的重心,从而OAB OAC OBC S S S ∆∆∆==∴AOB ∆与AOC ∆的面积之比为1,选A .【正解】∵230OA OB OC ++=u u u r u u u r u u u r r,令2,3,OB OB OC OC ''==u u u r u u u r u u u u r u u u r所以0OA OB OC ''++=u u u r u u u r u u u u r r,则O 为AB C ''∆的重心,从而:OAB OAC OB C S S S S ''''∆∆∆===,∴12OAB S S ∆=, 13OAC S S ∆=, ∴AOB ∆的面积与AOC ∆的面积之比为3:2.【答案】B4.设a r ,b r是非零向量,“a b a b ⋅=r r r r ”是“//a b r r ”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【解析】||||cos ,a b a b a b •=•<>r r r r r r ,由已知得cos ,1a b <>=r r ,即,0a b <>=r r ,//a b r r .而当//a b rr 时,,a b <>r r 还可能是π,此时||||a b a b •=-r r r r ,故“a b a b ⋅=r rr r ”是“//a b r r ”的充分而不必要条件,故选A . 【答案】A5.如图,在正方形ABCD 中,点E 是DC 的中点,点F 是BC 的一个三等分点,那么EF =( )A .AD AB 3121- B .AD AB 2141+ C .AD AB 2131+ D .AD AB 3221- 【解析】在CEF ∆中,CFEC EF+=,点E 是DC 的中点,有DC EC21=,又因为F 点是BC 的一个三等分点,所以有CB CF32=, 所以有AD AB DA AB CB DC EF322132213221-=+=+=.【答案】D 6.如图,正方形ABCD 中,E 为DC 的中点,若,则的值为( )EA BCDA .B .C .D .【解析】因为E 是DC 的中点,所以1()2AE AC AD =+u u u r u u u r u u u r,∴2AD AC AE =-+u u u r u u u r u u u r ,∴1,2λμ=-=,123λμ-=--=-. 【答案】D7.已知向量a 与b 不共线,且b a AB+=λ,b a AC μ+=,则点A ,B ,C 三点共线应满足 ()A .=2λμ+B .=1λμ-C .λμ=-1D .λμ=1【解析】若A ,B ,C 三点共线,则AC k AB =,即b a +λ()b a k μ+=,所以b a +λb k a k μ+=,所以λ=k ,1=μk ,故λμ=1. 【答案】D8.在ABC △中,点M ,N 满足2AM MC =u u u u r u u u u r ,BN NC =u u u r u u u r .若MN x AB y AC =+u u u u r u u u r u u u r,则x = ;y = .【解析】法一:在三角形ABC 中有AC AB CB -=,在三角形CMN 中,有CN MC MN +=,并且有2AM MC =u u u u r u u u u r ,=u u u r u u u rBN NC ,所以有AD AC AE λμ=+u u u r u u u r u u u rλμ-3213-()AC AB AC AB AC CB AC MN 612121312131-=-+=+=,.6121AC AB AC y AB x MN -=-=所以有.61,21-==y x【答案】.61,21-法二:特殊化,不妨设3,4,==⊥AC AB AB AC,利用坐标法,以A 为原点,AB 为x 轴,AC 为y 轴,建立直角坐标系,()()()()⎪⎭⎫⎝⎛23,2,0,4,3,0,2,0,0,0N B C M A ,()(),3,0,0,4,21,2==⎪⎭⎫ ⎝⎛=AC AB MN ,则()()3,00,4212y x +=⎪⎭⎫ ⎝⎛-,,.61,21,213,24-==-==y x y x .【答案】.61,21-9.直线l 过Y ABCD 的两条对角线AC 与BD 的交点O ,与AD 边交于点N ,与AB 的延长线交于点M .又知AB u u u r = m AM u u u u r ,AD u u ur =n AN ,则m n += .【解析】据题意,点O 为BD 的中点.1()2AO AB AD ∴=+u u u r u u u r u u u rQ AB u u u r = m AM u u u u r ,AD u u ur =n AN1()222m n AO mAM nAN AM AN ∴=+=+u u u r u u u u r u u u r u u u ur u u u r又,,M O N Q 三点共线,∴由平面内三点共线的向量式定理可得:122m n+= 2m n ∴+=.【答案】2 10.设向量a r ,b r 不平行,向量a b λ+r r 与2a b +r r平行,则实数λ=_________.【解析】因为向量a b λ+r r 与2a b +r r 平行,所以2a b k a b λ+=+r r r r (),则12,k k λ=⎧⎨=⎩,所以12λ=.【答案】1211.如图,经过OAB ∆的重心G 的直线与OA OB ,分别交于点P Q ,,设OP →=m OA →,OQ →=n OB →,m n ∈R ,,则1n +1m 的值为________. 【解析】 设OA →=a ,OB →=b , 由题意知OG →=23×12(OA →+OB →)=13(+a b ), PQ →=OQ →-OP →=n m b a -,PG →=OG →-OP →=(13-m )a +13b , 由P G Q 、、三点共线得,存在实数λ,使得PQ →=λPG →,即n m b a -=λ(13-m )a +13λb , 从而 1()313m m n λλ⎧-=-⎪⎪⎨⎪=⎪⎩消去λ得1n +1m =3. 12.已知椭圆的中心在原点,离心率为,一个焦点(,0)F m - (m 是大于0的常数).(1)求椭圆的方程; (2)设Q 是椭圆上的一点,且过点F Q 、的直线l 与y 轴交于点M ,若2MQ QF =u u u u r u u u r ,求直线l 的斜率.解:(1)设所求椭圆方程为22221(0)x y a b a b+=>>, 由已知得1,,2,32c c m a m b m a ==∴==, 故所求的椭圆方程是2222143x y m m+=. (2)设00(,)Q x y ,直线l 的方程为() y k x m =+,则点()0M km ,,由已知得F Q M 、、三点共线,且 2MQ QF =u u u u r u u u r ,∴2MQ QF =±u u u u r u u u r .当2MQ QF =u u u u r u u u r 时,由于()0F m -,,()0M km ,,由定比分点坐标公式,得21,33Q Q x m y km =-=又Q 在椭圆2222143x y m m +=上,∴有211927k +=,解得26k =±;21。
第1讲 平面向量的概念及线性运算4种题型(解析版)

第1讲 平面向量的概念及线性运算4种题型【考点分析】考点一:向量的基本概念①定义:既有大小又有方向的量叫做向量.②向量的模:向量AB 的大小,也就是向量AB 的长度,叫做向量的模,记作||AB . ③零向量:长度为0的向量,其方向是任意的. ④单位向量:长度等于1个单位的向量.⑤平行向量:方向相同或相反的非零向量.平行向量又叫共线向量.规定:0与任一向量平行. ⑥相等向量:长度相等且方向相同的向量. ⑦相反向量:长度相等且方向相反的向量. 考点二:向量的线性运算和向量共线定理 ①向量的线性运算考点三:向量共线定理①如果λ=a b 且0≠b ,则a b ∥;反之a b ∥且0≠b ,则一定存在唯一一个实数λ,使λ=a b . 推论:①三点A ,B ,C 共线⇔AB ,AC 共线(功能:证明三点共线);①向量PA ,PB ,PC 中三个向量的终点A ,B ,C 共线⇔存在实数λ,μ使得PA PB PC λμ=+,且1.λμ+=①BD DC λ=,111AD AC AC λλλ=+++. 【题型目录】题型一: 平面向量的概念 题型二: 平面向量的加法、减法 题型三: 平面向量的线性运算与共线定理 题型四: 由平面向量的性质判断图形的形状 【典型例题】题型一: 平面向量的概念【例1】给出下列说法:①零向量是没有方向的;①零向量的长度为0;①零向量的方向是任意的;①单位向量的模都相等.其中正确的有( ) A .1个 B .2个C .3个D .4个【答案】C【分析】根据零向量及单位向量的概念即可求解. 【详解】解:对①:零向量的方向是任意的,故①错误; 对①:零向量的长度为0,故①正确; 对①:零向量的方向是任意的,故①正确; 对①:单位向量的模都等于1,故①正确. 故选:C.【例2】下列命题中正确的是( )A .两个有共同起点且相等的向量,其终点必相同B .两个有公共终点的向量,一定是共线向量C .两个有共同起点且共线的向量,其终点必相同D .若AB 与CD 是共线向量,则点A ,B ,C ,D 必在同一条直线上 【答案】A【分析】根据向量相等与共线的概念即可解决.【详解】两个相等的向量方向相同且长度相等,因此起点相同时终点必相同,故A 正确; 两个有公共终点的向量,可能方向不同,也可能模长不同,故B 错误;两个有共同起点且共线的向量可能方向不同,也可能模长不同,终点未必相同,故C 错误;AB 与CD 是共线向量,也可能是AB 平行于CD ,故D 错误.故选:A【例3】有下列结论:①表示两个相等向量的有向线段,若它们的起点相同,则终点也相同; ①若a b ≠,则a ,b 不是共线向量;①若AB DC =,则四边形ABCD 是平行四边形; ①若m n =,n k =,则m k =;①有向线段就是向量,向量就是有向线段. 其中,错误的个数是( ) A .2 B .3C .4D .5,若a b ≠也有可能a ,b 长度不等,但方向相同或相反,即共线,AB DC =,则AB ,DC 不一定相等,所以四边形,若m n =,n k =,则m k =,①正确;,有向线段不是向量,向量可以用有向线段表示,综上,错误的是①①①,共3个. 【例4】设0a 为单位向量,①若a 为平面内的某个向量,则a =|a |0a ;②若a 与0a 平行,则a =|a |0a ;③若a 与0a 平行且|a |=1,则a =0a .上述命题中,假命题的个数是A .0B .1C .2D .3 【答案】D【详解】单位向量的模为1,方向可以是不同方向,所以①错 ;若a 与0a 平行,则两个向量可以同向,也可以反向,方向不一定相同,所以①错;①错因此选D 【例5】下列命题中,正确的个数是( )①单位向量都相等;①模相等的两个平行向量是相等向量; ①若,a b 满足||||a b >,且a 与b 同向,则a b >①若两个向量相等,则它们的起点和终点分别重合; ①若,a b b c ∥∥,则a c ∥ A .0个 B .1个C .2个D .3个【答案】A【分析】根据平面向量的基本概念,对选项中的命题进行分析、判断正误即可. 【详解】单位向量的大小相等,但方向不一定相同,故①错误; 模相等的两个平行向量是相等向量或相反向量,故①错误; 向量有方向,不能比较大小,故①错误;向量是可以自由平移的矢量,当两个向量相等时,它们的起点与终点不一定相同,故①错误; 当0b =时,可满足,a b b c ∥∥,但a 与c 不一定平行,故①错误; 综上,正确的个数是0, 故选:A .【例6】下面关于向量的说法正确的是( ) A .单位向量:模为1的向量B .零向量:模为0的向量,零向量没有方向C .平行(共线)向量:方向相同或相反的向量D .相等向量:模相等,方向相同的向量 【答案】ACD【分析】根据平面向量的基本定义逐个辨析即可.【详解】根据向量的定义可得,模为1的向量为单位向量,模为0的向量为零向量,零向量的方向是任意的,方向相同或相反的向量为共线向量,模相等,方向相同的向量为相等向量,ABCD 均正确, 故选:ACD .【例7】下列叙述中错误的是( ) A .若a b =,则32a b > B .若a b ∥,则a 与b 的方向相同或相反 C .若a b ∥,b c ∥,则a c ∥ D .对任一非零向量a ,||aa 是一个单位向量 【答案】ABC【分析】对于A ,根据向量的概念判断,对于BCD ,举例判断.【详解】因为是既有大小又有方向的量,所以向量不能比较大小,故A 错误;由于零向量与任意向量共线,且零向量的方向是任意的,故,若b 为零向量,则a 与c 可能不是共线向量,故,对任一非零向量a ,||aa 表示与a ABC 【题型专练】1.下列命题正确的是( )A .向量AB 与BA 是相等向量 B .共线的单位向量是相等向量C .零向量与任一向量共线D .两平行向量所在直线平行 【答案】C【详解】A 选项方向不同,所以错 ;B 选项共线向量是方向相同或者相反,所以错;C 选项,规定零向量的方向是任意的,所以C 对;D 选项向量共线可以在一条直线上,直线平行不能共线,所以D 错 2.下列命题中正确的个数是( )①若向量AB 与CD 是共线向量,则A 、B 、C 、D 必在同一直线上; ①若向量a 与向量b 平行,则a ,b 方向相同或相反;①若非零向量AB 与CD 是共线向量,则它们的夹角是0°或180°; ①若a b =,则a ,b 是相等向量或相反向量. A .0 B .1C .2D .3,根据模长的定义,可知方向不确定,可得答案.【详解】①错误,平行向量又叫共线向量,向量AB 与CD 是共线向量,则AB 与CD 平行或共线;错误,a 与b 至少有一个为零向量时,结论不成立;由向量的夹角可知正确; 错误,由a b =,只能说明a ,b 的长度相等,确定不了方向.3.给出下列命题:①共线向量一定在同一条直线上;①若A ,B ,C ,D 是不共线的四点,则AB DC =是四边形ABCD 为平行四边形的充要条件;①a b =的充要条件是||a b |=|且//a b .其中正确命题的序号是_______.【答案】①【详解】①不正确,共线向量不一定在同一条直线上,也可能在两条平行直线上; ①正确 ①AB DC =,①||||AB DC =且//AB DC , 又A ,B ,C ,D 是不共线的四点, ①四边形ABCD 为平行四边形.反之,若四边形ABCD 为平行四边形,则//AB DC 且||||AB DC =,①AB DC =;①不正确,当//a b 且方向相反时,||||a b =,但不能得到a b =,故||||a b =且//a b 不是a b =的充要条件,而是必要不充分条件. 故答案为:①4.把所有单位向量的起点平移到一点O ,则其终点构成的图形是_____________. 【答案】以O 为圆心的单位圆设终点为A ,则1AO =,则终点构成的图形是以O 为圆心的单位圆. 故答案为:以O 为圆心的单位圆. 5.下列说法中正确的是( ) A .若12,e e 为单位向量,则12e e = B .若a 与b 共线,则a b =或a b =-C .若0a =,则0a =D .a a是与非零向量a 共线的单位向量中,向量12,e e 的方向不一定相同,所以中,向量a 与b 的长度不一定相等,所以0a =,根据零向量的定义,可得0a =,所以C 1a a a a =⋅,可得a a与向量a 同向,a a的模等于a a是与非零向量a 共线的单位向量,所以故选:CD.6.下列说法中正确的是( )A .力是既有大小,又有方向的量,所以是向量B .若向量//AB CD ,则//AB CDC .在四边形ABCD 中,若向量//AB CD ,则该四边形为平行四边形 D .速度、加速度与位移的合成与分解,实质上就是向量的加减法运算 【答案】AD【分析】根据向量的定义,共线向量的定义,逐项判定,即可求解.【详解】对于A 中,根据向量的定义,力是既有大小,又有方向的量,所以是向量,所以A 正确; 对于B 中,向量//AB CD ,则//AB CD 或AB 与CD 共线,所以B 错误;对于C 中,在四边形ABCD 中,若向量//AB CD 、则只有一组对边平行,不一定是平行四边形,所以C 错误;对于D 中,根据向量的运算法则,可得速度、加速度与位移的合成与分解,实质上就是向量的加减法运算,所以D 正确. 故选:AD.7.下列结论中正确的是( ) A .若a b =,则a b = B .若,a b b c ==,则a c =C .若A ,B ,C ,D 是不共线的四点,则“AB DC =”是“四边形ABCD 为平行四边形”的充要条件 D .“a b =”的充要条件是“a b =且a b ∥” 是不共线的四点,则当AB DC =时,,故且,AB DC 同向,故AB DC =,故C ,当a b 且方向相反时,即使a b =,也不能得到a b =,故D 错误;8.下列结论中正确的是( ) A .a 与b 是否相等与a ,b 的方向无关 B .零向量相等,零向量的相反向量是零向量 C .若a ,b 都是单位向量,则a b = D .向量AB 与BA 相等【答案】AB【分析】由向量的模、零向量、单位向量、相等向量的定义判断各选项.【详解】对于C ,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等;对于D ,向量AB 与BA 互为相反向量,由向量模的定义,零向量的定义AB 正确. 故选:AB .题型二: 平面向量的加法、减法【例1】AO OB OC CA BO ++++等于( )A .AB B .0C .BCD .AC【答案】B【分析】根据平面向量加法的运算律计算可得; 【详解】解:AO OB OC CA BO ++++ ()()AO OC CA BO OB =++++000=+=故选:B【例2】化简下列各式: (1)AO OB CA CB ++-; (2)MN MD NQ DQ -+-.【答案】(1)0;(2)0【分析】(1)由向量的加法法则与减法法则求解即可; (2)由向量的加法法则与减法法则求解即可;(1)()()AO OB CA CB AO OB CA CB ++-=++-0AB BA =+=;(2)()()MN MD NQ DQ MN MD NQ QD -+-=-++0DN ND =+= 【例3】正方形ABCD 的边长为1,则AB AD +为( ) A.1 BC .3D .根据向量加法的平行四边形法则,AB AD AC +=, 212AB A AD C +==,故选:B.【例4】在ABC 中,M 是BC 的中点,则AB AC +等于( ) A .12AM B .AM C .2AM D .MA【答案】C【分析】根据向量的加法法则计算.【详解】如图,作平行四边形ABEC ,因为M 是BC 的中点,所以M 也是AE 的中点,则2AB AC AE AM +==. 故选:C.【例5】如图为正八边形ABCDEFGH ,其中O 为正八边形的中心,则OC HG FH ++=( )A .OB B .ODC .OFD .OH【答案】A【分析】根据平面向量的概念及加法的运算法则,准确运算,即可求解.【详解】由平面向量的运算法则,可得OC HG FH OC FG OC CB OB ++=+=+=. 故选:A.【例6】设M 是平行四边形ABCD 的对角线的交点,O 为平面上任意一点,则OA OB OC OD +++=( ) A .4OM B .3OM C .2OM D .OM【分析】分别在OAC 和OBD 【详解】解:在OAC 所以1()2OM OA OC =+,即2OA OC OM +=.在OBD 中,因为M 是平行四边形ABCD 的对角线的交点,所以1()2OM OB OD =+,即2OB OD OM +=. 所以4OA OB OC OD OM +++=. 故选:A .【例7】若74AB AC ==,,则BC 的取值范围是( )A .[3,7]B .()37,C .[]311, D .(311), 【分析】根据向量的减法的几何意义,确定向量,AC AB 共线时取得最值,即可求得答案74AB AC ==,,且||BC AC AB -=,当,AC AB 同向时,BC 取得最小值,|||||||4||BC AC AB AC AB ===---当,AC AB 反向时,BC 取得最大值,|||||||||4BC AC AB AC AB -+===+当,AC AB 不共线时,BC 取得最小值,3||||||||||1||||1AC AB BC AC AB =<-<+=,BC 的取值范围是[]311,, 故选:C【例8】已知ABC 为正三角形,则下列各式中成立的是___________.(填序号)AC AB =-①AB CA BC AB -=-;①AB CA CA BC -=-;①CA BC AB AC -=-. AB AC CB BC -==,故①分别为,,AB BC AC 的中点,32AB , 23AB CA AB AC AE AB -=+==, 23BC AB BC BA BF BA -=+==,所以AB CA BC AB -=-,故①成立;对于①,23CA BC CA CB CD AB -=+==, 所以AB CA CA BC -=-,故①正确;①,AB AC CB AB CA BC -==≠-,故①不成立故答案为:①①①.【题型专练】1.32AB BC AC +-=( ) A .AB AC + B .AB AC - C .AB D .BA【答案】A【分析】根据向量的运算法则,准确化简,即可求解.【详解】由向量的运算法则,可得3222AB BC AC AB BC AB AC +-=++- 2AC CB AB AC =+=+.故选:A.2.下列能化简为PQ 的是( ) A .QC QP CQ -+ B .()AB PA BQ ++C .()()AB PC BA QC ++- D .PA AB BQ +-【答案】ABC【分析】根据向量运算对选项进行分析,从而确定正确答案. 【详解】A 选项,QC QP CQ PC CQ PQ -+=+=,A 选项正确. B 选项,()AB PA BQ AB AQ BQ PA PA PQ ++=+=+=+,B 选项正确.C 选项,()()AB PC BA QC AB BA PC QC CQ CP PQ ++-=++-=-=,C 选项正确. D 选项,()PA AB BQ PB BQ BP BQ BP BQ PQ +-=-=--=-+≠,D 选项错误. 故选:ABC3. 在四边形ABCD 中,若CA CB CD =+,则( ) A .四边形ABCD 是矩形 B .四边形ABCD 是菱形 C .四边形ABCD 是正方形 D .四边形ABCD 是平行四边形【答案】D【分析】根据平面向量加法的运算法则及向量相等的充要条件判断即可;【详解】解:CA CB CD =+,CA CB BA =+,∴CB BA CB CD +=+∴BA CD =,//AB DC ∴且AB DC =,∴四边形ABCD 是平行四边形.故选:D .4. 在平面四边形ABCD 中,E ,F 分别为AD ,BC 的中点,则下列向量与AB DC +不相等的是( ) A .2EF B .AC DB + C .EB EC + D .FA FD +所以11,22AE ED AD BF FC BC ====, 因为EF EA AB BF =++,EF ED DC CF =++ 2EF ED DC CF EA AB BF AB DC =+++++=+, A 正确,因为,DC DA AC AB AD DB =+=+,所以DC AB DA AC AD DB AC DB +=+++=+,所以B 正确,因为,DC DE EC AB AE EB =+=+,所以DC AB DE EC AE EB EC EB +=+++=+,所以因为()FA FD FB BA FC CD BA CD AB DC +=+++=+=-+, D 错误, 故选:D5.在四边形ABCD 中,给出下列四个结论,其中一定正确的是( ) A .AB BC CA +=B .AB AD BD -=C.AB AD AC+=D.BC CD BD+=【答案】D【分析】由向量加法的三角形法则可判断AD,由向量减法的运算法则可判断B,由向量加法的平行四边形法则可判断C.【详解】根据三角形法则可得AB BC AC+=,所以A错误;根据向量减法的运算法则可得AB AD DB-=,所以B错误;四边形ABCD不一定是平行四边形,所以不一定有AB AD AC+=,C错误;根据三角形法则可得BC CD BD+=正确,所以D正确.故选:D.6.在四边形ABCD中,AB DC=,若AD AB BC BA-=-,则四边形ABCD是()A.菱形B.矩形C.正方形D.不确定【分析】由AB DC=,可得四边形为平行四边形,又BD AC=,从而即可求解【详解】解:在四边形ABCD因为AB DC=,所以四边形AD AB BC BA-=-,即BD AC=,所以平行四边形ABCD为矩形,故选:B.7.在ABC中,D,E,F分别是边BC,CA,AB的中点,点G为ABC的重心,则下列结论中正确的是()A.AB BC CA-=B.1()3AG AB AC=+C.0AF BD CE++=D.0GA GB GC++=【答案】BCD【分析】由向量的线性运算结合三角形的重心的性质求解即可.【详解】解:如图:,2AB BC AB CB EB AC-=+=≠,即选项为ABC的重心,则2211()()3323AG AD AB AC AB AC==⨯+=+,即选项,1()02AF BD CE AB BC CA++=++=,即选项C正确;,122()2GA GD GB GC=-=-⨯+,即0GA GB GC++=,即选项D正确,8.如图,E,F,G,H分别是梯形ABCD的边AB,BC,CD,DA的中点,化简下列各式:(1)DG EA CB++;(2)EG CG DA EB+++.【答案】(1)GE;(2)0.【分析】(1)(2)根据图形中相关线段的位置关系,结合向量加法的几何意义化简目标式.(1)DG EA CB GC BE CB GB BE GE+++++===;(2)EG CG DA EB EG GD DA AE ED DE==+=++++++.题型三:平面向量的线性运算与共线定理【例1】[多选题]下列命题是真命题的是().A.若A,B,C,D在一条直线上,则AB与CD是共线向量B.若A,B,C,D不在一条直线上,则AB与CD不是共线向量C.若向量AB与CD是共线向量,则A,B,C,D四点必在一条直线上D.若向量AB与AC是共线向量,则A,B,C三点必在一条直线上【答案】AD【分析】向量平行与共线是同一个概念,对四个命题依次判断即可.【详解】A 项为真命题,A,B,C,D在一条直线上,则向量AB,CD的方向相同或相反,因此AB与CD是共线向量;B 项为假命题,A ,B ,C ,D 不在一条直线上,则AB ,CD 的方向不确定,不能判断AB 与CD 是否共线;C 项为假命题,因为AB ,CD 两个向量所在的直线可能没有公共点, 所以A ,B ,C ,D 四点不一定在一条直线上;D 项为真命题,因为AB ,AC 两个向量所在的直线有公共点A , 且AB 与AC 是共线向量,所以A ,B ,C 三点共线. 故选:AD .【例2】已知向量a ,b ,且2AB a b =+,56BC a b =-+,72CD a b =-,则一定共线的三点是( ) A .A ,B ,D B .A ,B ,CC .B ,C ,DD .A ,C ,D【分析】由已知,分别表示出选项对应的向量,然后利用平面向量共线定理进行判断即可完成求解【详解】因为2AB a b =+,BC 56a b =-+,72CD a b =-,,2AB a b =+,(56)(72)24B a b D B D b C a C b a ++-+==-+=,若A ,B 则AB BD λ=,即2(24)a b a b λ+=+,解得12λ=,故该选项正确; 选项B ,2AB a b =+,BC 56a b =-+,若A ,B ,C 三点共线,则AB BC λ=,即2(56)a b a b λ+=-+,解得不存在,故该选项错误;选项C ,BC 56a b =-+,72CD a b =-,若B ,三点共线,则BC BD λ=,即56(72)a b a b λ-+=-,不存在,故该选项错误;,(2)(56)48a b a A b AB BC a b C ++=+=+-=-+,72CD a b =-,若A ,C ,D 三点共线,则AC CD λ=,48(72)a b a b λ+=-,解得λ不存在,故该选项错误; 故选:A.【例3】下列说法正确的是( )A .a 与b 是非零向量,则a 与b 同向是a b =的必要不充分条件B .,,A BC 是互不重合的三点,若AB 与BC 共线,则,,A B C 三点在同一条直线上 C .a 与b 是非零向量,若a 与b 同向,则a 与b -反向D .设,λμ为实数,若a b λμ=,则a 与b 共线 【答案】ABC选项:根据向量共线的性质,可知A 、选项:a 与b 同向,则a 与b -反向,显然正确; 选项:如果0λμ==,则无法得知a 与b 共线.【详解】a 与b 同向,但a 不一定与b 相等,∴a b ≠,若a b =,则a 与b 同向, a =b ,∴a 与b 同向是a b =的必要不充分条件,A 正确.AB 与BC 共线,则有AB =BC λ,故一定有,,A B C 三点在同一条直线上,B 正确.a 与b 同向,则a 与b -反向,C 正确.0λμ==时,a 与b 不一定共线,D 错误.故选:ABC【例4】“AB CD ∥”是“A ,B ,C ,D 四点共线”的________条件. 【答案】必要不充分【分析】根据向量平行的定义结合充分性、必要性的定义判断即可. 【详解】当AB CD ∥时,直线AB 与CD 的位置关系有可能是平行或共线, 当二者平行时A ,B ,C ,D 四个点分别位于两条平行线上而不是四点共线, 则“AB CD ∥”无法推出“A ,B ,C ,D 四点共线”;当A ,B ,C ,D 四点共线时,直线AB 与CD 的位置关系为重合,此时,AB CD ∥, 则“A ,B ,C ,D 四点共线”可以推出“AB CD ∥”,因此“AB CD ∥”是“A ,B ,C ,D 四点共线”的必要不充分条件. 故答案为:必要不充分.【例5】设向量,a b 不平行,向量λ+a b 与2+a b 平行,则实数λ= ___. 【答案】21 【解析】因向量λ+a b 与2+a b 平行,所以()b a b a b a μμμλ22+=+=+,所以⎩⎨⎧==μμλ21,解得⎪⎩⎪⎨⎧==2121μλ 【例6】已知P 是①ABC 所在平面内的一点,若CB PB PA λ-=,其中λ①R ,则点P 一定在( ) A .AC 边所在的直线上 B .BC 边所在的直线上 C .AB 边所在的直线上D .①ABC 的内部【答案】A【分析】根据向量的线性运算整理可得,再结合向量共线分析即可. 【详解】①CB PB PA λ-=,PB PC CB =+①()CB PC CB PA λ-+=,则PC -=λPA ,则CP PA λ= ①CP PA ∥①P 点在AC 边所在直线上. 故选:A .【例7】在①ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB =A .3144AB AC - B .1344AB AC - C .3144+AB ACD .1344+AB AC【答案】A【解析】根据向量的运算法则,可得()111111222424BE BA BD BA BC BA BA AC =+=+=++ 1113124444BA BA AC BA AC =++=+① 所以3144EB AB AC =-①故选A.【例8】在ABC 中,AD 为BC 边上的中线,E 为AD 的中点,且EB AB AC λμ=+,则λ=________,μ=_________.【答案】3414-【解析】如下图所示:D 为BC 的中点,则()()111222AD AB BD AB BC AB AC AB AB AC =+=+=+-=+,E 为AD 的中点,所以,()1124AE AD AB AC ==+,因此,()131444EB AB AE AB AB AC AB AC =-=-+=-,即34λ=,14μ=-. 故答案为:34;14-.【例9】在ABC 中,4AC AD =,P 为BD 上一点,若13AP AB AC λ=+,则实数λ的值( ) A .18B .316C .16D .38【答案】C 【解析】4AC AD =,14AD AC ∴=,则14BD AD AB AC AB =-=-, 1233BP AP AB AB AC AB AC AB λλ⎛⎫=-=+-=- ⎪⎝⎭,由于P 为BD 上一点,则//BP BD ,设BP k BD =,则21344kAC AB k AC AB AC k AB λ⎛⎫-=-=- ⎪⎝⎭, 所以423k k λ⎧=⎪⎪⎨⎪=⎪⎩,解得16λ=.【例10】在ABC ∆中,点P 满足3BP PC =,过点P 的直线与AB 、AC 所在的直线分别交于点M 、N ,若AM AB λ=,()0,0AN AC μλμ=>>,则λμ+的最小值为( )A.12+ B1 C .32D .52【答案】B【解析】如下图所示:3BP PC =,即()3AP AB AC AP -=-,1344AP AB AC∴=+, AM AB λ=,()0,0AN AC μλμ=>>,1AB AM λ∴=,1AC ANμ=, 1344AP AM ANλμ∴=+,M 、P 、N 三点共线,则13144λμ+=. ()133********λμλμλμλμμλ⎛⎫∴+=++=++≥=+ ⎪⎝⎭,当且仅当μ=时,等号成立,因此,λμ+1+,故选:B. 【例11】已知M 为ABC 的边AB 的中点,N 为ABC 内一点,且13AN AM BC =+,则AMN BCNS S =△△( ) A .16B .13C .12D .23【答案】B【解析】因为13AN AM BC =+,所以13MN BC =, 所以MN ①BC ,又因为 M 为边AB 的中点,所以点A 到MN 的距离等于点N 到BC 的距离, 所以13AMN BCN MN S S BC==△△,【题型专练】1.已知()1221123,,2AB e e CB e e CD e e =+=-=+,则下列结论中成立的是( )A .A ,B ,C 三点共线B .A ,B ,D 三点共线C .A ,D ,C 三点共线D .D ,B ,C 三点共线 【答案】C【分析】根据平面向量的线性运算可得2AC CD =,从而可求解.【详解】解:()()1221123422AC AB CB e e e e e e CD -=-=+-=+=,所以A ,D ,C 三点共线.故选:C.2.已知向量a ,b 是两个不共线的向量,且35OA a b =+,47OB a b =+,OC a mb =+,若A ,B ,C 三点共线,则m =( )A .1B .1-C .2D .2- 【答案】A【解析】法一:b a b a b a OB AO AB 27453+=++--=+=,()b m a b m a b a OC BO BC 7374-+-=++--=+=,因A ,B ,C 三点共线,所以AB 与BC 共线,所以()[]()b m a b m a b a 73732-+-=-+-=+λλλ,所以()⎩⎨⎧-=-=7231m λλ,解得⎪⎩⎪⎨⎧=-=131m λ 法二:由,,A B C 三点共线,得(1)(4)(72)OC xOA x OB x a x b =+-=-+-,故41,72,x x m -=⎧⎨-=⎩解得1m =. 3.设12e e ,是两个不共线的向量,若向量12m e ke =-+(k ∈R )与向量212n e e =-共线,则 A .0k =B .1k =C .2k =D .12k = 【答案】D【解析】因为向量12=-+m e ke (k ∈R )与向量212=-n e e 共线,所以存在实数λ,使得λ=m n , 所以有2211(2)λ-+=-e ke e e ,因此12k λλ=⎧⎨-=-⎩,解得12k =. 4.在ABC △中,D 是AB 边上的中点,则CB =( )A .2CD CA +B .2CD CA -C .2CD CA - D .2CD CA +【答案】C【解析】:CA CD AC CD CD AC CD AD CD DB CD CB -=+=++=+=+=225.在ABC 中,点P 为AC 中点,点D 在BC 上,且3BD DC =,则DP =( )A .1144AB AC + B .1144AB AC -- C .1144AB AC - D .1144AB AC-+ 【答案】B【解析】①点P 为AC 中点,①12AP AC =,①3BD DC =,()3AD AB AC AD ∴-=-, ①1344AD AB AC =+,①113244DP AP AD AC AB AC =-=--=1144AB AC --,故选:B. 6.设,,D E F 分别为ABC 的三边BC,CA,AB 的中点,则EB FC +=( ) A .ADB .12ADC .12BCD .BC 【答案】A【解析】111()()()222EB FC BA BC CA CB AB AC AD +=-+-+=+=,故选:A7.设D 为①ABC 所在平面内的一点,若3,AD BD CD CA CB λμ==+,则μλ=_____. 【答案】3-【解析】如图所示:3CD CA AD CA BD =+=+,CA =+3(CD CB -),即有CD =﹣1322CA CB +, 因为CD CA CB λμ=+,所以λ=﹣12,μ=32,则μλ=﹣3,故答案为:﹣3. 8.如图,在ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB ,AC 于不同的两点M N ,,若AB mAM =,AC nAN =,则m n +=( )A .1B .32C .2D .3【答案】C 【解析】连接AO ,由O 为BC 中点可得,1()222m n AO AB AC AM AN =+=+, M 、O 、N 三点共线,122m n ∴+=,2m n ∴+=.故选:C.9.在ABC 中,2AB =,4BC =,60ABC ∠=︒,AD 为BC 边上的高,O 为AD 的中点,若AO AB BC λμ=+,则λμ+=( )A .13B .23C .38 D .58【答案】D【解析】AD 是BC 边上的高,∴90ADB ∠=︒,在ADB △中,1cos 22BD BD ABD AB ∠===,解得1BD =,4BC =,∴14BD BC =, ∴14AD AB BD AB BC =+=+,O 为AD 中点, ∴1111122428AO AD AB BC AB BC ⎛⎫==+=+ ⎪⎝⎭,AO AB BC λμ=+, ∴1128AB BC AB BC λμ+=+,∴12λ=,18μ=, ∴115288λμ+=+=. 10.已知O 是ABC 所在平面内一点,D 为BC 边中点,且20OA OB OC ++=,那么( ) A .AO OD = B .2AO OD = C .3AO OD = D .4?AO OD【答案】A【解析】D 为BC 边中点,①2OB OC OD +=,①20OA OB OC ++=,①0OA OD =+,即AO OD =.11.设,,D E F 分别是ABC 的三边BC,CA,AB 上的点,且2,2,2DC BD CE EA AF FB ===,则AD BE CF ++与BC ( )A .反向平行B .同向平行C .互相垂直D .既不平行也不垂直 首先根据平面向量基本定理表示2133AD AB BD AB AC =+=+,2133BE BA BC =+,2133CF CB CA =+,【详解】()11213333AD AB BD AB BC AB AC AB AB AC =+=+=+-=+ 同理:2133BE BA BC =+,2133CF CB CA =+, 所以212121333333AD BE CF AB AC BA BC CB CA ⎛⎫⎛⎫⎛⎫++=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭13CB , 所以AD BE CF ++与BC 反向平行.故选:A【点睛】本题主要考查向量共线定理和平面向量基本定理,重点考查向量的表示,属于基础题型题型四:由平面向量的性质判断图形的形状【例1】若O 是ABC ∆所在平面内一点,且满足2OB OC OB OC OA -=+-,则ABC ∆的形状为____【答案】直角三角形=OC OA OC +=+=-+,+= 所以ABC ∆的形状为直角三角形【例2】若113e ,5e AB CD ===,则四边形ABCD 是( )A .平行四边形B .菱形C .等腰梯形D .不等腰的梯形 ,结合AD BC =,即可判断四边形【详解】解:因为113e ,5e AB CD ==,所以35AB CD =-,所以//AB CD AB CD ≠,AD BC =,所以四边形ABCD 为等腰梯形.故选:C.【题型专练】1.在四边形ABCD 中,对角线AC 与BD 交于点O ,若2323OA OC OD OB +=+,则四边形ABCD 一定是( )A .矩形B .梯形C .平行四边形D .菱形 【答案】B【分析】由2323OA OC OD OB +=+化简可得23DA CB =,结合向量共线定理判断四边形ABCD 的形状.【详解】① 2323OA OC OD OB +=+,① 2()3()OA OD OB OC -=-,① 23DA CB =,① 四边形ABCD 一定是梯形. 故选:B.2.四边形ABCD 中,2AB a b =+,4BC a b =--,53CD a b =--,若a 、b 不共线,则四边形ABCD 为( )A .平行四边形B .矩形C .梯形D .菱形 【分析】由向量知识可知//AD BC ,AD BC ≠可得答案【详解】由已知得,2453822AD AB BC CD a b a b a b a b BC =++=+----=--= , 故//AD BC ,由AD BC ≠,所以四边形ABCD 是梯形.故选:C.3.在四边形ABCD 中,若CA CB CD =+,则( )A .四边形ABCD 是矩形B .四边形ABCD 是菱形C .四边形ABCD 是正方形D .四边形ABCD 是平行四边形 【答案】D 【分析】根据平面向量加法的运算法则及向量相等的充要条件判断即可;【详解】解:CA CB CD =+,CA CB BA =+,∴CB BA CB CD +=+ ∴BA CD =,//AB DC ∴且AB DC =,∴四边形ABCD 是平行四边形. 故选:D .4.下列有关四边形ABCD 的形状判断正确的是( )A .若AD BC =,则四边形ABCD 为平行四边形B .若13AD BC =,则四边形ABCD 为梯形 C .若AB DC =,且AB AD =,则四边形ABCD 为菱形D .若AB DC =,且AC BD ⊥,则四边形ABCD 为正方形 【分析】由向量平行与相等的关系确定四边形的边的关系得结论.【详解】AD BC =,则AD 13AD BC =,则//AD BC 若AB DC =,四边形ABCD AB AD =,即AB 若AB DC =,四边形ABCD 是平行四边形,AC BD ⊥,即AC 故选:ABC .。
2023新高考数学复习讲义 第30讲 平面向量的概念及线性运算(解析版)

第30讲 平面向量的概念及线性运算学校:___________姓名:___________班级:___________考号:___________【基础巩固】1.给出下列说法:①两个有共同起点的相等向量,其终点必相同; ②两个有共同终点的向量,一定是共线向量;③非零向量AB⃗⃗⃗⃗⃗ 与非零向量CD ⃗⃗⃗⃗⃗ 是共线向量,则点A ,B ,C ,D 必在同一条直线上; ④有向线段就是向量,向量就是有向线段.其中错误说法的个数是( )A .1B .2C .3D .4C [解析] 对于①,相等向量是大小相等,方向相同的向量,故两个有共同起点的相等向量,其终点必相同,故①正确;对于②,共线向量是指方向相同或相反的向量,两个有共同终点的向量,其方向可能既不相同又不相反,故②错误;对于③,共线向量是指方向相同或相反的向量,向量AB⃗⃗⃗⃗⃗ 与向量CD ⃗⃗⃗⃗⃗ 是共线向量,则线段AB 和CD 平行或共线,故③错误;对于④,有向线段是向量的表示形式,不能等同于向量,故④错误.4个说法中有3个错误,故选C . 2.下列各式不能化简为PQ ⃗⃗⃗⃗⃗ 的是 ( ) A .AB⃗⃗⃗⃗⃗ +(PA ⃗⃗⃗⃗⃗ +BQ ⃗⃗⃗⃗⃗ ) B .(AB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )+(BA ⃗⃗⃗⃗⃗ -QC ⃗⃗⃗⃗⃗ ) C .QC ⃗⃗⃗⃗⃗ -QP ⃗⃗⃗⃗⃗ +CQ ⃗⃗⃗⃗⃗ D .PA ⃗⃗⃗⃗⃗ +AB⃗⃗⃗⃗⃗ -BQ ⃗⃗⃗⃗⃗ D [解析] 对于A,AB ⃗⃗⃗⃗⃗ +(PA ⃗⃗⃗⃗⃗ +BQ ⃗⃗⃗⃗⃗ )=AQ ⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗ =PQ ⃗⃗⃗⃗⃗ ;对于B,(AB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )+(BA ⃗⃗⃗⃗⃗ -QC ⃗⃗⃗⃗⃗ )=PC ⃗⃗⃗⃗⃗ -QC ⃗⃗⃗⃗⃗ =PQ ⃗⃗⃗⃗⃗ ;对于C,QC ⃗⃗⃗⃗⃗ -QP ⃗⃗⃗⃗⃗ +CQ ⃗⃗⃗⃗⃗ =-QP⃗⃗⃗⃗⃗ =PQ ⃗⃗⃗⃗⃗ .故选D . 3.在△ABC 中,D 是AB 边上的中点,则CB ⃗⃗⃗⃗⃗ = ( ) A .2CD ⃗⃗⃗⃗⃗ +CA ⃗⃗⃗⃗⃗ B .CD ⃗⃗⃗⃗⃗ -2CA ⃗⃗⃗⃗⃗ C .2CD⃗⃗⃗⃗⃗ -CA ⃗⃗⃗⃗⃗ D .CD⃗⃗⃗⃗⃗ +2CA ⃗⃗⃗⃗⃗ C [解析] ∵在△ABC 中,D 是AB 边上的中点,∴CB ⃗⃗⃗⃗⃗ =CD ⃗⃗⃗⃗⃗ +DB ⃗⃗⃗⃗⃗⃗ =CD ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ =CD ⃗⃗⃗⃗⃗ +(AC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ )=2CD ⃗⃗⃗⃗⃗ -CA ⃗⃗⃗⃗⃗ .故选C . 4.在四边形ABCD 中,AB ⃗⃗⃗⃗⃗ =a +2b ,BC ⃗⃗⃗⃗⃗ =-4a -3b ,CD ⃗⃗⃗⃗⃗ =-5a -5b ,则四边形ABCD 的形状是 ( )A .矩形B .平行四边形C .梯形D .以上都不对C [解析] ∵AD⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ =-8a -6b ,∴AD ⃗⃗⃗⃗⃗ =2BC ⃗⃗⃗⃗⃗ ,∴AD ∥BC ,且AD ≠BC ,∴四边形ABCD 是梯形.故选C . 5.已知向量a ,b 不共线,且AB ⃗⃗⃗⃗⃗ =a +2b ,BC ⃗⃗⃗⃗⃗ =-5a +6b ,CD ⃗⃗⃗⃗⃗ =7a -2b ,则一定共线的三点是 ( ) A .A ,B ,DB .A ,B ,C C .B ,C ,DD .A ,C ,DA [解析] ∵BD ⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ =2a +4b ,∴BD ⃗⃗⃗⃗⃗⃗ =2AB ⃗⃗⃗⃗⃗ ,又BD ⃗⃗⃗⃗⃗⃗ ,AB ⃗⃗⃗⃗⃗ 有公共点B ,∴A ,B ,D 三点共线.故选A . 6.[2022·新乡二模] 在△ABC 中,AE ⃗⃗⃗⃗⃗ =310·(AB⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ),D 为BC 边的中点,则 ( ) A .3AE ⃗⃗⃗⃗⃗ =7ED ⃗⃗⃗⃗⃗ B .7AE ⃗⃗⃗⃗⃗ =3ED ⃗⃗⃗⃗⃗ C .2AE ⃗⃗⃗⃗⃗ =3ED ⃗⃗⃗⃗⃗ D .3AE⃗⃗⃗⃗⃗ =2ED ⃗⃗⃗⃗⃗ C [解析] 因为D 为BC 边的中点,所以AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ =2AD ⃗⃗⃗⃗⃗ ,因为AE ⃗⃗⃗⃗⃗ =310(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ),所以AE ⃗⃗⃗⃗⃗ =35AD ⃗⃗⃗⃗⃗ ,则2AE⃗⃗⃗⃗⃗ =3ED ⃗⃗⃗⃗⃗ .故选C .7.2020年10月27日,在距离长江口南支航道0.7海里的风机塔上,东海航海保障中心上海航标处顺利完成临港海上风电场AIS(船舶自动识别系统)基站的新建工作,该基站也是我国首个海上风机塔AIS 基站.已知风机的每个转子叶片的长度为20米,每两个叶片之间的夹角相同,风机塔(杆)的长度为60米,叶片随风转动,假设叶片与风机塔在同一平面内,如图所示,则|OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OM⃗⃗⃗⃗⃗⃗ |的最小值为 ( )A .40B .20√7C .20√10D .80A [解析] 由题知,OA⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =0,即OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ =CO ⃗⃗⃗⃗⃗ ,则OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OM ⃗⃗⃗⃗⃗⃗ =CO ⃗⃗⃗⃗⃗ +OM ⃗⃗⃗⃗⃗⃗ =CM ⃗⃗⃗⃗⃗⃗ ,则当叶片OC 旋转到最低点时,|CM⃗⃗⃗⃗⃗⃗ |最小,且其值为60-20=40. 8.如图,在△ABC 中,AD ⃗⃗⃗⃗⃗ =3DB⃗⃗⃗⃗⃗⃗ ,P 为CD 上一点,且AP ⃗⃗⃗⃗⃗ =m AC ⃗⃗⃗⃗⃗ +12AB ⃗⃗⃗⃗⃗ ,则m 的值为 ( )A .12B .13C .14D .15B [解析] ∵AD ⃗⃗⃗⃗⃗ =3DB ⃗⃗⃗⃗⃗⃗ ,∴AB ⃗⃗⃗⃗⃗ =43AD ⃗⃗⃗⃗⃗ ,又AP ⃗⃗⃗⃗⃗ =m AC ⃗⃗⃗⃗⃗ +12AB ⃗⃗⃗⃗⃗ ,∴AP ⃗⃗⃗⃗⃗ =m AC ⃗⃗⃗⃗⃗ +23AD ⃗⃗⃗⃗⃗ ,又C ,P ,D 三点共线,∴m+23 =1,解得m=13.故选B .9.(多选)如图,在四边形ABCD 中,AB ∥CD ,AB ⊥AD ,AB=2AD=2DC ,E 为BC 边上一点,且BC⃗⃗⃗⃗⃗ =3EC ⃗⃗⃗⃗⃗ ,F 为线段AE的中点,则下列结论正确的是 ( )A .BC ⃗⃗⃗⃗⃗ =-12AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ B .AF⃗⃗⃗⃗⃗ =13AB ⃗⃗⃗⃗⃗ +13AD ⃗⃗⃗⃗⃗ C .BF ⃗⃗⃗⃗⃗ =-23AB ⃗⃗⃗⃗⃗ +13AD ⃗⃗⃗⃗⃗ D .CF ⃗⃗⃗⃗⃗ =16AB ⃗⃗⃗⃗⃗ -23AD ⃗⃗⃗⃗⃗ABC [解析] 连接BD (图略),∵AB ∥CD ,AB ⊥AD ,AB=2AD=2DC ,∴BC⃗⃗⃗⃗⃗ =BD ⃗⃗⃗⃗⃗⃗ +DC ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ +DC ⃗⃗⃗⃗⃗ =-AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ +12AB ⃗⃗⃗⃗⃗ =-12AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ ,A 正确;∵BC ⃗⃗⃗⃗⃗ =3EC ⃗⃗⃗⃗⃗ ,∴BE ⃗⃗⃗⃗⃗ =23BC ⃗⃗⃗⃗⃗ =23 (-12AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ ) =-13AB ⃗⃗⃗⃗⃗ +23AD ⃗⃗⃗⃗⃗ ,∴AE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +(-13AB ⃗⃗⃗⃗⃗ +23AD ⃗⃗⃗⃗⃗ ) =23AB ⃗⃗⃗⃗⃗ +23AD ⃗⃗⃗⃗⃗ ,又F 为线段AE 的中点,∴AF ⃗⃗⃗⃗⃗ =12AE ⃗⃗⃗⃗⃗ =13AB ⃗⃗⃗⃗⃗ +13AD ⃗⃗⃗⃗⃗ ,B 正确;BF ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AF ⃗⃗⃗⃗⃗ =-AB ⃗⃗⃗⃗⃗ +13AB ⃗⃗⃗⃗⃗ +13AD ⃗⃗⃗⃗⃗ =-23AB ⃗⃗⃗⃗⃗ +13AD ⃗⃗⃗⃗⃗ ,C 正确;CF ⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +BF ⃗⃗⃗⃗⃗ =BF ⃗⃗⃗⃗⃗ -BC ⃗⃗⃗⃗⃗ =-23AB ⃗⃗⃗⃗⃗ +13AD ⃗⃗⃗⃗⃗ -(-12AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ ) =-16AB ⃗⃗⃗⃗⃗ -23AD ⃗⃗⃗⃗⃗ ,D 错误.故选ABC . 10.(多选)设点M 是△ABC 所在平面内一点,则下列说法正确的是 ( )A .若AM ⃗⃗⃗⃗⃗⃗ =12AB⃗⃗⃗⃗⃗ +12AC ⃗⃗⃗⃗⃗ ,则点M 是边BC 的中点 B .若AM⃗⃗⃗⃗⃗⃗ =2AB ⃗⃗⃗⃗⃗ -AC ⃗⃗⃗⃗⃗ ,则点M 在边BC 的延长线上 C .若AM ⃗⃗⃗⃗⃗⃗ =-BM ⃗⃗⃗⃗⃗⃗ -CM⃗⃗⃗⃗⃗⃗ ,则点M 是△ABC 的重心 D .若2CM⃗⃗⃗⃗⃗⃗ =CA ⃗⃗⃗⃗⃗ +CB ⃗⃗⃗⃗⃗ ,则△MBC 的面积是△ABC 面积的12ACD [解析] 若AM ⃗⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ +12AC ⃗⃗⃗⃗⃗ ,则点M 是边BC 的中点,故A 正确;若AM ⃗⃗⃗⃗⃗⃗ =2AB ⃗⃗⃗⃗⃗ -AC ⃗⃗⃗⃗⃗ ,则AM ⃗⃗⃗⃗⃗⃗ -AB ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ -AC ⃗⃗⃗⃗⃗ ,即BM⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ ,则点M 在边CB 的延长线上,故B 错误;若AM ⃗⃗⃗⃗⃗⃗ =-BM ⃗⃗⃗⃗⃗⃗ -CM ⃗⃗⃗⃗⃗⃗ ,即AM ⃗⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗ +CM ⃗⃗⃗⃗⃗⃗ =0,则点M 是△ABC 的重心,故C 正确;由2CM⃗⃗⃗⃗⃗⃗ =CA ⃗⃗⃗⃗⃗ +CB ⃗⃗⃗⃗⃗ ,可得M 为边AB 的中点,则△MBC 的面积是△ABC 面积的12,故D 正确.故选ACD . 11.已知向量a 与b 的方向相反,|a |=1,|b |=2,则|a -2b |= . 5 [解析] 因为向量a 与b 的方向相反,所以|a -2b |=|a |+2|b |=1+4=5.12.已知△ABC 所在的平面上有一点D 满足AD ⃗⃗⃗⃗⃗ =3AB⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ 4,且BD⃗⃗⃗⃗⃗⃗ =λCD ⃗⃗⃗⃗⃗ (λ∈R),则λ= . -13 [解析] 由AD ⃗⃗⃗⃗⃗ =3AB⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ 4,可得4AD ⃗⃗⃗⃗⃗ =3AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ,所以3AD ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ =3AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ,则3(AD ⃗⃗⃗⃗⃗ -AB ⃗⃗⃗⃗⃗ )=AC ⃗⃗⃗⃗⃗ -AD ⃗⃗⃗⃗⃗ ,所以3BD⃗⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ ,故BD⃗⃗⃗⃗⃗⃗ =-13CD ⃗⃗⃗⃗⃗ ,所以λ=-13. 13.[2022·河北五个一联盟二模] 点M 在△ABC 的内部,且满足2MA ⃗⃗⃗⃗⃗⃗ +3MB ⃗⃗⃗⃗⃗⃗ +4MC ⃗⃗⃗⃗⃗⃗ =0,则S △MAC ∶S △MAB = .3∶4 [解析] 根据题意,分别延长MA 至D ,MB 至E ,MC 至F ,使得MD=2MA ,ME=3MB ,MF=4MC ,如图所示:由2MA ⃗⃗⃗⃗⃗⃗ +3MB ⃗⃗⃗⃗⃗⃗ +4MC ⃗⃗⃗⃗⃗⃗ =0,得MD ⃗⃗⃗⃗⃗⃗ +ME ⃗⃗⃗⃗⃗⃗ +MF ⃗⃗⃗⃗⃗⃗ =0,连接DE ,DF ,EF ,所以点M 是△DEF 的重心,所以S △MDE =S △MEF =S △MFD ,设S △MDE =1,则S △MAB =12 13 1=16,S △MAC =12 14 1=18,所以S △MAC ∶S △MAB =18∶16=3∶4. 14.已知两个非零向量a 和b 不共线,OA ⃗⃗⃗⃗⃗ =2a -3b ,OB ⃗⃗⃗⃗⃗ =a +2b ,OC ⃗⃗⃗⃗⃗ =k a +12b . (1)若2OA⃗⃗⃗⃗⃗ -3OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =0,求k 的值; (2)若A ,B ,C 三点共线,求k 的值. 解:(1)∵2OA⃗⃗⃗⃗⃗ -3OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ =0, ∴2(2a -3b )-3(a +2b )+k a +12b =(1+k )a =0,又a ≠0,∴k+1=0,∴k=-1.(2)∵A ,B ,C 三点共线,∴设BC ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ , 即OC ⃗⃗⃗⃗⃗ -OB ⃗⃗⃗⃗⃗ =λ(OB ⃗⃗⃗⃗⃗ -OA⃗⃗⃗⃗⃗ ), ∴(k-1)a +10b =-λa +5λb ,又a ,b 不共线,∴{k -1=-λ,10=5λ,消去λ得k=-1.15.已知点G 是△ABO 的重心,M 是AB 边的中点. (1)求GA ⃗⃗⃗⃗⃗ +GB ⃗⃗⃗⃗⃗ +GO ⃗⃗⃗⃗⃗ ;(2)若PQ 过△ABO 的重心G ,且OA ⃗⃗⃗⃗⃗ =a ,OB ⃗⃗⃗⃗⃗ =b ,OP ⃗⃗⃗⃗⃗ =m a ,OQ ⃗⃗⃗⃗⃗⃗ =n b ,求证:1m +1n =3. 解:(1)连接GM (图略),因为GA ⃗⃗⃗⃗⃗ +GB ⃗⃗⃗⃗⃗ =2GM ⃗⃗⃗⃗⃗⃗ ,2GM ⃗⃗⃗⃗⃗⃗ =-GO ⃗⃗⃗⃗⃗ , 所以GA ⃗⃗⃗⃗⃗ +GB ⃗⃗⃗⃗⃗ +GO ⃗⃗⃗⃗⃗ =-GO ⃗⃗⃗⃗⃗ +GO ⃗⃗⃗⃗⃗ =0. (2)证明:易知OM⃗⃗⃗⃗⃗⃗ =12(a+b ), 因为G 是△ABO 的重心,所以OG ⃗⃗⃗⃗⃗ =23OM ⃗⃗⃗⃗⃗⃗ =13(a+b ).由P ,G ,Q 三点共线,设QG ⃗⃗⃗⃗⃗ =t QP ⃗⃗⃗⃗⃗ , 所以OG ⃗⃗⃗⃗⃗ -OQ ⃗⃗⃗⃗⃗⃗ =t (OP ⃗⃗⃗⃗⃗ -OQ ⃗⃗⃗⃗⃗⃗ ), 即OG ⃗⃗⃗⃗⃗ =t OP ⃗⃗⃗⃗⃗ +(1-t )OQ ⃗⃗⃗⃗⃗⃗ , 即13a +13b =mt a +(1-t )n b .由a ,b 不共线,得{mt =13,(1-t )n =13,所以1m +1n=3.【素养提升】1.已知P 为△ABC 所在平面内一点,AB ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =0,|AB ⃗⃗⃗⃗⃗ |=|PB ⃗⃗⃗⃗⃗ |=|PC ⃗⃗⃗⃗⃗ |=2,则△ABC 的面积为 ( ) A .√3B .2√3C .3√3D .4√3B [解析] 设BC 边的中点为D ,AC 边的中点为M ,连接PD ,MD ,BM (图略),则有PB⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =2PD ⃗⃗⃗⃗⃗ .由AB ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =0,得AB ⃗⃗⃗⃗⃗ =-2PD ⃗⃗⃗⃗⃗ ,又D 为BC 边的中点,M 为AC 边的中点,所以AB ⃗⃗⃗⃗⃗ =-2DM ⃗⃗⃗⃗⃗⃗ ,则PD ⃗⃗⃗⃗⃗ =DM ⃗⃗⃗⃗⃗⃗ ,则P ,D ,M 三点共线且D 为线段PM 的中点.又D 为BC 边的中点,所以四边形CPBM 为平行四边形.因为|AB ⃗⃗⃗⃗⃗ |=|PB ⃗⃗⃗⃗⃗ |=|PC ⃗⃗⃗⃗⃗ |=2,所以|MC ⃗⃗⃗⃗⃗⃗ |=|BP ⃗⃗⃗⃗⃗ |=2,则AC=4,且BM=PC=2,所以△AMB 为等边三角形,所以∠BAC=60°,则S △ABC =12 2 4 √32=2√3.故选B .2.在矩形ABCD 中,AB=3,AD=4,P 为矩形ABCD 所在平面上一点,且PB ⊥PD ,则|PA ⃗⃗⃗⃗⃗ |的最大值是 ,|PA ⃗⃗⃗⃗⃗ +PC⃗⃗⃗⃗⃗ |= . 5 5 [解析] 连接AC ,BD ,设对角线AC ,BD 的交点为O ,∵AB=3,AD=4,∴AC=BD=√9+16=5.∵P 为矩形ABCD 所在平面上一点,且PB ⊥PD ,∴点P 在以线段BD 为直径的圆上,即点P 的轨迹是以O 为圆心,AC 2=52为半径的圆(除去B ,D 两点),A ,C 两点也在圆上,则|PA ⃗⃗⃗⃗⃗ |的最大值为圆的直径,即|PA ⃗⃗⃗⃗⃗ |的最大值为5.连接PO ,则PA ⃗⃗⃗⃗⃗ +PC⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗ ,∴|PA ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ |=2|PO ⃗⃗⃗⃗⃗ |=5.。
2020-2021学年高考数学(理)考点:平面向量的概念及线性运算
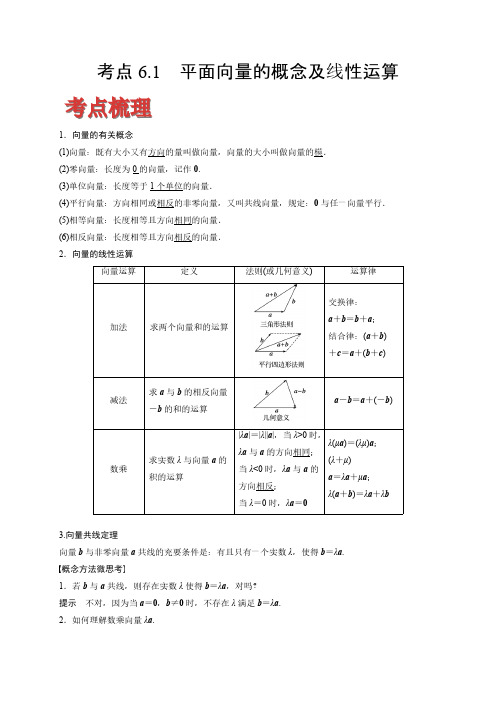
(5)相等向量:长度相等且方向相同的向量.
(6)相反向量:长度相等且方向相反的向量.
2.向量的线性运算
向量运算
定义
法则(或几何意义)
运算律
加法 求两个向量和的运算
交换律: a+b=b+a; 结合律:(a+b) +c=a+(b+c)
减法 数乘
求 a 与 b 的相反向量 -b 的和的运算
a-b=a+(-b)
考点 6.1 平面向量的概念及线性运算
考点梳理
1.向量的有关概念
(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的模.
(2)零向量:长度为 0 的向量,记作 0.
(3)单位向量:长度等于 1 个单位的向量.
(4)平行向量:方向相同或相反的非零向量,又叫共线向量,规定:0 与任一向量平行.
BC
3
3
3
33 3
9
99
.
故选 B.
13.(2020•湖北模拟)中,点为 BC 的中点,,为 AD 与 CE 的交点,若,则实数( )
A. 1 4
B. 1 3
C. 2 5
D. 1 2
【答案】D
【解析】如图, D 为 BC 的中点,
AD
1
AB
1
AC
,
22
又 AM AD ,且 AB 3AE ,
D.
2
a
2
b
1
c
332
【答案】B
【解析】因为空间四边形
OABC
如图,
OA
a
,
OB
b
,
OC
c
,
点 M 在线段 OA 上,且 OM 2MA , N 为 BC 的中点,
平面向量的概念及线性运算知识点讲解+例题讲解(含解析)

平面向量的概念及线性运算一、知识梳理1.向量的有关概念(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或模).(2)零向量:长度为0的向量,其方向是任意的.(3)单位向量:长度等于1个单位的向量.(4)平行向量:方向相同或相反的非零向量.平行向量又叫共线向量.规定:0与任一向量平行.(5)相等向量:长度相等且方向相同的向量.(6)相反向量:长度相等且方向相反的向量.2.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律:a+b=b+a.(2)结合律:(a+b)+c=a+(b+c)减法减去一个向量相当于加上这个向量的相反向量a-b=a+(-b)数乘求实数λ与向量a的积的运算(1)|λa|=|λ||a|;(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa=0λ(μa)=λμa;(λ+μ)a=λa+μa;λ(a+b)=λa+λb3.共线向量定理向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ,使得b=λa.结论:(1)O 为△ABC 的重心的充要条件是OA→+OB →+OC →=0;(2)四边形ABCD 中,E 为AD 的中点,F 为BC 的中点,则AB→+DC →=2EF →;(3)对于平面上的任一点O ,OA →,OB →不共线,满足OP →=xOA →+yOB →(x ,y ∈R ),则P ,A ,B 共线⇔x +y =1.二、例题精讲 + 随堂练习考点一 平面向量的概念【例1】 (1)设a ,b 都是非零向量,下列四个条件中,一定能使a |a |+b|b |=0成立的是( ) A.a =2b B.a ∥b C.a =-13bD.a ⊥b解析 (1)由a |a |+b |b |=0得a |a |=-b |b |≠0,即a =-b|b |·|a |≠0,则a 与b 共线且方向相反,因此当向量a 与向量b 共线且方向相反时,能使a |a |+b|b |=0成立.对照各个选项可知,选项A 中a 与b 的方向相同;选项B 中a 与b 共线,方向相同或相反;选项C 中a 与b 的方向相反;选项D 中a 与b 互相垂直.(2)给出下列四个命题: ①若|a |=|b |,则a =b ;②若A ,B ,C ,D 是不共线的四点,则“AB →=DC →”是“四边形ABCD 为平行四边形”的充要条件; ③若a =b ,b =c ,则a =c ; ④a =b 的充要条件是|a |=|b |且a ∥b . 其中正确命题的序号是( ) A.②③B.①②C.③④D.②④解析:(2)①不正确.两个向量的长度相等,但它们的方向不一定相同.②正确.∵AB →=DC →,∴|AB →|=|DC →|且AB →∥DC →,又A ,B ,C ,D 是不共线的四点,∴四边形ABCD 为平行四边形;反之,若四边形ABCD 为平行四边形,则|AB →|=|DC→|, AB→∥DC →且AB →,DC →方向相同,因此AB →=DC →. ③正确.∵a =b ,∴a ,b 的长度相等且方向相同,又b =c ,∴b ,c 的长度相等且方向相同,∴a ,c 的长度相等且方向相同,故a =c .④不正确.当a ∥b 且方向相反时,即使|a |=|b |,也不能得到a =b ,故|a |=|b |且a ∥b 不是a =b 的充要条件,而是必要不充分条件. 综上所述,正确命题的序号是②③. 答案 (1)C (2)A【训练1】 (1)如图,等腰梯形ABCD 中,对角线AC 与BD 交于点P ,点E ,F 分别在两腰AD ,BC 上,EF 过点P ,且EF ∥AB ,则下列等式中成立的是( )A.AD →=BC →B.AC →=BD →C.PE→=PF →D.EP→=PF → (2)给出下列说法:①非零向量a 与b 同向是a =b 的必要不充分条件; ②若AB→与BC →共线,则A ,B ,C 三点在同一条直线上; ③a 与b 是非零向量,若a 与b 同向,则a 与-b 反向; ④设λ,μ为实数,若λa =μb ,则a 与b 共线. 其中错误说法的序号是________.解析 (1)根据相等向量的定义,分析可得AD→与BC →不平行,AC →与BD →不平行,所以AD→=BC →,AC →=BD →均错误,PE →与PF →平行,但方向相反也不相等,只有EP →与PF →方向相同,且大小都等于线段EF 长度的一半,所以EP→=PF →.(2)根据向量的有关概念可知①②③正确,④错误. 答案 (1)D (2)④考点二 平面向量的线性运算 角度1 向量的线性运算【例2-1】 (2018·全国Ⅰ卷)在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB →=( ) A.34AB →-14AC → B.14AB →-34AC →C.34AB →+14AC →D.14AB →+34AC →解析 ∵E 是AD 的中点,∴EA →=-12AD →,∴EB→=EA →+AB →=-12AD →+AB →, 又知D 是BC 的中点, ∴AD→=12(AB →+AC →), 因此EB→=-14(AB →+AC →)+AB →=34AB →-14AC →. 答案 A角度2 利用向量线性运算求参数【例2-2】 (1)如图,在平行四边形ABCD 中,AC ,BD 相交于点O ,E 为线段AO 的中点.若BE→=λBA →+μBD →(λ,μ∈R ),则λ+μ等于( )A.1B.34C.23D.12解析 (1)∵E 为线段AO 的中点,∴BE→=12BA →+12BO →=12BA →+12×12BD →=12BA →+14BD →=λBA →+μBD →, ∴λ+μ=12+14=34.(2)在锐角△ABC 中,CM→=3MB →,AM →=xAB →+yAC →(x ,y ∈R ),则x y =________.解析:(2)由题设可得AM→=CM →-CA →=34CB →+AC →=34(AB →-A C →)+AC→=34AB →+14AC →, 则x =34,y =14.故x y =3. 答案 (1)B (2)3【训练2】 (1)如图所示,已知AB 是圆O 的直径,点C ,D 是半圆弧的两个三等分点,AB→=a ,AC →=b ,则AD →=( )A.a -12b B.12a -bC.a +12bD.12a +b解析 (1)连接CD ,由点C ,D 是半圆弧的三等分点, 得CD ∥AB 且CD→=12AB →=12a ,所以AD→=AC →+CD →=b +12a .(2)设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC .若DE →=λ1AB →+λ2AC →(λ1,λ2为实数),则λ1+λ2的值为________. 解析:(2)DE→=DB →+BE →=12AB →+23BC → =12AB →+23(AC →-AB →)=-16AB →+23AC →, ∵DE →=λ1AB →+λ2AC →,∴λ1=-16,λ2=23, 因此λ1+λ2=12. 答案 (1)D (2)12考点三 共线向量定理及其应用 【例3】 设两个非零向量a 与b 不共线.(1)若AB→=a +b ,BC →=2a +8b ,CD →=3(a -b ).求证:A ,B ,D 三点共线; (2)试确定实数k ,使k a +b 和a +k b 共线.(1)证明 ∵AB→=a +b ,BC →=2a +8b ,CD →=3(a -b ).∴BD →=BC →+CD →=2a +8b +3(a -b )=2a +8b +3a -3b =5(a +b )=5AB →.∴AB →,BD →共线,又它们有公共点B , ∴A ,B ,D 三点共线.(2)解 ∵k a +b 与a +k b 共线,∴存在实数λ, 使k a +b =λ(a +k b ),即k a +b =λa +λk b , ∴(k -λ)a =(λk -1)b .∵a ,b 是不共线的两个非零向量, ∴k -λ=λk -1=0,∴k 2-1=0,∴k =±1.【训练3】 (1)已知a ,b 是不共线的向量,AB →=λa +b ,AC →=a +μb ,λ,μ∈R ,则A ,B ,C 三点共线的充要条件为( ) A.λ+μ=2 B.λ-μ=1 C.λμ=-1D.λμ=1(2)已知A ,B ,C 是直线l 上不同的三个点,点O 不在直线l 上,则使等式x 2OA →+xOB →+BC →=0成立的实数x 的取值集合为( ) A.{0} B.∅ C.{-1}D.{0,-1}解析 (1)因为A ,B ,C 三点共线,所以AB →∥AC →,设AB →=mAC →(m ≠0),则λa +b =m (a +μb ),所以⎩⎨⎧λ=m ,1=mμ,所以λμ=1.(2)法一 若要x 2OA →+xOB →+BC →=0成立,BC →必须与x 2OA →+xOB →共线,由于OA →-OB→=BA →与BC →共线,所以OA →和OB →的系数必须互为相反数,则x 2=-x ,解得x =0或x =-1,而当x =0时,BC →=0,此时B ,C 两点重合,不合题意,舍去.故x=-1.法二 ∵BC→=OC →-OB →,∴x 2OA →+xOB →+OC →-OB →=0,即OC→=-x 2OA →-(x -1)OB →,∵A ,B ,C 三点共线, ∴-x 2-(x -1)=1,即x 2+x =0,解得x =0或x =-1.当x =0时,x 2OA →+xOB →+BC→=0,此时B ,C 两点重合,不合题意,舍去.故x =-1. 答案 (1)D (2)C三、课后练习1.判断下列结论正误(在括号内打“√”或“×”) (1)零向量与任意向量平行.( ) (2)若a ∥b ,b ∥c ,则a ∥c .( )(3)向量AB→与向量CD →是共线向量,则A ,B ,C ,D 四点在一条直线上.( )(4)当两个非零向量a ,b 共线时,一定有b =λa ,反之成立.( ) 解析 (2)若b =0,则a 与c 不一定平行.(3)共线向量所在的直线可以重合,也可以平行,则A ,B ,C ,D 四点不一定在一条直线上.答案 (1)√ (2)× (3)× (4)√2.给出下列命题:①零向量的长度为零,方向是任意的;②若a ,b 都是单位向量,则a =b ;③向量AB →与BA →相等.则所有正确命题的序号是( )A.①B.③C.①③D.①②解析 根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量AB →与BA →互为相反向量,故③错误. 答案 A3.设M 为平行四边形ABCD 对角线的交点,O 为平行四边形ABCD 所在平面内任意一点,则OA →+OB →+OC →+OD →等于( ) A.OM → B.2OM → C.3OM→D.4OM→ 解析 OA →+OB →+OC →+OD →=(OA →+OC →)+(OB →+OD →)=2OM →+2OM →=4OM →. 答案 D4.(2019·东莞调研)如图所示,已知AC →=3BC →,OA →=a ,OB →=b ,OC →=c ,则下列等式中成立的是( )A.c =32b -12aB.c =2b -aC.c =2a -bD.c =32a -12b解析 因为AC →=3BC →,OA →=a ,OB →=b ,所以OC →=OA →+AC →=OA →+32AB →=OA →+32(OB→-OA →)=32OB →-12OA →=32b -12a . 答案 A5.(2018·上海静安区月考)若四边形ABCD 满足AD →=12BC →且|AB →|=|DC →|,则四边形ABCD 的形状是( ) A.等腰梯形 B.矩形 C.正方形D.菱形解析 因为AD →=12BC →,所以AD →∥BC →,且|AD →|=12|BC →|,所以四边形ABCD 为以AD 为上底,BC 为下底的梯形.又|AB →|=|DC →|,所以梯形ABCD 的两腰相等.因此四边形ABCD 是等腰梯形. 答案 A6.(2019·菏泽调研)设a 与b 是两个不共线向量,且向量a +λb 与-(b -2a )共线,则λ=________.解析 依题意知向量a +λb 与2a -b 共线,设a +λb =k (2a -b ),则有(1-2k )a +(k +λ)b =0,所以⎩⎨⎧1-2k =0,k +λ=0,解得k =12,λ=-12. 答案 -127.已知点O ,A ,B 不在同一条直线上,点P 为该平面上一点,且2OP →=2OA →+BA →,则( )A.点P 在线段AB 上B.点P 在线段AB 的反向延长线上C.点P 在线段AB 的延长线上D.点P 不在直线AB 上解析 因为2OP →=2OA →+BA →,所以2AP →=BA →,所以点P 在线段AB 的反向延长线上,故选B.8.(2019·青岛二模)设D ,E ,F 分别为△ABC 三边BC ,CA ,AB 的中点,则DA →+2EB →+3FC →=( ) A.12AD →B.32AD →C.12AC →D.32AC →解析 因为D ,E ,F 分别为△ABC 三边BC ,CA ,AB 的中点,所以DA →+2EB →+3FC→=12(BA →+CA →)+2×12(AB →+CB →)+3×12×(AC →+BC →)=12BA →+AB →+CB →+32BC →+32AC →+12CA →=12AB →+12BC →+AC →=12AC →+AC →=32AC →. 答案 D9.已知△ABC 和点M 满足MA →+MB →+MC →=0,若存在实数m 使得AB →+AC →=mAM →成立,则m =________.解析 由已知条件得MB →+MC →=-MA →,如图,延长AM 交BC 于D 点,则D 为BC 的中点.同理E ,F 分别是AC ,AB 的中点,因此点M 是△ABC 的重心, ∴AM →=23AD →=13(AB →+AC →),则m =3.10.(2019·郑州模拟)设e 1与e 2是两个不共线向量,AB →=3e 1+2e 2,CB →=k e 1+e 2,CD →=3e 1-2k e 2,若A ,B ,D 三点共线,则k 的值为________. 解析 由题意,A ,B ,D 三点共线,故必存在一个实数λ,使得AB→=λBD →. 又AB →=3e 1+2e 2,CB →=k e 1+e 2,CD →=3e 1-2k e 2,所以BD →=CD →-CB →=3e 1-2k e 2-(k e 1+e 2)=(3-k )e 1-(2k +1)e 2,所以3e 1+2e 2=λ(3-k )e 1-λ(2k +1)e 2, 又e 1与e 2不共线,所以⎩⎨⎧3=λ(3-k ),2=-λ(2k +1),解得k =-94.11.在△ABC 中有如下结论:“若点M 为△ABC 的重心,则MA →+MB →+MC →=0.”设a ,b ,c 分别为△ABC 的内角A ,B ,C 的对边,点M 为△ABC 的重心. 若aMA →+bMB→+33cMC →=0,则内角A 的大小为________,当a =3时,△ABC 的面积为________.解析 由aMA →+bMB →+33cMC →=aMA →+bMB →+33c (-MA →-MB →)=⎝⎛⎭⎪⎫a -33c MA →+⎝⎛⎭⎪⎫b -33c MB →=0,且MA →与MB →不共线,∴a -33c =b -33c =0,∴a =b =33c .△ABC 中,由余弦定理可求得cos A =32,∴A =π6.若a =3,则b =3,c =33,S △ABC =12bc sin A =12×3×33×12=934.答案 π6 934。
数学高考平面向量的概念及线性运算专题复习题附答案

《数学高考平面向量的概念及线性运算专题复习题附答案.doc》长度等于0的向量叫做零向量,下面的是数学高考复习平面向量的概念及线性运算专题测试,...将本文的Word文档下载,方便收藏和打印推荐度:点击下载文档https://m./shiti/2043547.html下载说明:1. 下载的文档为doc格式,下载后可用word文档或者wps打开进行编辑;2. 若打开文档排版布局出现错乱,请安装最新版本的word/wps 软件;3. 下载时请不要更换浏览器或者清理浏览器缓存,否则会导致无法下载成功;4. 网页上所展示的文章内容和下载后的文档内容是保持一致的,下载前请确认当前文章内容是您所想要下载的内容。
付费下载付费后无需验证码即可下载限时特价:6.99元/篇原价20元免费下载仅需3秒1、微信搜索关注公众号:copy839点击复制2、进入公众号免费获取验证码3、将验证码输入下方框内,确认即可复制联系客服微信支付中,请勿关闭窗口微信支付中,请勿关闭窗口×温馨提示支付成功,请下载文档我知道了咨询客服×常见问题•1、支付成功后,为何无法下载文档?付费后下载不了,请核对下微信账单信息,确保付费成功;已付费成功了还是下载不了,有可能是浏览器兼容性问题。
•2、付费后能否更换浏览器或者清理浏览器缓存后下载?更换浏览器或者清理浏览器缓存会导致下载不成功,请不要更换浏览器和清理浏览器缓存。
•3、如何联系客服?扫描下方二维码关注公众号“网站在线小助理”,及时联系客服解决。
请把【付款记录详情】截图给客服,同时把您购买的文章【网址】发给客服。
客服会在24小时内把文档发送给您。
(客服在线时间为周一至周五9:00-12:30 14:00-18:30)。
2019高考数学考点突破——平面向量平面向量的概念及线性运算 Word版含解析
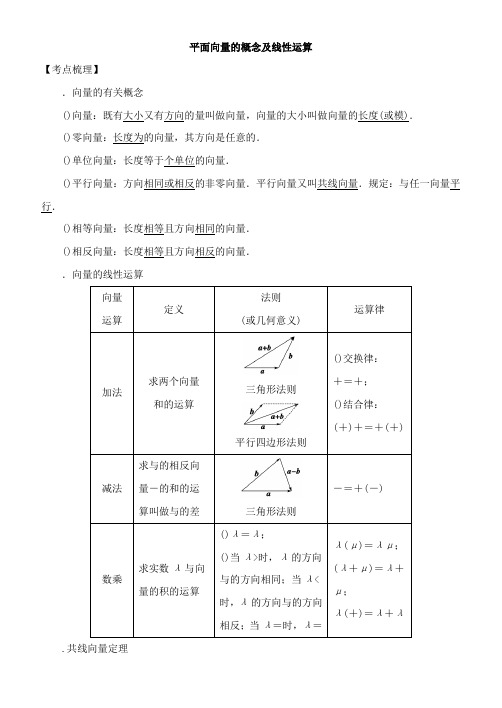
平面向量的概念及线性运算【考点梳理】.向量的有关概念()向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或模).()零向量:长度为的向量,其方向是任意的.()单位向量:长度等于个单位的向量.()平行向量:方向相同或相反的非零向量.平行向量又叫共线向量.规定:与任一向量平行.()相等向量:长度相等且方向相同的向量.()相反向量:长度相等且方向相反的向量..向量的线性运算平行四边形法则.共线向量定理向量(≠)与共线的充要条件是存在唯一一个实数λ,使得=λ.【考点突破】考点一、平面向量的有关概念【例】给出下列四个命题:①若=,则=;②若,,,是不共线的四点,则“=”是“四边形为平行四边形”的充要条件;③若=,=,则=;④=的充要条件是=且∥.其中正确命题的序号是( ).②③.①②.③④.②④[答案][解析]①不正确.两个向量的长度相等,但它们的方向不一定相同.②正确.∵=,∴=且∥,又,,,是不共线的四点,∴四边形为平行四边形;反之,若四边形为平行四边形,则=,∥且,方向相同,因此=.③正确.∵=,∴,的长度相等且方向相同,又=,∴,的长度相等且方向相同,∴,的长度相等且方向相同,故=.④不正确.当∥且方向相反时,即使=,也不能得到=,故=且∥不是=的充要条件,而是必要不充分条件.综上所述,正确命题的序号是②③.【类题通法】.相等向量具有传递性,非零向量的平行也具有传递性..共线向量即为平行向量,它们均与起点无关..向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象的移动混为一谈..非零向量与的关系:是与同方向的单位向量.【对点训练】给出下列六个命题:①若=,则=或=-;。
高三数学一轮复习:1015平面向量的概念及线性运算

例 1.(多选题)给出下列命题,正确的命题是( ) A.若|a|=|b|,则 a = b B. 若 A,B,C,D 不共线,则“A→B=D→C”是“四边形 ABCD 为平行四边形”的充要条件
C.若 a=b,b=c,则 a=c
D. “a=b”的充要条件是“|a|=|b|,且 a∥b”
例 2.(多选)给出下列命题,其中叙述错误的命题为( ) A.向量A→B的长度与向量B→A的长度相等 B.向量 a 与 b 平行,则 a 与 b 的方向相同或相反 C.|a|+|b|=|a-b|⇔a 与 b 方向相反 D.若非零向量 a 与非零向量 b 的方向相同或相反,则 a+b 与 a,b 之一的方向相同
S△ PBC PAC +S△
PABP→A=S△
S△ PAC PAC +S△
PABP→B+S△
S△ PAB PAC+S△
P→C,
PAB
∴S△PBC·P→A+S△PAC·P→B+S△PAB·P→C=→0 .
设点 O 在△ ABC 内,且有O→A+2O→B+3O→C=0,则△ ABC 面积和△ AOC 面积之比为( )
A.3
B.53
C.2
D.32
S△ PAC PAC +S△
PABP→B+S△
S△ PAB PAC+S△
P→C,
PAB
∵PPDA =SS△△ BBPPDA =SS△△ CCPPDA SS△△BBPPAD++SS△△CCPPDA=S△
S△ PBC PAC +S△
PAB,∴P→D=-S△
S△ PBC PAC +S△
P→A,
PAB
即- S△
A
O
B
C
如图,已知 P 为△ ABC 内一点,则有 S△PBC·P→A+S△PAC·P→B+S△PAB·P→C=→0 . A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点测试26 平面向量的概念及线性运算高考概览考纲研读1.了解向量的实际背景2.理解平面向量的概念,理解两个向量相等的含义3.理解向量的几何表示4.掌握向量加法、减法的运算,并理解其几何意义5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义6.了解向量线性运算的性质及其几何意义一、基础小题1.下列等式:①0-a=-a;②-(-a)=a;③a+(-a)=0;④a+0=a;⑤a-b=a+(-b).正确的个数是( )A.2 B.3 C.4 D.5答案 D解析由零向量和相反向量的性质知①②③④⑤均正确.2.若m∥n,n∥k,则向量m与向量k( )A.共线 B.不共线C.共线且同向 D.不一定共线答案 D解析如m∥0,0∥k,但k与m可能共线也可能不共线,故选D.3.如图,正六边形ABCDEF中,++=( )A.0B.C.D.答案 D解析++=++=.故选D.4.下列命题正确的是( )A.若|a|=|b|,则a=±b B.若|a|>|b|,则a>bC.若a∥b,则a=b D.若|a|=0,则a=0答案 D解析对于A,当|a|=|b|,即向量a,b的模相等时,方向不确定,故a=±b不一定成立;对于B,向量的模可以比较大小,但向量不可以比较大小,B不正确;C显然不正确.故选D.5.关于平面向量,下列说法正确的是( )A.零向量是唯一没有方向的向量B.平面内的单位向量是唯一的C.方向相反的向量是共线向量,共线向量不一定是方向相反的向量D.共线向量就是相等向量答案 C解析对于A,零向量是有方向的,其方向是任意的,故A不正确;对于B,单位向量的模为1,其方向可以是任意方向,故B不正确;对于C,方向相反的向量一定是共线向量,共线向量不一定是方向相反的向量,故C正确;对于D,由共线向量和相等向量的定义可知D不正确,故选C.6.已知m,n∈R,a,b是向量,有下列命题:①m(a-b)=ma-mb;②(m-n)a=ma-na;③若ma=mb,则a=b;④若ma=na,则m=n.其中正确的是( )A.①②③ B.①③④ C.②③④ D.①②答案 D解析由数乘向量的运算律知,数乘向量对数和向量都有分配律,所以①②正确;当m=0时,a,b不一定相等,当a=0时,m,n未必相等,所以③④错误.故选D.7.已知向量a=e1+2e2,b=2e1-e2,则a+2b与2a-b( )A.一定共线B.一定不共线C.当且仅当e1与e2共线时共线D.当且仅当e1=e2时共线答案 C解析由a+2b=5e1,2a-b=5e2可知,当且仅当e1与e2共线时,两向量共线.故选C.8.给出下列命题:①两个具有公共终点的向量,一定是共线向量;②λa=0(λ为实数),则λ必为零;③λ,μ为实数,若λa=μb,则a与b共线.其中错误的命题的个数为( )A.0 B.1 C.2 D.3答案 D解析①错误,两向量共线要看其方向而不是起点或终点;②错误,当a=0时,不论λ为何值,λa=0;③错误,当λ=μ=0时,λa=μb=0,此时a与b可以是任意向量.错误的命题有3个,故选D.9.已知向量a,b是两个不共线的向量,若向量m=4a+b与n=a-λb共线,则实数λ的值为( )A.-4 B.- C. D.4答案 B解析因为向量a,b是两个不共线的向量,所以若向量m=4a+b与n=a-λb共线,则4×(-λ)=1×1,解得λ=-,故选B.10.已知a,b是不共线的向量,=λa+b,=a+μb,λ,μ∈R,则A,B,C三点共线的充要条件为( )A.λ+μ=2 B.λ-μ=1C.λμ=-1 D.λμ=1答案 D解析∵A,B,C三点共线,∴∥,设=m(m≠0),则λa+b=m(a+μb),∴∴λμ=1,故选D.11.已知点M是△ABC的边BC的中点,点E在边AC上,且=2,则=( )A.+ B.+C.+ D.+答案 C解析如图,∵=2,∴=+=+=+(-)=+.故选C.12.已知在四边形ABCD中,O是四边形ABCD内一点,=a,=b,=c,=a-b+c,则四边形ABCD的形状为( )A.梯形 B.正方形C.平行四边形 D.菱形答案 C解析因为=a-b+c,所以=c-b,又=c-b,所以∥且||=||,所以四边形ABCD是平行四边形.故选C.二、高考小题13.(2015·全国卷Ⅰ)设D为△ABC所在平面内一点,=3,则( )A.=-+ B.=-C.=+ D.=-答案 A解析=+=++=+=+(-)=-+.故选A.14.(2018·全国卷Ⅰ)在△ABC中,AD为BC边上的中线,E为AD的中点,则=( ) A.- B.-C.+ D.+答案 A解析根据向量的运算法则,可得=-=-=-(+)=-,故选A.15.(2015·安徽高考)△ABC是边长为2的等边三角形,已知向量a,b满足=2a,=2a+b,则下列结论正确的是( )A.|b|=1 B.a⊥bC.a·b=1 D.(4a+b)⊥答案 D解析∵=2a,=2a+b,∴a=,b=-=,∵△ABC是边长为2的等边三角形,∴|b|=2,a·b=·=-1,故a,b不垂直,4a+b=2+=+,故(4a+b)·=(+)·=-2+2=0,∴(4a +b)⊥,故选D.16.(2015·北京高考)在△ABC中,点M,N满足=2,=.若=x+y,则x=________;y =________.答案-解析如图在△ABC中,=++=-++=-++(-)=-.∴x=,y=-.三、模拟小题17.(2018·河北张家口月考)如图,在正六边形ABCDEF中,++=( )A.0B.C.D.答案 A解析在正六边形ABCDEF中,CD∥AF,CD=AF,所以++=++=+=0,故选A.18.(2018·邯郸摸底)如图,在△ABC中,已知D为边BC的中点,E,F,G依次为线段AD 从上至下的3个四等分点,若+=4,则( )A.点P与图中的点D重合B.点P与图中的点E重合C.点P与图中的点F重合D.点P与图中的点G重合答案 C解析由平行四边形法则知+=2,又由+=4知2=4,即=2,所以P为AD的中点,即点P与点F重合.故选C.19.(2018·怀化一模)已知向量a,b不共线,向量=a+3b,=5a+3b,=-3a+3b,则( ) A.A,B,C三点共线 B.A,B,D三点共线C.A,C,D三点共线 D.B,C,D三点共线答案 B解析因为=+=2a+6b=2(a+3b)=2,所以,共线,又有公共点B,所以A,B,D三点共线.故选B.20.(2018·河南中原名校联考)如图,在直角梯形ABCD中,AB=2AD=2DC,E为BC边上一点,=3E,F为AE的中点,则=( )A.- B.-C.-+ D.-+答案 C解析=+=+=-+++=-+++=-+++(++)=-+.故选C.21.(2018·深圳模拟)如图所示,正方形ABCD中,M是BC的中点,若=λ+μ,则λ+μ=( )A. B.C. D.2答案 B解析因为=λ+μ=λ(+)+μ(+)=λ++μ(-+)=(λ-μ)+λ+μ,且=+,所以得所以λ+μ=,故选B.22.(2018·福建高三4月质检)庄严美丽的国旗和国徽上的五角星是革命和光明的象征.正五角星是一个非常优美的几何图形,且与黄金分割有着密切的联系:在如图所示的正五角星中,以A,B,C,D,E为顶点的多边形为正五边形,且=.下列关系中正确的是( )A.-= B.+=C.-= D.+=答案 A解析由题意得,-=-===,所以A正确;+=+==,所以B错误;-=-==,所以C错误;+=+,==-,若+=,则=0,不符合题意,所以D错误.故选A.23.(2018·银川一模)设点P是△ABC所在平面内一点,且+=2,则+=________.答案0解析因为+=2,由平行四边形法则知,点P为AC的中点,故+=0.24.(2018·衡阳模拟)在如图所示的方格纸中,向量a,b,c的起点和终点均在格点(小正方形顶点)上,若c与xa+yb(x,y为非零实数)共线,则的值为________.答案解析设e1,e2分别为水平方向(向右)与竖直方向(向上)的单位向量,则向量c=e1-2e2,a=2e1+e2,b=-2e1-2e2,由c与xa+yb共线,得c=λ(xa+yb),所以e1-2e2=2λ(x -y)e1+λ(x-2y)e2,所以所以则的值为.一、高考大题本考点在近三年高考中未涉及此题型.二、模拟大题1.(2018·山东莱芜模拟)如图,已知△OCB中,B,C关于点A对称,OD∶DB=2∶1,DC 和OA交于点E,设=a,=b.(1)用a和b表示向量,;(2)若=λ,求实数λ的值.解(1)由题意知,A是BC的中点,且=,由平行四边形法则,得+=2.∴=2-=2a-b,∴=-=(2a-b)-b=2a-b.(2)∵∥,=-=(2a-b)-λa=(2-λ)a-b,=2a-b,∴=,∴λ=.2.(2018·河南安阳模拟)如图所示,在△ABC中,在AC上取一点N,使得AN=AC,在AB 上取一点M,使得AM=AB,在BN的延长线上取点P,使得NP=BN,在CM的延长线上取点Q,使得=λ时,=,试确定λ的值.解∵=-=(-)=(+)=,=-=+λ.又∵=,∴+λ=,即λ=,∴λ=.。
