数组题型分析
五年级上学期数学第二单元位置知识点及基本题型解析
五年级上册第二单元位置知识点及基本题型解析
1、数对:由两个数组成,中间用逗号隔开,用括号括起来。
括号里面的数由左至右分别为列数和行数,即“先列后行”。
例1:小军坐在教室的第3列第4行,用(3,4)表示,小红坐在第1列第6行,用( 1 ,6 )来表示,用(5,2)表示的同学坐在第( 5 )列第( 4 )行。
2、作用:一组数对确定唯一一个点的位置。
经度和纬度就是这个原理。
例2:在方格图平面直角坐标系中用数对(3,5)表示(第三列,第五行)。
注:(1)在平面直角坐标系中X轴上的坐标表示列,y轴上的坐标表示行。
如:数对(3,2)表示第三列,第二行。
(2)数对(X,5)的行号不变,表示一条横线,(5,Y)的列号不变,表示一条竖线。
(有一个数不确定,不能确定一个点)
3、图形左右平移行数不变;图形上下平移列数不变。
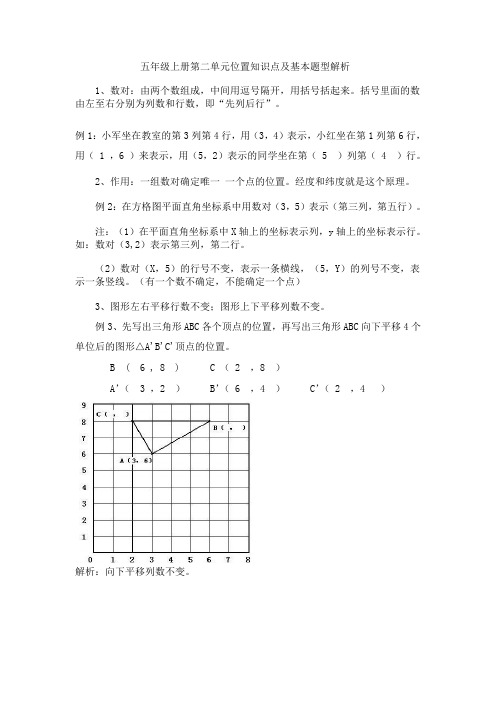
例3、先写出三角形ABC各个顶点的位置,再写出三角形ABC向下平移4个单位后的图形△A'B'C'顶点的位置。
B ( 6 , 8 )
C ( 2 ,8 )
A’( 3 ,2 ) B’( 6 ,4 ) C’( 2 ,4 )
解析:向下平移列数不变。
NOIP普及组历届试题分析

对于100%的数据,3 ≤ n ≤ 100 测验题给出的正整数大小不超过10,000。
试题分析
题意大意:给你n个数,在这n个数中,找 到满足A+B=C的C的个数,注意不是这个 等式的个数。
样例中,1,2,3,4有1+2=3,1+3=4两个。
由于本题数据规模n<=100,我们可以直接
枚举C, A, B,三层循环解决问题。
扫雷游戏 (noip2015普及组第二题)
输入样例 1 33 *?? ??? ?*? 输入样例 2 23 ?*? *??
输出样例 1 mine.out *10 221 1*1 输出样例 2 mine.out 2*1 *21
对于 100%的数据,1≤n≤100,1≤m≤100
问题分析:
本题也是简单的枚举类试题。 我们从雷区的第一行第一列(1,1)开始,判断它周围 有多少个地雷。 由于本题读入的是字符,读入时需要注意: readln(n,m); for i=1 to n do begin for j=1 to m do read(a[i][j]); readln; end;
比例简化 (noip2014普及组第二题)
在社交媒体上,经常会看到针对某一个观点同意与 否的民意调查以及结果。例如,对某 一观点表示 支持的有 1498 人,反对的有 902 人,那么赞同与 反对的比例可以简单的记为1498:902。 不过,如果把调查结果就以这种方式呈现出来,大 多数人肯定不会满意。因为这个比例的数值太大, 难以一眼看出它们的关系。对于上面这个例子,如 果把比例记为 5:3,虽然与 真实结果有一定的误差, 但依然能够较为准确地反映调查结果,同时也显得 比较直观。 现给出支持人数 A,反对人数 B,以及一个上限 L, 请你将 A 比 B 化简为 A’比 B’,要求在 A’和 B’均 不大于 L 且 A’和 B’互质(两个整数的最大公约数 是 1)的前提下,A’/B’ ≥ A/B 且 A’/B’ - A/B 的值 尽可能小。
数组经典题和解析

数组经典题和解析(原创版)目录1.数组经典题概述2.数组经典题的解题技巧3.数组经典题解析示例正文【数组经典题概述】数组经典题是计算机编程领域中常见的一类题目,主要考察程序员对数组数据结构的掌握程度以及相应的算法应用能力。
数组作为一种重要的数据结构,其操作涵盖了诸多方面,如排序、查找、插入、删除等。
因此,掌握数组经典题的解题技巧,对于提高编程水平具有重要意义。
【数组经典题的解题技巧】1.分析题目,确定数组操作需求:首先要对题目进行仔细阅读和分析,明确题目所要求的数组操作类型,如排序、查找等。
2.选择合适的算法:根据题目需求,选择合适的算法进行实现。
例如,对于排序问题,可以选择冒泡排序、快速排序、归并排序等不同类型的排序算法;对于查找问题,可以选择顺序查找、二分查找等方法。
3.注意数组边界条件:在实现数组操作时,要特别注意数组的边界条件,避免出现数组越界等错误。
4.优化算法性能:在保证算法正确的前提下,要尽量优化算法的性能,提高程序的运行效率。
【数组经典题解析示例】例题:给定一个整数数组,求数组中任意两个数之差的绝对值不超过1 的元素个数。
解题思路:1.遍历数组,对于每个元素,判断其与相邻元素之差的绝对值是否小于等于 1,如果是,则计数器加 1。
2.返回计数器的值,即为满足条件的元素个数。
具体代码实现如下:```pythondef countElements(arr):count = 0for i in range(len(arr) - 1):if abs(arr[i] - arr[i + 1]) <= 1:count += 1return count```总之,掌握数组经典题的解题技巧,可以帮助程序员更好地应对各种编程挑战,提高编程水平。
初中数学规律题题型与解题基本方法(初三)

初中数学规律题题型与解题方法(一)数列或数式的找规律一、基本方法——看增幅(一)如增幅相等(此实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n个数可以表示为:a+(n-1)b,其中a为数列的第一位数,b为增幅,(n-1)b为第一位数到第n位的总增幅。
然后再简化代数式a+(n-1)b。
强调:均匀变化的数列规律可用待定系数法来求一次函数的解析式来求解。
例:4、10、16、22、28、……,求第n位数。
分析:第二位数起,每位数都比前一位数增加6,增幅相都是6,所以,第n位数是:4+(n-1)×6=6n-2 (二)如增幅不相等,但是,增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数。
举例说明:2、5、10、17、……,求第n位数。
分析:数列的增幅分别为:3、5、7,增幅以同等幅度增加。
那么,数列的第n-1位到第n位的增幅是:3+2×(n-2)=2n-1,总增幅为:[3+(2n-1)]×(n-1)÷2=(n+1)×(n-1)=n2-1。
所以,第n位数是2+ n2-1= n2+1。
此解法虽然较烦,却是此类题的通用解法,当然此题也可用其它技巧,或用分析观察凑的方法求出。
强调:增幅不均匀变化的数列规律可尝试用待定系数法来求二次函数的解析式来求解,一定要验证。
(三)增幅不相等,且增幅也不以同等幅度增加(即增幅的增幅也不相等)。
此类题大概没有通用解法,只用分析观察的方法,但是,此类题包括第二类的题,如用分析观察法,也有一些技巧。
二、基本技巧(一)标出序列号:找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
国家二级C语言(数组)机试模拟试卷4(题后含答案及解析)

国家二级C语言(数组)机试模拟试卷4(题后含答案及解析)题型有:1. 选择题选择题1.若有定义:int x[10],*pt=x;,则对x数组元素的正确引用是( )。
A.pt+3B.*&x[10]C.*(pt+10)D.*(x+3)正确答案:D解析:没有A选项的引用形式。
*与&放在一起作用抵消,但x[10]下标10超出了数组下标范围,所以B选项错误。
最大只能引用到x[9],而*(pt+i)表示引用指针pt所指元素后的第i个元素,所以C选项错误,最大只能为*(pt+9)。
D 选项正确。
知识模块:数组2.有以下程序:#include<stdio.h>main( ){int i,s=0,t[]={1,2,3,4,5,6,7,8,9};for(i=0;i<9;i+=2)s+=*(t+i);printf(“%d\n”,s);}程序的运行结果是( )。
A.20B.25C.45D.36正确答案:B解析:统计1~9这9个数中的奇数和,此题考查指向数组的指针。
C语言规定数组名代表数组的首地址,也就是第一个元素的地址,因此*(t+i)代表数组的第i+1个元素。
程序的运行结果是1+3+5+7+9=25。
知识模块:数组3.有以下程序:#include<stdio.h>main( ){int s[12]={1,2,3,4,4,3,2,1,1,1,2,3},c[5]={0},i;for(i=0;i<12;i++)e[s[i]]++;for(i=1;i <5;i++)printf(“%d”,c[i]);printf(“\n”);}程序的运行结果是( )。
A.2 3 4 4B.4 3 3 2C.1 2 3 4D.1 1 2 3正确答案:B解析:在for(i=0;i<12;i++)c[s[i]]++中,数组元素s[i]的值作为数组c的下标,当退出循环时,数组c的4个元素的值分别为4、3、3、2,因此B选项正确。
知识模块:数组4.下列定义数组的语句中正确的是( )。
2023届新高考数学题型全归纳之排列组合专题02 排列数组合数的计算含解析

2023届新高考数学题型全归纳之排列组合专题2排列数组合数类型一、排列数组合数的简单计算【例1】对于满足〃213的正整数〃,)B. A:-【例2】计算A; =.【例3】计算A:0, A:;[例4】计算C”, C;=.【例5】计算C:0, C;:【例6】计算A;, A;。
, C:, C> C;9+C:9.【例7】已知A」I=140A;,求〃的值.【例8】解不等式式<64;2【例9】证明:A;-9A; + 8A; =A:.【例10】解方程A;、= 100A:.【例11】解不等式A;<6A「.【例12】解方程:11C:=24C1【例13]解不等式:C;>3邕.■【例14】设用表示不超过x的最大整数(如0=2, ( =1),对于给定的,定义C:=xe[l,+8),则当xe I,3、时,函数C;的值域是( ), Z■ 1 「、A. —, 28B. —, 5613 」[3 )/ X Z -1 /C. 4, yju [28, 56)D. 4, y U y, 28【例15】组合数C: (〃 > r 2 1, 〃、rw Z)恒等于()B. (/7 + l)(r+l)C- C 〃心;【例16]已知C>:C鬻:C%=3:5:5,求勿、〃的值.类型二、排列数组合数公式的应用【例17】已知求的值.【例18]若C^=C祟,SeN),则曾=【例19]若C;T :C: :C:x =3:4:5,贝ij〃一m=【例20】证明:〃C:=々+ 1尤7+AC: 1 1【例21】证明:y—c y=—yc M,.占j+1 “ 〃 +w+,【例22】求证:A'-1 =A a',1 +to -l)A fl:2 .【例23】证明:£圮:=〃・2"7. *-0【例24】证明:C1 +2C2 +X3 +L +/J C P=-C0+C1 +L +C “). n n n n 2 n n n【例25】求证:C;;+C;;,+C;;+2+L +C;' =C::;X;【例26】计算:器+%,C:+C;+C;+L +C:3【例27】证明:C°C* +Ci(/T +C2C〃-2+L +C*C° =C* .(其中AWm in , n}) to n m n a n a n〃♦k '7【例28】解方程C;»C;:;+C* + ;A>【例29】确定函数A:的单调区间.【例30】规定A: =xG-l)L G-卬+1),其中xeR , m为正整数,且A:=l,这是排列数A:(〃,勿是正整数,且加W〃)的一种推广.⑴求A二的值;⑵排列数的两个性质:①A:=〃A:二,②A:+R A:T=A:M(其中必,〃是正整数).是否都能推广到A:(xcR , m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由.专题2排列数组合数类型一、排列数组合数的简单计算【例1】对于满足〃213的正整数“,(〃-5)仅-6)...仅一12)=()A. A,B. A:_5C. A:D. A;,【解析】C.【例2】计算耳=.【解析】210【例3】计算A;。
七年级上册数学常考题型归纳

七年级上册数学常考题型归纳
一、数学运算题
1、基本运算:要求熟练掌握加减乘除的运算,正确率控制在100%以上。
2、综合运算:要求能够将课上学过的计算方法运用至实际综合问题的求解中。
3、运算能力:要求能够在规定的范围内,特殊情况下或其它时候能够运用相应的运算方法,把复杂问题变为简单问题。
二、分析题
1、假设分析:要求能够从假设证明的角度出发,分析与解决问题。
2、计算分析:要求能够去解决一些特殊的数学问题,根据给出的数据作出相应的数据分析。
3、综合分析:要求能够根据所提供的一系列数据作出判断,做出正确的综合分析,推出正确的结论。
三、图形题
1、几何图形:要求能够识别几何图形,进行快速分析;形状分析;结论推导,形成最佳解决方案。
2、几何运算:要求能够运用几何图形运算,如:斜率求解,直线求斜率,圆的运算等。
3、几何变换:要求能够使用几何变换,如旋转,平移,缩放,翻转等
来解决几何图形位置及大小等问题。
四、代数题
1、代数方程:要求能够解决一元二次方程、一次不定方程、不等式等各类代数方程。
2、函数计算:要求有一定的数学基本运算能力,能够规范计算函数图像以及函数在特定点值。
3、解析几何:要求能够正确把握几何几率与代数几何的区别,在解决坐标几何、原点几何等问题中有所施展。
五、数论题
1、数列数组:要求熟练掌握等差数列、等比数列、级数等数列的特点与计算,能够迅速求解数组。
2、等式的比较:要求能够熟练掌握数论计算中的比较大小规律,知道如何快速判断含有未知数的等式的真假。
3、质数:要求能够判断哪些是质数,哪些是合数,并且能够列出某个定范围内的质数表。
柯西不等式常见题型解法例说

上海中学数学2014年第3期柯西不等式常见题型解法例说315500浙江省奉化中学陈晴应向明柯西不等式≥:d;≥:研≥f≥]ni.6。
1‘是基本百鬲、百7而重要的不等式,是推证其他许多不等式的基础,不仅形式优美,而且还具有非常重要的应用价值.它原先只在数学竞赛中出现,但在2003年颁布的高中数学课程标准选修系列(4—5)《不等式选讲》里,已经加进了柯西不等式,也就是说它将成为选修学生的日常教学要求.用柯西不等式解决某些不等关系问题时往往比较简捷明了,但求解时灵活性较大,技巧性较强.其中一些常见的问题,其解决策略往往与其呈现方式直接相关.笔者就以其在近几年高考中的常见三维类型进行分类,例析对应的解决策略.三维的柯西不等式(盘;+丑;+口;)(躇+6;+鹾)≥(n。
6,+口:6:+a。
63)2揭示了任意两组数组即(n。
,n。
,n。
)、(6,,6。
,63)的平方和之积与实数积之和的平方的大小关系.应用时要解决的核心问题就是如何通过变换不等式,向柯西不等式“逼近”,构造出不等式所需要的两组数组(乜,,乜。
,以。
)、(6。
,6:,6。
),这也是运用柯西不等式解题的基本策略.1一次与二次例1(2013湖南高考)已知口、6、c∈R,盘+26 +3c一6,则n2+462+9c2的最小值为——.解:n+26+3c一6,由柯西不等式得(n2+462 +9c2)(12+12+12)≥(n+26+3c)2,可知n。
+462+9c。
≥婺一12,即最小值为12.例2设.r,y,z∈R,且满足T2+y2+z2—5,则Lr+2y+3z之最大值为——.解:(.f r+2y+32)2≤(L z’2+y2+z2)(12+22+ 32)一70,.‘.Ir+2y+3z最大值为√而.例3如啪2∈R且与≯+≮型+竖j翌一1,求T+y+z的最大值、最小值.解:与竽+≮型+半一,,由柯西不等式得[4z+渺+22]『c孚)2+c警)2+c字,2]≥…孚)惭(害)+z.(字)]2号25×1≥b+y+z一2)2≥5≥l L r+y+z一2≥一5≤z+y+z一2≤5..‘.一3≤T+y+z≤7.故T+y+z之最大值为7,最小值为一3.评注:这类题型的最大特征就是条件与结论中分别出现了一次式与两次式,而要实现一次与两次不等关系的关键就是根据柯西不等式的形态进行构造,让其中一个数组为常数组,这样问题往往可以奏效.2整式与分式2.1两组数组对应的数分别为倒数型例4(2012福建高考)已知函数厂(T)一m—z一2I,m∈R且,(z+2)≥o的解集为[一1,1].(1)求m的值;(2)若口,6,c∈R,且丢+去+去一m,求证:n+26+3c≥9.解:(1)厂(.r+2)一m—f.r},/(T+2)≥o等价于I T l≤m,由I T l≤m有解,得m≥O,且其解集为{丁l —m≤z≤m1),又,(z+2)≥o的解集为[一1,1],故m一1.(2)由(1)知丢+去+去一1,又&,6,c∈R,由柯西不等式得Ⅱ+26+3c一(n+26+3c)f丢+去+去)≥F‘去+何‘去+厄’去)2姐评注:这类题型从结构来讲,两组数组分别是整式类型(口,,n z,n。
高中数学经典题型-排列组合(含答案)

排列组合经典题型【编著】黄勇权【例题1】设有编号为1、2、3、4、5、6的六个桌子和编号为1、2、3、4、5、6的六个小球,将六个小球放在六个桌子上,恰有2个小球和桌子的编号相同的放法有()A.180种B.200种270种 D.360种解:第一步:准确把握“恰有2个”的意义:有2组编号相同,其他不相同第二步:6张桌子,6个小球,小球与桌子编号相同有6组,取其中2组,记作:C26我们假设1、2编号相同,其他的不相同。
下面讨论不同情况下有多少种放法①---③合计:1+2+6=9=270故选C总数:9C26【例题2】从6双不同颜色的鞋子中任取4只,其中恰好有1双同色的取法有()A.240种 B.180种 C.120种 D.60种解:准确理解“4只中,恰好有1双同色”的含义。
意思是:4只中有2只同颜色,2只不同颜色。
①“同颜色的2只”怎么来?1种取法,从6双鞋子中任选一双,则有C6②“不同颜色的2只”,又怎么来?2种,再从剩下的10只鞋子中,任选2只,则有C102中,包含了剩下的5套颜色相同的鞋子,所以要扣除。
因为C10扣除了这5套,其他均为不同颜色的。
即有:C102-5故总的选法数为C61(C102-5)=240种.故选A.【例题3】用0,1,2,3,4,5这六个数组成没有重复数字的四位偶数,将这些四位数从小到大排列起来,第71个数是()A、1240B、2048C、3140D、4020解:先考虑千位:千位为1的四位偶数有A13A24=36个;千位为2的四位偶数有A12A24=24个;千位为3的四位偶数有A13A24=36个;因36+24<71<36+24+36,所以第71个偶数的千位数字为3;再考虑百位:首位是3时,百位为0时有:A12•A13=3×2=6个,合计66个,千位是3.百位是1时,第的偶数依次为:3102,3104,3120.3124,3140,3140就是0,1,2,3,4,5这六个数组成没有重复数字的四位偶数,将这些四位数从小到大排列起来,第71个数.故答案为:3140.【例题4】将7只相同的小球分给4个小朋友,每个小朋友至少分得1球的方法有多少种?A、12B、16C、18D、20解:设4个小朋友为A、B、C、D,因为每个小朋友至少分得1球,那么先给每个人1个球,则还剩3个球。
离散数学题型梳理-第1章

离散数学常考题型梳理第1章 集合及其运算一、题型分析本章主要介绍集合论的基本概念和结论,集合的运算及其性质,以及利用运算性质进行集合表达式的化简和集合恒等式的证明等内容.经常涉及到的题型有:1-1集合与集合之间的包含、元素与集合之间的属于关系1-2幂集的计算1-3集合之间的运算1-4利用集合运算性质证明集合恒等式因此,在本章学习过程中希望大家要清楚地知道:1.集合与集合之间存在一种包含关系,当两个集合A 和B 存在关系A 包含B ,用A ⊇B 表示,或存在关系B 被A 包含,用B ⊆A 表示,这时称B 为A 的子集.注意空集∅是任意一个集合的子集,集合A 也是自己的子集.当B ⊆A 且B ≠A ,也就是说,只有B ⊂A 或A ⊃B 成立,则称B 为A 的真子集.若B 不是A 的子集,即B ⊆A 不成立时,则称A 不包含B ,记作B ⊆A .然而,元素与集合之间存在一种从属关系,当a 是集合A 中的元素,则称a 属于A ,记作a∈A ;若a 不是集合A 中的元素,则称a 不属于A ,记作a ∉A .因此,这两种关系一定不要混淆.2.由集合A 的所有子集组成的集合,称为A 的幂集,记作P (A )或2A .若集合A 是由n 个元素所组成的集合,则A 的幂集由2n 元素组成.当n =3时,A 的幂集由23=8个元素组成.例如,设集合A = {0, 1, 2 },则A 的全部子集由以下子集组成:0元子集(即空集):∅;1元子集:{0},{1},{2};2元子集:{0, 1},{0, 2},{1, 2};3元子集(即集合A ):{0, 1, 2}.因此,计算集合A 的幂集时,首先要按照上述方法写出集合A 的全部子集,然后检验写出的子集个数是否等于2n 个,其中n 是集合A 的元素个数.3.集合之间的运算有并(⋃)、交(⋂)、差(-)、补(~)和对称差(⊕)等五种运算,在做集合运算的题目时,一定要按照它们的定义进行计算.(1) 集合A 和B 的并集A B x x A ⋃=∈{或 x B ∈} 特点:由集合A 和B 的所有元素组成的集合.见图1 图1 图2(2) 集合A 和B 的交集A B x x A ⋂=∈{ 且 x B ∈}特点:由集合A 和B 的公共元素组成的集合.见图2(3) 集合A 与B 的差集A B -=∈∉{}x x A x B 且 特点:由属于A ,而不属于B 的所有元素组成的集合.见图3(4) 集合A 的补集~A ={}x x E x A ∈∉且特点:由属于全集E 但不属于集合A 的元素组成的集合.见图4补集总相对于一个全集而言,可以看作是全集E 与集合A 的差集.(5) 集合A 与B 的对称差A ⊕B =(A -B )⋃(B -A )或 A ⊕B =(A ⋃B )-(A ⋂B )特点:由分别属于集合A 与B 的元素但不属于它们公共元素组成的集合.见图5(6) 把集合A ,B 合成集合A ×B 叫做笛卡儿积,规定A ×B ={<x , y >∣x ∈A 且y ∈B }注意:由于有序对<x , y >中x ,y 的位置是确定的,因此A ×B 的记法也是确定的,不能写成B ×A..笛卡儿积的运算一般不能交换..虽然,笛卡儿积的内容是第2章2.1.1目的内容,是二元关系的预备知识,但我们认为把它作为集合的一种运算考虑更好些。
四位数问题

运行结果
Cnt=30
1231 1277 1283 1319 2543 2609 3793 3911 4013 4549 4817 4933 5591 5843 5939
6733 6791 6841 6871 6917 7297 7369 7703 8101 8221 8941 9013 9461 9689 9887
源程序
jsValue() { int i,j; int temp; for(i=0;i<300;i++) { if(isP(a[i])==1) { b[cnt++]=a[i]; } } for(i=0;i<cnt-1;i++) for(j=i+1;j<cnt;j++) { if(b[i]>b[j]) { temp=b[i]; b[i]=b[j]; b[j]=temp; } } }
运行结果
Cnt=18 pjz1=6681.22 Pjz2=5582.48
1-3实例
已知数据文件IN.DAT中存有300个四位数,并已调用读函数 READDAT()把这些数存入数组A中,请编制一函数JSVALUE(),其功能 是:求出所有这些四位数是素数的个数CNT,再求出所有满足此条件 的四位数平均值PJZ1,以及不满足条件的四位数平均值PJZ2,最后调 用写函数WRITEDAT()把结果CNT,PJZ1,PJZ2输出 到OUT.DAT文件. 例如:5591是素数,则该数满足条件计算平均值PJZ1,且个数 CNT=CNT+1. 9812是非素数,则该数不满足条件计算平均值PJZ2。
答案
jsValue() { int i; int g,s,bb,q; for(i=0;i<300;i++) { g=a[i]%10; s=a[i]/10%10; bb=a[i]/100%10; q=a[i]/1000; if(g+q==bb+s) { cnt++; pjz1+=a[i]; } else { pjz2+=a[i]; } } if(cnt!=0) pjz1=pjz1/cnt; if(cnt!=300) pjz2=pjz2/(300-cnt); }
全国计算机等级考试二级C语言题型分析

《全国计算机等级考试二级C语言》资格考试题型分析二级C考试分笔试和机试两部分,两部分总分均为100分,两部分考试均需60分以上才能合格发放证书。
若其中一科(笔试或机试)通过,另一科可在下一次考试中补考,若补考合格发放证书。
若二科均在85分以上,在合格证书上将加印“优秀”字样,若二科均在70分以上,在合格证书上将加印“良好”字样。
(一)笔试笔试内容分两部分。
公共基础知识考核内容:30分;C语言基础知识考核内容:70分。
题型分析如下:1、单向选择题40道题,共70分。
分值分布如下:其中(1)-(10)、(21)-(40)小题,每題2分,(11)-(20)小题,每题1分。
考核内容分布如下:(1)-(10)小题为公共基础知识考核内容,共计20分;(11)-(40)小题为C语言知识考核内容,共计50分。
2、填空题15个空,每空2分,共30分。
考核内容分布如下:(1)-(5)空为公共基础知识考核内容,共计10分;(6)-(15)空为C语言知识考核内容,共计20分。
(二)机试机试三道题:程序填空题,30分;程序修改题,30分;程序设计题,40分。
1、程序填空题通常会给出一段源代码,设计三个空需要你来填写。
每空10分。
例如:#include#include#define M 5#define N 20void fun(char (*ss)[N]){ int i, j, k=0, n, m, len;for(i=0; i{ len=strlen(ss[i]);if(i==0) n=len;if(len>n) {/**********found**********/n=len; ___1___=i;}}for(i=0; iif (i!=k){ m=n;len=strlen(ss[i]);/**********found**********/for(j=___2___; j>=0; j--)ss[i][m--]=ss[i][j];for(j=0; j/**********found**********/___3___='*';}}main(){ char ss[M][N]={"shanghai","guangzhou","beijing","tianjing","cchongqing"};int i;printf("\nThe original strings are :\n");for(i=0; iprintf("\n");fun(ss);printf("\nThe result:\n");for(i=0; i}2、程序修改题通常会给出一段源代码,设计2-3个错误需要你来修改。
专题23 数列的基本知识与概念 (学生版)高中数学53个题型归纳与方法技巧总结篇

高中数学53个题型归纳与方法技巧总结篇专题23数列的基本知识与概念【考点预测】1.数列的概念(1)数列的定义:按照一定顺序排列的一列数称为数列,数列中的每一个数叫做这个数列的项.(2)数列与函数的关系:从函数观点看,数列可以看成以正整数集N *(或它的有限子集{}12n ⋯,,,)为定义域的函数()n a f n =当自变量按照从小到大的顺序依次取值时所对应的一列函数值.(3)数列有三种表示法,它们分别是列表法、图象法和通项公式法.2.数列的分类(1)按照项数有限和无限分:(2)按单调性来分:111()n n n nn n a a a a a a C +++≥⎧⎪≥⎪⎨==⎪⎪⎩递增数列:递减数列: ,常数列:常数摆动数列 3.数列的两种常用的表示方法(1)通项公式:如果数列{}n a 的第n 项与序号n 之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.(2)递推公式:如果已知数列{}n a 的第1项(或前几项),且从第二项(或某一项)开始的任一项与它的前一项(或前几项)间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的递推公式.【方法技巧与总结】(1)若数列{}n a 的前n 项和为n S ,通项公式为n a ,则1112n n n S n a S S n n N*-=⎧⎪=⎨-≥∈⎪⎩ , , ,注意:根据n S 求n a 时,不要忽视对1n =的验证.(2)在数列{}n a 中,若n a 最大,则11n n n n a a a a -+≥⎧⎨≥⎩ , 若n a 最小,则11.n n nn a a a a -+≤⎧⎨≤⎩【题型归纳目录】题型一:数列的周期性题型二:数列的单调性题型三:数列的最大(小)项题型四:数列中的规律问题题型五:数列的最值问题【典例例题】题型一:数列的周期性例1.已知无穷数列{}n a 满足()21N n n n a a a x *++=-∈,且11a =,2a x =()x ∈Z ,若数列{}n a 的前2020项中有100项是0,则下列哪个不能是x 的取值()A .1147B .1148C .1142-D .1143-例2.若[]x 表示不超过x 的最大整数(如[]2.52=,[]44=,[]2.53-=-),已知2107n n a ⎡⎤=⨯⎢⎥⎣⎦,11b a =,()*110,2n n n b a a n n -=-∈≥N ,则2019b =()A .2B .5C .7D .8例3.数列{}n a 满足12a =,111nn na a a ++=-,其前n 项积为n T ,则10T 等于()A .16B .16-C .6D .6-例4.若数列{}n a 满足1222a a ==,且21n n n a a a ++=-,则{}n a 的前100项和为()A .67B .68C .134D .167例5.数列{}n a 满足112,0,2121,1,2n n n n n a a a a a +⎧≤<⎪⎪=⎨⎪-≤<⎪⎩若125a =,则2021a 等于()A .15B .25C .35D .45例6.已知数列{}n a 满足,()()111122,32n n n n n a a a a a ----⎧-+>⎪=⎨-⎪⎩ *(,1)n N n ∈>,若1(2,3)a ∈且记数列{}n a 的前n 项和为n S ,若2019=m S ,则2019S 的值为()A .60572B .3028C .60552D .3029例7.(2022·广东汕头·三模)已知数列{}n a 中,114a =-,当1n >时,111n n a a -=-,则2022a =()A .14-B .45C .5D .45-例8.(2022·河北·沧县中学高三阶段练习)已知数列{}n a 中,()1112n n n a a a n --=⋅+≥,12a =,则10a 等于()A .12-B .12C .-1D .2题型二:数列的单调性例9.(2022·四川达州·二模(理))已知单调递增数列{}n a 满足9,102121,109n n m n a m n n -⎧≥⎪=⎨⎛⎫+-< ⎪⎪⎝⎭⎩,则实数m 的取值范围是()A .[)12,+∞B .()1,12C .()1,9D .[)9,+∞例10.(2022·河南·温县第一高级中学高三阶段练习(文))已知函数()()633,7,7x a x x f x a x -⎧--≤=⎨>⎩,若数列{}n a 满足()()*n a f n n N =∈且{}n a 是递增数列,则实数a 的取值范围是()A .9,34⎛⎫ ⎪⎝⎭B .9,34⎡⎫⎪⎢⎣⎭C .()2,3D .[)2,3例11.(2022·浙江·高三专题练习)已知数列{}n a 的首项为11a =,2a a =,且121(2,)n n a a n n n N *++=+≥∈,若数列{}n a 单调递增,则a 的取值范围为()A .12a <<B .23a <<C .3522a <<D .1322a <<例12.(2022·全国·高三专题练习)已知等比数列{}n a 前n 项和n S 满足113n n S A +=-⋅(A R ∈),数列{}n b 是递增的,且2n b An Bn =+,则实数B 的取值范围为()A .2,3⎡⎫-+∞⎪⎢⎣⎭B .[)1,-+∞C .()1,-+∞D .1,3⎛⎫-+∞ ⎪⎝⎭例13.(2022·全国·高三专题练习(理))已知数列{}n a 满足()712,83,8n n a n n a n a n *-⎧⎛⎫-+>⎪ ⎪=∈⎝⎭⎨⎪≤⎩N ,若对于任意n *∈N 都有1n n a a +>,则实数a 的取值范围是()A .10,3⎛⎫ ⎪⎝⎭B .10,2⎛⎫ ⎪⎝⎭C .1,12⎛⎫ ⎪⎝⎭D .11,32⎛⎫ ⎪⎝⎭例14.(2022·全国·高三专题练习)设数列{}n a 的通项公式为2n a n bn =+,若数列{}n a 是单调递增数列,则实数b 的取值范围为()A .(2,)-+∞B .[2,)-+∞C .(3,)-+∞D .(,3)-∞-【方法技巧与总结】解决数列的单调性问题的3种方法作差比较法根据1n n a a +-的符号判断数列{}n a 是递增数列、递减数列或是常数列作商比较法根据1(>0<0)n n n na a a a +或与1的大小关系进行判断数形结合法结合相应函数的图象直观判断题型三:数列的最大(小)项例15.已知数列{}n a 的首项为1,且()()*111n n n a a n n ++=∈+N ,则na的最小值是()A .12B .1C .2D .3例16.已知数列{}n a 满足110a =,12n na a n+-=,则n a n 的最小值为()A .-1B .112C .163D .274例17.已知数列{}n a 的前n 项和n S ,且2(1)n n S a n -=-,22na nn b S =,则数列{}n b 的最小项为()A .第3项B .第4项C .第5项D .第6项例18.已知数列{}n a 的前n 项和2212,n S n n =-数列{||}n a 的前n 项和,n T 则nT n的最小值____例19.数列,1n =,2, ,中的最小项的值为__________.【方法技巧与总结】求数列的最大项与最小项的常用方法(1)将数列视为函数()f x 当x ∈N *时所对应的一列函数值,根据f (x )的类型作出相应的函数图象,或利用求函数最值的方法,求出()f x 的最值,进而求出数列的最大(小)项.(2)通过通项公式n a 研究数列的单调性,利用11()2n n nn a a a n a -+≥⎧⎨≥⎩≥,确定最大项,利用11()2n n nn a a a n a -+≤⎧⎨≤⎩≥,确定最小项.(3)比较法:若有1()()10n n a a f n f n -=+->+或0n a >时11n na a +>,则1n n a a +>,则数列{}n a 是递增数列,所以数列{}n a 的最小项为1(1)a f =;若有1()()10n n a a f n f n =-+-<+或0n a >时11n na a +<,则1n n a a <+,则数列{}n a 是递减数列,所以数列{}n a 的最大项为1(1)a f =.题型四:数列中的规律问题例20.蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以()f n 表示第n 幅图的蜂巢总数,则(4)f =();()f n =().A .352331n n +-B .362331n n -+C .372331n n -+D .382331n n +-例21.由正整数组成的数对按规律排列如下:()1,1,()1,2,()2,1,()1,3,()2,2,()3,1,()1,4,()2,3,()3,2,()4,1,()1,5,()2,4,⋅⋅⋅.若数对(),m n 满足()22222021m n -⋅-=,,m n N *∈,则数对(),m n 排在()A .第386位B .第193位C .第348位D .第174位例22.已知“整数对”按如下规律排列:()()()()()1,11,22,11,32,2,,,,,()()()3,11,42,3,,()3,2,,()4,1,…,则第68个“整数对”为()A .()1,12B .()3,10C .()2,11D .()3,9例23.将正整数排列如下:123456789101112131415……则图中数2020出现在A .第64行3列B .第64行4列C .第65行3列D .第65行4列题型五:数列的最值问题例24.(2022·北京市第十二中学高三期中)已知数列{}n a 满足32n a n n=+,则数列{}n a 的最小值为()A .343B .575C .D .12例25.(2022·全国·高三专题练习)已知数列{}n a ,2141n n a n n -=+-,则下列说法正确的是()A .此数列没有最大项B .此数列的最大项是3aC .此数列没有最小项D .此数列的最小项是2a 例26.(2022·河南·高三阶段练习(理))在数列{}n a 中,11a =,1n n a a n --=(N n +∈,2n ≥),则11n a n ++的最小值是()A .12B .34C .1D .32例27.(2022·辽宁·高三阶段练习)若数列{}n a 满足24122,n nn n n a T a a a -==⋅⋅⋅,则n T 的最小值为()A .92-B .102-C .112-D .122-例28.(2022·全国·高三专题练习)若数列{}n a 满足113a =,1n n n a a +-=,则na n的最小值为()A .235B .143C 12D .13例29.(2022·全国·高三专题练习)设221316n a n n =-+-,则数列{}n a 中最大项的值为()A .134B .5C .6D .132例30.(2022·浙江·高三专题练习)已知数列{}n a 的通项公式为211n aa n n n=-+,5a 是数列{}n a 的最小项,则实数a 的取值范围是()A .[]40,25--B .[]40,0-C .[]25,25-D .[]25,0-【过关测试】一、单选题1.(2022·陕西·交大附中模拟预测(理))函数()f x 定义如下表,数列{}()N n x n ∈满足02x =,且对任意的自然数n 均有()1n n x f x +=,则2022x =()x 12345()f x 51342A .1B .2C .4D .52.(2022·内蒙古赤峰·模拟预测(理))大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中曾经经历过的两仪数量总和,其中一列数如下:0,2,4,8,12,18,24,32,40,50,…….按此规律得到的数列记为{}n a ,其前n 项和为n S ,给出以下结论:①22122n a n n -=-;②182是数列{}n a 中的项;③21210a =;④当n 为偶数时,()2122n n n S S S n n *++-+=+∈N .其中正确的序号是()A .①②B .②③C .①④D .③④3.(2022·河南·模拟预测(理))观察数组()2,2,()3,4,()4,8,()5,16,()6,32,…,根据规律,可得第8个数组为()A .()9,128B .()10,128C .()9,256D .()10,2564.(2022·吉林长春·模拟预测(理))已知数列{}n a 满足()()11120n n a a +-++=,112a =,则数列{}n a 的前2022项积为()A .16-B .23C .6-D .325.(2022·江西·临川一中模拟预测(理))已知数列{}n a 满足()1112,21*+-==∈-n n n a a a n N a ,则2022=a ()A .13B .1C .2D .526.(2022·全国·高三专题练习)已知数列{}n a 的通项公式为n aa n n=+,则“21a a >”是“数列{}n a 单调递增”的()A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件7.(2022·全国·高三专题练习)已知数列{}n a 满足()2**2,5,,1,5,.n n tn n n a t n n n ⎧-+≤∈⎪=⎨->∈⎪⎩N N 且数列{}n a 是单调递增数列,则t 的取值范围是()A .919,24⎛⎫⎪⎝⎭B .9,2⎛⎫+∞ ⎪⎝⎭C .()5,+∞D .(]1,48.(2022·全国·高三专题练习)若数列{an }的前n 项和Sn =n 2-10n (n ∈N *),则数列{nan }中数值最小的项是()A .第2项B .第3项C .第4项D .第5项9.(2022·上海普陀·二模)数列{}n a 的前n 项的和n S 满足*1(N )n n S S n n ++=∈,则下列选项中正确的是()A .数列{}1n n a a ++是常数列B .若113a <,则{}n a 是递增数列C .若11a =-,则20221013S =D .若11a =,则{}n a 的最小项的值为1-10.(2022·北京四中三模)已知数列{n a }的通项为22n a n n λ=-,则“0λ<”是“*n ∀∈N ,1n n a a +>”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件二、多选题11.(2022·河北·衡水第一中学高三阶段练习)大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,是中国传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0,2,4,8,12,18,24,32,40,50,…,则下列说法正确的是()A .此数列的第20项是200B .此数列的第19项是180C .此数列偶数项的通项公式为222n a n=D .此数列的前n 项和为(1)n S n n =⋅-12.(2022·全国·高三专题练习)若数列{}n a 满足1112,012,1321,12n n n n n a a a a a a +⎧⎪⎪==⎨⎪-<<⎪⎩ ,则数列{}n a 中的项的值可能为()A .13B .2C .23D .4513.(2022·全国·高三专题练习)下列四个选项中,不正确的是()A .数列2345,,,3456,⋯的一个通项公式是1n n a n =+B .数列的图象是一群孤立的点C .数列1,1-,1,1-,⋯与数列1-,1,1-,1,⋯是同一数列D .数列11,24,⋯,12n是递增数列14.(2022·全国·高三专题练习)已知n S 是{}n a 的前n 项和,12a =,()1112n n a n a -=-≥,则下列选项错误的是()A .20212a =B .20211012S =C .331321n n n a a a ++⋅⋅=D .{}n a 是以3为周期的周期数列15.(2022·全国·高三专题练习)若数列{an }满足112,2712,62n n n n n a a a a a +⎧≤⎪⎪=⎨⎪->⎪⎩,123a =,则数列{an }中的项的值可能为()A .19B .16C .13D .4316.(2022·全国·高三专题练习)已知数列{}n a 满足112a =-,111n n a a +=-,则下列各数是{}n a 的项的有()A .2-B .23C .32D .317.(2022·全国·高三专题练习(文))南宋杨辉在他1261年所著的《详解九章算术》一书中记录了一种三角形数表,称之为“开方作法本源”图,即现在著名的“杨辉三角”.如图是一种变异的杨辉三角,它是将数列{}n a 各项按照上小下大,左小右大的原则写成的,其中{}n a 是集合{}220,,s ts t s t Z +≤<∈且中所有的数从小到大排列的数列,即13a =,25a =,36a =,49a =,510a =,…,则下列结论正确的是()A .第四行的数是17,18,20,24B .()11232-+=⋅n n n a C .()11221n n a n +=+D .10016640a =18.(2022·全国·高三专题练习)如图所示的数表中,第1行是从1开始的正奇数,从第2行开始每个数是它肩上两个数之和.则下列说法正确的是()A .第6行第1个数为192B .第10行的数从左到右构成公差为102的等差数列C .第10行前10个数的和为9952⨯D .数表中第2021行第2021个数为202060612⨯19.(2022·河北·石家庄实验中学高三开学考试)大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,是中国传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0,2,4,8,12,18,24,32,40,50,…,则下列说法正确的是()A .此数列的第20项是200B .此数列的第19项是182C .此数列偶数项的通项公式为222n a n=D .此数列的前n 项和为(1)n S n n =⋅-20.(2022·福建漳州·三模)已知数列{n a }的前n 项和为211n S n n =-,则下列说法正确的是().A .{}n a 是递增数列B .{}n a 是递减数列C .122n a n=-D .数列{}n S 的最大项为5S 和6S 21.(2022·湖南·长沙一中高三阶段练习)对于正整数n ,()n ϕ是小于或等于n 的正整数中与n 互质的数的数目.函数()n ϕ以其首名研究者欧拉命名,称为欧拉函数,例如()96ϕ=(1,2,4,5,7,8与9互质),则()A .若n 为质数,则()1n n ϕ=-B .数列(){}n ϕ单调递增C .数列()2n n ϕ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭的前5项和等于72D .数列(){}3nϕ为等比数列三、填空题22.(2022·北京·人大附中模拟预测)能说明命题“若无穷数列{}n a 满足()111,2,3,n na n a +>= ,则{}n a 为递增数列”为假命题的数列{}n a 的通项公式可以为n a =__________.23.(2022·陕西·宝鸡中学模拟预测)写出一个符合下列要求的数列{}n a 的通项公式:①{}n a 是无穷数列;②{}n a 是单调递减数列;③20n a -<<.这个数列的通项可以是__________.24.(2022·海南·模拟预测)写出一个同时具有下列性质①②③的数列{}n a 的通项公式:n a =__________.①10n n a a +<;②数列{}n a 是单调递减数列;③数列{}2nn a 是一个等比数列.25.(2022·江西·临川一中模拟预测(文))已知23n a n n =+,若2nn a λ≤对于任意*n ∈N 恒成立,则实数λ的取值范围是_______.26.(2022·天津市新华中学高三期末)在数列{}n a 中,()71()8n n a n =+,则数列{}n a 中的最大项的n =________.27.(2022·山西·模拟预测(理))数列{}n a 中,已知11a =,20a >,()*21n n n a a a n ++=-∈N ,则2022a 的取值范围是___________.28.(2022·四川成都·三模(理))已知数列{}n a 满足13a =,122n n n a a a ++=,则2022a 的值为______.29.(2022·全国·模拟预测)在数列{}na 中,11a =,1,231,nn n n n a a a a a +⎧⎪=⎨⎪+⎩为偶数为奇数,则1232021a a a a ++++= ___.。
全国信息学奥赛高中组入门基础讲解第六章数组(教学设计+源代码)

此外,在教学过程中,我注重了师生互动,鼓励学生积极参与讨论和提问。但反思后发现,课堂上的互动更多地集中在学生回答问题环节,而在学生自主学习和探究环节,互动相对较少。为了提高学生的自主学习能力,我计划在未来的教学中,增加小组合作环节,引导学生相互讨论、交流,培养他们的团队合作精神。
7. 作业布置(2分钟)
教师布置与数组相关的编程作业,要求学生在课后完成。作业难度要适中,旨在检验学生对课堂知识的掌握程度。
整个教学过程设计注重师生互动,充分调动学生的积极性、主动性和创造性。教学环节紧凑,突出重难点,注重实际应用,使学生在轻松愉快的氛围中掌握数组知识。
拓展与延伸
1. 提供与本节课内容相关的拓展阅读材料:
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
```
这些题型涵盖了数组的基本概念、声明与初始化、访问与引用、遍历、操作和排序等方面的知识点,能够帮助学生巩固和加深对数组的理解和掌握。通过解决这些实际问题,学生能够更好地将数组知识应用于编程实践。
2. 学生的学习兴趣、能力和学习风格:针对数组这一章节,学生可能对编程实践和问题解决具有较强的兴趣。在学习能力方面,学生应该具备一定的编程实践能力和逻辑思维能力。在学习风格上,学生可能更倾向于通过实践和案例分析来学习,因此需要提供丰富的编程实例和实际问题。
排列数、组合数公式常见题型例析

排列数、组合数公式常见题型例析广东省佛山市顺德区沙滘中学 528315 何健文纵观近10年高考,有关排列数、组合数公式的运用一直都是出题的冷点,试题偶有所见,大都是以选择题或填空题形式出现,属容易题,但2001年全国高考题的第一大题的出现,令众多考生束手无策,也引起了师生们的极大关注。
本文拟从以下两方面介绍有关排列数、组合数公式常见题型和解题分析,供广大读者参考。
一、 排列数、组合数公式及变形公式1、排列数公式mn A =n(n-1)(n-2)…(n-m+1)=)!(!m n n -,特别地nn A =n(n-1)(n-2)…3•2•1,规定0!=1;2、组合数公式=mn C 123)1()1()2)(1(⋅⋅⋅⋅⋅-+-⋅⋅⋅--m m m n n n n =m m mn A A =)!(!!m n m n -.注意:m n ≥且m n ,都是正整数,m 可以为0,即0n C =1.3、两个重要性质(1) =m n C mn n C -,为了简化计算,当m 2n >时,通常将m n C 转化为mn n C -; (2) m n C +1-m n C =m n C 1+.由这些性质可以得到几个常用变形公式(组合恒等式):(ⅰ) =m n C 11--m n C m n =1111++++m n C n m (ⅱ) 0n C +1n C +2n C +…+nn C =n 2.(ⅲ) (n+1)!=(n+1)﹒n!=n ﹒n!+n!. ⇒ n ﹒n!= (n+1)﹒n!-n!.(ⅳ) n n C +n n C 1++n n C 2++…+n m n C +=11+++n m n C 等等. 二、排列数、组合数公式常见题型例析 1、 求值例1 求n n C -7+nn C -+91的值.解:由题意可知, 原式中的正整数n 必须满足下列条件: 0≤7―n ≤n,0≤9-n ≤n+1, 解得4≤n ≤9. (n ∈N *) n ∈N *. ∴n=4, 5, 6, 7.将n=4, 5, 6, 7.代入n n C -7+nn C -+91可得到分别为5,25,41,29.评析 本题从组合数成立的条件(0≤m ≤n 且m n ,都是自然数)入手,既找到了解题路,又使问题 完满地得到了解决,可谓一举两得. 另一方面,我们从中又得到一个启发:利用组合数的性质解决某些问题,要比纯用组合数公式解决问题方便的多.例2 计算34C +35C +36C +…+310C . 解:利用组合数性质:m n C 1+=mn C +1-m n C . 原式=44C +34C +35C +36C +…+310C ―44C=45C +35C +36C +…+310C ―44C=…=411C ―1 =329.评析 正确使用组合数的性质及组合数的计算公式是解本题的关键。
排列组合题型分类(学生版)

排列组合题型分类一.元素分析法(位置分析法):1.亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项工作,其余三人均能从事这四项工作,则不同的选派方案共有()A. 36种B. 12种C. 18种D. 48种2.1名老师和4名获奖同学排成一排照相留念,若老师不站两端则有不同的排法有多少种?3.有七名学生站成一排,某甲不排在首位也不排在末位的排法有多少种?4.六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A.192种B.216种C.240种D.288种5.某班班会准备从含甲、乙的7人中选取4人发言,要求甲、乙两人至少有一人参加,且若甲、乙同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有()A.720种B.520种C.600种D.360种二.可重复排列6.有4名学生报名参加数学、物理、化学竞赛,每人限报一科,有多少种不同的报名方法?7.有4名学生参加争夺数学、物理、化学竞赛冠军,有多少种不同的结果?8.将3封不同的信投入4个不同的邮筒,则有多少种不同投法?9.把6名实习生分配到7个车间实习共有多少种不同方法?10.8名同学争夺3项冠军,获得冠军的可能性有()A、38B、83C、38AD、38C三.相邻问题11.停车场划出一排12个停车位置,今有8辆车需要停放.要求空车位置连在一起,不同的停车方法有多少种?12.永定土楼,位于中国东南沿海的福建省龙岩市,是世界上独一无二的神奇的山区民居建筑,是中国古建筑的一朵奇葩.2008年7月,成功列入世界遗产名录.它历史悠久、风格独特,规模宏大、结构精巧.土楼具体有圆形,方形,五角形,八角形,日字形,回字形,吊脚楼等类型.现有某大学建筑系学生要重点对这七种主要类型的土楼依次进行调查研究.要求调查顺序中,圆形要排在第一个或最后一个,方形、五角形相邻.则共有()种不同的排法.A.480B.240C.384D.1440四.不相邻问题13.七人并排站成一行,如果甲乙两个必须不相邻,那么不同的排法种数是14.马路上有编号为1,2,3…,9九只路灯,现要关掉其中的三盏,但不能关掉相邻的二盏或三盏,也不能关掉两端的两盏,求满足条件的关灯方案有多少种?五.相邻和不相邻综合问题24.已知六人排成一排拍照,其中甲、乙、丙三人两两不相邻,甲、丁两人必须相邻,则满足要求的排队方法数为()A.72B.96C.120D.28830.用1、2、3、4、5、6组成没有重复数字的六位数,要求1与2相邻,3与4相邻,5与6不相邻,这样的六位数有()个.A.24B.48C.96D.3615.3位男生和3位女生共6位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是()A. 360B. 288C. 216D. 96六.甲不乙不问题16.身穿兰、黄两种颜色衣服的各有两人,身穿红色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有()A.48种B.72种C.78种D.84种17.将甲、乙、丙、丁四位辅导老师分配到A、B、C、D四个班级,每个班级一位老师,且甲不能分配到A 班,丁不能分配到B 班,则共有分配方案的种数为( )A .10B .12C .14D .2418. 从星期一到星期六安排甲、乙、丙三人值班,每人值2天班,如果甲不安排在星期一,乙不安排在星期六,那么值班方案种数为( )A . 42B . 30C . 72D . 60七.坐凳子问题19. 3个人坐在一排8个椅子上,若每个人左右两边都有空位,则坐法的种数有多少种?20. 将A 、B 、C 、D 、E 五种不同文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屉至多放一种文件,则文件A 、B 被放在相邻抽屉内且文件C 、D 被放在不相邻的抽屉内的放法种数为( )A . 240B . 480C . 840D . 960八.多排问题 6个不同的元素排成前后两排,每排3个元素,那么不同的排法种数是( )A 、36种B 、120种C 、720种D 、1440种22. 把15人分成前后三排,每排5人,不同的排法种数为(A )510515A A (B )3355510515A A A A (C )1515A (D )3355510515A A A A23. 8个不同的元素排成前后两排,每排4个元素,其中某2个元素要排在前排,某1个元素排在后排,有多少种不同排法?九.环排问题24. 8人围桌而坐,共有多少种坐法?25. 8名学生平均分成两组,每组都围成一个个圆圈,有 种不同的围法.26. 7颗颜色不同的珠子,可穿成 种不同的珠子圈.27. 已知甲、乙、丙三位同学围成一个圆时,其中一个排列“甲乙丙”与该排列旋转一个或几个位置后得到的排列“乙丙甲”或“丙甲乙”是同一个排列.现有m 位同学,若站成一排,且甲同学在乙同学左边的站法共有60种,那么这m 位同学围成一个圆时,不同的站法总数为( )A .24B .48C .60D .12028. 5个女孩与6个男孩围成一圈,任意两个女孩中间至少站一个男孩,则不同排法有___种(填数字).29.如图,某手链由10颗较小的珠子(每颗珠子相同)和11颗较大的珠子(每颗珠子均不相同)串成,若10颗小珠子必须相邻,大珠子的位置任意,则该手链不同的串法有()A.种B.种C.种D.种30.如图,某伞厂生产的“太阳”牌太阳伞的伞蓬是由太阳光的七种颜色组成,七种颜色分别涂在伞蓬的八个区域内,且恰有一种颜色涂在相对区域内,则不同的颜色图案的此类太阳伞至多有()A.40320种B.5040种C.20160种D.2520种31.21个人按照以下规则表演节目:他们围坐一圈,按顺序从1到3循环报数,报数字“3”的人出来表演节目,并且表演过的人不再参加报数,那么在仅剩两个人没有表演过节目的时候,共报数的次数为()A.19B.38C.51D.57十.定序问题32.书架上某层有6本书,新买3本插进去,要保持原有6本书的顺序,有多少种不同的插法?33.将A、B、C、D、E、F这6个字母排成一排,若A、B、C必须按A在前,B居中,C在后的原则(A、B、C允许不相邻),有多少种不同的排法?34.身高互不相同的7名运动员站成一排,其中甲、乙、丙三人自左向右从高到矮排列的排法有种.(用数字填写答案)35.某学习小组A、B、C、D、E、F、G七名同学站成一排照相,要求A与B相邻,并且C在D的左边,E在D的右边,则不同的站队方法种数为()A.120B.160C.240D.36036.如图,迎面从左至右悬挂3串气球,分别有两串绑两只,一串绑3只,现在用枪射击气球,假设每枪均能命中一只气球,要求每次射击只能射击每串最下方的气球,则用7枪击爆这7只气球不同的次序有多少种.十一.错排问题(不配对问题)37.将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数,则每个方格的标号与所填数字均不相同的填法有()A、6种B、9种C、11种D、23种编号为1、2、3、4、5的五个人分别去坐编号为1、2、3、4、5的五个座位,其中有且只有两个的编号与座位号一致的坐法是()A 10种B 20种C 30种D 60种39.同室4人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则4张贺年卡不同的分配方式共有( )(A)6种(B)9种(C)11种(D)23种40.五个人排成一列,重新站队时,各人都不站在原来的位置上,那么不同的站队方式共有( )(A)60种(B)44种(C)36种(D)24种41.在编号为1,2,3,4的四块土地上分别试种编号为1,2,3,4的四个品种的小麦,但1号地不能种1号小麦,2号地不能种2号小麦,3号地不能种3号小麦,则共有______种不同的种植方案。
计算机科学考研必备数据结构与算法题型解析

计算机科学考研必备数据结构与算法题型解析数据结构和算法是计算机科学考研的重要内容,掌握好这些知识对于提高考试成绩至关重要。
本文将对计算机科学考研必备的数据结构和算法题型进行解析,帮助考生更好地理解和应对考试中的这些题目。
一、线性表线性表是最基本的数据结构之一,常见的线性表包括数组、链表和栈等。
考研中常出现与线性表相关的题目,要求考生熟练掌握线性表的基本操作和应用。
1. 数组数组是一种连续存储数据的线性表,具有随机访问的特性。
考研中可能出现与数组相关的题目,如数组的逆序、元素的插入和删除等操作。
2. 链表链表是一种动态存储数据的线性表,通过节点之间的指针链接起来。
考研中可能出现与链表相关的题目,如链表的逆序、节点的插入和删除等操作。
3. 栈栈是一种特殊的线性表,具有后进先出的特性。
考研中可能出现与栈相关的题目,如栈的应用、栈的实现等。
二、树与图树和图是常见的非线性数据结构,具有丰富的应用场景。
考研中涉及树与图的题目较多,要求考生掌握树和图的基本操作和相关算法。
1. 二叉树二叉树是一种特殊的树结构,每个节点最多只有两个子节点。
考研中可能出现与二叉树相关的题目,如二叉树的遍历、节点的插入和删除等操作。
2. 图图是由节点(顶点)和边组成的数据结构,用于描述各种实际问题的模型。
考研中可能出现与图相关的题目,如最短路径、最小生成树等算法的应用。
三、排序与查找排序和查找是算法中的经典问题,也是考研中常见的题型。
考生需要熟练掌握各种排序和查找算法,并能够分析其时间复杂度和空间复杂度。
1. 排序算法考研中常考察各种排序算法,如冒泡排序、选择排序、插入排序、快速排序等。
考生需要理解这些算法的原理和步骤,并能够分析其时间复杂度和空间复杂度。
2. 查找算法考研中可能出现与查找算法相关的题目,如二分查找、哈希查找、二叉查找树等。
考生需要了解这些算法的原理和应用场景,并能够分析其时间复杂度和空间复杂度。
四、动态规划与贪心算法动态规划和贪心算法是算法设计中的重要方法,也是考研中常见的题型。
计算机程序设计员实操考核题型详解

计算机程序设计员实操考核题型详解1. 考核目的计算机程序设计是计算机专业的核心课程之一,作为一名计算机程序设计员,能够熟练掌握各种常见编程语言、程序设计思路和解决问题的能力是非常重要的。
为了准确评估考生的实际编程能力,实操考核成为了计算机程序设计员考核的常见形式。
实操考核题型旨在通过实际编程任务,考察考生的综合编程能力、逻辑思维能力、问题解决能力和编码规范能力等方面。
本文将详细介绍几种常见的实操考核题型,并给出相应的解题思路和注意事项。
2. 基础题型2.1 编程题编程题是实操考核中最常见的一种题型,要求考生使用指定的编程语言编写程序,实现指定的功能。
根据难易程度的不同,编程题可以分为简单、中等和困难三个层次。
在解答编程题时,考生应做好以下准备工作:- 理解题目:仔细阅读题目要求,确保自己完全理解题目的意思、输入输出要求和功能需求。
- 分析问题:将问题分解为若干个小问题,确定编程任务的具体步骤和逻辑关系。
- 设计算法:根据问题要求和小问题的分析,设计出解决问题的算法和数据结构。
- 编写代码:根据算法和数据结构,使用合适的编程语言编写代码,通过编程语言提供的语法来实现设计的算法和数据结构。
- 调试测试:编写完代码后,需要进行调试和测试,确保程序能够按照题目要求正确运行,输出正确的结果。
2.2 调试题调试题是考察考生在理解和修复他人代码上的能力。
考生需要在给定的代码基础上,发现其中的错误,并予以修复。
在解答调试题时,考生应注意以下几个方面: - 理解代码:仔细阅读给定的代码,确保自己理解代码的功能和运行逻辑。
- 排查错误:通过观察、调试和测试,找出代码中的错误,并做出修复。
- 代码测试:修复代码后,进行测试,确保修复后的代码能够按照题目要求正确运行。
3. 高级题型3.1 排序算法实现排序算法实现题要求考生使用指定的排序算法对给定的数据进行排序,并输出排序后的结果。
在解答排序算法实现题时,需要考生具备以下能力和知识: - 排序算法的原理和运行机制:理解排序算法的原理和运行机制,如冒泡排序、选择排序、插入排序、快速排序等。
全国计算机二级C++程序设计题型

全国计算机二级C++程序设计题型关键信息项:1、选择题题型及占比单选题数量及分值多选题数量及分值2、操作题题型及占比基本操作题特点及分值简单应用题特点及分值综合应用题特点及分值3、考试时间分配选择题答题时间操作题答题时间4、考试知识点覆盖范围面向对象程序设计基础数据结构与算法模板异常处理等5、评分标准选择题评分细则操作题评分要点11 选择题题型111 全国计算机二级 C++程序设计的选择题部分包括单选题和多选题。
单选题数量通常为 40 道,每道题 1 分,总计 40 分。
多选题数量约为 10 道,每道题 2 分,共计 20 分。
112 选择题主要考查考生对 C++程序设计基础知识的掌握程度,涵盖了C++语言的基本语法、数据类型、控制结构、函数、数组、指针、结构体、类等方面的内容。
12 操作题题型121 基本操作题:此类题型主要考查考生对 C++程序基本语法和简单算法的运用能力。
通常要求考生根据给定的题目要求,编写一段相对简单的 C++程序,实现特定的功能。
题目分值约为 18 分。
122 简单应用题:在这一题型中,考生需要综合运用所学的 C++知识,解决较为复杂的编程问题。
可能涉及到数据结构的简单应用、函数的综合运用等,分值约为 24 分。
123 综合应用题:这是操作题中难度最大的部分,要求考生具备较强的编程能力和问题解决能力。
通常会给出一个较为复杂的实际问题,考生需要设计合理的算法和程序结构来解决,分值约为 18 分。
13 考试时间分配131 选择题答题时间建议控制在 30 分钟以内,以便为操作题留出充足的时间。
132 操作题答题时间约为 90 分钟。
其中,基本操作题建议花费 30分钟左右,简单应用题 40 分钟左右,综合应用题 20 分钟左右。
但考生应根据自身实际情况灵活调整。
14 考试知识点覆盖范围141 面向对象程序设计基础:包括类与对象、继承与多态、虚函数等重要概念。
142 数据结构与算法:如链表、栈、队列、二叉树等数据结构,以及排序、查找等算法在 C++中的实现。
php经典算法题型

php经典算法题型算法是我们学习的⼀⼤弱点,今天给⼤家整理了⼀份php经典算法题型,不要怕怀疑⼈⽣了,都跟着来学⼀学吧!1、⼀群猴⼦排成⼀圈,按1,2,…,n依次编号。
然后从第1只开始数,数到第m只,把它踢出圈,从它后⾯再开始数,再数到第m只,在把它踢出去…,如此不停的进⾏下去,直到最后只剩下⼀只猴⼦为⽌,那只猴⼦就叫做⼤王。
要求编程模拟此过程,输⼊m、n, 输出最后那个⼤王的编号。
function king($n, $m){$monkeys = range(1, $n); //创建1到n数组$i=0;while (count($monkeys)>1) { //循环条件为猴⼦数量⼤于1if(($i+1)%$m==0) { //$i为数组下标;$i+1为猴⼦标号unset($monkeys[$i]); //余数等于0表⽰正好第m个,删除,⽤unset删除保持下标关系} else {array_push($monkeys,$monkeys[$i]); //如果余数不等于0,则把数组下标为$i的放最后,形成⼀个圆形结构unset($monkeys[$i]);}$i++;//$i 循环+1,不断把猴⼦删除,或 push到数组}return current($monkeys); //猴⼦数量等于1时输出猴⼦标号,得出猴王}echo king(6,3);2、有⼀母⽜,到4岁可⽣育,每年⼀头,所⽣均是⼀样的母⽜,到15岁绝育,不再能⽣,20岁死亡,问n年后有多少头⽜。
function niu($y){static $num= 1; //定义静态变量;初始化⽜的数量为1for ($i=1; $i <=$y ; $i++) {if($i>=4 && $i<15){ //每年递增来算,4岁开始+1,15岁不能⽣育$num++;niu($y-$i); //递归⽅法计算⼩⽜$num,⼩⽜⽣长年数为$y-$i}else if($i==20){$num--; //20岁死亡减⼀}return $num;}3、杨辉三⾓<?php/* 默认输出⼗⾏,⽤T(值)的形式可改变输出⾏数 */class T{private $num;public function __construct($var=10) {if ($var<3) die("值太⼩啦!");$this->num=$var;}public function display(){$n=$this->num;$arr=array();//$arr=array_fill(0,$n+1,array_fill(0,$n+1,0));$arr[1]=array_fill(0,3,0);$arr[1][1]=1;echo str_pad(" ",$n*12," ");printf("%3d",$arr[1][1]);echo "<br/>";for($i=2;$i<=$n;$i++){$arr[$i]=array_fill(0,($i+2),0);for($j=1;$j<=$i;$j++){if($j==1)echo str_pad(" ",($n+1-$i)*12," ");printf("%3d",$arr[$i][$j]=$arr[$i-1][$j-1]+$arr[$i-1][$j]);echo " ";}echo"<br/>";}}}$yh=new T('3'); //$yh=new T(数量);$yh->display();>4.冒泡排序function maopao($arr){$len = count($arr);for($k=0;$k<=$len;$k++){for($j=$len-1;$j>$k;$j--){if($arr[$j]<$arr[$j-1]){$temp = $arr[$j];$arr[$j] = $arr[$j-1];$arr[$j-1] = $temp;}}}return $arr;}5.快速排序function quickSort($arr) {//先判断是否需要继续进⾏$length = count($arr);if($length <= 1) {return $arr;}//选择第⼀个元素作为基准$base_num = $arr[0];//遍历除了标尺外的所有元素,按照⼤⼩关系放⼊两个数组内//初始化两个数组$left_array = array(); //⼩于基准的$right_array = array(); //⼤于基准的for($i=1; $i<$length; $i++) {if($base_num > $arr[$i]) {//放⼊左边数组$left_array[] = $arr[$i];} else {//放⼊右边$right_array[] = $arr[$i];}}//再分别对左边和右边的数组进⾏相同的排序处理⽅式递归调⽤这个函数 $left_array = quickSort($left_array);$right_array = quickSort($right_array);//合并return array_merge($left_array, array($base_num), $right_array);}6.⼆分查找算法(折半查找算法)function binsearch($x,$a){$c=count($a);$lower=0;$high=$c-1;while($lower<=$high){$middle=intval(($lower+$high)/2);if($a[$middle]>$x){$high=$middle-1;} elseif($a[$middle]<$x){$lower=$middle+1;} else{return $middle;}}return false;}7.PHP奇异算法<?phpfunction test(){$a=1;$b=&$a;echo (++$a)+(++$a);}PHP7以下的版本返回的是 6,PHP7版本返回5 ,还真的算奇异,个⼈底层算法差,认为是PHP7以下版本的BUG8.字符集合:输⼊⼀个字符串,求出该字符串包含的字符集合,并按顺序排序(英⽂)function set($str){//转化为数组$arr = str_split($str);//去除重复$arr = array_flip(array_flip($arr));//排序sort($arr);//返回字符串return implode('', $arr);}9.遍历⼀个⽂件下的所有⽂件和⼦⽂件夹下的⽂件function AllFile($dir){if($dh = opendir($dir)){while (($file = readdir($dh)) !== false){if($file !='..' && $file !='.'){if(is_dir($dir.'/'.$file)){AllFile($dir.'/'.$file); //如果判断还是⽂件,则递归}else{echo $file; //输出⽂件名}}}}}10.从⼀个标准的Url提取出⽂件的扩展名function getExt($url){$arr = parse_url($url);$file = basename($arr['path']);// basename函数返回路径中的⽂件名部分$ext = explode('.', $file);return $ext[count($ext)-1];}11.有个⼈想上⼀个n级的台阶,每次只能迈1级或者迈2级台阶,问:这个⼈有多少种⽅法可以把台阶⾛完?例如:总共3级台阶,可以先迈1级再迈2级,或者先迈2级再迈1级,或者迈3次1级总共3中⽅式function jieti($num){ //实际上是斐波那契数列return $num<2?1:jieti($num-1)+jieti($num-2);}12.请写⼀段PHP代码,确保多个进程同时写⼊同⼀个⽂件成功<?php$fp = fopen("lock.txt","w+");if (flock($fp,LOCK_EX)) {//获得写锁,写数据fwrite($fp, "write something");// 解除锁定flock($fp, LOCK_UN);} else {echo "file is locking...";}fclose($fp);>13.⽆限级分类function tree($arr,$pid=0,$level=0){foreach ($arr as $v) {//如果是顶级分类,则将其存到$list中,并以此节点为根节点,遍历其⼦节点if ($v['pid'] == $pid) {$v['level'] = $level;$list[] = $v;tree($arr,$v['id'],$level+1);}}return $list;}14.获取上个⽉第⼀天和最后⼀天//获取上个⽉第⼀天date('Y-m-01',strtotime('-1 month'));//获取上个⽉最后⼀天date('Y-m-t',strtotime('-1 month'));15.随机输⼊⼀个数字能查询到对应的数据区间//把区间换成数组写法,⽤⼆分法查找区间function binsearch($x,$a){$c=count($a);$lower=0;$high=$c-1;while($lower<=$high){$middle=intval(($lower+$high)/2);if($a[$middle]>=$x){$high=$middle-1;}elseif($a[$middle]<=$x ){$lower=$middle+1;}}return '在区间'.$a[$high].'到'.$a[$lower];}$array = ['1','50','100','150','200','250','300'];$a = '120';echo binsearch($a,$array);16,现在有⼀个字符串,你要对这个字符串进⾏ n 次操作,每次操作给出两个数字:(p, l) 表⽰当前字符串中从下标为 p 的字符开始的长度为 l 的⼀个⼦串。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
※数组题型分析
29. 以下有关数组的说明中,错误的是。
(A)根据数组说明的方式,可将数组分为动态数组和静态数组
(B)在过程中,不能用Private语句定义数组
(C)利用ReDim语句重新定维时,不得改变已经定义说明过的数组的数据类型
(D)数组重新定维后,原有的数组元素内容将不予保留
答案:D
分析:要保留数组元素原有的内容用Preserve语句。
26.下面有关数组处理的叙述中,不正确的是
①在过程中用ReDim语句定义的动态数组,其下标的上下界可为赋了值的变量②在过程中,可以使用Dim、Private和Static语句定义数组
③用ReDim语句重新定义动态数组时,不得改变该数组的数据类型
④可用Public语句在窗体模块的通用说明处定义一个全局数组
(A)①②③④(B)①③④(C)①②③(D)②④
答案:D
分析:在过程中不能用Private定义数组;Public用在标准模块中定义数组。
31. 名为sort的Sub子过程的形式参数为一数组,以下的定义语句中正确的是。
(A)Private Sub sort(A() As Integer)
(B)Private Sub sort(A(10) As Integer)
(C)Private Sub sort(ByVal A() As Integer)
(D)Private Sub sort(A(,) As Integer)
答案:A
分析:数组参数必须为ByRef方式(传地址方式)传送。
27. 下列关于数组的叙述中,错误的是。
(A)在过程中可以用Dim语句对形参数组进行说明
(B)数组是同类变量的一个有序的集合
(C)数组元素可以是控件
(C)数组在使用之前,必须先用数组说明语句进行说明
答案:A
分析:形参中不使用Dim语句说明变量和数组。
31. 某过程的说明语句中,正确的数组说明语句是。
Const N As Integer=4
Dim L As Integer
①Dim X(L) As Integer
②Dim A(K) As Integer
Const K As Integer=3
③Dim B(N) As Integer
④Dim Y(2000 to 2008) As Integer
(A)①②④(B)①③④(C)③④(D)②③
答案:C
分析:在定义数组时,每一维的元素个数必须是常数,不能是变量或表达式。
(27)下列语句中的
(A)Private A(n) As Integer (B)Dim A() As Integer
(C)Dim A(,) As Integer (D)Dim A(1 to n)
答案:B
分析:给数组附以一个空维数表,这样就将数组声明为动态数组。
25.在窗体的通用声明处有语句Dim A() As Single,以下在某事件过程中重定义此数组的一组正确语句是:25 。
(A) ReDim A(3,3) (B) ReDim A(3,3)
ReDim A(4,4) As Integer ReDim Preserve A(4,4)
(C) ReDim A(3,3) (D) ReDim A(3,3)
ReDim A(3,3) As Integer ReDim Preserve A(3,4)
答案:D
分析:ReDim语句在用Preserve 关键字时,只能改变多维数组中最后一维的上界;如果改变了其它维或最后一维的下界,那么运行时就会出错。
28.定义两个过程Private Sub1(St() As String)和Private Sub2(Ch() As String*6),在调用过程中用Dim S(3) As String*6,A(3) As String定义了两个字符串数
组。
下面调用语句中正确的有28 。
①Call Sub1(S) ②Call Sub1(A) ③Call Sub2(A) ④Call Sub2(S)
(A)①②(B)①③(C)②③(D)②④
答案:D
分析:实参和形参的类型要对应。
27.以下有关控件数组的说法中错误的是_(27)_。
(A)控件数组由一组具有共同名称和相同类型的控件组成
(B)控件数组中的每一个控件共享同样的事件过程
(C)控件数组中的每个元素的下标由控件的Index属性指定
(D)同一控件数组中的元素只能有相同的属性设置值
答案:D
分析:
27.下列有关数组的说法中,不正确的是
(A)在窗体模块中不可以定义全局数组
(B)可以使用Erase语句释放所有数组所占据的存储空间
(C)语句Dim X(3.6+2) As Integer定义了一个维上界是6的一维的整形数组
(D)形参数组的类型可以是定长字符串类型
答案:B
分析:使用Erase语句重新初始化固定大小的数组中的元素,以及释放动态数组存储空间。
29.下面有关数组的说法中,错误的是。
A)数组必须先定义后使用
B)数组形参可以是定长字符串类型
C)Erase语句的作用是对已定义数组的值重新初始化
D)定义数组时,数组维界值可以不是整数
解析:Erase语句重新初始化大小固定的数组的元素,以及释放动态数组的存储空间。
答案:C
28. 以下有关数组的说法中,正确的是_____。
A.数组是有序变量的集合,序列中的变量类型可以不同
B.数组下标用以确定数组元素在数组中的位置,下标取值只能是0或1
C.在一定条件下动态数组可以反复改变其维数与大小
D.固定大小数组也可以使用ReDim语句改变其大小
答案:C
分析:固定大小数组不能使用ReDim语句改变其大小。
28.下面有关数组的说法中,
A) 在模块中由于未使用Option Explicit语句,所以数组不用先定义就可以使用,只不过是Variant类型
B) 过程定义中,形参数组可以是定长字符串类型
C) Erase语句的作用是对固定大小数组的值重新初始化或收回分配给动态数组的存储空间
D) 定义数组时,数组维界值可以不是整数
答案:C
24.以下说法不正确的是。
A) 使用不带关键字Preserve的ReDim语句可以重新定义数组的维数
B) 使用不带关键字Preserve的ReDim语句可以改变数组各维的上、下界
C) 使用不带关键字Preserve的ReDim语句可以改变数组的数据类型
D) 使用不带关键字Preserve的ReDim语句可以对数组中的所有元素进行初始化答案:C
27. 以下对数组参数的说明中,错误的是
A) 在过程中可以用Dim语句对形参数组进行声明
B) 形参数组只能按地址传递
C) 实参为动态数组时,可用ReDim 语句改变对应形参数组的维界
D) 只需把要传递的数组名作为实参,即可调用过程
答案:A
24.以下有关数组参数的说明中正确的是
A)在过程中也可用Dim语句对形参数组进行说明
B)动态数组作为实参时,可用ReDim语句在过程中改变对应形参数组的维界
C)调用过程时,数组名不能作为实参
D)数组可以按地址传递也可以按值传递
答案:B
30.下面有关数组的说法中,正确的是。
A) 数组的维下界不可以是负数
B) 模块通用声明处有Option Base 1,则模块中数组定义语句Dim A(0 To 5) 会与之冲突
C) 模块通用声明处有Option Base 1,模块中Dim A(0 To 5),则A 数组第一维维下界为0
D) 模块通用声明处有Option Base 1,模块中Dim A(0 To 5),则A 数组第一维维下界仍为1 答案:C
解析:以模块中Dim的定义为优先。
25.下面有关数组处理的叙述中,正确的是________。
A)在过程中使用ReDim语句可以改变动态数组的数据类型
B)在过程中,可以使用Dim、Private和Static语句来定义数组
C)用ReDim语句重新定义动态数组时,可以改变数组的大小,但不能改变数组的维数
D)不可以用Public语句在窗体模块的通用处说明一个全局数组
答案:D
25. 下列有关数组的叙述中,不正确的是(25)。
①在过程中使用ReDim语句定义的动态数组,其下标的上下界可以是变量
②数组作为形式参数时,传递的是每一个数组元素的值
③在窗体模块的通用说明处可以使用Public说明一个全局数组
④数组定义语句中可以用负数或小数来指定某一维的维下界或维上界的值
A)②③B)①③④C)①②③④D)③④
答案:A
27. 下列有关控件数组的说法中,错误的是(27)。
A)控件数组由一组具有相同名称和相同类型的控件组成,不同类型的控件无法组成控件数组
B)控件数组中的所有控件不得具有各自不同的属性设置值
C)控件数组中的所有控件共享同一个事件过程
D)控件数组中每个元素的下标由控件的Index属性指定
答案:B
25.以下说法中,错误的是25 。
A)使用缺省Preserve关键字的ReDim语句可以改变数组的维数和大小
B)ReDim语句只能出现在过程中
C)使用ReDim语句重新定义的动态数组,只能比原数组大
D)使用ReDim语句可以对动态数组的所有元素进行初始化
答案:C
4. 执行下面程序后,A(1,3)的值是,A(2,2)的值是,A(3,1)的值是。
