字母表示数思维导图 (1)
苏教版小学数学五年级上册单元思维导图
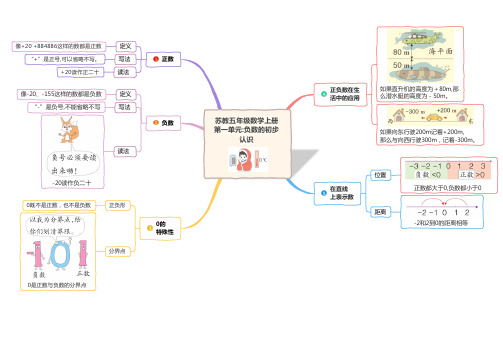
苏教五年级数学上册第一单元:负数的初步
认识
在直线上表示数
正数都大于0,负数都小于0如果直升机的高度为+80m,那
么潜水艇的高度为-50m。
如果向东行驶200m记着+200m,
那么与向西行驶300m,记着-300m。
负数
-20读作负二十
0的
特殊性0是正数与负数的分界点位置
距离
-2和2到0的距离相等
三角形面积等于等底等高的平
梯形
的面积S=(4+8)x3÷2=18(c㎡)不规则图
形的面积
举例
每个小方格表示1公
册第三单元:小数的意义和性质
小数的大小比较
小数的意义和读写方法
小数的计数单位和数位顺序
用“万”或“亿”作单位的小数表示大数
小数的性质
分母是10、100、1000·······小数的末尾添上“0”或去小数的近似数
册第四单元:小数的加法和减法小数加减法的验算
小数加法
小数减法用计算器算小数加减法
先把小数点对齐,再按照整数加法的方法进行计算,最
小数的近似数保留几位小数或精确到哪一位,要看那一位的下一位上的数字,
被减数的小数位数不够时,
苏教五年级数学上册第五单元:小数乘法
和除法
商的近似值
小数乘整数
一个数除以小数
除数是整数的小数除法
小数乘小数
小数四则混合运算
39.5÷10=3.95
苏教五年级数学上册第六单元:统计图和
条形统计图(二)复式
统计表复式条形统计图
找出不同的围法
找出比赛的场数
苏教五年级数学上册第八单元:用字母表示数。
七年级数学-秋季班-01-整式的基本概念-学生版

整式的基本概念★思维导图模块一:字母表示数★敲黑板!知识点!1.字母表示数字母可以表示运算律;字母可以表示公式;字母可以表示数量关系或方程里的求知量;字母可以表示探究得出规律的数. 2.字母表示数的规范要求(1)数字与字母及字母与字母间的乘号省略,且数字要写在字母之前; (2)当数字是带分数时,要写成假分数; (3)除法运算中的除号要用分数线来表示.★例题【例1】 下列用字母表示数的式子中,符合书写要求的有( ).①21x y ⋅ ②2ab c ÷ ③()2a b ⨯+ ④2ab ⋅ ⑤213xy⑥74a A .1个 B .2个 C .3个 D .4个【例2】 某种商品降价x %后,售价为a 元,则原售价是( ).A .100ax元 B .1100x a ⎛⎫+ ⎪⎝⎭元C .100ax元D .1100a x -元【例3】某次数学测试,班级中男生20名平均得a分,女生25名平均得b分,此次测验全班的平均分是多少?【例4】一个两位数为x,三位数为y,将x放在y的左边得到一个五位数,用含x.y代数式表示这个五位数.【例5】画一个正方形,使它的边长为2厘米,它的面积是_____平方厘米.再取各边中点,再连成第2个正方形,它的面积是_____平方厘米.再取第2个正方形的各边中点,连成第3个正方形,它的面积是_____平方厘米.如果依此方法画出第4个.第5个正方形······那么第20个正方形的面积是____平方厘米,第n个正方形的面积是______平方厘米.【例6】(1)一组按规律排列的式子:2ba-,52ba,83ba-,114ba,…(0ab≠),其中第7个式子是,第n个式子是(n为正整数).(2)搭建如图①的单顶帐篷需要17根钢管,这样的帐篷按图②.图③的方式串起来搭建,则串7顶这样的帐篷需要根钢管.①②③模块二:代数式★敲黑板!知识点!1.代数式(1)用运算符号和括号把数或字母连结而成的式子叫做代数式.(这里的运算符号一般指加、减、乘、除,以及以后要学的乘方,开方) (2)单独一个数字或者一个字母也是代数式.(3)因为等号和不等号不是运算符号,所以等式和不等式不是代数式.★例题【例7】 下列各式中,是代数式的有( ).①23xy②2R π ③2S r π=④b⑤512+>⑥2abA .3个B .4个C .5个D .6个【例8】 下列代数式中,书写规范的是().A .1573ab ⨯ B .226a b ⨯-C .69ab ÷D .213a b【例9】 下列代数式的值一定是正数的是( ).A .22x y + B .x y - C .223x +D .2()x y +【例10】 某项工程,甲队完成需要a 小时,乙队完成需要b 小时,则甲.乙两队合作1小时可完成该工程的( ).A .11a b +B .1a b + C .1abD .111a b ⎛⎫÷+ ⎪⎝⎭【例11】 用语言描述315a -的数量关系,其中错误的是().A .a 的3倍与15的差B .3a 与15的相反数的和C .a 与5的差的3倍D .a 与15的差的3倍【例12】 下列语句中,不正确的是( ).A .代数式22x y -的意义是x 与y 的平方差 .B .代数式()12x y -的意义是x 与y 的差的一半. C .x 的7倍与y 的和的一半,用代数式表示是72yx +.D .x 的16与y 的18差,用代数式表示是1168x y -.【例13】 用文字语言表示下列式子: (1)21a +; (2)3(2)a -;(3)5a -.【例14】 汽车每小时耗油10升,油箱中已装油a 升. (1)当80a =时,汽车行驶多少小时后,油箱中剩余油为20升? (2)用代数式表示汽车行驶x 小时后,油箱中剩余的油量y .【例15】 正方形的边长为a cm ,边长增加2cm 后,面积增加().A .24cmB .()224a cm +C .()222a cm +D .()2222a a cm ⎡⎤+-⎣⎦【例16】 船在静水中的速度为x 千米/时,水流速度为2千米/时()2x >,若A B 、两地相距s 千米,则在A B 、间往返一次共需__________小时.【例17】 浓度为80%的酒精a 克,加水10克后的浓度是多少?模块三:代数式的值★敲黑板!知识点!1.代数式的值用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果叫做代数式的值. 2、求代数式的值的方法直接代入法;整体代入法.★例题【例18】 当221x y +=,2322x y -=-时,24x y -的值是().A .2-B .1-C .3D .6【例19】 求代数式23x yx y-+的值,其中(1)2x =-,5y =-;(2)2x =,5y =.【例20】 若3a =,0.3b =,则132b a=____________.【例21】 如果()2320x y -+-=,则x y =_________.【例22】 如果25a ab +=,239b ab +=,则222a ab b --=_________.【例23】 若代数式2231a a ++的值是5,求代数式2698a a +-的值.【例24】 已知4a -与2a b +互为相反数,求代数式()()23310()89a b a b b a ---+-+ ()27b a -的值.【例25】 (1)当1a =,13b =及34a =,12b =时,分别计算222a ab b -+及2()a b -的值, 并观察所得代数式的值,有什么发现?可猜想出什么规? (2)应用你发现的规律,计算:22101.232101.23 1.23 1.23-⨯⨯+.【例26】 已知1998a b c +=+=+,求()()222()a b b c c a -+-+-.【例27】 已知:()3265432012345621x x a x a x a x a x a x a x a --=++++++.求:(1)0123456a a a a a a a ++++++的值;(2)0123456a a a a a a a -+-+-+的值; (3)0246a a a a +++的值.模块四:整式★敲黑板!知识点!1、单项式由数与字母的积或字母与字母的积所组成的代数式叫做单项式.单独一个数或字母也是单项式.单项式中的数字因数叫做这个单项式的系数,一个单项式中,所有字母的指数和叫做这个单项式的次数.2、多项式由几个单项式的和组成的代数式叫做多项式.在多项式中的每个单项式叫做多项式的项,不含字母的项叫做常数项,次数最高项的次数就是这个多项式的次数.3、多项式的升幂或降幂排列(1)把一个多项式按其一个字母的指数从高到低的顺序排列起来,叫做把多项式按这个字母降幂排列.(2)把一个多项式按某一个字母的指数从低到高的顺序排列起来,叫做把多项式按这个字母升幂排列.4、整式单项式.多项式统称为整式.★例题【例28】下列说法正确的是().A.12不是单项式B.ba是单项式C.x的系数是0D.322x y-是整式【例29】2005223x y是________次单项式.【例30】把多项式332356a ab b a b-+-按a的降幂排列为______________________.【例31】 已知31227n ab a b ---与22353x y π-的次数相等,则()11______n +-=.【例32】 多项式253246a b a b ab--+的一次项是__________,三次项系数是________,常数项是________.【例33】 多项式2313243n n n n x x x x -+-+--(n 是大于3的整数),按x 的升幂排列为_____________________.【例34】 m n 、都是正整数,多项式3m n m n x y +++的次数是( ) .A 22m n + .B m 或n .C m n + .D m n 、中的较大数【例35】 一个n 次多项式,它的任何一项次数都_______________.【例36】 若多项式4332531x ax x x bx x -+----不含x 的奇次项,求a b +的值.【例37】 若多项式4123n n x x -++-是三次三项式,求n 的值.【例38】 若关于x y 、的多项式()()()122324425a a a a a x y a x y b x y a y ----+-+-+是一个四次三项式,求a b 、的值,并写出此三项式.★练习【习题1】 将下列代数式分别填入相应的括号内:222221112113232333a x ab x x m n mn n x b x y x -+-+-+-+,,,,,,,单项式( ); 多项式( ); 二项式(); 二次多项式( ); 整式().【习题2】 已知关于x 的多项式()223m x mx --+中的x 的一次项系数为2-,则这个多项式是_____次______项式.【习题3】 在下列各式中,符合书写格式要求的有( ).2a ,1x ÷,112m ,3y -,()32x y ⨯+,231m n ,73ab,2ac b ÷.A .1个B .2个C .3个D .4个【习题4】 把多项式343225327x y y xy x y --+-(1)按x 的升幂排列__________________________________; (2)按y 的降幂排列__________________________________.【习题5】 某学生参加教育储蓄,把1000元存入银行,如果月利率是0.2%,那么x 个月后,本金与利息的和是_______元(教育储蓄不计利息税).【习题6】 买a 支水笔用了50元,毛笔每支比水笔贵2元,那么买a 支毛笔需____元钱.【习题7】 已知:311(13)26x =-÷⨯⨯,则代数式23201220131x x x x x ++++⋅⋅⋅++的值是( ).A .2013B .2012C .1D .0【习题8】 已知:242a ba b-=+,求代数式3(2)3(2)4(2)2a b a b a b a b -+++-的值.【习题9】 3232a b -的系数是___________,次数是_________.【习题10】 先观察多项式:234357x x x x --⋅⋅⋅⋅⋅⋅,,,,按这些单项式的系数和指数变化规 律写出第50个单项式;再求当1x =时,前50个单项式和的值.【习题11】 观察下列图形,则第(42)n +个图形中三角形的个数是___________ .……第1个第2个 第3个【习题12】 当1x =时,代数式31ax bx ++的值为2014,求当1x =-时代数式31ax bx ++的 值.【习题13】 点1A 、2A 、3A 、……、n A (n 为正整数)都在数轴上.点1A 在原点O 的左 边,且11AO =;点2A 在点1A 的右边,且212A A =;点3A 在点2A 的左边,且323A A =; 点4A 在点3A 的右边,且434A A =;……,依照上述规律,点2008A .2009A 所表示的数分别为( ). A .2008、2009- B .2008-、2009 C .1004、1005- D .1004、1004-【习题14】 如图,点A .B 对应的数是a .b ,点A 在3-.2-对应的两点(包括这两点)之间移动,点B 在1-.0对应的两点(包括这两点)之间移动,则以下四式的值,可 能比2008大的是( ).A .b a -B .1b a - C .11a b- D .2()a b -★温习【温习1】指出下列各式,哪些是代数式,哪些不是代数式? ① 21x + ② 23ab ③ 0 ④ 10n a ⨯ ⑤ a b b a +=+ ⑥ 32> ⑦ 2S R π= ⑧ 347+= ⑨ π【温习2】三个连续奇数,中间的一个是21n +,用代数式表示这三个连续奇数的和是_______;当2n =时,这个代数式的值是_______.【温习3】代数式()223x -+有( ).A .最大值B .最小值C .既有最大值,又有最小值D .既无最大值,也无最小值【温习4】某商品进价为每件a 元,商品按进价提高40%作为零售价销售,在销售旺季过后,又以8折价开展促销,求促销时每一件商品的售价.【温习5】找出下列各代数式中的单项式,并写出各单项式的系数和次数.223xy ;a -;a bc ;32mn +;572t ;233a b c -;2;xπ-【温习6】同时都含有a b c ,,,且系数为1的7次单项式共有( )个 A .4 B .12 C .15 D .25【温习7】当____a =时,式子39a b -+化简后是单项式.【温习8】当m 取什么值时,2123(2)3m m x y xy -+-是五次二项式?【温习9】一个多项式按x 的降幂排列,前几项如下:1098273234...x x y x y x y -+-+试写出它的第七项及最后一项,这个多项式是几次几项式?【温习10】已知()727012721...x a a x a x a x -=++++对任意x 的值都成立,求下列各式的值: (1)0127...a a a a ++++;(2)1357a a a a +++.【温习11】图1是一个水平摆放的小正方体木块,图2.图3是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是()A.25B.66C.91D.120图3图2图1。
五年级上册数学思维导图(共7张PPT)

初步体会 数形结合
的思想
位 置
受到辩证唯物 主义的启蒙教
育
在方格纸上用 数对确定物体
的位置
人教版五年级数学上册第二单元知识树
四舍五入法
一看二移三算 小数除以小数
实际应用
求积的近似值
实际应用
区分循环小数、
有限小数、无限小数ຫໍສະໝຸດ 小数除法商的近似值
循环小数
表示循环小数 求近似值
小数除以整数
解决问题
用循环小数 表示除法的商
用字母表示运算定律
和计算公式,并会计算
实际应用
用字母表示数
用字母表示数的意义
解简易方程
解稍复杂的方程
解稍复杂的方程
解决实际问题
简 易 方 程
人教版五年级数学上册第五单元知识树
h=2S÷a
a=2S÷h
计算公式
S=ah÷2
实际应用
实际应用
a=S÷h
计算公式
S=ah
平行四边形
面积
h=S÷a
三角形
面积
多 边 形 的 面 积
商的小数点与被除数
的小数点对齐
有余数添0再除
小 数
解决实际问题
进一法、去尾法
除
用计算器 探索规律
法
人教版五年级数学上册第三单元知识树
可能性 的大小
事件的确定性 和不确定性
可 能 性
人教版五年级数学上册第四单元知识树
等式的基本性质
方程的意义
解简易方程
±a=b 和 a =b
用含字母的式子 表示数量关系
五年级上册数学思维导图
四舍五入法
实际应用
求积的近似值
实际应用
五上简易方程思维导图
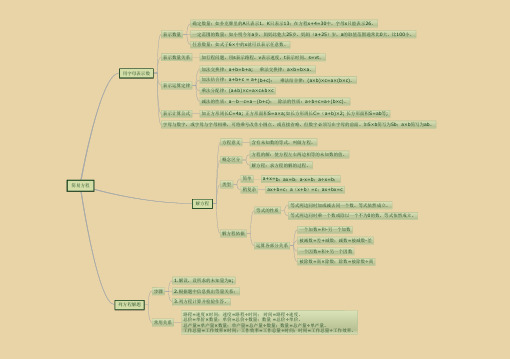
简易方程用字母表示数表示数量确定数量:如扑克牌里的A只表示1,K只表示13;在方程x+4=30中,字母x只能表示26。
一定范围的数量:如小明今年a岁,妈妈比他大25岁,妈妈(a+25)岁,a的取值范围通常比0大,比100小。
任意数量:如式子6×中的x就可以表示任意数。
表示数量关系如行程问题,用s表示路程,v表示速度,t表示时间,s=vt。
表示运算定律加法交换律:a+b=b+a; 乘法交换律:a×b=b×a。
加法结合律:a+b+c = a+(b+c); 乘法结合律:(a×b)×c=a×(b×c)。
乘法分配律:(a±b)×c=a×c±b×c减法的性质:a-b-c=a-(b+c); 除法的性质:a÷b÷c=a÷(b×c)。
表示计算公式如正方形周长C=4a; 正方形面积S=a×a;如长方形周长C=(a+b)×2; 长方形面积S=ab等;字母与数字,或字母与字母相乘,可将乘号改作小圆点,或直接省略,但数字必须写在字母的前面。
如5×b简写为5b;a×b简写为ab。
解方程方程意义含有未知数的等式,叫做方程。
概念区分方程的解:使方程左右两边相等的未知数的值。
解方程:求方程的解的过程。
类型简单a+x=b;ax=b;ax=b;a÷x=b;稍复杂ax+b=c;a(x+b)=c;ax+bx=c解方程依据等式的性质等式两边同时加或减去同一个数,等式依然成立。
等式两边同时乘一个数或除以一个不为0的数,等式依然成立。
运算各部分关系一个加数=和另一个加数被减数=差+减数;减数=被减数差一个因数=积÷另一个因数被除数=商×除数;除数=被除数÷商列方程解题步骤1.解设,设所求的未知量为x;2.根据题中信息找出等量关系;3.列方程计算并检验作答。
人教版五年级数学上册简易方程知识点寒假复习提升卷
知识点二:方程的意义及等式的性质
1.意义:含有未知数的等式叫做方程。
2.等式的性质
性质1:等式两边加上或者减去同一个数,左右两边仍然相等;
性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
注意:方程一定是等式,但等式不一定是方程。
(1)磁悬浮列车的速度比普通火车的速度快多少?
(2)如果同时行驶t小时,磁悬浮列车比普通火车多行驶多少千米?
3.甲书架上有x本书,乙书架上的书比甲书架上的1.5倍还多5本。用式子表示乙书架上有多少本书。当 时,乙书架上有多少本书?
4.王伯伯家有一块长方形菜地种了茄子和豆角(如下图)。
(1)这块菜地的面积是平方米。
4.稍微复杂的方程
(1)列方程解决实际问题的步骤:
首先,找出未知数,用字母X表示;
其次,分析实际问题中的数量关系,找出等量关系,列方程;
最后,解方程并检验作答。
(2)方程解法与算式解法的区别
列方程解决问题时,未知数用字母表示,参与列式,算式解法中未知数不参与列式;
列方程解决问题时根据题中的数量关系,列出含有未知数的等式,求未知数由解方程来完成,算术解法是根据题中已知数和未知数之间的关系确定解答步骤,再进行计算。
6.看图回答问题。
(1)图中哪一段表示(400-x)元,哪一段表示(400+y)元?
(2)根据上图,你能列出两个不同的方程吗?
7.小华买了1个文具盒和2支钢笔共花24元,买一个文具盒的钱可以买2支钢笔。1个文具盒和1支钢笔各多少元?(先画图,再解答。)
考点三:解方程及实际问题
8.解方程。
2.6x-1.8x=7.28x-4×8=8.80.5x÷2=2.5
七年级上册数学思维导图
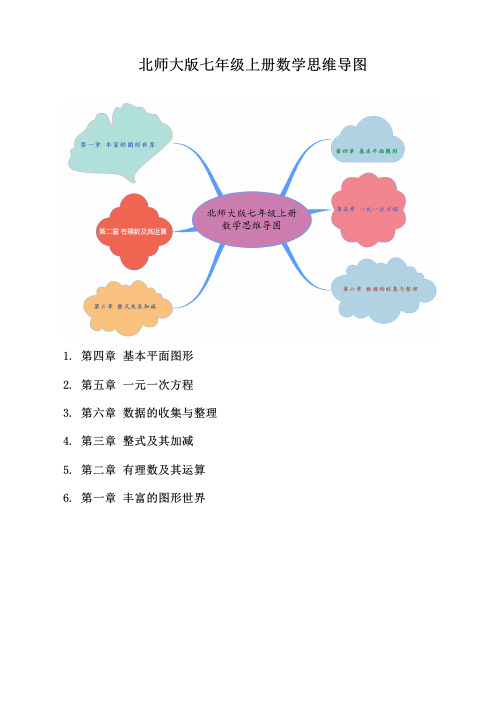
北师大版七年级上册数学思维导图1. 第四章基本平面图形2. 第五章一元一次方程3. 第六章数据的收集与整理4. 第三章整式及其加减5. 第二章有理数及其运算6. 第一章丰富的图形世界第一章丰富的图形世界1. 一、生活中的立体图形分类1.1. 柱体1.1.1. 圆柱1.1.2. 棱柱1.2. 锥体1.2.1. 圆锥1.2.2. 棱锥1.3. 台体1.3.1. 圆台1.3.2. 棱台1.4. 球体1.4.1. 由曲面围成2. 二、展开与折叠2.1. 1.常见立体图形的展开图2.1.1. ①圆柱:两个圆,一个长方形2.1.2. ②圆锥:一个圆,一个扇形2.1.3. ③三棱锥:四个三角形2.1.4. ④三棱柱:两个三角形,三个长方形2.1.5. ⑤正方体展开图:共有11种2.1.6. ⑥要展开一个正方体,需要切开7条棱2.1.7. ⑦正方体平面展开图找对立面:相间、Z端3. 三、截一个几何体3.1. 1.常见立体图形的截面3.2. 2.用一个平面去截一个正方体,可能得到三边形、四边形、五边形、六边形4. 四、三视图4.1. 主视图4.2. 左视图4.3. 俯视图5. 五、多边形的一些规律5.1. 1.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以把这个n边形分割成(n-2)个三角形5.2. 2.从一个n边形的一边上的一点出发,分别连接这个点与其余各顶点,可以把这个n边形分割成(n-1)个三角形5.3. 3.从一个n边形的内部的一个点出发,分别连接这顶点与其余各顶点,可以把这个n边形分割成n个三角形5.4. 4.从一个n边形一个顶点出发,可引( n-3)条对角线,n边形共有条对角线5.4.1. 4.从一个n边形一个顶点出发,可引( n-3)条对角线,n边形共有条对角线第二章:有理数及其运算1. 1.有理数的分类1.1. 整数1.1.1. 正整数1.1.2. 01.1.3. 负整数1.2. 分数1.2.1. 正分数1.2.2. 负分数2. 2.正负数2.1. 表示相反意义的量3. 3.相反数3.1. 互为相反数两数和为04. 4.数轴4.1. 三要素4.1.1. 原点4.1.2. 正方向4.1.3. 单位长度5. 5.倒数5.1. 乘积为1的两个有理数互为倒数6. 6.绝对值6.1. 正数的绝对值是它本身6.2. 0的绝对值是06.3. 负数的绝对值是它的相反数7. 7.有理数比较大小7.1. 正数>0>负数8. 8.有理数的运算8.1. 加法法则8.2. 减法法则8.3. 乘法法则8.4. 除法法则8.5. 有理数乘方9. 9.科学计数法9.1. 的形式第三章整式及其加减1. 一、字母表示数1.1. 字母可以表示任何数2. 二、代数式2.1. 1.代数式的概念2.2. 2.代数式的书写格式3. 三、整式3.1. 1.单项式3.1.1. 概念3.1.2. 系数3.1.3. 次数3.2. 2.多项式3.2.1. 概念3.2.2. 项3.2.3. 次数3.3. 3.同类项3.3.1. 所含字母相同,相同字母的指数也相同的项3.3.2. 合并同类项3.4. 4.去括号法则3.5. 5.整式的加减3.5.1. 先去括号3.5.2. 再合并同类项第四章:基本平面图形1. 一、直线、射线、线段1.1. 1. 概念以及它们的区别1.2. 2.直线公理:经过两点有且只有一条直线(两点确定一条直线)1.3. 3.字母表示图形1.4. 4.点和直线的关系1.5. 5.线段的性质2. 二、角2.1. 1.角的概念2.2. 2.角的表示2.3. 3.角的度量2.4. 4.角的平分线3. 三、多边形4. 四、圆5. 五、弧6. 六、扇形第五章一元一次方程1. 1.方程的概念1.1. 含有未知数的等式叫做方程2. 2.一元一次方程的概念2.1. 只含有一个未知数,并且未知数的最高次数是13. 3.方程的解4. 4.等式的性质5. 5.移项5.1. 把方程的一项从一边移动到另一边5.2. 移项的过程要更改符号6. 6.解一元一次方程的步骤6.1. ①去分母6.2. ②去括号6.3. ③移项6.4. ④合并同类项6.5. ⑤将未知数的系数化为17. 7.用一元一次方程解决实际问题7.1. ①找出等量关系式7.2. ②设未知数7.3. ③列方程7.4. ④解方程7.5. ⑤检验第六章数据的收集与整理1. 数据的收集方法1.1. 直接方法1.2. 间接方法2. 抽样调查2.1. 样本2.2. 样本容量3. 普查3.1. 总体3.2. 个体4. 数据的表示4.1. 扇形统计图4.2. 条形统计图4.3. 折线统计图。
初一上册数学思维导图
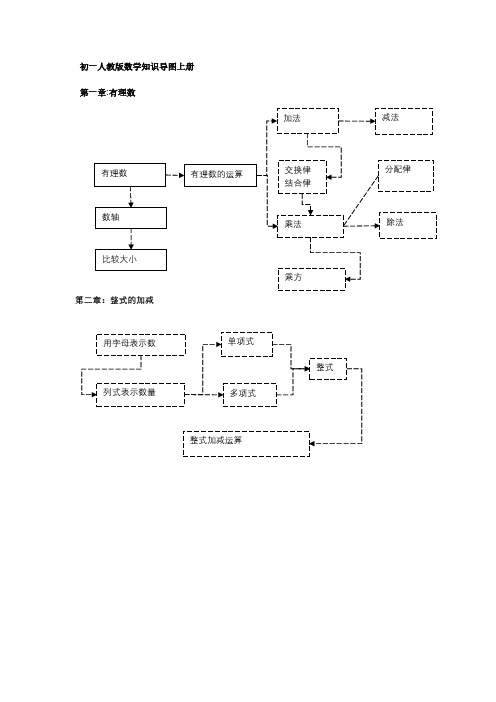
初一人教版数学知识导图上册
第一章:有理数
第二章:整式的加减
有理数
数轴
比较大小
有理数的运算
加法
交换律 结合律
乘法
乘方
减法
分配律
除法
用字母表示数
列式表示数量
单项式
多项式
整式
整式加减运算
第三章:一元一次方程
第四章:图形认识初步
实际问题
一元一次方程
实际问题的解答
一元一次方程的解(x=a )
几何图形
立体图形
平面图形
从不同方向看立体图形
展开立体图形
直线、射线、线段
角
角的度量
平面图形
角的比较与运算
余角和补角
角的平分线。
七年级数学第一章有理数思维导图
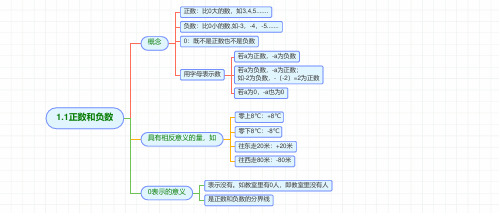
1.1正数和负数概念正数:比0大的数,如3,4,5.......负数:比0小的数,如-3,-4,-5.......0:既不是正数也不是负数用字母表示数若a为正数,-a为负数若a为负数,-a为正数;如-2为负数,-(-2)=2为正数若a为0,-a也为0具有相反意义的量,如零上8℃:+8℃零下8℃:-8℃往东走20米:+20米往西走80米:-80米0表示的意义表示没有。
如教室里有0人,即教室里没有人是正数和负数的分界线1.2有理数1.2.1有理数按意义分整数正整数负整数分数正分数负分数按性质符号分正有理数正整数正分数负有理数负整数负分数1.2.2数轴有原点、正方向、单位长度的一条直线任何有理数都能找到一个点与之对应,右边的数大于左边的数两点间距离:右边点对应的数减左边点对应的数1.2.3相反数只有符号不相同的两个数字互为相反数,a的相反数记为-a0的相反数是0,正数的相反数为负,负数的相反数为正一个数和它的相反数关于原点对称互为相反数的两个数相加等于01.2.4绝对值数轴上表示数a的点与原点的距离叫做数a 的绝对值,写为|a|互为相反数的两个数:绝对值相等两个负数,绝对值大的反而小,绝对值小的反而大若a>0,则|a|=a;若a<0,则|a|=-a;|0|=01.3有理数的加减法1.3.1加法同号两数相加:取相同的符号,绝对值相加;如-3+(-4)=-7异号两数相加:谁绝对值大,就取谁的符号;再用大绝对值减小绝对值;如-5+3=-2互为相反数的两数相加得0,任何数加0等于它本身1.3.2减法减去一个数,等于加上这个数的相反数;即a-b=a+(-b)如:5-(-3)=5+3=8加减混合相反数结合法:互为相反数的两个数相加等于0同分母结合法:把含相同分母的数或可通分的数结合在一起有带分数时先拆分为整数和分数,再结合分数和小数混合时统一为分数或统一为小数同号结合法:把符号相同的加数相结合(-23)-(-18)+(-15)-(+1)+(+23)原式=-23+(+18)+(-15)+(-1)+(+23)=(-23-25-1)+(18+23)=-7凑整法:把和为整数的加数相结合(+6.6)+(-5.2)-(-3.8)+(-2.6)-(+4.8)原式=(+6.6)+(-5.2)+(+3.8)+(-2.6)+(-4.8)=(6.6-2.6)+(-5.2-4.8)+3.8=-2.2分组结合法2-3-4+5+6-7-8+9…+66-67-68+69原式=(2-3-4+5)+(6-7-8+9)+…+(66-67-68+69)=0先拆项后结合(-2-4-6-8...-100)+(1+3+5+7 (99)原式=(-2+1)+(-4+3)+......+(-100+99)=-501.4有理数的乘除法1.4.1乘法两数相乘,同号得正,异号得负,并把绝对值相乘任何数乘0得0多个有理数相乘1.4.2除法除以一个数等于乘以这个数的倒数两数相除,同号得正,异号得负,并把绝对值相除0除以任何一个非0数,等于0;0不能作除数只要一个因数为0则积为0如果因数都不是0,则结果符号根据负数的个数来定:奇负偶正1.5.1有理数的乘方求n个相同因数的积的运算,叫做乘方在aⁿ中,a 叫做底数,n 叫做指数。
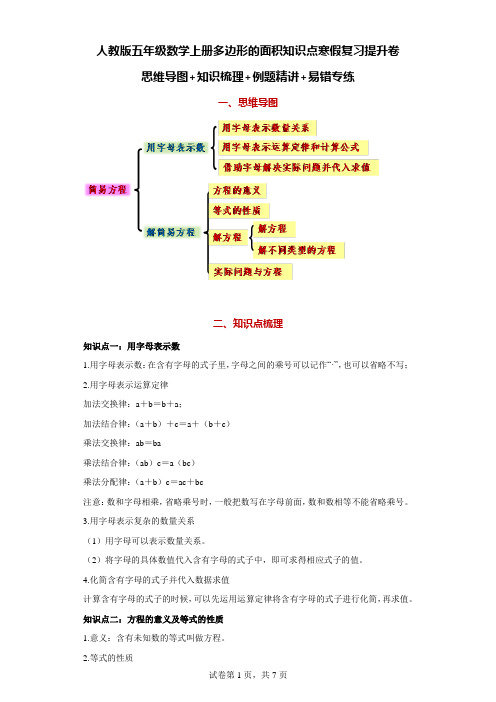
简易方程-五年级上册数学精品讲义(思维导图+知识梳理+例题精讲+易错专练) 人教版(含答案)

第5讲 简易方程(思维导图+学问梳理+例题精讲+易错专练)一、思维导图二、学问点梳理学问点一:用字母表示数1.用字母表示数:在含有字母的式子里,字母之间的乘号可以记作“.”,也可以省略不写;2.用字母表示运算定律加法交换律:a+b=b+a ;加法结合律:(a+b )+c=a+(b+c )乘法交换律:ab=ba乘法结合律:(ab )c=a (bc )乘法安排律:(a+b )c=ac+bc留意:数和字母相乘,省略乘号时,一般把数写在字母前面,数和数相等不能省略乘号。
3.用字母表示简单的数量关系(1)用字母可以表示数量关系。
(2)将字母的具体数值代入含有字母的式子中,即可求得相应式子的值。
简易方程用字母表示数方程的意义解方程解简易方程实际问题与方程解不同类型的方程解方程等式的性质4.化简含有字母的式子并代入数据求值计算含有字母的式子的时候,可以先运用运算定律将含有字母的式子进行化简,再求值。
学问点二:方程的意义及等式的性质1.意义:含有未知数的等式叫做方程。
2.等式的性质性质1:等式两边加上或者减去同一个数,左右两边仍旧相等;性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍旧相等。
留意:方程肯定是等式,但等式不肯定是方程。
学问点三:解方程及实际问题1.使方程左右相等的未知数的值,叫做方程的解,求方程的解的过程叫做解方程;2.依据等式的性质解不同形式的方程;3.把求得的未知数的值代入原方程,看方程左边的值是否等于右边的值,假如相等,所求的未知数的值就是原方程的解,否则就不是。
留意:解方程的依据是等式的性质;解方程时等号要上下对齐。
4.略微简单的方程(1)列方程解决实际问题的步骤:首先,找出未知数,用字母X表示;其次,分析实际问题中的数量关系,找出等量关系,列方程;最终,解方程并检验作答。
(2)方程解法与算式解法的区分列方程解决问题时,未知数用字母表示,参与列式,算式解法中未知数不参与列式;列方程解决问题时依据题中的数量关系,列出含有未知数的等式,求未知数由解方程来完成,算术解法是依据题中已知数和未知数之间的关系确定解答步骤,再进行计算。
字母表示数思维导图 (1)讲课教案

字母表示数思维导图
(1)
精品文档
收集于网络,如有侵权请联系管理员删除
分一分
教材分析
教学过程
教学目标
学生分析
经历字母表示数的过体会字母表示数的优越
发展抽象概括能
算术各部分间的关系、运算律
字母表示物
教学内容
前后联系
地位作用 核心概念 思维方法
用字母表示数 前
后
认识方程 解方程
算术思维发展到代数数学抽象 模型思想
知识基
生活经
学习障
字母表示数量的关
导入
探究 总结提巩固应用
游戏:数青蛙儿字母表示
a 只青蛙a 张字母表示
会用字母表示数及数量
加减、乘除互逆用字母表示运算
律 怎样把
字母的意义及取值范。
小学数学1-6年级思维导图

简单应用题的解题思路
缩小、缩小了、缩小到 综合法
求比一个 数多几的 数是多少
解答应用题 的 一般方法
已知一个数比另 一 个数少几,求 另一 个数是多少
弄清题意,分清已知条件和问题; 分析 题中的数量关系,把应用题 反映的实 际问题抽象为数学问题; 列出算式或方 程,进行计算或解 方程;检验,并写 出答语
_______________ ___J
1元亳
从制作材料上看,人 民币 分为纸币和硬币 人民币的基本单位是元
50元
小学数学思维导图03
小学数学第四章式与方程
使方程左右两边相等的未知数 的值, 叫做方程的解。求方程 的解的过程叫 做解方程
等式的左右两边同时加上或减 去同一 个数,等式仍然成立 等式的左右两边同时乘或者除以同 一个不 为0的数,等式仍然成立
一般应用题的意义;一般复合应用题的解题步骤
分数、 百分数 应甬题
整数、小 一般 数的复合 应用题 应甬题
简单 应角题
数量 关系
基本的数
典型应用题
量关系 部分量与总量;大数、小数与相差数
常见的数
每份数、份数与总数;倍数
量关系 单价、数量与总价;单产量、数量与总产量
应用题中 常见的一 些术语
工作效率、工作时间与工作总量 速度、时间与路程
整数的
数位与位值制 数位顺序表
负整数的读
因数 和 倍数
正整数的改写及求近似数 偶数
倍数的特征
奇数
整数的 大 小比较
最大公因数 小公倍数
分数的意义
分数的分 类及读写
分数的各部分名 称 及分数单位
分数与除法的关系
真分数 假分数
带分数
小学数学思维导图01
七年级数学思维导图3 (1)
合并同类项
系数化为1 列一元一次方程解应用题
点、线、面、体 立体图形 第四章 几何图形 平面图形 角的度量 角 角的比较与运算、角的平分线 余角和补角 从不同方向看立体图形 展开立体图形 线段的大小比较
直线、射线、线段 两点确定一条直线
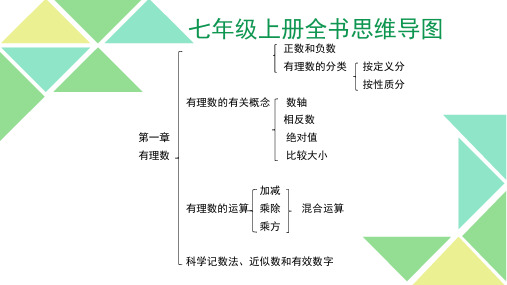
七年级上册全书思维导图
正数和负数 有理数的分类 按定义分 按性质分
有理数的有关概念
第一章
数轴
相反数 绝对值
有理数
加减
比较大小
有理数的运算 乘除
乘方
混合运算
科学记数法、近似数和有效数字
用字母表示数 整式 第二章 单项式项 去括号规律
整式加减的运算法则
方程
概念 一元一次方程
两点之间线段最短
七年级数学思维导图
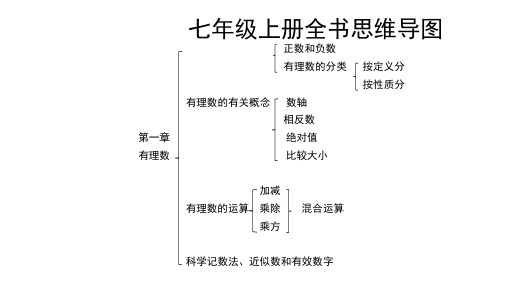
第三章 一元一次方程
方程 概念 一元一次方程
等式的性质 去分号 去括号
解一元一次方程的步骤 移项 合并同类项 系数化为1
列一元一次方程解应用题
点、线、面、体
立体图形 从不同方向看立体图形
第四章
展开立体图形
几何图形
线段的大小比较
直线、射线、线段 两点确定一条直线
平面图形
两点之间线段最短
角的度量
角 角的比较与运算、角的平分线
第一章 有理数
七年级上册全书思维导图
正数和负数 有理数的分类 按定义分
按性质分 有理数的有关概念 数轴
相反数 绝对值 比较大小
加减 有理数的运算 除
乘方
混合运算
科学记数法、近似数和有效数字
第二章 整式的加减
用字母表示数 整式 单项式
多项式
同类项 整式的加减 合并同类项
去括号规律 整式加减的运算法则
余角和补角
五年级简易方程思维导图
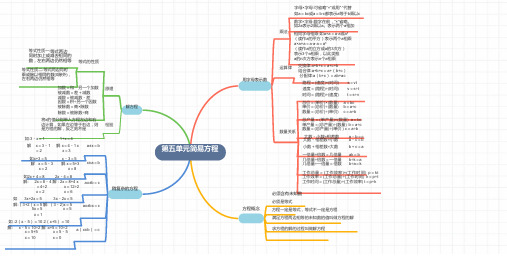
等式性质一:等式两边同时加上或减去相同的数,左右两边仍然相等等式性质二:等式两边同时乘或除以相同的数(0除外),左右两边仍然相等等式的性质用字母表示数乘法运算律字母×字母:可省略“×”或用“·”代替如a=bc或a=b·c都表示a等于b乘以c数字×字母:数字在前,“×”省略。
如2a表示2乘以a。
表示两个a相加相同字母相乘:如a×a=a·a或a²(读作a的平方)表示两个a相乘a×a×a=a·a·a=a³(读作a的立方或a的3次方)表示3个a相乘,以此类推a的n次方表示n个a相乘交换律:a+b+c=a+c+b结合律:a+b+c=a+(b+c)分配律:a(b+c)=ab+ac路程=(速度)×(时间) s=vt加数=和-另一个加数原理被减数=差+减数减数=被减数-差因数=积÷另一个因数被除数=商×除数除数=被除数÷商将x的值分别带入方程左边和右边计算,如果左边等于右边,则检验是方程的解,反之则不是如:3-x=1 1+x=4解方程数量关系速度=(路程)÷(时间) v=s÷t时间=(路程)÷(速度) t=s÷v总价=(单价)×(数量) a=bc单价=(总价)÷(数量) b=a÷c数量=(总价)÷(单价) c=a÷b总产量=(单产量)×(数量) a=bc单产量=(总产量)÷(数量) b=a÷c数量=(总产量)÷(单价) c=a÷b大数-小数=相差数a-b=c大数-相差数=小数a-c=b解x=3-1 解x=4-1 x=2 x=3如x+3=5 x-3=5解x=5-3 解x=5+3x=2 x=8如2x+4=8 2x-4=8解: 2x=8-4 解: 2x=8+4 x=4÷2 x=12÷2x=2 x=6如3x+2x=5 3x-2x=5解:(3+2)x=5 解: (3-2)x=55x=5 x=5x=1如:2(x-5)=10 2(x+5)=10a±x=bx±a=bax±b=cax±bx=c稍复杂的方程第五单元简易方程方程概念小数+相差数=大数b+c=a一倍量×倍数=几倍量ak=b几倍量÷倍数=一倍量b÷k=a几倍量÷一倍量=倍数b÷a=k工作总量=(工作效率)×(工作时间) p=kt工作效率=(工作总量)÷(工作时间) k=p÷t工作时间=(工作总量)÷(工作效率) t=p÷k必须含有未知数必须是等式方程一定是等式,等式不一定是方程满足方程两边相等的未知数的值叫做方程的解解: x-5=10÷2 解:x+5=10÷2x=5+5 x=5-5x=10 x=0a(x±b)=c求方程的解的过程叫做解方程。
