《数据结构与算法》课后习题答案(课件)

合集下载

数据结构与算法分析课后题答案

Chapter 5:Hashing5.1(a)On the assumption that we add collisions to the end of the list (which is the easier way if a hash table is being built by hand),the separate chaining hash table that results is shown here.4371132361734344419996791989123456789(b)96794371198913236173434441990123456789-25-w w w .k h d a w .com课后答案网(c)96794371132361734344198941990123456789(d)1989cannot be inserted into the table because hash 2(1989)=6,and the alternative locations 5,1,7,and 3are already taken.The table at this point is as follows:4371132361739679434441991234567895.2When rehashing,we choose a table size that is roughly twice as large and prime.In our case,the appropriate new table size is 19,with hash function h (x ) = x (mod 19).(a)Scanning down the separate chaining hash table,the new locations are 4371in list 1,1323in list 12,6173in list 17,4344in list 12,4199in list 0,9679in list 8,and 1989in list 13.(b)The new locations are 9679in bucket 8,4371in bucket 1,1989in bucket 13,1323in bucket 12,6173in bucket 17,4344in bucket 14because both 12and 13are already occu-pied,and 4199in bucket 0.-26-w ww .k h d a w.com课后答案网(c)The new locations are 9679in bucket 8,4371in bucket 1,1989in bucket 13,1323in bucket 12,6173in bucket 17,4344in bucket 16because both 12and 13are already occu-pied,and 4199in bucket 0.(d)The new locations are 9679in bucket 8,4371in bucket 1,1989in bucket 13,1323in bucket 12,6173in bucket 17,4344in bucket 15because 12is already occupied,and 4199in bucket 0.5.4We must be careful not to rehash too often.Let p be the threshold (fraction of table size)atwhich we rehash to a smaller table.Then if the new table has size N ,it contains 2pN ele-ments.This table will require rehashing after either 2N − 2pN insertions or pN deletions.Balancing these costs suggests that a good choice is p = 2/ 3.For instance,suppose we have a table of size 300.If we rehash at 200elements,then the new table size is N = 150,and we can do either 100insertions or 100deletions until a new rehash is required.If we know that insertions are more frequent than deletions,then we might choose p to be somewhat larger.If p is too close to 1.0,however,then a sequence of a small number of deletions followed by insertions can cause frequent rehashing.In the worst case,if p = 1.0,then alternating deletions and insertions both require rehashing.5.5(a)Since each table slot is eventually probed,if the table is not empty,the collision can beresolved.(b)This seems to eliminate primary clustering but not secondary clustering because all ele-ments that hash to some location willtry the same collision resolution sequence.(c,d)The running time is probably similar to quadratic probing.The advantage here is thatthe insertion can’t fail unless the table is full.(e)A method of generating numbers that are not random (or even pseudorandom)is given in the references.An alternative is to use the method in Exercise 2.7.5.6Separate chaining hashing requires the use of pointers,which costs some memory,and thestandard method of implementing calls on memory allocation routines,which typically are expensive.Linear probing is easily implemented,but performance degrades severely as the load factor increases because of primary clustering.Quadratic probing is only slightly more difﬁcult to implement and gives good performance in practice.An insertion can fail if the table is half empty,but this is not likely.Even if it were,such an insertion would be so expensive that it wouldn’t matter and would almost certainly point up a weakness in the hash function.Double hashing eliminates primary and secondary clustering,but the compu-tation of a second hash function can be costly.Gonnet and Baeza-Yates [8]compare several hashing strategies;their results suggest that quadratic probing is the fastest method.5.7Sorting the MN records and eliminating duplicates would require O (MN log MN )timeusing a standard sorting algorithm.If terms are merged by using a hash function,then the merging time is constant per term for a total of O (MN ).If the output polynomial is small and has only O (M + N )terms,then it is easy to sort it in O ((M + N )log (M + N ))time,which is less than O (MN ).Thus the total is O (MN ).This bound is better because the model is less restrictive:Hashing is performing operations on the keys rather than just com-parison between the keys.A similar bound can be obtained by using bucket sort instead of a standard sorting algorithm.Operations such as hashing are much more expensive than comparisons in practice,so this bound might not be an improvement.On the other hand,if the output polynomial is expected to have only O (M + N )terms,then using a hash table saves a huge amount of space,since under these conditions,the hash table needs only-27-w w w .k h d a w .c o m课后答案网O (M + N )space.Another method of implementing these operations is to use a search tree instead of a hash table;a balanced tree is required because elements are inserted in the tree with too much order.A splay tree might be particularly well suited for this type of a problem because it does well with sequential paring the different ways of solving the problem is a good programming assignment.5.8The table size would be roughly 60,000entries.Each entry holds 8bytes,for a total of 480,000bytes.5.9(a)This statement is true.(b)If a word hashes to a location with value 1,there is no guarantee that the word is in the dictionary.It is possible that it just hashes to the same value as some other word in the dic-tionary.In our case,the table is approximately 10%full (30,000words in a table of 300,007),so there is a 10%chance that a word that is not in the dictionary happens to hash out to a location with value 1.(c)300,007bits is 37,501bytes on most machines.(d)As discussed in part (b),the algorithm will fail to detect one in ten misspellings on aver-age.(e)A 20-page document would have about 60misspellings.This algorithm would be expected to detect 54.A table three times as large would still ﬁt in about 100K bytes and reduce the expected number of errors to two.This is good enough for many applications,especially since spelling detection is a very inexact science.Many misspelled words (espe-cially short ones)are still words.For instance,typing them instead of then is a misspelling that won’t be detected by any algorithm.5.10To each hash table slot,we can add an extra ﬁeld that we’ll call WhereOnStack, and we cankeep an extra stack.When an insertion is ﬁrst performed into a slot,we push the address (or number)of the slot onto the stack and set the WhereOnStack ﬁeld to point to the top of the stack.When we access a hash table slot,we check that WhereOnStack points to a valid part of the stack and that the entry in the (middle of the)stack that is pointed to by the WhereOn-Stack ﬁeld has that hash table slot as an address.5.14(2)000000100000101100101011(2)01010001011000010110111101111111(3)100101101001101110011110(3)1011110110111110(2)110011111101101111110000000001010011100101110111-28-w w w .k hd a w.c o m 课后答案网。

数据结构与算法课后习题解答

数据结构与算法课后习题解答数据结构与算法课后习题解答第一章绪论（参考答案）1.3 (1) O(n)(2) (2) O(n)(3) (3) O(n)(4) (4) O(n1/2)(5) (5) 执行程序段的过程中，x,y值变化如下：循环次数x y0（初始）91 1001 92 1002 93 100。

9 100 10010 101 10011 9112。

20 9921 91 98。

30 101 9831 91 97到y=0时，要执行10*100次，可记为O（10*y）=O（n）数据结构与算法课后习题解答1.5 2100 , (2/3)n , log2n , n1/2 , n3/2 , (3/2)n , nlog2n , 2 n , n! , n n第二章线性表(参考答案)在以下习题解答中，假定使用如下类型定义：（1）顺序存储结构：#define ***** 1024typedef int ElemType;// 实际上，ElemTypetypedef struct{ ElemType data[*****];int last; // last}sequenlist;（2*next；}linklist;（3）链式存储结构（双链表）typedef struct node{ElemType data;struct node *prior,*next；数据结构与算法课后习题解答}dlinklist;（4）静态链表typedef struct{ElemType data;int next;}node;node sa[*****];2.1 la，往往简称为“链表la”。

是副产品）2.2 23voidelenum个元素，且递增有序，本算法将x插入到向量A中，并保持向量的{ int i=0,j;while (ielenum A[i]=x) i++; // 查找插入位置for (j= elenum-1;jj--) A[j+1]=A[j];// 向后移动元素A[i]=x; // 插入元素数据结构与算法课后习题解答} // 算法结束24void rightrotate(ElemType A[],int n,k)// 以向量作存储结构，本算法将向量中的n个元素循环右移k位，且只用一个辅助空间。

数据结构+算法+第二版+课后+答案+部分

算法与数据结构课后习题答案第一章一、选择题CCADB二、判断题FFFFT三、简答题5.(1) n-1 (2)1 (3)n(n+1)/2 (4)if(a<b) n , a++ n/2(5)if(x>100) 11*100-1, x-=10;y-- 1006.(1)O(log3n) (2) O(n2) (3) O(n2)第二章一、选择题1~5: AADCD 6~10:BCBAD 11~12:BD二、判断题1~5:FTFTF 6~10:TFTTF 11~12:FF三、算法设计题1.#define arrsize 100int Inserseqx(datatype A[ ], int *elenum, datatype x ) { int i=*elenum-1;if(*elenum==arrsize) return 0;while(i>=0&&A[i]>=x ){ A[i+1]=A[i]; i--; }A[i+1]=x; *elenum ++;return 1;}6.typedef struct node{ dataype data;struct node *next;}LNode, *LinkList;int Inserlinkx(LinkList L,datatype x ){ LNode *p=L,*s;s=(LNode *)malloc(sizeof(LNode));if(!s) return 0;s->data=x;while(p->next&&p->next->data<=x) p=p->next;s->next=p->next; p->next=s;return 1;}第三章一、选择题1~5:CBDBB 6~10: CBDCC二、判断题1~5:TTTFF三、简答题4. 共14种顺序：4321 3214 3241 3421 2134 2143 23142341 2431 1234 1243 1324 1342 1432四、简答题1.#define MAXSIZE 1000typedef struct{datatype data[MAXSIZE];int top;}SeqStack;SeqStack *Init_SeqStack(); /*栈初始化*/int Empty_SeqStack(SeqStack *s)；/*判栈空*/int Push_SeqStack(SeqStack *s,datatype x); /*x入栈*/ int Pop_SeqStack(SeqStack *s,datatype *x); /*出栈*/int judgehuiwen(char *str)/*返回1表示是回文，否则不是*/{ SeqStack *s=Init SeqStack( );char *ch=str,ch1;while(*ch!=’@’){Push_SeqStack(s, *ch);ch++;}ch=str;while(!Empty_SeqStack(s)){ Pop_SeqStack(s,&ch1);if(*ch!=ch1) return 0;ch++;}return 1;}5.#define MAXSIZE 1000typedef struct{datatype data[MAXSIZE];int top;}SeqStack;SeqStack *Init_SeqStack(); /*栈初始化*/int Empty_SeqStack(SeqStack *s)；/*判栈空*/int Push_SeqStack(SeqStack *s,datatype x); /*x入栈*/ int Pop_SeqStack(SeqStack *s,datatype *x); /*出栈*/ int judge(char *str)/*返回1表示是匹配，否则不是*/{ SeqStack *s=Init SeqStack( );char *ch=str,ch1;while(*c h!=’\0’){ if（*ch==’(‘) Push_SeqStack(s, *ch);else if(*ch==’)‘)if(!Pop_SeqStack(s,&ch1)) return 0;ch++;}if(Empty_SeqStack(s)) return 1;else return 0;}4.typedef struct node{ dataype data;struct node *next;}Lqnode, *LqList;置空：LqList Init_lq(){ LqList rear=(LqList *)malloc(sizeof(LqList)); rear->next=rear;return rear;}入队：int in_lq(LqList *rear, datatype x){ Lqnode *p=(LqList *)malloc(sizeof(LqList)); if(!p) return 0;p->data=x;p->next=*rear->next; *rear->next=p; *rear=p; return 1;}出队：int out_lq(LqList *rear, datatype x){ Lqnode *p;if(*rear->next==*rear) return 0;p=*rear->next->next;if(p==*rear){*rear=*rear->next;*rear->next=*rear;} else *rear->next->next=p->next;free(p);return 1;}第四章一、选择题1-3：CBA 4：DAB 5:CCC 6:C二、判断题FTFFFFF三、简答题2.4. k=i+j-2+(i+1)%2 或k=i+j-1+i%26.第五章一、选择题：1~5：CCBBB 6~10:CBDAD 11~15:DCBDB3 5 6 7 98 13 17二、判断题：1~5：FTFFT 6~10:FFFTF 11~15:TFTFF 16~20:FTFFT 三、简答题：（(2)4、条件：森林中既没有孩子也没有右边的兄弟的结点11. 最大值：2h-1 最小值：2h-116.0.31 0.16 0.10 0.08 0.11 0.20 0.04 0.12 0.21 0.28 0.410.59a b c d e f ga:01 b:001 c:110 d:0000 e:111 f:10 g:0001四、算法设计题：typedef struct bitnode{ datatype data;struct bitnode *lchild, *rchild;}BiTNode, *BiTree;1.计算结点数目int counttotal(BiTree bt){ if(bt==NULL) return 0;return counttotal(bt->lchild)+counttotal(bt->rchild)+1;}计算度为1的结点数目：int countdegree1(BiTree bt){ if(bt==NULL) return 0;if( bt->lchild==NULL&& bt->rchild==NULL) return 0;if( bt->lchild==NULL|| bt->rchild==NULL)return countdegree1(bt->lchild)+ countdegree1(bt->rchild)+1; return countdegree1(bt->lchild)+ countdegree1(bt->rchild);}3.求深度;int depth(BiTree bt){ int ld,rd;if(bt==NULL) return 0;ld= depth(bt->lchild); rd=depth(bt->rchild);if( ld>=rd) return ld+1;return rd+1;}第6章作业讲评一、选择题1-4：BABC 5:BD 6-10:DBACB二、判断题1-5：FTTFF 6-10:TTFFT 11-15:FTFFF三、简答题1.（1）ID(1)=2 OD(1)=1ID(2)=2 OD(2)=2ID(3)=1 OD(3)=3ID(4)=3 OD(4)=0ID(5)=2 OD(5)=3ID(6)=1 OD(6)=2(2)0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 1 0(3) （4）54 3 2 1 0 54 3 2 1 0（5） 2. （1）0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 0 1 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 0 1 1 0（2）（4）（5）v1 v2 v3 v4 v5 v6 v73. 邻接矩阵表示图时，与顶点个数有关，与边的条数无关。

数据结构与算法分析习题与参考答案

大学《数据结构与算法分析》课程习题及参考答案模拟试卷一一、单选题（每题2分，共20分）1. 以下数据结构中哪一个是线性结构？（）A. 有向图B.队列C. 线索二叉树D. B树2. 在一个单链表HL中，若要在当前由指针p指向的结点后面插入一个由q指向的结点,则执行如下（）语句序列。

A. p=q; p_>n ext=q;B. p_>n ext=q; q_>n ext=p;C. p_>n ext=q _>n ext; p=q;D. q_>n ext=p->n ext; p_>n ext=q;3. 以下哪一个不是队列的基本运算？（）A. 在队列第i个元素之后插入一个元素B. 从队头删除一个元素C.判断一个队列是否为空D. 读取队头元素的值4. 字符A、B、C依次进入一个栈，按出栈的先后顺序组成不同的字符串，至多可以组成（）个不同的字符串？A. 14B.5C.6D.8由权值分别为3,8,6,2的叶子生成一棵哈夫曼树，它的带权路径长度为（）5.A. 11B.35C. 19D. 536.A. E、G F、 A C D BB. E、A、G C F、B、DC. E、A、C、B D G FD. E、G A、C D F、B7.A. A 、B、 C D E、G FB. E 、A、G C F、B、DC. E 、A、C B、D G FE. B D C '、AF、G E以下6-8题基于图1。

该二叉树结点的前序遍历的序列为该二叉树结点的中序遍历的序列为（8.该二叉树的按层遍历的序列为（）9.下面关于图的存储的叙述中正确的是 ()。

A .用邻接表法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关B .用邻接表法存储图，占用的存储空间大小与图中边数和结点个数都有关 C. 用邻接矩阵法存储图，占用的存储空间大小与图中结点个数和边数都有关 D .用邻接矩阵法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关10. 设有关键码序列(q , g , m z , a , n , p , x , h)，下面哪一个序列是从上述序列出发建堆的结果?()A. a , g , h , m n , p , q , x , zB. a ,g , m h , q , n , p , x , zC. g, m, q , a , n , p , x , h , z D. h,g , m p , a , n , q , x , z二、填空题(每空1分，共26分)1.数据的物理结构被分为、、和四种。

数据结构与算法设计课后习题及答案详解

第一章1.数据结构研究的主要内容包括逻辑结构、存储结构和算法。

2.数据元素是数据的基本单位，数据项是数据的最小标示单位。

3.根据数据元素之间关系的不同，数据的逻辑结构可以分为集合、树形、线性、图状。

4.常见的数据存储结构有四种类型：顺序、链式、索引、散列。

5.可以从正确性、可读性、健壮性、高效性四方面评价算法的质量。

6.在一般情况下，一个算法的时间复杂度是问题规模的函数。

7.常见时间复杂度有：常数阶O（1）、线性阶O（n）、对数阶O（log2 n）、平方阶O（n²）和指数阶O（2ⁿ）。

通常认为，具有常数阶量级的算法是好算法，而具有指数阶量级的算法是差算法。

8.时间复杂度排序由大到小（n+2）！>2ⁿ＋²>（n+2）4次方>nlog2 n>100000.问答题：1.什么叫数据元素？数据元素是数据的基本单位，是数据这个集合的个体，也称为元素、结点、顶点、记录。

2.什么叫数据逻辑结构？什么叫数据存储结构？数据逻辑结构：指数据元素之间存在的固有的逻辑结构。

数据存储结构：数据元素及其关系在计算机内的表示。

3.什么叫抽象数据类型？抽象数据类型是指数据元素集合以及定义在该集合上的一组操作。

4.数据元素之间的关系在计算机中有几种表示方法？顺序、链式、索引、散列。

5.数据的逻辑结构与数据的存储结构之间存在着怎样的关系？相辅相成，不可分割。

6.什么叫算法？算法的性质有哪些？算法：求解问题的一系列步骤的集合。

可行性、有容性、确定性、有输入、有输出。

7.评价一个算法的好坏应该从哪几方面入手？正确性、可读性、健壮性、高效性。

第二章1.线性表中，第一个元素没有直接前驱，最后一个元素没有直接后继。

2.线性表常用的两种存储结构分别是顺序存储结构和链式存储结构。

3.在长度为n的顺序表中，插入一个新元素平均需要移动表中的n/2个元素，删除一个元素平均需要移动（n-1）/2个元素。

4.在长度为n的顺序表的表头插入一个新元素的时间复杂度为O（n），在表尾插入一个新元素的时间复杂度为O（1）。

《数据结构与算法》习题与答案

《数据结构与算法》习题与答案（解答仅供参考）一、名词解释：1. 数据结构：数据结构是计算机存储、组织数据的方式，它不仅包括数据的逻辑结构（如线性结构、树形结构、图状结构等），还包括物理结构（如顺序存储、链式存储等）。

它是算法设计与分析的基础，对程序的效率和功能实现有直接影响。

2. 栈：栈是一种特殊的线性表，其操作遵循“后进先出”（Last In First Out, LIFO）原则。

在栈中，允许进行的操作主要有两种：压栈（Push），将元素添加到栈顶；弹栈（Pop），将栈顶元素移除。

3. 队列：队列是一种先进先出（First In First Out, FIFO）的数据结构，允许在其一端插入元素（称为入队），而在另一端删除元素（称为出队）。

常见的实现方式有顺序队列和循环队列。

4. 二叉排序树（又称二叉查找树）：二叉排序树是一种二叉树，其每个节点的左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。

这种特性使得能在O(log n)的时间复杂度内完成搜索、插入和删除操作。

5. 图：图是一种非线性数据结构，由顶点（Vertex）和边（Edge）组成，用于表示对象之间的多种关系。

根据边是否有方向，可分为有向图和无向图；根据是否存在环路，又可分为有环图和无环图。

二、填空题：1. 在一个长度为n的顺序表中，插入一个新元素平均需要移动______个元素。

答案：(n/2)2. 哈希表利用______函数来确定元素的存储位置，通过解决哈希冲突以达到快速查找的目的。

答案：哈希（Hash）3. ______是最小生成树的一种算法，采用贪心策略，每次都选择当前未加入生成树且连接两个未连通集合的最小权重边。

答案：Prim算法4. 在深度优先搜索（DFS）过程中，使用______数据结构来记录已经被访问过的顶点，防止重复访问。

答案：栈或标记数组5. 快速排序算法在最坏情况下的时间复杂度为______。

数据结构与算法习题及答案

精心整理第1章绪论习题1．简述下列概念：数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。

2．试举一个数据结构的例子，叙述其逻辑结构和存储结构两方面的含义和相互关系。

3．简述逻辑结构的四种基本关系并画出它们的关系图。

4．存储结构由哪两种基本的存储方法实现5A6{x=x-10;y--;}elsex++;（2）for(i=0;i<n;i++)for(j=0;j<m;j++)a[i][j]=0;（3）s=0;fori=0;i<n;i++)for(j=0;j<n;j++)s+=B[i][j];sum=s;（4）i=1;while(i<=n)i=i*3;（5）x=0;for(i=1;i<n;i++)for(j=1;j<=n-i;j++)x++;（6）x=n;n108 C63.5 C1 C-1 C1 Cext=s;(*s).next=(*p).next;C．s->next=p->next;p->next=s->next;D．s->next=p->next;p->next=s;2,=(rear+1)%=(rear+1)%(m+1)（13）最大容量为n的循环队列，队尾指针是rear，队头是front，则队空的条件是（）。

A.(rear+1)%n====frontC．rear+1==frontD.(rear-l)%n==front（14）栈和队列的共同点是（）。

A.都是先进先出B.都是先进后出C.只允许在端点处插入和删除元素D.没有共同点（15）一个递归算法必须包括（）。

A.递归部分B.终止条件和递归部分C.迭代部分D.终止条件和迭代部分（2）回文是指正读反读均相同的字符序列，如“abba”和“abdba”均是回文，但“good”不是回文。

试写一个算法判定给定的字符向量是否为回文。

(提示：将一半字符入栈)根据提示，算法可设计为：0’9’0’9’0’0’9’0’0’9’0’0’0’M-1]实现循环队列，其中M是队列长度。

数据结构与算法第六章课后答案第六章树和二叉树

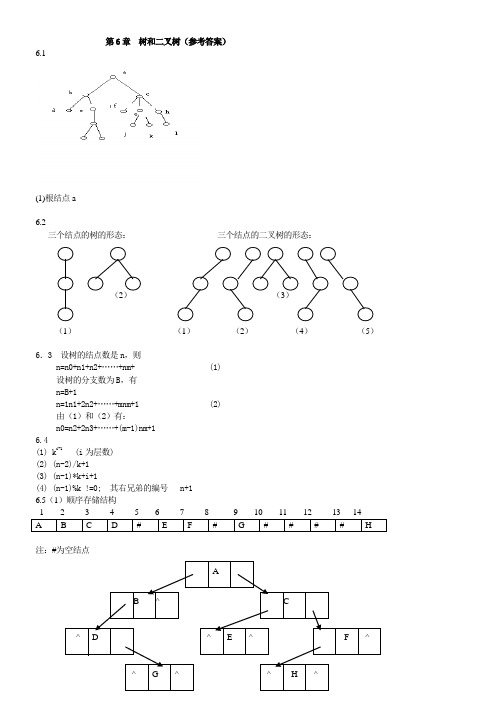
第6章树和二叉树（参考答案）6.1(1)根结点a6.2三个结点的树的形态：三个结点的二叉树的形态：（1）（1）（2）（4）（5）6．3 设树的结点数是n ，则n=n0+n1+n2+……+nm+ (1)设树的分支数为B ，有n=B+1n=1n1+2n2+……+mnm+1 (2)由（1）和（2）有：n0=n2+2n3+……+(m-1)nm+16.4(1) k i-1 (i 为层数)(2) (n-2)/k+1(3) (n-1)*k+i+1(4) (n-1)%k !=0; 其右兄弟的编号 n+16.5（1）顺序存储结构注：#为空结点6.6(1) 前序 ABDGCEFH(2) 中序 DGBAECHF(3) 后序 GDBEHFCA6.7(1) 空二叉树或任何结点均无左子树的非空二叉树(2) 空二叉树或任何结点均无右子树的非空二叉树(3) 空二叉树或只有根结点的二叉树6.8int height(bitree bt)// bt是以二叉链表为存储结构的二叉树，本算法求二叉树bt的高度{ int bl,br; // 局部变量，分别表示二叉树左、右子树的高度if (bt==null) return(0);else { bl=height(bt->lchild);br=height(bt->rchild);return(bl>br? bl+1: br+1); // 左右子树高度的大者加1（根） }}// 算法结束6.9void preorder(cbt[],int n,int i);// cbt是以完全二叉树形式存储的n个结点的二叉树，i是数// 组下标，初始调用时为1。

本算法以非递归形式前序遍历该二叉树{ int i=1,s[],top=0; // s是栈，栈中元素是二叉树结点在cbt中的序号 // top是栈顶指针，栈空时top=0if (n<=0) { printf(“输入错误”);exit（0）；}while (i<=n ||top>0){ while(i<=n){visit(cbt[i]); // 访问根结点if (2*i+1<=n) s[++top]=2*i+1; //若右子树非空，其编号进栈i=2*i;// 先序访问左子树}if (top>0) i=s[top--]; // 退栈，先序访问右子树} // END OF while (i<=n ||top>0)}// 算法结束//以下是非完全二叉树顺序存储时的递归遍历算法，“虚结点”用‘*’表示void preorder(bt[],int n,int i);// bt是以完全二叉树形式存储的一维数组，n是数组元素个数。

数据结构与算法分析课后习题答案

数据结构与算法分析课后习题答案【篇一：《数据结构与算法》课后习题答案】>2.3.2 判断题2．顺序存储的线性表可以按序号随机存取。

（√）4．线性表中的元素可以是各种各样的，但同一线性表中的数据元素具有相同的特性，因此属于同一数据对象。

（√）6．在线性表的链式存储结构中，逻辑上相邻的元素在物理位置上不一定相邻。

（√）8．在线性表的顺序存储结构中，插入和删除时移动元素的个数与该元素的位置有关。

（√）9．线性表的链式存储结构是用一组任意的存储单元来存储线性表中数据元素的。

（√）2.3.3 算法设计题1．设线性表存放在向量a[arrsize]的前elenum个分量中，且递增有序。

试写一算法，将x 插入到线性表的适当位置上，以保持线性表的有序性，并且分析算法的时间复杂度。

【提示】直接用题目中所给定的数据结构（顺序存储的思想是用物理上的相邻表示逻辑上的相邻，不一定将向量和表示线性表长度的变量封装成一个结构体），因为是顺序存储，分配的存储空间是固定大小的，所以首先确定是否还有存储空间，若有，则根据原线性表中元素的有序性，来确定插入元素的插入位置，后面的元素为它让出位置，（也可以从高下标端开始一边比较，一边移位）然后插入x ，最后修改表示表长的变量。

int insert (datatype a[],int *elenum,datatype x) /*设elenum为表的最大下标*/ {if (*elenum==arrsize-1) return 0; /*表已满，无法插入*/else {i=*elenum;while (i=0 a[i]x)/*边找位置边移动*/{a[i+1]=a[i];i--;}a[i+1]=x;/*找到的位置是插入位的下一位*/ (*elenum)++;return 1;/*插入成功*/}}时间复杂度为o(n)。

2．已知一顺序表a，其元素值非递减有序排列，编写一个算法删除顺序表中多余的值相同的元素。

数据结构与算法设计课后习题及答案详解

第一章1.数据结构研究的主要内容包括逻辑结构、存储结构和算法。

2.数据元素是数据的基本单位，数据项是数据的最小标示单位。

3.根据数据元素之间关系的不同，数据的逻辑结构可以分为集合、树形、线性、图状。

4.常见的数据存储结构有四种类型：顺序、链式、索引、散列。

5.可以从正确性、可读性、健壮性、高效性四方面评价算法的质量。

6.在一般情况下，一个算法的时间复杂度是问题规模的函数。

7.常见时间复杂度有：常数阶O（1）、线性阶O（n）、对数阶O（log2 n）、平方阶O（n²）和指数阶O（2ⁿ）。

通常认为，具有常数阶量级的算法是好算法，而具有指数阶量级的算法是差算法。

2.什么叫数据逻辑结构？什么叫数据存储结构？数据逻辑结构：指数据元素之间存在的固有的逻辑结构。

数据存储结构：数据元素及其关系在计算机内的表示。

3.什么叫抽象数据类型？抽象数据类型是指数据元素集合以及定义在该集合上的一组操作。

4.数据元素之间的关系在计算机中有几种表示方法？顺序、链式、索引、散列。

5.数据的逻辑结构与数据的存储结构之间存在着怎样的关系？相辅相成，不可分割。

6.什么叫算法？算法的性质有哪些？算法：求解问题的一系列步骤的集合。

可行性、有容性、确定性、有输入、有输出。

7.评价一个算法的好坏应该从哪几方面入手？正确性、可读性、健壮性、高效性。

第二章1.线性表中，第一个元素没有直接前驱，最后一个元素没有直接后继。

2.线性表常用的两种存储结构分别是顺序存储结构和链式存储结构。

3.在长度为n的顺序表中，插入一个新元素平均需要移动表中的n/2个元素，删除一个元素平均需要移动（n-1）/2个元素。

4.在长度为n的顺序表的表头插入一个新元素的时间复杂度为O（n），在表尾插入一个新元素的时间复杂度为O（1）。

《数据结构与算法》课后习题答案

2.3 课后习题解答2.3.2 判断题1．线性表的逻辑顺序与存储顺序总是一致的。

（×）2．顺序存储的线性表可以按序号随机存取。

（√）3．顺序表的插入和删除操作不需要付出很大的时间代价，因为每次操作平均只有近一半的元素需要移动。

（×）4．线性表中的元素可以是各种各样的，但同一线性表中的数据元素具有相同的特性，因此属于同一数据对象。

（√）5．在线性表的顺序存储结构中，逻辑上相邻的两个元素在物理位置上并不一定相邻。

（×）6．在线性表的链式存储结构中，逻辑上相邻的元素在物理位置上不一定相邻。

（√）7．线性表的链式存储结构优于顺序存储结构。

（×）8．在线性表的顺序存储结构中，插入和删除时移动元素的个数与该元素的位置有关。

（√）9．线性表的链式存储结构是用一组任意的存储单元来存储线性表中数据元素的。

（√）10．在单链表中，要取得某个元素，只要知道该元素的指针即可，因此，单链表是随机存取的存储结构。

（×）11．静态链表既有顺序存储的优点，又有动态链表的优点。

所以它存取表中第i个元素的时间与i无关。

（×）12．线性表的特点是每个元素都有一个前驱和一个后继。

（×）2.3.3 算法设计题1．设线性表存放在向量A[arrsize]的前elenum个分量中，且递增有序。

试写一算法，将x 插入到线性表的适当位置上，以保持线性表的有序性，并且分析算法的时间复杂度。

int insert (datatype A[],int *elenum,datatype x) /*设elenum为表的最大下标*/ {if (*elenum==arrsize-1) return 0; /*表已满，无法插入*/else {i=*elenum;while (i>=0 && A[i]>x) /*边找位置边移动*/{A[i+1]=A[i];i--;}A[i+1]=x; /*找到的位置是插入位的下一位*/(*elenum)++;return 1; /*插入成功*/}}时间复杂度为O(n)。

第5章数据结构与算法习题与答案

第五章习题（1）复习题1、试述数据和数据结构的概念及其区别。

数据是对客观事物的符号表示，是信息的载体；数据结构则是指互相之间存在着一种或多种关系的数据元素的集合。

（P113）2、列出算法的五个重要特征并对其进行说明。

算法具有以下五个重要的特征：有穷性：一个算法必须保证执行有限步之后结束。

确切性：算法的每一步骤必须有确切的定义。

输入：一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输入是指算法本身定除了初始条件。

输出：一个算法有一个或多个输出，以反映对输入数据加工后的结果。

没有输出的算法没有实际意义。

可行性：算法原则上能够精确地运行，而且人们用笔和纸做有限次运算后即可完成。

（P115）3、算法的优劣用什么来衡量？试述如何设计出优秀的算法。

时间复杂度空间复杂度（P117）4、线性和非线性结构各包含哪些种类的数据结构？线性结构和非线性结构各有什么特点？线性结构用于描述一对一的相互关系，即结构中元素之间只有最基本的联系，线性结构的特点是逻辑结构简单。

所谓非线性结构是指，在该结构中至少存在一个数据元素，有两个或两个以上的直接前驱（或直接后继）元素。

树型和图型结构就是其中十分重要的非线性结构，可以用来描述客观世界中广泛存在的层次结构和网状结构的关系。

（P118 P122）5、简述树与二叉树的区别；简述树与图的区别。

树用来描述层次结构，是一对多或多对一的关系；二叉树（Binary Tree）是个有限元素的集合，该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。

二叉树是有序的，即若将其左、右子树颠倒，就成为另一棵不同的二叉树。

图也称做网，是一种比树形结构更复杂的非线性结构。

在图中，任意两个节点之间都可能相关，即节点之间的邻接关系可以是任意的，图表示的多对多的关系。

（P121-P124）6、请举出遍历算法在实际中使用的例子。

提示：根据实际生活中需要逐个访问处理的情况举例。

数据结构与算法习题含参考答案

数据结构与算法习题含参考答案一、单选题（共100题，每题1分，共100分）1、要为 Word 2010 格式的论文添加索引，如果索引项已经以表格形式保存在另一个 Word文档中，最快捷的操作方法是：A、在 Word 格式论文中，逐一标记索引项，然后插入索引B、直接将以表格形式保存在另一个 Word 文档中的索引项复制到 Word 格式论文中C、在 Word 格式论文中，使用自动插入索引功能，从另外保存 Word 索引项的文件中插D、在 Word 格式论文中，使用自动标记功能批量标记索引项，然后插入索引正确答案：D2、下面不属于计算机软件构成要素的是A、文档B、程序C、数据D、开发方法正确答案：D3、JAVA 属于：A、操作系统B、办公软件C、数据库系统D、计算机语言正确答案：D4、在 PowerPoint 演示文稿中,不可以使用的对象是：A、图片B、超链接C、视频D、书签第 6 组正确答案：D5、下列叙述中正确的是A、软件过程是软件开发过程和软件维护过程B、软件过程是软件开发过程C、软件过程是把输入转化为输出的一组彼此相关的资源和活动D、软件过程是软件维护过程正确答案：C6、在 Word 中，不能作为文本转换为表格的分隔符的是：A、@B、制表符C、段落标记D、##正确答案：D7、某企业为了建设一个可供客户在互联网上浏览的网站，需要申请一个：A、密码B、门牌号C、域名D、邮编正确答案：C8、面向对象方法中，将数据和操作置于对象的统一体中的实现方式是A、隐藏第 42 组B、抽象C、结合D、封装正确答案：D9、下面属于整数类 I 实例的是A、-919B、0.919C、919E+3D、919D-2正确答案：A10、定义课程的关系模式如下：Course (C#, Cn, Cr，prC1#, prC2#)（其属性分别为课程号、课程名、学分、先修课程号 1和先修课程号 2），并且不同课程可以同名，则该关系最高是A、BCNFB、2NFC、1NFD、3NF正确答案：A11、循环队列的存储空间为 Q(1:100)，初始状态为 front=rear=100。

《数据结构与算法》课后习题答案

《数据结构与算法》课后习题答案一、算法分析和复杂度1.1 算法复杂度的定义算法的复杂度是指算法所需资源的度量，包括时间复杂度和空间复杂度。

时间复杂度描述了算法的执行时间随输入规模增长的增长速度，空间复杂度描述了算法执行期间所需的存储空间随输入规模增长的增长速度。

1.2 时间复杂度的计算方法时间复杂度可以通过估算算法的执行次数来计算。

对于循环结构，通常可以通过循环体内代码的执行次数来估算时间复杂度。

对于递归算法，则可以通过递归的深度和每次递归的复杂度来计算时间复杂度。

1.3 常见的时间复杂度在算法分析中，常见的时间复杂度有：O(1)、O(log n)、O(n)、O(n log n)、O(n^2)、O(n^3)等。

其中，O(1)表示算法的执行时间与输入规模无关，即常数时间复杂度；O(log n)表示算法的执行时间随输入规模呈对数增长；O(n)表示算法的执行时间随输入规模呈线性增长；O(nlog n)表示算法的执行时间随输入规模呈线性对数增长；O(n^2)表示算法的执行时间随输入规模呈平方增长；O(n^3)表示算法的执行时间随输入规模呈立方增长。

1.4 空间复杂度的计算方法空间复杂度可以通过估计算法执行过程中所需要的额外存储空间来计算。

对于递归算法，通常使用递归的深度来估算空间复杂度。

1.5 算法复杂度的应用算法的复杂度分析在实际应用中非常重要，可以帮助我们选择合适的算法来解决问题。

在时间复杂度相同的情况下，可以通过比较空间复杂度来选择更优的算法。

在实际开发中，我们也可以根据算法的复杂度来进行性能优化，减少资源的消耗。

二、搜索算法2.1 线性搜索算法线性搜索算法是一种简单直观的搜索算法，逐个比较待搜索元素和数组中的元素，直到找到匹配的元素或遍历完整个数组。

其时间复杂度为O(n)，空间复杂度为O(1)。

2.2 二分搜索算法二分搜索算法是一种高效的搜索算法，前提是数组必须是有序的。

算法首先取数组的中间元素进行比较，如果相等则返回找到的位置，如果大于中间元素则在右半部分继续搜索，如果小于中间元素则在左半部分继续搜索。

数据结构与算法分析习题与参考答案

大学《数据结构与算法分析》课程习题及参考答案模拟试卷一一、单选题（每题 2 分，共20分）1.以下数据结构中哪一个是线性结构？( )A. 有向图B. 队列C. 线索二叉树D. B树2.在一个单链表HL中，若要在当前由指针p指向的结点后面插入一个由q指向的结点，则执行如下( )语句序列。

A. p=q; p->next=q;B. p->next=q; q->next=p;C. p->next=q->next; p=q;D. q->next=p->next; p->next=q;3.以下哪一个不是队列的基本运算？（）A. 在队列第i个元素之后插入一个元素B. 从队头删除一个元素C. 判断一个队列是否为空D.读取队头元素的值4.字符A、B、C依次进入一个栈，按出栈的先后顺序组成不同的字符串，至多可以组成( )个不同的字符串？A.14B.5C.6D.85.由权值分别为3,8,6,2的叶子生成一棵哈夫曼树，它的带权路径长度为( )。

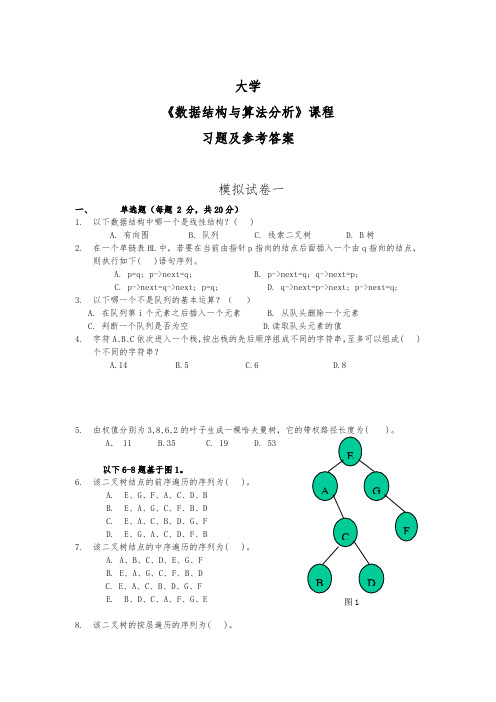
以下6-8题基于图1。

6.该二叉树结点的前序遍历的序列为( )。

A.E、G、F、A、C、D、BB.E、A、G、C、F、B、DC.E、A、C、B、D、G、FD.E、G、A、C、D、F、B7.该二叉树结点的中序遍历的序列为( )。

A. A、B、C、D、E、G、FB. E、A、G、C、F、B、DC. E、A、C、B、D、G、FE.B、D、C、A、F、G、E8.该二叉树的按层遍历的序列为( )。

A．E、G、F、A、C、D、B B. E、A、C、B、D、G、FC. E、A、G、C、F、B、DD. E、G、A、C、D、F、B9.下面关于图的存储的叙述中正确的是( )。

A．用邻接表法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关B．用邻接表法存储图，占用的存储空间大小与图中边数和结点个数都有关C. 用邻接矩阵法存储图，占用的存储空间大小与图中结点个数和边数都有关D．用邻接矩阵法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关10.设有关键码序列(q，g，m，z，a，n，p，x，h)，下面哪一个序列是从上述序列出发建堆的结果?( )A. a，g，h，m，n，p，q，x，zB. a，g，m，h，q，n，p，x，zC. g，m，q，a，n，p，x，h，zD. h，g，m，p，a，n，q，x，z二、填空题（每空1分，共26分）1.数据的物理结构被分为_________、________、__________和___________四种。

数据结构与算法教程习题答案作者朱明方吴及第5章习题解答.docx

第5章习题解答2- 9, 0-6, 4-9, 2-6, 6-4；(1) 请确定图中各个顶点的度； (2) 给出图的连通分量；(3)列出至少有三个顶点的简单路径。

［解答］由题意得到的图如图5-1所示。

［解答］如图5-2所示，分别为1个顶点，2个顶点，3个顶点，4个顶点，5个顶点和6个顶点的无向完全图。

5. 1 已知一个图有。

到9 一共10个顶点, 图中边为：3-7,1-4, 7-8, 0-5, 5-2, 3-8,(1)顶点:0 12 3 4 顶点的度：213232⑵连通分量1：连通分量2： (3)连通分量1：连通分量2中:4-6-0, 4-6-2, 6-2-5, 6-2-9, 9-2-6, 0-5-2,如图5-1 (b)所示。

如图5-1 (a)所示。

3- 7-8； 1-4-6, 1-4-9 4- 9-2, 6-0-5, 6-4一9, 9—2-5,共有13条。

5.2向完全图。

请分别画出1个顶点，2个顶点, 3个顶点，4个顶点，5个顶点和6个顶点的无图5-15.3 若无向图G有15条边，有3个度为4的顶点，其余顶点的度不大于3,图G至少有多少个顶点？［解答］设图G至少有x个顶点，根据握手定理有：3 X4 + 3 (x-3) =2X15, x=9(个)5.4 试证明有/个顶点的任何无环连通图均有V -1条边。

［解答］无环连通图即为树。

根据树的性质，有V个顶点的树均有V-1条边。

5.5对于一个有r个顶点和的无向完全图，请问一共有多少个子图？［解答］V 2一共有个子图。

i=05.6对于一个有V个顶点和E条边的无向图，请给出其连通分量个数的上界和下界。

［解答］根据无向图中顶点和边的关系可知，E必然满足0WEWK(片1)/2,由分析可得到：V-E if E<V-1 c = dmin［1 if E>V-1M=V-(l + Jl + 8E)/2 E<V(V-1)/2提示：在不形成环的情况下，连通分量数目达到最小值；当某个连通分量为完全图时, 连通分量数目达到最大值。

算法与数据结构1—5章课后习题

第一章绪论习题练习答案简述下列概念：数据、数据元素、数据类型、数据结构、逻辑结构、存储结构、线性结构、非线性结构。

●数据：指能够被计算机识别、存储和加工处置的信息载体。

●数据元素：就是数据的大体单位，在某些情况下，数据元素也称为元素、结点、极点、记录。

数据元素有时可以由若干数据项组成。

课后答案网数据类型：是一个值的集合和在这些值上概念的一组操作的总称。

通常数据类型可以看做是程序设计语言中已实现的数据结构。

●数据结构：指的是数据之间的彼此关系，即数据的组织形式。

一般包括三个方面的内容:数据的逻辑结构、存储结构和数据的运算。

●逻辑结构：指数据元素之间的逻辑关系。

●存储结构：数据元素及其关系在计算机存储器内的表示，称为数据的存储结构.●线性结构：数据逻辑结构中的一类。

它的特征是若结构为非空集，则该结构有且只有一个开始结点和一个终端结点，而且所有结点都有且只有一个直接前趋和一个直接后继。

线性表就是一个典型的线性结构。

栈、队列、串等都是线性结构。

●非线性结构：数据逻辑结构中的另一大类，它的逻辑特征是一个结点可能有多个直接前趋和直接后继。

数组、广义表、树和图等数据结构都是非线性结构。

试举一个数据结构的例子、叙述其逻辑结构、存储结构、运算三个方面的内容。

答：例如有一张学生体检情况记录表，记录了一个班的学生的身高、体重等各项体检信息。

这张记录表中，每一个学生的各项体检信息排在一行上。

这个表就是一个数据结构。

每一个记录(有姓名，学号，身高和体重等字段)就是一个结点，对于整个表来讲，只有一个开始结点(它的前面无记录)和一个终端结点(它的后面无记录)，其他的结点则各有一个也只有一个直接前趋和直接后继(它的前面和后面均有且只有一个记录)。

这几个关系就肯定了这个表的逻辑结构是线性结构。

这个表中的数据如何存储到计算机里，而且如何表示数据元素之间的关系呢? 即用一片持续的内存单元来寄存这些记录(如用数组表示)仍是随机寄存各结点数据再用指针进行链接呢? 这就是存储结构的问题。

《数据结构与算法》课后习题答案(课件)

数据结构与算法分析课后题答案

数据结构与算法课后习题解答

数据结构+算法+第二版+课后+答案+部分

数据结构与算法分析习题与参考答案

数据结构与算法设计课后习题及答案详解

《数据结构与算法》习题与答案

数据结构与算法习题及答案

数据结构与算法第六章课后答案第六章 树和二叉树

数据结构与算法分析课后习题答案

数据结构与算法设计课后习题及答案详解

《数据结构与算法》课后习题答案

第5章 数据结构与算法 习题与答案

数据结构与算法习题含参考答案

《数据结构与算法》课后习题答案

数据结构与算法分析习题与参考答案

数据结构与算法教程 习题答案 作者 朱明方 吴及 第5章习题解答.docx

算法与数据结构1—5章课后习题

数据结构与算法第六章课后答案第六章树和二叉树

第5章数据结构与算法习题与答案

数据结构与算法教程习题答案作者朱明方吴及第5章习题解答.docx