五年级奥数扇形周长与面积和弓形面积

合集下载

五年级奥数专题-不规则图形面积计算含解析

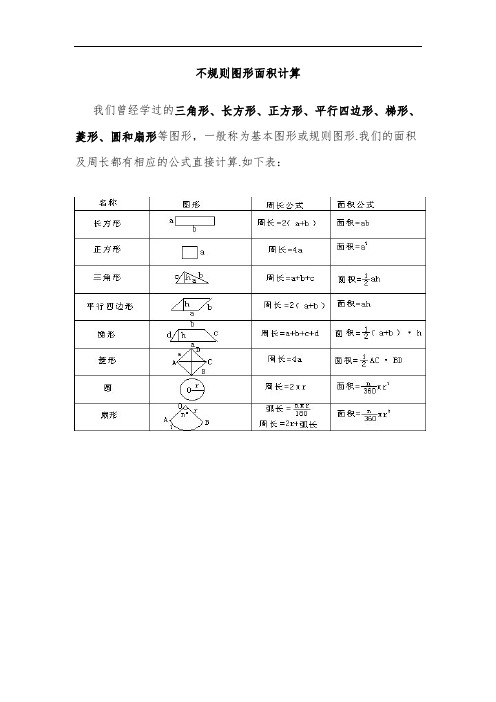
不规则图形面积计算我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

一、例题与方法指导例1 如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米.求阴影部分的面积。

思路导航：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2 如右图，正方形ABCD的边长为6厘米，△ABE、△ADF 与四边形AECF的面积彼此相等，求三角形AEF的面积.思路导航：∵△ABE 、△ADF 与四边形AECF 的面积彼此相等，∴四边形 AECF 的面积与△ABE 、△ADF 的面积都等于正方形ABCD 的13。

在△ABE 中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2， ∴△ECF 的面积为2×2÷2=2。

所以S △AEF=S 四边形AECF-S △ECF=12-2=10（平方厘米）。

例3 两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

思路导航：在等腰直角三角形ABC 中∵AB=10∵EF=BF=AB-AF=10-6=4，∴阴影部分面积=S △ABG-S △BEF=25-8=17（平方厘米）。

例4 如右图，A 为△CDE 的DE 边上中点，BC=CD ，若△ABC （阴影部分）面积为5平方厘米.求△ABD 及△ACE 的面积.B C思路导航：取BD中点F，连结AF.因为△ADF、△ABF和△ABC等底、等高，所以它们的面积相等，都等于5平方厘米.∴△ACD的面积等于15平方厘米，△ABD的面积等于10平方厘米。

五年级奥数专题-不规则图形面积计算含解析

不规则图形面积计算我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算般我们称这样的图形为不规则图形那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

一、例题与方法指导例1 如右图，甲、乙两图形都是正方形，它们的边长分别是10 厘米和12 厘米.求阴影部分的面积。

思路导航：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白三角形（△ ABG、△ BDE、△ EFG）的面积之和。

例2 如右图，正方形ABCD的边长为6 厘米，△ABE、△ADF 与四边形AECF的面积彼此相等，求三角形AEF的面积.思路导航：∵△ ABE、△ ADF与四边形AECF的面积彼此相等，∴四边形AECF的面积与△ ABE、△ ADF的面积都等于正方形1 ABCD的1。

3在△ ABE中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=，2∴△ ECF的面积为2×2÷ 2=2。

所以S△AEF=S四边形AECF-S△ ECF=12-2=1（0 平方厘米）。

例3两块等腰直角三角形的三角板，直角边分别是10 厘米和6 厘米。

如右图那样重合.求重合部分（阴影部分）的面积思路导航：在等腰直角三角形ABC中∵AB=10∵EF=BF=AB-AF=10-6=，4∴阴影部分面积=S△ ABG-S△BEF=25-8=1（7 平方厘米）例4 如右图，A 为△ CDE的DE边上中点，BC=CD，若△ ABC阴影部分）面积为5平方厘米.求△ ABD及△ ACE的面积.思路导航：取BD 中点F，连结AF.因为△ ADF、△ ABF和△ ABC等底、等高，所以它们的面积相等，都等于5平方厘米.∴△ ACD的面积等于15 平方厘米，△ ABD的面积等于10平方厘米。

扇形、三角形、弓形、菱形公式[整理版]

常用面积公式面积公式扇形面积公式00在半径为R的圆中，因为360°的圆心角所对的扇形的面积就是圆面积S=πR^2，所以圆心角为n°的扇形面积：00S=nπR²÷360 00比如：半径为1cm的圆，那么所对圆心角为135°的扇形的周长：00C=2R+nπR÷180 00=2×1+135×3.14×1÷180 00=2+2.355 00=4.355(cm)=43.55(mm) 00扇形的面积：00S=nπR²÷360 00=135×3.14×1×1÷360 00=1.1775(cm²)=117.75(mm²) 00扇形还有另一个面积公式00S=1/2lR 00其中l为弧长，R为半径00扇环面积00圆环周长:外圆的周长+内圆的周长(圆周率X(大直径+小直径)) 0圆环面积:外圆面积-内圆面积(圆周率X大半径的平方-圆周率X小半径的平方\圆周率X(大半径的平方-小半径的平方)) 00用字母表示：00S内+S外（∏R方）00S外—S内=∏(R方-r方）00还有第二种方法：00S=π[(R-r)×(R+r)] 00R=大圆半径00r=圆环宽度=大圆半径-小圆半径00还有一种方法：00已知圆环的外直径为D，圆环厚度（即外内半径之差）为d。

00d=R-r，00D-d=2R-（R-r）=R+r，00可由第一、二种方法推得S=π[(R-r)×(R+r)]=π(D-d)×d，0圆环面积S=π(D-d)×d 00这是根据外直径和圆环厚度（即外内半径之差）得出面积。

这两个数据在现实易于测量，适用于计算实物，例如圆钢管。

三角形面积公式00海伦公式00任意三角形的面积公式（海伦公式）：S²=p(p-a)(p-b)(p-c), p=（a+b+c）/2, a.b.c为三角形三边。

五年级奥数圆和扇形的周长与面积二

加油站
C B
答案：1
【例6】（★★★★）（北大附中“资优博雅杯”数学竞赛）（2）如图，阴影正方形的顶点分别是大正方形
各边的中点，分别以大正方形各边的一半为直径向外
各边的中点分别以大正方形各边的一半为直径向外
做半圆，再分别以阴影正方形的各边为直径向外作半
圆，形成个月牙形个月牙形
圆，形成8个“月牙形”。

这8个“月牙形”的总面积
为32平方厘米，问大正方形EFGH的面积是多少？
A
H
D
加加点睛
三个转化：化未知为已知；
化不规则为规则；为不可求为可求
四个基本方法：割补、变换、
差不变、整体、
重点例题：例1，例2，例3，例4，例5。

五年级奥数.几何.扇形周长与面积和弓形面积(A级).学生版

圆规和直尺圆规和直尺一块儿住进了文具盒。

圆规说：“我能画圆，你行吗？”“我横竖都会画，你行吗？”直尺很不服气。

文具盒听了，说：“别争了，谁能画一面扇形，谁就最行。

”圆规和直尺都为难了。

文具盒又说：“你俩一块儿合作，不就行了吗？” 圆规和直尺同心协力，很快画好了扇形。

从此，它们成了好朋友。

编后语：圆规和直尺各有自己的长处，也各有自己的不足，两者是不应互相瞧不起的。

后来，由于双方的真诚合作，充分发挥了各自的优势，创造了许多新的事物。

这则寓言告诉我们这样一个道理：一个人的智慧和力量是有限的，众人合作就会创造出新事物，新生活。

圆的知识：1. 当一条线段绕着它的一个端点O 在平面上旋转一周时，它的另一端点所画成的封闭曲线叫做圆，点O 叫做这个圆的圆心.2. 连结一个圆的圆心和圆周上任一点的线段叫做圆的半径.3. 连结圆上任意两点的线段叫做圆的弦.过圆心的弦叫做圆的直径.4. 圆的周长与直径的比叫做圆周率.圆周上任意两点间的部分叫做弧.5. 圆周长=直径×π.=半径×2π 圆面积=π×半径2.知识框架课前预习扇形的周长与面积和弓形面积扇形的知识：1. 扇形是圆的一部分，它是由圆心角的两条半径和圆心角所对的弧组成的图形.顶点在圆心的角叫做圆心角. 2. 我们经常说的12圆、14圆、16圆等等其实都是扇形，而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几．那么一般的求法是什么呢？关键是360n． 3. 扇形中的弧长= 180r nπ.扇形的周长= 180r n π+2r.扇形的面积=3602r n π =.弓形的知识：1. 弦与它所对的弧所组成的图形叫做弓形.【一般来说，弓形面积=扇形面积-三角形面积．(除了半圆)】重点：圆与扇形的面积和周长计算公式；弓形的面积公式。

难点：计算周长时，首先要分清围成这一图形的边有哪些，再正确计算。

计算面积时，首先要根据图形组合的形式，用会求的图形的面积去求的题目所要求的图形面积。

弧长、扇形、弓形的面积及侧面积

弧长、扇形面积及圆锥侧面积【知识要点】1．弧长公式：半径为R 的圆，其周长是R π2，将圆周分成360份，每一份弧就是1o的弧，1o弧的弧长应是圆周长的3601，而为1803602R R ππ=，因此，on 的弧的弧长就是180R n π，于是得到公式：)(180代表弧长l Rn l π=。

2．（1）扇形的定义：一条弧和经过这条弧的端点的两条半径组成的图形叫做扇形（如图）。

（2）扇形的周长：（3）扇形的面积：如图，阴影部分的面积即为扇形OAB 的面积。

S 扇形=)(3602为扇形圆心角的度数为半径，n R R n π 由上面两公式可知S 扇形=213602n R lR π=．可据已知条件灵活选用公式。

3．弓形的面积（1）由弦及其所对的劣弧组成的图形，S 弓形=S 扇形-S △OAB 。

（2）由弦及其所对的优弧组成的弓形，S 弓形=S 扇形+S △OAB 。

4．圆锥的有关概念:圆锥可以看做是一个直角三角形绕着直角边所在的直线旋转一周而形成的图形,另一条直角边旋转而成的面叫圆锥的底面,斜边旋转而成的面叫圆锥的侧面. 5．圆锥的侧面展开图:圆锥的侧面展开图是一个扇形,如果圆锥的母线长l ,底面半径为,那么这个扇形的半径为,弧长为,因此可得圆锥的侧面积: 圆锥的侧面积。

为底面圆半径为母线长，侧)(221r l rl r l S ππ=⋅=圆锥的表面积。

为底面圆半径为母线长，（底侧表))(r S S r l l r S +=+=π 【典型例题】例1如果一段弧的长度等于半径，则这段弧所对的圆心角的度数一定（）A 、小于60oB 、等于60oC 、大于60oD 、无法确定 AB AB l R l OB OA +=++2·O AB · A BO m· AB Om例2如图，在ABC △中，12023AB AC A BC =∠==，°，，A ⊙与BC 相切于点D ，且交AB AC 、于M N 、两点，则图中阴影部分的面积是（保留π）．例3 已知扇形的圆心角为120°，弧长为cm π20，这个扇形的面积是多少？例4 已知：如图所示，⊙O 中AB 的长度为4cm π，它所对的圆心角为120°，求弦AB 的长．例5 圆锥的母线长为5cm ，高为3cm ，在它的侧面展开图中，扇形的圆心角是多少度？例6 已知：圆锥的底面半径为r ，母线长为R ，侧面展开图的圆心角为︒n ，求证：︒n =︒⋅360Rr.例7如图，已知△ABC ，AC ＝BC ＝6，∠C ＝90°．O 是AB 的中点，⊙O 与AC 相切于点D 、与BC 相切于点E ．设⊙O 交OB 于F ，连DF 并延长交CB 的延长线于G ．（1）∠BFG 与∠BGF 是否相等？为什么？（2）求由DG 、GE 和弧ED 围成图形的面积（阴影部分）．A·O BA BC DEFGO ANCD BM例8.如图，圆心角都是90º的扇形OAB 与扇形OCD 叠放在一起，连结AC ，BD ．（1）求证：AC=BD ；（2）若图中阴影部分的面积是243cm π，OA=2cm ，求OC 的长．例9．图中的粗线CD 表示某条公路的一段，其中AmB 是一段圆弧，AC .BD 是线段，且AC .BD 分别与圆弧 AmB 相切于点A .B ，线段AB =180m ，∠ABD =150°．（1）画出圆弧 AmB 的圆心O ；（2）求A 到B 这段弧形公路的长．例10．如图，PA .PB 是半径为1的O ⊙的两条切线，点A .B 分别为切点，60APB OP AB C O D ∠=°，与弦交于点，与⊙交于点．（1）在不添加任何辅助线的情况下，写出图中所有的全等三角形；（2）求阴影部分的面积（结果保留π）．PAOBDCEFOA BC21OAB ClD 例11．如图，一个圆锥的高为33cm ，侧面展开图是半圆．求：（1）圆锥的母线长与底面半径之比；（2）求BAC ∠的度数；（3）圆锥的侧面积（结果保留π）．【经典练习】1、已知圆锥的底面半径是3cm ，母线长为6cm ，则侧面积为________cm 2．（结果保留π） 2.一个扇形的圆心角为90°．半径为2，则这个扇形的弧长为________． (结果保留π) 3．已知扇形的圆心角为120°，半径为15cm ，则扇形的弧长为 cm （结果保留π）．4. 如图，扇形OAB ，∠AOB=90︒，⊙P 与OA 、OB 分别相切于点F 、E ，并且与弧AB 切于点C ，则扇形OAB的面积与⊙P 的面积比是．5．如图，正方形ABCD 边长为4，以BC 为直径的半圆O 交对角线BD 于E ．则直线CD 与⊙O 的位置关系是，阴影部分面积为(结果保留π) ．6．如图，菱形ABCD 中，AB =2 ，∠C =60°,菱形ABCD 在直线l 上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过36次这样的操作菱形中心O 所经过的路径总长为．(结果保留π) A BO ChlrABCDOE（第15题）AB OABOA ’O ’图(十三)图(十四)Ｐ7.如图，四边形OABC 为菱形，点B 、C 在以点O 为圆心的⌒EF 上，若OA =1，∠1=∠2，则扇形OEF 的面积为（） A.6π B. 4π C. 3π D. 32π8.（2010年台湾省）如图(十三)，扇形AOB 中，OA =10， ∠AOB =36︒。

弓形面积公式简易

弓形面积公式简易好嘞，以下是为您生成的关于“弓形面积公式简易”的文章：咱今天就来好好唠唠这个弓形面积公式，这玩意儿听起来可能有点头疼，但别怕，跟着我一步步来，其实挺简单的。

先说说啥是弓形。

你看那圆，就像一个大披萨，切一刀没切到底，剩下那一块儿弯弯的，像个弓一样的，就是弓形啦。

比如说，你去蛋糕店买个圆形蛋糕，然后从边上切一块下来，没切到圆心，这一块就是弓形。

那怎么算这弓形的面积呢？咱们得先搞清楚几个概念。

想象一下，弓形就像是一个被折了一半的月亮，它是由圆弧和一条弦组成的。

这个弦呢，就像是把月亮给切成两半的那条直线。

而圆弧呢，就是那弯弯的部分。

咱们先从最简单的情况说起。

假如这个弓形对应的圆心角是90 度，就像一个直角扇形被切掉了一个三角形。

那这时候算它的面积就相对容易些。

我们先算出整个扇形的面积，扇形面积公式是圆心角的度数除以 360 度，再乘以圆的面积。

圆的面积咱都知道是πr² 嘛。

然后呢，再把那个被切掉的三角形面积算出来。

三角形的面积就是底乘以高除以 2。

这个底就是弦长，高就是从圆心到弦的距离。

我给你举个例子啊。

有一次我去朋友家，他家小孩正在做数学作业，就卡在这个弓形面积的问题上了。

我就给他讲，先把圆的半径假设成 5 厘米，然后算出整个圆的面积是25π 平方厘米。

因为圆心角是 90 度，所以扇形面积就是25π÷4 = 6.25π 平方厘米。

再看那弦长，通过勾股定理可以算出来是5√2 厘米，从圆心到弦的距离是5÷√2 = 5√2 / 2 厘米。

所以三角形的面积就是5√2 × 5√2 / 2 ÷ 2 = 25 / 2 平方厘米。

最后，用扇形面积减去三角形面积，就能得到弓形的面积啦，也就是6.25π - 25 / 2 平方厘米。

要是圆心角不是 90 度呢？也别慌。

咱们还是用同样的思路，先算出扇形面积，再算出三角形面积，一减就行。

只不过扇形面积里的圆心角度数变了而已。

五年级奥数几何专项十四扇形、弓形、割补法

专项十四扇形、弓形、割补法课前预习方形和圆形的故事世界上有两位魔法师，一个管方形，另一个管圆形，管方形的魔法师很稳重，管圆形的魔法师很机灵、活泼。

他们都用魔球来施魔法。

有一天，魔法师管辖下的方形和圆形吵起来了，他们吵起来的原因是：谁在生活当中最重要？自己都说自己是最重要的，圆形说：“你看，车轮是圆形的，盘子是圆形的，就连水杯都是圆形的！”方形说：“小学生用的书本是方形的，楼是方形的，就连国旗都是我的形状！”他们吵着吵着就睡着了。

魔法师知道了这件事，就怪他们不好好工作，反尔吵了起来，就想惩罚他们一下。

他们分别把方形和圆形放在不同的地方……等方形一睁开双眼发现世界都变成方形的了：火车的车轮变成方形的了，什么地方也去不了了；货车的车轮也变成了方形，货物都运不到指定的位子上，人们都饿着肚子，工厂里的材料和商场里的货物都运不到了。

想坐车的时候，车也跑不了了，想骑车呢？一骑就会摔跟头，人们都不理方形了，方形很伤心。

圆形呢？他睁开双眼看到车跑的飞快，他忽然从远处看到了一个小黑点，渐渐变大，向他扑了过来，他还像没有事是的问：“这是什么呀？一摇一晃的？”等他想出来是楼房的时候，他才大叫：“楼房快压着我了！”圆形说完这句话的时候，魔法师出现了，他们把所有的被改变的物体都恢复了原样。

他们俩回到家反思了一下，过了几天，他们又面了，他们总结出来一个道理：每个人都不要自以为是，每个人都要有尺有所短，寸有所长的思想。

知识框架圆的知识：1.当一条线段绕着它的一个端点O在平面上旋转一周时，它的另一端点所画成的封闭曲线叫做圆，点O叫做这个圆的圆心.2.连结一个圆的圆心和圆周上任一点的线段叫做圆的半径.3.连结圆上任意两点的线段叫做圆的弦.过圆心的弦叫做圆的直径.4.圆的周长与直径的比叫做圆周率.圆周上任意两点间的部分叫做弧.5.圆周长=直径×π.=半径×2π 圆面积=π×半径2.扇形的知识：1. 扇形是圆的一部分，它是由圆心角的两条半径和圆心角所对的弧组成的图形.顶点在圆心的角叫做圆心角.2. 我们经常说的12圆、14圆、16圆等等其实都是扇形，而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几．那么一般的求法是什么呢？关键是360n． 3. 扇形中的弧长= 180r n π.扇形的周长= 180r n π+2r.扇形的面积=3602r n π =.弓形的知识：弦与它所对的弧所组成的图形叫做弓形。

扇形的面积公式是什么？周长是什么

小编整理了初中数学里扇形面积和周长的计算的相关知识大家快来跟着小编一起来学习一下怎么计算
扇形的面积公式是什么?周长是什么
扇形面积
S扇=LR/2（L为扇形弧长，R为半径）
S扇=αR2/2（α为弧度制下的扇形圆心角，R为半径）
S扇=πnR2/360（n为圆心角的度数，R为半径）
S扇=π（R^2）*N/360（N扇形的度数）
扇形周长
若半径为r，直径为d，扇形所对的圆心角的度数为n°。
C=2r+（n÷360）πd=2r+（n÷180）πr
扇形所对的圆心角的度数为n°，大圆半径为R，小圆半径为r。
C=2*（R-r）+π（R+r）/180*n
如果两个圆不是同心圆，角度分别为n，m。大圆半径为R，小圆半径为r。
C=2*（R-r）+π（R*n+r*m）/180
扇形弧长
在圆上过2点的一段弧的长度叫做弧长。n是圆心角度数，r是半径，α是圆心角弧度。
l=nБайду номын сангаасr÷180
l=n/180·πr
l=|α|r
l=n°πR÷180°

爱提分圆和扇形的周长及面积公式(五年级)

一：周长与面积公式知识精讲在同一平面内，到定点的距离等于定长的点的集合叫做圆．点O就称为该圆的圆心；圆心与圆周上任意一点的连线（例如线段OA）叫做半径；通过圆心，并且两端都在圆上的线段叫做直径．直径长恰好是半径长的两倍．圆心确定了圆所在的位置，半径长度确定了圆的大小．一个圆只要确定了“圆心”和“半径”，就能完全确定下来．圆周长与直径的比值是一个固定不变的数，我们称之为圆周率，用希腊字母表示．圆周率是一个无限不循环小数，无法写成分数的形式．在实际问题的计算中，常常取近似值3.14．一．圆的周长与面积公式1．直径长度通常用字母d表示，半径长度通常用r表示，圆周长通常用C表示，圆面积通常用字母S表示．2．圆周长公式：蜜蜂飞行：无论小圆有多少个，大小是否相等，只要所有小圆的直径之和等于大圆的直径，那么它们的周长之和也等于大圆的周长．3．圆面积公式：二．扇形的周长与面积公式扇形是指圆上被两条半径和半径之间的弧所包围的部分．其中，圆的半径也称为扇形的半径，而两条半径所成的夹角称为扇形的圆心角．扇形是圆的一部分．要想知道扇形的弧长与面积，只要知道它是所在圆的几分之几就可以了．它是圆的几分之几，它的弧长就是圆周长的几分之几，它的面积也同样就是圆面积的几分之几．1．扇形弧长公式：2．扇形面积公式：3．温馨提示：扇形的弧长不是它的周长，扇形的周长还必须加上两条半径．三点剖析重难点：扇形周长公式，需要加上两条半径题模精讲题模一圆的周长与面积公式例1.1.1、已知一个圆的直径为2厘米，那么这个圆的周长为_________厘米，面积为_________平方厘米．答案：；解析：周长为厘米，面积为平方厘米．例1.1.2、已知一个圆的周长为50.24厘米，那么这个圆的直径为_________厘米．答案：16解析：直径为厘米．例1.1.3、有一个圆形花坛，直径为20米，一只小蜜蜂沿着花坛外周飞了一圈，请问它飞了多少米？如果小蜜蜂沿着图中的虚线，飞一个“8”字，路线构成过花坛圆心的两个小圆，那么这次它飞了多少米？（取3.14）答案：（1）62.8米（2）62.8米解析：小圆半径是5米，飞行路线为两个小圆周长，所以是米．无论小圆有多少个，大小是否相等，只要所有小圆的直径之和等于大圆，那么它们的周长之和也等于大圆．例1.1.4、如图，已知长方形的面积是12，则图中阴影部分的面积是多少？（取3.14）答案：2.58解析：长方形可以分成两个面积相等的正方形，面积都是6．方中圆，方和圆的面积比为，可求出小圆的面积是，那么阴影部分的面积是．例1.1.5、如图，在一块面积为28.26平方厘米的圆形铝板中，裁出了7个同样大小的圆铝板．问：余下的边角料的总面积是多少平方厘米？（取3.14）答案：6.28平方厘米解析：，大圆半径是3厘米．小圆半径是1厘米，所以边角料面积为平方厘米．例1.1.6、已知大圆的直径为10厘米，有四个大小不等的圆，圆心都在大圆的一条直径上，并且它们的直径之和与大圆相等．那么4个小圆的周长之和是________厘米．（取3.14）答案：31.4解析：假设中间4个小圆的直径分别为a、b、c、d，则有，4个小圆的周长之和为厘米．例1.1.7、如图，直角三角形的面积是40平方厘米，圆的面积是________平方厘米（π取3）．答案：240解析：直角三角形的直角边即为圆的半径，所以，，圆的面积是平方厘米．题模二扇形的周长与面积公式例1.2.1、如图3，圆P的直径OA是圆O的半径，，，则阴影部分的面积是__________．（π取3）答案：75解析：阴影部分的面积等于大圆面积的一半减去小圆的面积，即．例1.2.2、一个扇形的半径为6平方厘米，圆心角为60°，这个扇形的周长是__________厘米．（取3.14）答案：18.28解析：这个扇形是它所在圆的，所以这个扇形的弧长是cm，扇形的周长是厘米．例1.2.3、一个扇形的面积为6.28平方厘米，圆心角为45°，这个扇形的周长是_______厘米．（取3.14）答案：11.14解析：这个扇形是它所在圆的，所以这个圆的半径的平方是，所以这个圆的半径是4厘米，所以扇形的半径是4厘米，扇形的周长是厘米．例1.2.4、在荷兰的小镇卡茨赫弗尔，2013年6月建成了一个由三个半圆组成的城市雕塑，三个半圆的直径分别为24.2m，19.3m，4.9m．这个雕塑的原始图形来自于阿基米德《引理集》中的鞋匠刀形（Arbelos），即下图中阴影部分所示的图形．那么，该城市雕塑中的鞋匠刀形的周长为__________（圆周率用π表示）答案：24.2πm解析：鞋匠刀形的周长是由3条半圆形弧线组成，所以周长为m．例1.2.5、如图，等边三角形ABC的边长是1，依次以A、C、B为圆心，以BA、CD、BE为半径画扇形，那么三个扇形的面积和是多少？（结果保留π）答案：解析：各扇形圆心角均为，半径分别为1、2、3，因此三个扇形的面积和是．例1.2.6、一个半径为3分米的扇形，面积为6.28平方分米，那么它的圆心角是__________，它的弧长又是__________分米．答案：80°，4.15解析：根据题意得，，所以，所以圆心角是度．弧长为．例1.2.7、如图，边长为3cm与5cm的两个正方形并排放在一起，在大正方形中画一个以它的顶点B为圆心，边长为半径的圆弧，则阴影部分的面积是________（结果保留π）．答案：解析：连结AC、FB．易知，故，．例1.2.8、如图，有三个同心半圆，它们的直径分别为2，6，10，用线段分割成9块，如果每块字母代表这一块的面积并且相同的字母代表相同的面积，那么(A＋B)：C＝_______答案：55：48解析：设A的半径为，B的半径为，C的半径为A的面积：B的面积：3B=，．C的面积：5C=，．．题模三捆圆的周长和面积例1.3.1、已知下图中的每个小圆的半径均为1，这个图形的面积是__________．（取3.14）答案：35.14解析：如图，对图形进行分割后可知这个图形的面积相当于8个边长为2的正方形和一个半径为1的圆的面积的和．面积为．例1.3.2、如图，有8个半径为1的小圆，用它们圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心．那么花瓣图形的周长和面积分别是多少？答案：周长，面积解析：如图，做辅助线后可以看出周长为4个的圆弧加上4个半圆弧，所以周长为；而面积为正方形减去4个半圆加上4个圆，即．如图，每个圆的面积都为12.56，求该图形的外周长．答案：解析：圆半径为2．图形外周长可以分为三段长为4的线段和三段120°角的圆弧，则外周长为．例1.3.4、如图，有七根直径为5厘米的塑料管，用一根橡皮筋把它们扎成一捆，此时橡皮筋的长度是多少厘米？答案：解析：如图，作辅助线后可以发现外周长是由6段长度为5的线段和6个60°角的圆弧组成，所以皮筋长度为．随堂练习随练1.1、已知一个圆的直径是12厘米，那么这个圆的面积为__________平方厘米？（取3.14）答案：113.04解析：直径为12厘米，那么半径为6厘米，面积是平方厘米．随练1.2、已知一个圆的面积为314平方厘米，那么这个圆的直径为_______厘米？（取3.14）答案：20这个圆的半径为平方是，所以这个圆的半径是10厘米，直径是20厘米．随练1.3、半径分别为1、2、3、4厘米的四个圆的周长之和是多少厘米？（取3.14）答案：62.8厘米解析：圆的周长公式为，周长之和为厘米．随练1.4、如图，在一块面积为12.56平方厘米的纸板中，裁出了2个同样大小的圆纸板．问：余下的纸板的总面积是多少平方厘米？（取3.14）答案：6.28平方厘米解析：大圆的面积是12.56平方厘米，可求出大圆的半径是2厘米，那么小圆的半径是1厘米，面积是3.14平方厘米．阴影部分的面积是平方厘米．随练1.5、已知三个小圆的圆心在大圆同一直径上，周长分别为3、1、2厘米，则大圆周长为多少厘米？（π取近似值3.14）答案：6解析：大圆的直径等于三个小圆的直径之和，周长也恰为3个小圆周长之和．随练1.6、如图，边长为3cm与5cm的两个正方形并排放在一起，在大正方形中画一个以它的顶点B为圆心，边长为半径的圆弧，则阴影部分的面积是__________（结果保留π）．答案：解析：阴影部分面积为梯形ABFE与扇形ABC的面积之和减去三角形FEC的面积，易得为．随练1.7、已知一个扇形的半径是10厘米，圆心角是，那么：（1）这个扇形所在圆的周长是_________厘米，扇形的圆心角占圆周角的_________，它的弧长占圆周长的_________，这个扇形的弧长是_________厘米，周长是_________厘米．（2）这个扇形面积占它所在圆的面积的_________，是_________平方厘米．答案：（1）62.8；；；7.85；27.85（2）39.25；解析：（1）这个扇形所在圆的周长是厘米，扇形的圆心角占圆周角的，它的弧长占圆周长的，这个扇形的弧长是厘米，周长是．（2）这个扇形面积占它所在圆的面积的，面积是平方厘米．随练1.8、半径为10、20、30的三个扇形如下图放置，是的__________倍．答案：5解析：为，为，所以是的5倍．随练1.9、根据图中所给的数值，求这个图形的面积．（π取近似值3.14）答案：92.56解析：平方厘米．4个直角扇形的面积之和是4，因此整个圆角矩形的面积就是．随练1.10、如图，有七根直径为4厘米的塑料管，用一根橡皮筋把它们扎成一捆，此时橡皮筋的长度是多少厘米？（π取近似值3.14）答案：36.56解析：把圆角六边形的周长分为12个部分，由6条直线段和6段圆弧组成．6条直线段中，每段的长度都是5厘米，它们的长度和是厘米6段圆弧中，每段所对应的圆心角都是60°，每段的弧长都是圆周长的，6段圆弧恰好能拼成一个完整的圆周．它们的弧长之和就是圆周长，即厘米．圆角六边形的周长就是这两部分长度之和，即厘米．课后作业作业1、已知圆的直径为20米，那这个圆的周长为多少米？（π取近似值3.14）62.8解析：圆周长的计算公式为：C圆=π×D．作业2、把两根横截面半径都是10厘米的钢管用铁丝紧紧捆在一起，如果捆绑处不计，至少要用铁丝____________厘米．答案：102.8解析：厘米．作业3、一辆压路机的前轮是圆柱形，轮宽1.6米，直径是0.8米．前轮转动一周，压路的面积是______平方米．答案：3.84平方米解析：轮子压一周，周长为米，即压在路面上的长是2.4米，压路的面积=长×宽平方米．作业4、已知圆的面积是314平方米，那圆的周长是多少米？（π取近似值3.14）答案：62.8由圆的面积可以求出半径的平方，算出半径后可由公式计算圆的周长，为62.8．作业5、已知三个小圆的圆心在大圆同一直径上，周长分别为1、2、3厘米，则大圆周长为多少厘米？（π取近似值3.14）答案：6解析：大圆的直径等于三个小圆的直径之和，周长也恰为3个小圆周长之和．作业6、如图，在一块面积为36平方厘米的圆形铝板中，裁出了7个同样大小的圆铝板．问：余下的边角料的总面积是多少平方厘米？答案：8平方厘米解析：小圆的半径是整个大圆半径的，因此小圆的面积是大圆面积的，为平方厘米；大圆去掉7个小圆后剩下的面积是平方厘米．作业7、已知一个扇形的圆心角为120°，半径为2，这个扇形的面积是________，周长是________（π取3.14）．答案：面积，周长解析：扇形的面积；周长．作业8、如图，求各图中阴影部分的面积．（取3.14）答案：9.12解析：阴影部分面积为半径为4的半圆面积减去对角线为8的等腰直角三角形面积．阴影部分面积为．作业9、已知扇形的半径为3米，面积为14.13米，那扇形的圆心角为多少度？（π取近似值3.14）答案：180解析：扇形所在圆的面积≈3.14×32=28.26平方米，由此可知该扇形是它所在圆的．那么圆心角应该是360°的二分之一．作业10、已知一个扇形的半径为5厘米，弧长为6.28厘米，这个扇形的面积是多少？答案：15.7解析：因为扇形的弧长为厘米，所以，可得．扇形面积为平方厘米．作业11、根据图中所给的数值，求这个图形的面积．（π取近似值3.14）答案：23.14解析：平方厘米．4个直角扇形的面积之和是，因此整个圆角矩形的面积就是．作业12、如图，三个圆的半径都是4，那整个图形的外周长是多少？（π取近似值3.14）答案：49.12解析：整个外周长可以分为3段直线和3段弧形．作业13、如图，有七根直径为10厘米的塑料管，用一根橡皮筋把它们扎成一捆，此时橡皮筋的长度是多少厘米？（π取近似值3.14）答案：91.4解析：把圆角六边形的周长分为12个部分，由6条直线段和6段圆弧组成．6条直线段中，每段的长度都是5厘米，它们的长度和是厘米6段圆弧中，每段所对应的圆心角都是60°，每段的弧长都是圆周长的，6段圆弧恰好能拼成一个完整的圆周．它们的弧长之和就是圆周长，即厘米．圆角六边形的周长就是这两部分长度之和，即厘米．。

小学五年级奥数圆和扇形的周长与面积(一)

1.
本讲主线2.1.圆: 当一条线段绕着它的一个端点在平面内旋转一周时，它的另一个
端点的轨迹叫做圆
2圆直径
2.圆心、直径、半径
3.⑴圆心确定了圆所在的位置
⑵半径长度确定了圆的大小.
⑶圆周率：圆周长与直径是一个固定不变的数值，称为圆周率，用π
表示.
4.圆周长:
C＝πd
5.扇形:由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形
65
6. 扇形周长
C＝2r＋弧长
7.圆的面积
8. 扇形面积:
9. 其他扇形
弓形＝扇形－△
弯角
谷子
如图，是一个由2个半圆、2个扇形、1个正方形组成的“心型”。

已知半圆的直径为10，那么，“心型”的面积是___________。

(注：π取3.14)
图中四个圆的圆心恰好是正方形的四个顶点，如果每个圆的半径都是1厘米，那么阴影部分的总面积是多少？
求图中阴影部分的面积。

(圆周率取3.14 )
【超常大挑战】(★★★☆)
知识大总结
面积,。

扇形的周长面积公式

扇形的周长面积公式
扇形是一种几何图形，是圆的一部分，可以用于计算圆的周长和面积。

扇形的周长面积公式是一种计算圆面积和周长的公式，可用于计算椭圆、半圆和其他圆形图形的面积和周长。

圆的周长面积公式是：扇形的周长等于扇形的弧度乘以圆的半径，扇形的面积等于扇形的弧度乘以圆的半径的平方再乘以π。

在计算扇形的周长面积时，首先要确定扇形的弧度。

扇形的弧度是用弧长除以圆的半径得到的，也可以用角度乘以π除以180来计算。

例如，有一个半径为5厘米的圆，要计算一个弧长为20厘米的扇形，首先要求扇形的弧度，即20/5=4，然后计算扇形的周长，即
4*5=20，最后计算扇形的面积，即4*5*5*π=78.5π。

通过上述计算可以得到，一个半径为5厘米的圆，弧长为20厘米的扇形的周长是20厘米，面积是78.5π厘米平方。

从上述可以看出，扇形的周长面积公式可以用来快速计算圆的周长和面积，这对于工程中计算圆面积和周长有很大的帮助。

所以，扇形的周长面积公式被广泛应用于计算圆的周长和面积。

扇形周长和面积的不等式关系

扇形周长和面积的不等式关系扇形计算公式大全扇形周长公式因为扇形＝两条半径＋弧长若半径为R，扇形所对的圆心角为n°，那么扇形周长：C＝2R＋nπR÷180扇形面积公式在半径为R的圆中，因为360°的圆心角所对的扇形的面积就是圆面积S＝πR^2，所以圆心角为n°的扇形面积：S＝nπR^2÷360比如：半径为1cm的圆，那么所对圆心角为135°的扇形的周长：C＝2R＋nπR÷180＝2×1＋135×3.14×1÷180＝2＋2.355＝4.355(cm)＝43.55(mm)扇形的面积：S＝nπR^2÷360＝135×3.14×1×1÷360＝1.1775(cm^2)=117.75(mm^2)扇形还有另一个面积公式S=1/2lR其中l为弧长，R为半径本来S＝nπR^2÷360按弧度制.2π=360度.因为n的单位为度.所以l为角度为n时所对应的弧长.即.l=n*R所以.s=n*R*π*R/2π=1/2lR.扇形的弧长公式l=(n/180)*pi*r,l是弧长，n是扇形圆心角，pi是圆周率，r是扇形半径扇形的面积公式在半径为R的圆中，因为360°的圆心角所对的扇形的面积就是圆面积S＝πR^2，所以圆心角为n°的扇形面积：S＝nπR^2÷360扇形还有另一个面积公式S=1/2lR其中l为弧长，R为半径本来S＝nπR^2÷360按弧度制.2π=360度.因为n的单位为度.所以l为角度为n时所对应的弧长.即.l=n*R所以.s=n*R*π*R/2π=1/2lR.用弧度表示角度弧度制。

我们学习过角的度量。

规定周角的1/360为1°的角。

这种用度。

作为单位来度量角的单位制叫做角度制。

除此之外，在数学和其他科学中常用的另一种度量角的单位制弧度制，它的单位符号rad。

弓形计算公式

弓形计算公式好嘞，以下是为您生成的关于“弓形计算公式”的文章：咱先来说说啥是弓形。

想象一下，你手里拿着一根弯弯曲曲的绳子，然后把它两端一接，围成了一个封闭的曲线，这就有点像弓形啦。

比如说，你吃披萨的时候，切下来的那一块，要是从侧面看，是不是就有点像个弓形？弓形的计算，这里面可有不少门道。

先来说说弓形面积的计算公式吧。

弓形面积 = 扇形面积 - 三角形面积。

扇形面积的计算，就得用到圆心角的度数和半径啦。

假设圆心角是 n 度，半径是 r ，那扇形面积就是nπr²÷360 。

三角形面积呢，就简单多啦，底乘以高除以 2 。

我记得有一次，我去给我小侄子辅导功课，正好就碰到了弓形计算的题目。

那小家伙，眼睛瞪得大大的，一脸迷茫地看着我，嘴里还嘟囔着：“姑姑，这咋这么难啊！”我就耐心地跟他说：“别着急，咱们一步步来。

”我拿了一张纸，画了一个大大的弓形，然后指着图说：“你看啊，这个扇形就好比是一个大蛋糕，三角形呢，就是被切掉的那一块。

咱们先把大蛋糕的面积算出来，再把切掉的那部分减掉，剩下的就是咱们要的弓形面积啦。

”我一边说，一边在纸上写写画画。

小侄子好像有点明白了，也跟着我拿起笔，在纸上算起来。

再说弓形的弧长计算公式。

弧长= nπr÷180 ，这里的 n 还是圆心角的度数， r 还是半径。

这就好比你沿着弓形的边跑一圈，跑过的距离就是弧长。

学习弓形计算公式的时候，可别死记硬背，得理解着来。

比如说，你想想为啥扇形面积是那样算的，为啥弧长是这样算的。

多琢磨琢磨，就能记得更牢啦。

其实在生活中，弓形的计算也挺有用的。

像建筑设计里，有些屋顶的形状就是弓形的，设计师就得算出面积和弧长，才能确定材料的用量。

还有做手工的时候，要是想做个弓形的装饰品，也得先算算尺寸不是？总之，弓形计算公式虽然看起来有点复杂，但只要咱们用心学，多练习，就一定能掌握好。

就像我小侄子，经过那次辅导，后来再碰到弓形计算的题目，可就不那么犯愁啦！希望大家也都能轻松搞定弓形计算，让数学变得有趣又有用！。

五年级奥数专题-不规则图形面积计算含解析

一、例题与方法指导例1 如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米.求阴影部分的面积。

思路导航：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

在△ABE 中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2， ∴△ECF 的面积为2×2÷2=2。

所以S △AEF=S 四边形AECF-S △ECF=12-2=10（平方厘米）。

例3 两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

思路导航：在等腰直角三角形ABC 中∵AB=10∵EF=BF=AB-AF=10-6=4，∴阴影部分面积=S △ABG-S △BEF=25-8=17（平方厘米）。

五年级奥数思维训练圆与扇形的周长与面积计算

练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2 3 4
直径（d） 2 4 6 8
周长（C） 2π 4π 6π 8π
面积（S） 1π 4π 9π
25π
通过观察此表，回答：圆的半径扩大n倍，周长和面积分别扩大几倍？
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
直径（d） 2 4 6
周长（C） 2π 4π 6π 8π
面积（S） 1π 4π
25π
通过观察此表，回答：圆的半径扩大n倍，周长和面积分别扩大几倍？
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2 3
直径（d） 2 4 6
周长（C） 2π 4π 6π 8π
面积（S） 1π 4π 9π
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2
直径（d） 2 4 6
周长（C） 2π
8π
面积（S） 1π
25π
通过观察此表，回答：圆的半径扩大n倍，周长和面积分别扩大几倍？
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2
直径（d） 2 4 6
ห้องสมุดไป่ตู้
半径（r） 1 2
直径（d） 2
6
周长（C） 2π
8π
面积（S） 25π
通过观察此表，回答：圆的半径扩大n倍，周长和面积分别扩大几倍？
练一练
根据已知信息，将表格填补完整。（单位：厘米，π取3.14）
半径（r） 1 2
直径（d） 2

弓形面积最简单的方法

弓形面积最简单的方法引言弓形面积是数学中一个常见的概念，在各个领域都有着广泛的应用。

计算弓形面积经常用于物理学、工程学、计算机图形学等领域。

虽然计算弓形面积在一些特殊情况下可能比较复杂，但是在一般情况下，计算弓形面积是一个非常简单的任务。

本文将介绍一种简单的方法来计算弓形的面积，并且通过实例来进一步说明如何应用这种方法。

弓形面积计算方法计算弓形的面积可以通过将弓形划分为多个小的扇形来实现。

具体的步骤如下：1. 根据所给的弓形的半径和夹角，计算出弓形的弧长。

2. 将弓形的夹角等分为多个小的夹角，得到多个扇形。

3. 计算出每个扇形的面积。

4. 将所有扇形的面积加起来，得到弓形的面积。

下面我们通过一个具体的例子来演示这个方法。

实例演示假设我们要计算一个半径为10的弓形，其夹角为60度。

根据上述方法，我们可以按照以下步骤进行计算：1. 弓形的弧长可以通过公式: 弧长= 半径* 弧度计算得出。

由于夹角为60度，那么弧度为60 * (π/180) ≈1.047。

所以弧长= 10 * 1.047 ≈10.47。

2. 我们可以将夹角等分为6个小的夹角，每个小夹角为10度。

3. 接下来，我们计算每个扇形的面积。

扇形的面积可以通过公式: 面积= 1/2 * 半径^2 * 弧度计算得出。

其中，半径为10，弧度为10 * (π/180) ≈0.175。

所以每个扇形的面积= 1/2 * 10^2 * 0.175 ≈8.75。

4. 最后，我们将每个扇形的面积加起来，得到弓形的面积。

在本例中，由于共有6个扇形，所以弓形的面积为6 * 8.75 = 52.5。

结论如上所述，通过将弓形划分为多个扇形，我们可以很简单地计算出弓形的面积。

这种方法不仅简单而且适用于一般情况下的弓形，可以很方便地应用于各个领域。

当然，在某些特殊情况下，例如弓形的形状比较复杂或夹角较大时，使用此方法可能会比较困难。

但是在大多数情况下，这种方法是最简单且有效的。

5.1 圆扇形弓形及其组合图形的面积、周长解析

圆形周长和面积这一阶段，我们学习了圆：若它的半径为r,则周长为：2πr。

面积为：。

扇形:它是圆的一部分，若它的半径为r，圆心角为，则弧长为：2πr×，周长为：2πr×+2r。

面积为：×环形：由两个同心圆，圆周之间的部分组成。

以后在例题中，还会遇到弓形、“叶形”，将在题中一一说明。

求组合图形的面积、周长，可以用直接法、间接法、割补法、添补法、平移法、旋转法等等。

同学们在解题中一定要认真领会灵活运用，切实提高自己的观察、分析、综合能力。

下面看几个例题。

例1. 求阴影部分的面积。

(单位:厘米)例2. 正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)例3. 求图中阴影部分的面积。

(单位:厘米)例4.求阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米)例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。

(单位:厘米)例8.求阴影部分的面积。

(单位:厘米)例9.求阴影部分的面积。

(单位:厘米)例10.求阴影部分的面积。

(单位:厘米)例11.求阴影部分的面积。

(单位:厘米)例12.求等边三角形中阴影部分的面积。

(单位:厘米)例13.求阴影部分的面积。

(单位:厘米)例14.求阴影部分的面积。

(单位:厘米)例15.已知直角三角形面积是12平方厘米，求阴影部分的面积。

例17.图中圆的半径为5厘米,求阴影部分的面积。

(单位:厘米)例18.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。

例19.正方形边长为2厘米，求阴影部分的面积。

例20.如图，正方形ABCD的面积是36平方厘米，求阴影部分的面积。

例21.图中四个圆的半径都是1厘米，求阴影部分的面积。

例22. 如图，正方形边长为8厘米，求阴影部分的面积。

例23.图中的4个圆的圆心是正方形的4个顶点，，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少？例24.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。

奥数扇形和弧度(面积)

奥数扇形和弧度(面积)
什么是奥数扇形和弧度？
扇形是一个圆所对的两条半径和它们之间的弧组成的部分。

奥
数（奥林匹克数学竞赛）中常常涉及到扇形的性质和计算。

弧度是一种表达角度的单位，用于衡量角度的大小。

弧度数值
的计算基于圆的半径长度。

奥数中的扇形问题通常使用弧度来计算
扇形的面积。

如何计算奥数扇形的面积？
计算奥数扇形的面积需要使用扇形的角度和圆的半径的长度。

面积可以通过下列公式计算：
面积 = (角度 / 360度) × π × (半径的长度的平方)
其中，角度是扇形所对的角度，半径的长度是圆的半径的长度，π是一个常数，约等于3.。

举个例子
假设一个扇形的角度为60度，半径的长度为5厘米。

我们可以使用上述公式来计算扇形的面积：
面积 = (60度 / 360度) × 3. × (5厘米的平方) = 1/6 × 3. × 25 = 13.09平方厘米
因此，这个扇形的面积约为13.09平方厘米。

结论
奥数中的扇形和弧度是计算扇形面积的重要概念。

通过了解扇形的角度和圆的半径的长度，并使用相应的公式，我们可以计算出扇形的面积。

这些概念在解决奥数问题中非常有用，帮助我们理解和计算各种扇形相关的数学题目。

五年级奥数扇形周长与面积和弓形面积

五年级奥数专题-不规则图形面积计算含解析

五年级奥数专题-不规则图形面积计算含解析

扇形、三角形、弓形、菱形公式[整理版]

五年级奥数圆和扇形的周长与面积二

五年级奥数.几何.扇形周长与面积和弓形面积(A级).学生版

弧长、扇形、弓形的面积及侧面积

弓形面积公式简易

五年级奥数几何专项十四 扇形、弓形、割补法

扇形的面积公式是什么？周长是什么

爱提分圆和扇形的周长及面积公式(五年级)

小学五年级奥数 圆和扇形的周长与面积(一)

扇形的周长面积公式

扇形周长和面积的不等式关系

弓形计算公式

五年级奥数专题-不规则图形面积计算含解析

五年级奥数思维训练圆与扇形的周长与面积计算

弓形面积最简单的方法

5.1 圆 扇形 弓形及其组合图形的面积、周长解析

奥数扇形和弧度(面积)

五年级奥数几何专项十四扇形、弓形、割补法

小学五年级奥数圆和扇形的周长与面积(一)

5.1 圆扇形弓形及其组合图形的面积、周长解析