最新第六章单元测验

合集下载

人教版七年级数学下册第六章实数。单元测试题精选(Word版附答案)

人教版七年级数学下册第六章实数。

单元测试题精选(Word版附答案)人教版七年级数学第6章《实数》单元测试题精选完成时间：120分钟满分：150分得分评卷人：______________ 姓名：______________ 成绩：______________一、选择题（本大题10小题，每小题4分，共40分。

每小题给出的四个选项中，只有一个选项是符合题意的，请将该选项的标号填入表格内）题号 1 2 3 4 5 6 7 8 9 10答案 B A D A A C D C B B二、填空题（每题5分，共20分）11.m = 3.n = 1.(m+n)^5 = 243.12.(1) 0.000 521 7 (2) 0.002 284.13.3.14.x = 8.三、解答题（共90分）15.1) x = ±5/3;2) x = 3/5.16.1.17.a = 9.b = -8.3a+b的算术平方根为 5.18.已知 $m=\lfloor 313\rfloor$。

$n=0.13$，求 $m-n$ 的值。

19.如图，计划围一个面积为 $50\text{ m}^2$ 的长方形场地，一边靠旧墙（墙长为 $10$ m），另外三边用篱笆围成，并且它的长与宽之比为 $5:2$。

讨论方案时，XXX说：“我们不可能围成满足要求的长方形场地。

”小军说：“面积和长宽比例是确定的，肯定可以围得出来。

”请你判断谁的说法正确，为什么？解：设长为 $5x$，宽为 $2x$，则面积为 $10x^2$，另一条边长为 $10-5x$，由题意得 $10x^2=(10-5x)\times2x$，解得$x=1$，长为 $5$，宽为 $2$，可以围成满足要求的长方形场地，小军的说法正确。

20.若 $x+3+(y-3)^2=3$，则 $(xy)^{\frac{2015}{3}}$ 等于多少？解：移项得 $(y-3)^2=3-x-3=-x$，所以 $xy=\frac{3-x}{y-3}$，将其代入 $(xy)^{\frac{2015}{3}}$ 得 $\left(\frac{3-x}{y-3}\right)^{\frac{2015}{3}}$，根据乘方的运算法则，得$\left(\frac{3-x}{y-3}\right)^{671}$。

(最新)部编人教版地理七年级下册《第六章单元检测试题》(含答案解析)

第6章《我们生活的大洲-----亚洲》单元检测试题一．选择题（共24小题）1．我们目前发现的世界上最古老的彩色地图，出土在（）A．印度B．中国C．埃及D．希腊2．南亚大部分处于北纬10°～30°的低纬度地区，大部分地区属什么气候（）A．热带季风气候B．亚热带季风气候C．温带季风气候D．温带大陆性气候3．下列地理事物既是亚洲之最又是世界之最的是（）A．最长河流﹣﹣长江B．最深湖泊﹣﹣贝加尔湖C．最大平原﹣﹣西西伯利亚平原D．最大高原﹣﹣青藏高原4．陆地上高峻的山脉主要分布于（）A．环太平洋沿岸，美洲西岸山脉B．亚欧大陆南部，非洲北部C．环太平洋沿岸，亚欧大陆南部和非洲西北部D．太平洋东岸，太平洋西岸5．从世界看中国，我国位于（）A．东半球、南半球B．东半球、北半球C．西半球、南半球D．西半球、北半球6．读图，亚洲地形特点不包括以下的（）A．中部高四周低B．地势起伏很大C．地形复杂多样D．以高原为主，地面坦荡开阔7．中东地区处在印度洋和大西洋的重要国际航线上，沟通这两大洋的咽喉是（）A．苏伊士运河、马六甲海峡B．苏伊士运河、直布罗陀海峡C．巴拿马运河、土耳其海峡D．巴拿马运河、直布罗陀海峡8．日本最高峰位于（）A．北海道B．本州C．四国D．九州9．日本经济发达，但也面临一系列问题。

下列问题中，导致日本经济发展速度放缓的是（）①劳动力价格高②人口老龄化③环境污染④土地紧张⑤国内需求减少⑥教育发展迅速A．①②③④⑤B．②③④⑤⑥C．①③④⑤⑥D．①②③④⑥10．读世界轮廓图，图中数字①、②、③表示的大洋是（）A．太平洋、印度洋、大西洋B．太平洋、大西洋、印度洋C．大西洋、太平洋、印度洋D．印度洋、太平洋、大西洋11．下列各洲轮廓图中，实际面积最小的应是（）A．B．C．D．12．如图，亚洲缺乏的气候类型是（）A．A B．B C．C D．D13．下列叙述中，不符合欧美发达国家状况的是（）A．交通拥挤，人口增长快B．工农业生产发达，生产水平高C．市场繁荣，环境幽雅D．受教育程度高，生活质量好14．世界上季风气候面积最大的洲是（）A．亚洲B．非洲C．北美洲D．大洋洲15．亚洲和北美洲的分界线是（）A．苏伊士运河B．巴拿马运河C．白令海峡D．土耳其海峡16．亚洲唯一的发达国家是（）A．日本B．朝鲜C．马来西亚D．沙特阿拉伯17．连接地中海和黑海的海峡是（）A．白令海峡B．直布罗陀海峡C．土耳其海峡D．马六甲海峡18．下列说法错误的是（）A．目前，亚洲还没有发达国家B．欧洲西部是发达国家最为集中的地区C．发展中国家主要分布在亚洲、非洲和南美洲D．“南北对话”是指发达国家与发展中国家之间的政治、经济商谈19．波斯湾出入印度洋的门户是（）A．土耳其海峡B．霍尔木兹海峡C．直布罗陀海峡D．英吉利海峡20．关于甲、乙两大洲的叙述，正确的是（）A．甲大洲地势中间低，四周高B．乙大洲有湿润大洲之称C．甲大洲中部、北部人口稀疏D．乙大洲的刚果河是世界上水量最大的河流21．中国东南部和阿拉伯半岛纬度位置大致相同，两地大致相同的地理现象是（）①降水②昼夜长短③季节更替④正午太阳高度A．①②③B．①②④C．①③④D．②③④22．印度西北毗邻（）A．中国B．巴基斯坦C．尼泊尔D．不丹23．有关亚洲地形、地势特点的说法，正确的是（）A．地形复杂多样，地势起伏大B．地形以平原为主C．地势中部低，四周高D．拥有世界上最大的平原﹣﹣西西伯利亚平原24．下列景观图中属于印度的是（）A．B．C．D．二．解答题（共4小题）25．连接的海洋连线26．2018年6月上海合作组织成员国元首理事会第18次会议在青岛举行，部分成员国分布在亚洲中部地区。

(最新)部编人教版地理七年级下册《第六章单元检测试题》(含答案解析)

第六章《我们生活的大洲——亚洲》单元测试题一、单选题(每小题只有一个正确答案)1.下列有关亚洲位置的说法，错误的是（）A．亚洲的南面隔海与大洋洲相望 B．亚洲北临北冰洋、东临大西洋C．亚洲以白令海峡与北美洲为界 D．亚洲的西南以苏伊士运河与非洲为界2.有关亚洲地形地势的叙述，正确的是（）A．有世界上最大的亚马孙平原 B．地形以平原为主，高原山地面积较小C．地势东南高，西北低 D．既有世界最高峰，又有世界陆地表面最低处3.我们亚洲常常是“寒暑并存，干湿同在”，气候类型复杂多样，造成这种气候特征的主要原因是（）A．亚洲大部分处于高纬度地区 B．亚洲处在东半球C．亚洲纬度和经度跨度大 D．亚洲四面濒临海洋4.关于亚洲河流流向的说法，正确的是（）A．河流呈向心状流向中部的海洋 B．河流呈放射状流向周边的海洋C．北部、西部的河流全部注入大西洋 D．东部、南部的河流全部注入太平洋5.珠穆朗玛峰位于哪个大洲（）A．欧洲 B．亚洲 C．非洲 D．南美洲6.读“亚洲地形图”，影响亚洲气温南北差异大的主要原因是亚洲（）A．跨纬度大 B．地势起伏大 C．三面被大洋环绕 D．季风气候显著7.亚洲的主要地形是（）A．山地丘陵 B．高原山地 C．高原盆地 D．平原丘陵8.亚欧两洲分界线处的海峡是（）A．马六甲海峡 B．白令海峡 C．土耳其海峡 D．直布罗陀海峡9.下列关于亚洲自然地理特征的说法正确的是（）A．地势中部高，四周低 B．河流短小而湍急C．以热带雨林气候和热带草原气候为主 D．是世界上最湿润的大洲10.从所在的半球看，亚洲主要位于（）A．东半球、南半球 B．东半球、北半球C．西半球、南半球 D．西半球、北半球11.读“亚洲”图，E是亚洲最大的平原，它是（）A．湄公河三角洲 B．东北平原 C．西西伯利亚平原 D．恒河平原12.亚洲的地形类型多种多样，比重最大的是（）A．平原 B．丘陵 C．盆地 D．高原和山地13.亚洲的地势特点是（）A．西高东低 B．中部低，四周高 C．南低北高 D．中部高，四周低14.读如图“亚洲大陆沿30°N地形剖面示意图”和“亚洲大陆沿80°E地形剖面示意图”，亚洲南部河流主要注入（）A．太平洋 B．北冰洋 C．印度洋 D．大西洋15.亚洲气候的特征之一是复杂多样，亚洲缺少的气候类型是（）A．热带雨林气候、热带沙漠气候B．热带草原气候、温带海洋性气候C．地中海气候、热带季风气候D．热带沙漠气候、地中海气候16.下列有关亚洲和欧洲河流特征的描述，正确的是（）A．亚洲长河众多，欧洲河流流程较短 B．亚洲、欧洲的河流呈放射状发布C．亚洲多为内流河，欧洲多为外流河 D．亚洲河流稠密，欧洲河流稀少读亚洲气候图，完成下列问题。

第六章实数单元测试卷

第六章实数单元测试卷一、选择题1. 25 的平方根是 ( )A ． 5B ． −5C ． ±√5D ． ±5 2. 下列等式正确的是 ( )A ． ±√(−2)2=2B ． √(−2)2=−2C ． √−83=−2D ． √0.013=0.1 3. 下列各数中，无理数的个数是 ( )3.141，−227，√−273，π，0，0.1010010001⋯A ． 2B ． 3C ． 4D ． 5 4. 设 7−√10 的整数部分为 a ，小数部分为 b ，则 (a +√10)(b −1) 的值是 ( ) A ． 6 B ． 2−√10 C ． 1 D ． −1 5. 若 a ，b 为实数，且满足 ∣a −2∣+√3−b =0，则 b −a 的值为 ( ) A ． 1 B ． 0 C ． −1 D ．以上都不对 6. 计算 ∣∣√6−3∣∣+∣∣2−√6∣∣ 的值为 ( )A ． 5B ． 5−2√6C ． 1D ． 2√6−1 7. 下列说法不正确的有 ( )①任何数都有算术平方根；②一个数的算术平方根一定是正数；③ a 2 的算术平方根是 a ；④ (π−4)2 的算术平方根是 π−4；⑤算术平方根不可能是负数．A ． 5 个B ． 4 个C ． 3 个D ． 2 个 8. 若 √a 2=−a ，则实数 a 在数轴上的对应点一定在 ( )A ．原点左侧B ．原点右侧C ．原点或原点左侧D ．原点或原点右侧二、填空题9. 比较大小：√5−3 √5−22（填“>”“<”或“=”）．10. 下列关于 √13 的说法中，正确的有（填序号）．① 13 的平方根是 √13；② √13 是 13 的算术平方根；③ √13 是无理数；④ 3<√13<4．11. 若 √2+a 的值为有理数，请你写出一个符合条件的实数 a 的值． 12. 若 y =√x −12+√12−x −6，则 xy 的值为． 13. 若 a <√6<b ，且 a ，b 是两个连续的整数，则 a b = ．14. 大家知道 √2 是无理数，而无理数是无限不循环小数，因此 √2 的小数部分我们不可能全部写出来，于是小林用 √2−1 来表示 √2 的小数部分．事实上，小林的表示方法是有道理的，因为 1<√2<2，即 √2 的整数部分是 1，所以将这个数减去其整数部分就是小数部分．如果 √5 的小数部分为 a ，√13 的整数部分为 b ，那么 a +b −√5= ．15. 规定用符号 [m ] 表示一个实数 m 的整数部分，例如：[23]=0，[3.14]=3．按此规定，[√10+1] 的值为．三、解答题16. 把下列各数填入相应的大括号内．√3，−2，√93，0，√−83，16113，3.1415，3−π，√144，3−√29，3√2，0.2121121112⋯ 整数集合：{ ⋯}；非负数集合：{ ⋯}；无理数集合：{ ⋯}．17. 计算：(1) √144−√169+√83；(2) ∣∣√3−2∣∣+√3；(3) √−13−√16−√(−6)2+∣∣√2−1∣∣．18. 求 x 的值：(1) x 2−24=25； (2) 8x 3=125； (3) (x −2)2=25．19. 计算并回答问题：(1) √169= ，√1.69= ，√0.0169= ．(2) √21973= ，√2.1973= ，√0.0021973= ．(3) 根据上述结果你发现了什么规律？请用语言概括出来；(4) 根据你发现的规律填空：如果 √15≈3.873，√150≈12.25，√613≈3.936，√6103≈8.481，则 √1.5≈ ，√0.0613≈ ．20. 已知一个正方体的棱长是 7 cm ，要再做一个正方体，使它的体积是原正方体体积的 8倍，求新做的正方体的棱长．（提示：设未知数列方程）21. 若 √2a +b 与 √c −b 的值互为相反数，√1−3b 3 与 √b +13 互为相反数，求 a ，b ，c 的值．22. 已知 a 是 √10 的整数部分，b 是它的小数部分，求 (−a )3+(b +3)2 的值．23. 王老师给同学们布置了这样一道习题：一个数的算术平方根为 2m −6，它的平方根为±(m −2)，求这个数．小张的解法如下：依题意可知，2m −6 是 m −2，−(m −2) 两数中的一个． ⋯⋯（1）当 2m −6=m −2 时，解得 m =4． ⋯⋯（2）所以这个数为 2m −6=2×4−6=2． ⋯⋯（3）当 2m −6=−(m −2) 时，解得 m =83． ⋯⋯（4）所以这个数为 2m −6=2×83−6=−23． ⋯⋯（5）综上可得，这个数为 2 或 −23． ⋯⋯（6）王老师看后说，小张的解法是错误的．你知道小张错在哪里吗？为什么？请改正．24.先阅读，然后解答提出的问题．设a，b是有理数，且满足a+√2b=3−2√2，求b a的值．解：由题意得(a−3)+(b+2)√2=0，因为a，b都是有理数，所以a−3，b+2也是有理数，又因为√2是无理数，所以a−3=0，b+2=0，所以a=3，b=−2，所以b a=(−2)3=−8．问题：设x，y都是有理数，且满足x2−2y+√5y=10+3√5，求x+y的值．。

第六章实数单元测试-2022-2023学年七年级数学下册同步精品讲义(教师版)

第六章实数一、选择题（本大题共14个小题，每题2分，共28分，在每个小题的四个选项中只有一项是符合题目要求的）1．（2022秋·甘肃兰州·八年级统考期末）在实数2,0,7中，无理数有（）A ．1个B ．2个C ．3个D ．4个【答案】B 【分析】根据实数的分类：有理数和无理数，结合无理数的概念逐项进行辨别即可得到答案．【详解】解：∵2,0,1.41417是有理数；∴在所有数字中无理数有2个，故选：B ．【点睛】本题考查实数的分类、对无理数的辨别能力，关键是能准确理解并运用相关知识．2．（2022秋·福建莆田·八年级统考期中）下列说法正确的是（）A ．125的平方根是15B ．25-的算术平方根是5C ．()25-的平方根是5-D ．0的平方根和算术平方根都是0【答案】D【分析】根据一个正数有两个平方根，且这两个平方根互为相反数及算术平方根的定义即可判断各选项．【详解】解：A 、125的平方根为15±，故本选项不符合题意；B 、25-没有算术平方根，故本选项不符合题意；C 、()2525-=，25的平方根是5±，故本选项不符合题意；D 、0的平方根和算术平方根都是0，故本选项符合题意．故选D ．【点睛】本题考查了平方根和算术平方根的定义，一个正数有两个平方根，其中正的平方根称为算术平方根，负数没有平方根，0的平方根和算术平方根都是0．3．（2022秋·浙江·七年级专题练习）实数﹣20，﹣5中绝对值最大的数是（）A ．﹣2B C ．0D ．﹣5【答案】D【分析】根据绝对值的性质以及正实数和0的大小比较即可求解．【详解】∵20,55-=-=且025＜，∴所给的几个数中，绝对值最大的数是5-．故选：D ．【点睛】此题主要考查了实数大小比较的方法以及绝对值的性质，要熟练掌握．4．（2022秋·辽宁锦州·的值为（）A 5B ．5C ．1D 1【答案】C 【分析】根据绝对值以及立方根的定义进行化简，之后运算即可得到答案．321==故选：C【点睛】本题主要考查绝对值以及立方根的定义，掌握绝对值以及立方根的定义是解题的关键．5．（2022秋·江苏·八年级专题练习）如图，公园里有一个边长为8m 的正方形花坛．现在想扩大花坛的面积，使花坛面积增加280m 后仍为正方形，则边长应扩大（）A ．2mB ．3mC ．4mD ．5m【答案】C 【分析】设边长应扩大x 米，根据题意得到改造后花坛的边长长为（x ＋8）米，则其面积为（64＋80）平方米，然后根据正方形的面积（x ＋8）2＝（64＋80）平方米可得到答案．【详解】设边长应扩大x 米，根据题意，得：（x ＋8）2＝64＋80（x ＋8）2＝144∴x ＋812（负值舍去），∴x ＝4．故选：C ．【点睛】本题考查了算术平方根的应用．能够正确得出关系式（x ＋8）2＝（64＋80）是解题的关键．6．（2022春·安徽铜陵·七年级校考阶段练习）已知正方体A 的体积是棱长为4cm 的正方体B 的体积的127，则正方体A 的棱长是（）A ．43cm B ．34cm C ．427cm D ．49cm 【答案】A 【分析】可设正方体A 的棱长为x ，根据题目中的数量关系有331427x =´，解之即可.【详解】解：设正方体A 的棱长为x cm ，据题意得331427x =´，解得43x =.故选：A.【点睛】本题考查了用立方根解方程中的立体图形问题，寻找数量关系列出方程是解答关键.7．（2022·全国·七年级专题练习）如图所示的是一个大正方形，现从大正方形中剪去两个面积为24dm 和29dm 的小正方形，则余下的面积为（）2dm ．A ．12B ．10C ．8D ．6【答案】A 【分析】先求出剪去的正方形的边长，再根据长方形的面积公式计算即可．【详解】解：∵剪去的正方形的面积为24dm 和29dm ，，∴余下的面积为：223236612dm ´+´=+=，故选：A ．【点睛】本题考查了算术平方根的应用，求出剪去的正方形的边长是解题的关键．8．（2022秋·山东菏泽·21x =+，则x 的值为（）．A ．0B ．1-C ．12-D ．0，1-或12-【答案】D【分析】根据立方根的定义求解，因为立方根等于自身的数有01±，，据此求解即可【详解】Q 21x =+210x \+=或1±x \=0，1-或12-故选D【点睛】本题考查了立方根的定义，掌握立方根等于自身的数有01±，是解题的关键．9．（2022秋·八年级课时练习）一般地，如果n x a =（n 为正整数，且1n >），那么x 叫做a 的n 次方根，下列结论中正确的是（）A ．16的4次方根是2B ．32的5次方根是2±C ．当n 为奇数时，2的n 次方根随n 的增大而减小D ．当n 为奇数时，2的n 次方根随n 的增大而增大【答案】C【分析】根据题意n 次方根，列举出选项中的n 次方根，然后逐项分析即可得出答案．【详解】A.42=16Q 4(2)=16-，\16的4次方根是2±，故不符合题意；B.5232=Q ，5(2)32-=-，\32的5次方根是2，故不符合题意；C.设x y ==则155153232,28,x y ====1515,x y \> 且1,1,x y >>,x y \>\当n 为奇数时，2的n 次方根随n 的增大而减小，故符合题意；D.由C 的判断可得：D 错误，故不符合题意．故选C ．【点睛】本题考查了新概念问题，n 次方根根据题意逐项分析，得出正确的结论，在分析的过程中注意x 是否为负数,通过简单举例验证选项是解题关键．10．（2022·全国· 1.333» 2.872»约等于（）．A ．28.72B ．287.2C ．13.33D ．133.3【答案】A【分析】根据根号内的小数点移动规律即可求解，立方根的规律为，根号内的小数点移动3位，其结果的小数点移动一位，小数点的移动方向保持一致．2.872»,28.72»，故选A ．【点睛】本题考查了算术平方根与立方根的应用，掌握小数点的移动规律是解题的关键．11．（2022秋·4的数是（）A 44B ．4C ．4D ．44【答案】A【分析】分类讨论求解，向左就减，向右就加．4，4，故选A ．【点睛】本题考查了实数与数轴，分类讨论数解题的关键．12．（2022秋·全国·七年级专题练习）已知{}min ,,a b c 表示取三个数中最小的那个数，例加：min{1,2,3}3---=-，当}21min,81x x =时，则x 的值为（）A ．181B ．127C ．13D ．19【答案】D2,x x 都小于1且大于0，根据平方根求得x 的值即可求解．【详解】解：∵}21min ,81x x =2,x x 都小于1且大于02x x \<2181x \=19x \=（负值舍去）故选D2,x x 的范围是解题的关键．13．（2022秋·河南南阳·八年级校考阶段练习）小明是一个电脑爱好者，他设计了一个程序如图，当输入x的值为64时，输出的y 值是（）A B C ．2-D ．2【答案】A 【分析】直接根据流程图计算即可．【详解】64的算数平方根是8，是有理数，故将8取立方根为2，是有理数，将2，是无理数，故选A ．【点睛】本题考查了实数的判断和求一个数的算术平方根和立方根，解题的关键是正确按照流程图顺序计算．14．（2022秋·江苏南京·七年级校联考阶段练习）如图，在一条不完整的数轴上，从左到右的点A 、B 、C 把数轴分成①②③④四部分，点A 、B 、C 对应的实数分别是a 、b 、c ，若原点在第③部分，则下列结论：（1）0ab <，（2）0a b +<，（3）0a c -<（4）22a b >，其中，正确的是（）A ．（1）和（2）B ．（3）和（4）C ．（2）和（3）D ．（1）和（4）【答案】C 【分析】由点A 、B 、C 在数轴上点的位置判断a 、b 、c 的符号，按照运算法则进行判断即可【详解】解：若原点在第③部分，则a ＜0，b ＜0，c ＞0，a ＜b ＜0＜c ，（1）∵a ＜0，b ＜0，∴ 0ab >故（1）错误；（2）∵a ＜0，b ＜0，∴0a b +<故（2）正确；（3）∵a ＜0，c ＞0，∴0a c -<故（3）正确；（4）∵a ＜b ＜0，∴22a b<故（4）错误；故选：C【点睛】此题考查了数轴、数轴上的点表示的数的规律、相关运算法则等知识，解决本题的关键是数形结合思想的灵活应用．二、填空题（本题共4个小题；每个小题3分，共12分，把正确答案填在横线上）15．（2022秋·四川成都·八年级四川省成都市七中育才学校校考期中）如图，有五个小正方形，每个小正方形的边长为1，可通过“剪一剪”，“拼一拼”，将其拼成一个正方形，则这个正方形的边长是____________．【分析】由面积不变求出拼成的正方形的面积，再利用公式计算边长即可．【详解】解：∵拼成的正方形的面积为2155´=，【点睛】此题考查了有理数的乘方和乘法计算，算术平方根的实际应用，正确理解面积不变规律是解题的关键．16．（2022秋·四川宜宾·八年级统考期中）已知正实数b 的平方根是1a -与32a -，则b =______．【答案】1【分析】根据一个正数的平方根有两个，且互为相反数列方程求解即可．【详解】解：∵正实数b 的平方根是1a -与32a -，∴()()1320a a -+-=，解得：2a =，∴()2211b =-=，故答案为：1．【点睛】本题考查平方根、解一元一次方程，熟知一个正数的平方根有两个，且互为相反数是解答的关键．17．（2022秋·河南南阳·八年级统考期中）如果一个数的立方根是其本身，则这个数是_______．（写一个即可）【答案】1-、1、0（写出一个即可给分）【分析】根据1-、1、0的立方和立方根都是其本身即可解答；【详解】解：如果一个数的立方根是其本身，则这个数可以是1-、1、0，故答案为：1-、1、0（写出一个即可给分）【点睛】本题考查了立方根，熟记1-、1、0的立方和立方根都是其本身是解题关键．-的相反数是______________ ．18．（2022秋·甘肃酒泉·22##-【分析】先求出绝对值的值，根据相反数的定义，即可得出答案．22-=，-，∴其相反数是(222【点睛】本题考查化简绝对值，求一个数的相反数，掌握相反数的定义是本题的关键．三、解答题（本题共8道题，19-21每题6分，22-25每题8分，26题10分，满分60分）19．（2021春·浙江台州·七年级临海市学海中学校考期中）解答下列各题．(1)(2)解方程：()219x-=．【答案】2-x=-(2)4x=或2【分析】（1）根据求一个数的算术平方根，立方根，化简绝对值进行计算即可求解；（2）根据平方根的定义解方程即可求解．【详解】（1=-242=-；（2）∵()239±=，()219x -=∴13x -=±，解得：4x =或2x =-．【点睛】本题考查了实数的混合运算，平方根的定义，求一个数的算术平方根，立方根，化简绝对值，掌握以上知识是解题的关键．20．（2022秋·河南鹤壁·八年级鹤壁市外国语中学校考阶段练习）已知m M =3m +的算术平方根，24m N -=2n -的立方根，试求：(1)M 和N 的值；(2)M N +的平方根．【答案】(1)3，1(2)2和-2【分析】（1）根据算术平方根和立方根的意义列出方程求解即可；（2）求出M N +的值，再求平方根即可．【详解】（1）解：因为m M =3m +的算术平方根，24N m -=是2n -的立方根，所以可得：42m -=， 2433m n -+=，解得：6m =，3n =，把6m =，3n =代入39m +=，21n -=，所以可得3M =，1N =．（2）解：由（1）得4M N +=，4的平方根为2和-2．【点睛】本题考查了平方根和立方根，明确平方根和立方根的意义，熟练运用相关知识求解是解题关键．21．（2022秋·八年级单元测试）化简求值：(1)已知a 13=(2)已知：实数a ，b ||a b +-．【答案】(1)3±(2)3b -【分析】（11的取值范围，求出a 的值；3=，根据算术平方根的定义可求b ，再代（2）利用数轴得出各项符号，进而利用二次根式和绝对值的性质化简．【详解】（1<<∴45<<，∴314<-<，∴3a ×=，3=，∴9b =，9==，3±；（2）由数轴可得：101a b -<<<<，则10,10,0a b a b -<-<-<，||a b -12(1)()a b a b =--+-+-122a b a b=--+-+-3b =-．【点睛】本题考查了算术平方根与平方根的定义，以及估算无理数的大小，熟练掌握无理数的估算方法是解题的关键．22．（2022秋·浙江·七年级专题练习）“2=3”就是一个著名的数学“诡辩”，有人用下述方法“说明”这一结果是“正确”的．因为410=915--，所以2525410=91544-+-+，22225555222=3232222æöæö-´´+-´´+ç÷ç÷èøèø，22552=322æöæö--ç÷ç÷èøèø，552=322--，所以2=3．“2＝3”这个结果显然是不正确的，但问题出现在哪里呢？请你找一找，并与同学交流．【答案】错在由22552=322æöæö--ç÷ç÷èøèø得552=322--这一步【分析】由22x y =可得出x y =，但不能得出x y =，所以错在由22552=322æöæö--ç÷ç÷èøèø得552=322--这一步．【详解】解：错在由22552=322æöæö--ç÷ç÷èøèø得552=322--这一步，显然52<02-，5302->，所以5523022-¹->．【点睛】此题主要考查了利用平方根、平方运算法则解决阅读题目的问题，特别注意22x y =可得出x y =，但不能得出x y =，这是学生开平方时常犯的错误．23．（2022秋·浙江温州·七年级统考期中）观察下列一组算式的特征及运算结果，探索规律：（13==，（24=，（35==，（46==．(1)=______=______．(2)用含正整数n 的式子表示上述算式的规律：______．(3)L 【答案】(1)7， 212n ==+(3)1013【分析】（1）从数字找规律，即可解答；（2）从数字找规律，即可解答；（3）从数字找规律，进行计算即可解答．【详解】（17==21==，故答案为：7，21；（2）解：用含正整数n 2n ==+；2n ==+；（3L 34562023=-+-+¼+()110102023=-´+10102023=-+1013=．【点睛】本题考查了实数的运算，规律型：数字的变化类，从数字找规律是解题的关键．24．（2022秋·江苏·观察下表：(1)表格中的三个值分别为：x ＝；y ＝；z ＝；(2)用公式表示这一规律：当a ＝4×100n （n ＝；(3)利用这一规律，解决下面的问题：2.358»，则≈ ；≈ ．【答案】(1)0.220200；；(2)210n´(3)0.2358235.8；【分析】（1）直接利用算术平方根定义计算填表即可；（2（3）利用（2）得出的规律即可解答．【详解】（1）解：根据算术平方根定义可得：0.220200x y z ===；；．故答案为0.220200；；．（2）解：当4100n a =´（n 210n =´．故答案为210n ´．（3 2.358»，则0.2358»；235.8»．故答案为：0.2358235.8；．【点睛】本题主要考查了算术平方根、数字规律等知识点，熟练掌握算术平方根的定义是解本题的关键．25．（2022秋·八年级单元测试）数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人感觉十分惊奇，请华罗庚给大家解读其中的奥秘．你知道怎样迅速准确的计算出结果吗？请你按下面的问题试一试：①100==，又1000593191000000<<Q ，10100\<<，∴能确定59319的立方根是个两位数．②∵59319的个位数是9，又39729=Q ，∴能确定59319的立方根的个位数是9．③如果划去59319后面的三位319得到数59，<<34<，可得3040<<，由此能确定59319的立方根的十位数是3因此59319的立方根是39．（1）现在换一个数195112，按这种方法求立方根，请完成下列填空．①它的立方根是_______位数．②它的立方根的个位数是_______．③它的立方根的十位数是__________．④195112的立方根是________．（2）请直接填写结果：=________．=________．【答案】（1）①两；②8；③5；④58；（2）①24；②56．【分析】（1）①根据例题进行推理得出答案；②根据例题进行推理得出答案；③根据例题进行推理得出答案；④根据②③得出答案；（2）①先判断它的立方根是几位数，再判断个位、十位上的数字，即可得到结论；②先判断它的立方根是几位数，再判断个位、十位上的数字，即可得到结论.【详解】（1）①100==，10001951121000000<< ，∴10100<<，∴能确定195112的立方根是一个两位数，故答案为：两；②∵195112的个位数字是2，又∵38512=，∴能确定195112的个位数字是8，故答案为：8；③如果划去195112后面三位112得到数195，<，∴56<，可得5060<<，由此能确定195112的立方根的十位数是5，故答案为：5；④根据②③可得：195112的立方根是58，故答案为：58；（2）①13824的立方根是两位数，立方根的个位数是4，十位数是2，∴13824的立方根是24，故答案为：24；②175616的立方根是两位数，立方根的个位数是6，十位数是5，∴175616的立方根是56，故答案为：56.【点睛】此题考查立方根的性质，一个数的立方数的特点，正确理解题意仿照例题解题的能力，掌握一个数的立方数的特点是解题的关键.26．（2022秋·浙江嘉兴·七年级校联考期中）阅读材料：若点M ，N 在数轴上分别表示实数m ，n ，那么M ，N 之间的距离可表示为||m n -．例如|31|-，即表示3，1在数轴上对应的两点之间的距离；同样：|53||5(3)|+=--表示5，3-在数轴上对应的两点之间的距离．根据以上信息，完成下列题目：(1)已知A ，B ，C 为数轴上三点，点A C 对应的数为1．①若点B 对应的数为2-，则B ，C 两点之间的距离为；②若点A 到点B 的距离与点A 到点C 的距离相等，则点B 对应的数是．(2)对于|3||4|x x -++这个代数式．①它的最小值为；②若|3||4||1||2|10x x y y -+++-++=，则x y +的最大值为．【答案】(1)①3；②1(2)①7；②4【分析】（1）①根据两点间的距离公式解答即可；②根据两点间的距离公式解答即可；（2）①根据两点间的距离的几何意义解答；②根据两点间的距离公式填空．【详解】（1）解：①B ，C 两点之间的距离为|21|3--=；故答案为：3；②设点B 对应的数是x ，则有|1|x =，解得1x =-或1（舍去），故答案为：1；（2）解：①根据数轴的几何意义可得4-和3之间的任何一点均能使|3||4|x x -++取得的值最小，\当43x -……时，|3||4|x x -++的最小值为7．故答案为：7；②|3||4||1||2|10x x y y -+++-++=Q ，43x \-……，21y -……，64x y \-+……，x y \+的最大值为4．故答案为：4．【点睛】此题主要考查了绝对值的意义，实数与数轴，解题的关键是了解两点间的距离公式和两点间距离的几何意义．。

第六章实数单元测试及答案

第六章实数单元测试及答案一、选择题1．一列数1a ， 2a ， 3a ，…… n a ，其中1a =﹣1， 2a =111a -， 3a =211a -，……， n a =111n a --，则1a ×2a ×3a ×…×2017a =（）A ．1B ．-1C ．2017D ．-20172．圆的面积增加为原来的m 倍，则它的半径是原来的（）A ．m 倍B ．2m 倍 C倍 D ．2m 倍3．下列命题中，真命题是（）A ．实数包括正有理数、0和无理数B ．有理数就是有限小数C ．无限小数就是无理数D ．无论是无理数还是有理数都是实数4．下列说法中正确的个数有（）①0是绝对值最小的有理数；②无限小数是无理数；③数轴上原点两侧的数互为相反数；④相反数等于本身的数是0；⑤绝对值等于本身的数是正数；A ．2个B ．3个C ．4个D ．5个5．若a ，b均为正整数，且a >b <+a b 的最小值是（） A ．3 B ．4 C ．5 D ．66．有下列四种说法：①数轴上有无数多个表示无理数的点；②带根号的数不一定是无理数；③平方根等于它本身的数为0和1；④没有最大的正整数，但有最小的正整数；其中正确的个数是( )A ．1B ．2C ．3D ．47．已知|x |＝2，y 2＝9，且xy ＜0，则x +y 的值为（）A ．1或﹣1B ．-5或5C ．11或7D ．-11或﹣7830b -=）A ．0B ．±2C ．2D ．49．下列各数中3.14，0.1010010001…，﹣17，2π有理数的个数有（）A ．1个B ．2个C ．3个D ．4个10．已知m 是整数，当|m ﹣40|取最小值时，m 的值为（） A ．5 B ．6 C ．7 D ．8二、填空题11．若x +1是125的立方根，则x 的平方根是_________．12．若()2320m n ++-=，则m n 的值为 ____.13．估计51-与0.5的大小关系是：51-_____0.5．（填“＞”、“=”、“＜”） 14．观察下列各式：(1)123415⨯⨯⨯+=；(2)2345111⨯⨯⨯+=；(3)3456119⨯⨯⨯+=；根据上述规律，若121314151a ⨯⨯⨯+=，则a =_____．15．比较大小：512-__________0.5．（填“>”“<”或“=”） 16．已知31.35 1.105≈，3135 5.130≈，则30.000135-≈________．17．已知a 、b 为两个连续的整数，且a ＜19＜b ，则a +b ＝_____．18．如图，直径为1个单位长度的半圆，从原点沿数轴向右滚动一周，圆上的一点由原点O 到达点'O ，则点'O 对应的数是_______．19．若一个正数的平方根是21a +和2a +，则这个正数是____________．20．若x ，y 为实数，且|2|30x y ++-=，则(x+y) 2012的值为____________．三、解答题21．先阅读然后解答提出的问题：设a 、b 是有理数，且满足2322+=-a b b a 的值．解：由题意得(3)(20-++=a b ，因为a 、b 都是有理数，所以a ﹣3，b+2也是有理数，2是无理数，所以a-3=0，b+2=0，所以a=3，b=﹣2，所以3(2)8=-=-a b ．问题：设x 、y 都是有理数，且满足225y 1035x y -+=+x+y 的值．22．阅读下面文字：对于5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭可以如下计算：原式()()()5231591736342⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+++-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦ ()()()5231591736342⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-+-+-++-⎡⎤ ⎪ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦ 1014⎛⎫=+- ⎪⎝⎭ 114=- 上面这种方法叫拆项法，你看懂了吗？仿照上面的方法，计算：（1）115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭ （2）235120192018201720163462⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭ 23．阅读理解：计算1111234⎛⎫+++ ⎪⎝⎭×11112345⎛⎫+++ ⎪⎝⎭﹣111112345⎛⎫++++ ⎪⎝⎭×111234⎛⎫++ ⎪⎝⎭时，若把11112345⎛⎫+++ ⎪⎝⎭与111234⎛⎫++ ⎪⎝⎭分别各看着一个整体，再利用分配律进行运算，可以大大简化难度．过程如下：解：设111234⎛⎫++ ⎪⎝⎭为A ，11112345⎛⎫+++ ⎪⎝⎭为B ，则原式=B （1+A ）﹣A （1+B ）=B+AB ﹣A ﹣AB=B ﹣A=15．请用上面方法计算： ①11111123456⎛⎫+++++ ⎪⎝⎭×111111234567⎛⎫+++++ ⎪⎝⎭-1111111234567⎛⎫++++++ ⎪⎝⎭×1111123456⎛⎫++++ ⎪⎝⎭②111123n ⎛⎫++++ ⎪⎝⎭111231n ⎛⎫+++ ⎪+⎝⎭-1111231n ⎛⎫++++ ⎪+⎝⎭11123n ⎛⎫+++ ⎪⎝⎭． 24．你能找出规律吗？（1＝，＝；＝，＝．“＜”）．（2）请按找到的规律计算：；（3）已知：a，b＝（可以用含a ，b 的式子表示）．25．阅读理解．23．∴11＜21的整数部分为1，12．解决问题：已知a﹣3的整数部分，b﹣3的小数部分．（1）求a ，b 的值；（2）求（﹣a ）3+（b +4）22＝17．26．阅读下列解题过程：为了求23501222...2+++++的值，可设23501222...2S =+++++，则2345122222...2S =+++++，所以得51221S S -=-，所以5123505121:1222...221S =-+++++=-，即；仿照以上方法计算：（1）2320191222...2+++++= .（2）计算：2320191333...3+++++（3）计算：101102103200555...5++++【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】因为1a =﹣1,所以2a =11111112a ==---（）,3 a =21121112a ==--,4 a =3111112a ==---,通过观察可得:1 a ,2a ,3a ,4 a ……的值按照﹣1,1 2, 2三个数值为一周期循环,将2017除以3可得372余1,所以2017a 的值是第273个周期中第一个数值﹣1,因为每个周期三个数值的乘积为: 11212-⨯⨯=-,所以1a ×2a ×3a ×…×2017a =()()372111,-⨯-=-故选B. 2．C解析：C【分析】设面积增加后的半径为R ，增加前的半径为r ，根据题意列出关系式计算即可．【详解】设面积增加后的半径为R ，增加前的半径为r ，根据题意得：πR 2=mπr 2，∴，故选：C ．【点睛】此题主要考查了实数的运算，要注意，圆的面积和半径之间是平方关系而非正比例关系．3．D解析：D【分析】直接利用实数以及有理数、无理数的定义分析得出答案．【详解】A 、实数包括有理数和无理数，故此命题是假命题；B 、有理数就是有限小数或无限循环小数，故此命题是假命题；C 、无限不循环小数就是无理数，故此命题是假命题；D 、无论是无理数还是有理数都是实数，是真命题．故选：D ．【点睛】此题主要考查了命题与定理，正确掌握相关定义是解题关键．4．A解析：A【分析】分别利用绝对值的定义、无理数、有理数的定义、相反数的定义分别进行判断即可得出答案．【详解】①0是绝对值最小的有理数；根据绝对值的性质得出，故此选项正确；②无限小数是无理数；根据无限循环小数是有理数判断，故此选项错误；③数轴上原点两侧的数互为相反数；根据到原点距离相等的点是互为相反数，故此选项错误；④相反数等于本身的数是0；根据相反数的定义判断，故此选项正确；⑤绝对值等于本身的数是正数；还有0的绝对值也等于本身，故此选项错误.∴正确的个数有2个故选：A.【点睛】本题主要考查了绝对值的定义、无理数、有理数的定义、相反数的定义等知识，熟练掌握其性质是解题关键.5．B解析：B【分析】的范围，然后确定a、b的最小值，即可计算a+b的最小值．【详解】23．∵a a为正整数，∴a的最小值为3．12．∵b b为正整数，∴b的最小值为1，∴a+b的最小值为3+1=4．故选B．【点睛】本题考查了估算无理数的大小，解题的关键是：确定a、b的最小值．6．C解析：C【分析】根据实数的定义，实数与数轴上的点一一对应，平方根的定义可得答案．【详解】①数轴上有无数多个表示无理数的点是正确的；；2③平方根等于它本身的数只有0，故本小题是错误的；④没有最大的正整数，但有最小的正整数，是正确的．综上，正确的个数有3个，故选：C．【点睛】本题主要考查了实数的有关概念，正确把握相关定义是解题关键．7．A解析：A【分析】根据题意，利用平方根定义，绝对值的代数意义，以及有理数的乘法法则判断确定出x与y 的值即可．【详解】解：∵|x |＝2，y 2＝9，且xy ＜0，∴x=2或-2，y=3或-3，当x=2，y=-3时，x+y=2-3=-1；当x=-2，y=3时，原式=-2+3=1，故选：A ．【点睛】此题考查了有理数的乘方，绝对值，以及有理数的加法，熟练掌握运算法则是解本题的关键．8．C解析：C【分析】由算术平方根和绝对值的非负性，求出a 、b 的值，然后进行计算即可．【详解】解：根据题意，得a ﹣1＝0，b ﹣3＝0，解得：a ＝1，b ＝3，∴a +b ＝1+3＝4，∴2．故选：C ．【点睛】本题考查了算术平方根和绝对值的非负性，解题的关键是正确求出a 、b 的值．9．C解析：C【分析】直接利用有理数的定义进而判断得出答案．【详解】解：3.14，0.1010010001…，-17 ，2π 3.14，-17＝-2共3个.故选C ．【点睛】此题主要考查了有理数，正确把握有理数的定义是解题关键． 10．B解析：B【分析】根据绝对值是非负数，所以不考虑m 为整数,则m 取最小值是0，又0的绝对值为0，令0m=，得出m=m的整数可得：m ＝6．【详解】解：因为m取最小值，m∴=，∴=，m解得：m=240m=，∴<<，且m更接近6，67m∴当6m=时，m有最小值.故选：B．【点睛】本题考查绝对值的非负性，以及估算二次根式的大小，理解并熟练掌握绝对值的非负性是本题解题关键；在估算二次根式大小的时候，先算出二次根式的平方，再看这个平方在哪两个平方数之间，就相应的得出二次根式在哪两个整数之间，即可估算出二次根式的大小.二、填空题11．±2【分析】先根据立方根得出x的值，然后求平方根．【详解】∵x+1是125的立方根∴x+1=，解得：x=4∴x的平方根是±2故答案为：±2【点睛】本题考查立方根和平方根，注意一个正解析：±2【分析】先根据立方根得出x的值，然后求平方根．【详解】∵x+1是125的立方根∴x=4∴x的平方根是±2故答案为：±2本题考查立方根和平方根，注意一个正数的平方根有2个，算术平方根只有1个．12．【分析】根据非负数的性质列式求出m 、n 的值，然后代入代数式进行计算即可得解．【详解】由题意得，m+3=0，n-2=0，解得m=-3，n=2，所以，mn=（-3）2=9．故答案为9．【解析：【分析】根据非负数的性质列式求出m 、n 的值，然后代入代数式进行计算即可得解．【详解】由题意得，m+3=0，n-2=0，解得m=-3，n=2，所以，m n =（-3）2=9．故答案为9．【点睛】此题考查绝对值和算术平方根非负数的性质，解题关键在于掌握几个非负数的和为0时，这几个非负数都为0．13．>【解析】∵ . , ∴ , ∴ ,故答案为>.解析：>【解析】∵10.52-=-=20-> , ∴0> , ∴0.5> ,故答案为>.14．181【分析】观察各式得出其中的规律，再代入求解即可．【详解】由题意得将代入原式中故答案为：181．本题考查了实数运算类的规律题，掌握各式中的规律是解题的关键．解析：181【分析】观察各式得出其中的规律，再代入12n=求解即可．【详解】由题意得()31n n=⨯++将12n=代入原式中12151181a==⨯+=故答案为：181．【点睛】本题考查了实数运算类的规律题，掌握各式中的规律是解题的关键．15．＞【分析】首先把两个数采用作差法相减，根据差的正负情况即可比较两个实数的大小．【详解】∵，∵-2＞0，∴＞0．故＞0.5．故答案为：＞.【点睛】此题考查实数大小比较，解题关键在于解析：＞【分析】首先把两个数采用作差法相减，根据差的正负情况即可比较两个实数的大小．【详解】12＞0，∴22＞0．＞0.5．故答案为：＞.【点睛】此题考查实数大小比较，解题关键在于掌握比较两个实数的大小，可以采用作差法、取近似值法等．16．-0.0513【分析】根据立方根的意义，中，m的小数点每移动3位，n的小数点相应地移动1位．【详解】因为所以-0.0513故答案为：-0.0513【点睛】考核知识点：立方根．理解立方解析：-0.0513【分析】=中，m的小数点每移动3位，n的小数点相应地移动1位．n【详解】≈5.130≈-0.0513故答案为：-0.0513【点睛】考核知识点：立方根．理解立方根的定义是关键．17．9【分析】首先根据的值确定a、b的值，然后可得a+b的值．【详解】∵＜，∴4＜＜5，∵a＜＜b，∴a＝4，b＝5，∴a+b＝9，故答案为：9．【点睛】本题主要考查了估算无理数的解析：9【分析】a 、b 的值，然后可得a +b 的值．【详解】<∴45，∵a b ，∴a ＝4，b ＝5，∴a +b ＝9，故答案为：9．【点睛】本题主要考查了估算无理数的大小，关键是正确确定a 、b 的值． 18．【分析】点对应的数为该半圆的周长．【详解】解：半圆周长为直径半圆弧周长即故答案为：．【点睛】本题考查数轴上的点与实数的关系．明确的长即为半圆周长是解答的关键．解析：12π+【分析】点O '对应的数为该半圆的周长．【详解】解：半圆周长为直径+半圆弧周长即12π+ 故答案为：12π+．【点睛】本题考查数轴上的点与实数的关系．明确OO '的长即为半圆周长是解答的关键． 19．1【分析】一个正数有两个平方根，它们互为相反数，由此即可列式2a+1+a+2=0，求出a 再代回一个根再平方即可得到该正数.【详解】由题意得2a+1+a+2=0，解得a=-1,∴a+2=1解析：1【分析】一个正数有两个平方根，它们互为相反数，由此即可列式2a+1+a+2=0，求出a 再代回一个根再平方即可得到该正数.【详解】由题意得2a+1+a+2=0，解得a=-1,∴a+2=1,∴这个正数是22(2)11a +==，故答案为：1.【点睛】此题考查平方根的性质：一个正数有两个平方根，它们互为相反数，0的平方根是0，负数没有平方根.20．1【分析】先根据绝对值的非负性、算术平方根的非负性求出x 、y 的值，再代入计算有理数的乘方即可．【详解】由绝对值的非负性、算术平方根的非负性得：解得则故答案为：1．【点睛】本题考查了解析：1【分析】先根据绝对值的非负性、算术平方根的非负性求出x 、y 的值，再代入计算有理数的乘方即可．【详解】由绝对值的非负性、算术平方根的非负性得：2030x y +=⎧⎨-=⎩解得23x y =-⎧⎨=⎩则201220122012()(23)11x y +=-+==故答案为：1．【点睛】本题考查了绝对值的非负性、算术平方根的非负性、有理数的乘方运算，利用绝对值的非负性、算术平方根的非负性求解是常考知识点，需重点掌握．三、解答题21．7或-1.【分析】根据题目中给出的方法，对所求式子进行变形，求出x 、y 的值，进而可求x+y 的值.【详解】解：∵2210x y -=+∴()22100x y --+-=，∴2210x y --=0-=0∴x=±4，y=3当x=4时，x+y=4+3=7当x=-4时，x+y=-4+3=-1∴x+y 的值是7或-1.【点睛】本题考查实数的运算，解题的关键是弄清题中给出的解答方法，然后运用类比的思想进行解答.22．（1）14-（2）124- 【分析】（1）根据例子将每项的整数部分相加，分数部分相加即可解答；（2）根据例子将每项的整数部分相加，分数部分相加即可解答.【详解】（1）115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭()115112744362⎛⎫=--+-+--+- ⎪⎝⎭ 104⎛⎫=+- ⎪⎝⎭ 14=- （2）原式()235120192018201720163462⎛⎫=-+-++-+-+ ⎪⎝⎭ 124⎛⎫=-+- ⎪⎝⎭124=- 【点睛】此题考察新计算方法，正确理解题意是解题的关键，根据例子即可仿照计算.23．（1）17；（2）11n +. 【解析】【分析】①根据发现的规律得出结果即可；②根据发现的规律将所求式子变形，约分即可得到结果．【详解】（1）设1111123456⎛⎫++++ ⎪⎝⎭为A ，111111234567⎛⎫+++++ ⎪⎝⎭为B ，原式=（1+A ）B ﹣（1+B ）A=B+AB ﹣A ﹣AB=B ﹣A=17；（2）设11123n ⎛⎫+++ ⎪⎝⎭为A ，111231n ⎛⎫+++ ⎪+⎝⎭为B ，原式=（1+A ）B ﹣（1+B ）A=B+AB ﹣A ﹣AB=B ﹣A=11n +．【点睛】考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．24．（1）6，6，20，20，＝，＝；（2）①10，②4；（3）2a b【分析】（1)0,0a b =≥≥，据此判断即可．（2=10===，4===，据此解答即可．（3）根据a =b =2a b ==，据此解答即可．【详解】解：（1236=⨯=6==；4520=⨯=20==．==故答案为：6，6，20，20，＝，＝；（210===；4===；（3）∵a =b =2a b ==，故答案为：2a b ．【点睛】本题考查算数平方根，掌握求一个数算术平方根的方法为解题关键．25．（1）a ＝1，b ﹣4；（2）±4．【分析】（1）根据被开饭数越大算术平方根越大，可得a ，b 的值，（2）根据开平方运算，可得平方根．【详解】解：（1<，∴4<＜5，∴1﹣3＜2，∴a ＝1，b 4；（2）（﹣a ）3+（b+4）2＝（﹣1）3+﹣4+4）2＝﹣1+17＝16，∴（﹣a ）3+（b+4）2的平方根是：±4．【点睛】本题考查了估算无理数的大小，利用被开方数越大算术平方根越大得出4＜5是解题关键．26．（1）202021-；（2）2020312-；（3）201101554-. 【分析】仿照阅读材料中的方法求出所求即可．【详解】解：（1）根据2350511222...221+++++=-得：2320191222...2+++++=202021-（2）设2320191333...3S =+++++，则234202033333...3S =+++++，∴2020331S S -=-， ∴2020312S -= 即：2020232019311333 (32)-+++++= （3）设232001555...5S =+++++，则23420155555...5S =+++++，∴201551S S -=-，∴201514S -= 即：20123200511555 (5)4-+++++= 同理可求⸫10123100511555 (5)4-+++++= ∵1011021032002320023100555...51555...5)(1555...5)++++=+++++-+++++（ 201101201101101102103200515155555 (5444)---∴++++=-= 【点睛】此题考查了规律型：数字的变化类，弄清题中的规律是解本题的关键．。

第6章第6单元单元测验(下载版)

第六单元单元测验一、单项选择题1.甲上市公司在上市6个月时召开股东大会，该次股东大会通过的以下决议中，符合公司法律制度规定的是〔〕。

A.公司董事、监事、高级管理人员持有的本公司股份可以随时转让B.公司发起人持有的本公司股份自即日起可以对外转让C.公司收回本公司已发行股份的4％用于未来1年内奖励本公司职工D.决定与乙公司联合开发房地产，并要求乙公司以其持有的甲公司股份作为履行合同的质押担保2.根据公司法律制度的规定，除有继承等特殊情况外，以下有关股份股份转让限制的表述中，错误的选项是( )。

〔2007年〕A.公司发起人持有的本公司股份自公司成立之日起1年内不得转让B.公司高级管理人员离职后1年内不得转让其所持有的本公司股份C.公司监事所持本公司股份自公司股票上市交易之日起1年内不得转让D.公司董事在任职期间每年转让的股份不得超过其所持有本公司股份总数的25％二、多项选择题1.根据公司法律制度的规定，股份在发生以下事项时，可以收购本公司股份的有( )。

〔2006年〕A.减少公司注册资本B.与持有本公司股份的其他公司合并C.将股份奖励给本公司职工D.股东因对股东大会作出的公司合并、分立决议持异议，要求公司收购其股份2.根据公司法律制度的规定，股份可以收购本公司股份奖励给本公司职工。

以下有关该收购本公司股份事项的表述中，正确的有( )。

〔2007年〕A.该收购本公司股份事项，应当经股东大会决议B.因该事项所收购的股份，应当在2年内转让给职工C.用于该事项收购的资金，应当从公司的税后利润中支出D.因该事项收购的本公司股份，不得超过本公司已发行股份总额的10％参考答案及解析一、单项选择题1.【答案】C【解析】〔1〕选项C：股份可以收购本公司股份用于奖励给本公司职工，但不得超过本公司已发行股份总额的5％，用于收购的资金应当从公司的税后利润中支出，所收购的股份应当在1年内转让给职工；〔2〕选项D：股份不得接受以本公司的股票作为质押权的标的。

教科版《第六章-质量和密度》单元检测题(含答案)

教科版《第六章质量和密度》单元检测题及答案（时间60分钟满分100分）一、选择题。

（每题3分，共30分）1、一瓶啤酒放在冰箱冷冻室内，里面的啤酒结成冰后把瓶子胀破了，这是因为（）A、啤酒冻结后，质量不变，体积变大了B、啤酒冻结后，质量变大，体积也变大了C、啤酒冻结后，质量、体积均不变D、啤酒冻结后，质量变小，体积也变小了2、关于一块冰熔化成水，下列叙述中正确的是（）A、质量变大，体积不变，密度变大B、质量变小，体积变小，密度不变C、质量不变，体积变大，密度变小D、质量不变，体积变小，密度变大3、下列现象中质量发生变化的是（）A、铁水凝固成铁块B、将一块矿石由地球运到太空C、菜刀被磨光以后D、将铁丝用拔丝机拉长4、用天平测一枚大头针的质量，下面实验中正确的做法是（）A、将一枚大头针直接放在天平左盘中，测出其质量B、将100枚大头针放在天平左盘测出总质量，然后求出一枚大头针的质量C、将一枚大头针和一块铁块放在天平右盘称出总质量，然后减去铁块质量，就是大头针的质量D、以上三种做法各有道理，因此都可行5、以下各组器材中，不能测出长方体金属块密度的是（）A、刻度尺、水、细线、烧杯B、天平和砝码、量筒、水、细线C、弹簧测力计、刻度尺、细线D、刻度尺、天平和砝码6、在用天平和量筒测量形状不规则的石块密度的实验中，小明进行了以下操作，其中错误的是（）A、将天平标尺上的游码移至右端，再调节天平的横梁平衡B、用天平称出石块的质量mC、用细线系着石块放入盛有水的量筒中，测出石块的体积VD、用公式ρ=m/V算出石块的密度7、一个瓶子装满水时的总质量是400g，装满酒精时的总质量是350g．则瓶子的容积是（）（ρ水=1.0g/cm3，ρ酒精=0.8g/cm3）A、400cm3B、250cm3C、350cm3D、200cm38、（2011•烟台）右图是小明在探究甲、乙、丙三种物质质量与体积关系时作出的图象．分析图象可知（）A、ρ甲＞ρ乙＞ρ丙B、ρ甲＞ρ丙＞ρ乙C、ρ丙＞ρ乙＞ρ甲D、ρ乙＞ρ甲＞ρ丙9、在“测定液体密度”的实验中，液体的体积（V）及液体和容器的总质量（m总）可分别由量筒和天平测得．某同学通过改变液体的体积得到几组数据，画出有关图线，在下图中能正确反映液体和容器的质量跟液体的体积关系的是（）A、B、C、D、10、（2011•攀枝花）下面主要从密度的角度考虑选择材料的是（）A、用塑料做导线的绝缘皮B、用铅锑合金制作家庭电路的保险丝C、用水冷却汽车发动机D、用塑料泡沫搭建舞台表演中的道具房屋二、填空题。

初级会计实务(2022)第六章利润单元测试

初级会计实务(2022)第六章利润单元测试一、单项选择题1.综合收益总额是（）的合计金额。

A.净利润和其他综合收益B.利润总额和其他综合收益C.营业利润和其他综合收益D.营业收入和其他综合收益2.下列关于利润总额的计算公式，正确的是（）。

A.利润总额=营业利润-财务费用+营业外收入-营业外支出B.利润总额=净利润+营业外收入-营业外支出C.利润总额=营业利润+营业外收入-营业外支出D.利润总额=净利润-所得税费用3.下列各项中，属于应该直接计入当期利润的损失的是（）。

A.管理费用B.财务费用C.营业税金及附加D.营业外支出4.甲公司2022年6月主营业务收入为50万元，主营业务成本为40万元，管理费用为5万元，资产减值损失为3万元，公允价值变动收益为5万元，投资收益为6万元，营业外收入为8万元，营业外支出为5万元，所得税费用为5万元。

假定不考虑其他因素，该公司本月的利润总额为（）万元。

A.21B.11C.16D.105.2022年1月1日，财政局拨付甲公司240万元补助款（同日到账），用于购买环保设备1台，并规定若有结余，留归甲公司自行支配，3月20日，甲公司购入了设备，实际成本是150万元，使用寿命5年，则2022年4月应该计入营业外收入的金额是（）万元。

A.4B.2.5C.3D.1.56.甲公司2022年度的利润总额为1000万元，本年的国债利息收入100万元，业务招待费实际发生额为100万元，可扣除业务招待费为80万元，经查，甲公司当年营业外支出中有30万元为税收滞纳金，企业所得税税率为25%，不考虑其他事项，该公司2022年应交所得税为（）万元。

A.242.5B.237.5C.230D.2207.甲公司2022年递延所得税负债年初数是200万元，年末数是300万元，递延所得税资产年初数是150万元，年末数是100万元，则甲公司2022年的递延所得税为（）万元。

A.200B.100C.50D.1508.甲公司2022年利润总额为800万元，当年实际分配并发放给职工的工资为300万元，拨付的工会经费是5万元，发生的职工福利费支出是50万元，假定甲公司无其他纳税调整项目，企业所得税税率为25%，则甲公司2022年应交所得税为（）万元。

第六章频率与概率单元测试(含答案)

第六章频率与概率单元检测（时间：100分钟满分：100分）一、选择题（每题3分，共30分） 1、下列事件中，属于随机事件的是（）A.掷一枚普通正六面体骰子所得点数不超过6 ；B.买一张体育彩票中奖；C.太阳从西边落下；D.口袋中装有10个红球，从中摸出一个白球． 2、下列说法正确的是（）A 、可能性很大的事件必然发生;B 、可能性很小的事件也可能发生;C 、如果一件事情可能不发生，那么它就是必然事件;D 、如果一件事情发生的机会只有百分之一，那么它就不可能发生。

3、下列说法正确的是（）A ．一颗质地均匀的骰子已连续抛掷了2000次，其中，抛掷出5点的次数最少，则第2001 次一定抛掷出5点;B.某种彩票中奖的概率是1%，因此买100张该种彩票一定会中奖; C ．天气预报说明天下雨的概率是50％．所以明天将有一半时间在下雨; D.抛掷一枚图钉，钉尖触地和钉尖朝上的概率不相等.4、如图，一个小球从A 点沿制定的轨道下落，在每个交叉口都有向左或向右两种机会均等的结果，小球最终到达 H 点的概率是（）A. B. C. D. 5、在一个暗箱里放有a 个除颜色外其它完全相同的球，这a 个球中红球只有3个．每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在25%，那么可以推算出a 大约是（） A ．12B ．9C ．4D ．36. 小明在一只装有红色和白色球各一只的口袋中摸出一只球,然后放回搅匀再摸出一只球,反复多次实验后,发现某种“状况”出现的机会约为50%,则这种状况可能是 ( ) A 两次摸到红色球 B. 两次摸到白色球C. 两次摸到不同颜色的球D. 先摸到红色球,后摸到白色球7. 广告牌上“京都大酒店”几个字是霓虹灯，几个字一个接一个亮起来，直至全部亮起来再循环，当路人一眼望去，能够看到全亮的概率是（）．A ．B ．C ．D ．奖金（元） 1000 500 10050 10 21214161814151617109876543口袋数8、某市民政部门：“五一”期间举行“即开式福利彩票”的销售活动，发行彩票10万张（每张彩票2元），在这此彩票中，设置如下奖项：如果花2元钱购买1张彩票，那么所得奖金不少于50元的概率是（）A 、B 、C 、D 、 9、在元旦游园晚会上有一个闯关活动：将5张分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放，将有图形的一面朝下，从中任意翻开一张，如果翻开的图形是轴对称图形，就可以过关．那么一次过关的概率是（）Ａ．Ｂ．Ｃ．Ｄ．10、小张外出旅游时带了两件上衣(一件蓝色,一件黄色)和3条长裤(一件蓝色,一件黄色,一件绿色),他任意拿出一件上衣和一条长裤,正好是同色上衣和长裤的概率是 ( ) A. B. C. D. 二、填空题（每题3分共30分）11、根据天气预报，明天降水概率为20％，后天降水概率为80％，假如你准备明天或后天去放风筝，你选择天为佳．12、如图，每一个标有数字的方块均是可以翻动的木牌，其中只有两块木牌的背面贴有中奖标志，则随机翻动一块木牌中奖的概率为_______.13、在标有1，3，4，6，8的五张卡片中，随机抽取两张，和为奇数的概率为。

八年级物理下册第六章《常见光学仪器》单元测试题

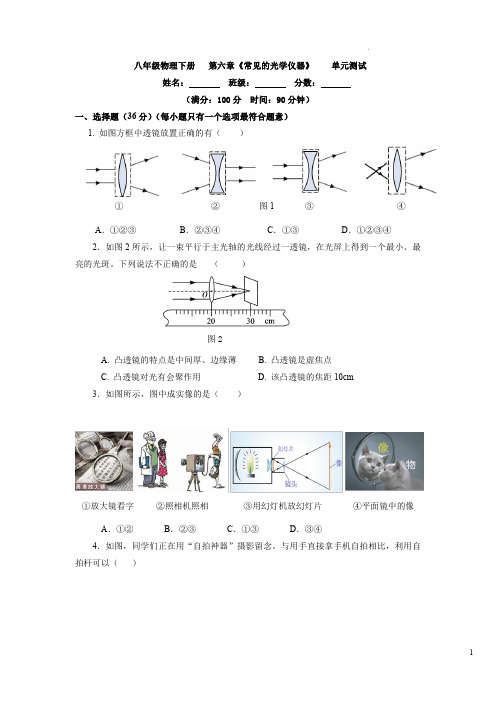
八年级物理下册第六章《常见的光学仪器》单元测试姓名：班级：分数：（满分：100分时间：90分钟）一、选择题（36分）（每小题只有一个选项最符合题意）1.如图方框中透镜放置正确的有（）①②图1③④A．①②③B．②③④C．①③D．①②③④2．如图2所示，让一束平行于主光轴的光线经过一透镜，在光屏上得到一个最小、最亮的光斑。

下列说法不正确的是（）图2A.凸透镜的特点是中间厚、边缘薄B.凸透镜是虚焦点C.凸透镜对光有会聚作用D.该凸透镜的焦距10cm3．如图所示，图中成实像的是（）①放大镜看字②照相机照相③用幻灯机放幻灯片④平面镜中的像A．①②B．②③C．①③D．③④4．如图，同学们正在用“自拍神器”摄影留念。

与用手直接拿手机自拍相比，利用自拍杆可以（）A．增大物距，减小像的大小，从而增大取景范围B．减小物距，减小像的大小，从而减小取景范围C．增大物距，增大像的大小，从而减小取景范围D．减小物距，增大像的大小，从而增大取景范围5．小乐用放大镜看指纹时，觉得指纹的像太小，为使指纹的像大一些，正确的做法是（）A．眼睛和手指不动，让放大镜离手指稍近些B．眼睛和手指不动，让放大镜离手指稍远些C．放大镜和手指不动，让眼睛离放大镜稍近些D．放大镜和手指不动，让眼睛离放大镜稍远些6．在探究凸透镜成像规律实验中，当烛焰位于距离凸透镜一倍焦距以内时，人眼观察到烛焰成像的情形是图中的（）7．如图所示，a、b、c、d在凸透镜主光轴上，F为焦点。

若保持凸透镜和光屏的位置不变，则物体放在哪个位置时，可能在光屏上观察到物体的像（）A．a点B．b点C．c点D．d点8．物体放在凸透镜前12cm时，在透镜另一侧的光屏上成一个倒立放大的像；则当物体距该透镜8cm时，所成的像可能是（）A倒立缩小的像B倒立等大的像C倒立放大的像D正立等大的虚像9．在“探究凸透镜成像的规律”实验中，下列说法正确的是（）A．将蜡烛移至a处时，移动光屏，可看见放大、正立的实像B．将蜡烛移至b处时，移动光屏，可看见缩小、倒立的实像C．将蜡烛移至c处时，移动光屏，可看见放大、倒立的实像D．将蜡烛移至d处时，移动光屏，可看见放大、正立的虚像10.小红同学学习了“小孔成像”、“平面镜成像”和“凸透镜成像”的知识后，总结出关于“实像”和“虚像”的一些特点，错误的是（）A．虚像不可以用光屏承接B．实像可以是放大的，也可以是缩小的C．既有等大实像，也有等大虚像D．观察实像时有光进入人眼，观察虚像时没有光进入人眼11．关于显微镜和天文望远镜所成的像和所观察到的像，下列说法中正确的是（）A.用显微镜观察到的是虚像，用望远镜看到的是实像B.用显微镜观察到的是实像，用望远镜看到的是虚像C.目镜成的是实像，物镜成的是虚像D.目镜成的是虚像，物镜成的是实像12．如图4所示，关于近视眼和远视眼，下列说法正确的是（）A．甲为近视眼，应佩戴凸透镜矫正B．乙为近视眼，应佩戴凹透镜矫正C．甲为远视眼，应佩戴凹透镜矫正D．乙为远视眼，应佩戴凸透镜矫正图4图513．在探究凸透镜成像规律的实验中，将蜡烛放在凸透镜前适当位置，调节光屏位置得到清晰的像。

(最新)数学七年级下册第六章《单元检测试题》含答案

七年级下册数学《第6章实数》单元测试题一．选择题（共10小题）1．4的平方根是（）A．2 B．﹣2 C．16 D．±22．的算术平方根是（）A．2 B．4 C．±2 D．±43．下列说法正确的是（）A．﹣81平方根是﹣9B．的平方根是±9C．平方根等于它本身的数是1和0D．一定是正数4．的值是（）A．2 B．﹣2 C．4 D．﹣45．下列各数：0.101001…（相邻两个1之间的0的个数逐次加1），，，，，中，无理数有（）A．1个B．2个C．3个D．4个6．无理数是（）A．带根号的数B．无限循环小数C．无限不循环小数D．开不尽方的数7．实数2019的相反数是（）A．2019 B．C．D．﹣20198．如图所示，直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A 点，则A点表示的数是（）A．﹣2π﹣1 B．﹣1+πC．﹣1+2πD．﹣π9．下列数中，比大的实数是（）A．﹣5 B．0 C．3 D．10．若k＜＜k+1（k是整数），则k等于（）A．7 B．8 C．9 D．10二．填空题（共8小题）11． +＝．12．若一个正数x的两个平方根分别是3m+1与﹣2m﹣3，则x的值是．13．如果一个数的立方根是4，那么这个数的算术平方根是．14．﹣的相反数是．15．实数a、b在数轴上如图所示，化简|a|﹣|a﹣b|＝．16．写一个比4小的无理数．17．将实数﹣，，π，﹣按从小到大的顺序排列，并用“＜”连接：．18．若x＜﹣1＜y且x，y是两个连续的整数，则x+y的值是．三．解答题（共7小题）19．计算++﹣|1﹣|20．求下列各式中x的值：（1）2x2＝8；（2）64x3+27＝021．把下列各数在数轴上表示出来，并把它们按从小到大的顺序用“＜”连接：，﹣1.2，|﹣2|，0，22．已知表示a，b两个实数的点在数轴上的位置如图所示，化简|a﹣b|+|a+b|．23．实数a，b互为相反数，c，d互为倒数，x的绝对值为3．求代数式x2+（a+b ﹣cd）x++的值．24．一个正数的两个平方根分别是2a﹣2和a﹣4，求这个正数．25．（1）在实数范围内定义运算“⊕”，其法则为：a⊕b＝a2﹣b2，求方程（4⊕3）⊕x＝24的解．（2）已知2a的平方根是±2，3是3a+b的立方根，求a﹣2b的值．参考答案一．选择题（共10小题）1．4的平方根是（）A．2 B．﹣2 C．16 D．±2【分析】根据平方根的定义即可求出答案．【解答】解：∵（±2）2＝4，∴4的平方根是±2，故选：D．【点评】本题考查平方根的定义，解题的关键是正确理解平方根的定义，本题属于基础题型．2．的算术平方根是（）A．2 B．4 C．±2 D．±4【分析】利用算术平方根定义计算即可得到结果．【解答】解：＝4，4的算术平方根是2，故选：A．【点评】此题考查了算术平方根，熟练掌握算术平方根的定义是解本题的关键．3．下列说法正确的是（）A．﹣81平方根是﹣9B．的平方根是±9C．平方根等于它本身的数是1和0D．一定是正数【分析】根据一个正数有两个平方根，这两个平方根互为相反数，零的平方根是零，负数没有平方根进行分析即可．【解答】解：A、﹣81没有平方根，故原题错误；B、＝9的平方根是±3，故原题错误；C、平方根等于它本身的数是0，故原题错误；D、一定是正数，故原题正确；故选：D．【点评】此题主要考查了平方根，关键是掌握平方根的性质．4．的值是（）A．2 B．﹣2 C．4 D．﹣4【分析】根据立方根的定义求出即可．【解答】解：＝﹣2，故选：B．【点评】本题考查了对立方根定义的应用，注意：a的立方根是．5．下列各数：0.101001…（相邻两个1之间的0的个数逐次加1），，，，，中，无理数有（）A．1个B．2个C．3个D．4个【分析】根据无理数的定义逐个判断即可．【解答】解：无理数有：0.101001…（相邻两个1之间的0的个数逐次加1），，，共3个，故选：C．【点评】本题考查了无理数的定义，能熟记无理数的定义的内容是解此题的关键，注意：无理数是指无限不循环小数．6．无理数是（）A．带根号的数B．无限循环小数C．无限不循环小数D．开不尽方的数【分析】根据无理数的概念：无限不循环小数叫无理数进行分析即可．【解答】解：无限不循环小数叫无理数，故选：C．【点评】此题主要考查了实数运算，关键是掌握无理数定义．7．实数2019的相反数是（）A．2019 B．C．D．﹣2019【分析】根据相反数的意义，直接可得结论．【解答】解：因为a的相反数是﹣a，所以2019的相反数是﹣2019．故选：D．【点评】本题考查了相反数的意义．理解a的相反数是﹣a，是解决本题的关键．8．如图所示，直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A 点，则A点表示的数是（）A．﹣2π﹣1 B．﹣1+πC．﹣1+2πD．﹣π【分析】先求出圆的周长π，即得到OA的长，然后根据数轴上的点与实数一一对应的关系即可得到点A表示的数．【解答】解：∵直径为单位1的圆的周长＝2π•＝π，∴OA＝π，∴点A表示的数为﹣π．故选：D．【点评】本题考查了实数与数轴：数轴上的点与实数一一对应．也考查了实数的估算．9．下列数中，比大的实数是（）A．﹣5 B．0 C．3 D．【分析】由于正数大于0，0大于负数，正数大于负数，根据实数大小比较法则求解即可．【解答】解：将四个选分别与进行比较，A、B、D中的数均比它小，只有C比它大．故选：C．【点评】此题主要考查了实数大小的比较，其中大小比较法则：（1）正数大于0，0大于负数，正数大于负数；（2）两个负数，绝对值大的反而小．10．若k＜＜k+1（k是整数），则k等于（）A．7 B．8 C．9 D．10【分析】估算确定出k的值即可．【解答】解：∵9＜10＜16，∴3＜＜4，即9＜3＝＜10，则k等于9，故选：C．【点评】此题考查了估算无理数的大小，弄清估算的方法是解本题的关键．二．填空题（共8小题）11． +＝ 5 ．【分析】直接利用算术平方根以及立方根的性质化简得出答案．【解答】解： +＝3+2＝5．故答案为：5．【点评】此题主要考查了实数运算，正确化简各数是解题关键．12．若一个正数x的两个平方根分别是3m+1与﹣2m﹣3，则x的值是49 ．【分析】根据平方根的定义即可求出答案．【解答】解：由题意可知：3m+1﹣2m﹣3＝0，解得：m＝2，∴3m+1＝7，∴x＝72＝49，故答案为：49．【点评】本题考查平方根，解题的关键是熟练运用平方根的定义，本题属于基础题型．13．如果一个数的立方根是4，那么这个数的算术平方根是8 ．【分析】根据立方跟乘方运算，可得被开方数，根据开方运算，可得算术平方根．【解答】解；43＝64，＝8，故答案案为：8．【点评】本题考查了立方根，先立方运算，再开平方运算．14．﹣的相反数是．【分析】根据相反数的定义进行填空即可．【解答】解：∵﹣的相反数是，故答案为．【点评】本题考查了实数的性质以及算术平方根，掌握相反数的定义是解题的关键．15．实数a、b在数轴上如图所示，化简|a|﹣|a﹣b|＝﹣b．【分析】观察数轴，可得出a＜0，a﹣b＜0，再结合绝对值的定义即可求出结论．【解答】解：观察函数图象，可知：a＜0＜b，∴a﹣b＜0，∴|a|﹣|a﹣b|＝﹣a+a﹣b＝﹣b．故答案为：﹣b．【点评】本题考查了实数与数轴以及绝对值，观察数轴找出a＜0，a﹣b＜0是解题的关键．16．写一个比4小的无理数π．【分析】找出一个小于4的无理数即可．【解答】解：比4小的无理数可以是π，故答案为：π【点评】此题考查了实数大小比较，以及无理数，熟练掌握无理数的定义是解本题的关键．17．将实数﹣，，π，﹣按从小到大的顺序排列，并用“＜”连接：﹣＜π．【分析】判断各数大小，用小于号连接即可．【解答】解：根据题意得：﹣＜﹣＜＜π，故答案为：﹣＜﹣＜＜π【点评】此题考查了实数大小比较，算术平方根，以及立方根，熟练掌握各自的性质是解本题的关键．18．若x＜﹣1＜y且x，y是两个连续的整数，则x+y的值是 3 ．【分析】估算得出的范围，进而求出x与y的值，即可求出所求．【解答】解：∵4＜6＜9，∴2＜＜3，即1＜﹣1＜2，∴x＝1，y＝2，则x+y＝1+2＝3，故答案为：3【点评】此题考查了估算无理数的大小，弄清估算的方法是解本题的关键．三．解答题（共7小题）19．计算++﹣|1﹣|【分析】原式利用二次用平方根、立方根定义，以及绝对值的代数意义计算即可求出值；【解答】解：原式＝﹣1﹣3+2﹣+1＝﹣1﹣；【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．20．求下列各式中x的值：（1）2x2＝8；（2）64x3+27＝0【分析】（1）将x2的系数化为1后利用平方根的定义求解可得；（2）将x3的系数化为1后，利用立方根的定义求解可得【解答】解：（1）∵2x2＝8，∴x2＝4，则x＝，即x＝±2；（2）∵64x3+27＝0，∴64x3＝﹣27，则x3＝﹣，∴x＝＝﹣．【点评】本题主要考查平方根与立方根，解题的关键是掌握平方根与立方根的定义．21．把下列各数在数轴上表示出来，并把它们按从小到大的顺序用“＜”连接：，﹣1.2，|﹣2|，0，【分析】先在数轴上表示各个数，再比较即可．【解答】解：＜﹣1.2＜0＜|﹣2|＜．【点评】本题考查了数轴和实数的大小比较，能熟记实数的大小比较法则的内容是解此题的关键，注意：在数轴上表示的数，右边的数总比左边的数大．22．已知表示a，b两个实数的点在数轴上的位置如图所示，化简|a﹣b|+|a+b|．【分析】根据数轴判定a、b与0的大小，然后根据绝对值的性质即可求出答案．【解答】解：由数轴知b＜a＜0，∴a﹣b＞0，a+b＜0，∴|a﹣b|＝a﹣b，|a+b|＝﹣（a+b）＝﹣a﹣b，∴原式＝a﹣b﹣a﹣b＝﹣2b．【点评】本题实数与数轴，解题的关键是根据数轴判断a、b与0的大小，本题属于基础题型．23．实数a，b互为相反数，c，d互为倒数，x的绝对值为3．求代数式x2+（a+b ﹣cd）x++的值．【分析】根据相反数、倒数、绝对值的性质即可求出答案．【解答】解：由题意可知：a+b＝0，cd＝1，x＝±3，∴原式＝9+（0﹣1）+0+1＝9﹣1+1＝9．【点评】本题考查学生的运算，解题的关键是正确理解相反数、倒数、绝对值的性质，本题属于基础题型．24．一个正数的两个平方根分别是2a﹣2和a﹣4，求这个正数．【分析】根据平方根的定义和相反数得出2a﹣2+a﹣4＝0，求出a＝2，求出2a﹣2＝2，即可得出答案．【解答】解：一个正数的两个平方根分别是2a﹣2和a﹣4，∴2a﹣2+a﹣4＝0，∴a＝2，∴2a﹣2＝2，∴这个正数为2的平方是4．【点评】本题考查了平方根和相反数的应用，解此题的关键是求出a的值，注意：一个正数有两个平方根，它们互为相反数．25．（1）在实数范围内定义运算“⊕”，其法则为：a⊕b＝a2﹣b2，求方程（4⊕3）⊕x＝24的解．（2）已知2a的平方根是±2，3是3a+b的立方根，求a﹣2b的值．【分析】（1）根据所给公式进行运算可得72﹣x2＝24，然后再解方程即可；（2）利用平方根的性质可得2a＝（±2）2，进而可得a的值，然后求出b，进而可得答案．【解答】解：（1）∵a⊕b＝a2﹣b2，∴（4⊕3）⊕x＝（42﹣32）⊕x＝7⊕x＝72﹣x2，∴72﹣x2＝24，∴x2＝25，∴x＝±5．（2）由题意，2a＝（±2）2，∴a＝2，当a＝2时，3a+b＝6+b，由于33＝6+b，∴b＝21，∴a﹣2b＝2﹣2×21＝﹣40．【点评】此题主要考查了实数运算，以及平方根和立方根，关键是掌握一个正数有两个平方根，这两个平方根互为相反数．。

人教版七年级下册第六章《实数》单元测试题及答案

第六章《实数》单元测试题一、用心填一填，一定能填对：（每空1分，共53分）1. 正数的平方根记作，正数的正的平方根记作，正数的负的平方根记作。

2. 如果2=4,则叫作4的，记作。

3。

81的平方根是，0。

64的算术平方根是。

5的平方根是，0的平方根是。

４。

的算术平方根的相反数是，平方根的倒数是，平方根的绝对值是。

５。

的相反数的倒数是，这个结果的算术平方根是。

６。

当时，有意义,当时，=0.７. 如果=5，则= .８。

如果一个正数的一个平方根是m，那么这个数的另一个平方根是 ,这个数的算术平方根是 ,两个平方根的和是 .９。

当>0时，表示的，当<0时，表示的 .10。

的负的平方根是，的平方根是。

11. 的平方根是 .12. 如果那么是的，是的.13。

0。

064的立方根是，的立方根是，3的立方根是，0的立方根是，的立方根是 .14．是5的，一个数的立方根是，则这个数是 .15． , ，。

16． .17．当时，有意义.18、若,则= ，若，则= 。

19．。

20．若是225的算术平方根，则的立方根是 .21。

的平方根是。

22。

若是的立方根,则的平方根是 .23。

的相反数是。

2４。

若，则。

25. 若有意义，则26。

比较大小: ， ,27. 数轴上离原点距离是的点表示的数是 .28. 无理数满足, 请写出两个你熟悉的无理数 .二、你很聪明,一定能选对:(每小题1分，共10分)1。

0。

0196的算术平方根是（）A 0.014B 0。

14CD ±0。

14２. 下列各式正确的是（）A B C D３. 下列语句、式子中① 4是16的算术平方根,即②4是16的算术平方根,即③—7是49的算术平方根，即④7是的算术平方根，即其中正确的是（）A ①③B ②③C ②④D ①④4。

下列说法错误的有（）①无限小数一定是无理数；②无理数一定是无限小数；③带根号的数一定是无理数；④不带根号的数一定是有理数.A ①②③B ②③④C ①③④D ①②④5. 的平方根是（ )A 9B 3C ±３D ±９6. 若一个数的算术平方根与它的立方根相同，则这个数是（）A 1B 0或1C 0D 非负数7. 下列语句正确的是( ）A 的立方根是2.B —3是27的负的立方根。

第六章人类与地理环境的协调发展单元测试题1

第六章人类与地理环境的协调发展单元测试题1第Ⅰ卷（选择题）本题共25小题，每小题2分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．关于环境问题分布特点的叙述，正确的是( )A．在城市地区，环境问题主要表现为生态破坏B．在广大的乡村地区，环境问题主要表现为环境污染C．从全球看，发达国家的环境问题比发展中国家更为严重D．有些环境问题不只影响某一个国家或地区，而且可能影响到其他国家甚至全球2．从总体上讲，环境问题的实质就是( )A．人口问题B．资源问题 C．生存问题D．发展问题3．联合国环境与发展大会通过的《气候变化框架公约》符合( )A．公平性原则B．持续性原则 C．共同性原则D．发展性原则4．下列做法，符合可持续发展思想的是( )①使用再生纸②垃圾分类回收利用③自备蓝子或布袋购物④将旧衣物、玩具、书籍捐赠给需要的人A．①③B．③④ C．②③④D．①②③④读图，回答5～6题。

5．图甲反映了人类与环境之间的何种关系( )①对立②统一③环境对人类的反馈作用④人类对环境资源的利用A．①③ B．②④ C．①④ D．②③6．图乙中能反映图甲的是( )A．A、B B．A、C C．D、B D．C、B目前，我国“速生鸡(在养殖过程中，超剂量、超范围违规使用抗生素)事件已经被媒体揭露。

现在越来越多的人期待厂家能生产更多更好的“绿色食品”。

据此回答7～8题。

7．肉制品厂家用牺牲人们健康来获取高利润的做法违背了可持续发展的A．公平性原则 B．持续性原则 C．共同性原则 D．公正性原则8．“绿色食品”是当今的热门话题。

为了生产“绿色食品”，下列措施正确的是①使用有剧毒的农药防治病虫害②引进抗病虫害的优良品种③在面粉中添加增白剂、防腐剂④利用作物害虫的天敌防治病虫害等A．①② B．②④ C．②③ D．③④下图是一座石碑，上面刻着美索不达米亚人的太阳神——萨玛斯正在接受礼拜。

据此完成9～10题。

9. 石碑所反映的时代是人类社会发展的四个阶段中的( )A．原始文明时代 B．农业文明时代 C．工业文明时代 D．环境文明时代10. 这幅石碑反映出当时的人类与环境的关系是( )A．人类对环境既崇拜又依赖B．人类与环境的对抗性明显增强，环境遭到破坏C．人地关系全面不协调D．人类正谋求与环境协调发展下图是某区域环境问题示意图，读图回答11～12题。

人教版七年级下册数学第六章实数单元测试训练卷含答案

22．方案一可行．
因为正方形胶合板的面积为 4 m2，所以正方形胶合板的边长为 4＝2(m)．
如图所示，沿着 EF 裁剪，因为 BC＝EF＝2 m，所以只要使 BE＝CF＝3÷2＝1.5(m)就满足条
件．
方案二不可行．理由如下：设所裁长方形装饰材料的长为 3x m、宽为 2x m. 则 3x·2x＝3，
11. 1－ 2 的相反数是_______，绝对值是_________．
12. 我们可以利用计算器求一个正数 a 的算术平方根，其操作方法是按顺序进行按键输入：
3 a ＝ .小明按键输入 3 1 6 ＝显示结果为 4，则他按键输入
3 1 6 0 0 ＝显示结果应为____. 13. 计算：| 2－ 3|＋ 2＝________. 14. 一个正数的平方根分别是 x＋1 和 x－5，则 x＝________． 15. 有两个正方体纸盒，已知小正方体纸盒的棱长是 5 cm，大正方体纸盒的体积比小正方体纸盒的体积大 91 cm3，则大正方体纸盒的棱长是__ __cm. 16. 现有两个大小不等的正方体茶叶罐，大正方体茶叶罐的体积为 1 000 cm3，小正方体茶叶罐的体积为 125 cm3，将其叠放在一起放在地面上(如图)，则这两个茶叶罐的最高点 A 到地面的距离是________cm.
()
A．2 倍 B．3 倍
C．4 倍 D．5 倍
7. 实数 a，b 在数轴上对应点的位置如图所示，则化简（a－1）2－（a－b）2＋b 的结果
是( )
A．1
B．b＋1
C．2a
D．1－2a
8. 制作一个表面积为 30 cm2 的无盖正方体纸盒，则这个正方体纸盒的棱长是( )
A. 6 cm B. 5 cm

七年级数学下册《第六章实数》单元检测卷(附带答案)

七年级数学下册《第六章实数》单元检测卷(附带答案)一、选择题(每题3分,共30分)1.9的平方根是（） A.3 B.-3C.±3D.不存在 2.38=（）A.2B.-2C.±2D.不存在3.下列说法正确的是（） A.-0.064的立方根是0.4 B.-9的平方根是±3 C.16316D.0.01的立方根是0.0000014．若a 3＝－27，则a 的倒数是( )A ．3B ．－3C.13D ．－135．面积为8的正方形的边长在( )5. ，且，则的值为（）A ．B ．C ．1D ．1或6. 已知x ，y ，则y x 的立方根是( )AB ．－2C ．－8D ．±27．下列命题中正确的是（）①0.027的立方根是0.3 不可能是负数 ③如果a 是b 的立方根，那么ab≥0 ④一个数的平方根与其立方根相同，则这个数是1． A ．①③ B ．②④ C ．①④ D ．③④8.一个数的算术平方根等于这个数的立方根，那么这个数是（）A.1B.0或1C.0D. ±19.下列实数317 -π 3.14159 8 327 12中无理数有（）A.2个B.3个C.4个D.5个10.如图，数轴上A ，B 两点对应的实数分别是1和3，若AB=BC ，则点C 所对应的实数是（）A.231B.13+C.23D.231二、填空题(每题3分,共24分) 11．4是_____的算术平方根．2316,27a b ==-||a b a b -=-+a b 1-7-7-()2320x y -+=363a12．25的算术平方根是_______.13．若一个正数的两个不同的平方根分别是2a﹣1和﹣a+2，则这个正数是．14．若a＜0，化简＝．15．已知10+的整数部分是x，小数部分是y，求x﹣y的相反数．16．已知x，y都是实数，且y＝x－3＋3－x＋4，则y x＝________.17．点A在数轴上和表示1的点相距6个单位长度，则点A表示的数为________．18．若两个连续整数x，y满足x＜5＋1＜y，则x＋y的值是________．三、解答题(满分46分,19题6分，20、21、22、23、24题每题8分)19．(6分)计算：(1)|－2|＋3－8－(－1)2017(2)9－（－6）2－3－27.20．(8分)求下列各式中x的值．(1)(x－3)2－4＝21 (2)27(x＋1)3＋8＝0.21．(本题8分)已知与互为相反数，求的平方根．22．你能找出规律吗？(1)计算：9×16＝________，9×16＝________ 25×36＝________，25×36＝________．(2)请按找到的规律计算：5×125 ②123×935.(3)已知a＝2，b＝10，用含a，b的式子表示40.23.如图，用两个面积为28cm的小正方形纸片剪拼成一个大的正方形．（1）大正方形的边长是________cm（2）请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为214cm的长方形纸片，使它的长宽之比为2:1，若能，求出这个长方形纸片的长和宽，若不能，请说明理由．24.已知：31a+的立方根是2-，21b-的算术平方根3，c43（1）求,,a b c的值（2）求922a b c-+的平方根．参考答案一.填空题题号12345678910答案C B C D B C A B A A二.选择题11．【答案】16【解析】试题解析：∵42=16∴4是16的算术平方根12．【答案】513．【解答】解：∵一个正数的两个平方根分别是2a﹣1与﹣a+2∴2a﹣1﹣a+2＝0解得：a＝﹣1故2a﹣1＝﹣3则这个正数是：（﹣3）2＝9故答案为：914．【答案】1﹣a15．【答案】16．【答案】6417．【答案】1－6或1＋6点拨：数轴上到某个点距离为a(a＞0)个单位长度的点有两个．注意运用数形结合思想，利用数轴帮助分析．18．【答案】7点拨：∵2＜5＜3，∴3＜5＋1＜4.∵x＜5＋1＜y，且x，y为两个连续整数，∴x＝3，y＝4.∴x＋y＝3＋4＝7.三.解答题19．【答案】解：(1)原式＝2－2＋1＝1.(4分)(2)原式＝3－6＋3＝0.(8分)20．【答案】解：(1)移项得(x－3)2＝25，∴x－3＝5或x－3＝－5，∴x＝8或－2.(5分)(2)移项整理得(x＋1)3＝－827，∴x＋1＝－23，∴x＝－53.(10分)21．【答案】解：根据相反数的定义可知：解得：a=-8,b=364的平方根是：22．【答案】解：(1)12 12 30 30(2)①原式＝5×125＝625＝25②原式＝53×485＝16＝4(3)40＝2×2×10＝2×2×10＝a2b.23．【答案】（1）4 （2）不能，理由见解析．【解析】（1）根据已知正方形的面积求出大正方形的边长即可（2）先设未知数根据面积=14（cm2）列方程，求出长方形的边长，将长方形的长与正方形边长比较大小再判断即可．解：（1）两个正方形面积之和为：2×8=16（cm2）∴拼成的大正方形的面积=16（cm 2） ∴大正方形的边长是4cm 故答案为：4（2）设长方形纸片的长为2xcm ，宽为xcm 则2x •x =14 解得：7x =2x 7>4∴不存在长宽之比为2:1且面积为214cm 的长方形纸片． 24．【答案】（1）3,5,6a b c =-== （2）其平方根为4± 【解析】（1）根据立方根，算术平方根，无理数的估算即可求出,,a b c 的值（2）将（1）题求出的值代入922a b c -+，求出值之后再求出平方根．解：（1）由题得318,219a b +=--= 3,5a b ∴=-= 364349<6437∴<6c ∴=3,5,6a b c ∴=-==（2）当3,5,6a b c =-==时()99223561622a b c -+=⨯--+⨯=∴其平方根为164±±。

人教版八年级上册物理第六章质量与密度单元试题(含答案)

第六章质量与密度章末测试卷一、单选题1．下列物体的质量最接近50kg的是（）A．一枚硬币B．一个鸡蛋C．一名中学生D．一支铅笔2．下列关于质量的说法，正确的是（）A．把铁块轧成薄铁片，质量变小B．冰箱里的一瓶矿泉水结冰，质量变小C．把物理课本放在平邑和放在北京的质量是一样的D．“神舟十三号”载人飞船从地球到空间站升空后，飞船内物资的质量变小3．关于托盘天平的使用方法，下列说法中正确的是（）A．调节横梁平衡时，指针指在分度盘左边，应向左调节平衡螺母B．在称物体质量前，应先估测被测物体的质量，以免超过量程C．称量时，被测物体放在右盘，砝码放在左盘D．称量时，向砝码盘中加砝码的顺序是由小到大4．在“用托盘天平称物体的质量”的实验中，下列操作中不正确的是A．调节天平横梁平衡时，应先将游码移至标尺左端的“0”刻度线上B．判断天平横梁是否平衡时，不一定要等指针完全静止下来C．称量时，发现指针偏左，应将左侧的平衡螺母向右调，右侧的平衡螺母向左调D．潮湿物体或化学药品都不能直接放在托盘中5．物理知识与生活联系非常紧密，下列关于密度的一些说法正确的是（）A．1kg的水和1kg的冰的密度相同B．可以利用密度来鉴别物质，因为不同物质的密度一定不同C．为减轻质量，航空器材常采用强度高、密度大的合金或新型合成材料D．发生火灾时，受困人员常采取弯腰甚至爬行的姿势撤离，是因为含有有害物质的空气温度较高，密度较小，大量聚集在房间的上方6．关于质量、密度，下列说法正确的是（）A．同种物质随着温度降低，密度会增大B．质量是指物体所含物质的多少C．固体的密度一定大于液体、气体的密度D．物体的质量随着它的形状、状态和位置的改变而改变7．如图所示是甲和乙两种物质的质量与体积关系图象，下列说法正确的是（）A．甲物质的密度随体积增大而增大B．当甲和乙两物质的质量相同时，乙物质的体积较大C．甲、乙两种物质的密度之比是4：1D．体积为5cm3的乙物质，质量为10g8．李华同学在实验室测量盐水的密度。

最新第六章单元测验

人教版七年级数学下册 第六章 实数。单元测试题精选(Word版附答案)

(最新)部编人教版地理七年级下册《第六章单元检测试题》(含答案解析)

(最新)部编人教版地理七年级下册《第六章单元检测试题》(含答案解析)

第六章实数单元测试卷

最新八年级数学第六章数据的分析单元测试题及答案

第六章 实数单元测试-2022-2023学年七年级数学下册同步精品讲义(教师版)

第六章 实数单元测试及答案

第6章第6单元单元测验(下载版)

教科版《第六章-质量和密度》单元检测题(含答案)

初级会计实务(2022)第六章利润单元测试

第六章 频率与概率单元测试(含答案)

八年级物理下册 第六章《常见光学仪器》单元测试题

(最新)数学七年级下册第六章《单元检测试题 》含答案

人教版七年级下册第六章《实数》单元测试题及答案

第六章人类与地理环境的协调发展单元测试题1

人教版七年级下册数学第六章实数 单元测试训练卷含答案

七年级数学下册《第六章 实数》单元检测卷(附带答案)

人教版八年级上册物理第六章质量与密度单元试题(含答案)

人教版七年级数学下册第六章实数。单元测试题精选(Word版附答案)

第六章实数单元测试-2022-2023学年七年级数学下册同步精品讲义(教师版)

第六章实数单元测试及答案

第六章频率与概率单元测试(含答案)

八年级物理下册第六章《常见光学仪器》单元测试题

(最新)数学七年级下册第六章《单元检测试题》含答案

人教版七年级下册数学第六章实数单元测试训练卷含答案

七年级数学下册《第六章实数》单元检测卷(附带答案)