初中数学奥林匹克初中训练题(032)
初中数学奥林匹克竞赛题包括答案.docx

初中数学奥林匹克竞赛题及答案奥数题一一、选择题(每题 1 分,共 10 分)1.如果 a,b 都代表有理数,并且a+b=0 ,那么 ( ) A.a,b 都是 0B.a,b 之一是 0C.a,b 互为相反数D. a,b 互为倒数答案: C解析:令 a=2 , b= - 2,满足 2+( - 2)=0 ,由此 a、b 互为相反数。
2.下面的说法中正确的是( )A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式答案: D3都是单项式.两个单项式33A。
两个单项式解析: x2, x x , x2之和为 x +x 2是多项式,排除x2, 2x2之和为3x2是单项式,排除 B。
两个多项式x3+x2 与 x3-x2之和为2x3 是个单项式,排除 C,因此选 D。
3.下面说法中不正确的是( )A.有最小的自然数B.没有最小的正有理数Word资料C.没有最大的负整数D.没有最大的非负数答案: C解析:最大的负整数是-1 ,故 C 错误。
4.如果 a,b 代表有理数,并且a+b 的值大于 a- b 的值,那么( ) A.a,b 同号B.a,b 异号C.a>0D. b> 0答案: D5.大于-π并且不是自然数的整数有( )A.2 个B.3 个C.4 个D.无数个答案: C解析:在数轴上容易看出:在-π右边0的左边(包括0 在)的整数只有-3,- 2,-1 ,0 共 4 个.选 C。
6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
Word资料这四种说法中,不正确的说法的个数是( )A.0 个B.1 个C.2 个D. 3 个答案: B解析:负数的平方是正数,所以一定大于它本身,故 C 错误。
7.a 代表有理数,那么, a 和- a 的大小关系是( )A.a 大于- aB.a 小于- aC.a 大于- a 或 a 小于- aD. a 不一定大于- a答案: D解析:令 a=0 ,马上可以排除A、 B、 C,应选 D。
初中数学奥林匹克训练题及答案五

又 AD ∥BC ,故 ∠ABC + ∠BAD = 180°,
即 ∠ADC + ∠BAD = 180°.
所以 ,AB ∥CD ,四边形 ABCD 是平行四边形.
5. (A) . 因为 aabb = 1 000 a + 100 a + 10 b + b
= 11 (100 a + b) , 由题意可设 100 a + b = 11 c2 ( c 是正整数) , 所以 ,101 < 100 a + b = 11 c2 < 999 , 即 9 < c2 < 90. 于是 ,4 ≤c ≤9. 经检验 , c = 8 时满足条件 ,此时 a = 7 , b = 4. 故 a + b = 11.
数学奥林匹克初中训练题
第一试
一 、选择题 (每小题 7 分 ,共 42 分) 1. 若 a 、b 都是质数 ,且 a2 + b = 2 003 , 则 a + b 的值等于 ( ) . (A) 1 999 (B) 2 000 (C) 2 001 (D) 2 002
2.设 a > 0 > b > c , a + b + c = 1 , M =
所以 , x - 8 = 30 ,知 x = 38.
即汽车在途中排除故障花了 38 min.
ab - ac = 360 ,则 abc 的最大值是 .
3. 若
abc
=
1
,
1
+
x a+
ab
+ 1+
x b+
bc
+
1
+
x c+
初中数学奥林匹克训练题及答案

初中数学奥林匹克训练题第一试一、选择题(每小题7分,共42分)1.已知m 、n 是两个连续正整数,m<n ,且a=mn ,设x=m -a n a ++,y=m -a n a -+.下列说法正确的是( ).(A)x 为奇数,y 为偶数 (B)x 为偶数,y 为奇数(C)x 、y 都为奇数 (D)x 、y 都为偶数2.设a 、b 、c 和S 分别为三角形的三边长和面积,关于x 的方程b 2x 2+(b 2+c 2-a 2)x+c 2=0的判别式为Δ.则Δ与S 的大小关系为( ).(A)Δ=16S 2 (B)Δ=-16S 2 (C)Δ=16S (D)Δ=-16S3.设a 为5353--+的小数部分,b 为336336--+的小数部分.则a b 12-的值为( ). (A) 6 + 2 -1 (B) 6- 2+1 (C) 6- 2-1 (D) 6+2+14.如图,D 、E 分别为△ABC 的边AB 、AC 上的点,△ACD 与△BCD的周长相等,△ABE 与△CBE 的周长相等,记△ABC 的面积为S.若∠ACB=90°,则AD ·CE 与S 的大小关系为( ).(A)S=AD·CE(B)S>AD·CE(C)S<AD ·CE(D)无法确定5.如图,在△ABC 中,AB=8,BC=7,AC=6,延长边BC 到点P ,使得△PAB 与△PCA 相似.则PC 的长是( ).(A)7 (B)8 (C)9 (D)106.如图,以PQ=2r(r ∈Q)为直径的圆与一个以R(R ∈Q)为半径的圆相切于点P.正方形ABCD 的顶点A 、B 在大圆上,小圆在正方形的外部且与边CD 切于点Q.若正方形的边长为有理数,则R 、r 的值可能是( ).(A)R=5,r=2 (B)R=4,r=3/2(C)R=4,r=2 (D)R=5,r=3/2二、填空题(每小题7分,共28分)1.已知方程x 2+x-1=0的两个根为α、β.则αββα33+的值为 . 2.把1,2,…,2 008个正整数分成1 004组:a 1,b 1;a 2,b 2;…;a 1 004,b 1 004,且满足a 1+b 1=a 2+b 2=…=a 1004+b 1004.对于所有的i(i=1,2,…,1 004),a i b i 的最大值为 .3.AD 、BE 、CF 为△ABC 的内角平分线.若BD+BF=CD+CE=AE+AF ,则∠BAC 的度数为 .4.下列四个命题:①一组对边相等且一组对角相等的四边形是平行四边形; ②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;③一组对角相等且这一组对角的顶点所联结的对角线被另一条对角线平分的四边形是平行四边形; ④一组对角相等且这一组对角的顶点所联结的对角线平分另一条对角线的四边形是平行四边形.其中,正确命题的序号是 .第二试一、(20分)已知△ABC 中,∠A>∠B>∠C ,且∠A=2∠B.若三角形的三边长为整数,面积也为整数,求△ABC 面积的最小值.二、(25分)已知G 是△ABC 内任一点,BG 、CG 分别交AC 、AB 于点E 、F.求使不等式S △BGF ·S △CGE ≤kS 2△ABC 恒成立的k 的最小值.三、(25分)已知(x+1y 2+)(y+1x 2+)=1.求证:x+y=0.初中数学奥林匹克训练题参考答案第一试一、1.C.x=n+m=m+m+1=2m+1,y=n-m=1.所以,x 、y 都是奇数.2.B.因为Δ=(b 2+c 2-a 2)2-4b 2c 2=(b 2+c 2-a 2+2bc)(b 2+c 2-a 2-2bc)=[(b+c)2-a 2][(b-c)2-a 2]=(b+c+a)(b+c-a)(b-c+a)(b-c-a).记p=21(a+b+c),所以,Δ=2p·2(p-a)·2(p-c)[-2(p-b)]=-16p(p-a)(p-b)(p-c).由海伦公式知S 2=p(p-a)(p-b)(p-c).故Δ=-16S 2.3.B.4.A.设BC=a ,CA=b ,AB=c.由题意知AD+AC=BC+CE=21(a+b+c).故AD=21(a+c-b),CE=21(b+c-a).则AD ·CE=41(a+c-b)(b+c-a)=41[c 2-(a-b)2]=41(c 2-a 2-b 2)+12ab.由∠ACB=90°,知a 2+b 2=c 2,S=21ab.于是,AD ·CE=S. 5.C.由题意知只能是△PAB ∽△PCA. 则有PA/PC=PB/PA=AB/AC=8/6=4/3.故PB=34PA ,PB=PC+BC=PC+7,PA=34PC.又PA 2=PB ·PCPC=9.6.D.辅助线如图.由题意知OA 2=OE 2+AE 2.设AB=2x ,则AE=x. 于是,R 2=[2x-(R-2r)]2+x 2.化简得5x 2-4(R-2r)x+4(r 2-Rr)=0.①要使AB 为有理数,只要x 为有理数,也即方程①的Δ=[-4(R-2r)]2-4×5×4(r2-Rr)=16(R 2+Rr-r 2)为完全平方式,也即只需R 2+Rr-r 2为完全平方式.经验证知,只有选项(D)符合题意.二、1.-7.令A=αββα33+,B=ββαα33+=α2+β2. 由已知有α+β=-1,αβ=-1.故B=(α+β)2-2αβ=1+2=3.①A+B=)=(α3+β3)(1/α+1/β)=-4.②由式①、②得A=-4-3=-7.2.1 009 020.注意到a i b i =41[(a i +b i )2-(a i -b i )2], a i +b i =(1+2 008)×1 004/1 004=2 009.要使a i b i 的值最大,须a i -b i 的值最小,而a i -b i 的最小值为1,此时a i +b i =2 009,a i -b i =1.于是,a i =1 005,b i =1 004,此时,a i b i 的最大值为1 005×1 004=1 009 020.3.60°.记BC=a ,CA=b ,AB=c.由内角平分线定理知 BD= c b ac +,CD=c b ab +,BF=b a ac +,CE=ca ab +. 由BD+BF=CD+CE ,.去分母并化简得a 2c+2ac 2+2bc 2+c 3=a 2b+2ab 2+2b 2c+b 3,即 (c-b)(a 2+2ac+2ab+b 2+c 2+3bc)=0.显然a 2+2ac+2ab+2bc+b 2+c 2+bc=(a+b+c)2+bc>0.于是,c-b=0,即b=c.同理,当CD+CE=AE+AF 时,有c=a.所以,a=b=c ,△ABC 为等边三角形.故∠BAC=60°.4.④.命题①、②、③可分别给出如下反例:命题①:如图5(a)中的四边形ABCD ,其中,△ABD △CDE.命题②:如图5(b),作等腰△ADE ,延长底边ED 到任意点O ,以O 为对角线的交点可作出 ABCE ,而此时四边形ABCD 满足条件AD=(AE=)BC ,且AO=CO ,但不是平行四边形.命题③:如图5(c)中的四边形ABCD ,其中,A 、C 是BD 垂直平分线上的任意两点.图5 以下证明命题④是正确的.如图5(d),已知∠BAD=∠DCB ,且OB=OD.以点O 为中心,将△ABD 逆时针旋转180°.因为OB=OD ,所以,点D 与B 重合, 点B 与D 重合,点A 与射线OC 上某点A 1重合.如果A 1不是C ,则∠BA 1D>∠BCD(A 1在线段OC 内部)或∠BA 1D<∠BCD(A 1在OC 的延长线上),都与∠BA 1D=∠BAD=∠BCD 矛盾,从而,A 1即是C ,即OA=OA 1=OC.所以,四边形ABCD 是平行四边形.第二试一、记BC=a ,CA=b ,AB=c.如图,作∠BAC 的平分线AD ,则∠BAD=∠DAC=∠B ,∠ADC=∠B+∠BAD=2∠B.故△ACD △BCA.于是,b/a=CD/b.①又由角平分线定理知b/c=CD/BD.从而,c b b +=BD CD CD + =a CD .② 由式①、②得a c b +=ba . 故a 2=b(b+c).若(b ,c)=d ,则由式①知d|a ,故不妨设(b ,c)=1.于是,可令b=m 2,b+c=n 2.则a=mn ,c=n 2-m 2.由∠A>∠B>∠C ,知a>b>c ,即mn>m 2>n 2-m 2.故m<n< 2 m.③又m 、n 为正整数,从而,2m-m>1,即m> 2 +1.④ 设△ABC 的面积为S ,由海伦公式知 S=41n(n+m)(n-m)·n)-n)(2m (2m +. 由式④知m ≥3.又由式③容易验证:当3≤m ≤7时,只有m=5时,n=6,n)-n)(2m (2m + =8(有理数),此时,S=14×6×11×1×8=132.下证当m ≥8,n ≥9时,S>162.由式③、④知(2m+n)(2m-n)>3m(2m- 2m)=(6-32)m 2>(6-42)m 2=(2-2)2m 2, n(n+m)(n-m)>n(1+22n)×1=21 (2+ 2)n 2. 由式⑤知 S>14×12(2+ 2)n 2(2- 2)m=14n 2则当m ≥8,n ≥9时,有S>162.故S 的最小值为132,此时,m=5,n=6.所以,a=30,b=25,c=11时,△ABC 面积最小,最小值为132.二、如图,设AF/AB=x ,AE/AC=y.则0<x 、y<1.在△ABE 中,由梅涅劳斯定理有BG/GE·EC/CA·AF/FB=1..从而,u 2+(t-2)u+2t=0在[0,2]内有实根,则Δ=(t-2)2-8t ≥0t ≥6+4 2或t ≤6-4 2.从而t ≤6-4 2.所以,tmax=6-4 2,此时u=2 2 -2.因此,当u=2 2-2,x=y ,即x=y=2-1时,(S △BFG ·S △CEG /S 2△ABC )max=41(6-4 2)2=17-12 2. 故k ≥17-12 2,kmin=17-12 2.三、用反证法证明.(1)先证x=0时y=0,或y=0时x=0.如若不然,假设x=0时,y>0.则 (x+1y 2+)(y+1x 2+)=1y 2+ (y+1)>1,与已知矛盾.当x=0,y<0时,又有 (x+1y 2+)(y+1x 2+)= 1y 2+ (y+1)< 12y 2+-y (1+y)=(1-y)(1+y)=1-y 2<1, 与已知矛盾.故x=0时,y=0. 同理,y=0时,x=0.(2)再证x ≠0,y ≠0时,x+y=0.为此先证xy<0.如若不然,则x>0,y>0或x<0,y<0.当x>0,y>0时,(x+1y 2+)(y+1x 2+)>1,与已知矛盾.当x<0,y<0时,(x+1y 2+)(y+1x 2+)=y)-1x x)(-1y ()y -1)(x x -1(y 222222++++ =y)-1x x)(-1y ()x -(y -122222++≤y)-1x x)(-1y (122++ .但(1y 2+-x>1,1x 2+-y>1,则y)-1x x)(-1y (122++<1,与已知矛盾.从而,xy<0.以下分两种情形讨论.(i)若x+y>0,由于原式关于x 、y 对称,不妨设x>0,y<0.则x>-y ,x2>y2,有(x+1y 2+)(y+1x 2+)>( 1y 2+-y)( 1y 2++y)=1,与已知矛盾.同理,当x<0,y>0时,也与已知矛盾.(ii)若x+y<0,不妨设x>0,y<0.则x<-y ,x 2<y 2,有(x+1y 2+)(y+1x 2+)<(1y 2+-y)( 1y 2++y)=1,与已知矛盾.由(i)、(ii)知,x+y>0和x+y<0均不成立.因此,x+y=0.综上知x+y=0.。
初中数学奥林匹克初中训练题(032)

数学奥林匹克初中训练题(032)第一试一、选择题(每小题7分,共42分)1.满足不等式|x -1|+|x -9|的整数x 的个数为().A .8B .9C .10D .112.如图,由钝角△ABC 的顶点A 作高AD ,以垂足D 为圆心,AD 为半径作圆,分别交AB 、AC 于M 、N ,如果AB =c ,AM =m ,AN =n ,那么,AC 边的长是( ).A .m +nB .C .D .()ncm mcn +n m m n3.已知一次函数y =ax +b (a 为整数)的图象过点(98,19),它与x 轴的交点为(p ,0),与y 轴的交点为(0,q ),若p 是质数,q 是正整数,那么满足条件的所有一次函数的个数为( ).A .0B .1C .2D .大于2的整数4.如图,在梯形ABCD 中,AB ∥CD ,并且AB =2CD ,M 、N 分别是对角线AC ,BD 的中点,设梯形ABCD 的周长为l 1,四边形CDMN 的周长为l 2,则l 1与l 2满足( ).A .l 1=2l 2B .l 1=3l 2C . l 2<l 1<2l 2D .2l 2<l 1<3l 25.设S .则与S 最接近的整数是( )A .1997B .1998C .1999D .20006.设n 是正整数,0<x ≤1,在△ABC 中,如果AB =n +x ,BC =n +2x ,CA =n +3x ,BC 边上的高AD =n ,那么,这样的三角形共有( )A .10个B .11个C .12个D .无穷多个二、填空题(每小题7分,共28分) .1.已知a 、b 为正整数,且满足.则a +b 的值等于___________.224=49a b a ab b +++2.如图,设ABCDE 是正五边形.直线MN 分别交边EA 、AB 于M 、N .如果AM +AN =AB ,那么,∠MAN +∠MBN +∠MCN +∠MDN +MEN =________.3.若n 是正整数,且n 2+9n +98恰好等于相邻的两个正整数的积,则n 的所有值是_______.4.已知如果满足(1)式的一切实数x 、y 、m 、n ,也满足(2)式,9(1)979(2)98x y m x y n x y m an x y bm cn +⎧=⎪+⎪⎨++⎪=⎪++⎩那么,a +b +c 的值等于_______.第二试一、(20分) 如图,在凸四边形ABCD 中,AC =BD =AB ,且AC ⊥BD ,垂足为E .设I 为△AEB 的内心,M 为AB 的中点.求证:MI 丄CD ,且MI =CD .12二、(25分) 已知关于x 的方程x 2+ax +6=0有两个不相等的实根.求证:方程x 4+ax 3 +(b -2)x 2-ax +1=0有四个互不相同的实数根.三、(25分) 六盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须以完全一样的面对接,最后得到的包装形状是一个长方形.已知磁带盒的长、宽、高尺寸分别是a =11cm ,b =7cm ,c =2cm .(1)请你给出一种能使表面积最小的打包方式,使其表面积最小,并画出其示意图;(2)若不给出a 、b 、c 的具体尺寸,只假定a ≥b ≥c ,问能否按照已知的打包方式,使其表面积最小?并说明理由.。
数学奥林匹克初中训练题(6套)

数学奥林匹克初中训练题(1)第 一 试一. 选择题.(每小题7分,共42分)( )1.已知33333a b c abc a b c++-=++,则22()()()()a b b c a b b c -+-+--的值为: (A)1 (B)2 (C)3 (D)4( )2.规定”Δ”为有序实数对的运算,如果(,)a b Δ(,)(,).c d ac bd ad bc =++如果对任意实数,a b 都有(,)a b Δ(,)(,),x y a b =则(,)x y 为:(A)(0,1) (B)(1,0) (C)(1,0)- (D)(0,1)-( )3.在ΔABC 中,211a b c=+,则∠A: (A)一定是锐角 (B)一定是直角 (C)一定是钝角 (D)非上述答案( )4.下列五个命题:①若直角三角形的两条边长为3与4,则第三边长是5;②2;a =③若点(,)P a b 在第三象限,则点1(,1)P a b --+在第一象限;④连结对角线垂直且相等的四边形各边中点的四边形是正方形;⑤两边及其第三边上的中线对应相等的两个三角形全等.其中正确的命题的个数是:(A)2个 (B)3个 (C)4个 (D)5个( )5.设P 为等腰Rt ΔABC 斜边AB 上或其延长线上一点,22S AP BP =+,那么:(A)22S CP (B)22S CP = (C)22S CP (D)不确定 ( )6.满足方程222()x y x y xy +=++的所有正整数解有:(A)一组 (B)二组 (C)三组 (D)四组二. 填空题.(每小题7分,共28分)1.一辆客车,一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等.走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上了客车.问再过分钟,货车追上了客车.2.若多项式2228171642070P a ab b a b =-+--+,那么P 的最小值是 .3.如图1, ∠AOB=30O , ∠AOB 内有一定点P,且OP=10.在OA 上有一点Q,OB 上有一点R.若ΔPQR 周长最小,则最小周长是 .4.已知二次函数2(1)y ax a =≥的图象上两点A,B 的横坐标分别为1,2-,O 是坐标原点,如果ΔAOB 是直角三角形,则ΔAOB 的周长为 .第 二 试一.(20分)已知实数,,a b c 满足不等式,a b c b c a ≥+≥+,c a b ≥+,求a b c ++的值.二.(25分)如图2,点D 在ΔABC 的边BC 上,且与B,C 不重合,过点D 作AC 的平行线DE 交AB 于E,作AB 的平行线DF 交AC 于点F.又知BC=5.(1) 设ΔABC 的面积为S.若四边形AEFD 的面积为25S .求BD 长.(2) 若,AC 且DF 经过ΔABC 的重心G,求E,F 两点的距离.三.(25分)已知定理:”若三个大于3的质数,,a b c 满足关系式25a b c +=,则a b c ++是整数n 的倍数.”试问:上述定理中整数n 的最大可能值是多少?并证明你的结论.数学奥林匹克初中训练题(2)第一试一. 选择题.(每小题7分,共42分)( )1.有铅笔,练习本,圆珠笔三种学习用品.若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本10本,圆珠笔1支共需4.2元.现购铅笔,练习本,圆珠笔各1件,共需:(A)1.2元 (B)1.05元 (C)0.95元 (D)0.9元( )2.三角形的三边,,a b c 都是整数,且满足7abc bc ca ab a b c ++++++=,则此三角形的面积等于:(A)2 (B)4 (C)4 (D)2( )3.如图1,ΔABC 为正三角形,PM ⊥AB,PN ⊥AC.设四边形AMPN, ΔABC 的周长分别是,m n ,则有: (A)1325m n (B)2334m n (C)80%83%m n (D)78%79%mn( )4.满足22(3)(3)6x y -+-=的所有实数对(,)x y ,使y x取最大值,此最大值为:(A)3+4+5+ (D)5( )5.设p .其中,,,a b c d 是正实数,且满足1a b c d +++=.则p 满足: (A)p >5(B)p <5 (C)p <2 (D)p <3( )6.如图2,点O 是正六边形ABCDEF 的中心,OM ⊥CD,N为OM 的中点.则:ABN BCN S S 等于:(A)9:5 (B)7:4 (C)5:3 (D)3:2二. 填空题.(每小题7分,共28分)1.若实数,x y 满足(1x y =,则x y += .2.如图3,CD 为直角ΔABC 斜边AB 上的高,DE ⊥AC.设ΔADE,ΔCDB,ΔABC 的周长分别是12,,p p p .当12p p p + 取最大值时,∠A= .3.若函数2543kx y kx kx +=++中自变量的取值范围是一切实数,则实数k 的取值范围是 .4.如图4所示,线段AB 与CD 都是⊙O 中的弦,其中108,,36,O O AB AB a CD CD b ====,则⊙O 的半径R= .第 二 试一.(共20分)n 是一个三位数,b 是一个一位数,且22,1a a b b ab ++都是整数,求a b +的最大值与最小值.二.(共25分)如图5,在ΔABC 中,∠A=60O ,O,I,H 分别是它的外心,内心,垂心.试比较ΔABC 的外接圆与ΔIOH 的外接圆的大小,证明你的论断.三.(共25分)求方程组33333x y z x y z ++=⎧⎨++=⎩的所有整数解.参考答案一.1.(B)数学奥林匹克初中训练题(四)第 一 试三. 选择题.(每小题7分,共42分)( )1.在11,,0.2002,7223πn 是大于3的整数)这5个数中,分数的个数为: (A)2 (B)3 (C)4 (D)5( )2.如图1,正方形ABCD 的面积为256,点F 在AD上,点E 在AB 的延长线上,Rt ΔCEF 的面积为200,则BE 的长为:(A)10 (B)11 (C)12 (D)15( )3.已知,,a b c 均为整数,且满足2223a b c +++<32ab b c ++.则以,a b c b +-为根的一元二次方程是:(A)2320x x -+= (B)2280x x +-=(C)2450x x --= (D)2230x x --=( )4.如图2,在Rt ΔABC 中,AF 是高,∠BAC=90O ,且BD=DC=FC=1,则AC 为:( )5.若222a b c a b c k c b a+++===,则k 的值为: (A)1 (B)2 (C)3 (D)非上述答案( )6.设0,0,26x y x y ≥≥+=,则224363u x xy y x y =++--的最大值是: (A)272(B)18 (C)20 (D)不存在四. 填空题.(每小题7分,共28分)1.方程222111013x x x x++=+的实数根是 . 2.如图3,矩形ABCD 中,E,F 分别是BC,CD 上的点,且2,3,4A B E C E F A D F S S S ===,则AEF S = .3.已知二次函数2(1)y x a x b =+++(,a b 为常数).当3x =时,3;y =当x 为任意实数时,都有y x ≥.则抛物线的顶点到原点的距离为 .4.如图4,半径为2cm ,圆心角为90O 的扇形OAB 的AB 上有一运动的点P.从点P 向半径OA 引垂线PH 交OA 于点H.设ΔOPH 的内心为I,当点P 在AB 上从点A 运动到点B 时,内心I 所经过的路径长为 .第 二 试一.(20分)在一个面积为1的正方形中构造一个如下的小正方形;将单位正方形的各边n 等分,然后将每个顶点和它相对应顶点最接近的分点连结起来,如图5所示.若小正方形的面积恰为13281,求n 的值. 二.(25分)一条笔直的公路l 穿过草原,公路边有一卫生站A,距公路30km 的地方有一居民点B,A,B 之间的距离为90km .一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是60/km h ,在草地上行驶的最快速度是30/km h .问司机应以怎样的路线行驶,所用的行车时间最短?最短时间是多少?三.(25分)从1,2,3,……,3919中任取2001个数。
数学奥林匹克初中训练题(含答案)

数学奥林匹克初中训练题第一试一、选择题(每小题7分,共42分)1.设z y x ++=+++6323,且x 、y 、z 为有理数.则xyz =( ).(A)3/4 (B)5/6 (C)7/12 (D)13/182.设二次函数f (x )=ax 2+ax +1的图像开口向下,且满足f (f (1))=f (3).则2a 的值为( ).(A)-3 (B)-5 (C)-7 (D)-93.方程|xy |+|x +y |=1的整数解的组数为( ).(A)2 (B)4 (C)6 (D)84.a 、b 是方程x 2+(m -5)x +7=0的两个根.则(a 2+ma +7)(b 2+mb +7)=( ).(A)365 (B)245 (C)210 (D)1755.如图,Rt △ABC 的斜边BC =4,∠ABC =30°,以AB 、AC 为直径分别作圆.则这两圆的公共部分面积为( )(A)2332+π (B) 33265-π (C) 365-π (D) 332-π 6.从1,2,…,13中取出k 个不同的数,使这k 个数中任两个数之差既不等于5,也不等于8.则k 的最大值为( ).(A)5 (B)6 (C)7 (D)8二、填空题(每小题7分,共28分)1.若整系数一元二次方程x 2+(a +3)x +2a +3=0有一正根x 1和一负根x 2,且|x 1|<|x 2|,则a = .2.当x =2329-时,代数式x 4+5x 3-3x 2-8x +9的值是 . 3.给定两组数,A 组为:1,2,…,100;B 组为:12,22,…,1002.对于A 组中的数x ,若有B组中的数y ,使x +y 也是B 组中的数,则称x 为“关联数”.那么,A 组中这样的关联数有个.4.已知△ABC 的三边长分别为AB =2576a 2+,BC =62514a a 2++,AC =62514a -a 2+,其中a >7.则△ABC 的面积为 .第二试一、(20分)解方程:(12x +5)2(6x -1)(x +1)=255.二、(25分)如图,四边形ABCD 中,∠ACB =∠ADB =90°,自对角线AC 、BD 的交点N 作NM ⊥AB 于点M ,线段AC 、MD 交于点E ,BD 、MC 交于点F ,P 是线段EF 上的任意一点.证明:点P 到线段CD 的距离等于点P 到线段MC 、MD 的距离之和.三、(25分)矩形玻璃台板碎裂成一些小玻璃片,每块碎片都是凸多边形,将其重新粘合成原矩形后,有交结点30个,其中20个点在原矩形的周界上(包括原矩形的四个顶点),其余10个点在矩形内部.在矩形的内部有45条粘缝(两个结点之间的线段算是一条粘缝,如图所示).试求该矩形台板所碎裂成的各种类型(指三角形、四边形、五边形等)的块数.说明:若凸多边形的周界上有n个点,就将其看成n边形,例如,图中的多边形ABCDE要看成五边形.数学奥林匹克初中训练题1参考答案第一试1.A .两边平方得3+2 +3+6=x +y +z +2xy +2yz +2xz . 根据有理数x 、y 、z 的对称性,可考虑方程组x +y +z =3,2xy = 2,2yz =3,2xz = 6.解得x =1,y =1/2,z =3/2.此时,xyz =3/4.2.B .注意到f (1)=2a +1,f (3)=12a +1,f (f (1))=a (2a +1)2+a (2a +1)+1.由f (f (1))=f (3),得 (2a +1)2+(2a +1)=12.所以,2a +1=3或-4.因a <0,故2a =-5.3.C .因x 、y 为整数,则|xy |、|x +y |为非负整数.于是,|xy |、|x +y |中一个为0,一个为1.分情形考虑得6组解.4.D .由ab =7,a 2+ma +7=5a ,b 2+mb +7=5b ,所以,(a 2+ma +7)(b 2+mb +7)=25ab =175.5.C .记两圆公共部分的面积为S .如图,易知S =S 扇形EAD +S 扇形F AD -S 四边形AEDF =5π/6-3 .6.B .将这13个数按照相邻两数的差为5或8排列于一个圆周上(如图5).若取出的数多于6个,则必有2个数在圆周上相邻.另一方面,可以取出适合条件的6个数(任取圆周上不相邻的6个数即可),因此,k 的最大值为6.二、1.-2.因方程的两根不等,故Δ>0,即(a +3)2>4(2a +3).解得a >3或a <-1.又由题设条件知,方程的两根和与积皆负,即-(a +3)<0,2a +3<0.从而,a >-3,a <-3/2,即-3<a <-3/2.而a 为整数,则a =-2. 2. 32297-. x =2329-是方程x 2+3x -5=0的根, 3.73.记x +y =a 2,y =b 2,则1≤b <a ≤100.而x=a2-b2=(a+b)(a-b)≤100,因a+b、a-b同奇偶,故a+b≥(a-b)+2.(1)若a-b=1,则a+b为奇数,且3≤a+b≤99.于是,a+b可取3,5,7,…,99,共49个值,这时,相应的x 也可取这49个值.(2)若a-b=2,则a+b为偶数,且4≤a+b≤50.于是,a+b可取4,6,8,…,50,共24个值,这时,相应的x 可取8,12,16,…,100这24个值.其他情况下所得的x值均属于以上情形.若a-b=奇数,则a+b=奇数.而x=a2-b2≥a+b≥3,归入(1).若a-b=偶数,则a+b=偶数.而x=(a-b)(a+b)为4的倍数,且a-b≥2,a+b≥4,故x≥8,归入(2).因此,这种x共有49+24=73个.4.168.注意到AB2=(2a)2+482,BC2=(a+7)2+242,AC2=(a-7)2+242.如图,以AB为斜边,向△ABC一侧作直角△ABD,使BD=2a,AD=48,∠ADB=90°.在BD上取点E,使BE=a+7,ED=a-7,又取AD的中点F,作矩形EDFC1.因BC21=BE2+EC21=(a+7)2+242=BC2,AC21=C1F2+AF2=(a-7)2+242=AC2,故点C与点C1重合.而S△ABD=48a,S△CBD=24a,S△ACD=24(a-7),则S△ABC=S△ABD-S△CBD-S△ACD=168.第二试一、将原方程变形得(12x+5)2(12x-2)(12x+12)=660.令12x+5=t,则t2(t-7)(t+7)=660,即t4-49t2=660.解得t2=60或t2=-11(舍去).由此得t=±2 15,即有12x+5=±215.因此,原方程的根为x1,2=121525-.二、如图,易知A、B、C、D四点共圆,B、C、N、M四点共圆,因此,∠ACD=∠ABD=∠MCN.故AC平分∠DCM.同理,BD平分∠CDM.如图,设PH⊥MC于点H,PG⊥MD于点G,PT⊥CD于点T;过点P作XY∥MC,交MD于点X,交AC于点Y;过点Y作YZ∥CD,交MD于点Z,交PT于点R;再作YH1⊥MC于点H1,YT1⊥CD 于点T1.由平行线及角平分线的性质得PH=YH1=YT1=RT.为证PT=PG+PH,只须证PR=PG.由平行线的比例性质得EP/EF=EY/EC=EZ/ED.因此,ZP∥DF.由于△XYZ与△MCD的对应边分别平行,且DF平分∠MDC,故ZP是∠XZY的平分线.从而,PR=PG.因此,所证结论成立.三、设全部碎片中,共有三角形a3个,四边形a4个,……,k边形a k个(a3,a4,…,a k为非负整数).记这些多边形的内角和为S角,于是,S角=a3×π+a4×2π+…+a k(k-2)π.另一方面,矩形内部有10个结点,对于每个点,围绕它的多边形顶角和为2π,10个内结点共获得10×2π弧度;矩形边界上(不含4个顶点)共有16个结点,在每个这种结点处,各多边形的顶角在此汇合成一个平角,16个这种结点共获得16π弧度;而原矩形的4个顶点处,共获得多边形碎片的2π弧度.因此,S角=20π+16π+2π=38π.于是,a3+2a4+…+(k-2)a k=38.①记这些多边形的边数和为S边.由于每个n边形有n条边,则S边=3a3+4a4+…+ka k.另一方面,在矩形内部的45条粘缝,每条都是两个多边形的公共边,故都计算了两次;矩形周界上的20条线段各被计算了一次,因此,S边=2×45+20=110.于是,3a3+4a4+…+ka k=110.②②-①得2(a3+a4+…+a k)=72.故a3+a4+…+a k=36.③①-③得a4+2a5+3a6+…+(k-3)a k=2.因所有a i∈N,故a6=a7=…=a k=0,a4+2a5=2.所以,或者a4=2,a5=0;或者a4=0,a5=1.综上,本题的解共有两种情况,即全部碎片共36块,其中,或含有34个三角形,2个四边形;或含有35个三角形,1个五边形.。
初二数学奥林匹克竞赛训练题

初中二年级数学奥林匹克竞赛训练题目录本内容适合八年级学生竞赛拔高使用。
注重中考与竞赛的有机结合,重点落实在中考中难以上题、奥赛方面的基础知识和基本技能培训和提高。
本内容难度适中,讲练结合,由浅入深,讲解与练习同步,重在提高学生的数学分析能力与解题能力。
另外在本次培训中,内容的编排大多大于120分钟的容量,因此在实际教学过程中可以根据学生的具体状况和层次,由任课教师适当的调整顺序和选择内容(如专题复习可以提前上)。
注:有(*) 标注的为选做内容。
本次培训具体计划如下,以供参考:第一讲如何做几何证明题第二讲平行四边形(一)第三讲平行四边形(二)第四讲梯形第五讲中位线及其应用第六讲一元二次方程的解法第七讲一元二次方程的判别式第八讲一元二次方程的根与系数的关系第九讲一元二次方程的应用第十讲专题复习一:因式分解、二次根式、分式第十一讲专题复习二:代数式的恒等变形第十二讲 专题复习三:相似三角形 第十三讲结业考试(未装订在内,另发)第十四讲 试卷讲评第一讲:如何做几何证明题【知识梳理】1、几何证明是平面几何中的一个重要问题,它对培养学生逻辑思维能力有着很大作用。
几何证明有两种基本类型:一是平面图形的数量关系;二是有关平面图形的位置关系。
这两类问题常常可以相互转化,如证明平行关系可转化为证明角等或角互补的问题.2、掌握分析、证明几何问题的常用方法:(1)综合法(由因导果),从已知条件出发,通过有关定义、定理、公理的应用,逐步向前推进,直到问题的解决;(2)分析法(执果索因)从命题的结论考虑,推敲使其成立需要具备的条件,然后再把所需的条件看成要证的结论继续推敲,如此逐步往上逆求,直到已知事实为止;(3)两头凑法:将分析与综合法合并使用,比较起来,分析法利于思考,综合法易于表达,因此,在实际思考问题时,可合并使用,灵活处理,以利于缩短题设与结论的距离,最后达到证明目的。
3、掌握构造基本图形的方法:复杂的图形都是由基本图形组成的,因此要善于将复杂图形分解成基本图形。
数学奥林匹克初中训练题
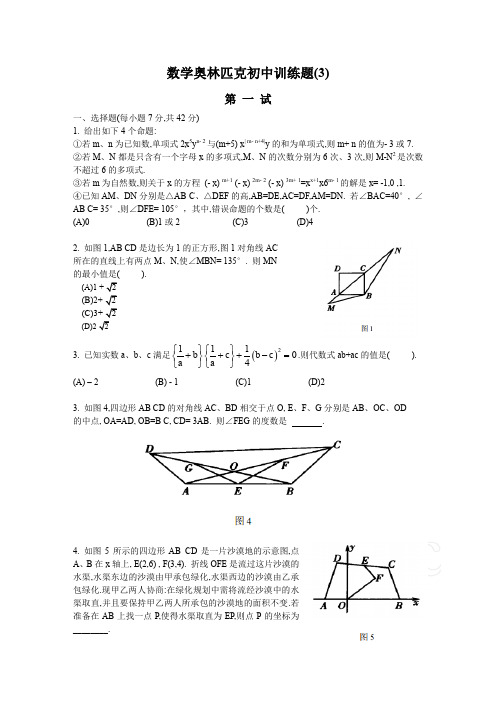
数学奥林匹克初中训练题(3)第 一 试一、选择题(每小题7分,共42分)1. 给出如下4个命题:①若m 、n 为已知数,单项式2x 5y n- 2与(m+5) x | m- n+4|y 的和为单项式,则m+ n 的值为- 3或7. ②若M 、N 都是只含有一个字母x 的多项式,M 、N 的次数分别为6次、3次,则M-N 2是次数不超过6的多项式.③若m 为自然数,则关于x 的方程 (- x) m+1 (- x) 2m- 2 (- x) 3m+ 1=x x+1x6m- 1的解是x= -1,0 ,1. ④已知AM 、DN 分别是△AB C 、△DEF 的高,AB=DE,AC=DF,AM=DN. 若∠BAC=40°, ∠AB C= 35°,则∠DFE= 105°,其中,错误命题的个数是( )个.(A)0 (B)1或2 (C)3 (D)42. 如图1,AB CD 是边长为1的正方形,图1对角线AC所在的直线上有两点M 、N,使∠MBN= 135°. 则MN的最小值是( ).3. 已知实数a 、b 、c 满足()211104b c b c a a ⎧⎫⎧⎫+++-=⎨⎬⎨⎬⎩⎭⎩⎭.则代数式ab+ac 的值是( ). (A) – 2 (B) - 1 (C)1 (D)23. 如图4,四边形AB CD 的对角线AC 、BD 相交于点O, E 、F 、G 分别是AB 、OC 、OD 的中点, OA=AD, OB=B C, CD= 3AB. 则∠FEG 的度数是.4. 如图5所示的四边形AB CD 是一片沙漠地的示意图,点A 、B 在x 轴上, E(2,6) , F(3,4). 折线OFE 是流过这片沙漠的水渠,水渠东边的沙漠由甲承包绿化,水渠西边的沙漠由乙承包绿化.现甲乙两人协商:在绿化规划中需将流经沙漠中的水渠取直,并且要保持甲乙两人所承包的沙漠地的面积不变.若准备在AB 上找一点P,使得水渠取直为EP,则点P 的坐标为________.。
初中数学奥林匹克训练题(1)

初中数学奥林匹克训练题(1)第一试一、 填空题1、计算:20033﹣20013﹣6×20032+24×1001= _________ .2、在△ABC 中,∠B 的平分线与∠C 的外角平分线相交于点D ,如果∠A=27°,那么∠BDC= _________ .3、已知0≤a ﹣b≤1,1≤a+b≤4,那么当a ﹣2b 达到最大值时,8a+2002b 的值等于 _________ .4、如果一个正整数等于它的数字和的4倍,那么我们就把这个正整数叫做四合数.所有四合数的总和等于 _________ .5、方程x 2﹣2|x+4|﹣27=0的所有根的和为 _________ .6、如果当m 取不等于0和1的任意实数时,抛物线2123m m y x x m m m--=+-错误!未找到引用源。
在平面直角坐标系上都过两个定点,那么这两个定点间的距离为 _________ .7、方程()32130x -++=错误!未找到引用源。
的三个根分别是 _________ .8、在Rt △ABC 中,∠A=30°,∠A 的平分线的长为1cm ,那么△ABC 的面积为 _________ .9、已知:商品利润率=错误!未找到引用源。
.某商人经营甲乙两种商品,每件甲种商品的利润率为40%,每件乙种商品的利润率为60%,当售出的乙种商品比售出的甲种商品的件数多50%时,这个商人得到的总利润率为50%,那么当售出的甲,乙两种商品的件数相等时,这个商人的总利润率是 _________ .10. 抛物线22y x =上两点()()1122,, ,A x y B x y 关于直线y x m =+对称,若1221x x =-,则2m 的值是____________二、解答题1.、已知a ,b ,c 是三个两两不同的奇质数,方程2()(2250b c x a ++++=有两个相等的实数根.(1)求a 的最小值;(2)当a 达到最小时,解这个方程.2、已知a 1,a 2,…,a 2002的值都是1或﹣1,设m 是这2002个数的两两乘积之和.(1)求m 的最大值和最小值,并指出能达到最大值、最小值的条件;(2)求m 的最小正值,并指出能达到最小正值的条件.3、在四边形ABCD 中,⊿ABD 、⊿BCD 、⊿ABC 的面积比是3∶4∶1,点M 、N 分别在AC 、CD 上满足AM ∶AC=CN ∶CD ,并且B 、M 、N 三点共线.求证:M 与N 分别是AC 与CD 的中点.4、试求最小的正整数,n 使得对于任何n 个连续正整数中,必有一数,其各位数字之和是7AB C DM N的倍数.初中数学奥林匹克训练题(1)第二试1、已知,,a b c 是实数, 二次函数2()f x ax bx c =++满足()02a b c f a --=,求证:-1与1中至少有一个是()0f x =的根.2、给定n 个共线的点,考虑点与点之间的距离,假设每个距离最多出现两次,证明:至少有2n ⎡⎤⎢⎥⎣⎦个距离分别只出现过一次.3、有一个m n p ⨯⨯的长方体盒子, 另有一个(2)(2)(2)m n p +⨯+⨯+的长方体盒子, 其中≤≤), 并且前者的体积是后者一半, 求p的最大值.m n p均为正整数(m n p,,4、求方程x2+x=y4+y3+y2+y的整数解.。
初中数学奥林匹克训练题及答案四

在 Rt △ABC 中 , A F
是 高 , ∠BAC = 90°,
且 BD = DC = FC =
1. 则 AC 为 ( ) . (A) 3 2 (B) 3
图2
(C) 2 (D) 3 3
5. 若
k
=
2a + c
b
=
2c + b
a
=
2
b+ a
c ,则
k
的值为 ( ) .
(A) 1 (B) 2 (C) 3 (D) 非上述答案 6. 设 x ≥0 , y ≥0 , 2 x + y = 6. 则 u = 4 x2 + 3 xy + y2 - 6 x - 3 y 的最大值是 ( ) .
则 S △AEF = S矩形ABCD - S △AB E - S △CEF - S △ADF =
7.
3.
1 4
221 .
把 x = 3 , y = 3 代入二次函数 y = x2 + ( a + 1) x
+ b得
b = - 3 a - 9.
当 x 为任意实数时 ,有 y ≥x ,即 x2 + ( a + 1) x + b ≥x. 把 b = - 3 a - 9 代入得 x2 + ax - 3 a - 9 ≥0. 则Δ = a2 - 4 ( - 3 a - 9) = ( a + 6) 2 ≤0. 所以 a = - 6 ,得 b = 9. 因此 ,二次函数解析式为 y = x2 - 5 x + 9 , 顶点
因为
k
=
2
a+ c
b
=
2c + b
数学奥林匹克初中训练题_123_

2
1 1 1 1 1 1 = + +…+ 3 4 4 5 n n +1 1 1 2 007 = = 3 n + 1 6 030 ] 1 = 3 = 1 ] n = 2 009. n + 1 6 030 2 010 3. 60 ° < C < 90 ° . 由已知得 AC = B C, ACP = B CP. 又 CP = CP , 因此 , △ACP △B CP , 有 CA P = CB P , 即 CA E = CB F. 再由 AC = B C ,得 △ACE △B CF , A E = B F. 所以 , △AB G 是以 AB 为底边的等腰三 角形 . 故 S △AB C = S △AB G Ζ A E = AC. (1)当 C 为直角或钝角时 , 在 △ACE 中 ,不论点 P 在 CH 何处 , 均有 A E > AC , 所 以 ,结论不成立 ; 1 ( 2 )当 C 为锐角时 , A =90° C, 2 而 CA E < A , 要使 A E = AC , 只需使 C = CEA ,此时 , CA E = 180 ° -2 C ,只须 1 180 ° -2 C < 90 ° C. 2 解得 60 ° < C < 90 ° . 411. x xy y 由 41 = 2 009, 得 41 = 2 009 . y 2y 2 又 7 = 2 009 ] 7 = 2 009 y 2 ] 49 = 2 009 ] 49xy = 2 0092 x.
xy xy xy 又 41 × 49 = 2 009 ] 41 × 49 = 2 009 . y 2x xy 故 2 009 × 2 009 = 2 009 ] 2 0092 x + y = 2 009xy ] 2 x + y = xy
数学奥林匹克初中训练题(132)

数学奥林匹克初中训练题(132)
李明;李一
【期刊名称】《中等数学》
【年(卷),期】2010(000)008
【摘要】@@ 第一试\r\n一、选择题(每小题7分,共42分)\r\n1.若关于x的方程\r\nx2+(1-2√2)x+3m-√2=0\r\n(m为有理数)有一个有理数根,则它的另一根为( ).
【总页数】4页(P35-38)
【作者】李明;李一
【作者单位】安徽省五河县第三中学,233300;安徽省五河县第三中学九年级八班,233300
【正文语种】中文
【中图分类】G424.79
【相关文献】
1.数学奥林匹克高中训练题(132) [J], 冯跃峰
2.数学奥林匹克初中训练题(186) [J], 罗家亮
3.数学奥林匹克初中训练题(190) [J], 陈迁;陈鸿飞
4.数学奥林匹克初中训练题(191) [J], 李耀文
5.数学奥林匹克初中训练题(192) [J], 陈迁
因版权原因,仅展示原文概要,查看原文内容请购买。
初中数学奥林匹克竞赛题4套带详解.pptx

于点.F.又知BC=5.
/A
(1) 设△ABC的面积为S.若四边形AEFD的面积为-£ .求
2
5 ED长.
⑵ 若AC = -J2AP,且DF经过△ ABC的重心G,求E, F两
点的距离,
=. (25分)已知定理:"若三个大于3的庙教貞,成二满足关系式2a-\-5b = c ,贝LI a +占+二
是整数点的倍数试问:上述定理中整数推的最大可能值是峯少T并证明你的结论.
fj£,(«+ ft + f):^yr 队&异曲乂 故("+ A + c):
s o.Mifti. n + t+ r=o. 二.如图7. W •:健:浦.网抓
,'-,2,稀#;s丄况4 s乙 ix:f.
记 S jtn = Si •
■ y .1.
①
,啓 HI) _ CD 一厅=商71 =此.
TH '/si g HD+IX: Bf: 于也
值与最小值. 二. (共狷分)如图5,在厶ABC中,ZA=60:J 0,
LH分别是它的外心,内心,垂心.试比较厶 ABC 的外接圆与厶IOH的外接圆的大小,证明 你的论 断.
x+y+z = 3 三. (共25分■)求方程组f 5 % 的所有
X3+/+Z3 = 3 整数解.
6
学海无涯
参考答案:2 没购铅宅、炼习本個球笔各I件分别元寸
4.已知二汶函数y=aX2(a>V)的圏象上两点A, B的橫坐标分别为-1,丄。是坐标原点,
如SAA0B是直角三角形,则AAOB的周长为____. 第二试
—.(20分)已知实数淳&二满足不等式园乏杓+二,冋乏Z+刘|, m |a+占|,求a+占+二
数学奥林匹克初中训练题(3)含答案

数学奥林匹克初中训练题(3)第 一 试一. 选择题.(每小题7分,共42分)( )1.在凸2005边形中,不大于111O 的内角最多有:(A)3个 (B)4个 (C)5个 (D)6个( )2.已知,a b 均为实数,且关于x 的不等式(2)21a x a b +-+的解集为13x -,则a b +的值为: (A)3或7 (B)3或13 (C)7或8 (D)8或13( )3.满足y =(,)x y :(A)只有一对 (B)恰有两对 (C)至少有三对 (D)不存在( )4.如图1,A,B,C 为⊙O 上的三个定点,AB=AC,P 为⊙O 上的动点.则当点P 从点B 按逆时针方向向点C 运动的过程中,PB PC PA+的值: (A)保持不变 (B)先减小后增大(C)先增大后减小 (D)无法判断( )5.设12,x x 是方程2200320050x x -+=的两个实根,实数 ,a b 满足:200320032004200412122003,2004,ax bx ax bx +=+=则2005200512ax bx +的值为:(A)2005 (B)2003 (C)2005- (D)2003-( )6.在同一平面上,正方形ABCD 的四个顶点到直线l 的距离只取四个值,其中一个值是另一个值的3倍,这样的直线l 可以有:(A)4条 (B)8条 (C)12条 (D)16条二. 填空题.(满分28分,每小题7分)7.抛物线2y ax =与直线1,2,1,2x x y y ====组成的正方形有公共 点, 则a 的取值范围是 .8.如图2,D 为ΔABC 的边BC 上一点,P 为线段AD 上一点,若若ΔAPB 的面积为9,ΔCPD 的面积为16,则ΔABC 面积的最小值是9.在由ΔABC 内的2005个点P 1,P 2,……P 2005及ΔABC 的三个顶点A,B,C 共2008个点所构成的三角形中,最多有 个三角形,它们恰好将ΔABC 完全分割成无任何重叠的三角形.10.如果点P 将⊙O 的弦AB 和CD 分成的四条线段PA,PB,PC,PD 的长度恰好是四个互不相同的正整数,则称点P 为⊙O 的”整分点”.现已知M 是半径为5的⊙O 上一点,则在半径OM 上有 个不同的整分点.第二试三. 解答题.(共70分)11.(满分20分)求所有的实数m,使得关于x的方程112121mx x x-=++-有且只有整数根.12.(满分25分)如图3,O,H分别是锐角ΔABC的外心和垂心,D是BC边上的中点.由H向∠A及其外角平分线作垂线,垂足分别是E,F.求证:D,E,F三点共线.13.(满分25分)能否将1,2,3……,12这12个正整数分成两组,使得其中第一组有3个数,第二组有9个数,并且第一组中3个数的积恰好等于第二组中9个数之和?若能,请给出所有的分组方法;若不能,请说明理由。
数学奥林匹克初中训练题2

数学奥林匹克初中训练题2第一试一、选择题(每小题7分,共42分)1.若x 、y 、z 均为实数,且满足1))(())(())((=++++++++z y y x zx y x x z yz x z z y xy , 则x 、y 、z 的取值情况是( ).(A)全为正数 (B)全为非负数 (C)全为负数 (D)有且仅有一个为零2.如图,在钝角△ABC 中,BC=1,∠A=30°,D 为边BC 的中点,G 为△ABC 的重心.若B 、C 为定点,当点A 运动时,线段GD 长度的取值范围是( ).(A)0<GD ≤613 (B)61<GD<613 (C)0<GD ≤632+ (D) 61≤GD ≤652+ 3.设a 、b 为正整数,且a+b 、a+5、b-2是某个直角三角形的三边长.则正整数对(a,b)的个数是( )个.(A)0 (B)1 (C)2 (D)34.已知抛物线y=a x 2+bx+c(a>0)与直线y=k(x-1)-4k 2.无论k 取任何实数,此抛物线与直线都只有一个公共点.那么,抛物线的解析式是( ).(A)y=x 2 (B)y=x 2-2x (C)y=x 2-2x+1 (D)y=2x 2-4x+25.若x 为实数,记{x}=x-[x]([x]表示不超过x 的最大整数),则方程2006x+{x}=00721的实根的个数是( ).(A)0 (B)1 (C)2 (D)大于2的整数6.如图,正方形ABCD 内接于⊙O,P 为劣弧CD 上一点,PA 交BD 于点M,PB交AC 于点N,记∠PAC=θ.若MN ⊥PA,则2cos 2θ-tan θ的值等于( ). (A)1 (B)2/2 (C)1/2 (D)2/4 二、填空题(每小题7分,共28分)1.已知x 、y 为实数,且满足(x+008 2x 2+)(y+008 2y 2+)=2 008.则x 2-3xy-4y 2-6x-6y+2 008的值等于 .2.设实数a 、b 、c 满足a+b+c=0,abc=2.则u=|a|3+|b|3+|c|3的最小值为 .3.在直角坐标平面内,已知A(-3 ,0)、B(3 ,0),点P 在直线y=33(x+4)+1上运动.当∠APB 最大时,PBPA 的值为 . 4.设Rt △ABC 的三边长分别为a 、b 、c,且a<b<c.若2017=+++b c a a c b .则a ∶b ∶c= .第二试一、(20分)已知m 、n 均为正整数,且m>n,2006m 2+m=2 007n 2+n.问m-n 是否为完全平方数?并证明你的结论.二、(25分)如图,在梯形ABCD 中,AB ∥CD,AD=12,E 是边CD 上一点,且45ED CE .设过A 、B 、C 、E 四点的⊙O 1的半径为R 1,过A 、C 、D 三点的⊙O 2的半径为R 2,且边BC 与⊙O 2相切.(1)求边CD 的长;(2)求21R R 的取值范围.三、(25分)求实数a的值,使得函数f(x)=(x+a)(|x-a+1|+|x-3|)-2x+4a的图像为中心对称图形.数学奥林匹克初中训练题2参考答案第一试一、1.D.显然,(x+y)(y+z)(z+x)≠0.去分母得xy(x+y)+yz(y+z)+zx(z+x)=(x+y)(y+z)(z+x).化简整理得xyz=0.所以,x 、y 、z 中至少有一个为零.若x 、y 、z 中有两个或三个为零,则x+y 、y+z 、z+x 中至少有一个为零,等式无意义. 故x 、y 、z 中有且仅有一个为零.2.B.因为∠A= 30°,且△ABC 为钝角三角形,所以,点A 在如图所示的不含端点的弧A 1B 、弧A 2C 上(其中,A 1B ⊥BC,A 2C ⊥BC).设G1为Rt △A 1BC 的重心,则31BD<GD<G1D. 易知A 1B= 3 ,则G1D=31A 1D=613.又31BD=1/6,所以,1/6<GD<613. 3.A.若a+b 为斜边长,则(a+b)2=(a+5)2+(b-2)2,即 2(ab-5a+2b)=29.上式左边为偶数,右边为奇数,矛盾.若a+5为斜边长,则(a+5)2=(a+b)2+(b-2)2,即 2(5a-ab-b 2+2b)=-21.矛盾.若b-2为斜边长,则(b-2)2=(a+b)2+(a+5)2,即 2(a 2+ab+5a+2b)=-21.矛盾.故满足条件的正整数对(a,b)不存在.4.C.由y=a x 2+bx+c,y=k(x-1)-k 2/4得a x 2+(b-k)x+c+k+k 2/4=0.①由题设知,方程①有两个相等的实根,则Δ=(b-k)2-4a( c+k+k 2/4)=0,即(1-a)k 2-2(2a+b)k+b 2-4ac=0.因为k 为任意实数,所以,抛物线的解析式为y=x 2-2x+1.5.C.因为x=[x]+{x},所以,原方程可化为2 006[x]+2 007{x}=1/2 007.又0≤2 007{x}<2 007,所以,[x]=-1或[x]=0.若[x]=-1,则{x}=2007 21007 2006 2+⨯=22007 21007 2-007 2+=1-20072006 2<1. 所以,x==-20072006 2. 若[x]=0,则{x}=1/2 0072,即x=1/2 0072.综上所述,x 1=-2 006/2 0072,x 2=1/2 0072.6.A.设⊙O 的半径为1,则AC=2.如图,联结PC.则∠APC=90°.从而,PA=ACcos θ=2cos θ. 在Rt △AOM 中,AM=OA/cos θ=1/cos θ;在Rt △AMN 中,MN=AM/tan θ=tan θ/cos θ;在Rt △PMN 中,因为∠MPN=∠APB=∠ADB=45°,所以,PM=MN=tan θcos θ.又AM+PM=PA,得1/cos θ+tan θ/cos θ=2cos θ.故2cos 2θ-tan θ=1.二、1.2 008.由题设得 (x+008 2x 2+))=2 008/(y+008 2y 2+).分母有理化得 x+008 2x 2+=008 2y 2+ -y.①同理,y+008 2y 2+=008 2x 2+-x.②①+②得x+y=0.故x 2-3xy-4y 2-6x-6y+2 008=(x+y)(x-4y)-6(x+y)+2 008=2 008.2.10.由题设知,a 、b 、c 必为一正两负.不妨设a>0、b<0、c<0.因为b+c=-a,bc=2/a,所以,b 、c 为方程x 2+ax+2/a=0的两个负根.于是,有Δ=a 2-8/a ≥0.解得a 3≥8.故u=a 3-b 3-c 3=a 3-(b+c)[(b+c)2-3bc]=a 3+a (a 2-6/a)=2a 3-6≥2×8-6=10.当且仅当a 3=8,即a=2时,上式等号成立.此时,b=c=-1.因此,u 的最小值为10. 3. 3 -1.如图,设直线与x 轴的交点为M.由平面几何知识即知,要使∠APB 最大,则过A 、B 、P 三点的圆必和直线相切于点P.因为∠MPA=∠MBP,所以,△MPA ∽△MBP.则有PA/PB=MP/MB.又由切割线定理得MP 2=MA·MB.故PA/PB=22MBMP =MA/MB. 因M(-4- 3 ,0)、A(-3,0)、B(3,0),所以, MA=4,MB=4+23.故PA/PB=3-1.4.8:15:17因为c 2-a 2=b 2,c 2-b 2=a 2,所以,a b c b a c bc b c a a c a c b b c a a c b -+-=--+--=+++=2222)()(2017 abc b a c ab b a b a c )()()(22-+=+-+= 又ab=2)(2)b (a -b)(a 222222c b a -+=++=21 (a+b+c)(a+b-c), 所以, cb ac ++=22017,即17(a+b)=23c. 两边平方得289(a 2+2ab+b 2)=529c 2=529(a 2+b 2).整理得(15a-8b)(8a-15b)=0.所以,a/b=8/15或a/b=15/8.又82+152=172,且a<b<c,故a ∶b ∶c=8∶15∶17.第二试一、m-n 为完全平方数.证明如下:设m=n+k(k 为正整数).代入2 006m 2+m=2 007n 2+n,得n 2-2×2 006kn -(2 006k 2+k)=0.因为n 为正整数,所以,Δ=4(2 006k)2+4(2 006k 2+k)为完全平方数.故Δ/4=k[(2 0062+2 006)k+1]为完全平方数.又因(k,(2 0062+2 006)k+1)=1,所以,k 与(2 0062+2006)k+1均为完全平方数.故m-n 为完全平方数.二、(1)因为BC 是⊙O 2的切线,所以,∠ACB=∠CDA.又AB ∥CD,则∠BAC=∠ACD.所以,△ABC ∽△CAD.从而,∠ABC=∠CAD.故AD 是⊙O 1的切线.由切割线定理得AD 2=DE ·DC.则122=94D C 2.解得CD=18. (2)由(1)知,△ABC ∽△CAD,CD=18.所以, R 1/R 2=AC/CD,即R 1/R 2=A C/18.因为6=CD-AD<AC<CD+AD=30,所以,1/3< R 1/R 2<5/3.又AC ≠CD(否则,四边形ABCD 为平行四边形),所以,R 1R 2≠1.故R 1R 2的取值范围是1/3< R 1/R 2<5/3,且R 1R 2≠1.三、为叙述方便,用max{a 1,a 2,…,a n }、min{a 1,a 2,…,a n }分别表示a 1,a 2,…,a n 中的最大数和最小数.当x ≤min{a-1,3}时,有f(x)=(x+a)(-2x+a+2)-2x+4a=-2x 2-ax+a 2+6a.当x ≥max{a-1,3}时,有f(x)=(x+a)(2x-a-2)-2x+4a=2x 2+(a-4)x-a 2+2a.当min{a-1,3}<x<max{a-1,3}时,f(x)为一次函数.可见,函数f(x)的图像在左、右两边为两段抛物线弧,而在中间这一段上为一条线段.当且仅当它的对称中心为中间这一线段的中点M,且左、右两端抛物线弧的顶点A 、B 也关于点M 对称时,函数f(x)的图像为中心对称图形.因为x M =231)-(a +=22a +,x A =-a/4,x B =-44-a , 所以,2x x B A + =xM,即-84-a a +=22a +. 解得a=-2/3.经检验,a=-2/3满足要求.。
数学奥林匹克初中训练题

’
则 k=
.
2 . 若 关 于 的方 程
+2( m +3) +m +3=0
若' t O=2 x 一2 y+ Z - , 则 W 的最 小值 为
( ) .
, , 1
的两 实数根分别为 . 、 , 则I x 一l l +I 2 一 l I 的最 小值 为 .
器j B C = .
所以, △A B C的周长为 5+ ̄ / / 1 0.
5 . B.
当 m=l时 , 原 方程 为 l Y 一1 I =3或 1
故有五个不同的实根 ± 2 , ± , 0 .
6 .R
如图 6 , 延 长 C A、 F M 交于点 P . 则C F:C P .
( D) 5+ 1 0
4 . 设 表示数 n 的个 位数字 . 则
l + 2 + … + X2 0 1 2=
— —
・
5 . 若关于 Y 的方程 l l Y 一 1 I 一 2 I = m恰
有五个 不 同 的实根 , 则r a=( ) .
一
第 二 试
、
( 2 0分 ) 如图 2 , 在等 腰 R t △A B C
( A) 0 ( B) 1 ( C) 2 ( D) 大于 2
6 . 如图 1 , 在△ A B C中 , A B: A C, C M 平
中, C= 9 0 。 , 点 D、 E在 边 B C上 , 点 在A C的延 长线 上 ,
且B E =E D =C F . 求
分 A C B, 与A B 交 于 点 M, A D _ l -B C 于 点 D, ME_ l _B C 于 点 E, MF上 MC与 B C 交 于 点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学奥林匹克初中训练题(032)
第一试
一、选择题(每小题7分,共42分)
1.满足不等式|x-1|+|x-9|
的整数x的个数为( ).
A.8 B.9 C.10 D.11
2.如图,由钝角△ABC的顶点A作高AD,以垂足D为圆心,AD为半径作圆,分别交AB、AC于M、N,如果AB=c,AM=m,AN=n,那么,AC边的长是( ).
A.m+n B.nc
m C.mc
n
D.(+
n m
m n
)
3.已知一次函数y=ax+b(a为整数)的图象过点(98,19),它与x轴的交点为(p,0),与y轴的交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为().
A.0 B.1 C.2 D.大于2的整数4.如图,在梯形ABCD中,AB∥CD,并且AB=2CD,M、N分别是对角线AC,BD 的中点,设梯形ABCD的周长为l1,四边形CDMN的周长为l2,则l1与l2满足( ).A.l1=2l2B.l1=3l2C.l2<l1<2l2D.2l2<l1<3l2
5.设S则与S最接近的整数是
( )
A.1997 B.1998 C.1999 D.2000
6.设n是正整数,0<x≤1,在△ABC中,如果AB=n+x,BC=n+2x,CA=n+3x,BC 边上的高AD=n,那么,这样的三角形共有()
A.10个B.11个C.12个D.无穷多个
二、填空题(每小题7分,共28分) .
1.已知a 、b 为正整数,且满足
224=49
a b a ab b +++.则a +b 的值等于___________. 2.如图,设ABCDE 是正五边形.直线MN 分别交边EA 、AB 于M 、N .如果AM +AN =AB ,
那么,∠MAN +∠MBN +∠MCN +∠MDN +MEN =________.
3.若n 是正整数,且n 2+9n +98恰好等于相邻的两个正整数的积,则n 的所有值是
_______.
4.已知9(1)
979(2)98x y m x y n x y m an x y bm cn +⎧=⎪+⎪⎨++⎪=⎪++⎩
如果满足(1)式的一切实数x 、y 、m 、n ,也满足(2)式,那么,a +b +c 的值等于_______.
第二试
一、(20分) 如图,在凸四边形ABCD中,AC=BD=AB,且AC⊥BD,垂足为E.设
CD.
I为△AEB的内心,M为AB的中点.求证:MI丄CD,且MI=1
2
二、(25分) 已知关于x的方程x2+ax+6=0有两个不相等的实根.求证:方程x4+ax3 +(b-2)x2-ax+1=0有四个互不相同的实数根.
三、(25分) 六盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须以完全一样的面对接,最后得到的包装形状是一个长方形.已知磁带盒的长、宽、高尺寸分别是a=11cm,b=7cm,c=2cm.
(1)请你给出一种能使表面积最小的打包方式,使其表面积最小,并画出其示意图;
(2)若不给出a、b、c的具体尺寸,只假定a≥b≥c,问能否按照已知的打包方式,使其表面积最小?并说明理由.。
