结构力学(王焕定第三版)教材习题第三章答案全解——哈工大老师提供
哈工大结构力学教材

哈工大结构力学教材
哈尔滨工业大学的结构力学教材有多个版本,包括:
1. 《结构力学教程》(上册、下册),由哈尔滨工业大学工程力学系编写组编写,高等教育出版社出版,1981年8月第一版,1990年6月第二版。
2. 《结构力学》(上册、下册),由戴鸿哲、盛兴、朱耀臻、李建中、王焕定等编写,哈尔滨工业大学出版社出版,2000年12月第一版。
3. 《结构力学》(上册、下册),由王焕定、祁皑主编,高等教育出版社和哈尔滨工业大学出版社出版,2007年5月第一版。
4. 《结构力学》(上册、下册),由唐锦春主编,高等教育出版社出版,2010年2月第二版。
这些教材在哈尔滨工业大学结构力学课程中被广泛使用。
如需了解更多版本,建议登陆学校官网或相关论坛查询。
结构力学王焕定答案

结构力学王焕定答案引言结构力学是工程学中一门重要的学科,它研究各种结构的力学性能和稳定性。
在结构设计和分析中,结构力学的基本原理和方法是必不可少的工具。
在结构力学领域,王焕定教授被公认为权威人物,他的研究和贡献对于该领域的发展起到了重要的推动作用。
本文将以王焕定教授的研究成果为基础,回答一些常见的结构力学问题。
1. 王焕定教授简介王焕定教授是中国工程院院士,同济大学结构工程系的教授。
他的研究领域主要是结构力学和抗震工程。
他在结构优化设计、结构动力学和结构抗震性能等方面做出了杰出的贡献。
他的研究成果不仅在国内具有广泛的应用,也对同行在国际上产生了积极的影响。
2. 结构力学基本原理结构力学的基本原理是力学的基础。
在结构设计和分析中,掌握这些基本原理是非常重要的。
以下是一些结构力学的基本原理:2.1. 受力分析结构受力分析是结构力学的起点。
它通过力的平衡原理和受力分解的方法,确定结构在不同载荷下的受力状态。
在受力分析中,常常使用静力学和力矩平衡原理来解决受力问题。
2.2. 应变和应力应变和应力是结构物力学性能的重要指标。
应变表示物体在外力作用下相对变形程度的大小,而应力表示单位面积上的力的大小。
结构力学中常常关注材料的线弹性行为,通过应力应变关系分析材料的变形和破坏情况。
2.3. 刚度和变形刚度是结构物抵抗变形的能力。
结构在受到外力作用时,常常会发生变形。
刚度常常用杨氏模量和截面惯性矩等指标来表征,它是结构力学分析中十分重要的参数。
刚度与自由度的数量相关联,它可以对结构的强度和稳定性进行评估。
2.4. 稳定性和挠度稳定性和挠度是结构力学的重要概念。
结构在不同载荷作用下,可能会发生不稳定破坏现象。
稳定性分析能够判断结构在外力作用下的抗承载能力,而挠度分析能够评估结构的变形程度。
结构的稳定性和挠度分析是结构设计和评估的重要内容。
3. 结构力学问题的解答王焕定教授通过多年的研究和实践,积累了丰富的经验和知识。
结构力学第三版王焕定第3章习题及参考答案
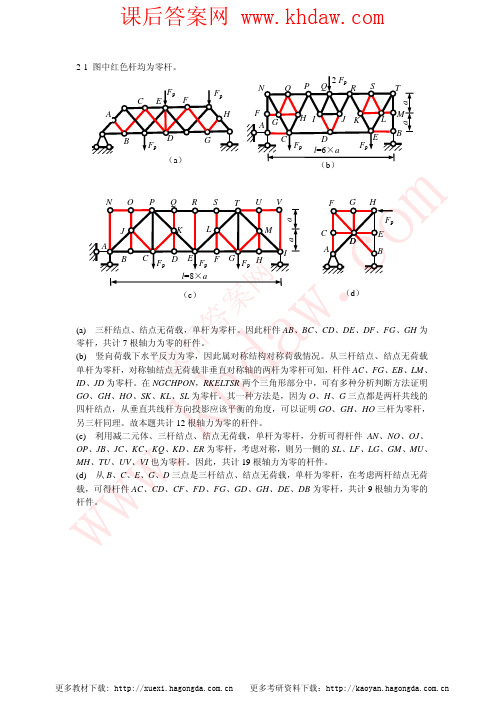
w.
cos α = 2 5
隔离体(b)
FN7 = FN8 = 35 kN
FN6 = FN5 = 65 kN
更多考研资料下载:
co
FN10
FN4
FN3
α α
隔离体(d)
m
40 kN FN4
课后答案网
2-2(b) Fp
θ
再取结点 B 作隔离体
FN4 = 26.67 kN
ww
更多教材下载:
w.
kh
更多考研资料下载:
da
课
后
答
w.
案 网
5 FN3 = − FN1 =33.33 kN 3 4 FN2 = FN1 = − 26.67 kN 3
1 0 8
12
13 6
4 5
7 4×2.5 m
17.5 kN 依次取结点为隔离体,受力图如下所示。 10 kN FN1 FN2
32.5 kN
2×1.25 m
2-2(a) 先求反力,结果如图所示。 10 kN 2
40 kN 3
α
FN8
FN1
α α
α
FN5
案 网
17.5 kN 隔离体(a)
FN9
32.5 kN 隔离体(c)
FN 2 = −30 2 kN=42.42 kN
FN3 = −15 2 kN= − 21.21 kN
更多教材下载:
更多考研资料下载:
co
FN4 45o FN1 FN3 (c)隔离体图
2-6(b)取 2、3 杆件相交的结点作隔离体图(a)所示,往FN2方向投影,列方程得:
( FN3 − FN4 ) sin 2α − 40 kN × cos α = 0, FN3 = 20 kN/sinα + FN4 = − 27.951 kN
结构力学(王焕定第三版)教材习题第三章答案全解——哈工大老师提供
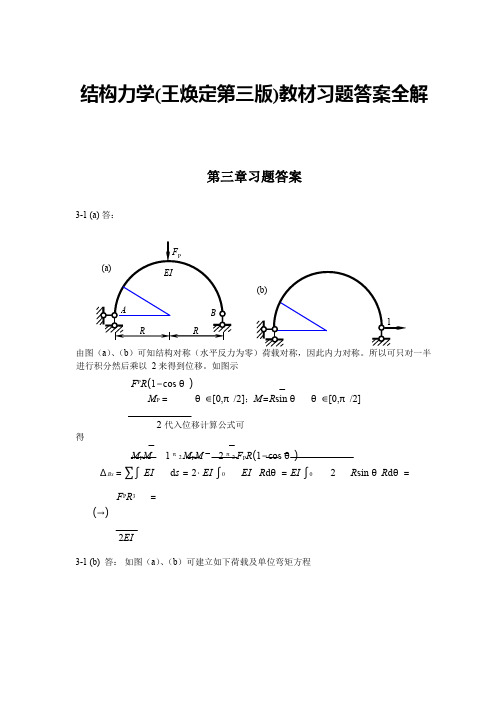
结构力学(王焕定第三版)教材习题答案全解第三章习题答案3-1 (a) 答:由图(a )、(b )可知结构对称(水平反力为零)荷载对称,因此内力对称。
所以可只对一半进行积分然后乘以 2 来得到位移。
如图示F P R (1−cos θ)M P = θ∈[0,π/2];M =R sin θ θ∈[0,π/2]2 代入位移计算公式可得M P M1 π2 M P M2 π2 F P R (1−cos θ)∆Bx = ∑∫ EId s = 2⋅ EI ∫0EI R d θ= EI ∫02 R sin θR d θ=F P R 3 =(→)2EI3-1 (b) 答: 如图(a )、(b )可建立如下荷载及单位弯矩方程EIBARRF P( a )1pR ∆Bx =∑∫ MEIM d s =∫0π2 MEI P M R d θ= q EI 4∫0π2(1−2cos θ+cos 2 θ)R d θqR 4 ⎡ θ 1⎤3π⎞ qR 4= EI ×⎢θ−2sin θ+ 2 + 4sin2θ⎥⎦0 =⎝⎜ 4 − 2⎠⎟ 2EI (→)2 ⎣3-2 答:作M P 图和单位力弯矩图如下图: 由此可得内力方程根据题意EI (x ) = EI (l + x )代入位移公式积分可得 2 2 P 0s i n ( ) d (1 c o s ) (1 c o s ) q M R q R M R θθ α α θθ − = = − = − ∫AqRBα θ1( a ) θ( b )ABlq 03 0 p 6 x q M M xl = = xP M 图2 0 6q l1lM 图 x5 83 82l 代入位移公式并积分(查积分表)可得M P M l 2 q0x4∆Bx =∑∫ EI d x =∫0 6EI(l + x) d x7q0l40.07 ql4= (ln 2−)× = (→)123EI EI3-3 答:分别作出荷载引起的轴力和单位力引起的轴力如下图所示:由此可得C 点的竖向为移为:F NP F N1F NP F N1 ∆Cy =∑∫EA d s=∑ EA l =65112.5 kN× ×6 m+2×(62.5 kN× ×5 m+125 kN× ×5 m+75 kN× ×6 m)= 88EA=8.485×10−4 m当求CD 和CE 杆之间的夹角改变使:施加如图所示单位广义力并求作出F N2 图,则F∆=∑∫ F NP EA F N2 ds =∑ NP EAF N2 l2×62.5 kN ×(−0.15)×5 m +(−112.5 kN)×0.25×6 m =EA=−1.4×10−4 rad( 夹角减小)3-4 (a)答:先作出M p和M 如右图所示。
结构力学—纸质作业答案[1]
![结构力学—纸质作业答案[1]](https://img.taocdn.com/s3/m/8580dec6a32d7375a5178094.png)
《结构力学》纸质作业谜底之阿布丰王创作第一章重点要求掌握:第一章介绍结构力学基本概念、结构力学研究对象、结构力学的任务、解题方法、结构计算简图及其简化要点、结构与基础间连接的简化、计算简图、杆件结构的分类、载荷的分类.要求掌握明确结构力学求解方法、会画计算简图,明确铰结点、刚结点、滚轴支座、铰支座、定向支座、固定支座的力学特点作业题:无第二章重点要求掌握:第二章介绍几何不变体系和几何可变体系的构造规律和判断方法,以及平面杆系体要求掌握几何不变体系的构造规律,会进行几何分析,判定静定结构和超静定结构作业题:2-1对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:从基础开始分析:将地基看成刚片,刚片AB与地基有三个链杆连接,三链杆不交同一点,组成几何不变体;刚片CD与扩年夜的地基有三个链杆连接三链杆不交同一点,组成几何不变体;刚片EF与扩年夜的地基有三个链杆连接三链杆不交同一点,组成几何不变体.总计,图示体系为几何不变体,没有多于约束2-2对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:从基础开始分析:A点由两个链杆固定在地基上,成为地基一部份;BC杆由三根不交同一点的链杆固定在基础上;D点由两根链杆固定在基础上,组成没有多于约束的几何不变体.2-3对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:把地基看成刚片,杆AB和杆BC是两外两个刚片,三个刚片由铰A、B、C链接,三铰共线,所示体系为几何瞬变体(几何可变体的一种)2-4对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:将ABC看成一个刚片,将CDE看成另一个刚片,地基是第三个刚片,三个刚片由铰A、C、E链接,三铰不共线,组成没有多于约束的几何不变体变体系,指出多于约束的数目解:用一根链杆将BB’连接起来,所示体系依照二元体规则,A、A’、E、E’点拆失落,然后,将体系依照H、D、D’、C、C’、G 顺序逐步拆完,剩下一个三角形BFB’(几何不变体),原来体系缺少一个需要约束(图中的BB’杆),所以原来体系是几何可变体.2-6对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:依照二元体规则,ADC可以看成刚片,与地基通过瞬铰F相连,同样,BEC可以看成刚片,与地基通过瞬铰G相连,刚片ADC和刚片BEC通过铰C相连,F、C、G三铰不共线,图示结构为没有多于约束的几何不变体.2-7对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:杆ADE和杆BE通过铰E相连,在通过铰A、B与地基相连,A、B、E三铰不共线,组成几何不变体成为扩年夜的地基,刚片CE通过两根杆与地基连接,所以图示体系缺少一个需要约束,是几何可变体.变体系,指出多于约束的数目解:将曲杆AC和曲杆BD看成刚片,两刚片通过瞬铰G相连,地基为第三个刚片,三个刚片通过A、B、G三铰相连,三铰不共线,所示体系是没有多于约束的几何不变体.2-9对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:从左侧开始分析,AE是固定在地基上,是基础的一部份,刚片BG通过链杆EF和铰B固定在地基上;刚片CH通过链杆GH和铰C固定在地基上;刚片DI通过链杆HI和铰D固定在地基上;所示体系为没有多于约束的几何不变体.2-10对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:杆AE和杆DI固定在地基上,成为地基的一部份,刚片CH通过铰C和链杆HI固定在基础上,成为不变体,刚片BG通过三根杆约束到地基上,整个体系是没有多于约束的几何不变体.2-11对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:节点D通过两根链杆固定在地基上,同样节点C、E分别通过两根链杆固定在地基上,构成几何不变体,扩年夜了基础,在从左向右分析,刚片FG通过不交一点的三根链杆连接到基础上,节点H、I、J分别用两根链杆约束,整个体系是没有多于约束的几何不变体.2-12对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:刚片AB由三根不交一点的小链杆固定在基础上,节点D有三根链杆固定,所以体系为有一个多于约束的几何不变体,即一次超静定结构.2-13对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:杆AC和BD固定在基础上,成为基础的一部份,CD杆为多于约束,整个结构是有一个多于约束的几何不变体,即一次超静定结构2-14对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:先分析内部,杆AC、AF、FD组成的三角形为一个刚片,杆BC、BG、GE组成的三角形为另一个刚片,EF为第三个刚片,三个刚片通过不再同一条直线上的三铰C、F、G相连,构成一个年夜刚片,年夜刚片再由三个小链杆与基础相连,整个体系是没有多于约束的几何不变体.2-15对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:先分析内部,杆AC、AD、DC组成的三角形为一个刚片,中间过剩一个链杆DF,杆BC、BE、EC组成的三角形为另一个刚片,中间过剩一个链杆EG,DE为第三个刚片,三个刚片通过不再同一条直线上的三铰D、E、C相连,构成一个年夜刚片,年夜刚片再由三个小链杆与基础相连,整个体系是有两个多于约束的几何不变体,即两次超静定结构2-16对图示体系作几何组成份析,如果是具有多于约束的几何不变体系,指出多于约束的数目解:约束对象(刚片或结点)的选择至关重要,若选择不妥将给构造分析带来很年夜困难,特别是在分析较复杂的三刚片体系时.这时,应考虑改变约束对象的选择方案.例如上图所示体系,一般容易将地基和ABD、BCF分别看作刚片Ⅰ、Ⅱ、Ⅲ(约束对象).此时刚片Ⅰ、Ⅲ之间既无实饺也无瞬铰连接,无法进行分析.若改变约束对象,将刚片Ⅱ换成杆DE(见上图),而链杆AB 、BD、DA酿成约束.于是,刚片I、Ⅱ由瞬铰E连接,刚片Ⅱ、Ⅲ由∞点瞬铰O相连,刚片Ⅰ、Ⅲ由瞬铰C相连.再判定三瞬铰是否共线即可获得正确结论.可以看出,新方案中每两个刚片间均以两链杆形成的瞬铰相连;原方案中刚片I、Ⅱ间和刚片Ⅱ、Ⅲ间均以实佼紧密相连,造成刚片Ⅰ、Ⅲ间无法实现有效连接.第三章重点要求掌握:本章结合几种经常使用的典范结构型式讨论静定结构的受力分析问题,涉梁、刚架、桁架、组合结构、拱等.内容包括支座反力和内力的计算、内力图、受力特性分析等,讲解内容是在资料力学等课程的基础上进行的,但在讨论问题的深度和广度上有显著的提高,要求掌握静定多跨梁和静定平面刚架的受力分析,静定平面桁架的受力分析,组合结构和三铰拱的受力分析,隔离体方法、构造和受力的对偶关系.作业题:3-1试作图示静定多跨梁的弯矩图和剪力图解:(1)求支座反力,此题为静定组合梁,ABE为基本部份,EC为附加部份,先分析附加部份40支撑,反过来,也就是说,基础部份在E点向上给附加部份kN340附加部份在E点给基础部份向下的压力kN3(2)求剪力,逐步取隔离体剪力图(3)求弯矩,采纳取隔离体方法,求出关键点弯矩,其中匀布载荷作用的DB部份,叠加上匀布载荷作用在简支梁的效果BD杆中点弯矩3-2试作图示静定多跨梁的弯矩图和剪力图解:(1)求支座反力,此题为静定组合梁,ABF为基本部份,GD为附加部份,先分析附加部份对ABF基本部份(2)求剪力,逐步取隔离体剪力图(3)求弯矩,采纳取隔离体方法,求出关键点弯矩,其中匀布载荷作用的FB部份,叠加上匀布载荷作用在简支梁的效果3-3试作图示静定多跨梁的弯矩图、剪力图和轴力图,并校核所得结果解:(1)支座反力(2)杆端剪力对DC杆对BC杆对AB杆剪力图(3)轴力对DC杆对BC 杆对AB 杆轴力图(4)弯矩图对DC 杆对BC 杆对AB 杆 )(60);(30右侧受拉外侧受拉m kN M m kN M AB BA ⋅=⋅= 弯矩图3-4试作图示静定多跨梁的弯矩图、剪力图和轴力图,并校核所得结果解:(1)支座反力(2)求杆端剪力取BD 杆作为隔离体取CB 杆作为隔离体取AB 杆作为隔离体剪力图(3)求杆端轴力取BD 杆作为隔离体取CB 杆作为隔离体取AB 杆作为隔离体轴力图(4)求杆端弯矩,画弯矩图取BD杆作为隔离体取CB杆作为隔离体取AB杆作为隔离体,因为杆AB上剪力为零,则弯矩坚持为常数3-7试作图示静定多跨梁的弯矩图、剪力图和轴力图,并校核所得结果解:(1)先求支座反力(2)求杆端弯矩取BC杆作为隔离体BC杆中点的弯矩再叠加上匀布载荷作用在剪质量上的效果,就获得BC杆的弯矩图取AC杆作为隔离体弯矩图(3)求杆端剪力取BC杆作为隔离体取AC杆作为隔离体剪力图(4)求杆端轴力取BC杆作为隔离体取AC 杆作为隔离体 轴力图3-8试作图示静定多跨梁的弯矩图、剪力图和轴力图,并校核所得结果解:(1)求支座反力(2)求杆端弯矩 取DC 杆为隔离体取BC杆为隔离体()上侧受拉m kN M M CB BC ⋅-=⨯-==60320取AB 杆为隔离体()()左侧受拉左侧受拉m kN M m kN M AB BA ⋅-=⎪⎭⎫⎝⎛⨯⨯⎪⎭⎫ ⎝⎛⨯⨯-⨯=⋅-=⨯-=1806316402132060320 剪力图轴力图户忽略3-9试作图示静定多跨梁的弯矩图、剪力图和轴力图,并校核所得结果 解:(1)求支座反力 (2)求杆端剪力取BE 作为隔离体 ql F ql F QEB QBE 41;41== 取DE 作为隔离体 ql F ql F QED QDE 41;41-=-= 取AD 作为隔离体 ql ql ql F ql F QDA QAD 4143;43-=-== 剪力图(3)求杆端轴力取BE 作为隔离体 ql F ql F NEB NBE 41;41-=-= 取DE 作为隔离体 ql F ql F NED NDE 41;41-=-=取AD作为隔离体 ql F ql F NDA NAD 41;41==轴力图(3)求杆端弯矩取BE 作为隔离体 ()右侧受拉241;0ql M M EB MBE == 取DE 作为隔离体取AD 作为隔离体 ()右侧受拉241;0ql M M DA MAD == 弯矩图3-14试作图示静定多跨梁的弯矩图、剪力图和轴力图,并校核所得结果 解:(1)求支座反力 剪力图 轴力图 弯矩图3-16试求图示三铰拱的支座反力,并求界面K 的内力 解:(1)支座反力 (2)K 点几何参数 (3)K 截面弯矩 (4)K 点剪力(5)K点轴力3-17试求图示抛物线三铰拱的支座反力,并求界面D和E的内力解:(1)根据几何条件,在图示坐标下,求抛物线方程.抛物线经过坐标原点,是抛物线方程为:bxy+=2,抛物线经ax过B(20,0)点.于是有C(10,4)为抛物线极点,2=b=ba⇒a+505+104=100解联立方程,获得抛物线方程:(2)求D点几何参数(3)求E点几何参数(4)支座反力(5)求D点内力D点弯矩D点剪力D点轴力(6)求E点内力E点弯矩E点剪力E点轴力弥补题1求x的值,是中间一跨的跨中弯矩与支座弯矩的绝对值相等解:CD 中点弯矩值()2281x l q - 支座弯矩()221221qx x x l q +-弥补题2图示体系为两跨梁,全长接受均布载荷作用,试求铰D 的位置,即确定图中x 的值,使负弯矩与正弯矩的峰值相等 解:以x 暗示较D 与支座B 之间的距离图b 图b\图b解:以x 暗示较D 与支座B 之间的距离.在图b 中,先计算附属部份AD ,求支座反力为2)(x l q -,做出弯矩图,跨中正弯矩峰值为8)(2x l q -再计算基本部份DC ,将附属部份在D 的所受的支承反力2)(x l q -,反其指向,当作载荷加于基本部份,支座B 处的负弯矩峰值为22)(2qx x x l q +-令正负弯矩峰值相等,获得 解之得:l x 172.0=铰的位置确定后,可作弯矩图c,其中正负弯矩峰值都即是2086.0ql ,如果使用两个跨度为l 的简支梁,弯矩峰值为281ql ,如图d,可见静定多跨梁的峰值比一系列简支梁要小. 弥补题3求作下面组合梁的内力图 解:支反力图 剪力图 弯矩图弥补题4求做图示简支梁的内力图 解:(1)计算支反力 (2)做剪力图注意AB 、BC 、EF 、FG 各段没有载荷作用,剪力为常数, 剪力图为水平线,CE 段有均布载荷, 剪力图是斜直线 (2)做弯矩图选A 、B 、C 、E 、F L 、、F R 、、G 为控制界面,求得如下弯矩值 或者依次定出折线各点,做出折线弯矩图,注意到CE 段有均布载荷,叠加上以CE 为简支梁在均布载荷作用下的弯矩图,获得最后的弯矩图D 点的弯矩值为注意到微分关系Q F dxdM=,弯矩的最年夜值发生在剪力即是零的处所,根据剪力图确定剪力即是零的位置,CH=2.25,如果以C 点为原点,C 1H 段方程为:弥补题5已知抛物线三铰拱轴线方程()x l x l fy -=24,求支座反力;截面D 、E 的内力 解:(1)支座反力(2)D 、E 点几何参数 (3)D 点的内力 (4)E 点的内力弥补题5求图示三铰拱,支座反力;D 、E 点的弯矩 解:(1)支座反力 (2)弯矩弥补题6求指定桁架杆的内力(轴力) 解:先求支座反力kN F kN F RB RA 30;50== 第四章重点要求掌握:1.掌握刚体系虚功原理与变形体虚功原理的内容及其应用条件:掌握广义位移与广义荷载的概念.2.掌握结构位移计算一般公式,并能正确应用于各类静定结构受荷载作用、支座移动等引起的位移计算.3. 熟练掌握梁和刚架位移计算的图乘法.4. 了解曲杆和拱的位移计算及温度变动时的位移计算.5.了解互等定理作业题:4-1a 求图示结构B 点的水平位移解:分别作已知载荷作用下结构的弯矩图和虚拟载荷作用下结构的弯矩图在已知载荷作用下,()150l x x F M P P ≤≤=,在单元虚拟载荷作用下x M =1B 点水用方向位移:4-1b 求图示结构B 点的水平位移解:分别作已知载荷作用下结构的弯矩图和虚拟载荷作用下结构的弯矩图在已知载荷作用下 BD 段弯矩 DC 段弯矩 CA 段弯矩 BD 段弯矩 DC 段弯矩 CA 段弯矩B 点水平位移,这里弯曲刚度 4-1c 求图示结构B 点的水平位移解:分别作已知载荷作用下结构的弯矩图和虚拟载荷作用下结构的弯矩图在已知载荷作用下 在单元虚拟载荷作用下 本题可以使用图乘法求解位移为求转角,先做单元虚拟弯距作用下的弯矩图 使用图乘法求解转角4-3a 试用图乘法求图示结构中B 处的转角和C 处的竖向位移本题适合用图乘法求解,先求在已知载荷作用下的弯矩图该弯矩图可以看成下面两种弯矩图叠加为求B点转角,在B点施加虚拟单元力偶,做出虚拟载荷作用下得弯矩图用图乘法求B点转角为求C点位移,在C点施加虚拟单元力,做出虚拟载荷作用下得弯矩图用图乘法求C点位移4-3b试用图乘法求图示结构中B处的转角和C处的竖向位移解:本题适合用图乘法求解,先求在已知载荷作用下的弯矩图该弯矩图可以看成C点集中载荷和AB匀布载荷两种载荷弯矩图的叠加,在集中载荷作用下的弯矩图如下AB匀布载荷作用下的弯矩图如下为求B点转角,在B点施加虚拟单元力偶,做出虚拟载荷作用下得弯矩图用图乘法求B点转角为求C点位移,在C点施加虚拟单元力,做出虚拟载荷作用下得弯矩图用图乘法求C点位移4-3c试用图乘法求图示结构中B处的转角和C处的竖向位移为求已知载荷作用下的弯矩图,先求支座反力 已知载荷作用下的弯矩图为求B 点的转角,在B 点加虚拟的单元弯矩,并做弯矩图 用图乘法求B 点转角为求C 点位移,在C 点施加虚拟单元力,做出虚拟载荷作用下的弯矩图4-4a 求图示结构C 点竖向位移解:1.建立虚拟状态如图示,即为求C 点的竖向位移,在C 点加一个竖向单元力.2.支反力:对实际载荷A 点支反力kN V A 40=,0=A H ,m kN M A ⋅-=⨯-⨯-=270540710对虚设载荷A 点支反力kN V A 1=,0=A H ,m kN M A ⋅-=⨯-=771 实际结构在已知集中载荷作用下的弯矩图实际结构在已知匀布载荷作用下的弯矩图 实际结构在虚拟载荷作用下的弯矩图 3.分段建立弯矩方程: 对CB 段,40≤≤x 对BA 段,74≤≤x对斜杆作变换dx ds 35=计算结果为正,暗示C 点竖向位移朝下,与虚拟载荷相同 4-4b 求图示结构C 点和A 点竖向位移 解:做已知载荷作用下的弯矩图为求C 点位移,在C 点加单元虚拟载荷,做虚拟载荷作用下得弯矩图,求C 点的位移,BC 段用积分法,BD 用图乘法为求A 点位移,在A 点加单元虚拟载荷,做虚拟载荷作用下得弯矩图,用图乘法求A 点的竖向位移 4-6求图示结构A点的竖向位移,已知46241036,1012,210m I m A GPa E --⨯=⨯==解:求支座在已知载荷作用下的反力 求CD 杆在已知载荷作用下的轴力 求已知载荷作用下得弯矩和CD 的轴力求支座在单元虚拟载荷作用下的反力 求CD 杆在单元虚拟载载荷作用下的轴力 求单元虚拟载载荷作用下得弯矩和CD 的轴力 求A 点的竖向位移4-7图示结构支座B 发生水平位移a 、竖向位移b,求由此发生的铰C 左右两截面的相对转角以及C 甸的竖向位移解:为求C 点左右两截面的相对转角,在C 点虚拟加单元弯矩,如下图所示,获得B 点的反力RBy RAy F F =,000=⇒=+⇒=∑RBy RBy RAy y F F F F所以,C 点左右两截面的相对转角为负号暗示转角方向与假设的方向相反为求C 点竖向位移,在C 点虚拟加单元竖向载荷,如下图所示,获得B 点的反力RBy RAy F F =,2110==⇒=+⇒=∑RBy RAy RBy RAy y F F F F F 所以,C 点竖向位移为弥补题弥补题1求悬臂梁A 点和C 点竖向位移和转角,忽略剪切变形的影响解:A 点竖向位移A 点的转角C 点竖向位移如果使用图乘法,CB 段P M 的形心很难确定,进而竖距无法确定,这里不应该使用图乘法C 点转角使用图乘法不论P M 图在CB 段的形心位值,它对应的竖距总是1,所以这里可以使用图乘法弥补题2求悬臂梁A 点和C 点竖向位移和转角,忽略剪切变形的影响解:A 点竖向位移A 点转角C 点竖向位移(将原点设在C 点)C 点转角(将原点设在C 点)弥补题3图示结构的杆AB由于资料收缩发生应变-ε,而杆BC由1于资料伸长发生应变ε.试求B点的水平位移△B和C点的水平位2移△C.解:(1)由于刚架各杆仅发生轴向应变,求刚架B点水平位移需在B点施加一个水平单元力,如图所示,得结构各杆虚轴力为F NAB=-2,F NBC=0.(2)由结构位移计算公式,得(3)求刚架B点水平位移需在C点施加一个水平单元力,如图所示,得结构各杆虚轴力为F NAB=-2,F NBC=-1可见,B、C两点的水平位移相差εa2弥补题4 刚架各杆的EI为常数,用图乘法求D点竖向位移和转角解:先做在实际载荷作用下的弯矩图,注意A点的弯矩为其中第一部份是C点载荷在A点发生的弯矩,第二部份是B 点竖向反力在A点发生的弯矩.再作在虚设载荷作用的弯矩图,注意AB段弯矩的计算弥补题5:求图示组合结构C点竖向位移,AC杆EI为常数,BD杆EA为常数解:分别给出组合结构在实际载荷作用下的弯矩图和在虚设载荷作用下的弯矩图,在实际载荷作用下,注意A点弯矩为零,所以B 点竖直方向反力12kN,BD杆受压,轴力在图上标出,同理求出虚设载荷作用下,BD杆的轴力弥补题6图示等截面梁,已知支座A下沉2cm,并发生转动,EI=500KNm2,D点竖向位移为零,问A点转角是几多?解:(1)作实际载荷作用下的弯矩图,先分析BD段,由B点弯矩为零,获得C点支座反力为19kN,再分析AB段,B点集中载荷为10kN,于是可以做出图示的弯矩图(2)作虚设载荷作用下的弯矩图,先分析BD段,由B点弯矩为零,获得C点支座反力为5/3,再分析AB段,B点集中载荷为2/3方向向上,,于是可以获得弯矩图和支座A的反力由弯矩引起的D点位移:由支座移动引起的D点位移:弥补题7:求图示结构A点截面转角,B点的竖向位移和水平位移解:注意A点有两个截面,可是截面转角相等,作出实际载荷作用下的弯矩图和虚设载荷作用下的弯矩图弥补题8求图示结构A、B两点的竖向位移解(1)先做弯矩图(2)计算位移弥补题10问取何值时候,E点的竖向位移为零解(1)先做弯矩图(2)计算位移第五章重点要求掌握1.掌握力法的基来源根基理及解题思路,重点在正确地选择力法基本体系,明确力法方程的物理意义.2.熟练掌握在荷载作用下超静定梁、刚架、排架内力的求解方法.3.掌握用力法求解在支座发生位移时梁和刚架内力的方法.4.能利用对称性进行力法的简化计算.5.能计算超静定结构的位移及进行变形条件的校核作业题5-1a确定超静定结构的次数解:去失落三个链杆,酿成静定的悬臂梁,所以本结构是3次超静定结构5-1b确定超静定结构的次数解:去失落A点链杆,结构酿成静定组合梁,所以本结构是1次超静定结构5-1c确定超静定结构的次数解:去失落A点两个链杆约束,结构酿成静定刚架,所以本结构是2次超静定结构5-1d确定超静定结构的次数解:去失落CF、CG、FG共3个链杆, A、B为固定支座改为铰支座,结构成为静定结构,所以本结构是5次超静定结构5-1e确定超静定结构的次数解:将圆环截断,结构成为静定结构,所以本结构是3次超静定结构5-1f确定超静定结构的次数解:将两个方框截断,去失落其中3个固定支座,结构成为静定结构,所以本结构是15次超静定结构5-1g确定超静定结构的次数解:将两个方框截断,结构成为静定结构,所以本结构是6次超静定结构5-1h确定超静定结构的次数解:将两个方框截断,去失落一个固定支座,结构成为静定结构,所以本结构是9次超静定结构5-1i确定超静定结构的次数解:AB是连接4个点的复链杆,相当于2n-3=5个单链杆,同理,BC相当于2n-3=5个单链杆,总计22各单链杆,地基外9个点,18个自由度,所以本结构是4次超静定结构5-1j确定超静定结构的次数解:将A、B、C改为铰支座,结构成为静定结构,所以本结构是3次超静定结构5-2a用力法计算下面结构,并绘出弯矩图解:这是一次超静定问题,由于B 点实际位移即是0,获得力法基本方程去失落B 点链杆支座,获得基本体系,去失落载荷获得基本结构做基本结构在已知载荷作用下的弯矩图做基本结构在单元载荷作用下的弯矩图用图乘法求得柔度系数用图乘法求得自由项解力法基本方程获得未知力根据公式P M X M M +=11得弯矩图5-2b 用力法计算下面结构,并绘出弯矩图解:这是一次超静定问题,由于B 点实际位移即是0,获得力法基本方程去失落B 点链杆支座,获得基本体系,去失落载荷获得基本结构做基本结构在已知载荷作用下的弯矩图做基本结构在单元载荷作用下的弯矩图用积分法求得柔度系数用积分法求得自由项解力法基本方程获得未知力根据公式P M X M M +=11得弯矩图5-2c 用力法计算下面结构,并绘出弯矩图解:这是一次超静定问题,由于A 点实际位移即是0,获得力法基本方程去失落A 点链杆支座,获得基本体系,去失落载荷获得基本结构做基本结构在已知载荷作用下的弯矩图做基本结构在单元载荷作用下的弯矩图图乘法求得柔度系数用图乘法求得自由项解力法基本方程获得未知力根据公式P M X M M +=11得弯矩图5-2d 用力法计算下面结构,并绘出弯矩图,EI 为常数解:本题为2次超静定问题,基本体系和基本结构见图力法基本方程系数和常数项意义见下图基本结构在已知载荷作用下得弯矩图基本结构在单元载荷11=X 作用下得弯矩图基本结构在单元载荷12=X 作用下得弯矩图柔度系数。
结构力学王焕定答案

结构力学王焕定答案引言结构力学是一门研究物体变形和受力行为的学科,是工程学中的重要基础学科。
结构力学的研究可以帮助我们了解结构物在受力时的行为,为工程设计和分析提供理论依据。
本文将介绍结构力学领域权威专家王焕定的相关问题答案。
问题1:简单支座和铰支座的区别是什么?答案:简单支座和铰支座是结构中常见的两种支座形式。
简单支座是指支座在所有方向上均能提供垂直支撑的一种支座形式,通常由一个平面或球面来提供支撑,可以阻止结构在任何方向上的平移和旋转。
铰支座则是指结构中的连接点允许在某些方向上发生旋转的一种支座形式,它只提供垂直支撑,不能阻止结构在平面内的移动。
简单支座所提供的支撑主要是通过摩擦力来实现的,而铰支座是通过连接点的旋转来实现的。
由于简单支座可以阻止结构在水平方向上的移动,因此它通常用于需要限制水平位移的结构中,如桥梁的支座。
而铰支座则适用于允许结构发生旋转或位移的情况,如房屋的支撑结构。
两种支座形式在结构分析和设计中起着不同的作用。
问题2:如何计算弹性变形?答案:弹性变形是指物体在受力作用下所发生的可逆形变。
它可以通过应力和材料的弹性模量来计算。
弹性模量是描述材料抵抗弹性变形的特征参数,记作E。
弹性变形可以用胡克定律来描述,即应变与应力成正比。
弹性变形的计算公式为:ε = σ / E其中,ε表示应变,σ表示应力,E表示材料的弹性模量。
在实际工程中,经常需要计算结构体的弹性变形。
例如,在计算梁的弯曲变形时,可以根据梁的几何形状、受力情况和材料的弹性模量来计算弯曲应变和弯曲角度。
这对于工程设计和结构分析来说非常重要。
问题3:什么是结构物的静力平衡?描述其应用领域。
答案:结构物的静力平衡是指结构物在受到外力作用时,所有受力部分的合力和合力矩均为零的一种平衡状态。
在结构力学中,静力平衡是分析和设计结构物的基本要求之一。
结构物的静力平衡可以应用于各种工程领域。
例如,在建筑结构设计中,静力平衡可以用来确定各个构件的受力情况,以确保结构的安全性和稳定性。
结构力学课后习题答案
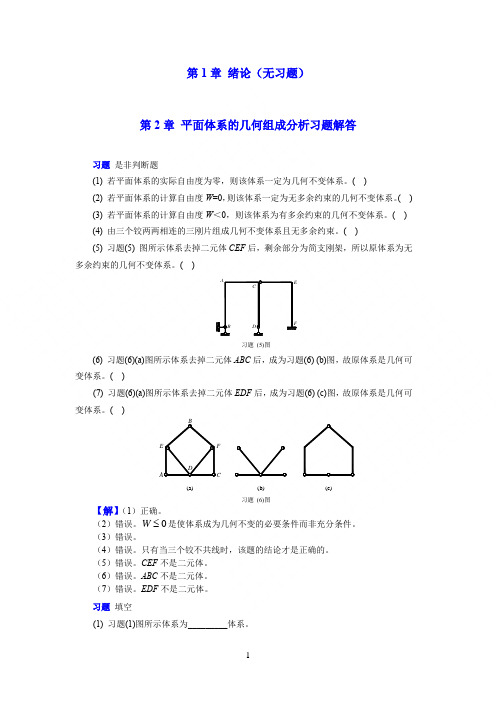
第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题 (5)图(6) 习题(6)(a)图所示体系去掉二元体ABC 后,成为习题(6) (b)图,故原体系是几何可变体系。
( )(7) 习题(6)(a)图所示体系去掉二元体EDF 后,成为习题(6) (c)图,故原体系是几何可变体系。
( )习题 (6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题 填空(1) 习题(1)图所示体系为_________体系。
B DACEF(a)(b)(c)D习题(1)图(2) 习题(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题(3)图(4) 习题(4)图所示体系的多余约束个数为___________。
习题(4)图(5) 习题(5)图所示体系的多余约束个数为___________。
习题(5)图(6) 习题(6)图所示体系为_________体系,有_________个多余约束。
习题(6)图(7) 习题(7)图所示体系为_________体系,有_________个多余约束。
结构力学三版课后习题答案

结构力学三版课后习题答案结构力学是一门研究物体在外力作用下的变形和破坏规律的学科。
它是工程力学的重要分支,广泛应用于建筑、桥梁、航空航天等领域。
而结构力学三版则是该学科的一本经典教材,它包含了大量的课后习题,帮助学生巩固所学知识。
本文将对结构力学三版课后习题进行解答,以帮助读者更好地理解和应用结构力学的知识。
1. 弹性力学弹性力学是结构力学的基础,它研究物体在外力作用下的弹性变形规律。
课后习题中的弹性力学问题涉及杆件、梁和板等不同形式的结构。
通过求解这些问题,可以掌握弹性力学的基本原理和计算方法。
2. 稳定性分析稳定性分析是结构力学的重要内容,它研究物体在外力作用下的稳定性和失稳规律。
在结构设计中,稳定性是一个关键问题,它决定了结构的安全性和可靠性。
课后习题中的稳定性问题涉及杆件、梁和框架等不同类型的结构。
通过求解这些问题,可以了解结构的稳定性分析方法和设计原则。
3. 动力学分析动力学分析是结构力学的进一步发展,它研究物体在外力作用下的振动和响应规律。
在工程实践中,动力学分析对于预测结构的振动特性和响应行为非常重要。
课后习题中的动力学问题涉及单自由度和多自由度系统的振动分析。
通过求解这些问题,可以掌握动力学分析的基本原理和计算方法。
4. 破坏力学破坏力学是结构力学的最终目标,它研究物体在外力作用下的破坏行为和破坏机制。
在结构设计和安全评估中,破坏力学的应用非常广泛。
课后习题中的破坏力学问题涉及杆件、梁和板等不同类型的结构。
通过求解这些问题,可以了解破坏力学的基本原理和计算方法。
总之,结构力学三版课后习题是学习和应用结构力学知识的重要工具。
通过解答这些习题,可以巩固理论知识、掌握分析方法,并培养解决实际工程问题的能力。
同时,课后习题还可以帮助读者深入理解结构力学的概念和原理,提高对结构行为的认识。
因此,建议读者认真对待结构力学三版课后习题,将其作为学习和实践的重要一环。
通过不断的练习和思考,相信读者一定能够在结构力学领域取得更好的成绩和进步。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构力学(王焕定第三版)教材习题答案全解第三章习题答案3-1 (a) 答:由图(a)、(b)可知结构对称(水平反力为零)荷载对称,因此内力对称。
所以可只对一半进行积分然后乘以 2 来得到位移。
如图示F P R(1cos θ)M P = θ∈[0,π/2];M=R sin θθ∈[0,π/2]2 代入位移计算公式可得M P M 1 π2 M P M 2π2 F P R(1cos θ)Bx = ∑∫ EI d s = 2 EI ∫0 EI R dθ= EI ∫0 2 R sin θR dθ=F P R3 =(→)2EI3-1 (b) 答:如图(a)、(b)可建立如下荷载及单位弯矩方程pR Bx =∑∫ MEIM d s =∫0π2 MEI P M R dθ= q EI 4 ∫0π2(12cosθ+cos 2θ)R dθqR 4θ 13π qR 4= EI ×θ2sinθ+ 2 + 4sin2θ0 = 4 2 2EI (→)23-2 答:作M P 图和单位力弯矩图如下图: 由此可得内力方程根据题意EI (x ) = EI (l + x )1 lM 图x3 0 p 6 x q M M x= = xP M 图2 06q l A Blq 0代入位移公式积分可得2 2 P 0s i n ( ) d (1c o s ) (1c o s ) q M R q R M R θθ α α θ θ == = ∫AqRBαθ1( a ) θ( b )5 8382l 代入位移公式并积分(查积分表)可得M P Ml2 q 0x 4Bx=∑∫ EI d x =∫0 6EI (l + x ) d x7q 0l 4 ql 4= (ln 2 )× =(→)12 3EI EI3-3 答:分别作出荷载引起的轴力和单位力引起的轴力如下图所示:由此可得 C 点的竖向为移为:F NP F N1 F NP F N1 Cy =∑∫ EA ds =∑ EAl =6 5kN× ×6 m+2× kN× ×5 m+125 kN× ×5 m+75 kN× ×6 m) = 8 8EA=×104 m当求 CD 和 CE 杆之间的夹角改变使:施加如图所示单位广义力并求作出F N2 图,则F =∑∫F NP EA F N2 ds =∑ NP EA F N2 l2× kN×(×5 m+( kN)××6 m =EA=×104 rad ( 夹角减小)3-4 (a)答:先作出M p和M 如右图所示。
利用图乘法计算。
按常规单位弯矩图M 的AK段为直线,KB段为零,KB段不用作图乘。
但M P图AK段形心不易求得,为了图乘简单,可将单位弯矩图AK段直线延长到KB段(如图虚线所示),这样可以用M P图的AB 段直接与M 图进行图乘(面积和形心对应的弯矩分别为A1、y1,如图中所示)。
但是,按照如此计算出的位移多计算了KB 部分的“贡献”(其面积和形心对应的弯矩分别为A2、y2,如图中所示)。
为此,根据叠加原理,必须再减去多计算的KB部分(也就是KB段作图乘)。
按上述分析思路进行图乘计算如下:M p M K y =∑∫ EI d sA1y1 A2 y 2= +EI EI17ql4= (↓)384EI3-4 (b) 答:先作出M p图和M 图如下所示。
2l82ly=KA B2/2ql8/2ql621qlA4=2248qlA=A KBPM图则根据图示的面积和对应的形心坐标,按位移计算公式计算可得M p M A1y1 + A2 y2 + A3 y3 + A4 y4 + A5 y5 23 F p l3 K y =∑∫ EI d s = EI = 3EI (↓)3-4 (c) 答:作出M p图和M 图如下图所示。
则根据图示的面积和对应的形心坐标,按位移计算公式计算可得M p M 2A1y1 + 2A2 y2 A3 y3 + A4 y4 5ql3AB =∑∫ EI d s = EI = 3EI2) 相对水平位移:则根据图示的面积和对应的形心坐标,按位移计算公式计算可得AB =∑∫ MEI P M d s = 2A1y1 +2A2yEI2 A3y3 + A4y4 = 5 6qlEI 4 ( 相互靠近)相对竖向位移为零:对称结构在对称荷载作用下的反对称位移等于零。
则根据图示的面积和对应的形心坐标,按位移计算公式计算可得M p MK y =∑∫ EI d s =1=1443-4(f)答:画出M p图和M 图如右所示。
A2=321272162A3=225PM图kN(m) 714y2=2y4=5.5y3=6M图y8=3A4=360则根据图示的面积和对应的形心坐标,按位移计算公式计算可得M p M 1y 1 A 2y 2 + A 3y 3 + A 4y 4 1985 C y =∑∫ EI d s =EI = EI (↓)3-5 答:在计算温度改变引起的位移时,注意要考虑轴向变形的影响。
Ct根据题意,轴线温度和温差分别为 t 0 = t = t1C 5 l5 5l M 图2按温度改变位移计算公式可得Cy= ∑∫αt 0F N d s +∑∫αhtM d s = ∑(±)αt 0A F N +∑(±)A M αh t3-6 答:与 3-5 一样要考虑轴向变形的影响。
按题意可求得BC 杆:t 0 = t 2 +t 1 =10°C t = t 2 t 1 = 40°C 2 AB 、CD 杆:t 0 = t 2 +t 1 = 10°C t = t 2 t 1 = 0°C2 代入位移计算公式A DC B 6mEI 2 =2 E I 1 EI 1 EI 1 -10o C 30C -10 o C1 0 m-10 o C内部 M 图6 mD6 m1 N F 图111DDy=∑∫αt 0F N d s +∑∫αtM d s = h=∑(±)αt 0AF N+∑(±)A M αh t =2400α=100α+= 2900α= m (←) h3-7 答:作出F N 图,本题 t 0 = t ,利用温度改变情况下的位移计算公式可得3-8 答:虚拟单位力状态与 3-7 题相同,单位力引起的轴力也相同(此处略,见上题)。
AK 杆的内力在其制造误差(变形虚位移——伸长位移)上所做的总虚变形功。
则根据虚功原理有:W e =K y W i = ×5mm= 5 2 mm( )N N 00 2d ( 2 0 . 5 2 ) 2 K y F t s t F l t d tdα α α α = = = ×× + × × = ↑ ∑ ∑∫N F 图25 2 2W e =W i K y = mm= mm (↑)3-9 答:求出单位水平力作用在 K 点时的支座反力,利用支座移动引起的位移计算公式有:3-10 答:本题是荷载、温度、支座移动和弹性支座多因素位移计算,可分别计算各单独因素的位移,然后叠加得到多因素结果,由此下面分别计算。
1)由于温度变化引起的 C 点竖向位移:m( ) ( ) 0 1 Ri KxiFc a b l a l== × + × + × =∑ →lt = t 2 t 1 = 30°C10°C = 20° CM d s = 120 α= 200 αhh2)由于荷载引起的 C 点竖向位移(将荷载下弹簧的变形作为虚变形,计算虚变形功):2M p M F RP A 1y 1 + A 2 y 2 A 3 y 3 A 4 y 4 F RP 60 105 585C y=∑∫ EI d s + F R k = EI + F R k = EI + 8EI = 8EI3)由于支座移动引起的 C 点竖向位移:F Ri ×c i = m将所有因素在 C 点产生的位移叠加:123585C y =C y +C y +C y = 200α+ m8EI3-11 答:因为要求考虑剪切变形的挠曲线,因此需分别作出荷载、单位力产生的弯矩图和剪力图。
又因是挠曲线计算,因此单位力状态作为在任意 x 截面位置。
根据所做的图形将内力代入位移计算公式积分即可得任意 x 截的位移——挠曲线。
ql qlBAqql22ql 1111xM 图F 图P M 图22ql 2 2ql x xF QP 图 QMEI P M x +∑ ∫ kFGA QP F Q d xy(x ) =∑∫ d1 x2 ql 2 x 2 x kql ×1 × x= E ×( ) + ×ql (l )+GAI 2 2 2 3= qxEI 2l l x + GA qlx (↓ ) x ∈[0,l ]4 63-12 答:因为 AB 杆应力-应变关系非线性,因此非线性杆需要根据式(3-4)计算22δε= σE F NP σ F NP= 对于 AB 杆件: EA ; 其他杆件:δε= E = EABx=∑∫ F N δεd xN F 图NP F 图∑ FNP F Nl +∫(F NP )2 F 2 N d x=EA(EA ) AB 杆件F P l (F NP )2 F N l = 2EA= + (EA )2 AB 杆件EA(EA )F P l 4(F P )2 l =+ 2(→)EA (EA )3-13 答:先求只有温度作用时的梁中点的挠度。
单位弯矩图如右下图所示按公式可得αt αt l 2t = t 2 t 1 = t (t ) = 2t t = ∑∫ h M d s = 1h再计算只有外力偶作用时的梁中点挠度,荷载与单位弯矩图如上图,可得M p M (±)A × y M 0l 2p=∑∫ EI d s =∑ EI = 8EI根据题目要求:t +P = 0,由此可解得M 0 =2αtEI 。
h1EIM 0M 0P M 图M 图( ) PP F l+×3-14 答:M 1 M 2MAB(a)(b)1M 1根据已知条件可以得到:θB =(M 2 )3EI 2 M 1因为图(b )情况θB = 0,由此解得:M 2 = ,代入θA 计算公式中,可得:2M 1 A =3-15 答: 由单位力状态求出支座反力、AC 杆件轴力和 BCD 杆的弯矩图如图示,与 3- 10 题一样先计算各单一因素的位移。
1)由 BCD 杆作成圆弧(假定向上凸)所引起的 D 点= F N ×= × m=转角为:1 ( ) ( 0 .5 1 3 m + 12 m ) d d( ) 200 mM DA M x M R R θ± × × × = = = = = ∑ ∑ ∑ ∫ ∫ 顺时针2 )由于 AC 杆件制造误差产生的 D 点转角为:D ABC单位力状态111533533EIAAθ lEIB1A3)由于支座移动产生的D 点转角为:3 = ∑F R i ×c i = (× m+× m)=D则向上凸时D 点转角为: D =D1 +D2 +D3 = (顺时针)同理向上凹时D 点转角为 D = 1D +D2 +D3 = (逆时针)3-16 答:本题已知A 截面转角,但F P 多大未知。
