由一道中考题想到的
合集下载
鉴古知今 继往开来——由一道中考试题得到的启示
一
一
【 评析及感悟 】
、
试题 所设 计的 三个 问题 之 间的 关 系
该题 以南水北 调工 程切人 ， 系河南 时政新 闻 ， 水 利工 程” 联 以“ 为
纽 带 ， 古今 三 大水 利项 目结合 在一 起 ， 过第 （） 、 （ ） 将 通 １问 第 ２ 问考查 学 生掌 握基 础知 识 的情况 ， 过第 （ ） 通 ３ 问引导 学 生立 足历 史 、 考现 思
由 一 道 中河 南省 中考历 史试 卷第 ２ 题 是一 道构思 巧 妙 的试 题 。 １ 笔 者初 见此 题 ， 深 深 感受 到 她 所洋 溢 的 引导 广 大 师生 关 注 国家 重 大 就 建 设项 目的热情 。题 目及参 考答 案如 下 ：
实。 这三个问题的设计展示了命题人宽阔的视野 、 跳跃的思维及强烈
的“ 鉴古知今 、 继往 开来 ” 的意识 ， 环相扣 、 环 层层递 进 。
中国 自古 以来就 是农业 大 国 ， 南省一 直是农业 大 省 。 为农业 河 作 大国， 水利建 设在农 业 生产发 展 中 ， 占有举 足轻 重 的地位 。无论 是传
视角看 ， 设计较为新颖。 由于“ 影响” 所涵盖的范围是广泛的 ， 有短期 、 长期的影响， 有直接 、 间接的影响 ， 有积极 、 消极的影响， 因此， 命题者
在设 计此题 时特别 限定 了 比较 思考 的范 围是 “ 当时的政权 ” 生 的 对 产
“ 响” 符合 初 中学 生 的认知 水平 ， 考虑 了一线教 学 的现 状 。 影 ， 也
考生通 过完成试 题 的第 （ ） ， １问 能够潜 移默 化地再 次感 受到水 利 工程 在 中国古代社会 发展 中的重要性 。材 料所 展示 的水利 工程在 历 史上都 有着不 可替代 、 可否认 的重要 功 能 ， 不 都对 当时的政 权产生 了 重要 影响 。第 （ ） ２ 问着 重考查 学生 比较分 析历史 现象 的能 力 ， 考查 从
一道中考题引起的教学思考
生 物学 教学 ２ ０ １ ３ 年（ 第３ ８ 卷） 第８ 期
－
５ ７・
一
道 中考题 引起 的教 学 思考
袁艳华 （ 江 苏 省 南 京 市 第 三 初 级 中 学２ １ ０ ０ ０ ２ ）
摘
要 就 学生在 中考 中一 道选择题错误 率高 的问题 ， 从教与学两方 面作了深省 ， 深悟 学生对概念 的模 糊实 为教 学的欠缺 ， 进而
８ 基 因 歧视
基因歧视 （ ｇ ｅ ｎ ｅ ｔ ｉ ｃ ｄ ｉ ｓ ｃ ｒ ｉ ｍ ｉ ｎ ａ ｔ ｉ ｏ ｎ ） 是指 随着科学 技
ห้องสมุดไป่ตู้
术 的发展 ， 人们 有可 能从 基 因 的角度对 人类 全体 的遗
传倾 向进行预测 ， 这些遗传信 息的揭示和公开 ， 将 对携
带某些 “ 不利基 因 ” 或“ 缺 陷基 因 ” 者 的升学 、 就业 、 婚
姻等社会活动产生不利 的影 响。基 因歧视可 以是针 对
一
［ １ ］ 安 国利． ２ ０ ０ ９ ． 细胞工程 （ 第 ２版） ． 北 京： 科学 出版社 ， １ ４ ６～ １ ４ ７ ［ ２ ］ 吴庆余． ２ ０ ０ ６ ． 基 础生命科学 （ 第 ２版 ） ． 北京 ： 高等教 育 出版社
２ ０ ０ ５年 ２月美 国参议 院 已通过 了禁 止基 因歧视 法案 。 随着基 因检测 的应用将 越来越 广泛 ， 我 国基 因歧 视现 象也很可能会 出现 ， 这并非杞人忧天 。
主要参考文献
者的离体 组织 细胞 ， 结果发 现这 些组 织细胞 能够 利用 半 乳糖。基因治 疗分体 内基 因治疗和体外基因治疗 。
习八下第 ８单元 “ 生物 技术 ” 时所 接触 到的具体 实例 ， 而选 项 ｃ中的植 物组织 培养 是在学 习八 上第 ５单 元
－
５ ７・
一
道 中考题 引起 的教 学 思考
袁艳华 （ 江 苏 省 南 京 市 第 三 初 级 中 学２ １ ０ ０ ０ ２ ）
摘
要 就 学生在 中考 中一 道选择题错误 率高 的问题 ， 从教与学两方 面作了深省 ， 深悟 学生对概念 的模 糊实 为教 学的欠缺 ， 进而
８ 基 因 歧视
基因歧视 （ ｇ ｅ ｎ ｅ ｔ ｉ ｃ ｄ ｉ ｓ ｃ ｒ ｉ ｍ ｉ ｎ ａ ｔ ｉ ｏ ｎ ） 是指 随着科学 技
ห้องสมุดไป่ตู้
术 的发展 ， 人们 有可 能从 基 因 的角度对 人类 全体 的遗
传倾 向进行预测 ， 这些遗传信 息的揭示和公开 ， 将 对携
带某些 “ 不利基 因 ” 或“ 缺 陷基 因 ” 者 的升学 、 就业 、 婚
姻等社会活动产生不利 的影 响。基 因歧视可 以是针 对
一
［ １ ］ 安 国利． ２ ０ ０ ９ ． 细胞工程 （ 第 ２版） ． 北 京： 科学 出版社 ， １ ４ ６～ １ ４ ７ ［ ２ ］ 吴庆余． ２ ０ ０ ６ ． 基 础生命科学 （ 第 ２版 ） ． 北京 ： 高等教 育 出版社
２ ０ ０ ５年 ２月美 国参议 院 已通过 了禁 止基 因歧视 法案 。 随着基 因检测 的应用将 越来越 广泛 ， 我 国基 因歧 视现 象也很可能会 出现 ， 这并非杞人忧天 。
主要参考文献
者的离体 组织 细胞 ， 结果发 现这 些组 织细胞 能够 利用 半 乳糖。基因治 疗分体 内基 因治疗和体外基因治疗 。
习八下第 ８单元 “ 生物 技术 ” 时所 接触 到的具体 实例 ， 而选 项 ｃ中的植 物组织 培养 是在学 习八 上第 ５单 元
总有简单的方法——一道中考压轴题引发的思考
０ Ｂ， Ｐ 交 Ｂ 与 点 Ｄ Ｃ
（） １求抛物线 的解 析式 ； （） ２ 点 是 Ａ Ｃ延 长线 上 一 点 ， ＢＥ Ｃ 的平 分 线 Ｃ 交 ｏ ， Ｄ ｏ 于点 Ｄ， 连接 Ｂ 求直 Ｄ， 线 Ｂ 的解析式 ； Ｄ （） （ ） 条件 ３在 ２ 的 下 ， 物 线 上 是 否 存 抛
Ｍ， 直线 ０ Ｍ 交 Ｂ 作 Ｄ 于点 Ⅳ， 证 Ｄ 肘 是 易 线段 Ｂ 的中垂 线 ， Ｄ 得 Ⅳ是线 段 Ｂ Ｄ的 中点 ， 易求点 Ⅳ 的 坐标 ， 求 得 直 线 ｏ Ⅳ 的 解 析 ， 式， 易求直线 Ｂ Ｃ的解 ／ 。 析 式 ， 得 直 线 ０ Ｎ 求 图 ３ 与直 线 Ｂ 的 交 点 Ｍ Ｃ 的坐标 ， 求直线 Ｄ 的解 析式 ， Ｍ 最后求直线 Ｄ 与抛 Ｍ 物线 的交点坐标 。 这种解 法很容易理解 ， 但计 算量大 。 方 法 三 ： 图 ４ 如 ，
￡ Ｏ ＤＫ —、 △ ＨＰＫ ．
ＢＧ ，
Ｂ ＡＧ ＝
Ａ
Ｃ Ｄ。易证 Ｃ Ｆ＝ Ｃ Ｄ， Ｂ 是 直径 ， Ａ Ｂ Ｂ Ｄ Ｂ Ａ Ｇ 是 直 角 ， Ｂ Ｇ＋ Ａ Ｇ ＝９￣ Ａ Ｇ ＋ Ｇ Ｋ ： Ａ Ｂ ０， Ｂ Ｂ ９ ， 得 Ｇ Ｋ＝ Ｃ Ｆ， Ｃ Ｄ ＝ Ｂ Ｇ＝ 。证 得 Ｂ Ｄ Ｆ Ｋ ９ △ Ｃ △ Ｇ Ｂ。 Ｃ 胁 Ｋ Ｆ：２ 得 Ｇ ， Ｋ：２ 得 Ｇ ７ 一４ ， ， （， ） Ｐ Ｂ交圆 ０ 于点 ， Ｄ 易证点 肘 和点 Ｇ关 于 轴
线。
，
得 ｘ号 一 ３ 吉２ ３ ＿ ＝
（ ）得 点 Ｐ坐标 为（４ ２ ） 坐标 为（ ， ） 一 ． １，５ ［ ３ 一８ 的 点不符合题 意 ， 舍去 ］ 。 方 法 二 ： 图 ３ 如 ， 作 Ｐ Ｂ＝ Ｃ Ｄ， Ｄ Ｂ 交 抛 物 线 于 点 Ｐ， Ｄ ＝
（） １求抛物线 的解 析式 ； （） ２ 点 是 Ａ Ｃ延 长线 上 一 点 ， ＢＥ Ｃ 的平 分 线 Ｃ 交 ｏ ， Ｄ ｏ 于点 Ｄ， 连接 Ｂ 求直 Ｄ， 线 Ｂ 的解析式 ； Ｄ （） （ ） 条件 ３在 ２ 的 下 ， 物 线 上 是 否 存 抛
Ｍ， 直线 ０ Ｍ 交 Ｂ 作 Ｄ 于点 Ⅳ， 证 Ｄ 肘 是 易 线段 Ｂ 的中垂 线 ， Ｄ 得 Ⅳ是线 段 Ｂ Ｄ的 中点 ， 易求点 Ⅳ 的 坐标 ， 求 得 直 线 ｏ Ⅳ 的 解 析 ， 式， 易求直线 Ｂ Ｃ的解 ／ 。 析 式 ， 得 直 线 ０ Ｎ 求 图 ３ 与直 线 Ｂ 的 交 点 Ｍ Ｃ 的坐标 ， 求直线 Ｄ 的解 析式 ， Ｍ 最后求直线 Ｄ 与抛 Ｍ 物线 的交点坐标 。 这种解 法很容易理解 ， 但计 算量大 。 方 法 三 ： 图 ４ 如 ，
￡ Ｏ ＤＫ —、 △ ＨＰＫ ．
ＢＧ ，
Ｂ ＡＧ ＝
Ａ
Ｃ Ｄ。易证 Ｃ Ｆ＝ Ｃ Ｄ， Ｂ 是 直径 ， Ａ Ｂ Ｂ Ｄ Ｂ Ａ Ｇ 是 直 角 ， Ｂ Ｇ＋ Ａ Ｇ ＝９￣ Ａ Ｇ ＋ Ｇ Ｋ ： Ａ Ｂ ０， Ｂ Ｂ ９ ， 得 Ｇ Ｋ＝ Ｃ Ｆ， Ｃ Ｄ ＝ Ｂ Ｇ＝ 。证 得 Ｂ Ｄ Ｆ Ｋ ９ △ Ｃ △ Ｇ Ｂ。 Ｃ 胁 Ｋ Ｆ：２ 得 Ｇ ， Ｋ：２ 得 Ｇ ７ 一４ ， ， （， ） Ｐ Ｂ交圆 ０ 于点 ， Ｄ 易证点 肘 和点 Ｇ关 于 轴
线。
，
得 ｘ号 一 ３ 吉２ ３ ＿ ＝
（ ）得 点 Ｐ坐标 为（４ ２ ） 坐标 为（ ， ） 一 ． １，５ ［ ３ 一８ 的 点不符合题 意 ， 舍去 ］ 。 方 法 二 ： 图 ３ 如 ， 作 Ｐ Ｂ＝ Ｃ Ｄ， Ｄ Ｂ 交 抛 物 线 于 点 Ｐ， Ｄ ＝
对一道中考试题的命制猜想与感悟
不变 ， 能感 受到数 学的无 穷魅力 ， 加深 美 的体验 ， 为学生 “ ” 爱 上数学 注入 了活性 剂． 在平 时的教 学 中 ， 要善 于捕
５ 几点感悟 ５ １ 重视教 材 。 ． 创造性地使用教材
教材是《 课程标准》 的载体 ， 是课程 目标 和课 程 内容
的物化 ， 是实施教 与学 的 “ 本 ” 同时 也是我 们施 教 的 蓝 ， 资源库 ， 当然 ， 重视教材并不 是要 做教材 的奴隶 ， 要敢 于
５ ４
中‘擞 ・ （ １年 －・ 中 ） ７ ７ ２ １ 第４ 初 版 ０ ｝ ￣ １
・ 试题赏析 ・
对 一道 中 考 试 题 的 命 制 猜 想 与 感悟
２ ００ 山 东 省 章 丘 市 第 六 中 学 袁翠香 ５２４ ２ ００ 山东省章丘市水寨镇中心中学 张卫东 ５２４
上取一点 Ⅳ， Ｃ Ｂ 直线 Ａ Ｃ 相交于点 Ｐ 使 Ｎ＝ Ｍ， Ｎ，Ｍ ．
பைடு நூலகம்
ＢＣＭ ．
图３
①请用量角 器度量 厶４ 的度 数为 朋 （ 精确到 １） 。； ②请用说理 的方法求 出ＬＡ Ｍ 的度数 ； Ｐ ③若 将 （ ） 的条 件 “ Ｃ＜ １中 Ｂ
Ａ ２ Ｃ 改 为“ Ｂ＞２ Ｃ ， Ｂ＜ Ｂ ” Ａ Ｂ ” 其他 条件不 变 ， 能 自己在 图 ２中 画 你
５ ２ 加强 图形变换教 学 。 “ 学好玩” ． 还 数 给学 生
点评
本题 源于题 目 ３ 是题 目 ３的横 向变衍 ， ， 它将
题 目３的强条件 （ 两个 等边 三角形 ） 当进行弱化 （ 适 有一
图形 变换 在新 教材中一亮相 ， 以势不 可挡 的态势 就 占据 了中考 的有利地 形 ， 为 中考 一道靓 丽 的风景 ， 成 同 时也使得 图形 的考查 变得 灵动起 来 ， 是 老态龙 钟 的 不再 “ 已知～求证一证 明” 的旧面孔． 图形 的平移 、 转、 旋 对称
５ 几点感悟 ５ １ 重视教 材 。 ． 创造性地使用教材
教材是《 课程标准》 的载体 ， 是课程 目标 和课 程 内容
的物化 ， 是实施教 与学 的 “ 本 ” 同时 也是我 们施 教 的 蓝 ， 资源库 ， 当然 ， 重视教材并不 是要 做教材 的奴隶 ， 要敢 于
５ ４
中‘擞 ・ （ １年 －・ 中 ） ７ ７ ２ １ 第４ 初 版 ０ ｝ ￣ １
・ 试题赏析 ・
对 一道 中 考 试 题 的 命 制 猜 想 与 感悟
２ ００ 山 东 省 章 丘 市 第 六 中 学 袁翠香 ５２４ ２ ００ 山东省章丘市水寨镇中心中学 张卫东 ５２４
上取一点 Ⅳ， Ｃ Ｂ 直线 Ａ Ｃ 相交于点 Ｐ 使 Ｎ＝ Ｍ， Ｎ，Ｍ ．
பைடு நூலகம்
ＢＣＭ ．
图３
①请用量角 器度量 厶４ 的度 数为 朋 （ 精确到 １） 。； ②请用说理 的方法求 出ＬＡ Ｍ 的度数 ； Ｐ ③若 将 （ ） 的条 件 “ Ｃ＜ １中 Ｂ
Ａ ２ Ｃ 改 为“ Ｂ＞２ Ｃ ， Ｂ＜ Ｂ ” Ａ Ｂ ” 其他 条件不 变 ， 能 自己在 图 ２中 画 你
５ ２ 加强 图形变换教 学 。 “ 学好玩” ． 还 数 给学 生
点评
本题 源于题 目 ３ 是题 目 ３的横 向变衍 ， ， 它将
题 目３的强条件 （ 两个 等边 三角形 ） 当进行弱化 （ 适 有一
图形 变换 在新 教材中一亮相 ， 以势不 可挡 的态势 就 占据 了中考 的有利地 形 ， 为 中考 一道靓 丽 的风景 ， 成 同 时也使得 图形 的考查 变得 灵动起 来 ， 是 老态龙 钟 的 不再 “ 已知～求证一证 明” 的旧面孔． 图形 的平移 、 转、 旋 对称
一道中考题的再思考
到正 佗 多边形的情形， 本文拟从 Ｚ Ｏ 的大小进 ｘ ｙ 行探索， 将问题进一步拓展．
＝ ＋ 。
＝
＝ ＋ 黑 ｎ＿ｔ ａ Ｃ ０
．
ａ ｃ） （ Ｏ． ＋ｔ 鲁
ＡＯＩ Ｃ中， 因为
在文 … 的各个变式 的解析中， 总是取 Ａ Ｂ的 中点 Ｍ ， 将问题转化为 △Ｏ Ｃ的三边关系， Ｍ 即 （Ｃ ≤ ０Ｍ ＋Ｍ Ｃ， 二 ｝ 由于 Ｄ 、Ｍ Ｃ均为定值，
当 （、 、 三点共线时， 二Ｉ ） 取等号； 又在 ＡＯ ＡＣ中，
接下来探讨 Ｚ Ｏｙ ｘ 为一般角的情况． 如图６ ， 设 Ｚ Ｏ 为定 角， ｘ ｙ 固定 的 △ＡＢ Ｃ的顶 点 和 Ｂ 分别在 Ｚ Ｏ 的两条边 Ｏ 、Ｏｙ ｘ ｙ ｘ 上滑动．以Ａ Ｂ 为弦、以 Ｚ Ｏ 为 圆周角作圆ｏ 过 圆心 ｘ ｙ ， 和顶 点 作直线， ｏ 与 交于点 Ｐ和 Ｑ．由于 Ｚ Ｏ ｘ ｙ 是定角， ＡＢ定长， 所以ｏ 是大 小固定 的圆， 又 由于 △ Ｅ 的大小 固定， 以ｏ △ 紧 Ｊ ； 所 和 Ｂ 密连在一起， 形成一个固定的图形． 这样 Ｐ、 Ｑ与
Ｂ 的两 侧 ， 则
ｏ △ＡＢ 和 的相对位置也就 固定下来， 伴随着
△ 口 移动而移动． 当 、 Ｂ在 Ｚ Ｏ 的边上滑 ｘ ｙ
（ 当０ ＜ １ 。 ＜１０ 一去 ） ８。 时，
动时， 始终通过顶点（， Ｐ和 Ｑ不断改 ｏ 二 ）
变位置， 但不改变大 小， 这样就有圆周 角 Ａ Ｆ ＯＪ ） 和 Ｚ ＯＱ不变， Ａ 这意味着 由Ｏ Ｐ和 Ｏ Ｑ决定的方 向ＯＭ 和 ＯⅣ不变．由于 ＰＱ是 ｏ 的直径， 所
２ ０＞ ６ 。 ＡＯＡ ０， Ｂ的外 心 在 Ｚ Ｃ 内， Ｉ Ａ Ｂ Ｏ ＝
面 ａ ， Ｃ＝ Ｉ
＝ ＋ 。
＝
＝ ＋ 黑 ｎ＿ｔ ａ Ｃ ０
．
ａ ｃ） （ Ｏ． ＋ｔ 鲁
ＡＯＩ Ｃ中， 因为
在文 … 的各个变式 的解析中， 总是取 Ａ Ｂ的 中点 Ｍ ， 将问题转化为 △Ｏ Ｃ的三边关系， Ｍ 即 （Ｃ ≤ ０Ｍ ＋Ｍ Ｃ， 二 ｝ 由于 Ｄ 、Ｍ Ｃ均为定值，
当 （、 、 三点共线时， 二Ｉ ） 取等号； 又在 ＡＯ ＡＣ中，
接下来探讨 Ｚ Ｏｙ ｘ 为一般角的情况． 如图６ ， 设 Ｚ Ｏ 为定 角， ｘ ｙ 固定 的 △ＡＢ Ｃ的顶 点 和 Ｂ 分别在 Ｚ Ｏ 的两条边 Ｏ 、Ｏｙ ｘ ｙ ｘ 上滑动．以Ａ Ｂ 为弦、以 Ｚ Ｏ 为 圆周角作圆ｏ 过 圆心 ｘ ｙ ， 和顶 点 作直线， ｏ 与 交于点 Ｐ和 Ｑ．由于 Ｚ Ｏ ｘ ｙ 是定角， ＡＢ定长， 所以ｏ 是大 小固定 的圆， 又 由于 △ Ｅ 的大小 固定， 以ｏ △ 紧 Ｊ ； 所 和 Ｂ 密连在一起， 形成一个固定的图形． 这样 Ｐ、 Ｑ与
Ｂ 的两 侧 ， 则
ｏ △ＡＢ 和 的相对位置也就 固定下来， 伴随着
△ 口 移动而移动． 当 、 Ｂ在 Ｚ Ｏ 的边上滑 ｘ ｙ
（ 当０ ＜ １ 。 ＜１０ 一去 ） ８。 时，
动时， 始终通过顶点（， Ｐ和 Ｑ不断改 ｏ 二 ）
变位置， 但不改变大 小， 这样就有圆周 角 Ａ Ｆ ＯＪ ） 和 Ｚ ＯＱ不变， Ａ 这意味着 由Ｏ Ｐ和 Ｏ Ｑ决定的方 向ＯＭ 和 ＯⅣ不变．由于 ＰＱ是 ｏ 的直径， 所
２ ０＞ ６ 。 ＡＯＡ ０， Ｂ的外 心 在 Ｚ Ｃ 内， Ｉ Ａ Ｂ Ｏ ＝
面 ａ ， Ｃ＝ Ｉ
一道中考题带给我们的教学启示
文 明对 物质 文 明的 巨大 推动 作用 等 。由于答 案 是 多
（） 系 上 述 材 料 ， 用 所 学 知 识 分 析 说 明 我 国 元 的 ，只 要 学 生 能 从 上 述 知 识 点 的 任 何 一 个 角 度 回 １联 运 答， 并能 围绕 人才 问题 的重 要 性加 以适 当的 阐述 ， 都 加 快 人 才培 养 的 重 要 性 。（ ） ９分
维普资讯
‘ 口 ，
Ｉ
所 需要 的 人 才？ （ ３分）
这 是 今年 绍兴 市 中考 的压轴 题 。就 两个 设 问而 言 ， 式 上 似乎 没什 么新 意 ， 却对 今后 的 中考改 革 形 但
碴 垣 由
和 学 科 教 学 起 到 了 积 极 的 导 向 作 用 ：一 是 它 把 教 材 讲 述 的 基 本 知 识 点 和 当 今 社 会 关 注 的 重 点 、热 点 问 题 有 机 地 融 合 在 了 一 起 ， 现 了社 会 、 治 学 科 的 时 体 政 代特 征 ；二是 它既 注重 考查 学 生对知 识 的调 控 和对 信息 的理解 处 理能 力 ， 蕴含 着很 好 的教育 价值 ， 又 体 现 了能力 立意 和教 育价 值 的 “ 密 ” 合 。但是 ， 亲 结 就 是这 样一道 看 似 常规 的题 目， 阅卷结 果上 看 ， 是 从 却 整 份 试 卷 中 得 分 率 最 低 的 一 题 。 抽 样 调 查 ， （） 据 第 １ 问
一
硼 ■＿ 题■ ● － 翟 ● 带 给
Ｉ Ｉ
平均 得分 仅 为 ３７分 ， （） ． 第 ２问平 均 分为 ２５ ．８分 ， 题 整 的难 度值 为 ０５ 。当然 ， 为压轴 题 ， ．２ 作 出题 者 的意 图 或许 是想 在本 题 中体 现较好 的 区分 度 ，达到 为高 一
一道中考试题引发的思考
D
C F
D
第一次翻折
C
D
第二次翻折
C AF
B E
E
120° 120°
E A B A
120°
A
B
图2
A
B
拓展2：如图2，在 ABCD中，∠A=120°，你能通过上 题的启示，用折纸的方法证明“直角三角形斜边中线 等于斜边一半吗？进而证明tan30°= 3 吗？
3
2012.10.31
本题需要我们抓住基本图形的特征，综合运用 轴对称的性质，勾股定理，等腰三角形的性质进行 探索，猜想。只要我们掌握了此类问题的本质，不 仅能以不变应万变，使问题迎刃而解，而且还能编 拟出一些好的题目，为学生的学习服务。
其次我们要在直角三角形中求出这个角所 对直角边与相临直角边的比值。
D
C F
翻折
全等
相等的边 相等的角
AB EB EAB AEB 45
O'
O
第一次翻折
E 第二次翻折 B
A
AE FE 1 FAE AFE AEB 22.5 2
D
C
而此题条件中没有给出任何边的长度. 但由前面对翻折过程的演示与分析， 我们已经知道AB=EB,AE=FE,
F
E A B
设AB x,则EB x, 由勾股定理得: AE AB 2 BE 2 x2 x2 2x
所以FE=AE=
2x
FB FE EB 2x x 所以tanFAB 2 1 AB AB x
2012.10.31
D
C F
设AB为x, 则EB x，
在RT三角形ABE中，由勾股定理得： AE AB EB x x 2x
一道中考作文题给我们的启示
（ ）命 题 应体 现 开 放性 。半 命 题 作文 把 考 生 的 思维 引 一
向了更 为 广 阔 的领 域 ，它 拓展 了考 生 的 思路 ，有 利 于考 生 联 述 、描 写 、 议论 、抒 情 等表 达 方 式 可灵 活 运 用 ，考 生 尽 可 以
系 自己的 生 活 实 际 ，调 动 自己 的生 活积 累 ，激 发 考 生 的真 情 选 用 自己擅 长 的方 式 挥 洒笔 墨 ，为 自己 的 内容选 择 最 佳 的表 实感 ，启 迪 考 生 的理 性 思 考 ，让 每 一位 考 生 都 能 有 话可 写 。 现 形式 。因 而 ，这 一 作 文命 题 符 合 《 文 课 程 标准 》 提 出 的 语 对 于该 题 目，考 生只 要 拓 展一 下思 路 ，便 会 发 现 可 写的 作 文 要 “ 少 对 学生 写 作 的 束缚 ”的 理念 ，有 利 于 学生 “ 减 有创 意
与学 生 对 写 作 的误 解 有 关 系 ，也 与 教师 平 时 的 引 导与 要 求有 在高 中生一般是每两周写一次作文 ，一学期下来最多能写七
很 大 关 系 。 在平 时的 写 作训 练 中， 既要 求 学 生 的作 文 有 较 高 八篇 文 章 ，再 加 上 有 的教 师 不 能 及 时批 改 讲评 ，这 根 本达 不 的境 界 ，又 要鼓 励 学 生 抒 发 自己的 真 实感 受 。教师 要 让 学 生 到提 高 写 作 水平 的 目的 。 明 白 ，写 作 并不 是 拒 绝 学 生表 达 自我 ，但 不 能 肆无 忌 惮 地 甚 总之 ，在 相 当一 部 分 高 中 生 当 中 ，普 遍 存 在着 写作 “ 心
校 名 、地 名 。
自己想 说 的话 ” ， “ 达 真 情 实 感 ” 。因 而 ， “ ”应是 作 表 真
由一道填幻方的中考题所想起的
６ ３
① ② ③ ④
口 口 口 口
图 ５— ５ 图 ５— ６ 图 ５— ７ 图 ５—８
口 口 口 口
图 ５— ９ 图 ５—１ ０ 图 ５— １ １ 图 ５—１ ２
① ＋ ＝ ＋ ， ＋１ ２ｘ ５ ② ③ ④ 得 ９＝ ９ ，
‘
．
．
：ｌ ． ７１
同的位置 ， 如下 图 ５ ：
口 口 口 口
图 ５—１ 图 ５— ２ 图 ５— ３ 图 ５— ４
为解决上 面 的两个 问题 ， 先来 了解 幻方 的两个 性
・ 数学园 ・ 地
十。 ７ （ｌ 第 期． 中 ） ７ 擞・ ２ｏ ２ 初 版 ｏ年
０＋ ｌ 戈 ｋ ｌ Ｃ＋ ＝ ａ ＋ ２ ９＝ ２ ｂ ＋１ ｋ ａ＋２ ９ ｌ 口 ＋ ５＝ｋ 口 ＋ｂ ＋ ５＝ Ｉ ２９ ｋ
（） ２ 中间填上 １０ 由已知 条件不难算得其余空格上 ０，
的数 ， 如图 ８所示
２ ４ １ ８１ ９ ５ ｌ ７１ １０ ０ ２ ９ １５ ０ ｌ ９ １６ ７
口 口 口 口
图 ５—１ ３ 图 ５ —１ ４ 图 ５一ｌ ５ 图 ５—１ ６
开头三个位置 中的 ３个数（ 图 ５—１５— ， — ） 见 ， ２５ ３ ，
列的和相 等 ， 一行 与一个斜对 角的三数 之和相 等 ， 第
可以得到两个方程， 通过解方程组解 出 ｙ的值． ，
解 （） １ 由已知得方程组
性质 ２ 与一个角上的数相邻的两个数之和等于对 角的一个数 的 ２ 倍． 如图 ４ 根据幻方 的定义 ， 照如图 ３ 则有 ， 对 ，
６
图 ３
图１
备用图
ａ ｌ 口 ＋ｎ ＝３ Ｉ＋ 笠 ＂ Ｓ， ０３ ｌ＋ｏ笠 ＋ｎ１ ３：３ Ｓ， ａｌ ２＋ａ ＋ａ ２＝３ 笠 ３ Ｓ，
对一道中考题的思考
电 压 表 示 数／ 电 流 表 示 数／ Ｖ Ａ 第 一 次 第 二 次 １４ ．８ Ｏ ９ ．ｌ ０ １ ．６ ０ ２ ．２
通过 计算 分 析 ， 认 为 这 个 传 感 器 是 否 你 仍 可使 用 ？此 时 ｎ ｂ问所 加 的电压 是 多少 ？ 、
（ ０ ９ 福建 省晋 江市 中考 题 ） ２０ ，
解 ： １ （） 器电阻 ＝ ＝３ ２
＝
题 的 每一个 步 骤 都 要 让别 人 看 明 白 ， 能 自 不
１ ｎ） 。（ ＿
己心里 有数 就行 ． 虽然 求 出 的结 果是 对 的 ， 这
是 因 为题 目的 条 件 巧合 ， 虑不 考 虑 电压 表 考
２
中学 教 与学
２０ ０９年 第 ８期
。试 题 研 究。
对
一
道
中
考
题
的
思
考
李 明
（ 东省 郓城 县 郓城 镇 初级 中学 ，７ ７０ 山 ２４ ０ ）
题 目 学 校
传感器额定电流 ， ： ： ． Ａ 传： Ｑ ０３（ ）
．
课 外 活 动 小 组 为 检测 某 传 感 器 而 设计 的电路如 图 １
ｕ传
ｊ
பைடு நூலகம்
（ ） 虑 到 电 流 表 的量 程 为 ０—０６Ａ， ２考 ． 滑动 变阻 器 允 许 通 过 的最 大 电流 为 １Ａ， 为
Ｓ
所示 ． 传感 器 上标
有 “ ０９Ｗ” ３Ｖ ．
图 １
确 保 电路各 部 分 的 安全 ， 电路 的最 大 电流 则
， ： Ｉ ＝０． ｘ ３ Ａ．
根 据第 二次 实验记 录数 据有
Ｕ＝， ２ ＋Ｕ ＝ ． ２ ＋ ． １ ｚ ０２ ０９ ． （
由一道中考试题引发的思考
约 定：“ 字形 线 路专 指 Ａ ＋ＡＢ， 中 ＡＣ ＜ 厂” 其
我们先介绍费马点知识 【 （ ４ 引用定义、 Ｊ 定理时我 们略作了改动） 以及相关的结论． 定义： 平面内到三角形三个顶点距离之和最
小的点叫三角形的费马点． 定理 １ 如图 ５ ＡＡ ， ＢＣ的所有 内角都小于 １０ ，则 《 点为 △ Ｂ ２。 二 ） Ｃ费马 点的 充要 条件是
考试题都是由课本题 目变化而来． 以， 所 日常教 学应 以课本为主， 深度挖掘课本题 目所反映 的基 本事实， 对一些典型图形进行深入 的研 究． 在习 题教学中， 教师不应该只就题论题、就题解题，
ｆ 人民教育出版社 中学数学室． ２ ） 几何证明选 讲 （ ４ １［ ． 选修 — ）Ｍ］北京： 人民教育出版社， ０７ ２０． ｆ 中华人 民共和国教育部． ３ ］ 普通高中数学课 程标准 （ 实验） ． ［ 北京： Ｍ１ 人民教育出版社， ０３ ２０．
图 ５
定理 ２ 如图 ５ ＡＡ ， ＢＣ的所有 内角都小于 １０ ， 、△ ＢＦ是正三 角形， ２ 。 △Ａ 若 Ｅ与 Ｆ交于 Ｄ点， 点 Ｄ是 △Ａ日 则 的 费马点， 该 点到 △ Ｃ三个顶点距离之和最 小， 且 ＝
Ｆ ＝ Ｏ Ａ ＋ ＯＢ ＋ Ｏ Ｃ ．
图 １
Ｐ为 污水 处理 厂的 位置 ， 由题 知 ＡＣ ＝ １ ＢＤ ＝ ，
２ ＣＤ ＝ ６ 设 ＰＣ ＝ Ｘ ， ， ，由 △ 得 Ａ＇ Ｃ Ｐ∽ ＡＢＤＰ
（） 图 ２ 、Ｊ两 个 化工 厂位 于 一段 直 线 ２如 ， Ｅ ｝
形 河堤 的 同侧 ， 工 厂到 河 堤 的距 离 ＡＣ为 ｌ ｍ， ｋ Ｂ工 厂到 河 堤 的距 离 ＢＤ 为 ２ ｉ ， ｋ 经测 量 河堤 上 ｎ
我们先介绍费马点知识 【 （ ４ 引用定义、 Ｊ 定理时我 们略作了改动） 以及相关的结论． 定义： 平面内到三角形三个顶点距离之和最
小的点叫三角形的费马点． 定理 １ 如图 ５ ＡＡ ， ＢＣ的所有 内角都小于 １０ ，则 《 点为 △ Ｂ ２。 二 ） Ｃ费马 点的 充要 条件是
考试题都是由课本题 目变化而来． 以， 所 日常教 学应 以课本为主， 深度挖掘课本题 目所反映 的基 本事实， 对一些典型图形进行深入 的研 究． 在习 题教学中， 教师不应该只就题论题、就题解题，
ｆ 人民教育出版社 中学数学室． ２ ） 几何证明选 讲 （ ４ １［ ． 选修 — ）Ｍ］北京： 人民教育出版社， ０７ ２０． ｆ 中华人 民共和国教育部． ３ ］ 普通高中数学课 程标准 （ 实验） ． ［ 北京： Ｍ１ 人民教育出版社， ０３ ２０．
图 ５
定理 ２ 如图 ５ ＡＡ ， ＢＣ的所有 内角都小于 １０ ， 、△ ＢＦ是正三 角形， ２ 。 △Ａ 若 Ｅ与 Ｆ交于 Ｄ点， 点 Ｄ是 △Ａ日 则 的 费马点， 该 点到 △ Ｃ三个顶点距离之和最 小， 且 ＝
Ｆ ＝ Ｏ Ａ ＋ ＯＢ ＋ Ｏ Ｃ ．
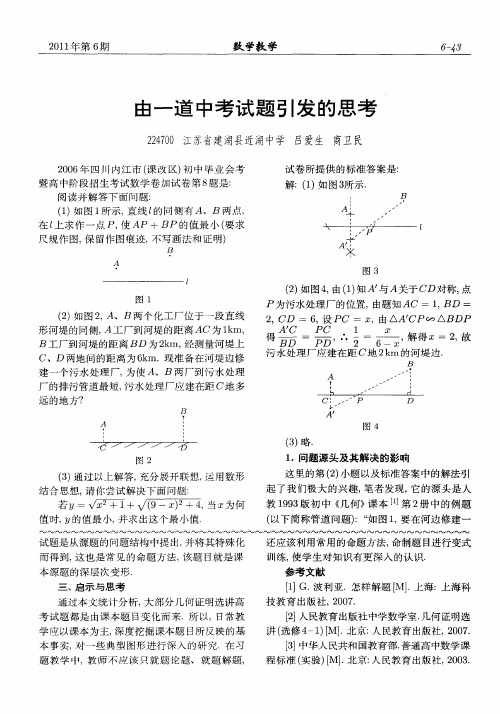
图 １
Ｐ为 污水 处理 厂的 位置 ， 由题 知 ＡＣ ＝ １ ＢＤ ＝ ，
２ ＣＤ ＝ ６ 设 ＰＣ ＝ Ｘ ， ， ，由 △ 得 Ａ＇ Ｃ Ｐ∽ ＡＢＤＰ
（） 图 ２ 、Ｊ两 个 化工 厂位 于 一段 直 线 ２如 ， Ｅ ｝
形 河堤 的 同侧 ， 工 厂到 河 堤 的距 离 ＡＣ为 ｌ ｍ， ｋ Ｂ工 厂到 河 堤 的距 离 ＢＤ 为 ２ ｉ ， ｋ 经测 量 河堤 上 ｎ
从一道源于课本的中考题谈起
又 ‘ ０＋ Ｃ Ｏ＋ ＬＢＣ ． ‘ Ｂ Ｏ＝ １ ０ ， ８ 。
ＡＢＣ＋ Ａ ．
’
将 上 式 理可 ： ＋ 四 以 三 整 ，得 Ｄ （Ａ
．
．
２ ０＋ ＬＯ Ｃ ＝ ＬＡ Ｃ＋ Ａ ， （ Ｂ ） Ｂ
・
．
－ ０＋ ＬＡ Ｃ＝ ＬＡ Ｃ ２ Ｂ Ｂ ＋ Ａ， 整理得
请 仿 照上 述解 法 ， 自己求 解 ，结 论 是 ：
１
图６
０ ＝ － Ａ ． －－ ６
Ｊ
解析： 由 Ａ ＝１ ０一 （ Ａ Ｃ ８ 。 曰 ＋ Ａ Ｂ ， Ｃ ）
将推广 ３ 与推广 ４结合可 以得 到推广 ８ ：
Ｌ０之 间的数量关 系．
．
。 ．
Ｌ ＋ （ ０一 ） ８。 Ｏ ÷ １ 。 ＝１ ， ８ ０ Βιβλιοθήκη Ｊ １ 。．
．
Ｚ０ ０ ＋÷ ＬＡ． ＝６ 。
ｊ
推 广 ２ 在ＡＡ Ｃ中， Ｂ
Ｃ
０ ． ＝
ｒ ｔ
Ａ ， ｃ
图 ３
ＬＡＣＯ＝ 上 厶 ４Ｃ
，
试探 求 Ａ 与 Ｄ之 间的
ｎ
．
．
Ｌ＋ （０ Ｌ）１。 Ｏ＋ １。 Ａ：８． ８一 ０
Ｌ Ｏ＝ ９ 。 Ｉ ＬＡ ０＋
．
与 ＬＯ之间的数量关 系．
厶４ 与 Ｄ之 间的数量关系为
Ｄ ： ｍ ８ ｏ １ ０ ＋ 二
ｎ ｎ
・
．
．
Ａ
．
下面从不 同的角度 ． 对该问题进行拓展．
一
从推广 １ 到推广 ３ ，关注 了问题 中数值 的
山东省 东营市胜利 第十一 中学 盖仕广
从一道中考题说开去——一个没有明确定义的概念
多次出现重合这 两个字 ． 在线段 的 比 如 较 与度 量 中 ． 把 线 段 Ａ 放 到 线 段Ａ 曰 “ Ｂ 上 ． 点Ａ与 点Ａ 重合 ． ”在 角 的 比 较 使 … ：
与 度 量 中 ． 把 ＡＯ 放 到 』 ０ Ｂ 上 ． “ Ｂ ４
２Ｊ题 ， ７ｂ 用反证法证 明“ ∥ｂ６ ， 若０ ，∥ｃ则
ａ
／ｃ 。 ／ ”第一步是假设 （
Ａ ｆｂ ｆ
Ｂ． 与 ｃ 交 相
）
有 重 合 ． 把 简 单 的 特 殊 问题 弄 得 很 复 会 杂 ． 周 角 在 几 何 圆 中 ． 心 角 是 可 能 而 圆
为 周 角 的．
Ｃ ｎ 不 平 行 ． 与ｃ
Ｄ ｎ 既不 平 行 义 不 相 交 ． 与ｃ
教学 研究 ＞ 课参考 备
数学教 学通 讯（ 教师版 ）
投稿部 ｓｊ ｖ ’３ｏ 籀： ｋ ｉ ６ ｒ ｘ＠ ｐ ｃｎ
矗鼍匿
从一道中考题说开去
一
个 没有 明确 定 义 的概 念
刘 克庆
舛一Ｍ 年 重一 一 ～删啊 己指 强
江 苏南京 浦 口第三 中学 ２ １ ０ １８０
论 不 成 立 ． 就 是 假 设。 不 平 行 ． 当 那 与ｃ 那
“ 重合 ” 一 概念 呢？ 是 否 真 的可 以忽 视 这
这一概念呢７
的接 受 能 力 和水 平 而设 置．其 中有 这 样
一
笔 者 认 为 在 几 何 教 学 中 ．重 合 ” “ 是
一
个 公 理 ： 在 同 一 平 面 内 ． 条 直 线 的 “ 两
犴嚯
脯 橼
前 几 年 南 京 市 中 考 题 第 四 大 题 第
它研 究 图 形 的 形 状 、大 小 和 位 置 关 系 ．
与 度 量 中 ． 把 ＡＯ 放 到 』 ０ Ｂ 上 ． “ Ｂ ４
２Ｊ题 ， ７ｂ 用反证法证 明“ ∥ｂ６ ， 若０ ，∥ｃ则
ａ
／ｃ 。 ／ ”第一步是假设 （
Ａ ｆｂ ｆ
Ｂ． 与 ｃ 交 相
）
有 重 合 ． 把 简 单 的 特 殊 问题 弄 得 很 复 会 杂 ． 周 角 在 几 何 圆 中 ． 心 角 是 可 能 而 圆
为 周 角 的．
Ｃ ｎ 不 平 行 ． 与ｃ
Ｄ ｎ 既不 平 行 义 不 相 交 ． 与ｃ
教学 研究 ＞ 课参考 备
数学教 学通 讯（ 教师版 ）
投稿部 ｓｊ ｖ ’３ｏ 籀： ｋ ｉ ６ ｒ ｘ＠ ｐ ｃｎ
矗鼍匿
从一道中考题说开去
一
个 没有 明确 定 义 的概 念
刘 克庆
舛一Ｍ 年 重一 一 ～删啊 己指 强
江 苏南京 浦 口第三 中学 ２ １ ０ １８０
论 不 成 立 ． 就 是 假 设。 不 平 行 ． 当 那 与ｃ 那
“ 重合 ” 一 概念 呢？ 是 否 真 的可 以忽 视 这
这一概念呢７
的接 受 能 力 和水 平 而设 置．其 中有 这 样
一
笔 者 认 为 在 几 何 教 学 中 ．重 合 ” “ 是
一
个 公 理 ： 在 同 一 平 面 内 ． 条 直 线 的 “ 两
犴嚯
脯 橼
前 几 年 南 京 市 中 考 题 第 四 大 题 第
它研 究 图 形 的 形 状 、大 小 和 位 置 关 系 ．
一道数学中考题引发的思考与感悟作文
一道数学中考题引发的思考与感悟作文“哎呀，这道数学中考题也太难了吧！”我忍不住抱怨起来。
那是一个周末的午后，我正在房间里做着数学练习题。
阳光透过窗户洒在桌子上，可我却完全没有心思享受这温暖。
“姐姐，陪我玩嘛！”弟弟跑过来缠着我。
“哎呀，等会儿啦，我这题还没做完呢！”我头也不抬地说道。
弟弟却不依不饶，“就玩一会儿嘛，一会儿就好。
”我无奈地放下笔，“好吧好吧，那玩什么呀？”弟弟兴奋地说：“我们玩过家家吧！”我哭笑不得，“你都多大了，还玩过家家呀。
”“就要玩就要玩！”弟弟开始撒娇。
没办法，我只好陪着他玩起了过家家。
我当妈妈，他当宝宝。
弟弟假装哇哇大哭，“妈妈，我饿了。
”我学着妈妈的样子说：“宝宝乖，妈妈给你做饭去。
”我拿起一些玩具假装做饭，弟弟在旁边看着，还时不时地捣乱。
玩了一会儿，我又想起了那道没做完的数学题，“哎呀，不行，我还是得去做题。
”弟弟不乐意了，“姐姐，再玩一会儿嘛。
”我哄着他说：“弟弟乖，姐姐把题做完再陪你玩好不好？”弟弟虽然不情愿，但还是点了点头。
我赶紧回到桌子前，继续研究那道数学题。
这道题就像一座大山一样横在我面前，怎么也过不去。
我抓耳挠腮，急得不行。
“怎么这么难呀！”我自言自语道。
这时，妈妈走了进来，“怎么啦，宝贝？”我指了指那道题，“妈妈，这道题我不会做。
”妈妈看了看题，笑着说：“这道题呀，你要换个思路想想。
”说着，妈妈给我讲了起来。
在妈妈的帮助下，我终于找到了解题的方法。
我不禁感慨，就像这道数学中考题一样，生活中也会遇到很多难题。
有时候我们自己怎么也想不明白，但是只要有人稍微指点一下，就会豁然开朗。
这不就像我和弟弟玩过家家一样吗？一个人玩可能会觉得无聊，但是两个人一起玩就会变得有趣多了。
学习也是这样，遇到困难不要只想着自己一个人去解决，可以多和同学、老师、家长交流交流，说不定就能找到新的思路呢。
所以呀，以后遇到难题我可不能再抱怨了，要多想想办法，多和别人交流。
我相信，只要我努力，就没有什么难题是解决不了的！。
自觉分析：让解题教学内涵更丰富——从一道中考试题说起
自觉 分 析 ： 让 解 题 教 学 内涵 更 丰 富
— —
从 一道 中考试题说起
张建 山
张建 山 江 苏省连 云港 市 东海县教 育局教研 室教研 员。
罗增儒 教授 在《 中学 数 学解 题 的理 论与
网格 中 ， 用 直 尺 和 三 角尺 画 出该 正 方 形 ， 并简 要 说 明 画 图方 法 （ 不 要 求 证 明） 。
、
与试题 有关的三次认知经历
（ 一） 初 接 触 时 的 不 解 与 迷 茫
罗增 儒教授 的“ 解题化 归论” 认为 ， “ 数学
解 题的过程 ， 就是 将 未知 的数 学 问题 转化 为
已经解 决的 问题 的化 归 过程 ” 。我 在初 接 触 这 道试题 的第（ ２ ） 问时 ， 能 在脑海 里涌现 出 的 “ 已经解决 的问题 ” 有： 三 角形 内接 矩形 （ 或正
讶， 以及 对 画 图途径 的迷 茫 。命 题 者 要着 力
考查 的知识模 型是 什 么？问题解 决的 突破 口
—
Ｐ ， ， ／１ Ｇ
’ 一
又在哪里 ？
（ 二） 再 研 讨 时 的尴 尬 与 顿 悟
，
：
／
一 ． ，， 一
带着初接触 时的疑 问 ， 在２ ０ １ ３ 年 全县 暑 期初 中数学 骨 干教 师解 题 教 学培 训 中 ， 我 将 自己的疑 问作 为本 次 活动 的一个 研 讨 内容 ， 以期集思广益 。３ Ｏ分钟的独立思考和研 讨交 流后 ， 参加活动 的 ７ ９位骨干 教师遭 遇 了一次 “ 才短思涩” 的尴尬 ， 大伙 只是 明 白了 参考 答
ቤተ መጻሕፍቲ ባይዱ
。
／ 一 一
— —
从 一道 中考试题说起
张建 山
张建 山 江 苏省连 云港 市 东海县教 育局教研 室教研 员。
罗增儒 教授 在《 中学 数 学解 题 的理 论与
网格 中 ， 用 直 尺 和 三 角尺 画 出该 正 方 形 ， 并简 要 说 明 画 图方 法 （ 不 要 求 证 明） 。
、
与试题 有关的三次认知经历
（ 一） 初 接 触 时 的 不 解 与 迷 茫
罗增 儒教授 的“ 解题化 归论” 认为 ， “ 数学
解 题的过程 ， 就是 将 未知 的数 学 问题 转化 为
已经解 决的 问题 的化 归 过程 ” 。我 在初 接 触 这 道试题 的第（ ２ ） 问时 ， 能 在脑海 里涌现 出 的 “ 已经解决 的问题 ” 有： 三 角形 内接 矩形 （ 或正
讶， 以及 对 画 图途径 的迷 茫 。命 题 者 要着 力
考查 的知识模 型是 什 么？问题解 决的 突破 口
—
Ｐ ， ， ／１ Ｇ
’ 一
又在哪里 ？
（ 二） 再 研 讨 时 的尴 尬 与 顿 悟
，
：
／
一 ． ，， 一
带着初接触 时的疑 问 ， 在２ ０ １ ３ 年 全县 暑 期初 中数学 骨 干教 师解 题 教 学培 训 中 ， 我 将 自己的疑 问作 为本 次 活动 的一个 研 讨 内容 ， 以期集思广益 。３ Ｏ分钟的独立思考和研 讨交 流后 ， 参加活动 的 ７ ９位骨干 教师遭 遇 了一次 “ 才短思涩” 的尴尬 ， 大伙 只是 明 白了 参考 答
ቤተ መጻሕፍቲ ባይዱ
。
／ 一 一
一道数学中考题引发的思考与感悟作文
一道数学中考题引发的思考与感悟作文《一道数学中考题引发的思考与感悟》
哎呀呀，提起那道数学中考题，可真是让我印象深刻极了呀！那是在我中考的时候，考场上我可紧张啦。
当我看到那道数学题时，我的大脑瞬间就有点懵了。
那道题就像是一个调皮的小精灵，在我眼前蹦来蹦去，就是不让我抓住它的解题思路。
我一边咬着笔头，一边在心里嘀咕：“这题咋这么难呢，这出题老师也太狠了吧！”我着急得就像热锅上的蚂蚁，汗水都快冒出来了。
我使劲回想老师讲过的知识点，又在草稿纸上不停地写写画画，可还是没啥头绪。
就在我快要绝望的时候，突然，我好像看到了一点曙光。
我发现这道题好像和我们之前做过的一道练习题有点类似，我赶紧抓住这个线索，一点点地推导。
嘿，你还别说，慢慢地，解题的思路就清晰起来啦。
最后，我终于算出了答案，那一刻，我心里那个高兴呀，就别提了。
这场考试结束后，我就一直在想啊，这道题让我明白了好多。
遇到难题不能慌张，得冷静去思考，要善于发现那些细微的线索，而且呀，平时的学习真得好好下功夫，把知识掌握扎实了，不然在关键时刻就抓瞎啦。
同时呢，
我也体会到了坚持的重要性，要是我当时轻易就放弃了，那可就真答不出来了。
现在回想起来，那道数学中考题就像是我人生路上的一个小挑战，虽然有点难，但也让我收获了好多。
我相信，以后遇到其他的难题，我也一定能像这次一样，勇敢地去面对，去找到解决的办法。
哈哈，这就是那道数学中考题带给我的思考和感悟哟！。
由一道中考题引发的探究和思考
交 线 段 ＡＢ 于 点 Ｄ ， 此 时 △ＡＣ Ｄ 与
△Ｂ Ｃ Ｄ都 为等腰 三角形， 则 直 线
图 ３
掌 饼
Ｃ Ｄ 把 △ＡＢ Ｃ恰 好 分割 成两 个 等 腰 三 角 形
②猜想 ： Ａ＋ Ｂ一９ ０ 。 ．
③验 证 ： Ａ一 ３ ０ 。 ， Ｂ一 ６ ０ 。 ，
２ ． 不 等 边 三 角形 ， 如图 ９ ．
版 如图 ４ ．
（ ２ ） ①作图 ： 如图 ５ ， 以 点 Ｂ为 顶 点， 以 ＡＢ 为 一 边 在 ＡＢ Ｃ 内 作
ＡＢ Ｅ一 Ａ＝２ ４ 。 ， 射线 Ｂ Ｅ 交 线 段 Ａ Ｃ 于 点 Ｅ， 此 时 则 △ ＡＢ Ｅ 与 △Ｂ Ｅ Ｃ都 为 等 腰 三 角 形 ， 则
Ｃ
１ ８Ｏ 。
２ ４ 。
Ｂ
ａ —＝ ＿ ＿一 ３ ６ ．
① ①作图 ： ②猜想 ： ③验证 ： （ ２ ） 如图 ２ ， 在 △ＡＢ Ｃ， Ｃ＝８ ４ 。 ，
。
图 １ ｒ
＝ ＝ ＝
② 当点 Ａ 为 顶 点 ， ＡＢ ＝Ａ Ｃ 且
Ａ， 即 ＜ ３ ａ＜ １ ８ Ｏ 。 一３ 一 口 ， 所 以 ０ 。 ＜Ｏ ｔ ＜
１ 口ｎ０
．
当 Ｂ Ｅ Ｃ ＝ Ｃ时 ， 即 ） ， 一２ ， 由 于 Ａ＜ Ａｌ Ｂ ｃ＜ Ｃ ，
ｆ
即口 ＜１ ８ ０ 。 ２ ａ — ＜ ２ ， 所以３ ６ 。 ＜ ＜４ ５ 。 ． 图 ６
到一条直线 ， 把 △ ＡＢ Ｃ恰 好 分 割 成 两 个 等 腰 三 角 形 （ 不 写 做
法， 但需保 留作 图痕 迹 ） ； 并 根据 每种 情 况分别 猜 想 ： Ａ 与
从一道中考试题中感悟高效数学课堂教学的着眼点
结合 ， 操作 与阅读理解并存 的好试题 ， 以三角形全 等作背 景材 料来考查 ， 先给 出问题 背景 ， 通过 阅读与理 解 ， 不 仅
要学生看懂背景 问题所提供 的分析思路框 图 ，还要 通过 类比、 转化 的方法 去灵活运用 ， 再拓展 延伸 ， 发 展思维 ， 步
后 ，老师 布置 了一 道课后 练 习 ：
点 Ｐ， Ｄ分 别 在 Ａ０和Ｂ Ｃ上 ， Ｐ Ｂ＝
Ｐ Ｄ， Ｄ Ｅ上Ａ Ｃ 于 点 ．
求证 ： ＡＢ Ｐ Ｏ Ａ肋 Ｅ
学 生获得对数学 理解 的同时 ， 在 思维能力 、 情 感态度与价 值 观等多方面得到进 步和发展． ” 另一方面也 向数 学教育 工作者进一步释放 出搞好数学课堂教学 的着眼点 ，笔 者
绎和类 比进行 推理 ， 而且会合 乎逻辑地 、 准确地阐述 自己
图２ ，满足 题 中条 件 的点Ｊ Ｄ 也 随之在 直线Ｂ Ｃ 上运动 到点
Ｄ ， 请直接 写 出Ｃ Ｄ 与Ａ Ｐ 的
数 量 关 系． （ 不 必 写 解 答 过
程）
一
道 好 的考 题 ， 不一定
（ Ｄ ）
略 的运用情况 ， 对学生 的思维给 以启发 ， 对初 中数学教 学
给 以指导． 这道 试题不偏 不怪 ， 它 是一 道难 度适 中 ， 动静
统性地进行思维能力 的适度训练 ，笔者经过多年 的探索 有感悟 ， 现 以一道 中考试题为例加 以剖析 ， 谈谈提高数学
课堂高效有益的几点举措． 题目 （ ２ ０ １ ３ 年浙 江 湖州 中考 题 ）第一 节 数学 课
蓬
中’ ？ 擞’ ７ 初 中 版。
２ ０ １ ４ 年１ 月
间结 论 ，全 过程 的解 答 较好地 检 测学 生学 会用 分析 法 和综 合法去 分析解决 问题 的能力 ． 教学 中针对 不 同题 型 可 以采用 不 同的分析 方法 ， 如排 序 、 列表 、 直线示 意 图 、 操作 实验 等来 强化分 析 的直觉 效果 ， 让 学 生通 过学 习 、 练习、 感悟 、 反思 ， 去掌握 分析方 法 ， 提 高解题 策 略． 在 学 生亲 身体验 和感 受通 过 自己的分析 使 问题 得 到解决 的
一道中考试题折射出课堂教学的误区
镜， 透过装水玻璃杯靠 近看物体 ， 会看到物体水平方 向被放大了 ； 而竖直 的专家学者精心编撰 的教材 ，已经为我们提供 了新课程实施的剧 ， 在
方 向厚度是一样的 ， 对物体没有放大作 用 ， 透过装水玻璃杯看 到的是和 课堂教学时必须演绎好这个 剧本 中的每一角色的每一场戏 ， 我们不能因 物体等高的像 。 然而， 初中学生是没有能力做 出上述推断的 ， 他们没有亲 为只是一个不起眼的角色就摒弃它。其实 ， 在给初二 学生上第一节物理 二 手去做一做 ， 通常会把盛满水的玻璃杯看作普通 的凸透 镜 ， 而根据普 时 ， 从 要让学生了解物理这一门学科 ， 激发学生学 习物理的兴趣 ， 老师们根 通凸透镜 的成像规律判断 出答案 Ｃ足正确 的 有少部分考生 “ 对 了， 本就不需要讲太多的东 睡， 蒙” 只要准备好教材安排 的实验活动所需 的器材 可能存在两种偶然因素： 一是有 的考生平时留心 观察过盛水玻璃杯 的成 （ 有条件的学校可以多安排几 个活动 ， 甚至让学生在实验室上课 ）把每 ． ．
绩， 不重视教材 的挖掘和使用的误 区。 通过这道题 目， 命题者的意图就是 有没有用好 我们 的教材 ， ： 按照教材去教 。 然而 ， 了应付考试身陷于题海 为
要 把跑 偏 了 的初 中物 理 课 堂 教 学 ， 回 到遵 循课 标 精 神 、 格按 照教 材 之中的老师们 ， 拉 严 ： 似乎 已经迷失 了方 向， 大部分老师在教学过程 中“ 忽略”
江苏省 ２ ０ ０ ９年中考物娜试卷一 最后 一道选择题 ， 目如下 ： ｝ ＝ 题
如 图所示 ， 小刚将盛满水 的圆柱形透 明玻璃 杯贴近书本 ， 透过玻璃 觉地去实施 ， 还有一段路要走 。为 了“ 挖掘” 学生的潜 能， 培养学生 的“ 能 ， 把 使 杯观看书上的鹦鹉图片（ 圆圈 中的鹦鹉 图与书本中的鹦鹉图实际大小相 力” 我们的老师可谓煞费苦心 ， 一个简单 的问题 设置许多的陷阱 ， 等）他所看到的虚像可能是 ，
方 向厚度是一样的 ， 对物体没有放大作 用 ， 透过装水玻璃杯看 到的是和 课堂教学时必须演绎好这个 剧本 中的每一角色的每一场戏 ， 我们不能因 物体等高的像 。 然而， 初中学生是没有能力做 出上述推断的 ， 他们没有亲 为只是一个不起眼的角色就摒弃它。其实 ， 在给初二 学生上第一节物理 二 手去做一做 ， 通常会把盛满水的玻璃杯看作普通 的凸透 镜 ， 而根据普 时 ， 从 要让学生了解物理这一门学科 ， 激发学生学 习物理的兴趣 ， 老师们根 通凸透镜 的成像规律判断 出答案 Ｃ足正确 的 有少部分考生 “ 对 了， 本就不需要讲太多的东 睡， 蒙” 只要准备好教材安排 的实验活动所需 的器材 可能存在两种偶然因素： 一是有 的考生平时留心 观察过盛水玻璃杯 的成 （ 有条件的学校可以多安排几 个活动 ， 甚至让学生在实验室上课 ）把每 ． ．
绩， 不重视教材 的挖掘和使用的误 区。 通过这道题 目， 命题者的意图就是 有没有用好 我们 的教材 ， ： 按照教材去教 。 然而 ， 了应付考试身陷于题海 为
要 把跑 偏 了 的初 中物 理 课 堂 教 学 ， 回 到遵 循课 标 精 神 、 格按 照教 材 之中的老师们 ， 拉 严 ： 似乎 已经迷失 了方 向， 大部分老师在教学过程 中“ 忽略”
江苏省 ２ ０ ０ ９年中考物娜试卷一 最后 一道选择题 ， 目如下 ： ｝ ＝ 题
如 图所示 ， 小刚将盛满水 的圆柱形透 明玻璃 杯贴近书本 ， 透过玻璃 觉地去实施 ， 还有一段路要走 。为 了“ 挖掘” 学生的潜 能， 培养学生 的“ 能 ， 把 使 杯观看书上的鹦鹉图片（ 圆圈 中的鹦鹉 图与书本中的鹦鹉图实际大小相 力” 我们的老师可谓煞费苦心 ， 一个简单 的问题 设置许多的陷阱 ， 等）他所看到的虚像可能是 ，
一道中考试题的启发
教 学 中 ，两 个 负 数 比较 时 ，绝对 值 大 的反 而小 。如有
是 直 角 边 。这 种 问题 在 学 生 的学 习 过 程 中经 常 遇 到 。 学 生 经 常 把 习 以为 常 的知 识 和 能 力 用 上 ，而 不 能 从 多
个 角 度 考 虑 问 题 。教 师应 该 在 教 学 过 程 中 提 醒 学 生 考 虑 问题 要 全 面 ，这样 才 能提 高 自己 的数 学 能力 。
算效率。 ５ 培 养 学 生 会 辨 析 问题 的能 力 。学 生 对 于 一 个 问 ． 题 的认 识 是 肤浅 的 ，比如 ：某 年 中考 有 这样 一 道 题 目： 已 知直 角 三 角 形 的 两 条 边 长 分 别 是 ３ ｍ 和 ４ ｒ，求 另 ｅ ｅ ａ
一
察 学 生解 决 问题 的应 变 能 力 和 解 法 的 多样 性 。 在 我 们
考 虑 到正 方形 又 是特 殊 的菱 形 。可 以利 用 菱 形 的 面 积 公式 ，即 ｓ １ ｘ ０ ２ ５ ＝０ １＋ ＝ ０ ４ 培养 学 生 观察 问题 的能 力 。观 察 不 仅 仅 是 一 种 ．
田
有以下几点 ：①上述计算错误 ；② 只将 Ｘ值写 上 ，不 合题 目要求 ；③把两个点的坐标都写上了 ，更 不符合
的这 种 能 力 不 能 集 中学 习 ，在 各 个 年 级 都 应 该渗 透 ， 有 时 可 以大 大 简 化 数 学 运算 。 比 如 在七 年 级 正 负 数 的
条边 的 长 ，结 果 很 多 学 生 填 了 ５ｒ，事 实 上 ， 已 知 ｅ ａ 的两 条 边 也 有 可 能 是 直 角 三 角 形 的斜 边 ，并 不 一 定 都
对 二 次 函数 解 析 式 的求 法 比较 熟 悉 ，解 答 大 部 分 是 将 各 个 点 的 坐标 代 人 解 析 式 ，然 后 求 得 ａ 、ｃ的值 ， 、ｂ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
24. 07 年 24. 在 直 角 梯 形 ABCD 中 , ∠C=900, 高 = CD=6cm(如图1). 动点P、Q同时从点 出发, P点 ( 如图1 动点 、 同时从点B出发, 点 同时从点 出发运动到C点停止 沿BA、AD、DC运动到 点停止, 点 Q沿BC运动到 、 、 运动到 点停止, 沿 运动到 停止， 点C停止，… 停止
变式2.如图,正方形ABCD的边长为10cm， 点E在边CB的延长线上，且EB=10cm。点 P在边DC上运动，EP与AB的交点为F，设 DP=xcm， △EFB与四边形AFPD的面积和 为ycm2 ，那么y与x之间的函数关系式
思考1.只有一个动点情况 思考 只有一个动点情况
思考1.只有一个动点情况 思考 只有一个动点情况
变式1.如图，△ABC中，BC=4， AC= 2 3， ∠ACB= 60°，P为BC上一点，过点P做PD ∥AC交BC于点D，连接AP，问点P在何处 时， △APD的面积最大？
变式2.如图,正方形ABCD的边长为10cm， 点E在边CB的延长线上，且EB=10cm。点 P在边DC上运动，EP与AB的交点为F，设 DP=xcm， △EFB与四边形AFPD的面积和 为ycm2 ，那么y与x之间的函数关系式
24. 07 年 24. 在 直 角 梯 形 ABCD 中 , ∠C=900, 高 = CD=6cm(如图1). 动点P、Q同时从点 出发, P点 ( 如图1 动点 、 同时从点B出发, 点 同时从点 出发 运动到C点停止 沿BA、AD、DC运动到 点停止, 点 Q沿BC运动到 、 、 运动到 点停止, 沿 运动到 停止， 点C停止，… 停止
y A D P B A D 30 M N
(1)
C
B
(2) Q
C
0
(3)
x
例1.正方形ABCD的边长为10cm,动点P、Q 分别从点出发，点M沿AB边向终点B移动，点 N沿边AD向终点D移动，速度都是1cm/s。移 动时间是x（s）。求△APQ的面积y（cm2） 关于x（s）的函数关系式。
例1.正方形ABCD的边长为10cm,动点P、Q 分别从点A出发，点M沿AB边向终点B移动， 点N沿边AD向终点D移动，速度都是1cm/s。 移动时间是x（s）。求△APQ的面积y（cm2） 关于x（s）的函数关系式。浙教版作业本八年级上（1）P38
思考2.有两个运动速度不同的动点 思考 有两个运动速度不同的动点
思考2.有两个运动速度不同的动点 思考 有两个运动速度不同的动点
思考三.有两个运动速度相同但方向不同的动点 思考三 有两个运动速度相同但方向不同的动点
思考三.有两个运动速度相同但方向不同的动点 思考三 有两个运动速度相同但方向不同的动点
24. 07 年 24. 在 直 角 梯 形 ABCD 中 , ∠C=900, 高 = CD=6cm(如图1). 动点P、Q同时从点 出发, P点 ( 如图1 动点 、 同时从点B出发, 点 同时从点 出发 运动到C点停止 沿BA、AD、DC运动到 点停止, 点 Q沿BC运动到 、 、 运动到 点停止, 沿 运动到 停止， 点C停止，… 停止
24. 07 年 24. 在 直 角 梯 形 ABCD 中 , ∠C=900, 高 = CD=6cm(如图1). 动点P、Q同时从点 出发, P点 ( 如图1 动点 、 同时从点B出发, 点 同时从点 出发 运动到C点停止 沿BA、AD、DC运动到 点停止, 点 Q沿BC运动到 、 、 运动到 点停止, 沿 运动到 停止， 点C停止，… 停止