Lagrange插值法
数值分析Chapter4_1_Lagrange插值

6 , x1
利用 x0
0
4
5 sin 50 L1 ( ) 0.77614 18 (2) f ( x ) 1 3 R1 ( x) ( x )( x ), sin x 2! 6 4 2 2
L1 ( x ) x / 4 1 + x / 6 1 / 6 / 4 2 / 4 / 6 2
f ( n+1) ( ) u ( x) (n + 1) !
例:已知 sin 1 , sin 1 , sin 3 6 2 4 2 3 2 分别利用 sin x 的1次、2次 Lagrange 插值计算
sin 50, 并估计误差。
解: n = 1 分别利用x0, x1 以及 x1, x2 计算
任意固定 x xi (i = 0, …, n), 考察
(t ) Rn (t ) u ( x) (t xi ) f (t ) Ln (t ) u ( x) (t xi )
i 0 i 0
n
n
(t)有 n+2 个不同的根 x0 … xn x
( n+1)
( x ) 0, x (a, b)
l0 ( x0 ) l1 ( x0 ) l0 ( x1 ) l1 ( x1 ) l0 ( xn ) l1 ( xn )
ln ( x0 ) c0 f ( x0 ) ln ( x1 ) c1 f ( x1 ) ln ( xn ) cn f ( xn )
因此得到插值多项式 pn(x)= f(x0)l0(x)+f(x1) l1(x)+…+ f(xn) ln(x)
拉格朗日(Lagrange)插值

Rn ( x ) = K ( Rn(x) 至少有 n+1 个根 ( x ) 充分光滑,x( x 0 )(= ( x)1 ) = 0 ,则 充分光滑, ) Π x xi Rolle’s Theorem: 若 i =0 ) 存在 ξ ∈ (x 0≠, x 1 )(i使得 ′(ξ), = 0 。 ( t ) = R ( t ) K ( x ) n ( t x ) …, n 任意固定 x xi = 0, 求导 考察 注意这里是对 t Π n i = ξ 0 ∈ ( x0 , x1 ), ξ1 ∈i ( 0 1 , x2 ) x 推广: 推广:若 ( x0 ) = ( x1 ) = ( x2 ) = 0 1) (x)有 n+2 个不同的根ξx0) …0xn x ξ ∈ (ξ , ( n)+使得 = ′′(,ξ )ξ= 0 ( a , b ) 有 使得 ′(ξ ) = ′( = (ξ x ) 0 x ∈ 0 ξ1 0 1
外插 的实际误差 ≈ 0.01001 利用 x1 = π , x2 = π 4 3 内插 的实际误差 ≈ 0.00596
~ 0.00538 < R1 5π < 0.00660 sin 50° ≈ 0.76008, ° 18
n=2
( x π )( x π ) 1 ( x π )( x π ) 1 ( x π )( x π ) 4 6 6 L2 ( x ) = π π π π3 × + π π π π3 × + π π π π4 × 3 ( 6 4 )( 6 3 ) 2 ( 4 6 )( 4 3 ) 2 ( 3 6 )( 3 4 ) 2
n 求 n 次多项式 Pn ( x ) = a0 + a1 x + L + a n x 使得
计算方法 插值法Lagrange插值

上的插值多项式。 则求插值多项式P(x)的问题就归结为求它的系数
ai, i 0, 1, . . . ,n
由插值条件
p(xi ) f(xi ),i = 0,1,2, … , n
可得:
n+1个未知数a0 , a1 ,…, an
an
x
n 0
an1x
n1 0
(2.1)式为插值条件。 越简单越好
插值函数
y (x)
y=f(x)
a x0
x1 x2
xn b
目的:使得 y ( x) 近似等于f(x).
而误差函数
R(x) f(x) (x)
称为插值余项, 区间[a, b]称为插值区间.
评论:
用 ( x)的值作为f(x)的近似值,不仅希望 ( x)能
较好地逼近f(x),而且还希望它计算简单 。
计算方法 (Numerical Analysis)
第1次 Lagrange插值
本讲内容
1. 插值法的基本概念 2. 拉格朗日(Lagrange)插值 3. Lagrange插值的例子 4. Lagrange插值的误差
插值法的基本概念
第二章 插值法
§1 引言 问题的提出
– 若函数f(x)的解析式未知,而通过实验观测得到的一组 数据, 即在某个区间[a, b]上给出一系列点的函数值 yi= f(xi)
B(x1, f(x1))
x0
x1
由解析几何知道,这条直线用点斜式表示为
改写为
p(x)
y0
y1 x1
y0 x0
(x
x0)
p(x)
x x1 x0 x1
y0
x x0 x1 x0
lagrange插值的原理

lagrange插值的原理
Lagrange插值是一种数值分析方法,用于在已知一些点上的函数值的情况下,通过一个多项式来近似这个函数。
其基本原理如下:
1. 首先,根据给定的插值节点和函数值,构造一个n次多项式。
2. 利用插值基函数的概念,构造n次Lagrange插值多项式。
插值基函数是n个线性无关的n次多项式,它们在插值节点上的值等于相应的函数值。
3. 通过插值基函数,构建一个关于待求点x的n次多项式。
待求点的近似值可以通过求解这个多项式在x处的值来得到。
Lagrange插值的优势在于,它可以根据给定的插值节点和函数值精确地构造出一个多项式,从而在插值节点附近实现较高的近似精度。
然而,Lagrange插值也存在一定的局限性,例如在插值节点外的预测精度可能会降低,而且计算复杂度较高。
需要注意的是,Lagrange插值不仅适用于一元函数的插值,还适用于多元函数的插值。
在实际应用中,Lagrange插值被广泛应用于数学、物理、工程等领域的问题求解。
拉格朗日(Lagrange)插值算法

拉格朗⽇(Lagrange)插值算法拉格朗⽇插值(Lagrange interpolation)是⼀种多项式插值⽅法,指插值条件中不出现被插函数导数值,过n+1个样点,满⾜如下图的插值条件的多项式。
也叫做拉格朗⽇公式。
这⾥以拉格朗⽇3次插值为例,利⽤C++进⾏实现:1//利⽤lagrange插值公式2 #include<iostream>3using namespace std;45double Lx(int i,double x,double* Arr)6 {7double fenzi=1,fenmu=1;8for (int k=0;k<4;k++)9 {10if (k==i)11continue;12 fenzi*=x-Arr[k];13 fenmu*=Arr[i]-Arr[k];14 }15return fenzi/fenmu;16 }1718int main()19 {20double xArr[4]={};21double yArr[4]={};22//输⼊4个节点坐标23 cout<<"请依次输⼊4个节点的坐标:"<<endl;24for (int i=0;i<4;i++)25 cin>>xArr[i]>>yArr[i];2627//输⼊要求解的节点的横坐标28 cout<<"请输⼊要求解的节点的横坐标:";29double x;30 cin>>x;31double y=0;32for (int i=0;i<4;i++)33 y+=Lx(i,x,xArr)*yArr[i];34 printf("x=%lf时,y=%lf\n",x,y);3536//分界,下⾯为已知y求x37 cout<<"请输⼊要求解的节点的纵坐标:";38 cin>>y;39 x=0;40for (int i=0;i<4;i++)41 x+=Lx(i,y,yArr)*xArr[i];42 printf("y=%lf时,x=%lf\n",y,x);4344 system("pause");45return0;46 }作者:耑新新,发布于转载请注明出处,欢迎邮件交流:zhuanxinxin@。
插值法(lagrange插值,牛顿插值)概要

对n=1及n=2时的情况前面已经讨论,用类
似的推导方法,可得到n次插值基函数为:
( x x0 )(x x1 ) ( x xk 1 )(x xk 1 ) ( x xn ) lk ( x ) ( xk x0 )(xk x1 ) ( xk xk 1 )(xk xk 1 ) ( xk xn )
拉格朗日( Lagrange )插值公式 ( 以下统称 • 此插值问题可表述为如下: n 多项式 Lagrange 插值公式 ) 的基本思想是,把 Ln ( x) ,使满足条件 • 为 问题 求作次数 Ln xi yi , (i 0,1,, n) pn(x) 的构造问题转化为 n+1 个插值基函数
且满足
Pn ( xi ) yi
i 0,1,2 ,, n
其中 a i为实数,就称P(x)为插值多项式,相应的插值法 称为多项式插值;若P(x)为分段的多项式,就称为分段 插值;若P(x)为三角多项式,就称为三角插值。
本章只讨论多项式插值与分段插值
2018/10/23 10
§ 2.2
拉格朗日插值
本章主要介绍有关插值法的一些基本概念, 及多项式插值的基础理论和几个常用的插 值方法:拉格朗日插值、分段线性插值、 牛顿插值、埃尔米特插值和三次样条插值.
2018/10/23
3
§ 2.1 引言
一、插值问题
对函数f ( x),其函数形式可能很复杂 , 且不利于在计算机上
运算, 假如可以通过实验或测 量, 可以获得f ( x)在区间 [ a , b] 上的一组n 1个不同的点
--------(2) --------(3)
7
且满足
2018/10/23
拉格朗日(Lagrange)插值

li ( x) = Ci ( x x0 )...(x xi )...(x xn ) = Ci ( x x j ) ji j =0 1 li ( xi ) = 1 Ci = j i ( xi xj )
l ( x) y
i =0 i
1
i
l0(x)
l1(x)
称为拉格朗日插值基函数 , 满足条件 li(xj)=ij /* Kronecker Delta */
n1
希望找到li(x),i = 0, …, n 使得 li(xj)=ij ;然后令
Pn ( x ) =
l (x) y
i=0 i
n
i
,则显然有Pn(xi) = yi 。
§4.2 拉格朗日(Lagrange)插值
n 求 n 次多项式 Pn ( x) = a0 a1 x an x 使得
Pn ( x i ) = y i ,
i = 0 , ... , n
条件:无重合节点,即 i j
xi x j
一. 插值多项式的存在唯一性 定理4.2.1 : 在 n 1 个互异节点 xk 处满足插值条件 Pn ( xk ) = yk
n
f
( n 1)
( n 1 ) ( x0 ) = = ( xn ) = 0( n 1 ) ( x ) Ln ( x ) K ( x )( n 1) ! = Rn ( x ) K ( x ) ( n 1) ! ( n) 存在 (a, b) 使得 ( ) = 0 ( n 1 ) n ( n 1 ) f ( ) x f ( x) Rn ( x ) = ( x xi ) = K ( x) (n 1) ! i =0 ( n 1) !
6-1 lagrange插值

其中a=(x0-x1)(x0-x2)
b=(x1-x0)(x1-x2) c=(x2-x0)(x2-x1)
3.三点二次插值多项式为:
总结:三点二次插值就是用过三点(x0,y0)、 (x1,y1)、(x2,y2)的抛物线来近似曲线y=f(x), 因此也称三点二次插值为抛物线插值。
3. 4点3次插值
3. 5点4次插值如何写?
二、Hermite (埃尔米特)插值
特点:不但节点处值相同,一阶导数也相同。 Hermite 插值多项式为: n
H(x)= ∑{[1-2(x-xi)*li’(xi)]*li2(x)*yi+(x-xi)*li2(x) *y’i} i=0
用hi(x)表示1-2(x-xi)*li’(xi)]*li2(x) 用ki(x)表示(x-xi)*li2 (x) 当n=1时,即两个节点x0、x1 Hermite 插值多项式为(分 段三次插值法):
x0-x1
x0-x1
将a0和a1的值带到插值多项中得到:
2点1次插值也叫线性插值。
4x)=a0+a1x+a2x2 , 满足: a0+a1x0+a2x02=y0 a0+a1x1+a2x12=y1
a0+a1x2+a2x22=y2
a0=x1x2y0/a+x0x2y1/b+x0x1y2/c a1=-(x1+x2)y0/a-(x0+x2)y1/b-(x0+x1)y2/c a2=y0/a+y1/b+y2/c
得 到 : H3(x)=2(1+2(x-1)(x-2)2+3(1-2(x-2))(x-1)2-(x-2)(x-1) 2=-3x3+13x2-17x+9 当x=1.5时函数值为:2.625 当x=1.7时函数值为:2.931
拉格朗日插值法
拉格朗日( Lagrange )插值可对插值函数选择多种不一样的函数种类,因为代数多项式拥有简单和一些优秀的特征,比如,多项式是无量圆滑的,简单计算它的导数和积分,故常采纳代数多项式作为插值函数。
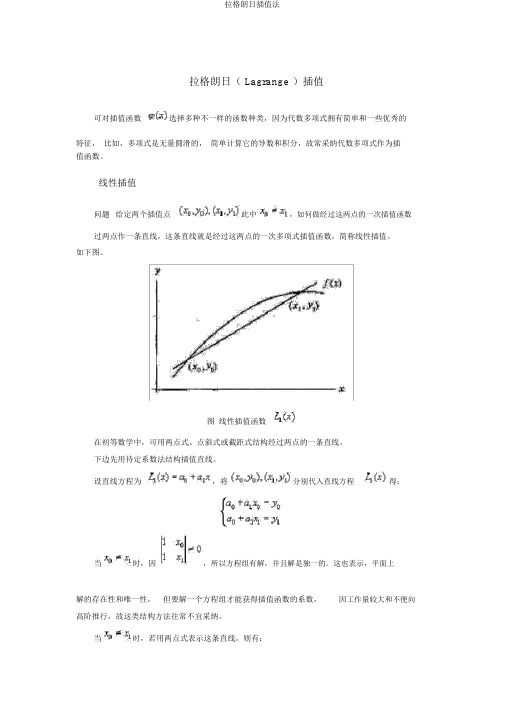
线性插值问题给定两个插值点此中,如何做经过这两点的一次插值函数过两点作一条直线,这条直线就是经过这两点的一次多项式插值函数,简称线性插值。
如下图。
图线性插值函数在初等数学中,可用两点式、点斜式或截距式结构经过两点的一条直线。
下边先用待定系数法结构插值直线。
设直线方程为,将分别代入直线方程得:当时,因,所以方程组有解,并且解是独一的。
这也表示,平面上解的存在性和唯一性,但要解一个方程组才能获得插值函数的系数,因工作量较大和不便向高阶推行,故这类结构方法往常不宜采纳。
当时,若用两点式表示这条直线,则有:()这类形式称为拉格朗日插值多项式。
,,称为插值基函数,计算,的值,易见()在拉格朗日插值多项式中可将看做两条直线,的叠加,并可看到两个插值点的作用和地位都是同等的。
拉格朗日插值多项式型式免去认识方程组的计算,易于向高次插值多项式型式推行。
线性插值偏差定理记为以为插值点的插值函数,。
这里,设一阶连续可导,在上存在,则对随意给定的,起码存在一点,使()证明令,因是的根,所以可设对任何一个固定的点,引进协助函数:则由定义可得别在和和,即。
,这样起码有上应用洛尔定理,可知和,对3个零点,不失一般性,假设在每个区间起码存在一个零点,不如记为在上应用洛尔定理,获得,分在上起码有一个零点,。
此刻对求二次导数,此中的线性函数),故有代入,得所以即二次插值问题给定三个插值点,, 此中互不相等,如何结构函数的二次的(抛物线)插值多项式平面上的三个点能确立一条次曲线,如下图。
图三个插值点的二次插值仿制线性插值的拉格朗日插值,即用插值基函数的方法结构插值多项式。
设每个基函数是一个二次函数,对来说,要求是它的零点,所以可设同理,也相对应的形式,得将代入,得同理将代入获得和的值,以及和的表达式。
第4章 Lagrange插值

x xi i 0 x j xi
i j
⑤
l j (x j ) 1 l j ( xi ) 0 i j
显然 l j ( x ) 满足{
Lagrange插值函数Ln(x)
定理 4.2 在[a、b]上有
2 n
span 1, x, x , , x span l0 ( x), l1 ( x), l2 ( x), , ln ( x)
这只是一张函数表;有的函数虽然有解析表达式,但由于计 算复杂,使用不方便,通常也构造一个函数表。如三角函数表、 对数表、平方根表、立方根表等等。
引言
科学实验得到数据: i , yi ) (x yi f ( xi ) (i 0,1,2,..., n), 它反映客观存在的函数y f ( x)在这些点的情况: (i 0,1,..., n) (i 0,1,2,..., n)。 但f ( x)时未知的。因此就想寻找函数 ( x ) f ( x ) 且保持 ( xi ) f ( xi ) yi 的插值函数。 称xi为节点, ( x)为f ( x)关于节点xi (i 0,1,2,..., n)
o i 0 i j n
2o v v l j y j ; 4) 输出 : u, v。
4.3 误差估计
定理 4.3 设函数 f ( x) C n [a, b] , f ( n1) ( x) 在开区间 (a,b)内存在,则 Lagrange 插值多项式 Ln( x) 的余式有如下估 计式
第4章 函数逼近的插值法 与曲线拟和法
引言
许多实际问题都用函数y f (x)来表示某种内在规律的数量
关系,其中相当一部分函数是通过实验或观测得到的.虽然 f (x)
在某个区间[a,b]上是存在的,有的还是连续的,但却只能 给出[a,b]上一系列点 xi的函数值yi f ( xi )
拉格朗日插值法知识讲解

拉格朗日插值法5.2 拉格朗日(Lagrange)插值可对插值函数选择多种不同的函数类型,由于代数多项式具有简单和一些良好的特性,例如,多项式是无穷光滑的,容易计算它的导数和积分,故常选用代数多项式作为插值函数。
5.2.1 线性插值问题5.1给定两个插值点其中,怎样做通过这两点的一次插值函数?过两点作一条直线,这条直线就是通过这两点的一次多项式插值函数,简称线性插值。
如图5.1所示。
图5.1 线性插值函数在初等数学中,可用两点式、点斜式或截距式构造通过两点的一条直线。
下面先用待定系数法构造插值直线。
设直线方程为,将分别代入直线方程得:当时,因,所以方程组有解,而且解是唯一的。
这也表明,平面上两个点,有且仅有一条直线通过。
用待定系数法构造插值多项式的方法简单直观,容易看到解的存在性和惟一性,但要解一个方程组才能得到插值函数的系数,因工作量较大和不便向高阶推广,故这种构造方法通常不宜采用。
当时,若用两点式表示这条直线,则有:(5.1)这种形式称为拉格朗日插值多项式。
,,称为插值基函数,计算,的值,易见(5.2)在拉格朗日插值多项式中可将看做两条直线,的叠加,并可看到两个插值点的作用和地位都是平等的。
拉格朗日插值多项式型式免除了解方程组的计算,易于向高次插值多项式型式推广。
线性插值误差定理5.1记为以为插值点的插值函数,。
这里,设一阶连续可导,在上存在,则对任意给定的,至少存在一点,使(5.3)证明令,因是的根,所以可设对任何一个固定的点,引进辅助函数:则。
由定义可得,这样至少有3个零点,不失一般性,假定,分别在和上应用洛尔定理,可知在每个区间至少存在一个零点,不妨记为和,即和,对在上应用洛尔定理,得到在上至少有一个零点,。
现在对求二次导数,其中的线性函数),故有代入,得所以即5.2.2 二次插值问题5.2给定三个插值点,,其中互不相等,怎样构造函数的二次的(抛物线)插值多项式?平面上的三个点能确定一条次曲线,如图5.2所示。
lagrange插值法

lagrange 插值法实验基本原理: lagrange 插值法是用来解决离散点的插值问题。
若给定两个插值点),(),,(1100y x y x 其10x x ≠,在公式中取1=n ,则La g r a n g e 插值多项式为:)()()()()()(001010010110101x x x x y y y x x x x y x x x x y x p ---+=--+--=是经过),(),,(1100y x y x 的一条直线,故此法称为线性插值法。
2、若函数给定三个插值点 2,1,0),,(=i y x i i ,,其中i x 互不相等,在公式中取1=n ,则Lagrange 插值多项式为: ))(())(())(())(())(())(()(1202102210120120102102x x x x x x x x y x x x x x x x x y x x x x x x x x y x p ----+----+----=是一个二次函数,若2,1,0),,(=i y x i i 三点不在一条直线上,则该曲线是一条抛物线,这种插值法称为二次插值或抛物插值。
为了解决这个问题,我们为此构造了这个矩阵⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----+---.........))(())(()())((12010212010212010x x x x x x x x x x x x x x x x 就可以找到相应系数。
实验结果分析:在应用拉格朗日插值法时应注意以下几个问题:1、在能获得原始资料时应尽量获取原始资料, 不能盲目地用组数据代入公式来估计未知数据。
2、在利用拉格朗日多项式进行插值估计时, 要求所研究范围的值的变化不受特殊或偶照因素的影响, 即的值是在正常条件下的。
3、如果有两组值(i x ,iy ),(j x ,j y ) 的i x =j x ;则这两组值只能取一组代入多项式计算, 否则便会出现 i y 与j y 的项分母为零的情况这种情况对于这种情况, 用哪组值代入多项式估计更好, 往往不易确定。
数学基础课里的lagrange插值公式

数学基础课里的lagrange插值公式lagrange插值公式:
1. Lagrange插值法是一种经典的插值方法,在数学和工程领域里都是一种常用的数值算法,也可以用来求解一元函数的极值点。
它实际上是对有n个数据点(比如:xi,yi)的函数f ( x) 进行拟合,形成n-1阶有理曲线,使得拟合曲线经过这些数据点。
2. Lagrange插值公式的可求性:在n个点的插值中,已知n个数据点(xi,yi),求使拟合曲线恰
好经过n个点的系数 ak 的问题。
3. Lagrange 插值公式:向量f (x) 和向量自变量x 可定义如下:f (x) = (f1 (x),f2 (x),…,fn-1 (x),fn (x));xi = (x1,x2,…,xn),那么有f (x) = Σ
j=1 n Lj(x).fj (*j = 1, 2,…, n*)
(其中Lj (x) 为Lagrangebasis 的基函数,可定义为:Lj (x) =Π(x/xj, i !=j))
4. Lagrange 插值公式的优点:
(1) Lagrange插值法简单易懂,实现简单;
(2) Lagrange插值法的拟合精度高;
(3) Lagrange插值法的拟合速度也是很快的,适用
性强。
5. Lagrange 插值公式的缺点:
(1) Lagrange插值法拟合数据点多时,计算量大;
(2) Lagrange插值法只适用于有n个数据点的插值,不能求解多元插值。
克里金插值法原理

克里金插值法原理
克里金插值法(也称作Lagrange插值法)是用于在特定的一组点上插入函数的方法,可以用来求解多元函数。
它是由Joseph-Louis Lagrange在18次世纪中发展出来的,因此它也被称为Lagrange插值法。
在拟合实验数据时,克里金插值法是常用的一种方法,它可以用来求解多元函数,以便评估函数之间的差异。
克里金插值法基于牛顿第三定律,其中第三定律规定,椭圆在椭圆上任意一点处,椭圆上所有点与此点的距离相等。
这就是克里金插值法的基本思想,求解一个函数的值,可以通过在一个椭圆上的多个点上的值求出来的。
它的计算方法是,在一个椭圆上的点上求出多个点,如已知每一点的函数值,用克里金插值法,可以求出椭圆上任意点的函数值。
克里金插值法的基本公式如下:
P(x)=∑n[L(x)f(x)]
其中P(x)表示函数值,L(x)表示拉格朗日多项式;f(x)表示被求函数值。
采用克里金插值法求解函数值的时候,首先要确定椭圆上的n+1个点,然后求出拉格朗日多项式L(x),最后从已知的f(x)的值,计算出函数值就可以了。
克里金插值法的优点在于它可以用来拟合较低次幂的多元阶数,不会受到解析解的限制,这使得拟合曲线更加准确。
克里金插值法也有一些缺点,如在椭圆上的点变多的时候,公式计算会变得复杂;如果有一个点出现数值错误,整个拟合结果也会失真。
总之,克里金插值法是求解多元函数的常用方法,它基于牛顿第三定律,可以用来拟合较低次幂的多元阶数,不会受到解析解的限制,因此,它是统计学中经常被使用的一种插值方法。
《Lagrange插值》课件

( j k 1, k 1);
( j k 1, k).
Lagrange插值多项式的构造
例如 : 求lk1( x),
因它
有
两个零
点xk
及xk
,故可表
1
示
为
lk1 ( x) A( x xk )( x xk1 ), 其中A为待定系数,可由条件lk1( xk1 ) 1
定出
A
( xk1
xk
若在 a,b上用Ln( x)近似 f ( x),则其截断误差 R(n x) f(x)Ln x,
被称为插值多项式的余项 关于插值余项估计有以下定理。
Lagrange插值余项与误差估计
定理2 设f (n)( x)在a, b上连续,f (n1)( x)在(a, b)内存在,
Ln( x)是满足条件Ln( x j )
从而 (t) 在[a,b]区间上有n 2个零点,由罗尔定理知:
'(t) 在(a,b)内至少有n 1个零点
''(t) 在(a,b)内至少有n个零点
(n1)(t) 在(a, b)内至少有1个零点
记 该零点为 (a,b),则有 (n1) ( ) f (n1) ( ) (n 1)! K( x) 0
L1( xk ) yk , L1( xk1) yk1.
yk
xk
y f (x)
y L1 ( x)
yk1
xk1
Lagrange插值多项式的构造
L1( x)
yk
yk 1 xk 1
yk xk
(x
xk )
( 点斜式),
L1( x)
x xk1 xk xk1
yk
x xk xk1 xk
yk1
实验四 Lagrange函数插值方法(新)
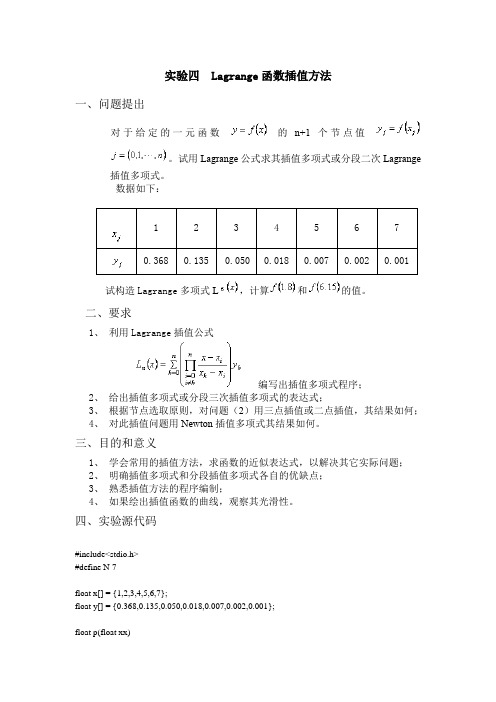
实验四 Lagrange函数插值方法一、问题提出对于给定的一元函数的n+1个节点值。
试用Lagrange公式求其插值多项式或分段二次Lagrange插值多项式。
数据如下:试构造Lagrange多项式L,计算和的值。
二、要求1、利用Lagrange插值公式编写出插值多项式程序;2、给出插值多项式或分段三次插值多项式的表达式;3、根据节点选取原则,对问题(2)用三点插值或二点插值,其结果如何;4、对此插值问题用Newton插值多项式其结果如何。
三、目的和意义1、学会常用的插值方法,求函数的近似表达式,以解决其它实际问题;2、明确插值多项式和分段插值多项式各自的优缺点;3、熟悉插值方法的程序编制;4、如果绘出插值函数的曲线,观察其光滑性。
四、实验源代码#include<stdio.h>#define N 7float x[] = {1,2,3,4,5,6,7};float y[] = {0.368,0.135,0.050,0.018,0.007,0.002,0.001};float p(float xx){int i,k;_______________for( i=0; i<N; i++ ){m1 = 1; m2 = 1;_______________if( k != i ) {________________ ________________________________ }return pp;}main(){printf( "f(1.8)=%lf\n", p(1.8) ); ____________________}五、实验结果六、实验心得与体会。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《Lagrange插值法》实验报告
1.实验名称
实验5 Lagrange插值法与最小二乘拟合法
2.实验题目
3.实验目的
验证Lagrange插值法对求插值多项式与近似值的数值结果,并用C++程序设计来实现该算法,加深对Lagrange插值法的优缺点的理解。
4.基础理论
5实验环境
Visual C++ 语言
6.实验过程
#include<iostream.h>
int main()
{
int n;
cout<<"节点的个数n=";cin>>n;
int i,j;
double x[20],y[20];
for( i=0;i<n;i++)
{
cout<<"节点"<<i+1<<":坐标x=";
cin>>x[i];
cout<<" 函数值y=";
cin>>y[i];
}
cout<<endl;
double yy=0,t=1;
double xx;
cout<<"xx="; cin>>xx;
for(i=0;i<n;i++)
{
t=y[i];
for(j=0;j<n;j++)
{
if(i!=j)
t=t*(xx-x[j])/(x[i]-x[j]);
}
yy=yy+t;
}
cout<<"节点"<<xx<<"处的函数值yy="<<yy<<endl;
return 0;
}。
