哈工大数据结构大作业——哈夫曼树生成、编码、遍历
数据结构实验哈夫曼树编码

实验四哈夫曼树编码一、实验目的1、掌握哈夫曼树的一般算法;2、掌握用哈夫曼树对字符串进行编码;3、掌握通过哈夫曼树对字符编码进行译码得过程。
二、实验基本要求1、设计数据结构;2、设计编码算法;3、分析时间复杂度和空间复杂度三、程序实现此程序中包含六个函数:Select()、HuffmanTree()、BianMa()、BianMa2()、YiMa()、Sum(),其功能及实现过程如下:#include <iostream.h>struct element//哈夫曼树结点类型{int weight;int lchild,rchild,parent;};struct Char//字符编码表信息{char node;int weight;char code[20];};void Select(element hT[],int &i1,int &i2,int k)//在hT[]中查找最小值及次小值{int min1=9999,min2=9999;i1=i2=0;for(int i=0;i<k;i++)if(hT[i].parent==-1)if(hT[i].weight<min1){min2=min1;i2=i1;min1=hT[i].weight;i1=i;}else if(hT[i].weight<min2){min2=hT[i].weight;i2=i;}}void HuffmanTree(element huffTree[],Char zifuma[],int n) //构建哈夫曼树{int i,k,i1,i2;for(i=0;i<2*n-1;i++) //初始化{huffTree[i].parent=-1;huffTree[i].lchild=-1;huffTree[i].rchild=-1;}for(i=0;i<n;i++) //构造n棵只含有根结点的二叉树huffTree[i].weight=zifuma[i].weight;for(k=n;k<2*n-1;k++) //n-1次合并{Select(huffTree,i1,i2,k); //在huffTree中找权值最小的两个结点i1和i2huffTree[i1].parent=k; //将i1和i2合并,则i1和i2的双亲是khuffTree[i2].parent=k;huffTree[k].weight=huffTree[i1].weight+huffTree[i2].weight;huffTree[k].lchild=i1;huffTree[k].rchild=i2;}}void BianMa(element huffTree[],Char zifuma[],int n)//根据哈夫曼树编码{int i,m,k,j,l;char temp[20];if(n==1){ zifuma[0].code[0]='0';zifuma[0].code[1]=0;}else {for(i=0;i<n;i++){j=0;k=huffTree[i].parent;l=i;while(k!=-1){if(huffTree[k].lchild==l)temp[j++]='0';else temp[j++]='1';l=k;k=huffTree[k].parent;}k=j-1;for(m=0;m<j;m++)zifuma[i].code[m]=temp[k--];zifuma[i].code[m]=0;}}void BianMa2(Char zifuma[],char zifu[],char bianma[],int n)//根据编码表对字符串编码{int i,j,k,m;i=k=0;while(zifu[i]){for(j=0;j<n;j++)if(zifu[i]==zifuma[j].node){m=0;while(zifuma[j].code[m])bianma[k++]=zifuma[j].code[m++];}i++;}bianma[k]=0;}void YiMa(element huffTree[],Char zifuma[],char bianma[],char yima[],int n)//根据编号的码元译成字符串{int i,j,k;i=j=0;if(n==1)while(bianma[i++])yima[j++]=zifuma[0].node;else{while(bianma[i]){k=2*(n-1);while(!(huffTree[k].lchild==-1&&huffTree[k].rchild==-1))if(bianma[i++]=='0')k=huffTree[k].lchild;elsek=huffTree[k].rchild;yima[j++]=zifuma[k].node;}}yima[j]=0;}void Sum(char zifu[],Char bianma[],int &n)//计算字符串中字符种类的个数及其出现次数{i=j=0;while(zifu[i]){for(int k=0;k<j;k++)if(bianma[k].node==zifu[i]){bianma[k].weight++;break;}if(k==j){bianma[j].node=zifu[i];bianma[j++].weight=1;}i++;}n=j;}void main(){int n,i;char a[50],b[200],c[50];element huffTree[100];Char w[50];cout<<"请输入需要编码的字符串:\n";cin.getline(a,49);Sum(a,w,n);cout<<"该字符串中共有"<<n<<"类字符。
数据结构:哈夫曼树和哈夫曼编码

数据结构:哈夫曼树和哈夫曼编码哈夫曼树哈夫曼树是⼀种最优⼆叉树,其定义是:给定n个权值作为n个叶⼦节点,构造⼀棵⼆叉树,若树的带权路径长度达到最⼩,这样的树就达到最优⼆叉树,也就是哈夫曼树,⽰例图如下:基本概念深⼊学习哈夫曼树前,先了解⼀下基本概念,并以上⾯的哈夫曼树图为例路径:树中⼀个结点到另⼀个结点之间的分⽀序列构成两个结点间的路径。
路径长度:路径中分⽀的数⽬,从根结点到第L层结点的路径长度为L-1。
例如100和80的路径长度为1,50和30的路径长度为2。
结点的权:树中结点的数值,例如100,50那些。
结点带权路径长度:根结点到该结点之间的路径长度与该结点的权的乘积。
如结点20的路径长度为3,该结点的带权路径长度为:3*20 = 60。
树的带权路径长度:所有叶⼦结点的带权路径长度之和,记为WPL。
例如上图树的WPL = 1100 + 280 +320 +310 = 350。
带权路径长度⽐较前⾯说到,哈夫曼树是最优⼆叉树,因为符合哈夫曼树特点的树的带权路径长度⼀定是最⼩的,我们将哈夫曼树和普通的⼆叉树做个⽐较,仍以上图为例,上图的哈夫曼树是结点10,20,50,100组成的⼆叉树,WPL是350,⽤这四个结点组成普通的⼆叉树,结果如下:不难计算,该⼆叉树的WPL = 210 + 220 + 250 + 2100 = 360,明显⽐哈夫曼树⼤,当然⼆叉树的组成结果不唯⼀,但WPL⼀定⽐哈夫曼树⼤。
所以说哈夫曼树是最优⼆叉树。
哈夫曼树的构造现在假定有n个权值,设为w1、w2、…、wn,将这n个权值看成是有n棵树的森林,根据最⼩带权路径长度的原则,我们可以按照下⾯步骤来将森林构造成哈夫曼树:1. 在森林中选出根结点的权值最⼩的两棵树进⾏合并,作为⼀棵新树的左、右⼦树,且新树的根结点权值为其左、右⼦树根结点权值之和;2. 从森林中删除选取的两棵树,并将新树加⼊森林;3. 重复1、2步,直到森林中只剩⼀棵树为⽌,该树即为所求得的哈夫曼树。
数据结构哈夫曼树的代码

数据结构哈夫曼树的代码数据结构哈夫曼树1.概述哈夫曼树(Huffman Tree)是一种经典的树形数据结构,用于编码和解码。
它根据各个字符出现的频率构建一个最优的前缀编码树,使得频率较高的字符具有较短的编码,频率较低的字符具有较长的编码。
2.哈夫曼树的构建2.1 频率统计首先,需要对给定的数据进行频率统计。
遍历数据集,记录每个字符的出现频率。
2.2 构建优先队列将频率统计得到的字符和各自的频率构建成一个优先队列。
队列中的每个元素都是一个字符及其频率的结构体。
2.3 构建哈夫曼树通过不断合并优先队列中频率最小的两个节点,构建出一棵哈夫曼树。
合并的过程中,新节点的频率为两个子节点频率之和。
2.4 构建哈夫曼编码从哈夫曼树的根节点出发,分别向左和向右遍历每个节点,直到叶子节点。
记录路径中经过的方向,0表示向左,1表示向右,获取每个字符的编码。
编码的长度即为该字符的出现频率。
3.哈夫曼树的应用3.1 数据压缩由于哈夫曼编码具有前缀码的特性,使得压缩后的数据可以唯一地解码回原始数据。
利用哈夫曼编码对数据进行压缩,可以减小存储空间的占用。
3.2 数据传输哈夫曼编码也广泛应用于数据传输领域。
由于编码的长度与频率成正比,频率较高的字符具有较短的编码,传输过程中能够减小数据传输的时间和带宽占用。
4.示例代码下面是一个用C++实现的简单哈夫曼树代码示例:________```cppinclude <iostream>include <queue>using namespace std。
struct Node {char data。
// 字符int freq。
// 频率Node left。
Node right。
}。
struct compare {bool operator(Node l, Node r) {return (l->freq > r->freq)}}。
void printCodes(Node root, string str) { if (!root)return。
哈夫曼树 哈夫曼编码(先序遍历方法)

for(i=0;i<2*n-1;i++)
{
printf("%d,", Huffman[i]->weight);
}
printf("\n");
for(i=0;i<2*n-1;i++)
{
printf("%d的左结点的下标为%d,右结点的下标为%d\n",Huffman[i]->weight,Huffman[i]->left,Huffman[i]->right);
{
if(i==1 && k==0 )
{
q[i] = Huffman[x];
s[i-1] = '*';
k++;
}
while(q[i]->left !=-1 && ls[i] == 0)
{
x =Huffman[x]->left;
ls[i] = 1; i++; k++;
q[i] = Huffman[x];
{
m1 = Huffman[j]->weight ;
x1 = j;
}
}
for(j=0;j<n+i;j++)
{
if( Huffman[j]->weight < m2 && Huffman[j]->parent == -1 && x1 != j)
{
m2 = Huffman[j]->weight ;
x2 = j;
tree Huffman[100];
哈夫曼树_实验报告

一、实验目的1. 理解哈夫曼树的概念及其在数据结构中的应用。
2. 掌握哈夫曼树的构建方法。
3. 学习哈夫曼编码的原理及其在数据压缩中的应用。
4. 提高编程能力,实现哈夫曼树和哈夫曼编码的相关功能。
二、实验原理哈夫曼树(Huffman Tree)是一种带权路径长度最短的二叉树,又称为最优二叉树。
其构建方法如下:1. 将所有待编码的字符按照其出现的频率排序,频率低的排在前面。
2. 选择两个频率最低的字符,构造一棵新的二叉树,这两个字符分别作为左右子节点。
3. 计算新二叉树的频率,将新二叉树插入到排序后的字符列表中。
4. 重复步骤2和3,直到只剩下一个节点,这个节点即为哈夫曼树的根节点。
哈夫曼编码是一种基于哈夫曼树的编码方法,其原理如下:1. 从哈夫曼树的根节点开始,向左子树走表示0,向右子树走表示1。
2. 每个叶子节点对应一个字符,记录从根节点到叶子节点的路径,即为该字符的哈夫曼编码。
三、实验内容1. 实现哈夫曼树的构建。
2. 实现哈夫曼编码和译码功能。
3. 测试实验结果。
四、实验步骤1. 创建一个字符数组,包含待编码的字符。
2. 创建一个数组,用于存储每个字符的频率。
3. 对字符和频率进行排序。
4. 构建哈夫曼树,根据排序后的字符和频率,按照哈夫曼树的构建方法,将字符和频率插入到哈夫曼树中。
5. 实现哈夫曼编码功能,遍历哈夫曼树,记录从根节点到叶子节点的路径,即为每个字符的哈夫曼编码。
6. 实现哈夫曼译码功能,根据哈夫曼编码,从根节点开始,按照0和1的路径,找到对应的叶子节点,即为解码后的字符。
7. 测试实验结果,验证哈夫曼编码和译码的正确性。
五、实验结果与分析1. 构建哈夫曼树根据实验数据,构建的哈夫曼树如下:```A/ \B C/ \ / \D E F G```其中,A、B、C、D、E、F、G分别代表待编码的字符。
2. 哈夫曼编码根据哈夫曼树,得到以下字符的哈夫曼编码:- A: 00- B: 01- C: 10- D: 11- E: 100- F: 101- G: 1103. 哈夫曼译码根据哈夫曼编码,对以下编码进行译码:- 00101110111译码结果为:BACGACG4. 实验结果分析通过实验,验证了哈夫曼树和哈夫曼编码的正确性。
哈夫曼树的编码和解码

哈夫曼树的编码和解码是哈夫曼编码算法的重要部分,下面简要介绍其步骤:
1. 编码:
哈夫曼编码是一种变长编码方式,对于出现频率高的字符使用较短的编码,而对于出现频率低的字符使用较长的编码。
具体步骤如下:(1)根据字符出现的频率,构建哈夫曼树。
频率相同的字符,按照它们在文件中的出现顺序排列。
(2)从哈夫曼树的叶子节点开始,从下往上逐步进行编码。
对于每个节点,如果该节点有左孩子,那么左孩子的字符编码为0,右孩子的字符编码为1。
如果该节点是叶子节点,则该节点的字符就是它的编码。
(3)对于哈夫曼树中的每个节点,都记录下它的左孩子和右孩子的位置,以便后续的解码操作。
2. 解码:
解码过程与编码过程相反,具体步骤如下:
(1)从哈夫曼树的根节点开始,沿着路径向下遍历树,直到找到一个终止节点(叶节点)。
(2)根据终止节点的位置信息,找到对应的字符。
(3)重复上述步骤,直到遍历完整个编码序列。
需要注意的是,哈夫曼编码是一种无损压缩算法,解压缩后的数据与原始数据完全相同。
此外,由于哈夫曼编码是一种变长编码方式,因此在解码时需要从根节点开始逐个解码,直到解码完成。
数据结构 哈夫曼编码实验报告

数据结构哈夫曼编码实验报告数据结构哈夫曼编码实验报告1. 实验目的本实验旨在通过实践理解哈夫曼编码的原理和实现方法,加深对数据结构中树的理解,并掌握使用Python编写哈夫曼编码的能力。
2. 实验原理哈夫曼编码是一种用于无损数据压缩的算法,通过根据字符出现的频率构建一棵哈夫曼树,并根据哈夫曼树对应的编码。
根据哈夫曼树的特性,频率较低的字符具有较长的编码,而频率较高的字符具有较短的编码,从而实现了对数据的有效压缩。
实现哈夫曼编码的主要步骤如下:1. 统计输入文本中每个字符的频率。
2. 根据字符频率构建哈夫曼树,其中树的叶子节点代表字符,内部节点代表字符频率的累加。
3. 遍历哈夫曼树,根据左右子树的关系对应的哈夫曼编码。
4. 使用的哈夫曼编码对输入文本进行编码。
5. 将编码后的二进制数据保存到文件,同时保存用于解码的哈夫曼树结构。
6. 对编码后的文件进行解码,还原原始文本。
3. 实验过程3.1 统计字符频率首先,我们需要统计输入文本中每个字符出现的频率。
可以使用Python中的字典数据结构来记录字符频率。
遍历输入文本的每个字符,将字符添加到字典中,并递增相应字符频率的计数。
```pythondef count_frequency(text):frequency = {}for char in text:if char in frequency:frequency[char] += 1else:frequency[char] = 1return frequency```3.2 构建哈夫曼树根据字符频率构建哈夫曼树是哈夫曼编码的核心步骤。
我们可以使用最小堆(优先队列)来高效地构建哈夫曼树。
首先,将每个字符频率作为节点存储到最小堆中。
然后,从最小堆中取出频率最小的两个节点,将它们作为子树构建成一个新的节点,新节点的频率等于两个子节点频率的和。
将新节点重新插入最小堆,并重复该过程,直到最小堆中只剩下一个节点,即哈夫曼树的根节点。
数据结构哈夫曼树实验报告

数据结构哈夫曼树实验报告一、实验内容本次实验的主要内容是哈夫曼树的创建和编码解码。
二、实验目的1. 理解并掌握哈夫曼树的创建过程;2. 理解并掌握哈夫曼编码的原理及其实现方法;3. 掌握哈夫曼树的基本操作,如求哈夫曼编码和哈夫曼解码等;4. 学习如何组织程序结构,运用C++语言实现哈夫曼编码和解码。
三、实验原理哈夫曼树的创建:哈夫曼树的创建过程就是一个不断合并权值最小的两个叶节点的过程。
具体步骤如下:1. 将所有节点加入一个无序的优先队列里;2. 不断地选出两个权值最小的节点,并将它们合并成为一个节点,其权值为这两个节点的权值之和;3. 将新的节点插入到队列中,并继续执行步骤2,直到队列中只剩下一棵树,这就是哈夫曼树。
哈夫曼编码:哈夫曼编码是一种无损压缩编码方式,它根据字符出现的频率来构建编码表,并通过编码表将字符转换成二进制位的字符串。
具体实现方法如下:1. 统计每个字符在文本中出现的频率,用一个数组记录下来;2. 根据字符出现的频率创建哈夫曼树;3. 从根节点开始遍历哈夫曼树,给左分支打上0的标记,给右分支打上1的标记。
遍历每个叶节点,将对应的字符及其对应的编码存储在一个映射表中;4. 遍历文本中的每个字符,查找其对应的编码表,并将编码字符串拼接起来,形成一个完整的编码字符串。
哈夫曼解码就是将编码字符串还原为原始文本的过程。
具体实现方法如下:1. 从根节点开始遍历哈夫曼树,按照编码字符串的位数依次访问左右分支。
如果遇到叶节点,就将对应的字符记录下来,并重新回到根节点继续遍历;2. 重复步骤1,直到编码字符串中的所有位数都被遍历完毕。
四、实验步骤1. 定义编码和解码的结构体以及相关变量;3. 遍历哈夫曼树,得到每个字符的哈夫曼编码,并将编码保存到映射表中;4. 将文本中的每个字符用其对应的哈夫曼编码替换掉,并将编码字符串写入到文件中;5. 使用哈夫曼编码重新构造文本,并将结果输出到文件中。
五、实验总结通过本次实验,我掌握了哈夫曼树的创建和哈夫曼编码的实现方法,也学会了如何用C++语言来组织程序结构,实现哈夫曼编码和解码。
哈夫曼树编码实训报告

一、实训目的本次实训旨在通过实际操作,让学生掌握哈夫曼树的基本概念、构建方法以及编码解码过程,加深对数据结构中树型结构在实际应用中的理解。
通过本次实训,学生能够:1. 理解哈夫曼树的基本概念和构建原理;2. 掌握哈夫曼树的编码和解码方法;3. 熟悉Java编程语言在哈夫曼树编码中的应用;4. 提高数据压缩和传输效率的认识。
二、实训内容1. 哈夫曼树的构建(1)创建叶子节点:根据给定的字符及其权值,创建叶子节点,并设置节点信息。
(2)构建哈夫曼树:通过合并权值最小的两个节点,不断构建新的节点,直到所有节点合并为一棵树。
2. 哈夫曼编码(1)遍历哈夫曼树:从根节点开始,按照左子树为0、右子树为1的规则,记录每个叶子节点的路径。
(2)生成编码:将遍历过程中记录的路径转换为二进制编码,即为哈夫曼编码。
3. 哈夫曼解码(1)读取编码:将编码字符串按照二进制位读取。
(2)遍历哈夫曼树:从根节点开始,根据读取的二进制位,在哈夫曼树中寻找对应的节点。
(3)输出解码结果:当找到叶子节点时,输出对应的字符,并继续读取编码字符串。
三、实训过程1. 准备工作(1)创建一个Java项目,命名为“HuffmanCoding”。
(2)在项目中创建以下三个类:- HuffmanNode:用于存储哈夫曼树的节点信息;- HuffmanTree:用于构建哈夫曼树、生成编码和解码;- Main:用于实现主函数,接收用户输入并调用HuffmanTree类进行编码和解码。
2. 编写代码(1)HuffmanNode类:```javapublic class HuffmanNode {private char data;private int weight;private HuffmanNode left;private HuffmanNode right;public HuffmanNode(char data, int weight) {this.data = data;this.weight = weight;}}```(2)HuffmanTree类:```javaimport java.util.PriorityQueue;public class HuffmanTree {private HuffmanNode root;public HuffmanNode buildHuffmanTree(char[] data, int[] weight) {// 创建优先队列,用于存储叶子节点PriorityQueue<HuffmanNode> queue = new PriorityQueue<>();for (int i = 0; i < data.length; i++) {HuffmanNode node = new HuffmanNode(data[i], weight[i]);queue.offer(node);}// 构建哈夫曼树while (queue.size() > 1) {HuffmanNode left = queue.poll();HuffmanNode right = queue.poll();HuffmanNode parent = new HuffmanNode('\0', left.weight + right.weight);parent.left = left;parent.right = right;queue.offer(parent);}root = queue.poll();return root;}public String generateCode(HuffmanNode node, String code) {if (node == null) {return "";}if (node.left == null && node.right == null) {return code;}generateCode(node.left, code + "0");generateCode(node.right, code + "1");return code;}public String decode(String code) {StringBuilder result = new StringBuilder();HuffmanNode node = root;for (int i = 0; i < code.length(); i++) {if (code.charAt(i) == '0') {node = node.left;} else {node = node.right;}if (node.left == null && node.right == null) { result.append(node.data);node = root;}}return result.toString();}}```(3)Main类:```javaimport java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);System.out.println("请输入字符串:");String input = scanner.nextLine();System.out.println("请输入字符及其权值(例如:a 2 b 3 c 5):"); String[] dataWeight = scanner.nextLine().split(" ");char[] data = new char[dataWeight.length / 2];int[] weight = new int[dataWeight.length / 2];for (int i = 0; i < dataWeight.length; i += 2) {data[i / 2] = dataWeight[i].charAt(0);weight[i / 2] = Integer.parseInt(dataWeight[i + 1]);}HuffmanTree huffmanTree = new HuffmanTree();HuffmanNode root = huffmanTree.buildHuffmanTree(data, weight); String code = huffmanTree.generateCode(root, "");System.out.println("编码结果:" + code);String decoded = huffmanTree.decode(code);System.out.println("解码结果:" + decoded);scanner.close();}}```3. 运行程序(1)编译并运行Main类,输入字符串和字符及其权值。
数据结构程序设计作业——《哈夫曼编码》

数据结构实验报告题目哈夫曼编码学生姓名王某某专业班级测控120X班学号U2012XXXXX1 问题描述输入一字符串,以字符串中各字符出现的频数为权值构造哈夫曼编码。
然后输入一0—1序列,根据生成的哈夫曼编码解码序列。
2 算法描述(1)哈夫曼树的表示设计哈夫曼树的结构体(htnode),其中包含权重、左右孩子、父母和要编码的字符。
用这个结构体(htnode)定义个哈夫曼数组(hfmt[])。
迷宫定义如下:typedef struct{int weight;int lchild;int rchild;int parent;char key;}htnode;typedef htnode hfmt[MAXLEN];(2)对原始字符进行编码初始化哈夫曼树(inithfmt)。
从终端读入字符集大小n,以及n个字符和n个权值,建立哈夫曼树。
并显示出每个字符的编码。
1.void inithfmt(hfmt t)//对结构体进行初始化2.void inputweight(hfmt t)//输入函数3.void selectmin(hfmt t,int i,int *p1,int *p2)//选中两个权值最小的函数4.void creathfmt(hfmt t)//创建哈夫曼树的函数5.void phfmnode(hfmt t)//对字符进行初始编码(3)对用户输入的字符进行编码void encoding(hfmt t)//对用户输入的电文进行编码{char r[1000];//用来存储输入的字符串int i,j;printf("\n\n请输入需要编码的字符:");gets(r);printf("编码结果为:");for(j=0;r[j]!='\0';j++)for(i=0;i<n;i++)if(r[j]==t[i].key)hfmtpath(t,i,j);printf("\n");}(4)对用户输入的字符进行编码void decoding(hfmt t)//对用户输入的密文进行译码{char r[100];int i,j,len;j=2*n-2;//j初始从树的根节点开始printf("\n\n请输入需要译码的字符串:"); gets(r);len=strlen(r);printf("译码的结果是:");for(i=0;i<len;i++){if(r[i]=='0'){j=t[j].lchild;if(t[j].lchild==-1){printf("%c",t[j].key);j=2*n-2;}}else if(r[i]=='1'){j=t[j].rchild;if(t[j].rchild==-1){printf("%c",t[j].key); j=2*n-2;}}}printf("\n\n");}3 程序设计流程图4 运行测试1.用户输入字符串,以回车键作为结束2.对字符统计打印统计结果、编码表和编码结果3.对一串数据解码4.统计编码前后的数据大小,计算压缩率5 实验收获代码编写完会有很多与预期不同的结果,耐心调试,修改代码,开始写代码的时候就认真的写,在调试时找出逻辑问题比较困难,做到一步到位。
哈夫曼树哈夫曼编码(先序遍历方法)

#include <stdio.h>#include <stdlib.h>typedef struct Tree{int weight;int left;int right;int parent;}*tree;void CreateHuffman(int n){int i;int m1,m2,x1,x2;tree Huffman[100];for(i=0;i< 2*n-1;i++){Huffman[i] = (tree) malloc(sizeof(struct Tree));}for(i=0;i<n;i++){scanf("%d",&Huffman[i]->weight);}for(i=0;i<2*n-1;i++){Huffman[i]->parent = -1;Huffman[i]->left = -1;Huffman[i]->right = -1;}int j;for(i=0;i<n-1;i++){m1= m2= 65536;x1 =x2 = 0;for(j=0;j<n+i;j++){if( Huffman[j]->weight < m1 && Huffman[j]->parent == -1){m1 = Huffman[j]->weight ;x1 = j;}}for(j=0;j<n+i;j++){if( Huffman[j]->weight < m2 && Huffman[j]->parent == -1 && x1 != j){m2 = Huffman[j]->weight ;x2 = j;}}Huffman[x1]->parent = n+i; Huffman[x2]->parent = n+i;Huffman[n+i]->weight =Huffman[x1]->weight + Huffman[x2]->weight ;Huffman[n+i]->left =x1; Huffman[n+i]->right =x2;}for(i=0;i<2*n-1;i++){printf("%d,", Huffman[i]->weight);}printf("\n");for(i=0;i<2*n-1;i++){printf("%d的左结点的下标为%d,右结点的下标为%d\n",Huffman[i]->weight,Huffman[i]->left,Huffman[i]->right);}char s[100]; int x; i--; x = i; int k; k=0;int rs[100];int ls[100]; i=1; tree q[100];int sum=0;for(j=0; j<100 ;j++){rs[j] =0;ls[j] =0; s[j]='\0';}while( i != 0){if(i==1 && k==0 ){q[i] = Huffman[x];s[i-1] = '*';k++;}while(q[i]->left !=-1 && ls[i] == 0){x =Huffman[x]->left;ls[i] = 1; i++; k++;q[i] = Huffman[x];s[i-1] ='0';ls[i] =0; rs[i] = 0;}if(( q[i]->left ==-1&& q[i]->right != -1 && rs[i] ==0 ) || (ls[i] ==1 && q[i]->right != -1&& rs[i] ==0 ) ){x =Huffman[x]->right;rs[i] =1; i++; k++;q[i] = Huffman[x];s[i-1] ='1';ls[i] =0; rs[i] = 0;}if( (q[i]->left ==-1 && q[i]->right ==-1 ) ){printf("%d:",q[i]->weight);for( j =1 ; j <i;j++)printf("%c",s[j]);printf("\n"); sum+= q[i]->weight *(i-1);}if( (q[i]->left ==-1 && rs[i] == 1 ) ||(q[i]->left ==-1 && q[i]->right == -1)||(q[i]->right ==-1 && ls[i] == 1 ) ||( rs[i] ==1&& ls[i] == 1 ) ){i--; k++;Huffman[x] =q[i];}}printf("带权长度为%d\n",sum);}void main(){int num; printf("输入叶子结点个数:");scanf("%d",&num);CreateHuffman( num);printf("\n");}。
哈夫曼树及其编码
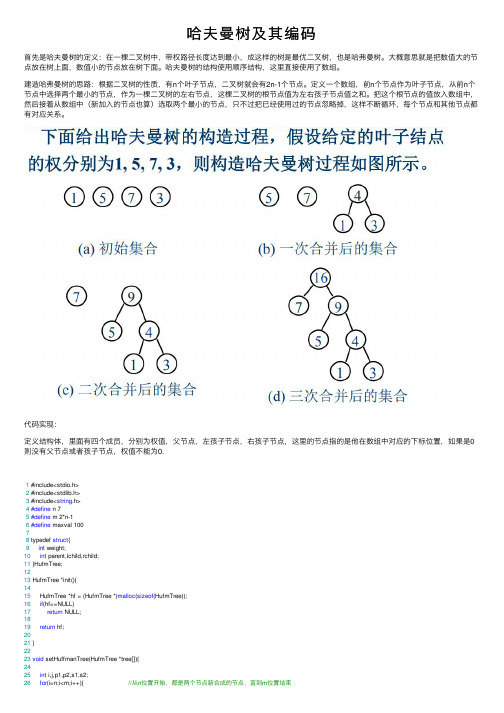
哈夫曼树及其编码⾸先是哈夫曼树的定义:在⼀棵⼆叉树中,带权路径长度达到最⼩,成这样的树是最优⼆叉树,也是哈弗曼树。
⼤概意思就是把数值⼤的节点放在树上⾯,数值⼩的节点放在树下⾯。
哈夫曼树的结构使⽤顺序结构,这⾥直接使⽤了数组。
建造哈弗曼树的思路:根据⼆叉树的性质,有n个叶⼦节点,⼆叉树就会有2n-1个节点。
定义⼀个数组,前n个节点作为叶⼦节点,从前n个节点中选择两个最⼩的节点,作为⼀棵⼆叉树的左右节点,这棵⼆叉树的根节点值为左右孩⼦节点值之和。
把这个根节点的值放⼊数组中,然后接着从数组中(新加⼊的节点也算)选取两个最⼩的节点,只不过把已经使⽤过的节点忽略掉,这样不断循环,每个节点和其他节点都有对应关系。
代码实现:定义结构体,⾥⾯有四个成员,分别为权值,⽗节点,左孩⼦节点,右孩⼦节点,这⾥的节点指的是他在数组中对应的下标位置,如果是0则没有⽗节点或者孩⼦节点,权值不能为0.1 #include<stdio.h>2 #include<stdlib.h>3 #include<string.h>4#define n 75#define m 2*n-16#define maxval 10078 typedef struct{9int weight;10int parent,lchild,rchild;11 }HufmTree;1213 HufmTree *init(){1415 HufmTree *hf = (HufmTree *)malloc(sizeof(HufmTree));16if(hf==NULL)17return NULL;1819return hf;2021 }2223void setHuffmanTree(HufmTree *tree[]){2425int i,j,p1,p2,s1,s2;26for(i=n;i<m;i++){ //从n位置开始,都是两个节点新合成的节点,直到m位置结束27 p1 = p2 = 0; //每次循环开始,都要数组从头开始遍历28 s1 = s2 = maxval;29for(j=0;j<=i-1;j++) //在所有节点中寻找,i后⾯没有数值的空位置⽤不到30if(tree[j]->parent==0) //此处的代码的作⽤是检查该节点是否已经使⽤过,因为使⽤过的节点肯定有⽗节点31if(tree[j]->weight<s1){ //寻找最⼩权值的节点32 s2 = s1;33 s1 = tree[j]->weight;34 p2 = p1;35 p1 = j;36 }37else if(tree[j]->weight<s2){//寻找次⼩权值的节点38 s2 = tree[j]->weight;39 p2 = j;40 }41 tree[p1]->parent = tree[p2]->parent = i; //把两个最⼩节点的⽗节点指向i42 tree[i]->weight = tree[p1]->weight + tree[p2]->weight; //⽗节点权值等于左右孩⼦权值之和43 tree[i]->lchild = p1; //指明⽗节点的左右孩⼦节点44 tree[i]->rchild = p2;45 }4647 }4849void display(HufmTree *tree[n]){5051int i;52for(i=0;i<m;i++){53 printf("%d ",tree[i]->weight);54 }55 printf("\n");56 }哈弗曼编码:使出现频率⾼的编码放在上⾯,频率低的编码放在下⾯。
(完整word版)哈工大数据结构大作业——哈夫曼树生成、编码、遍历

一、问题描述1.用户输入字母及其对应的权值,生成哈夫曼树;2.通过最优编码的算法实现,生成字母对应的最优0、1编码;3.先序、中序、后序遍历哈夫曼树,并打印其权值。
二、方法思路1。
哈夫曼树算法的实现§存储结构定义#define n 100 /*叶子树*/#define m 2*(n) –1 /* 结点总数*/typedef struct {/*结点型*/double weight ; /* 权值*/int lchild ;/* 左孩子链*/int rchild ;/* 右孩子链*/int parent; /*双亲链*/ 优点?}HTNODE ;typedef HTNODE HuffmanT[ m ];/*huffman树的静态三叉链表表示*/算法要点1)初始化:将T[0],…T[m—1]共2n-1个结点的三个链域均置空(—1 ),权值为0;2)输入权值:读入n 个叶子的权值存于T的前n 个单元T[0],…T[n],它们是n 个独立的根结点上的权值;3)合并:对森林中的二元树进行n—1次合并,所产生的新结点依次存放在T[i](n〈=i<=m—1)。
每次合并分两步:(1) 在当前森林中的二元树T [0],…T[i—1]所有结点中选取权值最小和次最小的两个根结点T[p1]和T[p2]作为合并对象,这里0<= p1,p2<= i –1;(2) 将根为T[p1]和T[p2]的两株二元树作为左、右子树合并为一株新二元树,新二元树的根结点为T[i]。
即T[p1].parent =T[p2].parent = i ,T[i].lchild= p1, T[i]。
rchild=p2, T[i].weight =T[p1]。
weight + T[p2].weight.2。
用huffman算法求字符集最优编码的算法:1) 使字符集中的每个字符对应一株只有叶结点的二叉树,叶的权值为对应字符的使用频率;2)利用huffman算法来构造一株huffman树;3) 对huffman树上的每个结点,左支附以0,右支附以1(或者相反),则从根到叶的路上的0、1序列就是相应字符的编码Huffman编码实现:存储结构typedef struct{char ch;//存储字符char bits[n+1];//字符编码位串}CodeNode;typedef CodeNode HuffmanCode[n];HuffmanCode H;3。
数据结构哈夫曼树的代码

数据结构哈夫曼树的代码数据结构哈夫曼树的代码实现:1·简介哈夫曼树(Huffman Tree),又称为最优二叉树,是一种用于数据压缩的树形结构。
它利用出现频率较高的字符采用较短的编码,而出现频率较低的字符采用较长的编码,从而实现数据的压缩和解压缩。
本文将详细介绍哈夫曼树的构建和编码解码的过程。
2·哈夫曼树的构建2·1 核心思想哈夫曼树的构建核心思想是根据字符的出现频率构建一棵树,使得频率高的字符离树根近,频率低的字符离树根远。
构建哈夫曼树的步骤如下:●创建一个包含所有字符的叶子结点集合。
●从集合中选择两个频率最低的结点(注意:频率越低,优先级越高),构建一个新的二叉树,根节点的频率等于这两个结点的频率之和。
●将新构建的二叉树的根节点加入集合中。
●重复上述操作,直到集合中只剩一个根结点,即构建完成。
2·2 代码实现下面是一个示例的哈夫曼树构建的代码:```pythonclass Node:def __init__(self, freq, char=None):self·freq = freqself·char = charself·left = Noneself·right = Nonedef build_huffman_tree(char_freq):leaves = [Node(freq, char) for char, freq in char_freq·items()]while len(leaves) > 1:leaves·sort(key=lambda x: x·freq)left = leaves·pop(0)right = leaves·pop(0)parent = Node(left·freq + right·freq)parent·left = leftparent·right = rightleaves·append(parent)return leaves[0]```3·哈夫曼树的编码3·1 核心思想哈夫曼树的编码过程是根据构建好的哈夫曼树,对每个字符进行编码。
哈夫曼树及哈夫曼编码的算法实现

哈夫曼树及哈夫曼编码的算法实现1. 哈夫曼树的概念和原理哈夫曼树是一种带权路径长度最短的树,也称最优二叉树。
它是由美国数学家大卫・哈夫曼发明的,用于数据压缩编码中。
哈夫曼树的构建原理是通过贪心算法,将权重较小的节点不断合并,直到所有节点都合并成为一个根节点,形成一棵树。
这样构建的哈夫曼树能够实现数据的高效压缩和解压缩。
2. 哈夫曼编码的概念和作用哈夫曼编码是一种可变长度编码,它根据字符在文本中出现的频率来进行编码,频率越高的字符编码越短,频率越低的字符编码越长。
这种编码方式能够实现数据的高效压缩,减小数据的存储空间,提高数据传输的效率。
3. 哈夫曼树和编码的算法实现在实现哈夫曼树和编码的算法过程中,首先需要统计文本中每个字符出现的频率,并根据频率构建哈夫曼树。
根据哈夫曼树的结构,确定每个字符的哈夫曼编码。
利用哈夫曼编码对文本进行压缩和解压缩。
4. 个人观点和理解哈夫曼树及哈夫曼编码算法是一种非常有效的数据压缩和编码方式,能够在保证数据完整性的前提下,减小数据的存储和传输成本。
在实际应用中,哈夫曼编码被广泛应用于通信领域、数据存储领域以及图像压缩等领域。
通过深入理解和掌握哈夫曼树及哈夫曼编码的算法实现,可以为我们在实际工作中处理大量数据时提供便利和效率。
5. 总结与回顾通过本篇文章的详细讲解,我深入了解了哈夫曼树及哈夫曼编码的算法原理和实现方式,对其在数据处理中的重要性有了更深刻的认识。
掌握了哈夫曼树及哈夫曼编码的算法实现,将为我未来的工作和学习提供更多的帮助和启发。
根据您提供的主题,本篇文章按照从简到繁、由浅入深的方式探讨了哈夫曼树及哈夫曼编码的算法实现。
文章共计超过3000字,深入剖析了哈夫曼树和编码的原理、实现方式以及应用场景,并结合个人观点进行了阐述。
希望本篇文章能够满足您的需求,如有任何修改意见或其他要求,欢迎随时告知。
哈夫曼树和哈夫曼编码是一种十分重要的数据压缩和编码方式,它们在实际的数据处理和传输中发挥着非常重要的作用。
数据结构——哈夫曼(Huffman)树+哈夫曼编码

数据结构——哈夫曼(Huffman)树+哈夫曼编码前天acm实验课,⽼师教了⼏种排序,抓的⼀套题上有⼀个哈夫曼树的题,正好之前离散数学也讲过哈夫曼树,这⾥我就结合课本,整理⼀篇关于哈夫曼树的博客。
哈夫曼树的介绍Huffman Tree,中⽂名是哈夫曼树或霍夫曼树,它是最优⼆叉树。
定义:给定n个权值作为n个叶⼦结点,构造⼀棵⼆叉树,若树的带权路径长度达到最⼩,则这棵树被称为哈夫曼树。
这个定义⾥⾯涉及到了⼏个陌⽣的概念,下⾯就是⼀颗哈夫曼树,我们来看图解答。
(01) 路径和路径长度定义:在⼀棵树中,从⼀个结点往下可以达到的孩⼦或孙⼦结点之间的通路,称为路径。
通路中分⽀的数⽬称为路径长度。
若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
例⼦:100和80的路径长度是1,50和30的路径长度是2,20和10的路径长度是3。
(02) 结点的权及带权路径长度定义:若将树中结点赋给⼀个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
例⼦:节点20的路径长度是3,它的带权路径长度= 路径长度 * 权 = 3 * 20 = 60。
(03) 树的带权路径长度定义:树的带权路径长度规定为所有叶⼦结点的带权路径长度之和,记为WPL。
例⼦:⽰例中,树的WPL= 1*100 + 2*50 +3*20 + 3*10 = 100 + 100 + 60 + 30 = 290。
⽐较下⾯两棵树上⾯的两棵树都是以{10, 20, 50, 100}为叶⼦节点的树。
左边的树WPL=2*10 + 2*20 + 2*50 + 2*100 = 360 右边的树WPL=350左边的树WPL > 右边的树的WPL。
你也可以计算除上⾯两种⽰例之外的情况,但实际上右边的树就是{10,20,50,100}对应的哈夫曼树。
⾄此,应该堆哈夫曼树的概念有了⼀定的了解了,下⾯看看如何去构造⼀棵哈夫曼树。
数据结构哈夫曼编码

数据结构哈夫曼编码
哈夫曼编码是一种用于数据压缩的算法,它基于哈夫曼树(HuffmanTree)进行编码。
哈夫曼编码的基本思想是:对于出现频率高的字符,其编码长度较短;而对于出现频率低的字符,其编码长度较长。
这样,通过调整字符的编码长度,可以有效地压缩数据。
哈夫曼编码的具体步骤如下:
1.统计原始数据中每个字符的出现频率。
2.构建哈夫曼树。
在构建过程中,每次将两个权值最小的节点合并,并将它们的权值相加。
同时,将新生成的节点的权值作为新字符的出现频率。
3.根据哈夫曼树生成哈夫曼编码。
对于哈夫曼树中的每个字符,从根节点到该字符所在节点的路径可以形成一个二进制编码。
通常约定左分支标记为0,右分支标记为1。
这样,从根节点到每个叶节点的路径就可以形成一个二进制编码,该编码即为对应字符的哈夫曼编码。
4.使用哈夫曼编码对原始数据进行压缩。
对于原始数据中的每个字符,根据其哈夫曼编码进行编码,最终得到压缩后的数据。
需要注意的是,哈夫曼编码是一种无损压缩算法,即压缩和解压过程中可以完全还原原始数据。
同时,由于哈夫曼编码是基于字符出现频率进行编码的,因此对于出现频率高的字符,其编码长度较短;而对于出现频率低的字符,其编码长度较长。
这样可以有效地减少数据的存储空间,提高数据压缩率。
数据结构实验哈夫曼树及哈夫曼编码c语言

数据结构实验报告:哈夫曼树及哈夫曼编码一、实验目的1. 理解哈夫曼树及哈夫曼编码的概念和原理;2. 掌握C语言中哈夫曼树及哈夫曼编码的实现方法;3. 分析和讨论哈夫曼编码在实际应用中的优势和不足。
二、实验内容和步骤1. 哈夫曼树的构建1.1 通过C语言实现哈夫曼树的构建算法;1.2 输入一组权值,按哈夫曼树构建规则生成哈夫曼树;1.3 输出生成的哈夫曼树结构,并进行可视化展示。
2. 哈夫曼编码的实现2.1 设计哈夫曼编码的实现算法;2.2 对指定字符集进行编码,生成哈夫曼编码表;2.3 对给定字符串进行哈夫曼编码,并输出编码结果。
三、实验过程及结果1. 哈夫曼树的构建在C语言中,通过定义结构体和递归算法实现了哈夫曼树的构建。
根据输入的权值,依次选择权值最小的两个节点构建新的父节点,直至构建完成整棵哈夫曼树。
通过调试和可视化展示,确认了程序正确实现了哈夫曼树的构建。
2. 哈夫曼编码的实现经过分析和设计,利用哈夫曼树的特点实现了哈夫曼编码的算法。
根据生成的哈夫曼树,递归地生成字符对应的哈夫曼编码,并输出编码结果。
对指定的字符串进行了编码测试,验证了哈夫曼编码的正确性和有效性。
四、实验结果分析1. 哈夫曼编码在数据传输和存储中具有较高的压缩效率和可靠性,能够有效减少数据传输量和存储空间;2. 哈夫曼树及哈夫曼编码在通信领域、数据压缩和加密等方面有着广泛的应用和重要意义;3. 在实际应用中,哈夫曼编码的构建和解码算法需要较大的时间和空间复杂度,对于大规模数据的处理存在一定的局限性。
五、实验总结通过本次实验,深入理解了哈夫曼树及哈夫曼编码的理论知识,并掌握了C语言中实现哈夫曼树及哈夫曼编码的方法。
对哈夫曼编码在实际应用中的优势和局限性有了更深入的认识,这对今后的学习和工作有着积极的意义。
六、参考文献1. 《数据结构(C语言版)》,严蔚敏赵现军著,清华大学出版社,2012年;2. 《算法导论》,Thomas H. Cormen 等著,机械工业出版社,2006年。
数据结构哈夫曼树实验报告

数据结构哈夫曼树实验报告一、实验目的本次实验的主要目的是深入理解和掌握哈夫曼树的数据结构及其相关算法,并通过实际编程实现来提高对数据结构的应用能力和编程技能。
二、实验环境本次实验使用的编程环境为具体编程语言名称,操作系统为具体操作系统名称。
三、实验原理哈夫曼树,又称最优二叉树,是一种带权路径长度最短的二叉树。
其基本原理是通过构建一棵二叉树,使得权值较大的节点距离根节点较近,权值较小的节点距离根节点较远,从而达到带权路径长度最小的目的。
在构建哈夫曼树的过程中,首先需要将所有的节点按照权值从小到大进行排序。
然后,选取权值最小的两个节点作为左右子树,构建一个新的父节点,该父节点的权值为左右子节点权值之和。
重复这个过程,直到所有的节点都被构建到哈夫曼树中。
哈夫曼编码是基于哈夫曼树的一种编码方式。
对于每个叶子节点,从根节点到该叶子节点的路径上,向左的分支编码为 0,向右的分支编码为 1,这样就可以得到每个叶子节点的哈夫曼编码。
四、实验步骤1、定义节点结构体```ctypedef struct HuffmanNode {char data;int weight;struct HuffmanNode left;struct HuffmanNode right;} HuffmanNode;```2、实现节点排序函数```cvoid sortNodes(HuffmanNode nodes, int n) {for (int i = 0; i < n 1; i++){for (int j = 0; j < n i 1; j++){if (nodesj>weight > nodesj + 1>weight) {HuffmanNode temp = nodesj;nodesj = nodesj + 1;nodesj + 1 = temp;}}}}```3、构建哈夫曼树```cHuffmanNode buildHuffmanTree(HuffmanNode nodes, int n) {while (n > 1) {sortNodes(nodes, n);HuffmanNode left = nodes0;HuffmanNode right = nodes1;HuffmanNode parent =(HuffmanNode )malloc(sizeof(HuffmanNode));parent>data ='\0';parent>weight = left>weight + right>weight;parent>left = left;parent>right = right;nodes0 = parent;nodes1 = nodesn 1;n;}return nodes0;}```4、生成哈夫曼编码```cvoid generateHuffmanCodes(HuffmanNode root, int codes, int index) {if (root>left) {codesindex = 0;generateHuffmanCodes(root>left, codes, index + 1);}if (root>right) {codesindex = 1;generateHuffmanCodes(root>right, codes, index + 1);}if (!root>left &&!root>right) {printf("%c: ", root>data);for (int i = 0; i < index; i++){printf("%d", codesi);}printf("\n");}}```5、主函数```cint main(){HuffmanNode nodes5 ={(HuffmanNode )malloc(sizeof(HuffmanNode)),(HuffmanNode )malloc(sizeof(HuffmanNode)),(HuffmanNode )malloc(sizeof(HuffmanNode)),(HuffmanNode )malloc(sizeof(HuffmanNode)),(HuffmanNode )malloc(sizeof(HuffmanNode))};nodes0>data ='A';nodes0>weight = 5;nodes1>data ='B';nodes1>weight = 9;nodes2>data ='C';nodes2>weight = 12;nodes3>data ='D';nodes3>weight = 13;nodes4>data ='E';nodes4>weight = 16;HuffmanNode root = buildHuffmanTree(nodes, 5);int codes100;generateHuffmanCodes(root, codes, 0);return 0;}```五、实验结果与分析通过运行上述程序,得到了每个字符的哈夫曼编码:A: 00B: 01C: 10D: 110E: 111分析实验结果可以发现,权值较小的字符A 和B 对应的编码较短,而权值较大的字符D 和E 对应的编码较长。
哈夫曼树与哈夫曼树编码实验原理

哈夫曼树与哈夫曼树编码实验原理哈夫曼树(Huffman Tree)是一种用于数据压缩的树形数据结构。
它的主要原理是通过构建一个最优的二叉树来实现编码和解码的过程。
以下是哈夫曼树和哈夫曼编码的实验原理:1. 构建哈夫曼树:- 给定一组需要进行编码的字符及其出现频率。
通常,这个频率信息可以通过统计字符在原始数据中的出现次数来得到。
- 创建一个叶节点集合,每个叶节点包含一个字符及其对应的频率。
- 从叶节点集合中选择两个频率最低的节点作为左右子节点,创建一个新的父节点。
父节点的频率等于左右子节点频率的和。
- 将新创建的父节点插入到叶节点集合中,并将原来的两个子节点从集合中删除。
- 重复上述步骤,直到叶节点集合中只剩下一个节点,即根节点,这个节点就是哈夫曼树的根节点。
2. 构建哈夫曼编码:- 从哈夫曼树的根节点开始,沿着左子树走一步就表示编码的0,沿着右子树走一步表示编码的1。
- 遍历哈夫曼树的每个叶节点,记录从根节点到叶节点的路径,得到每个字符对应的编码。
由于哈夫曼树的构建过程中,频率较高的字符在树中路径较短,频率较低的字符在树中路径较长,因此哈夫曼编码是一种前缀编码,即没有任何一个字符的编码是其他字符编码的前缀。
3. 进行数据压缩:- 将原始数据中的每个字符替换为其对应的哈夫曼编码。
- 将替换后的编码串连接起来,形成压缩后的数据。
4. 进行数据解压缩:- 使用相同的哈夫曼树,从根节点开始,按照压缩数据中的每个0或1进行遍历。
- 当遇到叶节点时,就找到了一个字符,将其输出,并从根节点重新开始遍历。
- 继续按照压缩数据的编码进行遍历,直到所有的编码都解压为字符。
通过构建最优的哈夫曼树和对应的编码表,可以实现高效的数据压缩和解压缩。
频率较高的字符使用较短的编码,从而达到减小数据大小的目的。
而频率较低的字符使用较长的编码,由于其出现频率较低,整体数据大小的增加也相对较小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、问题描述1.用户输入字母及其对应的权值,生成哈夫曼树;2.通过最优编码的算法实现,生成字母对应的最优0、1编码;3.先序、中序、后序遍历哈夫曼树,并打印其权值。
二、方法思路1.哈夫曼树算法的实现§存储结构定义#define n 100 /* 叶子树*/#define m 2*(n) –1 /* 结点总数*/typedef struct { /* 结点型*/double weight ; /* 权值*/int lchild ; /* 左孩子链*/int rchild ; /* 右孩子链*/int parent; /* 双亲链*/ 优点?}HTNODE ;typedef HTNODE HuffmanT[ m ] ;/* huffman树的静态三叉链表表示*/算法要点1)初始化:将T[0],…T[m-1]共2n-1个结点的三个链域均置空( -1 ),权值为0;2)输入权值:读入n 个叶子的权值存于T的前n 个单元T[0],…T[n], 它们是n 个独立的根结点上的权值;3)合并:对森林中的二元树进行n-1次合并,所产生的新结点依次存放在T[i](n<=i<=m-1)。
每次合并分两步:(1) 在当前森林中的二元树T [0],…T[i-1]所有结点中选取权值最小和次最小的两个根结点T[p1]和T[p2]作为合并对象,这里0<= p1,p2<= i –1;(2) 将根为T[p1]和T[p2]的两株二元树作为左、右子树合并为一株新二元树,新二元树的根结点为T[i]。
即T[p1].parent =T[p2].parent = i ,T[i].lchild= p1,T[i].rchild=p2,T[i].weight =T[p1].weight +T[p2].weight。
2.用huffman算法求字符集最优编码的算法:1) 使字符集中的每个字符对应一株只有叶结点的二叉树,叶的权值为对应字符的使用频率;2) 利用huffman算法来构造一株huffman树;3) 对huffman树上的每个结点,左支附以0,右支附以1(或者相反),则从根到叶的路上的0、1序列就是相应字符的编码Huffman编码实现:存储结构typedef struct{char ch; //存储字符char bits[n+1]; //字符编码位串}CodeNode;typedef CodeNode HuffmanCode[n];HuffmanCode H;3.二叉树遍历的递归定义先根顺序遍历二叉树:若二叉树非空则:{访问根结点;先根顺序遍历左子树;先根顺序遍历右子树;}中根顺序遍历二叉树:若二叉树非空则:{中根顺序遍历左子树;访问根结点;中根顺序遍历右子树;}后根顺序遍历二叉树:若二叉树非空则:{ 后根顺序遍历左子树;后根顺序遍历右子树;访问根结点;} ;三、主要数据结构及源程序代码及其注释1.扩充二叉树:内结点、外结点(增长树)2.哈夫曼树3.Huffman编码实现源程序代码及注释#include"stdafx.h"#include<stdio.h>#include<string.h>#include<stdlib.h>#define n 10#define m 2*(n)-1typedef struct//建立哈夫曼结点结构体{char data;float weight;int lchild;int rchild;int parent;}htnode;typedef struct//建立哈夫曼编码结构体{char ch;char bits[n+1];}htcode;void SelectMin(htnode T[m],int nn,int&p1,int&p2)//选择哈夫曼树所有结点中权值最小的两个根结点{int i,j;for(i=0;i<=nn;i++){if(T[i].parent==-1){p1=i;break;}}for(j=i+1;j<=nn;j++){if(T[j].parent==-1){p2=j;break;}}for(i=0;i<=nn;i++){if((T[p1].weight>T[i].weight)&&(T[i].parent==-1)&&(p2!=i))p1=i;}for(j=0;j<=nn;j++){if((T[p2].weight>T[j].weight)&&(T[j].parent==-1)&&(p1!=j))p2=j;}}void CreatHT(htnode T[m])//建立哈夫曼树{int i,p1,p2;for(i=0;i<m;i++){T[i].parent=T[i].lchild=T[i].rchild=-1;//赋初值}for(i=n;i<m;i++){SelectMin(T,i-1,p1,p2);T[p1].parent=T[p2].parent=i;if(T[p1].weight<T[p2].weight){T[i].lchild=p1;T[i].rchild=p2;}else{T[i].lchild=p2;T[i].rchild=p1;}T[i].weight=T[p1].weight+T[p2].weight;}}void HuffmanEncoding(htnode T[m],htcode C[n])//哈夫曼编码{int c,p,i;char cd[n+1];int start;cd[n]='\0';//结束表示for(i=0;i<n;i++){C[i].ch=T[i].data;start=n;c=i;while((p=T[c].parent)>=0){start=start-1;if(T[p].lchild==c){cd[start]='0';}else{cd[start]='1';}c=p;}strcpy(C[i].bits,&cd[start]);}}void preorder(htnode T[],int i)//先序遍历哈夫曼树:递归的办法{printf("%f",T[i].weight);if(T[i].lchild!=-1){preorder(T,T[i].lchild);preorder(T,T[i].rchild);}}void inorder(htnode T[],int i)//中序遍历哈夫曼树{if(T[i].lchild!=-1){inorder(T,T[i].lchild);printf("%f",T[i].weight);inorder(T,T[i].rchild);}else{printf("%f",T[i].weight);//防止左儿子为空,程序退出}}void postorder(htnode T[],int i)//后序遍历哈夫曼树{if(T[i].lchild!=-1){postorder(T,T[i].lchild);postorder(T,T[i].rchild);printf("%f",T[i].weight);}else{printf("%f",T[i].weight);//防止左儿子为空,程序退出}}void main(){int i;int j;j=m-1;htnode T[m];htcode C[n];htnode *b;printf("Input 10 elements and weights:");for (i=0;i<n;i++)//用户输入字母及对应的权值{printf("Input NO.%d element:\n",i);scanf(" %c",&T[i].data);printf("Input the weight of NO.%d element:\n",i);scanf(" %f",&T[i].weight);}CreatHT(T);//建立哈夫曼树HuffmanEncoding(T,C);//建立哈夫曼编码printf("Output Huffman coding:\n");for (i=0;i<n;i++){printf("%c:",C[i].ch);printf("%s\n",C[i].bits);}printf("Output Haffman Tress in preorder way:\n");preorder(T,j);//先序遍历哈夫曼树printf("\n");printf("Output Haffman Tress in inorder way:\n");//中序遍历哈夫曼树inorder(T,j);printf("Output Haffman Tress in postorder way:\n");//后序遍历哈夫曼树postorder(T,j);while(1);//运行结果停止在当前画面}四、运行结果#include"stdafx.h"#include<stdio.h>#include<string.h>#include<stdlib.h>#define n 10#define m 2*(n)-1typedef struct//建立哈夫曼结点结构体{char data;float weight;int lchild;int rchild;int parent;}htnode;typedef struct//建立哈夫曼编码结构体{char ch;char bits[n+1];}htcode;void SelectMin(htnode T[m],int nn,int&p1,int&p2)//选择哈夫曼树所有结点中权值最小的两个根结点{int i,j;for(i=0;i<=nn;i++){if(T[i].parent==-1){p1=i;break;}}for(j=i+1;j<=nn;j++){if(T[j].parent==-1){p2=j;break;}}for(i=0;i<=nn;i++){if((T[p1].weight>T[i].weight)&&(T[i].parent==-1)&&(p2!=i))p1=i;}for(j=0;j<=nn;j++){if((T[p2].weight>T[j].weight)&&(T[j].parent==-1)&&(p1!=j))p2=j;}}void CreatHT(htnode T[m])//建立哈夫曼树{int i,p1,p2;for(i=0;i<m;i++){T[i].parent=T[i].lchild=T[i].rchild=-1;//赋初值}for(i=n;i<m;i++){SelectMin(T,i-1,p1,p2);T[p1].parent=T[p2].parent=i;if(T[p1].weight<T[p2].weight){T[i].lchild=p1;T[i].rchild=p2;}else{T[i].lchild=p2;T[i].rchild=p1;}T[i].weight=T[p1].weight+T[p2].weight;}}void HuffmanEncoding(htnode T[m],htcode C[n])//哈夫曼编码{int c,p,i;char cd[n+1];int start;cd[n]='\0';//结束表示for(i=0;i<n;i++){C[i].ch=T[i].data;start=n;c=i;while((p=T[c].parent)>=0){start=start-1;if(T[p].lchild==c){cd[start]='0';}else{cd[start]='1';}c=p;}strcpy(C[i].bits,&cd[start]);}}void preorder(htnode T[],int i)//先序遍历哈夫曼树:递归的办法{printf("%f",T[i].weight);if(T[i].lchild!=-1){preorder(T,T[i].lchild);preorder(T,T[i].rchild);}}void inorder(htnode T[],int i)//中序遍历哈夫曼树{if(T[i].lchild!=-1){inorder(T,T[i].lchild);printf("%f",T[i].weight);inorder(T,T[i].rchild);}else{printf("%f",T[i].weight);//防止左儿子为空,程序退出}}void postorder(htnode T[],int i)//后序遍历哈夫曼树{if(T[i].lchild!=-1){postorder(T,T[i].lchild);postorder(T,T[i].rchild);printf("%f",T[i].weight);}else{printf("%f",T[i].weight);//防止左儿子为空,程序退出}}void main(){int i;int j;j=m-1;htnode T[m];htcode C[n];htnode *b;printf("Input 10 elements and weights:");for (i=0;i<n;i++)//用户输入字母及对应的权值{printf("Input NO.%d element:\n",i);scanf(" %c",&T[i].data);printf("Input the weight of NO.%d element:\n",i);scanf(" %f",&T[i].weight);}CreatHT(T);//建立哈夫曼树HuffmanEncoding(T,C);//建立哈夫曼编码printf("Output Huffman coding:\n");for (i=0;i<n;i++){printf("%c:",C[i].ch);printf("%s\n",C[i].bits);}printf("Output Haffman Tress in preorder way:\n");preorder(T,j);//先序遍历哈夫曼树printf("\n");printf("Output Haffman Tress in inorder way:\n");//中序遍历哈夫曼树inorder(T,j);printf("Output Haffman Tress in postorder way:\n");//后序遍历哈夫曼树postorder(T,j);while(1);//运行结果停止在当前画面}。
