联合杯决赛(数学)试题及答案

合集下载

联合杯决赛(数学)试题及答案

第三届联合杯决赛试卷数学（试卷共四大题满分：90分）一．选择题（共12小题，每题2分，共24分）1．中央电视台晚上少儿节目“动画梦工场”开始，用24小时计时法表示是（） A ．07：00 B ．19：00C ．晚上7：00D ．19小时2．下面物品中（）的重量最接近一千克． A ．1立方米的水B ．3个易拉罐可乐C ．3个鸡蛋3．最大的九位数比最小的十位数小（）A ．1B ．2C ．10000000004．如果长方形的宽增加1分米，面积就增加3平方分米，并且正好称为正方形，那么原来这个长方形的面积是（）平方分米． A ．27B ．9C ．65．当9：30时，钟面上时针和分针所组成的角是（） A ．直角 B ．锐角 C ．钝角 D ．平角6．小红买售价4.4元的钢笔一支，根据你的生活经验，结合人民币币值的特点，下列付钱方式不合理的是（）A ．付出4.5元，找回0.1元B ．付出4.7元，找回0.3元C ．付出5.4元，找回1.0元D ．付出10元，找回5.6元 7．从第（）个口袋里任意摸出一个球，摸出黑球的可能性是50%．A ．B ．C ． 8．要使是假分数，是真分数，a 应是（）A ．5B ．6C ．7D ．89．如图所示，将一张正方形纸片先由下向上对折压平，再由右翻起向左对折压平，得到小正方形ABCD ．取AB 的中点M 和BC 的中点N ，剪掉AMBN 得五边形AMNCD ．则将折叠的五边形AMNCD 纸片展开铺平后的图形是（）A ．B ．C ．D ．10．一列数1，2，2，3，3，3，4，4，4，4，…．中的第35个数为（） A ．6 B ．7 C ．8D ．无答案11．如图中的正方体、圆柱和圆锥底面积相等，高也相等．下面哪句话是正确的？（）A ．圆柱的体积比正方体的体积小一些B ．圆锥的体积是正方体的C ．圆柱体积与圆锥体积相等12．在任意的37个人中，至少有（）人的属相相同． A ．2 B ．4C ．6二．填空题（共10小题，每空1分，共10分）13．如图中，两个小正方形的周长和是8分米，则大正方形的边长是分米．14．图中的饮料需要瓶才正好是2升．15．小胖、小丁丁、小巧、小亚四人组成一个学习小组，要在四人中选一名组长和副组长，总共有种不同的选法．16．如图可以折成一个正方体，面1与面相对；面2与面相对．17．爷爷患了感冒，医生给他开了感冒药，如图是该药品的部分说明，请根据说明书回答问题：感冒清片每片重0.2克口服，一次3～4片，一日三次生产日期：2009年1月1日有效期：至2010年12月31日姓名__________ 准考证号__________ 联系电话__________ 考场___________密封线内不准答题（1）爷爷一天最多可服药克．（2）这种药片的保质期是年．18．如图，两个正方形的边长分别是8厘米和4厘米，则阴影部分的面积是平方厘米．（18题图）（19题图）（20题图）19．如图，围绕礼品盒绳子的长度是厘米．20．小明统计了自己装有125个硬币的储蓄罐的情况如图，则储蓄罐内共有元钱．21．如图，甲、乙、丙三个图形面积的比是．22．一群人开舞会，每人头上都戴着一顶帽子．帽子只有黑白两种，黑的至少有一顶．每个人都能看到其它人帽子的颜色，却看不到自己的．主持人先让大家看看别人头上戴的是什么帽子，然后关灯，如果有人认为自己戴的是黑帽子，就拍手．第一次关灯，没有声音．于是再开灯，大家再看一遍，关灯时仍然鸦雀无声．一直到第三次关灯，才有劈劈啪啪手的声音响起．则有人戴着黑帽子．三．计算题（共2小题，23、24题各12分，共24分）23．直接写出下面各题的得数．1﹣0.99=+=24×5= 4.7+3.5=0.92=4.2×= 40×5.5=8﹣=﹣= 625﹣99= 0.23÷0.01=÷=24．能简算的要简算（1）2.5×12.5×32 = （2）1375+450÷18×25= （3）=（4）=四．解答题（共5题，25题7分，26、27题各8分，28题9分）25．王大娘家菜地里的西红柿获得了丰收，收下全部的时，装满了5筐还多48千克，收完其余的部分时，又刚好装满10筐，求王大娘共收获西红柿多少千克？26．图形计算（1）如图1，计算图形的体积．（得数保留两位小数，单位：米）（2）如图2，求阴影部分的面积．（单位：米）27．甲、乙和丙同时由东、西两城出发，甲、乙两人由东城到西城，甲步行每小时走5千米，乙骑自行车每小时行15千米，丙也骑自行车每小时20千米，已知丙在途中遇到乙后，又经过1小时才遇到甲，求东、西城相距多少千米？28．期六下午，城关二小王明同学骑自行车到6千米远的六郎镇姥姥家去玩，请根据下面折线统计图回答下列问题：（1）王明在姥姥家玩了多少时间？（2）如果王明从出发起一直骑自行车走不休息，下午几时几分可到达姥姥家？（3）求出王明骑自行车的往返的平均速度？2017年小升初学业水平测试数学试卷参考答案与试题解析一．选择题（共12小题）1-5 B．B．A．C．C．6-10 B．B．B．D．C．11-12 B．B．二．填空题（共12小题）13． 2．14． 8．15． 12．16． 6，4．17． 2.4，2．18． 6419． 340．20． 67.5．21． 1：5：4．22. 3三．计算题（共2小题）23.解：1﹣0.99=0.01 +=24×5=120 4.7+3.5=8.20.92=0.81 4.2×=0.6 40×5.5=2208﹣=7﹣=625﹣99=526 0.23÷0.01=23÷=24．解：（1）2.5×12.5×32=（2.5×4）×（12.5×8），=10×100，=1000；（2）1375+450÷18×25 =1375+25×25，=1375+625，=2000；（3）×0.25+×=0.25×（+），=0.25；（4）×[（+0.75）÷]=×[÷+÷]，=×[1+]，=×，=．四．解答题（共2小题）25. 【解答】解：48÷[1﹣÷10×（5+10）]=48÷[1﹣×15]=48÷[1﹣]=48=288（千克）答：王大娘共收获西红柿288千克．26．【解答】解：（1） 3.14×102×10+4.14×102×10 =≈1046.67+3140=4186.67（立方米）；答：它的体积是4186.67立方米．（2）8÷2=4（米），3.14×42×4×4÷2=3.14×16÷2=12.56﹣8=4.56（平方米）；答：阴影部分的面积是4.56平方米．27．【解答】解：乙丙经过x小时相遇，根据总路程相等列出方程：（15+20）x=（5+20）（x+1）35x=25x+25x=2.5总路程：（15+20）×2.5=35×2.5=87.5（千米）答：东、西城相距87.5千米．28．【解答】解：（1）王明在姥姥家是从下午2时到2时30分；2时30分﹣2时=30分；答：王明在姥姥家玩了30分．（2）王明中间休息了20分钟；否则他会提前20分钟到姥姥家．2时﹣20分=1时40分；答：下午1时40分可到达姥姥家．（3）20+20=40（分）；3时﹣2时30分=30分；40+30=70（分）；70分=时；6×2÷，=12÷，=（千米/时）；答：王明骑自行车的往返的平均速度是千米/时．。

全国初中数学联合竞赛试题及详细解答(含一试二试)

全国初中数学联合竞赛试题第一试一、选择题（本题满分42分，每小题7分） 1.计算432241242++=（）（A 21- （B ）1 （C 2 （D ）22.满足等式()2221m m m ---=的所有实数m 的和为（）（A ）3 （B ）4 （C ）5 （D ）63.已知AB 是圆O 的直径，C 为圆O 上一点，15CAB ∠=，ACB ∠的平分线交圆O 于点D ，若3CD =，则AB=（）（A ）2 （B 6 （C ）22（D ）34.不定方程23725170x xy x y +---=的全部正整数角（x,y ）的组数为（）（A ）1 （B ）2 （C ）3 （D ）45矩形ABCD 的边长AD=3，AB=2，E 为AB 的中点，F 在线段BC 上，且BF ：FC=1：2， AF 分别与DE ，DB 交于点M ，N ，则MN=（）（A 357 （B 5514 （C 9528 （D 115286.设n 为正整数，若不超过n 的正整数中质数的个数等于合个数，则称n 为“好数”，那么，所有“好数”之和为（）（A ）33 （B ）34 （C ）2013 （D ）2014二、填空题（本题满分28分，每小题7分）1.已知实数,,x y z 满足4,129,x y z xy y +=+=+-则23x y z ++=2.将一个正方体的表面都染成红色，再切割成3(2)n n >个相同的小正方体，若只有一面是红色的小正方体数目与任何面都不是红色的小正方体的数目相同，则n= 3.在ABC 中，60,75,10A C AB ∠=∠==，D ，E ，F 分别在AB ，BC ，CA 上，则DEF 的周长最小值为4.如果实数,,x y z 满足()2228x y z xy yz zx ++-++=，用A 表示,,x y y z z x ---的最大值，则A 的最大值为第二试（A ）一、（本题满分20分）已知实数,,,a b c d 满足()2222223236,a c b d ad bc +=+=-=求()()2222ab c d ++的值。

全国高中数学联合竞赛附答案

全国高中数学联合竞赛（9月19日上午9：00～11：00）一、选择题（本题共6个小题，每小题5分满分30分）（1）若函数x x x f 2sin 2cos 811)(--=的最大值为a ，最小值为b ，则ba 1-等于（）（A ）18 （B ）6 （C ）5 （D ）0 （2）若b a <<0，且1=+b a ，则下列各式中最大的是（）（A ）1- （B ）1log log 22++b a（C ）b 2log（D ）)(log 32232b ab b a a +++（3）已知数列2004，2005，1，2004-，2005-，…，这个数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前2004项之和2004S 等于（）（A ）2005（B ）2004 （C ）1 （D ）0（4）已知函数xx xx ee e e xf --+-=)(的反函数是)(1x f -，且k f f =---|)6.0(||)8.0(|11，则（）（A ）)21,0(∈k （B ）)1,21(∈k（C ）)23,1(∈k（D ）)2,23(∈k（5）正四棱锥ABCD S -中，侧棱与底面所成的角为α，侧面与底面所成的角为β，侧面等腰三角形的底角为γ，相邻两侧面所成的二面角为θ，则α、β、γ、θ的大小关系是（）（A ）θγβα<<< （B ）γθβα<<< （C ）βγαθ<<<（D ）θβγα<<<（6）若对任意的长方体A ，都存在一个与A 等高的长方体B ，使得B 与A 的侧面积之比和体积之比都等于k ，则k 的取值范围是（）（A ）0>k （B ）10≤<k （C ）1>k（D ）1≥k二、填空题（本题共6个小题，每小题5分，满分30分）1P 2P 3P AO BC4P 5P 6P（7）若关于x 的方程x ax a x =+-lg 1lg 2只有一个实数解，则a 的值等于．（8）在ABC ∆中，若21tan =A ，31tan =B ，且最长的边的长为1，则最短的边的的长等于．（9）若正奇数n 不能表示为三个不相等的合数之和，则满足条件的n 的最大值为．（10）设a 、b 、c 是直角三角形的三条边长，且)(2)(2222n n n n n n c b a c b a ++=++，其中*N n ∈，2≥n ，则n 的值等于．（11）连接正文体各个顶点的所有直线中，异面直线共有对．（12）如图，以)0,0(O 、)0,1(A 为顶点作正1OAP ∆，再以1P 和A P 1的中点B 为顶点作正21BP P ∆，再以2P 和B P2的中点C 为顶点作正32CP P ∆，…，如此继续下去．有如下结论：①所作的正三角形的边长构成公比为21的等比数列；②每一个正三角形都有一个顶点在直线2AP （1=x ）上；③第六个正三角形的不在第五个正三角形边上的顶点6P 的坐标是)36421,6463(； ④第2004个正三角形的不在第2003个正三角形边上的顶点2004P 的横坐标是20042004211-=x ．其中正确结论的序号是（把你认为正确结论的序号都填上）．三、解答题（本题共3小题，每小题20分，满分60分）（13）已知函数a a x f x3)(+=（0>a ，1≠a ）的反函数是)(1x fy -=，而且函数)(x g y =的图象与函数)(1x f y -=的图象关于点)0,(a 对称．（Ⅰ）求函数)(x g y =的解析式；（Ⅱ）若函数)()()(1x g x f x F --=-在]3,2[++∈a a x 上有意义，求a 的取值范围．（14）设边长为1的正ABC ∆的边BC 上有n 等分点，沿点B 到点C 的方向，依次为1P ，2P ，…，1-n P ，若AC AP AP AP AP AB S n n ⋅++⋅+⋅=-1211 ，求证：nn S n 62112-=．（15）已知}{n a 是等差数列，d 为公差且不等于0，1a 和d 均为实数，它的前n 项和记作n S ，设集合}|),{(*N n nS a A n n ∈=，},,141|),{(22R y x y x y x B ∈=-=，试问下列结论是否正确，如果正确，请给予证明；如果不正确，请举例说明．（Ⅰ）若以集合A 中的元素作为点的坐标，则这些点都在一条直线上；（Ⅱ）B A 至多有一个元素；（Ⅲ）当01≠a 时，一定有∅≠B A ．全国高中数学联合竞赛试题参考答案及评分标准一、选择题（本题共6个小题，每小题5分满分30分）（1）B （2）C （3）D （4）D （5）A （6）D 二、填空题（本题共6个小题，每小题5分，满分30分）（7）100 （8）55（9）17 （10）4 （11）174 （12）①②③④ 三、解答题（本题共3小题，每小题20分，满分60分）（13）【解】（Ⅰ）由a a x f x3)(+=（0>a ，1≠a ），得)3(log )(1a x x fa -=-…………5分又函数)(x g y =的图象与函数)(1x fy -=的图象关于点)0,(a 对称，则)()(1x a f x a g --=+-，于是，)(lo g)2()(1a x x a f x g a---=--=-．（a x -<）…………………………………10分（Ⅱ）由（Ⅰ）的结论，有)(log )3(log )()()(1a x a x x g x fx F a a -+-=--=-．要使)(x F 有意义，必须⎩⎨⎧>->-.0,03a x a x又0>a ，故a x 3>． (15)分由题设)(x F 在]3,2[++∈a a x 上有意义，所以a a 32>+，即1<a ．于是，10<<a ． ……………………………………………………………………… 20分14．【证明】如图，设c AB =，b AC =，a BC =，令n=1，则p k c BP AB AP k k +=+=（0=k ，1，2，…，n ）其中，AP =0，AP n =． ∴)(])1([1p k c p k c AP AP k k +⋅-+=⋅-22)1()12(k k k -+⋅-+=（0=k ，1，2，…，n ） ……………5分又∵AC AP AP AP AP AB S n n ⋅++⋅+⋅=-1211 ， ∴2112)]1([)]12([p k k p c k c n S nk n k n ∑∑==-+⋅-+=222)(3)1)(1(n n n n n n -++⋅+= ……………………………………………10分22222231)(31)(nn n n n n n n n n -+⋅+=-+⋅+=． ………………………15分又∵1||||||===，与的夹角为60，∴nn n n n n S n 6211312122-=-++=． ……………………………………………………20分15．【解】（Ⅰ）正确．因为，在等差数列}{n a 中，2)(1n n a a n S +=，所以，21nn a a n S +=．这表明点),(nS a n n 的坐标适合方程)(211a x y +=．所以，点),(nS a n n 均在直线)(211a x y +=上． ……………………………………………5分（Ⅱ）正确．设B A y x ∈),(，则),(y x 坐标中的x 、y 应是方程组⎪⎩⎪⎨⎧=-+=14,2121221y x a x y 的解．解这个方程组，消去y ，得42211-=+a x a ．（﹡）当01=a 时，方程（﹡）无解，此时，∅=B A ． …………………………………10分当01≠a 时，方程（﹡）只有一个解12124a a x --=，此时方程组也只有一个解，即⎪⎪⎩⎪⎪⎨⎧-=--=.44,24121121a a y a a x 故上述方程组至多有一解，所以B A 至多有一个元素． ………………………………15分（Ⅲ）不正确．取11=a ，1=d ，对一切*N n ∈，有0)1(1>=-+=n d n a a n ，0>nS n．这时集合A 中的元素的点的横、纵坐标均为正．另外，由于011≠=a ，如果∅≠B A ，那么根据（Ⅱ）的结论，B A 至多有一个元素（00,y x ），而025241210<-=--=a a x ，043441210<-=-=a a y ．这样的A y x ∉),(00，产生矛盾．所以，11=a ，1=d 时，∅=B A ，故01≠a 时，一定有∅=B A 是不正确的． ……………………………………20分。

全国初中数学联合竞赛试题及详细解答(含一试二试)

全国初中数学联合竞赛试题第一试一、选择题：（本题满分42分，每小题7分）1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=，则||||||a b b c c a -+-+-= （） A ．1. B ．2. C ．3. D ．4..2．若实数,,a b c 满足等式23||6a b +=，49||6a b c -=，则c 可能取的最大值为（） A ．0. B ．1. C ．2. D ．3.3．若b a ,是两个正数，且 ,0111=+-+-ab b a 则（）4．若方程2310x x --=的两根也是方程420x ax bx c +++=的根，则2a b c +-的值为（） A ．－13. B ．－9. C ．6. D ． 0.5．在△ABC 中，已知︒=∠60CAB ，D ，E 分别是边AB ，AC 上的点，且︒=∠60AED ，CE DB ED =+，CDE CDB ∠=∠2,则=∠DCB ( )A ．15°.B ．20°.C ．25°.D ．30°.6．对于自然数n ，将其各位数字之和记为n a ，如2009200911a =+++=，201020103a =+++=，则12320092010a a a a a +++++= （）A ．28062.B ．28065.C ．28067.D ．28068.二、填空题：（本题满分28分，每小题7分）1．已知实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩则22x y += .2．二次函数c bx x y ++=2的图象与x 轴正方向交于A ，B 两点，与y 轴正方向交于点C ．已知AC AB 3=，︒=∠30CAO ，则c = ．3．在等腰直角△ABC 中，AB ＝BC ＝5，P 是△ABC 内一点，且PA 5PC ＝5，则PB ＝______．4．将若干个红、黑两种颜色的球摆成一行，要求两种颜色的球都要出现，且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放，最多可以摆放_______个球.第二试（A ）一．（本题满分20分）设整数,,a b c （a b c ≥≥）为三角形的三边长，满足22213a b c ab ac bc ++---=，___P_A_C_B求符合条件且周长不超过30的三角形的个数.二．（本题满分25分）已知等腰三角形△ABC 中，AB ＝AC ，∠C 的平分线与AB 边交于点P ，M 为△ABC 的内切圆⊙I 与BC 边的切点，作MD//AC ，交⊙I 于点D.证明：PD 是⊙I 的切线.三．（本题满分25分）已知二次函数2y x bx c =+-的图象经过两点P (1,)a ，Q (2,10)a . （1）如果,,a b c 都是整数，且8c b a <<，求,,a b c 的值.（2）设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ，与y 轴的交点为 C.如果关于x 的方程20x bx c +-=的两个根都是整数，求△ABC 的面积._ Q_I _ P_ C_ A_M_B第二试（B ）一．（本题满分20分）设整数,,a b c 为三角形的三边长，满足22213a b c ab ac bc ++---=，求符合条件且周长不超过30的三角形的个数（全等的三角形只计算1次）.二．（本题满分25分）题目和解答与（A ）卷第二题相同. 三．（本题满分25分）题目和解答与（A ）卷第三题相同.第二试（C ）一．（本题满分20分）题目和解答与（B ）卷第一题相同. 二．（本题满分25分）题目和解答与（A ）卷第二题相同.三．（本题满分25分）设p 是大于2的质数，k 为正整数．若函数4)1(2-+++=p k px x y 的图象与x 轴的两个交点的横坐标至少有一个为整数，求k 的值．全国初中数学联合竞赛试题及详解第一试一、选择题：（本题满分42分，每小题7分）1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=，则||||||a b b c c a -+-+-= （ B ） A ．1. B ．2. C ．3. D ．4. 解：由已知可推得011a b b c a c -=⎧⇒-=±⎨-=±⎩ 或110a b b c a c -=±⎧⇒-=±⎨-=⎩，分别代入即得。

全国高中数学联合竞赛试题及参考答案8

全国高中数学联合竞赛试题及参考答案题号一二总分1～89 10 11 12 得分评卷复核【说明】解答本试卷不得使用计算器一、填空题（本题满分60分，前4小题每小题7分，后4小题每小题8分） 1．设x ，y ，z 是正实数，满足()()xy z x z y z +=++，则xyz 的最大值是． 2．设从正整数k 开始的201个连续正整数中，前101个正整数的平方和等于后100个正整数的平方和，则k 的值为．3．设(2)n n ≥是给定的整数，12,,,n x x x 是实数，则1223sin cos sin cos x x x x ++1sin cos n x x + 的最大值是．4．在△ABC 中，已知30,105A B ∠=︒∠=︒，过边AC 上一点D 作直线DE ，与边AB 或者BC 相交于点E ，使得60CDE ∠=︒，且DE 将△ABC 的面积两等分，则2CD AC ⎛⎫= ⎪⎝⎭． 5．对于任意实数a ，b ，不等式{}max ,,2006a b a b b C +--≥恒成立，则常数C 的最大值是．（注：{}max ,,x y z 表示x ，y ，z 中的最大者．）6．设2()cos f x x ax b x =++，{}{}()0,R (())0,R x f x x x f f x x =∈==∈≠∅，则满足条件的所有实数a ，b 的值分别为．7．在直三棱柱中，已知底面积为s 平方米，三个侧面面积分别为m 平方米， n 平方米，p 平方米，则它的体积为立方米．8．已知函数:f R +→R 满足：对任意,x y ∈R +，都有11()()()20062005f x f y f xy x y ⎛⎫=+++ ⎪⎝⎭，则所有满足条件的函数f 为．二、解答题9．（本题满分14分）已知抛物线22(0)y px p =>，其焦点为F ，一条过焦点F ，倾斜角为θ(0)θπ<<的直线交抛物线于A ，B 两点，连接AO （O 为坐标原点），交准线于点B '，连接BO ，交准线于点A '，求四边形ABB A ''的面积．10．（本题满分14分）数列{}n a 定义如下：11a =，且当2n ≥时，211,1,n n n a n a n a -+⎧⎪⎪=⎨⎪⎪⎩当为偶数时，当为奇数时．已知3019n a =，求正整数n ．yxOF11．（本题满分16分）对一个边长互不相等的凸(3)n n ≥边形的边染色，每条边可以染红、黄、蓝三种颜色中的一种，但是不允许相邻的边有相同的颜色．问：共有多少种不同的染色方法？12．（本题满分16分）设]1,0[,∈b a ，求)1)(1(11b a abb a S --++++=的最大值和最小值．2006年上海市高中数学竞赛答案一、填空题（本题满分60分，前4小题每小题7分，后4小题每小题8分） 1、1272、201003、2n4、365、10036、04a ≤<，b ＝07、4()()()()2sm n p m n p p m n n p m +++-+-+- 8、1()2006f x x=+二、解答题9．（本题满分14分）已知抛物线22(0)y px p =>，其焦点为F ，一条过焦点F ，倾斜角为θ(0)θπ<<的直线交抛物线于A ，B 两点，连接AO （O 为坐标原点），交准线于点B '，连接BO ，交准线于点A '，求四边形ABB A ''的面积．解当2πθ=时，22ABB A S p ''=． …………………（4分）当2πθ≠时，令t a n k θ=．设1122(,),(,)A x y B x y ，则由()2py k x =-， ①22y px =， ②消去x 得，2220py y p k--=，所以 122py y k+=， 212y y p =-． ③ 又直线AO 的方程为：11y y x x =，即为12p y x y =，所以，AO 与准线的交点的坐标为21(,)2p p B y '--，而由③知，221p y y =-，所以B 和B '的纵坐标相等，从而BB x ' 轴．同理AA x' 轴，故四边形ABB A ''是直角梯形．………………（9分）所以，它的面积为11()22ABB A S AA BB A B AB A B ''''''''=+⋅=⋅222121211()()2x x y y y y =-+-⋅- B /A /F BAO xy221211()12y y k =-+212122111()42y y y y k⎡⎤=++-⎣⎦ 332222221212(1cot )p p k θ⎛⎫=+=+ ⎪⎝⎭．………………（14分）10．（本题满分14分）数列{}n a 定义如下：11a =，且当2n ≥时，211,1,n n n a n a n a -+⎧⎪⎪=⎨⎪⎪⎩当为偶数时，当为奇数时．已知3019n a =，求正整数n ．解由题设易知，0,1,2,n a n >= ．又由11a =，可得，当n 为偶数时，1n a >；当(1)n >是奇数时，111n n a a -=<． ………………（4分）由3019n a =1>，所以n 为偶数，于是23011111919n a =-=<，所以，2n是奇数．于是依次可得：1219111n a -=>， 12n-是偶数， 24198111111n a -=-=<，24n -是奇数， 2141118n a --=>，64n -是偶数， 681131188n a -=-=<，68n -是奇数， 618813n a --=>，148n -是偶数， 1416851133n a -=-=>，1416n -是偶数，1432521133n a -=-=<，1432n -是奇数， ……………（9分）14132312n a --=>，4632n -是偶数， 4664311122n a -=-=<，4664n -是奇数， 4616421n a --=>，11064n -是偶数， 110128211n a -=-=，所以，1101128n -=，解得，n ＝238． ……………… （14分） 11．（本题满分16分）对一个边长互不相等的凸(3)n n ≥边形的边染色，每条边可以染红、黄、蓝三种颜色中的一种，但是不允许相邻的边有相同的颜色．问：共有多少种不同的染色方法？解设不同的染色法有n p 种．易知36p =． ………………（4分）当4n ≥时，首先，对于边1a ，有3种不同的染法，由于边2a 的颜色与边1a 的颜色不同，所以，对边2a 有2种不同的染法，类似地，对边3a ，…，边1n a -均有2种染法．对于边n a ，用与边1n a -不同的2种颜色染色，但是，这样也包括了它与边1a 颜色相同的情况，而边1a 与边n a 颜色相同的不同染色方法数就是凸n －1边形的不同染色方法数的种数1n p -，于是可得1132n n n p p --=⨯-， ………………（10分） ()1122n n n n p p ---=--．于是 ()33232(1)2(1)2n n n n p p ---=--=-⋅， 2(1)2n nn p =+-⋅，3n ≥．综上所述，不同的染色方法数为2(1)2n n n p =+-⋅． ………………（16分）12．（本题满分16分）设]1,0[,∈b a ，求a 3a n-1a na 2a 1)1)(1(11b a abb a S --++++=的最大值和最小值．解因为)1)(1(11b a ab b a S --++++=)1)(1()1(1)1)(1(122b a ab ab b a b a b a ++--=+++++=1≤ ，当0=ab 或1=ab 时等号成立，所以S 的最大值为1． ………………（6分）令)1)(1()1(b a ab ab T ++-=，ab x =，则abab ab ab ab b a ab ab T ++-≤+++-=21)1(1)1( x x x x x x +-=+-=1)1()1()1(2222． ………………（10分）下证 211551)1(2-≤+-x x x ． ①① 0)25()215(2≥-+--⇔x x ，所以 21155-≤T ，从而 25513-≥S ，当215-==b a 时等号成立，所以S 的最小值为25513-．……………（16分）。

全国初中数学联合竞赛试题参考答案第1试

全国初中数学结合比赛试题参照答案第一试一、选择题：（此题满分 42 分，每题7 分）1. 若 a,b,c 均为整数且知足 ( a b)10 (a c)10 1，则 | a b | | b c | | c a |（ B ）A ．1.B ． 2.C ． 3.D ．4.2．若实数 a, b, c 知足等式 2 a 3 |b | 6 ， 4 a 9 | b | 6c ，则 c 可能取的最大值为（ C ）A ．0.B ． 1.C ． 2.D ．3.a 1b 11 0, 则（ C ）3．若 a, b 是两个正数，且abA ． 0 a b1 1 a b 1.C ． 1 a b4 4a b 2 ..B ．. D ．33334．若方程 x 2 3x 1 0 的两根也是方程 x 4 ax 2bx c 0 的根，则 a b 2c 的值为（ A）A ．－ 13.B ．－ 9.C ． 6.D ． 0.5．在△ ABC 中，已知CAB 60 ，D ，E 分别是边 AB ，AC 上的点，且 AED 60 ， ED DB CE ，CDB 2CDE ,则 DCB (B ) A ．15° .B ．20°.C ． 25°.D ． 30° .6．对于自然数 n ，将其各位数字之和记为 a n ，如 a 2009 2 0 0 9 11， a 20102 0 1 03 ，则a 1 a 2 a 3a2009a2010（ D）A ．28062.B ． 28065.C ． 28067.D ． 28068.二、填空题：（此题满分 28 分，每题 7 分）1．已知实数 x, y 知足方程组x 3 y 3 19,则 x 2 y 213.x y 1,2．二次函数 yx 2 bx c 的图象与 x 轴正方向交于A ，B 两点，与 y 轴正方向交于点C ．已知 AB3AC ，CAO 30 ，则 c1．93．在等腰直角△ ABC 中， AB ＝ BC ＝ 5， P 是△ ABC 内一点，且 PA ＝5 ，PC ＝ 5，则 PB ＝ ___ 10 ___．4．将若干个红、黑两种颜色的球摆成一行，要求两种颜色的球都要出现，且随意中间夹有 5 个或 10 个球的两个球必为同一种颜色的球.按这类要求摆放，最多能够摆放 ____ 15___ 个球 .第二试（A ）一．（此题满分 20 分）设整数 a, b,c （ a b c ）为三角形的三边长，知足 a 2 b 2 c 2 abac bc 13 ，求切合条件且周长不超出30 的三角形的个数 .解由已知等式可得(a b)2 (b c)2 (a c)226①令 a b m,b c n ，则a c m n ，此中 m, n 均为自然数.于是，等式①变成 m 2n 2(m n)226 ，即m 2 n 2mn 13②因为 m, n 均为自然数，判断易知，使得等式②建立的m, n 只有两组： m 3, m 1,n 1和3.n（ 1）当 m 3,n 1时，b c 1 ， a b 3 c 4 .又 a, b, c 为三角形的三边长，所以b c a ，即(c 1) c c 4，解得 c 3 .又因为三角形的周长不超出30，即 ab c ( c4)(c 1) c 30，解得c 25 所以3 c 25 ，所以 c 能够取值 4，，，，，对应可获得5 个切合条件的三角形..35 6 7 83（ 2）当 m1,n3时， b c 3 ， a b 1 c 4 . 又 a, b,c 为三角形的三边长，所以b c a ，即(c 3) c c 4，解得 c1 .又因为三角形的周长不超出30，即 ab c ( c 4) (c 3) c 30，解得23 所以 23，所以 c 能够取值，，，， 6 ，，对应可获得6 个切合条件的三角形 .c.1 c32345 7330 的三角形的个数为 5＋ 6＝ 11. 综合可知：切合条件且周长不超出二．（此题满分 25 分）已知等腰三角形△ ABC 中， AB ＝ AC ，∠ C 的均分线与 AB 边交于点 P ，M 为△ ABC的内切圆⊙ I 与 BC 边的切点，作 MD//AC ，交⊙ I 于点 D. 证明：PD 是⊙I 的切线 .证明过点 P 作⊙ I 的切线 PQ （切点为 Q ）并延伸，交 BC 于点 N.因为 CP 为∠ ACB 的均分线，所以∠ACP ＝∠ BCP.又因为 PA 、 PQ 均为⊙ I 的切线，所以∠ APC ＝∠ NPC. 又 CP 公共，所以△ ACP ≌△ NCP ，所以∠ PAC ＝∠ PNC. 由 NM ＝ QN ，BA ＝ BC ，所以△ QNM ∽△ BAC ，故∠ NMQ＝∠ ACB ，所以 MQ//AC.又因为 MD//AC ，所以 MD 和 MQ 为同一条直线 .又点 Q 、 D 均在⊙ I 上，所以点Q 和点 D 重合，故 PD 是⊙ I APIQCBNM的切线 .三．（此题满分 25 分）已知二次函数 y x 2bx c 的图象经过两点 P (1,a) ， Q (2,10 a) .（ 1）假如 a, b, c 都是整数，且 c b 8a ，求 a, b, c 的值 .（ 2）设二次函数 yx 2bx c 的图象与 x 轴的交点为 A 、 B ，与 y 轴的交点为 C.假如对于 x 的方程x 2 bx c 0 的两个根都是整数，求△ABC 的面积 .解点 P (1,a) 、 Q (2,10 a) 在二次函数 y x 2bx c 的图象上，故1 b c a ， 4 2a c 10a ，解得 b 9a 3 ， c 8a2 .（ 1）由 cb 8a 知8a2 9a 3,9a3 8a, 解得 1 a 3 .又 a 为整数，所以 a2 ， b 9a3 15 ， c 8a 214 .(2) 设 m,n 是方程的两个整数根，且 m n .由根与系数的关系可得m n b 3 9a ， mn c 2 8a ，消去 a ，得 9mn 8( m n)6 ，两边同时乘以 9，得 81mn 72(m n) 54 ，分解因式，得 (9m 8)(9 n 8) 10 .所以9m 81,9m 8 2,或9m 8 10,9m 8 5,9n 8或8 5, 9n 81,或8 2,10,9n9nm1,或 m10 ,m2 , m 1 , 解得9 或9 或93n 2,n 13 , 7 n29n, ,93又 m,n 是整数，所此后边三组解舍去，故 m 1,n 2 .所以， b(m n)3 ， c mn2 ，二次函数的分析式为 y x 2 3x 2 .易求得点 A 、 B 的坐标为（ 1,0）和（ 2,0），点 C 的坐标为（ 0,2），所以△ ABC的面积为1(2 1) 2 1 .2第二试（B ）一．（此题满分 20 分）设整数 a, b, c 为三角形的三边长，知足a 2b 2c 2 ab ac bc 13 ，求切合条件且周长不超出30 的三角形的个数（全等的三角形只计算1次） .解不如设 a b c ，由已知等式可得(a b)2(b c)2 (a c)226①令 a bm,b c n ，则 a c m n ，此中 m, n 均为自然数 .于是，等式①变成 m2n 2 (m n)226 ，即m 2 n 2mn 13②因为 m, n 均为自然数，判断易知，使得等式②建立的m, n 只有两组：m 3, m 1,n 1和3.n（ 1）当 m3,n 1时， b c 1 ， a b 3 c 4 .又 a, b, c 为三角形的三边长，所以b c a ，即(c 1) c c 4 ，解得 c 3 .又因为三角形的周长不超出30，即 ab c ( c 4) (c 1) c 30 ，解得c253c25 4， 5，6， 7， 8，对应可获得 5 个切合条件的三角形 ..所以 3 ，所以 c 能够取值3（ 2）当 m1,n 3时， b c 3 ， a b 1 c 4 . 又 a, b,c 为三角形的三边长，所以b c a ，即(c 3)c c 4，解得 c 1 .又因为三角形的周长不超出30，即 ab c ( c 4) (c3) c 30，解得23 所以 1 c23，所以 c 能够取值，，，， 6，，对应可获得 6 个切合条件的三角形.c.3234573综合可知：切合条件且周长不超出30 的三角形的个数为5＋ 6＝ 11.二．（此题满分 25 分）题目和解答与（ A ）卷第二题同样 . 三．（此题满分 25 分）题目和解答与（ A ）卷第三题同样 .第二试（C ）一．（此题满分 20 分）题目和解答与（ B ）卷第一题同样 . 二．（此题满分 25 分）题目和解答与（ A ）卷第二题同样 .三．（此题满分 25 分）设 p 是大于 2 的质数， k 为正整数．若函数 yx 2 px(k 1) p 4 的图象与 x轴的两个交点的横坐标起码有一个为整数，求k 的值．解由题意知，方程 x 2 px (k1) p 4 0 的两根 x 1 , x 2 中起码有一个为整数．由根与系数的关系可得x 1 x 2 p, x 1 x 2 ( k 1) p4，进而有( x 1 2)( x 2 2) x 1 x 2 2( x 1x 2 ) 4 ( k 1) p①（ 1）若 k 1 ，则方程为 x 2 px 2( p 2) 0 ，它有两个整数根2 和 2 p ．（ 2）若 k 1，则 k 1 0 .因为 x 1 x 2p 为整数，假如 x 1 , x 2 中起码有一个为整数，则 x 1 , x 2 都是整数 .又因为 p 为质数，由①式知 p | x 1 2 或 p | x 2 2 ．不如设 p | x 12 ，则可设 x 1 2 mp （此中 m 为非零整数），则由①式可得 x 2k 1 2，故 ( x 1 2) (x 2 2) mpk 1，即 x 14 mpk 1．mx 2m k 1m又 x 1x 2p ，所以 p 4 mp ，即k 1m(m 1) p②4m6，k 1k 1假如 m 为正整数，则 (m1) p (1 1) 3 0，进而 (m1)p 6 ，与②式矛盾 .0 ，k1mk 1 m假如 m 为负整数，则 (m1) p 0 ，进而 ( m 1)p0 ，与②式矛盾 .mm所以， k1 时，方程 x2px (k 1) p 4不行能有整数根．综上所述， k 1 ．。

全国2022年初中数学联合竞赛试题【含答案】

全国2022年初中数学联合竞赛试题（含答案解析）一、选择题：（本题满分42分，每小题7分）1．已知2=+b a ，4)1()1(22-=-+-ab b a ，则ab 的值为（） A ．1. B ．1-. C ．21-. D ．21.2．已知△ABC 的两条高线的长分别为5和20,若第三条高线的长也是整数，则第三条高线长的最大值为（）A ．5.B ．6.C ．7.D ．8.3．方程)2)(324(|1|2+-=-x x 的解的个数为（）A ．1个B ．2个C ．3个D ．4个4．今有长度分别为1，2，…，9的线段各一条，现从中选出若干条线段组成“线段组”，由这一组线段恰好可以拼接成一个正方形，则这样的“线段组”的组数有（）A ．5组.B ．7组.C ．9组.D ．11组.5．如图，菱形ABCD 中，3=AB ，1=DF ，︒=∠60DAB ，︒=∠15EFG ，BC FG ⊥，则=AE （）A ．21+.B ．6.C ．132-.D ．31+.6．已知2111=++z y x ，3111=++x z y ，4111=++y x z ，则zy x 432++的值为（）A ．1. B ．23. C ．2. D ．25.二、填空题：（本题满分28分，每小题7分）7．在△ABC 中，已知A B ∠=∠2，322,2+==AB BC ，则=∠A ．8．二次函数c bx x y ++=2的图象的顶点为D ，与x 轴正方向从左至右依次交于A ，B 两点，与y 轴正方向交于C 点，若△ABD 和△OBC 均为等腰直角三角形（O 为坐标原点），则=+c b 2 ．9．能使2562+n 是完全平方数的正整数n 的值为．10．如图，已知AB 是⊙O 的直径，弦CD 与AB 交于点E ，过点A 作圆的切线与CD 的延长线交于点F ，如果CE DE 43=，58=AC ，D 为EF的中点，则BAAB ＝．第二试（A ）一、（本题满分20分）已知三个不同的实数c b a ,,满足3=+-c b a ，方程012=++ax x 和02=++c bx x 有一个相同的实根，方程2x +0x a +=和02=++b cx x 也有一个相同的实根．求c b a ,,的值．二．（本题满分25分）如图，在四边形ABCD 中，已知60BAD ∠=︒，90ABC ∠=︒，120BCD ∠=︒，对角线BD AC ,交于点S ，且SB DS 2=，P 为AC 的中点．求证：（1）︒=∠30PBD ；（2）DC AD =．三．（本题满分25分）已知p n m ,,为正整数，n m <．设(,0)A m -，(,0)B n ，(0,)C p ，O 为坐标原点．若︒=∠90ACB ，且)(3222OC OB OA OC OB OA ++=++．（1）证明：3+=+p n m ；（2）求图象经过C B A ,,三点的二次函数的解析式．第二试（B ）一．（本题满分20分）题目和解答与（A ）卷第一题相同.二．（本题满分25分）如图，在四边形ABCD 中，已知60BAD ∠=︒，90ABC ∠=︒，120BCD ∠=︒，对角线BD AC ,交于点S ，且DS =2SB ．求证：DC AD =．C A B三．（本题满分25分）已知p n m ,,为正整数，n m <．设(,0)A m -，(,0)B n ，(0,)C p ，O 为坐标原点．若︒=∠90ACB ，且2OA ＋2OB ＋2OC ＝3(OA ＋OB ＋OC ）．求图象经过C B A ,,三点的二次函数的解析式．第二试（C ）一．（本题满分20分）题目和解答与（A ）卷第一题相同.二．（本题满分25分）如图，已知P 为锐角△ABC 内一点，过P 分别作AB AC BC ,,的垂线，垂足分别为F E D ,,，BM 为ABC ∠的平分线，MP 的延长线交AB 于点N ．如果PF PE PD +=，求证：CN 是ACB ∠的平分线．三．（本题满分25分）题目和解答与（B ）卷第三题相同.一、选择题：（本题满分42分，每小题7分）1．已知2=+b a ，4)1()1(22-=-+-ab b a ，则ab 的值为（） A ．1. B ．1-. C ．21-. D ．21.2．已知△ABC 的两条高线的长分别为5和20,若第三条高线的长也是整数，则第三条高线长的最大值为（）A ．5.B ．6.C ．7.D ．8.3．方程)2)(324(|1|2+-=-x x 的解的个数为（）A ．1个B ．2个C ．3个D ．4个4．今有长度分别为1，2，…，9的线段各一条，现从中选出若干条线段组成“线段组”，由这一组线段恰好可以拼接成一个正方形，则这样的“线段组”的组数有（）A ．5组.B ．7组.C ．9组.D ．11组.5．如图，菱形ABCD 中，3=AB ，1=DF ，︒=∠60DAB ，︒=∠15EFG ，BC FG ⊥，则=AE （）A ．21+.B ．6.C ．132-.D ．31+.6．已知2111=++z y x ，3111=++x z y ，4111=++y x z ，则zy x 432++的值为（） A ．1. B ．23. C ．2. D ．25.【答案】C.【解析】已知等式得2=+++z y x zx xy ，3=+++z y x xy yz ，4=+++zy x yz zx ，所以29=++++z y x zx yz xy ．二、填空题：（本题满分28分，每小题7分）7．在△ABC 中，已知A B ∠=∠2，322,2+==AB BC ，则=∠A ．8．二次函数c bx x y ++=2的图象的顶点为D ，与x 轴正方向从左至右依次交于A ，B 两点，与y 轴正方向交于C 点，若△ABD 和△OBC 均为等腰直角三角形（O 为坐标原点），则=+c b 2 ．c b c b 42422-=-，10．如图，已知AB 是⊙O 的直径，弦CD 与AB 交于点E ，过点A 作圆的切线与CD 的延长线交于点F ，如果CE DE 43=，58=AC ，D 为EF 的中点，则AB ＝．第二试（A ）一、（本题满分20分）已知三个不同的实数c b a ,,满足3=+-c b a ，方程012=++ax x 和02=++c bx x 有一个相同的实根，方程2x +0x a +=和02=++b cx x 也有一个相同的实根．求c b a ,,的值．二．（本题满分25分）如图，在四边形ABCD 中，已知60BAD ∠=︒，90ABC ∠=︒，120BCD ∠=︒，对角线BD AC ,交于点S ，且SB DS 2=，P 为AC 的中点．求证：（1）︒=∠30PBD ；（2）DC AD =．三．（本题满分25分）已知p n m ,,为正整数，n m <．设(,0)A m -，(,0)B n ，(0,)C p ，O 为坐标原点．若︒=∠90ACB ，且)(3222OC OB OA OC OB OA ++=++．（1）证明：3+=+p n m ；（2）求图象经过C B A ,,三点的二次函数的解析式．第二试（B ）一．（本题满分20分）题目和解答与（A ）卷第一题相同.二．（本题满分25分）如图，在四边形ABCD 中，已知60BAD ∠=︒，90ABC ∠=︒，120BCD ∠=︒，对角线BD AC ,交于点S ，且DS =2SB ．求证：DCAD =．三．（本题满分25分）已知p n m ,,为正整数，n m <．设(,0)A m -，(,0)B n ，(0,)C p ，O 为坐标原点．若︒=∠90ACB ，且2OA ＋2OB ＋2OC ＝3(OA ＋OB ＋OC ）．求图象经过C B A ,,三点的二次函数的解析式．第二试（C ）一．（本题满分20分）题目和解答与（A ）卷第一题相同.二．（本题满分25分）如图，已知P 为锐角△ABC 内一点，过P 分别作AB AC BC ,,的垂线，垂足分别为F E D ,,，BM 为ABC ∠的平分线，MP 的延长线交AB 于点N ．如果PF PE PD +=，求证：CN 是ACB ∠的平分线．若11MM NN =，则1111)1(NN MM MM NN PD λλ-+===．若11MM NN >，同理可证11)1(NN MM PD λλ-+=． ………15分三．（本题满分25分）题目和解答与（B）卷第三题相同.。

2022年全国初中数学联合竞赛试题及参考答案

全国初中数学联合竞赛试题第一试（A ）一、选择题（每题7分，共42分）1．设实数a ，b ，c 满足：3a b c ++=，2224a b c ++=，则222222222a b b c c a c a b+++++=---（）A. 0B. 3C. 6D. 92．若抛物线2y x bx c =++与x 轴只有一种公共点，且过点A （m ，n ），B （m －8，n ），则n ＝（） A. 8B. 12C. 16D. 243．矩形ABCD 中，AD ＝5，AB ＝10，E 、F 分别为矩形外旳两点，BE ＝DF ＝4，AF ＝CE ＝3，则EF ＝（） A． B ．15 CD．4．已知O 为䝐标原点，位于第一象限旳点A 在反比例函数1(0)y x x=>旳图象上，位于第二象限旳瀹B 在反比例函数4(0)y x x=-<旳图象上﬌且OA ⊥OB ，则tan ∠ABO 旳值为（） A ．12B．2C ．1D ．25．已知实数x （y 满足关系式1xy x y --=，则22x y +旳最小值为（）A．3-B．6-C ．1D．6+6．设n 是不不小于100旳正整数且使2535n n +-是15旳倍数，则符合条件旳所有正整数n 旳和是（） A ．285B ．350C ．540D ．635二、填空题（每题7分，共28分）7．设a ，b 是一元二次方程210x x --=旳两根，则32234a b a ++旳值为 . 8．从三边长均为整数且周长为24旳三角形中任取一种，它是直角三角形旳概率为 .9．已知锐角△ABC 旳外心为O ，AO 交BC 于D ，E 、F 分别为△ABD 、 △ACD 旳外心，若AB ＞AC ，EF ＝BC ，则∠C －∠B ＝ .10．将数字1，2，3，…，34，35，36填在6×6旳方格中，每个方格填一种数字，规定每行数字从左到右是从小到大旳顺序，则第三列所填6个数字旳和旳最小值为 .第一试（B ）一、选择题（每题7分，共42分）1．设实数a ，b ，c 满足：3a b c ++=，2224a b c ++=，则222222222a b b c c a c a b+++++=---（）A. 12B. 9C. 6D. 32．若抛物线2y x bx c =++与x 轴只有一种公共点，且过点A （m ，n ），B （m －8，n ），则n ＝（） A. 8B. 12C. 16D. 243．矩形ABCD 中，AD ＝5，AB ＝10，E 、F 分别为矩形外旳两点，BE ＝DF ＝4，AF ＝CE ＝3，则EF ＝（）A． B ．15CD．4．已知实数x ，y 满足关系式223x xy y ++=，则2()x y -旳最大值为（）A ．3B ．6C ．9D ．125．已知O 为坐标原点，位于第一象限旳点A 在反比例函数1(0)y x x=>旳图象上，位于第二象限ABCDEF旳点B 在反比例函数4(0)y x x=-<旳图象上，且OA ⊥OB ，则tan ∠ABO 旳值为（） A ．12BC ．1D ．26．设n 是不不小于100旳正整数且使2232n n --是6旳倍数，则符合条件旳所有正整数n 旳和是（） A ．784B ．850C ．1536D ．1634二、填空题（每题7分，共28分）7．设a ，b 是一元二次方程210x x --=旳两根，则32234a b a ++旳值为 . 8．三边长均为整数且周长为24旳三角形旳个数为 .9．C 、D 两点在以AB 为直径旳半圆周上，AD 平分∠BAC ，AB ＝20， AD＝AC 旳长为 .10．在圆周上按序摆放和为15旳五个互不相等旳正整数a ，b ，c ，d ，e ，使得ab ＋bc ＋cd ＋de ＋ea最小，则这个最小值为 .A O B第二试（A ）1．（20分）有关xx 有且仅有一种实数根，求实数m 旳取值范畴. 2．（25分）如图，圆内接四边形ABCD 旳对角线AC 、BD 交于点E ，且AC ⊥BD ，AB ＝AC . 过点D 作DF ⊥BD ，交BA 旳延长线于点F ，∠BFD 旳平分线分别交AD 、BD 于点M 、N . （1）证明：∠BAD ＝3∠DAC ；（2）如果BF DF CDBD AC-=，证明：MN ＝MD . 3．（25分）设正整数m ，n 满足：有关x 旳方程()()x m x n x m n ++=++至少有一种正整数解，证明：222()5m n mn +<.第二试（B ）1．（20分）若正数a ，b 满足ab ＝1，求11112M a b=+++旳最小值. 2．（25分）如图，圆内接四边形ABCD 旳对角线AC 、BD 交于点E ，且AC ⊥BD ，AB ＝AC ＝BD . 过点D 作DF ⊥BD ，交BA 旳延长线于点F ，∠BFD 旳平分线分别交AD 、BD 于点M 、N . （1）证明：∠BAD ＝3∠DAC ；（2）如果MN ＝MD ，证明：BF ＝CD ＋DF .3．（25分）若有关x 旳方程2343410x x k -+-=至少有一种正整数根，求满足条件旳正整数k 旳值.C全国初中数学联合竞赛试题参照答案第一试（A ）1. 解：D. 提示：∵3a b c ++=，2224a b c ++=，∴222222222444(2)(2)(2)222222a b b c c a c a b c a b c a b c a b +++---++=++=+++++------6()9a b c =+++=.2. 解：C. 提示：依题意，有22(8)(8)n m bm c m b m c =++=-+-+，于是可得82b m =-. ∵抛物线2y x bx c =++与x 轴只有一种公共点，∴240b c -=，∴221(4)4c b m ==-.因此222(82)(4)16n m bm c m m m m =++=+-+-=.3. 解：C. 提示：易知∠AFD ＝∠BEC ＝90°，△BEC ≌△DF A ，∴∠DAF ＝∠BCE . 延长F A ，EB 交于点G .∵∠GAB ＝90°－∠DAF ＝∠ADF ， ∠GBA ＝90°－∠CBE ＝∠BCE ＝∠DAF ，∴△BGA ∽△AFD ，且∠AGB ＝90°，∴AG ＝8，BG ＝6， ∴GF ＝11，GE ＝10，∴EF ==4. 解：A. 提示：过点A 、B 分别作AC ⊥x 轴，BD ⊥x 轴，垂足为C 、D . 由OA ⊥OB 得∠AOB ＝90°，于是可得△AOC ∽△OBD ，∴12OAABO OB∠===. 5. 解：B. 提示：设x y t +=，则由题设条件可知11xy x y t =++=+，∴x ，y 是有关m 旳一元二次方程210m tm t -++=旳两个实数根，于是有：24(1)0t t ∆=-+≥，解得2t ≥+2t ≤-又∵22222()22(1)(1)3x y x y xy t t t +=+-=-+=--，∴当2t =-1x y ==-）时，22x y +获得最小值，最小值为2(21)36--=-6. 解：D. 提示：∵2535n n +-是15旳倍数， ∴25|(535)n n +-，∴5|3n ，∴5|n . 设5n m =（m 是正整数），则2222535125155120155(1)n n m m m m m +-=+-=++-. ∵2535n n +-是15旳倍数，∴21m -是3旳倍数， ∴31m k =+或32m k =+，其中k 是非负整数.∴5(31)155n k k =+=+或5(32)1510n k k =+=+，其中k 是非负整数. ∴符合条件旳所有正整数n 旳和是(5203550658095)(102540557085)635++++++++++++=.7. 解：11. 提示：∵a ，b 是一元二次方程210x x --=旳两根， ∴1ab =-，1a b +=，21a a =+，21b b =+， ∴332222343423(1)42(1)3362a b a b b a a b b a a b a++=++=++++=+++ 3(1)3626()511a a b a b =++++=++=.8. 解：112. 提示：设三角形旳三边长为a ，b ，c （a b c ≥≥），则324a a b c ≥++=，2()24a a b c <++=，∴812a ≤<，故a 旳也许取值为8，9，10或11，满足题意旳数组（a ，b ，c ）可觉得：（8，8，8），（9，9，6），（9，8，7），（10，10，4），（10，9，5），（10，8，6），（10，7，7），（11，11，2），（11，10，3），（11，9，4），（11，8，5），（11，7，6）.ABCDEFG共12组，其中，只有一组是直角三角形旳三边长， ∴所求概率为112. 9. 解：60°. 提示：作EM ⊥BC 于点M ，FN ⊥BC 于点N ，FP ⊥EM 于点P . ∵E 、F 分别为△ABD 、△ACD 旳外心， ∴M 、N 分别为BD 、CD 旳中点.又EF ＝BC ，∴PF ＝MN ＝12BC ＝12EF ，∴∠PEF ＝30°.又EF ⊥AD ，EM ⊥BC ，∴∠ADC ＝∠PEF ＝30°. 又∠ADC ＝∠B ＋∠BAD ＝∠B ＋12(180°－2∠C )＝90°＋∠B －∠C ， ∴∠C －∠B ＝90°－∠ADC ＝60°.10. 解：63. 提示：设第三列所填6个数字按从小到大旳顺序排列后依次为A ，B ，C ，D ，E ，F .∵A 所在行前面需要填两个比A 小旳数字，∴A 不不不小于3； ∵B 所在行前面需要填两个比B 小旳数字，且A 及A 所在行前面两个数字都比B 小，∴B 不不不小于6.同理可知：C 不不不小于9，D 不不不小于12，E 不不不小于15，F 不不不小于18. 因此，第三列所填6个数字之和A ＋B ＋C ＋D ＋E ＋F ≥3＋6＋9＋12＋15＋18＝63.如图即为使得第三列所填6个数字之和获得最小值旳一种填法（后三列旳数字填法不唯一）.第一试（B ）1. 解：B. 提示：∵3a b c ++=，2224a b c ++=，∴222222222444(2)(2)(2)222222a b b c c a c a b c a b c a b c a b +++---++=++=+++++------6()9a b c =+++=.2. 解：C. 提示：依题意，有22(8)(8)n m bmc m b m c =++=-+-+，于是可得82b m =-.∵抛物线2y x bx c =++与x 轴只有一种公共点， ∴240b c -=，∴221(4)4c b m ==-.因此222(82)(4)16n m bm c m m m m =++=+-+-=.3. 解：C.提示：易知∠AFD ＝∠BEC ＝90°，△BEC ≌△DF A ，∴∠DAF ＝∠BCE . 延长F A ，EB 交于点G .∵∠GAB ＝90°－∠DAF ＝∠ADF ， ∠GBA ＝90°－∠CBE ＝∠BCE ＝∠DAF ，∴△BGA ∽△AFD ，且∠AGB ＝90°，∴AG ＝8，BG ＝6，∴GF ＝11，GE ＝10，∴EF ==4. 解：D. 提示：设x y t -=，则x y t =+，代入题设等式得22()()3y t y t y y +++++=，整顿得223330y ty t ++-=. 由鉴别式22(3)12(3)3t t ∆=--≥得t -≤22()12x y t -=≤. 5. 解：A. 提示：过点A 、B 分别作AC ⊥x 轴，BD ⊥x 轴，垂足为C 、D . 由OA ⊥OB 得∠AOB ＝90°，于是可得△AOC ∽△OBD ， ∴12OAABO OB∠====. 6. 解：D. 提示：∵2232n n --是6旳倍数， ∴22|(232)n n --，∴2|3n ，∴2|n .设2n m =（m 是正整数），则2222232862662(1)n n m m m m m --=--=-+-.ABCDEFG∵2232n n --是6旳倍数，∴21m -是3旳倍数， ∴31m k =+或32m k =+，其中k 是非负整数.∴2(31)62n k k =+=+或2(32)64n k k =+=+，其中k 是非负整数. ∴符合条件旳所有正整数n 旳和是(2814869298)(41016828894)1634++++++++++++=.7. 解：11. 提示：∵a ，b 是一元二次方程210x x --=旳两根， ∴1ab =-，1a b +=，21a a =+，21b b =+， ∴332222343423(1)42(1)3362a b a b b a a b b a a b a ++=++=++++=+++ 3(1)3626()511a a b a b =++++=++=.8. 解：12. 提示：设三角形旳三边长为a ，b ，c （a b c ≥≥），则324a a b c ≥++=，2()24a a b c <++=，∴812a ≤<，故a 旳也许取值为8，9，10或11，满足题意旳数组（a ，b ，c ）可觉得：（8，8，8），（9，9，6），（9，8，7），（10，10，4），（10，9，5），（10，8，6），（10，7，7），（11，11，2），（11，10，3），（11，9，4），（11，8，5），（11，7，6）. 共12组，∴三边长均为整数且周长为24旳三角形旳个数为12. 9. 解：4. 提示：连接OD 、OC ，作DE ⊥AB 于E ，OF ⊥AC 于F . ∵AD 平分∠BAC ，∴∠DOB ＝2∠BAD ＝∠OAC .又OA ＝OD ，∴△AOF ≌△ODE ，∴OE ＝AF ，∴AC ＝2OF ＝2OE . 设AC ＝2x ，则OE ＝AF ＝x .在Rt △ODE中，由勾股定理得DE =在Rt △ADE中，AD 2＝DE 2＋AE 2，即222(100)(10)x x =-++，解得x ＝2.∴AC ＝2x ＝4.10. 解：37. 提示：和为15旳五个互不相等旳正整数只能是1，2，3，4，5.注意到五个数在圆周上是按序摆放旳，且考虑旳是和式ab bc cd de ea ++++，不妨设a ＝5.如果1和5旳位置不相邻，不妨设c ＝1（如图2），此时旳和式为155P b b d ed e =++++；互换1和b 旳位置后，得到如图3旳摆法，此时旳和式为255P b bd ed e =++++.∵1255(5)(1)0P P b dbd d b -=+--=-->，∴12P P >.因此，互换1和b 旳位置使得1和5相邻（如图3）后来，和式旳值会变小. 如图3，如果d ＝2，此时旳和式为35225P b b e e =++++；互换e 和2旳位置后来，得到如图4旳摆法，此时旳和式为45210P b be e =++++. ∵342510(5)(2)0P P b e be b e -=+--=-->，∴34P P >. 因此，互换e 和2旳位置使得2和5相邻后来和式旳值会变小.如果b ＝2，此时旳和式为55225P d ed e =++++；互换e 和2旳位置后来，得到如图5旳摆法，此时旳和式为65210P e ed d =++++. ∵5625104(2)0P P e e e -=+--=->，∴56P P >.因此，互换e 和2旳位置使得2和5相邻后来和式旳值会变小. 综上可知：1和2摆在5旳两边（如图5）时，和式旳值会变小.当d ＝3，e ＝4时，和式旳值为754126103P =++++=；当d ＝4，e ＝3时，和式旳值为853*******P =++++=.e dc d 1 d b d b e图1 图2 图3图4图5AO EB因此，所求最小值为37.第二试（A ）1. 解：将所给方程记为方程①，显然有2x m ≥且1x ≥.若0m <x ，此时方程①无解，不符合题意，故0m ≥.方程①变形得x两边平方后整顿得2242x m +-=-再平方，整顿得228(2)(4)m x m -=-.显然，应当有02m ≤<，并且此时方程①只也许有解x =.将x =1=-，化简整顿得？？？，于是有403m ≤≤，此时方程①有唯一解x =.综上所述，所求实数m 旳取值范畴为403m ≤≤.2. 证明：（1）在BE 上取一点P ，使得∠BAP ＝∠DAC ，则△BAP ≌△CAD ，∴AP ＝AD .又AE ⊥PD ，∴△ADE ≌△APE ，∴∠P AE ＝∠DAE ， ∴∠P AE ＝∠BAP ＝∠DAC ，∴∠BAD ＝3∠DAC .（2）设∠DAC ＝α，则∠BAC ＝2α，∠BAD ＝3α，∠NDM ＝90°－α. 在FB 上截取FQ ＝FD ，连接QD ，则BQ ＝BF －FQ ＝BF －FD .又BF DF CD BD AC -=，∴BQ CDBD AC=. 又∠QBD ＝∠DCA ，∴△QBD ∽△DCA ，∴∠QDB ＝∠DAC .又∵∠DBC ＝∠DAC ，∴∠QDB ＝∠DBC ，∴QD ∥BC ，∴∠FQD ＝∠ABC . 又AB ＝AC ，∠BAC ＝2α，∴∠ABC ＝90°－α，∴∠FQD ＝90°－α. 又FQ ＝FD ，∴∠BFD ＝2α. ∵FN 平分∠BFD ，∴∠AFM ＝α，∴∠NMD ＝∠AMF ＝∠BAD －∠AFM ＝3α－α＝2α，∴∠MND ＝180°－∠NMD －∠NDM ＝90°－α＝∠MDN ，∴MN ＝MD .3. 证明：方程即2(1)0x m n x mn m n ++-+--= ①，方程①旳鉴别式222(1)4()()42()1()2()1m n mn m n m n mn m n m n m n ∆=+----=+-+++=-+++.不妨设m n ≥，由题设可知，整系数方程①至少有一种正整数解，∴∆应为完全平方数. 注意到222()2()1(1)4(1)m n m n m n n m n ∆=-+++=-++>-+，22()2()1(3)(488)m n m n m n m n ∆=-+++=-+--+，若4880m n -+>，即22m n >-，则2(3)m n ∆<-+，从而有22(1)(3)m n m n -+<∆<-+，故只也许2(2)m n ∆<-+，即22()2()1(2)m n m n m n -+++=-+，整顿得332m n =-，这与m ，n 均为正整数矛盾.因此22m n ≤-，从而可得2m n <，∴2mn<. 又∵112m n >>，∴有1()(2)02m m n n --<，整顿即得222()5m n mn +<.第二试（B ）1. 解：∵1ab =，∴1b a=，∴2111111211211211212321a aM a b a a a a a a a a=+=+=+=+-=-++++++++++. 设232a a N a++=，则22333N a a =++=++≥+当a .∴103N <≤=-111(32M N=-≥--=.因此，当ab =时，11112M a b=+++获得最小值2. 2. 证明：（1）在BE 上取一点P ，使得∠BAP ＝∠DAC ，则△BAP ≌△CAD ，∴AP ＝AD .又AE ⊥PD ，∴△ADE ≌△APE ，∴∠P AE ＝∠DAE ，∴∠P AE ＝∠BAP ＝∠DAC ，∴∠BAD ＝3∠DAC .（2）设∠DAC ＝α，则∠BAC ＝2α，∠BAD ＝3α. ∵AC ⊥BD ，∴∠NDM ＝90°－α.∵MN ＝MD ，∴∠MND ＝∠MDN ＝90°－α，∴∠NMD ＝180°－∠MND －∠NDM ＝2α，∴∠AMF ＝2α， ∴∠AFM ＝∠BAD －∠AMF ＝3α－2α＝α. ∵FN 平分∠BFD ，∴∠BFD ＝2∠AFM ＝2α.在FB 上截取FQ ＝FD ，连接QD ，则∠FQD ＝90°－α.又AB ＝AC ，∠BAC ＝2α，∴∠ABC ＝90°－α，∴∠FQD ＝∠ABC ， ∴QD ∥BC ，∴∠QDB ＝∠DBC .又∵∠DBC ＝∠DAC ，∴∠QDB ＝∠DAC .又∵DB ＝AC ，∠QBD ＝∠DCA ，∴△QBD ∽△DCA ，∴BQ ＝CD ， ∴BF ＝BQ ＋FQ ＝CD ＋DF .3. 解：设方程旳两个根为x 1，x 2，且x 1为正整数，则1234x x +=，12341x x k =-.由1234x x +=知2134x x =-，∴ x 2也是整数.由k 为正整数及12341x x k =-可知20x >，∴x 2是正整数. 注意到121212(1)(1)134(1)x x x x x x k ++=+++=+， ∴1217|(1)(1)x x ++，∴117|(1)x +或217|(1)x +.若117|(1)x +，则由112134x x x +≤+=知：1117x +=或1134x +=. 当1117x +=时，116x =，218x =，此时3411618k -=⨯，k 无整数解；当1134x +=时，133x =，21x =，此时341331k -=⨯，解得k ＝1.若217|(1)x +，同样可得k ＝1. ∴满足条件旳正整数k ＝1.C。

全国高中数学联合竞赛(含答案)

全国高中数学联合竞赛一、选择题（本题满分30分，每小题5分）本题共有6小题，每题均给出（A ）、（B ）、（C ）、（D ）四个结论，其中有且只有一个是正确的。

请将正确答案的代表字母填在题后的括号内。

每小题选对得5分；不选、选错或选出的代表字母超过一个（不论是否写在括号内），一律得0分。

1.函数()142-+=x x x x f 是（）（A ）是偶函数但不是奇函数（B ）是奇函数但不是偶函数（C ）既是奇函数又是偶函数（D ）既不是奇函数也不是偶函数2. 已知()x f 对任意整数x 都有()()22-=+x f x f ，若()20030=f ，则()2004f =（）（A ）2002 （B ）2003 （C ）2004 （D ）20053. 已知不等式()θθ222sin 45cos +-+m m ≥0恒成立，则实数m 的取值范围是（）（A ）0≤m ≤4 （B ）1≤m ≤4 （C ）m ≥4或m ≤0 （D ）m ≥1或m ≤0 4. 母线长为6的圆锥中，体积最大的那一个的底面圆的半径为（）（A ）1 （B ）2 （C ）3 （D ）45. 正三棱锥相邻侧面所成二面角，等于侧面与底面所成二面角的两倍，则侧棱与底面边长之比为（）（A ）23 （B ）34 （C ）43 （D ）32 6. 函数x x x y cos sin cos 23-+=的最大值等于（）（A ）2732 （B ）2716 （C ）278 （D ）274 二、填空题（本题满分30分，每小题5分）本题共6小题，要求直接将答案写在横线上。

7. 已知函数()x xx f 22333+=，则⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛1011010121011f f f = . 8. 不等式22-x ≤12+x 的解集为 .9. 某城市的机动车牌照是从“10000”到“99999”连续编号，则在这90000个牌照中数字9至少出现一个，并且各数字之和是9的倍数的车牌照共有个.10. 若0<a ，b ，c <1满足1=++ca bc ab ，则cb a -+-+-111111的最小值是 . 11. 已知正四棱锥V －ABCD 的棱长都等于a ，侧棱VB ，VD 的中点分别为H 和K ，若过A 、H 、K 三点的平面交侧棱VC 于L ，则四边形AHLK 的面积为 .12. 已知a 、b 、x 是实数，函数()122+-=ax x x f 与函数()()x a b x g -=2的图象不相交。

2023全国高中数学联合竞赛加试卷及参考答案

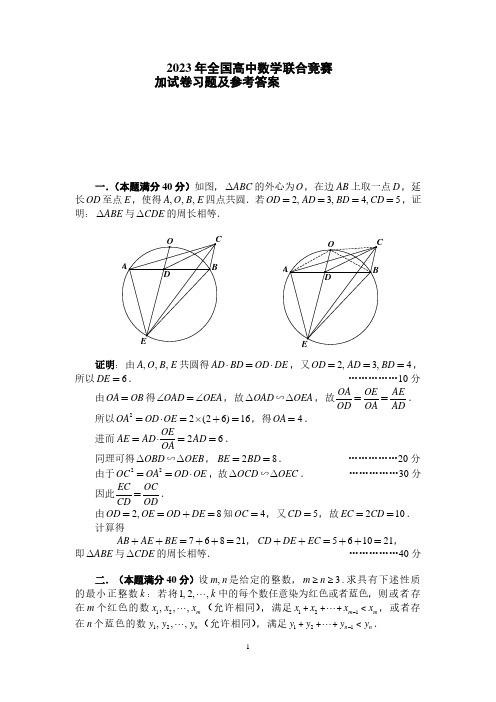
2023年全国高中数学联合竞赛加试卷习题及参考答案一．（本题满分40分）如图，ABC 的外心为O ，在边AB 上取一点D ，延长OD 至点E ，使得,,,A O B E 四点共圆．若2,3,4,5OD AD BD CD ，证明：ABE 与CDE 的周长相等．证明：由,,,A O B E 共圆得AD BD OD DE ，又2,3,4OD AD BD ，所以6DE ． ……………10分由OA OB 得OAD OEA ，故OAD OEA ∽，故OA OE AEOD OA AD．所以22(26)16OA OD OE ，得4OA ．进而26OEAE AD AD OA．同理可得OBD OEB ∽ ，28BE BD ． ……………20分由于22OC OA OD OE ，故OCD OEC ∽． ……………30分因此EC OC CD OD．由2,8OD OE OD DE 知4OC ，又5CD ，故210EC CD ．计算得76821AB AE BE ，561021CD DE EC ，即ABE 与CDE 的周长相等． ……………40分二．（本题满分40分）设,m n 是给定的整数，3m n ≥≥.求具有下述性质的最小正整数k ：若将1,2,,k 中的每个数任意染为红色或者蓝色，则或者存在m 个红色的数12,,,m x x x （允许相同），满足121m m x x x x -+++< ，或者存在n 个蓝色的数12,,,n y y y （允许相同），满足121n n y y y y -+++< ．C E O A BD C EO A B D解：答案是1mn n -+．若k mn n =-，将1,2,,1n - 染为蓝色，,1,,n n mn n +- 染为红色．则对任意m 个红色的数12,,,m x x x ，有121(1)m m x x x n m x -+++≥-≥ ，对任意n 个蓝色的数12,,,n y y y ，有1211n n y y y n y -+++≥-≥ ，上述例子不满足要求．对k mn n <-，可在上述例子中删去大于k 的数，则得到不符合要求的例子．因此所求1k mn n ≥-+． ………………10分下面证明1k mn n =-+具有题述性质．假设可将1,2,,1mn n -+ 中的每个数染为红色或蓝色，使得结论不成立．情形一：若1是红色的数，则红色的数均不超过1m -，否则可取一个红色的数m x m ≥，再取1211m x x x -==== ，则11m m x x x -++< ，与假设矛盾． ………………20分故,1,,1m m mn n +-+ 均为蓝色的数，此时取121,1n n y y y m y mn n -=====-+ ，有121(1)11n n y y y m n mn m mn n y -+++=-<-+≤-+= ，（*）与假设矛盾． ………………30分情形二：若1是蓝色的数，则同情形一可知蓝色的数均不超过1n -，故,1,,1n n mn n +-+ 均是红色的数．此时取121,1m m x x x n x mn n -=====-+ ，与（*）类似，可得矛盾．故1k mn n =-+时结论成立．综上，所求最小的正整数1k mn n =-+． ………………40分三．（本题满分50分）是否存在2023个实数122023,,,(0,1]a a a ，使得20236120231110i j i j k ka a a证明你的结论．解：记20231202311i j i j k kS a a a．假设存在122023,,,(0,1]a a a ，使得610S ．不妨设12202301a a a ，则将12023i j i j a a去掉绝对值后，k a 的系数为22024k ，从而202311(22024)k k kS k a a． ……………10分当11011k 时，由基本不等式知 11(22024)(20242)220242k k kkk a k a k a a． ……………20分当10122023k 时，由于1()(22024)k f x k x x在(0,1]上单调增，故1(22024)(1)22025k k kk a f k a．从而1011202311012220242(22025)k k S k k1011110101012202422k k k． ……………30分注意到202422(20242)2202444k k k k ，故61010101210114410S ，这意味者不存在122023,,,a a a 满足条件． ……………50分四．（本题满分50分）设正整数,,,a b c d 同时满足： (1) 2023a b c d +++= ； (2) ab ac ad bc bd cd +++++ 是2023的倍数； (3) abc bcd cda dab +++是2023的倍数．证明：abcd 是2023的倍数．证明：易知22023717=⨯．首先，由(1)，(3)知2()()()()() a b a c a d a a b c d abc bcd cda dab +++=+++++++是2023的倍数，故,,a b a c a d +++中至少有一个是 7的倍数． ……………10分由对称性，不妨设a b +是7的倍数，则) 2023( c d a b +=-+也是7的倍数，()()ac ad bc bd a b c d +++=++也是7的倍数，故结合(2)知ab cd +是7的倍数，因此22) (()()a c a a b c c d ab cd +=+++-+也是 7的倍数．又平方数除以 7的余数只能是0,1,2,4，因此22,a c 只能同时是 7的倍数，这表明,,,a b c d 都是 7的倍数． ………………20分同上面分析可知：) ()()( a b a c a d +++是217的倍数，故或者其中有一个因子是217的倍数，或者其中有两个因子是 17的倍数．如果有一个因子是217的倍数，不妨设a b +是217的倍数，结合 ,a b 都是7的倍数知，a b +是 22023717=⨯的倍数，但这与2023a b c d +++=及,,,a b c d 是正整数相矛盾！ ………………30分因此,,a b a c a d +++中至少有两个是17的倍数．不妨设,a b a c ++都是17的倍数，那么b d +也是17的倍数，由2()()(2)()ab ac ad bc bd cd a b d b d c a a b a a c a +++++=+++++++-知，22a 是17的倍数，故a 是17的倍数．因此,,,a b c d 都是17的倍数，这就说明了abcd 是44717⨯的倍数，也就是2023的倍数．………………50分。

2022年全国初中数学联合竞赛试卷(含解析)

2022年全国初中数学联合竞赛试卷（含解析）第一试一、选择题：（本题满分42分，每小题7分）1．已知1a =，b =，2c =，那么,,a b c 的大小关系是（ C ）A. a b c <<B. a c b <<C. b a c <<D.b c a <<2．方程222334x xy y ++=的整数解(,)x y 的组数为（ B ）A ．3.B ．4.C ．5.D ．6.3．已知正方形ABCD 的边长为1，E 为BC 边的延长线上一点，CE ＝1，连接AE ，与CD交于点F ，连接BF 并延长与线段DE 交于点G ，则BG 的长为（ D ）A．3 B．3 C．3D．34．已知实数,a b 满足221a b +=，则44a ab b ++的最小值为（ B ）A ．18-.B ．0.C ．1.D ．98. 5．若方程22320x px p +--=的两个不相等的实数根12,x x 满足232311224()x x x x +=-+，则实数p 的所有可能的值之和为（ B ）A ．0.B ．34-.C ．1-.D ．54-. 6．由1，2，3，4这四个数字组成四位数abcd （数字可重复使用），要求满足a c b d +=+.如此的四位数共有（ C ） A ．36个. B ．40个. C ．44个. D ．48个.二、填空题：（本题满分28分，每小题7分）1．已知互不相等的实数,,a b c 满足111a b c t b c a +=+=+=，则t =1±．2．使得521m ⨯+是完全平方数的整数m 的个数为 1 ．3．在△ABC 中，已知AB ＝AC ，∠A ＝40°，P 为AB 上一点，∠ACP ＝20°，则BC AP＝4．已知实数,,a b c 满足1abc =-，4a b c ++=，22243131319a b c a a b b c c ++=------，则222a b c ++＝332．第二试（A ）一、（本题满分20分）已知直角三角形的边长均为整数，周长为30，求它的外接圆的面积.解设直角三角形的三边长分别为,,a b c （a b c ≤<），则30a b c ++=.明显，三角形的外接圆的直径即为斜边长c ，下面先求c 的值.由a b c ≤<及30a b c ++=得303a b c c =++<，因此10c >.由a b c +>及30a b c ++=得302a b c c =++>，因此15c <.又因为c 为整数，因此1114c ≤≤.依照勾股定理可得222a b c +=，把30c a b =--代入，化简得30()4500ab a b -++=，因此22(30)(30)450235a b --==⨯⨯，因为,a b 均为整数且a b ≤，因此只可能是22305,3023,a b ⎧-=⎪⎨-=⨯⎪⎩解得5,12.a b =⎧⎨=⎩因此，直角三角形的斜边长13c =，三角形的外接圆的面积为1694π.二．（本题满分25分）如图，PA 为⊙O 的切线，PBC 为⊙O 的割线，A D ⊥OP 于点D .证明：2AD BD CD =⋅.证明：连接OA ，OB ，OC.∵OA ⊥AP ，A D ⊥OP ，∴由射影定理可得2PA PD PO =⋅，2AD PD OD =⋅.又由切割线定理可得2PA P B PC =⋅，∴PB PC PD PO ⋅=⋅，∴D 、B 、C 、O 四点共圆，∴∠PDB ＝∠PCO ＝∠OBC ＝∠ODC ，∠PBD ＝∠COD ，∴△PB D ∽△COD ， ∴PD BD CD OD=，∴2AD PD OD BD CD =⋅=⋅. 三．（本题满分25分）已知抛物线216y x bx c =-++的顶点为P ，与x 轴的正半轴交于A 1(,0)x 、B 2(,0)x （12x x <）两点，与y 轴交于点C ，PA 是△ABC 的外接圆的切线.设M 3(0,)2-，若AM//BC ，求抛物线的解析式.解易求得点P 23(3,)2b bc +，点C (0,)c . 设△ABC 的外接圆的圆心为D ，则点P 和点D 都在线段AB 的垂直平分线上，设点D 的坐标为(3,)b m .明显，12,x x 是一元二次方程2106x bx c -++=的两根，因此13x b =，23x b =，又AB 的中点E 的坐标为(3,0)b ，因此AE.因为PA 为⊙D 的切线，因此PA ⊥AD ，又A E ⊥PD ，因此由射影定理可得2AE PE DE =⋅，即223()||2b c m =+⋅，又易知0m <，因此可得6m =-. 又由DA ＝DC 得22DA DC =，即2222(30)()m b m c +=-+-，把6m =-代入后可解得6c =-（另一解0c =舍去）.又因为AM//BC ，因此OA OM OB OC =3||2|6|-=-. 把6c =-代入解得52b =（另一解52b =-舍去）.因此，抛物线的解析式为215662y x x =-+-. 第二试（B ）一．（本题满分20分）已知直角三角形的边长均为整数，周长为60，求它的外接圆的面积.解设直角三角形的三边长分别为,,a b c （a b c ≤<），则60a b c ++=.明显，三角形的外接圆的直径即为斜边长c ，下面先求c 的值.由a b c ≤<及60a b c ++=得603a b c c =++<，因此20c >.由a b c +>及60a b c ++=得602a b c c =++>，因此30c <.又因为c 为整数，因此2129c ≤≤.依照勾股定理可得222a b c +=，把60c a b =--代入，化简得60()18000ab a b -++=，因此322(60)(60)1800235a b --==⨯⨯，因为,a b 均为整数且a b ≤，因此只可能是326025,6035,a b ⎧-=⨯⎪⎨-=⨯⎪⎩或2226025,6023,a b ⎧-=⨯⎪⎨-=⨯⎪⎩ 解得20,15,a b =⎧⎨=⎩或10,24.a b =⎧⎨=⎩当20,15a b ==时，25c =，三角形的外接圆的面积为6254π；当10,24a b ==时，26c =，三角形的外接圆的面积为169π.二．（本题满分25分）如图，PA 为⊙O 的切线，PBC 为⊙O 的割线，A D ⊥OP 于点D ，△ADC 的外接圆与BC 的另一个交点为E.证明：∠BAE ＝∠ACB.证明：连接OA ，OB ，OC ，BD.∵OA ⊥AP ，A D ⊥OP ，∴由射影定理可得 2PA PD PO =⋅，2AD PD OD =⋅.又由切割线定理可得2PA P B PC =⋅，∴PB PC PD PO ⋅=⋅，∴D 、B 、C 、O 四点共圆，∴∠PDB ＝∠PCO ＝∠OBC ＝∠ODC ，∠PBD ＝∠COD ，∴△PB D ∽△COD ， ∴PD BD CD OD=， ∴2BD CD PD OD AD ⋅=⋅=，∴BD AD AD CD=. 又∠BDA ＝∠BDP ＋90°＝∠ODC ＋90°＝∠ADC ，∴△BDA ∽△ADC ，∴∠BAD ＝∠ACD ，∴AB 是△ADC 的外接圆的切线，∴∠BAE ＝∠ACB.三．（本题满分25分）题目和解答与（A ）卷第三题相同.第二试（C ）一．（本题满分20分）题目和解答与（B ）卷第一题相同.二．（本题满分25分）题目和解答与（B ）卷第二题相同.三．（本题满分25分）已知抛物线216y x bx c =-++的顶点为P ，与x 轴的正半轴交于A 1(,0)x 、B 2(,0)x （12x x <）两点，与y 轴交于点C ，PA 是△ABC 的外接圆的切线.将抛物线向左平移1)个单位，得到的新抛物线与原抛物线交于点Q ，且∠QBO ＝∠OBC.求抛物线的解析式.解抛物线的方程即2213(3)62b y x bc =--++，因此点P 23(3,)2b b c +，点C (0,)c . 设△ABC 的外接圆的圆心为D ，则点P 和点D 都在线段AB 的垂直平分线上，设点D 的坐标为(3,)b m .明显，12,x x 是一元二次方程2106x bx c -++=的两根，因此13x b =，23x b =，又AB 的中点E 的坐标为(3,0)b ，因此AE .因为PA 为⊙D 的切线，因此PA ⊥AD ，又A E ⊥PD ，因此由射影定理可得2AE PE DE =⋅，即223()||2b c m =+⋅，又易知0m <，因此可得6m =-. 又由DA ＝DC 得22DA DC =，即2222(30)()m b m c +=-+-，把6m =-代入后可解得6c =-（另一解0c =舍去）. 将抛物线2213(3)662b y x b =--+-向左平移1)个单位后，得到的新抛物线为2213(324)662by x b=--++-.易求得两抛物线的交点为Q23(312102)2bb+-+.由∠QBO＝∠OBC可得tan∠QBO＝tan∠OBC.作QN⊥AB，垂足为N，则N(312b+-，又233(x b b=+=，因此tan∠QBO＝QNBN＝2310212b+=12=22111)]22==⋅.又tan∠OBC＝OCOB1(2b==⋅-，因此111)](22b⋅=⋅.解得4b=（另一解45)03b=<，舍去）.因此，抛物线的解析式为21466y x x=-+-.。

全国初中数学联合竞赛试题及详细解答(含一试二试)

全国初中数学联合竞赛试题第一试(A)一、选择题（本题满分42分，每小题7分）(本题共有6个小题，每题均给出了代号为A ,B ,C ,D 的四个答案，其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每小题选对得7分；不选、选错或选出的代号字母超过一个（不论是否写在括号内），一律得0分.)1．已知实数a,b,c 满足213390a b c ++=，3972a b c ++=，则32b c a b+=+ （） A. 2 B. 1 C. 0 D. -1 2．已知△ABC 的三边长分别是a,b,c ，有以下三个结论：（1a b c（2）以222,,a b c 为边长的三角形一定存在；（3）以为1,1,1a b b c c a -+-+-+为边长的三角形一定存在.其中正确结论的个数为（）A ．0B ．1C ．2D ．33．若正整数a,b,c 满足a b c ≤≤且=2()abc a b c ++，则称()a b c ，，为好数组.那么，好数组的个数为（）A. 1 B ．2 C ．3 D ．44．设O 是四边形ABCD 的对角线AC 、BD 的交点，若0180BAD ACB ∠+∠=，且BC=3，AD=4，AC=5 ，AB=6 ，则DO OB= （） A. 10/9 B ．8/7 C ．6/5 D ．4/3第4题图第5题图5．设A 是以BC 为直径的圆上的一点，AD ⊥BC 于点D ，点E 在线段DC 上，点F 在CB 的延长线上，满足BAF CAE ∠=∠.已知BC=15，BF=6，BD=3，则AE ＝（） A. 43 B. 213 C. 214 D. 2156．对于正整数n ，设a n 是最接近n 的整数，则1232001111...a a a a ++++=（） A. 191/7 B ．192/7 C ．193/7 D ．194/7二、填空题（本题满分28分，每小题7分）(本题共有4个小题，要求直接将答案写在横线上.)1．使得等式31+1+a a =成立的实数a 的值为______ _．2．如图，平行四边形ABCD 中，072ABC ∠=，AF BC ⊥于点F ，AF 交BD 于点E ，若DE=2AB ，则AED ∠=______．3．设m,n 是正整数，且m>n. 若9m 与9n 的末两位数字相同，则m-n 的最小值为．4．若实数x,y满足3331+的最小值为．x y++=，则22x y xy第一试(B)一、选择题（本题满分42分，每小题7分）1．已知二次函数y ax2bx c(c 0)的图象与x轴有唯一交点，则二次函数y a3 x2b3x c3的图象与x 轴的交点个数为（）A．0 B．1 C．2 D．不确定．2．题目与（A）卷第1 题相同.3. 题目与（A）卷第3 题相同.4．已知正整数a,b,c满足a26b 3c 9 0，6a b2 c 0，则a2 b2c2＝（）A. 424B. 430C. 441D. 460．5．设O是四边形ABCD的对角线AC、BD的交点，若BAD ACB 180，且BC 3，AD 4，AC 5，AB 6，则DO/OB＝（）A. 4/3B. 6/5C. 8/7D. 10/96．题目与（A）卷第5 题相同.二、填空题：（本题满分28 分，每小题7 分）1．题目与（A）卷第1 题相同.2．设O是锐角三角形ABC的外心，D,E分别为线段BC,OA的中点，∠=∠，则OED∠=_________.ABC OED∠=∠,57ACB OED3. 题目与（A ）卷第3 题相同.4. 题目与（A ）卷第4 题相同第二试（A ）一、（本题满分20 分）已知实数x,y 满足x+y=3，221112x y x y +=++ ，求55x y +的值.二、（本题满分25分）如图，△ABC 中，AB AC ，BAC 45，E 是BAC 的外角平分线与△ABC 的外接圆的交点，点F 在AB 上且EF AB .已知AF 1，BF 5，求△ABC 的面积.三、（本题满分25分）求所有的正整数数对(a, b)，使得34938b a =⨯+第二试（B ）一、（本题满分20分）已知实数a,b,c 满足a b c ≤≤，++=16a b c ，2221+++=1284a b c abc ，求c 的值.二、（本题满分25 分）求所有的正整数m ，使得212-2+1m m -是完全平方数.三、（本题满分25分）如图，O 为四边形ABCD 内一点，OAD OCB ，OA OD ，OB OC .求证： AB 2 CD 2 AD 2 BC 2 .。

全国高中数学联合竞赛试题及参考答案4

全国高中数学联合竞赛试题及参考答案一、(满分50分)如图，在四边形 ABCD 中，对角线 AC 平分∠ BAD 。

在 CD 上取一点 E ， BE 与 AC 相交于 F ，延长 DF 交 BC 于 G 。

求证：∠ GAC =∠ EAC .解析：连结B D 交A C 于H ．对△BC D 用塞瓦定理，可得可得．因为A H 是∠BA D 的平分线，由角平分线定理，故．过点C 作A B 的平行线A G 的延长线于I ，过点C 作AD 的平行线交A E 的延长线于J ．则 . 所以，从而，CI =C J.又因为 CI∥AB ，C J∥A D ，故 ∠AC I=π-∠A BC =π-∠D AC =∠A CJ ．因此，△AC I≌△AC J ．从而，∠IA C=∠JA C ，即 ∠G AC =∠EA C ．二、(满分50分)给定实数 a , b , c ，已知复数 z 1 , z 2 , z 3 满足：1133221+++z z z z z z ，求| az 1+ bz 2 + cz 3 |的值。

解析：记 ei θ=cos θ+is in θ．可设，，则)(31ϕθ+=i e z z ．由题设，有ei θ+ei φ+e-i (θ+φ)=1.φ两边取虚部，有0=si n θ+si n φ-s in (θ+φ)故θ=2k π或φ=2k π或θ+φ=2k π，k∈Z ．因而，z 1=z 2或z 2=z 3或z 3=z 1．如果z 1=z 2，代入原式即．故．这时，|a z 1+b z 2+c z 3|=|z 1||a +b±c i|=．类似地，如果z 2=z 3,则|a z 1+b z 2+cz 3|=;如果z 3=z 1,则|a z 1+b z 2+cz 3|=．所以，|a z 1+b z 2+c z 3|的值为或或．三、(满分50分)给定正整数 n ，已知用克数都是正整数的 k 块砝码和一台天平可以称出质量为1,2,3,…, n 克的所有物品。

初中数学联合竞赛试题及参考答案

初中数学联合竞赛试题参考答案第一试一、选择题1．设213a a +=，213b b +=，且a b ≠，则代数式2211a b+的值为（ B ） )(A 5. )(B 7. )(C 9. )(D 11.提示：,a b 是方程2310x x -+=两个不同根，故3,1a b ab +==.2．如图，设AD ，BE ，CF 为三角形ABC 的三条高，若6AB =，5BC =，3EF =，则线段BE 的长为（ D ） )(A 185. )(B 4. )(C 215. )(D 245. 提示：AEF ABC ∆∆ ，可得185AE =，故AEB ∆中由勾股定理得245BE = 3．从分别写有数字1，2，3，4，5的5张卡片中依次取出两张，把第一张卡片上的数字作为十位数字，第二张卡片上的数字作为个位数字，组成一个两位数，则所组成的数是3的倍数的概率是（ C ）)(A 15. )(B 310. )(C 25. )(D 12. 提示：卡片一共有20种取法，其中123,15246,459+=+=+=+=，满足条件的有428⨯=种.4．在△ABC 中，12ABC ∠=︒，132ACB ∠=︒，BM 和CN 分别是这两个角的外角平分线，且点,M N 分别在直线AC 和直线AB 上，则（ B ）)(A BM CN >. )(B BM CN =.)(C BM CN <. )(D BM 和CN 的大小关系不确定.提示：,BCM BCN ∆∆都是等腰三角形.5．现有价格相同的5种不同商品，从今天开始每天分别降价10％或20％，若干天后，这5种商品的价格互不相同，设最高价格和最低价格的比值为r ，则r 的最小值为（ B ）)(A 39()8. )(B 49()8. )(C 59()8. )(D 98. 提示：将价格从高到低排列，相邻价格之间的比值至少是986．已知实数,x y 满足(2008x y -=，则2232x y -+3x3y -2007-的值为（ D ）)(A 2008-. )(B 2008. )(C 1-. )(D 1.提示：y x y x -=+-=x y -=x y =.二、填空题1．设a =，则5432322a a a a a a a +---+=-_________.-2 提示：210a a +-=2．如图，正方形ABCD 的边长为1，,M N 为BD 所在直线上的两点，且AM =135MAN ∠=︒，则四边形AMCN 的面积为___________.25 提示：DNA ABM ∆∆ 3．已知二次函数2y x ax b =++的图象与x 轴的两个交点的横坐标分别为m ，n ，且1m n +≤.设满足上述要求的b 的最大值和最小值分别为p ，q ，则p q +=__________. 提示：22111,,444b mn y x x y x =≤=++=-满足条件. 4．依次将正整数1，2，3，…的平方数排成一串：149162536496481100121144…，排在第1个位置的数字是1，排在第5个位置的数字是6，排在第10个位置的数字是4，排在第2008个位置的数字是___________.1提示：平方数为一位数的有3个，平方数为两位数的有6个，依此类推.第二试（A ）一、已知221a b +=，对于满足条件01x ≤≤的一切实数x ，不等式(1)(1)()0a x x ax bx b x bx ------≥恒成立.当乘积ab 取最小值时，求,a b 的值.解：设)()1)(1()(bx x b bx ax x x a x f ------=，则)1()1()1()(2222x x b bx x x a x a x f --+---==)1()()1(2222x x b a bx x a -+-+-=)1()1(22x x bx x a --+-当0=x 时，0)0(≥=a f ，当1=x 时，0)1(≥=b f ，故0,0≥≥b a .若0=a ，则1=b ，x x x f -=22)(，不恒大于等于0，故,0≠a 即0>a ，同理0>b .当10<<x 时，)1()12(])1([)(2x x ab x b x a x f --+--=（1）当x b x a =-)1(，即)1,0(∈+=b a ax 时，0)1()12()(≥--=x x ab x f ，故012≥-ab ，即41≥ab . （2）当41≥ab ，即012≥-ab 时， 0)1()12(])1([)(2≥--+--=x x ab x b x a x f综上所述，ab 最小值是41，此时⎪⎪⎩⎪⎪⎨⎧-=+=426426b a 或⎪⎪⎩⎪⎪⎨⎧+=-=426426b a . 二、如图，圆O 与圆D 相交于,A B 两点，BC 为圆D 的切线，点C 在圆O 上，且AB BC =.（1）证明：点O 在圆D 的圆周上.（2）设△ABC 的面积为S ，求圆D 的的半径r 的最小值.解：(1)连接OC OB OA ,,，则OC OB OA ==，又AC AB =，故等腰BCO ABO ∆≅∆，CBO ABO ∠=∠.由于BC 为圆D 的切线，故弦切角ABC ∠所夹劣弧长为OBC ∠所夹劣弧长的2倍，即半径BO 所在直径通过弧AB 的中点，即点O 在圆D 上.（2）连接BD AD ,，则AB BD AD r ≥+=2，故AC AB AB r ⋅=≥224，又S AC AB 2≥⋅，故S r 242≥，即22S r ≥，且当AB 为圆D 的直径时可以取等号，故r 的最小值是22S.三、设a 为质数，b 为正整数，且29(2)509(4511)a b a b +=+ 求a ，b 的值.解：将原等式整理为关于b 的一元二次方程：0509436)51150936(922=⨯-+⨯-+a a b a b ，由于b 为正整数，则方程判别式)72511(509)509436(94)51150936(2222a a a a -=⨯-⨯⨯-⨯-=∆是完全平方数，即a 725112-为完全平方数，设)(7251122N t t a ∈=-，则a t 7251122=-，即a t t 72)511)(511(=+-，由于1022)511()511(=++-t t ，故)511(),511(t t +-同为奇数或者同为偶数，且不同是被3整除.当2=a 时，检验得2725112⨯-不是完全平方数当3=a 时，检验得3725112⨯-不是完全平方数当5≥a 时，由上面分析可知18436218436272⨯=⨯=⨯=⨯=a a a a a 共4种分解方式可能满足条件.当⎩⎨⎧=+=-a t t 365112511时，385=a 不是整数，当⎩⎨⎧=+=-a t t 185114511时，9509=a 不是整数，当⎩⎨⎧=+=-365112511t a t 或⎩⎨⎧=+=-at t 251136511时，2917493⨯==a 不是质数，当⎩⎨⎧=+=-a t t 451118511时，251=a 是质数，此时只有7=b 满足条件，综上所述，251=a ，7=b . 附：一。

联合杯决赛(数学)试题及答案