FSAE悬架动力学仿真与优1

合集下载

FSAE赛车悬架的优化设计及分析

2、阻尼：阻尼的大小直接影响赛车的反弹速度和行驶平顺性。阻尼过大，赛车反弹过快，会影响赛车的操控性和稳定性；阻尼过小，则会导致赛车行驶平顺性降低。
3、几何形状：悬架的几何形状决定了赛车在不同行驶状态下的性能表现。例如，多连杆悬架可以提供更好的操控性和稳定性，但需要更高的技术要求和更复杂的结构设计。
二、大学生方程式赛车悬架的设计
1、确定悬架类型：大学生方程式赛车通常采用麦弗逊式独立悬架，这种悬架具有结构简单、重量轻、占用空间小等优点。
2、选择合适的材料：考虑到赛车的轻量化和刚度需求，通常会选择高强度铝合金作为悬架的主要材料。
3、确定弹簧刚度和阻尼：弹簧刚度需要根据赛车重量和赛道特性进行选择，而阻尼则需根据驾驶风格和赛道条件进行调整。
1、按照设计图纸进行前期准备
在制造阶段，首先要按照设计图纸进行前期准备，包括加工制造、组装等。要确保各个零部件的尺寸和性能符合设计要求，同时要对材料和加工工艺进行严格把关，确保赛车制造的质量。Biblioteka 2、安装动力装置和其他附件
在制造过程中，要安装发动机、变速器等动力装置，并连接相关管路和附件。在这个过程中，要保证各个零部件之间的连接牢固可靠，同时要确保管路和线路的布置合理，不会影响赛车的性能和安全性。
二、FSAE赛车悬架设计
FSAE赛车的悬架设计需要充分考虑赛车性能的要求和实际行驶情况。一般来说，FSAE赛车的悬架设计需要考虑以下几个方面：
1、刚度：悬架的刚度是决定赛车操控性和舒适性的关键因素。刚度过高会导致赛车过于僵硬，操控性虽然好，但舒适性会降低；刚度过低则会导致赛车过于软弱，操控性降低，同时也会影响赛车的稳定性。
2、性能测试与评估：在完成悬架设计后，需要进行实际的性能测试和评估。这包括在实验室进行振动测试、刚度测试等，以及在赛道上进行实际的驾驶测试。根据测试结果对设计进行相应的调整和优化。

悬架杠杆比简述【FSAE技术组资料】

悬架杠杆比简述1.悬架简介悬架是汽车的车架（或承载式车身）与车桥（或车轮）之间的一切传力连接装置的总称，其作用是传递作用在车轮和车架之间的力和力扭，并且缓冲由不平路面传给车架或车身的冲击力，并衰减由此引起的震动，以保证汽车能平顺地行驶，如图1所示。

图1 悬架示意图2.悬架简化模型我们将悬架的杆件运动简化为一个简单的曲柄摇杆机构。

在滑块上下运动的过程中，弹簧会随着三角块的旋转发生伸长或压缩。

我们将滑块的位移量与弹簧的伸长或压缩量的比值定义为悬架的杠杆比，如图2所示。

12图2 悬架简化机构图假设l 为滑块的位移量，d 为弹簧的伸长或压缩量，进过一系列的推导我们可以得知：011()()233ii i i i Lel el ele Le πααγπθθα+-+++=+（1）0110121()()22i i i x d l e l e l e αγθαγγθπθ+-++--=-- （2）其中部分变量的定义略去，我们可以得到弹簧的伸长或压缩量d 关于滑块的位移量l 的关系式。

通过一定的比例关系换算我们最总可以得到前、后悬架杠杆比示意图如图2 1-2 2所示：图2 1 前悬架杠杆比示意图。

横坐标是轮胎上下颠簸的位移，即简化示意图中滑块上下的位移，范围为（-25 4，+25 4），纵坐标为轮胎位移与减震弹簧压缩量之比。

3图2 2 后悬架杠杆比示意图。

横坐标是轮胎上下颠簸的位移，即简化示意图中滑块上下的位移，范围为（-25 4，+25 4），纵坐标为轮胎位移与减震弹簧压缩量之比。

3.simulink仿真Simulink是MATLAB最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。

在该环境中，无需大量书写程序，而只需要通过简单直观的鼠标操作，就可构造出复杂的系统。

Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点，并基于以上优点Simulink 已被广泛应用于控制理论和数字信号处理的复杂仿真和设计。

基于ADAMS的悬架系统动力学仿真分析与优化设计

基于ADAMS的悬架系统动力学仿真分析与优化设计一、概述本文以悬架系统为研究对象，运用多体动力学理论和软件，从新车型开发中悬架系统优化选型的角度，对悬架系统进行了运动学动力学仿真，旨在研究悬架系统对整车操纵稳定性和平顺性的影响。

文章提出了建立悬架快速开发系统平台的构想，并以新车型开发中的悬架系统优化选型作为实例进行阐述。

简要介绍了汽车悬架系统的基本组成和设计要求。

概述了多体动力学理论，并介绍了利用ADAMS软件进行运动学、静力学、动力学分析的理论基础。

基于ADAMSCar模块，分别建立了麦弗逊式和双横臂式两种前悬架子系统，多连杆式和拖曳式两种后悬架子系统，以及建立整车模型所需要的转向系、轮胎、横向稳定杆等子系统，根据仿真要求装配不同方案的整车仿真模型。

通过仿真分析，研究了悬架系统在左右车轮上下跳动时的车轮定位参数和制动点头量、加速抬头量的变化规律，以及汽车侧倾运动时悬架刚度、侧倾刚度、侧倾中心高度等侧倾参数的变化规律，从而对前后悬架系统进行初步评估。

1. 悬架系统的重要性及其在车辆动力学中的作用悬架系统是车辆的重要组成部分，对车辆的整体性能有着至关重要的作用。

它负责连接车轮与车身，不仅支撑着车身的重量，还承受着来自路面的各种冲击和振动。

悬架系统的主要功能包括：提供稳定的乘坐舒适性，保持车轮与路面的良好接触，以确保轮胎的附着力，以及控制车辆的姿态和行驶稳定性。

在车辆动力学中，悬架系统扮演着调节和缓冲的角色。

当车辆行驶在不平坦的路面上时，悬架系统通过其内部的弹性元件和阻尼元件，吸收并减少来自路面的冲击和振动，从而保持车身的平稳，提高乘坐的舒适性。

同时，悬架系统还能够根据车辆的行驶状态和路面的变化，自动调节车轮与车身的相对位置，确保车轮始终与路面保持最佳的接触状态，以提供足够的附着力。

悬架系统还对车辆的操控性和稳定性有着直接的影响。

通过合理的悬架设计，可以有效地改善车辆的操控性能，使驾驶员能够更加准确地感受到车辆的行驶状态，从而做出更为精确的操控动作。

基于ADAMS／Insight的FSAE赛车前悬架参数优化分析

束、主销内倾角为优化目标，运用了ＡＤＡＭＳ／Ｉｎｓｉｇｈｔ，采用二水平部分因子实验设计方法，对影响前轮定位参数因素进行灵敏度分析，优化了灵敏度较高的因素。优化后前轮定位参数随轮跳的变化得到了改善，有利于提高
整车的操纵稳定性。
ＯｐｔｉｍｉｚａｔｉｏｎＡｎａｌｙｓｉｓｏｆＦｒｏｎｔＳｕｓｐｅｎｓｉｏｎＰａｒａｍｅｔｅｒｏｆＦＳＡＥＲａｃｉｎｇＣａｒｗｉｔｈＡＤＡＭＳ／Ｉｎｓｉｇｈｔ
ａｎａｌｙｚｅｄｗｉｔｈｓｅｃｏｎｄｌｅｖｅｌｆａｃｔｏｉａｒｌｅｘｐｅｉｍｅｒｎｔｄｅｓｉｇｎｍｅｔｈｏｄ．Ｔｈｅｒｅｓｕｌｔｓｈｏｗｓｔｈａｔｔｈｅｃｈａｎｇｅｏｆｆｒｏｎｔｗｈｅｅｌｐｏｓｉｔｉｏｎ
［关键词］ＦＳＡＥ赛车；ＡＤＡＭＳ／Ｉｎｓｉｇｈｔ；前轮定位参数；优化设计［中图分类号］Ｕ４６１．６；Ｕ４６９．６＋９６［文献标志码］Ａ［文章编号］１６７３ — ３１４２（２０１３）０３ — ０００６ — ０３
第５１卷第３期
Ｖ０ｌ５ｌＮｏ．３
农业装备与车辆工程
ＡＧＲＩＣＵＬＴＵＲＡＬＥＱＵＩＰＭＥＮＴ＆ＶＥＨＩＣＬＥＥＮＧＩＮＥＥＲＩＮＧ

基于ADAMS的FSAE赛车双横臂悬架的仿真优化

的］。
１双横臂独立悬架仿真模型的建立悬架的建模主要是在ＡＤＡＭＳ／Ｃａｒ模块中完成
图１双横臂独立前悬架模型
的，为了建模的方便，应对前悬架系统进行适当简化和假设＿５］： ① 悬架中除橡胶元件和弹性元件外，所有零部件都认为是刚体，同时零部件之间的所有连接都简化为铰接，内部间隙不计； ② 认为左、右两侧非悬挂质量系统相同，关于赛车纵向中分面对称； ③车轮上下跳动时，假设车身相对于地面是静止的，即没有上下位移。从机械实物或者ＣＡＤ软件中获取硬点的空间坐标，给机械系统建立运动部件、施加相应的约束，并定义模型中的相关部件、弹性元件、铰链及相应的外界条件，从而建立起机械系统的运动学模型，如图１所示。
一
１．６６６３。～一０．５７８６。。
基于ＡＤＡＭＳ的ＦＳＡＥ赛车双横臂悬架的仿真优化
柳威，师忠秀，于渊，王甜甜
（青岛大学，山东青岛２６６０７１）
摘要：在ＡＤＡＭＳ／Ｃａｒ模块中建立ＦＳＡＥ赛车双横臂悬架模型，对模型进行运动学仿真，分析仿真结果，确
运动学性能得到改善。
关键词：ＦＳＡＥ赛车；ＡＤＡＭＳ）双横臂独立悬架；建模仿真；优化分析

基于ADAMS的FSAE赛车悬架优化设计

精度。本文基于ＡＤＡＭＳ软件，对某款ＦＳＡＥ赛
车悬架进行仿真并优化其结构参数以提高其性能。悬架的优化设计是汽车设计的热点问题之一
［１－２］。
汽车悬架由弹性元件、阻尼元件、导向机构和 Βιβλιοθήκη １、模型的建立
关键词：悬架；优化；仿真
中图分类号：Ｕ４６３．３３＋１文献标识码：Ａ文章编号：１６７１ — ７９８８（２０１３）０７－２７－０３
ＯｐｔｉｍｉｚａｔｉｏｎｏｆｔｈｅｓｕｓｐｅｎｓｉｏｎｏｆＦＳＡＥｒａｃｉｎｇｃａｒｂａｓｅｄｏｎＡＤＡＭＳ
Ｋｅｙｗｏｒｄｓ：ｓｕｓｐｅｎｓｉｏｎ，ｏｐｔｉｍｉｚａｔｉｏｎ，ｓｉｍｕｌａｔｉｏｎ．
ＣＬＣＮＯ．：Ｕ４６３．３３＋１ＤｏｃｕｍｅｎｔＣｏｄｅ：ＡＡｒｔｉｃｌｅＩＤ：１６７１－７９８８（２０１３）０７－２７－０３
减震器等组成，是汽车车身的一个重要总成，结构１．１参数的确定
复杂、精密。若按照传统设计模式在样机基础上进
由于赛车对车辆的操作稳定性要求很高，同时
行测试并改进优化，不仅成本巨大，而且悬架本身为了尽可能地降低整车质量，提高车辆的舒适性和性能也很难有显著地提升。随着计算机技术的发展，行驶稳定性，采用不等长双叉臂独立悬架作为本次为悬架的优化设计提供了便利，也涌现出很多新的赛车的前、后悬架。参考国内外赛车悬架的相关布优化算法，如刘顺安【３】的ＰＳＯ— ＢＰ网络算法对悬架进置并结合实际情况，本次赛车前、后悬架模型设计行优化，解来卿【４】采用磁力悬架并运用神经网络控初始参数如下：制的方法进行悬架的优化设计。将虚拟样机技术应 ① 前悬模型：前轮距１２００ｍｍ；上横臂每根杆长２４６．６ｍｍ，

基于ADAMS的FSAE赛车双横臂前悬架优化设计_杨岳

基于ＡＤＡＭＳ的ＦＳＡＥ赛车双横臂前悬架优化设计杨岳，邹铁方（长沙理工大学汽车与机械工程学院，湖南长沙　４１０００４）摘要：为了提高ＦＳＡＥ（中国大学生方程式汽车大赛）赛车的操纵稳定性，对赛车双横臂前悬架进行优化设计。

根据已建好的ＵＧ三维模型得到某赛车前悬架主要硬点坐标，然后利用ＡＤ－ＡＭＳ／Ｃａｒ建立前悬架虚拟样机模型并进行仿真试验，指出悬架设计的不足；利用ＡＤＡＭＳ／Ｉｎｓｉｇｈｔ进行优化分析，得到所考虑硬点位置对各项性能参数的影响灵敏度，再根据所得灵敏度对硬点位置进行优化，得到最合理的性能参数组合，进而获得最优的双横臂前悬架模型；最后对优化前后的模型进行仿真与对比，结果显示优化后悬架的运动学特性得到了一定改善。

关键词：汽车；ＦＳＡＥ赛车；双横臂前悬架；优化设计；ＡＤＡＭＳ中图分类号：Ｕ４６９．６文献标志码：Ａ文章编号：１６７１－２６６８（２０１３）０５－００２３－０５在ＦＳＡＥ（中国大学生方程式汽车大赛）赛车设计中，各车队在综合考虑各方面设计因素后，普遍采用双横臂推拉杆式独立前悬架。

悬架性能参数如车轮定位参数等对赛车的操纵稳定性起着很关键的作用。

在悬架设计过程中，利用多体动力学软件ＡＤ－ＡＭＳ对悬架性能进行优化设计成为一种普遍手段櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙櫙。

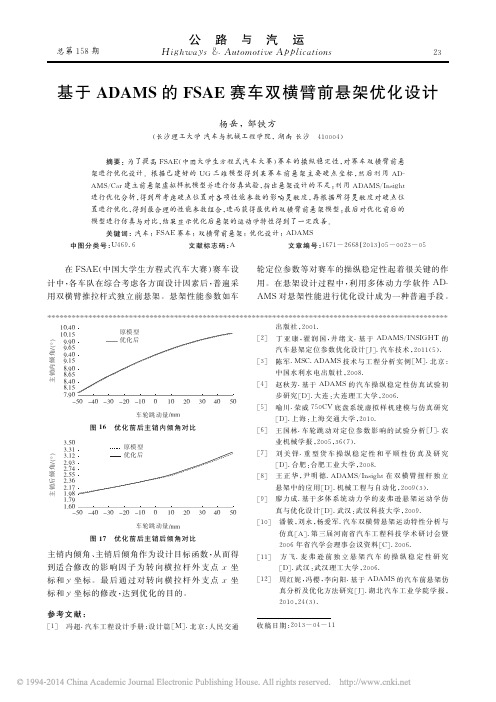
主销内倾角/（°）10.4010.159.909.659.409.157.905040302010-10-20-30-40-50车轮跳动量/mm原模型优化后8.908.658.408.15图１６　优化前后主销内倾角对比主销后倾角/（°）3.503.313.122.932.742.551.6050403020100-10-20-30-40-50车轮跳动量/mm原模型优化后2.362.171.981.79图１７　优化前后主销后倾角对比主销内倾角、主销后倾角作为设计目标函数，从而得到适合修改的影响因子为转向横拉杆外支点ｘ坐标和ｙ坐标。

FSAE实用赛车模拟器支架优化及关键部件设计

Mechanical Engineering and Technology 机械工程与技术, 2017, 6(4), 311-323Published Online October 2017 in Hans. /journal/methttps:///10.12677/met.2017.64038The Optimization of FSAE FunctionalRacing Simulator Bracket andthe Design of Its Main PartWenpu Wang, Ningning Liu, Yunjie YanSchool of Automotive Engineering, Shanghai University of Engineering Science, ShanghaiReceived: Oct. 8th, 2017; accepted: Oct. 24th, 2017; published: Oct. 30th, 2017AbstractIn this paper, a simulator bracket for driver training is designed and manufactured with the back-ground of 2016 Formula Student Electricity China. The whole design process is based on the rules of the competition, the maximum reduction of drivers in the car sitting posture, improve the driv-er’s situation reproduction ability, and to meet the requirements of the process to minimize the cost. The main work of this paper is to complete the design and calculation of the car simulator bracket, the utility analysis of the simulator bracket and the manufacture of the simulator bracket.The research and manufacture of this topic provide reference for the design of the training mode of FSAE driver in the future, and summarize the experience and lessons of the design and manu-facturing process, which has a certain engineering value.KeywordsSimulator Bracket, Driver Training, SAE 95%, Situation ReproductionFSAE实用赛车模拟器支架优化及关键部件设计王问璞，刘宁宁，严赟杰上海工程技术大学汽车学院，上海收稿日期：2017年10月8日；录用日期：2017年10月24日；发布日期：2017年10月30日王问璞等摘要本论文以2016 FSEC 中国大学生电动方程式汽车大赛为背景，设计并制造了一套用于车手训练的模拟器支架。

基于TTC轮胎数据的FSAE赛车悬挂系统设计-杨昌龙

2.2 主销、磨胎半径和机械拖距 ...................................................7
2.3 瞬时中心和侧倾中心 .............................................................8
2.4 阿卡曼转向 ......................................................................... 10
4.4.4 草图和硬点 ...................................................................... 37
4.5 本章小节 ............................................................................ 39
In this paper, first design the race car suspension systems by each parameter, and establish the suspension geometry. Use Matlab software application processing raw tire test data, selected tires through comparing, figure some of the tire’s features out. Than in ADAMS / CAR software to create a virtual prototype vehicle, and analyze the suspension system parameters how effect on the overall performance of the car. Each connected node of the force in the typical operating conditions arb outputted for finite element analysis. Finally, work with the team to c design the structural of suspension, then complete the RACE CAR design, to create a Formula Lengend of HIT.

大学生方程式赛车悬架系统的设计研究

大学生方程式赛车悬架系统的设计研究摘要：悬架是车架（或承载式车身）与车桥（或车轮）之间的一切传力装置的总称。

一般由弹性元件、减震器和导向机构组成，在多数的轿车和客车上还设有横向稳定杆。

悬架的功用是把路面作用于车轮上的垂直反力（支承力）、纵向反力（驱动力和制动力）和侧向反力以及这些反力所造成的力矩都传递到车架（或承载式车身）上，保证汽车的正常行驶。

关键词：悬架系统；刚度；横向稳定杆；计算1.悬架的设计要求具有合适的衰减震动的能力；保证汽车具有良好的操纵稳定性；汽车制动或加速时，要保证车身稳定，减少车身纵倾，转弯时车身侧倾角要合适；结构紧凑、占用空间尺寸要小；安装方便并易于调整；尽可能的传递车身与车轮之间的各种力和力矩，保证强度同时做到轻量化。

2.整车参数整车质量m（包含车手60）：300kg，前后轴距L：1550mm，前轮距B1：1250mm，后轮距B2：1200mm，质心高度h：300mm，前悬静态侧倾中心高度Z RF：15m，后悬静态侧倾中心高度Z RR：25mm，前后载荷比：45:55。

3.设计计算3.1 偏频选定汽车偏频是指汽车前、后部分车身的固有频率（用和表示）。

不同范围的偏频适用于不同类型、不同用途的汽车，一般的取值范围：普通轿车0.5~1.5，适中负升力赛车1.5~2.0，高负升力赛车3.0~5.0以上。

FSAE赛车的前后悬架偏频范围在2.4~3.5，且偏频的大小决定了悬架刚度的大小，影响赛车的舒适性和操纵性能。

综上考虑，前后悬架偏频定为：，。

3.2 悬架刚度计算（1）质心到侧倾轴线的距离计算：图1 横向载荷转移几何如图1所示，，，。

（2）悬架乘适刚度计算：（赛车簧下质量为60kg）赛车簧上质量，前轴左右单侧车轮的簧上质量，后轴左右单侧车轮的簧上质量，前轴左右单侧悬架的乘适刚度，后轴左右单侧悬架的乘适刚度。

（3）前后悬架传动比计算：（轮胎刚度）前后悬架的车轮中心刚度，，前悬架弹簧刚度为，后悬架弹簧刚度为，前悬架传动比，后悬架传动比。

基于响应面法的FSAE赛车悬架优化设计

基于响应面法的FSAE赛车悬架优化设计摘要:用响应面法对大学生方程式赛车悬架参数进行优化设计。

基于Adams/Car构建双叉臂悬架模型;在Adams/Insight模块中分析出影响各悬架参数的主要因子;对比优化前与优化后车轮定位参数可知,实现了外倾角和前束角的优化目的,其它车轮定位参数的变化范围也有所缩小。

在一定程度上提高了赛车的操纵稳定性,为实车的制造提供了可靠的数据依据。

关键词:响应面法Adams 双叉臂悬架优化设计Optimization of Suspension Design on FSAE Racing Car based on Response SurfaceAbstract:Response surface methodology has been used for the structure parameters optimization design of formula student racing car. Double wishbone suspension model was built based on ADAMS/Car.The main factors effecting alignment parameters were found out by using the Adams/Insight module.It is concluded by comparing the wheel alignment parameters before and after optimization that not only the optimization objective of toe-in and camber is achieved,but also the scope of change of other wheel alignment parameters is limited down.To a certain extent,improve the handling stability of the car,for real vehicle manufacturing provides a reliable data basis.Key Words:Response surface;Adams;Double wishbone suspension;Optimization design中国大学生方程式汽车大赛是由中国汽车工程学会主办,旨在由大学生构想、设计、制造一辆小型方程式赛车并参加比赛。

大学生方程式赛车制动系统设计与优化

大学生方程式赛车制动系统设计与优化王超;周岳斌【摘要】根据大学生方程式赛车(FSA E)的比赛规则对赛车制动性能的设计要求,确定了赛车制动系统方案和主要制动参数,对制动系统关键零部件进行了仿真分析及优化设计.实际测试和整车运行表明,所设计的制动系统具有较好的稳定性和操纵性,满足了赛车整体性能的需要,对大学生方程式赛车制动系统的设计有一定的指导意义和参考价值.【期刊名称】《装备制造技术》【年(卷),期】2016(000)010【总页数】4页(P68-71)【关键词】FSAE;制动系统;设计优化;仿真分析【作者】王超;周岳斌【作者单位】湖北文理学院机械与汽车工程学院,湖北襄阳 441053;湖北文理学院机械与汽车工程学院,湖北襄阳 441053【正文语种】中文【中图分类】TH122制动系统作为汽车底盘机构四大组成部分之一，其主要作用是使汽车按照驾驶员的要求减速或停止，对汽车起到重要的作用，对赛车更起着不可替代的作用，同时在紧急情况下保护赛车手的生命安全，并与赛车悬架系统和转向系统相配合，达到行驶和操作的稳定性。

制动系统对车手与赛车的安全保障至关重要，也是赛车发挥动力性和操纵稳定性的前提条件。

设计制造并调校出性能优异的制动系统是整车性能与安全的基本保证。

本文以2015年湖北文理学院TSD车队赛车为例，对大学生方程式赛车的制动系统进行了设计和优化。

方程式赛车制动系统设计最终目的就是达到规则要求的四轮同时抱死，同时对成本、轻量化等也有具体要求[1]。

为达到规则要求，同时兼顾安全和效能，湖北文理学院TSD赛车制动系统的制动回路布置如图1所示，制动回路采用H型并联液压双回路以及制动力分配可调的四轮盘式制动系统。

并联液压双回路可有效减小管路泄漏或失效带来的严重后果，便于前、后制动力的分配，液压制动布置简单且效率高、效果好。

通过制动力分配调节装置（平衡杆）可使赛车实现最佳前、后制动力分配并保证四轮同时抱死。

盘式制动器相对鼓式制动器质量轻，热稳定性好，具有更高的制动效率和制动效能[2]。

FSAE悬架

2011年4月机电技术77作者简介：郭刚(1985-)，男，硕士研究生，研究方向：汽车安全设计。

F-SAE 赛车后悬架优化赛车后悬架优化分析分析郭刚1 葛晓宏1，2 黄红武1，2(1.厦门大学机电系，福建厦门 361005；2.厦门理工学院，福建厦门 361024)摘要:运用多体动力学软件ADAMS/VIEW 模块建立F-SAE 赛车后悬架模型，并对模型进行仿真分析，研究分析FSAE 赛车运动中后悬架随车轮上下跳动时定位参数的变化规律，评价悬架数据合理性。

采用优化分析对悬架不合理数据进行优化，进一步改善悬架系统性能，以提高产品开发质量。

关键词：赛车独立悬架；ADAMS ；优化分析中图分类号：U463.33 文献标识码：A 文章编号：1672-4801(2011)02-077-03汽车悬架是车身和车轮之间的一切传力连接装置的总称，它把路面作用于车轮的支承力、牵引力、制动力和侧向力以及这些力所产生的力矩传递到车身上，以保证汽车的正常行驶。

悬架系统是汽车重要的组成部分，汽车悬架系统的性能是影响汽车行驶平顺性、操纵稳定性和安全性的重要因素。

由于汽车悬架部件之间运动关系复杂，一般都设计成主销内倾和后倾，并且控制臂轴也大多倾斜布置，这些都给悬架的运动学、动力学分析带来很大困难。

随着计算机技术不断提高，国内外研制开发了很多专门用于机械构件运动仿真分析及优化设计的专用软件，ADAMS 软件就是其中之一。

ADAMS 是虚拟样机分析的应用软件，用户可以运用该软件非常方便地对虚拟机械系统进行静力学、运动学和动力学分析；该软件还是虚拟样机分析开发工具，其开放性的程序结构和多种接口，可以成为特殊行业用户进行特殊类型虚拟样机分析的二次开发工具平台。

1 利用ADAMS/VIEW 创建汽车后悬架模型[5] [7] [9]1.1 悬架模型的建立由于较复杂的模型在计算机中难以建立，所以对所建立的模型做如下简化和假设：(1) 悬架中所有零部件都认为是刚体，同时零部件之间的所有连接都简化为铰链，内部间隙不计；(2) 减振器简化为线性弹簧和阻尼； (3) 各运动副内的摩擦力忽略不计； (4) 轮胎简化为刚性体。

电动方程式赛车悬架系统设计与仿真

10.16638/ki.1671-7988.2021.08.010电动方程式赛车悬架系统设计与仿真*万大千，李天宇，刘树民*，陈松利（内蒙古农业大学能源与交通工程学院，内蒙古呼和浩特010018）摘要：依托电动方程式赛车比赛要求，选取适合电动方程式赛车的悬架类型，对悬架进行合理的设计，并进行车轮定位参数的设定和刚度计算等，然后使用CATIA软件对悬架重要零部件进行建模，导入ANSYS软件对悬架的重要部件进行受应力分析。

分析结果表明，此悬架系统重要部件刚度强度符合要求，赛车安装后可以安全行驶。

关键词：电动方程式赛车；不等长双横臂式独立悬架；转向节；控制臂；摇臂；仿真分析中图分类号：U463.33 文献标识码：A 文章编号：1671-7988(2021)08-27-05Design and Simulation of Suspension System of Formula E Racing Car*Wan Daqian, Li Tianyu, Liu Shumin*, Chen Songli( College of Energy and Traffic Engineering, Inner Mongolia Agricultural University, Inner Mongolia Hohhot 010018 )Abstract:Relying on electric formula racing requirements, selecting suitable for electric formula of suspension type, reasonable design of suspension and wheel alignment parameters setting and stiffness calculation, etc., and then use the CATIA software modeling for the suspension important parts, import of ANSYS software by the stress analysis was carried out on the important parts of the suspension. The analysis results show that the stiffness and strength of the important components of the suspension system meet the requirements, and the car can drive safely after installation.Keywords: Formula E racing; Unequal length double wishbone type independent suspension; Steering knuckle; Control arm; Rocker arm; The simulation analysisCLC NO.: U463.33 Document Code: A Article ID: 1671-7988(2021)08-27-05前言悬架系统是赛车上尤为重要的部分之一，悬架系统的好坏，某种程度上决定了赛车的整体性能的优劣。

FSAE赛车空气动力学套件优化设计

文章编号： 1009 − 444X （2021）01 − 0053 − 08FSAE 赛车空气动力学套件优化设计李嘉寅，刘宁宁，沈钰豪，谭博文，陈　焕，薛雨晴，黄碧雄（上海工程技术大学机械与汽车工程学院，上海 201620）摘要：空气动力学作为赛车的关键领域，很大程度影响着赛车各方面性能. 在满足中国大学生方程式汽车大赛（Formular Student China ，FSC ）规则（2019赛季）的前提下，提出一种赛车空气动力学套件的改进优化方案. 使用数值累进法和控制变量法的优化方法，并通过计算流体动力学（Computational Fluid Dynamics, CFD ）进行仿真，设计完成一套性能优异的空气动力学套件.与2018赛季车辆相比，该设计使赛车的负升力和的升阻比分别提高81%和91%，极大提升了整车的动力学性能.关键词：大学生方程式汽车大赛；空气动力学；计算流体动力学中图分类号： TH 122 文献标志码： ADesign and Optimization of AerodynamicsParts on a FSAE VehicleLI Jiayin ，LIU Ningning ，SHEN Yuhao ，TAN Bowen ，CHEN Huan ，XUE Yuqing ，HUANG Bixiong（ School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China ）Abstract ：Aerodynamics, as a significant field of racing car, largely affects all aspects of racing performance.The aerodynamics properties of the new season was redesigned on the premise of meeting the rules of Formula Student China (FSC) in season 2019. By using numerical progressive methods and control variate method to optimize, and carrying computational fluid dynamics (CFD) to simulate, a set of aerodynamics parts with outstanding performance was designed and completed. The results show that compared to the season 2018, the new design not only increases the downforce and lift-to-drag ratio of the racing car respectively by 81% and 91%, but also greatly improves its kinetic performance.Key words ：formula society of automotive engineers (FSAE)；aerodynamics ；computational fluid dynamics (CFD)大学生方程式赛车大赛（Formula Society of Automotive Engineers ，FSAE) 由国际汽车工程师学会(Society of Automotive Engineers (SAE)International)于1978年开办，在当今世界内被视作大学生的“F1方程式赛车”，该赛事不只是单纯的竞速比赛，更是一项考察车辆性能设计的比赛.参赛者需要根据比赛规则在规定时间内设计制作一辆性能优异的方程式赛车.收稿日期： 2019 − 04 − 18基金项目：上海市大学生创新创业活动计划资助项目（E3-0800-18-01205）作者简介：李嘉寅（1998 − ），男，在读本科生，研究方向为车辆工程. E-mail ：****************通信作者：刘宁宁（1987 − ），男，实验师，硕士，研究方向为车辆NVH 测控技术. E-mail ：****************第 35 卷第 1 期上海工程技术大学学报Vol. 35 No. 12021 年 3 月JOURNAL OF SHANGHAI UNIVERSITY OF ENGINEERING SCIENCEMar. 2021赛车同其他车辆一样，是一种高度复杂的空气动力学装置. 由于其较小的离地间隙，导致周围的气流更加复杂，使得赛车在行驶中产生更多的阻力和紊流. 在悬架、轮胎、动力方面已经改进的情况下，良好的空气动力学套件（以下简称空套）则可以极大提高赛车性能. 其主要目标是在引进较小阻力的前提下提供较高的下压力来增加汽车的抓地力，产生牵引力. 空气动力学下压力作为赛车性能中最重要的因素之一，在制动、转向、加速度等方面有着无可比拟的作用[1].由于气动力不同于惯性力，空套可以在较小质量增加（套件的自重）的条件下，极大增加机械抓地力，从而提高轮胎的工作效率，获得更好的路面附着条件. 目前，国外的空气动力学套件设计已步入研究整车流场平衡的阶段，而国内的相关研究虽起步较早，但近几年发展缓慢，绝大部分对空套的设计研究仍只停留在简单的翼型选择和最大限度榨取总气动负升力（即下压力）上，很少关注气动平衡对车辆动力学以及赛车底盘调教策略产生的影响.上海工程技术大学锐狮电动方程式赛车队于2017年首次引入空气动力学套件，并完成整套设计、加工、装配流程. 本文基于往届赛车的设计基础，对组合翼各翼片攻角进行优化，并将研究重点深化至气动平衡上，在设计之初就将各套件之间的影响考虑在内，以期解决前后下压力的分配不合理、上游套件对下游套件影响过大等问题.1 研究方法赛车空气动力学套件最基础和主要的组成部分是翼型. 翼型参数包括弦长、倾角、攻角、展宽比、前后缘半径等. 考虑设计成本因素，优化攻角远比从数不尽的翼型库中挑选最合适的翼型有效率得多. 良好的攻角设计组合不仅可以提供较大的下压力，而且不会产生过多阻力. FSAE赛车多采用组合翼来提高翼片获取下压力的上限，组合翼中各个翼片存在相对几何关系：主翼攻角、襟翼相对攻角、缝道（Gap）水平距离、缝道竖直距离.然而在实际设计中，这些相对几何关系都较为复杂，与最后产生的下压力并不呈现明确的线性关系，这使得设计变成多变量问题.计算流体力学（Computational Fluid Dynamics，CFD）有限元分析方法能够执行CAD模型的理论测试计算. 虽然其精度比不上风洞试验，但却克服了后者的局限性. 目前，CFD可以分析从层流到湍流、定常到非定常、不可压到可压、无黏到有黏的几乎所有的流动现象[2]. 一般来讲，物体表面流体的未知量包括：流体在X、Y、Z方向上的速度、流体密度、温度和压强. 一般在赛车空气动力学中，密度和温度视为常量. 本质上，CFD通常是计算物体表面流速的改变. 本文将主要对各套件的组合翼攻角等进行优化设计分析，从而获得一套性能优异的空气动力学套件.2 模型建立及前处理2.1 三维模型2018赛季整车CAD模型如图1所示. 本研究在其设计基础上保留优良翼型及整体布置思路，然后在理论研究基础上，对空气动力学套件进行概念设计和优化选型；之后利用CATIA软件进行设计建模，前翼主翼选取升力系数和最大厚度较为均衡的AH 79-100B为翼型，通过宏命令精确导入到CATIA中. 为增大底板气流流量并减少底部能量的损失，主翼采用抬高前翼中部的变截面设计，建模使用多截面曲面功能一次成型. 襟翼的设计尽量在不损失前翼下压力的前提下减小近车身侧的弦长并提升内侧翼型的攻角，以达到将外侧气流抽吸至内侧的目的，在CATIA中同样采用变截面曲面来实现建模. 2019赛季整车CAD模型如图2所示.图 1 2018赛季整车CAD模型Fig. 1 CAD model of whole vehicle in season 2018考虑到CFD分析的时间效率，对车身及车体外部的驾驶员头盔和轮胎进行简化处理. 本文主要针对空气动力学套件进行设计分析，通过对阻· 54 ·上海工程技术大学学报第 35 卷塞比的计算得出计算域的大小：计算域长度为尾翼的10倍，高度为翼面半宽的5倍，以此保证不会出现回流，进而确保分析精度[3].2.2 控制方程和湍流模型结合赛事实际行驶工况，赛车车速一般为60 km/h ，空气密度变化不大，可以近似看成是常数，因此尾翼周围空气为不可压缩流体[4]. 根据雷诺理论，流动属于湍流，因而赛车空气动力学套件气动力的模拟属于求解湍流流动问题，采用的控制方程为三维不可压缩的雷诺平均连续方程和雷诺平均N-S 方程，即u ′i u ′j 式中：u i 为略去平均符号的雷诺平均速度分量；ρ为密度；p 为压强；、为脉动速度；σij 为应力张量分量.湍流模型采用Realizable k -ε模型[5]，该模型有利于代表各种不同尺度涡间能量谱的传递，可以有效用于不同类型的流动模拟. 该模型包括湍流动能（k ）方程和湍流耗散率（ε）方程. 关于k 的湍流动能方程为关于ε的湍流耗散方程为其中式中：μt 为湍流黏度；v 为运动黏度；ρ为密度；G k 为平均速度梯度引起的湍动能的生成项；G b 为浮力引起的湍动能的生成项；Y M 为可压缩湍流对总体耗散率的脉动膨胀的贡献项；C 2、C 1ε和C 3ε为常数；σk 与σε为关于k 与ε的湍流普朗特数；S k 与S ε为CFD 用户自定义源项；S 为平均应变率张量模量. 由于Realizable k -ε在湍流黏度计算中引入旋转和曲率有关的内容，并且ε方程的第3项不具有奇异性，这与Standard k -ε模型和RNG k -ε模型有很大区别[6].在CFD 模拟中对尾翼，前翼等空气动力学套件附近的流动特征、下压力和升阻比进行分析. 然后在完成优化的基础上进行整合计算，得到整车分析数据. 根据整车分析结果确定最终方案，并且将最终优化方案用于实车制造并进行实车性能测试.2.3 模型前处理使用STAR-CCM+完成计算域和网格的绘制，分析尾翼的计算域网格如图3所示.图 2 2019赛季整车CAD 模型Fig. 2 CAD model of whole vehicle in season 2019(a) 外部YZ X图 3 计算域网格Fig. 3 Computational domain grid第 1 期李嘉寅等：FSAE 赛车空气动力学套件优化设计· 55 ·网格大小的计算根据边界层计算器输入Y+=30，得出雷诺数Re=1×106. 下边界层总厚度d为0.021 6 m，计算得到外部体网格的单元格目标大小约为0.1 m. 由于不同的流动问题数值解法不同，需要的网格形式有一定的区别，但生成网格的方法基本一致. 网格可以分为结构网格(Structured Grid)和非结构网格(Unstructured Grid)两大类. 结构网格在空间上比较规范，网格往往是成行成列分布的，行线和列线明显；而非结构网格在空间分布上没有明显的行线和列线. 外流场计算常用的体网格类型有四面体网格(Tetrahedral Mesh)、Trimmed网格、多面体网格(Polyhedral Mesh)和边界层网格(Prism Mesh)[6].考虑到赛车造型复杂，使用非结构性网格，网格中的每个元素都可以是二维多边形或者三维多面体，其中最常见的是二维三角形以及三维四面体. 这里使用STAR-CCM+中多面体网格，其结合了四面体网格划分速度快和六面体网格精度高的特点，单个网格可同时与相邻的12或14个网格进行交互，这也极大减少了网格的数量，加快了计算效率，通常多面体网格的收敛速度比四面体要快接近一倍，比六面体也要快40%.2.4 边界条件参考文献[7]，边界类型有进口（Inlet），出口(Outlet)、对称面(Symmetry)和壁面(Wall). 进口设置为速度进口(Velocity inlet)，速度进口湍流强度为0.5%，湍流速率=4×计算域面积/计算域周长，流速u为16.67 m / s，出口设置为压力出口(Pressure outlet)，压力出口的湍流强度设置为0.5%，湍流速率=4×计算域面积/计算域周长. 为使仿真更贴近实际，地面设置为滑移壁面，滑移速度为16.67 m / s，车轮设置为旋转壁面，在地面上做纯滚动. 介质设定为空气.3 CFD优化分析3.1 前翼优化设计前翼是安装于赛车前部的空气动力学装置，为赛车前部提供下压力. 同时，前翼能够很大程度上影响前轮的升阻系数，其能够引导赛车前方的气流绕过前轮从而减少前轮大量的阻力.由于FSAE赛规中有前翼外侧离地250 mm的限制，从赛车的正投影面来看，前翼并无法完全遮挡前轮，所以需要特殊的设计来尽量引导气流绕过前轮. 就整车流场的层面而言，前翼所产生的升流会影响下游组件的工作效率，而前翼作为产生下压力的组件，这种影响不可避免，故设计中应在不过多减少下压力的情况下尽可能减小前翼的升流，前翼的下压力分配对于拥有不同转向特性的赛车也有所不同.2019年的新赛车采用前翼主要起引流作用并减少对下游组件干扰从而使侧翼下压力最大化的设计思路，同时通过尽可能多的外洗气流减少前轮迎风阻力并增加前翼的效能，设计效果如图4所示. 通过对变截面翼型的利用，减小前翼近车身侧的弦长和攻角从而减少前翼的上升气流对于下游组件的影响[6]. 该翼型还能有效增加前翼的外洗效应，减小轮胎的阻力.图 4 2019赛季赛车前翼Fig. 4 Front wing of season 2019前翼部分迹线图如图5所示. 图中深蓝色区域为前翼下翼面的低压区，由于三维流场中水平方向也存在压力流动，即翼尖涡效应，所以低压区并没有遍布整个下翼面. 为降低前翼对尾翼的影响，其攻角和弦长的减小必然会造成前翼下压力的减小，为弥补下压力的损失，主翼上安装竖直的旗翼，同时竖直旗翼能够进一步强化前翼端板对于该整体区域的气流外洗，起到减少前轮阻力，增强前翼的抽吸能力，从而在不改变弦长和攻角的情况下起到进一步提高前翼升力系数的作用.设计中为尽可能减小前翼对下游组件的影响，前翼中央采用负攻角并上抬翼面以减小前翼中部静压的大小，改善前翼对下游气流的损耗. 赛车前翼压力云图如图6所示. 从图中可以看出，中部静压明显小于侧边. 在CFD软件中，将迎风速度设置为16.67 m / s，得到2个版本赛车前翼的相关结果见表1. 与2018年赛车相比，2019年赛车前翼的下压力和对前轮的影响有相当程度的提高.· 56 ·上海工程技术大学学报第 35 卷1.713X Y Z7.44513.17818.91124.64330.376−1 200−868−536−204128460速度 / (m·s −1)压力系数图 5 赛车前翼部分迹线图Fig. 5 Part of track diagram of front wingXY Z −1 200−868−536−204128460压力系数图 6 赛车前翼压力云图Fig. 6 Pressure contour of front wing表 1 前翼分析数据表Table 1 Front wing analysis data table赛车版本负升力 / N 前轮迎风阻力 / N2018年120902019年210153.2 侧翼及扩散器优化设计侧面扩散器和尾部扩散器现已成为FSAE 赛车产生较大下压力的关键元素，其本身产生的阻力较小，在地面效应的影响下对整车的下压力提升有着至关重要的作用，且这部分设计在FSAE 中有很多应用前景，侧翼的添加，减少了扩散器壁面上气流的分离，提升临界扩散角的大小，能够有效提升侧面扩散器产生下压力的能力. 侧翼及扩散器的设计效果如图7所示. 侧翼最大程度上利用侧面空间，最大化扩散角的值，同时尽可能扩大扩散器入口的大小以获得更多气流的加速. 同时后轮附近的侧翼能够有效抑制后轮生成的乱流，减少后轮的阻力.3.3 尾翼优化设计尾翼一般使用组合翼的设计方案，通过各翼之间的引流可以让襟翼在较大的攻角下不会轻易失速，同时组合翼之间的位置调整也可以减少能量损失. 2019赛季赛车尾翼主要以获得最大的下压力作为主要目的，并具有对其他部件影响不敏感的特性. 因此通STAR-CCM+仿真试验了不同的翼型，相对攻角及间隙来确定组合翼之间的最优相对位置[8]，同时在分析中加入头枕及头盔模型使其更加接近尾翼真实的工况. 最终设计效果如图8所示.图 8 2019赛季尾翼Fig. 8 Rear wing in season 2019在尾翼翼型方面，主翼选取弯度较大且升力系数在低速时较大的CH10. 襟翼在弯度不同的翼型中通过控制变量试验得到；出于对节省计算资源的考虑，且尾翼试验流动复杂程度低，故使用1/2尾翼模型完成CFD 仿真，实际下压力为表格数据的2倍，仿真数据见表2.表 2 翼型分析数据表Table 2 Airfoil analysis data table翼型负升力（相同攻角和来流速度） / NS1223278.8Clark-Y132.8综上选用S1223作为襟翼的翼型. 考虑到CFD 分析效率及问题导向，在保证复合实际工况的条图 7 侧翼及扩散器Fig. 7 Sidepods and diffuser第 1 期李嘉寅等：FSAE 赛车空气动力学套件优化设计· 57 ·件下对分析对象进行简化，即取含头盔、座枕在内的尾翼区域局部模型进行分析，分析结果如图9和图10所示. 从图9可见，端板的保压效果非常可观，也从侧面反映了上下翼面的压力分布.−1 350−980−610−204130500压力系数XYZ图 9 尾翼局域分析压力云图Fig. 9 Local analysis pressure contour of rear wingX YZ −1 200−880−560−24080400压力系数图 10 压力云图截面图Fig. 10 Cross section of pressure contour同理，选取最佳的相对攻角. 假设主翼与第1片襟翼的相对攻角为∠1，第1片与第2片襟翼的相对攻角为∠2，仿真数据见表3. 使用1/2尾翼作为仿真对象，从表中可见，负升力为实际的一半.表 3 组合攻角分析数据表Table 3 Angle of attack analysis data ofmultiple-element wings序号∠1 / (°)∠2 / (°)负升力 / N 13236139.623336140.233436141.443437142.253438142.863439142.0由分析结果，最后选用34°、38°的相对攻角，1/2组合翼的负升力达到142.8 N ，即整体在16.67 m / s迎风速度下压力为285.6 N. 为增加扩散器的抽吸能力，提升扩散角的大小，在端板底端安装梁翼（Beam wing ），将尾翼整体的环量下移，在尽量不影响组合翼本身下压力的前提下，加强尾翼与扩散器的互相作用，提升整车的空气动力学效应. 本文中梁翼由于尺寸过小，并未起到较大的作用. 若想获得更好的效果，可以设计弦长更大的梁翼，但仍要考虑其对尾翼主翼下翼面压力分布的影响.从图10可知，驾驶员的头盔与头枕也对尾翼产生了些许影响，主翼前缘下部的低压区域呈现不自然的向后扭曲. 由于头枕位置和人机由总布置所定，并不能做太大变化，只能通过对尾翼的调整来尽可能地减小影响. 结合图10及空气动力学湍流理论可知，流体绕一定攻角的翼型流动时，会在翼型前缘背风面某处脱体，形成顺时针旋转的前缘涡，同时在后部尖缘处形成逆时针旋转的后缘涡，前缘涡与后缘涡之间存在剪切层. 随着前缘涡与后缘涡的发展和相互作用，翼体绕流的流态呈周期性变化，这一点在尾翼表现尤为明显. 为避免边界层分离，可以在后期引进被动流动控制技术，例如涡流发生器改善局部的流体状态.3.4 端板优化设计端板作为赛车中不可或缺的一部分，不只是用来隐藏翼型轮廓或作为赞助商标牌. 它最重要的一点是可以确保翼片不会出现较大的负升力损失，同时减少阻力. 如果没有端板，由于上翼型上下表面压差，空气会从高压侧迁移到低压侧造成压力损失[9]. 在端板布置方面，由于翼型上方静压升高比翼型下方静压降低要小得多，因此，机翼的影响在其下方比在其上方延伸得更远，这意味着需要在翼片的下方有更大的端板面积.前翼端板首要的目的是为了稳定压差进行保压，由于前翼安装位置的特殊性，其受到地面效应影响，所以端板保压作用好坏直接决定了前翼升力系数的大小，因此端板上安置有不同种类的保压条. 由前翼的CFD 仿真可得，在无保压组件的情况下，前翼负升力为189 N ；在有保压组件的情况下，前翼负升力为210 N ，提高将近11.11%的负升力. 同时前翼端板除了稳定压差外还需要拥有良好的引流特性，引导流向前轮的气流使其偏转到外侧或底部，从而达到减小前轮阻力的效果.尾翼端板同样可以通过一些附加组件或细节修改来加强其性能，2019与2018赛季赛车尾翼端· 58 ·上海工程技术大学学报第 35 卷板都加装了前缘缺口，如图11所示. 与前翼端板类似，尾翼端板的作用之一便是保压，而前缘缺口削减了端板的面积，从而降低了保压效果，并使得下压力小幅减少；但在侧风偏航车况下，前缘开口能成为来流进入尾翼的通道，缓解此工况下尾翼下压力由于来流不足而降低的问题，减小其空气动力学敏感度，增强了稳定性.X YZ−1 200−880−560−24080400压力系数图 11 2019赛季赛车尾翼端板压力云图Fig. 11 Pressure contour of rear wing’send plate in season 2019扩展来讲，理想的尾翼板大小取决于翼型的下压力水平，下压力较低的尾翼组合产生较小的压力变化，故对周围空气压力影响延伸的距离较小，可以使用较小的端板，反之亦然. 故2019年赛车的尾翼端板长度相较2018年的尾翼端板延长约30%.4 整车结果分析与对比图12为整车迹线图，由图可知，整车流线型良好，仅在车轮后方及车身尾部形成较大涡流. 前翼有明显外洗，中部上洗较少，符合预期设计，可有效降低前轮产生的紊流并增强前翼的抽吸作用，保证侧面扩散器有更多高能气流进入，且可看出相比尾翼影响不大. 3层尾翼的设计使气流能够更加贴合后方翼型，长端板保证了尾翼的保压效果，做到了先期预期能达到的最大下压力.2019年赛车在装配优化设计的空气动力学套件后，空气动力学指标都有较大提升，见表4. 首先负升力升高至原来的181%，增加明显，但是2019年赛车的阻力系数也增加33.66%，这是由于负升力的升高会导致压差阻力的升高，也可以说是获取下压力的代价之一. 升阻比是反映赛车空气动力学效率的一个重要指标，通过比较2版赛车可以发现，2019年赛车拥有更高效率的空气动力学套件，迎风面积的骤减也是其获得高效率的原因之一. 通过对赛车总布置以及造型的优化，相比2018年赛车，2019年赛车可有效减少过去只增加外形阻力的“无用”区域，并将它们转变为带有翼的空套部件区域.表 4 整车分析数据表Table 4 Vehicle analysis data sheet赛车版本负升力 / N阻力系数升阻比迎风面积 / m2 2018年380.1 1.01 1.45 1.3122019年686.5 1.35 2.77 1.046在气动平衡方面，2018年赛车未做出相关优化，风压中心（前后气动力平衡轴）相比重心位置（车长45∶55位置处）严重靠前，即前翼下压力占比过大. 2019年赛车对此进行了考量，最终的设计方案中，通过CFD软件去计算整车相对于过重心点水平轴气动力矩（C m）来判断风压中心距离重心的远近，最终经过软件计算所得气动力矩仅为10 N·m，可将其视为与重心基本重合.由此可见，通过正确的优化方法和设计思路来引导设计，最终能收获一套高性能的大学生方程式赛车的空套优化方案.5 结语本文分别对各空气动力学套件进行优化设计，并最终通过整车分析进行方案的验证. 结果表明：2019年赛车在负升力和升阻比的设计上进一XYZ6.11212.22418.53724.44930.561−1 000−750−500−2500250速度 / (m·s−1)压力系数图 12 整车迹线图Fig. 12 Full vehicle track diagram第 1 期李嘉寅等：FSAE赛车空气动力学套件优化设计· 59 ·步优化，负升力提升达到2018年的181%；前翼的外洗效应可以有效减少前轮紊流，并且能够显著提升前翼的升阻比和下压力；尾翼端板、相对攻角和间隙是影响其下压力的3个显著要素；侧翼和扩散器能对赛车的下压力提升起很大的作用，并同时提升前翼和尾翼的工作效率.2019年赛车的空气动力学套件的优化使得负升力和升阻比相比2018年赛车有较大的进步，对赛车性能有显著的提升，对赛车后续的设计优化具有指导实践意义.参考文献：MCBEATH S. Competition car aerodynamics [M ] . 3rdEdition. England: Veloce Publishing Limited, 2017: 8.［1］傅立敏. 汽车设计与空气动力学［M ］ . 北京. 机械工业出［2］版社, 2010: 1−25;.吕立坤. 扰流板对轿车气动特性改善的数值仿真［D ］ . 长春: 吉林大学, 2006.［3］王福军. 计算流体动力学分析［M ］ . 北京: 清华大学出版社, 2004: 185−253.［4］WILCOX D C. Turbulence modeling for CFD [M ] . 2ndEdition. La Canada: DCW Industries, 1998: 174.［5］孙文. 基于CFD 的低速赛车前后翼设计［D ］ . 长沙: 湖南大学, 2016.［6］杨炜, 谢睿轩, 曹子浩, 等. 大学生方程式赛车空气动力学套件改进［J ］ . 中国科技论文，2018，13（17）：2050 − 2054.［7］邓召文, 王兵. FSC 赛车空气套件CFD 优化设计［J ］ . 汽车实用技术，2014（3）：22 − 27.［8］曾飞云. 万得FSC 赛车空气动力学特性研究［D ］ . 锦州:辽宁工业大学, 2014.［9］（编辑：韩琳）• 科研快讯 •我校李文尧副教授带领的先进储能与传感材料团队在国内主办的中科院一区期刊Green Energy & Environment 上发表了以“Realizing optimal hydrogen evolution reaction properties via tuning phosphorous and transition metal interactions”为题的研究成果.20世纪以来，国内经济的快速发展和能源消耗，迫切需要大力发展清洁可再生的清洁能源推动未来经济发展，氢能作为一种可再生能源，成为未来能源发展的重要角色之一. 电解水析氢是氢能获取的主要途径，在这项研究工作中，该团队利用过渡金属掺杂和调控策略合成一种Co-Mo-P 化合物（非均相Co x Mo 1−x P 纳米阵列），发现通过掺杂形成的包含两种掺杂的化合物的金属磷化物和金属氧化物的纳米片层，以不完全磷化的状态和掺杂的氧化物共存的形式能有效提升电催化剂析氢能力，同时可通过调控不同金属的掺杂比例来优化催化性能. 发现Co 、Mo 金属掺杂的结构有效降低电解水析氢（阴极端）和析氧（阳极端）的电位. 最终，获得材料作为析氢催化剂获得的过电位只有51.2 mV （10 mA•cm −2时）. 同时，作为另一极电催化析氧催化剂也获得了较低的过电位353 mV （10 mA•cm −2时）. 此外，在20 h 稳定性测试过程中性能基本不变，并且作为电解水的阴阳极，获得的全水解的过电位只有1.603 V （10 mA•cm −2时），是性能优异的双功能催化剂. 该项工作得到国家自然科学基金、上海市“晨光计划”、中央高校创新基金以及英国工程和自然科学研究委员会基金的支持.· 60 ·上海工程技术大学学报第 35 卷。

基于FSAE车辆动力学的转向系统设计

第16期2019年6月No.16June ，2019苏禹帆，杨伟，颜宇，李垚（江苏大学汽车与交通工程学院，江苏镇江212013）基金项目：江苏大学2018年度大学生实践创新训练项目；项目编号：201810299459W 。

作者简介：苏禹帆（1999—），男，云南曲靖人，本科生；研究方向：车辆工程。

江苏科技信息Jiangsu Science &Technology Information基于FSAE 车辆动力学的转向系统设计摘要：为保证FSAE 方程式赛车的操纵稳定性，文章综合车辆动力学建模仿真，设计出一套符合赛事并且性能优良的转向系统。

仿真结果表明：设计得到的转向系统消除了绝大部分轮跳转向，转向梯形的优化也达到较好的效果，有效提高整车操控性能。

关键词：操纵稳定性；轮跳转向；转向梯形；车辆动力学中图分类号：U270.1+1文献标志码：A0引言大学生方程式汽车大赛（Formula Student China ，FSC ），简称FSAE ，是面向大学生的综合性工程教育赛事，开办30多年来已遍及15个国家，赛事发展越来越专业化，赛车操纵性要求越来越高，对转向系统的设计要求也不断提高。

国内外对FSAE 转向系统的研究已取得很大进展，但其在杆系布置和传动比确定选取方面与传统汽车有很大区别，在确定转向传动比、优化转向梯形结构方面仍然存在缺陷，降低了赛车的操纵性能。

首先，本文以整车动力学/车辆动力学为基础，介绍了一种适用于FSAE 赛车的转向系传动比确定方案，为赛车传动比设计提供了更可靠的理论基础。

其次，结合FSAE 赛车特点介绍了赛车轮跳转向优化和转向梯形优化过程，并且利用Catia ，Matlab 等软件设计工具联合设计，提高设计的计算精度。

最后，根据设计参数建立三维模型，在Optimum Kinematics 中进行运动学仿真，分析其性能是否符合赛事要求。

由此建立一套完整的具有参考价值的FSAE 转向系统设计流程［1］。

FSAE电动方程式赛车动力系统匹配及仿真

FSAE电动方程式赛车动力系统匹配及仿真郭忠庆;高聪聪;陈潮洲【摘要】电动汽车作为新能源汽车的典型代表,催生了中国大学生方程式电动赛车电动赛车运动的产生.本设计是为将要参加FSAE比赛的赛车匹配设计合适的动力系统.根据已确定电机、电池参数,利用CRUISE进行动力性的初步仿真分析.将仿真数据和理论数据做对比,证明本文的匹配设计符合要求并且是合理的.【期刊名称】《交通节能与环保》【年(卷),期】2019(015)004【总页数】4页(P19-22)【关键词】FSAE;动力匹配;CRUISE仿真;电动汽车【作者】郭忠庆;高聪聪;陈潮洲【作者单位】陕西职业技术学院,陕西西安 710100;陕西职业技术学院,陕西西安710100;交通运输部公路科学研究院,北京 100088【正文语种】中文【中图分类】U461.20 引言随着能源危机的加深和环境问题的日益凸显，使用新能源代替石化能源在汽车中的应用已成为不可逆转的趋势。

纯电动汽车将取代燃油车和混合动力汽车，将会成为下一代的主流。

电动汽车作为新能源汽车的典型代表，催生了FSAE电动赛车的产生。

FSAE电动赛车采用驱动电机和动力电池作为动力来源，配套电机控制器可使驱动电机进行无级传动，无需传统汽车的变速箱装置，大大简化了汽车传动结构[1]。

驱动电机传动效率较高，降低了能源消耗，减轻了环境污染[8]。

而电动赛车动力系统相当于传统赛车的发动机也就是赛车的动力源和心脏，如果一辆赛车没有合适且强大的心脏，那么很难在赛场中取得优秀的成绩，所以必须严格按照规则要求匹配赛车的动力系统。

然后根据确定的电机、电池参数，利用CRUISE进行初步的动力性仿真分析，并综合考虑赛车相关性能，合理分析得到适合赛车最优状态的匹配结果。

1 电动赛车动力系统参数计算电动赛车的动力系统主要包括电机、电池及传动系统，需要进行的计算参数有：电机相关参数、电池电量计算。

1.1 原车参数及FSAE电动赛车设计目标通过对往年比赛成绩的分析，然后根据本校车队实际情况确定FSAE电动赛车的动力性能，原车参数及电动赛车设计目标如表1所示[1]。