方位角计算

合集下载

坐标距离及方位角计算公式

坐标距离及方位角计算公式坐标距离计算公式：在平面坐标系中，可以使用勾股定理来计算两个点之间的距离。

给定两个点A(x1,y1)和B(x2,y2)，它们之间的距离可以由以下公式计算：距离=√((x2-x1)²+(y2-y1)²)在三维空间中，可以使用空间直角坐标系的距离计算公式。

给定两个点A(x1,y1,z1)和B(x2,y2,z2)，它们之间的距离可以由以下公式计算：距离=√((x2-x1)²+(y2-y1)²+(z2-z1)²)方位角计算公式：方位角是指从一个点到另一个点的方向角度。

在二维平面坐标系中，可以使用反正切函数来计算两点之间的方位角。

给定两个点A(x1,y1)和B(x2,y2)，它们之间的方位角可以由以下公式计算：方位角 = atan2(y2 - y1, x2 - x1)在三维空间中，可以使用球坐标系来计算两个点之间的方位角。

给定两个点A(r1,θ1,φ1)和B(r2,θ2,φ2)，其中r表示距离，θ表示纬度，φ表示经度，它们之间的方位角可以由以下公式计算：方位角= atan2(sin(φ2 - φ1) * cos(θ2), cos(θ1) * sin(θ2) - sin(θ1) * cos(θ2) * cos(φ2 - φ1))这些公式可以通过编程语言如Python或者使用地理信息系统软件如ArcGIS来实现。

总结：坐标距离计算公式通过平面直角坐标系或者球坐标系来计算两个点之间的距离。

方位角计算公式通过反正切函数或者球坐标系来计算从一个点到另一个点的方位角度。

这些公式对于地理和导航应用非常重要，可以帮助确定地理位置和导航方向。

方位角计算公式范文

方位角计算公式范文方位角是指从一个参考方向（通常是正北方向）起，按顺时针方向测量到其中一方向线的角度。

方位角通常用度数表示，范围从0度到360度。

下面介绍常见的方位角计算公式：1.方位角计算公式（两点坐标）：假设已知起点坐标A(x1,y1)和终点坐标B(x2,y2)，方位角θ的计算公式如下：θ = atan2(y2 - y1, x2 - x1)其中，atan2函数是一个双变量反正切函数，返回值为[-π, π]之间的角度值。

注意：上述公式计算得到的θ是以正北方向为参考的方位角。

如果要将方位角转换为以其他方向为参考的角度（如正东方向为0度），可以将θ减去相应的修正值。

2.方位角计算公式（两点经纬度）：假设已知起点的经度(lon1)、纬度(lat1)和终点的经度(lon2)、纬度(lat2)，方位角θ的计算公式如下：θ = atan2(sin(Δlon) * cos(lat2), cos(lat1) * sin(lat2) -sin(lat1) * cos(lat2) * cos(Δlon))其中，Δlon = lon2 - lon1是两点经度差。

注意：上述公式计算得到的θ是以正北方向为参考的方位角。

如果要将方位角转换为以其他方向为参考的角度（如正东方向为0度），可以将θ减去相应的修正值。

3.方位角计算公式（方向余弦矩阵）：方向余弦矩阵（Direction Cosine Matrix）是一种将方位角和俯仰角等转化为三维空间坐标旋转的方式。

方向余弦矩阵的计算公式如下：D=[ cos(θ) * cos(φ), sin(θ) * cos(φ), -sin(φ) ][ -sin(θ), cos(θ), 0 ][ cos(θ) * sin(φ), sin(θ) * sin(φ), cos(φ) ]其中，θ是方位角，φ是俯仰角。

D是一个3行3列的矩阵，表示坐标变换矩阵。

上述是常见的方位角计算公式，根据不同的应用场景和问题，可能还会有其他的计算公式。

方位角计算公式

4
辅助计算
点名 2 BM1 1
2
3
BM2
测站数 3 8 3 4 5
20
表 2-2 附合水准路线计算
观测高差 /m
改正数 /m
改正后高差 /m
4
5
6
+8.364
－ 0.014
+8.350
－ 1.433
－ 0.005
－ 1.438
－ 2.745
－ 0.007
－ 2.752
+4.661
－ 0.008
+4.653
+ 8.847
－ 0.034
一、直线定向
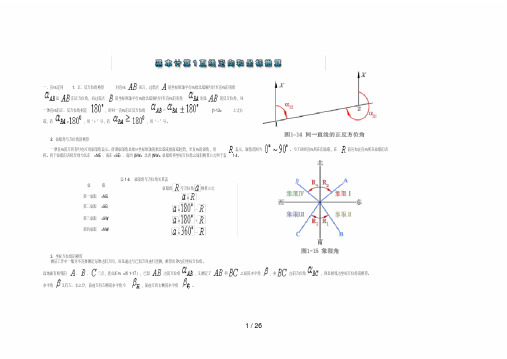
1、正、反方位角换算
对直线
而言，过始点
的坐标纵轴平行线指北端顺时针至直线的夹角
是
的正方位角，而过端点
的坐标纵轴平行线指北端顺时针至直线的夹角
则是
的反方位角，同
一条直线的正、反方位角相差
，即同一直线的正反方位角
＝
(1-13>
上式右
端，若
<
，用“＋”号，若
，用“－”号。
2、象限角与方位角的换算
算
各
待
定
点
的
高
程
。
如上所述，闭合水准路线的计算方法除高差闭合差的计算有所区别而外，其余与附合路线的计算完全相同。
二
、
举
例
1.
附
合
水
准
路
线
算
例
5 / 26
下图 2-18 所示附合水准路线为例，已知水准点 A 、 B 和待定点 1、2、3 将整个路线分为四个测段。
测段号 1 1 2 3

方位角的计算方法

方位角的计算方法：（已知方位角＋水平角大于540°－540°）已知方位角＋水平角±180°=方位角坐标增量的计算方法：平距×COS方位角=△X坐标增量平距×Sin方位角=△Y坐标增量坐标的计算方法：已知X坐标±△X坐标增量=X坐标已知Y坐标±△Y坐标增量=Y坐标高差、平距的计算方法：斜距×Sin倾角=高差斜距×COS倾角=平距高差÷Sin倾角=斜距平距÷cos已知度分秒=斜距高程的计算方法：已知高程－仪器高＋前视高±高差=该点的顶板高差原始记录计算方法：前视－后视相加÷2=水平角（前视不够－后视的＋360°再减）后视 00°00′00″ 180°00′09″前视92°49′02″272°49′13″水平角= 92°49′03″实测倾角：正镜－270°倒镜－90°（正、倒镜相加－360°）实例： 110°30′38″－90°= 00°30′38″实例： 270°30′38″－270°= 00°30′38″激光的计算方法：两点的高程相减：比如：5点高程1479、479－4点高程1471、052 = 8、427 两点之间的平距：60、673×tan7°19′25″=7、7988、427－7、797=0、629（上山前面的点一定高于后面的点，所以前面的点减后面的点）测量：1、先测后视水平角：归零，倒镜180°不能误差15′2、前视：先测水平角并读数记录，然后倒镜测倾角，水平角、平距、斜距、高差、量出仪器高，前视量出前视高。

要求方位角－已知方位角±180°=拨角方位画两千的图：展点用0.6正好.倾角的计算方法：180°以下的－90°270°－超过180°的两点的高差除平距按tan=倾角比如：2点1500、026－6点1484、096=15、932点～6点平距=127、8315、93÷127、83=接按第二功能键、接按tan接按=接按度分秒键完事。

测量学中坐标方位角计算公式

测量学中坐标方位角计算公式在测量学中，坐标方位角是用于描述目标物体或点在水平坐标系中的方向的数值。

坐标方位角是指从北方向顺时针旋转到目标点所需的角度。

在实际的测量工作中，计算坐标方位角是非常重要的，它可以帮助测量员准确地确定目标点在地图上的位置。

计算公式计算坐标方位角的主要公式是使用三角函数来实现的。

具体的计算公式如下：方位角 = arctan((Y2 - Y1) / (X2 - X1))在上述公式中，X1和Y1表示起点的水平坐标值，X2和Y2表示终点的水平坐标值。

arctan表示反正切函数，它可以将斜率转化为角度值。

通过使用这个计算公式，我们可以得到起点和终点之间的坐标方位角。

需要注意的是，上述公式仅适用于计算水平平面上的坐标方位角。

如果需要在垂直平面上计算坐标方位角，我们还需要考虑高程的影响。

在这种情况下，计算公式会稍有不同，需要引入高程差的概念。

示例为了更好地理解坐标方位角的计算过程，我们可以通过一个示例来说明。

假设我们有两个点A和B，它们的水平坐标分别为：点A：(X1, Y1) = (100, 200)点B：(X2, Y2) = (150, 280)现在我们来计算点A和点B之间的坐标方位角。

首先，我们将点A和点B的坐标值代入计算公式中：方位角 = arctan((280 - 200) / (150 - 100))接下来，我们计算分子和分母的差值：方位角 = arctan(80 / 50)然后，我们计算这两个差值的比值：方位角 = arctan(1.6)最后，使用反正切函数来计算坐标方位角的数值：方位角≈ 56.31°所以，根据计算结果，点A和点B之间的坐标方位角约为56.31°。

结论测量学中的坐标方位角是用于描述目标物体或点在水平坐标系中方向的数值。

通过使用三角函数计算公式，我们可以准确地确定起点和终点之间的坐标方位角。

在计算时需要注意坐标值的顺序和差值的计算方法。

通过实际的计算示例，我们可以更好地理解和应用坐标方位角的计算公式。

方位角计算公式

一、直线定向1、正、反方位角换算对直线而言，过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角，而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角，同一条直线的正、反方位角相差，即同一直线的正反方位角＝ (1-13)上式右端，若<，用“＋”号，若，用“－”号。

2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。

所谓象限角是指从坐标纵轴的指北端或指南端起始，至直线的锐角，用表示，取值范围为。

为了说明直线所在的象限，在前应加注直线所在象限的名称。

四个象限的名称分别为北东（NE）、南东（SE）、南西(SW)、北西(NW)。

象限角和坐标方位角之间的换算公式列于表1-4。

表1-4 象限角与方位角关系表象限角与方位角换算公式==－=＋=－3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向，而是通过与已知方向进行连测，推算出各边的坐标方位角。

设地面有相邻的、、三点，连成折线（图1-17），已知边的方位角，又测定了和之间的水平角，求边的方位角，即是相邻边坐标方位角的推算。

水平角又有左、右之分，前进方向左侧的水平角为，前进方向右侧的水平角。

设三点相关位置如图1-17()所示，应有＝＋＋ (1-14)设三点相关位置如图1-17()所示，应有＝＋＋－＝＋－ (1-15)若按折线前进方向将视为后边，视为前边，综合上二式即得相邻边坐标方位角推算的通式：＝＋(1-16)显然，如果测定的是和之间的前进方向右侧水平角，因为有＝－，代入上式即得通式＝－ (1-17)上二式右端，若前两项计算结果<，前面用“＋”号，否则前面用“－”号。

二、坐标推算 1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。

坐标正算，就是根据直线的边长、坐标方位角和一个端点的坐标，计算直线另一个端点的坐标的工作。

如图1所示，设直线AB 的边长DAB 和一个端点A 的坐标XA 、YA 为已知，则直线另一个端点B 的坐标为： XB=XA+ΔXAB YB=YA+ΔYAB式中，ΔXAB 、ΔYAB 称为坐标增量，也就是直线两端点A 、B 的坐标值之差。

测量方位角计算公式

测量方位角计算公式测量方位角是指通过其中一种方法求得一些目标物体相对于指定基准方向的角度。

方位角通常使用度数表示，以正北方向为基准，沿顺时针方向递增，范围为0到360度。

测量方位角在地理导航、测量工程、天文学等领域有着广泛的应用。

计算方位角的公式主要有以下几种：1. 方位角 = atan((E - E0) / (N - N0))其中，E、N为目标物体的东北坐标，E0、N0为基准点的东北坐标。

该公式适用于平面坐标系。

2. 方位角 = atan2(E - E0, N - N0)其中，E、N为目标物体的东北坐标，E0、N0为基准点的东北坐标。

该公式适用于平面坐标系，可以通过atan2函数直接得到方位角，避免了先计算斜率再反求角度的过程。

3. 方位角= atan((sin(ΔL) * cos(L2)) / (cos(L1) * sin(L2) - sin(L1) * cos(L2) * cos(ΔL)))其中，ΔL为目标物体经度减去基准点经度的差值，L1、L2分别为目标物体和基准点的纬度。

该公式适用于地理坐标系。

4. 方位角= arc tan((sin(Δλ) * cos(φ2)) / (cos(φ1) *sin(φ2) - sin(φ1) * cos(φ2) * cos(Δλ)))其中，Δλ为目标物体经度减去基准点经度的差值，φ1、φ2分别为目标物体和基准点的纬度。

该公式适用于地理坐标系，常用于计算大地方位角。

这些公式的推导及原理比较复杂，涉及到三角学和二元一次方程等知识。

在实际应用中，可以通过使用现成的工具或软件来计算方位角，如地图软件、GPS定位设备等。

这些工具会自动计算目标物体相对于基准方向的角度，准确性高、方便快捷，可以满足大部分测量需要。

需要注意的是，测量方位角是基于特定坐标系的，不同坐标系的方位角计算公式可能有所不同。

另外，由于地球是一个球体，使用平面坐标系进行测量会引入一定的误差，尤其是在较长的距离范围内。

掌握方位角计算公式

掌握方位角计算公式在测绘工作中，方位角是最基本的方位元素，也是导航定位和航空飞行等领域的重要元素。

所谓方位角，是指从北开始的顺时针旋转角度，指示了目标相对于真北的方位。

具体来说，我们可以将方位角分为真方位角和磁方位角两种。

真方位角以地球的真北方向为基准，而磁方位角则是以地球的磁北极方向为基准。

在实际测量中，我们通常使用磁罗盘测量得到的磁方位角。

方位角的计算方法有多种，最常用的是迭代法和正算法。

迭代法通过多次计算得到目标相对于真北的角度，而正算法则是直接计算出目标相对于真北的方向。

下面我们就来介绍一下计算方法。

1. 根据坐标值计算方位角：使用以下公式可以根据两个坐标值计算方位角：其中，AA为起点到终点的方位角，\text{起点}起点和\text{终点}终点为相应坐标的数值。

请注意，AA的值可能会受到所使用的坐标系的影响。

2.迭代法迭代法是一种比较常用的计算方位角的方法，它的基本思想是将目标点的坐标和起点的坐标代入以下公式：tan θ = (y2 - y1) / (x2 - x1)其中，θ表示角度，y2和y1分别表示目标点和起点的纬度，x2和x1则表示目标点和起点的经度。

通过多次迭代计算，即可得到目标点相对于起点的方位角。

3.正算法正算法是一种直接计算目标点相对于真北方向的计算方法，它主要借助了三角函数的知识。

假设目标点和起点的坐标均已知，我们可以使用以下公式进行计算：cos A = sinφ2 - sinφ1 * cos(λ2 - λ1) / cosφ1 * sin(λ2 - λ1)其中，A表示目标点相对于真北的方位角，φ1和φ2分别表示起点和目标点的纬度，λ1和λ2则表示起点和目标点的经度。

需要注意的是，在实际测量中，还需要考虑磁偏角和地球自转等因素的影响，这些影响会对方位角的计算产生一定的影响。

因此，我们在计算方位角时需要特别谨慎。

方位角的计算方法

方位角的计算方法方位角是指在平面直角坐标系中，特定点与正方向x轴之间逆时针方向的夹角。

它在数学、地理、航空航天等领域中都有广泛的应用。

计算方位角的方法主要有以下几种：1.基于直角坐标系的计算：假设有两个点A(x1, y1)和B(x2, y2)，首先需要计算出两点之间的直线斜率k = (y2 - y1) / (x2 - x1)。

然后利用反正切函数，通过求解arctan(k)得到弧度值θ。

最后利用单位换算，将弧度值θ转化为角度值α=θ * 180 / π，即为所求的方位角。

2.基于极坐标系的计算：在极坐标系中，一个点可以通过距离r和极角θ来表示。

假设有两个点A(r1,θ1)和B(r2,θ2)，要计算两点之间的方位角，首先需要将两点的极角θ转化为弧度制，然后通过计算Δθ=θ2-θ1得到两点之间的相对角度。

最后利用单位换算，将相对角度Δθ转化为角度值α=Δθ*180/π，即得到方位角。

3.基于方向向量的计算：假设有两个点A(x1, y1)和B(x2, y2)，可以将两点之间的连线看作一个方向向量。

首先需要计算出两点之间的方向向量V(x2 - x1, y2 - y1)。

然后利用反正切函数，通过求解arctan(Vy / Vx)得到弧度值θ。

最后利用单位换算，将弧度值θ转化为角度值α=θ * 180 / π，即为所求的方位角。

需要注意的是，在计算方位角时，可能会遇到特殊情况，例如：-当两点在同一直线上时，方位角为0或180度；-当两点重合时，方位角没有定义。

总结起来，方位角的计算方法有基于直角坐标系、极坐标系和方向向量三种方法，根据具体情况选择适合的方法进行计算。

(整理)方位角计算公式

2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。

所谓象限角是指从坐标纵轴的指北端或指南端起始，至直线的锐角，用表示，取值范围为。

为了说明直线所在的象限，在前应加注直线所在象限的名称。

四个象限的名称分别为北东（NE）、南东（SE）、南西(SW)、北西(NW)。

象限角和坐标方位角之间的换算公式列于表1-4。

表1-4 象限角与方位角关系表象限象限角与方位角换算公式=第一象限（NE）第二象限（SE）=－=＋第三象限（SW ）第四象限（NW）=－3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向，而是通过与已知方向进行连测，推算出各边的坐标方位角。

设地面有相邻的、、三点，连成折线（图1-17），已知边的方位角，又测定了和之间的水平角，求边的方位角，即是相邻边坐标方位角的推算。

水平角又有左、右之分，前进方向左侧的水平角为，前进方向右侧的水平角。

二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。

坐标正算，就是根据直线的边长、坐标方位角和一个端点的坐标，计算直线另一个端点的坐标的工作。

如图1所示，设直线AB的边长DAB和一个端点A的坐标XA、YA为已知，则直线另一个端点B的坐标为：XB=XA+ΔXABYB=YA+ΔYAB式中，ΔXAB、ΔYAB称为坐标增量，也就是直线两端点A、B的坐标值之差。

方位角计算坐标公式

方位角计算坐标公式方位角是指从某点的指北方向线起，依顺时针方向到目标方向线之间的水平夹角。

在数学、地理、工程等领域中，方位角的计算坐标公式可是相当重要的工具。

咱先来说说方位角的基本概念。

想象一下，你站在一个空旷的地方，面前有一个目标点，你要知道从你所在的位置看向那个目标点的方向角度，这就是方位角。

比如说，你正对着北方，然后顺时针转动到目标点的角度就是方位角啦。

那方位角计算坐标公式到底是啥呢？其实就是通过已知点的坐标和目标点的坐标来算出方位角。

具体的公式是：$tan\alpha = \frac{y_2 - y_1}{x_2 - x_1}$然后通过反正切函数就能得到方位角$\alpha$啦。

这里的$(x_1,y_1)$是已知点的坐标，$(x_2, y_2)$是目标点的坐标。

给大家举个例子哈。

比如说有两个点，A 点的坐标是(3, 4)，B 点的坐标是(7, 8)。

咱们来算算从 A 点看向 B 点的方位角。

首先，按照公式，$x_1 = 3$，$y_1 = 4$，$x_2 = 7$，$y_2 = 8$。

那么，$tan\alpha = \frac{8 - 4}{7 - 3} = \frac{4}{4} = 1$。

然后通过反正切函数，就知道$\alpha = 45°$。

这就意味着从 A 点看向 B 点的方位角是 45°。

在实际生活中，方位角的计算坐标公式用处可大了。

就拿建筑施工来说吧，工程师们要确定建筑物的朝向、道路的走向，就得靠这个公式来准确计算方位角。

我之前就碰到过这么个事儿，有一次去一个建筑工地，当时工人们正在打地基，但是因为方位角没算对，导致一开始的基础部分就有点偏差。

后来发现问题后，赶紧重新计算方位角，调整施工方案，这才避免了更大的错误。

你瞧，就这么一个小小的方位角计算，如果出错了，那带来的麻烦可不小。

在地理测量中，方位角也很关键。

比如测量山峰的位置、河流的走向等等。

还有导航系统，也是依靠方位角来为我们指引方向的。

方位角解析及计算

增量。
1
Vxi
f
x
D
Di
Vyi
f
y
D
Di
xˆi x Vxi yˆi x Vyi
1
970300
484318 A1
A
XA=536.27m
A
1122224
2
1051706
2
YA=328.74m
1233006
4 1014624
4
3
3
6、坐标计算
根据起始点的已知坐标和经改正的新的坐标增量，
-2 +2
545.62 490.05
2
-97.04
-2
-48.13
+1
-97.06
-48.11
448.56 441.94
3
+23.80 -91.33
-1 +1
+23.78 -91.32 472.34 350.62
4
+63.94 -21.89 +63.93 -21.88 536.27 328.74
A
1
ˆi i V
1
1
970300
484318 A1
A
XA=536.27m
A
1122224
2
1051706
2
YA=328.74m
1233006
4 1014624
4
3
3
3、按新的角值，推算各边坐标方位角。
4、按坐标正算公式，计算各边坐标增量。
5、坐标增量闭合差(closing error in coordination increment)计算与调整 1
48 43 18

方位角计算详细方法

K=
1 = 4000 D

<
1 2000
例题：
用EXCEL程序进行闭合导线计算
（四）附合导线平差计算
说明：与闭合导线基本相同，以下是两者的不同点:
1、角度闭合差的分配与调整
方法1：
（1）计算方位角闭合差： f α = α 终计算
α 终已知
（2）满足精度要求，若观测角为左角，则将fα反符号平均分配到各观测角上；若观测角为右角，则将fα同符号平均分配到各观测角上。
由A、B两点坐标来计算αAB、DAB
D AB = tgα AB = Δx
2 AB
X
YAB XAB AB DAB
B
+ Δy
2 AB
A
Δy AB Δx AB
0
y
αAB的具体计算方法如下：
（1）计算： Δy
Δx
AB AB
= xB = yB
xA yA
（2）计算：
α AB 锐 = arctg
Δy Δx
∑D
（2）分配坐标增量闭合差。
若K<1/2000（图根级），则将fx、fy以相反符号，按边长成正比分配到各坐标增量上去。并计算改正后的坐标
增量。
V Δxi = fx
1
∑D
fy
Di
A1 484318 A
1
970300 1051706 2
V Δyi =
∑D
Di
A
2
XA=536.27m YA=328.74m
图表：附合导线坐标计算表
点转折角改正后方位角边长坐标增量(米) 号 (右) D 转折角 (米) X Y 改正后坐标(米) 点增量(米) 号 X Y X Y

计算坐标与坐标方位角的基本公式

计算坐标与坐标方位角的基本公式在二维坐标系中，我们可以使用坐标表示一个点的位置。

一个点的坐标通常由一个有序的数对(x,y)表示，其中x表示点在x轴上的位置，y 表示点在y轴上的位置。

除了坐标，我们还可以使用方位角来表示点的位置。

方位角是一个极坐标系中的概念，通过一个长度和一个角度来确定一个点的位置。

在二维平面坐标系中，我们可以使用以下公式将坐标转换为方位角：1.计算长度（r）：r=√(x²+y²)2.计算角度（θ）：θ = arctan(y / x)其中，arctan(y / x)代表 y/x 的反正切值，θ表示点与 x 轴的夹角（逆时针方向为正）。

这样，我们就可以通过坐标计算得到点的方位角。

同样地，我们也可以使用方位角计算将方位角转换为坐标的公式：1.计算x坐标：x = r * cos(θ)2.计算y坐标：y = r * sin(θ)其中，cos(θ)代表角度θ 的余弦值，sin(θ)代表角度θ 的正弦值。

这样，我们就可以通过方位角计算得到点的坐标。

需要注意的是，上述公式中的θ是以弧度制表示的。

如果我们要将角度以度数制表示，可以用以下公式进行转换：角度（以度数制表示）=角度（以弧度制表示）*180/π除了上述基本公式，我们还可以通过方位角进行一些其他计算：1.两点之间的距离：d=√[(x₂-x₁)²+(y₂-y₁)²]其中，(x₁,y₁)和(x₂,y₂)是两个点的坐标。

2.两点之间的方位角：θ = arctan((y₂ - y₁) / (x₂ - x₁))这个公式可以用于计算两点之间的方位角，其中(x₁,y₁)和(x₂,y₂)是两个点的坐标。

在三维空间中，我们可以使用类似的方式计算坐标与方位角。

在三维空间中，一个点的坐标通常由一个有序的数三元组(x,y,z)表示，而方位角也变成了一个有序的数三元组(r,θ,φ)表示，其中r仍然表示长度，θ表示与x轴的夹角，φ表示与z轴的夹角。

方位角的计算公式

方位角的计算公式方位角是指从其中一点出发，顺时针方向到另一个点的位置角度。

它通常用度数来表示，以正北方向为基准，逆时针方向为正方向。

方位角的计算公式主要有两种，一种使用正弦和余弦函数，另一种使用向量运算。

1.使用正弦和余弦函数的计算公式：假设点A的坐标为(Ax, Ay)，点B的坐标为(Bx, By)。

首先需要计算两点之间的水平距离和垂直距离，即dx = Bx - Ax和dy = By - Ay。

然后可以计算方位角θ = arctan(dy/dx)。

但是由于arctan函数的值域是(-π/2, π/2)，只能表示-90°到90°之间的角度，为了得到完整的方位角计算结果，还需要根据点的位置进行调整。

- 如果dx > 0且dy > 0，即点B位于点A的右上方，此时方位角为θ。

- 如果dx > 0且dy < 0，即点B位于点A的右下方，此时方位角为360° + θ。

- 如果dx < 0，即点B位于点A的左侧，此时方位角为180° + θ。

- 如果dx = 0且dy > 0，即点B位于点A的正北方向，此时方位角为90°。

- 如果dx = 0且dy < 0，即点B位于点A的正南方向，此时方位角为270°。

这样就可以得到点A到点B的方位角。

2.使用向量运算的计算公式：向量的加减可以表示方向的改变，因此方位角的计算也可以通过向量运算来实现。

假设点A的坐标为(Ax,Ay)，点B的坐标为(Bx,By)。

首先构造向量AB，即将点B的坐标减去点A的坐标得到(ABx,ABy)。

然后可以计算该向量的方位角θ = arctan(ABy/ABx)，同样需要根据点的位置进行调整。

-如果ABx>0且ABy>0，即点B位于点A的右上方，此时方位角为θ。

-如果ABx>0且ABy<0，即点B位于点A的右下方，此时方位角为360°+θ。

方位角计算公式

方位角计算公式部门： xxx时间： xxx整理范文，仅供参考，可下载自行编辑一、直线定向1、正、反方位角换算对直线而言，过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角，而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角，同一条直线的正、反方位角相差，即同一直线的正反方位角＝ (1-13> 上式右端，若<，用“＋”号，若，用“－”号。

2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。

所谓象限角是指从坐标纵轴的指北端或指南端起始，至直线的锐角，用表示，取值范围为。

为了说明直线所在的象限，在前应加注直线所在象限的名称。

四个象限的名称分别为北东<NE）、南东<SE）、南西(SW>、北西(NW>。

象限角和坐标方位角之间的换算公式列于表1-4。

象限角与方位角换算公式==－=＋=－3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向，而是通过与已知方向进行连测，推算出各边的坐标方位角。

设地面有相邻的、、三点，连成折线<图1-17），已知边的方位角，又测定了和之间的水平角，求边的方位角，即是相邻边坐标方位角的推算。

水平角又有左、右之分，前进方向左侧的水平角为，前进方向右侧的水平角。

设三点相关位置如图1-17(>所示，应有＝＋＋ (1-14>设三点相关位置如图1-17(>所示，应有＝＋＋－＝＋－ (1-15>若按折线前进方向将视为后边，视为前边，综合上二式即得相邻边坐标方位角推算的通式：＝＋(1-16>显然，如果测定的是和之间的前进方向右侧水平角，因为有＝－，代入上式即得通式＝－ (1-17>上二式右端，若前两项计算结果<，前面用“＋”号，否则前面用“－”号。

二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。

坐标正算，就是根据直线的边长、坐标方位角和一个端点的坐标，计算直线另一个端点的坐标的工作。

方位角计算公式

2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。

所谓象限角是指从坐标纵轴的指北端或指南端起始，至直线的锐角，用表示，取值范围为。

为了说明直线所在的象限，在前应加注直线所在象限的名称。

四个象限的名称分别为北东（NE）、南东（SE）、南西(SW)、北西(NW)。

象限角和坐标方位角之间的换算公式列于表1-4。

表1-4 象限角与方位角关系表3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向，而是通过与已知方向进行连测，推算出各边的坐标方位角。

设地面有相邻的、、三点，连成折线（图1-17），已知边的方位角，又测定了和之间的水平角，求边的方位角，即是相邻边坐标方位角的推算。

水平角又有左、右之分，前进方向左侧的水平角为，前进方向右侧的水平角。

二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。

坐标正算，就是根据直线的边长、坐标方位角和一个端点的坐标，计算直线另一个端点的坐标的工作。

如图1所示，设直线AB的边长DAB和一个端点A的坐标XA、YA为已知，则直线另一个端点B的坐标为：XB=XA+ΔXABYB=YA+ΔYAB式中，ΔXAB、ΔYAB称为坐标增量，也就是直线两端点A、B的坐标值之差。