MATLAB与数学实验第七章习题
Matlab与数学实验(第二版)(张志刚 刘丽梅 版) 习题答案

Matlab与数学实验(第二版)(张志刚刘丽梅版)习题答案(1,3,4,5章)第一章d1zxt1用format的不同格式显示2*Pi,并分析格式之间的异同。
a=2*pi ;disp('***(1) 5位定点表示2*pi:')format short , a % 5位定点表disp('***(2) 15位定点表示2*pi:')format long , a % 15位定点表disp('***(3) 5位浮点表示2*pi:')format short e , a % 5位浮点表示disp('***(4) 15位浮点表示2*pi:')format long e , a % 15位浮点表示disp('***(5) 系统选择5位定点和5位浮点中更好的表示2*pi:')format short g , a % 系统选择5位定点和5位浮点中更好的表示disp('***(6) 系统选择15位定点和15位浮点中更好的表示2*pi:')format long g , a % 系统选择15位定点和15位浮点中更好的表disp('***(7) 近似的有理数的表示2*pi:')format rat , a % 近似的有理数的表disp('***(8) 十六进制的表示:')format hex , a % 十六进制的表disp('***(9) 用圆角分(美制)定点表示2*pi:')format bank , a % 用圆角分(美制)定点表示d1zxt2利用公式求Pi的值。
sum=0 ;n=21;for i = 1:4:n % 循环条件sum= sum+(1/i) ; % 循环体enddiff=0 ;for j = 3:4:(n-2) % 循环条件diff= diff+(1/j) ; % 循环体endpai=4*(sum-diff)d1zxt3 编程计算1!+3!+...+25!的阶乘。
数学实验(MATLAB)课后习题答案
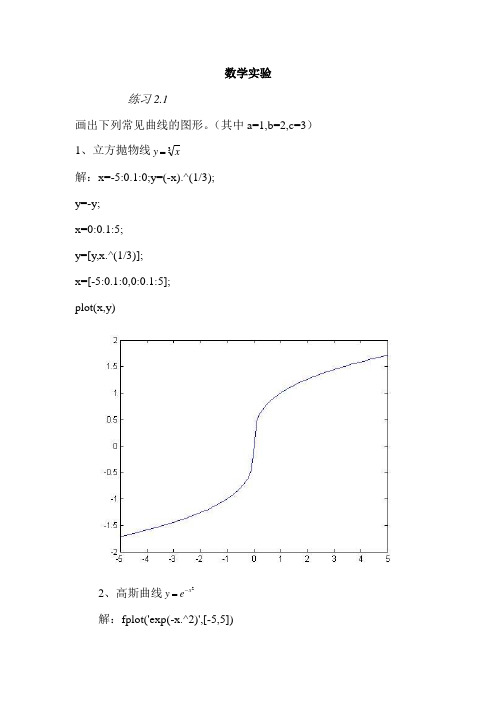
数学实验练习2.1画出下列常见曲线的图形。
(其中a=1,b=2,c=3)1、立方抛物线3xy=解:x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解:fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解:ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解:ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解:t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解:t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解:t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解:x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解:x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解:x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解:x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解:x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。
MATLAB数学实验答案(全)

MATLAB数学实验答案(全)第⼀次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作⼆维、三维⼏何图形,能够⽤Matlab 软件解决微积分、线性代数与解析⼏何中的计算问题。
补充命令vpa(x,n) 显⽰x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形在下⾯的题⽬中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx →∞-syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =,求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100x y edxdy +??dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +? syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//⾼阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最⾼次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=⽤循环语句编程给出该数列的前20项(要求将结果⽤向量的形式给出)。
MATLAB 实验七答案

实验七模型参数建立一、实验目的1、熟悉Matlab软件中数据拟合命令2、进一步熟悉用初等数学建模的一些方法3、掌握数学模型中参数的确定方法二、实验基本知识若数据(x1,y1),…(xn,yn)要拟合是m次多项式函数,y = a1xm + a2xm -1 + ... + amx + am +1则可用命令格式:a=polyfit(x,y,m)其中X,Y是数据向量,m是多项式的次数。
返回的a是系数构成的向量:a = [a1 a2 ...am am+1 ]二、实验内容1 有一只对温度敏感的电阻,已经测得了一组温度t 和电阻R的数据,试建立R 和t关系。
解先看一下温度与电阻大概存在什么关系:输入如下命令t=[20.5 32.7 51 73 95.7];R=[765 826 873 942 1032];plot(t,R,'r*')xlabel('t'),ylabel('R')aa=polyfit(t,R,1);说明R和t的关系是线性关系,则可用polyfit命令来拟合它的系数aa=polyfit(t,R,1);a=aa(1)b=aa(2)运行得:a=3.3987b=702.0968这样得到R与t的关系为:R=3.3987t+ 702.09682 一册书的成本费y 与印刷的册数x 有关,统计数据如下,试用 y=a+b/x 去拟合以上数据。
Matlab 程序: x=1:10; x1=1./x;y=[10.15 5.52 4.08 2.85 2.11 1.62 1.41 1.30 1.21 1.15]; A=polyfit(x1,y,1); x=1:10;y = 0.1382 + 10.2487./ x plot(x,y,'-r*')y = 0.1382 + 10.2487/x已知应力--应变关系可以用一条指数曲线来描述,即假设解 选取指数函数作拟合时,在拟合前需作变量代换,化为k 1,k 2的线性函数ε-ε=σ2k 1e kε-ε⨯=σ=⨯===-=-=+ε==-=εσ=ε-=εσ5209.4943231112010112021e 100275.45209.494k 100275.43009.8k ln a 5209.494k a a a z k ln a k a ln z k k ln ,,,,,k lna=[1.55 2.47 2.93 3.03 2.89]b=[500 1000 1500 2000 2375]*10^(-6) d=[3.103 2.465 1.953 1.517 1.219]*10^(3) c=log(d)aa=polyfit(b,c,1)。
MATLAB 数学实验 第七章

常微分方程组初值问题
dy = f (t , y ) dt y ( t 0 ) = y0
t ≥ t0
一阶常微分方程组初值问题数值求解方法 [T,y] = ode23(' F ',Tspan,y0) 其中, F是函数文件 表示 微分方程右端函数 其中 是函数文件, 是函数文件 Tspan = [t0 Tfinal] —— 求解区域 求解区域; y0 —— 初始条件 函数F(t,y) 必须返回列向量 必须返回列向量. 注: 函数 的每一行对应于列向量T中的每一行数据 数值解 y 的每一行对应于列向量 中的每一行数据
6/14
在平面坐标系中, 初始时刻点Q的坐标 的坐标(0, 在平面坐标系中 初始时刻点 的坐标 0), 点P的坐标 的坐标 以均匀速度v=1(m/min)沿Y轴 (100, 0).在时刻 tk , 点Q 以均匀速度 沿 轴 . 正向运动,而点 而点P以 的速度追赶 的速度追赶Q. 正向运动 而点 以2v的速度追赶 . 坐标为: 的坐标为: 时刻 tk ,点Q坐标为: (0, vk),点P的坐标为 (xk, yk) 坐标为 , 的坐标为 追击方向
5/14
时间步长法——模拟随时间变化的系统状态 时间步长法
追击问题模拟.设系统中有动点Q和动点 和动点P, 例7.7 追击问题模拟.设系统中有动点 和动点 ,点 Q从坐标原点出发以速度 从坐标原点出发以速度V=1(米/秒)沿y轴正向匀速直 从坐标原点出发以速度 米 沿 轴正向匀速直 线运动, 从坐标原点右侧100米处与 点同时出发, 米处与Q点同时出发 线运动,点P从坐标原点右侧 从坐标原点右侧 米处与 点同时出发, 速度紧盯Q点追赶 秒后P能否追上 以2V速度紧盯 点追赶.60秒后 能否追上 . 速度紧盯 点追赶. 秒后 能否追上Q 计算机模拟图 时间以步长dt 时间以步长 向前推 进时, 进时,系统中两个动 点在各个时刻的速度, 点在各个时刻的速度, 位移,位置和两点间 位移,位置和两点间 距离
MATLAB数学实验第二版课后练习题含答案

MATLAB数学实验第二版课后练习题含答案课后练习题MATLAB数学实验第二版的课后练习题如下:第一章课后练习题1.编写MATLAB程序,计算并输出下列公式的结果:y = \\frac{1}{\\sqrt{2\\pi\\sigma^2}} e^{-\\frac{(x-\\mu)^2}{2\\sigma^2}}其中,x, $\\mu$, $\\sigma$ 分别由用户输入。
要求输出结果精确至小数点后两位。
答案如下:x=input('请输入 x 的值:');mu=input('请输入 mu 的值:');sigma=input('请输入 sigma 的值:');y=1/sqrt(2*pi*sigma^2) *exp(-(x-mu)^2/ (2*sigma^2));fprintf('y = %.2f\', y);2.编写MATLAB程序,求解下列方程的解:4x + y = 11\\\\x + 2y = 7答案如下:A= [4,1;1,2];B= [11;7];X=inv(A) *B;fprintf('x = %.2f, y = %.2f\', X(1), X(2));第二章课后练习题1.编写MATLAB程序,计算下列多项式的值:P(x) = x^4 - 2x^3 + 3x^2 - x + 1其中,x 由用户输入。
要求输出结果精确至小数点后两位。
答案如下:x=input('请输入 x 的值:');y=x^4-2*x^3+3*x^2-x+1;fprintf('P(%.2f) = %.2f\', x, y);2.编写MATLAB程序,绘制下列函数的图像:f(x) = \\begin{cases} x + 1, & x < 0 \\\\ x^2, & 0 \\leq x < 1 \\\\ 2x - 1, & x \\geq 1 \\end{cases}答案如下:x=-2:0.01:2;y1=x+1;y2=x.^2.* ((x>=0) & (x<1));y3=2*x-1;plot(x,y1,x,y2,x,y3);legend('y1 = x + 1','y2 = x^2','y3 = 2x - 1');总结本文提供了《MATLAB数学实验第二版》的部分课后练习题及其答案。
matlab练习

《数学实验》在线习题1一、单项选择题(将选择答案写在答题纸上,每小题2分共20分)1.在MA TLAB 命令窗口中键入命令,Vname=prod(7:9)/prod(1:3),可计算组合数!6!3!939⨯=C ,如果省略了变量名Vname ,MA TLAB 表现计算结果将用下面的哪一变量名做缺省变量名AA )ans ;B )pi ;C )NaN ;D )eps2.宝石切割问题中,石料左右长度、前后长度、上下高度分别为a 1、a 2、a 3,即a 1×a 2×a 3(cm 3),而精品尺寸为b 1×b 2×b 3(cm 3)。
操作时,同向切割连续两次再旋转刀具。
某一切割方案的切割面积依次为:2a 1a 2→ 2a 1b 3 → 2b 2b 3,则这一切割方案为BA )左右→前后→上下;B )上下→前后→左右;C )前后→上下→左右;D )前后→ 左右→上下 3.机场指挥塔位置:北纬30度35.343分,东经104度2.441分,在MA TLAB 中用变量B=[30 35.343]表达纬度,L=[104 2.441]表达经度。
将数据转化为以度为单位的实数,下面正确的语句是A ) =B(1)+B(2)/60,Q=L(1)+L(2); B) P = 60*B(1) + B(2),Q=60*L(1)+L(2) C ) P = B(1) + B(2)/60,Q=L(1)+L(2)/60; D) P=B(1)+B(2),Q=L(1)+ L(2);。
4.用MA TLAB 随机产生60个1到365之间的正整数,应该使用下面的哪一条命令AA ) fix(365*rand(1,60));B )1+fix(366*rand(1,60));C )1+fix(364*rand(1,60));D )1+fix(365*rand(1,60))5.用A 、B 、C 表示三角形的三条边,用MA TLAB 表示条件“任意两条边之和大于第三条边”的逻辑表达式应该用下面哪一行语句AA ) A+B>C | A+C>B | B+C>A ; B ) A+B>=C | A+C>=B | B+C>=A ; C ) A+B>=C&A+C>=B&B+C>=A ;D ) A+B>C & A+C>B & B+C>A ; 6.在MA TLAB 命令窗口中,键入命令syms x ; y=int(6*x^4)。
数学实验matlab练习题

2015-2016数学实验练习题一、选择题1.清除Matlab工作空间(wordspace)变量的命令是(B )A. clcB. clearC. clfD.delete2. 清除当前屏幕上显示的所有内容,但不清除工作空间中的数据的命令是( A )A. clcB. clearC. clfD.delete3. 用来清除图形的命令( C )A. clcB. clearC. clfD.delete4. 在MATLAB程序中,使命令行不显示运算结果的符号是( A )A. ;B. %C. #D. &5. 在MATLAB程序中,可以将某行表示为注释行的符号是( B )A. ;B. %C. #D. &6.在循环结构中跳出循环,执行循环后面代码的命令为 ( B )A. returnB. breakC. continueD. Keyboard7.在循环结构中跳出循环,但继续下次循环的命令为( C )A. returnB. breakC. continueD. Keyboard8. MATLAB中用于声明全局变量的关键字是( C )A. infB. symsC. globalD. function9. 用户可以通过下面哪项获得指令的使用说明( A )A. helpB. loadC. demoD. lookfor10.在MATLAB命令窗口中键入命令S=zoros(3);可生成一个三行三列的零矩阵,如果省略了变量名S,MATLAB表现计算结果将用下面的哪一变量名做缺省变量名( A )A. ans;B. pi;C. NaN;D. Eps.11. 9/0的结果是( B )A. NAN;B. Inf;C. eps;D. 012.在MATLAB中程序或语句的执行结果都可以用不同格式显示,将数据结果显示为分数形式,用下面哪一条命令语句( D )A. format long;B. format long e;C. format bank;D. fromat rat13. 下列MATLAB命令中是构造1行3列的(-1,1)均匀分布随机矩阵的命令的是(D)A. randn(1,3);B. rand(1,3);C. ones(3);D. 以上都不对14. 产生四维元素都为1矩阵的语句为( A )A. ones(4)B. eye(4)C. zeros(4)D. rand(4)15. 用round 函数对数组[2.48 6.39 3.93 8.52]取整,结果为 ( C )A. [2 6 3 8]B. [2 6 4 8]C. [2 6 4 9]D. [3 7 4 9]16. y=dsolve(‘Dy=1/(1+x^2)-2*y^2’,’y(0)=0’,’x ’); ezplot(y)的功能是( A )A. 求微分方程特解并绘图;B. 解代数方程;C. 求定积分;D.求微分方程通解.17. MATLAB 命令roots([1,0,0,-1])的功能是 ( D )A. 产生向量[1,0,0,1];B. 求方程310x 的根;C. 求多项式31x的值; D. 求方程310x 的根。
数学实验七

取得最小值时候,我们可以认为这时候得到的 x,y 就是所要求的坐标 于是,我们在 matlab 中输入
然后,我们再定义一个函数: function f = question5(x,d,c) f=0; for i=1:52
f(i)=f+((x(1,d(i,1))-x(1,d(i,2))).^2+(x(2,d(i,1))-x(2,d(i,2))).^2-d(i, 3)).^2; end end
于是我们可以用线性最小二乘法拟合结果 我们令 q=ln Q , k=ln K l=ln L 在 matlab 中输入代码:
>> f=[k',l',ones(19,1)]; >> a1=inv(f’*f); >> b1=a1*f’; >> aa=b1*q' aa = 0.7824 0.6393 -0.098 于是,我么用线性最小二乘法拟合出来了表达式中的 αβa, 他们分别为 0.7834 0.6393 和 exp(-0.098),我认为,该表达式中的 alpha 就是资金对产值的影响指数,β是指劳动力对总 产值的影响指数。 下面,我们用非线性拟合的方式来求解式子中的相关系数。 function f = question7( x,L,K,Q ) f=x(1)*K.^(x2)*L.^(x(3));
end
然后输入代码 >> x0=[1,1,1]; >> x=lsqcurvefit(@question7,x0,L,K,Q) X= 0.9066 0.7824 0.6393 于是,在这里,我们很轻易的得到了所要非线性最小二乘法拟合的结果。 实验感悟与反思: 在这个实验中,我个人最大的收获就是在解第五题的过程中,如果一开始的初始值 x 设置为
MATLAB数学实验课后答案

数学实验MATLAB参考答案(重要部分)P20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值,b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明:编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明:编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)P20, ex2(1)a, b, c的值尽管都是1,但数据类型分别为数值,字符,逻辑,注意a 与c相等,但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码P20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813P20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500P20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6579 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3423 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59P 40 ex1先在编辑器窗口写下列M函数,保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124P 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度P 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocP 40 ex5c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)P 40 ex6(1)clear;fplot('x^2*sin(x^2-x-2)',[-2,2])x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2])(2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20);[theta,fai]=meshgrid(theta,fai); x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page41,ex8分别使用which trapz, type trapz, dir C:\MATLAB7\toolbox\matlab\datafun\ page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16];>> X=lyap(A,C)X =1.0000 -1.0000 -0.0000 -1.00002.0000 1.0000 -0.0000 1.0000 7.0000Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1];>> rank(A), rank([A,b]) ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]';>> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0 Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95];>> x1=a*x, x2=a^2*x, x10=a^10*x>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例,说明x是最大特征值对应的特征向量Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]'; >> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.0100 0.1200 0.0400 0.0900 >> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500 -0.0900 0.8000 -0.0100 -0.1200 -0.0400 0.9100 >> D=[17 17 17]';x=A\D x =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000-41.0000 25.0000 10.0000 -6.0000-17.0000 10.0000 5.0000 -3.000010.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)、(以n=5为例)%关键是矩阵的定义%方法一(三个for)n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二(一个for)n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三(不用for)n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286-0.0075 0.0376 -0.1429 0.4887 -0.5865 0.0015 -0.0075 0.0286 -0.0977 0.3173 >> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.9237 0.5546 -0.5546 -0.3771 -0.0000 0.3771-0.2614 -0.2614 0.0000 -0.1643 0.0000 0.0924 -0.0924 0.0628 -0.0000 -0.0628-0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a) v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关,可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关,不可对角化>> [v,d]=jordan(a)v =1 0 11 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的,所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组3>> b=a([1 2 4],:)';c=a([3 5],:)'; >> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; %i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0;1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3;0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\bans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467%Exercise 12>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3))fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013%Exercise 1(1)roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x'); fzero(fun,2)】%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))];[a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi; x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置,然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小,x(2)(4)(6)是局部极大,从最后一句知道x(1)全局最小, x(2)最大。
MATLAB程序设计与应用 实验答案 第七章

第七章1.(1)f=sym('x^9-1');factor(f)ans =(x-1)*(x^2+x+1)*(x^6+x^3+1)(2)f=sym('x^4+x^3+2*x^2+x+1');factor(f)ans =(x^2+1)*(x^2+x+1)(3)f=sym('125*x^6+75*x^4+15*x^2+1');factor(f)ans =(5*x^2+1)^3(4)syms x y z;f=x^2+y^2+z^2+2*(x*y+y*z+z*x);factor(f)ans =(x+y+z)^22.(1)syms x y;f=y/x+x/y;simplify(f)ans =(x^2+y^2)/x/y(2)syms a bf=sqrt((a+sqrt(a^2-b))/2)+sqrt((a-sqrt(a^2-b))/2);simplify(f)ans =1/2*(2*a+2*(a^2-b)^(1/2))^(1/2)+1/2*(2*a-2*(a^2-b)^(1/2))^(1/2) (3)sym x;f=2*cos(x)^2-sin(x)^2;simplify(f)ans =3*cos(x)^2-1(4)f=sqrt(3+2*sqrt(2));simplify(f)ans =2.41423.(1)sym x;f=(x^2+6*x+8)/(x^2-5*x+4);limit(f,x,4)ans =NaN(2)sym x;f=abs(x)/x;limit(f,x,0)ans =NaN(3)sym x;f=(sqrt(1+x^2)-1)/x;limit(f,x,0)ans =(4)sym x;f=(x+1/x)^x;limit(f,x,inf)ans =Inf4.(1)sym x;y=3*x^2-5*x+1;diff(y,x)diff(y,x,2)ans =6*x-5ans =6(2)sym x;y=sqrt(x+sqrt(x+sqrt(x)));diff(y,x)diff(y,x,2)ans =1/2/(x+(x+x^(1/2))^(1/2))^(1/2)*(1+1/2/(x+x^(1/2))^(1/2)*(1+1/2/x^(1/2))) ans =-1/4/(x+(x+x^(1/2))^(1/2))^(3/2)*(1+1/2/(x+x^(1/2))^(1/2)*(1+1/2/x^(1/2)))^2+1/2/(x+(x+x^(1/2))^(1/2))^(1/2)*(-1/4/(x+x^(1/2))^(3/2)*(1+1/2/x^(1/2))^2-1/8/(x+x^(1/2))^(1/2)/x^(3/2)) (3)sym x;y=sin(x)-x^2/2;diff(y,x)diff(y,x,2)ans =cos(x)-xans =-sin(x)-1(4)syms x y;z=x+y-sqrt(x^2+y^2);diff(z,x)*diff(z,y)-diff(z,x)/diff(z,y)ans =(1-1/(x^2+y^2)^(1/2)*x)*(1-1/(x^2+y^2)^(1/2)*y)ans =(-1+1/(x^2+y^2)^(1/2)*x)/(1-1/(x^2+y^2)^(1/2)*y)5.(1)x=sym('x');y=1/(x+a);int(y)ans =log(x+a)(2)x=sym('x');y=(1-3*x)^(1/3);int(y)ans =-1/4*(1-3*x)^(4/3)(3)x=sym('x');y=1/(sin(x)^2*cos(x)^2);int(y)ans =1/sin(x)/cos(x)-2/sin(x)*cos(x)(4)y=sym('x^2/(sqrt(a^2+x^2))');int(y)ans =1/2*x*(a^2+x^2)^(1/2)-1/2*a^2*log(x+(a^2+x^2)^(1/2)) 6.(1)数值法:y=inline('x.*(2-x.^2).^12');quadl(y,0,1)ans =315.0385符号法:y=sym('x*(2-x^2)^12');int(y,x,0,1)ans =8191/26(2)数值法:y=inline('x./(x.^2+x+1)');quadl(y,-1,1)ans =-0.3576符号法:y=sym('x/(x^2+x+1)');int(y,x,-1,1)ans =-1/6*3^(1/2)*pi+1/2*log(3)(3)数值法:y=inline('(x.*sin(x)).^2');quadl(y,0,pi)ans =4.3823符号法:y=sym('(x*sin(x))^2');int(y,x,0,pi)ans =-1/4*pi+1/6*pi^3(4)数值法:y=inline('abs(log(x))');quadl(y,1/exp(1),exp(1))ans =1.2642符号法:y=sym('abs(log(x))');int(y,1/exp(1),exp(1))ans =6627126856707895/18014398509481984*log(6627126856707895)-1403137728104727965/9007199254740992*log(2)-19566541956688519/18014398509481984+3060513257434037/1125899906842624*lo g(3060513257434037)7.(1)n=sym('n');symsum((2*n-1)/(2*n)*(-1)^(2*n-1),n,1,inf)-Inf(2)syms x,n;symsum((x^n)/n,n,x,inf)ans =x^x*LerchPhi(x,1,x)(3)sym n;symsum(1/((2*n-1))^2,n,1,inf)ans =1/8*pi^2(4)sym n;symsum(1/(n*(n+1)*(n+2)),n,1,inf)ans =1/48.(1)y=sym('x^4-5*x^3+x^2-3*x+4');taylor(y,x,inf,4)ans =-140+21*x+37*(x-4)^2+11*(x-4)^3+(x-4)^4(2)y=sym('exp(x)+exp(-x)/2');taylor(y,x,0,5)ans =3/2+1/2*x+3/4*x^2+1/12*x^3+1/16*x^4(3)y=sym('tan(x)');taylor(y,x,3,2)ans =tan(2)+(1+tan(2)^2)*(x-2)+tan(2)*(1+tan(2)^2)*(x-2)^2(4)y=sym('sin(x)^2');taylor(y,x,8,0)ans =x^2-1/3*x^4+2/45*x^6(5)y=sym('sqrt(x^3+x^2+5*x+3)');taylor(y,x,5,0)ans =3^(1/2)+5/6*3^(1/2)*x-13/72*3^(1/2)*x^2+137/432*3^(1/2)*x^3-2909/10368*3^(1/2)*x^49.(1)y=sym('a*x^2+b*x+c=0');x=solve(y)-1/2*(b-(b^2-4*a*c)^(1/2))/a-1/2*(b+(b^2-4*a*c)^(1/2))/a(2)y=sym('2*sin(3*x-pi/4)=1');x=solve(y)x =5/36*pi(3)y=sym('sin(x)-sqrt(3)*cos(x)=sqrt(2)');x=solve(y)x =-atan(2*(1/4*2^(1/2)-1/4*3^(1/2)*2^(1/2))*2^(1/2)/(1+3^(1/2)))-pi-atan(2*(1/4*2^(1/2)+1/4*3^(1/2)*2^(1/2))*2^(1/2)/(3^(1/2)-1))+pi(4)y=sym('x^2+10*(x-1)*sqrt(x)+14*x+1=0');x=solve(y)x =(2^(1/2)-1)^2(-4+17^(1/2))^210.(1)[x,y]=solve('ln(x/y)=9','exp(x+y)=3','x,y')x =exp(9)*log(3)/(exp(9)+1)y =log(3)/(exp(9)+1)(2)[x,y,z]=solve('4*x^2/(4*x^2+1)=y','4*y^2/(4*y^2+1)=z','4*z^2/(4*z^2+1)=x ','x,y,z')x =1/2-.20638628718333472422786438700877-.14591560496938088264289536925343*i.12180586017531728105257458866428+.19496067272379724816977143098554 *i-.55869011194229747835946156711686e-1-.22108561269887145278355886311693*i-.55869011194229747835946156711686e-1+.22108561269887145278355886311693*i.12180586017531728105257458866428-.19496067272379724816977143098554*i-.20638628718333472422786438700877+.14591560496938088264289536925343*iy =1/2.12180586017531728105257458866428+.19496067272379724816977143098554 *i-.55869011194229747835946156711680e-1+.22108561269887145278355886311692*i-.20638628718333472422786438700878+.14591560496938088264289536925342*i-.20638628718333472422786438700878-.14591560496938088264289536925342*i-.55869011194229747835946156711680e-1-.22108561269887145278355886311692*i.12180586017531728105257458866428-.19496067272379724816977143098554*iz =1/2-.55869011194229747835946156711683e-1+.22108561269887145278355886311691*i-.20638628718333472422786438700877-.14591560496938088264289536925342*i.12180586017531728105257458866428-.19496067272379724816977143098553*i.12180586017531728105257458866428+.19496067272379724816977143098553 *i-.20638628718333472422786438700877+.14591560496938088264289536925342*i-.55869011194229747835946156711683e-1-.22108561269887145278355886311691*i11.y=dsolve('x*D2y+(1-n)*Dy+y','y(0)=0','Dy(0)=0','t')y =12.[x,y]=dsolve('Dx=3*x+4*y','Dy=5*x-7*y','x(0)=0','y(0)=1','t')x =2/15*5^(1/2)*exp((-2+3*5^(1/2))*t)-2/15*5^(1/2)*exp(-(2+3*5^(1/2))*t)y =-1/6*5^(1/2)*exp((-2+3*5^(1/2))*t)+1/2*exp((-2+3*5^(1/2))*t)+1/6*5^(1/2)*exp(-(2+3*5^(1/2))*t)+1/2*exp(-(2+3*5^(1/2))*t)。
数学实验与数学建模MATLAB实验报告78

数学实验与数学建模MATLAB实验报告78数学实验与数学建模实验报告学院:信息科学与⼯程学院专业班级:姓名:学号:习题七1.求下列微分⽅程的通解(1)x y x y dx dy -+=(2)yxx y y +=cos ' (3)(xcosy+sin2y )y`=1 (4)x ey y y x2cos 3=-'+''(5) x y e y y x 2cos 3'''=-+解:(1)dsolve('Dy=(y+x)/(y-x)','x')(2)dsolve('Dy=cos(y/x)+x/y','x')(3)dsolve('(x*cos(y)+sin(2*y))*Dy=1','x')(4)dsolve('D2y+3*Dy-y=exp(x)*cos(2*x)','x')(5)dsolve('D2y+3*Dy-y=exp(x*cos(2*x))','x')ans=exp(1/2*(-3+13^(1/2))*x)*C2+exp(-1/2*(3+13^(1/2))*x)*C1-1/13*13^(1/2)*(-Int(exp (1/2*x*(3-13^(1/2)+2*cos(2*x))),x)*exp(x*13^(1/2))+Int(exp(1/2*x*(3+13^(1/2)+2*cos(2*x))),x))*exp(-1/2*(3+13^(1/2))*x) 2.求下列初值问题的解(1)==-++-+=10)2(212222y x y y x x dx dy xy xy (2)????===++==V dt dx x x a t t x dt dx n dt x d 000222,02解:(1) dsolve('x^2+2*x*y-y^2+(y^2+2*x*y-x^2)*Dy=0','y(1)=1','x')(2) dsolve('D2x+2*n*Dx+a^2*x=0','x(0)=x0','Dx(0)=V0','t')ans =1/2*(n*x0+(n^2-a^2)^(1/2)*x0+V0)/(n^2-a^2)^(1/2)*exp((-n+(n^2-a^2)^(1/2))*t )-1/2*(n*x0-(n^2-a^2)^(1/2)*x0+V0)/(n^2-a^2)^(1/2)*exp((-n-(n^2-a^2)^(1/2))*t)3.求微分⽅程组=--=++t te y x dtdy e y x dtdx 235的通解.解:[x,y]=dsolve('Dx+5*x+y=exp(t)','Dy-x-3*y=exp(2*t)','t')x =-4*exp((-1+15^(1/2))*t)*C2+exp((-1+15^(1/2))*t)*C2*15^(1/2)-4*exp(-(1+15^(1/2))*t)*C1-exp(-(1+15^(1/2))*t)*C1*15^(1/2)+2/11*exp(t)+1/6*exp(2*t) y =exp((-1+15^(1/2))*t)*C2+exp(-(1+15^(1/2))*t)*C1-1/11*exp(t)-7/6*exp(2*t) 4.求下列初值问题的解(1)⽅程组+=+=11x dtdy y dt dx满⾜=-=0)0(2)0(y x 的特解。
matlab数学实验练习题

Matlab 数学实验实验一 插值与拟合实验内容:预备知识:编制计算拉格朗日插值的M 文件。
1. 选择一些函数,在n 个节点上(n 不要太大,如5 ~ 11)用拉格朗日、分段线性、三次样条三种插值方法,计算m 个插值点的函数值(m 要适中,如50~100)。
通过数值和图形输出,将三种插值结果与精确值进行比较。
适当增加n ,再做比较,由此作初步分析。
下列函数任选一种。
(1)、 ;20,sin π≤≤=x x y (2)、;11,)1(2/12≤≤--=x x y (3)、;22,c o s10≤≤-=x x y(4)、22),exp(2≤≤--=x x y2.用电压V=10伏的电池给电容器充电,电容器上t 时刻的电压为)(0)()(τteV V V t v ---=,其中0V 是电容器的初始电压,τ是充电常数。
试由下面一组t ,V 数据确定0V 和τ。
实验二 常微分方程数值解试验实验目的:1. 用MATLAB 软件求解微分方程,掌握Euler 方法和龙格-库塔方法;2. 掌握用微分方程模型解决简化的实际问题。
实验内容: 实验三 地图问题1. 下图是一个国家的地图,为了计算出它的国土面积,首先对地图作如下测量:以由西向东方向为x 轴,由南到北方向为y 轴,选择方便的原点,并将从最西边界点到最东边界点在x 轴上的区间适当地划分为若干段,在每个分点的y 方向测出南边界点和北边界点的y 坐标y1和y2,这样就得到了表中的数据(单位mm )。
根据地图的比例我们知道18mm相当于40km,试由测量数据计算该国土2实验四狼追兔问题狼猎兔问题是欧洲文艺复兴时代的著名人物达.芬奇提出的一个数学问题。
当一个兔子正在它的洞穴南面60码处觅食时,一只恶狼出现在兔子正东的100码处。
当两只动物同时发现对方以后,兔子奔向自己的洞穴,狼以快于兔子一倍的速度紧追兔子不放。
狼在追赶过程中所形成的轨迹就是追击曲线。
狼是否会在兔子跑回洞穴之前追赶上兔子?为了研究狼是否能够追上兔子,可以先考虑求出狼追兔子形成的追击曲线,然后根据曲线来确定狼是否能够追上兔子。
MATLAB实验七--答案

数求解方程的根 ezplot('10*x+exp(x)-2') grid on 根所在区间为[0,2]; fzero('10*x+exp(x)-2',[0,2])
sin x y z 2 e x 4 0 4、求方程组 在(1,1,1)附近的解并对结果进行验证。要求编写 x yz 0 xy z 0
评语:
教师签字:
日期:
年
月
日
河南财经政法大学数学与信息科学学院
6
其中 k1 是药物量被吸收到血液中的速率系数,k 是血液中向体外排除的速率系数,D 是刚 开始胃中或肌肉中的药物总量。试用欧拉公式求上述微分方程数值解,并画出图形。(设 k1=0.6,k=0.2,D=200) clear f=sym('-0.2*x+0.6*200*exp(-0.6*t)'); a=0; b=60;h=4; n=(b-a)/h; t=0;x=0;szj=[t,x]; for i=1:n x=x+h*subs(f,{'t','x'},{t,x}); t=t+h; szj=[szj;t,x]; end szj plot(szj(:,1),szj(:,2),'*b-')
dy 3 y 3 x dx x x (e cos x) 2 x 10、求微分方程 的数值解,求解范围为区间[,2],并画出 2 3 y ( ) (e 1)
数值解和解析解的图形 数值解: fun=inline('((3*y)/x+x^3*(exp(x)+cos(x))-2*x)','x','y'); [x,y]=ode23(fun,[pi,2*pi],(exp(pi)+2/pi+1)*pi^3) plot(x,y,'r*') 解析解: y=dsolve('Dy=(3*y)/x+x^3*(exp(x)+cos(x))-2*x','y(pi)=(exp(pi)+2/pi)*pi^3','x') ezplot(y,[pi,2*pi]) 或者 x=[pi:0.1:2*pi]; y=x.^3.*(exp(x)+sin(x)+2./x); plot(x,y); hold on; fun=inline('3*y/x+x^3*(exp(x)+cos(x))-2*x','x','y'); [x,y]=ode23(fun,[pi,2*pi],(exp(pi)+2/pi+1)*(pi)^3); plot(x,y,'r'); xlabel('x'); ylabel('y');
MATLAB 程序设计教程第二版实验答案包括第七章

第二章:1.(1) w=sqrt(2)*(1+0.34245*10^(-6))w =1.4142(2) a=3.5;b=5;c=-9.8;x=(2*pi*a+(b+c)/(pi+a*b*c)-exp(2))/(tan(b+c)+a)x =0.9829(3) a=3.32;b=-7.9;y=2*pi*a^2*((1-pi/4)*b-(0.8333-pi/4)*a)y =-128.4271(4) t=[2,1-3i;5,-0.65];>> z=0.5*exp(2*t)*log(t+sqrt(1+t*t))z =1.0e+004 *0.0057 - 0.0007i 0.0049 - 0.0027i1.9884 - 0.3696i 1.7706 - 1.0539i2A=[-1,5,-4;0,7,8;3,61,7];B=[8,3,-1;2,5,3;-3,2,0]; >>(1) A+6*Bans =47 23 -1012 37 26-15 73 7>> A^2-B+eye-18 -216 1823 533 11022 868 526>>(2) A*Bans =14 14 16-10 51 21125 328 180>> A.*Bans =-8 15 40 35 24-9 122 0>> B*Aans =-11 0 -157 228 533 -1 28(3) A/Bans =1.2234 -0.92552.9787 -0.9468 2.3511 -0.9574 4.61703.8723 13.8936>> B\Aans =-0.5106 -8.6170 -1.1277 0.7340 17.5745 1.8085 -0.8830 -21.2128 0.4043>>(4) [A,B]ans =-1 5 -4 8 3 -10 7 8 2 5 33 61 7 -3 2 0>> [A([1,3],:);B^2]ans =-1 5 -43 61 773 37 117 37 13-20 1 9>>3A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14];(1) b=find(A>=10&A<=25);>> A(b)ans =2310(2) B=A(1:3,:)B =23.0000 10.0000 -0.7780 041.0000 -45.0000 65.0000 5.000032.0000 5.0000 0 32.0000C=A(:,1:2)C =23.0000 10.000041.0000 -45.000032.0000 5.00006.0000 -9.5400>> D=A(2:4,3:4)D =65.0000 5.0000 0 32.0000 54.0000 3.1400>> E=B*CE =1.0e+003 *0.9141 -0.22391.20802.71231.1330 -0.2103(3) E<Dans =0 10 00 1>> E&Dans =1 10 11 1>> E|Dans =1 11 11 1~E|~Dans =0 01 00 0第三章:2.(1)c=input('请输入成绩');if(c>=90&c<=100)disp 'A' ;elseif(c>=80)disp 'B';elseif(c>=70)disp 'C';elseif(c>60)disp 'D';elsedisp 'E';end请输入成绩55Ec=input('please enter:'); switch fix(c/10)case {9,10}disp('A');case {8}disp('B');case {7}disp('C');case {6}disp('D');case {0,1,2,3,4,5} disp('E');end>> asplease enter:55E>> asplease enter:67D(2)while(1)c=input('请输入成绩');if(c>=90&c<=100)disp 'A' ;elseif(c<90&c>=80)disp 'B';elseif(c<80&c>=70)disp 'C';elseif(c<70&c>=60)disp 'D';elseif(c<60&c>=0)disp 'E';elsedisp 'wrong'endend>> third请输入成绩113wrong请输入成绩-47wrong请输入成绩45E请输入成绩89B请输入成绩78C3.a=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] b=max(a)c=min(a)b=0c=0for i=1:20if a(i)>bb=a(i);endif a(i)<cc=a(i);endendbc6.A=rand(5,6)n=input('请输入矩阵:');if n>5n=5A(n,n)elseA(n)End6. a=rand(5,6);n=input('请输入n');if n==1disp(a(1,:))endif n==2disp(a(2,:))endif n==3disp(a(3,:))endif n==4disp(a(4,:))endif n==5disp(a(5,:))endif n>5disp(a(5,:))end第四章:1.(1)x=-12:0.001:12;y=x-x.^3/6;plot(x,y);xlabel('x轴');ylabel('y轴');title('Y=X-X^3/3!');(2)ezplot('x^2+2*y^2-64',[-8,8,-8,8])xlabel('x轴');ylabel('y轴');axis equaltitle('x^2+2y^2=64');4.(1)t=0:pi/100:2*pi;x=exp(-t/20).*cos(t);y=exp(-t/20).*sin(t);z=t;plot3(x,y,z)(2)[x,y]=meshgrid(-5:5);z=ones(11);surf(x,y,z);shading interp;第五章1.(1)A=randn(10,5);a=mean(A)a =0.0013 0.2310 0.0253 0.3588 -0.4197b=std(A)b =0.9034 0.8829 1.1898 0.7832 1.0821(2)max(max(A))ans =2.1832>> min(min(A))ans =-2.1707(3).sum(sum(A))ans =1.9666sum(A,1)ans =0.0128 2.3095 0.2528 3.5884 -4.1969(4).sort(A)ans =-1.6656 -0.8323 -1.5937 -1.2025 -2.1707-1.1465 -0.5883 -1.4410 -0.3999 -1.6041-0.4326 -0.1867 -1.3362 -0.1567 -1.0565-0.0376 -0.1364 -0.6918 -0.0198 -0.92190.1253 -0.0956 0.2944 0.6686 -0.80510.1746 0.0593 0.5711 0.6900 -0.05920.2877 0.1139 0.7143 0.7119 0.21930.3273 0.7258 0.8580 0.8156 0.25731.1892 1.0668 1.2540 1.1908 0.52871.19092.1832 1.6236 1.2902 1.4151>> sort(ans,2,'descend')ans =-0.8323 -1.2025 -1.5937 -1.6656 -2.1707-0.3999 -0.5883 -1.1465 -1.4410 -1.6041-0.1567 -0.1867 -0.4326 -1.0565 -1.3362-0.0198 -0.0376 -0.1364 -0.6918 -0.92190.6686 0.2944 0.1253 -0.0956 -0.80510.6900 0.5711 0.1746 0.0593 -0.05920.7143 0.7119 0.2877 0.2193 0.11390.8580 0.8156 0.7258 0.3273 0.25731.2540 1.1908 1.1892 1.0668 0.52872.1832 1.6236 1.4151 1.2902 1.19092.(2)n=1:10;a=n.*n;interp1(n,a,2.2,'cubic')ans =4.8133第七章(1)g=inline('sin(x)./x');>> [s,n]=quad(g,0,2)s =1.6054n =18(2)g=inline('1./((x-0.3).*(x-0.3)+0.01)-1./((x-0.9).*(x-0.9)+0.04)-6'); >> [s,n]=quad(g,0,1)s =11.7006n =145。
matlab第七章课后题答案

matlab第七章课后题答案第一题分解因式syms x y z>> A=x^9-1;>> factor(A)ans =(x-1)*(x^2+x+1)*(x^6+x^3+1) 解(1)>> B=x^4+x^3+2*x^2+x+1;>> factor(B)ans =(x^2+1)*(x^2+x+1) 解(2)> C=125*x^6+75*x^4+15*x^2+1;>> factor(C)ans =(5*x^2+1)^3 解(3)> D=x^2+y^2+z^2+z*(x*y+y*z+z*x);>> factor(D)ans =x^2+y^2+z^2+z*x*y+y*z^2+z^2*x 解(4)第二题化简表达式syms x y a b>> s=y/x+x/y;>> simplify(s)ans =(x^2+y^2)/x/y 解(1)s=sqrt(a+sqrt(a^2-b))/2+sqrt(a-sqrt(a^2-b))/2;ans =1/2*(a+(a^2-b)^(1/2))^(1/2)+1/2*(a-(a^2-b)^(1/2))^(1/2) 解(2)s=2*cos(x)^2*x-sin(x)^2*x;>> simplify(s)ans =x*(3*cos(x)^2-1) 解(3)s=sqrt(3+2*(sqrt2)) 第三题求函数的极限> syms x>> f=(x^2-6*x+8)/(x^2-5*x+4);> limit(f,x,4)ans =2/3 解(1)>> f=abs(x)/x;>> limit(f,x,0)ans =NaN 解(2)f=(sqrt(1+x^2)-1)/x;>> limit(f,x,0)ans =0 解(3)f=(x+1/x)^x;>> limit(f,x,inf,'left')ans =Inf 解(4)第四题求函数的符号导数f=3*(x^2)-5*x+1;>> diff(f)ans =6*x-5 解(1)y’>> diff(f,x,2)ans =6 解(1)> y=sqrt(x+sqrt(x+sqrt(x)));>> diff(y)ans =1/2/(x+(x+x^(1/2))^(1/2))^(1/2)*(1+1/2/(x+x^(1/2))^(1/2)* (1+1/2/x^(1/2))) 解(2)diff(y,x,2)ans =-1/4/(x+(x+x^(1/2))^(1/2))^(3/2)*(1+1/2/(x+x^(1/2))^(1/2)*(1+1 /2/x^(1/2)))^2+1/2/(x+(x+x^(1/2) )^(1/2))^(1/2)*(-1/4/(x+x^(1/2))^(3/2)*(1+1/2/x^(1/2))^2-1/8/(x+x^(1/2))^(1/2)/x^(3/2)) 解(2)y=sin(x)-x^2/2;> diff(y)ans =cos(x)-x 解(3)>> diff(y,x,2)ans =-sin(x)-1 解(3)syms x y z>> z=x+y-sqrt(x^2+y^2);>> diff(z,x,y)ans =1-1/(x^2+y^2)^(1/2)*y 解(4)>> diff(y,x)ans =0 解(4)第五题求不定积分x=sym('x');>> f=1/(x+a);>> int(f)ans =log(x+a) 解(1)>> f=(1-3*x)^3;>> int(f)ans =-1/12*(1-3*x)^4 解(2)>> f=(1/(sin(x)^2*cos(x)^2));>> int(f)ans =1/sin(x)/cos(x)-2/sin(x)*cos(x) 解(3)>> f=x^2/(sqrt(a^2+x^2));>> int(f)ans =1/2*x*(a^2+x^2)^(1/2)-1/2*a^2*log(x+(a^2+x^2)^(1/2)) 解(4)第六题求定积分> x=sym('x');> int((x*(2-sin(x)^2))^12,0,1)ans =-13072167041243000966100527033032931/1439431206610157 332070400000000000*sin(1)^19 *cos(1)-6398861758307370972493847449067915934618360845299932 3027852007/820274272 498737105178830959457441284892917760000000000*cos(1)*s in(1)+417844027386435896683 78350956709518241555640967463723429593/1230411408748 105657768246439186161927339376640000000000*sin(1)^3*cos(1)-6287598784304532394386769772554886862775718358540 017487607/179434997109098741757869272381315281070325 7600000000000*sin(1)^7*cos(1)-117903417317/3522410053632*sin(1)^23*cos(1)+93129118771 020938708526771772323524014639/1529945519744217245425650892800000000000*sin(1)^1 7*cos(1)-2677966496932891906 2789407028617562008014032541099/65676988573810175970 43504106365255680000000000* sin(1)^10-9093666156737053001410403050886921533204877134531540 1/53375584364747317 6140678428961747763200000000*cos(1)^2+2541573211/1467 67085568*sin(1)^24+940325057 70279736611460220749/16522396770089041920000000000*si n(1)^20+2704734082846637530 0822998906838403821858600396601/46703636319153902912 30936253415292928000000000*sin(1)^8+5542192477209543230894137867604219553503/255 75581466676109936796106752000000000*sin(1)^16+6290548805350754451916704658025155 325352197570086424587493/20 1864371747736084477602931428979691204116480000000000 0*sin(1)^9*cos(1)-74888453896 484988301898479573506809/175613581237857810540134400 0000000*sin(1)^18-66275838868 9551809679364987359346538465101954279/84285468669723 0591620583026983541145600000000*sin(1)^14+47417160064207694184289443781709965432 75038000761225969993/153801 4260935132072210308048982702409174220800000000000*sin(1)^5*cos(1)-273698005143037 11474211657412466731397670944577/1002665095819570213 96215456910540800000000000*sin(1)^15*cos(1)+18044178399358284974551495/22109663333 532016**********sin(1)^21*cos(1)+159018588498544047612814017616772807534595903672 788230889/18504234076875807 7437802687143231383603773440000000000*sin(1)^13*cos(1)-42990929319556261053136947 04999192498272936575705473777243/2220508089225096929 253632245718776603245281280000000000*sin(1)^11*cos(1)+7264479585721640057236136324 9893595045872001672201/160 1267530942419528422035286885243289600000000*sin(1)^4-179168559345113148705406926 00563709435304263998599/3002376620517036615791316162 909831168000000000*sin(1)^6-3 228431702614231399553/6979060395685611307008*sin(1)^22 +1809464903223467961506769 2014871302547716716561173/86693624917429432280974254 20402137497600000000*sin(1)^12+90821203400667453448262867129549773153665801090519 0650989336891/1066356554248 3582367324802472946736703607930880000000000 解(1)int(x/(x^2+x+1),-1,1)ans =1/2*log(3)-1/6*3^(1/2)*pi 解(2)> int((x*sin(x))^2,0,pi)ans =1/6*pi^3-1/4*pi 解(3)第七题求级数之和n=sym('n');>> s1=symsum((-1)*(2*n+1)/2^n,n,0,inf)s1 =-6 解(1)>> s2=symsum(x^(2*n-1)/2^n-1,n,1,inf)s2 =sum(x^(2*n-1)/(2^n)-1,n = 1 .. Inf) 解(2)s3=symsum(1/(2*n+1)^2,n,0,inf)s3 =1/8*pi^2 解(3)s4=symsum(1/n*(n+1)*(n+1),n,1,inf)s4 =Inf 解(4)第八题求泰勒展开式>> x=sym('x');f1=x^4-5*x^3+x^2-3*x+4;f2=(exp(x)+exp(-x))/2;f3=tan(x);f4=sin(x)^2;f5=sqrt(x^3+x^2+5*x+3);taylor(f1,4,4)ans =-140+21*x+37*(x-4)^2+11*(x-4)^3 解(1)taylor(f2,5,0)ans =1+1/2*x^2+1/24*x^4 解(2)taylor(f3,3,2)ans =tan(2)+(1+tan(2)^2)*(x-2)+tan(2)*(1+tan(2)^2)*(x-2)^2 解(3)taylor(f4,8,0)x^2-1/3*x^4+2/45*x^6 解(4)taylor(f5,5,0)ans =3^(1/2)+5/6*3^(1/2)*x-13/72*3^(1/2)*x^2+137/432*3^(1/2)*x^3-2909/10368*3^(1/2)* x^4 解(5)第九题求非线性方程的解x=solve(‘a*x^2+b*x+c=0’,’x’)x =1/2/a*(-b+(b^2-4*a*c)^(1/2))1/2/a*(-b-(b^2-4*a*c)^(1/2)) 解(1)x=solve(‘2*sin(3*x-pi/4)=1’,’x’)x =5/36*pi 解(2)x=solve(‘sin(x)-sqrt(3)*cos(x)=sqrt(2)’,’x’)x =-atan(2*(1/4*2^(1/2)+1/4*3^(1/2)*2^(1/2))*2^(1/2)/(3^(1/2)-1))+pi-atan(2*(1/4*2^(1/2)-1/4*3^(1/2)*2^(1/2))*2^(1/2)/(1+3^(1/2)))-pi 解(3)x=solve(‘x^2+10*(x-1)*sqrt(x)+14*x+1=0’,’x’)x =(2^(1/2)-1)^2(-4+17^(1/2))^2 解(4)第十题求方程组的解[x,y]=solve(‘ln(x/y)=9’,’exp(x+y)=3’,’x,y’)x =exp(9)*log(3)/(exp(9)+1)log(3)/(exp(9)+1) 解(1)[x,y,z]=solve(‘(4*x^2)/(4*x^2+1)=y’,’(4*y^2)/(4*y^2+1) =z’,’(4*z^2)/(4*z^2+ 1)=x’,’x,y,z’)x =y =0 解(2)z =第十一题求初值y=dsolve('x*(D2y)+(1-n)*(Dy)+y=0','y(0)=Dy(0)=0','x')第十二题,求特解[x,y]=dsolve(‘Dx=3*x+4*y’,’Dy=5*x-7*y’,’x(0)=0’,’y(0)=0’,’t’)x =y =解(1)。
MATLAB与数学实验 第七章习题

MATLAB与数学实验第七章习题第七章习题1.用MATLAB软件求下列数列极限:(?2)n?3n1 (2)lim(1)limx??(?2)n?1?3n?1x??(lnln)lnn11n?] (4)lim(n?2?2n?1?n)x??x??nn2答(1)syms nlimit(((-2)^n+3*n)/((-2)^(n+1)+3^(n+1)),n,inf) ans = 0 (2)(3)syms nlimit((1+1/n+1/n^2)^n,inf) ans = exp(1)(4)syms nlimit(sqrt(n+2)-2*sqrt(n+1)+sqrt(n),n,inf) ans = 02.用MATLAB软件求下列函数极限: (3)lim[1?1?x?1(1)limx?0x3233x?1?(x?1)3(2)limx??1x?1 (3)lim(sinx)tanxx??2x12x?3x?1(4)lim[(x?x?)ex?x6?1](5)lim() x???x??22x?1答(1)syms xlimit(((1+x)^1/3-1)/x,x,0) ans = NaN(2)syms xlimit((3^(x+1)-(x+1)^3)/(x+1),x,-1,'left') ans = -Inf (3)3.求下列函数的导数。
(1)y?x?x?x (2)y?4.求高阶导数。
x?2(3?x)41?sinx(4)y?xcos2xcox3x (3)y?(x?1)51?cosx(1)已知y?xsinbx,求y(3) (2)求y?x4cox7x 的40阶导数(3)已知y?xsin3x?v1tex?lnx 求y(3)。
5.已知抛射体运动轨迹的参数方程为:12y?v2t?gt2求抛射体在时刻t的运动速度的大小和方向。
dy6.求下列参数方程所确定的函数的导函数:dx (1)x=1-t2y=t-t3 (2)x=ln(1+t2)y=t-arctantdy dxdydxx?07.求由方程ey?xy?e?0 所确定的隐函数的导数8.求由方程y5?2y?x?3x7?0 所确定的隐函数在x=0处的导数?2z?2z?2z: 9.求下列函数的2,2,?x?y?x?y(1)z?sin(xy)?cos2(xy)(2)z?lntan?11?y x????y(3)z?arctan (4)z?e?xy?x10.求 grad1 22x?y11.设f(x,y,z)?x2?y2?z2, 求 gradf(1,?1,?2) 12.求下列函数的极值:1(1)f(x)?x(x2?8) (2)y?arctanx?ln(1?x2)(3)f(x)?x3?4x2?3x2(4)y?excosx,x?[0,2?](5)f(x)?231?3x12 lnx(6)y?x4?5x13.设有质量为5kg的物体,置于水平面上,受力F的作用而开始移动(如图所示)。
MATLAB数学实验练习题

MATLAB数学实验练习题“MATLAB”练习题要求:抄题、写出操作命令、运⾏结果,并根据要求,贴上运⾏图。
1、求230x e x -=的所有根。
(先画图后求解)(要求贴图)>> solve('exp(x)-3*x^2',0) > ezplot('exp(x)-3*x^2') >> grid on ans =-2*lambertw(-1/6*3^(1/2)) -2*lambertw(-1,-1/6*3^(1/2)) -2*lambertw(1/6*3^(1/2))2、求下列⽅程的根。
1) 5510x x ++=a=solve('x^5+5*x+1',0);a=vpa(a,6) a =1.10447+1.05983*i -1.00450+1.06095*i -.199936 -1.00450-1.06095*i 1.10447-1.05983*i 2)1sin 02x x -=⾄少三个根>> fzero('x*sin(x)-1/2', 3) ans =2.9726>> fzero('x*sin(x)-1/2',-3) ans =-2.9726>> fzero('x*sin(x)-1/2',0)ans =-0.74083)2sin cos 0x x x -= 所有根>> fzero('sin(x)*cos(x)-x^2',0) ans =>> fzero('sin(x)*cos(x)-x^2',0.6)ans =0.70223、求解下列各题: 1)30sin limx x xx->->> sym x;>> limit((x-sin(x))/x^3,x,0) ans = 1/62) (10)cos ,x y e x y =求 >> sym x>> diff(exp(x)*cos(x),10) ans =(-32)*exp(x)*sin(x)3)21/2(17x e dx精确到位有效数字)>> sym x>> vpa((int(exp(x^2),x,0,1/2)),17) ans =0.544987104183622224)42254x dx x +?>> sym x;>> int(x^4/(25+x^2),x) ans =125*atan(x/5) - 25*x + x^3/35)求由参数⽅程arctan x y t=?=所确定的函数的⼀阶导数dy dx 与⼆阶导数22d y dx 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章习题
1.用MATLAB 软件求下列数列极限:
(1)11(2)3lim
(2)3n n n x n ++→∞-+-+ ln 1
(2)lim (ln ln)n
x →∞ 2
11(3)lim[1]n
x n n →∞+
+
(4)x →∞
答(1)syms n
limit(((-2)^n+3*n)/((-2)^(n+1)+3^(n+1)),n,inf) ans = 0 (2)
(3)syms n
limit((1+1/n+1/n^2)^n,inf) ans = exp(1) (4)syms n
limit(sqrt(n+2)-2*sqrt(n+1)+sqrt(n),n,inf) ans = 0
2.用MATLAB 软件求下列函数极限:
01
(1)lim x x
→
13
13(1)(2)lim 1
x x x x +→--++ tan 2
(3)lim(sin )x x x π
→
13
2
(4)lim [()2x x x x x e →+∞++1
23(5)lim()21
x x x x +→∞++ 答(1)syms x
limit(((1+x)^1/3-1)/x,x,0) ans = NaN
(2)syms x
limit((3^(x+1)-(x+1)^3)/(x+1),x,-1,'left') ans = -Inf (3)
3.求下列函数的导数。
(1)y =
(2)y =
1sin (3)1cos x y x +=+(4)cos 23y x xcox x =
4.求高阶导数。
(1)已知sin y x bx =,求(3)y (2)求47y x cox x = 的40阶导数 (3
)已知y =求(3)y 。
5.已知抛射体运动轨迹的参数方程为:
12212
x v t
y v t gt
==+
求抛射体在时刻t 的运动速度的大小和方向。
6.求下列参数方程所确定的函数的导函数dy
dx
:
(1
) 23
x=1-t y=t-t (2) 2x=ln(1+t )
y=t-arctant
7.求由方程0y e xy e +-= 所确定的隐函数的导数
dy dx
8.求由方程57023y y x x =+-- 所确定的隐函数在x=0处的导数
x dy dx
=
9.求下列函数的22222,,
:z z z
x y x y ∂∂∂∂∂∂∂ 2(1)sin()cos ()z xy xy =+ (2)ln tan
y z x
= (3)tan y
z arc x
= 11(4)x y z e ⎛⎫
-+ ⎪⎝⎭=
10.求 22
1
grad
x y
+ 11.设222(,,),f x y z x y z =++ 求 (1,1,2)gradf -- 12.求下列函数的极值:
223
(1)()(8)f x x x =- 21
(2)arctan ln(1)2y x x =-+32(3)()43f x x x x =--
(4)cos ,[0,2]x y e x x π=∈2
1(5)()ln f x x x =
(6)y =
13.设有质量为5kg 的物体,置于水平面上,受力F 的作用而开始移动(如图所示)。
设摩擦系数μ=0.25。
问:力F 与水平线的交角α为多少时,才可使力F 的大小为最小?
14.求下列不定积分:
(1)
4sin cos 1sin x x
dx x +⎰ (2) 22723x dx x x +--⎰ (3) (4)sin x
xe xdx ⎰ (5)642
32242(1)x x x dx x x +--+⎰ (6) 15.求下列定积分:
(1)3
0⎰ (2)1222
0(23)x x dx -⎰ (3)720sin xdx π
⎰
(4)20
sin 5cos 4x xdx π
⎰ (5)1260
(1)x dx -⎰ (6)220
cos x xdx π
⎰
16.讨论下列积分的收敛性: (1)3
2
1
sin x dx x ⎰
(2)2
220
sin cos dx
x x
π
⎰
17.用三种方法求下列积分的数值解:
(6)10.5sin x
dx x
⎰
解:matlab 命令为: h=0.01;x=0.5:h:1; y=sin(x)./x; format long t=length(x);
z1=sum(y(1:(t-1)))*h z2=trapz(x,y)
z3=quad('sin(x)./x',0.5,1) 结果为:z1 =
0.45356139752127 z2 =
0.45297449705927 z3 =
0.45297565232213
18.用多种数值方法计算定积分4
1
1sin dx x
π
-⎰进行比较,观察不
同方法的误差。
进行比较, matlab 命令为: h=0.01;x=0:h:pi/4; y=1./(1-sin(x)); format long t=length(x);
z1=sum(y(1:(t-1)))*h z2=sum(y(2:y))*h z3=trapz(x,y)
z4=quad('1./(1-sinx)',0,pi/4) format short
u1=z1-sqrt(2),u2=z2-sqrt(2),u3=z3-sqrt(2),u4=z4-sqrt(2), 结果为:
z1 =
1.38411043673640 z2 =
0 z3 =
1.39596130696093 z4 =
1.53897101160451
u1 =
-0.0301 u2 =
-1.4142 u3 =
-0.0183 u4 =
0.1248
23.求函数
1
()ln
1
x
f x
x
+
=
-
在x=0处前7项的泰勒级数展开式。
解:matlab命令为:
syms x;
f=log((1+x)/(1-x));
taylor(f,x,7,0)
结果为:
ans =
2*x+2/3*x^3+2/5*x^5。
