电场的能量能量密度
电场能量密度公式

电场能量密度公式
电场能量密度是指一个电场中每单位体积所存在的电能量的大小。
电场能量密度的表达式为:U = 1/2 ρE2,它的单位是电子伏特的平方,其中ρ是电荷密度,E是电场强度。
电场能量密度可以用来计算在一定体积中有多少电能量。
例如,如果电场强度为5伏/厘米,电荷密度为5伏/厘米,则电场能量密度为25电子伏特的平方。
这意味着,在1立方厘米的体积中存在25电子伏特的电能量。
电场能量密度的另一个用途是计算电容器的工作能量。
电容器的电容量C可以用电容器的电场能量密度U来计算:U = 1/2Cv2,其中v是电压。
如果电容器的电压为5伏,那么电容器的工作能量就是25伏特的平方,也就是1/2Cv2。
电场能量密度不仅可以用来计算电能量和电容器的工作能量,还可以用来计算电磁场的能量。
如果电磁场的电场强度为E,磁场强度为H,则电磁场的能量密度可以表示为U = 1/2(E2 + H2)。
电场能量密度的量纲是电子伏特的平方,它可以用来计算一定体积中的电能量、电容器的工作能量和电磁场的能量。
因此,电场能量密度是电力学中非常重要的概念,在电子设备和电力系统的设计中都被广泛使用。
电场的能量

电场的能量
电场的能量是描述电场中电荷所具有的能量。
电场是由电荷产生的,它的存在和变化都与电荷的位置和状态有关。
电场的能量可以通过计算电场中电荷所受到的力,或者通过电势能和电场能量密度来描述。
在电场中,电荷受到电场力的作用,当电荷沿着电场方向移动时,电场力对电荷做功,从而将电势能转化为动能。
电场力的大小与电荷的电量和电场的强度有关。
当电场力与电荷的移动方向相同时,电场力对电荷做正功,电场能量增加;当电场力与电荷的移动方向相反时,电场力对电荷做负功,电场能量减少。
电场能量还可以通过电势能来描述。
电势能是指单位正电荷在电场中由于位置变化而具有的能量。
电场中的电势能与电荷的电量和电势差有关。
电场中的电势差是指单位正电荷从一个位置移动到另一个位置时所具有的能量变化。
电势差越大,电场能量越大。
除了电势能,电场能量还可以通过电场能量密度来描述。
电场能量密度是指单位体积内电场能量的大小。
在电场中,电场能量密度与电场强度的平方成正比。
电场能量密度越大,电场能量越大。
电场的能量在许多实际应用中起着重要作用。
例如,在电力系统中,电场能量可以用来传输电能;在电子设备中,电场能量可以用来驱动电子器件的工作;在化学反应中,电场能量可以用来促使电解反
应发生。
总结起来,电场的能量是描述电场中电荷所具有的能量。
它可以通过计算电场中电荷所受到的力、电势能和电场能量密度来描述。
电场的能量在许多实际应用中起着重要作用。
了解电场的能量可以帮助我们更好地理解电场的性质和应用。
电能密度和磁能密度

电能密度和磁能密度
电能密度和磁能密度是物理学中一个重要的概念,它们可以研究物质间相互作用的机制。
它们两个都是电磁学里最基本的概念,也是物理学中的重要概念。
电能密度是指电场的能量分布密度,它描述了单位体积内单位时间内所承受的电能量。
它
可以用矢量E表示,它的强度可以用V/m来衡量,静电场中,它仅在电场影响之外有效,
它可以定义为单位体积内所承受的电能量总和,它可以通过驱动电位来计算出来,它以牛
顿/千万伏特每立方厘米为单位计算。
磁能密度,即磁场能量密度,是指在某一点植物中所存在的磁场能量,它可以用矢量B表示,用斯坦比/立方米表示强度,它的单位为牛顿/千万伏特每立方厘米,它主要用来衡量
物体与场之间的互作用,其值受到场的强度和磁密度的影响,当场强度变化和磁密度变化时,磁能密度也随之改变。
电能密度和磁能密度都是电磁学最基本的概念,他们都可以研究物质之间的相互作用机制。
在相互影响下,它们的值发生变化,也控制了物质间的相互作用,电磁学研究中有着重要
的地位。
电场能量与能量密度

1 1 We E DdV D ndS 2 V 2 S'
第二章 静 电 场 式中V已经扩展到无穷大,故S′在无穷远处。对于分布在有限区域 的电荷,φ∝1/R,D∝1/R2, S′∝R2, 因此当R→∞时,上式中的面积 分为零,于是
1 We E DdV 2 V
第二章 静 电 场
2.8.2 能量密度
图 2 -15 能量密度
第二章 静 电 场
1 1 We dV SdS 2 V 2 S
将▽· D=ρ和D· n=ρS代入上式,有
1 1 We DdV D ndS 2 V 2 S
利用矢量恒等式
D (D) D (D) E D
第二章 静 电 场
2.8 电场能量与能量密度
2.8.1 电场能量
设每个带电体的最终电位为φ1、φ2、…、φn,最终电荷为q1、
q2 、… 、 qn 。带电系统的能量与建立系统的过程无关,仅仅与系
统的最终状态有关。假设在建立系统过程中的任一时刻,各个带 电体的电量均是各自终值的 α 倍 (α<1) ,即带电量为 αqi ,电位为 αφi,经过一段时间,带电体i的电量增量为d(αqi),外源对它所作 的功为αφid (αqi)。外源对n个带电体作功为
b
2
第二章 静 电 场
1 We S ( r ) ( r )dS S 2 1 We l ( r ) ( r )dl l2
We
i 1 n n
1 pij qi q j j 1 2 1 ij i j j 1 2
n
n
We
i 1
2 1 1 q We qU CU 2 2 2 2C
电容器的储能和电场能量密度

电容器的储能和电场能量密度近年来,随着可再生能源的快速发展,对能源储存的需求日益增加。
而电容器作为一种重要的储能器件,其在能量储存和释放方面具有独特的优势。
本文将探讨电容器的储能原理以及与之相关的电场能量密度。
一、电容器的储能原理电容器是由两个带电板和一个介质组成的器件,常见的有平行板电容器和球形电容器。
当电容器连接到电源时,带电板上的电荷会在电场的作用下产生电势差。
电容器的储能过程即是在电场的作用下,电荷从正极板移动到负极板的过程。
在充电过程中,正极板上的电荷被强电场驱使,穿过介质向负极板方向移动,这就是电容器储能的基本原理。
而在放电过程中,负极板上的电荷会受到电场力的作用,从负极板流向正极板,释放储存的能量。
二、电场能量密度的定义电场能量密度是指单位体积内电场能量的大小。
对于电容器而言,其电场能量主要集中在电介质中。
电场能量密度的计算公式为:E = 1/2 * ε * E^2其中,E为电场强度,ε为电介质的介电常数。
该公式表明,电场能量密度与电介质的介电常数以及电场强度的平方成正比。
三、影响电场能量密度的因素1. 介质的选择:电介质的介电常数决定了电场能量密度的大小。
介电常数越大,电场能量密度也就越大。
常见的介电常数较大的物质有聚合物、氧化物等。
2. 电场强度:电场强度越大,电场能量密度也就越大。
通过提高电场强度,可以增加电容器的储能量。
3. 电容器的结构:电容器的结构对电场能量密度也有一定的影响。
平行板电容器中,板间距越小,电场强度越大,电场能量密度也就越大。
四、电容器储能的应用电容器在储能方面有许多应用。
首先,它可以作为备用电源,在电网断电或电源故障时提供临时电力,以保障关键设备的正常运行。
其次,电容器还广泛应用于电动汽车领域。
电动汽车需要高峰时段的大功率输出和低峰时段的能量回收,而电容器的快速充放电特性非常适合这一需求。
此外,电容器还被应用于可再生能源的储能系统中。
通过将发电设备和储能设备相结合,可以实现发电稳定性和能源持续性的提高。
电场能量密度公式

电场能量密度公式
电场能量密度公式为:W=(1/2)UQ。
电场能量密度即单位体积内的电场能量。
静电场的能量是静电场的一个重要特征,对于静电场的能量,一般电磁学教材在讲述这一基本概念时,利用电容器的储能来说明能量定域在电场中,电场中的电介质要受到电场力的作用。
电场是电荷及变化磁场周围空间里存在的一种特殊物质。
这种物质与通常的实物不同,它虽然不是由分子原子所组成的,但它却是客观存在的特殊物质,具有通常物质所具有的力和能量等属性。
电场的力的性质表现为:电场对放入其中的电荷有作用力,这种力称为电场力。
电场的能的性质表现为:当电荷在电场中移动时,电场力对电荷做功,说明电场具有能量。
电场的能量密度

电场的能量密度
电场的能量密度是指单位体积电场中的能量。
在一个电场中,电荷会感受到电场力,从而在电场中运动。
在这个过程中,电荷会获取能量,而电场中也存储了能量。
这些能量被表示为电场的能量密度。
电场的能量密度可以通过以下公式计算:U = 0.5εE,其中,U
表示电场的能量密度,ε表示电场介质的介电常数,E表示电场强度。
这个公式表明,电场的能量密度与电场强度的平方成正比。
因此,当电场强度增加时,电场的能量密度也会增加。
此外,电场介质的介电常数也会影响电场的能量密度。
在相同的电场强度下,介电常数越大,电场的能量密度就越高。
电场的能量密度对于研究电场的性质和应用具有重要意义。
例如,在电容器中存储电荷时,电场的能量密度可以用来计算电容器的电能。
此外,在电磁波传播中,电场的能量密度也是重要的物理量之一。
综上所述,电场的能量密度是电场中存储的能量密度,它与电场强度和电场介质的介电常数有关。
它在研究电场的性质和应用方面具有重要意义。
- 1 -。
普通物理学 电场能量与能量密度

7-7 电场能量与能量密度一、4个重要基本公式①电介质下的电容C与真空下的电容C0的关系:C=C0εr②电场能量W e=12QU=12CU²③能量密度w e=12εE²=12DE④能量密度与电场能量的关系W e=w eVdV(V是电场体积,如果是平面采用二重积分)二、真空环境下与有介质环境下的各物理量间的关系引入:如图所示,已知真空下平行板电容器σ0,E0,U0,D0,C0,W e0,平行板电容器两板间距为d,求下面两种情况下电容器插入相对电容率为εr的σ,E,U,D,C,W e①充电后断开电源②充电后保持两板的电压不变①E=E0εr σ=Eε=E0εεr=E0ε0=σ0U=Ed=E0dεr=U0εrD=Eε=E0εrε0εr =E0ε0=σ0C=εr C0W e=12CU²=12εr C0(U0εr)²=W e0εr②保持电压不变,则:U=U0E=U0d =Ud=E0D= Eε=E0ε0εr=σ0εrσ=Eε=D=σ0εrC=εr C0W e=εr W e0小结:1、电容器的电容与电压大小无关,只和电介质相对电容率有关2、平行板电容器由于电荷增加而增加的能量,大于插入介质损失的能量,所以电场能量增加拓展:1、电位移矢量沿任何一个闭合曲面的通量为0,表明曲面内自由电荷代数和为0(D与E方向一致)2、介质中的电位移矢量和自由电荷与极化电荷的分布有关3、在自由电荷分布不发生变化时,含电介质的电容器电容一定是真空状态下的1ε0三、两个重要模型1、带电球壳电容器模型模型简述:如图所示,球形电容器的内、外半径分别为R 1和R 2,所带电荷为±Q .若在两球壳间充以电容率为ε的电介质,问此电容器贮存的电场能量为多少?解:根据笔记7-1,得到r 处的电场强度大小为E=Q4πεr能量密度w e =12× Q4πεr 2×ε=Q 232π2εr 那么根据第一幕的公式4,得到W e = w e V dV = dW e =Q 28πε drr ²R 2R 1=Q 28πε(1R 1−1R 2)回到笔记7-5的孤立导体,R 2趋近于无穷大,得到W e =Q 28πε1R 1是孤立导体的电场能量2、带电圆柱电容器模型模型简述:如图圆柱形电容器,中间是空气,空气的击穿场强是E b ,电容器外半径R 2.在空气不被击穿的情况下,内半径R 1为多少,可使电容器存储能量最多?解:根据7-3笔记得到任意圆柱面r 的电场强度是E=λ2πε0r带入击穿场强有λmax =E b 2πε0R 1 求出电容器电压U= λ2πε0r dr R 2R 1=λ2πε0ln R2R1根据能量公式得到W e =λl 2λ2πε0ln R 2R 1=λ²l 4πε0ln R 2R 1带入λmax =E b 2πε0R 1 得到:W e =πε0E b ²R 1²lnR 2R 1求导求出R 1取得的值使得W e 最大。
电场的能量能量密度

dq u
例1、求半径为R ,带电量为Q的孤立导体球的电能。
由: dA=Vdq 得:
q
dA
d的功为
W Q
A
q
dq q2
Q
Q2
0 40R
80R 0 80R
QR
r
由电场能量密度积分得:
r>R时电场的能量元为
dw120(4Q0r2)24r2dr
W
R
Q2
80r2
例2:平行板电容器带电量为 q,极板面积为 S,将极
板间距从 l 拉大到 l+d ,求外力作功 A,和电场能量的
增量。
解:拉力
F qEq
20
q
将极板拉开时外力作的功为
q q
Aq d q2 d 20 20S
电容器拉开后,其电能为
W q2
q2
2C 20S /(l d )
q2 (l d)
20S
例5:同轴电缆由内径为 R1、外径为 R2的两无限长金属圆柱面构成,单位长度带电量分别为 + 、 - ,其间充有 r 电介质。
例1:平行板电容器真空时参数如下
充电后保持电压不变,插入 r 介质;
2
W1 E V 1 ( q ) Sd q d 求这由:部电① 分 场两增能柱加量面的密间电度的场积场能分强量得恰:E0;等于2外力体 对系统作了功。0
例1、求半径为R ,带电量为Q的孤立导体球的电能。
四、应用举例
例1:平行板电容器真空时参数如
下
0,E0,V0,D0, C0,W0
①.充电后断开电源,插入介电常 数为 r 介质;
②.充电后保持电压不变,
插入 r 介质;
求: ,E,V,D,C,We
电场的能量与能量密度

电场具有方向和大小,是一个矢量场。
03
电场对电荷的作用力遵循库仑定律。
电场强度与电势差
电场强度是描述电场强弱的物理量,用E表示, 单位是牛/库仑(N/C)。
电势差是指电场中两点间的电势之差,用U表 示,单位是伏特(V)。
电场强度和电势差之间存在微分关系:E = grad(U)。
电场线及等势面
03
能量密度概念
能量密度定义
能量密度是指单位体积内的能量储存 量,用于描述电Байду номын сангаас、磁场等物理场中 的能量分布情况。
在电场中,能量密度表示电场能量的 空间分布情况,即单位体积内电场能 量的多少。
能量密度与电场关系
电场强度与能量密度成正比关系。电场强度越大,能量密度 也越大。
电场中的能量密度与电场的分布、电荷的分布以及电场的边 界条件等因素密切相关。
电场的能量与能量密 度
汇报人:XX 2024-01-20
目录
• 电场基本概念 • 电场能量 • 能量密度概念 • 电场能量与能量密度关系 • 不同类型电场中能量与能量密度表现 • 实际应用举例
01
电场基本概念
电场定义及性质
01
电场是存在于电荷周围的一种特殊物质,它对放入 其中的电荷产生力的作用。
高压输电线路周围环境影响评估
电场强度分布
高压输电线路周围存在强电场,其强度随距离的增加而迅 速减小。评估时需测量不同距离处的电场强度,以了解空 间分布情况。
对人体的影响
强电场可能对人体产生生理效应,如引发头痛、失眠等症 状。评估时需考虑电场对人体健康的影响,并制定相应的 防护措施。
对周围环境的影响
高压输电线路周围的强电场可能对周边设备、建筑物等产 生干扰或损坏。评估时需综合考虑电场对周围环境的影响 ,以确保输电线路的安全运行。
静电场的能量和能量密度
1 S
2d
(Ed )2
1 E 2Sd
2
电场能量密度
we
1 E 2
2
1 ED 2
物理意义 电场是一种物质,它具有能量.
电场空间所存储的能量
We
V wedV
1 E 2dV
V2
和的电R介例2,质1所,带如问电图此荷所电为示容,器球Q贮形存电.的容若电器在场的两能内球量、壳为外间多半充少径以?分电别容率为为R1
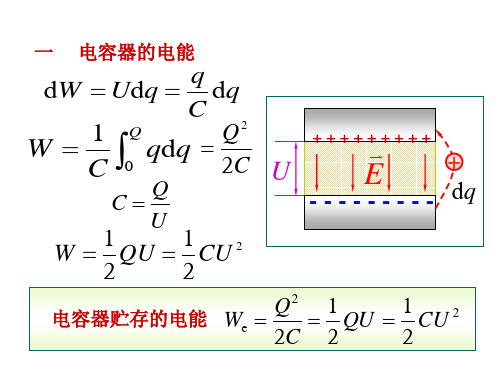
一 电容器的电能
dW Udq q dq
C
W 1
Q
qdq
Q2
C0
2C
CQ
U
+ + + + + + + + +
E
+
- - - - - - - - - dq
U
W 1 QU 1 CU 2
2
2
电容器贮存的电能
We
Q2 2C
1 QU 2
1 CU 2 2
二 静电场的能量 能量密度
We
1 CU 2
2
R2 R1
(球形电容器电容)
(2) R2
We
Q2
8π R1
(孤立导体球贮存的能量)
例2 如图圆柱形电容器,中间是空气,空气的击
穿场强是 Eb 3106 V m-,1 电容器外半径 R2 102 m.
在空气不被击穿的情况下,内半径
存储能量最多. ( 空气 r 1 )
R1
?
1
4π
Q r2
er
we
1 E 2
2
Q2
32π 2 r 4
R1 dr
电场能量密度公式中的d

电场能量密度公式中的d
电场能量密度公式中的d指的是电场的能量密度。
电场能量密度是电场中单位体积的能量,表示电场中的能量集中程度。
在电场中存在能量,当电场发生变化时,就会发生能量的转移和变化。
电场中的能量密度可以通过电场能量密度公式来计算,即U = 0.5εε0E^2,其中,U表示单位体积电场中的能量密度,ε表示电介质常数,ε0表示真空中的介电常数,E表示电场强度。
电场能量密度公式的意义在于,可以通过它来计算电场中的能量分布情况,揭示电场的能量变化规律。
这对于解决一些问题,如电场能量的传输和储存等,具有指导意义。
此外,电场能量密度公式还有着重要的实际应用。
例如,对于电场能量密度的测量和分析,可以帮助我们更好地理解电场的性质,进而提高电场的利用效率。
同时,在设计电场相关的设备和系统时,也可以根据电场能量密度公式,对电场能量密度进行合理分配和控制,以达到更好的性能和效果。
总之,电场能量密度公式中的d,即电场的能量密度,是电场中能量集中程度的重要描述指标,它的应用覆盖了电场领域的各个方面,对于研究和利用电场具有重要的参考和指导意义。
电场能量计算公式

电场能量计算公式
电场能量为电场所具有的能量,相当于其等效电容中的电能,公式:
w=1/2*u^2*c=1/2*q^2/c。
电场能量就是电场所具有的能量,电场能量等于电场能量密度对电场所处空间的积分,点电荷产生的静电场的能量正比于点电荷的带电量的平方。
电场能量为电场所具有的能量,相当于其等效电容中的电能,公式:
w=1/2*u^2*c=1/2*q^2/c。
电场能量就是电场所具备的能量,电场能量等同于电场能量密度对电场所处空间的分数,点电荷产生的静电场的能量正比于点电荷的磁铁量的平方。
对每个元电容不许考虑边缘效应,因为每个局部元电容中的场被周围元电容中的场加以保护。
这样任意一个自由空间是由无数个元电容组构成的一个电容结构,而每个元电容都相当于一个无限大平行板电容器。
所以用理想平行板电容器的均匀场研究空间电场能量分布具有普遍意义。
电容器在电路中的促进作用:
1、当电容器两端电压增加时,电容器从电源吸收能量并储存起来;
2、当电容器两端电压减少时,电容器便把它原来所储存的能量转化成。
3、即电容器本身只与电源进行能量交换,而并不损耗能量,因此电容器是一种储能元件。
能量密度计算公式 打印

能量密度计算公式打印
能量密度计算公式。
能量密度是指单位体积或单位质量的物质所含有的能量。
在物
理学和工程学中,能量密度通常用来描述电磁场、重力场、热力学
系统等的能量分布情况。
能量密度的计算公式可以根据具体的情况而有所不同,以下是
一些常见的能量密度计算公式:
1. 电磁场能量密度计算公式:
对于电磁场的能量密度,可以使用以下公式进行计算:
\[ u = \frac{1}{2}(\varepsilon E^2 + \frac{B^2}{\mu}) \]
其中,u表示能量密度,ε表示介电常数,E表示电场强度,B表示磁感应强度,μ表示磁导率。
2. 物质的能量密度计算公式:
对于物质的能量密度,可以使用以下公式进行计算:
\[ u = mc^2 \]
其中,u表示能量密度,m表示物质的质量,c表示光速。
3. 热力学系统的能量密度计算公式:
对于热力学系统的能量密度,可以使用以下公式进行计算: \[ u = \frac{1}{2} \rho v^2 \]
其中,u表示能量密度,ρ表示介质密度,v表示速度。
以上是一些常见的能量密度计算公式,它们在不同领域的物理学和工程学中有着重要的应用。
通过这些公式,我们可以更好地理解和描述能量在空间中的分布情况,为相关领域的研究和应用提供重要的理论基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
一、带电体系的能量
带电体系的带电过程可看成是从电势0点移动电荷到 带电体系的带电过程可看成是从电势 点移动电荷到 该带电体系,使带电体系带电。这个过程外界作的功, 该带电体系,使带电体系带电。这个过程外界作的功, 就是带电体系的能量 含互能、与自能) 带电体系的能量。 就是带电体系的能量。(含互能、与自能)
σ0
−σ0
εr
d
σ , E ,V , D, C,We
σ = σ0
K
充电后断开电源, ① 解:充电后断开电源,极板上 电量不变
V0
9
σ0 = 2.介质中场强:E = 介质中场强: 介质中场强 ε r ε rε 0
E0
3.电压:插入介质后 电压: 电压
σ0
−σ0
V = Ed =
E0
εr
d=
V0
εr
4.电位移矢量 插入介质后 电位移矢量:插入介质后 电位移矢量
将极板拉开时外力作的功为 2 σ q A=q d= d 2ε 0 2ε 0 S 电容器拉开后,其电能为 拉开后, 拉开后 q2 q2 W= = 2C 2ε 0 S /(l + d )
2
σ F = qE = q 2ε 0
+q
−q
−q
F l
q2 q2 q l+ d = (l + d ) = 2ε 0 S 2ε 0 S 2ε 0 S
Q
Q
Q
R
A=∫
0
q 4πε 0 R
dq =
q2
8πε 0 R 0
=
Q2 8πε 0 R
=W
r
由电场能量密度积分得:
r>R时电场的能量元为
1 Q dw = ε 0 ( ) 2 4πr 2 dr 2 4πε 0 r 2
2
W =∫
R
∞
Q
2
8πε 0 r
dr = −
Q
2
∞
8πε 0 r
=
R
Q2 8πε 0 R
d
7
= W0 + A
外力作正功,电容器能量增加。 外力作正功,电容器能量增加。
由上述的计算结果,在拉开极板时,电荷并没有增加, 由上述的计算结果,在拉开极板时,电荷并没有增加, 但电场能量增加了。增加的原因是极板拉开时, 但电场能量增加了。增加的原因是极板拉开时,外力 对系统作了功,使有电场的空间增大了。 对系统作了功,使有电场的空间增大了。这部分增加 的电场能量恰等于外力对系统作了功。 的电场能量恰等于外力对系统作了功。所以本例说明 静电能存储于电场中。 静电能存储于电场中。
1D 1 V体 W = EDV体 = 2 ε 2
2
1 1 2 1D W = εE V体 = EDV体 = V体 2 2 2 ε212源自ε rε 0 Sd
= ε r C0
6.能量 能量
2 0
q W0 = , 2C0
2 0
εr
d
2 q q0 W0 W= = = 2C 2ε rC0 ε r
K
V0
11
充电后保持电压不变, 介质; ②.充电后保持电压不变,插入 εr 介质; 充电后保持电压不变 不断开。 解:电压不变即电键 K 不断开。 1.电压 电压 2.场强 场强
1 q 2 q2 1 ) Sd = d ∆W = ε 0 E 2V体 = ε 0 ( 2 ε0S 2ε 0 S 2
该能量恰与电容器的能量增量相同。 该能量恰与电容器的能量增量相同。
q2 q2 W= l+ d 2ε 0 S 2ε 0 S
8
四、应用举例
例1:平行板电容器真空时参数如 : 下 σ 0 , E0 , V0 , D0 , C0 ,W0 充电后断开电源, ①.充电后断开电源,插入介电常 充电后断开电源 介质; 数为 εr 介质; ②.充电后保持电压不变, 充电后保持电压不变, 充电后保持电压不变 插入 εr 介质; 求:
−λ
15
解: ①极板间作高为 h 半径为 r 的高斯柱面, 的高斯柱面, 由介质中高斯定理: 由介质中高斯定理:
∫∫ D ⋅ dS = ∑ q 0
D2πrh = λh
λ
εr
h
R1 R2
r −λ
λ D= 2πr
场强
λ = E= ε 0ε r 2πε 0ε r r
D
16
②极间电压 R R U12 = ∫R E ⋅ dl = ∫R Edr λ dr R = ∫R 2πε 0ε r r
K
U0
14
例5:同轴电缆由内 : 径为 R1、外径为 R2 的两无限长金属圆柱 面构成, 面构成,单位长度带 电量分别为 +λ、 -λ, 电介质。 其间充有 εr 电介质。 求:①两柱面间的场 强 E;②电势差 U; ; ; ③单位长度电容 ; 单位长度贮存能量。 ④单位长度贮存能量。
λ
R1
εr
R2
移动 dq 作的元功
+q E
−q
dA = Vdq
极板带电量从 0 到Q 作功
A = ∫ dA = ∫0 Vdq = W
Q
Q
0
dq
外力所做的功A转化为带电体的 外力所做的功 转化为带电体的 能量W。 能量 。
u
2
例1、求半径为R ,带电量为Q的孤立导体球的电能。 由: dA=Vdq 得: q dA = dq 4πε 0 R 将导体球的电荷从0增加到Q,所作的功为
R1 R2
r −λ
18
λh R2 We = ln 4πε 0ε r R1
2
λ
εr
h
单位长度贮存能量
R1 R2
r −λ
We we = h
λ R2 = ln 4πε 0ε r R1
2
19
σ0
εr
−σ0
K
U0
20
1 ε 0ε rS 1 1 2 2 2 = ( Ed ) = ε 0ε r E Sd W = CU 2 d 2 2 1 2 = εE V体 2 由 D = εE 有
σ0
−σ0
εr
d
C = ε rC0
K
U0
13
6.电容器能量 电容器能量We 电容器能量
1 W0 = q0V0 2
σ0
εr
−σ0
1 1 W = qV0 = ε r q0V0 2 2
= ε rW0
由于q增多而增加的能量, 由于 增多而增加的能量,大 增多而增加的能量 于插入介质损失的能量, 于插入介质损失的能量,所以 W也增加。 也增加。 也增加
4
W
为电容器能量,单位:焦耳, 。 为电容器能量,单位:焦耳,J。
三、电场的能量
带电体系具有能量, 带电体系具有能量,这一能量也可以认为就 存在于电场之中。电场能量计算如下: 存在于电场之中。电场能量计算如下:
以充满介质的平行板电容器为例
1 ε 0ε r S 2 1 2 1 2 ( Ed ) = ε 0ε r E Sd 能量由: 能量由: W = CV = 2 2 d 2 1 2 = εE V体 2
2
2
λ
εr
h
1
1
2
R1 R2
r −λ
1
λ R2 = ln 2πε 0ε r R1
③单位长度电容
2πε 0ε r h h 长电容 C = = U12 ln( R2 / R1 )
λh
17
单位长度电容
λ
εr
h
C 2πε 0ε r c= = h ln( R2 / R1 )
④单位长度贮存能量 h 长贮存能量 1 We = qU12 2 1 λ R2 = λh ln 2 2πε 0ε r R1
V = V0
σ0
−σ0
Ed = E0d, ∴ E = E0
3.自由电荷面密度 3.自由电荷面密度
∵V = V0
σ0 σ = , ε 0 ε 0ε r σ = ε rσ 0
εr
d
K
V0
12
4.电位移矢量 电位移矢量D 电位移矢量
∵ D0 = σ 0
D = σ = ε rσ 0 = ε r D0
5.电容 5.电容 由于电容器电容与电量无关, 由于电容器电容与电量无关, 与介质有关, 与介质有关,充满介质时
3
二、电容器存储的能量: 电容器存储的能量: 电容器的电压由: 电容器的电压由:V = q C Q Q q dq A= Vdq = ∫0 0 C 1 Q2 = 2C
+q E
−q
∫
dq
V
外力作功等于电容器能量增量, 外力作功等于电容器能量增量,
CV 1Q A =W = = 2C 2
2
2
1 = QV 2
5
C=
ε 0ε r S
d
, V = Ed
三、电场的能量密度
1 2 W = εE V体 2
单位体积内的电场能量。 单位体积内的电场能量。 w = W V体
2 1 2 1 1D w = εE = ED = 2 2 ε 2
非均匀电场能量计算
W = ∫ wdV
V
只要确定 w 就可计算电场能量 W。 。
6
例2:平行板电容器带电量为 q,极板面积为 S,将极 : , , 板间距从 l 拉大到 l+d ,求外力作功 A,和电场能量 , 的增量。 的增量。 解:拉力
D = ε 0ε r E = ε 0ε r
E0
εr
d
εr
= ε 0 E0 = σ 0 = D0
K
不变, 也不变。 由于 D = σ0 ,断开电源后 σ0 不变,D 也不变。
V0
10
