十求图形面积的几种常用方法

合集下载

第四节图形面积-学而思培优

第四节图形面积一、课标导航二、核心纲要1.一些常用图形的面积公式正方形面积=边长×边长；长方形（矩形）面积=长×宽；平行四边形面积=底×高；三角形面积=;21高底⨯⨯ 梯形面积=.)(21高下底上底⨯+⨯ 2.计算图形的面积有以下常用方法(1)和差法：把图形面积用常见图形面积的和或差表示，通过常规图形面积公式计算．(2)割补法：有时直接求图形面积有困难，我们可以通过分割或补形，把图形转化为容易观察或解决的形状求解．(3)等积变换法：对某些图形，找出与所求图形面积相等或有关联的特殊图形，通过代换转化易求图形的面积．(4)等比法：将面积比转化为线段比． 3．在两个三角形中(1)同（等）高时，面积之比等于底之比． (2)同（等）底时，面积之比等于高之比． 4.等分三角形面积三角形一边中线平分三角形面积． 5．常见的基本模型本节重点讲解：图形面积的计算和证明．三、全能突破基础演练1．如图11-4—1所示，在△ABC 中，点D 、E 、F 分别为BC 、AD 、AC 的中点，且,16=∆ABC s 则DEF s ∆的面积为( )．2.A 8.B 4.C 1.D2．如图11-4 -2所示，在△ABC 中，,2,1==BC AB 则△ABC 的高AD: CE 为( )2:1.A 1:2.B 4:1.C 1:4.D3．已知△ABC 的面积为3，边BC 长为2，以点B 为原点，BC 所在的直线为z 轴建立平面直角坐标系，则点A 的纵坐标为( )3.A 3.-B 6.C 3.±D4．图ll-4-3(a)、(b)为两个相同的矩形，若图(a)阴影区域的面积为10，则图(b)的阴影面积等于( ) 40.A 30.B 20.C 10.D5．如图11-4 -4所示，已知BD AC ⊥于点CO D B O C A O B A O DO ∆∆∆∆、、、,的面积分别为、、、321s s s ,4S 设,,n BD m AC ==则下式中正确的是( )． mn s s s s A 21.4321=+++ mn s s s s B =+++4321. mn s s s S C 21.4321=⋅⋅⋅ mn S S s s D =⋅⋅⋅4321.6．如图11-4 -5所示，在△ABC 中，E 为BC 的中点，AD 上BC 于点D ，以下结论：;AE AD <①;CE BE =②;ACE ABE s s ∆∆>③ ,CDBDs s ACD ABD =∆∆④其中正确的命题为7．如图11-4 -6所示，在△ABC 中，AD 、BE 相交于点,1:2:,2:3:,==CE AE CD BD O 若,2=∆COD S 求：AO B Aoc BO C s s s ∆∆∆::)1(的值．(2)求⋅∆ABC s8．图11-4 -7所示是某个公园ABCDEF ，M 为AB 的中点，N 为CD 的中点，P 为DE 的中点，Q 为FA 的中点，其中游览区APEQ 与BNDM 的面积和是900平方米，中间的湖水AMDP 的面积为361平方米，其余的部分是草地，求草地的总面积．9．认真阅读，并回答下面问题：如图11-4 -8所示，AD 为△ABC 的中线，ABD S ∆与ADC s ∆相等吗？【解】过A 点作BC 边上的高h ， ∵ AD 为△ABC 的中线 .DC BD =∴.21,21h DC S h BD s ACD ABD ⋅=⋅=∆∆ ,ACD ABD s s ∆∆=∴(1)用一句简洁的文字表示上面这段内容的结论：(2)利用上面所得的结论，用不同的分割方法分别把下面两个三角形面积4等分（只要割线不同就算一种）． (3)已知：AD 为△ABC 的中线，点E 为AD 边上的中点，若△ABC 的面积为,4,20=BD 求点E 到BC 边的距离为多少？能力提升10.如图11-4 -9所示，三边均不相等的△ABC，若在此三角形内找一点0，使得△OAB、△OBC、△OCA 的面积均相等，判断下列作法正确的是( )． A.作中线AD ，再取AD 的中点0B ．分别作中线AD 、BE ，再取此两中线的交点0C ．分别作AB 、BC 的中垂线，再取此两中垂线的交点0D ．分别作∠A 、∠B 的角平分线，再取此两角平分线的交点011．如图11-4 -10所示，在正方形ABCD 中，DCE AB ∠=,2是正方形AB CD 的外角，P 是DCE ∠的角平分线CF 上任意一点，则△PBD 的面积等于( ) 1.A 5.1.B 2.C 5.2.D12.如图11-4 -11所示，△ABC 的面积为,182cm 点D 、E 、F 分别位于AB 、BC 、CA 上，,//AC DE 且,5,4cm DB cm AD ==则△ABE 的面积是( )． 8.A 9.B 10.C 12.D13.如图11-4 -12所示，在△ABC 中，点M 是BC 边上任意一点，D 、E 、F 分别是AM 、BD 、CE 的中点，且,1=∆ABC s 则=∆DEF s ( )．21.A 41.B 61.C 81.D14.如图11-4 -13所示，在长方形ABCD 中，E 是AD 的中点，F 是CE 的中点．三角形BDF 的面积是,62cm 则长方形ABCD 的面积为15.如图11-4 -14所示，面积为16的△ABC 中两中线AD ⊥BE ，若:2:=÷BE AD ,3则BE 的长为16.探索在图ll-4-15(a)至图11-4-15(c)中，△ABC 的面积为a ．(1)如图(a)所示，延长△ABC 的边BC 到点D ，使,BC CD =连接DA.若△ACD 的面积为,1s 则=1s （用含a 的代数式表示）；(2)如图(b)所示，延长△ABC 的边BC 到点D ，延长边CA 到点E ，使,,CA AE BC CD ==若△DEC 的面积为,2s 则=2s （用含a 的代数式表示），并写出理由；(3)在图(b)的基础上延长AB 到点F ，使,AB BF =连接FD 、FE ，得到△DEF(如图(c)所示）．若阴影部分的面积为,3S 则=3s （用含a 的代数式表示）．发现像上面那样，将△ABC 各边均顺次延长一倍，连接所得端点，得到△DEF(如图(c)所示），此时，我们称△ABC 向外扩展了一次，可以发现，扩展一次后得到的△DEF 的面积是原来△ABC 面积的倍．应用去年在面积为210m 的△ABC 空地上栽种了某种花卉．今年准备扩大种植规模，把△ABC 向外进行两次扩展，第一次由△ABC 扩展成△DEF，第二次由△DEF 扩展成△MGH(如图(d)所示）．求这两次扩展的区域（即阴影部分）面积共为多少平方米？17.已知，如图11-4 -16所示，,//,//BD CE AB DC 交AD 的延长线于点E ，求证：⋅⋅=∆∆∆D CE ABD BCD s s s 2)(18．(1)①问题1：如图ll-4-17(a)所示，已知△ABC，请你过点A 画一条直线，把△ABC 分成面积相等的两部分(在图(a)中画出来，简要写出作法）．②问题2：如图ll-4-17(b)所示，已知,//21l l 点A 、D 在1l 上，点B 、C 在2l 上，试说明△ABO 与△DCO 面积相等．(2)应用：如图ll-4-17(c)所示，在△ABC 中，点M 在AB 边上，过点M 画一条直线，将△ABC 的面积二等分（保留作图痕迹，不写作法）．(3)拓展：如图ll-4-17(d)所示，四边形ABCD 是一块土地的示意图，过点D 修一条直路，直路修好后，要保持直路两边的面积相等，请你确定出这条直路（不计直路的占地面积）． ①简要写出设计方案，并在图(d)中画出相应的图形．②说明方案的设计理由．19．如图11-4 -18所示，在△ABC 中，AC AC AB ,=边上的高.10cm BD =(1)如图(a)所示，求AB 边上的高CE 的长．(2)如图(b)所示，若点P 为BC 边上任意一点，AB PM ⊥于点AC PN M ⊥,于点N ，求PN PM +的值．(3)如图(c)所示，若点P 为BC 延长线上任意一点，AB PM ⊥于点AC PN M ⊥,于点N ，在.PN PM +①PN PM -②中有一个是定值，判断出来并求值．20．阅读理解如图ll-4-19(a)所示，在△ABC 中，D 是BC 的中点，如果用ABC S ∆表示△ABC 的面积，则由等底同高的三角形的面积相等，可得⋅==∆∆∆ARC ACD ABD s s s 21同理，如图(b)所示，在△ABC 中，D 、E 是BC 的三等分点，可得⋅===∆∆∆∆ABC c ADE ABD s s s s 31π 结论应用已知：△ABC 的面积为1，请利用上面的结论解决下列问题：(1)如图ll-4-20(a)所示，若D 、E 分别是AB 、AC 的中点，CD 与BE 交于点F ，则△DBF 的面积为类比推广(2)如图ll-4-20(b)所示，△ABC 的面积为1，D 、E 为AC 的三等分点，F 、G 为BC 的三等分点，四边形PECF 的面积．中考链接21.（2011．福州）如图11-4—21所示，在长方形网格中，每个小长方形的长为2，宽为1，A 、B 两点在网格格点上，若点C 也在网格格点上，以A 、B 、C 为顶点的三角形面积为2，则满足条件的点C 的个数是( )．2.A3.B4.C5.D22.（2011．随州）如图11-4 - 22所示，在△ABC 中，E 是BC 上的一点，,2BE EC =点D 是AC 的中点，设BEF ADF ABC ∆∆∆、、的面积分别为,BEF AD F ABC s s S 、、∆∆且,12=∆ABC s 则=-∆∆BEF ADF s S ( )1.A2.B3.C4.D巅峰突破23.如图11-4 - 23所示，在矩形ABCD 中，、、H E AB AD BF BG AE ,23121=====G 在同一条直线上，则阴影部分的面积等于( )． 8.A 12.B 16.C 20.D24.如图11-4 - 24所示，三角形ABC 内的线段BD 、CE 相交于点0，已知,2,OE OC OD OB ==设COD BOC BOE ∆∆∆、、和四边形AEOD 的面积分别为⋅4321s s s s 、、、(1)求31:s s 的值；(2)如果,22=s 求4S 的值．25.直角三角形的三条边长分别为3cm、4cm、5cm，在三角形内部有一点P，已知点P到三角形其中两条边的距离分别为3.2cm和0.5cm，求点P到三条边的距离.。

求图形面积的几种常用方法

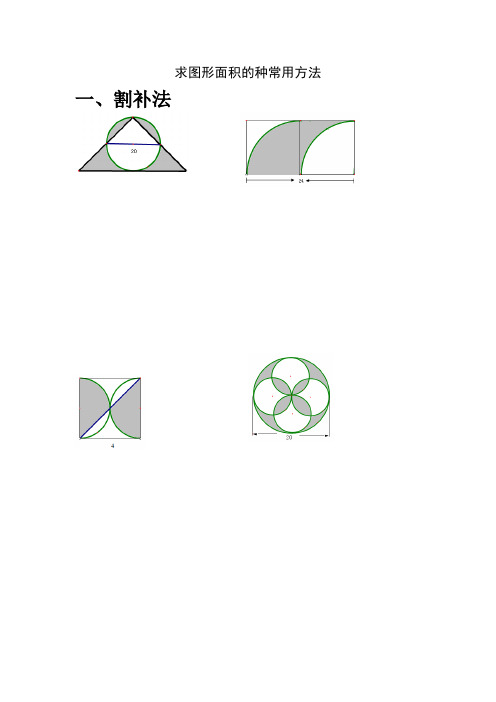
求图形面积的种常用方法一、割补法二、加减法律三、旋转法十、利用r2和r3的代换十二边形里每个空正三角形边长为3米四、等分法：4、下列每个正方六边形的面积都是36平方厘米，求阴影部分的面积各是多少5、四个相同的正六边形，每个面积为6，求三角形的面积C6、如图所示，四个等腰直角三角形的和一个正方形拼成一个长方形，已知正方形的面积是5平方厘米，求长方形的面积7、E 是长方形的中点，求阴影部分的面积与长方形面积的比是多少B8、长方形ABCD 的长是15厘米，E 、F9、正方形ABCD 的面积是12平方厘米，E 、F 、G 、H 分别是中点，求阴影部分的面积。

10、下面是由两个等腰直角三角形组成的图形，求阴影部分的面积占整个图形的几分之几。

8BFCBA五、抓不变量11、正方形ABCD 的边长为5厘米，△CEF的面积比△ABF 的面积大5平方厘米，求CE 的长。

12、已知长方形ABCD ，长是8是6积小平方厘米，求线段CE13、在平行四边形BCDG 中，米，直角三角形ABC 8面积大10平方厘米。

求BF FD C BA14、已知半圆的半径是4，阴影部分○比阴影部分○大，求BC 的长。

15、如图，三角形ABC 与三角形DEF 是两个完全一样的三角形，已知AB=12，BE=5，DG=4，求阴影部分的面积是多少FGD16、如图，OB 把半径为6厘米，圆心角为90度的扇形分成两部分，扇形OBC 的面积是扇形OAB 面积的2倍。

ODBE 是长方形，那么图中甲的面积比乙的面积大多少六、“一半”的应用17、已知长方形的长为8厘米，宽为6厘米，求阴影部分的面积。

18、已知平行四边形被分为4个三角形，已知其中3个三角形的面积分别为11平方厘米，30平方厘米，43平方厘米，那8么阴影部分的面积为多少平方厘米19、如图所示，已知平行四边形中的3个三角形面积分别为7平方厘米、2平方厘米、9平方厘米，那么阴影部分的面积为多少平方厘米20、如图所示，已知正方形图中的五块面积分别为65平方厘米，20平方厘米，50平方厘米，15平方厘米，70平方厘米，那么阴影部分的面积为多少平方厘米21、如图，在平行四边形ABCD 中，三角形ABP 的面积为15，三角形为3422、如图，ABCD 是正方形，EDGF 是长方形，CD=4厘米，DG=5厘米，求宽DE 。

求图形面积的几种常用方法

第十二讲求图形面积的几种常用方法在组合图形中，求阴影部分的面积的常用方法是：割补法、加减法、旋转法、构造法、等积的变换，抓不变量、等分、一半的应用、代换、比例等。

A、割补法：对于一些求不在一起的几块阴影面积的和，往往需要把它们通过剪割、拼补在一起，才便于计算，在剪割、拼补过程中，一定要注意割下来的图形和补上去的图形的形状、大小必须完全一样。

【例1】如图，每个小圆的半径是2厘米，求阴影部分的面积是多少平方厘米？【分析与解】如图，通过剪割、拼补，阴影部分的面积就变成了圆的面积减去正方形的面积，则阴影部分面积为：S=S圆－S正方形=π×42－4×4÷2×4=50.24－32=18.24(平阴影方厘米)【例2】右图中三个圆的半径都是4厘米，三个圆两两交于圆心。

求阴影部分的面积是多少平方厘米？【分析与解】如图，三个阴影部分的面积都相等，只需要求出其中一个面积即可，但非常困难。

这时我们可以考虑采用割补的方法，同时利用对称性，将其个半圆形，则阴影部分的面积=3。

14×4×4÷2=25。

12（平方厘米）B、加减法：注意观察，所求阴影部分的面积看是由哪几个图形相加，再减去哪个图形变可以得到。

我们把这种通过加、减就能求出它的面积的方法，我们的把它称为“加减法”。

【例3】如图，正方形的边长为4厘米，求阴影部分的面积是多少？【分析与解】如图，显然阴影部分的面积=扇形的面积－空白c的面积，而空白c的面积=正方形的面积－扇形的面积，即S阴影=S扇－（S正－S扇）= S扇－S正＋S扇= S扇＋S扇－S正即S扇＋S扇比S正的面积多了b那部分的面积，即b= [(b＋c)＋(b＋a)]－(a ＋b＋c)阴影部分的面积，S阴=π×42÷4×2ab－4×4=25.12－16=9.12(平方厘米)。

【例4】如图，长方形的长为12厘米，宽为8厘米，求阴影部分的面积是多少？【分析与解】如图，S 阴影= S 大扇－S a = S 大扇－(S 长－S 小扇) = S 大扇＋S小扇－S 长=π×122÷4＋π×82÷4－12×8=163.28－96=67.28（平方厘米）C 、旋转法：在求一些面积时，有时需要把某个图形进行一定方向的旋转，使之拼在一起，变成另一个比较方便求的图形。

阴影部分面积的求法

求图形面积的几种常用方法1、割补法：对于一些求不在一起的几块阴影面积的和，往往需要把它们通过剪割、拼补在一起，才便于计算，在剪割、拼补过程中，一定要注意割下来的图形和补上去的图形的形状、大小必须完全一样。

【例1】如图，每个小圆的半径是2厘米，求阴影部分的面积是多少平方厘米？【例2】右图中三个圆的半径都是4厘米，三个圆两两交于圆心。

求阴影部分的面积是多少平方厘米？2,重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可•例如，求下图中阴影部分面积3、加减法：注意观察，所求阴影部分的面积看是由哪几个图形相加，再减去哪个图形变可以得到。

我们把这种通过加、减就能求出它的面积的方法，我们的把它称为“加减法”【例3】如图，正方形的边长为4厘米，求阴影部分的面积是多少？使之组合成一个原来【例4】如图，长方形的长为 12厘米，宽为8厘米，求阴影部分的面积是多少?4.辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可例如，求下图中阴影部分面积5, 平移法：这种方法是将图形中某一部分切割下来平行移动到一恰当位置, 新的基本规则图形，便于求出面积•例如，如下图，求阴影部分面积6. 对称添补法：这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形图形面积就是这个新图形面积的一半 •例如，求下图中阴影部分的面积,7、旋转法：在求一些面积时，有时需要把某个图形进行一定方向的旋转，使之拼在一起, 变成另一个比较方便求的图形。

【例5】如图，梯形ABCD的上底是3厘米，下底是5厘米，高是4厘米，E是梯形的中点。

求阴影部分的面积是多少?8、等分法：就是将整个图形，平均分成若干份，再看所求的图形的面积占多少份，从而求得阴影部分的面积。

【例6】将三角形ABC的三条边分别向外延长一倍，得到一个大的六边形，已知三角形ABC【例7】如图，在正方形中，放置了两个小正方形，大正方形的面积是180平方厘米，求甲乙两个小正方形有面积各是多少?9、抓不变量：若甲比乙的面积大a，则甲和乙同时加上或减去相同的数，它们的大小不变，而图形发生变化，再通过变化后的图形进行求解，就可以使问题得到简便；若两个面积相等的图形，同时加上或差动相同的面积，则剩下的面积仍然相等。

展开面积的计算公式

展开面积的计算公式
展开面积指的是一个物体将其表面展开之后所占的面积，展开面
积的计算方法有多种，以下是其中几种常用方法：
1.平面图形法
利用平面图形的面积公式计算展开面积。

如果一个物体是由多个
平面图形组成的，可以将每个平面图形的面积加起来，就可以得到整
个物体的展开面积。

这种方法适用于形状简单的物体，如正方体、长
方体等。

2.参数方程法
利用参数方程计算展开面积。

将物体沿着某一方向展开，得到一
个平面曲线，然后将该曲线的参数方程代入到一个积分式中，就可以
求出展开面积。

这种方法适用于形状复杂的物体，如球体、立方体等。

3.三维曲面法
利用三维曲面的面积公式计算展开面积。

将物体展开之后，得到
一个复杂的三维曲面，可以利用该曲面的面积公式计算出展开面积。

这种方法适用于形状超出平面图形和参数方程的物体，如弯曲的管道、封闭的器皿等。

计算展开面积的公式和方法多种多样，但是无论采用哪种方法，
准确度都是非常重要的。

在具体计算时，需要注意单位换算，计算公
式的推导过程，以及对各种形状物体的特殊处理方法等。

同时，还需
要掌握一些常见物体的展开面积计算方法，以便在实际工作中快速准确地计算展开面积。

总之，展开面积计算是一个重要的数学问题，它在工程设计、制造等领域中都有着广泛的应用。

通过不断地学习和实践，我们可以更好地掌握展开面积的计算方法，为实际工作中的计算提供更加准确和可靠的结果。

2019中考数学《面积的计算》专题复习考点讲解(含答案)

面积的计算考点图解技法透析面积法是一种重要方法，计算图形面积是平面几何中最常见的基本问题之一，与面积相关的知识有：(1)常见图形的面积计算公式：正方形面积＝边长×边长；矩形的面积＝长×宽；平行四边形面积＝底×高；三角形面积＝底×高÷2；梯形面积＝（上底＋下底）×高÷2；圆的面积＝×半径的平方；扇形面积＝2360n r（n为圆心角，r为半径）(2)计算面积常常用到以下结论：①等底等高的两个三角形的面积相等；②等底的两个三角形的面积比等于对应高的比；③等高的两个三角形的面积比等于对应底的比；④三角形一边上的中线平分这个三角形的面积．(3)面积计算常用到以下方法：①和差法：把所求图形的面积转化为常见图形面积的和、差表示，运用常见图形的面积公式；②等积法：找出与所求图形面积相等的或者关联的特殊图形，通过代换转化来求出图形的面积；③运动法：通过平移、旋转、割补等方式，将图形中的部分图形运动起来，把图形转化为容易观察或解决的形状；④代数法：通过寻求图形面积之间的关系列方程（组）；把几何问题转化为代数问题．(4)非常规图形的面积计算往往采用“等积变换”，所谓“等积变换”就是不改变几何图形的面积，而是把它的形状改变成能够直接求出面积的图形，等积变换的主要目的，是把复杂的图形变成简单的图形，把不规则的图形变成规则的图形．(5)“等积变换”的方法①公式法，即运用某些图形的面积公式及其有关推论．②分割法，即把一个图形分割成熟知的若干部分图形．③割补法，即把一个图形的某一部分分割出来，然后用与其等积图形填补到某一位置．名题精讲考点1 用面积公式计算常规图形面积例1 如图，将直角三角形BC 沿着斜边AC 的方向平移到 △DEF 的位置（A 、D 、C 、F 四点在同一条直线上）．直角边DE 交BC 于点G ．如果BG ＝4，EF ＝12，△BEG 的面积等于4，那么梯形ABGD 的面积是 ( )A ．16B ．20C ．24D ．28【切题技巧】【规范解答】 B【借题发挥】把不能直接求出面积的图形通过转化或找出与它面积相等的特殊图形，从而能够求解．【同类拓展】 1．如图所示，A 是斜边长为m 的等腰直角三角形，B ，C ，D 都是正方形，则A ，B ，C ，D 的面积的和等于 ( )A ．94m 2B ．52m 2C ．114m 2D ．3m 2考点2 用面积的和、差计算非常规图形有面积例2 如图，P 是平行四边形ABCD 内一点，且S △PAB ＝5， S △PAD ＝2，请你求出S △PAC （即阴影部分的面积）．【切题技巧】 △APC 的底与高显然无法求，则应用已知三角形的面积的和或差来计算△APC 的面积．【规范解答】【借题发挥】对于不能直接求的图形可以把图形进行分解和组合，通过图形的面积和或差进行计算．【同类拓展】 2．如图，长方形ABCD 中，△ABP 的面积为a ， △CDG 的面积为b ，则阴影四边形的面积等于 ( )A ．a ＋bB ．a －bC ．2a bD ．无法确定考点3 列方程（组）求面积例3 如图所示，△ABC 的面积是1cm 2．AD ＝DE ＝EC ， BG ＝GF ＝FC ，求阴影四边形的面积．【切题技巧】条件中有两组等分点，易知△BCE，△ACF的面积为13，但仍然不能求阴影部分面积，因此，只要求出△BCE中另两块面积即可，【规范解答】如图，设AG与BE交于N，AF与BE交于P，连接NC，ND，PC，PD．设△NGB的面积为x，△NDE的面积为y，则有△NCG的面积为2x，△NEA的面积为2y．因为△ABC的面积是1cm2，且AD＝AE＝EC，BG＝GF＝FC．【借题发挥】求一些关系复杂的图形面积，列方程是一个重要方法，它不但可以使我们熟悉列方程和了解方程在几何中的应用，而且能清晰地表明图形面积之间的关系，从而可以化解或降低解题的难度．【同类拓展】3．如图，正方形ABCD中，E、F分别是BC、CD边上的点，AE、DE、BF、AF把正方形分成8小块，各小块的面积分别为S1、S2、…、S8，试比较S3与S2＋S7＋S8的大小，并说明理由．考点4 面积比与线段比的转化例4 如图所示，凸四边形ABCD中，对角线AC、BD相交于O点，若△AOD的面积是2，△COD的面积是1，△COB的面积是4，则四边形ABCD的面积是 ( )A．16 B．15 C．14 D．13【切题技巧】分析△AOD，△DOC，△AOB，△COB四个三角形的面积，只有通过线段比联系起来，相邻两个三角形的面积都存在着一种比例关系．【规范解答】【借题发挥】两三角形的高相等时，面积比等于对应底之比，则可以将面积比与对应线段比相互转化，这是．解答面积问题、线段比等问题的常用技巧．【同类拓展】 4．如图，点E 、F 分别是矩形ABCD 的边AB 、BC 的中点，连AF 、CE 交于点G ，则AGCD ABCDS S 四边形矩形等于 ( )A ．56B ．45C ．34D ．23考点5例5 如图所示，在四边形ABCD 中，AM ＝MN ＝ND ， BE ＝EF ＝FC ，四边形ABEM 、MEFN 、NFCD 的面积分别记为S 1，S 2和S 3．求213?S S S =+【切题技巧】把四边形分割成多个三角形，运用三角形等积变换定理即可求出，【规范解答】连接A ．E 、EN 、PC 和AC ．【借题发挥】等积变形的题目中，常将多边形面积转化为三角形面积，再运用等底同高来进行等积代换，因此，在转化时只要抓住题设中的等分点，就可以将多边形面积进行等积变换了．【同类拓展】 5．如图，张大爷家有一块四边形的菜地，在A 处有一口井，张大爷欲想从A 处引一条笔直的水渠，且这条笔直的水渠将四边形菜地分成面积相等的两部分，请你为张大爷设计一种引水渠的方案，画出图形并说明理由．考点6 格点多边形的面积例6 如图，五边形ABCDE 的面积为多少？我们把方格纸上两组互相平行且垂直的直线的交点叫格点．顶点在格点上的多边形叫格点多边形．可以通过图形的分割，转化为规则图形，再求面积．【规范解答】如图，标上字母F 、G 、H 、I 、J 点，使得△ABF ， △BCG ，△CDH ，△DEI ，△EAJ 为直角三角形，【借题发挥】格点多边形面积有如下计算规律：格点多边形的面积等于其所包含有格点个数，加上由其边界上的格点的个数之半，再减去1．此规律对凹多边形也适用．即：若格点多边形的面积为S ，格点多边形内部有且只有n 个格点，它各边上格点的个数和为x ．则S ＝12x ＋n －1．【同类拓展】 6．如图，在一个由4×4个小正方形组成的正方形格中，阴影部分面积与正方形ABCD 面积的比是 ( ) A ． 3：4 B ．5：8 C ．9：16 D ．1：2 参考答案1．A 2．A 3．S 3＝S 2＋S 7＋S 8． 4．D 5．S △ABF ＝S 四边形AFCD ． 6．B2019-2020学年数学中考模拟试卷一、选择题1．如图，小明书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A．SSS B．SAS C．ASA D．AAS2．甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：①A，B两城相距300千米；②乙车比甲车晚出发1小时，却早到1.5小时；③乙车出发后2.5小时追上甲车；④当甲、乙两车相距40千米时，t＝32或t＝72，其中正确的结论有（）A．1个B．2个C．3个D．4个3．点P（﹣3，m+1）在第二象限，则m的取值范围在数轴上表示正确的是（）A. B.C. D.4．如图，在平行四边形ABCD中，按以下步骤作图：①以A为圆心，AB长为半径画弧，交边AD于点F；②再分别以B，F为圆心画弧，两弧交于平行四边形ABCD内部的点G处；③连接AG并延长交BC于点E，连接BF，若3BF=， 2.5AB=，则AE的长为( )A.2B.4C.8D.55．如图，点是边长为1的菱形对角线上的一个动点，点，分别是边，的中点，则的最小值是( )A. B.1 C. D.26．方程组的解是( )A.B. C. D.7．多项式4x-x 3分解因式的结果是( ) A ．()2x 4x-B ．()()x 2x 2x -+C ．()()x x 2x 2-+D ．2x(2x)-8．一几何体的三视图如图所示，这个几何体是（）A ．四棱锥B ．圆锥C ．三棱柱D ．四棱柱9．如图，水平的讲台上放置的圆柱笔筒和长方体形粉笔盒，它的俯视图是（）A．B． C．D．10．从甲，乙，丙三人中任选一名代表，甲被选中的可能性是A.12B.1C.23D.1311．分解因式3a2b﹣6ab+3b的结果是（）A．3b（a2﹣2a）B．b（3a2﹣6a+1）C．3（a2b﹣2ab）D．3b（a﹣1）212．在整数范围内，有被除数＝除数×商+余数，即a＝bq+r(a≥b，且b≠0，0≤r＜b)，若被除数a和除数b确定，则商q和余数r也唯一确定，如：a＝11，b＝2，则11＝2×5+1此时q＝5，r＝1．在实数范围中，也有a＝bq+r(a≥b且b≠0，商q为整数，余数r满足：0≤r＜b)，若被除数是，除数是2，则q与r的和( )A．﹣4 B．﹣6 C．-4 D．-2二、填空题13．如图，矩形ABCD中，AB＝6，AD＝，点E是BC的中点，点F在AB上，FB＝2，P是矩形上一动点．若点P从点F出发，沿F→A→D→C的路线运动，当∠FPE＝30°时，FP的长为_____．14．计算：（﹣12）2=_____．15．如图，扇形纸扇完全打开后，∠BAC=120°，AB=AC=30厘米，则BC的长为_____厘米．（结果保留π）16．若关于x 的一元二次方程2230x x m -+-=有两个相等的实数根，则m 的值是______________.17．如图，已知△ABC 的周长是21，OB ，OC 分别平分∠ABC 和∠ACB ，OD ⊥BC 于D ，且OD ＝4，△ABC 的面积是_____．18．计算：（a+b ）（2a ﹣2b ）＝_____．三、解答题19．已知：△ABC 的两边AB 、BC 的长是关于x 的一元二次方程x 2﹣（2k+2）x+k 2+2k ＝0的两个实数根，第三边长为10．问当k 为何值时，△ABC 是等腰三角形？20．如图，已知⊙O 是等边三角形ABC 的外接圆,点D 在圆上，过A 作AE ∥BC 交CD 延长线于E.（1）求证：EA 是⊙O 的切线；（2）若BD 经过圆心O ，其它条件不变，则△ADE 与圆重合部分的面积为_____.(在备用图中画图后，用阴影标出所求面积)21．小张在网上销售一种成本为20元/件的T 恤衫，销售过程中的其他各种费用(不再含T 恤衫成本)总计40(百元)，若销售价格为x(元/件)，销售量为y(百件)，当30≤x≤50时，y 与x 之间满足一次函数关系，且当x ＝30时，y ＝5，有关销售量y(百件)与销售价格x(元/件)的相关信息如下：(1)请在表格中直接写出当30≤x≤50时，y与x的函数关系式；(2)求销售这种T恤衫的纯利润w(百元)与销售价格x(元/件)的函数关系式；(3)销售价格定为多少元/件时，获得的利润最大？最大利润是多少？22．如图，在Rt△ABC中，∠C＝90°，BD平分∠ABC，点O在AB上，以点O为圆心，OB 为半径的圆经过点D，交BC于点E（1）求证：AC是⊙O的切线；（2）若OB＝2，CD留π）．23．为考察甲、乙两种农作物的长势，研究人员分别抽取了6株苗，测得它们的高度（单位：cm）如下：甲：98，102，100，100，101，99；乙：100，103，101，97，100，99．（1）你认为哪种农作物长得高一些？说明理由；（2）你认为哪种农作物长得更整齐一些？说明理由．24．如图，在Rt△ABC中，∠ACB＝90°，D、E分别是AB、AC的中点，过C作CF∥AB交DE延长线于点F，连接AF、DC．求证：（1）DE＝FE；（2）四边形ADCF是菱形．25．已知，抛物线C1:y=- 12x2+mx+m+12（1）①当m=1时，抛物线与x轴的交点坐标为_______;②当m=2时，抛物线与x轴的交点坐标为________;（2）①无论m取何值，抛物线经过定点P________;②随着m的取值的变化，顶点M（x，y）随之变化，y是x的函数，记为函数C2，则函数C2的关系式为：________ ；（3）如图，若抛物线C1与x轴仅有一个公共点时，①直接写出此时抛物线C1的函数关系式；②请在图中画出顶点M满足的函数C2的大致图象，在x轴上任取一点C，过点C作平行于y轴的直线l分别交C1、C2于点A、B，若△PAB为等腰直角三角形，求点C的坐标；（4）二次函数的图象C2与y轴交于点N，连接PN，若二次函数的图象C1与线段PN有两个交点，直接写出m的取值范围．【参考答案】***一、选择题二、填空题14．415．20π16．417．4218．2a 2﹣2b 2三、解答题19．k ＝8或10【解析】【分析】因为方程有两个实根，所以△＞0，从而用k 的式子表示方程的解，根据△ABC 是等腰三角形，分AB ＝AC ，BC ＝AC ，两种情况讨论，得出k 的值．【详解】∵△＝[﹣(2k+2)]2﹣4(k 2+2k)＝4k 2+8k+4﹣4k 2﹣8k=4>0，∴x ＝()222k --+⎡⎤⎣⎦，∴x 1＝k+2，x 2＝k ，设AB ＝k+2，BC ＝k ，显然AB≠BC，而△ABC 的第三边长AC 为10，(1)若AB ＝AC ，则k+2＝10，得k ＝8，即k ＝8时，△ABC 为等腰三角形；(2)若BC ＝AC ，则k ＝10，即k ＝10时．△ABC 为等腰三角形．【点睛】本题考查了一元二次方程的根，公式法，解本题要充分利用条件，选择适当的方法求解k 的值，从而证得△ABC 为等腰三角形．20．（1）见解析；（2）23π．【解析】【分析】（1）根据等边三角形的性质可得：∠OAC=30°，∠BCA=60°，证明∠O AE=90°，可得：AE 是⊙O 的切线；（2）如备用图，根据等边三角形的性质得到BD ⊥AC ，∠ABD=∠CBD=30°，∠BAD=∠BCD=90°，根据平行线的性质得到∠AED=∠BCD=90°，解直角三角形得到AD=2，连接OA ，根据扇形和三角形的面积公式即可得到结论．(1)证明：如图1，连接OA，∵⊙O是等边三角形ABC的外接圆，∴∠OAC=30°，∠BCA=60°，∵AE∥BC，∴∠EAC=∠BCA=60°，∴∠OAE=∠OAC+∠EAC=30°+60°=90°，∴AE是⊙O的切线；（2）如备用图，∵△ABC是等边三角形，BD经过圆心O，∴BD⊥AC，∠ABD=∠CBD=30°，∠BAD=∠BCD=90°，∵EA是⊙O的切线，∴∠EAD=30°，∵AE∥BC，∴∠AED=∠BCD=90°，∵∴AD=2，∵OA=OB ，∴∠OAB=OBA=30°，∴∠AOD=60°，∴△ADE 与圆重合部分的面积=S 扇形AOD -S △AOD=260212236023ππ⋅⨯-⨯=故答案为：23π【点睛】本题考查了作图-复杂作图，切线的判定和性质，扇形的面积计算，正确的作出图形是解题的关键．21．(1)y ＝﹣110x+8；(2)见解析；(3)销售价格定为60元/件时，获得的利润最大，最大利润是60百元．【解析】【分析】（1）把x ＝50代入y ＝150x得y ＝3，设y 与x 的函数关系式为：y ＝kx+b ，把x ＝30，y ＝5；x ＝50，y ＝3，代入解方程组即可得到结论；（2）根据x 的范围分类讨论，由“总利润＝单件利润×销售量”可得函数解析式；（3）结合（1）中两个函数解析式，分别依据二次函数的性质和反比例函数的性质求其最值即可．【详解】(1)把x ＝50代入y ＝150x得y ＝3，设y 与x 的函数关系式为：y ＝kx+b ，∵当x ＝30时，y ＝5，当x ＝50时，y ＝3，∴530350k b k b =+⎧⎨=+⎩，解得：1k 10b 8⎧=-⎪⎨⎪=⎩，∴y 与x 的函数关系式为：y ＝﹣1x+8；故答案为：y ＝﹣110x+8； (2)当30≤x≤60时，w ＝(x ﹣20)(﹣0.1x+8)﹣40＝﹣0.1x 2+10x ﹣200；当60＜x≤80时，w ＝(x ﹣20)• 150x ﹣40＝﹣3000x+110； (3)当30≤x≤60时，w ＝﹣0.1x 2+10x ﹣200＝﹣0.1(x ﹣50)2+50，∴当x ＝50时，w 取得最大值50(百元)；当60＜x≤80时，w ＝﹣3000x +110， ∵﹣3000＜0，∴w 随x 的增大而增大，当x ＝60时，w 最大＝60(百元)，答：销售价格定为60元/件时，获得的利润最大，最大利润是60百元．【点睛】本题主要考查二次函数和反比例函数的应用，理解题意依据相等关系列出函数解析式，并熟练掌握二次函数和反比例函数的性质是解题的关键．22．（1）见解析；（2）23π-【解析】【分析】（1）欲证明AC 是⊙O 的切线，只要证明OD ⊥AC 即可．（2）证明△OBE 是等边三角形即可解决问题．【详解】（1）证明：连接OD ，如图，∵BD 为∠ABC 平分线，∴∠1＝∠2，∵OB ＝OD ，∴∠1＝∠3，∴∠2＝∠3，∵∠C ＝90°，∴∠ODA ＝90°，∴OD ⊥AC ，∴AC 是⊙O 的切线．（2）过O 作OG ⊥BC ，连接OE ，则四边形ODCG 为矩形，∴GC ＝OD ＝OB ＝2，OG ＝CD ，在Rt △OBG 中，利用勾股定理得：BG ＝1，∴BE ＝2，则△OBE 是等边三角形，∴阴影部分面积为260?2360π⨯﹣12＝23π- 【点睛】本题考查切线的判定和性质，等边三角形的判定和性质，思想的面积公式等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．23．甲组数据的平均数为100cm ；乙组数据的平均数为100cm ；（2）甲种农作物长得比较整齐．【解析】【分析】（1）根据平均数的计算公式分别把这6株农作物的高度加起来，再除以6即可；（2）先算出甲与乙的方差，再进行比较，方差越小的，农作物长势越整齐，即可得出答案．【详解】（1）甲组数据的平均数＝16×（98+102+100+100+101+99）＝100（cm ）；乙组数据的平均数＝16×（100+103+101+97+100+99）＝100（cm ）；（2）s 2甲＝16×[（98﹣100）2+（102﹣100）2+…+（99﹣100）2]＝53； s 2乙＝16×[（100﹣100）2+（103﹣100）2+…+（100﹣99）2]＝103． s 2甲＜s 2乙．所以甲种农作物长得比较整齐．【点睛】本题考查了平均数与方差，一般地设n 个数据，x 1，x 2，…x n 的平均数为x ，则方差大，波动性越大，反之也成立．24．（1）详见解析；（2）详见解析．【解析】【分析】（1）由“AAS ”可证AED CEF ∆≅∆，可得DE EF ＝；（2）由直角三角形的性质可得CD AD ＝，由对角线互相平分的四边形是平行四边形可证四边形ADCF 是平行四边形，即可证四边形ADCF 是菱形．【详解】（1）证明：∵CF AB ∥ ，∴DAC ACF ∠∠＝，又∵AE EC AED CEF ∠∠＝，＝，∴AED CEF AAS ≌（）， ∴DE EF ＝．（2）∵90ACB ∠︒＝，D 是AB 的中点，∴CD AD ＝∵DE EF AE EC ＝，＝∴四边形ADCF 是平行边形又∵AD CD ＝∴四边形ADCF 是菱形．【点睛】本题考查了菱形的判定和性质，全等三角形的判定和性质，直角三角形的性质，灵活运用这些性质进行推理是本题的关键．25．（1）（﹣1，0）（3，0）；（﹣1，0）（5，0）；（2）（-1，0）； y=12 (x+1)；（3）点C 的坐标为（1，0）或（-3，0）；（4）-12＜m≤0 【解析】【分析】（1）①把m=1,y=0分别代入抛物线C1，得到一个一元二次方程，解方程即可求出交点横坐标。

求圆环的面积的题典型

求圆环的面积的题典型求圆环的面积是一个常见的数学问题，可以通过一定的方法来计算得出。

下面将介绍一种常用的方法来求解圆环的面积。

我们需要明确圆环的定义。

圆环是由两个同心圆所围成的图形，其中内圆的半径为r1，外圆的半径为r2。

我们的目标是求解圆环的面积。

为了方便计算，我们可以把圆环拆分为两个圆，一个是外圆，一个是内圆。

我们可以先求解外圆的面积，再求解内圆的面积，最后用外圆的面积减去内圆的面积，即可得到圆环的面积。

求解圆的面积的方法是已知半径r，使用公式S=πr^2来计算。

其中，π是一个常数，近似等于3.14159。

我们求解外圆的面积。

根据题目要求，外圆的半径为r2，所以外圆的面积S2=πr2^2。

接下来，我们求解内圆的面积。

根据题目要求，内圆的半径为r1，所以内圆的面积S1=πr1^2。

我们用外圆的面积减去内圆的面积，即可得到圆环的面积。

圆环的面积S = S2 - S1 = πr2^2 - πr1^2。

需要注意的是，计算圆环的面积时，半径的单位必须一致。

如果半径的单位不一致，需要先进行单位转换再进行计算。

除了使用公式计算圆环的面积，还可以通过其他方法来求解。

例如，可以利用圆环的性质，将圆环分成多个扇形和三角形，然后分别计算每个扇形和三角形的面积，最后将它们相加即可得到圆环的面积。

在实际应用中，求解圆环的面积是非常常见的。

例如，建筑设计中经常会涉及到圆环形的结构，求解其面积可以帮助设计师合理规划空间。

另外，圆环的面积也常用于计算环形花坛、环形跑道等的面积。

求解圆环的面积是一个常见的数学问题，可以通过使用公式或其他方法来计算得出。

在实际应用中，对圆环的面积的求解有着重要的意义，能够帮助我们更好地应用数学知识解决实际问题。

小学数学常用解题方法与技巧15十五、平面图形的面积计算技巧(二)组合图形面积计算十法

平面图形的面积计算技巧（二）----组合图形面积计算技巧“十法”一、相加相减法【点拨】：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，相加求出整个图形的面积. 或者将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.【例题1】：求组合图形的面积。

（单位：厘米）【分析与解答】：上图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了.4÷2=2（米）4×4+2×2×3.14÷2=22.28（平方厘米）【例题2】：长方形长6厘米，宽4厘米，求阴影部分的面积。

【分析与解答】：上图中，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可.4÷2=2（米）6×4-2×2×3.14÷218.28（平方厘米）二、用比例知识求面积【点拨】：利用图形之间的比例关系解题。

【例题3】如图 OA=AB=BC=CD ，阴影部分面积之和为20平方厘米，求扇形ODH 的面积。

【分析与解答】：根据圆的半径之比的平方=面积之比，可得：四个扇形半径之比依次为1:2:3:4,则面积之比依次为: 22224:3:2:1即1:4:9:16，阴影面积对应份数为（4-1)+(16-9）=10份，因此，扇形ODH 的面积=20×1016=32平方厘米三、等分法【点拨】：根据所求图形的对称性，将所求图形面积平均分成若干份，先求出其中的一份面积，然后求总面积。

【例题4】：求阴影部分的面积（单位：厘米）【分析与解答】：把原图平均分成八分，就得到下图，先求出每个小扇形面积中的阴影部分：3.14×22÷4－2×2÷2=1.14(平方厘米 )阴影部分总面积为：1.14×8=9.12(平方厘米 )四、等积变形【点拨】：将题中的条件或问题替换成面积相等的另外的条件或问题，使原来复杂的图形变为简单明了的图形。

小学三年级下册数学“求图形面积”的10种方法,考试必考题型

小学三年级下册数学“求图形面积”的10种方法，考试必考题型！实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

先看三道例题感受一下例1 如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米.求阴影部分的面积。

一句话：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2 如右图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积.一句话：因为△ABE、△ADF与四边形AECF的面积彼此相等，都等于正方形ABCD面积的三分之一，也就是12厘米.解：S△ABE=S△ADF=S四边形AECF=12在△ABE中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2，∴△ECF的面积为2×2÷2=2。

所以S△AEF=S四边形AECF-S△ECF=12-2=10（平方厘米）。

例3 两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

一句话：阴影部分面积=S△ABG-S△BEF，S△ABG和S△BEF都是等腰三角形总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决。

常用的基本方法有：一、相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如：求下图整个图形的面积一句话：半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如：下图，求阴影部分的面积。

不规则图形的常用方法

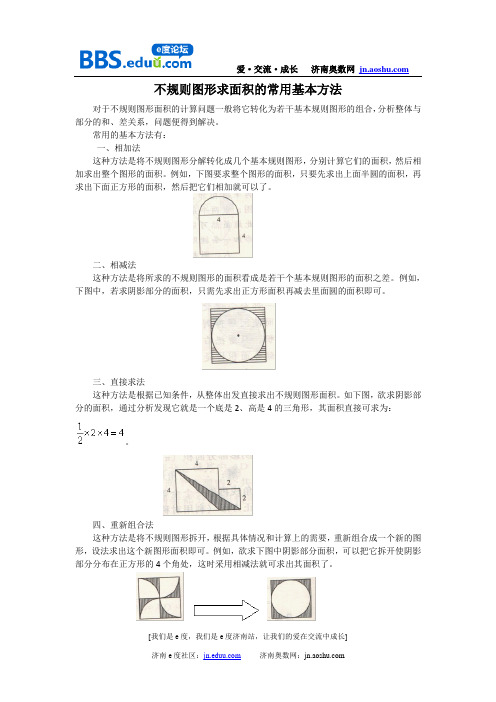
不规则图形求面积的常用基本方法对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决。

常用的基本方法有：一、相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积。

例如，下图要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了。

二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。

例如，下图中，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可。

三、直接求法这种方法是根据已知条件，从整体出发直接求出不规则图形面积。

如下图，欲求阴影部分的面积，通过分析发现它就是一个底是2、高是4的三角形，其面积直接可求为：。

四、重新组合法这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可。

例如，欲求下图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了。

五、辅助线法这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可。

如下图，求两个正方形中阴影部分的面积。

此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便。

六、割补法这种方法是把原图形的一部分切割下来补在图形中的另一部分，使之成为基本规则图形，从而使问题得到解决。

例如，如下图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半。

七、平移法这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积。

例如，如下图，欲求阴影部分面积，可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。

八、旋转法这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积，例如，欲求下图(1)中阴影部分的面积，可将左半图形绕B点逆时针方向旋转180°，使A与C重合，从而构成如下图(2)的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积。

重点五年级数学图形求面积十法

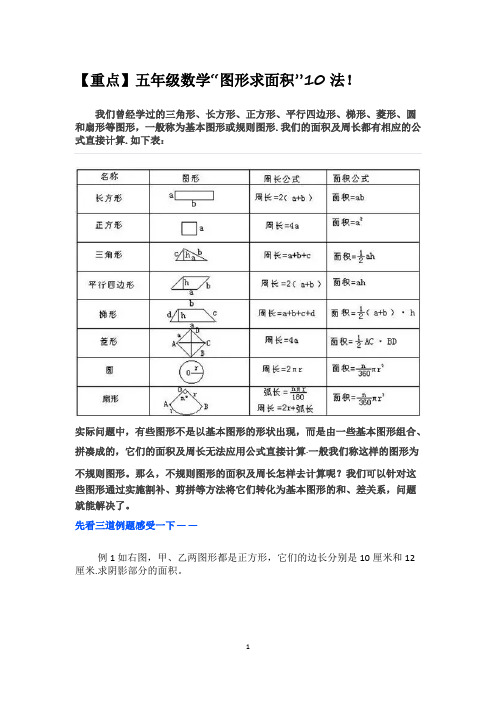
【重点】五年级数学“图形求面积”10法！我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

先看三道例题感受一下——例1 如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米.求阴影部分的面积。

一句话：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

所以S△AEF=S四边形AECF-S△ECF=12-2=10（平方厘米）。

例3 两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

(完整版)求阴影部分面积的几种常用方法

总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决.常用的基本方法有：一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，下图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了.二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，下图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可.三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分析发现它就是一个底是2、高是4的三角形，其面积直接可求为|：四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求下图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了.五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如下图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便.六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如下图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半.七、平移法：这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积.例如，如下图，欲求阴影部分面积，可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。

八、旋转法：这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积.例如，欲求下图（1）中阴影部分的面积，可将左半图形绕B 点逆时针方向旋转180°，使A与C 重合，从而构成如右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法：这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如，欲求下图中阴影部分的面积，沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。

简单几何图形的面积计算

简单几何图形的面积计算第二讲简单几何图形的面积计算一．常用的基本公式：1．正方形的边长为a，则正方形的面积是S=a2；2．长方形的长与宽分别是a、b，则长方形的面积是S=a×b。

3．平行四边形的底边长为a，高为h，则面积是S=a ×h。

4．三角形的三条边长分别为a、b、c，在它们上的高分别是h a、h b、h c，则三角形的面积S=a×h a÷2= b×h b÷2= c×h c÷2。

5．梯形的上底为a，下底为b，高为h，则梯形的面积是(a+b)×h÷2。

6．圆的半径为r，则圆的面积是S=π×r2。

其中π=3.14159265…。

二．几种常用的求面积的方法：1．直接利用公式计算；2．列出方程求图形的面积；3．添加辅助线计算图形面积；4．利用割补的办法变化图形，计算图形的面积。

5．用相等面积变换计算图形的面积。

（同底等高问题，等底等高问题）三．例题讲解：例1．如图，一块长方形耕地，它由四个小长方形拼合而成，其中三个长方形的面积分别是15、18、30公顷，则图中阴影部分的面积是公顷。

解：由题意知，a ×c =15，b ×c =18，b ×d =30，所以a ×d =(a ×c )×(b ×d )÷(b ×c )=15×30÷18=25(公顷)。

例2．如图所示，三角形ABC 是直角三角形，ACD 是以A 圆心，AC 为半径的扇形，图中阴影部分的面积是。

（π取3.14）6cm6cm D C B A解：阴影部分的面积是三角形面积减去扇形的面积，三角形ABC 的面积=6×6÷2=18，扇形的面积是圆的面积的八分之一，所以扇形面积是π×6×6÷8=4.5×π=14.13，所以阴影部分的面积是18–14.13=3.87（平方厘米）。

几何图形面积计算的几种常用方法

几何图形面积计算的几种常用方法吴仕为(福建省福鼎市第八中学ꎬ福建宁德３５５２１５)摘㊀要:几何图形面积问题是初中数学中的重难点部分ꎬ该部分知识在高中数学中也同样占据着重要地位.因此ꎬ对于初中学生而言ꎬ必须打好几何知识基础.在几何图形面积问题中ꎬ不规则图形面积或阴影部分面积的求解是十分常见的ꎬ学生在面对此类问题时ꎬ往往找不到正确的解题思路与方法.针对此种情况ꎬ便需要学生灵活应用常见几何图形面积的计算方法进行求解.基于此ꎬ文章主要分析与研究几何图形面积计算的几种常用方法ꎬ以期为广大师生提供解题参考与借鉴.关键词:几何图形ꎻ面积ꎻ常用方法中图分类号:Ｇ６３２㊀㊀㊀文献标识码:Ａ㊀㊀㊀文章编号:１００８－０３３３(２０２４)０８－００５２－０３收稿日期:２０２３－１２－１５作者简介:吴仕为(１９７３.９ )ꎬ男ꎬ福建省福鼎人ꎬ本科ꎬ中学一级教师ꎬ从事初中数学教学研究.㊀㊀与几何图形面积有关的计算问题主要考查学生的数学思维与计算能力ꎬ由于几何图形的变化灵活多样ꎬ从而导致大部分学生对这类问题感到困难与茫然ꎬ尤其是在计算不规则图形的面积时ꎬ学生很难快速获取解题突破口.实际上ꎬ解决与几何图形有关的面积问题时ꎬ只要充分掌握常用方法ꎬ熟悉常用解题套路ꎬ便能够高效完成问题解答.鉴于此ꎬ文章围绕典型的几何图形面积计算问题ꎬ分析求几何图形面积的几种常用方法.１巧用平移法计算几何图形的面积平移法ꎬ顾名思义是通过图形的横向㊁纵向水平运动进行解题ꎬ即把几何图形中的部分进行切割ꎬ然后使其横向或纵向水平运动到恰当位置ꎬ进而重新组合成常见的规则几何图形ꎬ然后利用规则图形的面积公式求解ꎬ以此达到简化解题难度的目的[１].在实际解题过程中ꎬ学生可以通过观察几何图形的结构特征ꎬ快速判断是否需要利用平移法计算面积.例１㊀如图１ꎬ现有一块长度为３２ｍ㊁宽度为２０ｍ的矩形地面ꎬ需在地面上按照阴影区域设计修建道路ꎬ其余非阴影区域用于绿化设计ꎬ若绿化设计面积为５４０ｍ２ꎬ请问道路修建的宽度应为ｍ.图１㊀矩形地面构造示意图学生在遇到此类不规则图形的面积问题时ꎬ通过观察已知图形便能够快速发现其结构特征ꎬ可考虑利用平移法ꎬ将不规则几何图形转化为规则的基本图形ꎬ然后利用规则图形的面积公式求解面积.基于此ꎬ本题有两种求解计算方法ꎬ求解过程如下.方法１㊀如图２ꎬ将不规则图形经过平移变为三个规则的矩形ꎬ通过平移与组合阴影部分的图形ꎬ能够得到两个规则的阴影矩形.假设道路的宽度为ｘｍꎬ结合题目条件能够列出(２０－ｘ)(３２－ｘ)＝５４０ꎬ这是一个关于ｘ的一元二次方程ꎬ解此方程即可得到问题的答案.解法１㊀设道路宽度为ｘｍ.根据题意ꎬ得(２０－ｘ)(３２－ｘ)＝５４０ꎬ即ｘ２－５２ｘ＋１００＝０ꎬ解得ｘ１＝５０(不合题意ꎬ舍去)ꎬｘ２＝２.故道路的宽度应为２ｍ.２５图２㊀平移变为三个规则的矩形方法２㊀如图３ꎬ将不规则图形平移变换为四个规则的矩形ꎬ此时绿化设计面积被分成四个规则的矩形ꎬ根据题目中的已知条件能够得到２０ˑ３２－(２０＋３２)ｘ＋ｘ２＝５４０ꎬ这是关于ｘ的一元二次方程式ꎬ解此方程即可得到问题的答案.图３㊀平移变换为四个规则的矩形解法２㊀设道路宽度为ｘｍ.根据题意ꎬ得２０ˑ３２－(２０＋３２)ｘ＋ｘ２＝５４０ꎬ即ｘ２－５２ｘ＋１００＝０ꎬ解得ｘ１＝５０(不合题意ꎬ舍去)ꎬｘ２＝２.故道路修建的宽度应为２ｍ.通过典型例题讲解可以发现ꎬ利用平移法解决不规则几何图形的面积问题时ꎬ平移的方式不同ꎬ可能会得到不同的解题思路.教师应抓住典型例题的一题多解思路ꎬ进一步拓展学生的数学逻辑思维ꎬ进而引导学生突破固有思维限制.２巧用旋转法计算几何图形面积旋转法主要应用于构造直角三角形㊁全等三角形等基本图形求面积问题ꎬ这种解法的基本原理是面积的旋转不变性[２].例２㊀如图４ꎬ点Ｐ是等边әＡＢＣ内的一点ꎬＰＡ＝３ꎬＰＢ＝４ꎬＰＣ＝５ꎬ则әＡＢＣ的面积是(㊀㊀).Ａ.９＋２５３４㊀㊀㊀㊀Ｂ.９＋２５３２Ｃ.１８＋２５３Ｄ.１８＋２５３２根据总结的旋转法解题技巧ꎬ应找到旋转中心.根据等边三角形边长的性质易知ＡＢ＝ＢＣꎬ故可考虑以点Ｂ为旋转中心ꎬ将әＢＰＣ逆时针旋转６０ʎꎬ可图４㊀等边әＡＢＣ示意图得到әＢＥＡꎬ如图５所示.由旋转的性质可得ＢＥ＝ＢＰ＝４ꎬøＰＢＥ＝６０ʎꎬ进而能够判断әＢＰＥ是等边三角形ꎬＰＢ＝ＰＥ＝４ꎬøＢＰＥ＝６０ʎ.此时ꎬ在әＡＥＰ中ꎬＡＥ＝５ꎬＡＰ＝３ꎬＰＥ＝４ꎬ利用勾股定理的逆定理能够判断әＡＰＥ是直角三角形ꎬ即øＡＰＥ＝９０ʎꎬ进而能够计算出øＡＰＢ的度数.过点Ａ作ＡＦʅＢＰꎬ交ＢＰ的延长线于点Ｆꎬ利用三角函数可计算出ＡＦ及ＰＦ边长ꎬ再次利用勾股定理可得出ＡＢ边长ꎬ最终利用三角形面积公式计算得到әＡＢＣ的面积.图５㊀旋转变换后的图形解㊀因为әＡＢＣ是等边三角形ꎬ所以ＢＡ＝ＢＣ.以Ｂ点为旋转中心ꎬ把әＢＰＣ逆时针旋转６０ʎ得到әＢＥＡꎬ连接ＥＰꎬ过点Ａ作ＡＦʅＢＰꎬ交ＢＰ的延长线于点Ｆꎬ则ＢＥ＝ＢＰ＝４ꎬＰＣ＝ＡＥ＝５ꎬøＰＢＥ＝６０ʎꎬ所以әＢＰＥ是等边三角形ꎬ所以ＰＢ＝ＰＥ＝４ꎬøＢＰＥ＝６０ʎ.在әＡＥＰ中ꎬＡＥ＝５ꎬＡＰ＝３ꎬＰＥ＝４ꎬ所以ＡＥ２＝ＰＥ２＋ＰＡ２ꎬ所以әＡＰＥ是直角三角形ꎬøＡＰＥ＝９０ʎꎬ所以øＡＰＢ＝１５０ʎꎬ所以øＡＰＦ＝３０ʎ.在әＡＰＦ中ꎬＡＦ＝１２ＡＰ＝３２ꎬＰＦ＝３２ＡＰ＝３２３.在әＡＢＦ中ꎬＡＢ２＝ＢＦ２＋ＡＦ２＝(４＋３２３)２＋(３２)２＝２５＋１２３ꎬ所以әＡＢＣ的面积为３４ＡＢ２＝３４(２５＋１２３)＝９＋２５３４.故正确选项为Ａ.３巧用分割法计算几何图形面积在计算几何图形面积的过程中ꎬ分割法较为常３５用ꎬ其本质是对原图添加合适的辅助线ꎬ从而达到将原图分隔为若干个规则的几何图形ꎬ如直角三角形㊁等腰三角形㊁正方形㊁长方形等ꎬ然后利用规则图形的面积公式解决问题ꎬ从而求得原图形的面积.例３㊀已知☉Ｏ为әＡＢＣ的内切圆ꎬ其中Ｆ㊁Ｄ㊁Ｅ分别是ＡＢ㊁ＢＣ㊁ＡＣ边上的切点ꎬ若ＢＣ＝ｘ㊁ＡＣ＝ｙ㊁ＡＢ＝ｚꎬ☉Ｏ的半径为Ｒꎬ请计算әＡＢＣ的面积Ｓ.解㊀如图６所示ꎬ将圆心Ｏ分别与点Ａ㊁Ｂ㊁Ｃ㊁Ｄ㊁Ｅ㊁Ｆ连接ꎬ形成әＣＯＢ㊁әＣＯＡ㊁әＢＯＡ三个三角形ꎬ这三个三角形的面积之和即为әＡＢＣ的面积Ｓ.因为Ｄ㊁Ｅ㊁Ｆ为☉Ｏ与ＣＢ㊁ＣＡ㊁ＢＡ边的切点ꎬ所以ＯＦʅＢＡꎬＯＥʅＣＡꎬＯＤʅＣＢ.因为☉Ｏ的半径为Ｒꎬ所以ＦＯ＝ＥＯ＝ＤＯ＝Ｒ.所以Ｓ＝ＳәＢＯＡ＋ＳәＣＯＢ＋ＳәＣＯＡ＝１２Ｒｚ＋１２Ｒｙ＋１２Ｒｘ＝１２ｚ＋ｙ＋ｘ()Ｒ.图６㊀分割后的әＡＢＣ示意图４巧用补法计算几何图形面积补方式与割方式相反ꎬ 割是指将原几何图形分割为若干个常见的规则图形ꎬ而补是指利用添加辅助线方式ꎬ将原不规则图形转化为规则图形ꎬ利用规则图形的面积公式直接求解ꎬ从而达到降低实际解题难度的目的.同时也能够根据不同的补的方式ꎬ将原不规则图形转化为多样化的规则图形ꎬ进而为学生提供多元化的解题路径.例４㊀如图７ꎬ将一个边长为３的正方形ＡＢＣＤ绕点Ａ逆时针旋转３０ʎꎬ得到ＡᶄＢᶄＣᶄＤᶄꎬ请计算图７中阴影部分的面积.图７㊀不规则阴影部分示意图分析㊀本题目主要考查正方形性质与旋转性质ꎬ故借助图形的旋转不变性㊁正方形的性质即可实现求解.如图８所示ꎬ这是基于补方式处理后的示意图.图８中ＡＥＣＢ为直角梯形ꎬ基于此便可以利用题目中所给条件与直角梯形相关公式完成阴影部分面积的分析与计算.图８㊀将阴影部分补成规则图形解㊀设ＣＤ与ＢᶄＣᶄ的交点为Ｅꎬ连接ＥＡ.根据已知条件ꎬ将正方形ＡＢＣＤ绕点Ａ逆时针方向旋转３０ʎ得到正方形ＡᶄＢᶄＣᶄＤᶄꎬ由旋转的性质可得ꎬøＢᶄＡＢ＝３０ʎ.因为ＡＢＣＤ为正方形ꎬ所以ＡＢᶄ＝ＡＤ.因为ＡＥ＝ＡＥꎬøＢᶄ＝øＤ＝９０ʎꎬ所以әＥＢᶄＡɸәＥＤＡ.因为øＤＡＢᶄ＝øＢＡＤ－øＥＡＢᶄꎬ且øＥＡＢᶄ＝３０ʎꎬ所以øＤＡＢᶄ＝６０ʎꎬøＥＡＤ＝３０ʎꎬ所以ＥＤ＝ＤＡｔａｎ３０ʎ＝３ˑ３３＝１.从而可知阴影部分面积Ｓ阴＝ＳＡＢＣＤ－２Ｓꎬ即Ｓ阴＝３ˑ３－２ˑ１ˑ３ˑ１２＝３－３.５结束语综上所述ꎬ解决几何图形面积计算问题ꎬ对提高初中生数学成绩㊁强化学生解题能力与数学思维十分有利.因此ꎬ教师应积极通过典型的几何图形面积计算问题的讲解与解析ꎬ帮助学生充分掌握常用的几何图形面积计算方法ꎬ进而总结解题方法和技巧ꎬ熟悉常规题型的解题套路ꎬ实现快速㊁正确解题.参考文献:[１]蒋艳ꎬ杨品方.例析解几中涉及三角形面积的多种题型[Ｊ].中学数学研究ꎬ２０２０(７):５９－６１. [２]李宏杰.关注几何面积探寻考查方式:以中考试题为例[Ｊ].中学数学教学参考ꎬ２０２３(３):７３－７５.[责任编辑:李㊀璟] ４５。

坐标的面积怎么算

坐标的面积计算方法在几何学中，坐标系是一个常用的工具，用来描述和测量点在平面上的位置。

当我们有一组坐标点时，可以使用特定的方法来计算这些点形成的图形的面积。

本文将介绍两种常用的计算坐标图形面积的方法：多边形面积计算和曲线下面积计算。

多边形面积计算多边形是由一组连接的线段组成的闭合图形。

计算多边形的面积是一种比较简单的方法，只需要根据多边形的顶点坐标进行计算。

下面介绍常见的计算多边形面积的方法。

方法一：面积累加法面积累加法是一种常用且简单的多边形面积计算方法。

具体步骤如下：1.将多边形的顶点坐标按顺时针或逆时针排序，确保多边形的点按顺序连接。

2.从多边形的第一个点开始，依次选择相邻的两个点，将这两个点和坐标原点（或其他固定点）组成的三角形的面积进行计算。

3.将每个三角形的面积累加，得到所有三角形的面积之和即为多边形的面积。

方法二：行列式法（叉积法）行列式法，也被称为叉积法，是一种使用向量的方法来计算多边形面积的准确而高效的方法。

具体步骤如下：1.将多边形的顶点坐标按顺时针或逆时针排序，确保多边形的点按顺序连接。

2.将多边形的顶点坐标依次表示为向量。

3.对于每个相邻的向量，计算它们的叉积。

4.将所有叉积的绝对值进行求和，并除以2，即得到多边形的面积。

曲线下面积计算对于一些不规则的图形或曲线，可以使用曲线下面积的计算方法来求解其面积。

下面介绍两种常见的曲线下面积计算方法。

方法一：分割法分割法是一种将曲线下面积划分为无数个矩形或梯形的方法，并对每个矩形或梯形的面积进行求和的计算方法。

具体步骤如下：1.将曲线下的区域分割为若干个矩形或梯形。

2.对于每个矩形或梯形，计算其面积。

3.将每个矩形或梯形的面积相加，得到曲线下的总面积。

方法二：积分法积分法是一种使用微积分基本原理来计算曲线下面积的方法。

具体步骤如下：1.将曲线方程表示为函数的形式。

2.设定曲线上的两个点，作为积分的上下限。

3.对于曲线方程，进行积分操作，根据定积分的定义，将积分结果求得。

菱形面积的求法

菱形面积的求法菱形是一种具有特殊形状的几何图形，它由四条相等长度的线段组成，两对对边相互平行且相交于90度角。

在几何学中，我们可以通过不同的方法来计算菱形的面积，下面将介绍两种常用的求解方法。

方法一：使用对角线长度求解菱形的面积菱形的对角线分别为d1和d2，根据对角线的长度可以求解出菱形的面积。

假设d1和d2分别为a和b，菱形的面积S可以通过以下公式计算：S = (d1 * d2) / 2其中，d1和d2表示菱形的对角线长度。

通过这个公式，我们可以轻松地求解出菱形的面积。

方法二：使用边长求解菱形的面积菱形的边长为a，可以通过边长来计算菱形的面积。

由于菱形可以看作是两个相互垂直的等腰三角形组成的，所以我们可以通过等腰三角形的面积公式来求解菱形的面积。

假设菱形的边长为a，菱形的面积S可以通过以下公式计算：S = a^2 / 2其中，a表示菱形的边长。

通过这个公式，我们可以快速计算出菱形的面积。

除了以上两种方法，还有其他的求解菱形面积的方法，比如使用高度和底边长度来计算等。

无论使用哪种方法，计算菱形面积都是比较简单的，只需要了解菱形的特点和相应的公式即可。

菱形面积的求解方法不仅在几何学中有应用，也可以在实际生活中得到应用。

比如，在铺设地板瓷砖时，如果地板的形状为菱形，我们可以通过计算菱形的面积来确定需要购买的瓷砖数量。

又比如，在制作菱形蛋糕时，我们可以通过计算菱形的面积来确定所需的蛋糕材料。

菱形的面积可以通过不同的方法来计算，包括使用对角线长度和边长等。

无论采用哪种方法，求解菱形面积都是比较简单的，只需要了解相应的公式和菱形的特点即可。

菱形面积的求解方法在几何学和实际生活中都有应用，对于解决相关问题具有重要意义。

十求图形面积的几种常用方法

第四节 图形面积-学而思培优

求图形面积的几种常用方法

求图形面积的几种常用方法

阴影部分面积的求法

展开面积的计算公式

2019中考数学《面积的计算》专题复习考点讲解(含答案)

求圆环的面积的题典型

小学数学常用解题方法与技巧15十五、平面图形的面积计算技巧(二)组合图形面积计算十法

小学三年级下册数学“求图形面积”的10种方法,考试必考题型

不规则图形的常用方法

重点五年级数学图形求面积十法

(完整版)求阴影部分面积的几种常用方法

简单几何图形的面积计算

几何图形面积计算的几种常用方法

坐标的面积怎么算

菱形面积的求法

第四节图形面积-学而思培优