lec5 Overdispersion in logistic regression
多分类有序反应变量Logistic回归及其应用

3、社会心理因素:老年人的心理状态、生活环境、生活习惯等也会对其睡 眠质量产生影响。例如,孤独、抑郁、生活压力等心理问题可能导致睡眠障碍。
有序多分类Logistic回归分析
为了探讨上述因素对老年人睡眠质量的影响,我们采用有序多分类Logistic 回归分析方法进行建模和分析。有序多分类Logistic回归是一种统计方法,它能 够根据有序类别变量的取值来估计多个类别的影响因素,并计算各因素的影响方 向和作用大小。
还应注意其他潜在影响因素的作用,以便更好地预防和改善公务员的亚健康 状况。
谢谢观看
பைடு நூலகம்
(2)数据拟合:将数据带入Logistic回归模型,用最大似然估计法对模型 参数进行估计。
(3)模型评估:通过交叉验证、准确率、AUC值等指标对模型进行评估,判 断其预测性能。
(4)模型优化:根据模型评估结果,对模型进行优化调整,包括特征选择、 参数调整等。
3、结果解读
多分类有序反应变量Logistic回归的结果解读包括以下几个方面:
影响因素
老年人睡眠质量受到多种因素的影响,包括身体健康状况、药物使用、社会 心理因素等。
1、身体健康状况:老年人往往存在各种健康问题,如慢性疾病、疼痛、呼 吸困难等,这些疾病会直接或间接影响睡眠质量。
2、药物使用:部分老年人在日常生活中需要使用药物来控制血压、治疗疼 痛等。然而,某些药物可能导致不良反应,从而影响睡眠质量。
1、因变量的处理:将亚健康状况分为5个等级(非常健康、健康、轻微不健 康、不健康、非常不健康),并将其作为有序分类变量进行统计处理。
2、自变量的选择:选择工作压力、生活方式、心理状况等作为自变量,并 将其进行标准化处理,以便进行比较和分析。
3、模型的建立:采用有序多分类logistic回归分析方法,建立模型并拟合 数据。通过模型的结果,可以观察各个自变量对因变量的影响程度及比较各个自 变量之间的相对重要性。
孕早期和孕中期抑郁状况及影响因素

中华疾病控制杂志2021年2月第25卷第2期Chin J I)is Cmmd Prev2021IGh25(2)•231••短篇论著"孕早期和孕中期抑郁状况及影响因素徐继红闫盼盼孙琛100081北京,国家卫生健康委科学技术研究所人类遗传资源中心(徐继红);261053山东,潍坊医学院心理学系(闫盼盼、孙琛)通信作者:徐继红,E-mail:gracexjh@DOI:10.16462/ki.zhjbkz.2021.02.021【摘要】目的探究孕早期和孕中期孕妇的抑郁状况及其影响因素方法2019年7月1日至12月31日,使用一般情况调查表、影响因素调查表和爱丁堡产后抑郁量表,通过在线调查系统追踪随访308名孕妇,采用Logistic线性回归分析模型分析相关影响因素「结果孕早期和孕中期抑郁的发生率分别为25.97%和23.70%回归分析结果显示,近期是否发生过应激性负性生活事件、孕后饮食满意度以及配偶对孕妇的关心情况是导致孕早期孕妇抑郁的影响因素(均有P<0.05)「近期是否发生应激性负性生活事件、配偶对孕妇的关心情况、对目前身体状况的担忧以及孕妇对所接受领导关心的满意度是导致孕中期孕妇抑郁的影响因素(均有P<0.()5)结论孕早期抑郁的发生率高于孕中期,孕早期和孕中期抑郁的影响因素既有共性也有不同「【关键词】抑郁;孕早期;孕中期【中图分类号】R715.3【文献标识码】A【文章编号】1674-3679(2021)02-0231-04基金项目:中央级公益性科研院所基本科研业务费专项重点项目(2019(;JZ()6)Depression status and influencing factors of pregnant women in early and mid-pregnancyXU Ji-hong,YAN Pan-pan,SUN ChenHuman Genetic Resources Center,National Research Institute for Health Commission,Beijing J00081,China(Xu JH);Department of Psychology,Weij'ang Medical University,Wei f ang261053,China(YanPP,Sun C)Corresponding author-XU Ji-hong,E-mail:gracexjh@[Abstract]Objective To investigate the depression status and influencing factors of pregnantwomen in early and mid-pregnancy,respectively.Methods From July I to December31,2019,308pregnant women were recruited through an onli ne survey system via the gen o ral situatio n questionnaire,influencing factor questionnaire and Edinburgh postpartum depression scale.Logistic liner regression analysis model was used to explore the influencing factors of depression in early and mid-pregnancy.Results The incidences of depression in early and mid-pregnancy were25.97%and23.70%,respectively.The results of regression analysis showed that the recent negative life events,dietiirv satisfaction afterpregnancy,and the spouse's concern were influencing factors of depression in early pregnancy(all P<0.05).The recent negative life events,the spouse's concern,wony about current physical conditions,and pregnant women's satisfaction with leaders'care were influencing factors of depression in mid-pregnancy(all P<0.()5).Conclusions The incidence of depression in early pregnancy is higher than that inmid-pregnancy.The influencing factors of depression during etirly and mi(l-|)regnancy have i)oth commonand unique factors.[Key words]Depression;Early-pregnancy;Mid-pregnancyFund program:Special Fund of the Chinese Central Government for Basic Scientific R(*search Operations(2019GJZ06)(Chin J Dis Control Prev2021,25(2):231-234)•232•中华疾病控制杂志2021年2月第25卷第2期Chin J四Control Prev2021Feh25(2)抑郁是女性孕期最常见的一种情绪反应。
riskclustr包的说明文档说明书

Package‘riskclustr’October14,2022Type PackageTitle Functions to Study Etiologic HeterogeneityVersion0.4.0Description A collection of functions related to the study of etiologic heterogeneity both across dis-ease subtypes and across individual disease markers.The included functions allow one to quan-tify the extent of etiologic heterogeneity in the context of a case-control study,and provide p-values to test for etiologic heterogeneity across individual risk factors.Begg CB,Za-bor EC,Bernstein JL,Bernstein L,Press MF,Seshan VE(2013)<doi:10.1002/sim.5902>. Depends R(>=4.0)License GPL-2URL /riskclustr/,https:///zabore/riskclustrBugReports https:///zabore/riskclustr/issuesEncoding UTF-8Imports mlogit,stringr,MatrixLanguage en-USLazyData trueRoxygenNote7.1.0VignetteBuilder knitrSuggests testthat,covr,rmarkdown,dplyr,knitr,usethis,spellingNeedsCompilation noAuthor Emily C.Zabor[aut,cre]Maintainer Emily C.Zabor<***************>Repository CRANDate/Publication2022-03-2301:00:02UTC12d R topics documented:d (2)dstar (3)eh_test_marker (4)eh_test_subtype (5)optimal_kmeans_d (7)posthoc_factor_test (8)subtype_data (9)Index11d Estimate the incremental explained risk variation in a case-controlstudyDescriptiond estimates the incremental explained risk variation across a set of pre-specified disease subtypesin a case-control study.This function takes the name of the disease subtype variable,the number of disease subtypes,a list of risk factors,and a wide dataset,and does the needed transformation on the dataset to get the correct format.Then the polytomous logistic regression model isfit using mlogit,and D is calculated based on the resulting risk predictions.Usaged(label,M,factors,data)Argumentslabel the name of the subtype variable in the data.This should be a numeric variable with values0through M,where0indicates control subjects.Must be suppliedin quotes,bel="subtype".quotes.M is the number of subtypes.For M>=2.factors a list of the names of the binary or continuous risk factors.For binary risk factors the lowest level will be used as the reference level.e.g.factors=list("age","sex","race").data the name of the dataframe that contains the relevant variables.ReferencesBegg,C.B.,Zabor,E.C.,Bernstein,J.L.,Bernstein,L.,Press,M.F.,&Seshan,V.E.(2013).A conceptual and methodological framework for investigating etiologic heterogeneity.Stat Med,32(29),5039-5052.doi:10.1002/sim.5902dstar3 Examplesd(label="subtype",M=4,factors=list("x1","x2","x3"),data=subtype_data)dstar Estimate the incremental explained risk variation in a case-only studyDescriptiondstar estimates the incremental explained risk variation across a set of pre-specified disease sub-types in a case-only study.The highest frequency level of label is used as the reference level,for stability.This function takes the name of the disease subtype variable,the number of disease sub-types,a list of risk factors,and a wide case-only dataset,and does the needed transformation on the dataset to get the correct format.Then the polytomous logistic regression model isfit using mlogit, and D*is calculated based on the resulting risk predictions.Usagedstar(label,M,factors,data)Argumentslabel the name of the subtype variable in the data.This should be a numeric variable with values0through M,where0indicates control subjects.Must be suppliedin quotes,bel="subtype".quotes.M is the number of subtypes.For M>=2.factors a list of the names of the binary or continuous risk factors.For binary risk factors the lowest level will be used as the reference level.e.g.factors=list("age","sex","race").data the name of the case-only dataframe that contains the relevant variables.ReferencesBegg,C.B.,Seshan,V.E.,Zabor,E.C.,Furberg,H.,Arora,A.,Shen,R.,...Hsieh,J.J.(2014).Genomic investigation of etiologic heterogeneity:methodologic challenges.BMC Med Res Methodol,14,138.4eh_test_marker Examples#Exclude controls from data as this is a case-only calculationdstar(label="subtype",M=4,factors=list("x1","x2","x3"),data=subtype_data[subtype_data$subtype>0,])eh_test_marker Test for etiologic heterogeneity of risk factors according to individualdisease markers in a case-control studyDescriptioneh_test_marker takes a list of individual disease markers,a list of risk factors,a variable name denoting case versus control status,and a dataframe,and returns results related to the question of whether each risk factor differs across levels of the disease subtypes and the question of whether each risk factor differs across levels of each individual disease marker of which the disease subtypes are comprised.Input is a dataframe that contains the individual disease markers,the risk factors of interest,and an indicator of case or control status.The disease markers must be binary and must have levels0or1for cases.The disease markers should be left missing for control subjects.For categorical disease markers,a reference level should be selected and then indicator variables for each remaining level of the disease marker should be created.Risk factors can be either binary or continuous.For categorical risk factors,a reference level should be selected and then indicator variables for each remaining level of the risk factor should be created.Usageeh_test_marker(markers,factors,case,data,digits=2)Argumentsmarkers a list of the names of the binary disease markers.Each must have levels0or 1for case subjects.This value will be missing for all control subjects. e.g.markers=list("marker1","marker2")factors a list of the names of the binary or continuous risk factors.For binary risk factors the lowest level will be used as the reference level.e.g.factors=list("age","sex","race")case denotes the variable that contains each subject’s status as a case or control.This value should be1for cases and0for controls.Argument must be supplied inquotes,e.g.case="status".data the name of the dataframe that contains the relevant variables.digits the number of digits to round the odds ratios and associated confidence intervals, and the estimates and associated standard errors.Defaults to2.ValueReturns a list.beta is a matrix containing the raw estimates from the polytomous logistic regression modelfit with mlogit with a row for each risk factor and a column for each disease subtype.beta_se is a matrix containing the raw standard errors from the polytomous logistic regression modelfit with mlogit with a row for each risk factor and a column for each disease subtype.eh_pval is a vector of unformatted p-values for testing whether each risk factor differs across the levels of the disease subtype.gamma is a matrix containing the estimated disease marker parameters,obtained as linear combina-tions of the beta estimates,with a row for each risk factor and a column for each disease marker.gamma_se is a matrix containing the estimated disease marker standard errors,obtained based on a transformation of the beta standard errors,with a row for each risk factor and a column for each disease marker.gamma_p is a matrix of p-values for testing whether each risk factor differs across levels of each disease marker,with a row for each risk factor and a column for each disease marker.or_ci_p is a dataframe with the odds ratio(95\factor/subtype combination,as well as a column of formatted etiologic heterogeneity p-values.beta_se_p is a dataframe with the estimates(SE)for each risk factor/subtype combination,as well as a column of formatted etiologic heterogeneity p-values.gamma_se_p is a dataframe with disease marker estimates(SE)and their associated p-values.Author(s)Emily C Zabor<****************>Examples#Run for two binary tumor markers,which will combine to form four subtypeseh_test_marker(markers=list("marker1","marker2"),factors=list("x1","x2","x3"),case="case",data=subtype_data,digits=2)eh_test_subtype Test for etiologic heterogeneity of risk factors according to diseasesubtypes in a case-control studyDescriptioneh_test_subtype takes the name of the variable containing the pre-specified subtype labels,the number of subtypes,a list of risk factors,and the name of the dataframe and returns results related to the question of whether each risk factor differs across levels of the disease subtypes.Input is a dataframe that contains the risk factors of interest and a variable containing numeric class labels that is0for control subjects.Risk factors can be either binary or continuous.For categorical risk factors,a reference level should be selected and then indicator variables for each remaining level of the risk factor should be created.Categorical risk factors entered as is will be treated as ordinal.The multinomial logistic regression model isfit using mlogit.Usageeh_test_subtype(label,M,factors,data,digits=2)Argumentslabel the name of the subtype variable in the data.This should be a numeric variable with values0through M,where0indicates control subjects.Must be suppliedin quotes,bel="subtype".M is the number of subtypes.For M>=2.factors a list of the names of the binary or continuous risk factors.For binary or categor-ical risk factors the lowest level will be used as the reference level.e.g.factors=list("age","sex","race").data the name of the dataframe that contains the relevant variables.digits the number of digits to round the odds ratios and associated confidence intervals, and the estimates and associated standard errors.Defaults to2.ValueReturns a list.beta is a matrix containing the raw estimates from the polytomous logistic regression modelfit with mlogit with a row for each risk factor and a column for each disease subtype.beta_se is a matrix containing the raw standard errors from the polytomous logistic regression modelfit with mlogit with a row for each risk factor and a column for each disease subtype.eh_pval is a vector of unformatted p-values for testing whether each risk factor differs across the levels of the disease subtype.or_ci_p is a dataframe with the odds ratio(95\factor/subtype combination,as well as a column of formatted etiologic heterogeneity p-values.beta_se_p is a dataframe with the estimates(SE)for each risk factor/subtype combination,as well as a column of formatted etiologic heterogeneity p-values.var_covar contains the variance-covariance matrix associated with the model estimates contained in beta.Author(s)Emily C Zabor<****************>optimal_kmeans_d7 Exampleseh_test_subtype(label="subtype",M=4,factors=list("x1","x2","x3"),data=subtype_data,digits=2)optimal_kmeans_d Obtain optimal D solution based on k-means clustering of diseasemarker data in a case-control studyDescriptionoptimal_kmeans_d applies k-means clustering using the kmeans function with many random starts.The D value is then calculated for the cluster solution at each random start using the d function,and the cluster solution that maximizes D is returned,along with the corresponding value of D.In this way the optimally etiologically heterogeneous subtype solution can be identified from possibly high-dimensional disease marker data.Usageoptimal_kmeans_d(markers,M,factors,case,data,nstart=100,seed=NULL)Argumentsmarkers a vector of the names of the disease markers.These markers should be of a type that is suitable for use with kmeans clustering.All markers will be missing forcontrol subjects.e.g.markers=c("marker1","marker2") M is the number of clusters to identify using kmeans clustering.For M>=2.factors a list of the names of the binary or continuous risk factors.For binary risk factors the lowest level will be used as the reference level.e.g.factors=list("age","sex","race")case denotes the variable that contains each subject’s status as a case or control.This value should be1for cases and0for controls.Argument must be supplied inquotes,e.g.case="status".data the name of the dataframe that contains the relevant variables.nstart the number of random starts to use with kmeans clustering.Defaults to100.seed an integer argument passed to set.seed.Default is NULL.Recommended to set in order to obtain reproducible results.8posthoc_factor_testValueReturns a listoptimal_d The D value for the optimal D solutionoptimal_d_data The original data frame supplied through the data argument,with a column called optimal_d_label added for the optimal D subtype label.This has the subtype assignment for cases,and is0for all controls.ReferencesBegg,C.B.,Zabor,E.C.,Bernstein,J.L.,Bernstein,L.,Press,M.F.,&Seshan,V.E.(2013).A conceptual and methodological framework for investigating etiologic heterogeneity.Stat Med,32(29),5039-5052.Examples#Cluster30disease markers to identify the optimally#etiologically heterogeneous3-subtype solutionres<-optimal_kmeans_d(markers=c(paste0("y",seq(1:30))),M=3,factors=list("x1","x2","x3"),case="case",data=subtype_data,nstart=100,seed=81110224)#Look at the value of D for the optimal D solutionres[["optimal_d"]]#Look at a table of the optimal D solutiontable(res[["optimal_d_data"]]$optimal_d_label)posthoc_factor_test Post-hoc test to obtain overall p-value for a factor variable used in aeh_test_subtypefit.Descriptionposthoc_factor_test takes a eh_test_subtypefit and returns an overall p-value for a specified factor variable.Usageposthoc_factor_test(fit,factor,nlevels)Argumentsfit the resulting eh_test_subtypefit.factor is the name of the factor variable of interest,supplied in quotes,e.g.factor= "race".Only supports a single factor.nlevels is the number of levels the factor variable in factor has.ValueReturns a list.pval is a formatted p-value.pval_raw is the raw,unformatted p-value.Author(s)Emily C Zabor<****************>subtype_data Simulated subtype dataDescriptionA dataset containing2000patients:1200cases and800controls.There are four subtypes,andboth numeric and character subtype labels.The subtypes are formed by cross-classification of two binary disease markers,disease marker1and disease marker2.There are three risk factors,two continuous and one binary.One of the continuous risk factors and the binary risk factor are related to the disease subtypes.There are also30continuous tumor markers,20of which are related to the subtypes and10of which represent noise,which could be used in a clustering analysis.Usagesubtype_dataFormatA data frame with2000rows–one row per patientcase Indicator of case control status,1for cases and0for controlssubtype Numeric subtype label,0for control subjectssubtype_name Character subtype labelmarker1Disease marker1marker2Disease marker2x1Continuous risk factor1x2Continuous risk factor2x3Binary risk factory1Continuous tumor marker1 y2Continuous tumor marker2 y3Continuous tumor marker3 y4Continuous tumor marker4 y5Continuous tumor marker5 y6Continuous tumor marker6 y7Continuous tumor marker7 y8Continuous tumor marker8 y9Continuous tumor marker9 y10Continuous tumor marker10 y11Continuous tumor marker11 y12Continuous tumor marker12 y13Continuous tumor marker13 y14Continuous tumor marker14 y15Continuous tumor marker15 y16Continuous tumor marker16 y17Continuous tumor marker17 y18Continuous tumor marker18 y19Continuous tumor marker19 y20Continuous tumor marker20 y21Continuous tumor marker21 y22Continuous tumor marker22 y23Continuous tumor marker23 y24Continuous tumor marker24 y25Continuous tumor marker25 y26Continuous tumor marker26 y27Continuous tumor marker27 y28Continuous tumor marker28 y29Continuous tumor marker29 y30Continuous tumor marker30Index∗datasetssubtype_data,9beta,5d,2,7dstar,3eh_test_marker,4eh_test_subtype,5kmeans,7mlogit,2,3,5,6optimal_kmeans_d,7posthoc_factor_test,8set.seed,7subtype_data,911。
The Cross-Section of Volatility and Expected Returns

The Cross-Section of V olatility and Expected Returns∗Andrew Ang†Columbia University,USC and NBERRobert J.Hodrick‡Columbia University and NBERYuhang Xing§Rice UniversityXiaoyan Zhang¶Cornell UniversityThis Version:9August,2004∗We thank Joe Chen,Mike Chernov,Miguel Ferreira,Jeff Fleming,Chris Lamoureux,Jun Liu,Lau-rie Hodrick,Paul Hribar,Jun Pan,Matt Rhodes-Kropf,Steve Ross,David Weinbaum,and Lu Zhang for helpful discussions.We also received valuable comments from seminar participants at an NBER Asset Pricing meeting,Campbell and Company,Columbia University,Cornell University,Hong Kong University,Rice University,UCLA,and the University of Rochester.We thank Tim Bollerslev,Joe Chen,Miguel Ferreira,Kenneth French,Anna Scherbina,and Tyler Shumway for kindly providing data. We especially thank an anonymous referee and Rob Stambaugh,the editor,for helpful suggestions that greatly improved the article.Andrew Ang and Bob Hodrick both acknowledge support from the NSF.†Marshall School of Business,USC,701Exposition Blvd,Room701,Los Angeles,CA90089.Ph: 2137405615,Email:aa610@,WWW:/∼aa610.‡Columbia Business School,3022Broadway Uris Hall,New York,NY10027.Ph:(212)854-0406, Email:rh169@,WWW:/∼rh169.§Jones School of Management,Rice University,Rm230,MS531,6100Main Street,Houston TX 77004.Ph:(713)348-4167,Email:yxing@;WWW:/yxing ¶336Sage Hall,Johnson Graduate School of Management,Cornell University,Ithaca NY14850. Ph:(607)255-8729Email:xz69@,WWW:/faculty/pro-files/xZhang/AbstractWe examine the pricing of aggregate volatility risk in the cross-section of stock returns. Consistent with theory,wefind that stocks with high sensitivities to innovations in aggregate volatility have low average returns.In addition,wefind that stocks with high idiosyncratic volatility relative to the Fama and French(1993)model have abysmally low average returns. This phenomenon cannot be explained by exposure to aggregate volatility risk.Size,book-to-market,momentum,and liquidity effects cannot account for either the low average returns earned by stocks with high exposure to systematic volatility risk or for the low average returns of stocks with high idiosyncratic volatility.1IntroductionIt is well known that the volatility of stock returns varies over time.While considerable research has examined the time-series relation between the volatility of the market and the expected re-turn on the market(see,among others,Campbell and Hentschel(1992),and Glosten,Jagan-nathan and Runkle(1993)),the question of how aggregate volatility affects the cross-section of expected stock returns has received less attention.Time-varying market volatility induces changes in the investment opportunity set by changing the expectation of future market returns, or by changing the risk-return trade-off.If the volatility of the market return is a systematic risk factor,an APT or factor model predicts that aggregate volatility should also be priced in the cross-section of stocks.Hence,stocks with different sensitivities to innovations in aggregate volatility should have different expected returns.Thefirst goal of this paper is to provide a systematic investigation of how the stochastic volatility of the market is priced in the cross-section of expected stock returns.We want to de-termine if the volatility of the market is a priced risk factor and estimate the price of aggregate volatility risk.Many option studies have estimated a negative price of risk for market volatil-ity using options on an aggregate market index or options on individual stocks.1Using the cross-section of stock returns,rather than options on the market,allows us to create portfolios of stocks that have different sensitivities to innovations in market volatility.If the price of ag-gregate volatility risk is negative,stocks with large,positive sensitivities to volatility risk should have low average ing the cross-section of stock returns also allows us to easily con-trol for a battery of cross-sectional effects,like the size and value factors of Fama and French (1993),the momentum effect of Jegadeesh and Titman(1993),and the effect of liquidity risk documented by P´a stor and Stambaugh(2003).Option pricing studies do not control for these cross-sectional risk factors.Wefind that innovations in aggregate volatility carry a statistically significant negative price of risk of approximately-1%per annum.Economic theory provides several reasons why the price of risk of innovations in market volatility should be negative.For example,Campbell (1993and1996)and Chen(2002)show that investors want to hedge against changes in mar-ket volatility,because increasing volatility represents a deterioration in investment opportuni-ties.Risk averse agents demand stocks that hedge against this risk.Periods of high volatility also tend to coincide with downward market movements(see French,Schwert and Stambaugh (1987),and Campbell and Hentschel(1992)).As Bakshi and Kapadia(2003)comment,assets 1See,among others,Jackwerth and Rubinstein(1996),Bakshi,Cao and Chen(2000),Chernov and Ghysels (2000),Burashi and Jackwerth(2001),Coval and Shumway(2001),Benzoni(2002),Jones(2003),Pan(2002), Bakshi and Kapadia(2003),Eraker,Johannes and Polson(2003),and Carr and Wu(2003).with high sensitivities to market volatility risk provide hedges against market downside risk. The higher demand for assets with high systematic volatility loadings increases their price and lowers their average return.Finally,stocks that do badly when volatility increases tend to have negatively skewed returns over intermediate horizons,while stocks that do well when volatil-ity rises tend to have positively skewed returns.If investors have preferences over coskewness (see Harvey and Siddique(2000)),stocks that have high sensitivities to innovations in market volatility are attractive and have low returns.2The second goal of the paper is to examine the cross-sectional relationship between id-iosyncratic volatility and expected returns,where idiosyncratic volatility is defined relative to the standard Fama and French(1993)model.3If the Fama-French model is correct,forming portfolios by sorting on idiosyncratic volatility will obviously provide no difference in average returns.Nevertheless,if the Fama-French model is false,sorting in this way potentially provides a set of assets that may have different exposures to aggregate volatility and hence different aver-age returns.Our logic is the following.If aggregate volatility is a risk factor that is orthogonal to existing risk factors,the sensitivity of stocks to aggregate volatility times the movement in aggregate volatility will show up in the residuals of the Fama-French model.Firms with greater sensitivities to aggregate volatility should therefore have larger idiosyncratic volatilities relative to the Fama-French model,everything else being equal.Differences in the volatilities offirms’true idiosyncratic errors,which are not priced,will make this relation noisy.We should be able to average out this noise by constructing portfolios of stocks to reveal that larger idiosyncratic volatilities relative to the Fama-French model correspond to greater sensitivities to movements in aggregate volatility and thus different average returns,if aggregate volatility risk is priced.While high exposure to aggregate volatility risk tends to produce low expected returns,some economic theories suggest that idiosyncratic volatility should be positively related to expected returns.If investors demand compensation for not being able to diversify risk(see Malkiel and Xu(2002),and Jones and Rhodes-Kropf(2003)),then agents will demand a premium for holding stocks with high idiosyncratic volatility.Merton(1987)suggests that in an information-segmented market,firms with largerfirm-specific variances require higher average returns to compensate investors for holding imperfectly diversified portfolios.Some behavioral models, 2Bates(2001)and Vayanos(2004)provide recent structural models whose reduced form factor structures have a negative risk premium for volatility risk.3Recent studies examining total or idiosyncratic volatility focus on the average level offirm-level volatility. For example,Campbell,Lettau,Malkiel and Xu(2001),and Xu and Malkiel(2003)document that idiosyncratic volatility has increased over time.Brown and Ferreira(2003)and Goyal and Santa-Clara(2003)argue that id-iosyncratic volatility has positive predictive power for excess market returns,but this is disputed by Bali,Cakici, Yan and Zhang(2004).like Barberis and Huang(2001),also predict that higher idiosyncratic volatility stocks should earn higher expected returns.Our results are directly opposite to these theories.Wefind that stocks with high idiosyncratic volatility have low average returns.There is a strongly significant difference of-1.06%per month between the average returns of the quintile portfolio with the highest idiosyncratic volatility stocks and the quintile portfolio with the lowest idiosyncratic volatility stocks.In contrast to our results,earlier researchers either found a significantly positive relation between idiosyncratic volatility and average returns,or they failed tofind any statistically sig-nificant relation between idiosyncratic volatility and average returns.For example,Lintner (1965)shows that idiosyncratic volatility carries a positive coefficient in cross-sectional regres-sions.Lehmann(1990)alsofinds a statistically significant,positive coefficient on idiosyncratic volatility over his full sample period.Similarly,Tinic and West(1986)and Malkiel and Xu (2002)unambiguouslyfind that portfolios with higher idiosyncratic volatility have higher av-erage returns,but they do not report any significance levels for their idiosyncratic volatility premiums.On the other hand,Longstaff(1989)finds that a cross-sectional regression coeffi-cient on total variance for size-sorted portfolios carries an insignificant negative sign.The difference between our results and the results of past studies is that the past literature either does not examine idiosyncratic volatility at thefirm level or does not directly sort stocks into portfolios ranked on this measure of interest.For example,Tinic and West(1986)work only with20portfolios sorted on market beta,while Malkiel and Xu(2002)work only with 100portfolios sorted on market beta and size.Malkiel and Xu(2002)only use the idiosyncratic volatility of one of the100beta/size portfolios to which a stock belongs to proxy for that stock’s idiosyncratic risk and,thus,do not examinefirm-level idiosyncratic volatility.Hence,by not di-rectly computing differences in average returns between stocks with low and high idiosyncratic volatilities,previous studies miss the strong negative relation between idiosyncratic volatility and average returns that wefind.The low average returns to stocks with high idiosyncratic volatilities could arise because stocks with high idiosyncratic volatilities may have high exposure to aggregate volatility risk, which lowers their average returns.We investigate this issue andfind that this is not a complete explanation.Our idiosyncratic volatility results are also robust to controlling for value,size, liquidity,volume,dispersion of analysts’forecasts,and momentum effects.Wefind the effect robust to different formation periods for computing idiosyncratic volatility and for different holding periods.The effect also persists in both bull and bear markets,recessions and expan-sions,and volatile and stable periods.Hence,our results on idiosyncratic volatility represent a substantive puzzle.The rest of this paper is organized as follows.In Section2,we examine how aggregate volatility is priced in the cross-section of stock returns.Section3documents thatfirms with high idiosyncratic volatility have very low average returns.Finally,Section4concludes.2Pricing Systematic Volatility in the Cross-Section2.1Theoretical MotivationWhen investment opportunities vary over time,the multi-factor models of Merton(1973)and Ross(1976)show that risk premia are associated with the conditional covariances between as-set returns and innovations in state variables that describe the time-variation of the investment opportunities.Campbell’s(1993and1996)version of the Intertemporal CAPM(I-CAPM) shows that investors care about risks from the market return and from changes in forecasts of future market returns.When the representative agent is more risk averse than log utility,assets that covary positively with good news about future expected returns on the market have higher average returns.These assets command a risk premium because they reduce a consumer’s abil-ity to hedge against a deterioration in investment opportunities.The intuition from Campbell’s model is that risk-averse investors want to hedge against changes in aggregate volatility because volatility positively affects future expected market returns,as in Merton(1973).However,in Campbell’s set-up,there is no direct role forfluctuations in market volatility to affect the expected returns of assets because Campbell’s model is premised on homoskedastic-ity.Chen(2002)extends Campbell’s model to a heteroskedastic environment which allows for both time-varying covariances and stochastic market volatility.Chen shows that risk-averse in-vestors also want to directly hedge against changes in future market volatility.In Chen’s model, an asset’s expected return depends on risk from the market return,changes in forecasts of future market returns,and changes in forecasts of future market volatilities.For an investor more risk averse than log utility,Chen shows that an asset that has a positive covariance between its return and a variable that positively forecasts future market volatilities causes that asset to have a lower expected return.This effect arises because risk-averse investors reduce current consumption to increase precautionary savings in the presence of increased uncertainty about market returns.Motivated by these multi-factor models,we study how exposure to market volatility risk is priced in the cross-section of stock returns.A true conditional multi-factor representation of expected returns in the cross-section would take the following form:r i t+1=a it+βim,t(r mt+1−γm,t)+βiv,t(v t+1−γv,t)+Kk=1βik,t(f k,t+1−γk,t),(1)where r it+1is the excess return on stock i,βim,tis the loading on the excess market return,βiv,tis the asset’s sensitivity to volatility risk,and theβik,tcoefficients for k=1...K representloadings on other risk factors.In the full conditional setting in equation(1),factor loadings, conditional means of factors,and factor premiums potentially vary over time.The model inequation(1)is written in terms of factor innovations,so r mt+1−γm,t represents the innovation in the market return,v t+1−γv,t represents the innovation in the factor reflecting aggregate volatility risk,and innovations to the other factors are represented by f k,t+1−γk,t.The conditional mean of the market and aggregate volatility are denoted byγm,t andγv,t,respectively,while the conditional mean of the other factors are denoted byγk,t.In equilibrium,the conditional mean of stock i is given by:a i t =E t(r it+1)=βim,tλm,t+βiv,tλv,t+Kk=1βik,tλk,t,(2)whereλm,t is the price of risk of the market factor,λv,t is the price of aggregate volatility risk, and theλk,t are prices of risk of the other factors.Note that only if a factor is traded is the conditional mean of a factor equal to its conditional price of risk.The main prediction from the factor model setting of equation(1)that we examine is that stocks with different loadings on aggregate volatility risk have different average returns.4How-ever,the true model in equation(1)is infeasible to examine because the true set of factors is unknown and the true conditional factor loadings are unobservable.Hence,we do not attempt to directly use equation(1)in our empirical work.Instead,we simplify the full model in equation (1),which we now detail.2.2The Empirical FrameworkTo investigate how aggregate volatility risk is priced in the cross-section of equity returns we make the following simplifying assumptions to the full specification in equation(1).First,we use observable proxies for the market factor and the factor representing aggregate volatility risk. We use the CRSP value-weighted market index to proxy for the market factor.To proxy innova-tions in aggregate volatility,(v t+1−γv,t),we use changes in the V IX index from the Chicago 4While an I-CAPM implies joint time-series as well as cross-sectional predictability,we do not examine time-series predictability of asset returns by systematic volatility.Time-varying volatility risk generates intertemporal hedging demands in partial equilibrium asset allocation problems.In a partial equilibrium setting,Liu(2001)and Chacko and Viceira(2003)examine how volatility risk affects the portfolio allocation of stocks and risk-free assets, while Liu and Pan(2003)show how investors can optimally exploit the variation in volatility with options.Guo and Whitelaw(2003)examine the intertemporal components of time-varying systematic volatility in a Campbell (1993and1996)equilibrium I-CAPM.Board Options Exchange(CBOE).5Second,we reduce the number of factors in equation(1) to just the market factor and the proxy for aggregate volatility risk.Finally,to capture the con-ditional nature of the true model,we use short intervals,one month of daily data,to take into account possible time-variation of the factor loadings.We discuss each of these simplifications in turn.Innovations in the V IX IndexThe V IX index is constructed so that it represents the implied volatility of a synthetic at-the-money option contract on the S&P100index that has a maturity of one month.It is constructed from eight S&P100index puts and calls and takes into account the American features of the option contracts,discrete cash dividends and microstructure frictions such as bid-ask spreads (see Whaley(2000)for further details).6Figure1plots the V IX index from January1986to December2000.The mean level of the daily V IX series is20.5%,and its standard deviation is7.85%.Because the V IX index is highly serially correlated with afirst-order autocorrelation of 0.94,we measure daily innovations in aggregate volatility by using daily changes in V IX, which we denote as∆V IX.Dailyfirst differences in V IX have an effective mean of zero(less than0.0001),a standard deviation of2.65%,and also have negligible serial correlation(the first-order autocorrelation of∆V IX is-0.0001).As part of our robustness checks in Section 2.3,we also measure innovations in V IX by specifying a stationary time-series model for the conditional mean of V IX andfind our results to be similar to using simplefirst differences. While∆V IX seems an ideal proxy for innovations in volatility risk because the V IX index is representative of traded option securities whose prices directly reflect volatility risk,there are two main caveats with using V IX to represent observable market volatility.Thefirst concern is that the V IX index is the implied volatility from the Black-Scholes 5In previous versions of this paper,we also considered sample volatility,following Schwert and Stambaugh (1987);a range-based estimate,following Alizadeh,Brandt and Diebold(2002);and a high-frequency estima-tor of volatility from Andersen,Bollerslev and Diebold(2003).Using these measures to proxy for innovations in aggregate volatility produces little spread in cross-sectional average returns.These tables are available upon request.6On September22,2003,the CBOE implemented a new formula and methodology to construct its volatility index.The new index is based on the S&P500(rather than the S&P100)and takes into account a broader range of strike prices rather than using only at-the-money option contracts.The CBOE now uses V IX to refer to this new index.We use the old index(denoted by the ticker V XO).We do not use the new index because it has been constructed by back-filling only to1990,whereas the V XO is available in real-time from1986.The CBOE continues to make both volatility indices available.The correlation between the new and the old CBOE volatility series is98%from1990-2000,but the series that we use has a slightly broader range.(1973)model,and we know that the Black-Scholes model is an approximation.If the true stochastic environment is characterized by stochastic volatility and jumps,∆V IX will reflect total quadratic variation in both diffusion and jump components(see,for example,Pan(2002)). Although Bates(2000)argues that implied volatilities computed taking into account jump risk are very close to original Black-Scholes implied volatilities,jump risk may be priced differ-ently from volatility risk.Our analysis does not separate jump risk from diffusion risk,so our aggregate volatility risk may include jump risk components.A more serious reservation about the V IX index is that V IX combines both stochastic volatility and the stochastic volatility risk premium.Only if the risk premium is zero or constant would∆V IX be a pure proxy for the innovation in aggregate volatility.Decomposing∆V IX into the true innovation in volatility and the volatility risk premium can only be done by writing down a formal model.The form of the risk premium depends on the parameterization of the price of volatility risk,the number of factors and the evolution of those factors.Each different model specification implies a different risk premium.For example,many stochastic volatility option pricing models assume that the volatility risk premium can be parameterized as a linear function of volatility(see,for example,Chernov and Ghysels(2000),Benzoni(2002),and Jones(2003)).This may or may not be a good approximation to the true price of risk.Rather than imposing a structural form,we use an unadulterated∆V IX series.An advantage of this approach is that our analysis is simple to replicate.The Pre-Formation RegressionOur goal is to test if stocks with different sensitivities to aggregate volatility innovations(prox-ied by∆V IX)have different average returns.To measure the sensitivity to aggregate volatility innovations,we reduce the number of factors in the full specification in equation(1)to two,the market factor and∆V IX.A two-factor pricing kernel with the market return and stochastic volatility as factors is also the standard set-up commonly assumed by many stochastic option pricing studies(see,for example,Heston,1993).Hence,the empirical model that we examine is:r i t =β0+βiMKT·MKT t+βi∆V IX·∆V IX t+εit,(3)where MKT is the market excess return,∆V IX is the instrument we use for innovations inthe aggregate volatility factor,andβiMKT andβi∆V IXare loadings on market risk and aggregatevolatility risk,respectively.Previous empirical studies suggest that there are other cross-sectional factors that have ex-planatory power for the cross-section of returns,such as the size and value factors of the Fama and French(1993)three-factor model(hereafter FF-3).We do not directly model these effectsin equation(3),because controlling for other factors in constructing portfolios based on equa-tion(3)may add a lot of noise.Although we keep the number of regressors in our pre-formation portfolio regressions to a minimum,we are careful to ensure that we control for the FF-3factors and other cross-sectional factors in assessing how volatility risk is priced using post-formation regression tests.We construct a set of assets that are sufficiently disperse in exposure to aggregate volatility innovations by sortingfirms on∆V IX loadings over the past month using the regression(3) with daily data.We run the regression for all stocks on AMEX,NASDAQ and the NYSE,with more than17daily observations.In a setting where coefficients potentially vary over time,a 1-month window with daily data is a natural compromise between estimating coefficients with a reasonable degree of precision and pinning down conditional coefficients in an environment with time-varying factor loadings.P´a stor and Stambaugh(2003),among others,also use daily data with a1-month window in similar settings.At the end of each month,we sort stocks into quintiles,based on the value of the realizedβ∆V IX coefficients over the past month.Firms in quintile1have the lowest coefficients,whilefirms in quintile5have the highestβ∆V IX loadings. Within each quintile portfolio,we value-weight the stocks.We link the returns across time to form one series of post-ranking returns for each quintile portfolio.Table1reports various summary statistics for quintile portfolios sorted by pastβ∆V IX over the previous month using equation(3).Thefirst two columns report the mean and standard deviation of monthly total,not excess,simple returns.In thefirst column under the heading ‘Factor Loadings,’we report the pre-formationβ∆V IX coefficients,which are computed at the beginning of each month for each portfolio and are value-weighted.The column reports the time-series average of the pre-formationβ∆V IX loadings across the whole sample.By con-struction,since the portfolios are formed by ranking on pastβ∆V IX,the pre-formationβ∆V IX loadings monotonically increase from-2.09for portfolio1to2.18for portfolio5.The columns labelled‘CAPM Alpha’and‘FF-3Alpha’report the time-series alphas of these portfolios relative to the CAPM and to the FF-3model,respectfully.Consistent with the negative price of systematic volatility risk found by the option pricing studies,we see lower average raw returns,CAPM alphas,and FF-3alphas with higher past loadings ofβ∆V IX.All the differences between quintile portfolios5and1are significant at the1%level,and a joint test for the alphas equal to zero rejects at the5%level for both the CAPM and the FF-3model.In particular,the5-1spread in average returns between the quintile portfolios with the highest and lowestβ∆V IX coefficients is-1.04%per month.Controlling for the MKT factor exacerbates the5-1spread to-1.15%per month,while controlling for the FF-3model decreases the5-1 spread to-0.83%per month.Requirements for a Factor Risk ExplanationWhile the differences in average returns and alphas corresponding to differentβ∆V IX loadings are very impressive,we cannot yet claim that these differences are due to systematic volatility risk.We will examine the premium for aggregate volatility within the framework of an uncon-ditional factor model.There are two requirements that must hold in order to make a case for a factor risk-based explanation.First,a factor model implies that there should be contemporane-ous patterns between factor loadings and average returns.For example,in a standard CAPM, stocks that covary strongly with the market factor should,on average,earn high returns over the same period.To test a factor model,Black,Jensen and Scholes(1972),Fama and French(1992 and1993),Jagannathan and Wang(1996),and P´a stor and Stambaugh(2003),among others,all form portfolios using various pre-formation criteria,but examine post-ranking factor loadings that are computed over the full sample period.While theβ∆V IX loadings show very strong patterns of future returns,they represent past covariation with innovations in market volatility. We must show that the portfolios in Table1also exhibit high loadings with volatility risk over the same period used to compute the alphas.To construct our portfolios,we took∆V IX to proxy for the innovation in aggregate volatil-ity at a daily frequency.However,at the standard monthly frequency,which is the frequency of the ex-post returns for the alphas reported in Table1,using the change in V IX is a poor approximation for innovations in aggregate volatility.This is because at lower frequencies,the effect of the conditional mean of V IX plays an important role in determining the unanticipated change in V IX.In contrast,the high persistence of the V IX series at a daily frequency means that thefirst difference of V IX is a suitable proxy for the innovation in aggregate volatility. Hence,we should not measure ex-post exposure to aggregate volatility risk by looking at how the portfolios in Table1correlate ex-post with monthly changes in V IX.To measure ex-post exposure to aggregate volatility risk at a monthly frequency,we follow Breeden,Gibbons and Litzenberger(1989)and construct an ex-post factor that mimics aggre-gate volatility risk.We term this mimicking factor F V IX.We construct the tracking portfolio so that it is the portfolio of asset returns maximally correlated with realized innovations in volatility using a set of basis assets.This allows us to examine the contemporaneous relation-ship between factor loadings and average returns.The major advantage of using F V IX to measure aggregate volatility risk is that we can construct a good approximation for innovations in market volatility at any frequency.In particular,the factor mimicking aggregate volatility innovations allows us to proxy aggregate volatility risk at the monthly frequency by simply cumulating daily returns over the month on the underlying base assets used to construct the mimicking factor.This is a much simpler method for measuring aggregate volatility innova-。
多水平logistic模型及其在流行病学调查数据中的应用

3
广东药学院硕士研究生学位论文
多水平 logistic 模型及其在流行病学调查数据中的应用
In this study, we focus on the rationale for using multilevel logsitic model in public health research and epidemiology, summarizes the statistical methodology, and highlights some of the research questions that have been addressed using these methods. The advantages and disadvantages of multilevel logsitic model compared with standard methods are reviewed. The use of multilevel logsitic model raises theoretical and methodological issues related to the theoretical model being tested, the conceptual distinction between group- and individual-level variables, the ability to differentiate “independent” effects, the reciprocal relationships between factors at different levels, and the increased complexity that these models imply. The potentialities and limitations of multilevel logsitic model, within the broader context of understanding.
Defining drug disposition determinants

Drug disposition is influenced by drug metabolizing enzymes (DMEs), drug transport proteins (DTPs), serum binding proteins and transcription factors that regulate DME and DTP expression (BOX 1). Foreknowledge of the specific proteins that influence the disposition of a new chemical entity (NCE) is an important goal of preclinical and early clinical drug develop‑ment. Early availability of this information enables mathematical modelling of the drug interaction potential of an NCE using quantitative kinetic parameters of specific DMEs1. This can therefore lead to better projection of doses for subsequent studies. Although tools exist to assess the roleof most of these proteins for the disposi‑tion of an NCE, drug developers typically learn only about a limited number of them (that is, several cytochrome P450s (CYPs), a few additional DMEs and the DTPP‑glycoprotein), and generally do not know the relative clinical importance of most of the more than 170 drug disposition pathways (TABLES 1,2;BOX 2; Supplementary information S1 (table), S2 (table), S3 (table), S4 (table)). Much of the knowledge aboutdrug disposition determinants comes fromacademic laboratories after a drug is marketed.Such knowledge has been highly beneficial forpatients; for example, when the prevalence ofsevere adverse events in thiopurine S‑methyl‑transferase (TPMT) poor metabolizers dosedwith thiopurines was identified2,3. However,for many drugs, the pathways that determinepharmacokinetic variation remain unknowneven years after regulatory approval. Thislimits the ability of drug developers to identify,manage and understand the consequences ofpharmacokinetic variability for efficacy, safetyand drug–drug interactions. For example,statins were used by many millions of peoplebefore it was discovered that their pharmaco‑kinetic variability, drug interactions, efficacyand safety might be dependent on the DTPsolute carrier organic anion transport protein1B1 (OATP1B1)4–6.Association between a gene variantand drug pharmacokinetics implies amechanistic role of the gene product indrug disposition, and the potential outcomeof making such associations is to learn theextent to which any of a wide range offactors influences the disposition of a drug.Increased knowledge and more accessibletechnology should now make it easier fordrug developers to study which pathwaysare responsible for the disposition of adrug. In this article, after a brief overviewof the preclinical characterization of drugdisposition, we summarize current know‑ledge on pharmacogenetics and drug dispo‑sition. We then propose a new approachin which pharmacogenetic results derivedfrom early clinical studies can both feedback to additional targeted in vitro studiesand feed forward to optimize later‑stage,larger clinical trials for NCEs, contribute tomore informative drug labels, and therebypotentially enable better drug use.Preclinical drug disposition assessmentPreclinical characterization of drug dis‑position generally involves the assessmentof individual proteins for their role in thedisposition of the NCE. A summary ofcurrently available tools for such studies,including purified or recombinantproteins, selective substrates and inhibitors isprovided in Supplementary information S5(table).Although many purified or recombinantDMEs — particularly members of thehuman CYP, flavin monooxygenase (FMO),monoamine oxidase (MAO), UDP glucu‑ronosyltransferase (UGT), sulphotransferase(SULT), N‑acetyltransferase (NAT) andglutathione S‑transferase (GST) families— are commercially available, there aresubstantial gaps in the availability of purifiedor recombinant DMEs from other families.Several DTPs have been functionallyexpressed in recombinant cell‑based assays,but these are generally not commerciallyavailable. When purified or recombinantprotein is not available, selective inhibitors(if known and commercially available) canbe useful to deconstruct the dispositionprocess in perfused organs, tissue slices,isolated cells or subcellular fractions.However, sufficiently selective inhibitors thatdistinguish between closely related proteinshave only been established for a few DMEor DTP families. Even among the CYPs, it isstill not possible to fully distinguish betweeno P i n i o nDefining drug dispositiondeterminants: a pharmacogenetic–pharmacokinetic strategyDavid A. Katz, Bernard Murray, Anahita Bhathena and Leonardo SahelijoAbstract | In preclinical and early clinical drug development, information about thefactors influencing drug disposition is used to predict drug interaction potential,estimate and understand population pharmacokinetic variability, and selectdoses for clinical trials. However, both in vitro drug metabolism studies andpharmacogenetic association studies on human pharmacokinetic parameters havefocused on a limited subset of the proteins involved in drug disposition. Furthermore,there has been a one-way information flow, solely using results of in vitro studiesto select candidate genes for pharmacogenetic studies. Here, we propose a two-way pharmacogenetic–pharmacokinetic strategy that exploits the dramatic recentexpansion in knowledge of functional genetic variation in proteins that influencedrug disposition, and discuss how it could improve drug development.NATUrE rEvIEWS |drug discovery vOLUME 7 | APrIL 2008 |293PersPectIves©2008Nature Publishing Groupthe four CYP3A enzymes, and selective inhibitors for some CYPs (for example, CYP2C18, CYP2G, CYP2r1, CYP2S1) have not been identified. Indeed, little is known at all about these and a number of other DMEs. When a selective inhibitor is not available, it may be possible to take advantage of tissue‑selective expression of particular isoforms within a protein family to learn the extent to which each can influence NCE disposition (for example, the roles of FMO1, FMO2 and FMO3 can be assessed separately in kidney, lung and liver using the same inhibitor). When neither recombinant protein nor selective inhibitor for a DME or DTP is available, observing that an NCE is a competitive inhibitor (in perfused organs, tissue slices, isolated cells or subcellular fractions) towards a known selective sub‑strate (again, if known and commercially available) might indicate that a particular DME or DTP is important for the NCE’sdisposition. If a drug induces DME or DTPexpression by a transcription factor bindingin a heterologous transcription activation assay,it might autoinduce its own disposition aswell as that of other drugs.To provide a comprehensive in vitrosurvey of drug disposition determinants,a laboratory needs the capability to per‑form the diverse assay types mentionedabove, many of which must be developedin‑house. Because of the current lack of acomprehensive toolset and the resourcesrequired — and also because there hasnot been a regulatory imperative foradditional investigation — a typical pre‑clinical in vitro survey has covered onlyseveral DMEs (mainly CYPs) and the DTPP‑glycoprotein. Knowing whether thesefactors can influence the disposition ofan NCE provides valuable but far fromcomprehensive information to predictdrug interaction potential, estimate andunderstand population pharmacokineticvariability, and select doses for subsequentclinical trials. Elucidation of the specific setof disposition pathways that are importantfor a particular NCE’s disposition has notbeen achieved, mainly because the neces‑sary resources have not been available.There is a need for an improved toolsetto identify the most important proteins thatinfluence the disposition of an NCE. Thistoolset should be more comprehensive incoverage of DMEs, DTPs and other factors;less diverse in assay types; feasible duringpreclinical or early clinical development; andaffordable. We propose that a strategy basedon the growing knowledge of the influenceof pharmacogenetic factors on drug disposi‑tion (summarized in the following section)can help provide that toolset.Pharmacogenetics and drug dispositionA genetic component of pharmacokineticvariability was postulated more than 100years ago by Archibald Garrod in studies ofpatients with alkaptonuria7. Half a centurylater, several drugs were shown to haveindistinguishable disposition in mono‑zygotic twins, but often distinct dispositionin dizygotic twins (for example, phenyl‑butazone8). These results established drugdisposition as a heritable trait. Deficienciesof the DMEs NAT and butyrylcholin‑esterase (BCHE) were later identified asrisk factors for adverse effects of isoniazid9and succinylcholine10, respectively, and thegenetic basis for these11–15 and other DMEpoor metabolizer phenotypes (for example,CYP2D616–20, TPMT21–23) were discoveredaround 1990.By the 1990s, there was an understand‑able reticence in the pharmaceutical industryto develop drugs that were substrates ofthese few polymorphic DMEs because of thelikelihood of variable pharmacokinetic anddrug–drug interactions. However, therewere exceptions: atomoxetine, a sensitiveCYP2D6 substrate, was approved for usein 2002 (REF. 24). Also in the 1990s, drugdevelopers began to utilize pharmacogeneticstudies to learn the magnitude of pharmaco‑kinetic variability of NCEs that could beattributed to genetic variation. In general,these studies focused on the few DMEs inwhich there were known polymorphisms,and were undertaken only when they wereconsidered necessary. That is, when in vitroresults indicated that the NCE was asubstrate of the polymorphic DME(hypothesis‑based experiments).P e r s P e c t i v e s294 | APrIL 2008 | vOLUME 7 /reviews/drugdisc©2008Nature Publishing GroupUntil recently, limited knowledge about functional genetic variation in DMEs (and none about polymorphism in other drugdisposition factors) substantially limited the scope of pharmacogenetics–pharmaco‑kinetics research. However, in the past few years, substantial knowledge in this field has been accumulated, and a review of the literature reveals that there are now over 170 gene products known or expected to have a role in drug disposition (BOX 3). These include not only numerous DMEs and DTPs, but also abundant serum binding proteins and regulatory (transcription) factors that control the expression of DMEs and DTPs. More than half of the corresponding genes are known to be poly‑morphic (TABLES 1,2;BOX 2; Supplementary information S1 (table)); most that are not known to contain common functional poly‑morphisms (Supplementary information S2 (table), S3 (table), S4 (table)) have not been adequately studied to state with certainty that they do not.The 16 proteins involved in drug disposition for which consistently replicated associations between variants in the corresponding genes and the human pharmacokinetics of at least one drug havebeen published are shown in TABLE 1. Withthe exception of FMO3, for which only tworeports showing relationship to sulindacpharmacokinetics were found, there werethree or more consistent reports for at leastone drug for each gene. FMO3 was includedin this group because the established associ‑ation of variants in this gene with fish-odoursyndrome25 is additional evidence supportingits relevance for xenobiotic disposition.Nearly all the genes listed in TABLE 1 encodeDMEs, although there is also a gene thatencodes a DTP (OATP1B1). There is robustscientific evidence showing that each genecontains common variants (combinedminor allele frequency of variants sharinga phenotype ≥5%), which have substantialeffects on human pharmacokinetics of oneor more drugs (see TABLE1 for references).However, this does not mean that the rele‑vance of these variants for clinical practicehas been established; in fact, dose adjust‑ments or contraindications based on onlyCYP2D6, CYP2C9, TPMT and UGT1A1 arecurrently included in US drug labels26.TABLE 2 shows the 18 genes for whichcommon variants are likely to have a role indrug disposition, having been shown to beassociated with the human pharmacokineticsof one or more drugs, albeit in single studies.Of these, 15 encode DMEs, 2 encode DTPsand 1 encodes a serum binding protein(α‑1 acid glycoprotein, gene = ORM1).The preponderance of DMEs in TABLE 1 andTABLE 2 reflects that DMEs were the solefocus of pharmacogenetics research relatedto drug disposition until recently. Many ofthe studies cited in TABLE 2 are relativelyrecent, and might therefore be replicatedin the near future. As this occurs, the rangeof genes established as polymorphic deter‑minants of human pharmacokinetics willexpand. In addition to pharmacokinetics,several of these genes have also beenassociated with drug efficacy or safety.Common variants of at least 55 genesencoding drug disposition factors have func‑tional effects on protein activity or expression(Supplementary information S1 (table);BOX 2), but have not yet been associated withhuman pharmacokinetics for any drug. It iscurrently unknown how many of these geneswill be found to have meaningful influenceon human pharmacokinetics. Several ofthem encode DMEs such as CYP3A4 and thetable 1 | Consistently replicated associations between genotype and clinical pharmacokineticsOnline Mendelian Inheritance in Man (OMIM) database web site: /sites/entrez?db=omim.P e r s P e c t i v e sNATUrE rEvIEWS |drug discovery vOLUME 7 | APrIL 2008 |295©2008Nature Publishing GroupP e r s P e c t i v e stable 2 | Associations between genotype and clinical pharmacokinetics*Online Mendelian Inheritance in Man (OMIM) database web site: /sites/entrez?db=omim. NsAID, non-steroidal anti-inflammatory drug; sNP, single nucleotide polymorphism.296 | APrIL 2008 | vOLUME 7 /reviews/drugdisc©2008Nature Publishing GroupUGTs, which are known to metabolize a wide range of drugs27,28, and these may be among those most likely to be found to be relevant for human pharmacokinetic variability. Finally, DMEs, DTPs and regulatory factors for which the relevance of genetic variation to drug disposition has not been established are shown in Supplementary information S2 (table), S3 (table) and S4 (table).Proposal for a new PG–PK strategyThe increase in knowledge about phar‑macogenetics and drug disposition sum‑marized above — coupled with technology advancements that have made genotyping more affordable (with costs of less than US$1 per genotype for multiple available technologies) in the past decade — have made broad application of pharmacogenet‑ics in most drug development programmes more feasible. Several platforms have been developed to screen the known functional variants that might influence drug disposi‑tion in the context of early clinical trials from which high‑quality pharmacokinetic data are also available.The approach we propose includes a broad evaluation of genotype–pharmaco‑kinetic relationships during early drug development, together with in vitro studies, to first generate and then confirm hypoth‑eses about the pathways that are majordisposition determinants of an NCE.Our core strategy for incorporation in NCE development comprises five steps (FIG. 1). The first step is to conduct in vitro experiments before clinical trials to assess whether, and to what extent, selected DMEs and DTPs might influence disposition of the NCE. This activity provides valuable information about the potential role of proteins that are known to influence the disposition of many drugs and to mediate a number of clinically important drug inter‑actions, such as CYP3A and P‑glycoprotein. These experiments have demonstrated utility in drug development planning and decision‑making. Additional in vitro assays may become standard on the basis of new information about drug disposition and interaction factors. For example, recent results from our group29 and others30–33 have demonstrated that the hepatic uptake DTP OATP1B1 (SLCO1B1) is a meaningful determinant of drug disposition for statins and other drugs, and that OATP1B1 inhibi‑tors may have drug interaction potential. recombinant OATP1B1 can be expressed in cell culture, and selective substrates and inhibitors are available (Supplementary information S5 (table)). Learning whetheran NCE is an OATP1B1 substrate or inhibi‑tor could become an ordinary preclinicalactivity.The second step is to conduct a broadsearch for associations of pharmacokineticswith genotypes during the first‑in‑humanstudy (BOX 4). The scope of this search couldinclude all relevant genes for which thereis reasonable expectation that a positiveresult can be obtained (based on studypower) and readily interpreted based oncurrent information about functionalvariants. This includes genes for which thereare well‑established (TABLE 1) or observed(TABLE 2) associations between genetic vari‑ants and human pharmacokinetics, as wellas genes for which in vitro evidence indicatesthat common variants alter the activityor expression of the gene product (BOX 2;Supplementary information S1 (table)).Defining the search scope in this way willinclude over half of known or suspecteddrug disposition determinants. For genes inwhich common variants are known but theirfunction is not (Supplementary informationS2 (table)), associations between genotypeand human pharmacokinetics might notbe readily interpreted without subsequentexperimentation to define the phenotype ofthe associated variant(s). These genes mightbe screened if there is preclinical evidencethat the NCE is a substrate or inhibitor,and perhaps not otherwise. Because first‑in‑human studies are generally not large,the likelihood of finding an associationbetween an uncommon functional variant(Supplementary information S3 (table))and human pharmacokinetics is low. Ifthere is preclinical evidence that the NCEis a substrate or inhibitor, a special study todetermine the clinical relevance of genotypetherein may be a better approach to assessthe effect of uncommon functional variantsthan the general strategy described here.Genes for which there is no publishedinformation regarding common geneticvariation (Supplementary information S3(table)) might be screened using singlenucleotide polymorphisms (SNPs) foundin online databases. Including these SNPswould enable some assessment of essentiallyevery known or expected drug dispositiondeterminant.P e r s P e c t i v e sNATUrE rEvIEWS |drug discovery vOLUME 7 | APrIL 2008 |297©2008Nature Publishing GroupThe third step is to replicate any observed associations during the multiple rising‑dose study (BOX 4). As large numbers of genes may be screened, replication of any observed association from a first‑in‑human study is essential to minimize the risk of making a decision based on false‑positive results. The fourth step is to confirm the gene product’s role using an in vitro assay (if the role was not already known from preclinical work) before or concurrently with Phase II clinical studies (BOX 4). When functional genetic variants affect protein activity (rather than expression), the activities of those variants towards the NCE should also be measured in the in vitro assay, as some variants have substrate‑dependent effects. For example, the *17 allele of CYP2D6 has normal catalytic activity towards codeine but reduced activity towards dextromethorphan and debrisoquin34. If different variants in the same gene were used jointly to classifyindividuals (for example, into poor metabo‑lizer or non‑poor metabolizer) for clinicalpharmacogenetic–pharmacokinetic associa‑tions, the classification should be confirmedby showing that the different variants sharea similar phenotype toward the compound(for example, SLCO1B1 and atrasentan29).The fifth step is to estimate the magni‑tude of genotype effect in a populationpharmacokinetics model during Phase IIclinical studies. At this point, genotype isused as a covariate in the population phar‑macokinetics model, just as sex or weightmight be used. It is often not feasible to usegenotype as a population pharmacokineticsmodel covariate before Phase II, becausethe number of subjects in Phase I clinicalstudies (BOX 4) is generally not large enoughto ensure an accurate estimate of the magni‑tude of genetic effect in a diverse population.Sufficient numbers of individuals havingrare genotypes might not be dosed with anNCE until Phase III clinical studies (BOX 4),or it might be necessary to conduct anenriched clinical study to appropriatelyinform the model.Knowledge about genetic variability rele‑vant to drug disposition can be applied inseveral ways, and these are discussed in thefollowing section.Applications of PG–PK knowledgePotent inhibitors or inducers of a polymor‑phic DME or DTP are likely to have effectsthat are proportional to the magnitude ofeffect of genotype (for example, CYP2C19and ticlopidine35). Thus, associationsbetween human pharmacokinetics of anNCE and genetic variation identifies apotential pathway for drug–drug inter‑actions, and hence the need for specific andadditional drug–drug interaction studies.By contrast, little or no effect of a well‑established genetic variant might show thatcertain drug–drug interaction studies arenot necessary. For example, a CYP2D6 inhib‑itor is unlikely to have a meaningful effecton a CYP2D6 substrate if that substrate’spharmacokinetics are not meaningfullyinfluenced by CYP2D6 genotype. Prioritizingdrug–drug interaction studies on the basis ofclinical pharmacogenetic effects will improveon the current approach of doing so on thebasis of in vitro experiments alone1.CYP2D6 can be used to exemplifyanother application of clinical pharmaco‑genetics: to increase confidence thatpharmacokinetic outliers are not likely tobe an issue in later development. Lack of asignificant effect of any genotype suggeststhat multiple distribution pathways arecontributing to drug disposition equally, andthat genetic pharmacokinetic outliers are atmost very rare (as they would have to carrymultiple rare genotypes). Pharmacogenetic–pharmacokinetic relationships can help todistinguish between ordinary populationvariability and true outliers in a limiteddataset — a relevant factor in decisions ofhow (or whether) to move a programmeforward. For example, in one study we iden‑tified that unusual pharmacokinetics of aCYP2D6 substrate was observed in a personwhose CYP2D6 genotype had a populationfrequency of <0.4% and was thus reasonablyconsidered an outlier36. In other situations,learning that one or more apparent outliersshare genetic constitution with other subjectssuggests a greater level of inter‑individualvariation rather than the existence of twoseparate populations.Box 3 | Survey of genetic variants in drug disposition factorsA search of the scientific literature and online resources was conducted to provide an overview ofthe variation in genes that encode drug metabolizing enzymes (DMEs), the drug transport proteins(DTPs), abundant plasma binding proteins, and factors that regulate DME and DTP expression.For each gene, at least the following sources were searched:• Online Mendelian Inheritance in Man (OMIM) (/entrez/query.fcgi?db=OMIM)• Medline (accessed through Dialog DataStar)was searched using the OMIM gene symbol.If this simple search yielded >100 articles, it was limited by applying the condition AND(pharmacogenetics OR polymorphism-genetic).• The Pharmacogenetics and Pharmacogenomics Knowledge Base ()genes were categorized as follows:• Consistently replicated association of variants with human pharmacokinetics of at least one drug(TABLE 1).• Association of variants with human pharmacokinetics of one or more drugs, but withoutconsistent replication for any drug (TABLE 2).• Functionality of common variants (≥5% combined frequency of variants of similar phenotype)demonstrated by in vitro methods, but no published association with human pharmacokinetics(BOX 2; see Supplementary information S1 (table)).• Common variants have been published, but functionality or association with humanpharmacokinetics have not (see Supplementary information S2 (table)).• Functionality of one or more rare (or unreported frequency) variants demonstrated (seeSupplementary information S3 (table)).• No information on variant functionality or association related to human pharmacokinetics;rare mutations in some of these genes have been linked to Mendelian metabolic disorders (seeSupplementary information S4 (table)).The aim of this overview is to provide a sense of the diversity of pharmacogenetics–pharmacokinetics knowledge. Although extensive, the tables are not necessarily comprehensive.We generally did not include reports of association unrelated to the pharmacokinetics of aspecific drug, even when a phenotype (such as cancer susceptibility) might be related toxenobiotic disposition. Literature citations are either to our choice of review articles orto primary literature supporting what we considered to be the most important sort of informationavailable. For example, if variants in a gene were associated with human pharmacokinetics in aclinical study we do not also cite work showing the molecular phenotype of those variants; if thephenotype of common variants in a gene is understood we do not also cite work concerning thephenotype of rare variants. We apologize in advance to any scientists whose relevantpublications are not cited.P e r s P e c t i v e s298 | APrIL 2008 | vOLUME 7 /reviews/drugdisc©2008Nature Publishing GroupNature Reviews | Drug DiscoveryAssess safety and tolerabilityin healthy volunteersDose verification andproof of conceptLong-term safetyand efficacy The use of genotype–pharmacokinetic associations can also enhance the design of special population or regional bridging studies (BOX 4). If a drug’s pharmacokinetic properties are sensitive to a polymorphism in a gene, success in special population studies may depend on including that gene in the design. How this is most efficiently done may vary between situations, depend‑ing in part on the strength of the effect and frequency of the genotype. For some studies, retrospective determination of whether an unbalanced representation of genotypes contributed to group differences may be sufficient. Sometimes, recruitment of geno‑type‑balanced cohorts or separate matched cohorts of different genotypes, or excluding individuals of a certain genotype, may be desirable to address the key clinical phar‑macology question. These approaches can be particularly relevant in regional bridging studies, as genetic variant frequencies are known to differ substantially betweenpopulations of different geographic origins (for example, CYP2C9 (REF . 37), CYP2C19 (REF . 38), CYP2A6 (REF . 39), UGT1A1 and UGT1A9 (REF . 40), NAT2 (REF . 41), OATP1B1 (REF . 42)).For example, suppose that pharmaco‑genetics–pharmacokinetics research in both first‑in‑human and multiple rising‑dose studies showed that, on average, individu‑als heterozygous for a low activity allele of CYP2A6 (intermediate metabolizers ) had higher levels of an NCE than those homozygous for the wild‑type allele of the gene (extensive metabolizers ). Furthermore,in vitro experiments conducted subsequently showed that the NCE is a CYP2A6 substrate and population pharmacokinetic analysis of Phase II clinical trial results confirm the influence of the CYP2A6 genotype on the pharmacokinetic properties of the NCE. To facilitate global development of the NCE, a pharmacokinetic bridging study between Japanese and Caucasians is a next step 2. Successful conduct of this study could elimi‑nate the need for a separate full development programme in Japan 43. Y et, because of highly different variant frequencies, individuals homozygous for low activity alleles (poor metabolizers) are common among Japanese but not in Caucasians. Hence, random recruitment of Japanese and Caucasians (the standard practice for regional bridging studies) is almost certain to fail to showequivalent pharmacokinetics between the two groups. There are several possible regional bridging trial designs that might provide the evidence to avert a requirement to conduct similar full development programmes in both groups, including recruitment of genotype‑matched cohorts of Japanese and Caucasians. However, there is currently a lack of public experience, and hence uncer‑tainty, as to whether this or other designs will be acceptable to regulatory agencies.Another way to use this information is in dose selection for pivotal studies (BOX 4). Understanding that the dose–exposure relationship differs between identifiable groups may lead to a decision to moveforward with a dose or doses that differ from what might have been selected considering a homogeneous population. For example, it may be desirable to increase the pivotal study dose to enhance efficacy among individuals who can be expected to have lower exposures (FIG. 2). The drug levels of some leading antidepressants (for example, paroxetine, venlafaxine) or antipsychotics (for example, olanzapine, aripiprazole) are moderately influenced by CYP2D6 genotype 44. These drugs are generally safe at a range of doses 45–48; however, there have been reports of poor efficacy related to low drug levels in CYP2D6 ultrarapid metabolizers 49–51. FIGURE 2a illustrates how pharmacogenetics might have been applied during the development of these drugs. Here, the ‘default’ dose represents the lowest dose that showed efficacy in pivotal studies and is generally the recommended starting dose in the drug’s labels. Suppose that the association between CYP2D6 genotype and pharmacokinetics had been established during Phase I and II clinical studies. Then, the developers of these drugs could have predicted that using a somewhat higher dose (the pharmacogenetics‑based dose) in pivotal studies would improve the efficacy profile in ultrarapid metabolizers and not meaningfully diminish the safety profile in other groups (including poor metabolizers). Perhaps they would have selected the phar‑macogenetics‑based doses for their pivotal studies. Because the drug label indicates doses studied in controlled efficacy trials, such a decision would have been reflected in the label and perhaps improved clinical practice using these drugs.Figure 1 | Flow chart of the proposed pharmacogenetic–pharmacokinetic strategy. In vitro experiments are conducted before clinical trials to assess whether, and to what extent, selected drug metabolizing enzymes (DMes) and drug transport proteins (DtPs) might influence the disposition of a new chemical entity (Nce). then, during the first-in-human study, a broad search for associations of pharmacokinetic (PK) properties with genotypes is conducted. Any observed associations are replicated during the multiple rising-dose study. Before or concurrently with Phase IIclinical studies, the gene product’s role is confirmed using an in vitro assay(if the role was not already known from preclinical work). the magnitude of genotype effect in a population pharmacokinetics model is then estimated during Phase II clinical studies.P e r s P e c t i v e sNATUrE rEvIEWS | drug discoveryvOLUME 7 | APrIL 2008 | 299© 2008Nature Publishing Group。
固相支撑液液萃取结合LC-MS

邓龙,周思,黄佳佳,等. 固相支撑液液萃取结合LC-MS/MS 快速测定生乳中32种农药残留[J]. 食品工业科技,2023,44(17):360−366. doi: 10.13386/j.issn1002-0306.2022120075DENG Long, ZHOU Si, HUANG Jiajia, et al. Determination of 32 Kinds of Pesticide Residues in Raw Milk by Supported Liquid Extraction with LC-MS/MS[J]. Science and Technology of Food Industry, 2023, 44(17): 360−366. (in Chinese with English abstract).doi: 10.13386/j.issn1002-0306.2022120075· 分析检测 ·固相支撑液液萃取结合LC-MS/MS 快速测定生乳中32种农药残留邓 龙1,周 思2, *,黄佳佳1,曾上敏1,张静文1(1.广东食品药品职业学院,广东广州 510520;2.广州市疾病预防控制中心,广东广州 510440)摘 要:将固相支撑液液萃取与超高效液相色谱串联质谱法结合,建立生乳中32种农药残留的快速检测方法,为保障生乳食品安全提供技术支持。
样品加入乙腈沉淀蛋白,高速离心分离,上清液用固相支撑液液萃取小柱净化,C 18色谱柱梯度洗脱分离后,经串联质谱电喷雾模式扫描,多反应监测模式检测,以基质匹配校准曲线外标法定量。
结果表明,32种目标物在一定范围内线性关系良好,相关系数大于0.9962,检出限为0.1~2.5 μg/kg ,定量限为0.3~7.5 μg/kg ,平均回收率为69.4%~113.8%,相对标准偏差(n=6)小于8.2%。
该方法简单、快速、可靠,适用于生乳中32种农药残留的测定。
年会互动 80题

年会互动 80题1. 2024年泰瑞沙晚期一线适应症的3S获益指的是哪3个S? *SIBOS(正确答案)RWS(正确答案)CNS(正确答案)2. 关于FLAURA序贯多重检验的描述正确的是? [单选题] *PFS→ORR→OSPFS→CNS PFS→OSPFS→OS→CNS PFS(正确答案)PFS→OS→基线合并脑转移患者的PFS3. 关于泰瑞沙晚期市场策略,以下表述正确的有 *从全国层面来看,一二代EGFR-TKI的竞品区隔已经不是一线主要份额来源新兴市场呼吸科的靶向诊疗观念仍有提升空间(正确答案)从过程管理角度,泰瑞沙晚期2024年重点关注肿瘤和呼吸科AB类客户扩面,以及贡献EM市场80%医院的扩面(正确答案)泰瑞沙晚期一线3S获益,既可以用于区隔国产三代竞品,也可以用于区隔一二代TKI(正确答案)4. 泰瑞沙晚期的重点市场活动包括 *完美战役-泰峰会系列(正确答案)完美战役-上下联动系列、肺跃全线系列(正确答案)一呼百应-介入学院/肺癌学院(正确答案)BEST OS系列城市会/院内会(正确答案)5. 在基线伴脑转移的SCLC患者中,英飞凡显示出较好的OS获益趋势 [单选题] * mOS: 11.7 vs 8.8(正确答案)mOS: 12.9 vs 10.4mOS: 11.5 vs 8.6mOS: 12 vs 96. 2024年SCLC优势病人 *脑转移(正确答案)高龄(正确答案)高质生活(正确答案)肝转移7. 英飞凡显著改善患者总生存,是目前唯一*将3年总生存率提升3倍以上的免疫检查点抑制剂 [单选题] *3-Yos 17.8% vs 5.6%)3-Yos 16.2% vs 4.8%)3-Yos 17.6% vs 5.8%)(正确答案)3-Yos 18.8% vs 5.8%)8. 度伐利尤单抗具有良好的的长期安全性与耐受性,免疫介导不良反应发生率低,3年随访SAE [单选题] *35.5% vs 37.5%)32.5% vs 36.5%)(正确答案)38.5% vs 38.5%)43.% vs 48%)9. 建立沃瑞沙治疗MET Exon14 NSCLC标准治疗地位,主要有哪些驱动力? * MET富集(正确答案)品牌引领(正确答案)扩大覆盖(正确答案)10. 2024扩大覆盖策略从以下哪些方面落地? *加速准入(正确答案)增加尝试者(正确答案)增加使用者(正确答案)增加倡导者11. 2023年沃瑞沙在化疗进展或不耐受MET-TKI中的市场份额(不包括克唑替尼)占比(),2024年目标占比达到() [单选题] *67%,80%53%,67%67%,84%(正确答案)53%,84%12. 2024年沃瑞沙的关键信息有哪些? *沃瑞沙®是首个获批的且纳入医保的特异性MET抑制剂(正确答案)沃瑞沙®快速起效,长久生存,各人群均实现OS获益(正确答案)沃瑞沙®口服便利,一日一次,安全性良好(正确答案)13. 泰瑞沙早期市场策略 *提升早期术后EGFR检测观念(正确答案)提高EGFR检测阳性率强化TKI辅助观念,推动辅助SoC(正确答案)强化泰瑞沙ADAURA优势,区隔竞品(正确答案)14. 对于完全切除术后EGFR敏感突变阳性的IB-IIIA期NSCLC患者的“3S获益“是指 *OS获益(正确答案)DFS获益(正确答案)SIB获益(正确答案)Safety获益15. 泰瑞沙早期关键战役包括 *术立典范(正确答案)A+2000(正确答案)完美战役一呼百应16. ADAURA关键信息包括 *泰瑞沙已参加3次国谈,是目前唯一**辅助治疗纳入医保目录的3G EGFR-TKI(正确答案)泰瑞沙是目前唯一能为IB-IIIA期EGFR敏感突变阳性NSCLC患者带来显著OS获益的EGFR-TKI,为患者带来治愈的希望(正确答案)泰瑞沙辅助治疗可带来压倒性DFS获益,中位DFS近5.5年,降低早期复发风险(正确答案)泰瑞沙是目前唯一适应症覆盖IB期患者,能给IB期患者带来DFS&OS双获益的EGFR-TKI(正确答案)17. 2024年英飞凡III期不可切除NSCLC市场策略是? *规范III期不可切诊疗路径,提高PACIFIC模式使用率(正确答案)提升英飞凡品牌份额(正确答案)提高USIII患者治疗率提高USIII患者5年生存率18. 2024年英飞凡III不可切除市场策略关注的比例有? *SIII%PACIFIC%(正确答案)IMFINZI%(正确答案)化疗%19. 2024英飞凡III期不可关键信息中包含以下哪些内容? *PACIFIC方案是USIII治疗金标准(正确答案)英飞凡是唯一*取得OS确证获益的免疫检查点抑制剂(正确答案)III期不等于IV期放化疗是基石20. 2024年英飞凡III期不可切除NSCLC关键信息是? *III期不等于IV期,具备临床治愈希望,放化疗是III期不可切NSCLC的基石PACIFIC方案降低45%的疾病进展风险英飞凡是目前唯一*在不可切除III期NSCLC中取得OS确证获益的免疫治疗药物,其显著(95% CI)延长中位OS至47.5个月,将5年生存率提高至43%,开启III期治愈新时代(正确答案)英飞凡PACIFIC方案是目前不可切除III期NSCLC标准治疗方案,并获得NCCN、CSCO等国内外指南一致推荐(最高级别)(正确答案)21. 如果遇到针对FLAURA研究中位PFS的挑战,以下哪一个回应策略对于品牌区隔是最有力的? [单选题] *不同的研究没有可比性FLAURA研究患者基线更重,所以在PFS数值上较低FLAURA研究的中国真实世界研究数据显示,中位PFS可达23.46个月强调唯一的OS获益,而不是PFS获益(正确答案)22. 以下哪些数据能说明奥希替尼组在一线治疗中的优势? *3 年时,仍在接受一线治疗的患者比例是吉非替尼或厄洛替尼组的 3 倍(正确答案) 1 年、 2 年和 3 年的 OS 率分别为89%、74%和54%(正确答案)1 年时、2 年时和3 年时,仍在接受一线治疗的患者比例分别为70%、42%和28%(正确答案)奥希替尼组的 3 年 OS 率仍超过 50%(正确答案)23. 2024年泰瑞沙晚期一线适应症的3S获益指的是哪3个S? *SIBOS(正确答案)RWS(正确答案)CNS(正确答案)24. 以下关于FLAURA研究的表述,不正确的有: *PFS和OS都是主要研究终点,因此OS的结果有统计学意义泰瑞沙是晚期一线NSCLC治疗唯一有显著OS获益的EGFR-TKI(正确答案)实验组的CNS CR (cFAS集)高达41%(正确答案)CNS PFS HR为0.48,但因为不是主要研究重点,所以没有统计学意义25. 对于三代EGFR-TKI二线治疗的mOS,以下表述正确的有 *AURA3研究的亚裔人群mOS达到30.2m(正确答案)相对于近年获批的三代EGFR-TKI,AURA3研究入组时间早,后续治疗方案少(化疗为主)(正确答案)AURA3对照组后续治疗以交叉至奥希替尼为主,高交叉率也可能影响了OS对比结果(正确答案)阿美替尼APOLLO研究的最新mOS为30.2个月,与AURA系列研究的循证等级及临床意义不相上下26. FLAURA与AURA3研究共同的特点是 *都允许纳入脑转移的患者(正确答案)2:1随机分层入组都是Ⅲ期注册临床研究(正确答案)都允许疾病进展后的交叉用药(正确答案)27. 针对国产三代友商产品传递其一线研究的PFS和泰瑞沙相比一致或更长,以下回应不妥当的有: [单选题] *泰瑞沙是目前晚期一线唯一有显著OS获益的EGFR-TKI,中位OS超过3年虽然阿美和伏美2024年大概率可能公布统计学显著的OS获益结果,但至少目前还没有(正确答案)评估活得更长的金标准是OS阿美和伏美的OS是不能下统计学结论的28. 关于国产三代友商产品传递所谓的“双重入脑”并藉此希望医生推荐患者一线尝试使用,以下回应不妥当的有: [单选题] *目前泰瑞沙的CR率最高,无论是cFAS集还是cEFR集泰瑞沙是目前晚期一线治疗唯一有显著CNS PFS获益的EGFR-TKIFLAURA研究 cFAS集中,泰瑞沙的CNS CR率可达41%放弃对脑转移人群的关注,毕竟脑转移在晚期一线患者中占比有限(正确答案)29. 以下关于FLAURA研究设计描述正确的是? [单选题] *FLAURA研究共纳入556例患者并按1:2随机分配FLAURA研究的主要研究终点是研究者评估的PFS(正确答案)FALURA研究按照按DFS→OS→CNS PFS的顺序进行检验FLAURA研究入为了更好控制II类错误(α=0.05),使用了序贯检验策略30. 关于FLAURA序贯多重检验的描述正确的是? [单选题] *PFS→ORR→OSPFS→CNS PFS→OSPFS→OS→CNS PFS(正确答案)PFS→OS→基线合并脑转移患者的PFS31. 泰瑞沙晚期市场策略中对于2024年过程KPI的关键词是什么 [单选题] *卷竞品扩医院·扩客户(正确答案)守份额推联合32. 泰瑞沙晚期市场的策略重点科室是 *胸外科肿瘤科(正确答案)呼吸科(正确答案)老年科33. 关于泰瑞沙晚期市场策略,以下表述错误的有 *EGFR检测率已经达到瓶颈,没有提升空间(正确答案)新兴市场呼吸科的靶向诊疗观念仍有提升空间从全国层面来看,一二代EGFR-TKI的竞品区隔已经不是一线主要份额来源(正确答案)泰瑞沙晚期一线3S获益,既可以用于区隔国产三代竞品,也可以用于区隔一二代TKI34. 泰瑞沙晚期的重点市场活动包括 *完美战役-泰峰会系列(正确答案)完美战役-上下联动系列、肺跃全线系列(正确答案)一呼百应-介入学院/肺癌学院(正确答案)BEST OS系列城市会/院内会(正确答案)35. 关于泰瑞沙晚期市场的过程和结果KPI,以下表述正确的有 *新兴市场全年同比销量增速达到35%(正确答案)2024Q2,泰瑞沙在晚期一线EGFR敏感突变人群中的的目标份额是45%(来源:PRISM调研)(正确答案)只有呼吸科需要关注AB类客户扩面的问题,肿瘤科不需要关注PRISM调研HCP关键信息自发回忆率的方法是,调研者给到HCP几个选项,请HCP从中选出该适应症的关键信息36. 2024年英飞凡III期不可切除NSCLC市场策略是? *规范III期不可切诊疗路径,提高PACIFIC模式使用率(正确答案)提升英飞凡品牌份额(正确答案)提高USIII患者治疗率提高USIII患者5年生存率37. 2024年英飞凡III不可切除市场策略关注的比例有? *SIII%PACIFIC%(正确答案)IMFINZI%(正确答案)化疗%38. 以下关于三期非小细胞肺癌的患者放化疗后的巩固治疗,描述正确的是? *根治性放化疗后选择不巩固治疗,远处复发转移是最大的风险,PFS和OS获益有限(正确答案)绝大多数患者在根治性放化疗后是PR或SD(CR患者比例极少)(正确答案)III期研究显示巩固化疗并未改善患者的PFS和OS,反而增加患者的毒性,因此巩固化疗不是标准治疗(正确答案)III期不等于IV期,具备临床治愈希望,放化疗是III期不可切NSCLC的基石(正确答案)39. 以下对PACIFIC研究描述正确的是? *与对照组比较,PACIFIC研究的中位PFS获益提升至3倍,近1/3患者肿瘤5年内无复发和进展(正确答案)与对照组比较,PACIFIC研中位TTDM延长近30个月,远处转移风险减低41%(正确答案)与对照组比较,PACIFIC研究可减少新病灶发生率(正确答案)PACIFIC研究5年OS率42.9%,近半患者实现”临床治愈“(正确答案)40. PACIFIC研究曾携英飞凡几度登陆新英格兰? *0次1次2次(正确答案)3次41. 针对III期不可切的NSCLC,放化疗后巩固治疗使用以下哪个免疫药物有唯一OS明确获益? [单选题] *帕博利珠单抗舒格利单抗度伐利尤单抗(正确答案)纳武利尤单抗42. 2024英飞凡III期不可关键信息中包含以下哪些内容? *PACIFIC方案是USIII治疗金标准(正确答案)英飞凡是唯一*取得OS确证获益的免疫检查点抑制剂(正确答案)III期不等于IV期放化疗是基石43. 2024年英飞凡III期不可切除NSCLC关键信息是? *III期不等于IV期,具备临床治愈希望,放化疗是III期不可切NSCLC的基石PACIFIC方案中位PFS达16.9个月,3倍获益,降低45%的疾病进展风险英飞凡是目前唯一*在不可切除III期NSCLC中取得OS确证获益的免疫治疗药物,其显著(95% CI)延长中位OS至47.5个月,将5年生存率提高至43%,开启III期治愈新时代(正确答案)英飞凡PACIFIC方案是目前不可切除III期NSCLC标准治疗方案,并获得NCCN、CSCO等国内外指南一致推荐(最高级别)(正确答案)44. durvalumab被哪些指南推荐用于III期不可切除NSCLC巩固免疫治疗? * CSCO(正确答案)CACA(正确答案)CMA(正确答案)NCCN(正确答案)45. 关于durvalumab以下描述正确的是? *durvalumab是NCCN指南唯一推荐的用于III期不可切除NSCLC的免疫治疗药物(正确答案)durvalumab是国内CSCO指南 I 级(最高级别)推荐的用于III期不可切除NSCLC 的免疫治疗药物(正确答案)durvalumab是国内CMA指南 I 类(最高级别)推荐的用于同步放化疗后未进展的III期不可切的巩固治疗药物(正确答案)durvalumab是国内CACA指南推荐用于III期不可切除同步放化疗后巩固治疗药物(正确答案)46. 肺的哪一侧叶数比较多? *左肺右肺(正确答案)两侧一样多无法确定47. OS总生存期的定义 *从随机化至治疗失败或退出试验的时间从随机化到任何因素导致患者死亡的时间(正确答案)从随机化至出现肿瘤客观进展的时间(不包括死亡)从随机化至出现肿瘤客观进展或全因死亡的时间48. 一代TKIs辅助治疗中常见的AE为 *皮疹(正确答案)腹泻(正确答案)呼吸系统疾病肝酶升高(正确答案)49. 以下对于奥希替尼辅助治疗说法正确的是 *ADAURA 研究证实无论既往是否接受过辅助化疗,奥希替尼辅助治疗 DFS 均显著获益(正确答案)ADAURA 研究纳入了 IB 患者,并证实 IB 期患者能从奥希替尼治疗中获益(正确答案)ADAURA 研究安全性良好,未影响患者的生活质量(正确答案)奥希替尼辅助治疗有效控制局部/远处复发,且CNS DFS 显著获益(正确答案) 50. ADAURA研究设计有哪些特点 *纳入ⅠB期患者,填补ⅠB期EGFR-TKI辅助研究空白(正确答案)由研究者决定辅助/不辅助化疗,更符合中国临床时间(正确答案)研究对比化疗,且取得阳性结果辅助时长3年,使更多患者渡过术后脑转移转移高峰期(正确答案)51. 对于奥希替尼突破脑部复发治疗局限,以下说法正确的是 *奥希替尼可穿透正常成年人的血脑屏障(正确答案)对伴有CNS转移的患者治疗疗效显著(正确答案)较一代TKI可显著降低CNS进展风险(正确答案)较一代TKI更易于穿透血脑屏障(正确答案)52. 2023年ASCO上公布了ADAURA的OS结果,针对完全切除术后NSCLC患者,描述正确的是 *II-IIIA期患者HR0.49(正确答案)IB期患者HR0.44(正确答案)II期患者HR0.63(正确答案)IIIA期患者HR0.3853. ADAURA研究中ⅢA期患者OS HR是多少 [单选题] *0.230.270.37(正确答案)0.4654. 关于EVAN研究,以下说法正确的是 *OS有获益且为主要研究终点之一2年DFS为主要研究终点(正确答案)α=0.2,允许20%假阳性(正确答案)mDFS仅为探索性研究结果(正确答案)55. 一代TKIs的治疗模式局限,其主要局限原因是 *一代TKI适应症局限(正确答案)一代没有化疗序贯证据(正确答案)一代TKIs对照化疗有显著获益一代的中位DFS仅三年左右(正确答案)56. 泰瑞沙早期关键战役包括 *完美战役一呼百应术立典范(正确答案)A+2000(正确答案)57. 泰瑞沙早期市场策略 *提升早期术后EGFR检测观念(正确答案)强化TKI辅助观念,推动辅助SoC(正确答案)提高EGFR检测阳性率强化泰瑞沙ADAURA优势,区隔竞品(正确答案)58. 早期市场活动包括以下哪些? *内外兼修(正确答案)手术大赛(正确答案)中外交流(正确答案)质控(正确答案)59. 对于完全切除术后EGFR敏感突变阳性的IB-IIIA期NSCLC患者的“3S获益“是指 *OS获益(正确答案)DFS获益(正确答案)Safety获益SIB获益(正确答案)60. ADAURA关键信息包括 *泰瑞沙已参加3次国谈,是目前唯一**辅助治疗纳入医保目录的3G EGFR-TKI(正确答案)泰瑞沙是目前唯一能为IB-IIIA期EGFR敏感突变阳性NSCLC患者带来显著OS获益的EGFR-TKI,为患者带来治愈的希望(正确答案)泰瑞沙辅助治疗可带来压倒性DFS获益,中位DFS近5.5年,降低早期复发风险(正确答案)泰瑞沙是目前唯一适应症覆盖IB期患者,能给IB期患者带来DFS&OS双获益的EGFR-TKI(正确答案)61. 建立沃瑞沙治疗MET Exon14 NSCLC标准治疗地位,主要有哪些驱动力? * MET富集(正确答案)品牌引领(正确答案)扩大覆盖(正确答案)加速准入62. 目前赛沃替尼在MET-TKI市场份额占比(),2024年目标占比() [单选题] * 67%,80%53%,67%67%,84%(正确答案)53%,84%63. 2024年MET 14外显子跳变检测率目标为: [单选题] *70%80%85%(正确答案)90%64. 对MET 14外显子跳变患者的治疗,赛沃替尼相比谷美替尼,其优势在于? * 1L mPFS更长,13.8vs11.7(正确答案)无头痛AE的发生(正确答案)脑转移患者成熟的OS数据(正确答案)65. 对MET 14外显子跳变患者的治疗,赛沃替尼相比伯瑞替尼,其优势在于? *疗效稳健(正确答案)脑转移患者成熟OS数据(正确答案)无特殊AE的发生66. 在2023 WCLC大会上,公布了赛沃替尼IIIb期1L治疗MET 14外显子跳变的数据,其中PFS为? *11.7m12.9m13.8m(正确答案)15m67. 2024年MET富集策略的关键信息有哪些? *沃瑞沙®️作为首个获批的且纳入医保的特异性MET抑制剂(正确答案)疗效确切,长久生存,被CSCO指南Ⅰ级推荐(正确答案)国内外指南/共识一致推荐晚期NSCLC进行MET外显子14跳变基因检测(正确答案)沃瑞沙®口服便利,一日一次,安全性良好68. 2024年品牌引领策略的关键信息有哪些? *沃瑞沙®是首个获批的且纳入医保的特异性MET抑制剂(正确答案)沃瑞沙®快速起效,长久生存,被CSCO指南Ⅰ级推荐(正确答案)沃瑞沙®口服便利,一日一次,安全性良好(正确答案)69. 2024年扩大覆盖策略的关键信息有哪些? *沃瑞沙®是首个获批的本土原研且纳入医保的特异性MET抑制剂,患者自付费用节省超8成(正确答案)沃瑞沙®快速起效,长久生存,被CSCO指南Ⅰ级推荐(正确答案)沃瑞沙®口服便利,一日一次,安全性良好70. 自2021年6月赛沃替尼获批上市后,受到国内哪些权威指南的一致推荐? * 2022/2023版 CSCO非小细胞肺癌指南(正确答案)2022版中华医学会指南(正确答案)2022中国肿瘤整合诊治指南非小细胞肺癌(正确答案)2022版中国卫健委原发性肺癌诊疗规范(正确答案)71. 2024年SCLC策略驱动 *聚焦CASPIAN优势人群(正确答案)提升免疫治疗率累积小肺真实世界经验(正确答案)区隔稳核心72. 广泛期SCLC有脑转移获益趋势的免疫抑制剂有 *阿得贝利单抗阿替利珠单抗度伐利尤单抗(正确答案)斯鲁利单抗(正确答案)73. 在基线伴脑转移的SCLC患者中,英飞凡显示出较好的OS获益趋势 [单选题] * mOS: 11.7 vs 8.8(正确答案)mOS: 12.9 vs 10.4mOS: 11.5 vs 8.6mOS: 12 vs 974. 2024年SCLC品牌组关键项目 *英有尽有(正确答案)星火燎原后浪计划(正确答案)一呼百应75. 2024年SCLC优势病人 *脑转移(正确答案)高龄(正确答案)高质生活(正确答案)肝转移76. 2024年LS-SCLC报阳的研究是 [单选题] *DURABLELEADTRIDENTADRIATIC(正确答案)77. 英飞凡显著改善患者总生存,是目前唯一*将3年总生存率提升3倍以上的免疫检查点抑制剂 [单选题] *3-Yos 17.8% vs 5.6%)3-Yos 16.2% vs 4.8%)3-Yos 17.6% vs 5.8%)(正确答案)3-Yos 18.8% vs 5.8%)78. 度伐利尤单抗具有良好的的长期安全性与耐受性,免疫介导不良反应发生率低,3年随访SAE [单选题] *35.5% vs 37.5%)32.5% vs 36.5%)(正确答案)38.5% vs 38.5%)43.% vs 48%)79. 2024年策略驱动聚焦CASPIAN优势人群对应项目 [单选题] *英有尽有星火燎原后浪计划(正确答案)一呼百应80. 2024年Q1呼吸肿瘤AB客户覆盖目标 *40%(正确答案)30%20%60%。
logistic回归模型的分类评估及r语言实现 -回复

logistic回归模型的分类评估及r语言实现-回复logistic回归模型的分类评估及R语言实现引言在机器学习中,logistic回归是一种常用的分类算法。
该算法用于预测二分类问题的概率,能够根据自变量的线性组合估计出目标类别的概率。
本文将介绍logistic回归模型的评估指标,并使用R语言实现相关代码。
一、分类评估指标1. 准确率(Accuracy)准确率是最常见的分类模型评估指标之一。
它表示分类器正确分类的样本数量占总样本数量的比例。
计算公式如下:准确率= (TP + TN) / (TP + TN + FP + FN)其中,TP(True Positive)表示真正例的数量,即阳性样本分类正确的数量;TN(True Negative)表示真反例的数量,即阴性样本分类正确的数量;FP(False Positive)表示假正例的数量,即阴性样本被错误地分类为阳性的数量;FN(False Negative)表示假反例的数量,即阳性样本被错误地分类为阴性的数量。
2. 精确率(Precision)精确率表示分类器将正例(阳性样本)正确分类的能力。
计算公式如下:精确率= TP / (TP + FP)精确率越高,表示分类器将阳性样本误判为阴性样本的概率较低。
3. 召回率(Recall)召回率表示分类器对阳性样本的识别能力,即将阴性样本误判为阳性样本的概率较低。
计算公式如下:召回率= TP / (TP + FN)召回率越高,表示分类器对阳性样本的识别能力越强。
4. F1分数(F1 Score)F1分数是精确率和召回率的调和平均值,综合了两者的性能。
计算公式如下:F1分数= 2 * (精确率* 召回率) / (精确率+ 召回率)F1分数越高,表示分类器的综合性能越好。
5. ROC曲线与AUCROC曲线(Receiver Operating Characteristic Curve)是以假阳性率(False Positive Rate)为横坐标,真阳性率(True Positive Rate)为纵坐标的曲线。
浅谈家用杀虫剂中有机氯含量检测方法

浅谈家用杀虫剂中有机氯含量检测方法1 概述而氯化乙酰苯胺类及有机氯杀虫剂在文献中曾使用过的前处理法包括固相萃取法(Solid Phase Extraction,SPE)、固相微萃取法(Solid Phase Microextraction,SPME)、微辅助萃取法(Microwave-Assisted Extraction,MAE)、液-液萃取法(Liquid–Liquid Extraction,LLE)等方法。
2 萃取法2.1 液-液萃取法(Liquid-Liquid Extraction,LLE)液-液萃取法是一种广泛使用的样品前处理方式,是将水样置于分液漏斗中再加入有机萃取溶剂,摇晃一段时间之后便可取出分层萃取液,是一种操作简易的萃取方法。
其原理是源自于Nernst所提出的分配理论(partition theory),主要是在固定的温度下,待测的物质于两不互溶的溶剂中依分配系数的不同来完成萃取。
其浓度比值为分配系数K(distribution coefficient):液-液萃取法的优点在于适用的范围广,对于基质复杂的样品皆适用,但缺点是在不互溶的两相间容易发生乳化现象,容易造成待测物的流失,且萃取过程需使用大量的有机溶剂,容易造成环境污染。
2.2 固相萃取法(Solid-Phase Extraction,SPE)固相萃取法是利用固相萃取管柱内填充具吸附能力的正相(normal phase)或逆相(reverse phase)吸附剂当作静相,例如C8、C18、PSDVB、GCBs等不同物化性物质。
上述这些吸附物与分析物经由分配原理,利用静相吸附分析物,再用适当的溶剂将分析物冲提出来,结合气相层析仪或液相层析仪等仪器进行分析。
2.3 固相微萃取法(Solid Phse Microextraction,SPME)固相微萃取法是由Pawliszyn教授实验室在1990年所设计,并于1993年由Supelco公司推出商业化的产品。
Method and Device for Transporting and Processing
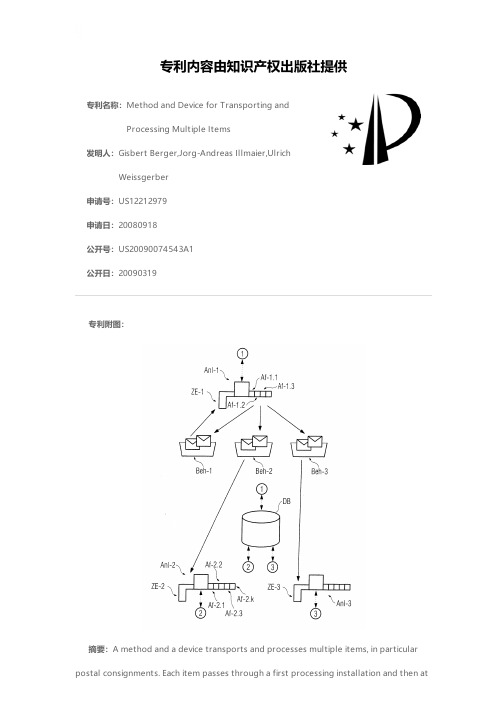
专利名称:Method and Device for Transporting andProcessing Multiple Items发明人:Gisbert Berger,Jorg-Andreas Illmaier,UlrichWeissgerber申请号:US12212979申请日:20080918公开号:US20090074543A1公开日:20090319专利内容由知识产权出版社提供专利附图:摘要:A method and a device transports and processes multiple items, in particular postal consignments. Each item passes through a first processing installation and then atleast one second processing installation. The first processing installation measures in each case a processing attribute and two values which two predefined features assume for the item, and generates a data record for the item. Data records for items that the second processing installation subjects to a predefined treatment are selected. The second processing installation measures at a first time point the value which the first feature assumes and later the value of the other feature. It searches for a selected data record and uses the feature value measured initially. When it finds such a data record, it subjects the item concerned to the predefined treatment.申请人:Gisbert Berger,Jorg-Andreas Illmaier,Ulrich Weissgerber地址:Berlin DE,Kreuzlingen CH,Konstanz DE国籍:DE,CH,DE更多信息请下载全文后查看。
多元有序logistic回归模型 条件 李克特五级量表

多元有序logistic回归模型条件李克特五级量
表
多元有序logistic回归模型是一种用于处理有序分类变量的统计模型,常用于分析李克特五级量表等有序测量数据。
以下是对这两个概念的简要解释:
1. 李克特五级量表(Likert Scale):李克特五级量表是一种常用的调查问卷测量工具,用于评估受访者对于某个观点或陈述的态度或意见。
它通常由五个等距离散的选项组成,例如“非常同意”、“同意”、“中立”、“不同意”、“非常不同意”,受访者选择其中一个选项来表达自己的态度。
2. 多元有序logistic回归模型:多元有序logistic回归模型是一种广义线性模型(Generalized Linear Model,GLM)的扩展,用于分析有序分类因变量和一个或多个自变量之间的关系。
它基于logistic函数,可以估计不同自变量对于有序分类变量的影响。
该模型考虑了有序分类变量的顺序性和概率分布,并通过最大似然估计进行参数估计。
使用多元有序logistic回归模型可以分析李克特五级量表等有序测量数据,了解自变量对于不同态度或意见的影响程度,并进行统计推断和预测。
在实际应用中,可以使用统计软件(如R、Python 等)来拟合多元有序logistic回归模型,并对结果进行解释和推断。
无序多元logistic回归方程

无序多元logistic回归方程
有序多分类logistic回归模型
因变量为水平数大于2的有序多分类的资料,对这种资料可通过拟合因变量水平数n-1个logistic回归模型,称为累计logistic模型。
实质是依次将因变量按不同的取值水平分割成两个等级,对这两个等级建立因变量为二分类的logistic 回归模型,但模型中的各自变量系数\beta_{i} 都保持不变,只改变常数项(前提条件,需要验证)。
以4个水平的因变量为例,其对应的概率为P_{i} ,对n 个自变量拟合3个模型(拟合累加模型),因变量有序取值水平的累计概率:logit\frac{P_{1}}{1-P_{1}}=logit\frac{P_{1}}{P_{2}+P_{3}+P_{4}}=-\alpha_{1} +\beta_{1} x_{1}+...+\beta_{n} x_{n}
logit\frac{P_{1}+P_{2}}{1-
(P_{1}+P_{2})}=logit\frac{P_{1}+P_{2}}{P_{3}+P_{4}}=-\alpha_{2} +\beta_{1} x_{1}+...+\beta_{n} x_{n}2 logit\frac{P_{1} }{1-P_{1}-P_{2}-P_{3}}=logit\frac{P_{1}+P_{2}+P_{3}}{ P_{4}}=-\alpha_{3} +\beta_{1} x_{1}+...+\beta_{n} x_{n}
此时的OR值是自变量每改变一个单位,因变量提高一个及一个以上等级的比数比。
老年共病患者服药依从性及其影响因素研究

·论著·慢性病共病专题研究·扫描二维码【摘要】 背景 随着老龄化程度的加剧,慢性病共病患者在老年群体中出现的比例越来越高,慢性病共病患者能否严格遵医嘱服药影响着共病管理的效果。
目的 调查广东省老年共病患者服药依从性,并分析其影响因素,为老年共病患者的共病管理提供依据。
方法 2022年10月—2023年3月,采取多阶段分层整群随机抽样方法从广东省27个社区抽取998例60岁及以上共病患者进行调查。
利用社区全科门诊、居民集中座谈的形式对共病患者进行面对面的询问方式完成匿名问卷调查。
以服药依从性为因变量,以患者性别、年龄、婚姻状况、居住状况、文化程度、个人年收入、家人督促服药、家庭医生帮助、患病数量、病情了解度、药物关注度、BMI、吸烟、饮酒作为自变量,采用多因素Logistic回归模型分析广东省老年共病患者服药依从性的影响因素。
结果 本次调查共发放1 000份问卷,回收有效问卷998份,有效回收率为99.8%。
在998例广东省老年共病患者中,服药依从性好719例(72.0%),服药依从性差279例(28.0%);男性512例(51.3%),女性486例(48.7%)。
多因素Logistic回归分析结果显示:文化程度(高中/中专:OR=0.298,95%CI=0.117~0.762;大专及以上:OR=0.325,95%CI=0.127~0.831)、个人年收入(>3万~5万元:OR=7.694,95%CI=2.071~28.582;>5万~10万元:OR=12.408,95%CI=3.229~47.686;>10万~20万元:OR=4.893,95%CI=1.174~20.397)、家人督促服药频率(偶尔:OR=1.842,95%CI=1.222~2.779)、家庭医生帮助(略有帮助:OR=2.537,95%CI=1.531~4.205)、病情了解度(大部分了解:OR=3.015,95%CI=1.948~4.667;比较了解:OR=3.510,95%CI=1.955~6.300;了解一些/不了解:OR=3.469,95%CI=1.338~8.994)、药物关注度(大部分关注:OR=4.928,95%CI=3.336~7.278;比较关注:OR=3.670,95%CI=1.915~7.033;关注一些/不关注:OR=8.560,95%CI=2.497~29.339)、BMI(过低:OR=2.303,95%CI=1.154~4.598;超重/肥胖:OR=0.598,95%CI=0.390~0.915)、饮酒(OR=1.959,95%CI=1.270~3.022)是广东省老年共病患者服药依从性的影响因素(P<0.05)。
gradientboostingregressor原理

gradientboostingregressor原理Gradient Boosting Regressor是一种机器学习算法,属于集成学习方法中的增强学习(Boosting)算法。
本文将详细介绍Gradient Boosting Regressor的原理,从基本概念出发,一步一步回答关于这一算法的问题。
1. 什么是Gradient Boosting Regressor?Gradient Boosting Regressor是一种用于回归问题的机器学习算法。
它是以决策树为基分类器的增强学习算法。
该算法通过迭代地训练一系列决策树,每棵树都尝试纠正前一棵树的预测结果,最终获得更准确的预测模型。
2. Gradient Boosting Regressor的基本原理是什么?Gradient Boosting Regressor的基本原理是通过梯度下降法来最小化损失函数。
当损失函数对于当前模型的预测结果的梯度(gradient)为零时,说明当前模型的预测结果已经达到最佳,此时算法停止迭代。
算法的目标是找到使损失函数达到最小的预测模型。
3. Gradient Boosting Regressor的训练过程是怎样的?Gradient Boosting Regressor的训练过程分为多个阶段,每个阶段都训练一棵决策树。
首先,初始化模型为一个常数值,通常是训练集样本目标值的平均值。
然后,依次迭代每个阶段,每个阶段都要计算残差(target值与当前模型预测值之差),并将残差作为下一棵决策树的训练目标。
4. 每棵决策树如何拟合数据?每棵决策树的拟合过程可以看做是一个回归问题。
目标是寻找一个函数,能够最小化残差的平方和。
通常使用最小二乘法或最小平方残差法,通过选择每个决策树的分裂节点和划分规则,来最小化残差。
5. Gradient Boosting Regressor中如何纠正前一棵树的预测结果?在每个阶段,当前训练的决策树需要尝试纠正前一棵树的预测结果。
logistic回归 逐步法

logistic回归逐步法摘要:1.引言2.Logistic 回归的概念和原理3.逐步法的概念和原理4.Logistic 回归与逐步法的关系5.Logistic 回归在实际应用中的案例6.结论正文:1.引言Logistic 回归是一种用于分类问题的统计分析方法,其应用广泛,包括了生物学、社会科学、医疗健康等领域。
在解决实际问题时,我们通常需要通过建立模型来分析和预测数据,这就需要选择合适的变量。
而逐步法作为一种逐步筛选变量的方法,可以帮助我们找到影响分类结果的关键变量。
本文将从Logistic 回归和逐步法的概念、原理以及在实际应用中的关系进行探讨。
2.Logistic 回归的概念和原理Logistic 回归是一种用于解决分类问题的线性模型,其基本原理是利用sigmoid 函数将线性模型的输出映射到0 到1 之间,表示为某一类的概率。
Logistic 回归模型主要包括两个部分:一部分是线性部分,另一部分是sigmoid 函数部分。
其数学表达式为:P(Y=1|X=x) = 1 / (1 + e^(-z)),其中,z = β0 + β1x1 + β2x2 +...+ βn*xn。
3.逐步法的概念和原理逐步法是一种逐步筛选变量的方法,其基本思想是在每一步中,通过比较当前模型和去掉一个变量后的模型的预测效果,决定是否保留该变量。
逐步法主要有两种:一种是向前逐步法,也称为加法法;另一种是向后逐步法,也称为减法法。
向前逐步法是从一个没有变量的模型开始,每步加入一个变量,直到不再加入变量为止;向后逐步法则是从一个包含所有变量的模型开始,每步去掉一个变量,直到不再去掉变量为止。
4.Logistic 回归与逐步法的关系在实际应用中,我们通常需要通过建立Logistic 回归模型来分析和预测数据。
而在建立模型时,我们面临的一个重要问题是如何选择变量。
这时,逐步法就派上用场了。
通过逐步法,我们可以筛选出对分类结果影响较大的变量,从而提高模型的预测准确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Lecture5:Overdispersion in logistic regressionClaudia CzadoTU M¨u nchenOverview•Definition of overdispersion•Detection of overdispersion•Modeling of overdispersionOverdispersion in logistic regressionCollett(2003),Chapter6Logistic model:Y i∼bin(n i,p i)independentp i=e x t iβ/(1+e x t iβ)⇒E(Y i)=n i p i V ar(Y i)=n i p i(1−p i)If one assumes that p i is correctly modeled,but the observed variance is larger or smaller than the expected variance from the logistic model given by n i p i(1−p i), one speaks of under or overdispersion.In application one often observes only overdispersion,so we concentrate on modeling overdispersion.How to detect overdispersion?If the logistic model is correct the asymptotic distribution of the residual deviance D∼χ2n−p.Therefore D>n−p=E(χ2n−p)can indicate overdispersion. Warning:D>n−p can also be the result of-missing covariates and/or interaction terms;-negligence of non linear effects;-wrong link function;-existance of large outliers;-binary data or n i small.One has to exclude these reasons through EDA and regression diagnostics.Residual deviance for binary logistic models Collett(2003)shows that the residual deviance for binary logistic models canbe written asD=−2ni=1(ˆp i lnˆp i1−ˆp i+ln(1−ˆp i)),whereˆp i=e x i tˆβ/(1+e x i tˆβ).This is independent of Y i,therefore not useful to assess goodness offit.Need to group data to use residual deviance as goodness offit measure.Reasons for overdispersion Overdispersion can be explained by-variation among the success probabilities or-correlation between the binary responsesBoth reasons are the same,since variation leads to correlation and vice versa. But for interpretative reasons one explanation might be more reasonable than the other.Variation among the success probabilitiesIf groups of experimental units are observed under the same conditions,the success probabilities may vary from group to group.Example:The default probabilities of a group of creditors with same conditions can vary from bank to bank.Reasons for this can be not measured or imprecisely measured covariates that make groups differ with respect to their default probabilities.Correlation among binary responsesLet Y i=n ij=1R ij R ij=1success0otherwiseP(R ij=1)=p i⇒V ar(Y i)=n ij=1V ar(R ij)p i(1−p i)+n ij=1k=jCov(R ij,R ik)=0=n i p i(1−p i)=binomial varianceY i has not a binomial distribution.Examples:-same patient is observed over time-all units are from the same family or litter(cluster effects)Modeling of variability among successprobabilitiesWilliams(1982)Y i=Number of successes in n i trials with random success probability v i, i=1,...,nAssume E(v i)=p i V ar(v i)=φp i(1−p i),φ≥0unknown scale parameter.Note:V ar(v i)=0if p i=0or1v i∈(0,1)is unobserved or latent random variableConditional expectation and variance of Y i:E(Y i|v i)=n i v iV ar(Y i|v i)=n i v i(1−v i)SinceE(Y)=E X(E(Y|X))V ar(Y)=E X(V ar(Y|X))+V ar X(E(Y|X)), the unconditional expectation and variance isE(Y i)=E vi (E(Y i|v i))=E vi(n i v i)=n i p iV ar(Y i)=E vi (n i v i(1−v i))+V ar vi(n i v i)=n i[E vi (v i)−E vi(v2i)]+n2iφp i(1−p i)=n i(p i−φp i(1−p i)−p2i)+n2iφp i(1−p i) =n i p i(1−p i)[1+(n i−1)φ]Remarks-φ=0⇒no overdispersion-φ>0⇒overdispersion if n i>1-n i=1(Bernoulli data)⇒no information aboutφavailable,this model is not usefulModelling of correlation among the binaryresponsesY i=n ij=1R ij,R ij=1success0otherwiseP(R ij=1)=p i⇒E(Y i)=n i p ibut Cor(R ij,R ik)=δk=j⇒Cov(R ij,R ik)=δV ar(R ij)V ar(R ik)=δp i(1−p i)⇒V ar(Y i)=n ij=1V ar(R ij)+n ij=1k=jCov(R ij,R ik)=n i p i(1−p i)+n i(n i−1)[δp i(1−p i)] =n i p i(1−p i)[1+(n i−1)δ]Remarks-δ=0⇒no overdispersion-δ>0⇒overdispersion if n i>1δ<0⇒underdispersion.-Since we need1+(n i−1)δ>0δcannot be too small.For n i→∞⇒δ≥0.-Unconditional mean and variance are the same ifδ≥0for both approaches, therefore we cannot distinguish between both approachesEstimation ofφY i|v i∼bin(n i,v i)E(v i)=p i V ar(v i)=φp i(1−p i)i=1,...,g Special case n i=n∀iV ar(Y i)=np i(1−p i)[1+(n−1)φ]σ2heterogenity factorOne can show thatE(χ2)≈(g−p)[1+(n−1)φ]=(g−p)σ2where p=number of parameters in the largest model to be considered andχ2=gi=1(y i−nˆp i)2nˆp i(1−ˆp i).⇒ˆσ2=χ2g−p⇒ˆφ=ˆσ2−1n−1Estimation ofβremains the sameAnalysis of deviance when variability among the success probabilities are presentmodel df deviance covariates1ν1D1x i1,...,x iν12ν2D2x i1,...,x iν1,x i(ν1+1),...,x iν20ν0D0x i1,...,x iνFor Y i|v i∼bin(n i,v i),i=1,...,g.Since E(χ2)≈σ2(g−p)we expectχ2a∼σ2χ2g−p and D a∼χ2a∼σ2χ2g−p χ2Statistic distribution⇒(D1−D2)/(ν2−ν1)D0/ν0a∼χ2ν2−ν1χ2νa∼Fν2−ν1,ν0→no change to ordinary caseEstimated standard errors in overdispersed modelsse0(ˆβj),se(ˆβj)=ˆσ·wherese0(ˆβj)=estimated standard error in the model without overdispersion This holds since V ar(Y i)=σ2n i p i(1−p i)and in both cases we have EY i=p i.Beta-Binomial models v i=latent success probability∈(0,1)v i∼Beta(a i,b i)f(v i)=1B(a i,b i)v a i−1i(1−v i)b i−1,a i,b i>0densityB(a,b)=1x a−1(1−x)b−1dx−Beta functionE(v i)=a ia i+b i=:p iV ar(v i)=a i b i(a i+b i)2(a i+b i+1)=p i(1−p i)/[a i+b i+1]=p i(1−p i)τiτi:=1a i+b i+1If a i>1,b i>1∀i we have unimodality and V ar(v i)<p i(1−p i)13.Ifτi=τ,the beta binomial model is equivalent to the model with variability among success probabilities withφ=τ<13(⇒more restrictive).(Marginal)likelihoodl(β)=ni=11f(y i|v i)f(v i)dv i=ni=1n iy i1B(a i,b i)v y ii(1−v i)n i−y i v a i−1i(1−v i)b i−1dv iwhere p i=e x t iβ/(1+e x t iβ)p i=a ia i+b i=ni=1n iy iB(y i+a i,n i−y i+b i)B(a i,b i)needs to be maximized to determine MLE ofβ. Remark:no standard software existsRandom effects in logistic regression Let v i=latent success probability with E(v i)=p ilogv i1−v i=x tiβ+δi“random effect”δi measures missing or measured imprecisely covariates.When an intercept is included we can assume E(δi)=0.Further assumeδi i.i.d.with V ar(δi)=σ2δLet Z i i.i.d.with E(Z i)=0and V ar(Z i)=1⇒δi D=γZ i withγ=σ2δ≥0Thereforelogv i1−v i=x tiβ+γZ iRemark:this model can also be used for binary regression dataEstimation in logistic regression with randomeffectsIf Z i∼N(0,1)i.i.d.the joint likelihood forβ,γ,Z i is given byL(β,γ,Z)=ni=1n iy iv y ii(1−v i)n i−y i=ni=1n iy iexp{x t iβ+γZ i}y i[1+exp{x t iβ+γZ i}]n ip+1+n parametersToo many parameters,therefore maximize marginal likelihood L(β,γ):=R nL(β,γ,Z)f(Z)d Z=ni=1n iy i∞−∞exp{x t iβ+γZ i}y i[1+exp{x t iβ+γZ i}]n i1√2πe−12Z2i dZ iThis can only be determined numerically.One approach is to use a Gauss-Hermite approximation given by∞−∞f(u)e−u2du≈mj=1c j f(s j)for known c j and s j(see tables in Abramowitz and Stegun(1972)). m≈20is often sufficient.Remarks for using random effects-no standard software for maximization-one can also use a non normal random effect-extension to several random effects are possible.Maximization over high dim.integrals might require Markov Chain Monte Carlo(MCMC)methods -random effects might be correlated in time or space,when time series or spatial data considered.ReferencesAbramowitz,M.and I. A.Stegun(1972).Handbook of mathematical functions with formulas,graphs,and mathematical tables.10th printing, with corr.John Wiley&Sons.Collett,D.(2003).Modelling binary data(2nd edition).London:Chapman &Hall.Williams,D.(1982).Extra binomial variation in logistic linear models.Applied Statistics31,144–148.。
