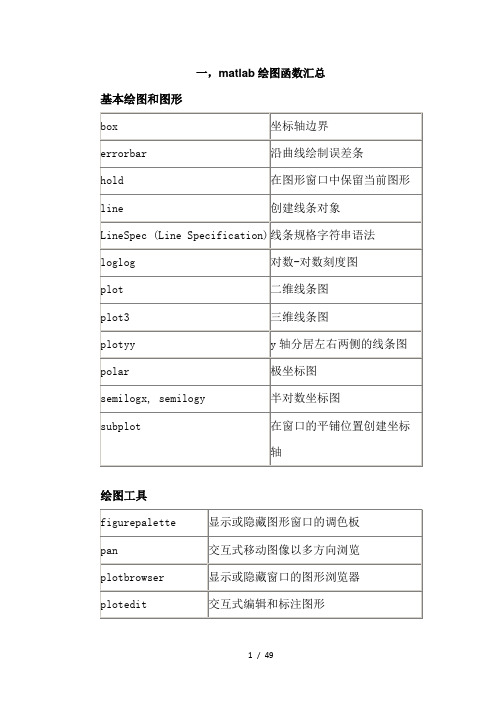
matlab在数学建模中的应用——第一章程序代码
matlab数学建模程序代码

matlab数学建模程序代码【实用版】目录1.MATLAB 数学建模概述2.MATLAB 数学建模程序代码的基本结构3.常用的 MATLAB 数学建模函数和命令4.MATLAB 数学建模程序代码的编写流程5.MATLAB 数学建模程序代码的示例正文一、MATLAB 数学建模概述MATLAB(Matrix Laboratory)是一款强大的数学软件,广泛应用于数学建模、数据分析、可视化等领域。
通过 MATLAB,用户可以方便地进行数学计算、编写程序以及绘制图表等。
在数学建模领域,MATLAB 为研究人员和工程师提供了丰富的工具箱和函数,使得数学模型的构建、求解和分析变得更加简单高效。
二、MATLAB 数学建模程序代码的基本结构MATLAB 数学建模程序代码通常分为以下几个部分:1.导入 MATLAB 库:在建模过程中,可能需要使用 MATLAB 提供的某些库或工具箱,需要在代码开头进行导入。
2.定义变量和参数:在建模过程中,需要定义一些变量和参数,用于表示模型中的各个要素。
3.建立数学模型:根据实际问题,编写相应的数学表达式或方程,构建数学模型。
4.求解模型:通过调用 MATLAB 内置函数或使用自定义函数,对数学模型进行求解。
5.分析结果:对求解结果进行分析,提取所需的信息,例如计算均值、方差等统计量。
6.可视化结果:使用 MATLAB 绘制图表,将结果以直观的形式展示出来。
三、常用的 MATLAB 数学建模函数和命令MATLAB 提供了丰富的数学建模函数和命令,例如:1.线性规划:使用`linprog`函数求解线性规划问题。
2.非线性规划:使用`fmincon`或`fsolve`函数求解非线性规划问题。
3.优化问题:使用`optimize`函数求解优化问题。
4.数据处理:使用`mean`、`std`等函数对数据进行统计分析。
5.图表绘制:使用`plot`、`scatter`等函数绘制各种图表。
Matlab在数学建模中的应用3页word

Matlab在数学建模中的应用一、前言由实验数据建立数学模型,我们通常采用回归分析,在热油管道运行优化软件的开发中,需要根据不同油品的粘温数据,回归出粘温关系数学模型,以计算出不同温度下的油品粘度。
二、热油管道运行优化软件简介1. 功能需求本软件的功能为已知输油管道系统的运行参数,寻求在特定输油任务的前提下,输油费用最小值时的工况组态,并可选择输出各工况组态的运行参数和相应费用。
2. 编程语言及开发环境本软件的功能侧重于数值计算,在寻优过程中需要进行大量的数据处理,为了能够快速得到寻优结果,需要软件具有较高的执行效率,因此本软件编程语言选择C++语言。
C++语言程序生成代码质量高,一般只比汇编程序生成的目标代码效率低10~20%,且具有指针操作功能,能够象汇编语言一样对位、字节和地址进行操作,使程序的算法更加灵活。
本软件采用Visual C++ 6.0作为软件开发环境,这是一种可视化编程工具,界面友好,逻辑清晰,调试方便,界面编制能力很强,开发的软件可以在Windows系列操作系统上良好运行。
3、软件界面本软件运行后,主界面如下图所示三、在VC++中通过调用Matlab实现回归分析1. 在VC++中调用Matlab方法简介Matlab是一种功能非常强大的数学分析软件,它广泛应用于线性代数、自动控制理论、数理统计、动态系统仿真等领域,具有扩展性好、易学易用、方便快捷等优点,但Matlab语言是一种解释性语言,它实时效率差、不可以脱离其环境独立运行,而在VC++中调用Matlab,既能保留Matlab的优良算法,又能保持VC++的高效率性, 能大大缩短本功能模块的开发周期,在VC++中调用Matlab 主要有以下两种方法:(1) 利用Matlab引擎 Matlab引擎采用客户机和服务器的计算方式,在运行中,VC++开发的程序为前端客户机,它向Matlab引擎传递命令和数据信息,并从Matlab引擎中接收数据信息,这种方法调用Matlab 采用较少的代码即可实现,但不能脱离Matlab 运行环境,且运行速度缓慢。
matlab数学建模程序代码

matlab数学建模程序代码
当进行数学建模时,MATLAB是一个强大的工具,用于实现和测试模型。
下面是一个简单的MATLAB代码示例,演示如何使用MATLAB进行一维线性回归建模:
```matlab
%生成示例数据
x=[1,2,3,4,5];
y=[2.8,3.9,4.8,5.5,6.3];
%进行一维线性回归
coefficients=polyfit(x,y,1);
slope=coefficients(1);
intercept=coefficients(2);
%绘制原始数据和回归线
scatter(x,y,'o','DisplayName','原始数据');
hold on;
plot(x,polyval(coefficients,x),'r-','DisplayName','回归线');
hold off;
%添加标签和图例
xlabel('X轴');
ylabel('Y轴');
title('一维线性回归建模示例');
legend('show');
%输出回归方程的系数
fprintf('回归方程:y=%.2fx+%.2f\n',slope,intercept);
```
此代码生成了一些示例数据,然后使用一维线性回归对数据进行建模。
回归方程的系数将被计算,并且原始数据与回归线将在图上显示。
请注意,这只是一个简单的示例,实际上,你可能需要根据你的具体问题修改代码。
Matlab在数学建模中的应用

x=[0:0.01:2*pi] y=abs(1000*sin(4*x))+1 semilogy(x,y); 单对数Y轴绘图命令
1.2特殊坐标图形
• 二、 极坐标图
函数polar(theta,rho)用来绘制极坐标图,theta为 极坐标角度,rho为极坐标半径
4.4 三维图形
• 三、surf函数
• surf用于绘制三维曲面图,各线条之间的补面用颜色 填充。surf函数和mesh函数的调用格式一致。
• 函数格式: surf (x,y,z)
• 其中x,y控制X和Y轴坐标,矩阵z是由x,y求得的曲 面上Z轴坐标。
•【例11】 下列程序绘制三维曲面图形 •x=[0:0.15:2*pi];
• y=sin(x);
• z=cos(x); • plot(x,y,'b');
• hold on;
• plot(x,z,'g'); 弦曲线
%绘制正弦曲线 %设置图形保持状态 %保持正弦曲线同时绘制余
• axis ([0 2*pi -1 1]);
• legend('cos','sin');
• hold off
• 【例5】 为正弦、余弦曲线增加图例
1.1 二维图形
二、 subplot函数 • (一)subplot(m,n,p) • 该命令将当前图形窗口分成m×n个绘图
区,即每行n个,共m行,区号按行优先 编号,且选定第p个区为当前活动区。
【例6】 在一个图形窗口中同时绘制正弦、 余弦、正切、余切曲线
1.1 二维图形
• 一、阶梯图形
• 函数stairs(x,y)可以绘制阶梯图形,如下列程序段:
数学建模算法的matlab代码
二,hamiton回路算法提供一种求解最优哈密尔顿的算法---三边交换调整法,要求在运行jiaohuan3(三交换法)之前,给定邻接矩阵C和节点个数N,结果路径存放于R中。
bianquan.m文件给出了一个参数实例,可在命令窗口中输入bianquan,得到邻接矩阵C和节点个数N以及一个任意给出的路径R,,回车后再输入jiaohuan3,得到了最优解。
由于没有经过大量的实验,又是近似算法,对于网络比较复杂的情况,可以尝试多运行几次jiaohuan3,看是否能到进一步的优化结果。
%%%%%%bianquan.m%%%%%%%N=13;for i=1:Nfor j=1:NC(i,j)=inf;endendfor i=1:NC(i,i)=0;endC(1,2)=6.0;C(1,13)=12.9;C(2,3)=5.9;C(2,4)=10.3;C(3,4)=12.2;C(3,5)=17.6;C(4,13)=8.8;C(4,7)=7.4;C(4,5)=11.5;C(5,2)=17.6;C(5,6)=8.2;C(6,9)=14.9;C(6,7)=20.3;C(7,9)=19.0;C(7,8)=7.3;C(8,9)=8.1;C(8,13)=9.2;C(9,10)=10.3;C(10,11)=7.7;C(11,12)=7.2;C(12,13)=7.9;for i=1:Nfor j=1:Nif C(i,j) < infC(j,i)=C(i,j);endendendfor i=1:NC(i,i)=0;endR=[4 7 6 5 3 2 1 13 12 11 10 9 8];<pre name="code" class="plain">%%%%%%%%jiaohuan3.m%%%%%%%%%%n=0;for I=1:(N-2)for J=(I+1):(N-1)for K=(J+1):Nn=n+1;Z(n,:)=[I J K];endendendR=1:Nfor m=1:(N*(N-1)*(N-2)/6)I=Z(m,1);J=Z(m,2);K=Z(m,3); r=R;if J-I~=1&K-J~=1&K-I~=N-1 for q=1:(J-I)r(I+q)=R(J+1-q);endfor q=1:(K-J)r(J+q)=R(K+1-q);endendif J-I==1&K-J==1r(K)=R(J);r(J)=R(K);endif J-I==1&K-J~=1&K-I~=N-1 for q=1:(K-J)r(I+q)=R(I+1+q); endr(K)=R(J);endif K-J==1&J-I~=1&K~=Nfor q=1:(J-I)r(I+1+q)=R(I+q); endr(I+1)=R(K);endif I==1&J==2&K==Nfor q=1:(N-2)r(1+q)=R(2+q);endr(N)=R(2);endif I==1&J==(N-1)&K==Nfor q=1:(N-2)r(q)=R(1+q);endr(N-1)=R(1);endif J-I~=1&K-I==N-1for q=1:(J-1)r(q)=R(1+q);endr(J)=R(1);endif J==(N-1)&K==N&J-I~=1r(J+1)=R(N);for q=1:(N-J-1)r(J+1+q)=R(J+q);endendif cost_sum(r,C,N)<cost_sum(R,C,N)R=rendendfprintf('总长为%f\n',cost_sum(R,C,N))%%%%%%cost_sum.m%%%%%%%%functiony=cost_sum(x,C,N)y=0;for i=1:(N-1)y=y+C(x(i),x(i+1));endy=y+C(x(N),x(1));三,灰色预测代码<pre name="code" class="plain">clearclcX=[136 143 165 152 165 181 204 272 319 491 571 605 665 640 628];x1(1)=X(1);X1=[];for i=1:1:14x1(i+1)=x1(i)+X(i+1);X1=[X1,x1(i)];endX1=[X1,X1(14)+X(15)]for k=3:1:15p(k)=X(k)/X1(k-1);p1(k)=X1(k)/X1(k-1);endp,p1clear kZ=[];for k=2:1:15z(k)=0.5*X1(k)+0.5*X1(k-1);Z=[Z,z(k)];endZB=[-Z',ones(14,1)]Y=[];clear ifor i=2:1:15Y=[Y;X(i)];endYA=inv(B'*B)*B'*Yclear ky1=[];for k=1:1:15y(k)=(X(1)-A(2)/A(1))*exp(-A(1)*(k-1))+A(2)/A(1); y1=[y1;y(k)];endy1clear kX2=[];for k=2:1:15x2(k)=y1(k)-y1(k-1);X2=[X2;x2(k)];endX2=[y1(1);X2]e=X'-X2m=abs(e)./X's=e'*en=sum(m)/13clear ksyms ky=(X(1)-A(2)/A(1))*exp(-A(1)*(k-1))+A(2)/A(1)Y1=[];for j=16:1:21y11=subs(y,k,j)-subs(y,k,j-1);Y1=[Y1;y11];endY1%程序中的变量定义:alpha是包含α、μ值的矩阵;%ago是预测后累加值矩阵;var是预测值矩阵;%error是残差矩阵; c是后验差比值function basicgrey(x,m) %定义函数basicgray(x)if nargin==1 %m为想预测数据的个数,默认为1 m=1;endclc; %清屏,以使计算结果独立显示if length(x(:,1))==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换x=x';endn=length(x); %取输入数据的样本量x1(:,1)=cumsum(x); %计算累加值,并将值赋及矩阵be for i=2:n %对原始数列平行移位 Y(i-1,:)=x(i,:);endfor i=2:n %计算数据矩阵B的第一列数据z(i,1)=0.5*x1(i-1,:)+0.5*x1(i,:);endB=ones(n-1,2); %构造数据矩阵BB(:,1)=-z(2:n,1);alpha=inv(B'*B)*B'*Y; %计算参数α、μ矩阵for i=1:n+m %计算数据估计值的累加数列,如改n+1为n+m可预测后m个值ago(i,:)=(x1(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1, :)*(i-1))+alpha(2,:)/alpha(1,:);endvar(1,:)=ago(1,:);f or i=1:n+m-1 %可预测后m个值var(i+1,:)=ago(i+1,:)-ago(i,:); %估计值的累加数列的还原,并计算出下m个预测值end[P,c,error]=lcheck(x,var); %进行后验差检验[rela]=relations([x';var(1:n)']); %关联度检验ago %显示输出预测值的累加数列alpha %显示输出参数α、μ数列var %显示输出预测值error %显示输出误差P %显示计算小残差概率 c %显示后验差的比值crela %显示关联度judge(P,c,rela) %评价函数显示这个模型是否合格<pre name="code" class="plain">function judge(P,c,rela) %评价指标并显示比较结果if rela>0.6'根据经验关联度检验结果为满意(关联度只是参考主要看后验差的结果)'else'根据经验关联度检验结果为不满意(关联度只是参考主要看后验差的结果)'endif P>0.95&c<0.5'后验差结果显示这个模型评价为“优”'else if P>0.8&c<0.5'后验差结果显示这个模型评价为“合格”'else if P>0.7&c<0.65'后验差结果显示这个模型评价为“勉强合格”' else'后验差结果显示这个模型评价为“不合格”' endendendfunction [P,c,error]=lcheck(x,var)%进行后验差检验n=length(x);for i=1:nerror(i,:)=abs(var(i,:)-x(i,:)); %计算绝对残差c=std(abs(error))/std(x); %调用统计工具箱的标准差函数计算后验差的比值cs0=0.6745*std(x);ek=abs(error-mean(error));pk=0;for i=1:nif ek(i,:)<s0pk=pk+1;endendP=pk/n; %计算小残差概率%附带的质料里有一部分讲了关联度function [rela]=relations(x)%以x(1,:)的参考序列求关联度[m,n]=size(x);for i=1:mfor j=n:-1:2x(i,j)=x(i,j)/x(i,1);endfor i=2:mx(i,:)=abs(x(i,:)-x(1,:)); %求序列差endc=x(2:m,:);Max=max(max(c)); %求两极差Min=min(min(c));p=0.5; %p称为分辨率,0<p<1,一般取p=0.5for i=1:m-1for j=1:nr(i,j)=(Min+p*Max)/(c(i,j)+p*Max); %计算关联系数endendfor i=1:m-1rela(i)=sum(r(i,:))/n; %求关联度end四,非线性拟合function f=example1(c,tdata)f=c(1)*(exp(-c(2)*tdata)-exp(-c(3)*tdata));<pre name="code" class="plain">function f=zhengtai(c,x) f=(1./(sqrt(2.*3.14).*c(1))).*exp(-(x-c(1)).^2./(2.*c( 2)^2));x=1:1:12;y=[01310128212]';c0=[2 8];for i=1:1000c=lsqcurvefit(@zhengtai,c0,x,y);c0=c;endy1=(1./(sqrt(2.*3.14).*c(1))).*exp(-(x-c(1)).^2./(2.*c (2)^2));plot(x,y,'r-',x,y1);legend('实验数据','拟合曲线')x=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16]';y=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4]';f=@(c,x)c(1)*(exp(-c(2)*x)-exp(-c(3)*x));c0=[114 0.1 2]';for i=1:50opt=optimset('TolFun',1e-3);[c R]=nlinfit(x,y,f,c0,opt)c0=c;hold onplot(x,c(1)*(exp(-c(2)*x)-exp(-c(3)*x)),'g')endt=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16];y=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4];c0=[1 1 1];for i=1:50 c=lsqcurvefit(@example1,c0,t,y);c0=c;endy1=c(1)*(exp(-c(2)*t)-exp(-c(3)*t));plot(t,y,' +',t,y1);legend('实验数据','拟合曲线')五,插值拟合相关知识在生产和科学实验中,自变量及因变量间的函数关系有时不能写出解析表达式,而只能得到函数在若干点的函数值或导数值,或者表达式过于复杂而需要较大的计算量。
MATLAB在数学建模中的应用

M AT L A B 在 教 育 和 研 究 领 域 的 应 用 前 景
促进数学建模教 育:MATL AB提 供了丰富的工具 和资源,帮助学 生和教师更容易 地学习和教授数 学建模。
支持科研工作: 科学家和研究人 员使用MATL AB 进行数据分析和 可视化,算法开 发,以及模拟和 建模。
案例:使用MATL AB求解非线性最小二乘问题,通过迭代算法找到最优解。
优势:MATL AB提供了高效的优化工具箱,可以进行大规模的优化计算。
应用领域:非线性优化问题在许多领域都有应用,如机器学习、图像处理、控制系统 等。
微分方程的求解
描述了使用MATL AB求解微分方程的基本步骤 提供了使用MATL AB求解微分方程的示例代码 介绍了使用MATL AB求解微分方程的优势和局限性 总结了MATL AB在数学建模中求解微分方程的应用场景和效果
如何使用MATLAB 进行数学建模
M AT L A B 的 基 本 语 法 和 操 作
变量定义:使用变量名和赋值符号(=)定义变量 矩阵运算:使用方括号[]进行矩阵的创建和运算 函数定义:使用function关键字定义函数,输入输出参数用逗号分隔 控制流语句:使用if、else、for、while等控制流语句进行程序流程控制
M AT L A B 的 起 源 : 由 C l e v e M o l e r 于1980年代初开发,旨在为线性 代数课程提供一种更有效的方法。
M AT L A B 的 发 展 : 经 过 多 年 的 不 断 发 展 和 完 善 , M AT L A B 已 经 成 为 一 个功能强大的数学计算软件,广泛 应用于科学、工程和数学领域。
MATLAB及在数学建模中应用

第1讲MATLAB及在数学建模中的应用• MatLab简介及基本运算•常用计算方法•应用实例一、 MatLab简介及基本运算1.1 MatLab简介1.2 MatLab界面1.3 MatLab基本数学运算1.4 MatLab绘图1.1 MatLab简介•MATLAB名字由MATrix和 LABoratory 两词组成。
20世纪七十年代后期, 美国新墨西哥大学计算机科学系主任Cleve Moler教授为减轻学生编程负担,为学生设计了一组调用LINPACK和EISPACK库程序的“通俗易用”的接口,此即用FORTRAN编写的萌芽状态的MATLAB。
•经几年的校际流传,在Little的推动下,由Little、Moler、Steve Bangert合作,于1984年成立了MathWorks公司,并把MATLAB正式推向市场。
从这时起,MATLAB的内核采用C语言编写,而且除原有的数值计算能力外,还新增了数据图视功能。
•1997年春,MATLAB5.0版问世,紧接着是5.1、5.2、5.3、6.0、6.1、6.5、7.0版。
现今的MATLAB拥有更丰富的数据类型和结构、更友善的面向对象、更加快速精良的图形可视、更广博的数学和数据分析资源、更多的应用开发工具。
•20世纪九十年代的时候,MATLAB已经成为国际控制界公认的标准计算软件。
•MATLAB具有用法简易、可灵活运用、程式结构强又兼具延展性。
以下为其几个特色:①可靠的数值运算和符号计算。
在MATLAB环境中,有超过500种数学、统计、科学及工程方面的函数可使用。
②强大的绘图功能。
MATLAB可以绘制各种图形,包括二维和三维图形。
③简单易学的语言体系。
④为数众多的应用工具箱。
1.2MatLab界面1.3 MatLab基本数学运算•MATLAB的基本算术运算有:+(加)、-(减)、*(乘)、/(右除)、\(左除)、^(乘方) 还有一种特殊的运算,点运算:.*、./、.\和.^。
matlab数学建模程序代码

matlab数学建模程序代码摘要:1.引言2.Matlab数学建模简介3.Matlab数学建模程序代码实例a.线性规划模型b.非线性规划模型c.动态规划模型d.排队论模型e.图论模型f.神经网络模型4.结论正文:Matlab是一种广泛应用于科学计算和数据分析的编程语言。
在数学建模领域,Matlab也发挥着重要的作用。
本文将介绍Matlab数学建模的基本知识,并通过实例代码展示不同类型的数学建模问题的解决方法。
首先,我们需要了解Matlab数学建模的基本概念。
Matlab提供了一系列用于解决各种数学建模问题的工具箱和函数。
例如,线性规划(LP)、非线性规划(NLP)、动态规划(DP)、排队论(QT)、图论(GT)和神经网络(NN)等。
这些工具箱和函数可以帮助我们快速地构建和求解数学模型。
接下来,我们将通过实例代码展示如何使用Matlab解决不同类型的数学建模问题。
1.线性规划模型线性规划是一种常见的优化问题,它的基本形式可以表示为:$minimize quad c^Tx$$subject quad to:$$Ax leq b$$x geq 0$在Matlab中,我们可以使用intlinprog函数求解线性规划问题。
下面是一个实例:```matlabf = [-1, 1, 1; -1, 2, 1; -1, 1, 2]; % 目标函数系数向量A = [1, 1, 1; 1, 1, 1; 1, 1, 1]; % 约束条件系数矩阵b = [3, 3, 3]; % 约束条件右端向量lb = [0, 0, 0]; % 变量下限[x, fval] = intlinprog(f, [], [], A, b, lb);disp(x);disp(fval);```2.非线性规划模型非线性规划问题的一般形式为:$minimize quad g(x)$$subject quad to:$$h_i(x) leq 0, i = 1, ..., m$$x in X$在Matlab中,我们可以使用fmincon函数求解非线性规划问题。
Matlab软件在数学建模中的应用

Matlab软件在数学建模中的应用摘要随着社会和计算机技术的发展,数学科学与计算机技术相结合,在社会各领域发挥着越来越重要的作用,能够方便、高效的解决各种实际问题。
从实例出发,论述数学软件Matlab在数学建模中的应用,以提高对Matlab软件的认识和数学建模的效率,提高解决实际问题的能力。
关键词Matlab软件;数学建模;最优化数学在其发展的早期主要是作为一种实用技术工具,用于处理人类生活及社会活动中的各种实际问题。
近年来,随着社会的发展以及计算机技术的迅速发展,人们对数学的重要作用有了新的认识。
数学在社会各领域中的应用越来越广泛,不但运用于自然科学的各个领域,而且渗透到经济、军事、管理以至于社会科学和社会活动的各领域,在许多方面发挥着越来越重要的作用。
数学建模就是对我们在科学研究、技术改革、经济管理等现实生活中所遇到的实际问题加以分析、抽象、简化,用数学语言进行描述、用数学方法寻求解决方案、办法,并通过解释、验证,最终应用于实际的过程。
计算机作为一种高科技的工具,大大推进了数学建模的进程,是数学建模中的不可缺少的重要工具。
数学科学与计算机技术相结合,使各领域复杂的实际问题得以快速的解决。
在数学建模中Matlab软件发挥了重要的作用,借助于Matlab的强大数据处理、图形处理能力可以方便、快捷、高效的解决数学建模中各种问题。
本文主要通过具体的实例介绍计算机软件Matlab在数学建模中的应用,以提高数学建模的质量和效率,增强解决实际问题的能力。
1Matlab的功能和特点Matlab的数值计算功能在数学类软件中首屈一指。
它可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
Matlab具有如下特点:1.1友好的工作平台Matlab由一系列工具组成。
这些工具方便用户使用Matlab的函数和文件,其中许多工具采用的是图形用户界面。
数学模型程序代码-Matlab-姜启源-第一章-建立数学模型

数学模型程序代码-M a t l a b-姜启源-第一章-建立数学模型-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第1章 建立数学模型1.(求解,编程)如何施救药物中毒p10~11人体胃肠道和血液系统中的药量随时间变化的规律(模型):d ,(0)1100d (,0)d ,(0)0d xx x ty x y y tλλμλμ⎧=-=⎪⎪>⎨⎪=-=⎪⎩ 其中,x (t )为t 时刻胃肠道中的药量,y (t )为t 时刻血液系统中的药量,t =0为服药时刻。
1.1(求解)模型求解p10~11要求:① 用MATLAB 求解微分方程函数dsolve 求解该微分方程(符号运算)。
② 用MATLAB 的化简函数simplify 化简所得结果。
③ 结果与教材P11上的内容比较。
提示:dsolve 和simplify 的用法可用help 查询。
建议在命令窗口中操作。
1.2(编程)结果分析p11已知λ=0.1386, μ=0.1155,将上题中得到x (t )和y (t )两条曲线画在同一个图形窗口内。
参考图形如下。
MATLAB命令plot, fplot, hold on/off, grid on/off, xlabel, ylabel, text 。
★ 编写的程序和运行结果:2.(编程,验证)商人们怎样安全过河p8~9三名商人各带一个随从乘船渡河,一只小船只能容纳二人,由他们自己划行。
随从们密约,在河的任一岸,一旦随从的人数比商人多,就杀人越货。
但是如何乘船的大权掌握在商人们手中。
商人们怎样才能安全渡河呢?[模型构成]决策:每一步(此岸到彼岸或彼岸到此岸)船上的人员。
要求:在安全的前提下(两岸的随从数不比商人多),经有限步使全体人员过河。
x k第k次渡河前此岸的商人数y k第k次渡河前此岸的随从数x k , y k=0,1,2,3; k=1,2,⋯过程的状态s k=(x k , y k)允许状态集合S={(x, y)|x=0, y=0,1,2,3; x=3, y=0,1,2,3; x=y=1,2}u k第k次渡船上的商人数v k第k次渡船上的随从数u k , v k=0,1,2; k=1,2,⋯决策d k=(u k , v k)允许决策集合D={(u , v)|u+v =1, 2}状态转移律s k+1=s k+(-1)k d k[多步决策问题]求d k∈D(k=1, 2, ⋯, n), 使s k∈S, 并按转移律由s1=(3,3) 到达s n+1=(0,0)。
matlab在数学建模中的应用

Matlab在数学建模中的应用
Matlab是世界上最广泛使用的数学建模工具之一,在过去的几十年里,它一直在帮助分析师,工程师和学者处理复杂的数学模型和科学问题。
Matlab的功能强大,它可以完成符号计算,计算和图形,以及几乎任
何数学任务。
在数学建模中,Matlab为其用户提供了一系列强大的编程函数,允许
用户快速建立,评估和优化参数。
除了编程函数,Matlab也提供一系
列强大的符号计算工具,如微积分和线性代数计算,以帮助用户深入
研究未来的建模方案。
Matlab的另一个重要功能是可视化功能,它可以让用户对复杂的数学
函数有更全面的认识。
用户可以生成2D和3D图形,可视化多变量函数,以及在微积分中可视化积分。
这些功能让用户能够更好地理解和
注释自己的建模,以及他们的结果并查看建模情况。
Matlab还提供较高级的插件提供一些更复杂的功能,如假设检验,线
性模型,贝叶斯建模和多义性研究。
这些插件可以大大提高用户的建
模能力,使其能够完成更复杂的工作,以获得更精确的结果。
最后,Matlab的在线资源也是其有力的支持者。
Matlab官方网站提供
了大量文档和教程,以帮助新手和高级用户充分利用其建模功能。
此外,社区也提供了大量交流空间,从而为Matlab用户提供更多的参考
资料,有助于他们深入了解其功能和开发新的方案。
总而言之,Matlab是一款强大的数学建模工具,它可以帮助分析师,
工程师和学者快速实现高质量的建模结果。
通过快速的参数优化,符
号计算和可视化技术,Matlab可以帮助用户实现复杂的数学建模任务,并减少工作量。
数学建模竞赛培训之编程MATLAB实用教程

数学建模竞赛培训之编程MATLAB实用教程在当今的学术和工程领域,数学建模竞赛越来越受到重视,而MATLAB 作为一款强大的数学计算和编程软件,在其中发挥着至关重要的作用。
如果你正在为数学建模竞赛做准备,那么掌握 MATLAB 的编程技巧将为你在竞赛中取得优异成绩提供有力的支持。
接下来,让我们一起开启 MATLAB 编程的实用教程之旅。
一、MATLAB 基础首先,我们来了解一下 MATLAB 的基本操作界面。
当你打开MATLAB 时,会看到一个命令窗口,这是我们输入命令和查看结果的地方。
变量是编程中的重要概念,在 MATLAB 中,变量无需事先声明类型,直接赋值即可使用。
例如,我们可以输入`x = 5` ,此时`x` 就被赋值为 5 。
MATLAB 支持多种数据类型,如数值型(包括整数和浮点数)、字符型、逻辑型等。
二、矩阵操作矩阵在数学建模中经常用到,MATLAB 对矩阵的操作非常方便。
可以通过直接输入元素来创建矩阵,比如`A = 1 2 3; 4 5 6` 就创建了一个 2 行 3 列的矩阵`A` 。
矩阵的运算也十分简单,加法、减法、乘法等都有相应的运算符。
例如,两个矩阵相加可以直接使用`A + B` 。
三、函数的使用MATLAB 拥有丰富的内置函数,大大提高了编程效率。
比如求矩阵的行列式可以使用`det()`函数,求矩阵的逆可以使用`inv()`函数。
我们还可以自己定义函数,语法如下:```matlabfunction output_args = function_name(input_args)%函数体end```四、绘图功能在分析数据和展示结果时,绘图是必不可少的。
MATLAB 能够绘制各种类型的图形,如折线图、柱状图、饼图等。
以绘制简单的折线图为例,使用`plot()`函数,如`plot(x,y)`,其中`x` 和`y` 是数据向量。
五、数值计算在数学建模中,常常需要进行数值计算,如求解方程、求积分等。
matlab在数学建模中的应用

matlab在数学建模中的应用1 引言Matlab是一种思考数学建模的功能强大的工具,其高级语言和可视化功能,使其成为解决机器学习,数值优化和科学计算问题的理想工具。
Matlab所提供的友好用户界面,可以帮助使用者更好地理解和处理数学模型,并得出正确的结论。
2 模型建立Matlab最重要的用途之一是建立数学模型。
使用Matlab可以简单快速地构建算法,它可以帮助使用者快速分析模型的潜在结果,因此可以更快地确定有效的解决方案。
Matlab提供了许多工具,其中包括可以帮助使用者构建不同类型的模型,并实时展示结果。
3 模型仿真Matlab也可以用于模拟物理系统,运动学和动力学系统,以及工程设计模型。
Matlab使用者可以根据实际应用场景,建立模型,从而研究影响结果的参数变化和探究其他未知因素对结果的影响。
Matlab 可以帮助使用者进行大量仿真,以找出最优的解决方案。
4 数据分析Matlab也可以用于数据分析,使用Matlab可以快速检测数据的结构和特征,并快速处理数据。
它可以用于可视化数据以帮助使用者更好地探究重要信息,Matlab也可以帮助使用者执行机器学习任务,让使用者从大量数据中发现潜在模式。
5 优化Matlab也可以用于优化,可以根据用户定义的目标函数,搜索解空间以找出最优解。
Matlab提供了一些内置优化工具,使用者可以快速找到优化解,提高系统性能。
6 结论从以上可以看出,Matlab在数学建模中有着重要的意义,无论是在建模,模拟,数据分析还是优化方面,Matlab都可以提供全面的支持。
Matlab现在已经成为研究数学建模的首选平台。
数学建模的MATLAB课件(1-6章)

2013-8-21
17
1.3.2 主窗口及子窗口
Matlab主窗口是Matlab的主要工作界面。主窗口除了嵌入一些子 窗口外,还主要包括菜单栏和工具栏。 1.菜单栏 在Matlab 6.5主窗口的菜单栏,共包含File、Edit、View、Web、 Window和Help 6个菜单项。 (1) File菜单项:File菜单项实现有关文件的操作。 (2) Edit菜单项:Edit菜单项用于命令窗口的编辑操作。 (3) View菜单项:View菜单项用于设置Matlab集成环境的显示方 式。 (4) Desktop菜单项:在MATLAB中,Desktop主菜单用于设置工作 空间和工具栏等的显示项。单击Desktop主菜单或按下快捷键 Alt+D,可以弹出Desktop下拉菜单。 (5) Window菜单项:主窗口菜单栏上的Window菜单,只包含一个 子菜单Close all,用于关闭所有打开的编辑器窗口,包括Mfile、Figure、Model和GUI窗口。 (6) Help菜单项:Help菜单项用于提供帮助信息。
2013-8-21
10
1.2.2 Matlab的安装
安装Matlab 7.0系统,需运行系统自带的安装程序setup.exe,一般只
要用鼠标双击安装图标,就会启动安装程序,你只需按照安装提示 正确输入(或粘贴)安装序列号后点击《确认》键,并按提示修改 安装路径(或默认安装到C盘)就能完成安装。 安装完毕后,在开始-程序-Matlab.exe菜单中,双击Matlab图标,即可 运行程序。
MATLAB在数学建模中的应用

>> a=[1 -1 4 -2;1 -1 -1 2;3 1 7 -2;1 -3 -12 6];
>> rref(a) 将矩阵A化为最简阶梯形
1 0 0 0 RREF Reduced row
ans = 0 1 0 0 0010
echelon form R(A)=4=n;
0 0 0 1 所以方程组只有零解。
X = 0.0010 -1.5708 0.0008 FVAL =-2.5000
MATLAB在《微积分》中的应用 5、求积分
例9 求不定积分 cos2xcos3xdx
>> int(cos(2*x)*cos(3*x))
Integrate:积分
ans =1/2*sin(x)+1/10*sin(5*x)
MATLAB的功能
➢ MATLAB产品组是从支持概念设计、算法开发、建模仿真,
到实时实现的集成环境,可用来进行:
➢ 数据分析 ➢ 数值与符号计算 ➢ 工程与科学绘图 ➢ 控制系统设计 ➢ 数字图像信号处理 ➢ 建模、仿真、原型开发 ➢ 财务工程、应用开发、图形用户界面设计
MATLAB语言特点
➢ 编程效率高,允许用数学的语言来编写程序 ➢ 用户使用方便,把程序的编辑、编译、连接和执行融为一体 ➢ 高效方便的矩阵和数组运算 ➢ 语句简单,内涵丰富 ➢ 扩充能力强,交互性,开放性 ➢ 方便的绘图功能 ➢ 该软件由c语言编写,移植性好
0
>> int(exp(-x^2/2),0,1)
erf (x) 2 xet2dt
0
ans =
1/2*erf(1/2*2^(1/2))*2^(1/2)*pi^(1/2)
ans 2 2 2et2dt
matlab在数学建模中的应用

Matlab在数学建模中的应用数学建模是通过对实际问题的抽象和简化,引入一些数学符号、变量和参数,用数学语言和方法建立变量参数间的内在关系,得出一个可以近似刻画实际问题的数学模型,进而对其进行求解、模拟、分析检验的过程。
它大致分为模型准备、模型假设、模型构成、模型求解、模型分析、模型检验及应用等步骤。
这一过程往往需要对大量的数据进行分析、处理、加工,建立和求解复杂的数学模型,这些都是手工计算难以完成的,往往在计算机上实现。
在目前用于数学建模的软件中,matlab 强大的数值计算、绘图以及多样化的工具箱功能,能够快捷、高效地解决数学建模所涉及的众多领域的问题,倍受数学建模者的青睐。
1 Matlab在数学建模中的应用下面将联系数学建模的几个环节,结合部分实例,介绍matlab 在数学建模中的应用。
1.1 模型准备阶段模型准备阶段往往需要对问题中的给出的大量数据或图表等进行分析,此时matlab的数据处理功能以及绘图功能都能得到很好的应用。
1.1.1 确定变量间关系例1 已知某地连续20年的实际投资额、国民生产总值、物价指数的统计数据(见表),由这些数据建立一个投资额模型,根据对未来国民生产总值及物价指数的估计,预测未来的投资额。
表1 实际投资额、国民生产总值、物价指数的统计表记该地区第t年的投资为z(t),国民生产总值为x(t),物价指数为y(t)。
赋值:z=[90.9 97.4 113.5 125.7 122.8 133.3 149.3 144.2 166.4 195 229.8 228.7 206.1 257.9 324.1 386.6 423 401.9 474.9 424.5]' x=[596.7 637.7 691.1 756 799 873.4 944 992.7 1077.6 1185.9 1326.4 1434.2 1549.2 1718 1918.3 2163.9 2417.8 2631.6 2954.7 3073]'y=[0.7167 0.7277 0.7436 0.7676 0.7906 0.8254 0.8679 0.91450.9601 1 1.0575 1.1508 1.2579 1.3234 1.4005 1.5042 1.63421.7842 1.95142.0688]'先观察x与z之间,y与z之间的散点图plot(x,z,'*')plot(y,z,'*')由散点图可以看出,投资额和国民生产总值与物价指数都近似呈线性关系,因此可以建立多元线性回归模型012z x y βββε=+++直接利用统计工具箱直接计算[b,bint,r,rint,stats]=regress(z,X,alpha)输入z :n 维数据向量X:[ones(20,1) x y],这里的1是个向量,元素全为常数1,即为ones(n,1)Alpha:置信水平,一般为0.05输出b :β的估计值bint:b 的置信区间r :残差向量z-Xbrint: r 的置信区间Stats:检验统计量2R ,F , p代入上述公式[b,bint,r,rint,stats]=regress(z,X,0.05)有b =322.80.4168-859.2322.75630.61850.859.479=+-z x y由stats =0.2672 920.7 0知z的99.085%可由模型确定,F远超过F检验的临界值,p远小于α=0.05 .bint =224. 421.70.0184 0.8151-1121. -597.5b的置信区间不包含零点,x,y对z影响都是显著的。
MATLAB在数学建模中的应用

MATLAB在数学建模中的应用随着科学技术的不断进步,数学建模在许多领域得到了广泛的应用。
其中,MATLAB作为一种功能强大的计算软件,具有很多优势,使其成为数学建模中的重要工具之一。
本文将介绍MATLAB在数学建模中的应用。
一、MATLAB的基本特点MATLAB是一种用于数学计算、数据分析、可视化和编程的高级技术计算软件。
它提供了许多方便且易于使用的功能,包括数值分析、矩阵计算、信号处理、图像处理、统计分析和数据可视化等等。
MATLAB的高度集成性、易于编程、优雅的编程语言和强大的可视化功能,使其广泛应用于工程领域、科学研究、数学建模等领域。
二、MATLAB在数学建模中的应用1.求解数学模型MATLAB提供了一组广泛的数学函数和工具箱,用于求解各种数学模型。
例如微分方程、线性代数、函数逼近和数值积分等等。
通过这些工具箱可方便地进行数学建模,完成各种数学问题的求解。
同时,MATLAB的计算速度非常快,可以大大缩短计算时间,提高求解精度。
2.绘制图像MATLAB可以生成各种类型的图形和图表,从二维和三维函数图到统计图和数据可视化。
因为MATLAB支持向量和矩阵计算,因此绘制图像非常方便,可以准确地显示数学模型的参数变化。
这对于数学建模的理解和分析,以及对结果的解释和演示非常有帮助。
3.设计算法MATLAB是一种基于高级编程语言的环境。
因此,它为数学建模者提供了编写自己的算法的机会。
MATLAB不仅提供了许多内置的算法,而且还可以自定义算法,以满足特定的需求。
这给数学建模者带来了更多的灵活性和自主性。
4.交互式研究MATLAB提供了交互式控制台,将数值计算和可视化相结合。
数学建模者可以通过这个控制台和模型进行交互式研究,并在过程中进行参数设置和模型调整。
这种交互方式可以及时观察模型的性能和结果,以便及时调整模型参数。
同时它也可以帮助数学建模者更加深入地理解模型本身。
三、MATLAB在数学建模中的优势MATLAB具有许多出色的特点,使得它成为数学建模中的首选工具。
MATLAB R2015b数学建模 第1章 MATLAB与数学建模基础知识

1.1.2 MATLAB的特点
作为一个强大的计算功能软件,MATLAB具有以下的特性: ● 用于数值计算、可视化和应用程序开发的高级语言; ● 可实现迭代式探查、设计及问题求解的交互式环境; ● 用于线性代数、统计、傅立叶分析、筛选、优化、数值积分以及常 微分方程求解的数学函数; ● 用于数据可视化的内置图形以及用于创建自定义绘图的工具; ● 用于改进代码质量和可维护性并最大限度地发挥性能的开发工具; ● 用于构建自定义图形界面应用程序的工具; ● 可实现基于 MATLAB 的算法与外部应用程序和语言(如 C、Java、 .NET 以及 Microsoft Excel)集成的函数。
1.2 MATLAB组成结构
MATLAB的工作界面主要由选项卡、命令窗口、历史命令窗口、当前 工作目录窗口和工作空间管理窗口组成
1.3 MATLAB计算基础
MATLAB语言也是一门计算语言,它的运算指令和语法基 于一系列基本的矩阵运算以及它们的扩展运算,还支持复数这一 数值元素,这也是MATLAB区别于其他高级语言的最大特点之一, 它给许多领域的计算带来了极大的方便。
1.1.1 MATLAB的发展史
为了提高MATLAB在数值算法、界面设计和外部接口等诸多 方面的功能,MathWorks公司在2000年10月底推出了MATLAB 6.0。2003年,MATLABR6.5采用最新的JIT加速技术,为 MATLAB程序提供了更快的执行速度。
在MATLAB6.5版本中,Simulink升级为5.0版本,该版本创 建出完整的嵌入式系统设计环境。开发者可以在单一的环境下 完成工程,同时还可以选择自动将算法及应用程序转换成C++等 程序代码。
第1章 MATLAB与数学建模基础知识
