LZW编码

合集下载

LZW编码

4）如果字典中已有W1，则将W1作为当前单词W，返回第三步。如果字典中没有W1(发现一个新单词)；先将原单词W的序号输出，再加新单词W1增加到字典中，然后把刚刚读入的字符CH作为当前单词W，返回第三步；
5）结束程序。
四、实验目的：
(1)进一步熟悉Huffman编码过程；(2)掌握C语言递归程序的设计和调试技术。以巩固课堂所学编码理论的相关知识。
2）动态数据初始化：初始化新单词存放位置指针P。将它指向字典的第一个位置。例如P 256(即0X100)，读入被压缩文件的第一个字符cha，作为待处理单词W。单词的前缀Q为空，即Q 4095，尾字符就是cha，码字就是cha的序号；
3）如果文件中再没有字符了，输出当前单词W的序号。编码结束。如果文件中还有字符，把当前单词W作为前缀，再从被压缩文件中读入一个字符CH，把CH作为尾字符，得到一个单词W1；
将压缩文件中所有使用到的单字节字符放入字典中为了压缩任何类型的文件可以将字典的前256个位置0x000到0x0ff依次分配给0x000到0x0ff的256个单字节字符
实验４：LZW编码
学生姓名：
学号：
一、实验室名称：信息与编码课程组
二、实验项目名称：LZW编码
三、实验原理：
1）字典初始化：将压缩文件中所有使用到的单字节字符放入字典中，为了压缩任何类型的文件，可以将字典的前256个位置(0X000到0X0FF)依次分配给0X000到0X0FF的256个单字节字符；
五、实验内容：
对于给定的信源符号序列AB CA，利用LZW编码方法编出其中一种定长码。
六、实验器材（设备、元器件）：
PC机一台，装有VC++6.0或其它C语言集成开发环境。
七、实验步骤及操作：

常见的文本压缩算法

常见的文本压缩算法1. Huffman 编码：Huffman 编码是一种基于概率分布的编码方法，通过统计文本中字符出现的频率，然后构建一个 Huffman 树，按照编码规则对每个字符进行编码。

频率较高的字符使用较短的编码，频率较低的字符使用较长的编码，这样可以实现对文本的压缩。

2. Lempel-Ziv-Welch (LZW) 编码：LZW 编码是一种基于字典的编码方法。

它使用滑动窗口技术来寻找文本中的重复子串，并将其替换为短的编码。

在编码过程中，不断更新和扩展字典，以便能够更好地压缩文本。

3. Burrows-Wheeler Transform (BWT)：BWT 是一种重排文本字符的方法。

它通过将字符重新排序，使得文本中相邻的字符具有更高的相似性，从而方便后续的压缩工作。

BWT 常常与 Move-To-Front (MTF) 编码结合使用，MTF 编码根据字符上一次出现的位置来对字符进行编码。

4. Arithmetic Coding：算术编码是一种根据字符的概率分布来进行编码的方法。

它将整个文本视为一个连续的区间，根据字符的概率来更新区间的范围，并将最终的区间编码为一个二进制数。

算术编码可以实现非常高效的压缩，但也需要较大的计算量。

5. Run-Length Encoding (RLE)：RLE 是一种简单的压缩算法，它将连续重复的字符序列替换为一个字符和重复次数的组合。

例如，字符串"AAAAABBBBCCCC" 可以被压缩为 "A5B4C4"。

6. Huffman-RLE：Huffman-RLE 是 Huffman 编码和 RLE 的结合。

它首先使用 RLE 对文本进行预处理，将连续重复的字符序列替换为一个字符和重复次数的组合，然后再使用 Huffman 编码对处理后的文本进行压缩。

这些算法都有各自的优缺点，适用于不同的压缩场景。

在实际应用中，常常会将它们结合起来使用，以提高压缩效率。

计算机应用基础数据压缩和解压缩的原理与方法

计算机应用基础数据压缩和解压缩的原理与方法数据压缩和解压缩在计算机应用中扮演着重要的角色，它可以有效地减少数据的存储空间和网络传输所需的带宽。

本文将介绍数据压缩和解压缩的原理与方法。

一、数据压缩的原理数据压缩的基本原理是通过消除冗余信息来减少数据的存储空间和传输带宽。

下面将介绍几种常见的数据压缩原理。

1.1 无损压缩无损压缩是指在数据压缩的过程中不会丢失原始数据的任何信息。

其中最常用的无损压缩算法是哈夫曼编码和LZW编码。

1.1.1 哈夫曼编码哈夫曼编码是一种变长编码，根据字符出现的频率来构建编码表。

频率较高的字符使用较短的编码，频率较低的字符使用较长的编码。

在压缩的过程中，将原始数据替换为对应的编码，从而减少数据的大小。

1.1.2 LZW编码LZW编码是一种字典编码，将一系列连续的字符序列映射为短的编码。

在压缩的过程中，使用一个字典来存储已经出现的字符序列及其对应的编码。

当遇到新的字符序列时，将其添加到字典中，并输出其对应的编码。

1.2 有损压缩有损压缩是指在压缩的过程中会有一定程度上的信息丢失。

有损压缩常用于图像、音频和视频等多媒体数据的压缩。

其中最常用的有损压缩算法是JPEG和MP3。

1.2.1 JPEGJPEG是一种常用的图像压缩格式，它通过舍弃图像中的一些高频信息来减少数据的大小。

在压缩的过程中，JPEG将图像分为不同的8x8像素块，并对每个块进行离散余弦变换（DCT），然后对DCT系数进行量化，并使用熵编码进行进一步压缩。

1.2.2 MP3MP3是一种常用的音频压缩格式，它通过删除音频中的一些听觉上不明显的信息来减少数据的大小。

在压缩的过程中，MP3首先对音频进行傅里叶变换，并将频谱分割为不同的子带。

然后对每个子带进行量化，并使用熵编码进行进一步压缩。

二、数据解压缩的原理数据解压缩的过程是数据压缩的逆过程，它可以将压缩后的数据恢复为原始的数据。

解压缩的原理和压缩的原理相对应，下面将介绍几种常见的数据解压缩原理。

lzw编码原理

lzw编码原理
LZW（Lempel-Ziv-Welch）编码是一种无损压缩算法，基于字典的压缩算法。

它的原理如下：
1. 初始化字典：创建一个初始字典，其中包含所有单个输入符号（字符）作为键，对应的编码为它们的ASCII码值。

2. 分割输入：将输入字符串分割为一个个输入符号的序列。

3. 初始化缓冲区：将第一个输入符号加入到缓冲区中。

4. 处理输入序列：从第二个输入符号开始，重复以下步骤直到处理完所有输入符号：
- 将当前输入符号与缓冲区中的符号连接，得到一个新的符号。

- 如果新的符号在字典中存在，则将其加入到缓冲区中，继续处理下一个输入符号。

- 如果新的符号不在字典中，则将缓冲区中的符号编码输出，将新的符号添加到字典中，并将新的符号作为下一个缓冲区。

5. 输出编码：当所有输入符号处理完后，将缓冲区中的符号（不包括最后一个输入符号）编码输出。

LZW编码的核心思想是使用字典记录出现过的符号及其编码，以减少编码的长度。

在处理输入序列时，如果新的符号在字典中存在，则将其添加到缓冲区，并继续处理下一个输入符号；如果新的符号不在字典中，则将缓冲区中的符号编码输出，并将新的符号添加到字典中。

由于LZW编码使用了字典记录已编码的符号，因此在解码时只需根据字典中的编码逆向查找对应的符号即可恢复原始输入序列。

lzw

21
贪婪分析算法
• LZW采用greedy parsing algorithm
– 每一次分析都要串行地检查来自字符流(Charstream) 的字符串，从中分解出已经识别的最长的字符串，也就是已经在词典中出现的最长的前缀(Prefix)。 – 用已知的前缀(Prefix)加上下一个输入字符C也就是当前字符(Current character)作为该前缀的扩展字符，形成新的扩展字符串。 – 判断新的串是否在词典中
12
LZ78编码算法
• 步骤1：将词典和当前前缀P都初始化为空。 • 步骤2：当前字符C:=字符流中的下一个字符。 • 步骤3：判断P＋C是否在词典中 • （1）如果“是”，则用C扩展P，即让P:=P＋C，返回到步骤2。 • （2）如果“否”，则输出与当前前缀P相对应的码字W和当前字符C，即（W，C）； • 将P＋C添加到词典中； • 令P:=空值，并返回到步骤2
吃葡萄不吐葡萄皮，不吃葡萄倒吐葡萄皮。
2
LZ77算法
• 第一类词典编码里：所指的“词典”是指用以前处理过的数据来表示编码过程中遇到的重复部分。 • 这类编码中的所有算法都是以Abraham Lempel和 Jakob Ziv在1977年开发和发表的称为LZ77算法为基础的 • Jacob Ziv, Abraham Lempel, A Universal Algorithm for Sequential Data Compression, IEEE Transactions on Information Theory, 23(3):337-343, May 1977.
11
在介绍LZ78算法之前，首先说明在算法中用到的几个术语：
字符流(Charstream)：待编码的数据序列。字符(Character)：字符流中的基本数据单元。前缀(Prefix)：在一个字符之前的字符序列。缀-符串(String)：前缀＋字符。码字(Code word)：码字流中的基本数据单元，代表词典中的一串字符。码流(Codestream)：码字和字符组成的序列，是编码器的输出。词典(Dictionary)：缀-符串表。按照词典中的索引号对每条缀-符串(String)指定一个码字(Code word)。当前前缀(Current prefix)：在编码算法中使用，指当前正在处理的前缀，用符号P表示。当前字符(Current character)：在编码算法中使用，指当前前缀之后的字符，用符号C表示。当前码字(Current code word)：在译码算法中使用，指当前处理的码字，用W 表示当前码字，String.W表示当前码字的缀-符串。

LZW编码算法详解

LZW编码算法详解LZW(Lempel-Ziv & Welch)编码又称字串表编码，是Welch将Lemple和Ziv所提出来的无损压缩技术改进后的压缩方法。

GIF图像文件采用的是一种改良的LZW 压缩算法，通常称为GIF-LZW压缩算法。

下面简要介绍GIF-LZW的编码与解码方程解：例现有来源于二色系统的图像数据源（假设数据以字符串表示）：aabbbaabb，试对其进行LZW编码及解码。

1）根据图像中使用的颜色数初始化一个字串表（如表1），字串表中的每个颜色对应一个索引。

在初始字串表的LZW_CLEAR和LZW_EOI分别为字串表初始化标志和编码结束标志。

设置字符串变量S1、S2并初始化为空。

2）输出LZW_CLEAR在字串表中的索引3H(见表2第一行)。

3）从图像数据流中第一个字符开始，读取一个字符a，将其赋给字符串变量S2。

判断S1+S2=“a”在字符表中，则S1=S1+S2=“a”（见表2第二行）。

4）读取图像数据流中下一个字符a，将其赋给字符串变量S2。

判断S1+S2=“aa”不在字符串表中，输出S1=“a”在字串表中的索引0H，并在字串表末尾为S1+S2="aa"添加索引4H，且S1=S2=“a”（见表2第三行）。

5）读下一个字符b赋给S2。

判断S1+S2=“ab”不在字符串表中，输出S1=“a”在字串表中的索引0H，并在字串表末尾为S1+S2=“ab”添加索引5H，且S1=S2=“b”（见表2第四行）。

6）读下一个字符b赋给S2。

S1+S2=“bb”不在字串表中，输出S1=“b”在字串表中的索引1H，并在字串表末尾为S1+S2=“bb”添加索引6H，且S1=S2=“b”（见表2第五行）。

7）读字符b赋给S2。

S1+S2=“bb”在字串表中，则S1=S1+S2=“bb”（见表2第六行）。

8）读字符a赋给S2。

S1+S2=“bba”不在字串表中，输出S1=“bb”在字串表中的索引6H，并在字串表末尾为S1+S2=“bba”添加索引7H，且S1=S2=“a”（见表2第七行）。

无损压缩算法的比较和分析

无损压缩算法的比较和分析常见的无损压缩算法包括LZ77、LZ78、LZW、Huffman编码、算术编码等。

下面对这些算法进行比较和分析。

1.LZ77LZ77算法是一种字典编码方法，通过寻找重复出现的数据片段，并用指针和长度来表示这些片段，从而实现无损压缩。

与其他算法相比，LZ77算法在压缩速度方面较快，但压缩率相对较低。

2.LZ78LZ78算法是一种基于字典编码的压缩算法，它将重复出现的片段替换为对应的指针，并在字典中新增新的片段。

与LZ77相比，LZ78算法具有更好的压缩效果，但压缩和解压缩的速度较慢。

3.LZWLZW算法是LZ78的改进版本，也是一种字典编码方法。

LZW算法通过将重复出现的片段编码为对应的指针，并将这些片段以及对应的指针存储在字典中，来实现压缩。

与LZ78相比，LZW算法在压缩效果上更好，但对字典的管理较复杂，导致压缩和解压缩速度较慢。

4. Huffman编码Huffman编码是一种基于字符出现频率的编码算法。

它通过统计字符出现的频率来构建一个最优前缀编码的树结构，从而实现无损压缩。

Huffman编码的压缩率较高，但压缩和解压缩的速度相对较慢。

5.算术编码算术编码是一种基于字符出现概率的编码算法。

它通过使用一个区间来表示整个数据流，将出现频率较高的字符用较短的区间表示，从而实现无损压缩。

算术编码的压缩率通常比Huffman编码更高，但压缩和解压缩的速度更慢。

综合比较上述算法，可以得出以下结论：1.LZ77和LZ78算法适用于实时压缩，因为它们在压缩和解压缩的速度方面较快，但压缩率较低。

2.LZW算法在压缩效果上较好，但对字典的管理较复杂，导致压缩和解压缩的速度较慢。

3. Huffman编码和算术编码在压缩率上较高，但压缩和解压缩的速度相对较慢。

根据具体需求，可以选择适合的无损压缩算法。

如果需要更快的压缩和解压缩速度，可以选择LZ77或LZ78算法；如果需要更好的压缩效果，可以选择LZW算法、Huffman编码或算术编码。

lzw和霍夫曼编码

lzw和霍夫曼编码LZW（Lempel-Ziv-Welch）编码和Huffman编码是常见的无损数据压缩算法。

它们可以将数据以更高效的方式表示，并减少数据所占用的存储空间。

虽然两种编码算法有一些相似之处，但它们的工作原理和实施方法略有不同。

1.LZW编码：LZW编码是一种基于字典的压缩算法，广泛应用于文本和图像等数据的压缩。

它的工作原理是根据已有的字典和输入数据，将连续出现的字符序列转换为对应的索引，从而减少数据的存储空间。

LZW编码的过程如下：•初始化字典，将所有可能的字符作为初始词条。

•从输入数据中读取字符序列，并检查字典中是否已有当前序列。

•如果字典中存在当前序列，则继续读取下一个字符，将该序列与下一个字符连接成一个长序列。

•如果字典中不存在当前序列，则将当前序列添加到字典中，并输出该序列在字典中的索引。

•重复以上步骤，直到输入数据全部编码完成。

LZW编码的优点是可以根据实际数据动态更新字典，适用于压缩包含重复模式的数据。

2.霍夫曼编码：霍夫曼编码是一种基于频率的前缀编码方法。

它根据字符出现的频率构建一个最优二叉树（霍夫曼树），将出现频率较高的字符用较短的二进制码表示，出现频率较低的字符用较长的二进制码表示。

霍夫曼编码的过程如下：•统计输入数据中各个字符的频率。

•使用字符频率构建霍夫曼树，频率较高的字符在树的较低层，频率较低的字符在树的较高层。

•根据霍夫曼树，为每个字符分配唯一的二进制码，保持没有一个字符的编码是另一个字符编码的前缀。

•将输入数据中的每个字符替换为相应的霍夫曼编码。

•输出霍夫曼编码后的数据。

霍夫曼编码的优点是可以根据字符频率进行编码，使高频字符的编码更短，适用于压缩频率差异较大的数据。

总的来说，LZW编码和霍夫曼编码都是常见的无损数据压缩算法，用于减少数据的存储空间。

它们的选择取决于具体的场景、数据特点和应用需求。

LZW编码算法详解

LZW编码算法详解LZW是一种字典压缩算法，用于无损数据压缩。

它是由Terry Welch在1977年提出的，主要用于无损压缩图像和文本数据。

LZW算法的特点是算法实现简单，压缩率高效。

LZW算法的基本原理是利用字典来存储已出现的文本片段，并使用字典中的索引来替代重复出现的片段。

初始时，字典中包含所有的单个字符。

算法从输入数据的第一个字符开始，不断扩充字典，直到处理完完整的数据流。

具体来说，LZW算法的编码流程如下：1.创建一个空字典，初始化字典中包含所有的单个字符。

2.读取输入数据流的第一个字符，将其作为当前字符。

3.从输入数据流中读取下一个字符，将其与当前字符进行拼接，得到当前字符串。

4.检查当前字符串是否在字典中，如果在字典中，则将当前字符串作为新的当前字符串，并继续读取下一个字符。

5.如果当前字符串不在字典中，将当前字符串的索引输出，并将当前字符串添加到字典中作为新的条目。

6.重复步骤3-5，直到处理完整的输入数据流。

LZW算法的解码流程与编码流程相似，但需要注意解码时字典的初始化方式。

解码时，初始字典只包含单个字符，不包含任何字符串。

解码算法的具体流程如下：1.创建一个空字典，初始化字典中包含所有的单个字符。

2.从输入编码流中读取第一个索引值，并将其作为上一个索引值。

3.在字典中找到当前索引值所对应的字符串，并输出。

4.如果已经读取完整个编码流，则解码结束。

5.否则，从输入编码流中读取下一个索引值，并将其作为当前索引值。

6.检查当前索引值是否在字典中，如果在字典中，则将上一个索引值和当前索引值对应的字符串进行拼接，得到新的解码字符串，并将其输出。

7.如果当前索引值不在字典中，将上一个索引值对应的字符串和上一个索引值拼接，得到新的解码字符串，并将其输出。

然后将新解码字符串添加到字典中作为新的条目。

8.将当前索引值作为上一个索引值，并继续重复步骤4-7，直到解码完成。

LZW算法的优点是能够在保持数据完整性的同时，显著减小数据的大小。

字符串压缩算法

字符串压缩算法字符串压缩算法是一种常用的数据压缩算法，它的原理是利用字符串的重复子序列，通过有效地压缩字符串长度，从而节约存储空间和传输带宽。

它可以有效地将字符串缩短一般2~5倍,最大可达到20倍以上。

字符串压缩算法一般指使用某种编码技术将字符串中的特殊字符和重复字符进行压缩,从而减少存储和传输的空间。

它的压缩算法可以大致分为无损和有损压缩两种。

一、无损压缩无损压缩法是指用一定的规则对字符串进行压缩，不破坏原有的字符信息，用无损压缩法进行压缩，字符串压缩率一般不会超过50%，但压缩之后可以保证完整性和正确性，不会出现乱码等情况。

无损压缩有很多种方法，其中种常用的有LZW（Lempel-Ziv-Welch）算法和Huffman算法，它们都是早期字符串压缩算法，但仍被广泛使用。

1、LZW（Lempel-Ziv-Welch）算法LZW（Lempel-Ziv-Welch）算法是一种基于词频的哈夫曼编码，它的基本原理是把重复出现的子串用一个索引号的形式表示，以减少字符数量，增加压缩比。

它的工作过程是：先初始化一个索引表，然后把字符串中每个字符都和索引表中的字符进行比较，如果字符串中的字符和索引表中某个字符相等，则将该字符所表示的索引号作为结果保存。

如果字符串中的字符不在索引表中，则将该字符添加到索引表中，并且给出一个新的索引号作为结果保存。

然后，以此类推，依次把字符编码成索引号，就可以得到一个编码后的字符串，这就实现了字符串的压缩。

2、Huffman算法Huffman算法也是一个基于词频的编码方法，它的原理是把出现频率最高的字符搭配编码长度最短的编码，而出现频率低的字符搭配编码长度较长的编码，这样总的编码长度最短，从而达到最小的压缩比。

它的工作过程是：首先，利用某种方法计算出字符串中每个字符出现的次数，然后，把这些字符按出现次数的多少重新排列，排列的结果就是一个霍夫曼树。

之后，把这棵树按照特定的方式进行遍历，从根节点到叶子节点，每次遍历到一个字符节点，就根据遍历路径给出一个编码，然后，把每个字符节点的编码都保存下来，就可以得到一个字符串的Huffman编码，这就实现了字符串的压缩。

lzw编码分析

LZW 编码分析导航L ZW 编码分析 (1)缘起： (1)名词规范： (1)本文完成的主要工作 (1)L ZW编码原理 (2)L ZW解码原理 (3)问题及改进： (4)算法实现及分析 (6)关于作业以外的延拓： (10)参考文献： (11)缘起：LZW 是一种无损数据压缩算法，是对1978 年发表的LZ78 的改进。

LZW应用于Unix 系统的标准工具、GIF图片格式以及TIFF格式等。

同时LZW压缩算法对于较大规模的英文文本的压缩具有良好的效果，一般可以压缩到原来大小的一半。

然而LZW的专利曾一度限制了其使用范围，不过，LZW专利于2003年过期。

对事物的好奇心驱使我深入学习LZW 压缩和解压缩算法。

本文绝大部分的陈述来自于Dobb博士的论文以及技术博客、论坛以及维基百科。

名词规范：码书编解码时供查询、插入的字符串和整数索引的集合{(STRING,INDEX)}文本需要进行编码的数据结构编码序列编码后的整数序列码字表示字符串及其索引值的一种数据结构(STRING,INDEX)本文完成的主要工作当码书很大时，查询和编码的效率将有所下降。

查询的效率可以很直观的理解，编码效率的下降是指编码的结果是整数序列，其中将会出现较大的整数，如果不进行后续处理，需要较多的比特才能对其进行编码。

本文将结合TIF格式中的压缩原理，对Dobb博士所提及的LZW算法进行适当的改进，即，当码书容量达到一个容限值时，比如4096 = 210(13bit)，清空码书，并在编码序列中插入清除标志CLEAR，为原始数据字长(255 = 28)加1，并插入结束标志END，其大小为清除标志CLEAR加1，然后重新构造码书。

LZW编码原理LZW压缩编码如下所示1.STRING = get input character2.WHILE there are still input characters DO3. CHARACTER = get input character4. IF STRING+CHARACTER is in the string table then5. STRING = STRING+character6. ELSE7. output the code for STRING8. add STRING+CHARACTER to the string table9.IF table size reaches up to the predetermined MAX_SIZE10. renew table and append CLEAN and END label to the output11.END of IF12. STRING = CHARACTER13. END of IF14.END of WHILE15.output the code for STRING其中9~11行根据TIF格式压缩原理而添加的步骤，图1是其编码示例，由于输入文本很短，不会导致码书容量达到上限值，因而不会运行9~11行所示代码。

LZW编码算法

班级 __ __ 学号__姓名 __ ___评分__________1．实验名称LZW编码与解码算法2．实验目的2.1通过实验进一步掌握LZW编码的原理；2.2 用C/C++等高级程序设计语言实现LZW编码。

3．实验内容步骤或记录（包括源程序或流程和说明等）3.1 实验原理（1）在压缩过程中动态形成一个字符列表（字典）。

（2）每当压缩扫描图像发现一个词典中没有的字符序列，就把该字符序列存到字典中，并用字典的地址（编码）作为这个字符序列的代码，替换原图像中的字符序列，下次再碰到相同的字符序列，就用字典的地址代替字符序列3.2实验步骤LZW编码算法的具体执行步骤如下：步骤1：开始时的词典包含所有可能的根(Root)，而当前前缀P是空的；步骤2：当前字符(C) ：=字符流中的下一个字符；步骤3：判断缀-符串P+C是否在词典中(1) 如果“是”：P ：= P+C // (用C扩展P) ；(2) 如果“否”①把代表当前前缀P的码字输出到码字流;②把缀-符串P+C添加到词典;③令P ：= C //(现在的P仅包含一个字符C);步骤4：判断码字流中是否还有码字要译(1) 如果“是”，就返回到步骤2；(2) 如果“否”①把代表当前前缀P的码字输出到码字流;②结束。

3.3 源程序#include<iostream>#include<string>using namespace std;const int N=200;class LZW{private: string Dic[200];//存放词典int code[N];//存放编码过的码字public: LZW(){//设置词典根Dic[0]='a';Dic[1]='b';Dic[2]='c';string *p=Dic;//定义指针指向词典中的字符} void Bianma(string cs[N]);//进行编码int IsDic(string e);//判断是否在词典中int codeDic(string f);void display(int g);//显示结果};void LZW::Bianma(string cs[N]){string P,C,K;P=cs[0];int l=0;for(int i=1;i<N;i++){C=cs[i];//当前字符(C) ：=字符流中的下一个字符 K=P+C;if(IsDic(K)) P=K;//P+C在词典中，用C扩展P else{//P+C不在词典中code[l]=codeDic(P);Dic[3+l]=K;//将P+C加入词典P=C;l++;}if(N-1==i)//如果字符流中没有字符需要编码code[l]=codeDic(P);}display(l);}int LZW::IsDic(string e){//如果字符流中还有字符需要编码for(int b=0; b<200; b++){ if(e==Dic[b]) return 1; }return 0;}int LZW::codeDic(string f){int w=0;for(int y=0;y<200;y++)if(f==Dic[y]){w=y+1;break;}return w;}void LZW::display(int g){cout<<"经过LZW编码后的码字如下："<<endl;for(int i=0;i<=g;i++)cout<<code[i];cout<<endl;cout<<"经LZW编码后的词典如下："<<endl;for(int r=0;r<g+3;r++)cout<<r+1<<Dic[r]<<endl;}int main(){LZW t;string CSstream[N];// 存放要进行LZW编码的字符序列int length;// 要进行LZW编码的字符序列长度cout<<"请输入所求码子序列的长度：";cin>>length;while(length>=N){cout<<"该长度太长，请重新输入：";cin>>length;}cout<<"请输入要进行LZW编码的字符序列："<<endl; for(int a=0;a<length;a++)cin>>CSstream[a];t.Bianma(CSstream);return 0;}4．实验环境（包括软、硬件平台）硬件：装有32M以上内存MPC；软件：Windows XP操作系统、Visual C++高级语言环境。

LZW-编码详解

采用算术编码每个符号的平均编码长度可以为小数。
待编码的数据序列为“dacab”，信源中各符号出现的概率依次为P(a)=0.4，P(b)=0.2，P(c)=0.2， P(d)=0.2。
数据序列中的各数据符号在区间［0, 1］内的间隔（赋值范围）设定为:
a=［0, 0.4） b=［0.4, 0.6） c=［0.6, 0.8） d=［0.8, 1.0 ]
8)读入code=3H,解码完毕。
解码过程
行号
1 2 3 4 5 6 7 8
输入数据 code 2H 0H 0H 1H 6H 4H 6H 3H
新串
aa ab bb bba aab
输出结果 oldcode 生成新字符及索引
a
0H
a
0H aa<4H>
b
1H ab<5H>
bb
6H bb<6H>
aa
4H bba<7H>
输出S1=“aa”在字串表中的索引4H，并在字符串表末尾
为S1+S2=“aab”添加索引8H，且S1= S2=“b”
序号输入数据 S1+S2 输出结果 S1
生成新字符及索引
S2
1 NULL
NULL 2H
NULL
2a
a
a
3a
aa
0H
a
aa<4H>
4b
ab
0H
b
ab<5H>
5b
bb
1H
b
bb<6H>
6b
4)读入code=1H,输出“b”,然后将 oldcode=0H所对应的字符串“a”加上 code=1H对应的字符串的第一个字符”b”, 即”ab”添加到字典中，其索引为5H，同时oldcode=code=1H

数据结构与算法――电文的编码和译码

数据结构与算法――电文的编码和译码电文的编码和译码在信息传输中起着重要的作用。

在传统的通信方式中，电文的编码和译码主要通过人工来完成，但是随着科技的发展，自动编码和译码系统也逐渐应用到各个领域中。

本文将介绍电文的编码和译码的常用算法和数据结构。

1.ASCII编码ASCII（American Standard Code for Information Interchange）编码是一种常用的字符编码方案，其中规定了128个常用字符的编码方式。

在ASCII编码中，每个字符用一个8位的二进制数表示，所以可以表示的字符范围是0-127、比如字符“A”的ASCII编码是65，字符“a”的ASCII编码是97、ASCII编码采用定长编码方式，编码的长度总是8位。

ASCII编码的优点是简单明了，但是只适用于表示英文字符。

2. Huffman编码Huffman编码是一种可变长度编码方式。

它根据字符出现的频率来进行编码，出现频率高的字符编码短，出现频率低的字符编码长。

Huffman编码的原理是通过构建Huffman树来实现的。

首先统计字符出现的频率，然后根据频率构建Huffman树，最后根据Huffman树生成字符的编码。

Huffman编码的长度不固定，根据字符的出现频率进行变长编码，可以更高效地利用存储空间。

Huffman编码广泛应用于无损压缩算法中。

3.LZW编码LZW（Lempel-Ziv-Welch）编码是一种基于字典的压缩算法，它通过将输入的字符序列映射为更短的编码来实现压缩。

LZW编码的原理是建立一个字典，在字典中存储常用的字符序列和对应的编码。

开始时，字典只包含单个字符；然后，从输入的字符序列中读取字符，查找是否存在字典中；如果存在，继续读取下一个字符并拼接到当前编码后面，然后继续查找；如果不存在，将当前编码输出，并将当前字符作为新的编码插入字典中。

LZW编码可以根据输入的字符序列动态生成字典，可以适用于任意类型的数据。

图像编码常用方法介绍(三)

图像编码是将图像转化为数字信号的过程，通过压缩图像，可以减少存储空间和传输带宽的需求。

在图像编码领域，有许多常用方法，本文将介绍其中的几种。

1. 无损编码：无损编码是一种压缩图像的方法，它不丢失任何图像信息。

常见的无损编码方法有：（1）Run-Length Encoding (RLE)：该方法通过将重复的像素值替换为像素值和重复次数的组合来压缩图像。

这种方法在图像中有大量相邻重复像素值的情况下表现良好。

（2）Huffman 编码：Huffman 编码是一种变长编码方法，通过将出现频率较高的像素值用较短的编码表示，出现频率较低的像素值用较长的编码表示来压缩图像。

Huffman 编码在统计图像中像素值分布的情况下可以取得较好的压缩效果。

（3）LZW 编码：LZW 编码是一种字典编码方法，它将连续的像素值序列作为字典项，出现频率较高的连续序列用较短的编码表示，出现频率较低的连续序列用较长的编码表示来压缩图像。

LZW 编码在处理连续重复出现的序列时效果较好。

2. 有损编码：有损编码是一种压缩图像的方法，它在压缩过程中会丢弃一些图像信息，以达到更高的压缩比。

常见的有损编码方法有：（1）JPEG 编码：JPEG 编码是一种基于离散余弦变换的编码方法，它通过将图像分成多个 8x8 尺寸的像素块，然后对每个块应用离散余弦变换，再将变换后的系数进行量化和编码来压缩图像。

JPEG 编码广泛应用于静态图像的压缩。

（2）JPEG2000 编码：JPEG2000 是 JPEG 编码的升级版，它在离散小波变换的基础上进行编码。

JPEG2000 编码使用基于小波变换的空间频率分解，将图像分为多个不同分辨率的子带，并对每个子带进行独立的编码。

这种方法可以提供更好的压缩质量和可扩展性。

（3）WebP 编码：WebP 编码是一种针对网络应用的图像编码方法，它结合了无损和有损编码的特点。

WebP 编码可以根据图像内容的复杂程度自动选择使用无损或有损编码来进行图像压缩，以达到更好的压缩效果和更快的加载速度。

实验三LZW编码

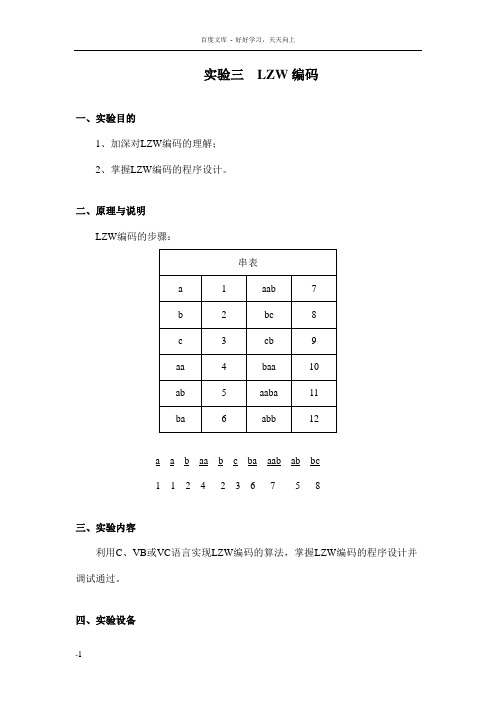
实验三LZW编码一、实验目的1、加深对LZW编码的理解；2、掌握LZW编码的程序设计。

二、原理与说明LZW编码的步骤：a ab aa bc ba aab ab bc1 12 4 23 6 7 5 8三、实验内容利用C、VB或VC语言实现LZW编码的算法，掌握LZW编码的程序设计并调试通过。

四、实验设备计算机程序如下：#include<>#include""#include""#include""#include""#define BIRS 12#define HASHING_SHIFT BITS-8#define MAX_V ALUE(1<<BITS)-1#define MAX_CODE MAX_V ALUE-1 #if BITS==14#define TABLE_SIZE 18041#endif#if BITS==13#define TABLE_SIZE 9029#endif#if BITS<=12#define TABLE_SIZE 5021int *code_value;unsigned int *prefix_code;unsigned char *append_character; unsigned char decode_stack[4000];char ok;find match(int hash_perfix,unsigned int hash_character){int index;int offset;index=(hash_character<<HASHING_SHIFT)^hash_prefix;if(index==0)offset=1;elseoffset=TABLE_SIZE-index;while(1){if(code_value[index]==-1)return(index);if(prefix_code[index]==hash_prefix&&append_character[index]==hash_character) return(index);index-=offset;if(index<0)index+=TABLE_SIZE;}}input_code(FILE*input){unsigned int return_value;static int input_bit_count=0;static unsigned long input_bit_buffer=0L;while(input_bit_count<=24){input_bit_buffer|=(unsigned long)getc(input)<<(24-input_bit_count);input_bit_count+=8;}return_value=input_bit_buffer>>(32-BITS);input_bit_buffer<<=BITS;input_bit_count-=BITS;return(return_value);}void output_code(FILE*output,unsigned int code){static int output_bit_count=0;static unsigned long output_bit_buffer=0L;output_bit_buffer|=(unsigned long)code<<(32-BITS-output_bit_count);output_bit_count+=BITS;while(output_bit_count>=8)putc(output_bit_buffer>>24,output);output_bit_buffer<<=8;output_bit_count-=8;}}void compress(FILE *input,FILE *output){unsigned int next_code;unsigned int character;unsigned int string_code;unsigned int index;int i;next_code=256;for(i=0;i<TABLE_SIZE;i++)code_value[i]=-1;i=0;printf("\n\nCompressing...\n);string_code=getc(input);while((character=getc(input))!=(unsigned)EOF) {index=find_match(string_code,character);if(code_value[index]!=-1)string_code=code_value[index];{if(next_code<=MAX_CODE){code_value[index]=next_code++;prefix_code[index]=string_code;append_character[index]=character;}output_code(output,string_code);string_code=character;}}output_code(output,string_code);output_code(output,MAX_V ALUE);output_code(output,0);printf("\n");getchar();void expand(FILE*input,FILE*output){unsigned int next_code;unsigned int nex_code;unsigned int old_code;int character;unsigned char*string;char*decode_string(unsigned char*buffer,unsigned int code)lnext_code=256;counter=0;printf("\n\nExpanding...\n");old_code=input_code(input);character=old_code;putc(old_code,output);while((nex_code=input_code(input))!=(MAX_V ALUE)){if(new_code>=next_code){*decode_stack=character;string=(unsigned char*)decode_string(decode_stcak+1,old_code);}elsestring=(unsigned char*)decode_string(decode_stck,nex_code);character=*string;while(string>=decode_stack)putc(*string--,output);if(next_code<=MAX_CODE){append_character[next_code]=character;next_code++;}old_code=nex_code;}printf("\n");getchar();}char *decode_string(unsigned char*buffer,unsigned int code) {int i;i=0;while(code>255){*buffer++=append_character[code];code=prefix_code[code];if(i++>=4094){printf("Fatal error during code expansion.\n");exit(0);}}*buffer=code;int main(int argc,char*argv[]){FILE*input_file;FILE*output_file;FILE*lzw_file;char input_file_name[81];int select;character=*string;while(string>=decode_stack)putc(*string--,output);if(next_code<=MAX_CODE){prefix_code[next_code]=old_code;append_character[next_code]=character;next_code++;}old_code=new_code;}printf("\n");getchar();}printf("**\n");printf("**********************\n");scanf("%d",&select);if(select==1){if(argc>1)strcpy(input_file_name,argv[1]);else{printf("\nInput file name?");scanf("%s",input_file_name);printf("\nCompressed file name?");scanf("%s",compressed_file_name);}input_file=fopen(input_file_name,"rb");lzw_file=fopen(compressed_filename,"wb");while(input_file==NULL||lzw_file==NULL){printf("Fatal error opening files!\n");printf("\nInput file names?");scanf("%s",input_file_name);printf("\nCompressed file name?");scanf("%s",compressed_file_name);input_file=fopen(input_file_name,"rb");};compress(input_file,lzw_file);fclose(input_file);fclode(lzw_file);free(code_value);else if(select==2){printf("\nOnput file names?");scanf("%s",onput_filename);printf("\nExpanded file name?");scanf("%s",expanded_filename);input_file=fopen(onput_filename,"rb");lzw_file=fopen(expanded_filename,"wb");while(lzw_file==NULL||output_file==NULL){printf("Fatal error opening files!\n");printf("\nOnput file names?");scanf("%s",onput_filename);printf("\nExpanded file name?");scanf("%s",expanded_filename);input_file=fopen(onput_filename,"rb");lzw_file=fopen(expanded_filename,"wb");};expand(lzw_file,output_file);fclose(lzw_file);-11fclose(output_file);}else{exit(0);}printf("\nContinue or not(y/n)?");scanf("%c",&ok);getchar();if(ok=='y'){goto loop;}else{printf("Complete......\n\nPress any key to continue");getchar();free(prefix_code);free(append_character);}return 0;}}-12。

栅格数据存储压缩编码方法

栅格数据存储压缩编码方法
栅格数据存储压缩编码是现今计算机技术中用来将大量的栅格数据以最小的存储空间存储的方法。

这种方法通常在地理信息系统、遥感与卫星图像处理以及数字地球等领域被广泛运用。

目前，常用的栅格数据格式有TIFF、JPEG2000、PNG与GeoTIFF等。

这些格式中比较常用的是GeoTIFF，该格式可以通过GeoTools、GDAL与Esri ArcGIS等平台进行读写，同时支持多种数据类型与压缩方式。

为了减小栅格数据存储空间，通常会采用压缩算法来对数据进行无损压缩。

常用的压缩算法有Run-Length Encoding（RLE）、Huffman编码、Lempel-Ziv-Welch（LZW）编码和Deflate编码等。

RLE是最简单的压缩算法，它通过将相邻的重复值替换为一个值和一个计数来减小数据体积。

然而，RLE算法在处理随机数据时效果不佳，而且压缩率较低。

Huffman编码是一种基于字典的编码方法，它通过树形结构将频繁出现的字符替换为较短的码字，这样可以减少数据存储。

LZW编码和Deflate编码是常用的数据压缩算法，它们可以通过分析数据块中连续的模式来压缩数据。

在栅格数据存储中，压缩算法的选择取决于存储需求和数据类型。

对于图像中大量连续出现的颜色块，RLE和Huffman编码可显著降低存储空间，而对于多变的地形数据，LZW 或Deflate算法将更为有效。

总体来说，采用压缩编码方法可以极大地缩小栅格数据的存储空间，降低数据存储成本，提高数据传输的效率。

同时，在选择相应压缩算法时，需要针对不同的数据类型选择最合适的算法来达到最佳的压缩效果。

单片机能用的压缩算法

单片机能用的压缩算法标题：单片机中常用的压缩算法简介：本文将介绍在单片机中常用的压缩算法，包括哈夫曼编码、LZW算法和RLE算法，旨在提供对于单片机压缩算法的基本理解和应用。

正文：在单片机应用中，由于资源的有限性和存储容量的限制，压缩算法成为一种重要的解决方案。

压缩算法可以通过减小数据的存储空间和传输带宽来优化单片机应用的性能。

首先介绍的是哈夫曼编码，这是一种经典的无损压缩算法。

它根据数据出现的频率来构建一棵哈夫曼树，将出现频率高的字符用较短的编码表示，而出现频率低的字符用较长的编码表示。

通过这种方式，可以有效地减少数据的存储空间。

在单片机中，可以利用哈夫曼编码对传感器采集的数据进行压缩，从而节省存储空间和传输带宽。

另一个常用的压缩算法是LZW算法。

LZW算法是一种字典压缩算法，它通过建立一个字典来记录出现的字符串，并用较短的编码替代较长的字符串。

在单片机中，LZW算法可以应用于图像压缩，将图像中的连续像素序列转换为较短的编码，从而减小图像的存储空间和传输带宽。

此外，还有一种简单且高效的压缩算法是RLE算法。

RLE算法是一种基于重复数据的压缩算法，它将连续出现的相同数据用一个计数值和该数据表示。

在单片机中，RLE算法可以应用于音频数据的压缩，将连续相同的音频采样数据用一个计数值表示，从而减小音频数据的存储空间和传输带宽。

综上所述，单片机中常用的压缩算法包括哈夫曼编码、LZW算法和RLE算法。

这些压缩算法可以在有限的资源条件下优化单片机应用的性能。

使用这些算法可以减小数据的存储空间和传输带宽，提高单片机应用的效率和响应速度。

通过合理选择和应用压缩算法，可以充分利用单片机的资源，并满足对存储和传输效率的要求。

在实际应用中，需要根据具体的场景和需求选择最适合的压缩算法，并根据实际情况进行参数调节和优化。