1.磁路
第一章 磁路

第一章磁路电机是一种机电能量转换装置,变压器是一种电能传递装置,它们的工作原理都以电磁感应原理为基础,且以电场或磁场作为其耦合场。
在通常情况下,由于磁场在空气中的储能密度比电场大很多,所以绝大多数电机均以磁场作为耦合扬。
磁场的强弱和分布,不仅关系到电机的性能,而且还将决定电机的体积和重量;所以磁场的分析扣计箅,对于认识电机是十分重要的。
由于电机的结构比校复杂,加上铁磁材料的非线性性质,很难用麦克斯韦方程直接解析求解;因此在实际工作中.常把磁场问题简化成磁路问题来处理。
从工程观点来说,准确度已经足够。
本章先说明磁路的基本定律,然后介绍常用铁磁材料及其性能,最后说明磁路的计算方法。
1-1 磁路的基本定律一、磁路的概念磁通所通过的路径称为磁路。
图1—1表示两种常见的磁路,其中图a为变压器的磁路,图b为两极直流电机的磁路。
在电机和变压器里,常把线圈套装在铁心上。
当线圈内通有电流时、在线圈周围的空间(包括铁心内、外)就会形成磁场。
由于铁心的导磁性能比空气要好得多,所以绝大部分磁通将在铁心内通过,并在能量传递或转换过程中起耦合场的作用,这部分磁通称为主磁通。
围绕裁流线圈、部分铁心和铁心周围的空间,还存在少量分散的磁通,这部分磁通称为漏磁通。
主磁通和漏磁通所通过的路径分别构成主磁路和漏磁路,图1—l中示意地表出了这两种磁路。
用以激励磁路中磁通的载流线圈称为励磁线圈(或称励磁绕组),励磁线圈中的电流称为励磁电流(或激磁电流)。
若励磁电流为直流,磁路中的磁通是恒定的,不随时间而变化,这种磁路称为直流磁路;直流电机的磁路就属于这一类。
若励磁电流为交流(为把交、直流激励区分开,本书中对文流情况以后称为激磁电流),磁路中的磁通随时间交变变化,这种磁路称为交流磁路;交流铁心线圈、变压器和感应电机的磁路都属于这一类。
二、磁路的基本定律进行磁路分析和计算时,往往要用到以下几条定律。
安培环路定律 沿着任何一条闭合回线L ,磁场强度H 的线积分值dlH L∙⎰ 恰好等于该闭合回线所包围的总电流值∑i ,(代数和).这就是安培环路定律(图l —2)。
什么是磁路-什么是电路-电路与磁路的区别

什么是磁路?什么是电路?电路与磁路的区别我们首先来看两个概念:磁路和电路。
那么什么是磁路,什么是电路呢,只有搞清楚这两个概念是什么,我们才能分析二者之间到底有什么区别。
我们先来看什么是电路:在电动势或者电压的作用下,电流所流经的路径叫电路。
电路的组成是由电源、负载和开关三部分结构。
而电路又分为直流电路和交流电路。
流经电路的电流的大小和方向不随时间变化的电路,叫做直流电路。
流经电路的电流的大小和方向随时间变化的电路,叫做交流电路。
看完了电路,我们再来讲讲磁路。
当通电线圈中具有铁芯时,磁动势所产生的磁通,主要集中在由铁芯所规定的路径内,这种路径就叫做磁路。
而磁路也是分为直流磁路和交流磁路。
由直流电流励磁的磁路,叫做直流磁路,由交流电流励磁的磁路,叫做交流磁路。
电路与磁路相同点确实没有什么可说的。
在电路中,电流是电动势产生的,在磁路中,磁通是由磁动势产生的。
在电路中,电流经过电阻便产生电压降,在磁路中,磁通经过磁阻便产生磁压降。
在电路中,用欧姆定律来表示电流、电阻和电压降之间的关系,在磁路中,用与电路相似的磁路欧姆定律来表示磁通、磁阻和磁动势之间的关系。
但是,电路与磁路二者有本质上的区别,主要区别如下:a.在电路中,没有电动势时,电流等于零。
而在磁路没有磁动势时,由于磁滞现象,总是或多或少地存在剩磁。
b.电流代表电荷的移动,而磁通却不代表任何质点移动。
磁通通过滋阻时,不象电流通过电阻那样要消耗能量,维持恒定磁通也并不需要消耗任何能童。
因此,在电路中可以有断路情况,在磁路中却没有断路的情况,只要有磁动势存在,总会引起相应的磁通,磁通总是连续的。
c.由于铁磁材料具有磁饱和现象,所以磁路的磁阻都是非线性,这与一般情况下电路电阻都是线性电阻是不一样的。
因此,磁路欧姆定律一般只能用来对磁路进行定性分析。
d.在电路中,导电材料的电导率一般比绝缘材料的电导率大儿千万倍以上,所以电路的漏电非常小,完全可以忽略不计。
在磁路中,铁磁材料的磁导率一般比非铁磁材料的磁导率只大几千倍甚至更小。
1 磁路

但是,电路和磁路只是形式上的相似,本质上是有区别的。 在电路中有真正的带电粒子在做定向运动,而在磁路中却没 有什么东西沿着闭合回路流动。
对电来讲,存在电的导体和绝缘体,电流可以集中在导体 中流过,可是不存在磁的导体,和磁的绝缘体。因此,磁路 概念并不象电路概念那样简明。
9
不过由于磁材料的磁导率很大,能使绝大部分磁通 集中在一定的回路中通过,因此从工程计算的角度 来看,为了简单方便,将磁场的问题简化成磁路来 处理,在大多数情况下,准确度已经足够了。
从上述的磁化过程可以看出,B的变化总是落后于H 的变化,这种现象就称为磁滞。
22
左图的闭合曲线称为磁滞回线。 Bm越大,磁滞回线面积也越大。 从左图曲线可以看出,当H下降 到零时,B并不下降到零而是保 持一定数值,这是因为外磁场虽 然消失了,但磁畴还不能恢复原 来状态,还保留一定磁性,称为 剩磁。
在磁场强度H由零开始逐 渐增加时,磁感应强度也 随着逐渐增加, 这种B=f(H)曲线就称为原 始磁化曲线,其形状如右 图所示。
铁磁材料与非铁磁材料的磁化曲线
20
在Oa段,H值增加时,B值 增加较快,这是因为随着H 值的增加,有越来越多的 磁畴趋向于外磁场的方向, 使磁场增强。 在ab段,随着H值的继续增 加,大部分磁畴已趋向外 磁场的方向,可以转向的 磁畴越来越少,故B值增加 越来越慢,这段曲线称为 磁化曲线的膝部。
(2) I2=H2l/N=924×0.5/200=2.31A
12
二. 磁路的基尔霍夫第一定律 下图中,如果在中间铁芯柱的线圈中通以电流,则产 生磁通,其路径如虚线所示,从图中显然可以看出:
1 2
A
3
1
或
0
1 2 3
第一章 磁路基础知识

l1 l2 3l 15 10 2 m 两边磁路长度:
气隙磁位降: B 1.211 2H 2 2 2.5 10 3 A 4818 A 0 4π 10 7
1.211 (2 0.25) 2 B T 1.533T 中间铁心磁位降: 3 4 A 4 10
磁路基础知识
1.2.3涡流与涡流损耗 1、涡流 2、涡流损耗:涡流在铁心中引起的损耗 3、注意:为减小涡流损耗,电机和变压器的铁心都用 含硅量较高的薄硅钢片叠成。 4、铁心损耗:磁滞损耗+涡流损耗
2 pFe f 1.3 BmG
南通大学《电机学》
磁路基础知识
1.3直流磁路的计算
磁路计算正问题——给定磁通量,计算所需的励磁磁动势 磁路计算逆问题——给定励磁磁势,计算磁路内的磁通量 磁路计算正问题的步骤: 1)将磁路按材料性质和不同截面尺寸分段; 2)计算各段磁路的有效截面积Ak和平均长度lk; 3)计算各段磁路的平均磁通密度Ak ,Bk=Φk/Ak; 4)根据Bk求出对应的Hk;
Φ
RmFe
N
F
Rm
i
Φ
串联磁路 南通大学《电机学》 磁路基础知识
模拟电路图
解:铁心内磁通密度为 BFe 0.0009 T 1T
AFe 0.0009
从铸钢磁化曲线查得:与BFe对应的HFe=9×102A/m
H FelFe 9 10 2 0.3A 270 A 铁心段的磁位降:
查磁化曲线:H1 H 2 215 A/m
H1l1 H 2l2 215 15 10 2 A 32.25A
总磁动势和励磁电流为:
Ni 2H H l
3 3
H 1l1
电机学第1章磁路

涡流损耗
铁芯是有阻值的,当磁通交变时,铁芯中就会感应交变的电 势,进而在铁心内引起环流。这些环流通作涡流状流动,称 为涡流涡流引起的损耗,称为涡流损耗。
pw k w f B
2
2 m
思考:如何尽量减小涡流损耗?
• 为减小涡流损耗, 电机和变压器的铁 心都用含硅量较高 的薄硅钢片叠成。
后于磁场强度变化,通常在电机内也可理解为磁通落后于 激磁电流的现象,称为磁滞现象)。
磁滞回线:磁场强度H缓慢地循环变化,B-H曲线封 闭曲线 • 磁滞现象是铁磁材料的另一个特性。
B
Bm
b
a
Br
Hc
c f e
Hc
H
Hm
Hm
d
Bm
图1-7 铁磁材料的磁滞回线
基本磁化曲线:
对同一铁磁材料,选择不同的磁场强度进行反复 磁化,可得一系列大小不同的磁滞回线,再将各 磁滞回线的顶点联接起来,所得的曲线。
2.磁化曲线和磁滞回线
磁化曲线:将一块尚未磁化的铁磁材料进行磁化,当磁 场强度H由零逐渐增大时,磁通密度B将随之增大, 得到曲线B=f(H)。 特性:①具有高的导磁性能;②磁化曲线呈非线性(饱 和特性)它的磁化曲线具有饱和性,磁导率μFe不 是常数,且随H的变化而变化。 磁滞回线在oa段:当H增大→B增大,但B增大速度较慢 在ab段:当H增大→B增大,B增大速度快; 在bc段:B随H增大的速度又较慢; 在cd段:为磁饱和区(又呈直线段)。其中拐弯点b称 为膝点;c点为饱和点。 • 过了饱和点c,铁磁材料的磁导率趋近μ0。
R
k
mk
Fm
• 磁路和电路的比拟仅是一种数学形式上的类似、 而不是物理本质的相似。
电机学第一章 磁路

H
随着磁场强度H的增大,饱和程度增加,μFe减 小,Rm增大,导磁性能降低.
B
c b
B = f ( H)
d
μFe = f ( H )
a
B = μ0 H
H
设计电机和变压器时,为使主磁路内得到较大的 磁通量而又不过分增大励磁磁动势.通常把铁心 内的工作磁通密度选择在膝点附近
B
c b
膝点 饱和点
B = f ( H)
四、铁心损耗
1.磁滞损耗
定义: 铁磁材料置于交变磁场中时,磁畴相 互间不停地摩擦、消耗能量、造成损耗,这种 损耗称为磁滞损耗。 公式: n h h m
p = C fB V
应用:由于硅钢片磁滞回线的面积较 小,故电机和变压器的铁心常用硅钢片叠成。
2.涡流损耗
¾涡流:铁磁材料在交变磁场将 有围绕磁通呈蜗旋状的感应电动 势和电流产生,简称涡流。 ¾涡流损耗:涡流在其流通路径 上的等效电阻中产生的I2R损耗 称为涡流损耗。 ¾涡流损耗与磁场交变频率f, 厚度d和最大磁感应强度Bm的平 方成正比,与材料的电阻率成反 比。 ¾要减小涡流损耗,首先应减小 厚度,其次是增加涡流回路中的 电阻。电工硅钢片中加入适量的 硅,制成硅钢片,显著提高电阻 率
表1.1 磁路和电路对比表 序 号 1 2 3 4 5 6 7 8 9 电 基本物理量 或基本定律 电 流 电 压 电 阻 电 导 电流密度 电导率 基尔霍夫 第一定律 基尔霍夫 第二定律 欧姆定律 路 符号或 定义 I U R=l/(γA) G=1/R J=I/A 单位 A V Ω S A/m2 S/m 磁 路 单 位 Wb A 1/H H Wb/m2(T) H/m 基本物理量或 符号或 基本定律 定义 磁 通 φ F 磁动势 磁 阻 磁 导 磁通密度 磁导率 磁通连续性 原理 Rm=l/(μA)
电机与拖动基础1

说明: 如果不是均匀磁场,则取B的平均值。
磁感应强度B 在数值上可以看成为与磁场方向垂 直的单位面积所通过的磁通,故又称磁通密度。
磁通 的单位:韦[伯](Wb)
1-4
3 磁场强度H
磁场强度H :介质中某点的磁感应强度 B 与介质
对于铁磁材料,磁导率μ除了比μ0大得多以外 ,还与磁场强度以及物质磁状态的历史有关,所以 铁磁材料的磁导率μ不是常数。
在工程计算时,事先将各种铁磁材料用试验的 方法,测得它们在不同磁场强度H下对应的磁通密 度B,绘制成B-H曲线,这条B-H曲线,就称为磁化 曲线。将未经磁化的铁磁材料进行磁化,磁场强度 H由零增大时,磁通密度B随之增大,所得的B=ƒ( H)曲线称为起始磁化曲线。
磁化曲线和 Fe f (H )曲线
1-21
分析磁化曲线
从图中可见,曲线分四段 在oa段:当H增大→B增
大,但B增大速度较慢;
在ab段:当H增大→B 增大,B增大速度快;
在bc段:B随H增大的 速度又较慢;
在cd段:为磁饱和区 (又呈直线段)。其中,a 点称为跗点;拐弯点b称为 膝点;c点为饱和点。
注意:尽管磁路和电路在物理量和基本定律上有一 一对应的关系,但是,磁路和电路仍有本质的区 别:
1)电路中可以有电动势而无电流,磁路中有磁动势 必有磁通
2)电路中有电流就有功率损耗,而在恒磁通下,磁 路中无损耗(直流磁路中有磁通但铁心中没有损耗)
3)电流只在导体中流过,而磁路中除了主磁通外还 必须考虑到漏磁通的影响(磁路中磁通没有绝磁体,磁通在除铁 心中外在周围空气中也有漏磁通)
在磁路(magnetic circuit)中根据磁通的连续性可得: 穿入任一闭合面的磁通必等于穿出该闭合面的磁通,即 磁路中通过任何闭合面上的磁通的代数和等于零,
磁路及交流铁心线圈

1.磁路的欧姆定律
式中
为磁阻,
2.磁路基尔霍夫第一定律
3.磁路基尔霍夫第二定律
为磁导。
二、交流铁芯线圈
励磁电流为直流时,称为直流铁心线圈(如直流电磁铁、 直流继电器的线圈),当励磁电流为交流时,称为交流铁心线 圈(如交流电机、变压器的线圈)。
i
+
– e
u –
e+–+
N
主磁通 :通过铁心闭合的 磁通。 与i不是线性关系。
O
到饱和值,这种现象称为磁 饱和性。从图中还可看出B 和H不成正比,所以磁性材 料的μ不是常数。
H
磁性材料的磁化曲线
(3)磁滞特性 若将磁性材料进行周期性磁化,磁感应强度 B随磁场强
度H 变化的曲线称为磁滞回线,如图所示。
从图中可见,当 H 已减到零 时, B 并未回到零值,而等于 Br 。这种磁感应强度滞后于磁场
磁路及交流铁心线圈
一、磁路及其基本定律
(一)磁路的概念 磁力线所通过的路径称为磁路。磁路主要由具有良好导 磁性能的磁性材料构成,如:硅钢片,铸铁等。
i1
u1 e1Βιβλιοθήκη N1N2e2
当线圈(通常被称为励磁线圈或励磁绕组)中通入电 流(通常被称为励磁电流)时,在线圈周围会形成磁场, 由于铁心的导磁性能比空气要好得多,所以绝大部分的磁 通将在铁心内通过,我们称它为主磁通或工作磁通;同时 有少量磁通会通过空气交链,我们称它为漏磁通,工程中 通常忽略不计。主磁通和漏磁通所通过的路径分别称为主 磁路和漏磁路。
或
3. 磁场强度H 磁场强度是计算磁场时所用的一个物理量,它也是个 矢量,根据安培环环路定理,沿任意闭合路径,磁场强度 的线积分等于该回路所包围的导体电流的代数和。
第一章磁路

第一章 磁路
电力拖动中广泛应用的电机、变压 器及部分控制电机都是依靠电与磁相 互作用而运行的,它们的工作原理既 涉及电路又涉及磁路。
电机学
1.1 1.2 1.3 1.4 1.5
磁场基本物理量 磁性材料 磁路的计算 交流铁心线圈 电磁铁
电机学
1.1 磁场的基本物理量
• 磁感应强度B
描述磁场强弱与方向的物理量 定义:单位正电荷以单位速度向垂直于磁场方向的方 向上运动时所受的机械力。 方向: B与产生磁场的电流方向符合右手螺旋定则。 单位:磁感应强度的单位: T(特斯拉) (高斯)
Φ2 B2
Φ3 B3 S3
2 B2S2 =1 6 10-4 =6 10-4 wb 截面S3中的磁通为: 3 1 2 10 104 6 104 4 104 wb 3 4 104 B3 0.8T 4 S3 5 10
电机学
例4:如图是一个对称磁路,中间柱截面积S3 是两边柱截面积S1或S2的两倍,假使N1I1=N2I2 , 求Φ1 ,Φ2,Φ3的大小关系和B1,B2,B3的大 小关系。
电机学
磁路
电路
磁动势F 磁通Φ 磁感应强度B 磁阻Rm=l/μS 欧姆定律φ=NI/Rm 克希荷夫磁通定律ΣΦk=0 克希荷夫定律磁压定律 ΣIN=Σ(H l)
电动势E 电流I 电流密度J 电阻R=l/rS 欧姆定律I=E/R 克希荷夫定律电流定律ΣI=0 克希荷夫定律电压定律 ΣE =Σ(IR)
1 2 , 3 21 2 2 B 1 =B 2 =B 3
电机学
例1.3.2 已知:l1=l3=60cm,l2=20cm, S2=S3=10cm2 , S1=20cm2 ,Φ3=5*10-4wb,材料为铸钢,求磁动势。
电机学讲义 (1)

DR510 D:电工钢板; R:热轧; 510:表示铁耗大小的数据,
5.1W/kG. DW310 D:电工钢板; W:无取向冷轧; 310:表示铁耗大小
的数据,3.1W/kG . DQ280 D:电工钢板; Q:有取向冷轧; 280:表示铁耗大小的
数据,2.8W/kW.
三、铁磁材料
1、软磁材料
2、硬磁材料
HL Ni
2、磁路的欧姆定律
作用在磁路上的磁动势 F 等于磁路内的磁通量 Φ乘以 磁阻 Rm
磁通量Φ等于磁通密度乘以面积
BdA BA
磁场强度等于磁通密度除以磁导率 H B /
于是
Ni lB / l /(A)
F Rm
[例1-1] 有一闭合铁心磁路,铁心的截面积A=9×10-4m2,
BFe
AFe
0.0009 0.0009
T
1T
从铸钢磁化曲线查得:与BFe对应的HFe=9×102A/m
铁心段的磁位降: H FelFe 9 10 2 0.3A 270 A
空气隙中: B
A
0.0009 3.052 10 4
T
0.967T
H
B
0
0.967
总磁动势和励磁电流为:
Ni 2H H3l3 H1l1
(4818 87.75 32.25)A 4938A
第四节 交流磁路的特点
交流磁路除了会在铁心中产生铁心损耗外,还有以 下两个效应: 1)磁通量随时间变化,在励磁线圈中产生感应电 动势。 2)磁饱和现象会导致电流、磁通和电动势波形畸 变。
[补]电机的铁心为什么常常用硅钢板叠成?
第一章磁路

铁磁物质的磁导率
非铁磁材料的磁导率接近真空磁导率0 ,铁 磁材料的磁导率比非铁磁材料的磁导率大得多, 即 0 。 常用铁磁材料的磁导率 铸钢: ≈1000 0 硅钢片:≈(6000 ~ 7000) 0 玻莫合金: ≈(20000 ~ 200000) 0
二、磁化曲线及磁滞回线
???
F Hl 159 0 .3 A 47 .7 A
励磁电流
iF
N
9.54 10 A
2
磁路的基本定律
磁路的基尔霍夫第一定律
磁路的基尔霍夫第一定律:穿出或进入 任一闭和面的总磁通量恒等于零(或者说, 进入任一闭合面的磁通量恒等于穿出该闭 合面的磁通量),这就是磁通连续性定律。
在电路中有电流时,就有功率损耗 I R ;而在直流磁路中,维持一 定的磁通量 ,铁心中没有功率损耗。
2
在电路中可以认为电流全部在导线中流过,导线外没有电流,在 磁路中,则没有绝对的磁绝缘体,除了铁心中的磁通外,实际上总 有一部分漏磁通散布在周围的空气中。 电路中导体的电阻率 在一定的温度下是不变的,而磁路中铁心 的磁导率 Fe却不是常值,它是随铁心的饱和程度大小而变化的。
2、磁路欧姆定律
对于一个等截面无分支的铁心磁路,如图 由于:Ф =∫BdA=BA H=B/μ F=Ni=Hl=(B/μ )l= Ф l/(μ A) 所以: F= ФRm
Ф i N A
Ф i N 磁路 A
F
磁路
Ф
Rm
相当于电路的欧姆定律: U= RI 模拟电路图如图。
模拟电路图 Ф F
Rm
公式:
- Φ1 Φ2 Φ3 0
Φ 0
Rm2
又称磁路的并联定律。
电机学第1章

if 1T Bm 1.8T then
pFe CFe f 1.3Bm2G
2020年1月23日星期四
20
1.3 磁路的计算
1.直流磁路的计算 2.直流电机的空载磁路和磁化曲线 3.永磁磁路的计算特点 4.交流磁路的特点
2020年1月23日星期四
15
3.铁磁材料
材料名称 磁性能
表1-1 永磁材料的磁性能
铝镍钴(AL 铁氧体(Y35) 稀土钴(YX 钕铁硼(N42
NICO 56/6)
G-26)
H)
剩磁T
1.35
0.39
1.03
1.33
矫顽力(kA/m)
60
200
765
907
最大磁能积
56
31.8
198
326
BH(kJ/)
2020年1月23日星期四
2
1.磁路的概念
图1-1 两种常见的磁路 a)变压器的磁路 b)四极直流电机的磁路
2020年1月23日星期四
3
2.磁路的基本定律
分析和计算磁场时,常常要用到两条基本定律: ➢ 安培环路定律, ➢ 磁通连续性定律
把这两条定律应用到磁路,可得磁路的 ➢ 欧姆定律 ➢ 磁路的基尔霍夫第一和第二定律
2020年1月23日星期四
图1-5 磁路的基尔霍夫第二定律
9
1.2 常用的铁磁材料及其特性
1.铁磁材料的磁化 2.磁化曲线和磁滞回线 3.铁磁材料 4.铁心损耗
2020年1月23日星期四
10
1.铁磁材料的磁化
磁化:铁磁材料在外磁场中呈现很强的磁性
图1-6 磁畴示意图 a)未磁化时 b)磁化后
电机与电力拖动第1章磁路
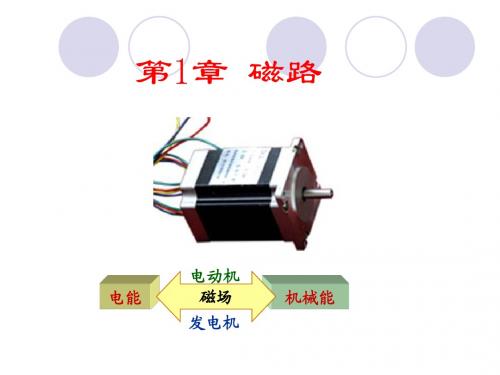
电势e正方向: 的正方向与Φ 电势 正方向:e 的正方向与Φ正方向符合右手螺旋关系 正方向
E m NωΦ m E= = = 2πfNΦ m = 4.44 fNΦ m 2 2
上一张下一张 上一张下一张
& 电动势与磁通的相位关系: & 电动势与磁通的相位关系: E = − j 4.44 fN Φ m
上一张下一张 上一张下一张
1.1 磁场的基本物理量
电流→ 磁场 ←用磁力线描述 电流 1. 磁感应强度 B
描述磁场中某点强弱和方向 的物理量,是一个矢量。 的物理量,是一个矢量。 磁力线是闭合的, 磁力线是闭合的,且围绕 着产生它的电流, 着产生它的电流,并满足 右手螺旋定则。 右手螺旋定则。 定义式: 定义式:
1. 高导磁性
铸钢: ※ 铸钢:
µ >> µ 0
µ ≈1 000 µ 0 硅钢片: 硅钢片: µ ≈ ( 6 000 ~ 7 000) µ 0 玻莫合金: 大几万倍。 玻莫合金:µ 比 µ 0 大几万倍。
上一张下一张 上一张下一张
磁性物质内部存在着很多很小的“磁畴” 磁性物质内部存在着很多很小的“磁畴”。
(a) Φ
(b)
涡流损耗
上一张下一张 上一张下一张
1.3 磁路和磁路定律
1.3.1 磁路的基本概念
磁力线经过的路径称为磁路。 磁力线经过的路径称为磁路。 主磁通:全部在磁路中闭合的磁通。 主磁通:全部在磁路中闭合的磁通。
N
电机空载磁路
S
漏磁通: 漏磁通:部分经过磁路周围物质闭合的磁通以及全部不在 磁路中闭合的磁通。 磁路中闭合的磁通。
上一张下一张 上一张下一张
5、磁路的基尔霍夫第一定律 、 任何磁路中, 任何磁路中,流进节点的磁通代数和为零 A Φ1 节点A: Φ2 Φ3 节点 : Φ1+ Φ2+ Φ3=0
磁 路

以说磁路是封闭在一定范围里的磁场,所以描述磁场的物理量也适用
于磁路。
1.1 磁场的基本物理量
1.磁感应强度
磁感应强度是表示磁场内某点的磁场强弱和方向的物理量,是个矢量,
用符号B表示。
对于电流产生的磁场,磁感应强度的方向和电流方向满足右手螺旋定
则,其大小可用式(1.1)表示
B=F/lI
(1.1)
材料的磁滞性。
1.3 磁路的基本定律
1.安培环路定律(全电流定律)
安培环路定律可用来确定磁场与电流之间的关系,是计算磁路的基本
公式。其数学表达式为
H dl I
(1.5)
2.磁路的欧姆定律
磁路欧姆定律是分析磁路的基本定律。以图1.1铁心线圈为例。媒质
是均匀的,磁导率为,根据式(1.5)得
式(1.1)中F表示磁通势,l表示磁路平均长度,I表示电流。感应强 度的单位是特斯拉(T)即韦伯/米2。
如果磁场内各点磁感应强度大小相等,方向相同的磁场,这样的称为
匀强磁场。
2. 磁通
磁感应强度B与垂直于磁场方向面积S的乘积,称为通过该面积的磁
通。用符号Φ表示,单位是Wb(韦伯)。在均匀磁场中
在没有外磁场作用时,小磁畴排列无序,对外部不显示磁性。在外磁
场作用下,一些小磁畴就会顺向外磁场方向而形成规则的排列,此时
磁性材料对外显示出磁性。随着外磁场的增强,大量磁畴都转到与外
磁场相同的方向,这样便产生了一个很强的与外磁场同方向的磁化磁
场,使磁性材料内的磁感应强度大大增强。磁性材料的磁化如图1.2
NI Hl B l l S
ቤተ መጻሕፍቲ ባይዱ
(N为线圈匝数)
(1.6)
因此,有
NI F l Rm S
电机学第五版第1章 磁路ppt课件

涡流损耗 涡流在铁心中引起的损耗。 公式:
pe=CeD2f2Bm 2V
应用:C为e — 减小涡涡流流损 损耗耗,系 电机数和变 压器的铁心都用含硅量较高的薄硅钢片 (0.35~0.5mm)叠成。
.
41..铁2心损常耗用的铁磁材料及其特性
磁滞损耗 铁磁材料置于交变磁场中时,材料被反复交变磁化, 与此同时,磁畴相互间不停地摩擦造成损耗,这种损耗称为磁滞损耗。
公式: ph = Ch fBmnV
Ch —磁滞损耗系数
应用:由于硅钢片磁滞回线的面积较小,故电机和变压器的铁心 常用硅钢片叠成。
.
41..铁2心损常耗用的铁磁材料及其特性
图1-17 直流电机的磁化曲线
.
3.永磁磁路的计算特点
(1)气隙内的磁位降Hδδ,是由永磁体内所形成的或者说所提供的,FM=-HMlM; 永磁体内的工作磁场强度HM和长度lM愈大,永磁体提供的磁动势就愈大。 (2)永磁体·的磁场HM总是负值,也就是说,它总是工作在永磁材料磁滞回线 的第二象限这段曲线上,这段曲线通常称为退磁曲线,如图1-19中段所示。 (3)若磁路中没有气隙,δ=0,则HMlM=0,于是HM=0,从退磁曲线可见,此时 永磁体内的磁通密度为剩磁Br,如图1-19中的R点所示。 。
???
图1-14 气隙磁场的边缘效应
.
1.3 磁路的计算
解 用磁路的基尔霍夫第二定律来求解。
铁心内的磁场强度: H F e=m B F F e e=5000创 4 1 p10 -7=159A /m
气隙磁场强度:
Hd=m B0d =41´p´3.130025-27 =77?104A/m
电机学:第一章 磁路2
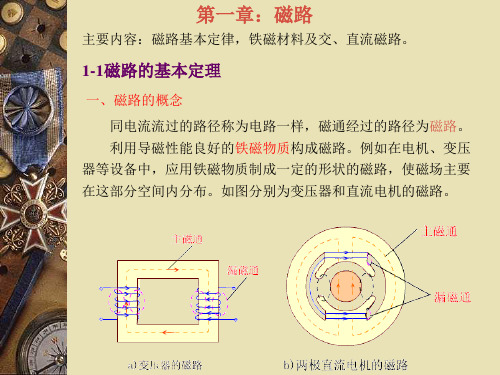
主要内容:磁路基本定律,铁磁材料及交、直流磁路。
1-1磁路的基本定理
一、磁路的概念 同电流流过的路径称为电路一样,磁通经过的路径为磁路。 利用导磁性能良好的铁磁物质构成磁路。例如在电机、变压
器等设备中,应用铁磁物质制成一定的形状的磁路,使磁场主要 在这部分空间内分布。如图分别为变压器和直流电机的磁路。
用直流励磁 用交流励磁
磁路中磁通恒定 磁路中磁通交变
直流磁路 直流电机 交流磁路 变压器、感应电机
二、磁路的基本定律
磁路的基本定律有 安培环路定律,磁路的欧姆定律,磁路的基尔霍 夫第一定律,磁路的基尔霍夫第二定律。 1、安培环路定理(或称全电流定理)
在磁路中沿任一闭合路径L,磁场H的线积分等于该闭合回路所包围 的总电流,即:
基尔霍夫第二定律
Ni Hl Rm
电动势 E=IR 电流 I 电阻 R=L/σA =ρL/A 电导 G=1/R
电导率
欧姆定律 I= E R
基尔霍夫第一定律 i 0
基尔霍夫第二定律
e iR
电路与磁路的不同点:
1、电路中有电流就有功率损耗。磁路中恒定磁通下没有功率损耗。 2、电流全部在导体中流动,而在磁路中没有绝对的磁绝缘体,除
范围内。所以电机和变压器的铁心用导磁率较高的铁磁材料组成。
一、铁磁物质的磁化
1 、铁磁物质
铁磁物质的磁导率都很大,一般是
的几千倍。
0
铁磁物质
金属
铁、钴、镍: B高,居里温度高。缺点是电阻率 低,涡流耗严重。
非金属 铁氧体: 电阻率高,涡流损耗小,抗锈防腐。
2、铁磁物质的磁化
缺点是B低,温度稳定性差。
I
Rm R F E
注:由于铁磁材料的磁导率不是常数,所以Rm一般不是常数。 3、磁路的基尔霍夫第一定律
磁路的三个基本定律

磁路的三个基本定律一、磁路的欧姆定律1. 内容- 磁路中的磁通Φ(单位为韦伯,Wb)与磁动势F(单位为安匝,At)成正比,与磁阻R_m(单位为H^-1)成反比,即varPhi=(F)/(R_m)。
2. 相关概念- 磁动势F:磁动势是产生磁通的激励,等于线圈的匝数N与通过线圈的电流I 的乘积,即F = NI。
例如,一个线圈匝数为100匝,通过的电流为2A,则磁动势F=100×2 = 200安匝。
- 磁阻R_m:磁阻表示磁路对磁通的阻碍作用,它与磁路的长度l(单位为米,m)成正比,与磁路的横截面积S(单位为平方米,m^2)和磁导率μ(单位为亨/米,H/m)成反比,即R_m=(l)/(μ S)。
例如,对于一段长度l = 0.5m,横截面积S=0.01m^2,磁导率μ = 4π×10^-7H/m的磁路,其磁阻R_m=(0.5)/(4π×10^-7)×0.01≈3.98×10^7H^-1。
二、磁路的基尔霍夫第一定律(磁通连续性定律)1. 内容- 对于磁路中的任一闭合面,进入该闭合面的磁通等于离开该闭合面的磁通,即∑varPhi = 0。
2. 理解与示例- 这一定律类似于电路中的基尔霍夫电流定律。
例如,在一个有分支的磁路中,假设一个节点处有三条磁路分支,磁通分别为varPhi_1、varPhi_2和varPhi_3,如果规定进入节点为正,离开节点为负,则varPhi_1-varPhi_2-varPhi_3 = 0。
也就是说,磁通在磁路的节点处是连续的,不会凭空产生或消失。
三、磁路的基尔霍夫第二定律(安培环路定律的推广)1. 内容- 在磁路的任一闭合回路上,磁动势的代数和等于各段磁路磁压降(Hl,其中H为磁场强度,单位为安/米,A/m)的代数和,即∑ F=∑ Hl。
2. 相关概念与示例- 磁场强度H:磁场强度与磁导率μ和磁感应强度B(单位为特斯拉,T)的关系为B = μ H。
磁路的基本概念 (1)

【课题名称】5.4 磁路的基本概念【课时安排】1课时(45分钟)【教学目标】1.了解磁路和磁动势的概念,了解主磁通和漏磁通的概念。
2.了解磁阻的概念,了解影响磁阻的因素。
3.了解充磁和消磁的概念,了解其在工程技术中的应用。
【教学重点】重点:磁路的基本概念;充磁和消磁在工程技术中的应用【教学难点】难点:磁路的基本概念【关键点】电生磁【教学方法】多媒体展示法、讲授法、谈话法、理论联系实际法【教具资源】多媒体课件、变压器【教学过程】一、导入新课教师可利用多媒体展示硅钢片中形成的磁路,引导学生仔细观察磁路的结构与组成,并设置一定的问题情境,从问题中引出本课的学习内容——磁路。
二、讲授新课教学环节1:磁路与磁动势教师活动:教师可利用多媒体展示硅钢片中形成的磁路,讲解磁路、磁动势的基本概念。
学生活动:学生可在教师的引导与讲解下,结合课本学习、理解磁路、磁动势的基本概念。
知识点:1.磁路:磁通经过的闭合路径。
2.磁动势:把通过线圈的电流和线圈匝数的乘积教学环节2:磁阻教师活动:教师可结合用多媒体展示的硅钢片中形成的磁路,讲解磁阻的概念以及影响磁阻的因素。
学生活动:学生可在教师的引导与讲解下,结合课本学习、认识磁阻的基本概念。
知识点:R表示。
1.磁阻:表示磁通通过磁路时所受到的阻碍作用,用符号m2.影响磁阻的因素:磁路中磁阻的大小与磁路的长度l成正比,与磁路的横截面积S成反比,并与组成磁路的材料的性质有关,写成公式为Sl R m μ=教学环节3:充磁与消磁 教师活动:教师可例举充磁和消磁在实践中的应用,引导学生明白充磁、消磁的概念及在日常生活和工作中的应用。
学生活动:学生在教师的引导下,了解充磁和消磁的应用。
三、课堂小结1.磁路和磁动势的概念。
2.磁阻的概念,影响磁阻的因素。
3.充磁和消磁的概念。
四、课堂练习再次认真阅读教材理解各种概念。
五、课后作业“学习辅导与练习”同步训练中的5.4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
磁畴:在铁磁材料内,由于自发磁化作用,某一区域 内的所有原子磁矩都按一定的规则排列,这一区域称 为磁畴。
磁畴(磁化前)
磁畴(磁化后)
磁性物质的高导磁性被广泛应用于变压器 和电机中。
第一章 磁路
2. 磁饱和性
B = H ( ≠常数)
起始磁化曲线
在一块未磁化的铁磁材料上绕上 线圈,通入电流,从零开始逐渐 增大,则铁磁物质中穿过横截面 的磁通密度将随之增大,测得对 应于不同的电流(不同的H)下的 B值。可逐点描绘出B-H曲线。即 为起始磁化曲线。
例:如右图,磁路由三段组成,两段为截面积 不同的铁磁材料,一段为空气,磁动势为NI, 则应用磁路的基尔霍夫第二定律有:
第一章 磁路
磁位差Um (磁压降) Um = Hmlm
Um = F
第一章 磁路
5、电路与磁路的区别
(1)电路中有电流就有功率损耗。磁路中恒定磁通下没有 功率损耗; (2)电流全部在导体中流动,而在磁路中没有绝对的磁绝 缘体; (3)对于线性电路可应用叠加原理,而当磁路饱和时为非 线性,不能应用叠加原理。 可见,磁路与电路仅是形式上的类似,而本质是不同的。
i方向和L参考方向符合右手法则。 若沿L,磁场强度H处处相等,则:
H۰L=N۰i N۰i为安匝数,表征磁势的大小。
安培环路定律
第一章 磁路
2、磁路的欧姆定律
不分支磁路的磁通等于作用于该磁路的磁势与磁阻之 比,即为磁路欧姆定律。由以下式子推导:
BdA BA
B H
H Ni l
第一章 磁路
三、基本电磁定律
1、电磁感应定律
e d N d
dt
dt
方向由右手定则判定(发电机准则)。
为实验定律(也称楞次定律)。
2、电磁力定律
方向由左手定则判定(电动机准则)。
第一章 磁路
1.2 常用铁磁材料及其特性
按磁导率分类:非磁性物质、磁性物质。
非磁性物质
≈ 0
0 =4 10-7 H / m
用以产生磁路中磁通的载流线圈称为励磁线圈,其电流 称为励磁电流(或激磁电流)。
用直流励磁 磁路中磁通恒定 直流磁路 直流电机 用交流励磁 磁路中磁通交变 交流磁路 变压器
感应电机
第一章 磁路
二、磁路的基本定律
1、安培环路定律(全电流定律) 在磁场中沿任一闭合路径L,磁场强
度H的线积分等于该闭合回路所包围的 总电流,即
减小涡流及其损耗 。
③用很薄的硅钢片叠成铁心,
减小涡流及其损耗 。
Φ
(b)
涡流损耗
第一章 磁路
1.3 磁路计算
1. 直流磁路
励磁 U → I → N I→
I
电压与电流的关系:
+
Φ
I=
U R
UΦຫໍສະໝຸດ -线圈的功率:P = R I2
第一章 磁路
2. 交流磁路
(1) 电磁关系
励磁:u → i →N i →Φ →e =-N
第一章 磁路
1.1 磁路的基本定律
一. 磁路的概念
工程上,为得到较强磁场,
广泛利用铁磁物质,在电机、 变压器等设备中应用铁磁物质
+
i
u
制成一定形状,人为的构成磁 -
通的路径,使磁场主要在这部
分空间内分布,这种磁通所通
过的路径称之为磁路。
Φ Φ
主磁通 磁路
漏磁通
第一章 磁路
引入磁路的概念,就把分布在整个空间的磁场问题,简 化为局限在一定范围内的磁路问题。由于铁心的导磁性比 空气好得多,所以绝大部分磁通在铁心中通过,这部分磁 通称为主磁通。经过空气隙闭合的磁路为漏磁通。
2
=
0.002 2
Wb
Φ1 I1
N1 Φ3
所以
= 0.001 Wb
B1 =
1
A1
=
0.001 8×10-4
T = 1.25 T
Φ2 I2
N2
第一章 磁路
B3 =
3
A3
=
0.002 20×10-4
T=1T
由磁化曲线查得:
H1 = 6.5 A/m
H3 = 3 A/m 最后求得
F1 = F2 = Um1+Um3 = H1l1+H3l3 = (6.5×30+3×10) A
3-2-1 = 0
Um1+Um3 = F1 Um2+Um3 = F2 已知: F1 = F2 ,l1 = l2 可得: Um1 = Um2
Φ1 I1
Φ2 I2
N1 Φ3
N2
第一章 磁路
即 因此 由于
H1 l1 = H2 l2 H1 = H2 B1 = B2
1 = 2
1 = 2 =
3
B B = f (H)
O H
起始磁化曲线
第一章 磁路
非铁磁材料的磁化曲线—直线
铁磁材料的磁化曲线—曲线 oa 起始段 ab 直线段 bc 饱和段 cd 过饱和段 b 膝点
B d
c B f (H) b
Fe f (H)
a
0
B 0 H
H
第一章 磁路
3. 磁滞性-磁滞回线
若对铁磁材料进行周期性的
= 225 A
第一章 磁路
本章结束!
Ce为涡流损耗系数,取决于材料电阻率;
Δ为电工硅钢片厚度。
第一章 磁路
(3)交变磁场中,由于存在磁滞效应,涡流效应等, 引起损耗功率,在电机、变压器中称为铁耗。
铜损耗使线圈发热, 铁损耗使铁心发热。0.35mm 减小铁损耗的方法:00..3207mmmm ① 使用软磁材料减小P0h.2。2mm ② 增大铁心的电阻率,
Ni
1
l A
F
Rm F Rm
l
Rm A F Ni
Rm为磁阻,磁路截 面愈大,路径愈长, 磁阻愈大。类似于电 阻,但本质不同。 F=N*i为作用在铁心 磁路上的安匝数,称 为磁路的磁动势。
i
N
A
l
a)无分支铁心磁路
Ф
F
Rm
b)模拟电路图
第一章 磁路
3、磁路的基尔霍夫第一定律
Um1 = H1 l1 = 9.2×30 A = 276 A
Um2 = H2 l2
= 14×12 A = 168 A
(5) 磁通势
l0/2
F = Um0+Um2+Um2 = ( 7 960+276+168 ) A
= 8 404 A
II
l1 A1
A2
l2
第一章 磁路
总结: 给定磁通,计算所需的励磁磁动势,计算步骤如下:
d
dt
→e =-N
d
dt
=-L
di dt
u = Ri-e-e
i
+e
u -
e
Φ Φ
第一章 磁路
【例 题】 图示磁路是由两块铸钢铁心及它们之间的
一段空气隙构成。各部分尺寸为:l0/2 = 0.5 cm , l1 = 30 cm ,l2 = 12 cm ,A0 = A1 = 4*4 cm2 , A2 = 8 cm2 。 线圈中的电流为直流电流。今要求在空气隙处的磁感应强
设计电机、变压器时, 为使主磁路内的磁通较 大而又不过分增大励磁 磁动势,一般把工作磁 通密度选在膝点附近。
基本磁化曲线
第一章 磁路 电机中常用铁磁材料的基本磁化曲线
第一章 磁路
5. 铁心损耗
(1)磁滞损耗 在铁芯被交变磁化过程中,铁芯内磁畴来回翻转,
互相摩擦,一方面使得磁通的变化落后于磁势的变化, 出现磁滞现象。另一方面,这些磁畴翻转摩擦使得铁芯 发热,消耗电源有功功率,称为磁滞损耗。
(1)将磁路按材料性质和不同截面分成数段 (2)计算各段的有效面积和平均长度Ai,Li (3)根据各段中的Φi计算各段对应的Bi (4)由Bi->Hi对铁磁材料查磁化曲线;
对空气磁路,按线性对待,B=µ0H
(5)计算出各段的磁压降HiLi,最后求F= Hm Li=NI
第一章 磁路
【例题】 图示磁路由硅钢制成。磁通势 F1 =
(2) 软磁物质 B-H 曲线窄, Br 小、Hc 小。 用于制造变压器、电机等电器的铁心。
(3) 矩磁物质 B-H 曲线形状接近矩形, Br 大、Hc 小。 用于计算机中,作记忆单元。
第一章 磁路
4. 基本磁化曲线
对同一铁磁材料,选用不同的Hm进行反复磁化,可得 到大小不同的磁滞回路,将各磁滞回路顶点连接起来, 即为基本磁化曲线。
度达到 B0 = 1 T,问需要多大的磁通势?忽略边缘效应。
解:(1) 磁路中的磁通
= B0A0
= 1×0.0016 Wb
II
l1
= 0.0016 Wb
A1
(2) 各段磁路磁感应强度
A2
B0 = 1 T
l0/2
B1 =
A1
=
00..00001166T = 1 T
l2
第一章 磁路
B2 =
A2
=
0.0016 0.000 8
T=2T
(3) 各段磁路的磁场强度
H0
=
B0
0
=
1 4×10-7
A/m
= 796 000 A/m
= 7 960 A/cm
由磁化曲线查得:
H1 = 9.2 A/cm
l0/2
H2 = 14 A/cm
II
l1 A1
A2
l2
第一章 磁路
(4) 各段磁路的磁位差
Um0 = H0 l0 = 7 960×1 A = 7 960 A
(1) 顺磁物质(如空气): 略大于 0 。
