先进PID控制及其MATLAB仿真
基于matlab的pid控制仿真课程设计

这篇文章是关于基于Matlab的PID控制仿真课程设计的,主要内容包括PID控制的基本原理、Matlab的应用、课程设计的目的和意义、课程设计的具体步骤和具体操作步骤。
文章采用客观正式的语气,结构合理,旨在解释基于Matlab的PID控制仿真课程设计的重要性和实施方法。
1. 简介PID控制是一种常见的控制算法,由比例项(P)、积分项(I)和微分项(D)组成,可以根据被控对象的实际输出与期望输出的偏差来调整控制器的输出,从而实现对被控对象的精确控制。
Matlab是一种强大的数学建模与仿真软件,广泛应用于工程领域,尤其在控制系统设计和仿真方面具有独特优势。
2. PID控制的基本原理PID控制算法根据被控对象的实际输出与期望输出的偏差来调整控制器的输出。
具体来说,比例项根据偏差的大小直接调整输出,积分项根据偏差的积累情况调整输出,微分项根据偏差的变化速度调整输出。
三者综合起来,可以实现对被控对象的精确控制。
3. Matlab在PID控制中的应用Matlab提供了丰富的工具箱,其中包括控制系统工具箱,可以方便地进行PID控制算法的设计、仿真和调试。
利用Matlab,可以快速建立被控对象的数学模型,设计PID控制器,并进行系统的仿真和性能分析,为工程实践提供重要支持。
4. 课程设计的目的和意义基于Matlab的PID控制仿真课程设计,旨在帮助学生深入理解PID控制算法的原理和实现方法,掌握Matlab在控制系统设计中的应用技能,提高学生的工程实践能力和创新思维。
5. 课程设计的具体步骤(1)理论学习:学生首先需要学习PID控制算法的基本原理和Matlab在控制系统设计中的应用知识,包括控制系统的建模、PID控制器的设计原理、Matlab的控制系统工具箱的基本使用方法等。
(2)案例分析:学生根据教师提供的PID控制实例,在Matlab环境下进行仿真分析,了解PID控制算法的具体应用场景和性能指标。
(3)课程设计任务:学生根据所学知识,选择一个具体的控制对象,如温度控制系统、水位控制系统等,利用Matlab建立其数学模型,设计PID控制器,并进行系统的仿真和性能分析。
学生--PID控制MATLAB仿真实验

计算机控制技术实验指导书(MATLAB版)机电学院杨蜀秦编2012-11-19实验一 连续系统的模拟PID 仿真一、基本的PID 控制 在模拟控制系统中,控制器最常用的控制规律是PID 控制。
模拟PID 控制系统原理框图如图1-1所示。
图1-1 模拟PID 控制系统原理框图PID 控制规律为:⎪⎪⎭⎫⎝⎛++=⎰dt t de T dt t e T t e k t u DtI p )()(1)()(0或写成传递函数的形式⎪⎪⎭⎫ ⎝⎛++==s T s T k s E s U s G D I p 11)()()( Ex1 以二阶线性传递函数ss 251332+为被控对象,进行模拟PID 控制。
输入信号)2.0*2sin()(t t r π=,仿真时取3,1,60===d i p k k k ,采用ODE45迭代方法,仿真时间10s 。
仿真方法一:在Simulink 下进行仿真,PID 控制由Simulink Extras 节点中的PID Controller 提供。
仿真程序:ex1_1.mdl ,如图1-2所示。
图1-2 连续系统PID 的Simulink 仿真程序连续系统的模拟PID 控制正弦响应结果如图1-3所示。
图1-3 连续系统的模拟PID 控制正弦响应仿真方法二:在仿真一的基础上,将仿真结果输出到工作空间中,并利用m 文件作图。
仿真程序:ex1_2.mdl ,程序中同时采用了传递函数的另一种表达方式,即状态方程的形式,其中[]0,01,1330,25010==⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=D C B A ,如图1-4所示。
m 文件作图程序:ex1_2plot.mclose all ;plot(t,rin,'k',t,yout,'k'); xlabel('time(s)'); ylabel('r,y');二、线性时变系统的PID 控制 Ex2 设被控对象为Jss Ks G +=2)(,其中)2sin(300400),6sin(1020t K t J ππ+=+=,输入信号为)2sin(5.0t π。
PID控制和其MATLAB仿真

序号,k=1,2,……,e (k-1)和e (k)分别为第(k-
1)和第k时刻所得旳偏差信号。
1.3.1 位置式PID控制算法
• 位置式PID控制系统
1.3.1 位置式PID控制算法
根据位置式PID控制算法得 到其程序框图。
在仿真过程中,可根据实 际情况,对控制器旳输出 进行限幅:[-10,10]。
• 变速积分旳基本思想是,设法变化积分项旳累加 速度,使其与偏差大小相相应:偏差越大,积分 越慢;反之则越快,有利于提升系统品质。
• 设置系数f(e(k)),它是e(k)旳函数。当 ∣e(k)∣增大时,f减小,反之增大。变速积分 旳PID积分项体现式为:
ui (k )
ki
k
1
e(i)
f
e(k )e(k )T
i0
1.3.8 变速积分算法及仿真
• 系数f与偏差目前值∣e(k)∣旳关系能够是线性 旳或是非线性旳,例如,可设为
1
f
e(k
)
A
e(k A
)
B
0
e(k) B B e(k) A B e(k) A B
1.3.8 变速积分算法及仿真
• 变速积分PID算法为:
u(k)
k
p e(k )
ki
1.3.4 增量式PID控制算法及仿真
• 增量式PID阶跃跟踪成果
1.3.5 积分分离PID控制算法及仿真
• 在一般PID控制中,引入积分环节旳目旳主要是为了 消除静差,提升控制精度。但在过程旳开启、结束或 大幅度增减设定时,短时间内系统输出有很大旳偏差 ,会造成PID运算旳积分积累,致使控制量超出执行机 构可能允许旳最大动作范围相应旳极限控制量,引起 系统较大旳振荡,这在生产中是绝对不允许旳。
模糊自适应整定PID控制matlab仿真程序(刘金锟-先进PID控制及其MATLAB仿真)

模糊自适应整定PID控制matlab仿真程序(刘金锟-先进PID控制及其MATLAB仿真)2这个例子的程序百度文库里有很多版本,但我下了很多都有错误,运行不了。
以下程序我一字一字的敲出来的,已经成功运行,绝对无误。
仿真实例,被控对象为p G (s)=ss s 1047035.8752350023++ 采样时间为1ms ,采用模糊PID 控制进行阶跃响应,在第300个采样时间时控制器输出加1.0的干扰,相应的运行结果如图1~13所示。
仿真程序如下:将以下程序保存为fuzzypid.m 文件,即可得到仿真结果。
%fuzzy tunning PID controlclear all ;clear all ;a=newfis('fuzzpid');a=addvar(a,'input','e',[-3,3]); %parameter ea=addmf(a,'input',1,'NB','zmf',[-3,-1]);a=addmf(a,'input',1,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PM','trimf',[0,2,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);a=addvar(a,'input','ec',[-3,3]); %parameter eca=addmf(a,'input',2,'NB','zmf',[-3,-1]);a=addmf(a,'input',2,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',2,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',2,'Z','trimf',[-2,0,2]);a=addmf(a,'input',2,'PS','trimf',[-1,1,3]);a=addmf(a,'input',2,'PM','trimf',[0,2,3]);a=addmf(a,'input',2,'PB','smf',[1,3]);a=addvar(a,'output','kp',[-0.3,0.3]); %parameter kpa=addmf(a,'output',1,'NB','zmf',[-0.3,-0.1]);a=addmf(a,'output',1,'NM','trimf',[-0.3,-0.2,0]);a=addmf(a,'output',1,'NS','trimf',[-0.3,-0.1,0.1]);a=addmf(a,'output',1,'Z','trimf',[-0.2,0,0.2]);a=addmf(a,'output',1,'PS','trimf',[-0.1,0.1,0.3]);a=addmf(a,'output',1,'PM','trimf',[0,0.2,0.3]);a=addmf(a,'output',1,'PB','smf',[0.1,0.3]);a=addvar(a,'output','ki',[-0.06,0.06]); %parameter ki a=addmf(a,'output',2,'NB','zmf',[-0.06,-0.02]);a=addmf(a,'output',2,'NM','trimf',[-0.06,-0.04,0]);a=addmf(a,'output',2,'NS','trimf',[-0.06,-0.02,0.02]); a=addmf(a,'output',2,'Z','trimf',[-0.04,0,0.04]);a=addmf(a,'output',2,'PS','trimf',[-0.02,0.02,0.06]);a=addmf(a,'output',2,'PM','trimf',[0,0.04,0.06]);a=addmf(a,'output',2,'PB','smf',[0.02,0.06]);a=addvar(a,'output','kd',[-3,3]); %parameter kda=addmf(a,'output',3,'NB','zmf',[-3,-1]);a=addmf(a,'output',3,'NM','trimf',[-3,-2,0]);a=addmf(a,'output',3,'NS','trimf',[-3,-1,1]);a=addmf(a,'output',3,'Z','trimf',[-2,0,2]);a=addmf(a,'output',3,'PS','trimf',[-1,1,3]);a=addmf(a,'output',3,'PM','trimf',[0,2,3]);a=addmf(a,'output',3,'PB','smf',[1,3]);rulelist=[1 1 7 1 5 1 1;1 2 7 1 3 1 1;1 3 62 1 1 1;1 4 62 1 1 1;1 5 5 3 1 1 1;1 6 4 42 1 1;1 7 4 4 5 1 1;2 1 7 1 5 1 1;2 2 7 13 1 1;2 3 6 2 1 1 1;2 4 53 2 1 1;2 5 53 2 1 1;2 6 4 43 1 1;2 734 4 1 1;3 1 6 14 1 1;3 2 6 2 3 1 1;3 3 6 3 2 1 1;3 4 5 3 2 1 1;3 54 4 3 1 1;3 6 3 5 3 1 1;3 7 3 54 1 1;4 1 6 2 4 1 1;4 2 6 2 3 1 1;4 35 3 3 1 1;4 4 4 4 3 1 1;4 5 3 5 3 1 1;4 6 2 6 3 1 1;4 7 2 6 4 1 1;35 1 5 2 4 1 1;5 2 5 3 4 1 1;5 3 4 4 4 1 1;5 4 3 5 4 1 1;5 5 3 5 4 1 1;5 6 2 6 4 1 1;5 7 2 7 4 1 1;6 1 5 47 1 1;6 2 4 4 5 1 1;6 3 3 5 5 1 1;6 4 2 5 5 1 1;6 5 2 6 5 1 1;6 6 27 5 1 1;6 7 1 7 7 1 1;7 1 4 4 7 1 1;7 2 4 4 6 1 1;7 3 2 5 6 1 1;7 4 2 6 6 1 1;7 5 2 6 5 1 1;7 6 1 7 5 1 1;7 7 1 7 7 1 1];a=addrule(a,rulelist);a=setfis(a,'DefuzzMethod','mom');writefis(a,'fuzzpid');a=readfis('fuzzpid');%PID controllerts=0.001;sys=tf(5.235e005,[1,87.35,1.047e004,0]); dsys=c2d(sys,ts,'tustin');[num,den]=tfdata(dsys,'v');u_1=0.0;u_2=0.0;u_3=0.0;y_1=0;y_2=0;y_3=0;x=[0,0,0]';4error_1=0;e_1=0.0;ec_1=0.0;kp0=0.40;kd0=1.0;ki0=0.0;for k=1:1:500time(k)=k*ts;rin(k)=1;%using fuzzy inference to tunning PIDk_pid=evalfis([e_1,ec_1],a);kp(k)=kp0+k_pid(1);ki(k)=ki0+k_pid(2);kd(k)=kd0+k_pid(3);u(k)=kp(k)*x(1)+kd(k)*x(2)+ki(k)*x(3);if k==300 %adding disturbance(1.0v at time 0.3s)u(k)=u(k)+1.0;endif u(k)>=10u(k)=10;endif u(k)<=-10u(k)=-10;endyout(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(1)*u(k)+num(2)*u_1+num(3)*u_2+num(4)*u_3;error(k)=rin(k)-yout(k);%%%%%%%%%%%%%%%%%%%%%%%%%return of pid parameters%%%%%%%%%%%%%%%%%%%%%%%% u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=yout(k);5x(1)=error(k); %calculating Px(2)=error(k)-error_1; %calculating Dx(3)=x(3)+error(k); %calculating De_1=x(1);ec_1=x(2);error_2=error_1;error_1=error(k);endshowrule(a)figure(1);plot(time,rin,'b',time,yout,'r'); xlabel('time(s)');ylabel( 'rin,yout');figure(2);plot(time,error,'r');xlabel('time(s)');ylabel( 'error ');figure(3);plot(time,u,'r');xlabel('time(s)');ylabel( 'u ');figure(4);plot(time,kp,'r');xlabel('time(s)');ylabel( 'kp ');figure(5);plot(time,ki,'r');xlabel('time(s)');ylabel( 'ki ');figure(6);plot(time,kd,'r');xlabel('time(s)');ylabel( 'kd ');figure(7);plotmf(a,'input',1);figure(8);plotmf(a,'input',2);figure(9);plotmf(a,'output',1);figure(10);plotmf(a,'output',2);figure(11);plotmf(a,'output',3);plotfis(a);fuzzy fuzzpid.fis6仿真运行结果:789。
二先进PID控制及其MATLAB仿真

1.3.6抗积分饱和PID控制算法及仿真
积分饱和现象
所谓积分饱和现象是指若系统存在一个方向的 偏差,PID控制器的输出由于积分作用的不断累加 而加大,从而导致u(k)达到极限位置。此后若控制 器输出继续增大,u(k)也不会再增大,即系统输出 超出正常运行范围而进入了饱和区。一旦出现反向 偏差,u(k)逐渐从饱和区退出。 进入饱和区愈深则退饱和时间愈长。此段时间 内,系统就像失去控制。这种现象称为积分饱和现 象或积分失控现象。
1.3.5 积分分离PID控制算法及仿真
积分分离式PID阶跃跟
采用普通PID阶跃跟踪
1.3.5 积分分离PID控制算法及仿真
Simulink主程序
1.3.5 积分分离PID控制算法及仿真
阶跃响应结果
1.3.5 积分分离PID控制算法及仿真
需要说明的是,为保证引入积分作用后系统 的稳定性不变,在输入积分作用时比例系数 Kp可进行相应变化。此外,β值应根据具体 对象及要求而定,若β过大,则达不到积分 分离的目的;β过小,则会导致无法进入积 分区。如果只进行PD控制,会使控制出现 余差。(为什么是β?)
控制工程与控制理论课程设计讲座
先进PID控制及其 MATLAB仿真
主讲人 付冬梅 自动化系
第1章 数字PID控制
1.1 PID控制原理 1.2 连续系统的模拟PID仿真
1.3 数字PID控制
1.1 PID控制原理
模拟PID控制系统原理框图
1.1 PID控制原理
PID是一种线性控制器,它根据给定值rin(t)与实 际输出值yout(t)构成控制方案:
积分分离控制算法可表示为:
u () k k e () k k e ( j ) T ke ( () k e ( k 1 ) ) / T p i d
pid控制及其matlab仿真-详细

在MATLAB中搭建仿真模型,验证PID控制器对复杂系统的控制 效果。
PID控制器的参数优化
参数优化方法
采用智能优化算法(如遗传算法、粒子群算法等)对PID 控制器参数进行优化,以进一步提高控制性能。
01
MATLAB实现
在MATLAB中编写优化算法程序,通过 Simulink仿真模型进行测试和验证。
积分控制
02
03
微分控制
通过累积输入信号的变化量来控 制输出信号,以减小输出信号的 误差。
通过预测输入信号的变化趋势来 控制输出信号,以减小输出信号 的超调和响应时间。
PID控制器的参数整定
比例系数
影响控制器的增益,比例系数越 大,控制器的增益越大,输出信 号变化越快。
积分系数
影响积分控制的强度,积分系数 越大,积分控制作用越强,误差 减小越快。
温度控制系统中的应用
温度控制系统是PID控制器的另一个重要应用领域。在工 业和科学实验中,温度控制对于保持恒定的实验条件和产 品质量至关重要。
PID控制器用于温度控制系统的目的是通过自动调节加热 元件的功率或冷却介质的流量,将温度维持在设定的范围 内。
PID控制器通过比较温度传感器的实际测量值与期望值之 间的误差,来调整加热元件或冷却介质的控制信号,以减 小误差并实现稳定的温度控制。
pid控制及其 matlab仿真-详细
目 录
• PID控制理论简介 • MATLAB仿真环境介绍 • PID控制器在MATLAB中的实现 • PID控制器的性能分析 • PID控制器的应用实例 • 结论与展望
01
CATALOGUE
PID控制理论简介
经典-先进PID控制及其MATLAB仿真(刘金锟)-315页[315页]
![经典-先进PID控制及其MATLAB仿真(刘金锟)-315页[315页]](https://img.taocdn.com/s3/m/ea40db3183c4bb4cf7ecd1f5.png)
免积分版,学习交流用,如需要请购买正版!先进PID控制及其MATLAB仿真刘金琨 著电 子 工 业 出 版 社内 容 简 介本书从MATLAB仿真角度系统地介绍了PID控制的基本理论、基本方法和应用技术,是作者多年来从事控制系统教学和科研工作的结晶,同时融入了国内外同行近年来所取得的新成果。
全书共分十章,包括连续系统和离散系统的PID控制,常用数字PID控制,专家PID 和模糊PID控制,神经PID控制,遗传算法PID控制,多变量解耦PID控制,几种先进的PID控制,灰色PID控制,伺服系统PID控制,PID实时控制,每种方法都通过MATLAB仿真程序进行了说明。
本书各部分内容既相互联系又相互独立,读者可根据自己需要选择学习。
本书适用于从事生产过程自动化、计算机应用、机械电子和电气自动化领域工作的工程技术人员阅读,也可作为大专院校工业自动化、自动控制、机械电子、自动化仪表、计算机应用等专业的教学参考书。
序 言在实际的过程控制与运动控制系统中,PID家族占有相当的地位,据统计,工业控制的控制器中PID类控制器占有90%以上(K J Åström and T. Hägglund. PID Controllers: Theory, Design and Tuning. Instrument Society of America, 1995)。
PID控制器是最早出现的控制器类型,因为其结构简单,各个控制器参数有着明显的物理意义,调整方便,所以这类控制器很受工程技术人员的喜爱。
此外,随着控制理论的发展,出现了各种分支,如专家系统、模糊逻辑、神经网络、灰色系统理论等,它们和传统的PID控制策略相结合又派生出各种新型的PID类控制器,形成庞大的PID家族,很多算法大大改进了传统PID控制器的性能。
拜读了刘金琨博士的新作《先进PID控制及其MATLAB仿真》,顿觉耳目一新。
国际上近年有大量的文章介绍各种新型的PID控制系统,也出现了一些介绍PID控制的专著,和同类专著相比较,这部力著有如下特色:z内容新颖:以新型的PID控制器为主加以介绍,包括一般连续及离散的PID控制器、专家系统整定的PID控制器、模糊逻辑PID控制器、各种神经网络PID控制器、基于遗传算法整定的PID控制器、多变量解耦PID控制器、非线性鲁棒PID控制器、灰色PID控制器,这是PID类专著中较少见的。
PID控制及其MATLAB仿真--详细解读

PID控制参数为:Kp=8,Ki=0.10,Kd=10
1.3.4 增量式PID控制算法及仿真
增量式PID阶跃跟踪结果
1.3.5 积分分离PID控制算法及仿真
在普通PID控制中,引入积分环节的目的主要是为了 消除静差,提高控制精度。但在过程的启动、结束或 大幅度增减设定时,短时间内系统输出有很大的偏差, 会造成PID运算的积分积累,致使控制量超过执行机 构可能允许的最大动作范围对应的极限控制量,引起 系统较大的振荡,这在生产中是绝对不允许的。 积分分离控制基本思路是,当被控量与设定值偏差较 大时,取消积分作用,以免由于积分作用使系统稳定 性降低,超调量增大;当被控量接近给定量时,引入 积分控制,以便消除静差,提高控制精度。
其中,A=1.0,f=0.20Hz 被控对象模型选定为:
133 G ( s) 2 s 25s
1.2 连续系统的基本PID仿真
连续系统PID的Simulink仿真程序
1.2 连续系统的基本PID仿真
连续系统的模拟PID控制正弦响应
1.3 数字PID控制
1.3.1 1.3.2 1.3.3 1.3.4 1.3.5 1.3.6 1.3.7 1.3.8 位置式PID控制算法 连续系统的数字PID控制仿真 离散系统的数字PID控制仿真 增量式PID控制算法及仿真 积分分离PID控制算法及仿真 抗积分饱和PID控制算法及仿真 梯形积分PID控制算法 变速积分PID算法及仿真
k
式中,Ki=Kp/Ti,Kd=KpTd,T为采样周期,K 为采样序号,k=1,2,……,e (k-1)和e (k) 分别为第(k-1)和第k时刻所得的偏差信号。
1.3.1 位置式PID控制算法
基于MATLAB的数字PID控制器设计及仿真分析资料

基于MATLAB的数字PID控制器设计及仿真分析摘要PID控制作为历史最为悠久,生命力最强的控制方式一直在生产过程自动化控制中发挥着巨大的作用。
PID控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好和可靠性高,被广泛用于过程控制和运动控制中。
数字PID控制算法是将模拟PID离散化而得到的,各参数有着明显的物理意义,而且调整方便,所以PID控制器很受工程技术人员的喜爱。
本论文主要实现基于MATLAB的数字PID控制器设计及仿真。
首先介绍了传统的模拟PID控制方法,包括比例控制方法、比例积分控制方法、比例积分微分控制方法等。
接下来,介绍了数字PID控制。
随着时代的发展,科技的进步,传统的模拟PID控制方法不能满足人们的需求,数字PID控制的改进算法也便随之而来。
本文最后,应用MATLAB软件,在实验的环境下实现了其设计及仿真。
本次毕业设计用来完成数字PID控制器的设计,并通过MATLAB实现其仿真同时加以分析。
通过查阅文献得知,与传统模拟PID控制器相比较,该控制器具有良好的灵活性,而且可得到精确的数学模型。
另外,基于MATLAB的数字PID 控制器设计及仿真,充分的利用了MATLAB的实验环境,整个设计验证了数字PID的广泛可实现性及准确性。
关键词:PID控制;模拟PID控制器;数字PID控制器;MATLAB仿真;Design and simulation analysis of Digital PID ControllerMATLAB-basedAbstractAs the most age-old and powerful control mode, PID control always has had a great effect on the automatic control of the production process. PID control is one of the first developed control strategy, because of thesimple algorithm,great robust and high reliability, it is widely used in process control and motor control. Digital PID control algorithm is gotten by discreting the analog PID control, and the parameters have obvious physical meaning and facility adjustment, so PID controller is popular with engineering and technical personnel.In the paper, the main idea is to accomplish MATLAB-based digital PID controller design and simulation analysis. In the first place, the traditional analog PID control methods is introduced, including proportional control methods, proportional integral control and proportional integral differential control. In the second place, the digital PID control methods are offered. With the development of the times, the advancement of technology, traditional analog PID control method cannot make a satisfaction, then digital PID control is followed. At last,the application of MATLAB software to achieve their design and simulation is easy to accomplish.The graduation project is to complete the digital PID controller design and simulation through MATLAB simulation and analysis. It is known that through the literature, compare with traditional PID controller, the controller has good flexibility and precision of the mathematical models available. In addition, in the number of MATLAB-based PID controller design and simulation, the MATLAB experiment environment is used comprehensively. The entire design is confirmed the wide range and accuracy of digital PID controller.Key words:PID control;analog PID controller;digital PID controller;MATLAB simulatio目录摘要 (I)ABSTRACT...................................................................... I I 第1章绪论.. (1)1.1课题目的及意义 (1)1.2数字PID控制器的研究现状 (2)第2章 PID控制器 (3)2.1传统PID控制器概述 (3)2.2PID控制器的基本原理 (5)2.2.1 比例(P)调节 (6)2.2.2 比例积分(PI)调节 (7)2.2.3 比例积分微分(PID)调节 (9)第3章数字PID控制器 (13)3.1数字PID控制系统 (13)3.2数字PID控制的基本算法 (14)3.2.1 位置式PID控制算法 (14)3.2.2 增量式PID控制算法 (16)3.2.3 位置算式与增量算式的比较 (17)第4章数字PID的改进算法 (19)4.1积分算法的改进 (20)4.1.1 积分分离法 (21)4.1.2 变速积分法 (24)4.1.3 遇限消弱积分法 (25)4.1.4 梯形积分法 (26)4.2微分算法的改进 (27)4.2.1 不完全微分PID控制算法 (27)4.2.2 微分先行PID控制算法 (30)4.3带死区的PID控制算法 (32)第5章基于MATLAB的数字PID控制器设计及仿真 (34)5.1位置式PID控制算法仿真实例 (34)5.2增量式PID控制算法仿真实例 (35)参考文献 (37)谢辞 (37)第1章绪论1.1 课题目的及意义PID控制器又称为PID调节器,是按偏差的比例P、积分I、微分进行控制的调节器的简称,它主要针对控制对象来进行参数调节。
基于matlab的pid控制仿真课程设计

基于matlab的pid控制仿真课程设计PID(比例-积分-微分)控制器是一种常见的控制算法,被广泛应用于工业控制系统中。
在本文中,我们将介绍基于MATLAB的PID控制仿真课程设计。
首先,我们将简要介绍PID控制器的原理和特点,然后介绍如何使用MATLAB进行PID控制的仿真。
PID控制器是一种反馈控制器,可以通过比例、积分和微分三部分来调节控制系统的输出。
比例部分根据误差的大小进行调节,积分部分用于消除稳态误差,微分部分用于抑制系统振荡。
通过调节PID控制器的参数,可以使系统的稳定性、响应速度和稳态误差达到预期的要求。
在MATLAB中,可以使用控制系统工具箱来进行PID控制的仿真。
首先,我们需要定义一个系统模型,可以是连续时间系统或离散时间系统。
然后,我们可以使用PID控制器对象来创建一个PID控制器。
PID控制器的参数可以通过试错法、模型辨识等方法进行调节。
一旦系统模型和PID控制器被定义,我们可以使用MATLAB中的仿真工具来进行PID控制器的仿真。
通常,我们将输入信号作为控制器的参考信号,将输出信号作为系统的输出,并将控制器的输出作为系统的输入。
然后,我们可以观察系统的响应,并根据需要调整控制器的参数。
在进行PID控制仿真实验时,我们可以通过选择不同的控制器参数、改变控制器的结构、调整参考信号等方式来研究控制系统的性能。
例如,我们可以改变比例增益来改变系统的稳定性和响应速度,增加积分时间常数来减小稳态误差,增加微分时间常数来抑制系统振荡等。
在课程设计中,我们可以设计不同的控制实验,并分析不同参数对系统性能的影响。
例如,可以研究比例增益对系统稳定性和响应速度的影响,或者研究积分时间常数对稳态误差的影响等。
同时,我们还可以通过比较PID控制和其他控制算法(如PI控制、PD控制等)来评估PID控制的优势和局限性。
在进行PID控制仿真实验时,我们应该注意以下几点。
首先,选择合适的系统模型,确保模型能够准确地描述实际系统的行为。
控制系统pid参数整定方法的matlab仿真

控制系统pid参数整定方法的matlab仿真
控制系统PID参数整定方法的MATLAB仿真,可以分为以下几个步骤:
1. 建立模型。
在MATLAB中建立你要进行PID参数整定的模型,比如电机速度控制系统或温度控制系统。
2. 设计控制器。
根据建立的模型,设计出对应的PID控制器,并将其加入到系统中。
3. 确定初始参数。
在进行PID参数整定前,需要确定PID控制器的初始参数。
通常可以选择Ziegler-Nichols方法、Chien-Hrones-Reswick方法等经典的PID参数整定法则来确定初始参数。
4. 仿真模拟。
使用MATLAB中的仿真工具,对整定后的PID控制器进行仿真模拟,并记录下系统的响应曲线和各项性能指标。
5. 调整参数。
根据仿真结果,对PID控制器的参数进行适当的调整,以达到更理想的控制效果。
6. 再次仿真模拟。
调整完参数后,再次使用MATLAB中的仿真工具,对整定后的PID控制器进行仿真模拟,并比较其与上一次仿真的差异,以确认调整是否合理。
7. 实现控制。
最后,将优化后的PID控制器应用到实际控制系统中,进行控制。
总的来说,PID参数整定是一个相对复杂的过程,需要根据具体情况选择合适的方法和工具。
MATLAB作为一种强大的数学计算软件,可以提供丰富的工具和函数,方便进行控制系统的建模和仿
真,也可以帮助我们更好地进行PID参数整定。
先进PID控制MATLAB仿真

1.3.2 连续系统的数字PID控制仿真
本方法可实现D/A及A/D的功能,符合数字 实时控制的真实情况,计算机及DSP的实时 PID控制都属于这种情况。 采用MATLAB语句形式进行仿真。被控对象 为一个电机模型传递函数: 1 G(s) Js 2 Bs
式中,J=0.0067,B=0.10
k
式中,Ki=Kp/Ti,Kd=KpTd,T为采样周期,K 为采样序号,k=1,2,……,e (k-1)和e (k) 分别为第(k-1)和第k时刻所得的偏差信号。
1.3.1 位置式PID控制算法
位置式PID控制系统
1.3.1 位置式PID控制算法
根据位置式PID控制算法得 到其程序框图。 在仿真过程中,可根据实 际情况,对控制器的输出 进行限幅:[-10,10]。
1.1 PID控制原理
PID控制器各校正环节的作用如下:
比例环节:成比例地反映控制系统的偏差信号e(t),偏差 一旦产生,控制器立即产生控制作用,以减小偏差。 积分环节:主要用于消除静差,提高系统的无差度。积 分作用的强弱取决于积分时间常数T,T越大,积分作用 越弱,反之则越强。 微分环节:反映偏差信号的变化趋势,并能在偏差信号 变得太大之前,在系统中引入一个有效的早期修正信号, 从而加快系统的动作速度,减少调节时间。
控制工程与控制理论课程设计讲座
先进PID控制及其 MATLAB仿真
主讲人 付冬梅 自动化系
第1章 数字PID控制
1.1 PID控制原理 1.2 连续系统的模拟PID仿真
1.3 数字PID控制
1.1 PID控制原理
模拟PID控制系统原理框图
1.1 PID控制原理
PID是一种线性控制器,它根据给定值rin(t)与实 际输出值yout(t)构成控制方案:
MATLAB和基本PID控制系仿真

3.2 PID控制系统仿真
例:基本PID控制SIMULINK仿真
仿真时取kp=60,ki=1,kd=3,输入指令为rin(k)=sin(0.4*pi*t) 采用ODE45迭代措施,仿真时间为10s。
Signal Generator
Sum
PID
PID Controller
133 s2+25 s Transfer Fcn
措施一
clear all;
close all;
ts=0.001;
sys=tf(523407,[1,86.85,10465,0]);
dsys=c2d(sys,ts,'z');
[num,den]=tfdata(dsys,'v');
u_1=0.0;u_2=0.0;u_3=0.0;
y_1=0.0;y_2=0.0;y_3=0.0;
Mux
Mux
Scope
参数设置
仿真曲线
3.2.1 数字PID
1、离散系统旳数字PID控制仿真:
离散PID控制算法:
u (k )
k perror(k) ki
k
error( j)T
j0
kd
error(k) error(k T
1)
例:被控对象为:G(s)
523407
s3 86.85s 2 10465s
(5)从频域角度来看,PID控制是经过积分作用于系统旳 低频段,以提升系统旳稳态性能,而微分作用于系统旳中 频段,以改善系统旳动态性能。
Байду номын сангаас
PID参数整定规律
几条基本旳PID参数整定规律: (1)增大百分比系数一般将加紧系统旳响应,在有静差旳情
PID控制算法的matlab仿真
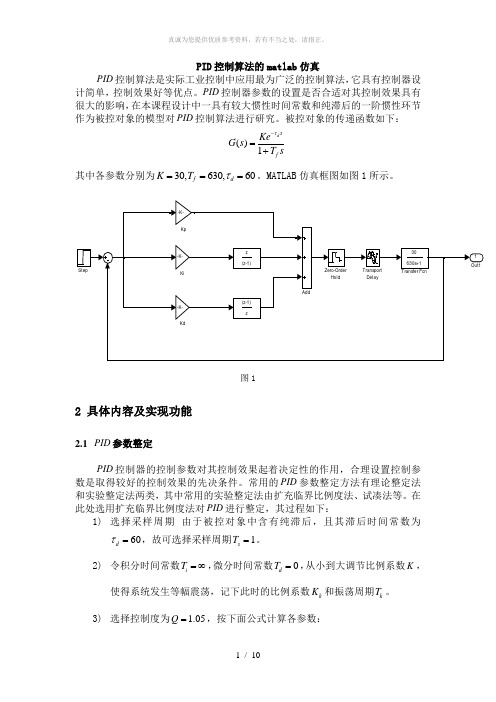
PID 控制算法的matlab 仿真PID 控制算法是实际工业控制中应用最为广泛的控制算法,它具有控制器设计简单,控制效果好等优点。
PID 控制器参数的设置是否合适对其控制效果具有很大的影响,在本课程设计中一具有较大惯性时间常数和纯滞后的一阶惯性环节作为被控对象的模型对PID 控制算法进行研究。
被控对象的传递函数如下:()1d sf Ke G s T sτ-=+ 其中各参数分别为30,630,60f d K T τ===。
MATLAB 仿真框图如图1所示。
图12 具体内容及实现功能2.1 PID 参数整定PID 控制器的控制参数对其控制效果起着决定性的作用,合理设置控制参数是取得较好的控制效果的先决条件。
常用的PID 参数整定方法有理论整定法和实验整定法两类,其中常用的实验整定法由扩充临界比例度法、试凑法等。
在此处选用扩充临界比例度法对PID 进行整定,其过程如下:1) 选择采样周期 由于被控对象中含有纯滞后,且其滞后时间常数为60d τ=,故可选择采样周期1s T =。
2) 令积分时间常数i T =∞,微分时间常数0d T =,从小到大调节比例系数K ,使得系统发生等幅震荡,记下此时的比例系数k K 和振荡周期k T 。
3) 选择控制度为 1.05Q =,按下面公式计算各参数:0.630.490.140.014p k i k d k s kK K T T T T T T ====通过仿真可得在1s T =时,0.567,233k k K T ==,故可得:0.357,114.17,32.62, 3.262p i d s K T T T ====0.0053.57p s i i p d d sK T K T K T K T ====按此组控制参数得到的系统阶跃响应曲线如图2所示。
010020030040050060070080090010000.20.40.60.811.21.41.61.8图2由响应曲线可知,此时系统虽然稳定,但是暂态性能较差,超调量过大,且响应曲线不平滑。
pid控制器matlab仿真

基于MATLAB的PID控制系统参数调节的仿真分析1、引言PID控制是最早发展的自动控制策略之一,PID控制系统由比例单元(P)、积分单元(I)和微分单元(D)组成。
具有简单易懂,使用中不需精确的系统模型等先决条件,因而成为应用最为广泛的控制器。
PID控制的参数自动调整是通过智能化调整或自校正、自适应算法来实现。
当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。
即当我们不完全了解一个系统和被控对象,或不能通过有效的测量手段来获得系统参数时,最适合用PID控制技术。
PID控制,实际中也有PI和PD控制。
PID控制器就是根据系统的误差,利用比例、积分、微分计算出控制量进行控制的。
本文首先从PID理论出发,建立模型,讨论系统的稳定性,快速性,准确性。
利用MATLAB对PID控制的参数进行仿真,设计不同的参数,以使系统满足所要求的性能指标。
2、控制领域有一个很重要的概念是反馈,它通过各种输出值和它们各自所需值的实时比较的度量—各种误差,再以这些误差进行反馈控制来减少误差。
这样形成的因果链是输入、动态系统、输出、测量、比较、误差、输入构成的一个环路,因而也构成了包含原动态系统在内的一个新的动态闭环系统。
采用反馈的基本原因是要在不确定性存在的条件下达到性能目标。
许多情况下,对于系统的了解是不全面的,或者可用的模型是基于许多简化的假设而使它们变得不透彻。
系统也可能承受外界干扰,输出的观测常受噪声干扰。
有效的反馈能减少这些不确定性的影响,因为它们可以补偿任何原因引起的误差。
反馈概括了很广泛的概念,包括当前系统中的许多回路、非线性和自适应反馈,以及将来的智能反馈。
广义的讲,反馈可以作为描述和理解许多复杂物理系统中发生的循环交互作用的方式。
在实际的过程控制和运动控制系统中,PID占有相当的地位,据统计,工业控制中 PID 类控制器占有 90%以上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
先进PID控制及其MATLAB仿真刘金琨 著电 子 工 业 出 版 社内 容 简 介本书从MATLAB仿真角度系统地介绍了PID控制的基本理论、基本方法和应用技术,是作者多年来从事控制系统教学和科研工作的结晶,同时融入了国内外同行近年来所取得的新成果。
全书共分十章,包括连续系统和离散系统的PID控制,常用数字PID控制,专家PID 和模糊PID控制,神经PID控制,遗传算法PID控制,多变量解耦PID控制,几种先进的PID控制,灰色PID控制,伺服系统PID控制,PID实时控制,每种方法都通过MATLAB仿真程序进行了说明。
本书各部分内容既相互联系又相互独立,读者可根据自己需要选择学习。
本书适用于从事生产过程自动化、计算机应用、机械电子和电气自动化领域工作的工程技术人员阅读,也可作为大专院校工业自动化、自动控制、机械电子、自动化仪表、计算机应用等专业的教学参考书。
序 言在实际的过程控制与运动控制系统中,PID家族占有相当的地位,据统计,工业控制的控制器中PID类控制器占有90%以上(K J Åström and T. Hägglund. PID Controllers: Theory, Design and Tuning. Instrument Society of America, 1995)。
PID控制器是最早出现的控制器类型,因为其结构简单,各个控制器参数有着明显的物理意义,调整方便,所以这类控制器很受工程技术人员的喜爱。
此外,随着控制理论的发展,出现了各种分支,如专家系统、模糊逻辑、神经网络、灰色系统理论等,它们和传统的PID控制策略相结合又派生出各种新型的PID类控制器,形成庞大的PID家族,很多算法大大改进了传统PID控制器的性能。
拜读了刘金琨博士的新作《先进PID控制及其MATLAB仿真》,顿觉耳目一新。
国际上近年有大量的文章介绍各种新型的PID控制系统,也出现了一些介绍PID控制的专著,和同类专著相比较,这部力著有如下特色:z内容新颖:以新型的PID控制器为主加以介绍,包括一般连续及离散的PID控制器、专家系统整定的PID控制器、模糊逻辑PID控制器、各种神经网络PID控制器、基于遗传算法整定的PID控制器、多变量解耦PID控制器、非线性鲁棒PID控制器、灰色PID控制器,这是PID类专著中较少见的。
z系统性强:在介绍各种算法时,首先较好地介绍其理论背景,然后通过例子介绍该PID 控制器设计与仿真,展示仿真效果,很有说服力。
本书选材较全面,内容深入浅出,易于理解和直接应用。
z计算机实现直观实用:每种介绍的算法均有MATLAB语言实现,适合于通用化,用户可以对所附的程序稍作修改,就可以直接解决自己的控制器设计与仿真问题,这也往往是其他专著所缺乏的。
z直接面向工程应用:介绍了MATLAB/Simulink模型的C语言转换和工程应用,很有实际应用的价值。
本书作者多年来一直从事PID控制类的研究与教学,积累了大量的经验和第一手材料,取材恰当,叙述清晰,结构合理,适合于工程应用和理论研究。
本人在评审博士、硕士论文时经常发现,许多学生往往将自己的控制算法与策略和传统的PID控制算法相比较,来演示自己算法的优越性。
这样的比较有时有些偏颇,因为论文中的算法常常和目前公认的效果不佳的Ziegler-Nichols整定算法比较,所以本人认为这样的比较很不客观,因为他们比较的对象不是最好的PID控制器。
此外,由于其他新型PID控制器实现与仿真的代码十分匮乏,也极大影响了研究者选择适当比较的对象。
相信这部著作及其所编写的程序可以作为PID控制领域的标准,也可以作为论文中算法比较的参照物。
众所周知,MATLAB在控制界之所以成为最受欢迎的语言,除了有其自身在科学运算与可视化方面的优势外,最大的特点还在于其开放性,正因为这个原因,许多控制界的名家编写出各种各样的工具箱,这些工具箱已经成为各自领域的标准。
迄今为止,尚没有被广泛认可的关于PID控制器的工具箱,所以可以预见,如果对本书中的程序进行较好的封装,并适当地扩充,将有望形成很有竞争力的PID工具箱,在国际上也将有很大的影响。
综上所述,本书是在PID控制器设计与实现领域的不可多得的优秀著作,故不揣冒昧,为本著作写此序言,乐于将其推荐给国内的同行和学生,望引起国内PID控制的研究者与应用者的注意,推进PID类控制器在我国的实际应用。
薛定宇 谨识2002年11月2日于东北大学前 言PID控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好和可靠性高,被广泛应用于过程控制和运动控制中,尤其适用于可建立精确数学模型的确定性控制系统。
然而实际工业生产过程往往具有非线性、时变不确定性,难以建立精确的数学模型,应用常规PID控制器不能达到理想的控制效果,而且在实际生产现场中,由于受到参数整定方法烦杂的困扰,常规PID控制器参数往往整定不良、性能欠佳,对运行工况的适应性很差。
随着计算机技术和智能控制理论的发展,为复杂动态不确定系统的控制提供了新的途径。
采用智能控制技术,可设计智能PID和PID的智能整定。
有关智能PID控制等新型PID控制理论及其工程应用,近年来已有大量的论文发表。
作者多年来一直从事智能控制方面的研究和教学工作,为了促进PID控制和自动化技术的进步,反映PID控制设计与应用中的最新研究成果,并使广大工程技术人员能了解、掌握和应用这一领域的最新技术,学会用MATLAB语言进行PID控制器的设计,作者编写了这本书,以抛砖引玉,供广大读者学习参考。
本书是在总结作者多年研究成果的基础上,进一步理论化、系统化、规范化、实用化而成的,其特点是:(1) PID控制算法取材新颖,内容先进,重点置于学科交叉部分的前沿研究和介绍一些有潜力的新思想、新方法和新技术,取材着重于基本概念、基本理论和基本方法; (2) 针对每种PID算法给出了完整的MATLAB仿真程序,这些程序都可以在线运行,并给出了程序的说明和仿真结果。
具有很强的可读性,很容易转化为其它各种实用语言;(3) 着重从应用领域角度出发,突出理论联系实际,面向广大工程技术人员,具有很强的工程性和实用性。
书中有大量应用实例及其结果分析,为读者提供了有益的借鉴;(4) 所给出的各种PID算法完整,程序设计结构设计力求简单明了,便于自学和进一步开发。
本书共分十章。
第一章介绍连续系统PID控制和离散系统数字PID控制的几种基本方法,通过仿真和分析进行了说明;第二章介绍了常用的数字PID控制系统,主要包括串级计算机控制系统的PID控制、纯滞后控制系统Dahlin算法、基于Smith预估的PID控制;第三章介绍了专家PID和模糊PID整定的基本算法和程序设计方法,其中模糊PID包括模糊自适应整定PID控制和模糊免疫PID控制算法,并进行了仿真分析;第四章介绍了神经PID的几种方法,包括单神经网络PID的设计、神经网络并行PID控制、PID的几种神经网络整定方法,并通过仿真进行了说明;第五章介绍了基于遗传算法的PID控制,主要包括基于遗传算法整定的PID控制和基于遗传算法摩擦模型参数辨识的PID控制;第六章介绍了多变量解耦PID 控制的几种方法,主要包括PID解耦控制、 基于单神经元 PID 解耦控制和基于DRNN神经网络整定的PID解耦控制;第七章介绍了几种先进的PID控制算法,包括基于干扰观测器的PID鲁棒控制、基于NCD优化的非线性PID控制、非线性参数整定的PID控制、基于重复控制的PID高精度控制和基于零相差前馈补偿的PID控制,每种方法都通过仿真程序进行了说明;第八章介绍了灰色PID控制算法和仿真方法,包括基于连续系统的灰色PID控制和基于离散系统的灰色PID控制;第九章介绍了伺服系统的PID控制,包括伺服系统在低速摩擦条件下的PID控制、单质量伺服系统PID控制和二质量伺服系统PID控制,并进行了仿真说明;第十章介绍了PID在实时控制中的应用实例,并给出了PID控制的MATLAB程序和相应的Borland C++语言实时控制程序。
本书是基于MATLAB 5.3环境下开发的,各个章节的内容具有很强的独立性,读者可以结合自己的方向深入地进行研究。
本书由北京航空航天大学尔联洁教授提出了许多宝贵意见,东北大学薛定宇教授给予了大力支持和帮助,在此一并表示感谢。
作者在仿真研究中,得到实验室许多同仁的帮助。
在神经网络设计方面得到扈宏杰博士的帮助,在遗传算法和零相差设计方面得到刘强博士的帮助,在灰色系统设计方面得到李水清硕士的帮助,在PID实时控制方面得到刘涛硕士的帮助,在此一一表示感谢。
本书的出版得到了电子工业出版社高平同志的大力支持,特别是龚兰方同志对本书进行了细致的编辑,在此深表谢意。
本书的研究工作得到了国家自然科学基金(编号:69874037)和航空基金(编号:00E51022)的资助。
由于作者水平有限,书中难免存在一些不足和错误之处,欢迎广大读者批评指正。
作者: 刘金琨2002年10月于北京航空航天大学目 录前 言第1章 数字PID控制 (1)1.1PID控制原理 (1)1.2 连续系统的模拟PID仿真 (2)1.3 数字PID控制 (3)1.3.1 位置式PID控制算法 (3)1.3.2 连续系统的数字PID控制仿真 (4)1.3.3 离散系统的数字PID控制仿真 (8)1.3.4 增量式PID控制算法及仿真 (14)1.3.5 积分分离PID控制算法及仿真 (16)1.3.6 抗积分饱和PID控制算法及仿真 (20)1.3.7 T型积分PID控制算法 (24)1.3.8 变速积分PID算法及仿真 (24)1.3.9 带滤波器的PID控制仿真 (28)1.3.10 不完全微分PID控制算法及仿真 (33)1.3.11 微分先行PID控制算法及仿真 (37)1.3.12 带死区的PID控制算法及仿真 (42)1.3.13 基于前馈补偿的PID控制算法及仿真 (45)1.3.14 步进式PID控制算法及仿真 (49)第2章 常用的数字PID控制系统 (53)2.1 单回路PID控制系统 (53)2.2 串级PID控制 (53)2.2.1 串级PID控制原理 (53)2.2.2 仿真程序及分析 (54)2.3 纯滞后系统的大林控制算法 (57)2.3.1 大林控制算法原理 (57)2.3.2 仿真程序及分析 (57)2.4 纯滞后系统的Smith控制算法 (59)2.4.1 连续Smith预估控制 (59)2.4.2 仿真程序及分析 (61)2.4.3数字Smith预估控制 (63)2.4.4仿真程序及分析 (64)第3章 专家PID控制和模糊PID控制 (68)3.1 专家PID控制 (68)3.1.1 专家PID控制原理 (68)3.1.2 仿真程序及分析 (69)3.2 模糊自适应整定PID控制 (72)3.2.1 模糊自适应整定PID控制原理 (72)3.2.2 仿真程序及分析 (76)3.3 模糊免疫PID控制算法 (87)3.3.1 模糊免疫PID控制算法原理 (88)3.3.2 仿真程序及分析 (89)第4章 神经PID控制 (94)4.1 基于单神经元网络的PID智能控制 (94)4.1.1 几种典型的学习规则 (94)4.1.2 单神经元自适应PID控制 (94)4.1.3 改进的单神经元自适应PID控制 (95)4.1.4 仿真程序及分析 (95)4.1.5 基于二次型性能指标学习算法的单神经元自适应PID控制 (99)4.1.6 仿真程序及分析 (100)4.2 基于BP神经网络整定的PID控制 (103)4.2.1基于BP神经网络的PID整定原理 (103)4.2.2 仿真程序及分析 (106)4.3 基于RBF神经网络整定的PID控制 (112)4.3.1 RBF神经网络模型 (112)4.3.2 RBF网络PID整定原理 (114)4.3.3 仿真程序及分析 (114)4.4 基于RBF神经网络辨识的单神经元PID模型参考自适应控制 (120)4.4.1 神经网络模型参考自适应控制原理 (120)4.4.2 仿真程序及分析 (121)4.5 基于CMAC神经网络与PID的并行控制 (126)4.5.1 CMAC网络 (126)4.5.2 CMAC与PID复合控制算法 (127)4.5.3 仿真程序及分析 (128)4.6 基于SIMULINK的CMAC与PID并行控制 (133)4.6.1 SIMULINK仿真方法 (133)4.6.2 仿真程序及分析 (134)第5章 基于遗传算法整定的PID控制 (139)5.1遗传算法基本原理 (139)5.2 遗传算法的优化设计 (140)5.2.1 遗传算法的构成要素 (140)5.2.2 遗传算法的应用步骤 (140)5.3 遗传算法求函数极大值 (140)5.3.1 遗传算法求函数极大值实例 (140)5.3.2 仿真程序及分析 (142)5.4 基于遗传算法的PID整定 (145)5.4.1 基于遗传算法的PID整定原理 (146)5.4.2 基于实数编码遗传算法的PID整定 (147)5.4.3 仿真程序及分析 (148)5.4.4 基于二进制编码遗传算法的PID整定 (153)5.4.5 仿真程序及分析 (153)5.5 基于遗传算法摩擦模型参数辨识的PID控制 (157)5.5.1仿真实例 (157)5.5.2 仿真程序及分析 (158)第6章 PID解耦控制 (165)6.1 PID多变量解耦控制 (165)6.1.1 PID解耦控制原理 (165)6.1.2仿真程序及分析 (165)6.2 单神经元PID解耦控制 (168)6.2.1单神经元PID解耦控制原理 (168)6.2.2 仿真程序及分析 (169)6.3 基于DRNN神经网络整定的PID解耦控制 (173)6.3.1 基于DRNN神经网络参数自学习PID解耦控制原理 (173)6.3.2 DRNN神经网络的Jacobian信息辨识 (174)6.3.3仿真程序及分析 (176)第7章 几种先进PID控制方法 (185)7.1 基于干扰观测器的PID控制 (185)7.1.1 干扰观测器设计原理 (185)7.1.2连续系统的控制仿真 (188)7.1.3 离散系统的控制仿真 (190)7.2 非线性系统的PID鲁棒控制 (195)7.2.1 基于NCD优化的非线性优化PID控制 (195)7.2.2 基于NCD与优化函数结合的非线性优化PID控制 (197)7.3 一类非线性PID控制器设计 (199)7.3.1 非线性控制器设计原理 (199)7.3.2仿真程序及分析 (201)7.4 基于重复控制补偿的高精度PID控制 (208)7.4.1 重复控制原理 (208)7.4.2 基于重复控制补偿的PID控制 (209)7.4.3仿真程序及分析 (209)7.5 基于零相差前馈补偿的高精度PID控制 (214)7.5.1 零相差控制原理 (214)7.5.2 基于零相差前馈补偿的PID控制 (215)7.5.3仿真程序及分析 (217)第8章 灰色PID控制 (229)8.1 灰色控制原理 (229)8.1.1 生成数列 (229)8.1.2 GM灰色模型 (230)8.2 灰色PID控制 (231)8.2.1 灰色PID控制的理论基础 (231)8.2.2 连续系统灰色PID控制 (233)8.2.3 仿真程序及分析 (235)8.2.4离散系统灰色PID控制 (240)8.2.5 仿真程序及分析 (242)8.3灰色PID的位置跟踪 (247)8.3.1连续系统灰色PID位置跟踪 (247)8.3.2 仿真程序及分析 (250)8.3.3 离散系统灰色PID位置跟踪 (254)8.3.4 仿真程序及分析 (256)第9章 非线性PID控制 (261)9.1 伺服系统低速摩擦条件下PID控制 (261)9.1.1 Stribeck摩擦模型描述 (261)9.1.2 一个典型伺服系统描述 (261)9.1.3 仿真程序及分析 (262)9.2 伺服系统的三环PID控制 (269)9.2.1 伺服系统三环的PID控制原理 (269)9.2.2 仿真程序及分析 (271)9.3 二质量伺服系统的PID控制 (276)9.3.1二质量伺服系统的PID控制原理 (276)9.3.2 仿真程序及分析 (278)第10章 PID 实时控制的 C++ 语言设计及应用 (283)10.1 M语言的 C++ 转化 (283)10.2 基于 C++ 的三轴飞行模拟转台伺服系统 PID 实时控制 (285)10.2.1 控制系统构成 (285)10.2.2 系统各部分功能的软件设计 (286)10.2.3 仿真程序及分析 (287)参考文献 (298)。
