jsff01(数值计算方法)
超级简易的JS计算器(实现加减乘除)
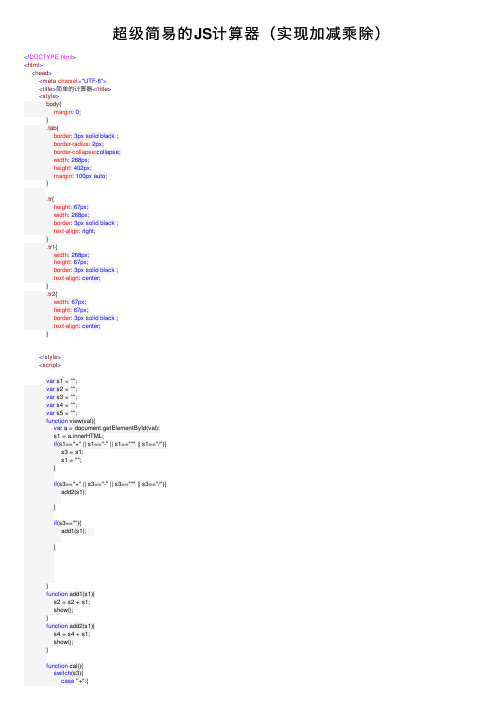
超级简易的JS计算器(实现加减乘除)<!DOCTYPE html><html><head><meta charset="UTF-8"><title>简单的计算器</title><style>body{margin: 0;}.tab{border: 3px solid black ;border-radius: 2px;border-collapse:collapse;width: 268px;height: 402px;margin: 100px auto;}.tr{height: 67px;width: 268px;border: 3px solid black ;text-align: right;}.tr1{width: 268px;height: 67px;border: 3px solid black ;text-align: center;}.tr2{width: 67px;height: 67px;border: 3px solid black ;text-align: center;}</style><script>var s1 = "";var s2 = "";var s3 = "";var s4 = "";var s5 = "";function view(val){var a = document.getElementById(val);s1 = a.innerHTML;if(s1=="+" || s1=="-" || s1=="*" || s1=="/"){s3 = s1;s1 = "";}if(s3=="+" || s3=="-" || s3=="*" || s3=="/"){add2(s1);}if(s3==""){add1(s1);}}function add1(s1){s2 = s2 + s1;show();}function add2(s1){s4 = s4 + s1;show();}function cal(){switch(s3){case "+":{s5 = (String)((parseFloat(s2)+parseFloat(s4)).toFixed(2));result.innerHTML = s5;break;}case "-":{s5 = (String)((parseFloat(s2)-parseFloat(s4)).toFixed(2));result.innerHTML = s5;break;}case "*":{s5 = (String)((parseFloat(s2)*parseFloat(s4)).toFixed(2));result.innerHTML = s5;break;}case "/":{s5 = (String)((parseFloat(s2)/parseFloat(s4)).toFixed(2));result.innerHTML = s5;break;}}}function show(){var result = document.getElementById("result");result.innerHTML = s2+s3+s4;}</script></head><body><table class="tab"><tr class = "tr2"><td colspan="4">简易计算器</td></tr><tr class="tr"><td id="result" colspan="4"></td></tr><tr ><td id="+" class="tr1" onclick="view('+')">+</td><td id="-" class="tr1" onclick="view('-')">-</td><td id="*" class="tr1" onclick="view('*')">*</td><td id="/" class="tr1" onclick="view('/')">/</td></tr><tr ><td id="7" class="tr1" onclick="view('7')">7</td><td id="8" class="tr1" onclick="view('8')">8</td><td id="9" class="tr1" onclick="view('9')">9</td><td id="0" class="tr1" onclick="view('0')">0</td></tr><tr><td id="4" class="tr1" onclick="view('4')">4</td><td id="5" class="tr1" onclick="view('5')">5</td><td id="6" class="tr1" onclick="view('6')">6</td><td id="." class="tr1" onclick="view('.')">.</td></tr><tr><td id="1" class="tr1" onclick="view('1')">1</td><td id="2" class="tr1" onclick="view('2')">2</td><td id="3" class="tr1" onclick="view('3')">3</td><td id="=" class="tr1" onclick="cal()">=</td></tr></table></body></html>对于这个程序来说,判断的顺序⾮常重要,不然就会把"+"号存在s2,s4中⽽不是s3中。
用javascript输出加减乘除算术题

题目:用JavaScript输出加减乘除算术题一、引言在现代社会中,计算机技术已经成为人们日常生活和工作中必不可少的一部分。
而JavaScript作为一种强大的脚本语言,被广泛应用于网页开发、移动应用开发等领域。
今天,我们将探讨如何利用JavaScript来输出加减乘除算术题,帮助读者更好地应用JavaScript。
二、使用JavaScript输出加减乘除算术题的方法在JavaScript中,我们可以利用以下几种方法来输出加减乘除算术题:1. 使用alert()方法输出算术题alert()方法是JavaScript中常用的弹窗方法,我们可以利用它来输出加减乘除算术题,并在弹窗中显示给用户。
例如:```javascriptvar num1 = 10;var num2 = 5;alert("加法题:" + num1 + " + " + num2 + " = " + (num1 +num2));alert("减法题:" + num1 + " - " + num2 + " = " + (num1 -num2));alert("乘法题:" + num1 + " * " + num2 + " = " + (num1 *num2));alert("除法题:" + num1 + " / " + num2 + " = " + (num1 /num2));```通过以上代码,我们可以利用alert()方法依次输出加减乘除算术题,并显示计算结果,让用户在弹窗中直观地看到算术题和答案。
2. 使用console.log()方法输出算术题除了利用alert()方法显示算术题外,我们还可以使用console.log()方法在浏览器的控制台中输出算术题。
js数据处理方法

js数据处理方法JavaScript 是一种广泛使用的编程语言,其灵活性和动态性使其成为数据处理的理想语言。
JavaScript 提供了许多数据结构和方法来处理各种类型的数据,从简单的数字和字符串到更复杂的对象和数组。
本文将介绍 JavaScript 中常见的数据处理方法,以帮助读者更好地理解 JavaScript 编程语言。
一、JavaScript中的数据类型基本数据类型包括:- 数字(Number)- 字符串(String)- 布尔值(Boolean)- null(空)- undefined(未定义)- 数组(Array)- 对象(Object)- 函数(Function)在 JavaScript 中,可以使用 typeof 运算符来查看变量的类型。
例如:```typeof 123; // 返回 "number"typeof "hello"; // 返回 "string"typeof true; // 返回 "boolean"typeof null; // 返回 "object"typeof undefined; // 返回 "undefined"typeof []; // 返回 "object"typeof {}; // 返回 "object"typeof function(){}; // 返回 "function"```JavaScript 中的数据类型可以互相转换。
可以使用 Number() 函数将字符串转换为数字,使用 String() 函数将数字转换为字符串。
1. 转换为数字可以使用 Number() 函数将其他数据类型转换为数字。
- 如果该值是数字,返回数字本身。
- 如果该值是布尔值 true,返回数字 1。
js解析数学表达式

在JavaScript中,可以使用不同的方法来解析和计算数学表达式。
以下是一些常见的方法:
1. 使用eval函数:
eval() 函数可以将包含数学表达式的字符串作为参数,并返回该表达式的计算结果。
例如:
var expression = "2 * (3 + 4)";
var result = eval(expression); // 结果为14
但是需要注意的是,eval() 函数存在安全风险,因为它会执行传入的任意代码,可能导致代码注入等安全问题,因此在实际开发中需要谨慎使用。
2. 使用Function构造函数:
可以使用Function构造函数动态创建一个函数来计算数学表达式。
例如:
var expression = "2 * (3 + 4)";
var calculate = new Function('return ' + expression);
var result = calculate(); // 结果为14
3. 使用第三方库:
也可以使用第三方的数学表达式解析库,例如math.js、expr-eval等。
这些库提供了更丰富的功能和更安全的表达式解析方法。
在实际开发中,建议根据具体的需求和安全考虑选择合适的方法来解析和计算数学表达式。
javascript 数学运算题

文章标题:探索JavaScript中的数学运算题在JavaScript编程中,数学运算是我们经常需要处理的一个重要部分。
无论是简单的加减乘除,还是复杂的数学函数计算,都需要我们对JavaScript中的数学运算有着深入的理解和掌握。
下面,我将以“javascript 数学运算题”为主题,深入探讨JavaScript中的数学运算,帮助您更好地理解并掌握这一内容。
1. JavaScript中的基本数学运算在JavaScript中,基本的数学运算包括加减乘除四则运算。
我们可以使用加号(+)进行加法运算,减号(-)进行减法运算,星号(*)进行乘法运算,斜杠(/)进行除法运算。
还可以使用Math对象提供的方法进行更复杂的数学运算,比如求平方根、取整、四舍五入等。
2. JavaScript中的数学函数除了基本的四则运算外,JavaScript还提供了丰富的数学函数,如Math.sqrt()用于求平方根,Math.pow()用于求幂运算,Math.abs()用于求绝对值等等。
这些数学函数在实际编程中经常会用到,了解和熟练运用这些函数,可以帮助我们更高效地进行数学运算。
3. JavaScript中的数学运算符优先级在进行复杂的数学运算时,了解运算符的优先级是非常重要的。
JavaScript中的运算符优先级遵循数学计算的习惯,比如乘除优先于加减。
如果不清楚运算符的优先级,很容易出现错误的计算结果,因此我们需要特别注意运算符的优先级规则。
4. JavaScript中的数学运算题实例分析接下来,让我们通过实例来进一步深入探讨JavaScript中的数学运算。
假设我们需要解决一个复杂的数学运算题,如求解一个三角函数的值,或者求解一个复杂的数学公式。
我们可以借助JavaScript的数学运算符和数学函数来进行计算,然后得到我们想要的结果。
通过实例分析,我们可以更好地理解和掌握JavaScript中数学运算的应用。
5. 个人观点和总结从以上讨论可以看出,JavaScript中的数学运算是程序员在日常编程中必不可少的一部分。
javascript中解析四则运算表达式的算法和示例

javascript中解析四则运算表达式的算法和⽰例在编写代码时我们有时候会碰到需要⾃⼰解析四则运算表达式的情况,本⽂简单的介绍使⽤JavaScript实现对简单四则运算表达式的解析。
⼀、熟悉概念中缀表⽰法(或中缀记法)是⼀个通⽤的算术或逻辑公式表⽰⽅法,操作符是以中缀形式处于操作数的中间(例:3 + 4)。
也就是我们最常⽤的算术表达式,中缀表达式对于⼈类来说⽐较容易理解,但是不易于计算机解析。
逆波兰表⽰法(Reverse Polish notation,RPN,或逆波兰记法),是⼀种是由波兰数学家扬·武卡谢维奇1920年引⼊的数学表达式⽅式,在逆波兰记法中,所有操作符置于操作数的后⾯,因此也被称为后缀表⽰法。
逆波兰记法不需要括号来标识操作符的优先级。
逆波兰表⽰法容易使⽤堆栈结构对表达式进⾏解析并计算,所以,这⾥我们解析四则元素表达式,是先从中缀表达式,转换为逆波兰表达式。
然后再计算值。
⼆、转换流程中缀表达式转换为后缀表达式(调度场算法)1.输⼊队列弹出⼀个记号2.如果记号为数字,添加到输出队列中3.如果是⼀个操作符(+-*/)则⽐较它与输出堆栈中栈顶的操作符,如果优先级⼩于或等于栈顶的操作符,那么将栈顶的操作符弹出并加⼊输出队列(循环,直到上述条件不满⾜),最后将本次的操作符压⼊堆栈。
4.如果是⼀个左括号,压⼊堆栈5.如果是⼀个右括号,从栈中不断的弹出操作符,并加⼊输出队列,知道栈顶的元素为左括号。
弹出左括号,不加⼊输出队列。
如果没有发现左括号,说明原来的表达式中括号不对称,有错误。
6.如果输⼊队列为空,⽽栈中尚有操作符时,如果栈顶的操作符为左括号,则说明原表达式有不匹配的括号。
将栈中的操作符逐个弹出,加⼊输出队列。
7.完成三、转换代码实现function isOperator(value){var operatorString = "+-*/()";return operatorString.indexOf(value) > -1}function getPrioraty(value){switch(value){case '+':case '-':return 1;case '*':case '/':return 2;default:return 0;}}function prioraty(o1, o2){return getPrioraty(o1) <= getPrioraty(o2);}function dal2Rpn(exp){var inputStack = [];var outputStack = [];var outputQueue = [];for(var i = 0, len = exp.length; i < len; i++){var cur = exp[i];if(cur != ' ' ){inputStack.push(cur);}}console.log('step one');while(inputStack.length > 0){var cur = inputStack.shift();if(isOperator(cur)){if(cur == '('){outputStack.push(cur);}else if(cur == ')'){var po = outputStack.pop();while(po != '(' && outputStack.length > 0){outputQueue.push(po);po = outputStack.pop();}if(po != '('){throw "error: unmatched ()";}}else{while(prioraty(cur, outputStack[outputStack.length - 1]) && outputStack.length > 0){outputQueue.push(outputStack.pop());}outputStack.push(cur);}}else{outputQueue.push(new Number(cur));}}console.log('step two');if(outputStack.length > 0){if(outputStack[outputStack.length - 1] == ')' || outputStack[outputStack.length - 1] == '('){throw "error: unmatched ()";}while(outputStack.length > 0){outputQueue.push(outputStack.pop());}}console.log('step three');return outputQueue;}console.log(dal2Rpn('1 + 2'));console.log(dal2Rpn('1 + 2 + 3'));console.log(dal2Rpn('1 + 2 * 3'));console.log(dal2Rpn('1 + 2 * 3 - 4 / 5'));console.log(dal2Rpn('( 1 + 2 )'));console.log(dal2Rpn('( 1 + 2 ) * ( 3 - 4 ) / 5'));console.log(dal2Rpn('( 1 + 2 ) * (( 3 - 4 ) / 5)'));四、逆波兰表达式求值1.从输⼊队列中弹出⼀个记号2.如果是操作数,加⼊输出堆栈3.如果是⼀个操作符,从输出堆栈中弹出两个操作数并进⾏计算,并将计算得到的值压⼊输出堆栈。
js 处理数字转换成金额的方法

js 处理数字转换成金额的方法在JavaScript中,将数字转换为金额通常需要遵循一些特定的格式和规则,特别是涉及到货币符号、小数点、千位分隔符等。
以下是一个简单的例子,说明如何实现这个转换。
首先,我们假设你有一个数字,例如 `.89`,你想将它转换成 `¥1,234,` 的格式。
下面是一个简单的JavaScript函数,可以将数字转换为这种金额格式:```javascriptfunction numberToCNYMoney(num) {var fraction = ['角', '分'];var digit = ['零', '壹', '贰', '叁', '肆', '伍', '陆', '柒', '捌', '玖'];var unit = [['元', '万', '亿'], ['', '拾', '佰', '仟']];var head = num < 0? '欠': '';num = (num);var s = '';for (var i = 0; i < ; i++) {s += (digit[(num 10 (10, i)) % 10] + fraction[i]).replace(/零./, ''); }s = s '整';num = (num);for (var i = 0; i < unit[0].length && num > 0; i++) {var p = '';for (var j = 0; j < unit[1].length && num > 0; j++) {p = digit[num % 10] + unit[1][j] + p;num = (num / 10);}s = (/(零.)零$/, '').replace(/^$/, '零') + unit[0][i] + s;}return head + (/(零.)零元/, '元').replace(/(零.)+/g, '零').replace(/^整$/, '零元整');}```你可以这样使用这个函数:```javascript(numberToCNYMoney.89)); // 输出:¥壹百贰十三万肆仟伍佰陆十七元捌角玖分```请注意,这只是一个简单的示例,并不涵盖所有可能的边界情况。
javascript实现简易计算器的代码_

javascript实现简易计算器的代码_ 下面我就为大家带来一篇javascript实现简易计算器的代码我觉得挺不错的,现在分享给大家,也给大家做个参考。
今日闲来无聊,想写点什么,突然想到用javascript写一个计算器。
程序还存在许多的Bug,先在这里记录一下,以后慢慢更正。
代码如下:!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "l1/DTD/xhtml1-transitional.dtd" html xmlns="l"headmeta http-equiv="Content-Type" content="text/html; charset=utf-8" /titlejavascript实现简易计算器的代码_脚本之家/titlestyle type="text/css"input{width:30px;height:20px;text-align:center;}#tbCalculator td{text-align:center;vertical-align:middle;}/stylescript type="text/javascript"var result; //保存点击运算符之前输入框中的数值var operator; //保存运算符var isPressEqualsKey = false; //记录是否按下”=“键 //数字键大事function connectionDigital(control){var txt = document.getElementById('txtScream'); if(isPressEqualsKey){txt.value = ""; //已进行过计算,则清空数值输入框重新开头isPressEqualsKey = false;}//数值输入已经存在小数点,则不允许再输入小数点if(txt.value.indexOf('.') -1 control.value == '.')return false;txt.value += control.value; //将控件值赋给数值输入框中}//退格键大事function backspace(){var txt = document.getElementById('txtScream'); txt.value = txt.value.substring(0,txt.value.length - 1);}//ce键大事:清空数字输入框function clearAll(){document.getElementById('txtScream').value = ""; result = "";operator = "";}// +、-、*、/ 大事function calculation(control){//将运算符保存入全局变量中operator = control.value;var txt = document.getElementById('txtScream'); if(txt.value == "")return false; //数值输入框中没有数字,则不能输入运算符//将数值输入框中的值保存到计算表达式中result = txt.value;//清空输入框,以待输入操作值txt.value = "";}//计算结果function getResult(){var opValue;//计算表达式中存在运算符var sourseValue = parseFloat(result);var txt = document.getElementById('txtScream'); if(operator == '*')opValue = sourseValue * parseFloat(txt.value); else if(operator == '/')opValue = sourseValue / parseFloat(txt.value);else if(operator == '+')opValue = sourseValue + parseFloat(txt.value);else if(operator == '-')opValue = sourseValue - parseFloat(txt.value);txt.value = opValue;isPressEqualsKey = true;result = "";opValue = "";}/script/headbodytable id="tbCalculator" width="200" border="1" align="center" cellpadding="0" cellspacing="0" bordercolor="#0066FF"trtd height="30" colspan="4" align="center"input type="text" name="txtScream" id="txtScream" style="width:180px; border-style:none; text-align:right;" readonly="readonly" / /td/trtrtd height="30" colspan="2"input type="button" name="btnCE" id="btnCE" value="C E" style="width:80px;" align="right"; onclick="clearAll();" //tdtd height="30" colspan="2"input type="button" name="btn10" id="btn10" value="Backspace" style="width:80px;" align="right"; onclick="backspace();" //td/trtrtd height="30"input type="button" name="btn7" id="btn7" value="7" onclick="connectionDigital(this);" //tdtdinput type="button" name="btn8" id="btn8" value="8" onclick="connectionDigital(this);"//tdtdinput type="button" name="btn9" id="btn9" value="9" onclick="connectionDigital(this);" //td tdinput type="button" name="btn6" id="btn6" value="/" onclick="calculation(this);" //td/trtrtd height="30"input type="button" name="btn4" id="btn4" value="4" onclick="connectionDigital(this);"//tdtdinput type="button" name="btn5" id="btn5" value="5" onclick="connectionDigital(this);"//tdtdinput type="button" name="btn6" id="btn6" value="6" onclick="connectionDigital(this);"//tdtdinput type="button" name="btn13" id="btn13" value="*" onclick="calculation(this);" //td/trtrtd height="30"input type="button" name="btn1" id="btn1" value="1" onclick="connectionDigital(this);"//tdtdinput type="button" name="btn2" id="btn2" value="2" onclick="connectionDigital(this);"//tdtdinput type="button" name="btn3" id="btn3" value="3" onclick="connectionDigital(this);"//tdtdinput type="button" name="btn18" id="btn18" value="-" onclick="calculation(this);" //td/trtrtd height="30"input type="button" name="btn0"id="btn0" value="0" onclick="connectionDigital(this);"//tdtdinput type="button" name="btndot" id="btndot" value="." onclick="connectionDigital(this);" //td tdinput name="btn22" type="button" id="btn22" value="=" onclick="getResult();" //tdtdinput type="button" name="btn23" id="btn23" value="+" onclick="calculation(this);" //td/tr/table/body/html以上这篇javascript实现简易计算器的代码就是我分享给大家的全部内容了,盼望能给大家一个参考...。
js关于精度的函数处理加减乘除方法

js关于精度的函数处理加减乘除方法在JavaScript中,由于浮点数的特性,进行简单的加减乘除运算时可能会出现精度丢失的问题。
为了解决这个问题,我们可以使用一些函数来处理。
对于加法运算,我们可以使用toFixed函数来保留指定小数位数的精度。
该函数可以接收一个参数,即要保留的小数位数。
例如,如果我们要计算0.1 + 0.2的结果并保留一位小数,可以使用以下代码:```javascriptvar result = (0.1 + 0.2).toFixed(1);console.log(result); // 输出 0.3```对于减法运算,由于JavaScript没有提供类似toFixed的函数,我们可以借助一个第三方库,如decimal.js或big.js来处理。
这些库可以提供更精确的减法运算。
例如,使用decimal.js库的代码如下:```javascriptvar Decimal = require('decimal.js');var result = new Decimal(0.3).minus(0.1);console.log(result.toString()); // 输出 0.2```对于乘法运算,我们可以使用toPrecision函数来保留指定有效数字位数的精度。
该函数接收一个参数,表示保留的有效数字位数。
例如,如果我们要计算2.1乘以1.3的结果并保留两位有效数字,可以使用以下代码:```javascriptvar result = (2.1 * 1.3).toPrecision(2);console.log(result); // 输出 2.7```对于除法运算,我们可以使用toPrecision函数来保留指定有效数字位数的精度,或使用toFixed函数来保留指定小数位数的精度。
例如,如果我们要计算3除以2的结果并保留两位有效数字,可以使用以下代码:```javascriptvar result = (3 / 2).toPrecision(2);console.log(result); // 输出 1.5var result2 = (3 / 2).toFixed(2);console.log(result2); // 输出 1.50```总之,通过使用toFixed、toPrecision以及借助第三方库,我们可以在JavaScript中处理加减乘除运算时更精确地控制精度,避免出现精度丢失的问题。
js自增自减运算例题详解

js自增自减运算例题详解JavaScript(简称JS)是一种广泛应用于网页开发的脚本语言,它可以为网页添加动态效果和交互功能。
在JS中,自增自减运算是一种常见的操作,本文将详细解析自增自减运算的例题。
一、自增运算自增运算符(++)用于将变量的值增加1。
它可以用在变量前面(前缀自增)或变量后面(后缀自增)。
下面是一个例子:```javascriptvar num = 5;console.log(++num); // 输出6console.log(num); // 输出6```在这个例子中,变量`num`的值先加1,然后输出。
再次输出`num`的值时,它已经变成了6。
二、自减运算自减运算符(--)用于将变量的值减少1。
它也可以用在变量前面(前缀自减)或变量后面(后缀自减)。
下面是一个例子:```javascriptvar num = 5;console.log(--num); // 输出4console.log(num); // 输出4```在这个例子中,变量`num`的值先减1,然后输出。
再次输出`num`的值时,它已经变成了4。
三、自增自减运算的应用自增自减运算在实际开发中有很多应用场景,比如循环控制、条件判断等。
下面是一些例题,通过解析这些例题,我们可以更好地理解自增自减运算的使用方法。
例题1:循环输出```javascriptfor (var i = 0; i < 5; i++) {console.log(i);}```在这个例题中,变量`i`的初始值为0,每次循环结束后,`i`的值会自增1。
当`i`的值小于5时,循环会一直执行,输出0、1、2、3、4。
例题2:条件判断```javascriptvar num = 10;if (num++ > 10) {console.log("大于10");} else {console.log("小于等于10");}```在这个例题中,变量`num`的初始值为10,通过后缀自增运算符,`num`的值会先参与判断,然后再自增1。
js数字转科学计数法

js数字转科学计数法摘要:1.科学计数法的概念2.JavaScript 中数字转科学计数法的方法3.实例演示4.总结正文:科学计数法是一种表示非常大或非常小的数字的方法,其使用基数为10 的指数来表示数字的值。
在JavaScript 中,我们可以使用一些方法将数字转换为科学计数法表示。
以下是JavaScript 中数字转科学计数法的方法:1.使用`toExponential()`方法`toExponential()`方法将数字转换为科学计数法表示,其返回一个字符串,表示为`a x 10^b`的形式,其中`a`是一个介于1 和10 之间的数字,`b`是一个整数。
例如,将数字123 转换为科学计数法表示,可以使用以下代码:```javascriptconst num = 123;const result = num.toExponential(); // 结果为"1.23 x 10^2"```2.使用`toFixed()`方法`toFixed()`方法将数字四舍五入为指定小数位数的数字,其返回一个字符串。
我们可以使用该方法来将数字转换为科学计数法表示。
例如,将数字123.456 转换为科学计数法表示,可以使用以下代码:```javascriptconst num = 123.456;const result = num.toFixed(1).replace(/^0+/, "").replace(/.0+$/, "").replace(/./g, "x").replace(/x$/, "10^x"); // 结果为"1.235 x 10^2"```在实际应用中,我们可以根据需要选择不同的方法来将数字转换为科学计数法表示。
js数字转科学计数法

js数字转科学计数法在JavaScript中,可以使用科学计数法来表示较大或较小的数字。
要将一个数字转换为科学计数法,可以使用toExponential()方法。
toExponential()方法接受一个参数,用于指定转换为科学计数法后的小数位数。
如果不提供参数,则默认使用尽可能多的小数位数。
下面是一个例子,演示如何将一个数字转换为科学计数法:javascript.let number = 1000000000;let scientificNotation = number.toExponential();console.log(scientificNotation); // 输出: 1e+9。
let number2 = 0.000000001;let scientificNotation2 = number2.toExponential();console.log(scientificNotation2); // 输出: 1e-9。
在上面的例子中,第一个数字1000000000被转换为1e+9,表示10的9次方;而第二个数字0.000000001被转换为1e-9,表示10的负9次方。
如果想要指定转换后的小数位数,可以将一个数字作为参数传递给toExponential()方法。
例如,将数字转换为科学计数法并保留两位小数:javascript.let number = 1000000000;let scientificNotation = number.toExponential(2);console.log(scientificNotation); // 输出: 1.00e+9。
let number2 = 0.000000001;let scientificNotation2 = number2.toExponential(2);console.log(scientificNotation2); // 输出: 1.00e-9。
javascript运算符——位运算符

javascript运算符——位运算符前⾯的话 位运算符是⾮常底层的运算,由于其很不直观,所以并不常⽤。
但是,其速度极快,且合理使⽤能达到很好的效果。
本⽂将介绍javascript中常常被忽视的运算符——位运算符⼆进制表⽰ ECMAScript中的所有数值都以IEEE-754 64位格式存储,但位操作符并不直接操作64位的值,⽽是以32位带符号的整数进⾏运算的,并且返回值也是⼀个32位带符号的整数 这种位数转换使得在对特殊的NaN和Infinity值应⽤位操作时,这两个值都会被当成0来处理 如果对⾮数值应⽤位操作符,会先使⽤Number()将该值转换成数值再应⽤位操作,得到的结果是⼀个数值//'|'表⽰按位或,⼀个整数与0按位或运算可以得到它本⾝,⼀个⼩数与0按位或运算可以得到取整效果console.log( 1.3 | 0);//1console.log( 1.8 | 0);//1console.log( Infinity | 0);//0console.log( -Infinity | 0);//0console.log( NaN | 0);//0console.log('12px' | 0);//0console.log('12' | 0);//12 有符号整数使⽤32位中的前31位表⽰整数数值,⽤第32位表⽰整数符号,0表⽰正数,1表⽰负数。
表⽰符号的位叫做符号位,符号位的值决定了其他位数值的格式。
其中,正数以纯⼆进制格式存储,31位中的每⼀位都表⽰2的幂。
第⼀位(叫做位0)表⽰2的0次,第⼆位表⽰2的1次,以此类推。
没有⽤到的位以0填充,即忽略不计 例如,数值18的⼆进制表⽰是00000000000000000000000000010010,或者更简洁的10010。
这是5个有效位,这5位本⾝就决定了实际的值console.log((18).toString(2));//"10010"console.log(0b00000000000000000000000000010010);//18 负数同样以⼆进制存储,但使⽤的格式是⼆进制补码。
js进制转换算法

在JavaScript中,进制转换通常涉及十进制与其他进制的转换。
以下是这两种类型的一些基本算法:1.十进制转其他进制(例如二进制、八进制或十六进制):2.javascript复制代码function decimalToOtherBase(decimalNumber, base) {var map = {2: "01",8: "01234567",16: "0123456789ABCDEF"};var result = "";while(decimalNumber > 0) {result = map[base].charAt(decimalNumber % base) + result;decimalNumber = Math.floor(decimalNumber / base);}return result;}使用方法:console.log(decimalToOtherBase(10, 2));输出:1010(十进制的10转为二进制的结果)2. 其他进制转十进制:javascript复制代码function otherBaseToDecimal(number, base) {var map = {2: {toDecimal: function(n){return n}},8: {toDecimal: function(n){return parseInt(n, 8)}, fromDecimal:function(n){return parseInt(n, 10)}} ,16: {toDecimal: function(n){return parseInt(n, 16)}, fromDecimal: function(n){return parseInt(n, 10)}}};return map[base].fromDecimal(number);}使用方法:console.log(otherBaseToDecimal('A', 16));输出:10(十六进制的'A'转为十进制的结果)注意,这些函数只处理整数,不处理小数。
js中的位运算

js中的位运算js中的位运算⼀、总结⼀句话总结:> 按位与(&)、按位或(|)、按位⾮(~)、按位异或(^)> 有符号左移(<<)、有符号右移(>>)> ⽆符号右移(>>>)⼆、js中的位运算我们可能很少在编程中⽤位运算,如果没深⼊学习,可能也很难理解。
平时的数值运算,其实是要先转换成⼆进制再进⾏运算的,⽽位运算就是直接进⾏⼆进制运算,所以位运算的执⾏效率肯定是更⾼的。
下⾯通过⼀些实例来加深对位运算的理解。
按位与(&)&&运算符我们都知道,只有两个都为真,结果才为真。
&道理是⼀样的,只有两个数的值为1时,才返回1。
例如1和3的按位与操作:0001& 0011---------0001只有对应的数为1时,结果才为1,其他都为0。
判断⼀个数是奇数还是偶数,我们会⽤求余数来判断:function assert(n) {if (n % 2 === 1) {console.log("n是奇数");} else {console.log("n是偶数");}}assert(3); // "n是奇数"我们也可以⽤⼀个数和1进⾏按位&操作来判断,⽽且速度更快:function assert(n) {if (n & 1) {console.log("n是奇数");} else {console.log("n是偶数");}}assert(3); // "n是奇数"下⾯是位运算过程:1 = 00013 = 0011--------& = 0001奇数的⼆进制码的最后⼀位数肯定是1,⽽1只有最后⼀位为1,按位&操作之后,结果肯定只有最后⼀位数为1。
⽽偶数的⼆进制表⽰的最后⼀位数是0,和1进⾏按位&操作,结果所有位数都为0。
js float计算 误差

js float计算误差摘要:1.JavaScript浮点数计算误差概述2.浮点数计算误差的原因3.解决浮点数计算误差的方法4.实战案例:精确计算两个浮点数的和正文:在前端开发中,JavaScript的浮点数计算误差是一个常见的问题。
本文将介绍浮点数计算误差的原因、解决方法以及实战案例。
一、JavaScript浮点数计算误差概述由于计算机内部表示浮点数时采用的科学计数法和小数点后数字的位数限制,导致了浮点数计算时出现误差。
例如,0.1 + 0.2 的结果并不等于0.3,而是稍微大于0.3。
这是因为计算机内部将0.1和0.2转换为科学计数法表示后,相加得到的结果再转换回普通数字时,小数点位置发生了变化。
二、浮点数计算误差的原因1.计算机内部表示:计算机内部用科学计数法表示浮点数,例如0.1 表示为1.0x10^-1,0.2 表示为1.0x10^-2。
因此,在计算过程中,可能会出现精度损失。
2.运算符优先级:JavaScript中的运算符优先级从高到低依次为:指数运算符、乘除运算符、加减运算符。
这导致在复杂数学运算中,浮点数计算误差可能会被放大。
3.数字类型转换:在JavaScript中,数字与字符串进行运算时,会自动转换为数字类型。
例如,"10" + 2 的结果为12,而不是10.2。
这种类型转换也可能导致浮点数计算误差。
三、解决浮点数计算误差的方法1.乘以10的幂:将参与计算的浮点数乘以10的幂,使得计算过程中避开浮点数运算。
例如,计算0.1 + 0.2,可以转换为计算10 * 0.1 + 10 * 0.2,最后再除以10的2次方。
2.使用第三方库:有一些第三方库专门处理JavaScript中的浮点数计算误差,如decimal.js、bignumber.js等。
这些库提供了一些方法来解决浮点数计算问题,如加法、减法、乘法、除法等。
3.自定义函数:可以编写自定义函数来处理浮点数计算误差。
js加减乘除的正则表达式

js加减乘除的正则表达式
在JavaScript中,我们可以使用正则表达式来进行加、减、乘、除等数学运算。
例如,下面是一个加法运算的正则表达式:
/(d+)+(d+)/
这个正则表达式可以匹配形如 '1+2' 的字符串,并将其中的两个数字提取出来,方便我们进行加法运算。
类似地,我们可以使用以下正则表达式进行减法、乘法、除法运算:
减法:/(d+)-(d+)/
乘法:/(d+)*(d+)/
除法:/(d+)/(d+)/
需要注意的是,由于正则表达式只能进行字符串匹配,因此在进行数学运算时,我们需要将匹配到的字符串转换成数字类型,以便进行实际的运算。
- 1 -。
js选择条件生成计算公式

js选择条件生成计算公式摘要:1.计算机编程与数学的结合2.JavaScript 的作用3.选择条件生成计算公式的方法4.实际应用案例5.总结正文:计算机编程与数学的结合在现代科技飞速发展的时代,计算机编程和数学的结合愈发紧密。
编程不仅能帮助人们解决各种实际问题,还能辅助数学研究,甚至成为数学研究的一种新工具。
在众多编程语言中,JavaScript 是一种广泛应用于网页开发的脚本语言。
它能帮助开发者更方便地实现网页的动态效果,为用户提供更丰富的交互体验。
JavaScript 的作用JavaScript 在网页开发中的作用举足轻重,它能实现各种动态效果,如验证表单、制作导航栏、实现图片轮播等。
此外,JavaScript 还可以通过计算公式来处理数据,从而帮助用户更好地理解数据,分析问题。
选择条件生成计算公式的方法在JavaScript 中,我们可以通过条件语句来实现选择条件生成计算公式。
例如,我们可以根据用户的选择,生成不同的计算公式。
如果用户选择了加法运算,那么计算公式就是两个数相加;如果用户选择了乘法运算,那么计算公式就是两个数相乘。
这样,用户可以根据自己的需求,随时调整计算公式。
实际应用案例假设我们开发了一个在线计算器,用户可以根据自己的需求选择不同的运算方式。
我们可以通过JavaScript 来实现这个功能。
首先,我们需要创建一个HTML 表单,让用户选择运算方式。
然后,我们通过JavaScript 获取用户的选择,并根据用户的选择生成相应的计算公式。
最后,我们将计算结果展示给用户。
总结随着计算机编程和数学的结合越来越紧密,JavaScript 等编程语言在数学研究中的应用也越来越广泛。
通过条件语句,我们可以在JavaScript 中实现选择条件生成计算公式的功能,为用户提供更便捷的服务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f ′( x0 ) = lim
h→ 0
f ( x 0 + h) − f ( x 0 ) h
f ( x 0 + h) − f ( x 0 ) 取差商 f [ x0 , x0 + h] = h
近似替代 f ′( x0 )
13
5、化整为零(将连续问题离散化):如定积分的
计算,当被积函数的原函数无法求得或被积函数为表 格函数(无解析表达式)时,就应做离散处理。
2、迭代法:迭代法也称为逐次逼近法。迭代法 迭代法: 的使用是为了逐次改进前面的计算结果,使之按 给定的精度逼近于问题的准确解。
10
例如求非线性方程f )=0的根,可将方程改写为 例如求非线性方程f(x)=0的根,可将方程改写为 等价形式 x=g(x),以形成迭代格式: xk+1=g(xk)
给定初始值x ,计算x 给定初始值x0,计算x1=g(x0) , x2=g(x1) ,……, ……, (给定精度控制量),x 直到| 直到|xk+1-xk|<ε(给定精度控制量),xk+1即为近似根。
7位阶码 阶码符号位 尾数符号位
23位尾数 23位尾数
Байду номын сангаас
例如,上图表示的二进制数据为:
2(1111111) 2 × (0.1111111111 1111111111 111) 2
相当于十进制数: 1.701412 ×1038 × 0.8388607
18
也就是按此种方式所能表示的最大浮点数。故对 十进制浮点数而言,小数点后最多能保留7 十进制浮点数而言,小数点后最多能保留7位。 如:x1=0.12345674 x2=0.12345675 如:x1=0.12345674和x2=0.12345675均不属计算 机数系,则计算机按如下形式接收: X1=0.1234567, X1=0.1234567,X2=0.1234568 所产生的误差即为舍入误差 所产生的误差即为舍入误差。 舍入误差。 4、截断误差(方法误差) 截断误差(方法误差) 对数学公式做简化处理后所产生的误差,如计 算函数e 在某点的值,由于e 算函数ex在某点的值,由于ex的展开式:
16
3、舍入误差(计算误差) 舍入误差(计算误差) 因计算机的数系不全、在接收和运算数据的舍 入处理中产生的误差,它是《数值计算方法》 入处理中产生的误差,它是《数值计算方法》 必须关注的问题。 要理解计算机的舍入误差,请思考: 要理解计算机的舍入误差,请思考:
(1)实数集是有限还是无限?是稠密还是离散? (2)计算机所能表示的数(称为计算机的数系) )计算机所能表示的数(称为计算机的数系) 是有限还是无限?是稠密还是离散? (3)如果数据不属于计算机的数系,那么计算机 如何接收和处理这一数据?
4
研究数值计算方法 研究数值计算方法的必要性: 数值计算方法的必要性: 很多数学问题在理论上严密、有精确解,但实际 计算时或者没有计算公式,或者套用计算公式无法 完成计算,或者根本无法得到其精确解。例如: 问题1 求非线性方程cosx =0的根(无求根公式); 问题1 求非线性方程cosx-x=0的根(无求根公式); 问题2 求解一个20阶线性方程组(克莱姆法则? 问题2 求解一个20阶线性方程组(克莱姆法则?); 问题3 问题3 求解下面的定积分(找不到原函数):
y
y=f(x)
o a
xi
xi+1
b
x
可将[ b]等分成n 可将[a , b]等分成n 个小区间 [xi , xi+1],其中xi =a+ih,x0=a, ,其中x ih, xn=b,i=0,1,…,n-1,h=(b–a)/n ,在每个小区间上以直代曲。 =0,1,…,n =(b a)/
14
I = ∫ f ( x )dx = ∑ ∫
17
浮点运算是计算机最重要的数值运算。设机器 浮点运算是计算机最重要的数值运算。设机器 字长为32位,浮点数(如C中的float型)在计算机 字长为32位,浮点数(如C中的float型)在计算机 中如何存储:
0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
注意:以上6 注意:以上6种思想方法并非万能,均有其使用条件 和局限性,不能盲目套用,否则会出现谬误。例如 递推法:必须考虑误差的积累和传播是否加剧; 递推法:必须考虑误差的积累和传播是否加剧; 迭代法:必须考虑迭代格式是否收敛于所求解; 迭代法:必须考虑迭代格式是否收敛于所求解; 直代曲:必须考虑是否会使有解变为无解; 直代曲:必须考虑是否会使有解变为无解; 离散化:必须综合考虑精确度、计算量和舍入误差。 离散化:必须综合考虑精确度、计算量和舍入误差。
8
方法之二: 方法之二: 秦九韶法(霍纳法),将P 秦九韶法(霍纳法),将P(x)写成如下形式:
P ( x ) = (L ((a n x + a n −1 ) x + a n − 2 ) x + L + a1 ) x + a0
采用递推法计算,用递推公式表示计算过程: bn=an,bi=ai+bi+1x,i=n-1,…,1,0 所需存储单元:n+2个;乘法次数为n 所需存储单元:n+2个;乘法次数为n。
x2 x3 xn ex = 1+ x + + +L+ +L 2! 3! n!
19
用其展开式中的前n 用其展开式中的前 n+1项近似代替无穷项来计算所产生的 误差就是截断误差 误差就是截断误差。是《数值计算方法》必须关注的误差。 截断误差。 数值计算方法》必须关注的误差。
1、绝对误差与误差限 设x*为准确值,x为其近似值,则称∆x=x*-x为近似 为准确值, 为其近似值,则称∆ 值x的绝对误差,简称误差。 绝对误差,简称误差 误差。 准确值通常未知,故误差∆ 一般也不可知, 准确值通常未知,故误差∆x一般也不可知,为此引 入误差限来对误差进行估计。 误差限来对误差进行估计。 称满足| 称满足| ∆x |=|x*-x|≤ε 的正数 ε 为近似值的误差限。 |=|x 为近似值的误差限 误差限。 误差限 ε 给出了准确值x*的所在范围x-ε ≤x*≤ x+ε, 给出了准确值x 的所在范围x x*≤ 显然,误差限 ε 越小,近似值越精确。
o
x* x3
x2
x1
x0 x
牛顿迭代法
几何意义: 几何意义: 从初值x 出发,过点( 从初值x0出发,过点(xk,f(xk))作曲线f(x)的切线, ))作曲线f 得到与x轴的交点x 以逐步逼近根x 得到与x轴的交点xk+1,以逐步逼近根x*。
12
4、以差商代微商(导数):如果无法按常规方 以差商代微商(导数):如果无法按常规方 法求导函数精确值,则可根据导数定义
9
秦九韶递推算法表示如下:
INPUT OUTPUT n ,n+1 个系数a (i),(i =0,1,2,…, n, ),x的值 个系数a ,(i ),x 多项式的值p 多项式的值p (x)。
Step1 Step2
Step3 STOP
b = a (n) For i =n-1 DownTo 0 b=a (i) +bx +bx End For i OUTPUT ( ‘p (x)=’ , b)
20
2、准确位数与有效数字
先讨论长度测量问题。设直尺刻度为m 长度为l 先讨论长度测量问题。设直尺刻度为m,长度为l。
1m 2m 3m
近似值 l =2.4m 2.4
则绝对误差 | ∆l |=| l*-l| ≤ ε = 0.5m 。 l*同理, 同理,在不同刻度下长度近似值有如下误差限: 刻度为dm : 刻度为dm: | ∆l |=| l*-l| ≤ ε = 0.05m =0.5×10-1m l*05m 刻度为cm 刻度为cm : | ∆l |=| l*-l| ≤ ε = 0.005m =0.5×10-2m l*005m 刻度为mm 刻度为mm : | ∆l |=| l*-l| ≤ ε = 0.0005m =0.5×10-3m l*0005m
I ( x) = ∫
x 0
t3 dt t e −1
5
数值计算方法: 数值计算方法: 把对数学问题的解法归结为有限次数加减乘 除等基本运算并有确定运算顺序的完整、准确、 有效的描述,称为数值计算方法。 有效的描述,称为数值计算方法。 算法: 算法: 研究数值计算方法的软件实现的问题。即用 流程图、数学语言或自然语言、计算机语言 (计算机程序)对数学问题的数值计算方法作 出准确的描述。
b a i =0 n −1 a i +1
ai
h f ( x )dx = ∑ I i ≈ ∑ [ f ( x i ) + f ( x i +1 )] i =0 i =0 2
n −1
n −1
6、外推法(Richardson外推思想的应用) 外推法(Richardson外推思想的应用) (在《数值微积分》 (在《数值微积分》中详述)
1
《数值计算方法》课程简介 数值计算方法》
数值计算方法— 数值计算方法—研究并解决数学问题近似解的 方法,是在计算机上使用的解数学问题的方法。 方法,是在计算机上使用的解数学问题的方法。 计算对象— 计算对象—在理论上有解而难于或无法用手工 完成计算的数学问题。 应用领域— 应用领域—广泛用于科学研究和工程技术,如 地质勘探、汽车制造、桥梁设计、天气预报、汉 字字样设计、数码成像技术等等。 课程特点— 课程特点—既有严密的理论性,又具很强的实 践性,所构造的方法要由计算机来实现。 先行课程— 先行课程—高等数学、线性代数、高级语言
