阻力区的确定
《工程流体力学》第四章 流动损失

层流受到扰动后 主导作用:粘性稳定作用 粘性稳定作用:使扰动衰减下来 流动:变为层流 主导作用:惯性扰动作用 粘性作用:无法使扰动衰减下来 流动:变为紊流
雷诺数正是反映了惯性力和粘性力的对比关系, 能判别流态。
在波峰上侧断面受压缩,流动截面积A变小,流速V增加, 压强p变小 在波峰下侧与上侧相反,A增加,V变小,p增加
在波谷上侧断面,A增加,V变小,p增加 在波谷下侧断面,A变小, V增加,p变小
结果出现由波谷指向波峰的两种压差Dp,Dp’
其中Dp使波动弯曲加剧,波幅增大; 而Dp’大到一定程度后,使流线两侧产生从波谷向另一波 峰流动的二次流,其作用是使波谷处受吸力,波峰处有惯 性力。
2、运动参数的时均值: 时均流速V:某点瞬时速度V在足够长时间段内的平均值
流速脉动->切应力、压强也产生脉动 如,对压强同样有:
对时均流动和脉动流动分别进行研究。
定常紊流流动:对时均流动,时均速度和时均压强不随时 间而变的紊流流动。 有关定常流动规律,如连续方程、伯努利方程等都可用。
但紊流中还要考虑脉动影响 脉动->横向掺混->各流层间质量、动量、热量和悬浮 含量的分布大大平均化 动量交换->紊流阻力大大增加 紊流脉动速度时均值:0 在工程上采用紊流度概念:表示紊流随机性质
Q流速高于VK的流动状态:极不稳定,稍有扰动,就转变 为紊流,对实际工程来说,总是有扰动的。 上临界速度对工程实际没有意义,而下临界速度就成为 判断流态的界限。 下临界速度也被称为临界速度。
雷诺实验还揭示了不同流动状态下流动损失规律。 不同流速下截面1到截面2的流动损失hw:画在对数坐标上
流体力学5-6沿程阻力

17
旧钢管及旧铸铁管
当v<1.2m/s
0.0179 d 0.3
1
0.867 v
0.3
当v >1.2m/s
0.021
d 0.3
舍维列夫公式是在水温为10oC,运动粘滞系数 ν=1.3×10-6m2/s的条件下得出的,前式适用于紊流过渡区, d 以m计,v 以m/s计;后式适用于阻力平方区, d 以m计
1932年尼古拉兹根据实验结果提
出了此式,n 为指数随雷诺数Re而变
化。该指数公式完全是经验性的,但 因公式形式简单,被广泛应用
u um ax
y r0
n
8
三、λ的半经验公式
1、尼古拉兹光滑管公式
1 2 lg Re
2.51
2、尼古拉兹粗糙管公式
1 2 lg 3.7d
Re vd
d l
2g v2
hf
算出若干组Re和λ值,将其点绘 在双对数坐标纸上,就得到=f(Re, ks /d)曲线,即尼古拉兹曲线图
2
3
尼古拉兹实验曲线
I.ab线层流区, =f(Re) ,=64/Re, Re<2300 II. bc线范围窄, =f(Re) , Re=2300~4000,层流向紊流
光滑区速度分布半经验公式
u 5.75lg yv 5.5
v
7
2.紊流粗糙区
u v
1
ln
y ks
c2
自然根对据数尼换古成常拉用兹对实数验,取便β=得0.4到、c2=8.48代入上式,并把
粗糙区速度分布半经验公式 u 5.75lg y 8.48
谈管道沿程阻力系数的计算

项 目名称 : 棉花产后增值 关键技术装备研发与产业化示范
! ! 堡 墅 墅 垦 8 1 l ! 堕蔓 ! 塑
薰
●戳精弼
( 二) 过渡 区
速2 4 m / s , 绝对 粗糙度 0 . 2 mm, 则 = 5 7 l 4 2 9 , 显然
为过渡状态 , R e >4 0 0 0 为紊流状态 , R e >1 0 0 0 0 为 完全紊流状态 。 二、 雷诺 数 的计算 雷诺数计算公式
d: Re : pv
—
主要依据是 雷诺数 。 雷诺 实验
一
堕
、
雷诺通过实验发现液体在流动 中存在两种内部 结构完全不同的流态 : 层流和紊流。同时也发现 , 层 流 的沿程水头损失 肺与流速一次方成正 比, 紊 流的
粗糙表面全部暴露出来 , 沿程阻力系数与 R e 无关 ,
先 确定 流 态 。
动力黏度系数 , P a ・ S ,
2 0℃时 , :1 8 . 2 0 x 1 0 ~ P a ・ s ;
运动黏度系数 , m 2 / s ,
2 0℃时 , 9 = 1 5 . 1 2 x 1 0 m2 / s ;
d 一管道的断面特征尺寸 , I n 。 对于圆形管道来说 , 特征尺寸即为圆管直径 ; 非
( 四) 粗糙 管 区
6 4
===
( 二) 过渡 区
A = 0 . 0 0 2 5 ( 扎依琴柯公式 )
( 三) 光滑 管 区
当 8 0 罟 ≤ R ≤ 4 1 6 0 ( - 2  ̄ - ) 。 时, 随 着 R e 的 增 大,
层 流层 逐 渐 减 少 , 以至 于不 能 覆 盖 粗糙 不 平 的管 壁 式)
流量与管径、压力、流速之间关系计算公式-孔径 压强 流速关系

流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管径的平方X流速(立方米/小时)。
其中,管径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式这里:Q ——断面水流量(m3/s)C ——Chezy糙率系数(m1/2/s)A ——断面面积(m2)R ——水力半径(m)S ——水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:h f——沿程水头损失(mm3/s)f ——Darcy-Weisbach水头损失系数(无量纲)l ——管道长度(m)d ——管道径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
1.1 管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用围和条件,一般都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜采用数值做为判别式,目前国管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
沿程水头损失水力计算公式和摩阻系数表1达西公式是管道沿程水力计算基本公式,是一个半理论半经验的计算通式,它适用于流态的不同区间,其中摩阻系数λ可采用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用围广泛,被认为紊流区λ的综合计算公式。
化工原理-1.4 边界层与阻力公式

3、摩擦系数 1)层流
范宁公 R式 : dl u22 f(d,u,,)
8 w u 2
64u u2d
64 Re
( w
8u )
d
代入范宁公式:
pf
l
d
u2 64u l u2 2 u2dd 2
32lu
d2
哈根-泊谡叶方程
pf
32lu
d2
用于层流,pf u pf 1 d2
2)湍流条件下的摩擦系数
影响因素复杂,一般由实验确定。
0.00005
0.009
0.008
102
103
104 Re
105
0.00001
106
107
摩擦系数λ与Re、ε/l关系图
摩擦因子图(莫狄图)
分四个区域:
层流区 Re 2000
64Re
pf
3d22luu
过渡流区 2000Re 4000
问题:1、过渡流,按哪种流型查λ
按湍流查λ,安全系数大;
2、对待过渡流的工程观点
倾斜变径管
(pA pB)(gz1 gz2)
pf
2
(u22
u12)
反映管段的总势能差、或者阻力损失与动能差
2)特例:
* 变径管中范宁公式的使用
必须按照不同管径,分别使用
范宁公 R式 : dl u22
2、不同管道中压差计读数R反映的信息
水平等径管 水平变径管 倾斜等径管
倾斜变径管
静 pA pB
pA pB
1.4 流体流动阻力
提出问题?
1、流动阻力产生的外因和内因 判断:* 牛顿型流体层流时所受的剪应力与法向
速度梯度成正比,与法向压力无关,其
第4章船体阻力确定方法

4.3 能量观点
是将船体总阻力划分为尾流阻力和波形阻力Rwp。尾流阻力由 粘性阻力Rν 和破波阻力Rwb组成,即总阻力为:
尾流阻力可通过尾流测量法确定,波形阻力则可使用波形分 析法确定。
琼斯(Jones)尾流测量法
该方法是通过测量船模后方尾流场的压力分布来得到尾流阻力的。
根据相对运动原理,假设船模不动,流体由远前方以船模运动 速度u0流向船模,流场内压力为P0。由于流体的粘性作用,流体绕 过船模后,其速度和压力均发生变化。
s 3
Sm
m
佛汝德换算方法也称为二因次换算法。
二因次换算法使用方便,所得结果与实船阻力相当接近,曾被世 界各国水池广泛使用,直到现在还受到一些水池的青睐。
佛汝德观点
合理之处:
二
因
1)使用该方法预报实船阻力与实际值基本吻合,能够较准确地
次 满足实际工程上的需要;
换 算 法
2)后来由Prandtl的边界层理论解释了其合理之处:首先,与Re 有关的摩擦阻力只在物体近表面的边界层内才有意义,界层以外可以
的 看作是无粘性的理想流体,或者说边界层以外没有较大的速度梯度;
合 其次,物面曲率半径较边界层厚度大得多时,就边界层的形成原因而
理 言,受物面曲率的影响较小,所以摩擦阻力可以按照相当平板公式进
与 行计算。
不
合
3)粘压阻力在船舶总阻力中的比重较小,且其与Re数的关系也
理 不大,将其并入剩余阻力系数并适用比较定律,也不致产生明显的误
为来流动压力。
由伯努利方程:
G称为总压头。设足够远处的压力为大气压力p0 ,p∞=p0,则有:
琼斯(Jones)尾流测量法
取G1=G-P0为S1截面上的相对总压力, P1=P1-P0为S1截面上的相对静 压力,则有:
《流体力学》第四章 流动阻力和能量损失4.6-4.7
第七节
非圆管的沿程损失
怎么把非圆管折合成圆管? 水力半径 当量直径 A R 水力半径:过流断面面积和湿周之比。
1 2 d d 对于圆管: R A 4 d 4
de = 4 R
2ab 对于矩形管: d e = a+ b
对于方形管:
de = a
非圆管流中的流态判断的临界雷诺
λ计算公式
紊流光滑区: 1 2 lg Re 2.51 (尼古拉兹 光滑区公式)
紊流粗糙区: (尼古拉兹 粗糙区公式)
0.3164 0.25 Re
(布拉修斯公式)
K 0.11 d
0.25
1
3.7d 2 lg K
(希弗林松公式)
半经验公式
纯经验公式
紊流过渡区
0.06 0.04 A
Ⅱ
Ⅴ Ⅲ Ⅳ
B A
0.02
2×103 5 104
C 2 5
2
l
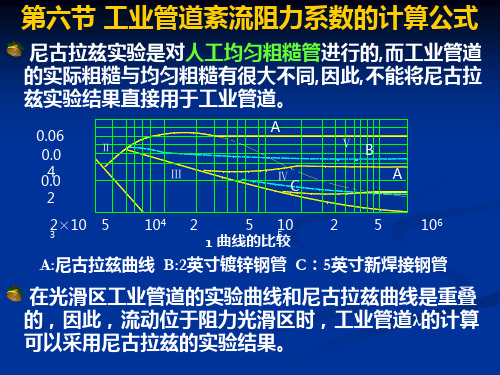
曲线的比较
5
105
106
A:尼古拉兹曲线 B:2英寸镀锌钢管 C:5英寸新焊接钢管
在光滑区工业管道的实验曲线和尼古拉兹曲线是重叠 的,因此,流动位于阻力光滑区时,工业管道λ的计算 可以采用尼古拉兹的实验结果。
在粗糙区,工业管道和尼古拉兹的实验曲线都是 与横坐标轴平行。这就存在用尼古拉兹粗糙区公式 计算工业管道的可能性。问题在于如何确定工业管 道的K值。 当量糙粒高度:和工业管道粗糙区λ值相等的同 直径尼古拉兹粗糙管的糙粒高度。
数仍为2000。 应用当量直径计算非圆管的能量损 失,并不适用于所有情况。
对矩形、方形、三角形结果接近, 但对长缝形和星形断面差别较大。 应用于层流时,误差较大。
《工程流体力学》第四章 流动损失

1、运动参数的脉动: 紊流特征:旋涡结构 紊流运动:旋涡迁移掺混的随机运动
精密测速仪测定流场中M点瞬时速度:随机变化曲线 运动参数的脉动(脉动现象):在足够长时段T内,随机 值具有围绕某一“平均值”而上下变动的现象
紊流脉动:各空间点的速度、压强等物理量,随时间围 绕某一“平均值”作不规则变化的流动现象。
(b)继续开大阀门C:B管中流速增大,有色液体的流动并 无变化,仍为层流。
当B管中平均流速达到某一值时,层流开始转变紊流 —— 临界状态(临界区)。
临界状态:流束发生动荡、分散、个别地方出现中断。
(c)再稍开大阀门C:B管中流速超过临界值VK’,则有色 液体不再呈现流束动荡和分散中断,而破碎掺混变成一种 紊乱的流动状态,有色流体质点布满B管中—紊流。
管中水流为紊流。
(2)保持层流的最大流速就是临界流速:
流态分析:
层流:各流层互不掺混,只有粘性引起的各流层间的滑动 摩擦阻力。
紊流:许多大大小小的涡体动荡于各流层间,有粘性阻力, 惯性阻力。(由质点掺混,互相碰撞所引起的)
紊流阻力>>层流阻力
层流到紊流的转变过程:
假设流体原来作直线层流运动,由于某种原因干扰,流层 发生波动。
水力半径:截面面积A与流体湿周长c之比 水力半径表征截面的流通能力: A增加,c变小,则流体流通能力增加。
几种断面的水力半径:
当量直径de:当非圆管的水力半径 = 圆管的水力半径时, 这时圆管的直径就是非圆管的当量直径。 如当非圆管的水力半径R = 圆管的水力半径d/4时, 则圆管的直径d = 4R为非圆管的当量直径de。
上临界速度VK’不稳定:受试验设备,周围环境影响很大 (1)当管壁光滑,入口平滑,周围干扰较小时:VK’可达到 较高值。即速度较大时,层流才转变为紊流 (2)当管壁粗糙,周围干扰较大时, VK’可达到的值较小。 即速度较小时,层流就转变为紊流
水流阻力系数的确定方法

水流阻力系数的确定方法
水流阻力系数的确定方法有多种,以下列举三种常用的方法:
1.理论公式法:根据流体力学原理,当流体在直管中流动时,阻力系数可以表示
为ξ=fi⋅dL,其中fi为摩擦系数,L为直管的长度,d为直管的内径。
当流体的流动状态为层流时,摩擦系数可以从流体力学推导而得:fi=Re64。
而当流体的流动状态为湍流时,摩擦系数无法采用理论分析方法完全推导而得,一般需要实验的方法。
2.实验测定法:通过实验测量得到水流的阻力系数。
在实验中,可以设置一系列
不同管径和流速的直管,记录每个管径和流速下的压力降和流速,然后根据公式Δp=ξ⋅ρ⋅2u2计算阻力系数。
3.经验数据法:根据实际应用中的经验数据确定水流阻力系数。
在实际应用中,
可以通过对已有的管道系统进行测量和计算,得到水流阻力系数的经验值。
这些经验值可以作为新管道系统设计时的参考。
需要注意的是,水流阻力系数的确定方法应根据具体情况选择。
在工程应用中,一般采用实验测定法和经验数据法来确定水流阻力系数。
同时,对于特殊的水流条件或需要精确计算的情况,可以采用理论公式法进行计算。
支撑位和阻力位

支撑位和阻力位以及分析方法之前我们一直在发表关于K线的基本知识,相信看见我之前的文章的朋友,应该对K线都有一定的认识了。
在整个K线中,我们也经常听见支撑位、阻力位到底什么是支撑位、阻力位今天小编就对这个做一个解释,希望对大家有作用。
定义1、支撑位是指在股价下跌时可能遇到支撑,从而止跌回稳的价位;阻力位则是指在股价上升时可能遇到压力,从而反转下跌的价位。
2、在股价运行时,阻力与支撑是可以互换的。
具体地说,如果重大的阻力位被有效突破,那么该阻力位则反过来变成未来重要的支撑位;反之,如果重要的支撑位被有效击穿,则该价位反而变成今后股价上涨的阻力位了。
3、多数情况下,高价或低价会集中在一定的区域,而不是一个点;由此该区域是“支撑区”或“阻力区”。
注意该区间不能太大,否则对投资者没有参考意义。
有效性分析:`1。
成交量的密集程度。
2。
价格在两个区间所经历的时间、堆积的成交量。
(某区间运行时间长,量多,阻力、支撑就大)3。
形成的时间与现在的远近(越远,越无效)4。
形成时的成交量与现在的成交量对比。
(如果放量拉升后,再也不放量就不可以突破)5、波浪,计算波段目标位,同时数波段内细浪,三点落在一起的支撑阻力是比较接近实际的。
研究的方法:一:均线阻力位:主要指5、10、20、30、60、120、250日等均线对股价的压力。
股价上穿均线都需要成交量放大配合,这其中以60、120、250日均线对股价的压力尤为重要,因此要特别关注这三条均线对股价的压力。
二:高点(波峰)压力位:前期两个以上高点(波峰)的连线构成高点阻力位。
股价突破此连线也需成交量放大配合。
(循环顶更厉害)三:低点(波谷)压力位;股价跌破前期两个以上低点(波谷)连线后,如果反弹,这条连线对股价将产生压力,这条连线就叫低点压力位。
(循环底厉害)四、前期密集成交区五:某些形态形成的压力/支撑:颈线压力位:双底(W底)、头肩底、N形底、双顶(M顶)等形态颈线对股价上涨或反弹都有压力。
支撑线与阻力线

支撑线的原理与运用市场上的商品价格在达到某一水平时,往往不再继续上涨或下跌,似乎在此价格上有一条对商品价格起阻拦或支撑作用的抵抗线,我们分别称之为阻力线与支撑线。
所谓阻力线是指商品价格上升至某一高度时,有大量的卖盘供应或是买盘接手薄弱,从而使商品价格的继续上涨受阻。
支撑线则是指商品价格下跌到某一高度时,买气转旺而卖气渐弱,从而使商品价格停止继续下跌。
从供求关系的角度看,“支撑”代表了集中的需求,而“阻力”代表了集中的供给,商品价格上供求关系的变化.导致了对商品价格变动的限制。
阻力线和支撑线都是图形分析的重要方法。
一般若商品价格在某个区域内上下波动,并且在该区域内累积成交量极大,那么如果商品价格冲过或跌破此区域,它便自然成为支撑线或阻力线。
这些曾经有过大成交量的价格时常由阻力线变为支撑线或由支撑线变为阻力线:阻力线一旦被冲过,便会成为下个跌势的支撑线;而支撑线一经跌破,将会成为下一个涨势的阻力线。
在K线图上,只要最低价格在同一微小区间多次出现,则连接两个相同最低价格并延长即成一支撑线,它形象地描述了商品价格在某一价格区间内,需求大于供给的不平衡状态。
当买卖价格跌入这一区间时,因买气大增,卖方惜售,使得商品价格调头回升。
其内在实质是:价格区间,累积了较大的成交量,当行情由上而下向支撑线靠拢时,卖出者获利筹码已清,手中已无卖出打压筹码;买进者持币趁低吸纳,形成需求;举棋不定者套牢已深,筹码锁定不轻易斩仓。
故在这一价格区间供应小于需求,自然形成了强有力的支撑基础。
另外,由于行情多次在此回头,也确立了广大投资者的心理支撑价格区间,只要无特大不利价格上涨消息出台,行情将获撑反弹。
技术分析将有较大累积成交量的价格区间定义为“成交密集区”,亦即在此密集区有很高的换手率。
密集区进货者欲获利则需待商品价格升至这一成本区间以上,这些进货者即持有筹码者,只要没有对后势失去信心,是不会在这一价格区间抛出筹码的,正因为持有筹码者惜售,故行情难以跌破这一价格。
第一章 流体的流动 思考简答题

第一章流体的流动思考简答题1.什么事连续性假设?质点的含义是什么?答:连续性介质假定是将流体视为无数流体微团或质点组成的连续介质。
流体致电是有大量分子组成的分子集合,在宏观上其几何尺寸很小,但包含足够多的分子,在微观上其尺寸度远大于分子的平均自由程。
2.不可压缩流体在半径ri的水平管内流动,试写出以duz/dr表示牛顿粘度定律的表达式,其中r为管中心算起的径向距离坐标,ur为r处的流体流速。
答:????duz/dr3.黏性流体在静止时有无剪应力?理想流体在运动时有无剪应力?若流体在静止时无剪应力,是否意味着它们没有黏性?答:(1)黏性流体在静止时无剪应力;(2)理想流体无剪应力;(3)黏性是流体的固有特性,在静止或运动时都有黏性。
4.静压力有什么特性?答:静压力的方向与其作用面相垂直,且在各个方向的数值相同,即静压力为标量。
5.流体在均匀直管内作定态流动时,其平均数度u沿流程保持定值,并不因摩擦而减速,这一说法是否正确?为什么?答:不正确。
根据连续性方程,流体在直管中向下定态流动时,其平均流速随管截面积和流体密度而变。
但流体不可压缩时,该说法是正确的。
6.在满流的条件下,水在垂直直管中向下定态流动。
则对沿管长不同位置处的平均流速而言,是否会因重力加速度而使下部的速度大于上部的速度?答:不会。
7.在应用机械能衡算方程解题时需要注意哪些问题?答:(1)所选控制面的上下游都应与流动方向垂直;(2)流体在两截面间应是连续的待求的未知量应在截面上或两截面之间;(3)截面上的物理量均取截面上的平均值;(4)位压头的基准面应是水平面,且z值是指截面中心点与基准水平面之间的距离;(5)物理量的单位要一致。
8.雷诺数的物理意义是什么?答:惯性力与黏性力之比。
9.湍流与层流有何不同,湍流的主要特点是什么?答:层流时,流体质点沿流线向下游作规则的流动,质点之间无宏观混合;流体分子在不同流速的流体层之间作随机热运动产生黏性力——内摩擦力。
管道摩擦阻力计算

长距离输水管道水力计算公式的选用之马矢奏春创作1. 经常使用的水力计算公式:供水工程中的管道水力计算一般均依照均匀流计算,目前工程设计中普遍采取的管道水力计算公式有: 达西(DARCY )公式:gd v l h f 22**=λ (1)谢才(chezy )公式:i R C v **= (2)海澄-威廉(HAZEN-WILIAMS )公式:87.4852.1852.167.10d C lQ h h f ***= (3) 式中hf------------沿程损失,m λ―――沿程阻力系数 l――管段长度,m d-----管道计算内径,m g----重力加速度,m/s2 C----谢才系数 i----水力坡降; R―――水力半径,mQ―――管道流量m/s2 v----流速 m/sCn----海澄――威廉系数其中大西公式,谢才公式对于管道和明渠的水力计算都适用。
海澄-威廉公式影响参数较小,作为一个传统公式,在国内外被广泛用于管网系统计算。
三种水力计算公式中,与管道内壁粗糙程度相关的系数均是影响计算结果的重要参数。
2.规范中水力计算公式的规定3.查阅室外给水设计规范及其他各管道设计规范,针对分歧的设计条件,推荐采取的水力计算公式也有所差别,见表1:表1 各规范推荐采取的水力计算公式4. 公式的适用范围:3.1达西公式达西公式是基于圆管层流运动推导出来的均匀流沿程损失普遍计算公式,该式适用于任何截面形状的光滑或粗糙管内的层流和紊流。
公式中沿程阻力系数λ值的确定是水头损失计算的关键,一般采取经验公式计算得出。
舍维列夫公式,布拉修斯公式及柯列勃洛克(C.F.COLEBROOK )公式均是针对工业管道条件计算λ值的著名经验公式。
舍维列夫公式的导出条件是水温10℃,运动粘度1.3*10-6 m2/s,适用于旧钢管和旧铸铁管,紊流过渡区及粗糙度区.该公式在国内运用教广. 柯列勃洛可公式)Re 51.27.3lg(21λλ+∆*-=d (Δ为当量粗糙度,Re 为雷诺数)是根据大量工业管道试验资料提出的工业管道过渡区λ值计算公式,该式实际上是泥古拉兹光滑区公式和粗糙区公式的结合,适用范围为4000<Re<108.大量的试验结果标明柯列勃洛克公式与实际商用圆管的阻力试验结果吻合良好,不但包含了光滑管区和完全粗糙管区,而且覆盖了整个过渡粗糙区,该公式在国外得到及为广泛的应用. 布拉修斯公式25.0Re 316.0=λ是1912年布拉修斯总结光滑管的试验资料提出的,适用条件为4000<Re<105,一般用于紊流光滑管区的计算. 3.2 谢才公式该式于1775年由CHEZY 提出,实际是达西公式的一个变形,式中谢才系数C 一般由经验公式y e R n C *=1计算得出,其中61=y 时称为曼宁公式,y 值采取)1.0(75.013.05.2---=n R n y (n 为粗糙系数)公式计算时称为巴浦洛夫斯基,这两个公式应用范围均较广.就谢才公式自己而言,它适用于有压或无压均匀流动的各阻力区,但由于计算谢才系数C 的经验公式只包含反映管壁粗糙状况的粗糙系数n 和水力半径R,而没有包含流速及运动年度,也就是与雷诺数Re 无关,因此该式一般仅适用于粗糙区.曼宁公式的适用条件为n<0.02,R<0.5m;巴浦洛夫斯基公式的适用条件为0.1m≤R≤3m;0.011≤n≤0.04.3.3 海澄-威廉公式是在直径≤3.66m 工业管道的大量测试数据基础上建立的著名经验公式,适用于常温的清水输送管道,式中海澄-威廉系数Ch 与分歧管材的管壁概况粗糙程度有关.因为该式参数取值简单,易用,也是得到广泛应用的公式之一.此公式适用范围为光滑区至部分粗糙度区,对应雷诺数Re 范围介于104-2*106. 通过对各相关规范所推荐计算公式的比较,除混凝土管仍然推荐采取谢才公式外,其它管材大多推荐采取达西公式.在新版《室外给水设计规范》中取消舍维列夫公式的相关条文,笼统采取达西公式,但未明确要求计算λ值采取的经验公式.由于舍维列夫公式是建立在对旧钢管及旧铸铁管研究的基础上,然而现在一般采取的钢或铸铁材质管道,内壁通常需进行防腐内衬,经过涂装的管道内壁概况均比旧钢管,旧铸铁管内壁光滑得多,也就是Δ值小得多,采取舍维列夫公式显然也就会发生较大得计算误差,该公式得适用范围相应较窄.经过内衬得金属管道采取柯列勃洛克公式或谢才公式计算更为合理.PVC-U,PE等塑料管道,或者内衬塑料得金属管道,因为其内壁Δ值很低,一般处于0.0015-0.015,管道流态大多位于紊流光滑区,采取适用光滑区得布拉修斯公式以及柯列勃洛克公式一般均能够得到与实际接近得计算结果.因此,《埋地硬聚氯乙稀给水管道工程技术规程》及《埋地聚乙稀给水管道工程技术规程》中对塑料管道水力计算公式均是合理得且与《室外给水设计规范》其实不矛盾.海澄-威廉公式可以适用于各种分歧材质管道得水力计算,其中海澄-威廉系数Ch得取值应根据管材确定.对于内衬水泥砂浆或者涂装有比较光滑得内防腐涂层得管道,其海澄-威廉系数应该参考类似工程经验参数或者实测数据,合理取用.因此,无论采取达西公式,谢才公式或者海澄-威廉公式计算,分歧管材得差别均表示在管内壁概况当量粗糙程度得分歧上,各公式中与粗糙度相关系数得取值是影响计算结果得重要因素.值得一提得是,同种材质管道由于采取分歧得加工工艺,其内概况得粗糙度也可能有所差别,这一因素在设计过程种也应重视(经常使用管材得粗糙度系数参考值见表2)表2 罕见管材粗糙度相关系数参考值根据雷诺数计算公式vVd Re ,雷诺数与流速v,管径d 成正比,与运动粘度成反比,因此对应管道得分歧设计条件应对所使用计算公式得适用范围进行复核.包管计算得准确性.大多说供水工程得设计依照水温10℃,运动粘度1.3*10-5 m2/s 得条件考虑,因此雷诺数实际受流速及管道口径得影响.以塑料管道为例,在正常设计流速范围条件下,管道内径大于100mm 时,虽然管道仍然处于紊流光滑区,但其雷诺数Re>105,也就是说已经超出了布拉修斯公式得适用范围,而且误差大小与雷诺数成正比.对PVC-U 管,采取布拉修斯公式与柯列勃洛克公式对比计算,当管内径为500mm ,流速1.5 m/s 时,采取布拉修斯公式得出得水力坡降比柯列波列克得结果低11%以上.采取《埋地硬聚氯乙稀给水管道工程技术规程》推荐得修正公式与柯式对比计算,修正公式计算结果,小口径管偏平安,中等口径与柯式符合较好,大口径管得负误差达5%以上.因此笔者认为,大口径塑料管或采取塑料内衬管不宜采取布拉修斯公式计算,而更宜于采取如柯列波洛克公式等适用条件更宽得其它经验公式,或应通过试验等对其进行修正.与上述情况类似,采取谢才公式计算时,如果管道内径大于2m 时则不采取曼宁公式计算谢才系数.如果采取巴甫洛夫斯基公式,其适用管径可以达到12m,对一般输水工程管道已完全足够了.海澄-威廉公式的数据基础是WILLIAMS和HAZEN在大量工业管道现场或试验丈量或得的.该公式因为简单易用,被广泛运用在管网水力计算中,国内外很多管道水力计算软件均采取该公式编制.由此可见,对于口径大于2m得管道应尽量防止采取海澄-威廉公式计算以策平安.6.值得提出得是,上述所有水力计算公式中采取得管径均为计算内径,各种管道均应采取管道净内空直径计算,对于采取水泥砂浆内衬得金属管道应考虑内衬层厚度得影响.大口径管道计算应尽量防止采取海澄-威廉公式,建议采取柯列勃洛克公式计算,大量试验结果证明该公式计算结果与实际工业管道符合性好,水力条件适用范围广,虽然运用该式需要进行多次迭代计算才干得到λ值,较为麻烦,不过运用计算机简单编程既能方便地得到较为准确地结果,手工计算时也可以通过查表或者查询蓦迪图辅助计算.。
阻力平方区的沿程水头损失系数与断面平均流速

阻力平方区的沿程水头损失系数与断面平均流速一、引言在流体力学领域中,阻力平方区的沿程水头损失系数与断面平均流速是一个重要的研究课题。
在工程实践中,我们常常需要计算管道或渠道内的水流情况,而水头损失系数与断面平均流速就是其中关键的参数。
本文将围绕这一主题展开讨论,通过深度和广度的分析,帮助读者更好地理解与应用这一概念。
二、阻力平方区的沿程水头损失系数1.概念介绍阻力平方区的沿程水头损失系数,简称水头损失系数,是指在管道或渠道内,单位长度的水头损失与单位长度的水力坡降之比。
它的大小与流体的黏性、管道的摩擦阻力以及流速等因素密切相关。
通常用λ表示,是一个无量纲的物理量。
2.计算方法水头损失系数的计算通常借助于经验公式或实验数据,常见的方法包括Darcy-Weisbach公式、Manning公式、Strickler公式等。
这些方法都是通过观测实验数据和理论推导,得出与管道条件、流体性质相关的数值关系,以便工程实践中的应用。
3.影响因素水头损失系数受到多个因素的影响,包括管道材质、管道粗糙度、流速、管道长度等。
尤其是管道内表面的粗糙度对水头损失系数影响较大,粗糙度越大,水头损失系数也越大。
三、断面平均流速1.概念介绍断面平均流速是指管道或渠道内,横截面上各点流速的平均值。
在流体流动过程中,由于管道内的摩擦阻力和流体的惯性作用,流速分布往往不是均匀的,因此需要通过断面平均流速来描述流体在横截面上的整体流动情况。
2.计算方法断面平均流速的计算通常涉及积分计算或流量测量等方法。
在工程实践中,我们可以通过流速剖面测量仪器进行实地测量,或者借助实验数据和模型计算出断面平均流速的数值。
3.变化规律断面平均流速受到多种因素的影响,包括流体的粘性、管道横截面形状、流速分布等。
通常情况下,断面平均流速在管道内会随着管道长度的增加而逐渐减小,这与水头损失系数的增加是紧密相关的。
四、阻力平方区的沿程水头损失系数与断面平均流速的关系1.理论分析从理论上来看,水头损失系数与断面平均流速之间存在着密切的关系。
实验三局部阻力系数的测定

实验三局部水头损失量测实验一、实验目的1.观察突扩管旋涡区测管水头线,以及其它各种边界突变情况下的测管水头变化情况,加深对局部水头损失的感性认识。
2.掌握测定管道局部水头损失系数的方法,并将突扩管的实测值与理论值比较,将突缩管的实测值与经验值比较。
3.学习用测压管测量压强和用体积法测流量的实验技能。
二、实验原理有压管道恒定流遇到管道边界的局部突变→ 流动分离形成剪切层→ 剪切层流动不稳定,引起流动结构的重新调整,并产生旋涡→ 平均流动能量转化成脉动能量,造成不可逆的能量耗散(图1)。
与沿程因摩擦造成的分布损失不同,这部分损失可以看成是集中损失在管道边界的突变处,每单位重量流体承担的这部分能量损失称为局部水头损失。
图1 流道的局部突变示意图根据能量方程,局部水头损失,这里我们认为因边界突变造成的能量损失全部产生在1-1,2-2两断面之间,不再考虑沿程损失。
上游断面1-1应取在由于边界的突变,水流结构开始发生变化的渐变流段中,下游2-2断面则取在水流结构调整刚好结束,重新形成渐变流段的地方。
总之,两断面应尽可能接近,又要保证局部水头损失全部产生在两断面之间。
经过测量两断面的测管水头差和流经管道的流量,进而推算两断面的速度水头差,就可测得局部水头损失。
局部水头损失系数是局部水头损失折合成速度水头的比例系数,即当上下游断面平均流速不同时,应明确它对应的是哪个速度水头?例如,对于突扩圆管就有和之分。
其它情况的局部损失系数在查表或使用经验公式确定时也应该注意这一点。
通常情况下对应下游的速度水头。
局部水头损失系数随流动的雷诺数而变,即(Re)f ζ=。
但当雷诺数大到一定程度后, 值成为常数。
在工程中使用的表格或经验公式中列出的就是指这个X 围的数值。
局部水头损失的机理复杂,除了突扩圆管的情况以外,一般难于用解析方法确定,而要通过实测来得到各种边界突变情况下的局部水头损失系数。
对于突扩圆管的情况,局部水头损失系数有理论结果,推导如下:流动经过突扩圆管的局部水头损失,取1-1,2-2两断面如图2, 这里要特别注意1-1断面取为突扩开始的断面,2-2断面则取在水流结构调整刚好结束,重新形成渐变流段的地方。
1.4 边界层和阻力公式

x 0
dp / dy 0, 认为是实际流体流动 , 产生流动阻力
u x u0,du dy 0, * 边界层外, y , 看作是理想流体流动 , 无流动阻力
层流边界层 u∞ u∞ δ A x0 u∞
y 0、ux 0 * 壁面处,
湍流边界层
层流边界层 湍流边界层Biblioteka u 0.99uu∞
u∞
u∞
A
δ 层流内层 平板上的流动边界层
例:
x0
20C的空气以10m/s流过平板时,在距离平板前
缘100mm处,边界层厚度约为1.8mm
1、平板上流体的流动边界层 边界层意义:
流动阻力及速度梯度,主要集中在边界层内 边界层内, y ,u u
p:任意两点间的压力差
2、总阻力 直管阻力(粘滞力引起) 局部阻力(形体阻力) 总阻力=直管阻力+局部阻力
Pi2
FIC
Pi1
一、圆形直管内的阻力损失 1、范宁公式 公式推导: 稳态流动流体 作受力分析
F F F
P
G
Ff 0
压力差:FP ( p1 p2 ) A
重力:FG gpV cos gA( z1 z2 )
其中,n f ( Re )
Re: 1.1105 3.2 106时,n 1 7 u 0.82 (常用公式) umax
书P39 图1.4.12:给出算图,查取平均流速 坐标:
Re u Re,max umax
问题:求平均流速的方法
1、速度分布未知
2、速度分布已知
qV u S u 0.5umax (层流)
提出问题?
3、强化传递过程的流动条件及其代价。 湍流时传热、传质,传递阻力↓↓,强化过程。 代价: 流动阻力↑↑,动力消耗↑。
平方阻力区

平方阻力区是指当速度增加时,阻力与速度的平方成正比。
这意味着,如果速度加倍,阻力将变为原来的四倍。
这种关系在流体力学中很常见,例如空气和水等流体。
平方阻力区通常用于描述飞机、汽车和其他交通工具在高速行驶时所受到的空气阻力。
平方阻力区的物理原理是空气分子之间的碰撞。
当物体在空气中运动时,它会使周围的空气分子产生扰动。
这些扰动会导致空气分子之间的碰撞频率增加,从而产生阻力。
根据牛顿第三定律,每个碰撞都会对物体施加一个反向的力,这个力就是阻力。
在低速运动时,空气分子之间的碰撞频率较低,因此阻力相对较小。
然而,随着速度的增加,空气分子之间的碰撞频率会急剧增加,导致阻力迅速增大。
这就是为什么高速行驶的车辆需要更大的动力来克服空气阻力的原因。
平方阻力区的一个重要应用是在飞机设计中。
飞机需要在大气层中高速飞行,因此必须考虑空气阻力对其性能的影响。
为了减小空气阻力,飞机设计师采用了多种方法,例如优化机翼形状、使用轻质材料和减少机身表面积等。
此外,飞机还可以通过改变飞行高度和速度来调整空气阻力。
除了飞机之外,平方阻力区还适用于其他交通工具,如汽车、火车和船舶等。
对于汽车来说,空气阻力主要影响其燃油效率和最高速度。
为了减小空气阻力,汽车制造商采用了各种措施,例如安装气动套件、降低车身高度和优化车身外形等。
平方阻力区不仅适用于交通工具,还可以用来解释自然界中的一些现象。
例如,飓风的形成和发展就与平方阻力区有关。
飓风是一种强大的热带气旋,其特点是中心气压极低,周围环绕着强风和暴雨。
飓风的形成是由于海洋表面温度升高导致的热对流。
当热空气上升时,它会形成一个低压区域,吸引周围的空气流入。
这些流入的空气会受到平方阻力区的影响,导致它们旋转并形成飓风的核心。
总之,平方阻力区是一个非常重要的概念,它有助于我们更好地理解和预测各种物体在流体中的行为。
无论是在交通工具的设计中,还是在自然界现象的解释中,平方阻力区都发挥着重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从供求关系角度讲,阻力位无非是大量卖单聚集的地方,它不是简单的一个价位而是一个地区。
阻力区有水平阻力区和轨道阻力区,这里我们主要讨论水平阻力区。
水平阻力区的确定方法之一是:在卖盘占主导地位的背景下,垂直供应柱的顶部是重要阻力区,因为在那个价位出现过剩的卖盘,这些过剩的卖盘导致价格垂直下跌。
这种阻力区有三个功能:
∙第一个是出场点,如果价格恢复到这个阻力区的时候,一种可能就是大量卖盘把价格压下去。
∙第二是进场点,在价格恢复过程中,如果需求足够大并吸收了阻力区的所有卖盘,需求开始控制市场,我们可以在小幅回落中买入。
∙第三个功能就是它提供了做空机会。
以德赛电池日线为例:
图中三个箭头处都是垂直供应柱。
我们看最下面的一个箭头(1月26日),它的特点是供应吸收了需求,并直线下跌。
这个结论我们可以从它垂直越过支撑区和扩大的成交量看出。
扩大成交量说明在支撑区,流入市场的卖盘远远大于买单(其中主要原因由于下跌扫掉了抄底者的止损单,那些止损单被触及后,自动变成卖单)。
这个垂直供应柱的顶部就为我们提供了阻力区。
2月17日价格恢复到这个区的时候,我们首先要假设大量卖单会出现,并把价格压下去,然后耐心观察双方较量的结果。
我们观察底部(1月28日)到2月17日的上涨特点,先问自己大量需求是否进入市场。
从这种小碎步的涨势来看,我们知道需求没有进入,也就是说主力买家还没兴趣介入。
我们由此得出结论,需求还没有控制市场,也就说市场背景中供应依然占主导地位。
在这种背景下,我们可以在阻力区做空。
我们再看最右边的垂直供应柱(2月25日),它是对供应继续控制市场的直接确认,也是对我们做空的确认。
它的阴线长度和扩大成交量给我们提供了一个新的阻力区。
在4月7日,价格回到这个阻力区,这是过剩的需求吸收了阻力区的所有卖盘,并使价格脱离了阻力区。
这个行为说明需求开始进入主导地位,这告诉我们后面的操作要以做多为主。
现在看第一个箭头,很显然,这也是个垂直供应柱。
4月价格回到这里的时候,大量买单已经准备好突破阻力。
但是4月11日的上冲回落显示了卖盘依然强大,说明这个阻力区依然有效,但是接下来几天的回落中卖盘耗尽告诉我们需求依然控制市场,市场还有机会向上发展。
下面我们看一下深天马的行情。
假如你在2015年9月根据判断抄底买入了,在利润不断增加的情况下,你开始考虑出场位置的问题。
你知道需求控制的市场背景下,供应必须扩大才能把目前的牛市压下来。
带着这种概念,我们看一下深天马周线图。
在深天马周线图上你看到了2015年7月第一周是垂直供应柱,同时你也发现8月21日那一周也是垂直供应柱。
从这两周的市场行为你判断它们之间(24~25)的卖盘聚集量很大,是出场重点关注的价格区。
然后你开始在日线观察价格回到这个阻力区时候的供求关系(这篇文章没有显示日线,大家看自己的电脑)。
2015年11月20日,价格进入周线阻力区。
从9月涨到这里,这一天的成交量是天量,很有可能是抢购高潮。
既然价格以天量接触阻力区,我们暂且认为它是强大需求准备突破阻力区。
不过你要有所警惕,毕竟抢购高潮的可能还在,而且抢购高潮等于供应进入。
接下来你会观察需求是否持续控制市场,同时观察供应是否继续进入并压制需求。
11月25日是你出场的日子,为什么?因为这一天的市场行为告
诉你供应继续扩大并压制需求,这种结果是在你的出场计划中写好了的,所以看到这种行为应该出场。
垂直供应柱为我们提供了重要的市场信息,它可以让我们提前按照市场行为做出场或者进场准备。
在我们实际交易中,这种行为一旦出现,我们必须重视并记住它的重要性。
