七年级下学期几何专题(附参考答案)
人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题(含答案)

人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题1、如图,已知∠2=∠3,∠C=∠D,求证:∠A=∠F.证明:∵∠2=∠3,∠1=∠2,∴∠1=∠3.∴DB∥CE.∴∠DBA=∠C.∵∠D=∠C,∴∠D=∠DBA.∴DF∥AC.∴∠A=∠F.2、如图,已知EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD的度数.解:∵EF∥AD,∴∠2=∠3(两直线平行,同位角相等).∵∠1=∠2,∴∠1=∠3(等量代换).∴AB∥DG(内错角相等,两直线平行).∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).3、如图,∠1=115°,∠2=50°,∠3=65°,EG为∠NEF的平分线.求证:AB∥CD,EG∥FH.证明:∵∠1=115°,∴∠FCD=180°-∠1=180°-115°=65°.∵∠3=65°,∴∠FCD=∠3.∴AB∥CD.∵∠2=50°,∴∠NEF=180°-∠2=180°-50°=130°.∵EG为∠NEF的平分线,∴∠GEF=12∠NEF=65°.∴∠GEF=∠3.∴EG∥FH.4、如图,已知∠B=∠D,∠E=∠F,判断BC与AD的位置关系,并说明理由.解:BC∥AD,理由:∴BE∥FD.∴∠B=∠BCF.又∵∠B=∠D,∴∠BCF=∠D.∴BC∥AD.5、如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.求证:AD平分∠BAC.证明:∵AD⊥BC,EG⊥BC,∴∠ADC=∠EGC=90°.∴AD∥EG.∴∠1=∠2,∠E=∠3.∵∠E=∠1,∴∠2=∠3.∴AD平分∠BAC.6、如图,B,C,E三点在一条直线上,A,F,E三点在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.证明:∵AB∥CD,∴∠4=∠BAE.∴∠3=∠BAE.∵∠1=∠2,∴∠1+∠CAF=∠2+∠CAF,即∠BAE=∠CAD.∴∠3=∠CAD.∴AD∥BE.7、如图,已知AB∥CD,试判断∠B,∠BED和∠D之间的关系,并说明理由.解:∠BED=∠B+∠D.理由如下:过点E作EF∥AB,则∠B=∠BEF.∵AB∥CD,∴EF∥CD.∴∠DEF=∠D.∵∠BED=∠BEF+∠DEF,∴∠BED=∠B+∠D.8、如图,∠AEF+∠CFE=180°,∠1=∠2,EG与HF平行吗?为什么?解:平行.理由:∵∠AEF+∠CFE=180°,∴AB∥CD.∴∠AEF=∠EFD.∴∠AEF -∠1=∠EFD -∠2,即∠GEF =∠HFE.∴EG ∥HF.9、如图,A ,B ,C 三点在同一直线上,∠1=∠2,∠3=∠D ,试判断BD 与CF 的位置关系,并说明理由.解:BD ∥CF.理由如下:∵∠1=∠2,∴AD ∥BF.∴∠D =∠DBF.∵∠3=∠D ,∴∠3=∠DBF.∴BD ∥CF.10、如图,∠ABC =∠ADC ,BF ,DE 分别是∠ABC ,∠ADC 的平分线,∠1=∠2,试说明:DC ∥AB.解:∵BF ,DE 分别是∠ABC ,∠ADC 的平分线,∴∠3=12∠ADC ,∠2=12∠ABC. ∵∠ABC =∠ADC ,∴∠3=∠2.∵∠1=∠2,∴∠1=∠3.∴DC∥AB.11、如图,AD平分∠BAC,AD⊥BC于D,点E,A,C共线,∠DAC=∠EFA,延长EF 交BC于点G.求证:EG⊥BC.证明:∵AD平分∠BAC,∴∠DAC=∠DAB.又∵∠DAC=∠EFA,∴∠DAB=∠EFA.∴AD∥EG.∴∠ADC=∠EGD.∵AD⊥BC,∴∠ADC=90°.∴∠EGD=90°.∴EG⊥BC.12、已知AB∥CD,点E为AB,CD之外任意一点.(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;(2)如图2,探究∠CDE与∠B,∠BED的数量关系,并说明理由.解:(1)∠B=∠BED+∠D.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠BEF=∠B,∠D=∠DEF.∵∠BEF=∠BED+∠DEF,∴∠B=∠BED+∠D.(2)∠CDE=∠B+∠BED.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠B+∠BEF=180°,∠CDE+∠DEF=180°.又∵∠DEF=∠BEF-∠BED,∴∠CDE+∠BEF-∠BED=∠B+∠BEF,即∠CDE=∠B+∠BED.13、如图,把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′和C′的位置上,ED′与BC的交点为G.若∠EFG=50°,求∠1,∠2,∠3的度数.解:根据折叠的性质可知,∠DEF=∠D′EF,∠EFC=∠EFC′.∵∠EFG=50°,∴∠EFC=180°-50°=130°.∴∠EFC′=∠EFC=130°.∴∠3=∠EFC′-∠EFG=130°-50°=80°.∵AD∥BC,∴∠DEF=∠EFG=50°.∴∠DED′=2∠DEF=100°.∴∠1=180°-∠DED′=180°-100°=80°.∵AD∥BC,∴∠1+∠2=180°.∴∠2=180°-∠1=100°.故∠1=80°,∠2=100°,∠3=80°.14、如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.解:(1)证明:∵AE⊥BC,FG⊥BC,∴AE∥GF.∴∠2=∠A.∵∠1=∠2,∴∠1=∠A.∴AB∥CD.(2)∵AB∥CD,∴∠D+∠CBD+∠3=180°.∵∠D =∠3+60°,∠CBD =70°,∴∠3=25°.∵AB ∥CD ,∴∠C =∠3=25°.15、(1)如图1,AB ∥CD ,则∠E +∠G 与∠B +∠F +∠D 有何关系?(2)如图2,若AB ∥CD ,又能得到什么结论?请直接写出结论.解:(1)过点E 作EM ∥AB ,过点F 作FN ∥AB ,过点G 作GH ∥CD. ∵AB ∥CD ,∴AB ∥EM ∥FN ∥GH ∥CD.∴∠1=∠B ,∠2=∠3,∠4=∠5,∠6=∠D.∴∠1+∠2+∠5+∠6=∠B +∠3+∠4+∠D ,即∠BEF +∠FGD =∠B +∠EFG +∠D.(2)∠B +∠F 1+∠F 2+…+∠F n -1+∠D =∠E 1+∠E 2+…+∠E n .16、已知E ,F 分别是AB ,CD 上的动点,P 也为一动点.(1)如图1,若AB ∥CD ,求证:∠P =∠BEP +∠PFD ;(2)如图2,若∠P =∠PFD -∠BEP ,求证:AB ∥CD ;(3)如图3,AB ∥CD ,移动E ,F ,使∠EPF =90°,作∠PEG =∠BEP ,则∠AEG∠PFD =2.证明:(1)过点P作PG∥AB,则∠EPG=∠BEP.∵AB∥CD,∴PG∥CD.∴∠GPF=∠PFD.∴∠EPF=∠EPG+∠FPG=∠BEP+∠PFD.(2)过点P作PQ∥AB,则∠QPE=∠BEP.∵∠EPF=∠PFD-∠BEP,∴∠PFD=∠EPF+∠BEP=∠EPF+∠QPE=∠FPQ. ∴DC∥PQ.∴AB∥CD.。
七年级数学下册期末几何压轴题试题(带答案) (一)解析

一、解答题1.如图,在平面直角坐标系中,()()()A 1,0,B 3,0,C 0,2-,CD//x 轴,CD=AB .(1)求点D 的坐标:(2)四边形OCDB 的面积S 四边形OCDB ;(3)在y 轴上是否存在点P ,使S △PAB =S 四边形OCDB ;若存在,求出点P 的坐标,若不存在,请说明理由.2.如图1,把一块含30°的直角三角板ABC 的BC 边放置于长方形直尺DEFG 的EF 边上. (1)根据图1填空:∠1= °,∠2= °;(2)现把三角板绕B 点逆时针旋转n °.①如图2,当n =25°,且点C 恰好落在DG 边上时,求∠1、∠2的度数;②当0°<n <180°时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n 的值和对应的那两条垂线;如果不存在,请说明理由.3.已知:如图,直线AB //CD ,直线EF 交AB ,CD 于P ,Q 两点,点M ,点N 分别是直线CD ,EF 上一点(不与P ,Q 重合),连接PM ,MN .(1)点M,N分别在射线QC,QF上(不与点Q重合),当∠APM+∠QMN=90°时,①试判断PM与MN的位置关系,并说明理由;②若PA平分∠EPM,∠MNQ=20°,求∠EPB的度数.(提示:过N点作AB的平行线)(2)点M,N分别在直线CD,EF上时,请你在备用图中画出满足PM⊥MN条件的图形,并直接写出此时∠APM与∠QMN的关系.(注:此题说理时不能使用没有学过的定理)4.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.小明的思路是:过P作PE∥AB,通过平行线性质,可得∠APC=∠APE+∠CPE=50°+60°=110°.问题解决:(1)如图2,AB∥CD,直线l分别与AB、CD交于点M、N,点P在直线I上运动,当点P 在线段MN上运动时(不与点M、N重合),∠PAB=α,∠PCD=β,判断∠APC、α、β之间的数量关系并说明理由;(2)在(1)的条件下,如果点P在线段MN或NM的延长线上运动时.请直接写出∠APC、α、B之间的数量关系;(3)如图3,AB∥CD,点P是AB、CD之间的一点(点P在点A、C右侧),连接PA、PC,∠BAP和∠DCP的平分线交于点Q.若∠APC=116°,请结合(2)中的规律,求∠AQC 的度数.5.如图,∠EBF=50°,点C是∠EBF的边BF上一点.动点A从点B出发在∠EBF的边BE 上,沿BE方向运动,在动点A运动的过程中,始终有过点A的射线AD∥BC.(1)在动点A运动的过程中,(填“是”或“否”)存在某一时刻,使得AD平分∠EAC?(2)假设存在AD平分∠EAC,在此情形下,你能猜想∠B和∠ACB之间有何数量关系?并请说明理由;(3)当AC ⊥BC 时,直接写出∠BAC 的度数和此时AD 与AC 之间的位置关系.6.已知,AB ∥CD ,点E 为射线FG 上一点.(1)如图1,若∠EAF =25°,∠EDG =45°,则∠AED = .(2)如图2,当点E 在FG 延长线上时,此时CD 与AE 交于点H ,则∠AE D 、∠EAF 、∠EDG 之间满足怎样的关系,请说明你的结论;(3)如图3,当点E 在FG 延长线上时,DP 平分∠EDC ,∠AED =32°,∠P =30°,求∠EKD 的度数.7.阅读下面的文字,解答问题 22的小数部分我们不可能全部212 21,将这个数减去其整数部分,差就是小数部分. 479273,∴7272)请解答:(157整数部分是 ,小数部分是 .(211a 7b ,求|a ﹣b 11(3)已知:5x +y ,其中x 是整数,且0<y <1,求x ﹣y 的相反数.8.对任意一个三位数n ,如果n 满足各数位上的数字互不相同,且都不为零,那么称这个数为“梦幻数”,将一个“梦幻数”任意两个数位上的数字对调后可以得到三个不同的新三数,把这三个新三位数的和与111的商记为K (n ),例如123n =,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213321132666++=,6661116÷=,所以()1236K =.(1)计算:()342K 和()658K ;(2)若x 是“梦幻数”,说明:()K x 等于x 的各数位上的数字之和;(3)若x ,y 都是“梦幻数”,且1000x y +=,猜想:()()K x K y +=________,并说明你猜想的正确性.9.阅读下面的文字,解答问题:是无理数,而无理数是无限不循环小数,的小数部分我们不可能全部写出来,而121.请解答下列问题:_______,小数部分是_________;(2)的小数部分为a b ,求a b +(3)已知:100x y +=+,其中x 是整数,且01y <<,求24x y -的平方根. 10.规定:求若千个相同的有理数(均不等于0)的除法运算叫做除方,如()()()()2223333÷÷-÷-÷-÷-,等,类比有理数的乘方,我们把222÷÷记作()32,读作“2的圈3次方”,()()()()3333-÷-÷-÷-记作()()43-,读作“3-的圈4次方”,一般地,把n a a a a a↑÷÷÷⋯⋯÷记作()n a ,读作“a ”的圈n 次方.(初步探究)(1)直接写出计算结果:()()32=- ;()()42=- ;(2)关于除方,下列说法错误的是( )A .任何非零数的圈2次方都等于1B .对于任何正整数(),1=1n nC .()()433=4D .负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数 (深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(3)试一试:()()()2446113=5=35⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,,依照前面的算式,将()93,()1012⎛⎫- ⎪⎝⎭的运算结果直接写成幂的形式是()93= ,()101=2⎛⎫- ⎪⎝⎭; (4)想一想:将一个非零有理数a 的圆n 次方写成幂的形式是:()n a = ; (5)算一算:()()()()4652311122333⎛⎫⎛⎫÷-⨯---÷ ⎪ ⎪⎝⎭⎝⎭.11.我们知道,正整数按照能否被2整除可以分成两类:正奇数和正偶数,小华受此启发,按照一个正整数被3除的余数把正整数分成了三类:如果一个正整数被3除余数为1,则这个正整数属于A 类,例如1,4,7等;如果一个正整数被3除余数为2,则这个正整数属于B 类,例如2,5,8等;如果一个正整数被3整除,则这个正整数属于C 类,例如3,6,9等.(1)2020属于 类(填A ,B 或C );(2)①从A 类数中任取两个数,则它们的和属于 类(填A ,B 或C );②从A 、B 类数中任取一数,则它们的和属于 类(填A ,B 或C );③从A 类数中任意取出8个数,从B 类数中任意取出9个数,从C 类数中任意取出10个数,把它们都加起来,则最后的结果属于 类(填A ,B 或C );(3)从A 类数中任意取出m 个数,从B 类数中任意取出n 个数,把它们都加起来,若最后的结果属于C 类,则下列关于m ,n 的叙述中正确的是 (填序号). ①2m n +属于C 类;②m n -属于A 类;③m ,n 属于同一类.12.观察下面的变形规律:;;;….解答下面的问题:(1)仿照上面的格式请写出= ; (2)若n 为正整数,请你猜想= ; (3)基础应用:计算:. (4)拓展应用1:解方程:=2016 (5)拓展应用2:计算:. 13.如图1在平面直角坐标系中,大正方形OABC 的边长为m 厘米,小正方形ODEF 的边长为n 厘米,且|m ﹣4|+2n -=0.(1)求点B 、点D 的坐标.(2)起始状态如图1所示,将大正方形固定不动,小正方形以1厘米/秒的速度沿x 轴向右平移,如图2.设平移的时间为t 秒,在平移过程中两个正方形重叠部分的面积为S 平方厘米.①当t =1.5时,S = 平方厘米;②在2≤t ≤4这段时间内,小正方形的一条对角线扫过的图形的面积为 平方厘米; ③在小正方形平移过程中,若S =2,则小正方形平移的时间t 为 秒.(3)将大正方形固定不动,小正方形从图1中起始状态沿x 轴向右平移,在平移过程中,连接AD ,过D 点作DM ⊥AD 交直线BC 于M ,∠DAx 的角平分线所在直线和∠CMD 的角平分线所在直线交于N (不考虑N 点与A 点重合的情形),求∠ANM 的大小并说明理由. 14.如图,直线//PQ MN ,一副直角三角板,ABC DEF ∆∆中,90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=.(1)若DEF ∆如图1摆放,当ED 平分PEF ∠时,证明:FD 平分EFM ∠.(2)若,ABC DEF ∆∆如图2摆放时,则PDE ∠=(3)若图2中ABC ∆固定,将DEF ∆沿着AC 方向平移,边DF 与直线PQ 相交于点G ,作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H (如图3),求GHF ∠的度数.(4)若图2中DEF ∆的周长35,5cm AF cm =,现将ABC ∆固定,将DEF ∆沿着CA 方向平移至点F 与A 重合,平移后的得到''D E A ∆,点D E 、的对应点分别是''D E 、,请直接写出四边形'DEAD 的周长.(5)若图2中DEF ∆固定,(如图4)将ABC ∆绕点A 顺时针旋转,1分钟转半圈,旋转至AC 与直线AN 首次重合的过程中,当线段BC 与DEF ∆的一条边平行时,请直接写出旋转的时间.15.如图,在平面直角坐标系中,点A B 、的坐标分别为(1,0)、(-2,0),现同时将点A B 、分别向上平移2个单位,再向左平移1个单位,分别得到点AB 、的对应点CD 、,连接AC 、BD 、CD .(1)若在y 轴上存在点M ,连接MA MB 、,使S △ABM =S □ABDC ,求出点M 的坐标; (2)若点P 在线段BD 上运动,连接PC PO 、,求S =S △PCD +S △POB 的取值范围; (3)若P 在直线BD 上运动,请直接写出CPO DCP BOP ∠∠∠、、的数量关系.16.对x ,y 定义一种新的运算P ,规定:,()(,),()mx ny x y P x y nx my x y +≥⎧=⎨+<⎩(其中0mn ≠).已知(2,1)7P =,(1,1)1P -=-.(1)求m 、n 的值;(2)若0a >,解不等式组(2,1)4111,523P a a P a a -<⎧⎪⎨⎛⎫---≤- ⎪⎪⎝⎭⎩. 17.如图1,在平面直角坐标系中,点A 为x 轴负半轴上一点,点B 为x 轴正半轴上一点,()0,C a ,(),D b a ,其中a 、b 满足关系式:24(1)0a b a ++--=.()1a =______,b =______,BCD 的面积为______;()2如图2,石AC BC ⊥于点C ,点P 是线段OC 上一点,连接BP ,延长BP 交AC 于点.Q 当CPQ CQP ∠=∠时,求证:BP 平分ABC ∠;(提示:三角形三个内角和等于180) ()3如图3,若AC BC ⊥,点E 是点A 与点B 之间上一点连接CE ,且CB 平分.ECF ∠问BEC ∠与BCO ∠有什么数量关系?请写出它们之间的数量关系并请说明理由.18.如图,在下面直角坐标系中,已知()0,A a ,(),0B b ,(),C b c 三点,其中a ,b ,c 满足关系式()22340a b c ---=.(1)求a ,b ,c 的值;(2)如果在第二象限内有一点1,2P m ⎛⎫ ⎪⎝⎭,请用含m 的式子表示四边形ABOP 的面积; (3)在(2)的条件下,是否存在点P ,使四边形ABOP 的面积与三角形ABC 的面积相等?若存在,求出点P 的坐标,若不存在,请说明理由.19.先阅读下面材料,再完成任务:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x ,y 满足35x y -=,……①,237x y +=,……②,求4x y -和75x y +的值. 本题常规思路是将①②两式联立组成方程组,解得x ,y 的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①-②可得42x y -=-,由①+②×2可得7519x y +=,这样的解题思想就是通常所说的“整体思想”解决问题:(1)已知二元一次方程组322233x y x y -=-⎧⎨-=-⎩,则x y -=______,x y +=______; (2)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记木共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?(3)对于实数x ,y ,定义新运算:x y ax by c *=++,其中a ,b ,c 是常数,等式右边是通常的加法和乘法运算.已知3515*=,4728*=,那么11*=______.20.阅读下列材料,解答下面的问题:我们知道方程2312x y +=有无数个解,但在实际生活中我们往往只需求出其正整数解.例:由2312x y +=,得:1222433x x y -==-,(x 、y 为正整数) ∴01220x x >⎧⎨->⎩,则有06x <<.又243x y =-为正整数,则23x 为正整数.由2与3互质,可知:x 为3的倍数,从而x=3,代入2423x y =-=∴2x+3y=12的正整数解为32x y =⎧⎨=⎩ 问题:(1)请你写出方程25x y +=的一组正整数解: .(2)若62x -为自然数,则满足条件的x 值为 .(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?21.某校规划在一块长AD为18 m、宽AB为13 m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮,如图所示,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM∶AN=8∶9,问通道的宽是多少?22.某公园的门票价格如下表所示:某中学七年级(1)、(2)两个班计划去游览该公园,其中(I)班的人数较少,不足 50 人;(2) 班人数略多,有 50 多人.如果两个班都以班为单位分别购票,则一共应付 1172 元,如果两个班联合起来,作为一个团体购票,则需付 1078 元.(1)列方程求出两个班各有多少学生;(2)如果两个班联合起来买票,是否可以买单价为 9 元的票?你有什么省钱的方法来帮他们买票呢?请给出最省钱的方案.23.小明为班级购买信息学编程竞赛的奖品后,回学校向班主任李老师汇报说:“我买了两种书,共30本,单价分别为20元和24元,买书前我领了700元,现在还余38元.”李老师算了一下,说:“你肯定搞错了.”(1)李老师为什么说他搞错了?试用方程的知识给予解释;(2)小明连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本.但笔记本的单价已模糊不清,只能辨认出应为小于10元的整数,如果单价为20元的书多于24元的书,请问:笔记本的单价为多少元?24.对a,b定义一种新运算T,规定:T(a,b)=(a+2b)(ax+by)(其中x,y均为非零实数).例如:T(1,1)=3x+3y.(1)已知T(1,﹣1)=0,T(0,2)=8,求x,y的值;(2)已知关于x,y的方程组()()113028T aT a⎧-=-⎪⎨=⎪⎩,,,若a≥﹣2,求x+y的取值范围;(3)在(2)的条件下,已知平面直角坐标系上的点A(x,y)落在坐标轴上,将线段OA 沿x轴向右平移2个单位,得线段O′A′,坐标轴上有一点B满足三角形BOA′的面积为9,请直接写出点B的坐标.25.某校为了丰富同学们的课外活动,决定给全校20个班每班配4副乒乓球拍和若干乒乓球,两家体育用品商店对同一款乒乓球拍和乒乓球推出让利活动,甲商店买一副乒乓球拍送10个乒乓球,乙商店所有商品均打九折(按标价的90%)销售,已知2副乒乓球拍和10个乒乓球110元,3副乒乓球拍和20个乒乓球170元。
人教版数学七年级下册:第五章 相交线与平行线——专题练习(附答案)

小专题(一)平行线中的“拐点”问题模型1 M型【例1】如图,已知AB∥CD,则∠B,∠BED,∠D之间有何数量关系?请说明理由.【思路点拨】由已知条件知,AB∥CD,但图形中没有截这两条平行线的第三条直线,因而不能直接用平行线的性质解决.为此可构造第三条直线,即过点E 作EF∥AB,于是BE,DE就可以作为第三条直线了.变式当点E运动到平行线的外侧1.已知AB∥CD,点E为AB,CD之外任意一点.(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;(2)如图2,探究∠CDE与∠B,∠BED的数量关系,并说明理由.2.(1)如图1中,AB∥CD,则∠E+∠G与∠B+∠F+∠D有何关系?(2)在图2中,若AB∥CD,又能得到什么结论?如果出现多个拐点时,可以作多条平行线,从而将多拐点问题转化为一个拐点问题来处理.M型最终的结论为:朝左的角之和等于朝右的角之和.模型2 铅笔型【例2】如图,直线AB∥CD,∠B,∠BED,∠D之间有什么关系呢?为什么?3.(1)①如图1,MA1∥NA2,则∠A1+∠A2=度;②如图2,MA1∥NA3,则∠A1+∠A2+∠A3=度;③如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=度;④图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=度;从上述结论中你发现了什么规律?(2)如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=度.小专题(二) 利用平行线的性质求角的度数类型1 直接利用平行线的性质与判定求角度1.如图,OC是∠AOB的平分线,l∥OB.若∠1=52°,则∠2的度数为( ) A.52° B.54° C.64° D.69°2.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,则∠AOF 的度数是( )A.20° B.25° C.30° D.35°3.如图,AB∥CD,CB∥DE,∠B=50°,则∠D=.4.如图,已知EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD的度数.类型2 借助学具的特征求角度5.如图,将直尺与30°角的三角尺叠放在一起.若∠1=40°,则∠2的大小是( )A.40° B.60° C.70° D.80°6.如图,一块直角三角板的两锐角的顶点刚好落在平行线l1,l2上,已知∠C是直角,则∠1+∠2的度数等于( )A.75° B.90° C.105° D.120°类型3 折叠问题中求角度7.将一个长方形纸片折叠成如图所示的图形.若∠ABC=26°,则∠ACD=.8.如图,一个四边形纸片ABCD,∠B=∠D=90°,∠C=130°.把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,则∠AEB的度数是.类型4 抽象出平行线模型求角度(建模思想)9.如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入经平面镜反射后,反射光线落在OB上的点E处,已知∠ADC=∠ODE.则∠DEB的度数是度.10.如图1是我们常用的折叠式小刀,图2中刀柄外形是一个梯形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2所示的∠1与∠2,则∠1与∠2的度数和是.小专题(三) 平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13):完成下面的证明.(1)如图1,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF ∥CA.求证:∠FDE=∠A.证明:∵DE∥BA,∴∠FDE=.∵DF∥CA,∴∠A=.∴∠FDE=∠A.(2)如图2,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD.求证AC∥BD.证明:∵∠C=∠COA,∠D=∠BOD,又∠COA=∠BOD( ),∴∠C=.∴AC∥BD(内错角相等,两直线平行).(1)判定两直线平行的方法有五种:①平行线的定义;②平行公理的推论;③同位角相等,两直线平行;④内错角相等,两直线平行;⑤同旁内角互补,两直线平行.(2)判定两直线平行时,定义一般不常用,其他四种方法要灵活运用,推理时要注意书写格式.(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补,解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角,同时要学会简单的几何说理,做到每一步有理有据.1.如图,已知AD⊥BC,EF⊥BC,垂足分别为D,F,∠2+∠3=180°.试说明:∠GDC=∠B.下面是不完整的说理过程,请你将横线上的过程和括号里的理由补充完整.解:因为AD⊥BC,EF⊥BC(已知),①所以∠ADB=∠EFB= (垂直的定义).②所以 (同位角相等,两直线平行).③所以∠1+∠2= (两直线平行,同旁内角互补).④又因为∠2+∠3=180°( ),⑤所以∠1=∠3( ).⑥所以AB∥DG( ).⑦所以∠GDC=∠B( ).2.如图,点G在射线BC上,射线DE与AB,AG分别交于点H,M.若DF∥AB,∠B=75°,∠D=105°,求证:∠AME=∠AGC.3.如图,AB∥CD,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.求证:AD ∥BC.4.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的平分线.你能判断DF 与AB的位置关系吗?请说明理由.5.如图,AB⊥BD于点B,点E是BD上的点,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.求证:CD⊥BD.6.如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点为G,点D,C分别落在D′,C′的位置上.若∠EFG=55°,求∠1,∠2的度数.7.如图,已知BC∥GE,∠AFG=∠1=50°.(1)求证:AF∥DE;(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACQ的度数.参考答案:小专题(一)平行线中的“拐点”问题模型1 M型【例1】如图,已知AB∥CD,则∠B,∠BED,∠D之间有何数量关系?请说明理由.【思路点拨】由已知条件知,AB∥CD,但图形中没有截这两条平行线的第三条直线,因而不能直接用平行线的性质解决.为此可构造第三条直线,即过点E 作EF∥AB,于是BE,DE就可以作为第三条直线了.【解答】∠BED=∠B+∠D.理由:过点E作EF∥AB,则EF∥CD.∴∠B=∠BEF,∠D=∠DEF.∴∠BED=∠BEF+∠DEF=∠B+∠D.变式当点E运动到平行线的外侧1.已知AB∥CD,点E为AB,CD之外任意一点.(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;(2)如图2,探究∠CDE与∠B,∠BED的数量关系,并说明理由.解:(1)∠B=∠BED+∠D.理由如下:过点E作EF∥AB,则AB∥CD∥EF.∴∠BEF=∠B,∠D=∠DEF.∵∠BEF=∠BED+∠DEF,∴∠B=∠BED+∠D.(2)∠CDE=∠B+∠BED.理由如下:过点E作EF∥AB,则AB∥CD∥EF.∴∠B+∠BEF=180°,∠CDE+∠DEF=180°.又∵∠DEF=∠BEF-∠BED,∴∠CDE+∠BEF-∠BED=∠B+∠BEF,即∠CDE=∠B+∠BED.拓展平行线间有多个拐点2.(1)如图1中,AB∥CD,则∠E+∠G与∠B+∠F+∠D有何关系?(2)在图2中,若AB∥CD,又能得到什么结论?解:(1)∠BEF+∠FGD=∠B+∠EFG+∠D.理由:过点E,F,G分别作EM∥AB,FN∥AB,GH∥AB,由AB∥CD,得AB∥EM∥FN∥GH∥CD.∴∠BEM=∠B,∠MEF=∠EFN,∠NFG=∠FGH,∠HGD=∠D.∴∠BEF+∠FGD=∠BEM+∠MEF+∠FGH+∠HGD=∠B+∠EFN+∠NFG+∠D=∠B+∠EFG+∠D.(2)在图2中,有∠E1+∠E2+∠E3+…+∠En=∠B+∠F1+∠F2+…+∠Fn-1+∠D.如果出现多个拐点时,可以作多条平行线,从而将多拐点问题转化为一个拐点问题来处理.M型最终的结论为:朝左的角之和等于朝右的角之和.模型2 铅笔型【例2】如图,直线AB∥CD,∠B,∠BED,∠D之间有什么关系呢?为什么?【解答】∠B+∠BED+∠D=360°.理由:过点E作EF∥AB.∵AB∥CD,∴AB∥CD∥EF.∴∠B+∠BEF=180°,∠D+∠DEF=180°. ∴∠B+∠BEF+∠D+∠DEF=360°,即∠B+∠BED+∠D=360°.拓展平行线间有多个拐点3.(1)①如图1,MA1∥NA2,则∠A1+∠A2=180度;②如图2,MA1∥NA3,则∠A1+∠A2+∠A3=360度;③如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=540度;④图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=720度;从上述结论中你发现了什么规律?(2)如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=180(n-1)度.解:每增加一个角,度数增加180°.小专题(二) 利用平行线的性质求角的度数类型1 直接利用平行线的性质与判定求角度1.如图,OC是∠AOB的平分线,l∥OB.若∠1=52°,则∠2的度数为( C ) A.52° B.54° C.64° D.69°2.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,则∠AOF 的度数是( D )A.20° B.25° C.30°D.35°3.如图,AB∥CD,CB∥DE,∠B=50°,则∠D=130°.4.如图,已知EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD的度数.解:∵EF∥AD,∴∠2=∠3(两直线平行,同位角相等).∵∠1=∠2,∴∠1=∠3(等量代换).∴AB∥DG(内错角相等,两直线平行).∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).∵∠BAC=80°,∴∠AGD=100°.类型2 借助学具的特征求角度5.如图,将直尺与30°角的三角尺叠放在一起.若∠1=40°,则∠2的大小是( D )A.40° B.60° C.70° D.80°6.如图,一块直角三角板的两锐角的顶点刚好落在平行线l1,l2上,已知∠C是直角,则∠1+∠2的度数等于( B )A.75° B.90° C.105° D.120°类型3 折叠问题中求角度7.将一个长方形纸片折叠成如图所示的图形.若∠ABC=26°,则∠ACD=128°.8.如图,一个四边形纸片ABCD,∠B=∠D=90°,∠C=130°.把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,则∠AEB的度数是65°.类型4 抽象出平行线模型求角度(建模思想)9.如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从点C射入经平面镜反射后,反射光线落在OB上的点E处,已知∠ADC=∠ODE.则∠DEB的度数是76度.10.如图1是我们常用的折叠式小刀,图2中刀柄外形是一个梯形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2所示的∠1与∠2,则∠1与∠2的度数和是90°.小专题(三) 平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13):完成下面的证明.(1)如图1,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF ∥CA.求证:∠FDE=∠A.证明:∵DE∥BA,∴∠FDE=∠BFD(两直线平行,内错角相等).∵DF∥CA,∴∠A=∠BFD(两直线平行,同位角相等).∴∠FDE=∠A.(2)如图2,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD.求证AC∥BD.证明:∵∠C=∠COA,∠D=∠BOD,又∠COA=∠BOD(对顶角相等),∴∠C=∠D.∴AC∥BD(内错角相等,两直线平行).(1)判定两直线平行的方法有五种:①平行线的定义;②平行公理的推论;③同位角相等,两直线平行;④内错角相等,两直线平行;⑤同旁内角互补,两直线平行.(2)判定两直线平行时,定义一般不常用,其他四种方法要灵活运用,推理时要注意书写格式.(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补,解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角,同时要学会简单的几何说理,做到每一步有理有据.1.如图,已知AD⊥BC,EF⊥BC,垂足分别为D,F,∠2+∠3=180°.试说明:∠GDC=∠B.下面是不完整的说理过程,请你将横线上的过程和括号里的理由补充完整.解:因为AD⊥BC,EF⊥BC(已知),①所以∠ADB=∠EFB=90°(垂直的定义).②所以AD∥EF(同位角相等,两直线平行).③所以∠1+∠2=180°(两直线平行,同旁内角互补).④又因为∠2+∠3=180°(已知),⑤所以∠1=∠3(同角的补角相等).⑥所以AB∥DG(内错角相等,两直线平行).⑦所以∠GDC=∠B(两直线平行,同位角相等).2.如图,点G在射线BC上,射线DE与AB,AG分别交于点H,M.若DF∥AB,∠B=75°,∠D=105°,求证:∠AME=∠AGC.证明:∵DF∥AB(已知),∴∠D=∠BHM(两直线平行,同位角相等).又∵∠B=75°,∠D=105°(已知),∴∠B+∠BHM=75°+105°=180°.∴DE∥BC(同旁内角互补,两直线平行).∴∠AME=∠AGC(两直线平行,同位角相等).3.如图,AB∥CD,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.求证:AD ∥BC.证明:∵AE平分∠BAD(已知),∴∠1=∠2(角平分线的定义).∵AB∥CD(已知),∴∠1=∠CFE(两直线平行,同位角相等).又∵∠1=∠2(已证),∠CFE=∠E(已知),∴∠2=∠E(等量代换).∴AD∥BC(内错角相等,两直线平行).4.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的平分线.你能判断DF 与AB的位置关系吗?请说明理由.解:DF∥AB.理由:∵BE是∠ABC的平分线,∴∠1=∠2(角平分线的定义).∵∠E=∠1(已知),∴∠E=∠2(等量代换).∴AE∥BC(内错角相等,两直线平行).∴∠A+∠ABC=180°(两直线平行,同旁内角互补).∵∠3+∠ABC=180°(已知),∴∠A=∠3(等量代换).∴DF∥AB(同位角相等,两直线平行).5.如图,AB⊥BD于点B,点E是BD上的点,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.求证:CD⊥BD.证明:∵AE平分∠BAC,CE平分∠ACD(已知),∴∠BAC=2∠1,∠ACD=2∠2(角平分线的性质).∴∠BAC+∠ACD=2∠1+2∠2=2(∠1+∠2).∵∠1+∠2=90°(已知),∴∠BAC+∠ACD=180°.∴AB∥CD(同旁内角互补,两直线平行).∴∠B+∠D=180°(两直线平行,同旁内角互补).∴∠D=180°-∠B(等式的性质).∵AB⊥BD(已知),∴∠B=90°(垂直的定义).∴∠D=90°,即CD⊥BD.6.如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点为G,点D,C分别落在D′,C′的位置上.若∠EFG=55°,求∠1,∠2的度数.解:∵AD∥BC,∠EFG=55°,∴∠2=∠GED,∠DEF=∠EFG=55°(两直线平行,内错角相等).由折叠,知∠GEF=∠DEF=55°.∴∠GED=110°.∴∠2=110°.∴∠1=180°-∠2=70°(两直线平行,同旁内角互补).7.如图,已知BC∥GE,∠AFG=∠1=50°.(1)求证:AF∥DE;(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACQ的度数.解:(1)证明:∵BC∥GE,∴∠E=∠1=50°.∵∠AFG=∠1=50°,∴∠E=∠AFG=50°.∴AF∥DE.(2)过点A作AP∥GE,∵BC∥GE,∴AP∥GE∥BC.∴∠FAP=∠AFG=50°,∠PAQ=∠Q=15°.∴∠FAQ=∠FAP+∠PAQ=65°.∵AQ平分∠FAC,∴∠CAQ=∠FAQ=65°.∴∠CAP=80°.∴∠ACQ=180°-∠CAP=100°.。
七年级数学几何体的展开图(专题)(含答案)

几何体的展开图(专题)一、单选题(共10道,每道10分)1.如图是一个正方体纸盒的表面展开图,下列选项中的正方体能由它折叠而成的是( )A. B.C. D.答案:D解题思路:根据正方体纸盒的表面展开图可得折起来之后面“○”与面“□”是相对的,因此不能相邻,也就是说折成正方体后,面“○”与面“□”两个面能且只能看到一个面,排除选项A,B,C.故选D.试题难度:三颗星知识点:找相对面相邻面2.下列各图都是正方体的表面展开图,若将它们折成正方体,则其中两个正方体各面图案完全一样的是( )A.(1)(2)B.(2)(3)C.(3)(4)D.(2)(4)答案:D解题思路:因为其中有两个正方体折叠之后各面图案完全一样,因此它们对应的平面展开图的相对面必须完全一样.先分析面“△”的相对面:(1)面“△”与面“#”相对;(2)面“△”与面“+”相对;(3)面“△”与面“+”相对;(4)面“△”与面“+”相对;因此可排除含有(1)的选项,故排除A;第二步分析面“☆”的相对面:(2)面“☆”与面“”相对;(3)面“☆”与面“○”相对;(4)面“☆”与面“”相对;因此排除含有(3)的选项,故排除B,C.经验证(2)和(4)折成的两个正方体各面图案完全一样,故选D.试题难度:三颗星知识点:找相对面相邻面3.一个正方体的表面展开图如图所示,每一个面上都写有一个数,并且相对两个面上所写的两个数之和都相等,那么( )A.a=7,b=5B.a=6,b=9C.a=1,b=5D.a=5,b=7答案:D解题思路:这是一个(2,3,1)型的正方体表面展开图,其相对面如图所示,又因为相对两个面上所写的两个数之和都相等,则4+b=8+3=6+a,所以a=5,b=7.故选D.试题难度:三颗星知识点:找相对面相邻面4.明明用如图所示的硬纸片折成了一个正方体的盒子,里面装了一瓶墨水,只凭观察,墨水可能在哪个盒子中?思路分析判断正方体的展开与折叠问题时,我们按照面、棱、顶点的顺序分析.如图,首先观察面,展开图中上下两个空白面为相对面,因此排除______和______.其次研究棱的对应,面ABCD与面“○”有一条公共棱DC,即相邻的部分是空白三角形,故排除_________,应选___________.以上横线处依次所填正确的是( )A.①④②③B.①④③②C.①③②④D.①②④③答案:B解题思路:参考题目中的思路分析,横线处依次所填正确的是①④③②,故选B.试题难度:三颗星知识点:找相对面相邻面5.如图所示的正方体的表面展开图可能是( )思路分析首先根据“相邻面不可能相对”,排除_______和_______.其次研究棱和顶点的对应,排除_________,应选___________.以上横线处依次所填正确的是( )A.①④②③B.①④③②C.②④①③D.④②③①答案:C解题思路:先从面开始分析,,,三个面是相邻面,可以排除②,④;观察发现①,③的区别在于,是面中的阴影小正方形跟和有公共顶点,还是面中的空白小正方形跟和有公共顶点,根据题中所给的正方体可以看出阴影小正方形跟和有公共顶点,排除①,应选③.因此横线处依次所填正确的是②④①③,故选C.试题难度:三颗星知识点:找相对面相邻面6.如图是一个正方体的表面展开图,则这个正方体是( )A. B.C. D.答案:C解题思路:如图,先从面开始分析,a,b,“○”所在的面为相邻面,因此从面上无法排除;然后从棱开始分析,分析的时候从拐角处出发(有两条棱连着的),再分析有一条棱连着的.由图分析可得在折叠之后的正方体中a所在的面与“○”所在的面有一条公共棱BC,a与棱BC 垂直;b所在的面与“○”所在的面有一条公共棱AB,b与棱AB平行,故选C.试题难度:三颗星知识点:找相对面相邻面7.如图,点M,N,P分别是正方体三条相邻棱的中点,沿着M,N,P三点所在的平面将该正方体的一个角切掉,然后将其展开,其表面展开图可能是( )A. B.C. D.答案:D解题思路:根据正方体的十一种表面展开图可知,没有(3,1,2)型,故排除A;分析该正方体,缺角的三个面是相邻面,根据相邻面不可能相对排除B;还可以知道展开之后缺的地方有公共顶点,接着从棱和点开始分析,分析的时候先找出一组相对面标上字母,然后根据边的重合与点的重合标出其他点.C选项中,标出各点的字母如下:缺的地方没有公共顶点,故C错误;D选项中,标出各点的字母如下:缺的地方有公共顶点,故选D.试题难度:三颗星知识点:找相对面相邻面8.一个小立方块的六面分别标有字母A,B,C,D,E,F,如图是从三个不同方向看到的情形,则A,B,E的相对面分别是( )A.E,D,FB.E,F,DC.F,E,BD.F,D,C答案:D解题思路:正方体6个面中,每一个面和四个面相邻,和一个面相对.首先找图中出现次数最多的,分别是“A”,“C”,“D”;①不妨先看“A”:从图中的三个正方体可以看到“A”和“B”,“C”,“D”,“E”相邻,所以“A”的相对面是“F”.②接下来看“C”,在剩下的四个面中,“C”和“B”,“D”相邻,所以“C”的相对面是“E”;③所以剩余的“B”和“D”是相对面.综上所述:“A”,“B”,“E”的相对面分别是“F”,“D”,“C”.故选D.试题难度:三颗星知识点:找相对面相邻面9.一个正方体,六个面上分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为3,6,7,则六个整数的和为( )A.27B.28C.33D.34答案:C解题思路:能看到的三个整数是3,6,7,由于是六个连续的整数,由题意分析可知其中的五个数字3,4,5,6,7,所以剩余的一个数字可能是2或者8,如果是2的话,根据每个相对面上的两个数之和相等,那么3与6相对,而图中3和6是相邻面,因此第六个数字只能是8,此时3与8相对,4与7相对,5与6相对,满足题中的条件,所以六个整数的和是3+4+5+6+7+8=33.故选C.试题难度:三颗星知识点:找相对面相邻面10.在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,按照如图所示拼成一个长方体,那么涂黄、白两种颜色的面的对面分别涂有( )颜色.A.蓝、红B.蓝、黑C.蓝、绿D.绿、白答案:B解题思路:本题通过相邻面确定相对面,正方体的每一个面与4个面相邻,1个面相对.首先找图中出现次数较多的,先从“红”开始,从第二个正方体看出“红”与“蓝”相邻,从第三个正方体看出“红”与“白”相邻,从第四个正方体看出“红”与“黄”,“黑”相邻,所以“红”与“蓝”,“白”,“黄”,“黑”相邻,那么与“绿”相对;同样的方法可以判断“黄”与“蓝”相对,“白”与“黑”相对,所以涂黄、白两种颜色的面的对面分别涂有蓝、黑两种颜色.故选B.试题难度:三颗星知识点:找相对面相邻面。
初一下册数学角度几何解析题以及练习题(附答案)

七年级下册数学几何解析题以及练习题(附答案)9.(2011·扬州)如图,C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从C 岛看A 、B 两岛的视角∠ACB =________.答案 105°解析 如图,∵(60°+∠CAB )+(45°+∠ABC )=180°,∴∠CAB +∠ABC =75°,在△ABC 中,得∠C =105°.12.如图所示,在△ABC 中,∠A =80°,∠B =30°,CD 平分∠ACB ,DE ∥AC .(1)求∠DEB 的度数; (2)求∠EDC 的度数.解 (1)在△ABC 中,∠A =80°,∠B =30°,∴∠ACB =180°-∠A -∠B =70°. ∵DE ∥AC ,∴∠DEB =∠ACB =70°. (2)∵CD 平分∠ACB , ∴∠DCE =12∠ACB =35°.∵∠DEB =∠DCE +∠EDC , ∴∠EDC =70°-35°=35°.13.已知,如图,∠1=∠2,CF ⊥AB 于F ,DE ⊥AB 于E ,求证:FG ∥BC .(请将证明补充完整)证明 ∵CF ⊥AB ,DE ⊥AB (已知),∴ED ∥FC ( ). ∴∠1=∠BCF ( ). 又∵∠1=∠2(已知), ∴∠2=∠BCF (等量代换),∴FG∥BC( ).解在同一平面内,垂直于同一直线的两条直线互相平行;两直线平行,同位角相等;内错角相等,两直线平行.14.如图,已知三角形ABC,求证:∠A+∠B+∠C=180°.分析:通过画平行线,将∠A、∠B、∠C作等角代换,使各角之和恰为一平角,依辅助线不同而得多种证法,如下:证法1:如图甲,延长BC到D,过C画CE∥BA.∵BA∥CE(作图所知),∴∠B=∠1,∠A=∠2(两直线平行,同位角、内错角相等).又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),∴∠A+∠B+∠ACB=180°(等量代换).如图乙,过BC上任一点F,画FH∥AC,FG∥AB,这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗?请你试一试.解∵FH∥AC,∴∠BHF=∠A,∠1=∠C.∵FG∥AB,∴∠BHF=∠2,∠3=∠B,∴∠2=∠A.∵∠BFC=180°,∴∠1+∠2+∠3=180°,即∠A+∠B+∠C=180°.15.(2010·玉溪)平面内的两条直线有相交和平行两种位置关系.(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD.又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b 中,将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ,如图c ,则∠BPD 、∠B 、∠D 、∠BQD 之间有何数量关系?(不需证明) (3)根据(2)的结论求图d 中∠A +∠B +∠C +∠D +∠E +∠F 的度数.解 (1)不成立,结论是∠BPD =∠B +∠D .延长BP 交CD 于点E , ∵AB ∥CD ,∴∠B =∠BED . 又∠BPD =∠BED +∠D , ∴∠BPD =∠B +∠D .(2)结论:∠BPD =∠BQD +∠B +∠D . (3)设AC 与BF 交于点G .由(2)的结论得:∠AGB =∠A +∠B +∠E .又∵∠AGB =∠CGF ,∠CGF +∠C +∠D +∠F =360°,∴∠A +∠B +∠C +∠D +∠E +∠F =360°.14.把一副常用的三角板如图所示拼在一起,那么图中∠ADE 是 度.2.如图,在△ABC 和△ABD 中,现给出如下三个论断:①AD =BC ;②∠C =∠D ;③∠1=∠2。
人教版七年级数学下册《相交线与平行线中的四种几何模型》专项练习题-附含答案

人教版七年级数学下册《相交线与平行线中的四种几何模型》专项练习题-附含答案类型一、猪脚模型例.问题情境:如图① 直线AB CD ∥ 点E F 分别在直线AB CD 上.(1)猜想:若1130∠=︒ 2150∠=︒ 试猜想P ∠=______°;(2)探究:在图①中探究1∠ 2∠ P ∠之间的数量关系 并证明你的结论;(3)拓展:将图①变为图② 若12325∠+∠=︒ 75EPG ∠=︒ 求PGF ∠的度数. 【答案】(1)80︒(2)36012P ∠=︒-∠-∠;证明见详解(3)140︒【详解】(1)解:如图过点P 作MN AB ∥∵AB CD ∥∵AB MN CD ∥∥.∵1180EPN ∠+∠=︒2180FPN ∠+∠=︒.∵1130∠=︒ 2150∠=︒∵12360EPN FPN ∠+∠+∠+∠=︒∵36013015080EPN FPN ∠+=︒-︒-︒=︒.∵P EPN FPN ∠=∠+∠∵∵P =80°.故答案为:80︒;(2)解:36012P ∠=︒-∠-∠ 理由如下:如图过点P 作MN AB ∥∵AB CD ∥∵AB MN CD ∥∥.∵1180EPN ∠+∠=︒2180FPN ∠+∠=︒.∵12360EPN FPN ∠+∠+∠+∠=︒∵EPN FPN P ∠+∠=∠36012P ∠=︒-∠-∠.(3)如图分别过点P 、点G 作MN AB ∥、KR AB ∥∵AB CD ∥∵AB MN KR CD ∥∥∥.∵1180EPN ∠+∠=︒180NPG PGR ∠+∠=︒2180RGF ∠+∠=︒.∵12540EPN NPG PGR RGF ∠+∠+∠+∠++∠=︒∵75EPG EPN NPG ∠=∠+∠=︒PGR RGF PGF ∠+∠=∠12325∠+∠=︒∵12540PGF EPG ∠+∠+∠+∠=︒∵54032575140PGF ∠=︒-︒-︒=︒故答案为:140︒.【变式训练1】已知直线a b ∥ 直线EF 分别与直线a b 相交于点E F 点A B 分别在直线a b 上 且在直线EF 的左侧 点P 是直线EF 上一动点(不与点E F 重合)设∵P AE =∵1 ∵APB =∵2 ∵PBF =∵3.(1)如图1 当点P 在线段EF 上运动时 试说明∵1+∵3=∵2;(2)当点P 在线段EF 外运动时有两种情况.①如图2写出∵1 ∵2 ∵3之间的关系并给出证明;②如图3所示 猜想∵1 ∵2 ∵3之间的关系(不要求证明).【答案】(1)证明见详解(2)①312∠=∠+∠;证明见详解;②123∠=∠+∠;证明见详解【详解】(1)解:如图4所示:过点P 作PC a ∥∵a b ∥∵PC a b ∥∥∵1APC ∠=∠ 3BPC ∠=∠∵2APC BPC ∠=∠+∠∵213∠=∠+∠;(2)解:①如图5过点P 作PC a ∥∵a b ∥∵PC a b ∥∥∵3BPC ∠=∠ 1APC ∠=∠∵2BPC APC ∠=∠+∠∵312;②如图6过点P 作PC a ∥∵a b ∥∵PC a b ∥∥∵1APC ∠=∠ 3BPC ∠=∠∵2APC BPC ∠=∠+∠∵123∠=∠+∠.【变式训练2】阅读下面内容 并解答问题.已知:如图1 AB CD 直线EF 分别交AB CD 于点E F .BEF ∠的平分线与DFE ∠的平分线交于点G .(1)求证:EG FG ⊥;(2)填空 并从下列①、②两题中任选一题说明理由.我选择 题.①在图1的基础上 分别作BEG ∠的平分线与DFG ∠的平分线交于点M 得到图2 则EMF ∠的度数为 .②如图3 AB CD 直线EF 分别交AB CD 于点E F .点O 在直线AB CD 之间 且在直线EF 右侧 BEO ∠的平分线与DFO ∠的平分线交于点P 则EOF ∠与EPF ∠满足的数量关系为 . GH ABAB CD AB GH CD ∴BEG EGH DFG FGH ∠∠∠∠∴==,180BEF DFE ∴∠+∠=︒EG 平分GEB ∴∠=GEB ∴∠+在EFG ∆中EGF ∴∠=EM 平分BEM ∴∠45EMF BEM MFD ∴∠=∠+∠=︒故答案为:45︒;②结论:2EOF EPF ∠=∠.理由:如图3中 由题意 EOF BEO DFO ∠=∠+∠ EPF BEP DFP ∠=∠+∠PE 平分BEO ∠ PF 平分DFO ∠2BEO BEP ∴∠=∠ 2DFO DFP ∠=∠2EOF EPF ∴∠=∠故答案为:2EOF EPF ∠=∠.【变式训练3】如图:(1)如图1 AB CD ∥ =45ABE ∠︒ 21CDE ∠=︒ 直接写出BED ∠的度数.(2)如图2 AB CD ∥ 点E 为直线AB CD 间的一点 BF 平分ABE ∠ DF 平分CDE ∠ 写出BED ∠与F ∠之间的关系并说明理由.(3)如图3 AB 与CD 相交于点G 点E 为BGD ∠内一点 BF 平分ABE ∠ DF 平分CDE ∠ 若60BGD ∠=︒ 95BFD ∠=︒ 直接写出BED ∠的度数. 【答案】(1)∵BED =66°;(2)∵BED =2∵F 见解析;(3)∵BED 的度数为130°.【详解】(1)解:(1)如图 作EF ∵AB∵直线AB ∵CD∵EF ∵CD∵∵ABE =∵1=45° ∵CDE =∵2=21°∵∵BED =∵1+∵2=66°;(2)解:∵BED =2∵F理由是:过点E作EG∥AB延长DE交BF于点H∵AB∥CD∵AB∥CD∥EG∵∵5=∵1+∵2∵6=∵3+∵4又∵BF平分∵ABE DF平分∵CDE∵∵2=∵1∵3=∵4则∵5=2∵2∵6=2∵3∵∵BED=2(∵2+∵3)又∵F+∵3=∵BHD∵BHD+∵2=∵BED∵∵3+∵2+∵F=∵BED综上∵BED=∵F+12∵BED即∵BED=2∵F;(3)解:延长DF交AB于点H延长GE到I∵∵BGD=60°∵∵3=∵1+∵BGD=∵1+60° ∵BFD=∵2+∵3=∵2+∵1+60°=95°∵∵2+∵1=35° 即2(∵2+∵1) =70°∵BF平分∵ABE DF平分∵CDE∵∵ABE=2∵2∵CDE=2∵1∵∵BEI=∵ABE +∵BGE=2∵2+∵BGE∵DEI=∵CDE+∵DGE=2∵1+∵DGE ∵∵BED=∵BEI+∵DEI=2(∵2+∵1)+( ∵BGE+∵DGE)=70°+60°=130°∵∵BED的度数为130°.类型二、铅笔模型例.问题情景:如图1 AB ∵CD ∵P AB =140° ∵PCD =135° 求∵APC 的度数.(1)丽丽同学看过图形后立即口答出:∵APC =85° 请补全她的推理依据.如图2 过点P 作PE ∵AB因为AB ∵CD 所以PE ∵CD .( )所以∵A +∵APE =180° ∵C +∵CPE =180°.( )因为∵P AB =140° ∵PCD =135° 所以∵APE =40° ∵CPE =45°∵APC =∵APE +∵CPE =85°.问题迁移:(2)如图3 AD ∵BC 当点P 在A 、B 两点之间运动时 ∵ADP =∵α ∵BCP =∵β 求∵CPD 与∵α、∵β之间有什么数量关系?请说明理由.(3)在(2)的条件下 如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合) 请直接写出∵CPD 与∵α、∵β之间的数量关系.【答案】(1)平行于同一条直线的两条直线平行(或平行公理推论) 两直线平行 同旁内角互补;(2)CPD αβ∠=∠+∠ 理由见解析;(3)CPD βα∠=∠-∠或CPD αβ∠=∠-∠【详解】解:(1)如图2 过点P 作PE ∵AB因为AB ∵CD 所以PE ∵CD .(平行于同一条直线的两条直线平行)所以∵A +∵APE =180° ∵C +∵CPE =180°.(两直线平行同旁内角互补)因为∵P AB=140° ∵PCD=135°所以∵APE=40° ∵CPE=45°∵APC=∵APE+∵CPE=85°.故答案为:平行于同一条直线的两条直线平行;两直线平行同旁内角互补;(2)∵CPD=∵α+∵β理由如下:如图3所示过P作PE∵AD交CD于E∵AD∵BC∵AD∵PE∵BC∵∵α=∵DPE∵β=∵CPE∵∵CPD=∵DPE+∵CPE=∵α+∵β;(3)当P在BA延长线时如图4所示:过P作PE∵AD交CD于E同(2)可知:∵α=∵DPE∵β=∵CPE∵∵CPD=∵β-∵α;当P在AB延长线时如图5所示:同(2)可知:∵α=∵DPE∵β=∵CPE∵∵CPD=∵α-∵β.综上所述∵CPD与∵α、∵β之间的数量关系为:∵CPD=∵β-∵α或∵CPD=∵α-∵β.【变式训练1】已知直线AB∥CD(1)如图(1)点G为AB、CD间的一点联结AG、CG.若∵A=140° ∵C=150° 则∵AGC 的度数是多少?(2)如图(2)点G为AB、CD间的一点联结AG、CG.∵A=x° ∵C=y° 则∵AGC的度数是多少?(3)如图(3)写出∵BAE、∵AEF、∵EFG、∵FGC、∵GCD之间有何关系?直接写出结论.【答案】(1)70°;(2)∵AGC=(x+y)°;(3)∵BAE+∵EFG+∵GCD=∵AEF+∵FGC.【详解】解:(1)如图过点G作GE∥AB∵AB∥GE∵∵A+∵AGE=180°(两直线平行同旁内角互补).∵∵A=140°∵∵AGE=40°.∵AB∥GE AB∥CD∵GE∥CD.∵∵C+∵CGE=180°(两直线平行同旁内角互补).∵∵C=150°∵∵CGE=30°.∵∵AGC=∵AGE+∵CGE=40°+30°=70°.(2)如图过点G作GF∥AB∵AB∥GF∵∵A=AGF(两直线平行内错角相等).∵AB∥GF AB∥CD∵GF∥CD.∵∵C=∵CGF.∵∵AGC=∵AGF+∵CGF=∵A+∵C.∵∵A=x° ∵C=y°∵∵AGC=(x+y)°.(3)如图所示过点E作EM∥AB过点F作FN∥AB过点G作GQ∥CD∵AB∥CD∵AB∥EM∥FN∥GQ∥CD.∵∵BAE=∵AEM∵MEF=∵EFN∵NFG=∵FGQ∵QGC=∵GCD(两直线平行内错角相等).∵∵AEF=∵BAE+∵EFN∵FGC=∵NFG+GCD.∵∵EFN+∵NFG=∵EFG∵∵BAE+∵EFG+∵GCD=∵AEF+∵FGC.【变式训练2】问题情境:如图1 AB∵CD∵P AB=130° ∵PCD=120° 求∵APC度数.思路点拨:小明的思路是:如图2 过P作PE∵AB通过平行线性质可分别求出∵APE、∵CPE的度数从而可求出∵APC的度数;小丽的思路是:如图3 连接AC通过平行线性质以及三角形内角和的知识可求出∵APC的度数;小芳的思路是:如图4 延长AP交DC的延长线于E通过平行线性质以及三角形外角的相关知识可求出∵APC的度数.问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算你求得的∵APC的度数为°;问题迁移:(1)如图5 AD∵BC点P在射线OM上运动当点P在A、B两点之间运动时∵ADP=∵α ∵BCP=∵β.∵CPD、∵α、∵β之间有何数量关系?请说明理由;(2)在(1)的条件下如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合)请你直接写出∵CPD、∵α、∵β间的数量关系.【答案】问题解决:110°;问题迁移:(1)∵CPD=∵α+∵β 理由见解析;(2)∵CPD=∵β﹣∵α 理由见解析【详解】解:小明的思路:如图2 过P作PE∵AB∵AB∵CD∵PE∵AB∵CD∵∵APE=180°﹣∵A=50° ∵CPE=180°﹣∵C=60°∵∵APC=50°+60°=110°故答案为:110;(1)∵CPD=∵α+∵β 理由如下:如图5 过P作PE∵AD交CD于E∵AD∵BC∵AD∵PE∵BC∵∵α=∵DPE∵β=∵CPE∵∵CPD=∵DPE+∵CPE=∵α+∵β;(2)当P在BA延长线时∵CPD=∵β﹣∵α;理由:如图6 过P作PE∵AD交CD于E∵AD∵BC∵AD∵PE∵BC∵∵α=∵DPE∵β=∵CPE∵∵CPD=∵CPE﹣∵DPE=∵β﹣∵α;当P在BO 之间时 ∵CPD =∵α﹣∵β.理由:如图7 过P 作PE ∵AD 交CD 于E∵AD ∵BC∵AD ∵PE ∵BC∵∵α=∵DPE ∵β=∵CPE∵∵CPD =∵DPE ﹣∵CPE =∵α﹣∵β.类型三、锄头模型例.已知 AB ∵CD .点M 在AB 上 点N 在CD 上.(1)如图1中 ∵BME 、∵E 、∵END 的数量关系为: ;(不需要证明) 如图2中 ∵BMF 、∵F 、∵FND 的数量关系为: ;(不需要证明)(2)如图3中 NE 平分∵FND MB 平分∵FME 且2∵E +∵F =180° 求∵FME 的度数;(3)如图4中 ∵BME =60° EF 平分∵MEN NP 平分∵END 且EQ ∵NP 则∵FEQ 的大小A BC D P123是否发生变化若变化请说明理由若不变化求出∵FEQ的度数.【答案】(1)∵BME=∵MEN﹣∵END;∵BMF=∵MFN+∵FND;(2)120°;(3)不变30°【详解】解:(1)过E作EH∵AB如图1∵∵BME=∵MEH∵AB∵CD∵HE∵CD∵∵END=∵HEN∵∵MEN=∵MEH+∵HEN=∵BME+∵END即∵BME=∵MEN﹣∵END.如图2 过F作FH∵AB∵∵BMF=∵MFK∵AB∵CD∵FH∵CD∵∵FND=∵KFN∵∵MFN=∵MFK﹣∵KFN=∵BMF﹣∵FND即:∵BMF=∵MFN+∵FND.故答案为∵BME=∵MEN﹣∵END;∵BMF=∵MFN+∵FND.(2)由(1)得∵BME=∵MEN﹣∵END;∵BMF=∵MFN+∵FND.(2)观察图(2)已知AB∵CD猜想图中的∵BPD与∵B、∵D的关系并说明理由.(3)观察图(3)和(4)已知AB∵CD猜想图中的∵BPD与∵B、∵D的关系不需要说明理由.【答案】(1)∵B+∵BPD+∵D=360° 理由见解析;(2)∵BPD=∵B+∵D理由见解析;(3)∵BPD=∵D-∵B或∵BPD=∵B-∵D理由见解析【详解】解:(1)如图(1)过点P作EF∵AB∵∵B+∵BPE=180°∵AB∵CD EF∵AB∵EF∵CD∵∵EPD+∵D=180°∵∵B+∵BPE+∵EPD+∵D=360°∵∵B+∵BPD+∵D=360°.(2)∵BPD=∵B+∵D.理由:如图2 过点P作PE∵AB∵AB∵CD∵PE∵AB∵CD∵∵1=∵B∵2=∵D∵∵BPD=∵1+∵2=∵B+∵D.(3)如图(3)∵BPD=∵D-∵B.理由:∵AB∵CD∵∵1=∵D∵∵1=∵B+∵BPD∵∵D=∵B+∵BPD即∵BPD=∵D-∵B;如图(4)∵BPD=∵B-∵D.理由:∵AB ∵CD∵∵1=∵B∵∵1=∵D +∵BPD∵∵B =∵D +∵BPD即∵BPD =∵B -∵D .【变式训练2】已知//AM CN 点B 为平面内一点 AB BC ⊥于B .(1)如图1 点B 在两条平行线外 则A ∠与C ∠之间的数量关系为______; (2)点B 在两条平行线之间 过点B 作BD AM ⊥于点D . ①如图2 说明ABD C ∠=∠成立的理由;②如图3 BF 平分DBC ∠交DM 于点,F BE 平分ABD ∠交DM 于点E .若180,3FCB NCF BFC DBE ∠∠∠∠+=︒= 求EBC ∠的度数.【答案】(1)∵A +∵C =90°;(2)①见解析;②105°【详解】解:(1)如图1 AM 与BC 的交点记作点O∵AM ∵CN∵∵C =∵AOB∵AB ∵BC∵∵A +∵AOB =90°∵∵A +∵C =90°;(2)①如图2 过点B作BG∵DM∵BD∵AM∵DB∵BG∵∵DBG=90°∵∵ABD+∵ABG=90°∵AB∵BC∵∵CBG+∵ABG=90°∵∵ABD=∵CBG∵AM∵CN BG∵DMBG CN//,∵∵C=∵CBG∵ABD=∵C;②如图3 过点B作BG∵DM∵BF平分∵DBC BE平分∵ABD∵∵DBF=∵CBF∵DBE=∵ABE由(2)知∵ABD=∵CBG∵∵ABF=∵GBF设∵DBE=α∵ABF=β则∵ABE=α∵ABD=2α=∵CBG∵GBF=∵AFB=β∵BFC=3∵DBE=3α∵∵AFC=3α+β∵∵AFC+∵NCF=180° ∵FCB+∵NCF=180° ∵∵FCB=∵AFC=3α+β∵BCF中由∵CBF+∵BFC+∵BCF=180°得:2α+β+3α+3α+β=180°∵AB∵BC∵β+β+2α=90°∵α=15° ∵∵ABE=15°∵∵EBC=∵ABE+∵ABC=15°+90°=105°.类型四、齿距模型例.如图AB∵EF设∵C=90° 那么x y z的关系式为______.【答案】y=90°-x+z.【详解】解:作CG//AB DH//EF∵AB//EF∵AB//CG//HD//EF∵∵x=∵1 ∵CDH=∵2 ∵HDE=∵z∵∵BCD=90°∵∵1+∵2=90°∵y=∵CDH+∵HDE=∵z+∵2∵∵2=90°-∵1=90°-∵x∵∵y=∵z+90°-∵x.即y=90°-x+z.【变式训练1】如图1 已知AB ∵CD ∵B =30° ∵D =120°;(1)若∵E =60° 则∵F = ;(2)请探索∵E 与∵F 之间满足的数量关系?说明理由;(3)如图2 已知EP 平分∵BEF FG 平分∵EFD 反向延长FG 交EP 于点P 求∵P 的度数.【答案】(1)90︒;(2)30F E ∠=∠+︒ 理由见解析;(3)15︒【详解】(1)解:如图1 分别过点E F 作//EM AB //FN AB////EM AB FN ∴30B BEM ∴∠=∠=︒ MEF EFN ∠=∠又//AB CD //AB FN//CD FN ∴180D DFN ∴∠+∠=︒又120D ∠=︒60DFN ∴∠=︒30BEF MEF ∴∠=∠+︒ 60EFD EFN ∠=∠+︒60EFD MEF ∴∠=∠+︒3090EFD BEF ∴∠=∠+︒=︒;故答案为:90︒;(2)解:如图1 分别过点E F 作//EM AB //FN AB////EM AB FN ∴30B BEM ∴∠=∠=︒ MEF EFN ∠=∠又//AB CD //AB FN//CD FN ∴又120D ∠=60DFN ∴∠=BEF MEF ∴∠=∠EFD MEF ∴∠=∠(3)解:如图设2BEF ∠=EP 平分PEF ∴∠=//FH EP HFG ∠=【变式训练2】如图1 点A 、B 分别在直线GH 、MN 上 GAC NBD ∠=∠ C D ∠=∠.(1)求证://GH MN ;(提示:可延长AC 交MN 于点P 进行证明) (2)如图2 AE 平分GAC ∠ DE 平分BDC ∠ 若AED GAC ∠=∠ 求GAC ∠与ACD ∠之间的数量关系;(3)在(2)的条件下 如图3 BF 平分DBM ∠ 点K 在射线BF 上 13KAG GAC ∠=∠ 若AKB ACD ∠=∠ 直接写出GAC ∠的度数.∵ACD C ∠=∠∵//AP BD∵NBD NPA ∠=∠∵GAC NBD ∠=∠∵GAC NPA ∠=∠∵//GH MN ;(2)延长AC 交MN 于点P 交DE 于点Q∵180E EAQ AQE ∠+∠+∠=° 180AQE AQD ∠+∠=° ∵AQD E EAQ ∠=∠+∠∵//AP BD∵AQD BDQ ∠=∠∵BDQ E EAQ ∠=∠+∠∵AE 平分GAC ∠ DE 平分BDC ∠∵2GAC EAQ ∠=∠ 2CDB BDQ ∠=∠∵2CDB E GAC ∠=∠+∠∵AED GAC ∠=∠ ACD CDB ∠=∠∵23ACD GAC GAC GAC ∠=∠+∠=∠;(3)当K 在直线GH 下方时 如图 设射线BF 交GH 于I⎫.⎪⎭上方时如图-∠(180GAC⎫.⎪⎭°︒。
七年级下学期数学几何难题(最新整理)
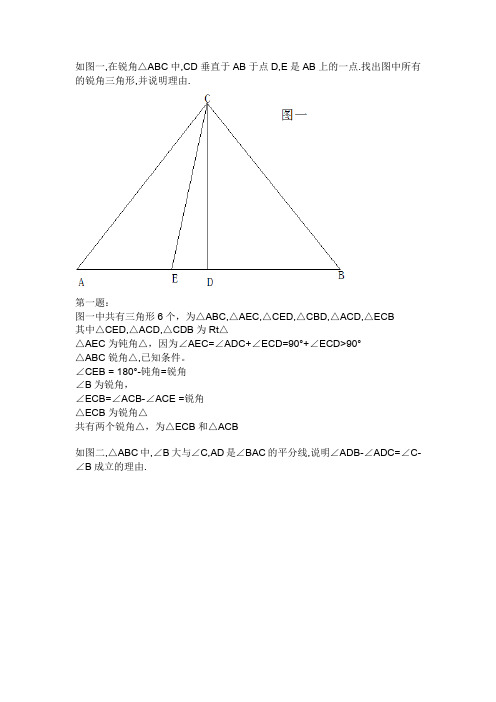
如图一,在锐角△ABC中,CD垂直于AB于点D,E是AB上的一点.找出图中所有的锐角三角形,并说明理由.第一题:图一中共有三角形6个,为△ABC,△AEC,△CED,△CBD,△ACD,△ECB其中△CED,△ACD,△CDB为Rt△△AEC为钝角△,因为∠AEC=∠ADC+∠ECD=90°+∠ECD>90°△ABC锐角△,已知条件。
∠CEB = 180°-钝角=锐角∠B为锐角,∠ECB=∠ACB-∠ACE =锐角△ECB为锐角△共有两个锐角△,为△ECB和△ACB如图二,△ABC中,∠B大与∠C,AD是∠BAC的平分线,说明∠ADB-∠ADC=∠C-∠B成立的理由.第二题:∵AD是∠BAC的平分线∴∠BAD=∠DAC∵三角形内角和为180°∴∠BAD+∠B+∠ADB=∠DAC+∠ADC+∠C∴∠B+∠ADB=∠ADC+∠C∴∠ADB-∠ADC=∠C-∠B如图三,已知BO平分∠CBA,CO平分∠ACB,MN‖BC,AB=12,AC=18,求△AMN 的周长.第三题∵MN‖BC∴∠MOB=∠OBC∴∠NOC=∠OCB∵BO平分∠CBA∴∠MBO=∠OBC∵CO平分∠ACB∴∠NCO=∠OCB∴∠MOB=∠MBO∴∠NCO=∠OCB∵∠MOB=∠MBO∴BM=OM∵∠NCO=∠OCB∴ON=NC∴AM+MN+NA = (AM+BM)+(AN+CN)=AB+AC=12+18=30∵△AMN的周长= 30图五,已知AB=AC,AD=AE,∠1=∠2,问CE=BD吗?说明理由.如图四,已知△ABC中,AD是BC边上的高线,AE是∠BAC的平分线,若设∠EAD=a,求∠C-∠B.(用a的代数式表示)第四题∠C=90°-∠DAC = 90°-[(1/2)∠BAC-a]∠B=∠AEC-∠BAE = 90°- a-∠BAE = 90°- a-(1/2)∠BAC∠C-∠B=90°-[(1/2)∠BAC-a]-{90°- a-(1/2)∠BAC}=2a如图六,由正方形ABCD边BC、CD向外作等边三角形BCE和CDF,连结AE、AF、EF,求证:△AEF为等边三角形。
北师大版七年级数学下册几何常见模型练习题(有答案)

全等三角形判定的三种类型已知一边一角型一次全等型1.已知,如图△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.2.如图,在△ABC中,D是BC边上的一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.求证:AD是△ABC的中线.两次全等型3.如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC =∠BEC.4.如图,在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,AE⊥BD于F交BC于E.(1)求证:∠ABD=∠CAE.(2)求证:∠ADB=∠CDE.(3)直接写出BD、AE、ED之间满足的数量关系.已知两边型一次全等型5.如图,点B,F,C,E在直线l上(点F,点C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.(1)求证:△ABC≌△DEF;(2)指出图中所有平行的线段,并说明理由.两次全等型6.如图所示,AB=CB,AD=CD,E是BD上任意一点,求证:AE=CE.7.如图:已知AE交BD于点C,∠DAC=∠EBC=∠BAC,AB=AC.试说明:DC与BE有怎样的数量关系.已知两角型一次全等型8.如图,已知∠BDC=∠CEB=90°,BE、CD交于点O,且AO平分∠BAC,求证:OB=OC.三角形中的四种常见说理类型说明相等关系1.如图,△ABC中,AB=AC,D是BC的中点,E、F分别是AB、AC上的点,且AE=AF,求证:DE=DF.说明位置关系说明平行关系2.已知△ABC为等边三角形,点P在AB上,以CP为边长作等边三角形△PCE.求证:AE∥BC.说明垂直关系3.如图,△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,且BD=CF,BE=CD,G是EF的中点,求证:DG⊥EF.说明倍分关系说明角的倍分关系4.如图,△ABC中,AB=AC,BD⊥AC于D.猜想:∠DBC与∠BAC之间的数量关系,并予以证明.说明线段的倍分关系5.如图,△ABC中,AB=AC,AD和BE是高,它们相交于H,且AE=BE.(1)求∠C的度数.(2)求证:AH=2BD.说明和、差关系6.如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC.线段垂直平分线与角平分线的应用类型典例例1.已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.(1)求证:AE=BF;(2)求线段DG的长.利用线段垂直平分线的性质求线段的长1.如图,已知AB比AC长3cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,求AB和AC的长.利用线段垂直平分线的性质求角的度数2.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连接AD.(1)若△ADC的周长为16,AB=12,求△ABC的周长;(2)若AD将∠CAB分成两个角,且∠CAD:∠DAB=2:5,求∠ADC的度数.利用线段垂直平分线的性质解决实际问题3.某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?利用线段垂直平分线的性质说明线段的数量关系4.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P放在射线OM上,两直角边分别与OA,OB交于点C,D.(1)证明:PC=PD.(2)若OP=4,求OC+OD的长度.利用线段垂直平分线的性质说明线段的位置关系5.如图所示,AD为△ABC的角平分线,DE⊥AC于点E,DF⊥AB于点F,EF交AD于点M,求证:AM ⊥EF.全等三角形判定的三种类型1.证明:如右图所示,∵BD=DC,∴∠3=∠4,又∵∠1=∠2,∴∠1+∠3=∠2+∠4,即∠ABC=∠ACB,∴△ABC是等腰三角形,∴AB=AC,在△ABD和△ACD中,∴△ABD≌△ACD(SAS),∴∠BAD=∠CAD,∴AD平分∠BAC.2.证明:∵BE⊥AD,CF⊥AD,∴∠BED=∠F=90°,在△BED和△CFD中,,∴△BED≌△CFD,∴BD=CD,∴AD是△ABC的中线.3.证明:在△ACD和△ACB中,,∴△ACD≌△ACB,(ASA)∴BC=CD,在△DCE和△BCE中,,∴△DCE≌△BCE(ASA),∴∠DEC=∠BEC.4.(1)证明:∵AE⊥BD,∴∠AFB=∠BAC=90°,∴∠ABD+∠BAF=90°,∠BAF+∠CAE=90°,∴∠ABD=∠CAE.(2)证明:过C作CM⊥AC,交AE的延长线于M,则∠ACM=90°=∠BAC,∴CM∥AB,∴∠MCE=∠ABC=∠ACB,∵∠BAF=∠ADB,∠ADB+∠F AD=90°,∠ABD+∠BAF=90°,∴∠ABD=∠CAM,在△ABD和△CAM中,,∴△ABD≌△CAM(ASA),∴∠ADB=∠M,AD=CM,BD=AM,∵D为AC中点,∴AD=DC=CM,在△CDE和△CME中,,∴△CDE≌△CME(SAS),∴∠M=∠CDE,∴∠ADB=∠CDE.(3)解:结论:BD=AE+DE.理由:∵△CDE≌△CME,∴ME=DE,∵AM=AE+ME=AE+DE,∵BD=AM,∴BD=AE+DE.5.(1)证明:∵BF=CE,∴BF+FC=FC+CE,即BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(SSS);(2)解:结论:AB∥DE,AC∥DF.理由:∵△ABC≌△DEF,∴∠ABC=∠DEF,∠ACB=∠DFE,∴AB∥DE,AC∥DF.6.证明:在△ABD与△CBD中,∴△ABD≌△CBD(SSS),∴∠ABD=∠CBD,在△ABE与△CBE中,△ABE≌△CBE(SAS),∴AE=CE.7.解:DC=BE,∵∠EBC=∠BAC,∠ACD=∠BAC+∠ABC,∠ABE=∠EBC+∠ABC,∴∠ACD=∠ABE,在△ACD和△ABE中,,∴△ACD≌△ABE(ASA),∴DC=BE.8.证明:∵∠BDC=∠CEB=90°,∴CD⊥AB,BE⊥AC,∵AO平分∠BAC,∴OD=OE,在△BDO和△CEO中∴△BDO≌△CEO(ASA),∴OB=OC.三角形中的四种常见说理类型1.证明:连接AD,∵AB=AC,D是BC的中点,∴∠EAD=∠F AD,在△AED和△AFD中,,∴△AED≌△AFD(SAS),∴DE=DF.2、证明:∵△ABC与△PCE为等边三角形,∴AC=BC,EC=PC,∠BCA=∠PCE=60°,∴∠BCP=∠ACE,在△BCP和△ACE中,,∴△CBP≌△CAE(SAS),∴∠CAE=∠B=60゜=∠ACB,∴AE∥BC.3.证明:连ED,DF,∵AB=AC,∴∠B=∠C,在△BED和△CDF中,,∴△BDE≌△CFD(SAS),∴DE=DF,∵G是EF的中点,∴DG⊥EF.4.解:∠DBC=∠BAC.设∠C=β,∵AB=AC,∴∠ABC=∠C=β,∴∠BAC=180°﹣2β,∠BAD=∠ABC+∠C=2β,∵BD⊥AC,∴∠ABD=90°﹣2β,∴∠DBC=90°﹣β,∴∠DBC=∠BAC.5.(1)解:∵AE=BE,BE⊥AC,∴∠BAE=45°,又∵AB=AC,∴∠C=(180°﹣∠BAE)=(180°﹣45°)=67.5°;(2)证明:∵AB=AC,AD⊥BC,∴BC=2BD,∠1+∠C=90°,∵BE⊥AC,∴∠2+∠C=90°,∴∠1=∠2,在△AEH和△BEC中,,∴△AEH≌△BEC(ASA),∴AH=BC,∴AH=2BD.6.证明:如图,在AC上截取AE=AB,∵AD平分∠BAC,∴∠CAD=∠BAD,在△ABD和△AED中,,∴△ABD≌△AED(SAS),∴DE=BD,∠AED=∠ABC,∵∠AED=∠C+∠CDE,∠ABC=2∠C,∴∠CDE=∠C,∴CE=DE,∵AE+CE=AC,∴AB+BD=AC.线段垂直平分线与角平分线的应用类型例1.(1)证明:连接AD、BD,∵AD是∠BCA的平分线,DE⊥AC,DF⊥BC,∴DE=DF,∵DG是AB边的垂直平分线,∴AD=DB,在Rt△AED和Rt△DFB中,,∴Rt△AED≌Rt△BFD(HL),∴AE=BF;(2)由(1)得:CE=CF==7,∴AE=EC﹣AC=1,∵∠ECD=∠EDC=45°,∴DE=CE=7,由题意可得:AG=BG=5,∴AD2=AE2+DE2=50,∴DG2=AD2﹣AG2=25,∴DG=5.1.解:∵DE是BC的垂直平分线,∴CD=BD,∴△ACD的周长=AC+AD+CD=AC+BD+AD=AC+AB,由题意得,,解得.∴AB和AC的长分别为8.5cm,5.5cm.2.解:(1)∵DE是AB的垂直平分线,∴AD=BD,又∵△ADC的周长为16,∴AD+CD+AC=16,即BD+CD+AC=BC+AC=16,又AB=12,∴AB+BC+AC=16+12=28,则△ABC的周长为28;(2)∵AD=BD,∴∠BAD=∠ABD,∵∠CAD:∠DAB=2:5,设一份为x,即∠CAD=2x,∠DAB=∠ABD=5x,又∠C=90°,∴∠ABD+∠BAC=90°,即2x+5x+5x=90°,解得:x=7.5°,∵∠ADC为△ABD的外角,∴∠ADC=∠DAB+∠ABD=5x+5x=10x=75°.3.解:如图,这所中学建在P点位置(点P为△ABC的外心).连结AB、BC、AC,作AB和BC的垂直平分线,两垂直平分线相交于点P,则点P到点A、B、C的距离相等.4.证明:(1)如图,过点P作PE⊥OA于点E,PF⊥OB于点F,∴∠PEC=∠PFD=90°.∵OM是∠AOB的平分线,∴PE=PF,∵∠AOB=90°,∠CPD=90°,∴∠PCE+∠PDO=360°﹣90°﹣90°=180°.而∠PDO+∠PDF=180°,∴∠PCE=∠PDF在△PCE和△PDF中∴△PCE≌△PDF(AAS)∴PC=PD;(2)∵∠AOB=90°,OM平分∠AOB,∴△POE与△POF为等腰直角三角形,∴OE=PE=PF=OF,∵OP=4,∴OE=2,由(1)知△PCE≌△PDF ∴CE=DF ∴OC+OD=OE+OF=2OE=4.5.证明:∵DE⊥AC于点E,DF⊥AB于点F,∴∠AED=∠AFD=90°,∵AD为三角形ABC的角平分线,∴∠EAD=∠F AD,而AD=AD,∴△AED≌△AFD∴ED=DF,AE=AF∴△AEF为等腰三角形,AM为∠BAC的平分线∴AM是△AEF的高,即AM⊥EF.。
七年级下学期几何专题(附参考答案)

七年级下学期几何专题一、精心选一选,慧眼识金!1.过五边形的一个顶点可作()条对角线A.1B.2C.3D.42.三角形的三个内角( )A、至少有两个锐角B、至少有一个直角C、至多有两个钝角D、至少有一个钝角3.下列图形中具有稳定性的是( )A、菱形B、钝角三角形C、长方形D、正方形4.下列图形中,是属于轴对称图形的是()A. B. C. D.●5.如图:BE、CF是ABC∆的角平分线,0∠,A=40则=∠BDC( D )11065 C. 095 D. 0A.050 B. 06.以下列长度的三条线段为边,不能组成三角形的是()A.4,4,5 B.3,2,5 C.3,12,13 D.6,8,107. 下列说法:①等边三角形是等腰三角形;②在三角形中至少有二个锐角;③三角形的一个外角等于两个内角的和;④钝角三角形的三条高相交于三角形外一点,其中正确的个数有()A、1个B、2个C、3个D、4个8. 下列图形:①角;②线段;③等腰三角形;④等边三角形;⑤平行四边形中是轴对称图形的个数是()A、1个B、2个C、 3个D、4个9.平面内三条直线最少有()个交点A.3B.2C.1D.0●10.已知Rt△ABC,∠A=30°,则∠B=( C )A.60°B.90°C.60°或90°D.30°11.如图,由AB∥CD,能推出正确结论的是( B ) A 、∠1=∠2 B 、∠3=∠4 C 、∠A=∠C D 、AD∥BC12.下列命题为真命题的是( D ) A.内错角相等B.点到直线的距离即为点到直线的垂线段C.如果∠A+∠B+∠C=180°,那么∠A 、∠B 、∠C 互补D.同一平面内,垂直于同一直线的两直线平行。
13.用同一种下列形状的图形地砖不能进行平面镶嵌的是( C ) A.正三角形 B.长方形 C.正八边形 D.正六边形14.当多边形的边数增加时,其外角和( C ) A 、增加 B 、减少 C 、不变 D 、不能确定● 15.已知:一光线沿平行于AB经镜面AC 、AB 反射后,如图所示, 若∠A=40°则∠MNA=( B ) A.90° B.100° C.60° D.80°● 16.已知:如图B 处在A 处的南偏西40C 处在A 处的南偏东15°方向上,C 处在B 处的北偏东80°方向,则∠ACB=( B )A.90°B.85°C.40°D.60° 17.若一个三角形中的其中一个外角等于与它相邻的内角,则此三角形是( A ) A 、直角三角形 B 、锐角三角形 C 、钝角三角形 D 、无法确定18.点到直线的距离是指这点到这条直线的( D )A 、垂线段B 、垂线C 、垂线的长度D 、垂线段的长度二、巧心填一填,一锤定音!19.已知∠a 的对顶角是58°,则∠a=______。
[必刷题]2024七年级数学下册几何证明专项专题训练(含答案)
![[必刷题]2024七年级数学下册几何证明专项专题训练(含答案)](https://img.taocdn.com/s3/m/e2aed845c4da50e2524de518964bcf84b8d52d05.png)
[必刷题]2024七年级数学下册几何证明专项专题训练(含答案)试题部分一、选择题:1. 在下列几何图形中,哪一个图形可以通过旋转90度后与自身重合?()A. 矩形B. 等边三角形C. 正方形D. 梯形2. 下列哪个条件可以证明两个三角形全等?()A. 两边和其中一边的对角相等B. 两角和其中一角的对边相等C. 两边和它们的夹角相等D. 两角和其中一边相等3. 在直角坐标系中,点A(2,3)关于原点对称的点是()A. (2,3)B. (2,3)C. (2,3)D. (3,2)4. 下列哪个条件可以证明两个角相等?()A. 两角的度数相等B. 两角的对边相等C. 两角的邻边相等D. 两角的余角相等5. 若一个等腰三角形的底边长为10cm,腰长为13cm,则该三角形的周长为()A. 32cmB. 42cmC. 46cmD. 52cm6. 在平行四边形ABCD中,若AB=6cm,BC=8cm,则对角线AC的取值范围是()A. 2cm < AC < 14cmB. 2cm < AC < 6cmC. 2cm < AC < 8cmD. 6cm < AC < 14cm7. 下列哪个条件可以证明两个平行四边形全等?()A. 一组对边平行且相等B. 两组对边平行C. 一组对边平行,另一组对边相等D. 一组对边平行且相等,另一组对边也相等8. 在三角形ABC中,若AB=AC,∠B=60°,则三角形ABC的周角为()A. 120°B. 180°C. 240°D. 360°9. 下列哪个图形是轴对称图形?()A. 等腰梯形B. 直角梯形C. 等腰三角形D. 一般四边形10. 若一个正方形的对角线长为10cm,则该正方形的面积是()A. 50cm²B. 100cm²C. 200cm²D. 500cm²二、判断题:1. 若两个三角形的两边和夹角分别相等,则这两个三角形全等。
(完整版)七年级下册数学期末几何压轴题试卷含答案(一)

一、解答题1.在平面直角坐标系xOy 中描出下列两组点,分别将每组里的点用线段依次连接起来.第一组:(3,3)-A 、(4,3)C ;第二组:(2,1)D --、(2,1)E .(1)线段AC 与线段DE 的位置关系是;(2)在(1)的条件下,线段AC 、DE 分别与y 轴交于点B ,F .若点M 为射线OB 上一动点(不与点O ,B 重合).①当点M 在线段OB 上运动时,连接AM 、DM ,补全图形,用等式表示CAM ∠、AMD ∠、MDE ∠之间的数量关系,并证明.②当ACM △与DEM △面积相等时,求点M 的坐标.2.已知,如图:射线PE 分别与直线AB 、CD 相交于E 、F 两点,PFD ∠的角平分线与直线AB 相交于点M ,射线PM 交CD 于点N ,设PFM α∠=︒,EMF β∠=︒且()2350αβα-+-=.(1)α=________,β=________;直线AB 与CD 的位置关系是______;(2)如图,若点G 是射线MA 上任意一点,且MGH PNF ∠=∠,试找出FMN ∠与GHF ∠之间存在一个什么确定的数量关系?并证明你的结论.(3)若将图中的射线PM 绕着端点P 逆时针方向旋转(如图)分别与AB 、CD 相交于点1M 和点1N 时,作1PM B ∠的角平分线1M Q 与射线FM 相交于点Q ,问在旋转的过程中1FPN Q∠∠的值变不变?若不变,请求出其值;若变化,请说明理由.3.阅读下面材料:小亮同学遇到这样一个问题:已知:如图甲,AB //CD ,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED . 求证:∠BED =∠B +∠D .(1)小亮写出了该问题的证明,请你帮他把证明过程补充完整.证明:过点E 作EF //AB ,则有∠BEF = .∵AB //CD ,∴ // ,∴∠FED = .∴∠BED =∠BEF +∠FED =∠B +∠D .(2)请你参考小亮思考问题的方法,解决问题:如图乙,已知:直线a //b ,点A ,B 在直线a 上,点C ,D 在直线b 上,连接AD ,BC ,BE 平分∠ABC ,DE 平分∠ADC ,且BE ,DE 所在的直线交于点E .①如图1,当点B 在点A 的左侧时,若∠ABC =60°,∠ADC =70°,求∠BED 的度数; ②如图2,当点B 在点A 的右侧时,设∠ABC =α,∠ADC =β,请你求出∠BED 的度数(用含有α,β的式子表示).4.如图,直线//PQ MN ,点C 是PQ 、MN 之间(不在直线PQ ,MN 上)的一个动点.(1)如图1,若1∠与2∠都是锐角,请写出C ∠与1∠,2∠之间的数量关系并说明理由; (2)把直角三角形ABC 如图2摆放,直角顶点C 在两条平行线之间,CB 与PQ 交于点D ,CA 与MN 交于点E ,BA 与PQ 交于点F ,点G 在线段CE 上,连接DG ,有BDF GDF ∠=∠,求AEN CDG ∠∠的值; (3)如图3,若点D 是MN 下方一点,BC 平分PBD ∠, AM 平分CAD ∠,已知25PBC ∠=︒,求ACB ADB ∠+∠的度数.5.(1)(问题)如图1,若//AB CD ,40AEP ∠=︒,130PFD ∠=︒.求EPF ∠的度数; (2)(问题迁移)如图2,//AB CD ,点P 在AB 的上方,问PEA ∠,PFC ∠,EPF ∠之间有何数量关系?请说明理由;(3)(联想拓展)如图3所示,在(2)的条件下,已知EPF α∠=,PEA ∠的平分线和PFC ∠的平分线交于点G ,用含有α的式子表示G ∠的度数.6.如图1,已AB ∥CD ,∠C =∠A .(1)求证:AD ∥BC ;(2)如图2,若点E 是在平行线AB ,CD 内,AD 右侧的任意一点,探究∠BAE ,∠CDE ,∠E 之间的数量关系,并证明.(3)如图3,若∠C =90°,且点E 在线段BC 上,DF 平分∠EDC ,射线DF 在∠EDC 的内部,且交BC 于点M ,交AE 延长线于点F ,∠AED +∠AEC =180°,①直接写出∠AED 与∠FDC 的数量关系: .②点P 在射线DA 上,且满足∠DEP =2∠F ,∠DEA ﹣∠PEA =514∠DEB ,补全图形后,求∠EPD 的度数7.阅读材料,解答问题:如果一个四位自然数,十位数字是千位数字的2倍与百位数字的差,个位数字是千位数字的2倍与百位数字的和,则我们称这个四位数“依赖数”,例如,自然数2135,其中3=2×2﹣1,5=2×2+1,所以2135是“依赖数”.(1)请直接写出最小的四位依赖数;(2)若四位依赖数的后三位表示的数减去百位数字的3倍得到的结果除以7余3,这样的数叫做“特色数”,求所有特色数.(3)已知一个大于1的正整数m 可以分解成m =pq+n 4的形式(p≤q ,n≤b ,p ,q ,n 均为正整数),在m 的所有表示结果中,当nq ﹣np 取得最小时,称“m =pq+n 4”是m 的“最小分解”,此时规定:F (m )=q n p n++,例:20=1×4+24=2×2+24=1×19+14,因为1×19﹣1×1>2×4﹣2×1>2×2﹣2×2,所以F (20)=2222++=1,求所有“特色数”的F (m )的最大值. 8.阅读下列解题过程: 为了求23501222...2+++++的值,可设23501222...2S =+++++,则2345122222...2S =+++++,所以得51221S S -=-,所以5123505121:1222...221S =-+++++=-,即;仿照以上方法计算:(1)2320191222...2+++++= .(2)计算:2320191333...3+++++(3)计算:101102103200555...5++++9.阅读下列材料:小明为了计算22019202012222+++++的值,采用以下方法: 设22019202012222s =+++++ ① 则22020202122222s =++++ ②②-①得,2021221s s s -==-请仿照小明的方法解决以下问题:(1)291222++++=________;(2)220333+++=_________; (3)求231n a a a a ++++的和(1a >,n 是正整数,请写出计算过程).10.观察下列两个等式:5532321,44133+=⨯-+=⨯-,给出定义如下:我们称使等式1a b ab +=-成立的一对有理数,a b 为“白马有理数对”,记为(,)a b ,如:数对5(3,2),4,3⎛⎫ ⎪⎝⎭都是“白马有理数对”.(1)数对3(2,1),5,2⎛⎫- ⎪⎝⎭中是“白马有理数对”的是_________; (2)若(,3)a 是“白马有理数对”,求a 的值;(3)若(,)m n 是“白马有理数对”,则(,)n m --是“白马有理数对”吗?请说明理由.(4)请再写出一对符合条件的“白马有理数对”_________(注意:不能与题目中已有的“白马有理数对”重复)11.已知,在计算:()()12++++N N N 的过程中,如果存在正整数N ,使得各个数位均不产生进位,那么称这样的正整数N 为“本位数”.例如:2和30都是“本位数”,因为2349++=没有进位,30313293++=没有进位;15和91都不是“本位数”,因为15161748++=,个位产生进位,919293276++=,十位产生进位.则根据上面给出的材料:(1)下列数中,如果是“本位数”请在后面的括号内打“√”,如果不是“本位数”请在后面的括号内画“×”.106( );111( );400( );2015( ). (2)在所有的四位数中,最大的“本位数”是 ,最小的“本位数”是 .(3)在所有三位数中,“本位数”一共有多少个?12.观察下列两个等式:5532321,44133+=⨯-+=⨯-,给出定义如下:我们称使等式1a b ab +=-成立的一对有理数,a b 为“白马有理数对”,记为(,)a b ,如:数对5(3,2),4,3⎛⎫ ⎪⎝⎭都是“白马有理数对”.(1)数对3(2,1),5,2⎛⎫- ⎪⎝⎭中是“白马有理数对”的是_________; (2)若(,3)a 是“白马有理数对”,求a 的值;(3)若(,)m n 是“白马有理数对”,则(,)n m --是“白马有理数对”吗?请说明理由.(4)请再写出一对符合条件的“白马有理数对”_________(注意:不能与题目中已有的“白马有理数对”重复)13.如图①,在平面直角坐标系中,点(0,)A a ,(,0)C b ,其中,a 是16的算术平方根,38b =,线段GO 由线段AC 平移所得,并且点G 与点A 对应,点O 与点C 对应.(1)点A 的坐标为 ;点C 的坐标为 ;点G 的坐标为 ;(2)如图②,F 是线段AC 上不同于AC 的任意一点,求证:OFC OAF AOF ∠∠∠=+;(3)如图③,若点F 满足FOC FCO ∠=∠,点E 是线段OA 上一动点(与点O 、A 不重合),连CE 交OF 于点H ,在点E 运动的过程中,2OHC ACE OEC ∠∠∠+=是否总成立?请说明理由.14.如图,已知AM //BN ,点P 是射线AM 上一动点(与点A 不重合),BC BD 、分别平分ABP ∠和PBN ∠,分别交射线AM 于点,C D .(1)当60A ∠=︒时,ABN ∠的度数是_______;(2)当A x ∠=︒,求CBD ∠的度数(用x 的代数式表示);(3)当点P 运动时,ADB ∠与APB ∠的度数之比是否随点P 的运动而发生变化?若不变化,请求出这个比值;若变化,请写出变化规律.(4)当点P 运动到使ACB ABD =∠∠时,请直接写出14DBN A +∠∠的度数.15.如图所示,A (1,0)、点B 在y 轴上,将三角形OAB 沿x 轴负方向平移,平移后的图形为三角形DEC ,且点C 的坐标为(﹣3,2).(1)直接写出点E 的坐标 ;(2)在四边形ABCD 中,点P 从点B 出发,沿“BC→CD”移动.若点P 的速度为每秒1个单位长度,运动时间为t 秒,回答下列问题:①当t= 秒时,点P 的横坐标与纵坐标互为相反数;②求点P 在运动过程中的坐标,(用含t 的式子表示,写出过程);③当点P 运动到CD 上时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x ,y ,z 之间的数量关系能否确定?若能,请用含x ,y 的式子表示z ,写出过程;若不能,说明理由.16.我们定义,关于同一个未知数的不等式A 和B ,若A 的解都是B 的解,则称A 与B 存在“雅含”关系,且A 不等式称为B 不等式的“子式”.如:0A x <,:1B x <,满足A 的解都是B 的解,所以A 与B 存在“雅含”关系,A 是B 的“子式”.(1)若关于x 的不等式:21A x +>,:3B x >,请问A 与B 是否存在“雅含”关系,若存在,请说明谁是谁的“子式”;(2)已知关于x 的不等式11:23x a C -+<,():233D x x --<,若C 与D 存在“雅含”关系,且C 是D 的“子式”,求a 的取值范围; (3)已知2m n k +=,3m n -=,12m ≥,1n <-,且k 为整数,关于x 的不等式:64P kx x +>+,():62142Q x x -≤+,请分析是否存在k ,使得P 与Q 存在“雅含”关系,且Q 是P 的“子式”,若存在,请求出k 的值,若不存在,请说明理由.17.如图1,在直角坐标系中直线AB 与x 、y 轴的交点分别为(),0A a ,()0,B b ,且满足80a b a b ++-+=.(1)求a 、b 的值;(2)若点M 的坐标为()1,m 且2ABM AOM S S =,求m 的值;(3)如图2,点P 坐标是()1,2--,若ABO 以2个单位/秒的速度向下平移,同时点P 以1个单位/秒的速度向左平移,平移时间是t 秒,若点P 落在ABO 内部(不包含三角形的边),求t 的取值范围.18.在平面直角坐标系中,O 为坐标原点.已知两点(),0A a ,(), 0B b 且a 、b 满足430a b ++-=;若四边形ABCD 为平行四边形,//CD AB 且CD AB = ,点()0,4C 在y 轴上.(1)如图①,动点P 从C 点出发,以每秒2个单位长度沿y 轴向下运动,当时间t 为何值时,三角形ABP 的面积等于平行四边形ABCD 面积的四分之一;(2)如图②,当P 从O 点出发,沿y 轴向上运动,连接PD 、PA ,CDP ∠、APD ∠、PAB ∠存在什么样的数量关系,请说明理由(排除P 在O 和C 两点的特殊情况).19.数学活动课上,小新和小葵各自拿着不同的长方形纸片在做数学问题探究.(1)小新经过测量和计算得到长方形纸片的长宽之比为3:2,面积为30,请求出该长方形纸片的长和宽;(2)小葵在长方形内画出边长为a ,b 的两个正方形(如图所示),其中小正方形的一条边在大正方形的一条边上,她经过测量和计算得到长方形纸片的周长为50,阴影部分两个长方形的周长之和为30,由此她判断大正方形的面积为100,间小葵的判断正确吗?请说明理由.20.题目:满足方程组3512332x y k x y k+=+⎧⎨+=-⎩的x 与y 的值的和是2,求k 的值. 按照常规方法,顺着题目思路解关于x ,y 的二元一次方程组,分别求出xy 的值(含有字母k ),再由x +y =2,构造关于k 的方程求解,从而得出k 值.(1)某数学兴趣小组对本题的解法又进行了探究利用整体思想,对于方程组中每个方程变形得到“x +y ”这个整体,或者对方程组的两个方程进行加减变形得到“x +y ”整体值,从而求出k 值请你运用这种整体思想的方法,完成题目的解答过程.(2)小勇同学的解答是:观察方程①,令3x =k ,5y =1解得y =15,3x +y =2,∴x =95 ∴k =3×95=275把x =95,y =15代入方程②得k =﹣35 所以k 的值为275或﹣35. 请诊断分析并评价“小勇同学的解答”.21.如图,学校印刷厂与A ,D 两地有公路、铁路相连,从A 地购进一批每吨8000元的白纸,制成每吨10000元的作业本运到D 地批发,已知公路运价1.5元/(t •km ),铁路运价1.2元/(t •km ).这两次运输支出公路运费4200元,铁路运费26280元.(1)白纸和作业本各多少吨?(2)这批作业本的销售款比白纸的购进款与运输费的和多多少元?22.如图,α∠和β∠的度数满足方程组2230320αβαβ∠+∠=︒⎧⎨∠-∠=︒⎩,且//CD EF ,AC AE ⊥. (1)用解方程的方法求α∠和β∠的度数;(2)求C ∠的度数.23.某企业用规格是170cm ×40cm 的标准板材作为原材料,按照图①所示的裁法一或裁法二,裁剪出甲型与乙型两种板材(单位:cm).(1)求图中a 、b 的值;(2)若将40张标准板材按裁法一裁剪,5张标准板材按裁法二裁剪,裁剪后将得到的甲型与乙型板材做侧面或底面,做成如图②所示的竖式与横式两种无盖的装饰盒若干个(接缝处的长度忽略不计).①一共可裁剪出甲型板材 张,乙型板材 张;②恰好一共可以做出竖式和横式两种无盖装饰盒子多少个?24.甲从A 地出发步行到B 地,乙同时从B 地步行出发至A 地,2小时后在中途相遇,相遇后,甲、乙步行速度都提高了1千米/小时.若设甲刚出发时的速度为a 千米/小时,乙刚出发的速度为b 千米/小时.(1)A 、B 两地的距离可以表示为 千米(用含a ,b 的代数式表示); (2)甲从A 到B 所用的时间是: 小时(用含a ,b 的代数式表示);乙从B 到A 所用的时间是: 小时(用含a ,b 的代数式表示).(3)若当甲到达B 地后立刻按原路向A 返行,当乙到达A 地后也立刻按原路向B 地返行.甲乙二人在第一次相遇后3小时36分钟又再次相遇,请问AB 两地的距离为多少? 25.阅读材料:关于x ,y 的二元一次方程ax+by=c 有一组整数解00x x y y =⎧⎨=⎩,则方程ax+by=c 的全部整数解可表示为00x x bt y y at =-⎧⎨=+⎩(t 为整数).问题:求方程7x+19y=213的所有正整数解. 小明参考阅读材料,解决该问题如下:解:该方程一组整数解为0069x y =⎧⎨=⎩,则全部整数解可表示为61997x t y t =-⎧⎨=+⎩(t 为整数). 因为61909+70.t t ->⎧⎨>⎩,解得96719t -<<.因为t 为整数,所以t =0或-1.所以该方程的正整数解为69x y =⎧⎨=⎩和252x y =⎧⎨=⎩. (1)方程3x-5y=11的全部整数解表示为:253x t y t θ=+⎧⎨=+⎩(t 为整数),则θ= ; (2)请你参考小明的解题方法,求方程2x+3y=24的全部正整数解;(3)方程19x+8y=1908的正整数解有多少组? 请直接写出答案.26.在平面直角坐标系中,点(),1A a ,(),6B b ,(),3C c ,且a ,b ,c 满足231321b c a a c b +=+⎧⎨+=+⎩.(1)请用含a 的式子分别表示B ,C 两点的坐标;(2)当实数a 变化时,判断ABC 的面积是否发生变化?若不变,求其值;若变化,求其变化范围;(3)如图,已知线段AB 与y 轴相交于点E ,直线AC 与直线OB 交于点P ,若2PA PC ≤,求实数a 的取值范围.27.阅读下列材料:我们知道||x 的几何意义是在数轴上数x 对应的点与原点的距离,即|||0|x x =-,也就是说,12||x x -表示在数轴上数1x 与数2x 对应的点之间的距离;例 1.解方程||2x =,因为在数轴上到原点的距离为2的点对应的数为2±,所以方程||2x =的解为2x =±.例 2.解不等式|1|2x ->,在数轴上找出|1|2x -=的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为1-或3,所以方程|1|2x -=的解为1x =-或3x =,因此不等式|1|2x ->的解集为1x <-或3x >.参考阅读材料,解答下列问题:(1)方程|3|5x +=的解为 ;(2)解不等式:|2|3x -≤;(3)解不等式:428x x -++>.28.某超市投入31500元购进A 、B 两种饮料共800箱,饮料的成本与销售价如下表:(单位:元/箱)类别 成本价 销售价 A 42 64 B3652(1)该超市购进A 、B 两种饮料各多少箱? (2)全部售完800箱饮料共盈利多少元?(3)若超市计划盈利16200元,且A 类饮料售价不变,则B 类饮料销售价至少应定为每箱多少元?29.某水果店到水果批发市场采购苹果,师傅看中了甲、乙两家某种品质一样的苹果,零售价都为8元/千克,批发价各不相同,甲家规定:批发数量不超过100千克,全部按零价的九折优惠;批发数量超过100千克全部按零售价的八五折优惠,乙家的规定如下表: 数量范围(千克) 不超过50的部分 50以上但不超过150的部分 150以上的部分 价格(元)零售价的95%零售价的85%零售价的75%(1)如果师傅要批发240千克苹果选择哪家批发更优惠?(2)设批发x 千克苹果(100x >),问师傅应怎样选择两家批发商所花费用更少? 30.在平面直角坐标系中,已知线段AB ,点A 的坐标为()1,2-,点B 的坐标为()3,0,如图1所示.(1)平移线段A B 到线段C D ,使点A 的对应点为,点B 的对应点为C ,若点C 的坐标为()2,4-,求点D 的坐标;(2)平移线段A B 到线段C D ,使点C 在y 轴的正半轴上,点D 在第二象限内(A 与D 对应, B 与C 对应),连接BC BD ,,如图2所示.若(7BCD BCD S S ∆∆=表示△BCD 的面积),求点C 、D 的坐标;(3)在(2)的条件下,在y 轴上是否存在一点P ,使(23PCD PCD BCD S S S ∆∆∆=表示△PCD 的面积)?若存在,求出点P 的坐标; 若不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)AC∥DE;(2)①∠CAM+∠MDE=∠AMD,证明见解析;②点M的坐标为(0,1711)或(0,253).【分析】(1)根据两点的纵坐标相等,连线平行x轴进行判断即可;(2)①过点M作MN∥AC,运用平行线的判定和性质即可;②设M(0,m),分两种情况:(i)当点M在线段OB上时,(ii)当点M在线段OB的延长线上时,分别运用三角形面积公式进行计算即可.【详解】解:(1)∵A(−3,3)、C(4,3),∴AC∥x轴,∵D(−2,−1)、E(2,−1),∴DE∥x轴,∴AC∥DE;(2)①如图,∠CAM+∠MDE=∠AMD.理由如下:过点M作MN∥AC,∵MN∥AC(作图),∴∠CAM =∠AMN (两直线平行,内错角相等), ∵AC ∥DE (已知), ∴MN ∥DE (平行公理推论),∴∠MDE =∠NMD (两直线平行,内错角相等),∴∠CAM +∠MDE =∠AMN +∠NMD =∠AMD (等量代换). ②由题意,得:AC =7,DE =4, 设M (0,m ),(i )当点M 在线段OB 上时,BM =3−m ,FM =m +1, ∴S △ACM =12AC •BM =12×7×(3−m )=2172m-, S △DEM =12DE •FM =12×4×(m +1)=2m +2, ∵S △ACM =S △DEM , ∴2172m-=2m +2, 解得:m =1711, ∴M (0,1711); (ii )当点M 在线段OB 的延长线上时,BM =m −3,FM =m +1, ∴S △ACM =12AC •BM =12×7×(m −3)=7212m -, S △DEM =12DE •FM =12×4×(m +1)=2m +2, ∵S △ACM =S △DEM , ∴7212m -=2m +2, 解得:m =253, ∴M (0,253); 综上所述,点M 的坐标为(0,1711)或(0,253).【点睛】本题考查了三角形面积,平行坐标轴的直线上的点的坐标的特征,平行线的判定和性质等,解题关键是运用数形结合思想和分类讨论思想.2.(1)35,35,平行;(2)∠FMN +∠GHF =180°,证明见解析;(3)不变,2 【分析】(1)根据(α-35)2+|β-α|=0,即可计算α和β的值,再根据内错角相等可证AB ∥CD ; (2)先根据内错角相等证GH ∥PN ,再根据同旁内角互补和等量代换得出∠FMN +∠GHF =180°;(3)作∠PEM 1的平分线交M 1Q 的延长线于R ,先根据同位角相等证ER ∥FQ ,得∠FQM 1=∠R ,设∠PER =∠REB =x ,∠PM 1R =∠RM 1B =y ,得出∠EPM 1=2∠R ,即可得1FPN Q∠∠=2. 【详解】解:(1)∵(α-35)2+|β-α|=0, ∴α=β=35,∴∠PFM =∠MFN =35°,∠EMF =35°, ∴∠EMF =∠MFN , ∴AB ∥CD ;(2)∠FMN +∠GHF =180°; 理由:由(1)得AB ∥CD , ∴∠MNF =∠PME , ∵∠MGH =∠MNF , ∴∠PME =∠MGH , ∴GH ∥PN , ∴∠GHM =∠FMN , ∵∠GHF +∠GHM =180°, ∴∠FMN +∠GHF =180°; (3)1FPN Q∠∠的值不变,为2, 理由:如图3中,作∠PEM 1的平分线交M 1Q 的延长线于R , ∵AB ∥CD , ∴∠PEM 1=∠PFN ,∵∠PER =12∠PEM 1,∠PFQ =12∠PFN , ∴∠PER =∠PFQ , ∴ER ∥FQ ,∴∠FQM 1=∠R ,设∠PER =∠REB =x ,∠PM 1R =∠RM 1B =y , 则有:122y x Ry x EPM ⎧⎨⎩=+∠=+∠,可得∠EPM 1=2∠R , ∴∠EPM 1=2∠FQM 1,∴11EPM FQM ∠∠=1FPN Q∠∠=2.【点睛】本题主要考查平行线的判定与性质,熟练掌握内错角相等证平行,平行线同旁内角互补等知识是解题的关键.3.(1)∠B ,EF ,CD ,∠D ;(2)①65°;②180°﹣1122a β+【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图1,过点E 作EF ∥AB ,当点B 在点A 的左侧时,根据∠ABC =60°,∠ADC =70°,参考小亮思考问题的方法即可求∠BED 的度数;②如图2,过点E 作EF ∥AB ,当点B 在点A 的右侧时,∠ABC =α,∠ADC =β,参考小亮思考问题的方法即可求出∠BED 的度数. 【详解】解:(1)过点E 作EF ∥AB , 则有∠BEF =∠B , ∵AB ∥CD , ∴EF ∥CD , ∴∠FED =∠D ,∴∠BED =∠BEF +∠FED =∠B +∠D ; 故答案为:∠B ;EF ;CD ;∠D ;(2)①如图1,过点E 作EF ∥AB ,有∠BEF =∠EBA .∵AB ∥CD , ∴EF ∥CD . ∴∠FED =∠EDC .∴∠BEF +∠FED =∠EBA +∠EDC . 即∠BED =∠EBA +∠EDC , ∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠EBA =12∠ABC =30°,∠EDC =12∠ADC =35°, ∴∠BED =∠EBA +∠EDC =65°. 答:∠BED 的度数为65°;②如图2,过点E 作EF ∥AB ,有∠BEF +∠EBA =180°.∴∠BEF =180°﹣∠EBA , ∵AB ∥CD , ∴EF ∥CD . ∴∠FED =∠EDC .∴∠BEF +∠FED =180°﹣∠EBA +∠EDC . 即∠BED =180°﹣∠EBA +∠EDC , ∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠EBA =12∠ABC =12α,∠EDC =12∠ADC =12β,∴∠BED =180°﹣∠EBA +∠EDC =180°﹣1122a β+.答:∠BED 的度数为180°﹣1122a β+.【点睛】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质. 4.(1)见解析;(2)12;(3)75° 【分析】(1)根据平行线的性质、余角和补角的性质即可求解. (2)根据平行线的性质、对顶角的性质和平角的定义解答即可. (3)根据平行线的性质和角平分线的定义以及三角形内角和解答即可. 【详解】解:(1)∠C =∠1+∠2,证明:过C 作l ∥MN ,如下图所示,∵l ∥MN ,∴∠4=∠2(两直线平行,内错角相等), ∵l ∥MN ,PQ ∥MN , ∴l ∥PQ ,∴∠3=∠1(两直线平行,内错角相等), ∴∠3+∠4=∠1+∠2,(2)∵∠BDF=∠GDF,∵∠BDF=∠PDC,∴∠GDF=∠PDC,∵∠PDC+∠CDG+∠GDF=180°,∴∠CDG+2∠PDC=180°,∴∠PDC=90°-12∠CDG,由(1)可得,∠PDC+∠CEM=∠C=90°,∴∠AEN=∠CEM,∴190(90)90122CDGAEN CEM PDCCDG CDG CDG CDG︒-︒-∠∠∠︒-∠====∠∠∠∠,(3)设BD交MN于J.∵BC平分∠PBD,AM平分∠CAD,∠PBC=25°,∴∠PBD=2∠PBC=50°,∠CAM=∠MAD,∵PQ∥MN,∴∠BJA=∠PBD=50°,∴∠ADB=∠AJB-∠JAD=50°-∠JAD=50°-∠CAM,由(1)可得,∠ACB=∠PBC+∠CAM,∴∠ACB+∠ADB=∠PBC+∠CAM+50°-∠CAM=25°+50°=75°.【点睛】本题考查了平行线的性质、余角和补角的性质,解题的关键是根据平行找出角度之间的关系.5.(1)90°;(2)∠PFC=∠PEA+∠P;(3)∠G=12α【分析】(1)根据平行线的性质与判定可求解;(2)过P点作PN∥AB,则PN∥CD,可得∠FPN=∠PEA+∠FPE,进而可得∠PFC=∠PEA+∠FPE,即可求解;(3)令AB与PF交点为O,连接EF,根据三角形的内角和定理可得∠GEF+∠GFE=1 2∠PEA+12∠PFC+∠OEF+∠OFE,由(2)得∠PEA=∠PFC-α,由∠OFE+∠OEF=180°-∠FOE=180°-∠PFC可求解.【详解】解:(1)如图1,过点P作PM∥AB,又∠AEP=40°,∴∠1=40°.∵AB∥CD,∴PM∥CD,∴∠2+∠PFD=180°.∵∠PFD=130°,∴∠2=180°-130°=50°.∴∠1+∠2=40°+50°=90°.即∠EPF=90°.(2)∠PFC=∠PEA+∠P.理由:过P点作PN∥AB,则PN∥CD,∴∠PEA=∠NPE,∵∠FPN=∠NPE+∠FPE,∴∠FPN=∠PEA+∠FPE,∵PN∥CD,∴∠FPN=∠PFC,∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;(3)令AB与PF交点为O,连接EF,如图3.在△GFE中,∠G=180°-(∠GFE+∠GEF),∵∠GEF=12∠PEA+∠OEF,∠GFE=12∠PFC+∠OFE,∴∠GEF+∠GFE=12∠PEA+12∠PFC+∠OEF+∠OFE,∵由(2)知∠PFC=∠PEA+∠P,∴∠PEA=∠PFC-α,∵∠OFE+∠OEF=180°-∠FOE=180°-∠PFC,∴∠GEF+∠GFE=12(∠PFC−α)+12∠PFC+180°−∠PFC=180°−12α,∴∠G=180°−(∠GEF+∠GFE)=180°−180°+12α=12α.【点睛】本题主要考查平行线的性质与判定,灵活运用平行线的性质与判定是解题的关键.6.(1)见解析;(2)∠BAE+∠CDE=∠AED,证明见解析;(3)①∠AED-∠FDC=45°,理由见解析;②50°【分析】(1)根据平行线的性质及判定可得结论;(2)过点E作EF∥AB,根据平行线的性质得AB∥CD∥EF,然后由两直线平行内错角相等可得结论;(3)①根据∠AED+∠AEC=180°,∠AED+∠DEC+∠AEB=180°,DF平分∠EDC,可得出2∠AED+(90°-2∠FDC)=180°,即可导出角的关系;②先根据∠AED=∠F+∠FDE,∠AED-∠FDC=45°得出∠DEP=2∠F=90°,再根据∠DEA-∠PEA=514∠DEB,求出∠AED=50°,即可得出∠EPD的度数.【详解】解:(1)证明:AB∥CD,∴∠A+∠D=180°,∵∠C=∠A,∴∠C+∠D=180°,∴AD∥BC;(2)∠BAE+∠CDE=∠AED,理由如下:如图2,过点E作EF∥AB,∵AB∥CD∴AB∥CD∥EF∴∠BAE=∠AEF,∠CDE=∠DEF即∠FEA+∠FED=∠CDE+∠BAE∴∠BAE+∠CDE=∠AED;(3)①∠AED-∠FDC=45°;∵∠AED+∠AEC=180°,∠AED+∠DEC+∠AEB=180°,∴∠AEC=∠DEC+∠AEB,∴∠AED=∠AEB,∵DF平分∠EDC∠DEC=2∠FDC∴∠DEC=90°-2∠FDC,∴2∠AED+(90°-2∠FDC)=180°,∴∠AED-∠FDC=45°,故答案为:∠AED-∠FDC=45°;②如图3,∵∠AED=∠F+∠FDE,∠AED-∠FDC=45°,∴∠F=45°,∴∠DEP=2∠F=90°,∵∠DEA-∠PEA=514∠DEB=57∠DEA,∴∠PEA=27∠AED,∴∠DEP=∠PEA+∠AED=97∠AED=90°,∴∠AED=70°,∵∠AED+∠AEC=180°,∴∠DEC+2∠AED=180°,∴∠DEC=40°,∵AD∥BC,∴∠ADE=∠DEC=40°,在△PDE中,∠EPD=180°-∠DEP-∠AED=50°,即∠EPD=50°.【点睛】本题主要考查平行线的判定和性质,熟练掌握平行线的判定和性质,角平分线的性质等知识点是解题的关键.7.(1)1022;(2)3066,2226;(3)67 36【分析】(1)由于千位不能为0,最小只能取1;根据题目得出相应的公式:十位=2×千位﹣百位,个位=2×千位+百位,分别求出十位和个位,即可求出最小的四位依赖数;(2)设千位数字是x ,百位数字是y ,根据“依赖数”定义,则有:十位数字是(2x ﹣y ),个位数字是(2x+y ),依据题意列出代数式然后表示为7的倍数加余数形式,然后求出x 、y 即可,从而求出所有特色数;(3)根据最小分解的定义可知: n 越小,p 、q 越接近,nq ﹣np 才越小,才是最小分解,此时F (m )=q n p n ++,故将(2)中特色数分解,找到最小分解,然后将n 、p 、q 的值代入F (m )=q n p n++,再比较大小即可. 【详解】解:(1)由题意可知:千位一定是1,百位取0,十位上的数字为:2×1-0=2,个位上的数字为:2×1+0=2则最小的四位依赖数是1022;(2)设千位数字是x ,百位数字是y ,根据“依赖数”定义,则有:十位数字是(2x ﹣y ),个位数字是(2x+y ),根据题意得:100y+10(2x ﹣y )+2x+y ﹣3y =88y+22x =21(4y+x )+(4y+x ),∵21(4y+x )+(4y+x )被7除余3,∴4y+x =3+7k ,(k 是非负整数)∴此方程的一位整数解为:x=4,y=5(此时2x+y >10,故舍去);x =3,y =7(此时2x ﹣y <0,故舍去);x =3,y =0;x =2,y =2;x =1,y =4(此时2x ﹣y <0,故舍去); ∴特色数是3066,2226.(3)根据最小分解的定义可知: n 越小,p 、q 越接近,nq ﹣np 才越小,才是最小分解,此时F (m )=q n p n ++, 由(2)可知:特色数有3066和2226两个,对于3066=613×5+14=61×50+24∵1×613-1×5>2×61-2×50,∴3066取最小分解时:n=2,p=50,q=61∴F (3066)=61263=50252++ 对于2226=89×25+14=65×34+24,∵1×89-1×25>2×65-2×34,∴2226取最小分解时:n=2,p=34,q=65∴F (2226)=6365267=342++ ∵63675236< 故所有“特色数”的F (m )的最大值为:6736. 【点睛】此题考查的是新定义类问题,理解题意,并根据新定义解决问题是解决此题的关键. 8.(1)202021-;(2)2020312-;(3)201101554-. 【分析】仿照阅读材料中的方法求出所求即可.【详解】解:(1)根据2350511222...221+++++=-得:2320191222...2+++++=202021-(2)设2320191333...3S =+++++,则234202033333...3S =+++++,∴2020331S S -=-, ∴2020312S -= 即:2020232019311333 (32)-+++++= (3)设232001555...5S =+++++,则23420155555...5S =+++++,∴201551S S -=-, ∴201514S -= 即:20123200511555 (5)4-+++++= 同理可求⸫10123100511555 (54)-+++++= ∵1011021032002320023100555...51555...5)(1555...5)++++=+++++-+++++( 201101201101101102103200515155555 (5444)---∴++++=-= 【点睛】此题考查了规律型:数字的变化类,弄清题中的规律是解本题的关键.9.(1)1021-;(2)21332-;(3)111n a a +-- 【分析】(1)设式子等于s ,将方程两边都乘以2后进行计算即可;(2)设式子等于s ,将方程两边都乘以3,再将两个方程相减化简后得到答案; (3)设式子等于s ,将方程两边都乘以a 后进行计算即可.【详解】(1)设s=291222++++①, ∴2s=29102222++++②,②-①得:s=1021-,故答案为:1021-;(2)设s=220333+++①,∴3s=22021333+++②,②-①得:2s=2133-, ∴21332s -=, 故答案为: 21332-; (3)设s=231n a a a a ++++①, ∴as=231n n a a a a a +++++②, ②-①得:(a-1)s=11n a +-,∴s=111n a a +--. 【点睛】此题考查代数式的规律计算,能正确理解已知的代数式的运算规律是难点,依据规律对于每个式子变形计算是关键.10.(1)35,2⎛⎫ ⎪⎝⎭;(2)2;(3)不是;(4)(6,75) 【分析】(1)根据“白马有理数对”的定义,把数对3(2,1),5,2⎛⎫- ⎪⎝⎭分别代入1a b ab +=-计算即可判断;(2)根据“白马有理数对”的定义,构建方程即可解决问题;(3)根据“白马有理数对”的定义即可判断;(4)根据“白马有理数对”的定义即可解决问题.【详解】(1)∵-2+1=-1,而-2×1-1=-3,∴-2+1≠-3,∴(-2,1)不是“白马有理数对”,∵5+32=132,5×32-1=132, ∴5+32=5×32-1, ∴35,2⎛⎫ ⎪⎝⎭是“白马有理数对”, 故答案为:35,2⎛⎫ ⎪⎝⎭; (2)若(,3)a 是“白马有理数对”,则a+3=3a-1,解得:a=2,故答案为:2;(3)若(,)m n 是“白马有理数对”,则m+n=mn-1,那么-n+(-m)=-(m+n)=-(mn-1)=-mn+1,∵-mn+1≠ mn-1∴(-n,-m)不是“白马有理数对”,故答案为:不是;(4)取m=6,则6+x=6x-1,∴x=75,∴(6,75)是“白马有理数对”,故答案为:(6,75).【点睛】本题考查了“白马有理数对”的定义,有理数的加减运算,一次方程的列式求解,理解“白马有理数对”的定义是解题的关键.11.(1)×,√,×,×;(2)3332;1000;(3)36(个).【分析】(1)根据“本位数”的定义即可判断;(2)要想保证不进位,千位、百位、十位最大只能是3,个位最大只能是2,故最大的四位“本位数”是3332;千位最小为1,百位、十位、个位最小为0,故最小的“本位数”是1000;(3)要想构成“本位数”,百位可以为1,2,3,十位可以为0,1,2,3,个位可以为0,1,2,所有的三位数中,“本位数”一共有34336⨯⨯=(个).【详解】解:(1)106107108321++=有进位;111112113336++=没有进位;4004014021203++=有进位;2015201620176048++=有进位;故答案为:×,√,×,×.(2)要想保证不进位,千位、百位、十位最大只能是3,个位最大只能是2,故最大的四位“本位数”是3332;千位最小为1,百位、十位、个位最小为0,故最小的“本位数”是1000,故答案为:3332,1000.(3)要想构成“本位数”,百位可以为1,2,3,十位可以为0,1,2,3,个位可以为0,1,2,所有的三位数中,“本位数”一共有34336⨯⨯=(个).【点睛】本题考查了新定义计算题,准确理解新定义的内涵是解题的关键.12.(1)35,2⎛⎫⎪⎝⎭;(2)2;(3)不是;(4)(6,75)【分析】(1)根据“白马有理数对”的定义,把数对3(2,1),5,2⎛⎫- ⎪⎝⎭分别代入1a b ab +=-计算即可判断;(2)根据“白马有理数对”的定义,构建方程即可解决问题;(3)根据“白马有理数对”的定义即可判断;(4)根据“白马有理数对”的定义即可解决问题.【详解】(1)∵-2+1=-1,而-2×1-1=-3,∴-2+1≠-3,∴(-2,1)不是“白马有理数对”,∵5+32=132,5×32-1=132, ∴5+32=5×32-1, ∴35,2⎛⎫ ⎪⎝⎭是“白马有理数对”, 故答案为:35,2⎛⎫ ⎪⎝⎭; (2)若(,3)a 是“白马有理数对”,则a+3=3a-1,解得:a=2,故答案为:2;(3)若(,)m n 是“白马有理数对”,则m+n=mn-1,那么-n+(-m )=-(m+n )=-(mn-1)=-mn+1,∵-mn+1≠ mn-1∴(-n ,-m )不是“白马有理数对”,故答案为:不是;(4)取m=6,则6+x=6x-1,∴x=75,∴(6,75)是“白马有理数对”,故答案为:(6,75).【点睛】本题考查了“白马有理数对”的定义,有理数的加减运算,一次方程的列式求解,理解“白马有理数对”的定义是解题的关键.13.(1)(0,4),(2,0),(2,4)-;(2)证明见解析;(3)成立,理由见解析【分析】(1)根据算术平方根、立方根得(0,4)A 、(2,0)C ;再根据直角坐标系、平移的性质分析,即可得到答案;(2)根据平移的性质,得//OG CA ;根据平行线性质,分别推导得OFC GOA AOF ∠∠∠=+,GOA OAF ∠∠=,从而完成证明;(3)结合题意,根据平行线的性质,推导得90GOA ACO ∠∠+=︒、AOF OAC ∠∠=;结合(2)的结论,通过计算即可完成证明.【详解】(1)连接GA∵a 是16的算术平方根∴4a =∴(0,4)A∴4AO =∵38b =∴2b =∴(2,0)C∴2OC =∵线段GO 由线段AC 平移所得,并且点G 与点A 对应,点O 与点C 对应∴2GA OC ==,//GA OC∴(2,4)G -故答案为:(0,4),(2,0),(2,4)-;(2)∵线段GO 由线段AC 平移所得∴//OG CA ,∴OFC GOF ∠∠=∵GOF GOA AOF ∠∠∠=+∴OFC GOA AOF ∠∠∠=+∵//OG CA∴GOA OAF ∠∠=∴OFC OAF AOF ∠∠∠=+(3)∵//OG CA∴180GOC ACO ∠+∠=︒∵GOC GOA AOC ∠∠∠=+∴180GOA AOC ACO ∠∠∠++=︒∵90AOC ∠=︒∴90180GOA ACO ∠∠+=︒+︒,即90GOA ACO ∠∠+=︒∵//OG CA∴GOA OAC ∠∠=∴90OAC ACO ∠+∠=︒∵90AOC AOF FOC ∠∠∠=+=︒∴AOF FOC OAC ACO ∠∠∠∠+=+∵FOC FCO ∠=∠,ACO FCO ∠∠=∴AOF OAC ∠∠=由(2)的结论得:OHC OEH EOH ∠∠∠=+,OEC EAC ACE ∠∠∠=+∵OEH OEC ∠∠=,EOH AOF OAC ∠∠∠==∴OHC OEC OAC ∠∠∠=+∴OHC ACE OEC OAC ACE ∠∠∠∠∠+=++∵EAC OAC ∠=∠∴OEC OAC ACE ∠∠∠=+∴2OHC ACE OEC ∠∠∠+=∴在点E 运动的过程中,2OHC ACE OEC ∠∠∠+=总成立.【点睛】本题考查了算术平方根、立方根、平行线、平移、直角坐标系的知识;解题的关键是熟练掌握直角坐标系、平移、平行线的性质,从而完成求解.14.(1)120°;(2)90°-12x °;(3)不变,12;(4)45°【分析】(1)由平行线的性质:两直线平行同旁内角互补可得;(2)由平行线的性质可得∠ABN =180°-x °,根据角平分线的定义知∠ABP =2∠CBP 、∠PBN =2∠DBP ,可得2∠CBP +2∠DBP =180°-x °,即∠CBD =∠CBP +∠DBP =90°-12x °; (3)由AM ∥BN 得∠APB =∠PBN 、∠ADB =∠DBN ,根据BD 平分∠PBN 知∠PBN =2∠DBN ,从而可得∠APB :∠ADB =2:1;(4)由AM ∥BN 得∠ACB =∠CBN ,当∠ACB =∠ABD 时有∠CBN =∠ABD ,得∠ABC +∠CBD =∠CBD +∠DBN ,即∠ABC =∠DBN ,根据角平分线的定义可得∠ABP =∠PBN =12∠ABN =2∠DBN ,由平行线的性质可得12∠A +12∠ABN =90°,即可得出答案.【详解】解:(1)∵AM ∥BN ,∠A =60°,∴∠A +∠ABN =180°,∴∠ABN =120°;(2)∵AM ∥BN ,∴∠ABN +∠A =180°,∴∠ABN =180°-x °,∴∠ABP +∠PBN =180°-x °,∵BC 平分∠ABP ,BD 平分∠PBN ,。
初中七年级下册平面几何证明之全等三角形之辅助线习题(含答案发))

初中七年级下册平面几何证明之全等三角形之辅助线习题(含答案发))AB∥CD(已知)___∠ACD(平行线夹角相等)AD∥BC(已知)___∠BCA(平行线夹角相等)ABC∽△CDA(AA)___又因为AC=BD,所以___AB+AD=BD+CDABCD是平行四边形又因为AB∥CD,所以∠ABD=∠CDA在△ABD和△CDA中AB CD(已知)BD AD(证明得出)ABD=∠CDA(证明得出)ABD≌△CDA(SAS)AB=CD,AD=BC(全等三角形对应边相等)3.证明:如图,连接BF、CF在△BFC和△DFC中BC ED(已知)___∠___∠___(已知)BF DF(公共边)BFC≌△DFC(SAS)___∠CFD(全等三角形对应角相等)又因为BC=ED,所以___又因为AB=AE,所以∠AFE=∠BAF在△___和△BAF中AF AF(公共边)AFE=∠BAF(证明得出)AE AB(已知)AFE≌△BAF(SAS)AFB=∠AFE(全等三角形对应角相等)又因为∠___∠CFD,所以∠AFB=∠CFD AFB=∠______⊥BD4.证明:如图,连接BC在△ABC中B=∠C(已知)AB=AC(等角对应边相等)5.证明:如图,连接BD,BE在△ABD和△___中AB EB(共边)ABD=∠___(已知)BD BC(已知)ABD≌△EBC(SAS)BD=BE(全等三角形对应边相等)6.证明:如图,连接BF,CF,AE,DE 在△ABD和△ECD中AE BD(已知)AED=∠ABD(公共角)EC DC(已知)AED≌△ABD(SAS)___∠AFE(全等三角形对应角相等)又因为BF=DF,所以BF+FD=DF+DE 又因为AE=BD,所以AF+FD=BFAF+FD=DF+DEAF-DE=DF-FDAF-DE=DF-FC又因为EC=CD,所以∠ECD=∠CDE在△ECD和△___中EC BC(已知)ECD=∠CDE(证明得出)CD FC(已知)ECD≌△___(SAS)BF=DE(全等三角形对应边相等)又因为BF=DF,所以BF-DE=DF-DEBF-DE=DF-FCBE=CF又因为∠___∠AFE,所以∠BAF+∠___∠AFE+∠CAF ___∠___又因为BE=CF,所以∠___∠CAF___∠CAF___⊥BD7.因为BD,CE是△ABC的高,所以∠ABD=90°,∠ACE=90°又因为BP=AC,CQ=AB,所以___BPC∽△CQA(SAS)又因为∠___∠CQA=90°,所以△BPC和△CQA是直角三角形又因为BP=AC,CQ=AB,所以BP+CQ=AB+AC=BCBP+CQ=BC又因为___,所以BP/BC=AC/(AB+AC)BP/BC=AC/BCBP=AC又因为BP=AC,所以___CQ/BC=AB/ACCQ=AB又因为BP=AC,CQ=AB,所以BP+CQ=AB+AC=BCAP=BQ=BC/2又因为BD,CE是△___的高,所以AP⊥BD,___⊥CE ___⊥BD,___⊥CEAP∥BQ又因为AP=BQ,所以APBQ是平行四边形AP=BQ,AP∥BQ2+∠4=90°又因为AB=AC,所以△ABP≌△ACQ(ASA)AP=AQ又因为AP⊥AQ,所以APQ为等腰直角三角形PAQ=45°8.解:如图。
(完整版)初一下册数学角度几何解析题以及练习题(附答案).doc

七年级下册数学几何解析题以及练习题(附答案)9.(2011 ·扬州 ) 如图,C岛在A岛的北偏东60°方向,在B岛的北偏西 45°方向,则从C岛看 A、 B 两岛的视角∠ ACB=________.答案105°解析如图,∵ (60 °+∠CAB)+(45 °+∠ABC)=180°,∴∠CAB+∠ABC=75°,在△ ABC中,得∠ C=105°.12.如图所示,在△ABC中,∠ A=80°,∠ B=30°, CD平分∠ ACB, DE∥AC.(1)求∠ DEB的度数;(2)求∠ EDC的度数.解(1) 在△ABC中,∠A=80°,∠B=30°,∴∠ ACB=180°-∠ A-∠ B=70°.∵ DE∥AC,∴∠ DEB=∠ ACB=70°.(2)∵ CD平分∠ ACB,1∴∠ DCE=2∠ ACB=35°.∵∠ DEB=∠ DCE+∠ EDC,∴∠ EDC=70°-35°=35°.13.已知,如图,∠1=∠ 2,CF⊥AB于F,DE⊥AB于E,求证:FG∥BC.( 请将证明补充完整 )证明∵ CF⊥ AB, DE⊥ AB(已知),∴ ED∥FC() .∴∠ 1=∠BCF() .又∵∠ 1=∠ 2( 已知 ) ,1∴ FG ∥BC () .解 在同一平面内, 垂直于同一直线的两条直线互相平行;两直线平行, 同位角相等;内错角相等,两直线平行.14.如图,已知三角形ABC ,求证:∠ A +∠ B +∠ C =180°.分析:通过画平行线,将∠A 、∠B 、∠C 作等角代换,使各角之和恰为一平角,依辅助线不同而得多种证法,如下:证法 1:如图甲,延长 BC 到 D ,过 C 画 CE ∥ BA .∵BA ∥ CE ( 作图所知 ) ,∴∠ B =∠ 1,∠ A =∠ 2( 两直线平行,同位角、内错角相等) .又∵∠ BCD =∠ BCA +∠ 2+∠ 1=180°( 平角的定义 ) ,∴∠ A +∠ B +∠ ACB =180°( 等量代换 ) .如图乙,过 BC 上任一点 F ,画 FH ∥AC , FG ∥ AB ,这种添加辅助线的方法能证明∠A +∠B +∠C =180°吗?请你试一试.解 ∵ FH ∥AC ,∴∠ BHF =∠ A ,∠ 1=∠ C .∵ FG ∥AB ,∴∠ BHF =∠ 2,∠ 3=∠ B ,∴∠ 2=∠ A .∵∠ BFC =180°,∴∠ 1+∠ 2+∠ 3=180°,即∠ A +∠ B +∠ C =180°.15.(2010 ·玉溪 ) 平面内的两条直线有相交和平行两种位置关系.(1) 如图 a ,若 AB ∥ CD ,点 P 在 AB 、 CD 外部,则有∠ B =∠ BOD .又因∠ BOD 是△ POD的外角,故∠ BOD =∠ BPD +∠ D ,得∠ BPD =∠ B -∠ D . 将点 P 移到 AB 、CD 内部,如图 b ,以上结论是否成立?若成立,说明理由;若不成立,则∠、∠ 、∠ D 之BPD B间有何数量关系?请证明你的结论;(2) 在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点 Q,如图 c,则∠ BPD、∠ B、∠ D、∠ BQD之间有何数量关系?( 不需证明 )(3)根据 (2) 的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.解(1) 不成立,结论是∠BPD=∠B+∠D.延长 BP交 CD于点 E,∵ AB∥CD,∴∠ B=∠ BED.又∠ BPD=∠ BED+∠ D,∴∠ BPD=∠ B+∠ D.(2)结论:∠ BPD=∠ BQD+∠ B+∠ D.(3)设 AC与 BF交于点 G.由 (2) 的结论得:∠AGB=∠ A+∠ B+∠ E.又∵∠ AGB=∠ CGF,∠ CGF+∠ C+∠ D+∠ F=360°,∴∠ A+∠ B+∠ C+∠D+∠ E+∠ F=360°.A 14.把一副常用的三角板如图所示拼在一起,那么图中∠ADE是度. DEBC第 14 题2.如图,在△ ABC和△ ABD中,现给出如下三个论断:①AD=BC;②∠C=∠D;③∠1=∠2。
2022-2023学年人教版数学七年级下册期末几何解答题专题练习

2022-2023学年人教版七年级下学期期末数学几何解答题专题练习1、如图,AB∥CD,∠A=∠C,BE平分∠ABC交AD的延长线于点E,(1)证明:AD∥BC;(2)若∠ADC=118°,求∠E的度数.2、如图,已知∠1=∠BDC,∠2+∠3=180°.(1)AD与EC平行吗?试说明理由.(2)若DA平分∠BDC,CE⊥AE于点E,∠1=80°,试求∠F AB的度数.3、小聪把一副三角尺ABC,DCE按如图1的方式摆放,其中边BC,DC在同一条直线上,过点A向右作射线AP∥DE.(1)如图2,求∠P AC的度数;(2)如图3,点Q是线段BC上一点,若∠AQB=53∠PAQ,求∠QAB的度数.4、已知:在四边形ABCD中,AD∥BC,AE平分∠DAB交BC于点E,点M为线段BC上一点,且AM∥DC.(1)如图(1),若点M与点E重合,求证:∠C=∠BAE;(2)如图(2),若AN平分∠BAM交BC于点N,且∠NAE=25°,求∠C的度数;(3)在(1)的条件下,F为线段BA的延长线上一点,∠DCB=75°,若∠DCB的三等分线与∠F AD的角平分线交于点P,请直接写出∠APC的度数.5、直线AB∥CD,BE﹣EC是一条折线段,BP平分∠ABE.(1)如图1,若BP∥CE,求证:∠BEC+∠DCE=180°;(2)CQ平分∠DCE,直线BP,CQ交于点F.①如图2,写出∠BEC和∠BFC的数量关系,并证明;②当点E在直线AB,CD之间时,若∠BEC=40°,直接写出∠BFC的大小.6、如图1,AB∥CD,点E在AB上,点H在CD上,点F在直线AB,CD之间,连接EF,FH,∠BEF=α,∠FHD=β.(1)直接写出∠EFH的度数为;(2)如图2,若HM平分∠CHF,MN平分∠BEF,证明:∠EFH+2∠M=180°;(3)如图3,若∠BEN=1n∠BEF,∠MHC=1n∠FHC,则∠M=.(用含有n,α,β的式子表示)7、如图,已知A(0,a),B(b,0),且满足|a−4|+√b+6=0.(1)求A、B两点的坐标;(2)点P(m,n)在线段AB上,当PB=2P A时,求P点的坐标;(3)若点M(c,6),△ABM的面积记作S△ABM,当S△ABM>10时,直接写出c的取值范围.8、在平面直角坐标系中,已知点A(a,0),B(0,b),若a,b满足(a﹣b+6)2+|2a﹣3b+14|=0.(1)求点A,B的坐标;(2)将线段AB向右平移2个单位至CD,线段CD与y轴交于点E,求点E的坐标;(3)点P为直线CD上一动点,连接BC,PB,若4≤S△BCP<6,则点P的横坐标x P的取值范围是.9、如图,已知AB∥CD,M,N分别是直线AB,CD上一点,点E在直线AB,CD之间.(1)如图1,求证:∠BME+∠DNE=∠MEN;(2)如图2,F是EM上一点,NE平分∠FND,FH平分∠NFE,试探究∠NHF与∠BME 之间的数量关系?并证明你的结论;(3)如图3,P为直线MN上一动点(不与点N重合),过点P作PG⊥MN交直线CD 于点G,∠PNG的角平分线和∠PGC的角平分线交于点O,则∠O的度数为(直接写出结果).10、平面直角坐标系中,A(a,0),B(0,b),a,b均为整数,且满足b=√2a−4−√4−a,点C在y轴负半轴上且S△ABC=10,将线段AB平移到DE,其中点A的对应点是点D.(1)请直接写出点A ,B ,C 的坐标;(2)如图(1),若点D 的坐标为(﹣1,0),点F (m ,n )为线段DE 上一点,且△ACF 的面积大于12,求m 的取值范围;(3)如图(2),若DE 与y 轴的交点G 在B 点上方,点P 为y 轴上一动点,请直接写出∠EBO ,∠BPD ,∠PDA 之间的数量关系.11、在平面直角坐标系中,A (a ,0),B (1,b ),a ,b 满足|a +b ﹣1|+√2a −b +10=0,连接AB 交y 轴于C .(1)直接写出a = ,b = ;(2)如图1,点P 是y 轴上一点,且三角形ABP 的面积为12,求点P 的坐标;(3)如图2,直线BD 交x 轴于D (4,0),将直线BD 平移经过点A ,交y 轴于E ,点Q (x ,y )在直线AE 上,且三角形ABQ 的面积不超过三角形ABD 面积的13,求点Q 横坐标x 的取值范围.12、已知,AB ∥DE ,点C 是直线AB ,DE 下方一点,连接BC ,DC .(1)如图1,求证:∠B +∠D ﹣∠C =180°;(2)如图2,若BF ,DG 分别平分∠ABC 和∠CDE ,BF 、DG 所在的直线相交于点H ,若∠H =α°,求∠C 的度数;(用含α的式子表示)(3)如图3,若BF ,DG 分∠ABC 和∠CDE 为两部分,且∠ABF =n ∠FBC ,∠EDG =n ∠CDG ,直线BF ,DG 相交于点H ,则∠H = .(用含n 和∠C 的式子表示)13、已知,在平面直角坐标系中,点A 在y 轴上,OA =a ,点B (b ,b ),且a 、b 满足√a +b −8+(a −b −4)2=0.(1)则a = ;b = ;(2)如图1,在x 轴上是否存在点C ,使三角形ABC 的面积等于三角形ABO 面积的一半?若存在,请求出点C 的坐标;若不存在,请说明理由;(3)如图2,将线段AB 向左平移m 个单位(m >0),得到线段A 'B ',其中点A ,点B 的对应点分别为点A ',点B '.若点N (﹣1,n )在射线A 'B '上,连接ON ,BN 得到三角形BON ,若三角形BON 的面积大于三角形ABO 面积的12并且小于三角形ABO 面积,则m 的取值范围是 .14、如图1,已知点A (﹣2,0),B (0,﹣4),C (﹣4,﹣6),过点C 作x 轴的平行线m ,一动点P 从C 点出发,在直线m 上以1个单位长度/秒的速度向右运动,与此同时,直线m 以2个单位长度/秒的速度竖直向上运动.(1)直接写出:运动1秒时,点P 的坐标为 ;运动t 秒时,点P 的坐标为 ;(用含t 的式子表示)(2)若点P 在第三象限,且S △ABP =8,求点P 的坐标;(3)如图2,如果将直线AB 沿y 轴负半轴向下平移n 个单位长度,恰好经过点C ,求n 的值.15、已知BE 平分∠ABD ,DE 平分∠BDC ,且∠BED =∠ABE +∠EDC .(1)如图1,求证:AB ∥CD ;(2)如图2,若∠ABE =3∠ABF ,且∠BFD =30°时,试求∠CDF ∠FDE 的值;(3)如图3,若H 是直线CD 上一动点(不与D 重合),BI 平分∠HBD ,画出图形,并探究出∠EBI 与∠BHD 的数量关系.问题探究:(1)如图1,∠CFP +∠EPF =∠AEP ,证明:AB ∥CD ;问题拓展:(2)如图2,AB ∥CD ,∠AEP 的角平分线EK 所在的直线和∠DFP 的角平分线FR 所在的直线交于Q 点,请写出∠EPF 和∠EQF 之间的数量关系,并证明.问题迁移:(3)如图3,AB ∥CD ,直线MN 分别交AB ,CD 于点M ,N ,若点H 在线段MN 上,且∠MEF =α,请直接写出∠HFE ,∠MEH 和∠EHF 之间满足的数量关系(用含α的式子表示).16、当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等例如:在图①、图②中,都有∠1=∠2,∠3=∠4.设镜子AB 与BC 的夹角∠ABC =α.(1)如图①,若α=90°,判断入射光线EF 与反射光线GH 的位置关系,并说明理由.(2)如图②,若90°<α<180°,入射光线EF 与反射光线GH 的夹角∠FMH =β.探索α与β的数量关系,并说明理由.(3)如图③,若α=120°,设镜子CD 与BC 的夹角∠BCD =γ(90°<γ<180°),入射光线EF 与镜面AB 的夹角∠1=m (0°<m <90°),已知入射光线EF 从镜面AB 开始反射,经过n (n 为正整数,且n ≤3)次反射,当第n 次反射光线与入射光线EF 平行时,请直接写出γ的度数.(可用含有m 的代数式表示)17、在平面直角坐标系中,点A ,C 均在x 轴上,点B 在第一象限,直线AB 上所有点的坐标(x ,y )都是二元一次方程x ﹣y =﹣2的解,直线BC 上所有点的坐标(x ,y )都是二元一次方程2x +y =8的解.(1)求B 点的坐标时,小明是这样想的:先设B 点坐标为(m ,n ),因为B 点在直线AB 上,所以(m ,n )是方程x ﹣y =﹣2的解;又因为B 点在直线BC 上,所以(m ,n )也是方程2x +y =8的解,从而m ,n 满足{m −n =−22m +n =8.据此可求出B 点坐标为 ,再求出A 点坐标为 ;C 点坐标为 .(均直接写出结果)(2)若线段BC 上存在一点D ,使S △OCD =12S △ABC (O 为原点),求D 点坐标;(3)点E (a ,﹣3)是坐标平面内的动点,若满足S △ABE ≤13S △ABC ,求a 的取值范围.18、已知:点E 在直线AB 上,点F 在直线CD 上,AB ∥CD .(1)如图1,连EF ,EP 平分∠AEF ,FP 平分∠CFE ,求∠P 的度数.(2)如图2,若∠EGF =160°,射线EH ,FH 分别在∠AEG ,∠CFG 的内部,且∠EHF =40°,当∠AEG =4∠AEH 时,求∠GFH ∠CFG 的值.(3)如图3,在(1)的条件下,在直线CD 上有一动点M (点M 不与点F 重合),EN 平分∠MEF ,若∠PEN =α(0°<α<90°),请直接写出∠EMF = (结果用含α的式子表示).19、在平面直角坐标系中,A (a ,0),B (b ,b ),C (0,c ).(其中a ,b ,c 均为正数),且a ,b ,c 满足{3a −b +2c =8a −2b −c =−9,若√b 的算术平方根为√2. (1)求a ,b ,c 的值.(2)如图1,在第二象限内有一点P (m ,12),若四边形ACPO 的面积与△ABC 的面积相等,求不等式:x−32≥2x−m 3的解集.(3)如图2,BO 平分∠AOC ,过点C 作CD ∥AB 交BO 的延长线于点D ,AE 平分∠BAX ,AE 的反向延长线交BO 的延长线于点F ,设∠CDB =α,∠F =β(其中α,β均为锐角),请直接写出:α+2β3= .23.(10分)如图1,已知直线l1∥l2,点A、B在直线l1上,点C、D在l2上,线段AD交线段BC于点E,且∠BED=60°.(1)求证:∠ABE+∠EDC=60°;(2)如图2,当F、G分别在线段AE、EC上,且∠ABF=2∠FBE,∠EDG=2∠GDC,标记∠BFE为∠1,∠BGD为∠2.①若∠1﹣∠2=16°,求∠ADC的度数;②当k=时,(k∠1+∠2)为定值,此时定值为.24.(12分)如图1,在平面直角坐标系中,已知A(a,1),B(0,b),且实数a,b满足√a+b−2+|a+2b|=0.(1)直接写出两点坐标:A(),B();(2)如图2,将线段AB沿着横坐标均为m的点组成的直线l对折,A与C对应,B与D 对应,若凸四边形ABDC的面积为18,求m的值;(3)如图3,点P在第二、四象限的角平分线上,设P点坐标为(h,﹣h),其中h≠0.①当P在线段AB上时,求h的值;②若S△ABP≥2+32S△OBP.直接写出h的取值范围.。
2024年数学七年级下册几何基础练习题(含答案)

2024年数学七年级下册几何基础练习题(含答案)试题部分一、选择题(每题2分,共20分)1. 在一个等边三角形中,每个角的度数是()。
A. 60°B. 90°C. 120°D. 180°2. 下列哪个图形是一个四边形?()A. 圆B. 三角形C. 正方形D. 直线3. 一个三角形的两个角分别是30°和60°,那么第三个角的度数是()。
A. 30°B. 60°C. 90°D. 120°4. 下列哪个图形是一个平行四边形?()A. 矩形C. 正方形D. 菱形5. 一个等腰三角形的底边长度是10厘米,腰长是12厘米,那么这个三角形的周长是()厘米。
A. 22B. 24C. 26D. 286. 下列哪个图形是一个圆形?()A. 正方形B. 长方形C. 椭圆D. 三角形7. 一个三角形的两个边长分别是5厘米和8厘米,那么这个三角形的周长最小可能是()厘米。
A. 10B. 12C. 13D. 148. 下列哪个图形是一个梯形?()A. 正方形B. 矩形C. 平行四边形9. 一个等腰三角形的底边长度是8厘米,腰长是10厘米,那么这个三角形的周长是()厘米。
A. 18B. 20C. 22D. 2410. 下列哪个图形是一个正方形?()A. 长方形B. 梯形C. 菱形D. 圆二、判断题(每题2分,共10分)1. 一个等边三角形的每个角都是60°。
()2. 一个四边形的内角和是360°。
()3. 一个等腰三角形的两个腰长相等。
()4. 一个正方形的四个角都是90°。
()5. 一个三角形的两个边长分别是5厘米和8厘米,那么这个三角形的周长最小可能是13厘米。
()以上是一个练习题的示例,你可以根据实际情况进行调整和扩展。
希望对你有所帮助!一、选择题(每题2分,共20分)1. 在一个等边三角形中,每个角的度数是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级下学期几何专题
一、精心选一选,慧眼识金!
1.过五边形的一个顶点可作()条对角线
A.1
B.2
C.3
D.4
2.三角形的三个内角( )
A、至少有两个锐角
B、至少有一个直角
C、至多有两个钝角
D、至少有一个钝角
3.下列图形中具有稳定性的是( )
A、菱形
B、钝角三角形
C、长方形
D、正方形
4.下列图形中,是属于轴对称图形的是()
A. B. C. D.
●5.如图:BE、CF是ABC
∆的角平分线,0
∠,
A
=
40
则=
∠BDC( D )
110
65 C. 0
95 D. 0
A.0
50 B. 0
6.以下列长度的三条线段为边,不能组成三角形的是()
A.4,4,5 B.3,2,5 C.3,12,13 D.6,8,10
7. 下列说法:①等边三角形是等腰三角形;②在三角形中至少有二个锐角;③三角形的一个外角等于两个内角的和;④钝角三角形的三条高相交于三角形外一点,其中正确的个数有()
A、1个
B、2个
C、3个
D、4个
8. 下列图形:①角;②线段;③等腰三角形;④等边三角形;⑤平行四边形中是轴对称图形的个数是()
A、1个
B、2个
C、 3个
D、4个
9.平面内三条直线最少有()个交点
A.3
B.2
C.1
D.0
●10.已知Rt△ABC,∠A=30°,则∠B=( C )
A.60°
B.90°
C.60°或90°
D.30°
11.如图,由AB∥CD,能推出正确结论的是( B ) A 、∠1=∠2 B 、∠3=∠4 C 、∠A=∠C D 、AD∥BC
12.下列命题为真命题的是( D ) A.内错角相等
B.点到直线的距离即为点到直线的垂线段
C.如果∠A+∠B+∠C=180°,那么∠A 、∠B 、∠C 互补
D.同一平面内,垂直于同一直线的两直线平行。
13.用同一种下列形状的图形地砖不能进行平面镶嵌的是( C ) A.正三角形 B.长方形 C.正八边形 D.正六边形
14.当多边形的边数增加时,其外角和( C ) A 、增加 B 、减少 C 、不变 D 、不能确定
● 15.已知:一光线沿平行于AB
经镜面AC 、AB 反射后,如图所示, 若∠A=40°则∠MNA=
( B ) A.90° B.100° C.60° D.80°
● 16.已知:如图B 处在A 处的南偏西40C 处在A 处的南偏东15°方向上,
C 处在B 处的北偏东80°方向,
则∠ACB=( B )
A.90°
B.85°
C.40°
D.60° 17.若一个三角形中的其中一个外角等于与它相邻的内角,则此三角形是( A ) A 、直角三角形 B 、锐角三角形 C 、钝角三角形 D 、无法确定
18.点到直线的距离是指这点到这条直线的( D )
A 、垂线段
B 、垂线
C 、垂线的长度
D 、垂线段的长度
二、巧心填一填,一锤定音!
19.已知∠a 的对顶角是58°,则∠a=______。
B
A C
20.在同一平面内,若直线a∥c,b∥c,则a_____b 。
21.七边形的内角和等于________,十二边形的外角和为_________
22.经过一点________一条直线垂直于已知直线。
● 23.如图所示,CE 垂直平分BD ,∠A =∠DBA , AC =16,ΔBCD 的周长是25,则BD 的长是 。
24.已知:直线AB 、CD 被 直线L 所截,∠1=∠2=85°,
则∠1的同位角度数为
25.
: ______________________________________
● 26、已知:AB//CD ,
∠A=140°,∠E=30°, 则∠C=________
● 27、若等腰三角形的边长分别为4和6,则它的周长为_______。
28、已知:Rt △ABC ,∠BAC=90°
AD ⊥BC 于D ,则图中相等的 锐角共有 对。
29、已知:△ABC ,∠A 比∠B 大50°,∠C=30°,则△ABC 为
________三角形。
30、已知:如图,AD ⊥BC 于D , 则图中共有 个以AD 为 高的三角形。
● 31.一个n 边形除一个内角外,其余各个内角的和为1680度,那么这个多
边形的边数是 ,这个内角是 度。
32. 在平面镜里看到背后墙上,电子钟示数如图所示,则这时的时间应是 .
A C B
E D A
C
B D A B D
C E 2
1
A B C D
l
C
B
A
公路
A 公路
三、专心作一作,美丽成形!
(保留作图过程和作图的痕迹)
33.如图,作出△ABC 关于直线l 的对称图形;
34.“西气东输”是造福子孙后代的创世纪工程。
现有两条高速公路和A 、B 两个城镇(如图),准备建立一个燃气中心站P ,使中心站到两条公路距离相等,并且到两个城镇距离相等,请你画出中心站位置。
35.如图(2),根据下列条件,利用网格点和三角板画图: (1)将△AB C 向左平移6个单位长度,得到△A′B ′C ′ (2)画出AB 边上的中线CD (3)画出BC
边上的高线AE
四、细心算一算,马到成功!
36.已知:如图所示的长方形ABCD 沿EF 折叠至D 1、C 1位置, 若∠C 1FE=115°,求∠AED 1度数。
37.已知:如图(4),直线AE∥BF,∠EAC=28°,∠FBC=50°,求 ∠ACB 的度数。
A
B
D
1
38.求下图(5)中x 的值
39.如图(1),在下列括号中填写推理理由 ∵∠l=135°(已知)
∴∠3=∠135°( ) 又∵∠2=45°(已知)
∴∠2+∠3=45°+135°=180°
∴a∥b( )
五、静心想一想,耐心做一做,天道酬勤!
● 40. 已知:如图(3),CD⊥AB 于D ,点E 为BC 边上的任意一点,EF⊥ AB 于F ,且∠l=∠2,那么BC 与DG 平行吗?请说明理由。
● 41.已知:AE 平分△ABC 的外角,且
AE//BC , (1)试判断∠B 、∠C 的大小关系,并说明理由
(2)在(1)的基础上,若边AB 的垂直平分线FM
与边AC 相交于点M ,且∠C=70°, 求∠CBM 的度数。
A C
B
D
E
F
M
42.已知:△ABC ,射线BE 、CF 分别平分∠ABC 和∠ACB ,且BE 、CF
相交于点O 。
探索:
(1)若∠ABC=40,∠ACB=50°,则∠BOC =_______
(2)若∠ABC+∠ACB=lO0°,则∠BOC=________ 。
(3)若∠A=70°,则∠BOC=_________。
(4)若∠BOC=140°,则∠A=________。
(5)你能发现∠BOC 与∠A 之间有什么数量关系吗? 请说明理由。
证明:求证:∠BOC=90°+2
1
∠A
B C O F A
拓展:(6)若将条件“CF平分∠ACB”改为“CF平分与∠ACB相邻的外角”,其它条件不变。
试问(5)中的结论是否仍成立?若成立说明理由;若不成立,请找出∠BOC与∠A的关系并予证明。
祝贺你已圆满完成本专题!请你认真复查,不要留下遗憾哦!
参考答案
一、1~5 BABBD 6~10 BCDDC 11~15 BDCCB 16~18 BAD
二、19.58° 20.11 21. 900°360° 22. 有且和只有 23. 7 24. 95°
25.如果两个角相等,那么这两个角的补角也相等。
26. ∠C=110°
27. 14 或 16 28. 2 29.钝角 30.6 31.12 120° 32. 21︰05
三、略
四、36.25° 37. 78° 38.60° 39. 同位角相等同旁内角互补,两直线平行
五、40.平行 41.(1) ∠B=∠C (2) ∠CBM=30° 42. (1) 135° (2) 130°
(3) 125° (4) 100° (5) ∠BOC=90°+1
2∠A (6) ∠BOC=
1
2∠A。
