2012年蚌埠市高三年级三质检_数学试题
2024届安徽省蚌埠市高三下学期第三次质量检查数学试题及答案

蚌埠市2024届高三年级第三次教学质量检查考试数 学本试卷满分150分,考试时间120分钟注意事项:1 答卷前,务必将自己的姓名和座位号填写在答题卡和试卷上。
2 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,务必擦净后再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1 已知集合A={1,3,5,7,9},B={3,6,9,12},则A∩B=A {3,9}B {1,3,5,6,7,9,12}C {1,5,7}D {6,12}2 已知平面向量a=(1,m),b=(-2,4),且a∥b,则m=A 2B12C -12D -23 已知曲线C∶x24+y2m=1(m≠0),则“m∈(0,4)”是“曲线C的焦点在x轴上”的A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件4 在△ABC中,角A,B,C的对边分别为a,b,c,已知a=acosB+bcosA=1,sinC=槡22,则A b=1B b槡=2C c槡=2D c槡=35 记数列{an}的前n项和为Sn,若Sn{}n是等差数列,S2=-8,S6=0,则a3+a4=A -8B -4C 0D 46 (1-x+x2)2·(1+x)3的展开式中,x4的系数为A 1B 2C 4D 57 在一组样本数据中,1,2,3,4出现的频率分别为p1,p2,p3,p4,且∑4i=1pi=1,则下面四种情形中,对应样本的标准差最小的一组是A p1=0 1,p2=0 2,p3=0 3,p4=0 4B p1=0 4,p2=0 3,p3=0 2,p4=0 1C p1=p4=0 1,p2=p3=0 4D p1=p4=0 4,p2=p3=0 18 已知抛物线C∶y2=4x,过其焦点F的直线交C于A,B两点,M为AB中点,过M作准线的垂线,垂足为N,若|AF|=4,则|NF|=A43B 槡433C83D 槡833二、选择题:本题共3小题,每小题6分,共18分。
安徽省蚌埠市高考数学三模试卷(理科)
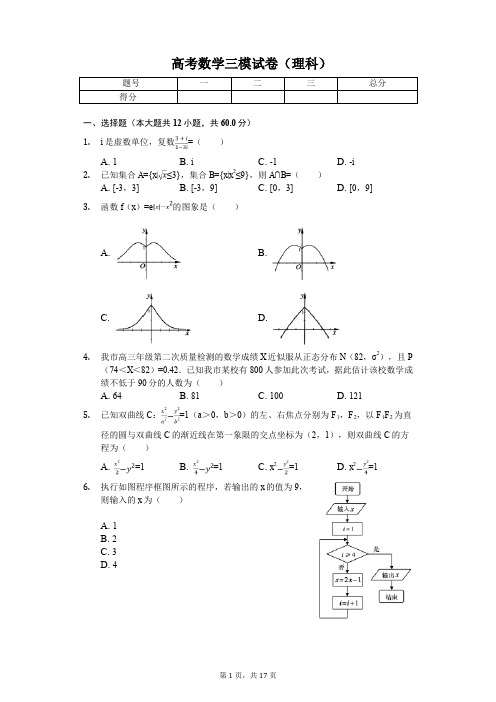
高考数学三模试卷(理科)一、选择题(本大题共12小题,共60.0分)1.i是虚数单位,复数=()A. 1B. iC. -1D. -i2.已知集合A={x|≤3},集合B={x|x2≤9},则A∩B=()A. [-3,3]B. [-3,9]C. [0,3]D. [0,9]3.函数f(x)=e的图象是()A. B.C. D.4.我市高三年级第二次质量检测的数学成绩X近似服从正态分布N(82,σ2),且P(74<X<82)=0.42.已知我市某校有800人参加此次考试,据此估计该校数学成绩不低于90分的人数为()A. 64B. 81C. 100D. 1215.已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1,F2,以F1F2为直径的圆与双曲线C的渐近线在第一象限的交点坐标为(2,1),则双曲线C的方程为()A. =1B. =1C. x2=1D. x2=16.执行如图程序框图所示的程序,若输出的x的值为9,则输入的x为()A. 1B. 2C. 3D. 47.如图,网格纸上小正方形的边长均为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A.B.C.D.8.若二项式(x6)n的展开式中含有常数项,则n的值可以是()A. 8B. 9C. 10D. 119.已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<)图象的相邻两条对称轴之间的距离为,将函数f(x)的图象向左平移个单位长度后,得到函数g(x)的图象.若函数g(x)为偶函数,则函数f(x)在区间[-]上的值域是()A. [-1,]B. (-2,1)C. (-1,)D. [-2,1]10.如图,在四棱锥P-ABCD中,BC∥AD,AD=2BC,点E是棱PD的中点,PC与平面ABE交于F点,设PF=λFC,则λ=()A. 4B. 3C. 2D. 111.设抛物线C:y2=2px(p>0)的焦点为F,点M在抛物线C上,|MF|=2.若以MF为直径的圆过点(0,1),则抛物线C的焦点到准线距离为()A. 2B. 2或4C. 8D. 8或1612.已知函数f(x)=x+,过点(1,0)作曲线f(x)的两条切线,切点为A(x1,f(x1)),B(x2,f(x2)),其中0<x1<x2.若在区间(x1,x2)中存在唯一整数,则a的取值范围是()A. (-∞,-2)B. [-1,-2)C. [-)D. (-)二、填空题(本大题共4小题,共20.0分)13.已知向量=(x,2),=(-1,1),若||=||,则x的值为______.14.在△ABC中,角A,B,C所对的边分别为a,b,c,若2sin2A+c(sin C-sin A)=2sin2B,且△ABC的面积S=abc.则角B=______.15.回收1吨废纸可以生产出0.8吨再生纸,可能节约用水约100吨,节约用煤约1.2吨,回收1吨废铅蓄电池可再生铅约0.6吨,可节约用煤约0.8吨,节约用水约120吨,回收每吨废铅蓄电池的费用约0.9万元,回收1吨废纸的费用约为0.2万元.现用于回收废纸和废铅蓄电池的费用不超过18万元,在保证节约用煤不少于12吨的前提下,最多可节约用水约______吨.16.已知球D的半径为3,圆A与圆C为该球的两个小圆,MN为圆A与圆C的公共弦,MN=2,若点B是弦MN的中点,则四边形ABCD的面积的最大值为______.三、解答题(本大题共7小题,共82.0分)17.已知数列{a n}中,a1=3,且n(n+1)(a n-a n+1)=2,其中n∈N*.(1)求数列{a n}的通项公式;(2)设b n=,求数列{b n}的前n项和S n.18.如图,在以P为顶点,母线长为的圆锥中,底面圆O的直径AB长为2,C是圆O所在平面内一点,且AC是圆O的切线,连接BC交圆O于点D,连接PD,PC.(1)求证:平面PAC⊥平面PBC;(2)若E是PC的中点,连接OE,ED,当二面角B-PO-D的大小为120°时,求平面PAC与平面DOE所成锐二面角的余弦值.19.已知点E(-2,0),F(2,0),P(x,y),是平面内一动点,P可以与点E,F重合.当P不与E,F重合时,直线PE与PF的斜率之积为.(1)求动点P的轨迹方程;(2)一个矩形的四条边与动点P的轨迹均相切,求该矩形面积的取值范围.20.某地种植常规稻α和杂交稻β,常规稻α的亩产稳定为485公斤,今年单价为3.70元/公斤,估计明年单价不变的可能性为10%,变为3.90元/公斤的可能性为70%,变为4.00元/公斤的可能性为20%.统计杂交稻β的亩产数据,得到亩产的频率分布直方图如图①.统计近10年杂交稻β的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为(x i,y i)(i=1,2,..10),并得到散点图如图②.(1)根据以上数据估计明年常规稻α的单价平均值;(2)在频率分布直方图中,各组的取值按中间值来计算,求杂交稻β的亩产平均值;以频率作为概率,预计将来三年中至少有二年,杂交稻β的亩产超过795公斤的概率;(3)①判断杂交稻β的单价y(单位:元/公斤)与种植亩数x(单位:万亩)是否线性相关?若相关,试根据以下的参考数据求出y关于x的线性回归方程;②调查得知明年此地杂交稻β的种植亩数预计为2万亩.若在常规稻α和杂交稻β中选择,明年种植哪种水稻收入更高?统计参考数据:,,,,附:线性回归方程,.21.已知函数f(x)=-x,其中a≥1.(1)求函数f(x)的单调区间;(2)讨论函数f(x)的零点个数.22.在平面直角坐标系xOy中,曲线C的参数方程为(α为参数),直线l的参数方程为(t为参数,0≤β<π),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.(1)求曲线C的极坐标方程;(2)已知直线l与曲线C相交于A,B两点,且|OA|-|OB|=2,求β.23.已知:a2+b2=1,其中a,b∈R.(1)求证:≤1;(2)若ab>0,求(a+b)(a3+b3)的最小值.答案和解析1.【答案】B【解析】解:===i,故选:B.根据复数运算的除法运算法则,分子分母同乘以1+3i,进行运算.本题考查了复数的除法运算,掌握运算法则是关键.本题属于基础题.2.【答案】C【解析】解:因为集合A={x|≤3}={x|0≤x≤9},B={x|x2≤9}={x|-3≤x≤3},所以A∩B={x|0≤x≤3},故选:C.通过解不等式,把集合A,B化简,然后求出A∩B.本题考查了不等式的解法,交集的基本运算,正确求解不等式是本题的关键,属于基础题.3.【答案】A【解析】解:f(0)=1,排除选项C,D;由指数函数图象的性质可得函数f(x)>0恒成立,排除选项B,故选:A.先根据函数值f(0)=1排除选项C,D;再根据指数函数图象的性质可得f(x)>0恒成立,即可得到答案.本题主要考查函数图象的判断,结合函数的性质是解决本题的关键.,图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.4.【答案】A【解析】解:因为数学成绩X近似服从正态分布N(82,σ2),所以数学成绩X关于X=82对称,∵P(74<X<82)=0.42.∴P(82<X<90)=0.42.P(X≥90)=P(X≤74)==0.08,所以我市某校有800人参加此次考试,据此估计该校数学成绩不低于90分的人数为0.08×800=64,故选:A.通过数学成绩X近似服从正态分布N(82,σ2),所以数学成绩X关于X=82对称,通过P(74<X<82)=0.42.可以计算出P(82<X<90)=0.42.利用对称性即可得出P (X≥90)=P(X≤74),这样就可以估计出我市某校有800人参加此次考试,该校数学成绩不低于90分的人数.本题考查了正态分布的对称性及其应用,考查了推理能力与计算能力,属于基础题.5.【答案】B【解析】解:设P(2,1),F1(-c,0),F2(c,0),由题意可知:点P在y=x上,所以a=2b,又P在以F1F2为直径的圆上,所以OF2=OP=(O为坐标原点),即c=,又a2+b2=c2=5,a=2b,解得a=2,b=1,所以双曲线方程为-y2=1,故选:B.设P(2,1),由题意可知:点P在y=上,再由OP=OF2列方程组,结合c2=a2+b2即可求出a,b的值.本题考查了求双曲线标准方程,解题的关键是应用向量构造等式.6.【答案】B【解析】解:执行程序框图,输入x,当i=1时,得到2x-1;当i=2时,得到2(2x-1)-1=4x-3,当i=3时,得到4(2x-1)-3=8x-7,当i=4时,退出循环,输出8x-7=9,解得x=2,故选:B.直接利用程序框图的循环结构的应用求出结果.本题考查循环结构的程序框图的输出结果的计算问题,着重考查推理与运算能力,属于基础题.7.【答案】A【解析】解:通过三视图可知,该几何体是由一个球和一个三棱柱组合而成,因此:=.故选:A.通过三视图可知,该几何体是由一个球和一个三棱柱组合而成,分别求出它们的体积相加即可.本题考查了通过三视图求几何体的体积问题,关键是识别出几何体的形状.主要考察学生的运算能力和转换能力,属于基础题.8.【答案】C【解析】解:二项式(x6)n的第r+1项为:T r+1=•(-1)r•,由题意可知含有常数项,所以只需4n-5r=0,对照选项当n=10时,r=8,故选:C.写出二项式展开式的通项,化简,令x的指数为零,对照选项,求出答案.本题考查了二项式定理的应用,解题的关键是应用二项式的展开式的通项公式,属于基础题.9.【答案】D【解析】解:因为函数f(x)=2sin(ωx+φ)(ω>0,|φ|<),图象的相邻两条对称轴之间的距离为,所以T=π,而ω>0,解得:ω=2,又因为函数f(x)的图象向左平移个单位长度后,得到函数g(x)的图象,所以g(x)=2sin[ω(x+)+φ],由函数g(x)为偶函数,可得(k∈Z),而|φ|<,所以:φ=-,因此:,由于:,所以:,所以:.所以函数f(x)在区间上的值域是[-2,1].故选:D.通过函数f(x)=2sin(ωx+φ)(ω>0,|φ|<)图象的相邻两条对称轴之间的距离为,可以求出周期,进而可以求出ω的值,函数f(x)的图象向左平移个单位长度后,得到函数g(x)的图象,因此g(x)=2sin[ω(x+)+φ],函数g(x)为偶函数,有,结合已知|φ|<,求出φ,再利用正弦函数的性质,求出函数f(x)在区间[]上的值域.本题综合考查了正弦型函数的图象和单调性.解决本题的关键是对函数g(x)为偶函数的理解,写出等式.主要考察学生的运算能力和转换能力,属于基础题型.10.【答案】C【解析】解:延长DC和AB交于一点G,连接EG交PC于点F,平面ABE即为平面AEG,连接PG,因为AD=2BC,且AD∥BC,可得点C,B分别是DG和AG的中点,又点E是PD的中点,即GE和PC分别为△PDG的中线,从而可得点F为△PDG的重心,即PF=2FC,可得λ=2,故选:C.延长DC和AB交于一点G,连接EG交PC于点F,由已知可确定点F为三角形的重心,从而可得答案.本题考查平面的确定和三角形的重心的性质,考查分析和推理能力,属于中档题.11.【答案】A【解析】解:设点M的坐标为(,y0),A(0,1),抛物线的焦点F(,0),抛物线的准线为x=-,由抛物线的定义可知:|MF|=+=2,①,因为以MF为直径的圆过点A(0,1),∴=-1,解得y0=2,代入①中得p=2,∴抛物线C的焦点到准线距离为2,故选:A.设出M的坐标为(,y0),A(0,1),根据MF=2可得到|=+=2,①,再由直线垂直,进而可以求出y0的值,代入①,求出p即可.本题考查了抛物线的定义以及p的几何意义.重点是由以MF为直径的圆过点(0,1),想到直线垂直.12.【答案】C【解析】解:由f(x)=x+,得f′(x)=1-,切点为A(x1,f(x1))的切线的斜率为f′(x1)=1-,∴切点为A(x1,f(x1))的切线方程为:,同理可求得切点为B(x2,f(x2))的切线方程为:,两条切线过点(1,0),把(1,0)代入两条切线方程得:①,②,∴可以把x1,x2看成2x2+2ax-a=0的两个根,∵0<x1<x2,∴③,即-a>2,∵0<x1<x2,∴,>>1,在区间(x1,x2)中存在唯一整数必须满足:,得-2<a≤,结合③,可得a的取值范围是[-).故选:C.对函数求导,然后求出过点(1,0)作曲线f(x)的两条切线,把(1,0)代入两条切线方程,得到,,可以把x1,x2看成2x2+2ax-a=0的两个根,由0<x1<x2,得,解出a的取值范围,可以证明出x2>1,在区间(x1,x2)中存在唯一整数,必须要满足,解出a的取值范围.本题考查了导数的几何意义、求曲线方程的切线.本题重点考查了在区间上方程有唯一整数解问题,考查了转化思想、方程思想,是中档题.13.【答案】2【解析】解:根据题意,若||=||,则||2=||2,变形可得:•=0,又由向量=(x,2),=(-1,1),则•=-x+2=0,解可得:x=2;故答案为:2根据题意,由||=||,结合向量数量积的计算公式可得•=0,进而由数量积的坐标计算公式计算可得答案.本题考查向量数量积的计算,关键是分析向量、的关系,属于基础题.14.【答案】【解析】解:由于S=abc,可得:abc=ab sin C,解得:c=2sin C,代入2sin2A+c(sin C-sin A)=2sin2B中,得sin2A+sin2C-sin A sin C=sin2B,由正弦定理,可将上式化简为,a2+c2-ac=b2,由余弦定理可知:b2=a2+c2-2ac cos B,所以:cos B=,又因为B∈(0,π),所以角B=.故答案为:.△ABC的面积S=abc,结合面积公式,可得c=2sin C,代入已知等式中,得到sin2A+sin2C-sin A sin C=sin2B,先用正弦定理,后用余弦定理,最后求出角B的值.本题考查了面积公式、正弦定理、余弦定理.解题的关键在于对公式的模型特征十分熟悉,属于基础题.15.【答案】9000【解析】解:设回收废纸x吨,回收废铅蓄电池y吨,可节约用水z吨,由已知条件可得,z=100x+120y,作出不等式组表示的可行域,如图所示,z=,平移直线可得当直线过点A时,在y轴的截距最大,即z最大,由图可得点A(90,0),此时z取得最大值为9000.故答案为:9000.设回收废纸x吨,回收废铅蓄电池y吨,由题意列出不等式组及目标函数,转化成求目标函数的最值问题.本题考查简单线性规划的应用,属于基础题解决线性规划的应用题时,其一般步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件;②由约束条件画出可行域;③分析目标函数z与直线截距之间的关系;④使用平移直线法求出最优解;⑤还原到现实问题中.16.【答案】2【解析】解:如下图所示:点B是弦MN的中点,由DB⊥MN,得DB=,又∵DA⊥AB,∴DA2+AB2=4,∴DA2+AB2=4≥2DA•AB,得,当且仅当DA=AB=时,等号成立,同理S△CAB≤1,当且仅当DC=CB=时,等号成立,因此四边形ABCD的面积的最大值为2.故答案为:2.利用球的性质可以推出DA⊥AB,得到DA2+AB2=4,这样可以得到S△DAB≤1,同理S△DAB≤1,这样求出四边形ABCD的面积的最大值.本题考查了球的性质.重点考查了重要不等式,关键是构造直角三角形,得到两线段长度的平方和是定值,是中档题.17.【答案】解:由题意知,n(n+1)(a n-a n+1)=2,a n-a n+1==2(-),即有a n+1-=a n-,进而a n-=a n-1-=…=a1-=1,即a n=1+;(2)a n=1+=,a1a2…a n=•…•=,于是b n===-,前n项和S n=-+-+…+-=2-.【解析】(1)由n(n+1)(a n-a n+1)=2,可以变形为a n+1-=a n-,根据等差数列的定义可以求出数列{a n}的通项公式;(2)根据(1)可以求出b n===-,应用裂相消法求出{b n}的前n项和S n.本题考查数列递推公式求出等差数列的通项公式.重点考查了裂相相消法求数列的前n 项和,属于中档题.18.【答案】证明:(1)AB是圆O的直径,AC与圆O切于点A,AC⊥AB,PO⊥底面圆O,∴PO⊥AC,PO∩AB=O,AC⊥平面PAB,∴AC⊥PB.又∵在△PAB中,PA=PB=AB,∴PA⊥PB,∵PA∩AC=A,∴PB⊥平面PAC,从而平面PAC⊥平面PBC.解:(2)∵OB⊥PO,OD⊥PO,∴∠BOD为二面角B-PO-D的平面角,∴∠BOD=120°,如图建立空间直角坐标系,由题意得OB=1,则A(0,-1,0),B(0,1,0),D(,-,0),C(,-1,0),P(0,0,1),E(,-),由(1)知==(0,-1,1)为平面PAC的一个法向量,设平面ODE的法向量为=(x,y,z),=(,-),=(,-),∵,∴,取z=1,得=(),∴cos<>==-.∴平面PAC与平面DOE所成锐二面角的余弦值为.【解析】(1)由AB是圆O的直径,AC与圆O切于点A,可得AC⊥AB,由PO⊥底面圆O,可得PO⊥AC,利用线面垂直的判定定理可知,AC⊥平面PAB,即可推出AC⊥PB.又在△PAB中,PA=PB=AB,可推出PA⊥PB,利用线面垂直的判定定理可证PB⊥平面PAC,从而利用面面垂直的判定定理可证出平面PAC⊥平面PBC.(2)由OB⊥PO,可知∠BOD为二面角B-PO-D的平面角,建立空间直角坐标系,利用向量法能求出平面PAC与平面DOE所成锐二面角的余弦值.本题考查了通过线面垂直证明面面垂直.重点考查了利用空间向量法求二面角的问题,是中档题.19.【答案】解:(1)当P与点E,F不重合时,设P(x,y),得,即,当P与点E,F重合时,适合上式,综上,动点P的轨迹方程为;(2)记矩形面积为S,当矩形一边与坐标轴平行时,易知S=8.当矩形各边均不与坐标轴平行时,根据对称性,设其中一边所在直线方程为y=kx+m,则对边方程为y=kx-m另一边所在的直线为y=-x+n,则对边方程为y=-x-n,∴矩形的邻边长为,b=,由得(1+4k2)x2+8kmx+4(m2-1)=0,则△=0,得4k2+1=m2,同理:,∴S=ab=×==4=4=4∈(8,10]综上:S∈(8,10].【解析】(1)当P与点E,F不重合时,根据斜率之积可直接求出动点P的轨迹方程;考虑到P与点E,F重合的情况,最后写出动点P的轨迹方程;(2)记矩形面积为S,当矩形一边与坐标轴平行时,易知S=8;当矩形各边均不与坐标轴平行时,根据对称性,设其中一组对边所在直线方程为y=kx±m,另一组对边所在的直线为,则由平行线间距离得矩形长宽a,b,联立直线与椭圆方程,由判别式为0可得k与m,n的关系式,代入面积算式结合不等式可得最值.本题考查了直译法求曲线的轨迹方程.重点考查了求椭圆外切矩形的面积的取值问题,考查了基本不等式的应用.(),估计明年常规稻α的单价平均值为3.9(元/公斤);(2)杂交稻β的亩产平均值为:[(750+810+820)×0.005+(760+800)×0.01+(770+790)×0.02+780×0.025]×10=782.依题意知杂交稻β的亩产超过795公斤的概率P=0.1+0.05×2=0.2,则将来三年中至少二年,杂交稻β的亩产超过795公斤的概率为:;(3)①∵散点图中各点大致分布在一条直线附近,∴可以判断杂交稻β的单价y与种植亩数x线性相关,由题中提供的数据得:,,∴线性回归方程为;②估计明年杂交稻β的单价元/公斤;估计明年杂交稻β的每亩平均收入为782×2.50=1955元/亩,估计明年常规稻α的每亩平均收入为485×E(ξ)=485×3.9=1891.5元/亩,∵1955>1891.5,∴明年选择种杂交稻β收入更高.【解析】(1)设明年常规稻α的单价为ξ,列出ξ的分布列,计算E(ξ);(2)根据频率分布直方图中,各组的取值按中间值来计算,所以可以求出杂交稻β的亩产平均值;根据以频率作为概率,可以预计出将来三年中至少有二年,杂交稻β的亩产超过795公斤的概率;(3)①根据题中给的数据和分式,可以求出线性回归方程;②估计明年杂交稻β的单价,进而可以估计明年杂交稻β的每亩平均收入,估计明年常规稻α的每亩平均收入,两者进行比较,可以得出明年选择种杂交稻β收入更高.本题考查了求离散型随机变量的分布列及均值、求线性回归方程并依据线性回归方程做出预测,是中档题.21.【答案】解:(1),x∈R令f'(x)=0得x1=1,x2=ln a,①当ln a=1,即a=e时,f'(x)≥0恒成立,∴f(x)在(-∞,+∞)上增;②当ln a<1,即1≤a<e时,令f'(x)>0,得x>1或x<ln a,令f'(x)<0,得ln a<x<1,∴f(x)在(-∞,ln a)上增,在(ln a,1)上减,在(1,+∞)上增;③当ln a>1即a>e时,令f'(x)>0,得x>ln a或x<1,令f'(x)<0,得1<x<ln a,∴f(x)在(-∞,1)上增,在(1,ln a)上减,在(ln a,+∞)上增;综上,当a≤0时,函数f(x)的减区间为(-∞,1),增区间为(1,+∞);当a=e时,f(x)的单调增区间为(-∞,+∞);当0<a<e时,f(x)的单调增区间为(-∞,ln a),(1,+∞),单调减区间为(ln a,1);当a>e时,f(x)的单调增区间为(-∞,1),(ln a,+∞),单调减区间为(1,ln a).(2)(i)由(1)知,当a=e时,f(x)单调递增,又f(0)=0,故1个零点;(ii)当a>e或1≤a<e时,,①当a=1时,f(x)在(-∞,0)上增,在(0,1)上减,在(1,+∞)上增,∵f(0)=0,,,此时2个零点;②当a>e时,f(x)在(-∞,1)上增,在(1,ln a)上减,在(ln a,+∞)上增;,又f(0)=0,此时1个零点;③当1<a<e时,f(x)在(-∞,ln a)上增,在(ln a,1)上减,在(1,+∞)上增;,,,f(0)=0,∵,∴当时,,有1个零点;当时,,有2个零点;当时,,有3个零点;综上所述:当时,有1个零点;当a=1或时,有2个零点;当时,有3个零点.【解析】(1)求导,令导函数为零,解出方程,根据根之间的大小关系,进行分类讨论,求出函数f(x)的单调区间;(2)(i)由(1)知,当a=e时,f(x)单调递增,可以判断有一个零点;(ii)当a>e或时,f(ln a)=,结合(1)中的结论,对a分类讨论,利用单调性,判断零点的个数.本题考查了利用导数研究函数的单调性和零点问题,解题的关键是根据单调性,求出极值点,而后分类讨论,求出函数零点的个数,属难题.22.【答案】解:(1)由曲线C的参数方程(α为参数),可得普通方程为(x-4)2+y2=9,即x2+y2-8x+7=0,∴曲线C的极坐标方程为ρ2-8ρcosθ+7=0;(2)由直线l的参数方程(t为参数,0≤β<π),可得直线的极坐标方程为θ=β(ρ∈R),∵直线l与曲线C相交于A,B两点,∴设A(ρ1,β),B(ρ2,β),联立,可得ρ2-8ρcosβ+7=0,∵△=64cos2β-28>0,即,ρ1+ρ2=8cosβ,ρ1ρ2=7.∴|OA|-|OB|=|ρ1-ρ2|==,解得cos,∴或.【解析】(1)利用平方和为1消去参数α得普通方程,利用x2+y2=ρ2,x=ρcosθ,将直角坐标方程转为极坐标方程.(2)将直线l和曲线C的极坐标方程联立,根据极径的几何意义可得|OA|-|OB|=|ρ1-ρ2|,即可得结果.本题考查极坐标方程,直角坐标方程以及参数方程之间的转化,考查极径几何意义的应用,属于中档题.23.【答案】解:(1)证明:根据题意,≤1⇒|a-b|≤|1-ab|⇒(a-b)2≤(1-ab)2,变形可得:(a2-1)(1-b2)≤0,又由a2+b2=1,则a2≤1,b2≤1,则有(a2-1)(1-b2)≤0,故原不等式成立.(2)根据题意,(a+b)(a3+b3)=a4+ab3+a3b+b4≥a4+2+b4=(a2+b2)2=1,当且仅当a=b=或-时,等号成立,则(a+b)(a3+b3)的最小值为1.【解析】(1)根据题意,分析可得所证不等式等价于|a-b|≤|1-ab|,进而变形可得(a-b)2≤(1-ab)2,进而可得可得:(a2-1)(1-b2)≤0,结合a、b的范围分析可得证明;(2)根据题意,分析可得(a+b)(a3+b3)=a4+ab3+a3b+b4≥a4+2+b4,进而利用基本不等式分析从而可求得最值.本题考查不等式的证明方法,涉及利用基本不等式求最值问题,属于中档题.。
安徽省蚌埠市2012届高三3月第二次质检试题(理综)word版解读

安徽省蚌埠市2012届高三3月第二次质检试题理综第I卷(选择题120分)1、下列有关细胞衰老、凋亡、坏死与癌变的叙述,正确的是A、凡细胞凋亡受基因控制;细胞癌变不受基因控制B、细胞衰老,代谢减弱;细胞癌变,代谢增强C、细胞坏死,膜通透性降低;细胞癌变,膜粘着性增强D、细胞癌变,细胞周期变短;细胞凋亡,细胞周期变长2、对下列四个曲线图中a、b两点的有关叙述,正确的是A、图甲中,a,b两点叶绿体的C3含量的变化趋势相反B、图乙中,a,b两点神经纤维膜内外电位差不相等C、图丙中,a,b两点细胞呼吸产生CO2酒精的量均相等A、图丁中,a,b两点可分别表示茎向光弯曲时向光侧和背光侧的生长素浓度3、下列甲表示家系中某遗传病的谱图(图中有阴影的为患者),图乙是对发病基因的测定结果,已知控制性状的基因是位于人类性染色体的同源部分,则II4的有关基因组成应是乙图中的4、图甲为细胞膜的结构示意图,图乙为突触结构示意图,下列相关叙述正确的是A、图甲中A,B分别表示蛋白质分子与磷脂分子,两者均属内环境成分B、若图甲中的M侧为肠道,那么N侧是毛细血管腔C、若图乙中C为抑制性递质,C与D结合后突触后膜的膜电位可由外正内负转变为外负内正D、若图乙中C,D分别表示神经递质与受体,C的释放体现了突触前膜的结构特点5、下表选项中,甲、乙、丙三者关系能用右下图表示的是6、下列有关酶特性的相关实验设计中,最科学、严谨的一项是7、化合物A是近年来采用的锅炉水添加剂,其结构简式如右图,A能除去锅炉水中溶解的氧气,下列说法正确的是A、A分子中所有原子都在同一平面内B、A分子中所含的σ键与π键个数之比为10:1C、1 mol A所含有的电子数为44N A(N A表示阿伏伽德罗常数)D、1 molA与O2反应生成CO2、N2、H2O的物质的量之比为1:2:38、在实验中进行下列实验,括号内的实验用品都能用到的是A、除去苯中的、苯酚(溴水、漏斗、玻璃棒)B、溶液中FE3-的校验(试管、氯水、KSCN溶液)C、测定Na2Co3和NaHCO3混合物中Na2CO3的质量分数(试管、酒精灯、托盘天平)D、用NaOH标准溶液确定未知尝试的硫酸溶液(石蕊试液、碱式滴定管、锥形瓶)9、室温下,下列各组粒子在指定溶液中能大量共存的是A、在PH=11的溶液中:K+,Na2-,CO32-,SO32-B、含有大量ClO+的溶液:H+,Mg2+,I+,SO210、下列说法正确的是A、相同温度下,等体积的任何气体所含的气体分子数相同B、原子间形成化学健,既与核外电子有关,又与原子核有关C、为同一主簇元素,所形成的最高价氧化物的晶体类型相同D、向饱和FeCl3溶液中滴加过量的氮水可抽取氢氧化铁胶体11、银锌碱性电池的电解质溶液为KOH溶液,电池放电时发生的总反应为下列说法正确的是A、放电时OH+向正极移动B 、Ag 2O 2在反应中既是氧化剂又是还原剂C 、每生成1mol Ag 外电路转移1 mol 电子D 、负极反应为12、向甲、乙两容积均为1L 的恒容容器中分别充入时,发生如下反应测得窗口中n (PCL 4)随时间t 的变化如图所示,下列叙述错误的是A 、在0-10min 内甲容器中PCl 3的反应速率为B 、在7°C 时,该反应的平衡常数K 甲=K 乙C 、若向平衡后的乙容器中充入PCl 3(g ),则再次达到平衡时PCl 3的体积分数增大D 、升高甲容器的温度,可以使甲容器中各物质的体积分数与乙容器的相同13、常温下,PH =3的醋酸溶液和PH =13的NaOH 溶液等体积充分混合,恰好完全中和(忽略溶液体积的变化),则下列说法正确的是A 、反应后溶液呈中性B 、原醋酸溶液的浓度等于原NaOH 的浓度C 、原醋酸溶液中有10%的CH 3COOH 发生电离D 、反应后的溶液中:14、某物体在恒力F (F ≠0)的作用下沿直线运动,以下各图分别表示物体的位移s ,速度v ,加速度a 和受到的冲量l 随时间变化的图象,其中不可能的是15、将一小球坚直上抛,假设小球运动时受到空气阴力且大小不变,如果小球到达电高点前的最后一秒和离开最高点后的第一秒时间内通过的中和分别为x 1和x 2,速度变化量的大小分别为1v ∆和2v ∆,则16、如图所示,小球在坚直向下的力F 作用下,静止在弹簧上端,某时刻起将力F 撤去,小球向上弹起,不计空气阻力,则从撤去力F 开始到小球运动到最高点的过程中A 、小球的动能最大时弹簧的弹性势能最小B 、小球的机械能先增大后减小C 、小球的重力势能与弹簧的弹性势能之和先减小后增大D 、小球的动能与弹簧的弹性势能之和先增大后减小17、如图,半圆形玻璃砖置于光屏PQ 的左下方,一束白光沿半径方向从A 点身入玻璃砖,在O 点发生反射的折射,折射光在白光屏上呈现七色光带。
安徽省蚌埠市高三数学第三次教学质量检查考试试题 理

蚌埠市2015届高三年级第三次教学质量检查考试数学试卷(理工类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考 试时间120分钟.第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的A 、B 、C 、D 的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置. 1.已知全集{}0,1,2,3,4U =, 集合{}2,3,4M =, {}0,1,4N =, 则集合{}0,1可以表示为( ) A.MN B.()U M N ð C.()UM N ð D.()()UUM N 痧1.【答案】B 【解析】2.复数21iz i-=+(其中i 是虚数单位),则z 的共轭复数z =( ) A.1322i - B.1322i -- C.1322i + D.1322i -+ 2.【答案】C3.双曲线()222214x y m Z m m+=∈-的离心率为( )23 3.【答案】B【解析】由题意240m -<,得22m -<<,故1m =或1-,所以221a m ==,()22244c m m =-+=,得2ce a==.故选B. 4.已知d R ∈,命题:p 对于任意n N *∈,21n n a a d ++-=;命题:q 数列{}n a 是公差为d 的等差数列,则p ⌝是q ⌝的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 4.【答案】A【解析】本题也就是找q 是p 的什么条件,因为数列{}n a 是公差为d 的等差数列⇒对于任意n N *∈,21n n a a d ++-=,反之不能得出.5.已知()(),f x g x 分别是定义在R 上的偶函数和奇函数,且()()322f x g x x x -=-,则()()22f g +=( )A.16B.16-C.8D.8- 5.【答案】B【解析】由题意得,分别令2x =和2x =-,可得()()220f g -=且()()2216f g ---=-,即()()2216f g +=-,则()()228f g ==-,故选B. 6.执行如图所示的程序框图,则输出结果S =( ) A.15 B.25C.50D.100 6.【答案】C【解析】根据程序框图,()()()1357979950S =-++-+++-+=,输出的S 为50.7.如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )A.47122π+B.1223π+C.1224π+D.45122π+7.【答案】A【解析】该几何体是半个圆台中间被挖掉一个半个圆柱, 表面积为120547204884122332ππππππ⎛⎫+⨯⨯-⨯+--+=+ ⎪⎝⎭ 8.将函数()()3sin 2,22f x x ππθθ⎛⎫=+-<< ⎪⎝⎭的图象向右平移()0ϕϕ>个单位长度后得到函数()g x 的图象,若()(),f x g x 的图象都经过点P ⎛ ⎝⎭,则ϕ的值不可能是( )A.34π B.π C.54π D.74π 8.【答案】C【解析】把0,2P ⎛ ⎝⎭代入()()3si n 2f x x θ=+,得s i n 2θ=,故4πθ=,所以()3s i n 224g x x πϕ⎛⎫=+- ⎪⎝⎭,把0,2P ⎛ ⎝⎭代入得s i n 242πϕ⎛⎫-=- ⎪⎝⎭,k ϕπ=或()4k k Z πϕπ=-∈,观察选项,故选C.9.若变量,x y 满足:2202403110x y x y x y -+≤⎧⎪+-≥⎨⎪-+≥⎩,且满足(1)(2)0t x t y t ++++=,则参数t 的取值范围为( ) A.423t -<<-B.423t -<≤-C.423t -≤≤-D.423t -≤<- 9.【答案】C【解析】:(1)(2)0l t x y x y ++++=,所以直线恒过定点()2,1-,画出可行域,由题意知,直线恒过定点()2,1-点及可行域内一点,直线l 方程可改写成:(2)(1)t y t x t +=-+-,①由图知,当斜率不存在时,符合题意;②当斜率存在时,11,22t k t +⎡⎫⇒=-∈+∞⎪⎢+⎣⎭⇒423t -<≤-;综上:423t -≤≤-. 10.如图,四面体D ABC -的体积为14,且满足060ACB ∠=,1BC =,2AD +=,则四面体D ABC -中最长棱的长度为( )B.2D.310.【答案】B 【解析】因为111sin 60324D ABC AD BC AC V -⎛⎫⋅⋅⋅⋅≥= ⎪⎝⎭, 即1AD ≥,因为22AD =+≥=,当且仅当1AD ==时,等号成立,这时1AC AD ==,且AD ⊥面ABC ,所以2CD =,AB =60DAC得BD =2.第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在答题卷相应横线上. 11.在921x x ⎛⎫- ⎪⎝⎭的二项展开式中,常数项的值为_______.11.【答案】84【解析】法一:()()9218319911rrr rrr r T C xC xx --+⎛⎫=-=- ⎪⎝⎭,令1830r -=,得6r =,故常数项为6349984T C C ===;法二:按比例分配2x 与1x-这两项中x 的次数之比为2:1,所以把9分为1:2两份,前项用1份,后项用2份,才会出现常数项,所以常数项为3984C =.12.在极坐标系中,O 是极点,设点,A B 的极坐标分别是2,3,63ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,则O 点到直线AB 的距离是 .12.【解析】,A B 的直角坐标分别是(3,2⎛- ⎝⎭,故直线AB 的方程为)3y x -=-,即120x +-=,所以O 点到直线AB 的距离是=13.某种产品的加工需要A ,B ,C ,D ,E 五道工艺,其中A 必须在D 的前面完成(不一定相邻),其它工艺的顺序可以改变,但不能同时进行,为了节省加工时间,B 与C 必须相邻,那么完成加工该产品的不同工艺的排列顺序有____种. (用数字作答) 13.【答案】24【解析】将B ,C 两道工序看成一个整体与A , D ,E 三道工序全排列共有44A 不同排列法,再将B ,C 两道工序全排列有22A ,因为A 和D 只有两钟可能,要么在左,要么在右,故A 必须在D 的前且B 与C 必须相邻的不同排列顺序为4242124.2A A ⋅= 14.已知函数()11f x x =+,点O 为坐标原点, 点()()(),n A n f n n N *∈,向量()0,1=i ,nθ是向量n OA 与i 的夹角,则912129cos cos cos sin sin sin θθθθθθ+++= . 14.【答案】910【解析】画图像可知912129cos cos cos 111,,,sin 12sin 23sin 910θθθθθθ===⨯⨯⨯, 所以912129cos cos cos 11111sin sin sin 122391010θθθθθθ+++=+++=-⨯⨯⨯910=. 15.已知函数)(x f y =,I x ∈,若存在I x ∈0,使得00)(x x f =,则称0x 为函数)(x f y =的不动点;若存在I x ∈0,使得00))((x x f f =,则称0x 为函数)(x f y =的稳定点.则下列结论中正确的是 . (填上所有正确结论的序号) ①1,12-是函数2()21g x x =-有两个不动点; ②若0x 为函数)(x f y =的不动点,则0x 必为函数)(x f y =的稳定点; ③若0x 为函数)(x f y =的稳定点,则0x 必为函数)(x f y =的不动点; ④函数2()21g x x =-共有三个稳定点;⑤若函数)(x f y =在定义域I 上单调递增,则它的不动点与稳定点是完全相同. 15.【答案】①②⑤【解析】对于①,令()g x x =,可得12x =-或1x =,故①正确; 对于②,因为00)(x x f =,所以000)())((x x f x f f ==, 即00))((x x f f =,故0x 也是函数)(x f y =的稳定点,故②正确;对于③④,2()21g x x =-,令x x =--1)12(222,因为不动点必为稳定点,所以该方程一定有两解1,21-=x ,由此因式分解,可得0)124)(12)(1(2=-++-x x x x 还有另外两解451±-=x ,故函数()g x 的稳定点有1,21-,451±-,其中451±-是稳定点,但不是不动点,故③④错误;对于⑤,若函数)(x f y =有不动点0x ,显然它也有稳定点0x ;若函数)(x f y =有稳定点0x ,即00))((x x f f =,设00)(y x f =,则00)(x y f =即),(00y x 和),(00x y 都在函数)(x f y =的图象上,假设00y x >,因为)(x f y =是增函数,则)()(00y f x f >,即00x y >,与假设矛盾; 假设00y x <,因为)(x f y =是增函数,则)()(00y f x f <,即00x y <,与假设矛盾; 故00y x =,即00)(x x f =,)(x f y =有不动点0x ,故⑤正确.三、解答题:本大题共6小题,共75分.解答须写出说明、证明过程和演算步骤. 16.(本小题满分12分)在ABC ∆中,内角,,A B C 所对的边分别是,,a b c ,已知sin tan 1cos CA=C-,c =(Ⅰ)求b a;(Ⅱ)若三角形ABC ∆的面积为6,求角C .17.(本小题满分12分)从某中学高三某个班级第一组的7名女生,8名男生中,随机一次挑选出4名去参加体育达标测试.(Ⅰ)若选出的4名同学是同一性别,求全为女生的概率; (Ⅱ)若设选出男生的人数为X ,求X 的分布列和EX .18.(本小题满分12分)设*n N ∈,函数ln ()n x f x x =,函数e ()xn g x x=,(0,)x ∈+∞.(Ⅰ)求函数()f x 的最大值及函数()g x 的单调区间;(Ⅱ)若存在直线:l y c =()c R ∈,使得曲线()y f x =与曲线()y g x =分别位于直线l 的两侧,求n 的最大值. (参考数据:ln 4 1.386,ln5 1.609≈≈)19. (本小题13分)如图,在五面体ABCDEF 中,四边形ABCD 是边长为4的正方形,//EF AD , 平面ADEF ⊥平面ABCD ,且2BC EF =, AE AF =,点G 是EF 的中点. (Ⅰ)证明:AG ⊥平面ABCD ;(Ⅱ)若直线BF 与平面ACE所成角的正弦值为9,求AG 的长.20.(本小题满分13分)已知数列{}n a 共有()22,k k k Z ≥∈项,11a =,前n 项和为n S ,前n 项乘积为n T ,且()112n n a a S +=-+()1,2,,21n k =-,其中2212k a -=,数列{}n b满足2log n b =(Ⅰ)求数列{}n b 的通项公式; (Ⅱ)若122123333322222k k b b b b --+-++-+-≤,求k 的值.21. (本小题14分)设()()0000,0A x y x y ⋅≠是椭圆()22:101x y m m τ+=>+上一点,它关于y 轴、原点、x 轴的对称点依次为,,B C D .E 是椭圆τ上不同于A 的另外一点,且AE AC ⊥,如图所示.(Ⅰ) 若点A 横坐标为2,且BD AE ∥, 求m 的值;(Ⅱ)求证:直线BD 与CE 的交点Q 总在椭圆21x y m ++yBFA CDG E蚌埠市2015届高三年级第二次教学质量检查考试数学试卷(理工类)参考答案及评分标准二、填空题: 11.84;12.7;13.24;14.910;15.①②⑤.三、解答题: 16.(本小题满分12分) 【解析】(Ⅰ)由题,sin sin cos 1cos A C=A C-,即有sin sin cos sin cos sin A=A C +C A=B 故1ba=;………………………………6分 (Ⅱ)有2222sin 32cos 2a C a a C a ⎧=⎪⎪⎨+-⎪=⎪⎩, 得cos 1C C =,1cos 2C =-,解得120C =.………………………………12分17. (本小题满分12分)【解析】(Ⅰ)若4人全是女生,共有4735C =种情况;若4人全是男生,共有4870C =种情况;故全为女生的概率为47448730170353C C C ==++.………………………6分 (Ⅱ)共15人,任意选出4名同学的方法总数是415C ,选出男生的人数为0,1,2,3,4X =………………………………7分01874151(0)39C C P X C ===;13874158(1)39C C P X C ===;(2)P X =22874152865C C C ==;318741556(3)195C C P X C ===; 43874152(4)39C C P X C ===.………………………………10分故X012343939651953915EX =⨯+⨯+⨯+⨯+⨯=.………………………12分 18. (本小题满分12分)【解析】(Ⅰ)结论:函数()f x 求导,得 11ln ()n n xf x x+-'=, 令 ()0f x '=,解得1e n x =. 当x 变化时,()f x '与()f x 的变化如下表所示:所以函数()f x 在区间10,ne ⎛⎫ ⎪⎝⎭上为单调递增,区间1,n e ⎛⎫+∞ ⎪⎝⎭上为单调递减.故函数()1max 1n f x f een⎛⎫== ⎪⎝⎭.………………………………3分函数()g x 求导,得 ()1()x n e x n g x x+-'=, 令 ()0g x '=,解得x n =. 当x 变化时,()g x '与()g x 的变化如下表所示:所以函数()g x 在区间()0,n 上为单调递减,区间(),n +∞上为单调递增. ………………………………6分(Ⅱ)由(1)知 ()()min nn e g x g n n==,因为存在直线:l y c =()c R ∈,使得曲线()y f x =与曲线()y g x =分别位于直线l 的两侧,所以1n n e n en≥,即11n n e n +-≥,可得()11ln n n n +≥-,………………………………8分当1n =时,成立, 当2n ≥时,1ln 1n n n +≥-,即21ln 01n n +-≥-, 令()()21ln 21h n n n n =+-≥-,则()h n 是减函数,所以继续验证, 当2n =时, 3ln 20->,………………………………10分 当3n =时, 2ln 30->,当4n =时,55ln 4 1.4033->-> 当5n =时, 33ln 5 1.6022-<-<,所以max 4n =.………………………………12分19. (本小题满分12分)【解析】(Ⅰ)证明:因为AE AF =,点G 是EF 的中点, 所以 AG EF ⊥. 又因为 //EF AD , 所以 AG AD ⊥.………………………………3分因为平面ADEF ⊥平面ABCD ,平面ADEF平面ABCD AD =,AG ⊂平面ADEF ,所以 AG ⊥平面ABCD . ………………………………6分(Ⅱ)因为AG ⊥平面ABCD ,AB AD ⊥,所以,,AG AD AB 两两垂直. 以A 为原点,以AB ,AD ,AG 分别为x 轴、y 轴和z 轴,如图建立空间直角坐标系 则(0,0,0)A ,(4,0,0)B ,(4,4,0)C , 设(0)AG t t =>,则(0,1,)E t ,(0,1,)F t -,所以(4,1,)BF t =--,(4,4,0)AC =,(0,1,)AE t =.……………………………8分 设平面ACE 的法向量为(,,)n x y z =, 由 0AC n ⋅=,0AE n ⋅=,得440,0,x y y tz +=+=⎧⎨⎩令 1z =, 得(,,1)n t t =-.因为BF 与平面ACE 所成角的正弦值为9,所以 6cos ,9||||BF n BF n BF n ⋅<>==⋅,………………………………10分即=, 解得21t =或2172t =.所以1AG = 或 2. ………………………………12分20.(本小题满分13分)【解析】(1)当1n =时,22a a =,则21a a a =; 当221n k ≤≤-时,()112n n a a S +=-+,()112n n a a S -=-+,所以()11n n n a a a a +-=-,故1n na a a +=,即数列{}n a 是等比数列,12n n a a -=, 可得()()1121211222n n n n nk n n T a a a a-+++++-=⋅⋅⋅==,()11112121n n n n b n n k k -⎡⎤-=+=+⎢⎥--⎣⎦; ………………………………7分(2)令32n b ≤,则12n k ≤+,又n N *∈,故当n k ≤时,32n b <, 当1n k ≥+时,32n b >.………………………………8分1221233332222k k b b b b --+-++-+- 12123333322222k k k b b b b b +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-+-++- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭………………10分()()()()212111210122212121k k k k k k k k k b b b b k k k k k +⎡⎤⎡⎤+-+-⎢⎥⎢⎥=++-++=+-+=⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦由23212k k ≤-,得22630k k -+≤,3322k ≤≤,……………………12分 又2k ≥,且k N *∈,所以2k =.………………………………13分21.(本小题满分14分)【解析】(Ⅰ)因为BD AC ∥,AE AC ⊥, 所以BD AC ⊥,可知A ⎝⎭,……………………………… 4分 故311m =+,2m =;………………………………6分 (Ⅱ)由对称性可知()00,B x y -,()00,C x y --,()00,D x y -,四边形ABCD 为矩形, 设()11,E x y ,由于,A E 均在椭圆τ上,则()()220022111111x m y m x m y m ⎧++=+⎪⎨++=+⎪⎩①②由②-①得:()()()()()1010101010x x x x m y y y y +-+++-=,……… 8分 显然10x x ≠,从而1010010100111111111AC AE y y x x y k x x m y y m k m m x +-=-⋅=-⋅=⋅=⋅++-+++,………………………………10分 因为AE AC ⊥,所以1AE AC k k ⋅=-,所以()()00100000100:1:1BDCE y l y x x y y y l y y x x x x x x m x ⎧=-⎪⎪⎨+⎪+=+=⋅+⎪++⎩,解得0022m x x m m y y m +⎧=⎪⎪⎨+⎪=-⎪⎩,………………………………12分代入椭圆方程,知22212x m y m m ⎛⎫+= ⎪++⎝⎭.………………………………14分(以上各题其它解法请参考以上评分标准酌情赋分)。
安徽省蚌埠市高三数学第三次教学质量检查试题 文

12 3 11 1 12正视图侧视图蚌埠市2016届高三年级第三次教学质量检查考试数学试卷(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考 试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的A 、B 、C 、D 的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置. 1.若复数z 满足(1)22(z i i i +=-为虚数单位),则||z =( ) A.1 B.2C.3D.22.已知全集为R ,集合{}{}20,1,2,3,4,320A B x x x ==-+≤,则()R A B =I ð( )A.{}0,1,4B.{}1,2,4C.{}0,3,4D.{}1,2,3 3.抛物线2y mx =的焦点为()1,0-,则m =( )A.4-B.4C.2-D.24.已知0a >,且1a ≠,下列函数中,在其定义域内是单调函数而且又是奇函数的是( )A.sin y ax =B.2log a y x =C.x xy a a -=- D.tan y ax =5.设实数x ,y 满足约束条件230,230,3x y x y x --≤⎧⎪+-≤⎨⎪≥-⎩, 则23z x y =-+的取值范围是( )A.[]6,17-B.[]5,15-C.[]6,15-D.[]5,17- 6. 已知两个非零向量a ,b 满足a ·(a -b )=0,且2|a |=|b |,则向量a ,b 的夹角为( ) A.30oB.60oC.120oD.150o7.执行如图所示的程序框图,如果输入3x =,则输出k 的值为 A.6 B.8 C.10 D.12 8.在ABC ∆中,角,,A B C 的对边分别为,,a b c .已知2a =,2c =2cos 4A =-. 则b 的值为( )A.1B.2C.32D.629.一个几何体的三视图如右图所示, 则该几何体的侧视图的面积为( ) A.22B.23开始k =23x x =+ 2k k =+结束输入x是否输出k 100?x >C.4D.510.已知()cos 12a f x b x x π⎛⎫=+ ⎪-⎝⎭,()221=-f , 则()=+21f ( )A.0B.2-C.4-D.6-11.设21,F F 为双曲线1:2222=-by a x C 的左,右焦点,P ,Q 为双曲线C 右支上的两点,若Q F PF 222=,且01=⋅PQ Q F ,则该双曲线的离心率是( ) A.153 B.173 C.52 D.7212.如图,已知直线y kx m =+与曲线()y f x =相 切于两点,则()()F x f x kx =-有( ) A.2个零点 B.3个极值点 C.2个极大值点 D.3个极大值点第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分,第13题-21题为必考题,每个试题考生都必须作答,第22题-24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.请将答案填在答题卷相应横线上.13.一个总体中有60个个体,随机编号0,1,2,…,59,依编号顺序平均分成6个小组,组号依次为1,2,3,…,6.现用系统抽样方法抽取一个容量为6的样本,若在第1组随机抽取的号码为3,则在第5组中抽取的号码是 .14.已知函数22,0(),0x x f x x x ⎧≥=⎨-<⎩,若2()(2)f a f a <-,则实数a 的取值范围是 .15.在四面体ABCD 中,2AB CD ==,2AC BD AD BC ====, 则该四面体的外接球的表面积为 .16.在ABC ∆中,点D 在边AB 上,CD BC ⊥,53AC =,5CD =,2BD AD =,则AD 的长为 .三、解答题:本大题共6小题,共70分.解答须写出说明、证明过程和演算步骤. 17.(本小题满分12分)已知数列{}n a 是等比数列,24a =,32a +是2a 和4a 的等差中项. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设22log 1n n b a =-,求数列{}n n a b ⋅的前n 项和n T .Oy xy kx m=+()y f x =第12题图18.(本小题满分12分)从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[)55,65,[)65,75,[]75,85内的频率之比为4:2:1.(Ⅰ)求这些产品质量指标值落在区间[]75,85内的频率;(Ⅱ)用分层抽样的方法在区间[)45,75 内抽取一个容量为6的样本,将该样本看成一 个总体,从中任意抽取2件产品,求这2件产 品都在区间[)45,65内的概率.19.(本小题满分12分)如图,在三棱锥BCD A -中,4=====CD BC AD AC AB ,24=BD , F E ,分别为CD AC ,的中点,G 为线段BD 上一点,且//BE 平面AGF .(Ⅰ)求BG 的长;(Ⅱ)当直线//BE 平面AGF 时,求四棱锥BCFG A -的体积.20.(本小题满分12分)已知函数()(1)ln f x a x x x =-+在点()()1,1f 处的切线斜率为1(Ⅰ)求()()1f xg x x =-的单调区间; (Ⅱ)若1m n >>mnn n mm >.21.(本小题满分12分)已知21,F F 分别是椭圆)0(12222>>=+b a by a x 的左,右焦点,B A ,分别为椭圆的上,下顶点.过椭圆的右焦点2F 的直线在y 轴右侧..交椭圆于C ,D 两点.CD F 1∆的周长 为8,且直线BC AC ,的斜率之积为41-. (Ⅰ)求椭圆的方程;(Ⅱ)设四边形ABCD 的面积为S ,求S 的取值范围.DABCE FG第19题图xyOADF 1F 2 质量指标值0.0120.0040.019 0.030 15 25 35 45 55 65 75 85 0频率 组距请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号 22. (本小题满分10分)选修4-1:几何证明选讲090,,ABC ACD ACB ADC BAC CAD ∆∆∠=∠=∠=∠如图,在和中,圆O 是以AB 为直径的圆,延长AB 与DC 交于E 点.(Ⅰ)求证:DC 是圆O 的切线;(Ⅱ)6,62EB EC ==若,求BC 的长.23. (本小题满分10分)选修4—4:坐标系与参数方程已知直线l 的参数方程为21222x t y t⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数),曲线C 的极坐标方程是2sin cos θρθ=,以极点为原点,极轴为x 轴正方向建立直角坐标系,点(1,0)M -,直线l 与曲线C 交于A 、B 两点.(Ⅰ)写出直线l 的极坐标方程与曲线C 的普通方程; (Ⅱ)求线段MA 、MB 长度之积MA MB ⋅的值.24. (本小题满分10分)选修4-5不等式证明选讲设函数()2x a x bf x +-+=,(Ⅰ)当10,2a b ==-时,求使)(x f 2≥的x 取值范围; (Ⅱ)若1()16f x ≥恒成立,求a b -的取值范围.蚌埠市2016届高三年级第三次教学质量检查考试数学(文史类)答案及评分标准题号 1 2 3 4 5 6 7 8 9 10 1112 答案 D B A C C B C A B B B D二、填空题:13.43 14.21a -<< 15.3π 16.5三、解答题:17.(本小题满分12分)解:(Ⅰ)设数列{}n a 的公比为q ,因为24a =,所以34a q =,244a q =.ADBCO第22题图因为32a +是2a 和4a 的等差中项,所以()32422a a a +=+. 即()224244q q +=+,化简得220q q -=. 因为公比0q ≠,所以2q =.所以222422n n nn a a q --==⨯=(*n ∈N ). ……………………………………6分(Ⅱ)因为2n na =,所以22log 121n nb a n =-=-.所以()212nn n a b n =-.…………………………………………………………8分 则()()231123252232212n n n T n n -=⨯+⨯+⨯+⋅⋅⋅+-+-, ① ()()23412123252232212n n n T n n +=⨯+⨯+⨯+⋅⋅⋅+-+-. ②①-②得,()2312222222212n n n T n +-=+⨯+⨯+⋅⋅⋅+⨯--分()()()11142221262321212n n n n n ++-=+⨯--=-----,所以()16232n n T n +=+-.…………………………………………………………12分18. (本小题满分12分)解:(Ⅰ)设区间[]75,85内的频率为x ,则区间[)55,65,[)65,75内的频率分别为4x 和2x .…………………………1分 依题意得()0.0040.0120.0190.03010421x x x +++⨯+++=,…………3分 解得0.05x =.所以区间[]75,85内的频率为0.05.……………………………………………4分 (Ⅱ)由(Ⅰ)得,区间[)45,55,[)55,65,[)65,75内的频率依次为0.3,0.2,0.1.用分层抽样的方法在区间[)45,75内抽取一个容量为6的样本,则在区间[)45,55内应抽取0.3630.30.20.1⨯=++件,记为1A ,2A ,3A .在区间[)55,65内应抽取0.2620.30.20.1⨯=++件,记为1B ,2B .在区间[)65,75内应抽取0.1610.30.20.1⨯=++件,记为C .…………………6分设“从样本中任意抽取2件产品,这2件产品都在区间[)45,65内”为事件M ,则所有的基本事件有:{}12,A A ,{}13,A A ,{}11,A B ,{}12,A B ,{}1,A C ,{}23,A A ,{}21,A B ,{}22,A B ,{}2,A C ,{}31,A B ,{}32,A B ,{}3,A C ,{}12,B B ,{}1,B C ,{}2,B C ,共15种. ………………………………………………………8分事件M 包含的基本事件有:{}12,A A ,{}13,A A ,{}11,A B ,{}12,AB ,{}23,A A , {}21,A B ,{}22,A B ,{}31,A B ,{}32,A B ,{}12,B B ,共10种.………………10分所以这2件产品都在区间[)45,65内的概率为102153=. ……………………12分19. (本小题满分12分)解:(Ⅰ)连DE 交AF 于M ,则M 为ACD ∆的重心,且12=ME DM Θ//BE 平面AGF ,∴BE//GM ,21DG BG = A∴423BG =……………………………6分 (Ⅱ)取BD 的中点为O ,连AO ,CO ,则22==CO AO ,∴OC AO ⊥,BD AO ⊥,从而⊥AO 平面BCD∴321622442131=⨯⨯⨯⨯=-BCD A V , ∴BCD A FDG A V V --=31,从而BCD A BCFG A V V --=32=9232. ………………12分20. (本小题满分12分) 解:(Ⅰ)()(1)ln 1ln f x a x a x '=-++=+ ,而(1)1f '=,因而1a =()ln f x x x =,()ln ()11f x x xg x x x ==--,2(1)ln ()(1)x x g x x --'=- ……………2分 设()h x =1ln x x --,其中0x >,则1()1h x x'=-则()0h x '=得1x =当01x <<时()0h x '<,()h x 单调递减 当1x >时()0h x '>,()h x 单调递增,()h x 的最小值为0,因而()0h x ≥,即2(1)ln ()0(1)x xg x x --'=≥- 那么()g x 在(0,)+∞上单调递增. ………………………………………………6分 (Ⅱ)若证明mnn nm m >,1m n >>,两边取对数, 则需证明11ln ln ln ln n m n m m n ->-即证明ln ln 11m m n n m n >--,由(1) ()g x 在(0,)+∞上单调递增, ∴1m n >>时ln ln 11m m n nm n >--成立, mnn n mm >成立. ……………………………………………………………12分21. (本小题满分12分) 解:(Ⅰ)设),(),,(2211y x D y x C ,由题意得),0(),,0(b B b A -,且2,84==a a由4122212211111-=-=-=+⨯-=⋅ab x b y x b y x b y k k BCAC , 得14122==a b ,∴椭圆的方程为1422=+y x . …………………………6分 (Ⅱ)由(Ⅰ)知,)0,3(2F ,故设直线3:+=my x CD ,代入1422=+y x 得0132)4(22=-++my y m ,则41,432221221+-=+-=+m y y m m y y 4142221++=-m m y y , 由,0,021>>x x 得302<≤m 43832)(22121+=++=+m y y m x x∴面积=++=∆∆∆OCD BOC AOD S S S S 21⨯⨯++⨯3214382m 41422++m m =4)21(3222+++m m……………………………………… 10分令)4,3[,212∈++=t m t ,则47323)2(322-+=+-=tt t tS 在)4,3[∈t 上递减 所以]233,738(∈S . ………………………………………………………… 12分 22. (本题满分10分)解:(Ⅰ),90,AB O ACB C O ︒∠=∴Q e e 是的直径点在上, OC OCA OAC DAC ∠=∠=∠连接可得,OC AD ∴∥,,AD DC DC OC ⊥∴⊥Q 又,OC DC O ∴Q e 为半径是的切线;……………………………………………5分(Ⅱ)2, DC O EC EB EA ∴=Q e g 是的切线6,62,12,6,, 222EB EC EA AB ECB EAC CEB AEC ECB EAC BC EC AC BC AC EA ====∠=∠∠=∠∴∆∆∴===Q Q :又又即, 22236, 3. AC BC AB BC +==∴=Q 又…………………………………10分23. (本题满分10分)解:(Ⅰ)直线l 2cos()14πρθ+=-,曲线C 的普通方程为2y x =;………………………………………………………5分(Ⅱ)(方法一)将21222x y ⎧=-+⎪⎪⎨⎪=⎪⎩代入2y x =得23220t t -+=,12||2MA MB t t ⋅==.(方法二)显然直线:10l x y -+=,联立得210x y y x-+=⎧⎨=⎩, 消去y 得210x x --=,所以11522x =+,21522x =-,不妨设1535(2222A --,1535(2222B ++则352()22MA =-,352()22MB =+, 所以35352()2()22222MA MB ⋅=-⋅+=.………………………………10分24. (本题满分10分)解:(Ⅰ)由于2xy =是增函数,)(x f 2≥等价于1122x x --≥ ① 当12x ≥时,1122x x --=,则①式恒成立,当102x <<时,11222x x x --=-,①式化为21x ≥,即x ∈∅,当0x ≤时,1122x x --=-,①式无解.综上,x 取值范围是1,2⎡⎫+∞⎪⎢⎣⎭……………………………………………… 5分(Ⅱ)1()||||416f x x a x b ≥⇔+-+≥- ②而由||||||||x a x b x a x b a b +-+≤+--=-⇒||||||||a b x a x b a b --≤+-+≤-∴要②恒成立,只需||4a b --≥-,可得a b -的取值范围是[]4,4-.…………………………………………10分(其他解法请参考以上评分标准酌情赋分)。
安徽省蚌埠市2024届高三第三次教学质量检查数学试题(原卷版)

蚌埠市2024届高三年级第三次教学质量检查考试数学本试卷满分150分,考试时间120分钟注意事项:1.答卷前,务必将自己的姓名和座位号填写在答题卡和试卷上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,务必擦净后再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上.写在本试卷上无效。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{1,3,5,7,9},{3,6,9,12}A B ==,则A B =( )A .{3,9}B .{1,3,5,6,7,9,12}C .{1,5,7}D .{6,12}2.己知平面向量(1,),(2,4)a m a ==-,且a b ∥,则m =( )A .2B .12C .12- D .2- 3.已知曲线22:1(0)4x y C m m+=≠,则“(0,4)m ∈”是“曲线C 的焦点在x 轴上”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件4.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c 已知2cos cos 1,sin a a B b A C =+==,则( ) A .1b = B .2b = C .2c = D .3c =5.记数列{}n a 的前n 项和为n S ,若n S n ⎧⎫⎨⎬⎩⎭是等差数列,268,0S S =-=,则34a a +=( ) A .8- B .4- C .0 D .46.()2231(1)x x x -+⋅+的展开式中,4x 的系数为( )A .1B .2C .4D .57.在一组样本数据中,1,2,3,4出现的频率分别为1234,,,p p p p ,且411i i p ==∑,则下面四种情形中,对应样本的标准差最小的一组是( )A .12340.1,0.2,0.3,0.4p p p p ====B .12340.4,0.3,0.2,0.1p p p p ====C .14230.1,0.4p p p p ====D .14230.4,0.1p p p p ====8.已知抛物线2:4C y x =,过其焦点F 的直线交C 于A ,B 两点,M 为AB 中点,过M 作准线的垂线,垂足为N ,若||4AF =,则||NF =( )A .43B .433C .83D .833 二、选择题:本题共3小题,每小题6分,共18分。
安徽省蚌埠市高三数学第三次质量检测试题(理)

安徽省蚌埠市2020 届高三年级第一次教课质量检查考试数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150 分,考试时间为120 分钟第Ⅰ卷(选择题,共60 分)一、选择题(本大题共12 小题,每题 5 分,共 60 分。
在每题给出的四个选项中,只有一项为哪一项切合题目要求的,)1、已知全集U{1,2,3,4,5}, A { 1,2,3}, B {3,4} ,则 C U (A I B)A 、 {3}B、 {4 ,5}C、 {1 , 2,4,5}D、 {1,2,3,4}2、已知函数y e x的图像与函数y f ( x) 的图像对于直线y x对称,则A 、f (2 x)e2x (x R)B、C、 f (2 x) 2e x ( x R)D、f (2 x) ln 2gln x( x 0) f (2 x) ln 2 ln x( x 0)3、若函数 f (x 2) tan x , x 0,则 f ( 2)gf ( 98) 等于lg( x), x 0 41B 、1C、 2D、 2A 、224 l平面,直线 m 平面,给出以下命题:①// l m;②、已知直线l // m ;③ l // m ;④ l m // ,此中正确命题的序号是A 、①②③B、②③④C、②④D、①③5、已知{ a n}是等比数列,a2 2, a5 1,则 a1a2 a2 a3 a n a n 1 4A 、16(1 4 n ) B、16(1 2 n ) C、32 (1 4 n ) D、32 (1 2 n )3 36、设命题 p:命题“x R, x2 x 1 0 ”的否认是“x R, x2 x 1 0 ”;命题q:“ x 2”是“| x 1| 1 ”的充足不用要条件,则A 、“p或q”为真B、“p且q”为真C、p真q假D、p, q均为假命题7、假如平面的一条斜线和它在这个平面上的射影的方向向量分别是v va (1,01),b (0,1,1)那么这条斜线与平面所成的角是A、900B、600C、450D、3008、已知函数y sin x cos x ,给出以下四个命题,此中为真命题的是A、若C、直线x [0, ] ,则y [0, 2]B、在区间[ ,5] 上是增函数2 4 4x 是函数图象的一条对称轴4D 、函数的图象可由y 2 sin x 的图象向右平移个单位获得4x 4cos为参数)的长轴为 A1A2 ,短轴为 B1 B2,将椭圆沿y轴折成一个9、椭圆(y 2 3 sin二面角,使得A1点在平面 B1 A2 B2上的射影恰巧为椭圆的右焦点,则该二面角的大小为A、750B、600C、450D、30010、已知图中一组函数图象,它们分别与后来所列的一个现真相境相般配:①②③④情境 A :一份 30 分钟前从冰箱里拿出来,而后被防到微波炉里加热,最后放到餐桌上的食品的温度(将 0 时辰确立为食品从冰箱里被拿出来的那一刻)情境 B :一个 1970 年生产的留声机从它刚开始的售价到此刻的价值(它被一个喜好者珍藏,而且被保留的很好);情境 C:从你刚开始防水沐浴,到你洗完后把它排掉这段时间浴缸里水的高度;情境 D :依据乘客人数,每辆公交车一趟运营的收益。
安徽省蚌埠市高三数学第三次教学质量检查考试试题 理-人教版高三全册数学试题

蚌埠市2015届高三年级第三次教学质量检查考试数学试卷(理工类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考 试时间120分钟.第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的A 、B 、C 、D 的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置. 1.已知全集{}0,1,2,3,4U =, 集合{}2,3,4M =, {}0,1,4N =, 则集合{}0,1可以表示为( ) A.MN B.()U M N C.()UM N D.()()U UM N1.【答案】B 【解析】2.复数21iz i-=+(其中i 是虚数单位),则z 的共轭复数z =( ) A.1322i - B.1322i -- C.1322i + D.1322i -+ 2.【答案】C3.双曲线()222214x y m Z m m+=∈-的离心率为( )23 3.【答案】B【解析】由题意240m -<,得22m -<<,故1m =或1-,所以221a m ==,()22244c m m =-+=,得2ce a==.故选B. 4.已知d R ∈,命题:p 对于任意n N *∈,21n n a a d ++-=;命题:q 数列{}n a 是公差为d 的等差数列,则p ⌝是q ⌝的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 4.【答案】A【解析】本题也就是找q 是p 的什么条件,因为数列{}n a 是公差为d 的等差数列⇒对于任意n N *∈,21n n a a d ++-=,反之不能得出.5.已知()(),f x g x 分别是定义在R 上的偶函数和奇函数,且()()322f x g x x x -=-,则()()22f g +=( )A.16B.16-C.8D.8- 5.【答案】B【解析】由题意得,分别令2x =和2x =-,可得()()220f g -=且()()2216f g ---=-,即()()2216f g +=-,则()()228f g ==-,故选B. 6.执行如图所示的程序框图,则输出结果S =( ) A.15 B.25 C.50 D.100 6.【答案】C【解析】根据程序框图,()()()1357979950S =-++-+++-+=,输出的S 为50.7.如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )A.47122π+B.1223π+C.1224π+D.45122π+7.【答案】A【解析】该几何体是半个圆台中间被挖掉一个半个圆柱, 表面积为120547204884122332ππππππ⎛⎫+⨯⨯-⨯+--+=+ ⎪⎝⎭ 8.将函数()()3sin 2,22f x x ππθθ⎛⎫=+-<< ⎪⎝⎭的图象向右平移()0ϕϕ>个单位长度后得到函数()g x 的图象,若()(),f x g x 的图象都经过点320,2P ⎛⎫⎪ ⎪⎝⎭,则ϕ的值不可能是( )A.34π B.π C.54π D.74π 8.【答案】C 【解析】把0,2P ⎛⎫⎪⎪⎝⎭代入()()3sin 2f x x θ=+,得sin 2θ=,故4πθ=,所以()3sin 224g x x πϕ⎛⎫=+- ⎪⎝⎭,把0,2P ⎛⎫ ⎪ ⎪⎝⎭代入得sin 24πϕ⎛⎫-= ⎪⎝⎭,k ϕπ=或()4k k Z πϕπ=-∈,观察选项,故选C.9.若变量,x y 满足:2202403110x y x y x y -+≤⎧⎪+-≥⎨⎪-+≥⎩,且满足(1)(2)0t x t y t ++++=,则参数t 的取值范围为( ) A.423t -<<-B.423t -<≤-C.423t -≤≤-D.423t -≤<- 9.【答案】C【解析】:(1)(2)0l t x y x y ++++=,所以直线恒过定点()2,1-,画出可行域,由题意知,直线恒过定点()2,1-点及可行域内一点,直线l 方程可改写成:(2)(1)t y t x t +=-+-,①由图知,当斜率不存在时,符合题意;②当斜率存在时,11,22t k t +⎡⎫⇒=-∈+∞⎪⎢+⎣⎭⇒423t -<≤-;综上:423t -≤≤-. 10.如图,四面体D ABC -的体积为14,且满足060ACB ∠=,1BC =,2AD +=,则四面体D ABC -中最长棱的长度为( )B.2D.310.【答案】B 【解析】因为111sin 60324D ABC AD BC AC V -⎛⎫⋅⋅⋅⋅≥= ⎪⎝⎭, 即1AD ≥,因为22AD =≥=,当且仅当1AD ==时,等号成立,这时1AC AD ==,且AD ⊥面ABC ,所以2CD =,AB =,60DACB得BD =,故最长棱的长为2.第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在答题卷相应横线上. 11.在921x x ⎛⎫- ⎪⎝⎭的二项展开式中,常数项的值为_______.11.【答案】84 【解析】法一:()()9218319911rrr rrr r T Cx C xx --+⎛⎫=-=- ⎪⎝⎭,令1830r -=,得6r =,故常数项为6349984T C C ===;法二:按比例分配2x 与1x-这两项中x 的次数之比为2:1,所以把9分为1:2两份,前项用1份,后项用2份,才会出现常数项,所以常数项为3984C =.12.在极坐标系中,O 是极点,设点,A B 的极坐标分别是2,3,63ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,则O 点到直线AB 的距离是 .12.【答案】7【解析】,A B 的直角坐标分别是(3,,22⎛- ⎝⎭,故直线AB 的方程为)3y x -=-,即120x +-=,所以O 点到直线AB 的距离是=. 13.某种产品的加工需要A ,B ,C ,D ,E 五道工艺,其中A 必须在D 的前面完成(不一定相邻),其它工艺的顺序可以改变,但不能同时进行,为了节省加工时间,B 与C 必须相邻,那么完成加工该产品的不同工艺的排列顺序有____种. (用数字作答) 13.【答案】24【解析】将B ,C 两道工序看成一个整体与A , D ,E 三道工序全排列共有44A 不同排列法,再将B ,C 两道工序全排列有22A ,因为A 和D 只有两钟可能,要么在左,要么在右,故A 必须在D 的前且B 与C 必须相邻的不同排列顺序为4242124.2A A ⋅= 14.已知函数()11f x x =+,点O 为坐标原点, 点()()(),n A n f n n N *∈,向量()0,1=i ,nθ是向量n OA 与i 的夹角,则912129cos cos cos sin sin sin θθθθθθ+++= . 14.【答案】910【解析】画图像可知912129cos cos cos 111,,,sin 12sin 23sin 910θθθθθθ===⨯⨯⨯, 所以912129cos cos cos 11111sin sin sin 122391010θθθθθθ+++=+++=-⨯⨯⨯910=. 15.已知函数)(x f y =,I x ∈,若存在I x ∈0,使得00)(x x f =,则称0x 为函数)(x f y =的不动点;若存在I x ∈0,使得00))((x x f f =,则称0x 为函数)(x f y =的稳定点.则下列结论中正确的是 . (填上所有正确结论的序号) ①1,12-是函数2()21g x x =-有两个不动点; ②若0x 为函数)(x f y =的不动点,则0x 必为函数)(x f y =的稳定点; ③若0x 为函数)(x f y =的稳定点,则0x 必为函数)(x f y =的不动点; ④函数2()21g x x =-共有三个稳定点;⑤若函数)(x f y =在定义域I 上单调递增,则它的不动点与稳定点是完全相同. 15.【答案】①②⑤【解析】对于①,令()g x x =,可得12x =-或1x =,故①正确; 对于②,因为00)(x x f =,所以000)())((x x f x f f ==, 即00))((x x f f =,故0x 也是函数)(x f y =的稳定点,故②正确;对于③④,2()21g x x =-,令x x =--1)12(222,因为不动点必为稳定点,所以该方程一定有两解1,21-=x ,由此因式分解,可得0)124)(12)(1(2=-++-x x x x 还有另外两解451±-=x ,故函数()g x 的稳定点有1,21-,451±-,其中451±-是稳定点,但不是不动点,故③④错误;对于⑤,若函数)(x f y =有不动点0x ,显然它也有稳定点0x ;若函数)(x f y =有稳定点0x ,即00))((x x f f =,设00)(y x f =,则00)(x y f =即),(00y x 和),(00x y 都在函数)(x f y =的图象上,假设00y x >,因为)(x f y =是增函数,则)()(00y f x f >,即00x y >,与假设矛盾; 假设00y x <,因为)(x f y =是增函数,则)()(00y f x f <,即00x y <,与假设矛盾; 故00y x =,即00)(x x f =,)(x f y =有不动点0x ,故⑤正确.三、解答题:本大题共6小题,共75分.解答须写出说明、证明过程和演算步骤. 16.(本小题满分12分)在ABC ∆中,内角,,A B C 所对的边分别是,,a b c ,已知sin tan 1cos CA=C-,c =(Ⅰ)求b a;(Ⅱ)若三角形ABC ∆,求角C .17.(本小题满分12分)从某中学高三某个班级第一组的7名女生,8名男生中,随机一次挑选出4名去参加体育达标测试.(Ⅰ)若选出的4名同学是同一性别,求全为女生的概率; (Ⅱ)若设选出男生的人数为X ,求X 的分布列和EX .18.(本小题满分12分)设*n N ∈,函数ln ()n x f x x=,函数e ()xn g x x =,(0,)x ∈+∞.(Ⅰ)求函数()f x 的最大值及函数()g x 的单调区间;(Ⅱ)若存在直线:l y c =()c R ∈,使得曲线()y f x =与曲线()y g x =分别位于直线l 的两侧,求n 的最大值. (参考数据:ln 4 1.386,ln5 1.609≈≈)19. (本小题13分)如图,在五面体ABCDEF 中,四边形ABCD 是边长为4的正方形,//EF AD , 平面ADEF ⊥平面ABCD ,且2BC EF =, AE AF =,点G 是EF 的中点. (Ⅰ)证明:AG ⊥平面ABCD ;(Ⅱ)若直线BF 与平面ACE所成角的正弦值为9,求AG 的长.20.(本小题满分13分)已知数列{}n a 共有()22,k k k Z ≥∈项,11a =,前n 项和为n S ,前n 项乘积为n T ,且()112n n a a S +=-+()1,2,,21n k =-,其中2212k a -=,数列{}n b满足2log n b =(Ⅰ)求数列{}n b 的通项公式; (Ⅱ)若122123333322222k k b b b b --+-++-+-≤,求k 的值.21. (本小题14分)设()()0000,0A x y x y ⋅≠是椭圆()22:101x y m m τ+=>+上一点,它关于y 轴、原点、x 轴的对称点依次为,,B C D .E 是椭圆τ上不同于A 的另外一点,且AE AC ⊥,如图所示.(Ⅰ) 若点A 横坐标为2,且BD AE ∥, 求m 的值;(Ⅱ)求证:直线BD 与CE 的交点Q 总在椭圆21x y m ++yBFA CDG E蚌埠市2015届高三年级第二次教学质量检查考试数学试卷(理工类)参考答案及评分标准二、填空题: 11.84;;13.24;14.910;15.①②⑤.三、解答题: 16.(本小题满分12分) 【解析】(Ⅰ)由题,sin sin cos 1cos A C=A C-,即有sin sin cos sin cos sin A=A C+C A=B 故1ba=;………………………………6分 (Ⅱ)有2222sin 32cos 2a C a a C a ⎧=⎪⎪⎨+-⎪=⎪⎩, 得cos 1C C =,1cos 2C =-,解得120C =.………………………………12分17. (本小题满分12分)【解析】(Ⅰ)若4人全是女生,共有4735C =种情况;若4人全是男生,共有4870C =种情况;故全为女生的概率为47448730170353C C C ==++.………………………6分 (Ⅱ)共15人,任意选出4名同学的方法总数是415C ,选出男生的人数为0,1,2,3,4X =………………………………7分01874151(0)39C C P X C ===;13874158(1)39C C P X C ===;(2)P X =22874152865C C C ==;318741556(3)195C C P X C ===; 43874152(4)39C C P X C ===.………………………………10分 故X012343939651953915EX =⨯+⨯+⨯+⨯+⨯=.………………………12分 18. (本小题满分12分)【解析】(Ⅰ)结论:函数()f x 求导,得 11ln ()n n xf x x+-'=, 令 ()0f x '=,解得1e n x =. 当x 变化时,()f x '与()f x 的变化如下表所示:所以函数()f x 在区间10,n e ⎛⎫⎪⎝⎭上为单调递增,区间1,n e ⎛⎫+∞ ⎪⎝⎭上为单调递减.故函数()1max 1nf x f e en ⎛⎫== ⎪⎝⎭.………………………………3分函数()g x 求导,得 ()1()x n e x n g x x +-'=, 令 ()0g x '=,解得x n =.当x 变化时,()g x '与()g x 的变化如下表所示:所以函数()g x 在区间()0,n 上为单调递减,区间(),n +∞上为单调递增. ………………………………6分(Ⅱ)由(1)知 ()()min nn e g x g n n==,因为存在直线:l y c =()c R ∈,使得曲线()y f x =与曲线()y g x =分别位于直线l 的两侧,所以1n n e n en≥,即11n n e n +-≥,可得()11ln n n n +≥-,………………………………8分当1n =时,成立, 当2n ≥时,1ln 1n n n +≥-,即21ln 01n n +-≥-, 令()()21ln 21h n n n n =+-≥-,则()h n 是减函数,所以继续验证, 当2n =时, 3ln 20->,………………………………10分 当3n =时, 2ln30->,当4n =时,55ln 4 1.4033->-> 当5n =时, 33ln 5 1.6022-<-<,所以max 4n =.………………………………12分19. (本小题满分12分)【解析】(Ⅰ)证明:因为AE AF =,点G 是EF 的中点, 所以 AG EF ⊥. 又因为 //EF AD , 所以 AG AD ⊥.………………………………3分因为平面ADEF ⊥平面ABCD ,平面ADEF平面ABCD AD =,AG ⊂平面ADEF ,所以 AG ⊥平面ABCD . ………………………………6分(Ⅱ)因为AG ⊥平面ABCD ,AB AD ⊥,所以,,AG AD AB 两两垂直. 以A 为原 点,以AB ,AD ,AG 分别为x 轴、y 轴和z 轴,如图建立空间直角坐标系 则(0,0,0)A ,(4,0,0)B ,(4,4,0)C , 设(0)AG t t =>,则(0,1,)E t ,(0,1,)F t -,所以(4,1,)BF t =--,(4,4,0)AC =,(0,1,)AE t =.……………………………8分 设平面ACE 的法向量为(,,)n x y z =, 由 0AC n ⋅=,0AE n ⋅=,得440,0,x y y tz +=+=⎧⎨⎩令 1z =, 得(,,1)n t t =-.因为BF 与平面ACE 所成角的正弦值为9,所以 6cos ,9||||BF n BF n BF n ⋅<>==⋅,………………………………10分即=, 解得21t =或2172t =.所以1AG = 或2. ………………………………12分20.(本小题满分13分)【解析】(1)当1n =时,22a a =,则21a a a =; 当221n k ≤≤-时,()112n n a a S +=-+,()112n n a a S -=-+,所以()11n n n a a a a +-=-,故1n na a a +=,即数列{}n a 是等比数列,12n n a a -=, 可得()()1121211222n n n n nk n n T a a a a-+++++-=⋅⋅⋅==,()11112121n n n n b n n k k -⎡⎤-=+=+⎢⎥--⎣⎦; ………………………………7分 (2)令32n b ≤,则12n k ≤+,又n N *∈,故当n k ≤时,32n b <,当1n k ≥+时,32n b >.………………………………8分 1221233332222k k b b b b --+-++-+- 12123333322222k k k b b b b b +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-+-++- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭………………10分()()()()212111210122212121k k k k k k k k k b b b b k k k k k +⎡⎤⎡⎤+-+-⎢⎥⎢⎥=++-++=+-+=⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦由23212k k ≤-,得22630k k -+≤k ≤≤12分 又2k ≥,且k N *∈,所以2k =.………………………………13分 21.(本小题满分14分)【解析】(Ⅰ)因为BD AC ∥,AE AC ⊥,所以BD AC ⊥,可知22A ⎛ ⎝⎭,……………………………… 4分故311m =+,2m =;………………………………6分 (Ⅱ)由对称性可知()00,B x y -,()00,C x y --,()00,D x y -,四边形ABCD 为矩形, 设()11,E x y ,由于,A E 均在椭圆τ上,则()()220022111111x m y m x m y m ⎧++=+⎪⎨++=+⎪⎩①②由②-①得:()()()()()1010101010x x x x m y y y y +-+++-=,……… 8分 显然10x x ≠,从而1010010100111111111AC AE y y x x y k x x m y y m k m m x +-=-⋅=-⋅=⋅=⋅++-+++,………………………………10分 因为AE AC ⊥,所以1AE AC k k ⋅=-,所以()()00100000100:1:1BDCE y l y x x y y y l y y x x x x x x m x ⎧=-⎪⎪⎨+⎪+=+=⋅+⎪++⎩,解得0022m x x m m y y m +⎧=⎪⎪⎨+⎪=-⎪⎩,………………………………12分 代入椭圆方程,知22212x m y m m ⎛⎫+= ⎪++⎝⎭.………………………………14分(以上各题其它解法请参考以上评分标准酌情赋分)。
安徽省蚌埠市2023-2024学年高三下学期第三次教学质量检查数学试题答案

蚌埠市2024届高三年级第三次教学质量检查考试数学参考答案及评分标准一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
题 号12345678答 案ADABCBCB二、选择题:本题共3小题,每小题6分,共18分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得6分,部分选对的得部分分,有选错的得0分。
题 号91011答 案ABCBCABD三、填空题:本题共3小题,每小题5分,共15分。
12 (0,1)13 0或4;(槡2-2,槡2+2)∪{4}(答对第一空给2分,答对第二空给3分)14 1四、解答题:本题共5个小题,共77分。
解答应写出说明文字、证明过程或演算步骤。
15 (13分)解:(1)由题意知a=1,且ba=1,∴b=1,2分………………………………………………∴c=a2+b槡2槡=2,所以双曲线的离心率e=ca槡=2 5分………………………………………………(2)由(1)知双曲线方程为x2-y2=1,将y=12x-12即x-1=2y代入x2-y2=1,得3y2+4y=0,9分…………………因而y1=0,y2=-43,所以|PQ|=1+2槡2·y1-y2=43槡5 13分………………………………………16 (15分)解:(1)依题意,p1=1,p2=0 5,p3=p2×0 5+(1-p2)×(1-0 4)=0 6-0 1p2=0 55 6分……………………依题意pn=pn-1×0 5+(1-pn-1)×(1-0 4)=0 6-0 1pn-1整理得pn-611=-110pn-1-6()11,又p1-611=511≠0,所以pn-6{}11是首项为511,公比为-110的等比数列 9分…………………………(2)由(1),寒假第n天不下雪的概率pn=511-1()10n-1+611,11分……………………从而小明寒假第n天跑步的概率为qn=pn×0 6+(1-pn)×0 2=0 2+0 4pn=2355+211-1()10n-1,13分……………则他第n天通过运动锻炼消耗能量为330qn+220(1-qn)=220+110qn=266+20(-110)n-115分……………………17 (15分)解:(1)由题意知AD=BC=PA=2,则在△ABC中,cos∠ABC=AB2+BC2-AC22AB·BC=42+22-(槡27)22×4×2=-12,∵∠ABC∈(0,π)∴∠ABC=2π3,从而∠DAB=π3,3分……………………………△ABD中,BD2=AD2+AB2-2AD·AB·cosπ3=22+42-2×2×4×12=12,则BD2+AD2=12+4=16=AB2∴BD⊥AD,5分………………………………………………………………………又BD⊥AE,AD∩AE=A,所以BD⊥平面PAD,而BD 平面ABCD,∴平面PAD⊥平面ABCD 8分……………………………………………………… 第17题答案图(2)由(1)知BD⊥平面PAD,PD 平面PAD,∴BD⊥PD,∴PD=PB2-BD槡2=2,所以△PAD为等边三角形,10分………如图,在平面PAD内作DH⊥AD,则DH⊥平面ABCD,以DA,DB,DH分别为x轴,y轴,z轴建立空间直角坐标系(如图所示),则D(0,0,0),B(0,槡23,0),C(-2,槡23,0),P(1,0,槡3),12分………………………从而BP→=(1,槡-23,槡3),BC→=(-2,0,0)显然平面ABC的一个法向量为n=(0,0,1)设平面PBC的法向量为m=(x,y,z),则BP→·m=0,BC→·m=0{,即x槡-23y槡+3z=0,-2x=0{,取m=(0,1,2),记二面角P-BC-A的平面角为α,则cosα=cos〈m,n〉=|m·n||m|·|n|=1×2槡1×5=槡255即二面角P-BC-A的余弦值为槡25515分………………………………………18 (17分)解:(1)记g(x)=tanx-x,则g′(x)=1cos2x-1,2分………………………………………因为x∈0,π()2,所以cosx∈(0,1),所以g′(x)>0,所以g(x)单调递增,从而g(x)>g(0)=0,即tanx>x 4分………………………………………………当a=1时x>xf(x)等价于x>sinx,记h(x)=x-sinx,则h′(x)=1-cosx>0,h(x)单调递增,6分………………………………………所以h(x)>h(0)=0,即x>sinx 综上,当a=1,x∈0,π()2时,tanx>x>xf(x) 8分…………………………………(2)xtanx<f(x)等价于xtanx<asinxx,记F(x)=xtanx-asinxx,则F(-x)=F(x),所以题设等价于当x∈0,π()2时,F(x)<0即x2cosx-asin2x<0 当a≤0时,F(x)>0,不合题意 10分………………………………………………当0<a<1时,x2cosx-asin2x>x2cosx-ax2=x2(cosx-a)存在θ∈0,π()2,cosθ-a=0,因此当x∈(0,θ),x2cosx-asin2x>0,即F(x)<0不成立,不合题意 13分……当a≥1时,x2cosx-asin2x≤x2cosx-sin2x,记G(x)=x2cosx-sin2x,x∈0,π()2,由于tanx>x,所以sinx>xcosx,故G′(x)=2xcosx-x2sinx-2sinxcosx<2sinx-x2sinx-2sinxcosx=-sinx[x2-2(1-cosx)]=-sinxx2-4sin2x()2=-4sinxx()22-sin2x[]2<0从而G(x)在0,π()2单调递减,G(x)<G(0)=0,F(x)<0恒成立,符合题意 综上,实数a的取值范围是[1,+∞)17分………………………………………19 (17分)解:(1)令x=0,则e(0)=1 由e(x)e(y)=e(x+y),令y=-x,则e(x)e(-x)=e(0)=1 因为e(x)≠0,故e(-x)=1e(x)5分………………………………………………(2)证明:因为(ix)4n(4n)!+(-ix)4n(4n)!=x4n(4n)!+x4n(4n)!=2x4n(4n)!,(ix)4n+1(4n+1)!+(-ix)4n+1(4n+1)!=ix4n+1(4n+1)!+-ix4n+1(4n+1)!=0,(ix)4n+2(4n+2)!+(-ix)4n+2(4n+2)!=-x4n+2(4n+2)!+-x4n+2(4n+2)!=-2x4n+2(4n+2)!,(ix)4n+3(4n+3)!+(-ix)4n+3(4n+3)!=-ix4n+3(4n+3)!+ix4n+3(4n+3)!=0,e(ix)+e(-ix)=∑∞n=02x4n(4n)!-2x4n+2(4n+2[])!=∑∞k=02(-1)k(2k)!x2k=2∑∞k=0(-1)k(2k)!x2k=2c(x),所以c(x)=e(ix)+e(-ix)211分……………………………………………………(3)证明:令g(x)=xe(x)-1,则有g(-x)-g(x)=-xe(-x)-1-xe(x)-1=-x1e(-x)-1+1e(x)[]-1=-x·[e(x)-1]+[e(-x)-1][e(-x)-1][e(x)-1]=-x·e(x)+e(-x)-22-e(x)-e(-x)=x,14分…………因此x=g(-x)-g(x)=∑∞n=0Bnn!(-x)n-∑∞n=0Bnn!xn=-2∑∞k=0B2k+1(2k+1)!x2k+1=-2B1x+∑∞k=1B2k+1(2k+1)!x2k[]+1故B1=-12且∑∞k=1B2k+1(2k+1)!x2k+1=0,即B2k+1=0(k=1,2,3,…) 17分…………(以上答案仅供参考,其它做法请参考以上评分标准赋分)。
安徽省蚌埠市2012届高三年级第三次教学质量检查考试文科综合试题

安徽省蚌埠市2012届高三年级第三次教学质量检查考试文科综合试题12.安徽地区的先贤们在中华民族精神主体、中国古典文化的构建过程中,都经做出不可磨灭的贡献。
下列表述正确的是①《逍遥游》表达了老子力图在乱世保持独立的人格,追求逍遥无恃的精神自由思想②吴敬梓的《儒林外史》是我国清代一部杰出的现实主义长篇讽刺小说③李鸿章践行了“中体西用”思想,促进了中国近代化的发展④陈独秀的《文学改良刍议》体现了解放思想、探索新知、再造文明的精神A.①②B.①③C.②③D.③④13.1514年,广东布政司参议陈伯献上奏说:“近许官府抽分(注:征收进口税),公为贸易,遂使奸民数千,驾造巨舶,私置兵器,纵横海上”。
据此可知A.陈伯献反对海禁政策B.明政府加强海禁力度C.明代东南沿海遭到西方侵略D.明政府曾经放松海禁14.隋唐时官方对曹操的评价以肯定为主,认为他是大英雄;到了北宋则完全相反,从官方到民间对他的评价都以否定为主。
形成这种变化的主要原因是A.宋代商品经济高度发展促进思想解放B.宋代统治者强化中央集权的需要C.理学发展为官方统治哲学的结果D.宋代市民文学发展的结果15.小周同学在学习了盂德斯鸠的思想后认为,“三权分立”的主张和董仲舒的“天人感应”有一致之处。
这是因为它们A.都主张权力制约B.都强调权力集中C.都主张分权制衡D.都认可君权无限16.当光绪帝把变法的想法通过庆亲王奕勖转告给太后时,太后就曾对光绪皇帝的变法愿望和志向予以赞同。
她表示,“变法乃素志”,“苟可以致富强者,儿自为之,吾不内制也。
”而她的条件是“戒帝毋操之过蹙而已。
”由此可以推断慈禧后来反对变法的原因可能是A.维新派变法措施过于激进B.慈禧顽固守旧,一贯反对改革C.慈禧一向善变,出尔反尔D.维新派保守软弱,改革效果不佳A.17.造成表1中米价变化的主要原因是表1:1946年1月-6月中国几个主要城市的米价(单位:百元/市石)A.抗战胜利,粮食丰收B.自然灾害,粮食减产C.内战在即,通货膨胀D.国共和谈,经济好转18.图2摄于20世纪50年代后期的中国。
安徽省蚌埠市高三数学3月第二次质检试题 理

安徽省蚌埠市2012届高三3月第二次质检试题数学(理)一、选择题(50分)1、已知全集U =R ,集合A ={x |x 2-x =0},B ={x |-1<x <1},则A ∩B = A 、{0} B 、{1} C 、{0,1} D 、φ 2、最小二乘法的原理是 A 、使得1[()]n iii y a bx =-+∑最小 B 、使得21[()]niii y a bx =-+∑最小C 、使得221[()]nii i ya bx =-+∑最小 D 、使得21[()]ni i i y a bx =-+∑最小3、设p :x <-1或x >1,q :x <-2或x >1,则p ⌝是⌝q 的 A 、充分不必要条件 B 、必要不充分条件A 、充要条件 A 、既不充分也不必要条件4、若2(2,)N ξσ--,且P (-4<ξ<-2==0.3,则P (ξ>0)的值为A 、0.2B 、0.3C 、0.7D 、0.8 5、给出下列四个例题,期中正确的命题是 A 、各侧面都是正方形的棱柱一定是正棱柱 B 、若直线l ⊥平面α,l ∥平面β,则α⊥βC 、若平面α与平面β的交线为m ,平面α内的直线n ⊥直线m ,则直线n ⊥平面βD 、一个二面角的两个半平面所在平面分别垂直于另一个二面角的两个半平面所在平面,则这两个二面角的平面角互为补角 6、已知函数f (x )===2,(10)1)x x x --≤≤⎧⎪<≤,则下列的图象错误的是7、已知圆的参数方程为2cos 2sin x y θθ=⎧⎨=⎩(θ为参数),给出以下函数,其中函数图象能平分该圆面积的是A 、f(x)=cosx B.f(x)=e x-1 C.f(x)=sinx D.f(x)=xsinx8、在三角形ABC 中,()AB AC AB AC ∙=-=6,M 为BC 边的中点,则中线AM 的长为 ABCD9、已知正项等比数列{n a }满足:7652a a a =+,若存在两项,m n a a使得1,则41m n+的最小值为 A 、1 B 、3 C 、9 D 、不存在 10、已知两定点M (-2,0),N (2,0),若直线上存在 点P ,使得|PM |-|PN |=2,则称该直线为“A 型直线”,给出下列直线: ①y=x+1 ②③y=-x+3 ④y=-2x其中是“A 型直线”的序号是A 、①④B 、③④C 、②③D 、①③第II 卷(非选择题,共100分)二、填空题(25分)11、设x,y 满足约束条件0201x x y x y ≥⎧⎪-≥⎨⎪-≤⎩,则z =2x +y 的最大值是_____12、若(x +2)n展开式的二项式系数之和等于64,则第三项是__13、已知函数f(x)=2sinx+3x+1,若f (6-a 2)>f(5a),则实数a 的取值范围是____14、程序框图如图所示,则输出a 的最后一个数值为____ 15、某同学对函数f(x)=xcosx 进行研究后,得出以下五个结论: ①函数y=f(x)的图象是中心对称图形; ②对任意实数x,|f(x)|≤|x|均成立;③函数y=f(x)的图象与x 轴有无穷多个公共点,且任意相邻两公共点间的距离相等;④函数y =f(x)的图象与直线y=x 有无穷多个公共点,且任意相邻两公共点间的距离相等⑤当常数k 满足|k|>1时,函数y=f(x)的图象与直线y=kx 有且仅有一个公共点。
安徽省蚌埠市高三数学第三次月考试题 理 新人教A版

怀远一中2012-2013学年度高三年级第三次月考数 学 试 题(理 科)(本试卷满分150分,时间120分钟) 选择题:本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一个是符合题目要求的.1.复数11i+在复平面上对应的点的坐标是( ) A .(1,1) B .(1,1)- C .(1,1)-- D .(1,1)-2.已知向量(2,1),(1,)a a b k =+=rr r ,若//a b r r ,则实数k =( ) A .12B .-2C .-7D .33.已知sin()2sin()2ππ-∂=-+∂,则sin cos ∂⋅∂=( )A.25 B. 25- C. 25或25- D. 15-4. 设函数()f x 是R 上可导的偶函数,且满足5()()2f x f x +=-,则曲线()y f x =在5x =处的切线的斜率为( )A .15- B .0 C .15D .5 5. 命题“存在04,2<-+∈a ax x R x 使为假命题”是命题“016≤≤-a ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6. 函数()()()⎩⎨⎧≥<+-=1log 13822x x x ax x x f a 在R x ∈内单调递减,则a 的范围是( )A .⎥⎦⎤ ⎝⎛21,0 B. )1,21[ C .⎥⎦⎤⎢⎣⎡85,21 D .⎪⎭⎫⎢⎣⎡1,857.若将函数sin()(0)4y wx w π=+>的图象向右平移4π个单位长度后,与函数sin()3y wx π=+的图象重合,则w 的最小值为( )A .1B . 2C .112D .2338. 设,,a b c 分别是方程122log x x =,121()log 2x x =,21()log 2xx =的实数根,则有( )A. a b c <<B. c b a <<C. b a c <<D. c a b <<9. 锐角ABC ∆中,,,a b c 分别是三内角,,A B C 的对边,设2B A =,则ba的取值范围是 ( )A. ()2,2-B. ()0,2C.)2D.10.已知函数()y f x =的周期为2,当[0,2]x ∈时,2()(1)f x x =-,如果()()5log |1|g x f x x =--,则函数()y g x =的所有零点之和为( )A .2B .4C .6D .8二、填空题:本大题共5小题,每小题5分,共25分,将答案填在答题卷中相应位置.11. 已知23cos()sin 6παα+-=,则7sin()6πα-的值是12. 若点P 是ABC ∆的外心,且0=++PC PB PA λ,0120=∠C ,则实数λ的值为13. ABC ∆中,,,a b c 分别是三内角,,A B C 的对边,若1,3,2a b A C B ==+=,则sin C =14. 已知函数)(log 221a ax x y +-=在区间]2,(-∞上是增函数,则实数a 的取值范围是15.已知定义在R 上函数()y f x =满足条件()(1)1f x f x +-=,当[]0,1x ∈时2()f x x =.给出以下四个命题:(1)函数()f x 是以2为周期的函数; (2)当[]1,2x ∈时,2()2f x x x =-;(3)函数()f x 为R 上的偶函数; (4)3(2005.5)4f -=. 其中真命题的序号为三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卷上指定区域. 16.(本小题满分12分)已知函数()2cos (sin cos )1,f x x x x x R =-+∈. (1)求函数()f x 的最小正周期; (2)求函数()f x 在区间3,84ππ⎡⎤⎢⎥⎣⎦上的最值.17. (本小题满分12分)在ABC ∆中,,,a b c 分别是角,,A B C 的对边,已知2,3c C π==.(1)若ABC ∆3,a b ;(2)若sin sin()2sin 2C B A A +-=,求ABC ∆的面积.18. (本小题满分12分)已知函数()f x 满足322()'()3f x x f x x c =+-+(其中c 为常数) (I )若方程()f x =0有且只有两个不等的实根,求常数c ;(II )在(I )的条件下,若1()03f ->,求函数()f x 的图像与X 轴围成的封闭图形的面积.19. (本小题满分12分)设锐角ABC ∆ 的内角,,A B C 的对边分别是,,a b c ,且2sin a b A =. (1)求B 的大小;(2)求cos sin A C +的取值范围.20. (本小题满分13分)已知2(1,cos ),(1sin ,cos )3a x b x x ==+r r ,0,2x π⎡⎤∈⎢⎥⎣⎦,2()2sin 3f x a b m x ⎛⎫=-+ ⎪⎝⎭r r g(1)当m =2时,求()f x 的值域;(2)若()f x 的最大值为3.求实数m 的值.21、(本小题满分14分)已知A 、B 、C 是直线l 上不同的三点,O 是l 外一点,向量OC OB OA,, 满足:.]y )x 32[ln()1x 23(2=⋅-+-⋅+-记()y f x =.(Ⅰ)求函数()y f x =的解析式:(Ⅱ)若对任意],3161[,∈x 不等式|a -ln x |-[]ln ()3f x x '->0恒成立,求实数a 的取值范围:(Ⅲ)若关于x 的方程()2f x x b =+在(]0,1上恰有两个不同的实根,求实数b 的取值范围.怀远一中2012-2013学年度高三年级第三次月考数 学 答 案(理 科)一、选择题:1----5 DABDC 6----10 BDACB 二、填空题:11、 1 12、 0 13、 -1 14、2315、(2)(3) 三、解答题:16、(12分) 解:(1)2211sin sin 4223()2(1cos )s ab C ab ab c a b ab C π⎫===⇒=⎪⇒⎬⎪=+-+⎭V 25a b '==L L(2)依题得sin()sin()4sin cos B A B A A A ++-= cos (2sin sin )0A A B ⇒-=①当cos 0A =即2A π=时,6B b π=⇒=此时182s bc '==V L ②当2sin sin A B =即2a b =时,再由2222cos c a b ab C =+-得a b ==此时1sin 2s ab C ==V故12s '=V L L L L L L L 17、(12分) 解:(1)1()sin )sin cos 22f x wx wx wx wx =++21wx =+()16f x ⎡'∴∈⎣L L L(2)易得 函数()y f x =的增区间为,,844k k k Z w w w w ππππ⎡⎤'-++∈⎢⎥⎣⎦L L 又()y f x =在区间3,42ππ⎡⎤-⎢⎥⎣⎦上单调递增,34410122430w w ww ππππ⎧-≤-⎪⎪⎪'∴≤⇒<≤⎨⎪>⎪⎪⎩L L18、(12分) 解:(1)由正弦定理得1sin sin 2sin sin 25sin 060,2B A B A B A B ππ⎫=⎪=⎫⎪'⇒⇒=⎬⎬≠⎛⎫⎭⎪∈ ⎪⎪⎝⎭⎭L L (2)A B C π++=Q 56A C π∴+= ∴5623202C A A A πππππ⎫=-<⎪⎪⇒<<⎬⎪<<⎪⎭所 以5cos sin cos sin())1063A C A A A ππ'+=+-=+L L 又25336A πππ<+<3cos sin 1222A C ⎛⎫'∴+∈ ⎪ ⎪⎝⎭L L 19、(12分) 解:(1) ()()ln 2ln 1ln 2(1)x x f x a a x a a a x a '=+-=-+> 易 知 0x >时()0f x '> 0x <时 ()0f x '< 所以()y f x =的单调递减区间为(),0-∞,单调递增区间为()0,+∞ 故 min ()(0)16f x f '==L L L L L (2)依题得 ()1()1f x t f x t -=⇒=+ 或()1f x t =-1121211t t t +>⎧'⇒⇒>⎨->⎩L L L L L20、(13分)解:(1)依题得22()(sin )2f x x m m =-+++22()(sin 2)6m f x x =⇒=-++ 又[][]sin 0,1()3,26x f x '∈∴∈-L L (2)22()(sin )2f x x m m =-+++ 令sin t x = 则 []22()()2,0,1g t t m m t =-+++∈①当0m -≤即0m ≥时, max ()(0)23g t g ==≠ 不符题意 ②当1m -≥即1m ≤-时, max ()(1)31g t g m ==⇒=-③当01m <-<即10m -<<时,2max ()()23g t g m m =-=+= 无 解综上知:113m '=-L L L L L L L L21、(14分)(2),3323)(x x x f ++='Θ ∴原不等式为.0)323ln(|ln |>+--xx a所以 ,323ln ln x x a +-<或,323ln ln xx a ++>①……6分设,323ln 323ln ln )(,332ln 323lnln )(2xxx x x h x x x x x g +=++=+=+-=依题意知 a <g (x )或a >h (x ) 在 x ∈]31,61[ 上 恒 成 立,又 ,03262)62(31323)('22>++=+⋅+=xx xx x x x g Θ,0)32(2)32(33)32(3332)('2>+=+⋅-+⋅+=x x x x x x x x h∴g (x )与h (x )在]31,61[上都是增函数,要使不等式①成立,当且仅当)61(g a <或),31(h a > ∴5ln 36a < 或31ln >a .……14分。
安徽省蚌埠市2012届高三第一次教学质量检查试题(数学理)

蚌埠市2012届高三年级第一次教学质量检查考试数学(理工类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的A 、B 、C 、D 的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卡上.(不用答题卡的,填在第Ⅱ卷中相应的答题栏内)1.已知集合M 满足条件{1,2} M={1,2,3},则集合M 可能是A .{1,2}B .{1,3}C .{1}D .{2}2.已知x 为实数,条件p :x 2<x ,条件q :x1≥1,则p 是q 的 A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知等差数列{n α}中,α2=6,α5=15,若b n =α2,则数列{b n }的前5项和等于A .30B .45C .180D .904.若函数⎩⎨⎧<-≥=+0),lg(0,tan )2(x x x x x f ,则)98()24(-∙+f f π等于 A .21 B .-21 C .2 D .一2 5.阅读右侧的程序框图,输出的结果S 的值为A. 0 B .23C .3 D.-23 6.以下关于函数x x x f 2cos 2sin )(-=的命题,正确的是A .函数)(x f y =在区间(0,π32)上单调递增 B .直线8π=x 是函数)(x f y =图像的一条对称轴 C .点(4π,0)是函数)(x f y =图像的一个对称中心D .将函数)(x f y =的图像向左平移8π个单位,可得到x y 2sin 2=的图像 7.投掷一枚正方体骰子(六个面上分别标有1,2,3,4,5,6),向上的面上的数字记为α,又n (A) 表示集合的元素个数,A={x |x 2+αx +3=1,x ∈R},则n (A)=4的概率为 A .31 B .21 c .32 D .61 8.函数)(sin ππ≥≤-=x e y x 的大致图像为9.在正方体ABCD-A 1B 1C 1D 1中,E 、F 分别为棱AA 1、CC 1的中点,则在空间中与三条直线A 1D 1、EF 、CD 都相交的直线A .不存在B .有且只有两条 C.有且只有三条 D.有无数条10.设∠POQ=60°在OP 、OQ 上分别有动点A ,B ,若·=6,△OAB 的重心是G ,则|| 的最小值是A.1 B .2 C .3 D .4第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分.请将答案直接填在题中横线上11.计算等ii +-221= . 12.一个总体分为A ,B 两层,其个体数之比为4:1,用分层抽样法从总体中抽取一个容量为10 的样本,已知B 层中甲、乙都被抽到的概率为281,则总体中的个体数是 . 13.在平面直角坐标系中,若不等式组⎪⎩⎪⎨⎧≤≥+-≥+k x y x y x 020(k 为常数)表示的平面区域面积是16,那么实数k 的值为 .14.已知二项式(51cos )(+θx 的展开式中2x 项的系数与445)(+x 。
安徽省蚌埠市2024届高三下学期第三次教学质量检查数学试题

一、单选题二、多选题三、填空题1. 函数的最小正周期是( )A.B .C.D.2. 已知:,:,若是的充分不必要条件,则的取值范围为( )A.B.C.D.3. 已知抛物线的焦点为F ,直线与抛物线交于两点,则直线FA 与直线FB 的斜率之和为( )A .0B .2C .-4D .44. 已知集合,则( )A.B.C.D.5. 复数的模为( )A .1B.C.D .36. 已知,,则实数a ,b ,c 的大小关系为( )A .c >a >bB .a >b >cC .a >c >bD .c >b >a7.已知实数满足,则的最小值为( )A .2B .4C.D .68.椭圆的一个焦点是,那么( )A.B .-1C .1D.9. 已知正方形的边长为,向量,满足,,则( )A.B.C.D.10.设正实数满足,则下列说法正确的是( )A.的最小值为6B .的最大值为C.的最小值为2D .的最小值为11. 已知曲线的方程为,则下列结论正确的是( )A .当时,曲线为椭圆,其焦距为B .当时,曲线为双曲线,其离心率为C .存在实数使得曲线为焦点在轴上的双曲线D .当时,曲线为双曲线,其渐近线与圆相切12.在平面四边形中,,,,,将沿折成三棱锥,当三棱锥的体积最大时,三棱锥外接球的体积为______.13. 在平面内将点绕原点按逆时针方向旋转,得到点,则点的坐标为__________.安徽省蚌埠市2024届高三下学期第三次教学质量检查数学试题四、填空题五、填空题六、解答题七、解答题八、解答题九、解答题14. 城区某道路上甲、乙、丙三处设有信号灯,汽车在这三处因遇绿灯而通行的概率分别为,,则汽车在这三处因遇红灯或黄灯而停车一次的概率为________.15. 已知曲线是平面内到定点和定直线的距离之和等于3的动点的轨迹,则曲线的一条对称轴方程是________,的最小值是________.16. 直线与轴交于点,交圆于,两点,过点作圆的切线,轴上方的切点为,则__________;的面积为__________.17.已知数列的前项和为,且,记,则________;若数列满足,则的最小值是________.18. 已知函数.(1)求f (x )的最小正周期和在的单调递增区间;(2)已知,先化简后计算求值:19. 在四棱锥中,平面,且底面为边长为2的菱形,,.(1)记在平面内的射影为(即平面),试用作图的方法找出M点位置,并写出的长(要求写出作图过程,并保留作图痕迹,不需证明过程和计算过程);(2)求二面角的余弦值.20.如图所示,在棱台中,平面,,(1)求证:;(2)求二面角的大小21. 为提升教师的命题能力,某学校将举办一次教师命题大赛,大赛分初赛和复赛,初赛共进行3轮比赛,3轮比赛命制的题目分别适用于高一,高二,高三年级,每轮比赛结果互不影响.比赛规则如下:每一轮比赛,限时60分钟,参赛教师要在指定的知识范围内,命制非解答题,解答题各2道,若有不少于3道题目入选,将获得“优秀奖”,3轮比赛中,至少获得2次“优秀奖”的教师将进入复赛.为能进入复赛,教师甲赛前多次进行命题模拟训练,指导老师从教师甲模拟训练命制的题目中,随机抽取了4道非解答题和4道解答题,其中有3道非解答题和2道解答题符合入选标准.(1)若从模拟训练命制的题目中所抽取的8道题目中,随机抽取非解答题,解答题各2道,由此来估计教师甲在一轮比赛中的获奖情况,试预十、解答题测教师甲在一轮比赛中获“优秀奖”的概率;(2)若以模拟训练命制的题目中所抽取的8道题目中两类题目各自入选的频率作为每道该类题目入选的概率,经指导老师对教师甲进行赛前强化训练后,每道非解答题入选的概率不变,每道解答题入选的概率比强化训练前大,以获得“优秀奖”次数的期望作为判断依据,试预测教师甲能否进入复赛?22. 已知函数.(1)当时,求的极值;(2)若,求的取值范围.。
