2018-2019北京四中初三数学第一次月考
2018-2019学年北京市第四中学初三第一学期统一练习(二) 数学试卷(含答案)

北京四中2018-2019 学年度第一学期初三数学统一练习(二)数学试卷一、选择题(每小题2分,满分16分)1.抛物线y=(x﹣1)2+2的对称轴为()A.直线x=1B.直线x=﹣1C.直线x=2D.直线x=﹣22.在Rt△ABC中,∠C=90°,若BC=1,AB=,则tan A的值为()A.B.C.D.23.如图所示,将△ABC的三边分别扩大一倍得到△A1B1C1,(顶点均在格点上),它们是以P点为位似中心的位似图形,则P点的坐标是()A.(﹣4,﹣3)B.(﹣3,﹣3)C.(﹣4,﹣4)D.(﹣3,﹣4)4.如图,AC是⊙O的直径,B,D是圆上两点,连接AB,BC,AD,BD.若∠CAB=55°,则∠ADB的度数为()A.55°B.45°C.35°D.25°5.如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是()A.3B.2.5C.2D.16.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是()A.B.C.D.7.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系p=at2+bt+c(a、b、c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为()A.3.50分钟B.3.75分钟C.4.00分钟D.4.25分钟8.如图,一条抛物线与x轴相交于M、N两点(点M在点N的左侧),其顶点P在线段AB 上移动.若点A、B的坐标分别为(﹣2,3)、(1,3),点N的横坐标的最大值为4,则点M的横坐标的最小值为()A.﹣1B.﹣3C.﹣5D.﹣7二、填空题(每题2分,共16分)9.已知锐角α满足tanα=,则α=°.10.如图,∠DCE是圆内接四边形ABCD的一个外角,如果∠DCE=75°,那么∠BAD的度数是.11.请写出一个图象为开口向下,并且与y轴交于点(0,﹣1)的二次函数表达式.12.利用复印机的缩放功能,将原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,则放大前后的两个三角形的面积比为.13.如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,若AB=4,AD=3,则CF的长为.14.已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)图象上部分点的横坐标x与纵坐那么BC=.16.如图,⊙O的半径为3,A,P两点在⊙O上,点B在⊙O内,tan∠APB=,AB⊥AP.如果OB⊥OP,那么OB的长为.三、解答题17.(5分)计算:sin60°﹣4cos230°+sin45°•tan60°.18.(5分)如图,△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,求tan C 的值.19.(5分)已知二次函数的解析式是y=x2﹣2x﹣3.(1)与y轴的交点坐标是,顶点坐标是.2y的取值范围是.20.(5分)如图,在平面直角坐标系xOy中,△ABC的三个顶点分别为A(2,6),B(4,2),C(6,2).(1)在第一象限内,以原点O为位似中心,将△ABC缩小为原来的,得到△DEF,请画出△DEF.(2)在(1)的条件下,点A的对应点D的坐标为,点B的对应点E的坐标为.21.(5分)在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB的长.请你解答这个问题.22.(5分)如图,在△ABC中,点D在BC边上,∠DAC=∠B.点E在AD边上,CD=CE.(1)求证:△ABD∽△CAE;(2)若AB=6,AC=,BD=2,求AE的长.23.(5分)奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)24.(5分)一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.(1)建立适当的平面直角坐标系,求抛物线的表达式;(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.25.(5分)如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.(1)求证:∠PCE=∠PEC;(2)若AB=10,ED=,sin A=,求PC的长.26.(7分)在平面直角坐标系xOy中,抛物线C1:y=mx2﹣2mx+m+4与y轴交于点A(0,3),与x轴交于点B、C(点B在点C左侧).(1)求该抛物线的解析式;(2)求点B的坐标;(3)若抛物线C2:y=a(x﹣1)2﹣1(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.27.(8分)在△ABC中,BA=BC,∠ABC=α(0°<α<180°),点P为直线BC上一动点(不与点B,C重合),连接AP,将线段P A绕点P顺时针旋转α度得到线段PQ,连接CQ.(1)当α=90°,且点P在线段BC上时,过P作PF∥AC交直线AB于点F,如图1,图中与△APF全等的一个三角形是,∠ACQ=°.(2)当点P在BC延长线上,AB:AC=m:n时,如图2,试求线段BP与CQ的比值;(3)当点P在直线BC上,α=60°,∠APB=30°,CP=4时,请直接写出线段CQ的长.28.(8分)在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P,Q两点为同族点.下图中的P,Q 两点即为同族点.(1)已知点A的坐标为(﹣3,1),①在点R(0,4),S(2,2),T(2,﹣3)中,为点A的同族点的是;②若点B在x轴上,且A,B两点为同族点,则点B的坐标为;(2)直线l:y=x﹣3,与x轴交于点C,与y轴交于点D,①M为线段CD上一点,若在直线x=n上存在点N,使得M,N两点为同族点,求n的取值范围;②M为直线l上的一个动点,若以(m,0)为圆心,为半径的圆上存在点N,使得M,N两点为同族点,直接写出m的取值范围.参考答案一、选择题1.解:∵y=(x﹣1)2+2,∴对称轴为直线x=1,故选:A.2.解:∵Rt△ABC中,∠C=90°,若BC=1,AB=,∴AC==2;∴tan A==;故选:C.3.解:由图中可知,点P的坐标为(﹣4,﹣3),故选A.4.解:∵AB是⊙O的直径,∴∠ABC=90°,∵∠CAB=55°,∴∠ACB=35°,∴∠ADB=∠ACB=35°.故选:C.5.解:连接OA,设CD=x,∵OA=OC=5,∴OD=5﹣x,∵OC⊥AB,∴由垂径定理可知:AB=4,由勾股定理可知:52=42+(5﹣x)2∴x=2,∴CD=2,故选:C.6.解:根据题意得:AB==,AC=,BC=2,∴AC:BC:AB=:2:=1::,A、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;B、三边之比为::3,图中的三角形(阴影部分)与△ABC不相似;C、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.故选:C.7.解:根据题意,将(3,0.7)、(4,0.8)、(5,0.5)代入p=at2+bt+c,得:,解得:,即p=﹣0.2t2+1.5t﹣2,当t=﹣=3.75时,p取得最大值,故选:B.8.解:根据题意知,点N的横坐标的最大值为4,此时对称轴过B点,点N的横坐标最大,此时的M点坐标为(﹣2,0),当对称轴过A点时,点M的横坐标最小,此时的N点坐标为(1,0),M点的坐标为(﹣5,0),故点M的横坐标的最小值为﹣5,故选:C.二、填空题(每题2分,共16分)9.解:∵tanα=,∴α=30°.故答案为:30.10.解:∵四边形ABCD是⊙O的内接四边形,且∠DCE=75°,∴∠BAD=∠DCE=75°,故答案为:75°.11.解:∵图象为开口向下,并且与y轴交于点(0,﹣1),∴a<0,c=﹣1,∴二次函数表达式为:y=﹣x2+2x﹣1(答案不唯一).故答案为:y=﹣x2+2x﹣1(答案不唯一).12.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,所以放大前后的两个三角形的面积比为1:16,故答案为:1:16.13.解:∵四边形ABCD为矩形,∴AB=CD,AD=BC,AB∥CD,∴∠F AE=∠FCD,又∵∠AFE=∠CFD,∴△AFE∽△CFD,∴==2.∵AC==5,∴CF=•AC=×5=.故答案为:.14.解:从表格看出,函数的对称轴为x=1,图象开口向下,函数与x轴的一个交点式(﹣1,0),由对称轴x=1,推出函数与x轴另外一个交点为(3,0),当y>0时,x的取值范围是为﹣3<x<1,故答案是﹣3<x<1.15.解:∵AB,AC都是⊙O的弦,OM⊥AB,ON⊥AC,∴N、M分别为AC、AB的中点,即MN为△ABC的中位线,∵MN=2.5,∴BC=2MN=5.故答案为5.16.解:如图,连接OA,作AM⊥OB交OB的延长线于M,作PN⊥MA交MA的延长线于N.则四边形POMN是矩形.∵∠POB=∠P AB=90°,∴P、O、B、A四点共圆,∴∠AOB=∠APB,∴tan∠AOM=tan∠APB==,设AM=4k,OM=3k,在Rt△OMA中,(4k)2+(3k)2=32,解得k=(负根已经舍弃),∴AM=,OM=,AN=MN﹣AM=∵∠MAB+∠ABM=90°,∠MAB+∠P AN=90°,∴∠ABM=∠P AN,∵∠AMB=∠PNA=90°,∴△AMB∽△PNA,∴=,∴=,∴BM=,∴OB=OM﹣BM=1.故答案为1三、解答题17.解:原式=×﹣4×()2+×=﹣3+=.18.解:∵△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,∴∠ADB=∠ADC=90°,∴AB=2BD,∴BD=6,∴CD=BC﹣BD=15﹣6=9,∴AD=,∴tan C=.即tan C的值是.19.解:(1)令x=0,则y=﹣3.所以抛物线y=x2﹣2x﹣3与y轴交点的坐标为(0,﹣3),y=x2﹣2x﹣3=(x﹣1)x2﹣4,所以它的顶点坐标为(1,﹣4);故答案为(0,﹣3),(1,﹣4);2;(3)当﹣2<x<1时,﹣4<y<5;当1<x<2时,﹣4<y<﹣3.故答案为:当﹣2<x<1时,﹣4<y<5;当1<x<2时,﹣4<y<﹣3.20.解:(1)如图所示:△DEF,即为所求;(2)由(1)得:点A的对应点D的坐标为:(1,3),点B的对应点E的坐标为:(2,1).故答案为:(1,3),(2,1).21.解:如图所示,连接OC.∵弦CD⊥AB,AB为圆O的直径,∴E为CD的中点,又∵CD=10寸,∴CE=DE=CD=5寸,设OC=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,由勾股定理得:OE2+CE2=OC2,即(x﹣1)2+52=x2,解得:x=13,∴AB=26寸,即直径AB的长为26寸.22.(1)证明:∵CD=CE,∴∠CDE=∠CED.∵∠AEC+∠CED=180°=∠BDA+∠CDE,∴∠AEC=∠BDA.又∵∠DAC=∠B,∴△ABD∽△CAE.(2)∵△ABD∽△CAE,∴=,∴AE=•BD=×2=.23.解:∵∠B=45°,AD⊥DB,∴∠DAB=45°,∴BD=AD,设DC=x,则BD=BC+DC=90+x,∴AD=90+x,∴tan58°===1.60,解得:x =150,∴AD =90+150=240(米),答:最高塔的高度AD 约为240米. 24.解:(1)本题答案不唯一,如:以AB 所在直线为x 轴,以抛物线的对称轴为y 轴建立平面直角坐标系xOy ,如图所示. ∴A (﹣4,0),B (4,0),C (0,6). 设这条抛物线的表达式为y =a (x ﹣4)(x +4). ∵抛物线经过点C , ∴﹣16a =6.∴a =﹣∴抛物线的表达式为y =﹣x 2+6,(﹣4≤x ≤4).(2)当x =1时,y =,∵4.4+0.5=4.9<,∴这辆货车能安全通过这条隧道.25.解:(1)∵PC 是圆O 的切线, ∴∠PCA =∠B .∵AB 是圆O 的直径, ∴∠ACB =90°. ∴∠A +∠B =90°. ∵PD ⊥AB ,∴∠A +∠AED =90°. ∴∠AED =∠B . ∵∠PEC =∠AED , ∴∠PCE =∠PEC .(2)如图所示,过点P 作PF ⊥AC ,垂足为F .∵AB =10,sin A =,∴BC =AB •=6.∴AC ==8.∵DE =,sin A =,∴AE =.∴EC =AC ﹣AE =8﹣=.∵PC =PE ,PF ⊥EC ,∴EF =.∵∠AED =∠PEF ,∠EDA =∠EFP , ∴△AED ∽△PEF .∴,.解得:EP =.∴PC =.26.解:(1)把A (0,3)代入y =mx 2﹣2mx +m +4得m +4=3,解得m =﹣1,所以抛物线的解析式为y =﹣x 2+2x +3;(2)当y =0时,﹣x 2+2x +3=0,解得x 1=﹣1,x 2=3, 所以B (﹣1,0);(3)抛物线C 2:y =a (x ﹣1)2﹣1(a ≠0)的顶点坐标为(1,﹣1), 因为抛物线C 2与线段AB 恰有一个公共点,则开口向上,当抛物线C 2与线段AB 的公共点为B 点时,a 最小,把B (﹣1,0)代入y =a (x ﹣1)2﹣1得4a ﹣1=0,解得a =;当抛物线C 2与线段AB 的公共点为A 点时,a 最大,把A (0,3)代入y =a (x ﹣1)2﹣1得a ﹣1=3,解得a =4,所以a的取值范围为≤a≤4.27.【解答】解:(1)如图①,∵∠ABC=90°,AB=CB,∴△ABC是等腰直角三角形,∵PF∥AC,∴∠BPF=∠BFP=45°,∴△BPF是等腰直角三角形,∴BF=BP,∴AF=CP,由旋转可得,AP=PQ,∠APQ=90°,而∠BPF=45°,∴∠QPC=45°﹣∠APF,又∵∠P AF=∠PFB﹣∠APF=45°﹣∠APF,∴∠P AF=∠QPC,∴△APF≌△PQC(SAS)∴∠PCQ=∠AFP=135°,又∵∠ACB=45°,∴∠ACQ=90°,故答案为:△PQC,90;(2)如图②,过P作PF∥AC,交BA的延长线于F,则,又∵AB=BC,∴AF=CP,又∵∠F AP=∠ABC+∠APB=α+∠APB,∠CPQ=∠APQ+∠APB=α+∠APB,∴∠F AP=∠CPQ,由旋转可得,P A=PQ,∴△AFP≌△PCQ(SAS),∴FP=CQ,∵PF∥AC,∴△ABC∽△FBP,∴∴;(3)如图,当P在CB的延长线上时,∵∠CPQ=∠APQ﹣∠APB=60°﹣30°=30°,∴∠APC=∠QPC,又∵AP=QP,PC=PC,∴△APC≌△QPC(SAS),∴CQ=AC,又∵BA=BC,∠ABC=60°,∴△ABC是等边三角形,∴∠ABC=60°,∠BAP=∠ABC﹣∠APB=30°,∴BP=AB=BC=PC=2,∴QC=AC=BC=2;如图,当P在BC的延长线上时,连接AQ,由旋转可得,AP=QP,∠APQ=∠ABC=60°,∴△APQ是等边三角形,∴AQ=PQ,∠APQ=60°=∠AQ P,又∵∠APB=30°,∠ACB=60°,∴∠CAP=30°,∠CPQ=90°,∴∠CAP=∠AP A,∴AC=PC,且AQ=PQ,CQ=CQ∴△ACQ≌△PCQ(SSS)∴∠AQC=∠PQC=∠AQP=30°,∴Rt△PCQ中,CQ=2CP=8.综上所述,线段CQ的长为2或8.28.解:(1)①∵点A的坐标为(﹣3,1),∴3+1=4,点R(0,4),S(2,2),T(2,﹣3)中,0+4=4,2+2=4,2+3=5,∴点A的同族点的是R,S;故答案为:R,S;②∵点B在x轴上,∴点B的纵坐标为0,设B(x,0),则|x|=4,∴x=±4,∴B(﹣4,0)或(4,0);故答案为:(﹣4,0)或(4,0);(2)①由题意,直线y=x﹣3与x轴交于C(3,0),与y轴交于D(0,﹣3).点M在线段CD上,设其坐标为(x,y),则有:x≥0,y≤0,且y=x﹣3.点M到x轴的距离为|y|,点M到y轴的距离为|x|,则|x|+|y|=x﹣y=3.∴点M的同族点N满足横纵坐标的绝对值之和为3.即点N在右图中所示的正方形CDEF上.∵点E的坐标为(﹣3,0),点N在直线x=n上,∴﹣3≤n≤3.②如图,设P(m,0)为圆心,为半径的圆与直线y=x﹣3相切,∵PN=,∠PCN=∠CPN=45°,∴PC=2,∴OP=1,观察图形可知,当m≥1时,若以(m,0)为圆心,为半径的圆上存在点N,使得M,N 两点为同族点,再根据对称性可知,m≤﹣1也满足条件,∴满足条件的m的范围:m≤﹣1或m≥1.。
2018-2019学年北京四中九年级(上)期中数学试卷-含详细解析

2018-2019学年北京四中九年级(上)期中数学试卷副标题题号四总分得分一、选择题(本大题共8小题,共16.0分)1.抛物线y = -2(x - 3尸一 4的顶点坐标()B. (—3,—4)2.3.4.5. A. (-3,4)C. (3,-4)如图,在中,ZC = 90°. AB = 10, AC = 8,siM 等于()A・5D. (3,4)如图,在ZMBC 中,DE//BC,。
£分别与施,AC 相交于点若4D = 4, DB = 2.则 DE : 8C 的值为()A -3C.-若为(一4,无),3(—1,无),C (2,),3)为二次函数y = —(x + 2)2 + 3的图象上的三点,则无,光,%小关系是()A. yi<y 2< 无B. y 3< y 2< yiC. y 3 <y±< y 2D・ y 2<yi< >3如图是一个抛物线形桥拱的示意图,在所给出的平而直角坐标系中,当水位在位置时,水面宽度为10也.此时水面到桥供的距离是4小.则抛物线的表达式为()B.-C.;D •:6.7.A 25 2A. y = —x^B.y = _%2C.y = _&/如图,己知匕1 =匕2,若再增加一个条件不一定能使结论△ADEdABC 成立,则这个条件是()A. Z.D = l B B・X c・X 己知函^y = ax 2+bx+c (a*0)的图象如图.给出下列4个结论:①abc > 0: @b 2 > 4ac: @4a + 2b + c > 0:④2Q + b=0只中正确的有()个・A. 1B. 2C. 3D. y D.48.二次函数y = ax 2 +bx 的图象如图所示,若一元二次方程。
亍+ bx +m-l = 0有两个不相等的实数根,则整数力的最小值为()A.O D. 2二、填空题(本大题共8小题,共16.0分)9.在AtZk/BC 中,ZC = 90°. BC = 4. tanA =贝UC =10.若当 = :,则?=11.如图是一位同学设计的用手电简来测量某古城瑙高度的示意图.点户处放一水平的平面镜,光线从点A 出 发经平面镜反射后刚好到古城墙CD 的顶端C 处,己知CD LBD.测得= 2米.BP = 3米.PD = 12米.那么该古城墙的高度CD 是______米.12.抛物线y = —2x2先向右平移1个单位,再向下平移2个单位,所得抛物线的解析式是______13.已知二次函fty = x -x+im- 1的图象与]轴有公共点,则〃,的取值范围是214.如图,抛物线y=a”与直线、=故+。
2018-2019学年北京四中九年级(上)期中数学模拟试卷(二)含答案解析

2018-2019学年北京四中九年级(上)期中数学模拟试卷(二)一、选择题:1.(3分)(2016•重庆)△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为()A.1:2B.1:3C.1:4D.1:162.(3分)(2018秋•香洲区期末)已知反比例函数y的图象过点P(2,﹣3),则该反比例函数的图象位于()A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限3.(3分)(2018秋•西城区校级期中)已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则y x的值是()A.2B.C.4D.84.(3分)(2016•攀枝花)若x=﹣2是关于x的一元二次方程x2ax﹣a2=0的一个根,则a的值为()A.﹣1或4B.﹣1或﹣4C.1或﹣4D.1或45.(3分)(2019•阿城区二模)在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为()A.7sin35°B.7cos35°C.7tan35°D.6.(4分)(2008•大兴安岭)对于抛物线y(x﹣5)2+3,下列说法正确的是()A.开口向下,顶点坐标(5,3)B.开口向上,顶点坐标(5,3)C.开口向下,顶点坐标(﹣5,3)D.开口向上,顶点坐标(﹣5,3)7.(3分)(2018秋•西城区校级期中)如图,已知DE∥BC,EF∥AB,在下面的比例式中,正确的有()①;②;③;④;⑤;⑥.A.①③B.①②③C.④⑤⑥D.①③⑤8.(3分)(2018秋•西城区校级期中)黄山市某塑料玩具生产公司,为了减少空气污染,国家要求限制塑料玩具生产,这样有时企业会被迫停产,经过调研预测,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=﹣n2+14n﹣24,则企业停产的月份为()A.2月和12月B.2月至12月C.1月D.1月、2月和12月9.(3分)(2015•攀枝花)关于x的一元二次方程(m﹣2)x2+(2m+1)x+m﹣2=0有两个不相等的正实数根,则m的取值范围是()A.m>B.m>且m≠2C.<m<2D.<m<2 10.(4分)(2018秋•西城区校级期中)抛物线y=﹣2(x﹣1)2的图象上有三个点A(﹣1,y1),B(1,y2),C(2,y3),则y1,y2,y3的大小关系是()A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y2>y3>y1二、填空题11.(3分)(2019•朝阳区模拟)请写出一个开口向下,并且与y轴交于点(0,2)的抛物线的解析式,y=.12.(3分)(2015•岳池县模拟)如果关于x的二次函数y=x2﹣2x+k与x轴只有1个交点,则k=.13.(3分)(2008秋•番禺区期末)小颖用几何画板软件探索方程ax2+bx+c=0的实数根,作出了如图所示的图象,观察得一个近似根为x1=﹣4.5,则方程的另一个近似根为x2=(精确到0.1).14.(3分)(2009•连云港模拟)如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A =45°,AC1=4米,点D2的坐标为(﹣13,﹣1.69),则桥架的拱高OH=米.15.(3分)(2016•聊城模拟)在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2n A2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是.16.(3分)(2007•丽水)廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是米.(精确到1米)三、简答题(共8个题,共78分)17.(8分)(2018秋•西城区校级期中)解方程(1)x2﹣2x﹣8=0(用因式分解法)(2)(x﹣2)(x﹣5)=﹣2.18.(8分)(2018秋•富顺县期中).已知抛物线y=x2+bx+c的对称轴为x=2,且过点C(0,3)(1)求此抛物线的解析式;(2)证明:该抛物线恒在直线y=﹣2x+1上方.19.(8分)(2014•伊春模拟)已知二次函数y x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积和周长.20.(8分)(2012•厦门模拟)设a,b,c是△ABC的三条边,关于x的方程x2x+c a =0有两个相等的实数根,方程3cx+2b=2a的根为x=0.(1)试判断△ABC的形状.(2)若a,b为方程x2+mx﹣3m=0的两个根,求m的值.21.(12分)(2014秋•横县期中)某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.(1)求y与x的函数关系式.(2)设商场老板每月获得的利润为P(元),求P与x之间的函数关系式;(3)如果想要每月获得2400元的利润,那么销售单价应定为多少元?22.(5分)(2018秋•西城区校级期中)如图,△ABC中,∠ACB=90°,D为AB上一点,CE⊥CD,且,.求证:△ACD∽△ECF.23.(10分)(2019•沂南县模拟)在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由;(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.2018-2019学年北京四中九年级(上)期中数学模拟试卷(二)参考答案与试题解析一、选择题:1.(3分)(2016•重庆)△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为()A.1:2B.1:3C.1:4D.1:16【解答】解:∵△ABC与△DEF的相似比为1:4,∴△ABC与△DEF的周长比为1:4;故选:C.2.(3分)(2018秋•香洲区期末)已知反比例函数y的图象过点P(2,﹣3),则该反比例函数的图象位于()A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限【解答】解:∵反比例函数y(k≠0)的图象经过点P(2,﹣3),∴k=2×(﹣3)=﹣6<0,∴该反比例函数经过第二、四象限.故选:C.3.(3分)(2018秋•西城区校级期中)已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则y x的值是()A.2B.C.4D.8【解答】解:∵点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,∴x﹣2+x+4=0,y﹣5=﹣3,解得:x=﹣1,y=2,则y x=2﹣1.故选:B.4.(3分)(2016•攀枝花)若x=﹣2是关于x的一元二次方程x2ax﹣a2=0的一个根,则a的值为()A.﹣1或4B.﹣1或﹣4C.1或﹣4D.1或4【解答】解:根据题意,将x=﹣2代入方程x2ax﹣a2=0,得:4﹣3a﹣a2=0,即a2+3a﹣4=0,左边因式分解得:(a﹣1)(a+4)=0,∴a﹣1=0,或a+4=0,解得:a=1或﹣4,故选:C.5.(3分)(2019•阿城区二模)在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为()A.7sin35°B.7cos35°C.7tan35°D.【解答】解:在Rt△ABC中,cos B,∴BC=AB•cos B=7cos35°,故选:B.6.(4分)(2008•大兴安岭)对于抛物线y(x﹣5)2+3,下列说法正确的是()A.开口向下,顶点坐标(5,3)B.开口向上,顶点坐标(5,3)C.开口向下,顶点坐标(﹣5,3)D.开口向上,顶点坐标(﹣5,3)【解答】解:∵抛物线y(x﹣5)2+3,∴a<0,∴开口向下,∴顶点坐标(5,3).故选:A.7.(3分)(2018秋•西城区校级期中)如图,已知DE∥BC,EF∥AB,在下面的比例式中,正确的有()①;②;③;④;⑤;⑥.A.①③B.①②③C.④⑤⑥D.①③⑤【解答】解:∵DE∥BC∴△ADE∽△ABC∴∴∵EF∥AB∴△CEF∽△CAB∴∴,∴,则①③⑤正确,②④⑥错误故选:D.8.(3分)(2018秋•西城区校级期中)黄山市某塑料玩具生产公司,为了减少空气污染,国家要求限制塑料玩具生产,这样有时企业会被迫停产,经过调研预测,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=﹣n2+14n﹣24,则企业停产的月份为()A.2月和12月B.2月至12月C.1月D.1月、2月和12月【解答】解:∵y=﹣n2+14n﹣24=﹣(n﹣2)(n﹣12),1≤n≤12且n为整数,∴当y=0时,n=2或n=12,当y<0时,n=1,故选:D.9.(3分)(2015•攀枝花)关于x的一元二次方程(m﹣2)x2+(2m+1)x+m﹣2=0有两个不相等的正实数根,则m的取值范围是()A.m>B.m>且m≠2C.<m<2D.<m<2【解答】解:根据题意得m﹣2≠0且△=(2m+1)2﹣4(m﹣2)(m﹣2)>0,解得m>且m≠2,设方程的两根为a、b,则a+b>0,ab1>0,而2m+1>0,∴m﹣2<0,即m<2,∴m的取值范围为<m<2.故选:D.10.(4分)(2018秋•西城区校级期中)抛物线y=﹣2(x﹣1)2的图象上有三个点A(﹣1,y1),B(1,y2),C(2,y3),则y1,y2,y3的大小关系是()A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y2>y3>y1【解答】解:∵y=﹣2(x﹣1)2,﹣2<0,∴当x<1时,y随x的增大而增大,当x>1时,y随x的增大而减小,∵抛物线y=﹣2(x﹣1)2的图象上有三个点A(﹣1,y1),B(1,y2),C(2,y3),∴y2>y3>y1,故选:D.二、填空题11.(3分)(2019•朝阳区模拟)请写出一个开口向下,并且与y轴交于点(0,2)的抛物线的解析式,y=﹣x2+2(答案不唯一).【解答】解:函数解析式为y=﹣x2+2(答案不唯一).故答案为:﹣x2+2(答案不唯一).12.(3分)(2015•岳池县模拟)如果关于x的二次函数y=x2﹣2x+k与x轴只有1个交点,则k=1.【解答】解:∵二次函数y=x2﹣2x+k的图象与x轴有且只有一个交点,∴△=b2﹣4ac=4﹣4k=0,∴k=1.故答案为:1.13.(3分)(2008秋•番禺区期末)小颖用几何画板软件探索方程ax2+bx+c=0的实数根,作出了如图所示的图象,观察得一个近似根为x1=﹣4.5,则方程的另一个近似根为x2=2.5(精确到0.1).【解答】解:由函数图象可知,此函数的对称轴为x=﹣1,设函数的另一根为x,则1,解得x=2.5.14.(3分)(2009•连云港模拟)如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A =45°,AC1=4米,点D2的坐标为(﹣13,﹣1.69),则桥架的拱高OH=7.24米.【解答】解:设抛物线D1OD8的解析式为y=ax2,将x=﹣13,y=﹣1.69代入,解得a∵横梁D1D8=C1C8=AB﹣2AC1=36m∴点D1的横坐标是﹣18,代入y x2里可得y=3.24又∵∠A=45°,∴D1C1=AC1=4m∴OH=3.24+4=7.24m.15.(3分)(2016•聊城模拟)在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2n A2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,).【解答】解:∵△OA1B1是边长为2的等边三角形,∴A1的坐标为(1,),B1的坐标为(2,0),∵△B2A2B1与△OA1B1关于点B1成中心对称,∴点A2与点A1关于点B1成中心对称,∵2×2﹣1=3,2×0,∴点A2的坐标是(3,),∵△B2A3B3与△B2A2B1关于点B2成中心对称,∴点A3与点A2关于点B2成中心对称,∵2×4﹣3=5,2×0﹣(),∴点A3的坐标是(5,),∵△B3A4B4与△B3A3B2关于点B3成中心对称,∴点A4与点A3关于点B3成中心对称,∵2×6﹣5=7,2×0,∴点A4的坐标是(7,),…,∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,∴A n的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,∵当n为奇数时,A n的纵坐标是,当n为偶数时,A n的纵坐标是,∴顶点A2n+1的纵坐标是,∴△B2n A2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,).故答案为:(4n+1,).16.(3分)(2007•丽水)廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是18米.(精确到1米)【解答】解:由“在该抛物线上距水面AB高为8米的点”,可知y=8,把y=8代入y x2+10得:x=±4,∴由两点间距离公式可求出EF=818(米).三、简答题(共8个题,共78分)17.(8分)(2018秋•西城区校级期中)解方程(1)x2﹣2x﹣8=0(用因式分解法)(2)(x﹣2)(x﹣5)=﹣2.【解答】解:(1)分解因式得:(x﹣4)(x+2)=0,可得x﹣4=0或x+2=0,解得:x1=4,x2=﹣2;(2)方程整理得:x2﹣7x+12=0,分解因式得:(x﹣3)(x﹣4)=0,可得x﹣3=0或x﹣4=0,解得:x1=3,x2=4.18.(8分)(2018秋•富顺县期中).已知抛物线y=x2+bx+c的对称轴为x=2,且过点C(0,3)(1)求此抛物线的解析式;(2)证明:该抛物线恒在直线y=﹣2x+1上方.【解答】解:(1)∵抛物线y=x2+bx+c的对称轴为x=2,∴2,得,b=﹣4,∵抛物线y=x2+bx+c过点C(0,3),∴c=3,∴此抛物线的解析式为:y=x2﹣4x+3;(2)证明:设y1=x2﹣4x+3,y2=﹣2x+1,则y1﹣y2=(x2﹣4x+3)﹣(﹣2x+1)=x2﹣2x+2=(x﹣1)2+1>0,∴y1>y2,∴该抛物线恒在直线y=﹣2x+1上方.19.(8分)(2014•伊春模拟)已知二次函数y x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积和周长.【解答】解:(1)把(2,0)、(0,﹣6)代入二次函数解析式,可得,解得,故解析式是y x2+4x﹣6;(2)∵对称轴x4,∴C点的坐标是(4,0),∴AC=2,OB=6,AB=2,BC=2,∴S△ABC AC•OB2×6=6,△ABC的周长=AC+AB+BC=2+22.20.(8分)(2012•厦门模拟)设a,b,c是△ABC的三条边,关于x的方程x2x+c a =0有两个相等的实数根,方程3cx+2b=2a的根为x=0.(1)试判断△ABC的形状.(2)若a,b为方程x2+mx﹣3m=0的两个根,求m的值.【解答】解:(1)∵x2x+c a=0有两个相等的实数根,∴△=()2﹣4(c a)=0,整理得a+b﹣2c=0 ①,又∵3cx+2b=2a的根为x=0,∴a=b②,把②代入①得a=c,∴a=b=c,∴△ABC为等边三角形;(2)a,b是方程x2+mx﹣3m=0的两个根,∴方程x2+mx﹣3m=0有两个相等的实数根∴△=m2﹣4×(﹣3m)=0,即m2+12m=0,∴m1=0,m2=﹣12.当m=0时,原方程的解为x=0(不符合题意,舍去),∴m=﹣12.21.(12分)(2014秋•横县期中)某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.(1)求y与x的函数关系式.(2)设商场老板每月获得的利润为P(元),求P与x之间的函数关系式;(3)如果想要每月获得2400元的利润,那么销售单价应定为多少元?【解答】解:(1)设y与x的函数关系式为:y=kx+b(k≠0),由题意得,解得.故y=﹣4x+360(40≤x≤90);(2)由题意得,p与x的函数关系式为:p=(x﹣40)(﹣4x+360)=﹣4x2+520x﹣14400,(3)当P=2400时,﹣4x2+520x﹣14400=2400,解得:x1=60,x2=70,故销售单价应定为60元或70元.22.(5分)(2018秋•西城区校级期中)如图,△ABC中,∠ACB=90°,D为AB上一点,CE⊥CD,且,.求证:△ACD∽△ECF.【解答】证明:∵CE⊥CD,∴∠ECD=90°,∴∠ACB=∠ECD,又∵,∴△ACB∽△ECD,∴∠A=∠E,∵∠ACB=∠ECD=90°,∴∠ACB﹣∠BCD=∠ECD﹣∠BCD,即∠ACD=∠ECF,∴△ACD∽△ECF.23.(10分)(2019•沂南县模拟)在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由;(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.【解答】解:(1)如图1,延长EB交DG于点H,∵ABCD和AEFG为正方形,∴在Rt△ADG和Rt△ABE中,,∴Rt△ADG≌Rt△ABE,∴∠AGD=∠AEB,∵∠HBG=∠EBA,∴∠HGB+∠HBG=90°,∴DG⊥BE;(2)如图2,过点A作AP⊥BD交BD于点P,∵ABCD和AEFG为正方形,∴在△DAG和△BAE中,,∴△DAG≌△BAE(SAS),∴DG=BE,∵∠APD=90°,∴AP=DP,∵AG=2,∴PG,∴DG=DP+PG,∵DG=BE,∴BE.。
2018年10用北京四中初三上月考数学试题及答案

20. (5 分)2014 年,“即墨古城”在即墨区破土重建,2016 年建成,现已成为 青岛北部一个重要的旅游景点,为了测量古城“潮海”门的高度,在数学课 外实践活动中,小明分别在如图所示的 A,B 两点处,利用测角仪对“潮海” 门的最高点 C 进行了测量,测得∠A=30°,∠CBD=45°,若 AB=22 米,求“潮 海”门的最高点 C 到地面的高度为多少米?(结果精确到 1 米,参考数据:
3 (第 7 题图)
1/6
2018-2019 学年度第一学期北京四中初三数学统一练习(一)
7. 二次函数 y = ax2 + bx + c(a 0) 的图象如图所示,给出下列结论:
① abc 0 ; ② 2a + b = 0 ; ③ a − b + c 0 ;④ b2 − 4ac 0 .
(1)求这个二次函数的解析式. (2)连接 BC,求线段 BC 的长. (3)若点 P 在 x 轴上,且△PBC 为等腰三角形,
请直接写出符合条件的所有点 P 的坐标.
23. (10 分)抛物线 y = − 1 x2 + 2 x +1 的顶点为 D,它与 x 轴交于 A,B 两点(点 33
A 在点 B 的左侧),与 y 轴交于点 C. (1)求点 A,B,C,D 的坐标; (2)求直线 BC 的解析式; (3)求△BCD 的面积; (4)在直线 BC 上方的抛物线上是否存在一点 P,使△PBC 面积为 1?若存在,
m 的取值范围是(
A. − 25 m 3 4
C. −2 m 3
)
B. − 25 m 2 4
初三第一次月考数学试卷4

初三第一次月考数学试卷3 初三第一次月考数学试卷3总分150分时间120分钟_.9.27 成绩_________一.选择题(每题3分,共42分)1.式子成立的条件是( )A.≥3B.≤1C.1≤≤3D.1<≤32.和是同类二次根式的是( )( A) ( B) (C)( D)3.对于任意实数,下列等式成立的是( )A.B. C.D.4.已知,,则与的关系是( )A.B.C. D.5.等于( )(A) 2 (B) (C) (D)6.的算术平方根是( )A.6B.-6C.D.7.如果1≤≤,则的值是( )A.B.C. D.18.下列方程中,无论取何值,总是关于的一元二次方程的是( )(A)(B)(C)(D)9.要使分式的植为0,则应该等于( )(A)4或1(B)4(C)1(D)或10.若与互为倒数,则实数为( )(A)±(B)±1(C)±(D)±11. 关于的一元二次方程有实数根,则( )(A)<0(B)>0(C)≥0(D)≤012.下列图形中,既是中心对称图形,又是轴对称图形的是(_shy; )(A)平行四边形_shy;(B)等边三角形_shy; (C)矩形_shy; (D)等腰梯形13.四边形ABCD的对角线交于O点,能判定四边形是正方形的条件是( )(A)AC=BD,AB=CD,AB∥CD.(2)AD∥BC,∠A=∠C.(C)AO=BO=CO=DO,AC⊥BD.(D)AO=CO,BO=DO,AB=BC.14.如果等边三角形的边长为3,那么连结各边中点所成的三角形的周长为( ).(A)9 (B)6 (C)3 (D)二.填空(答案填在后面的答案纸上)(每题4分,共24分)1.最简根式和是同类二次根式,则a= _________2.一元二次方程化为一般形式为:,二次项系数为: ,一次项系数为: ,常数项为: .3.已知平行四边形ABCD中,AB=14cm,BC=16cm,则此平行四边形的周长为_____cm.4.正方形的对称轴有___条.5.( )( )=_______6._______________三.计算 1.选用合适的方法解下列方程 (每题4分,共12分).(1) (2) (3)_2-4_-5=02.解方程2(用配方法)(4分)3.计算(1) (2) (每题4分,共8分)4.化简:(每题5分,共10分) (1)(2)先化简,再求值:,其中,四.(本题8分)观察下列各式:, ,请你将猜到的规律用含有自然数n的代数式表示出来并证明你的猜想.五.(12分)写出命题〝角平分线上的点到角两边的距离相等〞的逆命题,这个逆命题是真命题吗?请证明你的判断逆命题:图形已知:求证:证明六.(6分)如图,把边长为2 cm的正方形剪成四个大小.形状完全一样的直角三角形.请用这四个直角三角形拼成符合下列要求的图形(全部用上,互不重叠且不留空隙),并把你的拼法画图示意:(1)不是正方形的菱形:(2)不是正方形的矩形:(3)不是矩形和菱形的平行四边形:七.(6分)在□ABCD中,已知AC.BD相交于点O,两条对角线的和为30cm, △OCD的周长为20cm,求AB的长.八.等腰梯形ABCD中,AD∥BC,∠DBC=45_ordm;.翻折梯形ABCD,使点B重合于点D, 折痕分别交边AB.BC于点F.E.若AD=2,BC=8.(如图)(6分)求:(1)BE的长.(2)CD:DE的值.九.如图是规格为8_8的正方形网格,请在所给网格中按下列要求操作:(本题满分12分)⑴ 请在网格中建立平面直角坐标系, 使A点坐标为(-2,4),B点坐标为(-4,2);⑵ 在第二象限内的格点上画一点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是, △ABC的周长是(结果保留根号);⑶ 画出△ABC以点C为旋转中心.旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.自我评价: 总结与反思:。
2019北京四中初三(上)月考数 学

2019北京四中初三(上)月考数 学(考试时间:120分钟,试卷满分:100分)班级: 学号: 姓名:一、选择题(本题共16分,每小题2分)1. 下列标志图中,既是轴对称图形,又是中心对称图形的是( )A. B. C. D.2. 抛物线()21232y x =--的顶点坐标是( ) A. ()2,3B. ()2,3-C. ()2,3-D. ()2,3--3. 若将抛物线y =5x 2先向右平移2个单位,再向上平移1个单位,得到的新抛物线的表达式为( )A. B.C.D.4. 二次函数y =ax 2+bx +c 的图象如图所示,根据图象可得a ,b ,c 与0的大小关系是( )A. , ,B. , ,C. , ,D. , ,5. 如图, 在△ABC 中, ∠B =40°, 将△ABC 绕点A 逆时针旋转, 得到△ADE ,点D 恰好落在BC 的延长线上,则旋转角的度数为( )A. 70°B. 80°C. 90°D.100°6. 以原点为中心,把点P (1,3)顺时针旋转90°,得到的点P ′的坐标为( )A.B.C. D.7. 已知二次函数y =ax 2+bx +c 的y 与x 的部分对应值如下表:①该函数图象是抛物线,且开口向下;②该函数图象关于直线x =1对称;③当x <1时,函数值y 随x 的增大而增大;④方程ax 2+bx +c =0有一个根大于3.其中正确的结论有( )A. 1个B. 2个C. 3个D. 4个8. 抛物线2y ax bx c =++经过点(-2,0),且对称轴为直线,其部分图象如图所示.对于此抛物线有如下四个结论: ①; ②;③若, 则 时的函数值小于时的函数值; ④点不在此抛物线上. 其中正确结论的序号是( )A .①②B .②③C .②④D .③④二、填空题(本题共16分,每小题2分)9. 请写出一个开口向下, 且与y 轴的交点坐标为(0, 1)的抛物线的表达式: . 10. 已知抛物线的对称轴是x =n , 若该抛物线过A (-2, 5), B (4, 5) 两点, 则n 的值为 . 11. 点A (-3, y 1), B (2, y 2) 在抛物线y =x 2-5x 上, 则y 1______y 2.(填“>”,“<”或“=”)12. 如图, 直线1y kx n =+ (k ≠0)与抛物22y ax bx c =++(a ≠0)分别交于A(-1,0),B(2,-3) 两点,则关于x 的方程2=kx n ax bx c +++的解为 . 13. 如果函数24y x x m =+-的图象与x 轴有公共点,那么m 的取值范围是_______.14. 如图,在△ABC 中,∠CAB =70°,将△ABC 绕点A 逆时针旋转到△AB ′C ′的位置,使得CC ′∥AB ,则∠BAB ′的度数是______________.15. 如图,若被击打的小球飞行高度h (单位:m )与飞行时间t (单位:s )之间具有的关系为h =20t -5t 2,则小球从飞出到落地所用的时间为______s .(第14题图) (第15题图)16. 如图, 已知△ABC 中, ∠C =90°, AC =BC = 将△ABC 绕点A 顺时针方向旋转60°到△AB ′C ′的位置, 连接BB ′,则BB ′的长为 ,连接C ′B, 则C ′B 的长为 .1x =0ac >1640a b c ++=0m n >>1x m =+1x n =-(,0)2ca--23二、解答题(本题共68分)17. (5分) 已知抛物线的顶点为(-1,2),且经过点(0,4),求抛物线的解析式.18. (8分) 已知二次函数y =ax 2+bx +c 的图象如图所示.(1) 对称轴方程为____________;(2) 当x 时,y 随x 的增大而减小; (3) 求函数解析式.19. (5分) 在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,△ABC 是格点三角形 (顶点在网格线的交点上).(1) 先作△ABC 关于原点O 成中心对称的△A 1B 1C 1, 再把△A 1B 1C 1向上平移4个单位长度得到△A 2B 2C 2,请在图中画出△A 1B 1C 1及△A 2B 2C 2;(2) 可以看出△A 2B 2C 2与△ABC 关于某点成中心对称, 直接写出对称中心的坐标 .20. (5分) 如图, 等腰Rt △ABC 中, BA =BC ,∠ABC =90°, 点D 在AC 上, 将△ABD 绕点B 沿顺时针方向旋转90°后, 得到△CBE .(1) ∠DCE 的度数为_____________; (2) 若AB =4, CD =3AD , 求DE 的长.21. (6分) 已知二次函数()233y kx k x =-++图象的对称轴为:直线2x =.(1) 求该二次函数的表达式;(2) 画出该函数的图象,并结合图象直接写出: ①当y <0时,自变量x 的取值范围; ②当0≤ x <3时,y 的取值范围是多少?22. (5分) 如图,已知△ABC 中,AB =AC ,把△ABC 绕A 点沿顺时针方向旋转得到△ADE ,连接BD ,CE 交于点F . (1) 求证:△AEC ≌△ADB ;(2) 若AB =2, ∠BAC =45°, 当四边形ADFC 是平行四边形时,求BF 的长.23. (6分) 秋风送爽,学校组织同学们去颐和园秋游,昆明湖西堤六桥中的玉带桥最是令人喜爱,如图所示,玉带桥的桥拱是抛物线形.水面宽度AB =10m, 桥拱最高点C 到水面的距离为6m . (1) 建立适当的平面直角坐标系,求抛物线的表达式;(2) 现有一艘游船高度是4.5m ,宽度是4m ,为了保证安全,船顶距离桥拱顶部至少0.5m ,通过计算说明这艘游船能否安全通过玉带桥.24. (5分)如图, 直线l :2y x m =-+与x 轴交于点A (2-, 0), 抛物线:与x 轴的一个交点为B (点B 在点A 的左侧). 过点B 作BD 垂直x 轴交直线l 于点D . (1) 求m 的值和点B 的坐标;(2) 将△ABD 绕点A 顺时针旋转90°,点B ,D 的对应点分别为点E ,F . ①点F 的坐标为____________;②将抛物线沿x .轴.向右平移使它经过点F ,此时得到的抛物线记为,直接写出抛物线的表达式.25. (10分) 抛物线223y x x =-++的顶点为D , 它与x 轴交于A ,B 两点 (点A 在点B 的左侧), 与y 轴交于点C .(1) 求顶点D 的坐标;1C 243y x x =++1C 2C 2C(2)求直线BC的解析式;(3)求△BCD的面积;(4)当点P在直线BC上方的抛物线上运动时,△PBC的面积是否存在最大值?若存在,请求出这个最大值,并且写出此时点P的坐标;若不存在;请说明理由.26. (6分) 已知抛物线G: (k为常数).k=时,用配方法求抛物线G的顶点坐标;(1) 当3P x y.(2) 若记抛物线G的顶点坐标为(,)①分别用含k的代数式表示x,y,②请在①的基础上继续用含x的代数式表示y,③由①②可得, 顶点P的位置会随着k的取值变化而变化,但点P总落在的图象上.A.一次函数 B.反比例函数 C.二次函数(3) 小明想进一步对 (2) 中的问题进行如下改编:将 (2) 中的抛物线G改为抛物线H:(k为常数), 其中N为含k的代数式, 从而使这个新抛物线H满足:无论k取何值,它的顶点总落在某个一次函数的图象上. 请按照小明的改编思路,写出一个符合以上要求的新抛物线H的函数表达式: (用含k的代数式表示), 它的顶点=+(a,b为常数,a≠0)中, a= ,b= .所在的一次函数图象的表达式y ax b27. (7分) 在正方形ABCD中, 点P是直线BC上的一点, 连接AP, 将线段PA绕点P顺时针旋转90°, 得到线段PE, 连接CE.(1) 如图1, 点P在线段CB的延长线上.①请根据题意补全图形;②用等式表示BP和CE的数量关系,并证明.(2) 若点P在射线BC上,直接写出CE,CP,CD三条线段的数量关系为图1 备用图。
2018-2019北京四中 初三数学一模 几何综合汇编
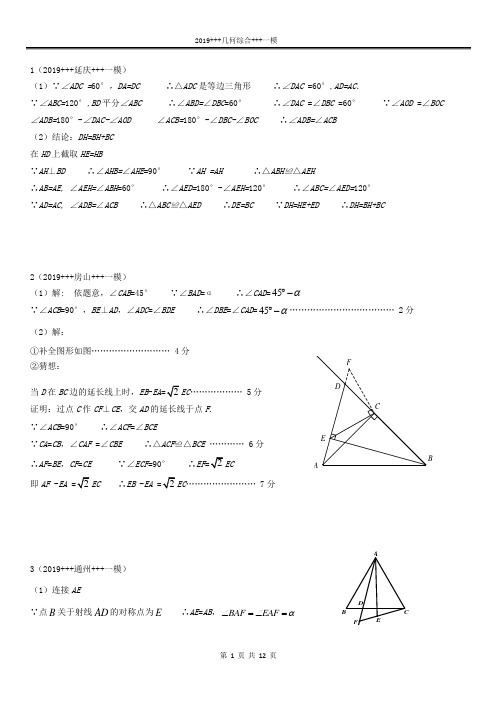
1(2019+++延庆+++一模)(1)∵∠ADC =60°,DA=DC ∴△ADC是等边三角形∴∠DAC =60°,AD=AC.∵∠ABC=120°,BD平分∠ABC ∴∠ABD=∠DBC=60°∴∠DAC =∠DBC =60°∵∠AOD =∠BOC ∠ADB=180°-∠DAC-∠AOD∠ACB=180°-∠DBC-∠BOC ∴∠ADB=∠ACB(2)结论:DH=BH+BC在HD上截取HE=HB∵AH⊥BD ∴∠AHB=∠AHE=90°∵AH =AH ∴△ABH≌△AEH ∴AB=AE,∠AEH=∠ABH=60°∴∠AED=180°-∠AEH=120°∴∠ABC=∠AED=120°∵AD=AC, ∠ADB=∠ACB ∴△ABC≌△AED ∴DE=BC ∵DH=HE+ED ∴DH=BH+BC2(2019+++房山+++一模)(1)解: 依题意,∠CAB=45°∵∠BAD=α∴∠CAD=45α︒-∵∠ACB=90°,BE⊥AD,∠ADC=∠BDE ∴∠DBE=∠CAD=45α︒-……………………………… 2分(2)解:①补全图形如图……………………… 4分②猜想:当D在BC边的延长线上时,EB-EA EC……………… 5分证明:过点C作CF⊥CE,交AD的延长线于点F.∵∠ACB=90°∴∠ACF=∠BCE∵CA=CB,∠CAF =∠CBE ∴△ACF≌△BCE………… 6分∴AF=BE,CF=CE ∵∠ECF=90°∴EF EC即AF -EA EC ∴EB -EA…………………… 7分3(2019+++通州+++一模)(1)连接AE∵点B关于射线AD的对称点为E∴AE=AB,BAF EAFα∠=∠=∵ABC △是等边三角形 ∴AB AC =,60BAC ACB ∠=∠=︒ ∴602EAC α∠=︒-,AE AC =………1分∴()1180602602ACE αα∠=︒-︒-=︒+⎡⎤⎣⎦ ∴6060BCF ACE ACB αα∠=∠-∠=︒+-︒=……………2分另解:借助圆 (2)AF EF CF -=证明:如图,作60FCG ∠=︒交AD 于点G ,连接BF ……………3分 ∵BAF BCF α∠=∠=,ADB CDF ∠=∠ ∴60ABC AFC ∠=∠=︒ ∴△FCG 是等边三角形 ∴GF =FC ……………… 4分 ∵ABC △是等边三角形 ∴BC AC =,60ACB ∠=︒∴ACG BCF α∠=∠= 在△ACG 和△BCF 中CA CB ACG BCF CG CF =⎧⎪∠=∠⎨⎪=⎩,,, ∴△ACG ≌△BCF∴AG BF =……………5分 ∵点B 关于射线AD 的对称点为E ∴BF EF =……………6分 ∴AF AG GF -= ∴AF EF CF -=………………7分 另一种证法:作60FAH ∠=︒交FC 的延长线于点H ,连接BF4(2019+++平谷+++一模) (1)∠BCD =120°-α (2)解:方法一:延长BA 使AE=BC ,连接DE 由(1)知△ADC 是等边三角形 ∴AD=CD ∵∠DAB +∠DCB =∠DAB +∠DAE =180°∴∠DAB =∠DAE ∴△ADE ≌△CDB ∴BD=BE ∴BD=AB+BC 方法二:延长AB 使AF=BC ,连接CF∠BDC =∠ADE ∵∠ABC =120° ∴∠CBF =60°∴△BCF 是等边三角形 ∴BC=CF ∵∠DCA =∠BCF =60°∴∠DCA +∠ACB =∠BCF +∠ACB 即∠DCB =∠ACF ∵CA=CD ∴△ACF ≌△DCB ∴BD=AF ∴BD=AB+BC (3)AC ,BD 的数量关系是:2AC BD 位置关系是:AC ⊥BD 于点P5(2019+++门头沟+++一模)(1)补全图形(如图1)…………… 1分 证明:略………… 3分(2)线段OE ,OP 和OF 之间的数量关系是OF +OE OP …… 4分 证明:如图2,作PQ ⊥PO 交OB 于Q∴∠2+∠3=90°,∠1+∠2=90° ∴∠1=∠3 又∵OC 平分∠AOB ,∠AOB =90° ∴∠4=∠5=45°又∵∠5+∠6=90° ∴∠6=45° ∴∠4=∠6 ∴PO =PQ ∴△EPO ≌ △FPQ …………… 5分 ∴PE =PF ,OE =FQ 又∵OQ =OF +FQ =OF +OE又∵OQ ∴OF+OE …………… 6分(3)线段OE ,OP 和OF 之间的数量关系是OF- OE …………… 7分6(2019++石景山+++一模) (1)补全的图形如图1所示 (2)△ABC 是等边三角形∴AB BC CA ==,60ABC BCA CAB ∠=∠=∠=︒由平移可知ED ∥BC ,ED =BC ……… 2分60ADE ACB ∴∠=∠=︒ 90GMD ∠=︒ 2DG DM DE ∴==…… 3分DE BC AC == DG AC ∴= AG CD ∴=……… 4分(3)线段AH 与CG 的数量关系:AH = CG ……… 5分 如图2,连接BE ,EF,ED BC =ED ∥BC BEDC ∴四边形是平行四边形 BE CD CBE ADE ABC ∴=∠=∠=∠, GM ED 垂直平分EF DF ∴= DEF EDF ∴∠=∠ ED ∥BCBFE DEF BFH EDF ∴∠=∠∠=∠, BFE BFH ∴∠=∠BF BF = BEF BHF ∴△≌△………… 6分BE BH CD AG ∴===AB AC = AH CG ∴=……… 7分7(2019+++西城+++一模)D8(2019+++燕山+++一模)(1)①补全的图形如图的所示………1分 ②证明:∵∠ADE =∠B =90°∴∠EDC +∠ADB =∠BAD +∠ADB =90° ∴∠EDC =∠BAD ……………3分 (2)①CE BD ……………4分 ②想法1:如图,过点E 作EF ⊥BC ,交BC 延长线于点F ∴∠F =90° 在△ADB 和△DEF 中,∠B =∠F =90°,∠EDC =∠BAD ,AD =DE ∴△ADB ≌△DEF ∴AB =DF ,BD =EF ∵AB =BC ∴DF =BC 即DC +CF =BD +DC ∴CF =BD =EF ∴△CEF 是等腰直角三角形∴CECF BD ……………7分 想法2:证明:在线段AB 上取一点F ,使得BF =BD ,连接DF∵∠B =90°,AB =BC ∴DF BD ∵AB =BC ,BF =BD ∴AB -BF =BC -BD 即AF =DC 在△ADF 和△DEC 中AF =DC ,∠BAD =∠EDC ,AD =DE ∴△ADF ≌△DEC∴CE=DF BD ……………7分 想法3:证明:延长AB 到F ,使得BF =BD ,连接DF ,CF∵∠B =90°∴DF 在Rt △ABD 和Rt △CBF 中 ∠ABD =∠CBF =90°,AB =BC ,BD =BF ∴△ABD ≌△CBFFABECD∴AD=CF,∠BAD=∠BCF ∵AD=DE ∴DE=CF∵∠EDC=∠BAD ∴∠EDC=∠BCF ∴DE∥CF∴四边形DFCE为平行四边形∴CE=DF BD……………7分9(2019+++丰台+++一模)10(2019+++密云+++零模)(1)补全图形AD与BE的数量关系为AD=BE(2)∵∠ACB=∠DCE= 60°∴∠ACD=∠BCE 又∵AC=BC,CD=CE ∴△ACD≌△BCE ∴AD=BE, ∠CBE=∠CAD=60°∴∠ABF=180°-∠ABC-∠CBE=60°在Rt AFB∆中,AFAB=∴ABDB AH O DBA1已知:四边形ABCD 中,120ABC ∠=︒,60ADC ∠=︒,AD =CD ,对角线AC ,BD 相交于点O ,且BD 平分∠ABC ,过点A 作AH BD ⊥,垂足为H (1)求证:ADB ACB ∠=∠(2)判断线段BH ,DH ,BC 之间的数量关系;并证明 2已知:Rt △ABC 中,∠ACB =90°,AC =BC(1) 如图1,点D 是BC 边上一点(不与点B ,C 重合),连接AD ,过点B 作BE ⊥AD ,交AD 的延长线于点E ,连接CE . 若∠BAD =α,求∠DBE 的大小 (用含α的式子表示)(2) 如图2,点D 在线段BC 的延长线上时,连接AD ,过点B 作BE ⊥AD ,垂足E 在线段AD 上,连接CE . ①依题意补全图2 ②用等式表示线段EA ,EB 和EC 之间的数量关系,并证明AA3如图,在等边ABC △中,点D 是线段BC 上一点.作射 线AD ,点B 关于射线AD 的对称点为E .连接CE 并 延长,交射线AD 于点F(1)设BAF α∠=,用α表示BCF ∠的度数(2)用等式表示线段AF 、CF 、EF 之间的数量关系, 并证明 4在△ABC 中,∠ABC =120°,线段AC 绕点A 逆时针旋转60°得到线段AD ,连接CD ,BD 交AC 于P (1)若∠BAC =α,直接写出∠BCD 的度数 (用含α的代数式表示) (2)求AB ,BC ,BD 之间的数量关系 (3)当α=30°时,直接写出AC ,BD 的关系5如图,∠AOB = 90°,OC 为∠AOB 的平分线,点P 为OC 上一个动点,过点P 作射线PE 交OA 于点E .以点P 为旋转 中心,将射线PE 沿逆时针方向旋转90°,交OB 于点F (1)根据题意补全图1,并证明PE = PF(2)如图1,如果点E 在OA 边上,用等式表示线段OE ,OP 和OF 之间的数量关系,并证明 (3)如图2,如果点E 在OA 边的反向延长线上,直接写出线段OE ,OP 和OF 之间的数量关系6如图,在等边△ABC 中,D 为边AC 的延长线上一点()CD AC ,平移线段BC ,使点C 移动到点D ,得到线段ED ,M 为ED 的中点,过点M 作ED 的垂线,交BC 于点F ,交AC 于点G (1)依题意补全图形 (2)求证:AG = CD(3)连接DF 并延长交AB 于点H ,用等 式表示线段AH 与CG 的数量关系,并证明PPEECCBBOOAADB A7如图,在△ABC 中,∠ABC =90°,BA=BC .将线段AB 绕点A 逆时针旋转90°得到线段AD ,E 是边BC 上的一动点,连接DE 交AC 于点F ,连接BF(1) 求证:FB=FD(2) 点H 在边BC 上,且BH=CE ,连接AH 交BF 于点N①判断AH 与BF 的位置关系,并证明你的结论②连接CN .若AB =2,请直接写出线段CN 长度的最小值8如图,在△ABC 中,AB =BC ,∠B =90°,点D 为线段BC上一个动点(不与点B ,C 重合),连接AD ,将线段AD 绕点 D 顺时针旋转90°得到线段DE ,连接EC(1) ① 依题意补全图1② 求证:∠EDC =∠BAD (2) ① 小方通过观察、实验,提出猜想:在点D 运动的过程中,线段CE 与BD 的数量关系始终不变,用等式表示为 ② 小方把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法想法1:过点E 作EF ⊥BC ,交BC 延长线于点F ,只需证△ADB ≌△DEF .想法2:在线段AB 上取一点F ,使得BF =BD ,连接DF ,只需证△ADF ≌△DEC .想法3:延长AB 到F ,使得BF =BD ,连接DF ,CF ,只需证四边形DFCE 为平行四边形.……请你参考上面的想法,帮助小方证明①中的猜想(一种方法即可)备用图AB C D 图1 D C B A9在ABC ∆中,090=∠ACB ,AC=BC ,D 为AB 的中点,点E 为AC 延长线上一点,连接DE ,过点D 作DF ⊥DE交CB 的延长线于点F(1)求证:BF=CE(2)若CE=AC ,用等式表示线段DF 与AB 的数量关系,并证明10已知ABC ∆为等边三角形,点D 是线段AB 上一点(不与A 、B 重合).将线段CD 绕点C 逆时针旋转60︒得到线段CE.连结DE 、BE(1)依题意补全图1并判断AD 与BE 的数量关系(2)过点A 作AF EB ⊥交EB 延长线于点F ,用等式表示线段EB 、DB 与AF 之间的数量关系并证明图2D C BA 图1ABC D。
