基于ARIMA模型的湖北省CPI时间序列分析及预测
基于ARIMA模型对湖北省能源消费的预测

拆借,进一步加剧了资金的东流。
而西部地区由于以重工业为主的工业结构对资金的倚赖性要远大于以轻工业为主的东部地区,所以资金倒流的边际效应的影响是很大的,对西部地区大部分资源省份的发展产生了明显的抑制作用,进一步加大了西部经济发展的困难。
3结论本文运用动态面板数据的广义矩方法考察了1980-2006年期间我国金融中介发展与经济增长关系的区域差异性。
结果显示,经济发达地区金融中介发展很好的促进了经济增长,而欠发达地区金融中介的发展并没有对经济增长有明显贡献。
也就是说,金融中介的发展与经济增长之间不存在稳定一致的关系,在经济发展程度不同的地区,其作用效果是有差异的。
参考文献:[1]LIANG,Q.&TENG,J..Financial development and economic growth: Evidence from China[J].China Economic Review,2006,17.[2]Rioja,F.,&Valev,N.Does One Size Fit all?A reexamination of the finance and growth relationship[J].Journal of Development Eco-nomics,2004,74.[3]韩廷春,夏金霞.中国金融发展与经济增长经验分析[J].经济与管理研究,2005,(4).[4]周好文,钟永红.中国金融中介发展与地区经济增长:多变量VAR 系统分析[J].金融研究,2004,(6).(责任编辑/易永生)邢瑞军1,刘丽英2(1.中国人民大学统计学院,北京100872;2.邯郸学院,河北邯郸056005)摘要:能源影响着我国社会经济的稳定持续发展,对未来能源消耗的准确预测具有重要意义。
文章以我国湖北省为例,利用1980~2005年的能源消费总量数据为基础,运用ARIMA模型进行能源消费的预测,达到了最小方差意义下的最优预测的效果。
基于ARIMA模型的湖北省城镇居民人均可支配收入预测

区域创新基于ARIMA 模型的湖北省城镇居民人均可支配收入预测张婷婷(中南民族大学经济学院湖北武汉430074)摘要:为了研究湖北省城镇居民人均可支配收入的情况,选取湖北省2000-2015年16年的数据,采用基于R 软件的时间序列分析方法对这部分数据进行检验和分析。
预测之前首先对非平稳的原始数据进行对数化处理,再作二阶差分得到平稳序列,之后建立ARIMA 模型(差分自回归移动平均模型),然后利用已经通过检验的模型对2016-2025年这10年数据进行预测。
从预测结果看出,2016-2025年未来10年湖北省城镇居民人均可支配收入依然呈现明显上涨 趋势。
最后给出政策性建议和总结,这对湖北省的经济发展有着很重要的使用价值。
关键词:时间序列;R软件;ARIMA 模型;预测doi :10.3969/j .issn .1665-2272.2017.14.002斯(Jenkins )于20世纪70年代初提出的一■者名时间序列预测方法,所以又称为box -jenkinS 模型、博克思-詹金斯法,该模型是指将非平稳时间序列转化为平稳时 间序列,然后将因变量仅对它的滞后值以及随机误差 项的现值和滞后值进行回归所建立的模型。
其中ARIMA (p ,d ,q )称为差分自回归移动平均模型,AR 为 自回归,责为自回归项,MA 为移动平均,择为移动平均 项数,d 为非平稳时间序列成为平稳时所做的差分次 数。
ARIMA 是残差进入模型,提高了模型的精度,但是 ARIMA 模型法自身包含一种假设,它假定时间序列为未来模式与过去的趋势一致,不能预测到某些特殊情 况的发生,通常被用于短期预测。
1数据的处理与平稳性检验1.1数据平稳性检验在预测之前首先需要对时间序列数据进行平稳性 检验,本文中通过取对数、做差分等数据转换的方法将 非平稳的时间序列转化为零均值的平稳随机时间序 列,表1为湖北省城镇居民人均可支配收入2000-2015 年数据,图1为2000-2015年数据的时间序列图。
湖北省人均GDP的ARIMA模型及预测

对于处理后的平稳序列进行分析,应用 SAS 程序的 PROC ARIMA 过程,分析其自相关系数(ACF) 和偏自相关系数(PACF)的变化趋势并估计自相关阶数 p 和移动平均阶数 q 的值。选择模型的原则如 表:
-.11682 |
.
**|
.
|
0.247116
Autocorrelation Check for White Noise
To
Chi-
Pr >
Lag
Square DF ChiSq --------------------Autocorrelations--------------------
6
16.98
1984
676
1996
5122
2008
19858
1985
808
1997
5899
2009
22677
1986
891
1998
6289
2010
27906
1987 1988 1989
1031 1228 1383
1999 2000 2001
6514 7188 7813
2011 2012 2013
34197 38572 42613
6 0.0093 0.476 0.133 0.020 -0.198 -0.265 -0.258
12
24.74 12 0.0161 -0.305 -0.196 -0.093 -0.073 -0.051 -0.117
湖北省社会消费品零售总额ARIMA模型与预测

湖北省社会消费品零售总额ARIMA模型与预测【摘要】本文首先根据1999年1月至2008年12月湖北省社会消费品零售总额数据建立了时间序列分析模型:ARIMA(2,1,1)(1,1,1)12,并利用该模型对2009和2010年的社会消费品零售总额进行了预测和分析。
【关键词】社会消费品零售总额时间序列ARIMA模型在全球金融海啸影响下,2009年的中国经济增长将更加依赖“内需”的提振。
因此,对反映消费能力和水平的社会消费品零售总额进行分析与预测,将有助于对湖北全省经济走向进行分析并进行相关决策。
一、问题的提出将湖北省1999年1月至2008年12月社会消费品零售总额的月度数据记为CONSUMPTION。
在文中对CONSUMPTION进行ARIMA模型建立与预测分析(数据来源于湖北省统计局网站和《湖北省国民经济统计月报》)。
模型建立及分析如下。
1、特征分析由时间序列数据绘制的折线图(图略)可知,湖北省社会消费品零售总额具有向上的趋势,并且包含周期为12的周期性特征。
为消除时间序列的异方差性,对时间序列取对数:lc=log(Consumption)。
从时间序列lc的自相关和偏相关函数图(图略)可以看出,序列仍然存在周期,表明季节性存在;自相关系数没有很快的趋于0,表明该序列是非平稳的。
为消除季节性并使得时间序列趋于平稳,对时间序列lc做一阶差分,差分的时间序列名为dlc=lc-lc(-1),折线图如图一所示。
由该图可知,时间序列的趋势基本消除;但在该序列的自相关和偏相关函数图中,季节性仍然存在。
对时间序列dlc做季节差分,得到新的时间序列sdlc=dlc-dlc(-12),该序列的自相关和偏相关系数见图2。
由图2可知,自相关系数(Autocorrelation)和偏相关系数(Partial Correlation)落入了随机区间,但在K=12时系数仍然较大。
对sdlc继续作一阶差分,季节性并没有较大改善,因此对时间序列lc最终只作一阶十二步差分——即时间序列sdlc。
时间序列分析与ARIMA模型

时间序列分析与ARIMA模型时间序列分析是一种研究时间上连续测量所构成的数据的方法。
它可以用来分析数据中的趋势、周期性和随机性,并预测未来的走势。
ARIMA(自回归滑动平均模型)是时间序列分析中常用的模型之一。
本文将介绍时间序列分析的基本概念以及ARIMA模型的原理和应用。
一、时间序列分析的基本概念时间序列是按照时间顺序排列的一组连续观测数据。
在时间序列分析中,我们常常关注序列中的趋势(trend)、季节性(seasonality)和周期性(cycle)等特征。
趋势是指长期上升或下降的走势;季节性是指数据在相同周期内波动的规律性;周期性是指超过一年的时间内出现的规律性波动。
二、ARIMA模型的原理ARIMA模型是由自回归(AR)和滑动平均(MA)模型组成的。
AR模型用过去的观测值来预测未来的值,滑动平均模型则用过去的噪声来预测未来的值。
ARIMA模型是将这两种模型结合起来,对时间序列进行建模和预测。
ARIMA模型包括三个主要部分:自回归阶数(p)、差分阶数(d)和滑动平均阶数(q)。
p表示模型中的自回归项数目,d表示需要进行的差分次数,q表示模型中的滑动平均项数目。
通过对时间序列的观测值进行差分,ARIMA模型可以将非平稳的序列转化为平稳的序列。
然后,可以通过对平稳序列的自回归和滑动平均建模,预测未来的值。
三、ARIMA模型的应用ARIMA模型在实际应用中被广泛使用。
它可以用于经济学、金融学、气象学等领域中的时间序列预测和分析。
以股票市场为例,投资者可以利用ARIMA模型对历史股价进行分析,预测未来股价的走势。
在气象学中,ARIMA模型可以用于预测未来的天气情况。
除了ARIMA模型,时间序列分析还包括其他模型,如季节性分解、移动平均、指数平滑等。
这些模型都有各自的优点和应用领域。
在实际应用中,根据不同的数据特点和研究目的,选择合适的模型进行分析和预测是十分重要的。
总结时间序列分析和ARIMA模型是研究时间数据的重要方法。
基于时间序列分析的ARIMA模型分析及预测

生产, 有效地节约能源, 避免浪费具有重要意义。
1模 型分 析 与建模
时 间序列分 析主要使 用统计推 断的方法 , 从己知东西 中获 知 一些未知 的东西 , 据概率分 布的某种特 征保 持不变性 , 根 推 导 出不 同类平稳性 的假定 。时 间序列 的主要性质有 : ( 1 )白噪声 , 如果随机过程 f I 足 1 X满
分布。 序列预测方法 , 基本思想是 : 将预测对象随时问推移而形成的数
序列 , 这个模型 一旦被识 别后就可 以从时 间序 列的过去值及现
从以上性质可 以看 出 , 严平稳是一 种条件 比较苛刻 的平 稳
时间的推 移而发 生变化 时 , 序列才 能被认为是 平稳 的 , 在 该 这
据序列视 为一个 随机序列 , 用一定的数学模型来 近似描述这个 性定义 。按这一定义 , 只有 当序列所有的统计 性质 都不 会随着 在值来预测未来值 。本文使用 ARMA模型对 电力系统月负荷 实际应用中是难 以办 到的。 I
数据进行分析 , 出规律 , 得 从而作 出预测 。该预测对 指导将来 的
( 相 关性 , 3 ) 对线性 时间 序列 { 我们研 究不 同时刻 t x1 , 与
其对应的随机变量 x【 间的线性关系 。自相关系数描述 了x , 之 与 x之间的相依程度。而偏相关系数是x x分别对 x … , 和 1 , x 进行 线性 回归后的残差的相 关性 。
计算机 时代 2 1 年 第 2 0 1 期
基于ARIMA模型算法的频谱时间序列预测分析

基于ARIMA模型算法的频谱时间序列预测分析摘要:结合频谱时间序列的特点,选择ARIMA模型作为预测模型,通过ARIMA模型算法的流程分析,初步论证预测模型及预测精度的可靠性。
关键词:ARIMA模型频谱时间序列时间序列就是按时间顺序取得的一系列观测值,具有如下特点:首先,时间序列的数据或数据点的位置依赖于时间,即数据的取值依赖于时间的变化,但不一定是时间t的严格函数;其次,每一时刻上的取值或数据点的位置具有一定的随机性,不可能完全准确地用历史值进行预测;第三,前后时刻(不一定是相邻时刻)的数值或数据点的位置有一定的相关性,这种相关性就是系统的动态规律性。
1 频谱时间序列的特点由于电磁环境的复杂多样性以及许多未知因素和不确定因素的影响,频谱占用是一个复杂多变的过程,频谱数据具有高度的非线性特点。
目前多数学者认为,频谱时间序列一般由确定分量和随机分量组成,确定分量具有一定的物理含义,随机分量由不规则的振荡和随机影响造成,具有高度的非线性特点,在进行频谱数据分析时,应根据频谱时间序列的特点找出一种精度较高的预测模型。
2 基于ARIMA模型算法的流程分析ARIMA模型算法分析流程图如图1所示。
2.1 平稳性检验平稳时间序列因为有很好的统计特性,首先检验所观测样本的平稳性,然后根据其是否具有平稳性来建立相适应的模型,主要使用自相关系数和自相关图检验。
运用自相关分析图判定时间序列平稳性的一般准则是:若时间序列的自相关系数基本上(通常为p>3时)都落入置信区间,且逐渐趋于零,则该时间序列具有平稳性;若时间序列的自相关系数更多的落在置信区间外面,则该时间序列就不具有平稳性。
2.2 纯随机性检验如果序列值之间没有任何相依性,过去的行为对将来的发展没有任何丝毫影响,这种序列称为纯随机序列。
从统计的观点来看,纯随机序列是没有任何分析价值的序列,因此需要对平稳序列进行纯随机性检验。
就说明该序列不是纯随机序列,该序列间隔k期的序列值之间存在着一定程度的相互影响关系,统计上称为相关信息。
基于ARIMA模型的中国CPI走势预测分析_郭晓峰

E
(εt,
εs)
=
0,
s
≠
t
1.2 数据预处理
本文使用中国 2001 年 1 月至 2011 年 10 月最新的月度 CPI(上年同期=100)作为研究对象,数据(详见表 1)来源
于国家统计局官方网站 /,所有的计
算过程使用 EViews6.0 软件完成。
写成相应的数据表达式为: ΔCPI = 0.042068 - 0.527426ΔCPIt - 12 + 0.248972ut - 2
(1.277187) (-7.036495) (2.889591) -0.300765ut - 20 + ut
(-3.351763)
S.E=0.541355,F=22.28468,SC=1.738539,AIC=1.644106
图 3 DCPI 的 AC 和 PAC 图
图 4 模型的残差序列检验
当然这样判断明显依然比较粗糙,具有很大的主观
性。为了提高模型的精度,本文建立了多个模型,进行了
数 10 次的建模尝试,同时利用 ACI 和 SC 准则对模型进行
比较,最终确定最优模型为 ARIMA(12,1,20)模型(表 2)。
表2
演到未来;也就是通过对时间序列的处理来研究预测目标 自身的变化趋势,以此准确预测该目标对象的未来变化情
况。时间序列进行分析的基本思想是:某些时间序列可以 看作是随着时间 t 而随机变化的变量,该时序的单个构成
序列值虽然不确定,但是整个序列却呈现一定的变化规律, 可以用数学模型去近似地描述。现实社会中,人们常常运
居民消费者价格指数受到多种因子的制约,并且因子 间又保持着极其复杂的关系,特别是在后国际金融危机时 代,中国经济运行不确定性和不稳定性在上升,面临这样 的情势,市场上对中国经济接下来发展态势的担忧声音继 续弥漫。在这样的背景下,更是增加了影响因子的“不确 定性”。因而运用结构性因果模型对消费者价格指数走势 进行预测,一般难以达到较为理想的预测效果。自回归求 积移动平均(ARIMA)模型是一种目前应用广泛最的线性 时间序列建模工具之一,ARIMA 模型又称博克斯-詹金 斯预测模型(theBox-JenkinsModel),简称 B-J 模型,它是以 美国统计学家 GeogreE.P.Box 和英国统计学家 GwilymM. Jenkins 的名字命名的一种时间序列预测方法。本文拟选 择以中国 2001 年 1 月至 2011 年 10 月最新的月度 CPI 数据 作为研究对象,构建 ARIMA(12,1,20)模型,在模型拟合 效果优良的基础上,预测 CPI 的未来走势,以期为政府决 策部门有效实施物价调控政策提供数量上的依据。
消费者物价指数的时间序列模型与研究

消费者物价指数的时间序列模型与研究一、引言消费者物价指数(Consumer Price Index,简称CPI)是衡量物价水平变动的重要指标,对于国家宏观经济政策的制定和市场调节具有重要意义。
本文将基于时间序列模型,对CPI进行分析和研究,旨在揭示CPI的长期趋势和短期波动规律,为经济决策提供参考。
二、时间序列模型简介时间序列模型是一种分析和预测时间序列数据的方法。
它基于统计学理论,通过对历史数据的分析,寻找数据内部的规律和趋势,进而预测未来的发展趋势。
常用的时间序列模型包括ARIMA模型、ARCH 模型等。
三、CPI的时间序列模型构建1. 数据收集与预处理为构建CPI的时间序列模型,首先需要收集CPI的历史数据,并进行预处理。
预处理包括去除异常值、填补缺失值等,确保数据的准确性和完整性。
2. 数据分析与探索对预处理后的CPI数据进行分析和探索,了解CPI的基本特征和趋势。
可以使用统计图表、描述性统计等方法,对CPI数据进行可视化和概括,以便更好地理解数据的特点。
3. 模型选择与建立根据CPI数据的特点和分析结果,选择适合的时间序列模型进行建立。
可以根据CPI数据的平稳性、自相关性等进行模型的选择和检验,确保选择的模型拟合性好且具有可解释性。
4. 模型参数估计与检验在选择并建立时间序列模型后,需要进行参数的估计与检验。
根据CPI数据,利用极大似然估计等方法,估计模型的参数,并进行显著性检验,判断模型的拟合效果和可靠性。
5. 模型预测与应用基于已建立并检验通过的时间序列模型,进行CPI的预测和应用。
可以利用模型进行未来一段时间内CPI的预测,提供决策者参考,同时也可以应用模型对CPI的波动和变动原因进行解释和分析,为相关政策的制定提供依据。
四、时间序列模型研究的意义与局限性1. 研究意义时间序列模型的研究可以揭示CPI的长期趋势和短期波动规律,为经济决策提供参考。
通过模型的预测和解释,可以帮助决策者制定合理的经济政策,稳定物价水平,维护社会稳定。
基于ARIMA模型的中国消费物价指数研究

基于ARIMA模型的中国消费物价指数研究摘要居民消费价格指数(CPI)是反映通货膨胀程度的重要指标,也是国民经济核算中的缩减指标。
居民消费价格指数反映的市场价格信号真实,带动价格舆论导向正确,则有利于改善价格的总水平调控。
目前,医疗、教育、交通等垄断行业价格上涨过快,导致居民大量增加储蓄,使正常消费受到压抑,消费结构变形,影响经济增长。
通货膨胀是中央银行制定货币政策必不可少的一个变量。
本文在对外国通货膨胀研究的基础上,收集了1987年1月至2015年10月的月度数据,对我国通货膨胀率进行分析,并做短期预测。
实证结果表明,ARIMA(1,1,1)模型对CPI 拟合预测结果良好。
若根据通货膨胀率的预测结果制定货币政策,中央银行的货币政策将更行之有效。
关键词CPI ARIMA模型残差时间序列AbstractThe consumer price index (CPI) is used to determine the relative number of changes in the price of consumer goods and services in a certain period of time. This indicator affects the government to develop monetary, fiscal, consumption, prices, wages and social security policies, but also a direct impact on the living standards of residents and Evaluation. The consumer price index reflects the true market price signals, driving the price correct guidance of public opinion, it will help to improve the general level of price regulation. Currently, health care, education, transportation and other monopoly industries prices rose too fast, resulting in a substantial increase in resident deposits, so that normal consumption suppressed, consumption structure deformation, affecting economic growth. Inflation is the central bank monetary policy an essential variable. Inflation based on the study in a foreign country, the paper collected from January 1987 to October 2015 monthly data on China's inflation rate was analyzed, and make short-term predictions. The empirical results show that, ARIMA (1,1,1) model to fit the CPI forecast good results. If monetary policy based on inflation forecast, the central bank's monetary policy will be more effective.Keyword CPI ARIMA model Residuals Time Series第1章序言1.1 研究意义和目的1.1.1 研究意义1、理论意义根据我国经济发展的特点,结合区域经济发展的复杂消费结构,主要从内部消费物价指数构成的成本,分析了我国物价上涨的主要驱动力。
基于ARIMA模型的武汉市居民价格消费指数研究

根 据 表 3以 AI C和 S C信 息 准 则 作 为 判 断 估 计 模 型 的 B
作者简介 : 杨翱 (9 9 ) 男 , 北 荆 州人 , 南财 经 政 法 大 学 统 计 与数 学 学 院 , 究方 向 : 量 经 济 学 。 18一 , 湖 中 研 数
一
7 2 —
N 0.1 201 4, 1
现代 商贸工业 M o enB s es rd d s y d r ui s T aeI ut n n r
21 0 1年 第 1 4期
优 劣 , 过 反 复 试 验 和 对 比 , 去 不 显 著 变 量 , 后 选 择 经 删 最
型。
由于武汉市统 计 年 鉴 缺 少基 于 15 9 2年 武 汉 市 居 民 消 费 指
1. 2 8 27 1. 0 8 3 7
l . 5 8 37 1 .8 8 34
0 0 2 . 3 0 0 0 . 5
0 0 3 . 7 0. 0 15
为 了 对模 型 进 行 预 测 时 检 验 模 型 的 精 确 度 , 们 对 15 — 我 92
2 0 年 的数 据 进 行 二 阶差 分 处 理 , 理 后 的 趋 势 图如 下 : 07 处
3I ( 2I ( 1 0
一
0 J】 f
一
一
2) ( 3 0
4【 】 5J (
—
一
都 比 较 小 。根 据 自相 关 和 偏 自相 关 的 特 点 , 行 模 型 的 定 进
图 1
( 阶 差 分 处理 ) 二
阶 。考 虑 到 偏 自相 关 图 中 只 有 延 迟 1阶 和 4阶 的 偏 自相 关 系 数 显 著 大 于 2倍 标 准 差 , 以 考 虑 构 造 疏 系 数 模 型 , 合 所 综 考 虑前 面 的 差 分 运 算 , 际 上 是 对 原 序 列 拟 合 疏 系 数 模 型 , 实
基于ARIMA模型的CPI实证分析及预测

司等都 曾 对 世 界 主要 国 家 的 C P I 进 行 预 测[ 3 ] 。 对C P I 的准 确 预 测 有 助 于把 握 未 来 经 济 发 展 和
人 民生 活状况 , 从 而更 能有效 制定 政策 , 对 国 民经
居 民消 费价 格 指 数 ( C o n s u me r P r i c e I n d e x , C P I ) , 是 一个 反 映居 民家 庭 所 购买 的生 活消 费 品
3 ) mo d e 1 i S we l l i l l u s t r a t e d i n CPI a n d p r o v i d e b e t t e r f o r e c a s t s . wh i c h p r o v i d e s o me r e f e r e n c e f o r t h e f o r mu l a t i o n a n d i mp l e me n t a t i o n o f t h e g o v e r n me n t ’ S m a c r o e c o n o mi c
( 1 . Re s e a r c h Ce n t e r f o r S EZ,S h e n z h e n Un i v e r s i t y ,S h e n z h e n 5 1 8 0 6 1 , Ch i n a ;2 . Co l l e g e o f Ma n a g e me n t , S h a n g q i u En g i n e e r i n g o l C l e g e ,S h a n g q i u 4 7 6 1 0 0 ,C h i n a )
Ab s t r a c t : ARI M A mo d e l wa s b u i l t a n d u s e d t o a n a l y z e a n d s h o r t —t e r m f o r e c a s t Ch i n a ’ S CPI
基于ARIMA模型的时间序列预测准确优化

基于ARIMA模型的时间序列预测准确优化时间序列预测是指根据过去的数据模式和趋势,去预测未来一段时间内的数值变化。
ARIMA(自回归积分滑动平均模型)是最常用的时间序列预测方法之一。
它通过对时间序列数据的自相关性和偏相关性进行分析,构建出能够预测未来数值变化的模型。
然而,ARIMA模型在实际应用中存在一定的准确性问题,需要进行优化。
一、ARIMA模型的基本原理ARIMA模型采用的是线性回归方法,建立一个自回归模型,同时,通过差分操作对时间序列进行平稳化处理。
ARIMA模型具有三个参数:p、d和q,分别表示自回归阶数、差分阶数和滑动平均阶数。
1. 自回归(AR)模型自回归模型是基于时间序列的过去数值进行预测未来数值的方法。
其中,p表示自回归阶数,即使用前p个时间步长的数值进行预测。
2. 积分(I)模型积分模型是为了平稳化时间序列而进行的差分操作。
差分操作可以消除时间序列的季节性和趋势性,使其更容易建立模型进行预测。
3. 滑动平均(MA)模型滑动平均模型是基于时间序列的过去数值与误差项的滞后值进行的线性组合。
其中,q表示滑动平均阶数,即使用前q个误差项的滞后值进行预测。
二、ARIMA模型准确性问题的原因尽管ARIMA模型在时间序列预测中被广泛应用,但其准确性在一些特定情况下可能存在问题。
以下是几个可能导致ARIMA模型准确性问题的原因:1. 数据质量问题ARIMA模型的准确性很大程度上依赖于数据的质量。
存在异常值、缺失值或离群值等数据质量问题可能会对ARIMA模型的准确性产生较大影响。
2. 趋势性和季节性变动ARIMA模型在处理具有趋势性和季节性变动的时间序列时,预测较为困难。
这是因为ARIMA模型是基于线性回归的方法,对于非线性趋势和季节变动的数据,准确性会有所下降。
3. 参数选择问题ARIMA模型的准确性还受参数选择的影响。
确定ARIMA模型的参数(例如p、d和q)需要根据经验和模型拟合的结果来调整,不同的参数选择可能会导致不同的预测效果。
基于ARIMA模型的中国CPI指数预测研究

---------------------------------------------------------------范文最新推荐------------------------------------------------------ 基于ARIMA模型的中国CPI指数预测研究摘要居民消费价格指数CPI一直以来都被我们公认为用来衡量通货膨胀水平的关键指标,它时刻与人民的日常生活紧密相关,在整个国家的国民经济价格体系中扮演着不可替代的角色。
随着我国经济渐渐地发展,CPI指数在居民生活中越来越受到人们的重视和关注,它在我国现代社会经济中也占据着越来越举足轻重的地位。
因此,对我国居民消费价格指数的发展趋势进行系统的分析与预测,不仅有利于维持物价水平稳定,而且对经济平稳发展是具有重要意义的。
5010本文中我们对居民消费价格指数CPI的概念、作用意义、编制方法以及影响因素等几个方面进行系统的简述后,再简单介绍了时间序列相关的理论知识。
由于CPI指数是具有较强的季节性与趋势性的时间序列数据,因此本中我们采用时间序列季节乘法模型对我国居民消费价格指数进行了实证分析与预测,得出相1 / 20关结论与建议。
关键词:居民消费价格指数;季节乘法模型;趋势预测Abstract The consumer price index CPI has long been recognized as an important indicator to measure the level of inflation, it is closely related to People's Daily life, in the whole national economy plays an irreplaceable role in price system. Along with our country economy development gradually, the CPI index in people life more and more attention and concern, it is in our modern society is occupying more and more important role in the economy. Therefore, the development trend of China's consumer price index system analysis and forecasting, is not only beneficial to maintain a stable price level, but is is of great significance to the steady economic development.This article, we in the consumer price index concept and function of the CPI, significance, methods and influencing factors from several aspects such as system briefly, and---------------------------------------------------------------范文最新推荐------------------------------------------------------then simply introduces the theory of knowledge of time series. Because the CPI is a strong seasonal and the trend of time series data, this article USES the seasonal time series multiplication model of China's consumer price index has carried on the empirical analysis and prediction, draw relevant conclusions and recommendations.时间序列分析在很久以前就开始一直被专家和学者广泛地运用于与数量有关的分析当中,它主要被用于对事物数量随时间的推进而发生变化的规律进行描述与探索。
基于ARIMA 模型的武汉市居民价格消费指数研究

基于ARIMA 模型的武汉市居民价格消费指数研究模型对时间序列的趋势有较好的拟合效果,介绍自回归移动平均模型的建模方法及Eviews实现。
建立模型对1952年到2008年武汉市居民价格消费指数进行了拟合和研究,在三种不同的模型下,对和进行比较分析,选出了最优拟合模型。
发现武汉市居民价格消费指数的波动具有记忆性,随着时间变化而增加。
将ARIMA模型应用于武汉市居民历年CPI数据的分析与预测,得到较为满意的结果。
标签:ARIMA;价格消费指数;预测1 研究背景目前,对于CPI的实证研究主要集中于两个方面:一是从影响CPI的各种因素出发,寻找CPI与这些因素之间存在的关系,也被称为基础因素分析法;一是从CPI本身的运动出发,研究其作为一个金融时间序列的运动特性。
现实中,大量研究结果表明,基础分析法难以预测CPI走势,并且对于短期CPI波动的解释能力低下。
本文拟利用1952年到2008年武汉市居民价格消费指数数据,应用ARIMA疏系数模型,在比较各模型的和值后选择两种模型,最后通过比较两种模型预测精确度来分析数据,找出最优拟合模型,对武汉市居民2009年和2010年的CPI进行预测。
2 ARMA模型在居民消费价格指数研究中的应用2.1 样本数据选择与处理本文选用武汉市统计局公布的武汉市居民消费价格指数作为观测值,时间从1952到2008年,以1952年的消费价格指数为标准值,共有57个观测值。
1952-1918年居民消费价格指数基本维持在一个相对稳定的状态,1978年后居民消费指数上升,有明显的递增趋势,该序列不是平稳序列。
为了对模型进行预测时检验模型的精确度,我们对1952-2007年的数据进行二阶差分处理,处理后的趋势图如下:从表1中可见,ADF检验结果表明,在1%显著性水平下,经过二阶差分后的序列不存在单位根,是一个平稳的时间序列,由检验结果可以看出CPI指数适用于模型ARIMA(p,2,q)。
因此,经过处理而得到的稳定的时间序列可运用ARIMA模型进行分析.2.2 模型的建立用Eviews软件对二阶差分后的序列的自相关函数(ACF)和偏相关函数(PACF)进行分析,得如下结果:表2显示延迟4阶之后,自相关系数基本上都在零值附近波动,可以认为自相关系数有可能存在拖尾,该差分后序列平稳。
中国CPI指数的时间序列分析
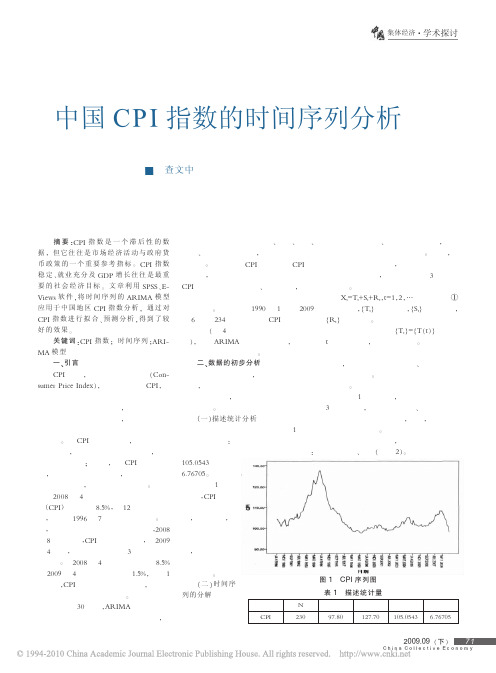
Xt=Tt+St+Rt,t=1 ,2 ,… ① 其 中 , {Tt} 是 趋 势 项 , {St} 是 季 节 项 , {Rt} 是随机项 。
通 常 认 为 趋 势 项 {Tt}={T (t )} 是 时 间
CPI 指 数 进 行 拟 合 、 预 测 分 析 , 得 到 了 较
好的效果。 关 键 词 :CPI 指 数 ; 时 间 序 列 ;ARI-
自相关 。 自 相关程 度 由 自 相 关 系 数 γk 度 量 , 表示时间序列中相隔 k 期 的观测值 之
xt, 在给 定 xt-1,xt-2, …,xt-k+1 的 条 件 下 ,xt 与 xt-k 之间的条件相关关系 。 其相关程度 用偏自相关系数 覬kk 度量 , 有 -1≤覬kk≤1 。
内外的学者将其运用于经济 、 旅游 、 能源 、 医 学 、环 境 等 许 多 领 域 ,出 现 了 一 批 较 好 的 成 果 。 以 每 月 的 CPI 指 数 构 成 CPI 指 数序列, 运用时间序列的建模方法对该
都 表 现 出 趋 势 性 、季 节 性 和 随 机 性 ,或 者 只表现出三者中的其二或 其一 。 这样 , 可 以认为每个时间序列 , 或经过适当 的函数 变换的时间序列 , 都可以分解 成 3 个部分 的叠加 。
CPI N 230
2008 年 4 月 份 中 国 居 民 消 费 价 格 指 数 (CPI)同比上涨 8.5% , 为 12 年以来的新 高 ,超过了 1996 年 7 月份创下的高点 。 然 而 ,由于受全球性的金融危机的影响 ,2008 年 8 月份开始 ,CPI 指数一路下滑 ,到 2009 年 4 月份 , 更是出现了连续 3 个月的同比 负增长 。 从 2008 年 4 月份的同比上涨 8.5% 到 2009 年 4 月份的同比下降 1.5%, 短短 1 年时间 ,CPI 指数如此大幅的波动 , 引发了
基于ARIMA模型对我国CPI指数的分析预测

流通经济基于ARIMA模型对我国CPI指数的分析预测中央民族大学经济学院 孙晓丹摘 要:通货膨胀代表一国物价总水平的持续上升,严重时可能会造成社会供需失衡,导致货币信任危机,因此有必要对通货膨胀水平进行衡量和预测。
CPI指数是衡量通货膨胀水平的重要指标,本文通过选取2000年1月至2021年1月共253个月份的CPI数据,构建ARIMA(13,0,0)模型对CPI指数进行分析和预测,以得出2021年我国的通货膨胀情况。
研究结果表明,CPI指数具有较长的滞后阶项,并且在经济形势逐渐好转之后,国内通货膨胀水平将会呈现出稳定增长态势。
关键词:ARIMA模型;通货膨胀率;CPI指数本文索引:孙晓丹.基于ARIMA模型对我国CPI指数的分析预测[J].商展经济,2021(15):015-017.中图分类号:F202 文献标识码:ADOI:10.12245/j.issn.2096-6776.2021.15.052020年世界经济遭遇了严峻的挑战,物价水平也出现了大幅下跌的情形。
如今,经济活动在持续衰退之后重新走向扩张,大宗商品价格持续上涨,通货膨胀现象再次浮现,给全球经济的复苏蒙上了一层阴影。
通货膨胀是指由于物价全面持续的上涨而造成一国货币的贬值,造成这一现象的直接原因通常是一国发行的实际货币量超过了其需要货币量。
消费者物价指数(CPI)是衡量通货膨胀情况的重要指标之一,如果一段时间内CPI指数持续、全面地上涨,则表明发生了通货膨胀。
国内学术界对通货膨胀的预测方面有着丰富的研究成果。
陈伟、牛霖琳(2013)运用贝叶斯模型平均方法对样本外通胀进行预测,并证明了货币量的增加会直接导致通胀增加。
田新(2015)利用ARIMA(3,1,(1,2,3,7))对2014-2015年的CPI指数进行了预测,结论表明,我国通货膨胀有较长的滞后期,其预测过程不受其他因素的干扰。
霍忻、刘黎明(2017)选取1985-2015的通货膨胀数据,利用ARIMA(3,2,2)模型对我国“十三五”时期通货膨胀的趋势进行了预测,结果表明,我国通胀率将继续保持平稳增长的态势。
居民消费价格指数预测的分解模型研究_以武汉市时间序列数据为例

对居民消费价格指数进行准确地预测,是合理制定宏观经济政策的前提。
本文选取武汉市2003年1月至2009年11月居民消费价格指数的月度定基比数据,采用时间序列分解法建立模型并进行预测。
从居民消费价格指数中分解出季节因素和长期趋势因素,并对居民消费价格指数的变化做出准确的预测,以期为宏观经济分析和决策提供参考。
一、武汉市居民消费价格指数时间序列分析时间序列分解模型的基本思想是序列的各种变化受到长期趋势、周期性循环要素、季节性变化和不规则变动这四个因素的影响。
其中(1)长期趋势因素(T):反映经济现象在一个较长时间内的发展方向,它可以在一个相当长的时间内表现为一种近似直线的持续向上或持续向下或平稳的趋势。
(2)周期性循环要素(C):是一种周期性变动,它是受各种经济因素影响的上下起伏不定的波动。
(3)季节性要素(S):是受季节变动影响所形成的一种长度和幅度固定的周期性波动。
(4)不规则要素(I):是受各种偶然因素影响所形成的不规则变动。
时间序列可以表示为上述四个因素的函数。
时间序列分解模型有很多,最常用的有加法模型:时间序列Y等于以上四个因素之和;乘法模型:时间序列Y等于以上四个因素的乘积;混合模型:时间序列Y等于长期趋势与季节性要素的乘积再加上循环要素与不规则要素之和。
本文选取武汉市2003年1月至2009年11月居民消费价格指数的月度定基比数据Y,由于是定基比数据,因此在各期之间具有可比性。
其时间序列如图1所示。
从图1可以看出,武汉市居民消费价格指数基本上是每年的2月达到最高,每年的6-7月达到最低;且不同年份的居民消费价格指数有逐年增长的趋势。
从2003年11月开始至2006年6月呈现逐渐上涨的趋势,2006年7月开始加速上涨,到2008年2月达到最高值,同比上涨9.8%,这主要是受到强雨雪天气影响,2月份食品价格环比上涨10.4%,同时,受上年价格“翘尾”的因素影响价格总水平上涨3.6%。
2008年3月武汉居民消费价格指数总水平比上月下将2.1%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年第5期下旬刊(总第445期)时 代 金 融Times FinanceNO.5,2011(CumulativetyNO.445)一、研究背景居民消费价格指数(Consumer Price Index,CPI)是反映居民家庭购买生活消费品和支出服务项目费用价格变动趋势和程度的相对数。
其目的在于观察居民生活消费品及服务项目价格的变动对城乡居民生活的影响,为各级党政领导掌握居民消费状况,研究和制定居民消费价格政策、工资政策以及为新国民经济核算体系中有消除价格变动因素的不变价格核算提供科学依据。
居民消费价格指数还是反映通货膨胀的重要指标。
2008年,席卷全球的金融危机,使全球经济受到了很大的打击。
金融危机后,伴随着世界经济的快速增长,通货膨胀问题越来越严重,物价上涨厉害。
为了研究金融危机后湖北省的物价指数变化,为党政领导提供一定的建议,笔者着手建立金融危机后湖北省居民消费价格指数变化的经济学模型,撰写此文。
二、文献综述目前,国内研究CPI 数据变化趋势并进行预测的文章比较多。
单化玉、周艳丽在《湖北省CPI 时间序列分析及预测》一文中用ARIMA(1,1,0)模型拟合了湖北省2002-2009年这8年的CPI 月度数据,并进行了预测。
汪淼、郑舒婷在《基于ARIMA 模型的中国消费者价格指数时间序列分析》一文中对中国1990年1月至2009年11月的CPI 月度数据序列采用了ARIMA (1,1 1)×(11)12季节乘积模型进行拟合,并进行了预测。
王黎明、李光明在《中国CPI 时间序列预测模型》一文中用ARIMA(1,1,2)模型拟合了我国1990-2008年的月度CPI 数据,对2009年1-5月的CPI 进行了预测。
上述学者在各自选用的方法虽然都较好地达到了各自研究的目的,但是他们的方法还是存在一定问题的。
首先,对于时间跨度较长(5年以上)的月度时间序列,并不能直接采用同期比指数来进行分析,应该采用以2000年为固定对比基期的居民消费价格指数,即消费价格定基比指数,来进行分析。
再者,他们研究的数据跨度时间太长,我国每5年会对计算CPI 的各成分修改一次权重,所以经过多次修正权重的数据放在一起研究,显然不是一个明智的选择。
最后,他们的研究数据都较陈旧。
金融危机后的中国变化速度加快,经济增长的同时通货膨胀问题也越来越严重,因此需要一个专门对后金融危机时代的研究来填补空缺。
当然,还有一些学者对此问题进行了研究,在此不再赘述。
本文从实际出发,采用金融危机席卷全球后的湖北省月度CPI 数据进行分析、预测,这便较为新颖。
三、基于eviews 软件的实证分析本文研究所采用的样本数据为2008年9月至2011年4月湖北省居民消费价格指数CPI 数值,共32个样本数据。
本文数据来自国家统计局网站及湖北省统计局网站。
为了拟合CPI 序列的走势,先来观测其走势图,如图1所示。
由图1可知,CPI 序列随着时间变化,存在着明显的先短暂下降后一直上升的趋势,故可推想该序列不平稳。
图1(1)单位根检验。
由于只有平稳的时间序列才能够用eviews 软件进行拟合,为了从理论上确定CPI 序列是否平稳,先运用ADF 单位根检验方法对CPI 序列做平稳性检验。
有检验结果可知,CPI 序列并不平稳。
于是再对其一阶差分序列D(CPI)做ADF 单位根检验,差分序列在1%的显著性水平下是平稳的。
具体的检验结果见表1。
表1 CPI 数据序列单位根检验结果变量ADF 值1% 临界值5% 临界值10% 临界值是否平稳CPI -2. 925858-4.284580-3.562882-3.215267不平稳D(CPI)-4.468096-1.952473-3.529758-1.610211平稳(2)一阶差分序列白噪声检验。
由于只有非白噪声序列才有可提取的信息,才存在研究价值,故应对一阶差分序列D(CPI)进行白噪声检验。
观察其自相关图可知,第3、4、5阶相关系数的P 值小于0.05,故在5%的显著性水平下拒绝原假设,认为D(CPI)序列并非白噪声序列。
3.模型估计。
接着,对D(CPI)序列进行模型估计。
由D(CPI)的自相关图可知,明显落在两倍标准误差外的是第三阶自相关系数、偏相关系数以及第十阶偏相关系数。
我们运用eviews 对D(CPI)序列估计ARIMA(10,1,3)模型。
在逐渐删除非显著变量并进行多种模型尝试后,得到疏系数模型ARIMA ((1,3,10),1,(2,3))拟合最好。
D(CPI)=0.2344-0.671AR(1)+0.521AR(3)-0.372AR(10)-1.463MA(2)-3.446MA(3)S.E(0.051)(0.096)(0.150)(0.033) (0.912) (1.099)其中,S.E 表示的是各估计系数的标准差。
拟合优度R 2值为0.94;各估计系数在10%的显著性水平上都显著;AIC、SC 值很小,分别为-1.075和-0.777;DW 值(2.14)非常接近2;F 值47, Prob(F-statistic)概率为0。
所有指标都说明模型拟合得非常好。
4.残差序列白噪声检验。
为了确定模型的有效性,对其残差序列进行白噪声检验,确定其信息已充分提取。
在eviews 中生成序列u=resid,对序列u 做单位根检验,其检验的T 值为-4.712435,概率p 为0.0001,说明序列是平稳的;观察序列u 的自相关图(图-3)知,其各阶相关系数的p 值都很大,远远超过0.05,说明u 已经是白噪声序列,也说明原始序列CPI 里的有效信息已被充分提取。
基于ARIMA 模型的湖北省CPI 时间序列分析及预测周美英(中南财经政法大学统计与数学学院,湖北 武汉 430073)【摘要】金融危机后,伴随着世界经济的快速增长,通货膨胀问题越来越严重,物价上涨厉害。
本文利用湖北省2008年9月至2011年这4年(32个月)的月度数据,对湖北省CPI 序列建立求和自回归移动平均(ARIMA)模型。
结果表明,疏系数模型ARIMA((1,3,10) ,1,(2,3))是描述湖北省CPI 变化趋势较优的时间序列模型。
本文利用此模型对2011年5、6、7月的湖北省CPI 指标进行了预测并提出了相应的建议。
【关键字】 CPI 疏系数ARIMA 模型 预测模型 单位根检验 白噪声检验(下转第110页)常发生在其有创新意识、与传统文化不相容的人才群体,结果导致企业朝表面趋同方向蜕变,缺乏创新精神。
当企业考虑这些成本因素后,往往发现维持现有契约关系不变是相对明智的选择。
此外,在雇主与雇员之间围绕利益分配问题的经常性讨价还价行为产生的谈判成本,也在一定程度上需要有关职位分配和工资报酬等刚性安排来降低交易成本。
(二)知识专用性和岗位特殊性的存在决定了内部劳动力市场的长期契约性如前所述特殊人力资本可以是企业对雇员进行特殊技能训练的结果,也可以是由于雇佣关系终止而引致的成本损失,第三种情况我们可以把特殊人力资本看做是工人和企业匹配的质量。
Jovanvic(1979)认为[12],特定工人和企业匹配的生产率是不断变化的,并且事先不可观察,需要雇佣期限的增加而不断被了解。
该模型得出了一个匹配质量的性质:如果工人对预期的匹配质量要低于工人的保留匹配质量,工人就会迟职。
在匹配的早期,工人对匹配质量的不确定性很高,离职寻找新工作的工作代价很大。
由于预期匹配质量变高的可能性很大,即使早期匹配质量低,工人也呆在原企业。
工作时间更长后,工人对匹配质量的不确定性降低,保留匹配质量上升,在这一点,离职率上升,不良匹配被清除。
剩余匹配都是离职率低的高质量的匹配。
该模型解释了劳动力市场上雇佣关系终止比率开始很低,然后变高,随后又非常低的客观现象。
也说明了为了减少无效的质量匹配,提高劳动生产率,需要内部劳动力市场的长期契约性。
从以上分析可以看出,内部劳动力市场的长期契约性有利于特殊人力资本的积累,可以有效地缓解劳资双方的机会主义行为,可以减少经济上无效率离职带来的效率损失,也有利于减少无效的质量匹配,提高劳动生产率。
(三)劳动力买卖双方信息不对称和不完全决定了内部劳动力市场的长期契约性在雇员进入内部劳动力市场的过程中,存在两种信息不对称问题,一种是“事前”的信息不对称,由于信息搜集和信号甄别问题的存在,企业无法观察到雇员的行为,既道德风险,或企业无法获知雇员所拥有的关于成本或价值的私人信息,这就是逆向选择问题,企业和雇员之间存在信息不对称问题;一种是“事后”的信息不对称,在进入“入口处”之后,仍然存在一方很难观察或监督另外一方的投入或产出的信息不对称问题。
同样,当员工处于专用性人力资本补偿阶段的时候,企业通过隐报市场绩效,可以借机解雇处于延期补偿阶段的员工,以降低工资成本。
可见,由于合同的不完全性,在信息不对称的条件下,雇佣双方之间短期的、临时性的市场交易往往难以形成合作的激励,机会主义可能成为一种普遍的理性行为。
因此,有必要通过一定的契约设计来协调二者之间的关系,在一定程度上保证内部劳动力市场的经济效率。
如利用内部晋升和延期支付等长期契约关系设计,使企业和雇员之间的博弈关系由一次性和短期性变成重复性和长期性的博弈关系,以强化声誉对双方机会主义行为的约束,实现尽量降低交易费用的目的。
在企业内部长期雇佣合约预期和劳资双方重复博弈条件下,“信誉”或“声誉”机制将发生作用,当事人中任何一方的违约或欺诈行为必然遭到另一面的惩罚,而任何一方的诚信行为也都有足够的时间赢得回报。
所以长期契约不仅有助于降低双方在确定劳动关系时的事前交易成本和管理成本,而且通过增强双方的合作激励又可以降低雇佣关系维持过程中的管理和监督成本。
此外,因为有了长期雇佣的预期,内部劳动力市场的合作能为企业带来当期收益和未来收益,这当然使内部员工有了长期合作下去的愿望。
参考文献[1]赵增耀.内部劳动市场的经济理性及其在我国的适用性[J].经济研究,2002(3).[2]张凤林等.西方内部劳动力市场理论评述[J],经济学动态, 2003(7).[3]陈晓燕.长期雇佣合约的选择与企业内部劳动力市场建设[J].理论月刊,2004(4).[4]蒋长流.长期雇佣关系对人力资本形成的激励效应[J].郑州航空工业管理学院学报,2007(4).[5]王迪钊,黎煦.长期雇佣:一个人力资本理论的解释[J].商业研究,2005(1).[6]施海晓.企业长期雇佣契约的优劣性分析[J].中国科技信息,2005(24).[7]张凤林等:《希望内部劳动力市场理论评述》,经济学动态, 2003(7).[8]陈晓燕:《长期雇佣合约的选择与企业内部劳动力市场建设,理论月刊,2004(4).[9]交易成本学说来源于:陈晓燕:《长期雇佣合约的选择与企业内部劳动力市场建设》,理论月刊,2004(4).[10]参见科斯,哈特等:《契约经济学》,北京:经济科学出版社,1999.[11]参见科斯,哈特等:《契约经济学》,北京:经济科学出版社,1999.[12]王迪钊,黎煦:《长期雇佣:一个人力资本理论的解释》,商业研究,2005(1).作者简介:王鑫,男,辽宁铁岭人,东北财经大学研究生院世界经济专业在读博士,研究方向:世界经济。
