2014年七年级下册数学竞赛试题及答案
2014年七年级下册数学竞赛试题及答案

2013~20XX 七年级下学期数学竞赛试题一. 选择题(每小题5分,共30分)1.若a<0 , ab<0 , 那么51---+-b a a b 等于( )A . 4B .-4C . -2a+2b+6 D. 19962.数轴上坐标是整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2009厘米的线段AB,则线段AB 盖住的整点的个数是( )A.2008 或2009B . 2008或 2010C . 2009 或2010D . 2010 或20113.已知{ax b y ==是方程组{5272=+=+y x y x 的解,则a-b 的值为( )A . 2B . 1 C. 0 D. -14.若a<3 , 则不等式(a-3)x<a-3的解集是( )A. x>1 B .x<1 C . x>-1 D . x<-15.方程2x+y=7的正整数解有( )A. 一组 B .二组 C .三组 D . 四组6.不等式组{5335+<-<x x a x 的解集为x<4,则a 满足的条件是( )A. a<4 B .a=4 C .a ≤4 D .a ≥4二. 填空题(每小题4分,共24分)1.不等式组{4252>+<-a x b x 的解集是0<x<2,则a+b 的值等于_______2.已知543zy x ==,且10254=+-z y x ,则z y x +-52的值等于________3.计算200920081431321211⨯+⋅⋅⋅+⨯+⨯+⨯ = _________4.一个角的补角的31等于它的余角,则这个角等于_____度.5.计算〔1+715131++〕×-91715131⎪⎪⎭⎫ ⎝⎛+++〔1+91715131+++〕×〔715131++〕=.6。
b b a -=+22若,______622=+-+ba b a 则三. 解答题:(,共46分).1〔本题6分〕解方程组345238x y x y -=⎧⎨+=-⎩,.2.〔本题10分〕已知: 0634=--z y x ,072=-+z y x ()0≠xyz , 求代数式222222103225zy x z y x ---+的值3〔本题10分〕.如图,已知CD ⊥AB ,DE ∥BC,∠1=∠2求证:FG ⊥AB21G F E D CB A4.〔本题10分〕在平面直角坐标系中,已知三点()()()b c C b B a A ,,0,,,0,其中c b a ,,满足关系式()a b c b a -==-+-2,0322;〔1〕求c b a ,,的值,〔2〕请你将三点()()()b c C b B a A ,,0,,,0在平面直角坐标系中描出来,并计算出ABC ∆的面积。
大江口中学2014年七年级下数学竞赛试题及答案

大江口中学2014年七年级下数学竞赛试题及答案时量:120分钟 满分:120分 一、选择题:(共8个小题,每小题5分,共40分)1. 方程4x +5y =98的正整数解的个数是( B )A .4B .5C .6D .72. 已知32x y =⎧⎨=⎩是方程组12ax cy cx by +=-⎧⎨-=-⎩的解,那么a 、b 之间的关系是( A )A .4b+9a=1B .4b-9a=1C .3a+2b=1D .4b+9a=-13. 已知23a =,26b =,212c =,则下列关系正确的是( B )A .2a =b +cB .2b =a +cC .2c =a +bD .c =2a +b4. 设a 1,a 2,…,a 10是在1-,0,1这三个整数中取值的数,若a 1+a 2+…+a 10=2,且(a 1+1)2+(a 2+1)2+…+(a 10+1)2=22,则a 1,a 2,…,a 10中取零的个数共有( B ) A .1个 B .2个 C .3个 D .4个5. 如果x 3+ax 2+bx +8有两个因式x +1和x +2,则a +b =( D )A .7B .8C .15D .2l6. 如图1,下列说法中不正确的是( A )A .因为AB ∥CD ,所以∠1=∠3 B .因为∠2=∠4,所以AE ∥CFC .因为AE ∥CF ,所以∠2=∠4D .因为∠1=∠3,∠2=∠4,所以AB ∥CD图1 图2 图37. 如图2,在△PMN 中,PM =PN ,AB 是线段PM 的对称轴,分别交PM 于A ,PN 于B ,若△PMN 的周长为60cm ,△BMN 的周长为36cm ,则MA 的长为( B )A .6cmB .12cmC .24cmD .36cm8. 如图3,△ABC 是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC 成轴对称且也以格点为顶点的三角形共有( D )A .2个B .3个C .4个D .5个二、填空题:(共8个小题,每小题5分,满分40分)9. 如图,已知AB CD ∥,直线EF 分别交AB 、CD 于点E 、F ,EG 平分BEF ∠交CD 于点G ,如果150∠=︒,那么2∠的度数是 65 度.图456图1H2图。
2014全国初中数学联合竞赛试题答案及评分标准

2014年全国初中数学联合竞赛试题参考答案及评分标准第一试一、选择题:(本题满分42分,每小题7分) 1.已知,x y 为整数,且满足22441111211()()()3x y x y x y++=--,错误!未找到引用源。
则x y +的可能的值有( )A. 1个B. 2个C. 3个D. 4个 【答】 C.由已知等式得2244224423x y x y x y xy x y x y++-? ,显然,x y 均不为0,所以x y +=0或32()xy x y =-. 若32()xy x y =-,则(32)(32)4x y +-=-.又,x y 为整数,可求得12,x y ì=-ïí=ïî,或21.x y =-⎧⎨=⎩,所以1x y +=或1x y +=-.因此,x y +的可能的值有3个.2.已知非负实数,,x y z 满足1x y z ++=,则22t xy yz zx =++的最大值为 ( ) A .47 B .59 C .916 D .1225【答】 A.21222()2()()4t xy yz zx x y z yz x y z y z =++=++≤+++212(1)(1)4x x x =-+-2731424x x =-++2734()477x =--+,易知:当37x =,27y z ==时,22t xy yz zx =++取得最大值47.3.在△ABC 中,AB AC =,D 为BC 的中点,BE AC ⊥于E ,交AD 于P ,已知3BP =,1PE =,则错误!未找到引用源。
=( )ABCD【答】 B .因为A D B C ⊥,BE AC ⊥,所以,,,P D C E 四点共圆,所以12BD BC BP BE ⋅=⋅=,又2B C B D =,所以BD =DP =.又易知△AEP ∽△BDP ,所以AE PEBD DP =,从而可得PE AE BD DP =⋅==. 4.6张不同的卡片上分别写有数字2,2,4,4,6,6,从中取出3张,则这3张卡片上所写的数字可以作为三角形的三边长的概率是 ( )A .12 B .25 C .23 D .34【答】 B.若取出的3张卡片上的数字互不相同,有2×2×2=8种取法;若取出的3张卡片上的数字有相同的,有3×4=12种取法.所以,从6张不同的卡片中取出3张,共有8+12=20种取法.要使得三个数字可以构成三角形的三边长,只可能是:(2,4,4),(4,4,6),(2,6,6),(4,6,6),由于不同的卡片上所写数字有重复,所以,取出的3张卡片上所写的数字可以作为三角形的三边长的情况共有4×2=8种.因此,所求概率为82205=. 5.设[]t 表示不超过实数t 的最大整数,令{}[]t t t =-.已知实数x 满足33118x x +=,则1{}{}x x+= ( )A .12 B.3 C.1(32D .1 【答】 D . 设1x a x +=,则32223211111()(1)()[()3](3)x x x x x a a x x x x x+=++-=++-=-,所以2(3)18a a -=,因式分解得2(3)(36)0a a a -++=,所以3a =.由13x x +=解得1(32x =,显然10{}1,0{}1x x <<<<,所以1{}{}x x +=1. 6.在△ABC 中,90C ∠=︒,60A ∠=︒错误!未找到引用源。
2014年全国初中数学联合竞赛试题参考答案

2014年全国初中数学联合竞赛试题参考答案第一试一、选择题:(本题满分42分,每小题7分) 1.已知,x y 为整数,且满足22441111211()()()3x y x y x y++=--,则x y +的可能的值有( ) A. 1个 B. 2个 C. 3个 D. 4个【答】 C.由已知等式得2244224423x y x y x y xy x y x y++-⋅=⋅,显然,x y 均不为0,所以x y +=0或32()xy x y =-. 若32()xy x y =-,则(32)(32)4x y +-=-.又,x y 为整数,可求得12,x y =-⎧⎨=⎩,或21.x y =-⎧⎨=⎩,所以1x y +=或1x y +=-.因此,x y +的可能的值有3个.2.已知非负实数,,x y z 满足1x y z ++=,则22t xy yz zx =++的最大值为 ( ) A .47 B .59 C .916 D .1225【答】 A.21222()2()()4t xy yz zx x y z yz x y z y z =++=++≤+++212(1)(1)4x x x =-+-2731424x x =-++2734()477x =--+,易知:当37x =,27y z ==时,22t xy yz zx =++取得最大值47.3.在△ABC 中,AB AC =,D 为BC 的中点,BE AC ⊥于E ,交AD 于P ,已知3BP =,1PE =,则AE = ( )ABCD【答】 B .因为AD BC ⊥,BE AC ⊥,所以,,,P D C E 四点共圆,所以12BD BC BP BE ⋅=⋅=,又2BC BD =,所以BD =DP =.又易知△AEP ∽△BDP ,所以AE PEBD DP =,从而可得PE AE BD DP =⋅== 4.6张不同的卡片上分别写有数字2,2,4,4,6,6,从中取出3张,则这3张卡片上所写的数字可以作为三角形的三边长的概率是 ( )A .12 B .25 C .23 D .34【答】 B.若取出的3张卡片上的数字互不相同,有2×2×2=8种取法;若取出的3张卡片上的数字有相同的,有3×4=12种取法.所以,从6张不同的卡片中取出3张,共有8+12=20种取法.要使得三个数字可以构成三角形的三边长,只可能是:(2,4,4),(4,4,6),(2,6,6),(4,6,6),由于不同的卡片上所写数字有重复,所以,取出的3张卡片上所写的数字可以作为三角形的三边长的情况共有4×2=8种.因此,所求概率为82205=. 5.设[]t 表示不超过实数t 的最大整数,令{}[]t t t =-.已知实数x 满足33118x x +=,则1{}{}x x+= ( )A .12 B.3 C.1(32- D .1 【答】 D . 设1x a x +=,则32223211111()(1)()[()3](3)x x x x x a a x x x x x+=++-=++-=-,所以2(3)18a a -=,因式分解得2(3)(36)0a a a -++=,所以3a =.由13x x +=解得1(32x =,显然10{}1,0{}1x x <<<<,所以1{}{}x x+=1. 6.在△ABC 中,90C ∠=︒,60A ∠=︒,1AC =,D 在BC 上,E 在AB 上,使得△ADE 为等腰直角三角形, 90ADE ∠=︒ ,则BE 的长为 ( )A.4- B.2 C.11)2D1【答】 A.过E 作EF BC ⊥于F ,易知△ACD ≌△DFE ,△EFB ∽△ACB . 设EF x =,则2BE x =,22AE x =-,)DE x =-,1DF AC ==,故2221)]x x +=-,即2410x x -+=.又01x <<,故可得2x =.故24BE x ==-二、填空题:(本题满分28分,每小题7分) 1.已知实数,,a b c 满足1a b c ++=,1111a b c b c a c a b++=+-+-+-,则abc =____.【答】 0. 由题意知1111121212c a b++=---,所以 (12)(12)(12)(12)(12)(12)(12)(12)(12)a b b c a c a b c --+--+--=---整理得22()8a b c abc -++=,所以abc =0. 2.使得不等式981715n n k <<+对唯一的整数k 成立的最大正整数n 为 .A【答】144. 由条件得7889k n <<,由k 的唯一性,得178k n -≤且189k n +≥,所以2118719872k k n n n +-=-≥-=,所以144n ≤.当144n =时,由7889k n <<可得126128k <<,k 可取唯一整数值127. 故满足条件的正整数n 的最大值为144.3.已知P 为等腰△ABC 内一点,AB BC =,108BPC ∠=︒,D 为AC 的中点,BD 与PC 交于点E ,如果点P 为△ABE 的内心,则PAC ∠= .【答】48︒.由题意可得PEA PEB CED AED ∠=∠=∠=∠,而180PEA PEB AED ∠+∠+∠=︒,所以60PEA PEB CED AED ∠=∠=∠=∠=︒, 从而可得30PCA ∠=︒.又108BPC ∠=︒,所以12PBE ∠=︒,从而24ABD ∠=︒. 所以902466BAD ∠=︒-︒=︒, 11()(6630)1822PAE BAD CAE ∠=∠-∠=︒-︒=︒,所以183048PAC PAE CAE ∠=∠+∠=︒+︒=︒.4.已知正整数,,a b c 满足:1a b c <<<,111a b c ++=,2b ac =,则b = . 【答】36.设,a c 的最大公约数为(,)a c d =,1a a d =,1c c d =,11,a c 均为正整数且11(,)1a c =,11a c <,则2211b ac d a c ==,所以22|d b ,从而|d b ,设1b b d =(1b 为正整数),则有2111b a c =,而11(,)1a c =,所以11,a c 均为完全平方数,设2211,a m c n ==,则1b mn =,,m n 均为正整数,且(,)1m n =,m n <.又111a b c ++=,故111()111d a b c ++=,即22()111d m n mn ++=. 注意到222212127m n mn ++≥++⨯=,所以1d =或3d =.若1d =,则22111m n mn ++=,验算可知只有1,10m n ==满足等式,此时1a =,不符合题意,故舍去.若3d =,则2237m n mn ++=,验算可知只有3,4m n ==满足等式,此时27,36,48a b c ===,符合题意.因此,所求的36b =.第二试D一、(本题满分20分)设实数,a b 满足22(1)(2)40a b b b a +++=,(1)8a b b ++=,求2211a b +的值.解 由已知条件可得222()40a b a b ++=,()8ab a b ++=.设a b x +=,ab y =,则有2240x y +=,8x y +=, 联立解得(,)(2,6)x y =或(,)(6,2)x y =.若(,)(2,6)x y =,即2a b +=,6ab =,则,a b 是一元二次方程2260t t -+=的两根,但这个方程的判别式2(2)24200∆=--=-<,没有实数根;若(,)(6,2)x y =,即6a b +=,2ab =,则,a b 是一元二次方程2620t t -+=的两根,这个方程的判别式2(6)8280∆=--=>,它有实数根.所以2222222222211()262282a b a b ab a b a b a b ++--⨯+====.二.(本题满分25分)如图,在平行四边形ABCD 中,E 为对角线BD 上一点,且满足ECD ACB ∠=∠, AC 的延长线与△ABD 的外接圆交于点F . 证明:DFE AFB ∠=∠.证明 由ABCD 是平行四边形及已知条件知ECD ACB DAF ∠=∠=∠. 又A 、B 、F 、 D 四点共圆,所以BDC ABD AFD ∠=∠=∠,所以△ECD ∽△DAF , 所以ED CD ABDF AF AF==. 又EDF BDF BAF ∠=∠=∠,所以△EDF ∽△BAF ,故 DFE AFB ∠=∠.三.(本题满分25分)设n 是整数,如果存在整数,,x y z 满足3333n x y z xyz =++-,则称n 具有性质P .在1,5,2013,2014这四个数中,哪些数具有性质P ,哪些数不具有性质P ?并说明理由.FBD解 取1x =,0y z ==,可得33311003100=++-⨯⨯⨯,所以1具有性质P . 取2x y ==,1z =,可得33352213221=++-⨯⨯⨯,所以5具有性质P . 为了一般地判断哪些数具有性质P ,记333(,,)3f x y z x y z xyz =++-,则33(,,)()3()3f x y z x y z xy x y xyz =++-+- 3()3()()3()x y z x y z x y z xy x y z =++-+++-++=3()3()()x y z x y z xy yz zx ++-++++2221()()2x y z x y z xy yz zx =++++--- 2221()[()()()]2x y z x y y z z x =++-+-+-. 即(,,)f x y z 2221()[()()()]2x y z x y y z z x =++-+-+- ①不妨设x y z ≥≥,如果1,0,1x y y z x z -=-=-=,即1,x z y z =+=,则有(,,)31f x y z z =+; 如果0,1,1x y y z x z -=-=-=,即1x y z ==+,则有(,,)32f x y z z =+; 如果1,1,2x y y z x z -=-=-=,即2,1x z y z =+=+,则有(,,)9(1)f x y z z =+; 由此可知,形如31k +或32k +或9k (k 为整数)的数都具有性质P . 因此,1,5和2014都具有性质P .若2013具有性质P ,则存在整数,,x y z 使得32013()3()()x y z x y z xy yz zx =++-++++.注意到3|2013,从而可得33|()x y z ++,故3|()x y z ++,于是有39|()3()()x y z x y z xy yz zx ++-++++,即9|2013,但2013=9×223+6,矛盾,所以2013不具有性质P .。
2014学年第二学期七年级四科联赛数学试卷附答案

2014学年第二学期七年级四科联赛数学试卷附答案出卷人:高伟芳 审核:八年级数学备课组考生须知:1. 全卷共4页, 有三大题, 23小题。
满分120分, 考试时间90分钟。
2. 本卷答案必须做在答题纸的对应位置上,做在试题卷上无效。
温馨提示: 请仔细审题, 细心答题, 相信你一定会有出色的表现.一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应格子内。
1.下图最左边的图案通过平移得到的图案是()2.一辆汽车在笔直的公路上行驶,在两次转弯后,前进的方向仍与原来相同,那么这两次 转弯的角度可以是( ) A . 先右转60°,再左转120° B . 先左转120°,再右转120° C . 先左转60°,再左转120° D . 先右转60°,再右转60°3.为了了解萧山区2014年数学学业考试各分数段成绩分布情况,从中抽取 1500名考生的学业考试数学成绩进行统计分析.在这个问题中,样本容量是指( ) A .1500 B .被抽取的1500名考生C .被抽取的1500名考生的学业考试数学成绩D .义乌市2013年学业考试数学成绩 4.方程的根是( )A .﹣1 B .2 C . ﹣1或2D . 1或25.“小马虎”在下面的计算中只做对一道题,他做对的题目是( )A.22)(ab ab =B. 623)(a a =C.235x y xy +=D.1243a a a =⋅6.已知m+n=2,mn=﹣2,则(1﹣m )(1﹣n )的值为( ) A . ﹣3 B . ﹣1 C .1 D .5 7.若02(3)2(36)x x ----有意义,那么x 的取值范围是 ( ) A.3x > B.2x < C.32x x ≠≠或 D.32x x ≠≠且8.如图,有下列判定,其中正确的有 ( ) ①若∠1=∠3,则AD∥BC ②若AD∥BC,则∠1=∠2=∠3③若∠1=∠3,AD∥BC,则∠1=∠2④若∠C+∠3+∠4=180°,则AD∥BCA .1个B .2个C .3个D .4个9.如图,已知直线L 交直线a,b 于A,B 两点,且a ∥b,E 是a 上的点,F 是b 上的点,满足∠DAE=13∠BAE, ∠DBF=13∠ABF,则∠ADB 的度数是 ( ) A. 045 B. 050 C. 060 D.无法确定Aab LDBEF(第9题)10、用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现在仓库里有m 张正方形纸板和n 张长方形纸板,如果做两种纸盒若干个,恰好使库存的纸板用完,则m+n 的值可能是( )A.2003B.2004C.2005D.2006二、认真填一填(本题有6个小题,每小题4分,共24分) 11.已知23x y =⎧⎨=-⎩是方程mx+3y=1的一个解,则m 的值是 .12. 某种细胞的平均半径是0.0036m ,用科学记数法可表示为 m . 13.若分式=0,则x= ;若分式有意义,则x 应满足的条件是 .14.若x ,y 均为正整数,且2x •8•4y=256,则x+y 的值为 .15.有两个正方形A,B 现将B 放在A 的内部得到图甲,将A,B并列放置,后构造新的正方形得图乙,若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B 的面积之和为___________BABA16.如图a 是长方形纸带,∠DEF=17°,将纸带沿EF 折叠成图b ,再沿BF 折叠成图c ,则 图c 中的∠CFE 的度数是 .三、全面答一答(本题有7个小题,共66分)解答应写出必要的文字说明、证明过程或推演步骤。
2014年全国初中数学竞赛试题参考答案及评分标准

2014年全国初中数学竞赛试题参考答案及评分标准一、选择题(共10小题,每小题6分,满分60分.) 1.已知x 、y 、z 满足2x =3y-x =5z+x ,则5x-yy+2z的值为( )(A )1 (B )13 (C )-13 (D )12【答】B .解:设 2x =3y-x =5z+x =1k 则x=2k ,y-z=3k ,z+x=5k ,即x=2k ,y=6k ,z=3k 。
所以5x-y y+2z =5·2k-6k 6k+6k =13,故选B.2.已知等腰三角形的周长为12,则腰长a 的取值范围是( )(A )a >3 (B )a <6 (C )3<a <6 (D )4<a <7 【答】C.解:腰长为a ,则底长为12-2a ,由2a >12-2a 及12-2a >0可得3<a <6 故选C. 3.设 21x x 、 是一元二次方程032=-+x x的两根,则 1942231+-x x 等于( )(A )-4 (B )8 (C )6 (D )0 【答】D.解:将21x x 、代入方程,将目标整式降次,利用两根之和求解.4.如果a b ,为给定的实数,且1a b <<,那么1121a a b a b ++++,, ,这四个数据的平均数与中位数之差的绝对值是( ) (A )1 (B )214a - (C )12 (D )14【答】D.解:由题设知,1112a a b a b <+<++<+,所以这四个数据的平均数为1(1)(1)(2)34244a ab a b a b+++++++++=, 中位数为 (1)(1)44224a ab a b++++++=, 于是 4423421444a b a b ++++-=. 故选D.5. 如图,正方形A BCD 和EFGC 中,正方形EFGC 的边长为a ,用a 的代数式表示阴影部分△AEG 的面积为( )(A )232a (B )223a (C )212a (D )2a【答】C .6.若△ABC 的三条边a,b,c 满足关系式a 4+b 2c 2- a 2c 2-b 4=0,则△ABC 的形状是( ) (A )等腰三角形 (B )等边三角形(C )直角三角形 (D )等腰三角形或直角三角形 【答】D.解法一:原方程左边变形为 (a 4-b 4)+(b 2c 2-a 2c 2)=0, (a 2+b 2)(a 2-b 2)+(b 2-a 2+)c 2=0,∴(a 2-b 2)(a 2+b 2-c 2)=0, ∴a=b 或c 2=a 2+b 2.∴△ABC 为等腰三角形或直角三角形. 解法二:应用配方法a 4+b 2c 2- a 2c 2-b 4=0, (a 4-a 2c 2)-(-b 2c 2+b 4)=0 (a 2-22c )2 -(22c -b 2)2=0 ∴(a 2-b 2)(a 2+b 2-c 2)=0, ∴a 2-b 2=0,或a 2+b 2-c 2=0. ∴a=b 或c 2=a 2+b 2. ∴△ABC 为等腰三角形或直角三角形. 故选D.7.一批志愿者组成了一个“爱心团队”,以募集爱心基金.第一个月他们就募集到资金1万元,随着影响的扩大,第n (n ≥2)个月他们募集到的资金都将会比上个月增加20%,则当该月所募集到的资金首次突破10万元时(参考数据: 51.22.5≈,61.2 3.0≈,71.2 3.6≈),相应的n 的值为( )(A )11 (B )12 (C )13 (D )14 【答】D.8.如图:点D 是△ABC 的边BC 上一点,若∠CAD = ∠DAB = 60°,AC = 3 ,AB = 6,则AD 的长度是( )(A )2 (B )2.5 (C )3 (D )3.5 【答】A.解:如图,作BE ⊥AC 交CA 的延长线于E ,在Rt △ABE 中, ∠BAE= 60° ∴∠ABE= 30° ∴AE=21AB = 3 由勾股定理得BE =33∴21BCA s △AC ·BE =329 ∵∠CAD = ∠DAB = 60°同理得△ADC 和△ABD 中AD 边上的高分别是323和33 ∴=CD A s △343AD ,=B DA s △323AD 又CD A s △+B DA s △=BC A s △ ∴343AD + 323AD =329 ∴AD = 2 故选A9.若m=20132+20132×20142+20142,则m ( )(A )是完全平方数,还是奇数 (B )是完全平方数,还是偶数 (C )不是完全平方数,但是奇数 (D )不是完全平方数,但是偶数 【答】A.解 :原式=20132-2×2013×2014+20142+2×2013×2014+20132×20142=(2013-2014)2+2×2013×2014+(2013×2014)2=1+2×2013×2014+(2013×2014)2=(2013×2014+1)2所以(2013×2014+1)2是一个完全平方数,末尾数字是9,所以也是奇数. 故选A. 10、设非零实数a ,b ,c 满足2302340a b c a b c ++=⎧⎨++=⎩,,则222ab bc caa b c ++++的值为( ) (A )12-(B )0 (C )12(D )1 【答】A.解:由已知得(234)(23)0a b c a b c a b c ++=++-++=,故 2()0a b c ++=.于是 2221()2ab bc ca a b c ++=-++, 所以22212ab bc ca a b c ++=-++.故选A.二、填空题(共5小题,每小题6分,满分30分)11.已知整数1234a a a a ⋅⋅⋅,,,,满足下列条件:10a =,21|1|a a =-+,32|2|a a =-+,43|3|a a =-+,…,依次类推,则2012a 的值为 .【答】1006-12.如图,四边形ABCD 中,AB =BC ,∠ABC =∠CDA =90°, BE ⊥AD 于点E ,且四边形ABCD 的面积为8,则BE = .【答】解:.如图,可以通过旋转变换将△ABE 绕点B 逆时针旋转90°,得到△CBF.证明出四边形BFDE 是正方形,且它的面积是8,则边长是或者过点B 作BF ⊥BE ,交DC 延长线于F. 证明△ABE ≌△CBF ,其余思路同上。
2014年下七年级数学竞赛试题及答案
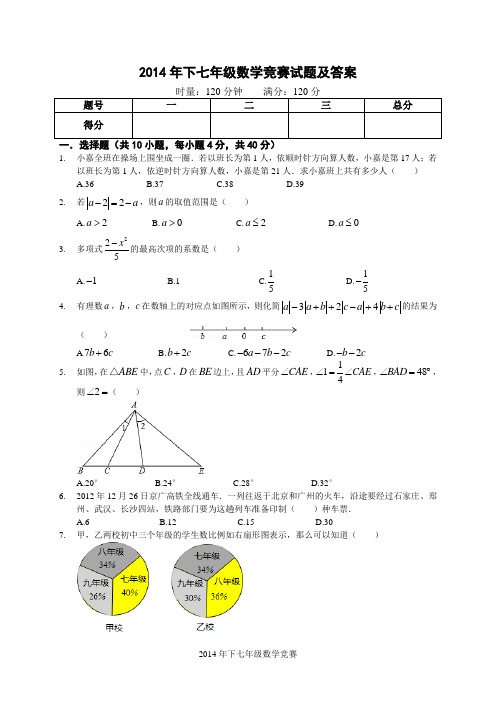
2014年下七年级数学竞赛试题及答案1. 小嘉全班在操场上围坐成一圈.若以班长为第1人,依顺时针方向算人数,小嘉是第17人;若以班长为第1人,依逆时针方向算人数,小嘉是第21人.求小嘉班上共有多少人( ) A.36 B .37 C.38 D.39 2. 若22a a -=-,则a 的取值范围是( )A.2a >B.0a >C.2a ≤D.0a ≤3. 多项式225x -的最高次项的系数是( )A.1-B.1C.15 D.15- 4. 有理数a ,b ,c 在数轴上的对应点如图所示,则化简324a a b c a b c -++-++的结果为( )A 76b c + B.2b c + C.672a b c --- D.2b c --5. 如图,在ABE △中,点C ,D 在BE 边上,且AD 平分CAE ∠,114CAE ∠=∠,48BAD ∠=︒,则2∠=( )A.20°B.24°C.28°D.32°6. 2012年12月26日京广高铁全线通车.一列往返于北京和广州的火车,沿途要经过石家庄、郑州、武汉、长沙四站,铁路部门要为这趟列车准备印制( )种车票. A.6 B.12 C.15 D.307. 甲,乙两校初中三个年级的学生数比例如右扇形图表示,那么可以知道( )A .甲校九年级人数比乙校九年级人数少B .甲校八年级人数和乙校七年级人数一样多C .甲校八年级人数比七,九年级人数的平均数少D .乙校七年级人数比八,九年级人数的平均数多8. 小明从家里骑自行车到学校,每小时骑15km ,可早到10分钟,每小时骑12km 就会迟到5分钟.问他家到学校的路程是多少km ?设他家到学校的路程是x km ,则据题意列出的方程是( )A.10515601260x x +=- B. 10515601260x x -=+ C. 10515601260x x -=- D. 1051512x x +=- 9. 若关于x 的方程521136x m x +-+=的解为正数,则实数m 的取值范围是( ) A.74m < B.74m > C.12m < D.1m <-10. 某商品2002年比2001年涨价5%,2003年又比2002年涨价10%,2004年比2003年降价12%,则2004年比2001年( )A.涨价3%B.涨价1.64%C.涨价1.2%D.降价1.2%二.填空题(共8小题,每小题5分,共40分)11. 如图,将一副直角三角板叠在一起,使直角顶点重合于点O ,若28DOC ∠=︒,则AOB ∠= °.第11题图 第12题图12. 如图,O 是直线AB 上一点,90AOE FOD ∠=∠=︒,OB 平分COD ∠,图中与DOE ∠互余的有 ,与DOE ∠互补的角有 . 13. 在2时和3时之间,若时针与分针成直角,则此时的时间是 _________ . 14. 观察下列等式(式子中的“!”是一种数学运算符号)1!1=,2!21=⨯,3!321=⨯⨯,4!4321=⨯⨯⨯,…,那么计算:2013!2014!= . 15. 若23na b 与45m a b -的差仍是单项式,则其差为 .16. 一个长方形操场的周长是322351x x x +-+,其中一条边长是2927x x -+,另一边的边长为 . 17. 方程201012233420102011x x x x++++=⨯⨯⨯⨯的解为x = .18. 若()m n +人完成一项工程需要m 天,则n 个人完成这项工程需要 _________ 天.(假定每个人的工作效率相同)三.解答题(共4小题,每小题10分,共40分)19. 如图,从点O 引出6条射线OA 、OB 、OC 、OD 、OE 、OF ,且100AOB ∠=︒,OF 平分BOC ∠,AOE DOE ∠=∠,140EOF ∠=︒,求COD ∠的度数.20. 如图B 、C 两点把线段AD 分成2:3:4三部分,M 是AD 的中点,8CD =,求MC 的长.21. 已知关于x 的方程()2360m m xm -++=①与()53nx x n -=-②的解相同,其中方程①是一元一次方程,求代数式()()2014221m x m n x n ++-+的值.22. 在计算代数式()()33252351x ax y b bx x y +-+--+-的值时,甲同学把“2x =-,3y =”误写成“2x =,3y =”,其结果也是正确的. (1)请你分析原因,并得出正确的结果.(2)在(1)的条件下,计算()222222752324a b ab a b abab a b ⎡⎤---+-+-⎣⎦的值.七年级参考答案二.填空题(共8小题,每小题5分,共40分)11.152°.12.∠EOF、∠BOD、∠BOC,∠BOF、∠EOC.13.14..15.8a2b4.16.3215113222x x x--- .17.2011.18.三.解答题(共4小题,每小题10分,共40分)19.解:设∠COD=x,∠BOC+∠AOD=y,由题意知OF平分∠BOC,OE平分∠AOD,∵∠EOF=140°,∠AOB=100°∴x+y=140°①,∵六个角之和为360°,∴x+y+100°=360°②,联立①②解得:x=20°,∴∠COD的度数为20°.20.解:设AB=2x,BC=3x,CD=4x,∴AD=9x,MD=x,则CD=4x=8,x=2,MC=MD﹣CD=﹣4x==×2=1.O21.解;因为方程①是一元一次方程,所以3021mm+≠⎧⎪⎨-=⎪⎩.解得m=3.所以方程①可化为6x+18=0,解得x=﹣3.把x=﹣3代入nx﹣5=x(3﹣n),得﹣3n﹣5=﹣3(3﹣n),解得n=.当m=3,n=,x=﹣3时,(m+x+1)2014•(﹣m2n+xn2)=(3﹣3+1)2014•[﹣32×+(﹣3)×()2]=﹣6+(﹣)=﹣.22、解:(1)(2x3+ax-5y+b)-(2bx3-3x+5y-1)=2x3+ax-5y+b-2bx3+3x-5y+1=(2-2b) x3+(a+3)x-10y+b+1甲同学把“x=-2,y=3”误写成“x=2,y=3”,其结果也是正确的.其原因只能是化简后与x无关,不含x 的项了,因此2-2b=0,a+3=0,故a=-3,b=1.原式=2x3-3x-5y+1-2x3+3x-5y+1=-10y+2当x=-2,y=3时,-10y+2=-10×3+2=-28.(2)-[-7a2b-5ab2+(2a2b-3ab2)+2ab2]-4a2b=-[-7a2b-5ab2+2a2b-3ab2 +2ab2]-4a2b=7a2b+5ab2-2a2b+3ab2 -2ab2 -4a2b=a2b+6ab2故当a=-3,b=1时.a2b+6ab2=(-3)2×1+6×(-3) ×12=9-18=-9.。
2014年全国初中数学联合竞赛初一试题(浙江卷)参考答案

2014 年全国初中数学联合竞赛初一试题(浙江卷)参考答案第一试一、选择题:(本题满分 42 分,每小题 7 分)1. 1.设,则 abcd < 0a| a | + b | b | + c | c | + d | d | + abcd | abcd | 的大于 0 的值等于( ) A. 1 B. 2 C. 3 D.4【答案】A【解析】因为 ,所以其中有一个,三个小于 0.由于大于 0, 所以,一个小于abcd < 00.2.已知 a =20142013 ,b = 20132014 , c = 20132014 d = 20142013 ,则 a ,b , c ,2013 2014 2013 2014d 大小关系是( )A .a >b >c >dB .c >a >d >bC .a >d >c >bD .a >c >d >b【答案】D【解析】因为 20142013 > 20132014 ,所以a = 20142013 > c =20132014 ,20132013同理: b < d 又因为c =2013⨯10000 + 2014 = 10000 + 2014 , d = 2014⨯10000 + 2013 = 10000 +20132013 2013 2014 2014所以c > d .故选D3、 12 + 1 -11 + 2 1 31 + 4 1 - 5 1 + 6 1 - 7 1 + 8 1 - 9 1 +10 1 -111的值为( )23 2 3 2 32 3 2 3 2 3A. 5B. 6C. 7D. 8【答案】C【解析】12 + 1 -11 + 2 1 - 31 + 4 1 - 5 1 + 6 1 - 7 1 + 8 1 - 9 1 +10 1 -1112 3 2 3 2 3 2 3 2 3 2 3= 12 + 1 - (1 + 1) + (2 + 1) - (3 + 1) + (4 + 1) - (5 + 1) + (6 + 1)2 3 2 3 2 3 2- (7 + 1) + (8 + 1) - (9 + 1) + (10 + 1) - (11+ 1) = (1+ 1 - 1) ⋅ 6 = 73 2 3 2 3 2 34. 有 2014 个数排成一行,其中任意相邻三个数中,中间的数等于它前后两数的和, 若第一个数和第二个数都是 1,则这 2014 个数的和等于( )A.2014 B.1 C.0 D.-1 【答案】B.【解析】由已知可知,前n 个数的排列顺序为1,1,0,-1,-1,0,1,1,0,…由此可见,从第7个数开始循环,即每隔6个数循环,这6个数的和等于0.又因为2014=6×335+4,所以这2014 个数的和等于1,故选B.5.假设时间用十进制表示,即每天有10 个小时,每小时有100 分钟.按照十进制生产出来的新电子闹钟读数为:午夜前为9:99;午夜对应0:00;1:25 对应凌晨3:00;7:50 对应下午6:00.在十进制下,如果一个人想在早上6:36 醒来,那么他应该将新电子闹钟定时在()A.2:00 B.2:25 C.2:50 D.2:75【答案】D.【解析】正常情况下,每天有60⨯ 24 =1440 分钟.早上6:36 表示午夜后396 分钟.在十进制下,每天有1000 分钟,因此早上6:36 对应午夜后396 ⨯1000 = 275 分钟.从而,1440新电子闹钟应该设定的时间为2:75,故选D.6、甲、乙、丙、丁的衬衫上各印有一个号码,甲说“我是2号,乙是3号”;乙说“我是2号,丙是4号”;丙说“我是3号,丁是2号”;丁说“我是1号,乙是3号”;他们四人都只说对一半,则甲是()A. 4 号B. 3 号C. 2 号D. 1 号【答案】D【解析】如果甲说“我是2 号,乙是3 号”中乙是3 号为真,由乙说丙是4 号为真,则由丙说丁是2 号为真,则乙是3 号,丙是4 号,丁为2 号,所以甲为1 号。
2014年全国初中数学竞赛试题及答案

中国教育学会中学数学教学专业委员会2014年全国初中数学竞赛试题答题时注意:1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线; 3.草稿纸不上交.一、选择题(共5小题,每小题7分,共35分.每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的.请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设非零实数a ,b ,c 满足2302340a b c a b c ++=⎧⎨++=⎩,,则222ab bc caa b c ++++的值为( ). (A )12-(B )0 (C )12(D )12.已知关于x 的不等式组255332x x x t x +⎧->-⎪⎨+⎪-<⎩,恰有5个整数解,则t 的取值范围是( ).(A )6-<t <112-(B )6-≤t <112-(C )6-<t ≤112-(D )6-≤t ≤112-3.如图,在Rt △ABC 中,已知O 是斜边AB 的中点,CD ⊥AB ,垂足为D ,DE ⊥OC ,垂足为E .若AD ,DB ,CD 的长度都是有理数,则线段OD ,OE ,DE ,AC 的长度中,不.一定..是有理数的为( ). (A )OD (B )OE (C )DE(D )AC4.如图,已知△ABC 的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且4BC CF =,DCFE 是平行四边形,则图中阴影部分的面积为( ).(A )3 (B )4 (C )6(D )85.对于任意实数x ,y ,z ,定义运算“*”为:()()32233333451160x y x y xy x y x y +++*=+++-,且()x y z x y z **=**,则2013201232****的值为( ). (A )607967(B )1821967(C )5463967(D )16389967二、填空题(共5小题,每小题7分,共35分)6.设33a =,b 是a 的小数部分,c 是2a 的小数部分,则(4)b b c ++的值为 .7.一个质地均匀的正方体的六个面上分别标有数1,2,3,4,5,6.掷这个正方体三次,则其朝上的面的数和为3的倍数的概率是 .8.已知正整数a ,b ,c 满足2220+--=a b c ,2380-+=a b c ,则abc 的最大值为 .9.实数a ,b ,c ,d 满足:一元二次方程20x cx d ++=的两根为a ,b ,一元二次方程20x ax b ++=的两根为c ,d ,则所有满足条件的数组(),,,a b c d 为 .10.444444222222121231991001121231991001++++++++++-+-+-…的值为 .三、解答题(共4题,每题20分,共80分)11.如图,抛物线y=23ax bx+-,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线113y x=-+与y轴交于点D.求∠DBC ∠CBE.12.设△ABC的外心、垂心分别为O H、,若B C H O、、、共圆,对于所有的△ABC,求BAC∠所有可能的度数.13.如图,设点D 在△ABC 外接圆上,且为BC 的中点,点X 在BD 上,E 是AX 的中点,过△ABC 的内心I 作直线R T 平行于DE ,分别与BC ,AX 交于点R ,T ,设直线DR 与ET 交于点S .证明:点S 在△ABC 的外接圆上.14.如果将正整数M 放在正整数m 左侧,所得到的新数可被7整除,那么称M 为m 的“魔术数”(例如,把86放在415的左侧,得到的数86415能被7整除,所以称86为415的魔术数).求正整数n 的最小值,使得存在互不相同的正整数12n a a a ,,…,,满足对任意一个正整数m ,在12n a a a ,,…,中都至少有一个为m 的魔术数.中国教育学会中学数学教学专业委员会2013年全国初中数学竞赛试题参考答案一、选择题 1.A解:由已知得(234)(23)0a b c a b c a b c ++=++-++=,故2()0a b c ++=.于是2221()2ab bc ca a b c ++=-++,所以22212ab bc ca a b c ++=-++. 2.C解:根据题设知不等式组有解,解得,32t -<x <20.由于不等式组恰有5个整数解,这5个整数解只能为15,16,17,18,19,因此14≤32t -<15,解得6-<t ≤112-. 3.D解:因AD ,DB ,CD 的长度都是有理数,所以,OA =OB =OC =2AD BD+是有理数.于是,OD =OA -AD 是有理数.由Rt △DOE ∽Rt △COD ,知2OD OE OC =,·DC DODE OC =都是有理数,而AC=·AD AB 不一定是有理数. 4.C解:因为DCFE 是平行四边形,所以DE //CF ,且EF //DC .连接CE ,因为DE //CF ,即DE //BF ,所以S △DEB = S △DEC ,因此原来阴影部分的面积等于△ACE 的面积.连接AF ,因为EF //CD ,即EF //AC ,所以S △ACE = S △ACF .因为4BC CF =,所以S △ABC = 4S △ACF .故阴影部分的面积为6.5.C解:设201320124m ***=,则()20132012433m ****=*32323339274593316460m m m m m m ⨯+⨯+⨯+==++++-, 于是()201320123292****=*3223333923929245546310360967⨯⨯+⨯⨯+⨯+==+-.二、填空题 6.2解:由于2123a a <<<<,故1=-b a ,22=-c a .所以223(4)(1)(124)(1)(1)12b b c a a a a a a a ++=--+-+=-++=-=.7.13解:掷三次正方体,朝上的面的数和为3的倍数的是3,6,9,12,15,18,且3=1+1+1,6=1+1+4=1+2+3=2+2+2,9=1+2+6=1+3+5=1+4+4=2+2+5=2+3+4=3+3+3, 12=1+5+6=2+4+6=2+5+5=3+3+6=3+4+5=4+4+4, 15=3+6+6=4+5+6=5+5+5, 18=6+6+6.记掷三次正方体面朝上的数分别为x ,y ,z .则使x +y +z 为3的倍数的(x ,y ,z )中,3个数都不相等的有8组,恰有两个相等的有6组,3个数都相等的有6组.故所求概率为83263616663⨯⨯+⨯+=⨯⨯.8.2013解:由已知2220+--=a b c ,2380-+=a b c 消去c ,并整理得()228666b a a -++=.由a 为正整数及26a a +≤66,可得1≤a ≤3.若1a =,则()2859b -=,无正整数解; 若2a =,则()2840b -=,无正整数解;若3a =,则()289b -=,于是可解得11=b ,5b =. (i )若11b =,则61c =,从而可得311612013abc =⨯⨯=; (ii )若5b =,则13c =,从而可得3513195abc =⨯⨯=. 综上知abc 的最大值为2013.9.(1212),,,--,(00),,,-t t (t 为任意实数) 解:由韦达定理得,,,.+=-⎧⎪=⎪⎨+=-⎪=⎪⎩a b c ab d c d a cd b 由上式,可知b a c d =--=.若0b d =≠,则1==d a b ,1==bc d ,进而2b d a c ==--=-.若0b d ==,则c a =-,有()(00),,,,,,=-a b c d t t (t 为任意实数). 经检验,数组(1212)--,,,与(00),,,-t t (t 为任意实数)满足条件. 10解:设0k >,那么=11111(1)1k k k k ⎤⎫=+=+-⎪⎥++⎝⎭⎣⎦. 上式对1=k ,2,…,99求和,得原式11991100100100⎫⎫=+-=-=⎪⎪⎝⎭⎝⎭.三、解答题11.解:将0x =分别代入y =113x -+,23y ax bx =+-知,D (0,1),C (0,3-),所以B (3,0),A (1-,0).直线y =113x -+过点B .将点C (0,3-)的坐标代入y =(1)(3)a x x +-,得1a =.…………5分抛物线223y x x =--的顶点为E (1,4-).于是由勾股定理得BC =32,CE =2,BE =25. 因为BC 2+CE 2=BE 2,所以,△BCE 为直角三角形,90BCE ∠=︒.…………10分因此tan CBE ∠=CE CB =13.又tan ∠DBO =13OD OB =,则∠DBO =CBE ∠.所以,45DBC CBE DBC DBO OBC ∠-∠=∠-∠=∠=︒.…………20分12.解:分三种情况讨论. (i )若△ABC 为锐角三角形.因为1802BHC A BOC A ∠=︒-∠∠=∠,,所以由BHC BOC ∠=∠,可得1802A A ︒-∠=∠,于是60A ∠=︒.…………5分(ii )若△ABC 为钝角三角形.当90A ∠>︒时,因为()1802180BHC A BOC A ∠=︒-∠∠=︒-∠,,所以由180BHC BOC ∠+∠=︒,可得()3180180A ︒-∠=︒,于是120A ∠=︒;当90A ∠<︒时,不妨假设90B ∠>︒,因为2BHC A BOC A ∠=∠∠=∠,,所以由180BHC BOC ∠+∠=︒,可得3180A ∠=︒,于是60A ∠=︒.…………15分(iii )若△ABC 为直角三角形.当90A ∠=︒时,因为O 为边BC 的中点,B C H O ,,,不可能共圆,所以A ∠不可能等于90︒;当90A ∠<︒时,不妨假设90B ∠=︒,此时点B 与H 重合,于是总有B C H O ,,,共圆,因此A ∠可以是满足090A ︒<∠<︒的所有角.综上可得,A ∠所有可能取到的度数为所有锐角及120︒.…………20分13.证明:如图,设DR 与△ABC 的外接圆交于点S ',AX 与S E '交于点T ',连接S C CD S A AE AD '',,,,.由D 为BC 的中点知,A ,I ,D 三点共线,且∠CS D '=∠RCD ,△S CD '∽△CRD ,所以S D CDCD RD'=, ① 即2CD S D RD '=⋅. ②…………5分由E 为AX 的中点知,∠AS E '=∠T AE ',△AS E '∽△T AE ',所以S E AEAE T E'=', ③ 即2AE S E T E ''=⋅. ④由IR ∥DE ,知180IRD S'DE S'AE ∠=︒-∠=∠.又因为IDR S DA S EA ''∠=∠=∠,所以△IRD ∽△S AE ',则有ID S ERD AE'=. ⑤ …………10分由I 为△ABC 的内心,连接CI ,由CID CAI ACI DCB BCI ICD ∠=∠+∠=∠+∠=∠知ID CD =.由式①,⑤,得S D S ECD AE''=, 即S D CDS E AE'='. ⑥ 由式②,④,得22CD S D RDAE S E T E'⋅=''⋅. ⑦ 由式⑥,⑦得S D RDS E T E'='', …………15分于是RT '∥DE .又RT ∥DE ,故点T '与T 重合,即点S '在直线ET 上.从而,点S '与S 重合,即点S 在△ABC 的外接圆上.…………20分14.解:若n ≤6,取m =1,2,…,7,根据抽屉原理知,必有12na a a ,,…,中的一个正整数M 是(1i j ,≤i <j ≤7)的公共的魔术数,即7|(10M i +),7|(10M j +).则有7|(j i -),但0<j i -≤6,矛盾.故n ≥7.…………10分又当12n a a a ,,…,为1,2,…,7时,对任意一个正整数m ,设其为k 位数(k 为正整数).则10k i m +(12i =,,…,7)被7除的余数两两不同.若不然,存在正整数i ,(1j ≤i <j ≤7),满足7|[(10)(10)]k k j m i m +-+,即7|10()k j i -,从而7|()j i -,矛盾.故必存在一个正整数i (1≤i ≤7),使得7|(10)k i m +,即i 为m 的魔术数. 所以,n 的最小值为7.…………20分。
2014奥林匹克数学竞赛(中国区)选拔赛试题 七年级数学

考生须知:本卷考试时间90分钟,共100分,不得使用计算工具或手机。
七年级试卷
一.选择题(共5题,每题5分,共25分)
(有4个备选答案,只选一个答案,把字母填在横线上)
1.如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、B、C、D对应的数分别是整数a、b、c、d,且d-2a=10,那么数轴的原点应该是()点。
A. A B. B C. C D. D
2.设A=(-1)□(-1)□(-1)□(-1)□(-1)□(-1)□(-1)在□
中只准填入“+”或“×”,则A的最大值是()。
A.1 B.2 C.5 D.6
3.在 中最简二次根式的个数是()。
A.1个B.2个C.3个D.4个
4.如图,⊙O的半径为2,弦AB= ,点C在弦AB上,AC= AB,则OC的长为()。
11.已知多项式 ,若多项式的值与字母 的取值无关,则 =________.
12. 的最小值是________.
13.已知关于 的方程 的解与 的解相同, =________.
14.已知数轴上有A、B、C三点,分别代表-24、-10、10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行。甲的速度为4个单位/秒。_________秒后甲到A、B、C的距离和为40个单位。
15.若 为定值,关于 的一元一次方程 ,无论 为何值时,它的解总是 ,那么 =________.
三.简答题(共2题,第16题20分,第17题5分,共25分)
16.设(2x-1)5=ax5+bx4+cx3+dx2+ex+f,求:
(1)f的值;
(2)a+b+c+d+e+f的值;
14—15学年下学期七年级学科竞赛数学(附答案)

七年级数学学科竞赛试卷一、选择题(每小题3分,共30分)1、如图1,A 、B 、C 、D 中的哪幅图案可以通过图1平移得到( )2、下列各式由左到右变形中,是因式分解的是( )A.a (x +y )=ax +ayB. x 2-4x +4=x (x -4)+4C.10x 2-5x =5x (2x -1)D. x 2-16+3x =(x -4)(x +4)+3x 3、如图, 下列各判断错误的是 ( )A. ∠A +∠ADC =180°→AB ∥CDB. AD ∥BC →∠3=∠4C. AB ∥CD →∠ABC +∠C =180°D. ∠1=∠2→AD ∥BC 4、用加减法解方程组372 5.x y x y -=⎧⎨+=⎩,时,要使方程组中同一个未知数的系数相等或互为相反数,必须适当变形。
以下四种变形中正确的是( ) ①6272 5.x y x y -=⎧⎨+=⎩, ②373615.x y x y -=⎧⎨+=⎩, ③62142 5.x y x y -=⎧⎨+=⎩, ④3736 5.x y x y -=⎧⎨+=⎩,A .①②B .②③C .①③D .④5、下面是小马虎同学在一次数学测验中的计算摘录,其中正确的是( ) A .()()23a a a -=-÷- B .()523a a = C .()532623x x x -=-⋅ D .()623ab ab =6、若分式2312+--x x x 的值为0,则x 等于( )A 、-1或1B 、1或2C 、1D 、-17、某市期末考试中,甲校满分人数占4%,乙校满分人数占5%,比较两校满分人数( ) A .甲校少于乙校 B . 甲校与乙校一样多 C .甲校多于乙校 D . 不能确定8、如果把分式23xyx y+中的x ,y 都扩大5倍,那么分式的值 ( )(图)ABDC123 4(A )扩大5倍 (B).缩小5倍 (C)不变 (D)扩大10倍 9、已知方程组2313359x y x y -=⎧⎨+=-⎩ 的解是23x y =⎧⎨=-⎩ , 则方程组2(1)3(2)133(1)5(2)9x y x y --+=⎧⎨-++=-⎩的解是 ( )A 、35x y =⎧⎨=-⎩B 、23x y =⎧⎨=-⎩C 、15x y =⎧⎨=-⎩D 、31x y =⎧⎨=-⎩10、若分式方程a x ax =-+1无解,则a 的值是 ( ) A.-1 B. 1 C. ±1 D.-2 二、填空题(每小题3分,共24分)11、计算:02132-⎛⎫-⨯=⎪⎝⎭12、用科学记数方法表示0000907.0= 13、已知a m =4,a n =8,则a 2m -n =___________.14、将一条两边沿互相平行的纸带如图折叠。
2014年七年级下期数学竞赛试卷

2014年七年级数学下册竞赛考试卷一、选择题:(每题4分共20分)1、若nmyxyxyx nnmm34,992213-=⋅++-则等于()A、8B、9C、10D、无法确定2、nabba,0,≠互为相反数,且为正整数,则下列两数互为相反数的是() A、nn ba与 B、nn ba22与C、1212--nn ba与 D、2222))(----nn ba与(3、已知多项式cbxx++22分解因式为)1)(3(2+-xx,则cb,的值为() A、1,3-==cb B、2,6=-=cbC、4,6-=-=cb D、6,4-=-=cb4、下列命题正确的是()A.若∠MON+∠NOP=90º则∠MOP是直角B.若α与β互为补角,则α与β中必有一个为锐角,另一个为钝角C.两锐角之和是直角D.若α与β互为余角,则α与β均为锐角5、已知∠AOB=30°,点P在∠AOB的内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2是()A.含30°角的直角三角形;B.顶角是30的等腰三角形;C.等边三角形 D.等腰直角三角形.二、填空:(每题4分,共20分)6、49x2+ +y2=( -y)2.7、若4a=2a+3,则(a–4)2003= .8、观察下列各式(x-1)(x+1)=x2-1 (x-1)(x2+x+1)=x3-1 (x-1)(x3+x2+x+1)=x4-1根据规律可得(x-1)(x n-1+……+x +1)= (其中n为正整数)9、如果2xa=,3ya=,则23x ya+=___________ 。
10、如图所示,把△ABC绕点C顺时针旋转35°,得到△11A B C,11A B交AC于点D,若∠1A DC=90°,则∠A=.三.解答题(共60分)11、先化简,再求值:(12分)22)()())((2babababa-++--+,其中21,2==ba12、将下列各式分解因式(15分)(1)、2222)1(2axxa-+(2)、21222++xx第(15)题户数/tGFE D C BA 21(3)b a b a 4422+--13、 如图,设DE ∥BC,∠1=∠2,CD ⊥AB,请说明 (1)FG ⊥AB. (12分)(2)若把题设中的“DE ∥BC ”与结论中的“FG ⊥AB ”对调后,还正确吗?试说明.14、为了丰富同学们的课外活动,某校组织了部分学生到郊外进行(1)冠军钓了15条鱼;(2)钓到3条或更多条鱼的选手平均每人钓到6条;(3)钓到12条或更少的选手平均每人钓到5条鱼. 问:整个比赛中共钓到多少条鱼?15、我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t ),并将调查结果绘成了如下的条形统计图.(Ⅰ)求这10个样本数据的平均数、众数和中位数;(9分)(Ⅱ)根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t 的约有多少户.(3分)。
2014年上期七年级数学下学期竞赛试卷_北师大版

仔细审题,认真思考,考出好成绩! 白中七数竞赛试题第 页1 2014年上期七年级数学竞赛试题(北师大版七年级下册第1-3章)考试说明考试时间:100分钟。
题型:全部是选择题。
共30题。
答案请填写到最后一页的答题卡........中。
每题只有一个答案。
总分120分,每小题4分,选对一题得4分,不选或选错不得分。
) 1. 一个角的余角是46°,这个角的补角是( ) A.134° B.136° C.156° D.144°2.如图,已知AB ∥CD ,点E 是AB 上一点,DE 平分∠BEC 交CD 于D ,∠BEC=100°,则∠D 的度数是( )A .100°B .50°C .45°D .40°3. (-0.125)2005×(-8)2006的值为( )A 、-4B 、4C 、-8D 、84. 观察这一列数:34-,57, 910-, 1713,3316-,依此规律下一个数是( )A. 4521B. 4519C. 6521D. 65195. 如果四个互不相同的正整数m ,n ,p ,q 满足(6-m)(6-n)(6-p)(6-q)=4, 那么m+n+p+q=( ). A 、24 B 、25 C 、26 D 、286.若()()232y y y my n +-=++,则m 、n 的值分别为( ).A .5m =,6n =B .1m =,6n =-C .1m =,6n =D .5m =,6n =- 7.计算)32)(32(z y x z y x -+++的值是( ).A .22294z y x -+B .222944z y xy x -+- C. 222944z y xy x -++ D. 222944z y xy x +++8. 已知关于x 的方程()x m mx -=+22的解满足121=-x ,则m 的值是( ). A. 7 B. 8 C. 9 D. 109.已知2n +2-n =k (n 为正整数),则4n + 4-n =( )(用含k 的代数式表示)A .2kB . k 2+2C . k 2-2D .2k-210. 如果()()422=--+b a b a ,则a 和b 的关系是 ( )A 、互为相反数B 、相等C 、互为倒数D 、互为负倒数班级:姓名:仔细审题,认真思考,考出好成绩! 白中七数竞赛试题第 页2 11.现已知有两个角,锐角α,钝角β,赵,钱,孙,李四位同学分别计算1()4αβ+的结果,分别为68.5º,22º,51.5º, 72º ,其中只有一个答案是正确的,那么这个正确的答案是( )A. 68.5ºB. 22ºC.51.5ºD.72º 12.若要使4192++my y 是完全平方式,则m 的值应为( ) A .31± B .3+ C .31- D .3±13. 如右图,把一张长方形纸条按如图所示的方式折叠,∠1的度数等于( )。
2014年春季七年级下册数学竞赛试卷(含答案)

2014年春季七年级数学竞赛试卷一、选择题(本大题有10小题,每小题3分,共30分)1、如下图,AB ∥EF ∥CD ,∠ABC=46°,∠CEF=154°,则∠BCE 等于( ) A.23° B.16° C.20° D.26°第1题图 第4题图 第7题图 第8题图2、一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则这两次拐弯的角度可以是( ) A.第一次向右拐40°,第二次向左拐140° B.第一次向左拐40°,第二次向右拐40° C.第一次向左拐40°,第二次向左拐140° D.第一次向右拐40°,第二次向右拐40°3、若定义),(),(),,(),(n m n m g b a b a f -=-=.例如:)5,4()5,4(),2,1()2,1(--=--=g f ,则))3,2((-f g =( ) A.(2,-3) B.(-2,3) C. (2,3) D. (-2,-3)4、如上图,长方形ABCD 中,,b S a S CDO ABP ==∆∆,则阴S 等于( )A.2b a + B.b a - C. b a + D.无法确定5、已知n 是奇数,m 是偶数,方程组⎩⎨⎧=+=+my x ny 28112014有整数解0x ,0y ,则( )A.0x ,0y 均为偶数B.0x ,0y 均为奇数C.0x 是偶数,0y 是奇数D.0x 是奇数,0y 均为偶数6、已知0=++c b a 且0≠abc ,则abc ac b bc a 222++的值为( ) A.0 B.1 C. 2 D. 37、某汽车维修公司的维修点环形分布如上图,公司在年初分配给A 、B 、C 、D 四个维修点某种配件各50件.在使用前发现需将A 、B 、C 、D 四个维修点的这批配件分别调整为40,45,54,61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n 件配件从一个维修点调整到相邻维修点的调动件次为n)为( )A.15B.16C.17D.188、如上图,平面中两条直线l 1和l 2相交于点O ,对于平面上任意一点M ,若p 、q 分别是M 到直线l 1和l 2的距离,则称有序非负实数对(p ,q )是点M 的“距离坐标”.根据上述定义,有以下几个结论,其中正确说法的个数有( )①“距离坐标”是(0,1)的点有1个; ②“距离坐标”是(5,6)的点有4个; ③“距离坐标”是(a ,a )(a 为非负实数)的点有4个. A.0 B.1 C. 2 D. 39、如果211=+=+=-c a c b b a ,,,则c b a 2++等于( )A.0B.1C. 2D. 3 10、某班有50人,在一次数学考试中,得分均为整数,全班最低分为48分,最高分为96分,那么这次考试中( ) A .至少有两人得分相同 B .不会出现得分相同的人 C .至多有两人得分相同 D .以上说法都不对二、填空题(本大题有6小题,每小题5分,共30分)11、长为4cm ,宽为3cm 的邮票300枚,不重不漏摆成一个正方形,这个正方形的边长等于 cm 。
2014年七年级数学竞赛试题

七年级数学竞赛试题(考试时间:90分钟 总分110分)班级_______ 姓名__________ 座号_______ 成绩_______一、选择题(本题有12小题,每小题3分,共36分)1、a 是最大的负整数,b 是绝对值最小的有理数,a+b= ( )A 、-1B 、0C 、1D 、2 2、方程x-3=2006 , x 的解是( )A 、x=2006B 、x=2007C 、x=20008D 、x=2009 3、如果m 是大于1的偶数,那么m 一定小于它的( ) A 、相反 B 、倒数 C 、绝对值 D 、平方4、当x =-2时, x+y 的值为9,则当x=2时, x+y 的值是( ) A 、-13 B 、-17 C 、13 D 、175、如图所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是 ( )6、如果有2005名学生排成一列,按1、2、3、4、3、2、1、2、3、4、3、2、1……的规律报数,那么第2005名学生所报的数是……………………………………………………………… ( ) A 、1 B 、2 C 、3 D 、47、若每人每天浪费水0.32升,那么100万人每天浪费的水,用科学记数法表示为( )A 、 0.32⨯105升B 、3.2⨯⨯105升C 、3.2⨯106升D 、3.2⨯107升8、在一个停车场内有24辆车,其中汽车有4个轮子,摩托车有3 个轮子,且停车场上只有汽车和摩托车,这些车共有86个轮子,那么摩托车应为( ) A 、14辆 B 、 10辆 C 、 16辆 D 、 12辆 9、某粮店出售的三种品牌的面粉袋上,分 别标有质量为(25±0.1)kg 、(25±0.2)kg 、(25±0.3)kg 的字样,从中任意拿出两袋,它们的质量最多相差( ) A 、0.8kg B 、0.6kg C 、0.5kg D 、0.4kg10、文具店的老板均以60元的价格卖了两个计算器,其中一个赚了20%,另一个亏了20%,则该老板( )A 、赚了5元B .亏了25元C 、赚了25元D 、亏了5元A .B .C .D .11、.若有理数a 、b 满足ab >0,且a + b <0,则下列说法正确的是( ) A 、a 、b 可能一正一负 B 、 a 、b 都是正数C 、 a 、b 都是负数D 、 a 、b 中可能有一个为012、为了节约用水,某市规定:每户居民每月用水不超过15立方米,按每立方米1.6元收费,超过15立方米,则超过部分按每立方米2.4元收费。
2014年初一(下)数学全科竞赛试卷

杭州长河中学七年级——学科全科竞赛试卷一、选择题。
(本题有10小题,每小题3分,共30分.请选出一个符合题意的正确选项,不选、多选、错选,均不给分)1、下列方程属于二元一次方程的是:( )A .1=+y x B.45=+xy C. x y =-832 D. 21=+yx 2、要反映杭州市一周内每天的最高气温的变化情况,宜采用( )A.条形统计图B.折线统计图C.扇形统计图D.频数分布直方图3、下列分解因式正确的是( )A .()222x xy x x y -=- B.()222xy xy y y xy x -+-=-- C.()2228822x x x -+=- D.()2313x x x x --=-- 4、如图,已知∠1=∠B ,∠2=∠C ,则下列结论不成立的是( )A.2B C ∠=∠B. AD ∥BCC.2180B ∠+∠=︒D.AB ∥CD5、在等式()()22a b a b --=-中,括号里应填的多项 式是( )A .a b -B .a b +C .a b --D .b a -6、有两块面积相同的小麦试验田,分别收获小麦9000kg 和15000kg .已知第一块试验田每公顷的产量比第二块少3000kg ,若设第一块试验田每公顷的产量为x kg ,根据题意,可得方程:( )A .xx 1500030009000=+ B. 3000150009000-=x x C. 3000150009000+=x x D. xx 1500030009000=- 7、解方程组278ax by cx y +=⎧⎨-=⎩时,一学生把c 看错而得22x y =-⎧⎨=⎩,而正确的解是32x y =⎧⎨=-⎩那么,a 、b 、c 的值是:( )A .不能确定 B. a =4,b =5,c =-2C. a 、b 不能确定,c =-2D. a =4,b =7,c =29、若长方形的周长为6,面积为1,以此长方形的长与宽为边分别作两个正方形,则此两个正 方形的面积之和是:( )A .7 B. 9 C. 5 D. 1110、如图,将边长为5个单位的等边△ABC 沿边BC 向右平移4个单位得到△A′B′C′,则四边形AA′C′B 的周长为( )A .22B .23C .24D .25二、填空题。
2014年全国初中数学联赛试题及答案(修正版)

2014年全国初中数学联赛试题及答案(修正版)2014年全国初中数学联合竞赛试题参考答案第一试一、选择题:1.已知x ,y 为整数,且满足(1x +1y ) (1x 2+1y2)=-23(1x 4-1y4),则x +y 的可能的值有( ) A. 1个 B. 2个 C. 3个 D. 4个2.已知非负实数x ,y ,z 满足x +y +z =1,则t =2xy +yz +2xz 的最大值为( )A .47B .59C .916D .12253.在△ABC 中,AB =AC ,D 为BC 的中点,BE ⊥AC 于E ,交AD 于P ,已知BP =3,PE =1,则AE =( )A .62B .2等腰直角三角形,∠ADE=90° ,则BE的长为()A.4-23B.2-3C.12(3-1)D.3-1二、填空题:1.已知实数a,b,c满足a+b+c=1,1a+b-c+1a+c-b+1b+c-a=1,则abc=__2.使得不等式917<nn+k<815对唯一的整数k成立的最大正整数n为________.3.已知P为等腰△ABC内一点,AB=BC,∠BPC=108°,D为AC的中点,BD与PC交于点E,如果点P为△ABE的内心,则∠PAC=________.4.已知正整数a ,b ,c 满足: 1<a <b <c ,a +b +c =111,b 2=ac ,则b =________.第一试 参考答案一、选择题1.C2.A3.B4.B5.D6.A 二、填空题1. 02. 1443. 48°4. 36第二试 (A )一、 设实数,a b 满足22(1)(2)40a bb b a +++=,(1)8a b b ++=,求2211a b+的值.FCA BDE 二、如图,在□ABCD 中, D 为对角线BD 上一点,且满足∠ECD =∠ACB , AC 的延长线与△ABD 的外接圆交于点F . 证明:∠DFE =∠AFB三、设n 是整数,如果存在整数x ,y ,z 满足n =x 3+y 3+z 3-3xyz ,则称n 具有性质P .在1,5,2013,2014这四个数中,哪些数具有性质P ,哪些数不具有性质P ?并说明理由.第二试 (A )答案一、解 由已知条件可得222()40a ba b ++=,()8ab a b ++=.设a b x +=,ab y =,则有2240xy +=,8x y +=,联立解得(,)(2,6)x y =或(,)(6,2)x y =.若(,)(2,6)x y =,即2a b +=,6ab =,则,a b 是一元二次方程2260tt -+=的两根,但这个方程的判别式2(2)24200∆=--=-<,没有实数根;若(,)(6,2)x y =,即6a b +=,2ab =,则,a b 是一元二次方程2620t t -+=的两根,这个方程的判别式2(6)8280∆=--=>,它有实数根.所以2222222222211()262282a b a b ab a b a b a b ++--⨯+====.二、证明 由ABCD 是平行四边形及已知条件知ECD ACB DAF∠=∠=∠.又A 、B 、F 、 D 四点共圆,所以BDC ABD AFD∠=∠=∠,所以△ECD∽△DAF,所以ED CD AB DF AF AF==.又EDF BDF BAF ∠=∠=∠,所以△EDF ∽△BAF ,故DFE AFB∠=∠.三、解 取1x =,0y z ==,可得33311003100=++-⨯⨯⨯,所以1具有性质P .取2x y ==,1z =,可得33352213221=++-⨯⨯⨯,所以5具有性质P .为了一般地判断哪些数具有性质P ,记333(,,)3f x y z x y z xyz=++-,则33(,,)()3()3f x y z x y z xy x y xyz=++-+-3()3()()3()x y z x y z x y z xy x y z =++-+++-++=3()3()()x y z x y z xy yz zx ++-++++2221()()2x y z x y z xy yz zx =++++---2221()[()()()]2x y z x y y z z x =++-+-+-.即(,,)f x y z 2221()[()()()]2x y z x y y z z x =++-+-+-①不妨设x y z ≥≥, 如果1,0,1x y y z x z -=-=-=,即1,x z y z=+=,则有(,,)31f x y z z =+;如果0,1,1x y y z x z -=-=-=,即1x y z ==+,则有(,,)32f x y z z =+;如果1,1,2x y y z x z -=-=-=,即2,1x z y z =+=+,则有FMHN AOBCD(,,)9(1)f x y z z =+;由此可知,形如31k +或32k +或9k (k 为整数)的数都具有性质P .因此,1,5和2014都具有性质P .若2013具有性质P ,则存在整数,,x y z 使得32013()3()()x y z x y z xy yz zx =++-++++.注意到3|2013,从而可得33|()x y z ++,故3|()x y z ++,于是有39|()3()()x y z x y z xy yz zx ++-++++,即9|2013,但2013=9×223+6,矛盾,所以2013不具有性质P .第二试 (B )试题及答案一.同(A )卷第一题.二.如图,已知O 为△ABC 的外心,AB AC =,D 为△OBC的外接圆上一点,过点A 作直线OD 的垂线,垂足为H .若7BD =,3DC =,求AH .解延长BD交⊙O于点N,延长OD交⊙O于点E,由题意得NDE ODB OCB OBC CDE∠=∠=∠=∠=∠,所以DE为BDC∠的平分线.又点D在⊙O的半径OE上,点C、N在⊙O上,所以点C、N关于直线OE对称,DN DC=.延长AH交⊙O于点M,因为O为圆心,AM OD⊥,所以点A、M关于直线OD对称,AH MH=.因此==.MN AC AB又FNM FAB∠=∠,所以△ABF≌△NMF,∠=∠,FBA FMN所以MF BF=.=,FN AF因此,AM AF FM FN BF BN BD DN BD DC=+=+==+=+AH=.AH=,所以57310=+=,即210三.设n 是整数,如果存在整数x ,y ,z 满足n =x 3+y 3+z 3-3xyz ,则称n 具有性质P ..(1)试判断1,2,3是否具有性质P ; (2)在1,2,3,…,2013,2014这2014个连续整数中,不具有性质P 的数有多少个?解 取1x =,0y z ==,可得33311003100=++-⨯⨯⨯,所以1具有性质P ;取1x y ==,0z =,可得33321103110=++-⨯⨯⨯,所以2具有性质P ;若3具有性质P ,则存在整数,,x y z 使得33()3()()x y z x y z xy yz zx =++-++++,从而可得33|()x y z ++,故3|()x y z ++,于是有39|()3()()x y z x y z xy yz zx ++-++++,即9|3,这是不可能的,所以3不具有性质P .(2)记333(,,)3f x y z xy z xyz=++-,则33(,,)()3()3f x y z x y z xy x y xyz =++-+-3()3()()3()x y z x y z x y z xy x y z =++-+++-++=3()3()()x y z x y z xy yz zx ++-++++2221()()2x y z x y z xy yz zx =++++---2221()[()()()]2x y z x y y z z x =++-+-+-.即(,,)f x y z 2221()[()()()]2x y z x y y z z x =++-+-+-①不妨设x y z ≥≥, 如果1,0,1x y y z x z -=-=-=,即1,x z y z=+=,则有(,,)31f x y z z =+;如果0,1,1x y y z x z -=-=-=,即1x y z ==+,则有(,,)32f x y z z =+; 如果1,1,2x y y z x z -=-=-=,即2,1x z y z =+=+,则有(,,)9(1)f x y z z =+;由此可知,形如31k +或32k +或9k (k 为整数)的数都具有性质P .又若33|(,,)()3()()f x y z x y z x y z xy yz zx =++-++++,则33|()x y z ++,从而3|()x y z ++,进而可知39|(,,)()3()()f x y z x y z x y z xy yz zx =++-++++.综合可知:当且仅当93n k =+或96n k =+(k 为整数)时,整数n 不具有性质P .又2014=9×223+7,所以,在1,2,3,…,2013,2014这2014个连续整数中,不具有性质P的数共有224×2=448个.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013~2014年七年级下学期数学竞赛试题
1.若a<0 , ab<0 , 那么51---+-b a a b 等于( )A . 4 B .-4 C . -2a+2b+6 D. 1996
2.数轴上坐标是整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2009厘米的线段AB,则线段AB 盖住的整点的个数是( )
A.2008 或2009 B . 2008或 2010 C . 2009 或2010 D . 2010 或2011
3.计算2009
20081431321211⨯+⋅⋅⋅+⨯+⨯+
⨯ = _________ 4.一个角的补角的31等于它的余角, 则这个角等于_____度. 5.计算(1+715131++)×-91715131⎪⎪⎭
⎫ ⎝⎛+++(1+91715131+++)×(715131++)= 6。
b b a -=+22若,______622=+-+b
a b a 则
7.如图,已知CD ⊥AB ,DE ∥BC,∠1=∠2
求证:FG ⊥AB
8.某学校准备组织290名学生进行野外考察活动,行李共有100件,学校计划租用甲乙两种型号的汽车共8辆,经了解,甲种汽车每辆最多能载40人和10件行李, 乙种汽车每辆最多能载30人和20件行李, ⑴设租用甲种汽车x 辆,请你帮助学校设计所有可能的租车方案;
⑵如果甲乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案
2
1G F E D C
B A
参考答案:
一选择题
1B 2C 3A 4A 5C 6D
一. .填空题 1 ; -45 ; 2009
2008 45 ;91,-4 三. 解答题
1、解:由①×2-②×3得:y=-2……③ ……3分
把③代入①得:x=-1 ……5分
∴原方程组的解为12x y =-⎧⎨=-⎩
,. ……6分 2. 解{z
y x z y x 63472=-=+得{z
x z y 32== 代入原式得, 原式 = -13
3. 证∵DE ∥BC , ∴ ∠1=∠BCD , 又∠1=∠2 ∴
∠2=∠BCD ∴FG ∥CD 又CD ⊥AB ∴FG ⊥AB
4.(本题10分)(1)a=2,b=3,c=4(2)作图(略);ABC ∆的面积=
5.5
5.解⑴:由题意得 {
解得: 5≤x ≤6 即共有两种租车方案: 第一种是租用甲种汽车5辆, 乙种汽车3辆 第二种是租用甲种汽车6辆, 乙种汽车2辆
⑵第一种租车方案的费用为:5×2000+3×1800=15400 第二种租车方案的费用为:6×2000+2×1800=15600 所以第一种租车方案更省钱
40X+30(8-X) ≥290 10X+20(8-X) ≥100。
