二次函数基本知识点基本方法专题训练
二次函数知识点总结和相关练习

二次函数知识点总结和相关练习知识点1: 配方:练习:1、将二次函数72412-+-=x x y 配成顶点式,并求对称轴和最值。
2、将二次函数251325012+--=x x y 配成顶点式,并求顶点坐标和最值。
知识点2:平移、对称、旋转变换:抓顶点和开口方向 练习:1、函数342--=x x y 关于X 轴对称的函数的解析式为 ;关于Y轴对称的函数的解析式为2、将二次函数的图像向下平移2个单位,再向右平移3个单位,得到抛物 ,则3、若抛物线 向左又向上各平移4个单位,再绕顶点旋转 180°,得到新的图像的解析式是________.知识点3:二次函数图像与系数c b a 、、之间的关系:①a 决定抛物线的形状和大小,a 的正负决定开口方向。
② b a 、共同决定对称轴:同左异右③ c 决定抛物线与y 轴交点位置④ac b 42-=∆的正负决定抛物线与x 轴的交点个数 ⑤伟达定理:a c a b x x x x =⋅-=+2121,练习:1、二次函数图象如图所示,则下列结论:① 0<++c b a ②1>+-c b a ③0>abc ④024<+-c b a ⑤1>-a c2、二次函数c bx ax y ++=2图象如图,则下例结论不正确的是( )A .0<a B. 0>abc C. 0>++c b a D 042>-ac b3、二次函数322-+=x ax y 图象与轴有一个交点在0、1之间,a 范围是( )A 、a >31B 、0<a <1C 、a >1D 、a >-31 且a 0≠ 4、二次函数c bx ax y ++=2图象如图,则下例结论正确的是( )A 、0<acB 、当1=x 时,0>yC 、方程02=++c bx ax (0≠a )有两个大于1的实根D 、存在一个大于1的实数x 0,使x x 0<时,y 随x 的增大而减少,当x x 0> 时,y 随x 增大而增大。
(完整版)二次函数知识点及经典例题详解最终
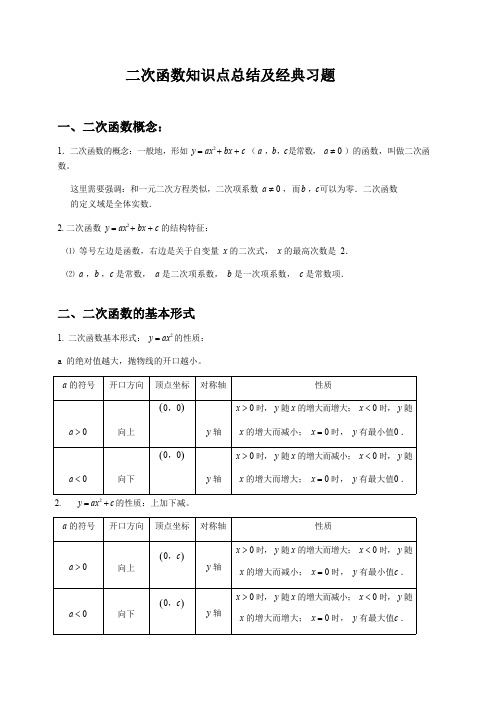
二次函数知识点总结及经典习题一、二次函数概念:1.二次函数的概念:一般地,形如y =ax2 +bx +c (a ,b,c是常数,a ≠ 0 )的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数a ≠ 0 ,而b ,c 可以为零.二次函数的定义域是全体实数.2. 二次函数y =ax2 +bx +c 的结构特征:⑴等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2.⑵ a ,b ,c 是常数, a 是二次项系数, b 是一次项系数, c 是常数项.二、二次函数的基本形式1.二次函数基本形式:y =ax2 的性质:a 的绝对值越大,抛物线的开口越小。
a 的符号开口方向顶点坐标对称轴性质a > 0向上(0,0)y 轴x > 0 时,y 随x 的增大而增大;x < 0 时,y 随x 的增大而减小;x = 0 时,y 有最小值0 .a < 0向下(0,0)y 轴x > 0 时,y 随x 的增大而减小;x < 0 时,y 随x 的增大而增大;x = 0 时,y 有最大值0 .2.y =ax2 +c 的性质:上加下减。
a 的符号开口方向顶点坐标对称轴性质a > 0向上(0,c)y 轴x > 0 时,y 随x 的增大而增大;x < 0 时,y 随x 的增大而减小;x = 0 时,y 有最小值c .a < 0向下(0,c)y 轴x > 0 时,y 随x 的增大而减小;x < 0 时,y 随x 的增大而增大;x = 0 时,y 有最大值c .3.y = a (x - h )2的性质:左加右减。
a 的符号开口方向顶点坐标对称轴性质a > 0向上(h ,0)X=hx > h 时, y 随 x 的增大而增大; x < h 时, y 随x 的增大而减小; x = h 时, y 有最小值0 .a < 0向下(h ,0)X=hx > h 时, y 随 x 的增大而减小; x < h 时, y 随x 的增大而增大; x = h 时, y 有最大值0 .4.y = a (x - h )2+ k 的性质:a 的符号开口方向顶点坐标对称轴性质a > 0向上(h ,k )X=h x > h 时, y 随 x 的增大而增大;x < h 时, y 随x 的增大而减小; x = h 时, y 有最小值 k .a < 0向下(h ,k )X=hx > h 时, y 随 x 的增大而减小;x < h 时, y 随x 的增大而增大; x = h 时, y 有最大值 k .三、二次函数图象的平移1.平移步骤:⑴ 将抛物线解析式转化成顶点式 y = a (x - h )2+ k ,确定其顶点坐标(h ,k );⑵ 保持抛物线 y = ax 2 的形状不变,将其顶点平移到(h ,k )处,具体平移方法如下:2.平移规律在原有函数的基础上“ h 值正右移,负左移; k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”.四、二次函数 y = a (x - h )2+ k 与 y = ax 2 + bx + c 的比较从解析式上看, y = a (x - h )2+ k 与 y = ax 2 + bx + c 是两种不同的表达形式,后者通过配方可以得到前者,即 y = a +,其中h= - ,k=(b2a )24ac - b 24ab2a 4ac - b 24a 五、二次函数 y = ax 2 + bx + c 的性质当 a > 0 时,抛物线开口向上,对称轴为,顶点坐标为.b2a (‒b 2a ,4ac ‒ b 24a)当x < - 时,y 随x 的增大而减小;b2a当x > - 时,y 随x 的增大而增大;b2a 当x =- 时,y 有最小值 .b 2a 4ac ‒ b 24a 2. 当α<0时,抛物线开口向下,对称轴为x =- , 顶点坐标为.当b2a(‒b 2a ,4ac ‒ b 24a)x < -时, y 随 x 的大而增大y;当随 x > - 时,y 随 x 的增大而减小;当x =- 时 , y 有最大值.b2ab 2a b 2a 4ac ‒ b 24a六、二次函数解析式的表示方法1.一般式: y = ax 2 + bx + c ( a , b , c 为常数, a ≠ 0 );2.顶点式: y = a (x - h )2 + k ( a , h , k 为常数, a ≠ 0 );3.两根式(交点式): y = a (x - x 1 )(x - x 2 ) ( a ≠ 0 , x 1 , x 2 是抛物线与 x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式, 只有抛物线与 x 轴有交点,即b 2 - 4ac ≥ 0 时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1.二次项系数 a ⑴ 当 a > 0 时,抛物线开口向上, a 的值越大,开口越小,反之 a 的值越小,开口越大;⑵ 当 a < 0 时,抛物线开口向下, a 的值越小,开口越小,反之 a 的值越大,开口越大.2.一次项系数b 在二次项系数 a 确定的前提下, b 决定了抛物线的对称轴.(同左异右b 为 0 对称轴为 y 轴)3.常数项c⑴ 当c > 0 时,抛物线与 y 轴的交点在 x 轴上方,即抛物线与 y 轴交点的纵坐标为正;⑵ 当c = 0 时,抛物线与 y 轴的交点为坐标原点,即抛物线与 y 轴交点的纵坐标为0 ;⑶ 当c < 0 时,抛物线与 y 轴的交点在 x 轴下方,即抛物线与 y 轴交点的纵坐标为负. 总结起来, c 决定了抛物线与 y 轴交点的位置.八、二次函数与一元二次方程:1.二次函数与一元二次方程的关系(二次函数与 x 轴交点情况):一元二次方程 ax 2 + bx + c = 0 是二次函数 y = ax 2 + bx + c 当函数值 y = 0 时的特殊情况. 图象与 x 轴的交点个数:① 当 ∆ = b 2 - 4ac > 0 时,图象与 x 轴交于两点 A (x 1 ,0),B (x 2 ,0 ) (x 1 ≠ x 2 ) ,其中的 x 1 ,x 2是一元二次方程 ax 2 + bx + c = 0(a ≠ 0)的两根.②当∆= 0 时,图象与x 轴只有一个交点;③当∆< 0 时,图象与x 轴没有交点.1' 当a > 0 时,图象落在x 轴的上方,无论x 为任何实数,都有y > 0 ;2 ' 当a < 0 时,图象落在x 轴的下方,无论x 为任何实数,都有y < 0 .2.抛物线y =ax2 +bx +c 的图象与y 轴一定相交,交点坐标为(0 ,c) ;中考题型例析1.二次函数解析式的确定例 1求满足下列条件的二次函数的解析式(1)图象经过 A(-1,3)、B(1,3)、C(2,6);(2)图象经过 A(-1,0)、B(3,0),函数有最小值-8;(3)图象顶点坐标是(-1,9),与 x 轴两交点间的距离是 6.分析:此题主要考查用待定系数法来确定二次函数解析式.可根据已知条件中的不同条件分别设出函数解析式,列出方程或方程组来求解.(1)解:设解析式为 y=ax 2+bx+c,把 A(-1,3)、B(1,3)、C(2,6)各点代入上式得解得 {3=a ‒b +c 3=a +b +c 6=4a +2b +c {a =1b =0c =2∴解析式为 y=x 2+2.(2)解法1:由 A(-1,0)、B(3,0)得抛物线对称轴为 x=1,所以顶点为(1,-8). 设解析式为 y=a(x-h)2+k,即 y=a(x-1)2-8.把 x=-1,y=0 代入上式得 0=a(-2)2-8,∴a=2. 即解析式为 y=2(x-1)2-8,即 y=2x 2-4x-6.解法2:设解析式为 y=a(x+1)(x-3),确定顶点为(1,-8)同上, 把 x=1,y=-8 代入上式得-8=a(1+1)(1-3).解得 a=2,∴解析式为 y=2x 2-4x-6.解法 3:∵图象过 A(-1,0),B(3,0)两点,可设解析式为:y=a(x+1)(x-3)=ax 2-2ax-3a.∵函数有最小值-8.∴ =-8.4a (‒3a )‒(2a)24a又∵a≠0,∴a=2.⎬∴解析式为 y=2(x+1)(x-3)=2x 2-4x-6.(3)解:由顶点坐标(-1,9)可知抛物线对称轴方程是 x=-1, 又∵图象与 x 轴两交点的距离为 6,即 AB=6.由抛物线的对称性可得 A 、B 两点坐标分别为 A(-4,0),B(2,0), 设出两根式 y=a(x-x 1)·(x-x 2),将 A(-4,0),B(2,0)代入上式求得函数解析式为 y=-x 2-2x+8.点评:一般地,已知三个条件是抛物线上任意三点(或任意 3 对 x,y 的值)可设表达式为y=ax 2+bx+c,组成三元一次方程组来求解; 如果三个已知条件中有顶点坐标或对称轴或最值,可选用 y=a(x-h)2+k 来求解;若三个条件中已知抛物线与 x 轴两交点坐标,则一般设解析式为 y=a(x-x 1)(x-x 2).2.二次函数的图象例 2y=ax 2+bx+c(a≠0)的图象如图所示,则点 M(a,bc)在().A.第一象限B.第二象限C.第三象限D.第四象限分析:由图可知:抛物线开口向上⇒ a>0.抛物线与y 轴负半轴相交 ⇒ c < 0b ⇒ bc>0.对称轴x = - 2a 在y 轴右侧 ⇒ b < 0∴点 M(a,bc)在第一象限. 答案:A.点评:本题主要考查由抛物线图象会确定 a 、b 、c 的符号.例 3 已知一次函数 y=ax+c 二次函数 y=ax 2+bx+c(a≠0),它们在同一坐标o系中的大致图象是().分析:一次函数 y=ax+c,当 a>0 时,图象过一、三象限;当 a<0 时,图象过二、 四象限;c>0 时, 直线交 y 轴于正半轴; 当 c<0 时, 直线交 y 轴于负半轴; 对于二次函数y= ax 2+bx+c(a≠0)来讲:⎧开口上下决定a 的正负⎪左同右异(即对称轴在y 轴左侧,b 的符号⎪⎨与a 的符号相同;)来判别b 的符号⎪抛物线与y 轴的正半轴或负半轴相交确定⎪⎩c 的正负解:可用排除法,设当 a>0 时,二次函数 y=ax 2+bx+c 的开口向上,而一次函数 y= ax+c 应过一、三象限,故排除 C;当 a<0 时,用同样方法可排除 A;c 决定直线与 y 轴交点;也在抛物线中决定抛物线与y 轴交点,本题中c 相同则两函数图象在y 轴上有相同的交点,故排除B.答案:D.3.二次函数的性质例 4对于反比例函数 y=-与二次函数 y=-x 2+3, 请说出他们的两个相同点:2x ①, ②; 再说出它们的两个不同点:① ,②.分析:本小题是个开放性题目,可以从以下几点性质来考虑①增减性②图象的形状③ 最值④自变量取值范围⑤交点等.解:相同点:①图象都是曲线,②都经过(-1,2)或都经过(2,-1);不同点:①图象形状不同,②自变量取值范围不同,③一个有最大值,一个没有最大值. 点评:本题主要考查二次函数和反比例函数的性质,有关函2数开放性题目是近几年命题的热点.4.二次函数的应用例 5 已知抛物线 y=x 2+(2k+1)x-k 2+k,(1)求证:此抛物线与 x 轴总有两个不同的交点.(2)设 x 1、x 2 是此抛物线与 x 轴两个交点的横坐标,且满足 x 12+x 2=-2k 2+2k+1.①求抛物线的解析式.②设点 P (m 1,n 1)、Q(m 2,n 2)是抛物线上两个不同的点, 且关于此抛物线的对称轴对称. 求 m+m 的值.分析:(1)欲证抛物线与 x 轴有两个不同交点,可将问题转化为证一元二次方程有两个不相等实数根,故令 y=0,证△>0 即可.(2)①根据二次函数的图象与x 轴交点的横坐标即是一元二次方程的根.由根与系数的关系,求出 k 的值,可确定抛物线解析式;②由 P 、Q 关于此抛物线的对称轴对称得 n 1=n 2, 由 n 1=m 12+m 1,n 2=m 22+m 2得 m 12+m 1=m 22+m 2,即(m 1-m 2)(m 1+m 2+1)=0 可求得 m 1+m 2= - 1.解:(1)证明:△=(2k+1)2-4(-k 2+k)=4k 2+4k+1+4k 2-4k=8k 2+1.∵8k 2+1>0,即△>0,∴抛物线与 x 轴总有两个不同的交点.(2) ①由题意得 x 1+x 2=-(2k+1), x 1· x 2=-k 2+k.∵x 1 2+x 2 2=-2k 2+2k+1,∴(x 1+x 2)2-2x 1x 2=- 2k 2+2k+1, 即(2k+1)2-2(-k 2+k)=-2k 2+k+1, 4k 2+4k+1+2k 2-2k= - 2k 2+2k+1.∴8k 2=0, ∴k=0,∴抛物线的解析式是 y=x 2+x.22②∵点 P 、Q 关于此抛物线的对称轴对称,∴n 1=n 2.又 n 1=m 12+m 1,n 2=m 2+m 2.∴m 12+m 1=m 2+m 2,即(m 1-m 2)(m 1+m 2+1)=0.∵P 、Q 是抛物上不同的点,∴m 1≠m 2,即 m 1-m 2≠0.∴m 1+m 2+1=0 即 m 1+m 2=-1.点评:本题考查二次函数的图象(即抛物线)与 x 轴交点的坐标与一元二次方程根与系数的关系.二次函数经常与一元二次方程相联系并联合命题是中考的热点.二次函数对应练习试题一、选择题1.二次函数 y = x 2- 4x - 7 的顶点坐标是()A.(2,-11)B.(-2,7)C.(2,11)D. (2,-3)2.把抛物线 y = -2x 2 向上平移 1 个单位,得到的抛物线是()A. y = -2(x +1)2B. y = -2(x -1)2C. y = -2x 2+1D. y = -2x 2-13.函数 y = kx 2- k 和 y = k(k ≠ 0) 在同一直角坐标系中图象可能是图中的()x4.已知二次函数 y = ax 2+ bx + c (a ≠ 0) 的图象如图所示,则下列结论: ①a,b同号;② 当 x = 1和 x = 3时,函数值相等;③ 4a + b = 0 ④当 y = -2时, x 的值只能取0.其中正确的个数是( )A.1 个B.2 个C. 3 个D.4 个5.已知二次函数 y = ax 2+ bx + c (a ≠ 0) 的顶点坐标(-1,-3.2)及部分图象(如图),由图象可知关于 x 的一元二次方程ax 2+ bx + c = 0 的两个根分别是 x 1 = 1.3和x 2 =()A.-1.3 B.-2.3 C.-0.3 D.-3.36. 已知二次函数 y = ax 2 + bx + c 的图象如图所示,则点(ac , bc ) 在( )A .第一象限B .第二象限C .第三象限D .第四象限7.方程 2x - x 2= 的正根的个数为()2xA.0 个B.1 个C.2 个.3个08.已知抛物线过点 A(2,0),B(-1,0),与 y 轴交于点 C,且 OC=2.则这条抛物线的解析式为A. y = x 2 - x - 2B. y = -x 2+ x + 2C. y = x 2- x - 2 或 y = -x 2+ x + 2 D. y = -x 2- x - 2 或 y = x 2+ x + 2二、填空题9.二次函数 y = x 2+ bx + 3 的对称轴是 x = 2 ,则b = 。
二次函数知识点梳理及经典练习(超详细)
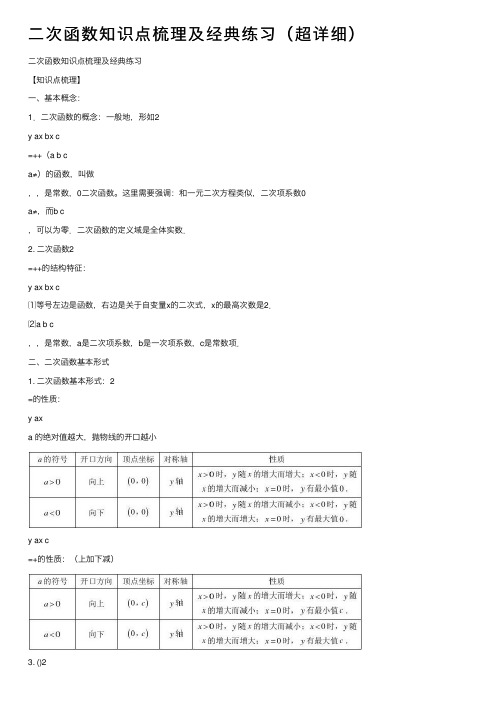
⼆次函数知识点梳理及经典练习(超详细)⼆次函数知识点梳理及经典练习【知识点梳理】⼀、基本概念:1.⼆次函数的概念:⼀般地,形如2y ax bx c=++(a b ca≠)的函数,叫做,,是常数,0⼆次函数。
这⾥需要强调:和⼀元⼆次⽅程类似,⼆次项系数0a≠,⽽b c,可以为零.⼆次函数的定义域是全体实数.2. ⼆次函数2=++的结构特征:y ax bx c⑴等号左边是函数,右边是关于⾃变量x的⼆次式,x的最⾼次数是2.⑵a b c,,是常数,a是⼆次项系数,b是⼀次项系数,c是常数项.⼆、⼆次函数基本形式1. ⼆次函数基本形式:2=的性质:y axa 的绝对值越⼤,抛物线的开⼝越⼩y ax c=+的性质:(上加下减)3. ()2y a x h =-的性质:(左加右减)4.()2y a x h k =-+的性质:三、⼆次函数图象的平移 1. 平移步骤:⽅法1:⑴将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,;⑵保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移⽅法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位⽅法2:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位, c bx ax y ++=2变成 c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)2. 平移规律: “h 值正右移,负左移;k 值正上移,负下移”.即“左加右减,上加下减”.四、⼆次函数()2y a x h k =-+与2y ax bx c =++的⽐较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配⽅可以得到前者,即22424b ac b y a x a a -?=++,其中2424b ac b h k a a -=-=,.五、⼆次函数2y ax bx c =++图象的画法五点绘图法:利⽤配⽅法将⼆次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开⼝⽅向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.⼀般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,、()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下⼏点:开⼝⽅向,对称轴,顶点,与x 轴的交点,与y 轴的交点. 六、⼆次函数2y ax bx c =++的性质1. 当0a >时,抛物线开⼝向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ??--,.当2bx a<-时,y 随x 的增⼤⽽减⼩;当2bx a>-时,y 随x 的增⼤⽽增⼤;当2bx a=-时,y 有最⼩值244ac b a -.2. 当0a <时,抛物线开⼝向下,对称轴为2bx a =-,顶点坐标为2424b ac b a a ??--,.当2bx a<-时,y 随x 的增⼤⽽增⼤;当2bx a>-时,y 随x 的增⼤⽽减⼩;当2bx a=-时,y 有最⼤值244ac b a -.七、⼆次函数解析式的表⽰⽅法 1.⼆次函数解析式表⽰⽅法:(1)⼀般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);(2)顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);(3)两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 注意:任何⼆次函数的解析式都可以化成⼀般式或顶点式,但并⾮所有的⼆次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以⽤交点式表⽰.⼆次函数解析式的这三种形式可以互化. 2.⼆次函数解析式的确定:根据已知条件确定⼆次函数解析式,通常利⽤待定系数法.⽤待定系数法求⼆次函数的解析式必须根据题⽬的特点,选择适当的形式,才能使解题简便.⼀般有如下⼏种情况:(1)已知抛物线上三点的坐标,⼀般选⽤⼀般式;(2)已知抛物线顶点或对称轴或最⼤(⼩)值,⼀般选⽤顶点式;(3)已知抛物线与x 轴的两个交点的横坐标,⼀般选⽤两根式;(4)已知抛物线上纵坐标相同的两点,常选⽤顶点式.⼋、⼆次函数的图象与各项系数之间的关系 1. ⼆次项系数a : 0a ≠.⑴当0a >时,抛物线开⼝向上,a 的值越⼤,开⼝越⼩,反之a 的值越⼩,开⼝越⼤;⑵当0a <时,抛物线开⼝向下,a 的值越⼩,开⼝越⼩,反之a 的值越⼤,开⼝越⼤.总结:a 决定了抛物线开⼝的⼤⼩和⽅向,a 的正负决定开⼝⽅向,a 的⼤⼩决定开⼝⼤⼩. 2. ⼀次项系数b : 在⼆次项系数a 确定的前提下,b 决定了抛物线的对称轴.⑴在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧;当0b =时,02ba-=,即抛物线的对称轴就是y 轴;当0b <时,02ba->,即抛物线对称轴在y 轴的右侧.⑵在0a <的前提下,结论刚好与上述相反,即当0b >时,02ba->,即抛物线的对称轴在y 轴右侧;当0b =时,02ba-=,即抛物线的对称轴就是y 轴;当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧.总结:在a 确定的前提下,b 决定了抛物线对称轴的位置.▲ab 符号判定:对称轴ab x 2-=在y 轴左边则0>ab ,在y 轴的右侧则03. 常数项c⑴当0c >时,抛物线与y 轴的交点在x 轴上⽅,即抛物线与y 轴交点的纵坐标为正;⑵当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0;⑶当0c <时,抛物线与y 轴的交点在x 轴下⽅,即抛物线与y 轴交点的纵坐标为负.总结:c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯⼀确定的.九、⼆次函数图象的对称⼆次函数图象的对称⼀般有五种情况,可以⽤⼀般式或顶点式表达 1. 关于x 轴对称:2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;2. 关于y 轴对称:2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称:2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 4. 关于顶点对称:(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称: ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然⽆论作何种对称变换,抛物线的形状⼀定不会发⽣变化,因此永远不变.求抛物线的对称抛物线的表达式时,习惯上先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开⼝⽅向,再确定其对称抛物线的顶点坐标及开⼝⽅向,然后再写出其对称抛物线的表达式.⼗、⼆次函数与⼀元⼆次⽅程:1.⼆次函数与⼀元⼆次⽅程的关系(⼆次函数与x 轴交点情况):⼀元⼆次⽅程20ax bx c ++=是⼆次函数2y ax bx c =++当函数值0y =时的特殊情况. 图像与x 轴的交点个数:(1)当240b ac ?=->时,图像与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是⼀元⼆次⽅程()200ax bx c a ++=≠的两根.这两点间的距离21AB x x =-=.(2)当0?=时,图像与x 轴只有⼀个交点;(3)当0?<时,图像与x 轴没有交点.①当0a >时,图像落在x 轴的上⽅,⽆论x 为任何实数,都有0y >;②当0a <时,图像落在x 轴的下⽅,⽆论x 为任何实数,都有0y <.2. 抛物线2y ax bx c =++的图像与y 轴⼀定相交,交点坐标为(0,)c ;3. ⼆次函数常⽤解题⽅法总结:⑴求⼆次函数的图像与x 轴的交点坐标,需转化为⼀元⼆次⽅程;⑵求⼆次函数的最⼤(⼩)值需要利⽤配⽅法将⼆次函数由⼀般式转化为顶点式;⑶根据图像的位置判断⼆次函数2y ax bxc =++中a ,b ,c 的符号,或由⼆次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷⼆次函数的图像关于对称轴对称,可利⽤这⼀性质,求和已知⼀点对称的点坐标,或已知与x 轴的⼀个交点坐标,可由对称性求出另⼀个交点坐标.⑸与⼆次函数有关的还有⼆次三项式,⼆次三项式2(0)ax bx c a ++≠本⾝就是所含字母x 的⼆次函数;下⾯以0a >时为例,揭⽰⼆次函数、⼆次三项式和⼀元⼆次⽅程之间的内在联系:【基础题型概览】⼀、⼆次函数的基本概念 1、y=mx m2+3m+2是⼆次函数,则m 的值为()A 、0,-3B 、0,3C 、0D 、-32、关于⼆次函数y=ax 2+b ,命题正确的是() A 、若a>0,则y 随x 增⼤⽽增⼤ B 、x>0时y 随x 增⼤⽽增⼤。
二次函数培优专题

二次函数培优专题一、二次函数的基本概念1. 二次函数的定义- 一般地,形如y = ax^2+bx + c(a,b,c是常数,a≠0)的函数,叫做二次函数。
- 例如y = 2x^2+3x - 1,这里a = 2,b = 3,c=-1。
- 题目解析:判断一个函数是否为二次函数,关键看其是否符合y = ax^2+bx + c(a≠0)的形式。
比如y=3x + 2就不是二次函数,因为它不符合二次函数的定义形式,其中x的最高次数是1;而y=(1)/(x^2)也不是二次函数,因为它不是整式函数。
2. 二次函数的图象- 二次函数y = ax^2+bx + c(a≠0)的图象是一条抛物线。
- 当a>0时,抛物线开口向上;当a < 0时,抛物线开口向下。
- 例如,对于二次函数y = x^2,a = 1>0,其图象开口向上;对于y=-2x^2,a=-2 < 0,其图象开口向下。
- 题目解析:给定二次函数,判断其图象开口方向是常见题型。
如y = 3x^2-2x + 1,因为a = 3>0,所以图象开口向上。
对于二次函数图象开口方向的理解,可以从二次函数的增减性角度来看,当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a < 0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小。
3. 二次函数的对称轴和顶点坐标- 对于二次函数y = ax^2+bx + c(a≠0),其对称轴公式为x =-(b)/(2a),顶点坐标公式为(-(b)/(2a),frac{4ac - b^2}{4a})。
- 例如,对于二次函数y = 2x^2-4x + 3,a = 2,b=-4,c = 3。
对称轴x=-(-4)/(2×2)=1,顶点纵坐标y=frac{4×2×3-(-4)^2}{4×2}=(24 - 16)/(8)=1,所以顶点坐标为(1,1)。
初中数学《二次函数》知识点归纳及相关练习题

九上数学二次函数知识点归纳及相关练习题(一)定义:一般地,如果y =ax 2+bx +c (a ,b ,c 是常数,a ≠0),那么y 叫做x 的二次函数.【名师推荐你做】1.判断下列函数是否为二次函数,如果是,指出其二次项系数、一次项系数和常数项:(1)d =12n 2-32n ;(2)2y x =-;(3)y =1-x 2.2.判断①y =5x -4,②t =23x 2-6x ,③y =2x 3-8x 2+3,④y =38x 2-1,⑤y =2312x x-+是否为二次函数,如果是,指出其二次项系数、一次项系数和常数项.3.已知2(1)31k ky k x x +=-++是关于x 的二次函数,求k 的值.【答案与解析】1.【解析】(1)d =12n 2-32n 是二次函数,二次项系数、一次项系数和常数项分别为12、32-、0;(2)2y x =-是一次函数,不是二次函数;(3)y =1-x 2是二次函数,二次项系数、一次项系数和常数项分别为-1、0、1.2.【解析】①y =5x -4,③y =2x 3-8x 2+3,⑤y =2312x x-+不符合二次函数解析式,②t =23x 2-6x ,④y =38x 2-1符合二次函数解析式,②t =23x 2-6x 的二次项系数、一次项系数和常数项分别为23、-6、0,④y =38x 2-1的二次项系数、一次项系数和常数项分别为38、0、-1.3.【答案】-2.【解析】∵函数2(1)31k ky k xx +=-++是关于x 的二次函数,∴2102k k k -≠⎧⎨+⎩=,解得k =-2.(二)二次函数y =ax 2的性质(1)抛物线y =ax 2的顶点是坐标原点,对称轴是y 轴.(2)函数y =ax 2的图像与a 的符号关系.①当a >0时⇔抛物线开口向上⇔顶点为其最低点;②当a <0时⇔抛物线开口向下⇔顶点为其最高点.(3)顶点是坐标原点,对称轴是y 轴的抛物线的解析式形式为y =ax 2(a ≠0).【名师推荐你做】1.观察函数y =3x 2与y =-3x 2的图像,回答:抛物线的开口方向,对称轴,顶点坐标及函数的单调性.【解析】(1)抛物线y =3x 2的开口方向是向上,对称轴是y 轴,顶点坐标是(0,0),当x ≠0时,抛物线上的点都在x 轴上方;当x >0时,曲线自左向右逐渐上升,当x <0时,曲线自左向右逐渐下降;二次函数y =-3x 2的开口方向是向下,对称轴是y 轴,顶点坐标是(0,0),当x ≠0时,抛物线上的点都在x 轴下方;当x >0时,曲线自左向右逐渐下降,当x <0时,曲线自左向右逐渐上升.(三)二次函数c bx ax y ++=2、k ax y +=2、()2h x a y -=、()kh x a y +-=2A.二次函数c bx ax y ++=2的图像是对称轴平行于(包括重合)y 轴的抛物线.B.二次函数c bx ax y ++=2用配方法可化成:()k h x a y +-=2的形式,其中a b ac k abh 4422-=-=,.C.二次函数由特殊到一般,可分为以下几种形式:①y =ax 2;②y =ax 2+k ;③y =a (x -h )2;④y =a (x -h )2+k ;⑤y =ax 2+bx +c .【名师推荐你做】1.将抛物线y =-2x 2向右平移3个单位,再向上平移5个单位,得到的抛物线解析式是()A.y =-2(x -3)2-5B.y =-2(x +3)2-5C.y =-2(x +3)2+5D.y =-2(x-3)2+5【答案与解析】1.【答案】D【解析】由“左加右减”的原则将函数y =-2x 2的图象向右平移3个单位,所得二次函数的解析式为:y =-2(x -3)2;由“上加下减”的原则将函数y =-2(x-3)2的图象向上平移5个单位,所得二次函数的解析式为:D.y =-2(x -3)2+5.所以选D.(四)抛物线A.抛物线的三要素:开口方向、对称轴、顶点.(1)a 的符号决定抛物线的开口方向:当0>a 时,开口向上;当0<a 时,开口向下;a 越大,抛物线的开口越小;a 越小,抛物线的开口越大。
二次函数基本知识点梳理与训练(最新)

二次函数考点一一般地,如果y = ax2+ bx+ c(a、b、c是常数,0),那么y叫做x的二次函数.1 •结构特征:①等号左边是函数,右边是关于自变量x的二次式;②x的最高次数是 2③二次项系数2 .二次函数的三种基本形式一般形式: y= ax2+ bx + c(a、b、c 是常数,且0);顶点式:y= a(x — h)2+ k(a丰0),它直接显示二次函数的顶点坐标是(h, k);交点式:y = a(x —x“(x — x?)(a z 0),其中x2是图象与 x轴交点的横坐标.考点二二次函数的图象和性质考点三2y=axy=a^^kv=a{x-hf-^k可求得使y >1成立的x 的取值范围是(二次函数y = ax2 + bx + c 的图象特征与 a 、b 、c 及b2 — 4ac 的符号之间的关系字母的符号图象的特征 甘 字扁、字母的符号 图彖的特征 L :^=0繆过原点 61d>{)开口向上 40与》轴正半轴和立 J<O开口向下与、•轴億半-WJ+II 空b对称轴为*轴// 一 4[tc用一4皿=心与上轴47啡交点C 顶展■)血>0(也与b 同号)对称轴北却轴左侧 用一4口40与技轴有两个交点与 b 异号)对称轴在y 轴右侧H — 4 H 弋轴液有交点考点四任意抛物线y = a(x — h)2+ k 可以由抛物线y = ax 2经过平移得到,具体平移方法如下:考点五1. 设一般式:y= ax 2+ bx+ c(a^ 0). 若已知条件是图象上三个点的坐标.则设一般式y= ax 2+ bx + c(a* 0),将已知条件代入,求出a 、b 、c 的值.2 .设交点式:y= a(x — x i )(x — X 2)(a 丰 0).若已知二次函数图象与 x 轴的两个交点的坐标, 则设交点式:y= a(x — x i )(x — X 2)(a 工0),将第三点的坐标或其他已知条件代入,求出待定系数 a,最后将解析式化为一般式. 23 .设顶点式:y= a(x — h) + k(a 丰0). 若已知二次函数的顶点坐标或对称轴方程与最大值或最小值,则设顶点式: y= a(x — h)2+ k(a^ 0),将已知条件代入,求出待定系数化为一般式 考点六二次函数的应用包括两个方法① 用二次函数表示实际问题变量之间关系.② 用二次函数解决最大化问题 (即最值问题),用二次函数的性质求解,同时注意自变量的取值范围. (1) 二次函数y = — 3x 2— 6x + 5的图象的顶点坐标是( )A . (— 1,8)B . (1,8) C. ( — 1,2)D . (1 , — 4)(2) 将二次函数y = x 2— 2x + 3化为y = (x — h)2+ k 的形式,结果为()A . y = (x + 1)2+ 4B . y = (x — 1)2+ 4 C. y= (x + 1)2+ 2 D .y = (x — 1)2+ 2向上卜QwO 评移UI 个叫』匕加卜一减 向右毒:>|=左奇人总平移匚不单迤向右各V©•左=入=¥移一竺牛单位左加右械向上下认vO }乎稿*|个单位 上加h'M⑶函数y= x2— 2x — 2的图象如下图所示,根据其中提供的信息,A . 1B . 2C . 31 .二次函数y = (x — 1)2+ 2的最小值是( A . 2B . 12. 抛物线y = (x — 2)2+ 3的顶点坐标是(A . (2,3)B . (— 2,3)C. C . — 1D . — 2)(2 , — 3) D . ( — 2, — 3)A . — 1w x w 3 B. — 1<x<3 C. x<— 1 或 x>3 D. x w — 1 或 x A 3 ⑷已知二次函数y= ax 2+ bx + c(a^ 0)的图象如图所示,有下列结论:①b 2— 4ac>0 :② abc>0 :③ 8a+ c>0 :④ 9a+ 3b + c<0.其中,正确结论的个数是( )(5)为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政 府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数 y (台)与补贴款额x (元)之间大致满 足如图①所示的一次函数关系.随着补贴款额 x 的不断增大,销售量也不断增加,但每台彩电的收益 z (元)会相应 降低且z 与x 之间也大致满足如图②所示的一次函数关系.(1) 在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元? (2) 在政府补贴政策实施后,分别求出该商场销售彩电台数 y 和每台家电的收益 z 与政府补贴款额 x 之间的函 数关系式;(3)要使该商场销售彩电的总收益 w (元)最大,政府应将每台补贴款额 x 定为多少元?并求出总收益 w 的最大值.【举一反三】3.抛物线y= a(x + 1)(x — 3)(a^ 0)的对称轴是直线()A . x = 1B . x=— 1C . x=— 3D . x = 34. 二次函数y=— 2x2+ 4x + 1的图象如何平移就得到 y = — 2x2的图象()A .向左平移1个单位,再向上平移 3个单位A . y 1<y 2<y 3B . y 2<y 1<y 3C . y 3<y 1<y 2D . y 〔<y 3<y 2B .向右平移1个单位,再向上平移 3个单位C. 向左平移1个单位,再向下平移 3个单位D. 向右平移1个单位,再向下平移 3个单位5.把二次函数 y=— 4x 2-x + 3用配方法化成 y = a (x — h )2+ k 的形式()1 2 1 2A . y = — 4(x — 2)+ 2B. y= 4(x — 2)+ 4C . y = — 4(x + 2)2+ 4D. y= gx —甘+ 36. 二次函数y= ax 2+ bx + c 的图象如图所示,则下列关系式不正确..的是()A . a v 0B . abc >0C . a + b + c >0d QCA7. 若A ( — —,y 1)、B ( — 4,y 2)、C (4,汨为二次函数y= x 2+ 4x — 5的图象上的三个点,贝yy ?、"的大小关系是( )8 .已知二次函数y= x 2— 2x — 3的图象与x 轴交于A 、B 两点(A 在B 的左侧),与y 轴交于点C,顶点为D.(1) 求点A 、B 、C 、D 的坐标,并在下面直角坐标系中画出该二次函数的大致图象.(2) 说出抛物线y= x 2— 2x — 3可由抛物线y= x 2如何平移得到?⑶求四边形OCDB 的面积.、选择题(每小题3分,共36分)1 .已知抛物线y= ax 2+ bx+ c 的开口向下,顶点坐标为(2, — 3),那么该抛物线有()A .最小值—3B.最大值—3C.最小值2D.最大值22.在平面直角坐标系中,抛物线y = x 2— 1与x 轴的交点的个数是()④y\i i |i i i i ■ > i■ * 十 1—^-A . 3B . 2C . 1D . 03 .若二次函数 y = x 2+ bx + 5配方后为y = (x — 2)2+ k ,贝V b 、k 的值分别为( ) A . 0,5 B . 0,1 C .— 4,5 D . — 4,14.抛物线y = x 2+ bx + c 的图象向右平移2个单位,再向下平移 3个单位,所得图象的解析式为 y = x 2— 2x —3,则b 、c 的值为( A . b = 2, c = 2D . b =— 3, c = 25 .如图,已知抛物线 y = x 2+ bx + c 的对称轴为x = 2,点A 、B 均在抛物线上,且 AB 与x 轴平行,其中点 A 的坐标为(0,3),则点B 的坐标为()A . (2,3)B . (3,2)C . (3,3)D . (4,3)a6.二次函数y = ax 2+ bx + c 的图象如图所示,反比例函数y =-与正比例函数y = (b + c)x 在同一坐标系中的大x致图象可能是( )7 . A . 8 . =x 2— 4上的一个点是( ) (4,4) B . (1 , — 4) C . (2,0) D . (0,4)已知二次函数y = ax 2+ bx + c 的图象如图所示,则下列结论正确的是 ( )a>0 B . c<0 C .k对于反比例函数 y = 一,当x>0时,y 随x 的增大而增大,则二次函数y = kx 2+ kx 的大致图象是( )x110 .二次函数y =— 2(x — 4)2+ 5的图象的开口方向、顶点坐标分别是( )A.向上、(4,5)B.向上、(一4,5)C.向下、(4,5)D.向下、(一4,5)11 .抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )B . b = 2, c = 0在抛物线yx = 1,若其与x 轴一交点为 A(3,0),12. 在Rt △ ABC 中,/ C = 90° AC = 4 cm , BC = 6 cm ,动点 P 从点C 沿CA 以1 cm/s 的速度向点 A 运动, 同时动点Q 从点C 沿CB 以2 cm/s 的速度向点B 运动,其中一个动点到达终点时, 另一个动点也停止运动. 则运动过程中所构成的△ CPQ 的面积y(cm 2)与运动时间x(s)之间的函数图象大致是()13.若二次函数 y= — x 2+ 2x + k 的部分图象如图所示,则关于 x 的一元二次方程一x 2+ 2x + k= 0的一个解x 1= 3,另一个解 x 2= ___________________ .14. ____________________________________________ 函数y = (x — 2)(3 — x)取得最大值时,x = .15. 已知二次函数 y= ax 2+ bx + c(a^ 0),其中a 、b 、c 满足a+ b+ c= 0和9a — 3b+ c= 0,则该二次函数图象 的对称轴是直线 _________ .16.如图,是二次函数 y = ax 2+ bx+ c 图象的一部分,其对称轴为直线则由图象可知,不等式 ax 2+ bx+ c<0的解集是 __________ .17. 如右上图,小明的父亲在相距 2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状, 身高1米的小明距较近的那棵树 0.5米时,头部刚好接触到绳 子,则绳子的最低点距地面的距离为 ___________ 米.三、解答题洪44分)18. (15分)已知抛物线y=— x 2+ 2x + 2.B . y = - 2x 2+2D . y = — x +x +2yfcm 1) y(cm 2)、填空题(每小题4分,共20分)(1)该抛物线的对称轴是________ ,顶点坐标_________(2)选取适当的数据填入下表,并在下图的直角坐标系内描点画出该抛物线的图象; ⑶若该抛物线上两点 A (X I , y i )、B (X 2,y 2)的横坐标满足x i >x 2>i ,试比较y i 与y 2的大小.乂B V- V■ • ■yV V- V・• ■1 2y = -2X 2+ bx + c 的图象经过 A(2,0)、B(0,- 6)两点.(1) 求这个二次函数的解析式;(2) 设该二次函数的对称轴与 X 轴交于点C,连结BA 、BC,求△ ABC 的面积.19.。
二次函数知识点归纳及相关习题(含答案)
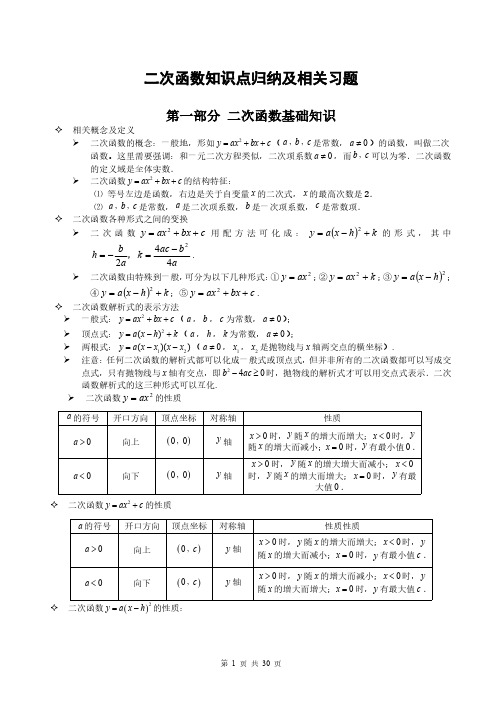
a 的符号
开口方向 向上
顶点坐标
对称轴
性质
a0
0 ,0 0 ,0
y轴
x 0 时, y 随 x 的增大而增大; x 0 时, y 随 x 的增大而减小;x 0 时,y 有最小值 0 . x 0 时, y 随 x 的增大增大而减小; x 0 时, y 随 x 的增大而增大; x 0 时, y 有最 大值 0 .
2
二次函数图象的对称:二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达
关于 x 轴对称 y ax 2 bx c 关于 x 轴对称后,得到的解析式是 y ax 2 bx c ;
y a x h k 关于 x 轴对称后,得到的解析式是 y a x h k ;
2
二次函数由特殊到一般, 可分为以下几种形式: ① y ax ; ② y ax k ; ③ y ax h ;
2 2
2
b 4ac b 2 . ,k 2a 4a
2
顶点式: y a( x h) 2 k ( a , h , k 为常数, a 0 ) ; 两根式: y a( x x1 )( x x2 ) ( a 0 , x1 , x2 是抛物线与 x 轴两交点的横坐标). 注意:任何二次函数的解析式都可以化成一般式或顶点式, 但并非所有的二次函数都可以写成交 2 点式,只有抛物线与 x 轴有交点,即 b 4ac 0 时,抛物线的解析式才可以用交点式表示.二次 函数解析式的这三种形式可以互化. 二次函数 y ax 的性质
抛物线与 x 轴的交点:二次函数 y ax bx c 的图像与 x 轴的两个交点的横坐标 x1 、 x 2 ,
二次函数的基础知识和经典练习题
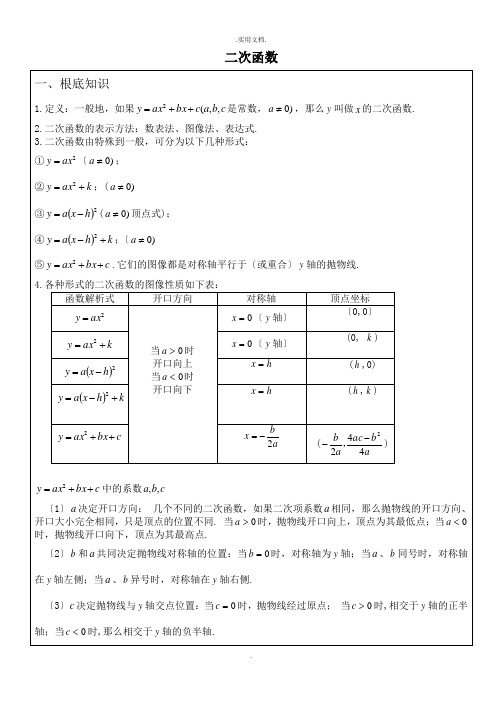
二次函数2.求抛物线的顶点、对称轴的方法〔1〕公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,顶点是),(a b ac a b 4422--,对称轴是直线abx 2-=.〔2〕配方法:运用配方的方法,将抛物线c bx ax y ++=2的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.其中ab ac k a b h 4422-=-=,.〔3〕运用抛物线的对称性:抛物线是轴对称图形,所以对称点的连线的垂直平分线就是抛物线的对称轴,对称轴与抛物线的交点是顶点.. 3.用待定系数法求二次函数的解析式〔1〕一般式:c bx ax y ++=2.图像上三点或三对x 、y 的值,通常选择一般式. 〔2〕顶点式:()k h x a y +-=2.图像的顶点或对称轴,通常选择顶点式.〔3〕两点式:图像与x 轴的交点坐标1x 、2x ,通常选用交点式:()()21x x x x a y --=.x 轴的交点设二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ,是对应一元二次方程02=++c bx ax x 轴的交点情况可以由对应的一元二次方程的根的判别式来判定:〔1〕240b ac ->⇔抛物线与x 轴有两个交点;〔2〕240b ac -=⇔抛物线与x 轴有一个交点〔顶点在x 轴上〕; 〔3〕240b ac -<⇔抛物线与x 轴没有交点.一、c bx ax y ++=2的性质1.二次函数772--=x kx y 与x 轴有交点,那么k 的取值范围是 。
解:2.二次函数c bx ax y ++=2的图象如图,那么直线bc ax y +=的图象不经过第 象限。
理由:c bx ax y ++=2的图象如图,试判断a 、b 、c 和∆的符号。
解:c bx ax y ++=2的图象如图,以下结论〔1〕c <0;〔2〕b >0;〔3〕4a+2b+c >0;〔4〕〔a+c 〕2<0,其中正确的选项是:〔 〕A .1个B .2个C .3个D .4个 理由:5. 二次函数c bx ax y ++=2的图象如图,那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中,值为正数的有〔 〕A .4个B .3个C .2个D .1个 理由:6. 直线b ax y +=的图象经过第一、二、三象限,那么12++=bx ax y 的图象为〔 〕A .B .C .D .7.函数4212--=x x y ,当函数值y 随x 的增大而减小时,x 的取值范围是( ) A .x <1 B .x >1 C .x >-2 D .-2<x <48.二次函数y =a (x +k )2+k ,当k 取不同的实数值时,图象顶点所在的直线是( )A .y =xB .x 轴C .y =-xD .y 轴9.二次函数y =ax 2+bx +c 的图象如右图所示,那么( )A .a >0,c >0,b 2-4ac <0B .a >0,c <0,b 2-4ac >0C .a <0,c >0,b 2-4ac <0D .a <0,c <0,b 2-4ac >010.二次函数y =ax 2+bx +c 的图象如以下列图所示,那么( )A .b >0,c >0,∆=0B .b <0,c >0,∆=0C .b <0,c <0,∆=0D .b >0,c >0,∆>011.二次函数y =mx 2+2mx -(3-m )的图象如以下列图所示,那么m 的取值范围是( )A .m >0B .m >3C .m <0D .0<m <312.在同一坐标系内,函数y =kx 2和y =kx -2(k ≠0)的图象大致如图( )13.函数xaby b ax y =+=221,(ab <0)的图象在以下四个示意图中,可能正确的选项是( )14.图中有相同对称轴的两条抛物线,以下关系不正确的选项是( )A .h =mB .k >nC .k =nD .h >0,k >015.二次函数y =ax 2+bx +c (a ≠0)的图象如下列图,有以下结论:①abc >0;②a +b +c =2;21>a ③;④b <1.其A .①②B .②③C .②④D .③④16.以下命题中,正确的选项是( )①假设a +b +c =0,那么b 2-4ac <0;②假设b =2a +3c ,那么一元二次方程ax 2+bx +c =0有两个不相等的实数根;③假设b 2-4ac >0,那么二次函数y =ax 2+bx +c 的图象与坐标轴的公共点的个数是2或3; ④假设b >a +c ,那么一元二次方程ax 2+bx +c =0,有两个不相等的实数根. A .②④ B .①③ C .②③ D .③④二、c bx ax y ++=2的最值1. 心理学家发现,学生对概念的接受能力y 和提出概念所用的时间x 〔单位:分〕之间大体满足函数关系式:436.21.02++-=x x y 〔0≤x ≤30〕。
二次函数知识点分类专题训练(专项练习2)(基础篇)

二次函数知识点分类专题训练(专项练习2)(基础篇)一、单选题知识点一、二次函数性质综合1.已知二次函数y=ax2+bx+c的部分图象如图所示,下列关于此函数图象的描述中,错误的是()A.对称轴是直线x=1B.当x<0时,函数y随x增大而增大C.图象的顶点坐标是(1,4)D.图象与x轴的另一个交点是(4,0)2.已知二次函数224=-++,则下列关于这个函数图象和性质的说法,正确的是()y x x1,3A.图象的开口向上B.图象的顶点坐标是()C.当1x<时,y随x的增大而增大D.图象与x轴有唯一交点3.关于二次函数2=+-,下列说法正确的是()y x x2410,1B.图像的对称轴在y轴的右侧A.图像与y轴的交点坐标为()x<时,y的值随x值的增大而减小D.y的最小值为-3C.当04.已知抛物线y=-x2+1,下列结论:①抛物线开口向上;①抛物线与x轴交于点(-1,0)和点(1,0);①抛物线的对称轴是y轴;①抛物线的顶点坐标是(0,1);①抛物线y=-x2+1是由抛物线y=-x2向上平移1个单位得到的.其中正确的个数有()A.5个B.4个C.3个D.2个知识点二、二次函数图象与各项系数符号5.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是()A.a>0B.b>0C.c<0D.a+b+c<0 6.如果二次函数2(0)y ax bx c a=++≠的图像如图所示,那么()A.a0,b0,c0<>>B.0,0,0a b c>>>C.0,0,0a b c><<D.0,0,0a b c>><7.如图是二次函数2y ax bx c=++图象的一部分,对称轴为12x=,且经过点(2,0).下列说法:①0abc<;① 20b c-+=;①240b ac-<;①若15(,)2y-,25(,)2y是抛物线上的两点,则12y y<.其中说法正确的是()A.①①①B.①①C.①①D.①①8.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中正确的是()A.ac>0B.2a+b=0C.b2﹣4ac<0D.b<0知识点三、一次函数、二次函数图象综合判断9.在同一直角坐标系中,a≠0,函数y=ax与y=ax2的图象可能正确的有()A.0B.1C.2D.310.已知函数y=ax+b的大致图象如图所示,那么二次函数y=ax2+bx+1的图象可能是A .B .C .D .11.二次函数2y ax bx c =++的图象如下左图,则一次函数24y ax b ac =+-与反比例函数b cy x+=.在同一坐标系内的图象大致为( )A .B .C .D .12.在同一平面直角坐标系中,二次函数2y ax =与一次函数y bx c =+的图象如图所示,则二次函数2y ax bx c =++的图象可能是( )A .B .C .D .知识点四、两个二次函数图象综合判断13.已知二次函数21y ax bx c =++和22y bx ax c =++,a b >,则下列说法正确的是( ) A .当0x <时,12y y < B .当01x <<时,12y y < C .当01x <<时,12y y >D .当1x >时12y y <14.对于二次函数y =﹣(x ﹣1)2+2的图象,下列说法正确的是( ) A .图象有最低点,其坐标是(1,2) B .图象有最高点,其坐标是(﹣1,2) C .当x <1时,y 随x 的增大而减小D .当x >1时,y 随x 的增大而减小15.在同一平面直角坐标系中,若抛物线22124()y x m x m =+-+-与2(3)y x m n x n =--++关于x 轴对称,则符合条件的m ,n 的值为( ) A .518,77m n ==-B .5,6m n ==-C .1,6m n =-=D .1,2m n ==-16.如果两个不同的二次函数的图象相交,那么它们的交点最多有( ) A .1 个B .2 个C .3 个D .4 个知识点五、根据二次函数图象判断代数式符号17.已知二次函数y =ax 2+bx+c (a≠0)的图象如图所示,则下列结论:①c <0;①2a+b =0;①a+b+c <0;①b 2﹣4ac <0,其中正确的有( )A .1个B .2个C .3个D .4个18.如图,已知顶点为(﹣3,﹣6)的抛物线y =ax 2+bx +c 经过点(﹣1,﹣4),则下列结论 ①6a ﹣b =0; ①abc >0;①若点M (﹣2,m )与点N (﹣5,n )为抛物线上两点,则m >n ; ①ax 2+bx +c ≥﹣6;①关于x 的一元二次方程ax 2+bx +c =﹣4的两根为﹣5和﹣1.其中正确结论有( )A .5B .4C .3D .219.如图二次函数y =ax 2+bx +c 的图象经过点A (2,0),B (6,0),下列说法正确的是( )A .b 2﹣4ac <0B .4a ﹣2b +c <0C .c <0D .对称轴是直线x =420.已知函数2(0)y ax bx c a =++≠的对称轴为直线4x =-.若12,x x 是方程20ax bx c ++=的两个根,且122,12x x x <<<,则下列说法正确的是( )A .120x x >B .1109x -<<-C .240b ac -<D .0abc >知识点六、二次函数图象的对称性21.已知点(1,)m 在函数224y x x c =--+的图象上,则下列选项中的点也在该函数图象上的是( ) A .(1,1)m -+B .(1,)m -C .(3,)m -D .(3,3)m -+22.抛物线y =ax 2+bx +c (a ≠0)与x 轴的交点是(1,0),(﹣3,0),则这条抛物线的对称轴是( ) A .x =1B .x =﹣1C .x =2D .x =﹣323.已知二次函数228y x x c =-++的图象过点()13,A y -,()21,B y -,()36,C y ,则1y ,2y ,3y 的大小关系是( ) A .213y y y <<B .321y y y <<C .132y y y <<D .123y y y <<24.已知二次函数231215y x x =+-,若点()15,t y -+,()21,t y -,()32,y -在此二次函数图象上,则1y ,2y ,3y 的大小关系正确的是( ) A .312y y y <<B .321y y y >>C .312y y y ≤=D .312y y y ≥=知识点七、二次函数图象的最值25.如图,已知二次函数的图象(0≤x ≤1+22).关于该函数在所给自变量取值范围内,下列说法正确的是( )A .有最小值﹣2,无最大值B .有最小值﹣2,有最大值﹣1.5C .有最小值﹣2,有最大值2D .有最小值﹣1.5,有最大值226.关于函数y =(mx +m ﹣1)(x ﹣1).下列说法正确的是( ) A .无论m 取何值,函数图象总经过点(1,0)和(﹣1,﹣2) B .当m ≠12时,函数图像与x 轴总有2个交点 C .若m >12,则当x <1时,y 随x 的增大而减小 D .若m >0时,函数有最小值是14-m﹣m +1 27.如图,直线y 34=-x +3分别与x 轴,y 轴交于点A 、点B ,抛物线y =x 2+2x ﹣2与y 轴交于点C ,点E 在抛物线y =x 2+2x ﹣2的对称轴上移动,点F 在直线AB 上移动,CE +EF 的最小值是( )A .4B .4.6C .5.2D .5.628.如图,在抛物线2y x =-上有A ,B 两点,其横坐标分别为1,2;在y 轴上有一动点C ,当BC AC +最小时,则点C 的坐标是( )A .(0.0)B .(0,1-)C .(0,2)D .(0,2-)知识点八、二次函数的解析式29.如图,抛物线y =﹣x 2+2x +c 与x 轴正半轴,y 轴正半轴分别交于点A ,B 且OA =OB ,则c 的值为( )A .0B .1C .2D .330.已知抛物线24y x x c =-++经过点(4,3),那么下列各点中,该抛物线必经过的点是( ) A .(0,2)B .(0,3)C .(0,4)D .(0,5)31.下表中列出的是一个二次函数的自变量x 与函数y 的几组对应值:下列各选项中,正确的是 A .这个函数的图象开口向下B .这个函数的图象与x 轴无交点C .这个函数的最小值小于-6D .当1x >时,y 的值随x 值的增大而增大32.二次函数2y ax bx c =++(a ,b ,c 为常数,且0a ≠)中的x 与y 的部分对应值如下表:下列结论:①0ac <;①30a b +=;①当1x >时,y 随着x 的增大而减小;①-1和3是方程()210ax b x c +-+=的根,其中正确的个数为( ) A .1个 B .2个C .3个D .4个二、填空题知识点一、二次函数性质综合33.一抛物线和另一抛物线y =﹣2x 2的形状和开口方向完全相同,且顶点坐标是(﹣2,1),则该抛物线的解析式为_____.34.抛物线2y ax bx c =++上部分点的横坐标x ,纵坐标y 的对应值如下表:从上表可知,下列说法中正确的是________.(填写序号)①抛物线与x 轴的一个交点为(3,0);①函数2y ax bx c =++的最大值为6; ①抛物线的对称轴是12x =; ①在对称轴左侧,y 随x 增大而增大. 35.抛物线y =3(x -2)2的开口方向是______,顶点坐标为______,对称轴是______.当x ______时,y 随x 的增大而增大;当x =______时,y 有最______值是______,它可以由抛物线y =3x 2向______平移______个单位得到. 36.下列说法中正确的序号是_____________ ①在函数y =﹣x 2中,当x =0时y 有最大值0; ①在函数y =2x 2中,当x >0时y 随x 的增大而增大①抛物线y =2x 2,y =﹣x 2,y =﹣212x 中,抛物线y =2x 2的开口最小,抛物线y =﹣x 2的开口最大①不论a 是正数还是负数,抛物线y =ax 2的顶点都是坐标原点知识点二、二次函数图象与各项系数符号37.若抛物线2y ax bx c =++(0a ≠)的示意图如图所示,则a ____0,b a ____0,c a ____0(填“>”,“=”或“<”).38.如图为二次函数() 20y ax bx c a =++≠的图象,则下列说法:①0a >;①20a b +=;①0a b c ++>;①420a b c -+>,其中正确的有___________.(填序号)39.二次函数2y ax bx c =++的图象如图所示,则下列四个结论:①0a >;①0c <;①0a b c ++<;①240b ac ->.其中正确的有______.(填写番号)40.如图是二次函数()20y ax bx c a =++≠的图象的一部分,给出下列命题:①0a b c ++=;①2b a >;①20ax bx c ++=的两根为3-和1;①420a b c -+>;①关于x 的一元二次方程240ax bx c a +++=有两个相等的解,其中正确的命题是______.(只要求填写正确命题的序号)知识点三、一次函数、二次函数图象综合判断41.如图是二次函数21y ax bx c =++ 和一次函数y 2=kx +t 的图象,当y 1≥y 2时,x 的取值范围是_____.42.函数y =x 2+bx +c 与y =x 的图象如图所示,有以下结论:①bc >0;①b 2﹣4c >0;①b +c +1=0;①3b +c +6=0;①当1<x <3时,x 2+(b ﹣1)x +c <0.其中正确的是_____.43.如图已知二次函数y 1=x 2+c 与一次函数y 2=x+c 的图象如图所示,则当y 1<y 2时x 的取值范围_____.44.如图,在平面直角坐标系xOy 中,()A 1,1,()B 3,1,如果抛物线2y ax (a 0)=>与线段AB 有公共点,那么a 的取值范围是______.知识点四、两个二次函数图象综合判断45.二次函数y =ax 2+bx +c (a ≠0)的图象如图,若|ax 2+bx +c |=k 有两个不相等的实数根,则k 的取值范围是____.46.如图,平行于x 轴的直线AC 分别交抛物线21x y =(x≥0)与22x y 5=(x≥0)于B 、C 两点,过点C 作y 轴的平行线交y 1于点D ,直线DE①AC ,交y 2于点E ,则DE AB =_.47.已知抛物线2222y x kx k k =-++-的顶点在坐标轴上,则k =________.48.如图,抛物线2122y x x =-+的顶点为A ,抛物线2122y x x =+的顶点为B ,作AC x ⊥轴于点C ,BD y ⊥轴于点D ,则阴影部分的面积之和为___________.知识点五、根据二次函数图象判断代数式符号49.二次函数y =ax 2+bx +c (a ≠0)的图象如图,给出下列结论:①4ac ﹣b 2<0;①4a +c <2b ;①b ﹣2a =0;其中正确结论是_____(填序号).50.如图,二次函数2(0)y ax bx c a =++≠的图象,则下列结论中正确的有_____.①0abc <;①20a b +=;①240b ac -<;①930a b c ++>;①80c a +<.51.二次函数2y ax bx c =++的图象如图所示,有下列结论:①当122x x >>时,12y y >;①0abc <;①40a b +=;①420a b c -+>.其中,正确结论的序号是________.52.二次函数2y ax bx c =++的图象如上图所示,则下列结论:① 0;abc <①240;b ac ->①20;a b c -+>4①0;a b c ++>①对称轴为1x =-,其中正确结的确序号是_________.知识点六、二次函数图象的对称性53.已知二次函数2y ax bx c =++中,函数y 与自变量x 的部分对应值如表:则二次函数2y ax bx c =++图象的顶点坐标是____________.54.抛物线2y ax bx c =++与x 轴的公共点是(1,0),(5,0)-,则这条抛物线的对称轴是直线x =_____.55.已知二次函数2y x bx c =++中,函数y 与自变量x 的部分对应值如表:()14,A m y -,()26,B m y +两点都在该函数的图象上,若12y y =,则m 的值为________.56.若二次函数21y ax =+,当x 取1x ,2x (12x x ≠)时,函数值相等,则当x 取12x x +时,函数值为_____. 知识点七、二次函数图象的最值57.已知抛物线223y x x =--与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,点(4,)D y 在抛物线上,E 是该抛物线对称轴上一动点.当BE DE +的值最小时,ACE 的面积为__________.58.如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC①x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为_____.59.若二次函数y=﹣x2+mx在﹣1≤x≤2时的最大值为3,那么m的值是_________________.60.当﹣1≤x≤1时,函数y=﹣x2﹣2mx+2n+1的最小值是﹣4,最大值是0,则m、n的值分别是_____.知识点八、二次函数的解析式61.若二次函数21y ax bx=--的图像经过点(2,1),则代数式20182a b-+的值等于______.62.如图,二次函数2(0)y x m m=-+>的图像经过一个顶点在原点的正方形的另三个顶点,则m=_______.63.已知抛物线1C:()221y x=-+,抛物线2C与抛物线1C关于y轴对称,则抛物线2C的表达式是__________.64.已知,抛物线()20y ax bx c a=++≠经过原点,其顶点为()(),0A m n m≠.(1)当1,3m n==时,抛物线的解析式为_________.(2)当点A在抛物线21y x x=-+上,且17m≤≤时,a的取值范围是______.参考答案1.D【分析】利用二次函数的图像与性质,判断选项的正误即可.【详解】由函数图像可知,对称轴是直线x =1故选项A 正确;当x <0时,函数y 随x 增大而增大,故选项B 正确;图象的顶点坐标是(1,4),故选项C 正确;图象与x 轴的另一个交点是(3,0),故选项D 错误.故选D【点拨】本题考查了二次函数的图像与性质,熟练掌握性质是解题的关键.2.C【分析】先利用配方法得到2(1)5y x =--+,可根据二次函数的性质可对A 、B 、C 进行判断;通过解方程2240x x -++=可对D 进行判断.【详解】解:2224(1)5y x x x =-++=--+,∴抛物线的开口向下,顶点坐标为(1,5),抛物线的对称轴为直线1x =,当 1x <时,y 随x 的增大而增大, 令0y =,则2240x x -++=,解方程解得 115x =+,215x =-, ∴①44(1)4200=-⨯-⨯=>, ∴抛物线与x 轴有两个交点.故选:C .【点拨】本题考查了二次函数的性质和二次函数的顶点式的知识点,熟悉相关性质是解题的关键. 3.D【详解】分析:根据题目中的函数解析式可以判断各个选项中的结论是否成立,从而可以解答本题.详解:①y=2x 2+4x -1=2(x+1)2-3,①当x=0时,y=-1,故选项A 错误,该函数的对称轴是直线x=-1,故选项B 错误,当x <-1时,y 随x 的增大而减小,故选项C 错误,当x=-1时,y 取得最小值,此时y=-3,故选项D 正确,故选D .点睛:本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质解答. 4.B【分析】根据a 确定抛物线的开口方向;令y=0解方程得到与x 轴的交点坐标;根据抛物线的对称轴、顶点坐标以及平移的性质,对各小题分析判断后即可得解.【详解】①①a=-1<0,①抛物线开口向下,故本小题错误;①令y=0,则-x 2+1=0,解得x 1=1,x 2=-1,所以,抛物线与x 轴交于点(-1,0)和点(1,0),故本小题正确; ①抛物线的对称轴2b x a =-=0,是y 轴,故本小题正确; ①抛物线的顶点坐标是(0,1),故本小题正确; ①抛物线y=-x 2+1是由抛物线y=-x 2向上平移1个单位得到,故本小题正确; 综上所述,正确的有①①①①共4个. 故选B . 【点拨】本题考查了二次函数的性质,理解二次函数图象与系数关系是关键. 5.D【分析】根据开口方向可判断A ;根据对称轴位置可判断B ;根据与y 轴的交点可判断C ;令x =1,可判断D .【详解】解:①由图象知,开口向下,①a <0,故A 错误;①对称轴在y 轴的左侧,①b <0,故B 错误;由图象知,与y 轴的交点在正半轴,①c >0,故C 错误;当x =1时,y =a +b +c <0,故D 正确;故选:D .【点拨】本题考查二次函数的图象与各项系数间的关系,熟知二次函数的图象与各项字母系数之间的关系是解答的关键.6.C【分析】首先根据开口方向确定a 的符号,再依据对称轴和a 的符号即可判断b 的符号,然后根据与y 轴的交点即可判断c的正负,由此得出答案即可.【详解】解:①图象开口方向向上,①a >0;①图象的对称轴在y 轴的右边上, ①2b a ->0, ①a >0, ①b <0; ①图象与y 轴交点在y 轴的负半轴上, ①c <0; ①a >0,b <0,c <0. 故选:C .【点拨】本题主要考查二次函数的图象与系数的关系,能根据图象正确确定各个系数的符号是解决此题的关键,运用了数形结合思想.7.A【分析】利用抛物线开口方向得到a <0,利用抛物线的对称轴方程得到b=-a >0,利用抛物线与y 轴的交点在x 轴上方得到c >0,则可对①进行判断;利用抛物线经过点(2,0)得到4a+2b+c=0,同时得到c=-2a ,加上b=-a ,则可对①进行判断;利由抛物线与x 轴有两个交点结合根的判别式,即可得出b 2-4ac >0,,则可对①进行判断;通过比较点(-52,y 1)到直线x=12的距离与点(52,y 2)到直线x=12的距离的大小可对①进行判断. 【详解】解:①抛物线开口向下,①a <0,①抛物线的对称轴为直线x=2b a -=12, ①b=-a >0,①抛物线与y 轴的交点在x 轴上方,①c >0,①abc <0,所以①正确;①抛物线经过点(2,0),①4a+2b+c=0,①c=-2a ,①-2b+c=2a -2a=0,所以①正确;①抛物线与x 轴有两个交点,①①=b 2-4ac >0,所以①错误;①点(52-,y 1)到直线x=12的距离比点(52,y 2)到直线x=12的距离大, ①y 1<y 2;所以①正确. 故选:A . 【点拨】本题考查二次函数图象与系数的关系,观察二次函数图象,逐一分析四条说法的正误是解题的关键. 8.B 【分析】 根据函数的图象得出图象的开口向下,与y 轴的交点在y 轴的正半轴上,对称轴是直线x =1,并利用抛物线的对称性逐个判断即可. 【详解】 图象的开口向下,与y 轴的交点在y 轴的正半轴上,0,0a c ∴<>, 0ac ∴< 故A 错误,对称轴是1x =,12b a∴-=, 20a b ∴+=,故B 正确,20b a ∴=->故D 错误,抛物线与x 轴有两个交点,240b ac ∴->故C 错误,综上,正确的是B 选项,故选B .【点拨】本题考查了二次函数的图象和性质,能根据图象得出正确信息是解此题的关键,数形结合是解题的关键.9.C【分析】分a >0和a <0时,分别判断两函数的图象即可求得答案.解:当a >0时,则函数y =ax 中,y 随x 的增大而增大,函数y =ax 2开口向上,故①正确,①错误;当a <0时,则函数y =ax 中,y 随x 的增大而减小,函数y =ax 2开口向下,故①不正确,①正确;①两函数图象可能是①①,故选:C .【点拨】本题主要考查了一次函数的图象和二次函数的图象,掌握一次函数的图象和二次函数的图象是解题的关键.10.D【分析】根据y=ax+b 的函数图象得到a>0,b<0,即可确定二次函数y=ax 2+bx+1的图象.【详解】根据一次函数的图象可得a>0,b<0.则二次函数开口向上,对称轴在y 轴的右侧.故选D .【点拨】此题考查函数图象与系数之间的关系.11.C【分析】根据二次函数图像,确定二次函数系数的符号,再确定一次函数与反比例函数的系数,即可求得.【详解】解:二次函数图像开口向上,得到0a >二次函数图像与x 轴有两个交点,得到240b ac ->二次函数的与y 轴交点在x 轴的下方,得到0c < 二次函数的对称轴b x 02a =->,得到0b < ①0b c +< ①一次函数24y ax b ac =+-图像经过一、二、三象限反比例函数b c y x+=的图像经过二、四象限 故选:C .【点拨】此题主要考查了一次函数、反比例函数与二次函数图像与系数的关系,熟练掌握相关知识是解题的关键.12.D【分析】根据二次函数2y ax =与一次函数y bx c =+的图象可知0a >,0b >,0c <,从而判断出二次函数2y ax bx c =++的【详解】解:①二次函数2y ax =的图象开口向上,①0a >,①次函数y bx c =+的图象经过一、三、四象限,①0b >,0c <,对于二次函数2y ax bx c =++的图象,①0a >,开口向上,排除A 、B 选项;①0a >,0b >,①对称轴02b x a =-<, ①D 选项符合题意; 故选:D . 【点拨】本题考查了一次函数的图象以及二次函数的图象,根据二次函数的图象和一次函数图象经过的象限,找出0a >,0b >,0c <是解题的关键. 13.B 【分析】 分两种情况讨论,通过解不等式22ax bx c bx ax c ++>++和22ax bx c bx ax c ++<++,可对各项进行判断.【详解】解:当12y y >时,22ax bx c bx ax c ++>++,整理得()()20a b x a b x --->,a b >,20x x ∴->,解得0x <或1x >;当12y y <时,22ax bx c bx ax c ++<++,整理得()()20a b x a b x ---<,a b >,20x x ∴-<,解得01x <<.故选:B.【点拨】本题考查了二次函数与不等式(组):利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,可作图利用交点直观求解,也可把两个函数解析式列成不等式求解.14.D【分析】根据二次函数的性质即可求出答案.【详解】解:A、由于a=﹣1<0,所以开口向下,有最大值,故A不符合题意.B、由二次函数y=﹣(x﹣1)2+2可知顶点为(1,2),故B不符合题意.C、由二次函数y=﹣(x﹣1)2+2可知对称轴为x=1,当x<1时,y随x的增大而增大,故C不符合题意.D、二次函数y=﹣(x﹣1)2+2可知对称轴为x=1,当x>1时,y随x的增大而减小,故D符合题意.故选:D.【点拨】本题考查二次函数,解题的关键是熟练运用二次函数的性质,本题属于基础题型.15.B【分析】根据关于x轴对称,函数值y互为相反数,将抛物线22124()y x m x m=+-+-化成关于x轴对称的抛物线的解析式为22)124(y x m x m=----+,列出方程组,求解即可得出结论.【详解】解:①抛物线22124()y x m x m=+-+-与2(3)y x m n x n=--++关于x轴对称,①22(124)y x m x m -=----+,①22)124(y x m x m =----+与2(3)y x m n x n =--++相同,①21324m m n m n -=+⎧⎨-+=⎩, 解得56m n =⎧⎨=-⎩, 故选:B .【点拨】本题考查了二次函数图象与几何变换,根据关于x 轴对称的坐标特征把抛物线22124()y x m x m =+-+-化成关于x 轴对称的抛物线的解析式是解题的关键.16.B【分析】根据二次函数图像的特点进一步求解即可.【详解】①二次函数的图像为抛物线,①两个不同二次函数的图像的交点最多只能有2个,故选:B.【点拨】本题主要考查了二次函数图像的性质与特点,熟练掌握相关概念是解题关键.17.C【分析】由抛物线的开口方向判断a 与0的关系,由抛物线与y 轴的交点判断c 与0的关系,然后根据对称轴及抛物线与x 轴交点情况进行推理,进而对所得结论进行判断.【详解】①如图所示,抛物线与y 轴交于负半轴,则c <0,故①正确;①如图所示,对称轴x =﹣2b a =1,则2a+b =0. 故①正确; ①如图所示,当x =1时,y <0,即:a+b+c <0.故①正确;①如图所示,抛物线与x 轴有两个不同的交点,则b 2﹣4ac >0.故①错误.【点拨】主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a 与b 的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.18.C【解析】【分析】根据题意和函数图象,可以判断各个小题中的结论是否正确,本题得以解决.【详解】解:①①抛物线的顶点坐标为(﹣3,﹣6),①﹣2b a =﹣3, ①b =6a , ①6a ﹣b =0,结论①正确; ①①抛物线开口向上,与y 轴交于负半轴, ①a >0,b =6a >0,c <0, ①abc <0,结论①错误;①①抛物线的顶点坐标为(﹣3,﹣6),点M (﹣2,m )在抛物线上,①点(﹣4,m )在抛物线上.①在x <﹣3上,y 随x 值的增大而减小,点N (﹣5,n )在抛物线上,①m <n ,结论①错误;①①抛物线的顶点坐标为(﹣3,﹣6),抛物线开口向上,①ax 2+bx +c ≥﹣6,结论①正确;①①抛物线y =ax 2+bx +c 经过点(﹣1,﹣4),抛物线的顶点坐标为(﹣3,﹣6),①抛物线y =ax 2+bx +c 经过点(﹣5,﹣4),①关于x 的一元二次方程ax 2+bx +c =﹣4的两根为﹣5和﹣1,结论①正确.故选:C .【点拨】本题考查二次函数图象与系数的关系,解答本题的关键是明确题意,利用二次函数的性质和数形结合的思根据抛物线与x 轴的交点即可判断A ;由x =﹣2时,y >0,即可判断B ;抛物线与y 轴的交点即可判断C ,根据对称性求得对称轴即可判断D .【详解】解:A 、①抛物线与x 轴有两个交点,①b 2﹣4ac >0,故错误;B 、当x =﹣2时,y =4a ﹣2b +c >0,故错误;C 、抛物线交y 轴的正半轴,则c >0,故错误;D 、①次函数y =ax 2+bx +c 的图象经过点A (2,0),B (6,0),①抛物线的对称轴为直线x =262+=4,故正确; 故选:D . 【点拨】本题考查了二次函数图象与系数的关系,抛物线与x 轴的交点,二次函数的性质,数形结合是解题的关键. 20.B 【分析】 利用函数图象分别得出抛物线与x 轴交点的横坐标的关系,进而判断四个结论得出答案. 【详解】 解:①x 1,x 2是一元二次方程ax 2+bx +c =0的两个根, ①x 1、x 2是抛物线与x 轴交点的横坐标, ①抛物线的对称轴为直线x =-4,x 1<x 2,1<x 2<2,①-10<x 1<-9,故选项B 正确;x 1x 2<0,故选项A 错误;①抛物线与x 轴有两个交点,①b 2-4ac >0,故选项C 错误;①抛物线开口向上,①a >0,①抛物线的对称轴为直线x =-4,①42b a-=-, ①b =8a >0,①抛物线与y 轴交于负半轴,【点拨】本题主要考查二次函数与一元二次方程之间的关系,会利用对称轴的值求抛物线与x 轴交点的横坐标间的数量关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.21.C【分析】先求出对称轴,然后根据对称性即可得到答案.【详解】224y x x c =--+的对称轴为x =-1根据对称性函数在x =1时的函数值与x =-3时的函数值一样故当点(1,)m 在函数224y x x c =--+的图象上时,(3,)m -也在函数图象上故选C .【点拨】本题主要考查二次函数的对称性,能够求出对称轴是解题关键.22.B【分析】根据“抛物线与x 轴的两个交点到对称轴的距离相等”进行填空.【详解】解:①抛物线y =ax 2+bx+c 与x 轴的交点是(1,0),(﹣3,0),①这条抛物线的对称轴是:x =312-+=-1, 即x =-1. 故选:B . 【点拨】本题考查了求抛物线与x 轴的交点问题,关键是掌握抛物线与x 轴的两交点关于对称轴对称; 23.C 【分析】根据二次函数图象具有对称性和二次函数图象上点的坐标特征,可以判断y 1、y 2、y 3的大小,从而可以解答本题.【详解】解:①228y x x c =-++①函数228y x x c =-++的对称轴为直线2x =,开口向下,当x <2时,y 随x 的增大而增大,当x >2时,y 随x 的增大而减小,①-3<-1<2①12y y <,①3212-<-<-<①132y y y <<故选C .【点拨】本题考查了二次函数的增减性.当二次项系数a >0时,在对称轴的左边,y 随x 的增大而减小,在对称轴的右边,y 随x 的增大而增大;a <0时,在对称轴的左边,y 随x 的增大而增大,在对称轴的右边,y 随x 的增大而减小.24.C【分析】 由题意易得二次函数的对称轴为直线22b x a =-=-,进而可得点()15,t y -+,()21,t y -关于抛物线的对称轴对称,然后根据二次函数的性质可排除选项. 【详解】 解:①二次函数231215y x x =+-, ①二次函数的对称轴为直线22b x a =-=-, ①点()32,y -为二次函数的顶点,①点()15,t y -+,()21,t y -,①根据二次函数的对称性可得:5122t t x -++-==-, ①12y y =,①3>0,①二次函数的开口向上,①312y y y ≤=;故选C .【点拨】本题主要考查二次函数图象与性质,熟练掌握二次函数的图象与性质是解题的关键.25.C【分析】由函数图象可看出其最大值和最小值,可求得答案.【详解】解:由图象可知当x =1时,y 有最小值-2,当122x =+时,y 有最大值2,①函数有最小值-2,有最大值2,【点拨】本题主要考查了二次函数的最值,正确识别函数图象、理解最值的意义是解题的关键.26.D【分析】根据函数的图象和性质逐一求解即可.【详解】解:A 、当m =0时,()()111y mx m x x =+--=-+,当x =-1时,y =2,则不经过(-1,-2),故错误;B 、()()2111y mx m x mx x m =+--=--+,当m =0时,1y x =-+,函数图像与x 轴只有1个交点,故错误;C 、22111124y mx x m m x m m m ⎛⎫=-+-=-+-- ⎪⎝⎭, 函数的对称轴为直线x =12m , 当m >12时,12m <1,故当x <12m时,y 随x 的增大而减小,故错误; D 、当m >0时,函数开口向上,函数的最小值是114m m--+,故正确; 故选D .【点拨】本题考查的是抛物线与x 轴的交点,主要考查函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.27.C【分析】C 点关于对称轴对称的点C',过点C'作直线AB 的垂线,交对称轴与点E ,交直线AB 于点F ,则C'F 即为所求最短距离.【详解】①y =x 2+2x ﹣2的对称轴为21221b x a =-=-=-⨯,C (0,﹣2), ①C 点关于对称轴对称的点C '(﹣2,﹣2),过点C '作直线AB 的垂线,交对称轴与点E ,交直线AB 于点F ,①CE =C 'E ,则C 'F =CE +EF =C 'E +EF 是CE +EF 的最小值;①直线y34=-x +3, 设直线C 'F 的解析式为43y x b =+, 将C '(﹣2,﹣2)代入得:()4223b -=⨯-+, 解得:23b =, ①C 'F 的解析式为y 43=x 23+, 解方程组4233334y x y x ⎧=+⎪⎪⎨⎪=-+⎪⎩, 得:28255425x y ⎧=⎪⎪⎨⎪=⎪⎩, ①F (2825,5425), ①C 'F 22285426(2)(2) 5.225255=+++==. 故选:C .【点拨】本题考查二次函数与一次函数的图象及性质;利用点的对称性,点到直线的垂线段最短,确定最短距离为线段C'F 的长是解题的关键.28.D【详解】解:如图,点A 关于y 轴的对称点A ′的横坐标为﹣1,连接A ′B 与y 轴相交于点C ,点C 即为使AC +BC 最短的点,当x =﹣1时,y =﹣1,所以,点A ′(﹣1,﹣1),B (2,﹣4),设直线A′B 为y kx b =+124k b k b -+=-⎧∴⎨+=-⎩ 1k ∴=- 2b =-2y x ∴=--当x=0时,y=-2即C (0,-2)故选D【点拨】本题考查了轴对称确定最短路线问题,二次函数的性质,熟记确定出最短路径的方法和二次函数的对称性确定出点C 的位置是解题的关键.29.D【分析】依题知,抛物线y =﹣x 2+2x +c 与x 轴正半轴,y 轴正半轴分别交于点A ,B ;可得B 点坐标,又OB=OA ,可得A 点坐标,然后将A 的坐标代入函数解析式即可;【详解】依题:抛物线y =﹣x 2+2x +c 与x 轴正半轴,y 轴正半轴分别交于点A ,B ,① B (0,c ),① OB =c ,① OA =OB ,① OA =c ,① A (c ,0),①﹣c 2+2c +c =0,解得c =3或c =0(舍去),故选:D【点拨】本题考查二次函数待定系数法,重点在理解和熟练求解过程的转化.30.B将已知点的坐标代入24y x x c =-++确定抛物线的解析式,再计算出自变量为0时所对应的函数值即可求解.【详解】解:①抛物线24y x x c =-++经过点(4,3),①31616c =-++,①3c =,①物线的解析式为:243y x x =-++,①0x =时,3y =,①抛物线必经过的点是(0,3).故选:B .【点拨】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式,解题的关键是明确题意,利用二次函数的性质解答.31.C【分析】利用表中的数据,求得二次函数的解析式,再配成顶点式,根据二次函数的性质逐一分析即可判断.【详解】解:设二次函数的解析式为2y ax bx c =++,依题意得:42646a b c c a b c -+=⎧⎪=-⎨⎪++=-⎩,解得:134a b c =⎧⎪=-⎨⎪=-⎩,①二次函数的解析式为234y x x =--=232524x ⎛⎫-- ⎪⎝⎭, ①10a =>, ①这个函数的图象开口向上,故A 选项不符合题意; ①()()2243414250b ac =-=--⨯⨯-=>,①这个函数的图象与x 轴有两个不同的交点,故B 选项不符合题意;①10a =>,①当32x =时,这个函数有最小值2564-<-,故C 选项符合题意; ①这个函数的图象的顶点坐标为(32,254-), ①当32x >时,y 的值随x 值的增大而增大,故D 选项不符合题意; 故选:C .。
二次函数知识整理及基础训练

1.定义:形如: (其中a,b,c是常数,且a≠0)的函数是二次函数。
2.图象:抛物线,抛物线是轴对称图形,对称轴和抛物线的交点叫做抛物线的顶点。
3.二次项的系数a对抛物线的影响:a决定抛物线的开口大小和方向,即抛物线的形状。
当a>0时,开口向上,当a<0时,开口向下; 越大开口越小,越接近y轴。
4.一次项的系数b对抛物线的影响:a,b决定抛物线的左右位置。
当b=0时,抛物线的对称轴是y轴;当a,b同号时,对称轴在y轴的左边;
当a,b异号时,对称轴在y轴的右边。即“左同右异”
5.常数项c对抛物线的影响:c决定抛物线的上下位置,即抛物线与y轴的交点。
当c>0时,抛物线与y轴的交点在y轴的正半轴;当c<0时,抛物线与y轴的交点在y轴的负半轴;当c=0时,抛物线经过原点.
15、函数y=9-4x2,当x=_________时有最大值________.
16、已知二次函数 的图象如图所示,则a0,b0,c0。
17、抛物线 的图象过原点,则 为
18、二次函数 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是
19、如果一条抛物线经过平移之后能够和抛物线 重合,且顶点坐标为(4,2),
9.二次函数 对称轴为直线 ,顶点坐标为
10.抛物线 在x轴上截得的线段的长度,就是方程 的两个解的差的绝对值 。
二次函数的解析式有如下三种形式:
二次函数练习题
1、下列关系式中,属于二次函数的是(x为自变量)()
A、 B、 C、 D、
2、抛物线y=x2-1的顶点坐标是( ).
A、(0,1) B、(0,一1) C、(1,0) D、(一1,0)
7、与抛物线 的形状大小开口方向相同,只有位置不同的抛物线是()
二次函数知识点总结及练习
二次函数知识点总结及练习知识点1:二次函数的概念(1)一般地,形如 (a,b,c 是常数, )的函数,叫做二次函数。
注意:①a ②最高次数为 ③代数式一定是 (2)二次函数的一般形式是 (a,b,c 是常数, ) 是二次项系数, 是一次项系数, 是常数项.练习:1.已知函数35)1(12-+-=+x x m y m 是二次函数,求m 的值。
2.若函数y=(m 2+2m-7)x 2+4x+5是关于x 的二次函数,则m 的取值范围为 。
知识点2:二次函数的图像和性质(1)y=ax 2的图像和性质:练习:1. y=-2x 2的对称轴是 ,顶点坐标是 ;当 时,y 的值随x 值的增大而减小 2.当m= 时,抛物线mm x m y +-=2)1(开口向下,对称轴为 ,当x<0时,y 随x 的增大而 ;当x>0时,y 随x 的增大而 .3.已知点(x 1,y 1),(x 2,y 2)在二次函数y=-2x 2图象上,当x 1>x 2>0时,则y 1与y 2的大小关系是 .4.已知点(-1,y 1),(2,y 2),(-3,y 3)都在函数y=5x 2的图象上,则则y 1与y 2,y 3的大小关系是 . (2)y=ax 2+c 的图像和性质:1.二次函数y=-2x 2+6图象的对称轴是 ,顶点坐标是 ,当 时,y 随x 的增大而增大. 2.已知y=ax 2+c 的图象上有A(-3,y 1),B(1,y 2),C(2,y 3)三点,且y 2<y 3<y 1,则a 的取值范围是 . 3.将二次函数y=2x 2-1的图象沿y 轴向上平移2个单位长度,所得图象对应的函数表达式为 .4.已知抛物线y=(m-1)x 2+m 2-2m-2的开口方向向下,且经过点(0,1). (1)求m 的值;(2)求此抛物线的顶点坐标及对称轴; (3)当x 为何值时,y 随x 的增大而增大?(3)y=a(x-h)2+k 的图像和性质:1.抛物线y=-12(x +4)2的顶点坐标为 ,当x >-4时,y 随x 的增大而 .2.抛物线y=-2(x-1)2-3的开口方向是 ,其顶点坐标是 ,对称轴是直线 ,当 时,函数值y 随自变量x 的值的增大而减小.3.若抛物线y=(x-m)2+(m +1)的顶点在第一象限,则m 的取值范围为 .4.已知A(1,y 1)、B(-12,y 2)、C(-2,y 3)在函数y=a(x +1)2+k(a>0)的图象上,则y 1、y 2、y 3的大小关系是 .(4)二次函数c bx ax y ++=2(a ≠0)的图像和性质练习:1.抛物线3842-+-=x x y 的开口方向向 ,对称轴是 ,最高点的坐标是 , 函数值得最大值是 。
二次函数知识点分类专题训练(专项练习3)(基础篇)

二次函数知识点分类专题训练(基础篇)一、单选题知识点一、抛物线与坐标轴交点坐标1.抛物线2(1)(3)y x x =-+-与x 轴的交点坐标为( ) A .(1,0),(3,0)-B .(1,0),(3,0)C .(1,0),(3,0)-D .(1,0),(3,0)--2.若抛物线y =x 2+bx+c 与x 轴只有一个公共点,且过点A(m ,n ),B(m ﹣8,n),则n 的值为( ) A .8B .12C .15D .163.抛物线2243y x x =-+与y 轴的交点坐标是( ) A .()3,0B .()3,0-C .()0,3D .()0,3-4.抛物线y =x 2-2x +1与坐标轴的交点个数是 A .0.B .1.C .2.D .3.知识点二、由函数值求自变量的值5.根据下表中的对应值:判断方程2320x x +-=的一个解的范围是( ) A .0.30.4x <<B .0.40.5x <<C .0.50.6x <<D .0.60.7x <<6.已知二次函数2y ax bx c =++的自变量x 与函数y 的部分对应值列表如下:则关于x 的方程20ax bx c ++=的解是( ) A .10x =,22x =B .122x x ==C .120x x ==D .不能确定7.二次函数21(2)12y x a =--+的图象上有两点()()121,,5,y y -,则12y y -的值是( ) A .负数B .零C .正数D .不能确定8.若抛物线2y x bx =+的对称轴是直线2x =,则方程25x bx +=的解是( ) A .11x =,25x =B .11x =,25x =-C .11x =-,25x =D .11x =-,25x =-知识点三、抛物线与一元二次方程关系9.对于二次函数2y x 2x 3=-++,下列说法不正确的是( ) A .当1x =时,y 有最大值2 B .当1≥x 时,y 随x 的增大而减小 C .开口向下D .函数图象与x 轴交于点()-1,0和()3,010.若二次函数2y x bx c =-++中函数y 与自变量x 之间的部分对应值如下表点()11,A x y 点()22,B x y 在该函数图象上,当12101,23,x x y <<<<与2y 的大小关系是( ) A .12y y <B .12y y >C .12y y ≥D .12y y ≤11.已知二次函数y=x 2﹣x+14m ﹣1的图象与x 轴有交点,则m 的取值范围是( )A .m≤5B .m≥2C .m <5D .m >212.二次函数263y kx x =-+的图象与x 轴有交点,则k 的取值范围是( ) A .3k < B .3k <且0k ≠ C .3k ≤D .3k ≤且0k ≠知识点四、抛物线与一元二次不等式关系13.抛物线y =ax 2+bx +c 的部分图象如图所示,对称轴为直线x =﹣1,则当y <0,x 的取值范围是( )A .x <1B .x >﹣1C .﹣3<x <1D .﹣4≤x ≤114.如图,二次函数2y ax bx c =++的图象与x 轴相交于(2,0)-和(4,0)两点,当函数值0y <时,自变量x 的取值范围是( )A .2x <-B .4x >C .24x -<<D .2x <-或4x >15.如图,抛物线2y ax c =+与直线y mx n =+交于(1,),(3,)A p B q -两点,则不等式2ax c mx n +>+的解集为( )A .1x >-B .3x <C .13xD .1x <-或3x >16.如图,己知抛物线()(0)y ax x t a =+≠经过点(3,3)A --,0t ≠.当抛物线的开口向上时,t 的取值范围是( )A .3t >B .3t >-C .3t >或3t <-D .3t <-知识点五、抛物线与x 轴的截距17.如图,一条抛物线与x 轴相交于M 、N 两点(点M 在点N 的左侧),其顶点P 在线段AB 上移动.若点A 、B 的坐标分别为(﹣2,3)、(1,3),点N 的横坐标的最大值为4,则点M 的横坐标的最小值为( )A .﹣1B .﹣3C .﹣5D .﹣718.老师出示了小黑板上的题后(如图),小华说:过点(3,0);小彬说:过点(4,3);小明说:a=1;小颖说:抛物线被x 轴截得的线段长为2.你认为四人的说法中,正确的有( )A .1个B .2个C .3个D .4个19.抛物线224y x x =--在x 轴上截得的线段长度是( ) A .25B .2C .35D .520.二次函数2y ax bx c =++的值永远为负值的条件是( ) A .0a >,240b ac -< B .0a <,240b ac -> C .0a >,240b ac ->D .0a <,240b ac -<知识点六、实际问题与二次函数21.国家决定对某药品分两次降价,若设平均每次降价的百分比为x ,该药品的原价为33元,降价后的价格为y 元,则y 与x 之间的函数关系为( ) A .()3321y x =⨯- B .()23321y x =⨯-C .()2331y x =⨯-D .()331y x =-22.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为( )人 A .56B .55C .54D .5323.如图,在ABC 中,90B ∠=︒,4cm AB =,8cm BC =.动点P 从点A 出发,沿边AB 向点B 以1cm/s 的速度移动(不与点B 重合),同时动点Q 从点B 出发,沿边BC 向点C 以2cm /s 的速度移动(不与点C 重合).当四边形APQC 的面积最小时,经过的时间为( )A .1sB .2sC .3sD .4s24.如图,矩形OABC 中,()30A -,,()0,2C ,抛物线()221y x m m =---+的顶点M 在矩形OABC 内部或其边上,则m 的取值范围是( )A .30m -≤≤B .31m -≤≤-C .12m -≤≤D .10m -≤≤知识点七、二次函数几何问题25.如图所示,矩形ABCD 中,8,6AB BC ==,P 是线段BC 上一点(P 不与B 重合),M 是DB 上一点,且BP DM =,设,BP x MBP =的面积为y ,则y 与x 之间的函数关系式为( )A .224(06)5y x x x =-+<≤B .224(06)5y x x x =-+≤≤C .233(06)10y x x x =-+<≤ D .233(06)10y x x x =-+≤≤ 26.如图,在菱形ABCD 中,AB =1,∠B =60°,点E 在边BC 上(与B 、C 不重合)EF ∠AC ,交AB 于点F ,记BE =x ,∠DEF 的面积为S ,则S 关于x 的函数图象是( )A .B .C .D .27.如图,Rt OAB △的顶点(2,4)A -在抛物线2y ax =上,将Rt OAB △绕点O 顺时针旋转90︒,得到OCD ,边CD 与该抛物线交于点P ,则点P 的坐标为( ).A .(2,2)B .(2,2)C .(2,2)D .(2,2)28.如图,∠ABC 是直角三角形,∠A=90°,AB=8cm ,AC=6cm .点P 从点A 出发,沿AB 方向以2cm/s 的速度向点B 运动,同时点Q 从点A 出发,沿AC 方向以1cm/s 的速度向点C 运动,其中一个动点到达终点则另一个动点也停止运动,则∠APQ 的最大面积是( )A .0cm 2B .8cm 2C .16cm 2D .24 cm 2二、填空题知识点一、抛物线与坐标轴交点坐标29.将抛物线2113=+y x 向上平移2个单位后,得到的新抛物线与y 轴交点的坐标为____.30.抛物线()2221y x k x k =+--(k 为常数)与坐标轴交点的个数是______.31.如图所示为抛物线y =ax 2+2ax ﹣3的图象,则一元二次方程ax 2+2ax ﹣3=0的两根为_____________.32.抛物线y =x 2﹣bx +1与x 轴只有一个交点,那么b =_____.知识点二、由函数值求自变量的值33.抛物线y=x 2+2x ﹣2018过点(m ,0),则代数式m 2+2m+1=_____.34.已知二次函数y =ax 2+bx +c (a≠0)中,函数值y 与自变量x 的部分对应值如下表:则关于x 的一元二次方程ax 2+bx +c =﹣2的根是_____.35.飞机着陆后滑行的距离y (单位:m )关于滑行时间t (单位:s )的函数解析式是250y t t =-,则经过________s 后,飞机停止滑行.36.已知二次函数223y x x =--+,当3m x m ≤≤+时,y 的取值范围是04y ≤≤,则m 的值为______.知识点三、抛物线与一元二次方程关系37.如图,抛物线2y ax bx =+与直线y mx n =+相交于点(3,6)A --,(1,2)B -,则关于x 的方程2ax bx mx n +=+的解为_______________ .38.抛物线()2221y x k x k =+--(k 为常数)与x 轴交点的个数是__________.39.若二次函数24y x x n =-+的图象与x 轴只有一个公共点,则实数n =______.40.二次函数y=﹣x 2+2x+k 的部分图象如图所示,则关于x 的一元二次方程﹣x 2+2x+k=0的一个解x 1=3,另一个解x 2=___.知识点四、抛物线与一元二次不等式关系41.如图,已知抛物线21y x bx c =++与直线2y kx m =+相交于()()-2,3、3,-1A B 两点,则12y y ≥时x 的取值范围是________________________.42.已知抛物线2y x bx c =++的部分图象如图所示,当3y <-时,x 的取值范围是______.43.已知函数y =ax 2+2bx ﹣c (a >0)的图象与x 轴交于A (2,0)、B (6,0)两点,则不等式cx 2+2bx ﹣a <0的解集为___.44.如图是二次函数21y ax bx c =++和一次函数2y kx t =+的图象,则关于x 的不等式2ax bx c kx t +++≤的解为________.知识点五、抛物线与x 轴的截距45.如图,抛物线()240y ax ax c a =-+<向下平移c 个单位后,交x 轴于O ,A 两点,则OA 的长为______.46.已知抛物线2y ax bx c =++与x 轴交于A 、B 两点,设抛物线顶点为P ,若30PAB ∠=,则24b ac -的值为________. 47.抛物线y=x 2﹣5x+6与x 轴交于A 、B 两点,则AB 的长为__.48.若抛物线y =x 2-2x -3与x 轴分别交于A ,B 两点,则AB 的长为 ________.知识点六、实际问题与二次函数49.如图,在水平的地面BD 上有两根与地面垂直且长度相等的电线杆AB ,CD ,以点B 为坐标原点,直线BD 为x 轴建立平面直角坐标系.已知电线杆之间的电线可近似地看成抛物线20.8 3.26y x x =-+则电线最低点离地面的距离是_______米.50.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y (单位:m )与它距离喷头的水平距离x (单位:m )之间满足函数关系式2241y x x =-++,喷出水珠的最大高度是______m .51.如图,以两条互相垂直的街道为坐标轴,某“理想社区”分布形如抛物线259y x x =-+,若建公交站点D (在抛物线上),使公交车行驶到十字路口(原点O )的路线最短(公交车只能平行或垂直于街道行驶)则该路线的长度为________.52.随着国内新冠疫情逐渐好转,市场对口罩的需求量越来越少,据统计,某口罩厂6月份出货量仅为4月份的40%,设4月份到6月份口罩出厂量平均每月的下降率为x ,则可列方程为___.知识点七、二次函数几何问题53.如图,在Rt ABC 中,90BAC ∠=︒,22AB AC ==,AD 为BC 边上的高,动点P 在AD 上,从点A 出发,沿A D →方向运动,设AP x =,ABP △的面积为1S ,矩形PDFE 的面积为2S ,12y S S =+,则y 与x 的关系式是________.54.如图,已知AB =12,P 为线段AB 上的一个动点,分别以AP 、PB 为边在AB 的同侧作菱形APCD 和菱形PBFE ,点P 、C 、E 在一条直线上,∠DAP =60°.M 、N 分别是对角线AC 、BE 的中点.当点P 在线段AB 上移动时,点M 、N 之间的距离最短为______.(结果留根号)55.如图,在平面直角坐标系中,抛物线y =x 2﹣2x ﹣1交y 轴于点A ,过点A 作AB∠x 轴交抛物线于点B ,点P 在抛物线上,连结PA 、PB ,若点P 关于x 轴的对称点恰好落在直线AB 上,则∠ABP 的面积是_____.56.如图,在平面直角坐标系中,点A在抛物线()224=-+上运动,过点A作AB∠x轴于点B,以AB为斜边y x作Rt∠ABC,则AB边上的中线CD的最小值为_________.参考答案1.C【分析】通过解方程2(1)(3)0x x -+-=即可得到抛物线2(1)(3)y x x =-+-的与x 轴交点的坐标.【详解】解:当y=0时,2(1)(3)0x x -+-=,解得x 1=-1,x 2=3,所以抛物线2(1)(3)y x x =-+-的与x 轴交点的坐标是(-1,0),(3,0).故选C .【点拨】本题考查了抛物线与x 轴的交点:把求二次函数y=ax 2+bx+c (a ,b ,c 是常数,a≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程.2.D【分析】由题意b 2﹣4c =0,得b 2=4c ,又抛物线过点A (m ,n ),B (m ﹣8,n ),可知A 、B 关于直线x =2b -对称,所以A (2b -+4,n ),B (2b -﹣4,n ),把点A 坐标代入y =x 2+bx+c ,化简整理即可解决问题. 【详解】 解:由题意b 2﹣4c =0,∠b 2=4c ,又∠抛物线过点A (m ,n ),B (m ﹣8,n ),∠A 、B 关于直线x =2b -对称, ∠A (2b -+4,n ),B (2b -﹣4,n ), 把点A 坐标代入y =x 2+bx+c ,n =(2b -+4)2+b (2b -+4)+c =14-b 2+16+c , ∠b 2=4c ,∠n =16.故选:D .【点拨】本题考查二次函数的性质,关键在于熟悉性质,灵活运用.3.C令x=0,求出y 的值即可.【详解】解:令x=0,则y=3,∠抛物线y=2x 2-4x+3与y 轴交点坐标为(0,3).故选:C .【点拨】本题考查的是二次函数图象上点的坐标特点,熟知y 轴上点的坐标特点是解答此题的关键.4.C【分析】当0x =时,求出与y 轴的纵坐标;当0y =时,求出关于x 的一元二次方程2210x x -+=的根的判别式的符号,从而确定该方程的根的个数,即抛物线221y x x =-+与x 轴的交点个数.【详解】解:当0x =时,1y =,则与y 轴的交点坐标为()0,1,当0y =时,2210x x -+=,∠()224110=--⨯⨯=,所以,该方程有两个相等的解,即抛物线221y x x =-+与x 轴有1个点.综上所述,抛物线221y x x =-+与坐标轴的交点个数是2个.故选:C .【点拨】此题考查了抛物线与x 轴的交点,以及一元二次方程的解法,其中令抛物线解析式中0x =,求出的y 值即为抛物线与y 轴交点的纵坐标;令0y =,求出对应的x 的值,即为抛物线与x 轴交点的横坐标.5.C【分析】 求抛物线的对称轴为32x =-,根据a =1>0,抛物线开口向上,在对称轴的右侧,y 随x 的增大而增大,根据表格确定函数值的符号, y=0时,有0.5<x<0.6,满足2320x x +-=.【详解】解:令y =232+-x x ,∠抛物线的对称轴为322b x a =-=-, ∠a =1>0,抛物线开口向上,在对称轴的右侧,y 随x 的增大而增大,根据表格x=0.5,y=-0.25<0,x=0.6时,y=0.16>0,故选择C .【点拨】本题考查一元二次方程与抛物线的关系,掌握函数的性质,一元二次方程根与抛物线与x 轴相交的关系是解题关键.6.A【分析】根据题意得到函数对称轴为直线x=1,而因此得到m=0,据此即可判断.【详解】由题意得:函数的对称轴为直线x=1∠当x=2时y 的值,和x=0时y 的值相等∠m=0∠方程20ax bx c ++=的解为10x =,22x =. 故选A .【点拨】本题考查了二次函数和一元二次方程的关系,熟练掌握二次函数与一元二次方程的关系,与不等式的关系是解决二次函数重难点题型的关键.7.B【分析】直接把各点坐标代入二次函数的解析式,求出y 1,y 2的值即可.【详解】∠二次函数y =−112(x −2)2+a 的图象上有两点(-1,y 1),(5, y 2), y 1 =-112(-1-2)2 +a , y 2 = 112-(5-2)2+a , ∠y 1-y 2=-112(-1-2)2+a + 112(5-2)2-a =-112×9+112×9=0,函数的图像和性质是解题的关键.8.C【分析】利用对称轴公式求出b 的值,然后解方程.【详解】 解:由题意:22b x =-= 解得:b=-4 ∠25x bx += 2450x x --= (5)(1)0x x -+= 解得:11x =-,25x =故选:C【点拨】本题考查抛物线对称轴公式及解一元二次方程,熟记公式正确计算是本题的解题关键.9.A【分析】先把一般式配成顶点式得到y =-(x -1)2+4,再根据二次函数的性质可对A 、B 、C 进行判断;通过解方程-x 2+2x +3=0得抛物线与x 轴的交点坐标,可对D 进行判断.【详解】解:∠y =-x 2+2x +3=-(x -1)2+4,-1<0,∠抛物线开口向下,顶点坐标为(1,4),故C 正确,不符合;当x ≥1时,y 随x 的增大而减小,故B 正确,不符合;当x =1时,y 有最大值4,故A 错误,符合;当y =0时,-x 2+2x +3=0,解得x 1=-1,x 2=3,∠抛物线与x 轴的交点坐标为(-1,0),(3,0),故D 正确,不符合;故选:A .【点拨】本题考查了抛物线与x 轴的交点:把求二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程.也考查了二次函数的性质.10.A【分析】根据表格数据判断出对称轴为直线x =2,再根据二次项系数小于0判断出函数图象开口向下,然后根据x 的取值范解:由表可知,抛物线的对称轴为直线x=2,∠a=-1<0,∠函数图象开口向下,∠0<x1<1,2<x2<3,∠y1<y2.故选A.【点拨】本题考查了二次函数图象上点的坐标特征,判断出对称轴和开口方向是解题的关键.11.A【详解】【分析】由题意可知∠=(-1) 2-4×1×(14m-1)≥0,解不等式即可求得m的取值范围.【详解】∠二次函数y=x2﹣x+14m﹣1的图象与x轴有交点,∠∠=(-1) 2-4×1×(14m-1)≥0,解得:m≤5,故选A.【点睛】本题考查了抛物线与x轴的交点,能根据题意得出关于m的不等式是解此题的关键.二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点个数与∠=b2-4ac的关系,∠>0抛物线y=ax2+bx+c(a≠0)的图象与x轴有2个交点;∠=0抛物线y=ax2+bx+c(a≠0)的图象与x轴有1个交点;∠<0抛物线y=ax2+bx+c(a≠0)的图象与x轴没有交点.12.D【分析】利用kx2-6x+3=0有实数根,根据判别式可求出k取值范围.【详解】∠二次函数y=kx2−6x+3的图象与x轴有交点,∠方程kx2−6x+3=0(k≠0)有实数根,即∠=36−12k∠0,k∠3,由于是二次函数,故k≠0,则k的取值范围是k∠3且k≠0.故选D.【点拨】此题考查抛物线与坐标轴的交点,解题关键在于掌握其性质定义.13.C【分析】轴的下方,从而可得答案.【详解】解:由抛物线的对称轴为:1,x =- 且过()1,0,所以抛物线与x 轴的另一个交点的坐标为:()3,0,-当y <0时,函数图像在x 轴的下方,所以:3-<x <1,故选:.C【点拨】本题考查的是抛物线的对称性,利用抛物线的图像写不等式的解集,掌握以上知识是解题的关键. 14.D【分析】由抛物线与x 轴的交点坐标,结合图象即可解决问题.【详解】解:∠二次函数2y ax bx c =++的图象与x 轴交于(2,0)-和(4,0)两点,函数开口向下,∠函数值0y <时,自变量x 的取值范围是2x <-或4x >,故选:D .【点拨】本题考查的是二次函数的基本性质,熟悉相关性质是解题的关键.15.D【分析】观察两函数图象的上下位置关系,即可得出结论.【详解】解:∠抛物线y =ax 2+c 与直线y =mx +n 交于A (-1,p ),B (3,q )两点,由图可知:抛物线y =ax 2+c 在直线y =mx +n 上方时,x 的范围是:x <-1或x >3,即ax 2+c >mx +n 的解集是x <-1或x >3,故选D .【点拨】本题考查二次函数与不等式,解答本题的关键是明确题意,利用数形结合的思想解答.16.A【分析】根据抛物线()(0)y ax x t a =+≠经过点(3,3)A --,求出13t a =+,由抛物线的开口向上,可得10a >,可得1=3+3t a>即可.解:∠抛物线()(0)y ax x t a =+≠经过点(3,3)A --,∠()33(3)(0)a t a -=--+≠,13t a =+, ∠抛物线的开口向上, ∠0a >,10a >, ∠1=3+3t a >. 故选择A . 【点拨】本题考查抛物线性质,利用抛物线经过点求出关于t 的代数式,利用抛物线开口方向确定10a >是解题关键. 17.C 【分析】 根据顶点P 在线段AB 上移动,又知点A 、B 的坐标分别为(﹣2,3)、(1,3),分别求出对称轴过点A 和B 时的情况,即可判断出M 点横坐标的最小值.【详解】解:根据题意知,点N 的横坐标的最大值为4,此时对称轴过B 点,点N 的横坐标最大,此时的M 点坐标为(﹣2,0), 当对称轴过A 点时,点M 的横坐标最小,此时的N 点坐标为(1,0),M 点的坐标为(﹣5,0),故点M 的横坐标的最小值为﹣5,故选:C .【点拨】本题考查了抛物线与x 轴的交点,二次函数的图象与性质,解答本题的关键是理解二次函数在平行于x 轴的直线上移动时,两交点之间的距离不变.18.C【分析】首先求出抛物线的解析式,然后逐一进行判断即可得出答案.【详解】解:∠抛物线过(1,0),对称轴是x =2, ∠ 30b 22aa b ++=⎧⎪⎨-=⎪⎩ ,解得a =1,b =-4, ∠y =x 2-4x +3,当x =3时,y =0,所以小华正确,当x =4时,y =3,小彬正确,a =1,小明也正确,答案不唯一,所以小颖也错误,故答案为:C .【点拨】本题主要考查抛物线,掌握二次函数的性质是解题的关键.19.A【分析】令解析式0y =,求解出抛物线与x 轴交点的横坐标,再作差即可.【详解】由2240x x --=解得115x =-,215x =+, ()()21151525x x -=+--=, 故选:A .【点拨】本题考查了抛物线在x 轴上截得的线段长,熟记基本公式,灵活计算是解题关键.20.D【分析】二次函数2y ax bx c =++的值永远为负即函数图象的开口向下且函数与x 轴没有交点,根据此即可算出a 和24b ac -的取值.【详解】解:因为二次函数2y ax bx c =++的值永远为负值,所以函数图象的开口向下,所以0a <.此外,函数与x 轴没有交点,所以240b ac -<,所以二次函数2y ax bx c =++的值永远为负值的条件是0a <,240b ac -<.故选D.【点拨】本题主要考查对于二次函数图象的理解,同时还要掌握函数图象与x 轴没有交点的性质.21.C【分析】原价为33,第一次降价后的价格是33(1)x ⨯-,第二次降价是在第一次降价后的价格的基础上降价的为:233(1)(1)33(1)x x x ⨯-⨯-=-,则函数解析式即可求得.【详解】解:根据题意:平均每次降价的百分比为x ,该药品的原价为33元,降价后的价格为y 元,可得y 与x 之间的函数关系为:233(1)y x =-.22.B【分析】设旅行团人数为x 人,此时的营业额为y 元,根据优惠规定可建立y 与x 之间的函数关系式,再利用二次函数的性质即可得.【详解】解:设旅行团人数为x 人,此时的营业额为y 元,则30x ≥,由题意得:[]280010(30)10(55)30250y x x x =--=--+,由二次函数的性质可知,在30x ≥内,当55x =时,y 取得最大值,即若这个旅行社要获得最大营业额,此时旅行团人数为55人,故选:B .【点拨】本题考查了二次函数的实际应用,正确建立函数关系式是解题关键.23.B【分析】根据图形得到ABC PBQ APQC S SS =-四边形列出函数关系,再将函数关系化为顶点式,根据性质求出结果. 【详解】解:设运动的时间为x 秒(04x ≤<),四边形APQC 的面积为y 2()cm ,则:1()AP x x cm =⋅=,2()BQ x cm =,∠(4)()BP AB AP x cm =-=-, ∠1122ABC PBQ y S S BC AC BQ BP =-=⋅⋅-⋅⋅, ∠2211842(4)416(2)1222y x x x x x =⨯⨯-⨯⨯-=-+=-+, ∠10a => ,∠抛物线开口向上,y 有最小值,∠当2x =时,,y 有最小值,,最小值是12,∠当四边形APQC 的面积最小时,经过的时间为2秒.故选:B .【点拨】本题主要考查了根据点的运动问题列出函数关系式以及二次函数的性质,关键是根据图形明确四边形的面积等于大三角形的面积减去小三角形的面积,列出函数关系.24.D【分析】解:抛物线()221y x m m =---+的顶点坐标M 为(m ,-m +1), ∠()30A -,,()0,2C , ∠30012m m -≤≤⎧⎨≤-+≤⎩, ∠-1≤m ≤0,故选:D .【点拨】本题考查二次函数与实际问题,解题的关键是熟知抛物线的性质.25.A【分析】根据勾股定理可得10BD =,因为DM x =,所以10BM x =-,过点M 作ME BC ⊥于点E ,可得BME BDC ∽,然后根据相似三角形的性质得到ME BM DC BD =,由此可用x 表示ME ,最后根据三角形的面积公式即可确定函数关系. 【详解】 解:∠8,6AB BC ==, ∠8CD =,∠10BD =, ∠DM x =,∠10BM x =-,如图,过点M 作ME BC ⊥于点E ,∠//ME DC ,∠BME BDC ∽,∠ME BM DC BD=, ∠485ME x =-,而12MBP S BP ME =⨯⨯, ∠2245y x x =-+,P 不与B 重合,那么0x >,可与点C 重合,那么6x ≤. 故y 与x 之间的函数关系式为224(06)5y x x x =-+<≤.故答案选A .26.A【分析】根据∠DEF 的面积=菱形的面积-∠ADF 的面积-∠CDE 的面积-∠BEF 的面积,据此表示出DEF 的面积即可.【详解】∠菱形ABCD 中,∠B=60°,∠∠ABC 是等边三角形,∠EF∠AC ,∠∠BFE 是等边三角形BE BF x ∴==BE x =2133224BEF x S x x ∴=⋅= 1AB = 1EC AF x ∴==- 1333(1)2244AFD CED S S x x ∴==-⋅=- 1331224ABCD S =⨯⨯=菱形 ()22333332144444DEF S x x x ⎛⎫∴=---=-- ⎪ ⎪⎝⎭(其中01x <<)故选A【点拨】本题考查了等边三角形的性质、平行线的性质,二次函数和几何图形综合,解决本题的关键是用x 将每个图形的面积表示出来.27.C【分析】先根据待定系数法求得抛物线的解析式,然后根据题意求得D (0,2),且DC∠x 轴,从而求得P 的纵坐标为2,代入求得的解析式即可求得P 的坐标.【详解】∠Rt ∠OAB 的顶点A (−2,4)在抛物线2y ax =上,∠4=4a ,解得a =1,∠抛物线为2y x =,∠OB =2,∠将Rt ∠OAB 绕点O 顺时针旋转90︒,得到∠OCD ,∠D 点在y 轴上,且OD =OB =2,∠D (0,2),∠DC ∠OD ,∠DC ∠x 轴,∠P 点的纵坐标为2,代入2y x =,得22x =, 解得2x =±, ∠P ()2,2 故答案为:() 2,2. 【点拨】考查二次函数图象上点的坐标特征, 坐标与图形变化-旋转,掌握旋转的性质是解题的关键. 28.C【解析】根据题意,沿AB 方向以2cm/s 的速度向点B 运动;同时点Q 从点A 出发,沿AC 方向以1cm/s 的速度向点C 运动,∠AP=2t ,AQ=t ,S ∠APQ =t 2,∠0<t∠4,∠三角形APQ 的最大面积是16.故选C.点睛:本题主要考查二次函数的应用,借助三角形的面积建立函数,利用函数探讨最值问题.29.(0,3)【分析】根据二次函数的平移规律得出新抛物线的解析式,再令x=0即可得出答案;【详解】解:∠抛物线2113=+y x 向上平移2个单位得到新抛物线的解析式为2133y x =+, ∠当x =0,则y =3,∠得到的新抛物线图象与y 轴的交点坐标为:(0,3).故答案为:(0,3).的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.30.3个【分析】先令y =0,得出关于x 的一元二次方程,由∠>0得方程有两个不相等的实数根,即抛物线与x 轴有两个不同的交点,与y 轴有一个交点.【详解】解:∠抛物线y =2x 2+2(k -1)x -k (k 为常数),∠当y =0时,0=2x 2+2(k -1)x -k ,∠∠=[2(k -1)]2-4×2×(-k )=4k 2+4>0,∠0=2x 2+2(k -1)x -k 有两个不相等的实数根,∠抛物线y =2x 2+2(k -1)x -k (k 为常数)与x 轴有两个交点,∠抛物线y =2x 2+2(k -1)x -k (k 为常数)与y 轴有一个交点,所以,抛物线()2221y x k x k =+--(k 为常数)与坐标轴交点有3个,故答案为:3个.【点拨】本题考查抛物线与x 、y 轴的交点,解答本题的关键是明确题意,利用二次函数的性质解答.31.x 1=1,x 2=﹣3【分析】根据题意可得抛物线的对称轴为:x =﹣1,又根据抛物线与x 轴的一个交点坐标为(﹣3,0),即可求出抛物线与x 轴的另一个交点坐标,即可求解.【详解】解:抛物线的对称轴为:x =22a a - =﹣1, 由图象可知,抛物线与x 轴的一个交点坐标为(﹣3,0), ∠抛物线与x 轴的另一个交点坐标为(1,0),∠一元二次方程ax 2+2ax ﹣3=0的两根为x 1=1,x 2=﹣3,故答案为:x 1=1,x 2=﹣3.【点拨】本题主要考查了抛物线与x 轴的交点坐标问题,利用数形结合找到抛物线与x 轴的另一个交点坐标是解题的关键.32.±2【分析】根据二次函数y =x 2﹣bx +1的图象与x 轴只有一个公共点,可知y =0时,方程x 2﹣bx +1=0有两个相等的实数根,解:∠二次函数y =x 2﹣bx +1的图象与x 轴只有一个公共点,∠y =0时,方程y =x 2﹣bx +1=0有两个相等的实数根.∠∠=(﹣b )2﹣4×1×1=0.解得,b =±2,故答案是:±2.【点拨】本题考查抛物线与x 轴的交点,解题的关键是明确二次函数21y x bx =-+的图象与x 轴只有一个公共点就是y =0时,方程21y x bx =-+有两个相等的实数根.33.2019【分析】利用二次函数图象上的坐标特征得到222018m m +=,然后利用整体代入得方法即可求解.【详解】将点(m ,0)代入抛物线y=x 2+2x ﹣2018可得:2220180m m +-=,∠222018m m +=∠221201812019m m ++=+=故答案为:2019【点拨】本题考查二次函数图象上的坐标特征,解题的关键是熟练掌握二次函数图象上的坐标满足二次函数解析式.34.x 1=0,x 2=﹣4【分析】从表格看,函数的对称轴为x =−2,根据函数的对称性,当x =0时和x =−2时,y 均为−2,即可求解.【详解】解:从表格看,函数二次函数y =ax 2+bx +c (a≠0)的对称轴为x =−2,根据函数的对称性,当x =0时和x =−2时,y 均为−2.故一元二次方程ax 2+bx +c =−2的根x =0或−4.故答案为:x 1=0,x 2=−4.【点拨】本题考查了二次函数与一元二次方程的关系,确定函数的对称轴是解题的关键.35.25【分析】要求飞机从滑行到停止的路程,即求出函数取最大值时,t 的值即可,因此将函数化为顶点式即可.【详解】解:()()222505062562525625y t t t t t =-=--++=--+即第25秒时,飞机滑行最大距离625m 停下来,故答案为:25.【点拨】本题主要考查了二次函数的应用,掌握二次函数求最值的方法,即公式法或配方法是解题关键. 36.-3或-2【解析】【分析】利用配方法将二次函数解析式由一般式变形为顶点式,结合y 的取值范围即可得出关于m 的一元一次不等式组,解之即可得出m 的取值范围,代入y=0求出x 的值,结合当m≤x≤m+3时y 的取值范围是0≤y≤4,即可得出m 的值,验证后即可得出结论.【详解】解:∠y=-x 2-2x+3=-(x+1)2+4,当y=0时,有-x 2-2x+3=0,解得:x 1=-3,x 2=1,由题意y 的取值范围是04y ≤≤,∠m=-3或m+3=1,则能使得y 的取值范围是04y ≤≤,∠m=-3或-2.故答案为:-3或-2.【点拨】本题考查了二次函数的性质以及二次函数图象上点的坐标特征,利用二次函数图象上点的坐标特征找出m 的值是解题的关键.37.x 1=﹣3,x 2=1【分析】关于x 的方程ax 2+bx =mx +n 的解为抛物线y =ax 2+bx 与直线y =mx +n 交点的横坐标,由此即可得到答案.【详解】∠抛物线y =ax 2+bx 与直线y =mx +n 相交于点A (﹣3,﹣6),B (1,﹣2),∠关于x 的方程ax 2+bx =mx +n 的解为x 1=﹣3,x 2=1.故答案为x 1=﹣3,x 2=1.【点拨】本题考查了抛物线与x 轴的交点:把求二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)与x 轴的交点坐标问题转化解关于x 的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.38.2【分析】求出∆的值,根据∆的值判断即可.【详解】∠抛物线与x轴有2个交点.故答案为:2.【点拨】本题考查了二次函数与坐标轴的交点问题,二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象与x轴的交点横坐标是一元二次方程ax2+bx+c=0的根.当∆=0时,二次函数与x轴有一个交点,一元二次方程有两个相等的实数根;当∆>0时,二次函数与x轴有两个交点,一元二次方程有两个不相等的实数根;当∆<0时,二次函数与x 轴没有交点,一元二次方程没有实数根.39.4.【详解】】解:y=x2﹣4x+n中,a=1,b=﹣4,c=n,b2﹣4ac=16﹣4n=0,解得n=4.故答案为4.40.-1【解析】试题分析:根据二次函数的图象与x轴的交点关于对称轴对称,直接求出x2的值由图可知,对称轴为x=1,根据二次函数的图象的对称性,=1,解得,x2=﹣1考点:抛物线与x轴的交点点评:此题考查了抛物线与x轴的交点,要注意数形结合,熟悉二次函数的图象与性质41.x≤-2或x≥3【分析】直接根据两函数图象的交点为A(-2,3)、B(3,-1)两点,进而结合函数图象得出y1≥y2时x的取值范围.【详解】解:如图所示:∠抛物线y1=x2+bx+c与直线y2=kx+m相交于A(-2,3)、B(3,-1)两点,∠y1≥y2时x的取值范围是:x≤-2或x≥3.故答案为:x≤-2或x≥3.42.0<x <2【分析】根据函数图象和二次函数的性质,可以得到(0,-3)关于对称轴对称的点,再结合图像可得x 的范围.【详解】解:由图象可得,该抛物线的对称轴为直线x =1,与y 轴的交点为(0,-3),故(0,-3)关于对称轴对称的点为(2,-3),故当y <-3时,x 的取值范围是0<x <2,故答案为:0<x <2.【点拨】本题考查了二次函数的图像和性质,解题的关键是理解3y <-,结合函数的对称性得到结果. 43.x <12-或x >16- 【分析】 根据原函数经过A ,B ,得到对应方程的两根,根据根与系数的关系得到b =-4a ,c =-12a ,将不等式cx 2+2bx -a <0化为12x 2+8x +1>0,解之即可.【详解】解:∠函数y =ax 2+2bx -c (a >0)的图象与x 轴交于A (2,0)、B (6,0)两点,∠ax 2+2bx -c =0(a >0)的两个实数根分别为x 1=2,x 2=6,∠2268b a -=+=,2612c a -=⨯=, ∠b =-4a ,c =-12a ,∠cx 2+2bx -a <0可化为-12ax 2-8ax -a <0,又a >0,∠12x 2+8x +1>0,令12x 2+8x +1=0,解得:x =16-或x =12-, ∠12>0,∠不等式的12x 2+8x +1>0解集为x <12-或x >16-. 【点拨】本题考查了二次函数与一元二次方程的关系,根与系数的关系,解题的关键是根据已知得到a ,b ,c 的关系.44.x ≤-1或x ≥2【分析】。
二次函数知识点总结及典型例题和练习(极好)

二次函数知识点总结及典型例题和练习(极好)知识点一:二次函数的概念和图像 1、二次函数的概念一般地,如果)0,,(2≠++=a c b a c bx ax y 是常数,,特别注意a 不为零,那么y 叫做x 的二次函数。
)0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。
2、二次函数的图像二次函数的图像是一条关于abx 2-=对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向;②有对称轴;③有顶点。
3、二次函数图像的画法--------五点作图法:(1)先根据函数解析式,求出顶点坐标,在平面直角坐标系中描出顶点M ,并用虚线画出对称轴(2)求抛物线c bx ax y ++=2与坐标轴的交点:当抛物线与x 轴有两个交点时,描出这两个交点A,B 及抛物线与y 轴的交点C ,再找到点C 的对称点D 。
将这五个点按从左到右的顺序连接起来,并向上或向下延伸,就得到二次函数的图像。
当抛物线与x 轴只有一个交点或无交点时,描出抛物线与y 轴的交点C 及对称点D 。
由C 、M 、D 三点可粗略地画出二次函数的草图。
如果需要画出比较精确的图像,可再描出一对对称点A 、B ,然后顺次连接五点,画出二次函数的图像。
【例1】 已知函数y=x 2-2x-3,(1)写出函数图象的顶点、图象与坐标轴的交点,以及图象与 y 轴的交点关于图象对称轴的对称点。
然后画出函数图象的草图;(2)求图象与坐标轴交点构成的三角形的面积:(3)根据第(1)题的图象草图,说 出 x 取哪些值时,① y=0;② y<0;③ y>0二次函数的解析式有三种形式:(1)一般式:)0,,(2≠++=a c b a c bx ax y 是常数,(2) 交点式:当抛物线c bx ax y ++=2与x 轴有交点时,即对应的一元二次方程02=++c bx ax 有实根1x 和2x 存在时,根据二次三项式的分解因式))((212x x x x a c bx ax --=++,二次函数c bx ax y ++=2可转化为两根式))((21x x x x a y --=。
二次函数基础练习题大全(含答案)(完整资料).doc

【最新整理,下载后即可编辑】二次函数基础练习题练习一 二次函数1、 一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离s (米)与时间t (秒)的数据如下表:写出用t 表示s 的函数关系式:2、 下列函数:① 23y x ;② 21y x x x ;③ 224y x x x;④ 21yx x ; ⑤ 1y x x ,其中是二次函数的是 ,其中a ,b ,c3、当m 时,函数2235y m x x (m 为常数)是关于x 的二次函数4、当____m 时,函数2221m m y m m x 是关于x 的二次函数5、当____m 时,函数2564m m y m x +3x 是关于x 的二次函数6、若点 A ( 2, m ) 在函数 12-=x y 的图像上,则 A 点的坐标是____.7、在圆的面积公式 S =πr 2 中,s 与 r 的关系是( )A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系 8、正方形铁片边长为15cm ,在四个角上各剪去一个边长为x (cm )的小正方形,用余下的部分做成一个无盖的盒子.(1)求盒子的表面积S (cm 2)与小正方形边长x (cm )之间的函数关系式;(2)当小正方形边长为3cm 时,求盒子的表面积.9、如图,矩形的长是 4cm ,宽是 3cm ,如果将长和宽都增加 x cm , 那么面积增加 ycm 2, ① 求 y 与 x 之间的函数关系式.② 求当边长增加多少时,面积增加 8cm 2.10、已知二次函数),0(2≠+=a c ax y 当x=1时,y= -1;当x=2时,y=2,求该函数解析式.11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料,建造猪舍三间,如图,它们的平面图是一排大小相等的长方形.(1) 如果设猪舍的宽AB 为x 米,则猪舍的总面积S(米2)与x 有怎样的函数关系?(2) 请你帮富根老伯计算一下,如果猪舍的总面积为32米2,应该如何安排猪舍的长BC 和宽AB 的长度?旧墙的长度是否会对猪舍的长度有影响?怎样影响?练习二 函数2ax y =的图像与性质1、填空:(1)抛物线221x y =的对称轴是(或 ),顶点坐标是 ,当x时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小,当x= 时,该函数有最 值是 ;(2)抛物线221x y -=的对称轴是 (或 ),顶点坐标是 ,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小,当x= 时,该函数有最 值是 ;2、对于函数22x y =下列说法:①当x 取任何实数时,y 的值总是正的;②x 的值增大,y 的值也增大;③y 随x 的增大而减小;④图像关于y 轴对称.其中正确的是 .3、抛物线 y =-x 2 不具有的性质是( )A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点4、苹果熟了,从树上落下所经过的路程 s 与下落时间 t 满足 S =12gt 2(g =9.8),则 s 与 t 的函数图像大致是( )B C D5、函数2ax y =与b ax y +-=的图像可能是( )A .B .C .D .6、已知函数24m m y mx 的图像是开口向下的抛物线,求m 的值.7、二次函数12-=m mx y 在其图像对称轴的左侧,y 随x 的增大而增大,求m 的值. 8、二次函数223x y -=,当x 1>x 2>0时,求y 1与y 2的大小关系.9、已知函数()422-++=m m x m y 是关于x 的二次函数,求:(1) 满足条件的m 的值;(2) m 为何值时,抛物线有最低点?求出这个最低点,这时x 为何值时,y 随x 的增大而增大; st O st O s t O s t O(3) m 为何值时,抛物线有最大值?最大值是多少?当x 为何值时,y 随x 的增大而减小?10、如果抛物线2y ax 与直线1y x 交于点,2b ,求这条抛物线所对应的二次函数的关系式.练习三 函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小.2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标 、 .3、任给一些不同的实数k ,得到不同的抛物线k x y +=2,当k 取0,1±时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最底点.其中判断正确的是 .4、将抛物线122-=x y 向上平移4个单位后,所得的抛物线是 ,当x= 时,该抛物线有最 (填大或小)值,是 .5、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称,则m =________;6、二次函数c ax y +=2()0≠a 中,若当x 取x 1、x 2(x 1≠x 2)时,函数值相等,则当x 取x 1+x 2时,函数值等于 .练习四 函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ,顶点坐标是 ,当x 时,y 随x 的增大而减小, 函数有最 值 .2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标.(1)右移2个单位;(2)左移32个单位;(3)先左移1个单位,再右移4个单位.3、请你写出函数()21+=x y 和12+=x y 具有的共同性质(至少2个).4、二次函数()2h x a y -=的图象如图:已知21=a ,OA=OC ,试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为A ,与y 轴交点为B ,求A 、B 两点坐标及⊿AOB 的面积.6、二次函数2)4(-=x a y ,当自变量x 由0增加到2时,函数值增加6.(1)求出此函数关系式.(2)说明函数值y 随x 值的变化情况.7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上,求k 的值.练习五 ()k h x a y +-=2的图象与性质1、请写出一个二次函数以(2, 3)为顶点,且开口向上.____________.2、二次函数 y =(x -1)2+2,当 x =____时,y 有最小值.3、函数 y =12 (x -1)2+3,当 x ____时,函数值 y 随 x 的增大而增大.4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向 平移3个单位,再向 平移2个单位得到.5、 已知抛物线的顶点坐标为2,1,且抛物线过点3,0,则抛物线的关系式是6、 如图所示,抛物线顶点坐标是P (1,3),则函数y 随自变量x 的增大而减小的x 的取值范围是( )A 、x>3B 、x<3C 、x>1D 、x<17、已知函数()9232+--=x y .(1) 确定下列抛物线的开口方向、对称轴和顶点坐标;(2)当x= 时,抛物线有最值,是.(3)当x 时,y随x的增大而增大;当x 时,y随x 的增大而减小.(4)求出该抛物线与x轴的交点坐标及两交点间距离;(5)求出该抛物线与y轴的交点坐标;(6)该函数图象可由23x=的图象经过怎样的平移得到的?y-8、已知函数()412-y.=x+(1)指出函数图象的开口方向、对称轴和顶点坐标;(2)若图象与x轴的交点为A、B和与y轴的交点C,求△ABC的面积;(3)指出该函数的最值和增减性;(4)若将该抛物线先向右平移2个单位,在向上平移4个单位,求得到的抛物线的解析式;(5)该抛物线经过怎样的平移能经过原点.(6)画出该函数图象,并根据图象回答:当x取何值时,函数值大于0;当x取何值时,函数值小于0.练习六c=2的图象和性质y++bxax1、抛物线942+y的对称轴是.x+=x2、抛物线2522+12y的开口方向是,顶点坐标x=x-是 .3、试写出一个开口方向向上,对称轴为直线x=-2,且与y 轴的交点坐标为(0,3)的抛物线的解析式 .4、将 y =x 2-2x +3 化成 y =a (x -h)2+k 的形式,则 y =____.5、把二次函数215322y x x 的图象向上平移3个单位,再向右平移4个单位,则两次平移后的函数图象的关系式是6、抛物线1662--=x x y 与x 轴交点的坐标为_________;7、函数x x y +-=22有最____值,最值为_______;8、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位,再沿y 轴向上平移3个单位,得到的图象的函数解析式为122+-=x x y ,则b 与c 分别等于( )A 、6,4B 、-8,14C 、-6,6D 、-8,-149、二次函数122--=x x y 的图象在x 轴上截得的线段长为( )A 、22B 、23C 、32D 、3310、通过配方,写出下列函数的开口方向、对称轴和顶点坐标:(1)12212+-=x x y ; (2)2832-+-=x x y ; (3)4412-+-=x x y 11、把抛物线1422++-=x x y 沿坐标轴先向左平移2个单位,再向上平移3个单位,问所得的抛物线有没有最大值,若有,求出该最大值;若没有,说明理由.12、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标 13、已知一次函数的图象过抛物线223y x x 的顶点和坐标原点1) 求一次函数的关系式;2) 判断点2,5是否在这个一次函数的图象上14、某商场以每台2500元进口一批彩电.如每台售价定为2700元,可卖出400台,以每100元为一个价格单位,若将每台提高一个单位价格,则会少卖出50台,那么每台定价为多少元即可获得最大利润?最大利润是多少元? 练习七 c bx ax y ++=2的性质1、函数2y x px q 的图象是以3,2为顶点的一条抛物线,这个二次函数的表达式为2、二次函数2224y mx x m m 的图象经过原点,则此抛物线的顶点坐标是3、如果抛物线2y ax bx c 与y 轴交于点A (0,2),它的对称轴是1x ,那么ac b4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点,与y 轴交于点C ,且线段AB 的长为1,△ABC 的面积为1,则b 的值为______.5、已知二次函数c bx ax y ++=2的图象如图所示,则a___0,b___0,c___0,ac b 42-____0;6、二次函数c bx ax y ++=2的图象如图,则直线bc ax y +=的图象不经过第 象限.7、已知二次函数2y ax bx c (0≠a )的图象如图所示,则下列结论: 1),a b 同号;2)当1x 和3x 时,函数值相同;3)40a b ;4)当2y 时,x 的值只能为0;其中正确的是(第5题) (第6题) (第7题) (第10题)8、已知二次函数2224m mx x y +--=与反比例函数xm y 42+=的图象在第二象限内的一个交点的横坐标是-2,则m=9、二次函数2y x ax b 中,若0a b ,则它的图象必经过点( )A1,1 B 1,1 C 1,1 D 1,110、函数b ax y +=与c bx ax y ++=2的图象如上图所示,则下列选项中正确的是( )A 、0,0>>c abB 、0,0><c abC 、0,0<>c abD 、0,0<<c ab11、已知函数c bx ax y ++=2的图象如图所示,则函数b ax y +=的图象是( )12、二次函数c bx ax y ++=2的图象如图,那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中,值为正数的有( )A .4个B .3个C .2个D .1个13、抛物线的图角如图,则下列结论:①>0;②;③>;④<1.其中正确的结论是( ).(A )①② (B )②③ (C )②④ (D )③④14、二次函数2y ax bx c 的最大值是3a ,且它的图象经过1,2,1,6两点,求a 、b 、c 的值。
二次函数知识点及重点题练习答案解析
答案
基础训练
1
3
1.函数 y= 的大致图象是( B ).
【解析】取值验证可知,函数
1
y= 3 的大致图象是选项
B 中的图象.
答案
解析
2
2.若二次函数 y=-2x -4x+t 的图象的顶点在 x 轴上,则 t 的值是( C ).
A.-4
B.4
C.-2
D.2
【解析】∵二次函数的图象的顶点在 x 轴上,∴Δ=16+8t=0,可
2.五种常见幂函数的图象
答案
3.幂函数的性质
(1)当 α>0 时,幂函数 y=xα 的图象过点 (0,0) 和 (1,1) ,在(0,+∞)上
是 增函数 .在第一象限内,当 α>1 时,图象下凹,当 0<α<1 时,图象上凸.
(2)当 α<0 时,幂函数 y=xα 的图象过点 (1,1) ,在(0,+∞)上是 减函数 .
4
2
∴h(m)=
-2m +
2
17 3
4
, < m ≤ 1,
4
3
-3 + 4m + 2,0 < m ≤ .
4
点拨:解决二次函数最值问题的关键是抓住“三点一轴”,其中“三点”
是指区间的两个端点和抛物线的顶点,“一轴”指的是对称轴,结合配方法,
根据函数的单调性及分类讨论思想即可解题.
点拨
【追踪训练 2】已知函数 f(x)=-x2+2ax+1-a 在[0,1]上的最大值为 2,求
当 a≠0 时,f(x)图象的对称轴为直线
3-
x= ,
二次函数各知识点、考点、典型例题及练习

二次函数各知识点、考点、典型例题及练习二次函数各知识点、考点、典型例题及对应练习(超全)【典型例题】题型 1 二次函数的概念例1(基础).二次函数2365=--+的图像的顶点坐标是y x x()A.(-1,8) B.(1,8)C(-1,2)D (1,-4)点拨:本题主要考察二次函数的顶点坐标公式例2.(拓展,2008年武汉市中考题,12)下列命题中正确的是○1若b2-4ac>0,则二次函数y=ax2+bx+c的图象与坐标轴的公共点的个数是2或3○2若b2-4ac=0,则二次函数y=ax2+bx+c的图象与x轴只有一个交点,且这个交点就是抛物线顶点。
○3当c=-5时,不论b为何值,抛物线y=ax2+bx+c一定过y轴上一定点。
○4若抛物线y=ax2+bx+c与x轴有唯一公共点,则方程ax2+bx+c=0有两个相等的实数根。
○5若抛物线y=ax2+bx+c与x轴有两个交点A、B,与y 轴交于c点,c=4,S=6,则抛物线解析式为y=x2△ABC-5x+4。
○6若抛物线y=ax2+bx+c(a≠0)的顶点在x轴下方,则一元二次方程ax2+bx+c=0有两个不相等的实数根。
○7若抛物线y=ax 2+bx+c (a ≠0)经过原点,则一元二次方程ax 2+bx+c=0必有一根为0。
○8若a -b+c=2,则抛物线y=ax 2+bx+c (a ≠0)必过一定点。
○9若b 2<3ac ,则抛物线y=ax 2+bx+c 与x 轴一定没有交点。
○10若一元二次方程ax 2+bx+c=0有两个不相等的实数根,则函数y=cx 2+bx+a 的图象与x 轴必有两个交点。
○11若b=0,则抛物线y=ax 2+bx+c 与x 轴的两个交点一个在原点左边,一个在原点右边。
点拨:本题主要考查二次函数图象及其性质,一元二次方程根与系数的关系,及二次函数和一元二次方程二者之间的联系。
复习时,抓住系数a 、b 、c 对图形的影响的基本特点,提升学生的数形结合能力,抓住抛物线的四点一轴与方程的关系,训练学生对函数、方程的数学思想的运用。
二次函数专题训练(带答案)

二次函数知识点第一节 二次函数的定义、图像、性质1.下列函数解析式中,一定为二次函数的是( ) A.13-=x yB.c bx ax y ++=2C.1222+-=t t sD.xx y 12+= 【解答】解:A 、y=3x ﹣1是一次函数,故A 错误;B 、y=ax 2+bx+c (a ≠0)是二次函数,故B 错误; C 、s=2t 2﹣2t+1是二次函数,故C 正确;D 、y=x 2+不是二次函数,故D 错误;故选:C .2.下列函数是二次函数的是( ) A.12+=x yB.12+-=x yC.22+=x yD.221-=x y 【解答】解:A 、y=2x+1,是一次函数,故此选项错误;B 、y=﹣2x+1,是一次函数,故此选项错误; D 、y=x 2+2是二次函数,故此选项正确;D 、y=x ﹣2,是一次函数,故此选项错误.故选:C .3.下列函数关系中,是二次函数的是( ) A.在弹性限度内,弹簧的长度y 与所挂物体质量x 之间的关系B.当距离一定时,火车行驶的时间t 与速度v 之间的关系C.等边三角形的周长C 与边长a 之间的关系D.圆心角为︒120的扇形面积S 与半径R 之间的关系【解答】解:A 、y=mx+b ,当m ≠0时(m 是常数),是一次函数,错误;B 、t=,当s ≠0时,是反比例函数,错误;C 、C=3a ,是正比例函数,错误;D 、S=πR 2,是二次函数,正确.故选:D .4.二次函数722-+=x x y 的函数值是8,那么对应的x 的值是( )A.3B.5C.-3和5D.3和-5【解答】解:根据题意,得x 2+2x ﹣7=8,即x 2+2x ﹣15=0,解得x=3或﹣5,故选:D .5.已知一次函数c x ab y +=的图象如图,则二次函数c bx ax y ++=2在平面直角坐标系中的图象可能是( )A. B. C.D.【解答】解:观察函数图象可知:<0、c >0,∴二次函数y=ax 2+bx+c 的图象对称轴x=﹣>0,与y 轴的交点在y 轴负正半轴.故选:A .6.如图,函数122+-=x ax y 和a ax y -=(a 是常数,且0≠a )在同一平面直角坐标系的图象可能是( )A. B. C. D.【解答】解:A 、由一次函数y=ax ﹣a 的图象可得:a <0,此时二次函数y=ax 2﹣2x+1的图象应该开口向下,故选项错误;B 、由一次函数y=ax ﹣a 的图象可得:a >0,此时二次函数y=ax 2﹣2x+1的图象应该开口向上,对称轴x=﹣>0,故选项正确;C 、由一次函数y=ax ﹣a 的图象可得:a >0,此时二次函数y=ax 2﹣2x+1的图象应该开口向上,对称轴x=﹣>0,和x 轴的正半轴相交,故选项错误;D 、由一次函数y=ax ﹣a 的图象可得:a >0,此时二次函数y=ax 2﹣2x+1的图象应该开口向上,故选项错误.故选:B .7.函数)(k x k y -=与2kx y =,)0(≠=k xky ,在同一坐标系上的图象正确的是( )A. B.C. D.【解答】解:一次函数y=k (x ﹣k )=kx ﹣k 2,∵k ≠0,∴﹣k 2<0,∴一次函数与y 轴的交点在y 轴负半轴. A 、一次函数图象与y 轴交点在y 轴正半轴,A 不正确;B 、一次函数图象与y 轴交点在y 轴正半轴,B 不正确;C 、一次函数图象与y 轴交点在y 轴负半轴,C 可以;D 、一次函数图象与y 轴交点在y 轴正半轴,D 不正确.故选:C .8.如图,二次函数bx ax y +=2的图象开口向下,且经过第三象限的点P .若点P 的横坐标为-1,则一次函数b x b a y +-=)(的图象大致是()A .B .C .D .【解答】解:由二次函数的图象可知,a <0,b <0,当x=﹣1时,y=a ﹣b <0, ∴y=(a ﹣b )x+b 的图象在第二、三、四象限,故选:D .9.已知二次函数33222+++=a ax ax y (其中x 是自变量),当2≥x 时,y 随x 的增大而增大,且12≤≤-x 时,y 的最大值为9,则a 的值为( )A.1或﹣2B.2-或2C.2D.1【解答】解:∵二次函数y=ax 2+2ax+3a 2+3(其中x 是自变量),∴对称轴是直线x=﹣=﹣1,∵当x ≥2时,y 随x 的增大而增大,∴a >0,∵﹣2≤x ≤1时,y 的最大值为9,∴x=1时,y=a+2a+3a 2+3=9, ∴3a 2+3a ﹣6=0,∴a=1,或a=﹣2(不合题意舍去).故选:D .10.抛物线5)2(32+-=x y 的顶点坐标是( )A.(-2,5)B.(-2,-5)C.(2,5)D.(2,-5)【解答】解:抛物线y=3(x ﹣2)2+5的顶点坐标为(2,5),故选:C .11.关于二次函数1422-+=x x y ,下列说法正确的是( )A.图象与y 轴的交点坐标为(0,1)B.图象的对称轴在y 轴的右侧C.当0<x 时,y 的值随x 值的增大而减小D.y 的最小值为-3【解答】解:∵y=2x 2+4x ﹣1=2(x+1)2﹣3,∴当x=0时,y=﹣1,故选项A 错误,该函数的对称轴是直线x=﹣1,故选项B 错误,当x <﹣1时,y 随x 的增大而减小,故选项C 错误, 当x=﹣1时,y 取得最小值,此时y=﹣3,故选项D 正确,故选:D .12.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA ,O 恰为水面中心,安置在柱子顶端A 处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA 的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y (m)与水平距离x (m)之间的关系式是322++-=x x y ,则下列结论:(1)柱子OA 的高度为3m ;(2)喷出的水流距柱子1m 处达到最大高度;(3)喷出的水流距水平面的最大高度是4m ;(4)水池的半径至少要3m 才能使喷出的水流不至于落在池外.其中正确的有( )A.1个B.2个C.3个D.4【解答】解:∵y=﹣x 2+2x+3=﹣(x ﹣1)2+4,∴当x=0时,y=3,即OA=3m ,故(1)正确, 当x=1时,y 取得最大值,此时y=4,故(2)和(3)正确,当y=0时,x=3或x=﹣1(舍去),故(4)正确,故选:D . 13.如图,抛物线()02≠++=a c bx ax y 的对称轴为直线1=x ,与x 轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①ac b 42-;②方程02=++c bx ax 的两个根是11-=x ,32=x ;③3ca->;④当0>y 时,x 的取值范围是31≤<-x ;⑤当0>x 时,y 随x 增大而增大. 上述五个结论中正确的有 (填序号)【解答】解:∵抛物线与x 轴有2个交点,∴b 2﹣4ac >0,即b 2>4ac ,所以①正确; ∵抛物线的对称轴为直线x=1,而点(﹣1,0)关于直线x=1的对称点的坐标为(3,0), ∴方程ax 2+bx+c=0的两个根是x 1=﹣1,x 2=3,所以②正确;∵x=﹣=1,即b=﹣2a ,而x=﹣1时,y=0,即a ﹣b+c=0,∴a+2a+c=0,∴3a+c=0,即a=﹣,所以③错误;∵抛物线与x 轴的两点坐标为(﹣1,0),(3,0),∴当﹣1<x <3时,y >0,所以④错误; ∵抛物线的对称轴为直线x=1,∴当x <1时,y 随x 增大而增大,所以⑤错误. 故答案为①②. 14.已知二次函数()()m x m x y ---=22(m 为常数).(1)求该二次函数图象与x 轴的交点坐标; (2)求该二次函数图象的顶点P 的坐标;(3)如将该函数的图象向左平移3个单位,再向上平移1个单位,得到函数2x y =的图象,直接写出m的值.【解答】解:(1)当y=0时,(x ﹣m )2﹣2(x ﹣m )=0,(x ﹣m )(x ﹣m ﹣2)=0,解得x 1=m ,x 2=m+2,∴该二次函数图象与x 轴的交点坐标为(m ,0),(m+2,0);(2)∵y=[x ﹣(m+1)]2﹣1,∴该二次函数图象的顶点P 的坐标为(m+1,﹣1);(3)∵该函数的图象向左平移3个单位,再向上平移1个单位,∴平移的顶点坐标为(m+1﹣3,﹣1+1),即顶点坐标为(m ﹣2,0),∵平移后的抛物线为y=x 2,即平移后的抛物线顶点坐标为(0,0), ∴m ﹣2=0,∴m=2.第二节 待定系数法、图像与系数关系1.已知二次函数的图象过(0,1),(2,4),(3,10)三点,求这个二次函数的解析式.2.已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2).求此二次函数的解析式.3.已知二次函数c bx ax y ++=2,当4=x 时,3=y ;当1-=x 时,8-=y ;当2=x 时,1=y .求这个二次函数的解析式.4.已知二次函数图象的顶点坐标为(1,-1),且过原点(0,0),求该二次函数的解析式.5.已知一个二次函数的图象与x 轴的两个交点的坐标分别为(-1,0)和(2,0),与y 轴的交点坐标为(0,-2),求这个二次函数的解析式.6.如图所示,已知二次函数c bx x y ++=2过点)0,1(A ,)3,0(-C .(1)求此二次函数的解析式;(2)在抛物线上存在一点P 使ABP ∆的面积为10,请直接写出点P 的坐标.7.如图,直线l 过点)0,4(A 和)4,0(B 两点,它与二次函数2ax y =的图象在第一象限内交于点P ,若29=∆AOPS ,求二次函数的解析式.8.抛物线c bx x y ++-=231经过点)0,33(A 和点)3,0(B ,且这个抛物线的对称轴为直线l ,顶点为C .(1)求抛物线的解析式; (2)连接AB 、AC 、BC ,求△ABC ABC ∆的面积.【解答】解:(1)∵抛物线经过A、B (0,3)∴由上两式解得∴抛物线的解析式为:;(2)由(1)抛物线对称轴为直线x=把x=代入,得y=4则点C 坐标为(,4)设线段AB 所在直线为:y=kx+b 解得AB 解析式为:∵线段AB 所在直线经过点A 、B (0,3)抛物线的对称轴l 于直线AB 交于点D∴设点D 的坐标为D 将点D代入,解得m=2∴点D 坐标为,∴CD=CE ﹣DE=2过点B 作BF ⊥l 于点F ∴BF=OE=∵BF+AE=OE+AE=OA=∴S △ABC =S △BCD +S △ACD =CD •BF+CD •AE∴S △ABC =CD (BF+AE )=×2×=9.已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,下列结论:①0>abc ;②02>+b a ;③042>-ac b;④0>+-c b a ,其中正确的个数是( )A.1B.2C.3D.4解:①∵抛物线对称轴是y 轴的右侧,∴ab <0,∵与y 轴交于负半轴,∴c <0,∴abc >0,故①正确; ②∵a >0,x=﹣<1,∴﹣b <2a ,∴2a+b >0,故②正确;③∵抛物线与x 轴有两个交点,∴b 2﹣4ac >0,故③正确; ④当x=﹣1时,y >0,∴a ﹣b+c >0,故④正确.故选:D . 10.如图,已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,有下列5个结论:①0>abc ;②c a b >-;③024>++c b a ;④c a ->3;⑤)(b am m b a +>+(1≠m 的实数).其中正确结论的有( )A.①②③B.②③⑤C.②③④D.③④⑤【解答】解:①∵对称轴在y 轴的右侧,∴ab <0,由图象可知:c >0,∴abc <0,故①不正确; ②当x=﹣1时,y=a ﹣b+c <0,∴b ﹣a >c ,故②正确;③由对称知,当x=2时,函数值大于0,即y=4a+2b+c >0,故③正确; ④∵x=﹣=1,∴b=﹣2a ,∵a ﹣b+c <0,∴a+2a+c <0,3a <﹣c ,故④不正确;⑤当x=1时,y 的值最大.此时,y=a+b+c ,而当x=m 时,y=am 2+bm+c ,所以a+b+c >am 2+bm+c (m ≠1),故a+b >am 2+bm ,即a+b >m (am+b ),故⑤正确.故②③⑤正确.故选:B .11.已知二次函数c bx ax y ++=2的图象如图所示,则下列说法正确的是( )A.0<acB.0<bC.042<-ac bD.0<++c b a【解答】解:∵抛物线开口向上,∴a >0,∵抛物线交于y 轴的正半轴,∴c >0,∴ac >0,A 错误; ∵﹣>0,a >0,∴b <0,∴B 正确;∵抛物线与x 轴有两个交点,∴b 2﹣4ac >0,C 错误;当x=1时,y >0,∴a+b+c >0,D 错误;故选:B .12.已知二次函数c bx ax y ++=2的图象如图所示,OC OA =,则由抛物线的特征写出如下含有c b a ,,三个字母的等式或不等式:①1442-=-ab ac ;②01=++b ac ;③0>abc ;④0>+-c b a .其中正确的个数是( )A.4个B.3个C.2个D.1个【解答】解:①=﹣1,抛物线顶点纵坐标为﹣1,正确;②ac+b+1=0,设C (0,c ),则OC=|c|,∵OA=OC=|c|,∴A (c ,0)代入抛物线得ac 2+bc+c=0,又c ≠0,∴ac+b+1=0,故正确; ③abc >0,从图象中易知a >0,b <0,c <0,故正确;④a ﹣b+c >0,当x=﹣1时y=a ﹣b+c ,由图象知(﹣1,a ﹣b+c )在第二象限,∴a ﹣b+c >0,故正确.故选:A .13.若抛物线c bx x y ++-=2经过点(-2,3),则942--b c 的值是( )A.5B.-1C.4D.18【解答】解:∵抛物线y=﹣x 2+bx+c 经过点(﹣2,3),∴﹣(﹣2)2﹣2b+c=3,整理得,﹣2b+c=7, ∴2c ﹣4b ﹣9=2(c ﹣2b )﹣9=2×7﹣9=5,故选:A .14.已知抛物线)0(2>=a ax y 过),2(1y A -、),1(2y B 两点,则下列关系式一定正确的是( )A.210y y >> B.120y y >>C.021>>y yD.012>>y y【解答】解:∵抛物线y=ax 2(a >0),∴A (﹣2,y 1)关于y 轴对称点的坐标为(2,y 1). 又∵a >0,0<1<2,∴y 2<y 1.故选:C .15.将抛物线322++=x x y 向下平移3个单位长度后,所得到的抛物线与直线3=y 的交点坐标是( )A.(0,3)或(-2,3)B.(-3,0)或(1,0)C.(3,3)或(-1,3)D.(-3,3)或(1,3)【解答】解:将抛物线y=x 2+2x+3向下平移3个单位长度后,所得到的抛物线为y=x 2+2x当该抛物线与直线y=3相交时,x 2+2x=3解得:x 1=﹣3,x 2=1则交点坐标为:(﹣3,3)(1,3)故选:D .16.将抛物线2x y =向左平移2个单位,再向下平移5个单位,平移后所得新抛物线的表达式为( )A.5)2(2-+=x yB.5)2(2++=x yC.5)2(2--=x yD.5)2(2+-=x y【解答】解:抛物线y=x 2的顶点坐标为(0,0),先向左平移2个单位再向下平移5个单位后的抛物线的顶点坐标为(﹣2,﹣5),所以,平移后的抛物线的解析式为y=(x+2)2﹣5.故选:A .第三节 最值问题、一元二次方程、实际应用1.已知二次函数2)(h x y --=(h 为常数),当自变量x 的值满足52≤≤x 时,与其对应的函数值y 的最大值为-1,则h 的值为( ) A.3或6B.1或6C.1或3D.4或6【解答】解:当h <2时,有﹣(2﹣h )2=﹣1,解得:h 1=1,h 2=3(舍去);当2≤h ≤5时,y=﹣(x ﹣h )2的最大值为0,不符合题意;当h >5时,有﹣(5﹣h )2=﹣1, 解得:h 3=4(舍去),h 4=6.综上所述:h 的值为1或6.故选:B .2.当1+≤≤a x a 时,函数122+-=x x y 的最小值为1,则a 的值为( )A.-1B.2C.0或2D.-1或2【解答】解:当y=1时,有x 2﹣2x+1=1,解得:x 1=0,x 2=2.∵当a ≤x ≤a+1时,函数有最小值1,∴a=2或a+1=0,∴a=2或a=﹣1,故选:D . 3.函数c bx ax y ++=2的图象如图所示,那么关于x 的一元二次方程032=-++c bx ax 的跟的情况是( )A.有两个不相等的实数根B.有两个异号的实数根C.有两个相等的实数根D.没有实数根4.在平面直角坐标系中,二次函数c bx x y ++=221的图像如图所示,关于x的方程m c bx x =++221有实数根,则m 的取值范围是5.某大学生利用课余时间在网上销售一种成本为50元/件的商品,每月的销售量y (件)与销售单价x (元/件)之间的函数关系式为4404+-=x y ,要获得最大利润,该商品的售价应定为()A .60元B .70元C .80元D .90元【解答】解:设销售该商品每月所获总利润为w , 则w=(x ﹣50)(﹣4x+440) =﹣4x 2+640x ﹣22000 =﹣4(x ﹣80)2+3600,∴当x=80时,w 取得最大值,最大值为3600,即售价为80元/件时,销售该商品所获利润最大,故选:C .6.竖直向上发射的小球的高度)(m h 关于运动时间)(s t 的函数表达式为bt ath +=2,其图象如图,若小球在发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( ) A.第3秒 B.第3.5秒 D.第4.2秒 D.第6.5秒7.如图,ABC ∆是直角三角形,︒=∠90A ,cm AB 8=,cm AC 6=点P 从点A 出发,沿AB 方向以s cm /2的速度向点B 运动;同时点Q 从点A 出发沿AC 方向以s cm /1的速度向点C 运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ 的最大面积是( )A.28cm B.216cm C.224cm D.232cm8.跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系()02≠++=a c bx ax y .如图记录了某运动员起跳后的x 与y 的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离是多少?【解答】解:根据题意知,抛物线y=ax 2+bx+c (a ≠0)经过点(0,54.0)、(40,46.2)、(20,57.9),则解得,所以x=﹣==15(m ).9.已知二次函数c bx x y ++-=2163的图象经过()3,0A ,⎪⎭⎫ ⎝⎛--29,4B 两点.(1)求c b ,的值. (2)二次函数c bx x y ++-=2163的图象与x 轴是否有公共点?若有,求公共点的坐标;若没有,请说明情况.【解答】解:(1)把A (0,3),B (﹣4,﹣)分别代入y=﹣x 2+bx+c ,得,解得;(2)由(1)可得,该抛物线解析式为:y=﹣x 2+x+3.△=()2﹣4×(﹣)×3=>0,所以二次函数y=﹣x 2+bx+c 的图象与x 轴有公共点.∵﹣x 2+x+3=0的解为:x 1=﹣2,x 2=8∴公共点的坐标是(﹣2,0)或(8,0).10.设二次函数()b a bx ax y +-+=2(a ,b 是常数,0≠a ).(1)判断该二次函数图象与x 轴的交点的个数,说明理由. (2)若该二次函数图象经过()4,1-A ,()1,0-B ,()1,1C 三个点中的其中两个点,求该二次函数的表达式.(3)若0<+b a ,点()m P,2()0>m 在该二次函数图象上,求证:0>a .【解答】解:(1)设y=0∴0=ax 2+bx ﹣(a+b )∵△=b 2﹣4•a[﹣(a+b )]=b 2+4ab+4a 2=(2a+b )2≥0 ∴方程有两个不相等实数根或两个相等实根.∴二次函数图象与x 轴的交点的个数有两个或一个(2)当x=1时,y=a+b ﹣(a+b )=0∴抛物线不经过点C 把点A (﹣1,4),B (0,﹣1)分别代入得解得∴抛物线解析式为y=3x 2﹣2x ﹣1(3)当x=2时m=4a+2b ﹣(a+b )=3a+b >0①∵a+b <0∴﹣a ﹣b >0② ①②相加得:2a >0∴a >011.已知二次函数()()312---=m x x y (m 为常数).(1)求证:不论m 为何值,该函数的图象与x 轴总有公共点; (2)当m 取什么值时,该函数的图象与y 轴的交点在x 轴的上方?【解答】(1)证明:当y=0时,2(x ﹣1)(x ﹣m ﹣3)=0, 解得:x 1=1,x 2=m+3.当m+3=1,即m=﹣2时,方程有两个相等的实数根; 当m+3≠1,即m ≠﹣2时,方程有两个不相等的实数根. ∴不论m 为何值,该函数的图象与x 轴总有公共点; (2)解:当x=0时,y=2(x ﹣1)(x ﹣m ﹣3)=2m+6, ∴该函数的图象与y 轴交点的纵坐标为2m+6,∴当2m+6>0,即m >﹣3时,该函数的图象与y 轴的交点在x 轴的上方.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数知识点基本方法专项训练一.解析式的理解1.顶点式:y=a (x-h )2-k 中a 的作用—————————————— h 的作用————————————,k 的作用——————————顶点是——————————————,当x=_______时,y 最大值_______ 抛物线必须在顶点式的条件下进行,先将y=ax 2向_______再向_______在________________________条件时,选择设抛物线解析式为顶点式 2.求下列抛物线与x 轴的交点坐标,并说明你发现Y=2(x-1)(x-3) y=-5(x-3)(x-2) y= -7(x-8)(x-9)你的发现是________________________已知抛物线与x 轴的两交点(x 1,0) (x 2,0)则有解析式:y=a(x-x 1)(x-x 2) 当条件中有_____________________时可设解析式为交点式3.一般式y=ax 2+bx+c 当已知抛物线上的三个点时可设解析式为一般式得到一个三元一次方程组(1)a 的作用确定抛物线的开口,形状,增减性,抛物线是由y=ax 2平移得到的 (2)a,b 由公式x=ab2-确定对称轴 (3)a.b.c 由公式_____________________确定顶点,由公式_____________________确定最值(4)c 的作用确定抛物线与y 轴的交点坐标为_____________________ (5)由∆=b 2-4ac 确定抛物线与x 轴交点的个数当∆>0时__________________∆<时________当∆=0时________(6)当x=1时有函数值y=________,当x= -1时,有函数值y= ________ 练习一1.抛物线y=ax 2+bx +c (a ≠0)的对称轴是x=2,且经过点P (3,0),则a +b +c 的值为( )A .-1B .0C .1D .22.函数y=-x 2+bx +c 的图象最高点是(1,-4),则b 、c 的值分别是( ) A .2,5 B .-2,-5 C .-2,5 D .2,-5 3.二次函数y=ax 2+bx +c 的图象如图所示,下列结论: ①a +b +c >0;②a -b +c >0;③abc <0;④2a -b=0, 其中正确的个数是( )A .1个B .2个C .3个D .4个 4.抛物线y=41(x +2)2-1是则函数y=41x 2+4x +19的图象先向上平移b 个单位,再向左平移a 个单位得到的,则a 、b 的值分别为( )A .a=4,b=6B .a=6,b=4C .a=2,b=-1D .无法确定 5.已知抛物线y=ax 2+bx +c 经过点(1,2)与(-1,4),则a +c 的值是 6.抛物线y=ax 2+bx+c 如右图,则c 的取值范围 二.在二次函数中常用的求点的坐标1求抛物线与x 轴交点。
方法把y=0代入解析式2.求y 轴交点坐标,方法把x=0代入解析式,当解析式为y=ax 2+bx +c 时,抛物线与y 轴的交点为(0,c )3.求两图象的交点,方法联立解析式解方程组4.用对称性求点的坐标;抛物线上的两个对称点(x 1,y )(x 2,y)对称轴x=221x x + 练习二1.求抛物线y=-2x 2+4x +6x 与x 轴的交点与y 轴的交点 与直线y=-2x-4的交点2. 已知抛物线y=x 2-bx+c 与x 轴一个交点坐标是(2,0)当x=-1时y 有最小值,则抛物线与x 轴的另一个交点是 三.求对称轴的方法 1.在一般式中用公式:x=-ab2 2.当已知抛物线上的两个对称点(x 1,y )(x 2,y)可用公式对称轴x=221x x + 3.在顶点式中直接得对称轴 四.一般式中∆=b 2-4ac 的作用 1.确定抛物线与x 轴交点的个数 2.可以确定函数值的符号3.可以确定二次不等式的解集 练习三1.抛物线y=2x 2-3x+5,∆= 抛物线与x 轴有 个交点,图象大致为无论x 取何值时,函数值恒 于0,一元二次不等式2x 2-3x+5〈0的解集五.有关解析式y=x 2-bx+c 中符号的确定 1.a 的符号由开口方向和增减性来确定 2.b 的符号由对称轴来确定3.c 的符号由抛物线与y 轴的交点位置确定4. ∆的符号是由抛物线与x 轴的交点个数和图象的位置来确定 练习三20.已知二次函数c bx ax y ++=2(0≠a )的图象如图所示 ,与y 轴相交一点C ,与x 轴负半轴相交一点A ,且OC OA =,有下列5个结论:①0>abc ;②c a b +<; ③024>++c b a ;④02=+b a ;⑤21-=+ac ,其中正确的结论有____________.六.二次函数与一元二次方程和一元二次不等式的关系1.抛物线与x 轴的两个交点的横坐标是一元二次方程ax 2+bx +c=0的两根2.求一元二次不等式ax 2+bx +c <0 与 ax 2+bx +c >0的解集 当a <0时________________________当a >0时________________________练习四求下列不等式的解集01322≥+-x x 0322≤--y y 542+-x x <0七.解析式的选择1.当有条件顶点,对称轴,最值时选择顶点式2.当有与x 轴的两交点时选择交点式3.当已知任意的三点时选择一般式 练习五根据下列条件求抛物解析式1.图象过(1,0)(-1,-4)(0,3) 2.图象顶点是(2,-1)且过(1,2)3.图象与横轴的交点是(-1,0)(3,0)且最大值是1xxO x练习六 一.选择题1.二次函数247y x x =-+的最小值为( ) A 2 B -2 C 3 D -32.把二次函数122--=x x y 配方成顶点式为( ) A .2)1(-=x y B . 2)1(2--=x y C .1)1(2++=x yD .2)1(2-+=x y3.直角坐标平面上将二次函数y =-2(x -1)2-2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )A.(0,0)B.(1,-2)C.(0,-1)D.(-2,1) 4.函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是( ) A .3<kB .03≠<k k 且C .3≤kD .03≠≤k k 且5.二次函数c bx x y ++=2的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )A .x =4 B. x =3 C. x =-5 D. x =-1。
6.二次函数26y x x =+-的图象与x 轴交点的横坐标是( ) A .2和3-B .2-和3C .2和3D .2-和3-7.已知22y x =的图象是抛物线,若抛物线不动,把x 轴,y 轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( ). A.22(2)2y x =-+ B.22(2)2y x =+-C.22(2)2y x =--D.22(2)2y x =++8.已知函数222y x x =--的图象如图所示,根据其中提供的信息,可求得使1y ≥成立的x 的取值范围是( ) A.13x -≤≤B.31x -≤≤C.3x -≥D.1x -≤或3x ≥9.已知抛物线2(1)(0)y a x h a =-+≠与x 轴交于1(0)(30)A x B ,,,两点,则线段AB 的长度为( )A.1 B.2 C.3D.410.小明从右边的二次函数2y ax bx c =++图象中,观察得出了下面的五条信息:①0a <,②0c =,③函数的最小值为3-,④当0x <时,0y >,⑤当1202x x <<<时,12y y >.你认为其中正确的个数为( ) A.2 B.3C.4 D.511.在同一平面直角坐标系中,一次函数y ax b =+和二次函数2y ax bx =+的图象可能为( )填空12.抛物线m x x y +-=42的顶点在x 轴上,其顶点坐标是 ;13.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 14.函数22y x bx =+在第一象限内y 的值随着x 的值增大而增大,则b 的取值范值是.15.已知二次函数2(0)y ax bx c a =++≠,其中a b c ,,满足0a b c ++=和930a b c -+=,则该二次函数图象的对称轴是直线 .16.请选择一组你喜欢的a b c ,,的值,使二次函数2(0)y ax bx c a =++≠的图象同时满足下列条件:①开口向下,②当2x <时,y 随x 的增大而增大;当2x >时,y 随x 的增大而减小.这样的二次函数的解析式可以是.17.有一个抛物线形拱桥,其最大高度为16m ,跨度为40m ,现把它的示意图放在平面直角坐标系中如图(4),求抛物线的解析式是_______________23-xyyO xyOxy OxyOxA. B. C. D.18.已知抛物线经过如图的位置的三点,可得a____0,c _______0 b _______0 b 2-4ac _______ 0 a-b+c _______o19.已知二次函数y =ax 2+bx +c 的图象与x 轴交于A (1,0),B (3,0)两点,与y 轴交于点C (0,3),则二次函数的解析式是 . 三.解答20.求函数.y =4x 2+24x +35的图像的对称轴、顶点坐标及与x 轴的交点坐标.;21.已知一个二次函数的图象经过点(1,-1),(0,1),(-1,13),求这个二次函数的解析式;22.(10分)已知抛物线42)4(2++-+-=m x m x y 与x 轴交于点)0,(1x A ,)0,2(B 两点,与y 轴交于点C . 若点A 关于y 轴对称点是点D . (1)求C 、D 两点坐标.(2)求过点B 、C 、D 三点的抛物线的解析式.(3)若P 是(2)中所求抛物线的顶点,H 是这条抛物线上异于点C 的另一点,且BDP ABH S S ∆∆=24,求直线PH 的解析式.xyD CB F E A23.某商场以每件20元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x (元)满足关系:m =140-2x .(1)写出商场卖这种商品每天的销售利润y 与每件的销售价x 间的函数关系式;(2)如果商场要想每天获得最大的销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?24.已知:如图,在Rt△ABC 中,∠C =90°,BC =4,AC =8,点D 在斜边AB 上, 分别作DE ⊥AC ,DF ⊥BC ,垂足分别为E 、F ,得四边形DECF ,设DE =x ,DF =y . (1)用含y 的代数式表示AE . (2)求y 与x 之间的函数关系式,并求出x 的取值范围.(3)设四边形DECF 的面积为S ,求出S 的最大值.。
