中考数学专题：函数图像

合集下载

九年级数学中考专项复习——函数图像与实际问题应用题(附答案)

中考专项复习——函数与实际问题1. 甲、乙两车从A 城出发前往B 城．在整个行程中，甲车离开A 城的距离1km y 与甲车离开A 城的时间 h x 的对应关系如图所示．乙车比甲车晚出发1h 2，以60 km/h 的速度匀速行驶．（Ⅰ）填空：① A ，B 两城相距km② 当02x ≤≤时，甲车的速度为 km/h ③ 乙车比甲车晚 h 到达B 城 ④ 甲车出发4h 时，距离A 城km⑤ 甲、乙两车在行程中相遇时，甲车离开A 城的时间为 h（Ⅱ）当2053x ≤≤时，请直接写出1y 关于x 的函数解析式．（Ⅲ）当1352x ≤≤时，两车所在位置的距离最多相差多少km ？y 1/ km 53232. 已知聪聪家、体育场、文具店在同一直线上，下面的图象反映的过程是：聪聪从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家．图中x 表示过程中聪聪离开家的时间，y 表示聪聪离家的距离．请根据相关信息，解答下列问题：（Ⅰ）填表：离开家的时间/min 6 10 20 46 离家的距离/km12.5（Ⅱ）填空：① 聪聪家到体育场的距离为______km② 聪聪从体育场到文具店的速度为______km/min ③ 聪聪从文具店散步回家的速度为______ km/min④ 当聪聪离家的距离为2 km 时，他离开家的时间为______min （Ⅲ）当10045≤≤x 时，请直接写出y 关于x 的函数解析式．3.同一种品牌的空调在甲、乙两个电器店的标价均是每台3000元.现甲、乙两个电器店优惠促销，甲电器店的优惠方案：如果一次购买台数不超过5台时，价格为每台3000元，如果一次购买台数超过5台时，超过部分按六折销售；乙电器店的优惠方案：全部按八折销售.设某校在同一家电器店一次购买空调的数量为x （x 为正整数）. （Ⅰ）根据题意，填写下表：一次购买台数（台） 2 6 15 … 甲电器店收费（元） 6000 … 乙电器店收费（元）4800…（Ⅱ）设在甲电器店购买收费y 1元，在乙电器店购买收费y 2元，分别写出y 1、y 2关于x 的函数关系式；（Ⅲ）当x > 6时，该校在哪家电器店购买更合算？并说明理由.4.已知小明的家、体育场、文化宫在同一直线上．下面的图象反映的过程是：小明早上从家跑步去体育场，在那里锻炼了一阵后又走到文化宫去看书画展览，然后散步回家．图中x 表示时间（单位是分钟）y 表示到小明家的距离（单位是千米）．请根据相关信息，解答下列问题：（Ⅰ）填表：小明离开家的时间/min 5 10 15 30 45 小明离家的距离/km131（Ⅱ）填空：（i ）小明在文化宫停留了_____________min（ii ）小明从家到体育场的速度为_______________km /min （iii ）小明从文化宫回家的平均速度为_______________km /min（iv ）当小明距家的距离为0.6km 时，他离开家的时间为_________________min （Ⅲ）当0≤x ≤45时，请直接写出y 关于x 的函数解析式.5.共享电动车是一种新理念下的交通工具：主要面向的出行市场，现有A 两种品牌的共享电动车，给出的图象反映了收费元与骑行时间min 之间的对应关系，其中品牌收费方式对应，品牌的收费方式对应．请根据相关信息，解答下列问题：（Ⅰ）填表：骑行时间/min 10 20 25 A 品牌收费/元 8 B 品牌收费/元8（Ⅱ）填空：①B 品牌10分钟后，每分钟收费元；②如果小明每天早上需要骑行A 品牌或B 品牌的共享电动车去工厂上班，已知两种品牌共享电动车的平均行驶速度均为，小明家到工厂的距离为，那么小明选择品牌共享电动车更省钱；③直接写出两种品牌共享电动车收费相差3元时的值是．（Ⅲ）直接写出，关于的函数解析式．3~10km B y x A 1y B 2y 300m /min 9km x 1y 2y x y /元O 10 20 x /min8 66. 小明的父亲在批发市场按每千克1.5元批发了若干千克的西瓜进城出售,为了方便他带了一些零钱备用．他先按市场价售出一些后，又降价出售．售出西瓜千克数x 与他手中持有的钱数y 元（含备用零钱）的关系如图所示，请根据相关信息，解答下列问题：（Ⅰ）填表：售出西瓜x /kg 0 10 20 30 40 80手中持有的钱数y /元 50______120155190 ______（Ⅱ）填空：①降价前他每千克西瓜出售的价格是________元②随后他按每千克下降1元将剩余的西瓜售完，这时他手中的钱（含备用的钱）是450 元，他一共批发了_________千克的西瓜（Ⅲ）当0≤x ≤80 时求y 与x 的函数关系式．7. 工厂某车间需加工一批零件，甲组工人加工中因故停产检修机器一次，然后以原来的工作效率继续加工，由于时间紧任务重，乙组工人也加入共同加工零件．设甲组加工时间为t （时），甲组加工零件的数量为 y 甲（个），乙组加工零件的数量为 y 乙（个），其函数图象如图所示．（I ）根据图象信息填表：（Ⅱ）填空：①甲组工人每小时加工零件个 ②乙组工人每小时加工零件个③甲组加工小时的时候，甲、乙两组加工零件的总数为480个（Ⅲ）分别求出 y 甲、y 乙与t 之间的函数关系式．加工时间t （时） 3 4 8 甲组加工零件的数量（个）a ＝8. 4月23日是“世界读书日”，甲、乙两个书店在这一天举行了购书优惠活动．在甲书店所有书籍按标价总额的折出售．在乙书店一次购书的标价总额不超过元的按标价总额计费，超过元后的部分打折．设在同一家书店一次购书的标价总额为（单位：元，）．（Ⅰ）根据题意，填写下表：一次购书的标价总额/元… 在甲书店应支付金额/元 … 在乙书店应支付金额/元…（Ⅱ）设在甲书店应支付金额元，在乙书店应支付金额元，分别写出、关于的函数关系式；（Ⅲ）根据题意填空：① 若在甲书店和在乙书店一次购书的标价总额相同，且应支付的金额相同，则在同一个书店一次购书的标价总额元；② 若在同一个书店一次购书应支付金额为元，则在甲、乙两个书店中的书店购书的标价总额多； ③ 若在同一个书店一次购书的标价总额元，则在甲、乙两个书店中的书店购书应支付的金额少．9. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．已知小明家、体育场、文具店依次在同一条直线上. 体育场离家，文具店离家．周末小明从家出发，匀速跑步到体育场；在体育场锻炼后，匀速走了到文具店；在文具店停留买笔后，匀速走了返回家．给出的图象反映了这个过程中小明离开家的距离与离开家的时间之间的对应关系．请根据相关信息，解答下列问题：（I ）填表：离开家的时间/min离开家的距离/ km（II ）填空：① 体育场到文具店的距离为______ ② 小明从家到体育场的速度为______ ③ 小明从文具店返回家的速度为______④ 当小明离家的距离为时，他离开家的时间为______ （III ）当时，请直接写出关于的函数解析式．81001006x 0x 501503*********y 2y 1y 2y x 2801203km 1.5km 15min 15min 15min 20min 30min km y min x 6122050701.23km km /min km /min 0.6km min 045x ≤≤y x10. 一个有进水管与出水管的容器，从某时刻开始4分钟内只进水不出水，在随后的8分钟内既进水又出水，12分钟后关闭进水管，放空容器中的水，每分钟的进水量和出水量是两个常数．容器内水量y （单位：L ）与时间x （单位：min ）之间的关系如图所示．请根据相关信息，解答下列问题：（Ⅰ）填表：（Ⅱ）填空：①每分钟进水______升，每分钟出水______升 ②容器中储水量不低于15升的时长是_________分钟（Ⅲ）当0≤x ≤12时，请直接写出y 关于x 的函数解析式.11. 明明的家与书店、学校依次在同一直线上，明明骑自行车从家出发去学校上学，当他骑了一段路时，想起要买某本书，于是又返回到刚经过的书店，买到书后继续去学校.下面图象反映了明明本次上学离家距离y （单位：m ）与所用时间x （单位：min ）之间的对应关系.请根据相关信息，解决下列问题：（Ⅰ）填表：（Ⅱ）填空：①明明家与书店的距离是 m②明明在书店停留的时间是min③明明与家距离900m 时，明明离开家的时间是 min（Ⅲ）当6≤t 14≤时，请直接写出y 与x 的函数关系式. 时间/min23412容器内水量/L1020离开家的时间/min25811离家的距离/m400 60012. 甲，乙两车从A 城出发前往B 城．在整个行程中，甲乙两车都以匀速行驶，汽车离开A 城的距离ykm 与时刻t 的对应关系如下图所示．请根据相关信息，解答下列问题：（I ）填表：（II ）填空：①A ，B 两城的距离为 km②甲车的速度为 km/h 乙车的速度为 km/h ③乙车追上甲车用了 h 此时两车离开A 城的距离是 km ④当9:00时，甲乙两车相距 km⑤ 当甲车离开A 城120km 时甲车行驶了 h ⑥ 当乙车出发行驶 h 时甲乙两车相距20km13.大部分国家都使用摄氏温度，但美国、英国等国家的天气预报仍然使用华氏温度．两种计量之间有如下对应：（Ⅰ）如果两种计量之间的关系是一次函数，设摄氏温度为x （ °C ）时对应的华氏温度为y （ °F ），请你写出华氏温度关于摄氏温度的函数表达式；（Ⅱ）求当华氏温度为0°F 时，摄氏温度是多少°C ？（Ⅲ）华氏温度的值与对应的摄氏温度的值有可能相等吗？若可能求出此值；若不可能请说明理由 .从A 城出发的时刻到达B 城的时刻甲 5:00 乙9:00摄氏温度/°C 0 10 20 30 40 华氏温度/°F32506886104参考答案1. 解：（Ⅰ）①360 ②60 ③56④6803⑤52或196（Ⅱ）当0≤x ≤2时 160y x =当2223x <≤时 1120y =当222533x <≤时 1280803y x =-（Ⅲ）当1352x ≤≤时由题意，可知甲车在乙车前面，设两车所在位置的距离相差y km则2801908060302033y x x x =---=-（）（） ∵ 200>∴ y 随x 的增大而增大 ∴ 当5x =时y 取得最大值1103答：两车所在位置的距离最多相差1103km2.解：（Ⅰ） 1.5（Ⅱ）①2.5 ②③ ④12或（Ⅲ）当时当时3. 解：（Ⅰ）16800 33000 14400 36000（Ⅱ）当0＜≤5时当＞5时，即；=⎩⎪⎨⎪⎧3000x （0＜x ≤5且x 为正整数），1800x ＋6000（x ＞5且x 为正整数）.（x ＞0且x 为正整数）531153702756545≤≤x 5.1=y 10065≤<x 730703+-=x y x 13000y x x 1300053000605y x％（）118006000y x1y 23000802400y x x ％（Ⅲ）设与的总费用的差为元. 则即. 当时即解得.∴当时选择甲乙两家电器店购买均可 ∵＜0∴随的增大而减小∴当6＜x ＜10时1y ＞2y 在乙家电器店购买更合算当x ＞10时＜在甲家电器店购买更合算4. 解：（Ⅰ）1 0.5（Ⅱ）填空：（i ） 25 （ii ）（iii ）（iv ）9或42（ii ）（Ⅲ）y ＝⎩⎪⎨⎪⎧x （0≤x ≤15），1（15＜x ≤30）， x ＋2（30＜x ≤ 45）.5.解：（Ⅰ）（Ⅱ）①0.2 ②B ③152或35 （Ⅲ）10.4 (0)y x x =≥ 26 0100.24 10x y x x ⎧=⎨+⎩，≤≤．，，＞6. 解：（Ⅰ）85 330（Ⅱ）3.5 128（Ⅲ）设y 与x 的函数关系式是)0(≠+=k b kx y ∵图象过），（500和）（330,80∴⎩⎨⎧+==b k b8033050 1y 2y y 180060002400y x x 6006000y x 0y60060000x10x10x 600y x 1y 2y 23115160115130-解得⎩⎨⎧==505.3b k ∴y 与x 的函数关系式为505.3+=x y )800(≤≤x7. （Ⅰ）（II ） ① 40 ② 120 ③ 7 (III ) （1）当时当时当时∵图象经过（4 120）则解得：∴ 当时∴（2）设把分别代入得解得 ∴与时间t 之间的函数关系式为：8. 解：（Ⅰ）40 240 50 220 （Ⅱ）10.8y x =（0x >）当0100x <≤时 2y x =当100x >时 21000.6100y x =+⨯-（）即20.640y x =+ （Ⅲ）① 200 ② 乙 ③ 甲03t t y 40=甲43≤t ＜120=甲y 84≤t ＜140b t y +=甲1440120b +⨯=401-=b 84≤t ＜4040-=t y 甲⎪⎩⎪⎨⎧≤-≤≤≤=)84(404043(120)3040t t t t t y ＜）＜（甲2b kt y +=乙(5,0)(8,360)⎩⎨⎧+=+=22836050b k b k ⎩⎨⎧-==6001202b k y 乙）乙85(600120≤≤-=t t y9. 解：（Ⅰ）2.4 1.5 1.25（Ⅱ）①1.5 ②0.2 ③0.05 ④3或83（Ⅲ）当015≤≤x 时 0.2=y x当1530<≤x 时 3=y当3045<≤x 时 0.16=-+y x10. （Ⅰ）填表：（Ⅱ）①5 3.75 ②13（Ⅲ）当04x ≤<时5y x =当412x <≤时5154y x =+11. 解：（Ⅰ）1000 600（Ⅱ）①600 ②4 ③4.5或7或338 （Ⅲ）300300068600812450480014x x y x x x -+≤≤⎧⎪=≤⎨⎪-≤⎩（）（＜）（12＜） 12. 解：（I ）甲 10:00 乙 6:00（II ）①300 ②60 100 ③1.5 150④60 ⑤2 ⑥ 1或213. 解：（Ⅰ）过程略 ∴华氏温度关于摄氏温度的函数表达式为1832y .x （Ⅱ）令0=y 则0328.1=+x 解得9160-=x ∴当华氏温度为0 °F 时摄氏温度是1609°C （Ⅲ）令x y =则x x =+328.1解得40-=x答：当华氏温度为- 40 °F 时，摄氏温度为-40°C 时，华氏温度的值与对应的摄氏温度的值相等. 时间/min 2 3 4 12 容器内水量/L 10 15 20 30。

2024年中考数学专题复习：一次函数的图像与性质-试卷

2024年中考数学专题复习：一次函数的图像与性质一、选择题（本大题共10道小题）1. (2023•沈阳)一次函数y ＝-3x+1的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限2. (2023八上·太原期中)课堂上,同学们研究正比例函数y=-x 的图象时,得到如下四个结论,其中错误的是( )A.当x=0时,y=0,所以函数y=-x 的图象经过原点B.点P(t,-t)一定在函数y=-x 的图象上C.当x>0时,y<0,当x<0时,y>0,所以函数y=-x 的图象经过二、四象限D.将函数的图象向左平移2个单位,即可得到函数y=-x+2的图象3. (2023·太原模拟)已知y 是x 的正比例函数,当x ＝3时,y ＝－6,则y 与x 的函数关系式为( )A.y ＝2xB.y ＝－2xC.y ＝12 xD.y ＝－12x 4. (2023•柳州)若一次函数y ＝kx+b 的图象如图所示,则下列说法正确的是( )A.k ＞0B.b ＝2C.y 随x 的增大而增大D.x ＝3时,y ＝0 5. (2023·贵州毕节·二模)已知正比例函数y=kx(k ≠0)的图象过点(2,3),把正比例函数y=kx(k ≠0)的图象平移,使它过点(1,-1),则平移后的函数图象大致是( )A. B. C.D. 6. (2023秋•会宁县)已知关于x 的一次函数y ＝(k 2+1)x-2图象经过点A(3,m)、B(-1,n),则m,n 的大小关系为( )A.m ≥nB.m ＞nC.m ≤nD.m ＜n7. (2023·随州模拟)如图,在平面直角坐标系中,动点A,B 分别在x 轴上和函数y ＝x 的图象上,AB ＝4,CB ⊥AB,BC ＝2,则OC 的最大值为( )A.222B.224C.2 5D.2528. (2023·鄂州中考)数形结合是解决数学问题常用的思想方法.如图,直线y ＝2x －1与直线y ＝kx ＋b(k ≠0)相交于点P(2,3).根据图象可知,关于x 的不等式2x －1＞kx ＋b 的解集是( )A.x ＜2B.x ＜3C.x ＞2D.x ＞39. (2023•贵阳)小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线y ＝k n x+b n (n ＝1,2,3,4,5,6,7),其中k 1＝k 2,b 3＝b 4＝b 5,则他探究这7条直线的交点个数最多是( )A.17个B.18个C.19个D.21个10. (2023·湖南永州·中考真题)已知点P(x 0,y 0)和直线y=kx+b,求点P 到直线y=kx+b 的距离d 可用公式0021kx y b d k -+=+计算.根据以上材料解决下面问题:如图,⊙C 的圆心C 的坐标为(1,1),半径为1,直线l 的表达式为y=-2x+6,P 是直线l 上的动点,Q 是⊙C 上的动点,则PQ 的最小值是( )A.355B.3515-C.6515-D.2二、填空题（本大题共8道小题）11. (2023•毕节市)将直线y ＝-3x 向下平移2个单位长度,平移后直线的解析式为 .12. (2023·四川成都市)在正比例函数y=kx 中,y 的值随着x 值的增大而增大,则点P(3,k)在第_____象限.13. (2023·贵州黔西·二模)如图,平面直角坐标系中,经过点B(-4,0)的直线y ＝kx+b 与直线y ＝mx+2相交于点3(,1)2A --,则关于x 的方程mx+2＝kx+b 的解为________.14. (2023秋•宁化县)若函数y ＝4x ﹣1与y ＝﹣x+a 的图象交于x 轴上一点,则a 的值为( )A.4B.﹣4C.D.±415. (2023黔西南州)如图,正比例函数的图象与一次函数y ＝－x ＋1的图象相交于点P,点P 到x 轴的距离是2,则这个正比例函数的解析式是 .16. (2023·湖南湘西·中考真题)在平面直角坐标系中,O 为原点,点A(6,0),点B 在y 轴的正半轴上,∠ABO=30o .矩形CODE 的顶点D,E,C 分别在OA,AB,OB 上,OD=2.将矩形CODE 沿x 轴向右平移,当矩形CODE 与△ABO 重叠部分的面积为63时,则矩形CODE 向右平移的距离为___________.17. (2023•毕节市)如图,在平面直角坐标系中,点N 1(1,1)在直线l:y ＝x 上,过点N 1作N 1M 1⊥l,交x 轴于点M 1;过点M 1作M 1N 2⊥x 轴,交直线于N 2;过点N 2作N 2M 2⊥l,交x 轴于点M 2;过点M 2作M 2N 3⊥x 轴,交直线l 于点N 3;…,按此作法进行下去,则点M 2023的坐标为 .18. (2023•泰安)如图,点B 1在直线l:y ＝21x 上,点B 1的横坐标为2,过点B 1作B 1A 1⊥l,交x 轴于点A 1,以A 1B 1为边,向右作正方形A 1B 1B 2C 1,延长B 2C 1交x 轴于点A 2;以A 2B 2为边,向右作正方形A 2B 2B 3C 2,延长B 3C 2交x 轴于点A 3;以A 3B 3为边,向右作正方形A 3B 3B 4C 3,延长B 4C 3交x 轴于点A 4;…;照这个规律进行下去,则第n 个正方形A n B n B n+1∁n 的边长为 (结果用含正整数n 的代数式表示).三、解答题（本大题共6道小题）19. (2023秋•安徽月考)已知经过点A(4,-1)的直线y ＝kx+b 与直线y ＝-x 相交于点B(2,a),求两直线与x 轴所围成的三角形的面积.20. (2023春•西丰县)如图,一次函数y＝kx+b的图象经过A(2,4),B(﹣2,﹣2)两点,与y轴交于点C.(1)求k,b的值,并写出一次函数的解析式;(2)求点C的坐标.21. (2023秋•兰州)如图,直线l1:y＝-x+4分别与x轴,y轴交于点D,点A,直线l2:y x+1与x轴交于点C,两直线l1,l2相交于点B,连AC.(1)求点B的坐标和直线AC的解析式;(2)求△ABC的面积.22. (2023•滨州)如图,在平面直角坐标系中,直线y x﹣1与直线y＝﹣2x+2相交于点P,并分别与x轴相交于点A、B.(1)求交点P的坐标;(2)求△PAB的面积;(3)请把图象中直线y＝﹣2x+2在直线y x﹣1上方的部分描黑加粗,并写出此时自变量x的取值范围.23. (2023·河北中考真题)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l ,如图.而某同学为观察k,b 对图象的影响,将上面函数中的k 与b 交换位置后得另一个一次函数,设其图象为直线l '.(1)求直线l 的解析式; (2)请在图上画出．．直线l '(不要求列表计算),并求直线l '被直线l 和y 轴所截线段的长; (3)设直线y=a 与直线l ,l '及y 轴有三个不同的交点,且其中两点关于第三点对称,直接．．写出a 的值.24. (2023•黑龙江)如图,矩形ABOC 在平面直角坐标系中,点A 在第二象限内,点C 在y 轴正半轴上,OA 2-9x+20＝0的两个根.解答下列问题:(1)求点A 的坐标;(2)若直线MN 分别与x 轴,AB,AO,y 轴交于点D,M,F,N,E,S △AMN ＝2,tan ∠AMN ＝1,求直线MN 的解析式;(3)在(2)的条件下,点P 在第二象限内,使以E,F,P,Q 为顶点的四边形是正方形？若存在;若不存在,请说明理由.。

中考数学专题复习函数及其图像

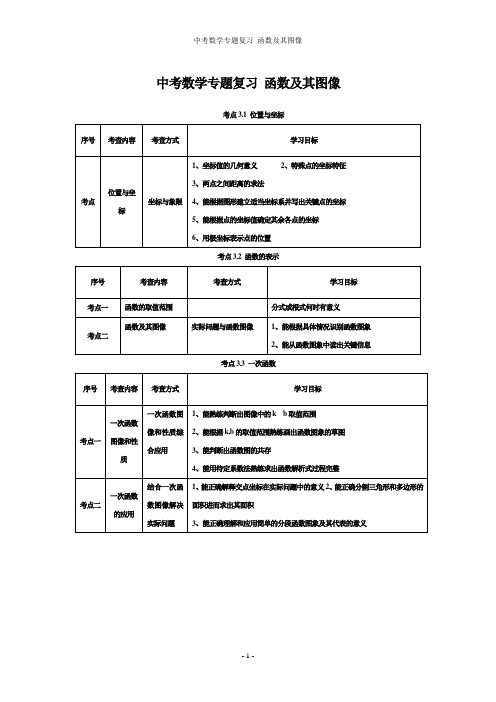
中考数学专题复习函数及其图像考点3.1 位置与坐标序号考查内容考查方式学习目标考点位置与坐标坐标与象限1、坐标值的几何意义2、特殊点的坐标特征3、两点之间距离的求法4、能根据图形建立适当坐标系并写出关键点的坐标5、能根据点的坐标值确定其余各点的坐标6、用极坐标表示点的位置考点3.2 函数的表示序号考查内容考查方式学习目标考点一函数的取值范围分式或根式何时有意义考点二函数及其图像实际问题与函数图像1、能根据具体情况识别函数图象2、能从函数图象中读出关键信息考点3.3 一次函数序号考查内容考查方式学习目标考点一一次函数图像和性质一次函数图像和性质综合应用1、能熟练判断出图像中的k b取值范围2、能根据k,b的取值范围熟练画出函数图象的草图3、能判断出函数图的共存4、能用待定系数法熟练求出函数解析式过程完整考点二一次函数的应用结合一次函数图像解决实际问题1、能正确解释交点坐标在实际问题中的意义2、能正确分割三角形和多边形的面积进而求出其面积3、能正确理解和应用简单的分段函数图象及其代表的意义考点3.4 反比例函数序号考查内容考查方式学习目标考点一反比例函数解析式的确定确定比例系数1、能从不同的表达式中分离出比例系数2、能根据比例系数画出函数草图待定系数法求解析式利用比例系数的几何意义确定反比例函数解析式k值的几何意义反映到函数中要结合具体的象限来确定值k考点二反比例函数的应用一次函数与反比例函数的综合应用考点3.5 二次函数序号考查内容考查方式学习目标考点一二次函数图像和性质确定二次函数图像的对称轴和顶点、与x轴的交点的坐标1、能准确化为一般形式，并指出其系数2、能熟练进行配方写出其顶点坐标式3、能熟练从三种解析式几个方面值的确定考点二二次函数的应用画二次函数图像及应用能熟练画出草图并进行分析应用考点三二次函数与实际问题（二次函数的应用题）确定解析式、求极值（解答题）能根据已知条件熟练写出解析式，并进行五个方面的相关计算考点3.6 用函数观点看方程（组）和不等式序号考查内容考查方式学习目标考点一函数与方程二次函数与一元二次方程理解二次函数与一元二次方程的联系，并能正确地将二次函数问题转化为一元二次方程，能用一元二次方程的根解释图象中的交点坐标考点二函数与不等式一次函数与一元一次不等式1、能根据图象正确判断不等式的解集2、理解交点坐标的意义3、能根据交点坐标正确写出方程或方程组反比例函数与不等式一次函数、反比例函数与不等式同上。

中考数学考点10一次函数图像与性质总复习(解析版)

一次函数的图像与性质【命题趋势】在中考中.主要以选择题、填空题和解答题形式出现.主要考查一次函数的图像与性质.确定一次函数的解析式.一次函数与方程（组）、不等式的关系。

一次函数与二次函数、反比例函数综合也是中考重点之一。

【中考考查重点】一、结合具体情景体会一次函数的意义.能根据已知条件确定一次函数的表达式；二、利用待定系数法确定一次函数的表达式；三、根据一次函数画出图像.探索并理解k＞0和k＜0时.图像的变化情况；四、体会一次函数与二元一次方程的关系考点一：一次函数及其图像性质概念一般地.形如y=kx+b(k,b为常数.k≠0）的函数.叫做一次函数.当b=0十.即y=kx.这时称y是x的正比例函数（一次函数的特殊形式）增减性k＞0k＜0从左向右看图像呈上升趋势.y随x的增大而增大从左向右看图像呈下降趋势.y随x的增大而较少图像（草图）b＞0b=0b＜0b＜0b=0 b＜0经过象限一、二、三一、三一、三、四一、二、四二、四二、三、四与y轴的交点位置b＞0.交点在y轴正半轴上；b=0,交点在原点；b＜0.交点在y轴负半轴上【提分要点】：1.若两直线平行.则；2.若两直线垂直.则1．（2021春•大安市期末）一次函数y＝2x﹣1图象经过象限（）A．一、二、三B．一、二、四C．二、三、四D．一、三、四【答案】D【解答】解：∵一次函数y＝2x﹣1.k＝2＞0.b＝﹣1＜0.∴该函数图象经过一、三、四象限.故选：D．2．（2021秋•肃州区期末）对于一次函数y＝x+6.下列结论错误的是（）A．函数值随自变量增大而增大B．函数图象与x轴正方向成45°角C．函数图象不经过第四象限D．函数图象与x轴交点坐标是（0.6）【答案】D【解答】解：A、∵一次函数y＝x+6中k＝1＞0.∴函数值随自变量增大而增大.故A 选项正确；B、∵一次函数y＝x+6与x、y轴的交点坐标分别为（﹣6.0）.（0.6）.∴此函数与x轴所成角度的正切值＝＝1.∴函数图象与x轴正方向成45°角.故B选项正确；C、∵一次函数y＝x+6中k＝1＞0.b＝6＞0.∴函数图象经过一、二、三象限.故C选项正确；D、∵令y＝0.则x＝﹣6.∴一次函数y＝x+6与x轴的交点坐标分别为（﹣6.0）.故D选项错误．故选：D．3．（2021秋•东港市期中）点A（﹣1.y1）和点B（﹣4.y2）都在直线y＝﹣2x上.则y1与y2的大小关系为（）A．y1＞y2B．y1＜y2C．y1＝y2D．y1≥y2【答案】B【解答】解：∵k＝﹣2＜0.∴y随x的增大而减小.又∵点A（﹣1.y1）和点B（﹣4.y2）都在直线y＝﹣2x上.且﹣1＞﹣4.∴y1＜y2．故选：B4．（2021秋•三水区期末）若一次函数y＝kx+b的图象经过第一、二、四象限.则一次函数y＝bx+k的图象大致是（）A．B．C．D．【答案】D【解答】解：一次函数y＝kx+b过一、二、四象限.则函数值y随x的增大而减小.因而k＜0；图象与y轴的正半轴相交则b＞0.因而一次函数y＝bx﹣k的一次项系数b＞0.y随x的增大而增大.经过一三象限.常数项k＜0.则函数与y轴负半轴相交.因而一定经过一三四象限.故选：D．考点二：一次函数解析式的确定方法待定系数法步骤1.设：一般式y=kx+b（k≠0）（题干中未给解析式需设）2.代：找出一次函数图像上的两个点.并且将点坐标代入函数解析式.得到二元一次方程组；3.求：解方程（组）求出k、b的值；4.写：将k、b的值代入.直接写出一次函数解析式5．（2021秋•尤溪县期中）已知一次函数y＝x+b过点（﹣1.﹣2）.那么这个函数的表达式为（）A．y＝x﹣1B．y＝x+1C．y＝x﹣2D．y＝x+2【答案】A【解答】解：把（﹣1.﹣2）代入y＝x+b得：﹣2＝﹣1+b.解得：b＝﹣1.则一次函数解析式为y＝x﹣1.故选：A．6．（2021春•海珠区期末）已知一次函数y＝mx﹣4m.当1≤x≤3时.2≤y≤6.则m的值为（）A．3B．2C．﹣2D．2或﹣2【答案】C【解答】解：当m＞0时.一次函数y随x增大而增大.∴当x＝1时.y＝2且当x＝3时.y＝6.令x＝1.y＝2.解得m＝.不符题意.令x＝3.y＝6.解得m＝﹣6.不符题意.当m＜0时.一次函数y随x增大而减小.∴当x＝1时.y＝6且当x＝3时.y＝2.令x＝1.y＝6.解得m＝﹣2.令x＝3.y＝2.解得m＝﹣2.符合题意.∴故选：C．7．（2021秋•萧山区月考）已知y与x﹣2成正比例.且当x＝1时.y＝1.则y与x之间的函数关系式为．【答案】y＝﹣x+2【解答】解：设y＝k（x﹣2）（k≠0）.将x＝1时y＝1代入.得1＝k（1﹣2）.解得k＝﹣1.所以y＝﹣x+2；故答案为：y＝﹣x+2．8．（2021春•古丈县期末）某个一次函数的图象与直线y＝x+6平行.并且经过点（﹣2.﹣4）.则这个一次函数的解析式为（）A．y＝﹣x﹣5B．y＝x+3C．y＝x﹣3D．y＝﹣2x﹣8【答案】C【解答】解：由一次函数的图象与直线y＝x+6平行.设直线解析式为y＝x+b.把（﹣2.﹣4）代入得：﹣4＝﹣1+b.即b＝﹣3.则这个一次函数解析式为y＝x﹣3．故选：C．考点三：一次函数图像的平移平移前平移方式（m＞0）平移后简记y=kx+b 向左平移m个单位长度y=k（x+m）+bx左加右减向右平移m个单位长度y=k（x-m）+b向上平移m个单位长度y=kx+b+m等号右端整体上加下减向下平移m个单位长度y=kx+b-m9．（2021秋•金安区校级期中）将直线y＝2x向右平移1个单位.再向上平移1个单位后.所得直线的表达式为（）A．y＝2x﹣1B．y＝2x C．y＝2x+4D．y＝2x﹣2【答案】A【解答】解：将直线y＝2x向右平移1个单位.再向上平移1个单位后.所得直线的解析式为y＝2（x﹣1）+1.即y＝2x﹣1．故选：A．10．（2021春•米易县期末）一次函数y＝2x﹣4的图象由正比例函数y＝2x的图象（）A．向左平移4个单位长度得到B．向右平移4个单位长度得到C．向上平移4个单位长度得到D．向下平移4个单位长度得到【答案】D【解答】解：将正比例函数y＝2x的图象向下平移4个单位即可得到y＝2x﹣4的图象．故选：D．11．（2021秋•长丰县月考）已知点A（2.4）沿水平方向向左平移3个单位长度得到点A'.若点A'在直线y＝x+b上.则b的值为（）A．1B．3C．5D．﹣1【答案】C【解答】解：∵点A（2.4）沿水平方向向左平移3个单位长度得到点A'.∴点A'的坐标为（﹣1.4）．又∵点A'在直线y＝x+b上.∴4＝﹣1+b.∴b＝5．故选：C考点四：一次函数与方程（组）、不等式与一元一次方程的关系方程ax+b=0（a≠0）的解是一次函数y=ax+b(a≠0）的函数值为0时自变量的取值.还是直线y=ax+b(a≠0）与x轴交点的横坐标与二元一次方程组的关系方程组的解时直线的交点坐标与一元一次不等式的关系1.从“数”来看（1）kx+b＞0的解集是y=kx+b中.y＞0时x的取值范围（2）kx+b＞＜0的解集是y=kx+b中.y＜0时x的取值范围2.从“形”上看（1）kx+b＞0的解集是y=kx+b函数图像位于x上方部分对应的点的横坐标（2）kx+b＜0的解集是y=kx+b函数图像位于x下方部分对应的点的横坐标12．（2021秋•乐平市期中）一次函数y＝kx+b的图象如图所示.则关于x的方程kx+b ＝0的解为（）A．x＝0B．x＝3C．x＝﹣2D．x＝﹣3【答案】B【解答】解：∵直线与x轴交点坐标为（3.0）.∴kx+b＝0的解为x＝3.故选：B．13．（2021秋•安徽期中）已知一次函数y＝ax﹣1与y＝mx+4的图象交于点A（3.1）.则关于x的方程ax﹣1＝mx+4的解是（）A．x＝﹣1B．x＝1C．x＝3D．x＝4【答案】C【解答】解：∵一次函数y＝ax﹣1与y＝mx+4的图象交于点A（3.1）.∴ax﹣1＝mx+4的解是x＝3．故选：C．14．（2021春•沧县期末）如图.直线y＝x+5和直线y＝ax+b相交于点P（20.25）.根据图象可知.方程x+5＝ax+b的解是（）A．x＝20B．x＝5C．x＝25D．x＝15【答案】A【解答】解：∵直线y＝x+5和直线y＝ax+b相交于点P（20.25）.∴方程x+5＝ax+b的解为x＝20．故选：A．15．（2020秋•建湖县期末）如图.一次函数y＝kx+b（k≠0）的图象经过点A（﹣1.﹣2）和点B（﹣2.0）.一次函数y＝2x的图象过点A.则不等式2x＜kx+b≤0的解集为（）A．x≤﹣2B．﹣2≤x＜﹣1C．﹣2＜x≤﹣1D．﹣1＜x≤0【答案】B【解答】解：∵由图象可知：正比例函数y＝2x和一次函数y＝kx+b的图象的交点是A（﹣1.﹣2）.∴不等式2x＜kx+b的解集是x＜﹣1.∵一次函数y＝kx+b的图象与x轴的交点坐标是B（﹣2.0）.∴不等式kx+b≤0的解集是x≥﹣2.∴不等式2x＜kx+b＜0的解集是﹣2≤x＜﹣1.故选：B．16．（2021秋•兴宁区校级月考）如图.直线y＝kx+b交x轴于点A（﹣2.0）.直线y＝mx+n交x轴于点B（5.0）.这两条直线相交于点C（2.c）.则关于x的不等式组的解集为（）A．x＜5B．1＜x＜5C．﹣2＜x＜5D．x＜﹣2【答案】D【解答】解：y＝kx+b＜0.则x＜﹣2.y＝mx+n＞0.则x＜5.关于x的不等式组的解集为：x＜﹣2.故选：D．17．（2020秋•西林县期末）如图所示是函数y＝kx+b与y＝mx+n的图象.则方程组的解是（）A．B．C．D．【答案】C【解答】解：∵函数y＝kx+b与y＝mx+n的图象交于点（3.4）.∴方程组的解是．故选：C．1．（2021春•扎兰屯市期末）将直线y＝﹣2x﹣2向右平移1个单位长度.可得直线的表达式为（）A．y＝2x B．y＝﹣2x﹣4C．y＝﹣2x D．y＝﹣2x+4【答案】C【解答】解：由“左加右减”的原则可知.把直线y＝﹣2x﹣2向右平移1个单位长度.可得直线的解析式为：y＝﹣2（x﹣1）﹣2.即y＝﹣2x．故选：C．2．（2021春•玉田县期末）下列有关一次函数y＝﹣6x﹣5的说法中.正确的是（）A．y的值随着x值的增大而增大B．函数图象与y轴的交点坐标为（0.5）C．当x＞0时.y＞﹣5D．函数图象经过第二、三、四象限【答案】D【解答】解：∵y＝﹣6x﹣5.﹣6＜0.﹣5＜0.∴y随x的增大而减小.故选项A不符合题意；当x＝0时.y＝﹣6×0﹣5＝﹣5.即函数图象与y轴的交点坐标为（0.﹣5）.故选项B不符合题意；当x＞0时.y＜﹣5.故选项C不符合题意；函数图象经过第二、三、四象限.故选项D符合题意；故选：D．3．（2021春•红寺堡区期末）点P1（x1.y1）.点P2（x2.y2）是一次函数y＝﹣4x+3图象上的两个点.且x1＜x2.则y1与y2的大小关系是（）A．y1＞y2B．y1＞y2＞0C．y1＜y2D．y1＝y2【答案】A【解答】解：∵k＝﹣4＜0.∴y随x的增大而减小.又∵x1＜x2.∴y1＞y2．故选：A．4．（2021秋•运城期中）在平面直角坐标系中.一次函数y＝kx+3（k≠0）的图象经过点A（2.﹣1）.则这个一次函数的表达式是（）A．y＝﹣2x+3B．y＝x+3C．y＝2x+3D．y＝x+3【答案】A【解答】解：∵一次函数y＝kx+3（k≠0）的图象经过点A（2.﹣1）.∴2k+3＝﹣1解得k＝﹣2.∴一次函数的表达式是y＝﹣2x+3．故选：A．5．（2021秋•南海区期中）如图.一次函数y＝kx+b的图象经过点（2.0）、（0.1）.则下列结论正确的是（）A．k＝1B．关于x的方程kx+b＝0的解是x＝2C．b＝2D．关于x的方程kx+b＝0的解是x＝1【答案】B【解答】解：A．∵一次函数y＝kx+b的图象经过点（2.0）、（0.1）.∴.解得：.故选项A不符合题意；B．由图象得：关于x的方程kx+b＝0的解为x＝2正确.故选项B符合题意；C．由图象得：当x＝0时.y＝1.即b＝1.故选项C不符合题意；D．由图象得：y＝0.即kx+b＝0时.x＝2.∴关于x的方程kx+b＝0的解是x＝2.故选项D不符合题意；故选：B．6．（2021秋•滕州市期中）直线y＝ax+b（a≠0）过点A（0.2）.B（1.0）.则关于x的方程ax+b＝0的解为（）A．x＝0B．x＝2C．x＝1D．x＝3【答案】C【解答】解：方程ax+b＝0的解.即为函数y＝ax+b图象与x轴交点的横坐标.∵直线y＝ax+b过B（1.0）.∴方程ax+b＝0的解是x＝1.故选：C．7．（2021秋•龙凤区期末）一次函数y＝mx﹣n（m.n为常数）的图象如图所示.则不等式mx﹣n≥0的解集是（）A．x≥2B．x≤2C．x≥3D．x≤3【答案】D【解答】解：由图象知：不等式mx﹣n≥0的解集是x≤3.故选：D．8．（2020秋•开化县期末）如图.直线y＝2x+n与y＝mx+3m（m≠0）的交点的横坐标为﹣1.则关于x的不等式2x+n＜mx+3m＜0的整数解为（）A．﹣1B．﹣2C．﹣3D．﹣3.5【答案】B【解答】解：∵直线y＝2x+n与y＝mx+3m（m≠0）的交点的横坐标为﹣1.∴关于x的不等式2x+n＜mx+3m的解集为x＜﹣1.∵y＝x+3＝0时.x＝﹣3.∴mx+3m＜0的解集是x＞﹣3.∴2x+n＜mx+3m＜0的解集是﹣3＜x＜﹣1.所以不等式2x+n＜mx+3m＜0的整数解为﹣2.故选：B．9．（2021春•单县期末）已知方程组的解为.则直线y＝﹣x+2与直线y ＝2x﹣7的交点在平面直角坐标系中位于（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】D【解答】解：∵方程组的解为.∴直线y＝﹣x+2与直线y＝2x﹣7的交点坐标为（3.﹣1）.∵x＝3＞0.y＝﹣1＜0.∴交点在第四象限．故选：D．10．（2021春•武陵区期末）对于实数a.b.我们定义符号max{a.b}的意义为：当a≥b 时.max{a.b}＝a；当a＜b时.max{a.b}＝b；如：max{4.﹣2}＝4.max{3.3}＝3.若关于x 的函数为y＝max（2x﹣1.﹣x+2}.则该函数的最小值是（）A．2B．1C．0D．﹣1【答案】B【解答】解：当2x﹣1≥﹣x+2时.解得：x≥1.此时y＝2x﹣1.∵2＞0.∴y随x的增大而增大.当x＝1时.y最小为1；当2x﹣1＜﹣x+2时.解得：x＜1.此时y＝﹣x+2.∵﹣1＜0.∴y随x的增大而减小.综上.当x＝1时.y最小为1.故选：B．11．（2020秋•成安县期末）如图.若直线y＝kx+b与x轴交于点A（﹣4.0）.与y轴正半轴交于B.且△OAB的面积为4.则该直线的解析式为（）A．B．y＝2x+2C．y＝4x+4D．【答案】A【解答】解：∵A（﹣4.0）.∴OA＝4.∵×4×OB＝4.解得OB＝2.∴B（0.2）.把A（﹣4.0）.B（0.2）代入y＝kx+b.∴.解得.∴直线解析式为y＝x+2．故选：A．12．（2021春•饶平县校级期末）已知2y﹣3与3x+1成正比例.则y与x的函数解析式可能是（）A．y＝3x+1B．C．D．y＝3x+2【答案】C【解答】解：∵2y﹣3与3x+1成正比例.则2y﹣3＝k（3x+1）.当k＝1时.2y﹣3＝3x+1.即y＝x+2．故选：C．13．（2021秋•榆林期末）已知直线l1交x轴于点（﹣3.0）.交y轴于点（0.6）.直线l2与直线l1关于x轴对称.将直线l1向下平移8个单位得到直线l3.则直线l2与直线l3的交点坐标为（）A．（﹣1.﹣4）B．（﹣2.﹣4）C．（﹣2.﹣1）D．（﹣1.﹣1）【答案】A【解答】解：设直线l1为y＝kx+b.∵直线l1交x轴于点（﹣3.0）.交y轴于点（0.6）.∴.解得.∴b＝﹣4.∴直线l1为y＝2x+6.将直线l1向下平移8个单位得到直线l3：y＝2x+6﹣8＝2x﹣2.∵直线l2与直线l1关于x轴对称.∴直线l2交x轴于点（﹣3.0）.交y轴于点（0.﹣6）.∴直线l2为y＝﹣2x﹣6.解得.∴直线l2与直线l3的交点坐标为（﹣1.﹣4）.故选：A．1．（2021•长沙）下列函数图象中.表示直线y＝2x+1的是（）A．B．C．D．【答案】B【解答】解：∵k＝2＞0.b＝1＞0.∴直线经过一、二、三象限．故选：B．2．（2021•嘉峪关）将直线y＝5x向下平移2个单位长度.所得直线的表达式为（）A．y＝5x﹣2B．y＝5x+2C．y＝5（x+2）D．y＝5（x﹣2）【答案】A【解答】解：将直线y＝5x向下平移2个单位长度.所得的函数解析式为y＝5x﹣2．故选：A．3．（2021•陕西）在平面直角坐标系中.将直线y＝﹣2x向上平移3个单位.平移后的直线经过点（﹣1.m）.则m的值为（）A．﹣1B．1C．﹣5D．5【答案】D【解答】解：将直线y＝﹣2x向上平移3个单位.得到直线y＝﹣2x+3.把点（﹣1.m）代入.得m＝﹣2×（﹣1）+3＝5．故选：D．4．（2021•抚顺）如图.直线y＝2x与y＝kx+b相交于点P（m.2）.则关于x的方程kx+b ＝2的解是（）A．x＝B．x＝1C．x＝2D．x＝4【答案】B【解答】解：∵直线y＝2x与y＝kx+b相交于点P（m.2）.∴2＝2m.∴m＝1.∴P（1.2）.∴当x＝1时.y＝kx+b＝2.∴关于x的方程kx+b＝2的解是x＝1.故选：B．5．（2020•牡丹江）两个一次函数y＝ax+b和y＝bx+a.它们在同一个直角坐标系的图象可能是（）A．B．C．D．【答案】B【解答】解：当a＞0.b＞0时.一次函数y＝ax+b和y＝bx+a的图象都经过第一、二、三象限.当a＞0.b＜0时.一次函数y＝ax+b的图象经过第一、三、四象限.函数y＝bx+a的图象经过第一、二、四象限.当a＜0.b＞0时.一次函数y＝ax+b的图象经过第一、二、四象限.函数y＝bx+a的图象经过第一、三、四象限.当a＜0.b＜0时.一次函数y＝ax+b和y＝bx+a的图象都经过第二、三、四象限.由上可得.两个一次函数y＝ax+b和y＝bx+a.它们在同一个直角坐标系的图象可能是B中的图象.故选：B．6．（2021•乐山）如图.已知直线l1：y＝﹣2x+4与坐标轴分别交于A、B两点.那么过原点O且将△AOB的面积平分的直线l2的解析式为（）A．y＝x B．y＝x C．y＝x D．y＝2x【答案】D【解答】解：如图.当y＝0.﹣2x+4＝0.解得x＝2.则A（2.0）；当x＝0.y＝4.则B（0.4）.∴AB的中点坐标为（1.2）.∵直线l2把△AOB面积平分∴直线l2过AB的中点.设直线l2的解析式为y＝kx.把（1.2）代入得2＝k.解得k＝2.∴l2的解析式为y＝2x.故选：D．7．（2021•娄底）如图.直线y＝x+b和y＝kx+4与x轴分别相交于点A（﹣4.0）.点B（2.0）.则解集为（）A．﹣4＜x＜2B．x＜﹣4C．x＞2D．x＜﹣4或x＞2【答案】A【解答】解：∵当x＞﹣4时.y＝x+b＞0.当x＜2时.y＝kx+4＞0.∴解集为﹣4＜x＜2.故选：A．8．（2019•苏州）若一次函数y＝kx+b（k.b为常数.且k≠0）的图象经过点A（0.﹣1）.B （1.1）.则不等式kx+b＞1的解集为（）A．x＜0B．x＞0C．x＜1D．x＞1【答案】D【解答】解：如图所示：不等式kx+b＞1的解为：x＞1．故选：D．9．（2021•德阳）关于x.y的方程组的解为.若点P（a.b）总在直线y＝x上方.那么k的取值范围是（）A．k＞1B．k＞﹣1C．k＜1D．k＜﹣1【答案】B【解答】解：解方程组可得..∵点P（a.b）总在直线y＝x上方.∴b＞a.∴＞﹣k﹣1.解得k＞﹣1.故选：B．10．（2021•呼和浩特）在平面直角坐标系中.点A（3.0）.B（0.4）．以AB为一边在第一象限作正方形ABCD.则对角线BD所在直线的解析式为（）A．y＝﹣x+4B．y＝﹣x+4C．y＝﹣x+4D．y＝4【答案】A【解答】解：过D点作DH⊥x轴于H.如图.∵点A（3.0）.B（0.4）．∴OA＝3.OB＝4.∵四边形ABCD为正方形.∴AB＝AD.∠BAD＝90°.∵∠OBA+∠OAB＝90°.∠OAB+∠DAH＝90°.∴∠ABO＝∠DAH.在△ABO和△DAH中..∴△ABO≌△DAH（AAS）.∴AH＝OB＝4.DH＝OA＝3.∴D（7.3）.设直线BD的解析式为y＝kx+b.把D（7.3）.B（0.4）代入得.解得.∴直线BD的解析式为y＝﹣x+4．故选：A．11．（2019•江西）如图.在平面直角坐标系中.点A.B的坐标分别为（﹣.0）.（.1）.连接AB.以AB为边向上作等边三角形ABC．（1）求点C的坐标；（2）求线段BC所在直线的解析式．【答案】（1）（.2）（2）y＝x+．【解答】解：（1）如图.过点B作BH⊥x轴.∵点A坐标为（﹣.0）.点B坐标为（.1）.∴|AB|＝＝2.∵BH＝1.∴sin∠BAH＝＝.∴∠BAH＝30°.∵△ABC为等边三角形.∴AB＝AC＝2.∴∠CAB+∠BAH＝90°.∴点C的纵坐标为2.∴点C的坐标为（.2）．（2）由（1）知点C的坐标为（.2）.点B的坐标为（.1）.设直线BC的解析式为：y＝kx+b.则.解得.故直线BC的函数解析式为y＝x+．1．（2021•庐阳区校级一模）一次函数y＝﹣2x﹣3的图象和性质．叙述正确的是（）A．y随x的增大而增大B．与y轴交于点（0.﹣2）C．函数图象不经过第一象限D．与x轴交于点（﹣3.0）【答案】C【解答】解：∵一次函数y＝﹣2x﹣3.∴该函数y随x的增大而减小.故选项A错误；与y轴交于点（0.﹣3）.故选项B错误；该函数图象经过第二、三、四象限.不经过第一象限.故选项C正确；与x轴交于点（﹣.0）.故选项D错误；故选：C．2．（2021•陕西模拟）平面直角坐标系中.直线y＝﹣2x+m沿x轴向右平移4个单位后恰好经过（1.2）.则m＝（）A．﹣1B．2C．﹣4D．﹣3【答案】C【解答】解：直线y＝﹣2x+m沿x轴向右平移4个单位后得到y＝﹣2（x﹣4）+m.∵经过（1.2）.∴2＝﹣2（1﹣4）+m.解得m＝﹣4.故选：C．3．（2021•商河县校级模拟）若一次函数y＝kx+b的图象经过一、二、四象限.则一次函数y＝﹣bx+k的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】A【解答】解：一次函数y＝kx+b过一、二、四象限.则函数值y随x的增大而减小.因而k＜0；图象与y轴的正半轴相交则b＞0.因此一次函数y＝﹣bx+k的一次项系数﹣b＜0.y随x的增大而减小.经过二四象限.常数项k＜0.则函数与y轴负半轴相交.因此一定经过二三四象限.因此函数不经过第一象限．故选：A．4．（2021•萧山区一模）已知y﹣3与x+5成正比例.且当x＝﹣2时.y＜0.则y关于x的函数图象经过（）A．第一、二、三象限B．第一、二、四象限C．第一、三、四象限D．第二、三、四象限【答案】D【解答】解：∵y﹣3与x+5成正比例.∴设y﹣3＝k（x+5）.整理得：y＝kx+5k+3．当x＝﹣2时.y＜0.即﹣2k+5k+3＜0.整理得3k+3＜0.解得：k＜﹣1．∵k＜﹣1.∴5k+3＜﹣2.∴y＝kx+5k+3的图象经过第二、三、四象限．故选：D．5．（2021•陕西模拟）一次函数y＝kx+b的图象经过点A（2.3）.每当x增加1个单位时.y 增加3个单位.则此函数表达式是（）A．y＝x+3B．y＝2x﹣3C．y＝3x﹣3D．y＝4x﹣4【答案】C【解答】解；由题意可知一次函数y＝kx+b的图象也经过点（3.6）.∴.解得∴此函数表达式是y＝3x﹣3.故选：C．6．（2021•蕉岭县模拟）在平面直角坐标系中.一次函数y＝mx+b（m.b均为常数）与正比例函数y＝nx（n为常数）的图象如图所示.则关于x的方程mx＝nx﹣b的解为（）A．x＝3B．x＝﹣3C．x＝1D．x＝﹣1【答案】A【解答】解：∵两条直线的交点坐标为（3.﹣1）.∴关于x的方程mx＝nx﹣b的解为x＝3.故选：A．7．（2021•奉化区校级模拟）八个边长为1的正方形如图摆放在平面直角坐标系中.经过原点的一条直线l将这八个正方形分成面积相等的两部分.则该直线l的解析式为（）A．y＝﹣x B．y＝﹣x C．y＝﹣x D．y＝﹣x【答案】D【解答】解：设直线l和八个正方形的最上面交点为A.过A作AB⊥OB于B.B过A 作AC⊥OC于C.∵正方形的边长为1.∴OB＝3.∵经过原点的一条直线l将这八个正方形分成面积相等的两部分.∴S△AOB＝4+1＝5.∴OB•AB＝5.∴AB＝.∴OC＝.由此可知直线l经过（﹣.3）.设直线方程为y＝kx.则3＝﹣k.k＝﹣.∴直线l解析式为y＝﹣x.故选：D．8．（2021•遵义一模）如图.直线y＝kx+b（k＜0）与直线y＝x都经过点A（3.2）.当kx+b＞x时.x的取值范围是（）A．x＜2B．x＞2C．x＜3D．x＞3【答案】C【解答】解：由图象可知.当x＜3时.直线y＝kx+b在直线y＝x上方.所以当kx+b＞x时.x的取值范围是x＜3．故选：C．9．（2021•饶平县校级模拟）如图.函数y＝ax+b和y＝﹣x的图象交于点P.则根据图象可得.关于x.y的二元一次方程组中的解是（）A．B．C．D．【答案】C【解答】解：当y＝1时.﹣x＝1.解得x＝﹣3.则点P的坐标为（﹣3.1）.所以关于x.y的二元一次方程组中的解为．故选：C．10．（2021•杭州模拟）已知直线l：y＝kx+b经过点A（﹣1.a）和点B（1.a﹣4）.若将直线l向上平移2个单位后经过原点.则直线的表达式为（）A．y＝2x+2B．y＝2x﹣2C．y＝﹣2x+2D．y＝﹣2x﹣2【答案】D【解答】解：将直线l向上平移2个单位后经过原点.则点A（﹣1.a）和点B（1.a﹣4）平移后对应的点的坐标为（﹣1.a+2）和（1.a﹣2）.∵将直线l向上平移2个单位后经过原点.∴点（﹣1.a+2）和点（1.a﹣2）关于原点对称.∴a+2+a﹣2＝0.∴a＝0.∴A（﹣1.0）.B（1.﹣4）.把A、B的坐标代入y＝kx+b得..解得.∴直线AB的解析式为y＝﹣2x﹣2.故选：D．11．（2021•南山区校级二模）我国古代很早就对二元一次方程组进行了研究.古著《九章算术》记载用算筹表示二元一次方程组.发展到现代就是用矩阵式＝来表示二元一次方程组.而该方程组的解就是对应两直线（不平行）a1x+b1y＝c1与a2x+b2y＝c2的交点坐标P（x.y）据此.则矩阵式＝所对应两直线交点坐标是．【答案】（﹣1.2）【解答】解：依题意.得.解得.∴矩阵式＝所对应两直线交点坐标是（﹣1.2）．故答案为：（﹣1.2）．12．（2021•杭州模拟）已知直线y＝kx+b经过点A（5.0）.B（1.4）．（1）求直线AB的解析式；（2）若直线y＝2x﹣4与直线AB相交于点C.求点C的坐标；（3）根据图象.写出关于x的不等式2x﹣4＞kx+b的解集．【答案】（1）y＝﹣x+5 （2）C（3.2）（3）x＞3【解答】解：（1）∵直线y＝kx+b经过点A（5.0）.B（1.4）.∴.解得.∴直线AB的解析式为：y＝﹣x+5；（2）∵若直线y＝2x﹣4与直线AB相交于点C.∴．解得.∴点C（3.2）；（3）根据图象可得x＞3.。

中考数学考点14二次函数图像与性质及与a、b、c的关系(解析版)

二次函数图像与性质及与a 、b 、c 的关系【命题趋势】在中考中.二次函数的图像与性质常在选择题和填空题常考；二次函数图像与系数a 、b 、c 的关系常在选择题或填空题的最后一题出现。

【中考考查重点】一、会用描点法画出二次函数的图像.通过图像了解二次函数的性质；二、会用配方法将数字系数的二次函数的表达式化为k ax +=-)h (2y 的形式.并能由此得到二次函数图像的顶点坐标.说出图像的开口方向.画出图像的对称轴。

考点一：二次函数的概念及三种解析式概念形如的函数叫二次函数三种解析式 1. 一般式：；2. 顶点式：（a ≠0）其中（h,k ）为二次函数的顶点坐标3. 交点式：.其中为抛物线与x 轴交点的横坐标图像画法列表、描点、连线1．（2021秋•黔西南州期末）下列各式中.y 是关于x 的二次函数的是（） A ．y ＝4x +2 B ．y ＝（x ﹣1）2﹣x 2 C ．y ＝3x 2+5﹣4x D ．y ＝【答案】C【解答】解：A ．y ＝4x +2.是一次函数.故A 不符合题意； B ．y ＝（x ﹣1）2﹣x 2＝﹣2x +1.是一次函数.故B 不符合题意； C ．y ＝3x 2+5﹣4x ＝3x 2﹣4x +5.是二次函数.故C 符合题意； D ．y ＝等号右边是分式.不是二次函数.故D 不符合题意；故选：C ．考点二：二次函数的图像与性质2．（2021春•岳麓区校级期末）已知二次函数的解析式为y ＝x 2﹣4x +5.则该二次函数图象的顶点坐标是（） A ．（﹣2.1） B ．（2.1）C ．（2.﹣1）D ．（1.2）【答案】B【解答】解：∵二次函数的解析式为y ＝x 2﹣4x +5. ∴x ＝﹣＝﹣＝2.y ＝＝＝1.二次函数图象的顶点坐标为（2.1）. 故选：B ．3．（2020秋•莫旗期末）对于二次函数y ＝（x ﹣1）2+2的图象.下列说法正确的是（）A ．开口向下B ．当x ＝﹣1时.y 有最大值是2C ．对称轴是直线x ＝﹣1解析式对称轴直线（还可以利用.其中为y 值相等的两个点对应的横坐标）求解）顶点坐标2424b ac b a a ⎛⎫-- ⎪⎝⎭，增减性当时.在对称轴左侧.y 随x 的增大而减少；在对称轴右侧.y 随x 的增大而增大当a ＜0时.在对称轴左侧.y 随x 的增大而增大；在对称轴右侧.y 随x的增大而减少最值当时.y 有最小值当2bx a =-时.y 有最小值244ac ba-．当a ＜0时.y 有最大值当时.y 有最大值D．顶点坐标是（1.2）【答案】D【解答】解：二次函数y＝（x﹣1）2+2的图象的开口向上.故A错误；当x＝1时.函数有最小值2.故B错误；对称轴为直线x＝1.故C错误；顶点坐标为（1.2）.故D正确．故选：D．4．（2021秋•越秀区期末）在同一平面直角坐标系xOy中.一次函数y＝ax与二次函数y ＝ax2﹣a的图象可能是（）A．B．C．D．【答案】C【解答】解：选项A.直线下降a＜0.抛物线开口向上.a＞0.不符合题意．选项B.直线下降.a＜0.抛物线开口向下a＜0.抛物线与y轴交点在x轴下方.﹣a＜0.即a＞0.不符合题意．选项C.直线上升.a＞0.抛物线开口向上a＞0.抛物线与y轴交点在x轴下方.﹣a＜0.即a＞0.符合题意．选项D.直线上升.a＞0.抛物线开口向下a＜0.不符合题意．故选：C．5．（2021秋•南召县期末）已知（﹣3.y1）.（1.y2）.（5.y3）是抛物线y＝﹣2x2﹣4x+m 上的点.则（）A．y1＞y2＞y3B．y2＞y1＞y3C．y1＝y2＞y3D．y1＞y2＝y3【答案】C【解答】解：∵y＝﹣2x2﹣4x+m＝﹣2（x+1）2+2+m.∴抛物线的开口向下.对称轴是直线x＝﹣1.∴当x＞﹣1时.y随x的增大而减小.∵（﹣3.y1）.（1.y2）.（5.y3）是抛物线y＝﹣2x2﹣4x+m上的点.∴点（﹣3.y1）关于对称轴x＝﹣1的对称点是（1.y3）.∵1＜5.∴y1＝y2＞y3.故选：C6．（2021秋•昭阳区期中）已知二次函数y＝﹣（x﹣k）2+h.当x＞2时.y随x的增大而减小.则函数中k的取值范围是（）A．k≥2B．k≤2C．k＝2D．k≤﹣2【答案】B【解答】解：抛物线的对称轴为直线x＝k.因为a＝﹣1＜0.所以抛物线开口向下.所以当x＞k时.y的值随x值的增大而减小.而x＞2时.y的值随x值的增大而减小.所以k≤2．故选：B．考点三：二次函数图像与a、b、c的关系a、b、c的正负数判断二次函数图像二次项系数a 决定抛物线的开口方向及开口大小⑴当0a>时.抛物线开口向上⑵当0a<时.抛物线开口向下一次项系数b 决定对称轴的位置在二次项系数a确定的前提下.b决定了抛物线的对称轴．（同左异右b为对称轴为y轴）2.根据二次函数图像判断a 、b 、c 关系式与0的关系7．（2021秋•新抚区期末）如图.已知点A （﹣1.0）和点B （1.1）.若抛物线y ＝x 2+c 与线段AB 有公共点.则c 的取值范围是（）A ．﹣1≤c ≤0B ．﹣1≤c ≤C ．﹣1≤c ≤D ．0≤c ≤常数项系数c决定抛物线与y 轴的交点的位置⑴ 当0c >时.抛物线与y 轴的交点在x 轴上方⑵ 当0c =时.抛物线与y 轴的交点为坐标原点⑶ 当0c <时.抛物线与y 轴的交点在x 轴下方ac 4b2-决定抛物线与x 轴的交点个数b2－4ac ＞0时.抛物线与x 轴有2个交点;b2－4ac ＝0时.抛物线与x 轴有1个交点; b2－4ac ＜0时.抛物线与x 轴没有交点决定抛物线与x 轴的交点个数关系式实质2a+b实质式结合a 的正负比较a2b-与1关系 2a+b实质式结合a 的正负比较a2b-与-1关系 a+b+c 实质是令x=1.看纵坐标正负 a -b+c 实质是令x=-1.看纵坐标正负 4a+2b+c 实质是令x=2.看纵坐标正负 4a -2b+c实质是令x=-2.看纵坐标正负【答案】C【解答】解：设AB所在直线为y＝kx+b.将（﹣1.0）.（1.1）代入y＝kx+b得.∴y＝x+.如图.当抛物线与线段AB相切时.令x+＝x2+c.整理得x2﹣x﹣+c＝0.∴Δ＝（﹣）2﹣4（﹣+c）＝0.解得c＝.c减小.抛物线向下移动.当抛物线经过点A（﹣1.0）时.将（﹣1.0）代入y＝x2+c得0＝1+c.解得c＝﹣1.∴﹣1≤c≤满足题意．故选：C．8．（2021秋•肃州区期末）已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示.在下列五个结论中：①2a﹣b＜0；②abc＜0；③a+b+c＜0；④a﹣b+c＞0；⑤4a+2b+c＞0．其中正确的个数有（）A．1个B．2个C．3个D．4个【答案】C【解答】解：∵抛物线开口向上.∴a＞0.∵0＜﹣＜1.∴b＜0.2a﹣b＞0.①不正确.不符合题意．∵抛物线与y轴交点在x轴下方.∴c＜0.∴abc＞0.②不正确.不符合题意．∵x＝1时.y＜0.∴a+b+c＜0.③正确.符合题意．∵x＝﹣1时.y＞0.∴a﹣b+c＞0.④正确.符合题意．∵x＝2时.y＞0.∴4a+2b+c＞0.⑤正确.符合题意．故选：C1．（2021秋•五常市期末）抛物线y＝x2+2x﹣3的对称轴是直线（）A．x＝﹣2B．x＝﹣1C．x＝1D．x＝2【答案】B【解答】解：∵y＝x2+2x﹣3.∴抛物线对称轴为直线x＝﹣＝﹣1.故选：B．2．（2021秋•呼和浩特期末）关于二次函数y＝2x2+4x﹣1.下列说法正确的是（）A．图象与y轴的交点坐标为（0.1）B．当x＜1时.y的值随x值的增大而减小C．图象的顶点坐标为（﹣1.﹣3）D．图象的对称轴在y轴的右侧【答案】C【解答】解：∵y＝2x2+4x﹣1＝2（x+1）2﹣3.∴当x＝0时.y＝﹣1.故选项A错误.该函数的对称轴是直线x＝﹣1.当x＜﹣1时.y随x的增大而减小.故选项B错误.图象的顶点坐标为（﹣1.﹣3）.故选项C正确.图象的对称轴在y轴的左侧.故选项D错误.故选：C．3．（2021春•岳麓区校级期末）已知抛物线y＝﹣（x+1）2上的两点A（﹣4.4.y1）和B （﹣3.3.y2）.那么下列结论一定成立的是（）A．0＜y2＜y1B．0＜y1＜y2C．y1＜y2＜0D．y2＜y1＜0【答案】C【解答】解：∵y＝﹣（x+1）2.∴二次函数图象开口向下.对称轴为直线x＝﹣1.顶点为（﹣1.0）.∵A（﹣4.4.y1）和B（﹣3.3.y2）.∴|﹣1+4.4|＞|﹣1+3.3|.∴y1＜y2＜0.故选：C．4．（2021秋•克东县期末）抛物线y＝x2﹣2x﹣4的顶点M关于坐标原点O的对称点为N.则点N的坐标为（）A．（1.﹣5）B．（1.5）C．（﹣1.5）D．（﹣1.﹣5）【答案】C【解答】解：∵抛物线y＝x2﹣2x﹣4＝（x﹣1）2﹣5.∴该抛物线的顶点M的坐标为（1.﹣5）.∴顶点M关于坐标原点O的对称点为N的坐标为（﹣1.5）.故选：C．5．（2021秋•龙江县期末）对称轴为直线x＝1的抛物线y＝ax2+bx+c（a、b、c为常数.且a≠0）如图所示.现有结论：①abc＜0.②b2＞4ac.③3a+c＞0.④ac﹣bc+c2＜0．其中结论正确的有（）A．1个B．2个C．3个D．4个【答案】C【解答】解：∵抛物线开口向上.∴a＞0.∵抛物线对称轴为直线x＝﹣＝1.∴b＝﹣2a＜0.∵抛物线与y轴交点在x轴下方.∴c＜0.∴abc＞0.①错误．∵抛物线与x轴有2个交点.∴b2﹣4ac＞0.∴b2＞4ac.②正确．∵b＝﹣2a.∴y＝ax2﹣2ax+c.由图象可得x＝﹣1时y＞0.∴a+2a+c＝3a+c＞0.③正确．∵c＜0.∴ac﹣bc+c2＜0可整理为a﹣b+c＞0.∵x＝﹣1时y＞0.∴a﹣b+c＞0.④正确．故选：C．1．（2021•兰州）二次函数y＝x2+4x+1的图象的对称轴是（）A．x＝2B．x＝4C．x＝﹣2D．x＝﹣4【答案】C【解答】解：∵二次函数y＝x2+4x+1.∴抛物线对称轴为直线x＝﹣＝﹣2．故选：C．2．（2021•广州）抛物线y＝ax2+bx+c经过点（﹣1.0）、（3.0）.且与y轴交于点（0.﹣5）.则当x＝2时.y的值为（）A．﹣5B．﹣3C．﹣1D．5【答案】A【解答】解：如图∵抛物线y＝ax2+bx+c经过点（﹣1.0）、（3.0）.且与y轴交于点（0.﹣5）.∴可画出上图.∵抛物线对称轴x＝＝1.∴点（0.﹣5）的对称点是（2.﹣5）.∴当x＝2时.y的值为﹣5．故选：A．3．（2021•常州）已知二次函数y＝（a﹣1）x2.当x＞0时.y随x增大而增大.则实数a 的取值范围是（）A．a＞0B．a＞1C．a≠1D．a＜1【答案】B【解答】解：∵二次函数y＝（a﹣1）x2.当x＞0时.y随x增大而增大.∴a﹣1＞0.∴a＞1.故选：B．4．（2021•阜新）如图.二次函数y＝a（x+2）2+k的图象与x轴交于A.B（﹣1.0）两点.则下列说法正确的是（）A．a＜0B．点A的坐标为（﹣4.0）C．当x＜0时.y随x的增大而减小D．图象的对称轴为直线x＝﹣2【答案】D【解答】解：∵二次函数y＝a（x+2）2+k的图象开口方向向上.∴a＞0.故A错误.∵图象对称轴为直线x＝﹣2.且过B（﹣1.0）.∴A点的坐标为（﹣3.0）.故B错误.D正确.由图象知.当x＜0时.由图象可知y随x的增大先减小后增大.故C错误.故选：D．5．（2021•深圳）二次函数y＝ax2+bx+1的图象与一次函数y＝2ax+b在同一平面直角坐标系中的图象可能是（）A．B．C．D．【答案】A【解答】解：A、由抛物线可知.a＞0.b＜0.c＝1.对称轴为直线x＝﹣.由直线可知.a ＞0.b＜0.直线经过点（﹣.0）.故本选项符合题意；B、由抛物线可知.对称轴为直线x＝﹣.直线不经过点（﹣.0）.故本选项不符合题意；C、由抛物线可知.对称轴为直线x＝﹣.直线不经过点（﹣.0）.故本选项不符合题意；D、由抛物线可知.对称轴为直线x＝﹣.直线不经过点（﹣.0）.故本选项不符合题意；故选：A．6．（2021•阿坝州）二次函数y＝ax2+bx+c的图象如图所示.下列说法错误的是（）A．a＜0.b＞0B．b2﹣4ac＞0C．方程ax2+bx+c＝0的解是x1＝5.x2＝﹣1D．不等式ax2+bx+c＞0的解集是0＜x＜5【答案】D【解答】解：由图象可知.抛物线开口向下.所以a＜0；对称轴为直线x＝﹣＝2.所以b＝﹣4a.所以b＞0.故A正确．因为抛物线与x轴有两个交点.所以b2﹣4ac＞0.故B正确．由图象和对称轴公式可知.抛物线与x轴交于点（5.0）和（﹣1.0）.所以方程ax2+bx+c ＝0的解是x1＝5.x2＝﹣1.故C正确．由图象可知.不等式ax2+bx+c＞0的解集是﹣1＜x＜5.故D错误．故选：D．7．（2021•雅安）定义：min{a.b}＝.若函数y＝min{x+1.﹣x2+2x+3}.则该函数的最大值为（）A．0B．2C．3D．4【答案】C【解答】解：x+1＝﹣x2+2x+3.解得x＝﹣1或x＝2．∴y＝.把x＝2代入y＝x+1得y＝3.∴函数最大值为y＝3．故选：C．8．（2021•烟台）如图.二次函数y＝ax2+bx+c的图象经过点A（﹣1.0）.B（3.0）.与y 轴交于点C．下列结论：①ac＞0；②当x＞0时.y随x的增大而增大；③3a+c＝0；④a+b≥am2+bm．其中正确的个数有（）A．1个B．2个C．3个D．4个【答案】B【解答】解：把点A（﹣1.0）.B（3.0）代入二次函数y＝ax2+bx+c.可得二次函数的解析式为：y＝ax2﹣2ax﹣3a.∵该函数图象开口方向向下.∴a＜0.∴b＝﹣2a＞0.c＝﹣3a＞0.∴ac＜0.3a+c＝0.①错误.③正确；∵对称轴为直线：x＝﹣＝1.∴x＜1时.y随x的增大而增大.x＞1时.y随x的增大而减小；②错误；∴当x＝1时.函数取得最大值.即对于任意的m.有a+b+c≥am2+bm+c.∴a+b≥am2+bm.故④正确．综上.正确的个数有2个.故选：B．9．（2021•徐州）如图.点A、B在y＝x2的图象上．已知A、B的横坐标分别为﹣2、4.直线AB与y轴交于点C.连接OA、OB．（1）求直线AB的函数表达式；（2）求△AOB的面积；（3）若函数y＝x2的图象上存在点P.使△P AB的面积等于△AOB的面积的一半.则这样的点P共有个．【答案】（1）y＝+2 （2）6 （3）4【解答】解：（1）∵点A、B在y＝x2的图象上.A、B的横坐标分别为﹣2、4.∴A（﹣2.1）.B（4.4）.设直线AB的解析式为y＝kx+b.∴.解得.∴直线AB的解析式为y＝+2；（2）在y＝+2中.令x＝0.则y＝2.∴C的坐标为（0.2）.∴OC＝2.∴S△AOB＝S△AOC+S△BOC＝+＝6．（3）过OC的中点.作AB的平行线交抛物线两个交点P1、P2.此时△P1AB的面积和△P2AB的面积等于△AOB的面积的一半.作直线P1P2关于直线AB的对称直线.交抛物线两个交点P3、P4.此时△P3AB的面积和△P4AB的面积等于△AOB的面积的一半.所以这样的点P共有4个.故答案为4．1．（2021•龙湾区模拟）下列函数中.是二次函数的是（）A．y＝6x2+1B．y＝6x+1C．y＝D．y＝﹣+1【答案】A【解答】解：A．是二次函数.故本选项符合题意；B．是一次函数.不是二次函数.故本选项不符合题意；C．是反比例函数.不是二次函数.故本选项不符合题意；D．等式的右边是分式.不是整式.不是二次函数.故本选项不符合题意；故选：A．2．（2021•安徽模拟）在平面直角坐标系中.A的坐标为（1.﹣2）.B的坐标为（﹣1.﹣5）.若y关于x的二次函数y＝﹣x2+2mx﹣m2﹣1在﹣1≤x≤1段的图象始终在线段AB 的下方.则m的取值范围是（）A．m＜﹣3B．m＞2C．m＜﹣2或m＞2D．m＜﹣3或m＞2【答案】D【解答】解：∵y关于x的二次函数为y＝﹣x2+2mx﹣m2﹣1.∴顶点式为y＝﹣（x﹣m）2﹣1.∴抛物线顶点为（m.﹣1）.当﹣1≤m≤1时.∵﹣1＞﹣2＞﹣5.∴顶点在线段AB的上方.不符合题意；当m＜﹣1时.若二次函数的图象与线段AB交于点B.则当x＝﹣1时.y＝﹣（﹣1﹣m）2﹣1＝﹣5.解得：m1＝﹣3.m2＝1（舍去）.∴要使二次函数的图象在线段AB的下方.则需要将图象向左平移.∴m＜﹣3.当m＞1时.若二次函数图象与线段AB交于点A.则当x＝1时.y＝﹣（1﹣m）2﹣1＝﹣2.解得：m1＝2.m2＝0（舍去）.∴而要使二次函数始终在线段AB下方.则需要将图象向右平移.∴m＞2.综上所述：m＜﹣3或m＞2．故选：D．3．（2021•陕西模拟）如图.若二次函数y＝ax2+bx+c（a≠0）图象的对称轴为x＝1.与y 轴交于点C．与x轴交于点A、点B（﹣1.0）．则：①二次函数的最大值为1；②4a ﹣2b+c＞0；③b2﹣4ac＞0；④当y＜0时.x＜﹣1或x＞3．其中错误的个数是（）A．I B．2C．3D．4【答案】B【解答】解：∵对称轴为直线x＝1.∴b＝﹣2a.∵B（﹣1.0）.∴A（3.0）.∴a﹣b+c＝0.∴c＝﹣3a.∴y＝ax2﹣2ax﹣3a；①当x＝1时.函数的最大值是a+b+c.故①不正确；②当x＝﹣2时.y＜0.∴4a﹣2b+c＜0.故②不正确；③∵函数与x轴有两个不同的交点.∴Δ＝b2﹣4ac＞0.故③正确；④由图象可知当y＜0时.x＜﹣1或x＞3.故④正确；故选：B．。

专题03 函数图像的压轴真题训练(解析版)-2023年中考数学解答题压轴真题汇编

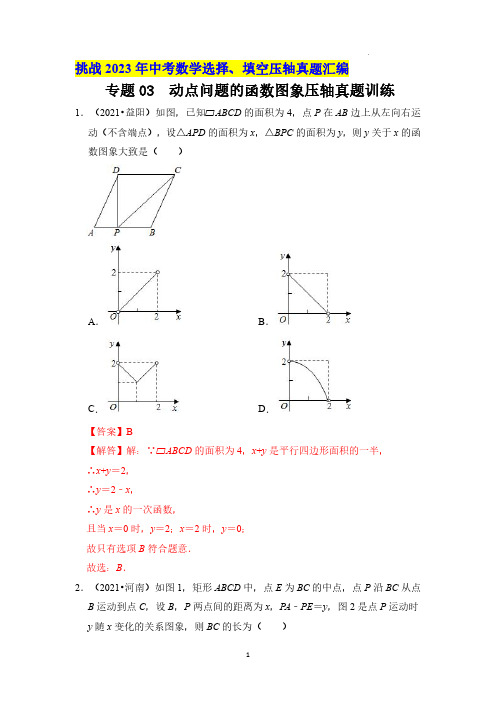
挑战2023年中考数学选择、填空压轴真题汇编专题03动点问题的函数图象压轴真题训练1．（2021•益阳）如图，已知▱ABCD的面积为4，点P在AB边上从左向右运动（不含端点），设△APD的面积为x，△BPC的面积为y，则y关于x的函数图象大致是（）A．B．C．D．【答案】B【解答】解：∵▱ABCD的面积为4，x+y是平行四边形面积的一半，∴x+y＝2，∴y＝2﹣x，∴y是x的一次函数，且当x＝0时，y＝2；x＝2时，y＝0；故只有选项B符合题意．故选：B．2．（2021•河南）如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x，PA﹣PE＝y，图2是点P运动时y随x变化的关系图象，则BC的长为（）A．4B．5C．6D．7【答案】C【解答】解：由函数图象知：当x＝0，即P在B点时，BA﹣BE＝1．利用三角形两边之差小于第三边，得到P A﹣PE≤AE．∴y的最大值为AE，∴AE＝5．在Rt△ABE中，由勾股定理得：BA2+BE2＝AE2＝25，设BE的长度为t，则BA＝t+1，∴（t+1）2+t2＝25，即：t2+t﹣12＝0，∴（t+4）（t﹣3）＝0，由于t＞0，∴t+4＞0，∴t﹣3＝0，∴t＝3．∴BC＝2BE＝2t＝2×3＝6．故选：C．3．（2022•鞍山）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝4cm，CD⊥AB，垂足为点D，动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B，同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动．当点M停止运动时，点N也随之停止，连接MN．设运动时间为ts，△MND的面积为Scm2，则下列图象能大致反映S与t之间函数关系的是（）A．B．C．D．【答案】B【解答】解：∵∠ACB＝90°，∠A＝30°，AB＝4，∴∠B＝60°，BC＝AB＝2，AC＝BC＝6，∵CD⊥AB，∴CD＝AC＝3，AD＝CD＝3，BD＝BC＝，∴当M在AD上时，0≤t≤3，MD＝AD﹣AM＝3﹣t，DN＝DC+CN＝3+t，∴S＝MD•DN＝（3﹣t）（3+t）＝﹣t2+，当M在BD上时，3＜t≤4，MD＝AM﹣AD＝t﹣3，∴S＝MD•DN＝（t﹣3）（3+t）＝t2﹣，故选：B．4．（2022•菏泽）如图，等腰Rt△ABC与矩形DEFG在同一水平线上，AB＝DE ＝2，DG＝3，现将等腰Rt△ABC沿箭头所指方向水平平移，平移距离x是自点C到达DE之时开始计算，至AB离开GF为止．等腰Rt△ABC与矩形DEFG 的重合部分面积记为y，则能大致反映y与x的函数关系的图象为（）A．B．C．D．【答案】B【解答】解：如图，作CH⊥AB于点H，∵AB＝2，△ABC是等腰直角三角形，∴CH＝1，当0≤x≤1时，y＝×2x•x＝x2，当1＜x≤3时，y＝＝1，当3＜x≤4时，y＝1﹣＝﹣（x﹣3）2+1，故选：B．5．（2022•鄂尔多斯）如图①，在正方形ABCD中，点M是AB的中点，点N 是对角线BD上一动点，设DN＝x，AN+MN＝y，已知y与x之间的函数图象如图②所示，点E（a，2）是图象的最低点，那么a的值为（）A．B．2C．D．【答案】A【解答】解：如图，连接AC交BD于点O，连接NC，连接MC交BD于点N′．∵四边形ABCD是正方形，∴O是BD的中点，∵点M是AB的中点，∴N′是△ABC的重心，∴N′O＝BO，∴N′D＝BD，∵A、C关于BD对称，∴NA＝NC，∴AN+MN＝NC+MN，∵当M、N、C共线时，y的值最小，∴y的值最小就是MC的长，∴MC＝2，设正方形的边长为m，则BM＝m，在Rt△BCM中，由勾股定理得：MC2＝BC2+MB2，∴20＝m2+（m）2，∴m＝4，∴BD＝4，∴a＝N′D＝BD＝×4＝，故选：A．6．（2021•鞍山）如图，△ABC是等边三角形，AB＝6cm，点M从点C出发沿CB方向以1cm/s的速度匀速运动到点B，同时点N从点C出发沿射线CA方向以2cm/s的速度匀速运动，当点M停止运动时，点N也随之停止．过点M 作MP∥CA交AB于点P，连接MN，NP，作△MNP关于直线MP对称的△MN′P，设运动时间为ts，△MN′P与△BMP重叠部分的面积为Scm2，则能表示S与t之间函数关系的大致图象为（）A．B．C．D．【答案】A【解答】解：如图1中，当点N′落在AB上时，取CN的中点T，连接MT．∵CM＝t（cm），CN＝2t（cm），CT＝TN，∴CT＝TN＝t（cm），∵△ABC是等边三角形，∴∠C＝∠A＝60°，∴△MCT是等边三角形，∴TM＝TC＝TN，∴∠CMN＝90°，∵MP∥AC，∴∠BPM＝∠A＝∠MPN＝60°，∠BMP＝∠C＝60°，∠C+∠CMP＝180°，∴∠CMP＝120°，△BMP是等边三角形，∴BM＝MP，∵∠CMP+∠MPN＝180°，∴CM∥PN，∵MP∥CN，∴四边形CMPN是平行四边形，∴PM＝CN＝BM＝2t，∴3t＝6，∴t＝2，如图2中，当0＜t≤2时，过点M作MK⊥AC于K，则MK＝CM•sin60°＝t，∴S＝•（6﹣t）•t＝﹣t2+t．如图3中，当2＜t≤6时，S＝•MQ•PQ＝×（6﹣t）×（6﹣t）＝×（6﹣t）2，观察图象可知，选项A符合题意，故选：A．7．（2021•威海）如图，在菱形ABCD中，AB＝2cm，∠D＝60°，点P，Q同时从点A出发，点P以1cm/s的速度沿A﹣C﹣D的方向运动，点Q以2cm/s 的速度沿A﹣B﹣C﹣D的方向运动，当其中一点到达D点时，两点停止运动．设运动时间为x（s），△APQ的面积为y（cm2），则下列图象中能大致反映y与x之间函数关系的是（）A．B．C．D．【答案】A【解答】解：∵四边形ABCD为菱形，∴AB＝BC＝CD＝DA＝2cm，∠B＝∠D＝60°．∴△ABC、△ACD都是等边三角形，∴∠CAB＝∠ACB＝∠ACD＝60°．如图1所示，当0≤x≤1时，AQ＝2xcm，AP＝xcm，作PE⊥AB于E，∴PE＝sin∠PAE×AP＝（cm），∴y＝AQ•PE＝×2x×＝，故D选项不正确；如图2，当1＜x≤2时，AP＝xcm，CQ＝（4﹣2x）cm，作QF⊥AC于点F，∴QF＝sin∠ACB•CQ＝（cm），∴y＝＝＝，故B选项不正确；如图3，当2＜x≤3时，CQ＝（2x﹣4）cm，CP＝（x﹣2）cm，∴PQ＝CQ﹣CP＝2x﹣4﹣x+2＝（x﹣2）cm，作AG⊥DC于点G，∴AG＝sin∠ACD•AC＝×2＝（cm），∴y＝＝＝．故C选项不正确，故选：A．8．（2021•日照）如图，平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成，点P在线段AB上，PQ⊥AB，且PQ交AD或交于点Q．设AP＝x（0＜x＜2），图中阴影部分表示的平面图形APQ（或APQD）的面积为y，则函数y关于x的大致图象是（）A．B．C．D．【答案】D【解答】解：当Q在AD上时，即点P在AO上时，有0＜x≤1，此时阴影部分为等腰直角三角形，∴y＝，该函数是二次函数，且开口向上，排除B，C选项；当点Q在弧BD上时，补全图形如图所示，阴影部分的面积等于等腰直角△AOD的面积加上扇形BOD的面积，再减去平面图形PBQ的面积即减去弓形QBF的面积，设∠QOB＝θ，则∠QOF＝2θ，＝﹣S△QOF，∴，S弓形QBF＝﹣＝﹣，当θ＝45°时，AP＝x＝1+≈1.7，S弓形QBFy＝+﹣（﹣）＝≈1.14，＝﹣＝﹣，当θ＝30°时，AP＝x≈1.87，S弓形QBFy＝+﹣（﹣）＝≈1.24，当θ＝60°时，AP＝x≈1.5，y≈0.98，在A，D选项中分别找到这两个特殊值，对比发现，选项D符合题意．故选：D．法二、当1＜x＜2时，即P在OB之间时，设∠QOD＝θ，则θ∈（0，），则PQ＝cosθ，OP＝sinθ，则弧QD的长为θπ，此时S阴影＝+θπ+sinθcosθ＝+θ+sin2θ，∴y随x的增大而增大，而且增加的速度越来越慢，分析四个选项中的图象，只有选项D符合．故选：D．9．（2021•辽宁）如图，在矩形ABCD中，AB＝6，AD＝4，E是CD的中点，射线AE与BC的延长线相交于点F，点M从A出发，沿A→B→F的路线匀速运动到点F停止．过点M作MN⊥AF于点N．设AN的长为x，△AMN的面积为S，则能大致反映S与x之间函数关系的图象是（）A．B．C．D．【答案】B【解答】解：如图，∵E是CD的中点，∴CE＝DE，∵四边形ABCD是矩形，∴∠D＝∠DCF＝90°，AD＝BC＝4，在△ADE与△FCE中，，∴△ADE≌△FCE（SAS），∴CF＝AD＝4，∴BF＝CF+BC＝8，∴AF＝，当点M在AB上时，在Rt△AMN和Rt△AFB中，tan∠NAM＝，∴NM＝x＝x，∴△AMN的面积S＝×x×x＝x2，∴当点M在AB上时，函数图象是开口向上、经过原点的抛物线的一部分；当点M在BF上时，如图，AN＝x，NF＝10﹣x，在Rt△FMN和Rt△FBA中，tan∠F＝，∴＝﹣，∴△AMN的面积S＝＝﹣，∴当点M在BF上时，函数图象是开口向下的抛物线的一部分；故选：B．10．（2021•苏州）如图，线段AB＝10，点C、D在AB上，AC＝BD＝1．已知点P从点C出发，以每秒1个单位长度的速度沿着AB向点D移动，到达点D后停止移动．在点P移动过程中作如下操作：先以点P为圆心，PA、PB 的长为半径分别作两个圆心角均为60°的扇形，再将两个扇形分别围成两个圆锥的侧面，设点P的移动时间为t（秒），两个圆锥的底面面积之和为S，则S关于t的函数图象大致是（）A．B．C．D．【答案】D【解答】解：∵AB＝10，AC＝BD＝1，∴CD＝10﹣1﹣1＝8，∵PC＝t，∴AP＝t+1，PB＝8﹣t+1＝9﹣t，设围成的两个圆锥底面圆半径分别为r和R则：2πr＝；．解得：r＝，R＝，∴两个圆锥的底面面积之和为S＝＝＝，根据函数关系式可以发现该函数图象是一个开口向上的二次函数．故选：D．11．（2021•甘肃）如图1，在△ABC中，AB＝BC，BD⊥AC于点D（AD＞BD）．动点M从A点出发，沿折线AB→BC方向运动，运动到点C停止．设点M的运动路程为x，△AMD的面积为y，y与x的函数图象如图2，则AC的长为（）A．3B．6C．8D．9【答案】B【解答】解：由图2知，AB+BC＝2，∵AB＝BC，∴AB＝，∵AB＝BC，BD⊥AC，∴AC＝2AD，∠ADB＝90°，在Rt△ABD中，AD²+BD²＝AB²＝13①，设点M到AC的距离为h，＝AD•h，∴S△ADM∵动点M从A点出发，沿折线AB→BC方向运动，∴当点M运动到点B时，△ADM的面积最大，即h＝BD，由图2知，△ADM的面积最大为3，∴AD•BD＝3，∴AD•BD＝6②，①+2×②得，AD²+BD²+2AD•BD＝13+2×6＝25，∴（AD+BD）²＝25，∴AD+BD＝5（负值舍去），∴BD＝5﹣AD③，将③代入②得，AD（5﹣AD）＝6，∴AD＝3或AD＝2，∵AD＞BD，∴AD＝3，∴AC＝2AD＝6，故选：B．12．（2021•百色）如图，矩形ABCD各边中点分别是E、F、G、H，AB＝2，BC＝2，M为AB上一动点，过点M作直线l⊥AB，若点M从点A开始沿着AB方向移动到点B即停（直线l随点M移动），直线l扫过矩形内部和四边形EFGH外部的面积之和记为S．设AM＝x，则S关于x的函数图象大致是（）A．B．C．D．【答案】D【解答】解：①当M点运动在AE段，+S△GHD﹣S△EOM﹣S△GPS，此时S＝S△HAE∵四边形ABCD是矩形，直线l⊥AB，H、E、F、G为AD、AB、BC、CD的中点，＝S△GHD，S△EOM＝S△GPS，∴AH＝AD＝＝1，AE＝AB＝，S△HAE﹣2S△EOM，∴S＝2S△HAE＝AE•AH＝；∴S△HAE∵直线l⊥AB，∴∠OME＝∠A＝90°，∠HEA＝∠OEM，∴△HAE∽△OME，∴，∴OM＝，又∵ME＝AE﹣AM＝﹣x，∴OM＝ME＝，＝，∴S△EOM﹣2S△EOM＝，∴S＝2S△HAE此时，对应抛物线开口向下；②当M点运动到在BE段，+S△GHD+S△EO1M1+S△GP1S1，此时，S＝S△HAE+2S△EO1M1，即S＝2S△HAE与①同理，O1M1＝，又∵M1E＝AM1﹣AE＝x﹣，∴O1M1＝M1E＝，＝，∴S△EO1M1+2S△EO1M1＝，∴S＝2S△HAE此时，对应抛物线开口向上，故选：D．13．（2021•鄂尔多斯）如图①，在矩形ABCD中，H为CD边上的一点，点M 从点A出发沿折线AH﹣HC﹣CB运动到点B停止，点N从点A出发沿AB运动到点B停止，它们的运动速度都是1cm/s，若点M、N同时开始运动，设运动时间为t（s），△AMN的面积为S（cm2），已知S与t之间函数图象如图②所示，则下列结论正确的是（）①当0＜t≤6时，△AMN是等边三角形．②在运动过程中，使得△ADM为等腰三角形的点M一共有3个．③当0＜t≤6时，S＝．④当t＝9+时，△ADH∽△ABM．⑤当9＜t＜9+3时，S＝﹣3t+9+3．A．①③④B．①③⑤C．①②④D．③④⑤【答案】A【解答】解：由图②可知：点M、N两点经过6秒时，S最大，此时点M在点H处，点N在点B处并停止不动，如图，①∵点M、N两点的运动速度为1cm/s，∴AH＝AB＝6cm，∵四边形ABCD是矩形，∴CD＝AB＝6cm．∵当t＝6s时，S＝9cm2，∴×AB×BC＝9．∴BC＝3cm．∵当6≤t≤9时，S＝且保持不变，∴点N在B处不动，点M在线段HC上运动，运动时间为（9﹣6）秒，∴HC＝3cm，即点H为CD的中点．∴BH＝cm．∴AB＝AH＝BH＝6cm，∴△ABM为等边三角形．∴∠HAB＝60°．∵点M、N同时开始运动，速度均为1cm/s，∴AM＝AN，∴当0＜t≤6时，△AMN为等边三角形．故①正确；②如图，当点M在AD的垂直平分线上时，△ADM为等腰三角形：此时有两个符合条件的点；当AD＝AM时，△ADM为等腰三角形，如图：当DA＝DM时，△ADM为等腰三角形，如图：综上所述，在运动过程中，使得△ADM为等腰三角形的点M一共有4个．∴②不正确；③过点M作ME⊥AB于点E，如图，由题意：AM＝AN＝t，由①知：∠HAB＝60°．在Rt△AME中，∵sin∠MAE＝，∴ME＝AM•sin60°＝tcm，∴S＝AN×ME＝cm2．∴③正确；④当t＝9+时，CM＝cm，如图，由①知：BC＝3cm，∴MB＝BC﹣CM＝2cm．∵AB＝6cm，∴tan∠MAB＝，∴∠MAB＝30°．∵∠HAB＝60°，∴∠DAH＝90°﹣60°＝30°．∴∠DAH＝∠BAM．∵∠D＝∠B＝90°，∴△ADH∽△ABM．∴④正确；⑤当9＜t＜9+3时，此时点M在边BC上，如图，此时MB＝9+3﹣t，∴S＝×AB×MB＝×6×（9+3﹣t）＝27+9﹣3t．∴⑤不正确；综上，结论正确的有：①③④．故选：A．14．（2021•通辽）如图，在矩形ABCD中，AB＝4，BC＝3，动点P，Q同时从点A出发，点P沿A→B→C的路径运动，点Q沿A→D→C的路径运动，点P，Q的运动速度相同，当点P到达点C时，点Q也随之停止运动，连接PQ．设点P的运动路程为x，PQ2为y，则y关于x的函数图象大致是（）A．B．C．D．【答案】C【解答】解：当0≤x≤3时，在Rt△APQ中，∠QAP＝90°，AP＝AQ＝x，∴PQ2＝2x2．∴y＝PQ2＝2x2；当3≤x≤4时，DQ＝x﹣3，AP＝x，∴y＝PQ2＝32+32＝18；当4≤x≤7时，CP＝7﹣x，CQ＝7﹣x，∴y＝PQ2＝CP2+CQ2＝2x2﹣28x+98．故选：C．15．（2021•湖北）如图，AC为矩形ABCD的对角线，已知AD＝3，CD＝4，点P沿折线C﹣A﹣D以每秒1个单位长度的速度运动（运动到D点停止），过点P作PE⊥BC于点E，则△CPE的面积y与点P运动的路程x间的函数图象大致是（）A．B．C．D．【答案】D【解答】解：∵BC∥AD，∴∠ACB＝∠DAC，∵∠PEC＝∠D＝90°，∴△PCE∽△CAD，∴＝＝，∵AD＝3，CD＝4，∴AC＝＝5，∴当P在CA上时，即当0＜x≤5时，PE＝＝x，CE＝＝x，∴y＝PE•CE＝＝x2，当P在AD上运动时，即当5＜x≤8时，PE＝CD＝4，CE＝8﹣x，∴y＝PE•CE＝×4×（8﹣x）＝16﹣2x，综上，当0＜x≤5时，函数图象为二次函数图象，且y随x增大而增大，当5＜x≤8时，函数图象为一次函数图象，且y随x增大而减小，故选：D．16．（2021•衡阳）如图1，菱形ABCD的对角线AC与BD相交于点O，P、Q 两点同时从O点出发，以1厘米/秒的速度在菱形的对角线及边上运动．点P的运动路线为O﹣A﹣D﹣O，点Q的运动路线为O﹣C﹣B﹣O．设运动的时间为x秒，P、Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，当点P在A﹣D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为厘米．【答案】（2+3）【解答】解：由图分析易知：当点P从O→A运动时，点Q从O→C运动时，y不断增大，当点P运动到A点，点Q运动到C点时，由图象知此时y＝PQ＝2cm，∴AC＝2cm，∵四边形ABCD为菱形，∴AC⊥BD，OA＝OC＝＝cm，当点P运动到D点，Q运动到B点，结合图象，易知此时，y＝BD＝2cm，∴OD＝OB＝BD＝1cm，在Rt△ADO中，AD＝＝＝2（cm），∴AD＝AB＝BC＝DC＝2cm，如图，当点P在A﹣D段上运动，点P运动到点E处，点Q在C﹣B段上运动，点Q运动到点F处时，P、Q两点的距离最短，此时，OE＝OF＝＝，AE＝CF＝＝＝，∴当点P在A﹣D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为：（cm），故答案为：（2+3）．17．（2021•武汉）如图（1），在△ABC中，AB＝AC，∠BAC＝90°，边AB 上的点D从顶点A出发，向顶点B运动，同时，边BC上的点E从顶点B出发，向顶点C运动，D，E两点运动速度的大小相等，设x＝AD，y＝AE+CD，y关于x的函数图象如图（2），图象过点（0，2），则图象最低点的横坐标是．【答案】﹣1【解答】解：∵图象过点（0，2），即当x＝AD＝BE＝0时，点D与A重合，点E与B重合，此时y＝AE+CD＝AB+AC＝2，∵△ABC为等腰直角三角形，∴AB＝AC＝1，过点A作AF⊥BC于点F，过点B作NB⊥BC，并使得BN＝AC，如图所示：∵AD＝BE，∠NBE＝∠CAD，∴△NBE≌△CAD（SAS），∴NE＝CD，又∵y＝AE+CD，∴y＝AE+CD＝AE+NE，当A、E、N三点共线时，y取得最小值，如图所示，此时：AD＝BE＝x，AC＝BN＝1，∴AF＝AC•sin45°＝，\又∵∠BEN＝∠FEA，∠NBE＝∠AFE∴△NBE∽△AFE∴，即，解得：x＝，∴图象最低点的横坐标为：﹣1．故答案为：．18．（2022•营口）如图1，在四边形ABCD中，BC∥AD，∠D＝90°，∠A＝45°，动点P，Q同时从点A出发，点P以cm/s的速度沿AB向点B运动（运动到B点即停止），点Q以2cm/s的速度沿折线AD→DC向终点C运动，设点Q的运动时间为x（s），△APQ的面积为y（cm2），若y与x之间的函数关系的图象如图2所示，当x＝（s）时，则y＝cm2．【答案】【解答】解：过点D作DE⊥AB，垂足为E，在Rt△ADE中，∵∠AED＝90°，∠EAD＝45°，∴，∵点P的速度为cm/s，点Q的速度为2cm/s，∴AP＝x，AQ＝2x，∴，在△APQ和△AED中，＝，∠A＝45°，∴△AED∽△APQ，∴点Q在AD上运动时，△APQ为等腰直角三角形，∴AP＝PQ＝x，∴当点Q在AD上运动时，y＝AP•AQ＝×x×x＝x2，由图像可知，当y＝9此时面积最大，x＝3或﹣3（负值舍去），∴AD＝2x＝6cm，当3＜x≤4时，过点P作PF⊥AD于点F，如图：＝S△APF+S四边形PQDF﹣S△ADQ，此时S△APQ在Rt△APF中，AP＝x，∠PAF＝45°，∴AF＝PF＝x，FD＝6﹣x，QD＝2x﹣6，＝x2+（x+2x﹣6）•（6﹣x）﹣×6×（2x﹣6），∴S△APQ即y＝﹣x2+6x，当x＝时，y＝﹣（）2+6×＝，故答案为：．。

中考数学专题函数图象选择题的几种解法

专题复习一一．专题复习 1. 探索型问题 2. 开放型问题二. 常见的问题的类型：1. 条件探索型——结论明确，而需探索发现使结论成立的条件的题目。

2. 结论探索型——给定条件，但无明确结论或结论不惟一。

3. 存在探索型——在一定条件下，需探索发现某种数学关系是否存在。

4. 规律探索型——发现数学对象所具有的规律性与不变性的题目。

三. 常用的解题切入点：1. 利用特殊值（特殊点、特殊数量、特殊线段、特殊位置）进行归纳、概括，从而得出规律。

2. 反演推理：根据假设进行推理，看推导出矛盾的结果还是能与已知条件一致。

3. 分类讨论：当命题的题设和结论不惟一确定时，则需对可能出现的情况做到既不重复，也不遗漏，分门别类地加以讨论求解，将不同结论综合归纳得出正确结论。

以上四种常见解题方法在本周的练习提纲中均有体现，同学们在解完本练习后，可细细对照参考答案，用心体会。

一. 填空题（每空4分，共48分）1. 请你写出：（1）一个比-1大的负数：____________；（2）一个二次三项式：____________。

2. 请你写出：（1）经过点（0，2）的一条直线的解析式是________________________；（2）经过点（0，2）的一条抛物线的解析式是________________________。

3. 如果菱形的面积不变，它的两条对角线的长分别是x 和y ，那么y 是x 的____________函数。

（填写函数名称）4. 如图，△ADE 和△ABC 有公共顶点A ，∠1＝∠2，请你添加一个条件：___________，使△ADE ∽△ABC 。

ABCE D215. 有一列数：1，2，3，4，5，6，……，当按顺序从第2个数数到第6个数时，共数了_______个数；当按顺序从第m 个数数到第n 个数（n m >）时，共数了_______个数。

6. 请你在“2，-3，4，-5，6”中任意挑选4个数，添加“＋，－，×，÷”和括号进行运算，使其计算结果为24，这个算式是_____________________。

中考数学--函数的图像与性质(较难)

专题6：函数的图象与性质一、选择题1.已知一次函数y ax b =+的图象过第一、二、四象限，且与x 轴交于点（2，0），则关于x 的不等式(1)0a x b -->的解集为A. 1x <-B. 1x >-C. 1x >D.1x <2.如图，直线 6y x =- 交x 轴、y 轴于A 、B 两点，P 是反比例函数4(0)y x x=>图象上位于直线下方的一点，过点P 作x 轴的垂线，垂足为点M ，交AB 于点E ，过点P 作y 轴的垂线，垂足为点N ，交AB 于点F 。

则AF·BE=A. 8B.6C. 4D. 623.已知直线l 经过点A(1，0)且与直线y x =垂直，则直线l 的解析式为 A ．1y x =-+ B ．1y x =-- C ．1y x =+ D ． 1y x =-4.有下列函数：①3y x =- ②1y x =- ③1(0)y x x=-> ④221y x x =++，其中函数值y 随自变量x 增大而增大的函数有A ．①②B ．②④C ．②③D ．①④5.已知二次函数y=ax 2+bx+c 的图象如图，其对称轴x=﹣1，给出下列结果①b 2＞4ac ；②abc ＞0；③2a +b=0；④a+b+c ＞0；⑤a ﹣b+c ＜0，则正确的结论是 A 、①②③④ B 、②④⑤ C 、②③④ D 、①④⑤6.如图，直线b x y +-=（b ＞0）与双曲线xky =（x ＞0）交于A 、B 两点，连接OA 、OB ，AM ⊥y 轴于M ，BN ⊥x 轴于N ；有以下结论：①OA=OB ，②△AOM ≌△BON ，③若∠AOB=45°，则S △AOB =k ，④当AB=2时，ON －BN=1；其中结论正确的个数为A ．1B ．2C ．3D ．47.若二次函数2()1y x m =--，当1x ≤时，y 随x 的增大而减小，则m 的取值范围是 A 、1m =B 、1m >C 、1m ≥D 、1m ≤8.反比例函数y ＝－1－a 2x (a 是常数)的图象分布在A ．第一、二象限B ．第一、三象限C ．第二、四象限D ．第三、四象限9.在平面直角坐标系中，如果抛物线y ＝3x 2不动，而把x 轴、y 轴分别向上、向右平移3个单位，那么在新坐标系中此抛物线的解析式是 A ．y ＝3(x －3)2＋3 B ．y ＝3(x －3)2－3 C ．y ＝3(x ＋3)2＋3 D ．y ＝3(x ＋3)2－310.若是方程（x －a ）（x －b ）= 1（a ＜b ）的两个根，则实数x 1，x 2，a ，b 的大小关系为A ．x 1＜x 2＜a ＜bB ．x 1＜a ＜x 2＜bC ．x 1＜a ＜b ＜x 2D ．a ＜x 1＜b ＜x 211.小明乘车从南充到成都，行车的平均速度v （km/h ）和行车时间t （h ）之间的函数图象是12小明的父亲饭后出去散步，从家中出发走20分钟到一个离家900米的报亭看报10分钟后，用15分钟返回家，下列图中表示小明的父亲离家的距离y （米）与离家的时间x （分）之间的函数关系的是13.（已知二次函数y=ax 2+bx+c （a ，b ，c 为常数，a≠0）的图象如图所示，有下列结论：①abc ＞0，②b 2﹣4ac ＜0，③a ﹣b+c ＞0，④4a ﹣2b+c ＜0，其中正确结论的个数是A 、1B 、2C 、3D 、4二、填空题1.在平面直角坐标系xOy 中，已知反比例函数2(0)ky k x=≠满足：当0x <时，y 随x 的增大而减小。

中考数学三轮专题冲刺7：利用函数图像解决实际问题综合(含答案)

中考数学第三轮压轴题专题冲刺复习：利用函数图像解决实际问题综合1、甲、乙两车分别从A 、B 两地同时出发，甲车匀速前往B 地，到达B 地立即以另一速度按原路匀速返回到A 地；乙车匀速前往A 地，设甲、乙两车距A 地的路程为y （千米），甲车行驶的时间为x （时），y 与x 之间的函数图象如图所示（1）求甲车从A 地到达B 地的行驶时间；（2）求甲车返回时y 与x 之间的函数关系式，并写出自变量x 的取值范围；（3）求乙车到达A 地时甲车距A 地的路程．2、由于持续高温和连日无雨，某水库的蓄水量随时间的增加而减少，已知原有蓄水量y 1（万m 3）与干旱持续时间x （天）的关系如图中线段l 1所示，针对这种干旱情况，从第20天开始向水库注水，注水量y 2（万m 3）与时间x （天）的关系如图中线段l 2所示（不考虑其它因素）．（1）求原有蓄水量y 1（万m 3）与时间x （天）的函数关系式，并求当x=20时的水库总蓄水量．（2）求当0≤x ≤60时，水库的总蓄水量y （万m 3）与时间x （天）的函数关系式（注明x 的范围），若总蓄水量不多于900万m 3为严重干旱，直接写出发生严重干旱时x 的范围．3、某物流公司引进A 、B 两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A 种机器人于某日0时开始搬运，过了1小时，B 种机器人也开始搬运，如图，线段OG 表示A 种机器人的搬运量A y （千克）与时间x （时）的函数图像，线段EF 表示B 种机器人的搬运量B y （千克）与时间x （时）的函数图像，根据图像提供的信息，解答下列问题：（1）求B y 关于x 的函数解析式；（2）如果A、B两种机器人各连续搬运5个小时，那么B种机器人比A种机器人多搬运了多少千克？4、有一科技小组进行了机器人行走性能试验，在试验场地有A、B、C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A、B两点同时同向出发，历时7分钟同时到达C点，乙机器人始终以60米/分的速度行走，如图是甲、乙两机器人之间的距离y（米）与他们的行走时间x（分钟）之间的函数图象，请结合图象，回答下列问题：（1）A、B两点之间的距离是米，甲机器人前2分钟的速度为米/分；（2）若前3分钟甲机器人的速度不变，求线段EF所在直线的函数解析式；（3）若线段FG∥x轴，则此段时间，甲机器人的速度为米/分；（4）求A、C两点之间的距离；（5）直接写出两机器人出发多长时间相距28米．5、快、慢两车分别从相距180千米的甲、乙两地同时出发，沿同一路线匀速行驶，相向而行，快车到达乙地停留一段时间后，按原路原速返回甲地．慢车到达甲地比快车到达甲地早小时，慢车速度是快车速度的一半，快、慢两车到达甲地后停止行驶，两车距各自出发地的路程y（千米）与所用时间x（小时）的函数图象如图所示，请结合图象信息解答下列问题：（1）请直接写出快、慢两车的速度；（2）求快车返回过程中y（千米）与x（小时）的函数关系式；（3）两车出发后经过多长时间相距90千米的路程？直接写出答案．6、某企业接到一批粽子生产任务，按要求在19天内完成，约定这批粽子的出厂价为每只4元，为按时完成任务，该企业招收了新工人，设新工人李红第x天生产的粽子数量为y只，y与x满足如下关系：y=（1）李红第几天生产的粽子数量为260只？（2）如图，设第x天生产的每只粽子的成本是p元，p与x之间的关系可用图中的函数图象来刻画，若李红第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大？最大利润是多少元？（利润=出厂价﹣成本）7、某市为节约水资源，制定了新的居民用水收费标准.按照新标准，用户每月缴纳的水费y（元）与每月用水量x（3m）之间的关系如图所示.（1）求y关于x的函数解析式；（2）若某用户二、三月份共用水340m（二月份用水量不超过325m），缴纳水费79.8元，则该用户二、三月份的用水量各是多少3m？8、某公司组织员工到附近的景点旅游，根据旅行社提供的收费方案，绘制了如图所示的图象，图中折线ABCD表示人均收费y（元）与参加旅游的人数x（人）之间的函数关系．（1）当参加旅游的人数不超过10人时，人均收费为元；（2）如果该公司支付给旅行社3600元，那么参加这次旅游的人数是多少？9、某周日上午8：00小宇从家出发，乘车1小时到达某活动中心参加实践活动．11：00时他在活动中心接到爸爸的电话，因急事要求他在12：00前回到家，他即刻按照来活动中心时的路线，以5千米/小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家x（小时）后，到达离家y（千米）的地方，图中折线OABCD 表示y与x之间的函数关系．（1）活动中心与小宇家相距千米，小宇在活动中心活动时间为小时，他从活动中心返家时，步行用了小时；（2）求线段BC所表示的y（千米）与x（小时）之间的函数关系式（不必写出x所表示的范围）；（3）根据上述情况（不考虑其他因素），请判断小宇是否能在12：00前回到家，并说明理由．10、甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．甲公司方案：每月的养护费用y （元）与绿化面积x （平方米）是一次函数关系，如图所示．乙公司方案：绿化面积不超过1000平方米时，每月收取费用5500 元；绿化面积超过1000平方米时，每月在收取5500元的基础上，超过部分每平方米收取4元．（1）求如图所示的y 与x 的函数解析式：（不要求写出定义域）；（2）如果某学校目前的绿化面积是1200平方米，试通过计算说明：选择哪家公司的服务，每月的绿化养护费用较少．11、湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养天的总成本为万元；放养天的总成本为万元（总成本=放养总费用+收购成本）．（1）设每天的放养费用是万元，收购成本为万元，求和的值；（2）设这批淡水鱼放养天后的质量为（），销售单价为元/．根据20000kg 1030.42030.8a b a b t m kg y kg以往经验可知：与的函数关系为；与的函数关系如图所示．①分别求出当和时，与的函数关系式；②设将这批淡水鱼放养天后一次性出售所得利润为元，求当为何值时，最大？并求出最大值．（利润=销售总额-总成本）12、如图1，在△ABC中，∠A=30°，点P从点A出发以2cm/s的速度沿折线A —C—B运动，点Q从点A出发以a(cm/s)的速度沿AB运动，P，Q两点同时出发，当某一点运动到点B时，两点同时停止运动.设运动时间为x(s)，△APQ的面积为y(cm2)，y关于x的函数图象由C1， C2两段组成，如图2所示.(1)求a的值；(2)求图2中图象C2段的函数表达式；(3)当点P运动到线段BC上某一段时△APQ的面积，大于当点P在线段AC上任意一点时△APQ的面积，求x的取值范围.13、在甲、乙两城市之间有一服务区，一辆客车从甲地驶往乙地，一辆货车从乙地驶往甲地．两车同时出发，匀速行驶，客车、货车离服务区的距离y1（千米），y 2（千米）与行驶的时间x（小时）的函数关系图象如图1所示．m t()()200000501001500050100tmt t≤≤⎧⎪=⎨+<≤⎪⎩y t 050t≤≤50100t<≤y tt W tW（1）甲、乙两地相距千米．（2）求出发3小时后，货车离服务区的路程y 2（千米）与行驶时间x （小时）之间的函数关系式．（3）在客车和货车出发的同时，有一辆邮政车从服务区匀速去甲地取货后返回乙地（取货的时间忽略不计），邮政车离服务区的距离y 3（千米）与行驶时间x（小时）之间的函数关系图线如图2中的虚线所示，直接写出在行驶的过程中，经过多长时间邮政车与客车和货车的距离相等？14、雷雷服饰有限公司生产了一款夏季服装，通过实验商店和网上商店两种途径进行销售，销售一段时间后，该公司对这种商品的销售情况，进行了为期30天的跟踪调查，其中实体商店的日销售量1y （百件）与时间t （t 为整数，单位：天）的部分对应值如下表所示；网上商店的日销售量2y （百件）与时间t （t 为整数，单位：天）的关系如下图所示.y与t （1）请你在一次函数、二次函数和反比例函数中，选择合适的函数能反映1y与t的函数关系式及自变量t的取值范围；的变化规律，并求出1y与t的函数关系式，并写出自变量t的取值范围；（2）求2（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为y（百件），求y与t的函数关系式；当t为何值时，日销售总量y达到最大，并求出此时的最大值.15、荆州市某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，销售单价p（元/千克）与时间第t（天）之间的函数关系为：，日销售量y（千克）与时间第t（天）之间的函数关系如图所示：（1）求日销售量y与时间t的函数关系式？（2）哪一天的日销售利润最大？最大利润是多少？（3）该养殖户有多少天日销售利润不低于2400元？（4）在实际销售的前40天中，该养殖户决定每销售1千克小龙虾，就捐赠m（m ＜7）元给村里的特困户．在这前40天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求m的取值范围．参考答案2021年中考数学第三轮压轴题专题冲刺复习：利用函数图像解决实际问题综合1、甲、乙两车分别从A 、B 两地同时出发，甲车匀速前往B 地，到达B 地立即以另一速度按原路匀速返回到A 地；乙车匀速前往A 地，设甲、乙两车距A 地的路程为y （千米），甲车行驶的时间为x （时），y 与x 之间的函数图象如图所示（1）求甲车从A 地到达B 地的行驶时间；（2）求甲车返回时y 与x 之间的函数关系式，并写出自变量x 的取值范围；（3）求乙车到达A 地时甲车距A 地的路程．【解答】解：（1）300÷（180÷1.5）=2.5（小时），答：甲车从A 地到达B 地的行驶时间是2.5小时；（2）设甲车返回时y 与x 之间的函数关系式为y=kx+b ，∴，解得：，∴甲车返回时y 与x 之间的函数关系式是y=﹣100x+550；（3）300÷[（300﹣180）÷1.5]=3.75小时，当x=3.75时，y=175千米，答：乙车到达A 地时甲车距A 地的路程是175千米．2、由于持续高温和连日无雨，某水库的蓄水量随时间的增加而减少，已知原有蓄水量y 1（万m 3）与干旱持续时间x （天）的关系如图中线段l 1所示，针对这种干旱情况，从第20天开始向水库注水，注水量y 2（万m 3）与时间x （天）的关系如图中线段l 2所示（不考虑其它因素）．（1）求原有蓄水量y 1（万m 3）与时间x （天）的函数关系式，并求当x=20时的水库总蓄水量．（2）求当0≤x ≤60时，水库的总蓄水量y （万m 3）与时间x （天）的函数关系式（注明x 的范围），若总蓄水量不多于900万m 3为严重干旱，直接写出发生严重干旱时x 的范围．【解答】解：（1）设y1=kx+b，把（0，1200）和（60，0）代入到y1=kx+b得：解得，∴y1=﹣20x+1200当x=20时，y1=﹣20×20+1200=800，（2）设y2=kx+b，把（20，0）和（60，1000）代入到y2=kx+b中得：解得，∴y2=25x﹣500，当0≤x≤20时，y=﹣20x+1200，当20＜x≤60时，y=y1+y2=﹣20x+1200+25x﹣500=5x+700，y≤900，则5x+700≤900，x≤40，当y1=900时，900=﹣20x+1200，x=15，∴发生严重干旱时x的范围为：15≤x≤40．3、某物流公司引进A、B两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A种机器人于某日0时开始搬运，过了1小时，B种机器人也开始搬运，如图，线段OG表示A种机器人的搬运量Ay（千克）与时间x（时）的函数图像，线段EF表示B种机器人的搬运量By（千克）与时间x（时）的函数图像，根据图像提供的信息，解答下列问题：（1）求By关于x的函数解析式；（2）如果A、B两种机器人各连续搬运5个小时，那么B种机器人比A种机器人多搬运了多少千克？解：（1）设B y 关于x 的函数解析式为1B y k x b =+（10k ≠），由线段EF 过点(1,0)E 和点(3,180)P ，得1103180k b k b +=⎧⎨+=⎩，解得19090k b =⎧⎨=-⎩，所以B y 关于x 的函数解析式为9090B y x =-（16x ≤≤）；（2）设A y 关于x 的函数解析式为2A y k x =（20k ≠），由题意，得21803k =，即260k = ∴60A y x =；当5x =时，560300A y =⨯=（千克），当6x =时，90690450B y =⨯-=（千克），450300150-=（千克）；答：如果A 、B 两种机器人各连续搬运5小时，那么B 种机器人比A 种机器人多搬运了150千克4、有一科技小组进行了机器人行走性能试验，在试验场地有A 、B 、C 三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A 、B 两点同时同向出发，历时7分钟同时到达C 点，乙机器人始终以60米/分的速度行走，如图是甲、乙两机器人之间的距离y （米）与他们的行走时间x （分钟）之间的函数图象，请结合图象，回答下列问题：（1）A 、B 两点之间的距离是 70 米，甲机器人前2分钟的速度为 95 米/分；（2）若前3分钟甲机器人的速度不变，求线段EF 所在直线的函数解析式；（3）若线段FG ∥x 轴，则此段时间，甲机器人的速度为 60 米/分；（4）求A 、C 两点之间的距离；（5）直接写出两机器人出发多长时间相距28米．【解答】解：（1）由图象可知，A、B两点之间的距离是70米，甲机器人前2分钟的速度为：（70+60×2）÷2=95米/分；（2）设线段EF所在直线的函数解析式为：y=kx+b，∵1×（95﹣60）=35，∴点F的坐标为（3，35），则，解得，，∴线段EF所在直线的函数解析式为y=35x﹣70；（3）∵线段FG∥x轴，∴甲、乙两机器人的速度都是60米/分；（4）A、C两点之间的距离为70+60×7=490米；（5）设前2分钟，两机器人出发xs相距28米，由题意得，60x+70﹣95x=28，解得，x=1.2，前2分钟﹣3分钟，两机器人相距28米时，35x﹣70=28，解得，x=2.8，4分钟﹣7分钟，两机器人相距28米时，（95﹣60）x=28，解得，x=0.8，0.8+4=4.8，答：两机器人出发1.2s或2.8s或4.8s相距28米．5、快、慢两车分别从相距180千米的甲、乙两地同时出发，沿同一路线匀速行驶，相向而行，快车到达乙地停留一段时间后，按原路原速返回甲地．慢车到达甲地比快车到达甲地早小时，慢车速度是快车速度的一半，快、慢两车到达甲地后停止行驶，两车距各自出发地的路程y（千米）与所用时间x（小时）的函数图象如图所示，请结合图象信息解答下列问题：（1）请直接写出快、慢两车的速度；（2）求快车返回过程中y（千米）与x（小时）的函数关系式；（3）两车出发后经过多长时间相距90千米的路程？直接写出答案．【解答】解：（1）快车速度：180×2÷（）=120千米/时，慢车速度：120÷2=60千米/时；（2）快车停留的时间：﹣×2=（小时），+=2（小时），即C（2，180），设CD的解析式为：y=kx+b，则将C（2，180），D（，0）代入，得，解得，∴快车返回过程中y（千米）与x（小时）的函数关系式为y=﹣120x+420（2≤x ≤）；（3）相遇之前：120x+60x+90=180，解得x=；相遇之后：120x+60x﹣90=180，解得x=；快车从甲地到乙地需要180÷120=小时，快车返回之后：60x=90+120（x﹣﹣）解得x=综上所述，两车出发后经过或或小时相距90千米的路程．6、某企业接到一批粽子生产任务，按要求在19天内完成，约定这批粽子的出厂价为每只4元，为按时完成任务，该企业招收了新工人，设新工人李红第x天生产的粽子数量为y只，y与x满足如下关系：y=（1）李红第几天生产的粽子数量为260只？（2）如图，设第x天生产的每只粽子的成本是p元，p与x之间的关系可用图中的函数图象来刻画，若李红第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大？最大利润是多少元？（利润=出厂价﹣成本）【解答】解：（1）设李红第x天生产的粽子数量为260只，根据题意得20x+60=260，解得x=10，答：李红第10天生产的粽子数量为260只；（2）根据图象得当0≤x≤9时，p=2；当9＜x≤19时，设解析式为y=kx+b，把（9，2），（19，3）代入得，解得，所以p=x+，①当0≤x ≤5时，w=（4﹣2）•32x=64x ，x=5时，此时w 的最大值为320（元）； ②当5＜x ≤9时，w=（4﹣2）•（20x+60）=40x+120，x=9时，此时w 的最大值为480（元）；③当9＜x ≤19时，w=[4﹣（x+）]•（20x+60）=﹣2x2+52x+174=﹣2（x ﹣13）2+786，x=13时，此时w 的最大值为786（元）；综上所述，第13天的利润最大，最大利润是786元．7、某市为节约水资源，制定了新的居民用水收费标准.按照新标准，用户每月缴纳的水费y （元）与每月用水量x （3m ）之间的关系如图所示.（1）求y 关于x 的函数解析式；（2）若某用户二、三月份共用水340m （二月份用水量不超过325m ），缴纳水费79.8元，则该用户二、三月份的用水量各是多少3m ？【答案】：（1）当015x <<时，设y mx =，则1527m =，所以 1.8m =， 1.8y x =当15x ≥时，设y kx b =+，则15272039k b k b +=⎧⎨+=⎩，解得 2.49k b =⎧⎨=-⎩，所以y 与x 的关系式是 1.8,0152.49,15x x y x x <<⎧=⎨-≥⎩.8、某公司组织员工到附近的景点旅游，根据旅行社提供的收费方案，绘制了如图所示的图象，图中折线ABCD表示人均收费y（元）与参加旅游的人数x（人）之间的函数关系．（1）当参加旅游的人数不超过10人时，人均收费为元；（2）如果该公司支付给旅行社3600元，那么参加这次旅游的人数是多少？【答案】（1）观察图象可知：当参加旅游的人数不超过10人时，人均收费为240元．故答案为240．（2）∵3600÷240=15，3600÷150=24，∴收费标准在BC段，设直线BC的解析式为y=kx+b，则有10240 25150k bk b+=⎧⎨+=⎩，解得6300kb=-⎧⎨=⎩，∴y=﹣6x+300，由题意（﹣6x+300）x=3600，解得x=20或30（舍弃）答：参加这次旅游的人数是20人．9、某周日上午8：00小宇从家出发，乘车1小时到达某活动中心参加实践活动．11：00时他在活动中心接到爸爸的电话，因急事要求他在12：00前回到家，他即刻按照来活动中心时的路线，以5千米/小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家x（小时）后，到达离家y（千米）的地方，图中折线OABCD 表示y与x之间的函数关系．（1）活动中心与小宇家相距22 千米，小宇在活动中心活动时间为 2 小时，他从活动中心返家时，步行用了0.4 小时；（2）求线段BC所表示的y（千米）与x（小时）之间的函数关系式（不必写出x所表示的范围）；（3）根据上述情况（不考虑其他因素），请判断小宇是否能在12：00前回到家，并说明理由．【解答】解：（1）∵点A的坐标为（1，22），点B的坐标为（3，22），∴活动中心与小宇家相距22千米，小宇在活动中心活动时间为3﹣1=2小时．（22﹣20）÷5=0.4（小时）．故答案为：22；2；0.4．（2）根据题意得：y=22﹣5（x﹣3）=﹣5x+37．（3）小宇从活动中心返家所用时间为：0.4+0.4=0.8（小时），∵0.8＜1，∴所用小宇12：00前能到家．10、甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．甲公司方案：每月的养护费用y（元）与绿化面积x（平方米）是一次函数关系，如图所示．乙公司方案：绿化面积不超过1000平方米时，每月收取费用5500 元；绿化面积超过1000平方米时，每月在收取5500元的基础上，超过部分每平方米收取4元．（1）求如图所示的y 与x 的函数解析式：（不要求写出定义域）；（2）如果某学校目前的绿化面积是1200平方米，试通过计算说明：选择哪家公司的服务，每月的绿化养护费用较少．【解答】解：（1）设y=kx+b ，则有，解得， ∴y=5x+400．（2）绿化面积是1200平方米时，甲公司的费用为6400元，乙公司的费用为5500+4×200=6300元，∵6300＜6400∴选择乙公司的服务，每月的绿化养护费用较少．11、湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养天的总成本为万元；放养天的总成本为万元（总成本=放养总费用+收购成本）．（1）设每天的放养费用是万元，收购成本为万元，求和的值；（2）设这批淡水鱼放养天后的质量为（），销售单价为元/．根据以往经验可知：与的函数关系为；与的函数关系如图所示．①分别求出当和时，与的函数关系式；20000kg 1030.42030.8a b a b t m kg y kg m t ()()200000501001500050100t m t t ≤≤⎧⎪=⎨+<≤⎪⎩y t 050t ≤≤50100t <≤y t②设将这批淡水鱼放养天后一次性出售所得利润为元，求当为何值时，最大？并求出最大值．（利润=销售总额-总成本）试题解析：（1）由题意得解得答：a 的值为0.04，b 的值为30.当50＜t ≤100时，设y 与t 的函数关系式为y=k 2t+n 2把点（50，25）和（100，20）的坐标分别代入y=k 2t+n 2，得解得 t W tW 1030.42030.8a b a b +=⎧⎨+=⎩0.0430a b =⎧⎨=⎩2222255020100k n k n =+⎧⎨=+⎩2211030k n ⎧=-⎪⎨⎪=⎩∴y 与t 的函数关系式为y=t+30 ②由题意得，当0≤t ≤50时，W=20000×（t+15）-（400t+300000）=3600t ∵3600＞0，∴当t=50时，W 最大值=180000（元）当50＜t ≤100时，W=（100t+15000）（t+30）-（400t+300000）=-10t 2+1100t+150000=-10（t-55）2+180250∵-10＜0，∴当t=55时，W 最大值=180250综上所述，当t 为55天时，W 最大，最大值为180250元.12、如图1，在△ABC 中，∠A=30°，点P 从点A 出发以2cm/s 的速度沿折线A —C —B 运动，点Q 从点A 出发以a(cm/s)的速度沿AB 运动，P ，Q 两点同时出发，当某一点运动到点B 时，两点同时停止运动.设运动时间为x(s)，△APQ 的面积为y(cm 2)，y 关于x 的函数图象由C 1 ， C 2两段组成，如图2所示.(1)求a 的值；(2)求图2中图象C 2段的函数表达式；(3)当点P 运动到线段BC 上某一段时△APQ 的面积，大于当点P 在线段AC 上任意一点时△APQ 的面积，求x 的取值范围.【答案】（1）解：在图1中，过P 作PD ⊥AB 于D ，∵∠A=30°，PA=2x ， ∴PD=PA ·sin30°=2x · =x ，∴y= = .由图象得，当x=1时，y= ，则 = . 110-15110-∴a=1.（2）解：当点P在BC上时（如图2），PB=5×2-2x=10-2x. ∴PD=PB·sinB=(10-2x)·sinB，∴y= AQ·PD= x·（10-2x）·sinB.由图象得，当x=4时，y= ,∴×4×（10-8）·sinB= ，∴sinB= .∴y= x·（10-2x）·= .（3）解：由C1， C2的函数表达式，得= ，解得x1=0（舍去），x2=2，由图易得，当x=2时，函数y= 的最大值为y= . 将y=2代入函数y= ，得2= .解得x1=2，x2=3，13、在甲、乙两城市之间有一服务区，一辆客车从甲地驶往乙地，一辆货车从乙地驶往甲地．两车同时出发，匀速行驶，客车、货车离服务区的距离y1（千米），y2（千米）与行驶的时间x（小时）的函数关系图象如图1所示．（1）甲、乙两地相距480 千米．（2）求出发3小时后，货车离服务区的路程y2（千米）与行驶时间x（小时）之间的函数关系式．（3）在客车和货车出发的同时，有一辆邮政车从服务区匀速去甲地取货后返回乙地（取货的时间忽略不计），邮政车离服务区的距离y3（千米）与行驶时间x （小时）之间的函数关系图线如图2中的虚线所示，直接写出在行驶的过程中，经过多长时间邮政车与客车和货车的距离相等？【解答】解：（1）360+120=480（千米）故答案为：480；（2）设3小时后，货车离服务区的路程y2与行驶时间x之间的函数关系式为y2=kx+b，由图象可得，货车的速度为：120÷3=40千米/时，则点B的横坐标为：3+360÷40=12，∴点P的坐标为（12，360），，得，即3小时后，货车离服务区的路程y2与行驶时间x之间的函数关系式为y2=40x﹣120；（3）v客=360÷6=60千米/时，v邮=360×2÷8=90千米/时，设当邮政车去甲地的途中时，经过t小时邮政车与客车和货车的距离相等，120+（90﹣40）t=360﹣（60+90）tt=1.2（小时）；设当邮政车从甲地返回乙地时，经过t小时邮政车与客车和货车的距离相等，40t+60t=480解得t=4.8，综上所述，经过1.2或4.8小时邮政车与客车和货车的距离相等．14、雷雷服饰有限公司生产了一款夏季服装，通过实验商店和网上商店两种途径进行销售，销售一段时间后，该公司对这种商品的销售情况，进行了为期30天y（百件）与时间t（t为整数，单位：的跟踪调查，其中实体商店的日销售量1y（百件）与时间t（t为天）的部分对应值如下表所示；网上商店的日销售量2整数，单位：天）的关系如下图所示.y与t （1）请你在一次函数、二次函数和反比例函数中，选择合适的函数能反映1y与t的函数关系式及自变量t的取值范围；的变化规律，并求出1y与t的函数关系式，并写出自变量t的取值范围；（2）求2（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为y（百件），求y与t的函数关系式；当t为何值时，日销售总量y达到最大，并求出此时的最大值.【答案】（3）依题意得y=y 1+y 2，当0≤t ≤10时，得到y 最大=80；当10＜t ≤30时，得到y 最大=91.2，于是得到结论．试题解析：（1）根据观察可设y 1=at 2+bt+c ，将（0，0），（5，25），（10，40）代入得：0,25525,1001040c a b a b =⎧⎪+=⎨⎪+=⎩，解得1,56,0a b c ⎧=-⎪⎪=⎨⎪=⎪⎩， ∴y 1与t 的函数关系式为：y 1=﹣15-t 2+6t （0≤t ≤30，且为整数）；（2）当0≤t ≤10时，设y 2=kt ，∵（10，40）在其图象上，∴10k=40，∴k=4， ∴y 2与t 的函数关系式为：y 2=4t ，当10≤t ≤30时，设y 2=mt+n ，将（10，40），（30，60）代入得1040,3060m n m n +=⎧⎨+=⎩，解得1,30m n =⎧⎨=⎩，∴y 2与t 的函数关系式为：y 2=t+30，综上所述，()()24010301030,t t t y t t t ⎧≤≤⎪=⎨+<≤⎪⎩，且为整数且为整数；（3）依题意得y=y 1+y 2，当0≤t ≤10时，y=15-t 2+6t+4t=15-t 2+10t=15-（t ﹣25）2+125，∴t=10时，y 最大=80；当10＜t ≤30时，y=15-t 2+6t+t+30=15-t 2+7t+30=15-（t ﹣352）2+3654， ∵t 为整数，∴t=17或18时，y 最大=91.2，∵91.2＞80，∴当t=17或18时，y 最大=91.2（百件）．15、荆州市某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，销售单价p（元/千克）与时间第t（天）之间的函数关系为：，日销售量y（千克）与时间第t（天）之间的函数关系如图所示：（1）求日销售量y与时间t的函数关系式？（2）哪一天的日销售利润最大？最大利润是多少？（3）该养殖户有多少天日销售利润不低于2400元？（4）在实际销售的前40天中，该养殖户决定每销售1千克小龙虾，就捐赠m（m ＜7）元给村里的特困户．在这前40天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求m的取值范围．【解答】解：（1）设解析式为y=kt+b，将（1，198）、（80，40）代入，得：，解得：，∴y=﹣2t+200（1≤x≤80，t为整数）；（2）设日销售利润为w，则w=（p﹣6）y，①当1≤t≤40时，w=（t+16﹣6）（﹣2t+200）=﹣（t﹣30）2+2450，=2450；∴当t=30时，w最大②当41≤t≤80时，w=（﹣t+46﹣6）（﹣2t+200）=（t﹣90）2﹣100，=2301，∴当t=41时，w最大∵2450＞2301，∴第30天的日销售利润最大，最大利润为2450元．（3）由（2）得：当1≤t≤40时，w=﹣（t﹣30）2+2450，令w=2400，即﹣（t﹣30）2+2450=2400，解得：t1=20、t2=40，由函数w=﹣（t﹣30）2+2450图象可知，当20≤t≤40时，日销售利润不低于2400元，而当41≤t≤80时，w最大=2301＜2400，∴t的取值范围是20≤t≤40，∴共有21天符合条件．（4）设日销售利润为w，根据题意，得：w=（t+16﹣6﹣m）（﹣2t+200）=﹣t2+（30+2m）t+2000﹣200m，其函数图象的对称轴为t=2m+30，∵w随t的增大而增大，且1≤t≤40，∴由二次函数的图象及其性质可知2m+30≥40，解得：m≥5，又m＜7，∴5≤m＜7．。

夯实基础-2023年九年级中考数学考点专题集训系列一次函数图像信息问题

夯实基础-2023年中考数学考点专题集训系列（一次函数图像信息问题）1.在一条笔直的公路上有A，B两地，甲、乙二人同时出发，甲从A地步行匀速前往B地，到达B地后，立刻以原速度沿原路返回A地．乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动)，甲、乙二人之间的距离y(米)与出发时间x(分钟)之间的函数关系如图所示，请结合图象解答下列问题：(1)A，B两地之间的距离是________米，乙的步行速度是________米/分钟；(2)图中a＝________，b＝________，c＝________；(3)求线段MN的函数表达式；(4)在乙运动的过程中，何时两人相距80米？(直接写出答案即可)2.A、B两地相距240km，甲货车从A地以40km/h的速度匀速前往B地，到达B地后停止．在甲出发的同时，乙货车从B地沿同一公路匀速前往A地，到达A地后停止．两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线CD-DE-EF所示，其中点C的坐标是（0,240），点D的坐标是（2.4,0），则点E的坐标是多少．3．一天早晨，小玲从家出发匀速步行到学校，小玲出发一段时间后，她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲，妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来速度的一半，小玲继续以原速度步行前往学校，妈妈与小玲之间的距离y（米）与小玲从家出发后步行的时间x（分）之间的关系如图所示（小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计）．当妈妈刚回到家时，小玲离学校的距离为多少米．4．“低碳生活，绿色出行”的理念已深入人心，现在越来越多的人选择骑自行车上下班或外出旅游．周末，小红相约到郊外游玩，她从家出发0.5小时后到达甲地，玩一段时间后按原速前往乙地，刚到达乙地，接到妈妈电话，快速返回家中．小红从家出发到返回家中，行进路程y（km）随时间x（h）变化的函数图象大致如图所示．（1）小红从甲地到乙地骑车的速度为km/h；（2）当1.5≤x≤2.5时，求出路程y（km）关于时间x（h）的函数解析式；并求乙地离小红家多少千米？5．周末，自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练，甲、乙分别以不同的速度匀速骑行，乙比甲早出发5分钟．乙骑行25分钟后，甲以原速的85继续骑行，经过一段时间，甲先到达B地，乙一直保持原速前往B地．在此过程中，甲、乙两人相距的路程y（单位：米）与乙骑行的时间x（单位：分钟）之间的关系如图所示，则乙比甲晚多少分钟到达B地．6．某农科所为定点帮扶村免费提供一种优质瓜苗及大鹏栽培技术．这种瓜苗早期在农科所的温室中生长，长到大约20cm时，移至该村的大棚内，沿插杆继续向上生长．研究表明，60天内，这种瓜苗生长的高度y（cm）与生长时间x（天）之间的关系大致如图所示．（1）求y与x之间的函数关系；（2）当这种瓜苗长到大约80cm时，开始开花结果，试求这种瓜苗移至大棚后，继续生长大约多少天，开始开花结果？7．某工厂甲、乙两车间接到加工一批零件的任务，从开始加工到完成这项任务共用了9天，乙车间在加工2天后停止加工，引入新设备后继续加工，直到与甲车间同时完成这项任务为止，设甲、乙车间各自加工零件总数为y（件），与甲车间加工时间x（天），y与x之间的关系如图（1）所示．由工厂统计数据可知，甲车间与乙车间加工零件总数之差z（件）与甲车间加工时间x（天）的关系如图（2）所示．（1）甲车间每天加工零件为_____件，图中d值为_____．（2）求出乙车间在引入新设备后加工零件的数量y与x之间的函数关系式．（3）甲车间加工多长时间时，两车间加工零件总数为1000件？8．A，B两地相距200千米.早上8：00货车甲从A地出发将一批物资运往B地，行驶一段路程后出现故障，即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发去接运甲车上的物资.货车乙遇到甲后，用了18分钟将物资从货车甲搬运到货车乙上，随后开往B地，两辆货车离开各自出发．．．．地的路程y(千米)与时间x(小时)的函数关系如图所示．(通话等其他时间忽略不计)（1）求货车乙在遇到货车甲前，它离开出发地的路程y关于x的函数表达式.（2）因实际需要，要求货车乙到达B地的时间比货车甲按原来的速度正常到达B 地的时间最多晚1个小时，问货车乙返回B地的速度至少为每小时多少千米？9.暑期将至，某健身俱乐部面向学生推出暑期优惠活动，活动方案如下.方案一:购买一张学生暑期专享卡，每次健身费用按六折优惠；方案二:不购买学生暑期专享卡，每次健身费用按八折优惠.设某学生暑期健身x (次)，按照方案一所需费用为1y (元)，且11y k x b =+；按照方案二所需费用为2y (元)，且22y k x =.其函数图象如图所示.(1)求1k 和b 的值，并说明它们的实际意义；(2)求打折前的每次健身费用和2k 的值；(3)八年级学生小华计划暑期前往该俱乐部健身8次，应选择哪种方案所需费用更少?说明理由.x kg之间10．某商店代理销售一种水果，六月份的销售利润y（元）与销售量()函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息，解答下列问题：日期销售记录6月1日库存600kg，成本价8元/kg，售价10元/kg（除了促销降价，其他时间售价保持不变）.6月9日从6月1日至今，一共售出200kg.6月10、11日这两天以成本价促销，之后售价恢复到10元/kg.6月12日补充进货200kg，成本价8.5元/kg.6月30日800kg水果全部售完，一共获利1200元.（1）截止到6月9日，该商店销售这种水果一共获利多少元？（2）求图像中线段BC所在直线对应的函数表达式.11．某市制米厂接到加工大米任务，要求5天内加工完220吨大米，制米厂安排甲、乙两车间共同完成加工任务，乙车间加工中途停工一段时间维修设备，然后改变加工效率继续加工，直到与甲车间同时完成加工任务为止．设甲、乙两车间各自加工大米数量y（吨）与甲车间加工时间s（天）之间的关系如图（1）所示；未加工大米w（吨）与甲加工时间x（天）之间的关系如图（2）所示，请结合图象回答下列问题：（1）甲车间每天加工大米吨，a=．（2）求乙车间维修设备后，乙车间加工大米数量y（吨）与x（天）之间函数关系式．（3）若55吨大米恰好装满一节车厢，那么加工多长时间装满第一节车厢？再加工多长时间恰好装满第二节车厢？12.如图1，在平面直角坐标系中，▱ABCD在第一象限，且BC∥x轴.直线y=x 从原点0出发沿x轴正方向平移.在平移过程中，直线被▱ABCD截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示，那么▱ABCD的面积为多少。

辽宁省各市中考数学分类解析专题6：函数的图像与性质

辽宁各市中考数学试题分类解析汇编专题6：函数的图像与性质锦元数学工作室编辑一、选择题1. （辽宁鞍山3分）如图，点A 在反比例函数()3y=x 0x>的图象上，点B 在反比例函数()ky=x 0x>的图象上，AB⊥x 轴于点M ，且AM ：MB=1：2，则k 的值为【】A ． 3B ．－6C ．2D ．6 【答案】B 。

【考点】反比例函数图象上点的坐标特征。

【分析】如图，连接OA 、OB ．∵点A 在反比例函数()3y=x 0x>的图象上，点B 在反比例函数()ky=x 0x>的图象上，AB⊥x 轴于点M ， ∴S △AOM =32，S △BOM =k 2。

∴S △AOM ：S △BOM =32：k 2=3：|k|。

∵S △AOM ：S △BOM =AM ：MB=1：2，∴3：|k|=1：2。

∴|k|=6。

∵反比例函数()ky=x 0x>的图象在第四象限，∴k＜0。

∴k=－6。

故选B 。

2. （辽宁鞍山3分）如图，二次函数y=ax 2+bx+c （a≠0）的图象与x 轴交于A 、B 两点，与y 轴交于点C ，点B 坐标（﹣1，0），下面的四个结论：①OA=3；②a+b+c＜0；③ac＞0；④b 2﹣4ac ＞0．其中正确的结论是【】A．①④ B．①③ C．②④ D．①②【答案】A。

【考点】二次函数图象与系数的关系，二次函数的性质，一元二次方程根的判别式。

【分析】∵由图象知，点B坐标（﹣1，0），对称轴是直线x=1，∴A的坐标是（3，0）。

∴OA=3。

∴结论①正确。

∵由图象知：当x=1时，y＞0，∴把x=1代入二次函数的解析式得：y=a+b+c＞0。

∴结论②错误。

∵抛物线的开口向下，与y轴的交点在y轴的正半轴上，∴a＜0，c＞0。

∴ac＜0。

∴结论③错误。

∵抛物线与x轴有两个交点，∴b2﹣4ac＞0。

∴结论④正确。

综上所述，结论①④正确。

故选A。

3. （辽宁本溪3分）如图，已知点A在反比例函数4y=x图象上，点B在反比例函数ky=x(k≠0)的图象上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为C、D，若OC=13OD，则k的值为【】A、10B、12C、14D、16 【答案】B。

中考数学专题函数及图像

2．(2010· 长沙)函数 y＝ A．x>－1 1 的自变量 x 的取值范围是( x＋1 B．x<－1 C．x≠－1 D．x≠1 )
举一反三
【解析】由 x＋1≠0 得 x≠－1.
考点训练
【答案】C
目录
首页
上一页
下一页
末页
宇轩图书
3．(2010· 眉山)某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗考点衣机内无水)，在这三个过程中洗衣机内水量 y(升)与时间 x(分)之间的函数关系对应的图象大知致为( ) 识精讲
考点知识精讲中考典例精析
7．某游泳池的横截面如图所示，用一水管向池内持续注水．若单位时间内注入的水量保持不变，则在注水过程中，下列图象能反映深水区水深 h 与注水时间 t 之间关系的是( A )
举一反三
考点训练
目录
首页
上一页
下一页
末页
宇轩图书
考点知 8．如图，乌鸦口渴到处找水喝，它看到了一个装有水的瓶子，但水位较低，且瓶口又小，识精乌鸦喝不着水，沉思一会后，聪明的乌鸦衔来一个个小石子放入瓶中，水位上升后，乌鸦喝讲到了水．在这则乌鸦喝水的故事中，从乌鸦看到瓶的那刻起开始计时并设时间为 x，瓶中水中考典例精析
举一反三
考点训练
目录
首页
上一页
下一页
末页
宇轩图书
考点知识精讲中考典例精析
举一反三
(2010· 丹东)星期天，小明与小刚骑自行车去距家 50 千米的某地旅游，匀速行驶 1.5 小时的时候，其中一辆自行车出故障，因此二人在自行车修理点修车，用了半个小时，然后以原速继续前行，行驶 1 小时到达目的地．请在右面的平面直角坐标系中，画出符合他们行驶的路程 s(千米)与行驶时间 t(时)之间的函数图象．

2023年中考数学--- a,b,c和二次函数图像的九种考法例题解析

2023年中考数学--- a ，b ，c 和二次函数图像的九种考法例题解析如图，二次函数的图像关于直线对称，与x 轴交于，两点，若考法解决方法本题结果①a,b,ca:二次函数图像开口向上时，a ＞0；开口向下，则a ＜0；b ：和a 共同决定了函数对称轴的位置，“左同右异”，当对称轴在y 轴左侧时，a ，b 同号，当对称轴在y 轴右侧时，a ，b 异号。

c ：c 为图像和y 轴交点的纵坐标。

a ＞0b ＜0c ＜0②b 2−4ac当图像和x 轴有两个交点时，b 2−4ac ＞0；当图像和x 轴有一个交点时，b 2−4ac =0；当图像和x 轴没有交点时，b 2−4ac ＜0。

b 2−4ac ＜0 ③a+b+c a-b+c 4a+2b+c 4a-2b+c 9a+3b+c 9a-3b+c 用特殊值进行判断：a+b+c 即为当x=1时的函数值； 4a-2b+c 即为当x=-2时的函数值。

a+b+c ＜0 a-b+c ＜0④3a+2b只有a ，b 时，用对称轴代换，消去一个未知数进行判断∵−b2a = 1，∴b=- 2а，∴3a ＋2b= 3a-4a= -a ，∵a ＞0，∴3a+2b<0⑤c+a 只有a ，c 或只有b ，c 时，先用对称轴代换，消去一个未知数，然后利用④中的结果判断结果∵a －b ＋c<0，∴a ＋c<b ，∵a ＞0， ∴b=-2a<0，∴a ＋c<0， ⑥b+2c若c 的系数不是1，可以先化成1再进行上述计算,或这把③中的某个式子中的c 的系数变成题里的形式。

∵−b 2a=1,∴2a =−b , ∵a+b ＋c<0，∴2a+2b ＋2c<0，-b+2b ＋2c<0，b ＋2c<0 ⑦am 2+bm 和a +b 的小小关系同时加上c ，am 2+bm+c ，a +b+c第一个式子是当x=m 时的函数值，第二个am 2+bm ≥a+b式子是当x=1时的函数值；由图可知，x=1时函数取最小值。

中考数学压轴题专题--函数图象中点的存在性问题（很好的一个专题训练并有试题详细解析及参考答案）

中考数学压轴题专题--函数图象中点的存在性问题（很好的⼀个专题训练并有试题详细解析及参考答案）1、如图1，在平⾯直⾓坐标系xOy 中，顶点为M 的抛物线y ＝ax 2＋bx （a ＞0）经过点A 和x 轴正半轴上的点B ，AO ＝BO ＝2，∠AOB ＝120°．（1）求这条抛物线的表达式；（2）连结OM ，求∠AOM 的⼤⼩；（3）如果点C 在x 轴上，且△ABC 与△AOM 相似，求点C 的坐标．图1．详细解析及参考答案：（1）如图2，过点A 作AH ⊥y 轴，垂⾜为H ．在Rt △AOH 中，AO ＝2，∠AOH ＝30°，所以AH ＝1，OH 3A (13)-．因为抛物线与x 轴交于O 、B (2,0)两点，设y ＝ax (x －2)，代⼊点A (13)-，可得3a =．图2 所以抛物线的表达式为23323(2)y x x =-=．（2）由22323331)y x x ==- 得抛物线的顶点M 的坐标为3(1,．所以3tan BOM ∠=．所以∠BOM ＝30°．所以∠AOM ＝150°．（3）由A (13)-、B (2,0)、M 3(1,，得3tan 3ABO ∠=，23AB =233OM =．所以∠ABO ＝30°，3OAOM=因此当点C 在点B 右侧时，∠ABC ＝∠AOM ＝150°．△ABC 与△AOM 相似，存在两种情况：①如图3，当BA OABC OM ==时，2BC ===．此时C (4,0)．②如图4，当BC OABA OM==时，6BC ===．此时C (8,0)．图3 图4考点伸展：在本题情境下，如果△ABC 与△BOM 相似，求点C 的坐标．如图5，因为△BOM 是30°底⾓的等腰三⾓形，∠ABO ＝30°，因此△ABC 也是底⾓为30°的等腰三⾓形，AB ＝AC ，根据对称性，点C 的坐标为(－4,0)．图52、如图1，已知抛物线211(1)444by x b x =-++（b 是实数且b ＞2）与x 轴的正半轴分别交于点A 、B （点A 位于点B 是左侧），与y 轴的正半轴交于点C ．（1）点B 的坐标为______，点C 的坐标为__________（⽤含b 的代数式表⽰）；（2）请你探索在第⼀象限内是否存在点P ，使得四边形PCOB 的⾯积等于2b ，且△PBC 是以点P 为直⾓顶点的等腰直⾓三⾓形？如果存在，求出点P 的坐标；如果不存在，请说明理由；（3）请你进⼀步探索在第⼀象限内是否存在点Q ，使得△QCO 、△QOA 和△QAB 中的任意两个三⾓形均相似（全等可看作相似的特殊情况）？如果存在，求出点Q 的坐标；如果不存在，请说明理由．图1详细解析及参考答案：（1）B 的坐标为(b , 0)，点C 的坐标为(0,4b )．（2）如图2，过点P 作PD ⊥x 轴，PE ⊥y 轴，垂⾜分别为D 、E ，那么△PDB ≌△PEC ．因此PD ＝PE ．设点P 的坐标为(x, x)．如图3，联结OP ．所以S 四边形PCOB ＝S △PCO ＋S △PBO ＝1152428b x b x bx ??+??=＝2b ．解得165x =．所以点P 的坐标为(1616,55)．图2 图3 （3）由2111(1)(1)()4444b y x b x x x b =-++=--，得A (1, 0)，OA ＝1．①如图4，以OA 、OC 为邻边构造矩形OAQC ，那么△OQC ≌△QOA ．当BA QA QA OA =，即2QA BA OA =?时，△BQA ∽△QOA ．所以2()14bb =-．解得8b =±Q 为(1,2．②如图5，以OC 为直径的圆与直线x ＝1交于点Q ，那么∠OQC ＝90°。

中考数学精讲篇专题突破五新函数图象及其性质探究题

12 ①函数 y＝（x－1）2＋2的图象关于直线 x＝1 对称；( )
12 ②当 x＝1 时，函数 y＝（x－1）2＋2有最大值，最大值为 6；( ) ③在自变量的取值范围内，函数 y 的值随自变量 x 的增大而增大．( )
(3)已知函数 y＝23x＋83的图象如图所示．结合你所画 12 2 8
类型二：曲线式函数图象的性质探究
(重庆：A 卷，B 卷 2021—2020T22)
3．(2021·九龙坡区校级模拟)函数图象在探索函数的性质中有非常重要的作用．现在就一类特殊的
a 函数展开探索：y＝x＋x，探索函数图象和性质过程如下：
x … －6 －4 －2 －1 1 n 4 6 …
y
… －230 m
x … －3 －2 －1 0 1 2 3 … y … －6 －4 －2 0 －2 －4 －6 …
(1)观察发现：三个函数的图象都是由两条射线组成的轴对称图形；三个函数解析式中绝对值前面的系数相同，则图象的开口方向和形状完全相同，只有最高点和对称轴发生了变化，写出点 A，B 的坐标和函数 y＝－ 2|x＋2|的对称轴； (2)探索思考：平移函数 y＝－2|x|的图象可以得到函数 y＝－2|x|＋2 和 y＝－2|x＋2|的图象，分别写出平移的方向和距离； (3)拓展应用：在所给的平面直角坐标系内画出函数 y＝－2|x－3|＋1 的图象．若点(x1，y1)和(x2，y2)在该函数图象上，且 x2>x1>3.比较 y1，y2 的大小．
的函数图象，直接写出不等式（x－1）2＋2＞3x＋3的解集．
解：(1)2；6；函数图象如图所示． (2)①√；②√；③×.
(3)x<－3 或－1<x<2.
解：(1)A(0，2)，B(－2，0)，对称轴为直线 x＝－2；

中考题数学一次函数图像应用题

第1题图（1）第1题图（2）中考题数学----一次函数图像应用题1/．已知某种水果的批发单价与批发量的函数关系如图（1）所示．（1）请说明图中①、②两段函数图象的实际意义．（2）写出批发该种水果的资金金额w （元）与批发量m （kg ）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．（3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商拟每日售出60kg 以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．）分2、邮递员小王从县城出发，骑自行车到A 村投递，途中遇到县城中学的学生李明从A 村步行返校．小王在A 村完成投递工作后，返回县城途中又遇到李明，便用自行车载上李明，一起到达县城，结果小王比预计时间晚到1分钟．二人与县城间的距离s (千米)和小王从县城出发后所用的时间t (分)之间的函数关系如图，假设二人之间交流的时间忽略不计，求：（1）小王和李明第一次相遇时，距县城多少千米？请直接写出答案．（2）小王从县城出发到返回县城所用的时间．（3）李明从A 村到县城共用多长时间？3、(本小题满分8分）甲、乙两人骑自行车前往A 地，他们距A 地的路程s （km ）与行驶时间t （h ）之间的关系如图所示，请根据图象所提供的信息解答下列问题：（1）甲、乙两人的速度各是多少？（2）求出甲距A 地的路程s 与行驶时间t 之间的函数关系式．（3）在什么时间段内乙比甲离A 地更近？4、（本小题满分8分）甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时（从甲车出发时开始计时）．图中折线OABC、线段DE分别表示甲、乙两车所行路程y（千米）与时间x（小时）之间的函数关系对应的图象（线段AB表示甲出发不足2小时因故停车检修）．请根据图象所提供的信息，解决如下问题：（1）求乙车所行路程y与时间x的函数关系式；（2）求两车在途中第二次相遇时，它们距出发地的路程；（3）乙车出发多长时间，两车在途中第一次相遇？（写出解题过程）5．南宁市狮山公园计划在健身区铺设广场砖．现有甲、乙两个工程队参加竞标，甲工程队铺设广场砖的造价y（元）与铺设面积()2m x的函数关系如图12所示；乙工程队铺设广场甲砖的造价y 乙（元）与铺设面积()2m x 满足函数关系式：y kx =乙．（1）根据图12写出甲工程队铺设广场砖的造价y 甲（元）与铺设面积()2m x 的函数关系式；（2）如果狮山公园铺设广场砖的面积为21600m ，那么公园应选择哪个工程队施工更合算？6、（本小题满分7分）为迎接2008年北京奥运会，某学校组织了一次野外长跑活动，参加长跑的同学出发后，另一些同学从同地骑自行车前去加油助威。