高中数学函数的图像专题拔高训练
高考数学函数的图像专题卷
高考数学函数的图像专题卷一、单选题(共28题;共56分)1. ( 2分) (2020高三上·兴宁期末)函数y=xcos x+sin x的图象大致为( ).A. B.C. D.2. ( 2分) (2021高三上·宝安月考)函数的图象大致为()A. B.C. D.3. ( 2分) (2021高三上·河南月考)函数的大致图象为()A. B.C. D.4. ( 2分) (2021高三上·河北期中)函数的图象大致为()A. B.C. D.5. ( 2分) (2021高三上·湖北期中)函数的图象大致为()A. B.C. D.6. ( 2分) (2021·芜湖模拟)函数的部分图象可能为()A. B.C. D.7. ( 2分) (2020高三上·天津月考)函数的图象大致是()A. B. C. D.8. ( 2分) 函数的图象大致为()A. B.C. D.9. ( 2分) (2020高三上·杭州期中)函数的部分图象大致为()A. B.C. D.10. ( 2分) (2021高三上·赣州期中)已知函数,则函数的大致图象为()A. B.C. D.11. ( 2分) (2021高三上·湖州期中)函数的图象可能是()A. B. C. D.12. ( 2分) (2021高三上·金华月考)已知,函数,,则图象为上图的函数可能是()A. B. C. D.13. ( 2分) (2021高三上·杭州期中)函数的图象可能是()A. B.C. D.14. ( 2分) (2021高三上·陕西月考)在同一直角坐标系中,函数,,(,且)的图像可能是()A. B.C. D.15. ( 2分) (2021高三上·贵州月考)函数f(x)= 的大致图象不可能是()A. B.C. D.16. ( 2分) (2020高三上·温州月考)函数的图像可能是()A. B.C. D.17. ( 2分) (2021·四川模拟)函数及,则及的图象可能为()A. B.C. D.18. ( 2分) 已知函数f(x)=ka x﹣a﹣x(a>0且a≠1)在R上是奇函数,且是增函数,则函数g(x)=log a (x﹣k)的大致图象是()A. B. C. D.19. ( 2分) (2021高三上·重庆月考)函数的大致图象如图所示,则a,b,c 大小顺序为()A. B. C. D.20. ( 2分) (2021·株洲模拟)若函数的大致图象如图所示,则()A. B. C. D.21. ( 2分) (2020高三上·浙江开学考)已知函数的图像如图所示,则下列判断正确的个数是()(1),(2),(3),(4)A. 1个B. 2个C. 3个D. 4个22. ( 2分) 如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,﹣),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为()A. B.C. D.23. ( 2分) (2021·新乡模拟)如图,在正方形中,点M从点A出发,沿向,以每2个单位的速度在正方形的边上运动;点N从点B出发,沿方向,以每秒1个单位的速度在正方形ABCD的边上运动.点M与点N同时出发,运动时间为t(单位:秒),的面积为(规定共线时其面积为零,则点M第一次到达点A 时,的图象为()A. B.C. D.24. ( 2分) (2017高三上·九江开学考)如图,圆C:x2+(y﹣1)2=1与y轴的上交点为A,动点P从A点出发沿圆C按逆时针方向运动,设旋转的角度∠ACP=x(0≤x≤2π),向量在=(0,1)方向的射影为y(O为坐标原点),则y关于x的函数y=f(x)的图象是()A. B.C. D.25. ( 2分) 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为()A. B. C. D.26. ( 2分) 如图,正△ABC的中心位于点G(0,1),A(0,2),动点P从A点出发沿△ABC的边界按逆时针方向运动,设旋转的角度∠AGP=x(0≤x≤2π),向量在=(1,0)方向的射影为y(O为坐标原点),则y关于x的函数y=f(x)的图象是()A. B.C. D.27. ( 2分) (2013·江西理)如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1,l2之间,l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2,则函数y=f(x)的图象大致是()A. B.C. D.28. ( 2分) (2016高三上·崇明期中)如图所示的图形是由一个半径为2的圆和两个半径为1的半圆组成,它们的圆心分别为O,O1,O2.动点P从A点出发沿着圆弧按A→O→B→C→A→D→B的路线运动(其中A,O1,O,O2,B五点共线),记点P运动的路程为x,设y=|O1P|2,y与x的函数关系为y=f (x),则y=f(x)的大致图象是()A. B.C. D.答案解析部分一、单选题1.【答案】D【考点】函数的图象【解析】【解答】由于函数y=xcosx+sinx为奇函数,故它的图象关于原点对称,所以排除B,由当时,y=1>0,当x=π时,y=π×cosπ+sinπ=−π<0.由此可排除A和C,故正确的选项为D.故答案为:D.【分析】利用奇函数的定义证出函数为奇函数,再利用奇函数的图象关于原点对称的性质结合特殊值法及函数值与0的大小关系,再利用排除法得出函数y=xcos x+sin x的大致图象。
高考数学专题《函数的图象》习题含答案解析

专题3.7 函数的图象1.(2021·全国高三专题练习(文))已知图①中的图象是函数()y f x=的图象,则图②中的图象对应的函数可能是()A.(||)y f x=B.|()|y f x=C.(||)y f x=-D.(||)y f x=--【答案】C【解析】根据函数图象的翻折变换,结合题中条件,即可直接得出结果.【详解】图②中的图象是在图①的基础上,去掉函数()y f x=的图象在y轴右侧的部分,然后将y轴左侧图象翻折到y轴右侧,y轴左侧图象不变得来的,∴图②中的图象对应的函数可能是(||)y f x=-.故选:C.2.(2021·浙江高三专题练习)函数()lg1y x=-的图象是()A.B.C.练基础D .【答案】C【解析】将函数lg y x =的图象进行变换可得出函数()lg 1y x =-的图象,由此可得出合适的选项.【详解】将函数lg y x =的图象先向右平移1个单位长度,可得到函数()lg 1y x =-的图象,再将所得函数图象位于x 轴下方的图象关于x 轴翻折,位于x 轴上方图象不变,可得到函数()lg 1y x =-的图象.故合乎条件的图象为选项C 中的图象.故选:C.3.(2021·全国高三专题练习(理))我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔离分家万事休.”在数学的学习和研究中,经常用函数的图象来研究函数的性质,也经常用函数的解析式来研究函数图象的特征.若函数()y fx =在区间[],a b 上的图象如图,则函数()y f x =在区间[],a b 上的图象可能是( )A .B .C .D .【答案】D【解析】先判断出函数是偶函数,根据偶函数的图像特征可得选项.【详解】 函数()y f x =是偶函数,所以它的图象是由()y f x =把0x ≥的图象保留,再关于y 轴对称得到的.结合选项可知选项D 正确,故选:D .4.(2021·全国高三专题练习(文))函数()5xf x x x e =-⋅的图象大致是( ). A . B .C .D .【答案】B【解析】由()20f >和()20f -<可排除ACD ,从而得到选项.【详解】由()()2223222160f e e =-=->,可排除AD ;由()()2223222160f e e ---=-+=-<,可排除C ;故选:B.5.(2021·陕西高三三模(理))函数x y b a =⋅与()log a y bx =的图像在同一坐标系中可能是()A .B .C .D .【答案】C【解析】根据指数函数和对数函数的单调性,以及特殊点函数值的范围逐一判断可得选项.【详解】令x f x b a ,()()log a g x bx =,对于A 选项:由x f xb a 得>1a ,且()00>1f b a b ==⋅,所以log >0a b ,而()1log 0a g b =<,所以矛盾,故A 不正确;对于B 选项:由x f xb a 得>1a ,且()001f b a b ⋅=<=,所以log 0a b <,而()1log >0a g b =,所以矛盾,故B 不正确;对于C 选项:由x f xb a 得>1a ,且()001f b a b ⋅=<=,所以log 0a b <,又()1log 0a g b =<,故C 正确;对于D 选项:由x f xb a 得>1a ,且()00>1f b a b ==⋅,而()()log a g x bx =中01a <<,所以矛盾,故D 不正确;故选:C . 6.(2021·宁夏吴忠市·高三其他模拟(文))已知函数()()()ln 2ln 4f x x x =-+-,则( ). A .()f x 的图象关于直线3x =对称B .()f x 的图象关于点()3,0对称C .()f x 在()2,4上单调递增D .()f x 在()2,4上单调递减【答案】A【解析】先求出函数的定义域.A :根据函数图象关于直线对称的性质进行判断即可;B :根据函数图象关于点对称的性质进行判断即可;C :根据对数的运算性质,结合对数型函数的单调性进行判断即可;D :结合C 的分析进行判断即可.【详解】 ()f x 的定义域为()2,4x ∈,A :因为()()()()3ln 1ln 13f x x x f x +=++-=-,所以函数()f x 的图象关于3x =对称,因此本选项正确;B :由A 知()()33f x f x +≠--,所以()f x 的图象不关于点()3,0对称,因此本选项不正确;C :()()()2ln 2ln 4ln(68)x x x f x x =-+-=-+- 函数2268(3)1y x x x =-+-=--+在()2,3x ∈时,单调递增, 在()3,4x ∈时,单调递减,因此函数()f x 在()2,3x ∈时单调递增,在()3,4x ∈时单调递减,故本选项不正确;D :由C 的分析可知本选项不正确,故选:A7.(2021·安徽高三二模(理))函数()n xf x x a =,其中1a >,1n >,n 为奇数,其图象大致为( ) A . B .C .D .【答案】B【解析】分析()f x 在()0,∞+、(),0-∞上的函数值符号,及该函数在()0,∞+上的单调性,结合排除法可得出合适的选项.【详解】对任意x ∈R ,0x a >,由于1n >,n 为奇数,当0x <时,0n x <,此时()0f x <,当0x >时,0n x >,此时()0f x >,排除AC 选项;当0x >时,任取1x 、()20,x ∈+∞且12x x >,则120x x a a >>,120n n x x >>,所以()()12f x f x >,所以,函数()f x 在()0,∞+上为增函数,排除D 选项.故选:B.8.(2021·浙江高三专题练习)已知函数f (x )=1331,,log 1x x x x ⎧≤⎪⎨>⎪⎩则函数y =f (1-x )的大致图象是( ) A . B .C .D .【答案】D【解析】由()f x 得到()1f x -的解析式,根据函数的特殊点和正负判断即可.【详解】因为函数()f x 133,1log ,1x x x x ⎧≤⎪=⎨>⎪⎩, 所以函数()1f x -()1133,0log 1,0x x x x -⎧≥⎪=⎨-<⎪⎩, 当x =0时,y =f (1)=3,即y =f (1-x )的图象过点(0,3),排除A ;当x =-2时,y =f (3)=-1,即y =f (1-x )的图象过点(-2,-1),排除B ;当0x <时,()1311,(1)log 10x f x x ->-=-<,排除C ,故选:D .9.【多选题】(2021·浙江高一期末)如图,某池塘里浮萍的面积y (单位:2m )与时间t (单位:月)的关系为t y a =.关于下列法正确的是( )A .浮萍每月的增长率为2B .浮萍每月增加的面积都相等C .第4个月时,浮萍面积不超过280mD .若浮萍蔓延到22m 、24m 、28m 所经过的时间分别是1t 、2t 、3t ,则2132t t t =+【答案】AD【解析】根据图象过点求出函数解析式,根据四个选项利用解析式进行计算可得答案.【详解】由图象可知,函数图象过点(1,3),所以3a =,所以函数解析式为3ty =, 所以浮萍每月的增长率为13323233t t tt t +-⨯==,故选项A 正确; 浮萍第一个月增加的面积为10332-=平方米,第二个月增加的面积为21336-=平方米,故选项B 不正确;第四个月时,浮萍面积为438180=>平方米,故C 不正确;由题意得132t =,234t =,338t =,所以13log 2t =,23log 4t =,33log 8t =,所以2133333332log 2log 8log (28)log 16log 42log 42t t t +=+=⨯====,故D 正确.故选:AD10.(2020·全国高一单元测试)函数()2x f x =和()3g x x =的图象如图所示,设两函数的图象交于点11(,)A x y ,22(,)B x y ,且12x x <.(1)请指出图中曲线1C ,2C 分别对应的函数;(2)结合函数图象,比较(3)f ,(3)g ,(2020)f ,(2020)g 的大小.【答案】(1)1C 对应的函数为()3g x x =,2C 对应的函数为()2x f x =;(2)(2020)(2020)(3)(3)f g g f >>>.【解析】(1)根据指数函数和一次函数的函数性质解题;(2)结合函数的单调性及增长快慢进行比较.【详解】(1)1C 对应的函数为()3g x x =,2C 对应的函数为()2x f x =.(2)(0)1f =,(0)0g =,(0)(0)f g ∴>,又(1)2f =,(1)3g =,(1)(1)f g ∴<,()10,1x ∴∈;(3)8f =,(3)9g =,(3)(3)f g ∴<,又(4)16f =,(4)12g =,(4)(4)f g ∴>,()23,4x ∴∈.当2x x >时,()()f x g x >,(2020)(2020)f g ∴>.(2020)(2020)(3)(3)f g g f ∴>>>.1.(2021·湖南株洲市·高三二模)若函数()2()mx f x e n =-的大致图象如图所示,则( )A .0,01m n ><<B .0,1m n >>C .0,01m n <<<D .0,1m n <>【答案】B【解析】令()0f x =得到1ln x n m =,再根据函数图象与x 轴的交点和函数的单调性判断.【详解】令()0f x =得mx e n =,即ln mx n =,解得1ln x n m =,由图象知1l 0n x m n =>,当0m >时,1n >,当0m <时,01n <<,故排除AD ,当0m <时,易知mx y e =是减函数,当x →+∞时,0y →,()2f x n →,故排除C故选:B2.(2021·甘肃高三二模(理))关于函数()ln |1|ln |1|f x x x =++-有下列结论,正确的是( ) A .函数()f x 的图象关于原点对称 B .函数()f x 的图象关于直线1x =对称 练提升C .函数()f x 的最小值为0D .函数()f x 的增区间为(1,0)-,(1,)+∞【答案】D 【解析】A.由函数的奇偶性判断;B.利用特殊值判断;C.利用对数函数的值域求解判断;D.利用复合函数的单调性判断. 【详解】2()ln |1|ln |1|ln |1|f x x x x =++-=-,由1010x x ⎧+>⎪⎨->⎪⎩,解得1x ≠±,所以函数的定义域为{}|1x x ≠±, 因为()ln |1|ln |1|ln |1|ln |1|()f x x x x x f x -=-++--=++-=,所以函数为偶函数,故A 错误. 因为(0)ln |1|0,(3)ln8f f =-==,所以(0)(3)f f ≠,故B 错误;因为 ()2|1|0,x -∈+∞,所以()f x ∈R ,故C 错误;令2|1|t x =-,如图所示:,t 在(),1,[0,1)-∞-上递减,在()(1,0],1,-+∞上递增,又ln y t =在()0,∞+递增,所以函数()f x 的增区间为(1,0)-,(1,)+∞,故D 正确; 故选:D3.(2021·吉林长春市·东北师大附中高三其他模拟(理))函数ln xy x=的图象大致为( )A .B .C .D .【答案】C 【解析】 求出函数ln xy x=的定义域,利用导数分析函数的单调性,结合排除法可得出合适的选项. 【详解】 对于函数ln xy x =,则有0ln 0x x >⎧⎨≠⎩,解得0x >且1x ≠, 所以,函数ln xy x=的定义域为()()0,11,+∞,排除AB 选项;对函数ln x y x =求导得()2ln 1ln x y x -'=.当01x <<或1x e <<时,0y '<;当x e >时,0y '>. 所以,函数ln xy x=的单调递减区间为()0,1、()1,e ,单调递增区间为(),e +∞, 当01x <<时,0ln xy x =<,当1x >时,0ln x y x=>,排除D 选项. 故选:C.4.(2021·海原县第一中学高三二模(文))函数2xx xy e+=的大致图象是( )A .B .C .D .【答案】D 【解析】利用导数可求得2xx xy e+=的单调性,由此排除AB ;根据0x >时,0y >可排除C ,由此得到结果. 【详解】 由题意得:()()222211x xxxx e x x e x x y e e +-+-++'==,令0y '=,解得:1x =,2x =,∴当11,,22x ∞∞⎛⎛⎫+∈-⋃+ ⎪ ⎪⎝⎭⎝⎭时,0y '<;当11,22x ⎛+∈ ⎝⎭时,0y '>;2x x x y e +∴=在1,2⎛--∞ ⎝⎭,1,2⎛⎫++∞ ⎪ ⎪⎝⎭上单调递减,在1122⎛⎫-+ ⎪ ⎪⎝⎭上单调递增,可排除AB ; 当0x >时,0y >恒成立,可排除C. 故选:D.5.(2021·天津高三三模)意大利画家列奥纳多·达·芬奇的画作《抱银鼠的女子》(如图所示)中,女士颈部的黑色珍珠项链与她怀中的白貂形成对比.光线和阴影衬托出人物的优雅和柔美.达·芬奇提出:固定项链的两端,使其在重力的作用下自然下垂,形成的曲线是什么?这就是著名的“悬链线问题”.后人研究得出,悬链线并不是抛物线,而是与解析式为2x x e e y -+=的“双曲余弦函数”相关.下列选项为“双曲余弦函数”图象的是( )A .B .C .D .【答案】C 【解析】分析函数2x xe e y -+=的奇偶性与最小值,由此可得出合适的选项.【详解】令()e e 2x x f x -+=,则该函数的定义域为R ,()()2x xe ef x f x -+-==,所以,函数()e e 2x xf x -+=为偶函数,排除B 选项.由基本不等式可得()112f x ≥⨯=,当且仅当0x =时,等号成立,所以,函数()f x 的最小值为()()min 01f x f ==,排除AD 选项. 故选:C.6.(2021·浙江高三月考)函数()3log 01a y x ax a =-<<的图象可能是( )A .B .C .D .【答案】B 【解析】先求出函数的定义域,判断函数的奇偶性,构造函数,求函数的导数,利用是的导数和极值符号进行判断即可. 【详解】根据题意,()3log a f x x ax =-,必有30x ax -≠,则0x ≠且x ≠即函数的定义域为{|0x x ≠且x ≠,()()()()33log log a a x a x x f f x ax x ---=--==,则函数3log a y x ax =-为偶函数,排除D ,设()3g x x ax =-,其导数()23g x x a '=-,由()0g x '=得x =±,当3x >时,()0g x '>,()g x 为增函数,而()f x 为减函数,排除C ,在区间,33⎛⎫- ⎪ ⎪⎝⎭上,()0g x '<,则()g x 在区间,33⎛⎫- ⎪ ⎪⎝⎭上为减函数,在区间3⎛⎫+∞ ⎪ ⎪⎝⎭上,()0g x '>,则()g x 在区间3⎛⎫+∞ ⎪ ⎪⎝⎭上为增函数,0g=,则()g x 存在极小值33339g a ⎛⎛⎫=-⨯=- ⎪ ⎪⎝⎭⎝⎭,此时()g x ()0,1,此时()0f x >,排除A , 故选:B.7.(2019·北京高三高考模拟(文))当x∈[0,1]时,下列关于函数y=2(1)mx -的图象与y =的图象交点个数说法正确的是( ) A .当[]m 0,1∈时,有两个交点 B .当(]m 1,2∈时,没有交点 C .当(]m 2,3∈时,有且只有一个交点 D .当()m 3,∞∈+时,有两个交点【答案】B 【解析】设f (x )=2(1)mx -,g (x ) ,其中x∈[0,1]A .若m=0,则()1f x =与()g x =[0,1]上只有一个交点(1,1),故A 错误.B .当m∈(1,2)时,111()(0)1,()(0)1()()2f x f g x g f x g x m<<∴≤=≥=>∴<即当m∈(1,2]时,函数y=2(1)mx -的图象与y =x∈[0,1]无交点,故B 正确,C .当m∈(2,3]时,2111()(1)(1),()(1)32f x f mg x g m <<∴≤=-≤=2(1)m >-时()()f x g x <,此时无交点,即C 不一定正确.D .当m∈(3,+∞)时,g (0)1,此时f (1)>g (1),此时两个函数图象只有一个交点,故D 错误,故选:B.8.(2021·浙江高三专题练习)若关于x的不等式34log2xax-≤在10,2x⎛⎤∈ ⎥⎝⎦恒成立,则实数a的取值范围是()A.1,14⎡⎫⎪⎢⎣⎭B.10,4⎛⎤⎥⎝⎦C.3,14⎡⎫⎪⎢⎣⎭D.30,4⎛⎤⎥⎝⎦【答案】A 【解析】转化为当10,2x⎛⎤∈ ⎥⎝⎦时,函数342xy=-的图象不在log ay x=的图象的上方,根据图象列式可解得结果.【详解】由题意知关于x的不等式34log2xax-≤在10,2x⎛⎤∈ ⎥⎝⎦恒成立,所以当10,2x⎛⎤∈ ⎥⎝⎦时,函数342xy=-的图象不在log ay x=的图象的上方,由图可知0111log 22a a <<⎧⎪⎨≥⎪⎩,解得114a ≤<. 故选:A9.对a 、b ∈R ,记{},max ,,a a b a b b a b⎧=⎨<⎩≥,函数{}2()max ||,24()f x x x x x =--+∈R .(1)求(0)f ,(4)f -.(2)写出函数()f x 的解析式,并作出图像.(3)若关于x 的方程()f x m =有且仅有3个不等的解,求实数m 的取值范围.(只需写出结论) 【答案】见解析.【解析】解:(1)∵{},max ,,a a b a b b a b⎧=⎨<⎩≥,函数{}2()max ||,24f x x x x =--+,∴{}(0)max 0,44f ==,{}(4)max 4,44f -=-=.(2)(3)5m =或m 10.(2021·全国高一课时练习)函数()2xf x =和()()30g x xx =≥的图象,如图所示.设两函数的图象交于点()11A x y ,,()22B x y ,,且12x x <.(1)请指出示意图中曲线1C ,2C 分别对应哪一个函数;(2)结合函数图象,比较()8f ,()8g ,()2015f ,()2015g 的大小. 【答案】(1)1C 对应的函数为()()30g x xx =≥,2C 对应的函数为()2x f x =;(2)()()()()2015201588f g g f >>>.【解析】(1)根据图象可得结果;(2)通过计算可知1282015x x <<<,再结合题中的图象和()g x 在()0+∞,上的单调性,可比较()8f ,()8g ,()2015f ,()2015g 的大小.【详解】(1)由图可知,1C 的图象过原点,所以1C 对应的函数为()()30g x xx =≥,2C 对应的函数为()2x f x =.(2)因为11g =(),12f =(),28g =(),24f =(),()9729g =,()9512f =,()101000g =,()101024f =,所以11f g >()(),22f g <()(),()()99f g <,()()1010f g >.所以112x <<,2910x <<.所以1282015x x <<<.从题中图象上知,当12x x x <<时,()()f x g x <;当2x x >时,()()f x g x >,且()g x 在()0+∞,上是增函数,所以()()()()2015201588f g g f >>>.1. (2020·天津高考真题)函数241xy x =+的图象大致为( ) 练真题A .B .C .D .【答案】A 【解析】由函数的解析式可得:()()241xf x f x x --==-+,则函数()f x 为奇函数,其图象关于坐标原点对称,选项CD 错误; 当1x =时,42011y ==>+,选项B 错误. 故选:A.2.(2019年高考全国Ⅲ卷理)函数3222x xx y -=+在[]6,6-的图像大致为( ) A . B .C .D .【答案】B【解析】设32()22x xx y f x -==+,则332()2()()2222x x x x x x f x f x ----==-=-++,所以()f x 是奇函数,图象关于原点成中心对称,排除选项C .又34424(4)0,22f -⨯=>+排除选项D ; 36626(6)722f -⨯=≈+,排除选项A , 故选B .3.(2020·天津高考真题)已知函数3,0,(),0.x x f x x x ⎧=⎨-<⎩若函数2()()2()g x f x kx xk =--∈R 恰有4个零点,则k 的取值范围是( ) A .1,(22,)2⎛⎫-∞-+∞ ⎪⎝⎭B .1,(0,22)2⎛⎫-∞- ⎪⎝⎭C .(,0)(0,22)-∞D .(,0)(22,)-∞+∞【答案】D 【解析】注意到(0)0g =,所以要使()g x 恰有4个零点,只需方程()|2|||f x kx x -=恰有3个实根 即可, 令()h x =()||f x x ,即|2|y kx =-与()()||f x h x x =的图象有3个不同交点. 因为2,0()()1,0x x f x h x x x ⎧>==⎨<⎩, 当0k =时,此时2y =,如图1,2y =与()()||f x h x x =有2个不同交点,不满足题意; 当k 0<时,如图2,此时|2|y kx =-与()()||f x h x x =恒有3个不同交点,满足题意; 当0k >时,如图3,当2y kx =-与2yx 相切时,联立方程得220x kx -+=,令0∆=得280k -=,解得k =,所以k >综上,k 的取值范围为(,0)(22,)-∞+∞.故选:D.4.(2019年高考全国Ⅱ卷理)设函数()f x 的定义域为R ,满足(1) 2 ()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-.若对任意(,]x m ∈-∞,都有8()9f x ≥-,则m 的取值范围是A .9,4⎛⎤-∞ ⎥⎝⎦B .7,3⎛⎤-∞ ⎥⎝⎦C .5,2⎛⎤-∞ ⎥⎝⎦D .8,3⎛⎤-∞ ⎥⎝⎦【答案】B【解析】∵(1) 2 ()f x f x +=,()2(1)f x f x ∴=-. ∵(0,1]x ∈时,1()(1)[,0]4f x x x =-∈-;∴(1,2]x ∈时,1(0,1]x -∈,1()2(1)2(1)(2),02f x f x x x ⎡⎤=-=--∈-⎢⎥⎣⎦; ∴(2,3]x ∈时,1(1,2]x -∈,()2(1)4(2)(3)[1,0]f x f x x x =-=--∈-,如图:当(2,3]x ∈时,由84(2)(3)9x x --=-解得173x =,283x =,若对任意(,]x m ∈-∞,都有8()9f x ≥-,则73m ≤.则m 的取值范围是7,3⎛⎤-∞ ⎥⎝⎦.故选B.5.(2017·天津高考真题(文))已知函数f(x)={|x|+2,x <1x +2x ,x ≥1.设a ∈R ,若关于x 的不等式f(x)≥|x 2+a|在R 上恒成立,则a 的取值范围是 A .[−2,2] B .[−2√3,2] C .[−2,2√3] D .[−2√3,2√3] 【答案】A【解析】满足题意时f (x )的图象恒不在函数y =|x2+a|下方,当a =2√3时,函数图象如图所示,排除C,D 选项;当a =−2√3时,函数图象如图所示,排除B 选项,本题选择A 选项.6.(2018·全国高考真题(文))设函数()2010x x f x x -⎧≤=⎨>⎩,,,则满足()()12f x f x +<的x 的取值范围是( )A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,【答案】D 【解析】分析:首先根据题中所给的函数解析式,将函数图像画出来,从图中可以发现若有()()12f x f x +<成立,一定会有2021x x x <⎧⎨<+⎩,从而求得结果.详解:将函数()f x 的图像画出来,观察图像可知会有2021x x x <⎧⎨<+⎩,解得0x <,所以满足()()12f x f x +<的x 的取值范围是()0-∞,,故选D .。
高中数学函数的图像经典专题拔高训练(附答案)
高中数学函数的图像专题拔高训练一.选择题1.(2014?鹰潭二模)如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t 变化的可能图象是()A .B.C. D .2.(2014?河东区一模)若方程f(x)﹣2=0 在(﹣∞,0)内有解,则(x)的图象是()A .B.C. D .3.(2014?福建模拟)现有四个函数:①?②?③?④? 号安排正确的一组是()x的图象(部分)如下,则按照从左到右图象对应的函数序A .① ④③②B.④①②③C.①④②③ D .③④②①4.(2014?漳州一模)已知函数,则函数(x)的大致图象为()A .B.C. D .5.(2014?遂宁一模)函数f(x)的图象大致是()2A .B.C. D .6.(2014?西藏一模)函数的大致图象是()A .B.C. D .7.(2014?湖南二模)若函数(x)的图象如图所示,则函数(1﹣x)的图象大致为()A .B.C. D .8.(2014?临沂三模)函数的图象大致为()A .B.C. D .9.(2014?大港区二模)如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:①f(x);②f(x)21;③ f(x)=2();④f(x).其中“同簇函数”的是()A .① ②B.①④C.②③ D .③④10.(2014?潍坊模拟)已知函数f(x)﹣﹣|,则函数(1)的大致图象为()A .B.C. D .211.(2014 ?江西一模)平面上的点P(x,y ),使关于t 的二次方程t 0 的根都是绝对值不超过 1 的实数,那么这样的点P 的集合在平面内的区域的形状是()A .B.C. D .12.(2014?宜春模拟)如图,半径为 2 的圆内有两条半圆弧,一质点M 自点 A 开始沿弧 A ﹣B ﹣C﹣O﹣A ﹣D﹣C 做匀速运动,则其在水平方向(向右为正)的速度(t)的图象大致为()A B C D....13.(2014?江西模拟)如图正方形边长为4,E 为的中点,现用一条垂直于的直线l 以0.4 的速度从l 1 平行移动到l 2,则在t 秒时直线l 扫过的正方形的面积记为F(t)(m2),则F(t)的函数图象大概是()y14.( 2014?临汾模拟)如图可能是下列哪个函数的图象()A .2x x 2﹣ 1 B .C . ( x 22x ) D .15.( 2014?芜湖模拟)如果两个方程的曲线经过若干次平移或对称变换后能够完全重合,则称这两个方程为 “互为生成方程对 ”.给出下列四对方程: ① 和1;② 2﹣x 22=2 和 x 22 2﹣ y =2; ③ y =4x 和 x =4y ; ④ (x ﹣ 1)和 1.其中是 “互为生成方程对 ”有( )A .1 对B . 2 对C . 3 对D .4 对16.(2014 ?上饶二模)如图,不规则图形中:和是线段,和是圆弧,直线 l ⊥于 E ,当 l 从左至右移动(与线段有公共点)时,把四边形分成两部分,设,左侧部分面积为y ,则 y 关于 x 的大致图象为()A .B .C .D .17.( 2014?乌鲁木齐三模)已知函数 f ( x )在定义域 R 上的值不全为零,若函数f ( 1)的图象关于( 1, 0)对称,函数 f ( 3)的图象关于直线 1 对称,则下列式子中错误的是()A .f (﹣ x )( x )B . f ( x ﹣ 2)(6)C . f (﹣ 2)(﹣ 2﹣ x ) =0D .f (3)( 3﹣ x ) =018.( 2014?凉山州一模)函数的图象大致是()﹣﹣19.(2014?安阳一模)已知 f (x)= ,则下列叙述中不正确的一项是()A .B.C. D .f(﹣x)的图象 f ()的图象f (x﹣1)的图象(x)|的图象20.如图,在正四棱柱﹣ A 1B1C1D 1 中,1=2,1,M 、N 分别在1,上移动,并始终保持∥平面1D 1,设,,则函数(x)的图象大致是()A .B.C. D .21.(2012?青州市模拟)如图,有一直角墙角,两边的长度足够长,在P 处有一棵树与两墙的距离分别是 a m(0 <a<12)、4m,不考虑树的粗细.现在想用16m 长的篱笆,借助墙角围成一个矩形的花圃.设此矩形花圃的最大2面积为S,若将这棵树围在花圃内,则函数(a)(单位m )的图象大致是()22.(2009?江西)如图所示,一质点P(x,y)在平面上沿曲线运动,速度大小不变,其在x 轴上的投影点Q(x,0)的运动速度(t)的图象大致为()A .B.C. D .23.(2010?湖南)用{a ,b} 表示a,b 两数中的最小值.若函数f(x){ ,} 的图象关于直线对称,则t 的值为()A .﹣2 B.2 C.﹣1 D .124.已知函数f(x)的定义域为[a,b] ,函数(x)的图象如下图所示,则函数f()的图象是()A .B.C. D .25.(2012?泸州二模)点P 从点O 出发,按逆时针方向沿周长为l 的图形运动一周,O,P 两点连线的距离y 与点P 走过的路程x 的函数关系如右图所示,那么点P 所走的图形是()二.填空题(共 5 小题)26.(2006?山东)下列四个命题中,真命题的序号有(写出所有真命题的序号).①将函数1|的图象按向量(﹣1,0)平移,得到的图象对应的函数表达式为.22②圆x +4x ﹣21=0 与直线相交,所得弦长为2.③若(α+β)= ,(α﹣β)= ,则αβ=5.④如图,已知正方体﹣ A 1B1C1D1,P 为底面内一动点,P 到平面1D 1D 的距离与到直线 1 的距离相等,则P 点的轨迹是抛物线的一部分.27.如图所示,f(x)是定义在区间[﹣c,c](c>0)上的奇函数,令g(x )(x),并有关于函数g(x)的四个论断:①若a>0,对于[﹣1,1]内的任意实数m,n(m<n),恒成立;②函数g(x)是奇函数的充要条件是0;③若a≥1,b<0,则方程g(x)=0 必有 3 个实数根;④? a∈R,g(x)的导函数g′(x)有两个零点;其中所有正确结论的序号是.28.定义域和值域均为[﹣a,a](常数a>0)的函数(x)和(x)的图象如图所示,给出下列四个命题:① 方程f[g (x)]有且仅有三个解;② 方程g[f (x)]有且仅有三个解;③ 方程f[f (x)] 有且仅有九个解;④方程g[g(x)] 有且仅有一个解.那么,其中正确命题的个数是.29.如图所示,在直角坐标系的第一象限内,△是边长为 2 的等边三角形,设直线(0≤t≤2)截这个三角形可得位于此直线左方的图形的面积为f(t),则函数(t)的图象(如图所示)大致是.(填序号).30.(2010?北京)如图放置的边长为 1 的正方形沿x 轴滚动.设顶点P(x,y)的轨迹方程是(x ),则f(x)的最小正周期为;(x)在其两个相邻零点间的图象与x 轴所围区域的面积为.参考答案与试题解析一.选择题1.(2014?鹰潭二模)如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t 变化的可能图象是()A .B.C. D .考点:函数的图象与图象变化.专题:压轴题;数形结合.分析:根据几何体的三视图确定几何体的形状是解决本题的关键,可以判断出该几何体是圆锥,下面细上面粗的容器,判断出高度h 随时间t 变化的可能图象.解答:解:该三视图表示的容器是倒放的圆锥,下面细,上面粗,随时间的增加,可以得出高度增加的越来越慢.刚开始高度增加的相对快些.曲线越“竖直”,之后,高度增加的越来越慢,图形越平稳.故选 B .点评:本题考查函数图象的辨别能力,考查学生对两变量变化趋势的直观把握能力,通过曲线的变化快慢进行筛选,体现了基本的数形结合思想.2.(2014?河东区一模)若方程f(x)﹣2=0 在(﹣∞,0)内有解,则(x)的图象是()A .B.C. D .考点:函数的图象与图象变化.专题:作图题;数形结合;转化思想.分析:根据方程f(x)﹣2=0 在(﹣∞,0)内有解,转化为函数f(x)的图象和直线 2 在(﹣∞,0)上有交点.解答:解:A:与直线 2 的交点是(0,2),不符合题意,故不正确;B :与直线 2 的无交点,不符合题意,故不正确;C:与直线 2 的在区间(0,+∞)上有交点,不符合题意,故不正确;D :与直线 2 在(﹣∞,0)上有交点,故正确.故选D.点评:考查了识图的能力,体现了数形结合的思想,由方程的零点问题转化为函数图象的交点问题,体现了转化的思想方法,属中档题.3.(2014?福建模拟)现有四个函数:①?②?③?④? 号安排正确的一组是()x的图象(部分)如下,则按照从左到右图象对应的函数序A .① ④③②B.④①②③C.①④②③ D .③④②①考点:函数的图象与图象变化.专题:综合题.分析:从左到右依次分析四个图象可知,第一个图象关于Y 轴对称,是一个偶函数,第二个图象不关于原点对称,也不关于Y 轴对称,是一个非奇非偶函数;第三、四个图象关于原点对称,是奇函数,但第四个图象在Y 轴左侧,函数值不大于0,分析四个函数的解析后,即可得到函数的性质,进而得到答案.解答:解:分析函数的解析式,可得:①?为偶函数;②?为奇函数;③?为奇函数,④?2x为非奇非偶函数且当x<0 时,③?≤0 恒成立;则从左到右图象对应的函数序号应为:①④②③ 故选:C.2点评:本题考查的知识点是函数的图象与图象变化,其中函数的图象或解析式,分析出函数的性质,然后进行比照,是解答本题的关键.4.(2014?漳州一模)已知函数,则函数(x)的大致图象为()A .B.C. D .考点:函数的图象与图象变化.专题:函数的性质及应用.分析:由函数不是奇函数图象不关于原点对称,排除A、C,由x>0 时,函数值恒正,排除D.解答:解:函数(x)是一个非奇非偶函数,图象不关于原点对称,故排除选项 A 、C,又当﹣1 时,函数值等于0,故排除D,故选B.点评:本题考查函数图象的特征,通过排除错误的选项,从而得到正确的选项.排除法是解选择题常用的一种方法.5.(2014?遂宁一模)函数f(x)的图象大致是()A .B.C. D .考点:函数的图象与图象变化;对数函数的图像与性质.专题:计算题.分析:由于f(﹣x)=﹣f(x),得出f(x)是奇函数,其图象关于原点对称,由图象排除C,D,利用导数研究根据函数的单调性质,又可排除选项B,从而得出正确选项.解答:解:∵函数f(x ),可得f(﹣x)=﹣f(x),f (x)是奇函数,其图象关于原点对称,排除C,D ,又f′(x)1,令f′(x)>0 得:x>,得出函数f(x)在(,+∞)上是增函数,排除B,故选 A点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题6.(2014?西藏一模)函数的大致图象是()A .B.C. D .考点:函数的图象与图象变化;函数的图象.专题:计算题;数形结合.分析:先研究函数的奇偶性知它是非奇非偶函数,从而排除 A 、C 两个选项,再看此函数与直线的交点情况,即可作出正确的判断.解答:解:由于f(x),∴f(﹣x)=﹣,∴f(﹣x)≠f(x),且f(﹣x)≠﹣f(x ),故此函数是非奇非偶函数,排除③④;又当时,,即f(x)的图象与直线的交点中有一个点的横坐标为,排除①.故选 B .点评:本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力,属于中档题.7.(2014?湖南二模)若函数(x)的图象如图所示,则函数(1﹣x)的图象大致为()A .B.C. D .考点:函数的图象与图象变化.专题:压轴题;数形结合.分析:先找到从函数(x)到函数(1﹣x)的平移变换规律是:先关于y 轴对称得到(﹣x ),再整体向右平移 1 个单位;再画出对应的图象,即可求出结果.解答:解:因为从函数(x)到函数(1﹣x)的平移变换规律是:先关于y 轴对称得到(﹣x ),再整体向右平移 1 个单位即可得到.即图象变换规律是:①→②.故选: A .点评:本题考查了函数的图象与图象的变换,培养学生画图的能力,属于基础题,但也是易错题.易错点在于左右平移,平移的是自变量本身,与系数无关.8.(2014?临沂三模)函数的图象大致为()A .B.C. D .考点:函数的图象与图象变化.专题:函数的性质及应用.分析:求出函数的定义域,通过函数的定义域,判断函数的奇偶性及各区间上函数的符号,进而利用排除法可得答案.解答:解:函数的定义域为(﹣∞,0)∪(0,+∞),且f(﹣x)﹣=﹣f(x)故函数为奇函数,图象关于原点对称,故 A 错误由分子中3x 的符号呈周期性变化,故函数的符号也呈周期性变化,故 C 错误;不x∈(0,)时,f(x)>0,故 B 错误故选: D点评:本题考查函数的图象的综合应用,对数函数的单调性的应用,考查基本知识的综合应用,考查数形结合,计算能力.判断图象问题,一般借助:函数的定义域、值域、单调性、奇偶性、周期性、以及函数的图象的变化趋势等等.9.(2014?大港区二模)如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:①f(x);②f(x)21;③ f(x)=2();④f(x).其中“同簇函数”的是()A .① ②B.①④C.②③ D .③④考点:函数的图象与图象变化.专题:函数的性质及应用.分析:由于f(x)2(),再根据函数图象的平移变换规律,可得它与f(x)=2()的图象间的关系.而其余的两个函数的图象仅经过平移没法重合,还必须经过横坐标(或纵坐标)的伸缩变换,故不是“同簇函数”.解答:解:由于①f (x)2x 与②f(x)21 的图象仅经过平移没法重合,还必须经过纵坐标的伸缩变换,故不是“同簇函数”.由于①f(x)2x 与④f(x)2()的图象仅经过平移没法重合,还必须经过横坐标的伸缩变换,故不是“同簇函数”.② f ( x ) 21 与③ f ( x )=2( ) 的图象仅经过平移没法重合,还必须经过横坐标的伸缩变换,故不是 “同簇函数 ”. 由于 ④ f ( x )2() =2 (),故把 ③ f ( x )=2 ( )的图象向左平移,可得 f ( x ) =2() 的图象,故③ 和④ 是“同簇函数 ”, 故选: D .点评: 本题主要考查行定义,函数图象的平移变换规律,属于基础题.10.( 2014?潍坊模拟)已知函数 f ( x )﹣﹣ |,则函数( 1)的大致图象为( )A .B .C .D .考点 : 函数的图象与图象变化. 专题 : 函数的性质及应用. 分析:化简函数 f (x )的解析式为,而 f ( 1)的图象可以认为是把函数f ( x )的图象向左平移 1 个单位得到的,由此得出结论. 解答:解:∵函数 f ( x )﹣﹣|,∴当 x ≥1 时,函数 f (x )﹣( x ﹣ ) = .当 0< x < 1 时,函数 f ( x ) = ﹣(﹣ ),即 f ( x ) =.函数( 1)的图象可以认为是把函数 f ( x )的图象向左平移 1 个单位得到的,故选 A .点评: 本小题主要考查函数与函数的图象的平移变换,函数(1)的图象与函数 f (x )的图象间的关系,属于基础题.211.(2014 ?江西一模)平面上的点 P ( x ,y ),使关于 t 的二次方程 t 0 的根都是绝对值不超过1 的实数,那么这样的点 P 的集合在平面内的区域的形状是( ) A .B .C .D .考点 : 函数的图象与图象变化. 专题 : 计算题;数形结合.20 的根都是绝对值不超过 1 的实数转化成 t 等式,最后画出图形即可.20 的根在﹣ 1 到 1 之间,然后根据根的分布建立不解答: 解: 2t 0 的根都是绝对值不超过 1 的实数,分析: 先根据条件 t2则t 0 的根在﹣1 到1 之间,∴即画出图象可知选项 D 正确.故选D.点评:本题主要考查了二次函数根的分布,以及根据不等式画出图象,同时考查数形结合的思想,属于基础题.12.(2014?宜春模拟)如图,半径为 2 的圆内有两条半圆弧,一质点M 自点 A 开始沿弧 A ﹣B ﹣C﹣O﹣A ﹣D﹣C 做匀速运动,则其在水平方向(向右为正)的速度(t)的图象大致为()A B C D....考点:函数的图象与图象变化.专题:函数的性质及应用.分析:根据位移的定义与路程的概念,以及速度是位移与时间的比值,分析质点M 的运动情况与速度v 的关系,选出符合题意的答案.解答:解:∵弧弧弧弧×π2×2=π,弧弧×π2×1=π,∴质点M 自点 A 开始沿弧 A ﹣B ﹣C﹣O﹣A ﹣D ﹣C 做匀速运动时,所用的时间比为1:1:1:1:1:1;又∵在水平方向上向右的速度为正,∴速度在弧段为负,弧段为正,弧段先正后负,弧段先负后正,弧段为正,弧段为负;∴满足条件的函数图象是B.故选:B.点评:本题考查路程及位移、平均速度与平均速率的定义,注意路程、平均速率为标量;而位移、平均速度为矢量.13.(2014?江西模拟)如图正方形边长为4,E 为的中点,现用一条垂直于的直线l 以0.4 的速度从l 1 平行移动到l 2,2则在t 秒时直线l 扫过的正方形的面积记为F(t)(m ),则F(t)的函数图象大概是()A .B.C. D .考点:函数的图象与图象变化.专题:函数的性质及应用.分析:分析出l 与正方形边有交点时和l 与正方形边有交点时,函数图象的凸凹性,进而利用排除法可得答案.解答:解:当l 与正方形边有交点时,此时直线l 扫过的正方形的面积随t 的增大而增大的速度加快,故此段为凹函数,可排除 A ,B,当l 与正方形边有交点时,此时直线l 扫过的正方形的面积随t 的增大而增大的速度不变,故此段为一次函数,图象就在为直线,可排除C,故选: D点评:本题考查的知识点是函数的图象与图象变化,其中分析出函数图象的凸凹性是解答的关键.14.(2014?临汾模拟)如图可能是下列哪个函数的图象()﹣ x ﹣ x ﹣ ﹣ yA .2x ﹣ x 2﹣ 1B .C . ( x 22x ) D .考点 : 函数的图象与图象变化. 专题 : 函数的性质及应用. 分析: A 中 2x﹣ x 21 可以看成函数 2x 与 2+1 的差,分析图象是不满足条件的;B 中由是周期函数,知函数的图象是以 x 轴为中心的波浪线,是不满足条件的;2C 中函数 ﹣ 2x 与的积,通过分析图象是满足条件的;D 中的定义域是( 0, 1)∪( 1, +∞),分析图象是不满足条件的.解答: 解: A 中,∵ 2x21,当 x 趋向于﹣ ∞时,函数 2x的值趋向于 0, 2∴函数 2x21 的值小于 0,∴ A 中的函数不满足条件;B 中,∵是周期函数,∴函数 的图象是以 x 轴为中心的波浪线,∴ B 中的函数不满足条件;C 中,∵函数 2﹣2( x ﹣ 1) 2﹣ 1,当 x < 0 或 x >1 时, y > 0,当 0< x < 1 时, y < 0; 且> 0 恒成立,∴( x 2﹣ 2x )的图象在 x 趋向于﹣ ∞时, y >0, 0< x < 1 时, y < 0,在 x 趋向于 +∞时, y 趋向于 +∞; ∴ C 中的函数满足条件;D 中, 的定义域是( 0, 1)∪( 1, +∞),且在 x ∈(0, 1)时,< 0,∴<0,∴ D 中函数不满足条件. 故选: C .点评: 本题考查了函数的图象和性质的应用问题,解题时要注意分析每个函数的定义域与函数的图象特征,是综合性题目.15.( 2014?芜湖模拟)如果两个方程的曲线经过若干次平移或对称变换后能够完全重合,则称这两个方程为 “互为生成方程对 ”.给出下列四对方程: ① 和1;② 2﹣x 22=2 和 x 22 2﹣ y =2; ③ y =4x 和 x =4y ; ④ (x ﹣ 1)和 1.其中是 “互为生成方程对 ”有( )A .1 对B . 2 对C . 3 对D .4 对考点 : 函数的图象与图象变化. 专题 : 函数的性质及应用.分析: 根据函数的平移个对称即可得出结论. 解答:解: ①,1;故 ① 是,﹣﹣+1 的值趋向 +∞,② y 2﹣x22=2 令,,则x22 2﹣y =2;和x22﹣y2=2 完全重合,故② 是,③ y =4x ;令,,则x =4y 和x =4y 完全重合,故③是,④(x﹣1)和 1 是一反函数,而互为反函数图象关于对称,故④是,故“互为生成方程对”有4 对.故选:D.点评:本题是基础题,实质考查函数图象的平移和对称变换问题,只要掌握基本知识,领会新定义的实质,不难解决问题.16.(2014 ?上饶二模)如图,不规则图形中:和是线段,和是圆弧,直线l⊥于E,当l 从左至右移动(与线段有公共点)时,把四边形分成两部分,设,左侧部分面积为y,则y 关于x 的大致图象为()A .B.C. D .考点:函数的图象与图象变化.专题:函数的性质及应用.分析:根据左侧部分面积为y,随x 的变化而变化,最初面积增加的快,后来均匀增加,最后缓慢增加,问题得以解决.解答:解:因为左侧部分面积为y,随x 的变化而变化,最初面积增加的快,后来均匀增加,最后缓慢增加,只有D 选项适合,故选D.点评:本题考查了函数的图象,关键是面积的增加的快慢情况,培养真确的识图能力.17.(2014?乌鲁木齐三模)已知函数f(x)在定义域R 上的值不全为零,若函数f(1)的图象关于(1,0)对称,函数f(3)的图象关于直线 1 对称,则下列式子中错误的是()A .f (﹣x )(x)B.f(x﹣2)(6)C.f(﹣2)(﹣2﹣x)=0 D .f (3)(3﹣x)=0考点:函数的图象与图象变化.专题:函数的性质及应用.分析:由已知条件求得f(4﹣x)=﹣f(x)①、f(4)(4﹣x)②、f(8)(x)③.再利用这 3 个结论检验各个选项是否正确,从而得出结论.解答:解:∵函数f(1)的图象关于(1,0)对称,∴函数f(x)的图象关于(2,0)对称,令F(x)(1),则F(x)=﹣F(2﹣x ),故有f(3﹣x)=﹣f(1),f(4﹣x)=﹣f(x)①.令G(x)(3﹣x),∵其图象关于直线 1 对称,∴G(2)(﹣x),即f(5)(3﹣x ),∴f(4)(4﹣x)②.由①②得,f(4)=﹣f(x ),∴f(8)(x)③.∴f(﹣x )(8﹣x )(4+4﹣x ),由② 得f[4+ (4﹣x)] [4 ﹣(4﹣x)](x ),∴f(﹣x )(x ),∴ A 对.由③得f(x﹣2+8)(x﹣2),即 f (x﹣2)(6),∴B对.由①得,f(2﹣x)(2)=0,又f(﹣x)(x ),∴f(﹣2﹣x)(﹣2)(2﹣x )(2)=0 ,∴ C 对.若f(3)(3﹣x)=0,则f(6)=﹣f(x),∴ f(12)(x ),由③可得f(12)(4),又f(4)=﹣f(x ),∴f(x)=﹣f(x ),∴f(x)=0,与题意矛盾,∴ D 错,故选:D.点评:本题主要考查函数的奇偶性、单调性、周期性的应用,函数的图象及图象变换.18.(2014?凉山州一模)函数的图象大致是()A .B.C. D .考点:函数的图象与图象变化.专题:函数的性质及应用.分析:求出函数的定义域,通过函数的定义域,判断函数的奇偶性及各区间上函数的符号,进而利用排除法可得答案.解答:解:函数f(x)的定义域为(﹣∞,﹣)∪(﹣,0)∪(0,)∪(,+∞),四个图象均满足;又∵f(﹣x)(x ),故函数为偶函数,故函数图象关于y 轴对称,四个图象均满足;当x∈(0,)时,<0,可排除 B ,D 答案;当x∈(,+∞)时,>0,可排除 C 答案;故选:A点评:本题考查函数的图象的综合应用,对数函数的单调性的应用,考查基本知识的综合应用,考查数形结合,计算能力.判断图象问题,一般借助:函数的定义域、值域、单调性、奇偶性、周期性、以及函数的图象的变化趋势等等.19.(2014?安阳一模)已知 f (x)= ,则下列叙述中不正确的一项是()A .B.C. D .f(﹣x)的图象 f ()的图象f (x﹣1)的图象(x)|的图象考点:函数的图象与图象变化.专题:函数的性质及应用.分析:作出函数f(x)的图象,利用函数与f(x)之间的关系即可得到结论.解答:解:作出函数f(x)的图象如图:A .将f(x)的图象向右平移一个单位即可得到f(x﹣1)的图象,则 A 正确.B .∵f(x)>0,∴(x)(x ),图象不变,则 B 错误.C.(﹣x)与(x)关于y 轴对称,则 C 正确.D .f()是偶函数,当x ≥0,f()(x ),则D 正确,故错误的是 B ,故选: B点评:本题主要考查函数图象之间的关系的应用,比较基础.20.如图,在正四棱柱﹣ A 1B1C1D 1 中,1=2,1,M 、N 分别在1,上移动,并始终保持∥平面1D 1,设,,则函数(x)的图象大致是()A .B.C. D .考点:函数的图象与图象变化;直线与平面平行的性质.专题:压轴题;数形结合.分析:由∥平面1D 1,我们过M 点向做垂线,垂足为E,则2,由此易得到函数(x)的解析式,分析函数的性质,并逐一比照四个答案中的图象,我们易得到函数的图象.解答:解:若∥平面1D1,则即函数(x)的解析式为f (x)= (0≤x≤1)其图象过(0,1)点,在区间[0 ,1] 上呈凹状单调递增故选 C点评:本题考查的知识点是线面平行的性质,函数的图象与性质等,根据已知列出函数的解析式是解答本题的关键.21.(2012?青州市模拟)如图,有一直角墙角,两边的长度足够长,在P 处有一棵树与两墙的距离分别是 a m(0 <a<12)、4m,不考虑树的粗细.现在想用16m 长的篱笆,借助墙角围成一个矩形的花圃.设此矩形花圃的最大2面积为S,若将这棵树围在花圃内,则函数(a)(单位m )的图象大致是()A .B.C. D .考点:函数的图象与图象变化.专题:压轴题;分类讨论.分析:为求矩形面积的最大值S,可先将其面积表达出来,又要注意P 点在长方形内,所以要注意分析自变量的取值范围,并以自变量的限制条件为分类标准进行分类讨论.解答:解:设长为x,则长为16﹣x又因为要将P 点围在矩形内,∴a≤x≤12则矩形的面积为x(16﹣x),当0<a≤8时,当且仅当8 时,64当8<a<12 时,(16﹣a)分段画出函数图形可得其形状与 C 接近故选C.点评:解决本题的关键是将S 的表达式求出来,结合自变量的取值范围,分类讨论后求出S 的解析式.22.(2009?江西)如图所示,一质点P(x,y)在平面上沿曲线运动,速度大小不变,其在x 轴上的投影点Q(x,0)的运动速度(t)的图象大致为()A .B.C. D .考点:函数的图象与图象变化;导数的几何意义.专题:压轴题.分析:对于类似于本题图象的试题,可以考虑排除法,由图象依次分析投影点的速度、质点p 的速度等,逐步排除即可得答案.解答:解:由图可知,当质点P(x,y)在两个封闭曲线上运动时,投影点Q(x,0)的速度先由正到0,到负数,再到0,到正,故 A 错误;质点P(x,y)在终点的速度是由大到小接近0,故 D 错误;质点P(x,y)在开始时沿直线运动,故投影点Q(x,0)的速度为常数,因此 C 是错误的,故选 B .点评:本题考查导数的几何意义在函数图象上的应用.23.(2010?湖南)用{a ,b} 表示a,b 两数中的最小值.若函数f(x){ ,} 的图象关于直线对称,则t 的值为()A .﹣2 B.2 C.﹣1 D .1考点:函数的图象与图象变化.专题:作图题;压轴题;新定义;数形结合法.分析:由题设,函数是一个非常规的函数,在同一个坐标系中作出两个函数的图象,及直线,观察图象得出结论解答:解:如图,在同一个坐标系中做出两个函数与的图象,函数f(x){ ,} 的图象为两个图象中较低的一个,分析可得其图象关于直线﹣对称,要使函数f(x){ ,} 的图象关于直线对称,则t 的值为 1故应选D.点评:本题的考点是函数的图象与图象的变化,通过新定义考查学生的创新能力,考查函数的图象,考查考生数形结合的能力,属中档题.24.已知函数f(x)的定义域为[a,b] ,函数(x)的图象如下图所示,则函数f()的图象是()A .B.C. D .考点:函数的图象与图象变化.专题:作图题;压轴题;数形结合;运动思想.分析:由函数(x)的图象和函数f()的图象之间的关系,()的图象是由(x)把x>0 的图象保留,x<0 部分的图象关于y 轴对称而得到的.解答:解:∵()是偶函数,∴()的图象是由(x)把x>0 的图象保留,x<0 部分的图象关于y 轴对称而得到的.故选 B .点评:考查函数图象的对称变换和识图能力,注意区别函数(x)的图象和函数f()的图象之间的关系,函数(x)的图象和函数(x)|的图象之间的关系;体现了数形结合和运动变化的思想,属基础题.25.(2012?泸州二模)点P 从点O 出发,按逆时针方向沿周长为l 的图形运动一周,O,P 两点连线的距离y 与点P 走过的路程x 的函数关系如右图所示,那么点P 所走的图形是()A .B.C. D .考点:函数的图象与图象变化.专题:数形结合.分析:本题考查的是函数的图象与图象变化的问题.在解答时首先要充分考查所给四个图形的特点,包括对称性、圆滑性等,再结合所给O,P 两点连线的距离y 与点P 走过的路程x 的函数图象即可直观的获得解答.解答:解:由题意可知:O,P 两点连线的距离y 与点P 走过的路程x 的函数图象为:由图象可知函数值随自变量的变化成轴对称性并且变化圆滑.由此即可排除A、B、C.故选D.点评:本题考查的是函数的图象与图象变化的问题.在解答的过程当中充分体现了观察图形、分析图形以及应用图形的能力.体现了函数图象与实际应用的完美结合.值得同学们体会反思.二.填空题(共 5 小题)26.(2006?山东)下列四个命题中,真命题的序号有③④(写出所有真命题的序号).①将函数1|的图象按向量(﹣1,0)平移,得到的图象对应的函数表达式为.22②圆x +4x ﹣21=0 与直线相交,所得弦长为2.③若(α+β)= ,(α﹣β)= ,则αβ=5.④如图,已知正方体﹣ A 1B1C1D1,P 为底面内一动点,P 到平面1D 1D 的距离与到直线 1 的距离相等,则P 点的轨迹是抛物线的一部分.考点:函数的图象与图象变化;两角和与差的正弦函数;直线和圆的方程的应用;点、线、面间的距离计算.专题:压轴题.分析:逐个进行验正,排除假命题,从而得到正确命题.解答:解:①错误,得到的图象对应的函数表达式应为﹣2|②错误,圆心坐标为(﹣2,1),到直线的距离为>半径2,故圆与直线相离,③正确,(α+β)αβαβ(α﹣β)αβ﹣αβ=两式相加,得2αβ= ,两式相减,得2αβ= ,故将上两式相除,即得αβ=5④正确,点P 到平面 1 的距离就是点P 到直线的距离,点P 到直线 1 就是点P 到点 C 的距离,由抛物线的定义可知点P 的轨迹是抛物线.故答案为:③④.点评:排除法是解决这类问题的有效方法.27.如图所示,f(x)是定义在区间[﹣c,c](c>0)上的奇函数,令g(x )(x),并有关于函数g(x)的四个论断:。
【高考专题】2019年 高考数学 函数图像 专项练习32题(含答案)

2019年 高考数学 函数图像 专项练习32题一、选择题1.函数y=5-|x|的图象是( )2.函数的图象可能是( ).3.函数y=2x -x 2的图像大致是( )4.函数的图像大致为( )5.函数)1(>=a xxa y x 的图象的大致形状是( )6.函数)1ln(23x x x y -++=的图象大致为( )7.函数y=e ∣x ∣-4cosx(e 为自然对数的底数)的图象可能是( )8.函数的图象大致为( )9.函数的图像大致为( )10.函数,则y=f(x+1)的图象大致是( )11.已知函数f(x)=4-x2,y=g(x)是定义在R上的奇函数,当x>0时,g(x)=logx,则函数f(x)·g(x)的大致2图象为( )12.函数y=-x4+x2+2的图像大致为( )13.已知a是常数,函数的导函数的图像如图所示,则函数的图像可能是( )14.已知lga+lgb=0,则函数y=a x与函数y=-logx的图象可能是( )b15.已知函数,则函数的大致图象是( )16.函数的大致图象为( )17.函数y=2x+1-2x2的图象大致是( )18.函数的部分图象大致为( )19.设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能的是 ( )20.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为( )21.已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),下面四个图象中y=f(x)的图象大致是( )22.设函数y=f(x)在定义域内可导,其图象如图所示,则导函数y=f′(x)的大致图象为( )23.函数f(x)在其定义域内可导,其图象如图所示,则导函数y=f′(x)的图象可能为( )24.已知函数f(x)=0.25x2+cosx,f/(x)是函数f(x)的导函数,则f/(x)的图象大致是( )25.函数y=sinx2的图象是( )26.函数的图象大致是( )27.函数f(x)=log∣2x-1∣的图象大致是( )228.幂函数f(x)=x a满足f(2)=4,那么函数g(x)=∣log(x+1)∣的图象大致为( )a29.函数y=e-∣x-1∣的图象大致形状是 ( )30.函数f(x)=-e-ln∣x∣+x的大致图象为( )31.函数f(x)=2-∣x∣+1的图像大致为 ( )32.函数在同一平面直角坐标系内的大致图象为 ( )参考答案1.D2.D3.A4.B5.B6.B7.C8.D9.C10.B11.D12.D13.D14.D15.A16.D17.B18.A19.C20.D21.C.22.D.23.C.24.A25.D26.D27.A28.C29.B30.B31.A32.C。
专题:函数图像精选训练题(有答案)

专题:函数图像训练题精选一、选择题1.下列函数图象中,函数y a a a x =>≠()01且,与函数y a x =-()1的图象只能是( )y y y yO x O x O x O xA B C D11112.若函数()()22m xf x x m-=+的图象如图所示,则m 的取值范围是( )A.(),1-∞-B. ()1,2C. ()1,2-D. ()0,23.已知函数()y f x =的图象与ln y x =的图象关于直线y x =对称,则()2f =( )A .1B .eC .2eD .()ln 1e -4.函数()2cos ln f x x x =-⋅的部分图象大致是( )5.将()y f x =的图象的横坐标伸长为原来的3倍,纵坐标缩短为原来的13,则所得函数的解析式为( ) A .3(3)y f x = B .11()33y f x =C .1(3)3y f x =D .13()3y f x = 6.如图所示的四个容器高度都相同,将水从容器顶部一个小孔以相同的速度注入其中,注满为止.用下面对应的图像显示该容器中水面的高度h 和时间t 之间的关系,其中不正确的....是A .1个B .2个C .3个D .4个7.在同一坐标系中,函数1()x y a=与)(log x y a -=(其中0a >且1a ≠)的图象只可能是( )8.如图,函数()y f x =的图象为折线ABC ,设()()g x f f x =⎡⎤⎣⎦, 则函数()y g x =的图象为( )9.如图,函数y =f (x )的图像为折线ABC ,设f 1(x )=f (x ),f n+1(x )=f [f n+1(x )], n ∈N *,则函数y =f 4(x )的图像为yxo 1 1 yx o 1 1 yx o 1-1 yx o 1-1ABCD10.已知1a >,函数x y a =与log ()a y x =-的图像可能是( )11.若函数)1,0()1()(≠>--=-a a a a k x f x x 在R 上既是奇函数,又是减函数,则)(log )(k x x g a +=的图像是( )12.函数|1|||ln --=x e y x 的图象大致是 ( )13.),10(log )(,)(2≠>==-a a x x g a x f a x 且,0)4()4(<-⋅g f 若则)(),(x g y x f y ==在同一坐标系内的大致图象是第5题14.已知函数2()4f x x =-,()y g x =是定义在R 上的奇函数,当0x >时,2()log g x x =,则函数()()f x g x ⋅的大致图象为 ( )15.已知f (x )=a x ,g (x )=log a x (a >0且a ≠1),若f (3)g (3)<0,则f (x )与g (x )在同一坐标系里的图像是( )16.当0<a <1时,在同一坐标系中,函数x y a -=与log a y x =的图象是( )17.函数1||2)(+-=x x f 的图像大致为 ( ▲ )y xy yy xxxoo o-1 1-1 1 2-112 1 o-1 112 121 B A C D18.函数||2x y =的定义域为],[b a ,值域为]16,1[,则点),(b a 表示的图形可以是( ▲ )19.设A={|02x x ≤≤}, B={|02y y ≤≤}, 下列各图中能表示集合A 到集合B 的映射是20.二次函数bx ax y +=2与指数函数xab y )32(=的图象,只有可能是下列中的哪个选项21.已知函数bx ax y +=2和xbay =|)| || ,0(b a ab ≠≠在同一直角坐标系中的图象不可能... 是( )BC DAxy123123 B.xy123123 C.xy0123123 A.A .B .C .D .22.已知函数9()4,(0,4)1f x x x x =-+∈+,当x a =时,()f x 取得最小值b ,则函数b x )a ()x (g +=1的图象为( )23.已知0,1a a >≠,函数log ,,x a y x y a y x a ===+在同一坐标系中的图象可能是24.函数()112xf x =-的图像是1xy11xy11xy 1-01xy1-25.函数()()112122x x f x ⎡⎤=+--⎣⎦的图象大致为26.若直角坐标平面内的两个不同点M 、N 满足条件:① M 、N 都在函数()y f x =的图像上; ② M 、N 关于原点对称. 则称点对[,]M N 为函数()y f x =的一对“友好点对”. (注:点对[,]M N 与[,]N M 为同一“友好点对”)已知函数32log (0)()4(0)x x f x x x x >⎧=⎨-- ⎩≤,此函数的“友好点对”有A. 0对B. 1对C. 2对D. 3对27.已知定义在区间[0,2]上的函数=()y f x 的图象如图所示,则=(2-)y f x 的图象为28.已知函数x x x f sin 21)(2+=,则)('x f 的大致图象是( )29.下列函数图象中,正确的是30.已知函数32()(,0)f x ax bx x a b R ab =++∈≠且的图像如图,且12||||x x >,则有( )A .0,0a b >>B .0,0a b <<C .0,0a b <>D .0,0a b ><31.如下图,设点A 是单位圆上的一定点,动点P 从点A 出发在圆上按逆时针方向旋转一周,点P 所旋转过的弧AP 的长为l ,弦AP 的长为d ,则函数d =f (l )的图象大致是( )32.已知二次函数()x f 的图象如图1所示 , 则其导函数()x f '的图象大致形状是( )33.已知对数函数()log a f x x =是增函数,则函数(||1)f x +的图象大致是( )34.已知0lg lg =+b a ,则函数x a x f =)(与函数x x g b log )(-=的图象可能( )35.已知函数sin (0)y ax b a =+>的图象如图所示,则函数log ()a y x b =+的图象可能是( )A .B . C. D.36.已知函数log (1)3,a y x =-+(01)a a >≠且的图像恒过点P ,若角α的终边经过点P ,则2sin sin2αα- 的值等于( )A.133 B.135 C. 133- D. 135- 37.已知函数的图象如图所示则函数的图象是( )38.如右图,一个直径为l 的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M 和N 是小圆的一条固定直径的两个端点.那么,当小圆这样滚过大圆内壁的一周,点M ,N 在大圆内所绘出的图形大致是( )39.已知在函数||y x =([1,1]x ∈-)的图象上有一点(,||)P t t ,该函数的图象与 x 轴、直线x =-1及 x =t 围成图形(如图阴影部分)的面积为S ,则S 与t 的函数关系图可表示为( )40.函数|)1lg(|-=x y 的图象是( )41.函数2()log 2f x x =与1()2x g x -=在同一直角坐标系下的图象大致是( )42.已知,()()()a b f x x a x b >=--函数的图象如右图,则函数()log ()a g x x b =+的图象可能为43.函数lg ||x y x=的图象大致是二、填空题44.已知函数211x y x -=-的图像与函数2y kx =-的图像恰有两个交点,则实数k 的取值范围是 .45.当直线y kx =与曲线|ln ||2|x y e x =--有3个公共点时,实数k 的取值范围是 .46.已知函数8log (3)9a y x =+-(0,1a a >≠)的图像恒过定点A ,若点A 也在函数()3x f x b =+的图像上,则b = 。
高三数学函数图像试题答案及解析

高三数学函数图像试题答案及解析1.函数在上的图像大致为()【答案】A【解析】函数是奇函数,所以C,D被排除;当时,,,由此判断,函数原点右侧开始时应该是正数,所以选A.【考点】函数的图像与性质2.如图,已知l1⊥l2,圆心在l1上、半径为1 m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cos x,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )【答案】B【解析】通过圆心角α将弧长x与时间t联系起来.圆半径为1,设弧长x所对的圆心角为α,则α=x,如图所示,cos=1-t,即cos=1-t,则y=cos x=2cos2-1=2(1-t)2-1=2(t-1)2-1(0≤t≤1).其图象为开口向上,在[0,1]上的一段抛物线.3.若函数的图像如右图所示,则下列函数图像正确的是()【答案】B【解析】由题意可得.所以函数是递减的即A选项不正确.B正确. 是递减,所以C不正确. 图象与关于y轴对称,所以D不正确.故选B.【考点】函数的图象.4.已知函数f(x)=|lgx|,若a≠b,且f(a)=f(b),则a+b的取值范围是()A.(1,+∞)B.[1,+∞)C.(2,+∞)D.[2,+∞)【答案】C【解析】函数f(x)=|lgx|的图象如图所示,由图象知a,b一个大于1,一个小于1,不妨设a>1,0<b<1.∵f(a)=f(b),∴f(a)=|lga|=lga=f(b)=|lgb|=-lgb=lg.∴a=.∴a+b=b+>2=2.5.设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围为________.【答案】【解析】由题意知,y=f(x)-g(x)=x2-5x+4-m在[0,3]上有两个不同的零点.在同一直角坐标系下作出函数y=m与y=x2-5x+4(x∈[0,3])的图像如图所示,结合图像可知,当x∈[2,3]时,y=x2-5x+4∈,故当m∈时,函数y=m与y=x2-5x+4(x∈[0,3])的图像有两个交点.6.函数y=2a x﹣1(0<a<1)的图象一定过点()A.(1,1)B.(1,2)C.(2,0)D.(2,﹣1)【答案】B【解析】因为函数y=a x(0<a<1)的图象一定经过点(0,1),而函数y=2a x﹣1(0<a<1)的图象是由y=a x(0<a<1)的图象向右平移1个单位,然后把函数y=a x﹣1(0<a<1)的图象上所有点的横坐标不变,纵坐标扩大到原来的2倍得到的,所以函数y=2a x﹣1(0<a<1)的图象一定过点(1,2).故选B.7.函数y=2x﹣x2的图象大致是()【答案】A【解析】因为当x=2或4时,2x﹣x2=0,所以排除B、C;当x=﹣2时,2x﹣x2=,故排除D,所以选A.8.函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=e x关于y轴对称,则f(x)=()A.e x+1B.e x﹣1C.e﹣x+1D.e﹣x﹣1【答案】D【解析】函数y=e x的图象关于y轴对称的图象的函数解析式为y=e﹣x,而函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=e x的图象关于y轴对称,所以函数f(x)的解析式为y=e﹣(x+1)=e﹣x﹣1.即f(x)=e﹣x﹣1.故选D.9.已知,则函数的零点个数为()A.1B.2C.3D.4【答案】D【解析】由题意可知,要研究函数的零点,只要研究函数与函数的交点个数,画出两个函数的图象,如图,很明显是4个交点.【考点】1.函数的零点;2.函数的图象.10.函数的图象大致是().【答案】C【解析】不难知道,函数是奇函数,故排除A;又,令得,而此方程有无穷个解,且在每个解的两边函数值不同号,所以函数有无穷多个极值点,故可排除B,D.11.已知,点在曲线上,若线段与曲线相交且交点恰为线段的中点,则称为曲线关于曲线的一个关联点.记曲线关于曲线的关联点的个数为,则( ) A.B.C.D.【答案】B【解析】设则的中点为所以有,因此关联点的个数就为方程解得个数,由于函数在区间上分别单调增及单调减,所以只有一个交点,即.【考点】函数图像12.如图,不规则四边形ABCD中,AB和CD是线段,AD和BC是圆弧,直线于E,当从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设,左侧部分面积为,则关于的图像大致为( )【答案】C【解析】由直线的变化可知,开始时圆弧那段变化较慢,所以排除A,B选项,由于左边的面积始终在增大,所以D选项不正确.【考点】1.图形的变化规律.2.关注局部图形的变化.13.已知函数y=f(x)的图象如图所示,请根据已知图象作出下列函数的图象:①y=f(x+1);②y=f(x)+2;【答案】【解析】(1)将函数y=f(x)的图象向左平移一个单位得到y=f(x+1)的图象(如图①所示),将函数y=f(x)的图象向上平移两个单位得到y=f(x)+2的图象(如图②所示).14.已知函数,,若在区间内,函数与轴有3个不同的交点,则实数的取值范围是()A.B.C.D.【答案】C【解析】∵,∴,∴,∴,∴,∴当时,,∵函数与x轴有3个不同交点,∴函数与有3个不同的交点,函数的图像如图所示,直线与相切是一个边界情况,直线过时是一个边界情况,符合题意的直线需要在这2条直线之间,∵,∴,∴,所以切线方程为,与相同,即,当过点时,,综上可得:,故选C.【考点】1.导数的运算;2.函数图像;3.曲线的切线.15.函数y=lnx-1的图象关于直线y=x对称的图象大致是 ( )A. B. C. D.【答案】A【解析】因为关于直线y=x对称点的关系为,所以函数y=lnx-1的关于直线y=x对称的函数的解析式为.即相当于将函数的图像向左平移一个单位,显然B,D不正确,C 选项中的图像在y轴的交点过低,所以不正确.故选A.【考点】1.函数的对称性.2.指数函数的图像.3.函数图像的平移知识.16.下列函数图象与x轴均有公共点,其中能用二分法求零点的是().【答案】C【解析】只有零点两侧的函数值符号相反且在零点附近连续时才可用二分法.17.函数y=的图象大致是().【答案】D【解析】由y=知为奇函数,排除A,B.根据函数有两个零点x=±1,排除C.18.函数y=-2sin x的图象大致是 ().【答案】C【解析】当x=0时,y=0-2sin 0=0,故函数图象过原点,可排除A.又∵y′=-2cos x,当x在y轴右侧趋向0时,f′(x)<0,此时函数为减函数;当x=2 π时,f′(2 π)=-2 cos 2 π=-<0,所以x=2 π应在函数的减区间上,故选C19.函数的图象大致是( )【答案】D【解析】因为的定义域为,且,故可排除,所以应选D.【考点】1、函数的定义域;2、函数的性质;函数的图象.20.函数的图象大致是( )【答案】A【解析】,故此函数在上为增函数,在为减函数;且只有一个根,故只有一个零点.所以选A.【考点】函数的性质与图像.21.随着生活水平的提高,私家车已成为许多人的代步工具。
高三数学函数图像试题答案及解析
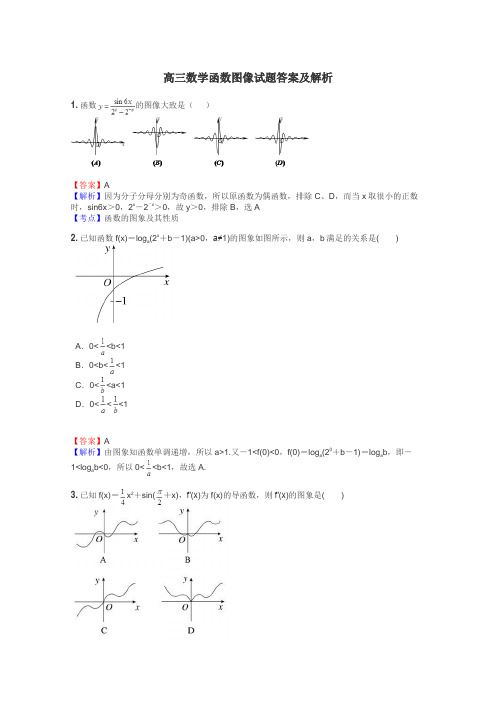
高三数学函数图像试题答案及解析1.函数的图像大致是()【答案】A【解析】因为分子分母分别为奇函数,所以原函数为偶函数,排除C、D,而当x取很小的正数时,sin6x>0,2x-2-x>0,故y>0,排除B,选A【考点】函数的图象及其性质2.已知函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是()A.0<<b<1B.0<b<<1C.0<<a<1D.0<<<1【答案】A【解析】由图象知函数单调递增,所以a>1.又-1<f(0)<0,f(0)=loga (20+b-1)=logab,即-1<logab<0,所以0<<b<1,故选A.3.已知f(x)=x2+sin(+x),f′(x)为f(x)的导函数,则f′(x)的图象是()【答案】A【解析】f(x)=x2+sin(+x)=x2+cosx,f′(x)=x-sinx.易知该函数为奇函数,所以排除B、D.当x=时,f′()=×-sin=-<0,可排除C.选A.4.(2013•浙江)已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象是()A.B.C.D.【答案】B【解析】由导数的图象可得,导函数f′(x)的值在[﹣1,0]上的逐渐增大,故函数f(x)在[﹣1,0]上增长速度逐渐变大,故函数f(x)的图象是下凹型的.导函数f′(x)的值在[0,1]上的逐渐减小,故函数f(x)在[0,1]上增长速度逐渐变小,图象是上凸型的,故选B.5.函数y=2a x﹣1(0<a<1)的图象一定过点()A.(1,1)B.(1,2)C.(2,0)D.(2,﹣1)【答案】B【解析】因为函数y=a x(0<a<1)的图象一定经过点(0,1),而函数y=2a x﹣1(0<a<1)的图象是由y=a x(0<a<1)的图象向右平移1个单位,然后把函数y=a x﹣1(0<a<1)的图象上所有点的横坐标不变,纵坐标扩大到原来的2倍得到的,所以函数y=2a x﹣1(0<a<1)的图象一定过点(1,2).故选B.6.函数y=2x﹣x2的图象大致是()【答案】A【解析】因为当x=2或4时,2x﹣x2=0,所以排除B、C;当x=﹣2时,2x﹣x2=,故排除D,所以选A.7.函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=e x关于y轴对称,则f(x)=()A.e x+1B.e x﹣1C.e﹣x+1D.e﹣x﹣1【答案】D【解析】函数y=e x的图象关于y轴对称的图象的函数解析式为y=e﹣x,而函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=e x的图象关于y轴对称,所以函数f(x)的解析式为y=e﹣(x+1)=e﹣x﹣1.即f(x)=e﹣x﹣1.故选D.8.若函数满足,当x∈[0,1]时,,若在区间(-1,1]上,方程有两个实数解,则实数m的取值范围是A.0<m≤B.0<m<C.<m≤l D.<m<1【答案】【解析】有两个零点,即曲线有两个交点.令,则,所以.在同一坐标系中,画出的图象(如图所示):直线过定点,所以,满足即选.【考点】分段函数,函数的图象,函数的零点.9.如图:正方体的棱长为,分别是棱的中点,点是的动点,,过点、直线的平面将正方体分成上下两部分,记下面那部分的体积为,则函数的大致图像是()【答案】C【解析】由题意可得下面那部分的是一个高为AB的三棱柱或四棱柱,当时.所以函数在大致图像是C、D选项.当时,令.所以上面的体积为.所以下面体积.所以函数的图象大致为C所示.故选C.【考点】1.空间几何.2.函数及图象.3.函数与立几交汇.10.对实数a和b,定义运算“”:,设函数.若函数的图象与x轴恰好有两个共公点,则实数c的取值范围是()A.B.C.D.【答案】B【解析】若即时,.若即或时,.画出的图象(如图)∵函数的图象与x轴恰好有两个共公点方程有两解函数与函数有两个不同的交点∴由图象可知或.11.为了得到函数的图像,只需把函数的图像上所有的点()A.向左平移3个单位长度,再向上平移1个单位长度B.向右平移3个单位长度,再向上平移1个单位长度C.向左平移3个单位长度,再向下平移1个单位长度D.向右平移3个单位长度,再向下平移1个单位长度【答案】C【解析】A.,B.,C.,D..12.已知函数,若关于的方程有三个不同的实根,则实数的取值范围是_.【答案】【解析】如图,直线y=x-a与函数的图象在处有一个切点,切点坐标为(0,0),此时;直线与函数的图象在处有两个切点,切点坐标分别是和,此时相应的,,观察图象可知,方程有三个不同的实根时,实数的取值范围是。
三角函数的图像与性质专项训练(解析版)

三角函数的图像与性质专项训练一、单选题1.(23-24高一上·浙江宁波·期末)为了得到πsin 53y x ⎛⎫=+ ⎪⎝⎭的图象,只要将函数sin 5y x =的图象()A .向左平移π15个单位长度B .向右平移π15个单位长度C .向右平移π3个单位长度D .向左平移π3个单位长度2.(23-24高一上·浙江丽水·期末)已知函数()()2sin f x x ωϕ=+的图象向左平移π6个单位长度后得到函数π2sin 23y x ⎛⎫=+ ⎪⎝⎭的图象,则ϕ的一个可能值是()A .0B .π12C .π6D .π33.(23-24高一下·浙江杭州·期末)为了得到函数()sin2f x x =的图象,可以把()cos2g x x =的图象()A .向左平移π2个单位长度B .向右平移π2个单位长度C .向左平移π4个单位长度D .向右平移π4个单位长度4.(23-24高一上·浙江宁波·期末)已知函数()()sin 0,π2f x x ϕωϕω⎛⎫=+>< ⎪⎝⎭.若π8f x ⎛⎫- ⎪⎝⎭为奇函数,π8f x ⎛⎫+ ⎪⎝⎭为偶函数,且()f x 在π0,6⎛⎫⎪⎝⎭上没有最小值,则ω的最大值是()A .2B .6C .10D .145.(23-24高一上·浙江湖州·期末)我们知道,每一个音都是由纯音合成的,纯音的数学模型是sin y A x ω=.已知某音是由3个不同的纯音合成,其函数为()11sin sin 2sin 323f x x x x =++,则()A .π3f ⎛⎫=⎪⎝⎭B .()f x 的最大值为116C .()f x 的最小正周期为2π3D .()f x 在π0,6⎛⎫⎪上是增函数6.(23-24高一上·浙江杭州·期末)已知函数()*2sin 6f x x ωω⎛⎫=+∈ ⎪⎝⎭N 有一条对称轴为23x =,当ω取最小值时,关于x 的方程()f x a =在区间,63ππ⎡⎤-⎢⎥⎣⎦上恰有两个不相等的实根,则实数a 的取值范围是()A .(2,1)--B .[1,1)-6⎣7.(23-24高一下·浙江丽水·期末)已知函数1()2sin(32f x x x π=ω-ω>∈,R),若()f x 的图象的任意一条对称轴与x 轴交点的横坐标均不属于区间(3π,4π),则ω的取值范围是()A .1287(,[]2396B .1171729(,][,]2241824C .52811[,][,]93912D .11171723[,][]182418248.(23-24高一下·浙江杭州·期末)已知函数()()sin ,0f x x ωω=>,将()f x 图象上所有点向左平移π6个单位长度得到函数()y g x =的图象,若函数()g x 在区间π0,6⎡⎤⎢⎥⎣⎦上单调递增,则ω的取值范围为()A .(]0,4B .(]0,2C .30,2⎛⎤⎥⎝⎦D .(]0,1【答案】C【详解】因为函数()()sin ,0f x x ωω=>,二、多选题9.(23-24高一上·浙江台州·期末)已知函数()ππsin cos sin cos 44f x x x x x ⎛⎫⎛⎫=+++ ⎪ ⎝⎭⎝⎭,则()A .函数()f x 的最小正周期为2πB .点π,08⎛⎫- ⎪⎝⎭是函数()f x 图象的一个对称中心C .函数()f x 在区间π5π,88⎡⎤⎢⎥上单调递减D .函数()f x 的最大值为110.(23-24高一上·浙江湖州·期末)筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,现有一个筒车按逆时针方向匀速转动.每分钟转动5圈,如图,将该筒车抽象为圆O ,筒车上的盛水桶抽象为圆O 上的点P ,已知圆O 的半径为4m ,圆心O 距离水面2m ,且当圆O 上点P 从水中浮现时(图中点0P )开始计算时间,点P 的高度()h t 随时间t (单位秒)变化时满足函数模型()()sin h t A t b ωϕ=++,则下列说法正确的是()A .函数()h t 的初相为π6B .1秒时,函数()h t 的相位为0故选:BC .11.(23-24高一上·浙江丽水·期末)已知函数π()tan(2)6f x x =-,则()A .()f x 的最小正周期是π2B .()f x 的定义域是π{|π,Z}3x x k k ≠+∈C .()f x 的图象关于点π(,0)12对称D .()f x 在ππ(,)32上单调递增三、填空题12.(23-24高一上·浙江金华·期末)函数()π2π200cos 30063f n n ⎛⎫=++ ⎪⎝⎭({}1,2,3,,12n ∈⋅⋅⋅为月份),近似表示某地每年各个月份从事旅游服务工作的人数,游客流量越大所需服务工作的人数越多,则可以推断,当n =时,游客流量最大.13.(23-24高一上·浙江湖州·期末)已知()3sin 4f x x ϕ⎛⎫=+ ⎪⎝⎭,其中0,2ϕ⎛⎫∈ ⎪⎝⎭,且ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,若函数()f x 在区间2π,3θ⎛⎫⎪上有且只有三个零点,则θ的范围为.14.(23-24高一上·浙江温州·期末)已知函数()π2sin (0)6f x x ωω⎛⎫=+> ⎪⎝⎭,对x ∀∈R 都有()π3f x f ⎛⎫⎪⎝⎭≤,且在,163⎛⎫ ⎪⎝⎭上单调,则ω的取值集合为四、解答题15.(23-24高一下·浙江丽水·期末)已知函数22()sin2f x x x x =.(1)求函数()f x 的最小正周期及单调递减区间;(2)将函数()f x 的图象上每个点的纵坐标缩短到原来的12,横坐标也缩短到原来的12,得到函数()g x 的图象,若函数()y g x m =-在区间π0,4⎡⎤⎢⎥内有两个零点,求实数m 的取值范围.16.(23-24高一下·浙江衢州·期末)已知函数()cos2f x x x =+.(1)求函数()f x 的最小正周期和对称中心;(2)求函数()f x 在π0,2⎡⎤⎢⎥上的值域.17.(23-24高一上·浙江杭州·期末)已知函数22()sin 2sin cos 3cos ,R f x x x x x x =++∈.求:(1)函数()f x 的最小值及取得最小值的自变量x 的集合;(2)函数()f x 的单调增区间.18.(23-24高一下·浙江杭州·期末)已知实数0a <,设函数22()cos sin2f x x a x a =+-,且()64f =-.(1)求实数a ,并写出()f x 的单调递减区间;(2)若0x 为函数()f x 的一个零点,求0cos2x .19.(23-24高一上·浙江嘉兴·期末)已知函数()24cos 2f x x x a x =--.(1)若1a =-,求函数()f x 在[]0,2上的值域;(2)若关于x 的方程()4f x a =-恰有三个不等实根123,,x x x ,且123x x x <<,求()()131278f x f x x --的最大值,并求出此时实数a 的值.,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学函数的图像专题拔高训练
1.(2014•河东区一模)若方程f(x)﹣2=0在(﹣∞,0)内有解,则y=f(x)的图象是()A.B.C.D.
2.(2014•福建模拟)现有四个函数:①y=x•sinx②y=x•cosx③y=x•|cosx|④y=x•2x的图象(部分)如下,则按照从左到右图象对应的函数序号安排正确的一组是()
A.①④③②B.④①②③C.①④②③D.③④②①
3.(2014•漳州一模)已知函数,则函数y=f(x)的大致图象为()A.B.C.D.
4.(2014•遂宁一模)函数f(x)=xln|x|的图象大致是()
A.B.C.D.
5.(2014•西藏一模)函数y=x+cosx的大致图象是()
A.B.C.D.
6.(2014•湖南二模)若函数y=f(x)的图象如图所示,则函数y=f(1﹣x)的图象大致为()
A.B.C.D.
7.(2014•大港区二模)如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:
①f(x)=sinxcosx;
②f(x)=sin2x+1;
③f(x)=2sin(x+);
④f(x)=sinx+cosx.
其中“同簇函数”的是()
A.①②B.①④C.②③D.③④
8.(2014•凉山州一模)函数y=的图象大致是()
A.B.C.D.
9.(2014•安阳一模)已知f(x)=,则下列叙述中不正确的一项是()
A.
f(x﹣1)的图象B.
|f(x)|的图象
C.
f(﹣x)的图象
D.
f(|x|)的图象
10.已知函数f(x)的定义域为[a,b],函数y=f(x)的图象如下图所示,则函数f(|x|)的图象是()
A.B.C.D.。
