第1章_习题解答
《电子电路基础》习题解答第1章

第一章习题解答题 电路如题图所示,试判断图中二极管是导通还是截止,并求出AO两端的电压UAO。
设二极管是理想的。
解:分析:二极管在外加正偏电压时是导通,外加反偏电压时截止。
正偏时硅管的导通压降为~。
锗管的导通压降为~。
理想情况分析时正向导通压降为零,相当于短路;反偏时由于反向电流很小,理想情况下认为截止电阻无穷大,相当于开路。
分析二极管在电路中的工作状态的基本方法为“开路法”,即:先假设二极管所在支路断开,然后计算二极管的阳极(P 端)与阴极(N 端)的电位差。
若该电位差大于二极管的导通压降,该二极管处于正偏而导通,其二端的电压为二极管的导通压降;如果该电位差小于导通压降,该二极管处于反偏而截止。
如果电路中存在两个以上的二极管,由于每个二极管的开路时的电位差不等,以正向电压较大者优先导通,其二端电压为二极管导通压降,然后再用上述“开路法”法判断其余二极管的工作状态。
一般情况下,对于电路中有多个二极管的工作状态判断为:对于阴极(N 端)连在一起的电路,只有阳极(P 端)电位最高的处于导通状态;对于阳极(P 端)连在一起的二极管,只有阴极(N 端)电位最低的可能导通。
图(a )中,当假设二极管的VD 开路时,其阳极(P 端)电位P U 为-6V ,阴极(N 端)电位N U 为-12V 。
VD 处于正偏而导通,实际压降为二极管的导通压降。
理想情况为零,相当于短路。
所以V U AO 6-=;图(b )中,断开VD 时,阳极电位V U P 15-=,阴极的电位V U N12-=,∵ N PUU < ∴ VD 处于反偏而截止∴ VU AO 12-=; 图(c ),断开VD1,VD2时∵ V U P 01= V U N 121-= 11N P U U > V U P 152-= V U N 122-= 22N P U U<∴ VD1处于正偏导通,VD2处于反偏而截止V U AO 0=;或,∵ VD1,VD2的阴极连在一起∴ 阳极电位高的VD1就先导通,则A 点的电位V U AO 0=,而 A N P U UV U =<-=2215∴ VD2处于反偏而截止 图(d ),断开VD1、VD2,∵ V U P 121-= V U N 01= 11N P U U < V U P 122-= VU N 62-= 22N P U U <;∴ VD1、VD2均处于反偏而截止。
电子技术及应用习题解答第1章

思考与练习1-、选择题:(请将唯一正确选项的字母填入对应的括号内)1、如图1-1所示,电路中所有的二极管都为理想二极管(即二极管正向压降可忽略不计),则哪个选项对D1、D2和D3的工作状态判断正确?( )(A )D1、D2导通,D3截止 (B )D1、D3导通,D2截止 (C )D1、D2截止,D3导通 (D )D1、D3截止,D2导通D 10V4V图1-1 题1.1图答案:C 。
原因:3D 的负极所接电压为-7V ,是最低电压,所以3D 导通。
3D 导通后1D 和2D 承受反向电压而截止。
2、如图1-2所示,电路中所有的二极管都为理想二极管,且L1、L2、L3、L4四盏灯都相同,则哪个灯最亮?( )(A )L1 (B )L2 (C )L3 (D )L4R图1-2题1.2图答案:D 。
原因:当电源~220V 正半周时,只有4D 承受正向电压导通,L4不亮;1D 、2D 和3D 承受反向电压截止,L1、L2和L3同时点亮;当电源~220V 负半周时,只有4D 承受反向电压截止,只有L4点亮;1D 、2D 和3D 承受正向电压导通,L1、L2和L3同时不亮;由此可见,灯泡L4最亮。
3、在如图1-3所示的电路中,已知10V E 稳压管Z1D 和Z2D 的稳定电压分别为5V 和3V ,正向压降都是0.7V ,则A 、B 两点间的电压O U 为多少?( )(A )-2.3V (B )4.3V (C )2.3V (D )-4.3VED Z 22图1-3 题1.3图答案:C 。
原因:A 点电位:A 100.79.3V V =-=;B 点电位:1037B V V =-=;所以,9.37 2.3O A B U V V V=-=-=4、下面关于二极管表述不正确的是?( ) (A )具有单向导电性; (B )由硅材料或锗材料构成;(C )既有点接触型二极管,也有面接触型二极管;(D )只能工作在反向击穿区,不能加正向电压。
大学物理第一章习题解答

a
at
an
dv dt
et
v2 R
en
1-6 已知质点沿x轴作直线运动,其运动方程为
x 2 6t 2 2t3
k
t2
v Rt2
2rad s3
(t) 2t2
t' 0.5s: 2t2 tt 2t2 0.5rad s1
d 4t,
dt
tt 4t' 2.0rad s2
at R, at tt 20.5 1.0m s2
和垂线成 750 角下降。求雨滴下落的速度 v2 。
(设下降的雨滴作匀速运动)
解:以地面为基本参照系
旅火, v客车雨看相地到对雨地v雨滴面火下:v落火v地的火速地雨度滴:v相雨火对地面:v雨地v火地
v雨地
v火地 tan 75o
5.36m s1
v雨火
v雨地
dy vy dt 15 40t
ax
dvx dt
60m s2
ay
dvy dt
40m s2
a
ax2
a
2 y
72.1m s2
设 a 与 x 轴正向的夹角为
tan ay 2
ax 3
33041'
1-13 质点沿直线运动,加速度 a 4 t2 ,式
a A Bv dv dt
电路理论习题解答 第一章

1.5
u /V
内阻不为零
+ us
R0
I
+
u
RL
−
伏安关系曲线
−
I/A 0.15
0
1.5
u /V
注:这里的伏安关系曲线只能在第一象限,原因也是,一旦出了第一象限, u 和 I 的比值就 变为负的了,反推出的 RL 就变为负值了,与题意不符。
V
V
1.5V
1.5V
R 内阻为零时 内阻不为零时
R
1-9 附图是两种受控源和电阻 RL 组成的电路。现以 RL 上电压作为输出信号,1)求两电路的电 压增益(A,gmRL);2)试以受控源的性质,扼要地说明计算得到的结果。
1) 如果不用并联分压(在中学就掌握的东西),当然也可以用两个回路的 KVL 方程和顶部 节点的 KCL 方程,得出上面的 H(jω)的表达式,但是显然这样做是低效的。 2) 事实上,本课程的目的是希望学习者能够根据不同的题目,尽可能采用多种方法中的一 种最简单的方法去解决问题。因此, a) 只要没有要求,任意的逻辑完整的解题思路都是可取的; b) 学习者可以视自己的练习目的选择一种简单熟悉的方法、或者一种较为系统的方法、 或者多种方法来完成习题。
第一章习题答案 1-1 已知电路中某节点如图,I1=-1A,I2=4A,I4=-5A,I5=6A,用 KCL 定律建立方程并求解 I3 ( 4A )
图 1-1 解:由 KCL 定律:任一集中参数电路中的任一节点,在任一时刻,流入该节点的电流之和与 流出该节点的电流之和相同。 即: I1+I3+I4+I5=I2 =〉-1+(-5)+6+I3=4 =〉I3=4(A)
1 2
信号与系统(应自炉)习题答案第1章 习题解重点

(222222j t k j t j t j k f t k e
e
e
e
f t π
π
π
πππ+++++==⨯==
∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.
求信号( 14sin( 110cos(2--+=t t t f的基波周期。
解:cos(101 t +的基波周期为15
π,s i n (4
1-8.
用阶跃函数写出题图1-8所示各波形的函数表达式。
t
t
t
(a (
bc
题图1-8
解:(a)((((((3[31]2[11]f t t u t u t u t u t =++-+++-- (((3[13]t u t u t +-+---
(((((
(3 3(1 1(1 1(3 3f
t t u t t u t t u t t u t =+++--++-+-+--(b)([( (1]2[(1 (2]4(2 f t u t u t u t u t u t =--+---+-
1 t -的基波周期为
1
2
π二者的最小公倍数为π,故( 14sin( 110cos(2--+=t t t f的基波周期为π。
1-3.
设(3, 0<=tt f ,对以下每个信号确定其值一定为零的t值区间。
(1)(t f -1(2)((t f t f -+-21(3)((t f t f --21(4)(t f 3(5)(f
运筹学教程(第三版)习题答案(第一章)

b 3/2 1
c x1 0 1 0
d x2 1 0 0
0 x3 5/14
0 x4 -3/4
-2/14 10/35 -5/14d+2/14c 3/14d-10/14c
School of Management
运筹学教程
第一章习题解答
之间时最优解为图中的A点 当c/d在3/10到5/2之间时最优解为图中的 点 ; 当 在 到 之间时最优解为图中的 c/d大于 且c大于等于 时最优解为图中的 点;当c/d 大于5/2且 大于等于 时最优解为图中的B点 大于等于0时最优解为图中的 大于 小于3/10且 d大于 时最优解为图中的 点 ; 当 c/d大于 大于0时最优解为图中的 小于 且 大于 时最优解为图中的C点 大于 5/2且c小于等于 时或当 小于 小于等于0时或当 小于3/10且d小于 时最优解 小于0时最优解 且 小于等于 时或当c/d小于 且 小于 为图中的原点。 为图中的原点。
page 7 14 March 2012
School of Management
运筹学教程
第一章习题解答
对下述线性规划问题找出所有基解, 1.3 对下述线性规划问题找出所有基解,指出哪 些是基可行解,并确定最优解。 些是基可行解,并确定最优解。
max Z = 3 x1 + x 2 + 2 x 3 12 x1 + 3 x 2 + 6 x 3 + 3 x 4 = 9 8 x + x − 4 x + 2 x = 10 1 2 3 5 st 3 x1 − x 6 = 0 x j ≥ 0( j = 1, L , 6) ,
School of Management
《电磁场与电磁波》课后习题解答第一章

n(x2
y2
z2)
(x2 y2 z2)2 (x2 y2 z2)
(n 3)rn
【习题 1.20 解】
1
已知 r (x2 y2 z2 )2
r xex yey zez
所以
(1)
r
(ex
x
ey
y
ez
z
)
(
xex
yey
zez )
ex ey ez
xyz
Bx ex By ey Bz ez
取一线元: dl exdx eydy ezdz
则有
B dl
ex ey ez Bx By Bz 0 dx dy dz
则矢量线所满足的微分方程为
dx dy dz Bx By Bz
或写成
dx dy dz =k(常数) a2 z a3 y a3x a1z a1 y a2x
对(3)(4)分别求和
(4)
d (a1x) d (a2 y) d (a3 z) 0 xdx ydy zdz 0
d (a1x a2 y a3 z) 0 d(x2 y2 z2) 0
所以矢量线方程为
a1x a2 y a3 z k1
x2 y2 z2 k2
【习题 1.6 解】
ex ey ez A B (ex 9ey ez ) (2ex 4ey 3ez ) 1 9 1
2 4 3
31ex 5ey 14ez
【习题 1.3 解】
已知 A ex bey cez , B ex 3ey 8ez ,
(1)要使 A B ,则须散度 A B 0
所以从 A B 1 3b 8c 0 可得: 3b 8c 1
即 12ex 9ey ez • aex bey 12a 9b 0 ⑴
第1章 电机的基本原理 《电机学(第2版)》王秀和、孙雨萍(习题解答)

第一章电机的基本原理习题解答:1、何为相对磁导率?答:材料的磁导率定义为该位置处的磁通密度与磁场强度之比,决定于磁场所在点的材料特性,单位为H/m。
根据材料的导磁性能,可将其分为铁磁材料和非铁磁材料。
非铁磁材料的磁导率可认为与真空的磁导率μ0相同,为4π⨯10-7H/m。
铁磁材料主要是铁、镍、钴以及它们的合金,其磁导率是非铁磁材料磁导率的几十倍至数千倍。
由于材料的磁导率变化范围很大,常采用相对磁导率μr来表征材料的导磁性能,μr为材料的磁导率与真空磁导率的比值。
2、磁路的磁阻如何计算?答:磁路的磁阻可用公式R m=L/(μA)计算,其中L为磁路的长度,单位为m,μ为材料的磁导率,单位为H/m,A为磁路的截面积,单位为m2。
从公式可以看出,磁路的磁阻主要取决于磁路的几何尺寸和材料的磁导率,大小上与磁路长度成正比,与磁路的截面积和磁导率成反比。
3、叙述磁路与电路的类比关系。
答:从电路和磁场的方程上看,两者形式上非常相似。
电路和磁路的类比关系可用下表表示:4、为什么希望磁路中的空气隙部分尽可能小?答:与磁路中铁磁材料相比,空气的磁导率小得多,如果磁路中的气隙部分长度增加,使得磁路的总磁阻大大增大,要想产生同样大小的磁通,需要的磁动势大大增加。
5、何为铁磁材料?为什么铁磁材料的磁导率高?答:铁磁材料包括铁、镍、钴及它们的合金、某些稀土元素的合金和化合物、铬和锰的一些合金等。
根据铁磁材料的磁化过程可知,当铁磁材料放置到磁场中之后,磁场会显著增强,表现为铁磁材料的导磁能力更强,因此磁导率大。
6、何为铁磁材料的饱和现象和磁滞现象?答:将未磁化的铁磁材料置于外磁场中,当磁场强度很小时,外磁场只能使少量磁畴转向,磁通密度增加不快,此时磁导率 较小;随着外磁场的增强,大量磁畴开始转向,磁通密度增加很快,磁导率很大;当外磁场增大到一定程度时,大部分磁畴已经转向,未转向的磁畴较少,继续增大外磁场时,磁通密度增加缓慢,磁导率逐渐减小,这种现象称为饱和。
高等数学第1章课后习题答案(科学出版社)

第一章 函数、极限、连续习题1-11.求下列函数的自然定义域:(1)321x y x=+-(2) 1arctany x=+(3) 1arccosx y -=;(4) 313 , 1x y x ⎧≠⎪=⎨⎪=⎩. 解:(1)解不等式组23010x x +≥⎧⎨-≠⎩得函数定义域为[3,1)(1,1)(1,)---+∞U U ; (2)解不等式组230x x ⎧-≥⎨≠⎩得函数定义域为[U ;(3)解不等式组2111560x x x -⎧-≤≤⎪⎨⎪-->⎩得函数定义域为[4,2)(3,6]--U ; (4)函数定义域为(,1]-∞.2.已知函数()f x 定义域为[0,1],求(cos ),()() (0)f f x f x c f x c c ++->的定义域.解:函数f要有意义,必须01≤≤,因此f 的定义域为[0,1];同理得函数(cos )f x 定义域为[2π-,2π]22k k ππ+;函数()()f x c f x c ++-要有意义,必须0101x c x c ≤+≤⎧⎨≤-≤⎩,因此,(1)若12c <,定义域为:[],1c c -;(2)若12c =,定义域为:1{}2;(3)若12c >,定义域为:∅. 3.设21()1,||x a f x x x a ⎛⎫-=- ⎪-⎝⎭0,a >求函数值(2),(1)f a f .解:因为21()1||x a f x x x a ⎛⎫-=- ⎪-⎝⎭,所以 21(2)104a f a a a ⎛⎫=-= ⎪⎝⎭,22 ,>1,11(1)10 ,0<<111a a f a a ⎛⎫⎧-=-= ⎪⎨ ⎪-⎩⎝⎭. 4. 证明下列不等式:(1) 对任何x R ∈有 |1||2|1x x -+-≥; (2) 对任何n Z +∈有 111(1)(1)1n n n n++>++;(3) 对任何n Z +∈及实数1a >有 111na a n--≤.证明:(1)由三角不等式得|1||2||1(2)|1x x x x -+-≥---= (2)要证111(1)(1)1n n n n++>++,即要证111n +>+= 111(1)(1)(1)11111n n n n n +++++++<=+++L 得证。
第1章 部分习题解答

第一章 部分习题解答(数字信号处理(第二版),刘顺兰,版权归作者所有,未经许可,不得在互联网传播) 1.1 序列)(n x 示意如图T1-1,请用各延迟单位脉冲序列的幅度加权和表示。
)(n图T1-1解: )3(2)1(3)()3(2)(−+−+−+−=n n n n n x δδδδ1.3 判断下列每个序列是否是周期性的,若是周期性的,试确定其周期。
(1)873cos()(ππ−=n A n x (2))313sin()(n A n x π=(3))6()(n j en x −=π(4) )18/sin()12/cos()(ππn n n x += 解 (a) 873cos()(ππ−=n A n x314722,7311===πωππω为有理数 所以该序列为周期序列,其周期143314=×=N (b ))313sin()(n A n x π=13631322,31322===ππωππω为有理数 所以该序列为周期序列,其周期613136=×=N (c ))6()(n j e n x −=πππωπω2122,133===为无理数 所以该序列为非周期序列。
1.12有一连续正弦信号)2cos(ϕπ+ft ,其中6,20πϕ==Hz f 。
(1) 求其周期0T ;(2) 在nT t =时刻对其采样,s T 02.0=,写出采样序列)(n x 的表达式; 求)(n x 的周期N 。
解: 6,20πϕ==Hz f(1)其周期ms s s f T 5005.020110====(2)s T 02.0=,)68.0cos()2cos()(ππϕπ+=+=n fnT n x(3)252,8.000==ωππω 则)(n x 的周期5225=×=N 1.13 今对三个正弦信号t t x πα2cos )(1=,t t x πα6cos )(2−=,t t x πα10cos )(3=进行理想采样,采样频率为π8=Ωs ,求三个采样输出序列,比较这三个结果,画出)(1t x α、)(2t x α、)(3t x α的波形及采样点位置并解释频谱混淆现象。
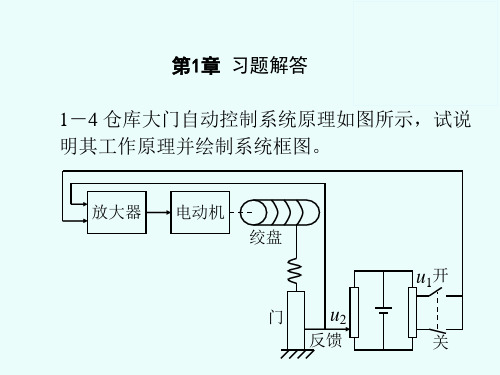
(完整版)自动控制原理_第一章课后习题解答

第一章1.1 图1.18是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c维持不变,试说明系统工作原理并画出系统方块图。
c+-SM___ 1Q浮浮浮浮浮浮2Q浮浮浮浮浮浮浮浮浮浮浮浮fi-+解:系统的控制任务是保持液面高度不变。
水箱是被控对象,水箱液位是被控变量。
电位器用来设置期望液位高度*c(通常点位器的上下位移来实现) 。
当电位器电刷位于中点位置时,电动机不动,控制阀门有一定的开度,使水箱的流入水量与流出水量相等,从而使液面保持在希望高度*c上。
一旦流出水量发生变化(相当于扰动),例如当流出水量减小时,液面升高,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一定的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液体流量减少。
这时,水箱液位下降.浮子位置相应下降,直到电位器电刷回到中点位置为止,系统重新处于平衡状态,液位恢复给定高度。
反之,当流出水量在平衡状态基础上增大时,水箱液位下降,系统会自动增大阀门开度,加大流入水量,使液位升到给定高度*c。
系统方框图如图解1. 4.1所示。
1.2恒温箱的温度自动控制系统如图1.19所示。
(1) 画出系统的方框图;(2) 简述保持恒温箱温度恒定的工作原理;(3) 指出该控制系统的被控对象和被控变量分别是什么。
M放大器电机减速器调压器 220~热电偶电阻丝- +- +图1.19 恒温箱的温度自动控制系统解:恒温箱采用电加热的方式运行,电阻丝产生的热量与调压器电压平方成正比,电压增高,炉温就上升。
调压器电压由其滑动触点位置所控制,滑臂则由伺服电动机驱动.炉子的实际温度用热电偶测量,输出电压作为反馈电压与给定电压进行比较,得出的偏差电压经放大器放大后,驱动电动机经减速器调节调压器的电压。
在正常情况下,炉温等于期望温度T ,热电偶的输出电压等于给定电压。
此时偏差为零,电动机不动,调压器的滑动触点停留在某个合适的位置上。
控制工程基础课后习题解答
(R1
R2
)C
d dt
uo
(t
)
uo
(t
)
R2C
d dt
ui
(t
)
ui
(t)
xi
xo
K1 K2 B f)
K1(
xi
xo
)
K2
(
xo
x)
B
dx dt
(K1
K2)B
d dt
xo
(t)
K1K 2 xo
(t)
K1B
d dt
xi
(t)
K1K 2 xi
(t)
易见:a)与b)、c)与d)、e)与f)为相似系统。
第2章 习题解答
dx2 dt
B2
dx2 dt
K 2 x2
m2
d 2x2 dt 2
第2章 习题解答
m1m2
d 4x2 dt 4
(m1B2
m1B3
m2 B1
m2 B3 )
d 3x2 dt3
(m1K2
m2 K1
B1B2
B1B3
B2 B3 )
d 2x2 dt 2
( K1B2
K1B3
K 2 B1
K 2 B3 )
dx2 dt
故:G2 (s)
X o (s) Xi (s)
(B1s K1)(B2s K2 ) (B2s K2 )(B1s K1) K1B1s
B1 K1 s 1 B2 K2 s 1
B1 K1 s 1 B2 K2 s 1 B1 K2 s
显然:两系统具有相同形式的传递函数。
第2章 习题解答
2-8 按信息传递和转换过程,绘出图示两机械系 统的方框图。
第一章习题解答

第一章习题解答(P37)2、设机器字长为6 位,写出下列各数的原码、补码、反码和移码。
10101 11111 10000-10101 -11111 -10000解: ① [10101]原=[10101]补=[10101]反=010101B[10101]移=2n-1-1+010101=11111+10101=110100B② [-10101]原=110101B[-10101]反=101010B[-10101]补=101011B[-10101]移=11111-10101=001010B③ [11111]原=[11111]补= [11111]反=011111B[11111]移=11111+11111=111110B④ [-11111]原=111111B[-11111]反=100000B[-11111]补=100001B[-11111]移=11111-11111=000000B⑤ [10000]原=[10000]补=[10000]反=010000B[10000]移=11111+10000=101111B⑥ [-10000]原=110000B[-10000]反=101111B[-10000]补=110000B[-10000]移=11111-10000=001111B3、利用补码进行加减法运算比用原码进行运算有何优越性?答: 利用补码进行加减法运算比用原码进行运算的优越性主要表现在只用一套加法器电路就可以进行加减法运算,简化了电路,降低了运算器的成本。
5、设机器字长为8 位,最高位为符号位,试对下列各算式进行二进制补码运算。
(1) 16+6=?解:∵ [16]补=10H[6]补=06H∴ [16+6]补=[16]补+[6]补=10H+06H=16H(2) 8+18=?解:∵ [8]补=08H[18]补=12H∴ [8+18]补=[8]补+[18]补=08H+12H=1AH(3) 9+(-7)=?解:∵ [9]补=09H[-7]补=F9H∴ [9+(-7)]补=[9]补+[-7]补=09H+F9H=02H(4)-25+6=?解:∵ [-25]补=E7H[6]补=06H∴ [-25+6]补=[-25]补+[6]补=E7H+06H=EDH(5) 8-18=?解:∵ [8]补=08H[-18]补=EEH∴ [8-18]补=[8]补+[-18]补=08H+EEH=F6H(6) 9-(-7)=?解:∵ [9]补=09H[-(-7)]补=07H∴ [9-(-7)]补=[9]补+[-(-7)]补=09H+07H=10H (7) 16-6=?解:∵ [16]补=10H[-6]补=FAH∴ [16-6]补=[16]补+[-6]补=10H+FAH=0AH(8) -25-6=?解:∵ [-25]补=E7H[-6]补=FAH∴ [-25-6]补=[-25]补+[-6]补=E7H+FAH=E1H6、设机器字长为8 位,最高位为符号位,试用“双高位”法判别下述二进制运算有没有溢出产生。
完整版高等代数习题解答(第一章)

完整版高等代数习题解答(第一章)高等代数题解答第一章多项式补充题1.当a,b,c取何值时,多项式f(x)=x-5与g(x)=a(x-2)^2+b(x+1)+c(x^2-x+2)相等?提示:比较系数得a=-1,b=-1,c=6.补充题2.设f(x),g(x),h(x)∈[x],f^2(x)=xg^2(x)+x^3h^2(x),证明:假设f(x)=g(x)=h(x)不成立。
若f(x)≠0,则∂(f^2(x))为偶数,又g^2(x),h^2(x)等于或次数为偶数,由于g^2(x),h^2(x)∈[x],首项系数(如果有的话)为正数,从而xg^2(x)+x^3h^2(x)等于或次数为奇数,矛盾。
若g(x)≠0或h(x)≠0,则∂(xg^2(x)+x^3h^2(x))为奇数,而f^2(x)为偶数,矛盾。
综上所证,f(x)≠g(x)或f(x)≠h(x)。
1.用g(x)除f(x),求商q(x)与余式r(x):1)f(x) =x^3-3x^2-x-1,g(x) =3x^2-2x+1;2)f(x) =x^4-2x+5,g(x) =x^2-x+2.1)解法一:待定系数法。
由于f(x)是首项系数为1的3次多项式,而g(x)是首项系数为3的2次多项式,所以商q(x)必是首项系数为1的1次多项式,而余式的次数小于2.于是可设q(x)=x+a,r(x)=bx+c。
根据f(x)=q(x)g(x)+r(x),即x^3-3x^2-x-1=(x+a)(3x^2-2x+1)+bx+c,右边展开,合并同类项,再比较两边同次幂的系数,得a=-1/3,b=-2/3,c=-1,故得q(x)=x-1/3,r(x)=-x-1/3.2)解法二:带余除法。
用长除法得商q(x)=x^2+x-1,余式r(x)=-5x+7.2.m,p,q适合什么条件时,有1)x^2+mx-1/x^3+px+q;2)x^2+mx+1/x^4+px^2+q.解:1)将x^3+px+q除以x^2+mx-1得商为x+m+1/(x+m-1),所以当m≠1时有解。
概率论第一章习题解答(全)

10 9 8 120 ; 3 2 1
事件 A 所包含基本事件数(即 5 固定,再从 6,7,8,9,10 这 5 个数中任选 2 个) :
C52
5 4 10 2
事件 B 所包含的基本事件数(即 5 固定,再从 1,2,3,4 这 4 个数中任选 2 个) :
故
43 6 2 10 1 6 1 P ( A) ; P( B) 120 12 120 20
1 1 1 1 1 1 1 17 ; 2 3 5 10 15 20 30 20 17 3 (ⅳ) P ( ABC ) P ( A B C ) 1 P ( A B C ) 1 ; 20 20
(ⅴ) 且 因为 ABC ( A B )C ( s ( A B ))C C ( AC BC )
P ( ABC ) P (( A B )C ) P (C ) P ( AC ) P ( BC ) 1 1 1 7 5 15 20 60
(ⅵ)
因为
P ( AB C ) P ( AB ) P (C ) P ( ABC )
已知 P ( AB )
4 7 , P ( ABC ) ,故 15 60
而 故
ABC AB , P ( AB ) 0 ,所以
P ( ABC ) 0
P ( A B C ) P ( A) P ( B ) P (C ) P ( AB ) P ( AC ) P ( BC ) P ( ABC ) 1 1 1 1 5互不相容,所以 AB , AB A , P ( AB ) P ( A) (ⅱ)因为 A A( B B ) AB AB ,且 AB AB , 所以
第1章物质聚集状态习题

第一章 物质聚集状态 习 题解答(教材)1.计算在15℃和97 kPa 压力下,15 g 氮气所占有的体积。
解:330132.01097)15273(314.82515PV m nRT =⨯+⨯⨯==2.在20℃和97 kPa 压力下,0.842 g 某气体的体积是0.400 L ,这气体的摩尔质量是多少?解: RT m V M p =13386.52104.010********.8842.0M --⋅=⨯⨯⨯⨯⨯==molg pRT Vm3. 407℃时,2.96 g 氯化汞在 l .00 L 的真空器中蒸发,压力为60 kPa ,求氯化汞的摩尔质量和化学式。
解:由公式PRT Mρ=得,9.278100.110602933148842.0M 33=⨯⨯⨯⨯⨯=-.g ⋅mol -1,M(Hg)=200.59 g ⋅mol -1,25.35==Cl n又25.35131169≈-=x ,所以分子式为HgCl 24.在30℃和 102 kPa 压力下,用 47.0 g 铝和过量的稀硫酸反应可以得到多少升干燥的 氢气?如果上述氢气是在相同条件下的水面上收集的,它的体积是多少? (已知,30℃,液态水的饱和蒸气压为4. 24k kPa )[解:设p 为总压,即常压。
2Al+3H 2SO 4 ==== Al 2(SO 4 )3 + 3H 2 37 347 x 37 :3=47: x x=2.61mol333105.641010215.303314.861.222mPRT n VH H -⨯=⨯⨯⨯== 或)5.64(Lp 总 =O H p 2+P`P` = 102-4. 24k=97.76kPa T 一定,P`V`= P V LP PV V 3.6776.975.64102``=⨯==5,在100 kPa 和 100℃下,混合0.300 L 氢与 0.100 L 氧,然后使之爆炸。
如果爆炸后压力和温度不变,则混合气体的体积是多少? 解: H 2(g) + 1/2O 2(g) = H 2O(l) 0.3 0.10.2 0.1 V(H 2)=0.2L 混合气体的体积0.3L6.在25℃时,初始压力相同的5.0 L 氮和 15 L 氧压缩到体积为 10.0L 的真空容器中, 混合气体的总压力是 150 kPa 试求:(1)两种气体的初始压力;()混合气体中氮和氧的分 压;(3)如果把温度升到210℃,容器的总压力。
概率论第一章习题解答

概率论第一章习题解答一、填空题:1.设,()0.1,()0.5,A B P A P B ⊂==则()P AB = ,()P A B = , ()P A B = 。
分析:()(,)0.1;A P B P AB A ==⊂()()0.5;P A B P B ==()()()1()0.9P A B P A B P AB P AB ===-=2.设在全部产品中有2%是废品,而合格品中有85%是一级品,则任抽出一个产品是一级品的概率为 。
分析:设A 为抽正品事件,B 为抽一级品事件,则条件知()1()0.98P A P A =-=,()0.85P B A =,所求为()()()0.980.850.833P B P A P B A ==⨯=;3.设A ,B ,C 为三事件且P(A)=P(B)=P(C)=41,81)(,0)()(===AC P BC P AB P ,则A,B,C 中至少有一个发生的概率为 .分析:,()()0,()0ABC AB P ABC P AB P ABC ⊆≤=∴= 所求即为5()()()()()()()()8P A B C P A P B P C P AB P BC P AC P ABC =++---+=; 4.一批产品共有10个正品和2个次品,不放回的抽取两次,则第二次取到次品的概率 为 .分析:第二次取到次品的概率为112111211C C ⨯或者为111110*********C C C C +=⨯ 5. 设A ,B 为两事件, ()0.4,()0.7,P A P A B == 当A ,B 不相容时, ()P B = 当A ,B 相互独立时, ()P B = 。
分析: (1)当A ,B 不相容时, ()0P AB =;()()()()P A B P A P B P AB =+- 由;则()()()()0.3P B P A B P A P AB =⋃-+=;(2)当A ,B 相互独立时, ()()()()()()()P AB P A P B P A B P A P B P AB =⎧⎨=+-⎩ ;则()(()(()))P A B P A P P P B B A =+- 由,代入求得()0.5P B =二.、选择题2.每次试验成功的概率为p (0< p <1),进行重复试验,直到第10次试验才取得4次成功的概率为( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F D
RD
NAx A
B
第1章
习题解答
B
.4.
2011年 2011年6月8日星期三
整体受力图: 整体受力图:
F NAx A C D
NAy
RD
RB NCx C NCy F D
NAx A
B
NCy C NCx
RD
NAy
RB
第1章
习题解答
G 720 G
.5.
2011年 2011年6月8日星期三
1-7
400 A
第1章
习题解答
A B Q Q C
.14.
2011年 2011年6月8日星期三
D F
F
N2 = F −Q =10-4 = 6 KN
N2 6×103 σ2 = = = 60 MPa A 100
N2 ⋅ l2 6×103 ×200 ∆l2 = = = 0.06 m m 5 EA 2×10 ×100
第1章
.27.
2011年 2011年6月8日星期三
1-15(b)
A C RA
P B
(1)求支座反力: (1)求支座反力: 求支座反力
l
a
RC
∑M
c
= 0 RA ⋅ l − P×a = 0
RA = Pa l RC = P( l + a) l
第1章
习题解答
.28.
2011年 2011年6月8日星期三
C RA x2 RC
B
第1章
习题解答
.29.
2011年 2011年6月8日星期三
Fs ( x1 ) = −RA = − Pa l M ( x1 ) = −RA ⋅ x1 = − Pax1 l A
P C RA RC B
Fs ( x2 ) = P M ( x2 ) = −P⋅ ( l + a − x2 )
( a ≤ x2 ≤ 2a)
第1章
习题解答
.31.
2011年 2011年6月8日星期三
Fs ( x1 ) = P − P = 0 M ( x1 ) = P⋅ ( 2a − x1 ) − P( a − x1 ) = Pa
( 0 ≤ x1 ≤ a)
Fs ( x2 ) = −P M ( x2 ) = P( 2a − x2 )
1 5 9 = − q x − a + qa 2 2 4 32
2
第1章
习题解答
.34.
2011年 2011年6月8日星期三
qa Fs ( x1 ) = 4 ( 0 ≤ x1 ≤ a) M ( x ) = qa x 1 1 4 3qa Fs ( x2 ) = − + q( 2a − x2 ) 4
NBC = 4.32KN
第1章
习题解答
.6.
2011年 2011年6月8日星期三
G A NAx
45°
G B
∑ Fx = 0 N BC ⋅ cos 45° − N Ax = 0
NAx = 3.05KN
NAy
NBC
C
∑F
y
= 0 N BC ⋅ sin 45° − G − G − N Ay = 0
NAy = −5.95KN
1-9(b)
C D P P
3
2
1
N3 = P + 2P − 2P = P N2 = P − 2P = −P N1 = P
第1章
习题解答
A B 2P P
.11.
2011年 2011年6月8日星期三
C 2P P
D P
P
P
第1章
习题解答
.12.
2011年 2011年6月8日星期三
补充: 补充:知A=100mm2、E= 2×105MPa,F=10KN、Q=4KN, MPa, 10KN、 4KN, 画轴力图,求应力、 画轴力图,求应力、变形
第1章
习题解答
.24.
2011年 2011年6月8日星期三
1-14
331 M = 9549 × = 10535.7 ( N.m ) 300
τ max φmax
T 10535.7 ×10 = = ≤ 40 d ≥ 110.3mm 3 Wt π d 16
3
T 10535.7 180° = = × ≤ 0.5 9 4 GI p 80 × 10 × π d 32 π
= 0 : FNBC ⋅ cos 30° − FNAB = 0
⇒ FNBC = 2G = 40 KN
x
FNAB FNBC
B
G
⇒ FNAB = 20 3KN
第1章
习题解答
.19.
2011年 2011年6月8日星期三
强度校核: 强度校核: FN 由: σ = ≤ [σ ] 可得 A
FNAB 20 3 × 10 3 AB杆: σ = = =110.3MP a ≤ [σ ] 2 AAB (π × 20 ) 4
习题解答
A B Q Q
.15.
2011年 2011年6月8日星期三
C
D F
F
N3 = F =10 KN
N3 10×103 σ3 = = =100 MPa A 100
N3 ⋅ l3 10×103 ×200 = 0.1 m m ∆l3 = = 5 EA 2×10 ×100
第1章
习题解答
.16.
2011年 2011年6月8日星期三
总变形: 总变形:
∆l = ∆l1 + ∆l2 + ∆l3 = 0.1 + 0.06 + 0.1 = 0.26mm
轴力图: 轴力图:
A F B Q Q C D F
10KN
6KN
10KN
第1章
习题解答
.17.
2011年 2011年6月8日星期三
1-11
分析:支架要安全, 分析:支架要安全, 则要保证AB AB、 则要保证AB、BC 杆均安全。 杆均安全。
1-15(d)
qa CB段: 段 4 3qa Fs ( x2 ) = − + q( 2a − x2 )
4
x2
3qa 4
( 2a − x2 ) 1 3qa M ( x2 ) = ( 2a − x2 ) − q ( 2a − M x2 ) ⋅ 4 2 2 1 2 5 1 2 = − qx2 + qax2 − qa 2 4 2
45°
G A NAx B NAy
45°
G B
NBC
C C 1、判断BC为二力杆,取AB为研究对象,画其受力图: 、判断 为二力杆 为二力杆, 为研究对象, 为研究对象 画其受力图: 2、建立坐标,列平衡方程: 、建立坐标,列平衡方程:Leabharlann ∑MA=0
N BC ×1120 × sin 45° − G × 400 − G × 1120 = 0
习题解答
B P C P 2
.8.
2011年 2011年6月8日星期三
1-9(a)
A D
N3 = P − P = 0 N2 = −P
N1 = 0
3 1
第1章
习题解答
A P B C
.9.
2011年 2011年6月8日星期三
D P
P
第1章
习题解答
A B 2P 2P
.10.
2011年 2011年6月8日星期三
FNBC 40 × 10 3 BC 杆: σ = = =31.8MP a ≤ [σ ] 2 ABC (π × 40 ) 4
所以,支架安全。 所以,支架安全。
第1章
习题解答
10KN.m
.20.
2011年 2011年6月8日星期三
1-12(a)
20KN.m
15KN.m 15KN.m 5KN.m
30KN.m
FN 由: σ = ≤ [σ ] 可知要求二杆轴力 A
第1章
习题解答
.18.
2011年 2011年6月8日星期三
判断:AB、BC均为二 判断:AB、BC均为二 力杆, 力杆,取B铰为研究 对象,其受力图为: 对象,其受力图为: 由平衡方程可得: 由平衡方程可得:
∑F
∑F
y
= 0 : FNBC ⋅ sin 30° − G = 0
d ≥ 111.3mm
∴ d = 112mm
第1章
习题解答
.25.
2011年 2011年6月8日星期三
Q、M正负号的规定: 、 正负号的规定 正负号的规定:
以该截面( 为界, 1、对于剪力Fs--以该截面(如n-n)为界,如左段相对右 对于剪力 --以该截面 段向上滑移(简称左上右下),则剪力为 左上右下),则剪力为正 反之为负。 段向上滑移(简称左上右下),则剪力为正;反之为负。 --若梁在该截面附近弯成上凹下凸, 2、对于弯矩M--若梁在该截面附近弯成上凹下凸,则弯 对于弯矩 --若梁在该截面附近弯成上凹下凸 矩为正;反之为负。 矩为正 反之为负。
Fs
Fs′
Fs
Fs′
第1章
习题解答
.26.
2011年 2011年6月8日星期三
1-15(a)
Fs ( x ) = −ql − qx
x M ( x ) = − qlx − qx ⋅ 2
x
Fs max = 2ql 3 2 M max = ql 2
ql
2ql
3ql 2
2
第1章
习题解答
第1章
习题解答
.7.
2011年 2011年6月8日星期三
补充: 补充: q
D NAx A NAy
M B NB
